Α. ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΚΡΟΣΚΟΠΙΑ Η ΕΝΝΟΙΑ ΤΗΣ ΜΕΓΕΘΥΝΣΗΣ 1. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΗΣ ΓΕΩΜΕΤΡΙΚΗΣ ΟΠΤΙΚΗΣ
|
|
|
- Ευδώρα Γιαννακόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 1 Α. ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΚΡΟΣΚΟΠΙΑ Η ΕΝΝΟΙΑ ΤΗΣ ΜΕΓΕΘΥΝΣΗΣ 1. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΤΗΣ ΓΕΩΜΕΤΡΙΚΗΣ ΟΠΤΙΚΗΣ 1.1 Η φύση του φωτός Το φως είναι εγκάρσια ηλεκτροµαγνητικά κύµατα, τα οποία ξεκινούν από τη φωτεινή πηγή και διαδίδονται προς όλες τις κατευθύνσεις στο χώρο. ηλαδή, µεταβολές ηλεκτρικού και µαγνητικού πεδίου που διαδίδονται στο χώρο ως κύµα. Οι συχνότητες αυτών των µεταβολών για το σύνολο των ηλεκτροµαγνητικών κυµάτων συνιστούν το ηλεκτροµαγνητικό φάσµα, µέρος του οποίου αντιστοιχεί στο ορατό φως. Πρωτογενείς πηγές της ηλεκτροµαγνητικής ακτινοβολίας κάθε είδους είναι ηλεκτρικά φορτία σε επιταχυνόµενη κίνηση. Η ταχύτητα διάδοσης του φωτός στο κενό είναι µια παγκόσµια σταθερά, εξ ορισµού ίση µεc m/s, ή, προσεγγιστικά, c = m/s. Κατά τη διάδοση ενός κύµατος φωτός (ή γενικότερα ενός κύµατος), τα σηµεία στα οποία η φάση της ταλάντωσης είναι η ίδια ορίζουν µια επιφάνεια που ονοµάζεται µέτωπο κύµατος. Στην περίπτωση σηµειακής πηγής που εκπέµπει προς όλες τις διευθύνσεις στο χώρο (τριδιάστατο κύµα), το µέτωπο κύµατος είναι σφαιρική επιφάνεια που διαστέλλεται µε ταχύτητα ίση µε την ταχύτητα διάδοσης του κύµατος (Σχ. 1.1α). Οι ακτίνες φωτός (ή φωτεινές ακτίνες) είναι γραµµές κατά την κατεύθυνση όδευσης του κύµατος, κάθετες στο µέτωπο κύµατος. Αν το φωτεινό κύµα είναι µονοδιάστατο, το µέτωπο κύµατος είναι επίπεδο κάθετο στη διεύθυνση διάδοσης και οι ακτίνες αποτελούν δέσµη παραλλήλων ευθειών, τότε έχουµε επίπεδο κύµα (Σχ. 1.1β). Σχήµα 1.1. (α) (β) Αρκετά µακριά από µια σηµειακή πηγή και σε περιορισµένη έκταση γύρω από ένα σηµείο µπορούµε να προσεγγίσουµε το σφαιρικό µέτωπο µε το εφαπτόµενο επίπεδο, δηλαδή το σφαιρικό µε ένα επίπεδο κύµα. Για την περιγραφή αρκετών οπτικών φαινοµένων είναι επαρκής η παράσταση ενός φωτεινού κύµατος µε τη βοήθεια των φωτεινών ακτίνων. Ο κλάδος αυτός της οπτικής ονοµάζεται γεωµετρική Οπτική. Ο κλάδος που πραγµατεύεται τα οπτικά φαινόµενα µε βάση την κυµατική συµπεριφορά του φωτός ονοµάζεται φυσική Οπτική. Για τη µελέτη των φαινοµένων της ανάκλασης και της διάθλασης του φωτός θα παραστήσουµε τα φωτεινά κύµατα ως δέσµες παράλληλων φωτεινών ακτίνων και χάριν απλότητας θα σχεδιάσουµε, όπως συχνά γίνεται, µια µόνον ακτίνα για κάθε δέσµη.
2 Η αρχή του Huygens καιη αρχή του Fermat για τη διάδοση του φωτός Η αρχή του Huygens µπορεί να χρησιµοποιηθεί για την περιγραφή της διάδοσης του φωτός στο χώρο. Σύµφωνα µε την αρχή αυτή, ένα κύµα φωτός θεωρείται ως ένα µέτωπο κύµατος, κάθε σηµείο του οποίου λειτουργεί ως πηγή δευτερευόντων κυµάτων, η περιβάλλουσα των οποίωνδίνει τη νέα θέση του κύµατος (Σχ. 1.2). Σχήµα1.2. Η αρχή του Hyugens για τη διάδοση του φωτός. (α) Η γεωµετρική κατα σκευή του νέου µετώπου κύµατος. (β) Περίθλαση κυµάτων στην επιφάνεια νερού, καθώς αυτά περνούν από στενή σχισµή. Στο όριο σχισµής µηδενικού εύρους, έχουµε την πλήρη εικόνα της αρχής του Hyugens. Η αρχή του Huygens αγνοεί τη διάδοση των δευτερευόντων κυµάτων προς τα πίσω ή πλαγίως. Επίσης, µε την αρχή δεν περιγράφεται η µεταβολή της έντασης του κύµατος συναρτήσει της θέσης. Με την αρχή αυτή µπορούν να εξαχθούν οι νόµοι της ανάκλασης και της διάθλασης του φωτός. Όπως αναφέρθηκε πιο πάνω, ένα µέτωπο φωτός, ή ηλεκτροµαγνητικού κύµατος γενικότερα, είναι µια ισοφασική επιφάνεια. Μια φυσική απόσταση δx µέσα σε ένα µέσον µε δείκτη διάθλασης n ισοδυναµεί µε οπτική απόσταση που ορίζεται ως nδx. Ο χρόνος που απαιτείται για να τη διανύσει το φως είναι δt= δx/υ= nδx/c, όπου υ η ταχύτητα του φωτός στο µέσον και c η ταχύτητα του φωτός στο κενό. Κάθε σηµείο της ισοφασικής επιφάνειας απέχει την ίδια οπτική απόσταση από την πηγή. Το φως χρειάστηκε τον ίδιο χρόνο για να φθάσει σε κάθε σηµείο του µετώπου κύµατος. Σύµφωνα µε την αρχή του Fermat, η διαδροµή που ακολουθεί το φως ανάµεσα σε δύο σηµεία είναι εκείνη για την οποία το µήκος του οπτικού δρόµου έχει ακρότατη τιµή (συνήθως ελάχιστη). Έτσι, ο χρόνος που χρειάζεται το φως για να διαδοθεί από ένα σηµείο σε ένα άλλο είναι ο ελάχιστος δυνατός. Κατά συνέπεια, αν το µέσον έχει σταθερό δείκτη διάθλασης, τότε η διαδροµή που ακολουθεί το φως είναι ευθεία. Για µέσον µε δείκτη διάθλασης που εξαρτάται από τη θέση, η διαδροµή είναι τέτοια ώστε να ελαχιστοποιείται ο χρόνος που χρειάζεται το φως για να τη διανύσει. Με την αρχή του Fermat είναι δυνατή η ερµηνεία των νόµων της ανάκλασης και της διάθλασης.
3 3 1.3 Η ανάκλαση του φωτός Για τη µελέτη του φαινόµενου της ανάκλασης του φωτός θα παραστήσουµε τα φωτεινά κύµατα ως δέσµες παράλληλων φωτεινών ακτίνων και χάριν απλότητας θα σχεδιάσουµε, όπως συχνά γίνεται, µια µόνον ακτίνα για κάθε δέσµη. Όταν ένα φωτεινό κύµα προσπέσει στη λεία επιφάνεια ενός κατόπτρου, ανακλάται. Το ανακλώµενο κύµα είναι ένα νέο κύµα που επιστρέφει πίσω στο ίδιο µέσον στο οποίο διαδιδόταν το αρχικό κύµα (Σχ. 1.3).Το φαινόµενο της ανάκλασης του φωτός διέπεται από τον ακόλουθο πειραµατικό νόµο της ανάκλασης: Οι διευθύνσεις πρόσπτωσης και ανάκλασης βρίσκονται στο ίδιο επίπεδο, το οποίο είναι κάθετο στη διαχωριστική επιφάνεια και άρα περιέχει την κάθετο επιφάνεια. Η γωνία πρόσπτωσης, θ i, είναι ίση µε τη γωνία ανάκλασης, θ r : θ i =θ r (1.1) Σχήµα 1.3: Η ανάκλαση µιας ακτίνας φωτός από επίπεδη επιφάνεια. 1.4 Η διάθλαση του φωτός Για τη µελέτη του φαινόµενου της διάθλασης του φωτός θα παραστήσουµε τα φωτεινά κύµατα ως δέσµες παράλληλων φωτεινών ακτίνων και χάριν απλότητας θα σχεδιάσουµε, όπως συχνά γίνεται, µια µόνον ακτίνα για κάθε δέσµη. Όταν ένα φωτεινό κύµα συναντά µια οµαλή επιφάνεια που διαχωρίζει δύο διαφανή υλικά, π.χ. αέρα και γυαλί ή νερό και γυαλί, τότε το κύµα εν µέρει ανακλάται και εν µέρει διαθλάται. Το διαθλώµενο κύµα είναι το κύµα που µεταδίδεται µέσα στο δεύτερο µέσον. Ο δείκτης διάθλασης ενός (οπτικού) υλικού, n, είναι ο λόγος της ταχύτητας του φωτός στο κενό, c, προς την ταχύτητά του Σχήµα στο 1.4.: ιάθλαση υλικό, υ, και αποτελεί σηµαντικό µέγεθος για τη γεωµετρική οπτική. c n= (1.2) u Η ταχύτητα διάδοσης του φωτός σε ένα µέσον εξαρτάται από τις ιδιότητες του µέσου. Για το κενό ισχύει n=1. Επειδή η ταχύτητα του φωτός µέσα σε ένα υλικό είναι πάντα µικρότερη από τηνταχύτητά του στο κενό, είναι n>1 για οποιοδήποτε υλικό. Το φαινόµενο της διάθλασης του φωτός διέπεται από τον ακόλουθο πειραµατικό νό- µο της διάθλασης ή νόµο του Snell: Οι διευθύνσεις πρόσπτωσης και διάθλασης βρίσκονται σε επίπεδο κάθετο στη διαχωριστική επιφάνεια το οποίο περιέχει εποµένως και την κάθετο στην επιφάνεια στο σηµείο πρόσπτωσης.
4 4 Ο λόγος του ηµιτόνου της γωνίας πρόσπτωσης προς το ηµίτονο της γωνίας διάθλασης είναι σταθερός και ίσος µε το αντίστροφο του λόγου των δεικτών διάθλασης των δύο µέσων n 1 και n 2 : sinθ1 n2 = sinθ 2 n1 ή n 1 sinθ 1 = n 2 sinθ 2. (1.3) Σύµφωνα µε την Εξ. (1.3), όταν µια ακτίνα διέρχεται από ένα υλικό (1) µέσα σε ένα άλλο υλικό (2) µεγαλύτερου δείκτη διάθλασης (n 1 < n 2 ), η ακτίνα κάµπτεται και προσεγγίζει την κάθετο. Όταν η προσπίπτουσα ακτίνα είναι κάθετη στη διαχωριστική επιφάνεια (θ 1 =0, sinθ 1 =0), η διερχόµενη ακτίνα δεν κάµπτεται καθόλου (θ 2 =0). Οι νόµοι της ανάκλασης και της διάθλασης εκφράζουν πειραµατικά αποτελέσµατα, αλλά είναι δυνατόν να εξαχθούν και θεωρητικώς χρησιµοποιώντας το κυµατικό µοντέλο για τη διάδοση του φωτός και τις εξισώσεις Maxwell του Ηλεκτροµαγνητισµού. Τα περισσότερα είδη γυαλιού που χρησιµοποιούνται στα οπτικά όργανα έχουν δείκτη διάθλασης µε τιµές περίπου από 1,5 ως 2,0. Ο δείκτης διάθλασης εξαρτάται από τη φύση του υλικού και από το µήκος κύµατος του φωτός. Το νερό έχει δείκτη διάθλασης ίσο µε 1,333. Ο δείκτης διάθλασης του αέρα υπό κανονικές συνθήκες πίεσης και θερµοκρασίας είναι περίπου 1,0003, οπότε σε πολλές περιπτώσεις θεωρείται ίσος µε τη µονάδα. Όταν το φως διέρχεται από ένα υλικό σε κάποιο άλλο, η συχνότητα f του κύµατος δεν µεταβάλλεται. Για κάθε υλικό ισχύει για την ταχύτητα διάδοσης του φωτός, υ, µέσα σε αυτό υ=λf, όπου λ το µήκος κύµατος του φωτός. Αφού η συχνότητα f του κύµατος σε κάθε υλικό έχει την τιµή που έχει και στο κενό, ενώ η ταχύτητα υ είναι πάντοτε µικρότερη από την ταχύτητα του κύµατος στο κενό, c, το µήκος κύµατος θα µειώνεται επίσης αντίστοιχα, οπότε: f = c/λ 0 = υ/λ, όπου λ 0 το µήκος κύµατος στο κενό, και σε συνδυασµό µε την Εξ.(1.2): λ = λ 0 /n. Οι νόµοι της ανάκλασης και της διάθλασης που διατυπώθηκαν ισχύουν τοπικά, α- κόµη και όταν ούτε το µέτωπο κύµατος ούτε η διαχωριστική επιφάνεια είναι επίπεδα, επειδή γύρω από κάθε σηµείο είτε του µετώπου κύµατος είτε της διαχωριστικής επιφάνειας υπάρχει µια µικρή περιοχή που µπορεί να θεωρηθεί ως επίπεδη προσεγγιστικά και όπου οι ακτίνες θα συµπεριφέρονται όπως αναφέρθηκε πιο πάνω. 1.5 Ανάκλαση σε επίπεδη επιφάνεια -Σχηµατισµός ειδώλου Όταν φως από κάποια πηγή προσπίπτει σε ένα επίπεδο κάτοπτρο (µια ανακλαστική επιφάνεια), η ανάκλαση του φωτός οδηγεί στο σχηµατισµό ειδώλου της πηγής. Στο Σχ. 1.5α, από το σηµείο Ρ πηγάζουν ακτίνες που ανακλώνται σε ένα επίπεδο κάτοπτρο, σύµφωνα µε το νόµο της ανάκλασης. Αφού ανακλασθούν, οι τελικές κατευθύνσεις των ακτίνων είναι αυτές που θα είχαν αν είχαν προέλθει από το σηµείο Ρ. Ονοµάζουµε το σηµείο Ρ σηµειακό αντικείµενο, το σηµείο Ρ αντίστοιχο σηµειακό είδωλο, και λέµε ότι το κάτοπτρο σχηµατίζει ένα είδωλο του σηµείου Ρ.
5 5 (α) (β) (γ) Σχήµα 1.5. Ο σχηµατισµός ειδώλου από επίπεδο κάτοπτρο. Οι εξερχόµενες ακτίνες (εκείνες που αποµακρύνονται από το κάτοπτρο) δεν προέρχονται πραγµατικά από το σηµείο Ρ, αλλά οι κατευθύνσεις τους συµπίπτουν µε τις κατευθύνσεις που θα είχαν αν προέρχονταν από αυτό το σηµείο. Ένας παρατηρητής που βλέπει µόνο τις αποµακρυνόµενες από την επιφάνεια ακτίνες, αφού ανακλαστούν σε αυτή, έχει την εντύπωση ότι προέρχονται από το σηµειακό είδωλο Ρ. ηλαδή το σηµειακό είδωλο παρέχει ένα πρόσφορο τρόπο περιγραφής των κατευθύνσεων ανακλώµενων ακτίνων, όπως ακριβώς το σηµειακό αντικείµενο Ρ περιγράφει τις κατευθύνσεις των ακτίνων που φθάνουν στην επιφάνεια πριν την ανάκλασή τους. Στο Σχ.1.5β φαίνεται ο τρόπος µε τον οποίο προσδιορίζεται η θέση του ειδώλου Ρ. Ονοµάζουµε την απόσταση s απόσταση αντικειµένου και την απόσταση s απόσταση ειδώλου. Στις περιπτώσεις όπως αυτή του σχήµατος, όπου οι εξερχόµενες ακτίνες δεν προέρχονται πραγµατικά από το σηµείο Ρ, το είδωλο Ρ ονοµάζεται φανταστικό είδωλο. Σε επόµενη ενότητα θα αναφερθούµε σε περιπτώσεις όπου οι εξερχόµενες ακτίνες διέρχονται πραγµατικά από σηµειακό είδωλο και τότε θα ονοµάσουµε το σχηµατιζόµενο είδωλο πραγµατικό είδωλο. Στο Σχ.1.5γ φαίνεται ο τρόπος δηµιουργίας του ειδώλου ενός εκτεταµένου αντικειµένου. 1.6 Ολική εσωτερική ανάκλαση Όπως προκύπτει από το νόµο της διάθλασης, sinθ 2 = (n 1 /n 2 ) sinθ 1. Αν θεωρήσουµε µια φωτεινή ακτίνα που διέρχεται από ένα µέσον µε δείκτη διάθλασης n 1 σε µέσον µε δείκτη διάθλασης n 2 < n 1, θα υπάρχει κάποια τιµή της γωνίας πρόσπτωσης θ 1 <90 ο, για τηνοποία προκύπτει sinθ 2 =1 και θ 2 =90 ο. Η γωνία πρόσπτωσης για την οποία η διαθλώµενη ακτίνα αναδύεται εφαπτοµενικά προς τη διαχωριστική επιφάνεια ονοµάζεται κρίσιµη γωνία (ή ορική γωνία), θcrit. Αν η γωνία πρόσπτωσης είναι µεγαλύτερη από την κρίσιµη γωνία η ακτίνα δεν µπορεί να εισχωρήσει στο δεύτερο υλικό (sinθ 2 >1) και ανακλάται εξ ολοκλήρου εσωτερικά στη διαχωριστική επιφάνεια. Το φαινόµενο αυτό ονοµάζεται ολική εσωτερική ανάκλαση. Για την κρίσιµη γωνία ισχύει: n2 θ crit = arcsin. (1.4) Σχήµα 1.6.: Ολική εσωτερική ανάκλαση. n 1
6 6 Για επιφάνεια γυαλιού-αέρα, µε n 1 = 1,52 για το γυαλί και n 2 = 1 για τον αέρα, θ crit = 41,1 ο Το γεγονός ότι η θ crit προκύπτει λίγο µικρότερη των 45 ο κάνει δυνατή τη χρησιµοποίηση ενός τριγωνικού πρίσµατος µε γωνίες 45 ο, 45 ο και 90 ο ως ολικώς ανακλώσας επιφάνειας (Σχ. 1.7α). Η ολική εσωτερική ανάκλαση έχει πολλές εφαρµογές στην Οπτική. Στο περισκόπιο και στα κιάλια, το φως ανακλάται µέσα στο σωλήνα υφιστάµενο ολική εσωτερική ανάκλαση σε πρίσµατα. Σε µια οπτική ίνα, το φως διαδίδεται κατά µήκος µιας λεπτής ράβδου (ίνας) από διαφανές υλικό, υφιστάµενο πολλές διαδοχικές εσωτερικές ανακλάσεις. H ίνα δρα ως σωλήνας φωτός (Σχ. 1.7β). Σχήµα ιασπορά ή διασκεδασµός του φωτός Όπως αναφέρθηκε πιο πάνω, ο δείκτης διάθλασης ενός υλικού εξαρτάται από το µήκος κύµατος. Η εξάρτηση του δείκτη διάθλασης ενός υλικού, και συνεπώς και της ταχύτητας διάδοσης του φωτός σ αυτό το υλικό, από το µήκος κύµατος του φωτός, ονοµάζεται διασπορά ή διασκεδασµός του φωτός. Το Σχ. 1.8 δείχνει τη µεταβολή του δείκτη διάθλασης συναρτήσει του µήκους κύµατος σε µερικά ευρέως χρησιµοποιούµενα οπτικά υλικά, (α) στην περιοχή του ορατού φωτός και (β) σε ευρύτερη περιοχή µηκώνκύµατος. Η τιµή του δείκτη διάθλασης n συνήθως µειώνεται όταν αυξάνεται το µήκος κύµατος του φωτεινού κύµατος. Φως µεγαλύτερου µήκους κύµατος έχει συνήθως µεγαλύτερη ταχύτητα σε ένα υλικό από φως µικρότερου µήκους κύµατος. Σχήµα 1.8 α. Ο δείκτης διάθλασης διαφόρων κοινών οπτικών υλικών συναρτήσει του µήκους κύµατος του φωτός, στην περιοχή του ορατού φωτός
7 7 Σχήµα 1.8 β. Οδείκτης διάθλασης διαφόρων υλικών συναρτήσει του µήκους κύµατος του φωτός (The Harshaw Chemical Co.). 2. ΜΙΚΡΟΣΚΟΠΙΑ 2.1 Γενικές αρχές Ως οπτικά ή φωτονικά αναφέρονται τα µικροσκόπια εκείνα όπου χρησιµοποιούν το τµήµα του ηλεκτροµαγνητικού φάσµατος που είναι ορατό, δηλαδή από nm. Ανάλογα µε την διάταξη των φακών και τον τρόπο παρατήρησης τα οπτικά µικροσκόπια διακρίνονται σε µικροσκόπια φωτεινού πεδίου, αντίθεσης φάσεως, µικροσκόπια σκοτεινού πεδίου, πολωτικά µικροσκόπια, µικροσκόπια αντίθεσης διαφορικής συµβολής, µικροσκόπια φθορισµού και άλλα. Η µεγέθυνση ενός οπτικού µικροσκοπίου δίνεται από τον τύπο : Μ=m 1 *m 2 (2.1) όπου m 1 και m 2 είναι οι εγκάρσιες µεγεθύνσεις των δύο φακών, δηλαδή του προσοφθάλµιου και του αντικειµενικού. Οι µεγεθύνσεις m 1 και m 2 αναγράφονται από τον κατασκευαστή στα αντίστοιχα στοιχεία του µικροσκοπίου και µε κατάλληλο συνδυασµό επιτυγχάνεται η επιθυµητή ολική µεγέθυνση. Εποµένως θα µπορούσαµε να πούµε ότι βάζοντας δυνατότερους φακούς θα ήταν δυνατόν να πετύχουµε µεγαλύτερες µεγεθύνσεις. Πράγµατι µε αυτό το σκεπτικό θα βλέπαµε το παρασκεύασµά µας µεγαλύτερο χωρίς όµως να έχουµε πιο µεγάλη ευκρίνεια της εικόνας (άδεια µεγέθυνση), όπως ακριβώς συµβαίνει όταν µεγεθύνουµε πολύ µια φωτογραφία έτσι που να φαίνονται οι κόκκοι του film. Υπάρχει µε άλλα λόγια µία µέγιστη χρήσιµη µεγέθυνση που είναι συνάρτηση της διακριτικής ικανότητας του οργάνου που ορίζεται ως ικανότητά του να διακρίνει δύο σηµειακές φωτεινές πηγές που βρίσκονται πολύ κοντά η µία µε την άλλη.η διακριτική ικανότητα (d) ενός οπτικού συστήµατος δίνεται από τον τύπο:
8 8 λ d = 0.61 (2.2) nsin a όπου d είναι η διακριτική ικανότητα, 0.61 ένας σταθερός αριθµός, λ το µήκος κύµατος του φωτός (ή της ακτινοβολίας) που χρησιµοποιούµε, n ο δείκτης διάθλασης του µέσου µεταξύ παρασκευάσµατος και φακού και το α το µισό της γωνίας του φωτεινού κώνου που δέχεται ο φακός. Η συνάρτηση (2.3) λέγεται και αριθµητικό άνοιγµα (Α) του φακού και εξαρτάται αποκλειστικά από τη κατασκευή του φακού. Α= n sinα (2.3) Εφόσον λοιπόν το φως που χρησιµοποιούν τα οπτικά µικροσκόπια συνήθως έχει ένα µέσο µήκος κύµατος λ=500 nm και το αριθµητικό άνοιγµα (Α) ενός πολύ καλού φακού είναι 1.6, τότε η διακριτική ικανότητα του οπτικού µικροσκοπίου δε µπορεί να ξεπεράσει τα d=200 nm = 0.2 µm και η «χρήσιµη µεγέθυνση» περίπου την τιµή 1600Χ. Ένας πρόχειρος, πρακτικός τρόπος υπολογισµού της χρήσιµης µεγέθυνσης που µπορεί να µας δώσει ένας αντικειµενικός φακός, δίνεται από τον τύπο: χ.µ.=1000*α. Ο τύπος λοιπόν (2.2) µας λέει πως για να καλυτερέψουµε τη διακριτική ικανότητα θα πρέπει να µικρύνουµε το λ και να αυξήσουµε το Α. Επειδή όµως οι οπτικοί (γυάλινοι) φακοί, από πλευράς ποιότητας κατασκευής, είναι σχεδόν τέλειοι, το Α δεν µπορεί να αυξηθεί άλλο. Έτσι µας µένει µόνο το µήκος κύµατος του φωτός (ή της ακτινοβολίας) το οποίο όµως όταν µικρύνει πολύ γίνεται αόρατο! Κατά καιρούς γίνανε διάφορες προσπάθειες βελτίωσης της διακριτικής ικανότητας του µικροσκοπίου χρησιµοποιώντας ακτινοβολίες µε µήκος κύµατος µικρότερο εκείνου του ορατού φωτός µε αποτέλεσµα την κατασκευή διαφόρων τύπων µικροσκοπίων όπως το υπεριώδες µικροσκόπιο, το µικροσκόπιο ακτινών Χ και άλλων µεταξύ των οποίων και το ηλεκτρονικό µικροσκόπιο στις διάφορες παραλλαγές του.στην πράξη τα µικροσκόπια που συναντάµε συνήθως σε ένα εργαστήριο έχουν φακούς που στην καλύτερη περίπτωση έχουν αριθµητικό άνοιγµα Α=1.4. Οι φακοί µε µεγαλύτερο αριθµητικό άνοιγµα (Α=1.6) έχουν δύο µεγάλα µειονεκτήµατα, τη πολύ υψηλή τιµή αγοράς αλλά και το πολύ µικρό βάθος εστίασης, κάτι που τους κάνει ιδιαίτερα δύσχρηστους.
9 9 2.2 Ο µεγεθυντικός φακός Απλό µικροσκόπιο Ένας µεγεθυντικός φακός, ή απλό µικροσκόπιο, είναι ένας συγκλίνων φακός σχετικά µικρής εστιακής απόστασης. Το αντικείµενο που παρατηρείται τοποθετείται πολύ κοντά στο µάτι και η λειτουργία του µεγεθυντικού φακού είναι να σχηµατίσει ένα φανταστικό είδωλο σε απόσταση ίση ή µεγαλύτερη από την ελάχιστη απόσταση ευκρινούς οράσεως (Σχ. 2.1), στην οποία το µάτι µπορεί να το παρατηρήσει άνετα. Σχήµα 2.1: Ο µεγεθυντικός φακός, ή απλό µικροσκόπιο. Αν το αντικείµενο έχει µέγεθος H και παρατηρείται µε γυµνό οφθαλµό (Σχ. 2.1.α), θα φαίνεται ευκρινώς και όσο γίνεται µεγαλύτερο αν βρίσκεται σε απόσταση ίση µε την ελάχιστη απόσταση ευκρινούς οράσεως. Σε αυτήν την περίπτωση, η γωνία που υποτείνει το αντικείµενο στο κέντρο του µατιού είναι περίπου ίση µε θ = H (2.1) Αν τώρα ο φακός τοποθετηθεί πολύ κοντά στο µάτι και το αντικείµενο σε απόσταση s από αυτό, τέτοια ώστε να σχηµατιστεί ένα είδωλο του αντικειµένου σε απόσταση ίση µε (Σχ. 2.1.β), το γωνιακό µέγεθος του ειδώλου θα είναι: h Η θ ' = (2.2) s
10 10 Η µεγέθυνση που επιτυγχάνεται µε αυτόν τον τρόπο είναι: θ ' H / s M = = =. θ H / s (2.3) Όµως, σύµφωνα µε τον τύπο των φακών, ισχύει η σχέση: 1 f 1 1 = + (2.4) s και εποµένως η µεγέθυνση που επιτυγχάνεται µε τον µεγεθυντικό φακό είναι: M = 1 + (2.5) f Βεβαίως, το είδωλο του παρατηρούµενου αντικειµένου µπορεί να σχηµατιστεί σε οποιαδήποτε άλλη απόσταση από το µάτι, µεγαλύτερη από. Στην άλλη ακραία περίπτωση, που το είδωλο σχηµατίζεται σε άπειρη απόσταση από το µάτι (Σχ. 2.1.γ), το αντικείµενο πρέπει να τοποθετηθεί στην εστία του φακού και τότε είναι. H θ '. Στη νπερίπτωση αυτή, η γωνιακή µεγέθυνση που επιτυγχάνεται µε τον f φακό είναι: θ ' M = = θ H / f H / ή M = (2.6) f Για άλλες αποστάσεις του ειδώλου από το µάτι, η µεγέθυνση Μ είναι: f <Μ< 1 + (2.7) f Προφανώς, λόγω της εξάρτησης από την ελάχιστη απόσταση ευκρινούς οράσεως, η µεγέθυνση ή το όφελος που προκύπτει από τη χρήση του µεγεθυντικού φακού εξαρτώνται από τον παρατηρητή. Για ένα άτοµο µε υπερµετρωπία, που κανονικά για να παρατηρήσει ένα αντικείµενο πρέπει να το τοποθετήσει σε µεγάλη απόσταση, η χρήση του φακού προσφέρει σηµαντικότερο πλεονέκτηµα από ό,τι για ένα άτοµο που µε γυµνό οφθαλµό µπορεί να παρατηρήσει το αντικείµενο από πολύ µικρότερη απόσταση. Στις συνήθεις χρήσεις των µεγεθυντικών φακών, οι µεγεθύνσεις είναι µέχρι 8 περίπου. Για µεγαλύτερες µεγεθύνσεις, µέχρι περίπου 20, απαιτείται να γίνουν διορθώσεις των σφαλµάτων των φακών.
11 11 Σχήµα 2.2.: Μικροσκόπιο 2.3 Σύνθετο οπτικό µικροσκόπιο Η πρόοδος της ηλεκτρονικής και των µικροϋπολογιστών δεν άφησε ανέπαφη και τη µικροσκοπία. Τα σύγχρονα µικροσκόπια διαθέτουν πλήθος αυτοµατισµών και άλλων µηχανισµών που κάνουν τα µικροσκόπια πιο εύκολα στη χρήση ακόµα και από άτοµα χωρίς ειδικές γνώσεις. Η χρήση όµως αυτών των µικροσκοπίων περιορίζεται σχεδόν αποκλειστικά στην έρευνα και τη διάγνωση στην ιατρική λόγω µεγάλου κόστους αγοράς και συντήρησης. Το σύνθετο µικροσκόπιο είναι ένα οπτικό όργανο που χρησιµοποιείται για την παρατήρηση, υπό µεγέθυνση, αντικειµένων που βρίσκονται κοντά στον παρατηρητή. Το παρατηρούµενο αντικείµενο τοποθετείται πολύ κοντά σε ένα συγκλίνοντα φακό πολύ µικρής εστιακής απόστασης (τον α- ντικειµενικό ή αντοφθάλµιο φακό), ο οποίος σχηµατίζει ένα πραγµατικό είδωλό του. Το είδωλο αυτό µεγεθύνεται από έναν άλλο συγκλίνοντα φακό (τον προσοφθάλµιο φακό), ο οποίος σχηµατίζει ένα φανταστικό είδωλο σε µια απόσταση από το µάτι που βρίσκεται ανάµεσα στην ελάχιστη και τη µέγιστη απόσταση ευκρινούς οράσεως. Το µάτι παρατηρεί αυτό το είδωλο.
12 Μέρη µικροσκοπίου Για τη σωστή χρήση των µικροσκοπίων είναι απαραίτητο να γνωρίζουµε τα µέρη από τα οποία αποτελούνται. Τα µέρη των µικροσκοπίων χωρίζονται σε µηχανικά και οπτικά µερη. Πιο αναλυτικά: Σχήµα 2.3.: Τα τµήµατα ενός σύγχρονου οπτικού µικροσκοπίου 1.Προσοφθάλµιος φακός, τοποθετηµένος στο πάνω µέρος του σωλήνα. Υπάρχουν τέσσερις τύποι: Huygens, Ramsden, Kellner και αντισταθµιστικοί (compensating). Οι τελευταίοι είναι και οι πιο σύγχρονοι και επιτρέπουν την παρατήρηση χωρίς το µάτι να είναι σε επαφή µε φακό. Ο χαραγµένος αριθµός π.χ. 10Χ δείχνει τη µεγέθυνση του φακού που αν τον πολλαπλασιάσουµε µε τη µεγέθυνση του αντικειµενικού φακού µας δίνει την τελική µεγέθυνση του µικροσκοπίου. Σε όλους σχεδόν τους προσοφθάλµιους φακούς υπάρχει δυνατότητα τοποθέτησης κλίµακας µέτρησης µέσα στο φακό αφού τον ξεβιδώσουµε. Ο σωλήνας στην κορυφή του οποίου βρίσκεται ο προσοφθάλµιος φακός (κατακόρυφος στα παλιότερα µικροσκόπια και υπό γωνία στα πιο σύγχρονα), µπορεί να είναι µονός, στα µονοφθάλµια µικροσκόπια και διπλός στα διοφθάλµια για πιο άνετη (όχι στερεοσκοπική) παρατήρηση. Ο σωλήνας συνήθως µπορεί να αφαιρεθεί για να τοποθετηθεί σωλήνας άλλου τύπου π.χ. σωλήνας µε υποδοχή για φωτογραφική µηχανή video camera κλπ, ή να περιστραφεί για χρήση του µικροσκοπίου από εµπρός ή από πίσω. 2.Περιστρεφόµενη κεφαλή µε τους αντικειµενικούς φακούς. Συνήθως έχει θέσεις για 3-6 φακούς. Σε ορισµένα ερευνητικά µικροσκόπια η περιστρεφόµενη κεφαλή µπορεί να αφαιρεθεί εύκολα και να αντικατασταθεί µε άλλη που έχει διαφορετικό set φακών. Έτσι σχετικά εύκολα µπορεί το µικροσκόπιο να µετατραπεί σε αντίθεσης φάσης, φθορισµού κλπ. 3. Η τράπεζα του µικροσκοπίου που µπορεί να είναι τετράγωνη σταθερή ή στρογγυλή περιστρεφόµενη (για πολωτικά µικροσκόπια) και µε σύστηµα µικροµετρικών κοχλιών για τη µετακίνηση του παρασκευάσµατος. Το υλικό κατασκευής της τράπεζας είναι συνήθως κάποιο µέταλλο ενώ σε κάποια σύγχρονα καλά µικροσκόπια µπορεί να είναι από κεραµικό που είναι ανθεκτικό σε διάφορες διαβρωτικές ουσίες. Σε ορισµένα µικροσκόπια υπάρχει µηχανισµός αυτόµατης µετακίνησης της αντικειµενοφόρου πλάκας µε δυνατότητα συστηµατικής σάρωσής της ή και ακόµα µε τη δυνατότητα εναλλαγής αντικειµενοφόρων πλακών. Τα
13 13 συστήµατα αυτά είναι ιδιαίτερα χρήσιµα σε αυτοµατοποιηµένες αιµατολογικές και κυτταρολογικές εξετάσεις και βιοψίες. 4.Μοχλός ρύθµισης της ίριδας (διαφράγµατος). Η ίριδα περιορίζει τον φωτεινό κώνο που φωτίζει το παρασκεύασµα έτσι που αυτό να δέχεται τις ακτίνες που δεν προέρχονται από περίθλαση ή διάθλαση. Η ίριδα δεν πρέπει ποτέ να χρησιµοποιείται για την αύξηση ή ελάττωση της φωτεινής έντασης. Η ρύθµισή της είναι πολύ σηµαντική κυρίως όταν πρόκειται να φωτογραφίσουµε το παρασκεύασµα. Ο τρόπος ρύθµισης διαφέρει από κατασκευαστή σε κατασκευαστή και θα πρέπει πάντα να συµβουλευόµαστε τις οδηγίες χρήσης του οργάνου. 5.Συγκεντρωτής (ή συµπυκνωτής) φακός. Σκοπός του εξαρτήµατος αυτού είναι η εστίαση της φωτεινής πηγής στο επίπεδο του παρασκευάσµατος. Η κακή ρύθµιση του συµπυκνωτή έχει σαν αποτέλεσµα τον κατά πολύ περιορισµό της διακριτικής ικανότητας του οργάνου. Για συνεχή παρατήρηση σε χαµηλή µεγέθυνση (π.χ. 4Χ ή 10Χ) ο φακός αυτός µπορεί να αφαιρεθεί. 6.Κουµπί εστίασης (µεγάλο εξωτερικό για αδρή και µικρό στο κέντρο για λεπτή εστίαση). Σε πολλά µικροσκόπια υπάρχουν ξεχωριστά αυτοί οι δυο κοχλίες. Η κλίµακα που είναι χαραγµένη στο µικροµετρικό κοχλία εστίασης µας δείχνει την κατακόρυφη µετακίνηση του αντικειµενικού φακού και µπορεί να χρησιµοποιηθεί για τη µέτρηση του ύψους (βάθους) ενός παρασκευάσµατος. 7.Βάση µικροσκοπίου µε (συνήθως) ενσωµατωµένο σύστηµα φωτισµού. Στα περισσότερα µικροσκόπια σήµερα υπάρχει ρεοστάτης για τη ρύθµιση της έντασης του φωτός. Προσοχή όµως γιατί αλλάζοντας τη φωτεινή ένταση µε αυτόν τον τρόπο αλλάζουν και τα µήκη κύµατος που απαρτίζουν το φως. Αυτό δεν επηρεάζει την απλή παρατήρηση ή την ασπρόµαυρη φωτογράφηση, επηρεάζει όµως σηµαντικά την έγχρωµη φωτογράφηση. Στην τελευταία περίπτωση χρησιµοποιούµε τον φωτισµό στη µέγιστη ένταση και για τον περιορισµό της φωτεινής έντασης χρησιµοποιούµε ουδέτερα φίλτρα. 3. ΑΝΤΙΚΕΙΜΕΝΙΚΟΙ ΦΑΚΟΙ ΜΙΚΡΟΣΚΟΠΙΩΝ 3.1 Γενικά Οι αντικειµενικοί φακοί είναι τα πιο σηµαντικά εξαρτήµατα του συστήµατος σχηµατισµού εικόνας του µικροσκοπίου γιατί από αυτούς εξαρτάται η τελική διακριτική ικανότητα και η αρχική µεγέθυνση. Οι φακοί αυτοί έχουν κατασκευαστεί έτσι που οι εικόνες να µην έχουν σφαιρικά ή χρωµατικά σφάλµατα, και να µην έχουν αστιγµατισµό. Ο φακοί αυτοί έχουν χαραγµένες στο σώµα τους διάφορες ενδείξεις π.χ. Plan 40/ /0.17, που σηµαίνει φακός επίπεδος µεγέθυνσης 40Χ, αριθµητικό άνοιγµα 0.65, για χρήση σε µικροσκόπιο µε σωλήνα µήκους 160 mm, και µε καλυπτρίδα πάχους mm. Η ένδειξη d=0 σηµαίνει ότι ο φακός είναι σχεδιασµένος για να χρησιµοποιείται χωρίς καλυπτρίδα. Οι αντικειµενικοί φακοί των µικροσκοπίων µπορούν να ταξινοµηθούν ποιοτικά µε βάση το είδος του φακού (αχρωµατικός, αποχρωµατικός ή φθορίτη) και κατά πόσο είναι για χρήση σε αέρα (ξηροί φακοί) ή για λάδι καταδύσεως (καταδυτικοί φακοί). Σκοπός των αντικειµενικών φακών είναι η υπό µεγέθυνση πιστή αναπαραγωγή της παρατηρούµενης εικόνας που θα φτάσει ως πραγµατικό είδωλο στην εστία του προσοφθάλµιου συστήµατος. 3.2 Χαρακτηριστικά αντικειµενικών φακών Τα χαρακτηριστικά των αντικειµενικών φακών είναι η µεγέθυνση, το αριθµητικό άνοιγµα, η ελεύθερη απόσταση εργασίας, το βάθος εστίασης και η διακριτική ικανότητα. Ειδικότερα είναι: Μεγέθυνση: ονοµάζεται η τάξη µεγέθους µε την οποία η παρατηρούµενη
14 14 εικόνα µεγεθύνεται, καθώς το φως περνά από τον αντικειµενικό φακό. Ανάλογα µε το είδος της έρευνας µπορούν να χρησιµοποιηθούν φακοί διαφόρων µεγεθύνσεων. Η µεγέθυνση αναγράφεται στην πλευρά του φακού και τα τυπικά µεγέθη της είναι 5Χ, 10Χ µέχρι 125Χ. Αριθµητικό άνοιγµα: ονοµάζεται το µέτρο της διακριτικής ικανότητας και καθορίζει το βάθος εστίασης και το εύρος της χρησιµότητας της µεγέθυνσης. Μαθηµατικά εκφράζεται από την παρακάτω σχέση: AA =n*ηµφ (3.1) όπου n = δείκτης διάθλασης του µέσου µεταξύ τοµής (δοκιµίου) φακού. Φ = ½ του γωνιακού ανοίγµατος του φακού. Η τιµή του αριθµητικού ανοίγµατος του φακού η οποία κυµαίνεται ποσοτικά µεταξύ 0,04 και1,4, αναγράφεται στην πλευρά του φακού. Ελεύθερη απόσταση εργασίας: είναι η απόσταση µεταξύ της επιφάνειας το δοκιµίου και της επιφάνειας του φακού σε θέση εστιάσεως και είναι αντιστρόφως ανάλογη της µεγέθυνσης και του αριθµητικού ανοίγµατος του φακού. Βάθος εστίασης: είναι η περιοχή πριν και µετά τη θέση εστιάσεως, µέσα στην οποία το είδωλο είναι ακόµα σαφές. Το βάθος εστιάσεως είναι αντιστρόφως ανάλογο της µεγέθυνσης και του αριθµητικού ανοίγµατος του φακού. ιακριτική ικανότητα: είναι η µικρότερη απόσταση που µπορούν να έχουν δύο σηµεία του παρατηρούµενου αντικειµένου, τα οποία διακρίνονται µε το µάτι. Αξίζει να σηµειωθεί ότι η µέγιστη διακριτική ικανότητα του µατιού είναι 0,3 χιλιοστά, όταν η παρατήρηση του αντικειµένου γίνεται από απόσταση 25 εκατοστών (απόσταση ευκρινούς όρασης). Η µαθηµατική σχέση από την οποία υπολογίζεται η διακριτική ικανότητα του µικροσκοπίου είναι: λ D= 2n ηµα (3.2) 2 Όπου: λ είναι το µήκος κύµατος του χρησιµοποιούµενου φωτός, n είναι ο δείκτης διάθλασης (η τιµή του για τον αέρα είναι n=1), Co( ταχύτητα _ φωτός ) n( δε ίκτης _ διάθλασης ) = (3.3) C α είναι η γωνία πρόσπτωσης του φωτός. Μέγιστη διακριτική ικανότητα: Η µέγιστη διακριτική ικανότητα ενός µικροσκοπίου για παρατήρηση στον αέρα και µε χρήση λευκού φωτός (λ=6000 ο Α) δίνεται από τη σχέση: D max = = = 0.3µ m _ ή _ 0, 0003mm (3.4) 2*1*1 2 Ωστόσο η χρήσιµη µεγέθυνση ενός µικροσκοπίου για τις παραπάνω συνθήκες είναι: D1 M χρ = (3.5) D max Στην παραπάνω σχέση, όπου D1 είναι η µέγιστη διακριτική ικανότητα του γυµνού οφθαλµού η οποία είναι ίση µε 0,3 χιλιοστόµετρα. Έτσι προκύπτει η σχέση:
15 M max = = 1000 (3.6) Για τη βελτίωση της διακριτικής ικανότητας έχουν επινοηθεί ορισµένες µέθοδοι οι οποίες µπορούν να εφαρµοστούν στην κατασκευή του µικροσκοπίου, µε αποτέλεσµα τελικά τη χρησιµοποίηση µεγαλύτερων µεγεθύνσεων. Ο πρώτος τρόπος σχετίζεται µε τον φωτισµό του δείγµατος προς εξέταση. Αν δηλαδή ελαττώσουµε το λ (µήκος κύµατος) του φωτός έχουµε βελτίωση της διακριτικής ικανότητας (ελάττωση αυτής). Έτσι το δοκίµιο φωτίζεται µε ιώδες φως, το οποίο έχει το µικρότερο µήκος κύµατος της ορατής ακτινοβολίας. Ο δεύτερος τρόπος µείωσης της διακριτικής ικανότητας είναι η αύξηση του ανοίγµατος του αντικειµενικού φακού. Ωστόσο η διαδικασία αυτή δεν είναι απλή και πρέπει να γίνει µε ένα περίπλοκο σύστηµα φακών. Το σύστηµα αυτό των φακών είναι απαραίτητο, ώστε να ελαττωθούν οι εκτροπές της φωτεινής ακτινοβολίας οι οποίες στην περίπτωση αυτή είναι ιδιαίτερα εµφανείς. Τέλος, µπορεί να χρησιµοποιείται ειδικό λάδι (κεδρέλαιο) ώστε να αυξηθεί η µέγιστη µεγέθυνση σε 1500, αφού για το κεδρέλαιο ισχύει n=1,5. Το λάδι αυτό παρεµβάλλεται ανάµεσα στο δοκίµιο και τον αντικειµενικό φακό. Ωστόσο για να είναι η εικόνα στο µικροσκόπιο ικανοποιητική πρέπει η ολική µεγέθυνση να µην ξεπερνά τη χρήσιµη µεγέθυνση του οπτικού συστήµατος η οποία είναι πρακτικά 1000 φορές το αριθµητικό άνοιγµα του αντικειµενικού φακού. Αξίζει να σηµειωθεί πως η ελαιοκατάδυση (χρήση καταδυτικού φακού και κεδρελαίου) ελαττώνει την ανακλαστικότητα των δοκιµίων, αλλά ενισχύει τις χρωµατικές αντιθέσεις έτσι χρωµατικά φαινόµενα πολύ ασθενή να γίνονται ορατά. 3.3 Τύποι αντικειµενικών φακών. Οι διάφοροι κατασκευαστές µικροσκοπίων µπορεί να χρησιµοποιούν διαφορετικούς συµβολισµούς θα πρέπει πάντα να διαβάζουµε τις οδηγίες χρήσης του συγκεκριµένου οργάνου. Το χρώµα των γραµµάτων και συµβόλων που είναι χαραγµένα πάνω στον αντικειµενικό φακό επίσης είναι ενδεικτικά του οπτικού τύπου του φακού π.χ. κόκκινα γράµµατα συµβολίζουν φακό για πολωµένο φως ενώ πράσινα γράµµατα συµβολίζουν φακό αντίθεσης φάσης. Σχήµα 3.1: Τύποι αντικειµενικών φακών
16 16 Πολλές φορές ο τύπος του φακού και η µεγέθυνσή του συµβολίζονται και µε χρωµατιστά δαχτυλίδια χαραγµένα πάνω τους όπως αναφέρεται στον πιο κάτω Πίνακα 1. Μεγέθυνση Χρώµα µαύρο γκρι καφέ 4-5 κόκκινο πορτοκαλί κίτρινο ανοιχτό πράσινο σκούρο πράσινο ανοιχτό µπλε σκούρο µπλε 100, 125, 160 άσπρο Υγρό κατάδυσης φακού λάδι νερό γλυκερίνη άλλα υγρά Χρώµα µαύρο άσπρο πορτοκαλί κόκκινο Πίνακας 1.: Τι σηµαίνουν τα χρωµατιστά δαχτυλίδια που είναι χαραγµένα στους αντικειµενικούς φακούς. Άλλα σύµβολα που µπορεί να είναι χαραγµένα πάνω στους αντικειµενικούς φακούς: PH: φακός για διάταξη αντίθεσης φάσης, ο αριθµός που συνήθως ακολουθεί π.χ. ΡΗ2 σηµαίνει ότι ο φακός αυτός πρέπει να χρησιµοποιηθεί σε συνεργασία µε το διάφραγµα νούµερο 2 του συµπυκνωτή φακού. PLAN: σηµαίνει ότι ο φακός είναι επίπεδος, δηλαδή όλα τα σηµεία του οπτικού πεδίου εστιάζουν στο ίδιο επίπεδο, αντίθετα σε φακούς χωρίς αυτή την ένδειξη όταν το κέντρο του οπτικού πεδίου είναι εστιασµένο τα σηµεία στην περιφέρεια δεν είναι εστιασµένα. Είναι απαραίτητο να χρησιµοποιούνται τέτοιοι φακοί όταν πρόκειται να γίνει φωτογράφηση του παρασκευάσµατος. APO: σηµαίνει ότι ο φακός είναι αποχρωµατικός, δηλαδή τα χρωµατικά σφάλµατα του φακού έχουν ελαχιστοποιηθεί για τρία τουλάχιστον µήκη κύµατος (450, 550 και 650 nm) ενώ τα σφαιρικά σφάλµατα έχουν ελαχιστοποιηθεί για µήκος κύµατος περίπου 550 nm. Achromat: λίγο κατώτερης ποιότητας από τους φακούς ΑΡΟ γιατί τα χρωµατικά σφάλµατα είναι ελαχιστοποιηµένα για δυο µόνο µήκη κύµατος (περίπου 500 και 600 nm) ενώ η διόρθωση για σφαιρικά σφάλµατα είναι η ίδια µε εκείνη των φακών ΑΡΟ. POL: σηµαίνει ότι ο φακός είναι για πολωτικό µικροσκόπιο. Semi-apochromat: φακοί ποιότητας ενδιάµεσης µεταξύ του APO και του Achromat.
17 17 Fluorite, Neofluor: σηµαίνει ότι το γυαλί από το οποίο είναι κατασκευασµένος ο φακός δεν απορροφά την υπεριώδη ακτινοβολία και δεν φθορίζει. Αυτοί οι φακοί είναι κατάλληλοι για µικροσκοπία φθορισµού ενώ µπορούν να χρησιµοποιηθούν και µε κοινό φωτισµό. 4. ΑΡΙΘΜΗΤΙΚΟ ΑΝΟΙΓΜΑ ΚΑΙ ΙΑΚΡΙΤΙΚΗ ΙΚΑΝΟΤΗΤΑ (NUMERICAL APERTURE AND RESOLUTION) 4.1 Αριθµητικό Άνοιγµα (Numerical Aperture). Το αριθµητικό άνοιγµα ενός µικροσκοπίου είναι ένα µέγεθος το οποίο χαρακτηρίζει τη δυνατότητα του µικροσκοπίου να συλλέγει το φως και να αναλύει το δείγµα σε λεπτοµέρειες, όταν αυτό βρίσκεται σε µία σταθερή απόσταση από τον αντικειµενικό φακό. Το µήκος κύµατος του φωτός απεικόνισης περνά µέσα από το δείγµα και εισάγεται στον αντικειµενικό φακό µε την µορφή ενός ανεστραµµένου κώνου όπως φαίνεται στην εικόνα 1. Μία επιµήκης φέτα από τον κώνο φωτός δείχνει το γωνιακό άνοιγµα, µία τιµή που καθορίζεται από την εστιακή απόσταση του αντικειµενικού φακού. Σχήµα 4.1 Η γωνία µ είναι το µισό γωνιακό άνοιγµα του αντικειµενικού φακού (η κλίση ως προς τον οπτικό άξονα, των εξωτερικών ακτινών που συµµετέχουν στον σχηµατισµό της εικόνας) και σχετίζεται µε το αριθµητικό άνοιγµα όπως ορίζεται στην εξίσωση που ακολουθεί: Numerical Aperture (NA) =n*sin(µ) (4.1) Όπου n είναι ο δείκτης διάθλασης του µέσου που παρεµβάλλεται µεταξύ του αντικειµένου-δείγµατος και του αντικειµενικού φακού. Μία τιµή που κυµαίνεται από 1,00 στον αέρα µέχρι 1,51 στο κεδρέλαιο (λάδι καταδυτικού φακού). Από την παραπάνω εξίσωση είναι προφανές ότι όταν το µέσο διάδοσης είναι ο αέρας (όπου n=1), τότε το αριθµητικό άνοιγµα εξαρτάται µόνο απο τη γωνία µ, της οποίας η µέγιστη τιµή µπορεί να είναι 90 ο. Το sin της γωνίας µ έχει µέγιστη τιµή το 1 (sinµ=1) για αυτό έχω µ max = 90 ο. Tότε έχω το θεωρητικά µέγιστο αριθµητικό άνοιγµα ενός φακού, µε µέσο διάδοσης τον αέρα. Στην πράξη, ωστόσο, είναι δύσκολο να επιτευχθούν αριθµητικά ανοίγµατα µε τιµές πάνω από 0,95 µε ξηρούς φακούς. Το σχήµα 2 δείχνει µία σειρά φωτεινών κώνων που προέρχονται από φακούς µε διάφορα εστιακά µήκη και αριθµητικά ανοίγµατα. Καθώς ο κώνος φωτός αλλάζει, η γωνία µ αυξάνεται απο 7 ο (Σχήµα 2.α) σε 60 ο (Σχήµα 2.c) και συνεπώς µεταβάλλεται και το αριθµητικό άνοιγµα από 0,12 σε 0,87, δηλαδή κοντά στο όριο όταν το µέσο είανι ο αέρας.
18 18 Σχήµα 4.2 Εξετάζοντας την εξίσωση του αριθµητικού ανοίγµατος, είναι προφανές ότι ο δείκτης διάθλασης είναι ο περιοριστικός παράγοντας που µας εµποδίζει να επιτύχουµε αριθµητικό άνοιγµα µεγαλύτερο του 1(ΝΑ>1). Εποµένως προκειµένου να λάβουµε µεγαλύτερα αριθµητικά ανοίγµατα, ο δείκτης διάθλασης του µέσου που παρεµβάλλεται µεταξύ του δείγµατος και του αντικειµενικού φακού πρέπει να αυξηθεί. Οι αντικειµενικοί φακοί των µικροσκοπίων που είναι σήµερα διαθέσιµοι µας επιτρέπουν την απεικόνιση µε εναλλακτικά µέσα διάδοσης όπως στο νερό(n=1.33), στη γλυκερίνη(n=1.47) και στο κεδρέλαιο-λάδι καταδυτικoύ φακού- (n=1.51). Αυτοί οι φακοί πρέπει να χρησιµοποιούνται µε προσοχή, ώστε να προλαµβάνονται τυχόν λάθος αποτελέσµατα. Λάθος αποτελέσµατα µπορεί να προκύψουν αν οι φακοί χρησιµοποιηθούν σε ένα διαφορετικό καταδυτικό µέσο από αυτό για το οποίο έχουν κατασκευαστεί. Οι περισσότεροι φακοί µεγέθυνσης µεταξύ 60Χ και 100Χ (και µεγαλύτερης µεγέθυνσης ) έχουν σχεδιαστεί για χρήση µε κεδρέλαιο. Εξετάζοντας την εξίσωση του αριθµητικού ανοίγµατος, βρίσκουµε ότι το µεγαλύτερο θεωρητικά αριθµητικό άνοιγµα που µπορεί να επιτευχθεί µε χρήση κεδρελαίου είναι 1,51(όταν sinµ=1). Στην πράξη, ωστόσο, οι περισσότεροι φακοί κεδρελαίου έχουν µέγιστο αριθµητικό άνοιγµα 1,4. Συνήθως το αριθµητικό άνοιγµα σε αυτές τις περιπτώσεις κυµαίνεται από 1,0 µέχρι 1,35. Objective Numerical Apertures Magnification Plan Achromat (NA) Plan Fluorite (NA) Plan Apochromat (NA) 0.5x n/a n/a 1x 0.04 n/a n/a 2x 0.06 n/a x x x x x (oil) n/a x x (oil) n/a n/a x (oil) x n/a n/a 0.90 Πίνακας 2
19 19 Το αριθµητικό άνοιγµα ενός φακού εξαρτάται ως ένα βαθµό και από το «ποσό» αποκατάστασης της οπτικής εκτροπής. Φακοί υψηλής διόρθωσης εκτροπής τείνουν να έχουν πολύ µεγαλύτερο αριθµητικό άνοιγµα από αντίχτοιχους φακούς µεγέθυνσης, όπως φαίνεται και στον πίνακα 2. Για παράδειγµα, αν πάρουµε µία σειρά φακών µεγέθυνσης 10Χ, θα δούµε ότι για τους φακούς οριζόντιας επίπεδης διόρθωσης, οι αυξήσεις των αριθµητικών ανοιγµάτων οφείλονται στη διόρθωση για τη χρωµατική και σφαιρική εκτροπή: plan achromat N.A.= 0.25, plan fluorite N.A.=0.30, plan apochromat N.A.= Αυτό το χαρακτηριστικό της αύξησης του αριθµητικού ανοίγµατος, πέρα από την αύξηση του παράγοντα της οπτικής αποκατάστασης, ισχύει για όλα τα είδη αντικειµενικών φακών µε ίδια µεγέθυνση(η µεγέθυνση µπορεί να πάρει οποιαδήποτε τιµή) όπως δαίνεται και στον πίνακα 2. Οι περισσότεροι κατασκευαστές προσπαθούν να εξασφαλίσουν ότι οι φακοί τους έχουν την µεγαλύτερη αποκατάσταση εκτροπής και το µεγαλύτερο αριθµητικό άνοιγµα που είναι δυνατόν, για κάθε είδος φακού. 4.2 Σχέση αριθµητικού ανοίγµατος(να) και διακριτικής ικανότητας (Resolution). Η διακριτική ικανότητα (R)(resolution) ενός φακού µικροσκοπίου ορίζεται ως η ελάχιστη απόσταση µεταξύ δύο σηµείων του αντικειµένου δείγµατος, τα οποία είναι διακρίσιµα στην τελική εικόνα. Η διακριτική ικανότητα είναι ένα υποκειµενικό µέγεθος στην µικροσκοπία επειδή σε µεγάλες µεγεθύνσεις µία εικόνα µπορεί να εµφανιστεί unsharp, ωστόσο αναλύεται µε την µέγιστη ικανότητα του φακού. Το αριθµητικό άνοιγµα καθορίζει την δυνατότητα ανάλυσης ενός αντικειµενικού φακού, ωστόσο η συνολική ανάλυση ενός συστήµατος µικροσκοπίας καθορίζεται από το αριθµητικό άνοιγµα του συµπυκνωτή φακού. Γενικότερα, όσο µεγαλύτερο είναι το αριθµητικό άνοιγµα του συστήµατος µικροσκοπίας, τόσο καλύτερη είναι και η διακριτική ικανότητά του. Η σωστή ευθυγράµµιση του οπτικού συστήµατος των µικροσκοπίων είναι επίσης υψήστης σηµασίας για την εξασφάλιση της µέγιστης διακριτικής ικανότητας. Ο συµπυκνωτής φακός πρέπει να ταιριάζει απόλυτα µε τον αντικειµενικό φακό στο αριθµητικό άνοιγµα και στις ρυθµίσεις ανοίγµατος του διαφράγµατος για να έχουµε ακριβή σχηµατισµό του κώνου φωτός. Το φάσµα του µήκους κύµατος του φωτός που χρησιµοποιείται για την απεικόνιση του δείγµατος είναι επίσης ένας σηµαντικός παράγοντας για την διακριτική ικανότητα. Μικρότερα µήκη κύµατος είναι ικανά να αναλύουν λεπτοµέρειες σε µεγαλύτερο βαθµό από ότι τα µεγαλύτερα µήκη κύµατος. Υπάρχουν αρκετές εξισώσεις που εκφράζουν τη σχέση µεταξύ του αριθµητικού ανοίγµατος, του µήκους κύµατος και της διακριτικής ικανότητας. λ R = (4.2) 2 ΝΑ 0.61λ R = (4.3) ΝΑ 1.22λ R= ( ΝΑ( obj) + NA( cond)) (4.4) Όπου R: είναι η διακριτική ικανότητα, ΝΑ: το αριθµητικό άνοιγµα, λ: το µήκος κύµατος, ΝΑ(obj): το αριθµητικό άνοιγµα του αντικειµενικού φακού, NA(cond): το
20 20 αριθµητικό άνοιγµα του συµπυκνωτή φακού Παρατηρήστε ότι οι εξισώσεις (4.1) και (4.2) διαφέρουν στον παράγοντα πολλαπλασιασµού ο οποίος είναι 0,5 στιν εξίσωση (4.1) και 0,61 στην εξίσωση (4.2). Αυτές οι εξισώσεις είναι βασισµένες σε διάφορους παράγοντες (συµπεριλαµβανοµένων ποικίλων θεωρητικών υπολογισµών που γίνπονται από τους οπτικούς φυσικούς) που υπολογίζουν µετράνε την συµπεριφορά των αντικειµενικών και συµπυκνωτών φακών, και δεν πρέπει να θεωρούνται ως αναµφισβήτητη τιµή οποιουδήποτε γενικού, φυσικού νόµου. Σε µερικές περιπτώσεις, όπως στη συνεστιακή µικροσκοπία και στην µικροσκοπία φθορισµού, η διακριτική ικανότητα µπορεί πραγµατικά να υπερβεί τα όρια από οποιαδήποτε από τις τρεις παραπάνω εξισώσεις. Άλλοι παράγοντες όπως η µικρή αντίθεση των χρωµάτων του δείγµατος και ο εσφαλµένος φωτισµός, µπορεί να οδηγήσουν σε µείωση της διακριτικής ικανότητας, και πιο συχνά από ποτέ, η πραγµατική τιµή του R (περίπου 0,25 µm), ένα µεσαίο φάσµα µήκους κύµατος 550 nm και το αριθµητικό άνοιγµα από 1,35 µέχρι 1,40 δεν υλοποιούνται στην πράξη. Ο πίνακας 2 δείχνει µία λίστα από διάφορες τιµές που παίρνει η διακριτική ικανότητα και το αριθµητικό άνοιγµα για τους αντικειµενικούς φακούς µεγέθυνσης και αποκατάστασης εκτροπής. Resolution and Numerical Aperture by Objective Type Objective Type Plan Achromat Plan Fluorite Magnification N.A Resolution (µm) N.A Resolution (µm) Plan Apochromat N.A Resolution (µm) 4x x x x x x N.A. = Numerical Aperture Πίνακας 3 Όταν το µικροσκόπιο είναι σε τέλεια ευθυγράµµιση και ο αντικειµενικός φακός αντιστοιχίζεται κατάλληλα µε τον συµπυκνωτή φακό, τότε µπορούµε να αντικαταστήσουµε το αριθµητικό άνοιγµα του αντικειµενικού φακού στις εξισώσεις (4.1) και (4.2) µε το προστιθέµενο αποτέλεσµα µε το οποίο η εξίσωση (4.3) µειώνεται στην εξίσωση (4.2). Πρέπει να τονίσουµε ότι η µεγέθυνση δεν εµφανίζεται ως παράγοντας σε κάποια από αυτές τις εξισώσεις, επειδή µόνο το αριθµητικό άνοιγµα και το µήκος κύµατος του φωτός αναπαράστασης καθορίζουν την ανάλυση του δείγµατος. Όπως έχουµε επισηµάνει (και µπορούµε να δούµε στις εξισώσεις) το µήκος κύµατος του φωτός είναι ένας σηµαντικός παράγοντας για τη διακριτική ικανότητα του µικροσκοπίου. Μικρότερα µήκη κύµατος παράγουν µεγαλύτερη διακριτική ικανότητα (χαµηλότερες τιµές για το R). Η µεγαλύτερη «δύναµη» της διακριτικής ικανότητας στα οπτικά µικροσκόπια γίνεται αντιληπτή µε ένα υπεριώδες φως µικρού µήκους κύµατος, το πιο µικρό, αποτελεσµατικό µήκος κύµατος απεικόνισης. Το υπεριώδες φως µικρού µήκους κύµατος ακολουθείται από µπλε, πράσινο και τέλος κόκκινο φως και είναι ικανό να αναλύει κάθε λεπτοµέρεια του δείγµατος. Συνήθως οι χειριστές των µικροσκοπίων χρησιµοποιούν λευκό φως, το οποίο παράγεται από ένα βολβό βολφραµίου αλογόνου, για να φωτίσουν το δείγµα. Το κέντρο του φάσµατος του ορατού φωτός βρίσκεται περίπου στα 500nm, το κυρίαρχο µήκος κύµατος για το πράσινο φως(τα µάτια µας είναι πιο ευαίσθητα
21 21 στο πράσινο φως). Είναι αυτό το µήκος κύµατος που χρησιµοποιήθηκε για τον υπολογισµό της διακριτικής ικανότητας στον πίνακα 3. Η τιµή του αριθµητικού ανοίγµατος είναι επίσης σηµαντική στις εξισώσεις (4.1), (4.2) και (4.3). Μεγαλύτερα αριθµητικά ανοίγµατα παράγουν µεγαλύτερη διακριτική ικανότητα όπως φαίνεται και στον πίνακα (4.2). Η επίδραση του µήκους κύµατος του φωτός στην διακριτική ικανότητα, µε ένα σταθερό αριθµητικό άνοιγµα, φαίνεται στον πίνακα 4. Resolution versus Wavelength Wavelength (nanometers) Resolution (micrometers) Πίνακας 4 Όταν το φως από τα διάφορα σηµεία του δείγµατος περνά µέσα από τον αντικειµενικό φακό και ανασυγκροτείται σε µία εικόνα, τα διάφορα σηµεία του δείγµατος εµφανίζονται στην εικόνα σαν µικρά σχέδια (και όχι σηµεία). Αυτά τα σχέδια είναι γνωστά ως σχέδια του Airy. Αυτό το φαινόµενο προκύπτει από τη διάθλαση και τη διασπορά του φωτός καθώς αυτό περνά µέσα από τα µικροσκοπικά µέρη και κενά του δείγµατος και το κυκλικό πίσω άνοιγµα του αντικειµενικού φακού. Το κεντρικό µέγιστο των σχηµάτων Airy συχνά αναφέρεται και ως δίσκος του Airy, ο οποίος ορίζεται ως η περιοχή η οποία εσωκλείεται από το πρώτο ελάχιστο του σχήµατος Airy και περιέχει το 84% της φωτεινής ενέργειας. Αυτοί οι δίσκοι του Airy αποτελούνται από µικρούς, οµόκεντρους, φωτεινούς ή σκοτεινούς κύκλους αυξανόµενης ακτίνας και φθίνουσας αντιστοίχως έντασης, όπως φαίνεται και στην εικόνα 4.5. Η ένταση του φωτός συναρτήσει της απόστασης από το κέντρο του δίσκου φαίνεται στο Σχ Είναι γνωστό, από τη θεωρία της περίθλασης του φωτός, ότι ο πρώτος σκοτεινός δακτύλιος έχει ακτίνα ίση µε fλ r = 1.22 (4.5) D όπου λ: είναι το µήκος κύµατος του φωτός, D: η διάµετρος της οπής και f: η απόσταση του πετάσµατος από την οπή. Σχήµα 4.3: Η ένταση συναρτήσει της ακτίνας.
22 22 Η διάταξη και η κατανοµή της έντασης του φωτός φαίνονται στο Σχ Η γωνία που υποτείνεται από την ακτίνα αυτή στο κέντρο της οπής είναι r λ θ = = (4.6) f D Σχήµα 4.4: Περίθλαση από κυκλική οπή Η εικόνα 3 δείχνει τους δίσκους του Airy και την κατανοµή της έντασής τους συναρτήσει της απόστασης διαχωρισµού. Σχήµα 4.5 Η εικόνα 4.5.a απεικονίζει έναν υποθετικό δίσκο Airy που αποτελείται ουσιαστικά από ένα σχέδιο διάθλασης το οποίο περιέχει ένα κεντρικό µέγιστο (που ονοµάζεται τυπικά µέγιστο µηδενικής τάξης(zeroth order) ) που περιβάλλεται από οµόκεντρους κύκλους(1ος, 2ος, 3ος κ.λ.π.) ταξινοµηµένους διαδοχικά από την µεγαλύτερη προς την µικρότερη φωτεινότητα δείχνοντας την διανοµή της έντασης. ύο δίσκοι Airy και η διανοµή της έντασής τους φαίνονται στο σχήµα 4.5.b. Σε αυτό το κοµµάτι της εικόνας, ο διαχωρισµός ανάµεσα στους δύο δίσκους υπερβαίνει τις ακτίνες του και µπορούν να διακριθούν. Το όριο στο οποίο δύο δίσκοι Airy µπορούν να διακριθούν σε δύο ξεχωριστές οντότητες ονοµάζεται κριτήριο Rayleigh. Το σχήµα 4.5.c δείχνει δύο δίσκους Airy και τη διανοµή της έντασής τους σε µία κατάσταση όπου η απόσταση µεταξύ των δύο κέντρων των µέγιστων zeroth order είναι µικρότερη από το πλάτος των µέγιστων zeroth order και οι δύο δίσκοι δεν µπορούν να διακριθούν σε διαφορετικές οντότητες µε βάση το κριτήριο Rayleigh. Το κριτήριο του Rayleigh, χρησιµοποιείται για να αποφασισθεί πότε δύο είδωλα σηµειακών πηγών µπορούν να θεωρηθούν ότι διαχωρίζονται. Η ιδέα επεξηγείται στο Σχ. 4.6.
23 23 Σχήµα 4.6:. Εικόνες συµβολής δύο σηµειακών πηγών, όπως σχηµατίζονται από µια κυκλική οπή ή φακό. Στο Σχ. 4.6.α, τα κέντρα των δίσκων του Airy απέχουν µεταξύ τους γωνιακή απόσταση α= 2 θ, και τα είδωλα µπορούν να θεωρηθούν ως σαφώς διακριτά. Το ίδιο ισχύει και στο Σχ. 4.6.β, για το οποίο είναι α= 32 θ. Στο Σχ.4.6.γ φαίνεται η οριακή περίπτωση για α = θ. Σ αυτήν την περίπτωση, το κεντρικό µέγιστο κάθε δίσκου συµπίπτει µε τον πρώτο σκοτεινό δακτύλιο του άλλου. Ο Rayleigh πρότεινε αυτήν την περίπτωση ως µια λογική διαχωριστική γραµµή ανάµεσα στο να θεωρούνται δύο είδωλα ως διακριτά ή µη. Σύµφωνα µε το κριτήριο του Rayleigh, λοιπόν, δύο σηµειακές πηγές θεωρούνται ότι διαχωρίζονται από το όργανο, αν η γωνιακή τους απόσταση, α, είναι ίση ή µµεγαλύτερη από τη γωνία λ θ = 1, 22 (4.6) D Στο Σχ.4.7 φαίνεται ο σχηµατισµός, από ένα τηλεσκόπιο, των ειδώλων δύο σηµειακών πηγών, τα οποία µόλις διαχωρίζονται. Σχήµα 4.7: Ο σχηµατισµός από ένα τηλεσκόπιο, των ειδώλων δύο σηµειακών πηγών, τα οποία µόλις διαχωρίζονται. Όσο µικρότεροι είναι οι δίσκοι Airy που προβάλλονται από τον αντικειµενικό φακό κατά την διαµόρφωση της εικόνας, τόσο µεγαλύτερη είναι η λεπτοµέρεια του δείγµατος που γίνεται ευδιάκριτη. Οι αντικειµενικοί φακοί υψηλής διόρθωσης (fluorites και apochromats) παράγουν µικρότερους δίσκους Airy από τους αντικειµενικούς φακούς µικρότερης διόρθωσης. Με παρόµοιο τρόπο, οι αντικειµενικοί φακοί που έχουν µεγαλύτερο αριθµητικό άνοιγµα είναι επίσης ικανοί να παράγουν µικρότερους δίσκους Airy. Αυτός είναι ο κύριος λόγος για τον οποίο αντικειµενικοί φακοί µε µεγάλο αριθµητικό άνοιγµα και ολική διόρθωση της οπτικής εκτροπής µπορούν να διακρίνουν ακόµα και την πιο µικρή λεπτοµέρεια στο δείγµα.
24 24 Σχήµα 4.8 Το σχήµα 4.8 απεικονίζει την επίδραση του αριθµητικού ανοίγµατος στο µέγεθος των δίσκων Airy, οι οποίοι προκύπτουν από αντικειµενικούς φακούς που έχουν ίδιο εστιακό µήκος αλλά διαφορετικό αριθµητικό άνοιγµα. Για µικρά αριθµητικά ανοίγµατα, το µέγεθος των δίσκων Airy είναι µεγάλο όπως φαίνεται και στην εικόνα 4.8.a. Καθώς το αριθµητικό άνοιγµα και η γωνία του κώνου φωτός ενός αντικειµενικού φακού αυξάνονται, το µέγεθος των δίσκων Airy µειώνεται όπως φαίνεται και στις εικόνες 4.8.b και 4.8.c. Η προκύπτουσα εικόνα στο επίπεδο του διαφράγµατος προσοφθαλµίου είναι ένα µωσαϊκό των δίσκων Airy, το οποίο θεωρούµε ως φως και σκοτάδι. Όταν δύο δίσκοι είναι πάρα πολύ κοντά µεταξύ τους, τόσο πολύ ώστε τα κέντρα τους να επικαλύπτονται, οι δύο λεπτοµέρειες που αντιπροσωπεύονται από αυτούς τους επικαλυπτόµενους δίσκους δεν µπορούν να αναλυθούν ή να διαχωριστούν και έτσι εµφανίζονται σαν µία, εικόνα 4.5. Μία σηµαντική έννοια που πρέπει να καταλάβουµε για τον σχηµατισµό της εικόνας είναι η φύση των διαθλούµενων ακτίνων φωτός που εµποδίζονται από τον αντικειµενικό φακό. Μόνο στις περιπτώσεις όπου οι υψηλότερες τάξεις (1 η, 2 η, 3 η κ.λ.π.) των διαθλούµενων ακτινών αιχµαλωτίζονται, µπορεί η εργασία που παρεµβάλλεται να αναδηµιουργήσει την εικόνα σε µία ενδιάµεση κατάσταση, από την εικόνα του αντικειµένου. Όταν µόνο οι ακτίνες της τάξης zeroth αιχµαλωτίζονται, είναι ουσιαστικά αδύνατο να ανασυγκροτηθεί µία αναγνωρίσιµη εικόνα του δείγµατος. Όταν οι ακτίνες φωτός της 1 ης τάξης προστεθούν στις ακτίνες της τάξης zeroth η εικόνα γίνεται περισσότερο συναφής, αλλά λείπουν ακόµα σηµαντικές λεπτοµέρειες. Μόνο όταν οι ακτίνες της υψηλότερης τάξης επανασυνδεθούν, η εικόνα αντιπροσωπεύει την πραγµατική αρχιτεκτονική του δείγµατος. Αυτή είναι η βάση για την ανάγκη των µεγάλων αριθµητικών ανοιγµάτων (και συνεπώς για µικρότερους δίσκους Airy), για την επίτευξη υψηλής ευκρίνειας εικόνων µε ένα οπτικό µικροσκόπιο. Στην πραγµατικότητα, οι περισσότεροι χειριστές µικροσκοπίων δεν προσπαθούν να επιτύχουν την εικόνα µε την υψηλότερη ευκρίνεια που είναι δυνατή µε το µικροσκόπιό τους. Μόνο σε ειδικές περιστάσεις, όπως η υψηλή µεγέθυνση φωτεινού πεδίου, ο φθορισµός, DIC και η συνεστιακή µικροσκοπία προσπαθούν να φτάσουν στα όρια των µικροσκοπίων. Στις περισσότερες χρήσεις των µικροσκοπίων δεν είναι απαραίτητο να χρησιµοποιούνται αντικειµενικοί φακοί µε µεγάλο αριθµητικό άνοιγµα, διότι το δείγµα µπορεί να αναλυθεί ικανοποιητικά και µε τη χρήση αντικειµενικών φακών µε µικρότερα αριθµητικά ανοίγµατα. Αυτό είναι ιδιαίτερα σηµαντικό επειδή το µεγάλο αριθµητικό άνοιγµα και η υψηλή µεγέθυνση συνοδεύονται από τα µειονεκτήµατα του πολύ ρηχού βάθους ( αυτό αναφέρεται στην καλή εστίαση στην περιοχή ακριβώς κάτω ή ακριβώς πάνω από την περιοχή που εξετάζεται) και µικρή απόσταση εργασίας. Συνεπώς σε δείγµατα όπου η υψηλή
25 25 ανάλυση είναι λιγότερο κρίσιµη και η µεγέθυνση µπορεί να είναι µικρότερη, είναι προτιµότερο να χρησιµοποιούνται αντικειµενικοί φακοί µεγέθυνσης µε µέτριο αριθµητικό άνοιγµα προκειµένου να παραχθούν εικόνες µε µεγαλύτερη απόσταση εργασίας και µεγαλύτερο βάθος τοµέα. Ο προσεκτικός προσδιορισµός του ανοίγµατος του διαφράγµατος του συµπυκνωτή φακού είναι επίσης κρίσιµος στον έλεγχο του αριθµητικού ανοίγµατος και η άνευ διακρίσεως χρήση αυτού του διαφράγµατος µπορεί να οδηγήσει στην υποβάθµιση της ποιότητας της εικόνας. Άλλοι παράγοντες, όπως η αντίθεση και η απόδοση του φωτισµού, είναι επίσης στοιχεία κλειδιά τα οποία επηρεάζουν στην ανάλυση της εικόνας.
26 26 Β. ΦΘΟΡΙΣΜΟΣ - ΜΙΚΡΟΣΚΟΠΙΑ ΦΘΟΡΙΣΜΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ 1.1. ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΦΑΣΜΑ ΟΠΤΙΚΗ Η/Μ ΑΚΤΙΝΟΒΟΛΙΑ Η ηλεκτροµαγνητική ακτινοβολία αποτελείται από ένα ηλεκτρικό και ένα µαγνητικό πεδίο, τα οποία ταλαντώνονται έτσι ώστε τα διανύσµατα έντασης των πεδίων τους να είναι κάθετα µεταξύ τους. Ο συνδυασµός τους δηµιουργεί ένα διαδιδόµενο ηλεκτροµαγνητικό κύµα. Η διεύθυνση διάδοσης, είναι κάθετη στο επίπεδο που σχηµατίζουν οι διευθύνσεις των διανυσµάτων έντασης των δύο συνιστωσών του ηλεκτροµαγνητικού κύµατος. Η συχνότητα f και το µήκος κύµατος λ συνδέονται µε τη σχέση: c=λ x f (1.1) όπου c=3x10 8 m/sec είναι η ταχύτητα του φωτός στο κενό. Το µήκος κύµατος καθορίζει την περιοχή του ηλεκτροµαγνητικού φάσµατος, στην οποία αντιστοιχεί η ακτινοβολία, ενώ όταν βρισκόµαστε στην ορατή περιοχή του Η/Μ φάσµατος, προσδιορίζει και το χρώµα της ακτινοβολίας. Η περιοχή του ορατού εκτείνεται από τα 400 ως τα 750 nm. Σχήµα 1.1: Ηλεκτροµαγνητικό φάσµα. Από τις υπόλοιπες περιοχές του ηλεκτροµαγνητικού φάσµατος ενδιαφέρουσες στην δική µας περίπτωση είναι η υπεριώδης (για 100nm < λ < 400nm) και η υπέρυθρη (για 750nm < λ < 1000nm)(Σχήµα1.1). Οι βασικότεροι τρόποι αλληλεπίδρασης ύλης και ακτινοβολίας είναι η απορρόφηση, η σκέδαση και η εκποµπή. Αυτά τα φαινόµενα είναι κβαντικά, δηλαδή η ενέργεια κατανέµεται σε διακριτά πακέτα ενέργειας, τα φωτόνια. Τα φαινόµενα αυτά περιγράφονται από τους νόµους της κβαντοµηχανικής. Η ενέργεια Ε του φωτονίου δίνεται από τη σχέση: c Ε= h x f = h x (1.2) λ όπου h=6.62x10-27 erg x sec είναι η σταθερά του Planck. Από αυτή τη σχέση φαίνεται ότι η ενέργεια είναι αντιστρόφως ανάλογη µε το µήκος κύµατος ΟΜΗ ΤΗΣ ΥΛΗΣ Άτοµα Ως γνωστόν η ύλη αποτελείται από άτοµα και µόρια ( τα οποία είναι ενώσεις ατόµων). Τα βιολογικά µόρια αποτελούνται κυρίως από ενώσεις ατόµων άνθρακα C, υδρογόνου Η, οξυγόνου Ο και αζώτου Ν. Στον πίνακα που ακολουθεί φαίνεται η
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΚΡΟΣΚΟΠΗΣΗ Εργαστηριακές Ασκήσεις Βιολογίας I Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας Παξινού Ευγενία Για την επιστήμη της Βιολογίας, το μικροσκόπιο αποτέλεσε τη μεγαλύτερη
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΚΡΟΣΚΟΠΗΣΗ Εργαστηριακές Ασκήσεις Βιολογίας I Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας Παξινού Ευγενία Για την επιστήμη της Βιολογίας, το μικροσκόπιο αποτέλεσε τη μεγαλύτερη
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Να αιτιολογήσετε την απάντησή σας. Μονάδες 5
 2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
Μεγεθυντικός φακός. 1. Σκοπός. 2. Θεωρία. θ 1
 Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
Φύση του φωτός. Θεωρούμε ότι το φως έχει διττή φύση: διαταραχή που διαδίδεται στο χώρο. μήκος κύματος φωτός. συχνότητα φωτός
 Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
6.10 Ηλεκτροµαγνητικά Κύµατα
 Πρόταση Μελέτης Λύσε απο τον Α τόµο των Γ. Μαθιουδάκη & Γ.Παναγιωτακόπουλου τις ακόλουθες ασκήσεις : 11.1-11.36, 11.46-11.50, 11.52-11.59, 11.61, 11.63, 11.64, 1.66-11.69, 11.71, 11.72, 11.75-11.79, 11.81
Πρόταση Μελέτης Λύσε απο τον Α τόµο των Γ. Μαθιουδάκη & Γ.Παναγιωτακόπουλου τις ακόλουθες ασκήσεις : 11.1-11.36, 11.46-11.50, 11.52-11.59, 11.61, 11.63, 11.64, 1.66-11.69, 11.71, 11.72, 11.75-11.79, 11.81
Το οπτικό μικροσκόπιο και ο τρόπος χρήσης του
 Το οπτικό μικροσκόπιο και ο τρόπος χρήσης του Το ανθρώπινο μάτι μπορεί να διακρίνει λεπτομέρειες της τάξης των 50-200 μm. Ο άνθρωπος με τις πρωτοποριακές εφευρέσεις των Malpighi, Hooke, Van Leeuwenhook
Το οπτικό μικροσκόπιο και ο τρόπος χρήσης του Το ανθρώπινο μάτι μπορεί να διακρίνει λεπτομέρειες της τάξης των 50-200 μm. Ο άνθρωπος με τις πρωτοποριακές εφευρέσεις των Malpighi, Hooke, Van Leeuwenhook
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
Κεφάλαιο 35 ΠερίθλασηκαιΠόλωση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 35 ΠερίθλασηκαιΠόλωση ΠεριεχόµεναΚεφαλαίου 35 Περίθλαση απλής σχισµής ή δίσκου Intensity in Single-Slit Diffraction Pattern Περίθλαση διπλής σχισµής ιακριτική ικανότητα; Κυκλικές ίριδες ιακριτική
Κεφάλαιο 35 ΠερίθλασηκαιΠόλωση ΠεριεχόµεναΚεφαλαίου 35 Περίθλαση απλής σχισµής ή δίσκου Intensity in Single-Slit Diffraction Pattern Περίθλαση διπλής σχισµής ιακριτική ικανότητα; Κυκλικές ίριδες ιακριτική
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Όλα τα θέματα των εξετάσεων έως και το 2014 σε συμβολή, στάσιμα, ηλεκτρομαγνητικά κύματα, ανάκλαση - διάθλαση ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ
 ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ Ερωτήσεις Πολλαπλής επιλογής 1. To βάθος µιας πισίνας φαίνεται από παρατηρητή εκτός της πισίνας µικρότερο από το πραγµατικό, λόγω του φαινοµένου της: α. ανάκλασης β. διάθλασης γ. διάχυσης
ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ Ερωτήσεις Πολλαπλής επιλογής 1. To βάθος µιας πισίνας φαίνεται από παρατηρητή εκτός της πισίνας µικρότερο από το πραγµατικό, λόγω του φαινοµένου της: α. ανάκλασης β. διάθλασης γ. διάχυσης
Εφαρμοσμένη Οπτική. Γεωμετρική Οπτική
 Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΠΟΥ ΔΙΑΔΙΔΕΤΑΙ ΤΟ ΦΩΣ
 1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ανάκλαση. Κάτοπτρα. Διάθλαση. Ολική ανάκλαση. Φαινόμενη ανύψωση αντικειμένου. Μετατόπιση ακτίνας. Πρίσματα
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Ανάκλαση Κάτοπτρα Διάθλαση Ολική ανάκλαση Φαινόμενη ανύψωση αντικειμένου Μετατόπιση ακτίνας Πρίσματα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ - Ανάκλαση Επιστροφή σε «γεωμετρική οπτική» Ανάκλαση φωτός ονομάζεται
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Ανάκλαση Κάτοπτρα Διάθλαση Ολική ανάκλαση Φαινόμενη ανύψωση αντικειμένου Μετατόπιση ακτίνας Πρίσματα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ - Ανάκλαση Επιστροφή σε «γεωμετρική οπτική» Ανάκλαση φωτός ονομάζεται
Περίθλαση και εικόνα περίθλασης
 Περίθλαση και εικόνα περίθλασης Η περίθλαση αναφέρεται στη γενική συμπεριφορά των κυμάτων, τα οποία διαδίδονται προς όλες τις κατευθύνσεις καθώς περνούν μέσα από μια σχισμή. Ο όρος εικόνα περίθλασης είναι
Περίθλαση και εικόνα περίθλασης Η περίθλαση αναφέρεται στη γενική συμπεριφορά των κυμάτων, τα οποία διαδίδονται προς όλες τις κατευθύνσεις καθώς περνούν μέσα από μια σχισμή. Ο όρος εικόνα περίθλασης είναι
1ο Κριτήριο Αξιολόγησης ΦΥΣΗ ΤΟΥ ΦΩΤΟΣ-ΑΝΑΚΛΑΣΗ, ΙΑΘΛΑΣΗ- ΕΙΚΤΗΣ ΙΑΘΛΑΣΗΣ
 1 ο ΚΕΦΑΛΑΙΟ 1. Φύση του φωτός - Ανάκλαση, διάθλαση - είκτης διάθλασης 2. ιασκεδασµός - Ανάλυση του φωτός από πρίσµα 3. Επαναληπτικό στο 1ο κεφάλαιο 4. Επαναληπτικό στο 1ο κεφάλαιο 11. 12. 1ο Κριτήριο
1 ο ΚΕΦΑΛΑΙΟ 1. Φύση του φωτός - Ανάκλαση, διάθλαση - είκτης διάθλασης 2. ιασκεδασµός - Ανάλυση του φωτός από πρίσµα 3. Επαναληπτικό στο 1ο κεφάλαιο 4. Επαναληπτικό στο 1ο κεφάλαιο 11. 12. 1ο Κριτήριο
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Generated by Foxit PDF Creator Foxit Software http://www.foxitsoftware.com For evaluation only. ΑΣΚΗΣΗ 10 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ
 ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell, το φως είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Η θεωρία αυτή α. δέχεται ότι κάθε φωτεινή πηγή εκπέμπει φωτόνια.
ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell, το φως είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Η θεωρία αυτή α. δέχεται ότι κάθε φωτεινή πηγή εκπέμπει φωτόνια.
EΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΒΛΗΜΑΤΑ ΣΤΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ ΟΛΙΚΗ ΑΝΑΚΛΑΣΗ
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Ύλη ένατου µαθήµατος. Οπτικό µικροσκόπιο, Ηλεκτρονική µικροσκοπία σάρωσης, Ηλεκτρονική µικροσκοπία διέλευσης.
 ιάλεξη 9 η Ύλη ένατου µαθήµατος Οπτικό µικροσκόπιο, Ηλεκτρονική µικροσκοπία σάρωσης, Ηλεκτρονική µικροσκοπία διέλευσης. Μέθοδοι µικροσκοπικής ανάλυσης των υλικών Οπτική µικροσκοπία (Optical microscopy)
ιάλεξη 9 η Ύλη ένατου µαθήµατος Οπτικό µικροσκόπιο, Ηλεκτρονική µικροσκοπία σάρωσης, Ηλεκτρονική µικροσκοπία διέλευσης. Μέθοδοι µικροσκοπικής ανάλυσης των υλικών Οπτική µικροσκοπία (Optical microscopy)
sin 2 n = sin A 2 sin 2 2 n = sin A = sin = cos
 1 Σκοπός Βαθμός 9.5. Ηθελε να γραψω καλύτερα το 9 ερωτημα. Σκοπός αυτής της εργαστηριακής άσκησης είναι η μελέτη της ανάκλασης, διάθλασης και πόλωσης του φωτός. Προσδιορίζουμε επίσης τον δείκτη διάθλασης
1 Σκοπός Βαθμός 9.5. Ηθελε να γραψω καλύτερα το 9 ερωτημα. Σκοπός αυτής της εργαστηριακής άσκησης είναι η μελέτη της ανάκλασης, διάθλασης και πόλωσης του φωτός. Προσδιορίζουμε επίσης τον δείκτη διάθλασης
Κυματική οπτική. Συμβολή Περίθλαση Πόλωση
 Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
ΟΠΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ. Φως... Φωτομετρικά μεγέθη - μονάδες Νόμοι Φωτισμού
 ΟΠΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ Φως... Φωτομετρικά μεγέθη - μονάδες Νόμοι Φωτισμού Ηλεκτρομαγνητικά κύματα - Φως Θα διερευνήσουμε: 1. Τί είναι το φως; 2. Πως παράγεται; 3. Χαρακτηριστικά ιδιότητες Γεωμετρική οπτική:
ΟΠΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ Φως... Φωτομετρικά μεγέθη - μονάδες Νόμοι Φωτισμού Ηλεκτρομαγνητικά κύματα - Φως Θα διερευνήσουμε: 1. Τί είναι το φως; 2. Πως παράγεται; 3. Χαρακτηριστικά ιδιότητες Γεωμετρική οπτική:
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ
 ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ 1.. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ) και ποιες λανθασμένες (Λ); α. Στη διάθλαση όταν το φως διέρχεται από ένα οπτικά πυκνότερο υλικό σε ένα οπτικά αραιότερο
ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ 1.. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ) και ποιες λανθασμένες (Λ); α. Στη διάθλαση όταν το φως διέρχεται από ένα οπτικά πυκνότερο υλικό σε ένα οπτικά αραιότερο
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 14/09/2014 ΘΕΜΑ Α
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 14/09/2014 ΘΕΜΑ Α Α1. Κατά την ανάλυση λευκού φωτός από γυάλινο πρίσμα, η γωνία εκτροπής του κίτρινου χρώματος είναι:
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 14/09/2014 ΘΕΜΑ Α Α1. Κατά την ανάλυση λευκού φωτός από γυάλινο πρίσμα, η γωνία εκτροπής του κίτρινου χρώματος είναι:
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση d=0.20 mm είναι τοποθετημένο σε απόσταση =1,20 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση d=0.20 mm είναι τοποθετημένο σε απόσταση =1,20 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές
ΚΕΦΑΛΑΙΟ 3. Οπτικά όργανα. Α. Οι βασικοί νόµοι της Οπτικής
 ΚΕΦΑΛΑΙΟ 3 Οπτικά όργανα 3.1 Η φύση του φωτός Α. Οι βασικοί νόµοι της Οπτικής Το φως είναι ηλεκτροµαγνητικά κύµατα που διαδίδονται στο χώρο. ηλαδή, µεταβολές ηλεκτρικού και µαγνητικού πεδίου που διαδίδονται
ΚΕΦΑΛΑΙΟ 3 Οπτικά όργανα 3.1 Η φύση του φωτός Α. Οι βασικοί νόµοι της Οπτικής Το φως είναι ηλεκτροµαγνητικά κύµατα που διαδίδονται στο χώρο. ηλαδή, µεταβολές ηλεκτρικού και µαγνητικού πεδίου που διαδίδονται
Μέτρηση Γωνίας Brewster Νόμοι του Fresnel
 Μέτρηση Γωνίας Bewse Νόμοι του Fesnel [] ΕΙΣΑΓΩΓΗ Στο πείραμα, δέσμη φωτός από διοδικό lase ανακλάται στην επίπεδη επιφάνεια ενός ακρυλικού ημι-κυκλικού φακού, πολώνεται γραμμικά και ανιχνεύεται από ένα
Μέτρηση Γωνίας Bewse Νόμοι του Fesnel [] ΕΙΣΑΓΩΓΗ Στο πείραμα, δέσμη φωτός από διοδικό lase ανακλάται στην επίπεδη επιφάνεια ενός ακρυλικού ημι-κυκλικού φακού, πολώνεται γραμμικά και ανιχνεύεται από ένα
Εισαγωγή στο φως. Εισαγωγή
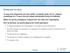 Εισαγωγή στο φως Το φως είναι απαραίτητο για όλες σχεδόν τις μορφές ζωής στη Γη. (Σήμερα γνωρίζουμε ότι) Το φως είναι μια μορφή ηλεκτρομαγνητικής ακτινοβολίας. Μέσω του φωτός μεταφέρεται ενέργεια από την
Εισαγωγή στο φως Το φως είναι απαραίτητο για όλες σχεδόν τις μορφές ζωής στη Γη. (Σήμερα γνωρίζουμε ότι) Το φως είναι μια μορφή ηλεκτρομαγνητικής ακτινοβολίας. Μέσω του φωτός μεταφέρεται ενέργεια από την
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος.
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
Περίθλαση από ακµή και από εµπόδιο.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
Κυματική Φύση του φωτός και εφαρμογές. Περίθλαση Νέα οπτικά μικροσκόπια Κρυσταλλογραφία ακτίνων Χ
 Κυματική Φύση του φωτός και εφαρμογές Περίθλαση Νέα οπτικά μικροσκόπια Κρυσταλλογραφία ακτίνων Χ Επαλληλία κυμάτων Διαφορά φάσης Δφ=0 Ενίσχυση Δφ=180 Απόσβεση Κάθε σημείο του μετώπου ενός κύματος λειτουργεί
Κυματική Φύση του φωτός και εφαρμογές Περίθλαση Νέα οπτικά μικροσκόπια Κρυσταλλογραφία ακτίνων Χ Επαλληλία κυμάτων Διαφορά φάσης Δφ=0 Ενίσχυση Δφ=180 Απόσβεση Κάθε σημείο του μετώπου ενός κύματος λειτουργεί
Ο15. Κοίλα κάτοπτρα. 2. Θεωρία. 2.1 Γεωμετρική Οπτική
 Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Περίθλαση από µία σχισµή.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 71 7. Άσκηση 7 Περίθλαση από µία σχισµή. 7.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την συµπεριφορά των µικροκυµάτων
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 71 7. Άσκηση 7 Περίθλαση από µία σχισµή. 7.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την συµπεριφορά των µικροκυµάτων
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΜΙΚΡΟΣΚΟΠΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ «ΒΙΟΛΟΓΙΑΣ ΚΥΤΤΑΡΟΥ» Ονοµατεπώνυµο...ΑΜ...
 ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΜΙΚΡΟΣΚΟΠΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ «ΒΙΟΛΟΓΙΑΣ ΚΥΤΤΑΡΟΥ» ΑΣΚΗΣΗ 2 η Μετρήσεις µε το µικροσκόπιο Κ. Φασσέας. Ονοµατεπώνυµο...ΑΜ... Σκοπός της άσκησης είναι: Να µάθουµε πώς γίνεται η
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΜΙΚΡΟΣΚΟΠΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ «ΒΙΟΛΟΓΙΑΣ ΚΥΤΤΑΡΟΥ» ΑΣΚΗΣΗ 2 η Μετρήσεις µε το µικροσκόπιο Κ. Φασσέας. Ονοµατεπώνυµο...ΑΜ... Σκοπός της άσκησης είναι: Να µάθουµε πώς γίνεται η
OΠΤIKH. Επειδή είναι πάντα υ<c (
 OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα. Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ
 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Η Φύση του Φωτός. Τα Β Θεματα της τράπεζας θεμάτων
 Η Φύση του Φωτός Τα Β Θεματα της τράπεζας θεμάτων Η ΦΥΣΗ ΤΟΥ ΦΩΤΟΣ Θέμα Β _70 Β. Μονοχρωματική ακτίνα πράσινου φωτός διαδίδεται αρχικά στον αέρα. Στη πορεία της δέσμης έχουμε τοποθετήσει στη σειρά τρία
Η Φύση του Φωτός Τα Β Θεματα της τράπεζας θεμάτων Η ΦΥΣΗ ΤΟΥ ΦΩΤΟΣ Θέμα Β _70 Β. Μονοχρωματική ακτίνα πράσινου φωτός διαδίδεται αρχικά στον αέρα. Στη πορεία της δέσμης έχουμε τοποθετήσει στη σειρά τρία
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
προς τα θετικά του x άξονα. Ως κύμα η ηλεκτρομαγνητική ακτινοβολία (άρα και το φως) ικανοποιούν τη βασική εξίσωση των κυμάτων, δηλαδή: c = λf (1)
 Φως 1 1 Φως 11 Η φύση του φωτός Το φως είναι το μέρος της ηλεκτρομαγνητικής ακτινοβολίας που διεγείρει τα κωνία και τα ραβδία του αμφιβληστροειδή χιτώνα του ματιού μας Αυτό έχει μήκος κύματος από λ 400
Φως 1 1 Φως 11 Η φύση του φωτός Το φως είναι το μέρος της ηλεκτρομαγνητικής ακτινοβολίας που διεγείρει τα κωνία και τα ραβδία του αμφιβληστροειδή χιτώνα του ματιού μας Αυτό έχει μήκος κύματος από λ 400
ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ. Ηλεκτροστατικοί και Μαγνητικοί Φακοί Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών
 ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΓΥΑΛΙΝΟΙ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΟΙ ΦΑΚΟΙ Οι φακοί χρησιμοποιούνται για να εκτρέψουν μία
ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΓΥΑΛΙΝΟΙ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΟΙ ΦΑΚΟΙ Οι φακοί χρησιμοποιούνται για να εκτρέψουν μία
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΦΩΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 04-05 ΠΟΡΕΙΑ ΑΚΤΙΝΑΣ. Β. Στο διπλανό
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΦΩΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 04-05 ΠΟΡΕΙΑ ΑΚΤΙΝΑΣ. Β. Στο διπλανό
1) Η εξάρτηση του δείκτη διάθλασης n από το μήκος κύματος για το κρύσταλλο του ιωδιούχου ρουβιδίου (RbI) παρουσιάζεται στο παρακάτω σχήμα.
 1) Η εξάρτηση του δείκτη διάθλασης n από το μήκος κύματος για το κρύσταλλο του ιωδιούχου ρουβιδίου (RbI) παρουσιάζεται στο παρακάτω σχήμα. Για τους δείκτες διάθλασης n 1 και n 2 ισχύει: n 2 = (11 / 10)
1) Η εξάρτηση του δείκτη διάθλασης n από το μήκος κύματος για το κρύσταλλο του ιωδιούχου ρουβιδίου (RbI) παρουσιάζεται στο παρακάτω σχήμα. Για τους δείκτες διάθλασης n 1 και n 2 ισχύει: n 2 = (11 / 10)
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 15/9/2013 ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 15/9/2013 ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟΥ 3
 ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟΥ 3 Η ταχύτητα του φωτός στο κενό ή στον αέρα είναι σταθερή και ίση με c o =3.10 8 m/s Η ταχύτητα του φωτός οπουδήποτε αλλού είναι c και ισχύει πάντα ότι c
ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟΥ 3 Η ταχύτητα του φωτός στο κενό ή στον αέρα είναι σταθερή και ίση με c o =3.10 8 m/s Η ταχύτητα του φωτός οπουδήποτε αλλού είναι c και ισχύει πάντα ότι c
ΟΡΟΣΗΜΟ ΓΛΥΦΑΔΑΣ. 7.1 Τι είναι το ταλαντούμενο ηλεκτρικό δίπολο; Πως παράγεται ένα ηλεκτρομαγνητικό
 ΚΕΦΑΛΑΙΟ 2 Ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικά κύματα 7. Τι είναι το ταλαντούμενο ηλεκτρικό δίπολο; Πως παράγεται ένα ηλεκτρομαγνητικό κύμα; 7.2 Ποιες εξισώσεις περιγράφουν την ένταση του ηλεκτρικού
ΚΕΦΑΛΑΙΟ 2 Ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικά κύματα 7. Τι είναι το ταλαντούμενο ηλεκτρικό δίπολο; Πως παράγεται ένα ηλεκτρομαγνητικό κύμα; 7.2 Ποιες εξισώσεις περιγράφουν την ένταση του ηλεκτρικού
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ερωτήσεις κλειστού τύπου. Ερωτήσεις ανοικτού τύπου
 ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
ΚΕΦΑΛΑΙΟ 11Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση
 ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
4. Όρια ανάλυσης οπτικών οργάνων
 4. Όρια ανάυσης οπτικών οργάνων 29 Μαΐου 2013 1 Περίθαση Οι αρχές ειτουργίας των οπτικών οργάνων που περιγράψαμε μέχρι στιγμής βασίζονται στη γεωμετρική οπτική, δηαδή την περιγραφή του φωτός ως ακτίνες
4. Όρια ανάυσης οπτικών οργάνων 29 Μαΐου 2013 1 Περίθαση Οι αρχές ειτουργίας των οπτικών οργάνων που περιγράψαμε μέχρι στιγμής βασίζονται στη γεωμετρική οπτική, δηαδή την περιγραφή του φωτός ως ακτίνες
7.1 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ
 7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
Άσκηση 1 η Το κοινό σύνθετο μικροσκόπιο και το φυτικό κύτταρο
 Εργαστήριο Φυσιολογίας και Μορφολογίας Φυτών Εργαστηριακές Ασκήσεις Βοτανικής (Συστηματική-Ανατομία) Άσκηση 1 η Το κοινό σύνθετο μικροσκόπιο και το φυτικό κύτταρο Λαβή. Είναι η χειρολαβή του οργάνου. Για
Εργαστήριο Φυσιολογίας και Μορφολογίας Φυτών Εργαστηριακές Ασκήσεις Βοτανικής (Συστηματική-Ανατομία) Άσκηση 1 η Το κοινό σύνθετο μικροσκόπιο και το φυτικό κύτταρο Λαβή. Είναι η χειρολαβή του οργάνου. Για
ΓΓ/Μ ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ. Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα
 ΓΓ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ' Τάξη
ΓΓ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ' Τάξη
ΠΕΡΙΘΛΑΣΗ H κυματική φύση του φωτός το πρόβλημα, η λύση
 ΠΕΡΙΘΛΑΣΗ H κυματική φύση του φωτός το πρόβλημα, η λύση ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Σύμφωνα με την καθημερινή μας εμπειρία, το φως φαίνεται σαν να ταξιδεύει ευθύγραμμα μέχρι να συναντήσει κάποιο αντικείμενο.
ΠΕΡΙΘΛΑΣΗ H κυματική φύση του φωτός το πρόβλημα, η λύση ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Σύμφωνα με την καθημερινή μας εμπειρία, το φως φαίνεται σαν να ταξιδεύει ευθύγραμμα μέχρι να συναντήσει κάποιο αντικείμενο.
ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 91 9. Άσκηση 9 ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό. 9.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε τα φαινόµενα
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 91 9. Άσκηση 9 ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό. 9.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε τα φαινόµενα
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ.
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ. ΑΝΤΙΚΕΙΜΕΝΟ : ΤΟ ΦΩΣ,( ΚΕΦ. Γ ΛΥΚΕΙΟΥ και ΚΕΦ.3 Β ΛΥΚΕΙΟΥ) ΘΕΜΑ Α Να επιλέξετε την σωστή πρόταση χωρίς να δικαιολογήσετε την απάντηση σας.. Οι Huygens
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ. ΑΝΤΙΚΕΙΜΕΝΟ : ΤΟ ΦΩΣ,( ΚΕΦ. Γ ΛΥΚΕΙΟΥ και ΚΕΦ.3 Β ΛΥΚΕΙΟΥ) ΘΕΜΑ Α Να επιλέξετε την σωστή πρόταση χωρίς να δικαιολογήσετε την απάντηση σας.. Οι Huygens
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ Θέμα1: Α. Η ταχύτητα διάδοσης ενός ηλεκτρομαγνητικού κύματος: α. εξαρτάται από τη συχνότητα ταλάντωσης της πηγής β. εξαρτάται
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΚΥΜΑΤΑ Θέμα1: Α. Η ταχύτητα διάδοσης ενός ηλεκτρομαγνητικού κύματος: α. εξαρτάται από τη συχνότητα ταλάντωσης της πηγής β. εξαρτάται
ΕΡΓΑΣΤΗΡΙΟ 2 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ
 ΕΡΓΑΣΤΗΡΙΟ 2 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ 1. Εισαγωγή. Η ενέργεια, όπως είναι γνωστό από τη φυσική, διαδίδεται με τρεις τρόπους: Α) δι' αγωγής Β) δια μεταφοράς Γ) δι'ακτινοβολίας Ο τελευταίος τρόπος διάδοσης
ΕΡΓΑΣΤΗΡΙΟ 2 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ 1. Εισαγωγή. Η ενέργεια, όπως είναι γνωστό από τη φυσική, διαδίδεται με τρεις τρόπους: Α) δι' αγωγής Β) δια μεταφοράς Γ) δι'ακτινοβολίας Ο τελευταίος τρόπος διάδοσης
Γεωμετρική Οπτική. Πρόκειται δηλαδή για μια ισοφασική επιφάνεια που ονομάζεται μέτωπο κύματος.
 Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής
 Φυσική Γ' Θετικής και Τεχνολογικής Κατ/σης ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ Θέματα Εξετάσεων 1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής 1. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο µέσων.
Φυσική Γ' Θετικής και Τεχνολογικής Κατ/σης ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ Θέματα Εξετάσεων 1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής 1. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο µέσων.
ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ. H γραφική αναπαράσταση ενός κύματος φωτός δίνεται στο Σχήμα 1(α) που ακολουθεί: ΣΧΗΜΑ 1
 ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ 1. ΟΡΙΣΜΟΙ Το φως είναι ένα σύνθετο κύμα. Με εξαίρεση την ακτινοβολία LASER, τα κύματα φωτός δεν είναι επίπεδα κύματα. Κάθε κύμα φωτός είναι ένα ηλεκτρομαγνητικό κύμα στο οποίο τα διανύσματα
ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ 1. ΟΡΙΣΜΟΙ Το φως είναι ένα σύνθετο κύμα. Με εξαίρεση την ακτινοβολία LASER, τα κύματα φωτός δεν είναι επίπεδα κύματα. Κάθε κύμα φωτός είναι ένα ηλεκτρομαγνητικό κύμα στο οποίο τα διανύσματα
Όλα τα θέματα των εξετάσεων έως και το 2014 σε συμβολή, στάσιμα, ηλεκτρομαγνητικά κύματα, ανάκλαση - διάθλαση Η/Μ ΚΥΜΑΤΑ. Ερωτήσεις Πολλαπλής επιλογής
 Η/Μ ΚΥΜΑΤΑ 1. Τα ηλεκτροµαγνητικά κύµατα: Ερωτήσεις Πολλαπλής επιλογής α. είναι διαµήκη. β. υπακούουν στην αρχή της επαλληλίας. γ. διαδίδονται σε όλα τα µέσα µε την ίδια ταχύτητα. δ. Δημιουργούνται από
Η/Μ ΚΥΜΑΤΑ 1. Τα ηλεκτροµαγνητικά κύµατα: Ερωτήσεις Πολλαπλής επιλογής α. είναι διαµήκη. β. υπακούουν στην αρχή της επαλληλίας. γ. διαδίδονται σε όλα τα µέσα µε την ίδια ταχύτητα. δ. Δημιουργούνται από
ΠΑΡΑΤΗΡΗΣΗ ΣΥΝΕΧΩΝ ΦΑΣΜΑΤΩΝ ΕΚΠΟΜΠΗΣ & ΑΠΟΡΡΟΦΗΣΗΣ ΣΤΕΡΕΟΥ
 1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΠΑΡΑΤΗΡΗΣΗ ΣΥΝΕΧΩΝ ΦΑΣΜΑΤΩΝ ΕΚΠΟΜΠΗΣ & ΑΠΟΡΡΟΦΗΣΗΣ ΣΤΕΡΕΟΥ Α. ΣΤΟΧΟΙ Η παραγωγή λευκού φωτός με τη χρήση λαμπτήρα πυράκτωσης. Η χρήση πηγών φωτός διαφορετικής
1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΠΑΡΑΤΗΡΗΣΗ ΣΥΝΕΧΩΝ ΦΑΣΜΑΤΩΝ ΕΚΠΟΜΠΗΣ & ΑΠΟΡΡΟΦΗΣΗΣ ΣΤΕΡΕΟΥ Α. ΣΤΟΧΟΙ Η παραγωγή λευκού φωτός με τη χρήση λαμπτήρα πυράκτωσης. Η χρήση πηγών φωτός διαφορετικής
Δίκτυα Τηλεπικοινωνιών. και Μετάδοσης
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Δίκτυα Τηλεπικοινωνιών και Μετάδοσης Σύστημα μετάδοσης με οπτικές ίνες Tο οπτικό φέρον κύμα μπορεί να διαμορφωθεί είτε από αναλογικό
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Δίκτυα Τηλεπικοινωνιών και Μετάδοσης Σύστημα μετάδοσης με οπτικές ίνες Tο οπτικό φέρον κύμα μπορεί να διαμορφωθεί είτε από αναλογικό
Βασικές διαδικασίες παραγωγής πολωμένου φωτός
 Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
Επαναληπτικό διαγώνισµα στα Κύµατα
 ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 12/02/12 ΛΥΣΕΙΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 011-01 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 1/0/1 ΥΣΕΙΣ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω ερωτήσεις
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 011-01 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 1/0/1 ΥΣΕΙΣ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω ερωτήσεις
7 σειρά ασκήσεων. Για την επίλυση των προβλημάτων να θεωρηθούν γνωστά: σταθερά του Planck 6,63 10-34 J s, ταχύτητα του φωτός στον αέρα 3 10 8 m/s
 η 7 σειρά ασκήσεων Για την επίλυση των προβλημάτων να θεωρηθούν γνωστά: σταθερά του Planck 6,63 10-34 J s, ταχύτητα του φωτός στον αέρα 3 10 8 m/s 1. Εξηγήστε γιατί, όταν φως διαπερνά μία διαχωριστική
η 7 σειρά ασκήσεων Για την επίλυση των προβλημάτων να θεωρηθούν γνωστά: σταθερά του Planck 6,63 10-34 J s, ταχύτητα του φωτός στον αέρα 3 10 8 m/s 1. Εξηγήστε γιατί, όταν φως διαπερνά μία διαχωριστική
ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ ΤΟ ΦΩΣ
 ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ ΤΟ ΦΩΣ Α] Τα ηλεκτρομαγνητικά κύματα Τι είναι τα ηλεκτρομαγνητικά κύματα Πρόκειται για μια σύνθεση που μπορεί να περιγραφεί με όρους ηλεκτρικού και μαγνητικού πεδίου. Πράγματι τα διανύσματα
ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ ΤΟ ΦΩΣ Α] Τα ηλεκτρομαγνητικά κύματα Τι είναι τα ηλεκτρομαγνητικά κύματα Πρόκειται για μια σύνθεση που μπορεί να περιγραφεί με όρους ηλεκτρικού και μαγνητικού πεδίου. Πράγματι τα διανύσματα
7α Γεωμετρική οπτική - οπτικά όργανα
 7α Γεωμετρική οπτική - οπτικά όργανα Εισαγωγή ορισμοί Φύση του φωτός Πηγές φωτός Δείκτης διάθλασης Ανάκλαση Δημιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/katsiki Ηφύσητουφωτός
7α Γεωμετρική οπτική - οπτικά όργανα Εισαγωγή ορισμοί Φύση του φωτός Πηγές φωτός Δείκτης διάθλασης Ανάκλαση Δημιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/katsiki Ηφύσητουφωτός
Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας
 Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας Τάξη : Γ Λυκείου Βασικές έννοιες και σχέσεις Μήκος κύματος - Μονοχρωματική ακτινοβολία - Συμβολή ηλεκτρομαγνητικών κυμάτων - Κροσσοί
Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας Τάξη : Γ Λυκείου Βασικές έννοιες και σχέσεις Μήκος κύματος - Μονοχρωματική ακτινοβολία - Συμβολή ηλεκτρομαγνητικών κυμάτων - Κροσσοί
Νέα Οπτικά Μικροσκόπια
 Νέα Οπτικά Μικροσκόπια Αντίθεση εικόνας (contrast) Αντίθεση πλάτους Αντίθεση φάσης Αντίθεση εικόνας =100 x (Ι υποβ -Ι δειγμα )/ Ι υποβ Μικροσκοπία φθορισμού (Χρησιμοποιεί φθορίζουσες χρωστικές για το
Νέα Οπτικά Μικροσκόπια Αντίθεση εικόνας (contrast) Αντίθεση πλάτους Αντίθεση φάσης Αντίθεση εικόνας =100 x (Ι υποβ -Ι δειγμα )/ Ι υποβ Μικροσκοπία φθορισμού (Χρησιμοποιεί φθορίζουσες χρωστικές για το
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell)
 Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell) 1. Σκοπός Αξιοποιώντας τις μετρήσεις των γωνιών πρόσπτωσης, διάθλασης α και δ αντίστοιχα μίας πολύ στενής φωτεινής δέσμης
Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell) 1. Σκοπός Αξιοποιώντας τις μετρήσεις των γωνιών πρόσπτωσης, διάθλασης α και δ αντίστοιχα μίας πολύ στενής φωτεινής δέσμης
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002 ÈÅÌÅËÉÏ
 ΘΕΜΑ 1ο ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί
ΘΕΜΑ 1ο ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί
10. Το ορατό φως έχει μήκη κύματος στο κενό που κυμαίνονται περίπου από: α nm β. 400nm - 600nm γ. 400nm - 700nm δ. 700nm nm.
 ΚΕΦΑΛΑΙΟ 1 ΤΟ ΦΩΣ ΓΡΗΓΟΡΗ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑ - ΑΣΚΗΣΕΙΣ 1. Με τον όρο ότι το φως έχει διπλή φύση εννοούμε ότι: α. είναι εγκάρσιο κύμα. β. αποτελείται από μικρά σωματίδια. γ. συμπεριφέρεται σαν κύμα και σαν
ΚΕΦΑΛΑΙΟ 1 ΤΟ ΦΩΣ ΓΡΗΓΟΡΗ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑ - ΑΣΚΗΣΕΙΣ 1. Με τον όρο ότι το φως έχει διπλή φύση εννοούμε ότι: α. είναι εγκάρσιο κύμα. β. αποτελείται από μικρά σωματίδια. γ. συμπεριφέρεται σαν κύμα και σαν
2. Οι ενεργειακές στάθµες του πυρήνα ενός στοιχείου είναι της τάξης α)µερικών ev γ)µερικών MeV
 ΙΑΓΩΝΙΣΜΑ Γ ΓΕΝΙΚΗΣ ΘΕΜΑ 1 ο 1. Αν ένα οπτικό µέσο Α µε δείκτη διάθλασης n Α είναι οπτικά πυκνότερο από ένα άλλο οπτικό µέσο Β µε δείκτη διάθλασης n Β και τα µήκη κύµατος του φωτός στα δυο µέσα είναι λ
ΙΑΓΩΝΙΣΜΑ Γ ΓΕΝΙΚΗΣ ΘΕΜΑ 1 ο 1. Αν ένα οπτικό µέσο Α µε δείκτη διάθλασης n Α είναι οπτικά πυκνότερο από ένα άλλο οπτικό µέσο Β µε δείκτη διάθλασης n Β και τα µήκη κύµατος του φωτός στα δυο µέσα είναι λ
ΦΑΣΜΑΤΑ ΕΚΠΟΜΠΗΣ ΑΠΟΡΡΟΦΗΣΗΣ
 ΚΒΑΝΤΙΚΗ ΦΥΣΙΚΗ: Τα άτομα έχουν διακριτές ενεργειακές στάθμες Τα άτομα και μόρια, βρίσκονται σε διακριτές ενεργειακές στάθμες και Υφίστανται μεταβάσεις μεταξύ αυτών των ενεργειακών σταθμών όταν αλληλεπιδρούν
ΚΒΑΝΤΙΚΗ ΦΥΣΙΚΗ: Τα άτομα έχουν διακριτές ενεργειακές στάθμες Τα άτομα και μόρια, βρίσκονται σε διακριτές ενεργειακές στάθμες και Υφίστανται μεταβάσεις μεταξύ αυτών των ενεργειακών σταθμών όταν αλληλεπιδρούν
Φυσική των οφθαλμών και της όρασης. Κική Θεοδώρου
 Φυσική των οφθαλμών και της όρασης Κική Θεοδώρου Περιεχόμενα Στοιχεία Γεωμετρικής Οπτικής Ανατομία του Οφθαλμού Αμφιβληστροειδής Ο ανιχνευτής φωτός του οφθαλμού Το κατώφλι της όρασης Φαινόμενα περίθλασης
Φυσική των οφθαλμών και της όρασης Κική Θεοδώρου Περιεχόμενα Στοιχεία Γεωμετρικής Οπτικής Ανατομία του Οφθαλμού Αμφιβληστροειδής Ο ανιχνευτής φωτός του οφθαλμού Το κατώφλι της όρασης Φαινόμενα περίθλασης
Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ34. Ιούλιος 2008 KYMATIKH. ιάρκεια: 210 λεπτά
 Κυµατική ΦΥΕ4 5/7/8 Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ4 Ιούλιος 8 KYMATIKH ιάρκεια: λεπτά Θέµα ο (Μονάδες:.5) A) Θεωρούµε τις αποστάσεις
Κυµατική ΦΥΕ4 5/7/8 Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ4 Ιούλιος 8 KYMATIKH ιάρκεια: λεπτά Θέµα ο (Μονάδες:.5) A) Θεωρούµε τις αποστάσεις
Φίλιππος Φαρμάκης Επ. Καθηγητής. Δείκτης διάθλασης. Διάδοση του Η/Μ κύματος μέσα σε μέσο
 9 η Διάλεξη Απόσβεση ακτινοβολίας, Σκέδαση φωτός, Πόλωση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Δείκτης διάθλασης Διάδοση του Η/Μ κύματος μέσα σε μέσο Η ταχύτητα διάδοσης μειώνεται κατά ένα παράγοντα n (v=c/n)
9 η Διάλεξη Απόσβεση ακτινοβολίας, Σκέδαση φωτός, Πόλωση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Δείκτης διάθλασης Διάδοση του Η/Μ κύματος μέσα σε μέσο Η ταχύτητα διάδοσης μειώνεται κατά ένα παράγοντα n (v=c/n)
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ
 13/02/2005 ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 2004-05 4 η ΕΡΓΑΣΙΑ Προθεσμία αποστολής 8/03/2005 ΑΣΚΗΣΕΙΣ Άσκηση 1 Α) Αν φωτίσουμε τα μέταλλα λίθιο (έργο εξαγωγής 2.3eV), βηρύλλιο (έργο εξαγωγής 3.9eV),
13/02/2005 ΕΛΛΗΝΙΚΟ ΑΝΟΙKΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 2004-05 4 η ΕΡΓΑΣΙΑ Προθεσμία αποστολής 8/03/2005 ΑΣΚΗΣΕΙΣ Άσκηση 1 Α) Αν φωτίσουμε τα μέταλλα λίθιο (έργο εξαγωγής 2.3eV), βηρύλλιο (έργο εξαγωγής 3.9eV),
ΔΙΑΣΚΕΔΑΣΜΟΣ & ΑΠΟΡΡΟΦΗΣΗ ΤΟΥ ΦΩΤΟΣ
 ΔΙΑΣΚΕΔΑΣΜΟΣ & ΑΠΟΡΡΟΦΗΣΗ ΤΟΥ ΦΩΤΟΣ Μάκης Αγγελακέρης 010 Εργαστήρια Οπτικής Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σκοπός της Άσκησης 1 o πείραμα: Να κατανοήσετε την έννοια του Διασκεδασμού
ΔΙΑΣΚΕΔΑΣΜΟΣ & ΑΠΟΡΡΟΦΗΣΗ ΤΟΥ ΦΩΤΟΣ Μάκης Αγγελακέρης 010 Εργαστήρια Οπτικής Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σκοπός της Άσκησης 1 o πείραμα: Να κατανοήσετε την έννοια του Διασκεδασμού
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ - ΤΥΠΟΛΟΓΙΟ
 ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ - ΤΥΠΟΛΟΓΙΟ 1 2 Ισχύς που «καταναλώνει» μια ηλεκτρική_συσκευή Pηλ = V. I Ισχύς που Προσφέρεται σε αντιστάτη Χαρακτηριστικά κανονικής λειτουργίας ηλεκτρικής συσκευής Περιοδική
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ - ΤΥΠΟΛΟΓΙΟ 1 2 Ισχύς που «καταναλώνει» μια ηλεκτρική_συσκευή Pηλ = V. I Ισχύς που Προσφέρεται σε αντιστάτη Χαρακτηριστικά κανονικής λειτουργίας ηλεκτρικής συσκευής Περιοδική
δ) Αν ένα σηµείο του θετικού ηµιάξονα ταλαντώνεται µε πλάτος, να υπολογίσετε την απόσταση του σηµείου αυτού από τον πλησιέστερο δεσµό. ΑΣΚΗΣΗ 4 Μονοχρ
 ΑΣΚΗΣΗ 1 Κατά µήκος µιας ελαστικής χορδής µεγάλου µήκους που το ένα άκρο της είναι ακλόνητα στερεωµένο, διαδίδονται δύο κύµατα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι µετρηµένα σε
ΑΣΚΗΣΗ 1 Κατά µήκος µιας ελαστικής χορδής µεγάλου µήκους που το ένα άκρο της είναι ακλόνητα στερεωµένο, διαδίδονται δύο κύµατα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι µετρηµένα σε
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ
 1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ 1. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο µέσων. Όταν η διαθλώµενη ακτίνα κινείται παράλληλα προς τη διαχωριστική
1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ 1. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο µέσων. Όταν η διαθλώµενη ακτίνα κινείται παράλληλα προς τη διαχωριστική
