2.2. ΘΝΗΣΙΜΟΤΗΤΑ ΚΑΤΑ ΑΙΤΙΕΣ ΘΑΝΑΤΟΥ
|
|
|
- Τερψιχόρη Ζέρβας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΚΕΦΑΛΑΙΟ 2 ΘΝΗΣΙΜΟΤΗΤΑ (MORTALITY) 2.1 ΕΙΣΑΓΩΓΗ Θα ήταν ίσως αναµενόµενο η παρουσίαση της γεννητικότητας να προηγηθεί εκείνης της θνησιµότητας εφ όσον η γέννηση σαν φυσικό γεγονός προηγείται του θανάτου. Η παρουσίαση εδώ είναι αντίστροφη για δύο λόγους. Ο πρώτος αφορά το γεγονός ότι η προσέγγιση της θνησιµότητας σαν δηµογραφικό φαινόµενο είναι ευκολότερη από την γεννητικότητα αφού στη πρώτη εµπλέκονται λιγότεροι παράγοντες που την επηρεάζουν - o θάνατος δεν αποτελεί συνήθως επιλογή, στη γέννηση αντίθετα εµπλέκεται σε µεγάλο βαθµό ο υποκειµενικός παράγοντας, η θέληση δηλαδή των ατόµων να αποκτήσουν παιδιά. Ο δεύτερος λόγος συνδέεται µε το γεγονός ότι η µελέτη της αναπαραγωγής ενός πληθυσµού προϋποθέτει τη µέτρηση της θνησιµότητας στην οποία υπόκειται ο πληθυσµός αυτός. Η θνησιµότητα, όπως και όλες οι άλλες πληθυσµιακές συνιστώσες, διαφοροποιείται κατά φύλο, ηλικία και σύµφωνα µε πληθώρα άλλων βιολογικών, κοινωνικών, οικονοµικών και περιβαλλοντικών χαρακτηριστικών του πληθυσµού όπως: η φυλή, η κληρονοµικότητα, η οικογενειακή κατάσταση, ο τόπος διαµονής, το κάπνισµα, η διατροφή, η κατανάλωση αλκοόλ, οι συνθήκες κατοικίας, η ιατροφαρµακευτική περίθαλψη, οι κλιµατολογικές συνθήκες. Οι µετρήσεις θνησιµότητας είναι αναγκαίες στη δηµογραφική έρευνα (ανάλυση θνησιµότητας, κατασκευή πινάκων επιβίωσης, ανάλυση γεννητικότητας, πληθυσµιακές προβολές κ.α.), στην έρευνα (Βιοστατιστική, Επιδηµιοµετρία κ.α.), στο δηµόσιο τοµέα (κρατικοί σχεδιασµοί, κοινωνική ασφάλιση κ.α.) και στον ιδιωτικό τοµέα (ασφαλιστικός κλάδος, φαρµακοβιοµηχανία κ.α.) ΘΝΗΣΙΜΟΤΗΤΑ ΚΑΤΑ ΑΙΤΙΕΣ ΘΑΝΑΤΟΥ Ένας από τους σηµαντικότερους πίνακες, που δηµοσιεύεται από τις εθνικές στατιστικές υπηρεσίες πολλών χωρών σε ετήσια βάση, αφορά στοιχεία που αναφέρονται σε αριθµούς θανάτων κατά φύλο, ηλικία και αιτία θανάτου. Η ταξινόµηση των θανάτων κατά αιτία γίνεται βάσει του δηµοσιεύµατος του Παγκόσµιου Οργανισµού Υγείας, ΠΟΥ (World Healh Orgaizaio, WHO): Maual of he Ieraioal Saisical Classificaio of iseases, Ijuries ad 32
2 Causes of eah γνωστό σαν I.C.. Αυτό το δηµοσίευµα περιέχει µια κατάσταση 50 βασικών οµάδων αιτιών θανάτου, η οποία ανανεώνεται και συµπληρώνεται τακτικά. Βιολογικοί παράγοντες όπως το φύλο, η ηλικία, η φυλή, η κληρονοµικότητα (τα δύο τελευταία καθορίζουν βιολογικές προδιαθέσεις) µπορεί να επηρεάσουν τη θνησιµότητα από τις διάφορες αιτίες θανάτου. Επίσης άλλοι παράγοντες που η επίδραση τους συνήθως διερευνάται σε µελέτες που αφορούν ειδική κατά αιτία θνησιµότητα είναι οικολογικοί, κλιµατολογικοί, η διατροφή, η απασχόληση κλπ. Χρειάζεται προσοχή σε συµπεράσµατα που αφορούν διαχρονικές µεταβολές θνησιµότητας από κάποια συγκεκριµένη αιτία καθώς είναι πιθανό η µεταβολή που παρατηρείται να αποτελεί απλά αποτέλεσµα της βελτίωσης των διαγνωστικών µέσων. Χρονολογικές σειρές στατιστικών δεδοµένων θνησιµότητας κατά φύλο και αιτίες θανάτου των χωρών µελών του Παγκόσµιου Οργανισµού Υγείας (Η.Π.Α., Καναδάς, χώρες της Ευρώπης, Αυστραλία, Νέα Ζηλανδία και Ιαπωνία και κάποιες χώρες της Λατινικής Αµερικής) αποτελούν τις βάσεις δεδοµένων του Παγκόσµιου Οργανισµού Υγείας και είναι διαθέσιµα στο διαδίκτυο στη διεύθυνση: hp://ifoserver.ciesi.org/ic/who/μoraliyaabase.hml 2.3. ΜΕΤΡΗΣΕΙΣ ΘΝΗΣΙΜΟΤΗΤΑΣ Ο Ακαθάριστος Συντελεστής Θνησιµότητας (Crude eah Rae), ο οποίος υπολογίζεται σαν τον λόγο του συνόλου των θανάτων () προς το µέσο πληθυσµό της χρονικής περιόδου αναφοράς ( ). Πολλαπλασιασµένος µε το 1000 εκφράζει το µέσο αριθµό θανάτων στα 1000 άτοµα του πληθυσµού: AΣΘ Ο ειδικός κατά ηλικία Συντελεστής Θνησιµότητας (Age-specific Moraliy Rae), οποίος υπολογίζεται από τον λόγο του αριθµού θανάτων ατόµων ηλικίας [, +) που συνέβησαν το έτος, προς το µέσο πληθυσµό ατόµων του ίδιου διαστήµατος ηλικίας το ίδιο έτος ( ). m Πολλαπλασιασµένος µε το 1000 εκφράζει το µέσο αριθµό θανάτων στα 1000 άτοµα του πληθυσµού ηλικιών του διαστήµατος [, +): 33
3 Σηµείωση: Εδώ ο δείκτης κάτω αριστερά, δεν αναφέρεται στη γενεά αλλά στο εύρος του διαστήµατος ηλικιών. Ο συντελεστής αναφέρεται σε δεδοµένα περιόδου (συνήθως ενός έτους) ΠΙΘΑΝΟΤΗΤΑ ΘΑΝΑΤΟΥ (robabiliy of dyig, risk of deah) Ας θεωρήσουµε ένα κλειστό πληθυσµό, έναν πληθυσµό δηλαδή που δεν εµφανίζει µεταναστευτική κίνηση, αλλά µεταβάλλεται µόνο από την επίδραση των φυσικών συµβάντων. Ας υποθέσουµε επίσης ότι σε αυτό τον πληθυσµό 120 άτοµα έκλεισαν τα 58 την και ακόµα ότι την έχουν επιβιώσει οι 112 από αυτούς. Άρα από τους 120 που ήταν εκτεθειµένοι στον κίνδυνο είχαµε 8 συµβάντα. Κατά συνέπεια, για κάθε έναν από τους 120, η πιθανότητα θανάτου το έτος 2002 θα ισούται µε: 2002 q ,67 Αν θεωρήσουµε ότι οι 8 θάνατοι επήλθαν οµοιόµορφα µέσα στο 2002 τότε µέχρι το µέσον του έτους 2002 θα έχουν συµβεί 4 θάνατοι. Κατά συνέπεια, ο πληθυσµός ηλικίας 58 του µέσου του έτους θα είναι: Γενικά λοιπόν η πιθανότητα θανάτου για την ηλικία θα ισούται µε: q Αν υπολογίσουµε τον ειδικό κατά ηλικία συντελεστή θνησιµότητας για τον πληθυσµό του παραδείγµατος, έχουµε: 2002 m ,069 Η διαφορά του ειδικού κατά ηλικία συντελεστή θνησιµότητας µε την πιθανότητα θανάτου, οφείλεται στο ότι το πρώτο µέτρο αναφέρεται στον πληθυσµό ηλικίας του µέσου του έτους (µέσο πληθυσµό), ενώ η πιθανότητα θανάτου αναφέρεται στον πληθυσµό ηλικίας της αρχής του έτους (τον πληθυσµό που εκτίθεται στον κίνδυνο του θανάτoυ κατά την διάρκεια του έτους ). 34
4 2.5. ΣΧΕΣΗ ΜΕΤΑΞΥ ΕΙ ΙΚΟΥ ΚΑΤΑ ΗΛΙΚΙΑ ΣΥΝΤΕΛΕΣΤΗ ΘΝΗΣΙΜΟΤΗΤΑΣ ΚΑΙ ΤΗΣ ΠΙΘΑΝΟΤΗΤΑΣ ΘΑΝΑΤΟΥ Αν υποθέσουµε ότι οι θάνατοι ατόµων ηλικίας του έτους είναι οµοιόµορφα κατανεµηµένοι κατά την διάρκεια του έτους, η πιθανότητα θανάτου στην ηλικία ισούται µε: q Αν διαιρέσουµε τη σχέση αυτή µε το µέσο πληθυσµό στην ηλικία,, τότε q Επειδή όµως m αντικαθιστώντας θα έχουµε: q m 2 m q 1 1+ m 2 + m 2 Αυτός o τελευταίος τύπος είναι ο κλασικός τύπος για τον υπολογισµό της πιθανότητας θανάτου, από τον αντίστοιχο ειδικό κατά ηλικία συντελεστή θνησιµότητας, που υπολογίζεται από τα εµπειρικά δεδοµένα (δεδοµένα απογραφών και της φυσικής και µεταναστευτικής κίνησης του πληθυσµού). Να σηµειωθεί ότι ο τύπος αυτός είναι προσεγγιστικός αφού στηρίζεται στην υπόθεση της οµοιόµορφης κατανοµής των συµβάντων µέσα σε κάθε διάστηµα ηλικίας [, +1). H υπόθεση όµως αυτή είναι επαρκώς ρεαλιστική για τις περισσότερες ηλικίες, µε εξαίρεση την ηλικία µηδέν και τις πολύ µεγάλες ηλικίες. Η πιθανότητα θανάτου για την ηλικία µηδέν εκτιµάται µε εναλλακτικό τρόπο που θα δούµε στη συνέχεια. Όσον αφορά τις ηλικίες από 85 και άνω, λόγω των λανθασµένων δηλώσεων ηλικιών των θανόντων σε αυτό το ηλικιακό διάστηµα ο αριθµός θανάτων δίνεται αθροιστικά για το σύνολο τους. Έτσι η πιθανότητα θανάτου δεν έχει κανένα πρόβληµα να υπολογιστεί γιατί θα είναι απλούστατα ίση 35
5 µε την µονάδα (το ενδεχόµενο κάποιος θνητός συγκεκριµένης ηλικίας να πεθάνει κάποτε στο µέλλον αποτελεί δυστυχώς ένα βέβαιο γεγονός) ΠΡΟΣΕΓΓΙΣΤΙΚΟ ΣΦΑΛΜΑ ΣΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΤΗΣ ΠΙΘΑΝΟΤΗΤΑΣ ΘΑΝΑΤΟΥ Εκτός της υπόθεσης της οµοιόµορφης κατανοµής θανάτων µέσα στο έτος αναφοράς (κάτι αβέβαιο!), µια άλλη πηγή συστηµατικού σφάλµατος στον υπολογισµό της πιθανότητας θανάτου προέρχεται από το γεγονός ότι αυτοί που πεθαίνουν σε ηλικία κατά την διάρκεια κάποιου έτους δεν ήταν όλοι ηλικίας ετών στην αρχή του έτους αυτού. Έτσι υπάρχει αναντιστοιχία αριθµητή και παρονοµαστή στο λόγο µε τον οποίο ορίζεται η πιθανότητα θανάτου. Το πλήθος ατόµων που περιλαµβάνονται στον αριθµητή δεν αποτελεί υποσύνολο του πληθυσµιακού συνόλου που αναφέρονται στον παρονοµαστή του κλάσµατος αυτού ΒΡΕΦΙΚΗ ΘΝΗΣΙΜΟΤΗΤΑ Βρεφική ηλικία θεωρούνται οι 12 πρώτοι µήνες ζωής. Η ηλικία αυτή αναφέρεται στην δηµογραφική ορολογία ως ηλικία 0 ή ηλικιακό διάστηµα [0,1). Ακριβής ηλικία µηδέν είναι η ηλικία κατά τη στιγµή της γέννησης. Το επίπεδο της νεογνικής και βρεφικής θνησιµότητας αντανακλά εντονότατα το επίπεδο ανάπτυξης µιας χώρας. Ο υπολογισµός του ειδικού συντελεστή βρεφικής θνησιµότητας διαφοροποιείται από τον υπολογισµό των ειδικών συντελεστών των άλλων ηλικιών. Θα µπορούσε να µετρηθεί από το λόγο του αριθµού θανάτων ατόµων ηλικίας µηδέν προς τον πληθυσµό ηλικίας µηδέν του µέσου του έτους. Όµως ο πληθυσµός ηλικίας µηδέν εκτός του έτους απογραφής υπολογίζεται από στοιχεία γεννήσεων. Έτσι ο ειδικός συντελεστής βρεφικής θνησιµότητας του έτους συνήθως υπολογίζεται από το λόγο του αριθµού θανάτων ατόµων ηλικίας µηδέν του έτους ( 0 ) προς τον αριθµό των γεννήσεων ζώντων ( B) του ίδιου έτους: B q 0 0 Με αυτό τον τρόπο βέβαια, αυτό που στην ουσία υπολογίζεται είναι η πιθανότητα θανάτου, εφ όσον ο παρονοµαστής του κλάσµατος είναι ο εκτεθειµένος στον κίνδυνο του θανάτου πληθυσµός ατόµων ηλικίας µηδέν µέσα στο έτος (τα άτοµα ακριβούς ηλικίας 0). Ακόµα να σηµειωθεί ότι αυτός ο τρόπος υπολογισµού ενέχει συστηµατικό σφάλµα, εφόσον οι θάνατοι ατόµων ηλικίας 0 το έτος δεν αναφέρονται µόνο στις γεννήσεις του έτους αλλά και σε όσους 36
6 γεννήθηκαν το προηγούµενο έτος -1, και πέθαναν πριν τα γενέθλια τους το έτος, ήταν λοιπόν τη στιγµή του θανάτου τους ακόµα ηλικίας 0. Έτσι έχουµε: q0 B ενώ ο σωστότερος τρόπος υπολογισµού θα ήταν: B q 0 B B Αυτό όµως είναι η πιθανότητα θανάτου ατόµων ηλικίας µηδέν της γενεάς του έτους και για να υπολογιστεί απαιτούνται τα στοιχεία θανάτων να παρέχονται όχι µόνο κατά ηλικία αλλά και κατά το έτος γέννησης θανόντος. Ο περιορισµός όµως για τον υπολογισµό αυτής της πιθανότητας είναι ότι µόνο σε εξαιρετικά ελάχιστες χώρες τα εµπειρικά δεδοµένα παρέχονται σε αυτή την αναλυτική µορφή, ενώ στις περισσότερες χώρες παρέχονται µόνο κατά ηλικία. Αξίζει να παρατηρηθεί ότι όπως φαίνεται από την σύγκριση των δύο προηγούµενων εκφράσεων αυτό που στην ουσία συµβαίνει στον κλασικό υπολογισµό της πιθανότητας θανάτου για την ηλικία 0, είναι ότι αντικαθίσταται + το 1 0 µε το 1 0. ηλαδή αντικαθίσταται ο αριθµός συµβάντων αυτών που γεννήθηκαν το έτος και πέθαναν πριν τα γενέθλιά τους το έτος +1, σε ηλικία µηδέν, µε τον αριθµό συµβάντων αυτών που γεννήθηκαν το έτος -1 και πέθαναν πριν τα γενέθλιά τους το έτος, σε ηλικία µηδέν. Αν όµως θεωρήσουµε ότι το µέγεθος και η κατά ηλικία σύνθεση του πληθυσµού καθώς και η µορφή και η ένταση της κατά ηλικία θνησιµότητας δε διαφοροποιείται σηµαντικά από ένα ηµερολογιακό έτος στο επόµενο, τότε το προσεγγιστικό σφάλµα του κλασικού τύπου υπολογισµού µπορεί να θεωρηθεί µη σηµαντικό. Εναλλακτικά, στην κοινή περίπτωση που τα εµπειρικά δεδοµένα θανάτων δίνονται µόνο κατά ηλικία τότε το q 0 µπορεί να προσεγγιστεί έµµεσα, αφού προηγούµενα υπολογιστεί ένας συντελεστής διαχωρισµού φ. Ο συντελεστής αυτός υπολογίζεται από αναλυτικά δεδοµένα κάποιου τυπικού πληθυσµού. Ο τυπικός πληθυσµός θα µπορούσε να είναι ο πληθυσµός κάποιου προηγούµενου έτους ( ) ή ο πληθυσµός κάποιας άλλης χώρας, για το οποίο υπάρχουν στοιχεία θανάτων σε αναλυτική µορφή (δεδοµένα και κατά έτος γέννησης και κατά ηλικία): φ o 37
7 όπου: 0 οι θάνατοι ατόµων ηλικίας 0, της γενιάς που συνέβησαν το έτος (το ίδιο έτος της γέννησης τους), 0 ο συνολικός αριθµός θανάτων ατόµων ηλικίας 0 της γενιάς (συνέβησαν τα έτη ή +1), οι θάνατοι ατόµων ηλικίας 0, της γενιάς που συνέβησαν το έτος +1 (τα άτοµα αυτά πέθαναν πριν τα πρώτα τους γενέθλια το έτος +1). Έτσι ο αριθµητής του συντελεστή θνησιµότητας ατόµων ηλικίας 0 το έτος, υπολογίζεται σαν σταθµικός µέσος των 0 και +1 0 µε συντελεστή στάθµισης τα φ και (1-φ): q o φ + (1 φ ) + Β όπου, οι θάνατοι ατόµων ηλικίας 0 το έτος, Β οι θάνατοι ατόµων ηλικίας 0 το έτος +1 και οι γεννήσεις ζώντων το έτος. Οι συντελεστές βρεφικής θνησιµότητας των διαφόρων χωρών έχουν εµφανίσει θεαµατική µείωση διαχρονικά. Ο Πίνακας 2.1 παρουσιάζει τιµές των συντελεστών κάποιων επιλεγµένων χωρών. 38
8 Πίνακας 2.1: Συντελεστής βρεφικής θνησιµότητας ΧΩΡΑ ΕΤΟΣ q AΓΓΛΙΑ , ΣΟΥΗ ΙΑ , , ΕΛΛΑ Α*** , , ,3 ΙΣΛΑΝ ΙΑ ,6* ΑΦΓΑΝΙΣΤΑΝ ,8** *Το χαµηλότερο του κόσµου ** Το υψηλότερο του κόσµου *** Οι δείκτες αυτοί πρέπει να αντιµετωπιστούν µε κάποια επιφύλαξη γιατί ενέχουν συστηµατικού σφάλµατος. Πολλοί θάνατοι αµέσως µετά την γέννηση, ιδιαίτερα στην επαρχία, δεν δηλώνονται ούτε σαν γέννηση ζώντος, ούτε σαν θάνατος στην ηλικία 0, µε αποτέλεσµα να παραποιείται η τιµή του δείκτη. Το πρόβληµα αυτό µε την πάροδο του χρόνου τείνει να εκλείψει ΝΕΟΓΝΙΚΗ ΚΑΙ ΠΕΡΙΓΕΝΝΗΤΙΚΗ ΘΝΗΣΙΜΟΤΗΤΑ Έχει παρατηρηθεί στους ανθρώπινους πληθυσµούς ότι το µεγαλύτερο ποσοστό των θανάτων του πρώτου έτους ζωής επέρχεται τις πρώτες εβδοµάδες ζωής. Στις περισσότερο ανεπτυγµένες χώρες σήµερα το 40% περίπου των θανάτων του πρώτου ηλικιακού έτους επέρχονται την πρώτη µέρα ζωής ενώ περίπου το 70% αυτών επέρχονται τις πρώτες τέσσερις εβδοµάδες. Για τις ανάγκες λοιπόν της µέτρησης της περιγεννητικής και νεογνικής θνησιµότητας συνήθως υπολογίζονται οι εξής συντελεστές: Συντελεστής πρώιµης νεογνικής θνησιµότητας: ο λόγος των θανάτων της πρώτης εβδοµάδας ζωής προς τις γεννήσεις του ηµερολογιακού έτους αναφοράς. Συντελεστής όψιµης νεογνικής θνησιµότητας: ο λόγος των θανάτων της 2ης, 3ης και 4ης εβδοµάδας ζωής προς τις γεννήσεις του ηµερολογιακού έτους αναφοράς. 39
9 Συντελεστής νεογνικής θνησιµότητας: To άθροισµα των δύο προηγουµένων. Συντελεστής περιγεννητικής θνησιµότητας: O λόγος των γεννήσεων νεκρών και θανάτων της πρώτης εβδοµάδας ζωής προς τις γεννήσεις του ηµερολογιακού έτους αναφοράς. 2.8 ΜΟΡΦΗ ΤΗΣ ΕΙ ΙΚΗΣ ΚΑΤΑ ΗΛΙΚΙΑ ΘΝΗΣΙΜΟΤΗΤΑΣ Στο διάγραµµα 2.1 εµφανίζονται οι ειδικοί κατά ηλικία συντελεστές θνησιµότητας δύο διαφορετικών πληθυσµών, δύο διαφορετικά ηµερολογιακά έτη. Είναι εµφανές ότι η εξέλιξη αυτή, η οποία είναι τυπική για όλους τους ανθρώπινους πληθυσµούς, εµφανίζει µια πολυπλοκότητα στη µορφή της. Θα µπορούσε να µελετηθεί καλύτερα αν χωρίζαµε το διάστηµα ηλικίας σε τρία µέρη: Νεογνική, βρεφική και παιδική θνησιµότητα Η ειδική κατά ηλικία θνησιµότητα από την γέννηση µέχρι την αρχή της εφηβείας (περίπου την ηλικία δέκα ετών) εµφανίζει µια φθίνουσα εκθετική εξέλιξη µε πολύ έντονο ρυθµό µείωσης. Η θνησιµότητα της ηλικίας µηδέν είναι πολύ υψηλή, αντιστοιχεί σε επίπεδα θνησιµότητας των ηλικιών στους σύγχρονους πληθυσµούς των ανεπτυγµένων χωρών, ενώ σε πληθυσµούς των υπό ανάπτυξη χωρών µπορεί να ξεπερνά τη θνησιµότητα της ηλικίας 80. Το τόσο υψηλό επίπεδο θνησιµότητας για το εύρος αυτών των ηλικιών οφείλεται κατά κύριο λόγο στην περιγεννητική και νεογνική θνησιµότητα. Γύρω στην ηλικία 10, το επίπεδο θνησιµότητας αγγίζει την ελάχιστη τιµή του. Θνησιµότητα νεαρών ενηλίκων Στο διάστηµα ηλικιών από τα 10 µέχρι τα 30 περίπου, η µορφή της κατά ηλικία θνησιµότητας εµφανίζει µια περισσότερο ή λιγότερο έντονη ανωµαλία γνωστή στην βιβλιογραφία µε τον όρο: accide hump (καµπύλη ατυχηµάτων). Οφείλεται κατά κύριο λόγο στη θνησιµότητα από αιτίες όπως: νεοπλάσµατα, καρδιακά, (παλαιότερα φυµατίωση και άλλες επιδηµίες), ατυχήµατα (εργατικά, τροχαία κ.α.) και επηρεάζεται από όλους εκείνους τους κινδύνους στους οποίους εκτίθενται οι έφηβοι και οι νεαροί ενήλικες λόγω της αυξηµένης φυσικής και κοινωνικής δραστηριότητας. Η θνησιµότητα αυτών των ηλικιών επηρεάζεται γενικά από διάφορους κοινωνικούς και περιβαλλοντολογικούς παράγοντες όπως τον τρόπο ζωής, την απασχόληση κ.λ.π. και διαφοροποιείται σηµαντικά κατά φύλο. Η εµπειρική 40
10 παρατήρηση έχει δείξει ότι η καµπύλη αυτή εµφανιζόταν εντονότερα στους ανδρικούς πληθυσµούς τουλάχιστον σε ότι αφορά τις ανεπτυγµένες χώρες τα προηγούµενα χρόνια, αλλά συναντάται ακόµη και σήµερα στους περισσότερους πληθυσµούς. Ο λόγος είναι κύρια η αυξηµένη δραστηριότητα των ανδρών σε σχέση µε τις γυναίκες. Αυτή η διαφοροποίηση στους σύγχρονους πληθυσµούς των ανεπτυγµένων χωρών τείνει να εκλείψει. Στους γυναικείους πληθυσµούς αυτή η καµπύλη ήταν σχεδόν ανύπαρκτη στο παρελθόν, ενώ εµφανίζεται πλέον έντονη σε νεότερους πληθυσµούς, κύρια λόγω της ένταξης των γυναικών στην αγορά εργασίας. Θνησιµότητα ωρίµων ενηλίκων Η ειδική κατά ηλικία θνησιµότητα των ωρίµων ενηλίκων, µετά από την ηλικία 30 ετών περίπου, εµφανίζει εξέλιξη αύξουσα εκθετική, µε ρυθµό που διαφοροποιείται µεταξύ πληθυσµών και φύλων. Στις ηλικίες αυτές η διαδικασία της φυσικής γήρανσης δρα µε συνεχώς αυξανόµενο ρυθµό για να αγγίξει την µέγιστη τιµή της στην µεγαλύτερη ηλικία που εµφανίζεται στον πληθυσµό. Ο ρυθµός αύξησης των επιπέδων θνησιµότητας είναι εντονότερος σε χρονολογικά νεότερους πληθυσµούς, σε γυναικείους πληθυσµούς και σε πληθυσµούς αναπτυγµένων χωρών. Αιτία αυτής της διαφοροποίησης αποτελεί το γεγονός ότι αν και τα κατά ηλικία επίπεδα θνησιµότητας διαφοροποιούνται µεταξύ των διαφόρων πληθυσµών, το ανώτατο όριο ζωής παραµένει αµετακίνητο σε όλους τους πληθυσµούς. Η εξέλιξη της ιατρικής και η ανάπτυξη του βιοτικού επιπέδου επιφέρει µείωση της κατά ηλικία θνησιµότητας στους διάφορους πληθυσµούς, έτσι ώστε όλο και µεγαλύτερο µέρος των πληθυσµών αυτών να περνά στη γήρανση. Εν τούτοις παρά τις εξελίξεις, δεν έχει κατορθωθεί να αυξηθεί η ανώτατη διάρκεια ζωής. Έτσι όσο χαµηλότερα είναι τα κατά ηλικία επίπεδα θνησιµότητας ενός πληθυσµού, τόσο ταχύτερα αυξάνεται η θνησιµότητα στις µεγάλες ηλικίες. ιάγραµµα 2.1. Ειδική κατά ηλικία θνησιµότητα log(q),05,04,03,02,01,005,004,003,002,001 Ialia males 1990,0005,0004,0003 Germa males 1988,0002 Ausralia, females 1960 age 41
11 2.9. ΣΥΓΚΡΙΣΕΙΣ ΘΝΗΣΙΜΟΤΗΤΑΣ ΜΕΘΟ ΟΙ ΤΥΠΟΠΟΙΗΣΗΣ (Sadardizaio mehods) Οι ακαθάριστοι συντελεστές θνησιµότητας για το έτος 1999 ήταν για διάφορες χώρες οι εξής: Σουηδία 11, Ελλάδα 10, ανία 11, Αλβανία 5, Μονακό 17. Βάσει αυτών των τιµών, η θνησιµότητα των περισσότερο αναπτυγµένων χωρών (Σουηδία, Μονακό) εµφανίζεται σε υψηλότερα επίπεδα από εκείνη της Ελλάδας, ενώ ακόµη και ο συντελεστής της Αλβανίας είναι δραµατικά µικρότερος εκείνων των ανεπτυγµένων χωρών. Ένα άλλο αξιοπερίεργο εµπειρικό εύρηµα είναι ότι η θνησιµότητα των Ελλήνων βάσει του ακαθάριστου συντελεστή, όπως αυτή αποτυπώνεται στο ιάγραµµα 2.2, διαχρονικά αυξάνεται σταθερά. ιάγραµµα 2.2 Ακαθάριστος συντελεστής θνησιµότητας του Ελληνικού Πληθυσµού Εν τούτοις είναι γνωστό ότι τα κατά ηλικία επίπεδα θνησιµότητας της Ελλάδας έχουν διαχρονικά δραµατικά µειωθεί. Αιτία αυτού του οξύµωρου φαινοµένου είναι ότι η ηλικιακή σύνθεση του πληθυσµού έχει µεταβληθεί έντονα µέσα σε αυτό το χρονικό διάστηµα. Ο πληθυσµός της Ελλάδας διαχρονικά ωριµάζει. Η κατά ηλικία σύνθεση του πληθυσµού διαµορφώνεται υπέρ των µεγάλων ηλικιών, η µέση ηλικία του πληθυσµού αυξάνεται σαν αποτέλεσµα της διαχρονικής µείωσης των κατά ηλικία επιπέδων θνησιµότητας και των επιπέδων γεννητικότητας. Επίσης το γεγονός ότι ο ακαθάριστος συντελεστής θνησιµότητας της Αλβανίας εµφανίζεται πολύ µικρότερος από τους αντίστοιχους των περισσότερων αναπτυγµένων χωρών οφείλεται στη διαφορετική κατά ηλικία σύνθεση των πληθυσµών. Οι περισσότερο αναπτυγµένες χώρες εµφανίζουν εντονότερα φαινόµενα δηµογραφικής γήρανσης λόγω µεγαλύτερης διαχρονικής αύξησης της προσδοκώµενης ζωής και πτώσης των επιπέδων γεννητικότητας. Έτσι, σε σχέση µε την Αλβανία, στους πληθυσµούς αυτούς πολύ µεγαλύτερο µέρος τους είναι ηλικιωµένοι. 42
12 Από αυτά τα παραδείγµατα γίνεται εµφανές ότι οι ακαθάριστοι συντελεστές θνησιµότητας είναι ακατάλληλα µέτρα για συγκρίσεις θνησιµότητας µεταξύ πληθυσµών όταν αυτοί οι πληθυσµοί εµφανίζουν διαφορετική κατά ηλικία σύνθεση. Οι ειδικοί κατά ηλικία συντελεστές θνησιµότητας είναι κατάλληλα µέτρα, αυτοί όµως είναι τόσοι πολλοί όσες και οι ηλικίες στον πληθυσµό (ή όσες οι οµάδες ηλικιών στις οποίες αναφέρονται) και αυτό κάνει τις συγκρίσεις πολύπλοκες. Είναι προφανές ότι κάποιο κατάλληλο µέτρο, που θα αναφέρεται στο σύνολο του πληθυσµού, είναι αναγκαίο για συγκρίσεις θνησιµότητας µεταξύ πληθυσµών ή για διαχρονικές συγκρίσεις θνησιµότητας κάποιου πληθυσµού Άµεση Τυποποίηση (irec sadardizaio) Ας θεωρήσουµε ένα παράδειγµα. Τα εµπειρικά δεδοµένα που παρουσιάζονται στον Πίνακα 2.2 αφορούν τον πληθυσµό της Ν. Ζηλανδίας το έτος Πίνακας 2.2. ηµογραφικά δεδοµένα του πληθυσµού της Ν. Ζηλανδίας Μαoρί Έποικοι (1) (2)* (3) (4) (5) (6)* (7) (8) (9) 0 39, ,44 267, , , ,91 505, , , ,53 401, , , ,52 597, , , ,90 487, , , ,59 219, ,50 201, , , ,09 * σε χιλιάδες Πηγή: ollard e. al όπου : ο µέσος πληθυσµός ηλικιών [, +) σε χιλιάδες ατόµων, % η κατά οµάδες ηλικιών ποσοστιαία, σύνθεση του πληθυσµού, ο αριθµός θανάτων ατόµων ηλικιών του διαστήµατος [, +), m ο ειδικός συντελεστής θνησιµότητας της οµάδας ηλικιών [, +). % m m % Θεωρώντας τις τιµές στις στήλες (5) και (9) του Πίνακα 2.2, παρατηρούµε ότι ενώ οι ειδικοί κατά ηλικία συντελεστές θνησιµότητας των εποίκων είναι συστηµατικά πολύ χαµηλότεροι από τους αντίστοιχους των Μαορί για όλες τις οµάδες ηλικιών, οι ακαθάριστοι συντελεστές θνησιµότητας συνδέονται µε αντίθετη σχέση. Ακόµα συγκρίνοντας τις τιµές στις στήλες (3) και (7) του Πίνακα 2.2 παρατηρούµε ότι η κατά ηλικία σύνθεση των δύο πληθυσµών διαφέρει αισθητά. Οι Μαορί είναι πολύ νεότερος πληθυσµός σε σχέση µε τους άποικους. 43
13 Γνωρίζουµε όµως ότι ο ακαθάριστος συντελεστής θνησιµότητας (ΑΣΘ) ορίζεται από τη σχέση: AΣΘ AΣΘ αλλά m m Άρα, m ΣΘ ΣΘ A A m Σε αυτή την τελευταία έκφραση είναι εµφανές ότι το Ακαθάριστος Συντελεστής Θνησιµότητας (ΑΣΘ) αποτελεί σταθµικό µέσο των επί µέρους ειδικών συντελεστών m µε συντελεστές στάθµισης τα αντίστοιχα ποσοστά πληθυσµού της κάθε οµάδας ηλικίας. Κατά συνέπεια, οι ΑΣΘ των δύο πληθυσµών είναι σταθµικοί µέσοι των επί µέρους m του κάθε πληθυσµού µε διαφορετικούς συντελεστές στάθµισης (τα αντίστοιχα µεγέθη του κάθε πληθυσµού) και ως εκ τούτου µη συγκρίσιµοι µεταξύ τους. Για να γίνουν συγκρίσιµα τα δύο αυτά µέτρα θα πρέπει να χρησιµοποιηθούν κοινοί συντελεστές στάθµισης στον υπολογισµό τους. Σαν τέτοιοι θα µπορούσαν να χρησιµοποιηθούν τα πληθυσµιακά µεγέθη του συνολικού πληθυσµού της Ν. Ζηλανδίας. Θεωρούµε λοιπόν το συνολικό πληθυσµό της χώρας σαν τυπικό (ή πρότυπο) πληθυσµό. Υπολογίζουµε µε αυτόν τον τρόπο έναν τυποποιηµένο συντελεστή θνησιµότητας για τον κάθε πληθυσµό, σαν ένα συνολικό συντελεστή θνησιµότητας που θα χαρακτήριζε τον πρότυπο πληθυσµό εάν σε αυτόν αντιστοιχούσαν, για την κάθε οµάδα ηλικιών, οι ειδικοί συντελεστές θνησιµότητας του υπό εξέταση πληθυσµού. Ο Τυποποιηµένος Συντελεστής Θνησιµότητας, (ΤΣΘ), είναι ο λόγος του αναµενόµενου αριθµού θανάτων του τυπικού πληθυσµού, αν ο πληθυσµός αυτός βίωνε τα ίδια κατά ηλικία επίπεδα θνησιµότητας µε αυτά του υπό εξέταση πληθυσµού, προς το συνολικό µέγεθος του τυπικού πληθυσµού. Έτσι για τον συνολικό πληθυσµό της Ν. Ζηλανδίας έχουµε τον πίνακα
14 Πίνακας 2.3. ηµογραφικά δεδοµένα συνολικού πληθυσµού Ν. Ζηλανδίας, για το έτος 1966 ( S ) ( S ) 0 306, , , , , , , , , , , , , ,89 (S): Sadard populaio - τυπικός ή πρότυπος πληθυσµός Τυποποιηµένοι συντελεστές θνησιµότητας για κάθε ένα από τους δύο υποπληθυσµούς της Ν. Ζηλανδίας, θα υπολογιστούν από τη σχέση: m ( S ) TΣΘ ( S) ( S) m Κάνοντας χρήση των πινάκων 2.2 και 2.3, o τυποποιηµένος συντελεστής των Μαορί είναι: ( ) 306,6 7, ,7 0, ,1 93,59 T ΣΘ M 2676,8 και αντιστοίχως των εποίκων: 13,88 ( ) T ΣΘ E 306,6 3, ,7 0, ,1 68, ,8 8,68 Παρατηρούµε ότι ενώ ο ΑΣΘ των Μαορί (6.41) εµφανίζεται µικρότερος από τον ΑΣΘ των εποίκων (9.09), οι αντίστοιχοι τυποποιηµένοι συντελεστές συνδέονται µε αντίθετη σχέση. (ΤΣΘ (Μ) > ΤΣΘ (Ε) 8.68). Αυτοί οι τελευταίοι δίνουν πιο σωστή εικόνα της σχέσης των γενικών επιπέδων θνησιµότητας των δύο πληθυσµών, η οποία συµπίπτει µε εκείνη που εµφανίζουν οι επί µέρους ειδικοί κατά ηλικία συντελεστές των δύο πληθυσµών Έµµεση Τυποποίηση (Ιdirec sadardizaio) Στο παράδειγµά µας υπολογίσαµε τους τυποποιηµένους συντελεστές θνησιµότητας των δύο πληθυσµών ως σταθµικούς µέσους των επί µέρους m του κάθε πληθυσµού µε κοινούς συντελεστές στάθµισης, τα πληθυσµιακά µεγέθη του τυπικού πληθυσµού κατά οµάδες ηλικιών. 45
15 Είναι προφανές ότι για αυτούς τους υπολογισµούς απαιτείται η γνώση των ειδικών κατά ηλικία συντελεστών θνησιµότητας του υπό εξέταση πληθυσµού ( m ). Αν αυτοί είναι άγνωστοι και αν το µόνο στοιχείο θνησιµότητας που είναι δεδοµένο για τον κάθε πληθυσµό είναι ο συνολικός αριθµός θανάτων των πληθυσµών αυτών, ο τυποποιηµένος συντελεστής θνησιµότητας µπορεί εναλλακτικά να υπολογιστεί από την έκφραση: T ΣΘ A m ΣΘ ( S) ( S ) όπου: ο συνολικός αριθµός θανάτων του υπό εξέταση πληθυσµού, ο µέσος πληθυσµός ηλικιών [, +) του υπό εξέταση πληθυσµού, (S ) m ο ειδικός συντελεστής θνησιµότητας της οµάδας ηλικιών [, +) του τυπικού πληθυσµού και (S ) AΣΘ ο ακαθάριστος συντελεστής θνησιµότητας του τυπικού πληθυσµού. Παρατηρούµε ότι αυτός ο συντελεστής υπολογίζεται σαν ο ακαθάριστος συντελεστής θνησιµότητας του τυπικού (πρότυπου) πληθυσµού πολλαπλασιασµένος µε το λόγο του πραγµατικού συνολικού αριθµού θανάτων του υπό εξέταση πληθυσµού προς τον αναµενόµενο συνολικό αριθµό θανάτων του υπό εξέταση πληθυσµού, αν θεωρήσουµε ότι αυτός υπόκεινται στην ίδια ειδική κατά ηλικία θνησιµότητα µε τον τυπικό πληθυσµό. Ο λόγος αυτός θα ισούται µε τη µονάδα αν η θνησιµότητα του πληθυσµού για τον οποίο υπολογίζεται είναι ίση µε εκείνη του πρότυπου πληθυσµού. Θα είναι µικρότερος της µονάδας αν η θνησιµότητα του πληθυσµού για τον οποίο υπολογίζεται είναι µικρότερη από εκείνη του πρότυπου πληθυσµού. Τέλος, θα είναι µεγαλύτερος της µονάδας στην αντίθετη περίπτωση. Έτσι ο ΤΣΘ του εκάστοτε πληθυσµού θα ξεπερνά ή θα υπολείπεται του ΑΣΘ του τυπικού πληθυσµού ανάλογα µε τη σχέση των γενικών επιπέδων θνησιµότητας των δύο πληθυσµών. Για το παράδειγµα µας: και ( ) T ΣΘ M ,5 4, ,7 0, ,9 68,94 8,89 15,00 ( ) T ΣΘ E ,89 8,67 267,1 4, ,0 0, ,2 68,9 Βάσει αυτού του τρόπου υπολογισµού βλέπουµε ότι το αποτέλεσµα συµπίπτει µε αυτό της άµεσης (ευθείας) τυποποίησης, δηλαδή ο τυποποιηµένος συντελεστής θνησιµότητας των Μαορί εµφανίζεται πολύ ψηλότερος από τον αντίστοιχο των εποίκων. 46
16 Σχόλια Οι τυποποιηµένοι συντελεστές δεν αποτελούν καθαρά µέτρα θνησιµότητας του πληθυσµού στον οποίο αναφέρονται, αφού για τον υπολογισµό τους δε χρησιµοποιούνται µόνο στοιχεία του πληθυσµού αυτού, αλλά και στοιχεία του πρότυπου πληθυσµού. Εν τούτοις λόγω της οµοιογένειας τους είναι κατάλληλοι για συγκρίσεις θνησιµότητας µεταξύ πληθυσµών. Πρέπει ακόµα να σηµειωθεί ότι δεν υπάρχει κάποιος γενικά αποδεκτός τρόπος επιλογής τυπικού πληθυσµού. Ο ερευνητής είναι ελεύθερος κατά την κρίση του να επιλέξει κάποιο πληθυσµό που θα χρησιµοποιηθεί σαν πρότυπος. Αυτός θα µπορούσε να είναι κάποιος γενικός πληθυσµός (κάποιος που οι πληθυσµοί τους οποίους θέλουµε να συγκρίνουµε αποτελούν υποσύνολα του) ή ακόµα, ο ένας από αυτούς τους πληθυσµούς ή κάποιος τρίτος ανεξάρτητος πληθυσµός. Η επιλογή πρότυπου πληθυσµού επηρεάζει βέβαια έντονα την τιµή των τυποποιηµένων συντελεστών, πολύ σπάνια όµως την κατεύθυνση της µεταξύ τους σχέσης. 47
ΚΕΦΑΛΑΙΟ 5 ΓΕΝΝΗΤΙΚΟΤΗΤΑ (FERTILITY)
 ΚΕΦΑΛΑΙΟ 5 ΓΕΝΝΗΤΙΚΟΤΗΤΑ (FERTILITY) Στην ξένη δηµογραφική βιβλιογραφία ο όρος feriliy αναφέρεται στην έκταση και την ένταση των γεννήσεων ζώντων σε ένα πληθυσµό. Αφορά λοιπόν το µέρος εκείνο της δηµογραφικής
ΚΕΦΑΛΑΙΟ 5 ΓΕΝΝΗΤΙΚΟΤΗΤΑ (FERTILITY) Στην ξένη δηµογραφική βιβλιογραφία ο όρος feriliy αναφέρεται στην έκταση και την ένταση των γεννήσεων ζώντων σε ένα πληθυσµό. Αφορά λοιπόν το µέρος εκείνο της δηµογραφικής
ΕΚΤΙΜΗΣΕΙΣ, ΠΡΟΒΛΕΨΕΙΣ ΚΑΙ ΠΡΟΒΟΛΕΣ ΠΛΗΘΥΣΜΟΥ (POPULATION PROJECTIONS)
 ΚΕΦΑΛΑΙΟ 8 ΕΚΤΙΜΗΣΕΙΣ, ΠΡΟΒΛΕΨΕΙΣ ΚΑΙ ΠΡΟΒΟΛΕΣ ΠΛΗΘΥΣΜΟΥ (OULATION ROJECTIONS) Η κύρια πηγή στατιστικών δεδοµένων που αφορούν το µέγεθος και τη σύνθεση του πληθυσµού είναι η απογραφή. Η απογραφή πληθυσµού
ΚΕΦΑΛΑΙΟ 8 ΕΚΤΙΜΗΣΕΙΣ, ΠΡΟΒΛΕΨΕΙΣ ΚΑΙ ΠΡΟΒΟΛΕΣ ΠΛΗΘΥΣΜΟΥ (OULATION ROJECTIONS) Η κύρια πηγή στατιστικών δεδοµένων που αφορούν το µέγεθος και τη σύνθεση του πληθυσµού είναι η απογραφή. Η απογραφή πληθυσµού
ΕΛΤΙΟ ΤΥΠΟΥ ΣΤΑΤΙΣΤΙΚΕΣ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΑΝΑΛΥΣΗ ΗΜΟΓΡΑΦΙΚΩΝ ΜΕΓΕΘΩΝ (ΓΑΜΩΝ ΓΕΝΝΗΣΕΩΝ ΘΑΝΑΤΩΝ)
 ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΕΘΝΙΚΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΤΗΣ ΕΛΛΑ ΟΣ Πειραιάς, 12-2-29 ΕΛΤΙΟ ΤΥΠΟΥ ΣΤΑΤΙΣΤΙΚΕΣ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΑΝΑΛΥΣΗ ΗΜΟΓΡΑΦΙΚΩΝ ΜΕΓΕΘΩΝ (ΓΑΜΩΝ ΓΕΝΝΗΣΕΩΝ ΘΑΝΑΤΩΝ) Από τη Γενική Γραµµατεία
ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΕΘΝΙΚΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΤΗΣ ΕΛΛΑ ΟΣ Πειραιάς, 12-2-29 ΕΛΤΙΟ ΤΥΠΟΥ ΣΤΑΤΙΣΤΙΚΕΣ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΑΝΑΛΥΣΗ ΗΜΟΓΡΑΦΙΚΩΝ ΜΕΓΕΘΩΝ (ΓΑΜΩΝ ΓΕΝΝΗΣΕΩΝ ΘΑΝΑΤΩΝ) Από τη Γενική Γραµµατεία
ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΑΚΡΙΒΕΙΑΣ ΤΩΝ ΗΜΟΓΡΑΦΙΚΩΝ Ε ΟΜΕΝΩΝ
 ΚΕΦΑΛΑΙΟ 9 ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΑΚΡΙΒΕΙΑΣ ΤΩΝ ΗΜΟΓΡΑΦΙΚΩΝ Ε ΟΜΕΝΩΝ Τα δηµογραφικά δεδοµένα τα οποία προέρχονται από τις απογραφές πληθυσµού, τις καταγραφές της φυσικής και µεταναστευτικής κίνησης του πληθυσµού
ΚΕΦΑΛΑΙΟ 9 ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΑΚΡΙΒΕΙΑΣ ΤΩΝ ΗΜΟΓΡΑΦΙΚΩΝ Ε ΟΜΕΝΩΝ Τα δηµογραφικά δεδοµένα τα οποία προέρχονται από τις απογραφές πληθυσµού, τις καταγραφές της φυσικής και µεταναστευτικής κίνησης του πληθυσµού
Στον πίνακα επιβίωσης θεωρούµε τον αριθµό ζώντων στην κάθε ηλικία
 ΚΕΦΑΛΑΙΟ 4 ΠΙΝΑΚΕΣ ΠΟΛΛΑΠΛΩΝ ΚΙΝ ΥΝΩΝ (MULTIPLE DECREMENT TABLES) Στον πίνακα επιβίωσης θεωρούµε τον αριθµό ζώντων στην κάθε ηλικία αρχίζοντας από µια οµάδα γεννήσεων ζώντων που αποτελεί την ρίζα του πίνακα
ΚΕΦΑΛΑΙΟ 4 ΠΙΝΑΚΕΣ ΠΟΛΛΑΠΛΩΝ ΚΙΝ ΥΝΩΝ (MULTIPLE DECREMENT TABLES) Στον πίνακα επιβίωσης θεωρούµε τον αριθµό ζώντων στην κάθε ηλικία αρχίζοντας από µια οµάδα γεννήσεων ζώντων που αποτελεί την ρίζα του πίνακα
ΕΛΤΙΟ ΤΥΠΟΥ ΣΤΑΤΙΣΤΙΚΕΣ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΑΝΑΛΥΣΗ ΗΜΟΓΡΑΦΙΚΩΝ ΜΕΓΕΘΩΝ (ΓΑΜΩΝ ΓΕΝΝΗΣΕΩΝ ΘΑΝΑΤΩΝ)
 ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΕΘΝΙΚΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΤΗΣ ΕΛΛΑ ΟΣ Πειραιάς, 2.04.2007 ΕΛΤΙΟ ΤΥΠΟΥ ΣΤΑΤΙΣΤΙΚΕΣ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΑΝΑΛΥΣΗ ΗΜΟΓΡΑΦΙΚΩΝ ΜΕΓΕΘΩΝ (ΓΑΜΩΝ ΓΕΝΝΗΣΕΩΝ ΘΑΝΑΤΩΝ) Η /νση Στατιστικών
ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΕΘΝΙΚΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΤΗΣ ΕΛΛΑ ΟΣ Πειραιάς, 2.04.2007 ΕΛΤΙΟ ΤΥΠΟΥ ΣΤΑΤΙΣΤΙΚΕΣ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΑΝΑΛΥΣΗ ΗΜΟΓΡΑΦΙΚΩΝ ΜΕΓΕΘΩΝ (ΓΑΜΩΝ ΓΕΝΝΗΣΕΩΝ ΘΑΝΑΤΩΝ) Η /νση Στατιστικών
Εργαστήριο Δημογραφικών & Κοινωνικών Αναλύσεων
 ΥΠΟΔΕΙΓΜΑΤΑ ΣΤΑΣΙΜΟΥ ΚΑΙ ΣΤΑΘΕΡΟΥ ΠΛΗΘΥΣΜΟΥ (ΕΛΕΥΘΕΡΙΑ ΑΝΔΡΟΥΛΑΚΗ) Η εξέταση των πολύπλοκων δεσμών που συνδέουν τα δημογραφικά φαινόμενα με τους πληθυσμούς από τους οποίους προέρχονται και τους οποίους
ΥΠΟΔΕΙΓΜΑΤΑ ΣΤΑΣΙΜΟΥ ΚΑΙ ΣΤΑΘΕΡΟΥ ΠΛΗΘΥΣΜΟΥ (ΕΛΕΥΘΕΡΙΑ ΑΝΔΡΟΥΛΑΚΗ) Η εξέταση των πολύπλοκων δεσμών που συνδέουν τα δημογραφικά φαινόμενα με τους πληθυσμούς από τους οποίους προέρχονται και τους οποίους
Ασφαλιστικά Μαθηµατικά Συνοπτικές σηµειώσεις
 Από την Θεωρία Θνησιµότητας Συνάρτηση Επιβίωσης : Ασφαλιστικά Μαθηµατικά Συνοπτικές σηµειώσεις Η s() δίνει την πιθανότητα άτοµο ηλικίας µηδέν, ζήσει πέραν της ηλικίας. όταν s() s( ) όταν o
Από την Θεωρία Θνησιµότητας Συνάρτηση Επιβίωσης : Ασφαλιστικά Μαθηµατικά Συνοπτικές σηµειώσεις Η s() δίνει την πιθανότητα άτοµο ηλικίας µηδέν, ζήσει πέραν της ηλικίας. όταν s() s( ) όταν o
ΠΡΟΒΟΛΕΣ ΠΛΗΘΥΣΜΟΥ ΕΛΛΑ ΟΣ
 ΠΡΟΒΟΛΕΣ ΠΛΗΘΥΣΜΟΥ ΕΛΛΑ ΟΣ 27-25 ΣΥΝΟΠΤΙΚΟ ΜΕΘΟ ΟΛΟΓΙΚΟ ΣΗΜΕΙΩΜΑ 1. Εισαγωγή Οι προβολές πληθυσµού καταρτίστηκαν µε βάση τον εκτιµώµενο πληθυσµό της 1 ης Ιανουαρίου 27 σε 3 σενάρια (χαµηλό, υψηλό, ενδιάµεσο)
ΠΡΟΒΟΛΕΣ ΠΛΗΘΥΣΜΟΥ ΕΛΛΑ ΟΣ 27-25 ΣΥΝΟΠΤΙΚΟ ΜΕΘΟ ΟΛΟΓΙΚΟ ΣΗΜΕΙΩΜΑ 1. Εισαγωγή Οι προβολές πληθυσµού καταρτίστηκαν µε βάση τον εκτιµώµενο πληθυσµό της 1 ης Ιανουαρίου 27 σε 3 σενάρια (χαµηλό, υψηλό, ενδιάµεσο)
ΜΕΘΟΔΟΙ ΠΡΟΤΥΠΟΠΟΙΗΣΗΣ
 ΜΕΘΟΔΟΙ ΠΡΟΤΥΠΟΠΟΙΗΣΗΣ είναι ο αριθμός των θανάτων - από κάθε αιτία - που συνέβησαν και καταγράφηκαν μέσα σε ένα ημερολογιακό έτος ανά 1 κατοίκους του μελετώμενου πληθυσμού. αριθμός θανάτων έτους t TBM/CDR
ΜΕΘΟΔΟΙ ΠΡΟΤΥΠΟΠΟΙΗΣΗΣ είναι ο αριθμός των θανάτων - από κάθε αιτία - που συνέβησαν και καταγράφηκαν μέσα σε ένα ημερολογιακό έτος ανά 1 κατοίκους του μελετώμενου πληθυσμού. αριθμός θανάτων έτους t TBM/CDR
ΑΝΑΣΤΑΣΙΑ ΚΩΣΤΑΚΗ Επίκουρος Καθηγήτρια Οικονοµικού Πανεπιστηµίου Αθηνών TEXNΙΚΕΣ ΗΜΟΓΡΑΦΙΚΗΣ ΑΝΑΛΥΣΗΣ
 ΑΝΑΣΤΑΣΙΑ ΚΩΣΤΑΚΗ Επίκουρος Καθηγήτρια Οικονοµικού Πανεπιστηµίου Αθηνών TEXNΙΚΕΣ ΗΜΟΓΡΑΦΙΚΗΣ ΑΝΑΛΥΣΗΣ Αθήνα 2003 I ΕΙΣΑΓΩΓΙΚΟ ΣΗΜΕΙΩΜΑ Πολλοί δηµογράφοι αντιµετωπίζουν τη ηµογραφία σαν ένα σύνολο τεχνικών.
ΑΝΑΣΤΑΣΙΑ ΚΩΣΤΑΚΗ Επίκουρος Καθηγήτρια Οικονοµικού Πανεπιστηµίου Αθηνών TEXNΙΚΕΣ ΗΜΟΓΡΑΦΙΚΗΣ ΑΝΑΛΥΣΗΣ Αθήνα 2003 I ΕΙΣΑΓΩΓΙΚΟ ΣΗΜΕΙΩΜΑ Πολλοί δηµογράφοι αντιµετωπίζουν τη ηµογραφία σαν ένα σύνολο τεχνικών.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΕΘΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΥΠΗΡΕΣΙΑ ΤΗΣ ΕΛΛΑΔΟΣ ΔΕΛΤΙΟ ΤΥΠΟΥ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΕΘΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΥΠΗΡΕΣΙΑ ΤΗΣ ΕΛΛΑΔΟΣ ΔΕΛΤΙΟ ΤΥΠΟΥ Πειραιάς, 13/09/.2006 ΣΤΑΤΙΣΤΙΚΕΣ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΑΝΑΛΥΣΗ ΔΗΜΟΓΡΑΦΙΚΩΝ ΜΕΓΕΘΩΝ (ΓΑΜΩΝ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΕΘΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΥΠΗΡΕΣΙΑ ΤΗΣ ΕΛΛΑΔΟΣ ΔΕΛΤΙΟ ΤΥΠΟΥ Πειραιάς, 13/09/.2006 ΣΤΑΤΙΣΤΙΚΕΣ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΑΝΑΛΥΣΗ ΔΗΜΟΓΡΑΦΙΚΩΝ ΜΕΓΕΘΩΝ (ΓΑΜΩΝ
Εργαστήριο Δημογραφικών & Κοινωνικών Αναλύσεων
 Το κείμενο που ακολουθεί είναι απόσπασμα από το βιβλίο του Β. Κοτζαμάνη, Στοιχεία Δημογραφίας, Πανεπιστημιακές Εκδόσεις Θεσσαλίας, Βόλος, 9, σσ. 95-99. IV.5 Υποδείγματα πληθυσμού: στάσιμος και σταθερός
Το κείμενο που ακολουθεί είναι απόσπασμα από το βιβλίο του Β. Κοτζαμάνη, Στοιχεία Δημογραφίας, Πανεπιστημιακές Εκδόσεις Θεσσαλίας, Βόλος, 9, σσ. 95-99. IV.5 Υποδείγματα πληθυσμού: στάσιμος και σταθερός
A. ΠΗΓΕΣ &ΜΕΛΕΤΗ ΔΙΑΧΡΟΝΙΚΩΝ ΤΑΣΕΩΝ ΒΑΣΙΚΕΣ ΠΡΟΒΟΛΕΣ ΣΥΝΟΛΙΚΟΥ ΠΛΗΘΥΣΜΟΥ
 A. ΠΗΓΕΣ &ΜΕΛΕΤΗ ΔΙΑΧΡΟΝΙΚΩΝ ΤΑΣΕΩΝ ΒΑΣΙΚΕΣ ΠΡΟΒΟΛΕΣ ΣΥΝΟΛΙΚΟΥ ΠΛΗΘΥΣΜΟΥ (πηγές) 1. ΕΛΣΤΑΤ : πληθυσμιακά μεγέθη και ηλικιακή δομή Απογραφές πληθυσμού 2001, 2011 (Σύνολο Χώρας, NUTS2-επίπεδο περιφέρειας)
A. ΠΗΓΕΣ &ΜΕΛΕΤΗ ΔΙΑΧΡΟΝΙΚΩΝ ΤΑΣΕΩΝ ΒΑΣΙΚΕΣ ΠΡΟΒΟΛΕΣ ΣΥΝΟΛΙΚΟΥ ΠΛΗΘΥΣΜΟΥ (πηγές) 1. ΕΛΣΤΑΤ : πληθυσμιακά μεγέθη και ηλικιακή δομή Απογραφές πληθυσμού 2001, 2011 (Σύνολο Χώρας, NUTS2-επίπεδο περιφέρειας)
Αναπαραγωγικότητα. Δρ. Δέσποινα Ανδριώτη
 Αναπαραγωγικότητα Δρ. Δέσποινα Ανδριώτη dandrioti@gmail.com Ορισμοί Σημασία Δείκτες Δομή του μαθήματος Παραδείγματα Αναπαραγωγικότητα ή γεννητικότητα ή γονιμότητα Κύριος παράγων διαμόρφωσης και εξέλιξης
Αναπαραγωγικότητα Δρ. Δέσποινα Ανδριώτη dandrioti@gmail.com Ορισμοί Σημασία Δείκτες Δομή του μαθήματος Παραδείγματα Αναπαραγωγικότητα ή γεννητικότητα ή γονιμότητα Κύριος παράγων διαμόρφωσης και εξέλιξης
Εισαγωγή στη Στατιστική- Κοινωνικές Στατιστικές. Διάλεξη
 Εισαγωγή στη Στατιστική- Κοινωνικές Στατιστικές Διάλεξη 24-4-2015 ΚΟΙΝΩΝΙΚΕΣ ΣΤΑΤΙΣΤΙΚΕΣ ΑΠΟΓΡΑΦΗ ΠΛΗΘΥΣΜΟΥ Για τη μελέτη των πληθυσμιακών εξελίξεων αντλούνται δεδομένα κυρίως από: Τις Απογραφές Πληθυσμού
Εισαγωγή στη Στατιστική- Κοινωνικές Στατιστικές Διάλεξη 24-4-2015 ΚΟΙΝΩΝΙΚΕΣ ΣΤΑΤΙΣΤΙΚΕΣ ΑΠΟΓΡΑΦΗ ΠΛΗΘΥΣΜΟΥ Για τη μελέτη των πληθυσμιακών εξελίξεων αντλούνται δεδομένα κυρίως από: Τις Απογραφές Πληθυσμού
Δημογραφία. Ενότητα 11.1: Παράδειγμα - Περιφερειακές διαφοροποιήσεις και ανισότητες του προσδόκιμου ζωής στη γέννηση
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Δημογραφία Ενότητα 11.1: Παράδειγμα - Περιφερειακές διαφοροποιήσεις και ανισότητες του προσδόκιμου ζωής στη γέννηση Μιχάλης Αγοραστάκης Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας &
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Δημογραφία Ενότητα 11.1: Παράδειγμα - Περιφερειακές διαφοροποιήσεις και ανισότητες του προσδόκιμου ζωής στη γέννηση Μιχάλης Αγοραστάκης Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας &
ΑΣΚΗΣΕΙΣ. (iii) ln(0.5) = , (iv) e =
 ΑΣΚΗΣΕΙΣ Να συµπληρωθεί ο παρακάτω πίνακας 47 48 49 50 5 l 348480 299692 d 43306 q 0.0 0.2 0.5 2 3 4 5 Η ένταση θνησιµότητας µ +t, 0 t, αλλάζει σε µ +t - c, όπου το c είναι θετικός σταθερός αριθµός. Να
ΑΣΚΗΣΕΙΣ Να συµπληρωθεί ο παρακάτω πίνακας 47 48 49 50 5 l 348480 299692 d 43306 q 0.0 0.2 0.5 2 3 4 5 Η ένταση θνησιµότητας µ +t, 0 t, αλλάζει σε µ +t - c, όπου το c είναι θετικός σταθερός αριθµός. Να
Πρόσφατες δηµογραφικές εξελίξεις σε περιφερειακό επίπεδο
 Πρόσφατες δηµογραφικές εξελίξεις σε περιφερειακό επίπεδο Βασιλική Στεφάνου, Προϊσταµένη /νσης Πληθυσµού, Ε.Σ.Υ.Ε. Χαρά Ζήκου, Προϊσταµένη Τµήµατος Φυσικής Κίνησης Πληθυσµού, /νση Πληθυσµού, Ε.Σ.Υ.Ε. Κων/νος
Πρόσφατες δηµογραφικές εξελίξεις σε περιφερειακό επίπεδο Βασιλική Στεφάνου, Προϊσταµένη /νσης Πληθυσµού, Ε.Σ.Υ.Ε. Χαρά Ζήκου, Προϊσταµένη Τµήµατος Φυσικής Κίνησης Πληθυσµού, /νση Πληθυσµού, Ε.Σ.Υ.Ε. Κων/νος
ΔΙΑΧΕΙΡΙΣΗ ΑΓΡΙΑΣ ΠΑΝΙΔΑΣ 8. ΓΕΝΝΗΤΙΚΟΤΗΤΑ ΘΝΗΣΙΜΟΤΗΤΑ
 ΔΙΑΧΕΙΡΙΣΗ ΑΓΡΙΑΣ ΠΑΝΙΔΑΣ 8. ΓΕΝΝΗΤΙΚΟΤΗΤΑ ΘΝΗΣΙΜΟΤΗΤΑ Γεννητικότητα Ρυθμός αναπαραγωγής: η παραγωγή νέων στον πληθυσμό μέσω της Γέννησης (στα θηλαστικά) Εκκόλαψης (πτηνά, ερπετά, αμφίβια, ψάρια) Γεννητικότητα:
ΔΙΑΧΕΙΡΙΣΗ ΑΓΡΙΑΣ ΠΑΝΙΔΑΣ 8. ΓΕΝΝΗΤΙΚΟΤΗΤΑ ΘΝΗΣΙΜΟΤΗΤΑ Γεννητικότητα Ρυθμός αναπαραγωγής: η παραγωγή νέων στον πληθυσμό μέσω της Γέννησης (στα θηλαστικά) Εκκόλαψης (πτηνά, ερπετά, αμφίβια, ψάρια) Γεννητικότητα:
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 31/01/2011 ΔΕΛΤΙΟ ΤΥΠΟΥ. Αύξηση πληθυσμού κατά 0,4 % ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ: Έτος 2009
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 31/01/2011 ΔΕΛΤΙΟ ΤΥΠΟΥ Αύξηση πληθυσμού κατά 0,4 % ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ: Έτος 2009 Την 1 η Ιανουαρίου του 2010 ο πληθυσμός της Ελλάδας εκτιμάται
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 31/01/2011 ΔΕΛΤΙΟ ΤΥΠΟΥ Αύξηση πληθυσμού κατά 0,4 % ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ: Έτος 2009 Την 1 η Ιανουαρίου του 2010 ο πληθυσμός της Ελλάδας εκτιμάται
Σηµειώσεις στις σειρές
 . ΟΡΙΣΜΟΙ - ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Σηµειώσεις στις σειρές Στην Ενότητα αυτή παρουσιάζουµε τις βασικές-απαραίτητες έννοιες για την µελέτη των σειρών πραγµατικών αριθµών και των εφαρµογών τους. Έτσι, δίνονται συστηµατικά
. ΟΡΙΣΜΟΙ - ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Σηµειώσεις στις σειρές Στην Ενότητα αυτή παρουσιάζουµε τις βασικές-απαραίτητες έννοιες για την µελέτη των σειρών πραγµατικών αριθµών και των εφαρµογών τους. Έτσι, δίνονται συστηµατικά
Ειδικά Θέματα Δημογραφίας: Χωρικές Διαστάσεις Δημογραφικών Δεδομένων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Ειδικά Θέματα Δημογραφίας: Χωρικές Διαστάσεις Δημογραφικών Δεδομένων Ενότητα 1.1: Αναλογίες, Πιθανότητες, Δείκτες - Πληθυσμιακές Δομές - Δομικοί Δείκτες Βύρων Κοτζαμάνης Τμήμα Μηχανικών
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Ειδικά Θέματα Δημογραφίας: Χωρικές Διαστάσεις Δημογραφικών Δεδομένων Ενότητα 1.1: Αναλογίες, Πιθανότητες, Δείκτες - Πληθυσμιακές Δομές - Δομικοί Δείκτες Βύρων Κοτζαμάνης Τμήμα Μηχανικών
Η μεταβλητή "χρόνος" στη δημογραφική ανάλυση - το διάγραμμα του Lexis
 Η μεταβλητή "χρόνος" στη δημογραφική ανάλυση - το διάγραμμα του Lexis Η αναφορά στο χρόνο Αναφερόμενοι στο χρόνο, θα πρέπει κατ αρχάς να τονίσουμε ότι αυτός μπορεί να είναι είτε το ημερολογιακό έτος, είτε
Η μεταβλητή "χρόνος" στη δημογραφική ανάλυση - το διάγραμμα του Lexis Η αναφορά στο χρόνο Αναφερόμενοι στο χρόνο, θα πρέπει κατ αρχάς να τονίσουμε ότι αυτός μπορεί να είναι είτε το ημερολογιακό έτος, είτε
«ΘΝΗΣΙΜΟΤΗΤΑ ΚΑΙ ΑΙΤΙΕΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΘΑΝΑΤΟΥ ΣΤΗΝ ΕΛΛΑΔΑ» ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΟ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΟ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΤΟΥ ΜΕΤΑΠΤΥΧΙΑΚΟΥ ΦΟΙΤΗΤΗ ΚΑΛΑΜΠΑΛΙΚΗ ΓΕΡΑΣΙΜΟΥ Α.Μ. 178 «ΘΝΗΣΙΜΟΤΗΤΑ ΚΑΙ ΑΙΤΙΕΣ ΘΑΝΑΤΟΥ ΣΤΗΝ ΕΛΛΑΔΑ» 1981 2000 ΥΠΕΥΘΥΝΟΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΟ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΤΟΥ ΜΕΤΑΠΤΥΧΙΑΚΟΥ ΦΟΙΤΗΤΗ ΚΑΛΑΜΠΑΛΙΚΗ ΓΕΡΑΣΙΜΟΥ Α.Μ. 178 «ΘΝΗΣΙΜΟΤΗΤΑ ΚΑΙ ΑΙΤΙΕΣ ΘΑΝΑΤΟΥ ΣΤΗΝ ΕΛΛΑΔΑ» 1981 2000 ΥΠΕΥΘΥΝΟΣ
ΔΕΛΤΙΟ ΤΥΠΟΥ ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ. Έτος 2014
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 30 Σεπτεμβρίου 2015 ΔΕΛΤΙΟ ΤΥΠΟΥ ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ Έτος 2014 Από την Ελληνική Στατιστική Αρχή ανακοινώνονται τα στατιστικά στοιχεία που αποτυπώνουν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 30 Σεπτεμβρίου 2015 ΔΕΛΤΙΟ ΤΥΠΟΥ ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ Έτος 2014 Από την Ελληνική Στατιστική Αρχή ανακοινώνονται τα στατιστικά στοιχεία που αποτυπώνουν
Ελληνικό ηµογραφικό ελτίο BU
 Ελληνικό ηµογραφικό ελτίο BU 06 2011 Εκτίµηση της µέσης ηλικίας ανδρών και γυναικών στον πρώτο γάµο µε τη χρήση απογραφικών δεδοµένων στην Ελλάδα και σε επιλεγµένες Ευρωπαϊκές χώρες κατά τα τέλη του 19
Ελληνικό ηµογραφικό ελτίο BU 06 2011 Εκτίµηση της µέσης ηλικίας ανδρών και γυναικών στον πρώτο γάµο µε τη χρήση απογραφικών δεδοµένων στην Ελλάδα και σε επιλεγµένες Ευρωπαϊκές χώρες κατά τα τέλη του 19
1. Τακτικές στατιστικές σειρές: στοιχεία με. 2. Ειδικές επιδημιολογικές έρευνες: περιγραφικές. 10/10/ Απογραφή πληθυσμού
 ΠΗΓΕΣ ΕΠΙΔΗΜΙΟΛΟΓΙΚΩΝ ΔΕΔΟΜΕΝΩΝ 1. Τακτικές στατιστικές σειρές: στοιχεία με ΠΗΓΕΣ ΣΤΟΙΧΕΙΩΝ Ανδρονίκη Νάσκα, Αναπλ. Καθηγήτρια επιδημιολογικό και βιοκοινωνικό ενδιαφέρον 2. Ειδικές επιδημιολογικές έρευνες:
ΠΗΓΕΣ ΕΠΙΔΗΜΙΟΛΟΓΙΚΩΝ ΔΕΔΟΜΕΝΩΝ 1. Τακτικές στατιστικές σειρές: στοιχεία με ΠΗΓΕΣ ΣΤΟΙΧΕΙΩΝ Ανδρονίκη Νάσκα, Αναπλ. Καθηγήτρια επιδημιολογικό και βιοκοινωνικό ενδιαφέρον 2. Ειδικές επιδημιολογικές έρευνες:
3. Οι αλλαγές στη σύνθεση της οικογένειας και των νοικοκυριών
 3. Οι αλλαγές στη σύνθεση της οικογένειας και των νοικοκυριών Η ανάλυση των διαχρονικών μεταβολών στη σύνθεση της οικογένειας και των νοικοκυριών προσκρούει πολύ συχνά στην αδυναμία μιας διαχρονικής στατιστικής
3. Οι αλλαγές στη σύνθεση της οικογένειας και των νοικοκυριών Η ανάλυση των διαχρονικών μεταβολών στη σύνθεση της οικογένειας και των νοικοκυριών προσκρούει πολύ συχνά στην αδυναμία μιας διαχρονικής στατιστικής
ΔΕΛΤΙΟ ΤΥΠΟΥ. ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ έτους 2013
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ ΔΕΛΤΙΟ ΤΥΠΟΥ Πειραιάς, 30 Σεπτεμβρίου 2014 ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ έτους 2013 Από την Ελληνική Στατιστική Αρχή ανακοινώνονται τα στατιστικά στοιχεία που αποτυπώνουν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ ΔΕΛΤΙΟ ΤΥΠΟΥ Πειραιάς, 30 Σεπτεμβρίου 2014 ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ έτους 2013 Από την Ελληνική Στατιστική Αρχή ανακοινώνονται τα στατιστικά στοιχεία που αποτυπώνουν
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ. Δημογραφία. Ενότητα 15: Προβολές Πληθυσμού. Βύρων Κοτζαμάνης Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας & Περιφερειακής Ανάπτυξης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Δημογραφία Ενότητα 15: Προβολές Πληθυσμού Βύρων Κοτζαμάνης Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας & Περιφερειακής Ανάπτυξης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Δημογραφία Ενότητα 15: Προβολές Πληθυσμού Βύρων Κοτζαμάνης Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας & Περιφερειακής Ανάπτυξης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Ο ΠΛΗΘΥΣΜΟΣ ΤΩΝ ΗΛΙΚΙΩΜΕΝΩΝ ΑΤΟΜΩΝ ΣΤΗΝ ΕΥΡΩΠΑΪΚΗ ΈΝΩΣΗ
 Ο ΠΛΗΘΥΣΜΟΣ ΤΩΝ ΗΛΙΚΙΩΜΕΝΩΝ ΑΤΟΜΩΝ ΣΤΗΝ ΕΥΡΩΠΑΪΚΗ ΈΝΩΣΗ Σύμφωνα με τα επίσημα στοιχεία της Eurostat οι πληθυσμοί της Ευρώπης γερνάνε γρήγορα λόγω του χαμηλού ποσοστού γεννήσεων και του αυξανόμενου προσδόκιμου
Ο ΠΛΗΘΥΣΜΟΣ ΤΩΝ ΗΛΙΚΙΩΜΕΝΩΝ ΑΤΟΜΩΝ ΣΤΗΝ ΕΥΡΩΠΑΪΚΗ ΈΝΩΣΗ Σύμφωνα με τα επίσημα στοιχεία της Eurostat οι πληθυσμοί της Ευρώπης γερνάνε γρήγορα λόγω του χαμηλού ποσοστού γεννήσεων και του αυξανόμενου προσδόκιμου
Ειδικά Θέματα Δημογραφίας: Χωρικές Διαστάσεις Δημογραφικών Δεδομένων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Ειδικά Θέματα Δημογραφίας: Χωρικές Διαστάσεις Δημογραφικών Δεδομένων Ενότητα 4.3: Οι δημογραφικές δομές και ο δημογραφικός δυναμισμός των ελληνικών δήμων (1999-2009) Μαρί-Νοέλ Ντυκέν,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Ειδικά Θέματα Δημογραφίας: Χωρικές Διαστάσεις Δημογραφικών Δεδομένων Ενότητα 4.3: Οι δημογραφικές δομές και ο δημογραφικός δυναμισμός των ελληνικών δήμων (1999-2009) Μαρί-Νοέλ Ντυκέν,
HOPEgenesis: Ελπίδα για την υπογεννητικότητα Οκτώβριος
 HOPEgenesis: Ελπίδα για την υπογεννητικότητα Οκτώβριος - 2018 Υπογεννητικότητα Υπογεννητικότητα υπάρχει σε μία χώρα, όταν ο αριθμός γεννήσεων ανά έτος είναι μικρότερος ή όχι σημαντικά μεγαλύτερος από τον
HOPEgenesis: Ελπίδα για την υπογεννητικότητα Οκτώβριος - 2018 Υπογεννητικότητα Υπογεννητικότητα υπάρχει σε μία χώρα, όταν ο αριθμός γεννήσεων ανά έτος είναι μικρότερος ή όχι σημαντικά μεγαλύτερος από τον
Δημογραφία. Ενότητα 5: Μέθοδοι ανάλυσης πληθυσμιακών δομών - Η Πυραμίδα των ηλικιών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Δημογραφία Ενότητα 5: Μέθοδοι ανάλυσης πληθυσμιακών δομών - Η Πυραμίδα των ηλικιών Βύρων Κοτζαμάνης Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας & Περιφερειακής Ανάπτυξης Άδειες Χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Δημογραφία Ενότητα 5: Μέθοδοι ανάλυσης πληθυσμιακών δομών - Η Πυραμίδα των ηλικιών Βύρων Κοτζαμάνης Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας & Περιφερειακής Ανάπτυξης Άδειες Χρήσης
ΠΛΗΘΥΣΜΟΣ ΤΟΥ ΝΟΜΟΥ ΡΑΜΑΣ
 39 ΚΕΦΑΛΑΙΟ 3 : ΗΜΟΓΡΑΦΙΚΑ ΣΤΟΙΧΕΙΑ ΝΟΜΟΥ ΡΑΜΑΣ 3.1 Πληθυσµιακά στοιχεία σε επίπεδο Ν. ΡΑΜΑΣ Πίνακας 3.1.1 : Πληθυσµός του Νοµού ράµας (1961-1991) ΠΛΗΘΥΣΜΟΣ ΤΟΥ ΝΟΜΟΥ ΡΑΜΑΣ ΣΤΟΙΧΕΙΑ \ ΕΤΗ 1961 1971 1981
39 ΚΕΦΑΛΑΙΟ 3 : ΗΜΟΓΡΑΦΙΚΑ ΣΤΟΙΧΕΙΑ ΝΟΜΟΥ ΡΑΜΑΣ 3.1 Πληθυσµιακά στοιχεία σε επίπεδο Ν. ΡΑΜΑΣ Πίνακας 3.1.1 : Πληθυσµός του Νοµού ράµας (1961-1991) ΠΛΗΘΥΣΜΟΣ ΤΟΥ ΝΟΜΟΥ ΡΑΜΑΣ ΣΤΟΙΧΕΙΑ \ ΕΤΗ 1961 1971 1981
ΔΕΛΤΙΟ ΤΥΠΟΥ. ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ έτους 2012
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 1.8.2013 ΔΕΛΤΙΟ ΤΥΠΟΥ ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ έτους 2012 Από την Ελληνική Στατιστική Αρχή ανακοινώνονται τα στατιστικά στοιχεία που αποτυπώνουν την
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 1.8.2013 ΔΕΛΤΙΟ ΤΥΠΟΥ ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ έτους 2012 Από την Ελληνική Στατιστική Αρχή ανακοινώνονται τα στατιστικά στοιχεία που αποτυπώνουν την
ΕΛΤΙΟ ΤΥΠΟΥ ΕΙ ΙΚΗ ΕΡΕΥΝΑ ΓΙΑ ΤΑ ΑΤΥΧΗΜΑΤΑ ΚΑΙ TA ΠΡΟΒΛΗΜΑΤΑ ΥΓΕΙΑΣ ΠΟΥ ΣΥΝ ΕΟΝΤΑΙ ΜΕ ΤΗΝ ΕΡΓΑΣΙΑ
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 21 Νοεµβρίου 2014 ΕΛΤΙΟ ΤΥΠΟΥ ΕΙ ΙΚΗ ΕΡΕΥΝΑ ΓΙΑ ΤΑ ΑΤΥΧΗΜΑΤΑ ΚΑΙ TA ΠΡΟΒΛΗΜΑΤΑ ΥΓΕΙΑΣ ΠΟΥ ΣΥΝ ΕΟΝΤΑΙ ΜΕ ΤΗΝ ΕΡΓΑΣΙΑ Σκοπός της έρευνας ήταν η συλλογή
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 21 Νοεµβρίου 2014 ΕΛΤΙΟ ΤΥΠΟΥ ΕΙ ΙΚΗ ΕΡΕΥΝΑ ΓΙΑ ΤΑ ΑΤΥΧΗΜΑΤΑ ΚΑΙ TA ΠΡΟΒΛΗΜΑΤΑ ΥΓΕΙΑΣ ΠΟΥ ΣΥΝ ΕΟΝΤΑΙ ΜΕ ΤΗΝ ΕΡΓΑΣΙΑ Σκοπός της έρευνας ήταν η συλλογή
2.3. Ασκήσεις σχ. βιβλίου σελίδας 100 104 Α ΟΜΑ ΑΣ
 .3 Ασκήσεις σχ. βιβλίου σελίδας 00 04 Α ΟΜΑ ΑΣ. Έξι διαδοχικοί άρτιοι αριθµοί έχουν µέση τιµή. Να βρείτε τους αριθµούς και τη διάµεσό τους. Αν είναι ο ποιο µικρός άρτιος τότε οι ζητούµενοι αριθµοί θα είναι
.3 Ασκήσεις σχ. βιβλίου σελίδας 00 04 Α ΟΜΑ ΑΣ. Έξι διαδοχικοί άρτιοι αριθµοί έχουν µέση τιµή. Να βρείτε τους αριθµούς και τη διάµεσό τους. Αν είναι ο ποιο µικρός άρτιος τότε οι ζητούµενοι αριθµοί θα είναι
στον πρωτογενή, δευτερογενή και τριτογενή τοµέα.
 ΡΑΣΗ: 1 ΟΡΓΑΝΩΣΗ ΤΗΣ ΕΡΓΑΣΙΑΣ ΚΑΙ ΙΑΧΕΙΡΙΣΗΣ ΤΗΣ ΕΝΕΡΓΟΥ ΓΗΡΑΝΣΗΣ ΑΠΟ ΤΙΣ ΕΠΙΧΕΙΡΗΣΕΙΣ ΣΤΟΝ ΠΡΩΤΟΓΕΝΗ, ΕΥΤΕΡΟΓΕΝΗ ΚΑΙ ΤΡΙΤΟΓΕΝΗ ΤΟΜΕΑ ράση 1: Μελέτη ανάλυσης της υφιστάµενης κατάστασης στον τοµέα της διαχείρισης
ΡΑΣΗ: 1 ΟΡΓΑΝΩΣΗ ΤΗΣ ΕΡΓΑΣΙΑΣ ΚΑΙ ΙΑΧΕΙΡΙΣΗΣ ΤΗΣ ΕΝΕΡΓΟΥ ΓΗΡΑΝΣΗΣ ΑΠΟ ΤΙΣ ΕΠΙΧΕΙΡΗΣΕΙΣ ΣΤΟΝ ΠΡΩΤΟΓΕΝΗ, ΕΥΤΕΡΟΓΕΝΗ ΚΑΙ ΤΡΙΤΟΓΕΝΗ ΤΟΜΕΑ ράση 1: Μελέτη ανάλυσης της υφιστάµενης κατάστασης στον τοµέα της διαχείρισης
ΚΕΦΑΛΑΙΟ 8 ΤΟ ΜΑΘΗΜΑ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 ΚΕΦΑΛΑΙΟ 8 ΤΟ ΜΑΘΗΜΑ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Εισαγωγή Στο Κεφάλαιο 8 υπολογίζονται και συγκρίνονται τα ποσοστά επιλογής του µαθήµατος στους ετήσιους πληθυσµούς, ανά φύλο και κατεύθυνση. Υπολογίζεται
ΚΕΦΑΛΑΙΟ 8 ΤΟ ΜΑΘΗΜΑ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Εισαγωγή Στο Κεφάλαιο 8 υπολογίζονται και συγκρίνονται τα ποσοστά επιλογής του µαθήµατος στους ετήσιους πληθυσµούς, ανά φύλο και κατεύθυνση. Υπολογίζεται
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΙΑ ΓΕΝΙΚΗΣ ΙΣΟΡΡΟΠΙΑΣ ΧΡΗΣΕΩΝ ΓΗΣ
 ΚΕΦΑΛΑΙΟ 8 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΙΑ ΓΕΝΙΚΗΣ ΙΣΟΡΡΟΠΙΑΣ ΧΡΗΣΕΩΝ ΓΗΣ Όταν εξετάζουµε µία συγκεκριµένη αγορά, πχ. την αστική αγορά εργασίας, η ανάλυση αυτή ονοµάζεται µερικής ισορροπίας. Όταν η ανάλυση µας περιλαµβάνει
ΚΕΦΑΛΑΙΟ 8 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΙΑ ΓΕΝΙΚΗΣ ΙΣΟΡΡΟΠΙΑΣ ΧΡΗΣΕΩΝ ΓΗΣ Όταν εξετάζουµε µία συγκεκριµένη αγορά, πχ. την αστική αγορά εργασίας, η ανάλυση αυτή ονοµάζεται µερικής ισορροπίας. Όταν η ανάλυση µας περιλαµβάνει
2. Το δημογραφικό πλαίσιο και η σημασία του για τη σύνθεση των νοικοκυριών και της οικογένειας
 2. Το δημογραφικό πλαίσιο και η σημασία του για τη σύνθεση των νοικοκυριών και της οικογένειας 2.1 Πτυχές των δημογραφικών εξελίξεων στη μεταπολεμική Ελλάδα με έμφαση στη γονιμότητα και τη θνησιμότητα
2. Το δημογραφικό πλαίσιο και η σημασία του για τη σύνθεση των νοικοκυριών και της οικογένειας 2.1 Πτυχές των δημογραφικών εξελίξεων στη μεταπολεμική Ελλάδα με έμφαση στη γονιμότητα και τη θνησιμότητα
κα π μ υλώ ν θνησιμότητας κα π μ ύλε ς θνησιμότητας
 ΔΗΜΟΓΡΑΦΙΑ Ως παλαιοδηµογραφία ορίζεται η µελέτη της δοµής και της δυναµικής πληθυσµών που έζησαν στο παρελθόν. Όπως και στη σύγχρονη δηµογραφία ο ερευνητής µελετά του ρυθµούς θανάτου, τις διάρκειες ζωής,
ΔΗΜΟΓΡΑΦΙΑ Ως παλαιοδηµογραφία ορίζεται η µελέτη της δοµής και της δυναµικής πληθυσµών που έζησαν στο παρελθόν. Όπως και στη σύγχρονη δηµογραφία ο ερευνητής µελετά του ρυθµούς θανάτου, τις διάρκειες ζωής,
ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ 5.1 5.8
 ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ 5. 5.8 5. Ένας υγειονοµικός σταθµός θέλει να ελέγξει αν ο µέσος αριθµός βακτηριδίων ανά µονάδα όγκου θαλασσινού νερού σε µια παραλία υπερβαίνει το επίπεδο ασφαλείας των 9 µονάδων. ώδεκα
ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ 5. 5.8 5. Ένας υγειονοµικός σταθµός θέλει να ελέγξει αν ο µέσος αριθµός βακτηριδίων ανά µονάδα όγκου θαλασσινού νερού σε µια παραλία υπερβαίνει το επίπεδο ασφαλείας των 9 µονάδων. ώδεκα
Η δημογραφική διάσταση της ενεργούς γήρανσης. Χρήστος Μπάγκαβος, Πάντειο Πανεπιστήμιο
 Η δημογραφική διάσταση της ενεργούς γήρανσης Χρήστος Μπάγκαβος, Πάντειο Πανεπιστήμιο Δύο μέρη 1. Δημογραφικές μεταβολές και πληθυσμός σε ηλικία εργασίας στην Ελλάδα (1970-2013), με έμφαση στα άτομα ηλικίας
Η δημογραφική διάσταση της ενεργούς γήρανσης Χρήστος Μπάγκαβος, Πάντειο Πανεπιστήμιο Δύο μέρη 1. Δημογραφικές μεταβολές και πληθυσμός σε ηλικία εργασίας στην Ελλάδα (1970-2013), με έμφαση στα άτομα ηλικίας
ΔΕΛΤΙΟ ΤΥΠΟΥ ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ: 2018
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 1 Οκτωβρίου 2019 ΔΕΛΤΙΟ ΤΥΠΟΥ ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ: 2018 Η Ελληνική Στατιστική Αρχή ανακοινώνει τα στατιστικά στοιχεία που αποτυπώνουν την εξέλιξη
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 1 Οκτωβρίου 2019 ΔΕΛΤΙΟ ΤΥΠΟΥ ΦΥΣΙΚΗ ΚΙΝΗΣΗ ΠΛΗΘΥΣΜΟΥ: 2018 Η Ελληνική Στατιστική Αρχή ανακοινώνει τα στατιστικά στοιχεία που αποτυπώνουν την εξέλιξη
ΣΕΙΡΕΣ TAYLOR. Στην Ενότητα αυτή θα ασχοληθούµε µε την προσέγγιση συναρτήσεων µέσω πολυωνύµων. Πολυώνυµο είναι κάθε συνάρτηση της µορφής:
 ΣΕΙΡΕΣ TAYLOR Στην Ενότητα αυτή θα ασχοληθούµε µε την προσέγγιση συναρτήσεων µέσω πολυωνύµων Πολυώνυµο είναι κάθε συνάρτηση της µορφής: p( ) = a + a + a + a + + a, όπου οι συντελεστές α i θα θεωρούνται
ΣΕΙΡΕΣ TAYLOR Στην Ενότητα αυτή θα ασχοληθούµε µε την προσέγγιση συναρτήσεων µέσω πολυωνύµων Πολυώνυµο είναι κάθε συνάρτηση της µορφής: p( ) = a + a + a + a + + a, όπου οι συντελεστές α i θα θεωρούνται
Σχήμα 20: Τύποι πληθυσμιακών πυραμίδων
 IV.3. Οι πληθυσμιακές πυραμίδες Στην ανάλυση των πληθυσμιακών δομών κεντρικό ρόλο έχουν οι πληθυσμιακές πυραμίδες και οι αποκαλούμενοι δομικοί δείκτες. Η κατανομή του συνόλου των ατόμων ενός πληθυσμού
IV.3. Οι πληθυσμιακές πυραμίδες Στην ανάλυση των πληθυσμιακών δομών κεντρικό ρόλο έχουν οι πληθυσμιακές πυραμίδες και οι αποκαλούμενοι δομικοί δείκτες. Η κατανομή του συνόλου των ατόμων ενός πληθυσμού
ΚΑΠΝΙΣΜΑ: Ιανουάριος ο Ενημερωτικό Σημείωμα
 Ιανουάριος 2018 14 ο Ενημερωτικό Σημείωμα Το 14 ο ενημερωτικό σημείωμα του Παρατηρητηρίου της Γενικής Γραμματείας Ισότητας των Φύλων (Γ.Γ.Ι.Φ.) εντάσσεται στο θεματικό πεδίο Γυναίκες και Υγεία. Συγκεκριμένα,
Ιανουάριος 2018 14 ο Ενημερωτικό Σημείωμα Το 14 ο ενημερωτικό σημείωμα του Παρατηρητηρίου της Γενικής Γραμματείας Ισότητας των Φύλων (Γ.Γ.Ι.Φ.) εντάσσεται στο θεματικό πεδίο Γυναίκες και Υγεία. Συγκεκριμένα,
2.6 ΟΡΙΑ ΑΝΟΧΗΣ. πληθυσµού µε πιθανότητα τουλάχιστον ίση µε 100(1 α)%. Το. X ονοµάζεται κάτω όριο ανοχής ενώ το πάνω όριο ανοχής.
 2.6 ΟΡΙΑ ΑΝΟΧΗΣ Το διάστηµα εµπιστοσύνης παρέχει µία εκτίµηση µιας άγνωστης παραµέτρου µε την µορφή διαστήµατος και ένα συγκεκριµένο βαθµό εµπιστοσύνης ότι το διάστηµα αυτό, µε τον τρόπο που κατασκευάσθηκε,
2.6 ΟΡΙΑ ΑΝΟΧΗΣ Το διάστηµα εµπιστοσύνης παρέχει µία εκτίµηση µιας άγνωστης παραµέτρου µε την µορφή διαστήµατος και ένα συγκεκριµένο βαθµό εµπιστοσύνης ότι το διάστηµα αυτό, µε τον τρόπο που κατασκευάσθηκε,
Ας θεωρήσουµε µια οµάδα αποτελούµενη από έναν αριθµό
 ΚΕΦΑΛΑΙΟ 3 ΠΙΝΑΚΕΣ ΕΠΙΒΙΩΣΗΣ (LIFE TABLES) Τα µέτρα θνησιµότητας που παρουσιάστηκαν στο προηγούµενο κεφάλαιο ικανοποιούν πολλές ανάγκες του ερευνητή στην προσπάθεια του να περιγράψει τη θνησιµότητα ενός
ΚΕΦΑΛΑΙΟ 3 ΠΙΝΑΚΕΣ ΕΠΙΒΙΩΣΗΣ (LIFE TABLES) Τα µέτρα θνησιµότητας που παρουσιάστηκαν στο προηγούµενο κεφάλαιο ικανοποιούν πολλές ανάγκες του ερευνητή στην προσπάθεια του να περιγράψει τη θνησιµότητα ενός
Συστημική προσέγγιση που εφαρμόζεται από τον Παγκόσμιο Οργανισμό Υγείας για τη βελτίωση της Υγείας Μητέρας-Παιδιού: Εφαρμογή στη χώρα Χ
 Συστημική προσέγγιση που εφαρμόζεται από τον Παγκόσμιο Οργανισμό Υγείας για τη βελτίωση της Υγείας Μητέρας-Παιδιού: Εφαρμογή στη χώρα Χ Έτος Δείκτες θνησιμότητας Δείκτες Αναπαραγωγικότητας Δείκτες Βρεφικής
Συστημική προσέγγιση που εφαρμόζεται από τον Παγκόσμιο Οργανισμό Υγείας για τη βελτίωση της Υγείας Μητέρας-Παιδιού: Εφαρμογή στη χώρα Χ Έτος Δείκτες θνησιμότητας Δείκτες Αναπαραγωγικότητας Δείκτες Βρεφικής
ΑΡΓΥΡΩ Ι. ΧΡΥΣΑΓΗ ΒΙΟΛΟΓΟΣ MSc Υποψήφια Διδάκτωρ Ιατρικής Σχολής Πανεπιστημίου Αθηνών Εργαστήριο Μοριακής Διάγνωσης ΙΑΣΩ
 ΑΡΓΥΡΩ Ι. ΧΡΥΣΑΓΗ ΒΙΟΛΟΓΟΣ MSc Υποψήφια Διδάκτωρ Ιατρικής Σχολής Πανεπιστημίου Αθηνών Εργαστήριο Μοριακής Διάγνωσης ΙΑΣΩ Κάποιοι ορισμοί.. Δημογραφία: επιστημονικός κλάδος που έχει ως αντικείμενο τη στατιστική
ΑΡΓΥΡΩ Ι. ΧΡΥΣΑΓΗ ΒΙΟΛΟΓΟΣ MSc Υποψήφια Διδάκτωρ Ιατρικής Σχολής Πανεπιστημίου Αθηνών Εργαστήριο Μοριακής Διάγνωσης ΙΑΣΩ Κάποιοι ορισμοί.. Δημογραφία: επιστημονικός κλάδος που έχει ως αντικείμενο τη στατιστική
Euro-SDMX δομή μεταδεδομένων (ESMS) Ονομασία: ΕΡΕΥΝΑ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ
 Χώρα: Ελλάδα Euro-SDMX δομή μεταδεδομένων (ESMS) Ονομασία: ΕΡΕΥΝΑ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΕΛΣΤΑΤ μεταδεδομένα Περιεχόμενα 1. Επικοινωνία 2. Ενημέρωση μεταδεδομένων 3. Στατιστική παρουσίαση 4. Μονάδα
Χώρα: Ελλάδα Euro-SDMX δομή μεταδεδομένων (ESMS) Ονομασία: ΕΡΕΥΝΑ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΕΛΣΤΑΤ μεταδεδομένα Περιεχόμενα 1. Επικοινωνία 2. Ενημέρωση μεταδεδομένων 3. Στατιστική παρουσίαση 4. Μονάδα
Βασικές έννοιες περιγραφικής επιδημιολογίας. Ιωάννα Τζουλάκη, Λέκτορας επιδημιολογίας
 Βασικές έννοιες περιγραφικής επιδημιολογίας Ιωάννα Τζουλάκη, Λέκτορας επιδημιολογίας Επιδημιολογία } Μελετά τη συχνότητα και των νόσων στους ανθρώπινους πληθυσμούς } Βασίζεται σε 2 υποθέσεις } Τα νοσήματα
Βασικές έννοιες περιγραφικής επιδημιολογίας Ιωάννα Τζουλάκη, Λέκτορας επιδημιολογίας Επιδημιολογία } Μελετά τη συχνότητα και των νόσων στους ανθρώπινους πληθυσμούς } Βασίζεται σε 2 υποθέσεις } Τα νοσήματα
ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ
 Χώρα: Ελλάδα Euro-SDMX δομή μεταδεδομένων (ESMS) Ονομασία: ΕΡΕΥΝΑ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΕΛΣΤΑΤ μεταδεδομένα Περιεχόμενα 1. Επικοινωνία 2. Ενημέρωση μεταδεδομένων 3. Στατιστική παρουσίαση 4. Μονάδα
Χώρα: Ελλάδα Euro-SDMX δομή μεταδεδομένων (ESMS) Ονομασία: ΕΡΕΥΝΑ ΦΥΣΙΚΗΣ ΚΙΝΗΣΗΣ ΠΛΗΘΥΣΜΟΥ ΕΛΣΤΑΤ μεταδεδομένα Περιεχόμενα 1. Επικοινωνία 2. Ενημέρωση μεταδεδομένων 3. Στατιστική παρουσίαση 4. Μονάδα
Marriages and births in Cyprus/el
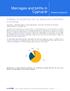 Marriages and births in Cyprus/el Statistics Explained Αναβολή της μητρότητας και της δημιουργίας οικογένειας στην Κύπρο Συγγραφέας : Στατιστική Υπηρεσία - Τομέας Δημογραφίας, Κοινωνικών Στατιστικών και
Marriages and births in Cyprus/el Statistics Explained Αναβολή της μητρότητας και της δημιουργίας οικογένειας στην Κύπρο Συγγραφέας : Στατιστική Υπηρεσία - Τομέας Δημογραφίας, Κοινωνικών Στατιστικών και
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β )
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΚΥΡΙΑΚΗ /0/0 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:ΕΝΝΕΑ (9) ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΜΑ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΚΥΡΙΑΚΗ /0/0 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:ΕΝΝΕΑ (9) ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΜΑ
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2015 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 05 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο R, να αποδείξετε ότι: f + g ' = f ' + g ', R Μονάδες 7 Α. Πότε λέµε ότι µια συνάρτηση
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 05 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο R, να αποδείξετε ότι: f + g ' = f ' + g ', R Μονάδες 7 Α. Πότε λέµε ότι µια συνάρτηση
ΣΤΑΤΙΣΤΙΚΗ ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ
 ΣΤΑΤΙΣΤΙΚΗ ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ Στα πλαίσια της ΣΤΑΤΙΣΤΙΚΗΣ ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑΣ προσπαθούµε να προσεγγίσουµε τα χαρακτηριστικά ενός συνόλου (πληθυσµός) δια της µελέτης των χαρακτηριστικών αυτών επί ενός µικρού
ΣΤΑΤΙΣΤΙΚΗ ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑ Στα πλαίσια της ΣΤΑΤΙΣΤΙΚΗΣ ΣΥΜΠΕΡΑΣΜΑΤΟΛΟΓΙΑΣ προσπαθούµε να προσεγγίσουµε τα χαρακτηριστικά ενός συνόλου (πληθυσµός) δια της µελέτης των χαρακτηριστικών αυτών επί ενός µικρού
ΚΑΤΑΣΤΑΣΗ ΥΓΕΙΑΣ ΚΑΙ ΠΡΟΣΔΟΚΩΜΕΝΗ ΖΩΗ ΧΩΡΙΣ ΠΡΟΒΛΗΜΑΤΑ ΥΓΕΙΑΣ
 ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΕΘΝΙΚΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΤΗΣ ΕΛΛΑΔOΣ Πειραιάς 22.5.2007 Δ Ε Λ Τ Ι Ο Τ Υ Π Ο Υ ΕΡΕΥΝΑ ΕΙΣΟΔΗΜΑΤΟΣ ΚΑΙ ΣΥΝΘΗΚΩΝ ΔΙΑΒΙΩΣΗΣ ΤΩΝ ΝΟΙΚΟΚΥΡΙΩΝ, ΕΤΟΥΣ 2004 ΚΑΤΑΣΤΑΣΗ ΥΓΕΙΑΣ ΚΑΙ ΠΡΟΣΔΟΚΩΜΕΝΗ
ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΕΘΝΙΚΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΤΗΣ ΕΛΛΑΔOΣ Πειραιάς 22.5.2007 Δ Ε Λ Τ Ι Ο Τ Υ Π Ο Υ ΕΡΕΥΝΑ ΕΙΣΟΔΗΜΑΤΟΣ ΚΑΙ ΣΥΝΘΗΚΩΝ ΔΙΑΒΙΩΣΗΣ ΤΩΝ ΝΟΙΚΟΚΥΡΙΩΝ, ΕΤΟΥΣ 2004 ΚΑΤΑΣΤΑΣΗ ΥΓΕΙΑΣ ΚΑΙ ΠΡΟΣΔΟΚΩΜΕΝΗ
ΕΛΤΙΟ ΤΥΠΟΥ. ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Μάρτιος 2014 ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ. Πειραιάς, 5 Ιουνίου 2014
 ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ ΕΛΤΙΟ ΤΥΠΟΥ Πειραιάς, 5 Ιουνίου 20 ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Μάρτιος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη ανεργίας για τον Μάρτιο
ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ ΕΛΤΙΟ ΤΥΠΟΥ Πειραιάς, 5 Ιουνίου 20 ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Μάρτιος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη ανεργίας για τον Μάρτιο
Γενικές ασκήσεις 2 ου κεφαλαίου (σελ )
 1 Γενικές ασκήσεις ου κεφαλαίου (σελ. 16 13) 1. Ο αριθµός των παιδιών σε ένα δείγµα 8 οικογενειών µιας πόλης δίνονται στον πίνακα. Αριθµός παιδιών 1 3 4 5 6 Οικογένειες 1 5 1 6 5 α) Να βρείτε τη µέση τιµή,την
1 Γενικές ασκήσεις ου κεφαλαίου (σελ. 16 13) 1. Ο αριθµός των παιδιών σε ένα δείγµα 8 οικογενειών µιας πόλης δίνονται στον πίνακα. Αριθµός παιδιών 1 3 4 5 6 Οικογένειες 1 5 1 6 5 α) Να βρείτε τη µέση τιµή,την
Αναλογία (Proportion)
 Μέτρα Νοσηρότητας Αναλογία (Proportion) Κλάσµα Αριθµητής ΣΥΜΠΕΡΙΛΑΜΒΑΝΕΤΑΙ ΑΠΑΡΑΙΤΗΤΩΣ στον παρανοµαστή Ποσότητες της ίδιας φύσης Κυµαίνεται πάντα µεταξύ 0 και 1 Ποσοστό = αναλογία x 100 κυµαίνεται: 0-100
Μέτρα Νοσηρότητας Αναλογία (Proportion) Κλάσµα Αριθµητής ΣΥΜΠΕΡΙΛΑΜΒΑΝΕΤΑΙ ΑΠΑΡΑΙΤΗΤΩΣ στον παρανοµαστή Ποσότητες της ίδιας φύσης Κυµαίνεται πάντα µεταξύ 0 και 1 Ποσοστό = αναλογία x 100 κυµαίνεται: 0-100
Γεννητικότητα-γονιμότητα
 Γεννητικότητα-γονιμότητα Α. Ορισμοί Γεννητικότητα: Ο όρος παραπέμπει συνήθως στη συχνότητα των γεννήσεων σε έναν πληθυσμό, δηλαδή στο αδρό ποσοστό της γεννητικότητας. Γονιμότητα: Ο όρος έχει διπλή έννοια:
Γεννητικότητα-γονιμότητα Α. Ορισμοί Γεννητικότητα: Ο όρος παραπέμπει συνήθως στη συχνότητα των γεννήσεων σε έναν πληθυσμό, δηλαδή στο αδρό ποσοστό της γεννητικότητας. Γονιμότητα: Ο όρος έχει διπλή έννοια:
Παραρτήματα Έκθεση Β. Εργαστήριο Δημογραφικών και Κοινωνικών Αναλύσεων (ΕΔΚΑ), Πανεπιστήμιο Θεσσαλίας Σεπτέμβριος 2016
 09.2016 1 Παραρτήματα Έκθεση Β Εργαστήριο Δημογραφικών και Κοινωνικών Αναλύσεων (ΕΔΚΑ), Πανεπιστήμιο Θεσσαλίας Σεπτέμβριος 2016 2 Περιεχόμενα ΠΑΡΑΡΤΗΜΑΤΑ 1. Μεθοδολογία ανάπτυξης προβλεπόμενων πινάκων
09.2016 1 Παραρτήματα Έκθεση Β Εργαστήριο Δημογραφικών και Κοινωνικών Αναλύσεων (ΕΔΚΑ), Πανεπιστήμιο Θεσσαλίας Σεπτέμβριος 2016 2 Περιεχόμενα ΠΑΡΑΡΤΗΜΑΤΑ 1. Μεθοδολογία ανάπτυξης προβλεπόμενων πινάκων
ΕΡΕΥΝΑ ΕΙΣΟΔΗΜΑΤΟΣ ΚΑΙ ΣΥΝΘΗΚΩΝ ΔΙΑΒΙΩΣΗΣ ΤΩΝ ΝΟΙΚΟΚΥΡΙΩΝ 2009
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 9/ 12/2010 Δ Ε Λ Τ Ι Ο Τ Υ Π Ο Υ ΕΡΕΥΝΑ ΕΙΣΟΔΗΜΑΤΟΣ ΚΑΙ ΣΥΝΘΗΚΩΝ ΔΙΑΒΙΩΣΗΣ ΤΩΝ ΝΟΙΚΟΚΥΡΙΩΝ 2009 Οικονομική ανισότητα Από την Ελληνική Στατιστική Αρχή
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 9/ 12/2010 Δ Ε Λ Τ Ι Ο Τ Υ Π Ο Υ ΕΡΕΥΝΑ ΕΙΣΟΔΗΜΑΤΟΣ ΚΑΙ ΣΥΝΘΗΚΩΝ ΔΙΑΒΙΩΣΗΣ ΤΩΝ ΝΟΙΚΟΚΥΡΙΩΝ 2009 Οικονομική ανισότητα Από την Ελληνική Στατιστική Αρχή
Τριµηνιαία ενηµέρωση για την απασχόληση και την οικονοµία Βασικά µεγέθη & συγκριτικοί δείκτες
 ΚΟΙΝΩΝΙΚΟ ΠΟΛΥΚΕΝΤΡΟ ιοσκούρων 4 & Πολυγνώτου ΑΘΗΝΑ 105 55 Τηλ. 2103310080, Fax: 2103310083 E-mail: info@kpolykentro.gr Τριµηνιαία ενηµέρωση για την απασχόληση και την οικονοµία Βασικά µεγέθη & συγκριτικοί
ΚΟΙΝΩΝΙΚΟ ΠΟΛΥΚΕΝΤΡΟ ιοσκούρων 4 & Πολυγνώτου ΑΘΗΝΑ 105 55 Τηλ. 2103310080, Fax: 2103310083 E-mail: info@kpolykentro.gr Τριµηνιαία ενηµέρωση για την απασχόληση και την οικονοµία Βασικά µεγέθη & συγκριτικοί
(f(x)+g(x)) =f (x)+g (x), x R
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑ ΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 0 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α. Αν οι συναρτήσεις, g είναι παραγωγίσιµες στο IR, να αποδείξετε ότι (()+g()) ()+g (), R Μονάδες 7 Α.
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑ ΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 0 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α. Αν οι συναρτήσεις, g είναι παραγωγίσιµες στο IR, να αποδείξετε ότι (()+g()) ()+g (), R Μονάδες 7 Α.
ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 7 Ιανουαρίου 2016 ΕΛΤΙΟ ΤΥΠΟΥ
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 7 Ιανουαρίου 2016 ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Οκτώβριος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 7 Ιανουαρίου 2016 ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Οκτώβριος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη
Ελλιπή δεδομένα. Εδώ έχουμε 1275. Στον πίνακα που ακολουθεί δίνεται η κατά ηλικία κατανομή 1275 ατόμων
 Ελλιπή δεδομένα Στον πίνακα που ακολουθεί δίνεται η κατά ηλικία κατανομή 75 ατόμων Εδώ έχουμε δ 75,0 75 5 Ηλικία Συχνότητες f 5-4 70 5-34 50 35-44 30 45-54 465 55-64 335 Δεν δήλωσαν 5 Σύνολο 75 Μπορεί
Ελλιπή δεδομένα Στον πίνακα που ακολουθεί δίνεται η κατά ηλικία κατανομή 75 ατόμων Εδώ έχουμε δ 75,0 75 5 Ηλικία Συχνότητες f 5-4 70 5-34 50 35-44 30 45-54 465 55-64 335 Δεν δήλωσαν 5 Σύνολο 75 Μπορεί
Εργαστήριο Δημογραφικών & Κοινωνικών Αναλύσεων
 Θνησιμότητα-πίνακες επιβίωσης-life Tables (ή πίνακες θνησιμότητας) A) Παρουσίαση των πινάκων επιβίωσης (Β. ΚΟΤΖΑΜΑΝΗΣ) Στο σημείο αυτό θα σταθούμε στη μελέτη της θνησιμότητας μέσω της παρουσίασης του ιδιότυπου
Θνησιμότητα-πίνακες επιβίωσης-life Tables (ή πίνακες θνησιμότητας) A) Παρουσίαση των πινάκων επιβίωσης (Β. ΚΟΤΖΑΜΑΝΗΣ) Στο σημείο αυτό θα σταθούμε στη μελέτη της θνησιμότητας μέσω της παρουσίασης του ιδιότυπου
ερµηνεύσετε τα αποτελέσµατα του ερωτήµατος (α).
 Ερωτήσεις ανάπτυξης. ** Για να υπολογίσει κάποιος την (0 ) χρησιµοποιεί για + προσέγγιση τον αριθµό +, ενώ ένας άλλος τον αριθµό. 3 α) Να εκτιµήσετε ποια από τις δύο προσεγγίσεις δίνει το ελάχιστο (απόλυτο)
Ερωτήσεις ανάπτυξης. ** Για να υπολογίσει κάποιος την (0 ) χρησιµοποιεί για + προσέγγιση τον αριθµό +, ενώ ένας άλλος τον αριθµό. 3 α) Να εκτιµήσετε ποια από τις δύο προσεγγίσεις δίνει το ελάχιστο (απόλυτο)
ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Αύγουστος 2015
 ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Αύγουστος 20 Πειραιάς, 12 Νοεµβρίου 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη ανεργίας για τον
ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Αύγουστος 20 Πειραιάς, 12 Νοεµβρίου 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη ανεργίας για τον
ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ τρίµηνο 2004
 ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΓΓ ΕΘΝΙΚΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΤΗΣ ΕΛΛΑ ΟΣ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ τρίµηνο 2004 Πειραιάς, 12 Απριλίου 2005 Η Γενική Γραµµατεία της Εθνικής Στατιστικής Υπηρεσίας
ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΓΓ ΕΘΝΙΚΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΤΗΣ ΕΛΛΑ ΟΣ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ τρίµηνο 2004 Πειραιάς, 12 Απριλίου 2005 Η Γενική Γραµµατεία της Εθνικής Στατιστικής Υπηρεσίας
Χαιρετισμός του Προέδρου Αντιναρκωτικού Συμβουλίου Κύπρου Δρα. Χρύσανθου Γεωργίου, στη διάσκεψη τύπου
 Χαιρετισμός του Προέδρου Αντιναρκωτικού Συμβουλίου Κύπρου Δρα. Χρύσανθου Γεωργίου, στη διάσκεψη τύπου της «4 ης Εβδομάδας Ευαισθητοποίησης για το Αλκοόλ Τετάρτη, 26 Οκτωβρίου 2016, 11.00 12.30 Έντιμοι
Χαιρετισμός του Προέδρου Αντιναρκωτικού Συμβουλίου Κύπρου Δρα. Χρύσανθου Γεωργίου, στη διάσκεψη τύπου της «4 ης Εβδομάδας Ευαισθητοποίησης για το Αλκοόλ Τετάρτη, 26 Οκτωβρίου 2016, 11.00 12.30 Έντιμοι
ΑΝΑ ΚΕΦΑΛΑΙΟ. geeconomy@yahoo.com. Γ Ι Ω Ρ Γ Ο Σ Κ Α Μ Α Ρ Ι Ν Ο Σ Ο Ι Κ Ο Ν Ο Μ Ο Λ Ο Γ Ο Σ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 1 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 ΑΝΑ ΚΕΦΑΛΑΙΟ Στο παρόν είναι συγκεντρωµένες όλες σχεδόν οι ερωτήσεις κλειστού τύπου που
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 1 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 ΑΝΑ ΚΕΦΑΛΑΙΟ Στο παρόν είναι συγκεντρωµένες όλες σχεδόν οι ερωτήσεις κλειστού τύπου που
ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ
 ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, Σεπτεμβρίου 20 ΔΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΔΥΝΑΜΙΚΟΥ: 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρμοσμένο δείκτη ανεργίας για τον Ιούνιο 20.
ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, Σεπτεμβρίου 20 ΔΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΔΥΝΑΜΙΚΟΥ: 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρμοσμένο δείκτη ανεργίας για τον Ιούνιο 20.
ΕΛΤΙΟ ΤΥΠΟΥ. Οι άνεργοι µειώθηκαν κατά άτοµα σε σχέση µε το Απρίλιο του 2014 (µείωση
 ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ ΕΛΤΙΟ ΤΥΠΟΥ Πειραιάς, 9 Ιουλίου 20 ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Απρίλιος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη ανεργίας για τον Απρίλιο
ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ ΕΛΤΙΟ ΤΥΠΟΥ Πειραιάς, 9 Ιουλίου 20 ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Απρίλιος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη ανεργίας για τον Απρίλιο
ηµογραφικά και κοινωνικά χαρακτηριστικά της αγοράς εργασίας στις περιφέρειες της Ελλάδας
 ηµογραφικά και κοινωνικά χαρακτηριστικά της αγοράς εργασίας στις περιφέρειες της Ελλάδας Γιάννα Φαρσάρη, Περιβαλλοντολόγος, Ινστιτούτο Υπολογιστικών Μαθηµατικών, Ίδρυµα Τεχ νολογίας και Έρευνας Κρήτης
ηµογραφικά και κοινωνικά χαρακτηριστικά της αγοράς εργασίας στις περιφέρειες της Ελλάδας Γιάννα Φαρσάρη, Περιβαλλοντολόγος, Ινστιτούτο Υπολογιστικών Μαθηµατικών, Ίδρυµα Τεχ νολογίας και Έρευνας Κρήτης
ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 12 Μαΐου 2016 ΕΛΤΙΟ ΤΥΠΟΥ
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 12 Μαΐου 20 ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Φεβρουάριος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 12 Μαΐου 20 ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Φεβρουάριος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη
ΠΑΡΟΥΣΙΑΣΗ ΚΑΙ ΚΡΙΤΙΚΗ ΒΙΒΑΙΟΥ από τον Σάββα Γ. Ρομπόλη
 Επιθεώρηση Κοινωνικών Ερευνών. 114. 2004. 205-211 ΠΑΡΟΥΣΙΑΣΗ ΚΑΙ ΚΡΙΤΙΚΗ ΒΙΒΑΙΟΥ από τον Σάββα Γ. Ρομπόλη Χρήστος Μπάγκαβος, 2003, Δημογραφικές μεταβολές, αγορά εργασίας και συντάξεις στην Ελλάδα και την
Επιθεώρηση Κοινωνικών Ερευνών. 114. 2004. 205-211 ΠΑΡΟΥΣΙΑΣΗ ΚΑΙ ΚΡΙΤΙΚΗ ΒΙΒΑΙΟΥ από τον Σάββα Γ. Ρομπόλη Χρήστος Μπάγκαβος, 2003, Δημογραφικές μεταβολές, αγορά εργασίας και συντάξεις στην Ελλάδα και την
ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 10 Ιουλίου 2014 ΕΛΤΙΟ ΤΥΠΟΥ
 ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 10 Ιουλίου 20 ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Απρίλιος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη ανεργίας για τον Απρίλιο
ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 10 Ιουλίου 20 ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Απρίλιος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη ανεργίας για τον Απρίλιο
ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 8 Σεπτεµβρίου 2016 ΕΛΤΙΟ ΤΥΠΟΥ
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 8 Σεπτεµβρίου 20 ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Ιούνιος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 8 Σεπτεµβρίου 20 ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ: Ιούνιος 20 Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρµοσµένο δείκτη
Επαγγελματική Επιδημιολογία
 Επαγγελματική Επιδημιολογία Η επιδημιολογία είναι η επιστήμη, που μελετά τη συχνότητα των νοσημάτων σε ανθρώπινους πληθυσμούς και διερευνά τους αιτιολογικούς παράγοντες και τους παράγοντες πρόγνωσης. Η
Επαγγελματική Επιδημιολογία Η επιδημιολογία είναι η επιστήμη, που μελετά τη συχνότητα των νοσημάτων σε ανθρώπινους πληθυσμούς και διερευνά τους αιτιολογικούς παράγοντες και τους παράγοντες πρόγνωσης. Η
Ηλικιακή σύνθεση πληθυσµού
 Ηλικιακή σύνθεση πληθυσµού Ηλικιακή πληθυσµιακή δοµή Χρήση διαγραµµάτων ηλικιακής δοµής 3 ηλικιακές κατηγορίες προαναπαραγωγική (0-14 ετών) αναπαραγωγική (15-44 ετών) µετα-αναπαραγωγική (45-85+ ετών) 1
Ηλικιακή σύνθεση πληθυσµού Ηλικιακή πληθυσµιακή δοµή Χρήση διαγραµµάτων ηλικιακής δοµής 3 ηλικιακές κατηγορίες προαναπαραγωγική (0-14 ετών) αναπαραγωγική (15-44 ετών) µετα-αναπαραγωγική (45-85+ ετών) 1
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ
 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Σύμβολα και Συντμήσεις... 13 Εισαγωγή Β' ΑΝΑΛΥΣΗ ΤΩΝ ΣΤΟΙΧΕΙΩΝ... 18 2. Γεννήσεις ζώντων... 19 3. Γεννήσεις νεκρών... 21 5. Βρεφική θνησιμότητα... 24 6. Πίνακες επιβίωσης... 24 7.
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Σύμβολα και Συντμήσεις... 13 Εισαγωγή Β' ΑΝΑΛΥΣΗ ΤΩΝ ΣΤΟΙΧΕΙΩΝ... 18 2. Γεννήσεις ζώντων... 19 3. Γεννήσεις νεκρών... 21 5. Βρεφική θνησιμότητα... 24 6. Πίνακες επιβίωσης... 24 7.
Δημογραφία. Ενότητα 13: Ανάλυση Γαμηλιότητας. Βύρων Κοτζαμάνης Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας & Περιφερειακής Ανάπτυξης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Δημογραφία Ενότητα 13: Ανάλυση Γαμηλιότητας Βύρων Κοτζαμάνης Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας & Περιφερειακής Ανάπτυξης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Δημογραφία Ενότητα 13: Ανάλυση Γαμηλιότητας Βύρων Κοτζαμάνης Τμήμα Μηχανικών Χωροταξίας, Πολεοδομίας & Περιφερειακής Ανάπτυξης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΕΠΗΡΕΑΖΕΤΑΙ Η ΕΝΔΟΝΟΣΟΚΟΜΕΙΑΚΗ ΘΝΗΣΙΜΟΤΗΤΑ ΑΠΟ ΠΑΡΑΜΕΤΡΟΥΣ ΠΟΥ ΣΧΕΤΙΖΟΝΤΑΙ ΜΕ ΤΗΝ ΕΠΟΧΙΚΟΤΗΤΑ ΚΑΙ ΤΟ ΩΡΑΡΙΟ ΛΕΙΤΟΥΡΓΙΑΣ;
 ΕΠΗΡΕΑΖΕΤΑΙ Η ΕΝΔΟΝΟΣΟΚΟΜΕΙΑΚΗ ΘΝΗΣΙΜΟΤΗΤΑ ΑΠΟ ΠΑΡΑΜΕΤΡΟΥΣ ΠΟΥ ΣΧΕΤΙΖΟΝΤΑΙ ΜΕ ΤΗΝ ΕΠΟΧΙΚΟΤΗΤΑ ΚΑΙ ΤΟ ΩΡΑΡΙΟ ΛΕΙΤΟΥΡΓΙΑΣ; Χαρδαλιάς Λεωνίδας Συκά Άννα Φίλιππα Μαρία Σιαφαρίκας Χρήστος Μπασούλης Δημήτρης
ΕΠΗΡΕΑΖΕΤΑΙ Η ΕΝΔΟΝΟΣΟΚΟΜΕΙΑΚΗ ΘΝΗΣΙΜΟΤΗΤΑ ΑΠΟ ΠΑΡΑΜΕΤΡΟΥΣ ΠΟΥ ΣΧΕΤΙΖΟΝΤΑΙ ΜΕ ΤΗΝ ΕΠΟΧΙΚΟΤΗΤΑ ΚΑΙ ΤΟ ΩΡΑΡΙΟ ΛΕΙΤΟΥΡΓΙΑΣ; Χαρδαλιάς Λεωνίδας Συκά Άννα Φίλιππα Μαρία Σιαφαρίκας Χρήστος Μπασούλης Δημήτρης
Ανάλυση Δεδοµένων µε χρήση του Στατιστικού Πακέτου R
 Ανάλυση Δεδοµένων µε χρήση του Στατιστικού Πακέτου R, Επίκουρος Καθηγητής, Τοµέας Μαθηµατικών, Σχολή Εφαρµοσµένων Μαθηµατικών και Φυσικών Επιστηµών, Εθνικό Μετσόβιο Πολυτεχνείο. Περιεχόµενα Εισαγωγή στη
Ανάλυση Δεδοµένων µε χρήση του Στατιστικού Πακέτου R, Επίκουρος Καθηγητής, Τοµέας Μαθηµατικών, Σχολή Εφαρµοσµένων Μαθηµατικών και Φυσικών Επιστηµών, Εθνικό Μετσόβιο Πολυτεχνείο. Περιεχόµενα Εισαγωγή στη
Υ: Νόσος. Χ: Παράγοντας Κινδύνου 1 (Ασθενής) 2 (Υγιής) Σύνολο. 1 (Παρόν) n 11 n 12 n 1. 2 (Απών) n 21 n 22 n 2. Σύνολο n.1 n.2 n..
 Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
Μέτρα Κινδύνου για Δίτιμα Κατηγορικά Δεδομένα Σε αυτή την ενότητα θα ορίσουμε δείκτες μέτρησης του κινδύνου εμφάνισης μίας νόσου όταν έχουμε δίτιμες κατηγορικές μεταβλητές. Στην πιο απλή περίπτωση μας
ΑΝΑΛΥΣΗ ΤΩΝ ΜΕΤΑΒΟΛΩΝ ΣΤΟ ΠΡΟΣΔΟΚΙΜΟ ΕΠΙΒΙΩΣΗΣ ΣΤΗΝ ΕΛΛΑΔΑ ΚΑΙ ΠΑΡΑΓΟΝΤΕΣ ΠΟΥ ΤΙΣ ΕΠΗΡΕΑΖΟΥΝ: 1991-2001
 Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Π Ε Ι Ρ Α Ι Ω Σ ΤΜΗΜΑ Σ Τ Α Τ Ι Σ Τ Ι Κ Η Σ ΚΑΙ ΑΣΦΑΛΙΣΤΙΚΗΣ Ε Π Ι Σ Τ Η Μ Η Σ Μ Ε Τ Α Π Τ Υ Χ Ι Α Κ Ο ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ Ε Φ Α Ρ Μ Ο Σ Μ Ε Ν Η Σ Τ Α Τ Ι Σ Τ Ι Κ Η ΑΝΑΛΥΣΗ ΤΩΝ
Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Π Ε Ι Ρ Α Ι Ω Σ ΤΜΗΜΑ Σ Τ Α Τ Ι Σ Τ Ι Κ Η Σ ΚΑΙ ΑΣΦΑΛΙΣΤΙΚΗΣ Ε Π Ι Σ Τ Η Μ Η Σ Μ Ε Τ Α Π Τ Υ Χ Ι Α Κ Ο ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ Ε Φ Α Ρ Μ Ο Σ Μ Ε Ν Η Σ Τ Α Τ Ι Σ Τ Ι Κ Η ΑΝΑΛΥΣΗ ΤΩΝ
ΚΑΜΠΥΛΗ ENGEL ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΖΗΤΗΣΗΣ ΚΑΤΑ MARSHALL ΚΑΙ HICKS. 1. Η καµπύλη Engel
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ ΚΑΜΠΥΛΗ ENGEL ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΖΗΤΗΣΗΣ ΚΑΤΑ ARSALL ΚΑΙ ICKS. Η καµπύλη Egel Η καµπύλη Egel παράγεται από την
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ ΚΑΜΠΥΛΗ ENGEL ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΖΗΤΗΣΗΣ ΚΑΤΑ ARSALL ΚΑΙ ICKS. Η καµπύλη Egel Η καµπύλη Egel παράγεται από την
Ειδικά Θέματα Δημογραφίας: Χωρικές Διαστάσεις Δημογραφικών Δεδομένων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Ειδικά Θέματα Δημογραφίας: Χωρικές Διαστάσεις Δημογραφικών Δεδομένων Ενότητα 4.1: Οι αλλοδαποί στην Ελλάδα. Χωρική ανάλυση των δημογραφικών τους χαρακτηριστικών και της συμβολής
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Ειδικά Θέματα Δημογραφίας: Χωρικές Διαστάσεις Δημογραφικών Δεδομένων Ενότητα 4.1: Οι αλλοδαποί στην Ελλάδα. Χωρική ανάλυση των δημογραφικών τους χαρακτηριστικών και της συμβολής
ΔΕΛΤΙΟ ΤΥΠΟΥ. ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΔΥΝΑΜΙΚΟΥ: Σεπτέμβριος 2016 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ. Πειραιάς, 8 Δεκεμβρίου 2016
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 8 Δεκεμβρίου ΔΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΔΥΝΑΜΙΚΟΥ: Σεπτέμβριος Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρμοσμένο δείκτη
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 8 Δεκεμβρίου ΔΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΔΥΝΑΜΙΚΟΥ: Σεπτέμβριος Η Ελληνική Στατιστική Αρχή (ΕΛΣΤΑΤ) ανακοινώνει τον εποχικά προσαρμοσμένο δείκτη
ΕΠΙΤΑΧΥΝΣΗ- ΕΠΙΤΑΧΥΝΟΜΕΝΗ ΚΙΝΗΣΗ
 ΕΠΙΤΑΧΥΝΣΗ- ΕΠΙΤΑΧΥΝΟΜΕΝΗ ΚΙΝΗΣΗ Η ταχύτητα συνήθως δεν παραµένει σταθερή Ας υποθέσουµε ότι ένα αυτοκίνητο κινείται σε ευθύγραµµο δρόµο µε ταχύτητα k 36. Ο δρόµος είναι ανοιχτός και ο οδηγός αποφασίζει
ΕΠΙΤΑΧΥΝΣΗ- ΕΠΙΤΑΧΥΝΟΜΕΝΗ ΚΙΝΗΣΗ Η ταχύτητα συνήθως δεν παραµένει σταθερή Ας υποθέσουµε ότι ένα αυτοκίνητο κινείται σε ευθύγραµµο δρόµο µε ταχύτητα k 36. Ο δρόµος είναι ανοιχτός και ο οδηγός αποφασίζει
ΔΕΛΤΙΟ ΤΥΠΟΥ ΟΙΚΟΝΟΜΙΚΗ ΑΝΙΣΟΤΗΤΑ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 22 / 6 / 2018 ΔΕΛΤΙΟ ΤΥΠΟΥ Έρευνα Εισοδήματος και Συνθηκών Διαβίωσης των Νοικοκυριών: Έτος 2017 (Περίοδος αναφοράς 2016) H Ελληνική Στατιστική Αρχή
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΑΡΧΗ Πειραιάς, 22 / 6 / 2018 ΔΕΛΤΙΟ ΤΥΠΟΥ Έρευνα Εισοδήματος και Συνθηκών Διαβίωσης των Νοικοκυριών: Έτος 2017 (Περίοδος αναφοράς 2016) H Ελληνική Στατιστική Αρχή
ΕΛΤΙΟ ΤΥΠΟΥ. ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ Γ τρίµηνο 2007
 ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΕΘΝΙΚΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΤΗΣ ΕΛΛΑ OΣ Πειραιάς, 19 εκεµβρίου 2007 ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ Γ τρίµηνο 2007 Η Γενική Γραµµατεία της Εθνικής Στατιστικής Υπηρεσίας της Ελλάδος
ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΕΘΝΙΚΗΣ ΣΤΑΤΙΣΤΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΤΗΣ ΕΛΛΑ OΣ Πειραιάς, 19 εκεµβρίου 2007 ΕΛΤΙΟ ΤΥΠΟΥ ΕΡΕΥΝΑ ΕΡΓΑΤΙΚΟΥ ΥΝΑΜΙΚΟΥ Γ τρίµηνο 2007 Η Γενική Γραµµατεία της Εθνικής Στατιστικής Υπηρεσίας της Ελλάδος
ΔΙΑΧΡΟΝΙΚΕΣ ΤΑΣΕΙΣ ΔΕΙΚΤΩΝ ΑΝΘΡΩΠΙΝΟΥ ΔΥΝΑΜΙΚΟΥ ΣΤΗΝ ΚΥΠΡΟ. Σύγκριση με Ευρωπαϊκή Ένωση 2 0 0 2-2 0 0 8 ΔΙΕΥΘΥΝΣΗ ΕΡΕΥΝΑΣ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 ΔΙΑΧΡΟΝΙΚΕΣ ΤΑΣΕΙΣ ΔΕΙΚΤΩΝ ΑΝΘΡΩΠΙΝΟΥ ΔΥΝΑΜΙΚΟΥ ΣΤΗΝ ΚΥΠΡΟ Σύγκριση με Ευρωπαϊκή Ένωση 2 0 0 2-2 0 0 8 ΔΙΕΥΘΥΝΣΗ ΕΡΕΥΝΑΣ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΑΡΧΗ ΑΝΑΠΤΥΞΗΣ ΑΝΘΡΩΠΙΝΟΥ ΔΥΝΑΜΙΚΟΥ ΔΕΚΕΜΒΡΙΟΣ 2008 Υπεύθυνοι
ΔΙΑΧΡΟΝΙΚΕΣ ΤΑΣΕΙΣ ΔΕΙΚΤΩΝ ΑΝΘΡΩΠΙΝΟΥ ΔΥΝΑΜΙΚΟΥ ΣΤΗΝ ΚΥΠΡΟ Σύγκριση με Ευρωπαϊκή Ένωση 2 0 0 2-2 0 0 8 ΔΙΕΥΘΥΝΣΗ ΕΡΕΥΝΑΣ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΑΡΧΗ ΑΝΑΠΤΥΞΗΣ ΑΝΘΡΩΠΙΝΟΥ ΔΥΝΑΜΙΚΟΥ ΔΕΚΕΜΒΡΙΟΣ 2008 Υπεύθυνοι
