ΠΑΚΕΤΟ ΟΠΤΙΚΗΣ ΕΚΔΟΣΕΙΣ ΔΙΕΡΕΥΝΗΤΙΚΗ ΜΑΘΗΣΗ ΓΕΩΡΓΙΟΥ ΒΛΑΧΟΥ 13, ΑΘΗΝΑ ΤΗΛ ΦΑΞ
|
|
|
- Γάννη Αναγνώστου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΚΕΤΟ ΟΠΤΙΚΗΣ ΕΚΔΟΣΕΙΣ ΔΙΕΡΕΥΝΗΤΙΚΗ ΜΑΘΗΣΗ ΓΕΩΡΓΙΟΥ ΒΛΑΧΟΥ 13, ΑΘΗΝΑ ΤΗΛ ΦΑΞ
2 ΠΑΚΕΤΟ ΟΠΤΙΚΗΣ Ενεργειακές απαιτήσεις -12V Εναλ./Συν. ρεύμα στα 2 έως 3 Amp. Το ΣΕΤ ΟΠΤΙΚΗΣ αποτελείται από μια πηγή ακτίνων φωτός και μια σειρά συσκευών που προκαλούν ανάκλαση, διάθλαση και χρωματική ανάμιξη στο φως. Έτσι καθίσταται εύκολη η πραγματοποίηση μετρήσεων και η εξαγωγή συμπερασμάτων. Η πηγή του φωτός είναι τοποθετημένη σε ένα ειδικά σχεδιασμένο Κουτί φωτός, το οποίο συνοδεύεται από έναν φακό εστίασης ακτινών. Στην αντίθετη πλευρά του κουτιού είναι προσαρμοσμένοι δύο περιστρεφόμενοι καθρέφτες, οι όποιοι αντανακλούν το φως που πηγάζει από τις πλαϊνές οπές. Η παρουσία διάφορων έγχρωμων φίλτρων καθιστά εφικτή την περιστροφή των δύο πλευρικών δεσμών, έτσι ώστε να επικαλύψουν και να αναμιχθούν με την προκαθορισμένης εστίασης κεντρική δέσμη. Το εφέ γίνεται εμφανές σε μια λευκή οθόνη, σε απόσταση περίπου 200 mm από το κουτί. Η παράλληλη δέσμη φωτός που αναδύεται από το εμπρόσθιο μέρος του κουτιού, μπορεί να σπάσει σε μία λεπτή δέσμη (για την παραγωγή φάσματος) ή εναλλακτικά σε μία, δύο, τρεις ή τέσσερις λεπτές ακτίνες, εφαρμόζοντας στην κατάλληλη εγκοπή το κατάλληλο εξάρτημα διαμόρφωσης οπών. Αυτές οι ακτίνες ή δέσμες μπορούν να χρωματιστούν με την τοποθέτηση ενός έγχρωμου φίλτρου στη μεγαλύτερη οπή, στην εμπρόσθια όψη του κουτιού. Αν θέλετε να έχετε ελαφρώς συγκλίνουσες ή αποκλίνουσες δέσμες, μπορείτε να μετακινήσετε τον φακό εστίασης με το ειδικό κουμπί ρύθμισης. Αυτή η αλλαγή μπορεί να γίνει πιο εμφανής αν χρησιμοποιήσετε το εξάρτημα διαμόρφωσης πολλαπλών οπών. Αν σε κάποιο πείραμα απαιτείται μεγαλύτερη σύγκλιση ή απόκλιση, χρησιμοποιήστε τους φακούς με τον παρακάτω τρόπο. ΠΡΟΕΤΟΙΜΑΣΙΑ ΓΙΑ ΤΟ ΠΕΙΡΑΜΑ Τοποθετήστε το Κουτί φωτός σε ένα τραπέζι με τη λυχνιολαβή στραμμένη προς τα επάνω. Η βάση του συστήματος εξασφαλίζει την απαιτούμενη σταθερότητα κατά τη διάρκεια του πειράματος. Συνδέστε το καλώδιο της λάμπας σε μια πρίζα 12V 3A. Η λάμπα (κοιτάξτε στα ανταλλακτικά) λειτουργεί και με υψηλότερες τάσεις (έως και 14 volt), αλλά αυτό δεν συνίσταται γιατί έτσι μειώνεται ο χρόνος ζωής της.
3 Προσαρμόστε ένα από τα εξαρτήματα διαμόρφωσης πολλαπλών οπών στην μπροστινή εσοχή. Μετακινήστε τον φακό εστίασης μέχρι να έχετε μια σειρά παράλληλων ακτίνων. Τοποθετήστε τους φακούς διαμόρφωσης, τα πρίσματα και τους καθρέφτες σε ένα απλό φύλλο χαρτί και σε διάφορες θέσεις, όπως υποδεικνύεται στα πειράματα. Να πιάνετε τους φακούς πάντα από την ειδική λαβή για να προστατεύετε την οπτική τους επιφάνεια από λεκέδες και χαρακιές. Η βάση κάθε φακού και πρίσματος είναι ειδικά φινιρισμένη για να προκαλεί την ανάκλαση των ακτίνων φωτός, ούτως ώστε να είναι ορατή η διαδρομή της κάθε ακτίνας μέσα από τη συσκευή. Φυσικά, θα έχετε καλύτερα οπτικά αποτελέσματα αν τα πειράματα γίνουν με ημίφως ή σκοτάδι. Καθώς οι συσκευές τοποθετούνται πολύ κοντά στο Κουτί φωτός, μπορεί να εμφανιστούν μέσα στους διαμορφωτές φωτεινές και εσωτερικά ανακλούμενες ακτίνες. Αυτό συμβαίνει λόγω των ακτίνων που εισέρχονται στον διαμορφωτή από την επάνω επιφάνεια και ανακλώνται εσωτερικά από την κάτω. Επιπλέον, οι ακτίνες που περνούν επάνω από το διαμορφωτή μπορεί να εμφανιστούν και σε κάποια απόσταση κάτω από αυτόν. Αυτά τα φαινόμενα μπορούν να εξαλειφθούν:- μετακινώντας τα πρίσματα και τους διαμορφωτές μακριά από το κουτί, τοποθετώντας το φύλλο χαρτιού όχι στο τραπέζι, αλλά σε ένα λεπτό βιβλίο, ή κλείνοντας τα άκρα των οπών για να μειωθεί το ύψος της ακτίνας. ΚΑΤΑΓΡΑΦΗ ΔΙΑΔΡΟΜΗΣ ΑΚΤΙΝΑΣ Για να καταγράψετε τη διαδρομή μιας ακτίνας, σημειώστε τη θέση του φακού, πρίσματος ή καθρέφτη που χρησιμοποιείτε περνώντας με ένα μολύβι την περίμετρό τους. Στη συνέχεια σημειώστε το κέντρο της ακτίνας που παρατηρείτε σε δύο θέσεις, μία τελεία κοντά στην επιφάνεια του φακού και μία όσο μακριά γίνεται. Εάν το σχέδιο των ακτίνων είναι πεπλεγμένο, με διασταυρούμενες ακτίνες, αριθμήστε τις τελείες που αντιστοιχούν στην κάθε ακτίνα ώστε να μπορείτε εύκολα να τις ακολουθήσετε. Αφαιρέστε τον φακό ή το πρίσμα και ενώστε προσεκτικά με γραμμές τις αριθμημένες τελείες για να δείξετε τις διαδρομές της ακτίνας από, προς και διαμέσου της συσκευής. Σημειώστε βελάκια στις γραμμές για να δείξετε τη διεύθυνση της μετάδοσης. Εάν έχετε αμφιβολίες για τη συνέχεια κάποιας γραμμής, τοποθετήστε τη συσκευή στην ακριβώς ίδια θέση και εντοπίστε ξανά την ακτίνα.
4 Πείραμα 1 Ανάκλαση - Μονή ακτίνα. Προβάλλετε μια μονή ακτίνα στο χαρτί και σημειώστε τα δύο άκρα της. Τοποθετήστε τον επίπεδο καθρέφτη στα μέσα αυτής της διαδρομής, να συναντά την ακτίνα υπό γωνία. Σημειώστε τις εξής θέσεις:- (a)την εμπρόσθια όψη του καθρέφτη. (b)την ανακλούσα πίσω όψη του καθρέφτη. (c)την ανακλώμενη ακτίνα (ή ακτίνες). Εξηγήστε γιατί η δεύτερη ακτίνα είναι πιο αχνή. Σχηματίστε μία κατακόρυφη στον καθρέφτη γραμμή στο σημείο της επιφάνειάς του όπου συναντώνται οι προσπίπτουσες και οι ανακλώμενες ακτίνες. Αυτή η κατακόρυφη γραμμή καλείται η ΚΑΘΕΤΟΣ στον καθρέφτη, στο συγκεκριμένο σημείο. Μετρήστε τη γωνία μεταξύ της ΠΡΟΣΠΙΠΤΟΥΣΑΣ ΑΚΤΙΝΑΣ και της ΚΑΘΕΤΟΥ. Αυτή η γωνία καλείται ΓΩΝΙΑ ΠΡΟΣΠΤΩΣΗΣ. Μετρήστε τη γωνία μεταξύ της ΑΝΑΚΛΩΜΕΝΗΣ ΑΚΤΙΝΑΣ και της ΚΑΘΕΤΟΥ. Αυτή η γωνία καλείται ΓΩΝΙΑ ΑΝΑΚΛΑΣΗΣ. Αυτές οι γωνίες μετρώνται σε σχέση με την ΚΑΘΕΤΟ γιατί στα επόμενα πειράματα θα ανακλάτε ακτίνες με καμπυλωμένους καθρέφτες. Εφόσον δεν μπορείτε να μετρήσετε τη γωνία μεταξύ της ακτίνας και της καμπυλωμένης επιφάνειας του καθρέφτη, πρέπει να σχεδιάσετε μία κάθετο στην καμπυλωμένη επιφάνεια και σύμφωνα με αυτή την ευθεία γραμμή να υπολογίσετε τις γωνίες πρόσπτωσης και ανάκλασης.
5 Πείραμα 2 Ανάκλαση - Αποκλίνουσα ακτίνα Τοποθετήστε το εξάρτημα διαμόρφωσης τριών οπών στην μπροστινή στενή εσοχή του Κουτιού. Προβάλλετε μια σειρά αποκλίνουσων ακτίνων σε ένα φύλλο χαρτί και σημειώστε τις διαδρομές. Τοποθετήστε έναν επίπεδο καθρέφτη έτσι ώστε να συναντά τις ακτίνες με γωνία διαφορετική των 90. Σημειώστε την ανακλαστική περιοχή του καθρέφτη και τις διαδρομές των ανακλώμενων ακτίνων. Σχεδιάστε καθέτους στην επιφάνεια του καθρέφτη, σε κάθε σημείο όπου γίνεται ανάκλαση. Μετρήστε τις γωνίες πρόσπτωσης και ανάκλασης σε κάθε σημείο ανάκλασης. Παραθέστε τα αποτελέσματά σας ως εξής: ΑΚΤΙΝ Α Α B C ΓΩΝΙΑ ΠΡΟΣΠΤΩΣ ΗΣ ΓΩΝΙΑ ΑΝΑΚΛΑΣ ΗΣ Η γωνία πρόσπτωσης είναι μεγαλύτερη, μικρότερη ή ίση με αυτή της ανάκλασης; Μόλις ανακαλύψατε έναν από τους νόμους της ανάκλασης ποιος είναι αυτός; Οι αποκλίνουσες ακτίνες συνέχισαν να αποκλίνουν και μετά τη ανάκλαση; Οι παράλληλες ακτίνες συνέχισαν να είναι παράλληλες και μετά την ανάκλαση; Δοκιμάστε το και δείτε. Οι συγκλίνουσες ακτίνες συνέχισαν να είναι συγκλίνουσες και μετά την ανάκλαση; Δοκιμάστε το και δείτε.
6 Πείραμα 3 Ανάκλαση - Πλευρική και κάθετη αναστροφή Ρυθμίστε το Κουτί ακτίνων για να προβάλλετε δύο παράλληλες ακτίνες. Τοποθετήστε ένα έγχρωμο φίλτρο (μπλε) στην αριστερή ακτίνα (όπως βλέπετε τη συσκευή από μπροστά) και χρωματίστε κόκκινη τη δεξιά ακτίνα. Προκαλέστε την ανάκλαση των δύο ακτίνων μέσω του επίπεδου καθρέφτη όπως και προηγουμένως. Κοιτάξτε τον καθρέπτη και παρατηρήστε την ανάκλαση των ακτίνων. Η αριστερή ακτίνα είναι κόκκινη ή μπλε; Σημειώστε τις ακτίνες με έγχρωμα μολύβια, υποδεικνύοντας ποια είναι η μπλε και ποια η κόκκινη. Τι παθαίνει ένα είδωλο όταν ανακλάται σε έναν επίπεδο καθρέφτη; Το είδωλο του εαυτού σας που βλέπετε εσείς στον καθρέφτη σας είναι το ίδιο με το είδωλο που βλέπουν οι φίλοι σας όταν σας κοιτούν; Αν το πρόσωπό σας είναι ανεστραμμένο από αριστερά προς τα δεξιά κατά την ανάκλαση, γιατί δεν συμβαίνει το ίδιο και από πάνω προς τα κάτω; Αν γείρετε το κεφάλι σας πλαγίως, έτσι ώστε να έρθει σε οριζόντια θέση, η ανάκλασή σας θα αναστραφεί κατακόρυφα. Δοκιμάστε το και δείτε. Τι εννοούμε με τη φράση "ΠΛΕΥΡΙΚΗ ΑΝΑΣΤΡΟΦΗ ΚΑΤΑ ΤΗΝ ΑΝΑΚΛΑΣΗ;" Αν κρατήσετε μια κάρτα που γράφει L to R έτσι ώστε να ανακλάται σε έναν καθρέφτη, ποιο από τα παρακάτω παραδείγματα θα είναι η ανάκλαση; Μην το προσπαθήσετε αν δεν έχετε προβλέψει το αποτέλεσμα. Όταν οι επιστήμονες πιστεύουν πως γνωρίζουν τους κανόνες σύμφωνα με τους οποίους συμβαίνει ένα φαινόμενο, τότε ισχυρίζονται πως έχουν μια θεωρία για το φαινόμενο κι έτσι μπορούν να προβλέψουν τι θα συμβεί υπό συγκεκριμένες συνθήκες. Στη συνέχεια πειραματίζονται για να δουν αν θα επαληθευτεί η πρόβλεψή τους. Ανάλογα με το αποτέλεσμα του πειράματος, δέχονται, απορρίπτουν ή αλλάζουν την θεωρία τους. Το πείραμα που κάνατε σας ώθησε να δεχθείτε, να αλλάξετε ή να απορρίψετε την θεωρία σας; Κάντε μια άλλη πρόβλεψη. Πώς θα είναι το ανακλώμενο είδωλο της ακόλουθης λέξης εάν τοποθετηθεί ένας επίπεδος καθρέφτης κατακόρυφα στην στικτή γραμμή και η παρατήρηση γίνει από μια θέση στο κάτω μέρος της σελίδας;
7 CARBON-DI-OXIDE Σχεδιάστε το αναμενόμενο είδωλο πριν προβείτε στο πείραμα. Ήταν σωστή η πρόβλεψή σας; Αυτή είναι η ΠΛΕΥΡΙΚΗ ΑΝΑΣΤΡΟΦΗ; Αν σας έλεγαν να κρατήσετε τη λέξη CARBON-DIOXIDE και να παρατηρήσετε το είδωλό της στον καθρέφτη, πώς ακριβώς θα την κρατούσατε; Με αυτόν τον τρόπο παρουσιάστηκε στον καθρέφτη στο προηγούμενο πείραμα; Αν η λέξη ήταν γραμμένη σε διάφανο χαρτί και παρουσιάζεται στον καθρέφτη με τους δύο τρόπους που περιγράφονται, πώς θα την βλέπατε εσείς αν κοιτάζατε στον καθρέφτη μέσα από το χαρτί; Δοκιμάστε το και δείτε. Η τελευταία αναστροφή οφείλεται στον καθρέφτη ή στον τρόπο με τον οποίο παρουσιάζεται η λέξη σε αυτόν; Γιατί μερικά από τα γράμματα φαίνονται ανεστραμμένα ενώ άλλα όχι; Εάν και τα δύο μισά ενός αντικειμένου ή ειδώλου είναι κατοπτρικά είδωλα το ένα του άλλου, τότε λέγονται ΣΥΜΜΕΤΡΙΚΑ. Το πρόσωπό σας είναι συμμετρικό; Τοποθετήστε έναν επίπεδο καθρέπτη έτσι ώστε να προεξέχει κάθετα από το πρόσωπό σας, στο κέντρο της μύτης, και κοιτάξτε το είδωλό σας σε έναν άλλο καθρέφτη. Φαίνεστε φυσιολογικός; Το πρόσωπό σας είναι κανονικό κατοπτρικό είδωλο; Ποιο ήμισυ σας αρέσει περισσότερο; Μετακινήστε τον καθρέφτη δίπλα από τη μύτη σας. Μήπως έχοντας δύο μύτες βλέπετε βελτίωση; Μετακινήστε τον καθρέφτη στην άλλη πλευρά της μύτης σας. Πώς σας φαίνεστε χωρίς μύτη με δύο μάτια το ένα πάνω στο άλλο;
8 Πείραμα 4 Ανάκλαση - Θέση σε επίπεδο καθρέφτη Όταν κοιτάζεστε στον καθρέφτη, το ανακλώμενο είδωλό φαίνεται σαν να είναι κάπου πίσω από τον καθρέφτη. Αν μετακινηθείτε προς τα πίσω κατά ένα μέτρο, το είδωλό σας απομακρύνεται και αυτό από εσάς. Το επόμενο πείραμα θα σας βοηθήσει να εντοπίσετε τη θέση του ειδώλου. Προβάλλετε μια σειρά συγκλινουσών ακτίνων σε ένα φύλλο χαρτί και καταγράψτε τις θέσεις τους καθώς και το εστιακό σημείο. Χρησιμοποιήστε τον παρακάτω συνδυασμό φακών και μετακινήστε τους έτσι ώστε να προσαρμόσετε την εστιακή σας απόσταση. Τοποθετήστε έναν επίπεδο καθρέφτη κάθετα στις ακτίνες με γωνία και καταγράψτε τις διαδρομές των ανακλώμενων ακτίνων. Καθώς κοιτάτε στον καθρέφτη την ανάκλαση των συγκλινουσών ακτίνων, σηκώστε τον καθρέφτη και παρατηρήστε τις πραγματικές συγκλίνουσες ακτίνες. Αφαιρέστε και επανατοποθετήστε τον καθρέφτη αρκετές φορές, παρατηρώντας τις ομοιότητες ανάμεσα στις πραγματικές και τις ανακλώμενες ακτίνες. Θα ισχυριζόσασταν πως το σημείο συνάντησης των πραγματικών ακτίνων είναι το είδωλο του σημείου συνάντησης των ανακλώμενων ακτίνων; Καταγράψτε αυτά τα δύο σημεία σύγκλισης καθώς και τη θέση της ανακλαστικής επιφάνειας του καθρέφτη. Ενώστε με μία γραμμή τα δύο σημεία σύγκλισης. Ποια γωνία σχηματίζει αυτή η γραμμή με τον καθρέφτη; Ποια είναι η απόσταση μεταξύ του πραγματικού σημείου σύγκλισης και του σημείου σύγκλισης των ανακλώμενων από τον καθρέφτη; Επαναλάβετε το πείραμα με ένα φύλλο χαρτιού, άλλη σειρά συγκλινουσών ακτίνων και τον καθρέφτη σε πιο κοντινή ή πιο μακρινή θέση από το σημείο σύγκλισης. Εντοπίστε τα σημεία σύγκλισης και τη θέση του καθρέφτη, και στη συνέχεια σχεδιάστε γραμμές και μετρήστε τις γωνίες όπως και προηγουμένως. Σφηνώστε μια πινέζα κάθετα στο χαρτί (χρησιμοποιώντας ένα χαρτόνι από κάτω) και ακριβώς στη θέση των δύο σημείων σύγκλισης. Τώρα έχετε μια πινέζα μπροστά από τον καθρέφτη και μία άλλη κρυμμένη πίσω από τον καθρέφτη. Σηκώστε κατακόρυφα τον καθρέφτη μέχρι να μπορείτε να δείτε την κρυμμένη πινέζα, επανατοποθετήστε τον και ξανασηκώστε τον αρκετές φορές. Η κρυμμένη πινέζα βρίσκεται στη θέση του ανακλώμενου ειδώλου της μπροστινής πινέζας; Εάν αλλάξετε τη θέση σας (του παρατηρητή) επηρεάζεται η θέση του ειδώλου;
9 Πείραμα 5α Ανάκλαση - Πολλαπλές ανακλάσεις Προκαλέστε την ανάκλαση μιας μονής ακτίνας από επίπεδο καθρέφτη με γωνία πρόσπτωσης 45 με 50. Παρατηρήστε προσεκτικά τις αντανακλάσεις. Πόσα ανακλώμενα είδωλα παράγονται; Ποιο είναι το πιο φωτεινό; Παρατηρήστε προσεκτικά τον καθρέφτη από πάνω και στη συνέχεια σχηματίστε ένα σχέδιο υποδεικνύοντας τον τρόπο σχηματισμού των τριών ανακλώμενων ακτίνων. Συμβαίνει κάτι ιδιαίτερο όταν η γωνία πρόσπτωσης είναι 90 ; Πειραματιστείτε για να ανακαλύψετε αν οι τρεις αντανακλάσεις συμβαίνουν και με άλλες γωνίες πρόσπτωσης, π.χ. 10, 20 κ.ο.κ. μέχρι 90. Ποια ανακλώμενη ακτίνα εξαφανίζεται και σε ποια γωνία συμβαίνει αυτό; Γιατί αυτή η ανάκλαση παράγει το πιο αχνό αποτέλεσμα από τις τρεις; Τοποθετήστε τον ορθογώνιο διαμορφωτή μπροστά από τον καθρέφτη και επαναλάβετε το πείραμα και τις παρατηρήσεις.
10 Πείραμα 5β Πολλαπλές ανακλάσεις Τοποθετήστε δύο καθρέφτες με γωνία 90 μεταξύ τους. Προβάλλετε μία μονή ακτίνα στον ένα καθρέφτη υπό γωνία, και στη θέση των 25 mm από τη γωνία στην οποία συναντιούνται οι δύο καθρέφτες. Παρατηρήστε την κυρίαρχη ανακλώμενη ακτίνα (όχι τις πιο αχνές δευτερεύουσες ανακλάσεις), όπως αυτή ανακλάται και από τους δύο καθρέφτες. Καταγράψτε αυτή τη θέση. Τι παρατηρείτε σχετικά με την κατεύθυνση της αρχικής ακτίνας και της ανακλώμενης ακτίνας; Το ίδιο αποτέλεσμα ισχύει με όλες τις γωνίες πρόσπτωσης; Κοιτάξτε μέσα στη γωνία των καθρεφτών. Τι βλέπετε; Αν αλλάξετε τη θέση σας συμβαίνει το ίδιο πράγμα; Αν υπάρχει ένας μεγαλύτερος επίπεδος καθρέφτης, τοποθετήστε τον οριζόντια στο τραπέζι και στηρίξτε τους άλλους δύο καθρέφτες επάνω του κάθετα, έτσι ώστε και οι τρεις καθρέφτες να είναι σε ορθή γωνία μεταξύ τους. Ένας τέτοιος ανακλαστήρας είχε τοποθετηθεί από τους αστροναύτες στη σελήνη. Μετακινηθείτε πλαγίως και πάνω-κάτω κοιτώντας πάντα την τριπλή γωνία από όλες τις κατευθύνσεις. Τι βλέπετε στη γωνία; Στοχεύστε μία δέσμη φωτός στη γωνία. Τι παρατηρείτε σχετικά με την ανάκλαση; Εξηγήστε γιατί ο ανακλαστήρας που τοποθετήθηκε στο φεγγάρι ήταν ένας τριπλός, ορθογώνιος ανακλαστήρας. Τι είδους δέσμη φωτός στοχεύθηκε επάνω του και ποιο ήταν το αποτέλεσμα; Εφόσον οι επιστήμονες γνωρίζουν ότι αυτό το είδος της ανάκλασης συμβαίνει στη γη, τι κέρδισαν με την τοποθέτηση του ανακλαστήρα στο φεγγάρι; Εξετάστε τους ανακλαστήρες στο πίσω μέρος αυτοκινήτων και ποδηλάτων. Τι σχήμα έχουν τα κοιλώματα στο γυαλί ή το πλαστικό;
11 Πείραμα 6 Ανάκλαση - Περιστροφή επίπεδου καθρέφτη Στοχεύστε μια μονή ακτίνα φωτός σε έναν επίπεδο καθρέφτη. Καταγράψτε την προσπίπτουσα ακτίνα, την ανακλούσα περιοχή της επιφάνειας του καθρέφτη (ονομάστε την M1) και την ανακλώμενη ακτίνα (ονομάστε τη R1). Τώρα περιστρέψτε τον καθρέφτη περίπου 5 γύρω από το σημείο της πρόσπτωσης, έτσι ώστε η προσπίπτουσα ακτίνα να συναντά τον καθρέφτη στο ίδιο σημείο, αλλά υπό διαφορετική γωνία. Καταγράψτε τη νέα ανακλούσα περιοχή ως M2 και τη νέα ανακλώμενη ακτίνα ως R2. Χρησιμοποιώντας μοιρογνωμόνιο, μετρήστε τη γωνία περιστροφής του καθρέφτη. (Τη γωνία ανάμεσα στις γραμμές M1 και M2.) Παρομοίως, μετρήστε τη γωνία περιστροφής της ανακλώμενης ακτίνας. (Τη γωνία ανάμεσα στις γραμμές R1 και R2). Συγκρίνετε τις δύο γωνίες. Προβλέψτε τι θα συμβεί στην R2 αν ο καθρέφτης περιστραφεί σε σχέση με την M2 άλλες 10. Ήταν σωστή η πρόβλεψή σας; Αυτή η τεχνική χρησιμοποιείται συχνά από τους επιστήμονες όταν θέλουν να μεγιστοποιήσουν ή να απλοποιήσουν μικρές κινήσεις στα μετρητικά όργανα, όπως π.χ. το μέτρο. Τοποθετήστε τον καθρέφτη σε τέτοια θέση ώστε η ανακλώμενη δέσμη να προσπίπτει σε έναν τοίχο ή σε μια κάρτα, σε απόσταση δύο μέτρων από τον καθρέφτη. Μετακινήστε ελάχιστα τον καθρέφτη, περίπου κατά 0,5. Τι παρατηρείτε στο μακρινό είδωλο; Ζητήστε από τον καθηγητή σας να σας δείξει ένα κατοπτρικό γαλβανόμετρο και παρατηρήστε πώς αυτό χρησιμοποιεί έναν καθρέφτη και μια ακτίνα φωτός ως προβολέα ακτίνων.
12 Πείραμα 7 Ανάκλαση - Είδωλα σε επίπεδο καθρέφτη - Παράλλαξη Σφηνώστε μια πινέζα κατακόρυφα σε ένα φύλλο χαρτιού χρησιμοποιώντας ένα χαρτόνι ως βάση. Τοποθετήστε τον επίπεδο καθρέφτη περίπου 40 mm πίσω από την πινέζα και παρατηρήστε την ανάκλαση της πινέζας στον καθρέφτη. Το είδωλο φαίνεται σαν να είναι πίσω από τον καθρέφτη. Για να εντοπίσετε τη θέση του ειδώλου, στοχεύστε μια μονή ακτίνα έτσι ώστε να συναντήσει τον καθρέφτη και να ανακλαστεί πίσω στην πινέζα. Το ανακλώμενο είδωλο της ακτίνας που βλέπετε στον καθρέφτη κατευθύνεται προς την ανάκλαση της πινέζας; Αν κοιτάξετε κάτω από την πινέζα και κατά μήκος της ακτίνας προς τη θέση του καθρέφτη, η ακτίνα είναι καμπυλωμένη ή ευθεία; Σημειώστε μόνο τη θέση του καθρέφτη και την προσπίπτουσα ακτίνα. Μετακινήστε το Κουτί ακτίνων σε διαφορετική θέση, στοχεύοντας πάλι την ανακλώμενη ακτίνα στην πινέζα όπως προηγουμένως. Καταγράψτε την προσπίπτουσα ακτίνα. Επαναλάβετε τη διαδικασία, μετακινώντας κάθε φορά την πηγή της ακτίνας σε διαφορετικές θέσεις και από τις δύο πλευρές της πινέζας. Καταγράψτε μόνο τις προσπίπτουσες ακτίνες. Αφαιρέστε τον καθρέφτη, σχεδιάστε τις προσπίπτουσες ακτίνες και προεκτείνετέ τις μέχρι να συναντηθούν. Συναντιούνται όλες μαζί σε κάποιο σημείο; Επανατοποθετήστε τον καθρέφτη. Οι γραμμές που σχεδιάσατε εμπρός και πίσω από τον καθρέφτη σας υποδεικνύουν τη θέση του ανακλώμενου ειδώλου της πινέζας; Εάν έχετε αμφιβολίες, σφηνώστε μια ψηλή πινέζα ή βελόνα πλεξίματος κατακόρυφα στο σημείο όπου συναντιούνται οι γραμμές πίσω από τον καθρέφτη, έτσι ώστε να μπορείτε να βλέπετε ταυτόχρονα τόσο την κορυφή της βελόνας όσο και την ανάκλαση της πινέζας. Είναι στοιχισμένες; Μετακινήστε το κεφάλι προς τη μία πλευρά και μετά την άλλη.. Οι ανακλάσεις της πινέζας και της πινέζας παραμένουν στοιχισμένες; Αυτό το φαινόμενο είναι γνωστό ως ΠΑΡΑΛΛΑΞΗ. Η Παράλλαξη είναι η φαινομενική πλάγια κίνηση ενός μακρινού αντικειμένου, σε σχέση με ένα κοντινό αντικείμενο, η οποία ακολουθεί την κατεύθυνση του παρατηρητή. Οι αστρονόμοι χρησιμοποιούν την παράλλαξη για να δείξουν ποια αστέρια είναι κοντά και ποια όχι. Καθώς η γη κινείται στη διαδρομή της τροχιάς της, τα μακρινά αστέρια φαίνονται σαν να μετακινούνται, σε σχέση πάντα με τα πιο κοντινά αστέρια, στην ίδια διεύθυνση με αυτή της Γης. Ενώστε με μία γραμμή τη θέση της πινέζας με τη θέση του ειδώλου της.
13 Αυτή η γραμμή "κόβει" τον καθρέφτη υπό ορθή γωνία; Η απόσταση του ειδώλου και αυτού καθαυτού του αντικειμένου σε από τον καθρέφτη είναι η ίδια; Μετακινήστε την πινέζα σε άλλη θέση και προβλέψτε τη θέση του νέου ειδώλου. Επαναλάβετε το προηγούμενο μέρος αυτού του πειράματος για να δείτε αν ήταν σωστή η πρόβλεψή σας.
14 Πείραμα 8 Ανάκλαση - Σε κυκλικό, κοίλο καθρέφτη. Επιλέξτε τον ημικυκλικό κοίλο καθρέφτη. Στοχεύστε μια σειρά παράλληλων ακτίνων στο κέντρο της εσωτερική καμπύλης του καθρέφτη έτσι ώστε οι ακτίνες να είναι παράλληλες με τον άξονα συμμετρίας του καθρέφτη. Καταγράψτε τις προσπίπτουσες και ανακλούμενες ακτίνες και σημειώστε σε ποιο σημείο συναντιούνται. Αυτό το σημείο καλείται ΕΣΤΙΑ του καθρέφτη. Πόσο μακριά βρίσκεται η εστία (ή ΕΣΤΙΑΚΟ ΣΗΜΕΙΟ) από τον καθρέφτη; Αυτή η απόσταση καλείται ΕΣΤΙΑΚΗ ΑΠΟΣΤΑΣΗ του καθρέφτη. Αν το εστιακό σημείο εμφανίζεται αχνό και εκτεταμένο, με πολλές ακτίνες να το επικαλύπτουν, εμποδίστε την έξοδο από το Κουτί των εξωτερικών ακτίνων και αφήστε να περάσουν μόνο οι κεντρικές. Πείραμα 9 Ανάκλαση - Κέντρο της κυρτότητας - Ακτίνα της κυρτότητας - Εστιακή απόσταση ενός κυκλικού καθρέφτη Προετοιμάστε το κουτί όπως και στο προηγούμενο πείραμα και χαράξτε επάνω στο χαρτί την εσωτερική ανακλώσα επιφάνεια του κοίλου καθρέφτη. Μετακινήστε τον καθρέφτη γύρω από την καμπύλη και συνεχίστε την καταγραφή μέχρι να έχετε έναν πλήρη κύκλο. Μετρήστε τη διάμετρο αυτού του κύκλου σε διάφορες κατευθύνσεις και υπολογίστε τον μέσο όρο. Ποια είναι η ακτίνα του κύκλου; Βρείτε το κέντρο της κυρτότητας, π.χ. το κέντρο του κύκλου. Πώς συγκρίνεται η ακτίνα με την εστιακή απόσταση που υπολογίσατε στο προηγούμενο πείραμα; Μια άλλη μέθοδος για να βρείτε το κέντρο της κυρτότητας είναι να στοχεύσετε μια μονή ακτίνα στην εσωτερική καμπύλη του καθρέφτη έτσι ώστε να ανακλάται πίσω στον εαυτό της. Για να το κάνετε αυτό, η ακτίνα πρέπει να συναντά την επιφάνεια στο σημείο της καθέτου ή να είναι κάθετη στην επιφάνεια σε εκείνο το σημείο και πρέπει να ανακλάται κατά μήκος αυτής της ακτινικής θέσης και διαμέσου του κέντρου της καμπυλότητας. Καταγράψτε τη θέση αυτής της ακτίνας και χωρίς να μετακινήσετε τον καθρέφτη, μετακινήστε το Κουτί σε άλλη θέση απ' όπου η ακτίνα ανακλάται και πάλι στον εαυτό της και καταγράψτε τη νέα θέση της. Επαναλάβετε τη διαδικασία για τρίτη φορά.
15 Πείραμα 10 Ανάκλαση - Σφαιρική παρέκκλιση Τι συμβαίνει όταν παράλληλες ακτίνες κατευθύνονται σε έναν κοίλο καθρέφτη ΠΑΡΑΛΛΗΛΑ προς τον άξονα συμμετρία, αλλά με μια πλάγια μετατόπιση; Χρησιμοποιήστε μόνο δύο ακτίνες από το κουτί φωτός. Καταγράψτε έξι θέσεις του εστιακού σημείου καθώς μετακινείτε το Κουτί σε διαφορετικές θέσεις, διατηρώντας όμως τις ακτίνες παράλληλες στον άξονα συμμετρίας. Τα διάφορα εστιακά σημεία βρίσκονται σε καμπύλη ή σε ευθεία γραμμή; Συναντιούνται σε κάποιο σημείο οι τέσσερις παράλληλες στον άξονα συμμετρίας ακτίνες; Χρησιμοποιώντας το εξάρτημα διαμόρφωσης 4 οπών, εμποδίστε τις δύο εσωτερικές ακτίνες και καταγράψτε τη θέση των δύο εξωτερικών καθώς και του εστιακού τους σημείου. Σημειώστε τη θέση του καθρέφτη. Εμποδίστε τις δύο εξωτερικές ακτίνες και καταγράψτε τις δύο εσωτερικές και το εστιακό τους σημείο. Ποιες ακτίνες συγκλίνουν πιο κοντά στον καθρέφτη οι εσωτερικές ή οι εξωτερικές; Χρησιμοποιώντας ένα άλλο φύλλο χαρτιού, επαναλάβετε τον εντοπισμό των εσωτερικών και εξωτερικών ακτίνων, με τέσσερις ακτίνες ΠΑΡΑΛΛΗΛΕΣ στον άξονα συμμετρία αλλά απεντοπισμένες πλαγίως. Η σφαιρική παρέκκλιση (δηλ. η αποτυχία σύγκλισης όλων των ακτίνων σε ένα σημείο) αυξάνεται ή μειώνετε αν μετακινήσετε τις ακτίνες προς τη μία πλευρά του άξονα συμμετρίας; Αφαιρέστε το διαμορφωτή οπών από το Κουτί και ρυθμίστε τον φακό εστίασης έτσι ώστε να προβάλλει μια αποκλίνουσα δέσμη. Κρατήστε το Κουτί επάνω από το τραπέζι και μετακινήστε το μακριά κατά 1 μέτρο. Προβάλλετε αυτή την πλατιά ακτίνα στον καθρέφτη, υπό ελαφρώς κατιούσα γωνία, και παρατηρήστε την έντονα φωτιζόμενη περιοχή. Σχεδιάστε το περίγραμμα αυτής της περιοχής. Αυτό το σχήμα λέγεται ΚΑΥΣΤΙΚΗ ΚΑΜΠΥΛΗ (Caustic Curve). Caustic σημαίνει Καυστικός. Γιατί ο μεγεθυντικός φακός καλείται συχνά καυστικός φακός (burning glass); Τι προκαλεί το σχήμα αυτής της καυστικής καμπύλης; Σύρετε τον διαμορφωτή μονής οπής πλαγίως και κατά μήκος του Κουτιού μέχρι η πλατιά δέσμη να σβήσει σταδιακά. Καθορίστε τις περιοχές όπου ανακλώνται τα διάφορα σημεία της δέσμης. Ένα σχήμα σαν αυτό της καυστικής καμπύλης, ουσιαστικά το περίγραμμα των θέσεων μιας κινούμενης γραμμής, καλείται και "φάκελος". Κάνοντας ανώτερα μαθηματικά θα συναντήσετε περισσότερους φακέλους και θα βρείτε τις εξισώσεις τους. Σε μία από τις καταγεγραμμένες ανακλάσεις, σχεδιάστε γραμμές από το κέντρο της κυρτότητας προς τα σημεία της ανάκλασης. Κάθε μία από αυτές τις γραμμές είναι μία ακτίνα και είναι κάθετη στην κοιλότητα του καθρέφτη. Για κάθε ανάκλαση, σημειώστε τη γωνία πρόσπτωσης (ανάμεσα στην προσπίπτουσα ακτίνα και την κάθετο) και τη γωνία ανάκλασης (ανάμεσα στην ανακλώμενη ακτίνα και την κάθετο). Οι γωνίες πρόσπτωσης είναι ίσες με τις αντίστοιχες γωνίες ανάκλασης;
16 Πείραμα 11 Ανάκλαση - Κυρτός καθρέφτης Προβάλλετε μια σειρά παράλληλων ακτίνων στην ΕΞΩΤΕΡΙΚΗ επιφάνεια του ημικυκλικού καθρέφτη, παράλληλα με τον άξονα συμμετρίας. Από πού φαίνονται να πηγάζουν οι αποκλίνουσες ακτίνες; Εντοπίστε αυτό το σημείο σχεδιάζοντας αυτές τις ακτίνες προς τα πίσω, μέσω της θέσης του καθρέφτη. Το σημείο απ' όπου πηγάζουν καλείται ΚΑΤΟΠΤΡΙΚΗ ΕΣΤΙΑ και η απόσταση αυτού του σημείου από τον καθρέφτη ΚΑΤΟΠΤΡΙΚΗ ΕΣΤΙΑΚΗ ΑΠΟΣΤΑΣΗ. Πώς συγκρίνεται αυτή η εστιακή απόσταση με αυτή της κυρτωμένης πλευράς του καθρέφτη; Πώς συγκρίνεται με την ακτίνα της κυρτότητας του καθρέφτη που βρήκατε προηγουμένως; Κατά πόσο διαφέρουν τα αποτελέσματα; Μπορεί αυτή η διαφορά να οφείλεται στην κατασκευή του καθρέφτη; Εξηγήστε γιατί οι ελαφρώς κυρτοί καθρέφτες χρησιμοποιούνται ως εσωτερικοί καθρέφτες αυτοκινήτων. Αν σχεδιάσετε μια γραμμή από το κέντρο της κυρτότητας προς το σημείο πρόσπτωσης της ακτίνας στον καθρέφτη, η γραμμή αυτή είναι κάθετη στην επιφάνεια. Σχεδιάστε αρκετές τέτοιες καθέτους. Για κάθε ανάκλαση, μετρήστε τη γωνία πρόσπτωσης (ανάμεσα στην προσπίπτουσα ακτίνα και την κάθετο) και τη γωνία ανάκλασης (ανάμεσα στην ανακλώμενη ακτίνα και την κάθετο). Οι γωνίες πρόσπτωσης είναι ίσες με τις αντίστοιχες γωνίες ανάκλασης; Πείραμα 12 Ανάκλαση - Παραβολικός ανακλαστήρας Παραβολή είναι μια ασυνήθιστα σχηματισμένη καμπύλη η οποία βρίσκεται με μία από τις παρακάτω μεθόδους:- Σχεδιάστε την καμπύλη της γραφικής παράστασης Υ = X 2 ή κάποιας άλλης δευτεροβάθμιας εξίσωσης. Καταγράψτε τη διαδρομή ενός βλήματος στον αέρα. Μετακινήστε ένα σημείο P έτσι ώστε να απέχει πάντα ίση απόσταση από ένα σημείο F (ΕΣΤΙΑ) και μια ευθεία γραμμή AB. Αυτή η γραμμή λέγεται ΔΙΕΥΘΥΝΟΥΣΑ γιατί υποδεικνύει προς τα που θα είναι στραμμένη η παραβολή. Κόψτε έναν κώνο στην κυρτή πλευρά για να σχηματιστεί μια διπλής όψης επίπεδη και παράλληλη επιφάνεια. Αυτό καλείται ΚΩΝΙΚΗ ΤΟΜΗ. Άλλες κωνικές τομές είναι οι
17 κύκλοι, οι ελλείψεις ή οι υπερβολές. Πώς κατασκευάζονται αυτές; Στοχεύστε μια σειρά παράλληλων ακτίνων σε έναν παραβολικό ανακλαστήρα έτσι ώστε οι ακτίνες να είναι παράλληλες με τον άξονα συμμετρίας του καθρέφτη. Σημειώστε τη θέση του καθρέφτη και τις διαδρομές των ακτίνων. Καταγράψτε την εστιακή απόσταση. Μετακινήστε πλαγίως το Κουτί διατηρώντας όμως τις ακτίνες παράλληλες με τον άξονα συμμετρίας. Το χαρτί "μιλιμετρέ "θα θα σας φανεί χρήσιμο στην ευθυγράμμιση του καθρέφτη με τις ακτίνες. Τι παρατηρείτε σχετικά με τη θέση του εστιακού σημείου; Στοχεύστε μία πλατιά, παράλληλα μετατοπισμένη δέσμη φωτός στον παραβολικό καθρέφτη και παρατηρήστε το αποτέλεσμα. Ποιο σχήμα καθρέφτη θα χρησιμοποιούσατε για να παράγετε είδωλα αστεριών, διασκορπισμένων σε όλες τις κατευθύνσεις του πεδίου της όρασης; Τι θα συμβεί αν μια σημειακή πηγή φωτός τοποθετηθεί στο εστιακό σημείο ενός παραβολικού καθρέφτη; Δοκιμάστε το και δείτε. Γιατί τα ραντάρ, τα ραδιοτηλεσκόπια, οι ανακλαστήρες στα μπροστινά φώτα των αμαξιών και οι ανακλαστήρες ακτινοβολίας, έχουν παραβολικό σχήμα αντί για κυκλικό ή σφαιρικό; Στα παραδείγματα που δίνονται, και όσον αφορά τον ανακλαστήρα, θα τοποθετούνταν η συσκευή λήψης, αποστολής ή ακτινοβολίας;
18 Πείραμα 13 Διάθλαση - Ημικυκλικός διαμορφωτής Στοχεύστε μια μονή ακτίνα υπό γωνία 90 στο κεντρικό σημείο της λείας πλευράς του ημικυκλικού διαμορφωτή. Καταγράψτε τη θέση του διαμορφωτή και τη διαδρομή της ακτίνας. Παρατηρείται κάποια παρέκκλιση στην πορεία της δέσμης; Εάν υπάρχει, η γωνία δεν είναι 90. Μετακινήστε το Κουτί έτσι ώστε η ακτίνα να κατευθύνεται στο ίδιο κεντρικό σημείο της λείας πλευράς του διαμορφωτή, αλλά υπό γωνία 10 σε σχέση με την κάθετο. Καταγράψτε τη διαδρομή της ακτίνας από και προς το διαμορφωτή, έτσι ώστε όταν αφαιρείται ο διαμορφωτής να μπορείτε να δείτε τη διαδρομή της ακτίνας μέσα από αυτόν, Μετακινήστε το Κουτί αρκετές φορές και σχεδιάστε με διαφορετικά χρώματα τις νέες διαδρομές των ακτίνων (όλες εισέρχονται από το ίδιο σημείο στο διαμορφωτή). Τι συμβαίνει όταν μια ακτίνα φωτός:- Περνά από ένα μέσο (αέρας) σε ένα άλλο (πλαστικό) υπό γωνία 90 ; Περνά όπως πριν, αλλά υπό γωνία διαφορετική των 90 0 ; (δηλ. η γωνία πρόσπτωσης δεν είναι μηδέν). Όταν περνά από το πλαστικό στον αέρα; Γιατί δεν η ακτίνα δεν διαθλάται όταν περνά μέσα από την ημικυκλική πρόσοψη ενώ διαθλάται όταν περνά μέσα από τη λεία πρόσοψη; Αφαιρέστε το διαμορφωτή μετά την προβολή έξι ακτίνων και σημειώστε τη θέση της λείας όψης του διαμορφωτή. (Οι ακτίνες μπορούν να προβληθούν και στις δύο πλευρές της καθέτου στη λεία επιφάνεια.) Σχεδιάστε προσεκτικά τις ακτίνες που συναντιούνται στο κεντρικό σημείο της λείας όψης και τις επακόλουθες πορείες τους. Σχεδιάστε έναν κύκλο διαμέτρου 100 mm, κέντρο του οποίου είναι το σημείο πρόσπτωσης. Προεκτείνετε προσεκτικά τις προσπίπτουσες και διαθλασμένες ακτίνες μέχρι να συναντήσουν τον κύκλο. Σχεδιάστε την κάθετο N στο σημείο της πρόσπτωσης. Σχεδιάστε κατακόρυφες προς την κάθετη γραμμή από τα σημεία που οι ακτίνες συναντούν τον κύκλο. Το διάγραμμά σας θα πρέπει να είναι κάπως έτσι:- Αυτές οι κατακόρυφοι ονομάζονται ΜΙΣΕΣ ΧΟΡΔΕΣ.
19 Συμπληρώστε έναν πίνακα με τις παρατηρήσεις σας ως ακολούθως: ΑΡ. ΑΚΤΙΝΑΣ ΑΡ. ΑΚΤΙΝΑΣ ΓΩΝΙΑ ΠΡΟΣΠΤΩΣΗΣ i ΑΝΑΛΟΓΙΑ ΜΙΣΗΣ ΧΟΡΔΗΣ i/μιση ΧΟΡΔΗ r ΓΩΝΙΑ ΔΙΑΘΛΑΣΗΣ r ΔΙΑΦΟΡΑ ΜΕΤΑΞΥ i-r ΑΝΑΛΟΓΙΑ I/r ΜΗΚΟΣ ΤΗΣ ΜΙΣΗΣ ΧΟΡΔΗΣ I ΜΗΚΟΣ ΤΗΣ ΜΙΣΗΣ ΧΟΡΔΗΣ r Ημιτ. i Ημιτ. r ΑΝΑΛΟΓΙΑ Ημιτ. I / Ημιτ. r Εάν δεν έχετε διδαχθεί τριγωνομετρία ή λογαρίθμους, μάλλον δεν θα είστε σε θέση να συμπληρώσετε τις τρεις τελευταίες στήλες, αλλά αυτό δεν έχει σημασία. Είναι απλά ένας πιο ακριβής τρόπος για τον έλεγχο του αποτελέσματος της 4ης στήλης. Η διαφορά μεταξύ της γωνίας i και r είναι πάντα η ίδια; Η αναλογία: γωνία i/ γωνία r είναι πάντα η ίδια; Η αναλογία: μισή χορδή i/μισή χορδή d είναι πάντα περίπου ίδια; Η αναλογία: ημιτ. i/ ημιτ. r είναι πάντα η ίδια; Ο άνθρωπος που ανακάλυψε αυτό το φαινόμενο λέγεται Snell. Ο νόμος του Snell λέει ότι:- (a) Όταν μια φωτεινή ακτίνα περνά από ένα μέσο (υλικό) σε ένα άλλο υπό γωνία (όχι κάθετα στην επιφάνεια), υφίσταται μια εκτροπή (ΔΙΑΘΛΑΣΗ) και η αναλογία: ημιτ. i/ημιτ. r (ή η αναλογία των μισών χορδών) είναι σταθερή γι' αυτά τα δύο μέσα. (b) Η προσπίπτουσα ακτίνα, η κάθετος στην επιφάνεια και η διαθλώμενη ακτίνα, βρίσκονται σε ένα επίπεδο (γι' αυτό λέγονται και ΟΜΟΕΠΙΠΕΔΕΣ). Η αναλογία: ημιτ. i/ημιτ. r καλείται ΔΕΙΚΤΗΣ ΔΙΑΘΛΑΣΗΣ για τα δύο υλικά. Ποιος είναι ο δείκτης διάθλασης για πέρασμα από τον αέρα σε πλαστικό; Για να παρατηρήσετε και να καταγράψετε τις διαφορετικές διαθλαστικές ιδιότητες υλικών εκτός του ακρυλικού πλαστικού, χρησιμοποιήστε ένα χοντρό γυαλί στη θέση του πλαστικού ή έναν αβαθή, ημικυκλικό πλαστικό δίσκο γεμισμένο ως τη μέση με νερό, κηροζίνη, παραφίνη ή κάποιο άλλο καθαρό υγρό. Άσχετα από το τι θα συμβεί τελικά στις ακτίνες, καταγράψτε μόνο την πρώτη περίπτωση διάθλασης.
20 Πείραμα 14 Διάθλαση - Παράλληλος διαμορφωτής Τοποθετήστε τον ορθογώνιο διαμορφωτή με την επιμήκη πλαϊνή κατακόρυφο σε μια μονή ακτίνα. Παρατηρείται διάθλαση στις περιοχές πρόσπτωσης ή σε αυτές της προβολής; Αν όχι, γιατί; Η ακτίνα περνά από το ένα μέσο (αέρας) στο δεύτερο (ακρυλικό πλαστικό) στην πρώτη διεπιφάνεια και αντιστρόφως στη δεύτερη διεπιφάνεια. Επομένως τι άλλο πρέπει να συμβαίνει, εκτός από το πέρασμα της ακτίνας από το ένα μέσο στο άλλο, για να έχουμε διάθλαση της ακτίνας; Μετακινήστε το Κουτί τόσο ώστε η ακτίνα να χτυπήσει στο κέντρο της μεγάλης πλευράς του διαμορφωτή, με γωνία πρόσπτωσης 10. Άρα 80 ως προς την επιφάνεια. Καταγράψτε τις προσπίπτουσες και τις αναδυόμενες ακτίνες. Αφαιρέστε το διαμορφωτή και σχεδιάστε: (a) Τη διαδρομή της ακτίνας μέσα από το διαμορφωτή. (a) Την υποθετική πορεία της ακτίνας αν δεν είχε μεσολαβήσει ο διαμορφωτής. Η αναδυόμενη ακτίνα είναι παράλληλη στην προσπίπτουσα και την προέκτασή της; Τώρα σχεδιάστε τις καθέτους στη διεπιφάνεια όπου εισήλθαν και αναδύθηκαν από το διαμορφωτή οι ακτίνες. Μετρήστε τις γωνίες πρόσπτωσης και διάθλασης (από τις καθέτους) και στις δύο διεπιφάνειες. Σχεδιάστε βελάκια στην ακτίνα αν έχετε αμφιβολίες για το ποια είναι η προσπίπτουσα ακτίνα στη δεύτερη διεπιφάνεια. Με ένα μοιρογνωμόνιο, μετρήστε και ονομάστε τις γωνίες πρόσπτωσης και διάθλασης των δύο διαθλάσεων. Το ποσοστό της διάθλασης στην πρώτη διεπιφάνεια είναι το ίδιο αλλά αντίστροφο στη δεύτερη; Σχεδιάστε κύκλους, όπως στο Πείραμα 13, γύρω από κάθε σημείο διάθλασης και σχεδιάστε και μετρήστε τις μισές χορδές στις καθέτους σε αυτά τα σημεία. Με τον τύπο: Δείκτης διάθλασης = Ημιτ. i/ημιτ. r ή ΜΙΣΗ ΧΟΡΔΗ i /ΜΙΣΗ ΧΟΡΔΗ r, βρείτε το δείκτη διάθλασης από τον αέρα στο πλαστικό και αντιστρόφως. Ποιος είναι μεγαλύτερος από 1; Ποιος είναι μικρότερος από 1? Μήπως το ένα είναι το αντίστροφο του άλλου; Αν ο δείκτης διάθλασης από τον αέρα στο γυαλί είναι 1,5, (δηλ. 3/2), ποιος είναι ο δείκτης διάθλασης από το γυαλί στον αέρα; Αν ο δείκτης διάθλασης από τον αέρα στο νερό είναι 1,33, (δηλ. 4/3), ποιος είναι ο δείκτης διάθλασης από το νερό στον αέρα; Χρησιμοποιήθηκε μόνο μία γωνία πρόσπτωσης (περίπου 10 ) για να βρεθεί ο δείκτης διάθλασης. Υπήρξε η ανάγκη χρησιμοποίησης κάποιας άλλης γωνίας πρόσπτωσης; Αν όχι, γιατί;
21 Πείραμα 15 Διάθλαση - Ολική εσωτερική ανάκλαση Με τον ημικυκλικό διαμορφωτή Ρυθμίστε τον ημικυκλικό διαμορφωτή έτσι ώστε μία μονή ακτίνα φωτός να χτυπά την κοίλη επιφάνεια στο σημείο της μεσοκαθέτου και να περνά από το κέντρο της λείας επιφάνειας. Παρατηρείται διάθλαση σε κάποια από τις δύο διεπιφάνειες; Αν όχι, γιατί; Σημειώστε τη θέση του κέντρου της λείας επιφάνειας του διαμορφωτή και στρέψτε τον ελαφρά γύρω από αυτό το σημείο μέχρι που η ακτίνα στο εσωτερικό του διαμορφωτή να συναντά την λεία πλευρά υπό γωνία. Η ακτίνα σε αυτή τη λεία όψη διαθλάται και απομακρύνεται ή πλησιάζει την κάθετο στο σημείο πρόσπτωσης; Στρέψτε ξανά το διαμορφωτή γύρω από το κεντρικό σημείο της λείας όψης του και παρατηρήστε την αναδυόμενη ακτίνα από τη νέα θέση. Συνεχίστε την περιστροφή του διαμορφωτή μέχρι που να μην αναδύεται διαθλασμένη ακτίνα από τη λεία επιφάνεια. Ποια είναι η γωνία πρόσπτωσης στη λεία επιφάνεια όταν συμβαίνει αυτό; Περιστρέψτε το διαμορφωτή λίγο περισσότερο. Τι συμβαίνει στην ακτίνα που είχε πριν διαθλαστεί; Στρέψτε το προς τα πίσω ξανά μέχρι η ακτίνα να πάψει να ανακλάται εσωτερικά και να έχουμε ξανά διάθλαση. Βρείτε και πάλι τη γωνία πρόσπτωσης στην οποία σταματάει η διάθλαση και ξεκινά η εσωτερική ανάκλαση. Μετρήστε αυτή τη γωνία πρόσπτωσης η οποία καλείται και ΚΡΙΣΙΜΗ ΓΩΝΙΑ γι' αυτό το υλικό. Ο ορισμός είναι: Η κρίσιμη γωνία για κάποιο υλικό είναι η γωνία πρόσπτωσης πέρα από την οποία μια φωτεινή ακτίνα, η οποία περνά από ένα πυκνό σε ένα ελαφρύ μέσο, δεν διαθλάται πια έξω από το μέσο, αλλά έχουμε το φαινόμενο της ολικής εσωτερικής ανάκλασης. Σχεδιάστε έναν κύκλο ακτίνας 100 mm γύρω από το σημείο πρόσπτωσης και καταγράψτε τις μισές χορδές της κρίσιμης γωνίας (λέγεται και ic). Υπολογίστε την αναλογία: μισή χορδή i/ακτίνα ή βρείτε το ημιτ. ic από την ακτίνα, κάποιο βιβλίο με μαθηματικούς πίνακες ή με κομπιουτεράκι. Χρησιμοποιώντας τα προηγούμενα πειραματικά σας αποτελέσματα, υπολογίστε: 1/δείκτης διαθλάσεως για ακρυλικό προς αέρα
22 Τι παρατηρείτε σχετικά με το: Μισή χορδή i/ακτίνα : ημιτ. ic :: 1/δείκτης διαθλάσεως για ακρυλικό προς αέρα Αν ο δείκτης διάθλασης από τον αέρα στο γυαλί είναι 1,5, (δηλ. 3/2), ποιο είναι το αντίστροφό του; Με τι ισούται τότε το ημίτονο από το γυαλί στον αέρα; Με τι ισούται τότε η κρίσιμη γωνία από το γυαλί στον αέρα; Αν ο δείκτης διάθλασης από τον αέρα στο νερό είναι 1,33, (δηλ. 4/3), ποιο είναι το αντίστροφό του; Με τι ισούται τότε η κρίσιμη γωνία από το νερό στον αέρα; Εάν υπάρχει η δυνατότητα, πάρτε ένα κομμάτι γυαλί και έναν ρηχό δίσκο με νερό και προβάλλετε επάνω τους διαδοχικά μία μονή ακτίνα. Βρείτε και τσεκάρετε τις κρίσιμες γωνίες για γυαλί προς αέρα και νερό προς αέρα. Εάν το γυαλί τοποθετηθεί μέσα σε νερό και έχουμε τη διεπιφάνεια γυαλί-νερό, η κρίσιμη γωνία θα εμφανιστεί κατά το πέρασμα από το νερό στο γυαλί ή από το γυαλί στο νερό. Ελέγξτε πειραματικά την απάντησή σας. Πώς χρησιμοποιείται η κρίσιμη γωνία ενός κομματιού ακρυλικού πλαστικού στην εύρεση του δείκτη διαθλάσεώς του;
23 Πείραμα 16 Διάθλαση - Ολική εσωτερική ανάκλαση Με τη βοήθεια των τριγωνικών πρισμάτων (α) Στοχεύστε μονή ακτίνα φωτός στην κοντύτερη πλευρά του ακρυλικού πρίσματος , έτσι ώστε η διαθλώμενη ακτίνα μέσα στο πρίσμα να συναντά την υποτείνουσα. Ρυθμίστε τις θέσεις του Κουτιού και του πρίσματος μέχρι να παρατηρηθεί το φαινόμενο της ολικής εσωτερικής ανάκλασης και η ακτίνα να αναδύεται από την τρίτη πλευρά. Καταγράψτε την πρώτη θέση στην οποία συμβαίνει αυτό και μετρήστε τη γωνία πρόσπτωσης από την κάθετο στην υποτείνουσα. Είναι ίδια με την κρίσιμη γωνία του προηγούμενου πειράματος; (β) Στοχεύστε τη μονή ακτίνα κατακόρυφα στην κοντύτερη πλευρά του ακρυλικού πρίσματος , έτσι ώστε η ακτίνα να χτυπάει την υποτείνουσα εκ των έσω. Έχουμε ανάκλαση; Καταγράψτε τις εισερχόμενες και εξερχόμενες ακτίνες, καθώς και τη θέση του πρίσματος. Στοχεύστε μία μονή ακτίνα κατακόρυφα στην υποτείνουσα του πρίσματος των 45, στο 1/4 περίπου της απόστασης από το ένα άκρο. Αυτή τη φορά η ακτίνα ανακλάται ολικά και εσωτερικά στο πρίσμα δύο φορές και επιστρέφει σε μια πορεία παράλληλη προς την αρχική, αλλά με αντίθετη διεύθυνση. Καταγράψτε τη θέση του πρίσματος και τη διαδρομή της ακτίνας μέσα από αυτό. (γ) Στοχεύστε 4 παράλληλες ακτίνες στην υποτείνουσα του πρίσματος των 45 (κοντά στο ένα άκρο), χρωματίστε διαδοχικά τις ακτίνες ("σκεπάζοντάς" τις με έγχρωμα φίλτρα) και χαράξτε τη θέση των διαφορετικά χρωματισμένων ακτίνων. Έχουν αναστραφεί οι θέσεις των ακτίνων από τις διπλές αντανακλάσεις; (δ) Στοχεύστε δύο παράλληλες ακτίνες σε δύο πρίσματα των 45, τοποθετημένα όπως στο διάγραμμα. Χρωματίστε διαδοχικά τις ακτίνες και χαράξτε την πορεία τους. Η τετραπλή ανάκλαση (διπλή σε κάθε πρίσμα) επαναφέρει τις ακτίνες στην αρχική τους θέση ή είναι ακόμα ανεστραμμένες; Ζεύγη πρισμάτων διαρρυθμισμένα με τέτοιο τρόπο χρησιμοποιούνται στα πρισματικά κιάλια, ούτως ώστε να μειώσουν το συνολικό μήκος του τηλεσκοπίου που φτάνει τα 0,5 με 0,75 μέτρα.
24 Πείραμα 17 Διάθλαση - Γωνία διπλής διάθλασης (Μηδενική παρέκκλιση) Στοχεύστε μια ακτίνα φωτός στη μία όψη του ισόπλευρου τριγωνικού πρίσματος ( ) έτσι ώστε η δέσμη να είναι περίπου παράλληλη με μια διπλανή πλευρά και η ακτίνα να εξέρχεται από την τρίτη πλευρά αφού έχει διαθλαστεί διπλά. Σημειώστε τη θέση του πρίσματος και τις διαδρομές των ακτίνων. Στοχεύστε την ακτίνα στο ίδιο σημείο της όψης του πρίσματος, αλλάζοντας όμως τη γωνία πρόσπτωσης. Παρατηρήστε την αλλαγή της διεύθυνσης της εξερχόμενης ακτίνας. Βρείτε τη θέση του πρίσματος και της ακτίνας που προκαλεί την μικρότερη απόκλιση αρχικής και τελικής θέσης στη δέσμη. Επαναλάβετε το πείραμα χρησιμοποιώντας το πρίσμα των 45 στη θέση Α και βρείτε τη γωνία μικρότερης απόκλισης. Επαναλάβετε το πείραμα χρησιμοποιώντας το πρίσμα των 90 στη θέση Α και βρείτε τη γωνία μικρότερης απόκλισης Επαναλάβετε το πείραμα χρησιμοποιώντας το πρίσμα των 30 στη θέση Α και βρείτε τη γωνία μικρότερης απόκλισης. Παραθέστε τα αποτελέσματά σας ως εξής: ΑΚΤΙΝΑ Α Β Γ ΓΩΝΙΑ ΠΡΟΣΠΤΩΣΗΣ ΓΩΝΙΑ ΑΝΑΚΛΑΣΗΣ Πώς επηρεάζει τη γωνία μικρότερης απόκλισης η γωνία του πρίσματος; Τι συμβαίνει όταν χρησιμοποιείται το 90' στη θέση Α;
25 Πείραμα 18 Διάθλαση - Διπλή διάθλαση παράλληλων ακτίνων (α) Όπως και στο προηγούμενο πείραμα, στοχεύστε μία μονή ακτίνα στο τριγωνικό πρίσμα. Ονομάστε τη γωνία στην κορυφή του πρίσματος γωνία Α και τη μία από τις δύο παρακείμενες ευθείες επίσης Α (βάση της γωνίας). Η διπλά διαθλασμένη ακτίνα πλησιάζει ή απομακρύνεται από τη βάση Α; Επαναλάβετε το πείραμα χρησιμοποιώντας ως γωνία Α την κάθε γωνία του κάθε πρίσματος. Η διεύθυνση της διάθλασης προς το μέρος της βάσης Α είναι ίδια για κάποια από τις γωνίες στη θέση Α; (β) Περάστε ένα ζεύγος παράλληλων ακτίνων μέσα από κάθε ένα από τα τριγωνικά πρίσματα διαδοχικά και παρατηρήστε τις εξερχόμενες ακτίνες. Οι εξερχόμενες ακτίνες είναι μεταξύ τους παράλληλες σε κάθε ένα από τα πρίσματα των 30, 45 και 60 ; Πείραμα 19 Διάθλαση - Διπλή διάθλαση με έγχρωμο σκεδασμό Προσαρμόστε το εξάρτημα διαμόρφωσης οπών για την πλατιά δέσμη. Περάστε μία πλατιά δέσμη μέσα από το ισόπλευρο πρίσμα, το οποίο πρέπει να προσαρμόσετε έτσι ώστε να επιτυγχάνεται η μέγιστη παρέκκλιση. Τοποθετήστε ένα λευκό χαρτόνι στη διαδρομή της ακτίνας. Η αρχική ακτίνα από το Κουτί είναι άχρωμη ή έγχρωμη; Υπάρχουν ενδείξεις χρώματος στην εξερχόμενη ακτίνα; Ποιο άκρο της ακτίνας είναι κόκκινο και ποιο μπλε; Εάν υπάρχουν και άλλα χρώματα εκτός του κόκκινου και του μπλε, καταγράψτε τη σειρά με την οποία εμφανίζονται. Ένα τέτοιο εκπέτασμα χρωμάτων, το οποίο προκαλείται από το σκεδασμό του λευκού φωτός λέγεται ΦΑΣΜΑ. Αυτό το φαινόμενο προκαλείται επειδή κάθε χρώμα καμπυλώνει σε ελαφρώς διαφορετικό βαθμό κατά τη διάθλαση. Όλα τα χρώματα μαζί συνθέτουν το λευκό φως και το πρίσμα μπορεί να τα ξεχωρίσει ξανά εξαιτίας αυτού του εκπληκτικού φαινομένου. Πείραμα 20 Διάθλαση - Απορρόφηση χρώματος με φίλτρα Με τη συσκευή ρυθμισμένη όπως και στο προηγούμενο πείραμα, τοποθετήστε ένα κόκκινο φίλτρο στην πλατιά οπή του Κουτιού. Τι συνέπειες έχει αυτό στο εξερχόμενο φάσμα; Αφαιρέστε το φίλτρο που βρίσκεται ανάμεσα στη πηγή του φωτός και το πρίσμα. Τώρα τοποθετήστε το φίλτρο έτσι ώστε η έγχρωμη διασκορπισμένη ακτίνα που εξέρχεται από το πρίσμα να περνά μέσα από το φίλτρο. Τι συμβαίνει με τα χρώματα που ΔΕΝ είναι κόκκινα; Επαναλάβετε αυτό το πείραμα και με τα υπόλοιπα φίλτρα. Πρώτα κάντε το πείραμα με ένα προς ένα τα φίλτρα και ύστερα δοκιμάστε διάφορα ζεύγη. Αντιγράψτε και συμπληρώστε τον παρακάτω πίνακα σημειώνοντας με τικ και σταυρούς τα κατάλληλα κουτιά.
26 ΚΟΚΚΙΝΟ ΦΙΛΤΡΟ ΜΠΛΕ ΦΙΛΤΡΟ ΚΙΤΡΙΝΟ ΦΙΛΤΡΟ ΦΙΛΤΡΟ ΚΤΛ. ΤΟ ΛΕΥΚΟ ΦΩΣ ΠΕΡΙΕΧΕΙ ΤΑ ΕΞΗΣ ΧΡΩΜΑΤΑ Εκπέμπει Απορροφά Εκπέμπει Απορροφά Εκπέμπει Απορροφά Εκπέμπει Απορροφά ΚΟΚΚΙΝΟ ΙΩΔΕΣ Πείραμα 21 Διάθλαση - Το πείραμα του Newton με το φάσμα Προβάλλετε ένα καθαρό φάσμα με το σκεδασμό του φωτός που προκαλείται από τη διπλή διάθλαση μέσω ενός πρίσματος Χρησιμοποιήστε στενή ακτίνα. Εκτελέστε το πείραμα του Isaac Newton τοποθετώντας ένα δεύτερο πρίσμα των 60 στη διαδρομή της δέσμης των σκεδασμένων χρωμάτων. Βεβαιωθείτε πως οι προσόψεις των δυο πρισμάτων είναι παράλληλες και σε κοντινή απόσταση. Με αυτόν τον τρόπο η ακτίνα διαθλάται πάλι προς την αντίθετη κατεύθυνση και επανενώνει τα χρώματα του φάσματος με αποτέλεσμα το σχηματισμό φωτός. Όταν ένας χρωματισμένος με όλα τα χρώματα του φάσματος δίσκος περιστρέφεται γρήγορα, το μάτι βλέπει μόνο ένα μίγμα αυτών των χρωμάτων και ο δίσκος φαίνεται σαν είναι λευκός. Ζητήστε από τον καθηγητή σας να σας δείξει ένα δίσκο του Newton
27 Πείραμα 22 Διάθλαση - Διπλή διάθλαση με αμφίκυρτο φακό Στο Πείραμα 18 ότι ένα μόνο πρίσμα δεν μπορεί να εστιάσει μια σειρά παράλληλων ακτίνων παραμένουν παράλληλες και μετά τη διάθλαση, παρόλο που παρατηρείται ένας μικρός σκεδασμός χρωμάτων. Ομάδες πρισμάτων, ωστόσο, μπορούν να εστιάσουν παράλληλες ευθείες σε ένα σημείο. Ρυθμίστε το Κουτί έτσι ώστε να παραχθούν δύο παράλληλες, πλατιές ακτίνες. Τοποθετήστε όπως στο διάγραμμα πρίσματα 60 και 30 και χαράξτε τη διαδρομή των εξερχόμενων ακτίνων. Επαναρυθμίστε τη θέση των πρισμάτων όπως φαίνεται στο παρακάτω διάγραμμα, αυτή τη φορά χρησιμοποιώντας δύο όμοια πρίσματα. (Δανειστείτε ένα από άλλο σετ.) Με αυτή τη μέθοδο μπορείτε να εστιάσετε δυο παράλληλες ακτίνες α και β στο ίδιο σημείο. Αν προστεθεί μια άλλη ακτίνα παράλληλη στην α και μία παράλληλη στη β εστιάζονται και αυτές στο ίδιο σημείο; Δοκιμάστε το και δείτε. Για να εστιάσετε όλες τις ακτίνες σε ένα σημείο, απαιτείται ένα διαφορετικής γωνίας πρίσμα για την γ και ένα για τη δ. Αυτό σημαίνει πως πρίσμα χρειάζεται εκεί όπου η γωνία αυξάνεται συνεχώς. Αυτό το αντικείμενο λέγεται ΦΑΚΟΣ. Στοχεύστε 4 παράλληλες ακτίνες στη μία όψη του λεπτότερου εκ των δύο φακών, όπως στο παρακάτω διάγραμμα. Καταγράψτε τη θέση του φακού, τη διαδρομή των ακτίνων και το εστιακό σημείο. Αν η εστιακή απόσταση ενός φακού είναι η απόσταση από το κέντρο του φακού μέχρι το εστιακό σημείο, ποια είναι η εστιακή απόσταση αυτού του φακού; Σε ένα ξεχωριστό φύλλο χαρτιού, βρείτε την εστιακή για το μεγαλύτερο φακό που βρίσκεται στο κουτί. Οι φακοί αυτού του σχήματος λέγονται Αμφίκυρτοι γιατί και οι δύο όψεις του σχηματίζουν εξόγκωμα προς τα έξω.
28 Πείραμα 23 Διάθλαση - Ακτίνα καμπυλότητας Χαράξτε το καμπύλο τμήμα της μίας όψης του λεπτότερου φακού στο χαρτί σας. Μετακινήστε την καμπυλωμένη επιφάνεια κατά μήκος της διαδρομής που χαράξατε, την οποία πρέπει να επεκτείνετε κάποιες φορές μέχρι να σχηματιστεί κύκλος. Μετρήστε τη διάμετρο του κύκλου και υπολογίστε την ακτίνα. Επαναλάβετε το πείραμα χρησιμοποιώντας το δεύτερο αμφίκυρτο φακό. Ποια είναι η ακτίνα του δεύτερου κύκλου; Κάθε μία από αυτές τις ακτίνες των κύκλων λέγεται Ακτίνα καμπυλότητας του συγκεκριμένου φακού, σύμφωνα με τον οποίο σχεδιάστηκε ο κύκλος. Χρησιμοποιώντας τα αποτελέσματα του Πειράματος 22, συγκρίνετε την ακτίνα καμπυλότητας κάθε φακού με την εστιακή του απόσταση. Πώς επηρεάζει η ακτίνα καμπυλότητας την εστιακή απόσταση; Αν απαιτείται φακός με εστιακή απόσταση 20 mm, ποια ακτίνα καμπυλότητας θα έπρεπε να χρησιμοποιηθεί; Η καμπυλότητα ενός φακού δεν χρειάζεται να είναι είναι η ίδια και στις δύο όψεις. Ένας φακός μπορεί να έχει το ίδιο σχήμα με αυτούς στον εξοπλισμό του κουτιού, ωστόσο κάποιοι είναι σχηματισμένοι με τρόπο παρόμοιο με αυτόν του παρακάτω διαγράμματος. Η καμπυλότητα στη μία όψη μπορεί να μην είναι ίδια με αυτή στην άλλη όψη, και η μία όψη μπορεί να είναι κυρτή (να εξέχει προς τα έξω) ενώ η άλλη κοίλη (προς τα μέσα). Ο παρακάτω τύπος δείχνει τη σχέση μεταξύ του δείκτη διάθλασης, της εστιακής απόστασης και της ακτίνας καμπυλότητας: Όπου:-1/f=(n-1) [1/R1 + 1/R2] t- εστιακή απόσταση του φακού n - δείκτης διάθλασης του υλικού R1 - ακτίνα καμπυλότητας της μίας όψης R2 - ακτίνα καμπυλότητας της άλλης όψης Ποιες είναι οι τιμές των R1 και R2 για τους δύο αμφίκυρτους φακούς του εξοπλισμού; Χρησιμοποιήστε μία από αυτές τις σειρές τιμών στον παραπάνω τύπο και υπολογίστε την τιμή του n για το πλαστικό υλικό του φακού. Χρησιμοποιήστε τη δεύτερη σειρά τιμών για να επαληθεύστε την τιμή του n γι' αυτό το υλικό. (Και οι δύο φακοί είναι από το ίδιο υλικό). Πώς συγκρίνεται η τιμή του n που υπολογίσατε με την τιμή που εξήχθη ως αποτέλεσμα του πειράματος 13;
29 Πείραμα 24 Διάθλαση - Εστιακή γραμμή ή Εστιακό επίπεδο ενός αμφίκυρτου φακού Τοποθετήστε έναν αμφίκυρτο φακό σε ένα φύλλο χαρτί και χαράξτε το περίγραμμά του. Χωρίς να αλλάξετε τη θέση του φακού, ρυθμίστε το Κουτί φωτός να προβάλλει δύο παράλληλες ακτίνες και μετακινήστε το έτσι ώστε να (α) Προβάλλει τις ακτίνες παράλληλα στον άξονα συμμετρίας του φακού. (β) Προβάλλει τις ακτίνες υπό μικρή γωνία σε σχέση με τον άξονα, αλλά κατευθείαν στο κέντρο του φακού. Πρώτα στην αριστερή πλευρά και μετά στη δεξιά. (γ) Προβάλλει τις ακτίνες υπό μεγαλύτερες γωνίες ως προς τον άξονα, αλλά πάντα στο κέντρο του φακού. Σχεδιάστε μια γραμμή ενώνοντας αυτή τη σειρά των εστιακών σημείων (FOCI). Τα σημεία αυτά σχηματίζουν ευθεία ή καμπύλη γραμμή; Αν υποθέσουμε ότι τα ζεύγη των παράλληλων ακτίνων προέρχονται από μακρινά αστέρια και περνούν μέσα από τον φακό μας, πού θα έπρεπε να τοποθετηθεί το φωτογραφικό φιλμ ώστε τα είδωλα των αστεριών να είναι εστιασμένα; Η θέση στην οποία παράλληλες ακτίνες, υπό οποιαδήποτε γωνία, εστιάζονται ονομάζεται Εστιακή επιφάνεια του φακού. Μερικές φωτογρ. μηχανές έχουν ένα "ρολό" το οποίο ανοίγει και κλείνει πάνω από αυτόν. Άλλες (οι οποίες έχουν αποσπώμενους ή περιορισμένου χρόνου ζωής φακούς) έχουν ένα ρολό το οποίο καλύπτει τον φακό όλη την ώρα, εκτός από τη στιγμή που ανοίγει για να ληφθεί η φωτογραφία. Αυτό το κάλυμμα λέγεται κάλυμμα Εστιακής επιφάνειας. Πείραμα 25 Διάθλαση - Χρωματική εκτροπή με αμφίκυρτο φακό Περάστε ακτίνες μέσα από τα εξωτερικά άκρα ενός αμφίκυρτου φακού. Παρατηρήστε ότι τα άκρα χρωματίζονται μετά τη διάθλαση. Ποιο άκρο είναι κόκκινο και ποιο μπλε; Περάστε δύο παράλληλες ακτίνες από τα εξωτερικά άκρα του φακού, έτσι ώστε να εστιαστούν στο ίδιο σημείο. Τοποθετήστε μια ορθογώνια λευκή κάρτα κοντά στο σημείο της εστίασης και μετακινήστε τη κοντά και μακριά από τον φακό. Σε ποια θέση της κάρτας σε σχέση με τον φακό, το είδωλο στην κάρτα έχει κοκκινωπό κέντρο και μπλε άκρες; Εξηγήστε για τα φτηνά κιάλια και τηλεσκόπια εμφανίζουν έγχρωμα περιγράμματα γύρω από τα είδωλα που παράγουν. Οι κατασκευαστές φακών για φωτογραφικές, τηλεσκόπια, κτλ. μπαίνουν σε μεγαλύτερο κόπο καθώς χρησιμοποιούν συνδυασμούς φακών με διαφορετικές καμπυλότητες, οι οποίοι είναι κατασκευασμένοι με γυαλιά διαφορετικών δεικτών διάθλασης, έτσι ώστε να εξασφαλίσουν ότι τα χρώματα θα εστιαστούν όλα στο ίδιο σημείο. Ένας συνδυασμός φακών, ο οποίος έχει όλα εκείνα τα σχεδιαστικά χαρακτηριστικά για να το κάνει αυτό λέγεται Αχρωματικός φακός.
30 Πείραμα 26 Διάθλαση - Αμφίκοιλοι φακοί Επιλέξτε τον φακό που έχει δύο κοίλες όψεις, οι οποίες καμπυλώνουν η μία προς την άλλη, κάτι που καθιστά τον φακό λεπτότερο στο κέντρο παρά στα άκρα του. Αυτό είναι ο Αμφίκοιλος φακός. Στοχεύστε 4 παράλληλες ακτίνες φωτός στον φακό, παράλληλα στον άξονα συμμετρίας του. Χαράξτε τη θέση του φακού καθώς και τις εισερχόμενες και εξερχόμενες ακτίνες. Αφαιρέστε τον φακό και επεκτείνετε τις γραμμές των εξερχόμενων ακτίνων προς τα πίσω, διαμέσου της θέσης του φακού και προς το Κουτί. Φαίνονται σαν να πηγάζουν από το ίδιο σημείο ή από περισσότερα; Ο αμφίκοιλος φακός είναι Αποκλίνων φακός και έχει Αρνητική εστιακή απόσταση, γιατί το σημείο απ' το οποίο φαίνεται να πηγάζει η ακτίνα δεν βρίσκεται κάτω από τον φακό αλλά μεταξύ της πηγής και του φακού. Ποια είναι η εστιακή απόσταση του φακού που χρησιμοποιήθηκε; Αυτοί οι φακοί είναι ιδιαίτερα χρήσιμοι στις περιπτώσεις πρεσβυωπίας. Αυτή είναι μια πάθηση κατά την οποία το είδωλο που σχηματίζει ο φακός του ματιού δεν ανταποκρίνεται στις απαιτήσεις του φωτο-ευαίσθητου αμφιβληστροειδούς. Αυτοί οι φακοί χρησιμοποιούνται επίσης και για να αυξήσουν την εστιακή απόσταση των συγκεντρωτικών φακών. Προσπαθήστε να θυμηθείτε τη μέθοδο που παρουσιάστηκε στην αρχή αυτού του οδηγού, με την οποία μπορείτε να προβάλλετε μια επιμήκη, συγκεντρωτική ακτίνα από το Κουτί. Πείραμα 27 Παρατήρηση χρωμάτων - Χρώματα αντικειμένων Στο Πείραμα 20, το λευκό φως μετατράπηκε σε φάσμα με τα χρώματα της ίριδας περνώντας μέσα από ένα πρίσμα. Τοποθετούνται διάφορα φίλτρα στην ακτίνα για να δούμε ποια από τα χρώματα εκπέμπονται από τα φίλτρα και ποια απορροφούνται. Το πίσω άκρο του Κουτιού έχει περιστρεφόμενους καθρέφτες και είναι έτσι σχεδιασμένο ώστε να φέρει τα έγχρωμα φίλτρα σε 3 διαφορετικές θέσεις. Χρησιμοποιώντας το πίσω άκρο του Κουτιού (όχι τους καθρέφτες) προβάλλετε μια δέσμη λευκού φωτός σε κάθε έναν από τους χρωματιστούς πίνακες του εξοπλισμού. Χρωματίστε τις προσπίπτουσες ακτίνες τοποθετώντας φίλτρα στις κατάλληλες οπές και παρατηρήστε τα διαφορετικά χρώματα των πινάκων όταν φωτίζονται με διαφόρων χρωμάτων ακτίνες. Αντιγράψτε και συμπληρώστε τον παρακάτω πίνακα. Το χρώμα ενός αντικειμένου εξηγείται από το θεώρημα ότι το λευκό φως αποτελείται από πολλά χρώματα και ένα λευκό αντικείμενο αντανακλά όλα αυτά τα χρώματα. Ένα κόκκινο
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα. Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ
 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Φύση του φωτός. Θεωρούμε ότι το φως έχει διττή φύση: διαταραχή που διαδίδεται στο χώρο. μήκος κύματος φωτός. συχνότητα φωτός
 Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ανάκλαση. Κάτοπτρα. Διάθλαση. Ολική ανάκλαση. Φαινόμενη ανύψωση αντικειμένου. Μετατόπιση ακτίνας. Πρίσματα
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Ανάκλαση Κάτοπτρα Διάθλαση Ολική ανάκλαση Φαινόμενη ανύψωση αντικειμένου Μετατόπιση ακτίνας Πρίσματα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ - Ανάκλαση Επιστροφή σε «γεωμετρική οπτική» Ανάκλαση φωτός ονομάζεται
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Ανάκλαση Κάτοπτρα Διάθλαση Ολική ανάκλαση Φαινόμενη ανύψωση αντικειμένου Μετατόπιση ακτίνας Πρίσματα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ - Ανάκλαση Επιστροφή σε «γεωμετρική οπτική» Ανάκλαση φωτός ονομάζεται
ΠΟΥ ΔΙΑΔΙΔΕΤΑΙ ΤΟ ΦΩΣ
 1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
EΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΒΛΗΜΑΤΑ ΣΤΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ ΟΛΙΚΗ ΑΝΑΚΛΑΣΗ
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
1. Ιδιότητες φακών. 1 Λεπτοί φακοί. 2 Απριλίου Βασικές έννοιες
 . Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
. Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34
 Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
Μελέτη συστήματος φακών με τη Μέθοδο του Newton
 Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
ΑΝΑΚΛΑΣΗ ΕΠΙΠΕΔΟΙ ΚΑΘΡΕΦΤΕΣ ΕΙΔΩΛΟ
 1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΑΝΑΚΛΑΣΗ ΕΠΙΠΕΔΟΙ ΚΑΘΡΕΦΤΕΣ ΕΙΔΩΛΟ Α. ΣΤΟΧΟΙ Η ικανότητα συναρμολόγησης μιας απλής πειραματικής διάταξης. Η ικανότητα χρήσης καθρέφτη και πηγής laser. Η κατανόηση
1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΑΝΑΚΛΑΣΗ ΕΠΙΠΕΔΟΙ ΚΑΘΡΕΦΤΕΣ ΕΙΔΩΛΟ Α. ΣΤΟΧΟΙ Η ικανότητα συναρμολόγησης μιας απλής πειραματικής διάταξης. Η ικανότητα χρήσης καθρέφτη και πηγής laser. Η κατανόηση
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση d=0.20 mm είναι τοποθετημένο σε απόσταση =1,20 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση d=0.20 mm είναι τοποθετημένο σε απόσταση =1,20 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές
ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
Σχηματισμός ειδώλων. Εισαγωγή
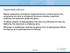 Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. G. Mitsou
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
ΓΓ/Μ ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ. Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα
 ΓΓ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ' Τάξη
ΓΓ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ' Τάξη
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ
 ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2017 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2017 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ
 ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2016 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2016 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΟ είναι η προσπίπτουσα ακτίνα. Ο είναι η διαθλωµένη ακτίνα. ΟΚ είναι η κάθετη στο σηµείο πρόσπτωσης. α : είναι η γωνία πρόσπτωσης δ : είναι η γωνία
 1 2 Ανάκλασης Νόµος Ανάκλασης Ακτίνα πρόσπτωσης Κάθετη Ακτίνα ανάκλασης Νόµος Ανάκλασης: η γωνία πρόσπτωσης (α) ισούται µε τη γωνία ανάκλασης (β) α = β α β Επίπεδο κάτοπτρο ε α β α: Γωνίαπρόσπτωσης β:γωνίαανάκλασης
1 2 Ανάκλασης Νόµος Ανάκλασης Ακτίνα πρόσπτωσης Κάθετη Ακτίνα ανάκλασης Νόµος Ανάκλασης: η γωνία πρόσπτωσης (α) ισούται µε τη γωνία ανάκλασης (β) α = β α β Επίπεδο κάτοπτρο ε α β α: Γωνίαπρόσπτωσης β:γωνίαανάκλασης
Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ
 ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΑ ΜΑΘΗΤΩΝ 1)... 2)... 3)... ΗΜΕΡΟΜΗΝΙΑ : Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ Με το πείραµα αυτό θα προσδιορίσουµε: Σκοπός
ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΑ ΜΑΘΗΤΩΝ 1)... 2)... 3)... ΗΜΕΡΟΜΗΝΙΑ : Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ Με το πείραµα αυτό θα προσδιορίσουµε: Σκοπός
Ο15. Κοίλα κάτοπτρα. 2. Θεωρία. 2.1 Γεωμετρική Οπτική
 Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗ 25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Το πρόβλημα Ένας φίλος σας βρήκε ένα μικρό, πολύ όμορφο τεμάχιο διαφανούς στερεού και ζητά τη γνώμη
ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗ 25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Το πρόβλημα Ένας φίλος σας βρήκε ένα μικρό, πολύ όμορφο τεμάχιο διαφανούς στερεού και ζητά τη γνώμη
7.1 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ
 7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
ΔΙΕΡΕΥΝΗΤΙΚΗ ΜΑΘΗΣΗ Α.Ε. ΓΕΩΡΓΙΟΥ ΒΛΑΧΟΥ 13, 11525 ΑΘΗΝΑ ΤΗΛ 210 6779 800 ΦΑΞ 210 6779 803 WWW.WHY.GR EMAIL: WHY@WHY.GR
 Α.Ε. ΓΕΩΡΓΙΟΥ ΒΛΑΧΟΥ 13, 11525 ΑΘΗΝΑ ΤΗΛ 210 6779 800 ΦΑΞ 210 6779 803 WWW.WHY.GR EMAIL: WHY@WHY.GR 2 ΠΕΡΙΕΧΟΜΕΝΑ ΕΓΧΕΙΡΙΔΙΟΥ ΕΝΟΤΗΤΑ Σελ. ΠΕΡΙΕΧΟΜΕΝΑ ΠΑΚΕΤΟΥ 2 ΜΕΘΟΔΟΛΟΓΙΚΟ ΛΕΞΙΛΟΓΙΟ 3-4 ΕΙΔΙΚΟ ΛΕΞΙΛΟΓΙΟ
Α.Ε. ΓΕΩΡΓΙΟΥ ΒΛΑΧΟΥ 13, 11525 ΑΘΗΝΑ ΤΗΛ 210 6779 800 ΦΑΞ 210 6779 803 WWW.WHY.GR EMAIL: WHY@WHY.GR 2 ΠΕΡΙΕΧΟΜΕΝΑ ΕΓΧΕΙΡΙΔΙΟΥ ΕΝΟΤΗΤΑ Σελ. ΠΕΡΙΕΧΟΜΕΝΑ ΠΑΚΕΤΟΥ 2 ΜΕΘΟΔΟΛΟΓΙΚΟ ΛΕΞΙΛΟΓΙΟ 3-4 ΕΙΔΙΚΟ ΛΕΞΙΛΟΓΙΟ
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ 5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2.. 3.. ΜΟΝΑΔΕΣ: Το πρόβλημα Μελέτη οπτικών ιδιοτήτων διαφανούς υλικού με τη βοήθεια πηγής φωτός laser Είστε στο δωμάτιό
ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ 5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2.. 3.. ΜΟΝΑΔΕΣ: Το πρόβλημα Μελέτη οπτικών ιδιοτήτων διαφανούς υλικού με τη βοήθεια πηγής φωτός laser Είστε στο δωμάτιό
Κυματική οπτική. Συμβολή Περίθλαση Πόλωση
 Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Εισαγωγή στο φως. Εισαγωγή
 Εισαγωγή στο φως Το φως είναι απαραίτητο για όλες σχεδόν τις μορφές ζωής στη Γη. (Σήμερα γνωρίζουμε ότι) Το φως είναι μια μορφή ηλεκτρομαγνητικής ακτινοβολίας. Μέσω του φωτός μεταφέρεται ενέργεια από την
Εισαγωγή στο φως Το φως είναι απαραίτητο για όλες σχεδόν τις μορφές ζωής στη Γη. (Σήμερα γνωρίζουμε ότι) Το φως είναι μια μορφή ηλεκτρομαγνητικής ακτινοβολίας. Μέσω του φωτός μεταφέρεται ενέργεια από την
Εφαρμοσμένη Οπτική. Γεωμετρική Οπτική
 Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
ΑΣΚΗΣΗ 8 Μελέτη φακών
 Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης
 3 Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης Μέθοδος Σε σώμα διαφανές ημικυλινδρικού σχήματος είναι εύκολο να επιβεβαιωθεί ο νόμος του Sell και να εφαρμοστεί
3 Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης Μέθοδος Σε σώμα διαφανές ημικυλινδρικού σχήματος είναι εύκολο να επιβεβαιωθεί ο νόμος του Sell και να εφαρμοστεί
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Σφάλματα φακών (Σφαιρικό - Χρωματικό).
 O12 Σφάλματα φακών (Σφαιρικό - Χρωματικό). 1. Σκοπός Στην άσκηση αυτή υπολογίζονται πειραματικά δυο από τα πιο σημαντικά οπτικά σφάλματα (η αποκλίσεις) που παρουσιάζονται όταν φωτεινές ακτίνες διέλθουν
O12 Σφάλματα φακών (Σφαιρικό - Χρωματικό). 1. Σκοπός Στην άσκηση αυτή υπολογίζονται πειραματικά δυο από τα πιο σημαντικά οπτικά σφάλματα (η αποκλίσεις) που παρουσιάζονται όταν φωτεινές ακτίνες διέλθουν
1. Σκοπός της άσκησης... 1. 2. Στοιχεία θεωρίας... 1. 2.1 Γεωμετρική οπτική... 1. 2.2 Ο νόμος της ανάκλασης... 1. 2.3 Ο νόμος της διάθλασης...
 1. Λεπτοί Φακοί Σελίδα 1. Σκοπός της άσκησης.... 1 2. Στοιχεία θεωρίας... 1 2.1 Γεωμετρική οπτική... 1 2.2 Ο νόμος της ανάκλασης... 1 2.3 Ο νόμος της διάθλασης... 2 2.4 Είδωλα & παραξονική προσέγγιση...
1. Λεπτοί Φακοί Σελίδα 1. Σκοπός της άσκησης.... 1 2. Στοιχεία θεωρίας... 1 2.1 Γεωμετρική οπτική... 1 2.2 Ο νόμος της ανάκλασης... 1 2.3 Ο νόμος της διάθλασης... 2 2.4 Είδωλα & παραξονική προσέγγιση...
Φυσική Εικόνας & Ήχου Ι (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 3: Γενικά περί φακών Αθανάσιος Αρααντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών Τεχνών Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 3: Γενικά περί φακών Αθανάσιος Αρααντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών Τεχνών Το περιεχόμενο
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος.
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
Φυσική των οφθαλμών και της όρασης. Κική Θεοδώρου
 Φυσική των οφθαλμών και της όρασης Κική Θεοδώρου Περιεχόμενα Στοιχεία Γεωμετρικής Οπτικής Ανατομία του Οφθαλμού Αμφιβληστροειδής Ο ανιχνευτής φωτός του οφθαλμού Το κατώφλι της όρασης Φαινόμενα περίθλασης
Φυσική των οφθαλμών και της όρασης Κική Θεοδώρου Περιεχόμενα Στοιχεία Γεωμετρικής Οπτικής Ανατομία του Οφθαλμού Αμφιβληστροειδής Ο ανιχνευτής φωτός του οφθαλμού Το κατώφλι της όρασης Φαινόμενα περίθλασης
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΕΚΦΕ ΕΥΒΟΙΑΣ. ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ
 ΕΚΦΕ ΕΥΒΟΙΑΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 Διάρκεια: 60 min ΣΑΒΒΑΤΟ 06/12/2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Μαθητές: Σχολική Μονάδα 1.
ΕΚΦΕ ΕΥΒΟΙΑΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 Διάρκεια: 60 min ΣΑΒΒΑΤΟ 06/12/2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Μαθητές: Σχολική Μονάδα 1.
ΓΓ/Μ ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ. Τεύχος 5ο: Φύση και Διάδοση φωτός Ανάκλαση του φωτός
 ΓΓ/Μ5 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 5ο: Φύση και Διάδοση φωτός Ανάκλαση του φωτός ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ'
ΓΓ/Μ5 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 5ο: Φύση και Διάδοση φωτός Ανάκλαση του φωτός ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ'
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΦΩΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 04-05 ΠΟΡΕΙΑ ΑΚΤΙΝΑΣ. Β. Στο διπλανό
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΦΩΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 04-05 ΠΟΡΕΙΑ ΑΚΤΙΝΑΣ. Β. Στο διπλανό
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Όλα τα θέματα των εξετάσεων έως και το 2014 σε συμβολή, στάσιμα, ηλεκτρομαγνητικά κύματα, ανάκλαση - διάθλαση ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ
 ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ Ερωτήσεις Πολλαπλής επιλογής 1. To βάθος µιας πισίνας φαίνεται από παρατηρητή εκτός της πισίνας µικρότερο από το πραγµατικό, λόγω του φαινοµένου της: α. ανάκλασης β. διάθλασης γ. διάχυσης
ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ Ερωτήσεις Πολλαπλής επιλογής 1. To βάθος µιας πισίνας φαίνεται από παρατηρητή εκτός της πισίνας µικρότερο από το πραγµατικό, λόγω του φαινοµένου της: α. ανάκλασης β. διάθλασης γ. διάχυσης
γ) Να σχεδιάσετε τις γραφικές παραστάσεις απομάκρυνσης - χρόνου, για τα σημεία Α, Β και Γ, τα οποία απέχουν από το ελεύθερο άκρο αντίστοιχα,,
 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
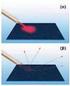 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
Generated by Foxit PDF Creator Foxit Software http://www.foxitsoftware.com For evaluation only. ΑΣΚΗΣΗ 10 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ
 ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
Μέτρηση Γωνίας Brewster Νόμοι του Fresnel
 Μέτρηση Γωνίας Bewse Νόμοι του Fesnel [] ΕΙΣΑΓΩΓΗ Στο πείραμα, δέσμη φωτός από διοδικό lase ανακλάται στην επίπεδη επιφάνεια ενός ακρυλικού ημι-κυκλικού φακού, πολώνεται γραμμικά και ανιχνεύεται από ένα
Μέτρηση Γωνίας Bewse Νόμοι του Fesnel [] ΕΙΣΑΓΩΓΗ Στο πείραμα, δέσμη φωτός από διοδικό lase ανακλάται στην επίπεδη επιφάνεια ενός ακρυλικού ημι-κυκλικού φακού, πολώνεται γραμμικά και ανιχνεύεται από ένα
Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell)
 Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell) 1. Σκοπός Αξιοποιώντας τις μετρήσεις των γωνιών πρόσπτωσης, διάθλασης α και δ αντίστοιχα μίας πολύ στενής φωτεινής δέσμης
Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell) 1. Σκοπός Αξιοποιώντας τις μετρήσεις των γωνιών πρόσπτωσης, διάθλασης α και δ αντίστοιχα μίας πολύ στενής φωτεινής δέσμης
Φυσική IΙ. Ενότητα 13: Γεωμετρική οπτική. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
Γεωμετρική Οπτική. Πρόκειται δηλαδή για μια ισοφασική επιφάνεια που ονομάζεται μέτωπο κύματος.
 Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 91 9. Άσκηση 9 ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό. 9.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε τα φαινόµενα
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 91 9. Άσκηση 9 ιάθλαση. Ολική ανάκλαση. ιάδοση µέσα σε κυµατοδηγό. 9.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε τα φαινόµενα
Να αιτιολογήσετε την απάντησή σας. Μονάδες 5
 2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
Μάθημα 4.10: Οπτικά Αποθηκευτικά Μέσα
 Κεφάλαιο 4 ο Ο Προσωπικός Υπολογιστής Μάθημα 4.10: Οπτικά Αποθηκευτικά Μέσα Όταν ολοκληρώσεις το κεφάλαιο θα μπορείς: Να εξηγείς τις αρχές λειτουργίας των οπτικών αποθηκευτικών μέσων. Να περιγράφεις τον
Κεφάλαιο 4 ο Ο Προσωπικός Υπολογιστής Μάθημα 4.10: Οπτικά Αποθηκευτικά Μέσα Όταν ολοκληρώσεις το κεφάλαιο θα μπορείς: Να εξηγείς τις αρχές λειτουργίας των οπτικών αποθηκευτικών μέσων. Να περιγράφεις τον
ΣΤΕΡΕΟΣΚΟΠΙΚΕΣ ΕΙΚΟΝΕΣ
 ΣΤΕΡΕΟΣΚΟΠΙΚΕΣ ΕΙΚΟΝΕΣ Η προοπτική εικόνα, είναι, όπως είναι γνωστό, η προβολή ενός χωρικού αντικειμένου, σε ένα επίπεδο, με κέντρο προβολής, το μάτι του παρατηρητή. Η εικόνα αυτή, θεωρούμε ότι αντιστοιχεί
ΣΤΕΡΕΟΣΚΟΠΙΚΕΣ ΕΙΚΟΝΕΣ Η προοπτική εικόνα, είναι, όπως είναι γνωστό, η προβολή ενός χωρικού αντικειμένου, σε ένα επίπεδο, με κέντρο προβολής, το μάτι του παρατηρητή. Η εικόνα αυτή, θεωρούμε ότι αντιστοιχεί
Αρκετές φορές θα έχεις τυφλώσει τους φίλους σου με τον ήλιο. Μπορείς να εξηγήσεις:
 ΠΑΡ. 7.1: ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ ΣΤΌΧΟΙ: Θα πρέπει ο μαθητής: 1) Να διακρίνει το φαινόμενο της ανάκλασης και της διάθλασης στη διαχωριστική επιφάνεια ενός υγρού από τον αέρα και να συνδέσοει το φαινόμενο με
ΠΑΡ. 7.1: ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ ΣΤΌΧΟΙ: Θα πρέπει ο μαθητής: 1) Να διακρίνει το φαινόμενο της ανάκλασης και της διάθλασης στη διαχωριστική επιφάνεια ενός υγρού από τον αέρα και να συνδέσοει το φαινόμενο με
ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ. Ηλεκτροστατικοί και Μαγνητικοί Φακοί Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών
 ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΓΥΑΛΙΝΟΙ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΟΙ ΦΑΚΟΙ Οι φακοί χρησιμοποιούνται για να εκτρέψουν μία
ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΓΥΑΛΙΝΟΙ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΟΙ ΦΑΚΟΙ Οι φακοί χρησιμοποιούνται για να εκτρέψουν μία
Ο μαθητής (σχεδιαστής) πρέπει να αναπτύξει την ικανότητα επικοινωνίας, με τη βοήθεια σχεδίων ή σκίτσων.
 ΓΡΑΦΙΚΗ ΕΠΙΚΟΙΝΩΝΙΑ Η Γραφική Επικοινωνία αναφέρεται στις γραφικές δεξιότητες και τεχνικές που χρησιμοποιούνται στην Τεχνολογία. Περιλαμβάνει σχέδιο, χρήση χρωμάτων, καταχώρηση πληροφοριών και παρουσίαση
ΓΡΑΦΙΚΗ ΕΠΙΚΟΙΝΩΝΙΑ Η Γραφική Επικοινωνία αναφέρεται στις γραφικές δεξιότητες και τεχνικές που χρησιμοποιούνται στην Τεχνολογία. Περιλαμβάνει σχέδιο, χρήση χρωμάτων, καταχώρηση πληροφοριών και παρουσίαση
Φυσικά Μεγέθη Μονάδες Μέτρησης
 ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
10. Το ορατό φως έχει μήκη κύματος στο κενό που κυμαίνονται περίπου από: α nm β. 400nm - 600nm γ. 400nm - 700nm δ. 700nm nm.
 ΚΕΦΑΛΑΙΟ 1 ΤΟ ΦΩΣ ΓΡΗΓΟΡΗ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑ - ΑΣΚΗΣΕΙΣ 1. Με τον όρο ότι το φως έχει διπλή φύση εννοούμε ότι: α. είναι εγκάρσιο κύμα. β. αποτελείται από μικρά σωματίδια. γ. συμπεριφέρεται σαν κύμα και σαν
ΚΕΦΑΛΑΙΟ 1 ΤΟ ΦΩΣ ΓΡΗΓΟΡΗ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑ - ΑΣΚΗΣΕΙΣ 1. Με τον όρο ότι το φως έχει διπλή φύση εννοούμε ότι: α. είναι εγκάρσιο κύμα. β. αποτελείται από μικρά σωματίδια. γ. συμπεριφέρεται σαν κύμα και σαν
Q 40 th International Physics Olympiad, Merida, Mexico, July 2009
 ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΟΥ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΦΩΤΟΣ ASER ΥΛΙΚΑ ΚΑΙ ΟΡΓΑΝΑ Επιπρόσθετα με τα υλικά 1), 2) και 3), αναμένεται να χρησιμοποιήσετε τα ακόλουθα: 4) Φακός ενσωματωμένος μέσα σε
ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΟΥ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΦΩΤΟΣ ASER ΥΛΙΚΑ ΚΑΙ ΟΡΓΑΝΑ Επιπρόσθετα με τα υλικά 1), 2) και 3), αναμένεται να χρησιμοποιήσετε τα ακόλουθα: 4) Φακός ενσωματωμένος μέσα σε
Q 40 th International Physics Olympiad, Merida, Mexico, July 2009
 ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 2 ΔΕΙΚΤΗΣ ΔΙΑΘΛΑΣΗΣ ΚΡΥΣΤΑΛΛΟΥ (MCA) Σκοπός αυτού του πειράματος είναι ο υπολογισμός του δείκτη διάθλασης ενός κρυσταλλικού υλικού (mica). ΟΡΓΑΝΑ ΚΑΙ ΥΛΙΚΑ Επιπρόσθετα από τα υλικά
ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 2 ΔΕΙΚΤΗΣ ΔΙΑΘΛΑΣΗΣ ΚΡΥΣΤΑΛΛΟΥ (MCA) Σκοπός αυτού του πειράματος είναι ο υπολογισμός του δείκτη διάθλασης ενός κρυσταλλικού υλικού (mica). ΟΡΓΑΝΑ ΚΑΙ ΥΛΙΚΑ Επιπρόσθετα από τα υλικά
sin 2 n = sin A 2 sin 2 2 n = sin A = sin = cos
 1 Σκοπός Βαθμός 9.5. Ηθελε να γραψω καλύτερα το 9 ερωτημα. Σκοπός αυτής της εργαστηριακής άσκησης είναι η μελέτη της ανάκλασης, διάθλασης και πόλωσης του φωτός. Προσδιορίζουμε επίσης τον δείκτη διάθλασης
1 Σκοπός Βαθμός 9.5. Ηθελε να γραψω καλύτερα το 9 ερωτημα. Σκοπός αυτής της εργαστηριακής άσκησης είναι η μελέτη της ανάκλασης, διάθλασης και πόλωσης του φωτός. Προσδιορίζουμε επίσης τον δείκτη διάθλασης
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
ΘΕΜΑ Β Β.1 Α) Μονάδες 4 Μονάδες 8 Β.2 Α) Μονάδες 4 Μονάδες 9
 Β.1 O δείκτης διάθλασης διαφανούς υλικού αποκλείεται να έχει τιμή: α. 0,8 β. 1, γ. 1,4 Β. Το ηλεκτρόνιο στο άτομο του υδρογόνου, έχει κινητική ενέργεια Κ, ηλεκτρική δυναμική ενέργεια U και ολική ενέργεια
Β.1 O δείκτης διάθλασης διαφανούς υλικού αποκλείεται να έχει τιμή: α. 0,8 β. 1, γ. 1,4 Β. Το ηλεκτρόνιο στο άτομο του υδρογόνου, έχει κινητική ενέργεια Κ, ηλεκτρική δυναμική ενέργεια U και ολική ενέργεια
4. Ανάκλαση & Διάθλαση του Φωτός
 4. Ανάκλαση & Διάθλαση του Φωτός Σελίδα 1. Σκοπός της άσκησης... 1. Στοιχεία θεωρίας... 1.1 Ανάκλαση & διάθλαση του φωτός: κρίσιμη γωνία πρόσπτωσης... 1. Συντελεστές ανακλαστικότητας & διαπερατότητας φωτεινής
4. Ανάκλαση & Διάθλαση του Φωτός Σελίδα 1. Σκοπός της άσκησης... 1. Στοιχεία θεωρίας... 1.1 Ανάκλαση & διάθλαση του φωτός: κρίσιμη γωνία πρόσπτωσης... 1. Συντελεστές ανακλαστικότητας & διαπερατότητας φωτεινής
ΟΡΟΣΗΜΟ ΓΛΥΦΑΔΑΣ. 7.1 Τι είναι το ταλαντούμενο ηλεκτρικό δίπολο; Πως παράγεται ένα ηλεκτρομαγνητικό
 ΚΕΦΑΛΑΙΟ 2 Ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικά κύματα 7. Τι είναι το ταλαντούμενο ηλεκτρικό δίπολο; Πως παράγεται ένα ηλεκτρομαγνητικό κύμα; 7.2 Ποιες εξισώσεις περιγράφουν την ένταση του ηλεκτρικού
ΚΕΦΑΛΑΙΟ 2 Ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικά κύματα 7. Τι είναι το ταλαντούμενο ηλεκτρικό δίπολο; Πως παράγεται ένα ηλεκτρομαγνητικό κύμα; 7.2 Ποιες εξισώσεις περιγράφουν την ένταση του ηλεκτρικού
ΟΠΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ. Φως... Φωτομετρικά μεγέθη - μονάδες Νόμοι Φωτισμού
 ΟΠΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ Φως... Φωτομετρικά μεγέθη - μονάδες Νόμοι Φωτισμού Ηλεκτρομαγνητικά κύματα - Φως Θα διερευνήσουμε: 1. Τί είναι το φως; 2. Πως παράγεται; 3. Χαρακτηριστικά ιδιότητες Γεωμετρική οπτική:
ΟΠΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ Φως... Φωτομετρικά μεγέθη - μονάδες Νόμοι Φωτισμού Ηλεκτρομαγνητικά κύματα - Φως Θα διερευνήσουμε: 1. Τί είναι το φως; 2. Πως παράγεται; 3. Χαρακτηριστικά ιδιότητες Γεωμετρική οπτική:
Με k1 = 1.220, k2 = 2.232, k3 = 3.238, and n = 1,2,3,
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ Ι ΠΟΜ 114(Ε) ΟΠΤΙΚΗ ιάθλαση φωτός µέσω σχισµής, γύρω από µικρό δοκάρι και µέσω µικρής οπής
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ Ι ΠΟΜ 114(Ε) ΟΠΤΙΚΗ ιάθλαση φωτός µέσω σχισµής, γύρω από µικρό δοκάρι και µέσω µικρής οπής
Προβλήματα φακών/κατόπτρων
 Προβλήματα φακών/κατόπτρων 1. Χρησιμοποιείστε την τεχνική των ακτινών και σχηματισμών ειδώλου για να βρείτε το είδωλο, που δημιουργείται από ένα κοίλο σφαιρικό κάτοπτρο, ενός αντικειμένου που τοποθετείται
Προβλήματα φακών/κατόπτρων 1. Χρησιμοποιείστε την τεχνική των ακτινών και σχηματισμών ειδώλου για να βρείτε το είδωλο, που δημιουργείται από ένα κοίλο σφαιρικό κάτοπτρο, ενός αντικειμένου που τοποθετείται
Η κατασκευή με τις δύο πινέζες και το νήμα
 Η κατασκευή με τις δύο πινέζες και το νήμα Στη δραστηριότητα αυτή θα εξερευνήσετε ίσως την πλέον κοινή μέθοδο κατασκευής μιας έλλειψης. Προκειμένου να θέσετε το πλαίσιο για την κατασκευή αυτή, πρέπει να
Η κατασκευή με τις δύο πινέζες και το νήμα Στη δραστηριότητα αυτή θα εξερευνήσετε ίσως την πλέον κοινή μέθοδο κατασκευής μιας έλλειψης. Προκειμένου να θέσετε το πλαίσιο για την κατασκευή αυτή, πρέπει να
7 σειρά ασκήσεων. Για την επίλυση των προβλημάτων να θεωρηθούν γνωστά: σταθερά του Planck 6,63 10-34 J s, ταχύτητα του φωτός στον αέρα 3 10 8 m/s
 η 7 σειρά ασκήσεων Για την επίλυση των προβλημάτων να θεωρηθούν γνωστά: σταθερά του Planck 6,63 10-34 J s, ταχύτητα του φωτός στον αέρα 3 10 8 m/s 1. Εξηγήστε γιατί, όταν φως διαπερνά μία διαχωριστική
η 7 σειρά ασκήσεων Για την επίλυση των προβλημάτων να θεωρηθούν γνωστά: σταθερά του Planck 6,63 10-34 J s, ταχύτητα του φωτός στον αέρα 3 10 8 m/s 1. Εξηγήστε γιατί, όταν φως διαπερνά μία διαχωριστική
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Άσκηση 4: Σφάλματα φακών: Ι Σφαιρική εκτροπή Εξεταζόμενες γνώσεις: σφάλματα σφαιρικής εκτροπής. Α. Γενικά περί σφαλμάτων φακών Η βασική σχέση του Gauss 1/s +1/s = 1/f που
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Άσκηση 4: Σφάλματα φακών: Ι Σφαιρική εκτροπή Εξεταζόμενες γνώσεις: σφάλματα σφαιρικής εκτροπής. Α. Γενικά περί σφαλμάτων φακών Η βασική σχέση του Gauss 1/s +1/s = 1/f που
Φυσική ΘΕΜΑ 1 ΘΕΜΑ 2 ΘΕΜΑ 3
 Φυσική ΘΕΜΑ 1 1) Υπάρχουν δύο διαφορετικά είδη φορτίου που ονομάστηκαν θετικό και αρνητικό ηλεκτρικό φορτίο αντίστοιχα. Τα σώματα που έχουν θετικό φορτίο λέμε ότι είναι θετικά φορτισμένα (π.χ. μια γυάλινη
Φυσική ΘΕΜΑ 1 1) Υπάρχουν δύο διαφορετικά είδη φορτίου που ονομάστηκαν θετικό και αρνητικό ηλεκτρικό φορτίο αντίστοιχα. Τα σώματα που έχουν θετικό φορτίο λέμε ότι είναι θετικά φορτισμένα (π.χ. μια γυάλινη
OΠΤIKH. Επειδή είναι πάντα υ<c (
 OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
 Ενότητα 4 Τριγωνομετρία Στην ενότητα αυτή θα μάθουμε: Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
Ενότητα 4 Τριγωνομετρία Στην ενότητα αυτή θα μάθουμε: Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
Περίθλαση από ακµή και από εµπόδιο.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
ΠΑΡΑΤΗΡΗΣΗ ΣΥΝΕΧΩΝ ΦΑΣΜΑΤΩΝ ΕΚΠΟΜΠΗΣ & ΑΠΟΡΡΟΦΗΣΗΣ ΣΤΕΡΕΟΥ
 1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΠΑΡΑΤΗΡΗΣΗ ΣΥΝΕΧΩΝ ΦΑΣΜΑΤΩΝ ΕΚΠΟΜΠΗΣ & ΑΠΟΡΡΟΦΗΣΗΣ ΣΤΕΡΕΟΥ Α. ΣΤΟΧΟΙ Η παραγωγή λευκού φωτός με τη χρήση λαμπτήρα πυράκτωσης. Η χρήση πηγών φωτός διαφορετικής
1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΠΑΡΑΤΗΡΗΣΗ ΣΥΝΕΧΩΝ ΦΑΣΜΑΤΩΝ ΕΚΠΟΜΠΗΣ & ΑΠΟΡΡΟΦΗΣΗΣ ΣΤΕΡΕΟΥ Α. ΣΤΟΧΟΙ Η παραγωγή λευκού φωτός με τη χρήση λαμπτήρα πυράκτωσης. Η χρήση πηγών φωτός διαφορετικής
Τίτλος: Διορθωτικά Γυαλιά Οράσεως. Ηλικία: Χρόνος: 90 Λεπτά (2 Μαθήματα) Θέματα: Διορθωτικά Γυαλιά οράσεως , χρονών
 Πλάνο Τίτλος: Διορθωτικά Γυαλιά Οράσεως Θέματα: Διορθωτικά Γυαλιά οράσεως Χρόνος: 90 Λεπτά (2 Μαθήματα) Ηλικία: 15 16, χρονών Διαφοροποίηση: Μπορεί να ζητηθεί από τους πιο ικανούς μαθητές, να υπολογίσουν
Πλάνο Τίτλος: Διορθωτικά Γυαλιά Οράσεως Θέματα: Διορθωτικά Γυαλιά οράσεως Χρόνος: 90 Λεπτά (2 Μαθήματα) Ηλικία: 15 16, χρονών Διαφοροποίηση: Μπορεί να ζητηθεί από τους πιο ικανούς μαθητές, να υπολογίσουν
Μεγεθυντικός φακός. 1. Σκοπός. 2. Θεωρία. θ 1
 Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Ιπτάμενες Μηχανές. Οδηγός για το Μαθητή
 Ιπτάμενες Μηχανές Οδηγός για το Μαθητή Το αεροσκάφος κάθετης απογείωσης Αφού βεβαιωθείτε ότι βρίσκεστε στο περιβάλλον του εκπαιδευτικού προγράμματος, επιλέξτε «Έναυσμα». Ακολουθώντας τις οδηγίες που παρουσιάζονται
Ιπτάμενες Μηχανές Οδηγός για το Μαθητή Το αεροσκάφος κάθετης απογείωσης Αφού βεβαιωθείτε ότι βρίσκεστε στο περιβάλλον του εκπαιδευτικού προγράμματος, επιλέξτε «Έναυσμα». Ακολουθώντας τις οδηγίες που παρουσιάζονται
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ερωτήσεις κλειστού τύπου. Ερωτήσεις ανοικτού τύπου
 ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 21 ΙΟΥΝΙΟΥ 2016 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 21 ΙΟΥΝΙΟΥ 2016 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με πέντε (5) αντικείμενα ΓΕΝΙΚΕΣ ΟΔΗΓΙΕΣ: Η σύνθεση περιλαμβάνει
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 21 ΙΟΥΝΙΟΥ 2016 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με πέντε (5) αντικείμενα ΓΕΝΙΚΕΣ ΟΔΗΓΙΕΣ: Η σύνθεση περιλαμβάνει
ΚΕΦΑΛΑΙΟ 11Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση
 ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
Κατά την φόρτιση πυκνωτή (Εξ. 37 στις σημειώσεις Ηλεκτρομαγνητισμού)
 1α Σε ένα κύκλωμα RC συνεχούς με διακόπτη, αντίσταση R = 650 Ω και πηγή 1 V όλα σε σειρά, ο διακόπτης κλείνει στο t = 0 και ο πυκνωτής είναι αρχικά αφόρτιστος. Η διαφορά δυναμικού στον πυκνωτή φτάνει στο
1α Σε ένα κύκλωμα RC συνεχούς με διακόπτη, αντίσταση R = 650 Ω και πηγή 1 V όλα σε σειρά, ο διακόπτης κλείνει στο t = 0 και ο πυκνωτής είναι αρχικά αφόρτιστος. Η διαφορά δυναμικού στον πυκνωτή φτάνει στο
Doppler Radar. Μεταφορά σήµατος µε την βοήθεια των µικροκυµάτων.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 101 10. Άσκηση 10 Doppler Radar. Μεταφορά σήµατος µε την βοήθεια των µικροκυµάτων. 10.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 101 10. Άσκηση 10 Doppler Radar. Μεταφορά σήµατος µε την βοήθεια των µικροκυµάτων. 10.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών
ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ
 ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Όταν προσπίπτει φως σε μια διεπιφάνεια που σχηματίζεται μεταξύ δύο οπτικά διαφορετικών μέσων, ένα μέρος του υφίσταται ανάκλαση ενώ το υπόλοιπο διέρχεται από το πρώτο στο δεύτερο
ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Όταν προσπίπτει φως σε μια διεπιφάνεια που σχηματίζεται μεταξύ δύο οπτικά διαφορετικών μέσων, ένα μέρος του υφίσταται ανάκλαση ενώ το υπόλοιπο διέρχεται από το πρώτο στο δεύτερο
1ο Κριτήριο Αξιολόγησης ΦΥΣΗ ΤΟΥ ΦΩΤΟΣ-ΑΝΑΚΛΑΣΗ, ΙΑΘΛΑΣΗ- ΕΙΚΤΗΣ ΙΑΘΛΑΣΗΣ
 1 ο ΚΕΦΑΛΑΙΟ 1. Φύση του φωτός - Ανάκλαση, διάθλαση - είκτης διάθλασης 2. ιασκεδασµός - Ανάλυση του φωτός από πρίσµα 3. Επαναληπτικό στο 1ο κεφάλαιο 4. Επαναληπτικό στο 1ο κεφάλαιο 11. 12. 1ο Κριτήριο
1 ο ΚΕΦΑΛΑΙΟ 1. Φύση του φωτός - Ανάκλαση, διάθλαση - είκτης διάθλασης 2. ιασκεδασµός - Ανάλυση του φωτός από πρίσµα 3. Επαναληπτικό στο 1ο κεφάλαιο 4. Επαναληπτικό στο 1ο κεφάλαιο 11. 12. 1ο Κριτήριο
Πειραματική μελέτη λεπτών σφαιρικών φακών
 Πειραματική μελέτη λεπτών σφαιρικών φακών Τάξη - Τµήµα: Ονόµατα µαθητών οµάδας: ) 2).. 3) 4) Πειραματική μελέτη λεπτών σφαιρικών φακών Στόχοι της εργαστηριακής άσκησης ) Μέτρηση των γεωµετρικών χαρακτηριστικών
Πειραματική μελέτη λεπτών σφαιρικών φακών Τάξη - Τµήµα: Ονόµατα µαθητών οµάδας: ) 2).. 3) 4) Πειραματική μελέτη λεπτών σφαιρικών φακών Στόχοι της εργαστηριακής άσκησης ) Μέτρηση των γεωµετρικών χαρακτηριστικών
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑΔΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO Σάββατο 7 Δεκεμβρίου Εξέταση στη Φυσική
 ΠΑΝΕΛΛΗΝΙΑ ΕΝΩΣΗ ΥΠΕΥΘΥΝΩΝ ΕΡΓΑΣΤΗΡΙΑΚΩΝ ΚΕΝΤΡΩΝ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ - «ΠΑΝΕΚΦE» 1ο και 2ο ΕΚΦΕ Ηρακλείου ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑΔΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO 2014 Σάββατο 7 Δεκεμβρίου
ΠΑΝΕΛΛΗΝΙΑ ΕΝΩΣΗ ΥΠΕΥΘΥΝΩΝ ΕΡΓΑΣΤΗΡΙΑΚΩΝ ΚΕΝΤΡΩΝ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ - «ΠΑΝΕΚΦE» 1ο και 2ο ΕΚΦΕ Ηρακλείου ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑΔΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO 2014 Σάββατο 7 Δεκεμβρίου
δ) Αν ένα σηµείο του θετικού ηµιάξονα ταλαντώνεται µε πλάτος, να υπολογίσετε την απόσταση του σηµείου αυτού από τον πλησιέστερο δεσµό. ΑΣΚΗΣΗ 4 Μονοχρ
 ΑΣΚΗΣΗ 1 Κατά µήκος µιας ελαστικής χορδής µεγάλου µήκους που το ένα άκρο της είναι ακλόνητα στερεωµένο, διαδίδονται δύο κύµατα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι µετρηµένα σε
ΑΣΚΗΣΗ 1 Κατά µήκος µιας ελαστικής χορδής µεγάλου µήκους που το ένα άκρο της είναι ακλόνητα στερεωµένο, διαδίδονται δύο κύµατα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι µετρηµένα σε
ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ. H γραφική αναπαράσταση ενός κύματος φωτός δίνεται στο Σχήμα 1(α) που ακολουθεί: ΣΧΗΜΑ 1
 ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ 1. ΟΡΙΣΜΟΙ Το φως είναι ένα σύνθετο κύμα. Με εξαίρεση την ακτινοβολία LASER, τα κύματα φωτός δεν είναι επίπεδα κύματα. Κάθε κύμα φωτός είναι ένα ηλεκτρομαγνητικό κύμα στο οποίο τα διανύσματα
ΠΟΛΩΣΗ ΤΟΥ ΦΩΤΟΣ 1. ΟΡΙΣΜΟΙ Το φως είναι ένα σύνθετο κύμα. Με εξαίρεση την ακτινοβολία LASER, τα κύματα φωτός δεν είναι επίπεδα κύματα. Κάθε κύμα φωτός είναι ένα ηλεκτρομαγνητικό κύμα στο οποίο τα διανύσματα
06/05/2017 Όνομα και Επώνυμο:.. Όνομα Πατέρα: Όνομα Μητέρας: Δημοτικό Σχολείο: Τάξη/Τμήμα:.
 06/05/2017 Όνομα και Επώνυμο:.. Όνομα Πατέρα: Όνομα Μητέρας: Δημοτικό Σχολείο: Τάξη/Τμήμα:. Θέμα 1ο Οι τέσσερις φίλοι απολαμβάνουν μια βόλτα με ποδήλατο. Ποια νομίζεις ότι είναι τα πλεονεκτήματα της χρήσης
06/05/2017 Όνομα και Επώνυμο:.. Όνομα Πατέρα: Όνομα Μητέρας: Δημοτικό Σχολείο: Τάξη/Τμήμα:. Θέμα 1ο Οι τέσσερις φίλοι απολαμβάνουν μια βόλτα με ποδήλατο. Ποια νομίζεις ότι είναι τα πλεονεκτήματα της χρήσης
Η Φύση του Φωτός. Τα Β Θεματα της τράπεζας θεμάτων
 Η Φύση του Φωτός Τα Β Θεματα της τράπεζας θεμάτων Η ΦΥΣΗ ΤΟΥ ΦΩΤΟΣ Θέμα Β _70 Β. Μονοχρωματική ακτίνα πράσινου φωτός διαδίδεται αρχικά στον αέρα. Στη πορεία της δέσμης έχουμε τοποθετήσει στη σειρά τρία
Η Φύση του Φωτός Τα Β Θεματα της τράπεζας θεμάτων Η ΦΥΣΗ ΤΟΥ ΦΩΤΟΣ Θέμα Β _70 Β. Μονοχρωματική ακτίνα πράσινου φωτός διαδίδεται αρχικά στον αέρα. Στη πορεία της δέσμης έχουμε τοποθετήσει στη σειρά τρία
