Vilniaus universitetas. Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS
|
|
|
- Ἄννα Βλαστός
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992
2 T U R I N Y S 1. Vektorinė erdvė Matricos rangas Vektorinės erdvės bazė Poerdviai, poerdviu suma bei sankirta Tiesiniu lygčiu sistemos Kvadratinės formos Euklido erdvė Tiesinės transformacijos Žordano forma Grupiu teorijos elementai Idealai, faktoržiedžiai, algebriniai plėtiniai Literatūra STANDARTINIAI ŽYMENYS N natūraliu aibė, Z sveiku žiedas, Q racionaliu kūnas, R n n-matė aritmetinė erdvė, K m n vienarūšiu m n-matricu erdvė virš kūno K, K kūno K multiplikacinė grupė, Z n n-osios eilės ciklinė grupė. 2
3 1. VEKTORINĖ ERDVĖ Apibrėžimas. Adicinė grupė V vadinama vektorine erdve virš kūno K, kai apibrėžta jos elementu daugybos iš kūno K elementu operacija, kuri turi tokias savybes: 1) asociatyvumo a (b α) = (a b) α ( a, b K, α V ); 2) distributyvumo grupės V elementu a (α + β) = a α + a β ( a K, α, β V ); 3) distributyvumo kūno K elementu (a + b) α = a α + b α ( a, b K, α V ); 4) kūno K vieneto e panaikinimo e α = α ( α V ). Vektorinės erdvės V elementus vadiname vektoriais ir žymime graikiškomis raidėmis, o kūno K elementus skaliarais ir žymime mažomis lotyniškomis raidėmis. Vektorinės erdvės sistema α 1, α 2,..., α m vadinama tiesiškai priklausoma, kai galima rasti tokius skaliarus c 1, c 2,..., c m, iš kuriu bent vienas nelygus 0, kad būtu teisinga lygybė c 1 α 1 + c 2 α c m α m = θ (θ nulinis vektorius). Jei pastara ja lygybe tenkina tik skaliarai c 1 = c 2 =... = c m = 0, tai sistema vadinama tiesiškai nepriklausoma. 1 teorema. Jei sistemos posistemis yra tiesiškai priklausomas, tai ir ta sistema yra tiesiškai priklausoma. Išvada. Jei sistema yra tiesiškai nepriklausoma, tai tiesiškai nepriklausomas ir bet kuris jos posistemis. Vektorinės erdvės vektorius α vadinamas tos erdvės α 1, α 2,..., α m tiesine kombinacija, kai galima rasti skaliarus a 1, a 2,..., a m, su kuriais yra teisinga lygybė α = a 1 α 1 + a 2 α a m α m. 2 teorema. Vektoriu sistema, sudaryta iš daugiau kaip vieno vektoriaus, yra tiesiškai priklausoma tada ir tik tada, kai bent viena jos galima užrašyti kitu tos sistemos tiesine kombinacija. 3
4 Vektoriu sistemos rangu vadinamas didžiausias jos tiesiškai nepriklausomu posistemiu skaičius. 3 teorema. Jei sistemos α 1, α 2,..., α r,..., α m rangas lygus r, o jos posistemis α 1, α 2,..., α r yra tiesiškai nepriklausomas, tai kiekviena sistemos galima užrašyti to posistemio tiesine kombinacija. 4 teorema. Prijungus prie sistemos jos tiesine kombinacija, gaunama to paties rango sistema. Vektoriu sistemos elementariaisiais pertvarkiais vadinami šie pertvarkiai: 1) bet kurio sistemos vektoriaus pakeitimas to vektoriaus ir nelygaus nuliui skaliaro sandauga; 2) sistemos vektoriaus pakeitimas suma to vektoriaus ir kito sistemos vektoriaus, padauginto iš bet kurio skaliaro. 5 teorema. Atlikus sistemos elementaru ji pertvarki, gaunama to paties rango sistema. PAVYZDŽIAI 1. Apibrėšime aritmetine vektorine erdve K n. Nagrinėjame sutvarkytus n kūno K elementu rinkinius α = (a 1, a 2,..., a n ). Dvie elementu sudėti apibrėšime pakomponenčiui: jei α = (a 1, a 2,..., a m ), β = (b 1, b 2,..., b n ), tai tu elementu suma laikome elementa α + β = (a 1 + b 1, a 2 + b 2,..., a n + b n ). Apibrėžtos sudėties operacijos atžvilgiu sudarytoji aibė yra adicinė grupė. Iš tikru : 1) operacija asociatyvi jei γ = (c 1, c 2,..., c n ), tai (α + β) + γ = ( (a 1 + b 1 ) + c 1, (a 2 + b 2 ) + c 2,..., (a n + b n ) + c n ) = = ( a 1 + (b 1 + c 1 ), a 2 + (b 2 + c 2 ),..., a n + (b n + c n ) ) = α + (β + γ); 2) egzistuoja nulinis elementas θ = (0, 0,..., 0): α + θ = (a 1 + 0, a 2 + 0,..., a n + 0) = α; 3) kartu su kiekvienu elementu α = (a 1, a 2,..., a n ) aibei priklauso ir jam priešingas elementas α = ( a 1, a 2,..., a n ): 4) operacija komutatyvi α + ( α) = (a 1 a 1, a 2 a 2,..., a n a n ) = θ; α + β = (a 1 + b 1, a 2 + b 2,..., a n + b n ) = = (b 1 + a 1, b 2 + a 2,..., b n + a n ) = β + α. Elemento daugyba iš skaliaro apibrėžiame taip pat pakomponenčiui aα = (aa 1, aa 2,..., aa n ). 4
5 Daugybos operacija turi tokias savybes: 5) asociatyvumo a(bα) = ( a(ba 1 ), a(ba 2 ),..., a(ba n ) ) = = ( (ab)a 1, (ab)a 2,..., (ab)a n ) = (ab)α; 6) distributyvumo a(α + β) = ( a(a 1 + b 1 ), a(a 2 + b 2 ),..., a(a n + b n ) ) = = (aa 1 + ab 1, aa 2 + ab 2,..., aa n + ab n ) = aα + aβ; 7) distributyvumo skaliaru (a + b)α = ( (a + b)a 1, (a + b)a 2,..., (a + b)a n ) = 8) kūno K vieneto panaikinimo = (aa 1 + ba 1, aa 1 + aa 2,..., aa n + ba n ) = aα + bα; eα = (ea 1, ea 2,..., ea n ) = (a 1, a 2,..., a n ) = α. 2. Apskaičiuosime aritmetinės vektorinės erdvės R 3 sistemos α 1 = (1, 1, 2), α 2 = (2, 1, 1), α 3 = (0, 1, 5) ranga, pasinaudoje tik jo apibrėžimu. Sprendžiame lygti x 1 α 1 + x 2 α 2 + x 3 α 3 = θ. I raše α 1, α 2, α 3, θ išraiškas ir atlike veiksmus, gauname (x 1 + 2x 2, x 1 x 2 + x 3, 2x 1 x 2 5x 3 ) = (0, 0, 0). Ši lygtis yra ekvivalenti tri tiesiniu lygčiu su trim nežinomaisiais sistemai { x1 +2x 2 =0, x 1 x 2 + x 3 =0, 2x 1 x 2 5x 3 =0. Pastaroji sistema turi bent viena nenulini sprendini, pavyzdžiui, (2, 1, 1), todėl nagrinėjamoji sistema yra tiesiškai priklausoma ir jos rangas r 2. Nagrinėjame posistemius, sudarytus iš dvie. Sprendžiame lygti x 1 α 1 + x 2 α 2 = θ. Atlike veiksmus, gauname ekvivalenčia lygčiu sistema { x1 +2x 2 =0, x 1 x 2 =0, 2x 1 x 2 =0. Ši sistema turi tik nulini sprendini, todėl posistemis α 1, α 2 yra tiesiškai nepriklausomas ir sistemos rangas r = 2. 5
6 UŽDAVINIAI 1.1. Ar sudaro vektorine erdve : 1) n-osios eilės kvadratinės matricos su elementais iš kūno K matricu sudėties ir daugybos iš skaliaro atžvilgiu; 2) aibė kūno K elementu virš jo paties tame kūne apibrėžtu operaci atžvilgiu; 3) aibė plėtinio L K elementu virš kūno K kūne L apibrėžtu operaci atžvilgiu; 4) n-osios eilės simetrinės matricos virš kūno K matricu sudėties ir daugybos iš skaliaro atžvilgiu; 5) aibė visu n-ojo laipsnio virš kūno K sudėties ir daugybos iš skaliaro atžvilgiu; 6) aibė visu virš kūno K, kuriu laipsniai ne didesni už natūralu ji n, sudėties ir daugybos iš skaliaro atžvilgiu; 7) aibė visu virš kūno K sudėties ir daugybos iš skaliaro atžvilgiu; 8) aibė visu tolydžiu kompleksiniu reikšmiu funkci virš kompleksiniu kūno funkci sudėties ir daugybos iš skaliaro atžvilgiu; 9) aibė visu plokštumos laisvu, kuriu galai priklauso vienai tiesei, sudėties ir daugybos iš skaliaro atžvilgiu? 1.2. Ar galima apibrėžti vektorinės erdvės struktūra : 1) realiu aibėje R; 2) teigiamu realiu aibėje R + ; 3) racionaliu aibėje Q; 4) natūraliu aibėje N; 5) aibėje R[t] visu f(t), tenkinančiu sa lyga 6) Dekarto sandaugoje Q Q; 7) Dekarto sandaugoje Z Z? f(3) = 2f(2); 1.3. I rodykite, kad aritmetinės erdvės K 3 bet kuri keturiu sistema yra tiesiškai priklausoma Ar galima apibrėžti elementu tiesinės priklausomybės sa voka Abelio grupėje? 1.5. I rodykite, kad aritmetinės erdvės R 4 sistema α 1, α 2,..., α m yra tiesiškai nepriklausoma ir apskaičiuokite šiu tiesine kombinacija α: 1) α 1 = (2, 1, 0, 1), α 2 = (1, 2, 1, 3), α 3 = (3, 4, 1, 2), α = 2α 1 3α 2 + 4α 3 ; 2) α 1 = (4, 3, 2, 1), α 2 = (5, 1, 3, 2), α = α 1 + 5α 2 ; 3) α 1 = (1, 1, 1, 2), α 2 = (2, 1, 1, 1), α 3 = (4, 1, 2, 3), α 4 = ( 3, 3, 2, 3), α = α 1 2α 2 3α 3 + 4α 4 ; 4) α 1 = (1, 2, 3, 1), α 2 = ( 1, 2, 3, 1), α 3 = (2, 3, 1, 1), α 4 = (1, 1, 1, 3), α = 2α 1 + α 2 3α 3 + 2α 4. 6
7 1.6. Patikrinkite, ar aritmetinės erdvės R n sistema α 1, α 2,..., α m yra tiesiškai priklausoma: 1) α 1 = (3, 4, 2), α 2 = (2, 1, 3), α 3 = (7, 2, 4); 2) α 1 = (2, 1, 3), α 2 = (3, 2, 1), α 3 = (1, 2, 3); 3) α 1 = (1, 4, 2, 1), α 2 = ( 2, 8, 4, 2); 4) α 1 = (2, 3, 1, 1), α 2 = (2, 3, 0, 1) Apskaičiuokite aritmetinės erdvės R 3 sistemos α 1, α 2, α 3 ranga, pasinaudoje tik jo apibrėžimu: 1) α 1 = (1, 1, 1), α 2 = (1, 2, 3), α 3 = ( 1, 1, 2); 2) α 1 = (1, 2, 1), α 2 = (2, 1, 3), α 3 = (4, 3, 5); 3) α 1 = (1, 1, 3), α 2 = (2, 1, 1), α 3 = (1, 2, 2); 4) α 1 = (1, 3, 1), α 2 = ( 2, 6, 2), α 3 = (3, 9, 3) Apskaičiuokite, kuriu laipsniai ne didesni už 5, erdvės R 5 [t] sistemos ranga, pasinaudoje tik jo apibrėžimu: 1) 2, 2 + t, 3 + 2t + t 2 ; 2) 1 + t + t 2, 1 + t 2 + t 3, 1 + t + t 2 2t 3 ; 3) 1 + t, 2 + t t 2, 3 + 2t t 3, 1 t 3 ; 4) 1 + t + t 3, 1 + t 2 t 3, 2 + t + t 2, 1 + t 3. ATSAKYMAI ) Taip; 2) taip; 3) taip; 4) taip; 5) ne; 6) taip; 7) taip; 8) taip; 9) taip, jei tiesės yra koordinačiu ašys; ne kitais atvejais ) Taip; 2) taip; 3) taip; 4) ne; 5) taip; 6) taip; 7) ne Taip ) α = (13, 24, 7, 1); 2) α = (21, 8, 17, 9); 3) α = ( 27, 12, 5, 3); 4) α = ( 3, 5, 8, 2) ) Taip; 2) ne; 3) taip; 4) ne ) r = 3; 2) r = 2; 3) r = 2; 4) r = ) r = 3; 2) r = 2; 3) r = 3; 4) r = 3. 7
Matematika 1 4 dalis
 Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
Matematika 1 3 dalis
 Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
X galioja nelygyb f ( x1) f ( x2)
 Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
FUNKCIJOS. veiksmu šioje erdvėje apibrėžkime dar viena. a = {a 1,..., a n } ir b = {b 1,... b n } skaliarine sandauga
 VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
Specialieji analizės skyriai
 Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Elektronų ir skylučių statistika puslaidininkiuose
 lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
AIBĖS, FUNKCIJOS, LYGTYS
 AIBĖS, FUNKCIJOS, LYGTYS Aibės sąvoka ir pavyzdžiai Atskirų objektų rinkiniai, grupės, sistemos, kompleksai matematikoje vadinami aibėmis. Šie atskiri objektai vadinami aibės elementais. Kai elementas
AIBĖS, FUNKCIJOS, LYGTYS Aibės sąvoka ir pavyzdžiai Atskirų objektų rinkiniai, grupės, sistemos, kompleksai matematikoje vadinami aibėmis. Šie atskiri objektai vadinami aibės elementais. Kai elementas
Dviejų kintamųjų funkcijos dalinės išvestinės
 Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
FDMGEO4: Antros eilės kreivės I
 FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
ANALIZINĖ GEOMETRIJA III skyrius (Medžiaga virtualiajam kursui)
 ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
1.4. Rungės ir Kuto metodas
 .4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
.4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
1 Tada teigini Ne visi šie vaikinai yra studentai galima išreikšti formule. 2 Ta pati teigini galima užrašyti ir taip. 3 Formulė U&B C reiškia, kad
 45 DISKREČIOJI MATEMATIKA. LOGIKA. PAVYZDŽIAI Raidėmis U, B ir C pažymėti teiginiai: U = Vitas yra studentas ; B = Skirmantas yra studentas ; C = Jonas yra studentas. 1 Tada teigini Ne visi šie vaikinai
45 DISKREČIOJI MATEMATIKA. LOGIKA. PAVYZDŽIAI Raidėmis U, B ir C pažymėti teiginiai: U = Vitas yra studentas ; B = Skirmantas yra studentas ; C = Jonas yra studentas. 1 Tada teigini Ne visi šie vaikinai
4.1 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n. Priminsime, kad šios erdvės elementai yra vektoriai vektoriu
 IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
2015 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pagrindinė sesija. I dalis
 PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
1 TIES ES IR PLOK TUMOS
 G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
I.4. Laisvasis kūnų kritimas
 I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
MATEMATINĖ LOGIKA. Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA
 LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
2009 m. matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 1 6 uždavinių atsakymai
 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA PATVIRTINTA Nacionalinio egzaminų centro direktoriaus -6- įsakymu Nr. (..)-V-8 m. matematikos valstybinio brandos egzamino VERTINIMO
M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA PATVIRTINTA Nacionalinio egzaminų centro direktoriaus -6- įsakymu Nr. (..)-V-8 m. matematikos valstybinio brandos egzamino VERTINIMO
I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI ATSAKYMAI
 008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas
 Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
ELEMENTARIOJI TEORIJA
 ELEMENTARIOJI TEORIJA Pirmosios kombinatorikos þinios siekia senàsias Rytø ðalis, kuriose mokëta suskaièiuoti këlinius bei derinius ir sudarinëti magiðkuosius kvadratus, ypaè populiarius viduramþiais.
ELEMENTARIOJI TEORIJA Pirmosios kombinatorikos þinios siekia senàsias Rytø ðalis, kuriose mokëta suskaièiuoti këlinius bei derinius ir sudarinëti magiðkuosius kvadratus, ypaè populiarius viduramþiais.
III. MATRICOS. DETERMINANTAI. 3.1 Matricos A = lentele žymėsime taip:
 III MATRICOS DETERMINANTAI Realiu ju skaičiu lentele 3 Matricos a a 2 a n A = a 2 a 22 a 2n a m a m2 a mn vadinsime m n eilės matrica Trumpai šia lentele žymėsime taip: A = a ij ; i =,, m, j =,, n čia
III MATRICOS DETERMINANTAI Realiu ju skaičiu lentele 3 Matricos a a 2 a n A = a 2 a 22 a 2n a m a m2 a mn vadinsime m n eilės matrica Trumpai šia lentele žymėsime taip: A = a ij ; i =,, m, j =,, n čia
Specialieji analizės skyriai
 Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Matematinės analizės konspektai
 Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
VIII. FRAKTALINĖ DIMENSIJA. 8.1 Fraktalinės dimensijos samprata. Ar baigtinis Norvegijos sienos ilgis?
 VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] )
![ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] ) ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] )](/thumbs/72/67447727.jpg) ATSITIKTINIAI PROCESAI (paskaitų konspektas 2014[1] ) Alfredas Račkauskas Vilniaus universitetas Matematikos ir Informatikos fakultetas Ekonometrinės analizės katedra Vilnius, 2014 Iš dalies rėmė Projektas
ATSITIKTINIAI PROCESAI (paskaitų konspektas 2014[1] ) Alfredas Račkauskas Vilniaus universitetas Matematikos ir Informatikos fakultetas Ekonometrinės analizės katedra Vilnius, 2014 Iš dalies rėmė Projektas
Spalvos. Šviesa. Šviesos savybės. Grafika ir vizualizavimas. Spalvos. Grafika ir vizualizavimas, VDU, Spalvos 1
 Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
eksponentinės generuojančios funkcijos 9. Grafu
 DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės indukcijos ir Dirichlė principai 2 Dauginimo taisyklė,,skaičiuok dukart principas
DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės indukcijos ir Dirichlė principai 2 Dauginimo taisyklė,,skaičiuok dukart principas
IV. FUNKCIJOS RIBA. atvira. intervala. Apibrėžimas Sakysime, kad skaičius b yra funkcijos y = f(x) riba taške x 0, jei bet kokiam,
 41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
1. Individualios užduotys:
 IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
DISKREČIOJI MATEMATIKA
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Valdas Diči ūnas Gintaras Skersys DISKREČIOJI MATEMATIKA Mokymo priemonė Vilnius 2003 Įvadas Išvertus iš lotynu kalbos
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Valdas Diči ūnas Gintaras Skersys DISKREČIOJI MATEMATIKA Mokymo priemonė Vilnius 2003 Įvadas Išvertus iš lotynu kalbos
Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra. Gintaras Skersys. Mokymo priemonė
 Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra Gintaras Skersys Klaidas taisančių kodų teorija Mokymo priemonė Vilnius 2005 I dalis Pagrindinės savokos 1 Įvadas Panagrinėkime
Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra Gintaras Skersys Klaidas taisančių kodų teorija Mokymo priemonė Vilnius 2005 I dalis Pagrindinės savokos 1 Įvadas Panagrinėkime
Algoritmai. Vytautas Kazakevičius
 Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
1. Vektoriu veiksmai. Vektoriu skaliarinė, vektorinė ir mišrioji sandaugos
 1. Vektoriu veiksmai. Vektoriu skaliarinė, vektorinė ir mišrioji sandaugos Vektoriu užrašymas MAPLE Vektorius MAPLE galime užrašyti daugeliu būdu. Juos grafiškai vaizduosime paketo Student[LinearAlgebra]
1. Vektoriu veiksmai. Vektoriu skaliarinė, vektorinė ir mišrioji sandaugos Vektoriu užrašymas MAPLE Vektorius MAPLE galime užrašyti daugeliu būdu. Juos grafiškai vaizduosime paketo Student[LinearAlgebra]
0.1. Bendrosios sąvokos
 .1. BENDROSIOS SĄVOKOS 1.1. Bendrosios sąvokos.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε =, xt;ε) C n T), T [,+ ), < ε ε ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε,
.1. BENDROSIOS SĄVOKOS 1.1. Bendrosios sąvokos.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε =, xt;ε) C n T), T [,+ ), < ε ε ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε,
1 Įvadas Neišspręstos problemos Dalumas Dalyba su liekana Dalumo požymiai... 3
 Skaičių teorija paskaitų konspektas Paulius Šarka, Jonas Šiurys 1 Įvadas 1 1.1 Neišspręstos problemos.............................. 1 2 Dalumas 2 2.1 Dalyba su liekana.................................
Skaičių teorija paskaitų konspektas Paulius Šarka, Jonas Šiurys 1 Įvadas 1 1.1 Neišspręstos problemos.............................. 1 2 Dalumas 2 2.1 Dalyba su liekana.................................
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA. Algoritmų teorija. Paskaitų konspektas
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
TEORIJA. RINKTINIAI MATEMATIKOS SKYRIAI (Informatikos spec., 2 srautas, magistrantūra, 1 semestras) PROGRAMA. su skaidžia savybe skaičiu
 GRAFU TEORIJA RINKTINIAI MATEMATIKOS SKYRIAI (Informatikos spec, 2 srautas, magistrantūra, 1 semestras) PROGRAMA 1 Pagrindinės sa vokos, pavyzdžiai Grafu veiksmai 2 Grafo parametru sa ryšiai 3 Jungiantysis
GRAFU TEORIJA RINKTINIAI MATEMATIKOS SKYRIAI (Informatikos spec, 2 srautas, magistrantūra, 1 semestras) PROGRAMA 1 Pagrindinės sa vokos, pavyzdžiai Grafu veiksmai 2 Grafo parametru sa ryšiai 3 Jungiantysis
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Matematinė logika. 1 skyrius Propozicinės formulės. žodį, Graikiškas žodis logos (λóγoς) reiškia
 1 skyrius Matematinė logika Graikiškas žodis logos (λóγoς) reiškia mintį, žodį, protą, sąvoką. Logika arba formalioji logika nagrinėja teisingo mąstymo dėsnius ir formas, kai samprotavimų turinys nėra
1 skyrius Matematinė logika Graikiškas žodis logos (λóγoς) reiškia mintį, žodį, protą, sąvoką. Logika arba formalioji logika nagrinėja teisingo mąstymo dėsnius ir formas, kai samprotavimų turinys nėra
2.5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS
 .5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS 5.. Pirmoji Bolcao Koši teorema. Jei fucija f tolydi itervale [a;b], itervalo galuose įgyja priešigų želų reišmes, tai egzistuoja tos tašas cc, ( ab ; ), uriame
.5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS 5.. Pirmoji Bolcao Koši teorema. Jei fucija f tolydi itervale [a;b], itervalo galuose įgyja priešigų želų reišmes, tai egzistuoja tos tašas cc, ( ab ; ), uriame
8. LENKIAMŲ PLOKŠTELIŲ ELEMENTAI
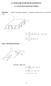 8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
TRANSPORTO PRIEMONIŲ DINAMIKA
 Marijonas Bogdevičius RANSPORO PRIEMONIŲ DINAMIKA Projekto kodas VP-.-ŠMM 7-K--3 Studijų programų atnaujinimas pagal ES reikalavimus, gerinant studijų kokybę ir taikant inovatyvius studijų metodus Vilnius
Marijonas Bogdevičius RANSPORO PRIEMONIŲ DINAMIKA Projekto kodas VP-.-ŠMM 7-K--3 Studijų programų atnaujinimas pagal ES reikalavimus, gerinant studijų kokybę ir taikant inovatyvius studijų metodus Vilnius
TEORIJOS PRADMENYS PROGRAMA
 DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės inducijos principas 2 Dauginimo taisylė 3 Gretiniai, ėliniai ir deriniai 4 Kartotiniai
DISKREČIOJI MATEMATIKA (2 semestras) KOMBINATORIKOS IR GRAFU TEORIJOS PRADMENYS PROGRAMA I KOMBINATORIKA 1 Matematinės inducijos principas 2 Dauginimo taisylė 3 Gretiniai, ėliniai ir deriniai 4 Kartotiniai
Ketvirtos eilės Rungės ir Kutos metodo būsenos parametro vektoriaus {X} reikšmės užrašomos taip:
 PRIEDAI 113 A priedas. Rungės ir Kuto metodas Rungės-Kutos metodu sprendiamos diferencialinės lygtys. Norint skaitiniu būdu išspręsti diferencialinę lygtį, reikia žinoti ieškomos funkcijos ir jos išvestinės
PRIEDAI 113 A priedas. Rungės ir Kuto metodas Rungės-Kutos metodu sprendiamos diferencialinės lygtys. Norint skaitiniu būdu išspręsti diferencialinę lygtį, reikia žinoti ieškomos funkcijos ir jos išvestinės
EKONOMETRIJA 1 (Regresinė analizė)
 EKONOMETRIJA 1 Regresinė analizė Kontrolinis Sudarė M.Radavičius 004 05 15 Kai kurių užduočių sprendimai KOMENTARAS. Kai kuriems uždaviniams tik nusakytos sprendimų gairės, kai kurie iš jų suskaidyti į
EKONOMETRIJA 1 Regresinė analizė Kontrolinis Sudarė M.Radavičius 004 05 15 Kai kurių užduočių sprendimai KOMENTARAS. Kai kuriems uždaviniams tik nusakytos sprendimų gairės, kai kurie iš jų suskaidyti į
Vilius Stakėnas. Kodavimo teorija. Paskaitu. kursas
 Vilius Stakėnas Kodavimo teorija Paskaitu kursas 2002 2 I vadas Informacija perduodama kanalais, kurie kartais iškraipo informacija Tarsime, kad tie iškraipymai yra atsitiktiniai, t y nėra nei sistemingi,
Vilius Stakėnas Kodavimo teorija Paskaitu kursas 2002 2 I vadas Informacija perduodama kanalais, kurie kartais iškraipo informacija Tarsime, kad tie iškraipymai yra atsitiktiniai, t y nėra nei sistemingi,
04 Elektromagnetinės bangos
 04 Elektromagnetinės bangos 1 0.1. BANGINĖ ŠVIESOS PRIGIMTIS 3 Šiame skyriuje išvesime banginę lygtį iš elektromagnetinio lauko Maksvelo lygčių. Šviesa yra elektromagnetinė banga, kurios dažnis yra optiniame
04 Elektromagnetinės bangos 1 0.1. BANGINĖ ŠVIESOS PRIGIMTIS 3 Šiame skyriuje išvesime banginę lygtį iš elektromagnetinio lauko Maksvelo lygčių. Šviesa yra elektromagnetinė banga, kurios dažnis yra optiniame
2008 m. matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija
 008 M MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA 008 m matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 7 uždavinių atsakymai I variantas Užd
008 M MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA 008 m matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 7 uždavinių atsakymai I variantas Užd
TIKIMYBIU TEORIJA HAMLETAS MARK AITIS MYKOLO ROMERIO UNIVERSITETAS 2010
 TIKIMYBIU TEORIJA HAMLETAS MARK AITIS MYKOLO ROMERIO UNIVERSITETAS 2010 Tikimybiu teorija nagrin eja atsitiktinius ivykius ir tu ivykiu tikimybes ivykio pasirodymo galimyb es mat, i²reik²t skai iumi p,
TIKIMYBIU TEORIJA HAMLETAS MARK AITIS MYKOLO ROMERIO UNIVERSITETAS 2010 Tikimybiu teorija nagrin eja atsitiktinius ivykius ir tu ivykiu tikimybes ivykio pasirodymo galimyb es mat, i²reik²t skai iumi p,
Diskrečioji matematika
 VILNIAUS UNIVERSITETAS Gintaras Skersys Julius Andrikonis Diskrečioji matematika Pratybų medžiaga Versija: 28 m. sausio 22 d. Vilnius, 27 Turinys Turinys 2 Teiginiai. Loginės operacijos. Loginės formulės
VILNIAUS UNIVERSITETAS Gintaras Skersys Julius Andrikonis Diskrečioji matematika Pratybų medžiaga Versija: 28 m. sausio 22 d. Vilnius, 27 Turinys Turinys 2 Teiginiai. Loginės operacijos. Loginės formulės
06 Geometrin e optika 1
 06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
Statistinė termodinamika. Boltzmann o pasiskirstymas
 Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
1 iš 15 RIBOTO NAUDOJIMO
 iš 5 PATVIRTINTA Nacionalinio egzaminų centro direktoriau 00-06-08 įakymu Nr. 6.-S- 00 m. matematiko valtybinio brando egzamino VERTINIMO INSTRUKCIJA Pagrindinė eija 8 uždavinių atakymai Užd. Nr. 5 6 7
iš 5 PATVIRTINTA Nacionalinio egzaminų centro direktoriau 00-06-08 įakymu Nr. 6.-S- 00 m. matematiko valtybinio brando egzamino VERTINIMO INSTRUKCIJA Pagrindinė eija 8 uždavinių atakymai Užd. Nr. 5 6 7
4.3. Minimalaus dengiančio medžio radimas
 SKYRIUS. ALGORITMAI GRAFUOSE.. Minimalaus dengiančio medžio radimas Šiame skyriuje susipažinsime su minimaliu dengiančiu medžių radimo algoritmais. Pirmiausia sudarysime dvi taisykles, leidžiančias pasirinkti
SKYRIUS. ALGORITMAI GRAFUOSE.. Minimalaus dengiančio medžio radimas Šiame skyriuje susipažinsime su minimaliu dengiančiu medžių radimo algoritmais. Pirmiausia sudarysime dvi taisykles, leidžiančias pasirinkti
0.1. Bendrosios sąvokos
 0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
5 paskaita. 5.1 Kompaktiškosios aibės Sąvokos
 5 pskit 5.1 Kompktiškosios ibės 5.1.1 Sąvokos Iš mtemtinės nlizės kurso žinome dvi svrbis prėžtu reliu ju skičiu ibiu svybes. Pirmoji Bolcno-Vejerštrso teorem: bet kuri beglinė prėžt reliu ju skičiu ibė
5 pskit 5.1 Kompktiškosios ibės 5.1.1 Sąvokos Iš mtemtinės nlizės kurso žinome dvi svrbis prėžtu reliu ju skičiu ibiu svybes. Pirmoji Bolcno-Vejerštrso teorem: bet kuri beglinė prėžt reliu ju skičiu ibė
Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė
 Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė dėst. T. Rekašius, 2012 m. lapkričio 19 d. 1 Duomenys Visi trečiam laboratoriniam darbui reikalingi duomenys yra tekstinio formato failuose http://fmf.vgtu.lt/~trekasius/destymas/2012/ekomet_lab3_xx.dat,
Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė dėst. T. Rekašius, 2012 m. lapkričio 19 d. 1 Duomenys Visi trečiam laboratoriniam darbui reikalingi duomenys yra tekstinio formato failuose http://fmf.vgtu.lt/~trekasius/destymas/2012/ekomet_lab3_xx.dat,
Taikomieji optimizavimo metodai
 Taikomieji optimizavimo metodai 1 LITERATŪRA A. Apynis. Optimizavimo metodai. V., 2005 G. Dzemyda, V. Šaltenis, V. Tiešis. Optimizavimo metodai, V., 2007 V. Būda, M. Sapagovas. Skaitiniai metodai : algoritmai,
Taikomieji optimizavimo metodai 1 LITERATŪRA A. Apynis. Optimizavimo metodai. V., 2005 G. Dzemyda, V. Šaltenis, V. Tiešis. Optimizavimo metodai, V., 2007 V. Būda, M. Sapagovas. Skaitiniai metodai : algoritmai,
Labai svarbi tiesiniu operatoriu šeima kompaktiškieji operatoriai. Jiems skirtas paskutinysis?? skyrelis.
 13 pskit 13.1 Tiesinii opertorii Šime skyriuje ngrinėjmos normuotu ju erdviu tiesinės funkcijos tiesinii opertorii. Bigtinės dimensijos erdvėms, kip mtysime, jie pršomi mtricomis. Tigi tiesiniu opertoriu
13 pskit 13.1 Tiesinii opertorii Šime skyriuje ngrinėjmos normuotu ju erdviu tiesinės funkcijos tiesinii opertorii. Bigtinės dimensijos erdvėms, kip mtysime, jie pršomi mtricomis. Tigi tiesiniu opertoriu
Matematinis modeliavimas
 ALGIRDAS AMBRAZEVIƒIUS Matematinis modeliavimas Vilniaus universitetas 2006 2 TURINYS 1 SKYRIUS PAPRASƒIAUSI MATEMATINIAI MODELIAI 4 11 Pagrindines s vokos 4 12 Fundamentaliu gamtos desniu taikymas 10
ALGIRDAS AMBRAZEVIƒIUS Matematinis modeliavimas Vilniaus universitetas 2006 2 TURINYS 1 SKYRIUS PAPRASƒIAUSI MATEMATINIAI MODELIAI 4 11 Pagrindines s vokos 4 12 Fundamentaliu gamtos desniu taikymas 10
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 1
 DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 1 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 9 d. Santrauka Pirmas laboratorinis darbas skirtas išmokti generuoti nesudėtingus
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 1 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 9 d. Santrauka Pirmas laboratorinis darbas skirtas išmokti generuoti nesudėtingus
III.Termodinamikos pagrindai
 III.ermodinamikos pagrindai III.. Dujų plėtimosi darbas egu dujos yra cilindre su nesvariu judančiu stūmokliu, kurio plotas lygus S, ir jas veikia tik išorinis slėgis p. Pradinius dujų parametrus pažymėkime
III.ermodinamikos pagrindai III.. Dujų plėtimosi darbas egu dujos yra cilindre su nesvariu judančiu stūmokliu, kurio plotas lygus S, ir jas veikia tik išorinis slėgis p. Pradinius dujų parametrus pažymėkime
M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS MATEMATIKOS KATEDRA Antanas Lapinskas M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D (MOKOMOJI KNYGA) AKADEMIJA 006 UDK 0049 (0754) Sudarė: doc dr Antanas
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS MATEMATIKOS KATEDRA Antanas Lapinskas M A T E M A T I K O S P R A K T I K U M A S S U M A T H C A D (MOKOMOJI KNYGA) AKADEMIJA 006 UDK 0049 (0754) Sudarė: doc dr Antanas
P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ
 P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
PNEUMATIKA - vožtuvai
 Mini vožtuvai - serija VME 1 - Tipas: 3/2, NC, NO, monostabilūs - Valdymas: Mechaninis ir rankinis - Nominalus debitas (kai 6 barai, Δp = 1 baras): 60 l/min. - Prijungimai: Kištukinės jungtys ø 4 žarnoms
Mini vožtuvai - serija VME 1 - Tipas: 3/2, NC, NO, monostabilūs - Valdymas: Mechaninis ir rankinis - Nominalus debitas (kai 6 barai, Δp = 1 baras): 60 l/min. - Prijungimai: Kištukinės jungtys ø 4 žarnoms
Gabija Maršalkaitė Motiejus Valiūnas. Astronomijos pratybų užduočių komplektas
 Gabija Maršalkaitė Motiejus Valiūnas Astronomijos pratybų užduočių komplektas Vilnius 2014 1 Įvadas 1.1 Astronomijos olimpiados Lietuvoje kylant moksleivių susidomėjimu astronomijos olimpiada buvo pastebėta,
Gabija Maršalkaitė Motiejus Valiūnas Astronomijos pratybų užduočių komplektas Vilnius 2014 1 Įvadas 1.1 Astronomijos olimpiados Lietuvoje kylant moksleivių susidomėjimu astronomijos olimpiada buvo pastebėta,
Vilijandas Bagdonavi ius. Julius Jonas Kruopis MATEMATIN E STATISTIKA
 VILNIAUS UNIVERSITETO MATEMATIKOS IR INFORMATIKOS FAKULTETAS Vilijandas Bagdonavi ius Julius Jonas Kruopis MATEMATIN E STATISTIKA Vadovelis IV DALIS DAUGIAMAT E STATISTIKA Vilniaus universiteto leidykla
VILNIAUS UNIVERSITETO MATEMATIKOS IR INFORMATIKOS FAKULTETAS Vilijandas Bagdonavi ius Julius Jonas Kruopis MATEMATIN E STATISTIKA Vadovelis IV DALIS DAUGIAMAT E STATISTIKA Vilniaus universiteto leidykla
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2
 DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 23 d. Santrauka Antras laboratorinis darbas skirtas išmokti sudarinėti daugialypės
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 23 d. Santrauka Antras laboratorinis darbas skirtas išmokti sudarinėti daugialypės
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Fizikos katedra. Juozas Navickas FIZIKA. I dalis MOKOMOJI KNYGA
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Fizikos katedra Juozas Navickas FIZIKA I dalis MOKOMOJI KNYGA KAUNAS, ARDIVA 8 UDK 53(75.8) Na95 Juozas Navickas FIZIKA, I dalis
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Fizikos katedra Juozas Navickas FIZIKA I dalis MOKOMOJI KNYGA KAUNAS, ARDIVA 8 UDK 53(75.8) Na95 Juozas Navickas FIZIKA, I dalis
KADETAS (VII ir VIII klasės)
 ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
Praeita paskaita. Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje. Praeita paskaita. 2D Transformacijos. Grafika ir vizualizavimas, VDU, 2010
 Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
5 klasė. - užduotys apie varniuką.
 5 klasė - užduotys apie varniuką. 1. Varniukas iš plastilino lipdė raides ir iš jų sudėliojo užrašą: VARNIUKO OLIMPIADA. Vienodas raides jis lipdė iš tos pačios spalvos plastelino, o skirtingas raides
5 klasė - užduotys apie varniuką. 1. Varniukas iš plastilino lipdė raides ir iš jų sudėliojo užrašą: VARNIUKO OLIMPIADA. Vienodas raides jis lipdė iš tos pačios spalvos plastelino, o skirtingas raides
ŠVIESOS SKLIDIMAS IZOTROPINĖSE TERPĖSE
 ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
Papildomo ugdymo mokykla Fizikos olimpas. Mechanika Dinamika 1. (Paskaitų konspektas) 2009 m. sausio d. Prof.
 Papildoo ugdyo okykla izikos olipas Mechanika Dinaika (Paskaitų konspektas) 9. sausio -8 d. Prof. Edundas Kuokštis Vilnius Paskaita # Dinaika Jei kineatika nagrinėja tik kūnų judėjią, nesiaiškindaa tą
Papildoo ugdyo okykla izikos olipas Mechanika Dinaika (Paskaitų konspektas) 9. sausio -8 d. Prof. Edundas Kuokštis Vilnius Paskaita # Dinaika Jei kineatika nagrinėja tik kūnų judėjią, nesiaiškindaa tą
1. Įvadas į sistemas ir signalus. 1. Signalas, duomenys, informacija ir žinios
 . Įvadas į sistemas ir signalus. Signalas, duomenys, informacija ir žinios Žodis signalas yra kilęs iš lotyniško žodžio signum ženklas. Signalas tai yra tai kas yra naudojama žiniai perduoti. Signalas
. Įvadas į sistemas ir signalus. Signalas, duomenys, informacija ir žinios Žodis signalas yra kilęs iš lotyniško žodžio signum ženklas. Signalas tai yra tai kas yra naudojama žiniai perduoti. Signalas
Atsitiktinių paklaidų įvertinimas
 4.4.4. tsitiktinių paklaidų įvertinimas tsitiktinės paklaidos įvertinamos nurodant du dydžius: pasikliaujamąjį intervalą ir pasikliaujamąją tikimybę. tsitiktinių paklaidų atveju, griežtai tariant, nėra
4.4.4. tsitiktinių paklaidų įvertinimas tsitiktinės paklaidos įvertinamos nurodant du dydžius: pasikliaujamąjį intervalą ir pasikliaujamąją tikimybę. tsitiktinių paklaidų atveju, griežtai tariant, nėra
Remigijus Leipus. Ekonometrija II. remis
 Remigijus Leipus Ekonometrija II http://uosis.mif.vu.lt/ remis Vilnius, 2013 Turinys 1 Trendo ir sezoniškumo vertinimas bei eliminavimas 4 1.1 Trendo komponentės vertinimas ir eliminavimas........ 4 1.2
Remigijus Leipus Ekonometrija II http://uosis.mif.vu.lt/ remis Vilnius, 2013 Turinys 1 Trendo ir sezoniškumo vertinimas bei eliminavimas 4 1.1 Trendo komponentės vertinimas ir eliminavimas........ 4 1.2
2 laboratorinis darbas. TIKIMYBINIAI MODELIAI
 laboratorns darbas laboratorns darbas. TIKIMYBINIAI MODELIAI DARBO TIKSLAS - šstudjuot atstktnų dydžų r vektorų skrstnus, skrstno (passkrstymo) funkcją, tanko funkcją, skatnes charakterstkas r jų savybes.
laboratorns darbas laboratorns darbas. TIKIMYBINIAI MODELIAI DARBO TIKSLAS - šstudjuot atstktnų dydžų r vektorų skrstnus, skrstno (passkrstymo) funkcją, tanko funkcją, skatnes charakterstkas r jų savybes.
Laboratorinis darbas Nr. 2
 M A T E M A T I N Ė S T A T I S T I K A Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2005 m. spalio 23 d. Reziumė Antras laboratorinis darbas skirtas išmokti generuoti tikimybinių skirstinių
M A T E M A T I N Ė S T A T I S T I K A Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2005 m. spalio 23 d. Reziumė Antras laboratorinis darbas skirtas išmokti generuoti tikimybinių skirstinių
Matematinės analizės egzamino klausimai MIF 1 kursas, Bioinformatika, 1 semestras,
 MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
II dalis Teisingas atsakymas į kiekvieną II dalies klausimą vertinamas 1 tašku g/mol
 PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 05 m. birželio 8 d. įsakymu Nr. (.3.)-V-73 05 M. CHEMIJOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA. Pagrindinė sesija I dalis Teisingas
PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 05 m. birželio 8 d. įsakymu Nr. (.3.)-V-73 05 M. CHEMIJOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA. Pagrindinė sesija I dalis Teisingas
Pav1 Žingsnio perdavimo funkcija gali būti paskaičiuota integruojant VIPF. Paskaičiavus VIPF FFT gaunamo amplitudinė_dažninė ch_ka.
 Įvadas į filtrus Skaitmeniniai filtrai, tai viena iš svarbiausių siganalų apdorojimo dalių. Kadangi skaitmeniniai filtrai turi nepalyginamai daugiau pranašumų nei analoginiai filtrai, tai nulėmė jų populiarumą.
Įvadas į filtrus Skaitmeniniai filtrai, tai viena iš svarbiausių siganalų apdorojimo dalių. Kadangi skaitmeniniai filtrai turi nepalyginamai daugiau pranašumų nei analoginiai filtrai, tai nulėmė jų populiarumą.
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
Arenijaus (Arrhenius) teorija
 Rūgštys ir bazės Arenijaus (Arrhenius) teorija Rūgštis: Bazė: H 2 O HCl(d) H + (aq) + Cl - (aq) H 2 O NaOH(k) Na + (aq) + OH - (aq) Tuomet neutralizacijos reakcija: Na + (aq) + OH - (aq) + H + (aq) + Cl
Rūgštys ir bazės Arenijaus (Arrhenius) teorija Rūgštis: Bazė: H 2 O HCl(d) H + (aq) + Cl - (aq) H 2 O NaOH(k) Na + (aq) + OH - (aq) Tuomet neutralizacijos reakcija: Na + (aq) + OH - (aq) + H + (aq) + Cl
V skyrius ĮVAIRŪS PALŪKANŲ APSKAIČIAVIMO KLAUSIMAI
 V skyrius ĮVAIRŪS PALŪKANŲ APSKAIČIAVIMO KLAUSIMAI Uždirbtų palūkanų suma priklauso ne tik nuo palūkanų normos dydžio, bet ir nuo palūkanų kapitalizavimo dažnio Metinė palūkanų norma nevisada atspindi
V skyrius ĮVAIRŪS PALŪKANŲ APSKAIČIAVIMO KLAUSIMAI Uždirbtų palūkanų suma priklauso ne tik nuo palūkanų normos dydžio, bet ir nuo palūkanų kapitalizavimo dažnio Metinė palūkanų norma nevisada atspindi
AUTOMATINIO VALDYMO TEORIJA
 Saulius LISAUSKAS AUTOMATINIO VALDYMO TEORIJA Projekto kodas VP1-.-ŠMM-7-K-1-47 VGTU Elektronikos fakulteto I pakopos studijų programų esminis atnaujinimas Vilnius Technika 1 VILNIAUS GEDIMINO TECHNIKOS
Saulius LISAUSKAS AUTOMATINIO VALDYMO TEORIJA Projekto kodas VP1-.-ŠMM-7-K-1-47 VGTU Elektronikos fakulteto I pakopos studijų programų esminis atnaujinimas Vilnius Technika 1 VILNIAUS GEDIMINO TECHNIKOS
LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 2014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ
 LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 014 m. birželio 5 d. matematikos valstybinį
LIETUVOS RESPUBLIKOS ÐVIETIMO IR MOKSLO MINISTERIJA NACIONALINIS EGZAMINØ CENTRAS 014 METŲ MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO REZULTATŲ STATISTINĖ ANALIZĖ 014 m. birželio 5 d. matematikos valstybinį
Riebalų rūgščių biosintezė
 Riebalų rūgščių biosintezė Riebalų rūgščių (RR) biosintezė Kepenys, pieno liaukos, riebalinis audinys pagrindiniai organai, kuriuose vyksta RR sintezė RR grandinė ilginama jungiant 2C atomus turinčius
Riebalų rūgščių biosintezė Riebalų rūgščių (RR) biosintezė Kepenys, pieno liaukos, riebalinis audinys pagrindiniai organai, kuriuose vyksta RR sintezė RR grandinė ilginama jungiant 2C atomus turinčius
Fizika. doc. dr. Vytautas Stankus. Fizikos katedra Matematikos ir gamtos mokslų fakultetas Kauno Technologijos Universitetas
 Fizika doc. dr. Vytautas Stankus Fizikos katedra Matematikos ir gamtos mokslų fakultetas Kauno Technologijos Universitetas Studentų 50 58 kab. Darbo tel.: 861033946 Vytautas.Stankus@ktu.lt Bendrosios fizikos
Fizika doc. dr. Vytautas Stankus Fizikos katedra Matematikos ir gamtos mokslų fakultetas Kauno Technologijos Universitetas Studentų 50 58 kab. Darbo tel.: 861033946 Vytautas.Stankus@ktu.lt Bendrosios fizikos
FRANKO IR HERCO BANDYMAS
 VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. FRANKO IR HERCO BANDYMAS Parengė A. Poškus 013-08-31 Turinys Darbo tikslas 1.
VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. FRANKO IR HERCO BANDYMAS Parengė A. Poškus 013-08-31 Turinys Darbo tikslas 1.
FIZ 313 KOMPIUTERINĖ FIZIKA. Laboratorinis darbas FIZIKOS DIFERENCIALINIŲ LYGČIŲ SPRENDIMAS RUNGĖS KUTOS METODU
 EUROPOS SĄJUNGA Europos socialinis fondas KURKIME ATEITĮ DRAUGE! 2004-2006 m. Bendrojo programavimo dokumento 2 prioriteto Žmogiškųjų išteklių plėtra 4 priemonė Mokymosi visą gyvenimą sąlygų plėtra Projekto
EUROPOS SĄJUNGA Europos socialinis fondas KURKIME ATEITĮ DRAUGE! 2004-2006 m. Bendrojo programavimo dokumento 2 prioriteto Žmogiškųjų išteklių plėtra 4 priemonė Mokymosi visą gyvenimą sąlygų plėtra Projekto
2.6. IŠVESTINĖ, DIFERENCIJAVIMAS
 6 IŠVESTINĖ DIFERENCIJAVIMAS 61 Išvestiės sąvok Fukcijos išvestiės sąvok yr mtemtikos istrumets kurio reikšmę suku įvertiti Glbūt ti glim plygiti su vidus degimo vriklio sukūrimu Diferecijuoti pprsčiusis
6 IŠVESTINĖ DIFERENCIJAVIMAS 61 Išvestiės sąvok Fukcijos išvestiės sąvok yr mtemtikos istrumets kurio reikšmę suku įvertiti Glbūt ti glim plygiti su vidus degimo vriklio sukūrimu Diferecijuoti pprsčiusis
1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai
 1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai 1.1. Branduolio nukleonų energijos diskretumo aiškinimas. Dalelė stačiakampėje potencialo duobėje Dalelės banginė funkcija tai koordinačių ir
1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai 1.1. Branduolio nukleonų energijos diskretumo aiškinimas. Dalelė stačiakampėje potencialo duobėje Dalelės banginė funkcija tai koordinačių ir
SIGNALAI TELEKOMUNIKACIJŲ SISTEMOSE
 VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra SIGNALAI TELEKOMUNIKACIJŲ SISTEMOSE Mokymo priemonė Parengė A. Poškus 4 Turinys. ĮVADAS..... Telekomunikaijų sistemos struktūrinė shema. Pagrindinės
VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra SIGNALAI TELEKOMUNIKACIJŲ SISTEMOSE Mokymo priemonė Parengė A. Poškus 4 Turinys. ĮVADAS..... Telekomunikaijų sistemos struktūrinė shema. Pagrindinės
1. Klasifikavimo su mokytoju metodai
 1. Klasifikavimo su mokytoju metodai Klasifikacijos uždavinys yra atpažinimo uždavinys, kurio esmė pagal pateiktus objekto (vaizdo, garso, asmens, proceso) skaitinius duomenis priskirti ji kokiai nors
1. Klasifikavimo su mokytoju metodai Klasifikacijos uždavinys yra atpažinimo uždavinys, kurio esmė pagal pateiktus objekto (vaizdo, garso, asmens, proceso) skaitinius duomenis priskirti ji kokiai nors
