Διπλωματική Εργασία. του φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και. Τεχνολογίας Υπολογιστών της Πολυτεχνικής Σχολής του. Πανεπιστημίου Πατρών
|
|
|
- Μελίνα Κρεστενίτης
- 5 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ: ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΕΡΓΑΣΤΗΡΙO: ΑΥΤΟΜΑΤΙΣΜΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ Διπλωματική Εργασία του φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών της Πολυτεχνικής Σχολής του Πανεπιστημίου Πατρών Γεωργίου Πανταζή του Νεκταρίου Αριθμός Μητρώου: Θέμα «Συγκριτική Μελέτη των Μεθόδων Ενεργειακής Διαχείρισης Βασισμένων στην Βελτιστοποίηση σε Υβριδικά Ηλεκτρικά Οχήματα» Επιβλέπων Κούσουλας Νικόλαος Αριθμός Διπλωματικής Εργασίας: Πάτρα, Απρίλιος
2 ΠΙΣΤΟΠΟΙΗΣΗ Πιστοποιείται ότι η Διπλωματική Εργασία με θέμα «Συγκριτική Μελέτη των Μεθόδων Ενεργειακής Διαχείρισης Βασισμένων στην Βελτιστοποίηση σε Υβριδικά Ηλεκτρικά Οχήματα» Του φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Γεωργίου Πανταζή του Νεκταρίου Αριθμός Μητρώου: Παρουσιάστηκε δημόσια και εξετάστηκε στο Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών στις.../../ Ο Επιβλέπων Κούσουλας Νικόλαος Ο Διευθυντής του Τομέα Κούσουλας Νικόλαος Αριθμός Διπλωματικής Εργασίας: 2
3 Θέμα: «Συγκριτική Μελέτη των Μεθόδων Ενεργειακής Διαχείρισης Βασισμένων στην Βελτιστοποίηση σε Υβριδικά Ηλεκτρικά Οχήματα» Φοιτητής: Πανταζής Γεώργιος Επιβλέπων: Κούσουλας Νικόλαος Περίληψη Στην παρούσα εργασία πραγματοποιήθηκε μία μελέτη των -βασισμένων στην βελτιστοποίηση- μεθόδων ενεργειακής διαχείρισης υβριδικών ηλεκτρικών οχημάτων. Αρχικά, αναλύθηκε η δυναμική και ενεργειακή ισορροπία του οχήματος. Στην συνέχεια, πραγματοποιήθηκε η περιγραφή των κύκλων οδήγησης, καθώς και η δομή και τα είδη τοπολογιών των υβριδικών ηλεκτρικών οχημάτων. Ακόμα, έγινε περιγραφή των βασικών υποσυστημάτων του οχήματος με σκοπό την ενεργειακή διαχείριση καθώς και σύγκριση των κύριων λογισμικών ανάπτυξης υβριδικών οχημάτων. Στην συνέχεια, εξετάστηκαν οι βασικές μέθοδοι ενεργειακής διαχείρισης αρχίζοντας από την μέθοδο του Δυναμικού Προγραμματισμού. Ως μία εναλλακτική λύση στην μη αιτιότητα και στην μεγάλη υπολογιστική πολυπλοκότητα του Δυναμικού Προγραμματισμού προτάθηκε η Αρχή Ελαχίστων του Pontryagin. Προχωρώντας, πραγματοποιήθηκε η θεωρητική ανάλυση πιο σύνθετων μεθόδων Ενεργειακής Διαχείρισης όπως ο Στοχαστικός Δυναμικός Προγραμματισμός (SDP), η Στρατηγική Ελάχιστης Ισοδύναμης Κατανάλωσης (ECMS) καθώς και η Προσαρμοζόμενη Στρατηγική Ελάχιστης Ισοδύναμης Κατανάλωσης (A-ECMS) και εξετάστηκαν οι δυνατότητές και οι αδυναμίες τους σε πραγματικές εφαρμογές. Τέλος, εξετάστηκε μία υπολογιστικά απλή μέθοδος ενεργειακής διαχείρισης βασισμένη σε ένα απλοποιημένο μοντέλο και χρησιμοποιήθηκε ένας βέλτιστος νόμος 3
4 ελέγχου με λιγότερες υπολογιστικές απαιτήσεις [4]. Για την μελέτη της λειτουργίας της η μέθοδος διερευνήθηκε για διαφορετικούς κύκλους οδήγησης. Summary In this thesis, a study of optimization-based energy management strategies in hybrid electric vehicles was conducted. The basic topologies, subsystems, modelling techniques were described. In addition, an analysis of available simulation software was conducted. Initially, basic energy management methods were examined such as Dynamic Programming. As an alternative to the non-causality and the high computational complexity of Dynamic Programming, a technique based on Pontryagin s Minimum Principle was proposed. Subsequently, more complex methods of energy management were theoretically analyzed, such as Stochastic Dynamic Programming (SDP), the Equivalent Consumption Minimization Strategy (ECMS) and the Adaptive Equivalent Consumption Minimization Strategy (A-ECMS) and their advantages as well as their weaknesses in actual applications were discussed. Finally, a computationally simple energy management method based on a simplified model was examined, and an optimal control law was used [4]. To confirm its functionality, the strategy was investigated under different driving profiles. 4
5 Ευχαριστίες Θα ήθελα αρχικά να ευχαριστήσω τον Διευθυντή του τομέα Συστημάτων και Αυτομάτου Ελέγχου κ.κούσουλα Νικόλαο που δέχτηκε να είναι ο επιβλέπων μιας διπλωματικής το θέμα της οποίας επιθυμούσα χρόνια να μελετήσω. Η πολύτιμη βοήθειά του καθώς και οι συμβουλές του για τον τρόπο με τον οποίο πρέπει να προσεγγίσω το πολύπλοκο αυτό ζήτημα στάθηκαν καθοριστικές για την ολοκλήρωση της εργασίας αυτής. Ακόμα, τον ευχαριστώ βαθύτατα για την ηθική υποστήριξη τόσο σε ακαδημαϊκά όσο και σε προσωπικά ζητήματα. Επίσης, θα ήθελα να ευχαριστήσω τους καθηγητές κ.μπιτσώρη Γεώργιο και κ.αλεξανδρίδη Αντώνιο που με δίδαξαν την συστημική προσέγγιση των φυσικών συστημάτων, καθώς και την θεωρία ελέγχου με τον δικό τους ξεχωριστό τρόπο. Οι συζητήσεις μας πάνω σε πληθώρα συστημάτων και μεθόδων ελέγχου, με έκαναν να δω τον κόσμο γύρω μου τελείως διαφορετικά και έκαναν την φοίτηση των τελευταίων χρόνων μια ιδιαίτερα ευχάριστη διαδικασία. Τέλος, ένα μεγάλο ευχαριστώ οφείλω στην οικογένειά μου για την αμέριστη υποστήριξή της όλα αυτά τα χρόνια. Η κατανόηση και συμπαράστασή τους ήταν η σημαντικότερη βοήθεια τόσο στη μαθητική όσο και στην φοιτητική μου πορεία. Πίνακας περιεχομένων Eισαγωγή... 8 Ενέργεια και Περιβάλλον... 8 Το Μέλλον της Αυτοκίνησης-Κίνητρα και Στόχοι... 9 Βασικά Πλεονεκτήματα και Μειονεκτήματα Υβριδικών Ηλεκτρικών Οχημάτων Κύκλοι Οδήγησης και Οδηγητικές Συνθήκες Κύκλοι Οδήγησης Ευρωπαϊκός Κύκλος Οδήγησης (EUDC) Κύκλος FTP-Highway (HWFET) Κύκλος City-II
6 Νέος Ευρωπαϊκός Κύκλος Οδήγησης (NEDC) Κύκλος FTP Δυναμική και Ενεργειακή Ισορροπία Οχήματος Δυνάμεις Ασκούμενες κατά την Οδήγηση Προσέγγιση Backward και Forward- Εξαγωγή της Ισορροπίας Ισχύος Aνάλυση της Μοντελοποίησης της Οδηγητικής Ισχύος μέσω Πραγματικών Μετρήσεων Δομή και Μέθοδοι Μοντελοποίησης Υβριδικών Οχημάτων Είδη Προσεγγίσεων Μοντελοποίησης Μέθοδος Μέσου Σημείου Ψευδοστατική Μέθοδος Δυναμική Μέθοδος Υποσυστήματα Παράλληλου Υβριδικού Οχήματος Μηχανή Εσωτερικής Καύσης Ηλεκτρική Μηχανή Μπαταρία Διαφορικό Κιβώτιο Ταχυτήτων και Μετάδοση Τοπολογίες Υβριδικών Ηλεκτρικών Οχημάτων Τοπολογία σε Σειρά...45 Τοπολογία εν Παραλλήλω Μεικτή Τοπολογία Εργαλεία Προσομοίωσης Υβριδικών Οχημάτων Easy AMESim Modellica Simscape Driveline QSS-Toolbox Advisor
7 Βελτιστοποίηση και Ενεργειακή Διαχείριση Υβριδικών Οχημάτων Κατηγορίες Βελτιστοποίησης Υβριδικών Οχημάτων Ανάλυση Συστήματος..58 Το Γενικό Πρόβλημα Ενεργειακής Διαχείρισης...59 Μαθηματική Διατύπωση του Γενικού Προβλήματος Ενεργειακής Διαχείρισης στο Συνεχή Χώρο Κατάστασης Η Μέθοδος του Δυναμικού Προγραμματισμού Δυναμικός Προγραμματισμός & Ενεργειακή Διαχείριση Ενδεικτικά Αποτελέσματα Μεθόδου Μειονεκτήματα του Δυναμικού Προγραμματισμού Αρχή Ελαχίστων του Pontryagin Αρχή Ελαχίστων του Pontryagin για προβλήματα χωρίς περιορισμούς κατάστασης Αρχή Ελαχίστων του Pontryagin για προβλήματα με περιορισμούς κατάστασης Προβλήματα Υλοποίησης Σημασία της Αρχικής Τιμής της Συμπληρωματικής Κατάστασης στο Πρόβλημα Ενεργειακής Διαχείρισης Ενδεικτικά Αποτελέσματα Μεθόδου και Συμπεράσματα Σύγχρονες Στρατηγικές Βασισμένες στον Δυναμικό Προγραμματισμό και στην Αρχή Ελαχίστων του Pontryagin Στοχαστικός Δυναμικός Προγραμματισμός (SDP) Στρατηγική Ελάχιστης Ισοδύναμης Κατανάλωσης Καυσίμου (ECMS) Προσαρμοζόμενη Στρατηγική Ελάχιστης Ισοδύναμης Κατανάλωσης Καυσίμου (Α-ECMS) Απλοποιημένη Μέθοδος για Ενεργειακή Διαχείριση Απλοποιημένο Μοντέλο Υβριδικού Ηλεκτρικού Οχήματος Βέλτιστος Νόμος Ελέγχου και Καταστάσεις Λειτουργίας Ανάλυση Μονοτονίας Χαμιλτονιανής Συνάρτησης Σχεδιασμός Περιοχών Λειτουργίας Αποτελέσματα και Συμπεράσματα Μεθόδου
8 1. Eισαγωγή 1.1 Ενέργεια & Περιβάλλον [42],[22],[8] H μεγάλη αύξηση του πληθυσμού καθώς και η χρήση μηχανημάτων για τις περισσότερες ανθρώπινες εργασίες είχαν ως αποτέλεσμα την ραγδαία αύξηση της κατανάλωσης των διαθέσιμων ενεργειακών πόρων για την κάλυψη των ανθρώπινων αναγκών. [66] Ωστόσο, η χρήση ορυκτών καυσίμων είναι μια λύση προσωρινή στο παγκόσμιο ενεργειακό πρόβλημα καθώς τα ορυκτά καύσιμα συμβάλλουν στην ρύπανση του περιβάλλοντος με μη αντιστρεπτά αποτελέσματα τόσο για το κλίμα και την ατμόσφαιρα όσο και για το έδαφος και τα ύδατα. Το πρόβλημα αυτό μπορεί να προληφθεί μόνο αν ληφθούν δραστικά μέτρα για την μείωση των ρύπων κατά περίπου 60% τις επόμενες 4-5 δεκαετίες. Ωστόσο, οι χαμηλές τιμές των ορυκτών καυσίμων, ωθούν τους καταναλωτές στην αύξηση της κατανάλωσής τους για την εξασφάλιση ενεργειακών αναγκών, γεγονός που δυσχεραίνει το πρόβλημα, ακόμα κι αν η στρατηγική μείωσης των ρύπων είναι βιώσιμη και εφικτή. [42], [22] Ευτυχώς, το πρόβλημα έχει εντοπιστεί γεγονός που γίνεται φανερό από την σημαντική αύξηση των επενδύσεων σε ανανεώσιμες πηγές ενέργειας. Συγκεκριμένα, το 2015 το 70% του συνολικού κεφαλαίου για παγκόσμια ενεργειακή κάλυψη αξιοποιήθηκε για την εξόρυξη ορυκτών καυσίμων. Το 2016 το ποσοστό αυτό μειώθηκε σε 60% ενώ σχεδόν το 20% του συνολικού κεφαλαίου επενδύθηκε σε ανανεώσιμες πηγές ενέργειας γεγονός που φανερώνει μια στροφή των επενδύσεων σε περιβαλλοντολογικά φιλικότερες και μονιμότερες ενεργειακές λύσεις. [8] Το βασικό κλειδί σε ένα ενεργειακά βιώσιμο μέλλον είναι η βελτίωση της απόδοσης των συστημάτων αυτών. Η πολυπλοκότητα των σημερινών συστημάτων καθιστά τον σχεδιασμό στρατηγικών με σκοπό την βελτίωση της απόδοσης ανέφικτο μόνο με χρήση της εμπειρίας. Η μαθηματική περιγραφή υπό την μορφή διαφορικών εξισώσεων προσφέρει μια πιο διεισδυτική ματιά τόσο στο σύστημα όσο και στο ίδιο το πρόβλημα. 8
9 Η παράλληλη εξέλιξη του τομέα της ενέργειας και της θεωρίας ελέγχου οδήγησε στον συνδυασμό των δύο αυτών κλάδων με σκοπό την εξασφάλιση υψηλών προδιαγραφών λειτουργίας μέσω αποδοτικών αλγορίθμων ελέγχου και την βελτιστοποίηση της ενεργειακής οικονομίας. Πλέον τα δύο αυτά πεδία είναι αδήριτα συνδεδεμένα σε πλήθος ενεργειακών εφαρμογών. 1.2 Το Μέλλον της Αυτοκίνησης-Κίνητρα και Στόχοι [8],[42] Σύμφωνα με την [8] κατά το έτος 2014 ο τομέας των μεταφορών ήταν υπεύθυνος σε ποσοστό περίπου 26% για την ποσότητα διοξειδίου του άνθρακα που εκλύεται στην ατμόσφαιρα λόγω των μηχανών εσωτερικής καύσης. Όπως αναφέρουν οι [42] και [23], οι μηχανές εσωτερικής καύσης χρησιμοποιούν την χημική ενέργεια του καυσίμου για να παράγουν μηχανική ενέργεια στον άξονα μέσω καύσης, μιας διαδικασίας που απελευθερώνει ενέργεια και κάποια άλλα προϊόντα της αντίδρασης. Στην ιδανική περίπτωση που πραγματοποιείται πλήρης καύση, τα προϊόντα (για την περίπτωση των υδρογονανθράκων) είναι το διοξείδιο του άνθρακα CO2 και το νερό H2O ενώ η ατελής καύση που είναι και πιο συχνή, οδηγεί στα λεγόμενα παραπροϊόντα καύσης. Επίσης το CO2 υπό συγκεκριμένες συγκεντρώσεις δεν αποτελεί ρύπο καθώς αξιοποιείται από τα φυτά κατά τη διαδικασία της φωτοσύνθεσης. Συνεπώς, το CO2 είναι απαραίτητο συστατικό για την ισορροπία του οικοσυστήματος [42], [23]. Ο μεγάλος αριθμός οχημάτων,ωστόσο, έχει ως αποτέλεσμα την έκλυση μεγάλων ποσοτήτων CO2 στο περιβάλλον, το οποίο μπορεί να προκαλέσει σημαντικά προβλήματα σε μεγαλύτερες του κανονικού ποσότητες. [65] Το διοξείδιο του άνθρακα αποτελεί το κύριο καυσαέριο του φαινομένου του θερμοκηπίου, καθώς συνέβαλλε με συμμετοχή 65% το 2010 [8] στην αύξηση θερμοκρασίας του πλανήτη και μέτρα για την μείωσή του πρέπει να ληφθούν άμεσα. 9
10 Εικόνα 1-Ποσοστό συμμετοχής του τομέα των μεταφορών στην έκλυση αερίων του θερμοκηπίου & σύσταση % των αερίων αυτών [8] Με βασικό σκοπό την μείωση του εκλυόμενου CO2, γίνεται μεγάλη προσπάθεια για την ανάπτυξη τεχνολογιών πιο φιλικών προς το περιβάλλον. Τα ηλεκτρικά και τα υβριδικά οχήματα συμβάλλουν στην επίτευξη του σκοπού αυτού. Πιο συγκεκριμένα, τα υβριδικά ηλεκτρικά οχήματα, που είναι και το αντικείμενο της εργασίας αυτής, συνδυάζουν δύο διαφορετικές πηγές ενέργειας που καλύπτουν το φορτίο ανάλογα με το ποια συμφέρει οικονομικά την εκάστοτε στιγμή. Πολλές αυτοκινητοβιομηχανίες αναπτύσσουν εδώ και χρόνια τέτοια μοντέλα με ιδιαίτερα ελπιδοφόρα αποτελέσματα για το μέλλον. Μάλιστα, στα plug-in υβριδικά οχήματα παρέχεται η δυνατότητα φόρτισης της μπαταρίας από ειδικούς σταθμούς φόρτισης. Αν η ηλεκτρική ενέργεια με την οποία φορτίζεται το όχημα προέρχεται από ανεμογεννήτριες ή φωτοβολταϊκά, τότε η φόρτιση του αυτοκινήτου και συνεπώς και η ηλεκτροκίνησή του παράγεται χωρίς να λαμβάνει χώρα καύση κάποιου ορυκτού καυσίμου. 10
11 Εικόνα 2-Διάγραμμα εκπομπών CO2 κατά τα έτη λόγω του τομέα των μεταφορών [8] 1.3 Τα Βασικά Πλεονεκτήματα και Μειονεκτήματα των Υβριδικών Ηλεκτρικών Οχημάτων [29] Η δομή του συστήματος μετάδοσης των υβριδικών ηλεκτρικών οχημάτων περιλαμβάνει, συνήθως, την συσκευή αποθήκευσης ηλεκτρικής ενέργειας, την μηχανή, τον ηλεκτροκινητήρα και το κιβώτιο ταχυτήτων ως βασικά υποσυστήματα. Μερικές διατάξεις χρησιμοποιούν και μία δεύτερη ηλεκτρική μηχανή που λειτουργεί ως γεννήτρια. Ως συσκευή αποθήκευσης ηλεκτρικής ενέργειας χρησιμοποιείται, συνήθως, μία ηλεκτροχημική μπαταρία, ενώ σπανιότερα χρησιμοποιούνται υπερπυκνωτές. Η πολυπλοκότητα του υβριδικού συστήματος μετάδοσης κίνησης κάνει την στρατηγική ελέγχου ενός υβριδικού οχήματος πολυπλοκότερη σε σχέση με αυτή ενός συμβατικού ή ηλεκτρικού οχήματος. Η βασική ιδιότητα που καθιστά τα υβριδικά οχήματα μία πολλά υποσχόμενη λύση για το μέλλον της αυτοκίνησης είναι η δυνατότητα συνδυασμού υψηλής πυκνότητας ισχύος και υψηλής ενεργειακής πυκνότητας λόγω των δύο πηγών ενέργειας. Συγκεκριμένα, ο ηλεκτροκινητήρας χαρακτηρίζεται από υψηλή πυκνότητα ισχύος. Η υψηλή του απόδοση τον καθιστά ιδανικό για την κάλυψη των μεταβατικών οδηγητικών αναγκών. Τα μεταβατικά φαινόμενα κατά την διάρκεια ενός κύκλου οδήγησης περιλαμβάνουν εντολές του οδηγού, όπως γκάζι και φρένο, καθώς και απότομες 11
12 μεταβολές ισχύος λόγω της διαδρομής. Ωστόσο, λόγω της περιορισμένης ενέργειας στην συσκευή αποθήκευσης, οι ηλεκτροκινητήρες μπορούν να καλύψουν ολοκληρωτικά τις οδηγητικές ανάγκες μόνο για ένα σχετικά μικρό εύρος της διαδρομής. Χαρακτηρίζονται,δηλαδή, από χαμηλή ενεργειακή πυκνότητα. [29] Το μειονέκτημα αυτό διορθώνεται με την χρήση της μηχανής όπου αυτό χρειάζεται. Η μηχανή χαρακτηρίζεται από μικρή απόδοση στα μεταβατικά φαινόμενα της οδήγησης και υψηλή απόδοση στις σταθερές ταχύτητες, ειδικά κοντά στην ονομαστική. Χαρακτηρίζεται,δηλαδή, από χαμηλή πυκνότητα ισχύος και υψηλή ενεργειακή πυκνότητα. Η χρήση του ηλεκτροκινητήρα στις μεταβατικές βοηθά την μηχανή να λειτουργεί στα βέλτιστα σημεία λειτουργίας της. Από την άλλη, η μηχανή καλύπτει τις μεγάλες σταθερές ενεργειακές απαιτήσεις με στόχο την αύξηση του εύρους οδήγησης. Συνεπώς, ο ηλεκτροκινητήρας και η μηχανή δρουν συμπληρωματικά σε μια προσπάθεια τα πλεονεκτήματα του ενός να αντισταθμίσουν τα μειονεκτήματα του άλλου. Η σχεδίαση της στρατηγικής ελέγχου πρέπει να είναι τέτοια ώστε να εκμεταλλεύεται στον βέλτιστο βαθμό τα πλεονεκτήματα αυτά.[29] Ωστόσο, πρέπει να αναφερθεί πως τα πλεονεκτήματα αυτά έρχονται με το τίμημα του επιπλέον βάρους και μιας πολυπλοκότερης δομής του συστήματος μετάδοσης κίνησης γεγονός που έχει ως αποτέλεσμα κάποιοι σχεδιασμοί υβριδικών οχημάτων να συμφέρουν ενώ κάποιοι άλλοι όχι. 2. Κύκλοι Οδήγησης & Οδηγητικές Συνθήκες 2.1 Κύκλοι Οδήγησης Προκειμένου να μελετήσουμε την συμπεριφορά του οχήματος καθώς και την κατανάλωση καυσίμου κατά την διάρκεια της οδήγησης έχουν επινοηθεί χαρακτηριστικοί κύκλοι οδήγησης που προσομοιώνουν τις απαιτήσεις σε ταχύτητα και σε ισχύ χαρακτηριστικών διαδρομών στον κόσμο. [38] Έτσι, υπάρχουν κύκλοι οδήγησης για την εθνική οδό και για οδήγηση πόλης αλλά και συνδυασμοί τους για χαρακτηριστικές διαδρομές της Ευρώπης, της Αμερικής, της Ιαπωνίας καθώς και άλλων χωρών. Για τις ανάγκες της εργασίας αυτής αναλύθηκαν οι χαρακτηριστικοί κύκλοι NEDC, EUDC, FTP-75, FTP-Highway και City-II. Οι κύκλοι αυτοί περιγράφονται 12
13 στις επόμενες ενότητες. Ο Ευρωπαϊκός κύκλος οδήγησης (EUDC) αναλύεται πλήρως έτσι ώστε να μας δώσει μια διεισδυτική ματιά της πρακτικής σημασίας των κύκλων οδήγησης. Για τους υπόλοιπους κύκλους γίνεται μία σύντομη αναφορά των βασικών χαρακτηριστικών τους Ευρωπαϊκός Κύκλος Οδήγησης (EUDC) [30] O κύκλος οδήγησης EUDC έχει σχεδιαστεί για να περιγράφει έντονες συνθήκες οδήγησης μεγάλης ταχύτητας. Η μεγαλύτερη ταχύτητα του κύκλου είναι 120km/h ενώ τα οχήματα χαμηλής ισχύος περιορίζονται στα 90km/h. Εικόνα 3-Κύκλος Οδήγησης EUDC και κύρια χαρακτηριστικά του στο περιβάλλον ADVISOR Μετά από ένα σταμάτημα διάρκειας 20 sec - εάν το όχημα διαθέτει μηχανικό κιβώτιο ταχυτήτων, στην 1η σχέση το αυτοκίνητο επιταχύνει αργά σε 70km/h σε 41sec και αφού κινηθεί με σταθερή ταχύτητα για 50sec (5η σχέση) επιβραδύνεται σε 50 km/h μέσα σε 13
14 8s (4s στην 5 η σχέση και 4s στην 4 η σχέση) και κινείται με σταθερή ταχύτητα για 69sec, στη συνέχεια επιταχύνει βραδέως σε 70 km / h σε 13 sec. Στα 201 sec, το όχημα κινείται με σταθερή ταχύτητα στα 70km/h για 50sec (5η σχέση), στη συνέχεια επιταχύνει βραδέως σε 100 km/h σε 35 sec και κινείται ξανά με σταθερή ταχύτητα για 30sec (5η ή 6η σχέση). Τέλος, στα 316sec το αυτοκίνητο επιταχύνει αργά σε 120 km / h σε 20 sec, και κινείται με σταθερή ταχύτητα για 10 s. Τότε σιγά-σιγά αρχίζει να φρενάρει και σταματά πλήρως μέσα σε 34 sec (5η ή 6η σχέση 10 sec με αποσύμπλεξη του συμπλέκτη), και η μηχανή παραμένει αναμμένη για άλλα 20 sec (σε νεκρά). Η συνολική διάρκεια είναι 400 sec (6 λεπτά 40 δευτερόλεπτα) και η θεωρητική απόσταση είναι 6956 μέτρα, με μέση ταχύτητα 62,44 km /h. Όπως παρατηρούμε ένας κύκλος οδήγησης εκτελεί διάφορα σενάρια οδήγησης κατά την διάρκεια του για να «δοκιμάσει» τις δυνατότητες του οχήματος σε πραγματικές συνθήκες δρόμου Κύκλος FTP-Highway (HWFET) [11],[12] Εικόνα 4-Κύκλος Οδήγησης FTP-Highway και κύρια χαρακτηριστικά του στο περιβάλλον ADVISOR [26] 14
15 Ο κύκλος οδήγησης FTP-Highway (Federal Test Procedure) είναι γνωστός και ως HWFET. Σκοπός του κύκλου είναι να κρίνει την οικονομία καυσίμου κατά την διάρκεια οδήγησης σε εθνική οδό. Ο κύκλος δεν έχει στάσεις, η μέση του ταχύτητα είναι 77km/h, ενώ η μέγιστή του ταχύτητα είναι 97km/h. Έχει διάρκεια 765 sec και συνολική απόσταση km Κύκλος City-II Πρόκειται για υποσύνολο του κύκλου οδήγησης FTP-75 από τα 500sec έως το 1400 sec που περιγράφεται αναλυτικά στην ενότητα Κύκλος NEDC [30] Εικόνα 5-Κύκλος Οδήγησης CIty-II (m/sec) O κύκλος οδήγησης NEDC (New European Driving Cycle) αποτελείται από τρεις κύκλους ECE-15 ακολουθούμενους από έναν κύκλο EUDC. H συνολική διάρκεια του κύκλου είναι 1180 ή 1220 sec, ενώ τα πρώτα 20sec το αυτοκίνητο μένει ακινητοποιημένο. Η συνολική απόσταση που διανύεται κατά την διάρκεια του κύκλου είναι θεωρητικά 11023m. 15
16 2.1.5 Κύκλος FTP-75 [12] Εικόνα 6-Κύκλος Οδήγησης NEDC (m/sec) Ο κύκλος οδήγησης FTP-75 ταυτίζεται με τον κύκλο οδήγησης UDDS ακολουθούμενο από έναν άλλο κύκλο UDDS διάρκειας 505sec. Σε πολλές εκδόσεις αυτού του κύκλου υπάρχει ένα διάστημα 800 sec μεταξύ του πρώτου UDDS και του δεύτερου κατά το οποίο το όχημα μένει ακίνητο. Εικόνα 7-Κύκλος Οδήγησης FTP-75 (m/sec) 16
17 Στην εργασία αυτή χρησιμοποιείται ο συνεχόμενος κύκλος χωρίς το σταμάτημα μεγάλης διάρκειας. Συνήθως, η διάρκεια του κύκλου είναι 1874 sec και η διανυόμενη απόσταση 17.77km. Η μέση ταχύτητα του κύκλου είναι 34.1km/h. 2.2 Δυναμική & Ενεργειακή Ισορροπία Οχήματος Ασκούμενες Δυνάμεις στο Αμάξωμα κατά την Οδήγηση [43] H μοντελοποίηση της δυναμικής και ενεργειακής ισορροπίας οχημάτων με σκοπό την ενεργειακή διαχείριση έχει αναπτυχθεί στην [43] και στα επόμενα δύο υποκεφάλαια πραγματοποιείται μια ανάλυσή της προσαρμοσμένη στις ανάγκες της εργασίας αυτής. Σύμφωνα με αυτή, το όχημα αντιμετωπίζεται ως σημειακό κέντρο μάζας και σύμφωνα με τον 1 ο νόμο του Newton για την δυναμική ισορροπία πρέπει να ικανοποιείται η εξίσωση: F T = F I + F R + F A + F G (2.1) Για τους υπολογισμούς δυνάμεων F I, F R, F A, F G είναι απαραίτητη η γνώση της μάζας M του οχήματος, των ιδιοτήτων των τροχών (αντίσταση κύλισης c R ), των αεροδυναμικών ιδιοτήτων του αμαξώματος (εμπρόσθια επιφάνεια οχήματος Α και αντίσταση αέρα c A ) καθώς και η αναλογία σχέσεων του τελικού συστήματος μετάδοσης. Παρακάτω περιγράφονται αναλυτικά οι δυνάμεις αυτές. Για λόγους ευκολίας από εδώ και στο εξής οι δυνάμεις αυτές θα χαρακτηρίζονται ως εξωτερικές δυνάμεις. Δύναμη λόγω αδράνειας FΙ Από τον 2 ο Νόμο του Newton προκύπτει: F I = M V (t) (2.2) Η δύναμη αδράνειας εξαρτάται άμεσα από την επιτάχυνση του οχήματος γεγονός που υποδεικνύει πως όταν : V (t) > 0 => F I > 0 : Κατά την επιταχυνόμενη κίνηση παίρνει θετικές τιμές. η δύναμη αδράνειας 17
18 V (t) < 0 => F I < 0 : Κατά την επιβραδυνόμενη κίνηση η δύναμη αδράνειας παίρνει αρνητικές τιμές. V (t) = 0 => F I = 0 : Στην περίπτωση σταθερής ταχύτητας η δύναμη αδράνειας είναι μηδενική. Πρόκειται για μία δύναμη συντηρητική καθώς εξαρτάται αποκλειστικά από την ταχύτητα. Δύναμη λόγω τριβής κύλισης FR H δύναμη αυτή εξαρτάται τόσο από την ταχύτητα του οχήματος όσο και από την κλίση του δρόμου και υπολογίζεται από την παρακάτω εξίσωση: F R = (c R1 V + c R2 ) Mgcos(θ) (2.3) Οι σταθερές c R1, c R2 είναι συντελεστές της τριβής κύλισης και υπολογίζονται πειραματικά. Όπως παρατηρούμε για σταθερή κλίση η σχέση μεταξύ της απαιτούμενης δύναμης και της ταχύτητας του οχήματος είναι γραμμική. Οι τιμές c R1 και c R2 κυμαίνονται συνήθως στο διάστημα (0.1 για χωμάτινο έδαφος) για το c R1 και ακόμα μικρότερες για το c R2. Πολλές φορές, ο δεύτερος συντελεστής αμελείται κατά την μοντελοποίηση. Συνεπώς, η αντίσταση κύλισης δεν είναι συνήθως παραπάνω από το 2% του συνολικού βάρους του οχήματος. Οι τιμές που παίρνει η δύναμη αυτή είναι πάντα θετικές όπως φαίνεται και από το συνημίτονο στην εξίσωση. Αφού αντιστέκεται συνεχώς στην κίνηση, πρόκειται για δύναμη απωλειών. Αεροδυναμική δύναμη FΑ Η δύναμη FΑ είναι ανάλογη του τετραγώνου της ταχύτητας και δίνεται από την σχέση F A = 1 ραc 2 AV 2 (2.4), όπου ρ η πυκνότητα του αέρα, Α η μπροστινή περιοχή του οχήματος, c A η αεροδυναμική σταθερά. Η δύναμη αυτή παίρνει πάντα θετικές τιμές. Αφού αντιστέκεται συνεχώς στην κίνηση πρόκειται για δύναμη απωλειών. 18
19 Δύναμη λόγω βαρύτητας FG Η δύναμη αυτή εξαρτάται από την κλίση του δρόμου και δίνεται από την σχέση : F G = Mgsin(θ) (2.5) Κατά την μοντελοποίησή της χρησιμοποιούμε ημίτονο, δηλαδή η δύναμη αυτή παίρνει θετικές τιμές καθώς το όχημα οδηγείται σε ανηφόρα, ενώ παίρνει αρνητικές τιμές στην κατηφόρα. Πρόκειται για συντηρητική δύναμη καθώς εξαρτάται αποκλειστικά από την ταχύτητα και την κλίση του δρόμου. Βάσει των σχέσεων (2.2), (2.3), (2.4), (2.5) η εξίσωση (2.1) παίρνει την ακόλουθη μορφή: F T = M V (t) + (c R1 V + c R2 ) Mgcos(θ) ρα c AV 2 + Mgsin(θ) (2.6) Ο πρώτος και τελευταίος όρος της παραπάνω εξίσωσης συμμετέχουν στην κινητική και στην δυναμική ενέργεια του οχήματος αντίστοιχα, ενώ ο δεύτερος και ο τρίτος όρος περιγράφουν τις δυνάμεις απωλειών του οχήματος κατά την διάρκεια του κύκλου. Εικόνα 8-Ενεργειακή Ισορροπία Κατά την Οδήγηση [28] οδήγησης. Η δύναμη φορτίου F T εμπεριέχει τις συνιστώσες F I και F G οι οποίες παίρνουν τόσο θετικές όσο και αρνητικές τιμές. Έτσι, το πρόσημο της δύναμης φορτίου παίρνει και αυτό με τη σειρά του θετικές ή αρνητικές τιμές ανάλογα με τις εξωτερικές δυνάμεις 19
20 που δρουν στο όχημα. Όταν πατιέται το γκάζι τότε F T > 0, ενώ όταν το όχημα φρενάρει τότε F T < 0. Στην περίπτωση που δεν πατιέται ούτε γκάζι ούτε φρένο τότε F T = 0. Κατά την διάρκεια του κύκλου οδήγησης, υπάρχει περίπτωση η δύναμη F T να είναι θετική αλλά λόγω των έντονων εξωτερικών δυνάμεων, η κίνηση του οχήματος να είναι επιβραδυνόμενη. Από την άλλη, σε μεγάλη κατηφόρα υπάρχει περίπτωση να έχουμε F T 0 ενώ στο όχημα να παρατηρείται επιταχυνόμενη κίνηση, καθώς η μεγάλη κλίση υπερνικά τις δυνάμεις αντίστασης και τις δυνάμεις φρένων Προσέγγιση Backward και Forward- Εξαγωγή της Ισορροπίας Ισχύος [43] Λύνοντας την σχέση (2.6) ως προς τον όρο M V (t) η εξίσωση παίρνει την μορφή: V (t) = F I M = 1 M ( F T (c R1 V + c R2 ) Mgcos(θ) 1 2 ρα c AV 2 Mgsin(θ) ) (2.7) Μολονότι οι εξισώσεις (2.6) και (2.7) φαίνονται ίδιες, στην ουσία περιγράφουν δύο διαφορετικές προσεγγίσεις μοντελοποίησης της ισορροπίας του οχήματος. Επειδή δεν υπάρχουν δόκιμοι όροι στα ελληνικά για τις προσεγγίσεις αυτές θα χρησιμοποιηθούν οι αγγλικοί όροι των μεθόδων. Η εξίσωση (2.7) περιγράφει την «Forward» προσέγγιση η οποία σε ελεύθερη μετάφραση σημαίνει προσέγγιση με κατεύθυνση προς τα εμπρός και έχει να κάνει με την πορεία που ακολουθούμε μέσα στην εξίσωση ισορροπίας για την εξαγωγή των αντίστοιχων μεγεθών. Στην (2.7) η επιτάχυνση του οχήματος V (t) υπολογίζεται μέσα από την δύναμη φορτίου που απαιτείται για την ικανοποίηση των εξωτερικών απαιτήσεων σε δύναμη. Στην συνέχεια, η ταχύτητα εξάγεται μέσω ολοκλήρωσης της επιτάχυνσης. Η δύναμη φορτίου είναι εκ των προτέρων γνωστή και δρα ως η αιτία, ενώ η ταχύτητα V υπολογίζεται μέσα από αυτήν και είναι το αποτέλεσμα. 20
21 Εικόνα 9-Forward Προσέγγιση[28] Η εξίσωση (2.6) περιγράφει την «Backward» προσέγγιση, κατά την οποία η πορεία που ακολουθείται για τον υπολογισμό των μεγεθών αυτών είναι η αντίστροφη. Στην προσέγγιση αυτή, η δύναμη φορτίου F T που απαιτείται για την κάλυψη των ενεργειακών απαιτήσεων του οχήματος υπολογίζεται μέσα από την αδρανειακή δύναμη M V (t) και από τις εξωτερικές δυνάμεις, υπό την υπόθεση ότι η ταχύτητα V του οχήματος είναι γνωστή και περιγράφεται από έναν κύκλο οδήγησης. Εικόνα 10-Backward Προσέγγιση [28] Εδώ αντιστρέφεται η σχέση μεταξύ αιτίου και αποτελέσματος. Γνωρίζοντας το αποτέλεσμα, δηλαδή την ταχύτητα V προσπαθούμε να βρούμε το αίτιο που την προκάλεσε δηλαδή την δύναμη φορτίου F T. Είναι προφανές πως μια στρατηγική με την λογική αυτή δεν είναι δυνατόν να εφαρμοστεί σε ένα πραγματικό όχημα. Η σημασία,ωστόσο, των μεθόδων αυτών στην μοντελοποίηση είναι μεγάλη. 21
22 Πολλαπλασιάζοντας την (2.1) με την ταχύτητα του οχήματος προκύπτει: V F T = V F I + V F R + V F A + V F G (2.8) P T = P I + P R + P A + P G (2.9) H σχέση αυτή υποδηλώνει την ισορροπία ισχύος στο όχημα. Κάθε ισχύς αντιστοιχεί στα φαινόμενα που έχουν ήδη περιγραφεί με την προσθήκη ότι τώρα πια υπάρχει μια εξάρτηση από την ταχύτητα του οχήματος. Είτε πρόκειται για ισχύ είτε για δύναμη, η φυσική σημασία των μεγεθών αυτών είναι παρεμφερής. Συγκεκριμένα, η ισχύς αδράνειας P I περιγράφει την ισχύ που απαιτείται για την επιτάχυνση του οχήματος, η ισχύς κύλισης P R περιγράφει την ισχύ που απαιτείται για να ξεπεραστεί η αντίσταση του δρόμου και η αεροδυναμική ισχύς P A περιγράφει την ισχύ που απαιτείται για να ξεπεραστεί η αντίσταση του αέρα. Τέλος η ισχύς λόγω κλίσης P G περιγράφει την ισχύ που απαιτείται για να ανέβει το όχημα μια ανηφόρα ή την ισχύ που απαιτείται να καταναλωθεί στα φρένα για να αποφευχθεί η επιτάχυνση του οχήματος σε μία κατηφόρα Aνάλυση της Μοντελοποίησης της Οδηγητικής Ισχύος μέσω Πραγματικών Μετρήσεων Mε απώτερο σκοπό να εκτιμήσουμε την αξιοπιστία της μαθηματικής εξίσωσης από την οποία υπολογίζουμε την απαιτούμενη οδηγητική ισχύ του οχήματος για έναν επιλεγμένο κύκλο οδήγησης, χρησιμοποιήθηκαν μετρήσεις της Argonne Labs για το όχημα Honda Insight. Η μεθοδολογία που ακολουθήθηκε έχει περιγραφεί για τον υπολογισμό των βασικών παραμέτρων υβριδικού ηλεκτρικού οχήματος μεικτής τοπολογίας και συγκεκριμένα του Toyota Prius. [29] Ο λόγος που επιλέχθηκε το Honda Insight στην περίπτωσή μας είναι επειδή η τοπολογία του προσομοιάζει περισσότερο από τα υπόλοιπα οχήματα της αγοράς στην παράλληλη τοπολογία που μελετάμε στην παρούσα εργασία. Όπως ήδη έχουμε περιγράψει η δύναμη φορτίου που ασκείται κατά την διάρκεια της οδήγησης έχει την γενική μορφή: F T = M V (t) + (c R1 V + c R2 ) Mgcos(θ) ρα c AV 2 + Mgsin(θ) (2.10) 22
23 H μορφή αυτή συμπεριλαμβάνει και την αντίσταση κύλισης. Ωστόσο, η αντίσταση κύλισης είναι δύσκολο να μετρηθεί κατά την διάρκεια των τεστ που γίνονται στο πραγματικό όχημα ειδικά αν οι μετρήσεις γίνονται με δυναμόμετρο στο σασί. Έτσι, στην προσπάθεια να εξαχθεί ένα μαθηματικό μοντέλο που να ταυτίζεται όσο το δυνατόν περισσότερο με τις μετρήσεις απαιτούμενης ισχύος που είναι διαθέσιμες από τα εργαστήρια της Argonne, έγινε κατανοητό πως η συνιστώσα της αντίστασης κύλισης έπρεπε να εξαιρεθεί καθώς αλλοίωνε τα αποτελέσματα. Τέλος, δεν λαμβάνεται υπόψιν η δύναμη του βάρους καθώς το όχημα δεν βρίσκεται υπό κλίση κατά την διάρκεια των τεστ. Έτσι η απλοποιημένη μαθηματική μορφή της απαιτούμενης ισχύος [29]: P T = V F T = V (M V (t) ρα c AV 2 ) (2.11) Ο τύπος αυτός, ωστόσο, δεν σημαίνει πως η αντίσταση κύλισης είναι αμελητέα στην πραγματικότητα. Αντιθέτως, η συνιστώσα αυτή είναι υπαρκτή και πάρα πολύ σημαντική στην μοντελοποίηση και ο μόνος λόγος που δεν την χρησιμοποιούμε προσωρινά είναι η αδυναμία του δυναμόμετρου να την μετρήσει καλά. Ωστόσο, το να την αμελήσουμε είναι ο μόνος τρόπος να εξετάσουμε την ταύτιση μετρήσεων και μοντέλου για τις υπόλοιπες συνιστώσες. Τα διαθέσιμα δεδομένα από την Downloadable Dynamometer Database είναι η δύναμη φορτίου (N), η ταχύτητα του οχήματος (mph), η γωνιακή ταχύτητα της μηχανής (rpm),ο ρυθμός κατανάλωσης καυσίμου (cc/s), η τάση (V) και το ρεύμα (A) του συστήματος αποθήκευσης ηλεκτρικής ενέργειας, η κατάσταση φόρτισης της μπαταρίας (%) και ο χρόνος με δειγματοληψία (Ts=0.1 sec). Για να μπορέσουμε να χρησιμοποιήσουμε τα δεδομένα αυτά για να εξάγουμε την πραγματική απαιτούμενη οδηγητική ισχύ P T μετατρέψαμε το μέγεθος της ταχύτητας σε km/h. Έτσι η υπολογίζεται ως εξής: Γνωρίζουμε πως η μετρούμενη ισχύς στις ρόδες είναι ένας συνδυασμός των δυνάμεων που δρουν στις ρόδες και μιας γνωστής ταχύτητας. Έτσι έχουμε: P T = T T ω Τ (2.12) Τ Τ = F T R (2.13) P T 23
24 ω Τ = V R (2.14) Συνεπώς, από τις παρακάτω σχέσεις προκύπτει : P T = F T V (2.15) Οι σχέση (2.15) δηλώνει ότι η απαιτούμενη οδηγητική ισχύς είναι ανεξάρτητη της ακτίνας του τροχού καθώς και ότι μπορεί να υπολογιστεί απευθείας από την δύναμη φορτίου και την ταχύτητα του οχήματος, που επιβάλλει ο κάθε κύκλος οδήγησης. Παρακάτω παρουσιάζονται τα βασικά χαρακτηριστικά του οχήματος και των συνθηκών οδήγησης, τα οποία θα μας βοηθήσουν να εκτιμήσουμε την απαιτούμενη ισχύ. Τα χαρακτηριστικά αυτά είναι κοντινά στα πραγματικά χαρακτηριστικά ενός παράλληλου υβριδικού οχήματος. Περιγραφή Σύμβολο Τιμή Μονάδα Μέτρησης Μάζα M 1600 kg Συντελεστής c R * - Αντίστασης Κύλισης Πυκνότητα Αέρα ρ 1.2 kg/m 3 Συντελεστής c A Αεροδυναμικής Τριβής Εμβαδόν Εμπρόσθιας Επιφάνειας Οχήματος A 1.65 m 2 Επιτάχυνσης της g 9.81 m/s 2 Βαρύτητας Ακτίνα Τροχών R 0.27 m 24
25 *Γενικά η τιμή c R1 =0.05 για αντίσταση κύλισης σημαίνει αρκετά κακές συνθήκες δρόμου. Ωστόσο, βάζουμε μια τέτοια τιμή για να δοκιμάσουμε το μοντέλο που αναπτύσσεται στις επόμενες παραγράφους υπό απαιτητικότερες συνθήκες οδήγησης μιας και στο μοντέλο της παραγράφου αυτής η αντίσταση κύλισης αμελείται. Με σκοπό να εκτιμηθεί καλύτερα από το μοντέλο η απαιτούμενη ισχύς, εισάγουμε στον 1 ο όρο της εξίσωσης έναν παράγοντα δ ως συντελεστή της περιστροφικής αδράνειας που σχετίζεται με την γωνιακή κίνηση των στρεφόμενων εξαρτημάτων. Έτσι η τελική εξίσωση εκτίμησης της απαιτούμενης ισχύος των εργαστηρίων της Argonne είναι [29]: P T = V F T = V (M δ V (t) ρα c AV 2 ) (2.16) Με σκοπό να δούμε πως ο συντελεστής δ επηρεάζει την ακρίβεια της εκτίμησης απεικονίζουμε γραφικά την μετρούμενη απαιτούμενη ισχύ και τις υπολογισμένες απαιτούμενες ισχείς για τρείς διαφορετικές τυπικές τιμές του δ (0.9, 1, 1.05), για να εξάγουμε τον καλύτερο συντελεστή. Χρησιμοποιείται ο κύκλος οδήγησης Highway (HWFET) από την ιστοσελίδα των Argonne Labs. Επειδή ο κύκλος οδήγησης περιέχει συνολικά περίπου δείγματα είναι πολύ δύσκολο να αποφανθούμε μέσω του γενικού διαγράμματος του κύκλου ποιο δ είναι το κατάλληλο για το μοντέλο μας. Για τον λόγο αυτό απεικονίζουμε μόνο μέρος του διαγράμματος, όπως φαίνεται στο σχήμα. Για να δούμε πως το μαθηματικό μοντέλο ακολουθεί το πραγματικό σε έντονες και γρήγορες μεταβολές, η περιοχή ενδιαφέροντος περιορίστηκε μεταξύ των δειγμάτων 160 και 320. Όπως φαίνεται και στο σχήμα, και οι τρεις τιμές του δ είναι ιδιαίτερα ικανοποιητικές. 25
26 Εικόνα 11-Υπολογισθείσα και Μετρούμενη Ισχύς Φορτίου για τρεις τιμές του δ Από το σχήμα παρατηρούμε πως πιο ακριβής από τις 3 είναι η μαντζέντα γραμμή που αντιστοιχεί στην τιμή δ=1.05. Δοκιμάστηκαν και άλλες τιμές και από πλευράς απόλυτου σχετικού σφάλματος, διαπιστώθηκε πως τιμές κοντά στην τιμή δ=0.95 έδιναν το καλύτερο αποτέλεσμα. 26
27 Εικόνα 12-Υπολογισθείσα και Μετρούμενη Ισχύς φορτίου για δ=1.05 Στο σχήμα,επίσης, παρατηρούμε κάποια spikes που προέκυψαν κατά την διάρκεια των υπολογισμών. Αυτά τα spikes οφείλονται κυρίως στην παράγωγο της ταχύτητας, καθώς χρειάστηκε να χρησιμοποιήσουμε αριθμητική μέθοδο για την εξαγωγή της παραγώγου σε κάθε σημείο, μιας και δεν υπήρχαν διαθέσιμα δεδομένα για την επιτάχυνση του συγκεκριμένου κύκλου, βάσει των μετρήσεων. Αν είχαμε ακριβείς μετρήσεις και για την επιτάχυνση από τα εργαστήρια της Argonne, εκτιμάται πως τα αποτελέσματα θα ήταν ακόμη πιο ακριβή. Ωστόσο, ακόμα και με αυτό το μικρό σφάλμα, μπορεί να επιβεβαιωθεί η σωστή λειτουργία του μοντέλου. Το σφάλμα είναι ιδιαίτερα μικρό και, μάλιστα, για δ=0.95 έχουμε σφάλματα μικρότερα του 0.5kW που δεν επηρεάζουν την γενική λειτουργία του οχήματος. Έτσι, μπορεί εύκολα να επιβεβαιωθεί η αξιοπιστία του μοντέλου ισορροπίας ισχύος. H διαδικασία που ακολουθήσαμε για την εκτίμηση της οδηγητικής ισχύος είναι πολύ μεγάλης σημασίας, καθώς έχοντας εκτιμήσει κατάλληλα τις σταθερές παραμέτρους της σχέσης για το όχημά μας, μπορούμε να υπολογίσουμε την απαιτούμενη ισχύ απευθείας από την ταχύτητα, αρκεί εκείνη να είναι γνωστή μέσα από τον κύκλο οδήγησης. Έτσι, μπορούμε να εκτιμήσουμε την ισχύ οποιουδήποτε κύκλου οδήγησης αρκεί να ξέρουμε την ταχύτητα, κάποια βασικά χαρακτηριστικά του και τις συνθήκες οδήγησης. Η σωστή εκτίμηση της επαληθεύεται από το μικρό σφάλμα μεταξύ μετρούμενης και υπολογισθείσας τιμής. 27
28 3.Δομή και Μέθοδοι Μοντελοποίησης Υβριδικών Οχημάτων 3.1 Είδη Προσεγγίσεων Μοντελοποίησης [13] Υπάρχουν 3 βασικές μέθοδοι μοντελοποίησης που αναπτύσσονται αναλυτικά στην [13] και περιγράφονται στην συνέχεια της υποενότητας αυτής. Σημαντικότερη από αυτές είναι η ψευδοστατική μέθοδος που είναι και η μέθοδος που συνήθως χρησιμοποιείται για την επίλυση προβλημάτων ενεργειακής διαχείρισης. Δοθέντος ενός συγκεκριμένου κύκλου οδήγησης, πρέπει στο μοντέλο μας να καθορίσουμε πώς θα αναπτύξουμε τα μοντέλα των υποσυστημάτων μας και πώς θα εκτιμήσουμε την κατανάλωση καυσίμου στο όχημα. Υπάρχουν τρεις βασικές προσεγγίσεις που χρησιμοποιούνται στην μοντελοποίηση οχημάτων. Οι προσεγγίσεις αυτές είναι η μέθοδος μέσου σημείου λειτουργίας, η Ψευδοστατική μέθοδος και η Δυναμική μέθοδος. Η Ψευδοστατική και η Δυναμική προσέγγιση συχνά ταυτίζονται σαν ορολογίες με την μέθοδο Backward και Forward αντίστοιχα του Κεφαλαίου 2. Ωστόσο, οι δύο ορολογίες έχουν μια βασική διαφορά καθώς οι Backward και Forward προσεγγίσεις περιγράφουν την κατεύθυνση με την οποία ρέει η πληροφορία μέσα στο όχημα. Οι προσεγγίσεις που περιγράφονται στην υποενότητα αυτή σχετίζονται περισσότερο με την λεπτομέρεια που εισάγεται στην μοντελοποίηση του οχήματος Μέθοδος Μέσου Σημείου Η προσέγγιση μέσου σημείου χρησιμοποιεί μόνο ένα σημείο, στο οποίο αντιστοιχίζεται μία συγκεκριμένη τιμή απόδοσης της μηχανής κατά την διάρκεια του κύκλου οδήγησης. Το μέσο σημείο λειτουργίας υπολογίζεται μέσα από την μέση τιμή της ισχύος που απαιτείται στους τροχούς. Κάθε υποσύστημα του οχήματος περιγράφεται από την μέση ισχύ του. Έτσι, ακολουθώντας την «Backward» προσέγγιση εκτιμάται η κατανάλωση καυσίμου. Η μέθοδος αυτή δεν εφαρμόζεται πλέον άμεσα στην εκτίμηση 28
29 της κατανάλωσης καυσίμου. Αξιοποιείται,ωστόσο, έμμεσα από μία πιο ισχυρή μέθοδο που χαρακτηρίζεται ως Ψευδοστατική Ψευδοστατική Μέθοδος Στην περίπτωση της Hμιστατικής Προσέγγισης (Quasistatic Approach) ο κύκλος οδήγησης χωρίζεται σε κομμάτια η χρονική διάρκεια των οποίων μπορεί να είναι ίδια ή και μεταβλητή. Τα χρονικά διαστήματα πρέπει να είναι τόσο μικρά ώστε η ταχύτητα, η επιτάχυνση και η κλίση του δρόμου να μπορούν να θεωρηθούν σταθερά. Σε κάθε ένα από τα χρονικά διαστήματα εφαρμόζεται η προσέγγιση μέσου σημείου. Κατά την Ψευδοστατική προσέγγιση θεωρούμε πως το όχημα ακολουθεί επακριβώς τον κύκλο οδήγησης. Η ταχύτητα και η επιτάχυνση για κάθε χρονικό διάστημα δίνονται από τις σχέσεις (3.1) και (3.2). Ως ταχύτητα θεωρούμε την μέση τιμή της αρχής και του τέλους κάθε διαστήματος. Ως επιτάχυνση θεωρούμε την διαφορά των δύο ταχυτήτων δια την διανυόμενη απόσταση h. V = V i + V i 1 2 (3.1) και α = V i V i 1 h (3.2) t [t i 1, t i ] Βάσει της ταχύτητας, της επιτάχυνσης και της κλίσης του δρόμου, υπολογίζεται η απαιτούμενη δύναμη στους τροχούς F T. Η δύναμη αυτή μετατρέπεται σε ισχύ φορτίου P T και βάσει της ισχύος αυτής υπολογίζεται η απαιτούμενη ενέργεια καυσίμου για την ικανοποίηση των οδηγητικών απαιτήσεων. Για την μοντελοποίηση των υποσυστημάτων του συστήματος μετάδοσης κίνησης, χρησιμοποιούνται χάρτες απόδοσης, χάρτες απωλειών ισχύος ή χάρτες κατανάλωσης καυσίμου. Συνήθως, στην μοντελοποίηση της ΜΕΚ χρησιμοποιούνται χάρτες κατανάλωσης καυσίμου καθώς ένας χάρτης απόδοσης δεν εκτιμά σωστά την ενέργεια καυσίμου στις χαμηλές ταχύτητες. Το κύριο πλεονέκτημά της Ψευδοστατικής μεθόδου είναι ο συνδυασμός ικανοποιητικών αποτελεσμάτων με την χαμηλή υπολογιστική πολυπλοκότητα και τον γρήγορο χρόνο εκτέλεσης. Η Ψευδοστατική προσέγγιση έχει επιβεβαιωθεί πειραματικά 29
30 ότι ισχύει για την ΜΕΚ. Κατά συνέπεια, ισχύει και για τον ηλεκτροκινητήρα καθώς οι σταθερές χρόνου των ηλεκτρικών συστημάτων είναι πολύ μικρότερες αυτών των ΜΕΚ. Η μέθοδος,ωστόσο, υστερεί στο γεγονός ότι ακολουθεί την Βackward προσέγγιση η οποία συνεπάγεται μη αιτιότητα και ανάγκη της εκ των προτέρων γνώσης του κύκλου οδήγησης για τον σχεδιασμό της στρατηγικής ελέγχου Δυναμική Μέθοδος Η δυναμική προσέγγιση βασίζεται στην περιγραφή κάθε υποσυστήματος του υβριδικού οχήματος υπό την μορφή δυναμικών εξισώσεων. Οι εξισώσεις αυτές περιγράφονται συνήθως στον χώρο κατάστασης και έχουν την γενική μορφή της σχέσης: d x(t) = f(x(t), u(t)), x(t) R, u(t) R (3.3) dx όπου x(t) οι μεταβλητές κατάστασης και u(t) οι είσοδοι ελέγχου του συστήματος. Δεν υπάρχει όριο στην λεπτομέρεια μοντελοποίησης με την προσέγγιση αυτή. Το μοντέλο μπορεί να είναι τόσο απλό ή τόσο λεπτομερές όσο οι μαθηματικές εξισώσεις που το περιγράφουν. Το γεγονός αυτό προσφέρει πληθώρα επιλογών στην μοντελοποίηση των υποσυστημάτων του οχήματος. Ακόμα, η αναλυτική φύση της σχέσης βοηθά στην περαιτέρω εμβάθυνση της δυναμικής συμπεριφοράς του οχήματος και των υποσυστημάτων, με ενδιαφέρον τόσο θεωρητικό όσο και πρακτικό, μιας οι είσοδοι στο δυναμικό μοντέλο του συστήματος είναι στην ουσία τα σήματα ελέγχου σε ένα πραγματικό σύστημα μετάδοσης. Με την προσέγγιση αυτή είναι δυνατός ο σχεδιασμός ελεγκτών πρόσωανατροφοδότησης για τον έλεγχο οχημάτων. Για να φέρουμε,όμως, ένα τόσο πολύπλοκο σύστημα σε μία μορφή που να μπορεί να περιγραφεί από την (3.3) και κυρίως να είναι υπολογιστικά εφικτή, είναι απαραίτητο να οριστεί ο σκοπός της μοντελοποίησης, να διερευνηθούν οι σχέσεις μεταξύ των μεταβλητών ενδιαφέροντος με άλλες δευτερεύουσες μεταβλητές και να εξαχθεί ένα μοντέλο που βασίζεται στην αλληλεπίδραση μόνο των μεταβλητών εκείνων που επηρεάζουν ουσιαστικά το σύστημά μας. Συνεπώς, η λεπτομέρεια δεν είναι πάντα η λύση στην μοντελοποίηση καθώς μετά 30
31 από ένα σημείο υπεισέρχονται προβλήματα υπολογιστικής και χρονικής πολυπλοκότητας. Συνήθως, η εξαγωγή ενός συστήματος με χαμηλό υπολογιστικό φόρτο μέσω της δυναμικής προσέγγισης είναι μια επίπονη διαδικασία και,πολλές φορές, μη πραγματοποιήσιμη. Έτσι, παρά την ελκυστικότητα της, η δυναμική προσέγγιση χρησιμοποιείται μόνο όπου η Ψευδοστατική προσέγγιση αποτυγχάνει. 3.2 Μοντελοποίηση Υποσυστημάτων Παράλληλου Υβριδικού Οχήματος Για την καλύτερη κατανόηση ενός υβριδικού οχήματος είναι απαραίτητο να αναλυθούν τα βασικά υποσυστήματα του. Στην παρούσα εργασία αναλύονται μόνο τα υποσυστήματα που αφορούν στην περίπτωση των υβριδικών οχημάτων παράλληλης συνδεσμολογίας, καθώς και διατάξεων παρεμφερών με αυτή την βασική κατηγορία. Η μοντελοποίηση των υποσυστημάτων αυτών γίνεται με σκοπό την ενεργειακή διαχείριση Μηχανή Εσωτερικής Καύσης [14],[44] Σύμφωνα με την [14], Οι βασικοί τύποι μηχανών εσωτερικής καύσης είναι οι παλινδρομικές εμβολοφόρες μηχανές, όπου το έμβολο κινείται εντός του κυλίνδρου και μεταβάλλει συνεχώς τον όγκο του αερίου καθώς κινείται. Ανάλογα με τους χρόνους που χρειάζεται η μηχανή για να ολοκληρώσει έναν κύκλο έχουμε τις εξής δύο κατηγορίες: Τετράχρονες ΜΕΚ: Απαιτούν 4 χρόνους για να συμπληρωθεί ένας κύκλος Δίχρονες ΜΕΚ: Aπαιτούν 2 χρόνους για να συμπληρωθεί ένας κύκλος 31
32 Εικόνα 13-Μηχανή Εσωτερικής Καύσης Ανάλογα με τον τρόπο με τον οποίο γίνεται η ανάφλεξη του μίγματος οι μηχανές εσωτερικής καύσης χωρίζονται στις εξής δύο κατηγορίες: Mηχανές Έναυσης μέσω σπινθηρισμού SI (Spark Ignition) Mηχανές Έναυσης μέσω συμπίεσης CI (Compression Ignition) O τρόπος με τον οποίο δημιουργείται το μίγμα καυσίμου-αέρα είναι διαφορετικός στις δύο μηχανές και τα εξαρτήματα που δημιουργούν και ρυθμίζουν το μείγμα ελέγχουν και τις στροφές τις μηχανής. Οι μηχανές συνήθως έχουν περισσότερους από έναν κυλίνδρους και η διάταξή τους έχει διάφορες μορφές. 32
33 Εικόνα 14-Κύκλοι τετράχρονης μηχανής [14] Ο λόγος του όγκου στο κάτω νεκρό σημείο V1 προς τον όγκο συμπίεσης στο άνω νεκρό σημείο Vο της μηχανής ορίζει τον λόγο συμπίεσης : r = V 1 V 0 (3.4) Έτσι, ο όγκος εκτόπισης δίνεται από την σχέση V d = V 1 V 0 = π 4 B2 s (3.5) Η μέση ταχύτητα του εμβόλου εκφράζεται ως : u = 2sn s (3.6) όπου n s οι στροφές της μηχανής. Η γωνιακή ταχύτητα του στροφάλου δίνεται από τον τύπο : ω = 2sn s 60 (3.7) 33
34 Εικόνα 15-Κύκλοι Δίχρονης Μηχανής [14] Ο συντελεστής απόδοσης της μηχανής εσωτερικής καύσης ορίζεται ως ο λόγος της μηχανικής ισχύος που παράγεται στην έξοδο προς την ισχύ καυσίμου που καταναλώθηκε για την επίτευξη της κίνησης όπως φαίνεται στην σχέση (3.8). Συνεπώς ο συντελεστής απόδοσης μιας μηχανής εξαρτάται κυρίως από την ροπή και την γωνιακή ταχύτητα που αναπτύσσει. Στην βιβλιογραφία έχουν προταθεί διάφοροι τρόποι εξαγωγής της απόδοσης μιας μηχανής που λαμβάνουν υπόψιν πληθώρα από ειδικά φαινόμενα. Ωστόσο, για τις ανάγκες της ενεργειακής διαχείρισης η συνάρτηση η ICE (Τ ICE, ω ICE ) όπως αναπτύσσεται και περιγράφεται στην [44] είναι αρκετή για να μοντελοποιήσει την μηχανή με σχετική ακρίβεια και για αυτό υιοθετείται στο παρόν κεφάλαιο αυτός ο τρόπος μοντελοποίησης. η ICE = τ ICE ω ICE P chem (3.8) Συνήθως, οι μηχανές εσωτερικής καύσης περιγράφονται από χάρτες μηχανής που συσχετίζουν την ροπή, την γωνιακή ταχύτητα και την κατανάλωση καυσίμου. 34
35 Eναλλακτικά, οι χάρτες μπορούν να εκφραστούν χρησιμοποιώντας την μέση ενεργό πίεση, την μέση ταχύτητα του πιστονιού και την απόδοση. Η μέση ενεργός πίεση ορίζεται ως : p me = 4π τ V ΙCE (3.9) d Όπου τ είναι η ροπή της μηχανής εσωτερικής καύσης και V d o συνολικός όγκος εκτόπισης. Η ταχύτητα του πιστονιού ορίζεται ως: c m = S p π ω ICE (3.10) Όπου S p η διαδρομή του πιστονιού και ω η γωνιακή ταχύτητα της μηχανής. Συνεπώς, η μηχανική ισχύς δίνεται από την σχέση: P mech = τ ICE ω ICE = V d c 4S m p, me (3.11) p Η ισχύς καυσίμου σχετίζεται με την ροή μάζας καυσίμου ανά μονάδα χρόνου μέσω της σχέσης: P chem = LHV m f (3.12) όπου LHV η κατώτερη θερμογόνος ικανότητα (Lower Heating Value) του καυσίμου. Ο βασικός τρόπος απεικόνισης της απόδοσης της μηχανής είναι μέσω διαγραμμάτων της μορφής η ICE = f(p me,c m ), η ICE = f(τ ICE,ω ICE ). Όπως αναφέρει η [44], συνήθως, μηχανές από τον ίδιο κατασκευαστή και της ίδιας οικογένειας έχουν την χαρακτηριστική ιδιότητα η σχέση μεταξύ των τριών μεγεθών της απόδοσης, της ροπής και της γωνιακής ταχύτητας (αντίστοιχα της απόδοσης, της μέσης ενεργού πίεσης και της ταχύτητας πιστονιού) να είναι ίδια. Συνεπώς, μπορούμε να χρησιμοποιήσουμε συντελεστές (όγκος εκτόπισης, μήκος πιστονιού, αριθμός κυλίνδρων) με τους οποίους αν πολλαπλασιάσουμε τους χάρτες της μηχανής να 35
36 πάρουμε τους αντίστοιχους χάρτες των άλλων μηχανών της οικογενείας. Οι συντελεστές αυτοί ονομάζονται συντελεστές μεγέθους (scaling factors). Η ιδιότητα αυτή των μηχανών εφαρμόζεται καλύτερα στις παλιότερες μηχανές σε σύγκριση με τις μοντέρνες. Αυτό συμβαίνει επειδή ο ηλεκτρονικός έλεγχος των σύγχρονων μηχανών εισάγει ασυνέχειες στους χάρτες. Οι ασυνέχειες αυτές δημιουργούν μεγάλο πρόβλημα στο να εξαχθούν οι χάρτες συγγενικών μηχανών καθώς δεν υπάρχει αντιστοιχία στα σημεία εκείνα. Ωστόσο, η μέθοδος αυτή είναι μέχρι στιγμής η μοναδική για να εκτιμήσουμε τον χάρτη απόδοσης παρόμοιων μηχανών αν έχουμε στην διάθεσή μας μόνο τον χάρτη μίας μηχανής του είδους. Εικόνα 16- Παράδειγμα Μοντέλου Μηχανής Εσωτερικής Καύσης στο περιβάλλον QSS Συχνά, χρησιμοποιείται για την μοντελοποίηση της μηχανής η εξίσωση Willans που συνδέει την απόδοση με την μέση ενεργό πίεση σύμφωνα με την προσεγγιστική σχέση : p me = e(ω ICE ) p mf p me0 (ω ICE )(3.13) Όπου p mf η μέση πίεση καυσίμου και απεικονίζει την μέση ενεργό ισχύ που μια μηχανή με απόδοση ίση με την μονάδα (η ICE = 1) θα παρήγαγε, καίγοντας μάζα m f καυσίμου με αναγωγή στην κατώτερη θερμογόνο δύναμη. Η μέση πίεση καυσίμου ορίζεται ως : p mf = LHV m f V d (3.14) 36
37 Το μέγεθος e(ω ICE ) απεικονίζει την απόδοση της μετατροπής από χημική ενέργεια σε πίεση μέσα στον κύλινδρο. Η μεταβλητή p me0 (ω ICE ) συμβολίζει τις απώλειες κατά την μετατροπή. Η έντονη εξάρτηση των μεγεθών αυτών από την γωνιακή ταχύτητα της μηχανής είναι ιδιαίτερα κρίσιμη για την απόδοσή της. Πολλές φορές για περαιτέρω απλοποίηση του συστήματος οι παράμετροι αυτοί θεωρούνται σταθερές. Παρά την απλότητά του το μοντέλο του Willans μπορεί να προσεγγίσει ιδιαίτερα ικανοποιητικά τους πραγματικούς χάρτες μηχανής. Ακόμα, το γεγονός ότι δεν εξαρτάται άμεσα από τα γεωμετρικά χαρακτηριστικά της μηχανής το καθιστά ικανό να περιγράψει χάρτες μηχανών κάθε μεγέθους μέσω μιας απλής αναλυτικής συνάρτησης.[44] Ηλεκτρικός Κινητήρας [45],[19] Η μοντελοποίηση των ηλεκτρικών μηχανών ως συστήματα για ενεργειακή διαχείριση γίνεται με τρόπο παρόμοιο με των μηχανών εσωτερικής καύσης. Εδώ, υιοθετείται η προσέγγιση των [19], [45]. Ανάλογα με τους σκοπούς για τους οποίους την χρειαζόμαστε η ηλεκτρική μηχανή μπορεί να λειτουργήσει είτε ως κινητήρας είτε ως γεννήτρια. Εικόνα 17- Εσωτερική Δομή Ηλεκτρικού Κινητήρα Μόνιμων Μαγνητών της General Motors 37
38 Λειτουργία ως Κινητήρας Ως είσοδο του μοντέλου στην περίπτωση αυτή θεωρείται η μηχανική ισχύς (P μηχανική > 0) ενώ η ηλεκτρική ισχύς P Ηλεκτρική την οποία αντιμετωπίζουμε ως έξοδο υπολογίζεται από τον ορισμό της απόδοσης ενός ηλεκτρικού κινητήρα ως εξής: P Ηλεκτρική = P μηχανική η = T Μηχω Μηχ η(t Μηχ, ω Μηχ ) (3.15) Οι απώλειες ισχύος για την λειτουργία του ηλεκτρικού κινητήρα δίνονται από τον τύπο: P απώλ. = P Ηλεκτρική P μηχανική = ω μηχτ μηχ η ω μηχ Τ μηχ = ( 1 η 1) ω μηχτ μηχ (3.16) Εικόνα 18-Moντελοποίηση ηλεκτρικής μηχανής ως γεννήτρια και ως κινητήρα για ενεργειακή διαχείριση[45] 38
39 Εικόνα 19-Παράδειγμα Μοντελοποίησης Ηλεκτροκινητήρα στο Περιβάλλον QSS Λειτουργία ως Γεννήτρια Ως είσοδο του μοντέλου στην περίπτωση αυτή θεωρούμε την ηλεκτρική ισχύ (P ηλεκτρική ) ενώ την μηχανική ισχύ (P μηχανική < 0) την υπολογίζουμε από τον ορισμό της απόδοσης της ηλεκτρικής γεννήτριας: P Μηχανική = P Ηλεκτρική η (3.17) Συνεπώς, η ροπή που απαιτείται για την συγκεκριμένη μηχανική ενέργεια προκύπτει από τον ακόλουθο τύπο: Τ μηχ = 1 P ηλεκτρική = 1 P ηλεκτρική ω μηχ η ω μηχ η(p ηλεκτρική, ω μηχ ) (3.18) Οι απώλειες ισχύος για την λειτουργία γεννήτριας είναι: P απωλ. = P ηλεκτρική P μηχανική = ηω μηχ Τ μηχ ω μηχ Τ μηχ = (η 1)ω μηχ Τ μηχ (3.19) 39
40 H απόδοση της γεννήτριας εξαρτάται από την ισχύ και από την γωνιακή ταχύτητα της ηλεκτρικής μηχανής Mπαταρία [45] Η ακριβής περιγραφή του μοντέλου της μπαταρίας είναι πάρα πολύ σημαντική κατά την διαδικασία μοντελοποίησης υβριδικών ή ηλεκτρικών οχημάτων. Από την άλλη, η μαθηματική μοντελοποίηση των μπαταριών αποτελεί μια εξαιρετικά δύσκολη διαδικασία λόγω της έντονα μη γραμμικής αλληλεξάρτησης των βασικών μεγεθών και χαρακτηριστικών της όπως του ρεύματος (i), της θερμοκρασίας (T), της τάσης (V) και ενός μεγέθους μεγάλης σημασίας που θα περιγραφεί παρακάτω και ονομάζεται κατάσταση φόρτισης (x(t)). Το μοντέλο μπαταρίας δύναται στην απλή μορφή του να περιγραφεί από την σχέση: dx(t) dt Ορισμός Κατάστασης Φόρτισης Μπαταρίας = i(t) Q batt (3.20) Ως κατάσταση φόρτισης μιας μπαταρίας ορίζουμε το πηλίκο του φορτίου της μπαταρίας μια δεδομένη χρονική στιγμή προς την συνολική χωρητικότητα φορτίου. Το μέγεθος αυτό είναι το πιο κρίσιμο μέγεθος στην ενεργειακή διαχείριση. 40
41 Εικόνα 20-Mπαταρία Αυτοκινήτου Η τάση της μπαταρίας μπορεί να γραφεί ως άθροισμα δύο τάσεων, της τάσης ανοικτοκυκλώματος V oc και της πτώσης τάσης V R λόγω αντίστασης, μεγέθη τα οποία εξαρτώνται από την κατάσταση φόρτισης και το ρεύμα της μπαταρίας αντίστοιχα σύμφωνα με την σχέση: V Φ = V oc (x(t)) + V R (i(t))(3.21) Όπως γνωρίζουμε, η ενέργεια της μπαταρίας είναι ανάλογη της τάσης ανοικτοκυκλώματος καθώς και από του φορτίο της εκείνη την χρονική στιγμή και δίνεται από την σχέση: Ε = V oc Q (3.22) Ένα άλλο μέγεθος που χρησιμοποιείται εναλλακτικά της κατάστασης φόρτισης σε κάποιες μεθόδους ενεργειακής διαχείρισης είναι η κατάσταση ενέργειας της μπαταρίας. Ορισμός Κατάστασης Ενέργειας Μπαταρίας Ως κατάσταση ενέργειας της μπαταρίας (State of Energy: SOE) ορίζουμε το πηλίκο της ενέργειας της μπαταρίας την δεδομένη χρονική στιγμή προς την συνολική χωρητικότητα ενέργειας της μπαταρίας και ορίζεται από την σχέση: SOE(t) = E E max = V oc Q V oc,max Q max = x(t) V oc V oc,max (3.23) 41
42 Συνήθως για την μοντελοποίηση της μπαταρίας χρησιμοποιείται το απλό μοντέλο της εικόνας εκτός κι αν απαιτείται ένα μοντέλο πιο λεπτομερές. Οι εξισώσεις που περιγράφουν το απλό μοντέλο είναι [40]: V Φ = V oc RI V i n i=1 (3.24) C i ( dv i dt ) = I V i R i (3.25) Εικόνα 21-Απλοποιημένο Μοντέλο Μπαταρίας [40] Ωστόσο, η πολυπλοκότητα της δυναμικής συμπεριφοράς της μπαταρίας καθώς και η έντονη μη γραμμικότητά των εσωτερικών της μεγεθών και παραμέτρων της αποτελούν πολλές φορές τροχοπέδη για την μοντελοποίησή της. Έτσι, παρά την μεγάλη σημασία του απλοποιημένου μοντέλου της μπαταρίας είναι απαραίτητο, πολλές φορές, να χρησιμοποιήσουμε χάρτες για την μπαταρία καθώς η αντίσταση φόρτισης και αποφόρτισης καθώς και η τάση ανοικτοκυκλώματος μεταβάλλονται μη γραμμικά με την κατάσταση φόρτισης, μια συμπεριφορά που δεν μπορεί να προβλέψει εύκολα ένα απλοποιημένο και υπολογιστικά εφικτό μοντέλο. Έτσι, όπως και στην περίπτωση της μηχανής και του ηλεκτροκινητήρα, έτσι κι εδώ οι χάρτες μπαταρίας βασισμένες σε ρεαλιστικές μετρήσεις είναι μία καλή λύση για την μοντελοποίηση του υποσυστήματος αυτού Διαφορικό[39] Το διαφορικό είναι μία καθαρά μηχανική συσκευή η οποία είναι απαραίτητη για την μετάδοση της κίνησης. Το πιο απλό δυνατό μοντέλο συνδέει την ταχύτητα και την ροπή 42
43 στον έναν άξονα με την ταχύτητα και ροπή αντίστοιχα στον άλλο άξονα σύμφωνα με την σχέση: ω αξ2 = N αξ1 N αξ2 ω αξ1 (3.26) Τ αξ2 = N αξ2 N αξ1 Τ αξ1 (3.27) Εικόνα 22-Κάτοψη Διαφορικού Αν στο μοντέλο μας θέλουμε να λάβουμε υπόψιν και τις απώλειες εισάγεται ένας συντελεστής απωλειών και η παραπάνω σχέση παίρνει την μορφή: Τ αξ2 = η απωλ. N αξ2 N αξ1 Τ αξ1 (3.28) Οι απώλειες ισχύος από τα γρανάζια υπολογίζονται ως: P απωλ. = ω αξ1 Τ αξ1 (1 η απωλ ) (3.29) Κιβώτιο Ταχυτήτων και Μετάδοση[39] Το κιβώτιο ταχυτήτων είναι στην ουσία ένα ζεύγος γραναζιών η αναλογία του οποίου αλλάζει κατά την διάρκεια της οδήγησης ανάλογα με τις απαιτήσεις ισχύος του κύκλου 43
44 οδήγησης. Tο μοντέλο χρησιμοποιεί την ίδια σχέση με το ζεύγος γραναζιών του διαφορικού με συντελεστή απωλειών, αλλά αυτή την φορά με μεταβλητή αναλογία γραναζιών καθώς και μεταβλητή απόδοση λόγω αυτού. Συνήθως, στην μοντελοποίηση λαμβάνεται υπόψιν και η καθυστέρηση λόγω της αλλαγής σχέσεων μέσω ενός κατάλληλα επιλεγμένου φίλτρου καθυστέρησης πρώτης τάξης. Εικόνα 23-Σύστημα Μετάδοσης Κίνησης Η μοντελοποίηση αυτή μπορεί να αξιοποιηθεί τόσο για χειροκίνητα κιβώτια ταχυτήτων όσο και για αυτόματα. Ωστόσο, αν θέλουμε οι μετρήσεις μας να είναι ακόμα πιο ακριβείς, είναι απαραίτητο να αναπτυχθεί ένα αναλυτικό μοντέλο μετάδοσης. 3.3 Τοπολογίες Υβριδικών Ηλεκτρικών Οχημάτων [29] Το κεφάλαιο αυτό στοχεύει στην αναγνώριση των βασικών χαρακτηριστικών που ξεχωρίζουν τις τοπολογίες μεταξύ τους. Ανάλογα με την συνδεσμολογία τα υποσυστήματα του οχήματος διαφέρουν ως προς το μέγεθος, την επιλογή και τις συνδέσεις. Οι συνδέσεις μπορούν να είναι είτε μηχανικές είτε ηλεκτρικές. Η ουσιαστική διαφορά κάθε τοπολογίας έγκειται στον τρόπο με τον οποίο γίνεται η ενεργειακή αλληλεπίδραση μεταξύ του κυρίου άξονα και των πηγών ενέργειας. Οι τρεις βασικές τοπολογίες υβριδικών οχημάτων είναι η τοπολογία σε σειρά, η τοπολογία εν παραλλήλω και η τοπολογία σε σειρά/εν παραλλήλω ή αλλιώς μεικτή. 44
45 3.3.1 Τοπολογία σε Σειρά Η συνδεσμολογία σε σειρά περιλαμβάνει δύο ηλεκτρικές μηχανές οι οποίες παρεμβάλλονται μεταξύ της μηχανής εσωτερικής καύσης και των τροχών. Η ηλεκτρική μηχανή 1 λειτουργεί ως γεννήτρια μετατρέποντας την μηχανική ενέργεια που παρέχει η μηχανή εσωτερικής καύσης σε ηλεκτρική. Η ηλεκτρική ενέργεια είτε αποθηκεύεται στην συσκευή αποθήκευσης ενέργειας είτε χρησιμοποιείται για άμεση ικανοποίηση των οδηγητικών απαιτήσεων σε ισχύ. Η ηλεκτρική μηχανή 2 χρησιμοποιείται κυρίως ως ηλεκτροκινητήρας για να ικανοποιήσει τις απαιτήσεις φορτίου και συνεπώς καθορίζει την απόδοση του οχήματος. Η χρήση της ηλεκτρικής μηχανής 2 απευθείας στο σύστημα μετάδοσης μειώνει την ανάγκη κιβωτίου ταχυτήτων καθώς ο ηλεκτροκινητήρας έχει πιο ευέλικτα περιθώρια ως προς την ροπή και την ταχύτητα και η μέση απόδοση του είναι μεγάλη. Εικόνα 24- Δομή Σειριακού Υβριδικού Οχήματος [27] Το κύριο πλεονέκτημα της συνδεσμολογίας αυτής είναι η έμμεση παροχή ισχύος από την ΜΕΚ στο σύστημα μετάδοσης γεγονός που εξασφαλίζει την λειτουργία της ΜΕΚ σε υψηλό συντελεστή απόδοσης ανεξαρτήτως της ταχύτητας του οχήματος. Ωστόσο, η μετατροπή της μηχανικής ενέργειας της ΜΕΚ σε ηλεκτρική αυξάνει τις απώλειες του 45
46 συστήματος. Βασικός στόχος της σειριακης τοπολογίας είναι η βελτιστοποίηση της απόδοσης λειτουργίας της ηλεκτρικής μηχανής Τοπολογία εν Παραλλήλω Στην διάταξη αυτή η μηχανή εσωτερικής καύσης και ο ηλεκτροκινητήρας δρουν στον ίδιο άξονα, δηλαδή η σύνδεση της ΜΕΚ με το υπόλοιπο σύστημα μετάδοσης είναι άμεση σε αντίθεση με το σειριακό υβριδικό. Σημαντικό πλεονέκτημα τις άμεσης σύνδεσης είναι οι μειωμένες απώλειες καθώς αποφεύγουμε την μετατροπή ενέργειας από μηχανική σε ηλεκτρική. Η μηχανική σύζευξη μεταξύ του ηλεκτροκινητήρα και της ΜΕΚ επιτρέπει στο σύστημα αποθήκευσης ενέργειας να φορτιστεί μέσω της ΜΕΚ χωρίς την μετατροπή της μηχανικής της ενέργειας σε ηλεκτρική. Εικόνα 25- Δομή Υβριδικού Οχήματος Παράλληλης Τοπολογίας [2] Τα πλήρως παράλληλα υβριδικά χρησιμοποιούν έναν ελεγχόμενο συμπλέκτη μεταξύ της μηχανής και του ηλεκτροκινητήρα, έτσι ώστε η μηχανή να μπορεί να αποζευγνύεται από το υπόλοιπο σύστημα μετάδοσης κίνησης. Το όχημα χαρακτηρίζεται ως ήπιο υβριδικό στην περίπτωση που ο συμπλέκτης αυτός απουσιάζει. Θεωρητικά, και πάλι η οδήγηση βασισμένη αποκλειστικά σε ηλεκτρική ενέργεια θα ήταν δυνατή. Ωστόσο, τότε 46
47 ο ηλεκτροκινητήρας θα πρέπει να «τραβάει» την ίδια την μηχανή γεγονός που θα αύξανε τις απώλειες και θα μείωνε την απόδοση. Συνεπώς, μια τέτοια τακτική είναι καλύτερο να αποφευχθεί στην περίπτωση ήπιων παράλληλων υβριδικών οχημάτων. Λόγω των δύο πηγών ενέργειας που συνδέονται άμεσα με το σύστημα μετάδοσης κίνησης παρέχεται η δυνατότητα στον ελεγκτή να επιλέξει την αναλογία με την οποία ικανοποιεί κάθε πηγή ενέργειας την απαιτούμενη ροπή κάθε χρονική στιγμή. Το πρόβλημα βελτιστοποίησης πρέπει να λυθεί με τρόπο τέτοιο ώστε η χρήση της αποθηκευμένης ηλεκτρικής ενέργειας και η χρήση ενέργειας καυσίμου να εκμεταλλεύονται με τον βέλτιστο τρόπο. Ωστόσο, στα υβριδικά αυτής της τοπολογίας πρέπει να ληφθούν υπόψιν οι περιορισμοί που εισάγει στην ΜΕΚ η άμεση σύνδεσή της με το σύστημα μετάδοσης κίνησης. Η ταχύτητα λειτουργίας της ΜΕΚ πρέπει να είναι ανάλογη με την ταχύτητα των τροχών. Για τον λόγο αυτό χρησιμοποιείται συνήθως κιβώτιο ταχυτήτων έτσι ώστε να υπάρχει ευελιξία στις ταχύτητες λειτουργίας της ΜΕΚ. Βασικός στόχος στην παράλληλη τοπολογία είναι ο συνδυασμός ΜΕΚ και ηλεκτροκινητήρα έτσι ώστε οι απώλειες στην μηχανή να είναι οι ελάχιστες δυνατές δηλαδή να λειτουργεί στο βέλτιστο σημείο λειτουργίας της Μεικτή Τοπολογία Εικόνα 26-Δομή Υβριδικού Οχήματος σε σειρά-εν παραλλήλω [3] 47
48 H σε σειρά/ εν παραλλήλω ή αλλιώς μεικτή τοπολογία είναι ένας συνδυασμός σειριακής και παράλληλης τοπολογίας. Θεωρητικά, εξαλείφει τα μειονεκτήματα και των δύο τοπολογιών χρησιμοποιώντας όπου συμφέρει την κατάλληλη λειτουργία. Το σημαντικότερο εξάρτημα της τοπολογίας αυτής είναι το πλανητικό μοντέλο γραναζιών (PGS) το οποίο συνδέει μεταξύ τους τις δύο ηλεκτρικές μηχανές και την ΜΕΚ. Μέσω αυτής της σύνδεσης η μεικτή τοπολογία παρέχει την επιλογή στην ΜΕΚ να λειτουργεί με μία συγκεκριμένη ταχύτητα ή να μεταφέρει ισχύ απευθείας στους τροχούς για την ικανοποίηση των οδηγητικών αναγκών. Έτσι, με την χρήση του πλανητικού συστήματος γραναζιών αποφεύγονται οι αυστηροί περιορισμοί λειτουργίας της ΜΕΚ της παράλληλης συνδεσμολογίας. Ακόμα, λόγω της άμεσης σύνδεσης της ΜΕΚ μέσω του PGS με το σύστημα μετάδοσης κίνησης οι απώλειες μετατροπής της σειριακής τοπολογίας αποφεύγονται. Ωστόσο, μία τέτοια τοπολογία πέραν του ότι αυξάνει το βάρος του οχήματος και το κόστος κεφαλαίου για την παραγωγή του, απαιτεί ταυτόχρονα έναν ιδιαίτερα πολύπλοκο και προσεκτικό σχεδιασμό στρατηγικής ελέγχου που να λαμβάνει υπόψιν του την άρρηκτη σχέση των υποσυστημάτων μεταξύ τους. Στην παρούσα διπλωματική εξετάζεται μόνον η περίπτωση του υβριδικού οχήματος παράλληλης τοπολογίας. Η παράλληλη τοπολογία είναι ιδανική για την σύγκριση των μεθόδων ενεργειακής διαχείρισης καθώς η απλούστερη μαθηματική περιγραφή του συγκριτικά με την μεικτή τοπολογία βοηθά περισσότερο στην ανάλυση των τεχνικών βελτιστοποίησης και ελέγχου που είναι και το κύριο αντικείμενο της εργασίας αυτής. Επίσης, λόγω μειωμένης πολυπλοκότητας οι αλγόριθμοι ελέγχου είναι πολύ πιο πιθανόν να λειτουργούν σε ένα πραγματικό όχημα σε σύγκριση με την περίπτωση του μεικτού υβριδικού όπου υπεισέρχονται διάφορα τεχνικά προβλήματα τα οποία συνήθως αντιμετωπίζονται με πατέντες στο σχεδιασμό παρά με κάποια στρατηγική ελέγχου. 4. Εργαλεία Προσομοίωσης Υβριδικών Οχημάτων [19] Στο κεφάλαιο αυτό περιγράφονται τα βασικά πακέτα προσομοίωσης υβριδικών οχημάτων. Τα λογισμικά αυτά έχουν συμβάλλει στην ακριβή μοντελοποίηση οχημάτων γεγονός που έχει βοηθήσει τόσο σε εφαρμογές στην βιομηχανία όσο και σε καινοτόμες 48
49 έρευνες πολλών πανεπιστημίων. Τα λογισμικά Easy5, AMESim, Modelica και Simscape Driveline περιγράφονται στην [19] ενώ εισάγονται και δύο νέα πιο σύγχρονα λογισμικά, το QSS toolbox καθώς και το λογισμικό ADVISOR. Η ανάλυση των εργαλείων προσομοίωσης αρχίζει με τα συγκριτικά πιο άγνωστα αλλά εξίσου σημαντικά για την εποχή τους πακέτα και προχωρά σταδιακά στα πιο δημοφιλή. 4.1 Easy5 [31] Το λογισμικό Easy5 αποτελεί προϊόν της MSC software και περιλαμβάνει βιβλιοθήκες για την δυναμική οχημάτων, την δυναμική μηχανών και ηλεκτροκινητήρων καθώς και διάφορα άλλα μηχανικά και ηλεκτρικά συστήματα. Αποτελεί ένα από τα πρώτα λογισμικά που παρείχαν στον χρήστη την δυνατότητα ενός GUI περιβάλλοντος για καλύτερο έλεγχο της στρατηγικής και των τεχνικών μοντελοποίησης. 4.2 AMESim[36] Το λογισμικό ΑΜΕSim της LMS περιλαμβάνει πληθώρα από εφαρμογές συμπεριλαμβανομένης και της μοντελοποίησης οχημάτων. Η δομή του είναι παρεμφερής με το Easy5 με την διαφορά ότι διαθέτει πιο ισχυρές μαθηματικές τεχνικές για την επίλυση δυναμικών εξισώσεων. Εικόνα 27-Έλεγχος Υβριδικού Οχήματος στο περιβάλλον AMESim 49
50 4.3 Modellica[32] Πρόκειται για γλώσσα προγραμματισμού που σχεδιάστηκε για την μοντελοποίηση πολύπλοκων συστημάτων, όπως π.χ. τα υβριδικά οχήματα. Η σπουδαία συνεισφορά της στην μοντελοποίηση συστημάτων είναι ο έξυπνος τρόπος με τον οποίο διασυνδέονται τα υποσυστήματα καθώς το κάθε σύστημα αντιλαμβάνεται με ευκολία την συμπεριφορά του άλλου. Η γλώσσα Modellica χρησιμοποιήθηκε ως βάση για την δημιουργία του γνωστού λογισμικού προσομοίωσης Dymola. Εικόνα 28- Απλό μοντέλο ενός drivetrain στο περιβάλλον Dymola Στην εικόνα παρουσιάζεται η υλοποίηση ενός PID ελεγκτή για τον έλεγχο ενός απλού συστήματος μετάδοσης στο περιβάλλον Dymola. Πρόκειται για λογισμικό ευρέως διαδεδομένο τόσο στην ακαδημαϊκή κοινότητα όσο και στην βιομηχανία. Η εύκολη σύνδεσή του με το περιβάλλον CATIA που χρησιμοποιείται στις βιομηχανίες καθιστά το λογισμικό αυτό ιδανικό για πραγματικές εφαρμογές. 50
51 4.4 Simscape Driveline [37] To λογισμικό Simscape Driveline έχει υλοποιηθεί στο Matlab/ Simulink και αποτελεί υποσύνολο ενός μεγαλύτερου toolbox που λέγεται Simscape. Οι χρήστες έχουν την δυνατότητα να ορίζουν οι ίδιοι την δυναμική των μοντέλων τους και τα διασυνδέουν με άλλα υποσυστήματα που είναι και αυτά υλοποιημένα στο περιβάλλον Simulink. Το περιβάλλον αυτό είναι εύκολο στον χρήστη και παρέχει ιδιαίτερα ικανοποιητικά αποτελέσματα. Εικόνα 29-Υβριδικό Όχημα Παράλληλης Τοπολογίας σε περιβάλλον SimDriveline 4.5 QSS-Toolbox [33] To περιβάλλον QSS προσφέρει την δυνατότητα απλής και ταυτόχρονα ακριβούς μοντελοποίησης των οχημάτων και των υποσυστημάτων του. Δημιουργήθηκε στο εργαστήριο Δυναμικής και Ελέγχου του ETH στην Ζυρίχη και κατέχει σαν λογισμικό οχημάτων δεσπόζουσα θέση στον ακαδημαϊκό χώρο. Πλήθος ερευνών χρησιμοποιούν το περιβάλλον αυτό ή πληροφορίες που εμπεριέχονται σε εκείνο. 51
52 Εικόνα 30- Μοντέλο Σειριακού Υβριδικού Οχήματος στο Περιβάλλον QSS-toolbox Παρέχει ευελιξία στον σχεδιασμό συστημάτων μετάδοσης κίνησης καθώς και στον υπολογισμό της κατανάλωσης καυσίμου. Όπως υπαγορεύει και το όνομά του (Quasistatic ), το περιβάλλον QSS βασίζεται στην Ψευδοστατική μέθοδο που έχει ήδη περιγραφεί στο Κεφάλαιο 3. Σε αυτή την μέθοδο οφείλει και την απλότητα και ακρίβειά του καθώς όλα τα blocks του βασίζονται σε εκείνη. Το λογισμικό διαθέτει, επίσης, μία έτοιμη βιβλιοθήκη με όλα τα βασικά υποσυστήματα ενός οχήματος συμβατικού και μη. Ωστόσο, το περιβάλλον δεν προτείνεται για μελέτη δυναμικών φαινομένων που περιγράφονται από διαφορικές εξισώσεις. Για την αποδοτική επίλυση αυτών των φαινομένων υπάρχουν πολύ αποδοτικές αριθμητικές μέθοδοι που δεν συμπεριλαμβάνονται στο λογισμικό. Συνεπώς, αν και πολύ ικανό σε απλούς υπολογισμούς που βασίζονται σε χάρτες, το περιβάλλον δεν έχει κατασκευαστεί για να επιλύει τέτοια δυναμικά προβλήματα. 4.6 ADVISOR (Advanced Vehicle Simulator) [26] Το λογισμικό ADVISOR υλοποιήθηκε σε περιβάλλον Matlab/Simulink. Μας δίνει την δυνατότητα μοντελοποίησης οποιουδήποτε οχήματος συμβατικού, υβριδικού και των τριών τοπολογιών, υβριδικού με κυψέλες καυσίμου καθώς και ειδικών τοπολογιών υβριδικών οχημάτων της αγοράς, όπως εκείνη του Toyota Prius και του Honda Insight. 52
53 Τα υποσυστήματα του οχήματος στο ADVISOR βασίζονται σε χάρτες που προσεγγίζουν όσο το δυνατόν καλύτερα την πραγματικότητα. Έτσι, τα αποτελέσματα της προσομοίωσης είναι πολύ πιο ρεαλιστικά από μία απλή μαθηματική περιγραφή όπως για παράδειγμα η προσέγγιση Willans στην μοντελοποίηση της ΜΕΚ. Όπως αναφέρει και η [29], συνδυάζει δύο διαφορετικούς τρόπους μοντελοποίησης. Η πρώτη μοντελοποίηση περιλαμβάνει την χρήση παραμετρικών μοντέλων. Η δεύτερη είναι πιο αναλυτική αλλά πιο υπολογιστικά ακριβή και συμπεριλαμβάνει και την δυναμική των συστημάτων. Χρησιμοποιεί παραμετρικά μοντέλα με σκοπό να ξεπεράσει τα προβλήματα πολύπλοκων αποκρίσεων σημάτων. Ακόμα, λαμβάνει υπόψιν την δυναμική συμπεριφορά, όπου απαιτείται η μοντελοποίηση των αλληλεπιδράσεων μεταξύ των υποσυστημάτων του οχήματος.[29] Για να το καταφέρει αυτό συνδυάζει τις προσεγγίσεις «Forward» και «Backward». Μέσω του συνδυασμού αυτού επιτυγχάνει γρήγορες αποκρίσεις των μεθόδων ελέγχου και βελτιστοποίησης λαμβάνοντας ταυτόχρονα υπόψιν τους περιορισμούς του κάθε υποσυστήματος. Χρησιμοποιώντας την «Backward» προσέγγιση υπολογίζεται η ροπή, η ισχύς και η ταχύτητα μέσω look-up tables. Για την υλοποίηση της δυναμικής απόκρισης με χρήση της «Forward» προσέγγισης, το ADVISOR υπολογίζει τις εισόδους του συστήματος. Οι είσοδοι αυτές ελέγχονται έτσι ώστε να ικανοποιούν τους απαραίτητους περιορισμούς. Το ADVISOR υπολογίζει, ταυτόχρονα, τις απαιτούμενες εξόδους μέσα από τις εισόδους (Forward) ενώ καθορίζει τις εισόδους που προκύπτουν μέσα από τις εξόδους (Backward). Έτσι, μπορούμε να έχουμε μια αλληλοεπικάλυψη των δύο προσεγγίσεων με αποτέλεσμα να μπορούμε να συνδυάζουμε τα πλεονεκτήματά τους. Τέλος, τα μοντέλα που χρησιμοποιεί είναι ιδιαίτερα αξιόπιστα και ακριβή και τα αποτελέσματα των προσομοιώσεων είναι ιδιαίτερα ρεαλιστικά.[29] Ανάλυση Υβριδικού Οχήματος με χρήση του λογισμικού ADVISOR Με κύριο σκοπό την καλύτερη περιγραφή του λογισμικού καθώς των δυνατοτήτων που προσφέρει αναλύεται στο περιβάλλον Advisor ένα χαρακτηριστικό μοντέλο υβριδικού ηλεκτρικού οχήματος της αγοράς του Honda Insight, του οποίου η τοπολογία προσεγγίζει σε μεγάλο βαθμό την παράλληλη. Στο περιβάλλον Advisor μπορούμε να 53
54 επιλέξουμε όχι μόνο την επιθυμητή τοπολογία αλλά και τα βασικά χαρακτηριστικά των υποσυστημάτων του οχήματος. Ένα ακόμα μεγάλο θετικό του Advisor είναι πως χρησιμοποιεί τους πραγματικούς χάρτες του Honda Ιnsight για να εκτελέσει την προσομοίωση, διαδικασία που συνήθως δίνει αποτελέσματα πολύ πιο κοντά στην πραγματικότητα. Ανάλογα με την τοπολογία του οχήματος (συμβατικό, υβριδικό σειριακής, παράλληλης ή μεικτής τοπολογίας) προτείνεται και η αντίστοιχη fixed στρατηγική ελέγχου για κάθε περίπτωση. Το πρόγραμμα απαγορεύει την χρήση μιας στρατηγικής ελέγχου διαφορετικής τοπολογίας στην παρούσα τοπολογία για τον προφανή λόγο, πως κάθε στρατηγική έχει σχεδιαστεί λαμβάνοντας υπόψιν τα υποσυστήματα και την εσωτερική δυναμική της ροής ενέργειας στην τοπολογία για την οποία σχεδιάστηκε. Για παράδειγμα, μια στρατηγική ελέγχου για υβριδικό όχημα σειριακής τοπολογίας δεν έχει νόημα να εφαρμοστεί σε ένα υβριδικό όχημα παράλληλης τοπολογίας. Στην εικόνα 31 φαίνεται το κυρίως μενού του περιβάλλοντος καθώς και η τοπολογία του επιλεγμένου οχήματος με τα χαρακτηριστικά του τα οποία συνοψίζονται στον πίνακα : Μέγιστη Ισχύς Απόδοση Μάζα Αμάξωμα+Eπιβάτες - - ( )kg Μηχανή 50 kw kg Ηλεκτρικός Κινητήρας 10kW kg Μπαταρία 25kW kg Σύστημα Μετάδοσης kg Για την προσομοίωση θεωρούμε ως βάρος επιβατών την τιμή 125kg. Στην συνέχεια επιλέγουμε τον κύκλο οδήγησης που θα ακολουθήσει το όχημα όπως φαίνεται στην εικόνα. 54
55 Εικόνα 31-Μοντέλο του Honda Insight στο περιβάλλον ADVISOR Κατά την οδήγηση επιλέγουμε μηδενική κλίση εδάφους και το όχημα να μην έχει επιπλέον βάρος. Τα αποτελέσματα της προσομοίωσης για τους κύκλους οδήγησης EUDC, FTP-Highway και EUDC παρουσιάζονται στις παρακάτω εικόνες. Όπως παρατηρούμε, το φορτίο διατηρείται από την αρχή στο τέλος της οδήγησης με απόκλιση στην τελική κατάσταση το πολύ της τάξης του (Περίπτωση FTP-75). Ειδικά στην περίπτωση του FTP-Highway, το φορτίο διατηρείται ακριβώς το ίδιο στην αρχή και στο τέλος του κύκλου ενώ στην διαδρομή EUDC οι διαφορές είναι αμελητέες. 55
56 Εικόνα 32-Κατάσταση Φόρτισης του Honda Insight κατά την διάρκεια του κύκλου EUDC Εικόνα 33-Κατάσταση Φόρτισης του Honda Insight κατά τον κύκλο FTP-Highway στο περιβάλλον Advisor 56
57 Εικόνα 34-Κατάσταση Φόρτισης του Honda Insight κατά τον κύκλο FTP-75 στο περιβάλλον Advisor Η οικονομία καυσίμου του Honda Insight κατά την διάρκεια των τριών αυτών κύκλων οδήγησης στο περιβάλλον Advisor φαίνεται στον πίνακα Ι. Τα αποτελέσματα αυτά είναι ιδιαίτερα ενθαρρυντικά και δείχνουν μια πολύ καλή συμπεριφορά από πλευράς οικονομίας καυσίμου ειδικά στην περίπτωση του κύκλου FTP-Highway. FTP-Highway EUDC FTP km/l km/l km/l Πίνακας Ι -Οικονομία Καυσίμου του Honda Insight κατά την διάρκεια τριών κύκλων οδήγησης στο περιβάλλον Advisor 5. Βελτιστοποίηση και Ενεργειακή Διαχείριση 5.1 Κατηγορίες Βελτιστοποίησης Υβριδικών Οχημάτων [44] Τα τρία βασικά επίπεδα βελτιστοποίησης υβριδικών οχημάτων που αναλύονται στην [44] και περιγράφονται περιληπτικά στο παρόν υποκεφάλαιο είναι: Α. Δομική Βελτιστοποίηση : 57
58 Σκοπός είναι η εύρεση της καλύτερης δομής του συστήματος πρόωσης ώστε να έχουμε την βέλτιστη ενεργειακή διαχείριση. Β. Παραμετρική Βελτιστοποίηση: Σκοπός είναι η εύρεση των καλύτερων δυνατών παραμέτρων για την βέλτιστη ενεργειακή διαχείριση δεδομένης μίας συγκεκριμένης δομής υβριδικού οχήματος. Γ. Βελτιστοποίηση Συστήματος Ελέγχου: Σκοπός είναι η εύρεση των καλύτερων δυνατών αλγορίθμων ελέγχου ώστε η ενέργεια να διαχειρίζεται με τον βέλτιστο τρόπο. Τα τρία βασικά επίπεδα βελτιστοποίησης δεν είναι απομονωμένα. Αντιθέτως, επηρεάζονται σε μεγάλο βαθμό το ένα από το άλλο. Τελευταία γίνονται μεγάλες προσπάθειες συνδυασμού των επιπέδων αυτών με σκοπό μια ολική μέθοδο βελτιστοποίησης, όπως στην σχετικά πρόσφατη διδακτορική διατριβή [46]. Η παρούσα εργασία στοχεύει κυρίως στην κατηγορία βελτιστοποίησης Γ. Τέλος, η έννοια βέλτιστη λύση πρέπει να αντιμετωπιστεί με σκεπτικισμό καθώς για την εξαγωγή της υιοθετούνται πολύ περιοριστικές υποθέσεις με αποτέλεσμα η λύση του προβλήματος να έχει απόκλιση από την βέλτιστη λύση ενός πραγματικού υβριδικού οχήματος. Για τον λόγο αυτό πρέπει οι υποθέσεις μας κατά την διατύπωση του προβλήματος να γίνονται με μεγάλη προσοχή ώστε το πρόβλημα προς επίλυση και το πρόβλημα πραγματικού χρόνου να μην παρουσιάζουν μεγάλες αποκλίσεις. Συνεπώς, το πρόβλημα διαχείρισης ενέργειας με βασικό σκοπό την ελαχιστοποίηση του καυσίμου που καταναλώνεται δεν είναι ένα απλό πρόβλημα που μπορεί να λυθεί με συμβατικές μεθόδους. Απαιτείται ένας μεγάλος αριθμός επαναλήψεων και μια γενική πρακτική αντίληψη κατά την δημιουργία του αλγορίθμου που χαρακτηρίζεται ιδιαίτερα κρίσιμη για την συμπεριφορά του ελεγκτή σε ειδικές περιπτώσεις λειτουργίας. Αν ληφθούν υπόψιν και οι εκπομπές ρύπων καθώς και ζητήματα όπως η οδηγησιμότητα, το πρόβλημα γίνεται ακόμα πιο πολύπλοκο. 5.2 Ανάλυση Συστήματος 58
59 Πριν προχωρήσουμε στο πρόβλημα ενεργειακής διαχείρισης είναι απαραίτητο να αναλύσουμε την φύση του συστήματός μας. Η κατανόησή του θα μας βοηθήσει να γίνουν αντιληπτά τα βασικά προβλήματα στην μαθηματική μοντελοποίηση του οχήματος καθώς και στον έλεγχό του. Το σύστημα του υβριδικού οχήματος αναλύεται σύμφωνα με βασικές έννοιες της θεωρίας συστημάτων. Ανάλυση της Μορφής του Συστήματος σύμφωνα με την θεωρία Συστημάτων [41] Όπως φαίνεται το σύστημα μας είναι μη γραμμικό. Αν και θα μπορούσαμε να γραμμικοποιήσουμε το σύστημα γύρω από κάποια σημεία λειτουργίας, η απόπειρα αυτή απλοποίησης του προβλήματος περισσότερο θα δυσχεράνει παρά θα βοηθήσει στην επίλυση του προβλήματος καθώς μέσω της γραμμικοποίησης χάνεται πληροφορία για σημαντικά χαρακτηριστικά του συστήματος, όπως η on/off διακοπτική λειτουργία της μηχανής μέσω του συμπλέκτη που επιβάλλει ασυνέχειες στην κατανάλωση καυσίμου. Ακόμα, το σύστημα είναι χρονικώς μεταβαλλόμενο αφού έχουμε μεταβολή της ροπής και της ταχύτητας κατά τη διάρκεια του κύκλου οδήγησης. Oι περιορισμοί του σήματος εισόδου που αναζητούμε είναι χρονικώς μεταβαλλόμενοι. Αυτό οφείλεται στο γεγονός ότι οι περιορισμοί αυτοί επηρεάζονται τόσο από άμεσους περιορισμούς όπως ο ηλεκτροκινητήρας, όσο και από έμμεσους όπως είναι η ισορροπία ισχύος που περιγράψαμε. 5.3 Το Γενικό Πρόβλημα Ενεργειακής Διαχείρισης Το πρόβλημα ενεργειακής διαχείρισης δύναται υπό συγκεκριμένες προϋποθέσεις να αναχθεί σε ένα πρόβλημα βέλτιστου ελέγχου. Σύμφωνα με την θεωρία ελέγχου ένας νόμος ελέγχου είναι βέλτιστος όταν εξασφαλίζει την ελαχιστοποίηση ενός κριτηρίου βελτιστοποίησης. Στην περίπτωση της ενεργειακής διαχείρισης υβριδικών ηλεκτρικών οχημάτων ο βέλτιστος νόμος ελέγχου αφορά στον καλύτερο δυνατό διαμοιρασμό ισχύος μεταξύ της μηχανής και του ηλεκτροκινητήρα για την ικανοποίηση των οδηγητικών 59
60 αναγκών. Ως κριτήριο βελτιστοποίησης χρησιμοποιείται η κατανάλωση καυσίμου κατά την διάρκεια ενός κύκλου οδήγησης. Για τον λόγο αυτό χρησιμοποιούμε ολοκλήρωμα από την αρχή του κύκλου οδήγησης μέχρι το τέλος του. Πολλές φορές το κριτήριο βελτιστοποίησης λαμβάνει υπόψιν του και άλλους παράγοντες εκτός της κατανάλωσης καυσίμου, όπως η εκπομπή ρύπων, καθώς και η εναλλαγή σχέσεων που παίζουν πολύ σημαντικό ρόλο στην κατανάλωση. Τα τελευταία χρόνια γίνεται επίσης μεγάλη προσπάθεια συνδυασμού θερμικής και ενεργειακής διαχείρισης [17], [18]. Η εξαγωγή ενός βέλτιστου νόμου ελέγχου θεωρεί γνωστό όλο τον κύκλο οδήγησης κάτι που δεν είναι εφικτό στην πραγματικότητα. Συνεπώς, τα αποτελέσματα του βέλτιστου νόμου ελέγχου σε εφαρμογές, όπου ο ορίζοντας δεν είναι πλήρως γνωστός, είναι πάντοτε υποβέλτιστα Μαθηματική Διατύπωση του Γενικού Προβλήματος Ενεργειακής Διαχείρισης στον Συνεχή Χώρο Κατάστασης [55] Το πρόβλημα βέλτιστου ελέγχου διατυπώνεται στον πίνακα Ι. Οι μεταβλητές x R n είναι οι μεταβλητές κατάστασης ενώ οι μεταβλητές u R p απεικονίζουν τις εισόδους ελέγχου. Στόχος του βέλτιστου νόμου ελέγχου είναι η ελαχιστοποίηση της συνάρτησης κόστους J στο χρονικό διάστημα [0, t f ] όπου ως t=0 θεωρούμε την έναρξη του κύκλου οδήγησης και ως t=t f το τέλος του. Πρόκειται για ένα πρόβλημα υπό περιορισμούς κατάστασης και περιορισμούς εισόδου. Όπως είναι φυσικό, η αρχική συνθήκη της μεταβλητής κατάστασης είναι κρίσιμη για τον προσδιορισμό της βέλτιστης τροχιάς της λύσης. t Αντικειμενική Συνάρτηση: J(x(t), u(t)) = f [L(x(t), u(t), t)dt] + Φ(x(t f ), t f ) 0 (5.1) min J(x(t), u(t)) (5.2) u(t) Σύστημα: x = F(x(t), u(t), t), x R n, u R p (5.3) Aρχική Συνθήκη: x(0) = x 0 (5.4) Περιορισμοί : x fmin x(t f ) x fmax (5.5) 60
61 x min x(t) x max (5.6) u min u(t) u max (5.7) Η συνάρτηση L(x(t), u(t), t) ονομάζεται Lagrangian συνάρτηση και απεικονίζει την στιγμιαία συνάρτηση κόστους. Η συνάρτηση Φ(x(t f ), t f ) απεικονίζει το τελικό κόστος στο τέλος του κύκλου οδήγησης. Συνήθως το τελικό κόστος εξασφαλίζει την διατήρηση της κατάστασης φόρτισης της μπαταρίας. Αν η κατανάλωση καυσίμου είναι ο μόνος σκοπός της βελτιστοποίησης, τότε η Lagrangian συνάρτηση αντιστοιχεί αποκλειστικά στο μέγεθος αυτό. Αν η βελτιστοποίηση συμπεριλαμβάνει και άλλους παράγοντες όπως η ελαχιστοποίηση των ρύπων και η εναλλαγή σχέσεων, τότε η στιγμιαία συνάρτηση κόστους συμπεριλαμβάνει και τα μεγέθη αυτά με την χρήση συντελεστών βάρους. Οι συντελεστές βάρους διατηρούν την αντικειμενικότητα της συνάρτησης μεταξύ διαφορετικών μεγεθών ενώ ταυτόχρονα συμβάλλουν στο να ξεχωρίσουμε ποια μεγέθη κρίνονται ως πιο σοβαρά στην βελτιστοποίηση. Οι περιορισμοί που εισάγονται στο πρόβλημα βελτιστοποίησης σχετίζονται με περιορισμούς στα υποσυστήματα του οχήματος, όπως στην μηχανή και τον ηλεκτροκινητήρα. Ένας άλλος σημαντικός περιορισμός είναι η κατάσταση φόρτισης της μπαταρίας στην αρχή και στο τέλος του κύκλου οδήγησης να είναι σχεδόν ίδια. Στο σημείο αυτό πρέπει να αποσαφηνιστούν δύο διαφορετικοί περιορισμοί τελικής κατάστασης που ως σκοπό έχουν την διατήρηση της κατάστασης φόρτισης της μπαταρίας στην ίδια στάθμη στην αρχή και στο τέλος του κύκλου οδήγησης. Επειδή δεν υπάρχουν δόκιμοι όροι στην ελληνική βιβλιογραφία για την περιγραφή των περιορισμών αυτών θα χρησιμοποιηθεί όπως και στην Forward και Backward προσέγγιση η αντίστοιχη αγγλική ορολογία.[55] Σκληρός Περιορισμός (Hard Constraint) Πρόκειται για έναν ισοτικό περιορισμό της μορφής x(0) = x(t f ). Χρησιμοποιείται συνήθως για την κατάσταση φόρτισης της μπαταρίας και επιβάλλει στο μέγεθος αυτό να έχει στην τελική κατάσταση τιμή ίση με την αρχική κατάσταση. Αναφέρεται ως hard δηλαδή «σκληρός» γιατί στην ουσία εξαναγκάζει την κατάσταση φόρτισης να έχει μια συγκεκριμένη τιμή στο τέλος του κύκλου οδήγησης ό,τι κι αν συμβαίνει στην διάρκειά του. 61
62 Μαλακός Περιορισμός (Soft Constraint) Πρόκειται για περιορισμό που εκφράζεται συνήθως υπό την μορφή μιας συνάρτησης τιμωρίας Φ(x(t f )). Η συνάρτηση αυτή, στην περίπτωση του υβριδικού οχήματος, δρα διορθωτικά στην τελική κατάσταση φόρτισης x(t f ) και χρησιμοποιείται για να διατηρήσει την τελική κατάσταση φόρτισης της μπαταρίας κοντά στην επιθυμητή τιμή x f. Θα μπορούσαμε να πούμε, πως η συνάρτηση αυτή δρα ουσιαστικά ως ένας απλός ελεγκτής για την τελική κατάσταση διορθώνοντας το σφάλμα όσο περισσότερο επιτρέπουν οι συνθήκες οδήγησης. Μια ενδεχόμενη απουσία της συνάρτησης τιμωρίας Φ(x(t f ) ή του ισοτικού περιορισμού της μορφής x(0)=x(t f ) από το κριτήριο κόστους οδηγεί στην αραίωση της μπαταρίας κατά την προσπάθεια του αλγορίθμου να ελαχιστοποιήσει την κατανάλωση καυσίμου. Η προσθήκη αυτή είναι υψίστης σημασίας καθώς οδηγεί σε μια λύση βιώσιμη από πλευράς μπαταρίας Μέθοδος του Δυναμικού Προγραμματισμού [51] Η μέθοδος του Δυναμικού Προγραμματισμού [47], [50] προτάθηκε από τον Richard Bellman το Πρόκειται για μία αριθμητική μέθοδο που χρησιμοποιείται για την επίλυση προβλημάτων λήψης αποφάσεων. Το βασικό πλεονέκτημα του Δυναμικού Προγραμματισμού έναντι των υπολοίπων μεθόδων είναι ότι μπορεί να εφαρμοστεί τόσο σε γραμμικά συστήματα όσο και σε μη γραμμικά, με ή και χωρίς περιορισμούς. Βασικός στόχος της μεθόδου είναι να διαχωρίσει ένα πολύπλοκο πρόβλημα σε απλούστερα υποπροβλήματα. Η αναδρομική απλοποίηση και επίλυση των υποπροβλημάτων οδηγούν στην λύση του αρχικού πολύπλοκου προβλήματος. Είναι απαραίτητο να τονιστεί πως ο Δυναμικός Προγραμματισμός δύναται να εφαρμοστεί μόνο σε διακριτά συστήματα. Για τον λόγο αυτό, είναι απαραίτητη η μετατροπή του συστήματος από συνεχές σε διακριτό πριν προχωρήσουμε στη διαδικασία της βελτιστοποίησης. Αρχικά, ο αλγόριθμος περιγράφεται επιγραμματικά για οποιοδήποτε διακριτό σύστημα και στην συνέχεια αναλύεται η εφαρμογή του στην διαχείριση ενέργειας υβριδικών οχημάτων. 62
63 Ο Δυναμικός Προγραμματισμός βασίζεται στην αρχή βελτιστότητας του Bellman. Η βασική φιλοσοφία της μεθόδου είναι η εξής [19]: Αν η βέλτιστη τροχιά ενός συστήματος περάσει από μία ενδιάμεση κατάσταση, τότε η βέλτιστη λύση του προβλήματος αρχίζοντας από αυτήν, πρέπει να είναι συνέχεια του ίδιου μονοπατιού. [49] Δηλαδή όποια κι αν ήταν η τροχιά στο παρελθόν, οι εναπομείνασες αποφάσεις πρέπει να διαγράφουν την βέλτιστη τροχιά ενώ λαμβάνουν υπόψιν τους τις προηγούμενες καταστάσεις [48]. Για την αναλυτικότερη περιγραφή της μεθόδου ας θεωρήσουμε το σύστημα διακριτού χρόνου πολλών εισόδων πολλών εξόδων, που περιγράφεται από την εξίσωση διαφορών: x(k + 1) = F(x(k), u(k)), x(0) = x 0 (5.8) και το κριτήριο κόστους που δίνεται από τη σχέση: N 1 J = L k (x(k), u(k)) + Φ(x(N)) (5.9) k=0 Όπου L k η στιγμιαία Lagrangian συνάρτηση που εκφράζει το στιγμιαίο κόστος (Το άθροισμα του κόστους στα διακριτά συστήματα είναι το αντίστοιχο του ολοκληρώματος στα συνεχή). Σύμφωνα με την αρχή της βελτιστοποίησης θα πρέπει για οποιαδήποτε χρονική στιγμή k=i και οποιαδήποτε κατάσταση x(i) η πολιτική ελέγχου από εκεί και πέρα να είναι βέλτιστη. Επομένως, με βάση το κριτήριο κόστους J ορίζουμε για κάθε x(i) και i την πολιτική βελτιστοποίησης με τη μαθηματική έκφραση [51]: V i (x(i)) = min { u(i) N 1 L k (x(k), u(k)) + Φ(x(N)) } (5.10) k=0 Σύμφωνα όμως με την Αρχή της Βελτιστοποίησης, έχουμε: V i (x(i)) = min { u(i) επειδή όμως προφανώς ισχύει: N 1 L i (x(i), u(i)) + L k (x(k), u(k)) + Φ(x(N)) } (5.11) k=i+1 63
64 V i+1 (x(i + 1)) = min { u(i) η τελική μορφή της εξίσωσης γίνεται: N 1 L k (x(k), u(k)) + Φ(x(N)) } (5.12) k=i+1 V i (x(i)) = min { L i (x(i), u(i)) + V i+1 (x(i + 1))} (5.13) u(i) με τελική τιμή στο i=n: V N (x(n)) = Φ(x(N)) (5.14) Η εξίσωση αυτή ονομάζεται Hamilton-Jacobi-Bellman και αποτελεί έναν επαναληπτικό αλγόριθμο που ξεκινάει από το όριο i=n, με τιμή V N (x(n)) = Φ(x(N)) και δίνει το βέλτιστο νόμο ελέγχου για συστήματα διακριτού χρόνου, σε κάθε βήμα, συναρτήσει του διανύσματος κατάστασης στο σημείο ελαχίστου της, δηλαδή εκεί όπου: u(i) {L i(x(i), u(i)) + V i+1 (x(i + 1))} = 0 (5.15) Με άλλα λόγια, είναι δυνατόν να καθορίσουμε την βέλτιστη ακολουθία δράσεων ελέγχου προχωρώντας από την τελική κατάσταση προς τα πίσω, επιλέγοντας σε κάθε βήμα το μονοπάτι εκείνο που ελαχιστοποιεί την συνάρτηση κόστους. Η διαδικασία εύρεσης της βέλτιστης ακολουθίας σημάτων ελέγχου από το τέλος προς την αρχή, που βασίζεται στην παραπάνω εξίσωση, ονομάζεται Δυναμικός Προγραμματισμός. Μία χαρακτηριστική εφαρμογή του Δυναμικού Προγραμματισμού που περιγράφεται στις [49] και [19] είναι η εύρεση του βέλτιστου μονοπατιού σε ένα Γράφο του οποίου οι ακμές έχουν διαφορετικά βάρη. Για παράδειγμα για να φτάσουμε από το σημείο Α στο σημείο Β για τον Γράφο της εικόνας 35 στον μικρότερο δυνατό χρόνο θεωρώντας πως το βάρος του κάθε κλάδου εκφράζει την χρονική διάρκεια που χρειάζεται για την μετάβαση από τον έναν κόμβο του στον άλλο. Αν το μέγεθος του προβλήματος δεν είναι πολύ μεγάλο μπορούμε να εξετάσουμε όλες τις πιθανότητες και στην συνέχεια να επιλέξουμε εκείνη την διαδρομή που αντιστοιχεί στον ελάχιστο χρόνο. Ωστόσο, κάτι τέτοιο θα ήταν ιδιαίτερα χρονοβόρο και πολύπλοκο, ειδικά καθώς το μέγεθος του προβλήματος μεγάλωνε, και πρακτικά ανεφάρμοστο σε πολύ μεγάλους Γράφους. [19] 64
65 Εικόνα 35-Απλό παράδειγμα εφαρμογής του Δυναιμού Προγραμματισμού [49], [19] Χρησιμοποιώντας αντί αυτού την αρχή βελτιστότητας κατά Bellman είναι δυνατόν να μειώσουμε τον αριθμό των υπολογισμών που απαιτούνται αρχίζοντας την διαδικασία αντίστροφα από το σημείο B. Αν το μονοπάτι περάσει από το x τότε ο βέλτιστος τρόπος για να φτάσουμε στο B είναι να πάμε πάνω από το x και μετά κάτω στο B (συνολική διαδρομή βάρους 16) παρά να πάμε κάτω και μετά πάνω (συνολική διαδρομή βάρους 18). Συνεπώς, το βέλτιστο κόστος για το σημείο x είναι 16 και το βέλτιστο μονοπάτι είναι εκείνο που αντιστοιχεί στο ελάχιστο αυτό κόστος. Αν επαναλάβουμε την ίδια λογική για κάθε κόμβο μέχρι να φτάσουμε το σημείο έναρξης Α, προκύπτει η ελάχιστη συνάρτηση κόστους για κάθε κόμβο. Το μονοπάτι που αντιστοιχεί στην ελαχιστοποίηση του κόστους είναι το βέλτιστο μονοπάτι. [19], [49] 65
66 5.3.3 Δυναμικός Προγραμματισμός & Διαχείριση Ενέργειας [52] Για να εφαρμοστεί ο δυναμικός προγραμματισμός πρέπει αρχικά να γίνει διακριτοποίηση του συστήματος. Το διακριτό μοντέλο του υβριδικού οχήματος περιγράφεται από την σχέση: x(k + 1) = F(x(k), u(k)) (5.16) Όπου u η είσοδος ελέγχου και x οι καταστάσεις του συστήματος. Σκοπός της βελτιστοποίησης είναι να βρεθεί η βέλτιστη ακολουθία εισόδων ελέγχου που να ελαχιστοποιεί το κριτήριο βελτιστοποίησης κατά την διάρκεια ενός κύκλου οδήγησης [41]. H είσοδος ελέγχου παριστάνει τον διαχωρισμό ισχύος μεταξύ της μηχανής εσωτερικής καύσης και του ηλεκτροκινητήρα κατά τα διαδοχικά βήματα από την αρχή του κύκλου οδήγησης μέχρι το τέλος του. Το κριτήριο βελτιστοποίησης μπορεί να αντιστοιχεί αποκλειστικά στην κατανάλωση καυσίμου είτε να συμπεριλαμβάνει και άλλους σημαντικούς παράγοντες. Αναλόγως με τις απαιτήσεις συνολικής ισχύος του οδηγού, καθώς και της κατάστασης στην οποία βρίσκονται την στιγμή εκείνη η μπαταρία ο ηλεκτροκινητήρας και η μηχανή εσωτερικής καύσης, καθορίζονται και οι ισχείς που πρέπει να ικανοποιηθούν μέσα από την είσοδο ελέγχου. Χρησιμοποιώντας την ταχύτητα του οχήματος καθώς και την επιτάχυνσή του μπορεί να υπολογιστεί η απαιτούμενη οδηγητική ισχύς στους τροχούς. Ανάλογα,τώρα, με τις απαιτήσεις σε συνολική ισχύ καθορίζεται η μέγιστη και ελάχιστη τιμή ισχύος που μπορούν να αποδώσουν τα υποσυστήματα του οχήματος. Αν η ισχύς υπερβαίνει τις δυνατότητες των υποσυστημάτων, τότε δεν έχει νόημα ο έλεγχος διαχωρισμού ισχύος καθώς τόσο η μηχανή όσο και ο ηλεκτροκινητήρας χρησιμοποιούνται στην μέγιστη ισχύ τους. Όμως, στην περίπτωση που η συνολική ισχύς δεν ξεπερνά την μέγιστη δυνατή, έχουμε άπειρους πιθανούς συνδυασμούς του ηλεκτροκινητήρα και της μηχανής προκειμένου να ικανοποιηθεί το φορτίο. Εδώ, είναι που χρειάζεται η επινόηση αλγορίθμων ελέγχου που είναι και το κύριο ζήτημα της εργασίας αυτής. Σε πολλούς αλγορίθμους, όπως και στον αλγόριθμο του δυναμικού προγραμματισμού, δεν επιλέγουμε όλες τις δυνατές λύσεις στον συνεχή χώρο αλλά 66
67 επιλέγουμε από ένα σύνολο διακριτών λύσεων. Ο λόγος για τον οποίο το κάνουμε αυτό είναι γιατί προσπαθούμε να έρθουμε σε έναν συμβιβασμό μεταξύ καλής ακρίβειας αποτελέσματος και σχετικά χαμηλής υπολογιστικής πολυπλοκότητας. Έτσι, είναι πολύ πιθανόν το ελάχιστο κόστος σε κάθε κατάσταση να μην συμπίπτει ακριβώς με το πραγματικό ελάχιστο κόστος και τα μεγέθη που προκύπτουν να παρουσιάζουν κάποιες ανακρίβειες. Συνεπώς, ακόμη και ο δυναμικός προγραμματισμός εκφυλλίζεται για λόγους υπολογιστικού φόρτου σε προσέγγιση της βέλτιστης συμπεριφοράς. Ωστόσο, αν τα σημεία αυτά επιλεγούν προσεκτικά παρέχουν μια λύση στο πρόβλημα βέλτιστου ελέγχου πολύ κοντά στην βέλτιστη. Ως κριτήριο κόστους στο πρόβλημα ενεργειακής διαχείρισης επιλέγεται η κατανάλωση καυσίμου [55]: N 1 J = fuel(x(k), u(k)) + Φ(x(N)) (5.9) k=0 Η διαδικασία υπολογισμού της βέλτιστης στρατηγικής μέσω του Δυναμικού Προγραμματισμού χωρίζεται σε δύο βασικά βήματα: I) Αρχικά, υπολογίζεται το τελικό κόστος για κάθε διαδρομή J N (x(n)) = Φ Ν (x(ν)) (5.17) II) Το πρόβλημα βελτιστοποίησης λύνεται προς τα πίσω στον χρόνο αρχίζοντας από το N-1 ως το 0 βάσει της εξίσωσης Hamilton-Jacobi-Bellman όπως αυτή περιγράφεται στην εξίσωση (5.13) με τελική τιμή στο i=n: J N (x(n)) = Φ N (x(n)) = a(soc(n) SOC f ) 2 (5.18) Στην περίπτωση που το αποτέλεσμα δεν ανήκει σε ένα από τα διακριτά σημεία χρησιμοποιείται η μέθοδος της παρεμβολής για τον κατάλληλο εντοπισμό του σημείου. Εναλλακτικά της σχέσης (5.18) μπορούμε να χρησιμοποιήσουμε τον σκληρό περιορισμό SOC(0)=SOC(tf). O όρος Φ(x(N) εισάγεται ως ένας τελικός περιορισμός κατάστασης. Ο περιορισμός αφορά την κατάσταση φόρτισης της μπαταρίας SOC και ορίζεται ως μία τετραγωνική συνάρτηση τιμωρίας (Penalty Function). Η συνάρτηση αυτή δρα διορθωτικά στην τελική κατάσταση φόρτισης SOC(N) και χρησιμοποιείται για να διατηρήσει την τελική 67
68 κατάσταση φόρτισης της μπαταρίας κοντά στην επιθυμητή τιμή SOC f. Μια ενδεχόμενη απουσία της συνάρτησης τιμωρίας από το κριτήριο κόστους οδηγεί στην αραίωση φορτίου της μπαταρίας κατά την προσπάθεια του αλγορίθμου να ελαχιστοποιήσει την κατανάλωση καυσίμου. Η προσθήκη αυτή είναι υψίστης σημασίας, καθώς οδηγεί σε μια λύση βιώσιμη από πλευράς φορτίου. Συνήθως το κέρδος του συντελεστή βάρους του τελικού περιορισμού είναι αρκετά μεγάλο (της τάξης του 10 6 ), έτσι ώστε η ανταπόκριση της βελτιστοποίησης να είναι μεγάλη και γρήγορη κατά την διάρκεια του κύκλου οδήγησης γεγονός που τελικά θα μας εξασφαλίσει ότι: SOC(0) = SOC(N). Η λύση του παραπάνω προβλήματος βελτιστοποίησης για έναν δεδομένο κύκλο οδήγησης μας δίνει την βέλτιστη ακολουθία εισόδου. Όπως έχουμε αναφέρει, η είσοδος αυτή εκφράζει την αναλογία με την οποία κατανέμεται η συνολική απαιτούμενη ισχύς μεταξύ της μηχανής και του ηλεκτροκινητήρα. Η έξοδος του αλγορίθμου είναι ένας χάρτης διακριτών τιμών της μεταβλητής ελέγχου. Μέσα από τον χάρτη αυτόν μπορούμε βρούμε το σήμα ελέγχου εκείνο που όταν το εφαρμόσουμε στο σύστημα διαγράφει την βέλτιστη τροχιά της κατάστασης ξεκινώντας από την αρχική συνθήκη. Δεδομένου ότι ο χάρτης περιέχει διακριτές τιμές στον χώρο κατάστασης, για να περάσουμε στο αντίστοιχο συνεχές σήμα πρέπει να χρησιμοποιήσουμε κάποια μέθοδο παρεμβολής Ενδεικτικά Αποτελέσματα Mεθόδου Για να εξαχθούν κάποια ενδεικτικά της μεθόδου αποτελέσματα χρησιμοποιήθηκε μηχανή εσωτερικής καύσης με σπινθήρα (SI) μέγιστης ισχύος 100kW μέσης απόδοσης 0.37 και ηλεκτροκινητήρας μόνιμων μαγνητών μέγιστης ισχύος 25kW μέσης απόδοσης Η χωρητικότητα της μπαταρίας που χρησιμοποιήθηκε είναι 10 Ah. Ακόμα, η αντίσταση φόρτισης Rdis και αποφόρτισης Rchg καθώς και η τάση ανοικτοκυκλώματος Voc είναι συναρτήσεις της κατάστασης φόρτισης SOC και η σχέση τους προκύπτει από πίνακες μετρήσεων και παρουσιάζεται στην εικόνα 36. Ως τελικός περιορισμός χρησιμοποιείται ο σκληρός περιορισμός (hard constraint) SOC(0)=SOC(tf)=0.7. Η απαιτούμενη ισχύς των κύκλων οδήγησης που επιβάλλονται στο όχημα έχει πολλαπλασιαστεί στην περίπτωση των κύκλων NEDC και EUDC επί έναν σταθερό παράγοντα κέρδους 1<K<2 έτσι ώστε να μελετηθεί η απόκρισή του οχήματος σε πιο ακραίες μεταβολές και καταστάσεις μεγαλύτερης ισχύος στους τροχούς. Ακόμα κι αν η 68
69 ισχύς φορτίου δεν παίζει πολύ σημαντικό ρόλο δεδομένου ότι κυμαίνεται σε σχετικά λογικά πλαίσια, αυτό έγινε πειραματικά επειδή θα ήταν καλύτερο για την εξέταση της λειτουργίας του οχήματος να υπάρχουν κάποιοι κύκλοι οδήγησης, όπου το όχημα να χρησιμοποιεί όλες τις δυνατότητές του για κάλυψη των αναγκών ισχύος. Ωστόσο, πρέπει να λάβουμε υπόψιν μας η απαιτούμενη ισχύς να μην ξεπερνά τις δυνατότητες σε ισχύ των δύο πηγών ενέργειας συνδυασμένων, καθώς σε μια τέτοια περίπτωση το όχημα δεν δύναται να καλύψει τις οδηγητικές του ανάγκες. Εικόνα 36- Καμπύλες αντίστασης φόρτισης-αποφόρτισης και τάση ανοικτοκυκλώματος της μπαταρίας συναρτήσει της κατάστασης φόρτισης Η μέθοδος του δυναμικού προγραμματισμού διερευνήθηκε για τον ευρωπαϊκό κύκλο οδήγησης EUDC, τον κύκλο FTP-Highway (HWFET), τον κύκλο πόλης City-II και τέλος τον κύκλο πόλης FTP-75 [34]. Παρακάτω παρουσιάζονται αποτελέσματα ενδεικτικά της λειτουργίας της μεθόδου. Τα σημαντικά χαρακτηριστικά της στρατηγικής για κάθε κύκλο οδήγησης είναι η κατάσταση φόρτισης της μπαταρίας, καθώς και ο λόγος με τον οποίο διαμοιράζεται η ολική απαιτούμενη ισχύς μεταξύ μηχανής και ηλεκτροκινητήρα. Παρατηρούμε πως το άθροισμα της ισχύος μηχανής και ηλεκτροκινητήρα δίνει κάποιες τιμές ισχύος ελαφρώς διαφορετικές από την ισχύ φορτίου που εισάχθηκε ως είσοδος στο σύστημα. Αυτό πιθανότατα οφείλεται κατά κύριο λόγο στις απώλειες ισχύος στο κιβώτιο ταχυτήτων καθώς και στην μετάδοση και στο διαφορικό. Δηλαδή, η ισχύς που πρέπει να ικανοποιούν η μηχανή και ο ηλεκτροκινητήρας συνολικά πρέπει να λαμβάνουν υπόψιν τους και τα υποσυστήματα αυτά για την ικανοποίηση των οδηγητικών αναγκών γεγονός που 69 οδηγεί σε μια ελαφρώς διαφορετική δυναμική συμπεριφορά και σε μια μεγαλύτερη κατά μέσο όρο σπατάλη ενέργειας λόγω των επιπλέον μηχανικών απαιτήσεων.
70 Τέλος, κάποιες μικροδιαφορές είναι πιθανόν να οφείλονται και στην διακριτοποίηση του συστήματός μας έτσι ώστε να μπορέσει να λυθεί με την μέθοδο του Δυναμικού Προγραμματισμού ή στο γεγονός ότι χρησιμοποιούμε χάρτες μηχανής για την υλοποίησή του αλγορίθμου που βασίζονται σε πειραματικά δεδομένα και αλλοιώνουν την πληροφορία που εισάγουμε, καθώς έχουν ασυνεχή μορφή. Σε κάθε περίπτωση, αφού οι απαιτήσεις σε ταχύτητα ικανοποιούνται, τέτοιες μικροδιαφορές δεν αλλοιώνουν την συνολική συμπεριφορά της ενεργειακής διαχείρισης. Εξάλλου, δεν έχει σημασία ο κύκλος οδήγησης αλλά πως αντιδρά η στρατηγική του οχήματός μας κατά την διάρκειά του. Με λίγα λόγια, οι κύκλοι οδήγησης έχουν μικρή σημασία στις λεπτομέρειές τους και την κύρια σημασία έχει η σύγκριση των στρατηγικών μας κάτω από τις ίδιες συνθήκες ταχύτητας και ισχύος. Στην ουσία, οι κύκλοι οδήγησης δεν είναι τίποτε άλλο παρά διαταραχές, που αντιπροσωπεύουν όσο πιο καλά μπορούν την πραγματική οδήγηση και οι στρατηγικές ελέγχου είναι οι αποφάσεις που πρέπει να ληφθούν για την καλύτερη αντιμετώπιση των διαταραχών από πλευράς ενεργειακής οικονομίας. Αν κυμαίνονται σε λογικά πλαίσια, οι διαταραχές αυτές είναι καθαρά υποκειμενικές και απλώς δοκιμάζουν την κάθε στρατηγική. Για τον λόγο αυτό, οι υπόλοιπες μέθοδοι μελετήθηκαν υπό τους ίδιους κύκλους-διαταραχές. Μάλιστα, για την τρίτη στρατηγική που αναλύεται στο Κεφάλαιο 7, δεν χρησιμοποιήθηκε η ισχύς φορτίου αλλά η συνολική ισχύς μηχανής και ηλεκτροκινητήρα που μπορεί να μετρηθεί λαμβάνοντας υπόψιν και τις απαιτήσεις της μετάδοσης, έτσι ώστε να αναδεικνύεται η παρεμφερής συμπεριφορά των μεθόδων. Τα αποτελέσματα της ενεργειακής διαχείρισης με την μέθοδο του Δυναμικού Προγραμματισμού παρουσιάζονται στις παρακάτω εικόνες: 70
71 Εικόνα 37- Διαγράμματα Κατάστασης Φόρτισης Μπαταρίας, Ισχύων Κινητήρα και Μηχανής και Συνολικής Ισχύος για τον κύκλο οδήγησης EUDC Κατά την διάρκεια του Ευρωπαϊκού Κύκλου Οδήγησης παρατηρούμε πως η κατάσταση φόρτισης υφίσταται μείωση όσο οι απαιτήσεις σε ταχύτητα μένουν σταθερές ή αυξάνονται, γεγονός που σημαίνει πως ο ηλεκτροκινητήρας αποφορτίζει την μπαταρία, προκειμένου να βοηθήσει την ΜΕΚ στην ικανοποίηση της οδηγητικής ισχύος. Αντίθετα, κατά την διάρκεια μείωσης ή μηδενισμού της ταχύτητας η κατάσταση φόρτισης αυξάνεται, καθώς μέρος της μηχανικής ισχύος της ΜΕΚ χρησιμοποιείται για 71
72 την επαναφόρτιση της μπαταρίας μέσω της ηλεκτρικής μηχανής που λειτουργεί ως γεννήτρια. Τέλος, από τα μέσα του κύκλου οδήγησης και μετά παρατηρείται μία τάση της ηλεκτρικής μηχανής να λειτουργεί ολοένα και περισσότερο ως γεννήτρια παρόλο που στον κύκλο οδήγησης παρατηρούνται μεγάλα διαστήματα σταθερής ταχύτητας και επιτάχυνσης (κατά το διάστημα ). Αυτό συμβαίνει καθώς στο πρόβλημα βελτιστοποίησης τέθηκε για την κατάσταση φόρτισης ο σκληρός περιορισμός SOC(0) = SOC(t f ). Έτσι, προκειμένου να ικανοποιήσει τον περιορισμό αυτό, ο αλγόριθμος έθεσε σε λειτουργία την ηλεκτρική μηχανή προκειμένου να φορτίσει την μπαταρία στην αρχική τιμή φορτίου. Αυτό φανερώνει την μεγάλη σημασία που έχει για το πρόβλημα ενεργειακής διαχείρισης ο τελικός περιορισμός καθώς και επιβεβαιώνει ότι ο αλγόριθμος ικανοποιεί την βιωσιμότητα από πλευράς φορτίου μπαταρίας. Η παραπάνω περιγραφή επιβεβαιώνει την ορθή λειτουργία του Δυναμικού Προγραμματισμού για τον ευρωπαϊκό κύκλο οδήγησης. 72
73 Εικόνα 38- Διαγράμματα Κατάστασης Φόρτισης Μπαταρίας, Ισχύων Κινητήρα και Μηχανής και Συνολικής Ισχύος για τον κύκλο οδήγησης FTP-Highway Ο κύκλος οδήγησης FTP (Federal Test Procedure) για λειτουργία εθνικής οδού επιλέχθηκε για να διερευνηθεί η βέλτιστη διαχείριση ενέργειας του υβριδικού οχήματος υπό συνθήκες μεγάλων απαιτήσεων σε ταχύτητα κατά την διάρκεια των οποίων, έχουμε απότομες αλλαγές στην ταχύτητα συγκριτικά με τον EUDC. Ο κύκλος αυτός θα μας οδηγήσει σε κάποια συμπεράσματα σχετικά με το πώς λειτουργεί η μέθοδος του Δυναμικού Προγραμματισμού υπό αυτές τις συνθήκες. Στην περίπτωση του κύκλου 73
74 FTP-Highway, οι μεταβολές στην ταχύτητα είναι τόσο έντονες που δεν είναι εύκολο να διακρίνουμε χαρακτηριστικές περιοχές φόρτισης και αποφόρτισης της μπαταρίας όπως στην περίπτωση του Ευρωπαϊκού κύκλου. Έτσι, το μόνο που μπορούμε να πούμε είναι πως η κατάσταση φόρτισης μειώνεται, κυρίως μέχρι το μέσον του κύκλου οδήγησης και στην συνέχεια αυξάνεται μέχρι που παίρνει την αρχική της τιμή. Εικόνα 39- Διαγράμματα Κατάστασης Φόρτισης Μπαταρίας, Ισχύων Κινητήρα και Μηχανής και Συνολικής Ισχύος για τον κύκλο οδήγησης City-II 74
75 Κατά την διάρκεια του κύκλου πόλης City-II παρατηρούμε μια συμπεριφορά του οχήματος που μπορεί να χαρακτηριστεί ως ενδιάμεση μεταξύ του κύκλου EUDC και του κύκλου FTP-Highway. Kαι στην περίπτωση αυτή, παρατηρούμε μικρά διαστήματα φόρτισης κατά την επιβράδυνση καθώς και εκφόρτιση και χρήση του κινητήρα στην διάρκεια μεγάλων απαιτήσεων σε φορτίο. Ταυτόχρονα, έχουμε ικανοποίηση του τελικού περιορισμού γεγονός που επιβεβαιώνει την βιωσιμότητα του αλγορίθμου από πλευράς φορτίου. Τέλος, ο κύκλος πόλης FTP-75 μελετά πως συμπεριφέρεται το όχημα σε πολύ μεγάλες και απότομες μεταβολές της ταχύτητας και της επιτάχυνσης. Όπως φαίνεται από το σχήμα, η μπαταρία αποφορτίζεται με μεγαλύτερο ρυθμό από ότι φορτίζεται. Έτσι, μακροσκοπικά παρατηρείται μια σταδιακή εκφόρτιση της μπαταρίας, ενώ στο τέλος ο τελικός περιορισμός επιβάλλει την επαναφόρτισή της έτσι ώστε το φορτίο της μπαταρίας να επανέλθει στην αρχική του τιμή. 75
76 Εικόνα 40- Διαγράμματα Κατάστασης Φόρτισης Μπαταρίας, Ισχύων Κινητήρα και Μηχανής και Συνολικής Ισχύος για τον κύκλο οδήγησης FTP-75 76
77 5.3.5 Μειονεκτήματα του Δυναμικού Προγραμματισμού Ο έλεγχος που προκύπτει από τον δυναμικό προγραμματισμό είναι ο βέλτιστος που μπορούμε να έχουμε για τον κύκλο οδήγησης στον οποίο εφαρμόζεται. Ωστόσο, υπάρχουν δύο σημαντικοί λόγοι οι οποίοι καθιστούν τον αλγόριθμο αυτό μη ρεαλιστικό στην πράξη [28], [61]: Ι) Τρέχει από το τέλος προς την αρχή. Συνεπώς, είναι απαραίτητη η εκ των προτέρων γνώση ολόκληρου του κύκλου οδήγησης ώστε να βρεθεί ο βέλτιστος νόμος ελέγχου. Η πληροφορία αυτή απουσιάζει από εφαρμογές πραγματικού χρόνου. Τέτοιου είδους μέθοδοι οι οποίες απαιτούν την εκ των προτέρων γνώση της διαταραχής, ώστε να εξάγουν τον νόμο ελέγχου ονομάζονται μη αιτιατές. ΙΙ) Έχει μεγάλη υπολογιστική πολυπλοκότητα γεγονός που τον καθιστά ακατάλληλο για εφαρμογές πραγματικού χρόνου. Παρά τα σοβαρά μειονεκτήματα από τα οποία υποφέρει ο δυναμικός προγραμματισμός και που τον καθιστούν ανεφάρμοστο σε πρακτικές εφαρμογές, ο αλγόριθμος προσφέρει την πιο κοντινή προσέγγιση βέλτιστης λύσης που θα μπορούσαμε να έχουμε. Χρησιμοποιείται τις περισσότερες φορές ως μέτρο σύγκρισης της οικονομίας καυσίμου για τους αιτιατούς αλγορίθμους.[28] Με απώτερο σκοπό την εφαρμογή σε πραγματικό όχημα είναι απαραίτητο να καταστρωθεί ένας νόμος ελέγχου ο οποίος να είναι αιτιατός και να προσεγγίζει όσο καλύτερα μπορεί το ολικό βέλτιστο που υπολογίσαμε μέσω του δυναμικού προγραμματισμού. 5.4 Η Αρχή Ελαχίστων του Pontryagin Η Αρχή Ελαχίστων του Pontryagin [47], [53] είναι ένα μαθηματικό θεώρημα το οποίο έθεσε την βάση για την σύγχρονη θεωρία ελέγχου. Σύμφωνα με το θεώρημα, για να έχουμε βέλτιστη λύση ενός συστήματος υπάρχουν κάποιες στιγμιαίες συνθήκες βελτιστότητας που πρέπει να ικανοποιούνται. [51] Οι συνθήκες αυτές δεν εξασφαλίζουν από μόνες τους βελτιστότητα. Ωστόσο, η βέλτιστη λύση είναι υποχρεωμένη να τις ικανοποιεί. Παρακάτω παρουσιάζεται η Αρχή Ελαχίστων του Pontryagin με και χωρίς περιορισμούς. 77
78 5.4.1 Αρχή Ελαχίστων του Pontryagin για προβλήματα χωρίς περιορισμούς κατάστασης [28], [41] Στην περίπτωση αυτή το διάνυσμα κατάστασης μπορεί να πάρει οποιαδήποτε τιμή μέσα στο πεδίο των πραγματικών αριθμών x(t) R n Για το σύστημα των εξισώσεων (5.3) σύμφωνα με την αρχή ελαχίστων του Pontryagin πρέπει να ικανοποιούνται οι παρακάτω συνθήκες για την βέλτιστη είσοδο u opt [54]: I) Η είσοδος u opt να ελαχιστοποιεί την Χαμιλτονιανή του συστήματος: H(t, u(t), x(t), λ(t)) = λ Τ f(t, u(t), x(t)) + L(t, u(t), x(t))(5.19) δηλαδή η βέλτιστη λύση ικανοποιεί την σχέση : u opt = min u U H (5.20) Όπου U είναι το σύνολο των επιτρεπτών εισόδων ελέγχου και λ(t) R n το διάνυσμα συμπληρωματικών καταστάσεων. ΙΙ) Η συμπληρωματική κατάσταση πρέπει να ικανοποιεί την εξίσωση : III) IV) λ = Η x, για u = uopt και x = x opt (5.21) H βέλτιστη τροχιά x opt πρέπει να ικανοποιεί τους οριακούς περιορισμούς: Φ(x(t f ), t f ) = 0 (5.22) Σε περίπτωση που δεν υπάρχουν τελικοί περιορισμοί τότε η τελική συνθήκη δίνεται από την συμπληρωματική κατάσταση : λ opt (t f ) = Φ(x(t f), t f ) x (5.23) 78
79 5.4.2 Αρχή Ελαχίστων του Pontryagin για προβλήματα με περιορισμούς κατάστασης [28],[39] Ένας από τους απλούστερους τρόπους περιγραφής της Αρχής Ελαχίστων του Pontryagin υπό περιορισμούς περιγράφεται στην [39] και ακολουθεί στη συνέχεια με τα απαραίτητα σχόλια για την κατανόηση της μεθόδου. Σε ένα τέτοιο πρόβλημα οι μεταβλητές κατάστασης έχουν σταθερούς ή χρονομεταβλητούς περιορισμούς. Συνεπώς, ανήκουν σε ένα σύνολο X το οποίο είναι υποσύνολο του R n και δηλώνει τον χώρο κατάστασης στον οποίο μπορούν να πάρουν τιμές οι μεταβλητές, ικανοποιώντας παράλληλα τους περιορισμούς. Έστω πως το σύνολο στο οποίο μπορεί να πάρει τιμές το διάνυσμα κατάστασης φράσσεται από τις συναρτήσεις περιορισμού G(x, t) με G: R n T R p, x R n, T [t 0, t f ]. Η συνάρτηση αυτή έχει ως μεταβλητή το διάνυσμα κατάστασης και τον χρόνο και εκφράζει για κάθε τιμή τους στον χώρο κατάστασης ένα σύνολο ανισοτικών περιορισμών που πρέπει να ικανοποιεί η κατάσταση κάθε χρονική στιγμή. Έτσι, οι επιτρεπόμενες καταστάσεις ανήκουν στο σύνολο: X = {x R n G(x(t), t) 0 } (5.24) Στην περίπτωση αυτή, τα όρια της κατάστασης πρέπει να ληφθούν υπόψιν στο κριτήριο βελτιστοποίησης, μέσω ενός παραπάνω όρου που εισάγει στο κριτήριο παραπάνω κόστος, όταν ο αλγόριθμος φτάνει τα όρια αυτά. Με αυτόν τον τρόπο, επιτυγχάνεται η αποφυγή καταστάσεων που θα μπορούσαν να έχουν καταστροφικές συνέπειες για το σύστημά μας. Με την παραπάνω προσθήκη η χαμιλτονιανή παίρνει την μορφή [39]: t f H = (L(x(t), u(t), t) + w Η(x(t), t)dt + Φ(x(t f ), t f ) (5.25) 0 Όπου η συνάρτηση H είναι ουσιαστικά μια σύνθετη Heaviside συνάρτηση, που ενεργοποιείται όταν παραβιάζονται οι περιορισμοί για να δώσει επιπλέον βάρος στο κόστος και να μην ακολουθηθεί έτσι η απαγορευμένη τροχιά. 79
80 Η συνάρτηση H ορίζεται ως: H(x(t), t) = { 0, G(x(t), t) 0 (ανενεργοί περιορισμοί) 1, G(x(t), t) > 0 (ενεργοί περιορισμοί), (5.26) Πολύ σημαντική σε αυτήν την περίπτωση είναι η παράμετρος βάρους w. Η τιμή της είναι αυτή που στην ουσία θα καθορίσει πόσο επιδρά ο επιπλέον όρος περιορισμών στο κριτήριο κόστους. Η τιμή της πρέπει να είναι αρκετή, έτσι ώστε ο επιπλέον όρος του κριτηρίου κόστους να καθιστά την κατάσταση που παραβιάζει τον περιορισμό μη αποδεκτή. Είναι προφανές, πως μία συνάρτηση κριτηρίου κόστους που εμπεριέχει μία συνάρτηση τύπου Heaviside θα οδηγήσει σε Χαμιλτονιανή συνάρτηση που θα εμπεριέχει ασυνέχειες. Αυτό σημαίνει πως θα υπάρχουν ασυνέχειες και στην συμπληρωματική κατάσταση αφού συνδέονται μέσω της σχέσης 5.19 και Συνεπώς, την χρονική στιγμή που η κατάσταση παραβιάζει τους περιορισμούς, την στιγμή εκείνη η συμπληρωματική κατάσταση αλλάζει ξαφνικά σε μία εντελώς διαφορετική τιμή, παρουσιάζοντας έτσι ασυνεχή συμπεριφορά. Η Αρχή Ελαχίστων του Pontryagin είναι μια πάρα πολύ ισχυρή τεχνική. Μας προσφέρει την δυνατόττητα να ορίσουμε το πρόβλημα ολικής βελτιστοποίησης ως πρόβλημα στιγμιαίας βελτιστοποίησης με τοπικούς περιορισμούς. Εκφράζει δε τις απαραίτητες συνθήκες βελτιστότητας, έτσι ώστε να βρεθούν υποψήφιοι νόμοι ελέγχου. Ωστόσο, δεν εξασφαλίζει την βέλτιστη λύση ή ακόμη και την ύπαρξή της. Δηλώνει,όμως, πως η βέλτιστη λύση, αν υπάρχει, ικανοποιεί της συνθήκες βελτιστότητας της αρχής. Αν το πρόβλημα βέλτιστου ελέγχου έχει μόνο μια λύση και αυτή ικανοποιεί τις συνθήκες αυτές τότε αυτή η λύση είναι και ο βέλτιστος έλεγχος. Αν, όμως, βρεθεί ένας αριθμός υποψήφιων βέλτιστων λύσεων, τότε πρέπει να εφαρμόσουμε κάθε λύση ξεχωριστά στο πρόβλημά μας και να διαλέξουμε εκείνη με την χαμηλότερη τιμή συνολικού κόστους. Η αναλυτική φύση του θεωρήματος σημαίνει πως πρέπει να εκφράσουμε το σύστημα μας όσο πιο απλοϊκά μπορούμε προκειμένου να μπορέσει να επιλυθεί γρήγορα. Από την άλλη, δεν πρέπει να χάνονται πολύτιμες πληροφορίες για το σύστημα κατά την απλοποίηση. Ψάχνουμε, συνεπώς, μια χρυσή τομή μεταξύ απλότητας και ακρίβειας της 80
81 μοντελοποίησης. Εκτός αυτού, συνήθως για να εφαρμόσουμε την αρχή ελαχίστων του Pontryagin απαιτείται η εκ των προτέρων γνώση ολόκληρου του ορίζοντα βελτιστοποίησης, που στην περίπτωσή μας είναι ο κύκλος οδήγησης. Συνεπώς, μία πραγματική εφαρμογή της στρατηγικής δεν είναι δυνατόν να πραγματοποιηθεί εκτός κι αν ο κύκλος οδήγησης είναι εξαρχής γνωστός ή μπορεί να προβλεφθεί Προβλήματα Υλοποίησης [41] To πρόβλημα βελτιστοποίησης της διαχείρισης ενέργειας είναι ένα ιδιαίτερα πολύπλοκο πρόβλημα το οποίο είναι αρκετά δύσκολο να λυθεί με την αρχή ελαχίστων του Pontryagin για τους εξής λόγους: To σύστημα είναι χρονικώς μεταβαλλόμενο. Υπάρχουν περιορισμοί κατάστασης και περιορισμοί τελικής κατάστασης Ένα τέτοιο πρόβλημα μπορεί να λυθεί με την παραπάνω μέθοδο μόνο αν είναι γνωστό σε ποια διαστήματα ενεργοποιούνται οι περιορισμοί. Το γεγονός ότι το σύστημα είναι χρονικώς μεταβαλλόμενο, κάνει τον εντοπισμό των διαστημάτων αυτών πολύ δύσκολη υπόθεση. Αν το σύστημα ήταν χρονικώς αμετάβλητο, τότε οι περιορισμοί θα ενεργοποιούνταν μόνο σε ένα διάστημα. Στην περίπτωσή μας, ωστόσο, η χρονική μεταβλητότητα του συστήματος απαγορεύει την εκ των προτέρων γνώση του πότε και πως ενεργοποιούνται οι περιορισμοί. Συνεπώς, για να μπορέσουμε να λύσουμε το πρόβλημα με την αρχή ελαχίστων του Pontryagin πρέπει αναγκαστικά να μην ληφθούν υπόψιν οι περιορισμοί εκτός κι αν γνωρίζουμε εκ των προτέρων πως μεταβάλλονται τα μεγέθη στον χρόνο. Υπό αυτήν την παραδοχή δεν μπορούμε να είμαστε σίγουροι αν η λύση μας θα ικανοποιεί ή θα παραβιάζει τους περιορισμούς. Από τις συνθήκες βελτιστότητας προκύπτει ότι το βέλτιστο σήμα ελέγχου κάθε χρονική στιγμή βρίσκεται ως το ολικό ελάχιστο της Χαμιλτονιανής συνάρτησης, κατά μήκος της βέλτιστης τροχιάς της κύριας και της συμπληρωματικής κατάστασης. Η ελαχιστοποίηση της Χαμιλτονιανής οδηγεί σε ένα πεπερασμένο σύνολο σημάτων βέλτιστου ελέγχου που ταυτόχρονα ανήκουν στο επιτρεπτό σύνολο σημάτων ελέγχου. Η 81
82 μέθοδος αυτή στηρίζεται στην ελαχιστοποίηση της τοπικής συνάρτησης κόστους αντί της ελαχιστοποίησης της ολοκληρωτικής συνάρτησης κόστους και τα αποτελέσματά της είναι πολύ κοντά στα βέλτιστα Σημασία της Αρχικής Τιμής της Συμπληρωματικής Κατάστασης στο Πρόβλημα Ενεργειακής Διαχείρισης Ιδιαίτερα κρίσιμη για την ορθή λειτουργία της Αρχής Ελαχίστων του Pontryagin είναι η επιλογή της κατάλληλης αρχικής συνθήκης της συμπληρωματικής κατάστασης. Η αρχική τιμή της συμπληρωματικής κατάστασης ουσιαστικά αλλάζει όλο τον ορίζοντα βελτιστοποίησης. Συνεπώς, η αρχική αυτή τιμή αλλάζει και την τιμή της χαμιλτονιανής αφού η χαμιλτονιανή είναι συνάρτηση της λ. Αφού το πρόβλημα είναι ανοικτό και δεν υπάρχουν περιορισμοί τερματισμού μπορούμε να επιλέξουμε την λ(0) ελεύθερα και από τις επιλογές μας να χρησιμοποιήσουμε εκείνη που είναι κατάλληλη. Συνήθως, η λ διατηρείται σχεδόν σταθερή με μικρές μεταβολές σε όλο τον ορίζοντα βελτιστοποίησης. Έτσι, η τιμή λ(0) καθορίζει την τιμή λ για όλο αυτό το διάστημα. Έτσι, μία υψηλή τιμή του λ(0) σημαίνει πώς η στρατηγική θα φορτίσει την μπαταρία στο μέγιστο και θα την χρησιμοποιεί μόνο κατά ένα μέρος κατά την διάρκεια του κύκλου. Μία χαμηλή τιμή του λ(0) σημαίνει πως η μπαταρία θα αποφορτίζεται πλήρως και θα φορτίζεται μόνο μέσω αναγεννητικής πέδησης.[19] Μία μέση λύση θα δώσει μια πάρα πολύ καλή ενεργειακή διαχείριση. Παρόλο που οι κύκλοι οδήγησης είναι αισθητά διαφορετικοί ο ένας από τον άλλον η βέλτιστη τιμή του λ θα προκύπτει η ίδια Ενδεικτικά Aποτελέσματα Mεθόδου και Συμπεράσματα Η αρχική αυτή συνθήκη επιλέχθηκε έτσι ώστε τα αποτελέσματα να είναι ικανοποιητικά ενώ ταυτόχρονα δεν οδηγούν σε προβλήματα μπαταρίας όπως υπερφόρτιση ή πλήρης αποφόρτιση. Η βέλτιστη αρχική τιμή συμπληρωματικής κατάστασης δίνει αποτελέσματα κοντινά με την μέθοδο του Δυναμικού Προγραμματισμού. Αυτό οφείλεται κυρίως στην βαθιά συγγενική σχέση των δύο μεθόδων από μαθηματικής σκοπιάς. Για μια κατάλληλα επιλεγμένη τιμή της αρχικής 82
83 συμπληρωματικής κατάστασης αλλά όχι της βέλτιστης, τα αποτελέσματα, τόσο της κατάστασης φόρτισης όσο και της οικονομίας καυσίμου, προκύπτουν σχετικά κοντά στον δυναμικό προγραμματισμό, δηλαδή ακόμα και χωρίς την βέλτιστη τιμή επιβεβαιώνεται η ορθή λειτουργία της μεθόδου. Τα αποτελέσματα της κατάστασης φόρτισης καθώς και των ισχύων που προέκυψαν για την αρχή ελαχίστων του Pontryagin χωρίς περιορισμούς κατά την διάρκεια του κύκλου οδήγησης FTP-Highway, παρουσιάζονται στις εικόνες 41 και 42. Παρατηρούμε ότι ακόμα και αν υπάρχουν κάποιες σημαντικές αποκλίσεις σε κάποια σημεία της κατάστασης φόρτισης, η συμπεριφορά των ισχύων είναι παραπλήσια. Η συνολική κατανάλωση καυσίμου με την Αρχή Ελαχίστων προκύπτει km/l. H αντίστοιχη οικονομία καυσίμου με χρήση του Δυναμικού προγραμματισμού προέκυψε km/l. Η διαφορά αυτή οφείλεται στο ότι χρησιμοποιείται μία αρκετά καλή αρχική τιμή της συμπληρωματικής κατάστασης αλλά διαφορετική από την βέλτιστη. Δηλαδή, ανάλογα με την επιλογή της αρχικής συνθήκης έχουμε διαφορετική συμπεριφορά της ενεργειακής διαχείρισης και συνεπώς, διαφορετική κατανάλωση καυσίμου. Αυτό φανερώνει και την κρισιμότητα της επιλογής της αρχικής συμπληρωματικής κατάστασης που παριστάνει στην ουσία τον συντελεστή ισοδυναμίας της κατανάλωσης όπως θα αναφέρουμε σε επόμενα κεφάλαια. Ταυτόχρονα, πρέπει να ληφθεί υπόψιν η μπαταρία να μην υπερφορτίζεται ή να εκφορτίζεται πλήρως δηλαδή να πληρούνται οι βασικοί περιορισμοί κατάστασης ακόμα κι αν δεν είναι μαθηματικά παρόντες. Επίσης, θεωρείται πως το λ είναι σταθερό καθ όλη την διάρκεια του κύκλου οδήγησης. Η πραγματικότητα,όμως, είναι ότι το λ ταλαντεύεται ελαφρώς γύρω από την αρχική τιμή του κατά την διάρκεια του κύκλου. Μάλιστα, όσο πιο απότομες είναι οι συνθήκες οδήγησης τόσο μεγαλύτερες εκτιμώνται οι ταλαντώσεις αυτές. [19] Αυτό το φαινόμενο δεν λαμβάνεται συνήθως υπόψιν δηλαδή η υπόθεση χάριν απλοποίησης περί σταθερού λ μπορεί να οδηγεί σε μία λύση που είναι ελαφρώς υποβέλτιστη σε σύγκριση με μία χρονομεταβλητή συμπληρωματική κατάσταση. Ωστόσο, οι διαφορές αυτές είναι,κανονικά, σχετικά αμελητέες και οι απλοποιήσεις βοηθούν στον γρήγορο υπολογισμό της βέλτιστης τροχιάς. 83
84 Εικόνα 41- Κατάσταση Φόρτισης της Μπαταρίας για τον κύκλο οδήγησης FTP-Highway με την μέθοδο Pontryagin ελαχίστων του Εικόνα 42-Ισχύς Μηχανής, Κινητήρα και Ολική Ισχύς για τον κύκλο οδήγησης FTP-Highway με την μέθοδο ελαχίστων του Pontryagin 84
85 Παρακάτω συνοψίζονται ενδεικτικά οι οικονομίες καυσίμου για την Αρχή Ελαχίστων του Pontryagin και τον Δυναμικό Προγραμματισμό. Τα αποτελέσματα παρουσιάζονται και κανονικοποιημένα ως προς την μέθοδο του Δυναμικού Προγραμματισμού για κάθε κύκλο οδήγησης. Επειδή έχουμε επιλέξει να απεικονίσουμε την οικονομία καυσίμου σε km/l η κανονικοποιημένη τιμή 1 δηλώνει την βέλτιστη λύση που βρίσκεται μέσω του δυναμικού προγραμματισμού. Οποιαδήποτε άλλη μέθοδος θα έχει ως υποβέλτιστη, κανονικοποιημένη τιμή μικρότερη της μονάδας. Οικονομία Καυσίμου για 3 κύκλους οδήγησης Πραγματικές Τιμές Kανονικοποιημένες Τιμές Αρχή Αρχή Δυναμικός Προγραμματισμός Ελαχίστων του Pontryagin Δυναμικός Προγραμματισμός Ελαχίστων του Pontryagin FTP km/l km/l Highway (3.92 L/100km) (4.02L/100km) EUDC km/l 26,73 km/l (3.68 L/100km) (3.74L/100km) FTP km/l km/l (4,06 L/100km) (4,11 L/100km) Τα αποτελέσματα είναι ικανοποιητικά ειδικά στην περίπτωση του κύκλου FTP-75. Οι τιμές οι οποίες προέκυψαν για την οικονομία καυσίμου είναι λογικές για ένα υβριδικό 85
86 όχημα. Αυτό μπορεί να επιβεβαιωθεί και από χαρακτηριστικές τιμές οικονομίας καυσίμου υβριδικών οχημάτων της αγοράς. Συγκεκριμένα, το Honda Insight πρώτης γενιάς είχε αυτονομία 3.9L/100km κατά την διάρκεια οδήγησης σε κύκλο πόλης και 3.5L/100km για οδήγηση σε εθνική οδό. Τα μεγέθη αυτά σε km/l μεταφράζονται σε και km/l [35]. Δεδομένου ότι από τους κύκλους οδήγησης που επιλέξαμε ο FTP-75 προσομοιώνει κατά κάποιο τρόπο την οδήγηση σε πόλη ενώ ο EUDC προσομοιώνει την οδήγηση στην εθνική οδό γίνεται φανερό πως οι μετρήσεις βρίσκονται αρκετά κοντά στην πραγματικότητα. Πρέπει να διευκρινιστεί στο σημείο αυτό, ότι οι μετρήσεις αυτές δεν είναι ίδιες με την οικονομία καυσίμου που μας έδωσε το Advisor για τον κύκλο FTP-Highway του Honda Insight αλλά αυτό είναι κάτι φυσιολογικό καθώς η μοντελοποίησή μας περιλαμβάνει τελείως διαφορετικά μεγέθη από του Honda Insight. Ωστόσο, χρειαζόμαστε κάποιες μετρήσεις του ως αναφορές απλώς για να δούμε αν το μοντέλο δουλεύει μέσα σε λογικά πλαίσια ενεργειακής διαχείρισης. Τα τελευταία χρόνια έχει πραγματοποιηθεί μία έντονη προσπάθεια τροποποίησης και εμπλουτισμού των δύο βασικών μη αιτιατών στρατηγικών του Δυναμικού Προγραμματισμού και της Αρχής Ελαχίστων του Pontryagin με σκοπό την δυνατότητα εφαρμογής τους σε προβλήματα πραγματικού χρόνου. Στα επόμενα κεφάλαια, πραγματοποιείται μια λεπτομερής περιγραφή των παράγωγων μεθόδων, καθώς επίσης αναλύονται τα θετικά και αρνητικά τους στοιχεία όσον αφορά στο επίπεδο των πραγματικών εφαρμογών. 6. Σύγχρονες Στρατηγικές Βασισμένες στον Δυναμικό Προγραμματισμό και στην Αρχή Ελαχίστων του Pontryagin 6.1 Στοχαστικός Δυναμικός Προγραμματισμός (SDP) [19] Όπως αναλύθηκε στο κεφάλαιο 5 ο δυναμικός προγραμματισμός παρά το γεγονός ότι δίνει βέλτιστες λύσεις στο πρόβλημα διαχείρισης ενέργειας, παρουσιάζει κάποια σοβαρά μειονεκτήματα που δεν γίνεται να αγνοηθούν καθώς απαγορεύουν ουσιαστικά την εφαρμογή του αλγορίθμου για διαχείριση πραγματικού χρόνου. Αρχικά, ο αλγόριθμος τρέχει για έναν συγκεκριμένο κύκλο οδήγησης και καθορίζει την βέλτιστη 86
87 στρατηγική για τον συγκεκριμένο μόνο κύκλο οδήγησης. Αν η ίδια στρατηγική ακολουθηθεί για έναν διαφορετικό κύκλο οδήγησης η ενεργειακή διαχείριση δεν θα είναι βέλτιστη και κινδυνεύει μάλιστα να μην είναι και βιώσιμη από πλευράς του φορτίου της μπαταρίας. Τέλος, η μεγάλη υπολογιστική του πολυπλοκότητα καθώς και το γεγονός πως είναι μη αιτιατός (απαιτείται εκ των προτέρων γνώση όλου του κύκλου οδήγησης) αποκλείουν την χρήση του στην πραγματική ζωή. Αν, όμως, ήταν εφικτό με κάποιο τρόπο να προβλέψουμε τον κύκλο οδήγησης στο μέλλον με καλή ακρίβεια χρησιμοποιώντας προβλεπτικά μοντέλα, ίσως να ήταν εφικτό ο αλγόριθμος να τροποποιηθεί έτσι ώστε να ικανοποιείται η συνθήκη της αιτιατότητας. Έτσι, με μια καλή πρόβλεψη του κύκλου οδήγησης και με δεδομένο τη συνεχή ανανέωση των πληροφοριών θα μπορούσαμε να χρησιμοποιήσουμε τον αλγόριθμο του δυναμικού προγραμματισμού για να βρούμε την βέλτιστη τροχιά βάσει του ορίζοντα πρόβλεψης. Αυτό που πρέπει να προσέξουμε κατά την εκτέλεση του αλγορίθμου είναι ότι δεν πρέπει να καθορίσουμε την βέλτιστη λύση για όλο τον ορίζοντα πρόβλεψης αλλά μόνο για την πρώτη είσοδο του ορίζοντα. Οι υπόλοιπες είσοδοι ελέγχου θα προκύπτουν καθώς ο ορίζοντας πρόβλεψης προχωρά στον χρόνο. Σε μια τέτοια περίπτωση είναι δυνατόν να απαλλαγούμε από την μη αιτιατότητα του δυναμικού προγραμματισμού ενώ ταυτόχρονα έχουμε μια λύση πολύ κοντά στην βέλτιστη. Ωστόσο, η σκέψη αυτή παρουσιάζει κάποιες αδυναμίες που εμποδίζουν την εφαρμογή της και είναι οι εξής: I. Υπερβολικά μεγάλος υπολογιστικός φόρτος για την λύση ενός ολόκληρου προβλήματος δυναμικού προγραμματισμού κάθε χρονική στιγμή. II. Αδυναμία ακριβούς πρόβλεψης των μελλοντικών καταστάσεων για έναν σχετικά μεγάλο ορίζοντα πρόβλεψης. Έτσι, οι δυνατότητες πρόβλεψης περιορίζονται σε πιο στενούς ορίζοντες οδηγώντας σε υποβέλτιστες λύσεις του προβλήματος ενεργειακής διαχείρισης. Για τους λόγους αυτούς και για να λύσουμε τα προβλήματα στα οποία οδηγούν είναι απαραίτητο να μεταβούμε από την αιτιοκρατική θεώρηση του δυναμικού προγραμματισμού στην στοχαστική. Αντί, λοιπόν, να βελτιστοποιήσουμε την διαχείριση ενέργειας για έναν συγκεκριμένο κύκλο οδήγησης προσπαθούμε να λύσουμε το πρόβλημα βελτιστοποίησης κατά την διάρκεια ενός κύκλου οδήγησης που αποτελείται 87
88 από όμοια αναμεμειγμένους τυχαίους κύκλους. Έτσι, διατυπώνουμε ένα πρόβλημα βελτιστοποίησης απείρου ορίζοντα το οποίο θα λυθεί με την μέθοδο του Στοχαστικού Δυναμικού Προγραμματισμού (Stochastic Dynamic Programming), μίας εξελιγμένης μορφής του Αιτιοκρατικού Δυναμικού Προγραμματισμού που είχε αναπτυχθεί ως τώρα. Ο Στοχαστικός Δυναμικός Προγραμματισμός είναι μία μέθοδος που μπορεί να εφαρμοστεί σε πραγματικό χρόνο και δίνει αποτελέσματα πολύ κοντινά στα βέλτιστα αν υλοποιηθεί σωστά. Για να μπορέσει να εφαρμοστεί σε πραγματικό χρόνο χρησιμοποιεί χάρτες με τις ιδιότητες και τις απαιτήσεις των κύκλων οδήγησης ως ένα look-up table. Βασισμένος σε αυτό, ο αλγόριθμος εξάγει την βέλτιστη ακολουθία ελέγχου. Η εκτίμηση της απαιτούμενης ισχύος γίνεται με την χρήση μιας μαθηματικής θεώρησης που ονομάζεται Μαρκοβιανή Αλυσίδα (Markov Chain). Εικόνα 43-α) Διάγραμμα u-pd-soc για ω=44rad/sec β) Χάρτης SDP ταχύτητα τροχών ω=39rad/sec [7] Μαρκοβιανές Αλυσίδες (Markov Chains) [15] Ένα Μαρκοβιανό σύστημα ή μια Μαρκοβιανή διαδικασία είναι ένα σύστημα το οποίο μπορεί να βρίσκεται σε μία κατάσταση από ένα σύνολο πεπερασμένων καταστάσεων και έχει την ιδιότητα να περνάει από την μία κατάσταση στην άλλη βάσει ενός σταθερού συνόλου πιθανοτήτων. Αυτό δίνει στα συστήματα Markov την ικανότητα οι μελλοντικές καταστάσεις, δοθείσας μίας κατάστασης στο παρόν, να μην επηρεάζονται καθόλου από τις παρελθοντικές καταστάσεις, μια ιδιότητα που δεν έχουμε συναντήσει 88
89 μέχρι στιγμής στις υπόλοιπες μεθόδους ενεργειακής διαχείρισης. Αυτό σημαίνει πως η κατάσταση στο παρόν εμπεριέχει όλες τις πληροφορίες εκείνες που απαιτούνται για να πάρουμε μια απόφαση στο μέλλον. Ωστόσο, στις μελλοντικές καταστάσεις αυτή τη φορά θα μεταπηδήσουμε στοχαστικά, δηλαδή βασισμένοι σε ένα σύνολο καλώς ορισμένων πιθανοτήτων[19]. Η ιδιότητα της ανεξαρτησίας του μέλλοντος από το παρελθόν για τα συστήματα Markov μπορεί να εκφραστεί μαθηματικά ως: P(X N = Α i,ν X N 1 = Α i,ν 1,, X 1 = Α i,1 ) = P(X N = Α i,ν X N 1 = Α i,ν 1 ) (6.1) Κατά μία Μαρκοβιανή διασικασία η πιθανότητα η διαδικασία να μεταπηδήσει από την κατάσταση i στην κατάσταση j δεν εξαρτάται από τον αριθμό καταστάσεων από τις οποίες πέρασε μέχρι να φτάσει στην τελική κατάσταση. Η ιδιότητα αυτή ονομάζεται ιδιότητα της αμνησίας και μας επιτρέπει να καθορίσουμε μία πιθανότητα μετάβασης από την κατάσταση i στην κατάσταση j που συμβολίζουμε με P(i, j). Ως ένα απλό παράδειγμα για μελετήσουμε τις μαρκοβιανές διαδικασίες επιλέγουμε την αλυσίδα κατά Markov του σχήματος: Οι πιθανότητες να βρισκόμαστε στην κατάσταση P1 ή στην κατάσταση P2 ανάλογα με τις συνθήκες μπορεί να αναπαρασταθεί μέσω της μήτρας διέλευσης: P = ( P(P 1, P 1 ) P(P 1, P 2 ) 0.2 ) = (0.8 P(P 2, P 1 ) P(P 2, P 2 ) ) (6.2) Ο πίνακας P απεικονίζει το μοντέλο κατά το οποίο μία κατάσταση P1 έχει πιθανότητα 0.8 να ακολουθηθεί από μια κατάσταση P1 και 0.2 πιθανότητα να μεταβεί στην κατάσταση P2. Από την άλλη βρισκόμενοι στην κατάσταση P2 υπάρχει μία πιθανότητα 0.6 να μεταβούμε σε μια κατάσταση P2 ενώ υπάρχει πιθανότητα 0.4 να μεταβούμε στην κατάσταση P1. Αν ένα στοιχείο του πίνακα διέλευσης είναι μηδέν αυτό σημαίνει πως δεν είναι δυνατή η μετάβαση από την συγκεκριμένη κατάσταση στην άλλη. Αφού η 89
90 μήτρα διέλευσης είναι στοχαστική, μία ιδιότητα που είναι απαραίτητο να εξασφαλίζεται στις αλυσίδες κατά Markov είναι: Προβλέποντας το Μέλλον [15] m P(P i, P j ) = 1 (6.3) j=1 Γνωρίζουμε πως η αρχική κατάσταση του μαρκοβιανού συστήματος είναι η P1. H κατάσταση αυτή μπορεί να απεικονιστεί από ένα διάνυσμα στο οποίο η πρώτη στήλη είναι η αρχική πιθανότητα για την κατάσταση P1 και η δεύτερη η αρχική πιθανότητα για την κατάσταση P2. Έτσι ορίζεται το διάνυσμα αρχικής κατάστασης: x (0) = [1 0] Στην επόμενη κατάσταση της αλυσίδας Markov το διάνυσμα κατάστασης γίνεται: x (1) = x (0) P = (1 0) ( ) = ( ) Συνεπώς, στην επόμενη κατάσταση η οποία θα μπορούσε να είναι σε χρονικό διάστημα για παράδειγμα 1 sec, 1min ή ακόμα και μίας ημέρας ή ενός χρόνου υπάρχει πιθανότητα 80% να βρισκόμαστε στην κατάσταση P1 και πιθανότητα 20% να βρισκόμαστε στην κατάσταση P2. Στην αμέσως επόμενη κατάσταση έχουμε: x (2) = x (1) P = x (0) P = (1 0) ( )2 = ( ) Υπάρχει δηλαδή πιθανότητα 72% να βρισκόμαστε στην κατάσταση P1 και πιθανότητα 28% να βρισκόμαστε στην κατάσταση P2. Αξίζει να παρατηρήσουμε πως οι μελλοντικές τιμές εξάγονται με την ιδιότητα της αμνησίας δηλαδή το μόνο που μας ενδιαφέρει για τον υπολογισμό τους είναι η αμέσως προηγούμενη κατάσταση. Φυσικά, μπορούμε να πούμε πως η πρόβλεψη του μέλλοντος συνδέεται έμμεσα με το παρελθόν αφού μπορούμε να υπολογίσουμε το αποτέλεσμα μέσω της αρχικής τιμής, αλλά αυτό 90
91 συμβαίνει μόνο επειδή το παρόν υπολογίζεται μέσω του παρελθόντος. Συνεπώς, όλη η πληροφορία για τις προβλέψεις μας βρίσκεται στο παρόν. Οι έξοδοι ενός συστήματος Markov μπορεί να είναι διαφορετικές από τις καταστάσεις του. Για τον λόγο αυτό ορίζεται ένας πίνακας εξόδων b ο οποίος εκφράζει την πιθανότητα να έχουμε την συγκεκριμένη έξοδο δεδομένου πως το σύστημα βρίσκεται σε μία συγκεκριμένη κατάσταση. Αν οι έξοδοι μιας Μαρκοβιανής αλυσίδας ταυτίζονται με τις καταστάσεις της τότε ο πίνακας εξόδων είναι ο μοναδιαίος πίνακας. Στοχαστικός Δυναμικός Προγραμματισμός & Ενεργειακή Διαχείριση [19] Ο Στοχαστικός Δυναμικός Προγραμματισμός που αναπτύσσεται στην [47] έχει βρει εφαρμογή σε αρκετές περιπτώσεις σε υβριδικά ηλεκτρικά οχήματα όπως γίνεται φανερό από την βιβλιογραφία όπως φαίνεται στις [7],[56],[57]. Η διαδικασία που πρέπει να ακολουθηθεί για την υλοποίηση μιας στρατηγικής ενεργειακής διαχείρισης υβριδικού ηλεκτρικού οχήματος βασισμένη στην μέθοδο του Στοχαστικού Δυναμικού Προγραμματισμού περιγράφεται στην [19] και περιλαμβάνει τα παρακάτω έξι βασικά βήματα: I. Συλλογή δεδομένων ταχύτητας και απαιτούμενης οδηγητικής ισχύος για έναν αριθμό κύκλων οδήγησης. II. Διακριτοποίηση των μεταβλητών κατάστασης και των εισόδων ελέγχου III. Μοντελοποίηση Μαρκοβιανού Συστήματος: Χρήση των δεδομένων ταχύτητας και ισχύος που συγκεντρώθηκαν από τους κύκλους οδήγησης για την κατάστρωση πιθανοτικής κατανομής ( εικόνα 43α ), τέτοιας ώστε να εξάγει με τυχαίο τρόπο κατάλληλη ακολουθία ταχύτητας και ισχύος που να προσεγγίζει τα χαρακτηριστικά του πραγματικού κύκλου. IV. Επίλυση του στοχαστικού δυναμικού προβλήματος σύμφωνα με την πιθανοτική κατανομή για κάθε πιθανό συνδυασμό καταστάσεων και εισόδων ελέγχου και αποθήκευση των αποτελεσμάτων σε έναν χάρτη ο οποίος περιέχει τις βέλτιστες εισόδους ελέγχου ως συνάρτηση των καταστάσεων σύμφωνα με την κατανομή αυτή (εικόνα 43β). 91
92 V. Χρήση του χάρτη για την εξαγωγή της βέλτιστης ακολουθίας εισόδου ελέγχου για τον πραγματικό κύκλο οδήγησης. VI. Εφαρμογή της βέλτιστης ακολουθίας και εξαγωγή αποτελεσμάτων για την οικονομία καυσίμου, τους ρύπους και την απόκριση του οχήματος. Τα βήματα που ακολουθούνται κατά την μέθοδο του Στοχαστικού Δυναμικού Προγραμματισμού συνοψίζονται στο διάγραμμα της εικόνας 44. Εικόνα 44- Διαδικασία Στοχαστικού Δυναμικού Προγραμματισμού [7] Για να υλοποιηθεί η μέθοδος πρέπει πρώτα να οριστούν οι μεταβλητές κατάστασης του συστήματος. Επειδή η απαιτούμενη ισχύς και η ταχύτητα είναι απαιτούμενα μεγέθη για την εξαγωγή του χάρτη, οι μεταβλητές κατάστασης του συστήματος είναι η κατάσταση φόρτισης, η ισχύς του κύκλου και η γωνιακή ταχύτητα στους τροχούς. Φυσικά, αυτό εξαρτάται από το μοντέλο υβριδικού οχήματος που χρησιμοποιούμε καθώς και τον τρόπο κατάστρωσης του αλγορίθμου του στοχαστικού δυναμικού προγραμματισμού. Εδώ θα ακολουθηθεί η ίδια περιγραφή του αλγορίθμου με την [19] δηλαδή αυτή βασισμένη στις [56], [7] για την βασική μοντελοποίηση του οχήματος και στην [47] για την μορφή του αλγορίθμου του στοχαστικού δυναμικού προγραμματισμού. Έτσι, το δυναμικό μας σύστημα περιγράφεται από τις καταστατικές εξισώσεις: 92
93 SOC(k + 1) = f(soc(k), u(k)) { ω wh (k + 1) = ω wh (k) + α (u(k), P T (k)) Δt (6.4) P T (k + 1) = r(p T (k), ω wh (k)) Όπου α η γωνιακή επιτάχυνση στους τροχούς και r μία στοχαστική συνάρτηση που περιγράφει την κατανομή του χάρτη της εικόνας 43a. Συνεπώς, το σύστημά μας εκτός της βασικής καταστατικής εξίσωσης της κατάστασης φόρτισης χρειάζεται και κάποιες στοχαστικές συμπληρωματικές εξισώσεις. Έτσι, η απαιτούμενη οδηγητική ισχύς P T υπολογίζεται από μία στοχαστική συνάρτηση r που βάσει της κατανομής της εικόνας 43a που χρησιμοποιεί την προηγούμενη τιμή ισχύος και ταχύτητας στους τροχούς. Η απαιτούμενη ισχύς και η στρατηγική ελέγχου θα καθορίσει τις επόμενες τιμές της ταχύτητας στους τροχούς. Συνεπώς, οι συμπληρωματικές εξισώσεις είναι βαθιά συζευγμένες καθώς ο υπολογισμός της μίας εξίσωσης εξαρτάται από τον υπολογισμό της άλλης. Είναι προφανές πως οι τρείς καταστάσεις παίρνουν τιμές σε ένα σύνολο πεπερασμένων και φραγμένων διακριτών τιμών. Η ισχύς του κύκλου οδήγησης δεν είναι εκ των προτέρων γνωστή συνεπώς πρέπει να καταστρωθεί μία στοχαστική διαδικασία δημιουργίας του κύκλου οδήγησης βασιζόμενοι στους χάρτες. Η τιμή της ισχύος υπολογίζεται από το σύστημα (6.4). Όπως και στις προηγούμενες μεθόδους η συνάρτηση κόστους προκύπτει ως το άθροισμα από τα στιγμιαία κόστη σε κάθε χρονικό βήμα. Ωστόσο, υπάρχει μια πολύ μεγάλη διαφορά σε σχέση με την μέθοδο του Δυναμικού Προγραμματισμού. Στην περίπτωση του Δυναμικού Προγραμματισμού ο ορίζοντας βελτιστοποίησης είναι γνωστός και καλώς ορισμένος αφού γνωρίζουμε όλο τον κύκλο οδήγησης. Στην περίπτωση,όμως, του Στοχαστικού Δυναμικού Προγραμματισμού ο κύκλος οδήγησης είναι άγνωστος και γίνεται εκτίμησή του μέσω της στοχαστικής σχέσης στην (6.4). Αυτό σημαίνει ότι ο ορίζοντας δεν είναι καλώς ορισμένος όπως στον Δυναμικό Προγραμματισμό. Για τον λόγο αυτό είμαστε αναγκασμένοι να θεωρήσουμε ένα πρόβλημα βελτιστοποίησης απείρου ορίζοντα στο οποίο πρέπει να βρούμε την βέλτιστη λύση u = u opt (x) που να ελαχιστοποιεί το κριτήριο: n 1 J(x 0 ) = lim E { γ k Κ(x(i), u(x(i))) } (6.5) n i=0 93
94 Όπου E{ } ο τελεστής αναμενόμενης τιμής, n ο συνολικός αριθμός των βημάτων Κ το στιγμιαίο κόστος για κάθε βήμα και γ ενας συντελεστής που παίρνει τιμές 0 < γ < 1 και χρησιμοποιείται για να εξασφαλίσει πως το κριτήριο κόστους θα οδηγηθεί κάποτε σε σύγκλιση. Στην ουσία αυτό που κάνει είναι να μειώνει με την πάροδο των βημάτων την ισχύ του στιγμιαίου κόστους πάνω στο συνολικό κόστος έτσι ώστε το κριτήριο να οδηγηθεί τελικά σε έναν σταθερό αριθμό που μπορεί να χρησιμοποιηθεί για να βρεθεί το ελάχιστο κόστος από όλες της πιθανές τιμές. Η αρχική τιμή της κατάστασης από την οποία θα αρχίσει το σύστημα παίζει πολύ σημαντικό ρόλο στην χρονική εξέλιξη του συνολικού κόστους. Για τον λόγο αυτό εκφράζουμε το συνολικό κόστος ως συνάρτηση της αρχικής κατάστασης. Το πρόβλημα του στοχαστικού δυναμικού προγραμματισμού πρέπει να λυθεί για ολόκληρο το σύνολο των διακριτών καταστάσεων: x ι = {x 1, x 2,, x nsoc n Pd n ωr } (6.6) Για την επίλυση του Στοχαστικού Δυναμικού Προγραμματισμού χρησιμοποιείται ένας επαναληπτικός αλγόριθμος. Ο αλγόριθμος αυτός περιγράφεται από τα εξής βήματα: 1. Υπολογισμός του κόστους J για στρατηγική ελέγχου u, δοθείσας μιας σταθερής αρχικής τιμής της κατάστασης x i. To συνολικό κόστος δίνεται από τον τελευταίο όρο του επαναληπτικού αλγορίθμου: J 1 (x i ) = K(x i, u(x i )) + J 0 (x i ) (6.7) J 2 (x i ) = K(x i, u(x i )) + E{γJ 1 (x i )} (6.8)... J n (x i ) = K(x i, u(x i )) + E{ γj n 1 (x )} (6.9) Όπου x η στοχαστική τιμή του x με την εφαρμογή της στρατηγικής u: x = f(x i, u(x i ), r) (6.10) 94
95 H διαδικασία επαναλαμβάνεται έως ότου J n (x i )-J n 1 (x ) <ε όπου ε μια μικρή ποσότητα. Λόγω του γ μέσα στον επαναληπτικό αλγόριθμο οι χαμηλότερης τιμής όροι μπορούν να αγνοηθούν και έτσι το αποτέλεσμα να υπολογιστεί πιο γρήγορα. 2. Εύρεση βελτιωμένης στρατηγικής Μετά την εύρεση του συνολικού κόστους της στρατηγικής u, η βελτίωση της στρατηγικής προκύπτει από την εξίσωση: u = arg min u U {K(x i, u)} + E{ γj(x )}(6.11) 3. Επανάληψη του βήματος (1) για την βελτιωμένη στρατηγική ελέγχου. 4. Επανάληψη των βημάτων (1)-(3) μέχρι η βελτίωση να αμελητέα Για να καταλάβουμε αν η βελτίωση είναι αμελητέα ή όχι ελέγχουμε αν η βελτίωση βρίσκεται μέσα σε ένα προκαθορισμένο διάστημα ανοχής. Αν κάτι τέτοιο ισχύει η βελτίωση από εκεί και πέρα θεωρείται αμελητέα και ο αλγόριθμος σταματά καθώς βρέθηκε η βέλτιστη στρατηγική. 6.2 Στρατηγική Ελάχιστης Ισοδύναμης Κατανάλωσης Καυσίμου (ECMS) [61],[24] H στρατηγική ελάχιστης ισοδύναμης κατανάλωσης καυσίμου παγκόσμια γνωστή και ως ECMS (Equivalent Consumption Minimization Strategy) εισάχθηκε για πρώτη φορά στις [59], [60] και εμπλουτίστηκε με τον χρόνο από άλλες έρευνες όπως η [62]. Είναι μία μέθοδος που μας δίνει την δυνατότητα το πρόβλημα ενεργειακής διαχείρισης να λυθεί ως ένα πρόβλημα στιγμιαίας βελτιστοποίησης που δεν απαιτεί πληροφορία για το μέλλον της διαδρομής. Πριν προχωρήσουμε πρέπει να τονιστεί ότι υπάρχουν πολλοί διαφορετικοί τρόποι να περιγραφεί μαθηματικά η ECMS. Στην συνέχεια του κεφαλαίου ακολουθείται η μέθοδος και οι μαθηματικές εξισώσεις που περιγράφονται στην [61] καθώς η μέθοδος αυτή περιγράφει με σαφήνεια την ουσιαστική συνεισφορά της στρατηγικής αυτής. Ωστόσο, όλες οι μέθοδοι είναι βασισμένες σε μια παρόμοια 95
96 μαθηματική φιλοσοφία. Η ανάλυση της πορείας σκέψης της [61] αναλύεται σε στάδια που εξηγούν αυτή την πορεία σκέψης και συμβάλλουν στην καλύτερη κατανόηση της μεθόδου. Πρόκειται για μια στρατηγική συγγενική με την Αρχή Ελαχίστων του Pontryagin καθώς και με την απλοποιημένη μέθοδο που αναπτύχθηκε στην συνέχεια. Η βάση της στρατηγικής αυτής στηρίζεται στην σκέψη πως στα υβριδικά ηλεκτρικά οχήματα που δεν είναι plug-in πρέπει η αρχική τιμή της κατάστασης φόρτισης να είναι ίδια με την τιμή της στο τέλος του κύκλου οδήγησης. Αυτό σημαίνει πως αν αντιμετωπίσουμε ολιστικά την συμπεριφορά της μπαταρίας κατά την διάρκεια του κύκλου οδήγησης μπορούμε να πούμε ότι δρα συνολικά σαν μονάδα αποθήκευσης σχεδόν της ίδιας ενέργειας. Αυτήν όμως την ενέργεια από κάπου πρέπει να την λάβει έτσι ώστε να οδηγηθούμε σε λύση βιώσιμη από πλευράς φορτίου. Η πηγή ενέργειας που δίνει στην μπαταρία την δυνατότητα αυτή είναι η ενέργεια καυσίμου. Μπορούμε συνεπώς να πούμε πως η μπαταρία λειτουργεί ως μια συσκευή που δέχεται και αποθηκεύει ενέργεια καυσίμου αντί να δίνει. Δηλαδή η ενέργεια που δίνεται για την πρόωση του οχήματος μέσω αποφόρτισης της μπαταρίας πρέπει μέχρι το τέλος του κύκλου οδήγησης να έχει προσφερθεί πίσω στην μπαταρία για να διατηρηθεί το φορτίο. Συνεπώς, κατά την διάρκεια του κύκλου οδήγησης θα υπάρχουν φάσεις που η μπαταρία αποφορτίζεται έτσι ώστε ο ηλεκτροκινητήρας να δράσει βοηθητικά της μηχανής στην πρόωση του οχήματος που οδηγούν σε εξοικονόμηση καυσίμου και υπάρχουν και φάσεις επαναφόρτισης της μπαταρίας που απαιτούν μηχανική ισχύ από την μηχανή και συνεπώς παραπάνω κατανάλωση καυσίμου. Δεδομένης της άμεσης σχέσης μεταξύ της ισχύος καυσίμου και της ηλεκτρικής ισχύος που αποθηκεύεται στην μπαταρία μπορούμε να επινοήσουμε έναν συντελεστή ο οποίος να μεταφράζει την ηλεκτρική ενέργεια σε ισοδύναμη ενέργεια καυσίμου ανάλογα με την περίσταση. O συντελεστής αυτός είναι ο γνωστός συντελεστής ισοδυναμίας s που συναντήσαμε και στην 2 η και 3 η μέθοδο. Στην ουσία η 3 η μέθοδος που υλοποιήσαμε μπορεί να θεωρηθεί ως μία στρατηγική ισοδύναμης κατανάλωσης καυσίμου για ένα απλοποιημένο μοντέλο και για σταθερό συντελεστή ισοδυναμίας. Εδώ η σκέψη αυτή γενικεύεται και παρουσιάζεται στην πλήρη μορφή της. Ο πυρήνας της στρατηγικής ισοδύναμης κατανάλωσης είναι να βρεθεί μία ορθή τιμή του συντελεστή ισοδυναμίας η οποία μπορεί να είναι είτε σταθερή ή να μεταβάλλεται ανάλογα με τις οδηγητικές συνθήκες. Στην ουσία η τιμή αυτή περιγράφει κατά πόσο 96
97 είναι αποδοτική η μηχανή και κατά πόσο είναι αποδοτική η μπαταρία υπό διαφορετικές συνθήκες και η επιλογή της επηρεάζει τόσο την βιωσιμότητα από πλευράς φορτίου όσο και την απόδοση του οχήματος. Πολλές φορές στον συντελεστή ισοδυναμίας εισάγουμε μία συνάρτηση τιμωρίας που δρα διορθωτικά στην κατάσταση φόρτισης και βοηθά στην βιωσιμότητα φορτίου. Στην [24] (στην οποία βασίζεται η ανάλυση της [61]) υλοποιείται μια τέτοια στρατηγική έτσι ώστε να γίνει η μετάβαση από την Αρχή Ελαχίστων του Pontryagin στην ECMS και από έναν συντελεστή ισοδυναμίας που είτε είναι ακαθόριστος, είτε απαιτεί όλο τον κύκλο οδήγησης, σε έναν συντελεστή ισοδυναμίας που διορθώνεται και προσαρμόζεται ανάλογα με την κατάσταση φόρτισης. Για να μεταβούμε από την Αρχή Ελαχίστων του Pontryagin στην ECMS αρχικά ορίζουμε το κριτήριο: J = 0 t f [ LHV m f(u(t), t) + w ( x ref(t) x(t) ) Δx q ] dt (6.12) Ο όρος w εισάγεται ως ένας συντελεστής βάρους για να ελέγχουμε πόσο επιδρά η απόκλιση της κατάστασης φόρτισης στην συνάρτηση κόστους. Το μέγεθος Δx κανονικοποιεί την απόκλιση της κατάστασης φόρτισης ενώ ο εκθέτης q εκφράζει την τάξη της συνάρτησης τιμωρίας. Η τιμή του q προτείνεται να είναι άρτια έτσι ώστε το πρόσημο της διαφοράς x ref (t) x(t) να είναι πάντα θετικό ή μηδέν. Αν ήταν περιττή το πρόσημο της απόκλισης θα άλλαζε κατά την διάρκεια του κύκλου οδήγησης γεγονός που θα προκαλούσε προβλήματα στην συνάρτηση κόστους. Η Χαμιλτονιανή συνάρτηση που προκύπτει από την νέα συνάρτηση κόστους είναι: H 2 (x(t), u(t), λ(t), t) = LHV m f(u(t), t) + w (x ref (t) x(t)) q λ(t) I batt(x(t), u(t), t) Q 0 (6.13) Ο βέλτιστος νόμος ελέγχου u* είναι όπως γνωρίζουμε από την θεωρία βέλτιστου ελέγχου η είσοδος εκείνη που ελαχιστοποιεί την Χαμιλτονιανή Συνάρτηση δηλαδή: u opt = min u H(x opt, u, λ opt ), (6.14) 97
98 Αν γνωρίζαμε την βέλτιστη συνάρτηση J opt (x(t), t) που αντιστοιχεί στο συναρτησιοειδές J θα μπορούσαμε να υπολογίσουμε την βέλτιστη συμπληρωματική κατάσταση μέσω του τύπου: λ opt (x, t) = J opt(x(t), t) x, (6.15) Όμως, αφού δεν έχουμε καμία πληροφορία για τις μελλοντικές συνθήκες οδήγησης δεν μπορούμε να υπολογίσουμε την συνάρτηση J opt (x(t), t). Το βασικό μας πρόβλημα στην αδυναμία υπολογισμού της συνάρτησης αυτής είναι η ιδιότητά της να μεταβάλλεται στον χρόνο. Μία λύση,συνεπώς, θα ήταν να εκτιμήσουμε μία συνάρτηση J s (x(t)) αντί για την J opt (x(t), t). Προφανώς, η συνάρτηση αυτή είναι υποβέλτιστη αλλά στην παρούσα φάση αυτό που κυρίως μας ενδιαφέρει είναι να βρούμε μια λύση εφαρμόσιμη και αρκετά κοντά στην βέλτιστη. Η συνάρτηση J s (x(t)) θα πρέπει να λαμβάνει υπόψιν της τόσο την ενέργεια καυσίμου όσο και την τιμωρία σε περίπτωση απόκλισης από την κατάσταση φόρτισης. Συνεπώς, η υποβέλτιστη συνάρτηση κόστους υπολογίζεται από τον παρακάτω τύπο : J s (x(t)) = J fuel (x(t)) + J batt (x(t)), (6.16) Για λόγους ευκολότερου υπολογισμού στην συνέχεια χωρίζουμε την συνάρτηση κόστους καυσίμου J fuel (x(t)) σε δύο μέρη: I) Την συνάρτηση κόστους καυσίμου που καταναλώνεται στους τροχούς J fuel,1.η συνάρτηση αυτή δεν εξαρτάται από την κατάσταση φόρτισης της μπαταρίας. II) Την συνάρτηση κόστους καυσίμου που καταναλώνεται για την φόρτιση της μπαταρίας J fuel,2 (x(t)) Έτσι, η συνάρτηση κόστους καυσίμου γίνεται : J fuel (x(t)) = J fuel,1 + J fuel,2 (x(t)), (6.17) και η συνολική συνάρτηση κόστους παίρνει την μορφή: 98
99 J s (x(t)) = J fuel,1 + J fuel,2 (x(t)) + J batt (x(t)) (6.18) Στόχος μας είναι να υπολογίσουμε την βέλτιστη τροχιά της συμπληρωματικής κατάστασης μέσω του νέου τύπου που βασίζεται στην υποβέλτιστη χρονικώς αμετάβλητη συνάρτηση κόστους μέσω του παρακάτω τύπου : λ s (x, t) = J s(x(t)) x (6.19) Άρα αφού σκοπός μας είναι ο υπολογισμός της παραγώγου και η συνάρτηση J fuel,1 είναι ανεξάρτητη του x δεν είναι απαραίτητο να υπολογίσουμε την J fuel,1 στη συνέχεια. Η ενέργεια που αποθηκεύεται στην μπαταρία σε κατάσταση φόρτισης x(t) και με τιμή αναφοράς x ref (t) υπολογίζεται από τον παρακάτω τύπο: x ref E batt = Q 0 V OC (x(t))dx x(t) (6.20) H ενέργεια αυτή είναι η ενέργεια που πρέπει να προσφερθεί από την μηχανή εσωτερικής καύσης στην μπαταρία προκειμένου να μηδενιστεί η απόκλιση της τρέχουσας κατάστασης φόρτισης με την τιμή αναφοράς. Συνεπώς, η ενέργεια καυσίμου που πρέπει να καταναλωθεί για να ικανοποιήσει την ενέργεια της μπαταρίας εξαρτάται από της απόδοση της μηχανής. Ο συντελεστής απόδοσης της μηχανής δίνεται από τον τύπο: η ICE = E batt E ICE (6.21) H ενέργεια που καταναλώνεται από την μηχανή εσωτερικής καύσης για την φόρτιση της μπαταρίας είναι η αντικειμενική συνάρτηση καυσίμου J fuel,2 (ξ(t)). Συνεπώς: η ICE = E batt J fuel,2 (6.22) και λύνοντας ως προς την ενέργεια καυσίμου: 99
100 x ref J fuel,2 (x) = E batt = Q 0 V η ICE η OC (x(t))dx ICE x(t) (6.23) O έλεγχος της SOC θέλουμε να είναι τέτοιος ώστε η x(t)να φτάνει στην x ref μέσα σε έναν προκαθορισμένο χρόνο Τ. Αυτό σημαίνει πως κάθε επόμενη κατάσταση x next (t) θα πρέπει να διορθώνει τόσο την x(t) κάθε χρονική στιγμή τ ώστε μετά από χρόνο T να έχουμε φτάσει στην x ref. Η συνάρτηση κόστους που αντιστοιχεί στην μπαταρία υπολογίζεται: Θεωρούμε : J SOC (x) = wt q + 1 (x ref x(t) Δx Συνεπώς η συνολική συνάρτηση κόστους είναι: q ) J s (x(t)) = J fuel,1 + J fuel,2 (x(t)) + J batt (x(t)) (6.24) = J fuel,1 + Q x ref 0 V η OC (ξ(t)) dx + wt ICE q + 1 (x ref x(t) Δξ x(t) Η συμπληρωματική κατάσταση υπολογίζεται από τον τύπο: λ s (x, t) = J s(x(t)) x = Q 0V OC (x) η c qtw (1 + q) k qtw (6.27) (1 + q)δxq Έτσι η συμπληρωματική κατάσταση παίρνει την μορφή: (x ref x(t)) q 1 λ s (ξ, t) = Q 0V OC (x) η c k (x ref x(t)) q 1 (6.28) q ) Δx q (6.26) (6.25) Άρα, ο συντελεστής συμπληρωματικής κατάστασης και συνεπώς και ο συντελεστής ισοδυναμίας μπορούν πλέον να ελέγχονται ανάλογα με την τιμή της κατάστασης φόρτισης. 100
101 Έχει αποδειχτεί πως μπορούμε να πετύχουμε αποτελέσματα αρκετά κοντά στον Δυναμικό Προγραμματισμό με χρήση δύο διαφορετικών σταθερών συντελεστών ισοδυναμίας έναν για την φόρτιση και έναν για την αποφόρτιση. [20] Oι συντελεστές αυτοί είναι διαφορετικοί για κάθε κύκλο οδήγησης και απαιτούν βελτιστοποίηση που μπορεί να γίνει μόνο αν ο κύκλος είναι εκ των προτέρων γνωστός. Δηλαδή η στρατηγική θα δουλέψει σωστά για κύκλους μόνο αρκετά κοντά στον κύκλο για τον οποίο έγινε η βελτιστοποίηση. Δηλαδή μια ECMS στρατηγική αυτής της μορφής ακόμα βασίζεται σε πληροφορία από το μέλλον της διαδρομής καθιστώντας την ως μία στρατηγική μεταξύ αιτιατότητας και μη αιτιατότητας. Υπό την απόπειρα να καλύψουμε την απαιτούμενη γνώση κάποιων μελλοντικών οδηγητικών συνθηκών στην ECMS προσπαθούμε να υλοποιήσουμε μια στρατηγική που να παίρνει την πληροφορία της μελλοντικής διαδρομής και να την χρησιμοποιεί για να προσαρμόσει ανάλογα τον συντελεστή ισοδυναμίας. 6.3 Προσαρμοζόμενη Στρατηγική Ελάχιστης Ισοδύναμης Κατανάλωσης (A-ECMS) H στρατηγική A-ECMS είναι μία εξέλιξη της ECMS έτσι ώστε οι συντελεστές ισοδύναμης κατανάλωσης να υπολογίζονται online με χρήση πληροφοριών του κύκλου όπως για παράδειγμα μέσω GPS. Παραδείγματα τέτοιων υλοποιήσεων μπορούν να βρεθούν στις [63] και [64]. Τα βασικά στοιχεία στρατηγικών τέτοιου τύπου εξηγούνται στην [19]. Βάσει αυτής, οι συντελεστές φόρτισης και αποφόρτισης υπολογίζονται επαναλαμβάνοντας την διαδικασία βελτιστοποίησης κάθε λίγα λεπτά πάνω σε ένα απλοποιημένο μοντέλο του οχήματος που υπάρχει μέσα στον ελεγκτή. Επίσης, η απλοποίηση είναι απαραίτητη γιατί αλλιώς ακόμα και για ορίζοντα λίγων λεπτών οι υπολογιστικές και χρονικές απαιτήσεις θα ήταν μη πραγματοποιήσιμες για real-time εφαρμογές. Η προσαρμοζόμενη στρατηγική δεν δίνει πολλές φορές φορές τόσο καλά αποτελέσματα όπως η κλασική ECMS για έναν καθορισμένο κύκλο οδήγησης.[19] Ωστόσο, τα αποτελέσματά της είναι ιδιαίτερα ικανοποιητικά και μπορεί να χρησιμοποιηθεί και σε κύκλους οδήγησης που αποκλίνουν αισθητά από τον καθορισμένο. 101
102 Εικόνα 45-Στρατηγική Ενεργειακής Διαχείρισης A-ECMS [62] Ωστόσο, η προσαρμοζόμενη στρατηγική εμφανίζει πολλές φορές προβλήματα σε online εφαρμογές λόγω του περιορισμένου ορίζοντα για τον οποίο μπορεί να γίνει η βελτιστοποίηση, του θορύβου ή λόγω λανθασμένων πληροφοριών από το σύστημα GPS. Στην παρούσα εργασία αναπτύσσεται και διερευνάται η λειτουργία ενός ελεγκτή που βασίζεται στην ελαχιστοποίηση της συνολικής ισχύος ενός απλοποιημένου μοντέλου. Ο βέλτιστος έλεγχος του απλοποιημένου μοντέλου μπορεί να χρησιμοποιηθεί αυτούσιος ως σύστημα ενεργειακής διαχείρισης ενός πραγματικού οχήματος, καθώς πρόκειται στην ουσία για μία ECMS στρατηγική βασισμένη σε ένα απλοποιημένο μοντέλο για γρηγορότερη απόκριση. Το απλοποιημένο μοντέλο μπορεί επίσης να ενσωματωθεί σε στρατηγικές, όπως η A-ECMS ή κάποιος προβλεπτικός έλεγχος (MPC) για πιο ακριβείς και γρηγορότερους υπολογισμούς καθώς και για αύξηση του ορίζοντα βελτιστοποίησής τους. 7. Απλοποιημένη Μέθοδος για Ενεργειακή Διαχείριση[4] 7.1 Απλοποιημένο Μοντέλο Υβριδικού Οχήματος [4],[25] Στην ενότητα αυτή αναλύεται και υλοποιείται ένας βέλτιστος ελεγκτής βασισμένος σε ένα απλοποιημένο μοντέλο υβριδικού οχήματος παράλληλης τοπολογίας που είχε αρχικά αναπτυχθεί στις [4] και [25] και η ελκυστικότητά του οφείλεται στο γεγονός ότι, 102
103 λόγω της απλότητάς του, θα μπορούσε, υπό προϋποθέσεις, να εφαρμοστεί σε πραγματικό χρόνο ακόμα και σε περιπτώσεις που οι προηγούμενες στρατηγικές αποτυγχάνουν, εξαιτίας της σύνθετης δομής τους. Πριν την υλοποίησή του και για την σε βάθος κατανόηση του υπό μελέτη ελεγκτή κρίθηκε σημαντική η ενδελεχής ανάλυση της πορείας σκέψης από μαθηματική σκοπιά και της ανάλυσης των εξισώσεων και της εξαγωγής του βέλτιστου ελεγκτή που περιγράφονται στην [4] καθώς μέσα από τα βήματα αυτά αποκαλύπτονται σημαντικές θεμελιώδεις πτυχές της ενεργειακής διαχείρισης και των σχέσεων που συνδέουν μαθηματικά τα επιμέρους υποσυστήματα. Οι εξισώσεις αυτές της [4] αναλύονται στο παρόν κεφάλαιο και τις ενότητές του. Στη συνέχεια, η μέθοδος εφαρμόστηκε για 4 βασικούς κύκλους οδήγησης για να μελετήσουμε την συμπεριφορά της και εξάχθηκε η οικονομία καυσίμου για κάθε κύκλο. Η δομή του απλοποιημένου μοντέλου φαίνεται στην εικόνα 46. Το εξαιρετικά ενδιαφέρον είναι ότι η προσέγγιση που ακολουθείται στην παράγραφο αυτή βασίζεται στην ισχύ για την εξαγωγή του βέλτιστου νόμου ελέγχου. Εικόνα 46-Δομή Απλοποιημένου Μοντέλου Η μπαταρία χρησιμοποιεί την αποθηκευμένη χημική ενέργεια έτσι ώστε να κινήσει τον ηλεκτροκινητήρα ο οποίος δρα βοηθητικά στην μηχανή εσωτερικής καύσης. Η απαιτούμενη ισχύς φορτίου P φ (t) όπως έχει περιγραφεί στο κεφάλαιο 1 μπορεί να πάρει και αρνητικές τιμές κατά την διάρκεια του κύκλου οδήγησης. Στην περίπτωση αυτή η ηλεκτρική μηχανή θα λειτουργήσει ως γεννήτρια φορτίζοντας την μπαταρία. Ακόμα, υπάρχει η δυνατότητα φόρτισης της μπαταρίας μέσω της μηχανής εσωτερικής καύσης. Για λόγους απλοποίησης ο συμπλέκτης αντικαθίσταται με έναν απλό διακόπτη Δ. Το σημαντικότερο μέγεθος στην προσέγγιση αυτή είναι η εσωτερική ενέργεια της 103
104 μπαταρίας E batt,int. (t) η οποία πρέπει στο τέλος του κύκλου οδήγησης να είναι ίση με την ενέργεια της μπαταρίας στην αρχή του. Χρησιμοποιήθηκε,δηλαδή, σκληρός περιορισμός (Hard Constraint) για την κατάσταση ενέργειας. Η απαιτούμενη ισχύς P φ (t) ορίζεται από τις συνθήκες και τον κύκλο οδήγησης. Η ικανοποίηση της οδηγητικής ισχύος καλύπτεται από τις δύο πηγές ισχύος του υβριδικού P ΜΕΚ (t) και P ΗΜ (t) έτσι ώστε: P ΜΕΚ (t) + P ΗΜ (t) = P φ (t) (7.1) Η σχέση (7.1) που καλείται και εξίσωση ισορροπίας ισχύος είναι από τις σημαντικότερες εξισώσεις της δυναμικής του υβριδικού οχήματος και πρέπει να ικανοποιείται t T, όπου T είναι το σύνολο των χρονικών στιγμών που ορίζονται από τον εκάστοτε κύκλο οδήγησης. Αδυναμία ικανοποίησης της εξίσωσης (7.1) οδηγεί σε μη κάλυψη των ενεργειακών αναγκών σε περίπτωση που P φ (t) < P ΜΕΚ (t) + P ΗΜ (t) ή P φ (t) > P ΜΕΚ (t) + P ΗΜ (t). Στην πρώτη περίπτωση η ισχύς που παρέχεται από την μηχανή και τον ηλεκτροκινητήρα δεν αρκεί για να ξεπεραστεί η απαιτούμενη οδηγητική ισχύς γεγονός που σε κάποιες περιπτώσεις θα μπορούσε να οδηγήσει σε κίνηση του οχήματος προς τα πίσω στην ανηφόρα ή στην αδυναμία επιτυχούς προσπέρασης στον δρόμο. Στην δεύτερη περίπτωση η ισχύς που παρέχεται από την μηχανή και τον ηλεκτροκινητήρα είναι μεγαλύτερη από την απαιτούμενη, γεγονός που δεν δίνει στον οδηγό τον πλήρη έλεγχο του οχήματος και υποβαθμίζει την οδηγησιμότητα του. Ευτυχώς, οι αποκλίσεις από την εξίσωση (7.1) είναι συνήθως πολύ μικρές κι έτσι δύσκολα γίνονται αντιληπτές σε πραγματικές εφαρμογές. Η τήρηση της σχέσης στην μοντελοποίησή που ακολουθούμε όχι μόνο είναι απαραίτητη για την ορθή λειτουργία του μοντέλου αλλά επίσης μας βοηθά στην εξαγωγή του βέλτιστου νόμου ελέγχου. Η ισχύς καυσίμου της μηχανής δίνεται από την σχέση (7.2). Μέρος της ισχύος καυσίμου (P καυσίμου ) μετατρέπεται σε ισχύ ικανή να ξεπεράσει τις τριβές της μηχανής (P ΜΕΚ,0 ) και η υπόλοιπη σε μηχανική ισχύ που θα περιστρέψει την μηχανή και θα κινήσει τους τροχούς (P ΜΕΚ ). Οι τιμές που μπορεί να πάρει ο συμπλέκτης Δ είναι 1 104
105 και 0 ανάλογα αν η μηχανή παραμένει συζευγμένη ή αποσυζευγμένη από το υπόλοιπο σύστημα μετάδοσης. P Καυσίμου (t) = Δ P ΜΕΚ(t) + P ΜΕΚ,0 η ΜΕΚ (7.2) Η ισχύς της μπαταρίας είναι διαφορετική κατά την φόρτιση και την αποφόρτιση δηλαδή ανάλογα με το αν η ηλεκτρική μηχανή λειτουργεί ως γεννήτρια ή ως κινητήρας. Στην περίπτωση που η ηλεκτρική μηχανή λειτουργεί ως κινητήρας ισχύει: η ΗΜ = P εξ. = P μηχ. = P ΗΜ (7.3) P εισ. P ηλ. P μπατ. Στην περίπτωση που η ηλεκτρική μηχανή λειτουργεί ως γεννήτρια ισχύει: η ΗΜ = P εξ. P εισ. = P ηλ.(t) P μηχ. (t) = P μπατ.(t) P ΗΜ (t) (7.4) Για να κάνουμε πιο εύκολη την περιγραφή του υβριδικού οχήματος περιγράφουμε τις σχέσεις (7.3) και (7.4) ως μία. Θεωρώντας ως θετική την ισχύ που παρέχει η ηλεκτρική μηχανή κατά την λειτουργία της ως κινητήρας και ως αρνητική για την λειτουργία της ως γεννήτρια οι δύο αυτές σχέσεις συμπτύσσονται στην παρακάτω: sign(p η ΗΜ (t)) P ΗΜ (t) ΗΜ = P μπατ. (t) (7.5) Λύνοντας ως προς την ισχύ της μπαταρίας προκύπτει η παρακάτω σχέση: Στο απλοποιημένο ενεργειακό sign(p P μπατ. (t) = η ΗΜ (t)) ΗΜ PΗΜ (t) (7.6) μοντέλο είναι καλύτερο να χρησιμοποιήσουμε ως μεταβλητή κατάστασης ένα μέγεθος που περιγράφει ενέργεια. Το μέγεθος αυτό είναι η εσωτερική ενέργεια της μπαταρίας Ε μπατ,εσωτ. και είναι στενά συνδεδεμένη με την κατάσταση φόρτισης. Προκειμένου να υπερβεί τις απώλειες ενέργειας λόγω της εσωτερικής αντίστασης και να αποδώσει την απαραίτητη εξωτερική ενέργεια, η εσωτερική ενέργεια της μπαταρίας E μπατ,εσωτ. (t) πρέπει να ισούται με την ενέργεια που 105
106 εισάγεται ή εξάγεται από αυτή Ε μπατ. συν τις απώλειες στην αντίσταση Ε απωλ. σύμφωνα με την σχέση (7.7). E μπατ,εσ. (t) = Ε μπατ. (t) Ε απωλ. (t) (7.7) Παραγωγίζοντας την σχέση αυτή ως προς τον χρόνο προκύπτει η εσωτερική ισχύς της μπαταρίας: P μπατ,εσ. (t) = d dt E μπατ,εσ.(t) = P μπατ. (t) P απωλ. (t) (7.8) Οι εξισώσεις (7.1),(7.2), (7.6) και (7.8) περιγράφουν την δυναμική του συστήματος. Οι απώλειες της μπαταρίας υπολογίζονται προσεγγιστικά με χρήση αναπτύγματος Taylor και ο βέλτιστος νόμος ελέγχου εξάγεται με ελαχιστοποίηση μιας Χαμιλτονιανής συνάρτησης που αναπτύσσεται στην [4]. Η μπαταρία αντιμετωπίζεται ως ένα απλό μοντέλο πηγής τάσης και εσωτερικής αντίστασης. Η ισχύς απωλειών βάσει του φαινομένου Joule προκύπτει: 2 P απωλ. = R μπατ I μπατ = R μπατ ( V oc V 2 2 oc 4R μπατ. P μπατ. ) 2R μπατ. = (V oc V oc 2 4R μπατ. P μπατ. ) 2 4R μπατ. (7.9) Συνεπώς, η ισχύς απωλειών μπορεί να περιγραφεί ως συνάρτηση της ισχύος της μπαταρίας P απωλ. = f(p μπατ. ). Η συνάρτηση απωλειών απλοποιείται περαιτέρω με χρήση του θεωρήματος Taylor γύρω από το σημείο ισορροπίας P μπατ. = 0: P απωλ. = f(p μπατ. ) = f(0) + P μπατ. 1! f (0) + P 2 μπατ. 2! f (0) + (7.10) Όταν η μπαταρία δεν παρέχει ή καταναλώνει ισχύ τότε οι απώλειες είναι μηδενικές. Αυτό επιβεβαιώνεται και από τον τύπο (7.10). Έτσι, P απωλ. (0) = f(0) = 0. O ρυθμός με τον οποίο μεταβάλλονται οι απώλειες ισχύος ως προς την ισχύ που καταναλώνει η μπαταρία είναι: 106
107 dp απωλ. = f (P dp μπατ. ) = 2 V oc V 2 oc 4R μπατ. P μπατ. (V μπατ. 4R oc V 2 oc 4R μπατ. P μπατ. ) μπατ. = = 2 V oc V oc 2 4R μπατ. P μπατ. 4R μπατ. 2R μπατ. 1 V oc 2 4R μπατ. P μπατ. = = V oc V oc 2 4R μπατ. P μπατ. V oc 2 4R μπατ. P μπατ. Έτσι, P απωλ. (0) = f (0) = 0 Ομοίως: d 2 P απωλ. = f (P dp2 μπατ. ) = ( V oc V 2 oc 4R μπατ. P μπατ. ) μπατ. V 2 oc 4R μπατ. P μπατ. 2V oc R μπατ. = (V 2 oc 4R μπατ. P μπατ. ) 3 Έτσι η σειρά (Taylor) γίνεται: P απωλ. = f(p μπατ. ) = 0 + P μπατ. 1! 0 + P 2 μπατ. 2! 2V ocr μπατ. + (7.11) (V 2 oc ) 3 Αγνοώντας τους όρους ανωτέρας τάξης καταλήγουμε στην παρακάτω σχέση: Βάσει της σχέσης (7.12) η σχέση (7.8) γίνεται: P απωλ. = f(p μπατ. ) = R μπατ. V oc 2 P μπατ. (7.12) P μπατ,εσ. (t) = d dt E μπατ,εσ.(t) = P μπατ. (t) R μπατ. P V2 μπατ. (t)(7.13) oc Βάσει των (7.1), (7.2), (7.6) η εξίσωση (7.14) παίρνει την τελική μορφή: de μπατ,εσ. dt = η ΗΜ sign(p ΗΜ ) P ΗΜ R μπατ. V oc 2 2sign(P η ΗΜ ) 2 ΗΜ P ΗΜ (7.14) 107
108 7.2 Βέλτιστος Νόμος Ελέγχου και Καταστάσεις Λειτουργίας [4] Ο βέλτιστος νόμος ελέγχου εξάγεται μέσω της ελαχιστοποίησης βελτιστοποίησης: του κριτηρίου t f J = P καυσίμου (t) dt 0 (7.15) Ως είσοδο του συστήματος θεωρούμε την ισχύ του κινητήρα P ΗM ενώ ως κατάσταση του συστήματος θεωρείται η εσωτερική ενέργεια της μπαταρίας. Τέλος, θέλουμε τόσο στην αρχή όσο και στο τέλος του κύκλου οδήγησης η εσωτερική ενέργεια της μπαταρίας να είναι μηδέν (Hard Constraint). Συνεπώς, η αρχική και τελική συνθήκη είναι: E batt,i (0) = E batt,i (t f ) = 0 (7.16) Η δυναμική του συστήματος περιγράφεται από την σχέση (4.15). Έτσι, η Χαμιλτονιανή συνάρτηση του συστήματος παίρνει την μορφή: H = P καυσίμου + λ de μπατ,εσ. dt (7.17) Όπως είναι φανερό, η χαμιλτονιανή εκφράζει την ισοδύναμη ισχύ καυσίμου του υβριδικού οχήματος κάθε χρονική στιγμή. Η ισχύς καυσίμου και η ισχύς της μπαταρίας προστίθενται για να σχηματίσουν μία συνάρτηση συνολικής ισχύος. Ο παράγοντας λ που στην θεωρία βέλτιστου ελέγχου ονομάζεται συντελεστής συμπληρωματικής κατάστασης παίζει τον ρόλο ενός συντελεστή ισοδυναμίας ισχύος. Πρακτικά, επειδή η ισχύς της χαμιλτονιανής αναφέρεται σε ισχύ καυσίμου είναι απαραίτητος ο παράγοντας ισοδυναμίας λ που να μετατρέπει την ηλεκτρική ισχύ της μπαταρίας σε μία ποσότητα ισοδύναμης ισχύος καυσίμου. Από τις σχέσεις (4.1) και (4.2) η ισχύς καυσίμου γίνεται: 108
109 P καυσίμου = Δ P ΜΕΚ,0 + P φ P ΗΜ η ΜΕΚ (7.18) Συνεπώς, η Χαμιλτονιανή του συστήματος παίρνει την μορφή: H = Δ P 0+P T P EM η ICE sign(p + λ ( η M/G ) M/G P EM R batt 2sign(P V2 η EM ) EM P 2 EM ) (7.19) oc Από την [4] και σύμφωνα με την αρχή ελαχίστων του Pontryagin οι συνθήκες που πρέπει να ικανοποιούνται για την βέλτιστη ισχύ ελέγχου P opt EM είναι οι παρακάτω: I. opt de μπατ,εσ. dt opt sign(p = η ΕΜ ) ΕΜ P opt EM R opt batt 2sign(P V2 η ΕΜ ) opt ΕΜ P 2 ΗM (7.20) oc II. III. IV. opt E μπατ,εσ. dλ opt dt opt (0) = E μπατ,εσ (t f ) (7.21) = Eμπατ,ες. H = 0 (7.22) H(P opt ΗM, λ opt, t) H(P ΗM, λ opt, t) (7.23) Στην ουσία το πρόβλημα βέλτιστου ελέγχου με την αρχή ελαχίστων του Pontryagin στο απλοποιημένο μοντέλο έχει ως βασικό στόχο την εύρεση της βέλτιστης ισχύος κινητήρα η οποία συμπληρωματικά με την ισχύ της μηχανής θα οδηγήσει στην ελαχιστοποίηση της Χαμιλτονιανής δηλαδή στην ελαχιστοποίηση της απαραίτητης ισχύος ενώ ταυτόχρονα ικανοποιούνται οι οδηγητικές απαιτήσεις. Από την εξίσωση (7.22) προκύπτει: λ opt = c, όπου c=σταθερά. Στην πραγματικότητα ο παράγοντας ισοδυναμίας είναι συνάρτηση του χρόνου δηλαδή έχουμε συνεχή μεταβολή του κατά την διάρκεια του κύκλου οδήγησης. Το απλοποιημένο μοντέλο μας δίνει την δυνατότητα να προσδιορίσουμε έναν σταθερό συντελεστή ισοδυναμίας καθ όλη τη διάρκεια του κύκλου γεγονός το οποίο είναι ιδιαίτερα βοηθητικό στους υπολογισμούς μας, όμως μπορεί να προκαλέσει προβλήματα σε περίπτωση που η λύση δεν δίνει στρατηγική βιώσιμη από πλευράς φορτίου. Κρίσιμος,συνεπώς, στην υλοποίηση της στρατηγικής αυτής είναι ο προσδιορισμός μιας κατάλληλης τιμής του συντελεστή ισοδυναμίας που να ικανοποιεί την βιωσιμότητα αυτή. 109
110 Για λόγους πρακτικούς αλλάζουμε το πρόσημο στον συντελεστή ισοδυναμίας. Έτσι, ο συντελεστής ισοδυναμίας ορίζεται ως το αντίθετο του συντελεστή συμπληρωματικής κατάστασης σύμφωνα με την σχέση: s = λ opt (7.24) Μπορούμε ακόμα να ορίσουμε τον ακόλουθο συντελεστή χάριν απλότητας: b = R batt V oc 2 (7.25) προκύπτει η τελική Γενική Χαμιλτονιανή συνάρτηση: H = Δ P 0 + P T P EM η ICE + s (η EM sign(p EM ) P EM + R batt V oc 2 2sign(P η EM ) EM P 2 EM ) (7.26) Ανάλογα με την κατάσταση λειτουργίας του Υβριδικού Ηλεκτρικού Οχήματος, η χαμιλτονιανή συνάρτηση μπορεί να αναλυθεί σε μια απλοποιημένη πολύκλαδη συνάρτηση. Για τον λόγο αυτό διακρίνουμε στις παρακάτω περιπτώσεις: 1. Κατάσταση Επαναφόρτισης με λειτουργία της μηχανής εσωτερικής καύσης : P EM 0, P EM < P T Εικόνα 47-διάγραμμα ροής ισχύος για την κατάσταση επαναφόρτισης με λειτουργία της μηχανής εσωτερικής καύσης H ισχύς ελέγχου του ηλεκτροκινητήρα είναι μη θετική και μικρότερη της απαιτούμενης οδηγητικής ισχύος. Στην περίπτωση αυτή sign(p EM ) < 0 και δεδομένου πως η ηλεκτρική μηχανή δεν δύναται να ικανοποιήσει μόνη της το απαιτούμενο φορτίο έχουμε σύμπλεξη της μηχανής για την επαλήθευση της σχέσης (7.1) δηλαδή B=1. Επειδή η ισχύς του ηλεκτροκινητήρα είναι αρνητική η μπαταρία φορτίζεται μέσω μέρους της ισχύος 110
111 της ΜΕΚ. Συνεπώς, βρισκόμαστε στην κατάσταση όπου η ΜΕΚ λειτουργεί κανονικά ενώ η ΗΜ φορτίζει την μπαταρία. H χαμιλτονιανή τότε παίρνει την μορφή: H = H ICEΟΝ +RCHG = Δ P ICE, 0 + P T + (s η η EM 1 ) P ICE η EM + s β η 2 EM P 2 EM )(7.27) ICE Ειδική περίπτωση της (1) είναι η ΗΜ να μην καταναλώνει ούτε να παράγει ισχύ. Σε αυτή την περίπτωση η χαμιλτονιανή εκφυλλίζεται στην μορφή: H = H ICE ON = Δ P ICE, 0 + P T η ICE (7.28) Στην κατάσταση αυτή λειτουργεί μόνο η ΜΕΚ και ονομάζεται αμιγώς θερμική λειτουργία. 2. Κατάσταση Ταυτόχρονης Λειτουργίας Μηχανής Εσωτερικής Καύσης και Ηλεκτροκινητήρα: P EM 0, P EM < P T Εικόνα 48- Διάγραμμα ροής της ισχύος για την ταυτόχρονη λειτουργία μηχανής εσωτερικής καύσης και ηλεκτροκινητήρα H ισχύς ελέγχου του ηλεκτροκινητήρα είναι μη αρνητική και μικρότερη της απαιτούμενης ενέργειας ισχύος. Στην περίπτωση αυτή sign(p EM ) > 0 και όπως και στην περίπτωση (1) δεδομένου πως ο ηλεκτροκινητήρας δεν δύναται να ικανοποιήσει μόνος του το απαιτούμενο φορτίο έχουμε B=1. Επειδή η ισχύς του ηλεκτροκινητήρα είναι θετική αυτό σημαίνει πως χρησιμοποιείται ηλεκτρική ενέργεια από την μπαταρία για την πρόωση του οχήματος. Ταυτόχρονα, η μηχανή εσωτερικής καύσης παρέχει τόση 111
112 ισχύ ώστε να ικανοποιείται η εξίσωση ισορροπίας (4.1). Συνεπώς, βρισκόμαστε στην κατάσταση όπου η μηχανή λειτουργεί κανονικά και ο ηλεκτροκινητήρας συμπληρώνει την ΜΕΚ σε ισχύ πρόωσης. Η χαμιλτονιανή παίρνει την μορφή: H = H ICEΟΝ +EM ON = Δ P ICE, 0 + P T η ICE + ( s 1 s β ) P η EM η EM + ICE η 2 P EM 2 ) (7.29) EM 3. Αμιγώς Ηλεκτρική Λειτουργία: P EM = P T 0 Εικόνα 49-διάγραμμα ροής της ισχύος για την αμιγώς ηλεκτρική λειτουργία H ισχύς ελέγχου του ηλεκτροκινητήρα είναι εκείνη που καλύπτει πλήρως την απαιτούμενη ισχύ οδήγησης. Στην περίπτωση αυτή η ηλεκτρική μηχανή οδηγεί ουσιαστικά το όχημα και η μηχανή εσωτερικής καύσης δεν είναι απαραίτητη, έχουμε δηλαδή αποσύμπλεξη (Β=0). Συνεπώς η Χαμιλτονιανή παίρνει την μορφή: H = H EMON = s s β P η EM + EM η 2 P EM 2 (7.30) EM 4. Κατάσταση επαναφόρτισης χωρίς την λειτουργία της ΜΕΚ :P EM = P T 0 112
113 Εικόνα 50- Διάγραμμα ροής ισχύος για την κατάσταση επαναφόρτισης χωρίς λειτουργία της μηχανής εσωτερικής καύσης Η ισχύς φορτίου παίρνει αρνητικές τιμές το οποίο συνήθως σημαίνει πέδηση. Η ηλεκτρική μηχανή χρησιμοποιεί την ισχύ φορτίου για να επαναφορτίσει την μπαταρία μέσω αναγεννητικής πέδησης. Η μηχανή δεν είναι απαραίτητη σε αυτήν την κατάσταση λειτουργίας συνεπώς B=0. Έτσι η Χαμιλτονιανή παίρνει την μορφή: H = H EMON +RCHG = s η EM P EM + η 2 2 EM s β P EM (7.31) Βάσει των 4 καταστάσεων λειτουργίας που αναπτύχθηκαν καθώς και της υποπερίπτωσης της αμιγώς θερμικής λειτουργίας προκύπτει η πολύκλαδη Χαμιλτονιανή συνάρτηση: H = Δ P ICE, 0 + P T + (s η η EM 1 ) P ICE η EM + s β η 2 EM P 2 EM ), P EM < 0, P EM < P T ICE Δ P ICE, 0 + P T η ICE, P EM = 0, P EM < P T Δ P ICE, 0 + P T + ( s 1 s β ) P η ICE η EM η EM + ICE η 2 P EM, EM P EM > 0, P EM < P T (7.32) s s β P η EM + EM η 2 P EM, EM P EM = P T > 0 { s η EM P EM + η 2 2 EM s β P EM P EM = P T < 0 Η πολύκλαδη χαμιλτονιανή συνάρτηση εξαρτάται από δύο βασικές μεταβλητές : Τον παράγοντα ισοδυναμίας s και την ισχύ του ηλεκτροκινητήρα P EM. Για την εύρεση του ελαχίστου της χαμιλτονιανής είναι απαραίτητη η ανάλυση της μονοτονίας και των τοπικών ακροτάτων των επιμέρους συναρτήσεων. Οι 3 πρώτοι κλάδοι της συνάρτησης 113
114 μπορούν να γραφούν ως 2 καθώς ο δεύτερος κλάδος είναι υποπερίπτωση του κλάδου 1 και του κλάδου 2. Συνεπώς μπορούμε να γράψουμε: H = Δ P ICE, 0 + P T + (s η η EM 1 ) P ICE η EM + s β η 2 EM P EM ), P EM 0, P EM < P T ICE Δ P ICE, 0 + P T + ( s 1 s β ) P η ICE η EM η EM + ICE η 2 P EM, EM P EM 0, P EM < P T (7.33) s s β P η EM + EM η 2 P EM, EM P EM = P T > 0 { s η EM P EM + η 2 2 EM s β P EM P EM = P T < Ανάλυση της Μονοτονίας της Χαμιλτονιανής Συνάρτησης [4] Αφού η εξίσωση ορίζεται στο σημείο P EM = 0, ορίζεται η παράγωγος για τους κλάδους (1) και (2). Παραγωγίζοντας τον πρώτο κλάδο προκύπτει: H ICEΟΝ +RCHG(P EM ) = (H ICE ΟΝ +RCHG) = (sη P EM 1 ) + 2sβη 2 EM η EM P EM (7.34) ICE Ανάλυση της μονοτονίας και των τοπικών ακροτάτων της H ICEΟΝ +RCHG: Θεωρώντας το s ως σταθερά βρίσκουμε για ποια τιμή του P EM προκύπτει τοπικό ελάχιστο της χαμιλτονιανής. H ICEΟΝ +RCHG(P EM ) 0 => (sη EM 1 ) + 2sβη η EM P EM 0 => ICE 1 η sη EM P EM ICE 2 (7.35) 2sβη EM 114
115 Εικόνα 51-Μονοτονία Χαμιλτονιανής για την κατάσταση Επαναφόρτισης με Λειτουργία της Μηχανής Εσωτερικής Καύσης Παραγωγίζοντας τον 2 ο κλάδο προκύπτει: H ICEΟΝ +EM ON (P EM ) = (H ICE ΟΝ +EM ON ) = ( s 1 ) + 2sβ P EM η EM η ICE Ανάλυση της μονοτονίας και των τοπικών ακροτάτων της H ICEΟΝ +EM ON : 2 P η EM EM Θεωρώντας το s ως σταθερά βρίσκουμε για ποια τιμή του P EM προκύπτει τοπικό ελάχιστο της χαμιλτονιανής: H ICEΟΝ +EM ON (P EM ) 0 => ( s 1 ) + 2sβ η EM η 2 P EM 0 => ICE η EM P EM η EM η EM η ICE s 2sβ (7.36) 115
116 Εικόνα 52-Μονοτονία Χαμιλτονιανής για την κατάσταση ταυτόχρονης λειτουργίας Ηλεκτροκινητήρα και Μηχανής Εσωτερικής Καύσης Μπορεί η ανάλυση να φαίνεται απλή,όμως, η εξάρτηση της χαμιλτονιανής από τον συντελεστή ισοδυναμίας s καθιστά την εύρεση ελαχίστου δύσκολη υπόθεση καθώς εξαρτάται από δύο μεταβλητές και τα υποψήφια ελάχιστα προκύπτουν από τις διαφορετικές καταστάσεις λειτουργίας. Εύρεση της Περιοχής του τοπικού ελαχίστου για s < η EM η ICE Για τον λόγο αυτόν είναι απαραίτητο να χωρίσουμε την χαμιλτονιανή σε διαστήματα του συντελεστή ισοδυναμίας s. Στην ουσία δηλαδή κάνουμε μια ανάλυση της δεύτερης μεταβλητής μέσα στην ανάλυση της πρώτης. Στα παρακάτω σχήματα απεικονίζονται οι χαμιλτονιανές συναρτήσεις H ICEΟΝ +EM ON και H ICEΟΝ +RCHG συναρτήσει της ισχύος του κινητήρα και του συντελεστή ισοδυναμίας για s < η EM η ICE στην περιοχή ενδιαφέροντος κοντά στο 0. Οι τιμές του συντελεστή ισοδυναμίας που επιλέχθηκαν είναι ποιοτικές και όχι ποσοτικές δηλαδή δεν περιγράφουν τις ακριβείς τιμές που χρησιμοποιήσαμε στην συνέχεια στους κύκλους οδήγησης. Ωστόσο, η συμπεριφορά των κλάδων της Χαμιλτονιανής είναι ίδια για οποιαδήποτε επιλογή των τιμών αυτών. Για να αναλύσουμε την συμπεριφορά της ισχύος του ηλεκτροκινητήρα στην περιοχή αυτή, επιλέγουμε ο ηλεκτροκινητήρας να παίρνει τιμές στο διάστημα [-350W,350W]. Όπως περιμέναμε, η καμπύλη είναι φθίνουσα και παίρνει την ελάχιστη τιμή της στο σημείο 0 το οποίο ταυτίζεται με την περιοχή αμιγώς θερμικής λειτουργίας. Στο σημείο αυτό πρέπει να τονιστεί πως σκοπός της απεικόνισης αυτής είναι να βρούμε σε ποια από τις δύο περιοχές παρουσιάζεται το ελάχιστο της Χαμιλτονιανής. Συνεπώς, αν η καμπύλη της κατάστασης λειτουργίας φθίνει ακόμα περισσότερο στην κατάσταση λειτουργίας πρόωσης με χρήση και των δύο πηγών, αυτό σημαίνει πως το ελάχιστο βρίσκεται στην περιοχή αυτή αφού γνωρίζουμε ήδη την μονοτονία των δύο συναρτήσεων. 116
117 Εικόνα 53- Απεικόνιση Χαμιλτονιανής H ως συνάρτηση της ισχύος ελέγχου του ηλεκτροκινητήρα P EM και του συντελεστή ισοδυναμίας s στην περιοχή ενδαφέροντος s < η EM η ICE. Υπό σταθερό s η πορεία της χαμιλτονιανής για P EM 0 είναι φθίνουσα. Όπως φαίνεται από το δεύτερο διάγραμμα η καμπύλη συνεχίζει και φθίνει ενώ έχει μπει στην κατάσταση λειτουργίας πρόωσης με χρήση και των δύο πηγών. Συνεπώς, η χαμιλτονιανή ελαχιστοποιείται στην κατάσταση αυτή για την συγκεκριμένη περιοχή του συντελεστή ισοδυναμίας. 117
118 Εικόνα 54-Απεικόνιση Χαμιλτονιανής H ως συνάρτηση της ισχύος ελέγχου του ηλεκτροκινητήρα P EM και του συντελεστή ισοδυναμίας s στην περιοχή ενδαφέροντος s < η EM η ICE. Υπό σταθερό s η πορεία της χαμιλτονιανής έως το σημείο P EM 0 είναι φθίνουσα. Εύρεση της Περιοχής του τοπικού ελαχίστου για η EM η ICE < s < 1 η EM η ICE Στην περίπτωση αυτή η χαμιλτονιανή για την λειτουργία επαναφόρτισης φαίνεται στο διάγραμμα όπου παρατηρείται η φθίνουσα πορεία της. Συνεπώς, αν η χαμιλτονιανή για την περιοχή πρόωσης με δύο πηγές ενέργειας φθίνει τότε γνωρίζουμε πώς το ελάχιστο βρίσκεται εκεί ενώ αν η συνάρτηση είναι αύξουσα δεν μπορούμε να αποφανθούμε χωρίς την ακριβή τοποθεσία του σημείου λειτουργίας στον χώρο ενώ υποψήφια γίνεται η περίπτωση της καθαρά θερμικής λειτουργίας. 118
119 Εικόνα 55-Απεικόνιση Χαμιλτονιανής H ως συνάρτηση της ισχύος ελέγχου του ηλεκτροκινητήρα P EM και του συντελεστή ισοδυναμίας s στην περιοχή ενδαφέροντος η EM 1 < s <. Υπό σταθερό s η πορεία της χαμιλτονιανής έως το σημείο η ICE η EM η ICE P EM 0 είναι φθίνουσα. Η χαμιλτονιανή στην περιοχή ενδαφέροντος η EM η ICE < s < 1 η EM η ICE για λειτουργία επαναφόρτισης φαίνεται στο διάγραμμα. Eίναι ξεκάθαρο πως υπό σταθερό s η μονοτονία έχει αλλάξει και η συνάρτηση είναι πλέον αύξουσα. Έτσι, στο διάστημα αυτό δεν είναι πλέον σαφές ποια λειτουργία δίνει την ελάχιστη χαμιλτονιανή γεγονός που σημαίνει πως η θέση του ελάχιστου σημείου εξαρτάται από εσωτερικούς παράγοντες κυριότεροι από τους οποίους είναι η ισχύς ελέγχου και ο συντελεστής ισοδυναμίας ενώ υποψήφιο ελάχιστο είναι και η καθαρά θερμική λειτουργία. 119
120 Εικόνα 56-Απεικόνιση Χαμιλτονιανής H ως συνάρτηση της ισχύος ελέγχου του ηλεκτροκινητήρα P EM και του συντελεστή ισοδυναμίας s στην περιοχή ενδαφέροντος η EM 1 < s <. Υπό σταθερό s η πορεία της χαμιλτονιανής έως το σημείο η ICE η EM η ICE P EM 0 είναι αύξουσα. Εύρεση της Περιοχής του τοπικού ελαχίστου για s > 1 η EM η ICE Στην περίπτωση αυτή η χαμιλτονιανή της περιοχής επαναφόρτισης με χρήση της μηχανής είναι αύξουσα. Η χαμιλτονιανή για την λειτουργία πρόωσης με χρήση της μηχανής και του ηλεκτροκινητήρα είναι επίσης αύξουσα. Συνεπώς, η συνάρτηση ελαχιστοποιείται στην περιοχή επαναφόρτισης. 120
121 Εικόνα 57-Απεικόνιση Χαμιλτονιανής H ως συνάρτηση της ισχύος ελέγχου του ηλεκτροκινητήρα P EM και του συντελεστή 1 ισοδυναμίας s στην περιοχή ενδαφέροντος s >. Υπό σταθερό s η πορεία της χαμιλτονιανής έως το σημείο P η EM η EM 0 ICE είναι αύξουσα. 121
122 Εικόνα 58-Απεικόνιση Χαμιλτονιανής H ως συνάρτηση της ισχύος ελέγχου του ηλεκτροκινητήρα P EM και του συντελεστή 1 ισοδυναμίας s στην περιοχή ενδαφέροντος s >. Υπό σταθερό s η πορεία της χαμιλτονιανής έως το σημείο P η EM η EM 0 ICE είναι αύξουσα. Ανάλογα με το πρόσημο της ισχύος φορτίου η συμπεριφορά του ελεγκτή πρέπει να είναι διαφορετική. Από τον ορισμό της Χαμιλτονιανής υπάρχει ασυνέχεια στο σημείο Pm=Pt. Συνεπώς, η τιμή αυτή μπορεί να είναι υποψήφιο ελάχιστο. Η κατάστρωση των σχημάτων έγινε για την περίπτωση θετικής P T. Συνεπώς τα συμπεράσματά μας για την χαμιλτονιανή αφορούν την P T >0. Όπως παρατηρήσαμε από τα διαγράμματα 1,2 το ελάχιστο της χαμιλτονιανής στην περίπτωση s < η EM η ICE αποκλείεται να βρίσκεται στην περιοχή λειτουργίας 1. Συνεπώς, οι υποψήφιες χαμιλτονιανές για την περίπτωση αυτή είναι οι H ICEΟΝ +EM ON, H EMON. Από τις χαμιλτονιανές συναρτήσεις H ICEΟΝ +EM ON και H ICE ON+RCHG μπορούμε εύκολα να βρούμε πως το ελάχιστο για την περιοχή η EM η ICE < s < 1 η EM η ICE βρίσκεται στο σημείο Pm=0 δηλαδή στην καθαρά θερμική λειτουργία. Συνεπώς, οι υποψήφιες Χαμιλτονιανές για την περιοχή αυτή είναι οι H ICE ON και H ΕΜΟΝ. Τέλος, στην περίπτωση s > 1 η EM η ICE επιβεβαιώσαμε πως το ελάχιστο δεν θα εμφανιστεί σίγουρα στην δεύτερη περιοχή. Συνεπώς, υποψήφιες Χαμιλτονιανές είναι οι H ICE ON+RCHG και H ΕΜΟΝ. 7.4 Σχεδιασμός Περιοχών Λειτουργίας [4] Τελικά, η ελαχιστοποίηση της Χαμιλτονιανής ως προς την ισχύ ελέγχου του ηλεκτροκινητήρα παίρνει την μορφή: min{h} = P EM { min{h ICEΟΝ +EM ON, H EMON }, min{h ICE ON, H EMON }, η EM η ICE < s < min{h ICE ON+RCHG, H EMON }, s > s < η EM η ICE 1 η EM η ICE 1 η EM η ICE (7.37) Όπως ήδη έχουμε υπολογίσει από την ανάλυση μονοτονίας και τοπικών ακροτάτων στα σημεία όπου ορίζεται η χαμιλτονιανή έχουμε: 122
123 η EM η s min{h ICEΟΝ +EM ON } => P EM = η EM ICE 2sβ 1 η sη EM min{h ICE ON+RCHG} => P EM = ICE 2 (7.38) 2sβη EM { min{h ICEΟΝ } => P EM = 0 Συνεπώς, ο βέλτιστος νόμος ελέγχου παίρνει την μορφή ενός ντετερμινιστικού ελέγχου βασισμένου σε κανόνες: P opt EM = { η EM η s min{p T, η EM ICE 2sβ }, s < η EM η ICE η EM 1 min{p T, 0}, < s < (7.39) η ICE η EM η ICE 1 η sη EM min{p T, ICE 1 2 }, s > 2sβη EM η EM η ICE Είναι φανερό πως στην περιοχή s < η EM η ICE η ελάχιστη χαμιλτονιανή θα είναι είτε η H ICEΟΝ +EM ON (P M (s)) είτε η H ΕΜΟΝ (P d ) γεγονός από το οποίο μπορούμε να εξάγουμε την απαραίτητη συνθήκη για καθαρά ηλεκτρική οδήγηση. Έτσι, το υβριδικό όχημα μπαίνει σε λειτουργία καθαρά ηλεκτρικής οδήγησης όταν : H ΕΜΟΝ (P d ) < H ICEΟΝ +EM ON (P M (s)) => ICE P T < P ΟΝ +EM ON M, = οριακό η 2 ( ( s 1 η EM η )+ 4sβP 0 ICE η 2 EM ηice 2 ) 2sβ (7.40) 123
124 Για την περιοχή η EM η ICE < s < οχήματος όταν: 1 η EM η ICE είναι φανερό πως έχουμε ηλεκτρική λειτουργία του H ΕΜΟΝ (P d ) < H ICEΟΝ (0) (7.41) Λύνοντας την ανίσωση αυτή από τις σχέσεις που περιγράφουν τις χαμιλτονιανές προκύπτει η συνθήκη για ηλεκτρική οδήγηση: ICE P T < P ΟΝ M, οριακό = η 2 ( ( s 1 )+ 4 s β P 0 η EM η ICE η 2 EM η 2 +( s 1 η ICE EM 2sβ 2 ) η ICE ) (7.42) Για την περιοχή s > οχήματος όταν: 1 η EM η ICE είναι φανερό πως έχουμε ηλεκτρική λειτουργία του H ΕΜΟΝ (P T ) < H ICEΟΝ +RCHG(P M ) (7.43) Λύνοντας την ανίσωση αυτή από τις σχέσεις που περιγράφουν τις χαμιλτονιανές προκύπτει η συνθήκη για ηλεκτρική οδήγηση: (7.44) ICE P T < P ΟΝ M, οριακό = η 2 ( ( s 1 )+ 4s β P 0 η EM η ICE η 2 EM ηice 2 +( s η 1 EM 2sβ 2 ) η ICE +( s 1 η EM η ICE η 2 2) ) EM Για την περίπτωση όπου η απαιτούμενη οδηγητική ισχύς παίρνει αρνητική τιμή ( P Τ < 0 ) τότε έχουμε φόρτιση της μπαταρίας στην περίπτωση που για τις χαμιλτονιανές ισχύει η παρακάτω ανίσωση: H ΕΜΟΝ+RCHG (P T ) < H ICEΟΝ +RCHG(P M ) (7.45) Λύνοντας την ανίσωση αυτή από τις σχέσεις που περιγράφουν τις χαμιλτονιανές προκύπτει η συνθήκη για ηλεκτρική οδήγηση: 124
125 2 β P0 (s η EM 1 )+ 4 s η EM η ICE η 2 EM P T < P ON+RCHG ICE M, οριακό = 2 s β η 2 (7.46) Έτσι, ο τελικός βέλτιστος νόμος ελέγχου για την ενεργειακή διαχείριση του οχήματος που καθορίζει τις καταστάσεις λειτουργίας του οχήματος κατά την διάρκεια ενός κύκλου οδήγησης απλοποιείται στον ντετερμινιστικό βασισμένο σε κανόνες νόμο ελέγχου που περιγράφεται παρακάτω: P M opt (P T, s) { η EM η EM η ICE s 2sβ, P T > 0 και s < η EM 0, P T > 0, P d > P M, οριακό 1 η ICE sη EM 2sβη EM 1 sη η EM ICE ICE ΟΝ, η EM η ICE < s < ICE 2, P T > 0, P d > P ΟΝ +RCHG M,, s > οριακό 2sβη EM P T, 2, P T < 0, P d > P M, οριακό ΕΜ ΟΝ+RCHG, 1 s > η ICE 1, η EM η ICE 1 η EM η ICE η EM η ICE αλλιώς (7.47) Για τον σχεδιασμό του χάρτη λειτουργίας του οχήματος χρησιμοποιήθηκαν οι τιμές που φαίνονται στον παρακάτω πίνακα για τις σταθερές παραμέτρους. Βασικές Παράμετροι Απλοποιημένου Μοντέλου V OC R batt 280 V 0.4 Ω η EM
126 η ICE 0.37 P W Στο σημείο αυτό πρέπει να υπολογίσουμε την τιμή εκείνη του συντελεστή ισοδυναμίας όπου σταματά η κατάσταση επαναφόρτισης με λειτουργία της μηχανής εσωτερικής καύσης και ενεργοποιείται η κατάσταση φόρτισης μόνο από αναγεννητική πέδηση. Η ζητούμενη τιμή υπολογίζεται επιλύοντας την εξίσωση για τα δεδομένα του πίνακα. η 2 ( ( s 1 )+ 4s β P 0 η EM η ICE η 2 EM ηice 2 +( s 2 η 1 ) +( s 1 EM η ICE η EM η ICE η 2 2) ) EM 2sβ = (s η EM 1 )+ 4 s η EM 2 β P0 η ICE η 2 ICE 2 s β η 2 (7.48) Οι λύσεις της παραπάνω εξίσωσης για τις τιμές του πίνακα είναι s= και s= Από αυτές τις δύο εκείνη που έχει το φυσικό νόημα για τον σχεδιασμό του χάρτη των καταστάσεων λειτουργίας είναι η s= Έτσι ο χάρτης καταστάσεων που προκύπτει είναι ο παρακάτω: 126
127 Εικόνα 59- Χάρτης Καταστάσεων Λειτουργίας ως συνάρτηση του συντελεστή ισοδυναμίας χωρίς περιορισμούς ισχύος για την μηχανή και τον ηλεκτροκινητήρα Στην περίπτωσή μας λόγω των προδιαγραφών της μηχανής και του ηλεκτροκινητήρα η απαιτούμενη ισχύς μπορεί να ικανοποιηθεί για κάθε κύκλο οδήγησης αποκλειστικά από την μηχανή. Στην περίπτωση που η μέγιστη ισχύς την οποία μπορούσε να παρέχει η μηχανή ήταν μικρότερη της ισχύος στους τροχούς θα έπρεπε η ηλεκτρική μηχανή να δράσει ως κινητήρας και να υποβοηθήσει την μηχανή στην πρόωση του οχήματος. Ακόμα, όταν η ισχύς που μπορεί να αντέξει ο κινητήρας ως γεννήτρια είναι μεγαλύτερη από την ονομαστική αρνητική τιμή του, πρέπει το όχημα να εισαχθεί σε λειτουργία αναγεννητικής πέδησης. 7.5 Αποτελέσματα και Συμπεράσματα Μεθόδου Έχοντας επιβεβαιώσει την ορθή εκτίμηση της απαιτούμενης ισχύος χρησιμοποιούμε το μαθηματικό αυτό μοντέλο για την εξαγωγή της ισχύος των κύκλων οδήγησης EUDC, FTP-Highway, FTP-75 και City-II. Ανάλογα με την ισχύ και σύμφωνα με την κατάστρωση του απλοποιημένου ελεγκτή ενεργοποιούνται διαφορετικές καταστάσεις λειτουργίας που σημαίνουν και διαφορετική συμπεριφορά του οχήματος σύμφωνα με τον χάρτη. Χρησιμοποιούμε τους ίδιους κύκλους ισχύος όπου οι κύκλοι NEDC και EUDC είναι πολλαπλασιασμένοι με το ίδιο κέρδος Κ για να εξετάσουμε την συμπεριφορά του ελεγκτή, καθώς και τις δυνατότητες πρόωσης με χρήση της μηχανής σε μεγαλύτερες απαιτήσεις. Ο συντελεστής ισοδυναμίας, που οδηγεί σε στρατηγική 127
128 βιώσιμη από πλευράς φορτίου, υπολογίστηκε μέσω της επίλυσης της αντίστοιχης εξίσωσης. Τα αποτελέσματα για κατάλληλο συντελεστή ισοδυναμίας για κάθε κύκλο παρουσιάζονται στα παρακάτω σχήματα. Εικόνα 60- Απαιτούμενη Ισχύς (μαύρο), Ισχύς Κινητήρα (κόκκινο), Ισχύς Μηχανής (μπλε) για τον κύκλο οδήγησης City-II υπό συντελεστή ισοδυναμίας s=
129 Εικόνα 61- Εσωτερική Ενέργεια της Μπαταρίας για τον κύκλο οδήγησης City-II υπό συντελεστή ισοδυναμίας s= Εικόνα 62- Απαιτούμενη Ισχύς (μαύρο), Ισχύς Κινητήρα (κόκκινο), Ισχύς Μηχανής (μπλε) για τον κύκλο οδήγησης EUDC υπό συντελεστή ισοδυναμίας s=
130 Εικόνα 63- Εσωτερική Ενέργεια Μπαταρίας για τον κύκλο οδήγησης EUDC υπό συντελεστή ισοδυναμίας s= Εικόνα 64- Απαιτούμενη Ισχύς (μαύρο), Ισχύς Κινητήρα (κόκκινο), Ισχύς Μηχανής (μπλε) για τον κύκλο οδήγησης FTP-Highway (HWFET) υπό συντελεστή ισοδυναμίας s=
131 Εικόνα 65- Εσωτερική Ενέργεια Μπαταρίας για τον κύκλο οδήγησης FTP-Highway (HWFET) υπό συντελεστή ισοδυναμίας s= Εικόνα 66- Απαιτούμενη Ισχύς (μαύρο), Ισχύς Κινητήρα (κόκκινο), Ισχύς Μηχανής (μπλε) για τον κύκλο οδήγησης FTP-75 υπό συντελεστή ισοδυναμίας s=
4 ΜΟΝΤΕΛΟ ΗΛΕΚΤΡΙΚΟΥ ΟΧΗΜΑΤΟΣ
 4 ΜΟΝΤΕΛΟ ΗΛΕΚΤΡΙΚΟΥ ΟΧΗΜΑΤΟΣ Στο κεφάλαιο αυτό παρουσιάζεται το προσομοιωτικό μοντέλο ενός ηλεκτρικού οχήματος όπως υλοποιήθηκε στο λογισμικό Matlab/Simulink. Για την υλοποίηση του μοντέλου του ηλεκτρικού
4 ΜΟΝΤΕΛΟ ΗΛΕΚΤΡΙΚΟΥ ΟΧΗΜΑΤΟΣ Στο κεφάλαιο αυτό παρουσιάζεται το προσομοιωτικό μοντέλο ενός ηλεκτρικού οχήματος όπως υλοποιήθηκε στο λογισμικό Matlab/Simulink. Για την υλοποίηση του μοντέλου του ηλεκτρικού
Η επαναπαραγόμενη ενέργεια μπορεί να χρησιμοποιηθεί για τη φόρτιση μπαταριών ενός EV ή ενός HEV.
 ΑΝΑΓΕΝΝΗΤΙΚΗ ΠΕΔΗΣΗ ΕΙΣΑΓΩΓΗ Ένα από τα πλεονεκτήματα της χρήσης των ηλεκτρικών κινητήρων για την κίνηση οχημάτων είναι η εξοικονόμηση ενέργειας κατά τη διάρκεια της πέδησης (φρεναρίσματος) του οχήματος.
ΑΝΑΓΕΝΝΗΤΙΚΗ ΠΕΔΗΣΗ ΕΙΣΑΓΩΓΗ Ένα από τα πλεονεκτήματα της χρήσης των ηλεκτρικών κινητήρων για την κίνηση οχημάτων είναι η εξοικονόμηση ενέργειας κατά τη διάρκεια της πέδησης (φρεναρίσματος) του οχήματος.
ΚΕΦΑΛΑΙΟ 4 ΑΝΑΓΕΝΝΗΤΙΚΗ ΠΕΔΗΣΗ
 ΚΕΦΑΛΑΙΟ 4 ΑΝΑΓΕΝΝΗΤΙΚΗ ΠΕΔΗΣΗ Ένα από τα πλεονεκτήματα της χρήσης των ηλεκτρικών κινητήρων για την κίνηση οχημάτων είναι η εξοικονόμηση ενέργειας κατά τη διάρκεια της πέδησης (φρεναρίσματος) του οχήματος.
ΚΕΦΑΛΑΙΟ 4 ΑΝΑΓΕΝΝΗΤΙΚΗ ΠΕΔΗΣΗ Ένα από τα πλεονεκτήματα της χρήσης των ηλεκτρικών κινητήρων για την κίνηση οχημάτων είναι η εξοικονόμηση ενέργειας κατά τη διάρκεια της πέδησης (φρεναρίσματος) του οχήματος.
ΘΕΜΑ: «Tα υβριδικά αυτοκίνητα»
 ΘΕΜΑ: «Tα υβριδικά αυτοκίνητα» Καράμπελα Καράπαπα Επιμέλεια εργασίας: Ζωή Ιωάννα ΤΙ ΕΙΝΑΙ ΤΟ ΥΒΡΙΔΙΚΟ ΑΥΤΟΚΙΝΗΤΟ; Αυτός ο τύπος αυτοκινήτου ονομάζεται έτσι επειδή συνδυάζει δύο μορφές ενέργειας για να
ΘΕΜΑ: «Tα υβριδικά αυτοκίνητα» Καράμπελα Καράπαπα Επιμέλεια εργασίας: Ζωή Ιωάννα ΤΙ ΕΙΝΑΙ ΤΟ ΥΒΡΙΔΙΚΟ ΑΥΤΟΚΙΝΗΤΟ; Αυτός ο τύπος αυτοκινήτου ονομάζεται έτσι επειδή συνδυάζει δύο μορφές ενέργειας για να
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 29 Μαρτίου 2017 1 Συναρτήσεις μεταφοράς σε
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 29 Μαρτίου 2017 1 Συναρτήσεις μεταφοράς σε
Το Ι.Ο.ΑΣ. «Πάνος Μυλωνάς» και η ΓΕΦΥΡΑ Α.Ε., Μέλος της Συμμαχίας «Δρόμοι στο Μέλλον» ενημερώνουν για τα οφέλη της Οικολογικής Οδήγησης
 Το Ι.Ο.ΑΣ. «Πάνος Μυλωνάς» και η ΓΕΦΥΡΑ Α.Ε., Μέλος της Συμμαχίας «Δρόμοι στο Μέλλον» ενημερώνουν για τα οφέλη της Οικολογικής Οδήγησης Γιατί Οικολογική Οδήγηση; Η έννοια της αυτοκίνησης είναι συνδεδεμένη
Το Ι.Ο.ΑΣ. «Πάνος Μυλωνάς» και η ΓΕΦΥΡΑ Α.Ε., Μέλος της Συμμαχίας «Δρόμοι στο Μέλλον» ενημερώνουν για τα οφέλη της Οικολογικής Οδήγησης Γιατί Οικολογική Οδήγηση; Η έννοια της αυτοκίνησης είναι συνδεδεμένη
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ Συνδυασμένη χρήση μοντέλων προσομοίωσης βελτιστοποίησης. Η μέθοδος του μητρώου μοναδιαίας απόκρισης Νικόλαος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΔΙΑΧΕΙΡΙΣΗ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ Συνδυασμένη χρήση μοντέλων προσομοίωσης βελτιστοποίησης. Η μέθοδος του μητρώου μοναδιαίας απόκρισης Νικόλαος
Τμήμα Ηλεκτρολόγων Μηχανικών ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΚΑΤΆ ΤΗ ΛΕΙΤΟΥΡΓΙΑ ΣΓ
 Όταν κατά τη λειτουργία μιας ΣΓ η ροπή στον άξονα της ή το φορτίο της μεταβληθούν απότομα, η λειτουργία της παρουσιάζει κάποιο μεταβατικό φαινόμενο για κάποια χρονική διάρκεια μέχρι να επανέλθει στη στάσιμη
Όταν κατά τη λειτουργία μιας ΣΓ η ροπή στον άξονα της ή το φορτίο της μεταβληθούν απότομα, η λειτουργία της παρουσιάζει κάποιο μεταβατικό φαινόμενο για κάποια χρονική διάρκεια μέχρι να επανέλθει στη στάσιμη
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Έργο Δύναμης Έργο σταθερής δύναμης
 Παρατήρηση: Σε όλες τις ασκήσεις του φυλλαδίου τα αντικείμενα θεωρούμε ότι οι δυνάμεις ασκούνται στο κέντρο μάζας των αντικειμένων έτσι ώστε αυτά κινούνται μόνο μεταφορικά, χωρίς να μπορούν να περιστραφούν.
Παρατήρηση: Σε όλες τις ασκήσεις του φυλλαδίου τα αντικείμενα θεωρούμε ότι οι δυνάμεις ασκούνται στο κέντρο μάζας των αντικειμένων έτσι ώστε αυτά κινούνται μόνο μεταφορικά, χωρίς να μπορούν να περιστραφούν.
Στο διάγραμμα αποδίδεται γραφικά η ταχύτητα ενός κινητού οε συνάρτηση με το χρόνο. Α. Να περιγράψετε την κίνηση του κινητού έως τη χρονική στιγμή 20s.
 ΣΧΟΛIKO BIBΛIO / ΑΣΚ 19. Στο διάγραμμα αποδίδεται γραφικά η ταχύτητα ενός κινητού οε συνάρτηση με το χρόνο. Α. Να περιγράψετε την κίνηση του κινητού έως τη χρονική στιγμή 0s. υ ( m/sec) Β. Να υπολογίσετε
ΣΧΟΛIKO BIBΛIO / ΑΣΚ 19. Στο διάγραμμα αποδίδεται γραφικά η ταχύτητα ενός κινητού οε συνάρτηση με το χρόνο. Α. Να περιγράψετε την κίνηση του κινητού έως τη χρονική στιγμή 0s. υ ( m/sec) Β. Να υπολογίσετε
2. Ανάλυση του βασικού κινηματικού μηχανισμού των εμβολοφόρων ΜΕΚ
 2. Ανάλυση του βασικού κινηματικού μηχανισμού των εμβολοφόρων ΜΕΚ Προαπαιτούμενες γνώσεις: (α) Γνώσεις των τμημάτων κινηματικού μηχανισμού Μηχανής Εσωτερικής Καύσης (β) Αριθμητικός υπολογισμός παραγώγου
2. Ανάλυση του βασικού κινηματικού μηχανισμού των εμβολοφόρων ΜΕΚ Προαπαιτούμενες γνώσεις: (α) Γνώσεις των τμημάτων κινηματικού μηχανισμού Μηχανής Εσωτερικής Καύσης (β) Αριθμητικός υπολογισμός παραγώγου
3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
 Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
Κεφάλαιο 10 Περιστροφική Κίνηση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 10 Περιστροφική Κίνηση Περιεχόμενα Κεφαλαίου 10 Γωνιακές Ποσότητες Διανυσματικός Χαρακτήρας των Γωνιακών Ποσοτήτων Σταθερή γωνιακή Επιτάχυνση Ροπή Δυναμική της Περιστροφικής Κίνησης, Ροπή και
Κεφάλαιο 10 Περιστροφική Κίνηση Περιεχόμενα Κεφαλαίου 10 Γωνιακές Ποσότητες Διανυσματικός Χαρακτήρας των Γωνιακών Ποσοτήτων Σταθερή γωνιακή Επιτάχυνση Ροπή Δυναμική της Περιστροφικής Κίνησης, Ροπή και
3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
 Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα ΦΥΣ102 1 Δύναμη είναι: Η αιτία που προκαλεί μεταβολή
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα ΦΥΣ102 1 Δύναμη είναι: Η αιτία που προκαλεί μεταβολή
ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της αρχής λειτουργίας των μηχανών συνεχούς ρεύματος, β) η ανάλυση της κατασκευαστικών
ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της αρχής λειτουργίας των μηχανών συνεχούς ρεύματος, β) η ανάλυση της κατασκευαστικών
1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά; Μονόμετρα ονομάζονται τα μεγέθη τα οποία, για να τα προσδιορίσουμε πλήρως, αρκεί να γνωρίζουμε
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά; Μονόμετρα ονομάζονται τα μεγέθη τα οποία, για να τα προσδιορίσουμε πλήρως, αρκεί να γνωρίζουμε
ΘΕΜΑ Α Παράδειγμα 1. Α1. Ο ρυθμός μεταβολής της ταχύτητας ονομάζεται και α. μετατόπιση. β. επιτάχυνση. γ. θέση. δ. διάστημα.
 ΘΕΜΑ Α Παράδειγμα 1 Α1. Ο ρυθμός μεταβολής της ταχύτητας ονομάζεται και α. μετατόπιση. β. επιτάχυνση. γ. θέση. δ. διάστημα. Α2. Για τον προσδιορισμό μιας δύναμης που ασκείται σε ένα σώμα απαιτείται να
ΘΕΜΑ Α Παράδειγμα 1 Α1. Ο ρυθμός μεταβολής της ταχύτητας ονομάζεται και α. μετατόπιση. β. επιτάχυνση. γ. θέση. δ. διάστημα. Α2. Για τον προσδιορισμό μιας δύναμης που ασκείται σε ένα σώμα απαιτείται να
ΠΘ/ΤΜΜΒ/ΕΘΘΜ - ΜΜ802 Γραπτή Δοκιμασία ώρα 12:00-14:30
 ΠΘ/ΤΜΜΒ/ΕΘΘΜ - ΜΜ80 Γραπτή Δοκιμασία.06.07 ώρα 1:00-14:30 Επισυνάπτεται διάγραμμα με ισουψείς ειδικής κατανάλωσης καυσίμου [g/psh] στο πεδίο λειτουργίας του κινητήρα Diesel με προθάλαμο καύσης, OM61 της
ΠΘ/ΤΜΜΒ/ΕΘΘΜ - ΜΜ80 Γραπτή Δοκιμασία.06.07 ώρα 1:00-14:30 Επισυνάπτεται διάγραμμα με ισουψείς ειδικής κατανάλωσης καυσίμου [g/psh] στο πεδίο λειτουργίας του κινητήρα Diesel με προθάλαμο καύσης, OM61 της
Ν. Κυρτάτος, Καθηγητής ΕΜΠ, Δ/ντής ΕΝΜ, Γ. Παπαλάμπρου, Λέκτορας ΕΜΠ, Σ. Τοπάλογλου, ΥΔ ΣΝΜΜ/ΕΜΠ
 Η ΝΕΑ ΜΕΓΑΛΗ ΠΕΙΡΑΜΑΤΙΚΗ ΚΛΙΝΗ ΔΟΚΙΜΩΝ ΥΒΡΙΔΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΠΡΟΩΣΗΣ ΠΛΟΙΩΝ ΜΕ ΘΕΡΜΙΚΟΥΣ ΚΑΙ ΗΛΕΚΤΡΙΚΟΥΣ ΚΙΝΗΤΗΡΕΣ ΚΑΙ ΣΥΣΤΗΜΑ ΑΠΟΡΡΥΠΑΝΣΗΣ ΚΑΥΣΑΕΡΙΩΝ, ΤΟΥ ΕΡΓΑΣΤΗΡΙΟΥ ΝΑΥΤΙΚΗΣ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΜΠ Ν. Κυρτάτος,
Η ΝΕΑ ΜΕΓΑΛΗ ΠΕΙΡΑΜΑΤΙΚΗ ΚΛΙΝΗ ΔΟΚΙΜΩΝ ΥΒΡΙΔΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΠΡΟΩΣΗΣ ΠΛΟΙΩΝ ΜΕ ΘΕΡΜΙΚΟΥΣ ΚΑΙ ΗΛΕΚΤΡΙΚΟΥΣ ΚΙΝΗΤΗΡΕΣ ΚΑΙ ΣΥΣΤΗΜΑ ΑΠΟΡΡΥΠΑΝΣΗΣ ΚΑΥΣΑΕΡΙΩΝ, ΤΟΥ ΕΡΓΑΣΤΗΡΙΟΥ ΝΑΥΤΙΚΗΣ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΜΠ Ν. Κυρτάτος,
1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
1. Δύναμη. Η ιδέα της Δύναμης δίνει μία ποσοτική περιγραφή της αλληλεπίδρασης α) μεταξύ δύο σωμάτων β) μεταξύ ενός σώματος και του περιβάλλοντος του.
 . Δύναμη Η ιδέα της Δύναμης δίνει μία ποσοτική περιγραφή της αλληλεπίδρασης α) μεταξύ δύο σωμάτων β) μεταξύ ενός σώματος και του περιβάλλοντος του. Υπάρχουν δυνάμεις οι οποίες ασκούνται ακόμη και όταν
. Δύναμη Η ιδέα της Δύναμης δίνει μία ποσοτική περιγραφή της αλληλεπίδρασης α) μεταξύ δύο σωμάτων β) μεταξύ ενός σώματος και του περιβάλλοντος του. Υπάρχουν δυνάμεις οι οποίες ασκούνται ακόμη και όταν
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ
 Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
Ευθύγραμμη ομαλή κίνηση
 Διάγραμμα s - Ευθύγραμμη Κίνηση (m) Μέση αριθμητική ταχύτητα (μονόμετρο) Μέση διανυσματική ταχύτητα Μέση επιτάχυνση 1 4 Διάγραμμα u - (sec) Απόσταση (x) ονομάζουμε την ευθεία που ενώνει την αρχική και
Διάγραμμα s - Ευθύγραμμη Κίνηση (m) Μέση αριθμητική ταχύτητα (μονόμετρο) Μέση διανυσματική ταχύτητα Μέση επιτάχυνση 1 4 Διάγραμμα u - (sec) Απόσταση (x) ονομάζουμε την ευθεία που ενώνει την αρχική και
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου
 Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
ΕΚΦΕ Χανίων «Κ. Μ. Κούμας» Νίκος Αναστασάκης Γιάννης Σαρρής
 ΕΚΦΕ Χανίων «Κ. Μ. Κούμας» Νίκος Αναστασάκης Γιάννης Σαρρής Σκοπός Στόχοι Άσκησης Οι μαθητές να: Αναγνωρίζουν τις δυνάμεις που ασκούνται στα σώματα και αντιλαμβάνονται τις σχέσεις μεταξύ τους,
ΕΚΦΕ Χανίων «Κ. Μ. Κούμας» Νίκος Αναστασάκης Γιάννης Σαρρής Σκοπός Στόχοι Άσκησης Οι μαθητές να: Αναγνωρίζουν τις δυνάμεις που ασκούνται στα σώματα και αντιλαμβάνονται τις σχέσεις μεταξύ τους,
ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΙ ΜΕΤΡΗΣΗ ΣΥΝΑΡΤΗΣΗΣ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΡΑΚΤΙΚΑ ΣΥΣΤΗΜΑΤΑ
 Κεφάλαιο ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΙ ΜΕΤΡΗΣΗ ΣΥΝΑΡΤΗΣΗΣ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΡΑΚΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Στη διαδικασία σχεδιασμού των Συστημάτων Αυτομάτου Ελέγχου, η απαραίτητη και η πρώτη εργασία που έχουμε να κάνουμε, είναι να
Κεφάλαιο ΥΠΟΛΟΓΙΣΜΟΣ ΚΑΙ ΜΕΤΡΗΣΗ ΣΥΝΑΡΤΗΣΗΣ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΡΑΚΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Στη διαδικασία σχεδιασμού των Συστημάτων Αυτομάτου Ελέγχου, η απαραίτητη και η πρώτη εργασία που έχουμε να κάνουμε, είναι να
Γ. Β Α Λ Α Τ Σ Ο Σ. 4ο ΓΥΜΝΑΣΙΟ ΛΑΜΙΑΣ 1. Γιώργος Βαλατσός Φυσικός Msc
 4ο ΓΥΜΝΑΣΙΟ ΛΑΜΙΑΣ 1 1. Πότε τα σώματα θεωρούνται υλικά σημεία; Αναφέρεται παραδείγματα. Στη φυσική πολλές φορές είναι απαραίτητο να μελετήσουμε τα σώματα χωρίς να λάβουμε υπόψη τις διαστάσεις τους. Αυτό
4ο ΓΥΜΝΑΣΙΟ ΛΑΜΙΑΣ 1 1. Πότε τα σώματα θεωρούνται υλικά σημεία; Αναφέρεται παραδείγματα. Στη φυσική πολλές φορές είναι απαραίτητο να μελετήσουμε τα σώματα χωρίς να λάβουμε υπόψη τις διαστάσεις τους. Αυτό
Άσκηση 4 Αρχή λειτουργίας Μηχανών DC
 Άσκηση 4 Αρχή λειτουργίας Μηχανών DC 4.1 Σκοπός της Άσκησης Σκοπός την Άσκησης είναι η μελέτη της αρχής λειτουργίας των μηχανών DC. Οι μηχανές DC μπορούν να λειτουργήσουν είτε ως γεννήτριες είτε ως κινητήρες.
Άσκηση 4 Αρχή λειτουργίας Μηχανών DC 4.1 Σκοπός της Άσκησης Σκοπός την Άσκησης είναι η μελέτη της αρχής λειτουργίας των μηχανών DC. Οι μηχανές DC μπορούν να λειτουργήσουν είτε ως γεννήτριες είτε ως κινητήρες.
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑΣ 2017
 ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑΣ 2017 ΚΕΦΑΛΑΙΟ 1 ο ΕΙΣΑΓΩΓΗ 1.3 Τα φυσικά μεγέθη και οι μονάδες τους 1. Ποια μεγέθη ονομάζονται θεμελιώδη; Θεμελιώδη ονομάζονται τα μεγέθη τα οποία δεν ορίζονται με
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑΣ 2017 ΚΕΦΑΛΑΙΟ 1 ο ΕΙΣΑΓΩΓΗ 1.3 Τα φυσικά μεγέθη και οι μονάδες τους 1. Ποια μεγέθη ονομάζονται θεμελιώδη; Θεμελιώδη ονομάζονται τα μεγέθη τα οποία δεν ορίζονται με
Υπολογισμός Κινητήρα
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΤΡΑ 2006 Εργασία στη Δυναμική Μηχανών και Μηχανισμών: Υπολογισμός Κινητήρα Φοιτητές: Ιωαννίδης Νικόλαος 4655 Σφακιανάκης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΠΑΤΡΑ 2006 Εργασία στη Δυναμική Μηχανών και Μηχανισμών: Υπολογισμός Κινητήρα Φοιτητές: Ιωαννίδης Νικόλαος 4655 Σφακιανάκης
Κεφάλαιο 1. Κίνηση σε μία διάσταση
 Κεφάλαιο 1 Κίνηση σε μία διάσταση Κινηματική Περιγράφει την κίνηση, αγνοώντας τις αλληλεπιδράσεις με εξωτερικούς παράγοντες που ενδέχεται να προκαλούν ή να μεταβάλλουν την κίνηση. Προς το παρόν, θα μελετήσουμε
Κεφάλαιο 1 Κίνηση σε μία διάσταση Κινηματική Περιγράφει την κίνηση, αγνοώντας τις αλληλεπιδράσεις με εξωτερικούς παράγοντες που ενδέχεται να προκαλούν ή να μεταβάλλουν την κίνηση. Προς το παρόν, θα μελετήσουμε
Προηγμένος έλεγχος ηλεκτρικών μηχανών
 Προηγμένος έλεγχος ηλεκτρικών μηχανών Ενότητα 3: Βαθμωτός Έλεγχος Ασύχρονων Μηχανών Επαμεινώνδας Μητρονίκας - Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών
Προηγμένος έλεγχος ηλεκτρικών μηχανών Ενότητα 3: Βαθμωτός Έλεγχος Ασύχρονων Μηχανών Επαμεινώνδας Μητρονίκας - Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών
Επεξεργαςία πειραματικών δεδομζνων
 Επεξεργαςία πειραματικών δεδομζνων Επεξεργασία μετρήσεων. Στα θέματα που ακολουθούν, η επεξεργασία των μετρήσεων στηρίζεται στη δημιουργία γραφημάτων α βαθμού, δηλαδή της μορφής ψ=α χ+β,και στην εξαγωγή
Επεξεργαςία πειραματικών δεδομζνων Επεξεργασία μετρήσεων. Στα θέματα που ακολουθούν, η επεξεργασία των μετρήσεων στηρίζεται στη δημιουργία γραφημάτων α βαθμού, δηλαδή της μορφής ψ=α χ+β,και στην εξαγωγή
Δυναμική Μηχανών I. Διάλεξη 5. Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ
 Δυναμική Μηχανών I Διάλεξη 5 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Περιεχόμενα: Μοντελοποίηση Μηχανικών- Ηλεκτρικών-Υδραυλικών-Θερμικών Συστημάτων Επανάληψη: Εξισώσεις Lagrange σε συστήματα
Δυναμική Μηχανών I Διάλεξη 5 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Περιεχόμενα: Μοντελοποίηση Μηχανικών- Ηλεκτρικών-Υδραυλικών-Θερμικών Συστημάτων Επανάληψη: Εξισώσεις Lagrange σε συστήματα
12. Δυναμομέτρηση Εμβολοφόρου Βενζινοκινητήρα με τη χρήση Υδραυλικής Πέδης Νερού
 12. Δυναμομέτρηση Εμβολοφόρου Βενζινοκινητήρα με τη χρήση Υδραυλικής Πέδης Νερού Προαπαιτούμενες γνώσεις: (α) Θεωρητικές γνώσεις κατάστρωσης Ενεργειακού Ισολογισμού Μ.Ε.Κ. και (β) Θεωρητικές γνώσεις για
12. Δυναμομέτρηση Εμβολοφόρου Βενζινοκινητήρα με τη χρήση Υδραυλικής Πέδης Νερού Προαπαιτούμενες γνώσεις: (α) Θεωρητικές γνώσεις κατάστρωσης Ενεργειακού Ισολογισμού Μ.Ε.Κ. και (β) Θεωρητικές γνώσεις για
ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση.
 ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση. Η δύναμη είναι ένα διανυσματικό μέγεθος. Όταν κατά την κίνηση ενός σώματος η δύναμη είναι μηδενική
ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση. Η δύναμη είναι ένα διανυσματικό μέγεθος. Όταν κατά την κίνηση ενός σώματος η δύναμη είναι μηδενική
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 23/9/2015 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ /9/015 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα κινείται σε ευθύγραμμη οριζόντια τροχιά με την ταχύτητά του σε συνάρτηση
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ /9/015 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα κινείται σε ευθύγραμμη οριζόντια τροχιά με την ταχύτητά του σε συνάρτηση
Touareg Hybrid Οδηγός συμπεριφοράς υβριδικού συστήματος
 Touareg Hybrid Οδηγός συμπεριφοράς υβριδικού συστήματος Πίνακας περιεχομένων 1 Συμπεριφορά υβριδικού συστήματος σε διαφορετικές θέσεις του επιλογέα ταχυτήτων...3 2 Συμπεριφορά του αυτοκινήτου στην επιτάχυνση...4
Touareg Hybrid Οδηγός συμπεριφοράς υβριδικού συστήματος Πίνακας περιεχομένων 1 Συμπεριφορά υβριδικού συστήματος σε διαφορετικές θέσεις του επιλογέα ταχυτήτων...3 2 Συμπεριφορά του αυτοκινήτου στην επιτάχυνση...4
Ασκήσεις στην ευθύγραμμη ομαλή κίνηση
 Ασκήσεις στην ευθύγραμμη ομαλή κίνηση 1. Κινητό που εκτελεί ΕΟΚ περνά από τη θέση x 1 =12m τη χρονική στιγμή t 1 =9s και από τη θέση x 2 =2m τη χρονική στιγμή t 2 =14s. Να βρείτε: α) την κατεύθυνση προς
Ασκήσεις στην ευθύγραμμη ομαλή κίνηση 1. Κινητό που εκτελεί ΕΟΚ περνά από τη θέση x 1 =12m τη χρονική στιγμή t 1 =9s και από τη θέση x 2 =2m τη χρονική στιγμή t 2 =14s. Να βρείτε: α) την κατεύθυνση προς
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 Η
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 Η τεχνολογία των Α/Γ Βασικά Τεχνικά χαρακτηριστικά και μεγέθη [1] Θεωρητικό Μέρος ΕΡΓΑΣΤΗΡΙΟ Α.Π.Ε Ι Κύρια μέρη της Ανεμογεννήτριας Φτερωτή (η στροφέα) που φέρει δύο η τρία πτερύγια.
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 9 Η τεχνολογία των Α/Γ Βασικά Τεχνικά χαρακτηριστικά και μεγέθη [1] Θεωρητικό Μέρος ΕΡΓΑΣΤΗΡΙΟ Α.Π.Ε Ι Κύρια μέρη της Ανεμογεννήτριας Φτερωτή (η στροφέα) που φέρει δύο η τρία πτερύγια.
ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ : ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση. Tο γιο-γιο του σχήματος έχει ακτίνα R και αρχικά είναι ακίνητο. Την t=0 αφήνουμε ελεύθερο το δίσκο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ : ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση. Tο γιο-γιο του σχήματος έχει ακτίνα R και αρχικά είναι ακίνητο. Την t=0 αφήνουμε ελεύθερο το δίσκο
Οδηγός βαθμολόγησης Εξεταστικού Δοκιμίου Α Λυκείου
 ΛΥΚΕΙΟ ΜΑΚΑΡΙΟΥ Γ ΛΑΡΝΑΚΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2014-15 Οδηγός βαθμολόγησης Εξεταστικού Δοκιμίου Α Λυκείου 1) Να γράψετε 3 διανυσματικά μεγέθη και 2 μονόμετρα μεγέθη καθώς και τις μονάδες μέτρησής τους (στο
ΛΥΚΕΙΟ ΜΑΚΑΡΙΟΥ Γ ΛΑΡΝΑΚΑΣ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2014-15 Οδηγός βαθμολόγησης Εξεταστικού Δοκιμίου Α Λυκείου 1) Να γράψετε 3 διανυσματικά μεγέθη και 2 μονόμετρα μεγέθη καθώς και τις μονάδες μέτρησής τους (στο
ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ
 ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ 1 ΝΟΜΟΣ ΤΟΥ OHM (ΩΜ) Για πολλά υλικά ο λόγος της πυκνότητας του ρεύματος προς το ηλεκτρικό πεδίο είναι σταθερός και ανεξάρτητος από το ηλεκτρικό
ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ 1 ΝΟΜΟΣ ΤΟΥ OHM (ΩΜ) Για πολλά υλικά ο λόγος της πυκνότητας του ρεύματος προς το ηλεκτρικό πεδίο είναι σταθερός και ανεξάρτητος από το ηλεκτρικό
ηλεκτρικό ρεύμα ampere
 Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
2. Μια μοτοσυκλέτα τρέχει με ταχύτητα 108 km/h. α) Σε πόσο χρόνο διανύει τα 120 m; β) Πόσα μέτρα διανύει σε 5 s;
 1. Αυτοκίνητο κινείται σε ευθύγραμμο δρόμο με σταθερή φορά και το ταχύμετρο του (κοντέρ) δείχνει συνεχώς 36 km/h. α) Τι είδους κίνηση κάνει το αυτοκίνητο; β) Να μετατρέψετε την ταχύτητα του αυτοκινήτου
1. Αυτοκίνητο κινείται σε ευθύγραμμο δρόμο με σταθερή φορά και το ταχύμετρο του (κοντέρ) δείχνει συνεχώς 36 km/h. α) Τι είδους κίνηση κάνει το αυτοκίνητο; β) Να μετατρέψετε την ταχύτητα του αυτοκινήτου
Φυσικά μεγέθη. Φυσική α λυκείου ΕΙΣΑΓΩΓΗ. Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα. Β.
 ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
Τμήμα Ηλεκτρολόγων Μηχανικών ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΡΟΠΗΣ ΤΑΧΥΤΗΤΑΣ ΕΠΑΓΩΓΙΚΩΝ ΚΙΝΗΤΗΡΩΝ
 Αν είναι γνωστή η συμπεριφορά των μαγνητικών πεδίων στη μηχανή, είναι δυνατός ο προσεγγιστικός προσδιορισμός της χαρακτηριστικής ροπής-ταχύτητας του επαγωγικού κινητήρα Όπως είναι γνωστό η επαγόμενη ροπή
Αν είναι γνωστή η συμπεριφορά των μαγνητικών πεδίων στη μηχανή, είναι δυνατός ο προσεγγιστικός προσδιορισμός της χαρακτηριστικής ροπής-ταχύτητας του επαγωγικού κινητήρα Όπως είναι γνωστό η επαγόμενη ροπή
β) Από τον νόμο του Νεύτωνα για την μεταφορική κίνηση του κέντρου μάζας έχουμε: Επομένως το κέντρο μάζας αποκτάει αρνητική επιτάχυνση σταθερού μέτρου
 ΣΥΝΘΕΤΗ ΚΙΝΗΣΗ 1) Συμπαγής κύλινδρος μάζας m και ακτίνας R δέχεται μια αρχική μεγάλη και στιγμιαία ώθηση προς τα πάνω σε κεκλιμένο επίπεδο γωνίας θ και μετά αφήνεται ελεύθερος. Κατά την παύση της ώθησης,
ΣΥΝΘΕΤΗ ΚΙΝΗΣΗ 1) Συμπαγής κύλινδρος μάζας m και ακτίνας R δέχεται μια αρχική μεγάλη και στιγμιαία ώθηση προς τα πάνω σε κεκλιμένο επίπεδο γωνίας θ και μετά αφήνεται ελεύθερος. Κατά την παύση της ώθησης,
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/2014
 minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014
 1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
ΜΕΛΕΤΗ ΤΗΣ ΚΙΝΗΣΗΣ ΡΑΒΔΟΥ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ ΜΕΤΡΗΣΗ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΤΗΣ ΡΑΒΔΟΥ
 ΜΕΛΕΤΗ ΤΗΣ ΚΙΝΗΣΗΣ ΡΑΒΔΟΥ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ ΜΕΤΡΗΣΗ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΤΗΣ ΡΑΒΔΟΥ Συνοπτική περιγραφή Μελετάμε την κίνηση μιας ράβδου που μπορεί να περιστρέφεται γύρω από σταθερό οριζόντιο άξονα,
ΜΕΛΕΤΗ ΤΗΣ ΚΙΝΗΣΗΣ ΡΑΒΔΟΥ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ ΜΕΤΡΗΣΗ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΤΗΣ ΡΑΒΔΟΥ Συνοπτική περιγραφή Μελετάμε την κίνηση μιας ράβδου που μπορεί να περιστρέφεται γύρω από σταθερό οριζόντιο άξονα,
ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Το έργο μίας από τις δυνάμεις που ασκούνται σε ένα σώμα. α. είναι μηδέν όταν το σώμα είναι ακίνητο β. έχει πρόσημο το οποίο εξαρτάται από τη γωνία
ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Το έργο μίας από τις δυνάμεις που ασκούνται σε ένα σώμα. α. είναι μηδέν όταν το σώμα είναι ακίνητο β. έχει πρόσημο το οποίο εξαρτάται από τη γωνία
1)Σε ένα πυκνωτή, η σχέση μεταξύ φορτίου Q και τάσης V μεταξύ των οπλισμών του, απεικονίζεται στο διάγραμμα.
 1)Σε ένα πυκνωτή, η σχέση μεταξύ φορτίου Q και τάσης V μεταξύ των οπλισμών του, απεικονίζεται στο διάγραμμα. Να επιλέξετε τη σωστή απάντηση. Η χωρητικότητα του πυκνωτή είναι: α. 5 F, β. 1 / 5 μf, γ. 5
1)Σε ένα πυκνωτή, η σχέση μεταξύ φορτίου Q και τάσης V μεταξύ των οπλισμών του, απεικονίζεται στο διάγραμμα. Να επιλέξετε τη σωστή απάντηση. Η χωρητικότητα του πυκνωτή είναι: α. 5 F, β. 1 / 5 μf, γ. 5
Δ3. Ο χρόνος από τη στιγμή που η απόστασή τους ήταν d μέχρι τη στιγμή που ακουμπά η μία την άλλη. Μονάδες 6
 ΘΕΜΑ Δ 1. Δύο αμαξοστοιχίες κινούνται κατά την ίδια φορά πάνω στην ίδια γραμμή. Η προπορευόμενη έχει ταχύτητα 54km/h και η επόμενη 72km/h. Όταν βρίσκονται σε απόσταση d, οι μηχανοδηγοί αντιλαμβάνονται
ΘΕΜΑ Δ 1. Δύο αμαξοστοιχίες κινούνται κατά την ίδια φορά πάνω στην ίδια γραμμή. Η προπορευόμενη έχει ταχύτητα 54km/h και η επόμενη 72km/h. Όταν βρίσκονται σε απόσταση d, οι μηχανοδηγοί αντιλαμβάνονται
Volvo fh με i-save ΠΟΤΈ Η ΕΞΟΙΚΟΝΌΜΗΣΗ ΚΑΥΣΊΜΟΥ ΔΕΝ ΉΤΑΝ ΤΌΣΟ ΑΠΛΉ
 Volvo fh με i-save ΠΟΤΈ Η ΕΞΟΙΚΟΝΌΜΗΣΗ ΚΑΥΣΊΜΟΥ ΔΕΝ ΉΤΑΝ ΤΌΣΟ ΑΠΛΉ Το απόλυτο φορτηγό μεγάλων αποστάσεων Όταν πρόκειται για οικονομία καυσίμου, το θέμα δεν είναι μόνο πόση οικονομία μπορείτε να κάνετε
Volvo fh με i-save ΠΟΤΈ Η ΕΞΟΙΚΟΝΌΜΗΣΗ ΚΑΥΣΊΜΟΥ ΔΕΝ ΉΤΑΝ ΤΌΣΟ ΑΠΛΉ Το απόλυτο φορτηγό μεγάλων αποστάσεων Όταν πρόκειται για οικονομία καυσίμου, το θέμα δεν είναι μόνο πόση οικονομία μπορείτε να κάνετε
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
2 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση
 2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
ψψαριαα0001.jpg ψψαριαα0001.jpg Κ.-Α. Θ. Θωμά
 Οι διαφάνειες που ακολουθούν είναι βοηθητικές για το μάθημα της Φυσικής που διδάσκεται στους φοιτητές του Βιολογικού Τμήματος του Πανεπιστημίου Πατρών. Επειδή, στο καλωσόρισμα, ακόμη και όταν πρόκειται
Οι διαφάνειες που ακολουθούν είναι βοηθητικές για το μάθημα της Φυσικής που διδάσκεται στους φοιτητές του Βιολογικού Τμήματος του Πανεπιστημίου Πατρών. Επειδή, στο καλωσόρισμα, ακόμη και όταν πρόκειται
Toyota Hybrid. Ηλίας Καραϊσκός Αγγελική Τσενέ
 Toyota Hybrid Ηλίας Καραϊσκός Αγγελική Τσενέ Η σημερινή μας agenda Toyota & Hybrid Η τεχνολογία Toyota Hybrid Μοναδικά οφέλη Toyota Hybrid Γκάμα Test Drive Η Toyota στον κόσμο Δηλαδή Kaizen προκαλώντας
Toyota Hybrid Ηλίας Καραϊσκός Αγγελική Τσενέ Η σημερινή μας agenda Toyota & Hybrid Η τεχνολογία Toyota Hybrid Μοναδικά οφέλη Toyota Hybrid Γκάμα Test Drive Η Toyota στον κόσμο Δηλαδή Kaizen προκαλώντας
Όπου m είναι η μάζα του σώματος και υ η ταχύτητά του.
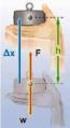 1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ ΙΣΧΥΣ Η ενέργεια είναι από εκείνες τις έννοιες που δύσκολα ορίζονται στη Φυσική. Ένα σώμα μπορεί να έχει, να παίρνει ή να δίνει ενέργεια. Η ίδια η ενέργεια μπορεί να μετατρέπεται από μια
1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ ΙΣΧΥΣ Η ενέργεια είναι από εκείνες τις έννοιες που δύσκολα ορίζονται στη Φυσική. Ένα σώμα μπορεί να έχει, να παίρνει ή να δίνει ενέργεια. Η ίδια η ενέργεια μπορεί να μετατρέπεται από μια
ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι
 Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 1.1- Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 015.
Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 1.1- Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 015.
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Μέτρηση της επιτάχυνσης της βαρύτητας με τη βοήθεια του απλού εκκρεμούς.
 Μ2 Μέτρηση της επιτάχυνσης της βαρύτητας με τη βοήθεια του απλού εκκρεμούς. 1 Σκοπός Η εργαστηριακή αυτή άσκηση αποσκοπεί στη μέτρηση της επιτάχυνσης της βαρύτητας σε ένα τόπο. Αυτή η μέτρηση επιτυγχάνεται
Μ2 Μέτρηση της επιτάχυνσης της βαρύτητας με τη βοήθεια του απλού εκκρεμούς. 1 Σκοπός Η εργαστηριακή αυτή άσκηση αποσκοπεί στη μέτρηση της επιτάχυνσης της βαρύτητας σε ένα τόπο. Αυτή η μέτρηση επιτυγχάνεται
Στο στάτη της μηχανής εφαρμόζεται ένα 3-φασικό σύστημα ρευμάτων το οποίο παράγει στο εσωτερικό της στρεφόμενο ομογενές μαγνητικό πεδίο
 Στον ΣΚ 2 πόλων το μαγνητικό πεδίο του δρομέα BR παράγεται από το ρεύμα διέγερσης IF Στο στάτη της μηχανής εφαρμόζεται ένα 3-φασικό σύστημα ρευμάτων το οποίο παράγει στο εσωτερικό της στρεφόμενο ομογενές
Στον ΣΚ 2 πόλων το μαγνητικό πεδίο του δρομέα BR παράγεται από το ρεύμα διέγερσης IF Στο στάτη της μηχανής εφαρμόζεται ένα 3-φασικό σύστημα ρευμάτων το οποίο παράγει στο εσωτερικό της στρεφόμενο ομογενές
Α) ΕΝΑ ΚΙΝΗΤΟ. 1) Πληροφορίες από διάγραμμα x-t.
 Α) ΕΝΑ ΚΙΝΗΤΟ 1) Πληροφορίες από διάγραμμα x-t Ένα κινητό κινείται ευθύγραμμα και στο σχήμα φαίνεται η μετατόπισή του σε συνάρτηση με τον χρόνο Ποιες από τις ακόλουθες προτάσεις είναι σωστές και ποιες
Α) ΕΝΑ ΚΙΝΗΤΟ 1) Πληροφορίες από διάγραμμα x-t Ένα κινητό κινείται ευθύγραμμα και στο σχήμα φαίνεται η μετατόπισή του σε συνάρτηση με τον χρόνο Ποιες από τις ακόλουθες προτάσεις είναι σωστές και ποιες
ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας του κινητήρα συνεχούς
ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας του κινητήρα συνεχούς
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ 1. Ο άνθρωπος ξεκινά τη στιγμή t=0 από τη θέση x=50 m και όπως φαίνεται στο παρακάτω διάγραμμα κινείται προς τα αριστερά. Στη συνέχεια σε κάθε σημειωμένη θέση στο
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ 1. Ο άνθρωπος ξεκινά τη στιγμή t=0 από τη θέση x=50 m και όπως φαίνεται στο παρακάτω διάγραμμα κινείται προς τα αριστερά. Στη συνέχεια σε κάθε σημειωμένη θέση στο
Μελέτη προβλημάτων ΠΗΙ λόγω λειτουργίας βοηθητικών προωστήριων μηχανισμών
 «ΔιερΕΥνηση Και Aντιμετώπιση προβλημάτων ποιότητας ηλεκτρικής Ισχύος σε Συστήματα Ηλεκτρικής Ενέργειας (ΣΗΕ) πλοίων» (ΔΕΥ.Κ.Α.Λ.Ι.ΩΝ) πράξη ΘΑΛΗΣ-ΕΜΠ, πράξη ένταξης 11012/9.7.2012, MIS: 380164, Κωδ.ΕΔΕΙΛ/ΕΜΠ:
«ΔιερΕΥνηση Και Aντιμετώπιση προβλημάτων ποιότητας ηλεκτρικής Ισχύος σε Συστήματα Ηλεκτρικής Ενέργειας (ΣΗΕ) πλοίων» (ΔΕΥ.Κ.Α.Λ.Ι.ΩΝ) πράξη ΘΑΛΗΣ-ΕΜΠ, πράξη ένταξης 11012/9.7.2012, MIS: 380164, Κωδ.ΕΔΕΙΛ/ΕΜΠ:
ΔΕΙΓΜΑ ΠΡΙΝ ΤΙΣ ΔΙΟΡΘΩΣΕΙΣ - ΕΚΔΟΣΕΙΣ ΚΡΙΤΙΚΗ
 Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
1 ο Διαγώνισμα Α Λυκείου Σάββατο 18 Νοεμβρίου 2017
 1 ο Διαγώνισμα Α Λυκείου Σάββατο 18 Νοεμβρίου 017 Διάρκεια Εξέτασης 3 ώρες Ονοματεπώνυμο. ΘΕΜΑ Α: Στις ερωτήσεις Α1 ως και Α4 επιλέξτε την σωστή απάντηση: Α1. Αν υ η ταχύτητα ενός κινητού και α η επιτάχυνσή
1 ο Διαγώνισμα Α Λυκείου Σάββατο 18 Νοεμβρίου 017 Διάρκεια Εξέτασης 3 ώρες Ονοματεπώνυμο. ΘΕΜΑ Α: Στις ερωτήσεις Α1 ως και Α4 επιλέξτε την σωστή απάντηση: Α1. Αν υ η ταχύτητα ενός κινητού και α η επιτάχυνσή
1. Μια σφαίρα κινείται ευθύγραμμα και στο παρακάτω σχήμα βλέπετε την θέση της Α για t=0.
 1. Μια σφαίρα κινείται ευθύγραμμα και στο παρακάτω σχήμα βλέπετε την θέση της Α για t=0. Αν η ταχύτητα της σφαίρας μεταβάλλεται όπως στο διπλανό διάγραμμα: A) Χαρακτηρίστε την κίνηση της σφαίρας: i) Από
1. Μια σφαίρα κινείται ευθύγραμμα και στο παρακάτω σχήμα βλέπετε την θέση της Α για t=0. Αν η ταχύτητα της σφαίρας μεταβάλλεται όπως στο διπλανό διάγραμμα: A) Χαρακτηρίστε την κίνηση της σφαίρας: i) Από
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/2013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m=0.1 Kg κινείται σε οριζόντιο δάπεδο ευθύγραμμα με την
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m=0.1 Kg κινείται σε οριζόντιο δάπεδο ευθύγραμμα με την
Honda Mobility MOBILITY
 Υβριδική Τεχνολογία Honda Εισηγητής: Νίκος Ξυδιάς Τεχνικός Εκπαιδευτής Honda 1 Honda Mobility MOBILITY 3 3 To Όραµα της Honda Επιθυµούµε να είµαστε µία Εταιρία την Ύπαρξη της οποίας θέλει η Κοινωνία (we
Υβριδική Τεχνολογία Honda Εισηγητής: Νίκος Ξυδιάς Τεχνικός Εκπαιδευτής Honda 1 Honda Mobility MOBILITY 3 3 To Όραµα της Honda Επιθυµούµε να είµαστε µία Εταιρία την Ύπαρξη της οποίας θέλει η Κοινωνία (we
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 10//10/01 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας 1 Kg βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας κλίσης 45º. Μεταξύ
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 10//10/01 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας 1 Kg βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας κλίσης 45º. Μεταξύ
Ασκήσεις υναµικής 6 η ενότητα: Eπίπεδη κίνηση στερεών σωµάτων: υνάµεις και επιταχύνσεις
 Ασκήσεις υναµικής 6 η ενότητα: Eπίπεδη κίνηση στερεών σωµάτων: υνάµεις και επιταχύνσεις 1. Η ράβδος µάζας 7-kg ΒC ενώνει ένα δίσκο (µε κέντρο το Α) µε στρόφαλο CD όπως δείχνει το σχήµα. Γνωρίζοτας ότι
Ασκήσεις υναµικής 6 η ενότητα: Eπίπεδη κίνηση στερεών σωµάτων: υνάµεις και επιταχύνσεις 1. Η ράβδος µάζας 7-kg ΒC ενώνει ένα δίσκο (µε κέντρο το Α) µε στρόφαλο CD όπως δείχνει το σχήµα. Γνωρίζοτας ότι
ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης
 ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 218-219 ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης ΘΕΜΑ 1 Διάρκεια εξέτασης 2 ώρες Υλικό σημείο κινείται ευθύγραμμα πάνω στον άξονα x με ταχύτητα,
ΕΞΕΤΑΣΕΙΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 218-219 ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ Διδάσκοντες: Βαρσάμης Χρήστος, Φωτόπουλος Παναγιώτης ΘΕΜΑ 1 Διάρκεια εξέτασης 2 ώρες Υλικό σημείο κινείται ευθύγραμμα πάνω στον άξονα x με ταχύτητα,
Γιάννης Γιάκας. Συστήματα αναφοράς και μονάδες μέτρησης Γραμμικά κινηματικά χαρακτηριστικά Γωνιακά κινηματικά χαρακτηριστικά Βλητική 2/12/2013
 Γιάννης Γιάκας Ύλη προόδου Συστήματα αναφοράς και μονάδες μέτρησης Γραμμικά κινηματικά χαρακτηριστικά Γωνιακά κινηματικά χαρακτηριστικά Βλητική 1 Συστήματα Αναφοράς M.K.S. ( m, Kg, sec ) C.G.S. ( cm, gr,
Γιάννης Γιάκας Ύλη προόδου Συστήματα αναφοράς και μονάδες μέτρησης Γραμμικά κινηματικά χαρακτηριστικά Γωνιακά κινηματικά χαρακτηριστικά Βλητική 1 Συστήματα Αναφοράς M.K.S. ( m, Kg, sec ) C.G.S. ( cm, gr,
Β ΛΥΚΕΙΟΥ - ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ
 Β ΛΥΚΕΙΟΥ - ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 1. Ποια η σημασία των παρακάτω μεγεθών; Αναφερόμαστε στην κυκλική κίνηση. Α. Επιτρόχια επιτάχυνση: Β. Κεντρομόλος επιτάχυνση: Γ. Συχνότητα: Δ. Περίοδος: 2. Ένας τροχός περιστρέφεται
Β ΛΥΚΕΙΟΥ - ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 1. Ποια η σημασία των παρακάτω μεγεθών; Αναφερόμαστε στην κυκλική κίνηση. Α. Επιτρόχια επιτάχυνση: Β. Κεντρομόλος επιτάχυνση: Γ. Συχνότητα: Δ. Περίοδος: 2. Ένας τροχός περιστρέφεται
ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ. Από τη Φυσική της Α' Λυκείου
 ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ Από τη Φυσική της Α' Λυκείου Δεύτερος νόμος Νεύτωνα, και Αποδεικνύεται πειραματικά ότι: Η επιτάχυνση ενός σώματος (όταν αυτό θεωρείται
ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ Από τη Φυσική της Α' Λυκείου Δεύτερος νόμος Νεύτωνα, και Αποδεικνύεται πειραματικά ότι: Η επιτάχυνση ενός σώματος (όταν αυτό θεωρείται
ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 1 ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο 1. Aν ο ρυθμός μεταβολής της ταχύτητας ενός σώματος είναι σταθερός, τότε το σώμα: (i) Ηρεμεί. (ii) Κινείται με σταθερή ταχύτητα. (iii) Κινείται με μεταβαλλόμενη
1 ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο 1. Aν ο ρυθμός μεταβολής της ταχύτητας ενός σώματος είναι σταθερός, τότε το σώμα: (i) Ηρεμεί. (ii) Κινείται με σταθερή ταχύτητα. (iii) Κινείται με μεταβαλλόμενη
Δυναμική Μηχανών I. Μοντελοποίηση της Αλληλεπίδρασης. Συστήματος με το Περιβάλλον του
 Δυναμική Μηχανών I Μοντελοποίηση της Αλληλεπίδρασης 3 4 Συστήματος με το Περιβάλλον του 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή
Δυναμική Μηχανών I Μοντελοποίηση της Αλληλεπίδρασης 3 4 Συστήματος με το Περιβάλλον του 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή
Φυσική Β Γυμνασίου - Κεφάλαιο 2: Κινήσεις ΚΕΦΑΛΑΙΟ 2: ΚΙΝΗΣΕΙΣ. Φυσική Β Γυμνασίου
 ΚΕΦΑΛΑΙΟ 2: ΚΙΝΗΣΕΙΣ Φυσική Β Γυμνασίου Εισαγωγή Τα πάντα γύρω μας κινούνται. Στο διάστημα όλα τα ουράνια σώματα κινούνται. Στο μικρόκοσμο συμβαίνουν κινήσεις που δεν μπορούμε να τις αντιληφθούμε άμεσα.
ΚΕΦΑΛΑΙΟ 2: ΚΙΝΗΣΕΙΣ Φυσική Β Γυμνασίου Εισαγωγή Τα πάντα γύρω μας κινούνται. Στο διάστημα όλα τα ουράνια σώματα κινούνται. Στο μικρόκοσμο συμβαίνουν κινήσεις που δεν μπορούμε να τις αντιληφθούμε άμεσα.
v = 1 ρ. (2) website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Εισαγωγή στην Τεχνολογία Αυτοματισμού
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑIΟΥ & ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ. Τμήματα Ναυτιλίας και Επιχειρηματικών Υπηρεσιών & Μηχ. Αυτοματισμού ΤΕ Εισαγωγή στην Τεχνολογία Αυτοματισμού Ενότητα # 2: Μαθηματική αναπαράσταση φυσικών συστημάτων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑIΟΥ & ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ. Τμήματα Ναυτιλίας και Επιχειρηματικών Υπηρεσιών & Μηχ. Αυτοματισμού ΤΕ Εισαγωγή στην Τεχνολογία Αυτοματισμού Ενότητα # 2: Μαθηματική αναπαράσταση φυσικών συστημάτων
NISSAN. e-nv200 EVALIA
 NISSAN e-nv200 EVALIA 40-60 min* ΤΑΧΕΙΑ ΦΟΡΤΙΣΗ ΑΥΤΟΝΟΜΙΑ ΜΙΚΤΟΣ ΚΥΚΛΟΣ 200 KM ΚΥΚΛΟΣ ΠΟΛΗΣ 301 KM (ΕΓΚΡΙΣΗ ΤΥΠΟΥ WLTP) 7H 30min WALLBOX 21H 30min ΦΟΡΤΙΣΗ ΣΕ ΟΙΚΙΑΚΗ ΠΡΙΖΑ *Ο χρόνος εξαρτάται από τις συνθήκες
NISSAN e-nv200 EVALIA 40-60 min* ΤΑΧΕΙΑ ΦΟΡΤΙΣΗ ΑΥΤΟΝΟΜΙΑ ΜΙΚΤΟΣ ΚΥΚΛΟΣ 200 KM ΚΥΚΛΟΣ ΠΟΛΗΣ 301 KM (ΕΓΚΡΙΣΗ ΤΥΠΟΥ WLTP) 7H 30min WALLBOX 21H 30min ΦΟΡΤΙΣΗ ΣΕ ΟΙΚΙΑΚΗ ΠΡΙΖΑ *Ο χρόνος εξαρτάται από τις συνθήκες
ΥΠΟΛΟΓΙΣΤΙΚΗ ΜΕΛΕΤΗ ΤΗΣ ΧΩΡΟ-ΧΡΟΝΙΚΗΣ ΑΠΟΚΡΙΣΗΣ ΤΑΛΑΝΤΟΥΜΕΝΩΝ ΗΛΕΚΤΡΟΧΗΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΕ ΔΙΑΜΟΡΦΩΣΕΙΣ ΔΥΟ ΚΑΙ ΤΡΙΩΝ ΗΛΕΚΤΡΟΔΙΩΝ
 ΥΠΟΛΟΓΙΣΤΙΚΗ ΜΕΛΕΤΗ ΤΗΣ ΧΩΡΟ-ΧΡΟΝΙΚΗΣ ΑΠΟΚΡΙΣΗΣ ΤΑΛΑΝΤΟΥΜΕΝΩΝ ΗΛΕΚΤΡΟΧΗΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΕ ΔΙΑΜΟΡΦΩΣΕΙΣ ΔΥΟ ΚΑΙ ΤΡΙΩΝ ΗΛΕΚΤΡΟΔΙΩΝ Παναγιώτης Σταματόπουλος, Αντώνης Καραντώνης Τομέας Επιστήμης και Τεχνικής
ΥΠΟΛΟΓΙΣΤΙΚΗ ΜΕΛΕΤΗ ΤΗΣ ΧΩΡΟ-ΧΡΟΝΙΚΗΣ ΑΠΟΚΡΙΣΗΣ ΤΑΛΑΝΤΟΥΜΕΝΩΝ ΗΛΕΚΤΡΟΧΗΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΕ ΔΙΑΜΟΡΦΩΣΕΙΣ ΔΥΟ ΚΑΙ ΤΡΙΩΝ ΗΛΕΚΤΡΟΔΙΩΝ Παναγιώτης Σταματόπουλος, Αντώνης Καραντώνης Τομέας Επιστήμης και Τεχνικής
ΗΛΕΚΤΡΟΝΙΚΑ ΙΣΧΥΟΣ ΗΜΥ 444
 ΗΛΕΚΤΡΟΝΙΚΑ ΙΣΧΥΟΣ ΗΜΥ 444 ΕΛΕΓΧΟΣ ΚΙΝΗΤΗΡΩΝ DC ΚΑΙ AC ΣΥΣΤΗΜΑΤΑ ΑΔΙΑΛΕΙΠΤΗΣ ΠΑΡΟΧΗΣ Δρ Ανδρέας Σταύρου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τα Θέματα
ΗΛΕΚΤΡΟΝΙΚΑ ΙΣΧΥΟΣ ΗΜΥ 444 ΕΛΕΓΧΟΣ ΚΙΝΗΤΗΡΩΝ DC ΚΑΙ AC ΣΥΣΤΗΜΑΤΑ ΑΔΙΑΛΕΙΠΤΗΣ ΠΑΡΟΧΗΣ Δρ Ανδρέας Σταύρου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τα Θέματα
ΤΑΛΑΝΤΩΣΗ ΗΛΕΚΤΡΙΚΟΥ ΦΟΡΤΙΟΥ ΣΕ ΚΕΚΛΙΜΕΝΟ ΕΠΙΠΕΔΟ
 A A N A B P Y T A ΡΑΛΛΟΥ ΦΑΣΟΥΡΑΚΗ (Β4) ΜΑΡΤΙΟΣ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 9 5 ΤΑΛΑΝΤΩΣΗ ΗΛΕΚΤΡΙΚΟΥ ΦΟΡΤΙΟΥ ΣΕ ΚΕΚΛΙΜΕΝΟ ΕΠΙΠΕΔΟ Γενίκευση της άσκησης (σελ 4) του σχολικού βιβλίου Φυσικής Κατεύθυνσης Β Λυκείου
A A N A B P Y T A ΡΑΛΛΟΥ ΦΑΣΟΥΡΑΚΗ (Β4) ΜΑΡΤΙΟΣ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ 9 5 ΤΑΛΑΝΤΩΣΗ ΗΛΕΚΤΡΙΚΟΥ ΦΟΡΤΙΟΥ ΣΕ ΚΕΚΛΙΜΕΝΟ ΕΠΙΠΕΔΟ Γενίκευση της άσκησης (σελ 4) του σχολικού βιβλίου Φυσικής Κατεύθυνσης Β Λυκείου
Κεφάλαιο 6α. Περιστροφή στερεού σώματος γύρω από σταθερό άξονα
 Κεφάλαιο 6α Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Στερεό (ή άκαμπτο) σώμα Τα μοντέλα ανάλυσης που παρουσιάσαμε μέχρι τώρα δεν μπορούν να χρησιμοποιηθούν για την ανάλυση όλων των κινήσεων. Μπορούμε
Κεφάλαιο 6α Περιστροφή στερεού σώματος γύρω από σταθερό άξονα Στερεό (ή άκαμπτο) σώμα Τα μοντέλα ανάλυσης που παρουσιάσαμε μέχρι τώρα δεν μπορούν να χρησιμοποιηθούν για την ανάλυση όλων των κινήσεων. Μπορούμε
Τμήμα Ηλεκτρολόγων Μηχανικών ΕΛΕΓΧΟΣ ΤΑΧΥΤΗΤΑΣ ΣΤΟΥΣ ΕΠΑΓΩΓΙΚΟΥΣ ΚΙΝΗΤΗΡΕΣ
 Το κανονικό εύρος λειτουργίας ενός τυπικού επαγωγικού κινητήρα (κλάσης Α, Β και C) περιορίζεται κάτω από 5% για την ολίσθηση ενώ η μεταβολή της ταχύτητας πέρα από αυτό το εύρος είναι σχεδόν ανάλογη του
Το κανονικό εύρος λειτουργίας ενός τυπικού επαγωγικού κινητήρα (κλάσης Α, Β και C) περιορίζεται κάτω από 5% για την ολίσθηση ενώ η μεταβολή της ταχύτητας πέρα από αυτό το εύρος είναι σχεδόν ανάλογη του
kg(χιλιόγραμμο) s(δευτερόλεπτο) Ένταση ηλεκτρικού πεδίου Α(Αμπέρ) Ένταση φωτεινής πηγής cd (καντέλα) Ποσότητα χημικής ουσίας mole(μόλ)
 ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
15. : (4) (10) 16. 225/45 R17 91 W 17.
 ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΓΙΑ ΠΛΗΡΩΣΗ ΚΕΝΩΝ ΘΕΣΕΩΝ ΤΕΧΝΙΚΟΥ ΣΤΟ ΤΜΗΜΑ Ο ΙΚΩΝ ΜΕΤΑΦΟΡΩΝ Θέµα: ΕΙ ΙΚΟ (Τεχνολογία Αυτοκινήτων)
ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΓΙΑ ΠΛΗΡΩΣΗ ΚΕΝΩΝ ΘΕΣΕΩΝ ΤΕΧΝΙΚΟΥ ΣΤΟ ΤΜΗΜΑ Ο ΙΚΩΝ ΜΕΤΑΦΟΡΩΝ Θέµα: ΕΙ ΙΚΟ (Τεχνολογία Αυτοκινήτων)
Παρουσίαση 2 η : Αρχές εκτίμησης παραμέτρων Μέρος 1 ο
 Εφαρμογές Ανάλυσης Σήματος στη Γεωδαισία Παρουσίαση η : Αρχές εκτίμησης παραμέτρων Μέρος ο Βασίλειος Δ. Ανδριτσάνος Αναπληρωτής Καθηγητής Γεώργιος Χλούπης Επίκουρος Καθηγητής Τμήμα Μηχανικών Τοπογραφίας
Εφαρμογές Ανάλυσης Σήματος στη Γεωδαισία Παρουσίαση η : Αρχές εκτίμησης παραμέτρων Μέρος ο Βασίλειος Δ. Ανδριτσάνος Αναπληρωτής Καθηγητής Γεώργιος Χλούπης Επίκουρος Καθηγητής Τμήμα Μηχανικών Τοπογραφίας
Α3. Όταν ένα σώμα ισορροπεί, η συνισταμένη των δυνάμεων είναι α) Θετική β) Αρνητική γ) Μηδέν
 Α ΛΥΚΕΙΟΥ ΝΕΟ ΕΞΕΤΑΣΤΙΚΟ ΣΥΣΤΗΜΑ ΦΥΣΙΚΗ Τρίτη 0 Μαΐου 014 Επιμέλεια: Φροντιστήρια «ΟΜΟΚΕΝΤΡΟ ΦΛΩΡΟΠΟΥΛΟΥ» ΦΥΣΙΚΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας δίπλα
Α ΛΥΚΕΙΟΥ ΝΕΟ ΕΞΕΤΑΣΤΙΚΟ ΣΥΣΤΗΜΑ ΦΥΣΙΚΗ Τρίτη 0 Μαΐου 014 Επιμέλεια: Φροντιστήρια «ΟΜΟΚΕΝΤΡΟ ΦΛΩΡΟΠΟΥΛΟΥ» ΦΥΣΙΚΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας δίπλα
6 Εισαγωγή στα Συστήματα Ηλεκτρικής Ενέργειας
 Πρόλογος Σ το βιβλίο αυτό περιλαμβάνεται η ύλη του μαθήματος «Εισαγωγή στα Συστήματα Ηλεκτρικής Ενέργειας» που διδάσκεται στους φοιτητές του Γ έτους σπουδών του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Πρόλογος Σ το βιβλίο αυτό περιλαμβάνεται η ύλη του μαθήματος «Εισαγωγή στα Συστήματα Ηλεκτρικής Ενέργειας» που διδάσκεται στους φοιτητές του Γ έτους σπουδών του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Κεφάλαιο 10 Περιστροφική Κίνηση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 10 Περιστροφική Κίνηση Περιεχόµενα Κεφαλαίου 10 Γωνιακές Ποσότητες Διανυσµατικός Χαρακτήρας των Γωνιακών Ποσοτήτων Σταθερή γωνιακή Επιτάχυνση Ροπή Δυναµική της Περιστροφικής Κίνησης, Ροπή και
Κεφάλαιο 10 Περιστροφική Κίνηση Περιεχόµενα Κεφαλαίου 10 Γωνιακές Ποσότητες Διανυσµατικός Χαρακτήρας των Γωνιακών Ποσοτήτων Σταθερή γωνιακή Επιτάχυνση Ροπή Δυναµική της Περιστροφικής Κίνησης, Ροπή και
