Επίδραση Καταστατικού Νόμου Μεμβράνης στη Δυναμική. Συμπεριφορά Μικροφυσαλίδας Τύπου Contrast Agent σε. Περιβάλλον Υπερήχου ΔΑΛΛΑ ΠΕΤΡΟΥ
|
|
|
- Αταλάντη Θεοδοσίου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ & ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ Διπλωματική Εργασία Επίδραση Καταστατικού Νόμου Μεμβράνης στη Δυναμική Συμπεριφορά Μικροφυσαλίδας Τύπου Contrast Agent σε Περιβάλλον Υπερήχου υπό ΔΑΛΛΑ ΠΕΤΡΟΥ Υπεβλήθη για την εκπλήρωση μέρους των απαιτήσεων για την απόκτηση του Διπλώματος Μηχανολόγου Μηχανικού Βιομηχανίας 2005
2 Πανεπιστήμιο Θεσσαλίας Υπηρεσία Βιβλιοθήκης & Πληροφόρησης Ειαικη Συλλογή «Γκρίζα Βιβλιογραφία» Αριθ. Εισ.: 3511/1 Ημερ. Εισ.: Δωρεά: Ταξιθετικός Κωδικός: Συγγραφέα ΠΤ-ΜΜΒ 2005 ΔΑΛ
3 2005 Δάλλας Πέτρος Η έγκριση της διπλωματικής εργασίας από το Τμήμα Μηχανολόγων Μηχανικών Βιομηχανίας της Πολυτεχνικής Σχολής του Πανεπιστημίου Θεσσαλίας δεν υποδηλώνει αποδοχή των απόψεων του συγγραφέα (Ν. 5343/32 αρ. 202 παρ. 2).
4 Εγκρίθηκε από τα Μέλη της Τριμελούς Εξεταστικής Επιτροπής: Πρώτος Εξεταστής (Επιβλέπων) Δρ. Νικόλαος Πελεκάσης Επίκουρος Καθηγητής, Τμήμα Μηχανολόγων Μηχανικών Βιομηχανίας, Πανεπιστήμιο Θεσσαλίας Δεύτερος Εξεταστής Δρ. Βασίλειος Μποντόζογλου Καθηγητής, Τμήμα Μηχανολόγων Μηχανικών Βιομηχανίας, Πανεπιστήμιο Θεσσαλίας Τρίτος Εξεταστής Δρ. Νικόλαος Βλάχος Καθηγητής, Τμήμα Μηχανολόγων Μηχανικών Βιομηχανίας, Πανεπιστήμιο Θεσσαλίας 111
5 Ευχαριστίες Πρώτα απ' όλα, θα ήθελα να εκφράσω τις ιδιαίτερες ευχαριστίες μου στον επιβλέποντα καθηγητή μου κ. Νικόλαο Πελεκάση για την εμπιστοσύνη που έδειξε στο πρόσωπο μου, για την υπομονή και επιμονή του όπως και για την επιστημονική καθοδήγηση του. Ακόμα θα ήθελα να ευχαριστήσω τον υποψήφιο διδάκτορα Κωνσταντίνο Τσιγκλιφή για την πολύτιμη βοήθεια και το χρόνο που αφιέρωσε για την διεκπεραίωση της διπλωματικής μου εργασίας. Ευχαριστώ τους φίλους μου Άγγελο, Αντώνη, Διονύση, Ζήση, Θοδωρή, Κωστή, Πέτρο και Σπήλιο για την ηθική υποστήριξή τους και τις όμορφες στιγμές που περάσαμε αυτά τα χρόνια. Τέλος θα ήθελα να ευχαριστήσω τους γονείς μου και τον αδερφό μου, στους οποίους και αφιερώνω την παρούσα διπλωματική εργασία, για την ολόψυχη αγάπη και υποστήριξη τους όλα αυτά τα χρόνια. Δάλλας Πέτρος
6 ΕΠΙΔΡΑΣΗ ΚΑΤΑΣΤΑΤΙΚΟΥ ΝΟΜΟΥ ΜΕΜΒΡΑΝΗΣ ΣΤΗ ΔΥΝΑΜΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΜΙΚΡΟΦΥΣΑΑΙΔΑΣ ΤΥΠΟΥ CONTRAST AGENT ΣΕ ΠΕΡΙΒΑΛΛΟΝ ΥΠΕΡΗΧΟΥ ΠΕΤΡΟΣ ΔΑΛΛΑΣ Πανεπιστήμιο Θεσσαλίας, Τμήμα Μηχανολόγων Μηχανικών Βιομηχανίας, 2005 Επιβλέπων Καθηγητής: Δρ. Πελεκάσης Νικόλαος, Επίκουρος Καθηγητής Υπολογιστικής Ρευστομηχανικής Περίληψη Οι μικροφυσαλίδες τύπου Contrast Agent βρίσκουν εφαρμογή τα τελευταία χρόνια στη διαγνωστική ιατρική για να βελτιώσουν την απεικόνιση συγκεκριμένων περιοχών των έμβιων οργανισμών όπως, π.χ τα αγγεία και οι ιστοί. Χρησιμοποιούνται επίσης για την θεραπεία διαφόρων ασθενειών αφού λειτουργούν ως συστήματα μεταφοράς φαρμάκων, πρωτεϊνών και γονιδίων. Παρόλο που οι παραπάνω εφαρμογές έχουν βασιστεί σε εκτεταμένες εργαστηριακές και κλινικές μετρήσεις, υπάρχουν αρκετά αναπάντητα ερωτήματα σχετικά με τη δυναμική συμπεριφορά των μικροφυσαλίδων και. τον τρόπο που αυτές αλληλεπιδρούν με τους υπέρηχους και τους γειτονικούς ιστούς. Στην παρούσα διπλωματική εργασία γίνεται προσπάθεια προσομοίωσης της δυναμικής συμπεριφοράς της μικροφυσαλίδας, θεωρώντας σφαιροσυμμετρικές ταλαντώσεις, όταν υπόκειταί' σε διαταραχή της εξωτερικής πίεσης και η μεμβράνη που την περικλείει περιγράφεται από τους μη γραμμικούς καταστατικούς νόμους τάσεων-παραμορφώσεων Mooney-Rivlin γιο: υλικά strain-softening και Skalak για υλικά strain-hardening. Στη συνέχεια γίνεται σύγκριση των αριθμητικών αποτελεσμάτων με τα αντίστοιχα αποτελέσματα του γραμμικού καταστατικού νόμου τάσεων-παραμορφώσεων Kelvin-Voigt kol τα αποτελέσματα από τα πειράματα. Στο πλαίσιο αυτό προκύπτει η σημασία του καταστατικού νόμου της ελαστικής μεμβράνης στην δυναμική των μικροφυσαλίδων και στην αποδοτικότερη διεξαγωγή των κλινικών μετρήσεων. Τέλος, προκαταρτική σύγκριση με πειραματικές μετρήσεις δείχνει ότι η τρέχουσα μοντελοποίηση, των μικροφυσαλίδων μπορεί να περιγράφει ποιοτικά τα φαινόμενα που εμπλέκονται στην χρήση υπερήχων όμως χρειάζονται αρκετές βελτιώσεις προκειμένου να υπάρξει η δυνατότητα ποσοτικής πρόβλεψης, ιδιαίτερα για μεγάλες εντάσεις των ακουστικών διαταραχών. ν
7 Περιεχόμενα Κεφάλαιο 1 Εισαγωγή Ιστορική Αναδρομή Λειτουργία των Contrast Agents Περιορισμοί των Contrast Agents Εφαρμογές των Contrast Agents Υπάρχοντα και μελλοντικά Contrast Agents Ιδιότητες των υπερήχων Ταχύτητα διάδοσης των υπερήχων Ακουστική Αντίσταση Σκέδαση Μοντέλο ακουστικής ανάκλασης Συχνότητα Συντονισμού Βιβλιογραφική Ανασκόπηση Οργάνωση Διπλωματικής Εργασίας Κεφάλαιο 2 Μοντελοποίηση της Μικροφυσαλίδας Θεωρητική Ανάλυση Κεφάλαιο 3 Αριθμητική Μεθοδολογία και Έλεγχος Ακρίβειας Γραμμικοποίηση του προβλήματος Αριθμητική Προσέγγιση Σύγκριση των μη γραμμικών μοντέλων με την αναλυτική λύση της γραμμικής θεωρίας...31 Κεφάλαιο 4 Αποτελέσματα και Συζήτηση Η Επίδραση της Εξωτερικής Διαταραχής Η Επίδραση της Εξωτερικής Διαταραχής νόμος Mooney-Rivlin Η Επίδραση της Εξωτερικής Διαταραχής νόμος Skalak Η Επίδραση της Εξωτερικής Διαταραχής νόμος Kelvin-Voigt Η Επίδραση του Μέτρου Διάτμησης της Μεμβράνης Η Επίδραση του Μέτρου Διάτμησης της Μεμβράνης νόμος Mooney-Rivlin Η Επίδραση του Μέτρου Διάτμησης της Μεμβράνης νόμος Skalak Η Επίδραση του Μέτρου Διάτμησης της Μεμβράνης νόμος Kelvin-Voigt Η Επίδραση του Ιξώδους της Μεμβράνης Η Επίδραση του Ιξώδους της Μεμβράνης νόμος Mooney-Rivlin Η Επίδραση του Ιξώδους της Μεμβράνης νόμος Skalak Η Επίδραση του Ιξώδους της Μεμβράνης νόμος Kelvin-Voigt Η Επίδραση του Πάχους της Μεμβράνης Η Επίδραση του Πάχους της Μεμβράνης νόμος Mooney-Rivlin Η Επίδραση του Πάχους της Μεμβράνης νόμος Skalak Η Επίδραση του Πάχους της Μεμβράνης νόμος Kelvin-Voigt Η Επίδραση του Μεγέθους της Μικροφυσαλίδας Η Επίδραση του Μεγέθους της Μικροφυσαλίδας νόμος Mooney-Rivlin Η Επίδραση του Μεγέθους της Μικροφυσαλίδας νόμος Skalak Η Επίδραση του Μεγέθους της Μικροφυσαλίδας νόμος Kelvin-Voigt νι
8 4.6 Η Επίδραση του Ιξώδους και της Συμπιεστότητας του Εξωτερικού Ρευστού Η Επίδραση του Ιξώδους και της Συμπιεστότητας του Εξωτερικού Ρευστού νόμος Mooney-Rivlin Η Επίδραση του Ιξώδους και της Συμπιεστότητας του Εξωτερικού Ρευστού νόμος Skalak Η Επίδραση του Ιξώδους και της Συμπιεστότητας του Εξωτερικού Ρευστού νόμος Kelvin-Voigt Η Επίδραση του Συντελεστή b του νόμου Mooney-Rivlin Η Επίδραση του Συντελεστή c του νόμου Skalak Η Επίδραση των Παραμένουσων Τάσεων της Μεμβράνης Η Επίδραση των Παραμένουσων Τάσεων της Μεμβράνης νόμος Mooney- Rivlin Η Επίδραση των Παραμένουσων Τάσεων της Μεμβράνης νόμος Skalak Η Επίδραση των Παραμένουσων Τάσεων της Μεμβράνης νόμος Kelvin- Voigt Σύγκριση με τις Ελεύθερες Φυσαλίδες Σύγκριση με Πειραματικά Αποτελέσματα...77 Κεφάλαιο 5 Συμπεράσματα & Προτάσεις για Μελλοντική Έρευνα Παράρτημα...85 I. Βιβλιογραφία-Αναφορές...85 II. Κώδικας Κατάλογος Σχημάτων Σχήμα 2.1: Γεωμετρικά χαρακτηριστικά φυσαλίδας σε κατάσταση ισορροπίας...14 Σχήμα 3.1: Η εξωτερική ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου σε κατάσταση συντονισμού. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, pi=998 kg/m3, S =0.04 Kg/s2, S2=0.005 kg/s2,s=0.045 Kg/s2 μρο.οοι kgnt's'1, C =1500 m/s, μ5=0.6 kgor's-1, Gs=35 MPa, Rba^MO^m, δ= 15*10*9 m, Ej f=0.05, ur(t = 0)r=I = ur(t = 0)r=a^ = Σχήμα 3.2 : Η εξωτερική ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου σε κατάσταση εκτός συντονισμού. Δεδομένα προσομοίωσης: γ=1.4, PjnrT01325 Pa, ρι=998 kg/m3, si=0.04 Kg/s2, S2=0.005 kg/s2,s=0.045 Kg/s2 μρο.οοι kgnt's'1, C =1500m/s, ps=0.6 kgrrf's'1, Gs=35 MPa, Rbai=3*10'6 m, δ=15*10'9 m, Einf=0.05, ur{t = 0) r=) = ur{t = θ)^( = Σχήμα 4.1: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για emf=0.05. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgrrt's'1, Q=1500 m/s, μ$=0.6 kgrtf s'1, Gs=35 MPa, r=3*10 6m, δ=15* 10 9 m, ur(t = 0)( = = ur{t = =0, b= Σχήμα 4.2: To oscn ως συνάρτηση της εξωτερικής συχνότητας για ε,πί=2.05. Δεδομένα προσομοίωσης: γ=1.4, Pjnt= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρο.οοι kgm''s'', Ci=1500 m/s, μ5=0.6 kgm''s ', Gs=35 MPa, r=3*10 6m, 6=15*10'9m, ur(t - 0) r = ur(t - 0) f=i^ =0, b= Σχήμα 4.3: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για ειη(=4.05. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρο.οοι kgm 1s l, C =l500 m/s, μ5=0.6 kgm'1s'1, Gs=35 MPa, r=3*10'6 m, δ=15*10 9 m, ur(t = - ur{t = = 0, b=0 36 Vll Vll
9 Σχήμα 4.4: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για ε(ηί=0.05. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μρο.οοι kgnt's'1, C =1500 m/s, μ5=0.6 kgm'v, Gs=35 MPa, r=3*10'6m, δ=15*10"9 m, ur(t - 0)^ = ur{t - θ)( =0, c=l...36 Σχήμα 4.5: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για ειηί=2.05. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρρ998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v, Q=1500 m/s, μ5=0.6 kgm 1s'1, Gs=35 MPa, r=3*10'6m, δ= 15*1 O'9 m, ur{t = 0)jr= ur(t = 0)(r_R =0, c=l...37 Σχήμα 4.6: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για emf=4.05. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'ls'1, C =l500 m/s, μ5=0.6 kgm'v, Gs=35 MPa, r=3*lct6 m, δ=15*10'9 m, ur(t = θ) = uat = θ), =0, c=l...37 Σχήμα 4.7: To σ5ο,η ως συνάρτηση της εξωτερικής συχνότητας για ε!η}=0.05. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, Si=0.04 Kg/s2, S2=0.005 kg/s, μρο.οοι kgm'ls'1, C =1500m/s, μ5=0.6 kgm''s', Gs=35 MPa, r=3*10' m, δ=15*10'9ιτι, M,(' = 0Ll =Wr(^ = Lata, = Σχήμα 4.8: To osc.n ως συνάρτηση της εξωτερικής συχνότητας για ε,ηρ2.05. Δεδομένα προσομοίωσης: γ=1.4, Ρ,ηΓ= Pa, ρι=998 kg/m3, spo.04 Kg/s2, S2=0.005 kg/s, μρθ.001 kgm'v, C =1500m/s, μ5=0.6 kgm'v, Gs=35 MPa, r=3*10' m, δ=15*10'9ηι, «.ML -MIL.-o...38 Σχήμα 4.9: To osc n ως συνάρτηση της εξωτερικής συχνότητας για ειπρ4.05. Δεδομένα προσομοίωσης: γ= 1.4, P;nf= Pa, ρρ998 kg/m3, spo.04 Kg/s2, S2=0.005 kg/s, μρθ.001 kgm'v, C =1500m/s, μ5=0.6 kgm'v, Gs=35 MPa, r=3*10' m, δ=15*10'9πι, r(i = 0L= ro=0) «w =0... Σχήμα 4.10: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=35 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pj pl01325 Pa, ρρ998 kg/m3, s=0.045 Kg/s2, μρο.οοι kgm'v, Ci=1500m/s, μ5=0.6 kgm'v, r=3*l O'6 m, δ=15*10'9 m, Sjnf=2.05,.ML- 4<-o)U,-o,b-o... Σχήμα 4.11: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=70 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pjnpl01325 Pa, ρρ998 kg/m3, s=0.045 Kg/s2, μρο.οοι kgm'ls'1, C =1500m/s, μ5=0.6 kgm'v, r=3*l0'6 m, δ=15*10'9 m, ajnf=2.05,».('=ol= 4'=0L, =.b= Σχήμα 4.12: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=105 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pjnpl01325 Pa, pr998 kg/m3, s=0.045 Kg/s2, gro.ool kgm'ls'1, C =1500m/s, μδ=0.6 kgm'v, r=3*10'6 m, δ= 15*1 O'9 m, Sinf=2.05, 4' - l, - n. b= Σχήμα 4.13: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=140 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, pi=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v, C =1500 m/s, gs=0.6 kgm'v, r=3*10"6 m, δ=15*10'9 m, ajnf=2.05, I'l.. -u.l; «1. ^ - :.b 0... Σχήμα 4.14: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=35 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μρο.οοι kgm'1s'1, Ci=l500 m/s, gs=0.6 kgm'ls'1, r=3*10'6 m, δ=15*10'9 m, Sjnf=2.05, w,(i=0l=^('=ol«w =0 c=1... Σχήμα 4.15: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=70 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v, C =l500 m/s, μδ=0.6 kgm'ls'1, r=3*10'6 m, δ=15*10'9 m, ajnr=2.05, «,(ΐ = 0)(Γ=1=ΜΓ(ί = 0^=Λω = 0, c=l Vlll
10 Σχήμα 4.16: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=105 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μ,=0.001 kgm'v1, C =1500 m/s, μ5=0.6 kgm'v1, r=3*10'6 m, δ=15*10'9 m, sinf=2.05, ur(t = OL =ur(t = 0)1^ = 0, c=l Σχήμα 4.17: To osc>n ως συνάρτηση της εξωτερικής συχνότητας για Gs=140 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, Cf=1500 m/s, μ5=0.6 kgm"1s'1, r=3*10'6 m, δ=15*10'9 m, sinf=2.05, ^(' = )L= r(' = 0)Lw =0 c= Σχήμα 4.18: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=35 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, pi=998 kg/m3, si=0.04 Kg/s2, s2=0.005 kg/s2, μ,=0.001 kgm'v1, C =1500m/s, μ5=0.6 kgm'v1, r=3*10'6 m, δ=15*10'9 m, Sjnf=2.05, ur( = Li = r(' = 0)Lw = Σχήμα 4.19: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=70 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, si=0.04 Kg/s2, s2=0.005 kg/s2, μρο.οοι kgm'v1, Ci=1500m/s, μ5=0.6 kgm'1s'1, r=3*10'6 m, δ=15*10'9 m, Sjnf=2.05, ur(t = 0 L =M,(' = 0La/ra, = Σχήμα 4.20: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=105 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, ρ(=998 kg/m3, S]=0.04 κε/s2, s2=0.005 kg/s2, μρο.οοι kgm'v1, C =1500m/s, μ5=0.6 kgm'1s'1, r=3*10'6 m, δ=15*10' m, 8j f=2.05, = 45 Σχήμα 4.21: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=140 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, ρρ998 kg/m3, Si =0.04 κε/s2, s2=0.005 kg/s2, μρο.οοι kgm'v1, Ci=1500m/s, μ5=0.6 kgm'ls'1, r=3*10'6 m, δ=15*10' m, 8jnf=2.05, «,(' = 0L= r(' = 0)U, = Σχήμα 4.22: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5=0.6 kgm'v1. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, s=0.045 Kg/s, μι=0.001 kgm'v1, C =l 500 m/s, Gs=35 MPa, r=3*10'6m, δ=15*10'9 m, 8inf=2.05, wr(/ = 0) f=i =i/r(i = 0j =0, b= Σχήμα 4.23: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5= 1.6 kgm'v1. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, pi=998 kg/m3, s=0.045 Kg/s, μι=0.001 kgm'1s'1, C =1500 m/s, Gs=35 MPa, r=3*10'6m, δ=15*10'9 m, είη1=2.05,.('=0l=.('=0l, =. >» Σχήμα 4.24: To Osc>n ως συνάρτηση της εξωτερικής συχνότητας για μ5=2.6 kgm'v1. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, s=0.045 Kg/s, μρθ.001 kgm'v1, Ci=l500 m/s, Gs=35 MPa, r=3*10'6m, δ=15*10'9 m, ειηί=2.05,,(' = 0)1, = 0,b Σχήμα 4.25: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5=3.6 kgm'v1. Δεδομένα προσομοίωσης: γ=1.4, Pinf=l Pa, pi=998 kg/m3, s=0.045 Kg/s, μι=0.001 kgm"is'1, C =l500 m/s, Gs=35 MPa, romo^m, δ=15*10'9 m, 8mf=2.05, ur if = 0)L = «, (f = Oj,.^ = 0, b= Σχήμα 4.26: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5=0.6 kgm'ls'1. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μρο.οοι kgm'v1, Ci=1500 m/s, Gs=35 MPa, r=3*10'6 m, δ=15*10'9 m, είη(=2.05, ur(t = = ur(t = θ) = 0, c=l...48 Σχήμα 4.27: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5=1.6 kgm'ls'1. Δεδομένα προσομοίωσης: γ=1.4, Pj f= Pa, pi=998 kg/m3, s=0.045 Kg/s, μι=0.001 kgm'ls'1, Q=1500 m/s, Gs=35 MPa, r=3*10'6m, δ=15*10'9 m, είηι=2.05,»,(< "L -0.C IX
11 Σχήμα 4.28: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για us=2.6 kgm'ls'1. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρ,=998 kg/m3, s=0.045 Kg/s, μρο.οοι kgm'v1, C =1500 m/s, Gs=35 MPa, r=3*10'6m, δ=15*10'9 m, είη(=2.05, Ur (* = L = Ur( = 0U, = 0 C= Σχήμα 4.29: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5=3.6 kgnt's'1. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρρ998 kg/m3, s=0.045 Kg/s2, μρο.οοι kgm'1s'1, Ci=l500 m/s, Gs=35 MPa, r=3*10'6m, δ=15*10'9 m, είη(=2.05, =Ur(t = )Lta, =0 C= Σχήμα 4.30: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5=0.6 kgm'ls'1. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, ρι=998 kg/m3, si=0.04 Kg/s2, s2=0.005 kg/s2, μρθ.001 kgnt's'1, Ci=1500 m/s, Gs=35 MPa, r=3*10'6m, δ= 15*1 O'9 m, 8jnf=2.05, ur(i = 0L = «,(' = 0)^ Σχήμα 4.31: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5=1.6 kgm'ls 1. Δεδομένα προσομοίωσης: γ=1.4, Pinf=l01325 Pa, ρι=998 kg/m3, si=0.04 Kg/s2, s2=0.005 kg/s2, μρθ.001 kgnt s'1, C =1500 m/s, Gs=35 MPa, r=3*10'6m, δ=15*10'9 m, 8jnf=2.05, ^ = 0L =Ur(t = 01=αω = Σχήμα 4.32: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5=2.6 kgm'1s'1. Δεδομένα προσομοίωσης: γ=1.4, Pinf=l01325 Pa, pi=998 kg/m3, si=0.04 Kg/s2, s2=0.005 kg/s2, μρθ.001 kgnt's'1, Ci=l 500 m/s, Gs=35 MPa, r=3*10'6m, δ= 15*1 O'9 m, Sjnf=2.05, r(f = 0j^ =ur(t = 0\=aM = Σχήμα 4.33: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5=3.6 kgnt's'1. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, si =0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm'ls'1, C =l 500 m/s, Gs=35 MPa, r=3*10'6m, δ=15*10'9 m, ainf=2.05, Σχήμα 4.34: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=15* ΙΟ'9. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm'ls'1, C =l500 m/s, μδ=0.6 kgnt's'1, Gs=35 MPa, r=3*10'6m, 8inp2.05, ur(t - 0)jr=i = ur(t = θ) r=r =0, b= Σχήμα 4.35: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=35* ΙΟ'9. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'ls'1, Ci=1500 m/s, μ5=0.6 kgnt's'1, Gs=35 MPa, r=3*10'6m, Sjnf=2.05, ur(t = 0) r=1 = ur(t = θ)(r=r =0, b= Σχήμα 4.36: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=55* ΙΟ'9. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgnt's'1, Ci=l500 m/s, gs=0.6 kgm'is'1, Gs=35 MPa, r=3*10'6m, 8jnf=2.05, ur(t = 0)(f=1 = ur(t = θ) r=r =0, b= Σχήμα 4.37: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=75* 10'9. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, pf=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm''s'', Q=1500 m/s, μ8=0.6 kgnt's'1, Gs=35 MPa, r=3*10'6m, 8jnf=2.05,H,.(i = 0)jr ] = ur(t = 0) r = = 0, b= Σχήμα 4.38: To ascn ως συνάρτηση της εξωτερικής συχνότητας για δ=15* ΙΟ'9. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm'ls'1, Ci=1500 m/s, μ5=0.6 kgnt's'1, Gs=35 MPa, r=3*10'6m, Sjnf=2.05, ur{t = 0) r=l = ur(t = 0) r=/?w =0,c=l Σχήμα 4.39: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=35* ΙΟ'9. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'1s'1, Ci=l500 m/s, μ5=0.6 kgnt's'1, Gs=35 MPa, r=3*10'6m, 8mf=2.05, ur(t = 0)jr= = u\t = θ) Γ=Λ =0, c=l x
12 Σχήμα 4.40: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=55* ΙΟ'9. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm''s, C,=1500 m/s, μ5=0.6 kgm'v, Gs=35 MPa, r=3*10'6m, ajnf=2.05, ur(t = 0))r=i = ur(t - 0)^ = 0,c=l Σχήμα 4.41: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=75* ΙΟ'9. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μρο.οοι kgm''s'', Ci=1500 m/s, μ5=0.6 kgm'v1, Gs=35 MPa, r=3*10'6m, sinf=2.05, ur(t = 0))r=i = ur(t = 0) r R =0,c=l...55 Σχήμα 4.42: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=15* ΙΟ'9 m. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρ,=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μ,=0.001 kgm'ls'1, Ci=1500m/s, μδ=0.6 kgm'v, Gs=35 MPa, r=3*10'6m, Sjnf=2.05, K(t = 0l=i=ur{t = 0l_^= Σχήμα 4.43: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=35* ΙΟ'9 m. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, ρι=998 kg/m3, si=0.04 Kg/s2, S2=0.005 kg/s2, μρο.οοι kgm'1s'1, Ci=1500m/s, μ5=0.6 kgm'v, Gs=35 MPa, r=3*10'6m, Sjnf=2.05, U^ = L =ur(t = 0l am = Σχήμα 4.44: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=55* ΙΟ'9 m. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, ρι=998 kg/m3, si=0.04 Kg/s2, S2=0.005 kg/s2, μι=0.001 kgm'v1, C =1500m/s, μ5=0.6 kgm'v, Gs=35 MPa, r=3*10'm, Sjnf=2.05, I'=!'L: = >(' ">. "...57 Σχήμα 4.45: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για δ=75* ΙΟ'9 m. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρι=998 kg/m3, sj=0.04 Kg/s2, S2=0.005 kg/s2, μρο.οοι kgm'v1, Ci=1500m/s, μ5=0.6 kgm''s', Gs=35 MPa, r=3*10' m, ε,ηί=2.05, >(' = L = 4' = i =...57 Σχήμα 4.46: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για r=3* ΙΟ'6 m. Δεδομένα προσομοίωσης: γ=1.4, P nf=l01325 Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρο.001 kgm'1s'1, Ci=l 500 m/s, Gs=35 MPa, μ5=0.6 kgm'1s'1, δ=15*1 O'9 m, aj f=2.05, urit = 0) r=1 =vr{t = θ) Γ=Λω = 0, b= Σχήμα 4.47: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για r=5* ΙΟ'6 m. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, C =1500 m/s, Gs=35 MPa, μδ=0.6 kgm'1s'1, δ=τ5*10'9 m, Sjnf=2.05, Ur(( = θ) Γ=1 =urii = θ) Γ=Λω = 0, b= Σχήμα 4.48: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για r=7* ΙΟ'6 m. Δεδομένα προσομοίωσης: γ=1.4, P nf= Pa, ρρ998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm'ls'1, C =1500 m/s, Gs=35 MPa, gs=0.6 kgm'1s'1, δ= 15*1 O'9 m, ainf=2.05, Ur{1 = 0) r=i =Urit = θ)(γ=λω 0 J b= Σχήμα 4-49: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για r=3* 10'6 m. Δεδομένα προσομοίωσης: γ=1.4, Pjnpl01325 Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm'ls'1, C =1500 m/s, Gs=35 MPa, μ5=0.6 kgm'ls'1, δ=15*10'9 m, Sjnf=2.05, = 0)Γ=1 =«,(' = 0 Γ=Λω =0,c=l Σχήμα 4.50: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για r=5* ΙΟ'6 m. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm'ls'1, Ci=l 500 m/s, Gs=35 MPa, gs=0.6 kgm'1s'1, δ=15*1 O'9 m, ainf=2.05, «,('=0)L =Ur(t = =0,C= Σχήμα 4.51: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για r=7* 10'6 m. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, pi=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm 1s'1, C =1500 m/s, Gs=35 MPa, μ5=0.6 kgm'1s'1, δ= 15*1 O'9 m, ajnt=2.05, ur{t = 0)(r=) = ur(t = O) = 0, c=l...60 XI
13 Σχήμα 4.52: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για r=3* 10'6 m. Δεδομένα προσομοίωσης: γ=1.4, Pinf=l01325 Pa, ρ,=998 kg/m3, sp=0.04 Kg/s2, s2=0.005 kg/s2, μ,=0.001 kgm''s'', Ci=1500 m/s, Gs=35 MPa, μ5=0.6 kgm'v1, 5=15*1 O'9 m, smf=2.05, r(t = L. = r(t = Σχήμα 4.53: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για r=5* 10 6 m. Δεδομένα προσομοίωσης: γ=1.4, Pinf=l Pa, ρ,=998 kg/m3, Si =0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm ls'1, C =l 500 m/s, Gs=35 MPa, μ5=0.6 kgm'v1, δ= 15*1 O'9 m, sinf=2.05, r(i = ol = = Σχήμα 4.54: To σβο,ηως συνάρτηση της εξωτερικής συχνότητας για r=7* ΙΟ'6 m. Δεδομένα προσομοίωσης: γ=1.4, Pinf=l01325 Pa, ρι=998 kg/m3, si =0.04 Kg/s2, s2=0.005 kg/s2, μρθ.001 kgm'v1, Ci=l 500 m/s, Gs=35 MPa, μ5=0.6 kgm'v1, 5=15*1 O'9 m, Sjnf=2.05, M,(' = L, =»,(* = 0 r=aw ~ Σχήμα 4.55: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για νερό (C =l 500 m/s, μρθ.001 kgm'v1). Δεδομένα προσομοίωσης: γ=1. 4, Pinf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, r=3* 1 O'6 m, Gs=35 MPa, μ5=0.6 kgm' s'1, δ= 15*1 O'9 m, Sjnf=2.05, ur{t = i=1 =ur(t = ),_J*W = 0 b= Σχήμα 4.56: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για αίμα (C =500 m/s, μι=0.004 kgm'v1). Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, pi=998 kg/m3, s=0.045 Kg/s2, i=3*10' m, Gs=35 MPa, μ5=0.6 kgm'v1, δ=15*1 O'9 m, Sjnf=2.05, «,(^0L=^(i = 0UM=0>b= Σχήμα 4.57: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για νερό (C =l 500 m/s, μι=0.001 kgm'v1). Δεδομένα προσομοίωσης: γ=1.4, Ρ,ρ Pa, pi=998 kg/m3, s=0.045 Kg/s2, r=3*10'6m, Gs=35 MPa, μ$=0.6 kgm'v1, δ=15* 10'9 m, είη{=2.05, Ur( = L = Ur( = 01=«Λ =» C= Σχήμα 4.58: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για αίμα (C =500 m/s, μι=0.004 kgm'1s'1). Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, -1-1 r=3*10 m, Gs=35 MPa, μ$=0.6 kgm's 5=15*10 m, Sjnf=2.05, < (' = 0)L = «,(* = 0] = 0, c=l Σχήμα 4.59: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για νερό (C =l 500 m/s, μι=0.001 kgm'1s'1). Δεδομένα προσομοίωσης: γ=1.4, Pm(= Pa, ρι=998 kg/m3, si=0.04 Kg/s2, s2=0.005 kg/s2, α=3* 10'6 m, Gs=35 MPa, μ5=0.6 kgm-'s'1, 5=15*1 O'9 m, 8jnf=2.05,Mr(i = 0)r=l =ur(t = 0) r=^ = Σχήμα 4.60: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για αίμα (C =500 m/s, μι=0.004 kgm'v1). Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, a=3*10'6 m, Gs=35 MPa, μ5=0.6 kgm-'s'1, δ=15*10'9 m, είηί=2.05, = = r(' = 0)Lw = Σχήμα 4.61: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για b=0. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, C =1500 m/s, Gs=35 MPa, μδ=0.6 kgm"1s'1, 5=15*1 O'9 m, Sjnf=2.05, ur(t = θ)( =] =ur(t = θ) r=r = 0, r=3* 1 O'6 m Σχήμα 4.62: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για b=0.5. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, pi=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm' s'1, C =l500 m/s, Gs=35 MPa, μ5=0.6 kgm-'s'1, 5=15*1 O'9 m, smf=2.05, = 0)L = ur(t = 1=Λω = 0, r=3*10'6 m Σχήμα 4.63: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για b=l. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l Pa, pi=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm-'s-1, C =l500 m/s, Gs=35 MPa, μ5=0.6 kgm-'s'1, δ=15*1 O'9 m, εΐηΐ=2.05, «,(' = 0)L =Ur(t = 0L*W = 0 > i^3*10'
14 Σχήμα 4.64: To oscn ως συνάρτηση της εξωτερικής συχνότητας για c=l. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρρ998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm'v, C =1500 m/s, Gs=35 MPa, μ5=0.6 kgm''s'', 5=15*1 O'9 m, ajnf=2.05, uxf = 0i=1 = A* = \=Ru = 0, r=3*10'6 m Σχήμα 4.65: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για c=5. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, pi=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'1s'1, C =1500 m/s, Gs=35 MPa, μ5=0.6 kgm'v, 5=15*1 O'9 m, Sjnf=2.05, UA* = 0 r=1 = "A* = θ Γ=Λω = 0, r=3*10'6 m Σχήμα 4.66: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για c=10. Δεδομένα προσομοίωσης: γ=1.4, Pinf=l01325 Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v, Ci=l500 m/s, Gs=35 MPa, μ5=0.6 kgm'v, 5=15*10 9 m, Sjnt=2.05, Ur(t = 0) r=1 = «,(* = = 0 r=3*10'6 m Σχήμα 4.67: Η ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη εκτός συντονισμού. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, pi=998, kg/m, s=0.045 Kg/s2, μρθ.001 kgm'v, C =1500m/s, μρθ.6 kgm''s'', Gs=35 MPa, r=3*10'6m, 5=15*1 O'9 m, a,np0.05,b= Σχήμα 4.68: Η ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη σε συντονισμό. Δεδομένα προσομοίωσης: γ=1.4, Pj f= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm'v, C =1500 m/s, μ5=0.6 kgm'1s'1, Gs=35 MPa, r=3*10'6m, δ=15*10'9 m, ainf=0.05,b= Σχήμα 4.69: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm'v, C =1500 m/s, a=3*10'6 m, Gs=35 MPa, μ5=0.6 kgm'ls'1, δ=15*10 9 m, ajnf=2.05, b= Σχήμα 4.70: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ=1.4, Pinpl01325 Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm'ls'1, C =1500 m/s, α=3*10'6 m, Gs=35 MPa, gs=0.6 kgm'v, 5=15*1 O'9 m, είη(=2.05, b= Σχήμα 4.71: To osc, ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm' s'', Ci=1500 m/s, a=3*10'6 m, Gs=35 MPa, μ5=0.6 kgm'1s'1, δ=15*10'9 m, ainf=2.05, b=l...71 Σχήμα 4.72: Η ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη εκτός συντονισμού. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, pi=998, kg/m, s=0.045 Kg/s2, μρθ.001 kgm'1s'1, C =l 500 m/s, μ5=0.6 kgm'ls'1, Gs=35 MPa, r=3*10'6m, δ=15*10'9 m, ainp0.05,b= Σχήμα 4.73: Η ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη σε συντονισμό. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm"1s'1, C =1500 m/s, gs=0.6 kgm'v, Gs=35 MPa, r=3*10'6m, δ=15* 10'9 m, ainp0.05,c=l...72 Σχήμα 4.74: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ=1.4, Ρ,ηρ Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm''s', Ci=1500 m/s, a=3*10'6 m, Gs=35 MPa, μ5=0.6 kgm'v, δ=15*10'9 m, ainf=2.05, c=l Σχήμα 4.75: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm''s'', C =1500 m/s, a=3*10"6 m, Gs=35 MPa, gs=0.6 kgm'ls'1, 5=15* 1 O'9 m, ajnf=2.05, c= Σχήμα 4.76: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μρθ.001 kgm''s'', C =1500 m/s, a=3*10'6 m, Gs=35 MPa, μ5=0.6 kgm'1s'1, δ=15*10'9 m, ajnf=2.05, c=
15 Σχήμα 4.77: Η εξωτερική ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη εκτός συντονισμού. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, pi=998 kg/m3, Si=0.04 Kg/s2, S2=0.005 kg/s2, μι=0.001 kgrrf's'1, C =1500 m/s, μ5=0.6 kgm'1s 1, Gs=35 MPa, a=3*10'6m, δ=15*10'9 m, είη(= Σχήμα 4.78: Η εξωτερική ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη σε συντονισμό. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, si=0.04 Kg/s2, S2=0.005 kg/s2, μι=0.001 kgmf's'1, Ci=l500 m/s, μ5=0.6 kgm 's 1, Gs=35 MPa, a=3*10'6m, δ=15*10'9 m, sinf= Σχήμα 4-79: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ=1.4, Pinr= Pa, pi=998 kg/m3, Si=0.04 Kg/s2, S2=0.005 kg/s2, μι=0.001 kgm'1s'1, CpT500 m/s, a=3*10'6 m, Gs=35 MPa, μ5=0.6 kgm'v1, δ=15*10 9 m, ainf= Σχήμα 4.80: Contrast Agent (μοντέλο Mooney-Rivlin). Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, pi=998 kg/m, s=0.045 Kg/s2, μρθ.001 kgm'1s'1, Cf=1500 m/s, a=3*10'6 m, Gs=35 MPa, μ5=0.6 kgmv, δ=15*10'9 m, einf=1.0, ur(t = 0) r=ur(t = 0) r_s = 0, b= Σχήμα 4.81: Contrast Agent (μοντέλο Skalak). Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l01325 Pa, pi=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, C =1500 m/s, a=3*10'6 m, Gs=35 MPa, μ5=0.6 kgm'v1, δ=15*10'9 m, ainf=1.0, ur(t - 0)jr= =ur(t-0) r=/( = 0,c=l...76 Σχήμα 4.82: Contrast Agent (μοντέλο Kelvin-Voigt). Δεδομένα προσομοίωσης: γ=1.4, Pinf=l01325 Pa, pi=998 kg/m, Si=0.04 Kg/s2, S2=0.005 kg/s2, μρθ.001 kgm'v1, C =1500m/s, a=3*10'6 m, Gs=35 MPa, gs=0.6 kgm'ls'1, δ=15*10'9 m, Sjnf=1.0 ur(t = 0)j -ur(t = 0) r=o = Σχήμα 4.83: Ελεύθερες φυσαλίδες. Δεδομένα προσομοίωσης: γ=1.4, Pint= Pa, pi=998 kg/m3, Si=0.072 Kg/s, S2=0.0 kg/s, μι=0.001 kgm"1s'1, C =1500 m/s, a=3*10 6 m, Gs=0 MPa, μ5=0.0 kgm'1s'1, δ=0 m, 8inf= Σχήμα 4.84: Η συγκέντρωση (κ.ο.) των μικροφυσαλίδων στο πείραμα των Jean - Marie Gorce et al Σχήμα 4.85: Ο συντελεστής h (backscatter coefficient) ως συνάρτηση της εξωτερικής συχνότητας a) Παρόν αριθμητικό μοντέλο για τους τρεις καταστατικούς νόμους μεμβράνης b) Πείραμα των Jean - Marie Gorce et al,. Δεδομένα προσομοίωσης: γ=1.4, Pjnf=l Pa, pi=998 kg/m3, si=0.04 Kg/s2, S2=0.005 kg/s2, Gs=36.67 MPa, μ5= kgm'ls'1^=15*10'9 m, Einf=0.5., ur(t = 0^r=i =ur(t = 0}^ Κατάλογος Πινάκων Πίνακας 1.1: Contrast Agents διαθέσιμα ή σε στάδιο κλινικού ελέγχου (Πηγή: Frinking et al., 2000)...6 Πίνακας 1.2: Ταχύτητα διάδοσης διαμηκών υπερήχων και ακουστική αντίσταση διαφόρων μέσων σε θερμοκρασία δωματίου και ατμοσφαιρική πίεση (Πηγή: (Repacholi,1985; Shung, 1992 and Pose, 1979)... 7 Πίνακας 1.3: Συμπιεστότητες και πυκνότητες για νερό και τρία αέρια των μικροφυσαλίδων που χρησιμοποιούνται εκτενώς (Πηγή: Shung, 1992)... 9 XIV
16 Κεφάλαιο Ιο Εισαγωγή Κεφάλαιο 1 Εισαγωγή Η μελέτη των μη προσιτών οργάνων του ανθρώπινου σώματος αποτελούσε πάντοτε πρόκληση για τους ιατρούς, τους επιστήμονες και αργότερα τους σχεδιαστές εμπορικών συσκευών. Η ανακάλυψη των ακτινών x στα τέλη του δεκάτου ενάτου αιώνα φάνηκε να είναι προς στιγμή το απόλυτο όργανο για τη μελέτη αυτή. Όμως, παρόλα αυτά, έγινε φανερό ότι η ραδιογραφία με ακτίνες χ είχε καταστροφικά αποτελέσματα στους ιστούς λόγω της ιονίζουσας ακτινοβολίας. Σήμερα, αν και οι ακτίνες x είναι περισσότερο ασφαλείς και εφαρμόζονται με μεγαλύτερη τεχνογνωσία, συνεχίζουν να προσδίδουν το ίδιο είδος ραδιενέργειας και να αποτελούν ρίσκο για την υγεία όπως στα προηγούμενα χρόνια. Την τελευταία δεκαετία οι διαγνωστικές εφαρμογές με χρήση υπερήχων έχουν γίνει ιδιαίτερα δημοφιλείς επειδή, μεταξύ άλλων, οι υπέρηχοι είναι περισσότερο ασφαλείς και λιγότερο δαπανηροί ως εφαρμογή από τις ακτίνες χ. Η διαγνωστική με χρήση υπερήχων εξελίχθηκε σε μια ιδιαίτερα επιτυχημένη μέθοδο της διαγνωστικής ιατρικής επειδή μπορεί να παρέχει, σε πραγματικό χρόνο, απεικονίσεις των ιστών και της ροής του αίματος χωρίς τη χρήση ιονίζουσας ακτινοβολίας. Συνήθως χρησιμοποιεί συχνότητες εύρους 1-10ΜΗζ, η χρήση των οποίων στην ιατρική αποτελεί πλέον μια σημαντική τεχνική διάγνωσης και θα συνεχίσει να παίζει σπουδαίο ρόλο στο μέλλον [ 1 ]. Ωστόσο, οι απεικονίσεις που δίνουν οι υπέρηχοι δεν έχουν σαφείς αντιθέσεις και μερικές φορές οι περιοχές που απεικονίζονται καλύπτονται από τις σκιές των ιστών. Το πρόβλημα αυτό μπορεί να επιλυθεί με τη χρήση μικροφυσαλίδων τύπου Contrast Agent. Οι μικροφυσαλίδες τύπου Contrast Agent που χρησιμολοιούνται στη διαγνωστική ιατρική περιέχουν αργής διάχυσης αέριο το οποίο είναι συνήθως διαλυτό στο αίμα και περιβάλλεται από εξωτερικό περίβλημα που παρουσιάζει ελαστικές ιδιότητες. Το περίβλημα αυτό αποτρέπει τη γρήγορη διάλυση των μικροφυσαλίδων κατά τη διάρκεια της εφαρμογής τους και επιτρέπει τη μεταφορά τους στο επιθυμητό σημείο δράσης χωρίς αλλοιώσεις [2], Ωστόσο τα νεότερα μοντέλα μικροφυσαλίδων περιέχουν αέρια με μικρή διαλυτότητα στο αίμα και έτσι αυξάνεται η διάρκεια ζωής τους. Η διάμετρος των μικροφυσαλίδων ποικίλει από 1 ως 10 μηι, γεγονός που τους επιτρέπει να διέρχονται μέσω των αγγείων, ενώ σε συνδυασμό με τον μικρό τους αριθμό ελαχιστοποιείται το ενδεχόμενο καρδιακής εμβολής. Επίσης, οι μικροφυσαλίδες εισάγονται στον οργανισμό με διάφορους τρόπους, π.χ. κάποιες δίδονται με τη μορφή ροφήματος ενώ άλλες εισάγονται ενδοφλέβια ή σε μορφή κλύσματος. Μετά την εξέταση Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 1
17 Κεφάλαιο Ιο Εισαγωγή κάποιες απορροφώνται αβλαβώς από χον οργανισμό και άλλες εκκρίνονται από τα ούρα ή από την εντερική οδό [3]. Από τα παραπάνω συμπεραίνουμε πως η εφαρμογή τους στο ανθρώπινο κυκλοφορικό σύστημα είναι ασφαλής 1.1 Ιστορική Αναδρομή Η ανακάλυψη των μικροφυσαλίδων τύπου Contrast Agent προήλθε από την τυχαία παρατήρηση του καρδιολόγου, Dr. Claude Joyner στα τέλη του 1960 [4], Ο Dr. Joyner κατά τη διάρκεια εκτέλεσης ηχο-καρδιογράμματος μεθόδου m προκειμένου να προσδιορίσει και να παρακολουθήσει την αορτική ρίζα, παρατήρησε παροδική αύξηση του υπερηχητικού σήματος έπειτα από κάθε υπερβαλβική έγχυση αλατούχου διαλύματος στην αορτή [4], Η πρώτη δημοσίευση σχετικά με την ηχο-καρδιογραφία με χρήση μικροφυσαλίδων τύπου Contrast Agent συναντάται σε ένα άρθρο το 1968 των Gramiak και Shah, όπου αναφέρεται έγχυση πράσινης βαφής ινδοκυανίνης στην καρδιά με σκοπό τη μελέτη του αυξημένου συντονισμού του αίματος που περιείχε τη βαφή [4], Επακολούθησε έρευνα από τους Gramiak και Fred Kremkau, του έδειξε ότι η βελτίωση στη μέθοδο των υπερήχων ήταν αποτέλεσμα σχηματισμού μικρών φυσαλίδων στην άκρη του καθετήρα και όχι λόγω της ίδιας της βαφής [5]. Το πρώτο υλικό που χρησιμοποιήθηκε για διάγνωση με χρήση υπερήχων ήταν αιωρήματα φυσαλίδων σε βιο-συμβατά υγρά όπως η πράσινη ινδοκυανίνη και η δεξτερόζη όπου πεπιεσμένος αέρας διασκορπιζόταν στο υγρό λίγο πριν την έγχυση του. Όμως, τα υλικά αυτά δεν μπορούσαν να αποθηκευθούν και έπρεπε να προετοιμάζονται πριν την μελέτη. Παρόλα αυτά, παρείχαν μια περιορισμένη βελτίωση της επανασκέδασης του ηχητικού σήματος [6]. Τα πιο προηγμένα υλικά που αναπτύχθηκαν συνιστούν σταθεροποιημένες μικροφυσαλίδες αποτελούμενες από χαμηλής διαλυτότητας αέρια τα οποία περιβάλλονται, είτε από σφαιρική μεμβράνη πολυμερούς που σχηματίζεται με ανάμειξη σε συνθήκες έντονης διάτμησης, είτε από λιπίδια ή άλλους σύνθετους υδρογονάνθρακες. Αυτού του είδους τα σωματίδια τροποποιούνται κατάλληλα προκειμένου να έχουν καθορισμένο στόχο, να λειτουργούν δηλαδή ως συστήματα διανομής φαρμάκων ή γονιδίων σε γονιδιακές θεραπείες και ακόμα να μπορούν να είναι θεραπευτικά μέσα που διαλύουν τους θρόμβους του αίματος. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 2 ΕΡ&Ι
18 Κεφάλαιο Ιο Εισαγωγή 1.2 Λειτουργία των Contrast Agents Τα σωματίδια αυτά βελτιώνουν σημαντικά την ακουστική επανασκέδαση του αίματος και αυτό βοηθά στην απεικόνιση των ανθρώπινων οργάνων και της ροής του αίματος, ενώ δίδουν τη δυνατότητα προσδιορισμού της θέσεως των οργάνων κατά την εφαρμογή διαγνωστικής μεθόδου με χρήση υπερήχων [7]. Η βελτίωση του επανασκεδαζόμενου σήματος οφείλεται στη συμπιεστότητα των περικλειομένων αερίων [1]. Η μικροφυσαλίδα ταλαντώνεται λόγω της διαταραχής του πεδίου της πίεσης με συγκεκριμένο πλάτος και συχνότητα, και στη συνέχεια εκπέμπει ένα σήμα πίεσης λόγω σκέδασης. Με ανάλυση του σήματος εξάγεται το φάσμα συχνοτήτων της ταλάντωσης [8]. Σε περίπτωση μικρής (γραμμικής) διαταραχής το φάσμα συχνοτήτων θα περιέχει μόνο την επιβαλλόμενη συχνότητα διαταραχής, ενώ σε περίπτωση που η διαταραχή είναι μεγάλη το φάσμα θα περιέχει και άλλες συχνότητες διαταραχής (υποαρμονικές ή υπεραρμονικές). Με τον τρόπο αυτό γίνεται η ταυτοποίηση του συγκεκριμένου σωματιδίου. Παράλληλα σε συνθήκες συντονισμού, όπου η εξωτερική συχνότητα συμπίπτει με την ιδιοσυχνότητα ταλάντωσης της μικροφυσαλίδας, το σκεδαζόμενο σήμα της πίεσης επηρεάζεται σημαντικά, γεγονός που αυξάνει τις δυνατότητες επεξεργασίας του. 1.3 Περιορισμοί των Contrast Agents Τα σωματίδια αυτά υπόκεινται σε αρκετούς περιορισμούς προκειμένου να βελτιωθεί η αποτελεσματικότητα της μεθόδου των υπερήχων. Έτσι λοιπόν τμ contrast agents πρέπει να αποτελούνται από σωματίδια που να μην έχουν διαλυτότητα στο νερό [9]. Το μέγεθος των αγγείων του αίματος κυμαίνεται από 4 ως 8 μιη, επομένως η διάμετρος των σωματιδίων που συνιστούν τα contrast agents θα πρέπει να έχει άνω όριο τα 8μπι ώστε να τους επιτρέπει να διασχίζουν τα αγγεία και να αποτρέπεται η φραγή των τελευταίων [10]. Επίσης, τη διαταραχή της πίεσης εκτός από τις μικροφυσαλίδες την αντιλαμβάνονται και τα ανθρώπινα όργανα τα οποία έχουν δικό τους φάσμα συχνοτήτων λόγω σκέδασης. Συνεπώς θα πρέπει να είναι γνωστό ένα τμήμα του φάσματος συχνοτήτων των μικροφυσαλίδων, ώστε να μπορεί να ταυτοποιηθεί η θέση τους αλλά και η τοποθεσία του ανθρώπινου ιστού, λόγω της αντίθεσης (contrast) του σκεδαζόμενου σήματος. Για να γίνεται πιο εύκολα η ταυτοποίηση της μικροφυσαλίδας θα πρέπει το σήμα που στέλνει πίσω να είναι όσο το δυνατόν μεγαλύτερο, γεγονός που συμβαίνει Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 3
19 Κεφάλαιο Ιο Εισαγωγή στην κατάσταση συντονισμού και για σχετικά μεγάλο πλάτος της ακουστικής διαταραχής. Συνεπώς θα πρέπει να είναι γνωστή η ιδιοσυχνότητα ταλάντωσης της και το πλάτος διαταραχής περιορισμένο για να μην επηρεαστούν οι γύρω ιστοί. Οι μικροφυσαλίδες θα πρέπει επίσης να είναι χημικά σταθερές και να σχεδιάζονται έτσι ώστε η μεμβράνη τους να λειτουργεί ως εμπόδιο του ρυθμού διάχυσης του αερίου έξω από τη φυσαλίδα [9]. 1.4 Εφαρμογές των Contrast Agents Οι μικροφυσαλίδες τύπου Contrast Agent χρησιμοποιούνται ευρέως στη διαγνωστική ιατρική μέσω της μεθόδου των υπερήχων, προκειμένου να τονίσουν συγκεκριμένες περιοχές του ανθρώπινου σώματος [11], π.χ. εφαρμόζονται για την καταγραφή της τροφοδοσίας της καρδιάς με αίμα και αποτελούν εργαλείο για την πρόβλεψη καρδιακών επεισοδίων. Επίσης οι μικροφυσαλίδες μπορούν να λειτουργούν ως συστήματα μεταφοράς φαρμάκων σε προβληματικές περιοχές του ανθρώπινου σώματος [12], Σύμφωνα με αυτή τη μέθοδο, λόγω των ιδιοτήτων της μεμβράνης τους, οι μικροφυσαλίδες προσκολλώνται επιλεκτικά στα άρρωστα κύτταρα ενώ έπειτα από εφαρμογή μεγάλης διαταραχής της πίεσης καταστρέφονται και το φάρμακο μεταφέρεται στα κύτταρα αυτά. Οι μικροφυσαλίδες θα πρέπει όμως να σχεδιάζονται με τέτοια χαρακτηριστικά ώστε η διαταραχή της πίεσης και της συχνότητας να τις καταστρέφει χωρίς να επηρεάζονται οι γύρω ιστοί, αφού η μέγιστη επιτρεπόμενη τιμή πίεσης στους έμβιους οργανισμούς δεν μπορεί να ξεπερνά τα 1.6 MPa (10 bar). Μια ακόμη εφαρμογή των μικροφυσαλίδων στην ιατρική είναι η δημιουργία πόρων στην επιφάνεια των κυττάρων (sonoporation) λόγω του ροϊκού πεδίου που προκαλούν οι ταλαντώσεις τους (microsteaming). Το ροϊκό πεδίο που δημιουργείται αυξάνει την απορροφητικότητα των κυττάρων, επομένως μπορούν να μεταφερθούν σε αυτά φάρμακα, πρωτεΐνες και γονίδια με αποτέλεσμα η θεραπεία να είναι αποδοτικότερη. Στην παραπάνω εφαρμογή επειδή η απορροφητικότητα των κυττάρων σχετίζεται με το σχηματιζόμενο ροϊκό πεδίο και κατά συνέπεια με τη συχνότητα ταλάντωσης της φυσαλίδας θα πρέπει να αποτρέπεται η κατάρρευση της. Είναι απαραίτητο λοιπόν να βρεθούν για τα συγκεκριμένα φυσικά χαρακτηριστικά της μικροφυσαλίδας το παράθυρο ασφαλείας σχετικά με το πλάτος και τη συχνότητα διαταραχής της πίεσης. Τέλος, στο πλαίσιο εφαρμογών που σχετίζονται με την εξειδικευμένη μεταφορά φαρμάκων ή γονιδίων σε συγκεκριμένους ιστούς και κύτταρα του ανθρώπινου σώματος, διεξάγεται έρευνα πάνω στον σχεδίασμά του ελαστικού περιβλήματος των μικροφυσαλίδων ώστε αυτές να κατευθύνονται και να Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 4
20 Κεφάλαιο Ιο Εισαγωγή αλληλεπιδρούν με παθολογικούς ιστούς. Έτσι η ελεγχόμενη ταλάντωσή ή και ενδεχόμενη θραύση τους απελευθερώνει ουσίες με θεραπευτικές ιδιότητες ή πολύτιμο γονιδιακό υλικό για γονιδιακή θεραπεία [14]. 1.5 Υπάρχοντα και μελλοντικά Contrast Agents Οι μικροφυσαλίδες τύπου Contrast Agent έχουν αποτελέσει μία σημαντική βελτίωση στην εφαρμογή της διαγνωστικής με τη μέθοδο των υπερήχων. Περισσότερες από 10 μικροφυσαλίδες βρίσκονται σε στάδιο ανάπτυξης και αρκετές υπόκεινται σε κλινικούς ελέγχους [15]. Κάποιες από αυτές τις μικροφυσαλίδες καταγράφονται στον παρακάτω πίνακα: Όνομα Κατασκευαστής Τύπος μεμβράνης/ αερίου Κατάσταση έγκρισης υδάτινα αιωρήματα συνδυασμού εγκεκριμένο στην Levovist Schering AG μικροσωματιδίων Ευρώπη και κλινικά γαλακτόζης και παλμιτικού ελεγμένο στην Ιαπωνία οςέως και τις ΗΠΑ 2% γαλάκτωμα εγκεκριμένο στην Echogen Sonus/ Abbot δωδεκαφθοροπεντανίου Ευρώπη φωσφολιπΐδια- σταθεροποιη μένες SonoVue Bracco μικροφυασαλίδες με θειικό εγκεκριμένο σε πέντε εςαφθοριούχο αέριςι 'ι ευρωπαϊκές χώρες υπερφθοράνθρακας- ορός Optison Molecular Biosystems με μικροσφαιρίδια εγκεκριμένο στις ΗΠΑ Inc./ Mallincrodt αλμπουμίνης σιμεθικόνη - επικαλυμμένη SonoRx Bracco σελουλόζη εγκεκριμένο στις ΗΠΑ μικροφυσαλίδες ε7ηκαλυμμένες με Definity Dupont/ ImaxRx φωσφολιπίδια που εγκεκριμένο στις ΗΠΑ περιβάλλουν αέριο υπερφθοράνθρακα Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 5
21 Κεφάλαιο Ιο Εισαγωγή αέριο υπερφθοροβουτάνιο Sonazoid Nycomed περιβαλλόμενο από κλινικοί έλεγχοι υπό σταθεροποιη μένη εξέλιξη στην Ευρώπη μεμβράνη λιπιδίου Απολυμαντική μεμβράνη που περιέχει κλινικοί έλεγχοι υπό Imagent Alliance/ Schering υπερφθοροεξάνιο - εξέλιξη στις ΗΠΑ πεπιεσμένος αέρας Πολυμερές (PLGA) του Α1-700 Acusphere Incorporated περιβάλλει χαμηλό υπερφθοράνθρακα κλινικοί έλεγχοι υπό εξέλιξη στις ΗΠΑ Πίνακας 1.1: Contrast Agents διαθέσιμα ή σε στάδιο κλινικού ελέγχου (Πηγή: Frinking et ah, 2000) 1.6 Ιδιότητες των υπερήχων Η υπερηχητική ακτινοβολία συμπεριλαμβάνεται στη λίστα της μη ιονίζουσας ακτινοβολίας. Ωστόσο διαφέρει από τα άλλα είδη μη ιονίζουσας ακτινοβολίας επειδή δεν είναι κύμα ηλεκτρομαγνητικό, αλλά μηχανικό. Ως επακόλουθο τα ηχητικά κύματα, σε αντίθεση με τα ηλεκτρομαγνητικά κύματα, χρειάζονται ένα μέσο για να μπορούν να μεταδοθούν. Τα ηχητικά κύματα παράγονται από διαταραχές σε ένα υλικό μέσο, προκαλώντας ταλάντωση στα σωματίδια που το αποτελούν [16]. Ανάλογα με τις ιδιότητες του μέσου, υπάρχουν οι ακόλουθοι τρόποι διάδοσης του υπερηχητικού κύματος: διαμήκη, εγκάρσια και επιφανειακά κύματα [16]. Οι υπέρηχοι ταξινομούνται ως ηχητικά κύματα με συχνότητα μεγαλύτερη των 20 khz. Οι άνθρωποι μπορούν να ακούσουν συνήθως ηχητικά κύματα των οποίων η συχνότητα έχει εύρος από 20Ηζ ως 20kHz. Τα υπερηχητικά κύματα βρίσκονται πέραν του εύρους συχνοτήτων που αντιλαμβάνεται η ανθρώπινη ακοή. Η διαγνωστική μέθοδος με χρήση υπερήχων χρησιμοποιεί συχνότητες μεταξύ ΙΜΗζ ως ΙΟΜΗζ. Σε ρευστό με μικρή ή καθόλου αντίσταση στη διάτμηση, διαδίδονται μόνο διαμήκη κύματα [17]. Αυτό σημαίνει ότι η διαταραχή θα ακολουθήσει την κατεύθυνση της διάδοσης του κύματος. Έτσι λοιπόν τα υπερηχητικά κύματα στο αίμα και σε μαλακούς ιστούς είναι διαμήκη. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 6
22 Κεφάλαιο Ιο Εισαγωγή 1.7 Ταχύτητα διάδοσης των υπερήχων Η ταχύτητα με την οποία ο ήχος διαδίδεται σε ένα μέσο εξαρτάται από τις φυσικές ιδιότητες του μέσου [16]. Στα υγρά, η ταχύτητα εξαρτάται από την πυκνότητα και την συμπιεστότητα. Το παραπάνω εκφράζεται από την εξής σχέση : (1-1) όπου c (m/s) η ταχύτητα του ήχου, ρ (kg/m3) η πυκνότητα του μέσου και β (kg/s2-m) το μέτρο διόγκωσης του μέσου [16]. Η ταχύτητα διάδοσης του ήχου στα στερεά μπορεί να εκφραστεί από την παρακάτω σχέση: όπου c (m/s) η ταχύτητα του ήχου, ρ (kg/nt) η πυκνότητα του μέσου και G (kg/s2 m) το μέτρο ακαμψίας του μέσου [18]. Η ταχύτητα του ήχου στο αίμα είναι 1550 m/s και η ταχύτητα του ήχου στο ήπαρ είναι λίγο μεγαλύτερη, 1570 m/s [19]. Μέσο Ταχύτητα (m/s) Ακουστική Αντίσταση x ΙΟ6 (kg-mv) αέρας δεκαφθοροβουτάνιο (aapiopfc) εξαφθοριούχο θείο (αέριο SF6) υδρογόνο νερό αίμα μυοκάρδιο λίπος ήπαρ νεφρό οστό κρανίου πλεξιγκλάς Πίνακας 1.2: Ταχύτητα διάδοσης διαμηκών υπερήχων και ακουστική αντίσταση διαφόρων μέσων σε θερμοκρασία δωματίου και ατμοσφαιρική πίεση (Πηγή: (Repacholi, 1985; Shung, 1992 and Pose, 1979) Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 7
23 Κεφάλαιο Ιο Εισαγωγή 1.8 Ακουστική Αντίσταση Η ακουστική αντίσταση περιγράφεται ως ο λόγος της ακουστικής πίεσης στη σωματιδιακή ταχύτητα και δίδεται από την παρακάτω εξίσωση: Ρ pc u (1-3) όπου ζ (Pa-s/m) η ακουστική αντίσταση, ρ (Pa) η ακουστική πίεση, u (m/s) η σχετική σωματιδιακή ταχύτητα, ρ (kg/m3) η πυκνότητα του μέσου κοα. c (m/s) η ταχύτητα του ήχου στο μέσο [16]. 1.9 Σκέδαση Η σκέδαση των υπερηχητικών κυμάτων αναφέρεται στο φαινόμενο της αναδιανομής της υπερηχητικής ενέργειας από ένα προσπίπτων κύμα σε κύματα που κινούνται σε άλλες διευθύνσεις. Σε περίπτωση που υπάρχει διεπιφάνεια μεταξύ δύο μέσων, η διάδοση των υπερήχων θα επηρεαστεί δραματικά. Όταν οι υπέρηχοι συναντήσουν αυτό το όριο, κάποια από τα προσπίπτοντα κύματα θα διαβιβαστούν στο δεύτερο μέσο ενώ τα υπόλοιπα θα ανακλαστούν πίσω [20]. Ο βαθμός του διαχωρισμού θα εξαρτηθεί επομένως από την ακουστική αντίσταση των δύο μέσων. Η σκέδαση μπορεί να παράγει τόσο διάδοση παλμών όσο και σήμα μείωσης της ηχητικής εντάσεως. Επίσης η σκέδαση μπορεί να προκόψει λόγω της αλληλεπίδρασης ενός ηχητικού σήματος με ένα μικρό αντικείμενο [18] Μοντέλο ακουστικής ανάκλασης Οι μικροφυσαλίδες τύπου Contrast Agent βελτιώνουν το επανασκεδαζόμενο σήμα των υπερήχων λόγω της μεγάλης διαφοράς της ακουστικής αντίστασης ανάμεσα στη φυσαλίδα και τη μεμβράνη. Υποθέτοντας ότι η θεωρία του Raleigh περί της σκέδασης είναι ορθή και χρησιμοποιώντας την προσέγγιση του Bom, η σκεδαζόμενη υπερηχητική ένταση μπορεί να εκφραστεί ως συνάρτηση της προσπίπτουσας έντασης I, και του συντελεστή επανασκέδασης σ (1-4) Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 8
24 Κεφάλαιο Ιο Εισαγωγή όπου Is (watt/rrt) η ένταση του σκεδαζόμενου υπερηχητικού σήματος, I, (watt/m2) η ένταση του προσπίπτοντος σήματος, σ (m2) ο συντελεστής σκέδασης του επιστρεφόμενου σήματος του ανακλαστήρα και d (m) η απόσταση ανάμεσα στον μετατροπέα (transducer) και του σκεδαστή (scatterer). Ο συντελεστής σ αναφέρεται πιο αναλυτικά στο επόμενο κεφάλαιο Συχνότητα Συντονισμού Όταν οι μικροφυσαλίδες εκτίθενται σε υπερηχητικά κύματα επιδεικνύουν συμπεριφορά συντονισμού που είναι αποτέλεσμα της συμπιεστότητας και της αδράνειάς τους [21], Η συμπιεστότητα είναι αποτέλεσμα της παλμικής κίνησης του αερίου όγκου μέσα στη φυσαλίδα, που προκαλείται όταν διαταράσσεται η ακτίνα ισορροπίας της [21]. Η αδράνεια οφείλεται κυρίως στις ταλαντώσεις του περιβάλλοντος μέσου [21]. Το φαινόμενο αυτό αυξάνει αποτελεσματικά την ένταση του επιστρεφόμενου κύματος της φυσαλίδας μέχρι και τρεις τάξεις έντασης του ήχου. Μια προσέγγιση της συχνότητας συντονισμού μιας φυσαλίδας μπορεί να γίνει από την παρακάτω εξίσωση: (1-5) μβ fr (1/s) τη συχνότητα αντήχησης, r (m) την ακτίνα της φυσαλίδας, ρ (kg/m3) την πυκνότητα του περιβάλλοντος μέσου, γ (σταθερά, 1.4 για ιδανικό αέριο) το λόγο της ειδικής θερμότητας υπό σταθερή πίεση προς την ειδική θερμότητα υπό σταθερό όγκο και ρ την πίεση μέσα στη φυσαλίδα [22], Η συχνότητα συντονισμού που υπολογίζεται για μικροφυσαλίδες μεγέθους Ιμιη ως 8μιυ, βρίσκεται στο διαγνωστικό εύρος των υπερήχων. Μείγμα Συμπιεστότητα κ (πγ/ν) Πυκνότητα ρ (kg/mj) Αέρας (80% Ν2) 7.05x10' (273Κ) C4F x10'& (273Κ) sf6 7.05x10' (293Κ) Νερό 4.6x10 ' 1000 (273Κ) Πίνακας 1.3: Συμπιεστότητες και πυκνότητες για νερό και τρία αέρια των μικροφυσαλίδων που χρησιμοποιούνται εκτενώς (Πηγή: Shung,1992) Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 9
25 Κεφάλαιο Ιο Εισαγωγή 1.12 Βιβλιογραφική Ανασκόπηση Τα τελευταία χρόνια υπάρχουν αρκετές μελέτες πάνω στις μικροφυσαλίδες τύπου Contrast Agent όταν αυτές υπόκεινται σε γραμμικές διαταραχές. Το πιο διαδεδομένο μοντέλο είναι αυτό των De Jong et al [23]. που βασίζεται στην τροποποιημένη διαφορική εξίσωση Rayleigh. Plesset, Noltingk, Neppiras and Poritsky (RPNNP). Στο μοντέλο αυτό χρησιμοποιείται η καταστατική εξίσωση Kelvin-Voigt για τη συσχέτιση των τάσεων με τις παραμορφώσεις της μεμβράνης, το πάχος της μεμβράνης θεωρείται αμελητέο και οι όροι που αναφέρονται στην ιξώδη και ακουστική σκέδαση της συνολικής ενέργειας μοντελοποιούνται βάση των αποτελεσμάτων της γραμμικής ανάλυσης για ταλαντώσεις ελεύθερης φυσαλίδας [24]. Έτσι λοιπόν ισχύει: prr + -pr2 =Pe go (/Ο 1/ [rj 2σ ( 1 η + Ρ - Ρ Sn - δ, coprr ~ PAc{t) (1-6) Ρ R \R0 με R την ακτίνα της μικροφυσαλίδας σε τυχαία χρονική στιγμή t, ρ την πυκνότητα του εξωτερικού ρευστού, Ro την ακτίνα της φυσαλίδας στην κατάσταση ισορροπίας. Pgo την πίεση του αερίου μέσα στη μικροφυσαλίδα στην κατάσταση ισορροπίας, γ την πολυτροπική σταθερά του αερίου, Ρν την τάση των ατμών, Pst τη στατική πίεση του περιβάλλοντος ρευστού, σ το συντελεστή επιφανειακής τάσης, PAc τη διαταραχή της πίεσης του περιβάλλοντος ρευστού, Sp την παράμετρο που αφορά την ελαστικότητα της μεμβράνης και 6t το συνολικό συντελεστή απόσβεσης που δίνεται από τη σχέση: $=$-+**+$*+*/, ο-7) και οφείλεται στη συμπιεστότητα Srad, στο ιξώδες δνιί και στην αντίσταση στην μεταφορά θερμότητας δώ του εξωτερικού ρευστού αλλάκαι στο ιξώδες της μεμβράνης δf. Το τελευταίο μπορεί να εκφραστεί από τη σχέση: Sf δί=~1~ (1-8) πιω όπου Sf είναι παράμετρος που χαρακτηρίζει το ιξώδες της μεμβράνης, ω η γωνιακή συχνότητα της εξωτερικής διέγερσης και m = 47iR2p η μάζα του συστήματος φυσαλίδας-ρευστού. Το μοντέλο αυτό ουσιαστικά έχει προκόψει από αυτό του Church [25], θεωρώντας αμελητέο το πάχος της μεμβράνης. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Conlrasl Agent σε περιβάλλον υπερήχου 10
26 Κεφάλαιο Ιο Εισαγωγή Πρόσφατα οι Khismatullin & Nadim [26] έλαβαν υπόψη τους το ιξώδες και τη συμπιεστότητα του ρευστού καθώς και την ελαστικότητα και το ιξώδες της μεμβράνης. Για γραμμικές διαταραχές και θεωρώντας πεπερασμένο το πάχος της μεμβράνης, υπολόγισαν τις συχνότητες συντονισμού και τους συντελεστές απόσβεσης. Ο συντονισμός επέρχεται σε υψηλότερες συχνότητες διαταραχών σε σχέση με τις ελεύθερες φυσαλίδες, για δεδομένο μέγεθος, λόγω της ελαστικότητας της μεμβράνης. Μόνο το μοντέλο των De Jong et al. έχει μελετήσει αριθμητικά την επίδραση της μη γραμμικότητας της διαταραχής στη συνεισφορά των υψηλότερων αρμονικών στο φάσμα συχνοτήτων, καθώς επίσης και ότι οι υψηλότερες αρμονικές είναι αρκετά αδύναμες στις μικροφυσαλίδες σε αντίθεση με τις ελεύθερες φυσαλίδες. Στην παρούσα διπλωματική εργασία γίνεται διερεύνηση της επίδρασης της μη γραμμικής διαταραχής, των ιδιοτήτων της μεμβράνης (ελαστικότητα και ιξώδες) και του εξωτερικού ρευστού (συμπιεστότητα και ιξώδες), στο φάσμα συχνοτήτων της μικροφυσαλίδας για σφαιροσυμμετρικές ταλαντώσεις. Επίσης, μελετάται η επίδραση των παραμενουσών τάσεων της μεμβράνης στην απόκριση της μικροφυσαλίδας,. Τα παραπάνω αναφέρονται στους μη γραμμικούς καταστατικούς νόμους τάσεων - παραμορφώσεων των Mooney-Rivlin kol Skalak Οργάνωση Διπλωματικής Εργασίας Το υπόλοιπο αυτής της διπλωματικής εργασίας χωρίζεται σε τέσσερις ενότητες που καταλαμβάνουν τα Κεφάλαιο 2-5, αντίστοιχα. Συγκεκριμένα: Στο Κεφάλαιο 2 αναλύεται το πρόβλημα που αφορά τις σφαιροσυμμετρικές ταλαντώσεις της μικροφυσαλίδας. Παρουσιάζονται οι ορισμού οι παραδοχές και οι εξισώσεις που περιγράφουν το πρόβλημα. Στο Κεφάλαιο 3 αναφέρεται η αριθμητική μέθοδος που χρησιμοποιείται για την επίλυση της μη γραμμικής εξίσωσης και για την παραγωγή του φάσματος συχνοτήτων. Επίσης γίνεται έλεγχος ακρίβειας, σύγκριση με τη γραμμική θεωρία και εφαρμόζεται γραμμική ανάλυση ευσταθείας στη μη γραμμική εξίσωση για να λάβουμε το φάσμα συχνοτήτων, όταν επιβάλλονται γραμμικές διαταραχές. Στο Κεφάλαιο 4 παρουσιάζονται τα αριθμητικά αποτελέσματα με χρήση των καταστατικών μοντέλων Mooney-Rivlin για υλικά strain-softening km Skalak για υλικά strainhardening. Επίσης γίνεται σύγκριση των αποτελεσμάτων με το μοντέλο των Kelvin-Voigt καί τα πειράματα. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 1 (
27 Κεφάλαιο Ιο Εισαγωγή Στο Κεφάλαιο 5 εξάγονται συμπεράσματα όσον αφορά την επίδραση των ιδιοτήτων της μεμβράνης στη δυναμική της σφαιροσυμμετρικής ταλάντωσης της μικροφυσαλίδας και γίνονται προτάσεις για μελλοντική έρευνα. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 12
28 Κεφάλαιο 2ο Μοντελοποίηση της Μικροφυσαλίδας Κεφάλαιο 2 Μοντελοποίηση της Μικροφυσαλίδας Στο παρόν κεφάλαιο θα γίνει η ανάλυση του προβλήματος που αφορά τις σφαιροσυμμετρικές ταλαντώσεις της μικροφυσαλίδας όταν η ελαστική μεμβράνη που την περιβάλλει περιγράφεται από τους καταστατικούς νόμους Mooney-Rivlin, για υλικά strainsoftening, κα Skalak, για υλικά strain-hardening. Παρουσιάζονται λοιπόν οι περιορισμοί, οι παραδοχές και οι εξισώσεις που περιγράφουν το πρόβλημα. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου \ 3
29 Κεφάλαιο 2ο Μοντελοποίηση της Μικροφυσαλίδας 2.1 Θεωρητική Ανάλυση Θεωρούμε αρχικά ότι μικροφυσαλίδα (Contrast Agent) εξωτερικής ακτίνας R=Rbai βρίσκεται σε ισορροπία μέσα σε νευτωνικό ρευστό πυκνότητας ρι, δυναμικού ιξώδους μι και στατικής πίεσης PSt (Σχήμα 1). Το ελαστο-ιξώδες υλικό της μεμβράνης θεωρείται ότι είναι ασυμπίεστο με μέτρο διάτμησης Gs και έχει συμπεριφορά νευτωνικού ρευστού με δυναμικό ιξώδες ps. Έστω ότι Runs είναι η εξωτερική ακτίνα της μικροφυσαλίδας, όταν δεν υπάρχουν παραμένουσες τάσεις στην μεμβράνη. Θα θεωρήσουμε ότι στην κατάσταση ισορροπίας υπάρχουν παραμένουσες τάσεις και ότι ur(t = θ) Γ=Λ είναι οι αντίστοιχες μετατοπίσεις που προκαλούν τις τάσεις αυτές. Τότε θα ισχύει: Κ αι=κη,+»λ' = θι^ (2-1) Στο εσωτερικό της μικροφυσαλίδας υπάρχει ιδανικό αέριο σε πίεση ισορροπίας Pg,bai> οι μεταβολές της οποίας θεωρούνται ότι γίνονται ομοιόμορφα και ακαριαία σε όλο το αέριο. Σχήμα 2-1: Γεωμετρικά χαρακτηριστικά φυσαλίδας σε κατάσταση ισορροπίας Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 14
30 Κεφάλαιο 2ο Μοντελοποίηση της Μικροφυσαλίδας Όταν διαταραχθεί η πίεση στο άπειρο τη χρονική στιγμή t = Ο : Κ (Ο = ρ [ι + ε sin(ay )], ω{ = 2πή, (2-2) όπου ε και f = 1-10 MHz το πλάτος και η συχνότητα της εξωτερικής διαταραχής, αντίστοιχα, η φυσαλίδα αρχίζει να ταλαντώνεται και να εκπέμπει σκεδαζόμενο κύμα πίεσης στο οποίο περιέχοντας εν γένει, διάφορες συχνότητες. Η ένταση (Scattering Cross Section - asc) του επιστρεφόμενου κύματος από τη μικροφυσαλίδα μπορεί να ποσοτικοποιηθεί από την παρακάτω σχέση [27]: k(r,«)dt =4πτ'^ (2-3) k* 0 όπου PAc(t) = spslsm(coft) η διαταραχή της πίεσης στο άπειρο και PSc(r,t)= P,(r,t)-Psl PAe(t) η σκεδαζόμενη πίεση μέσα στο περιβάλλον υγρό και σε απόσταση r από το κέντρο της μικροφυσαλίδας. Η ένταση αυτή, Osc, καθορίζει ουσιαστικά το πόσο δυνατό είναι το σήμα που επιστρέφει η φυσαλίδα. Προκειμένου να ταυτοποιηθούν οι διάφορες συχνότητες που εμπεριέχονται στο σήμα που εκπέμπει η μικροφυσαλίδα ορίζεται το παρακάτω μέγεθος [23]: ν (2-4) ο όπου Psc,n το πλάτος της νιοστής αρμονικής της πίεσης, σε απόσταση r από το κέντρο της μικροφυσαλίδας. Ουσιαστικά το μέγεθος αυτό δείχνει ξεχωριστά την συμμετοχή της κάθε αρμονικής στο συνολικό σήμα. Για ευκολία η σκεδαζόμενη πίεσή υπολογίζεται επάνω στην επιφάνεια της μικροφυσαλίδας. Η ταχύτητα διάδοσης της διαταραχής είναι πεπερασμένη και έστω Q, επειδή το ρευστό θεωρείται πως έχει συμπιεστότητα μακριά από τη φυσαλίδα, ενώ η ροή κοντά στη φυσαλίδα θεωρείται ασυμπίεστη. Για να ισχύει η παραπάνω υπόθεση το μήκος κύματος της διαταραχής θα πρέπει να είναι αρκετά μεγαλύτερο από την ακτίνα της φυσαλίδας. Στο πλαίσιο αυτό η μη γραμμική διαφορική εξίσωση για σφαιρική ταλάντωση φυσαλίδας μέσα σε συμπιεστό ρευστό, όπως περιγράφεται από τους Keller - Miksis [28], ισχύει στην παρούσα εργασία και δίνεται από τον τύπο: Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου J 5
31 Κεφάλαιο 2ο Μοντελοποίηση της Μικροφυσαλίδας R ' (δ R Λ RR + C.) κ 2 2C, j Ρι 1 + -*. C, P.c, dt pj (2-5) Ο - vs ', t A dr(t) D d2r{t) οπού R την ακτίνα της φυσαλιδας την τυχαία χρονική στιγμή t, R =, R = dt dt~ και Ρ, r=r η πίεση του εξωτερικού ρευστού υπολογισμένη στη διεπιφάνεια της φυσαλίδας με το υγρό. Η προσπάθεια μοντελοποίησης της μικροφυσαλίδας θα ολοκληρωθεί με τη συσχέτιση της Ρ, με την εσωτερική πίεση του αερίου Pg και τα χαρακτηριστικά της μεμβράνης. Για τον σκοπό αυτό θα θεωρήσουμε ότι η μεμβράνη έχει απειροελάχιστο πάχος, δ, υφίσταται μόνο ακτινικές μετατοπίσεις και ότι έχει συμπεριφορά ιξωδοελαστικού ρευστού που περιγράφεται από ένα εκ των δύο πιο ευρέως διαδεδομένων μη γραμμικών καταστατικών νόμων τάσεων-παραμορφώσεων, δηλαδή είτε από το μοντέλο Mooney-Rivlin είτε από το μοντέλο Skalak. Πιο πολλές λεπτομέρειες για την σημασία των παραπάνω δύο νόμων δίδονται στην εργασία των Barthes-Biesel et al., J. Fluid Mech. (2002) [29]. Ο καταστατικός νόμος των Mooney-Rivlin δίνεται από την παρακάτω σχέση [30,31]: Fmr =2Gs R -7 [l + b(e -l)] + 4M6^ (2-6) όπου e = 1 + η παραμόρφωση της μεμβράνης λόγω της ακτινικής της μετατόπισης και Runs 0<b< 1 μια σταθερά που εξαρτάται από το υλικό της μεμβράνης. Καθώς η σταθερά b τείνει στη μονάδα το υλικό μαλακώνει για την ίδιες μετατοπίσεις και ανακτάται το μοντέλο Kelvin- Voigt. Ο καταστατικός νόμος του Skalak δίνεται από την παρακάτω σχέση [29]: FSK = 2G. Γ(ΐ -c)e2 +ce6-l] + 4ps30 ^ (2-7) όπου e η παραμόρφωση της μεμβράνης λόγω της ακτινικής της μετατόπισης και Runs 0<c<oo μια σταθερά που εξαρτάται από το υλικό της μεμβράνης. Καθώς η σταθερά c μεγαλώνει οι αναπτυσσόμενες τάσεις στη μεμβράνη, για ίδιες μετατοπίσεις, μεγαλώνουν. Και οι δύο παραπάνω καταστατικοί νόμοι αφορούν την ελαστικότητα της μεμβράνης. Το ιξώδες Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 16
32 Κεφάλαιο 2ο Μοντελοποίηση της Μικροφυσαλίδας της τελευταίας, όπως φαίνεται και από τις εξισώσεις (2-6) καί (2-7), περιγράφεται με τον ίδιο τρόπο όπως και στον καταστατικό όμο Kelvin-Voigt που αναφέρεται παρακάτω. Το μοντέλο Kelvin-Voigt περιγράφει μεμβράνη στην οποία ισχύει γραμμικός καταστατικός νόμος τάσεων-παραμορφώσεων [8] και δίνεται από: =2 [Gty + M,y) (2-8) οπού r = Τ[ν«+(ν!ί)Γ] (2-9) και ί = \[γ.υ+(έ.υ)\ (2-10) Το ισοζύγιο ορθών τάσεων στη διεπιφάνεια αερίου - μεμβράνης και μεμβράνης - εξωτερικού ρευστού για τον νόμο των Mooney - Rivlin δίνεται από την παρακάτω εξίσωση: Ρ =Ρ. & ι + -Χ( ) ΓΤ r.r+f,r R (2-Π) όπου Fn συμβολίζει τις τάσεις που αναπτύσσονται πάνω στην μεμβράνη λόγω της ιξωδοελαστικής της συμπεριφοράς. δφ X (')... 4Α, 32Φ dr r=r Λ 3 dr2 r-r R (2-12) η συνιστώσα του τανυστή των ιξωδών τάσεων του εξωτερικού υγρού υπολογισμένη πάνω στην μεμβράνη (r=r) και Φ(τ,/) το δυναμικό ταχύτητας του υγρού. Από τη θεωρία της ιδανικής ροής γύρω από σφαίρα ακτίνας /?(ί), προκύπτει ότι: RR2 Φ(/%/)=-- (2-13) Επίσης σχετικά με τις μετατοπίσεις της ακτίνας, για τυχούσα χρονική στιγμή t ισχύει:»,l = Λ('Μ = (2-14) Για το αέριο θεωρούμε αδιαβατική συμπίεση - εκτόνωση, οπότε θα ισχύει η σχέση: ρ-15) Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 17
33 Κεφάλαιο 2ο Μοντελοποίηση της Μικροφυσαλίδας όπου Pgjbai, Vbai συμβολίζουν την πίεση και τον όγκο του αερίου σε συνθήκες ισορροπίας. Στην κατάσταση ισορροπίας ισχύει R = Ο, Ρ, r=r = PST οπότε για το νόμο Mooney - Rivlin η (2-11) δίνει: g,bal =Ρ + Λ ST + Rh, rrhal-ur(t = 0)1 λ G1 R, bal 1 + b R, bal v (2-16) R ḃal Rba, -Mr(/ = 0) r_. Rba! J ενώ αντίστοιχα για το νόμο Skalak παίρνουμε: P.^=P*r+ + g,bal 1 ST R bal 2 G5 R bal (1-, R, R-bal Ur Ψ ~ 0) r=r, bal J ' J Rh Rhal 11 r (t ~ 0) r=r, Bal J (2-17) Συνδυασμός των σχέσεων (2.11)-(2.16) για το νόμο Mooney - Rivlin δίνει: f R- V7 P, _R = v R j PST+ + 2Gs ^bal ^bal Rbal -Ur(t = 0) r=r(- 1 r=rw Rv 6 7 Rt 1 + b _ν R»i -,(< = 0) 2σ R R μ μ 3δ R ' R 1 R- 6 " 7 Rb, -ur(t = Q) r, )Ι 1 R -2G, b R R > _ν Rbal -Ur(t = 0) r=rbal y -1 ^ J -1 (2-18) em συνδυασμός των σχέσεων (2.11)-(2.15) και (2-17), για το νόμο Skalak αντιστοίχως, δίνει: Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου \ 8
34 Κεφάλαιο 2 ο Μοντελοποίηση της Μικροφυσαλίδας ρ I = Ri^ R Λ3, PST + + 2Gs ST ρ Ρ IV,. IV,. bal bal 2σ R R μ 3δ μ R 1 R R2 Ο-e) R. Rbal -Ur(t = 0) λ2 f V i -2G 1 R (1-c) R R + c Rbal-Ur(t=0)U J (Rba,-Ur(t=0) r; J + c R. Rba, -Ur(t=0) r., ^h*i J -1 J (2-19) Στη συνέχεια θα εφαρμόσουμε αδιαστατοποίηση στις εξισώσεις (2-18) και (2-19) του προέκυψαν από τους νόμους Mooney - Rivlin και Skalak. αντιστοίχως. Τα κατάλληλα χαρακτηριστικά μεγέθη είναι: Χαρακτηριστικό μήκος: R* = Rhal Χαρακτηριστικός χρόνος: t * =, επειδή η χρονική κλίμακα στην οποία θα αναπτυχθούν τα φαινόμενα καθορίζεται από την συχνότητα της εξωτερικής διέγερσης. Χαρακτηριστική πίεση: Ρ* = p,co2frlal Τα αδιάστατα μεγέθη που προκύπτουν είναι: P/U'R P.cOjRl, Αριθμός Reynolds εξωτερικού ρευστού: Re, = Μι Μ, Αριθμός Reynolds μεμβράνης: Res = p,u'r' p,cofr 3δμ5 3δμ5 6G. 5G. Μέτρο διάτμησης της μεμβράνης: G = RbalΡ* Pl frbal 2 d3 Αριθμός Weber: We - R'P' p,cofr bal u' oifr, flxbal Αριθμός Mach λόγω της συμπιεστότητας στο εξωτερικό ρευστό: Μ, = Ct C, Εφαρμόζοντας την αδιαστατοποίηση στην (2-18) για το νόμο Mooney - Rivlin προκύπτει: Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 19
35 1 -K (' = o)u \J (2-20) Κεφάλαιο 2ο Μοντελοποίηση της Μικροφυσαλίδας ρ Γ.I r~r ( 1 Λ7 Ρ' G ST We i-(i-«:(^o)r=1)6 1 + b R' 2 Λ' R' Λ R'We R' Re, R'2 Re 2G R' 1- i-«:a=o)u, R' \+b R' \2 i; -1 ενώ η (2-19) για το νόμο Skalak δίνει: Ρ' = 1 1 r=r r ι ν3υ R' ρ; G ST We (1-c) 2, R' R'._ WeR' R'Re, R': Re -2G- R' (i-c) R' V + cί i-u;(t=o) r=] j u-u'(t=o) rj i-u'(t = 0) rj V + cf R' (1-U;(t = 0) p -1 (2-21) Χρησιμοποιώντας τα παραπάνω κατάλληλα μεγέθη εφαρμόζουμε την αδιαστατοποίηση και στην εξίσωση Keller-Miksis, εξίσωση (2-5), για να πάρουμε την σχέση, ( \ 1 - R'M, R'R'+ \ 2 V R'M, R' (2-22) + -ep'st sin/') Στις σχέσεις (2-20),(2-21),(2-22) τα μεγέθη με τόνο είναι αδιάστατα. Στο εξής τα αδιάστατα μεγέθη θα εμφανίζονται χωρίς τόνο για ευκολία, εκτός αν δηλώνονται αλλιώς. Αντικαθιστώντας τη σχέση (2-20) στην (2-22) παίρνουμε τελικά: Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrasl Agent σε περιβάλλον υπερήχου 20
36 Κεφάλαιο 2ο Μοντελοποίηση της Μικροφυσαλίδας ί 1 - RM, R R + 3 RM, V R = ί ι λ 3 7 R) PST + We +2G, ί - (ι - un(t = o) T_, y Γ 1 + b _ν ι ur(t = 0) r., V M.R Η 2 4 R 4R ΡΪΤ - ερ,τ sm t RWe R Re, Re R2 ST 2G R 1- i u r (t = 0) r=, R 1 + b λ2 R l-ur(t = 0) r. J - 1 PST + We + RM, yR'3Y' R -2G [l - (l - ur (t = 0) r=1 )6j 1 + b (. 2 \ ί. 2 Λ 4 R R - R 4 R R - 2 R 2 R V 7 7, - ερςτ cos t WeR2 Re, R2 Res R ST V l-ur(t = 0) ri J -1-2G R br br 7 R (l - u (t = 0) ) R (i-ur(t = 0) r=1 )2 R2 RS 5b(l-ur(t = 0) r=1 )JR 7b (1 - ur (t = 0) ) R Rf Ra (2-23) καταλήγουμε Ομοίως για το νόμο του Skalak αντικαθιστούμε τη σχέση (2-21) στη (2-22) και Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 21
37 Κεφάλαιο 2ο Μοντελοποίηση της Μικροφυσαλίδας ( 1 - RM, RR + 3 RM, 2 2 R - ί ι Vr RJ Ρ + We +G (1-c) Λ2 ί 1 + C l-ur(t = 0) r J > J M.R 2 4 R 4 R Ρςτ - ερ sin t RWe R Re, Re R2 s ST -G (1-c) R 1 - ur(t = 0) r= ' J v r + c R 1 u r (t = 0) r= J -1-3YR-3r"' R + RM, < + 2 R WeR2 P + +G We (1-c) V f + c l-ur(t = 0) r., J 1^1 ur(t = 0)jr (... 2 A (. 2 \ 4 R R - R 4 R R - 2 R V y - spst cost Re, R2 Re R3 i J - 1 2R R 6R5 R -G (1-c) + c (l-u,(t = 0), ) (l- ur(t = 0),) (2-24) Οι εξισώσεις (2-23),(2-24) αποτελούν μη γραμμικές συνήθεις διαφορικές εξισώσας δεύτερης τάξης ως προς R(t), άρα απαιτούνται δύο αρχικές συνθήκες για την χρονική ολοκλήρωσή τους. Οι αρχικές συνθήκες θα είναι η αρχική ακτινική θέση και αρχική ακτινική ταχύτητα της μικροφυσαλίδας σε κατάσταση ισσοροπίας: R(t = 0) = Rbal R(t - Ο) = 0 (2-25) Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 22
38 Κεφάλαιο 2 ο Μοντελοποίηση της Μικροφυσαλίδας Η αριθμητική επίλυση της σχέσης (2-23) για το νόμο Mooney - Rivlin kol της σχέσης (2-24) για το νόμο Skalak θα δώσει την ακτίνα της μικροφυσαλίδας με το χρόνο. Στη συνέχεια με τη βοήθεια της σχέσης (2-20) για το νόμο Mooney - Rivlin και αντίστοιχα με τη σχέση (2-21) για το νόμο Skalak θα υπολογιστεί η πίεση του εξωτερικού ρευστού πάνω στη μεμβράνη ως συνάρτηση του χρόνου. Η μεταβλητή αυτή θα χρησιμοποιηθεί για τον υπολογισμό της Psc(R,t) και η οποία στη συνέχεια χρησιμοποιείται για τον υπολογισμό του 0Sc,n. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 23
39 Κεφάλαιο 3ο Αριθμητική Μέθοόολογία και Έλεγχος Ακρίβειας Κεφάλαιο 3 Αριθμητική Μεθοδολογία και Έλεγχος Ακρίβειας Στο κεφάλαιο αυτό εφαρμόζεται γραμμικοποίηση στις μη γραμμικές εξισώσεις του προβλήματος που εξήχθησαν στο προηγούμενο κεφάλαιο και λύνονται αναλυτικά οι γραμμικές δευτεροβάθμιες που προκύπτουν. Αναφέρεται επίσης η αριθμητική μέθοδος που χρησιμοποιείται για την επίλυση των μη γραμμικών εξισώσεων και τον υπολογισμού του φάσματος συχνοτήτων. Τέλος προκειμένου να γίνει έλεγχος ακρίβειας συγκρίνονται τα αριθμητικά αποτελέσματα με την αναλυτική λύση της γραμμικής θεωρίας. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 24
40 Κεφάλαιο 3 ο Αριθμητική Μέθοδολογία και Έλεγχος Ακρίβειας 3.1 Γραμμικοποίηση του προβλήματος Για να αποδώσουμε γραμμικά την εξίσωση (3-1) που προέκυψε από τον καταστατικό νόμο Mooney-Rivlin: 3 M,R 2 2 R2 + We. +Pst+2G l-(l-^,)6 1+fl (. \ 1A -1 Λ + +(ι+μ,λ) 2 4 R 4 R D d ' (A + 2G R v *, 1+6 ' Λ * νη, -lyrr^-'r (C+/*+2Cl -MJ* 1+6 (. A vh~«, -1 +RM, 4Λ2 8 R2 Wem R2 Re, R2 +Res jf ~ερ* <Χβ(ί)+ -2ηηι-η +_Μ_+(,_4)7( - ί,ί«^»( -,ί 1)4Λ (HJ If If (3-1),,, t> \ D 4Mi 4Mi 1 -Mi i+ i+-i- 1 I Re, Res R R όπου G = G S _ Plωf R-bal η/ _ Ρΐω/^ΙαΙ, Re, = VVeav kol Re, = f hal εφαρμόζουμε Pi^fKa, 3SPs crav _ μ, 'i πολύ μικρές διαταραχές στη βασική λύση η οποία είναι η κατάσταση ισορροπίας της μικροφυσαλίδας. Προκειμένου να απλοποιήσουμε την εξίσωση θεωρούμε ότι δεν υπάρχουν παραμένουσες τάσεις στη μεμβράνη ur(t = 0))^ =ur{t = 0)jr=/, = Ο. Με χρήση των: R = 1 + srd. / \,με ε«1 Ρ, =Ρ + sps, sm^/j (3-2) Διατηρώντας μόνο τους όρους πρώτης τάξης ως προς ε παίρνουμε: Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 25
41 Κεφάλαιο 3 ο Αριθμητική Μέθοδολογία και Έλεγχος Ακρίβειας + 12 CM, (3-3) η οποία είναι της μορφής : FxRd + F2Rd + F3Rd = -ερα sin(t)-epstml cos(/) (3-4) και έχει αναλυτική λύση: Rd [ή--βεσκ' cos(<r//)+:^^ e Rt sin(o //) + ^sin(/)+5cos(/) (3-5) οπού ~F\ + F2Mt + F3 A = -ερ F2 + F2-2FlFi + F2 FlMl ~F}M, +F2 Β = ερ s F2+F2-2FxF3 + F2 κοα σ = ar + ίσ, οι ρίζες του χαρακτηριστικού πολυωνύμου. To πραγματικό μέρος των ριζών, σλ, φανερώνει την απόσβεση του συστήματος και το φανταστικό, σ,, την κυκλική ιδιοσυχνότητα ταλάντωσης της μικροφυσαλίδας. Αν χρησιμοποιήσουμε την ίδια διαδικασία για την παρακάτω εξίσωση που προέκυψε από το νόμο Skalak: Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 26
42 Κεφάλαιο 3ο Αριθμητική Μέθοδολογία και Έλεγχος Ακρίβειας λ3 M.R' R We, -+R.+2G Kl~Ur=lJ λ >0 (\-ή +c 1-mI =1;,3r f(l+μ,ίή 2 4 R 4 R n n., v sp sm m + Wem,R Be Re, R S> Be Re5 R2 02 sf st V > + 2G R l-w 2 (l-c)+c A 1 -u -1-3yRr^-'R We, -+R.+2G 1~uLj (l-c)+c νη,-,ν -1 +RM, 2 R 4 R2 8 R2 D / \ +τ=^ ^Γ T r-^.cos Rf> 03 a W / + Wem. R2 Re, R2 Re, R 2{\-C)R (xrar -2G HJ (>-U (3-6) (\-M,R) R+?ML+^Li Re, Res<l R καταλήγουμε στην εξίσωση: R, 4Μ 4Μ 1η---- ί + Re, Re, 4 + 2Μ, _4 4 ίίέ Re, Re, +W^^P3]+4GH(1+2c) 4+ (3-7) -ή3λ +/J.We 3 f2g(2+4c) =-εξ sin(/) cos(/) Kelvin-Voigt [32]: Εργαζόμαστε ομοίως και για τη σχέση που προέκυψε από τον καταστατικό νόμο Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 27
43 Κεφάλαιο 3ο Αριθμητική Μεθοδολογία και'ελεγχος Ακρίβειας 3 M,R 2 2 R Γ> aj^\ We,a'bal + We^+Ps'~AG^ bal fa ^ ubat V a ) M,R 2 tfnl 2 4 R 4 (R2R R We, a We,R Re, R Res 1 a3 R + -4G Λ-1+«Λ lr=l Λ sin(i) +ΛΜ) f" -3/ *a/ ^ R2R L- ubal v α y a3 2 α^λ2/? 2 Λ 4ί 4 r23w2 3 R4R2 R2 i23 + We, a4 +We2R2+Re,R2 Res a3 a6 +R2 Λ2/? -4Gl ερ5, cos (?) R2 (3-8) Λ,,A\n 4M 4M -Mi Λ \ 'I Re, Res Λ -1 Λ D Ρ\ω{^αΙ n Ρΐω[^ΗαΙ ^ G P^f^h οπού Re, = , Re5 = , G = r^, We, = P, Ms Ρ,ω}Κ, σ^ πεπερασμένο, καταλήγουμε στην εξίσωση: Γ, Α Α\ '.,lk + Re, Res αί,, d / 5 \ bat J, We2 = P'-f-R kol δ + +: -Mi We,CrbaJ+We2+Ps' + 3 γμι atl 3λ fl ^ ^2 *J I 2Mt, 4 4 i+ We, a^ + Re/+ReJ J-e* +^_+pl_ ^ Weiabd -ep* sin(i)-^pv//cos(i) +4GM/ 2 2. J C? i, + j 1 +Α*Λ 4 + (3-9) Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 28
44 Κεφάλαιο 3 ο Αριθμητική Μέθοδολογία και Έλεγχος Ακρίβειας G, μ, Θεωρώντας δ -> 0, Gs =, μ$ = JiL, η εξίσωση (3-9) συμπίπτει με τη σχέση (3-3) δ 3δ και ο ελαστικός αριθμός, G = J sd,, και ο αριθμός Reynolds, Re = f h, της Ρ,ω{Κ, μεμβράνης όπως ορίζονται για μεμβράνη απειροελάχιστου πάχους με τους νόμους Mooney- Psd Rivlin και Skalak δίνουν τους αντίστοιχους αριθμούς, G = G, Ρ,ω}Κ ' bal p,coj-rhal kol Re, = , για Ps μεμβράνη πεπερασμένου πάχους που περιγράφεται από τον νόμο KV. Επίσης αν θέσουμε c=l στη σχέση (3-7) παρατηρούμε ότι συμπίπτει με τη σχέση (3-3). Συνεπώς η δυναμική συμπεριφορά της μικροφυσαλίδας είναι ανεξάρτητη από τον καταστατικό νόμο που ακολουθεί η μεμβράνη αν οι παραμορφώσεις είναι πολύ μικρές και οι παράμετροι που περιγράφουν το υλικό έχουν συγκεκριμένες τιμές. Επομένως έχει ενδιαφέρον η εξέταση της επίδρασης των καταστατικών νόμων της μεμβράνης για μεγάλες παραμορφώσεις. Αν υπολογισθεί το osc από τη σχέση: σ<=4 nrl- (3-10) \ρ]α με την βοήθεια της αναλυτικής επίλυσης του γραμμικού προβλήματος μετά το πέρας των μεταβατικών ταλαντώσεων, τότε θα προκύψει η σχέση: 4π«αΙ σ&κ) = λ > λ2 ω -1 KJ Ιι+μ] 2 \ +*,2Μ F{ «0. \ωί) Ft ' Ft (3-11) όπου coo=aio)f η ιδιοσυχνότητα ταλάντωσης της μικροφυσαλίδας, αη η εξωτερική επιβαλλόμενη συχνότητα, R ^ η ακτίνα της μικροφυσαλίδας στην ισορροπία και δι ο συνολικός συντελεστής απόσβεσης. 3.2 Αριθμητική Προσέγγιση Τόσο η εξίσωση (3-1) για το νόμο Mooney-Rivlin όσο και η εξίσωση (3-6) για το νόμο Skalak: αποτελούν γραμμικές διαφορικές εξισώσεις 2Ι,ς τάξης ως προς το χρόνο. Για την επίλυση αυτών των εξισώσεων χρησιμοποιήθηκε η μέθοδος Runge-Kutta 4,ς τάξης για συστήματα, και η οποία Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 29
45 Κεφάλαιο 3ο Αριθμητική Μέθοδολογία και Έλεγχος Ακρίβειας έχει ακρίβεια τάξης 0(dt4). Για να εφαρμοστεί η μέθοδος αυτή θα πρέπει να μετατραπούν οι μη γραμμικές διαφορικές εξισώσεις 2ης τάξης σε συστήματα διαφορικών εξισώσεων \ης τάξης. Αυτό επιτυγχάνεται αν θεωρηθούν τα εξής: R{t) = Z{t) (3-12) Ζ = F(Z(t),R(t),t) (3-13) και με αρχικές συνθήκες: R(t = 0) = 1 (3-14) Z(t = 0) = 0 (3-15) Επίσης το χρονικό βήμα της μεθόδου θεωρείται σταθερό και τέτοιο ώστε να επιτυγχάνεται σύγκλιση της μεθόδου. '/ Προκειμένου να υπολογίσουμε το ολοκλήρωμα jpsc,ndt εφαρμόζουμε την ταυτότητα Parseval ο πάνω στους συντελεστές του αναπτύγματος Fourier της ακουστικής πίεσης Psc X X psc (t) = a0 +Σ3 εοδ(ω 0 + Zb sin((o t). (3-16) Επειδή η σκεδαζόμενη πίεση δεν περιέχει την στατική πίεση ούτε την διαταραχή της, η μέση της τιμή αναμένεται να είναι περίπου μηδέν και ως εκ τούτου ao=0. Εφαρμόζοντας την σχέση του Parceval παίρνουμε. Psc (Of = }ρ (ί)<1ί = Σ an jcos2 (co t)dt + b2 Jsin2(ont)dt = -f J(a; +b2), (3-17) οπού ω = 2πη n = 1,2,3..., kol tf είναι η συνολική διάρκεια της χρονικής ολοκλήρωσης. Συνεπώς μπορεί να θεωρηθεί ότι το μερίδιο κάθε αρμονικής στο μέτίρο της σκεδαζόμενης πίεσης δίδεται από τη σχέση: ίρ2 dt = (a2 +b2) J Sc.n λ \ n n / 0 (3-18) όπου an, bn n -1,2,...oo είναι οι συντελεστές του αναπτύγματος Fourier του διανύσματος Psc(t). Ο αλγόριθμος που χρησιμοποιείται για να υπολογιστούν οι παραπάνω συντελεστές είναι ο Γρήγορος Μετασχηματισμός Fourier (FFT). Έχοντας υπολογίσει τους συντελεστές του αναπτύγματος Fourier του διανύσματος Psc(t) και διαιρώντας τον κάθε όρο της παραπάνω απειροσειράς με: Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 30
46 Κεφάλαιο 3ο Αριθμητική Μέθοδολογία και'ελεγχος Ακρίβειας J>> (3-19) Ο παίρνουμε τη συνεισφορά της αρμονικής Osc,n στο συνολικό συντελεστή σκέδασης. 3.3 Σύγκριση των μη γραμμικών μοντέλων με την αναλυτική λύση της γραμμικής θεωρίας Προκειμένου να εξεταστεί η ορθότητα της παραπάνω αριθμητικής μεθόδου έγιναν έλεγχοι για την περίπτωση μικρών διαταραχών της πίεσης. Έτσι λοιπόν συγκρίθηκαν τα αριθμητικά αποτελέσματα με την αναλυτική λύση της γραμμικής θεωρίας. Για μη γραμμικές διαταραχές της πίεσης επιβάλλεται να γίνει σύγκριση με τα πειραματικά αποτελέσματα. Στο σχήμα 3.1 φαίνεται η ακτίνα της φυσαλίδας ως συνάρτηση του χρόνου σε κατάσταση συντονισμού και στο σχήμα 3.2 σε κατάσταση εκτός συντονισμού, όταν επιβάλλεται ημιτονοειδής διαταραχή. Για λόγους απλούστευσης θεωρείται πως η μεμβράνη δεν έχει παραμένουσες τάσεις. Η μελέτη της επίδρασης των παραμενουσών τάσεων στο φάσμα συχνοτήτων της μικροφυσαλίδας για μη γραμμικές διαταραχές δίνεται στο επόμενο κεφάλαιο. Από τα σχήματα που προαναφέρθηκαν γίνεται φανερό πως υπάρχει συμφωνία ανάμεσα στο αριθμητικό μοντέλο και τη γραμμική θεωρία. Σχήμα 3.1: Η εξωτερική ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου σε κατάσταση συντονισμού. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa. Ρι=998 kg/m3, s,=0.04 Kg/s2, s2=0.005 kg/s2,s=0.045 Kg/s2 μ,=0.001 kgrn's, C,= 1500 m/s, μ5=0.6 kgm's'1, Gs=35 MPa. Rba =3*10'6 m, δ=15* 10 9 m, Einf=0.05, w,('= L=M'('=0Law =0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 3 1
47 Κεφάλαιο 3 ο Αριθμητική Μέθοδολογία και Έλεγχος Ακρίβειας Σχήμα 3.2: Η εξωτερική ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου σε κατάσταση εκτός συντονισμού. Δεδομένα προσομοίωσης: γ=1.4, Plnf= Pa, ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2,s=0.045 Kg/s2 μι=0.001 kgm's', Q=1500 m/s, μ5=0.6 kgrr/'s'1, Gs=35 MPa, Rbal=3*10 m, o=15* 10 J m, Elnf=0.05, Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 32
48 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Κεφάλαιο 4 Αποτελέσματα και Συζήτηση Στο παρόν κεφάλαιο παρουσιάζονται τα αριθμητικά αποτελέσματα που προέκυψαν από τη χρήση των νόμων Mooney-Rivlin για υλικά strain-softening και Skalak για υλικά strainhardening. Γίνεται επίσης σύγκριση με τα αριθμητικά αποτελέσματα του γραμμικού νόμου τάσεων-παραμορφώσεων Kelvin-Voigt [32]. Θα πρέπει να αναφερθεί ότι τόσο για το μοντέλο Mooney-Rivlin όσο και για το μοντέλο Skalak θεωρήσαμε το πάχος της μεμβράνης απειροελάχιστο, γεγονός που δεν ισχύει για το μοντέλο Kelvin-Voigt. Ωστόσο τα μοντέλα Mooney-Rivlin και Skalak ενσωματώνουν το πάχος της μεμβράνης δ στο μέτρο διάτμησης και το ιξώδες της μεμβράνης ως μ5 =, Gs = όπου μ5 είναι το ιξώδες της μεμβράνης για το 3δ δ μοντέλο Kelvin-Voigt, ps(j το ιξώδες της μεμβράνης για τα μοντέλα Mooney-Rivlin κοα Skalak, Gs το μέτρο διάτμησης της μεμβράνης του μοντέλου Kelvin-Voigt, GSd το μέτρο διάτμησης της μεμβράνης των μοντέλων Mooney-Rivlin κοα Skalak. Αξίζει να σημειωθεί ότι στο μοντέλο Kelvin-Voigt θεωρείται πεπερασμένο πάχος μεμβράνης ενώ στα μοντέλα Mooney-Rivlin και Skalak το πάχος της μεμβράνης λαμβάνεται ως απειροελάχιστο και ως εκ τούτου ενσωματώνεται στο μέτρο διάτμησης και στο ιξώδες της μεμβράνης. Επίσης, επειδή στο κεφάλαιο αυτό γίνεται σύγκριση των αριθμητικών αποτελεσμάτων με τα πειραματικά αποτελέσματα των Jean-Marie Gorse et al [33] (όπου μελετάται ένα υπάρχον Contrast Agent to SonoVue ), οι τιμές των μ^ και GSd που χρησιμοποιούνται στους δύο καταστατικούς νόμους που εξετάζονται στην παρούσα μελέτη έχουν ληφθεί από συσχετίσεις βασισμένες στις παραπάνω πειραματικές μετρήσεις. Τέλος, λόγω του ότι η βιβλιογραφία είναι περιορισμένη θα πρέπει να σημειωθεί πως οι τιμές των διαφόρων παραμέτρων που εξετάζονται στο παρόν κεφάλαιο, κυρίως των μ* και Gs, βρίσκονται στο εύρος τιμών που εξετάζεται στην εργασία των Khismatulin & Nadim [26]. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 3 3
49 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση 4.1 Η Επίδραση της Εξωτερικής Διαταραχής Όπως έχει αναφερθεί επιβάλλουμε ημιτονοειδείς διαταραχές της πίεσης στο άπειρο με συχνότητα C0f. Καθώς αυξάνεται το πλάτος της εξωτερικής διαταραχής αρχίζουν να εμφανίζονται στο φάσμα συχνοτήτων της μικροφυσαλίδας υψηλότερες αρμονικές ανεξάρτητα από τον καταστατικό νόμο. Η συχνότητα συντονισμού μετατοπίζεται σε χαμηλότερες τιμές για τους νόμους Mooney-Rivlin κοα. Kelvin-Voigt, ενώ για το νόμο Skalak σε υψηλότερες. Όμως και για τους τρεις νόμους η μετατόπιση της συχνότητας συντονισμού είναι πολλή μικρή. Για όμοιες μη γραμμικές διαταραχές ο ρόλος των υψηλότερων αρμονικών είναι πιο σημαντικός στη δυναμική της μικροφυσαλίδας όταν εφαρμόζεται ο νόμος Mooney-Rivlin απ ότι όταν εφαρμόζεται ο νόμος Skalak. Η συνεισφορά της επιβαλλόμενης συχνότητας στο Osc,n είναι μεγαλύτερη για το νόμο Skalak και μικρότερη για το νόμο Mooney-Rivlin. Φαίνεται πως ένα μέρος της ενέργειας της βασικής αρμονικής μεταφέρεται στις υψηλότερες αρμονικές όταν οι εξωτερική διαταραχή αυξάνεται και το υλικό είναι τύπου strain-softening. Το γεγονός αυτό, όπως και η μετατόπιση του συντονισμού σε υψηλότερες συχνότητες όταν χρησιμοποιείται ο νόμος Skalak, εξηγούνται αν λάβουμε υπόψη μας ότι μεγαλύτερη διαταραχή πίεσης σημαίνει μεγαλύτερη παραμόρφωση της μεμβράνης. Στο νόμο Skalak το μέτρο διάτμησης της μεμβράνης αυξάνει καθώς η παραμόρφωση της μεμβράνης μεγαλώνει και το υλικό σκληραίνει, ενώ στο νόμο Mooney-Rivlin το μέτρο διάτμησης παίρνει χαμηλότερες τιμές Η Επίδραση της Εξωτερικής Διαταραχής νόμος Mooney-Rivlin Στα σχήματα φαίνεται η επίδραση της εξωτερικής διαταραχής στο osc,n της μικροφυσαλίδας. Κατά την αύξηση της διαταραχής της πίεσης στο άπειρο η συχνότητα συντονισμού δεν επηρεάζεται σημαντικά και το φάσμα συχνοτήτων της μικροφυσαλίδας εμπλουτίζεται με υψηλότερες αρμονικές. Όταν η διαταραχή είναι μικρή τότε το osc,n συμπίπτει με αυτό της γραμμικής θεωρίας. Επίσης όσο αυξάνεται η διαταραχή παρατηρείται μικρή απόσβεση τόσο της επιβαλλόμενης συχνότητας στο osc,n όσο και των υψηλότερων αρμονικών. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 34
50 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.1: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για ε,ηγ=0.05. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v, C =l 500 m/s, μ5=0.6 kgm 's'1, Gs=35 MPa, r=3*10'6 m, 6=15*10'9m, (/ = 0)( =ur(t = 0)r K =0.b=0 Σχήμα 4.2: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για 8mf=2.05. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v, Ci=l500 m/s, μ =0.6 kgm''s ', Gs=35 MPa, r=3*10'6 m, 5=15*10 9m, «r(l = 0) r= = Ur (t = 0)jr_R = 0, b=0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 3 5
51 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση VHz> χίο6 Σχήμα 4.3: Το oscn ως συνάρτηση της εξωτερικής συχνότητας για emf=4.05. Δεδομένα προσομοίωσης: γ=1.4, Pi f= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgrrf's'1, C =1500 m/s, μ5=0.6 kgrrf's'1, Gs=35 MPa, r=3*10'6m, δ=15*10'9m, ur(t = 0) r=1 = ur(t = θ) =0,b= Η Επίδραση της Εξωτερικής Διαταραχής νόμος Skalak Στα σχήματα φαίνεται η επίδραση της εξωτερικής διαταραχής στο osc,n της μικροφυσαλίδας. Η αύξηση της διαταραχής της πίεσης στο άπειρο δεν επηρεάζει σημαντικά τη συχνότητα συντονισμού της μικροφυσαλίδας, όμως εμφανίζονται υψηλότερες αρμονικές των οποίων η συνεισφορά στο osc,n είναι μικρή. Επίσης όσο αυξάνεται η διαταραχή παρατηρείται μικρή απόσβεση της επιβαλλόμενης συχνότητας στο σ$ς,η Για μικρές διαταραχές το Osc,n συμπίπτει με αυτό της γραμμικής θεωρίας. Σχήμα 4.4: Το σ8ο>η ως συνάρτηση της εξωτερικής συχνότητας για ειη(=0.05. Δεδομένα προσομοίωσης: γ=1.4, P,n(= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm 's'1, C =l 500 m/s, μ8=0.6 kgm''s'', Gs=35 MPa, r=3*10'6 m, 5=15*10'9m, Mr(/ = 0 r=) = Ur(t = θ] =0,c=l Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrasl Agent σε περιβάλλον υπερήχου 36
52 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.5: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για smf=2.05. Δεδομένα προσομοίωσης: γ=1.4. Pinf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgirf's"1, C =l500 m/s, μ5=0.6 kgrtt's'1, Gs=35 MPa, r=3*10'6 m, 5=15*10'9m, Ur(t = 0) r=1 =ur(t = θ) = 0,c=l Σχήμα 4.6: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για 8lnf=4.05. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μ,=0.001 kgur's"1, Q=1500 m/s, ps=0.6 kgm 's'1, Gs=35 MPa, r=3*10'6 m, 6=15*10 9m, ur(t = θ) Γ=1 = Ur(t = 0)jr=ft = 0,c=l Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 3 7
53 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Η Επίδραση της Εξωτερικής Διαταραχής νόμος Kelvin-Voigt Σχήμα 4.7: To asc ως συνάρτηση της εξωτερικής συχνότητας για s,nf=0.05. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, Ρι=998 kg/m3, S =0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm"'s"1, C =1500 m/s, ps=0.6 kgm'ls'1, Gs=35 MPa, r=3*10'6m, 5=15*10'9m, ur(t = ti\r_χ = ur(t = θ) Γ=β =0 Σχήμα 4.8: To ascr, ως συνάρτηση της εξωτερικής συχνότητας για ειπ(=2.05. Δεδομένα προσομοίωσης: γ=1.4, P, f= Pa, Ρι=998 kg/m3, s,=0.04 Kg/s2, s2=0.005 kg/s2, pi=0.0()l kgrrf's'1, C =1500 m/s, ps=0.6 kgm 's'1, Gs=35 MPa, r=3*10'6m, 5=15*l(T9m, Mr(/ = 0)(r_1 = Ur(t = 0) r=e = 0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 3 8
54 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.9: To oscn ως συνάρτηση της εξωτερικής συχνότητας για 8,nf=4.05. Δεδομένα προσομοίωσης: 7=1.4, Ρ,ΠΓ= Pa, Ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm'1s'1, C =1500 m/s, /is=0.6 kgnv's'1, Gs=35 MPa, r=3*10 6m, 5=15*10 9m, ur(t = θ =ι = ur(t = θ) =η = Η Επίδραση του Μέτρου Διάτμησης της Μεμβράνης Η αύξηση του μέτρου διατμήσεως της μεμβράνης έχει δυο κύρια αποτελέσματα ανεξάρτητα του υλικού από το οποίο αποτελείται. Πρώτον, μετατοπίζει το συντονισμό σε υψηλότερες συχνότητες και δεύτερον, αυξάνει τη συνεισφορά της επιβαλλόμενης συχνότητας στο (Tsc,n Οι υψηλότερες αρμονικές δεν έχουν τόσο μεγάλη ισχύ γεγονός που φαίνεται περισσότερο σε υλικά τύπου strain-hardening. Η ενίσχυση της συνεισφοράς της επιβαλλόμενης συχνότητας στο osc,n> λόγω της αύξησης του μέτρου διάτμησης εξηγείται από το ισοζύγιο ενέργειας της μικροφυσαλίδας. Η ενέργεια που παρέχεται στη μικροφυσαλίδα μετατρέπεται σε κινητική ενέργεια, δυναμική ενέργεια του εσωτερικού ρευστού λόγω μεταβολής της πίεσης, ενέργεια λόγω της επιφανειακής τάσης μεταξύ μεμβράνης-εξωτερικού υγρού και μεμβράνηςεσωτερικού αερίου, ενέργεια της μεβράνης λόγω ελαστικότητας, απώλεια ενέργειας λόγω συμπιεστότητας και ιξώδους του εξωτερικού ρευστού. Όταν η ελαστικότητα μεγαλώνει μεγαλύτερο ποσοστό της ενέργειας αποθηκεύεται και ταυτόχρονα η ταχύτητα της μεμβράνης ελαττώνεται. Αυτό έχει ως συνέπεια την απόσβεση του πλάτους ταλάντωσής της και άρα της ολικής ενέργειας. Για το λόγο αυτό όταν εφαρμόζεται ο νόμος Skalak, η συνεισφορά της επιβαλλόμενης συχνότητας στο osc,n έχει μεγαλύτερες τιμές σε σχέση με τους άλλους νόμους. Καθώς η παραμόρφωση της μεμβράνης μεγαλώνει το φαινόμενο μέτρο ελαστικότητας αυξάνει όταν χρησιμοποιείται ο νόμος Skalak, λόγω της αύξησης της κλίσης της καμπύλης τάσης παραμόρφωσης, ενώ αντίθετα μειώνεται στην περίπτωση του νόμου Mooney-Rivlin. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 39
55 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Η Επίδραση του Μέτρου Διάτμησης της Μεμβράνης νόμος Mooney-Rivlin Από τα σχήματα φαίνεται πως η αύξηση του μέτρου διάτμησης της μεμβράνης αυξάνει κυρίως το σ&,η της επιβαλλόμενης συχνότητας, ενώ οι υψηλότερες αρμονικές αποσβένονται λίγο και το ποσοστό συμμετοχής τους στο osc,n μειώνεται αρκετά. Επίσης ο συντονισμός επέρχεται σε υψηλότερες συχνότητες. Σχήμα 4.10: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=35 MPa. Δεδομένα προσομοίωσης: γ=1.4, P,nf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm's'1, C =1500 m/s, μ5=0.6 kgnt's"1, rf MO'6 m, 5=15*1 O'9 m, iinf=2.05, Mr(/ = 0 r=[ = Ur(t = = 0, b=0 Σχήμα 4.11: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=70 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm's"1, Ci=l500 m/s, ps=0.6 kgm'v, r=3*10"6 m, 5=15* 10'9 m, jnf=2.05, ur(t = 0 r=1 =Μ,(ί = θ) Γ = 0, b=0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 40
56 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.12: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=105 MPa. Δεδομένα προσομοίωσης: γ= 1.4, Pinf= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, C]=l500 m/s, μ5=0.6 kgm''s'', r=3*10'6 m, δ=15*10'9 m, f,nf=2.05, ur{t = 0)^, =Ur(t = = 0, b=0 Σχήμα 4.13: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=140 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, /t>i=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, C,=1500 m/s, μ, =0.6 kgm'v1, r=3*10'6 m, δ=15*10'9 m, inf=2.05, Ur(t = =ur{t = = 0, b= Η Επίδραση του Μέτρου Διάτμησης της Μεμβράνης νόμος Skalak Από τα σχήματα φαίνεται πως η αύξηση του μέτρου διάτμησης της μεμβράνης αυξάνει κυρίως το Osc,n της επιβαλλόμενης συχνότητας, ενώ οι υψηλότερες αρμονικές αποσβένονται και το ποσοστό συμμετοχής τους στο osc,n είναι ελάχιστο. Επίσης ο συντονισμός επέρχεται σε υψηλότερες συχνότητες. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 41
57 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.14: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=35 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, μ=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgrrf's'1, C =1500 m/s, μ5=0.6 kgtrf's'1, r=3* 1 O'6 m, 5=15*1 O'9 m, tmf=2.05, Mf(/ = 0^=] =«,(/ = Ojj^ = 0, c=l Σχήμα 4.15: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=70 MPa. Δεδομένα προσομοίωσης: γ=1.4, P,nf=l01325 Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgnt's 1, Q=1500 m/s, μ$=0.6 kgnt's 1, r=3*10'6 m, 5= 15* 1 O'9 m, jnf=2.05, Ur(t = = Ur(t = Oj^ =0,c=l Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 42
58 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.16: Το σ5οη ως συνάρτηση της εξωτερικής συχνότητας για Gs=105 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pinf=l01325 Pa, Ρι=998 kg/m3, s=0.045 icg/s2, μι=0.001 kgm s'1, C =1500 m/s, μ$=0.6 kgnt's"1, r=3*10'6 m, δ=15*10'9 m,,n(=2.05, Mr(l = 0jf=1 =ur(t = 0\=R^ = 0,c=l Σχήμα 4.17: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=140 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρ,=998 kg/m3, s=0.045 /cg/s2, μ,=0.001 kgm'1s'1, C,=1500 m/s, μ5=0.6 kgnt's'1, r=3*10'6 m, δ= 15* 1 O'9 m, imf=2.05, (f = = Ur(t = =0,c=l Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 43
59 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Η Επίδραση του Μέτρου Διάτμησης της Μεμβράνης νόμος Kelvin-Voigt Σχήμα 4.18: To osc>n ως συνάρτηση της εξωτερικής συχνότητας για Gs=35 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, Ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm's'1, Q=1500 m/s, μ<=0.6 kgm'v1, r=3* 10-6 m, δ=15*10'9 m, mf=2.05, «r(i = 0) r=1 =ur(t = Ojr_a = 0 Σχήμα 4.19: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=70 MPa. Δεδομένα προσομοίωσης: γ=1.4, P, f=l01325 Pa, ρ,=998 kg/m3, s,=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm'v, Ci=1500m/s, μ5=0.6 kgm 's'1, r=3*10'6 m, δ=15*10'9 m, mf=2.05, Ur(t = 0) r=1 =ur(t = θ) =0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τόπου Contrast Agent σε περιβάλλον υπερήχου 44
60 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.20: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για Gs=105 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, Ρι=998 kg/m3, s,=0.04 Kg/s2, s2=0.005 kg/s2, μ,=0.001 kgm 's'1, C =1500 m/s, μ<=0.6 kgm'v1, 5=15*10'9m,,nf=2.05, Ur(t = 0) r=1 =ur(t = θ) =0 Σχήμα 4.21: To σ5ο,η ως συνάρτηση της εξωτερικής συχνότητας για Gs=140 MPa. Δεδομένα προσομοίωσης: γ=1.4, Pln(= Pa, Ρι=998 kg/m3, sι =0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm 's1, C =1500 m/s, μ,=0.6 kgm'v1, i=3*10'6 m, 6= 15*1 O'9 m,, r=2.05, Ur (t = Oj^ =Ur(t = 0)^ = Η Επίδραση του Ιξώδους της Μεμβράνης Η αύξηση του ιξώδους της μεμβράνης επηρεάζει όλες τις αρμονικές αποσβένοντας τις και ο συντονισμός τείνει να μετατοπιστεί σε λίγο μεγαλύτερες συχνότητες. Πιο συγκεκριμένα η αύξηση του ιξώδους της μεμβράνης ενισχύει την απώλεια της ενέργειας. Η απώλεια αυτή όταν Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 45
61 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση χρησιμοποιείται ο νόμος Skalak είναι μεγαλύτερη από των νόμων Mooney-Rivlin κοα Kelvin- Voigt Η Επίδραση του Ιξώδους της Μεμβράνης νόμος Mooney-Rivlin Από τα σχήματα φαίνεται πως το ιξώδες της μεμβράνης επηρεάζει όλες τις αρμονικές αποσβένοντας τις, ενώ παράλληλα μετατοπίζει το συντονισμό σε υψηλότερες συχνότητες, γεγονός που δεν είναι τόσο σημαντικό. Σχήμα 4.22: Το asc,n ως συνάρτηση της εξωτερικής συχνότητας για ps=0.6 kgm'1s'1. Δεδομένα προσομοίωσης: γ=1.4, Plnf=l01325 Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μ^ο.οοι kgm'1s'1, Q=1500 m/s, Gs=35 MPa, r=3*10 6 m, 6=15*10"9m, inf=2.05, Ur{t = 0]^ = Ur(t = 0^ = 0, b=0 \<H*> xio6 Σχήμα 4.23: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5= 1.6 kgnt s'1. Δεδομένα προσομοίωσης: 7=1.4, P,nf= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μ,=0.001 kgmv, C,=1500 m/s, Gs=35 MPa, r=3*10 6 m, 5= 15*10 9 m,,nf=2.05, wr(/ = 0) r=1 =Mf(/ = 0))r_R =0,b=0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 46
62 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.24: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για Ps=2.6 kgm 's'1. Δεδομένα προσομοίωσης: 7=1.4, Pm(= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm 's'1, Q=1500 m/s, Gs=35 MPa, r=3*10"6 m, 5=15*1 O'9 m,,nf=2.05, «,(/= 0)^ =Ur(t = =0,b=0 Σχήμα 4.25: To oscn ως συνάρτηση της εξωτερικής συχνότητας για μ,=3.6 kgnt's 1. Δεδομένα προσομοίωσης: 7=1.4, Plnf= Pa, ρ,=998 kg/m3, s=0.045 /cg/s2, μ,=0.001 kgm's'1, C,= 1500 m/s, Gs=35 MPa, ^ΙΟ"6 m, 5=15*10 9 m, f,nf=2.05, «(/= = Ur{t = = 0,b= Η Επίδραση του Ιξώδους της Μεμβράνης νόμος Skalak Από τα σχήματα φαίνεται πως το ιξώδες της μεμβράνης επηρεάζει όλες τις αρμονικές αποσβένοντας τις, ενώ παράλληλα μετατοπίζει το συντονισμό σε υψηλότερες συχνότητες, γεγονός που δεν είναι τόσο σημαντικό. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 47
63 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.26: To σ$ςη ως συνάρτηση της εξωτερικής συχνότητας για μ5=0.6 kgrrf's'1. Δεδομένα προσομοίωσης: 7=1.4, Pmf= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgnt's'1, Q=1500 m/s, Gs=35 MPa, r=3* 1 O'6 m, δ=15*10'9 m, imf=2.05, Ur(t = 0)fml = Ur{t = =0,c=l Σχήμα 4.27: To ascn ως συνάρτηση της εξωτερικής συχνότητας για μ3= 1.6 kgnt's'1. Δεδομένα προσομοίωσης: 7=1.4, Plnf=l01325 Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μ,=0.001 kgm 's1, C,= 1500 m/s, Gs=35 MPa, r=3*10'6 m, δ=15*10'9 m, einf=2.05, u At = θ) = uat = θ) = 0,c=l r v '< r=\ ' y -Ί r=rhai Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 48
64 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.28: To oscn ως συνάρτηση της εξωτερικής συχνότητας για μ5=2.6 kgm'v. Δεδομένα προσομοίωσης: 7=1.4, Pmf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm's'1, C;= 1500 m/s, Gs=35 MPa, r=3*10'6m, 6=15*1 O'9 m, i f=2.05, ur(t = 0)r=] = ur{t = 0\=R^ = 0,c=l Σχήμα 4.29: To σ5ο>η ως συνάρτηση της εξωτερικής συχνότητας για μ5=3.6 kgm'v. Δεδομένα προσομοίωσης: 7=1.4, Pinf=l01325 Pa, μ:=998 kg/m3, s=0.045 Kg/s2, μ,=0.001 kgm'v, C,=1500 m/s, Gs=35 MPa, r=3*10'6 m, δ=15*10'9 m, fmf=2.05, Wr(/ = 0) f=1 = Ur(t = =0,c=l Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 49
65 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Η Επίδραση του Ιξώδους της Μεμβράνης νόμος Kelvin-Voigt Σχήμα 4.30: To asc>n ως συνάρτηση της εξωτερικής συχνότητας για μ5=0.6 kgm'v1. Δεδομένα προσομοίωσης: γ=1.4, Plnf= Pa, ρ,=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm'v1, C =l 500 m/s, Gs=35 MPa, r=3* 1 O'6 m, δ=15* 10'9 m, lnf=2.05, (/ = θ) = Mr(/= 0) r= j =0 Σχήμα 4.31: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5= 1.6 kgm''s'. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρ,=998 kg/m3, s,=0.04 Kg/s2, s2=0.005 kg/s2, μ,=0.001 kgm'v1, C,= 1500 m/s, Gs=35 MPa, ^ lo^m, 6= 15*10 9 m, f,nf=2.05, Wr(/ = 0) r=1 =ur(t = θ) =0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 50
66 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.32: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για μ5=2.6 kgm'ls'1. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, Ρι=998 kg/m3, s, =0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgrrf's'1, C =1500 m/s, Gs=35 MPa, r=3*10 6 m, δ=15*10'9 m, ejnf=2.05, (/ = O) =1 = Ur(t = θ) Γ=β ^ =0 Σχήμα 4.33: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για Ps=3.6 kgrrf's'1. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρ,=998 kg/m3, s,=0.04 Kg/s2, s2=0.005 kg/s2, μ,=0.001 kgnf's'1, C,=1500 m/s, Gs=35 MPa, r=3*10'6m, 6=15*10'9rn, mf=2.05, (/ = θ) =J =Ur(t = 0) r=fl =0 4.4 Η Επίδραση του Πάχους της Μεμβράνης Η αύξηση του πάχους της μεμβράνης επηρεάζει τη συχνότητα συντονισμού η οποία μετατοπίζεται σε υψηλότερες συχνότητες και αποσβένει τη συνεισφορά των υψηλότερων αρμονικών και της επιβαλλόμενης συχνότητας στο osc,n, για κάθε υλικό. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 5 1
67 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Η Επίδραση του Πάχους της Μεμβράνης νόμος Mooney-Rivlin Από τα σχήματα φαίνεται πως η αύξηση του πάχους της μεμβράνης αποσβένει τη συνεισφορά των υψηλότερων αρμονικών και της επιβαλλόμενης συχνότητας στο asc,n Επίσης ο συντονισμός μετατοπίζεται σε υψηλότερες συχνότητες όσο αυξάνεται το πάχος της μεμβράνης. Σχήμα 4.34: To oscn ως συνάρτηση της εξωτερικής συχνότητας για δ=15*10"9. Δεδομένα προσομοίωσης: γ= 1.4, Plnf= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μ,=0.001 kgnt's'1, C,=1500 m/s, μ =0.6 kgmv, Gs=35 MPa, r=3*10 6 m,,nf=2.05, Ur(t = 0 r=1 =Ur(t = = 0, b=0 Σχήμα 4.35: To asc>n ως συνάρτηση της εξωτερικής συχνότητας για δ=35*10'9. Δεδομένα προσομοίωσης: γ= 1.4, Pln(= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μ,=0.001 kgnt's'1, C,=1500 m/s, μ5=0.6 kgnt's'1, Gs=35 MPa, r=3*10'6 m,,nf=2.05, «,(/ = 0 r=) = Ur (t = O)^ = 0, b=0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 52
68 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.36: To oscn ως συνάρτηση της εξωτερικής συχνότητας για δ=55*10'9. Δεδομένα προσομοίωσης: γ= 1.4, Pmf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm''s ', Ci=l500 m/s, ^=0.6 kgm''s ', Gs=35 MPa, r=3*10^ m,,nf=2.05, Ur(t = 0)r=, =Ur(t = Oj^ = 0, b=0 Σχήμα 4.37: To σ5ο,η ως συνάρτηση της εξωτερικής συχνότητας για δ=75*10'9. Δεδομένα προσομοίωσης: γ=1.4, P,nf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgnt's'1, C =l500 m/s, gs=0.6 kgtrf's'1, Gs=35 MPa, r=3*10 6 m, einf=2.05, ur (t = 0^=J =Ur(t = = 0, b= Η Επίδραση του Πάχους της Μεμβράνης νόμος Skalak Από τα σχήματα φαίνεται πως η αύξηση του πάχους της μεμβράνης αποσβένει τη συνεισφορά των υψηλότερων αρμονικών, οι οποίες είναι πολύ μικρές, και της επιβαλλόμενης συχνότητας στο osc,n Επίσης ο συντονισμός μετατοπίζεται σε υψηλότερες συχνότητες όσο αυξάνεται το πάχος της μεμβράνης. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 53
69 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.38: Το σ5ο,η ως συνάρτηση της εξωτερικής συχνότητας για δ=15*10'9. Δεδομένα προσομοίωσης: γ= 1.4, Pmf= Pa, p]=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, C(=l500 m/s, ps=0.6 kgrrf's'1, Gs=35 MPa, r=3*106 m, mf=2.05, Ur(t = 0)r=1 = Ur (t = = 0,c=l vf (Hz> xio6 Σχήμα 4.39: To oscn ως συνάρτηση της εξωτερικής συχνότητας για δ=35*10'9. Δεδομένα προσομοίωσης: γ= 1.4, Pmf= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, Q=1500 m/s, ps=0.6 kgm'v1, Gs=35 MPa, r=3*10'6 m, lnf=2.05, Ur(t = =Ur(t = = 0, c=l Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 54
70 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.40: Το ως συνάρτηση της εξωτερικής συχνότητας για δ=55*10'9. Δεδομένα προσομοίωσης: γ=1.4, Pin =l01325 Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgrrf's*1, Ci=l500 m/s, ps=0.6 kgm'v1, Gs=35 MPa, r=3* 10 6 m, einf=2.05, Ur(t = 0) r=1 = W,(/ = 0) r=r = 0,c=l Σχήμα 4.41: To ascn ως συνάρτηση της εξωτερικής συχνότητας για δ=75* Δεδομένα προσομοίωσης: γ= 1.4, Pini= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgrrf's'1, C =1500 m/s, μ<=0.6 kgrrf's'1, Gs=35 MPa, r=3*l(> * m, inf=2.05, Ur(t = 0 r=] = Ur(t = = 0, c=l Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 5 5
71 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Η Επίδραση του Πάχους της Μεμβράνης νόμος Kelvin-Voigt Σχήμα 4.42: To ffsc rl ως συνάρτηση της εξωτερικής συχνότητας ηιαδ=15*10'9ιτι. Δεδομένα προσομοίωσης: γ=1.4, P,nf= Pa, Ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgrrf's'1, C =1500 m/s, μ5=0.6 kgrrt's'1, Gs=35 MPa, r=3*10 6 m, 6,nf=2.05, ur(t = 0) r=1 =Ur(t = 0 r=(j = 0 MHz> xio6 Σχήμα 4.43: To asc,n ως συνάρτηση της εξωτερικής συχνότητας yia δ=35* 10'9 m. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm''s'', Q=1500 m/s, μ5=0.6 kgm'v, Gs=35 MPa, r=3*10'6 m, fmf=2.05, Ur(t = 0) r=l = Ur(t = 0))r=a = 0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τόπου Contrast Agent σε περιβάλλον υπερήχου 56
72 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.44: To asc,n ως συνάρτηση της εξωτερικής συχνότητας ήΐαό=55*10'9ηι. Δεδομένα προσομοίωσης: 7=1-4, Pinf= Pa, Ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm''s'', C =1500 m/s, μ3=0.6 kgnt's'1, Gs=35 MPa, r=3*10'6 m, elnf=2.05, U (i = 0) = u (t = θ\ =0 r v />r=1 ry r=aba, Σχήμα 4.45: To ascn ως συνάρτηση της εξωτερικής συχνότητας γιαδ=75*10'9ιη. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, Ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgnt's'1, C =1500 m/s, μ5=0.6 kgnt's'1, Gs=35 MPa, r=3*10'6m, lnf=2.05, Mr(/ = 0^=1 = ur(t = θ) =0 4.5 Η Επίδραση του Μεγέθους της Μικροφυσαλίδας Όσο μεγαλώνει το μέγεθος των μικροφυσαλίδων τόσο περισσότερο εμπλουτίζεται το asc.n όλων των αρμονικών. Επίσης ο συντονισμός επέρχεται σε μικρότερες συχνότητες καθώς μεγαλώνει η ακτίνα της μικροφυσαλίδας, ανεξαρτήτως καταστατικού νόμου. Πρέπει να επισημανθεί ότι η υποαρμονική εμφανίζεται κυρίως σε μεγάλες ακτίνες, όταν χρησιμοποιούνται οι νόμοι Mooney-Rivlin και. Kelvin-Voigt και επιβάλλονται μεγάλες διαταραχές. Όταν το υλικό Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 5 7
73 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση είναι τύπου strain-hardening η υποαρμονική έχει σχεδόν αμελητέα τιμή. Επιπλέον η υποαρμονική αποκτά σημαντική τιμή μετά την εμφάνιση των υψηλότερων αρμονικών Η Επίδραση του Μεγέθους της Μικροφυσαλίδας νόμος Mooney-Rivlin Όσο μεγαλύτερο είναι το μέγεθος των μικροφυσαλίδων τόσο πιο πλούσιο είναι το φάσμα συχνοτήτων σε υψηλές αρμονικές και υποαρμονικές, αν και το ποσοστό στο συνολικό Osc.n δεν αλλάζει σημαντικά. Επίσης η συχνότητα συντονισμού τείνει να γίνει μικρότερη για μεγαλύτερες μικροφυσαλίδες (σχήματα ). Σχήμα 4.46: To ffsc.n ως συνάρτηση της εξωτερικής συχνότητας yia r=3* 10 6 m. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgrrf's'1, Q=1500 m/s, Gs=35 MPa, ps=0.6 kgm'v, 5=15*10'9m, inf=2.05, Ur(t = 0) r=1 = ur(t = Q)\r=R =0, b=0 Σχήμα 4.47: To ascn ως συνάρτηση της εξωτερικής συχνότητας γ,α r=5*10^ m. Δεδομένα προσομοίωσης: "pl.4, Plnf= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm 's'1, Q=1500 m/s, Gs=35 MPa, ps=0.6 kgm 's'1, δ=15*10'9 m, einf=2.05, Ur{t = = Ur(t = Oj^ = 0, b=0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 58
74 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση ~10000 Π Ε e ν( (Hz) 9 10 χιο6 Σχήμα 4.48: To asc>n ως συνάρτηση της εξωτερικής συχνότητας yia. r=7*lο"6 m. Δεδομένα προσομοίωσης: γ=1.4, P,nf= Pa, Ρι=998 kg/m3, s=0.045 <cg/s2, μι=0.001 kgrrf s'1, Q=1500 m/s, Gs=35 MPa, μ5=0.6 kgnt's'1, 5=15*10'9m, mf=2.05, Ur(t = 0)jr=1 = wr(/= θ) Γ=Λ =0, b= Η Επίδραση του Μεγέθους της Μικροφυσαλίδας νόμος Skalak Όσο μεγαλύτερο είναι το μέγεθος των μικροφυσαλίδων τόσο πιο πλούσιο είναι το φάσμα συχνοτήτων σε υψηλές αρμονικές, αν και το ποσοστό στο συνολικό osc>n δεν αλλάζει σημαντικά. Επίσης η συχνότητα συντονισμού τείνει να γίνει μικρότερη για μεγαλύτερες μικροφυσαλίδες (σχήματα ). Σχήμα 4-49: To asc>n ως συνάρτηση της εξωτερικής συχνότητας y.a r=3*10'6 m. Δεδομένα προσομοίωσης: γ=\α, Pmf= Pa, ρ;=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgnt s'1, C =1500 m/s, Gs=35 MPa, μ$=0.6 kgm s'1, 5=15* 10'9 m, fmf=2.05, Ur(t = 0]^ = ur(t = 6}^ = 0, c=l Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Conlrast Agent σε περιβάλλον υπερήχου 59
75 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.50: To ascn ως συνάρτηση της εξωτερικής συχνότητας για r=5*10'6 m. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρ,=998 kg/m3, s=0.045 κφ2, μ,=0.001 kgm'v1, C,=1500 m/s, Gs=35 MPa, μ<=0.6 kgmv, δ=15*10'9 m, mf=2.05, ur(t = Q\r χ =Ur(t = O))^ = 0,c=l Σχήμα 4.51: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για r=7*10 6 m. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm 's'1, C =1500 m/s, Gs=35 MPa, /xs=0.6 kgrrt's 1, δ=15*10'9 m, einf=2.05, U At = θ)( = ur(t = 0)i =0,c=l V lr=* X lr=iibal Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 60
76 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Η Επίδραση του Μεγέθους της Μικροφυσαλίδας νόμος Kelvin-Voigt Σχήμα 4.52: To (JSc>n ως συνάρτηση της εξωτερικής συχνότητας γ,α r=3* 10'6 m. Δεδομένα προσομοίωσης: γ= 1.4, Pinf= Pa, ρ,=998 kg/m3, s,=0.04 Kg/s2, s2=0.005 kg/s2, μ,=0.001 kgnf's'1, C,=1500 m/s, Gs=35 MPa, μ5=0.6 kgrrf's'1, δ=15*10'9 m, elnf=2.05, ur(t- 0) r=1 =ur(t =6^ =a =0 Σχήμα 4.53: To asc, ως συνάρτηση της εξωτερικής συχνότητας ηια r=5*10 6 m. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgm"'s 1, Ci=l500 m/s, Gs=35 MPa, /is=0.6 kgtrf s'1, 5=15*10 9m, einf=2.05, ur{t θ) =1 =ur(t θ)( =η = 0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 61
77 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.54: To ffscn ως συνάρτηση της εξωτερικής συχνότητας yia r=7*10'6 m. Δεδομένα προσομοίωσης: γ=1.4, Ρι {= Pa, ρ,=998 kg/m3, s,=0.04 Kg/s2, s2=0.005 kg/s2, /i,=0.001 kgm'1s'1, C,=1500 m/s, Gs=35 MPa, Ps=0.6 kgm'ls 1, 5=15*10 9m, lnf=2.05, Ur(t = =ur(t = 0]r=a = Η Επίδραση του Ιξώδους και της Συμπιεστότητας του Εξωτερικού Ρευστού Καθώς μεγαλώνει το ιξώδες και η συμπιεστότητα του εξωτερικού υγρού ενισχύεται η απόσβεση των αρμονικών και ο συντονισμός επέρχεται σε λίγο μεγαλύτερες συχνότητες. Η αύξηση του ιξώδους και της συμπιεστότητας του εξωτερικού υγρού έχει ανάλογα αποτελέσματα με αυτά που προκύπτουν από την αύξηση του ιξώδους της μεμβράνης. Το είδος του υλικού δεν επηρεάζει αυτή τη συμπεριφορά εντούτοις η απώλεια ενέργειας είναι μεγαλύτερη όταν χρησιμοποιείται ο νόμος Skalak Η Επίδραση του Ιξώδους και της Συμπιεστότητας του Εξωτερικού Ρευστού νόμος Mooney-Rivlin Στα σχήματα 4.55 και 4.56 φαίνεται το osc,n όταν το εξωτερικό ρευστό είναι νερό (Ci=l 500 m/s, μι=0.001 kgm'v1) και αίμα (Q=500 m/s, μι=0.004 kgm'v1) αντίστοιχα. Από τα γραφήματα παρατηρείται ότι στο αίμα, σε σχέση με ότι συμβαίνει στο νερό, οι αρμονικές αποσβένουν και μετατοπίζεται ελάχιστα η τιμή της συχνότητας που επέρχεται ο συντονισμός. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 62
78 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.55: To oscn ως συνάρτηση της εξωτερικής συχνότητας για νερό (C =1500 m/s, μι=0.001 kgm 's'1). Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, r=3*10"6 m, Gs=35 MPa, p,=0.6 kgm-'s 1, δ=15*10"9 m,,nf=2.05, ur(t = 0^=1 =Ur(t = Oj^ = 0, b=0 VHz> x10e Σχήμα 4.56: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για αίμα (Cf=500 m/s, μι=0.004 kgnt s'1). Δεδομένα προσομοίωσης: γ= 1.4, Pinf=l01325 Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, r=3*10"6 m, Gs=35 MPa, μ^ο.6 kgm- s1, 5=15*10-9m, inf=2.05, ur(t = 0) r=1 =ur(t = θ) =0,b= Η Επίδραση του Ιξώδους και της Συμπιεστότητας του Εξωτερικού Ρευστού νόμος Skalak Στα σχήματα 4.57 καν 4.58 φαίνεται το asc,n όταν το εξωτερικό ρευστό είναι νερό (C]=1500 m/s, /i =0.001 kgm'v1) και αίμα (Ci=500 m/s, μι=0.004 kgm''s'') αντίστοιχα. Από τα γραφήματα παρατηρείται ότι στο αίμα, σε σχέση με ότι συμβαίνει στο νερό, το osc,n της Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 63
79 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση επιβαλλόμενης συχνότητας μειώνεται σημαντικά και οι υπόλοιπες αρμονικές παρόλο που είναι πολύ μικρές αποσβένουν. Επιπλέον δεν επηρεάζεται σημαντικά η συχνότητα συντονισμού. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, r=3*10'6 m, Gs=35 MPa, μ3=0.6 kgrrf s'1, 0=15*10-9m,6,nf=2.05, ur{t = 0^=] = «,(/ = Oj^ =0,c=l Σχήμα 4.58: To oscn ως συνάρτηση της εξωτερικής συχνότητας για αίμα (C =500 m/s, μι=0.004 kgm'ls'1). Δεδομένα προσομοίωσης: γ=1.4. P, r Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, r=3*10'6 m, Gs=35 MPa, μ,=0.6 kgm's'1, 6=15*10-9m,finf=2.05, Ur(t = 0)^ = Ur(t = θ) =0,c=l Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 64
80 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Η Επίδραση του Ιξώδους και της Συμπιεστότητας του Εξωτερικού Ρευστού νόμος Kelvin-Voigt Σχήμα 4.59: To ascn ως συνάρτηση της εξωτερικής συχνότητας για νερό (Q=1500 m/s, μι=0.001 kgrrt's'1). Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, Ρι=998 kg/m3, s,=0.04 Kg/s2, s2=0.005 kg/s2, cf=3*10 6 m, Gs=35 MPa, μ,=0.6 kgm 's'1, δ=15*10"9 m, mf=2.05,mr(/ = 0) r=1 = (/= 0) r=a =0 Σχήμα 4.60: To oscn ως συνάρτηση της εξωτερικής συχνότητας για αίμα (Q=500 m/s, μι=0.004 kgm'v). Δεδομένα προσομοίωσης: γ=1.4, P,nf= Pa, p =998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, 0^3*10 6 m, Gs=35 MPa, μ^ο.6 kgrtt's'1, δ=15*10'9 m, einf=2.05, «r(/ = 0) r=1 =Ur(t = 0) r=a =0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 65
81 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση 4.7 Η Επίδραση του Συντελεστή b του νόμου Mooney-Rivlin Όπως φαίνεται από τα σχήματα η αύξηση του συντελεστής b ενισχύει τη συνεισφορά της επιβαλλόμενης συχνότητας στο osc,n, ενώ παράλληλα οι υπόλοιπες αρμονικές αποσβένονται λίγο. Επίσης ο συντονισμός μετατοπίζεται σε λίγο υψηλότερες συχνότητες. Σχήμα 4.61: To Osc,n ως συνάρτηση της εξωτερικής συχνότητας για b=0. Δεδομένα προσομοίωσης: γ=1.4, P, f= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μ,=0.001 kgmv, C,=1500 m/s, Gs=35 MPa, μ=0.6 kgmv, 5= 15*1 O'9 m, elnf=2.05, wr(f = 0) f=1 = ur(t = 0]r=R =0,r=3*10 6m. Σχήμα 4.62: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για b=0.5. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm''s, C =1500 m/s, Gs=35 MPa, ps=0.6 kgm' s'', δ=15*10'9 m, in{=2.05, Ur(t = 0}r=] = Ur(t = =0,r=3*10'6m. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 66
82 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση ΜΗΖ> χΐοβ Σχήμα 4.63: Το oscn ως συνάρτηση της εξωτερικής συχνότητας για b=l. Δεδομένα προσομοίωσης: γ=1.4, Pmr= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, C =1500 m/s, Gs=35 MPa, μ5=0.6 kgrrf's'1, 5=15*10 9 m, fi f=2.05, Ur(t = 0)rl =Ur(t = θ) =0,r=3*l(r6m. 4.8 Η Επίδραση του Συντελεστή c του νόμου Skalak Η αύξηση του συντελεστής c επηρεάζει τη συνεισφορά της επιβαλλόμενης συχνότητας στο Osc.n και τη συχνότητα συντονισμού. Όσο αυξάνεται το c τόσο περισσότερο ενισχύεται η συνεισφορά της επιβαλλόμενης συχνότητας στο osc,n Επίσης η συχνότητα συντονισμού επέρχεται σε υψηλότερες συχνότητες για μεγάλα c. Σχήμα 4.64: To ascn ως συνάρτηση της εξωτερικής συχνότητας για c=l. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgrrt's'1, Q=1500 m/s, Gs=35 MPa, μ5=0.6 kgnt's'1, δ= 15*1 O'9 m, jnf=2.05, wr(i = 0) r=] = Ur(t = θ) = 0, r=3*10 6 m. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 67
83 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.65: To oscn ως συνάρτηση της εξωτερικής συχνότητας για c=5. Δεδομένα προσομοίωσης: γ=1.4, P,nf= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm's'1, Ci=1500 m/s, Gs=35 MPa, μ3=0.6 kgm's'1, 5= 15*1 O 9 m, einf=2.05, «r(/ = 0))r=1 =ur(t = 0]r=R = 0, r=3*10'6 m. Σχήμα 4.66: To oscn ως συνάρτηση της εξωτερικής συχνότητας για c=10. Δεδομένα προσομοίωσης: γ=1.4, Pinf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μ^ο.οοι kgnt's'1, C =1500 m/s, Gs=35 MPa, μ3=0.6 kgm 's'1, δ= 15*1 O'9 m, iinf=2.05, Ur(t = 0) r=1 = Ur(t = θ) =0,r=3*10'6m. 4.9 Η Επίδραση των Παραμένουσων Τάσεων της Μεμβράνης Η επίδραση των παραμένουσων στο osc,n είναι σχεδόν αμελητέα όταν οι καταστατικοί μόμοι Mooney-Rivlin και Kelvin-Voigt περιγράφουν τη συμπεριφορά του υλικού. Ο νόμος Mooney-Rivlin προβλέπει μικρότερη συνεισφορά της βασικής αρμονικής στο Osc,n ενώ και ο συντονισμός επέρχεται σε χαμηλότερη συχνότητα συγκριτικά με το νόμο Kelvin-Voigt, παρόλα αυτά οι διαφορές αυτές είναι πολύ μικρές. Καθώς ο συντελεστής b τείνει στη μονάδα ο νόμος Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 68
84 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Mooney-Rivlin δίνει αποτελέσματα παρόμοια με το νόμο Kelvin-Voigt. Επιπλέον εμφανίζονται υψηλότερες αρμονικές στο osc,n των δύο προηγούμενων νόμων, όταν εφαρμόζονται μη γραμμικές διαταραχές. Όταν το υλικό υπακούει στο νόμο Skalak τα αποτελέσματα του osc,n της μικροφυσαλίδας λόγω της επίδρασης των παραμένουσων τάσεων είναι διαφορετικά. Έτσι όσο πιο strain-hardening είναι ο τύπος του υλικού, τόσο περισσότερο ο συντονισμός μετατοπίζεται σε υψηλότερες συχνότητες και το osc,n αποκτά μεγαλύτερες τιμές και οι παραμένουσες τάσεις παίζουν σημαντικό ρόλο στην απόκριση της φυσαλίδας, μεταβάλλοντας το osc,n και τη συχνότητα συντονισμού. Η κατεύθυνση των αρχικών μετατοπίσεων που προκαλούν της παραμένουσες τάσεις έχουν μεγάλη σημασία ειδικά όταν εφαρμόζεται ο νόμος Skalak Η Επίδραση των Παραμένουσων Τάσεων της Μεμβράνης νόμος Mooney-Rivlin Στα σχήματα φαίνεται η μεταβολή της ακτίνας ως συνάρτηση του χρόνου σε κατάσταση εκτός και εντός συντονισμού αντίστοιχα. Παρατηρούμε πως τα αποτελέσματα είναι ίδια ανεξάρτητα από το αν υπάρχουν παραμένουσες τάσεις στη μεμβράνη. Τα σχήματα απεικονίζουν το osc,n όταν υπάρχουν παραμένουσες τάσεις στη μεμβράνη για τιμές του συντελεστή b του νόμου Mooney-Rivlin Ο, 0.5 και 1 αντίστοιχα. Είναι φανερό πως η επίδραση των παραμένουσων τάσεων στο osc.n Σχήμα 4.67: Η ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη εκτός συντονισμού. Δεδομένα προσομοίωσης: γ=1.4, Plnf= Pa, ρι=998, kg/m3, s=0.045 Kg/s2, μι=0.001 kgrtf's'1, Ci=1500m/s, μ5=0.6 kgm'v, Gs=35 MPa, r=3*10 6m, δ= 15*1 O'9 m, mf=0.05,b=0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 69
85 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.68: Η ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη σε συντονισμό. Δεδομένα προσομοίωσης: γ= 1.4, P,nf=l Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm's'1, Q=1500 m/s, μ$=0.6 kgnt s, Gs=35 MPa, r=3*10"6m, δ= 15*10"9 m, mf=0.05,b=0. Σχήμα 4.69: To osc, ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ= 1.4, P,nf= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'1 s'1, C =1500 m/s, o-3*10'6 m, Gs=35 MPa, μ^ο.6 kgmv, δ=15*10-9 m, einf=2.05, b=0. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 70
86 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.70: Το σ5οη ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ= 1.4, Plnf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgrrf s'1, C =1500 m/s, a=3*10"6 m, Gs=35 MPa, μ5=0.6 kgnt's'1, δ=15* 10'9 m, inf=2.05, b=0.5. vf (Hz) Σχήμα 4.71: To asc,n ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρ,=998 kg/m3, s=0.045 Kg/s2, μ,=0.001 kgm' s'', C,= 1500 m/s, α=3*10'6 m, Gs=35 MPa, μ,=0.6 kgm 's'1, 5= 15*1 O'9 m, mf=2.05, b=l. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου J1
87 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Η Επίδραση των Παραμένουσων Τάσεων της Μεμβράνης νόμος Skalak Στα σχήματα φαίνεται η μεταβολή της ακτίνας ως συνάρτηση του χρόνου σε κατάσταση εκτός και εντός συντονισμού αντίστοιχα. Παρατηρούμε πως τα αποτελέσματα έχουν μικρές διαφορές όταν υπάρχουν παραμένουσες τάσεις στη μεμβράνη. Τα σχήματα απεικονίζουν το osc.n όταν υπάρχουν παραμένουσες τάσεις στη μεμβράνη για τιμές του συντελεστή c του νόμου Skalak 1, 5 και 10 αντίστοιχα. Είναι φανερό πως η επίδραση των παραμένουσων τάσεων στο asc.n είναι ιδιαιτέρα σημαντική. Επίσης γίνεται αντιληπτό πως η κατεύθυνση των αρχικών μετατοπίσεων μεταβάλλει τη συχνότητα συντονισμού. Έτσι όταν η κατεύθυνση των αρχικών μετατοπίσεων έχει θετική φορά αυξάνεται το osc,n της επιβαλλόμενης συχνότητας και ο συντονισμός επέρχεται σε υψηλότερες συχνότητες. Σχήμα 4.72: Η ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη εκτός συντονισμού. Δεδομένα προσομοίωσης: γ=1.4, Plnf= Pa, Ρι=998, kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v, Ci=1500m/s, μ5=0.6 kgm's 1, Gs=35 MPa, r=3*10 6m, δ= 15*1 O'9 m, fmr=0.05,b= Time Σχήμα 4.73: Η ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη σε συντονισμό. Δεδομένα προσομοίωσης: γ=1.4, Pjnf= Pa, βι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm's1, C =1500m/s, μ5=0.6 kgm'v, Gs=35 MPa, r=3*10 6 m, o=15*10'9 m, inf=0.05,c=l. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Conlrasl Agent σε περιβάλλον υπερήχου 72
88 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.74: To osc n ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ=1.4, Pmf= Pa, ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, C = 1500 m/s, a=3*l 0 6 m, Gs=35 MPa, μ^ο.6 kgm's', 5=15*10_9m, elnf=2.05, c=l. Σχήμα 4.75: To σ5ο, ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ= 1.4, Pmf= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm 's'1, Q= 1500 m/s, o=3*10 6 m, Gs=35 MPa, ^=0.6 kgm''s'', ό=15* 10'9 m, mf=2.05, c=5. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τόπου Contrast Agent σε περιβάλλον υπερήχου 73
89 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.76: To osc,n ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ=1.4, P,nf= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'v1, C =1500 m/s, of3*10'6 m, Gs=35 MPa, ^=0.6 kgm 's'1, δ=15* 10'9 m, 6inf=2.05, c= Η Επίδραση των Παραμένουσων Τάσεων της Μεμβράνης νόμος Kelvin-Voigt Σχήμα 4-77: Η εξωτερική ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη εκτός συντονισμού. Δεδομένα προσομοίωσης: γ= 1.4, Pmf= Pa, ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgnt's"1, C =1500 m/s, ps=0.6 kgm 's'1, Gs=35 MPa, α=3* 10'6 m, 5=15*1 O'9 m,,nf=0.05. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 74
90 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Time Σχήμα 4-78: Η εξωτερική ακτίνα της μικροφυσαλίδας ως συνάρτηση του χρόνου με και χωρίς παραμένουσες τάσεις στη μεμβράνη σε συντονισμό. Δεδομένα προσομοίωσης: γ= 1.4, Pjnf= Pa, ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, gi=0.001 kgm'1s'1, C =1500 m/s, ps=0.6 kgm's'1, Gs=35 MPa, a=3*10'6 m, δ=15* 10'9 m. finf vf (Hz) xio6 Σχήμα 4-79: To asc n ως συνάρτηση της εξωτερικής συχνότητας για διάφορες τιμές των παραμένουσων τάσεων. Δεδομένα προσομοίωσης: γ= 1.4, Pi f=l01325 Pa, Ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgrrf's 1, C,= 1500 m/s, a=3*lo'6 m, Gs=35 MPa, μ5=0.6 kgm 's'1, δ=15*10'9 m, i,nf=2.05. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 75
91 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση 4.10 Σύγκριση με τις Ελεύθερες Φυσαλίδες Οι ελεύθερες μικροφυσαλίδες δεν έχουν μεμβράνη και το φάσμα συχνοτήτων που εμφανίζουν είναι πλούσιο σε υψηλότερες αρμονικές και υποαρμονικές. Ο συντονισμός τους επέρχεται σε χαμηλότερες συχνότητες σε σχέση με τις μικροφυσαλίδες τύπου Contrast Agent και η εμφάνιση υποαρμονικών λαμβάνει χώρα σε μικρότερα μεγέθη και διαταραχές πίεσης. Η χρήση μεμβράνης είναι επιτακτική επειδή η ταλάντωση της ελεύθερης μικροφυσαλίδας είναι ασταθής σε μεγάλες διαταραχές πίεσης, που έχει ως αποτέλεσμα την κατάρρευση της. Σχήμα 4.80: Contrast Agent (μοντέλο Mooney-Rivlin). Δεδομένα προσομοίωσης: γ=1.4, Plnf= Pa, Ρι=998 kg/m3, s=0.045 Kg/s2, μι=0.001 kgm'ls'1, Q=1500 m/s, a=3*10'6 m, Gs=35 MPa, ps=0.6 kgm"1s l, δ= 15*1 O'9 m, inf-1-0, Ur{t θ) Γ_ =Ur(t = 6)\r=R^ 0, b-0 Σχήμα 4.81: Contrast Agent (μοντέλο Skalak). Δεδομένα προσομοίωσης: 7=1.4, Pinf= Pa, pi=998 kg/m3, s=0.045 Kg/s2, pi=0.001 kgm'v1, C =1500 m/s, α=3* 10'6 m, Gs=35 MPa, μ5=0.6 kgm''s'', δ=15* 10'9 m, einf=1.0, ur{t = 0\^ =ur{t = 0 r= = 0,c=l Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 76
92 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.82: Contrast Agent (μοντέλο Kelvin-Voigt). Δεδομένα προσομοίωσης: γ=1.4, ΡιηΓ= Pa, Ρι=998 kg/m3, Si=0.04 Kg/s2, s2=0.005 kg/s2, μι=0.001 kgnr's"1, C =1500 m/s, a=3*10 6 m, Gs=35 MPa, /is=0.6 kgm'v1, δ=15*10'9 m, imf=1.0 Ur(t = θ) =ι =Ur(t = O) =0 Σχήμα 4.83: Ελεύθερες φυσαλίδες. Δεδομένα προσομοίωσης: γ= 1.4, Pinf= Pa, ρι=998 kg/m3, Si=0.072 Kg/s2, s2=0.0 kg/s2, μι=0.001 kgm''s'', Cf=1500 m/s, oe=3*10'6 m, Gs=0 MPa, gs=0.0 kgnt's'1, δ=0 m, emf= Σύγκριση με Πειραματικά Αποτελέσματα Οι μικροφυσαλίδες που χρησιμοποιούνται στα πειράματα και τις διάφορες εφαρμογές εμφανίζονται πάντα σε πληθυσμούς και το μέγεθος τους ακολουθεί συγκεκριμένη κατανομή. Για το λόγο αυτό ορίζεται ο συντελεστής επανασκέδασης: /!(v/)=^rzn('')ct&(v/ r) Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 77
93 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση όπου n(r) η συγκέντρωση των φυσαλίδων με ακτίνα r, συμβολίζει τον αριθμό φυσαλίδων που έχουν την συγκεκριμένη ακτίνα ισορροπίας r ως προς τον συνολικό όγκο του δείγματος των μικροφυσαλίδων. Όπως αναφέρθηκε από την παραπάνω ανάλυση το Osc,n εξαρτάται σε μεγάλο βαθμό από το μέγεθος της μικροφυσαλίδας. Επίσης, τα πειραματικά αποτελέσματα των Jean - Marie Gorce et al [33] έδειξαν παρομοίως ότι το asc εξαρτάται από τον συνολικό όγκο που καταλαμβάνουν οι μικροφυσαλίδες συγκεκριμένης ακτίνας και όχι από τον αριθμό των μικροφυσαλίδων με το ίδιο μέγεθος. Στο σχήμα 4.84 εμφανίζεται η συγκέντρωση κατ όγκο των μικροφυσαλίδων από το πείραμα των Jean - Marie Gorce et al [33] έχοντας θεωρήσει πέντε κλάσεις. Από το γράφημα φαίνεται ότι το 87% του όγκου των φυσαλίδων έχουν διάμετρο από μηι με μέση τιμή περίπου τα 6.4 μιτι. Diameter (μηι) Σχήμα 4.84: Η συγκέντρωση (κ.ο.) των μικροφυσαλίδων στο πείραμα των Jean - Marie Gorce et al. Προκειμένου να γίνει σύγκριση των αριθμητικών αποτελεσμάτων με τα πειραματικά, θεωρήθηκε η μέση τιμή του μεγέθους της μικροφυσαλίδας από κάθε κλάση και υπολογίσθηκε το asc για κάθε μέγεθος. Έπειτα, χρησιμοποιήθηκε η σχέση (4-1) για τον υπολογισμό του συντελεστή h, όπου n(r) θεωρήθηκε η συγκέντρωση κατ όγκο των μικροφυσαλίδων. Δεδομένα για το ιξώδες, το πάχος και το μέτρο ελαστικότητας της μεμβράνης προέκυψαν από τις μέσες τιμές των παραμέτρων που αναφέρονται στην ίδια εργασία (Gs=36.67 MPa, ^= kgm'v, δ=15 nm). Το μέσο μεταφοράς των ακουστικών διαταραχών ήταν το νερό, ενώ η διαταραχή της πίεσης που εφαρμόσθηκε ήταν Emf=0.5 (υπερπίεση 50 KPa). Στο σχήμα 4.85 δίδονται τα αριθμητικά και τα πειραματικά αποτελέσματα, όσον αφορά τον συντελεστή h. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 78
94 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Σχήμα 4.85: Ο συντελεστής h (backscatter coefficient) ως συνάρτηση της εξωτερικής συχνότητας a) Παρόν αριθμητικό μοντέλο για τους τρεις καταστατικούς νόμους μεμβράνης b) Πείραμα των Jean - Marie Gorce et al,. Δεδομένα προσομοίωσης: γ=1.4, Plnf= Pa. Pi=998 kg/m3, S =0.04 Kg/s2, s2=0.005 kg/s2, Gs=36.67 MPa, ^= kgnf1s-',5=15*10-9m,,nf=0.5., ur(t = 0\ml = Ur{t = =0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 79
95 Κεφάλαιο 4ο Αποτελέσματα & Συζήτηση Αξίζει να σημειωθεί ότι η συγκέντρωση, n(r), κάθε μίας από τις κλάσεις των μικροφυσαλίδων έχει υπολογιστεί με τον ακόλουθο τρόπο, /λ _ αριθμός μικροφυσαλίδων ακτίνας r συνολικός όγκος δείγματος n / ν _ αριθμός μικροφυσαλίδων ακτίνας r ^ ^ μέσος όγκος μικροφυσαλίδας x συνολικός αριθμός μικροφυσαλίδων, λ _ ποσοστό μικροφυσαλίδων ακτίνας r μέσος όγκος μικροφυσαλίδας όπου η μέση διάμετρος μικροφυσαλίδας στα πειράματα που απεικονίζονται στο Σχήμα 4.85β είναι r=6.4 μιη. Είναι φανερό ότι υπάρχει ποιοτική συμφωνία ανάμεσα στα πειραματικά αποτελέσματα και το αριθμητικό μοντέλο όσον αφορά τη συχνότητα συντονισμού. Οι σημαντικές διαφορές, όσον αφορά το μέγεθος και την διασπορά του συντελεστή h, ανάμεσα στο μοντέλο και τα πειραματικά αποτελέσματα μπορεί να οφείλονται στους παρακάτω παράγοντες: i. Το γεγονός ότι θεωρήσαμε μέσες τιμές για κάθε κλάση ελαττώνει την ακρίβεια. Είναι αναγκαίο να χρησιμοποιήσουμε τιμές για κάθε κλάση και ειδικά από αυτή με το μεγαλύτερο ποσοστό όγκου. Π. Τα δεδομένα για το ιξώδες της μεμβράνης, το μέτρο διάτμησης και το πάχος προήλθαν από μέσες τιμές παραμέτρων που δόθηκαν στην εργασία των Jean - Marie Gorce et al [33].Είναι απαραίτητο να χρησιμοποιήσουμε τιμές που μετρήθηκαν καθώς η απόκριση της μικροφυσαλίδας είναι ευαίσθητη στα χαρακτηριστικά της μεμβράνης. iii. Θεωρήσαμε αμελητέα την απόσβεση ενέργειας λόγω θερμότητας. Η απόσβεση αυτή λόγω θερμικών απωλειών από τη μικροφυσαλίδα πιθανώς να είναι σημαντική έπειτα από αρκετές περιόδους ταλαντώσεων. iv. Αγνοήθηκε η αλληλεπίδραση των μικροφυσαλίδων μεταξύ τους. ν. Τα πειραματικά δεδομένα, όπως ο όγκος του δείγματος, η κατανομή των φυσαλίδων και η διάρκεια των πειραματικών μετρήσεων, ώστε να θεωρηθεί ότι έχουν παρέλθει τυχόν μεταβατικά φαινόμενα στην απόκριση των μικροφυσαλίδων και συνεπώς έχει επέλθει μόνιμη κατάσταση, είναι ελλιπή, και αποτελούν αντικείμενο της τρέχουσας ερευνητικής προσπάθειας. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 80
96 Κεφάλαιο 5ο Συμπεράσματα & Προτάσεις για Μελλοντική Έρευνα Κεφάλαιο 5 Συμπεράσματα & Προτάσεις για Μελλοντική Έρευνα Στην παρούσα διπλωματική εργασία εξετάστηκε η επίδραση των καταστατικών νόμων μεμβράνης Mooney-Rivlin και Skalak στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent όταν υπόκειται σε ακουστικές διαταραχές της πίεσης στο άπειρο. Θεωρήσαμε ότι η διαταραχή της πίεσης στο άπειρο είναι ημιτονοειδής και οι ταλαντώσεις της μικροφυσαλίδας έχουν σφαιρική συμμετρία. Έτσι λοιπόν το μοντέλο βασίστηκε στην εξίσωση Keller-Miksis [28] που ισχύει για σφαιρικές ταλαντώσεις ελευθέρων φυσαλίδων και λαμβάνει υπόψη τη συμπιεστότητα και το ιξώδες του ρευστού στο οποίο βρίσκονται. Προκειμένου να μοντελοποιηθεί η ελαστικότητα της μεμβράνης χρησιμοποιήθηκαν οι παραπάνω μη γραμμικοί καταστατικοί νόμοι τάσεων-παραμορφώσεων. Η μελέτη του προβλήματος έδειξε ότι υπάρχει ποιοτική συμφωνία μεταξύ των αποτελεσμάτων του αριθμητικού μοντέλου και των πειραμάτων. Παρατηρήθηκε επίσης ότι τα χαρακτηριστικά της μεμβράνης παίζουν σπουδαίο ρόλο στην απόκριση της μικροφυσαλίδας. Για το μοντέλο που περιγράφεται από τον καταστατικό νόμο μεμβράνης Mooney-Rivlin καταλήξαμε λοιπόν στα εξής : Η αύξηση της εξωτερικής διαταραχής της πίεσης είχε ως αποτέλεσμα τον εμπλουτισμό του osc,n με υψηλότερες αρμονικές, τη μικρή απόσβεση της επιβαλλόμενης συχνότητας στο asc,n και την μικρή αύξηση της συχνότητας συντονισμού. Η αύξηση του μέτρου διάτμησης της μεμβράνης αυξάνει το osc,n της επιβαλλόμενη συχνότητας, αποσβένει λίγο τη συνεισφορά των υψηλότερων αρμονικών στο συνολικό asc,n και αυξάνει., την τιμή της συχνότητας συντονισμού. Η αύξηση του ιξώδους της μεμβράνης έχει ως συνέπεια την απόσβεση όλων των αρμονικών ενώ παράλληλα μετατοπίζει το συντονισμό σε υψηλότερες συχνότητες. Αύξηση του πάχους της μεμβράνης προκαλεί την απόσβεση της συνεισφοράς όλων των αρμονικών στο συνολικό osc,n ενώ ο συντονισμός μετατοπίζεται σε υψηλότερες συχνότητες. Η αύξηση του μεγέθους της μικροφυσαλίδας έχει ως αποτέλεσμα τη μείωση της συχνότητας συντονισμού και την αύξηση της συνεισφοράς τόσο των υποαρμονικών όσο και των υψηλότερων αρμονικών στο Osc,n Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 81
97 Κεφάλαιο 5ο Συμπεράσματα & Προτάσεις για Μελλοντική Έρευνα Η επίδραση του μέσου στο οποίο βρίσκεται η μικροφυσαλίδα επηρεάζει το συνολικό Osc,n και όχι τη συχνότητα συντονισμού. Έτσι λοιπόν όταν αυξάνεται η συμπιεστότητα και το ιξώδες του μέσου στο οποίο βρίσκεται η μικροφυσαλίδα μειώνεται η συνεισφορά όλων των αρμονικών στο συνολικό 0Sc,n Όσο αυξάνεται ο συντελεστής b, δηλαδή η μη γραμμικότητα του νόμου, ενισχύεται η συνεισφορά της επιβαλλόμενης συχνότητας στο osc,n, αποσβέννυνται ελάχιστα οι υπόλοιπες αρμονικές και μετατοπίζεται η συχνότητα συντονισμού σε λίγο μεγαλύτερες συχνότητες. Η ύπαρξη παραμενουσών τάσεων δεν επηρεάζει σημαντικά την απόκριση της μικροφυσαλίδας. Το φάσμα συχνοτήτων των ελευθέρων φυσαλίδων είναι πιο πλούσιο από των μικροφυσαλίδων τύπου Contrast Agent για ίδια τιμή της διαταραχής και ο συντονισμός τους επέρχεται σε χαμηλότερες συχνότητες. Για το μοντέλο που περιγράφεται από τον καταστατικό νόμο μεμβράνης Skalak οδηγηθήκαμε στα εξής συμπεράσματα: Η αύξηση της εξωτερικής διαταραχής της πίεσης είχε ως αποτέλεσμα ττ\ν εμφάνιση υψηλότερων αρμονικών στο συνολικό Osc,n των οποίων η συνεισφορά είναι ελάχιστη, τη μικρή απόσβεση της επιβαλλόμενης συχνότητας στο osc,n και την αμελητέα μεταβολή της συχνότητας συντονισμού. Η αύξηση του μέτρου διάτμησης της μεμβράνης αυξάνει το asc,n τηζ επιβαλλόμενη συχνότητας, αποσβένει λίγο τη συνεισφορά των υψηλότερων αρμονικών στο συνολικό osc,n παρόλο που η συνεισφορά τους είναι πολύ μικρή και αυξάνει την τιμή της συχνότητας συντονισμού. Η αύξηση του ιξώδους της μεμβράνης έχει ως συνέπεια την απόσβεση όλων των αρμονικών ενώ παράλληλα μετατοπίζει το συντονισμό σε υψηλότερες συχνότητες. Αύξηση του πάχους της μεμβράνης προκαλεί την απόσβεση της συνεισφοράς όλων των αρμονικών στο συνολικό osc,n ενώ ο συντονισμός μετατοπίζεται σε υψηλότερες συχνότητες. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 82
98 Κεφάλαιο 5ο Συμπεράσματα & Προτάσεις για Μελλοντική Έρευνα Η αύξηση του μεγέθους της μικροφυσαλίδας έχει ως αποτέλεσμα τη μεταφορά του συντονισμού σε χαμηλότερες συχνότητες και την αύξηση της συνεισφοράς τόσο των υποαρμονικών όσο και των υψηλότερων αρμονικών OTO 0Sc,n Η επίδραση του μέσου στο οποίο βρίσκεται η μικροφυσαλίδα επηρεάζει το συνολικό osc,n και όχι τη συχνότητα συντονισμού. Έτσι λοιπόν όταν αυξάνεται η συμπιεστότητα και το ιξώδες του μέσου στο οποίο βρίσκεται η μικροφυσαλίδα μειώνεται η συνεισφορά όλων των αρμονικών στο συνολικό 0Sc,n Όσο αυξάνεται ο συντελεστής c, δηλαδή το υλικό της μεβράνης γίνεται περισσότερο strain-hardening, ενισχύεται η συνεισφορά της επιβαλλόμενης συχνότητας στο osc,n και ο συντονισμός επέρχεται σε υψηλότερες συχνότητες. Η ύπαρξη παραμένουσων τάσεων επηρεάζει σημαντικά την απόκριση της μικροφυσαλίδας. Έτσι αναλόγως της φοράς των αρχικών μετατοπίσεων στη μεμβράνη μεταβάλλεται το συνολικό osc,n καθώς επίσης και η συχνότητα συντονισμού. Το φάσμα συχνοτήτων των ελευθέρων φυσαλίδων, για ίδια τιμή της διαταραχής, είναι πιο πλούσιο από των μικροφυσαλίδων τύπου Contrast Agent που περιγράφονται από το νόμο Skalak ενώ ο συντονισμός των πρώτων επέρχεται σε χαμηλότερες συχνότητες. Όσον αφορά τη σύγκριση των αποτελεσμάτων του αριθμητικού μοντέλου με αυτά των πειραμάτων παρατηρήθηκε ποιοτική συμφωνία. Ωστόσο, για να επιτύχουμε μεγαλύτερη συμφωνία θα μπορούσε η μορφή της διαταραχής του αριθμητικού μοντέλου να επεκταθεί ώστε να περιλαμβάνει ένα εύρος συχνοτήτων όπως συμβαίνει συνήθως στα πειράματα. Πρόσφατες έρευνες αφορούν την απόκριση μικροφυσαλίδας η οποία διαταράσσεται με μία συχνότητα αρχικά και έπειτα από ορισμένη φάση με διαφορετική συχνότητα [34]. Ακόμα, σημαντικό ρόλο παίζει και η διάρκεια των πειραμάτων ώστε να ολοκληρωθεί η μεταβατική φάση των ταλαντώσεων της μικροφυσαλίδας όπως συμβαίνει στις προσομοιώσεις. Τέλος, αναφορικά με την σύγκριση συγκεκριμένων πειραματικών μετρήσεων με προσομοιώσεις. Σχήματα 4.85 α, β, θα πρέπει να υπάρχουν αναλυτικά και αξιόπιστα στοιχεία σχετικά με τον όγκο του δείγματος, την κατανομή των μεγεθών των φυσαλίδων και την διάρκεια των πειραμάτων, πριν καταστεί δυνατή η ποσοτική σύγκριση. Εν γένει χρειάζεται μεγάλη προσοχή στην συμβατότητα των συνθηκών διεξαγωγής των πειραματικών μετρήσεων και των προσομοιώσεων. Όσον αφορά την Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 83
99 Κεφάλαιο 5ο Συμπεράσματα & Προτάσεις για Μελλοντική Έρευνα αξιοπιστία των προσομοιώσεων, χρειάζεται να διερευνηθεί η επίδραση και άλλων μηχανισμών απόσβεσης της ενέργειας, όπως π.χ. των θερμικών απωλειών, να εξετασθεί η επίδραση γειτονικών φυσαλίδων ή ιστών καθώς και να ληφθούν υπόψη τρισδιάστατες διαταραχές της σφαιρικής ή της αξονικής συμμετρίας του προβλήματος, προκειμένου να υπάρξει και ποσοτική συμφωνία με τις υπάρχουσες πειραματικές μετρήσεις. Σε αυτήν την κατεύθυνση και προκειμένου να μελετηθεί περαιτέρω η δυναμική συμπεριφορά των μικροφυσαλίδων που βρίσκονται σε περιβάλλον υπερήχων, προτείνονται οι εξής βελτιώσεις των μοντέλων προσομοίωσης μικροφυσαλίδων: Εξέταση των ταλαντώσεων της μικροφυσαλίδας που περιγράφονται από αξονοσυμμετρικό μοντέλο και μελέτη των παραμέτρων της μικροφυσαλίδας ώστε να προσδιορισθούν τα όρια συνοχής της καθώς και οι μηχανισμοί κατάρρευσης της. Μελέτη της αλληλεπίδρασης μεταξύ μικροφυσαλίδας και γειτονικής μικροφυσαλίδας ή μεμβράνης που αναπαριστά κύτταρο ή ιστό και εξέταση της πιθανότητας δημιουργίας πόρου στη μεμβράνη. Διεξαγωγή τρισδιάστατων προσομοιώσεων. Επέκταση των αποτελεσμάτων της δυναμικής συμπεριφοράς μιας μικροφυσαλίδας προκειμένου να προβλεφθεί η συμπεριφορά αιωρήματος μικροφυσαλίδων που υπόκεινται σε ακουστικές διαταραχές Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 84
100 Παράρτημα Παράρτημα I. Βιβλιογραφία-Αναφορές [1] Ν. de Jong and F.J. Ten Cate. New ultrasound contrast agents and technological innovations, Ultrasonics, 34: , 1996 [2] A. Bouakaz, P.J. A. Frinking, N. de Jong, and N. Bom. Noninvasive measurement of the hydrostatic pressure in a fluid-filled cavity based on the disappearance time of micrometer-sized free gas bubbles. Ultrasound Med. Biol., 25: , 1999 [3] Ιστοσελίδα της American Society of Radiologic Technologists [4] R.Gramiak and M.Shah. Echocardiography of the Aortic Root, Investigative Radiology, 3: , 1968 [5] B. Goldberg. Ultrasound Contrast Agents, Martin Dunitz Ltd, 1997 [6] A. Klibnov, Targeted Delivery of Gas-Filled Microbubbles. Contrast Agents for Ultrasound Imaging, Advanced Drug Delivery, 37: , 1999 [7] Forsberg, R. Basude, J. Lui, J. Alessandro, W. Shi, N. Rawool, B. Goldberg and M. Wheatley. Effect of filling gases on the backscatter from contrast microbubbles: Theory and in vivo measurements, Ultrasound in Medicine and Biology, 8: ,1999 [8] D. B. Khismatullin and A. Nadim. Radial oscillations of encapsulated microbubbles. Phys. Fluids, Vol. 14, No. 10, October 2002F. [9] L. Hoff. Acoustic properties of ultrasonic contrast agents, Ultrasonics 34: ,1996 [10] W. Shi, F. Frosberg, A. Tomes, J. Ostensen and B. Goldberg. Destruction of Contrast Microbubbles and the Association with Inertial Cavitation, Ultrasound in Medicine and Biology, Vol. 26, No. 6, ,2000 [11] G.M. Lanza, R. Trousil, K. Wallace, J. Rose, C. Hall, M. Scott, J. Miller, P. Eisenburg, P. Gaffney and S. Wickline. In vitro characterization of a novel, tissue-targeted ultrasonic contrast system with acoustic microscopy, Journal of the Acoustic Society of America, 104: ,1998 [12] V. Rouffiac, JS. Duret, P. Opolon, P. Peronneau, A. Roche. A new high intensity focused ultrasound (HIFU) system for tumor treatment and real - time Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 85
101 Παράρτημα control by Doppler sonography. Ex vivo and in vivo investigations. The Tenth European Symposium on Ultrasound Contrast Imaging. January 2005 [13] S. Theoharis, F. Fostira, A. George, M. Blomley. Optison Enhances gene delivery by increasing the uptake of plasmid DNA by cells. The Tenth European Symposium on Ultrasound Contrast Imaging. January 2005 [14] J. Babich and A. Fischman. Target imaging of infection, Advance Drug Delivery Reviews, 37: ,1997 [15] P. J. Frinking, A. Bouakaz, J. Kirkhom and F.J. Ten Cate. Ultrasound contrast imaging: Current and new potential methods. Ultrasound in Medicine and Biology, Vol. 26, No. 6, ,2000 [16] M. FI. Repacholi, M. Garandolfo and A. Rindi. Ultrasound: Medical Applications, Biological Effects and Hazard Potential, Plenum Press, New York, 1987 [17] R. H. Randall. An introduction to acoustics, Addison-Wesley Publishing Company, Inc., 1951 [18] J. L. Rose and B.B. Goldberg. Basic Physics in Diagnostic Ultrasound, Wiley Medical Publication, 1979 [19] K. K. Shung. Principle of Medical Imaging, Academic Press, San Diego, 1992 [20] M.Hussey. Basic Physics and Technology of Medical Diagnostic Ultrasound, Elsevier, 1984 [21] N. de Jong, P. Frinking, A. Bouakaz and F.J. Ten Cate. Detection Procedures of Ultrasound Contrast Agents, Ultrasonics, 38: 87-92,2000 [22] M. Minnaert. On musical air bubbles and the sound of running water, Phil. Magazine., 26: 121, 1936 [23] N. de Jong, A. Bouakaz, and C.T. Lancee. Higher harmonics of vibrating gas filled microspheres. Part one: Simulations, Ultrasonics, 32: , 1994 [24] A. Prosperetti. Thermal effects and damping mechanisms in forced radial oscillations of gas - bubbles in liquids. Journal of the Acoustical Society of America, 1977 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 86
102 Παράρτημα [25] C.C. Church. The effects of an elastic solid surface layer on the radial pulsations of gas bubbles. J. Acoust. Soc. Am., 97: , 1995 [26] D. B. Khismatullin and A. Nadim. Radial oscillations of encapsulated microbubbles. Phys. Fluids, Vol. 14, No. 10, October 2002 [27] V. Sboros, V. A. MacDonald, S.D. Pye, C.M. Moran, J. Gomatam and W.N. McDicken. The dependence of ultrasound contrast agents backscatter on acoustic pressure: Theory versus experiment. Ultrasonics, 40: , 2002 [28] J. B. Keller and M. Miksis. Bubble oscillations of large amplitude../. Acoust. Soc. Am. 68(2), Aug [29] D. Barthes-Biesel, A. Diaz and E. Dhenin. Effect of constitutive laws for two- dimensional membranew on flow-induced capsule deformation. J. Fluid Mech., 460: ,2002 [30] C. Pozrikidis. Boundary integral and singularity methods for linearized viscous flow. Cambridge University Press, 1992 [31] A. Diaz, D. Barthes-Biesel, N. A. Pelekasis. Effect of membrane viscosity on the dynamic response of an axisymmetric capsule. Physics of Fluids, volume 13, number 12, December 2001 [32] K. Τσιγκλιφής. Προσομοίωση δυναμικής μικροφυσαλίδας (Contrast Agents) σε περιβάλλον υπερήχων. Μεταπτυχιακή Εργασία, 2005 [33] Jean - Marie Gorce, Marcel Arditi, and Michel Schneider. Influence of Bubble Size Distribution on the Echogenicity of Ultrasound Contrast Agents. A Study of SonoVue. Investigative Radiology, volume 35,number 11, (2000) [34] R. Hansen, B. Angelsen, P. Bums, A. Bouakaz, J. Borsboom, M. Versluis, N. de Jong. Radial modulation imaging. The Tenth European Symposium on Ultrasound Contrast Imaging. January 2005 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τόπου Contrast Agent σε περιβάλλον υπερήχου 87
103 Παράρτημα 11. Κώδικας Ο κώδικας για το μοντέλο Mooney-Rivlin: PROGRAM CONTRAST ID IMPLICIT NONE INTEGER NUMSTEPJERR1,1,METR, VALUE,PERIODS,J REAL(8) STARTTIME,ENDTIME,RDRDT,GSDIMINITIAL,DGSDIM,GSDIMFINAL,EINFINITIAL,DEINF,EINFFINAL REAL(8)RB,AB,ABUNDIM,THICKNESS,GAMA,PINFDIM,EINF,FREQ,FREQINITIAL,DFREQ,FREQFINAL& REAL(8) CL,PL,ML,MSK,GSDIM,SAB,SRB,UDIM,B,U,MS,MSINITIAL,DMS,MSFINAL,RB IN ITIAL.DRB.RB FINAL,THICKNESSINITIAL& DTHICKNESS.THICKNESSFINAL REAL(8) PI,OMEGA,REL,RES,MACH,GS.WEBSAB,WEBSRB,PINF,VOLUMESDIM,VOLUMES,TSTEP REAL(8) TIME,R,A,DRDT,K1 (2),K2(2),K3(2),K4(2),ARADIUS,RRADIUS REAL(8) FREQUEN(5),SCSEN(5) REAL(8), ALLOCATABLE, DIMENSION (:):: PSCATTERVECTOR,FREQUENCY,POWPSCATTERVECTOR,SCS.RPOWPSCATTERVECTOR INTEGER, ALLOCATABLE,DIMENSION (:)::IPERM OPEN( 1,FILE-INPUTCONTRASTnew.DAT',STATUS UNKNOWN') OPEN(2,FILE='OUTCONTRAST 1. DAT',STATUS='UNKNOWN') OPEN(3,FILE= APOT. DAT,STATUS-UNKNOWN1) OPEN(4,FILE-POWER.DAT,STATUS UNKNOWN') OPEN(5,FILE-RESULTS.DAT'.STATUS UNKNOWN') OPEN(6,FILE-SCSRES.DAT,STATUS UNKNOWN') READ(I,*) STARTTIME.TSTEP.PERIODS,VALUE READ( 1,*) GAMA.PINFDIM READ(1,*) CL,PL,ML,SRB,UDIM,B READ(1,*) FREQINITIAL.DFREQ.FREQFINAL READ(1,*) MSINITIAL,DMS,MSFINAL READ( 1,*) GSDIMINITIAL,DGSDIM,GSDIMFINAL READ(I,*) RBINITIAL.DRB.RBFINAL READ(1,*) THICKNESSINITIAL,DTHICKNESS,THICKNESSFINAL READ(1,*) EINFIN1TIAL,DEINF,EINFFINAL PI=DACOS(-1.0D0) ENDTIME=STARTTIME+2.0D0*PI*PERIODS NUMSTEP=DNINT((ENDTIME-STARTTIME)/TSTEP) ALLOCATE (PSCATTERVECTOR(NUMSTEP),FREQUENCY(NUMSTEP),& POWPSCATTERVECTOR(NUMSTEP),SCS(NUMSTEP/2),IPERM(NUMSTEP/2),RPOWPSCATTERVECTOR(NUMSTEP/2)&,STAT = IERR1) IF(IERR1.NE.0)THEN WRITE(*,*)"WRONG MEMORY ALLOCATION STOP ENDIF EINF=EINFINITIAL DO WHILE(EINF.LE.EINFFINAL) THICKNESS=THICKNESSINITIAL DO WHILE(THICKNESS.LE.THICKNESSFINAL) RB=RB INITIAL DO WHILE(RB.LE.RBFINAL) GSDIM=GSDIMINITIAL DO WHILE(GSDIM.LE.GSDIMFINAL) MSK=MSINITIAL DO WHILE(MSK.LE.MSFINAL) FREQ=FREQINITIAL Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 88
104 Παράρτημα DO WHILE(FREQ.LE.FREQFINAL) MS=3*MSK*THICKNESS OMEGA=2.0D0*PI*FREQ REL=PL*OMEGA*RB**2,ODO/ML RES=PL*OMEGA*RB**3,ODO/MS MACH=OMEGA*RB/CL GS=GSDIM*THICKNESS/(PL*RB**3.0D0*OMEGA**2.0D0) WEBSRB=(PL*RB**3.0D0*OMEGA**2.0D0)/SRB PINF=PINFDIM/(PL*RB**2.0D0*OMEGA**2.0D0) U=UDIM/RB WRITE(2,*) OMEGA -.OMEGA WRITE(2,*) 'REYNOLDS NUMBER LIQUID =',REL WRITE(2,*) 'REYNOLDS NUMBER SOLID =',RES WRITE(2,*) 'MACH NUMBER =',MACH WRITE(2,*) 'SHEAR MODULUS UNDIM =',GS WRITE(2,*) 'WEBER NUMBER SRB =',WEBSRB WRITE(2,*) 'PRESSURE INFINITE UNDIM=',PINF WRITE(2,*) 'VOLUME OF SOLID DIM =,VOLUMESDIM WRITE(2,*) 'VOLUME OF SOLID UNDIM VOLUMES WRITE(2,*) TIMESTEP =,TSTEP I*********************** INITIAL VALUES* ************* * * ** TIME=ST ARTTIME R=RB/RB DRDT=O.ODO RDRDT=0.0D0 METR=1 t***********************initial VALUES****************** DO I=1,NUMSTEP K1=0 0D0 K2=O.ODO K3=O.ODO K4=fl.0D0 RRADIUS=R RDRDT=DRDT K1(1)=RDRDT K1 (2)=D2RDTF(TIME,RRADIUS,RDRDT) RRADIUS=R+0.5D0*TSTEP*K1 (1) RDRDT=DRDT+0.5D0*TSTEP*K1(2) K2(1)=RDRDT K2(2)=D2RDTF(TIME+0.5D0*TSTEP,RRADIUS,RDRDT) RRADIUS=R+0.5D0*TSTEP*K2( 1) RDRDT=DRDT+O.5D0*TSTEP*K2(2) K3(1)=RDRDT K3(2)=D2RDTF(TIME+0.5D0*TSTEP,RRADIUS,RDRDT) RRADIUS=R+TSTEP*K3(1) RDRDT=DRDT+TSTEP*K3(2) K4(1)=RDRDT K4(2)=D2RDTF(TIME+TSTEP,RRADIUS,RDRDT) R=R+TSTEP/6.0D0*(K1(1 )+2.0D0*K2( 1 H2.0D0*K3( 1 )+K4( 1)) DRDT=DRDT+TSTEP/6.0D0*(K1(2)+2.0D0*K2(2)+2.0D0*K3(2)+K4(2)) Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 89
105 Παράρτημα IF (METR.EQ. VALUE) THEN WRITE(3,1000) TIME,R.DRDT,PSCATTER(TIME,R,DRDT) METR=0 ENDIF PSCATTER VECTOR! I)=PSCATTER(TIME,R,DRDT) TIME=TIME+TSTEP METR=METR+1 ENDDO 1000 F0RMAT(1X,F15.6,1X,F15.6,1X,F15.6,1X,F15.6,1X,F15.7) CALL POWERSPECTRUM(NUMSTEP,TSTEP,PSCATTERVECTOR,FREQUENCY,POWPSCATTERVECTOR) POWPSCATTERVECTOR(l )=0.0D0 DO 1=1,NUMSTEP/2 SCS(I)=4.0D0*PI*(RB*10**6.0D0)**2.0D0*POWPSCATTERVECTOR(I)*»2.0D0/(EINF*PINF)**2.0D0!WRITE(4,*) FREQUENCY(I),POWPSCATTERVECTOR(I),SCS(I) ENDDO POWPSCATTERVECTOR=DABS(POWPSCATTER VECTOR) DO 1=1, NUMSTEP/2 IPERMdH ENDDO CALL DSVRGP(NUMSTEP/2,POWPSCATTERVECTOR! 1 :NUMSTEP/2),RPOWPSCATTERVECTOR,IPERM) WRITE(5,2000) CL,MSK,GSDIM,RB,THICKNESS,EINF, FREQ,UD1M.FREQUENCY(IPERM(NUMSTEP/2)),SCS(IPERM (NUMSTEP/2)),& FREQUENCY(IPERM(NUMSTEP/2-l )),& SCS(IPERM(NUMSTEP/2-l)),FREQUENCY(IPERM(NUMSTEP/2-2)),SCS(IPERM(NUMSTEP/2-2)),& FREQUENCY(lPERM(NUMSTEP/2-3)),SCS(IPERM(NUMSTEP/2-3)) 2000 F0RMAT(1X,F15.9,1X,F15.9,1X,F15.1,1X,F!5.12,1X,F15.12,1X,F15.9,1X,F15.1,1X,F15.12,1X,F15.9,1X,F15.9,1X,F15.9,1X,F15.9 &,1X,F15.9,1X,F15.9,1X,F15.9,1X,F15.9,1X,F15.9,1X,F15.9,1X,F15.9,1X,F15.9) FREQ=FREQ+DFREQ ENDDO MSK=MSK+DMS ENDDO GSDIM=GSD1M+DGSDIM END DO RB=RB+DRB ENDDO THICKNESS=THICKNESS+DTHICKNESS ENDDO EINF=EINF+DEINF ENDDO CONTAINS REAL(8) FUNCTION D2RDTF(TIME,R,DRDT) IMPLICIT NONE REAL(8) TIME.R.DRDT REAL(8) PIB,PIBA,PIBB,PIBR,OROS 1,OROS2,ARITH,PARON,ARITHI.ARITH2 PIB=O.ODO PIBA=O.0D0 PIBB=O.ODO PIBR=O.ODO OROS1=O.ODO OROS2=O.ODO Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 90
106 Παράρτημα ARITH=O.ODO PARON=O.ODO ARITH1=0.0D0 ARITH2=O.ODO OROS1=(1,ODO+DRDT*MACH) 0R0S2=(R*MACH) PIBA=( 1,0D0-( I ODO-U)* *6.0DO)*( 1,ODO+B*(-1 ODO+( 1 ODO/( 1 0D0-U))**2.0D0)) PIBB=(1.0D0-((1.0DO-U)/R)**6.0D0)*(l,0DO+B*(-1.0D0+(R/(1.0DO-U))**2.OD0))/R ARITHl=ARJTHl+(!.0DO/R) (3.0D0*GAMA)*(PINF+2.0DO/WEBSRB+2.0D0*GS*PIBA) ARITH1=ARITH1-2.0DO/(WEBSRB*R)-4.0DO*DRDT/(REL*R)-2.0DO*GS*PIBB/R-4.0DO*DRDT/(RES*R**2.0DO)-PINF- & EINF*PINF*DSIN(TIME)!ARITHl=ARITHl-2.0D0/(WEBSRB*R)-4.0DO*DRDT/(REL*R)-2.0D0*GS«PIBB-4.0D0*DRDT/(RES*R**2.0DO)-PINF-& EINF*PINF*DCOS(TIME) ARITH2=ARITH2-3.0D0*GAMA*DRDT»R**(-3.0D0*GAMA-1.0D0)*(PINF+2.0D0AVEBSRB+2.0D0*GS»PIBA) ARITH2=ARITH2+2.0D0*DRDT/(WEBSRB*R**2.0D0)+2.0DO*GS*DRDT/(R**2.0D0) ARITH2=ARITH2-2.0DO*GS*B*DRDT/((1.0D0-U)»*2.0DO)-2.ODO*GS*B*DRDT/(R**2.OD0) ARITH2=ARITH2-14.OD0*GS*DRDT*((1.0DO-U)**6.0D0)/(R**8.0DO) ARITH2=ARITH2-K).ODO*GS*B*DRDT*((l.ODO-U)**4.ODO)/(R**6.0DO>i-I4.0DO*GS*B*DRDT*((1.ODO-U)**6.ODO)/(R**8.ODO)-& E1NF*PINF*DC0S(TIME)!ARITH2=ARJTH2-10,0DO*GS*B*DRDT*((l.OD0-U)**4.0D0)/(R**6.0DO)+14.0D0*GS*B*DRDT*((l.ODO- & U)**6.0D0)/(R**8.0D0)+EINF*PINF*DSIN(TIME) ARITH=ARITH+OROS 1 *ARITH1+OROS2*ARITH2-(3.0DO/2,ODO- & DRDT«MACH/2.0DO)«(DRDT**2.0DO)+4.0DO*MACH*(DRDT**2.0DO)/(REL*R) ARITH=ARITH+8.0DO*MACH*(DRDT**2.0DO)/(RES*R**2.0DO) PARON=PARON+(l.0D0-DRDT*MACH)*R+4 0D0*MACH/(REL)+4.0D0*MACH/(RES*R) D2RDTF=ARITH/PARON END FUNCTION REAL(8) FUNCTION PSCATTER(TIME,R,DRDT) IMPLICIT NONE REAL(8) TIME,R,DRDT REAL(8) PIBW.PIBX PIBX=O.ODO PIBW=O.ODO PIBX=( 1,ODO-(( 1,ODO-U)/R)**6.0DO)*(1 0D0+B*(-1,0D0+(R/(1.ODO-U))**2,ODO)) PIBW=(1 ODO-(1 ODO-U)**6.0DO)*(1.0DO+B*(-1.0DO+(1.0DO/(1,0D0-U))**2.0D0)) PSCATTER=O.ODO PSCATTER=PSCATTER+PINF+((2.0D0)/(WEBSRB))+2.0D0*GS*PIBW PSCATTER=PSCATTER*(1.0D0/R)**(3.0DO*GAMA) PSCATTER=PSCATTER-(2.0D0y(WEBSRB*R) PSCATTER=PSCATTER-(4.0DO*DRDT)/(REL*R) PSCATTER=PSCATTER-(2.0DO*GS*PIBX/R) PSCATTER=PSCATTER^tODO*DRDT/(RES*R**2.0DO) PSCATTER=PSCATTER-PINF-EINF PINF*DSIN(TIME) END FUNCTION Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 91
107 Παράρτημα SUBROUTINE POWERSPECTRUM(NUMSTEP,TSTEP,PSCATTERVECTOR,FREQUENCY,POWPSCATTERVECTOR) IMPLICIT NONE INTEGERS) NUMSTEP,I REAL(8) PSCATTERVECTOR(NUMSTEP),POWPSCATTERVECTOR(NUMSTEP) REAL(8) FREQUENCY(NUMSTEP),TSTEP!REAL(8) FPSCATTERVECTOR(NUMSTEP) ICALL DFFTRF (NUMSTEP, PSCATTERVECTOR, FPSCATTERVECTOR) CALL DFFTRF (NUMSTEP, PSCATTERVECTOR, PSCATTERVECTOR) DO 1=1, NUMSTEP!POWPSCATTERVECTOR(I)=FPSCATTERVECTOR(I)*2.0DO/NUMSTEP POWPSCATTERVECTOR(I)=PSCATTERVECTOR(I)*2.0DO/NUMSTEP FREQUENCY(I)=PI»(I/(NUMSTEP*TSTEP)) ENDDO END SUBROUTINE END PROGRAM CONTRAST1D Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 92
108 Παράρτημα Αντίστοιχα για το μοντέλο Skalak ο κώδικας είναι: PROGRAM CONTRAST 1D IMPLICIT NONE INTEGER NUMSTEP.IERR 1,I,METR,VALUE,PERIODS,J REAL(8)STARTTIME.ENDTIME,RDRDT,GSDIMINITIAL,DGSDIM,GSDIMFINAL,EINFINITIAL,DEINF,EINFFINAL REA L(8)RB,AB,ABUNDIM,TH1CKNESS,GAMA,PINFDIM,EINF,FREQ,FREQINITIAL,DFREQ,FREQFINAL REAL(8)CL,PL,ML,MSK,GSDIM,SAB,SRB.UDIM,B,U,MS,MSINITIAL,DMS,MSFINAL,RBINITIAL,DRB,RBFINAL, & THICKNESSINITIAL,DTHICKNESS,THICKNESSFINAL REAL(8)PI,OMEGA,REL,RES,MACH,GS,WEBSAB,WEBSRB,PINF,VOLUMESDIM,VOLUMES,TSTEP REAL(8) TIME,R,A,DRDT,K1(2),K2(2),K3(2),K4(2),ARADRJS,RRADIUS REAL(8) FREQUEN(5),SCSEN(5) REAL(8), ALLOCATABLE, DIMENSION (:):: PSCATTERVECTOR.FREQUENCY.POWPSCATTERVECTOR.SCS.RPOWPSCATTERVECTOR INTEGER, ALLOCATABLE.DIMENSION (:)::IPERM OPEN( 1,FILE=,INPUTCONTRASTnew,DAT',STATUS='UN KNOWN ) 0PEN(2,FILE-0UTC0NTRAST1.DAT',STATUS='UN KNOWN') OPEN(3,FILE='APOT.DAT',STATUS UNKNOWN') OPEN(4,FILE-POWER. DAT.STATUS-UN KNOWN') OPEN(5,FILE='R ESULTS.DAT',STATUS-UNKNOWN') OPEN(6,FILE='SCSRES.DAT',STATUS-UNKNOWN') READ( 1,*) STARTTIME.TSTEP.PERIODS,VALUE READ(1,*) GAMA,PINFDIM READ(1,*) CL.PL,ML,SRB,UDIM,B READ(1,*) FREQINITIAL.DFREQ.FREQFINAL READ(1,*) MSINITIAL.DMS.MSFINAL READ( 1,*) GSDIMINITIAL,DGSDIM,GSDIMFINAL READ(I,*) RBINITIAL.DRB.RBFINAL READfl,*) THICKNESSINITIAL.DTHICKNESS.THICKNESSFINAL READ(1,*) EINFINITIAL.DEINF.EINFFINAL PI=DACOS(-l 0D0) ENDTIME=STARTTIME+2,ODO*PI*PERIODS NUMSTEP=DNINT((ENDTIME-STARTTIME)/TSTEP) ALLOCATE (PSCATTERVECTOR(NUMSTEP),FREQUENCY(NUMSTEP),& POWPSCATTERVECTOR(NUMSTEP),SCS(NUMSTEP/2),IPERM(NUMSTEP/2),RPOWPSCATTERVECTOR(NUMSTEP/2),& STAT = IERR1) IF(IERRl.NE.O) THEN WRITE(*,*)"WRONG MEMORY ALLOCATION STOP ENDIF EINF=EINFINITIAL DO WHILE(EINF.LE.EINFFINAL) THICKNESS=THICKNESSINITIAL DO WHILE(THICKNESS.LE.THICKNESSFINAL) RB=RB INITIAL DO WHILE(RB.LE.RBFINAL) GSDIM=GSDIMINITIAL DO WHILE(GSDIM.LE.GSDIMFINAL) MSK=MSINITIAL DO WHILE(MSK.LE.MSFINAL) FREQ=FREQINITIAL DO WHILE(FREQ.LE.FREQFINAL) MS=3*MSK*THICKNESS OMEGA=2.0D0*PI*FREQ REL=PL*OMEGA*RB**2,ODO/ML Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 93
109 Παράρτημα RES=PL*OMEGA*RB**3,ODO/MS MACH=OMEGA*RB/CL GS=GSDIM*THICKNESS/(PL*RB**3,ODO*OMEGA**2,ODO) WEBSRB=(PL*RB**3.0D0*OMEGA**2.0D0)/SRB PINF=PINFDIM/(PL*RB**2.0D0*OMEGA**2.0D0) U=UDIM/RB WRITE(2,*) OMEGA -.OMEGA WRITE(2,*) 'REYNOLDS NUMBER LIQUID =,REL WRITE(2,*) REYNOLDS NUMBER SOLID =,RES WRITE(2,*) MACH NUMBER =,ΜΑΟΗ WRITE(2,*) 'SHEAR MODULUS UNDIM =',GS WRITE(2,*) 'WEBER NUMBER SRB -.WEBSRB WRITE(2,*) 'PRESSURE INFINITE UNDIM=',PINF WRITE(2,*) 'VOLUME OF SOLID DIM =\VOLUMESDIM WRITE(2,*) 'VOLUME OF SOLID UNDIM =',VOLUMES WRITE(2,*) 'TIMESTEP =',TSTEP i***********************initial VALUES****************** TIME=STARTTIME R=RB/RB DRDT=O.ODO RDRDT=O.ODO METR=1 t ****** ****** ****** *****[]sjixial values****************** DO I=1,NUMSTEP K1=O.ODO K2=0.0D0 K3=0.0D0 K4=O.ODO RRADIUS=R RDRDT=DRDT K1(1)=RDRDT K1 (2)=D2RDTF(TIME,RRADIUS,RDRDT) RRADIUS=R+0.5D0*TSTEP*K 1(1) RDRDT=DRDT+0.5DO*TSTEP*K.1(2) K2(1)=RDRDT K2(2)=D2RDTF(TIME+0.5D0*TSTEP,RRADIUS,RDRDT) RRADIUS=R+0.5D0*TSTEP*K2( 1) RDRDT=DRDT+0.5D0*TSTEP*K2(2) K3(I)=RDRDT K3(2)=D2RDTF(TIME+0.5D0*TSTEP,RRADIUS,RDRDT) RRADIUS=R+TSTEP*K3( I) RDRDT=DRDT+TSTEP*K3(2) K4( 1 )=RDRDT K4(2)=D2RDTF(TIME+TSTEP,RRADIUS,RDRDT) R=R+TSTEP/6.0D0*(K 1 (1 )+2.0D0*K2( 1 }*-2.0D0*K3( 1 )+K4( 1)) DRDT=DRDT+TSTEP/6.0DO*(K1(2)+2.0DO*K2(2)+2.0DO*K3(2HC4(2)) IF (METR.EQ. VALUE) THEN WRITE(3,1000) TIME.R.DRDT.PSC ATTER(TIME,R,DRDT) METRO ENDIF Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 94
110 Παράρτημα PSCATTERVECTOR(I)=PSCATTER(TIME,R.DRDT) TIME=TIME+TSTEP METR=METR+1 ENDDO 1000 F0RMAT(1X,F15.6,1X,F15.6,1X,F15.6,1X,F15.6,1X,F15.7) CALL POWERSPECTRUM(NUMSTEP,TSTEP,PSCATTERVECTOR,FREQUENCY,POWPSCATTERVECTOR) POWPSCATTERVECTOR( 1 )=0.0D0 DO l=l,numstep/2 SCS(I)=4.0D0*PI*(RB*10**6.0D0)**2.0D0*POWPSCATTERVECTOR(I)**2.0D0/(EINF*PINF)**2.0D0!WRITE(4,*)FREQUENCY(I),POWPSCATTERVECTOR(I),SCS(I) ENDDO POWPSCATTERVECTOR=DABS(POWPSCATTER VECTOR) DO 1= 1,NUMSTEP/2 IPERM(I)=I ENDDO CALL DSVRGP(NUMSTEP/2,POWPSCATTERVECTOR! 1 :NUMSTEP/2),RPOWPSCATTERVECTOR,IPERM) WRJTE(5,2000) CL,MSK,GSDIM,RB,THICKNESS,EINF,FREQ,UDIM,FREQUENCY(IPERM(NUMSTEP/2)),SCS(IPERM(NUMSTEP/2)),& FREQUENCY(IPERM(NUMSTEP/2-l )),& SCS(IPERM(NUMSTEP/2-l)),FREQUENCY(IPERM(NUMSTEP/2-2)),SCS(IPERM(NUMSTEP/2-2)),& FREQUENCY(IPERM(NUMSTEP/2-3)),SCS(IPERM(NUMSTEP/2-3)) 2000 FORMAT(lX,F15.9,lX,F15.9,lX,F15.1,lX,F15,12,lX,F15.12,1X,F15.9,1X,F15.1, IX,FI 5.12,1 X.Fl 5.9,1 X,F15.9,1 X,F15.9,1 X.F15.9,1 X,& FI 5.9, IX, & F15.9,1X,F15.9,1X,F15.9,1X,F15.9,1X,F15.9,1X,F15.9,1X,F15.9) FREQ=FREQ+DFR Q ENDDO MSK=MSK+DMS ENDDO GSDIM=GSDIM+DGSD1M ENDDO RB=RB+DRB ENDDO THIC KN ESS=THICKN ESS+DTHIC KNESS ENDDO EINF=EINF+DEINF END DO CONTAINS REAL(8) FUNCTION D2RDTF(TIME,R,DRDT) IMPLICIT NONE REAL( 8) TIME,R,DRDT REAL(8) PIB,PIBA,PIBB,PIBR,OROS 1,OROS2,ARITH,PARON,ARITHl.ARITFL2 PIB=O.ODO PIBA=O.ODO PIBB=0.0D0 PIBR=O.ODO OROS1=O.ODO OROS2=O.ODO ARITH=0.0D0 PARON=OODO ARITH1=O.ODO ARITH2=0.0D0 Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 95
111 Παράρτημα OROS1 =( 1,0D0+DRDT*MACH) OROS2=(R*MACH) PIBA=(1.0DO-B)*(l.ODO/(l.ODO-U))**(2.ODO)+B*(l.OD0/(1.0DO-U))**(6.ODO)-1.0DO PIBR=(1.0DO-B)*(R/(1.0DO-U))**(2.ODO)+B*(R/(1.0DO-U))**(6.0D0)-1.0DO PIBB=2.OD0*(1.0DO-B)*R*DRDT/((l.OD0-U)**(2.0DO))+6.0D0*B*DRDT*(R**5.0D0)/((1.0DO-U)**(6.0D0)) ARITH1=AR1TH1+(1.ODO/R)**(3.0DO*GAMA)*(PINF+2.0DO/WEBSRB+2.0DO*GS*PIBA) ARITHl=ARITHl-2.0D0/(WEBSRB*R)-4.0DO*DRDT/(REL*R)-2.0DO*GS*PIBR/R-4.0D0*DRDT/(RES*R**2.ODO)-PINF-& EINF*PINF*DSIN(TIME)!ARITHl=ARITHl-2.0D0/(WEBSRB*R)-4.0D0*DRDT/(REL*R)-2.0D0*GS*PIBB-4.0D0»DRDT/(RES*R**2.0D0)-PINF-& EINF*PINF*DCOS(TIME) ARITH2=ARlTH2-3.0D0*GAMA*DRDT*R**(-3.0DO*GAMA-1.0DO)*(PINF+2.0DO/WEBSRB+2.0D0*GS*PIBA) ARITH2=ARITH2+2.0DO*DRDT/(WEBSRB*R**2.0DO)+4.0D0*(DRDT**2.0DO)/(REL*R**2.0D0) ARITH2=ARITH2-2.0DO*GS*PlBB/R+8.0DO»(DRDT»*2.0DO)/(RES*R**3.0D0) ARITH2=ARITH2-EINF*PINF*DCOS(TIME)!ARITH2=ARITH2-10.0DO*GS*B*DRDT*((1.0D0-U)**4.0DO)/(R**6.ODO)+14.0D0*GS»B*DRDT*((1.0D0-& U)**6.0D0)/(R**8.0DO)+EINF*PINF*DSIN(TIME) ARITH=ARITH+OROSI*ARITH1+OROS2*AR!TH2-(3.0DO/2,ODO-DRDT*MACH/2.0DO)*(DRDT**2.0DO) PARON=PARON+(l,0D0-DRDT*MACH)*R+4.0D0*MACH/(REL)+4.0D0*MACH/(RES*R) D2 RDTF=A RITH/P ARON END FUNCTION REAL(8) FUNCTION PSCATTER(TIME,R,DRDT) IMPLICIT NONE R AL(8) TIME,R,DRDT REAL(8) PIBW.PIBX PIBX=0.0D0 PIBW=O.ODO PIBX=((1.0DO-B)*(R/(1.0DO-U))*»(2.0DO)+B*(R/(1.0DO-U))**(6.0DO)-1.0DO) PIBW=((1.0DO-B)*(1.0DO/(1.0DO-U))**(2.ODO)+B*(l.ODO/(1.0DO-U))**(6.ODO)-l.ODO) PSCATTER=O.ODO PSCATTER=PSCATTER+PINF+((2.0D0)/(WEBSRB))+2.0D0*GS*PIBW PSCATTER=PSCATTER*( 1 0D0/R)*»(3.0D0*GAMA) PSCATTER=PSCATTER-{2.0D0y(WEBSRB*R) PSCATTER=PSCATTER-(4.0D0*DRDT)/(REL*R) PSCATTER=PSCATTER-(2.0D0*GS*PIBX/R) PSCATTER=PSCATTER-4.0DO*DRDT/(RES*R**2.0DO) PSCATTER=PSCATTER-PINF-EINF*PINF*DSIN(TIME) END FUNCTION Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 96
112 Παράρτημα SUBROUTINE POWERSPECTRUM(NUMSTEP,TSTEP,PSCATTERVECTOR, FREQUENCY,POWPSCATTERVECTOR) IMPLICIT NONE INTEGERS) NUMSTEP.I REAL(8)PSCATTERVECTOR(NUMSTEP),POWPSCATTERVECTOR(NUMSTEP) REAL,(8) FREQUENCY(NUMSTEP),TSTEP!REAL(8) FPSCATTERVECTOR(NUMSTEP) 1CALL DFFTRF (NUMSTEP, PSCATTERVECTOR, FPSCATTERVECTOR) CALL DFFTRF (NUMSTEP, PSCATTERVECTOR, PSCATTERVECTOR) DO 1=1,NUMSTEP!POWPSCATTERVECTOR(I)=FPSCATTERVECTOR(I)*2.0DO/NUMSTEP POWPSCATTERVECTOR(I)=PSCATTERVECTOR(I)*2.0DO/NUMSTEP FREQUENCY(I)=PI*(I/(NUMSTEP*TSTEP)) ENDDO END SUBROUTINE END PROGRAM CONTRAST ID Στον παραπάνω κώδικα η μεταβλητή c του νόμου Skalak έχει οριστεί ως b. Επίδραση καταστατικού νόμου μεμβράνης στη δυναμική συμπεριφορά μικροφυσαλίδας τύπου Contrast Agent σε περιβάλλον υπερήχου 97
113
114
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ & ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ. Διπλωιιατική Εργασία
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ & ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ Διπλωιιατική Εργασία Επίδραση μη γραμμικής διαταραχής στη δυναμική συμπεριφορά
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ & ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ Διπλωιιατική Εργασία Επίδραση μη γραμμικής διαταραχής στη δυναμική συμπεριφορά
Η Φυσική των ζωντανών Οργανισμών (10 μονάδες)
 Η Φυσική των ζωντανών Οργανισμών (10 μονάδες) Δεδομένα: Κανονική Ατμοσφαιρική Πίεση, P 0 = 1.013 10 5 Pa = 760 mmhg Μέρος A. Η φυσική του κυκλοφορικού συστήματος. (4.5 μονάδες) Q3-1 Στο Μέρος αυτό θα μελετήσετε
Η Φυσική των ζωντανών Οργανισμών (10 μονάδες) Δεδομένα: Κανονική Ατμοσφαιρική Πίεση, P 0 = 1.013 10 5 Pa = 760 mmhg Μέρος A. Η φυσική του κυκλοφορικού συστήματος. (4.5 μονάδες) Q3-1 Στο Μέρος αυτό θα μελετήσετε
Ευθυμίου Κωνσταντίνου
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ & ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ Διδακτορική Διατριβή: Αλληλεπίδραση μικροφυσαλίδας με ελαστικό περίβλημα (Contrast Agent)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ & ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ Διδακτορική Διατριβή: Αλληλεπίδραση μικροφυσαλίδας με ελαστικό περίβλημα (Contrast Agent)
ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ
 ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Γενικές Αρχές Φυσικής Κ. Χατζημιχαήλ ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Καλώς ήλθατε Καλή αρχή Υπερηχογραφία Ανήκει στις τομογραφικές μεθόδους απεικόνισης Δεν έχει ιονίζουσα
ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Γενικές Αρχές Φυσικής Κ. Χατζημιχαήλ ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Καλώς ήλθατε Καλή αρχή Υπερηχογραφία Ανήκει στις τομογραφικές μεθόδους απεικόνισης Δεν έχει ιονίζουσα
ΑΘΑΝΑΣΙΟΣ Ι. ΦΡΕΝΤΖΟΣ. 6 ο ΕΤΟΣ ΙΑΤΡΙΚΗΣ (2004-05) του Ε.Κ.Π.Α. ΕΡΓΑΣΙΑ
 ΑΘΑΝΑΣΙΟΣ Ι. ΦΡΕΝΤΖΟΣ 6 ο ΕΤΟΣ ΙΑΤΡΙΚΗΣ (2004-05) του Ε.Κ.Π.Α. ΕΡΓΑΣΙΑ 148 ΑΡΧΕΣ ΦΥΣΙΚΗΣ ΤΩΝ ΥΠΕΡΗΧΩΝ ΑΣΦΑΛΕΙΑ ΤΩΝ ΥΠΕΡΗΧΩΝ ΣΤΗ ΜΑΙΕΥΤΙΚΗ Γ ΜΑΙΕΥΤΙΚΗ ΚΑΙ ΓΥΝΑΙΚΟΛΟΓΙΚΗ ΚΛΙΝΙΚΗ ΑΝ. ΚΑΘΗΓΗΤΗΣ Δ. ΚΑΣΣΑΝΟΣ
ΑΘΑΝΑΣΙΟΣ Ι. ΦΡΕΝΤΖΟΣ 6 ο ΕΤΟΣ ΙΑΤΡΙΚΗΣ (2004-05) του Ε.Κ.Π.Α. ΕΡΓΑΣΙΑ 148 ΑΡΧΕΣ ΦΥΣΙΚΗΣ ΤΩΝ ΥΠΕΡΗΧΩΝ ΑΣΦΑΛΕΙΑ ΤΩΝ ΥΠΕΡΗΧΩΝ ΣΤΗ ΜΑΙΕΥΤΙΚΗ Γ ΜΑΙΕΥΤΙΚΗ ΚΑΙ ΓΥΝΑΙΚΟΛΟΓΙΚΗ ΚΛΙΝΙΚΗ ΑΝ. ΚΑΘΗΓΗΤΗΣ Δ. ΚΑΣΣΑΝΟΣ
ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΘΕΩΡΙΑ ο ΜΑΘΗΜΑ
 ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΘΕΩΡΙΑ 2017 7 ο ΜΑΘΗΜΑ Εισαγωγή Κύμα είναι η διάδοση των περιοδικών κινήσεων (ταλαντώσεων) που κάνουν τα στοιχειώδη σωματίδια ενός υλικού γύρω από τη θέση ισορροπίας
ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΘΕΩΡΙΑ 2017 7 ο ΜΑΘΗΜΑ Εισαγωγή Κύμα είναι η διάδοση των περιοδικών κινήσεων (ταλαντώσεων) που κάνουν τα στοιχειώδη σωματίδια ενός υλικού γύρω από τη θέση ισορροπίας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΑΣ. Μεταπτυχιακή Εργασία
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ & ΣΤΡΟΒΙΑΟΜΗΧΑΝΩΝ Μεταπτυχιακή Εργασία ΠΡΟΣΟΜΟΙΩΣΗ ΔΥΝΑΜΙΚΗΣ ΜΙΚΡΟΦΥΣΑΛΙΔΑΣ (Contrast Agents)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΒΙΟΜΗΧΑΝΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣ & ΣΤΡΟΒΙΑΟΜΗΧΑΝΩΝ Μεταπτυχιακή Εργασία ΠΡΟΣΟΜΟΙΩΣΗ ΔΥΝΑΜΙΚΗΣ ΜΙΚΡΟΦΥΣΑΛΙΔΑΣ (Contrast Agents)
Δομικά Υλικά Μάθημα ΙΙΙ. Ηχος & Ηχητικά Φαινόμενα
 Δομικά Υλικά Μάθημα ΙΙΙ Ηχος & Ηχητικά Φαινόμενα Ηχος: Μια μηχανική διαταραχή η οποία προκαλείται από μια πηγή και διαδίδεται με ορισμένη ταχύτητα σε ένα ελαστικό μέσο. Μια περιοδική ταλάντωση των μορίων
Δομικά Υλικά Μάθημα ΙΙΙ Ηχος & Ηχητικά Φαινόμενα Ηχος: Μια μηχανική διαταραχή η οποία προκαλείται από μια πηγή και διαδίδεται με ορισμένη ταχύτητα σε ένα ελαστικό μέσο. Μια περιοδική ταλάντωση των μορίων
ΦΥΣΙΚΗ ΚΑΙ ΟΡΓΑΝΟΛΟΓΙΑ ΥΠΕΡΗΧΩΝ
 ΦΥΣΙΚΗ ΚΑΙ ΟΡΓΑΝΟΛΟΓΙΑ ΥΠΕΡΗΧΩΝ 1. Η Doppler σάρωση έχει τη δυνατότητα να προσδιορίσει: α) Το βάθος της κινούμενης διεπιφάνειας. β) Την ταχύτητα της κινούμενης διεπιφάνειας. γ) Την κατεύθυνση της κινούμενης
ΦΥΣΙΚΗ ΚΑΙ ΟΡΓΑΝΟΛΟΓΙΑ ΥΠΕΡΗΧΩΝ 1. Η Doppler σάρωση έχει τη δυνατότητα να προσδιορίσει: α) Το βάθος της κινούμενης διεπιφάνειας. β) Την ταχύτητα της κινούμενης διεπιφάνειας. γ) Την κατεύθυνση της κινούμενης
1 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ
 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά
Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά
ΔΙΑΓΩΝΙΣΜΑ ΤΕΛΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 2014 ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ: ΚΟΛΟΣΙΩΝΗΣ ΔΗΜΗΤΡΗΣ
 1 ΔΙΑΓΩΝΙΣΜΑ ΤΕΛΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 2014 ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ: ΚΟΛΟΣΙΩΝΗΣ ΔΗΜΗΤΡΗΣ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό κάθε μιας από τις παρακάτω
1 ΔΙΑΓΩΝΙΣΜΑ ΤΕΛΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 2014 ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ: ΚΟΛΟΣΙΩΝΗΣ ΔΗΜΗΤΡΗΣ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό κάθε μιας από τις παρακάτω
Άσκηση 36 Μελέτη ακουστικών κυμάτων σε ηχητικό σωλήνα
 Μιχάλης Καλογεράκης 9 ο Εξάμηνο ΣΕΜΦΕ ΑΜ:911187 Υπεύθυνος Άσκησης: Κος Πέογλος Ημερομηνία Διεξαγωγής:3/11/25 Άσκηση 36 Μελέτη ακουστικών κυμάτων σε ηχητικό σωλήνα 1) Εισαγωγή: Σκοπός και στοιχεία Θεωρίας
Μιχάλης Καλογεράκης 9 ο Εξάμηνο ΣΕΜΦΕ ΑΜ:911187 Υπεύθυνος Άσκησης: Κος Πέογλος Ημερομηνία Διεξαγωγής:3/11/25 Άσκηση 36 Μελέτη ακουστικών κυμάτων σε ηχητικό σωλήνα 1) Εισαγωγή: Σκοπός και στοιχεία Θεωρίας
ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5)
 ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ - ΝΕΟ ΣΥΣΤΗΜΑ - Γ ΗΜΕΡΗΣΙΩΝ ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Στις ερωτήσεις Α - Α4
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ - ΝΕΟ ΣΥΣΤΗΜΑ - Γ ΗΜΕΡΗΣΙΩΝ ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Στις ερωτήσεις Α - Α4
ΙΑΤΡΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΚΑΤΑΤΑΚΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΑΚ.ΕΤΟΥΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ
 ΙΑΤΡΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΚΑΤΑΤΑΚΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΑΚ.ΕΤΟΥΣ 217-218 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ 1. Τι γνωρίζετε για τη νόσο των δυτών. Απάντηση: Η νόσος των δυτών είναι μία σοβαρή κατάσταση,
ΙΑΤΡΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΚΑΤΑΤΑΚΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΑΚ.ΕΤΟΥΣ 217-218 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ 1. Τι γνωρίζετε για τη νόσο των δυτών. Απάντηση: Η νόσος των δυτών είναι μία σοβαρή κατάσταση,
r r r r r r r r r r r
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑÏΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑÏΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 2019 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ
 Εισηγητής: Γκίκας Στ. Βασίλειος ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 2019 ΘΕΜΑ Α ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Να γράψετε στην κόλα σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Εισηγητής: Γκίκας Στ. Βασίλειος ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 2019 ΘΕΜΑ Α ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Να γράψετε στην κόλα σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΙΑΤΡΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΚΑΤΑΤΑΚΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΑΚ.ΕΤΟΥΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ
 ΙΑΤΡΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΚΑΤΑΤΑΚΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΑΚ.ΕΤΟΥΣ 2016-2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Περιγράψτε τη μικρή (πνευμονική) κυκλοφορία και τη μεγάλη (συστηματική) κυκλοφορία
ΙΑΤΡΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΚΑΤΑΤΑΚΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΑΚ.ΕΤΟΥΣ 2016-2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Περιγράψτε τη μικρή (πνευμονική) κυκλοφορία και τη μεγάλη (συστηματική) κυκλοφορία
Πολιτικός Μηχανικός Ph.D.
 Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Ηχομονωτική προστασία κτιρίου Πανεπιστήμιο Θεσσαλίας Πολυτεχνική Σχολή ΤμήμαΠολιτικών Μηχανικών Διάλεξη 11 η /2016 Ακουστική Ακουστική είναι η επιστήμη που
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Ηχομονωτική προστασία κτιρίου Πανεπιστήμιο Θεσσαλίας Πολυτεχνική Σχολή ΤμήμαΠολιτικών Μηχανικών Διάλεξη 11 η /2016 Ακουστική Ακουστική είναι η επιστήμη που
Παρουσίαση μέσων Φυσικοθεραπείας Ι (φυσικά μέσα και τεχνολογίες)
 Παρουσίαση μέσων Φυσικοθεραπείας Ι (φυσικά μέσα και τεχνολογίες) ρ. Παναγιώτης Β. Τσακλής Καθηγητής Εµβιοµηχανικής & Εργονοµίας ΤΕΦΑΑ - ΠΘ Res. Assoc Department of Molecular Medicine & Surgery Karolinska
Παρουσίαση μέσων Φυσικοθεραπείας Ι (φυσικά μέσα και τεχνολογίες) ρ. Παναγιώτης Β. Τσακλής Καθηγητής Εµβιοµηχανικής & Εργονοµίας ΤΕΦΑΑ - ΠΘ Res. Assoc Department of Molecular Medicine & Surgery Karolinska
ENOTHTA 1: ΚΡΟΥΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 5 Ο : ΚΡΟΥΣΕΙΣ ΦΑΙΝΟΜΕΝΟ DOPPLER ENOTHT 1: ΚΡΟΥΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ Κρούση: Κρούση ονομάζουμε το φαινόμενο κατά το οποίο δύο ή περισσότερα σώματα έρχονται σε επαφή για πολύ μικρό χρονικό διάστημα κατά
ΚΕΦΑΛΑΙΟ 5 Ο : ΚΡΟΥΣΕΙΣ ΦΑΙΝΟΜΕΝΟ DOPPLER ENOTHT 1: ΚΡΟΥΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ Κρούση: Κρούση ονομάζουμε το φαινόμενο κατά το οποίο δύο ή περισσότερα σώματα έρχονται σε επαφή για πολύ μικρό χρονικό διάστημα κατά
Επαναληπτικό Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου ~~ Διάρκεια: 3 ώρες ~~
 Επαναληπτικό Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου ~~ Διάρκεια: 3 ώρες ~~ Θέμα Α 1. Σε χορδή έχει δημιουργηθεί στάσιμο κύμα. Δύο σημεία Α και Β που δεν είναι δεσμοί απέχουν μεταξύ τους απόσταση
Επαναληπτικό Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου ~~ Διάρκεια: 3 ώρες ~~ Θέμα Α 1. Σε χορδή έχει δημιουργηθεί στάσιμο κύμα. Δύο σημεία Α και Β που δεν είναι δεσμοί απέχουν μεταξύ τους απόσταση
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 1 Ονοματεπώνυμο.. Υπεύθυνος Καθηγητής: Γκαραγκουνούλης Ιωάννης Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ > Κυριακή 20-3-2011 2 ΘΕΜΑ 1ο Να γράψετε στο
1 Ονοματεπώνυμο.. Υπεύθυνος Καθηγητής: Γκαραγκουνούλης Ιωάννης Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ > Κυριακή 20-3-2011 2 ΘΕΜΑ 1ο Να γράψετε στο
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 11 ΑΠΡΙΛΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 11 ΑΠΡΙΛΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. Στις ερωτήσεις Α1-Α4, να γράψετε στην κόλλα σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ Α & Β ΑΡΣΑΚΕΙΩΝ ΤΟΣΙΤΣΕΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΤΡΙΤΗ ΑΠΡΙΛΙΟΥ 07 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗΣ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Στις ερωτήσεις
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ Α & Β ΑΡΣΑΚΕΙΩΝ ΤΟΣΙΤΣΕΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΤΡΙΤΗ ΑΠΡΙΛΙΟΥ 07 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗΣ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Στις ερωτήσεις
Διαγώνισμα 1 Α στα Μηχανικά κύματα
 ΔΙΑΓΩΝΙΣΜΑ 4 5 ου ΚΕΦΑΛΑΙΟΥ ΘΕΜΑ 1 Από τις παρακάτω προτάσεις ποιες είναι σωστές και ποιες είναι λανθασμένες; α) Όταν ένα σώμα που ταλαντώνεται περνάει από τη θέση ισορροπίας, η τιμή της συνολικής δύναμης
ΔΙΑΓΩΝΙΣΜΑ 4 5 ου ΚΕΦΑΛΑΙΟΥ ΘΕΜΑ 1 Από τις παρακάτω προτάσεις ποιες είναι σωστές και ποιες είναι λανθασμένες; α) Όταν ένα σώμα που ταλαντώνεται περνάει από τη θέση ισορροπίας, η τιμή της συνολικής δύναμης
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ
 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
Μάθημα Ακουστικής. Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ
 Μάθημα Ακουστικής Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ Περιοδική Κίνηση Μία κίνηση χαρακτηρίζεται σαν περιοδική αν αναπαράγεται απαράλλακτα σε ίσα διαδοχικά χρονικά διαστήματα. Στο χρονικό αυτό
Μάθημα Ακουστικής Νικόλαος Παλληκαράκης Καθ. Ιατρικής Φυσικής ΠΠ Περιοδική Κίνηση Μία κίνηση χαρακτηρίζεται σαν περιοδική αν αναπαράγεται απαράλλακτα σε ίσα διαδοχικά χρονικά διαστήματα. Στο χρονικό αυτό
Ηχητικά κύματα Διαμήκη κύματα
 ΦΥΣ 131 - Διαλ.38 1 Ηχητικά κύματα Διαμήκη κύματα Τα ηχητικά κύματα χρειάζονται ένα μέσο για να μεταδοθούν π.χ. αέρας Δεν υπάρχει ήχος στο κενό Ηχητικές συχνότητες 20Ηz 20ΚΗz Τα ηχητικά κύματα διαδίδονται
ΦΥΣ 131 - Διαλ.38 1 Ηχητικά κύματα Διαμήκη κύματα Τα ηχητικά κύματα χρειάζονται ένα μέσο για να μεταδοθούν π.χ. αέρας Δεν υπάρχει ήχος στο κενό Ηχητικές συχνότητες 20Ηz 20ΚΗz Τα ηχητικά κύματα διαδίδονται
ΠΟΜΠΟΣ ΕΚΤΗΣ ΑΝΙΧΝΕΥΤΗΣ
 Σαν ήχος χαρακτηρίζεται οποιοδήποτε μηχανικό ελαστικό κύμα ή γενικότερα μία μηχανική διαταραχή που διαδίδεται σε ένα υλικό μέσο και είναι δυνατό να ανιχνευθεί από τον άνθρωπο μέσω της αίσθησης της ακοής.
Σαν ήχος χαρακτηρίζεται οποιοδήποτε μηχανικό ελαστικό κύμα ή γενικότερα μία μηχανική διαταραχή που διαδίδεται σε ένα υλικό μέσο και είναι δυνατό να ανιχνευθεί από τον άνθρωπο μέσω της αίσθησης της ακοής.
r r r r r r r r r r r
 http://edu.kliaka.g ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑÏΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ)
http://edu.kliaka.g ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑÏΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ)
Δομικά Υλικά Μάθημα ΙV. Ηχος & Ηχητικά Φαινόμενα II
 Δομικά Υλικά Μάθημα ΙV Ηχος & Ηχητικά Φαινόμενα II Συντελεστής Ανάκλασης r Συντελεστής Ανάκλασης r Ο λόγος της ανακλώμενης (W r ) ηχητικής ενέργειας από την επιφάνεια προς την προσπίπτουσα (W i ) Συντελεστής
Δομικά Υλικά Μάθημα ΙV Ηχος & Ηχητικά Φαινόμενα II Συντελεστής Ανάκλασης r Συντελεστής Ανάκλασης r Ο λόγος της ανακλώμενης (W r ) ηχητικής ενέργειας από την επιφάνεια προς την προσπίπτουσα (W i ) Συντελεστής
ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ
 ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Γενικές Αρχές Απεικόνισης 1 Κ. Χατζημιχαήλ ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Καλώς ήλθατε..δεν ξεχνώ Ιατρική Απεικόνιση-Υπερηχογραφία Υπέρηχοι Για τη διάδοση απαιτείται
ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Γενικές Αρχές Απεικόνισης 1 Κ. Χατζημιχαήλ ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Καλώς ήλθατε..δεν ξεχνώ Ιατρική Απεικόνιση-Υπερηχογραφία Υπέρηχοι Για τη διάδοση απαιτείται
και επιτάχυνση μέτρου 1 4m/s. Ποια από τις παρακάτω προτάσεις είναι η σωστή;
 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ Α Α1. Ένα σώμα εκτελεί απλή αρμονική ταλάντωση και χρειάζεται χρόνο Δt = πs για να διανύσει την απόσταση από τη μια ακραία θέση στην άλλη.
Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ Α Α1. Ένα σώμα εκτελεί απλή αρμονική ταλάντωση και χρειάζεται χρόνο Δt = πs για να διανύσει την απόσταση από τη μια ακραία θέση στην άλλη.
ΘΕΜΑ Α ΕΡΩΤΗΣΕΙΣ ΘΕΜΑ Α
 ΘΕΜΑ Α 1. Να επιλέξετε τη σωστή απάντηση. Μηχανικό ονομάζεται το κύμα στο οποίο: α. Μεταφέρεται ύλη στον χώρο κατά την κατεύθυνση διάδοσης του κύματος. β. Μεταφέρεται ορμή και ενέργεια στον χώρο κατά την
ΘΕΜΑ Α 1. Να επιλέξετε τη σωστή απάντηση. Μηχανικό ονομάζεται το κύμα στο οποίο: α. Μεταφέρεται ύλη στον χώρο κατά την κατεύθυνση διάδοσης του κύματος. β. Μεταφέρεται ορμή και ενέργεια στον χώρο κατά την
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ - ΤΥΠΟΛΟΓΙΟ
 ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ - ΤΥΠΟΛΟΓΙΟ 1 2 Ισχύς που «καταναλώνει» μια ηλεκτρική_συσκευή Pηλ = V. I Ισχύς που Προσφέρεται σε αντιστάτη Χαρακτηριστικά κανονικής λειτουργίας ηλεκτρικής συσκευής Περιοδική
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ - ΤΥΠΟΛΟΓΙΟ 1 2 Ισχύς που «καταναλώνει» μια ηλεκτρική_συσκευή Pηλ = V. I Ισχύς που Προσφέρεται σε αντιστάτη Χαρακτηριστικά κανονικής λειτουργίας ηλεκτρικής συσκευής Περιοδική
ΕΡΓΑΣΤΗΡΙΑΚΗ ΜΕΛΕΤΗ ΣΤΑΣΙΜΩΝ ΗΧΗΤΙΚΩΝ ΚΥΜΑΤΩΝ ΣΕ ΣΩΛΗΝΑ KUNDT
 ΕΚΦΕ Χανίων ΕΡΓΑΣΤΗΡΙΑΚΗ ΜΕΛΕΤΗ ΣΤΑΣΙΜΩΝ ΗΧΗΤΙΚΩΝ ΚΥΜΑΤΩΝ ΣΕ ΣΩΛΗΝΑ KUNDT Κώστας Θεοδωράκης Νίκος Αναστασάκης Φυσικοί 10 ο Συνέδριο ΕΕΦ & ΕΚΦ Κέρκυρα 3 Μαρτίου 2007 Θεωρία: Το αποτέλεσμα της συμβολής δύο
ΕΚΦΕ Χανίων ΕΡΓΑΣΤΗΡΙΑΚΗ ΜΕΛΕΤΗ ΣΤΑΣΙΜΩΝ ΗΧΗΤΙΚΩΝ ΚΥΜΑΤΩΝ ΣΕ ΣΩΛΗΝΑ KUNDT Κώστας Θεοδωράκης Νίκος Αναστασάκης Φυσικοί 10 ο Συνέδριο ΕΕΦ & ΕΚΦ Κέρκυρα 3 Μαρτίου 2007 Θεωρία: Το αποτέλεσμα της συμβολής δύο
max 0 Eκφράστε την διαφορά των δύο θετικών λύσεων ώς πολλαπλάσιο του ω 0, B . Αναλύοντας το Β σε σειρά άπειρων όρων ώς προς γ/ω 0 ( σειρά
 . Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
. Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου
 Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου Επιμέλεια Θεμάτων Σ.Π.Μαμαλάκης Ζήτημα 1 ον 1.. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο μέσων. Όταν η διαθλώμενη ακτίνα κινείται παράλληλα
Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου Επιμέλεια Θεμάτων Σ.Π.Μαμαλάκης Ζήτημα 1 ον 1.. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο μέσων. Όταν η διαθλώμενη ακτίνα κινείται παράλληλα
Θέμα Α (Μονάδες 25) α. με πλάτος Α και περίοδο Τ 2. β. με πλάτος Α 2
 ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Μ. ΤΕΤΑΡΤΗ 1 ΑΠΡΙΛΙΟΥ 017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Θέμα Α () Α1. Κατά τη διάρκεια μιας εξαναγκασμένης
ΠΡΟΣΟΜΟΙΩΣΗ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Μ. ΤΕΤΑΡΤΗ 1 ΑΠΡΙΛΙΟΥ 017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Θέμα Α () Α1. Κατά τη διάρκεια μιας εξαναγκασμένης
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ 2013 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ 2013 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Στις ερωτήσεις από Α1-Α4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και το γράµµα που αντιστοιχεί στην σωστή
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ 2013 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Στις ερωτήσεις από Α1-Α4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και το γράµµα που αντιστοιχεί στην σωστή
Προτεινόμενα θέματα για τις εξετάσεις 2011
 Προτεινόμενα θέματα για τις εξετάσεις 011 Τάξη: Γ Γενικού Λυκείου Μάθημα: Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης ΘΕΜΑ Α Α1-A4 Να επιλέξετε τη σωστή από τις απαντήσεις Α1. Ένα σώμα μάζας είναι στερεωμένο
Προτεινόμενα θέματα για τις εξετάσεις 011 Τάξη: Γ Γενικού Λυκείου Μάθημα: Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης ΘΕΜΑ Α Α1-A4 Να επιλέξετε τη σωστή από τις απαντήσεις Α1. Ένα σώμα μάζας είναι στερεωμένο
Μέτρηση της ταχύτητας του ήχου στον αέρα.
 Α2 Μέτρηση της ταχύτητας του ήχου στον αέρα. 1 Σκοπός Στο πείραμα αυτό θα μελετηθεί η συμπεριφορά των στάσιμων ηχητικών κυμάτων σε σωλήνα με αισθητοποίηση του φαινομένου του ηχητικού συντονισμού. Επίσης
Α2 Μέτρηση της ταχύτητας του ήχου στον αέρα. 1 Σκοπός Στο πείραμα αυτό θα μελετηθεί η συμπεριφορά των στάσιμων ηχητικών κυμάτων σε σωλήνα με αισθητοποίηση του φαινομένου του ηχητικού συντονισμού. Επίσης
Διδάσκων: Καθ. Αλέξανδρος Ρήγας Εξάμηνο: 9 ο
 Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Τομέας Τηλεπικοινωνιών και Διαστημικής Εργαστήριο Ηλεκτρομαγνητικής Θεωρίας Διδάσκων: Καθ. Αλέξανδρος Ρήγας Εξάμηνο:
Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Τομέας Τηλεπικοινωνιών και Διαστημικής Εργαστήριο Ηλεκτρομαγνητικής Θεωρίας Διδάσκων: Καθ. Αλέξανδρος Ρήγας Εξάμηνο:
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1 Χαρακτηριστικά Διάδοσης Κύματος Όλα τα κύματα μεταφέρουν ενέργεια.
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1 Χαρακτηριστικά Διάδοσης Κύματος Όλα τα κύματα μεταφέρουν ενέργεια.
ΚΥΜΑΤΑ 1. Νίκος Κανδεράκης
 ΚΥΜΑΤΑ 1 Νίκος Κανδεράκης Ταλάντωση Πλάτος x o Περίοδος T χρόνος για μία ταλάντωση Α Β Α Συχνότητα f αριθμός ταλαντώσεων σε 1s συχνότητα = αριθμός ταλαντώσεων/χρόνο ή f = N/t Αν Ν = 1 τότε t = T f = N/t
ΚΥΜΑΤΑ 1 Νίκος Κανδεράκης Ταλάντωση Πλάτος x o Περίοδος T χρόνος για μία ταλάντωση Α Β Α Συχνότητα f αριθμός ταλαντώσεων σε 1s συχνότητα = αριθμός ταλαντώσεων/χρόνο ή f = N/t Αν Ν = 1 τότε t = T f = N/t
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 4 ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ. ΗΜΕΡ/ΝΙΑ : 15/05/2015 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω
4 ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ. ΗΜΕΡ/ΝΙΑ : 15/05/2015 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω
ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ
 6/11/004 ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 004-05 η ΕΡΓΑΣΙΑ ΑΣΚΗΣΕΙΣ Προθεσμία παράδοσης 0/1/004 1) Εκκρεμές μήκους L και μάζας m 1 εκτελεί μικρές ταλαντώσεις γύρω από τη θέση ισορροπίας, έχοντας συνδεθεί
6/11/004 ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 004-05 η ΕΡΓΑΣΙΑ ΑΣΚΗΣΕΙΣ Προθεσμία παράδοσης 0/1/004 1) Εκκρεμές μήκους L και μάζας m 1 εκτελεί μικρές ταλαντώσεις γύρω από τη θέση ισορροπίας, έχοντας συνδεθεί
Ηλεκτρομαγνητικά Διαδίδονται στο κενό
 Κύμα: διαταραχή που διαδίδεται στο χώρο και στο χρόνο μεταφέροντας ενέργεια. Μηχανικά Μέσο διάδοσης Ηλεκτρομαγνητικά Διαδίδονται στο κενό Διαμήκη Διεύθυνση διάδοσης παράλληλη στη διαταραχή Εγκάρσια Διεύθυνση
Κύμα: διαταραχή που διαδίδεται στο χώρο και στο χρόνο μεταφέροντας ενέργεια. Μηχανικά Μέσο διάδοσης Ηλεκτρομαγνητικά Διαδίδονται στο κενό Διαμήκη Διεύθυνση διάδοσης παράλληλη στη διαταραχή Εγκάρσια Διεύθυνση
ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) U β A
 Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α και
Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α και
ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 2009
 ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 009 Θέμα 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από
ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 009 Θέμα 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ:
 ΦΥΣΙΚΗ KATΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΡΚΕΙΑ: 180min ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ:. ΘΕΜΑ 1 ο ΘΕΜΑ 2 ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΜΟΝΑΔΕΣ ΘΕΜΑ Α: 1. Δύο σύγχρονες πηγές δημιουργούν στην επιφάνεια υγρού εγκάρσια
ΦΥΣΙΚΗ KATΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΡΚΕΙΑ: 180min ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ:. ΘΕΜΑ 1 ο ΘΕΜΑ 2 ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΜΟΝΑΔΕΣ ΘΕΜΑ Α: 1. Δύο σύγχρονες πηγές δημιουργούν στην επιφάνεια υγρού εγκάρσια
Μέθοδοι έρευνας ορυκτών και πετρωμάτων
 Μέθοδοι έρευνας ορυκτών και πετρωμάτων Μάθημα 9 ο Φασματοσκοπία Raman Διδάσκων Δρ. Αδαμαντία Χατζηαποστόλου Τμήμα Γεωλογίας Πανεπιστημίου Πατρών Ακαδημαϊκό Έτος 2017-2018 Ύλη 9 ου μαθήματος Αρχές λειτουργίας
Μέθοδοι έρευνας ορυκτών και πετρωμάτων Μάθημα 9 ο Φασματοσκοπία Raman Διδάσκων Δρ. Αδαμαντία Χατζηαποστόλου Τμήμα Γεωλογίας Πανεπιστημίου Πατρών Ακαδημαϊκό Έτος 2017-2018 Ύλη 9 ου μαθήματος Αρχές λειτουργίας
2. Στο ηλιακό στέµµα η ϑερµότητα διαδίδεται µε αγωγιµότητα και η ϱοή ϑερµικής ενέργειας (heat flux)είναι
 4.6 Ασκήσεις 51 4.6 Ασκήσεις 1. Μελετήστε τον στάσιµο ( t = 0) ισόθερµο άνεµο σε επίπεδο, χρησιµοποιώντας πολικές συντεταγµένες και (α) Βρείτε τη χαρακτηριστική απόσταση από τον αστέρα r στην οποία γίνεται
4.6 Ασκήσεις 51 4.6 Ασκήσεις 1. Μελετήστε τον στάσιµο ( t = 0) ισόθερµο άνεµο σε επίπεδο, χρησιµοποιώντας πολικές συντεταγµένες και (α) Βρείτε τη χαρακτηριστική απόσταση από τον αστέρα r στην οποία γίνεται
Λύσεις 1ης σειράς ασκήσεων
 Λύσεις 1ης σειράς ασκήσεων 1-13 Άσκηση 1 η : Μετατρέπουμε τα δεδομένα από το αγγλοσαξονικό σύστημα στο SI: Διάμετρος άξονα: Dax 3 ice 3i.5 c i 7.6 c.76 Πλάτος περιβλήματος: Wi 6 ice 6i.5 c i 15. c.15 Διάκενο
Λύσεις 1ης σειράς ασκήσεων 1-13 Άσκηση 1 η : Μετατρέπουμε τα δεδομένα από το αγγλοσαξονικό σύστημα στο SI: Διάμετρος άξονα: Dax 3 ice 3i.5 c i 7.6 c.76 Πλάτος περιβλήματος: Wi 6 ice 6i.5 c i 15. c.15 Διάκενο
ιαγώνισμα στη Φυσική Γ Λυκείου Κατεύθυνσης Επαναληπτικό Ι
 Θέμα 1 ο ιαγώνισμα στη Φυσική Γ Λυκείου Κατεύθυνσης Επαναληπτικό Ι Στα ερωτήματα 1 5 του πρώτου θέματος, να μεταφέρετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα της απάντησης που θεωρείτε
Θέμα 1 ο ιαγώνισμα στη Φυσική Γ Λυκείου Κατεύθυνσης Επαναληπτικό Ι Στα ερωτήματα 1 5 του πρώτου θέματος, να μεταφέρετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα της απάντησης που θεωρείτε
Μονάδες 5. Μονάδες 5. Μονάδες 5. Μονάδες 5 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ
 ΘΕΜΑ ο ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ου ΓΕΛ ΠΕΤΡΟΥΠΟΛΗΣ ΔΕΥΤΕΡΑ 3 ΜΑΪΟΥ 200 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ () Να γράψετε στο τετράδιό
ΘΕΜΑ ο ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ου ΓΕΛ ΠΕΤΡΟΥΠΟΛΗΣ ΔΕΥΤΕΡΑ 3 ΜΑΪΟΥ 200 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ () Να γράψετε στο τετράδιό
Κεφάλαιο 5 ο : Μηχανικά Κύματα
 Κεφάλαιο 5 ο : Μηχανικά Κύματα Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan Εισαγωγή Η ενέργεια μεταφέρεται με Μεταφορά μάζας Κύματα Μέσω του σκοινιού ύδιαδίδεται δίδ ένα κύμα το
Κεφάλαιο 5 ο : Μηχανικά Κύματα Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan Εισαγωγή Η ενέργεια μεταφέρεται με Μεταφορά μάζας Κύματα Μέσω του σκοινιού ύδιαδίδεται δίδ ένα κύμα το
2. Κατά την ανελαστική κρούση δύο σωμάτων διατηρείται:
 Στις ερωτήσεις 1-4 να επιλέξετε μια σωστή απάντηση. 1. Ένα πραγματικό ρευστό ρέει σε οριζόντιο σωλήνα σταθερής διατομής με σταθερή ταχύτητα. Η πίεση κατά μήκος του σωλήνα στην κατεύθυνση της ροής μπορεί
Στις ερωτήσεις 1-4 να επιλέξετε μια σωστή απάντηση. 1. Ένα πραγματικό ρευστό ρέει σε οριζόντιο σωλήνα σταθερής διατομής με σταθερή ταχύτητα. Η πίεση κατά μήκος του σωλήνα στην κατεύθυνση της ροής μπορεί
2-1 ΕΙΣΑΓΩΓΗ 2-2 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΕΞΩΦΥΛΛΟ 43 Εικ. 2.1 Κύμα στην επιφάνεια της θάλασσας. 2-1 ΕΙΣΑΓΩΓΗ Η έννοια «κύμα», από τις πιο βασικές έννοιες της φυσικής, χρησιμοποιήθηκε για την περιγραφή φαινομένων που καλύπτουν ένα ευρύ φάσμα.
ΕΞΩΦΥΛΛΟ 43 Εικ. 2.1 Κύμα στην επιφάνεια της θάλασσας. 2-1 ΕΙΣΑΓΩΓΗ Η έννοια «κύμα», από τις πιο βασικές έννοιες της φυσικής, χρησιμοποιήθηκε για την περιγραφή φαινομένων που καλύπτουν ένα ευρύ φάσμα.
Το παρακάτω διάγραμμα παριστάνει την απομάκρυνση y ενός σημείου Μ (x Μ =1,2 m) του μέσου σε συνάρτηση με το χρόνο.
 ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα ζητούνται στο Θεωρητικό
ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα ζητούνται στο Θεωρητικό
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ
 ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΥΠΕΡΗΧΟ Δρ. Βουλγαράκη Χαριτίνη ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΒΙΟΜΗΧΑΝΙΚΟΥ 2016 ΠΕΡΙΕΧΟΜΕΝΑ 1.Μέθοδος των Υπερήχων 3 1.1. Φυσική των Υπερήχων 3 1.2. Τύποι
ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΥΠΕΡΗΧΟ Δρ. Βουλγαράκη Χαριτίνη ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΒΙΟΜΗΧΑΝΙΚΟΥ 2016 ΠΕΡΙΕΧΟΜΕΝΑ 1.Μέθοδος των Υπερήχων 3 1.1. Φυσική των Υπερήχων 3 1.2. Τύποι
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 Β ΦΑΣΗ ΣΥΝΕΙΡΜΟΣ
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ημερομηνία: Σάββατο 4 Μαΐου 09 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ημερομηνία: Σάββατο 4 Μαΐου 09 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό
ÊÏÑÕÖÇ ÊÁÂÁËÁ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΣΙΚΗ
 Επαναληπτικά Θέµατα ΟΕΦΕ 007 Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΣΙΚΗ ZHTHMA Στις ερωτήσεις έως 4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθµό το γράµµα που αντιστοιχεί
Επαναληπτικά Θέµατα ΟΕΦΕ 007 Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΣΙΚΗ ZHTHMA Στις ερωτήσεις έως 4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθµό το γράµµα που αντιστοιχεί
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
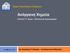 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Αέρια & Πίεση Αερίων 2 Ο αέρας είναι ένα τυπικό αέριο
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Αέρια & Πίεση Αερίων 2 Ο αέρας είναι ένα τυπικό αέριο
ΘΕΜΑ 1 ο. Φροντιστήριο «ΕΠΙΛΟΓΗ» Ιατροπούλου 12 & σιδ. Σταθμού - Καλαμάτα τηλ.: & 96390
 ΘΕΜΑ 1 ο ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 1 ΙΟΥΝΙΟΥ 006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Να γράψετε στο τετράδιό σας τον
ΘΕΜΑ 1 ο ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 1 ΙΟΥΝΙΟΥ 006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Να γράψετε στο τετράδιό σας τον
3 Μετάδοση Θερμότητας με Φυσική Μεταφορά και με Ακτινοβολία
 3 Μετάδοση Θερμότητας με Φυσική Μεταφορά και με Ακτινοβολία 3.1 Εισαγωγή Η μετάδοση θερμότητας, στην πράξη, γίνεται όχι αποκλειστικά με έναν από τους τρεις δυνατούς μηχανισμούς (αγωγή, μεταφορά, ακτινοβολία),
3 Μετάδοση Θερμότητας με Φυσική Μεταφορά και με Ακτινοβολία 3.1 Εισαγωγή Η μετάδοση θερμότητας, στην πράξη, γίνεται όχι αποκλειστικά με έναν από τους τρεις δυνατούς μηχανισμούς (αγωγή, μεταφορά, ακτινοβολία),
r r r r r r r r r r r Μονάδες 5 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΠΑΡΑΣΚΕΥΗ 0 ΜΑÏΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΠΑΡΑΣΚΕΥΗ 0 ΜΑÏΟΥ 011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ
Φυσική για Μηχανικούς
 Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 6 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 23/04/2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ο.Π ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 23/04/2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ο.Π ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο
Γκύζη 14-Αθήνα Τηλ :
 Γκύζη 14-Αθήνα Τηλ : 10.64.5.777 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 10 ΙΟΥΝΙΟΥ 014 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)
Γκύζη 14-Αθήνα Τηλ : 10.64.5.777 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 10 ΙΟΥΝΙΟΥ 014 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)
Γκύζη 14-Αθήνα Τηλ :
 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 22 ΜΑΪΟΥ 2013 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Στις ερωτήσεις Α1-Α4 να γράψετε
ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 22 ΜΑΪΟΥ 2013 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Στις ερωτήσεις Α1-Α4 να γράψετε
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 23 ΜΑΪOY 2016 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
ΘΕΜΑ 1ο Στις ερωτήσεις 1 4 να επιλέξετε τη σωστή απάντηση
 ΜΑΘΗΜΑ - ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΕΠΑΝΑΛ. ΔΙΑΓΩΝΙΣΜΑ 2018 ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΠΑΡΑΡΤΗΜΑ ΔΙΑΡΚΕΙΑ 3 ΩΡΕΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1 4 να επιλέξετε τη σωστή απάντηση Α1 Περιπολικό ακολουθεί αυτοκίνητο
ΜΑΘΗΜΑ - ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΕΠΑΝΑΛ. ΔΙΑΓΩΝΙΣΜΑ 2018 ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΠΑΡΑΡΤΗΜΑ ΔΙΑΡΚΕΙΑ 3 ΩΡΕΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1 4 να επιλέξετε τη σωστή απάντηση Α1 Περιπολικό ακολουθεί αυτοκίνητο
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 6 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΠΟΥ ΥΠΗΡΕΤΟΥΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 8 ΣΕΠΤΕΜΒΡΙΟΥ 016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΠΟΥ ΥΠΗΡΕΤΟΥΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 8 ΣΕΠΤΕΜΒΡΙΟΥ 016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ
Περι-Φυσικής. Βαθµολογία % E = E max ηµπ(10 15 t 2x )
 Εξέταση Προσοµοίωσης Γ τάξης Ενιαίου Λυκείου Τετάρτη 17 Απριλίου 2013 Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Σύνολο σελίδων : επτά (7) Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ηµιτελείς προτάσεις Α.1
Εξέταση Προσοµοίωσης Γ τάξης Ενιαίου Λυκείου Τετάρτη 17 Απριλίου 2013 Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Σύνολο σελίδων : επτά (7) Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ηµιτελείς προτάσεις Α.1
Απορρόφηση του φωτός Προσδιορισμός του συντελεστή απορρόφησης διαφανών υλικών
 Ο11 Απορρόφηση του φωτός Προσδιορισμός του συντελεστή απορρόφησης διαφανών υλικών 1. Σκοπός Η εργαστηριακή αυτή άσκηση αποσκοπεί α) στην μελέτη του φαινομένου της εξασθένησης του φωτός καθώς αυτό διέρχεται
Ο11 Απορρόφηση του φωτός Προσδιορισμός του συντελεστή απορρόφησης διαφανών υλικών 1. Σκοπός Η εργαστηριακή αυτή άσκηση αποσκοπεί α) στην μελέτη του φαινομένου της εξασθένησης του φωτός καθώς αυτό διέρχεται
ΘΕΜΑ 1 ο Στις ερωτήσεις 1 4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ 2013 Γ Λυκείου Θετική & Τεχνολογική Κατεύθυνση ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις ερωτήσεις 1 4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση 1. Σώμα
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ 2013 Γ Λυκείου Θετική & Τεχνολογική Κατεύθυνση ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις ερωτήσεις 1 4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση 1. Σώμα
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ ΕΣΠΕΡΙΝΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6)
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΜΟΝΟ ΝΕΟ ΣΥΣΤΗΜΑ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6)
Θέμα 1ο Να σημειώσετε τη σωστή απάντηση σε καθεμία από τις παρακάτω ερωτήσεις πολλαπλής επιλογής.
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΚΡΙΤΗΡΙΑ ΑΞΙΟΛΟΓΗΣΗΣ o ΕΠΑΝΑΛΗΠΤΙΚΟ ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ Θέμα ο Να σημειώσετε τη σωστή απάντηση σε καθεμία από τις παρακάτω ερωτήσεις πολλαπλής επιλογής. ) Σώμα εκτελεί ταυτόχρονα δύο απλές
ΕΠΑΝΑΛΗΠΤΙΚΑ ΚΡΙΤΗΡΙΑ ΑΞΙΟΛΟΓΗΣΗΣ o ΕΠΑΝΑΛΗΠΤΙΚΟ ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ Θέμα ο Να σημειώσετε τη σωστή απάντηση σε καθεμία από τις παρακάτω ερωτήσεις πολλαπλής επιλογής. ) Σώμα εκτελεί ταυτόχρονα δύο απλές
4ο Διαγώνισμα προσομοίωσης Γ' Λυκείου Θετικού προσανατολισμού
 1 4ο Διαγώνισμα προσομοίωσης Γ' Λυκείου Θετικού προσανατολισμού Θέμα Α: (Για τις ερωτήσεις Α.1 έως και Α.4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
1 4ο Διαγώνισμα προσομοίωσης Γ' Λυκείου Θετικού προσανατολισμού Θέμα Α: (Για τις ερωτήσεις Α.1 έως και Α.4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s.
 1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s. Να βρεθεί το μήκος κύματος. 2. Σε ένα σημείο του Ειρηνικού ωκεανού σχηματίζονται κύματα με μήκος κύματος 1 m και
1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s. Να βρεθεί το μήκος κύματος. 2. Σε ένα σημείο του Ειρηνικού ωκεανού σχηματίζονται κύματα με μήκος κύματος 1 m και
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2007 Πανεπιστήμιο Αθηνών Εργαστήριο Φυσικών Επιστημών, Τεχνολογίας, Περιβάλλοντος Γ Λυκείου
 Γ Λυκείου 21 Απριλίου 27 Θεωρητικό Μέρος Θέμα 1 ο : 1. Σε μια πειραματική άσκηση χρησιμοποιήσαμε τη διάταξη που φαίνεται στο διπλανό σχήμα. Γεμίσαμε με νερό μια προχοΐδα, την στηρίξαμε L κατακόρυφα και
Γ Λυκείου 21 Απριλίου 27 Θεωρητικό Μέρος Θέμα 1 ο : 1. Σε μια πειραματική άσκηση χρησιμοποιήσαμε τη διάταξη που φαίνεται στο διπλανό σχήμα. Γεμίσαμε με νερό μια προχοΐδα, την στηρίξαμε L κατακόρυφα και
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
ΑΓ.ΚΩΝΣΤΑΝΤΙΝΟΥ ΠΕΙΡΑΙΑΣ ΤΗΛ ,
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ 1 ΘΕΜΑ Α Στις προτάσεις που ακολουθούν να επιλέξετε τη σωστή απάντηση. 1. Δύο σώματα συγκρούονται πλαστικά. Τότε δεν
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ 1 ΘΕΜΑ Α Στις προτάσεις που ακολουθούν να επιλέξετε τη σωστή απάντηση. 1. Δύο σώματα συγκρούονται πλαστικά. Τότε δεν
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / Ε Π Ω Ν Υ Μ Ο :...
 Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / 2 0 1 8 Ε Π Ω Ν Υ Μ Ο :... Ο Ν Ο Μ Α : Τ Μ Η Μ Α : Ε Π Ι Μ Ε Λ Ε Ι Α Θ Ε Μ Α Τ Ω Ν : ΦΑΡΜΑΚΗΣ Π. ΜΠΑΡΛΙΚΑΣ Σ. ΘΕΜΑ A
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / 2 0 1 8 Ε Π Ω Ν Υ Μ Ο :... Ο Ν Ο Μ Α : Τ Μ Η Μ Α : Ε Π Ι Μ Ε Λ Ε Ι Α Θ Ε Μ Α Τ Ω Ν : ΦΑΡΜΑΚΗΣ Π. ΜΠΑΡΛΙΚΑΣ Σ. ΘΕΜΑ A
Θεωρητική Εξέταση. Τρίτη, 15 Ιουλίου /3
 Θεωρητική Εξέταση. Τρίτη, 15 Ιουλίου 2014 1/3 Πρόβλημα 2. Καταστατική Εξίσωση Van der Waals (11 ) Σε ένα πολύ γνωστό μοντέλο του ιδανικού αερίου, του οποίου η καταστατική εξίσωση περιγράφεται από το νόμο
Θεωρητική Εξέταση. Τρίτη, 15 Ιουλίου 2014 1/3 Πρόβλημα 2. Καταστατική Εξίσωση Van der Waals (11 ) Σε ένα πολύ γνωστό μοντέλο του ιδανικού αερίου, του οποίου η καταστατική εξίσωση περιγράφεται από το νόμο
Γενικές εξετάσεις Φυσική Γ λυκείου θετικής και τεχνολογικής κατεύθυνσης
 Γενικές εξετάσεις 0 Φυσική Γ λυκείου θετικής και τεχνολογικής κατεύθυνσης ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
Γενικές εξετάσεις 0 Φυσική Γ λυκείου θετικής και τεχνολογικής κατεύθυνσης ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 8 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΥΛΗ ΜΑΘΗΜΑΤΟΣ ΑΚΟΥΣΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ ΕΝΕΡΓΕΙΑ ΠΕΡΙΒΑΛΛΟΝ
 ΥΛΗ ΜΑΘΗΜΑΤΟΣ ΑΚΟΥΣΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ ΕΝΕΡΓΕΙΑ ΠΕΡΙΒΑΛΛΟΝ Περι... ήχου Ηχητικά κύματα -- ορισμοί ιάδοση ήχου στον αέρα Μέτρηση έντασης ήχου (decibel) Απορρόφηση ήχου σε δομικά υλικά Ακουστική μικρών χώρων
ΥΛΗ ΜΑΘΗΜΑΤΟΣ ΑΚΟΥΣΤΙΚΗ ΦΩΤΟΜΕΤΡΙΑ ΕΝΕΡΓΕΙΑ ΠΕΡΙΒΑΛΛΟΝ Περι... ήχου Ηχητικά κύματα -- ορισμοί ιάδοση ήχου στον αέρα Μέτρηση έντασης ήχου (decibel) Απορρόφηση ήχου σε δομικά υλικά Ακουστική μικρών χώρων
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θ Ε Μ Α 1 ο Οδηγία: Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θ Ε Μ Α 1 ο Οδηγία: Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 9 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΣΙΚΗ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 9 ΙΟΥΝΙΟΥ 003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΣΙΚΗ ΘΕΜΑ 1ο Στις προτάσεις 1.1 έως 1.4 να γράψετε στο τετράδιό σας
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 9 ΙΟΥΝΙΟΥ 003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΣΙΚΗ ΘΕΜΑ 1ο Στις προτάσεις 1.1 έως 1.4 να γράψετε στο τετράδιό σας
Κεφάλαιο 5 ο : Μηχανικά Κύματα
 Κεφάλαιο 5 ο : Μηχανικά Κύματα Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan g g Εισαγωγή Η ενέργεια μεταφέρεται με μεταφορά μάζας Αν ρίξεις μια μπάλα προς ένα αμαξάκι, το αμαξάκι
Κεφάλαιο 5 ο : Μηχανικά Κύματα Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan g g Εισαγωγή Η ενέργεια μεταφέρεται με μεταφορά μάζας Αν ρίξεις μια μπάλα προς ένα αμαξάκι, το αμαξάκι
Επαναληπτικό Διαγώνισμα Γ Λυκείου Φυσικής Θετικών Σπουδών
 Επαναληπτικό Διαγώνισμα Γ Λυκείου Φυσικής Θετικών Σπουδών ΘΕΜΑ Α Α1) Η μεταβολή της στροφορμής ενός στερεού σε σχέση με τον χρόνο φαίνεται στο διπλανό L σχήμα. Να σημειώσετε τη σωστή πρόταση: α. Ο ρυθμός
Επαναληπτικό Διαγώνισμα Γ Λυκείου Φυσικής Θετικών Σπουδών ΘΕΜΑ Α Α1) Η μεταβολή της στροφορμής ενός στερεού σε σχέση με τον χρόνο φαίνεται στο διπλανό L σχήμα. Να σημειώσετε τη σωστή πρόταση: α. Ο ρυθμός
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 24 ΑΠΡΙΛΙΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5)
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ΑΠΡΙΛΙΟΥ 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ΑΠΡΙΛΙΟΥ 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που
1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β.
 ΚΡΟΥΣΕΙΣ ΕΠΑΝΑΛΗΨΗ 1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β. Α) Αν η κρούση είναι μετωπική και ελαστική
ΚΡΟΥΣΕΙΣ ΕΠΑΝΑΛΗΨΗ 1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β. Α) Αν η κρούση είναι μετωπική και ελαστική
