Ενότητα: Ο κόσμος αύριο: προβλέψεις και υγειακό τοπίο
|
|
|
- Σωτηρία Φιλιππίδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Τίτλος Μαθήματος: Πολιτικές Υγείας Ενότητα: Ο κόσμος αύριο: προβλέψεις και υγειακό τοπίο Διδάσκοντες: Αν. Καθηγητής Γιάνης Δημολιάτης (υπεύθυνος), Επίκ. Καθ. Ευαγγελία Ντζάνη, Κωνσταντίνος Τσιλίδης Τμήμα: Ιατρικής
2 !"#$%&, '(%)*+%()(,, -)&./$%+,.01 2)$3$45&: 678.1µ&5#()."#$%$ 1!"#$%& '%µ()"#*%&, '%µ+*,%&!-)#,%&, '%µ+*,%& '%µ()"#*%& &!"#$$%& '%µ%*,./(0)(& 12334,"& «52$("» 3 2$- 30$26,"( 7%µ4"8*"9+&!! "#$%µ&' ()*+, 17, -./0* 12+01)31* )&2 "*4-#1µ0&2 5&/)6&2 +&1,/#),)*' )& 1990, -*0 "/&7$8"%)*0 +* %6+*0, 8, )& 2020 (Murray & Lopez 1996). 9 :*4-#1µ0*!/4;+<1, =4%6*' >%3/,1% ),+ *"%$%2>8/<1, *"# )& :.;( *(0 /()2µ(0 (#?0 *"$; *"# )&+ "#$%µ&) <' ),+ "/3), "/&@"#>%1, 40* 24%6*, <' ),+ -./0* *0)6* 24%6*': «<8,=& 4",+$% -*0 -&0+<+0-( A0-*0&1.+,,?</6' */-%)( )/&5( -*0 +%/#,?</6' %-"*6A%21, -*0 *B0&"/%"( -*)&0-6*, -*0?</6' +* A&>%6 1)&+ -*>8+* -*0 1% #$&2' 8+*'?/(10µ&' /#$&' 1),+ -&0+<+6* -0 8+* %"*/-8' %01#A,µ*, A%+ µ"&/%6 +* 2";/B%0 -*µ0; 24%6* 40* )&2' *+>/3"&2', -*µ0; "/*4µ*)0-( *+;")2B, -*0 -*µ0; -&0+<+0-( "/#&A&'. [ ]! /.)4µ(& %6+*0, "0& 1&7*/( *" #$%' )0' *"%0$8' -*); ),' 24%6*'. [ ] >",+$% A%+ %6+*0 *"$;, *"&216* "&$8µ&2. C6+*0 %"0"$8&+ µ0* >%)0-( *61>,1, %2%B6*' -*0 *15;$%0*' 40* )&2' *+>/3"&2' #$<+ )<+?</3+, "&2 )&2' A6+%0 ),+ %2-*0/6* +* -*>&/61&2+ %$%.>%/* )&+ "/&&/01µ# ),' D<(' )&2' -*0 +* %-").B&2+ "$(/<' )& *+>/3"0+& A2+*µ0-# )&2'. [ ] E% -;>%?3/* & *(µ2-& *%& 0?4=-& >* "/8"%0 +* "*6B%0,4%)0-# /#$& 1)0' "/&1";>%0%' "/&3>,1,' µ0*' 1)%+(' -*0 µ*-/#?/&+,' 12+%/4*16*' ";+< 1% "/&7$(µ*)* 24%6*' "&2 2"%/7*6+&2+ )* 4@$"9# 3A$(,-» (World Health Organization 1985). F' %"*44%$µ*)6%' 24%6*' &5%6$*µ% +* 8?&2µ% $#4& 40* )* 1.+&/*, &5%6$*µ% +* 2"%/7&.µ% )* «%>+0-; 1.+&/*» :/&7$,µ*)0D#µ*1)%,?/#+0* "&$$; (G,µ&$0;),' 1994), 40* )& /#$& )<+ 12+#/<+ 1% -2))*/0-# -*0 -&0+<+0-# %"6"%A&. H%-0+(1*µ% +* 1-%5)#µ*1)% )* 1.+&/* µ% *5&/µ( )&2' "&$8µ&2' "&2 µ*' )*$*+6D&2+, >%</3+)*' )* 2"*6)0* -*0 µ013+)*' )*: «+* -*)*/4,>&.+, +*,12?;1&2µ%!» I& A%.)%/& 7(µ* ()*+ *+*"#5%2-)&: *"?=$4*-" 3*% B"()(?=-; 8+*+ )&µ8* "&2 4+</6D&2µ% -;"<' -*$.)%/*. =";/?&2+ %-%6 1.+&/*; I& "/3)& 1&- ()*+ #)*+ 12+%0A,)&"&0(1*µ% #)0 &0-2))*/0-8' µ%µ7/;+%' A%+ %6+*0 "*/; 1.+&/&, )& 1.+&/& )<+ %+A&-2));/0<+ *"# )0' %B<-2));/0%' A&µ8'.!0 )</0+8' µ*' *"#J%0' 40* )& /#$& )<+ 12+#/<+ *"# ), 70&$&40-( 1-&"0; 61<' A%+ %6+*0 12µ7*)8' µ% )0' %"0-/*)&.1%' *"#J%0' 1?%)0-; µ% )* -&0+<+0-; #/0*. 9 70&$&40-( %B8$0B, %"8$%B% )* "0& *"&)%$%1µ*)0-; 121)(µ*)*, %+3 )* -/*)0-; 1.+&/* "&2, "*/*76*1( )&2' 01&A2+*µ%6 µ% "#$%µ& 5*6+%)*0 +* %6+*0 *"&)8$%1µ* A.+*µ,' ()& A6-*0& )&2 01?2/&)8/&2). G%+ %6µ*1)% %0A0-&6 ),' 1,µ%0<)0-(', >* >8$*µ% #µ<' ";/* "&$. +* *-&.1&2µ% "3' &0 ;$$&0 7$8"&2+ )* "/;4µ*)*. G0*01>*+#µ*1)% *-#µ, "<' *2); "&2 %µ%6' *"# ), 70&$&46* 4+</6D&2µ% (( «4+</6D&2µ%») >* %6+*0?/(10µ* 1% -%6+&2'. K%)*B. )<+ %"01),µ3+ (-*0 )<+ %"01),µ#+<+) 2";/?&2+ 1.+&/* &/&$&46*' µ;$$&+ "*/; %++&0&$&46*'. I* 1.+&/* 1)* -.))*/* -*0 ), 70&$&46* 61<' %6+*0 A0%"01),µ&+0-;?/(10µ*. 9 8+>%+ -*-%6>%+ µ%)*b. )<+ 12+#/<+ )<+ %"01),µ3+ A0%"01),µ&+0-( 31µ<1, µ*' 85%/% 1), L$3/0+* (M*$;/,' -.;. 2007). 1 N+*-&0+3>,-% 1)& 8& 12+8A/0& ),' C$$,+0-(' E,µ%0<)0-(' C)*0/6*' µ% >8µ* 7%µ4"8*"9+ 9-" "64()(?=4&: 3A$(,-, /4,":2,4"4&, 6"-3/(,2&, "&2 840+% 1), L$3/0+* )& I& -%6µ%+& )&.)& *"&)%$%6 )& )%$%2)*6& A&-6µ0& "&2 1);$>,-% 40* )* :/*-)0-; )&+ O&8µ7/0& )&
3 1-3A$(,- 3*% B"()(?=- 7*( 9A**-,( I* %>+0-; 1.+&/* A%+ )* B8/&2µ% -*$;. N2); "&2 B8/&2µ% -*$; (( -*$.)%/*) %6+*0 )* 70&$&40-; 1.+&/*. C6+*0, 7;1, ),' D<('. P</6' 1.+&/* A%+ µ"&/%6 +* 2";/B%0 D<(. 9 D<( 1)(+%)*0 ";+< 1)& 1.+&/&. K81* *" ), µ%µ7/;+, )&2-2));/&2 %6+*0 D<+)*+#, 8B< *"# ), µ%µ7/;+, %6+*0 µ, D<+)*+#. Q/* D<( 1,µ*6+%0 1.+&/&. E),+ C0-#+* 1 5*6+%)*0 1?,µ*)0-; 8+* -.))*/& 1% )&µ(. I& -2))*/#"$*1µ* "%/07;$$%)*0 *"# µ0* µ%µ7/;+,, "&2 B%?</6D%0 -*0 "/&1)*)%.%0 -*0 )*2)#?/&+* %+3+%0 )& -.))*/& *"#/µ% )& "%/07;$$&+ )&2: %6+*0 )& 1.+&/& "&2 &/6D%0 )& -.))*/&. N"&)%$%6)*0 *"# 8+* A0"$# 1)/3µ* 5<15&$0"0A6<+. C+1<µ*)<µ8+* 7/61-&+)*0 "&0-6$* µ#/0* "/<)%R+3+ "&2 A/&2+ 1*+ -*+;$0* -*0 *+)$6%' («"&/)08/,A%'») "&2 µ%)*-0+&.+ A0;5&/* µ#/0* "/&' )* µ81* ( "/&' )* 8B<. 9 µ%µ7/;+, %6+*0 «,µ0-"%/*)(», A0#)0 %"0)/8"%0 µ0* &216* +* "%/+; ( )%$%6<' %$%.>%/* ( 1% "%/0&/01µ8+, 8-)*1, ( +* µ,+ "%/+; -*>#$&2. E)0' %"05*+%0*-8' µ%µ7/;+%' 2";/?&2+ %"61,' "/<)%R+0-&6 2"&A&?%6', "/<)%S+%' "&2 *+*4+</6D&2+ %B<)%/0-; 1(µ*)* *"# µ#/0* #"<' &0 &/µ#+%' (".?. 2"&A&?%6' "&2 2"&A8?&+)*0 ), >2/&B6+, -*0 )& µ(+2µ* "&2 *2)( 58/+%0: «*.B,1% 3 -.))*/& )& µ%)*7&$01µ# 1&2»). >"9.$- 1: '"#?,-µµ- 4$.& *0/"9(A 409-,08*"9(A 90**#,(0, /(0 64=C$4" *- 0/(90**#,"- (,?-$=6"-: (1) /0,%$=39(&, (2) /0,+$-&, (3),";.38µ-, (4) 903*=6"(, (5) -6,. 4$6(/)-3µ-*"9. 6=9*0(, (6) *(0 Golgi, (7) 90**-,(394)4*.&, (8) )4=( 4$6(/)-3µ-*"9. 6=9*0(, (9) µ"*(c.$6,"-, (10) 94$(*./"(, (11) 90**-,./)-3µ-, (12) )03.38µ-, (13) 94$*,".)"-. D%?+: I* 1.+&/* %6+*0 %B*0/%)0-; %"0$%-)0-;: &0 "&/)08/,A%' %$84?&2+ "&0&' >* µ"%0, "&0&' >* 74%0, "#1& >* µ"%0, "#1& >* 74%0, "#1& >* 2";/?%0 µ81*, "#1& 8B<, "&$. -;$0& µ81*, "&$. +;)/0& 8B<, 7;D&2+ )& 8+*, 74;D&2+ )& ;$$&. T0 8)10 /2>µ6D&2+ ), D<(. N+?*$;1%0, *+)$6* "&2 )/*7;%0 )& +;)/0&, )& -.))*/& "%>*6+%0, A%+ 2";/?%0 D<(. Q/* >8$&2µ% 1.+&/*, A0#)0?</6' 1.+&/* A%+ 2";/?%0 D<(, *$$; )8)&0* "&2 +* µ"*0+&74*6+&2+ "/;4µ*)* %"0$%4µ8+* -*0 /2>µ0D#µ%+*. T*0 %"0$%4µ8+* -*6 /2>µ0D#µ%+*. G,$*A(, *2)&6 &0 "&/)08/,A%' "*6/+&2+ %+8/4%0*, -*)*+*$3+&2+ %+8/4%0*?/(µ*)* >* $84*µ% )& -&0+<+0-# 01&A.+*µ# ),' 40* +* &/4*+31&2+ *2)( )&2' ), A/;1,, -*)*+*$3+&2+ %+8/4%0* *"# )& -.))*/& -*0 74;D&2+ 8B< )& *+%"0>.µ,)& -*0 7;D&2+ µ81* )& %"0>2µ,)#, &.)<' 31)% +* A0*),/%6)*0, &µ&0&1)*16* "&2 /2>µ6D%0 ), D<(, "&2 -;+%0 )& -.))*/& D<+)*+#. M0* "*/;A%04µ*, "3' µ"*6+%0 & 16A,/&' µ81* 1)& -.))*/&; K% "&$$&.' -*0 "&$."$&-&2' µ,?*+01µ&.'. U)*+?/%0;D%)*0 16A,/&' )&+ 7;D&2µ% µ81*, #)*+ A%+?/%0;D%)*0 A%+ )&+ 7;D&2µ% -*0 µ"&/%6 -*0 +* )&+ 74;$&2µ% -0#$*'.! 16A,/&' 8?%0
4 "&$. "&$."$&-&2' "&/)08/,A%', A%+ 8?%0 µ#+&+ 8+*+, 20 "/<)%S+%' 12+%/4;D&+)*0 40* +* µ"%0 #1&' 16A,/&' "/8"%0 +* µ"%0. M+</6D&2µ% µ% *-/67%0* )&2' µ,?*+01µ&.'. =";/?&2+ *01>,)(/%' (18+1&/%') "&2 -*)*$*7*6+&2+, "&2 %$84?&2+ "#1& 16A,/& 8?&2µ% µ81* 1)& -.))*/& -*0 "#1&?/%0*D#µ*1)%, -*0 #)*+ -*)*$;7&2+ #)0 8?&2µ% $04#)%/&, )#)% µ0* "/<)%S+, ";%0 -*0 A8+%)*0 ";+< 1)& mrna )<+ "/<)%R+3+ "&2 %$84?&2+ ),+ %61&A& )&2 10A(/&2 -*0 )*2)#?/&+* *2B;+%0 ),+ %61&A# )&2 -*0 µ%03+%0 )0' *"&>(-%' 10A(/&2, &.)<' 31)% )* %+A&-2));/0* %"6"%A* +* *2B,>&.+. N+;"&A* 46+%)*0 #)*+ 2";/?%0 "&$.' 16A,/&' µ81* 1)& -.))*/&: )#)% *2B;+%0 )0' *"&>(-%' -*0 µ%03+%0 ),+ %61&A&, 40* +* />%0 ";$0 1),+ 6A0* 01&//&"6*. I& #)0 µ0$;µ%, )& #)0 4/;5&2µ%, )& #)0 A0*7;D&2µ% A%+ %6+*0 "*/; 8+* «"*04+6A0» 12+#/<+. P</6' ),+ "#$<1, -*0 ),+ %-"#$<1, ),' µ%µ7/;+,' )<+ +%2/ ));/<+, A%+ >* 2"(/?% &.)% &µ0$6* &.)% 4/*5(!!.)% -*+ 1-8J,. C2)2?3' "&2 2";/?&2+ 1.+&/*! K* µ% 8+*+ "%/6)%?+& µ,?*+01µ# %+%/4,)0-(' -*0 "*>,)0-(' A0#A&2-0 %"*+*A0#A&2 0#+)<+ *"# ), µ0* )&2' "$%2/; "/&' ),+ ;$$, E% %"6"%A& -2));/&2, $&0"#+, -.))*/& 61&+ 1.+&/&. P</6' 1.+&/& A%+ 2";/?%0 -.))*/& &0* ),' D<(' %6+* *1µ8+, µ% )& 1.+&/&. E#*8 -/. *( 9A**-,( T*)%7*6+&+)*' 8+* %"6"%A& -;)< *"# )& -.))*/&, µ"*6+&+)*' µ81* 1)& -.))*/&, 1)* 2"&-2));/0* &/4*+6A0* %"61,' 2";/?&2+ 1.+&/* (C0-#+* 1). N-/073' )& 6A0&. K81* )& -.))*/& A%+ %6+*0 &µ&0&4%+8'. =";/?&2+ µ%µ7/;+%' "&2 A0*?</6D&2+ )& -;>% A0*µ8/01µ*. T*0 %"61,' -*0 %-%6 2";/?&2+ "&/)08/,A%' "&2 %"0)/8"&2+ ( %+A%?&µ8+<' 7;D&2+ µ% )& D#/0 µ81* *2)# "&2?/%0;D%)*0 -*0 74;D&2+ µ% )& D#/0 8B< *2)# "&2 A%?/%0;D%)*0. T*0?/,10µ&"&0&.+ %+8/4%0* 40* +* )& -;+&2+ *2)#. I* µ0)&?#+a/0*, 40* "*/;A%04µ* (&0 "*/*4<4&6 %+8/4%0*' )&2-2));/&2), %6+*0 %+)%$3' A0*5&/%)0-; *"# )& -2))*/#"$*1µ* "&2 )* "%/07;$$%0. I* $21&13µ*)* (8+* 1*-6 "&2 8?%0 µ81* 2A/&$2)0-; 8+D2µ*, #,)0 µ"%0 µ81* %-%6 -*)*-%/µ*)6d%)*0) %"61,':, µ%µ7/;+, )<+ $21&1<µ;)<+ 8?%0 "&/)08/,A%' "&2 7;D&2+ µ81* "/<)#+0*, )* $21&13µ*)* 8?&2+?*µ,$# ph, -*0 B&A%.&2+ %+8/4%0* 40* +*?*µ,$31&2+ )& ph.! "2/(+*' "&2 "%/0-$%6%0 )& 4%+%)0-# 2$0-# )&2-2));/&2 ()& DNA) 8?%0 ), A0-( )&2 µ%µ7/;+, %2( )&2 Golgi A%+ %6+*0 "*/; µ0* µ%µ7/;+, -)$. Q/*, )* 1.+&/* 2";/?&2+ -*0 1)0' 2"&-2));/0%' (%+A&-2));/0%') A&µ8' -*0 %6+*0 *"#$2)*. F?9,=G- GH$% T*µ0; 5&/; A%+ %6+*0 )#1& B%-;>*/&, %6+*0 -;"<' A.1-&$& +* )/*7(B%0' ), (12+&/0*-() 4/*µµ( *+;µ%1* 1)& %µ%6' -*0 1)& ;$$&, 1)& D<+)*+# -*0 1)& µ, D<+)*+#. I0 %6+*0 )& 8+)%/# µ*'; V<+)*+#; N2)# "&2 2";/?%0 1)& %1<)%/0-# )&2, #,)0 "%/+;%0 *"# )& 1)#µ* -*0 5);+%0 1)& 1)&µ;?0 -*0 1), 12+8?%0* 1)& 8+)%/&, >* "/8"%0 +* >%</,>%6 µ, D<+)*+#. U,)0 µ"*6+%0 µ81* A%+ %6+*0 D<+)*+#, *$$; & &/4*+01µ#' )/*7;%0 #,)0 >8$%0 *"# *2)# -*0 )& %+1<µ*)3+%0 1)&+ %*2)# )&2, -0 #,)0 A% >8$%0 )& *5(+%0 -*0 5%.4%0: %6+*0 -;)0 µ%)*b. D<(' -*0 µ, D<('; :*/#)0 2";/?%0 µ81* 1 8+*+ D<+)*+# &/4*+01µ#, A21-&$%2#µ*1)% +*?*/*-),/61&µ% )& "%/0%?#µ%+& )&2 %+)8/&2 D<+)*+#. I* -.))*/* )&2 %+)8/&2 %6+*0 787*0* D<+)*+;, )& "%/0%?#µ%+# )&2 #µ<' µ;$$&+ #?0.!0 "+%.µ&+%' %6+*0 8+* *-#µ* "*/;A%04µ*: & *8/*' "&2 8?&2+ µ81* A%+ µ"&/%6 +* >%</,>%6 D<+)*+#'. T*0 1)* A.& "*/*A%64µ*)*, )* #/0* µ%)*b. )&2 D<+)*+&. -*0 )&2 µ, D<+)*+&., )& 1.+&/&, %6+*0 "0& µ81* *" #"&2 5*6+&+)*0 *"8B<, "0& µ81* *"# )*?%6$, µ*', "0& µ81* *"# ), µ.), µ*'. =";/?&2+ -0 %+A0;µ%1* 1);A0* µ%)*b. D<(' -*0 µ, D<('.!0 0&6, "*/*A%64µ*)&'?;/,, A%+ B8/&2µ% *+ %6+*0 D<+)*+&6 ( µ, D<+)*+&6.!0 0&6 A%+ 8?&2+
5 *-/073' µ%µ7/;+,, 8?&2+ 8+* -*J6A0&, -*0 A%+ 8?&2+ )& µ,?*+01µ# +* "&$$*"$*10;D&+)*0.!0 D<+)*+&6 &/4*+01µ&6 "&$$*"$*10;D&+)*0 *"# µ#+&0 )&2'W &0 0&6 "/8"%0 +* µ"& * -.))*/& -*0 +*?/,10µ&"&0(1&2+ )& 2$0-# )&2-2));/&2 40* +* "&$$*"$*10*1)&.+. U)*+ %6+*0 1)&+ *8/* %6+*0 µ, D<+)*+&6, "0>*+#+ +* µ%6+&2+ 40*?/#+0* 1)&+ *8/*, 40* %-*)&µµ./0*?/#+0* 61<', -*0 +* µ,+ ";>&2+ )6"&)*. U)*+ 7/&2+ 8+* -.))*/&, -&$$;+% ";+< )&2, 7;D&2+ µ81* )& 4%+%)0-# )&2' 2$0-#,?/,10µ&"&0&.+ )& µ,?*+01µ# )&2-2));/&2, -*0 "&$$*"$*10;D&+)*0. X?&2+ µ%+ 8+* -*J6A0& *"# "/<)%S+%', *$$; A%+ 8?&2+ µ%µ7/;+,, -*0 A%+ B8/&2µ% *+ %6+*0 D<+)*+&6 ( µ, D<+)*+&6 &/4*+01µ&6, 61<' -;)0 %+A0;µ%1& 5*6+%)*0 $&40-# +* 2";/?%0 )& 12+%?8' *"# )& µ, D<+)*+# 1)& D<+)*+#. X?&2µ% "&$$; "*/*A%64µ*)* 12+#/<+ "&2 A0*?</6D&2+ ), D<( *"# )&+ >;+*)&. YA0*6)%/* 1,µ*+)0-; %6+*0 )* 1.+&/* 1),+ -2))*/0-( «*2)&-)&+6*», ),+ *"#")<1,. E),+ "%/6")<1, *2)( "/&-*$%6)*0 µ0* &/4*+<µ8+, *2)&-*)*1)/&5( )<+ -2));/<+ "&2?*/*-),/6D%)*0 *"# )&+ -*)*-%/µ*)01µ# )&2' -*0 )& "/&1%-)0-# "*-%);/01µ* )<+ 121)*)0-3+ )&2' 1% %0A0-&.' 1;-&2' *"# µ%µ7/;+%' (1.+&/*), &0 &"&6%' %B<)%/0-; 8?&2+ A%6-)%' (5<15*)0A2$&-1%/6+%') "&2 A,$3+&2+ #)0 )* 121)*)0-; "/8"%0 +* ";+% 40* *+*-.-$<1,. E% *+)6>%), "%/6")<1,, #)*+ A,$*A( )* 121)*)0-; )<+ +%-/3+ -2));/<+ A0*?2>&.+ *+%B8$%4-)* 1)&+ "%/07;$$&+)*?3/&, "/&-*$&.+ 7$;7%' 1)* "*/*-%6µ%+* -.))*/*, *-/073' #"<' -*0, *+%B8$%4-), *"#//0J, 1-&2"0A03+ 1), 5.1,. D#$8 -/. *( 9A**-,( I* 1.+&/* A%+?</6D&2+ µ#+& )& -.))*/& *" )& "%/07;$$&+ )&2 -*0 )0' %+A&-2));/0%' A&µ8' *" )& -2))*/#"$*1µ*. E.+&/*?</6D&2+ -*0 )0' 2"%/-2));/0%' A&µ8' *" )& "%/07;$$&+ )&2'. N+ *+%7&.µ% 8+* %"6"%A& ";+< *"# )& -.))*/& (A, )& 8?&2µ% -;µ%0 µ0$3+)*' 40* )& 8+)%/&, 1)&2' "&$2-.))*/&2' &/4*+01µ&.', B*+*7/61-&2µ% 1.+&/*. Z1<' <' µ0* "/&8-)*1, )<+ %+A&-2));/0<+ -*0-2))*/ #/<+. I* #/4*+* $%0)&2/4&.+ µ81* 1)& 1.+&/# )&2':, -*/A0; 1)& "%/0-;/A0&, &0 "+%.µ&+%' 1)&+ 2"%D<-#)*, & %4-85*$&' 1), µ(+044* (1)0' µ(+044%' 40* ),+ *-/67%0*) -)$. :%/65,µ&' %6+*0 & *0µ*)%4-%5*$0-#' 5/*4µ#'W 150?)#, *+%$*1)0-#, 1?%A#+ *A0*"8/*1)& 1.+&/& *+;µ%1* 1)& *6µ* -*0 )&+ %4-85*$&W µ#+& &/01µ8+%'?,µ0-8' &216%', *"# )0'?0$0;A%' "&2-2-$&5&/&.+ 1)& *6µ*, %"0)/8"%)*0 +* )&+ A0*7&.+, -0 *2)8' 2"# *"#$2)& 8$%4?&: & %4-85*$&' A%+ %6+*0 "*6B%-48$*1%. N"# ),+ ;$$, µ%/0;,, -2J%$0A&)/0?&%0A0-( µ%µ7/;+, )<+ "+%2µ#+<+, #"&2 12+*+);)*0, %+1<µ*)<µ8+, *)µ#15*0/* (*+*"+%#µ%+&' *8/*') µ% ),+ %+1<µ*)<µ8+, 2A/#15*0/* (*6µ*, 1<µ*)&"&0,µ8+, >;$*11*), A%+ %6+*0 "*/; %-)%)*µ8+* (#1& 8+* 4("%A& )8+0'!) «)/."0*» 1.+&/*: «-;>%»?,µ0-( &216* "%/+;%0 1?%A#+ %$%.>%/* :0& 8B< *"# )& &$&5;+%/& 1.+&/& )&2 &/4*+01µ&. µ*', )& A8/µ*, 2";/?%0-0 8+* *#/*)&: -*+%6' µ*' A%+ %"0)/8"%0 1% -*+8+*+ +* µ*' "$,10;1%0 "%/011#)%/& *"#, *' "&.µ%, µ0* "*$;µ, *"# )& &/*)# 1.+&/& ),'."*/B(' µ*', *"# )& A8/µ* (Wainwright 1993). T;>% µ%4*$.)%/, %44.),)* %-$*µ7;+%)*0 <' %"6>%1, %+*+)6&+ ),' *-%/*0#),);' µ*', -*0, *2)#µ*),, «5210-(», *+)6A/*1( µ*' %6+*0, *+)%"6>%1, (, 12+,>81)%/*,, 524( ()/*70#µ*1)% "/&' )* "61<)W %-)#' *"# µ#+& A.& "%/0")31%0': *+ & %017&$8*' %6+*0 & µ% ),+ ;A%0; µ*' 40*)/#' µ*' (*2)&12+)(/,1( µ*') ( & %/<)0-#' µ*' 1.+)/&5&' (*+*"*/*4<4( µ*', *2)&12+)(/,1, )&2 %6A&2'). D#$8 -/. *($ (,?-$"3µ. X?&2+ )* A8+)/* µ%)*b. )&2' 1.+&/*; I* D3*; I* &0-&121)(µ*)*; C-%6 "&2-2+,4;%0, *$%"&. N -2+,4;%0 -*0, [; M6+&+)*0 "#$%µ&0 *+;µ%1; )&2'; :3' /2>µ6D%0 )& &0-&1.1),µ* )* µ%)*b. )<+ 1)&0?%6<+ )&2 #/0* -*0 12+-#/0*; E)& IA9("
6 µ%$ 9)-=*4 & %B%/%2+,)(' 1,µ;A%J% (87*$% 1.+&/*) )&?3/& 4./< *"# ), 1-,+( )&2 µ% )&+ )/#"& "&2 7$8"&2µ% -;>% µ8/* )* 1-2$0; +* -;+&2+: &2/3+)*'. «:%/65/*B%» #µ<' 8)10 µ81* 1),+ %"0-/;)%0; )&2 -*0 )& A/#µ& "&2 & $.-&' 8-*+% *"# ), 5<$0; )&2 1)& -2+(40. C-%6+, ),+,µ8/*, #)*+ #"<' -;>% µ8/* 85)*1% )/8?&+)*' 1)& *#/*)& 1.+&/&, 5/%+;/01% *"#)&µ*, µ./01%, *+*4+3/01% -*)*"*),)8', 8-*+% 4./<- 4./< -*0 12+8?01% )& A/#µ& )&2 (Mowat 1999 [1971]). E),+ &0-&$&46* 2";/?&2+ A0;5&/* 1.+&/* (Cox & Moore 1998). I* 7&2+;, 40* "*/;A%04µ*, -*0, >;$*11* *"&µ&+3+&2+ "$,>21µ&.', -*0 "/&1)*)%.&2+ *"# -;"&0&2' «A2+;µ%0» %?>/&.'. U)*+ "81&2+ )* «*A0*"8/*1)*» 1.+&/*, &0 12+8"%0%' %6+*0 12+(><' -*)*1)/&50-8' 40* )& &0-&1.1),µ*. N"# ),+ ;$$,, *+ )* 1.+&/* %6+*0 "%/*); (,µ0"%/*);, &0 4%0)&+0-&6 "$,>21µ&6 %"<5%$&.+)*0 *"# ),+ *+)*$$*4( 4&+0A6<+. G%+ %6+*0 ;1"/&-µ*./& (&.)% -0 %A3!) I& "/#7$,µ* µ% )* «*A0*"8/*1)*» 1.+&/* %6+*0 #)0 A%+ 2";/?%0 12+%B8$0B, )<+ %0A3+, &"&6*, %-)#' *"# "%/0")31%0' *µ&07*6*' 12µ76<1,' (#"<', %"0-&+6*1,), A6+%0 -*0 ), A2+*)#),)* +* *+*")2?>&.+ &0 1?%)0-8' ;µ2+%' -*0 +* 01&//&"(1&2+ &0 1?81%0' µ%)*b. )<+ &/4*+01µ3+. M0* "*/;A%04µ*, )* "&+)6-0* A% >* %-$%6J&2+ "&)8 <' %6A&', %B*0)6*' ),'."*/B,' 4*)3+. \#4< ),' µ*-/#?/&+,' 12+%B8$0B,' )* "&+)6-0* >* %6+*0 ";+)* 8+* 7(µ* µ"/&1); *"# )0' 4;)%', -*0 &0 "$,>21µ&6 )<+ A.& *2)3+ %0A3+ $64& "&$. >* *$$,$&%B*/)3+)*0 *+ >%</(1&2µ% "<' )* "&+)6-0* *"&)%$&.+ ),+ -./0* )/&5( )<+ 4*)3+ -*0 A%+ 8?&2+ ;$$&2' 1,µ*+)0-&.' >,/%2)8' (Biology Pages 2008). U"&2 *2); )* *A0*"8/*1)* 4%<4/*50-; 1.+&/* 8?&2+ -*)*//%.1%0 (12+(><' µ% *+>/3"0+, "*/8µ7*1,), &0 +)#"0&0 *"&µ&+<µ8+&0 "$,>21µ&6 12?+; 2"&58/&2+. 9 %01*4<4( -&2+%$03+ 1),+ N21)/*$6*, #"&2 A%+ %6?*+ -;"&0& 5210-# %?>/#, 1?%A#+ &A(4,1% 1),+ -*);//%21, )&2 $07*A0-&. &0-&121)(µ*)&'. I& "0& 4+<1)# #µ<' "*/;A%04µ* %6+*0 *2)# )&2 +)#+)& (dodo) 1)& K*2/6-0& (+,16 )&2 Y+A0-&. F-%*+&.), "&2 %B*$%65>,-% %"%0A( %B%$6?>,-% *"&µ&+<µ8+&: -*)*/?(+ A% 5&7#)*+ )&2' *+>/3"&2', #)*+ )&2' "/<)&12+;+),1% )& 1581, -0 8)10 ()*+ %.-&$&' 1)#?&'W µ%4*$.)%/& /#$& #µ<' 1),+ %B*5;+01( )&2 %6?%, %01*4<4( 1)& K*2/6-0& 4&2/&2+03+, */&2/*6<+, 1-.$<+, 4*)3+ -*0 µ*-;-<+, "&2 8)/<4*+ )* *24; )&2W )& +)#+)& A%+ %6?% "&)8 )8)&0&2 %6A&2' %?>/&.' -*0 8)10 8?)0D% ), 5<$0; )&2 1)&?3µ*?</6' -*µ6* "/&5.$*B, (1.+&/&): µ8?/0 )& 1700 %6?% %B*5*+01)%6. EA**-,-, (,?-$"3µ(=, ("9(303*+µ-*- 9-" 6"-:(,"92& 45"3H34"&! G%+ %6+*0 1)&2' 1-&"&.' )&2 ;/>/&2 *2)&. +* 2"%018$>%0 1% )%?+0-8' $%")&µ8/%0%'. ]* 1,µ%031&2µ% µ#+& #)0 & Meinhardt (1992) 1% 8+* 1,µ*+)0-# ;/>/& %"01-#",1,' "%/084/*J% µ% 8+* 1.1),µ* µ, 4/*µµ0-3+ µ%/0-3+ A0*5&/0-3+ %B0131%<+ )&+ -/610µ& /#$& "&2 "*6D&2+ )* 1.+&/* 40* ), 7%$)6<1, )<+ 8µ70<+ #+)<+ 1), A0*A0-*16* ),' %B8$0B,', )#1& 1)& %"6"%A& )&2-2));/&2 #1& -*0 1)* %"6"%A* )&2 &/4;+&2 -*0 )&2 &/4*+01µ&.. L*6+%)*0 #)0 01?.%0 )& 6A0& 1% #$* )* %"6"%A* ),' L.1,': *"# )& 1)&0?%03A%' 1<µ*)6A0& ),' -7*+)0-(' 5210-(' 2 -*0 )&+ *+#/4*+& -#1µ& 3 µ8?/0 )&+ &0-&$&40-# *+)*4<+01µ# )<+ %0A3+ -*0 ),+ 0-*+#),); )&2' +* 2 E)& µ0-/#-&1µ& )&2 +*+&µ8)/&2 ()&2 µ%48>&2' ), -7;+)<1, %B*/);)*0 *"# )&+ %4-$<701µ# 1% "%/0&?(. 3 ^A, )& 1952, $64& "/0+ )&+ )/*40-# >;+*)# )&2, & Turing "%/084/*J% )& /#$& ),' A0;?21,' A.& &2103+ µ% A0*5&/%)0-8' )*?.),)%' A0;?21,' 40* ), A,µ0&2/46* µ&/53+ (12+#/<+) µ% 8+* *"$# 1.1),µ* A0*5&/0-3+ %B0131%<+: dx/dt=5x-6y+1, dy/dt=6x-7y+1. CA3, -*)*+#,1, ),' A0*A0-*16*' *2)o&/4;+<1,' )<+ µ&/6<+ 1% 1.+&$* µ&/6<+ %6+*0 "&1&)0-( -*0 &0 1)&0?%03A%0' A0*A0-*16%' ),' *2)&-*);$21,' -*0 ),' "*/%µ"#a01,' A,µ0&2/4&.+
7 "%/05/&2/&.+ µ% A0;5&/%' 1)/*),40-8' )&?3/& )&2' (Patel & Lansey 2006) 4. 9 µ*>,µ*)0-( 8-5/*1, ),' )*?.),)*' u <' µ%)*7&$(' ),' "&1#),)*' µ0*' &+)#),)*' N µ% )&+?/#+& t, u=dn/dt, %6+*0, 7;1, 1),+ -*);1)/<1, )<+ A0*5&/0-3+ %B0131%<+ ),'?/&+&%B8$0B,' %+#' 121)(µ*)&' *"# &+)#),)%'. C;+ )& N %6+*0?,µ0-8' %+31%0' *5&/; *2)&&/4;+<1, µ&/6<+, *+ %6+*0 D<0-; ( 52)0-; %6A, *5&/; ),+ %B8$0B, *2)3+ )<+ %0A3+.!0 "/&1&µ&031%0' µ% ),+?/(1, µ*>,µ*)0-3+ µ&+)8$<+ 8?&2+ */-%); -*$( "/&7$%")0-( 0-*+#),)*W #)*+ 0-*+&"&0&.+)*0 -;"&0%' 1?81%0' µ%)*b. )<+ */?0-3+ "&1&)()<+ N, 2";/?%0 *+;")2B, *"# ),+ µ, &/4;+<1, (?;&') 1% µ6* ( "%/011#)%/%' *2)&&/4*+31%0', *$$03' µ% -;"&0%' ;$$%' "/&@"&>81%0' 8?&2µ% %B;$%0J, µ0*' *"# )0' *2)&o/4*+31%0', A,$*A( )* 1.+&/* µ%)*b. µ0*' *2)&&/4;+<1,' -*0 µ0*' ;$$,' %B*$%65&+)*0. I8$&',, %B61<1, Drake (1960) 1),+ *1)/&5210-( 8-*+% µ0* "/#7$%J, 40* ),+ %B<70&$&46* -*0 ),+ %B;"$<1, "&$0)01µ3+ 1)& E.µ"*+ 5 µ% ), A21µ%+( "/#4+<1, #)0 &0 )%?+&$&40-&6 "&$0)01µ&6 8?&2+ ),+ );1, +* -*)*//8&2+ (5*0+#µ%+& "&2 %6+*0 4+<1)# <' «)& "*/;A&B& )&2 Fermi») (Wikipedia 2008). I* 1.+&/* "*+)&. "*6D&2+ "&$21(µ*+)& /#$& 1),?/&+&%B8$0B, )<+ 121),µ;)<+ &+)&)()<+, %6)% %6+*0 1)&0?%03A, 1<µ;)0* %6)% µ#/0*, %6)% A0;5&/* %6A, 52)0-&. ( D<0-&. 7*10$%6&2, %6)% &$#-$,/&0 "&$0)01µ&6. J/. *% B"()(?=- 3*%$ E("$8$=- :3' "/&%-)%6+&+)*0 &0 &/4*+01µ&6 *2)&6 -*>*2)&6; CB%0A0-%2#µ%+&0. Z1<' 1)& *"3)*)& µ8$$&+ µ0* "&$0)%6* 1*+ ), L$3/0+* >* "*/;4%0 µ#+& "*"&.)10*, 8)10 #"<' µ0* "&$0)%6* 1*+ )&+ >2/%&%0A( *A8+* 5)0;?+%0 µ#+& &/µ#+%', >* 8?&2µ% A,$*A( )/&µ%/( %B%0A6-%21,. N2)# µ"&/%6 +* %0"<>%6 1*+ "/&8-)*1, 1)& -&0+<+0-# %"6"%A& *2)3+ "&2 12µ7*6+&2+ 1)& -2))*/0-#. G,$*A(, "3' 5);1*µ% 1)&+ ;+>/<"&; :/3)* ()*+ &0 µ&+&-.))*/&0 &/4*+01µ&6. V<+)*+&6 &/4*+01µ&6, 8+* -.))*/& #$& -0 #$&. K%); -#$$,1*+ µ*d6 -*0 8-*+*+ &$04&-.))*/&2' -*0 "&$2-.))*/&2' &/4*+01µ&.', -*0 1)& )8$&' )* D3* -*0 )&2' *+>/3"&2', "&2 *"&)%$&.+)*0 *"# #/4*+* µ% %+)%$3' %B%0A0-%2µ8+* -.))*/*. N"# )& 6A0& -.))*/& B%-0+;+% #$*, )& 4&+0µ&"&0,µ8+& <;/0&, "&2 A0"$*10;D%)*0, "&$$*"$*10;D%)*0, -*0 A0*5&/&"&0%6)*0, µ%/0-; 46+&+)*0 -.))*/* %4-%5;$&2, ;$$* 46+&+)*0 +.?0*, -0 ;$$* 46+&+)*0 µ2'. :*/#)0 8?&2+ )& 6A0& 4%+%)0-# 2$0-#, A0*5&/&"&0&.+)*0-0 %B%0A0-%.&+)*0 +* -;+&2+ µ0* 124-%-/0µ8+, A&2$0;. :0>*+#+ -0 &0 -&0+<+6%' 8)10 >* %B%$0?)&.+, *+ )&2' A&>%6 &?/#+&' -*0 A%+ -*)*1)/*5&.+ %+A0;µ%1*. ]* %B%0A0-%2)&.+ +* -;+&2+, -*>%µ0; µ0* 124-%-/0µ8+, A&2$0;. K0* "&$0)%6* >* µ"&/%6 +* 5)0;?+%0 µ#+& "*"&.)10*, )* -*$.)%/* #µ<', -*0 )*2)#?/&+* >* %6+*0 *"#$2)* %B*/),µ8+, *"# )0' ;$$%' "&$0)%6%', &0 &"&6%' µ% ), 1%0/; )&2' >* -;+&2+, -*>%µ0; -*0 A0*5&/%)0-# "/&R#+. N+, µ;$01)*, 1)*µ*)(1%0, "&$0)%6* *2)( +* 5)0;+%0 "*"&.)10*, >* "%>*6+%0W -*0 µ*d6 ),' #$%' &0 "&$0)%6%', #"<' ;µ* 1)*µ*)(1%0 )& ("*/ +* $%0)&2/4%6 )%$%03+%0 #$& )& 13µ*. E 8+* 7;>&'?/#+&2, A,$*A(, >* 46+&2µ% 1),+ "/*4µ*)0-#),)* 8+*' &/4*+01µ#' (µ%4*&/4*+01µ#'). ]%</3+)*' )& A0-# µ*' &/4*+01µ# 1*+ 8+* "%/0&A0-#),)%' µ&)67<+ µ% A0*5&/%)0-(?,µ0-( 1.1)*1, -*0 A0%"05;+%0%' (1.+&/*) µ%)*b. )&2'. 4 K0* 707$0&4/*50-( *+*D(),1, (10/10/07) 1)& scopus.com µ% )0' $8B%0' biology, boundary -*0 differential equation 8A<1% 26 ;/>/* "&2 12+A8&2+ "$,>21µ&.' D<0-3+ ( 52)0-3+ %0A3+ µ% "%0/*µ*)0-8' "*/*),/(1%0' -*0 µ*>,µ*)0-8' "/&7$8J%0' %"076<1,' -*0 -*)*1)/&5(' 1% 1?81, µ% )& )0 46+%)*0 *"# )&+ *+)*4<+01µ# µ% ;$$* %6A, -*0 ),+ 0-*+#),); )&2' +* "%/05/&2/&.+ µ% A0;5&/%' 1)/*),40-8' )&?3/& )&2'. 5 9 *1)/&70&$&46* ( %B<70&$&46* %6+*0, µ%$8), ),' *"*/?(', ),' %B8$0B,', ),' -*)*+&µ(' -*0 )&2 µ8$$&+)&' ),' D<(' 1)& E.µ"*+ (Jstrobiology 2008).
8 «-.))*/&», 1*+ µ6* µ&+;a*, µ0* -&0+<+6* *"&)%$%6)*0 *"# "&$$8' )8)&0%' µ&+;a%' #"&2 -;>% ;+>/<"&' *"&)%$%6 8+* -.))*/# ),'. T*0, -&0+<+6*, 6A0* µ"&/%6 %"61,' +* %6+*0 µ6* µ&+;a*. U"<' &0 µ&+&-.))*/&0 &/4*+01µ&6 85)0*B*+ )&2' "&$2-.))*/&2', 8)10, 1% µ0* %B%$0-)0-( "&/%6*, -*0 &0 µ&+&&/4*+01µ&6 5)0;?+&2+ )&2' "&$2&/4*+01µ&.'. C6µ*1)% (A, 1)& %"6"%A& )<+ "&$2&/4*+01µ3+. 9 &0-&48+%0* %6+*0 "&$2&/4*+01µ#'. G%+ %6µ*1)% #µ<' "&$. %B%$04µ8+&0 *-#µ*. E),+ */?( B%-6+,1% -;>% &0-&48+%0* +* %6+*0 *2)&A.+*µ,, +* 5)0;?+%0 )& 5*4,)# ),', +* 5)0;?+%0 )* "*"&.)10* ),', +* 5)0;?+%0 )& 1"6)0 ),', #$*. E04; 104; %B%0A0-%.),-*+W -*0 12+%?6D&2µ% +* %B%0A0-%2#µ*1)%. =";/?&2+ ;+>/<"&0 "&2 B8/&2+ µ#+& )&?/,µ*)01)(/0& -*0 D&2+ µ0*?*/;, *$$; A%+ B8/&2+ +* 5)0;B&2+ &.)% 8+* -/%µ.a0 ( 8+* -&)#"&2$&. L*6+%)*0 "<' "/&?</;µ% "/&' ),+ %B%0A6-%21,, #"<' #)*+ &0 µ&+&-.))*/&0 &/4*+01µ&6 85)0*B*+ "&$2-.))*/&2' µ% %B%0A0-%2µ8+* µ&+&-.))*/*. N+ *2)# %6+*0 )& µ8$$&+ µ*', >* "*6D&2+ )* 1.+&/* -;"&0& /#$& -*0 "&0&+; I* -&0+<+0-; 8+)&µ* %B%0A6-%21*+ )0' $%0)&2/46%' )&2' µ% )8)&0&+ )/#"& 31)% &0 A0;5&/&0 %0A0-&6 +* 1?,µ*)6D&2+ #$&0 µ*d6 8+* -&0+<+0-# 13µ*. I* -&0+<+0-; 8+)&µ*?/%0;D&+)*0 )& 8+* )& ;$$& -*0 A%+ µ"&/&.+ +* %"07031&2+ <' µ&+*?0-; 8+)&µ*. N+ *"&µ&+31&2µ% 8+* µ2/µ(4-0, >*?;1%0 ),+ #/%B( )&2, > *//<1)(1%0 -*0 >* "%>;+%0. T*); 8+*+ )/#"&, A%+ %6+*0 8+* &$&-$,/<µ8+& #+ -*>*2)#, *$$; 8+* «#/4*+&», 8+* µ8/&' )&2 -&0+<+0-&. )&2 13µ*)&' ),' -&0+<+6*' ),' µ2/µ,4-&5<$0;'. Z1<' 8+* µ2/µ(4-0 +* %6+*0 40* ),+ -&0+<+6* )&2 #,)0 8+* µ0)&?#+a/0& 40* )& -.))*/# )&2» (Sahtouris 1989). C6µ*1)% -&0+<+0-; #+)*;! 1-3A$(,- *(0 µ2))($*(& 9 *"&)%$%1µ*)0-#),)* %6+*0 )& -/0)(/0& 1), [0&$&46*. N"&)%$%1µ*)0-; 1.+&/* A0*?</6D&2+ )0' A&µ8' ),', 31)%, -*>%µ6* +* 7%$)01)&"&0%6 ), $%0)&2/46* ),'. C6+*0 )* )</0+; -/*)0-; 1.+&/* *"&)%$%1µ*)0-;; K;$$&+ %6+*0 *"&)%$81µ*)* A.+*µ,'. U"&0&' %6?% ), A.+*µ, %"87*$% 1.+&/* %-%6 "&2 85)*+%, A.+*µ( )&2. E)& -.))*/& A%+ )* -*>#/01%, A.+*µ,, )* -*>#/01%, *"&)%$%1µ*)0-#),)*. N+ >%</(1&2µ% )& -&0+<+0-# <' "/&8-)*1, )&2 70&$&40-&. 2"&A%64µ*)&', )* µ%$$&+)0-; 1.+&/* >* 8?&2+ 1?81, µ% ),+ *"&)%$%1µ*)0-#),)*. G,$*A(,, *"&µ#+<1, µ81* 1% 8+* 1.+&/& -*0, "/&1)*16* *"# 8+* 1.+&/&,, «µ#+<1,», >*?/%0;D%)*0 40* +* A&2$%.&2+ *"&)%$%1µ*)0-; )* µ8/,. L210-; A% µ0$;µ% 40* "/;4µ*)* "&2 >* 12µ7&.+ 1)0' µ8/%' µ*'. N"# ),+ %"&?( "&2 (µ*1)*+ µ&+&-.))*/&0, "&2 2"(/?*+ A,$*A( µ#+& µ&+&-.))*/&0 &/4*+01µ&6, µ8?/0 "&2 A.& -.))*/* 12+-A8>,-*+ µ*d6 -*0 85)0*B*+ )& "/3)& 124-.)0&, *2)# >* "/8"%0 +* "(/%?/#+&, "&$.?/#+&, ),' );B,' )<+ %-*)&µµ2/6<+ %)3+ 61<'. 9 M, 8?%0 )811%/* )%11%/;µ010 A01%-*)&µµ./0*?/#+0*. E)* µ01; *"# *2); 2";/?%0 D<(, )* "/3)* µ01; ()*+?</6' D<(. E)* )%$%2)*6* A2#µ010 A01%-*)&µµ./0*?/#+0* %B%$611%)*0, D<(. N+ >%</(1&2µ% ),+ 01)&/6* ),' M,' 1*+ 8+* 24</&, & ;+>/<"&' %µ5*+6d%)*0 1)0' 23 -*0 59, A,$*A( )& )%$%2)*6& $%")#. N+ )&2 "(/% 8+* $%")# 40* +* 5)0;B%0 1.+&/* µ% 7;1, ), A.+*µ,, +* µ, )&2 ";/%0-0 8+* $%")# (( 81)< A%2)%/#$%")&) 40* +* 5)0;B%0 1.+&/* µ% 7;1, ),+ *"&)%$%1µ*)0-#),)*; T&0+( 4*/, ).?, -*0 )& µ8$$&+ *#/*)&+! ^ µ;$$&+, "*/#)0 )& µ8$$&+ %6+*0 *#/*)& -*0 )* "*/*";+< A%+ *"&)%$&.+ "*/; %0-*16%' *"# "/&8-)*1, )&2 70&$&40-&. 1)& -&0+<+0-#,, ).?, #$<+ )<+ *+>/3"<+ ),'!-=-& %6+*0 µ;$$&+ -&0+(.
9 70µ/4,-3µ-*"9# V<( 1,µ*6+%0 1.+&/&. 9 70&$&46* A%+ %6+*0 "*/; 1.+&/*, 1.+&/*, 1.+&/*! E.+&/* µ81* 1)* 1.+&/*. N$$%";$$,$%' 1)/31%0' 12+#/<+. N"*/*6),), "/&@"#>%1, ),' D<(' %6+*0 )* 1.+&/*. 9 D<( %6+* *1µ8+, µ% )* 1.+&/*. P</6' 1.+&/* A%+ 2";/?%0 D<(. N$$; 1.+&/* "&2 %"0$84&2+ -*0 %$84?&2+ *21),/; )0, "#1& -*0 "#)% >* )* A0*7%6 "/&' ), µ0* ( ),+ ;$$, -*)%.>2+1,. U/0* 2"# #/&2'. '"4/"3*%µ($"9. 03*4,.?,-:( E)&+ ",4*0µ# 40* ), L$3/0+*, 74(-*µ% 8B< *" )& -*$&."0 µ*', *" )& -*7&.-0 µ*', *" )& 1.+&/# µ*', )& 1.+&/& ),' %"01)(µ,' )&2 & -*>8+*', -*0 "/&1"*>(1*µ% "/0+ *" #$* +* -*)*$;7&2µ% & 8+*' )&+ ;$$&+. K"&/%6 *2)# "&2 J;?+&2µ% +* %6+*0 (A, *"*+),µ8+& *" ),+ "*/*A6"$* %"01)(µ,! I& "*+%"01)(µ0& A%+ (>* 8"/%"% )&2$;?01)&+ +*) %6+*0 8+*' 1</#' µ&+%"01),µ6<+ µ% *A0*"8/*1)* 1.+&/* (G&2$4%/6A,' 2007) 1),+ «*$(>%0* )<+ -*0+&./40<+ 56$<+. I* [A0%"01),µ&+0-;] #/0* 2"&?</&.+. I& 1,µ*+)0-# "&2 *"&µ8+%0 %6+*0 &0 #/&0.» (T*µ0+;/, 2007) 6 «K%4;$* -0 2J,$; )/04./< µ&2 8-)01*+ )%6?, [ ] N! #)*+ 8-)0D*+ )* )%6?, "3' +* µ,+ "/&18B<; N+%"*01>()<' µ 8-$%01*+ *"# )&+ -#1µ&+ 8B<» («I* )%6?,», T. T*7;5,'). N+, A0*)(/,1, ),' 70&$&40-(' "&0-0$#),)*' %6+*0?/8&'.J01)&, %6+*0 ;/*4% µ0-/#)%/&, A0*)(/,1, ),' -&0+<+0-(' "&0-0$#),)*'; C6+*0 )& *6),µ* 40* «%>+0-( -*>*/#),)*» (*+)6 «%>+0-(' "&0-0$#),)*'») <' -*0 (%>+0-() *2)&-)&+6*; ^/>*µ% 1)& 12+8A/0& +* )& µ;>&2µ%, %0158/&+)*' ), A0-( µ*' *$(>%0*, *2)(+ ),' [0&$&46*', "&2 ), 4+</6D&2µ% -;"<' -*$.)%/*. 2)93)$4%&*5& Nstrobiology (2008). E)& ("/#17*1, 12/5/08). Biology Pages (2008). E)& ("/#17*1, 12/5/08). M*$;/,', G,µ()/,', M0;++,' G,µ,)/#"&2$&' & M0;++,' G,µ&$0;),' (2007). E.+&/*, "%/058/%0%', A0*1"&/8' 1), [0&$&46*. E)& 7%µ4"8*"9+ 9-" "64()(?=4&: 3A$(,-, /4,":2,4"4&, 6"-3/(,2&. :%/0$(J%0' 8&2 12+%A/6&2 C$$,+0-(' E,µ%0<)0-(' C)*0/6*', G,µ&$0;),', M0;++,' (1994). M0* µ0*+ %+*$$*-)0-( >%3/,1, )<+ 12+#/<+. F K2- L"9()(?=-, K;0&', G&2$4%/6A,', G,µ()/,' (2007). Y<;++,' 9$0#"&2$&', & %/%2+,)('. 1-C06,.µ(& 394 (3), T*7;5,', T<+1)*+)6+&' (?.?.). «I%6?,». D("+µ-*-. :*/&216*1, M03/4,' :0-/#'. N>(+*: C-A#1%0' M0;++,!0-&+#µ&2. T*µ0+;/,, K8$0++* (2007). X+* &A&0"&/0-# &/6<+ -*0 #/<+. M8*(?,#:(& 168, «I& )*B6A0 "/&' )* 1.+&/* µ&0;d%0 ";+)* *)8$%0<)& [ ] I* 1.+&/* ()*+ µ#+&, *5&/µ(. N2); µ*' 85%/*+ -&+);. I0 8µ%0+%; H A0*A0-*16*,, µ&+*a0-#),)* )<+ A0*5&/%)0-3+ )/#"<+ 1-8J,',, %"0-&0+<+6*,, *$(>%0* )<+ -*0+&./40<+ 56$<+. I* #/0* 2"&?</&.+. I& 1,µ*+)0-# "&2 *"&µ8+%0 %6+*0 &0 #/&0.!0 #/&0 "&2 )6>%+)*0 1)& "%A6& *+)0"*/;>%1,' #$<+ )<+ A0*5&/%)0-3+ -#1µ<+, #$<+ )<+ A0*5&/%)0-3+ "/*4µ*)0-&)()<+, #$<+ )<+ A0*5&/%)0-3+ %"01),µ3+» (T*µ0+;/, 2007).
10 Cox, C. Barry & Peter D. Moore (1998). Biogeography: An ecological and evolutionary approach. Blackwell Science. Meinhardt, 9ans (1992). Pattern formation in biology: a comparison of models and experiments. Reports on Progress in Physics 55 (6), Mowat, Farley (1999 [1971]). Never cry wolf/k)5/. M0&$;+)* \%76A,-\&.,. N>(+*: P*)D,+0-&$(. Murray, Christopher JL & Lopez, Alan D. (1996). The global burden of disease: A comprehensive assessment of mortality and disability from diseases, injuries and risk factors in 1990 and projected to [&1)#+,: Harvard University Press. Patel, Kunj & Jonathan Lansey (2006). Border properties of allopatric and sympatric plant species interactions. CAMS Report 0506-[10], (Fall 2005/Spring 2006), Center for Applied Mathematics and Statistics. Sahtouris, Elisabet (1989). Gaia. K)5/. N448$* [%/2-&-;-,-N/)8µ, (1999).!-=- - *( -$@,H/"$( *-5=6" -/. *( C#(& 3*($ 9.3µ(, N>(+*, O8* E.+&/*. Wainwright, Gordon (1993). Body language. K)5/. N$%B;+A/* O)*+;-* & M0;++,' G,µ&$0;),' (2007). F?)H33- *(0 3Hµ-*(& µ4 *% µ2@(6( *%& -0*(6"6-39-)=-&, N>(+*, T*1)*+03),'. Wikipedia (2008). E)& ("/#17*1, 12/5/08). World Health Organization (1985). Targets for health for all. Chapter 2: Prerequisites for health. Copenhagen. K)5/.-%"0µ. M0;+,' G,µ&$0;),' (2002). N?4=- 21: 0?4=-?"-.)(0& *($ 21( -"H$-, N>(+*: I2"<>()<.!"#$%& '%µ()"#*%& >/=9(0,(& E-@%?%*+& N?"4"$+& & >/"6%µ"()(?=-& O-*,"9+& 7C()+& D-$4/"3*%µ=(0 O8-$$=$8$ idimoliatis@gmail.com '%µ+*,%&!-)#,%& E-@%?%*+& B"()(?"9+& <%µ4=-& O-*,"9+& 7C()+& D-$4/"3*%µ=(0 O8-$$=$8$ dgalaris@uoi.gr '%µ+*,%& '%µ()"#*%& Environmental Consultant Hyder Consulting Pty Ltd Web: dimoliatis@gmail.com!"#$$%& '%µ%*,./(0)(& J$-/)%,8*+& E-@%?%*+& 1µ+µ- P%C-$"9H$ D)%,(:(,"9+& & 1%)4/"9("$8$"H$ 1(µ2-& >:-,µ(3µ2$%& D)%,(:(,"9+& D-$4/"3*+µ"( '0*"9+& P-946($=-& idimitr@uowm.gr
11 Ανοικτά Ακαδημαϊκά Μαθήματα Πανεπιστήμιο Ιωαννίνων Τέλος Ενότητας
12 Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το έργο «Ανοικτά Ακαδημαϊκά Μαθήματα στο Πανεπιστήμιο Ιωαννίνων» έχει χρηματοδοτήσει μόνο τη αναδιαμόρφωση του εκπαιδευτικού υλικού. Το έργο υλοποιείται στο πλαίσιο του Επιχειρησιακού Προγράμματος «Εκπαίδευση και Δια Βίου Μάθηση» και συγχρηματοδοτείται από την Ευρωπαϊκή Ένωση (Ευρωπαϊκό Κοινωνικό Ταμείο) και από εθνικούς πόρους. Σημειώματα Σημείωμα Αναφοράς Copyright Πανεπιστήμιο Ιωαννίνων, Διδάσκοντες: Αν. Καθηγητής Γιάνης Δημολιάτης (υπεύθυνος), Επίκ. Καθ. Ευαγγελία Ντζάνη, Κωνσταντίνος Τσιλίδης. «Πολιτικές Υγείας. Ο κόσμος αύριο: προβλέψεις και υγειακό τοπίο». Έκδοση: 1.0. Ιωάννινα Διαθέσιμο από τη δικτυακή διεύθυνση: Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά Δημιουργού - Παρόμοια Διανομή, Διεθνής Έκδοση 4.0 [1] ή μεταγενέστερη. [1]
Μικροβιολογία & Υγιεινή Τροφίμων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μικροβιολογία & Υγιεινή Τροφίμων Μικροοργανισμοί που ελέγχονται ανά είδος τροφίμου Διδάσκοντες: Καθ. Χρυσάνθη Παπαδοπούλου, Λέκτορας Ηρακλής Σακκάς Άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μικροβιολογία & Υγιεινή Τροφίμων Μικροοργανισμοί που ελέγχονται ανά είδος τροφίμου Διδάσκοντες: Καθ. Χρυσάνθη Παπαδοπούλου, Λέκτορας Ηρακλής Σακκάς Άδειες
Εκκλησιαστικό Δίκαιο. Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Τμήμα Νομικής Α.Π.Θ.
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 7η: Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 7η: Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Ιστορία της μετάφρασης
 ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Ηλεκτρισμός & Μαγνητισμός
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρισμός & Μαγνητισμός Αυτεπαγωγή Διδάσκων : Επίκ. Καθ. Ν. Νικολής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρισμός & Μαγνητισμός Αυτεπαγωγή Διδάσκων : Επίκ. Καθ. Ν. Νικολής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ. Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης
 Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Παράγωγοι και ολοκληρώματα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Ολοκληρώματα με το πρόγραμμα Maima Αθανάσιος
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Παράγωγοι και ολοκληρώματα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Ολοκληρώματα με το πρόγραμμα Maima Αθανάσιος
Γενικά Μαθηματικά Ι. Ενότητα 12: Κριτήρια Σύγκλισης Σειρών. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Κριτήρια Σύγκλισης Σειρών Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Κριτήρια Σύγκλισης Σειρών Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Εκκλησιαστικό Δίκαιο
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11η: Οργανισμοί της Εκκλησίας της Ελλάδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11η: Οργανισμοί της Εκκλησίας της Ελλάδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Πίνακες Νερού σε κατάσταση Κορεσμού. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
1 η Διάλεξη. Ενδεικτικές λύσεις ασκήσεων
 1 η Διάλεξη Ενδεικτικές λύσεις ασκήσεων 1 Περιεχόμενα 1 η Άσκηση... 3 2 η Άσκηση... 3 3 η Άσκηση... 3 4 η Άσκηση... 3 5 η Άσκηση... 4 6 η Άσκηση... 4 7 η Άσκηση... 4 8 η Άσκηση... 5 9 η Άσκηση... 5 10
1 η Διάλεξη Ενδεικτικές λύσεις ασκήσεων 1 Περιεχόμενα 1 η Άσκηση... 3 2 η Άσκηση... 3 3 η Άσκηση... 3 4 η Άσκηση... 3 5 η Άσκηση... 4 6 η Άσκηση... 4 7 η Άσκηση... 4 8 η Άσκηση... 5 9 η Άσκηση... 5 10
Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 10η: Απεσταλμένοι του Ρωμαίου Ποντίφικα και Ρωμαϊκή Κουρία Κυριάκος Κυριαζόπουλος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 10η: Απεσταλμένοι του Ρωμαίου Ποντίφικα και Ρωμαϊκή Κουρία Κυριάκος Κυριαζόπουλος
Γενικά Μαθηματικά Ι. Ενότητα 15: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Εκκλησιαστικό Δίκαιο
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8η: Ο νέος αντιρατσιστικός νόμος και ο ν.4301/2014 Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8η: Ο νέος αντιρατσιστικός νόμος και ο ν.4301/2014 Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Εφαρμοσμένη Στατιστική
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφαρμοσμένη Στατιστική Περιγραφική Στατιστική Διδάσκων: Επίκουρος Καθηγητής Κωνσταντίνος Μπλέκας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφαρμοσμένη Στατιστική Περιγραφική Στατιστική Διδάσκων: Επίκουρος Καθηγητής Κωνσταντίνος Μπλέκας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2)
 Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 7: Παράγωγος, ελαστικότητα, παραγώγιση συναρτήσεων (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 7: Παράγωγος, ελαστικότητα, παραγώγιση συναρτήσεων (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης
Διοικητική Λογιστική
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 10: Προσφορά και κόστος Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 10: Προσφορά και κόστος Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Ιστορία της μετάφρασης
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η μετάφραση των εβδομήκοντα, η εκπαίδευση των μεταφραστών κατά Κικέρωνα, η τέχνη της μετάφρασης από την αρχαιότητα μέχρι τα
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η μετάφραση των εβδομήκοντα, η εκπαίδευση των μεταφραστών κατά Κικέρωνα, η τέχνη της μετάφρασης από την αρχαιότητα μέχρι τα
Ηλεκτρονικοί Υπολογιστές I
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές I Ελαστικότητα και εφαρμογές Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές I Ελαστικότητα και εφαρμογές Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Ενδεικτικές λύσεις ασκήσεων διαχείρισης έργου υπό συνθήκες αβεβαιότητας
 Ενδεικτικές λύσεις ασκήσεων διαχείρισης έργου υπό συνθήκες αβεβαιότητας 1 Περιεχόμενα 1 η Άσκηση... 4 2 η Άσκηση... 7 3 η Άσκηση... 10 Χρηματοδότηση... 12 Σημείωμα Αναφοράς... 13 Σημείωμα Αδειοδότησης...
Ενδεικτικές λύσεις ασκήσεων διαχείρισης έργου υπό συνθήκες αβεβαιότητας 1 Περιεχόμενα 1 η Άσκηση... 4 2 η Άσκηση... 7 3 η Άσκηση... 10 Χρηματοδότηση... 12 Σημείωμα Αναφοράς... 13 Σημείωμα Αδειοδότησης...
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 11η: Σύγκριση Ρωσικής Ορθόδοξης Εκκλησίας και Καθολικής Εκκλησίας Κυριάκος Κυριαζόπουλος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 11η: Σύγκριση Ρωσικής Ορθόδοξης Εκκλησίας και Καθολικής Εκκλησίας Κυριάκος Κυριαζόπουλος
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας. Βιοστατιστική (Ε) Ενότητα 3: Έλεγχοι στατιστικών υποθέσεων
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 3: Έλεγχοι στατιστικών υποθέσεων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 3: Έλεγχοι στατιστικών υποθέσεων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας. Βιοστατιστική (Ε) Ενότητα 1: Καταχώρηση δεδομένων
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 1: Καταχώρηση δεδομένων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 1: Καταχώρηση δεδομένων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος διατίθεται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Πιθανότητες. Συνδυαστική Ανάλυση Διδάσκων: Επίκουρος Καθηγητής Κωνσταντίνος Μπλέκας
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Πιθανότητες Συνδυαστική Ανάλυση Διδάσκων: Επίκουρος Καθηγητής Κωνσταντίνος Μπλέκας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Πιθανότητες Συνδυαστική Ανάλυση Διδάσκων: Επίκουρος Καθηγητής Κωνσταντίνος Μπλέκας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εκκλησιαστικό Δίκαιο
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6η: Ελληνική νομολογία Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6η: Ελληνική νομολογία Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Μηχανολογικό Σχέδιο Ι
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα # 8: Άτρακτοι και σφήνες Μ. Γρηγοριάδου Μηχανολόγων Μηχανικών Α.Π.Θ. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα # 8: Άτρακτοι και σφήνες Μ. Γρηγοριάδου Μηχανολόγων Μηχανικών Α.Π.Θ. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας. Βιοστατιστική (Ε) Ενότητα 2: Περιγραφική στατιστική
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 2: Περιγραφική στατιστική Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 2: Περιγραφική στατιστική Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Σχεδιασμός & Αξιολόγηση Προγραμμάτων Εκπαίδευσης Ενηλίκων
 Σχεδιασμός & Αξιολόγηση Προγραμμάτων Εκπαίδευσης Ενηλίκων Ενότητα 3 η : Οργάνωση Προγραμμάτων ΙΙΙ Συντελεστές Θανάσης Καραλής Σχολή Ανθρωπιστικών και Κοινωνικών Επιστημών Τμήμα Επιστημών της Εκπαίδευσης
Σχεδιασμός & Αξιολόγηση Προγραμμάτων Εκπαίδευσης Ενηλίκων Ενότητα 3 η : Οργάνωση Προγραμμάτων ΙΙΙ Συντελεστές Θανάσης Καραλής Σχολή Ανθρωπιστικών και Κοινωνικών Επιστημών Τμήμα Επιστημών της Εκπαίδευσης
Αξιολόγηση μεταφράσεων ιταλικής ελληνικής γλώσσας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Αξιολόγηση μεταφράσεων ιταλικής ελληνικής γλώσσας Ενότητα 1: Αυτοαξιολόγηση μεταφραστών Κασάπη Ελένη Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Αξιολόγηση μεταφράσεων ιταλικής ελληνικής γλώσσας Ενότητα 1: Αυτοαξιολόγηση μεταφραστών Κασάπη Ελένη Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός
 Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.4: Ολοκλήρωση με Αντικατάσταση Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.4: Ολοκλήρωση με Αντικατάσταση Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Υπολογιστές Ι. Άδειες Χρήσης. Δομή του προγράμματος. Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης Υπολογιστές Ι Δομή του προγράμματος Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης Υπολογιστές Ι Δομή του προγράμματος Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται
Παράκτια Τεχνικά Έργα
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΔΙΑΘΕΣΗ ΥΓΡΩΝ ΣΤΗ ΘΑΛΑΣΣΑ ΥΠΟΒΡΥΧΙΟΙ ΑΓΩΓΟΙ Ενότητα 5 η : Κατασκευαστικά παραδείγματα Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΔΙΑΘΕΣΗ ΥΓΡΩΝ ΣΤΗ ΘΑΛΑΣΣΑ ΥΠΟΒΡΥΧΙΟΙ ΑΓΩΓΟΙ Ενότητα 5 η : Κατασκευαστικά παραδείγματα Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης Το παρόν εκπαιδευτικό
Λογιστική Κόστους Ενότητα 8: Κοστολογική διάρθρωση Κύρια / Βοηθητικά Κέντρα Κόστους.
 Λογιστική Κόστους Ενότητα 8: Κοστολογική διάρθρωση Κύρια / Βοηθητικά Κέντρα Κόστους. Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Λογιστική Κόστους Ενότητα 8: Κοστολογική διάρθρωση Κύρια / Βοηθητικά Κέντρα Κόστους. Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ Ενότητα # 17: Ταχύτητα Αντιδράσεων Ακρίβος Περικλής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ Ενότητα # 17: Ταχύτητα Αντιδράσεων Ακρίβος Περικλής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση - Συγχώνευση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση - Συγχώνευση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Φ 619 Προβλήματα Βιοηθικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Ο Πλάτων και ο Αριστοτέλης ως ιατροί. Οι ιατροφιλόσοφοι (Ιπποκράτης, Γαληνός, Κέλσος). Ελένη Καλοκαιρινού Φιλοσοφίας-Παιδαγωγικής
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Ο Πλάτων και ο Αριστοτέλης ως ιατροί. Οι ιατροφιλόσοφοι (Ιπποκράτης, Γαληνός, Κέλσος). Ελένη Καλοκαιρινού Φιλοσοφίας-Παιδαγωγικής
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Πίνακες Νερού Υπέρθερμου Ατμού. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού Υπέρθερμου Ατμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση Ποιότητας,
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού Υπέρθερμου Ατμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση Ποιότητας,
Γενικά Μαθηματικά Ι. Ενότητα 14: Ολοκλήρωση Κατά Παράγοντες, Ολοκλήρωση Ρητών Συναρτήσεων Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Ολοκλήρωση Κατά Παράγοντες, Ολοκλήρωση Ρητών Συναρτήσεων Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Ολοκλήρωση Κατά Παράγοντες, Ολοκλήρωση Ρητών Συναρτήσεων Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Εισαγωγή στην Διοίκηση Επιχειρήσεων
 Εισαγωγή στην Διοίκηση Επιχειρήσεων Ενότητα 7: ΑΣΚΗΣΕΙΣ ΜΕΓΕΘΟΥΣ ΕΠΙΧΕΙΡΗΣΗΣ Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εισαγωγή στην Διοίκηση Επιχειρήσεων Ενότητα 7: ΑΣΚΗΣΕΙΣ ΜΕΓΕΘΟΥΣ ΕΠΙΧΕΙΡΗΣΗΣ Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εισαγωγή στην Διοίκηση Επιχειρήσεων
 Εισαγωγή στην Διοίκηση Επιχειρήσεων Ενότητα 4: Στρατηγικοί προσανατολισμοί Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εισαγωγή στην Διοίκηση Επιχειρήσεων Ενότητα 4: Στρατηγικοί προσανατολισμοί Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Οικονομία των ΜΜΕ. Ενότητα 7: Μορφές αγοράς και συγκέντρωση των ΜΜΕ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Οικονομία των ΜΜΕ Ενότητα 7: Μορφές αγοράς και συγκέντρωση των ΜΜΕ Γιώργος Τσουρβάκας, Αναπληρωτής Καθηγητής Τμήμα Δημοσιογραφίας και
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Οικονομία των ΜΜΕ Ενότητα 7: Μορφές αγοράς και συγκέντρωση των ΜΜΕ Γιώργος Τσουρβάκας, Αναπληρωτής Καθηγητής Τμήμα Δημοσιογραφίας και
Διπλωματική Ιστορία Ενότητα 2η:
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2η: Η εμφάνιση των εθνών-κρατών και οι συνέπειες στο διεθνές σύστημα Ιωάννης Στεφανίδης, Καθηγητής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2η: Η εμφάνιση των εθνών-κρατών και οι συνέπειες στο διεθνές σύστημα Ιωάννης Στεφανίδης, Καθηγητής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Μυελού των Οστών Ενότητα #1: Ερωτήσεις κατανόησης και αυτόαξιολόγησης
 Δωρεά Κυττάρων Αίματος και Μυελού των Οστών Ενότητα #1: Ερωτήσεις κατανόησης και αυτόαξιολόγησης για τη Δωρεά Κυττάρων Αίματος και Μυελού των Οστών Αλέξανδρος Σπυριδωνίδης Σχολή Επιστημών Υγείας Τμήμα
Δωρεά Κυττάρων Αίματος και Μυελού των Οστών Ενότητα #1: Ερωτήσεις κατανόησης και αυτόαξιολόγησης για τη Δωρεά Κυττάρων Αίματος και Μυελού των Οστών Αλέξανδρος Σπυριδωνίδης Σχολή Επιστημών Υγείας Τμήμα
Χώρος και Διαδικασίες Αγωγής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η κοινωνική ποιότητα του χώρου Δημήτριος Γερμανός Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η κοινωνική ποιότητα του χώρου Δημήτριος Γερμανός Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Ηλεκτρισμός & Μαγνητισμός
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρισμός & Μαγνητισμός Ο νόμος των Biot-Savart Διδάσκων : Επίκ. Καθ. Ν. Νικολής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρισμός & Μαγνητισμός Ο νόμος των Biot-Savart Διδάσκων : Επίκ. Καθ. Ν. Νικολής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 12η: Αυτόνομες και ημιαυτόνομες εκκλησίες κ.ά. διατάξεις Κυριάκος Κυριαζόπουλος Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 12η: Αυτόνομες και ημιαυτόνομες εκκλησίες κ.ά. διατάξεις Κυριάκος Κυριαζόπουλος Άδειες
Οδοποιία IΙ. Ενότητα 14: Υπόδειγμα σύνταξης τευχών θέματος Οδοποιίας. Γεώργιος Μίντσης ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Οδοποιία IΙ Ενότητα 14: Υπόδειγμα σύνταξης τευχών θέματος Οδοποιίας Γεώργιος Μίντσης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Οδοποιία IΙ Ενότητα 14: Υπόδειγμα σύνταξης τευχών θέματος Οδοποιίας Γεώργιος Μίντσης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Βασικές Αρχές Φαρμακοκινητικής
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Βασικές Αρχές Φαρμακοκινητικής Βιοδιαθεσιμότητα και κάθαρση πρώτης διόδου. Προβλέποντας τις αλληλεπιδράσεις των φαρμάκων Διδάσκων: Αναπληρωτής Καθηγητής
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Βασικές Αρχές Φαρμακοκινητικής Βιοδιαθεσιμότητα και κάθαρση πρώτης διόδου. Προβλέποντας τις αλληλεπιδράσεις των φαρμάκων Διδάσκων: Αναπληρωτής Καθηγητής
Ιστορία της Αρχιτεκτονικής και των Στυλ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ιστορία της Αρχιτεκτονικής και των Στυλ Ενότητα 2: Γοτθικό στυλ Ιάκωβος Ποταμιάνος Τμήμα Θεάτρου Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ιστορία της Αρχιτεκτονικής και των Στυλ Ενότητα 2: Γοτθικό στυλ Ιάκωβος Ποταμιάνος Τμήμα Θεάτρου Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Προχωρημένα Θέματα Διδακτικής της Φυσικής
 Προχωρημένα Θέματα Διδακτικής της Φυσικής Ενότητα 2η: Ο τίτλος του κειμένου Κώστας Ραβάνης Σχολή Ανθρωπιστικών & Κοινωνικών Επιστημών Τμήμα Επιστημών της Εκπαίδευσης και της Αγωγής στην Προσχολική Ηλικία
Προχωρημένα Θέματα Διδακτικής της Φυσικής Ενότητα 2η: Ο τίτλος του κειμένου Κώστας Ραβάνης Σχολή Ανθρωπιστικών & Κοινωνικών Επιστημών Τμήμα Επιστημών της Εκπαίδευσης και της Αγωγής στην Προσχολική Ηλικία
Προγραμματισμός και Εφαρμογές Υπολογιστών
 Προγραμματισμός και Εφαρμογές Υπολογιστών Ενότητα 7: Διαχείριση Πινάκων 1/2 Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Κ.Π. Γιαλούρης Μαθησιακοί Στόχοι Κατανόηση της αναγκαιότητας των πινάκων (arrays).
Προγραμματισμός και Εφαρμογές Υπολογιστών Ενότητα 7: Διαχείριση Πινάκων 1/2 Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Κ.Π. Γιαλούρης Μαθησιακοί Στόχοι Κατανόηση της αναγκαιότητας των πινάκων (arrays).
Ιατρικά Μαθηματικά & Βιοστατιστική
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ιατρικά Μαθηματικά & Βιοστατιστική Μεταβλητές Διδάσκοντες: Ευάγγελος Ευαγγέλου, Kωνσταντίνος Τσιλίδης, Ιωάννης Δημολιάτης, Ευαγγελία Ντζάνη, Γεωργία Σαλαντή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ιατρικά Μαθηματικά & Βιοστατιστική Μεταβλητές Διδάσκοντες: Ευάγγελος Ευαγγέλου, Kωνσταντίνος Τσιλίδης, Ιωάννης Δημολιάτης, Ευαγγελία Ντζάνη, Γεωργία Σαλαντή
Εισαγωγή στη Διδακτική των Θετικών Επιστημών
 Εισαγωγή στη Διδακτική των Θετικών Επιστημών Ενότητα 1η: Η Διδακτική Θετικών Επιστημών στον κόσμο των Επιστημών Κώστας Ραβάνης Σχολή Ανθρωπιστικών & Κοινωνικών Επιστημών Τμήμα Επιστημών της Εκπαίδευσης
Εισαγωγή στη Διδακτική των Θετικών Επιστημών Ενότητα 1η: Η Διδακτική Θετικών Επιστημών στον κόσμο των Επιστημών Κώστας Ραβάνης Σχολή Ανθρωπιστικών & Κοινωνικών Επιστημών Τμήμα Επιστημών της Εκπαίδευσης
Κβαντική Επεξεργασία Πληροφορίας
 Κβαντική Επεξεργασία Πληροφορίας Ενότητα 4: Κλασσική και Κβαντική Πιθανότητα Σγάρμπας Κυριάκος Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Σκοπός της ενότητας
Κβαντική Επεξεργασία Πληροφορίας Ενότητα 4: Κλασσική και Κβαντική Πιθανότητα Σγάρμπας Κυριάκος Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Σκοπός της ενότητας
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Χαρακτηριστικό Πολυώνυµο Γινοµένου Πινάκων Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 4 Μέρος 1. Η οµή Ενός
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Χαρακτηριστικό Πολυώνυµο Γινοµένου Πινάκων Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 4 Μέρος 1. Η οµή Ενός
Διεθνείς Οικονομικές Σχέσεις και Ανάπτυξη
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διεθνείς Οικονομικές Σχέσεις και Ανάπτυξη Ενότητα 8: Η Οικονομική πολιτική της Ευρωπαϊκής Ένωσης Γρηγόριος Ζαρωτιάδης Άδειες Χρήσης Το
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διεθνείς Οικονομικές Σχέσεις και Ανάπτυξη Ενότητα 8: Η Οικονομική πολιτική της Ευρωπαϊκής Ένωσης Γρηγόριος Ζαρωτιάδης Άδειες Χρήσης Το
Εκκλησιαστικό Δίκαιο
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1η: Εισαγωγή Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1η: Εισαγωγή Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Προχωρημένα Θέματα Διδακτικής της Φυσικής
 Προχωρημένα Θέματα Διδακτικής της Φυσικής Ενότητα 8η: Τα συμπεράσματα της έρευνας Κώστας Ραβάνης Σχολή Ανθρωπιστικών & Κοινωνικών Επιστημών Τμήμα Επιστημών της Εκπαίδευσης και της Αγωγής στην Προσχολική
Προχωρημένα Θέματα Διδακτικής της Φυσικής Ενότητα 8η: Τα συμπεράσματα της έρευνας Κώστας Ραβάνης Σχολή Ανθρωπιστικών & Κοινωνικών Επιστημών Τμήμα Επιστημών της Εκπαίδευσης και της Αγωγής στην Προσχολική
Λογισμός 3. Ενότητα 19: Θεώρημα Πεπλεγμένων (γενική μορφή) Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 19: Θεώρημα Πεπλεγμένων (γενική μορφή) Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 19: Θεώρημα Πεπλεγμένων (γενική μορφή) Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Φ 619 Προβλήματα Βιοηθικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η Βιοηθική στη σύγχρονη εποχή. Ελένη Καλοκαιρινού Φιλοσοφίας-Παιδαγωγικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η Βιοηθική στη σύγχρονη εποχή. Ελένη Καλοκαιρινού Φιλοσοφίας-Παιδαγωγικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Εργαστήριο Χημείας Ενώσεων Συναρμογής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 9: Μέτρηση Αγωγιμότητας Διαλυμάτων Περικλής Ακρίβος Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 9: Μέτρηση Αγωγιμότητας Διαλυμάτων Περικλής Ακρίβος Άδειες Χρήσης Το παρόν εκπαιδευτικό
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 11: Διανύσματα (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων &
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 11: Διανύσματα (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων &
Οικονομετρία. Εξειδίκευση του υποδείγματος. Μορφή της συνάρτησης: Πολυωνυμική, αντίστροφη και αλληλεπίδραση μεταβλητών
 Οικονομετρία Εξειδίκευση του υποδείγματος Μορφή της συνάρτησης: Πολυωνυμική, αντίστροφη και αλληλεπίδραση μεταβλητών Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Λαζαρίδης Παναγιώτης Μαθησιακοί Στόχοι
Οικονομετρία Εξειδίκευση του υποδείγματος Μορφή της συνάρτησης: Πολυωνυμική, αντίστροφη και αλληλεπίδραση μεταβλητών Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Λαζαρίδης Παναγιώτης Μαθησιακοί Στόχοι
Βασικές Αρχές Φαρμακοκινητικής
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Βασικές Αρχές Φαρμακοκινητικής Κάθαρση Διδάσκων: Αναπληρωτής Καθηγητής Π. Παππάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Βασικές Αρχές Φαρμακοκινητικής Κάθαρση Διδάσκων: Αναπληρωτής Καθηγητής Π. Παππάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ενότητα: Δακτύλιοι, Ακέραιες Περιοχές, Σώματα. Διδάσκων: Καθηγητής Μαρμαρίδης Νικόλαος - Θεοδόσιος
 Τίτλος Μαθήματος: Αλγεβρικές Δομές ΙΙ Ενότητα: Δακτύλιοι, Ακέραιες Περιοχές, Σώματα Διδάσκων: Καθηγητής Μαρμαρίδης Νικόλαος - Θεοδόσιος Τμήμα: Μαθηματικών Κεφάλαιο 1 Προκαταρκτικές Έννοιες 1.1 Δακτύλιοι,
Τίτλος Μαθήματος: Αλγεβρικές Δομές ΙΙ Ενότητα: Δακτύλιοι, Ακέραιες Περιοχές, Σώματα Διδάσκων: Καθηγητής Μαρμαρίδης Νικόλαος - Θεοδόσιος Τμήμα: Μαθηματικών Κεφάλαιο 1 Προκαταρκτικές Έννοιες 1.1 Δακτύλιοι,
Εργαστήριο Χημείας Ενώσεων Συναρμογής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 4: Τοποθέτηση d ηλεκτρονίων σε οκτάεδρα Σύμπλοκα Περικλής Ακρίβος Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 4: Τοποθέτηση d ηλεκτρονίων σε οκτάεδρα Σύμπλοκα Περικλής Ακρίβος Άδειες Χρήσης Το παρόν
Φυσική Περιβάλλοντος
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Φυσική Περιβάλλοντος Φαινόμενο του θερμοκηπίου Διδάσκοντες: Καθηγητής Π. Κασσωμένος, Λέκτορας Ν. Μπάκας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Φυσική Περιβάλλοντος Φαινόμενο του θερμοκηπίου Διδάσκοντες: Καθηγητής Π. Κασσωμένος, Λέκτορας Ν. Μπάκας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα
 Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Ασκήσεις 1 Ανδριανός Ε. Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής Σελίδα 2 1. Σκοποί ενότητας... 5 2.
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Ασκήσεις 1 Ανδριανός Ε. Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής Σελίδα 2 1. Σκοποί ενότητας... 5 2.
Γεωργική Εκπαίδευση Ενότητα 9
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Σχεδιασμός εκπαιδευτικών προγραμμάτων για τον αγροτικό χώρο Αφροδίτη Παπαδάκη-Κλαυδιανού Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Σχεδιασμός εκπαιδευτικών προγραμμάτων για τον αγροτικό χώρο Αφροδίτη Παπαδάκη-Κλαυδιανού Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΥΠΟΛΟΓΙΣΤΕΣ ΙI. Άδειες Χρήσης. Δείκτες Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Δείκτες Διδάσκοντες: Αν Καθ Δ Παπαγεωργίου, Αν Καθ Ε Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Δείκτες Διδάσκοντες: Αν Καθ Δ Παπαγεωργίου, Αν Καθ Ε Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Γενικά Μαθηματικά Ι. Ενότητα 1: Συναρτήσεις και Γραφικές Παραστάσεις. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Συναρτήσεις και Γραφικές Παραστάσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Συναρτήσεις και Γραφικές Παραστάσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Διαφήμιση και Δημόσιες Σχέσεις Ενότητα 9: Σχέσεις διαφημιστή-διαφημιζόμενου
 Διαφήμιση και Δημόσιες Σχέσεις Ενότητα 9: Σχέσεις διαφημιστή-διαφημιζόμενου Θεοδωρίδης Προκόπης Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.)
Διαφήμιση και Δημόσιες Σχέσεις Ενότητα 9: Σχέσεις διαφημιστή-διαφημιζόμενου Θεοδωρίδης Προκόπης Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.)
Ιατρικά Μαθηματικά & Βιοστατιστική
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ιατρικά Μαθηματικά & Βιοστατιστική Στατιστικοί έλεγχοι για συνεχή και κατηγορικά δεδομένα Διδάσκοντες: Ευάγγελος Ευαγγέλου, Kωνσταντίνος Τσιλίδης, Ιωάννης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ιατρικά Μαθηματικά & Βιοστατιστική Στατιστικοί έλεγχοι για συνεχή και κατηγορικά δεδομένα Διδάσκοντες: Ευάγγελος Ευαγγέλου, Kωνσταντίνος Τσιλίδης, Ιωάννης
Ενότητα: Περιγραφική Στατιστική 1: Πίνακες - Διαγράμματα
 Τίτλος Μαθήματος: Στατιστική Ι Ενότητα: Περιγραφική Στατιστική 1: Πίνακες - Διαγράμματα Διδάσκων: Επίκ. Καθ. Αθανάσιος Λαπατίνας Τμήμα: Οικονομικών Επιστημών Διάλεξη 2: ΑΣΚΗΣΕΙΣ 1. Μια ερώτηση έχει τρεις
Τίτλος Μαθήματος: Στατιστική Ι Ενότητα: Περιγραφική Στατιστική 1: Πίνακες - Διαγράμματα Διδάσκων: Επίκ. Καθ. Αθανάσιος Λαπατίνας Τμήμα: Οικονομικών Επιστημών Διάλεξη 2: ΑΣΚΗΣΕΙΣ 1. Μια ερώτηση έχει τρεις
Μεθοδολογία Έρευνας Κοινωνικών Επιστημών Ενότητα 2: ΣΥΓΚΕΝΤΡΩΣΗ ΠΛΗΡΟΦΟΡΙΩΝ ΜΑΡΚΕΤΙΝΓΚ Λοίζου Ευστράτιος Τμήμα Τεχνολόγων Γεωπόνων-Kατεύθυνση
 Μεθοδολογία Έρευνας Κοινωνικών Επιστημών Ενότητα 2: ΣΥΓΚΕΝΤΡΩΣΗ ΠΛΗΡΟΦΟΡΙΩΝ ΜΑΡΚΕΤΙΝΓΚ Λοίζου Ευστράτιος Τμήμα Τεχνολόγων Γεωπόνων-Kατεύθυνση Αγροτικής Οικονομίας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Μεθοδολογία Έρευνας Κοινωνικών Επιστημών Ενότητα 2: ΣΥΓΚΕΝΤΡΩΣΗ ΠΛΗΡΟΦΟΡΙΩΝ ΜΑΡΚΕΤΙΝΓΚ Λοίζου Ευστράτιος Τμήμα Τεχνολόγων Γεωπόνων-Kατεύθυνση Αγροτικής Οικονομίας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Προγραμματισμός και Εφαρμογές Υπολογιστών
 Προγραμματισμός και Εφαρμογές Υπολογιστών Ενότητα 8: Διαχείριση Πινάκων 2/2 Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Κ.Π. Γιαλούρης Μαθησιακοί Στόχοι Κατανόηση του χειρισμού πινάκων δύο διαστάσεων
Προγραμματισμός και Εφαρμογές Υπολογιστών Ενότητα 8: Διαχείριση Πινάκων 2/2 Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Κ.Π. Γιαλούρης Μαθησιακοί Στόχοι Κατανόηση του χειρισμού πινάκων δύο διαστάσεων
Αερισμός. Ενότητα 1: Αερισμός και αιμάτωση. Κωνσταντίνος Σπυρόπουλος, Καθηγητής Σχολή Επιστημών Υγείας Τμήμα Ιατρικής
 Αερισμός Ενότητα 1: Αερισμός και αιμάτωση Κωνσταντίνος Σπυρόπουλος, Καθηγητής Σχολή Επιστημών Υγείας Τμήμα Ιατρικής Ολικός και κυψελιδικός αερισμός Η κύρια λειτουργία του αναπνευστικού συστήματος είναι
Αερισμός Ενότητα 1: Αερισμός και αιμάτωση Κωνσταντίνος Σπυρόπουλος, Καθηγητής Σχολή Επιστημών Υγείας Τμήμα Ιατρικής Ολικός και κυψελιδικός αερισμός Η κύρια λειτουργία του αναπνευστικού συστήματος είναι
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 6 η Άσκηση - DFS δένδρα Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 6 η Άσκηση - DFS δένδρα Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Εργαστήριο Χημείας Ενώσεων Συναρμογής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 6: Προσδιορισμός δ0 σε οκτάεδρα σύμπλοκα Περικλής Ακρίβος Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 6: Προσδιορισμός δ0 σε οκτάεδρα σύμπλοκα Περικλής Ακρίβος Άδειες Χρήσης Το παρόν εκπαιδευτικό
Εισαγωγή στην Διοίκηση Επιχειρήσεων
 Εισαγωγή στην Διοίκηση Επιχειρήσεων Ενότητα 9: ΑΣΚΗΣΕΙΣ ΕΠΙΛΟΓΗΣ ΤΟΠΟΥ ΕΓΚΑΤΑΣΤΑΣΗΣ Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Εισαγωγή στην Διοίκηση Επιχειρήσεων Ενότητα 9: ΑΣΚΗΣΕΙΣ ΕΠΙΛΟΓΗΣ ΤΟΠΟΥ ΕΓΚΑΤΑΣΤΑΣΗΣ Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Βάσεις Περιβαλλοντικών Δεδομένων
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Βάσεις Περιβαλλοντικών Δεδομένων Ενότητα 3: Μοντέλα βάσεων δεδομένων Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Βάσεις Περιβαλλοντικών Δεδομένων Ενότητα 3: Μοντέλα βάσεων δεδομένων Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται
Διδακτική της Περιβαλλοντικής Εκπαίδευσης
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διδακτική της Περιβαλλοντικής Εκπαίδευσης Ενότητα 08: Σχεδιασμός και Οργάνωση ενός Προγράμματος Περιβαλλοντικής Εκπαίδευσης Ι Πολυξένη
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διδακτική της Περιβαλλοντικής Εκπαίδευσης Ενότητα 08: Σχεδιασμός και Οργάνωση ενός Προγράμματος Περιβαλλοντικής Εκπαίδευσης Ι Πολυξένη
Κβαντική Επεξεργασία Πληροφορίας
 Κβαντική Επεξεργασία Πληροφορίας Ενότητα 12: Ιδιοτιμές και Ιδιοδιανύσματα Σγάρμπας Κυριάκος Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Ιδιοτιμές και Ιδιοδιανύσματα
Κβαντική Επεξεργασία Πληροφορίας Ενότητα 12: Ιδιοτιμές και Ιδιοδιανύσματα Σγάρμπας Κυριάκος Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Ιδιοτιμές και Ιδιοδιανύσματα
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 8: Εφαρμογές παραγώγων Μελέτη και βελτιστοποίηση συναρτήσεων μιας μεταβλητής (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 8: Εφαρμογές παραγώγων Μελέτη και βελτιστοποίηση συναρτήσεων μιας μεταβλητής (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων
Διοικητική Λογιστική
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 6: Μέθοδοι ς Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά Το έργο
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 6: Μέθοδοι ς Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά Το έργο
Οικονομία των ΜΜΕ. Ενότητα 9: Εταιρική διασπορά και στρατηγικές τιμολόγησης
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Εταιρική διασπορά και στρατηγικές τιμολόγησης Γιώργος Τσουρβάκας, Αναπληρωτής Καθηγητής Τμήμα Δημοσιογραφίας και ΜΜΕ Σχολή
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Εταιρική διασπορά και στρατηγικές τιμολόγησης Γιώργος Τσουρβάκας, Αναπληρωτής Καθηγητής Τμήμα Δημοσιογραφίας και ΜΜΕ Σχολή
Συγκριτικό Εκκλησιαστικό Δίκαιο
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Συγκριτικό Εκκλησιαστικό Δίκαιο Ενότητα 1η: Εισαγωγή Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Συγκριτικό Εκκλησιαστικό Δίκαιο Ενότητα 1η: Εισαγωγή Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 10 : Φυσιολογία φωνής (Μέρος Β ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 10 : Φυσιολογία φωνής (Μέρος Β ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου
Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου
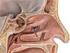 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 9 : Φυσιολογία φωνής (Μέρος Α ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 9 : Φυσιολογία φωνής (Μέρος Α ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου
Γενικά Μαθηματικά Ι. Ενότητα 5: Παράγωγος Πεπλεγμένης Συνάρτησης, Κατασκευή Διαφορικής Εξίσωσης. Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Παράγωγος Πεπλεγμένης Συνάρτησης, Κατασκευή Διαφορικής Εξίσωσης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Παράγωγος Πεπλεγμένης Συνάρτησης, Κατασκευή Διαφορικής Εξίσωσης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ
 Ε.Μ.Π. ΣΧΟΛΗ ΑΡΧΙΤΕΚΤΟΝΩΝ ΤΟΜΕΑΣ ΣΥΝΘΕΣΕΩΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΑΙΧΜΗΣ ΠΕΡΙΟΧΗ ΟΙΚΟΔΟΜΙΚΗΣ ntua ACADEMIC OPEN COURSES ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΤΗΣ ΟΙΚΟΔΟΜΙΚΗΣ II Β. ΤΣΟΥΡΑΣ Επίκουρος Καθηγητής Άδεια
Ε.Μ.Π. ΣΧΟΛΗ ΑΡΧΙΤΕΚΤΟΝΩΝ ΤΟΜΕΑΣ ΣΥΝΘΕΣΕΩΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΑΙΧΜΗΣ ΠΕΡΙΟΧΗ ΟΙΚΟΔΟΜΙΚΗΣ ntua ACADEMIC OPEN COURSES ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΤΗΣ ΟΙΚΟΔΟΜΙΚΗΣ II Β. ΤΣΟΥΡΑΣ Επίκουρος Καθηγητής Άδεια
Λογιστική Κόστους Ενότητα 11: Λογισμός Κόστους (1)
 Λογιστική Κόστους Ενότητα 11: Λογισμός Κόστους (1) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Λογιστική Κόστους Ενότητα 11: Λογισμός Κόστους (1) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Επιμέλεια μεταφράσεων και εκδοτικός χώρος
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Επιμέλεια μεταφράσεων και εκδοτικός χώρος 2 η ενότητα: Οργάνωση ημερίδας Ελένη Κασάπη Τμήμα Ιταλικής Γλώσσας και Φιλολογίας Άδειες Χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Επιμέλεια μεταφράσεων και εκδοτικός χώρος 2 η ενότητα: Οργάνωση ημερίδας Ελένη Κασάπη Τμήμα Ιταλικής Γλώσσας και Φιλολογίας Άδειες Χρήσης
ΗΜΙΑΓΩΓΑ ΥΛΙΚΑ: ΘΕΩΡΙΑ-ΔΙΑΤΑΞΕΙΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΗΜΙΑΓΩΓΑ ΥΛΙΚΑ: ΘΕΩΡΙΑ-ΔΙΑΤΑΞΕΙΣ Μέρος 1 ο : Στοιχεία Θεωρίας Ημιαγωγών Ενότητα 4 η : Φράγμα δυναμικού-φαινόμενο σήραγγας. Γεώργιος Λιτσαρδάκης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΗΜΙΑΓΩΓΑ ΥΛΙΚΑ: ΘΕΩΡΙΑ-ΔΙΑΤΑΞΕΙΣ Μέρος 1 ο : Στοιχεία Θεωρίας Ημιαγωγών Ενότητα 4 η : Φράγμα δυναμικού-φαινόμενο σήραγγας. Γεώργιος Λιτσαρδάκης
Διοίκηση Ολικής Ποιότητας & Επιχειρηματική Αριστεία Ενότητα 1.3.3: Μεθοδολογία εφαρμογής προγράμματος Ολικής Ποιότητας
 Διοίκηση Ολικής Ποιότητας & Επιχειρηματική Αριστεία Ενότητα 1.3.3: Ψωμάς Ευάγγελος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.) Υποενότητα
Διοίκηση Ολικής Ποιότητας & Επιχειρηματική Αριστεία Ενότητα 1.3.3: Ψωμάς Ευάγγελος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.) Υποενότητα
Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 5 : Στοματική κοιλότητα Φάρυγγας (Μέρος Α ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Ανατομία - Φυσιολογία Ακοής Ομιλίας Λόγου Ενότητα 5 : Στοματική κοιλότητα Φάρυγγας (Μέρος Α ) Ναυσικά Ζιάβρα 2 Ανοιχτά Ακαδημαϊκά Μαθήματα
