Chapter 10: Time and Global States Introduction Clocks,events and process states Synchronizing physical clocks Logical time and logical clocks Global

Transcript

1 Chapter 10: Time and Global States Introduction Clocks,events and process states Synchronizing physical clocks Logical time and logical clocks Global states Distributed debugging Summary

2 Time is an important issue in DS Time is a quantity we need to measure accurately E.g. e-commerce transaction involves events at a merchant s computer and at a bank computer. Thus, it is important for auditing purposes that these events are timestamped accurately. Algorithms depending on clock synchronization have been developed for several problems in distribution E.g. maintaining consistency of distributed data

3 There is no universe physical clock Physicist s view Newton s notation: absolute physical time Einstein s Relativity Theory People s approaches dealing with time Approximately synchronize Logical clocks

4 Model of a distributed system A collection of N processes p i, i = 1,2,.. N s i The state of p i E.g. variables Actions of p i Operations that transform p i s state Send or receive message between p j

5 Model of a distributed system e Event: occurrence of a single action (e.g., communication or processing action) i occur before in p i, e.g. e i e` (only if event e occurs before e` ) Total order of events in p i History of process p i history(p i ) = h i h i = <e i0, e i1, e i2, >

6 Clock skew and clock drift Each computer has its own clock Computer clocks tend not to be in perfect agreement Clock drift Crystal oscillate at different rate Clock drift can not be avoided Clock skew The instantaneous difference between the readings of any two clocks

7 Coordinated Universal Time (UTC) Computer clocks can be synchronized to external sources Coordinated Universal Time (UTC) is the international standard for timekeeping Broadcast UTC to the World E.g., by GPS or WWV

8 External & Internal synchronization C i : p i s clock I: an interval of real time External synchronization (to synchronize the clock with an external source of time) For a synchronization bound D > 0, and for a source S of UTC time, S(t)-C i (t) < D, for i = 1, 2, N and for all real times t in I Clocks C i are accurate to within the bound D

9 External & Internal synchronization (2) Internal synchronization (to synchronize the clocks of two computers) For a synchronization bound D > 0, C i (t)- C j (t) < D for i, j =1,2, N, and for all real times t in I Clocks C i agree within the bound D If accurate to within D, then agree within 2D

10 General synchronization issues (2) Clock failures Crash failure: stop ticking Arbitrary failure, e.g. Y2K bug

11 Synchronization in a synchronous system Protocol Sender: send M(t) Receiver: set time to t + T trans In a synchronous system, bounds are know min < T trans < max (constant) So, set T trans = (min+max) / 2 Receiver s clock = t + (min+max) / 2 Clock skew between sender and receiver (max min ) / 2 t t + min t +T trans t+max

12 Cristian s method of synchronizing clocks Applying circumstance Cristian observed that the round-trip times for messages exchanged between processes is relatively short Protocol Process p sends m r to request time and receives time t in message m t (t). It records the total T round to send message and receive reply (in the order ot milliseconds in LAN) Estimated time: t + T round /2 m r p m t Time server,s

13 Cristian s method of synchronizing clocks (2) Accuracy analysis If the minimum delay of a message transmission is min, then accuracy: ± (T round /2 min) t + min t +T round -min t t +T round /2 t +T round

14 The Berkeley algorithms Internal synchronization (developed for collections of computers running Berkeley UNIX) A coordinator computer (master) acts as coordinator. It periodically polls the other computers whose clocks are to be synchronized (called slaves) Protocol 1. The master polls the slaves clocks 2. The master estimates the slaves clocks by roundtrip time Similar to Christian s algorithm 3. Instead of considering only 1 slave, the master averages all the slaves clock values Advantage: Cancel out the individual clock s tendencies to run fast or slow

15 The Berkeley algorithms (2) 4. The master sends back to the slaves the amount that the slaves clocks should adjust by Positive or negative value Avoid further uncertainty due to the message transmission time Each slave adjusts its clock

16 Design aims of Network Time Protocol External synchronization Enable clients across the Internet to be synchronized accurately to UTC Reliability Can survive lengthy losses of connectivity Redundant server & redundant path between servers Scalability Enable clients to resynchronize sufficiently frequently to offset the rates of drift found in most computers Security Protect against interference with the time service

17 Network Time Protocol Architecture Note: Arrows denote synchronization control, numbers denote levels. Primary servers connected directly to a time source Secondary servers synchronized with primary servers, and so on Clocks belonging to higher levels may be less accurate (errors introduced at each level) Reconfigure when servers become unreachable

18 Synchronization measures NTP servers synchronize with one another in one of three modes: Multicast mode Intend for use on a high speed LAN Assuming a small delay Low accuracy but efficient Procedure-call mode Similar to Christian s (one server accepts requests from other computers which it processes by replying with its timestamp) Higher accuracy than multicast Symmetric mode A pair of servers operating in symmetric mode exchange messages with timing information The highest accuracy

19 Symmetric mode sync. implementation NTP servers retain 8 most recent pairs <o i,d i > The value o i of that corresponds to the minimum value d i is chosen to estimate o A NTP server exchanges with several peers in addition to with parent Peers with lower level numbers are favoured Peers with the lowest synchronization dispersion are favoured

20 Logical Time and Logical Clocks Lamport (1978) τόνισε ότι δεν µπορούµε να συγχρονίσουµε τέλεια ρολόγια σε ένα κατανεµηµένο σύστηµα, µπορούµε όµως να χρησιµοποιήσουµε ένα σύστηµα που να µοιάζει µε φυσική αιτιότητα (physical causality) για να ορίσουµε διάταξη σε γεγονότα που συµβαίνουν σε διαφορετικές διεργασίες

21 Happen-before relation HB1: If διεργασία p i : e i e`, then e e` HB2: For any message m, send(m) receive(m) HB3: IF e, e`and e`` είναι γεγονότα για τα οποία ισχύει ότι e e` and e` e``, τότε e e`` Causal ordering

22 Happen-before relation Δεν συσχετίζονται όλα τα γεγονότα µε τη σχέση Αυτά τα γεγονότα λέγονται παράλληλα γεγονότα a e Προβλήµατα Δεν είναι κατάλληλο για τις διαδικασίες συνεργασίας που δεν ανταλλάσουν µηνύµατα Capture potential causal ordering

23 Ιδέα Lamport επινόησε έναν απλό µηχανισµό µε τον οποίο η σχέση συνέβη-πριν (happenedbefore) µπορεί να συλληφθεί αριθµητικά, αυτό όνοµάζεται λογικό ρολόι Κάθε διεργασία έχει το δικό της λογικό ρολόι L i που χρησιµοποιεί σαν timestamp των γεγονότων. Εµείς χαρακτηρίζουµε το timestamp του γεγονότος e at p i by L i (e)

24 Lamport timestamps algorithm LC1 L i αυξάνεται κάθε φορά που ένα γεγονός συµβαίνει στην διεργασία p i : L i :=L i +1 LC2: (a) Οταν η διεργασία p i στέλνει µήνυµα m, µαζί µε το µήνυµα m βάζει και την τιµή t = L i (b) Οταν λαµβάνει το µήνυµα (m,t) µια διεργασία P j υπολογίζει το L j := max(l j, t) και µετά εκτελεί το LC1 πριν να βάλει timestamp στο γεγονός receive(m)

25 Lamport timestamps algorithm (2) e e` L(e) < L(e`) Το αντίθετο δεν είναι πάντα αλήθεια L(e) < L(e`) e e` or e e`

26 Totally ordered logical clocks Κάποια ζευγάρια των γεγονότων που παράγονται από διαφορετικές διαδικασίες, έχουν τα ίδια Lamport timestamps. Μπορούμε και τότε να δημιουργήσουμε μια συνολική διάταξη για τα γεγονότα ως εξής: Assumption T i : local timestamp of e that is an event occurring at p i T j : local timestamp of e` that is an event occurring at p j Define the timestamps of e, e` are (T i, i), (T j, j) Define < (T i, i) < (T j, j) if T i < T j, or T i = T j and i < j Χρήσιµο σε µερικές εφαρµογές (e.g. order processes to a critical section)

27 Διανυσµατικά Ρολόγια (Vector Clocks) Κάθε διεργασία p i έχει διάνυσµα vector clock V i VC1: Αρχικά, V i [j]=0, for i, j = 1,2, N VC2: Πριν η διεργασία p i timestamps ένα γεγονός, ορίζει V i [i] := V i [i] +1 VC3: p i ενσωµατώνει την τιµή t= V i σε κάθε µήνυµα που στέλνει VC4: Οταν η διεργασία p i λάβει το timestamp t σε ένα µήνυµα, ορίζει V i [j] :=max(v i [j], t[j]), for j=1,2,n

28 Vector Clocks - σηµασία Συγκρίνουµε vector timestamps ως εξής: V = V` iff V [j] = V`[j] for j = 1,2, N V <= V` iff V`[j]<=V`[j] for j = 1,2, N V < V` iff V`[j]< V`[j] for j = 1,2, N Otherwise V<>V V(e) < V(e`) e e`, V(e) <> V(e`) e e`

29 Vector Clocks - example

30 The problem of Global States Εξετάζουµε το πρόβληµα να διαπιστώσουµε αν µια συγκεκριµένη ιδιότητα είναι αληθής. Παραδείγµατα Distributed garbage collection Based on reference counting Should include the state of communication channels Distributed deadlock detection Look for waits-for relationship Distributed termination detection Look for state in which all processes are passive

31 Global states and consistent cuts The essential problem of Global states Absence of global time History of process p i h i = <e i0, e i1, e i 2 > Prefix of a process s history h i k = <e i0, e i1 e i k > Global history of processes set H = h 1 h 2 h N

32 The state (κατάσταση) of process p i s i k : η κατάσταση προτού το kth γεγονός συμβεί The state of channel between the p i and p j when transmit the massage A cut of a system execution A subset of its global history that is a union of prefixes of process histories. C = <h 1 c1, h 2 c2 h 3 c3 > A global state S = (s 1, s 2, s N ) s i corresponding to the cut of C is that of p i immediately after the last event processed by p i in the cut- e i ci

33 Global states and consistent cuts A cut C is consistent: For all events e C, f e f C < e 10, e 20 >, < e 12, e 22 >

34 Global states and consistent cuts A consistent global state: correspond to a consistent cut The s i corresponding to the cut C is that of p i immediately after the last event processed by p i in C Execution of a distributed system S 0 S 1 S 2

35 Global states and consistent cuts A run a total ordering of all the events in a global history that is consistent with each local history s ordering, i Not all runs pass through consistent global state A linearization (consistent) run an ordering of the events in a global history H that is consistent with this happened-before relation on H. Pass only consistent global state

36 Global states and consistent cuts S is reachable from a state S there is a linearization that pass through S and then S

37 The snapshot algorithm of Chandy and Lamport Σκοπός µας Να υπολογίσουµε consistent global state του κατανεµηµένου συστήµατος

38 The snapshot algorithm - assumptions Ούτε τα κανάλια, ούτε διαδικασίες αποτυγχάνουν Μονοκατευθυντικά κανάλια, FIFO παράδοση µηνυµάτων Πλήρης σύνδεση µεταξύ όλων των διεργασιών Κάθε διαδικασία µπορεί να ξεκινήσει µια παγκόσµια στιγµιότυπο (global snapshot) ανά πάσα χρονική στιγµή Οι διεργασίες µπορούν να συνεχίσουν την εκτέλεση και την αποστολή και λήψη µηνυµάτων, ενώ το κανονική στιγµιότυπο λαµβάνει χώρα

39 The snapshot algorithm - idea Οταν µια διεργασία καταγράψει µια κατάσταση S i, κάνε όλες τις διεργασίες να καταγράψουν τις καταστάσεις τους που έχουν προκληθεί από την S i

40 The snapshot algorithm - method Incoming channels, outgoing channels Process state + channel state Marker message Marker sending rule: µια διεργασία στέλνει ένα marker αφού έχει καταγράψει την κατάστασή της, και προτού στείλει άλλα µηνύµατα Marker receiving rule: µια διεργασία καταγράφει την κατάσταση της αν η κατάσταση της έχει αλλάξει από την τελευταία εγγραφή, διαφορετικά καταγράφει την κατάσταση των incoming channels

41 Marker receiving rule for process p i On p i s receipt of a marker message over channel c: if (p i has not yet recorded its state) it records its process state now; records the state of c as the empty set; turns on recording of messages arriving over other incoming channels; else p i records the state of c as the set of messages it has received over c since it saved its state. end if Marker sending rule for process p i After p i has recorded its state, for each outgoing channel c: p i sends one marker message over c (before it sends any other message over c).

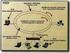
42 The snapshot algorithm - example p 1 trade p 2 in widget which is 10$ per item Initial state p 1 has sent 50$ to p 2 to buy 5 widget, and p 2 has received the order

43 Execution of the processes in the example 1. Global state S 0 2. Global state S 1 3. Global state S 2 4. Global state S 3 <$1000, 0> p 1 c 2 (empty) p 2 <$50, 2000> c 1 (empty) <$900, 0> p 1 c (Order 10, $100), M 2 p 2 <$50, 2000> c 1 (empty) <$900, 0> p 1 c (Order 10, $100), M 2 p 2 <$50, 1995> c 1 (five widgets) M <$900, 5> p 1 c 2 (Order 10, $100) p 2 <$50, 1995> c 1 (empty) (M = marker message) The final recorded state P 1 :<$1000, 0>; p 2 :<$50,1995>;c 1 :<(five widgets)>;c 2 :<>