ΠΡΟΦΟΡΙΚΗ ΑΡΙΘΜΗΣΗ: ΜΙΑ ΒΑΣΙΚΗ ΚΑΙ ΧΡΗΣΙΜΗ ΓΝΩΣΗ ΠΟΥ Η ΔΙΔΑΣΚΑΛΙΑ ΤΗΝ ΑΓΝΟΕΙ. Εισαγωγή
|
|
|
- Ἓσπερος Κούνδουρος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Το παρακάτω άρθρο δημοσιεύτηκε στο περιοδικό Διάσταση το Η πλήρης αναφορά είναι η εξής: Α. Γαγάτσης, Χ. Λεμονίδης (1994). Προφορική αρίθμηση: Μια βασική και χρήσιμη γνώση που η διδασκαλία την αγνοεί. Περιοδικό Διάσταση, Τεύχος 4, σσ ΠΡΟΦΟΡΙΚΗ ΑΡΙΘΜΗΣΗ: ΜΙΑ ΒΑΣΙΚΗ ΚΑΙ ΧΡΗΣΙΜΗ ΓΝΩΣΗ ΠΟΥ Η ΔΙΔΑΣΚΑΛΙΑ ΤΗΝ ΑΓΝΟΕΙ Εισαγωγή Α. Γαγάτσης Μαθηματικό Τμήμα Α.Π.Θ. Χ. Λεμονίδης Π.Τ.Δ.Ε. Φλώρινας Η παρουσίαση και η μάθηση του αριθμού εμφανίζει μια διπλή υπόσταση. Κατά πρώτον η αρίθμηση είναι ένα οργανωμένο και συγκεκριμένο σύστημα γνώσεων το οποίο λειτουργεί κάθε φορά μέσα στα πλαίσια ενός πολιτισμού. Είναι δηλαδή ένα αντικείμενο κοινωνικής και ιστορικής υπόστασης που καταρχήν είναι εξωτερικό ως προς το παιδί και πρέπει να αναλυθεί, να προσαρμοστεί και να εσωτερικευτεί από αυτό, ώστε να μπορεί να χρησιμοποιείται για τις ανάγκες του. Κατά δεύτερον το σύστημα αυτό αναφέρεται σε μερικές λογικομαθηματικές σχέσεις όπως η διάταξη, η πληθικότητα, η πρόσθεση κτλ., που δομούν και καθορίζουν την εσωτερική του οργάνωση. Οι σχέσεις αυτές αναφέρονται στις λογικές θεμελιώσεις του αριθμού και της αρίθμησης, οι οποίες δεν μπορούν να μεταδοθούν ως μια κοινωνική γνώση, όπως είναι για παράδειγμα η απαγγελία των πρώτων αριθμών της αριθμητικής ακολουθίας. Αυτές οι λογικομαθηματικές σχέσεις θα πρέπει να κατασκευαστούν από το ίδιο το παιδί. Βέβαια σ αυτήν την κατασκευή επιδρούν και την επηρεάζουν κοινωνικοί και πολιτισμικοί παράγοντες, χωρίς τα αποτελέσματά τους να είναι πολύ άμεσα.
2 Με βάση αυτήν τη διάκριση έχουν αναπτυχθεί δύο διαφορετικές αντιλήψεις όσον αφορά τη γένεση του αριθμού και της αρίθμησης. Υπάρχει δηλαδή μια πρώτη ομάδα από ερευνητές που βασίζονται σε εμπειρικά και πολιτισμικά ρεύματα και τονίζουν περισσότερο τη μάθηση της ακολουθίας των αριθμών και των ιδιοτήτων της. Η δεύτερη ομάδα των ερευνητών αναφέρεται περισσότερο στις λογικές ιδιότητες του αριθμού και ερευνά ουσιαστικά τους καθολικούς γνωστικούς μηχανισμούς οι οποίοι επηρεάζονται ελάχιστα ή και καθόλου από τις πολιτισμικές διαφοροποιήσεις. Αυτοί επιμένουν περισσότερο στην ανάπτυξη των λογικών βάσεων του αριθμού. Παρά τις διαφοροποιήσεις και τις δυσκολίες συνύπαρξης αυτών των δύο διαφορετικών ρευμάτων κατά τη διάρκεια των τελευταίων ετών παρατηρείται μια τάση σύνθεσης και χρησιμοποίησης στοιχείων και από τις δύο αντιλήψεις για τις έρευνες και την ερμηνεία της κατανόησης και μάθησης του αριθμού και της αρίθμησης. Επιγραμματικά αναφέρουμε ότι η σημερινή επίσημη διδασκαλία στην Ελλάδα όσον αφορά τον αριθμό και την αρίθμηση είναι εναρμονισμένη με το δεύτερο ρεύμα και τις αντιλήψεις του Πιαζέ που είναι ο κύριος εκφραστής του ρεύματος αυτού. Η διδασκαλία αυτή δηλαδή υπερτονίζει και αφιερώνει πολύ χρόνο για τις λογικές σχέσεις που συνθέτουν την έννοια του αριθμού (ταξινομήσεις, διατάξεις, εγκλεισμούς των τάξεων κτλ.) και ασχολείται ελάχιστα ή αγνοεί γνώσεις όπως η προφορική αρίθμηση που μπορούν να συμβάλλουν πολύ στην κατανόηση του αριθμού και την εκτέλεση των πράξεων και επιπλέον οι γνώσεις αυτές είναι δεδομένες στις περισσότερες περιπτώσεις από την κοινωνία. Δηλαδή, οι μαθητές από την προσχολική ηλικία ακόμη έχουν οι περισσότεροι πολλές γνώσεις όσον αφορά την απαγγελία της αριθμητικής ακολουθίας χωρίς να έχουν δεχτεί κάποια διδασκαλία γιαυτήν. Η καλή γνώση της προφορικής αριθμητικής ακολουθίας εκτός του ότι συμβάλλει πολύ στην κατανόηση του αριθμού και τη
3 λειτουργία της απαρίθμησης είναι βασική γνώση σε ένα πρώτο επίπεδο για την κατανόηση και την εκτέλεση των πράξεων. Για παράδειγμα έχει διαπιστωθεί (βλέπε Χ. Λεμονίδη, 1994) ότι οι μαθητές αλλά ακόμη και οι ενήλικες χρησιμοποιούν αρκετά τις διαδικασίες ευθείας ή αντίστροφης αρίθμησης για να εκτελούν απλές προσθέσεις ή αφαιρέσεις (π.χ. για να εκτελέσουν την αφαίρεση 13-5 αριθμούν αντίστροφα 5 βήματα αρχίζοντας από το 13, "12,11,10,9,8."). Στην εργασία αυτή αφού παρουσιάσουμε τις διάφορες χρήσεις των λέξεων-αριθμών που συγκροτούν την προφορική ακολουθία των αριθμών μέσα στα πλαίσια της έννοιας του εννοιολογικού πεδίου, θα δούμε την εξέλιξη της μάθησης της προφορικής αριθμητικής ακολουθίας βασιζόμενοι σε διάφορες σύγχρονες έρευνες. Στη συνέχεια θα δούμε κάποια εμπειρικά αποτελέσματα για τις γνώσεις των Ελλήνων μαθητών στην προφορική αρίθμηση και θα τα συγκρίνουμε με τα αντίστοιχα σε Αμερικανούς μαθητές. Οι λέξεις-αριθμοί και το εννοιολογικό πεδίο της χρήσης τους Λέξεις-αριθμούς ονομάζουμε τις ειδικές λέξεις που εκφράζουν τους αριθμούς και μπορούν να χρησιμοποιούνται σε διαφορετικές καταστάσεις στην καθημερινή ζωή. Οι καταστάσεις αυτές μπορεί να είναι διαφορετικές μεταξύ τους και από Μαθηματική άποψη. Μπορούμε να πούμε ότι υπάρχουν οι διάφορες καταστάσεις του εννοιολογικού πεδίου της έννοιας των λέξεων αριθμών που δίνουν νόημα στην έννοια αυτή. Το εννοιολογικό πεδίο έχει εισαχθεί ως όρος από το Γάλλο ψυχολόγο G. Vergnaud (1981) και θεωρεί ότι μια έννοια μπορεί να οριστεί ως μια τριάδα τριών συνόλων : C = (S, I, L) S : το σύνολο των καταστάσεων όπου εμφανίζεται και απ'όπου παίρνει το νόημα της η έννοια,
4 I : το σύνολο των αναλλοίωτων που δίνει νόημα στην έννοια (το σημαινόμενο). Οι αναλλοίωτοι είναι αντικείμενα, ιδιότητες ή σχέσεις. L : το σύνολο των γλωσσικών και μη γλωσσικών μορφών που μας επιτρέπουν να αναπαραστήσουμε συμβολικά την έννοια, τις ιδιότητες της, τις καταστάσεις και τις διαδικασίες χρήσης της (το σημαίνον). Μια κλασική εφαρμογή του εννοιολογικού πεδίου είναι οι προσθετικές σχέσεις που έχουν μελετηθεί και στον Ελληνικό χώρο (Γαγάτσης, 1994). Μέσα στα πλαίσια λοιπόν του εννοιολογικού πεδίου των λέξεων αριθμών υπάρχουν πολλές καταστάσεις που δίνουν διαφορετικές σημασίες και απαιτούν διαφορετικούς τρόπους χρησιμοποίησης αυτών των λέξεων. Σύμφωνα με την ανάλυση της Κ. Fuson (1988) οι μαθητές καταλαβαίνουν και χειρίζονται προοδευτικά τις λέξεις-αριθμούς μέσα στα πλαίσια επτά διαφορετικών καταστάσεων. Τρεις από αυτές τις καταστάσεις είναι Μαθηματικές: η πληθική μορφή, όπου η λέξη-αριθμός αναφέρεται στην ολότητα ενός συνόλου με διακριτά στοιχεία και δείχνει από πόσα στοιχεία αποτελείται. Παράδειγμα τέτοιας πρόωρης πληθικής χρήσης από τα μικρά παιδιά είναι φράσεις όπως "έχω τρεις καραμέλες". η διατακτική μορφή, όπου η λέξη-αριθμός αναφέρεται σ'ένα στοιχείο στα πλαίσια μιας συλλογής διατεταγμένων στοιχείων και περιγράφει τη σχετική θέση αυτού του στοιχείου, π.χ. "θέλω να πάω πρώτος" και η μετρική μορφή, όπου η λέξη-αριθμός αναφέρεται σε μια συνεχή ποσότητα και δείχνει πόσες μονάδες αντιστοιχούν σ'αυτήν π.χ. "είμαι τριών χρόνων". 'Αλλες δύο μορφές με τις οποίες παρουσιάζονται οι λέξειςαριθμοί είναι αυτές της ακολουθίας και της απαρίθμησης. Αυτές δίνουν τα πολιτιστικά εργαλεία που εγγυώνται την ακρίβεια της λέξης-αριθμού που χρησιμοποιείται μέσα σε πληθικά, διατακτικά και μετρικά πλαίσια.
5 Εάν οι λέξεις-αριθμοί λέγονται μόνο χωρίς καμία αναφορά σε αντικείμενα, τότε λέμε ότι χρησιμοποιούνται σε μια κατάσταση ακολουθίας. Στην περίπτωση αυτή υπάρχει μια σταθερή σειρά στις λέξεις-αριθμούς της ακολουθίας και οι λέξεις δεν έχουν καμία αναφορά και δεν περιγράφουν τίποτα. Εάν οι λέξεις-αριθμοί λέγονται σε μια κατάσταση οντοτήτων και κάθε λέξη-αριθμός αναφέρεται σε μια οντότητα, τότε η κατάσταση λέμε ότι είναι μια κατάσταση απαρίθμησης. Οι λέξεις της αρίθμησης αναφέρονται σε αντικείμενα στα οποία αντιστοιχούν από τη δραστηριότητα της απαρίθμησης, αλλά αυτές οι λέξεις δεν περιγράφουν τα αντικείμενα και δε δίνουν καμία πληροφορία γι αυτά. Η έκτη μορφή των λέξεων-αριθμών αναφέρεται στην ανάγνωσή τους και είναι η συμβολική μορφή που ανακαλεί την έκφραση μιας λέξης-αριθμού απομονωμένης χωρίς καμιά άλλη πληροφορία. "Αυτό είναι ένα πέντε" ανακοινώνουμε διαβάζοντας ένα 5. Αργότερα, οι αριθμοί παίρνουν μια σημασία πληθική, διατακτική, μετρική, μια σημασία αρίθμησης και μια σημασία ακολουθίας. Τέλος, οι λέξεις-αριθμοί χρησιμοποιούνται επίσης μέσα σε πλαίσια μη αριθμητικά ή το πολύ σε ημιαριθμητικά, όπως όταν σχηματίζουμε τους αριθμούς των τηλεφώνων, τις γραμμές των λεωφορείων, τα κανάλια της τηλεόρασης, σε ένα δρόμο τα νούμερα των σπιτιών και τους ταχυδρομικούς κώδικες. Τα μικρά παιδιά συναντούν τις λέξεις-αριθμούς μέσα στα επτά αυτά διαφορετικά πλαίσια και αρχίζουν να τις χρησιμοποιούν μέσα σ'αυτές τις ποικίλες καταστάσεις. Σε μια πρώτη περίοδο οι διαφορετικές σημασίες είναι ανεξάρτητες η μια από την άλλη. Με την πάροδο του χρόνου, τα παιδιά εγκαθιστούν μεταξύ των αριθμών συνάφειες τέτοιες ώστε η ανακοίνωση μιας μόνο λέξης-αριθμού να καλύπτει περισσότερες από μια σημασίες. Η μάθηση όλων αυτών των σχέσεων απαιτεί χρόνο που διαρκεί από τα 2 μέχρι τα 8 χρόνια στα περισσότερα παιδιά.
6 Ανάλυση και εξέλιξη της μάθησης της προφορικής αριθμητικής ακολουθίας Η εξέλιξη στο παιδί της μάθησης της προφορικής αριθμητικής ακολουθίας σύμφωνα με τους Fuson, Richards και Briars, (1982) ακολουθεί δύο φάσεις οι οποίες δεν είναι ανεξάρτητες και επικαλύπτονται η μια με την άλλη. Στη διάρκεια της πρώτης φάσης το παιδί μαθαίνει να λέει με αποστήθιση (απέξω) το πρώτο μέρος της ακολουθίας των λέξεων των αριθμών. Αργότερα έχουμε τη λειτουργική φάση της μάθησης όπου η προφορική ακολουθία αναπαράγεται με πιο σύνθετους και πολύπλοκους τρόπους. Στην περίοδο αυτήν κατασκευάζονται οι σχέσεις της ισοδυναμίας, της διάταξης και οι λειτουργίες της ακολουθίας των λέξεων-αριθμών. Οι Fuson και Hall (1983), Fuson, Richard & Briars (1982) πραγματοποιώντας πειράματα σε Αμερικανούς μαθητές βρήκαν ότι η μάθηση της προφορικής αριθμητικής ακολουθίας από το 1 μέχρι το 100 αρχίζει πολύ νωρίς, περίπου σε ηλικία δύο ετών και ολοκληρώνεται στις περισσότερες περιπτώσεις στο τέλος της πρώτης ή την αρχή της δευτέρας χρονιάς της δημοτικής εκπαίδευσης. Η ηλικία της μάθησης είναι πολύ διαφορετική από το ένα παιδί στο άλλο καθώς επίσης και οι περίοδοι ανάπτυξης σ'ένα μόνο παιδί είναι χρονικά πολύ μεταβλητές. Οι διαφορές αυτές σε μεγάλο βαθμό έχουν να κάνουν με τα διαφορετικά ερεθίσματα που δέχεται κάθε παιδί από το εξωτερικό του περιβάλλον. Παρατηρήθηκε ότι κατά τη διάρκεια της περιόδου της μάθησης με αποστήθιση οι προφορικές αριθμητικές ακολουθίες που δίνουν τα παιδιά για απάντηση στην ερώτηση "δείξε μου μέχρι πόσο ξέρεις να μετράς", αποτελούνται από τρία μέρη. Σ'ένα μόνο παιδί που απαντά διαδοχικά στην παραπάνω ερώτηση παρατηρούμε ότι στις απαντήσεις συνυπάρχουν: α) ένα πρώτο μέρος που είναι σταθερό και σωστό, ισοδύναμο μ αυτό των ενηλίκων.
7 β) ένα δεύτερο μέρος που είναι σταθερό αλλά λανθασμένο, εδώ δηλαδή, είτε είναι λάθος η σειρά των αριθμών είτε λείπουν στοιχεία, και γ) ένα τρίτο μέρος που δεν είναι ούτε σταθερό ούτε σωστό, γιατί μεταβάλλεται σε κάθε απάντηση που δίνει το παιδί. Η μάθηση της προφορικής αριθμητικής ακολουθίας συνεχίζεται για μεγάλο χρονικό διάστημα ακόμη και μετά που το παιδί είναι ικανό να απαγγέλλει σωστά τις λέξεις-αριθμούς. Αυτή η συνεχής λειτουργική μάθηση που διαρκεί σχεδόν από την ηλικία των 4 μέχρι 8 χρόνων εκδηλώνεται με τη διαδοχική εμφάνιση νέων ικανοτήτων στο παιδί. Οι Fuson και άλλοι (1982) μελέτησαν αυτές τις ικανότητες και προσδιόρισαν πέντε επίπεδα ανάπτυξης της λειτουργικής φάσης της προφορικής αριθμητικής ακολουθίας. Αυτά τα πέντε επίπεδα είναι τα εξής : α) Το επίπεδο της αλυσίδας, όπου οι λέξεις αριθμοί εμφανίζονται και λειτουργούν σαν ένα συμπαγές και αδιαχώριστο όλο, "εναδυοτριατέσσεραπέντε...". Εδώ πρόκειται για μια απαγγελία που αναφέρεται σ'ένα προφορικό μπλόκ που στερείται κάθε αριθμητικής σημασίας. β) Το επίπεδο της αδιαίρετης αλυσίδας, όπου οι λέξεις είναι διαχωρισμένες αλλά η ακολουθία αναγγέλλεται μόνο σε ευθεία κατεύθυνση και μπορεί να παράγεται μόνο αρχίζοντας από την αρχή. Στο επίπεδο αυτό δηλαδή το παιδί δεν μπορεί να αρχίζει την προφορική αρίθμηση από οποιοδήποτε αριθμό, πάντοτε ξεκινάει από το ένα. Αντίθετα, τώρα μπορεί να σταματάει σε ένα αριθμό που του ορίζουμε από την αρχή, π.χ. "μέτρα μέχρι το εννέα". γ) Το επίπεδο της διασπασμένης αλυσίδας, όπου μπορεί να παράγονται κομμάτια της προφορικής ακολουθίας αρχίζοντας από οποιοδήποτε στοιχείο, αντί να γίνεται η αρχή πάντοτε από το πρώτο στοιχείο. Τώρα επίσης το παιδί γίνεται ικανό να απαντά αυτόματα στην ερώτηση, "ποιος αριθμός βρίσκεται πριν ή μετά από ένα δεδομένο
8 αριθμό", χωρίς να απαγγέλλει την ακολουθία από την αρχή μέχρι το δεδομένο αριθμό όπως γινόταν στο προηγούμενο επίπεδο. Δύο άλλες ικανότητες που εδραιώνονται σ'αυτό το επίπεδο είναι το να μπορεί το παιδί να απαντάει στις ερωτήσεις: "μέτρησε ξεκινώντας από τον αριθμό ν" και "μέτρησε από το ν μέχρι το μ". δ) Το επίπεδο της αριθμήσιμης αλυσίδας, όπου οι λέξεις-αριθμοί γίνονται ακόμη πιο αφηρημένες και αποτελούν μονάδες με την αριθμητική έννοια, και έτσι κομμάτια της προφορικής ακολουθίας μπορούν να αναπαριστούν μια αριθμητική κατάσταση και μπορεί να αριθμούνται ή να αντιστοιχούνται. Στη διάρκεια του επιπέδου αυτού αναπτύσσεται στο παιδί η ικανότητα να μετράει, κατευθείαν ή αντίστροφα, ν στοιχεία αρχίζοντας από ένα στοιχείο α. Σ'αυτήν την περίπτωση δηλαδή το παιδί θα πρέπει να αριθμεί τα στοιχεία της αριθμητικής ακολουθίας διατηρώντας ταυτόχρονα στη μνήμη του τον αριθμό των στοιχείων τα οποία ήδη έχει αριθμήσει. ε) Το επίπεδο της διπλής κατεύθυνσης, όπου η προφορική ακολουθία μπορεί να παράγεται εύκολα και προς τις δύο κατευθύνσεις. Τα παιδιά μπορούν να μετράνε γρήγορα κατευθείαν ή αντίστροφα από οποιαδήποτε λέξη-αριθμό. Μπορούν εύκολα να αριθμούν αντίστροφα χωρίς τη βοήθεια της ευθείας αρίθμησης. Αυτά τα διαφορετικά επίπεδα χαρακτηρίζονται από μια αύξουσα σειρά ικανοτήτων. Έτσι ο μαθητής γίνεται προοδευτικά ικανός: να αρχίζει και να σταματάει την αρίθμηση σε οποιαδήποτε λέξη-αριθμό της ακολουθίας, να αριθμεί προς τα πάνω για ένα δεδομένο πλήθος από λέξεις-αριθμούς, και να αριθμεί αντίστροφα αρχίζοντας και σταματώντας σε οποιοδήποτε αριθμό ή να αριθμεί αντίστροφα για ένα δεδομένο πλήθος λέξεων-αριθμών. Διαμέσου αυτών των επιπέδων, λοιπόν, το παιδί αυξάνει την ικανότητά του στο να καταλαβαίνει και να παράγει τις σχέσεις της διάταξης των λέξεωναριθμών μέσα στην ακολουθία των αριθμών. Εμπειρικά δεδομένα από Έλληνες μαθητές όσον αφορά τη γνώση της προφορικής αριθμητικής ακολουθίας
9 Με σκοπό να διερευνήσουμε τις γνώσεις των Ελλήνων μαθητών στην αριθμητική ακολουθία πραγματοποιήσαμε μια έρευνα σε παιδιά του νηπιαγωγείου και της πρώτης τάξης του δημοτικού. Συνολικά εξετάσαμε 149 μαθητές νηπιαγωγείων (μικρά και μεγάλα νήπια) και 41 μαθητές από δύο τμήματα της πρώτης δημοτικού. Όλοι οι παραπάνω μαθητές ανήκαν σε σχολεία της πόλης της Φλώρινας. Κάθε μαθητής χωριστά υποβαλλόταν σε προσωπική εξέταση και οι απαντήσεις του μαγνητοφωνούνταν. Η εξέταση της πλειοψηφίας των μαθητών του νηπιαγωγείου και του ενός τμήματος της πρώτης τάξης πραγματοποιήθηκε στο τέλος της σχολικής χρονιάς (Μάϊο). 'Αρα αυτοί οι μαθητές είχαν διδαχθεί για τον αριθμό τα προβλεπόμενα από το αναλυτικό πρόγραμμα. Το δεύτερο τμήμα της πρώτης τάξης εξετάστηκε το μήνα Ιανουάριο και η διδασκαλία που είχε δεχτεί ως προς τον αριθμό δεν είχε ολοκληρωθεί και ήταν σχεδόν παρόμοια με αυτήν του νηπιαγωγείου. Όπως γνωρίζουμε σύμφωνα με το αναλυτικό πρόγραμμα στο νηπιαγωγείο προβλέπεται όσον αφορά τους αριθμούς, η αναγνώριση και η γραφή των αριθμών από το 1 μέχρι το 5 και απαρίθμηση συνόλων με αντικείμενα από 1 μέχρι 10. Δηλαδή, σύμφωνα με το πρόγραμμα τελειώνοντας το νηπιαγωγείο τα παιδιά θα πρέπει να ξέρουν να αριθμούν προφορικά μέχρι το 10. Στην πρώτη δημοτικού προβλέπεται η διδασκαλία των αριθμών μέχρι το 20 και στην δευτέρα μέχρι το 100. Στον παρακάτω πίνακα 1 παραθέτουμε τα ποσοστά των μαθητών του νηπιαγωγείου σύμφωνα με την ηλικία τους αλλά και στο σύνολό τους που αριθμούν σωστά απαγγέλλοντας την προφορική ακολουθία για ν<10, 10 ν<14,... αντίστοιχα, απαντώντας στην ερώτηση "Μέτρα όσο πιο πολύ μπορείς". Πίνακας 1
10 Μέγεθος/ Ηλικία ν< ν ν<14 14 ν ν<20 20 ν ν<30 30 ν ν<72 72 ν ν< ν ν< ν 4-4* ,5 15, *6-4*11 20,5 27, , * ,5 11 3, *6-5* ,5 23,5 26,5 8 2,5 0 18,5 6-6*5 8,5 25 8, ,5 Συνολικά Νήπια 16,5 19,5 21, ,5 3,5 0,5 0,5 Παρατηρούμε στον παραπάνω πίνακα ότι οι περισσότεροι από τους μισούς μαθητές ηλικίας μεταξύ 4 και 4*5 χρόνων ξέρουν τις ακολουθίες των λέξεων-αριθμών που είναι μικρότερες του 10, ένα σημαντικό ποσοστό (30,5%) των παιδιών αυτών φτάνει να αριθμεί σωστά μέχρι τους αριθμούς μεταξύ του 10 και του 14 και ένα μικρό ποσοστό (15,5%) μπορεί να αριθμεί σωστά μέχρι τους αριθμούς που βρίσκονται μεταξύ του 14 και 20. Στις ηλικίες μεταξύ 4*6 και 4*11 ετών παρατηρούμε ότι μειώνεται σημαντικά το ποσοστό (20,5%) των παιδιών που αριθμούν μέχρι αριθμούς που είναι μικρότεροι του 10 και σχεδόν το ένα τέταρτο των παιδιών αυτών μπορεί να αριθμεί σωστά μέχρι αριθμούς μεταξύ του 20 και 30. Γενικά παρατηρούμε ότι με την αύξηση της ηλικίας τα παιδιά γίνονται ικανά να αριθμούν προφορικά ολοένα και περισσότερους αριθμούς από την ακολουθία των αριθμών. Συνολικά για τα νήπια μπορούμε να πούμε ότι η πλειοψηφία των μαθητών φτάνει να αριθμεί μέχρι αριθμούς που είναι μικρότεροι του 20 ενώ το ένα τέταρτο περίπου των μαθητών φτάνει σε αριθμούς που βρίσκονται μεταξύ του 20 και 30. Λίγα νήπια (10,5%) ξέρουν να αριθμούν σωστά μέχρι αριθμούς που βρίσκονται μεταξύ του 30 και 72, και ελάχιστα (κάποιες μεμονωμένες περιπτώσεις) αριθμούν μέχρι το 100 ή και παραπάνω. Παρατηρούμε επίσης ότι ένα ποσοστό (16,5%) νηπίων δεν είναι ικανό να αριθμεί σωστά μέχρι το Ο συμβολισμός 4*5 σημαίνει ηλικία 4 ετών και 5 μηνών.
11 Παρακάτω στον πίνακα 2, παρουσιάζουμε τα αντίστοιχα ποσοστά επιτυχίας στην προφορική αρίθμηση για τους μαθητές της πρώτης τάξης, διαχωρίζοντας τα δύο τμήματα σύμφωνα με τη χρονική περίοδο που εξετάστηκαν. Πίνακας 2 Μέγεθος/ Ηλικία ν<10 10 ν ν<14 14 ν ν<20 20 ν ν<30 30 ν ν<72 72 ν ν< ν ν< ν Πρώτη Ιανου , , άριος Πρώτη Μάϊος 0 4, ,5 41 4,5 9 Συνολικά Πρώτη , ,5 22 2,5 5 Για την πρώτη τάξη του δημοτικού βλέποντας τον παραπάνω πίνακα μπορούμε να διαπιστώσουμε τα εξής: Καταρχήν δεν υπάρχουν μαθητές που να μην ξέρουν να αριθμούν προφορικά μέχρι το 10. Στην πρώτη τάξη του δημοτικού μέχρι τον Ιανουάριο, όσον αφορά στον αριθμό, ουσιαστικά η διδασκαλία επαναλαμβάνει την ύλη του νηπιαγωγείου αλλά με περισσότερη λεπτομέρεια και σε μεγαλύτερο βάθος, οι μαθητές μέχρι αυτήν τη χρονική περίοδο δεν έχουν προχωρήσει ακόμη στους αριθμούς από το 10 μέχρι το 20. Στο τμήμα λοιπόν της πρώτης τάξης που εξετάσαμε τον Ιανουάριο βλέπουμε ότι η πλειοψηφία των μαθητών ήξερε να αριθμεί μέχρι αριθμούς που βρίσκονται μεταξύ του 20 και 30 (37%) και του 30 και 72 (26,5%). Αντίθετα, στο τμήμα της πρώτης που εξετάσαμε στο τέλος της χρονιάς η πλειοψηφία των μαθητών ήξερε να αριθμεί μέχρι αριθμούς που βρίσκονται μεταξύ του 30 και 72 (22,5%) και του 72 και 101 (41%). Παρατηρούμε δηλαδή μια εξέλιξη της προφορικής
12 αρίθμησης προς μεγαλύτερους αριθμούς κατά τη διάρκεια της πρώτης τάξης. Συνολικά, παρατηρούμε για τους μαθητές της πρώτης τάξης ότι: σχεδόν οι μισοί μαθητές ξέρουν να αριθμούν προφορικά μέχρι αριθμούς που βρίσκονται μεταξύ του 20 και 30 (27%) και μεταξύ του 30 και 72 (24,5%). Ένα σημαντικό ποσοστό μαθητών (22%) ξέρει να αριθμεί μέχρι αριθμούς που βρίσκονται μεταξύ του 72 και του 101. Ένα μικρό ποσοστό μαθητών πετυχαίνει να αριθμεί μέχρι το 200 ή και παραπάνω. 'Οσον αφορά στην προφορική αρίθμηση 2-2 (2, 4, 6, 8,...) παρατηρήσαμε τα εξής: στο νηπιαγωγείο υπήρχε πλήρης αδυναμία των παιδιών να αριθμήσουν 2-2 στις περισσότερες περιπτώσεις τα παιδιά δεν καταλάβαιναν τι τους ζητούσαμε. Μόνο κάποιες μεμονωμένες περιπτώσεις παιδιών που ήξεραν να αριθμούν ένα-ένα πολύ καλά και μέχρι μεγάλους αριθμούς (π.χ. το 100 και πάνω) κατάφερναν να αριθμήσουν 2-2 το πολύ μέχρι το 20. Στο τμήμα της πρώτης τάξης που εξετάστηκε στο τέλος της χρονιάς από τους 22 μαθητές οι 10 (45,5%) δεν μπόρεσαν καθόλου να αριθμήσουν 2-2. Από τους υπόλοιπους μαθητές αν και οι περισσότεροι μπορούσαν να αριθμούν 1-1 περίπου μέχρι το 100, στην αρίθμηση 2-2 έφταναν σε αριθμούς γύρο στο 20. Επίσης, και για την αντίστροφη αρίθμηση θα πρέπει να πούμε ότι ήταν μια πολύ δύσκολη διαδικασία για τα νήπια και ήταν αδύνατο να την καταμετρήσουμε. Στην πρώτη τάξη επίσης τα παιδιά είχαν πολύ μεγάλη δυσκολία να μετρήσουν αντίστροφα και όσα από αυτά μπορούσαν στην πλειοψηφία τους ήταν ικανά να αριθμήσουν μόνο από το 10 και κάτω. Σύγκριση Ελλήνων και Αμερικανών μαθητών ως προς τη γνώση της προφορικής αριθμητικής ακολουθίας Στον πίνακα 3 παρουσιάζονται ποσοστά επιτυχίας από Αμερικανούς μαθητές αντίστοιχων ηλικιών που έχουν κωδικοποιηθεί με τις ίδιες ομάδες αριθμών: ν<10, 10 ν<14,
13 14 ν<20, κτλ. Τα δεδομένα στον πίνακα 3 προέρχονται από την εργασία των Fuson, Richards και Briars (σελ.38, 1982). Πίνακας 3 Μέγεθος/ Ηλικία ν<10 10 ν ν<14 14 ν ν<20 20 ν ν<30 30 ν ν<72 72 ν ν< ν ν< ν 4-4* *6-4* * *6-5* Νήπια Πρώτη Θα πρέπει να αναφέρουμε στο σημείο αυτό ότι τα Αμερικανικά προγράμματα, όσον αφορά τη διδασκαλία του αριθμού αφιερώνουν περισσότερο χρόνο και δίνουν μεγαλύτερη σημασία απ'ότι τα Ελληνικά στην προφορική αρίθμηση και την απαρίθμηση αντικειμένων. Αν συγκρίνουμε λοιπόν τα ποσοστά επιτυχίας στην προφορική αρίθμηση των Ελλήνων μαθητών από τους πίνακες 1 και 2 με τα αντίστοιχα των Αμερικανών από τον πίνακα 3, διαπιστώνουμε γενικά ότι στις αντίστοιχες ηλικίες οι Αμερικανοί μαθητές ξέρουν να αριθμούν προφορικά μεγαλύτερα κομμάτια της ακολουθίας των αριθμών απ'ότι οι Έλληνες μαθητές. Για παράδειγμα, αν συγκρίνουμε τα αντίστοιχα ποσοστά για την ηλικία μεταξύ των 5 και 5*5 ετών από τους πίνακες 1 και 3 διαπιστώνουμε ότι: Ενώ η πλειοψηφία των Ελλήνων μαθητών ξέρει να μετράει μέχρι τους αριθμούς που βρίσκονται μεταξύ του 14 και 20 (24%) και του 20 και 30 (33,5%), η πλειοψηφία των Αμερικανών μαθητών φτάνει μέχρι τους αριθμούς που βρίσκονται μεταξύ του 20 και 30 (13%) και του 30 και 72 (44%). Επίσης στην ηλικία αυτή στους Έλληνες μαθητές βρίσκουμε ένα ποσοστό (13%) που δεν ξέρει να μετράει μέχρι το 10 ενώ οι Αμερικανοί μαθητές ξέρουν όλοι να μετρούν πάνω από το 10.
14 Πιστεύουμε ότι σε γενικές γραμμές η καλύτερη απόδοση των Αμερικανών μαθητών στην προφορική αρίθμηση οφείλεται στην διαφορετική διδασκαλία που δέχονται και η οποία όπως αναφέραμε παραπάνω δίνει μεγαλύτερη βαρύτητα στην προφορική αρίθμηση. Συμπεράσματα Η μάθηση λοιπόν της προφορικής αρίθμησης όπως ήδη έχουμε τονίσει είναι μια μακρόχρονη διαδικασία: ξεκινάει από πολύ νωρίς με μορφή κοινωνικής γνώσης που στις περισσότερες περιπτώσεις προσφέρεται από την οικογένεια και μαθαίνεται με αποστήθιση πριν ακόμη το παιδί πάει στο σχολείο και δεχτεί κάποια οργανωμένη διδασκαλία και συνεχίζει μέχρι τις πρώτες τάξεις του δημοτικού όπου η μάθηση αυτή γίνεται πιο λειτουργική και σύμφωνη με τους κανόνες του αριθμητικού συστήματος. Από τα εμπειρικά δεδομένα που είδαμε προηγουμένως όσον αφορά στις γνώσεις των μαθητών στην προφορική αρίθμηση μπορούμε να κάνουμε τις εξής γενικές διαπιστώσεις: - Η κοινωνική προέλευση της προφορικής αρίθμησης γίνεται φανερή από το γεγονός ότι τα νήπια ακόμη και στις πιο μικρές ηλικίες ξέρουν να αριθμούν προφορικά μέχρι πολύ μεγαλύτερους αριθμούς από αυτούς που διδάσκονται. Τα περισσότερα παιδιά έχουν αυτές τις γνώσεις πριν ακόμη δεχτούν κάποια διδασκαλία. Επίσης η εξωσχολική προέλευση αυτής της γνώσης φαίνεται από το γεγονός ότι υπάρχουν έντονες διαφοροποιήσεις μεταξύ των παιδιών ως προς την ικανότητα της προφορικής αρίθμησης. Για παράδειγμα τα δύο παιδιά του νηπιαγωγείου που παρουσίασαν εκπληκτικές ικανότητες στην προφορική αρίθμηση (αρίθμηση ένα-ένα πάνω από το 100, ικανότητα αρίθμησης δύο-δύο και αντίστροφης αρίθμησης) ήταν παιδιά εκπαιδευτικών. - Σε γενικές γραμμές μπορούμε να παρατηρήσουμε ότι στο νηπιαγωγείο αλλά και στο δημοτικό η πλειοψηφία των μαθητών ξέρει να αριθμεί μέχρι αριθμούς που είναι πολύ μεγαλύτεροι από αυτούς που προβλέπονται μέσα στα προγράμματα διδασκαλίας.
15 - Το γεγονός ότι με την αύξηση της ηλικίας των παιδιών παρατηρείται ταυτόχρονα και μια μεγάλη αύξηση της ικανότητας προφορικής αρίθμησης προς ολοένα και μεγαλύτερους αριθμούς, μαρτυρεί ότι τα παιδιά αποκτούν και αναπτύσσουν την ικανότητα αυτή εύκολα. Συμπερασματικά όσον αφορά στην διδασκαλία μπορούμε να κάνουμε τις εξής παρατηρήσεις: Γενικά η διδασκαλία δε χρησιμοποιεί και δεν εκμεταλλεύεται όσο πρέπει τις γνώσεις των παιδιών στην προφορική αρίθμηση που στην αρχή έχουν χαρακτήρα κοινωνικό και προέρχονται έξω από το σχολικό σύστημα. Δηλαδή η διδασκαλία περιορίζει την προφορική αρίθμηση σε μικρούς αριθμούς (μέχρι το 10 στα νήπια, μέχρι το 20 στην πρώτη και μέχρι το 100 στη δευτέρα) εξαιτίας των πλαισίων που θέτει για τη γενικότερη διδασκαλία και κατανόηση του αριθμού. Τουλάχιστον για την προφορική αρίθμηση θα μπορούσε να επεκταθούν κατά πολύ τα μεγέθη των αριθμών. Πρέπει να γίνεται περισσότερη δουλειά και από πιο νωρίς πάνω στην ακολουθία των αριθμών αριθμώντας κατευθείαν και αντίστροφα, αρχίζοντας από τη νοερή απαγγελία της ακολουθίας και προχωρώντας στην ανάγνωση ή τη γραφή της. Το δείγμα των μαθητών που είχαμε για την πρώτη τάξη αν και ήταν πολύ μικρό για να βγάλουμε γενικά συμπεράσματα έδειχνε όμως χαρακτηριστικά την αδυναμία των μαθητών στην αντίστροφη αρίθμηση. Αυτό επιβεβαιώνεται επίσης αν δούμε το μικρό χώρο που αφιερώνει και τις αποσπασματικές περιπτώσεις στις οποίες αναφέρεται η αντίστροφη αρίθμηση στο σημερινό πρόγραμμα διδασκαλίας. ΑΝΑΦΟΡΕΣ Γαγάτσης Α. (1993). Προβλήματα προσθετικών σχέσεων σύμφωνα με τις εργασίες του G. Vergnaud. Διάσταση, 1-2, σελ , 1993.
16 Fuson, K.-C. (1988). Children's counting and concepts of number. New-York: Springer-verlag. Fuson, K., & Hall, J.W. (1983). The acquisition of early number word meaning: A conceptual analysis and review. In H.P. Ginsburg (Ed.), The development of mathematical thinking. New-York: Academic Press. Fuson K. C, Richards J. and Briars D. J. (1982). The acquisition and elaboration of the nomber word sequence. In C. Brainerd (Ed), Progress in cognitive development. (Vol 1). Children's logical and mathematical cognition. New-York: Springer-Verlag. Λεμονίδης Χ. (1994). Περίπατος στη μάθηση της στοιχειώδους αριθμητικής. Εκδόσεις Αδελφών Κυριακίδη Θεσ/νίκη. Vergnaud G. (1981). Quelques orientations theoriques et methodologiques des recherches francaises en didactique des Mathematiques, Recherches en Didactique des Mathematiques, 2.2, σελ
μπορούσαμε και θα έπρεπε να το αντισταθμίσουμε με νέες πολιτικές, με άλλες κατακτήσεις και ωφέλειες. Ο κίνδυνος της αποβιομηχάνισης ήταν βέβαια
 ΣΤΡΟΓΓΥΛΟ ΤΡΑΠΕΖΙ Κος ΘΩΜΑΔΑΚΗΣ Ευχαριστώ πάρα πολύ, συνάδελφε. Κυρίες και κύριοι, αντικρύζοντας τον τίτλο της σημερινής ημερίδας, 1962-2012, 50 χρόνια στην Ευρώπη, αναλογίστηκα αμέσως ότι το 62 ήμουν
ΣΤΡΟΓΓΥΛΟ ΤΡΑΠΕΖΙ Κος ΘΩΜΑΔΑΚΗΣ Ευχαριστώ πάρα πολύ, συνάδελφε. Κυρίες και κύριοι, αντικρύζοντας τον τίτλο της σημερινής ημερίδας, 1962-2012, 50 χρόνια στην Ευρώπη, αναλογίστηκα αμέσως ότι το 62 ήμουν
3. ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ ΜΕΛΕΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑ ΠΕΛΟΠΟΝΝΗΣΟΥ ΝΟΜΟΣ ΜΕΣΣΗΝΙΑΣ ΔΗΜΟΣ ΜΕΣΣΗΝΗΣ ΔΙΕΥΘΥΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΕΡΓΟ: ΕΠΙΣΚΕΥΗ ΚΟΙΝΟΤΙΚΟΥ ΚΑΤΑΣΤΗΜΑΤΟΣ ΣΤΡΕΦΙΟΥ Αριθμ. Μελέτης : 979-4/2014 ΠΡΟΫΠΟΛΟΓΙΣΜΟΣ:
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑ ΠΕΛΟΠΟΝΝΗΣΟΥ ΝΟΜΟΣ ΜΕΣΣΗΝΙΑΣ ΔΗΜΟΣ ΜΕΣΣΗΝΗΣ ΔΙΕΥΘΥΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΕΡΓΟ: ΕΠΙΣΚΕΥΗ ΚΟΙΝΟΤΙΚΟΥ ΚΑΤΑΣΤΗΜΑΤΟΣ ΣΤΡΕΦΙΟΥ Αριθμ. Μελέτης : 979-4/2014 ΠΡΟΫΠΟΛΟΓΙΣΜΟΣ:
3. ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ ΜΕΛΕΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑ ΠΕΛΟΠΟΝΝΗΣΟΥ ΝΟΜΟΣ ΜΕΣΣΗΝΙΑΣ ΔΗΜΟΣ ΜΕΣΣΗΝΗΣ ΔΙΕΥΘΥΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΕΡΓΟ: ΧΡΗΜΑΤΟΔΟΤΗΣΗ : ΕΠΙΣΚΕΥΗ ΚΑΙ ΔΙΑΜΟΡΦΩΣΗ ΚΟΙΜΗΤΗΡΙΟΥ ΤΟΠΙΚΗΣ ΚΟΙΝΟΤΗΤΑΣ ΜΗΛΙΩΤΙΟΥ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑ ΠΕΛΟΠΟΝΝΗΣΟΥ ΝΟΜΟΣ ΜΕΣΣΗΝΙΑΣ ΔΗΜΟΣ ΜΕΣΣΗΝΗΣ ΔΙΕΥΘΥΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΕΡΓΟ: ΧΡΗΜΑΤΟΔΟΤΗΣΗ : ΕΠΙΣΚΕΥΗ ΚΑΙ ΔΙΑΜΟΡΦΩΣΗ ΚΟΙΜΗΤΗΡΙΟΥ ΤΟΠΙΚΗΣ ΚΟΙΝΟΤΗΤΑΣ ΜΗΛΙΩΤΙΟΥ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΕΒΡΟΥ ΔΗΜΟΣ ΣΟΥΦΛΙΟΥ ΤΕΧΝΙΚΗ ΥΠΗΡΕΣΙΑ ΑΡ.ΜΕΛ: 74/2013
 1 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΕΒΡΟΥ ΔΗΜΟΣ ΣΟΥΦΛΙΟΥ ΤΕΧΝΙΚΗ ΥΠΗΡΕΣΙΑ ΑΡ.ΜΕΛ: 74/2013 ΔΗΜΟΣ ΣΟΥΦΛΙΟΥ ΕΡΓΟ: Βελτίωση υποδομών κέντρου ενημέρωσης Σουφλίου και περιβάλλοντος χώρου. ΑΝΑΛΥΤΙΚΟ ΤΙΜΟΛΟΓΙΟ 1 ΓΕΝΙΚΟΙ
1 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΕΒΡΟΥ ΔΗΜΟΣ ΣΟΥΦΛΙΟΥ ΤΕΧΝΙΚΗ ΥΠΗΡΕΣΙΑ ΑΡ.ΜΕΛ: 74/2013 ΔΗΜΟΣ ΣΟΥΦΛΙΟΥ ΕΡΓΟ: Βελτίωση υποδομών κέντρου ενημέρωσης Σουφλίου και περιβάλλοντος χώρου. ΑΝΑΛΥΤΙΚΟ ΤΙΜΟΛΟΓΙΟ 1 ΓΕΝΙΚΟΙ
ΘΡΙΑΣΙΟ ΗΜΕΡΗΣΙΑ ΕΚΔΟΣΗ ΓΙΑ ΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΘΡΙΑΣΙΟΥ ΠΕΔΙΟΥ & ΑΤΤΙΚΗΣ
 Σελ: 3 ΘΡΙΑΣΙΟ ΗΜΕΡΗΣΙΑ ΕΚΔΟΣΗ ΓΙΑ ΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΘΡΙΑΣΙΟΥ ΠΕΔΙΟΥ & ΑΤΤΙΚΗΣ ΑΡ. ΦΥΛΛΟΥ 2603 Δευτέρα 24 Νοεμβρίου 2014 Έτος 20ο email: info@thriassio.gr τηλ: 210 5571855 www.thriassio.gr Απόκλιση 146 εκ.
Σελ: 3 ΘΡΙΑΣΙΟ ΗΜΕΡΗΣΙΑ ΕΚΔΟΣΗ ΓΙΑ ΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΘΡΙΑΣΙΟΥ ΠΕΔΙΟΥ & ΑΤΤΙΚΗΣ ΑΡ. ΦΥΛΛΟΥ 2603 Δευτέρα 24 Νοεμβρίου 2014 Έτος 20ο email: info@thriassio.gr τηλ: 210 5571855 www.thriassio.gr Απόκλιση 146 εκ.
Φυσικό αέριο, χρήσεις, ασφάλεια και οικονομία Ομάδα Μαθητών: Συντονιστές Καθηγητές: Λύκειο Αγίου Αντωνίου Θεωρητικό υπόβαθρο Το Φυσικό αέριο
 1 Φυσικό αέριο, χρήσεις, ασφάλεια και οικονομία Ομάδα Μαθητών: Γεδεών Στέλλα, Θεοφάνους Ρογήρος, Γεωργίου Μαρίνα, Ξενοφώντος Άννα, Μιχαήλ Αντρέας, Δήμου Ιωάννης, Παύλου Ειρήνη Συντονιστές Καθηγητές: Νικόλας
1 Φυσικό αέριο, χρήσεις, ασφάλεια και οικονομία Ομάδα Μαθητών: Γεδεών Στέλλα, Θεοφάνους Ρογήρος, Γεωργίου Μαρίνα, Ξενοφώντος Άννα, Μιχαήλ Αντρέας, Δήμου Ιωάννης, Παύλου Ειρήνη Συντονιστές Καθηγητές: Νικόλας
Αριστοτέλης Ο πατέρας της Δυτικής Επιστήμης
 Αριστοτέλης Ο πατέρας της Δυτικής Επιστήμης Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Τμήμα Φυσικής ΕΚΠΑ Ο Αριστοτέλης γεννήθηκε το 384 π.χ. (15 χρόνια μετά τον θάνατο του Σωκράτη, και 3 χρόνια
Αριστοτέλης Ο πατέρας της Δυτικής Επιστήμης Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Τμήμα Φυσικής ΕΚΠΑ Ο Αριστοτέλης γεννήθηκε το 384 π.χ. (15 χρόνια μετά τον θάνατο του Σωκράτη, και 3 χρόνια
ΔΙΑΜΕΣΟΛΑΒΗΣΗ 194/2013. (Άρθρο 77 παρ. 3 Ν.3852/2010) Προς. 3. Kύριο *** *** *** Κοινοποίηση
 Διαμεσολάβηση 194/2013 Σελίδα 1 ΔΙΑΜΕΣΟΛΑΒΗΣΗ 194/2013 (Άρθρο 77 παρ. 3 Ν.3852/2010) Ι. Η καταγγελία Προς 1. Τμήμα Υποστήριξης Δημοτικού Συμβουλίου dimotikosymvoulio@cityofathens.gr 2. Διεύθυνση Οδοποιίας
Διαμεσολάβηση 194/2013 Σελίδα 1 ΔΙΑΜΕΣΟΛΑΒΗΣΗ 194/2013 (Άρθρο 77 παρ. 3 Ν.3852/2010) Ι. Η καταγγελία Προς 1. Τμήμα Υποστήριξης Δημοτικού Συμβουλίου dimotikosymvoulio@cityofathens.gr 2. Διεύθυνση Οδοποιίας
74 η ΣΥΝΟΔΟΣ ΠΡΥΤΑΝΕΩΝ & ΠΡΟΕΔΡΩΝ Δ.Ε. ΤΩΝ ΕΛΛΗΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΩΝ Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Θεσσαλονίκη, 12-13 Δεκεμβρίου 2013
 74 η ΣΥΝΟΔΟΣ ΠΡΥΤΑΝΕΩΝ & ΠΡΟΕΔΡΩΝ Δ.Ε. ΤΩΝ ΕΛΛΗΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΩΝ Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Θεσσαλονίκη, 12-13 Δεκεμβρίου 2013 ΟΜΟΦΩΝΟ ΨΗΦΙΣΜΑ ΓΙΑ ΤΑ ΘΕΣΜΙΚΑ ΘΕΜΑΤΑ ΤΩΝ ΠΑΝΕΠΙΣΤΗΜΙΩΝ 1. Θεσμικά
74 η ΣΥΝΟΔΟΣ ΠΡΥΤΑΝΕΩΝ & ΠΡΟΕΔΡΩΝ Δ.Ε. ΤΩΝ ΕΛΛΗΝΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΩΝ Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Θεσσαλονίκη, 12-13 Δεκεμβρίου 2013 ΟΜΟΦΩΝΟ ΨΗΦΙΣΜΑ ΓΙΑ ΤΑ ΘΕΣΜΙΚΑ ΘΕΜΑΤΑ ΤΩΝ ΠΑΝΕΠΙΣΤΗΜΙΩΝ 1. Θεσμικά
ΕΡΓΟ: 3ο 2/θέσιο & 21ο 2/θέσιο Ολοήμερο Ν/Γ Αγρινίου, με τη μέθοδο της προκατασκευής
 ΚΤΙΡΙΑΚΕΣ ΥΠΟΔΟΜΕΣ A.E. ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΕΡΓΩΝ ΔΙΕΥΘΥΝΣΗ ΥΠΟΣΤΗΡΙΞΗΣ ΕΡΓΩΝ ΤΜΗΜΑ ΤΕΥΧΩΝ, ΔΙΑΓΩΝΙΣΜΩΝ & ΣΥΜΒΑΣΕΩΝ ΕΡΓΟ: 3ο 2/θέσιο & 21ο 2/θέσιο Ολοήμερο Ν/Γ Αγρινίου, με τη μέθοδο της προκατασκευής ΠΡΟΫΠΟΛΟΓΙΣΜΟΣ:
ΚΤΙΡΙΑΚΕΣ ΥΠΟΔΟΜΕΣ A.E. ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΕΡΓΩΝ ΔΙΕΥΘΥΝΣΗ ΥΠΟΣΤΗΡΙΞΗΣ ΕΡΓΩΝ ΤΜΗΜΑ ΤΕΥΧΩΝ, ΔΙΑΓΩΝΙΣΜΩΝ & ΣΥΜΒΑΣΕΩΝ ΕΡΓΟ: 3ο 2/θέσιο & 21ο 2/θέσιο Ολοήμερο Ν/Γ Αγρινίου, με τη μέθοδο της προκατασκευής ΠΡΟΫΠΟΛΟΓΙΣΜΟΣ:
-ΠΡΑΓΜΑΤΟΓΝΩΜΟΣΥΝΗ ΑΤΥΧΗΜΑΤΟΣ- ΜΗΧΑΝΟΛΟΓΙΚΗΣ ΑΠΟΨΕΩΣ ΚΑΙ ΑΛΛΗΛΟΥΧΙΑ ΦΑΣΕΩΝ ΚΑΤΑΣΚΕΥΗΣ ΑΜΑΞΩΜΑΤΟΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΑΡΥΜΑ ΚΑΒΑΛΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΤΟΜΕΑΣ ΕΝΕΡΓΕΙΑΣ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ -ΠΡΑΓΜΑΤΟΓΝΩΜΟΣΥΝΗ ΑΤΥΧΗΜΑΤΟΣ- ΜΗΧΑΝΟΛΟΓΙΚΗΣ ΑΠΟΨΕΩΣ ΚΑΙ ΑΛΛΗΛΟΥΧΙΑ ΦΑΣΕΩΝ ΚΑΤΑΣΚΕΥΗΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΑΡΥΜΑ ΚΑΒΑΛΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΤΟΜΕΑΣ ΕΝΕΡΓΕΙΑΣ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ -ΠΡΑΓΜΑΤΟΓΝΩΜΟΣΥΝΗ ΑΤΥΧΗΜΑΤΟΣ- ΜΗΧΑΝΟΛΟΓΙΚΗΣ ΑΠΟΨΕΩΣ ΚΑΙ ΑΛΛΗΛΟΥΧΙΑ ΦΑΣΕΩΝ ΚΑΤΑΣΚΕΥΗΣ
ΥΠΟΣΤΗΡΙΖΟΜΕΝΗ ΑΠΑΣΧΟΛΗΣΗ ΣΤΗΝ ΕΛΕΥΘΕΡΗ ΑΓΟΡΑ ΕΡΓΑΣΙΑΣ
 ΥΠΟΣΤΗΡΙΖΟΜΕΝΗ ΑΠΑΣΧΟΛΗΣΗ ΣΤΗΝ ΕΛΕΥΘΕΡΗ ΑΓΟΡΑ ΕΡΓΑΣΙΑΣ Το Πρόγραμμα «Σκαπανέας» «ΚΑΛΕΙΔΟΣΚΟΠΙΟ» Αστική Μη Κερδοσκοπική Εταιρεία για την ψυχοκοινωνική αποκατάσταση ΑΘΗΝΑ 2012 Το σχέδιο στο εξώφυλλο είναι
ΥΠΟΣΤΗΡΙΖΟΜΕΝΗ ΑΠΑΣΧΟΛΗΣΗ ΣΤΗΝ ΕΛΕΥΘΕΡΗ ΑΓΟΡΑ ΕΡΓΑΣΙΑΣ Το Πρόγραμμα «Σκαπανέας» «ΚΑΛΕΙΔΟΣΚΟΠΙΟ» Αστική Μη Κερδοσκοπική Εταιρεία για την ψυχοκοινωνική αποκατάσταση ΑΘΗΝΑ 2012 Το σχέδιο στο εξώφυλλο είναι
Χαιρετισμός από τη Διευθύντρια του σχολείου κ. Σωτηρούλα Μενοίκου
 ΠΕΡΙΦΕΡΕΙΑΚΟ ΛΥΚΕΙΟ ΑΠΟΣΤΟΛΟΥ ΛΟΥΚΑ ΚΟΛΟΣΣΙΟΥ ΤΕΥΧΟΣ 1 ον Δεκέμβριος 2012 Φεβρουάριος 2013 Υπεύθυνη Ιδιοκτήτρια: Σωτηρούλα Μενοίκου, Διευθύντρια «Η πένα είναι πιο δυνατή από το ξίφος». Αγγλική παροιμία
ΠΕΡΙΦΕΡΕΙΑΚΟ ΛΥΚΕΙΟ ΑΠΟΣΤΟΛΟΥ ΛΟΥΚΑ ΚΟΛΟΣΣΙΟΥ ΤΕΥΧΟΣ 1 ον Δεκέμβριος 2012 Φεβρουάριος 2013 Υπεύθυνη Ιδιοκτήτρια: Σωτηρούλα Μενοίκου, Διευθύντρια «Η πένα είναι πιο δυνατή από το ξίφος». Αγγλική παροιμία
ΓΡΑΜΜΑΤΕΙΑ ΓΥΝΑΙΚΩΝ ΤΗΣ ΥΠΑΛΛΗΛΩΝ
 ΓΡΑΜΜΑΤΕΙΑ ΓΥΝΑΙΚΩΝ ΤΗΣ ΠΑΝΕΛΛΗΝΙΑΣ ΟΜΟΣΠΟΝΔΙΑΣ ΥΠΑΛΛΗΛΩΝ ΑΣΤΥΝΟΜΙΚΩΝ ΣΤΕΛΕΧΩΣΗ ΓΡΑΜΜΑΤΕΙΑΣ ΓΥΝΑΙΚΩΝ ΑΣΤΥΝΟΜΙΚΩΝ Α/Α Αξίωμα 'Ονοματεπώνυμο Ένωση 1 Γραμματέας Γυναικών ΓΙΑΝΝΑΚΟΠΟΥΛΟΥ Μαρία ΚΕΦΑΛΛΗΝΙΑ 2
ΓΡΑΜΜΑΤΕΙΑ ΓΥΝΑΙΚΩΝ ΤΗΣ ΠΑΝΕΛΛΗΝΙΑΣ ΟΜΟΣΠΟΝΔΙΑΣ ΥΠΑΛΛΗΛΩΝ ΑΣΤΥΝΟΜΙΚΩΝ ΣΤΕΛΕΧΩΣΗ ΓΡΑΜΜΑΤΕΙΑΣ ΓΥΝΑΙΚΩΝ ΑΣΤΥΝΟΜΙΚΩΝ Α/Α Αξίωμα 'Ονοματεπώνυμο Ένωση 1 Γραμματέας Γυναικών ΓΙΑΝΝΑΚΟΠΟΥΛΟΥ Μαρία ΚΕΦΑΛΛΗΝΙΑ 2
ΠΟΛΥΤΕΧΝΕΙΟ 73. Η λάμψη της εξέγερσης είναι παντοτινή...
 1 ΠΟΛΥΤΕΧΝΕΙΟ 73 Η λάμψη της εξέγερσης είναι παντοτινή... 2 ΠΕΡΙΕΧΟΜΕΝΑ Σελ.3 Το πολυτεχνείο δεν τέλειωσε ποτέ Σελ.5 Η σύγχρονη κοινοβουλευτική «χούντα» Σελ.9 Χρονικό της Εξέγερσης (Τετάρτη 14/11) Σελ.10
1 ΠΟΛΥΤΕΧΝΕΙΟ 73 Η λάμψη της εξέγερσης είναι παντοτινή... 2 ΠΕΡΙΕΧΟΜΕΝΑ Σελ.3 Το πολυτεχνείο δεν τέλειωσε ποτέ Σελ.5 Η σύγχρονη κοινοβουλευτική «χούντα» Σελ.9 Χρονικό της Εξέγερσης (Τετάρτη 14/11) Σελ.10
ΤΕΧΝΙΚΟ ΕΠΙΜΕΛΗΤΗΡΙΟ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΑΝΑΤΟΛΙΚΗΣ ΚΡΗΤΗΣ
 ΤΕΧΝΙΚΟ ΕΠΙΜΕΛΗΤΗΡΙΟ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΑΝΑΤΟΛΙΚΗΣ ΚΡΗΤΗΣ ΠΡΑΚΤΙΚΑ ΕΙΔΙΚΗΣ ΣΥΝΕΔΡΙΑΣΗΣ ΤΗΣ ΑΝΤΙΠΡΟΣΩΠΕΙΑΣ ΤΟΥ Τ.Ε.Ε./Τ.Α.Κ. Στις 17-2 - 2014 ΑΝΝΑ ΚΟΝΤΟΥ ΑΠΟΜΑΓΝΗΤΟΦΩΝΗΣΕΙΣ ΠΡΑΚΤΙΚΩΝ ΔΑΚΤΥΛΟΓΡΑΦΗΣΕΙΣ-ΜΕΤΑΦΡΑΣΕΙΣ
ΤΕΧΝΙΚΟ ΕΠΙΜΕΛΗΤΗΡΙΟ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΑΝΑΤΟΛΙΚΗΣ ΚΡΗΤΗΣ ΠΡΑΚΤΙΚΑ ΕΙΔΙΚΗΣ ΣΥΝΕΔΡΙΑΣΗΣ ΤΗΣ ΑΝΤΙΠΡΟΣΩΠΕΙΑΣ ΤΟΥ Τ.Ε.Ε./Τ.Α.Κ. Στις 17-2 - 2014 ΑΝΝΑ ΚΟΝΤΟΥ ΑΠΟΜΑΓΝΗΤΟΦΩΝΗΣΕΙΣ ΠΡΑΚΤΙΚΩΝ ΔΑΚΤΥΛΟΓΡΑΦΗΣΕΙΣ-ΜΕΤΑΦΡΑΣΕΙΣ
ΤΙΜΟΛΟΓΙΟ ΜΕΛΕΤΗΣ ΕΡΓΑΣΙΩΝ ΜΕ ΤΙΜΕΣ ΜΟΝΑΔΟΣ
 ΚΤΙΡΙΑΚΕΣ ΥΠΟΔΟΜΕΣ A.E. ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΕΡΓΩΝ ΔΙΕΥΘΥΝΣΗ ΥΠΟΣΤΗΡΙΞΗΣ ΕΡΓΩΝ ΤΜΗΜΑ ΤΕΥΧΩΝ, ΔΙΑΓΩΝΙΣΜΩΝ & ΣΥΜΒΑΣΕΩΝ ΕΡΓΟ: "ΕΙΔΙΚΟ ΔΗΜΟΤΙΚΟ ΚΑΙ ΝΗΠΙΑΓΩΓΕΙΟ ΖΑΚΥΝΘΟΥ-ΟΙΚΟΔΟΜΙΚΕΣ ΕΡΓΑΣΙΕΣ & Η/Μ ΕΓ- ΚΑΤΑΣΤΑΣΕΙΣ"
ΚΤΙΡΙΑΚΕΣ ΥΠΟΔΟΜΕΣ A.E. ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΕΡΓΩΝ ΔΙΕΥΘΥΝΣΗ ΥΠΟΣΤΗΡΙΞΗΣ ΕΡΓΩΝ ΤΜΗΜΑ ΤΕΥΧΩΝ, ΔΙΑΓΩΝΙΣΜΩΝ & ΣΥΜΒΑΣΕΩΝ ΕΡΓΟ: "ΕΙΔΙΚΟ ΔΗΜΟΤΙΚΟ ΚΑΙ ΝΗΠΙΑΓΩΓΕΙΟ ΖΑΚΥΝΘΟΥ-ΟΙΚΟΔΟΜΙΚΕΣ ΕΡΓΑΣΙΕΣ & Η/Μ ΕΓ- ΚΑΤΑΣΤΑΣΕΙΣ"
Μπορούμε να πούμε ότι η δεύτερη δύναμη είναι πολύ πιο ισχυρή από την πρώτη.
 ΣΚΑΦΟΣ Η μορφή των ιστιοφόρων σκαφών όπως εξελίχθηκε από τα αρχαία ξύλινα εμπορικά και πολεμικά πλοία έως τα σύγχρονα αγωνιστικά επηρεάζονταν από τους ίδιους παράγοντες. Είναι συνάρτηση της χρήσης τους,
ΣΚΑΦΟΣ Η μορφή των ιστιοφόρων σκαφών όπως εξελίχθηκε από τα αρχαία ξύλινα εμπορικά και πολεμικά πλοία έως τα σύγχρονα αγωνιστικά επηρεάζονταν από τους ίδιους παράγοντες. Είναι συνάρτηση της χρήσης τους,
ΔΗΜΟΣ ΑΓΡΙΝΙΟΥ ΟΙΚΟΝΟΜΙΚΗ ΕΠΙΤΡΟΠΗ ΑΠΟΣΠΑΣΜΑ. Από το πρακτικό της 37ης/2012 συνεδρίασης της Οικονομικής Επιτροπής Δήμου Αγρινίου
 ΔΗΜΟΣ ΑΓΡΙΝΙΟΥ ΟΙΚΟΝΟΜΙΚΗ ΕΠΙΤΡΟΠΗ ΑΠΟΣΠΑΣΜΑ Από το πρακτικό της 7ης/01 συνεδρίασης της Οικονομικής Επιτροπής Δήμου Αγρινίου Αριθμός Απόφασης 19/01 ΘΕΜΑ: «Σύνταξη Προϋπολογισμού και Ετήσιου Προγράμματος
ΔΗΜΟΣ ΑΓΡΙΝΙΟΥ ΟΙΚΟΝΟΜΙΚΗ ΕΠΙΤΡΟΠΗ ΑΠΟΣΠΑΣΜΑ Από το πρακτικό της 7ης/01 συνεδρίασης της Οικονομικής Επιτροπής Δήμου Αγρινίου Αριθμός Απόφασης 19/01 ΘΕΜΑ: «Σύνταξη Προϋπολογισμού και Ετήσιου Προγράμματος
Αλλά να μια άσπρη γραμμή από σκόνη σημαδεύεται πάνω στο δημόσιο δρόμο στο έβγα της Παραβόλας προς τη Μαντάνισσα (Παντάνασσα). Ταυτόχρονα ήχος μοτέρ
 Μάχη της Γουρίτσας Μια διήγηση του Νίκου Ε. Σκιαδά, από το βιβλίο του «Καπετάν Επαμεινώνδας» Το πρώτο δεκαήμερο του Ιουλίου το Αρχηγείο ΕΛΑΣ Τριχωνίδας βρίσκεται στον Αη- Βλάση. Εκεί πήρε στις επτά του
Μάχη της Γουρίτσας Μια διήγηση του Νίκου Ε. Σκιαδά, από το βιβλίο του «Καπετάν Επαμεινώνδας» Το πρώτο δεκαήμερο του Ιουλίου το Αρχηγείο ΕΛΑΣ Τριχωνίδας βρίσκεται στον Αη- Βλάση. Εκεί πήρε στις επτά του
ΣΥΝΕΝΤΕΥΞΗ ΤΥΠΟΥ ΜΑΝΟΛΗ ΚΕΦΑΛΟΓΙΑΝΝΗ ΥΠΟΥΡΓΟΥ ΕΜΠΟΡΙΚΗΣ ΝΑΥΤΙΛΙΑΣ
 ΥΠΟΥΡΓΕΙΟ ΕΜΠΟΡΙΚΗΣ ΝΑΥΤΙΛΙΑΣ ΓΡΑΦΕΙΟ ΕΠΙΚΟΙΝΩΝΙΑΣ ΚΑΙ Μ.Μ.Ε. ΣΥΝΕΝΤΕΥΞΗ ΤΥΠΟΥ ΜΑΝΟΛΗ ΚΕΦΑΛΟΓΙΑΝΝΗ ΥΠΟΥΡΓΟΥ ΕΜΠΟΡΙΚΗΣ ΝΑΥΤΙΛΙΑΣ ΤΕΤΑΡΤΗ 29 ΙΟΥΝΙΟΥ 2005 ΥΠΟΥΡΓΟΣ: Πρώτον. Το ταξίδι στην Κίνα θα φέρει καρπούς
ΥΠΟΥΡΓΕΙΟ ΕΜΠΟΡΙΚΗΣ ΝΑΥΤΙΛΙΑΣ ΓΡΑΦΕΙΟ ΕΠΙΚΟΙΝΩΝΙΑΣ ΚΑΙ Μ.Μ.Ε. ΣΥΝΕΝΤΕΥΞΗ ΤΥΠΟΥ ΜΑΝΟΛΗ ΚΕΦΑΛΟΓΙΑΝΝΗ ΥΠΟΥΡΓΟΥ ΕΜΠΟΡΙΚΗΣ ΝΑΥΤΙΛΙΑΣ ΤΕΤΑΡΤΗ 29 ΙΟΥΝΙΟΥ 2005 ΥΠΟΥΡΓΟΣ: Πρώτον. Το ταξίδι στην Κίνα θα φέρει καρπούς
Ενότητα 9 ΣΧΟΛΕΙΟ. Παρουσίαση της ενότητας. Περιεχόµενα της ενότητας
 Ενότητα 9 ΣΧΟΛΕΙΟ Παρουσίαση της ενότητας Σε αυτή την ενότητα, παρακολουθούµε την Κατερίνα και τη Βασιλική, δύο µητέρες µικρών κοριτσιών, σε διαλόγους επικοινωνίας µε τη δασκάλα των παιδιών τους και άλλους
Ενότητα 9 ΣΧΟΛΕΙΟ Παρουσίαση της ενότητας Σε αυτή την ενότητα, παρακολουθούµε την Κατερίνα και τη Βασιλική, δύο µητέρες µικρών κοριτσιών, σε διαλόγους επικοινωνίας µε τη δασκάλα των παιδιών τους και άλλους
ενώ πλέον είχαμε μπει στην πέμπτη δεκαετία από την απελευθέρωση της Θεσσαλονίκης, δεν βρέθηκε κάποιος να σηκώσει στην πλάτη του την χρόνια αυτή
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης, Παρασκευή 9 Μαίου 2014, ομιλία με αφορμή την τελετή των αποκαλυπτηρίων γλυπτού στη μνήμη των Εβραίων που εξοντώθηκαν στο Ολοκαύτωμα Θεσσαλονίκη, Οκτώβριος του 65.
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης, Παρασκευή 9 Μαίου 2014, ομιλία με αφορμή την τελετή των αποκαλυπτηρίων γλυπτού στη μνήμη των Εβραίων που εξοντώθηκαν στο Ολοκαύτωμα Θεσσαλονίκη, Οκτώβριος του 65.
ΣτΕ 4531/2009 Θέμα : [Νόμιμη απόρριψη αίτησης για οριοθέτηση ρέματος]
![ΣτΕ 4531/2009 Θέμα : [Νόμιμη απόρριψη αίτησης για οριοθέτηση ρέματος] ΣτΕ 4531/2009 Θέμα : [Νόμιμη απόρριψη αίτησης για οριοθέτηση ρέματος]](/thumbs/33/15841141.jpg) ΣτΕ 4531/2009 Θέμα : [Νόμιμη απόρριψη αίτησης για οριοθέτηση ρέματος] Περίληψη : Σκοπός της οριοθέτησης (μη πλεύσιμου) ποταμού ή του ρέματος, είναι η αποτύπωση της φυσικής κοίτης του ενόψει του χαρακτήρα
ΣτΕ 4531/2009 Θέμα : [Νόμιμη απόρριψη αίτησης για οριοθέτηση ρέματος] Περίληψη : Σκοπός της οριοθέτησης (μη πλεύσιμου) ποταμού ή του ρέματος, είναι η αποτύπωση της φυσικής κοίτης του ενόψει του χαρακτήρα
ΙΣΤΟΡΙΚΟ ΛΕΞΙΚΟ ΕΠΙΣΤΗΜΟΝΙΚΩΝ ΟΡΩΝ
 ΕΙΣΑΓΩΓΗ Γενικά Δεν υπάρχει αμφιβολία ότι θεμελιώδης αρχή της επιστήμης είναι η πίστη στην ύπαρξη ενός αντικειμενικού κόσμου ανεξάρτητου από το υποκείμενο (τον άνθρωπο) που επιδιώκει κάθε φορά την ερμηνεία
ΕΙΣΑΓΩΓΗ Γενικά Δεν υπάρχει αμφιβολία ότι θεμελιώδης αρχή της επιστήμης είναι η πίστη στην ύπαρξη ενός αντικειμενικού κόσμου ανεξάρτητου από το υποκείμενο (τον άνθρωπο) που επιδιώκει κάθε φορά την ερμηνεία
Σ Υ Λ Λ Ο Γ Ο Σ Ε Λ Λ Η Ν Ω Ν Α Ρ Χ Α Ι Ο Λ Ο Γ Ω Ν
 Σ Υ Λ Λ Ο Γ Ο Σ Ε Λ Λ Η Ν Ω Ν Α Ρ Χ Α Ι Ο Λ Ο Γ Ω Ν Ερμού 134-136, 105 53 Αθήνα - τηλ.-fax: 210 32 52 214, 6937075765. www.sea.org.gr Αθήνα, 11/2/2015 Αρ. Πρωτ.: 97 Προς: τον κ. Νικόλαο Ξυδάκη, Αναπληρωτή
Σ Υ Λ Λ Ο Γ Ο Σ Ε Λ Λ Η Ν Ω Ν Α Ρ Χ Α Ι Ο Λ Ο Γ Ω Ν Ερμού 134-136, 105 53 Αθήνα - τηλ.-fax: 210 32 52 214, 6937075765. www.sea.org.gr Αθήνα, 11/2/2015 Αρ. Πρωτ.: 97 Προς: τον κ. Νικόλαο Ξυδάκη, Αναπληρωτή
Στον Πανούλη. Γιάννης
 Στον Πανούλη Γιάννης Φίλη μαθήτρια, φίλε μαθητή, Στο βιβλίο δόθηκε ιδιαίτερη έμφαση στη μεθοδολογία αντιμετώπισης των θεμάτων που καλύπτουν την προς εξέταση ύλη. Αυτό επιτυγχάνεται με την επίλυση και τον
Στον Πανούλη Γιάννης Φίλη μαθήτρια, φίλε μαθητή, Στο βιβλίο δόθηκε ιδιαίτερη έμφαση στη μεθοδολογία αντιμετώπισης των θεμάτων που καλύπτουν την προς εξέταση ύλη. Αυτό επιτυγχάνεται με την επίλυση και τον
ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ. «Η ΟΡΓΑΝΩΣΕ ΤΟΥ ΤΜΙΙΜΑΤΟΣ ΠΡΟΜΗΘΕΙΩΝ ΣΕ ΜΙΑ ΕΠΙΧΕΙΡΗΣΗ i
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΑΒΑΛΑΣ ΣΧΟΛΗ: ΔΙΟΙΚΗΣΗΣ* ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ «Η ΟΡΓΑΝΩΣΕ ΤΟΥ ΤΜΙΙΜΑΤΟΣ ΠΡΟΜΗΘΕΙΩΝ ΣΕ ΜΙΑ ΕΠΙΧΕΙΡΗΣΗ i ΚΑΘΗΓΗΤΗΣ ΠΙΠ1ΛΙΑΓΚΟΠΟΥΑΟΣ ΜΙΧΑΑΗΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΑΒΑΛΑΣ ΣΧΟΛΗ: ΔΙΟΙΚΗΣΗΣ* ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ: ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ «Η ΟΡΓΑΝΩΣΕ ΤΟΥ ΤΜΙΙΜΑΤΟΣ ΠΡΟΜΗΘΕΙΩΝ ΣΕ ΜΙΑ ΕΠΙΧΕΙΡΗΣΗ i ΚΑΘΗΓΗΤΗΣ ΠΙΠ1ΛΙΑΓΚΟΠΟΥΑΟΣ ΜΙΧΑΑΗΣ
Οδηγία της ΕΟΚ για τη διατήρηση των φυσικών οικοτόπων και της άγριας πανίδας και αυτοφυούς χλωρίδας ΣΕΠΤΕΜΒΡΙΟΣ - ΟΚΤΩΒΡΙΟΣ 1993 ΘΕΣΣΑΛΟΝΙΚΗ ΤΕΥΧΟΣ 3
 φ ΔΙΜΗΝΙΑΙΑ ΕΚΔΟΣΗ ΤΟΥ ΕΛΛΗΝΙΚΟΥ ΚΕΝΤΡΟΥ ΒΙΟΤΟΠΩΝ-ΥΓΡΟΤΟΠΩΝ ΘΕΣΣΑΛΟΝΙΚΗ ΣΕΠΤΕΜΒΡΙΟΣ - ΟΚΤΩΒΡΙΟΣ 1993 ΤΕΥΧΟΣ 3 ΔΡΧ. 10 Η Οδηγία για το υ ς Ο ικοτύπους, πρόκληση για πρόοδο στη διατήρηση τη ς φύσης. Η εφ
φ ΔΙΜΗΝΙΑΙΑ ΕΚΔΟΣΗ ΤΟΥ ΕΛΛΗΝΙΚΟΥ ΚΕΝΤΡΟΥ ΒΙΟΤΟΠΩΝ-ΥΓΡΟΤΟΠΩΝ ΘΕΣΣΑΛΟΝΙΚΗ ΣΕΠΤΕΜΒΡΙΟΣ - ΟΚΤΩΒΡΙΟΣ 1993 ΤΕΥΧΟΣ 3 ΔΡΧ. 10 Η Οδηγία για το υ ς Ο ικοτύπους, πρόκληση για πρόοδο στη διατήρηση τη ς φύσης. Η εφ
Διπλωματική Εργασία του φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών της Πολυτεχνικής Σχολής του Πανεπιστημίου Πατρών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΕΡΓΑΣΤΗΡΙΟ Συστημάτων και Μετρήσεων (Γενικής Ηλεκτροτεχνίας) Διπλωματική Εργασία του φοιτητή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΕΡΓΑΣΤΗΡΙΟ Συστημάτων και Μετρήσεων (Γενικής Ηλεκτροτεχνίας) Διπλωματική Εργασία του φοιτητή
(μαθητική εργασία στη Νεοελληνική Γλώσσα από το τμήμα Β3 του Γυμνασίου) zxcvbnmσγqwφertyuioσδφpγρaηsόρ. [σχολικό έτος 2013-2014]
![(μαθητική εργασία στη Νεοελληνική Γλώσσα από το τμήμα Β3 του Γυμνασίου) zxcvbnmσγqwφertyuioσδφpγρaηsόρ. [σχολικό έτος 2013-2014] (μαθητική εργασία στη Νεοελληνική Γλώσσα από το τμήμα Β3 του Γυμνασίου) zxcvbnmσγqwφertyuioσδφpγρaηsόρ. [σχολικό έτος 2013-2014]](/thumbs/39/18898625.jpg) qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj «Ο ΤΟΠΟΣ ΜΑΣ,, Ο ΜΥΛΟΠΟΤΑΜΟΣ» klzxcvλοπbnαmqwertyuiopasdfghjkl (μαθητική
qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj «Ο ΤΟΠΟΣ ΜΑΣ,, Ο ΜΥΛΟΠΟΤΑΜΟΣ» klzxcvλοπbnαmqwertyuiopasdfghjkl (μαθητική
ΑΝΑΠΛΑΣΗ ΣΥΝΕΚΤΙΚΟΥ ΤΜΗΜΑΤΟΣ ΚΑΤΩ ΖΑΡΟΥ ΟΙΚΙΣΜΟΥ ΖΑΡΟΥ ΔΗΜΟΥ ΦΑΙΣΤΟΥ ΤΙΜΟΛΟΓΙΟ ΜΕΛΕΤΗΣ
 Ε Λ Λ Η Ν Ι Κ Η Δ Η Μ Ο Κ Ρ Α Τ Ι Α Ν Ο Μ Ο Σ Η Ρ Α Κ Λ Ε Ι Ο Υ Δ Η Μ Ο Σ Φ Α Ι Σ Τ Ο Υ ΑΝΑΠΛΑΣΗ ΣΥΝΕΚΤΙΚΟΥ ΤΜΗΜΑΤΟΣ ΚΑΤΩ ΖΑΡΟΥ ΟΙΚΙΣΜΟΥ ΖΑΡΟΥ ΔΗΜΟΥ ΦΑΙΣΤΟΥ ΤΙΜΟΛΟΓΙΟ ΜΕΛΕΤΗΣ ΗΡΑΚΛΕΙΟ 2011 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ
Ε Λ Λ Η Ν Ι Κ Η Δ Η Μ Ο Κ Ρ Α Τ Ι Α Ν Ο Μ Ο Σ Η Ρ Α Κ Λ Ε Ι Ο Υ Δ Η Μ Ο Σ Φ Α Ι Σ Τ Ο Υ ΑΝΑΠΛΑΣΗ ΣΥΝΕΚΤΙΚΟΥ ΤΜΗΜΑΤΟΣ ΚΑΤΩ ΖΑΡΟΥ ΟΙΚΙΣΜΟΥ ΖΑΡΟΥ ΔΗΜΟΥ ΦΑΙΣΤΟΥ ΤΙΜΟΛΟΓΙΟ ΜΕΛΕΤΗΣ ΗΡΑΚΛΕΙΟ 2011 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ
Έκθεση Εσωτερικής Αξιολόγησης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΠΟΛΙΤΙΣΜΙΚΩΝ ΣΠΟΥΔΩΝ Τμήμα Φιλολογίας Έκθεση Εσωτερικής Αξιολόγησης Πανεπιστήμιο Πελοποννήσου Σχολή Ανθρωπιστικών Επιστημών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΠΟΛΙΤΙΣΜΙΚΩΝ ΣΠΟΥΔΩΝ Τμήμα Φιλολογίας Έκθεση Εσωτερικής Αξιολόγησης Πανεπιστήμιο Πελοποννήσου Σχολή Ανθρωπιστικών Επιστημών
Η οικονομική κρίση και ύφεση ανασχεθούν δεν θα αποφύγει να μετεξελιχθεί οι προοπτικές της ευρω- ζώνης αναιμικές η Ευρώπη Κινητήρια δύναμη
 Σύνοψη συμπερασμάτων Η οικονομική κρίση και ύφεση σε συνδυασμό με τα προβλήματα που έχουν προκληθεί από τις ασκούμενες πολιτικές της εσωτερικής υποτίμησης, ιδιαίτερα, στον Νότο, θέτει τις ευρωπαϊκές ελίτ,
Σύνοψη συμπερασμάτων Η οικονομική κρίση και ύφεση σε συνδυασμό με τα προβλήματα που έχουν προκληθεί από τις ασκούμενες πολιτικές της εσωτερικής υποτίμησης, ιδιαίτερα, στον Νότο, θέτει τις ευρωπαϊκές ελίτ,
ΔΕΗ Ανανεώσιμες: Το μέλλον της ΔΕΗ Ομιλία του κ. Τάκη Αθανασόπουλου Προέδρου & Διευθύνοντος Συμβούλου ΔΕΗ Α.Ε. 6-11-2008
 ΔΕΗ Ανανεώσιμες: Το μέλλον της ΔΕΗ Ομιλία του κ. Τάκη Αθανασόπουλου Προέδρου & Διευθύνοντος Συμβούλου ΔΕΗ Α.Ε. 6-11-2008 Αγαπητοί εκπρόσωποι των Μέσων Μαζικής Ενημέρωσης, Αγαπητοί συνάδελφοι, Θα ήθελα
ΔΕΗ Ανανεώσιμες: Το μέλλον της ΔΕΗ Ομιλία του κ. Τάκη Αθανασόπουλου Προέδρου & Διευθύνοντος Συμβούλου ΔΕΗ Α.Ε. 6-11-2008 Αγαπητοί εκπρόσωποι των Μέσων Μαζικής Ενημέρωσης, Αγαπητοί συνάδελφοι, Θα ήθελα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΦΥΠΟΥΡΓΟΣ ΠΑΡΑ ΤΩ ΠΡΩΘΥΠΟΥΡΓΩ ΚΥΒΕΡΝΗΤΙΚΗ ΕΚΠΡΟΣΩΠΟΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΦΥΠΟΥΡΓΟΣ ΠΑΡΑ ΤΩ ΠΡΩΘΥΠΟΥΡΓΩ ΚΥΒΕΡΝΗΤΙΚΗ ΕΚΠΡΟΣΩΠΟΣ ΚΟΙΝΗ ΣΥΝΕΝΤΕΥΞΗ ΤΥΠΟΥ ΤΟΥ ΥΠΟΥΡΓΟΥ ΕΡΓΑΣΙΑΣ, ΚΟΙΝΩΝΙΚΗΣ ΑΣΦΑΛΙΣΗΣ & ΚΟΙΝΩΝΙΚΗΣ ΑΛΛΗΛΕΓΓΥΗΣ ΓΙΩΡΓΟΥ ΚΑΤΡΟΥΓΚΑΛΟΥ, ΤΟΥ ΑΝΑΠΛΗΡΩΤΗ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΦΥΠΟΥΡΓΟΣ ΠΑΡΑ ΤΩ ΠΡΩΘΥΠΟΥΡΓΩ ΚΥΒΕΡΝΗΤΙΚΗ ΕΚΠΡΟΣΩΠΟΣ ΚΟΙΝΗ ΣΥΝΕΝΤΕΥΞΗ ΤΥΠΟΥ ΤΟΥ ΥΠΟΥΡΓΟΥ ΕΡΓΑΣΙΑΣ, ΚΟΙΝΩΝΙΚΗΣ ΑΣΦΑΛΙΣΗΣ & ΚΟΙΝΩΝΙΚΗΣ ΑΛΛΗΛΕΓΓΥΗΣ ΓΙΩΡΓΟΥ ΚΑΤΡΟΥΓΚΑΛΟΥ, ΤΟΥ ΑΝΑΠΛΗΡΩΤΗ
ΜΕΡΟΣ Α ΒΙΒΛΙΟ ΕΡΓΑΣΙΩΝ ΟΝΟΜΑ.. ΤΑΞΗ...
 941205 ΜΕΡΟΣ Α ΒΙΒΛΙΟ ΕΡΓΑΣΙΩΝ ΟΝΟΜΑ.. ΤΑΞΗ... 2 ΔΙΕΡΕΥΝΗΤΙΚΗ ΜΑΘΗΣΗ ΦΥΛΛΑ ΕΡΓΑΣΙΩΝ ΓΙΑ ΜΑΘΗΤΕΣ ΕΡΕΥΝΩΝΤΑΣ ΤΗΝ ΠΥΚΝΟΤΗΤΑ ΠΕΡΙΕΧΟΜΕΝΑ Έρευνα Σελίδα 1. Γιατί τα αντικείμενα επιπλέουν ή βυθίζονται; 2 Πίνακας
941205 ΜΕΡΟΣ Α ΒΙΒΛΙΟ ΕΡΓΑΣΙΩΝ ΟΝΟΜΑ.. ΤΑΞΗ... 2 ΔΙΕΡΕΥΝΗΤΙΚΗ ΜΑΘΗΣΗ ΦΥΛΛΑ ΕΡΓΑΣΙΩΝ ΓΙΑ ΜΑΘΗΤΕΣ ΕΡΕΥΝΩΝΤΑΣ ΤΗΝ ΠΥΚΝΟΤΗΤΑ ΠΕΡΙΕΧΟΜΕΝΑ Έρευνα Σελίδα 1. Γιατί τα αντικείμενα επιπλέουν ή βυθίζονται; 2 Πίνακας
ΤΟ ΤΑΞΙΔΙ ΕΙΝΑΙ Η ΑΦΟΡΜΗ
 ΤΟ ΤΑΞΙΔΙ ΕΙΝΑΙ Η ΑΦΟΡΜΗ Το ταξίδι δίνει νόημα στην ζωή μας ή η αισθανόμαστε πως με το ταξίδι αποκτά νόημα η ζωή μας; Ο εξωτερικός κόσμος δίνει νόημα στην ζωή μας ή εμείς χρησιμοποιούμε τα στοιχεία του
ΤΟ ΤΑΞΙΔΙ ΕΙΝΑΙ Η ΑΦΟΡΜΗ Το ταξίδι δίνει νόημα στην ζωή μας ή η αισθανόμαστε πως με το ταξίδι αποκτά νόημα η ζωή μας; Ο εξωτερικός κόσμος δίνει νόημα στην ζωή μας ή εμείς χρησιμοποιούμε τα στοιχεία του
Από τα σπορ στην καθημερινή ζωή. Όλοι διαφορετικοί, όλοι ίσοι.
 Εφαρμογή Προγραμμάτων που προωθούν την Ισότητα στην Κοινωνία - ΚΑΛΛΙΠΑΤΕΙΡΑ Από τα σπορ στην καθημερινή ζωή. Όλοι διαφορετικοί, όλοι ίσοι. ΤΕΤΡΑΔΙΟ ΔΡΑΣΤΗΡΙΟΤΗΤΩΝ (Δ', Ε, ΣΤ' Δημοτικού) ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ
Εφαρμογή Προγραμμάτων που προωθούν την Ισότητα στην Κοινωνία - ΚΑΛΛΙΠΑΤΕΙΡΑ Από τα σπορ στην καθημερινή ζωή. Όλοι διαφορετικοί, όλοι ίσοι. ΤΕΤΡΑΔΙΟ ΔΡΑΣΤΗΡΙΟΤΗΤΩΝ (Δ', Ε, ΣΤ' Δημοτικού) ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ
ΕΚΘΕΣΗ ΔΙΕΡΕΥΝΗΣΗΣ ΚΑΙ ΑΞΙΟΛΟΓΗΣΗΣ ΕΝΑΛΛΑΚΤΙΚΩΝ ΓΙΑ ΤΗΝ ΧΩΡΟΘΕΤΗΣΗ ΔΙΚΑΣΤΙΚΟΥ ΜΕΓΑΡΟΥ ΒΟΛΟΥ
 ΕΚΘΕΣΗ ΔΙΕΡΕΥΝΗΣΗΣ ΚΑΙ ΑΞΙΟΛΟΓΗΣΗΣ ΕΝΑΛΛΑΚΤΙΚΩΝ ΛΥΣΕΩΝ ΓΙΑ ΤΗΝ ΧΩΡΟΘΕΤΗΣΗ ΔΙΚΑΣΤΙΚΟΥ ΜΕΓΑΡΟΥ ΒΟΛΟΥ Ιανουάριος 2014 ΟΜΑΔΑ ΕΡΓΑΣΙΑΣ Κωνσταντίνος Λαλένης, Αναπληρωτής καθηγητής, Τμ. Χωροταξίας, Πολεοδομίας
ΕΚΘΕΣΗ ΔΙΕΡΕΥΝΗΣΗΣ ΚΑΙ ΑΞΙΟΛΟΓΗΣΗΣ ΕΝΑΛΛΑΚΤΙΚΩΝ ΛΥΣΕΩΝ ΓΙΑ ΤΗΝ ΧΩΡΟΘΕΤΗΣΗ ΔΙΚΑΣΤΙΚΟΥ ΜΕΓΑΡΟΥ ΒΟΛΟΥ Ιανουάριος 2014 ΟΜΑΔΑ ΕΡΓΑΣΙΑΣ Κωνσταντίνος Λαλένης, Αναπληρωτής καθηγητής, Τμ. Χωροταξίας, Πολεοδομίας
ΤΑ ΕΡΓΑΤΙΚΑ ΑΤΥΧΗΜΑΤΑ ΣΤΗΝ ΕΛΛΑΔΑ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΓΕΝΙΚΟ ΤΜΗΜΑ-ΤΟΜΕΑΣ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΚΑΙΟΥ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΔΙΚΑΙΟΥ ΚΑΙ ΤΕΧΝΙΚΗΣ ΝΟΜΟΘΕΣΙΑΣ ΤΑ ΕΡΓΑΤΙΚΑ ΑΤΥΧΗΜΑΤΑ ΣΤΗΝ ΕΛΛΑΔΑ ΔΙΠΛΩΜΑΤΙΚΗ ΚΑΤΣΙΛΙΔΗΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΓΕΝΙΚΟ ΤΜΗΜΑ-ΤΟΜΕΑΣ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΚΑΙΟΥ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΔΙΚΑΙΟΥ ΚΑΙ ΤΕΧΝΙΚΗΣ ΝΟΜΟΘΕΣΙΑΣ ΤΑ ΕΡΓΑΤΙΚΑ ΑΤΥΧΗΜΑΤΑ ΣΤΗΝ ΕΛΛΑΔΑ ΔΙΠΛΩΜΑΤΙΚΗ ΚΑΤΣΙΛΙΔΗΣ
Ευαγγελινή Αθανασοπούλου Κωνσταντία Λαδοπούλου Στέλλα Χαριτάκη
 Κώδικας Δεοντολογίας Κώδικας Δεοντολογίας της Παιδοψυχιατρικής Εταιρείας Ελλάδος- Ένωσης Ψυχιάτρων Παιδιών και Εφήβων ΑΘΗΝΑ, 2009 Διοικητικό Συμβούλιο της Π.Ε.Ε. ΕΝΩ.ΨΥ.ΠΕ Πρόεδρος: Δημήτριος Γεωργιάδης
Κώδικας Δεοντολογίας Κώδικας Δεοντολογίας της Παιδοψυχιατρικής Εταιρείας Ελλάδος- Ένωσης Ψυχιάτρων Παιδιών και Εφήβων ΑΘΗΝΑ, 2009 Διοικητικό Συμβούλιο της Π.Ε.Ε. ΕΝΩ.ΨΥ.ΠΕ Πρόεδρος: Δημήτριος Γεωργιάδης
ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΤΕΙ ΣΕΡΡΩΝ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ
 ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΤΕΙ ΣΕΡΡΩΝ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ Υπολογισμός Φόρου για την Ατομική Επιχείρηση, Ομόρρυθμη Εταιρεία, Ετερόρρυθμη Εταιρεία, Κοινωνία Κληρονομικού
ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΤΕΙ ΣΕΡΡΩΝ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ Υπολογισμός Φόρου για την Ατομική Επιχείρηση, Ομόρρυθμη Εταιρεία, Ετερόρρυθμη Εταιρεία, Κοινωνία Κληρονομικού
Εξαρθρώθηκε κύκλωμα διαρρηκτών στη Φλώρινα
 ΕΤΟΣ 2o ΑΡ. ΦΥΛΛΟΥ 55 ΤΕΤΑΡΤΗ 10 ΦΕΒΡΟΥΑΡΙΟΥ 2010 ΤΙΜΗ ΦΥΛΛΟΥ 1,00 ΕΥΡΩ Η ηχώ σας εύχεται καλή Σαρακοστή! Εξαρθρώθηκε κύκλωμα διαρρηκτών στη Φλώρινα Υπογραφή Συμφωνίας ΔΕΥΑΦ & Θερμοϋδραυλικών για δωρεάν
ΕΤΟΣ 2o ΑΡ. ΦΥΛΛΟΥ 55 ΤΕΤΑΡΤΗ 10 ΦΕΒΡΟΥΑΡΙΟΥ 2010 ΤΙΜΗ ΦΥΛΛΟΥ 1,00 ΕΥΡΩ Η ηχώ σας εύχεται καλή Σαρακοστή! Εξαρθρώθηκε κύκλωμα διαρρηκτών στη Φλώρινα Υπογραφή Συμφωνίας ΔΕΥΑΦ & Θερμοϋδραυλικών για δωρεάν
ΘΕΜΑ: «Συζήτηση και λήψη αποφάσεων για τη διαθεσιμότητα υπαλλήλων, περικοπή πόρων, και δημιουργία Παρατηρητηρίου στον Δήμο μας».
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΠΡΕΒΕΖΑΣ ΔΗΜΟΣ ΠΡΕΒΕΖΑΣ ΑΥΤΟΤΕΛΕΣ ΓΡΑΦΕΙΟ ΥΠΟΣΤΗΡΙΞΗΣ ΑΙΡΕΤΩΝ ΟΡΓΑΝΩΝ ΓΡΑΜΜΑΤΕΙΑ ΔΗΜΟΤΙΚΟΥ ΣΥΜΒΟΥΛΙΟΥ Α Π Ο Σ Π Α Σ Μ Α Από το πρακτικό 17/2012 ΚΑΤΕΠΕΙΓΟΥΣΑΣ Συνεδρίασης ΔΗΜΟΤΙΚΟΥ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΠΡΕΒΕΖΑΣ ΔΗΜΟΣ ΠΡΕΒΕΖΑΣ ΑΥΤΟΤΕΛΕΣ ΓΡΑΦΕΙΟ ΥΠΟΣΤΗΡΙΞΗΣ ΑΙΡΕΤΩΝ ΟΡΓΑΝΩΝ ΓΡΑΜΜΑΤΕΙΑ ΔΗΜΟΤΙΚΟΥ ΣΥΜΒΟΥΛΙΟΥ Α Π Ο Σ Π Α Σ Μ Α Από το πρακτικό 17/2012 ΚΑΤΕΠΕΙΓΟΥΣΑΣ Συνεδρίασης ΔΗΜΟΤΙΚΟΥ
Από τον "Μύθο του Σίσυφου", μτφ. Βαγγέλη Χατζηδημητρίου, εκδόσεις Μπουκουμάνη, Αθήνα 1973.
 Αλμπέρ Καμύ Η ελπίδα και το Παράλογο στο έργο του Φραντς Κάφκα Από τον "Μύθο του Σίσυφου", μτφ. Βαγγέλη Χατζηδημητρίου, εκδόσεις Μπουκουμάνη, Αθήνα 1973. Ο Κάφκα σε υποχρεώνει να τον ξαναδιαβάσεις. Κι
Αλμπέρ Καμύ Η ελπίδα και το Παράλογο στο έργο του Φραντς Κάφκα Από τον "Μύθο του Σίσυφου", μτφ. Βαγγέλη Χατζηδημητρίου, εκδόσεις Μπουκουμάνη, Αθήνα 1973. Ο Κάφκα σε υποχρεώνει να τον ξαναδιαβάσεις. Κι
ΚΑΤΑΣΤΑΤΙΚΟ ΕΤΑΙΡΕΙΑ ΠΟΛΙΤΙΣΤΙΚΗΣ ΚΛΗΡΟΝΟΜΙΑΣ ΚΑΤΩΚΟΠΙΑΣ (KATOKOPIA CULTURAL HERITAGE ASSOCIATION)
 ΚΑΤΑΣΤΑΤΙΚΟ ΕΤΑΙΡΕΙΑ ΠΟΛΙΤΙΣΤΙΚΗΣ ΚΛΗΡΟΝΟΜΙΑΣ ΚΑΤΩΚΟΠΙΑΣ (KATOKOPIA CULTURAL HERITAGE ASSOCIATION) Άρθρο 1. ΕΠΩΝΥΜΙΑ Όνομα: ΕΤΑΙΡΕΙΑ ΠΟΛΙΤΙΣΤΙΚΗΣ ΚΛΗΡΟΝΟΜΙΑΣ ΚΑΤΩΚΟΠΙΑΣ Έδρα: ΛΕΥΚΩΣΙΑ Έτος Ίδρυσης: 2008
ΚΑΤΑΣΤΑΤΙΚΟ ΕΤΑΙΡΕΙΑ ΠΟΛΙΤΙΣΤΙΚΗΣ ΚΛΗΡΟΝΟΜΙΑΣ ΚΑΤΩΚΟΠΙΑΣ (KATOKOPIA CULTURAL HERITAGE ASSOCIATION) Άρθρο 1. ΕΠΩΝΥΜΙΑ Όνομα: ΕΤΑΙΡΕΙΑ ΠΟΛΙΤΙΣΤΙΚΗΣ ΚΛΗΡΟΝΟΜΙΑΣ ΚΑΤΩΚΟΠΙΑΣ Έδρα: ΛΕΥΚΩΣΙΑ Έτος Ίδρυσης: 2008
Α Π Ο Σ Π Α Σ Μ Α Από το πρακτικό 23/2013 Συνεδρίασης ΔΗΜΟΤΙΚΟΥ ΣΥΜΒΟΥΛΙΟΥ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΠΡΕΒΕΖΑΣ ΔΗΜΟΣ ΠΡΕΒΕΖΑΣ ΔΙΕΥΘΥΝΣΗ ΔΙΟΙΚΗΤΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΥΠΟΣΤΗΡΙΞΗΣ ΑΙΡΕΤΩΝ ΟΡΓΑΝΩΝ ΑΔΑ: ΒΙΕΟΩΞΧ-56Θ Α Π Ο Σ Π Α Σ Μ Α Από το πρακτικό 23/2013 Συνεδρίασης ΔΗΜΟΤΙΚΟΥ ΣΥΜΒΟΥΛΙΟΥ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΠΡΕΒΕΖΑΣ ΔΗΜΟΣ ΠΡΕΒΕΖΑΣ ΔΙΕΥΘΥΝΣΗ ΔΙΟΙΚΗΤΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΥΠΟΣΤΗΡΙΞΗΣ ΑΙΡΕΤΩΝ ΟΡΓΑΝΩΝ ΑΔΑ: ΒΙΕΟΩΞΧ-56Θ Α Π Ο Σ Π Α Σ Μ Α Από το πρακτικό 23/2013 Συνεδρίασης ΔΗΜΟΤΙΚΟΥ ΣΥΜΒΟΥΛΙΟΥ
ΤΑ ΕΘΝΟΜΑΘΗΜΑΤΙΚΑ ΚΑΙ Η ΔΙΔΑΣΚΑΛΙΑ ΜΟΤΙΒΩΝ: ΜΙΑ ΕΡΕΥΝΗΤΙΚΗ ΜΕΛΕΤΗ ΣΕ ΜΑΘΗΤΕΣ Ε ΤΑΞΗΣ
 45. Μιχαήλ, Μ., Λεμονίδης, Χ., (2007). Τα εθνομαθηματικά και η διδασκαλία μοτίβων: μια ερευνητική μελέτη σε μαθητές Ε τάξης. Πρακτικά 9 ου Παγκύπριου Συνεδρίου Μαθηματικής Παιδείας και Επιστήμης, Πάφος
45. Μιχαήλ, Μ., Λεμονίδης, Χ., (2007). Τα εθνομαθηματικά και η διδασκαλία μοτίβων: μια ερευνητική μελέτη σε μαθητές Ε τάξης. Πρακτικά 9 ου Παγκύπριου Συνεδρίου Μαθηματικής Παιδείας και Επιστήμης, Πάφος
ΕΠΙΣΗΜΗ ΕΦΗΜΕΡΙΔΑ ΤΗΣ ΚΥΠΡΙΑΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΚΥΡΙΟ ΜΕΡΟΣ ΤΜΗΜΑ Α
 ΕΠΙΣΗΜΗ ΕΦΗΜΕΡΙΔΑ ΤΗΣ ΚΥΠΡΙΑΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΚΥΡΙΟ ΜΕΡΟΣ ΤΜΗΜΑ Α Αριθμός 4695 Παρασκευή, 17 Μαΐου 2013 385 Αριθμός 301 ΔΙΟΡΙΣΜΟΣ ΔΙΚΑΣΤΗ ΤΟΥ ΑΝΩΤΑΤΟΥ ΔΙΚΑΣΤΗΡΙΟΥ Ο Πρόεδρος της Δημοκρατίας κ. Νίκος Αναστασιάδης,
ΕΠΙΣΗΜΗ ΕΦΗΜΕΡΙΔΑ ΤΗΣ ΚΥΠΡΙΑΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΚΥΡΙΟ ΜΕΡΟΣ ΤΜΗΜΑ Α Αριθμός 4695 Παρασκευή, 17 Μαΐου 2013 385 Αριθμός 301 ΔΙΟΡΙΣΜΟΣ ΔΙΚΑΣΤΗ ΤΟΥ ΑΝΩΤΑΤΟΥ ΔΙΚΑΣΤΗΡΙΟΥ Ο Πρόεδρος της Δημοκρατίας κ. Νίκος Αναστασιάδης,
Παρράσιο Πάρκο Πολιτιστικής Κληρονομιάς: Σχέδιο της Πρότασης
 Παρράσιο Πάρκο Πολιτιστικής Κληρονομιάς: Σχέδιο της Πρότασης Ο στόχος του παρόντος φυλλαδίου είναι να δώσει τις κατευθυντήριες γραμμές για τη δημιουργία και τη διαχείριση του Παρράσιου Πάρκου Πολιτιστικής
Παρράσιο Πάρκο Πολιτιστικής Κληρονομιάς: Σχέδιο της Πρότασης Ο στόχος του παρόντος φυλλαδίου είναι να δώσει τις κατευθυντήριες γραμμές για τη δημιουργία και τη διαχείριση του Παρράσιου Πάρκου Πολιτιστικής
ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ
 20129 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΠΕΡΙΕΧΟΜΕΝΑ ΑΠΟΦΑΣΕΙΣ Καθορισμός δικαιολογητικών και τρόπου πληρω μής των οικονομικών ενισχύσεων που προβλέ πονται στην υπ αριθμ. 47121/1.8.2006
20129 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΠΕΡΙΕΧΟΜΕΝΑ ΑΠΟΦΑΣΕΙΣ Καθορισμός δικαιολογητικών και τρόπου πληρω μής των οικονομικών ενισχύσεων που προβλέ πονται στην υπ αριθμ. 47121/1.8.2006
Πρόταση Διδακτικής για την Ενότητα. «Τα φύλα στη Λογοτεχνία» Εισήγηση. στο Σεμινάριο Φιλολόγων Νομού Φθιώτιδας 13/11/2012
 Πρόταση Διδακτικής για την Ενότητα «Τα φύλα στη Λογοτεχνία» Εισήγηση στο Σεμινάριο Φιλολόγων Νομού Φθιώτιδας 13/11/2012 Συνεδριακό Κέντρο Δήμου Λαμιέων Δρ Καλλιόπη Πολυμέρου Σχολική Σύμβουλος Φιλολόγων
Πρόταση Διδακτικής για την Ενότητα «Τα φύλα στη Λογοτεχνία» Εισήγηση στο Σεμινάριο Φιλολόγων Νομού Φθιώτιδας 13/11/2012 Συνεδριακό Κέντρο Δήμου Λαμιέων Δρ Καλλιόπη Πολυμέρου Σχολική Σύμβουλος Φιλολόγων
ΕΦΗΜΕΡΙΣΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ
 01001501507970024 6279 ΕΦΗΜΕΡΙΣΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣΕΛΛΗΝΙΚΗΣΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΠΡΩΤΟ Αρ. Φύλλου 150 15 Ιουλίου 1997 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΕΔΡΙΚΑ ΔΙΑΤΑΓΜΑΤΑ 174. Τροποποίηση π.δ. 186/95 "Προστασίατων εργαζομένων
01001501507970024 6279 ΕΦΗΜΕΡΙΣΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣΕΛΛΗΝΙΚΗΣΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΠΡΩΤΟ Αρ. Φύλλου 150 15 Ιουλίου 1997 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΕΔΡΙΚΑ ΔΙΑΤΑΓΜΑΤΑ 174. Τροποποίηση π.δ. 186/95 "Προστασίατων εργαζομένων
ΣΥΝΕΝΤΕΥΞΗ -Αρθρο ΠΡΕΣΒΗ ( ΕΠΙ ΤΙΜΗ) ΑΛΕΞΑΝΔΡΟΥ ΜΑΛΛΙΑ,
 ΣΥΝΕΝΤΕΥΞΗ -Αρθρο ΠΡΕΣΒΗ ( ΕΠΙ ΤΙΜΗ) ΑΛΕΞΑΝΔΡΟΥ ΜΑΛΛΙΑ, ΕΙΔΙΚΟΥ ΣΥΜΒΟΥΛΟΥ ΤΟΥ ΕΛΙΑΜΕΠ ΠΡΩΤΟΥ ΕΠΙΚΕΦΑΛΗΣ ΤΟΥ ΓΡΑΦΕΙΟΥ ΣΥΝΔΕΣΜΟΥ ΤΗΣ ΕΛΛΑΔΟΣ ΣΤΑ ΣΚΟΠΙΑ ( 1995-1999).ΠΡΩΗΝ ΠΡΕΣΒΗ ΤΗΣ ΕΛΛΑΔΟΣ ΣΤΑ ΤΙΡΑΝΑ ΚΑΙ
ΣΥΝΕΝΤΕΥΞΗ -Αρθρο ΠΡΕΣΒΗ ( ΕΠΙ ΤΙΜΗ) ΑΛΕΞΑΝΔΡΟΥ ΜΑΛΛΙΑ, ΕΙΔΙΚΟΥ ΣΥΜΒΟΥΛΟΥ ΤΟΥ ΕΛΙΑΜΕΠ ΠΡΩΤΟΥ ΕΠΙΚΕΦΑΛΗΣ ΤΟΥ ΓΡΑΦΕΙΟΥ ΣΥΝΔΕΣΜΟΥ ΤΗΣ ΕΛΛΑΔΟΣ ΣΤΑ ΣΚΟΠΙΑ ( 1995-1999).ΠΡΩΗΝ ΠΡΕΣΒΗ ΤΗΣ ΕΛΛΑΔΟΣ ΣΤΑ ΤΙΡΑΝΑ ΚΑΙ
ΓΝΜΔ 1164/20.6.2012 ΣΧΕΤ. Ν. 3019/2011 ΦΕΚ Α 32/02.03.2011. ΘΕΜΑ. Για τη συνταγματικότητα του Ν. 3919/2011. ΓΝΩΜΟΔΟΤΗΣΗ
 Δρ. ΧΑΡΗΣ Τ. ΠΟΛΙΤΗΣ ΔΙΚΗΓΟΡΟΣ ΣΕ Α.Π., Σ.τ.Ε., Δρ. ΙΑΤΡΙΚΗΣ Ε.Κ.Π.Α. ΕΠΙΣΚ. ΚΑΘ. ΙΑΤΡ. ΔΙΚΑΙΟΥ ΕΥΡ. ΠΑΝ. ΚΥΠΡΟΥ ΣΙΚΕΛΙΑΝΟΥ 15, 15451 ΨΥΧΙΚΟ, ΑΘΗΝΑ ΤΗΛ.: (210) 6756732, FAX: (210) 6729207, e-mail: chpolitis@gmail.com
Δρ. ΧΑΡΗΣ Τ. ΠΟΛΙΤΗΣ ΔΙΚΗΓΟΡΟΣ ΣΕ Α.Π., Σ.τ.Ε., Δρ. ΙΑΤΡΙΚΗΣ Ε.Κ.Π.Α. ΕΠΙΣΚ. ΚΑΘ. ΙΑΤΡ. ΔΙΚΑΙΟΥ ΕΥΡ. ΠΑΝ. ΚΥΠΡΟΥ ΣΙΚΕΛΙΑΝΟΥ 15, 15451 ΨΥΧΙΚΟ, ΑΘΗΝΑ ΤΗΛ.: (210) 6756732, FAX: (210) 6729207, e-mail: chpolitis@gmail.com
ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ
 ΑΝΑΘΕΤΟΥΣΑ ΑΡΧΗ ΔΗΜΟΣ ΚΑΒΑΛΑΣ ΔΗΜΟΤΙΚΗ ΚΟΙΝΩΦΕΛΗΣ ΕΠΙΧΕΙΡΗΣΗ ΚΑΒΑΛΑΣ ΔΗΜΩΦΕΛΕΙΑ ΕΡΓΟ ΕΠΙΣΚΕΥΗ ΔΑΠΕΔΟΥ ΣΤΟ ΔΩΜΑ ΤΗΣ ΔΗΜΟΤΙΚΗΣ ΑΓΟΡΑΣ ΚΑΒΑΛΑΣ ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ 1 ΓΕΝΙΚΟΙ ΟΡΟΙ 1.1 Αντικείμενο του παρόντος
ΑΝΑΘΕΤΟΥΣΑ ΑΡΧΗ ΔΗΜΟΣ ΚΑΒΑΛΑΣ ΔΗΜΟΤΙΚΗ ΚΟΙΝΩΦΕΛΗΣ ΕΠΙΧΕΙΡΗΣΗ ΚΑΒΑΛΑΣ ΔΗΜΩΦΕΛΕΙΑ ΕΡΓΟ ΕΠΙΣΚΕΥΗ ΔΑΠΕΔΟΥ ΣΤΟ ΔΩΜΑ ΤΗΣ ΔΗΜΟΤΙΚΗΣ ΑΓΟΡΑΣ ΚΑΒΑΛΑΣ ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ 1 ΓΕΝΙΚΟΙ ΟΡΟΙ 1.1 Αντικείμενο του παρόντος
ΕΠΙΤΡΟΠΗ ΔΗΜΟΣΙΑΣ ΔΙΟΙΚΗΣΗΣ ΔΗΜΟΣΙΑΣ ΤΑΞΗΣ ΚΑΙ ΔΙΚΑΙΟΣΥΝΗΣ
 ΕΠΙΤΡΟΠΗ ΔΗΜΟΣΙΑΣ ΔΙΟΙΚΗΣΗΣ ΔΗΜΟΣΙΑΣ ΤΑΞΗΣ ΚΑΙ ΔΙΚΑΙΟΣΥΝΗΣ ΠΡΑΚΤΙΚΟ Στην Αθήνα σήμερα, 4 Ιουλίου 1999 ημέρα Κυριακή και ώρα 16.30 στην Αίθουσα 150 του Μεγάρου της Βουλής, συνεδρίασε η Επιτροπή Δημόσιας
ΕΠΙΤΡΟΠΗ ΔΗΜΟΣΙΑΣ ΔΙΟΙΚΗΣΗΣ ΔΗΜΟΣΙΑΣ ΤΑΞΗΣ ΚΑΙ ΔΙΚΑΙΟΣΥΝΗΣ ΠΡΑΚΤΙΚΟ Στην Αθήνα σήμερα, 4 Ιουλίου 1999 ημέρα Κυριακή και ώρα 16.30 στην Αίθουσα 150 του Μεγάρου της Βουλής, συνεδρίασε η Επιτροπή Δημόσιας
«Σε μια ρώγα από σταφύλι» Εκπαιδευτικό Πρόγραμμα για το Αμπέλι, το Σταφύλι & το Κρασί
 «Σε μια ρώγα από σταφύλι» Εκπαιδευτικό Πρόγραμμα για το Αμπέλι, το Σταφύλι & το Κρασί Κάκκου Μαρία Γ 1 τάξη του 6 ου Δ.Σ. Μεσολογγίου Μεσολόγγι 2013 Εισαγωγή Πληροφοριακό υλικό Το αμπέλι και το κρασί είναι
«Σε μια ρώγα από σταφύλι» Εκπαιδευτικό Πρόγραμμα για το Αμπέλι, το Σταφύλι & το Κρασί Κάκκου Μαρία Γ 1 τάξη του 6 ου Δ.Σ. Μεσολογγίου Μεσολόγγι 2013 Εισαγωγή Πληροφοριακό υλικό Το αμπέλι και το κρασί είναι
Αστυνομική τέχνη. με όλες τις πηγές, ο Τζέισον Στρανκ
 Κεφάλαιο 1 Αστυνομική τέχνη Σ ύμφωνα με όλες τις πηγές, ο Τζέισον Στρανκ ήταν ένας ασήμαντος τύπος, άχρωμος και άοσμος, γύρω στα τριάντα, σχεδόν αόρατος για τους γείτονές του ίσως και άφωνος επίσης, αφού
Κεφάλαιο 1 Αστυνομική τέχνη Σ ύμφωνα με όλες τις πηγές, ο Τζέισον Στρανκ ήταν ένας ασήμαντος τύπος, άχρωμος και άοσμος, γύρω στα τριάντα, σχεδόν αόρατος για τους γείτονές του ίσως και άφωνος επίσης, αφού
ΕΜΦΥΤΕΥΣΙΜΟΙ ΚΑΡΔΙΟΜΕΤΑΤΡΟΠΕΙΣ- ΑΠΙΝΙΔΩΤΕΣ. ΤΙ ΠΡΕΠΕΙ ΝΑ ΓΝΩΡΙΖΟΥΜΕ.
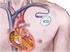 ΕΜΦΥΤΕΥΣΙΜΟΙ ΚΑΡΔΙΟΜΕΤΑΤΡΟΠΕΙΣ- ΑΠΙΝΙΔΩΤΕΣ. ΤΙ ΠΡΕΠΕΙ ΝΑ ΓΝΩΡΙΖΟΥΜΕ. 1) Τι είναι ο απινιδωτής; Ο εμφυτεύσιμος-καρδιομετατροπέας απινιδωτής (Implantable Cardioverter Defibrillator- ICD) είναι μία συσκευή
ΕΜΦΥΤΕΥΣΙΜΟΙ ΚΑΡΔΙΟΜΕΤΑΤΡΟΠΕΙΣ- ΑΠΙΝΙΔΩΤΕΣ. ΤΙ ΠΡΕΠΕΙ ΝΑ ΓΝΩΡΙΖΟΥΜΕ. 1) Τι είναι ο απινιδωτής; Ο εμφυτεύσιμος-καρδιομετατροπέας απινιδωτής (Implantable Cardioverter Defibrillator- ICD) είναι μία συσκευή
ΟΙΚΟΝΟΜΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΠΡΟΜΗΘΕΙΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΥΛΙΚΟΥ. ΤΗΛΕΦΩΝΟ: 210-4857719 ΦΑΞ: E mail:
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ----------------------------------------------------- Καλλιθέα: 20-10-2015 Ι Δ Ρ Υ Μ Α Αριθ. πρωτ.: 13194 ΣΙΒΙΤΑΝΙΔΕΙΟΣ ΔΗΜΟΣΙΑ ΣΧΟΛΗ ΤΕΧΝΩΝ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ----------------------------------------------------- Καλλιθέα: 20-10-2015 Ι Δ Ρ Υ Μ Α Αριθ. πρωτ.: 13194 ΣΙΒΙΤΑΝΙΔΕΙΟΣ ΔΗΜΟΣΙΑ ΣΧΟΛΗ ΤΕΧΝΩΝ
ΚΑΡΟΛΟΣ ΠΑΠΟΥΛΙΑΣ (Πρόεδρος της Δημοκρατίας): Κύριοι, σας καλωσορίζω ακόμη μία φορά. Είναι μία τελευταία προσπάθεια μήπως εξευρεθεί κάποια λύση για
 ΚΑΡΟΛΟΣ ΠΑΠΟΥΛΙΑΣ (Πρόεδρος της Δημοκρατίας): Κύριοι, σας καλωσορίζω ακόμη μία φορά. Είναι μία τελευταία προσπάθεια μήπως εξευρεθεί κάποια λύση για την αποφυγή εκλογών, που νομίζω ότι κανένας από εμάς
ΚΑΡΟΛΟΣ ΠΑΠΟΥΛΙΑΣ (Πρόεδρος της Δημοκρατίας): Κύριοι, σας καλωσορίζω ακόμη μία φορά. Είναι μία τελευταία προσπάθεια μήπως εξευρεθεί κάποια λύση για την αποφυγή εκλογών, που νομίζω ότι κανένας από εμάς
ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ
 1691 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΤΡΙΤΟ Αρ. Φύλλου 250 4 Μαρτίου 2014 ΟΡΓΑΝΙΣΜΟΙ ΛΟΙΠΟΙ ΦΟΡΕΙΣ Αριθμ. 8218 Προκήρυξη θέσης Καθηγητή του Τμήματος Γεωπονί ας (πρώην Γεωπονική
1691 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΤΡΙΤΟ Αρ. Φύλλου 250 4 Μαρτίου 2014 ΟΡΓΑΝΙΣΜΟΙ ΛΟΙΠΟΙ ΦΟΡΕΙΣ Αριθμ. 8218 Προκήρυξη θέσης Καθηγητή του Τμήματος Γεωπονί ας (πρώην Γεωπονική
ΓΙΑ ΤΑ ΕΠΑΓΓΕΛΜΑΤΙΚΑ ΔΙΚΑΙΩΜΑΤΑ ΤΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΟΝ ΠΟΛΥΝΟΜΟ ΤΟΥ ΑΠΡΙΛΗ
 ΓΙΑ ΤΑ ΕΠΑΓΓΕΛΜΑΤΙΚΑ ΔΙΚΑΙΩΜΑΤΑ ΤΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΟΝ ΠΟΛΥΝΟΜΟ ΤΟΥ ΑΠΡΙΛΗ Η διαφύλαξη του δημόσιου χαρακτήρα της Εκπαίδευσης, η ανάδειξη της πυραμίδας της τεχνικής εκπαίδευσης και η διασφάλιση αντίστοιχων
ΓΙΑ ΤΑ ΕΠΑΓΓΕΛΜΑΤΙΚΑ ΔΙΚΑΙΩΜΑΤΑ ΤΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΟΝ ΠΟΛΥΝΟΜΟ ΤΟΥ ΑΠΡΙΛΗ Η διαφύλαξη του δημόσιου χαρακτήρα της Εκπαίδευσης, η ανάδειξη της πυραμίδας της τεχνικής εκπαίδευσης και η διασφάλιση αντίστοιχων
ΜΕΛΙ: ΠΑΡΑΓΩΓΗ ΠΡΟΙΟΝΤΑ ΧΡΗΣΕΙΣ
 ΜΕΛΙ: ΠΑΡΑΓΩΓΗ ΠΡΟΙΟΝΤΑ ΧΡΗΣΕΙΣ ΔΗΜΙΟΥΡΓΙΑ ΜΕΛΙΟΥ ΑΠΟ ΤΗΝ ΜΕΛΙΣΣΑ Οι μέλισσες πετάνε από λουλούδι σε λουλούδι και συλλέγουν γύρη και νέκταρ. Όταν μαζέψουν αρκετό και το φορτίο τους γίνει βαρύ επιστρέφουν
ΜΕΛΙ: ΠΑΡΑΓΩΓΗ ΠΡΟΙΟΝΤΑ ΧΡΗΣΕΙΣ ΔΗΜΙΟΥΡΓΙΑ ΜΕΛΙΟΥ ΑΠΟ ΤΗΝ ΜΕΛΙΣΣΑ Οι μέλισσες πετάνε από λουλούδι σε λουλούδι και συλλέγουν γύρη και νέκταρ. Όταν μαζέψουν αρκετό και το φορτίο τους γίνει βαρύ επιστρέφουν
1. ΟΙ ΦΥΛΑΚΕΣ ΤΩΝ ΜΥΣΤΙΚΩΝ... 13 2. ΠΡΩΙΝΑ ΜΕΙΔΙΑΣΜΑΤΑ... 19
 Περιεχόμενα 1. ΟΙ ΦΥΛΑΚΕΣ ΤΩΝ ΜΥΣΤΙΚΩΝ... 13 2. ΠΡΩΙΝΑ ΜΕΙΔΙΑΣΜΑΤΑ... 19 3. ΤΟ «Γαλόπαιδο» 1... 27 4. Ο ΑΝΘΡΩΠΟΣ ΠΟΥ ΕΒΛΕΠΕ ΤΑ ΠΑΠΟΥΤΣΙΑ ΝΑ ΠΕΡΝΟΥΝ... 37 5. Ο ΔΕΚΑΤΟΣ ΤΡΙΤΟΣ ΟΡΟΦΟΣ... 51 6. Η ΕΠΙΣΦΡΑΓΙΣΗ
Περιεχόμενα 1. ΟΙ ΦΥΛΑΚΕΣ ΤΩΝ ΜΥΣΤΙΚΩΝ... 13 2. ΠΡΩΙΝΑ ΜΕΙΔΙΑΣΜΑΤΑ... 19 3. ΤΟ «Γαλόπαιδο» 1... 27 4. Ο ΑΝΘΡΩΠΟΣ ΠΟΥ ΕΒΛΕΠΕ ΤΑ ΠΑΠΟΥΤΣΙΑ ΝΑ ΠΕΡΝΟΥΝ... 37 5. Ο ΔΕΚΑΤΟΣ ΤΡΙΤΟΣ ΟΡΟΦΟΣ... 51 6. Η ΕΠΙΣΦΡΑΓΙΣΗ
ΑΓΙΑ ΓΑΛΗΝΗ ΤΕΥΧΟΣ 24 - ΙΟΥΝΙΟΣ 1992 ΕΚΔΟΣΗ ΣΥΛΛΟΓΟΥ «Λ ΓIΛ ΓΑΛΗΝΗ» ΣΤΗΝ ΑΘΗΝΑ
 ΤΕΥΧΟΣ 24 - ΙΟΥΝΙΟΣ 1992 ΕΚΔΟΣΗ ΣΥΛΛΟΓΟΥ «Λ ΓIΛ ΓΑΛΗΝΗ» ΣΤΗΝ ΑΘΗΝΑ Αγαπητοί Συγχωριανοί και φίλοι της Αγίας Γαλήνης, το Διοικητικό Συμβούλιο του Συλλόγου μας, θεω ρεί υποχρέωσή του, λόγω της λήξης της
ΤΕΥΧΟΣ 24 - ΙΟΥΝΙΟΣ 1992 ΕΚΔΟΣΗ ΣΥΛΛΟΓΟΥ «Λ ΓIΛ ΓΑΛΗΝΗ» ΣΤΗΝ ΑΘΗΝΑ Αγαπητοί Συγχωριανοί και φίλοι της Αγίας Γαλήνης, το Διοικητικό Συμβούλιο του Συλλόγου μας, θεω ρεί υποχρέωσή του, λόγω της λήξης της
Κοινωνική Οικονομία: Μια βιώσιμη εναλλακτική?
 Κοινωνική Οικονομία: Μια βιώσιμη εναλλακτική? Δρ. Διευθυντής, Ινστιτούτο Κοινωνικής Οικονομίας Περιεχόμενα ΕΙΣΑΓΩΓΗ... 3 Α. ΕΠΕΝΔΥΣΕΙΣ... 4 Α.1. Άμεσες Ξένες Επενδύσεις και Κοινωνικά Ομόλογα... 4 Α.2.
Κοινωνική Οικονομία: Μια βιώσιμη εναλλακτική? Δρ. Διευθυντής, Ινστιτούτο Κοινωνικής Οικονομίας Περιεχόμενα ΕΙΣΑΓΩΓΗ... 3 Α. ΕΠΕΝΔΥΣΕΙΣ... 4 Α.1. Άμεσες Ξένες Επενδύσεις και Κοινωνικά Ομόλογα... 4 Α.2.
Εβδομαδιαίος προγραμματισμός 9 η εβδομάδα 2 6/11/2015 Θέμα: «Η Ελιά και το Λάδι»
 1 Εβδομαδιαίος προγραμματισμός 9 η εβδομάδα 2 6/11/2015 Θέμα: «Η Ελιά και το Λάδι» Αφορμή Ερέθισμα Τώρα το Νοέμβριο σε πολλές περιοχές της πατρίδας μας, οι αγρότες ασχολούνται με το μάζεμα της ελιάς. Πώς
1 Εβδομαδιαίος προγραμματισμός 9 η εβδομάδα 2 6/11/2015 Θέμα: «Η Ελιά και το Λάδι» Αφορμή Ερέθισμα Τώρα το Νοέμβριο σε πολλές περιοχές της πατρίδας μας, οι αγρότες ασχολούνται με το μάζεμα της ελιάς. Πώς
«Δημοκρατικοί» παραλογισμοί... και χαράτσια
 «Δημοκρατικοί» παραλογισμοί... και χαράτσια Αναμφίβολα, είναι δεδομένος ο παραλογισμός της πολιτικής ηγεσίας της χώρας, στη λήψη των αποφάσεων της, αναφορικά με την αντιμετώπιση της οικονομικής κρίσης
«Δημοκρατικοί» παραλογισμοί... και χαράτσια Αναμφίβολα, είναι δεδομένος ο παραλογισμός της πολιτικής ηγεσίας της χώρας, στη λήψη των αποφάσεων της, αναφορικά με την αντιμετώπιση της οικονομικής κρίσης
Οδηγίες Χρήσεως DW 455 S. 9 σερβίτσια 10 σερβίτσια πρόγραμμα ½ φορτίου. Πλυντήριο Πιάτων
 Οδηγίες Χρήσεως DW 455 S Πλυντήριο Πιάτων 9 σερβίτσια 10 σερβίτσια πρόγραμμα ½ φορτίου Αγαπητέ πελάτη, Διαβάστε αυτό το εγχειρίδιο Διαβάσετε προσεχτικά τις οδηγίες που εμπεριέχονται στο παρόν φυλλάδιο
Οδηγίες Χρήσεως DW 455 S Πλυντήριο Πιάτων 9 σερβίτσια 10 σερβίτσια πρόγραμμα ½ φορτίου Αγαπητέ πελάτη, Διαβάστε αυτό το εγχειρίδιο Διαβάσετε προσεχτικά τις οδηγίες που εμπεριέχονται στο παρόν φυλλάδιο
The electronic version of the book is created by http://www.enverhoxha.ru for http://www.enverhoxha.info
 The electronic version of the book is created by http://www.enverhoxha.ru for http://www.enverhoxha.info ΕΝΒΕΡ ΧΟΤΖΑ ΕΝΒΕΡ ΧΟΤΖΑ ΣΚΕΨΕΙΣ ΓΙΑ ΤΗ ΜΕΣΗ ΑΝΑΤΟΛΗ 1958-1983 ΑΠΟ ΤΟ ΠΟΛΙΤΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΟΡΕΙΑ
The electronic version of the book is created by http://www.enverhoxha.ru for http://www.enverhoxha.info ΕΝΒΕΡ ΧΟΤΖΑ ΕΝΒΕΡ ΧΟΤΖΑ ΣΚΕΨΕΙΣ ΓΙΑ ΤΗ ΜΕΣΗ ΑΝΑΤΟΛΗ 1958-1983 ΑΠΟ ΤΟ ΠΟΛΙΤΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΟΡΕΙΑ
αντιπληροφορηση η γενικευμένη απαξία, η καταστολή, είναι εδώ για να θωρακίζουν την κατεχόμενη καθημερινότητά μας.
 αντιπληροφορηση θερσιτης στουσ δρομουσ του ίλιου-πετρούπολησ-άγιων ανάργυρων νοεμβρης 309 τευχοσ εφημεριδα δρομου πυγμή & Χρειάζεται πολύ αφέλεια, πολύ ματαιότητα και άλλη τόση αδράνεια για να συνεχίσει
αντιπληροφορηση θερσιτης στουσ δρομουσ του ίλιου-πετρούπολησ-άγιων ανάργυρων νοεμβρης 309 τευχοσ εφημεριδα δρομου πυγμή & Χρειάζεται πολύ αφέλεια, πολύ ματαιότητα και άλλη τόση αδράνεια για να συνεχίσει
Φροντιστήριο «ΕΠΙΛΟΓΗ» Ιατροπούλου 12 & σιδ. Σταθμού - Καλαμάτα τηλ.: 27210-95352 & 96390
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 25 ΜΑΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΡΧΑΙΑ ΕΛΛΗΝΙΚΑ ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ Α. Αφού λοιπόν η αρετή είναι δύο ειδών, η μια
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 25 ΜΑΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΡΧΑΙΑ ΕΛΛΗΝΙΚΑ ΘΕΩΡΗΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ Α. Αφού λοιπόν η αρετή είναι δύο ειδών, η μια
Κύριε Πρόεδρε, θα σας ρωτήσω ευθέως εάν πιστεύετε ότι η χώρα βρίσκεται στα πρόθυρα του εμφυλίου.
 Γ. ΠΡΕΤΕΝΤΕΡΗΣ: Κυρίες και κύριοι καλησπέρα σας. Απόψε, καλεσμένος μας είναι ο Πρωθυπουργός ο κ. Αντώνης Σαμαράς, του οποίου καλεσμένοι είμαστε εμείς στο γραφείο στο Μέγαρο Μαξίμου. Καλησπέρα κ. Πρόεδρε.
Γ. ΠΡΕΤΕΝΤΕΡΗΣ: Κυρίες και κύριοι καλησπέρα σας. Απόψε, καλεσμένος μας είναι ο Πρωθυπουργός ο κ. Αντώνης Σαμαράς, του οποίου καλεσμένοι είμαστε εμείς στο γραφείο στο Μέγαρο Μαξίμου. Καλησπέρα κ. Πρόεδρε.
ΔΙΑΚΗΡΥΞΗ ΠΡΟΧΕΙΡΟΥ ΔΙΑΓΩΝΙΣΜΟΥ ΓΙΑ ΤΗΝ ΠΡΟΜΗΘΕΙΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΩΝ ΣΥΣΚΕΥΩΝ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Βέροια, 6/11/2015 ΝΟΜΟΣ ΗΜΑΘΙΑΣ ΔΗΜΟΣ ΒΕΡΟΙΑΣ Αριθμ. Πρωτ.: 47006 ΔΙΑΚΗΡΥΞΗ ΠΡΟΧΕΙΡΟΥ ΔΙΑΓΩΝΙΣΜΟΥ ΓΙΑ ΤΗΝ ΠΡΟΜΗΘΕΙΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΩΝ ΣΥΣΚΕΥΩΝ Έχοντας λάβει
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Βέροια, 6/11/2015 ΝΟΜΟΣ ΗΜΑΘΙΑΣ ΔΗΜΟΣ ΒΕΡΟΙΑΣ Αριθμ. Πρωτ.: 47006 ΔΙΑΚΗΡΥΞΗ ΠΡΟΧΕΙΡΟΥ ΔΙΑΓΩΝΙΣΜΟΥ ΓΙΑ ΤΗΝ ΠΡΟΜΗΘΕΙΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΩΝ ΣΥΣΚΕΥΩΝ Έχοντας λάβει
Πολιτική κατάθεση του Χριστόφορου Κορτέση στο ειδικό δικαστήριο του Κορυδαλλού, 06/02/13
 Πολιτική κατάθεση του Χριστόφορου Κορτέση στο ειδικό δικαστήριο του Κορυδαλλού, 06/02/13 Όταν ξεκίνησε αυτή η διαδικασία στη δεύτερη συνεδρίαση στις 24 του Οκτώβρη (2011) με είχατε ρωτήσει αν έχω να κάνω
Πολιτική κατάθεση του Χριστόφορου Κορτέση στο ειδικό δικαστήριο του Κορυδαλλού, 06/02/13 Όταν ξεκίνησε αυτή η διαδικασία στη δεύτερη συνεδρίαση στις 24 του Οκτώβρη (2011) με είχατε ρωτήσει αν έχω να κάνω
Για να λύσουμε ένα πρόβλημα με τη βοήθεια εξισώσεων γενικά ακολουθούμε τα παρακάτω βήματα:
 Μέρος Α -1.4. ΕΠΙ ΠΡΟΒΛΗΜΑΤΩΝ ΜΕ ΤΗ ΧΡΗΣΗ ΕΞΙΣΩΣΕΩΝ 29 1.4 ΕΠΙ ΠΡΟΒΛΗΜΑΤΩΝ ΜΕ ΤΗ ΧΡΗΣΗ ΕΞΙΣΩΣΕΩΝ Γενικά Για να λύσουμε ένα πρόβλημα με τη βοήθεια εξισώσεων γενικά ακολουθούμε τα παρακάτω βήματα: Διαβάζουμε
Μέρος Α -1.4. ΕΠΙ ΠΡΟΒΛΗΜΑΤΩΝ ΜΕ ΤΗ ΧΡΗΣΗ ΕΞΙΣΩΣΕΩΝ 29 1.4 ΕΠΙ ΠΡΟΒΛΗΜΑΤΩΝ ΜΕ ΤΗ ΧΡΗΣΗ ΕΞΙΣΩΣΕΩΝ Γενικά Για να λύσουμε ένα πρόβλημα με τη βοήθεια εξισώσεων γενικά ακολουθούμε τα παρακάτω βήματα: Διαβάζουμε
Τ.Ε.Ι. ΚΑΛΑΜΑΤΑΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΜΟΝΑΔΩΝ ΤΟΠΙΚΗΣ ΑΥΤΟΔΙΟΙΚΗΣΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
 Τ.Ε.Ι. ΚΑΛΑΜΑΤΑΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΜΟΝΑΔΩΝ ΤΟΠΙΚΗΣ ΑΥΤΟΔΙΟΙΚΗΣΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ: «Ο ΔΑΝΕΙΣΜΟΣ ΤΗΣ ΤΟΠΙΚΗΣ ΑΥΤΟΔΙΟΙΚΗΣΗΣ ΣΤΗΝ ΕΛΛΑΔΑ. Η ΠΕΡΙΠΤΩΣΗ ΤΟΥ ΔΗΜΟΥ ΜΕΛΙΓΑΛΑ ΝΟΜΟΥ
Τ.Ε.Ι. ΚΑΛΑΜΑΤΑΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΜΟΝΑΔΩΝ ΤΟΠΙΚΗΣ ΑΥΤΟΔΙΟΙΚΗΣΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ: «Ο ΔΑΝΕΙΣΜΟΣ ΤΗΣ ΤΟΠΙΚΗΣ ΑΥΤΟΔΙΟΙΚΗΣΗΣ ΣΤΗΝ ΕΛΛΑΔΑ. Η ΠΕΡΙΠΤΩΣΗ ΤΟΥ ΔΗΜΟΥ ΜΕΛΙΓΑΛΑ ΝΟΜΟΥ
ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ
 33387 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΔΕΥΤΕΡΟ Αρ. Φύλλου 2828 23 Δεκεμβρίου 2015 ΑΠΟΦΑΣΕΙΣ Αριθμ. 133384/6587 Προδιαγραφές Σύνταξης των Μελετών Διαχείρισης Πάρκων και Αλσών. Ο
33387 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΕΥΧΟΣ ΔΕΥΤΕΡΟ Αρ. Φύλλου 2828 23 Δεκεμβρίου 2015 ΑΠΟΦΑΣΕΙΣ Αριθμ. 133384/6587 Προδιαγραφές Σύνταξης των Μελετών Διαχείρισης Πάρκων και Αλσών. Ο
ΠΡΟΚΗΡΥΞΗ ΠΡΟΣΦΟΡΑΣ. Αρ. Προσφοράς: 2014/9 Τελ. Ημερομ. Υποβ. Προσφ: 3 Σεμπτεμβριου 2014
 ΠΡΟΚΗΡΥΞΗ ΠΡΟΣΦΟΡΑΣ Αρ. Προσφοράς: 2014/9 Τελ. Ημερομ. Υποβ. Προσφ: 3 Σεμπτεμβριου 2014 Η εταιρεία Οργανισμός Συγκοινωνιών Επαρχίας Αμμοχώστου ζητά προσφορές για την Παροχή Υπηρεσιών για τη μεταφορά μαθητών
ΠΡΟΚΗΡΥΞΗ ΠΡΟΣΦΟΡΑΣ Αρ. Προσφοράς: 2014/9 Τελ. Ημερομ. Υποβ. Προσφ: 3 Σεμπτεμβριου 2014 Η εταιρεία Οργανισμός Συγκοινωνιών Επαρχίας Αμμοχώστου ζητά προσφορές για την Παροχή Υπηρεσιών για τη μεταφορά μαθητών
ΑΡΙΘΜΟΣ ΑΠΟΦΑΣΗΣ 1101/2015 ΤΟ ΕΙΡΗΝΟΔΙΚΕΙΟ ΑΘΗΝΩΝ
 ΕΙΡΗΝΟΔΙΚΕΙΟ ΑΘΗΝΩΝ ΔΙΑΔΙΚΑΣΙΑ ΕΡΓΑΤΙΚΩΝ ΔΙΑΦΟΡΩΝ ΑΡΙΘΜΟΣ ΑΠΟΦΑΣΗΣ 1101/2015 ΤΟ ΕΙΡΗΝΟΔΙΚΕΙΟ ΑΘΗΝΩΝ Συγκροτήθηκε από την Ειρηνοδίκη Ιωάννα Τουρή την οποία όρισε η Πρόεδρος του Τριμελούς Συμβουλίου Διοίκησης
ΕΙΡΗΝΟΔΙΚΕΙΟ ΑΘΗΝΩΝ ΔΙΑΔΙΚΑΣΙΑ ΕΡΓΑΤΙΚΩΝ ΔΙΑΦΟΡΩΝ ΑΡΙΘΜΟΣ ΑΠΟΦΑΣΗΣ 1101/2015 ΤΟ ΕΙΡΗΝΟΔΙΚΕΙΟ ΑΘΗΝΩΝ Συγκροτήθηκε από την Ειρηνοδίκη Ιωάννα Τουρή την οποία όρισε η Πρόεδρος του Τριμελούς Συμβουλίου Διοίκησης
ΤΡΙΗΡΗΣ. ΤΡΙΗΡΗΣ Σελίδα 1
 ΤΡΙΗΡΗΣ ΤΡΙΗΡΗΣ Σελίδα 1 ΤΡΙΗΡΗΣ Σελίδα 2 ΟΜΑ Α ΜΑΘΗΤΩΝ ΣΙΑΦΗ ΓΕΩΡΓΙΑ ΕΙΡΗΝΗ ΣΑΡΑΝΤΑΡΗ ΠΑΝΑΓΙΩΤΑ ΣΙΑΜΑΝΤΑ ΙΣΑΒΕΛΛΑ ΣΠΥΡΙ ΟΥΛΑ ΣΙΑΜΑΝΤΑ ΠΑΡΘΕΝΙΑ ΣΙΑΦΑΚΑ ΣΩΤΗΡΙΑ ΣΙΝΤΟΡΗΣ ΗΜΗΤΡΙΟΣ ΣΙΣΚΑΣ ΕΥΑΓΓΕΛΟΣ ΣΟΥΚΟΥΒΕΛΟΥ
ΤΡΙΗΡΗΣ ΤΡΙΗΡΗΣ Σελίδα 1 ΤΡΙΗΡΗΣ Σελίδα 2 ΟΜΑ Α ΜΑΘΗΤΩΝ ΣΙΑΦΗ ΓΕΩΡΓΙΑ ΕΙΡΗΝΗ ΣΑΡΑΝΤΑΡΗ ΠΑΝΑΓΙΩΤΑ ΣΙΑΜΑΝΤΑ ΙΣΑΒΕΛΛΑ ΣΠΥΡΙ ΟΥΛΑ ΣΙΑΜΑΝΤΑ ΠΑΡΘΕΝΙΑ ΣΙΑΦΑΚΑ ΣΩΤΗΡΙΑ ΣΙΝΤΟΡΗΣ ΗΜΗΤΡΙΟΣ ΣΙΣΚΑΣ ΕΥΑΓΓΕΛΟΣ ΣΟΥΚΟΥΒΕΛΟΥ
Το Μονόκλωνο γραμμικό σύστημα διαμόρφωσης των δένδρων κερασιάς
 Το Μονόκλωνο γραμμικό σύστημα διαμόρφωσης των δένδρων κερασιάς Κωνσταντίνος Καζαντζής 1 και Πασχάλης Αποστόλου 2 1 ΕΘ.Ι.ΑΓ.Ε., Ινστιτούτο Φυλλοβόλων Δένδρων, Τ.Θ. 122, 59200 Νάουσα 2 «Φυτώρια Αποστόλου»,
Το Μονόκλωνο γραμμικό σύστημα διαμόρφωσης των δένδρων κερασιάς Κωνσταντίνος Καζαντζής 1 και Πασχάλης Αποστόλου 2 1 ΕΘ.Ι.ΑΓ.Ε., Ινστιτούτο Φυλλοβόλων Δένδρων, Τ.Θ. 122, 59200 Νάουσα 2 «Φυτώρια Αποστόλου»,
Τέλος, θα ήθελα να ευχαριστήσω την οικογένειά μου και τους φίλους που με στήριξαν στην προσπάθειά μου αυτή.
 ΠΡΟΛΟΓΟΣ Η παρούσα Πτυχιακή Εργασία πραγματοποιήθηκε στα πλαίσια του προγράμματος σπουδών του τμήματος Κλωστοϋφαντουργίας της Σχολής Τεχνολογικών Εφαρμογών (Σ.Τ.Εφ.) του Τεχνολογικού Εκπαιδευτικού Ιδρύματος
ΠΡΟΛΟΓΟΣ Η παρούσα Πτυχιακή Εργασία πραγματοποιήθηκε στα πλαίσια του προγράμματος σπουδών του τμήματος Κλωστοϋφαντουργίας της Σχολής Τεχνολογικών Εφαρμογών (Σ.Τ.Εφ.) του Τεχνολογικού Εκπαιδευτικού Ιδρύματος
για τη ριζική ανανέωση και αλλαγή της δηµοκρατικής παράταξης και του πολιτικού συστήµατος
 Προχωράµε για τη ριζική ανανέωση και αλλαγή της δηµοκρατικής παράταξης και του πολιτικού συστήµατος για να πάει η Ελλάδα µπροστά Με πίστη και πεποίθηση υποστηρίζω την ύπαρξη στην ελληνική κοινωνία ενός
Προχωράµε για τη ριζική ανανέωση και αλλαγή της δηµοκρατικής παράταξης και του πολιτικού συστήµατος για να πάει η Ελλάδα µπροστά Με πίστη και πεποίθηση υποστηρίζω την ύπαρξη στην ελληνική κοινωνία ενός
ΤΕΧΝΟΛΟΓΙΚΟ ΕΡΓΟ ΣΤΟ ΜΑΘΗΜΑ ΤΗΣ «ΤΕΧΝΟΛΟΓΙΑΣ» ΤΕΧΝΟΛΟΓΙΚΗ ΕΝΟΤΗΤΑ «ΜΕΤΑΦΟΡΕΣ-ΕΠΙΚΟΙΝΩΝΙΕΣ» ΕΡΓΟ:ΑΕΡΟΣΤΑΤΟ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΡΓΟ ΣΤΟ ΜΑΘΗΜΑ ΤΗΣ «ΤΕΧΝΟΛΟΓΙΑΣ» ΤΕΧΝΟΛΟΓΙΚΗ ΕΝΟΤΗΤΑ «ΜΕΤΑΦΟΡΕΣ-ΕΠΙΚΟΙΝΩΝΙΕΣ» ΕΡΓΟ:ΑΕΡΟΣΤΑΤΟ Ονοματεπώνυμο: Αικατερίνα Τσιάβα Τάξη: Α Τμήμα:5ο Σχολικό Έτος:2ΟΟ9-2Ο10 1 1ο στάδιο Ανάλυση της
ΤΕΧΝΟΛΟΓΙΚΟ ΕΡΓΟ ΣΤΟ ΜΑΘΗΜΑ ΤΗΣ «ΤΕΧΝΟΛΟΓΙΑΣ» ΤΕΧΝΟΛΟΓΙΚΗ ΕΝΟΤΗΤΑ «ΜΕΤΑΦΟΡΕΣ-ΕΠΙΚΟΙΝΩΝΙΕΣ» ΕΡΓΟ:ΑΕΡΟΣΤΑΤΟ Ονοματεπώνυμο: Αικατερίνα Τσιάβα Τάξη: Α Τμήμα:5ο Σχολικό Έτος:2ΟΟ9-2Ο10 1 1ο στάδιο Ανάλυση της
Διασυνοριακές συγχωνεύσεις και διασπάσεις
 Διασυνοριακές συγχωνεύσεις και διασπάσεις Διασυνοριακές συγχωνεύσεις και διασπάσεις Διαβούλευση της Ευρωπαϊκής Επιτροπής (ΓΔ MARKT) ΕΙΣΑΓΩΓΗ Προκαταρκτική παρατήρηση Στόχος του ερωτηματολογίου αυτού είναι
Διασυνοριακές συγχωνεύσεις και διασπάσεις Διασυνοριακές συγχωνεύσεις και διασπάσεις Διαβούλευση της Ευρωπαϊκής Επιτροπής (ΓΔ MARKT) ΕΙΣΑΓΩΓΗ Προκαταρκτική παρατήρηση Στόχος του ερωτηματολογίου αυτού είναι
Η ΣΩΤΗΡΙΑ ΕΝ ΧΡΙΣΤΩ ΚΑΙ ΤΟ ΘΕΜΑ ΤΗΣ ΑΙΩΝΙΟΥ ΣΩΤΗΡΙΑΣ ΤΟΥ ΠΙΣΤΟΥ
 Ιωάννης ΜΠΑΛΤΑΤΖΗΣ Λόγοι διδακτοί Πνεύματος (1Κορ.2:13) Η ΣΩΤΗΡΙΑ ΕΝ ΧΡΙΣΤΩ ΚΑΙ ΤΟ ΘΕΜΑ ΤΗΣ ΑΙΩΝΙΟΥ ΣΩΤΗΡΙΑΣ ΤΟΥ ΠΙΣΤΟΥ (Σειρά Βιβλικών μελετών) Βρυξέλλες, 2015 - 2 - ΠΡΟΛΟΓΟΣ Η εκκλησία του Χριστού που
Ιωάννης ΜΠΑΛΤΑΤΖΗΣ Λόγοι διδακτοί Πνεύματος (1Κορ.2:13) Η ΣΩΤΗΡΙΑ ΕΝ ΧΡΙΣΤΩ ΚΑΙ ΤΟ ΘΕΜΑ ΤΗΣ ΑΙΩΝΙΟΥ ΣΩΤΗΡΙΑΣ ΤΟΥ ΠΙΣΤΟΥ (Σειρά Βιβλικών μελετών) Βρυξέλλες, 2015 - 2 - ΠΡΟΛΟΓΟΣ Η εκκλησία του Χριστού που
Εκπαίδευση Ατόμων με Ειδικές Εκπαιδευτικές Ανάγκες Σπονδυλωτό Εξ Αποστάσεως Πρόγραμμα Εξειδίκευσης
 Εκπαίδευση Ατόμων με Ειδικές Εκπαιδευτικές Ανάγκες Σπονδυλωτό Εξ Αποστάσεως Πρόγραμμα Εξειδίκευσης Αναλυτική Περιγραφή Θεματικών Ενοτήτων 1. Εισαγωγή στην Εκπαίδευση Ατόμων με Οπτική Αναπηρία Κωνσταντίνος
Εκπαίδευση Ατόμων με Ειδικές Εκπαιδευτικές Ανάγκες Σπονδυλωτό Εξ Αποστάσεως Πρόγραμμα Εξειδίκευσης Αναλυτική Περιγραφή Θεματικών Ενοτήτων 1. Εισαγωγή στην Εκπαίδευση Ατόμων με Οπτική Αναπηρία Κωνσταντίνος
Ι. ΛΕΙΤΟΥΡΓΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟΥ
 1. ΣΥΣΤΗΜΑ ΟΡΓΑΝΩΣΗΣ ΑΛΦΑ Ι. ΛΕΙΤΟΥΡΓΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟΥ Α. Διάρθρωση τμημάτων Τα τμήματα όλων των τάξεων δημιουργούνται με κύριο κριτήριο να είναι ομοιογενή από άποψη επιδόσεων των μαθητών. Δίνεται δηλαδή
1. ΣΥΣΤΗΜΑ ΟΡΓΑΝΩΣΗΣ ΑΛΦΑ Ι. ΛΕΙΤΟΥΡΓΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟΥ Α. Διάρθρωση τμημάτων Τα τμήματα όλων των τάξεων δημιουργούνται με κύριο κριτήριο να είναι ομοιογενή από άποψη επιδόσεων των μαθητών. Δίνεται δηλαδή
ΕΚΠΑΙΔΕΥΤΙΚΑ ΠΡΟΓΡΑΜΜΑΤΑ ΜΟΥΣΕΙΟΥ ΣΧΟΛΙΚΗΣ ΖΩΗΣ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗΣ ΠΡΟΓΡΑΜΜΑΤΑ ΓΙΑ ΠΑΙΔΙΑ ΚΑΙ ΓΟΝΕΙΣ
 ΕΚΠΑΙΔΕΥΤΙΚΑ ΠΡΟΓΡΑΜΜΑΤΑ ΜΟΥΣΕΙΟΥ ΣΧΟΛΙΚΗΣ ΖΩΗΣ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗΣ Από τον Ιανουάριο ξεκινάνε στο Μουσείο Σχολικής Ζωής και Εκπαίδευσης προγράμματα για παιδιά και γονείς. Με αυστηρά επιλεγμένα κριτήρια φιλοδοξούμε
ΕΚΠΑΙΔΕΥΤΙΚΑ ΠΡΟΓΡΑΜΜΑΤΑ ΜΟΥΣΕΙΟΥ ΣΧΟΛΙΚΗΣ ΖΩΗΣ ΚΑΙ ΕΚΠΑΙΔΕΥΣΗΣ Από τον Ιανουάριο ξεκινάνε στο Μουσείο Σχολικής Ζωής και Εκπαίδευσης προγράμματα για παιδιά και γονείς. Με αυστηρά επιλεγμένα κριτήρια φιλοδοξούμε
ΠΡΟΣΚΛΗΣΗ ΕΝΔΙΑΦΕΡΟΝΤΟΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΜΕΣΩΝ ΕΝΗΜΕΡΩΣΗΣ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΕΝΗΜΕΡΩΣΗΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ ΠΡΟΣΚΛΗΣΗ ΕΝΔΙΑΦΕΡΟΝΤΟΣ Πρόχειρος Διαγωνισμός για την προμήθεια δύο χιλιάδων οκτακοσίων (2.800) δεσμίδων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΜΕΣΩΝ ΕΝΗΜΕΡΩΣΗΣ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΕΝΗΜΕΡΩΣΗΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ ΠΡΟΣΚΛΗΣΗ ΕΝΔΙΑΦΕΡΟΝΤΟΣ Πρόχειρος Διαγωνισμός για την προμήθεια δύο χιλιάδων οκτακοσίων (2.800) δεσμίδων
ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΠΟΛΙΤΙΣΜΟΥ Αθήνα, 10 Απριλίου 2014 ΠΡΟΣΚΛΗΣΗ ΕΚΔΗΛΩΣΗΣ ΕΝΔΙΑΦΕΡΟΝΤΟΣ ΓΙΑ ΣΥΜΜΕΤΟΧΗ ΣΕ ΠΡΟΧΕΙΡΟ ΜΕΙΟΔΟΤΙΚΟ ΔΙΑΓΩΝΙΣΜΟ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΑΝΑΡΤΗΤΕΟ ΣΤΟ ΔΙΑΔΙΚΤΥΟ ΑΔΑ : ΒΙΗΔ469ΗΔΞ-721 ΥΠΟΥΡΓΕΙΟ ΠΟΛΙΤΙΣΜΟΥ & ΑΘΛΗΤΙΣΜΟΥ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΠΟΛΙΤΙΣΜΟΥ Αθήνα, 10 Απριλίου 2014 ΤΑΜΕΙΟ ΑΡΧΑΙΟΛΟΓΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΑΠΑΛΛΟΤΡΙΩΣΕΩΝ ΔΙΕΥΘΥΝΣΗ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΑΝΑΡΤΗΤΕΟ ΣΤΟ ΔΙΑΔΙΚΤΥΟ ΑΔΑ : ΒΙΗΔ469ΗΔΞ-721 ΥΠΟΥΡΓΕΙΟ ΠΟΛΙΤΙΣΜΟΥ & ΑΘΛΗΤΙΣΜΟΥ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΠΟΛΙΤΙΣΜΟΥ Αθήνα, 10 Απριλίου 2014 ΤΑΜΕΙΟ ΑΡΧΑΙΟΛΟΓΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΑΠΑΛΛΟΤΡΙΩΣΕΩΝ ΔΙΕΥΘΥΝΣΗ
Συνήγορος του Καταναλωτή Νομολογία ΠολΠρωτΑθ 2960/1996
 ΠολΠρωτΑθ 2960/1996 Προστασία καταναλωτή. Τηλεπικοινωνίες. ΟΤΕ. Χρέωση για αποτυχημένες κλήσεις. Έννοια προμηθευτή. Έγερση συλλογικής αγωγής. Ευθύνη παραγωγού, προϋποθέσεις. (.) Κατά την διάταξη του άρθρου
ΠολΠρωτΑθ 2960/1996 Προστασία καταναλωτή. Τηλεπικοινωνίες. ΟΤΕ. Χρέωση για αποτυχημένες κλήσεις. Έννοια προμηθευτή. Έγερση συλλογικής αγωγής. Ευθύνη παραγωγού, προϋποθέσεις. (.) Κατά την διάταξη του άρθρου
AΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ
 AΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΑΝΘΡΩΠΟΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝ (1.1., 1.2.) 1. Ο οργανισμός του ανθρώπου προκειμένου να διατηρεί σταθερό το εσωτερικό του περιβάλλον είναι υποχρεωμένος να τροποποιεί
AΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΑΝΘΡΩΠΟΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝ (1.1., 1.2.) 1. Ο οργανισμός του ανθρώπου προκειμένου να διατηρεί σταθερό το εσωτερικό του περιβάλλον είναι υποχρεωμένος να τροποποιεί
ΣΧΕΔΙΟ ΝΟΜΟΥ. Mέρος Α' Διατάξεις ουσιαστικού ποινικού δικαίου. Ι. Γενικό μέρος. Άρθρο 1. Εφαρμογή διατάξεων Ποινικού Κώδικα.
 ΣΧΕΔΙΟ ΝΟΜΟΥ «Προσαρμογή των διατάξεων του εσωτερικού δικαίου προς τις διατάξεις του καταστατικού του Διεθνούς Ποινικού Δικαστηρίου που κυρώθηκε με τον ν. 3003/2002 (ΦΕΚ Α 75)» Mέρος Α' Διατάξεις ουσιαστικού
ΣΧΕΔΙΟ ΝΟΜΟΥ «Προσαρμογή των διατάξεων του εσωτερικού δικαίου προς τις διατάξεις του καταστατικού του Διεθνούς Ποινικού Δικαστηρίου που κυρώθηκε με τον ν. 3003/2002 (ΦΕΚ Α 75)» Mέρος Α' Διατάξεις ουσιαστικού
καταλογίζονται η μείωση των επαναλαμβανόμενων επισκέψεων, ο κίνδυνος μείωσης της προσέλευσης του κοινού, η μείωση των εσόδων καθώς αποφεύγουν οι
 Τα σεμινάρια του συγκεκριμένου μαθήματος αναφέρονται α) στη διεθνή νομοθεσία για την προστασία της παγκόσμιας κληρονομιάς, β) στην ισχύουσα ελληνική νομοθεσία για την πρόσβαση και χρήση των μουσείων, γ)
Τα σεμινάρια του συγκεκριμένου μαθήματος αναφέρονται α) στη διεθνή νομοθεσία για την προστασία της παγκόσμιας κληρονομιάς, β) στην ισχύουσα ελληνική νομοθεσία για την πρόσβαση και χρήση των μουσείων, γ)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΠΟΛΙΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ & ΔΙΕΘΝΩΝ ΣΧΕΣΕΩΝ ΕΡΓΑΣΙΑ ΜΑΘΗΜΑ: ΕΛΛΗΝΙΚΟ ΠΟΛΙΤΙΚΟ ΣΥΣΤΗΜΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΠΟΛΙΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ & ΔΙΕΘΝΩΝ ΣΧΕΣΕΩΝ ΕΡΓΑΣΙΑ ΜΑΘΗΜΑ: ΕΛΛΗΝΙΚΟ ΠΟΛΙΤΙΚΟ ΣΥΣΤΗΜΑ ΔΙΔΑΣΚΟΝ : Κος. ΜΑΝΟΣ Γ. ΠΑΠΑΖΟΓΛΟΥ ΦΟΙΤΗΤΡΙΑ : ΚΟΥΧΑΡΣΚΑΓΙΑ ΟΛΓΑ E ΕΞΑΜΗΝΟ Α.Μ/3033201200115
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΠΟΛΙΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ & ΔΙΕΘΝΩΝ ΣΧΕΣΕΩΝ ΕΡΓΑΣΙΑ ΜΑΘΗΜΑ: ΕΛΛΗΝΙΚΟ ΠΟΛΙΤΙΚΟ ΣΥΣΤΗΜΑ ΔΙΔΑΣΚΟΝ : Κος. ΜΑΝΟΣ Γ. ΠΑΠΑΖΟΓΛΟΥ ΦΟΙΤΗΤΡΙΑ : ΚΟΥΧΑΡΣΚΑΓΙΑ ΟΛΓΑ E ΕΞΑΜΗΝΟ Α.Μ/3033201200115
