ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Δομές δεδομένων. Ενότητα 9: Ταξινόμηση Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών
|
|
|
- Καλόγερος Παπάζογλου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Ενότητα 9: Ταξινόμηση Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών
2 Ενότητα 9 Ταξινόμηση ΗΥ240 - Παναγιώτα Φατούρου 2
3 Ταξινόμηση Θεωρούμε έναν πίνακα Α[0..n-1] με n στοιχεία στα οποία έχει ορισθεί μια γραμμική διάταξη, δηλαδή ζεύγος στοιχείων x,y του Α, είτε x < y, ή x > y ή x = y. Η διαδικασία ταξινόμησης του Α συνίσταται στην αναδιάταξη των στοιχείων του, έτσι ώστε μετά το πέρας της διαδικασίας αυτής να ισχύει Α[0] Α[1] Α[n-1]. ΗΥ240 - Παναγιώτα Φατούρου 3
4 Ταξινόμηση Ταξινόμηση με Χρήση Ουρών Προτεραιότητας Δεδομένου ότι μια βιβλιοθήκη παρέχει ουρές προτεραιότητας, ζητείται αλγόριθμος που να ταξινομεί τα n στοιχεία του πίνακα Α. Αλγόριθμος Ταξινόμησης με Χρήση Ουράς Προτεραιότητας MakeEmptySet(S); for (j = 0; j < n; j++) εισαγωγή του στοιχείου Α[j] στην ουρά προτεραιότητας S; for (j = 0; j < n; j++) Print(DeleteMin(S)); Ποια είναι η χρονική πολυπλοκότητα του αλγορίθμου αυτού? Η πολυπλοκότητα εξαρτάται από την πολυπλοκότητα των λειτουργιών Insert() και DeleteMin() της ουράς προτεραιότητας. Αν η ουρά προτεραιότητας υλοποιείται ως σωρός, τότε η χρονική πολυπλοκότητα του αλγορίθμου είναι Ο(nlogn). ΗΥ240 - Παναγιώτα Φατούρου 4
5 Ταξινόμηση χρησιμοποιώντας άλλες Δομές Δεδομένων Αλγόριθμος Ταξινόμησης με Χρήση Ταξινομημένων Δένδρων MakeEmptyBinarySearchTree(T); for (j = 0; j < n; j++) BinarySearchTreeInsert(Τ, A[j]); Inorder(T) // με τη Visit() να εκτελεί μια εκτύπωση του κλειδιού του εκάστοτε κόμβου Χρονική Πολυπλοκότητα Η χρονική πολυπλοκότητα του παραπάνω αλγορίθμου είναι Ο(nh), όπου h το ύψος του ταξινομημένου δένδρου μετά από τις n εισαγωγές. Αν το ταξινομημένο δένδρο είναι AVL, (2-3) δένδρο ή κοκκινόμαυρο δένδρο τότε η χρονική πολυπλοκότητα του παραπάνω αλγορίθμου είναι Ο(nlogn) (αφού h = O(logn)). Χωρική Πολυπλοκότητα Τα n στοιχεία που είναι αποθηκευμένα στον πίνακα Α απαιτείται να αποθηκευτούν εκ νέου σε μια νέα δομή. Το ίδιο ισχύει και στην περίπτωση χρήσης ουράς προτεραιότητας. Αυτό προκαλεί σπατάλη μνήμης! ΗΥ240 - Παναγιώτα Φατούρου 5
6 Ταξινόμηση - Ο Αλγόριθμος InsertionSort Πρόβλημα Είσοδος Μια ακολουθία από n αριθμούς <a 1, a 2,..., a n >. Έξοδος (output): Μια μετάθεση (αναδιάταξη) < a 1, a 2,..., a n > της ακολουθίας εισόδου έτσι ώστε: a 1 a 2... a n Πως λειτουργεί ο αλγόριθμος αν A = <5,2,4,6,1,3>; Ο αλγόριθμος InsertionSort() και η πολυπλοκότητά του έχουν συζητηθεί αναλυτικά στην Ενότητα 1 του μαθήματος. Algorithm InsertionSort (Α[1..n]) { // Είσοδος: ένας μη-ταξινομημένος πίνακας Α // ακεραίων αριθμών // Έξοδος: ο πίνακας Α με τα στοιχεία του // σε αύξουσα διάταξη int key, i, j; for (j = 2; j n; j++) { key = A[j]; i = j-1; while (i > 0 && A[i] > key) { A[i+1] = A[i]; i = i-1; A[i+1] = key; return A; ΗΥ240 - Παναγιώτα Φατούρου 6
7 Ταξινόμηση - Ο αλγόριθμος InsertionSort() Algorithm InsertionSort (Α[1..n]) { int key, i, j; for (j = 2; j n; j++) { key = A[j]; i = j-1; while (i > 0 && A[i] > key) { A[i+1] = A[i]; i = i-1; A[i+1] = key; return A; Πως λειτουργεί ο αλγόριθμος αν A = <5,2,4,6,1,3>; Βασική Ιδέα Επαναληπτικά, επιλέγεται το επόμενο στοιχείο από το μηταξινομημένο κομμάτι Α[j..n-1] του πίνακα και τοποθετείται στην κατάλληλη θέση του ταξινομημένου κομματιού Α[0..j-1] του πίνακα. Η χρονική πολυπλοκότητα της InsertionSort() είναι Θ(n 2 ). ΗΥ240 - Παναγιώτα Φατούρου 7
8 Ταξινόμηση - Ο αλγόριθμος SelectionSort() Βασική Ιδέα Επαναληπτική αναζήτηση, στο μηταξινομημένο κομμάτι του πίνακα Α, του στοιχείου εκείνου που θα αποτελέσει το επόμενο στοιχείο στο ταξινομημένο κομμάτι του πίνακα (το μέγεθος του ταξινομημένου κομματιού του πίνακα αυξάνει κατά ένα μετά από κάθε επανάληψη). Πως λειτουργεί ο αλγόριθμος αν A = <5,2,4,6,1,3>; Procedure SelectionSort(table A[0..n- 1]) { // sort A by repeatedly selecting the smallest element // from the unsorted part for (i = 0; i < n-1; i++) { j = i; for (k = i+1; k < n; k++) if (A[k] < A[j]) j = k; swap(a[i], A[j]); i = 1, j = i = 0, j = i = 2, j = i = 3, j = 5 i = 4, j = Άσκηση για το σπίτι Αποδείξτε ότι η χρονική πολυπλοκότητα της SelectionSort() είναι Θ(n 2 ). ΗΥ240 - Παναγιώτα Φατούρου 8
9 Ταξινόμηση - Ο αλγόριθμος HeapSort() Αποδοτικότερη έκδοση του SelectionSort(): το μη-ταξινομημένο κομμάτι του Α διατηρείται ως ένας σωρός που το ελάχιστο στοιχείο του βρίσκεται στη θέση Α[n-1], ενώ τα υπόλοιπα στοιχεία είναι αποθηκευμένα με την κατάλληλη σειρά σε φθίνουσες θέσεις του A ξεκινώντας από την A[n-2]. Υποθέτουμε ότι αρχικά τα στοιχεία του πίνακα έχουν την ιδιότητα της μερικής διάταξης (αυτό επιτυγχάνεται με κλήση της διαδικασίας InitializeHeap()). Διατρέχουμε όλα τα στοιχεία του Α και για κάθε ένα από αυτά το ανταλλάσουμε με το στοιχείο Α[n-1] (δηλαδή το ελάχιστο του σωρού) και εκτελούμε τη διαδικασία Heapify(), η οποία επαναφέρει την ιδιότητα της μερικής διάταξης του σωρού. Procedure HeapSort( table A[0..n- 1]) { InitializeHeap(Α); // Η InitializeHeap() αναλαμβάνει τη // μερική ταξινόμηση του αρχικού //πίνακα ώστε αυτός να μετατραπεί // σε σωρό με ελάχιστο στην Α[n-1] for (i = 0; i < n-1; i++) { swap(a[i], A[n-1]); // επαναληπτική αποθήκευση του // μικρότερου στοιχείου του // σωρού στη θέση i του πίνακα Heapify(A[i+1 n-1]); // επαναφορά της μερικής // διάταξης του σωρού που μπορεί // να έχει καταστραφεί στη ρίζα ΗΥ240 - Παναγιώτα Φατούρου 9
10 procedure Heapify(table A[i..j]) { // Αρχικά, το κομμάτι Α[i..j-1] είναι μερικώς ταξινομημένο, ενώ μετά την εκτέλεση της Heapify() το κομμάτι A[i..j] είναι μερικώς ταξινομημένο m = j; while ((leftchild(m) i AND A[leftchild(m)] < A[m]) OR (rightchild(m) i AND A[rightchild(m)] < A[m]) { // αν υπάρχει αριστερό παιδί με μικρότερο κλειδί από του m ή αν // υπάρχει δεξιό παιδί με μικρότερο κλειδί από του m if (rightchild(m) i ) { if (A[leftchild(m)] < A[rightchild(m)]) p = leftchild(m) else p = rightchild(m); 3 Ταξινόμηση - Ο αλγόριθμος HeapSort() else p = i; swap(α[m], A[p]); m = p; Στον παραπάνω κώδικα ισχύει ότι: leftchild(m) = 2m-n rightchild(m) = 2m-n Παράδειγμα Εκτέλεσης της HeapSort(A) όπου A = [6,4,5,2,3 που είναι σωρός. 6 i = i = i = 1, πριν Heapify() i = i = 2, πριν Heapify() 5 4 πριν την εκτέλεση της Heapify() μετά την εκτέλεση της Heapify() i = 1, μετά Heapify() i = 2, μετά Heapify() i = 3, πριν Heapify() i = 3, μετά Heapify() i = 4, πριν Heapify() i = 4, μετά Heapify() ΗΥ240 - Παναγιώτα Φατούρου
11 Ταξινόμηση - Ο αλγόριθμος HeapSort() Procedure InitializeHeap(Τable A[0..n-1]) { // Μετατροπή του Α σε σωρό for (i=1; i < n; i++) Heapify(A[0..i]); αρχικά μετά ανακύκλωση i = 1 μετά ανακύκλωση i = 2 μετά ανακύκλωση i = i=1: τα φύλλα 3 και 2 δεν έχουν παιδιά η Heapify() δεν επιφέρει καμία αλλαγή! i=2: τα φύλλα 1, 3 και 2 δεν έχουν παιδιά η Heapify() δεν επιφέρει καμία αλλαγή! i=3: ο κόμβος 6 είναι ο μόνος που έχει παιδιά η Heapify() ανταλλάσει το 6 με το παιδί του, που έχει τιμή 2 και είναι μικρότερο. 2 1 μετά ανακύκλωση i = 4 μετά ανακύκλωση i = i=4: η ιδιότητα της μερικής ταξινόμησης καταστρατηγείται από το 5 η Heapify() ανταλλάσει το 5 με το i=5: η ιδιότητα της μερικής ταξινόμησης έχει καταστρατηγηθεί στη ρίζα η Heapify() ανταλλάσει το 4 με το 1 και στη συνέχεια το 4 με το 3. ΗΥ240 - Παναγιώτα Φατούρου
12 Ταξινόμηση - Ο αλγόριθμος HeapSort() Χρονική Πολυπλοκότητα της HeapSort() (Χρονική Πολυπλοκότητα της InitializeHeap()) + ((n-1) * Χρονική Πολυπλοκότητα της Heapify(A[0..n-1])) (Χρονική Πολυπλοκότητα της InitializeHeap()) (n-1) * (Χρονική Πολυπλοκότητα της Heapify(A[0..n-1])) Χρονική Πολυπλοκότητα της Heapify(A[0..n-1]) = O(logn). Επομένως: Χρονική Πολυπλοκότητα της HeapSort() = O(nlogn). Χωρική Πολυπλοκότητα της HeapSort() Τα στοιχεία αποθηκεύονται κάθε χρονική στιγμή στον ίδιο τον πίνακα Α. Ο αλγόριθμος είναι πολύ αποδοτικός ως προς την χωρική πολυπλοκότητα. O αλγόριθμος είναι βέλτιστος ως προς τη χρονική πολυπλοκότητά του. ΗΥ240 - Παναγιώτα Φατούρου 12
13 Ταξινόμηση - Ο αλγόριθμος MergeSort() Τεχνική «Διαίρει και Κυρίευε» Η τεχνική περιλαμβάνει τρία βήματα: 1. Διαίρεση του προβλήματος σε διάφορα υποπροβλήματα που είναι παρόμοια με το αρχικό πρόβλημα αλλά μικρότερου μεγέθους. 2. Κυριαρχία επί των υποπροβλημάτων, επιλύοντάς τα αναδρομικά, μέχρι αυτά να γίνουν αρκετά μικρού μεγέθους οπότε και τα επιλύουμε απευθείας. 3. Συνδυασμός των επιμέρους λύσεων των υποπροβλημάτων ώστε να συνθέσουμε μια λύση του αρχικού προβλήματος. Ο αλγόριθμος MergeSort() ακολουθεί το μοντέλο «Διαίρει και Κυρίευε»: 1. Διαίρεση: Η προς ταξινόμηση ακολουθία των n στοιχείων διαιρείται σε δύο υπακολουθίες των n/2 στοιχείων η κάθε μια. 2. Κυριαρχία: Οι δυο υπακολουθίες ταξινομούνται καλώντας αναδρομικά τη MergeSort() για κάθε μια από αυτές. Η αναδρομή εξαντλείται όταν η προς ταξινόμηση υπακολουθία έχει μήκος 1 (αφού κάθε υπακολουθία μήκους 1 είναι ταξινομημένη). 3. Συνδυασμός: Συγχωνεύουμε τις δύο ταξινομημένες υπακολουθίες ώστε να σχηματίσουμε την τελική ταξινομημένη ακολουθία. ΗΥ240 - Παναγιώτα Φατούρου 13
14 Ταξινόμηση - Ο αλγόριθμος MergeSort() Διαδικασία Συγχώνευσης Χρησιμοποιείται μια βοηθητική διαδικασία Merge(table A, int p,q,r), της οποίας οι παράμετροι είναι ένας πίνακας Α και τρεις ακέραιοι, δείκτες στον πίνακα, τ.ω. p q < r. H διαδικασία προϋποθέτει ότι οι υποπίνακες A[p..q] και A[q+1..r] είναι ταξινομημένοι και συγχωνεύει τα στοιχεία τους ώστε να σχηματίσει μια ενιαία ταξινομημένη υπακολουθία, η οποία αντικαθιστά την αρχική A[p..r]. Αποθηκεύουμε στο τέλος κάθε υποπίνακα έναν κόμβο φρουρό, void Merge(table A, int p,q,r) { n1 = q-p+1; n2 = r-q; // δημιουργία υποπινάκων L[0..n1] και R[0..n2] for (i= 0; i < n1; i++) L[i] = A[p+i]; for (i = 0; i < n2; i++) R[i] = A[q+1+i]; i = j = 0; L[n1] = R[n2] = ; // κόμβοι φρουροί των πινάκων for (k = p; k <= r; k++) { if (L[i] < R[j]) { A[k] = L[i]; i++; else { A[k] = R[j]; j++; ΗΥ240 - Παναγιώτα Φατούρου 14
15 Ταξινόμηση - Παράδειγμα εκτέλεσης της Merge Σχήμα 2.3: Cormen, Leiserson, Rivest & Stein, Εισαγωγή στους αλγόριθμους, Πανεπιστημιακές Εκδόσεις Κρήτης, 2006 Παράδειγμα εκτέλεσης της Merge(A, 9, 12, 16), όπου Α[9..16] = <2,4,5,7,1,2,3,6> Οι ελαφρά σκιασμένες θέσεις στον πίνακα Α έχουν λάβει τις τελικές τους τιμές, ενώ οι έντονα σκιασμένες θέσεις θα αντικατασταθούν στη συνέχεια από άλλες τιμές. ΗΥ240 - Παναγιώτα Φατούρου 15 Οι ελαφρά σκιασμένες θέσεις στους πίνακες L,R περιέχουν τιμές οι οποίες
16 Ταξινόμηση - Παράδειγμα εκτέλεσης της Merge Σχήμα 2.3: Cormen, Leiserson, Rivest & Stein, Εισαγωγή στους αλγόριθμους, Πανεπιστημιακές Εκδόσεις Κρήτης, 2006 ΗΥ240 - Παναγιώτα Φατούρου 16
17 Ταξινόμηση - Ο αλγόριθμος MergeSort() Συνθήκη που ισχύει αναλλοίωτη κατά την εκτέλεση της Merge() «Στην αρχή κάθε επανάληψης της 3ης for, ο υποπίνακας Α[p..k-1] περιέχει τα k-p μικρότερα στοιχεία των L[0..n1] και R[0..n2], ταξινομημένα. Επιπλέον, τα L[i] και R[j] είναι τα μικρότερα στοιχεία των υποπινάκων αυτών που δεν έχουν ακόμη καταχωρηθεί στον πίνακα Α.» Ο ισχυρισμός αυτός αποδεικνύεται με επαγωγή στο k. Η απόδειξη αφήνεται ως άσκηση για το σπίτι! Ποια είναι η χρονική πολυπλοκότητα της Merge(); Θ(n1+n2) = Θ(n). void Merge(table A, int p,q,r) { n1 = q-p+1; Θ(1) n2 = r-q; Θ(1) for (i=0; i < n1; i++) -- L[i] = A[p+i]; - Θ(n1) for (i = 0; i < n2; i++) -- R[i] = A[q+1+i]; - Θ(n2) i = j = 0; Θ(1) L[n1] = R[n2] = ; --- Θ(1) for (k = p; k <= r; k++) ΗΥ240 - Παναγιώτα Φατούρου 17 if (L[i] < R[j]) { Θ(n1+n2)
18 Ταξινόμηση - Ο αλγόριθμος MergeSort() void MergeSort(table A, int p, r) { if (p < r) { q = (p+r)/2 ; MergeSort(A,p,q); MergeSort(A,q+1,r); Merge(A,p,q,r); Σχήμα 2.4: Cormen, Leiserson, Rivest & Stein, Εισαγωγή στους αλγόριθμους, Πανεπιστημιακές Εκδόσεις Κρήτης, 2006 ΗΥ240 - Παναγιώτα Φατούρου 18
19 Ανάλυση Αλγορίθμων τύπου «Διαίρει και Κυρίευε» Έστω T(n) ο χρόνος εκτέλεσης ενός αλγορίθμου που λειτουργεί βάσει της τεχνικής «διαίρει και κυρίευε», όπου n είναι το μέγεθος της εισόδου. Αν το n είναι αρκετά μικρό, π.χ., n c, όπου c είναι μια σταθερά, η απευθείας λύση απαιτεί χρόνο Θ(1). Έστω ότι κατά τη διαίρεση του προβλήματος προκύπτουν a υποπροβλήματα που το καθένα έχει μέγεθος το 1/b του μεγέθους του πλήρους προβλήματος. Έστω ότι η διαίρεση του προβλήματος σε υποπροβλήματα απαιτεί χρόνο D(n) και ότι η σύνθεση των επιμέρους λύσεων των υποπροβλημάτων για το σχηματισμό της πλήρους λύσης απαιτεί χρόνο C(n). Τότε: (1) αν n c T( n) at ( n / b) D( n) C( n) ά ΗΥ240 - Παναγιώτα Φατούρου 19
20 Ανάλυση αλγορίθμου MergeSort() Υποθέτουμε ότι το n είναι κάποια δύναμη του 2 (για λόγους απλότητας). Η MergeSort() για ένα μόνο στοιχείο απαιτεί σταθερό χρόνο Θ(1). Όταν εκτελείται σε (υπο)πίνακα με n > 1 στοιχεία, αναλύουμε τη χρονική πολυπλοκότητα ως εξής: Διαίρει: D(n) = Θ(1) (υπολογισμός του μεσαίου στοιχείου του υποπίνακα σε χρόνο Θ(1)) Κυρίευε: Αναδρομική επίλυση δύο υπο-προβλημάτων μεγέθους n/2 τα καθένα. Άρα, το χρονικό κόστος του βήματος αυτού είναι 2Τ(n/2). Συνδύασε: Η κλήση της Merge() απαιτεί χρόνο Θ(n) C(n) = Θ(n). Η αναδρομική σχέση που περιγράφει τη χρονική πολυπλοκότητα της MergeSort() είναι: c1 αν n = 1, T( n) 2 Tn ( / 2) c2n αν n > 1, όπου c 1 και c 2 είναι σταθερές. Άσκηση για το σπίτι Αποδείξτε (είτε επαγωγικά ή με τη μέθοδο της αντικατάστασης) ότι T(n) = Θ(nlogn). ΗΥ240 - Παναγιώτα Φατούρου 20
21 Ταξινόμηση - Ο αλγόριθμος QuickSort() Βασίζεται στην τεχνική «Διαίρει και Κυρίευε». Διαίρεση: Επιλέγεται ένα στοιχείο x της προς ταξινόμηση ακολουθίας (π.χ., το τελευταίο) και η αρχική ακολουθία Α[p..r] χωρίζεται στις υπακολουθίες A[p..q-1] και Α[q+1..r] έτσι ώστε κάθε στοιχείο της Α[p..q-1] να είναι μικρότερο του x, ενώ κάθε στοιχείο της A[q+1..r] να είναι μεγαλύτερο του x. Μέρος του βήματος αυτού είναι και ο υπολογισμός της κατάλληλης θέσης q του πίνακα στην οποία θα πρέπει να βρίσκεται το στοιχείο x μετά την ταξινόμηση. Κυριαρχία: Ταξινομούμε τις δύο υπακολουθίες Α[p..q-1] και A[q+1..r] με αναδρομικές κλήσεις της QuickSort(). Συνδυασμός: Δεν χρειάζεται κάποια ιδιαίτερη ενέργεια για το συνδυασμό των δυο υπακολουθιών Α[p..q-1] και A[q+1..r], αφότου αυτές ταξινομηθούν (λόγω του τρόπου που αυτές δημιουργήθηκαν). Δηλαδή, η συνολική ακολουθία A[p..r] είναι και αυτή ταξινομημένη χωρίς την εκτέλεση περαιτέρω ενεργειών. ΗΥ240 - Παναγιώτα Φατούρου 21
22 Ταξινόμηση - Ο αλγόριθμος QuickSort() void QuickSort(Table A, int p, int r) { if (p < r) { q = Partition(A,p,r); QuickSort(A,p,q); QuickSort(A,q+1,r); int Partition(Table A, int p, int r) { int x, i, j; x = A[p]; i = p-1; j = r+1; while (TRUE) { repeat j = j-1; until A[j] <= x; repeat i = i+1; until A[i] >= x; if (i < j) swap(a[i],a[j]); else return j; α. β. γ. Figure 8.1: Cormen, Leiserson & Rivest, Introduction to Algorithms, MIT Press, 1990 δ. ε. ΗΥ240 - Παναγιώτα Φατούρου 22
23 Ταξινόμηση - Ο αλγόριθμος QuickSort() Ο χρόνος εκτέλεσης χειρότερης περίπτωσης της QuickSort() για ένα πίνακα n στοιχείων είναι Θ(n 2 ). Ο πίνακας είναι εξ αρχής ταξινομημένος. Η Partition() παράγει ένα τμήμα με n-1 στοιχεία και ένα τμήμα με 1 μόνο στοιχείο. int Partition(Table A, int p, int r) { int x, i, j; x = A[p]; i = p-1; j = r+1; while (TRUE) { repeat j = j-1; until A[j] <= x; repeat i = i+1; until A[i] >= x; if (i < j) swap(a[i],a[j]); else return j; Αν το προβληματικό αυτό σενάριο προκύψει σε κάθε εκτέλεση της Partition(), η αναδρομική σχέση που περιγράφει την QuickSort() είναι: Τ(1) = Θ(1) και T(n) = T(n-1) + Θ(n) = Θ(n 2 ). ΗΥ240 - Παναγιώτα Φατούρου 23
24 Ταξινόμηση - Ο αλγόριθμος QuickSort() Figure 8.2: Cormen, Leiserson & Rivest, Introduction to Algorithms, MIT Press, 1990 Δένδρο αναδρομής της QuickSort() όπου η Partition() διαμερίζει επαναληπτικά τον πίνακα σε ένα τμήμα μεγέθους 1 και σε ένα τμήμα μεγέθους n-1. ΗΥ240 - Παναγιώτα Φατούρου 24
25 QuickSort() Ο καλύτερος χρόνος εκτέλεσηςτης QuickSort() είναι Θ(nlogn). H Partition() παράγει δύο τμήματα με n/2 στοιχεία το καθένα. int Partition(Table A, int p, int r) { int x, i, j; x = A[p]; i = p-1; j = r+1; while (TRUE) { repeat j = j-1; until A[j] <= x; repeat i = i+1; until A[i] >= x; if (i < j) swap(a[i],a[j]); else return j; Η αναδρομική σχέση που περιγράφει τη χρονική πολυπλοκότητα της QuickSort() σε αυτή την περίπτωση είναι: Τ(1) = Θ(1) και Τ(n) = 2T(n/2) + Θ(n) = Θ(nlogn) ΗΥ240 - Παναγιώτα Φατούρου 25
26 Ταξινόμηση - Ο αλγόριθμος QuickSort() Figure 8.3: Cormen, Leiserson & Rivest, Introduction to Algorithms, MIT Press, 1990 Δένδρο αναδρομής της QuickSort() όπου η Partition() διαμερίζει επαναληπτικά τον πίνακα σε δύο τμήματα μεγέθους n/2 το καθένα. ΗΥ240 - Παναγιώτα Φατούρου 26
27 Ταξινόμηση - Ο αλγόριθμος QuickSort() log Figure 8.4: Cormen, Leiserson & Rivest, Introduction to Algorithms, MIT Press, 1990 Οποιαδήποτε διαμέριση του πίνακα (από την Partition()) σε δύο τμήματα τ.ω. η αναλογία μεταξύ των μηκών των δύο τμημάτων είναι σταθερή, οδηγεί σε Θ(logn) επίπεδα αναδρομικών κλήσεων που το καθένα κοστίζει Θ(n). ΗΥ240 - Παναγιώτα Φατούρου 27
28 Διαίσθηση για την Μέση Περίπτωση Υπόθεση Κάθε μετάθεση των προς ταξινόμηση αριθμών προκύπτει, ως είσοδος της QuickSort(), με την ίδια πιθανότητα όπως όλες οι υπόλοιπες μεταθέσεις. Παράδειγμα Οι διαμερίσεις που παράγουν εξισορροπημένα, ως προς το μέγεθος, τμήματα του πίνακα εναλλάσσονται με εκείνες που δεν το επιτυγχάνουν αυτό. Figure 8.5: Cormen, Leiserson & Rivest, Introduction to Algorithms, MIT Press, 1990 ΗΥ240 - Παναγιώτα Φατούρου 28
29 Έκδοση QuickSort() που χρησιμοποιεί τυχαιότητα Βασική Ιδέα Σε κάθε βήμα, πριν να εκτελεστεί η διαμέριση του πίνακα, ανταλλάσσουμε το στοιχείο A[p] με ένα άλλο στοιχείο του πίνακα που επιλέγεται με τυχαιότητα. Αυτό αναμένεται να οδηγήσει σε διαμέριση του πίνακα σε δύο τμήματα που είναι εξισορροπήμενα ως προς το μέγεθός τους. void RandomizedQuickSort(Table A, int p, int r) { if (p < r) { q = RandPartition(A,p,r); RandomizedQuickSort(A,p,q); RandomizedQuickSort(A,q+1,r); void RandomizedPartition(Table A, int p, int r) { i = random(p,r); swap(a[p], A[i]); return Partition(A,p,r); ΗΥ240 - Παναγιώτα Φατούρου 29
30 Αναφορές Το υλικό της ενότητας αυτής περιέχεται στα ακόλουθα βιβλία: Harry Lewis and Larry Denenberg, Data Structures and Their Algorithms, Harper Collins Publishers, Inc., New York, 1991 Chapter 11: Sorting (Section 11.3 Selection and Heap Sort) Cormen, Leiserson and Rivest, Introduction to Algorithms, MIT Press, Chapter 8: Quicksort Cormen, Leiserson, Rivest & Stein, Εισαγωγή στους Αλγορίθμους, Πανεπιστημιακές Εκδόσεις Κρήτης, 2006 Ενότητα 2.1 Ενθετική Ταξινόμηση Ενότητα 2.3 Σχεδίαση Αλγορίθμων ΗΥ240 - Παναγιώτα Φατούρου 30
31 Τέλος Ενότητας
32 Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το έργο «Ανοικτά Ακαδημαϊκά Μαθήματα στο Πανεπιστήμιο Κρήτης» έχει χρηματοδοτήσει μόνο τη αναδιαμόρφωση του εκπαιδευτικού υλικού. Το έργο υλοποιείται στο πλαίσιο του Επιχειρησιακού Προγράμματος «Εκπαίδευση και Δια Βίου Μάθηση» και συγχρηματοδοτείται από την Ευρωπαϊκή Ένωση (Ευρωπαϊκό Κοινωνικό Ταμείο) και από εθνικούς πόρους.
33 Σημειώματα
34 Σημείωμα αδειοδότησης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά Δημιουργού - Μη Εμπορική Χρήση - Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων». [1] Ως Μη Εμπορική ορίζεται η χρήση: που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί..
35 Σημείωμα Αναφοράς Copyright Πανεπιστήμιο Κρήτης, Παναγιώτα Φατούρου. «Δομές δεδομένων. Ενότητα 9: Ταξινόμηση». Έκδοση: 1.0. Ηράκλειο/Ρέθυμνο Διαθέσιμο από τη δικτυακή διεύθυνση:
ΗΥ240 - Παναγιώτα Φατούρου 2
 Ενότητα 8 Ταξινόµηση ΗΥ0 - Παναγιώτα Φατούρου Ταξινόµηση Θεωρούµε έναν πίνακα Α[0..n-] µε n στοιχεία στα οποία έχει ορισθεί µια γραµµική διάταξη, δηλαδή ζεύγος στοιχείων x,y του Α, είτε x < y, ή x > y
Ενότητα 8 Ταξινόµηση ΗΥ0 - Παναγιώτα Φατούρου Ταξινόµηση Θεωρούµε έναν πίνακα Α[0..n-] µε n στοιχεία στα οποία έχει ορισθεί µια γραµµική διάταξη, δηλαδή ζεύγος στοιχείων x,y του Α, είτε x < y, ή x > y
ΗΥ240 - Παναγιώτα Φατούρου 2
 Ενότητα 9 Ταξινόµηση ΗΥ0 - Παναγιώτα Φατούρου Ταξινόµηση Θεωρούµε έναν πίνακα Α[0..n-] µε n στοιχεία στα οποία έχει ορισθεί µια γραµµική διάταξη, δηλαδή ζεύγος στοιχείων x,y του Α, είτε x < y, ή x > y
Ενότητα 9 Ταξινόµηση ΗΥ0 - Παναγιώτα Φατούρου Ταξινόµηση Θεωρούµε έναν πίνακα Α[0..n-] µε n στοιχεία στα οποία έχει ορισθεί µια γραµµική διάταξη, δηλαδή ζεύγος στοιχείων x,y του Α, είτε x < y, ή x > y
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Δομές δεδομένων. Ενότητα 7η: Ουρές Προτεραιότητας Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Ενότητα 7η: Ουρές Προτεραιότητας Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητα 7 Ουρές Προτεραιότητας ΗΥ240 - Παναγιώτα Φατούρου 2 Ουρές
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Ενότητα 7η: Ουρές Προτεραιότητας Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητα 7 Ουρές Προτεραιότητας ΗΥ240 - Παναγιώτα Φατούρου 2 Ουρές
Αλγόριθμοι και πολυπλοκότητα Συγχωνευτική Ταξινόμηση
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Συγχωνευτική Ταξινόμηση Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Συγχωνευτική Ταξινόμηση (Merge Sort) 7 2 9 4 2 4 7 9 7 2 2 7 9 4
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Συγχωνευτική Ταξινόμηση Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Συγχωνευτική Ταξινόμηση (Merge Sort) 7 2 9 4 2 4 7 9 7 2 2 7 9 4
Δομές δεδομένων. Ενότητα 8: Ξένα Σύνολα που υποστηρίζουν τη λειτουργία της Ένωσης (Union-Find) Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Ενότητα 8: Ξένα Σύνολα που υποστηρίζουν τη λειτουργία της Ένωσης (Union-Find) Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητα 8 Ξένα Σύνολα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Ενότητα 8: Ξένα Σύνολα που υποστηρίζουν τη λειτουργία της Ένωσης (Union-Find) Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητα 8 Ξένα Σύνολα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Δομές Δεδομένων. Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές Δεδομένων Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές Δεδομένων Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού
Αλγόριθμοι και πολυπλοκότητα Ταχυταξινόμηση (Quick-Sort)
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Ταχυταξινόμηση (Quick-Sort) Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Ταχυταξινόμηση (Quick-Sort) 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Ταχυταξινόμηση (Quick-Sort) Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Ταχυταξινόμηση (Quick-Sort) 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών ΗΥ2, Ενότητα : Ασκήσεις και Λύσεις Άσκηση 1 Ενότητα : Υλοποίηση Λεξικών µε
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών ΗΥ2, Ενότητα : Ασκήσεις και Λύσεις Άσκηση 1 Ενότητα : Υλοποίηση Λεξικών µε
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης 1 Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητα 1: Εισαγωγή Ασκήσεις και Λύσεις Άσκηση 1 Αποδείξτε τη µεταβατική
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης 1 Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητα 1: Εισαγωγή Ασκήσεις και Λύσεις Άσκηση 1 Αποδείξτε τη µεταβατική
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 2
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 2 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 2 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Δομές Δεδομένων. Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές Δεδομένων Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές Δεδομένων Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού
Αλγόριθμοι και πολυπλοκότητα Διαίρει και Κυρίευε
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Διαίρει και Κυρίευε Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Διαίρει και Κυρίευε 7 9 4 4 7 9 7 7 9 4 4 9 7 7 9 9 4 4 Διαίρει και Κυρίευε
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Διαίρει και Κυρίευε Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Διαίρει και Κυρίευε 7 9 4 4 7 9 7 7 9 4 4 9 7 7 9 9 4 4 Διαίρει και Κυρίευε
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση - Συγχώνευση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση - Συγχώνευση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Εισαγωγή στους Αλγόριθμους
 Εισαγωγή στους Αλγόριθμους Ενότητα 16: Δυαδική αναζήτηση και ταξινόμηση με συγχώνευση Εύη Παπαϊωάννου Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διαχείρισης Πολιτισμικού Περιβάλλοντος και Νέων Τεχνολογιών
Εισαγωγή στους Αλγόριθμους Ενότητα 16: Δυαδική αναζήτηση και ταξινόμηση με συγχώνευση Εύη Παπαϊωάννου Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διαχείρισης Πολιτισμικού Περιβάλλοντος και Νέων Τεχνολογιών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης 3-4 Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητες 3 & 4: ένδρα, Σύνολα & Λεξικά Ασκήσεις και Λύσεις Άσκηση 1 Γράψτε
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης 3-4 Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητες 3 & 4: ένδρα, Σύνολα & Λεξικά Ασκήσεις και Λύσεις Άσκηση 1 Γράψτε
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 1
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 1 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 1 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Δομές δεδομένων. Ενότητα 4η: Σύνολα - Λεξικά Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Ενότητα 4η: Σύνολα - Λεξικά Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών ΕΝΟΤΗΤΑ 4 ΣΥΝΟΛΑ - ΛΕΞΙΚΑ ΗΥ240 - Παναγιώτα Φατούρου 2 Σύνολα (Sets) Τα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Ενότητα 4η: Σύνολα - Λεξικά Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών ΕΝΟΤΗΤΑ 4 ΣΥΝΟΛΑ - ΛΕΞΙΚΑ ΗΥ240 - Παναγιώτα Φατούρου 2 Σύνολα (Sets) Τα
Εισαγωγή στους Αλγορίθμους Ενότητα 10η
 Εισαγωγή στους Αλγορίθμους Ενότητα 10η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Ενότητα 10η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Προγραμματισμός Η/Υ. Βασικές Προγραμματιστικές Δομές. ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος
 Προγραμματισμός Η/Υ Βασικές Προγραμματιστικές Δομές ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος Δομή Ελέγχου Ροής (IF) Η εντολή IF χρησιμοποιείται όταν
Προγραμματισμός Η/Υ Βασικές Προγραμματιστικές Δομές ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος Δομή Ελέγχου Ροής (IF) Η εντολή IF χρησιμοποιείται όταν
Δομές Δεδομένων Ενότητα 4
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4: Ουρές Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4: Ουρές Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 6 η Άσκηση - DFS δένδρα Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 6 η Άσκηση - DFS δένδρα Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
1 η Διάλεξη. Ενδεικτικές λύσεις ασκήσεων
 1 η Διάλεξη Ενδεικτικές λύσεις ασκήσεων 1 Περιεχόμενα 1 η Άσκηση... 3 2 η Άσκηση... 3 3 η Άσκηση... 3 4 η Άσκηση... 3 5 η Άσκηση... 4 6 η Άσκηση... 4 7 η Άσκηση... 4 8 η Άσκηση... 5 9 η Άσκηση... 5 10
1 η Διάλεξη Ενδεικτικές λύσεις ασκήσεων 1 Περιεχόμενα 1 η Άσκηση... 3 2 η Άσκηση... 3 3 η Άσκηση... 3 4 η Άσκηση... 3 5 η Άσκηση... 4 6 η Άσκηση... 4 7 η Άσκηση... 4 8 η Άσκηση... 5 9 η Άσκηση... 5 10
Διοικητική Λογιστική
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 10: Προσφορά και κόστος Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 10: Προσφορά και κόστος Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Ενδεικτικές λύσεις ασκήσεων διαχείρισης έργου υπό συνθήκες αβεβαιότητας
 Ενδεικτικές λύσεις ασκήσεων διαχείρισης έργου υπό συνθήκες αβεβαιότητας 1 Περιεχόμενα 1 η Άσκηση... 4 2 η Άσκηση... 7 3 η Άσκηση... 10 Χρηματοδότηση... 12 Σημείωμα Αναφοράς... 13 Σημείωμα Αδειοδότησης...
Ενδεικτικές λύσεις ασκήσεων διαχείρισης έργου υπό συνθήκες αβεβαιότητας 1 Περιεχόμενα 1 η Άσκηση... 4 2 η Άσκηση... 7 3 η Άσκηση... 10 Χρηματοδότηση... 12 Σημείωμα Αναφοράς... 13 Σημείωμα Αδειοδότησης...
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
Δομές Δεδομένων Ενότητα 1
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Εισαγωγή Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Εισαγωγή Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 8: ΧΡΗΣΗ ΔΟΜΩΝ ΔΕΝΤΡΟΥ ΚΑΙ ΣΩΡΟΥ ΓΙΑ ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΟΣ ΤΑΞΙΝΟΜΗΣΗΣ ΑΛΓΟΡΙΘΜΟΣ HEAPSORT
 Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 8: ΧΡΗΣΗ ΔΟΜΩΝ ΔΕΝΤΡΟΥ ΚΑΙ ΣΩΡΟΥ ΓΙΑ ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΟΣ ΤΑΞΙΝΟΜΗΣΗΣ ΑΛΓΟΡΙΘΜΟΣ HEAPSORT Δημήτριος Κουκόπουλος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διαχείρισης
Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 8: ΧΡΗΣΗ ΔΟΜΩΝ ΔΕΝΤΡΟΥ ΚΑΙ ΣΩΡΟΥ ΓΙΑ ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΟΣ ΤΑΞΙΝΟΜΗΣΗΣ ΑΛΓΟΡΙΘΜΟΣ HEAPSORT Δημήτριος Κουκόπουλος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διαχείρισης
Βάσεις Περιβαλλοντικών Δεδομένων
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Βάσεις Περιβαλλοντικών Δεδομένων Ενότητα 2: Εισαγωγή Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Βάσεις Περιβαλλοντικών Δεδομένων Ενότητα 2: Εισαγωγή Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Πίνακες Νερού σε κατάσταση Κορεσμού. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Εισαγωγή στους Αλγορίθμους Ενότητα 10η Άσκηση Αλγόριθμος Dijkstra
 Εισαγωγή στους Αλγορίθμους Ενότητα 1η Άσκηση Αλγόριθμος Dijkra Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upara.gr Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 1η Άσκηση Αλγόριθμος Dijkra Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upara.gr Άδειες Χρήσης Το παρόν
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ενότητα 2 ιαίρει και Βασίλευε Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 2 1 / 24 Επιλογή Το πρόβληµα
Αλγόριθµοι και Πολυπλοκότητα Ενότητα 2 ιαίρει και Βασίλευε Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Καθηγητής: Ν. Μ. Μισυρλής Αλγόριθµοι και Πολυπλοκότητα - Ενότητα 2 1 / 24 Επιλογή Το πρόβληµα
Ψηφιακή Επεξεργασία Εικόνων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα # 14: Τμηματοποίηση με χρήση τυχαίων πεδίων Markov Καθηγητής Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Τμηματοποίηση εικόνων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα # 14: Τμηματοποίηση με χρήση τυχαίων πεδίων Markov Καθηγητής Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Τμηματοποίηση εικόνων
Εισαγωγή στους Αλγορίθμους Ενότητα 9η Άσκηση - Αλγόριθμος Prim
 Εισαγωγή στους Αλγορίθμους Ενότητα 9η Άσκηση - Αλγόριθμος Prim Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Emil: zro@ei.uptrs.r Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 9η Άσκηση - Αλγόριθμος Prim Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Emil: zro@ei.uptrs.r Άδειες Χρήσης Το παρόν
Ταξινόμηση. Παύλος Εφραιμίδης. Δομές Δεδομένων Ταξινόμηση 1
 Ταξινόμηση Παύλος Εφραιμίδης Δομές Δεδομένων Ταξινόμηση 1 Το πρόβλημα της ταξινόμησης Δομές Δεδομένων Ταξινόμηση 2 Ταξινόμηση Δίνεται πολυ-σύνολο Σ με στοιχεία από κάποιο σύμπαν U (πχ. U = το σύνολο των
Ταξινόμηση Παύλος Εφραιμίδης Δομές Δεδομένων Ταξινόμηση 1 Το πρόβλημα της ταξινόμησης Δομές Δεδομένων Ταξινόμηση 2 Ταξινόμηση Δίνεται πολυ-σύνολο Σ με στοιχεία από κάποιο σύμπαν U (πχ. U = το σύνολο των
Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2)
 Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Εισαγωγή στους Η/Υ. Ενότητα 2β: Αντίστροφο Πρόβλημα. Δημήτρης Σαραβάνος, Καθηγητής Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών
 Εισαγωγή στους Η/Υ Ενότητα 2β: Δημήτρης Σαραβάνος, Καθηγητής Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών Σκοποί ενότητας Εύρεση συνάρτησης Boole όταν είναι γνωστός μόνο ο πίνακας αληθείας.
Εισαγωγή στους Η/Υ Ενότητα 2β: Δημήτρης Σαραβάνος, Καθηγητής Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών Σκοποί ενότητας Εύρεση συνάρτησης Boole όταν είναι γνωστός μόνο ο πίνακας αληθείας.
Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 9: ΒΑΣΙΚΕΣ ΤΕΧΝΙΚΕΣ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΑΝΑΛΥΣΗΣ ΑΛΓΟΡΙΘΜΩΝ ΕΞΙΣΟΡΡΟΠΗΣΗ, ΔΙΑΙΡΕΙ ΚΑΙ ΒΑΣΙΛΕΥΕ
 Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 9: ΒΑΣΙΚΕΣ ΤΕΧΝΙΚΕΣ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΑΝΑΛΥΣΗΣ ΑΛΓΟΡΙΘΜΩΝ ΕΞΙΣΟΡΡΟΠΗΣΗ, ΔΙΑΙΡΕΙ ΚΑΙ ΒΑΣΙΛΕΥΕ Δημήτριος Κουκόπουλος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα
Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 9: ΒΑΣΙΚΕΣ ΤΕΧΝΙΚΕΣ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΑΝΑΛΥΣΗΣ ΑΛΓΟΡΙΘΜΩΝ ΕΞΙΣΟΡΡΟΠΗΣΗ, ΔΙΑΙΡΕΙ ΚΑΙ ΒΑΣΙΛΕΥΕ Δημήτριος Κουκόπουλος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα
Εισαγωγή στους Αλγορίθμους Ενότητα 5η
 Εισαγωγή στους Αλγορίθμους Ενότητα 5η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Ενότητα 5η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Ψηφιακή Επεξεργασία Εικόνων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα # 15: Τμηματοποίηση σε τοπολογικά συνεκτικές περιοχές Καθηγητής Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Διαμέριση σε συνεκτικές
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα # 15: Τμηματοποίηση σε τοπολογικά συνεκτικές περιοχές Καθηγητής Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Διαμέριση σε συνεκτικές
Εισαγωγή στους Αλγορίθμους Ενότητα 8η
 Εισαγωγή στους Αλγορίθμους Ενότητα 8η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Ενότητα 8η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας. Βιοστατιστική (Ε) Ενότητα 3: Έλεγχοι στατιστικών υποθέσεων
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 3: Έλεγχοι στατιστικών υποθέσεων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 3: Έλεγχοι στατιστικών υποθέσεων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας. Βιοστατιστική (Ε) Ενότητα 1: Καταχώρηση δεδομένων
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 1: Καταχώρηση δεδομένων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 1: Καταχώρηση δεδομένων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος διατίθεται
Εισαγωγή στον δομημένο προγραμματισμό
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στον δομημένο προγραμματισμό Ενότητα 5 η : Πίνακες (Προχωρημένα Θέματα) Αν. καθηγητής Στεργίου Κώστας e-mail: kstergiou@uowm.gr Τμήμα Μηχανικών Πληροφορικής
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στον δομημένο προγραμματισμό Ενότητα 5 η : Πίνακες (Προχωρημένα Θέματα) Αν. καθηγητής Στεργίου Κώστας e-mail: kstergiou@uowm.gr Τμήμα Μηχανικών Πληροφορικής
Αλγόριθμοι και πολυπλοκότητα Bucket-Sort και Radix-Sort
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Bucket-Sort και Radix-Sort Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Bucket-Sort και Radix-Sort 1, c 3, a 3, b 7, d 7, g 7, e B 0 1
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Bucket-Sort και Radix-Sort Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Bucket-Sort και Radix-Sort 1, c 3, a 3, b 7, d 7, g 7, e B 0 1
Λογιστική Κόστους Ενότητα 8: Κοστολογική διάρθρωση Κύρια / Βοηθητικά Κέντρα Κόστους.
 Λογιστική Κόστους Ενότητα 8: Κοστολογική διάρθρωση Κύρια / Βοηθητικά Κέντρα Κόστους. Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Λογιστική Κόστους Ενότητα 8: Κοστολογική διάρθρωση Κύρια / Βοηθητικά Κέντρα Κόστους. Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Δομές Δεδομένων. Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές Δεδομένων Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές Δεδομένων Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού
Εισαγωγή στους Υπολογιστές
 Εισαγωγή στους Υπολογιστές Εργαστήριο 2 Καθηγητές: Αβούρης Νικόλαος, Παλιουράς Βασίλης, Κουκιάς Μιχαήλ, Σγάρμπας Κυριάκος Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άσκηση 2 ου εργαστηρίου
Εισαγωγή στους Υπολογιστές Εργαστήριο 2 Καθηγητές: Αβούρης Νικόλαος, Παλιουράς Βασίλης, Κουκιάς Μιχαήλ, Σγάρμπας Κυριάκος Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άσκηση 2 ου εργαστηρίου
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας. Βιοστατιστική (Ε) Ενότητα 2: Περιγραφική στατιστική
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 2: Περιγραφική στατιστική Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 2: Περιγραφική στατιστική Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Εισαγωγή στους Αλγορίθμους Ενότητα 3η
 Εισαγωγή στους Αλγορίθμους Ενότητα 3η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Ενότητα 3η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Δομές Δεδομένων Ενότητα 2
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Θέματα Απόδοσης Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Θέματα Απόδοσης Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Βάσεις Περιβαλλοντικών Δεδομένων
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Βάσεις Περιβαλλοντικών Δεδομένων Ενότητα 3: Μοντέλα βάσεων δεδομένων Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Βάσεις Περιβαλλοντικών Δεδομένων Ενότητα 3: Μοντέλα βάσεων δεδομένων Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται
ΑΛΓΟΡΙΘΜΟΙ. Ενότητα 4: Διαίρει και Βασίλευε. Ιωάννης Μανωλόπουλος, Καθηγητής Αναστάσιος Γούναρης, Επίκουρος Καθηγητής Τμήμα Πληροφορικής ΑΠΘ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΛΓΟΡΙΘΜΟΙ Ενότητα 4: Διαίρει και Βασίλευε Ιωάννης Μανωλόπουλος, Καθηγητής Αναστάσιος Γούναρης, Επίκουρος Καθηγητής Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΛΓΟΡΙΘΜΟΙ Ενότητα 4: Διαίρει και Βασίλευε Ιωάννης Μανωλόπουλος, Καθηγητής Αναστάσιος Γούναρης, Επίκουρος Καθηγητής Άδειες Χρήσης Το παρόν
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός
 Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.4: Ολοκλήρωση με Αντικατάσταση Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.4: Ολοκλήρωση με Αντικατάσταση Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 7: Παράγωγος, ελαστικότητα, παραγώγιση συναρτήσεων (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 7: Παράγωγος, ελαστικότητα, παραγώγιση συναρτήσεων (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 5
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 5 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 5 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Προγραμματισμός Η/Υ. Αναζήτηση & Ταξινόμηση. ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος
 Προγραμματισμός Η/Υ Αναζήτηση & Ταξινόμηση ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος Αναζήτηση Το πρόβλημα της αναζήτησης (searching) ενός στοιχείου σε
Προγραμματισμός Η/Υ Αναζήτηση & Ταξινόμηση ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος Αναζήτηση Το πρόβλημα της αναζήτησης (searching) ενός στοιχείου σε
Προγραμματισμός Η/Υ. Συναρτήσεις & Υποπρογράμματα. ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος
 Προγραμματισμός Η/Υ Συναρτήσεις & Υποπρογράμματα ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος Τμηματικός Προγραμματισμός Η επίλυση ενός προβλήματος διευκολύνεται
Προγραμματισμός Η/Υ Συναρτήσεις & Υποπρογράμματα ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος Τμηματικός Προγραμματισμός Η επίλυση ενός προβλήματος διευκολύνεται
Ταξινόμηση με συγχώνευση Merge Sort
 Ταξινόμηση με συγχώνευση Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Πληροφορικής 1 Διαίρει και Βασίλευε Η μέθοδος του «Διαίρει και Βασίλευε» είναι μια γενική αρχή σχεδιασμού αλγορίθμων
Ταξινόμηση με συγχώνευση Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Πληροφορικής 1 Διαίρει και Βασίλευε Η μέθοδος του «Διαίρει και Βασίλευε» είναι μια γενική αρχή σχεδιασμού αλγορίθμων
Αλγόριθμοι και πολυπλοκότητα Δυναμικός Προγραμματισμός
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Δυναμικός Προγραμματισμός Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Δυναμικός Προγραμματισμός Δυναμικός Προγραμματισμός 1 Περίληψη
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Δυναμικός Προγραμματισμός Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Δυναμικός Προγραμματισμός Δυναμικός Προγραμματισμός 1 Περίληψη
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 3: Μη γραμμικές συναρτήσεις (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 3: Μη γραμμικές συναρτήσεις (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 11: Διανύσματα (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων &
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 11: Διανύσματα (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων &
Διεθνείς Οικονομικές Σχέσεις και Ανάπτυξη
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διεθνείς Οικονομικές Σχέσεις και Ανάπτυξη Ενότητα 8: Η Οικονομική πολιτική της Ευρωπαϊκής Ένωσης Γρηγόριος Ζαρωτιάδης Άδειες Χρήσης Το
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διεθνείς Οικονομικές Σχέσεις και Ανάπτυξη Ενότητα 8: Η Οικονομική πολιτική της Ευρωπαϊκής Ένωσης Γρηγόριος Ζαρωτιάδης Άδειες Χρήσης Το
Μηχανολογικό Σχέδιο Ι
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα # 8: Άτρακτοι και σφήνες Μ. Γρηγοριάδου Μηχανολόγων Μηχανικών Α.Π.Θ. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα # 8: Άτρακτοι και σφήνες Μ. Γρηγοριάδου Μηχανολόγων Μηχανικών Α.Π.Θ. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
a 1 a 2 a n. 3. i = j 1 5. A[i + 1] = A[i] 6. i = i 1
![a 1 a 2 a n. 3. i = j 1 5. A[i + 1] = A[i] 6. i = i 1 a 1 a 2 a n. 3. i = j 1 5. A[i + 1] = A[i] 6. i = i 1](/thumbs/62/47026969.jpg) Εισαγωγη στον Σχεδιασμο και Αναλυση αλγοριθμων Αλγοριθμοι Ταξινομησης Η ταξινόμηση μιας ακολουθίας αριθμών είναι από τα βασικά αποτελέσματα της θεωρίας αλγορίθμων. Μια ευρεία γκάμα τέτοιων αλγορίθμων έχουν
Εισαγωγη στον Σχεδιασμο και Αναλυση αλγοριθμων Αλγοριθμοι Ταξινομησης Η ταξινόμηση μιας ακολουθίας αριθμών είναι από τα βασικά αποτελέσματα της θεωρίας αλγορίθμων. Μια ευρεία γκάμα τέτοιων αλγορίθμων έχουν
Quicksort. ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Quicksort ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Quicksort ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Εισαγωγή στους Αλγορίθμους Ενότητα 9η Άσκηση - Αλγόριθμος Kruskal
 Εισαγωγή στους Αλγορίθμους Ενότητα 9η Άσκηση - Αλγόριθμος Kruskl Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Emil: zro@ei.uptrs.r Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 9η Άσκηση - Αλγόριθμος Kruskl Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Emil: zro@ei.uptrs.r Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 11η Άσκηση - Σταθμισμένος Χρονοπρογραμματισμός Διαστημάτων
 Εισαγωγή στους Αλγορίθμους Ενότητα η Άσκηση - Σταθμισμένος Χρονοπρογραμματισμός Διαστημάτων Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr
Εισαγωγή στους Αλγορίθμους Ενότητα η Άσκηση - Σταθμισμένος Χρονοπρογραμματισμός Διαστημάτων Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr
Ενότητα 7 Ουρές Προτεραιότητας
 Ενότητα 7 Ουρές Προτεραιότητας ΗΥ240 - Παναγιώτα Φατούρου Ουρές Προτεραιότητας Θεωρούµε ένα χώρο κλειδιών U και έστω ότι µε κάθε κλειδί Κ (τύπου Key) έχει συσχετισθεί κάποια πληροφορία Ι (τύπου Type).
Ενότητα 7 Ουρές Προτεραιότητας ΗΥ240 - Παναγιώτα Φατούρου Ουρές Προτεραιότητας Θεωρούµε ένα χώρο κλειδιών U και έστω ότι µε κάθε κλειδί Κ (τύπου Key) έχει συσχετισθεί κάποια πληροφορία Ι (τύπου Type).
Quicksort. Πρόβλημα Ταξινόμησης. Μέθοδοι Ταξινόμησης. Συγκριτικοί Αλγόριθμοι
 Πρόβλημα Ταξινόμησης Quicksort Διδάσκοντες: Σ. Ζάχος, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Είσοδος : ακολουθία n αριθμών (α 1, α 2,..., α n
Πρόβλημα Ταξινόμησης Quicksort Διδάσκοντες: Σ. Ζάχος, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Είσοδος : ακολουθία n αριθμών (α 1, α 2,..., α n
Εισαγωγή στους Αλγορίθμους Ενότητα 7η
 Εισαγωγή στους Αλγορίθμους Ενότητα 7η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Ενότητα 7η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΝΤΙΚΕΙΜΕΝΟΣΤΡΑΦΗΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων ΑΝΤΙΚΕΙΜΕΝΟΣΤΡΑΦΗΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 10: Πρότυπα Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων ΑΝΤΙΚΕΙΜΕΝΟΣΤΡΑΦΗΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 10: Πρότυπα Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Κβαντική Επεξεργασία Πληροφορίας
 Κβαντική Επεξεργασία Πληροφορίας Ενότητα 4: Κλασσική και Κβαντική Πιθανότητα Σγάρμπας Κυριάκος Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Σκοπός της ενότητας
Κβαντική Επεξεργασία Πληροφορίας Ενότητα 4: Κλασσική και Κβαντική Πιθανότητα Σγάρμπας Κυριάκος Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Σκοπός της ενότητας
ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 9: Αναδρομή
 ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 9: Αναδρομή Μιχάλης Δρακόπουλος Σχολή Θετικών επιστημών Τμήμα Μαθηματικών Αναδροµή 24 Αναδροµή Πληροφορική Ι Μ. ρακόπουλος 24 Αναδροµικές µέθοδοι Μια µέθοδος καλεί τον εαυτό της
ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 9: Αναδρομή Μιχάλης Δρακόπουλος Σχολή Θετικών επιστημών Τμήμα Μαθηματικών Αναδροµή 24 Αναδροµή Πληροφορική Ι Μ. ρακόπουλος 24 Αναδροµικές µέθοδοι Μια µέθοδος καλεί τον εαυτό της
Διοικητική Λογιστική
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 6: Μέθοδοι ς Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά Το έργο
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 6: Μέθοδοι ς Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά Το έργο
Προγραμματισμός Η/Υ. Αλγόριθμοι. ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος
 Προγραμματισμός Η/Υ Αλγόριθμοι ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος Ανάπτυξη Λογισμικού Η διαδικασία ανάπτυξης λογισμικού μπορεί να παρομοιαστεί
Προγραμματισμός Η/Υ Αλγόριθμοι ΤΕΙ Ιονίων Νήσων Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος Ανάπτυξη Λογισμικού Η διαδικασία ανάπτυξης λογισμικού μπορεί να παρομοιαστεί
Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 6: ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ: ΠΡΟΒΛΗΜΑ ΑΝΑΖΗΤΗΣΗΣ
 Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 6: ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ: ΠΡΟΒΛΗΜΑ ΑΝΑΖΗΤΗΣΗΣ Δημήτριος Κουκόπουλος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διαχείρισης Πολιτισμικού Περιβάλλοντος
Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 6: ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ: ΠΡΟΒΛΗΜΑ ΑΝΑΖΗΤΗΣΗΣ Δημήτριος Κουκόπουλος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διαχείρισης Πολιτισμικού Περιβάλλοντος
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 2: Γραμμικές συναρτήσεις (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 2: Γραμμικές συναρτήσεις (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
ΗΛΕΚΤΡΟΝΙΚΗ ΙIΙ Ενότητα 6
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΗ ΙIΙ Ενότητα 6: 1η εργαστηριακή άσκηση και προσομοίωση με το SPICE Χατζόπουλος Αλκιβιάδης Τμήμα Ηλεκτρολόγων Μηχανικών και
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΗ ΙIΙ Ενότητα 6: 1η εργαστηριακή άσκηση και προσομοίωση με το SPICE Χατζόπουλος Αλκιβιάδης Τμήμα Ηλεκτρολόγων Μηχανικών και
Προχωρημένες έννοιες προγραμματισμού σε C
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Διδάσκοντες: Στάθης Ζάχος (zachos@cs.ntua.gr) Νίκος Παπασπύρου (nickie@softlab.ntua.gr)
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Διδάσκοντες: Στάθης Ζάχος (zachos@cs.ntua.gr) Νίκος Παπασπύρου (nickie@softlab.ntua.gr)
Έλεγχος και Διασφάλιση Ποιότητας Ενότητα 4: Μελέτη ISO Κουππάρης Μιχαήλ Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας
 Έλεγχος και Διασφάλιση Ποιότητας Ενότητα 4: Μελέτη Κουππάρης Μιχαήλ Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας ISO 17025 5.9. ΔΙΑΣΦΑΛΙΣΗ ΤΗΣ ΠΟΙΟΤΗΤΑΣ ΤΩΝ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΔΟΚΙΜΩΝ (1) 5.9.1 Το Εργαστήριο
Έλεγχος και Διασφάλιση Ποιότητας Ενότητα 4: Μελέτη Κουππάρης Μιχαήλ Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας ISO 17025 5.9. ΔΙΑΣΦΑΛΙΣΗ ΤΗΣ ΠΟΙΟΤΗΤΑΣ ΤΩΝ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΔΟΚΙΜΩΝ (1) 5.9.1 Το Εργαστήριο
Μάρκετινγκ Αγροτικών Προϊόντων
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μάρκετινγκ Αγροτικών Προϊόντων Ενότητα 4 η : Οι Παραγωγοί Αγροτικών Προϊόντων Χρίστος Καμενίδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μάρκετινγκ Αγροτικών Προϊόντων Ενότητα 4 η : Οι Παραγωγοί Αγροτικών Προϊόντων Χρίστος Καμενίδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 8: Εφαρμογές παραγώγων Μελέτη και βελτιστοποίηση συναρτήσεων μιας μεταβλητής (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 8: Εφαρμογές παραγώγων Μελέτη και βελτιστοποίηση συναρτήσεων μιας μεταβλητής (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων
Αλγόριθμοι και πολυπλοκότητα Περιήγηση Πανεπιστημίων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Περιήγηση Πανεπιστημίων Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Περιήγηση Πανεπιστημίων 5/8/008 :46 AM Campus Tour Περίληψη και ανάγνωση
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Περιήγηση Πανεπιστημίων Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Περιήγηση Πανεπιστημίων 5/8/008 :46 AM Campus Tour Περίληψη και ανάγνωση
Πληροφορική ΙΙ Θεματική Ενότητα 5
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Πληροφορική ΙΙ Θεματική Ενότητα 5 Λογικοί Τελεστές Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Πληροφορική ΙΙ Θεματική Ενότητα 5 Λογικοί Τελεστές Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 8
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 8 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 8 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στην Διοίκηση Επιχειρήσεων
 Εισαγωγή στην Διοίκηση Επιχειρήσεων Ενότητα 7: ΑΣΚΗΣΕΙΣ ΜΕΓΕΘΟΥΣ ΕΠΙΧΕΙΡΗΣΗΣ Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εισαγωγή στην Διοίκηση Επιχειρήσεων Ενότητα 7: ΑΣΚΗΣΕΙΣ ΜΕΓΕΘΟΥΣ ΕΠΙΧΕΙΡΗΣΗΣ Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης 2 Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητα 2: Στοίβες Ουρές - Λίστες Ασκήσεις και Λύσεις Άσκηση 1 Έστω ότι µια
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Άσκηση αυτοαξιολόγησης 2 Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών Ενότητα 2: Στοίβες Ουρές - Λίστες Ασκήσεις και Λύσεις Άσκηση 1 Έστω ότι µια
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Δομές Δεδομένων. Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές Δεδομένων Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές Δεδομένων Ιωάννης Γ. Τόλλης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού
Εισαγωγή στους Αλγορίθμους Ενότητα 11η
 Εισαγωγή στους Αλγορίθμους Ενότητα 11η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Ενότητα 11η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 4
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 4 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 4 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Αλγόριθμοι και πολυπλοκότητα Μελανέρυθρα δεντρα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Μελανέρυθρα δεντρα Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Μελανέρυθρα δεντρα v 3 8 z Red-Black Trees 1 Περιγραφή και Διαβασμα Από
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Μελανέρυθρα δεντρα Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Μελανέρυθρα δεντρα v 3 8 z Red-Black Trees 1 Περιγραφή και Διαβασμα Από
Δομές δεδομένων. Ενότητα 5η: Υλοποίηση Λεξικών με Ισοζυγισμένα Δένδρα Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών
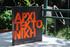 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Ενότητα 5η: Υλοποίηση Λεξικών με Ισοζυγισμένα Δένδρα Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών ΕΝΟΤΗΤΑ 5 ΥΛΟΠΟΙΗΣΗ ΛΕΞΙΚΩΝ ΜΕ ΙΣΟΖΥΓΙΣΜΕΝΑ ΔΕΝΔΡΑ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δομές δεδομένων Ενότητα 5η: Υλοποίηση Λεξικών με Ισοζυγισμένα Δένδρα Παναγιώτα Φατούρου Τμήμα Επιστήμης Υπολογιστών ΕΝΟΤΗΤΑ 5 ΥΛΟΠΟΙΗΣΗ ΛΕΞΙΚΩΝ ΜΕ ΙΣΟΖΥΓΙΣΜΕΝΑ ΔΕΝΔΡΑ
Ενδεικτικές λύσεις ασκήσεων διαγραμμάτων περίπτωσης χρήσης (1ο Μέρος)
 Ενδεικτικές λύσεις ασκήσεων διαγραμμάτων περίπτωσης χρήσης (1ο Μέρος) 1 Περιεχόμενα 1 η Άσκηση Λειτουργίες του βιβλίου διευθύνσεων σε ένα πρόγραμμα ηλεκτρονικού ταχυδρομείου... 4 2 η Άσκηση Λειτουργίες
Ενδεικτικές λύσεις ασκήσεων διαγραμμάτων περίπτωσης χρήσης (1ο Μέρος) 1 Περιεχόμενα 1 η Άσκηση Λειτουργίες του βιβλίου διευθύνσεων σε ένα πρόγραμμα ηλεκτρονικού ταχυδρομείου... 4 2 η Άσκηση Λειτουργίες
Ενότητα 9 Ξένα Σύνολα που υποστηρίζουν τη λειτουργία της Ένωσης (Union-Find)
 Ενότητα 9 (Union-Find) ΗΥ240 - Παναγιώτα Φατούρου 1 Έστω ότι S 1,, S k είναι ξένα υποσύνολα ενός συνόλου U, δηλαδή ισχύει ότι S i S j =, για κάθε i,j µε i j και S 1 S k = U. Λειτουργίες q MakeSet(X): επιστρέφει
Ενότητα 9 (Union-Find) ΗΥ240 - Παναγιώτα Φατούρου 1 Έστω ότι S 1,, S k είναι ξένα υποσύνολα ενός συνόλου U, δηλαδή ισχύει ότι S i S j =, για κάθε i,j µε i j και S 1 S k = U. Λειτουργίες q MakeSet(X): επιστρέφει
Προγραμματισμός Η/Υ. 8 η ενότητα: Περιβαλλοντικά και μαθηματικά προβλήματα. Τμήμα. Τεχνολόγων Περιβάλλοντος. ΤΕΙ Ιονίων Νήσων
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Προγραμματισμός Η/Υ 8 η ενότητα: Περιβαλλοντικά και μαθηματικά προβλήματα Τμήμα Τεχνολόγων Περιβάλλοντος ΤΕΙ Ιονίων Νήσων Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Προγραμματισμός Η/Υ 8 η ενότητα: Περιβαλλοντικά και μαθηματικά προβλήματα Τμήμα Τεχνολόγων Περιβάλλοντος ΤΕΙ Ιονίων Νήσων Το περιεχόμενο του μαθήματος διατίθεται
Διοίκηση Επιχειρήσεων
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η λήψη των αποφάσεων Ευγενία Πετρίδου Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η λήψη των αποφάσεων Ευγενία Πετρίδου Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΣΥΜΠΕΡΙΦΟΡΑ ΚΑΤΑΝΑΛΩΤΗ
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων ΣΥΜΠΕΡΙΦΟΡΑ ΚΑΤΑΝΑΛΩΤΗ Ενότητα 8: ΘΕΩΡΙΑ ΚΑΙ ΜΕΘΟΔΟΙ ΚΑΤΑΤΜΗΣΗΣ ΚΑΤΑΝΑΛΩΤΙΚΗΣ ΣΥΜΠΕΡΙΦΟΡΑΣ Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων ΣΥΜΠΕΡΙΦΟΡΑ ΚΑΤΑΝΑΛΩΤΗ Ενότητα 8: ΘΕΩΡΙΑ ΚΑΙ ΜΕΘΟΔΟΙ ΚΑΤΑΤΜΗΣΗΣ ΚΑΤΑΝΑΛΩΤΙΚΗΣ ΣΥΜΠΕΡΙΦΟΡΑΣ Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons
