for fracture orientation and fracture density on physical model data

HTML
DOWNLOAD

Μέγεθος: px

Εμφάνιση ξεκινά από τη σελίδα:

Download "for fracture orientation and fracture density on physical model data"

Καλλικράτης Κοσμόπουλος
7 χρόνια πριν
Προβολές:

1 AVAZ inversion for fracture orientation and fracture density on physical model data Faranak Mahmoudian Gary Margrave CREWES Tech talk, February 0 th, 0

$and azimuths) for fracture orientation$ $fracture planes Fracture density:$

2 Objective Inversion of prestack PP amplitudes (different incident angles and azimuths) for fracture orientation and fracture density. Fracture orientation: direction of fracture planes Fracture density: number of fractures in unit area

3 Anisotropic models Previous work Outline Jenner s method for fracture orientation Implementation on physical model data Conclusions Acknowledgements

4 VTI (vertical transverse isotropy) Horizontal isotropic planes Vertical symmetry axis 5 parameters to describe the medium (α, β, ε, δ, γ) X 3 α = β = P-vetical velocity S-vertical velocity ε γ = = VP( fast) VP( slow) V ( slow) P V ( fast) V ( slow) S V S S ( slow) Dominates the small angle δ = wave propagation ( A A ) ( A A ) A ( A A )

5 HTI (horizontal transverse isotropy) Simple model to describe vertical fractures Vertical isotropic plane Horizontal symmetry yaxis (α, β, ε, δ, γ) to describe X the medium α = β = P-vetical velocity S-vertical velocity ε = V Px V (Shear-wave V P z splitting parameter) VSx VSz γ = directly related to V Sz fracture density δ = Pz :Sv-wave in (x, ( A + A ) ( A A ) A ( A A ) x 3 ) plane

6 Determining elastic constants of phenolic layer (00 work) Phenolic layer HTI Transmission shot gathers on single layer Traveltime inversioni True (ε, δ, γ)

$along fracture$ system Large offset

7 AVAZ inversion for (ε, δ, γ) (0 work) Azimuth 90⁰ Acquisition coordinate system Acquisition coordinate system along fracture system Large offset data phenolic top

8 Amplitude corrections Water-plexiglas interface Spherical Zoeppritz picked amp Geometrical Speading Total-motion + Spreading Directivity + Total-motion + Spreading Rpp Incident angle (Degree) Geometrical spreading Free-surface Transmission loss emergence angle Source-receiver directivity

$5 Azimuth 90 (fracture$ plane) Azimuth 45 Azimuth

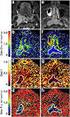
9 Phenolic top reflector corrected amplitudes Azimuth 90⁰ Azimuth 90 (fracture plane) Azimuth 45 Azimuth 0 (symmetry plane) phenolic top Rpp Incident angle (Degree)

$sin tan θ : incident angle φ: angle between source-receiver azimuth and fracture$

10 HTI: PP reflection coefficient (Rüger, 997) HTI R PP Δα 4β Δβ 4β Δρ ( θϕ, ) sin θ + sin θ cos θ α α β + α ρ ( 4 ) 4β cos ϕsin θ tan θ Δε + cos ϕsin θ Δγ + α cos sin cos sin sin tan θ : incident angle φ: angle between source-receiver azimuth and fracture symmetry axis ( ϕ θ + ϕ ϕ θ θ) φ Δδ Independent determination of (α, β, ρ) Inversion for (ε, δ, γ)

11 AVAZ inversion Successful inversion results for (ε, δ, γ) Azimuth φ Azimuth φ n Aϕ B ϕ C ϕ R Anϕ B nϕ C nϕ R n Δδ ε Δ = Δγ A (3 ) ϕ B m ϕ C m ϕ R m m A R n B nm m n C m n m ϕ ϕ ϕ ( nm ) ( nm 3) Gm = d T T m = ( G G + μ ) G d est

12 Fracture symmetry axis not known X φ φ 0 X : fracture system : acquisition coordinate φ : source-receiver azimuth φ 0 : fracture symmetry direction HTI R PP X 3 Δα 4β Δβ 4β Δρ ( θϕ, ) sin θ + sin θ cos θ α α β + α ρ ( 4 ) 4β cos ( ϕ ϕ0)sin θ tan θ Δ ε + cos ( ϕ ϕ 0)sin θ Δ γ + α ( cos ( ϕ )sin cos ( )sin ( ) 0 θ ϕ 0 ϕ 0 ϕ + ϕ ϕ sin θ tan θ) Δδ

13 HTI: PP reflection coefficient Small llincident id angle (θ<35⁰) HTI Δα 4β Δβ 4β Δρ R PP ( θϕ, ) sin θ + sin θ cos θ α α β α + ρ 4β + Δ γ + Δ δ cos ( ϕ ϕ 0)sin θ α HTI RPP ( θϕ, ) I + G G cos ( ϕ ϕ0) + sin θ Isotropic gradient Anisotropic gradient 4β G = Δγ + α Δδ

14 Estimate fracture orientation Jenner (00) HTI RPP ( θϕ, ) I + G Gcos ( ϕ ϕ0) + sin θ HTI RPP ( θϕ, ) I + Gsin ( ϕ ϕ0) ( G G)cos ( ϕ ϕ0) + + sin θ sin( ϕ ϕ0) = sin ϕcosϕ0 cosϕsin ϕ0 cos( ϕ ϕ0) = cosϕcosϕ0 + sinϕsinϕ0 HTI RPP ( θ, ϕ) I + W sin ϕ W sinϕcosϕ W cos ϕ + + sin θ = + + G 0.5( W W ( W W ) 4 W ) = ( ) + 4 G W W W ϕ 0 = tan W W + ( W W) + 4W W W, W, W33: function of φ 0

$fracture symmetry axis azimuth$

15 Test on physical model data, AVAZ inversion φ 0 =30⁰ φ 0 : fracture symmetry axis azimuth φ 0 X True φ 0 30⁰ Estimate φ 0 8.7⁰⁰

16 Testing different fracture orientations φ 0 : fracture symmetry axis azimuth True φ 0 0⁰ 5⁰ 0⁰ 0⁰ 30⁰ 40⁰ 50⁰ 60⁰ 70⁰ 80⁰ 90⁰ Estimate φ 0.5⁰ 3.7⁰ 8.7⁰ 8.7⁰ 8.7⁰ 38.7⁰ 48.7⁰ 58.7⁰ 68.7⁰ 78.7⁰ 88.7⁰

17 Estimate fracture density γ : directly related to fracture density Knowing the fracture orientation, do the AVAZ inversion of large offset data for (ε,δ,γ). HTI R PP Δα 4β Δβ 4β Δρ ( θϕ, ) sin θ + sin θ cos θ α α β + α ρ ( 4 ) 4β cos ϕsin θ tan θ Δε + cos ϕsin θ Δγ + α ( cos ϕ sin θ + cos ϕ sin ϕ sin θ tan θ) Δδ

18 AVAZ inversion of large offset data for (ε, δ, γ) % error Directly related to fracture density -0 δ ε γ Favourable results compared to those obtained previously by traveltime inversion

19 Conclusions Rüger equation for HTI, PP reflection coefficient, can be used in an inversion but fracture orientation must be known. Jenner s method reformulates to allow a linear inversion to determine fracture orientation. Implementation ti on physical model data gives results consistent with these theories. Fracture density can be estimated from AVAZ inversion of large-offset data after determining fracture orientation.

20 Acknowledgments CREWES sponsors Xinxiang Li Dr. Joe Wong David Henley David Cho Mahdi Almotlaq

Σχετικά έγγραφα

Dr. D. Dinev, Department of Structural Mechanics, UACEG

Lecture 4 Material behavior: Constitutive equations Field of the game Print version Lecture on Theory of lasticity and Plasticity of Dr. D. Dinev, Department of Structural Mechanics, UACG 4.1 Contents