General Linear Process. Autocovariance and Spectrum
|
|
|
- Σωφρονία Γεωργίου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 STAT 520 Linear Stationary and Nonstationary Models 1 General Linear Process Slide 1 Consider a general linear process of the form z t = a t + j=1 ψ ja t j = (1+ j=1 ψ jb j )a t = ψ(b)a t, where a t is a white noise process with var[a t ] = σ 2 a, B is the backward shift operator, Bz t = z t 1, B j z t = z t j, and ψ(b) is called the transfer function. Alternatively, one may write (1 j=1 π jb j )z t = π(b)z t = a t, where the current value of z t is regressed on the past values z t j. It is easily seen that π(b)ψ(b) = 1. It is known that any zero-mean stationary Gaussian process can be written in the MA form z t = ψ(b)a t with j=1 ψ j <. The transfer function ψ(b) defines a linear filter that transforms the input a t to output z t. The filter is stable with j=1 ψ j <. Autocovariance and Spectrum Slide 2 Set ψ 0 = 1 and ψ h = 0, h < 0. It is easy to calculate γ k = σa 2 j=0 ψ jψ j+k. Write γ(b) = k= γ kb k as the autocovariance generating function. It follows that γ(b) = σa 2 k j ψ jψ j+k B k = σa 2 j ψ jb j k ψ j+kb j+k = σaψ(b 2 1 )ψ(b), where B 1 = F is the forward shift operator. Recall the definition of the power spectrum, p(ω) = k= γ ke i2πkω. Substituting e i2πω for B in ψ(b), one has p(ω) = σ 2 aψ(e i2πω )ψ(e i2πω ) = σ 2 a ψ(e i2πω ) 2.
2 STAT 520 Linear Stationary and Nonstationary Models 2 Stationarity and Invertibility Slide 3 For the linear process z t = ψ(b)a t to be a valid stationary process, ψ(e i2πω ) = j=0 ψ je i2πωj must be convergent, i.e., ψ(b) be convergent for B 1. It suffices to have j=0 ψ j <. A process is invertible if π(b) is convergent for B 1. It suffices to have j=0 π j <. To illustrate the idea, consider the MA(1) process z t = (1 θb)a t. Since k 0 xj (1 x) = 1 x k+1, one has z t = k j=1 θj z t j +a t θ k+1 a t k 1. For θ < 1, one may let k and invert the process into an AR( ) process, with π j = θ j dying out as j 0. For θ 1, θ k+1 a t k 1 0. Also note that ρ 1 = 1/(θ +θ 1 ), so θ = b ±1 are not identifiable. Invertibility removes the ambiguity and assures practical sensibility. AR(p) Process: Stationarity Slide 4 An autoregressive process of order p (i.e., AR(p)) is defined by z t = φ 1 z t 1 + +φ p z t p +a t, or (1 φ 1 B φ p B p )z t = φ(b)z t = a t. The transfer function is given by ψ(b) = φ 1 (B). AR(p) is invertible by definition. Write φ(b) = p j=1 (1 G jb), where G 1 j are the roots of φ(b) = 0. One has (assuming distinctive roots), ψ(b) = p j=1 1 1 G j B = p j=1 K j 1 G j B, so one must have G i < 1 for ψ(b) to be convergent for all B 1. In other words, one needs the roots of φ(b) to lie outside of the unit circle for z t = φ 1 (B)a t to be stationary. To get the roots of 1+.6x+.5x 2, use polyroot(c(1,.6,.5)) in R.
3 STAT 520 Linear Stationary and Nonstationary Models 3 Examples: AR(1) and AR(2) Stationarity condition For AR(1), one needs φ 1 < 1. For AR(2), one needs g j < 1 in the expression Slide 5 φ(b) = (1 g 1 B)(1 g 2 B) = 1 (g 1 +g 2 )B ( g 1 g 2 )B 2. With g j real, (φ 1,φ 2 ) = (g 1 +g 2, g 1 g 2 ) over g 1,g 2 ( 1,1). With g j a conjugate pair Ae ±i2πω, one has (φ 1,φ 2 ) = (2Acos2πω, A 2 ) over ω ( 1/2,1/2), A (0,1). Autocorrelation For AR(1), ρ k = φ k 1, k 0. For AR(2), ρ k = φ 1 ρ k 1 +φ 2 ρ k 2, k > 0; ρ 0 = 1, ρ 1 = φ 1 /(1 φ 2 ). Examples: AR(1) and AR(2) Variance For AR(1), γ 0 = φ 1 γ 1 +σ 2 a, so γ 0 = σ 2 a/(1 φ 1 ρ 1 ) = σ 2 a/(1 φ 2 1). For AR(2), γ 0 = φ 1 γ 1 +φ 2 γ 2 +σ 2 a, so Slide 6 γ 0 = Power spectrum σ 2 a 1 φ 1 ρ 1 φ 2 ρ 2 = 1 φ 2 1+φ 2 σ 2 a {(1 φ 2 ) 2 φ 2 1 }. For AR(1), p(ω) = σ 2 a/ 1 φ 1 e i2πω 2 = σ 2 a/(1+φ 2 1 2φ 1 cos2πω). For AR(2), p(ω) = σ 2 a 1 φ 1 e i2πω φ 2 e i4πω 2 = σ 2 a 1+φ 2 1 +φ2 2 2φ 1(1 φ 2 )cos2πω 2φ 2 cos4πω.
4 STAT 520 Linear Stationary and Nonstationary Models 4 AR(p) Process: Yule-Walker Equations Taking expectations of the expression, z t k z t = φ 1 z t k z t 1 + +φ p z t k z t p +z t k a t, one has, after dividing by γ 0, Slide 7 ρ k = φ 1 ρ k 1 + +φ p ρ k p, k > 0. Substituting k = 1,...,p, one obtains the Yule-Walker equations 1 ρ 1 ρ 2... ρ p 1 φ 1 ρ 1 ρ 1 1 ρ 1... ρ p 2 φ 2 ρ =.,. ρ p 1 ρ p 2 ρ p φ p ρ p or P p φ = ρ p, and φ = P 1 p ρ p expresses φ j s in terms of ACF s. Partial Autocorrelation Function Consider a Gaussian stationary process. The partial autocorrelation function at lag k is defined by α k = corr[(z k E[z k z 1,...,z k 1 ]),(z 0 E[z 0 z 1,...,z k 1 ])]. Slide 8 For a general process, replace E[y z 1,...,z k 1 ] by the linear projection of y in {z 1,...,z k 1 }, ŷ = b 0 +b 1 z 1 + +b k 1 z k 1, with b j s chosen to minimize E(y ŷ) 2. It can be shown that α k equals the kth element of φ k = P 1 k ρ k, φ kk. Replacing ρ v by r v in the Yule-Walker equations, one gets the sample PACF ˆφ kk as the kth element of ˆφ 1 k = ˆP k ˆρ k. For AR(p) processes at lag k > p, one has φ kk = 0, and it can be shown that, asymptotically, ˆφ kk N(0, 1 N ). Sample PACF s can be calculated and plotted in R using acf with type="partial".
5 STAT 520 Linear Stationary and Nonstationary Models 5 Recursive Yule-Walker Solutions and PACF Slide 9 Let h = k 1. Partition P k = ( P h ρ h ρ T ), where ρ h 1 h is ρ h in reverse order, and write d = 1 ρ T h P 1. One has P 1 k = h ρ h = 1 ρt h P 1 h ρ h = 1 φt h ρ h ( P 1 h +d 1 P 1 h ρ h ρt h P 1 h d 1 ρ T h P 1 h d 1 P 1 h ρ h Write φ h = P 1 h ρ h. Straightforward algebra yields, φ k = P 1 k ρ h = ρ k φ h d 1 (ρ k φ T h ρ h ) φ h d 1 (ρ k φ T h ρ h ) d 1 = which gives the recursive formulas for Yule-Walker solutions. ). φ h φ kk φ h φ kk, Consider Gaussian process with σa 2 = 1. The conditional covariance matrix of (z 0,z k ) (z 1,...,z k 1 ) is given by ( ) 1 ρk ρ T ) ρ k 1 ( h P 1 ρ T h (ρ h, ρ h ). h It follows that α k = (ρ k ρ T h P 1 h ρ h )/(1 ρt h P 1 h ρ h ) = φ kk. Yule-Walker (Moment) Estimates for AR(p) Recall the Yule-Walker equations P p φ = ρ p and note the fact that γ 0 = p j=1 φ jγ j +σa. 2 Substituting the moment estimates ˆρ j = r j for ρ j, j = 1,...,p and ˆγ 0 = c 0 for γ 0, one has the Yule-Walker estimates ˆφ 1 p = ˆP p ˆρ p and ˆσ a 2 = c 0 (1 ˆφ T p ˆρ p) = ˆv p. Slide 10 Recall the recursive Yule-Walker solutions, one has φ kk = ρ k ρ T k 1 φ k 1 1 φ T k 1ρ k 1 = γ 0 (ρ k ρ T k 1 φ k 1 )/v k 1, φ k,k 1 = φ k 1 φ kk φk 1, v k = γ 0 (1 φ T kρ k ) = v k 1 (1 φ 2 kk), where φ T k = (φ T k,k 1,φ kk ). Putting hats on the parameters and starting with ˆφ 11 = r 1 and ˆv 1 = c 0 (1 r1), 2 one obtains the Durbin-Levinson algorithm for fitting AR models.
6 STAT 520 Linear Stationary and Nonstationary Models 6 Examples: AR(1), AR(2), and AR(3) Slide 11 The Y-W equations for AR(1), AR(2), and AR(3) are φ 1 = ρ 1, ( )( ) ( ) 1 ρ 1 ρ 2 φ 1 ρ 1 1 ρ 1 φ 1 ρ 1 =, and ρ 1 1 ρ 1 φ 2 = ρ 2. ρ 1 1 φ 2 ρ 2 ρ 2 ρ 1 1 φ 3 ρ 3 The Durbin-Levinson algorithm proceeds as follows: 1. φ 11 = r 1 ; v 1 = c 0 (1 r 2 1). 2. φ 22 = c 0 (r 2 ρ 1 φ 11 )/v 1 ; φ 21 = φ 11 φ 22 φ 11 ; v 2 = v 1 (1 φ 2 22). 3. φ 33 = c 0 (r 3 ρ 1 φ 22 ρ 2 φ 21 )/v 2 ; (φ 31,φ 32 ) = (φ 21,φ 22 ) φ 33 (φ 22,φ 21 ); v 3 = v 2 (1 φ 2 33). MA(q) Process: Invertibility Slide 12 A moving average process of order q (i.e., MA(q)) is defined by z t = a t θ 1 a t 1 θ q a t q, or z t = (1 θ 1 B θ q B q )a t = θ(b)a t. The transfer function is given by ψ(b) = θ(b). MA(q) is stationary by definition. Similar to the stationarity condition for AR(p), one needs the roots of θ(b) to lie outside of the unit circle for z t = θ(b)a t to be invertible. Let G 1 j be the roots of θ(b) and consider the spectrum p(ω) = q j=1 1 G je i2πω 2. For G j real, 1 G j e i2πω 2 (G j +G 1 j 2cos2πω), so G ±1 j are exchangeable. Similar arguments can be made for conjugate pairs of complex roots. Hence, MA(q) models come in 2 q -plet, of which only one is invertible, barring G j = 1.
7 STAT 520 Linear Stationary and Nonstationary Models 7 Examples: MA(1) and MA(2) Invertibility condition The invertibility of MA(1) and MA(2) is dual to the stationarity of AR(1) and AR(2). Slide 13 Variance and autocorrelation For MA(1), γ 0 = σ 2 a(1+θ 2 1); ρ 1 = θ 1 /(1+θ 2 1), ρ k = 0, k > 1. For MA(2), γ 0 = σ 2 a(1+θ 2 1 +θ 2 2); ρ 1 = θ 1(1 θ 2 ) 1+θ1 2, ρ 2 = +θ2 2 θ 2 1+θ1 2, ρ k = 0, k > 2. +θ2 2 Power spectrum Replacing φ 1 by θ 1 and φ 2 by θ 2 in the power spectrums of AR(1) and AR(2), and move the denominators to the numerators, one gets the power spectrums of MA(1) and MA(2). Multiplicity: MA(1) and MA(2) Consider z t = (1 2B)a t, which has the same autocorrelation function as the invertible z t = (1 0.5B)a t. Slide 14 Consider z t = (1 B B 2 )a t = ( B)( B)a t, which has the same autocorrelation function as the invertible z t = ( B 2 )a t = ( B)( B)a t, where 1/1.618 = The other two members of the family are z t = ( B 2 )a t = ( B)( B)a t and z t = (1+B B 2 )a t = ( B)( B)a t. The a t in different expressions are independent but may have different variances.
8 STAT 520 Linear Stationary and Nonstationary Models 8 ARMA(p, q) Process An ARMA(p,q) model is of the form z t φ 1 z t 1 φ p z t p = a t θ 1 a t 1 θ q z t q, Slide 15 or φ(b)z t = θ(b)a t, where φ(b) and θ(b) are polynomials of degree p and q in B. The stationarity and invertibility are governed by the roots of φ(b) and θ(b). For k > q, since φ(b)z t = θ(b)a t is uncorrelated with z t k, one has cov[φ(b)z t,z t k ] = φ(b)ρ k = 0, or more explicitly, ρ k = φ 1 ρ k 1 + +φ p ρ k p, k > q. With the transfer function ψ(b) = φ 1 (B)θ(B), the power spectrum of ARMA(p,q) is seen to be p(ω) = σ 2 a θ(e i2πω ) 2 / φ(e i2πω ) 2. Example: ARMA(1,1) Stationarity and invertibility condition For stationarity, one needs φ 1 < 1, for invertibility, θ 1 < 1. Slide 16 Variance and autocorrelation Note that E[z t a t ] = E[(φ 1 z t 1 +a t θ 1 a t 1 )a t ] = σ 2 a, one has γ 0 = E[(φ 1 z t 1 +a t θ 1 a t 1 ) 2 ] = φ 2 1γ 0 +σ 2 a +θ 2 1σ 2 a 2φ 1 θ 1 σ 2 a, so γ 0 = a 2 t(1+θ 2 1 2φ 1 θ 1 )/(1 φ 2 1). Similarly, one has ρ 1 = φ 1 θ 1 σ 2 a/γ 0 = (φ 1 θ 1 )(1 2φ 1 θ 1 ) 1+θ 2 1 2φ 1θ 1, ρ k = φ k 1 1 ρ 1, k > 1. Power spectrum p(ω) = σ 2 1 θ 1 e i2πω 2 a 1 φ 1 e i2πω 2 = σ2 a 1+θ 2 1 2θ 1 cos2πω 1+φ 2 1 2φ 1cos2πω.
9 STAT 520 Linear Stationary and Nonstationary Models 9 Moment Estimates for MA(q) and ARMA(p,q) Slide 17 For an MA(q) model, one has γ 0 = σa(1+ 2 q j=1 θ2 j ) and γ k = σa( θ 2 k + q k j=1 θ jθ j+k ), k 1. The moment estimates of σa, 2 θ q,..., θ 1 can be obtained through a simple iteration, σ 2 a = c 0 /(1+ q j=1 θ2 j), θ k = (c k /σ 2 a q k j=1 θ jθ j+k ), k = q,...,1. Remember that the solutions of θ j and σ 2 a are not unique. For an ARMA(p,q) model, one needs to use c j, j = 0,...,p+q. One can solve φ j from the equations, γ k = φ 1 γ k 1 + +φ p γ k p, k = q +1,...,q +p. Note that w t = φ(b)z t = θ(b)a t, and the ACF of w t is γ k = φt Γ k φ, where φ T = (1, φ 1,..., φ p ) and Γ k has (i,j)th entry γ k+j i. Use c k = ˆφ TˆΓkˆφ in the MA iteration above to get θj. Moment Estimates: ARMA(1,1) When applied to an ARMA(1,1) process (1 φb)z t = (1 θb)a t, the algorithm for moment estimates proceeds as follows: Slide Solve φ from r 2 = φr Calculate ( )( ) ( )( ) c c 0 c = (1, φ), c c 1 c = (1, φ). c 1 c 0 φ c 0 c 1 φ 3. Solve θ, σ 2 a from equations σa 2 = c 0 1+θ 2, θ = c 1 σa 2.
10 STAT 520 Linear Stationary and Nonstationary Models 10 Estimation of Mean Slide 19 Consider φ(b)z t = µ+θ(b)a t. It is easily seen that E[z t ] = µ/(1 φ 1 φ p ). Recall the large sample variance of the sample mean z, var[ z] = 1 n k= γ k = γ(1) n = σ2 a n ψ2 (1) = σ2 a θ 2 (1) n φ 2 (1) = p(0) n, where γ(b) = σ 2 aψ(b)ψ(b 1 ) is the covariance generating function and p(ω) is the power spectrum. The moment estimate of µ is thus ˆµ = ˆφ(1) z with approximate standard error ˆσ a ˆθ(1) / n. Fitting an ARMA(1,1) model to Series A, one has ˆφ =.8683, ˆθ =.4804, and ˆσ a 2 = Further, z = with s.e.[ z] ˆp(0)/n =.0882, and ˆµ = (1.8683)(17.06) = 2.25 with s.e.[ˆµ] = ˆσ a (1 ˆθ)/ n = Linear Difference Equation and ACF From the linear difference equation φ(b)ρ k = 0, k > q, one can obtain a general expression for ρ k. Slide 20 Write φ(b) = p j=1 (1 G jb), where G 1 j are the roots of φ(b). It is easy to verify that (1 G j B)G t j = 0, so ρ k has a term A j G k j. For a double root G 1 j, one also has (1 G j B) 2 (tg t j ) = 0, so ρ k has terms (A j,0 +A j,1 k)g k j. In general, a root G 1 j of multiplicity m contributes terms m 1 v=0 A j,vk v G k j. For pairs of conjugate complex roots G j 1 e ±iγ j, one has terms G j k (A j e iγ jk +Āje iγ jk ) = 2 G j k A j cos(kγ j +α j ). Assuming distinct roots, one has ρ k = p j=1 A jg k j, where A j s are determined by the initial values ρ q,...,ρ q p+1.
11 STAT 520 Linear Stationary and Nonstationary Models 11 Examples: AR(2) and ARMA(2,1) For (1 0.4B 0.21B 2 )z t = (1 0.7B)(1+0.3B)z t = a t, ρ k = A k +A 2 ( 0.3) k, k > 0, as φ(b)ρ k = 0, k > 0. A 1 and A 2 can be fixed via ρ 0 = 1 and ρ 1 = ρ 1 = φ 1 /(1 φ 2 ). Slide 21 For (1 0.8e iπ/3 B)(1 0.8e iπ/3 B)z t = (1 0.5B)a t, ρ k = A(0.8e iπ/3 ) k +Ā(0.8e iπ/3 ) k = A (0.8) k e i(α+kπ/3) + A (0.8) k e i(α+kπ/3) = (0.8) k 2 A cos(kπ/3+α) = (0.8) k {Bcos(kπ/3)+Csin(kπ/3)}, k > 1, where B and C can be fixed from ρ 0 = 1 and ρ 1 ; ρ 1 and κ = σa/γ 2 0 satisfy equations 1 = φ 2 1 +φ φ 1 φ 2 ρ 1 +(1+θ 2 2φ 1 θ)κ and ρ 1 = φ 1 +φ 2 ρ 1 θκ, where φ 1 = 0.8, φ 2 = 0.64, and θ = 0.5. Reverse Time Stationary Models A stationary process is characterized by its autocovariance and mean, independent of the time direction. In particular, models assuming forward or reverse time are mathematically equivalent. Slide 22 Recall the autocovariance generating function of z t = ψ(b)a t, γ(b) = σaψ(b)ψ(b 2 1 ). It is clear that z t = ψ(f)a t has the same autocovariance, where F = B 1 is the forward shift operator. For ARMA(p,q), let G 1 j be the roots of θ(b) and H 1 j those of φ(b). The same autocovariance is shared by all processes of the form p j=1 (1 H jb ±1 )z t = q j=1 (1 G jb ±1 )a t. Consider an MA(1) process z t = a t θa t 1. For θ > 1, one has z t = a t θa t 1 = ( θ)( θ 1 a t +a t 1 ) = ã t θ 1 ã t+1, an invertible reverse time MA(1) model, where ã t = θa t 1.
12 STAT 520 Linear Stationary and Nonstationary Models 12 Model Identification via ACF/PACF For k > q with an MA(q) process, ρ k = 0, E[r k ] 0, and var[r k ] (1+2 q j=1 ρ2 j )/N. Slide 23 For k > p with an AR(p) process, φ kk = 0, E[ˆφ kk ] 0, and var[ˆφ kk ] 1/N, where ˆφ kk is the Yule-Walker estimate of φ kk. For an stationary ARMA(p,q) process, ρ k damps out exponentially. If φ(b) has a near unit root G 1 i = (1 δ i ) 1, ρ k has a term A i (1 δ i ) k A i (1 kδ i ), damping out at a much slower linear rate. A slowly damping ρ k signifies nonstationarity. In practice, one inspect r k for stationarity, take differences if nonstationary, and repeat the process. The order identification of mixed ARMA model is not as straightforward. Model Selection via AIC or BIC To each observed series, one usually can fit several different models with similar goodness-of-fit. For example, suppose the ARMA(1,1) model (1+.2B)z t = (1.8B)a t is a good fit to the data. Since (1+.2B) 1 (1.8B) = 1 B +.2B 2.04B B +.2B 2, Slide 24 so an MA(2) fit z t = (1 B +.2B 2 )a t is also likely a good fit. AIC and BIC can be of assistance in the selection of competing models. Let l(γ z) be the log likelihood of the model and ˆγ be the MLE of γ, where γ consists of all model parameters including φ j, θ k, and σ 2 a. AIC and BIC are defined by AIC = 2l(ˆγ z)+2r, BIC = 2l(ˆγ z)+rlogn, where r is the number of parameters and n is the sample size. Models with smaller AIC or BIC are considered better ones.
13 STAT 520 Linear Stationary and Nonstationary Models 13 ARIMA(p,d,q) Processes To model nonstationary yet nonexplosive series, a popular device is the autoregressive integrated moving average (ARIMA) model, φ(b) d z t = ϕ(b)z t = θ(b)a t, Slide 25 where ϕ(b) = φ(b) d is a generalized AR operator. Note that d = (1 B) d has roots on the unit circle. A process with roots of ϕ(b) inside the unit circle is explosive. Assume stationarity and invertibility for d z t. An ARIMA model can be written in the AR( ) form π(b)z t = a t, where π(b) = 1 j=1 π jb j = θ 1 (B)φ(B)(1 B) d. For d > 0, since π(1) = 0, one has j=1 π j = 1. MA form of ARIMA Processes Symbolically, an ARIMA process can be written in a MA( ) form z t = ψ(b)a t, ψ(b) = 1+ i=1 ψ ib i, although {z t } is nonstationary and the filter unstable. From ϕ(b)ψ(b) = θ(b), one has Slide 26 ψ j = ϕ 1 ψ j 1 + +ϕ p+d ψ j p d θ j, j > 0, where ψ 0 = 1, ψ j = 0, j < 0. For j > q, ϕ(b)ψ j = 0. Take a time origin k < t and write z t = I k (t k)+c k (t k), where I k (t k) = t k 1 j=0 ψ j a t j. For t k > q, ϕ(b)i k (t k) = θ(b)a t, so ϕ(b)c k (t k) = 0. C k (t k) is called the complementary function, and is seen to be determined by the history up to time k. It follows that E[z t z k,z k 1,...] = C k (t k). Note that C k (t k) = C k 1 (t (k 1))+ψ t k a k.
14 STAT 520 Linear Stationary and Nonstationary Models 14 Example: ARIMA(1,1,1) Consider p = d = q = 1 with φ, θ < 1. ϕ(b) = (1 φb)(1 B). Since ϕ(b)ψ j = 0, j > 1, one has ψ j = A 0 +A 1 φ j, where A 0 = (1 θ)/(1 φ) and A 1 = (θ φ)/(1 φ) are determined from A 0 +A 1 = ψ 0 = 1 and A 0 +A 1 φ = ψ 1 = ϕ 1 θ = 1+φ θ. Slide 27 Since C k (t k) = b (k) 0 +b (k) 1 φt k for t k > 1, one has z t = t k 1 j=0 (A 0 +A 1 φ j )a t j +(b (k) 0 +b (k) 1 φt k ), where b (k) 0, b(k) 1 satisfy the initial conditions b (k) 0 +b (k) 1 = z k and b (k) 0 +b (k) 1 φ+a k+1 = z k+1 = (1+φ)z k φz k 1 +a k+1 θa k. Solving for b (k) 0, b(k) 1 from the equations, one has b (k) 0 = (z k φz k 1 θa k )/(1 φ), b (k) 1 = ( φ(z k z k 1 )+θa k )/(1 φ). With π(b) = (1 θb) 1 (1 φb)(1 B), it is easy to verify that π 1 = 1+φ θ, π j = (1 θ)(θ φ)θ j 2, j > 1. Example: IMA(0,2,2) Consider p = 0, d = q = 2 with θ(b) invertible. ϕ(b) = (1 B) 2. Since ϕ(b)ψ j = 0, j > 2, one has ψ j = A 0 +A 1 j, where A 0 = 1+θ 2 and A 1 = 1 θ 1 θ 2 are solved from A 0 +A 1 = ψ 1 = ϕ 1 θ 1 = 2 θ 1 and A 0 +2A 1 = ψ 2 = ϕ 1 ψ 1 +ϕ 2 θ 2 = 2(2 θ 1 ) (1+θ 2 ). Slide 28 Since C k (t k) = b (k) 0 +b (k) 1 (t k) for t k > 2, one has z t = a t + t k 1 j=1 (A 0 +A 1 j)a t j +(b (k) 0 +b (k) 1 (t k)), where b (k) 0, b(k) 1 satisfy the initial conditions b (k) 0 +b (k) 1 = z k+1 a k+1 and b (k) 0 +2b (k) 1 = z k+2 a k+2 ψ 1 a k+1. It follows that b (k) 1 = z k+2 z k+1 a k+2 (1 θ 1 )a k+1 = z k z k 1 (θ 1 +θ 2 )a k θ 2 a k 1 and b (k) 0 = z k+1 a k+1 b (k) 1 = z k +θ 2 a k. Note that C k (0) = z k b (k) 0. Since θ(b)π(b) = ϕ(b), one has π 1 = 2 θ 1, π 2 = π 1 θ 1 (1+θ 2 ) = θ 1 (2 θ 1 ) (1+θ 2 ), and θ(b)π j = 0, j > 2.
15 STAT 520 Linear Stationary and Nonstationary Models 15 ARIMA Processes with Added Noise The sum of independent MA processes of orders q and q 1 is itself an MA process of order max(q,q 1 ). Slide 29 Suppose one observes Z t = z t +b t, where φ(b) d z t = θ(b)a t and φ 1 (B)b t = θ 1 (B)α t with a t, α t being two independent white noise processes. It follows that φ 1 (B)φ(B) d Z t = φ 1 (B)θ(B)a t +φ(b)θ 1 (B) d α t, so Z t is of order (p 1 +p,d,max(p 1 +q,p+d+q 1 )). In particular, an IMA process with added white noise is of order (0,d,max(q,d)). If φ(b) and φ 1 (B) share some common roots, the orders will be lower. In general, an ARIMA model of form ϕ(b)z t = θ(b)a t is over-parameterized if ϕ(b) and θ(b) have common roots. Example: IMA(0,1,1) and Random Walk Consider Z t = z t +b t, where z t = a t θa t 1 and a t, b t are independent white noise with variances σ 2 a, σ 2 b. For the autocovariance of Z t = (1 θb)a t +(1 B)b t, one has Slide 30 γ 0 = σ 2 a(1+θ 2 )+2σ 2 b, γ 1 = θσ 2 a σ 2 b, γ k = 0, k > 1. Write Z t = u t Θu t 1 and equate γ 0 = σ 2 u(1+θ 2 ), γ 1 = Θσ 2 u, Θ = r(1+θ2 )+2 4r(1 θ) 2 +r 2 (1 θ 2 ) 2 2(1+rθ), σu 2 = θσ2 a +σ2 b Θ, where r = σa/σ 2 b 2. Consider a random walk with θ = 0. One has Θ = (r+2 4r+r 2 )/2, σ 2 u = σ 2 b /Θ. Hence, an IMA(0,1,1) process with Θ > 0 is seen to be a random walk buried in a white noise.
16 STAT 520 Linear Stationary and Nonstationary Models 16 Testing for Unit Root Slide 31 Consider an AR(1) process z t = φz t 1 +a t. Observing z 0,...,z n and minimizing the LS criterion n t=1 (z t φz t 1 ) 2, one has ˆφ = n t=1 z tz t 1 / n t=2 z2 t 1 = φ+ n t=1 z t 1a t / n t=1 z2 t 1. It can be shown through conditioning arguments that E[ n t=1 z t 1a t ] = 0, var[ n t=1 z t 1a t ] = σ 2 ae[ n t=1 z2 t 1]. For φ < 1, z t is stationary with γ 0 = var[z t ] = σ 2 a/(1 φ 2 ), so n/(1 φ2 )(ˆφ φ) = O p (1). For φ = 1, E[ n t=1 z2 t 1] = σ 2 an(n+1)/2, thus n(ˆφ 1) = O p (1). A test based on the t-statistic, ˆτ = (ˆφ 1)/ s 2 / n t=1 z2 t 1, where s 2 = n t=1 (z t ˆφz t 1 ) 2 /(n 1), was proposed by Dickey and Fuller, who derived its asymptotic null distribution under φ = 1. Testing for Unit Root Allowing for a constant, a linear trend, and possibly dependent but stationary innovations u t with autocovariance γ k, one has z t = β 0 +β 1 (t n/2)+φz t 1 +u t. Slide 32 The asymptotic distribution of the t-statistic, ˆτ = (ˆφ 1)/s.e.[ˆφ], was derived by Phillips and Perron under φ = 1, which depends on γ 0 and σ 2 = p u (0) = k= γ k. Consistent estimates of γ 0 and σ 2 are ˆγ 0 = n t=1û2 t/(n 3) and the Newey-West estimate, ˆσ 2 = n 1 n t=1û2 t +2n 1 l s=1 w sl n t=s+1ûtû t s, where û t are the residuals from the LS fit, w sl = 1 s/(l+1), and l, l 4 /n 0 as n. The test is implemented in PP.test. For φ(b) z t =θ(b)a t, z t =z t 1 + p j=1 φ jw t j +θ(b)a t =z t 1 +u t, where w t = z t. The process {u t } is stationary when {w t } is.
Module 5. February 14, h 0min
 Module 5 Stationary Time Series Models Part 2 AR and ARMA Models and Their Properties Class notes for Statistics 451: Applied Time Series Iowa State University Copyright 2015 W. Q. Meeker. February 14,
Module 5 Stationary Time Series Models Part 2 AR and ARMA Models and Their Properties Class notes for Statistics 451: Applied Time Series Iowa State University Copyright 2015 W. Q. Meeker. February 14,
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Lecture 2: ARMA Models
 Leture 2: ARMA Models Bus 41910, Autumn Quarter 2008, Mr Ruey S Tsay Autoregressive Moving-Average (ARMA) models form a lass of linear time series models whih are widely appliable and parsimonious in parameterization
Leture 2: ARMA Models Bus 41910, Autumn Quarter 2008, Mr Ruey S Tsay Autoregressive Moving-Average (ARMA) models form a lass of linear time series models whih are widely appliable and parsimonious in parameterization
Introduction to the ML Estimation of ARMA processes
 Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Stationary ARMA Processes
 Stationary ARMA Processes Eduardo Rossi University of Pavia October 2013 Rossi Stationary ARMA Financial Econometrics - 2013 1 / 45 Moving Average of order 1 (MA(1)) Y t = µ + ɛ t + θɛ t 1 t = 1,..., T
Stationary ARMA Processes Eduardo Rossi University of Pavia October 2013 Rossi Stationary ARMA Financial Econometrics - 2013 1 / 45 Moving Average of order 1 (MA(1)) Y t = µ + ɛ t + θɛ t 1 t = 1,..., T
HW 3 Solutions 1. a) I use the auto.arima R function to search over models using AIC and decide on an ARMA(3,1)
 HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
Asymptotic distribution of MLE
 Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Stationary ARMA Processes
 University of Pavia 2007 Stationary ARMA Processes Eduardo Rossi University of Pavia Moving Average of order 1 (MA(1)) Y t = µ + ǫ t + θǫ t 1 t = 1,...,T ǫ t WN(0, σ 2 ) E(ǫ t ) = 0 E(ǫ 2 t) = σ 2 E(ǫ
University of Pavia 2007 Stationary ARMA Processes Eduardo Rossi University of Pavia Moving Average of order 1 (MA(1)) Y t = µ + ǫ t + θǫ t 1 t = 1,...,T ǫ t WN(0, σ 2 ) E(ǫ t ) = 0 E(ǫ 2 t) = σ 2 E(ǫ
Durbin-Levinson recursive method
 Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
2. ARMA 1. 1 This part is based on H and BD.
 2. ARMA 1 1 This part is based on H and BD. 1 1 MA 1.1 MA(1) Let ε t be WN with variance σ 2 and consider the zero mean 2 process Y t = ε t + θε t 1 (1) where θ is a constant. MA(1). This time series is
2. ARMA 1 1 This part is based on H and BD. 1 1 MA 1.1 MA(1) Let ε t be WN with variance σ 2 and consider the zero mean 2 process Y t = ε t + θε t 1 (1) where θ is a constant. MA(1). This time series is
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
ARMA Models: I VIII 1
 ARMA Models: I autoregressive moving-average (ARMA) processes play a key role in time series analysis for any positive integer p & any purely nondeterministic process {X t } with ACVF {γ X (h)}, there
ARMA Models: I autoregressive moving-average (ARMA) processes play a key role in time series analysis for any positive integer p & any purely nondeterministic process {X t } with ACVF {γ X (h)}, there
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
5. Partial Autocorrelation Function of MA(1) Process:
 54 5. Partial Autocorrelation Function of MA() Process: φ, = ρ() = θ + θ 2 0 ( ρ() ) ( φ2, ) ( φ() ) = ρ() φ 2,2 φ(2) ρ() ρ() ρ(2) = φ 2,2 = ρ() = ρ() ρ() ρ() 0 ρ() ρ() = ρ()2 ρ() 2 = θ 2 + θ 2 + θ4 0
54 5. Partial Autocorrelation Function of MA() Process: φ, = ρ() = θ + θ 2 0 ( ρ() ) ( φ2, ) ( φ() ) = ρ() φ 2,2 φ(2) ρ() ρ() ρ(2) = φ 2,2 = ρ() = ρ() ρ() ρ() 0 ρ() ρ() = ρ()2 ρ() 2 = θ 2 + θ 2 + θ4 0
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
MAT Winter 2016 Introduction to Time Series Analysis Study Guide for Midterm
 MAT 3379 - Winter 2016 Introduction to Time Series Analysis Study Guide for Midterm You will be allowed to have one A4 sheet (one-sided) of notes date: Monday, Febraury 29, Midterm 1 Topics 1 Evaluate
MAT 3379 - Winter 2016 Introduction to Time Series Analysis Study Guide for Midterm You will be allowed to have one A4 sheet (one-sided) of notes date: Monday, Febraury 29, Midterm 1 Topics 1 Evaluate
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C
 DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
Stationary Univariate Time Series Models 1
 Stationary Univariate Time Series Models 1 Sebastian Fossati University of Alberta 1 These slides are based on Eric Zivot s time series notes available at: http://faculty.washington.edu/ezivot Example
Stationary Univariate Time Series Models 1 Sebastian Fossati University of Alberta 1 These slides are based on Eric Zivot s time series notes available at: http://faculty.washington.edu/ezivot Example
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
SOLVING CUBICS AND QUARTICS BY RADICALS
 SOLVING CUBICS AND QUARTICS BY RADICALS The purpose of this handout is to record the classical formulas expressing the roots of degree three and degree four polynomials in terms of radicals. We begin with
SOLVING CUBICS AND QUARTICS BY RADICALS The purpose of this handout is to record the classical formulas expressing the roots of degree three and degree four polynomials in terms of radicals. We begin with
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
w o = R 1 p. (1) R = p =. = 1
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Problem Set 9 Solutions. θ + 1. θ 2 + cotθ ( ) sinθ e iφ is an eigenfunction of the ˆ L 2 operator. / θ 2. φ 2. sin 2 θ φ 2. ( ) = e iφ. = e iφ cosθ.
 Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Written Examination. Antennas and Propagation (AA ) April 26, 2017.
 Written Examination Antennas and Propagation (AA. 6-7) April 6, 7. Problem ( points) Let us consider a wire antenna as in Fig. characterized by a z-oriented linear filamentary current I(z) = I cos(kz)ẑ
Written Examination Antennas and Propagation (AA. 6-7) April 6, 7. Problem ( points) Let us consider a wire antenna as in Fig. characterized by a z-oriented linear filamentary current I(z) = I cos(kz)ẑ
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Queensland University of Technology Transport Data Analysis and Modeling Methodologies
 Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Quadratic Expressions
 Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
 9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Exercise 2: The form of the generalized likelihood ratio
 Stats 2 Winter 28 Homework 9: Solutions Due Friday, March 6 Exercise 2: The form of the generalized likelihood ratio We want to test H : θ Θ against H : θ Θ, and compare the two following rules of rejection:
Stats 2 Winter 28 Homework 9: Solutions Due Friday, March 6 Exercise 2: The form of the generalized likelihood ratio We want to test H : θ Θ against H : θ Θ, and compare the two following rules of rejection:
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplementary Appendix
 Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Lecture 12: Pseudo likelihood approach
 Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Trigonometric Formula Sheet
 Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Econ Spring 2004 Instructor: Prof. Kiefer Solution to Problem set # 5. γ (0)
 Cornell University Department of Economics Econ 60 - Spring 004 Instructor: Prof. Kiefer Solution to Problem set # 5. Autocorrelation function is defined as ρ h = γ h γ 0 where γ h =Cov X t,x t h =E[X
Cornell University Department of Economics Econ 60 - Spring 004 Instructor: Prof. Kiefer Solution to Problem set # 5. Autocorrelation function is defined as ρ h = γ h γ 0 where γ h =Cov X t,x t h =E[X
Lecture 7: Overdispersion in Poisson regression
 Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS
 CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
 CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Introduction to Time Series Analysis. Lecture 16.
 Introduction to Time Series Analysis. Lecture 16. 1. Review: Spectral density 2. Examples 3. Spectral distribution function. 4. Autocovariance generating function and spectral density. 1 Review: Spectral
Introduction to Time Series Analysis. Lecture 16. 1. Review: Spectral density 2. Examples 3. Spectral distribution function. 4. Autocovariance generating function and spectral density. 1 Review: Spectral
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DIRECT PRODUCT AND WREATH PRODUCT OF TRANSFORMATION SEMIGROUPS
 GANIT J. Bangladesh Math. oc. IN 606-694) 0) -7 DIRECT PRODUCT AND WREATH PRODUCT OF TRANFORMATION EMIGROUP ubrata Majumdar, * Kalyan Kumar Dey and Mohd. Altab Hossain Department of Mathematics University
GANIT J. Bangladesh Math. oc. IN 606-694) 0) -7 DIRECT PRODUCT AND WREATH PRODUCT OF TRANFORMATION EMIGROUP ubrata Majumdar, * Kalyan Kumar Dey and Mohd. Altab Hossain Department of Mathematics University
ECE Spring Prof. David R. Jackson ECE Dept. Notes 2
 ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Empirical best prediction under area-level Poisson mixed models
 Noname manuscript No. (will be inserted by the editor Empirical best prediction under area-level Poisson mixed models Miguel Boubeta María José Lombardía Domingo Morales eceived: date / Accepted: date
Noname manuscript No. (will be inserted by the editor Empirical best prediction under area-level Poisson mixed models Miguel Boubeta María José Lombardía Domingo Morales eceived: date / Accepted: date
FORMULAS FOR STATISTICS 1
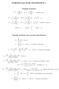 FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1 [1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg) 1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
TMA4115 Matematikk 3
 TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
