Lecture 7: Overdispersion in Poisson regression
|
|
|
- Ιόλη Λαμέρας
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
2 Overview Introduction Modeling overdispersion through mixing Score test for detecting overdispersion c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
3 Introduction McCullagh and Nelder (1989) p Overdispersion is present if V ar(y i ) > E(Y i ) Overdispersion can be modeled using a mixing approach: Y i Z i P oisson(z i ) Z i 0 ind. rv s with E(Z i ) = µ i c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
4 Distributional assumption for Z i 1) Z i Gamma with mean µ i and index φµ i Recall X Gamma(µ, ν) f X (x) = 1 Γ(ν) µ mean ν index E(X) = µ V ar(x) = µ 2 /ν ( ) ν ( νx µ exp νx µ ) 1 x Here f Zi (z i ) = 1 Γ(φµ i ) ( ) φµi ( ) φµi z i µ i exp φµ iz i µ i 1 z i E(Z i ) = µ i V ar(z i ) = µ2 i φµ i = µ i /φ c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
5 P (Y i = y i ) = 0 e z i(z i ) y i y i! 1 Γ(φµ i ) ( φµi z i µ i ) φµi exp{ φzi } 1 z i dz i = φ φµ i Γ(φµ i )y i! 0 e zi(1+φ) z (y i+φµ i 1) i dz i s i =z i (1+φ) = φ φµ i Γ(φµ i )y i! 0 e s i 1 s (y i+φµ i 1) 1 (1+φ) (y i +φµ i 1) i φ+1 ds i = = φ φµ i Γ(φµ i )y i!(1+φ) (y i +φµ i ) 0 e s is (y i+φµ i 1) i ds i φ φµ iγ(y i +φµ i ) Γ(φµ i )y i!(1+φ) (y i +φµ i ) = Γ(y i+φµ i ) Γ(φµ i )Γ(y i +1) ( ) φµ φ i ( ) φ 1 + φ }{{}}{{} 1 1/φ 1/φ+1 1/φ+1 y i c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
6 Negative binomial distribution X negbin(a, b) P (X = k) = Γ(a+k) Γ(a)Γ(k+1) ( 1 1+b ) a ( b 1+b) k k = 0, 1,... a, b 0 E(X) = ab V ar(x) = ab(1 + b) c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
7 is given by Marginal distribution of Y i Y i negbin(a i, b i ) with a i = φµ i b i = 1/φ E(Y i ) = φµ i φ = µ i und V ar(y i ) = φµ i φ (1 + 1/φ) = µ i(1 + 1/φ) Remarks: - V ar(y i ) > E(Y i ) if 1/φ > 0, i.e. overdispersion - φ = no overdispersion - To estimate β and φ jointly one needs to maximize the negative binomial likelihood. No standard software available but one can use the Splus library negbin() from http : //lib.stat.cmu.edu/s/ - V ar(y i ) = µ i (1 + 1/φ) is linear in µ i c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
8 2) Z i Gamma with mean µ i and index ν (exercise) Y i negbin(ν, µ i /ν) such that E(Y i ) = ν µ i /ν = µ i V ar(y i ) = µ i + µ 2 i /ν quadratic variance function in µ i c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
9 Multiplicative heterogeneity in Poisson regression Another approach for modeling overdispersion is to use Y i Z i P oisson(µ i Z i ) with E(Z i ) = 1 and V ar(z i ) = σ 2 Z, i.e. Z i i.i.d., Z i is called multiplicative random effect (exercise) E(Y i ) = µ i V ar(y i ) = µ i + σ 2 Z µ2 i If Z i Gamma with expectation 1 and index ν Y i is negbin(a i, b i ) a i = ν, b i = µ i ν c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
10 Summary 1) Y i Z i P oisson(z i ) E(Z i ) = µ i a) b) Z i Gamma(µ i, φµ i ) Y i Negbin(φµ i, 1/φ) E(Y i ) = µ i V ar(y i ) = µ i (1 + 1/φ) linear Z i Gamma(µ i, ν) Y i Negbin(ν, µ i /ν) E(Y i ) = µ i V ar(y i ) = µ i + µ 2 i /ν quadratic 2) Y i Z i P oisson(µ i Z i ) E(Z i ) = 1 Z i Gamma(1, ν) Y i Negbin(ν, µ i /ν) E(Y i ) = µ i V ar(y i ) = µ i + µ 2 i /ν quadratic c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
11 Test for overdispersion Dean (1992) Assume Y i P oisson(µ i ) with µ i = e x i t β θ i = ln(µ i ) = x t i β To model overdispersion we assume that the canonical parameters θ i are not fixed but random quantities θ i with E(θ i ) = θ i V ar(θ i ) = τk i(θ i ) > 0 for τ 0 and k i (θ i ) differentiable c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
12 To test for overdispersion, want to test H 0 : τ = 0 versus H 1 : τ > 0 Example: θi = xt i β + Z i with Z i i.i.d. E(Z i ) = 0 V ar(z i ) = τ < E(θi ) = θ i V ar(θi ) = τ i.e. k i(θ i ) = 1 Compare to: Y i Z i P oisson(µ i Z i ) E(Z i ) = 1 θ i = ln(µ iz i ) = ln(µ i ) + ln(z i ) E(ln(Z i )) 0 A score test will now be developed for H 0 : τ = 0 versus H 1 : τ > 0. c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
13 General score test Let Y 1,..., Y n ind. r.v. with densities f i (y, θ) θ Ω and H 0 : θ Ω 0 H 1 : θ Ω 1 Ω 0 + Ω 1 = Ω R d Ω 0 Ω1 = Loglikelihood: I(θ) := E l(θ) = n i=1 ( [ l(θ) θ l i (θ) l i (θ) = ln f i (y i ; θ) ] [ ] ) t l(θ) θ R d d Fisher information = E ( ) l 2 (θ) θ θ t under regularity conditions c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
14 We are interested in the following composite hypothesis for θ = (β t, τ) t : H 0 : τ = τ 0 versus H 1 : τ τ 0 Consider the score statistic T s = [ ] t θ l(θ) θ=ˆθ0 I 1 (ˆθ 0 ) [ ] θ l(θ) θ=ˆθ0 where ˆθ 0 is the MLE of θ in model θ = (β t, τ 0 ) t, i.e. ˆθ 0 = (ˆβ t, ˆτ 0 ) t satisfies θ l(θ) = ( l(β, τ) t, β ) t l(β, τ) τ θ=ˆθ0 = 0 Under regularity conditions we have T S χ 2 dimω dimω 0 under H 0. c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
15 Remark: There are regularity condition under which the standard asymptotic remains valid if τ 0 is at the boundary of Ω, as for example at H 0 : τ = 0 versus H 1 : τ > 0. Here: θ = (β t, τ) t For τ = 0 we have a Poisson GLM and one can show that ˆθ 0 = (ˆβ 0t, 0) t where ˆβ 0 is the MLE of the Poisson GLM. c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
16 Score test for overdispersion in count regression Y i θ i P oisson(eθ i ) with E(θ i ) = xt i β and V ar(θ i ) = τk i(θ i ) Let f(y i, θi ) be the conditional density of Y i given θi, then with Taylor we have f(y i, θ i ) = f(y i, θ i ) + θ i f(y i, θ i ) θ i =θ i (θ i θ i) θi 2 R = remainder term f(y i, θ i ) θ i =θ i (θ i θ i) 2 + R c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
17 f M (Y i, θ i ) = marginal likelihood of Y i = f(y i, θ i )f(θ i )dθ i = E θ i (f(y i, θ i )) = f(y i, θ i ) θi 2 [ = f(y i, θ i ) τk i(θ i )f 1 (Y i, θ i ) 2 f(y i, θi ) θi =θ i E[(θ i θ i ) 2 ] +R }{{} V ar(θi )=τk i(θ i ) θi 2 ] f(y i, θi ) θi =θ + Rf 1 (Y i i, θ i ) c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
18 Marginal log likelihood l(θ) = n i=1 l i (θ i ) = n i=1 = n [ln f(y i, θ i ) i=1 + ln l(θ) θ ln f M (Y i, θ i ) { τk i(θ i ) f 1 (Y i, θ i ) 2 θ=( ˆβ0t,0) t = l(β,τ) β l(β,τ) τ θi 2 β= ˆβ0,τ=0 β= ˆβ0,τ=0 } f(y i, θi ) θi =θ + Rf 1 (Y i i, θ i ) ] = 0 l(β,τ) τ β= ˆβ0,τ=0 θ i = x t i β ˆθ 0 i := x i tˆβ0 c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
19 We assume E((θ i θ i) r ) =: d r with d r = o(τ) for r 3 l(β,τ) τ β= ˆβ0,τ=0 n i=1 1 2 k i(θ i ) f 1 (Y i,θ i ) 2 θ i τ k i(θ i ) f 1 (Y i,θ i ) 2 f(y i,θ i ) θ i =θ i θ i 2 f(y i,θi ) θ i =θ i β= ˆβ0,τ=0 = n i=1 1 2 k i(ˆθ i 0 ) f 1 (Y i, ˆθ i 0 ) θi 2 f(y i, θi ) θ i =ˆθ i 0 }{{} 2 =:T i (ˆθ 0 i ) (denominator = 1, since τ=0) c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
20 Additionally I(ˆθ 0 ) = T s = ( ) Iββ I βτ I βτ I ττ [ ˆθ 0 = (ˆβ 0t, 0) t θ l(θ) θ=( ˆβ0,0)] t I 1 (ˆβ 0, 0) [ ] θ l(θ) θ=( ˆβ0,0) = ( l(β,τ) τ ) 2 ( ) β= ˆβ0,τ=0 I 1 (ˆβ 0, 0) ττ = [ n i=1 ] 2 ) T i (ˆθ i (I 0) 1 (ˆβ 0, 0) ττ since components corresponding to β are zero. Further I 1 (ˆβ 0, 0) = (I ττ I t βτ I 1 ββ I βτ) 1 (partioned matrixes) T S = [ n i=1 T i (ˆθ 0 i ) ] 2 / V 2, V 2 = (I ττ I t βτ I 1 ββ I βτ) c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
21 Overdispersion test Reject H 0 : τ = 0 versus H 1 : τ > 0 at level α T S > χ 2 1,1 α c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
22 Ex.: Poisson model with random effects θ i = xt i β + Z i E(Z i ) = 0 V ar(z i ) = τ Y i θ i P oisson(eθ i ) θi = ln µ i = x t i β E(Y i ) = E θ i (E(Y i θ i )) = E θ i (eθ i ) Eθ i (1 + θ i ) = 1 + θ i = 1 + ln µ i 1 + µ i 1 = µ i V ar(y i ) = E θ i (V ar(y i θi )) + V ar }{{} θ i (E(Y i θi )) }{{} E(Y i θi ) = E(Y i ) + (e θ i) 2 V ar(e Z i ) }{{} V ar(1+z i )=V ar(z i )=τ µ i + µ 2 i τ can model overdispersion e θ i c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
23 Overdispersion test in Poisson model with random effect Model: Y i θ i P oisson(eθ i ) θ i = x t i β + Z i E(Z i ) = 0 V ar(z i ) = σ 2 Score test: Reject H 0 : τ = 0 versus H 1 : τ > 0 n i=1 T i (ˆθ i 0 ) V = 1 2 n [(Y i ˆµ 0 i )2 ˆµ 0 i] n i=1 1 2 i=1 ˆµ 02 i > Z 1 α/2 c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
24 References Dean, C. (1992). Testing for overdispersion in Poisson and binomial regression models. JASA 87(418), McCullagh, P. and J. Nelder (1989). Generalized linear models. Chapman & Hall. c (Claudia Czado, TU Munich) ZFS/IMS Göttingen
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Theorem 8 Let φ be the most powerful size α test of H
 Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
HW 3 Solutions 1. a) I use the auto.arima R function to search over models using AIC and decide on an ARMA(3,1)
 HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
Empirical best prediction under area-level Poisson mixed models
 Noname manuscript No. (will be inserted by the editor Empirical best prediction under area-level Poisson mixed models Miguel Boubeta María José Lombardía Domingo Morales eceived: date / Accepted: date
Noname manuscript No. (will be inserted by the editor Empirical best prediction under area-level Poisson mixed models Miguel Boubeta María José Lombardía Domingo Morales eceived: date / Accepted: date
Introduction to the ML Estimation of ARMA processes
 Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Exercise 2: The form of the generalized likelihood ratio
 Stats 2 Winter 28 Homework 9: Solutions Due Friday, March 6 Exercise 2: The form of the generalized likelihood ratio We want to test H : θ Θ against H : θ Θ, and compare the two following rules of rejection:
Stats 2 Winter 28 Homework 9: Solutions Due Friday, March 6 Exercise 2: The form of the generalized likelihood ratio We want to test H : θ Θ against H : θ Θ, and compare the two following rules of rejection:
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Lecture 21: Properties and robustness of LSE
 Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
P AND P. P : actual probability. P : risk neutral probability. Realtionship: mutual absolute continuity P P. For example:
 (B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
(B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
An Introduction to Signal Detection and Estimation - Second Edition Chapter II: Selected Solutions
 An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
FORMULAS FOR STATISTICS 1
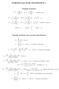 FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Lecture 12: Pseudo likelihood approach
 Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Last Lecture. Biostatistics Statistical Inference Lecture 19 Likelihood Ratio Test. Example of Hypothesis Testing.
 Last Lecture Biostatistics 602 - Statistical Iferece Lecture 19 Likelihood Ratio Test Hyu Mi Kag March 26th, 2013 Describe the followig cocepts i your ow words Hypothesis Null Hypothesis Alterative Hypothesis
Last Lecture Biostatistics 602 - Statistical Iferece Lecture 19 Likelihood Ratio Test Hyu Mi Kag March 26th, 2013 Describe the followig cocepts i your ow words Hypothesis Null Hypothesis Alterative Hypothesis
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Summary of the model specified
 Program: HLM 7 Hierarchical Linear and Nonlinear Modeling Authors: Stephen Raudenbush, Tony Bryk, & Richard Congdon Publisher: Scientific Software International, Inc. (c) 2010 techsupport@ssicentral.com
Program: HLM 7 Hierarchical Linear and Nonlinear Modeling Authors: Stephen Raudenbush, Tony Bryk, & Richard Congdon Publisher: Scientific Software International, Inc. (c) 2010 techsupport@ssicentral.com
More Notes on Testing. Large Sample Properties of the Likelihood Ratio Statistic. Let X i be iid with density f(x, θ). We are interested in testing
 Ulrich Müller Economics 2110 Fall 2008 More Notes on Testing Large Sample Properties of the Likelihood Ratio Statistic Let X i be iid with density f(x, θ). We are interested in testing H 0 : θ = θ 0 against
Ulrich Müller Economics 2110 Fall 2008 More Notes on Testing Large Sample Properties of the Likelihood Ratio Statistic Let X i be iid with density f(x, θ). We are interested in testing H 0 : θ = θ 0 against
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
ECE598: Information-theoretic methods in high-dimensional statistics Spring 2016
 ECE598: Information-theoretic methods in high-dimensional statistics Spring 06 Lecture 7: Information bound Lecturer: Yihong Wu Scribe: Shiyu Liang, Feb 6, 06 [Ed. Mar 9] Recall the Chi-squared divergence
ECE598: Information-theoretic methods in high-dimensional statistics Spring 06 Lecture 7: Information bound Lecturer: Yihong Wu Scribe: Shiyu Liang, Feb 6, 06 [Ed. Mar 9] Recall the Chi-squared divergence
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
An Inventory of Continuous Distributions
 Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
ESTIMATION OF SYSTEM RELIABILITY IN A TWO COMPONENT STRESS-STRENGTH MODELS DAVID D. HANAGAL
 ESTIMATION OF SYSTEM RELIABILITY IN A TWO COMPONENT STRESS-STRENGTH MODELS DAVID D. HANAGAL Department of Statistics, University of Poona, Pune-411007, India. Abstract In this paper, we estimate the reliability
ESTIMATION OF SYSTEM RELIABILITY IN A TWO COMPONENT STRESS-STRENGTH MODELS DAVID D. HANAGAL Department of Statistics, University of Poona, Pune-411007, India. Abstract In this paper, we estimate the reliability
Survival Analysis: One-Sample Problem /Two-Sample Problem/Regression. Lu Tian and Richard Olshen Stanford University
 Survival Analysis: One-Sample Problem /Two-Sample Problem/Regression Lu Tian and Richard Olshen Stanford University 1 One sample problem T 1,, T n 1 S( ), C 1,, C n G( ) and T i C i Observations: (U i,
Survival Analysis: One-Sample Problem /Two-Sample Problem/Regression Lu Tian and Richard Olshen Stanford University 1 One sample problem T 1,, T n 1 S( ), C 1,, C n G( ) and T i C i Observations: (U i,
Lecture 17: Minimum Variance Unbiased (MVUB) Estimators
 ECE 830 Fall 2011 Statistical Sigal Processig istructor: R. Nowak, scribe: Iseok Heo Lecture 17: Miimum Variace Ubiased (MVUB Estimators Ultimately, we would like to be able to argue that a give estimator
ECE 830 Fall 2011 Statistical Sigal Processig istructor: R. Nowak, scribe: Iseok Heo Lecture 17: Miimum Variace Ubiased (MVUB Estimators Ultimately, we would like to be able to argue that a give estimator
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Lecture 26: Circular domains
 Introductory lecture notes on Partial Differential Equations - c Anthony Peirce. Not to be copied, used, or revised without eplicit written permission from the copyright owner. 1 Lecture 6: Circular domains
Introductory lecture notes on Partial Differential Equations - c Anthony Peirce. Not to be copied, used, or revised without eplicit written permission from the copyright owner. 1 Lecture 6: Circular domains
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
5. Choice under Uncertainty
 5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data
 Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data Rahim Alhamzawi, Haithem Taha Mohammad Ali Department of Statistics, College of Administration and Economics,
Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data Rahim Alhamzawi, Haithem Taha Mohammad Ali Department of Statistics, College of Administration and Economics,
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
HOMEWORK#1. t E(x) = 1 λ = (b) Find the median lifetime of a randomly selected light bulb. Answer:
 HOMEWORK# 52258 李亞晟 Eercise 2. The lifetime of light bulbs follows an eponential distribution with a hazard rate of. failures per hour of use (a) Find the mean lifetime of a randomly selected light bulb.
HOMEWORK# 52258 李亞晟 Eercise 2. The lifetime of light bulbs follows an eponential distribution with a hazard rate of. failures per hour of use (a) Find the mean lifetime of a randomly selected light bulb.
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Econ Spring 2004 Instructor: Prof. Kiefer Solution to Problem set # 5. γ (0)
 Cornell University Department of Economics Econ 60 - Spring 004 Instructor: Prof. Kiefer Solution to Problem set # 5. Autocorrelation function is defined as ρ h = γ h γ 0 where γ h =Cov X t,x t h =E[X
Cornell University Department of Economics Econ 60 - Spring 004 Instructor: Prof. Kiefer Solution to Problem set # 5. Autocorrelation function is defined as ρ h = γ h γ 0 where γ h =Cov X t,x t h =E[X
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
STAT200C: Hypothesis Testing
 STAT200C: Hypothesis Testing Zhaoxia Yu Spring 2017 Some Definitions A hypothesis is a statement about a population parameter. The two complementary hypotheses in a hypothesis testing are the null hypothesis
STAT200C: Hypothesis Testing Zhaoxia Yu Spring 2017 Some Definitions A hypothesis is a statement about a population parameter. The two complementary hypotheses in a hypothesis testing are the null hypothesis
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Notes on the Open Economy
 Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Risk! " #$%&'() *!'+,'''## -. / # $
 Risk! " #$%&'(!'+,'''## -. / 0! " # $ +/ #%&''&(+(( &'',$ #-&''&$ #(./0&'',$( ( (! #( &''/$ #$ 3 #4&'',$ #- &'',$ #5&''6(&''&7&'',$ / ( /8 9 :&' " 4; < # $ 3 " ( #$ = = #$ #$ ( 3 - > # $ 3 = = " 3 3, 6?3
Risk! " #$%&'(!'+,'''## -. / 0! " # $ +/ #%&''&(+(( &'',$ #-&''&$ #(./0&'',$( ( (! #( &''/$ #$ 3 #4&'',$ #- &'',$ #5&''6(&''&7&'',$ / ( /8 9 :&' " 4; < # $ 3 " ( #$ = = #$ #$ ( 3 - > # $ 3 = = " 3 3, 6?3
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Additional Results for the Pareto/NBD Model
 Additional Results for the Pareto/NBD Model Peter S. Fader www.petefader.com Bruce G. S. Hardie www.brucehardie.com January 24 Abstract This note derives expressions for i) the raw moments of the posterior
Additional Results for the Pareto/NBD Model Peter S. Fader www.petefader.com Bruce G. S. Hardie www.brucehardie.com January 24 Abstract This note derives expressions for i) the raw moments of the posterior
Section 4: Conditional Likelihood: Sufficiency and Ancillarity in the Presence of Nuisance Parameters
 70 Section 4: Conditional Likelihood: Sufficiency and Ancillarity in the Presence of Nuisance Parameters In this section we will: (i) Explore decomposing information in terms of conditional and marginal
70 Section 4: Conditional Likelihood: Sufficiency and Ancillarity in the Presence of Nuisance Parameters In this section we will: (i) Explore decomposing information in terms of conditional and marginal
ON NEGATIVE MOMENTS OF CERTAIN DISCRETE DISTRIBUTIONS
 Pa J Statist 2009 Vol 25(2), 135-140 ON NEGTIVE MOMENTS OF CERTIN DISCRETE DISTRIBUTIONS Masood nwar 1 and Munir hmad 2 1 Department of Maematics, COMSTS Institute of Information Technology, Islamabad,
Pa J Statist 2009 Vol 25(2), 135-140 ON NEGTIVE MOMENTS OF CERTIN DISCRETE DISTRIBUTIONS Masood nwar 1 and Munir hmad 2 1 Department of Maematics, COMSTS Institute of Information Technology, Islamabad,
Supplementary Appendix
 Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
( )( ) ( ) ( )( ) ( )( ) β = Chapter 5 Exercise Problems EX α So 49 β 199 EX EX EX5.4 EX5.5. (a)
 hapter 5 xercise Problems X5. α β α 0.980 For α 0.980, β 49 0.980 0.995 For α 0.995, β 99 0.995 So 49 β 99 X5. O 00 O or n 3 O 40.5 β 0 X5.3 6.5 μ A 00 β ( 0)( 6.5 μa) 8 ma 5 ( 8)( 4 ) or.88 P on + 0.0065
hapter 5 xercise Problems X5. α β α 0.980 For α 0.980, β 49 0.980 0.995 For α 0.995, β 99 0.995 So 49 β 99 X5. O 00 O or n 3 O 40.5 β 0 X5.3 6.5 μ A 00 β ( 0)( 6.5 μa) 8 ma 5 ( 8)( 4 ) or.88 P on + 0.0065
Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines
![Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines](/thumbs/51/28406191.jpg) Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the
Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Solutions: Homework 3
 Solutios: Homework 3 Suppose that the radom variables Y,, Y satisfy Y i = βx i + ε i : i,, where x,, x R are fixed values ad ε,, ε Normal0, σ ) with σ R + kow Fid ˆβ = MLEβ) IND Solutio: Observe that Y
Solutios: Homework 3 Suppose that the radom variables Y,, Y satisfy Y i = βx i + ε i : i,, where x,, x R are fixed values ad ε,, ε Normal0, σ ) with σ R + kow Fid ˆβ = MLEβ) IND Solutio: Observe that Y
Asymptotic distribution of MLE
 Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
Dynamic types, Lambda calculus machines Section and Practice Problems Apr 21 22, 2016
 Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Dynamic types, Lambda calculus machines Apr 21 22, 2016 1 Dynamic types and contracts (a) To make sure you understand the
Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Dynamic types, Lambda calculus machines Apr 21 22, 2016 1 Dynamic types and contracts (a) To make sure you understand the
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
ENGR 691/692 Section 66 (Fall 06): Machine Learning Assigned: August 30 Homework 1: Bayesian Decision Theory (solutions) Due: September 13
 ENGR 69/69 Section 66 (Fall 06): Machine Learning Assigned: August 30 Homework : Bayesian Decision Theory (solutions) Due: Septemer 3 Prolem : ( pts) Let the conditional densities for a two-category one-dimensional
ENGR 69/69 Section 66 (Fall 06): Machine Learning Assigned: August 30 Homework : Bayesian Decision Theory (solutions) Due: Septemer 3 Prolem : ( pts) Let the conditional densities for a two-category one-dimensional
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
 1 1 1 2 1 2 2 1 43 123 5 122 3 1 312 1 1 122 1 1 1 1 6 1 7 1 6 1 7 1 3 4 2 312 43 4 3 3 1 1 4 1 1 52 122 54 124 8 1 3 1 1 1 1 1 152 1 1 1 1 1 1 152 1 5 1 152 152 1 1 3 9 1 159 9 13 4 5 1 122 1 4 122 5
1 1 1 2 1 2 2 1 43 123 5 122 3 1 312 1 1 122 1 1 1 1 6 1 7 1 6 1 7 1 3 4 2 312 43 4 3 3 1 1 4 1 1 52 122 54 124 8 1 3 1 1 1 1 1 152 1 1 1 1 1 1 152 1 5 1 152 152 1 1 3 9 1 159 9 13 4 5 1 122 1 4 122 5
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C
 DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
Biostatistics for Health Sciences Review Sheet
 Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
