Introduction to the ML Estimation of ARMA processes
|
|
|
- Πυθις Διαμαντόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics / 1
2 We consider the AR(p) model: Y t = c + φ 1 Y t φ p Y t p + ε t t = 1,..., T ε t WN(0, σ 2 ) where Y 0, Y 1,..., Y 1 p are given. Notation as a regression model Y t = z tθ + ε t with θ = (c, φ 1,..., φ p ) and z t = (1, Y t 1,..., Y t p ) : c Y 1 1 Y 0... Y 1 p θ 1. = Y T 1 Y T 1... Y T p θ p ε 1. ε T Rossi ARMA Estimation Financial Econometrics / 1
3 OLS Estimation of AR(p) The model is: The OLS estimator: y = Zθ + ε θ = (Z Z) 1 Z y = (Z Z) 1 Z (Zθ + ε) = θ + (Z Z) 1 Z ε ( ) 1 ( ) 1 1 = θ + T Z Z T Z ε OLS is no longer linear in y. Hence cannot be BLUE. In general OLS in no more unbiased. Small sample properties are analytically difficult to derive. Rossi ARMA Estimation Financial Econometrics / 1
4 OLS Estimation of AR(p) If Y t is a stable AR(p) process and ε t is a standard white noise, then the following results hold (Mann and Wald, 1943): 1 T (Z Z) Γ p ( ) 1 T T Z d ε N(0, σ 2 Γ) then consistency and asymptotic normality follows from Cramer s theorem: T ( θ θ) d N(0, σ 2 Γ 1 ) Rossi ARMA Estimation Financial Econometrics / 1
5 Impact of autocorrelation on regression results Necessary condition for the consistency of OLS estimator with stochastic (but stationary) regressors is that z t is asymptotically uncorrelated with ε t, i.e. plim ( 1 T Z ε t ) = 0: ( 1 plim θ θ = plim = Γ 1 plim T Z Z ) 1 ( 1 plim ( ) 1 T Z ε ) T Z ε OLS is no longer consistent under autocorrelation of the regression error as ( ) 1 plim T Z ε 0 Rossi ARMA Estimation Financial Econometrics / 1
6 OLS Estimation - Example Consider an AR(1) model with first-order autocorrelation of its errors Y t = φy t 1 + u t u t = ρu t 1 + ε t ε t WN(0, σ 2 ) such that Z = [Y 0,..., Y T 1 ]. Then E [ ] [ 1 1 T Z u = E T ] Y t 1 u t = 1 T t=1 E[Y t 1 (ρ(y t 1 φy t 2 ) + ε t )] t=1 since u t = ρ(y t 1 φy t 2 ) + ε t Rossi ARMA Estimation Financial Econometrics / 1
7 OLS Estimation - Example E [ ] 1 T Z u ( ) ( ) 1 = ρ E[Y 2 1 T t 1] φρ E[Y t 1 Y t 2 ] + T t=1 t=1 ( ) 1 E[Y t 1 ε t ] T t=1 = ρ [γ y (0) φγ y (1)] where γ y (h) is the autocovariance function of {Y t } which can be represented as an AR(2) process. Rossi ARMA Estimation Financial Econometrics / 1
8 MLE AR(1) For the Gaussian AR(1) process, Y t = c + φy t 1 + ε t φ < 1 the joint distribution of is the observations ε t NID(0, σ 2 ) Y T = (Y 1,..., Y T ) Y T N(µ, Σ) y (Y 1, Y 2,..., Y T ) are the single realization of Y T Rossi ARMA Estimation Financial Econometrics / 1
9 MLE AR(1) µ = µ. µ Y 1. Y T Σ = N (µ, Σ) γ 0... γ T γ T 1... γ 0 Rossi ARMA Estimation Financial Econometrics / 1
10 The p.d.f. of the sample y = (Y 1, Y 2,..., Y T ) is given by the multivariate normal density f Y (y; µ, Σ) = (2π) T 2 Σ 1 2 exp { 1 } 2 (y µ) Σ 1 (y µ) Denoting Σ = σ 2 y Ω with Ω ij = φ i j γ γ 0... γ T T 1 γ 0 Σ = = γ γ γ T 1... γ T 1 0 γ ρ(t 1) Σ = σy 2 Ω = σy ρ(t 1)... 1 Rossi ARMA Estimation Financial Econometrics / 1
11 ρ(j) = φ j Collecting the parameters of the model in θ = (c, φ, σ 2 ), the joint p.d.f. becomes: { f Y (y; θ) = (2πσy 2 ) T 2 Ω 1 2 exp 1 } 2σy 2 (y µ) Ω 1 (y µ) Collecting the parameters of the model in θ = (c, φ, σ 2 ), the sample log-likelihood function is given by L(θ) = T 2 log(2π) T 2 log(σ2 y ) 1 2 log( Ω ) 1 2σy 2 (y µ) Ω 1 (y µ) Rossi ARMA Estimation Financial Econometrics / 1
12 Sequential Factorization The prediction-error decomposition uses the fact that the ε t are independent, identically distributed: T f (ε 2,..., ε T ) = f ε (ε t ). and: t=2 [ T ] g Y (y T,..., y 1 ) = g Yt Y t 1 (y t y t 1 ) g Y1 (y 1 ) t=2 by the Markov property. We assume that the marginal density of Y 1 is that of ε 1 with E[Y 1 ] = µ = E[(Y 1 µ) 2 ] = σ 2 y = c 1 φ σ2 1 φ 2 Rossi ARMA Estimation Financial Econometrics / 1
13 Since then ε t = Y t (c + φy t 1 ) g Yt Y t 1 (y t y t 1 ) = f ε (y t y t 1 ) = f ε (ε t ) t = 2,..., T Rossi ARMA Estimation Financial Econometrics / 1
14 Hence: {[ T ] } g Y (y T,..., y 1 ) = f ε (y t y t 1 ) f ε (y 1 ) t=2 For ε t NID(0, σ 2 ), the log-likelihood is given by: L(θ) = log L(θ) = log f ε (y t y t 1 ; θ) + log f y (y 1 ; θ) t=2 { = T 2 log (2π) T 1 2 log (σ 2 ) + 1 2σ 2 { 1 2 log (σ2 y ) + 1 } 2σy 2 (y 1 µ) 2 } ε t t=2 Rossi ARMA Estimation Financial Econometrics / 1
15 where Y 1 N(µ, σy 2 ) with µ = c 1 φ and σ 2 2 y = σ2 1 φ. 2 Maximization of the exact log likelihood for an AR(1) process must be accomplished numerically. Rossi ARMA Estimation Financial Econometrics / 1
16 MLE AR(p) Gaussian AR(p): Y t = c + φ 1 Y t φ p Y t p + ε t ε t NID(0, σ 2 ) θ = (c, φ 1,..., φ p, σ 2 ) Exact MLE Using the prediction-error decomposition, the joint p.d.f is given by: [ T ] f Y (y 1, y 2,..., y T ; θ) = t=p+1 f ε (y t y t 1 ; θ) f Y1,...,Y p (y 1,..., y p ; θ) but only the p most recent observations matter f ε (y t y t 1 ; θ) = f ε (y t y t 1,..., y t p ; θ) Rossi ARMA Estimation Financial Econometrics / 1
17 MLE AR(p) The likelihood function for the complete sample is: [ T ] f Y (y 1, y 2,..., y T ; θ) = f ε (y t y t 1,..., y t p ; θ) f y (y 1,..., y p ; θ) t=p+1 With ε t NID(0, σ 2 ) [ 1 f ε (y t y t 1,..., y t p ; θ) = exp (yt c φ 1 y t 1... φ p y t p ) 2 ] 2πσ 2 2σ 2. The first p observations are viewed as the realization of a p-dimensional Gaussian variable with moments: E(Y p ) = µ p E [ (Y p µ p )(Y p µ p ) ] = Σ p Rossi ARMA Estimation Financial Econometrics / 1
18 MLE AR(p) γ 0 γ 1... γ p 1 Σ p = σ 2 γ 1 γ 0... γ p 2 V p = γ p 1 γ p 2... γ 0 [ f y (y 1,..., y p ; θ) = (2π) p 2 σ 2 Vp exp (Y ] p µ p ) Vp 1 (Y p µ p ) 2σ 2 Rossi ARMA Estimation Financial Econometrics / 1
19 MLE AR(p) The log-likelihood is: L(θ) = log f Y (y 1, y 2,..., y T ; θ) = log f ε (y t y t 1,..., y t p ; θ) + log f y (y 1,..., y p ; θ) t=p+1 = T 2 log (2π) T 2 log (σ2 ) + 1 log V 1 p 2 1 2σ 2 (Y p µ p ) Vp 1 (Y p µ p ) (y t c φ 1 y t 1... φ p y t p ) 2 2σ 2 t=p+1 The exact MLE follows from: θ = arg max L(θ) θ Rossi ARMA Estimation Financial Econometrics / 1
20 Conditional MLE AR(p) Conditional MLE = OLS Take y p = (y 1,..., y p ) as fixed pre-sample values Conditioning on Y p : θ = arg max f Y p+1,...,y T Y 1,...,Y p (y p+1,..., y T y p ; θ) θ T = arg max f ε (y t y t 1,..., y t p ; θ) θ t=p+1 L(θ) = log f Yp+1,...,Y T Y 1,...,Y p (y p+1,..., y T y p ; θ) = log f ε (ε t Y t 1 ; θ) t=p+1 = T p 2 log (2π) T p 2 log (σ 2 ) 1 2σ 2 t+p ε 2 t Rossi ARMA Estimation Financial Econometrics / 1
21 Conditional MLE AR(p) where ε t = Y t (c + φ 1 Y t φ p Y t p ) Thus the MLE of (c, φ 1,..., φ p ) results by minimizing the sum of squared residuals: arg max L(c, φ 1,..., φ p ) = arg (c,φ 1,...,φ p) min (c,φ 1,...,φ p) t=p+1 The conditional ML estimate of σ 2 turns out to be: σ 2 = 1 T p t=p+1 ε 2 t ε 2 t (c, φ 1,..., φ p ) Rossi ARMA Estimation Financial Econometrics / 1
22 Conditional MLE AR(p) The ML estimates γ = ( c, φ 1,..., φ p ) are equivalent to OLS estimates. ( c, φ 1,..., φ p ) are consistent estimators if {Y t } is stationary and T ( γ γ) is asymptotically normally distributed. The exact ML estimates and the conditional ML estimates have the same large-sample distribution. Rossi ARMA Estimation Financial Econometrics / 1
23 Conditional MLE AR(p) Asymptotically equivalent MLE of the mean-adjusted model Y t µ = φ 1 (Y t 1 µ) φ p (Y t p µ) + ε t where µ = (1 φ 1... φ p ) 1 c. OLS of (φ 1,..., φ p ) in the mean adjusted model, where µ = 1 T t=1 Y t Rossi ARMA Estimation Financial Econometrics / 1
24 Yule-Walker estimation Yule-Walker estimation of (φ 1,..., φ p ) φ 1. φ p = γ 0... γ p γ p 1... γ 0 1 γ 1. γ p where and γ h = (T h) 1 T t=h+1 µ = y = 1 T (y t y)(y t h y) t=1 y t Rossi ARMA Estimation Financial Econometrics / 1
25 MLE ARMA(p,q) Gaussian MA(q): Y t = µ + ε t + θ 1 ε t θ q ε t q ε t NID(0, σ 2 ) Conditional MLE = NLLS Conditioning on ε 0 = (ε 0, ε 1,..., ε 1 q ) = 0, we can iterate on: ε t = Y t (θ 1 ε t θ q ε t q ) for t = 1,..., T. The conditional likelihood is where θ = (µ, θ 1,..., θ q, σ 2 ). L(θ) = log f YT ε 0 =0(y T ε 0 = 0; θ) = T 2 log (2π) T 2 log (σ2 ) t=1 ε 2 t 2σ 2 Rossi ARMA Estimation Financial Econometrics / 1
26 MLE ARMA(p,q) The MLE of (µ, θ 1,..., θ q ) results by minimizing the sum of squared residuals. Analytical expressions for MLE are usually not available due to highly non-linear FOCs. MLE requires to apply numerical optimization techniques. Rossi ARMA Estimation Financial Econometrics / 1
27 MLE ARMA(p,q) Conditioning requires invertibility, i.e. the roots of 1 + θ 1 z + θ 2 z θ q z q = 0 lie outside the unit circle. For MA(1) process: t ε t = Y t µ θ 1 ε t 1 = ( θ 1 ) t ε 0 + ( θ 1 ) j [Y t j µ] j=1 Rossi ARMA Estimation Financial Econometrics / 1
28 MLE ARMA(p,q) Y t = c + φ 1 Y t φ p Y t p + ε t + θ 1 ε t θ q ε t q ε t NID(0, σ 2 ) Conditional MLE = NLLS Conditioning on Y 0 = (Y 0, Y 1,..., Y p+1 ) and ε 0 = (ε 0, ε 1,..., ε q+1 ) = 0, the sequence {ε 1, ε 2,..., ε T } can be calculated from {Y 1, Y 2,..., Y T } by iterating on: ε t = Y t (c + φ 1 Y t φ p Y t p ) (θ 1 ε t θ q ε t q ) for t = 1,..., T. Rossi ARMA Estimation Financial Econometrics / 1
29 The conditional log-likelihood is: L(θ) = log f YT Y 0,ε 0 (y T y 0, ε 0 ) = T 2 log (2π) T 2 log (σ2 ) t=1 ε 2 t 2σ 2 One option is to set the initial values equal to their expected values: Y s = (1 φ 1... φ p ) 1 c s = 0, 1,..., p + 1 ε s = 0 s = 0, 1,..., q + 1 Rossi ARMA Estimation Financial Econometrics / 1
30 Box and Jenkins (1976) recommended setting ε s to zero but y s equal to their actual values. The iteration is started at date t = p + 1, with Y 1, Y 2,..., Y p set to the observed values and ε p = ε p 1 =... = ε p q+1 = 0 Rossi ARMA Estimation Financial Econometrics / 1
HW 3 Solutions 1. a) I use the auto.arima R function to search over models using AIC and decide on an ARMA(3,1)
 HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Asymptotic distribution of MLE
 Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Stationary ARMA Processes
 Stationary ARMA Processes Eduardo Rossi University of Pavia October 2013 Rossi Stationary ARMA Financial Econometrics - 2013 1 / 45 Moving Average of order 1 (MA(1)) Y t = µ + ɛ t + θɛ t 1 t = 1,..., T
Stationary ARMA Processes Eduardo Rossi University of Pavia October 2013 Rossi Stationary ARMA Financial Econometrics - 2013 1 / 45 Moving Average of order 1 (MA(1)) Y t = µ + ɛ t + θɛ t 1 t = 1,..., T
Module 5. February 14, h 0min
 Module 5 Stationary Time Series Models Part 2 AR and ARMA Models and Their Properties Class notes for Statistics 451: Applied Time Series Iowa State University Copyright 2015 W. Q. Meeker. February 14,
Module 5 Stationary Time Series Models Part 2 AR and ARMA Models and Their Properties Class notes for Statistics 451: Applied Time Series Iowa State University Copyright 2015 W. Q. Meeker. February 14,
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Stationary ARMA Processes
 University of Pavia 2007 Stationary ARMA Processes Eduardo Rossi University of Pavia Moving Average of order 1 (MA(1)) Y t = µ + ǫ t + θǫ t 1 t = 1,...,T ǫ t WN(0, σ 2 ) E(ǫ t ) = 0 E(ǫ 2 t) = σ 2 E(ǫ
University of Pavia 2007 Stationary ARMA Processes Eduardo Rossi University of Pavia Moving Average of order 1 (MA(1)) Y t = µ + ǫ t + θǫ t 1 t = 1,...,T ǫ t WN(0, σ 2 ) E(ǫ t ) = 0 E(ǫ 2 t) = σ 2 E(ǫ
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
2. ARMA 1. 1 This part is based on H and BD.
 2. ARMA 1 1 This part is based on H and BD. 1 1 MA 1.1 MA(1) Let ε t be WN with variance σ 2 and consider the zero mean 2 process Y t = ε t + θε t 1 (1) where θ is a constant. MA(1). This time series is
2. ARMA 1 1 This part is based on H and BD. 1 1 MA 1.1 MA(1) Let ε t be WN with variance σ 2 and consider the zero mean 2 process Y t = ε t + θε t 1 (1) where θ is a constant. MA(1). This time series is
Lecture 12: Pseudo likelihood approach
 Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Lecture 21: Properties and robustness of LSE
 Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Econ Spring 2004 Instructor: Prof. Kiefer Solution to Problem set # 5. γ (0)
 Cornell University Department of Economics Econ 60 - Spring 004 Instructor: Prof. Kiefer Solution to Problem set # 5. Autocorrelation function is defined as ρ h = γ h γ 0 where γ h =Cov X t,x t h =E[X
Cornell University Department of Economics Econ 60 - Spring 004 Instructor: Prof. Kiefer Solution to Problem set # 5. Autocorrelation function is defined as ρ h = γ h γ 0 where γ h =Cov X t,x t h =E[X
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Queensland University of Technology Transport Data Analysis and Modeling Methodologies
 Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
5. Partial Autocorrelation Function of MA(1) Process:
 54 5. Partial Autocorrelation Function of MA() Process: φ, = ρ() = θ + θ 2 0 ( ρ() ) ( φ2, ) ( φ() ) = ρ() φ 2,2 φ(2) ρ() ρ() ρ(2) = φ 2,2 = ρ() = ρ() ρ() ρ() 0 ρ() ρ() = ρ()2 ρ() 2 = θ 2 + θ 2 + θ4 0
54 5. Partial Autocorrelation Function of MA() Process: φ, = ρ() = θ + θ 2 0 ( ρ() ) ( φ2, ) ( φ() ) = ρ() φ 2,2 φ(2) ρ() ρ() ρ(2) = φ 2,2 = ρ() = ρ() ρ() ρ() 0 ρ() ρ() = ρ()2 ρ() 2 = θ 2 + θ 2 + θ4 0
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Introduction to Time Series Analysis. Lecture 16.
 Introduction to Time Series Analysis. Lecture 16. 1. Review: Spectral density 2. Examples 3. Spectral distribution function. 4. Autocovariance generating function and spectral density. 1 Review: Spectral
Introduction to Time Series Analysis. Lecture 16. 1. Review: Spectral density 2. Examples 3. Spectral distribution function. 4. Autocovariance generating function and spectral density. 1 Review: Spectral
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data
 Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data Rahim Alhamzawi, Haithem Taha Mohammad Ali Department of Statistics, College of Administration and Economics,
Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data Rahim Alhamzawi, Haithem Taha Mohammad Ali Department of Statistics, College of Administration and Economics,
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Lecture 7: Overdispersion in Poisson regression
 Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
SECTION II: PROBABILITY MODELS
 SECTION II: PROBABILITY MODELS 1 SECTION II: Aggregate Data. Fraction of births with low birth weight per province. Model A: OLS, using observations 1 260 Heteroskedasticity-robust standard errors, variant
SECTION II: PROBABILITY MODELS 1 SECTION II: Aggregate Data. Fraction of births with low birth weight per province. Model A: OLS, using observations 1 260 Heteroskedasticity-robust standard errors, variant
A Bonus-Malus System as a Markov Set-Chain. Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics
 A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Durbin-Levinson recursive method
 Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
Higher Derivative Gravity Theories
 Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
An Introduction to Signal Detection and Estimation - Second Edition Chapter II: Selected Solutions
 An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Supplementary Appendix
 Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
ENGR 691/692 Section 66 (Fall 06): Machine Learning Assigned: August 30 Homework 1: Bayesian Decision Theory (solutions) Due: September 13
 ENGR 69/69 Section 66 (Fall 06): Machine Learning Assigned: August 30 Homework : Bayesian Decision Theory (solutions) Due: Septemer 3 Prolem : ( pts) Let the conditional densities for a two-category one-dimensional
ENGR 69/69 Section 66 (Fall 06): Machine Learning Assigned: August 30 Homework : Bayesian Decision Theory (solutions) Due: Septemer 3 Prolem : ( pts) Let the conditional densities for a two-category one-dimensional
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
FORMULAS FOR STATISTICS 1
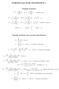 FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Theorem 8 Let φ be the most powerful size α test of H
 Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
ECE598: Information-theoretic methods in high-dimensional statistics Spring 2016
 ECE598: Information-theoretic methods in high-dimensional statistics Spring 06 Lecture 7: Information bound Lecturer: Yihong Wu Scribe: Shiyu Liang, Feb 6, 06 [Ed. Mar 9] Recall the Chi-squared divergence
ECE598: Information-theoretic methods in high-dimensional statistics Spring 06 Lecture 7: Information bound Lecturer: Yihong Wu Scribe: Shiyu Liang, Feb 6, 06 [Ed. Mar 9] Recall the Chi-squared divergence
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
5. Choice under Uncertainty
 5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Table 1: Military Service: Models. Model 1 Model 2 Model 3 Model 4 Model 5 Model 6 Model 7 Model 8 Model 9 num unemployed mili mili num unemployed
 Tables: Military Service Table 1: Military Service: Models Model 1 Model 2 Model 3 Model 4 Model 5 Model 6 Model 7 Model 8 Model 9 num unemployed mili mili num unemployed mili 0.489-0.014-0.044-0.044-1.469-2.026-2.026
Tables: Military Service Table 1: Military Service: Models Model 1 Model 2 Model 3 Model 4 Model 5 Model 6 Model 7 Model 8 Model 9 num unemployed mili mili num unemployed mili 0.489-0.014-0.044-0.044-1.469-2.026-2.026
w o = R 1 p. (1) R = p =. = 1
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Stationary Univariate Time Series Models 1
 Stationary Univariate Time Series Models 1 Sebastian Fossati University of Alberta 1 These slides are based on Eric Zivot s time series notes available at: http://faculty.washington.edu/ezivot Example
Stationary Univariate Time Series Models 1 Sebastian Fossati University of Alberta 1 These slides are based on Eric Zivot s time series notes available at: http://faculty.washington.edu/ezivot Example
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
= λ 1 1 e. = λ 1 =12. has the properties e 1. e 3,V(Y
 Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
LAD Estimation for Time Series Models With Finite and Infinite Variance
 LAD Estimatio for Time Series Moels With Fiite a Ifiite Variace Richar A. Davis Colorao State Uiversity William Dusmuir Uiversity of New South Wales 1 LAD Estimatio for ARMA Moels fiite variace ifiite
LAD Estimatio for Time Series Moels With Fiite a Ifiite Variace Richar A. Davis Colorao State Uiversity William Dusmuir Uiversity of New South Wales 1 LAD Estimatio for ARMA Moels fiite variace ifiite
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C
 DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Elements of Information Theory
 Elements of Information Theory Model of Digital Communications System A Logarithmic Measure for Information Mutual Information Units of Information Self-Information News... Example Information Measure
Elements of Information Theory Model of Digital Communications System A Logarithmic Measure for Information Mutual Information Units of Information Self-Information News... Example Information Measure
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Outline Analog Communications. Lecture 05 Angle Modulation. Instantaneous Frequency and Frequency Deviation. Angle Modulation. Pierluigi SALVO ROSSI
 Outline Analog Communications Lecture 05 Angle Modulation 1 PM and FM Pierluigi SALVO ROSSI Department of Industrial and Information Engineering Second University of Naples Via Roma 9, 81031 Aversa (CE),
Outline Analog Communications Lecture 05 Angle Modulation 1 PM and FM Pierluigi SALVO ROSSI Department of Industrial and Information Engineering Second University of Naples Via Roma 9, 81031 Aversa (CE),
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1 [1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg) 1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
Forced Pendulum Numerical approach
 Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Mean-Variance Analysis
 Mean-Variance Analysis Jan Schneider McCombs School of Business University of Texas at Austin Jan Schneider Mean-Variance Analysis Beta Representation of the Risk Premium risk premium E t [Rt t+τ ] R1
Mean-Variance Analysis Jan Schneider McCombs School of Business University of Texas at Austin Jan Schneider Mean-Variance Analysis Beta Representation of the Risk Premium risk premium E t [Rt t+τ ] R1
 1 1 1 2 1 2 2 1 43 123 5 122 3 1 312 1 1 122 1 1 1 1 6 1 7 1 6 1 7 1 3 4 2 312 43 4 3 3 1 1 4 1 1 52 122 54 124 8 1 3 1 1 1 1 1 152 1 1 1 1 1 1 152 1 5 1 152 152 1 1 3 9 1 159 9 13 4 5 1 122 1 4 122 5
1 1 1 2 1 2 2 1 43 123 5 122 3 1 312 1 1 122 1 1 1 1 6 1 7 1 6 1 7 1 3 4 2 312 43 4 3 3 1 1 4 1 1 52 122 54 124 8 1 3 1 1 1 1 1 152 1 1 1 1 1 1 152 1 5 1 152 152 1 1 3 9 1 159 9 13 4 5 1 122 1 4 122 5
Biostatistics for Health Sciences Review Sheet
 Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
