SUPPLEMENT TO SEQUENTIAL ESTIMATION OF STRUCTURAL MODELS WITH A FIXED POINT CONSTRAINT (Econometrica, Vol. 80, No. 5, September 2012, )
|
|
|
- Ζωή Ελευθερίου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Econometrca Supplementary Materal SULEMENT TO SEQUENTIAL ESTIMATION OF STRUCTURAL MODELS WITH A FIXED OINT CONSTRAINT (Econometrca, Vol. 80, No. 5, September 2012, ) BY HIROYUKI KASAHARA AND KATSUMI SHIMOTSU THIS SULEMENT contans the followng detals omtted from the man paper due to space constrants: (A) proof of the results n the paper, (B) auxlary results and ther proof, (C) addtonal alternatve sequental algorthms, (D) the convergence propertes of the NL algorthm for models wth unobserved heterogenety, and (E) addtonal Monte Carlo results. Throughout ths Supplement, let a.s. abbrevate almost surely, and let.o. abbrevate nfntely often. C denotes a generc postve and fnte constant that may take dfferent values n dfferent places. For matrx and nonnegatve scalar sequences of random varables {X M M 1} and {Y M M 1}, respectvely, we wrte X M = O(Y M ) (or o(y M ))a.s.f X M AY M for some (or all) A>0a.s.WhenY M belongs to a famly of random varables ndexed by τ T, we say X M = (Y M (τ)) (or o(y M (τ))) a.s.unformly n τ f the constant A>0 can be chosen the same for every τ T. For nstance, n roposton 7 below, we take τ = j 1 and Y M (τ) = j 1 ˆ NL. AENDIX A: ROOFS OF THERESULTS IN THE MAIN TEXT Throughout the proofs, the O( ) terms are unform, but we suppress the reference to ther unformty for brevty. ROOF OF ROOSITION 1: We suppress the subscrpt NL from ˆ NL.Let b>0 be a constant such that ρ(m Ψθ Ψ ) + 2b <1. From Lemma of Horn and Johnson (1985), there s a matrx norm α such that M Ψθ Ψ α ρ(m Ψθ Ψ )+b. Defne a vector norm β for x R L as x β = [x 0 0] α ; then a drect calculaton gves Ax β = A [x 0 0] α A α x β for any matrx A. From the equvalence of vector norms n R L (see, e.g., Corollary of Horn and Johnson (1985)), we can restate roposton 7 n terms of β as follows: there exsts c>0 such that j ˆ = M Ψθ Ψ ( j 1 ˆ) + O(M 1/2 j 1 ˆ β + j 1 ˆ 2 ) a.s. holds unformly n β j 1 { : 0 β <c}. We rewrte ths statement further so that t s amenable to recursve substtuton. Frst, note that M Ψθ Ψ ( j 1 ˆ) β M Ψθ Ψ α j 1 ˆ β (ρ(m Ψθ Ψ )+b) j 1 ˆ β. Second, rewrte the remander term as O(M 1/2 + j 1 ˆ β ) j 1 ˆ β.setc<b; then ths term s smaller than b j 1 ˆ β a.s. Thrd, snce ˆ s consstent, { : ˆ β <c/2} { : 0 β <c} a.s. Consequently, j ˆ β (ρ(m Ψθ Ψ ) + 2b) j 1 ˆ β holds a.s. for all 2012 The Econometrc Socety DOI: /ECTA8291
2 2 H. KASAHARA AND K. SHIMOTSU j 1 n { : ˆ β <c/2}. Because each NL updatng of (θ ) uses the same pseudo lkelhood functon, we may recursvely substtute for the j s, and hence lm k k = ˆ a.s. f 0 ˆ β <c/2. The stated result follows from applyng the equvalence of vector norms n R L to 0 ˆ β and 0 ˆ and usng the consstency of ˆ. Q.E.D. ROOF OF ROOSITION 2: We prove that the stated result holds f j 1 s n a neghborhood N NL c of ˆ NL. The stated result then follows from the strong consstency of ˆ NL. Because roposton 7 holds under the current assumpton, we have (5) j ˆ NL = M Ψθ Ψ 0 ( j 1 ˆ NL ) + f( j 1 ˆ NL ) where f(x) C(x 2 + M 1/2 x ) a.s. Let λ 1 λ 2 λ L be the egenvalues of M Ψθ Ψ 0 such that (6) λ 1 λ r > 1 λ r+1 λ L For any ɛ 0, we may apply a Jordan decomposton to M Ψθ Ψ 0 to obtan H 1 M Ψθ Ψ 0H = D + ɛj, whered = dag(λ 1 λ L ),andj s a matrx wth zeros and ones mmedately above the man dagonal (on the superdagonal) and zeros everywhere else. Defne y j = H 1 ( j ˆ NL ) and g(y) = H 1 f(hy); then multplyng (5) by H 1 gves y j = (D + ɛj)y j 1 + g(y j 1 ),wth g(y) C( y 2 + M 1/2 y ) a.s. Let y 1 j denote the frst r elements of y, and rewrte ths equaton as (7) ( ) ( y 1 j D1 0 = y 2 j 0 D 2 )( y 1 j 1 y 2 j 1 ) ( J1 0 + ɛ 0 J 2 )( y 1 j 1 y 2 j 1 ) + ( ) g1 (y j 1 ) g 2 (y j 1 ) where y 1 and g j 1 1(y j 1 ) are r 1 and D 1 and J 1 are r r wth D 1 = dag(λ 1 λ r ). We frst show that H 1 ( j ˆ NL ) > H 1 ( j 1 ˆ NL ) by provng that y 1 > j y1 j 1 under the stated assumptons. Applyng the trangle nequalty to the frst equaton of (7) gves (8) y 1 j D 1y 1 j 1 ɛj 1y 1 j 1 g 1(y j 1 ) For the frst two terms on the rght hand sde of (8), we have D 1 y 1 = j 1 ( r λ k=1 k 2 (y j 1 k ) 2 ) 1/2 (1 + 3δ) y 1 j 1 for some δ>0 from (6) and ɛj 1 y 1 j 1 δ y1 j 1 by choosng ɛ suffcently small. For the last term of (8), observe that j 1 V(c)f and only f y 1 j 1 c y2 j 1, and hence j 1 / V(c) y j 1 2 = y 1 j y 2 j 1 2 <(1 + c 2 ) y 1 j 1 2
3 ESTIMATION OF STRUCTURAL MODELS 3 Therefore, g 1 (y j 1 ) δ y 1 NL j 1 holds when Nc s suffcently small and M s suffcently large. It then follows from (8) that y 1 (1 + j δ) y1 > j 1 y1. j 1 It remans to show that j / V(c). Applyng the trangle nequalty to the second equaton of (7) gves y 2 D j 2y 2 + ɛj j 1 2y 2 + g j 1 2(y j 1 ). For the frst term on the rght hand sde, D 2 y 2 =( L λ j 1 k=r+1 k 2 (y j 1 k ) 2 ) 1/2 y 2 j 1 from (6). For the second term, smlarly to the updatng of y 1 j, by choosng ɛ and N NL c suffcently small, we have ɛj 2 y 2 + g j 1 2(y j 1 ) c 1 δ y 1 f j 1 j 1 N NL c \ V(c) and M s suffcently large. Therefore, y 2 j y2 + j 1 c 1 δ y 1 j 1 <c 1 (1 + δ) y 1 j 1 <c 1 y 1 j a.s., where the last two nequaltes use y 2 j 1 <c 1 y 1 and j 1 y1 < j 1 y1.thsproves j j / V(c). Q.E.D. ROOF OF ROOSITION 3: Frst, note that j for j 1 satsfes restrcton (2) because t s generated by Ψ(θ ). The restrctons (2) and (3) do not affect the valdty of ropostons 1 and 2 because () the fxed pont constrant n terms of Ψ(θ ) and of Ψ + (θ + ) are equvalent, and () the restrctons (2) and (3) do not affect the order of magntude of the dervatves of Ψ(θ ). For the equvalence of the egenvalues, takng the dervatve of (3) gves ( ) + Ψ Ψ(θ )= + (θ + ) 0 (9) E + Ψ + (θ + = (U ) 0 + Ψ + (θ + ) 0 ) and θ Ψ(θ ) = U θ Ψ + (θ + ). Substtutng ths nto M Ψθ Ψ 0,usngΨ 0 θ = UΨ + θ, and rearrangng terms gves M Ψθ Ψ 0 =[UM+ Ψ θ Ψ + + 0]. Therefore, the updatng formula of + and s gven by + j ˆ + NL = M + Ψ θ Ψ + + ( + j 1 ˆ + NL) + O(M 1/2 + j 1 ˆ + NL + + j 1 ˆ + NL 2 ) a.s. and j ˆ NL = E( + j ˆ NL), + respectvely. Fnally, the equvalence of the egenvalues follows from det(m Ψθ Ψ 0 λi dm()) = det(m + Ψ θ Ψ + λi + dm( + )) det( λi dm( )) and det(ψ 0 λi dm() ) = det(ψ + λi + dm( + )) det( λi dm( )). Q.E.D. ROOF OF EQUATION (4): The notaton follows page 10 of Agurregabra and Mra (2007; henceforth AM07). Let π (a x; θ) = a A (a )Π (a a x; θ) and e (a x; θ) = E[ε (a ) x ],wheree[ε (a ) x ] =E[ε (a ) x ] holds as dscussed on pages 9 10 of AM07. Let V (x) denote the soluton of frm s ntegrated Bellman equaton: (10) V (x) = { max π (a x; θ) + β } V (x )f (x x a ) + ε (a ) a A x X g(dε ; θ)
4 4 H. KASAHARA AND K. SHIMOTSU where f (x x a ) = a A (a )f (x x a a ). Let Π (a a ; θ), π (a ; θ), e (a ; θ), (a ),andv denote the vectors of dmenson X that stack the correspondng state-specfc elements of Π (a a x; θ), π (a x; θ), e (a x; θ), (a x),andv (x), respectvely. Defne the valuaton operator as Γ (θ ) (I βf ) 1 a A (a ) [π (a ; θ) + e (a ; θ)] where F s a matrx wth transton probabltes f (x x), and denotes the Hadamard product. Γ (θ ) gves the soluton of frm s ntegrated Bellman equaton gven θ and. Defne frm s best response mappng gven V and as (cf. equaton (15) of AM07) (11) [Υ (θ V )](a x) ( I a = arg max a A + ε (a) + β x X { π (a x; θ) }) V (x )f (x x a) g(dε ; θ) where f (x x a ) = a A (a )f (x x a a ). Then, the mappng Ψ and ts Jacoban matrx evaluated at (θ 0 0 ) are gven by ( ) ( ) Ψ1 (θ ) Υ1 (θ Γ Ψ(θ )= = 1 (θ ) 2 ) and Ψ 2 (θ ) Υ 2 (θ Γ 2 (θ ) 1 ) ( ) Ψ 0 = 0 2 Ψ 1 (θ 0 0 ) 1 Ψ 2 (θ 0 0 ) 0 where Ψ (θ 0 0 ) = 0 follows from Γ (θ ) = 0 (Agurregabra and Mra (2002), roposton 2). Q.E.D. ROOF OF ROOSITION 4: For part (a), let V denote the soluton of the Bellman equaton (10) gven,andlet be the condtonal choce probabltes assocated wth V.Sncex t = (S t a 1 t 1 a 2 t 1 ) holds and S t follows an exogenous process, we may verfy under Assumpton 3(c) that () V (S t a t 1 a ) = V t 1 (S t a t 1 a ) for t 1 a t 1 a, () V t 1 does not depend on, () Γ (θ ) = Γ (θ ) = V, and (v) Υ (θ V ) = Υ (θ V ) = for any and n the space of s. It follows from () (v) that the model becomes a sngle-agent model for each
5 ESTIMATION OF STRUCTURAL MODELS 5 player and that there exsts a unque Markov perfect equlbrum characterzed by a unque fxed pont = Ψ (θ ) = Υ (θ Γ (θ ) ) for = 1 2, where the fxed pont does not depend on the value of. Defne F(θ ) = Ψ(θ ).Snce F(θ ) = I Ψ(θ ) = I, we may apply the mplct functon theorem to F(θ ) = Ψ(θ ) at (θ ) = (θ ) under Assumpton 2(b), and there exsts an open set N θ contanng θ,anopensetn contanng, and a unque contnuously dfferentable functon (θ): N θ N such that (θ) = Ψ(θ (θ))for any θ N θ. Therefore, a Markov perfect equlbrum exsts n N when the true parameter θ 0 s n N θ. The mappng ρ(m Ψθ Ψ (θ (θ))) s a contnuous functon of θ N θ because (θ) s contnuous n θ N θ, Ψ(θ ) s contnuously dfferentable by Assumpton 2(b), M Ψθ < by Assumpton 2(b), and the spectral radus of a matrx s a contnuous functon of the elements of the matrx. The stated result then follows from Ψ(θ (θ )) = 0 (Remark 1) and the contnuty of ρ(m Ψθ Ψ (θ (θ))). For part (b), under Assumpton 3(d), θ = θ,andβ = 0, the model becomes a sngle-agent model for each player. Therefore, repeatng the argument for part (a) gves the stated result. Q.E.D. ROOF OF ROOSITION 5: Let λ = Re(λ) + Im(λ) = r cos θ + r sn θ be an egenvalue of Ψ 0. Then, the correspondng egenvalue of Λ s λ(α) = αr cos θ + αr sn θ + (1 α). Letf (α) = λ(α) 2 ; then the stated result holds because f(0) = 1and α f(0) = 2(r cos θ 1)<0frcos θ<1and α f(0)>0 f r cos θ>1. Q.E.D. AENDIX B: AUXILIARY RESULTS AND THEIR ROOF roposton 6 strengthens the weak consstency result of roposton 2 of AM07 to strong consstency. roposton 7 descrbeshow an NL step updates θ and. ROOSITION 6: Suppose that Assumpton 1 holds. Then, ( ˆθ NL ˆ NL ) (θ 0 0 ) a.s. ROOF: roposton 2 of AM07 showed weak consstency of ( ˆθ NL ˆ NL ). Therefore, strong consstency ( ˆθ NL ˆ NL ) follows from strengthenng n probablty and wth probablty approachng 1 statements n Steps 2 5 of the proof of roposton 2 of AM07 to almost surely. Frst, observe that AM07 (pp ) showed that Q M (θ ) converges to Q 0 (θ ) a.s. and unformly n (θ ). Thus, the events A M s defned nsteps2,3,and5ofam07satsfyr(a c M o ) = 0. In Step 2, we can strengthen r((θ M ) I) M 1ofAM07to(θ M M ) Ia.s. because AM07 (pp ) showed A M {(θ M ) I}and we have M r(ac M o ) = 0. In
6 6 H. KASAHARA AND K. SHIMOTSU Step 3, an analogous argument strengthens r(sup N( 0 ) θ M () θ 0 () < ε) 1nAM07tosup N( 0 ) θ M () θ 0 () <ε a.s. Smlarly, we can strengthen wth probablty approachng 1 n Steps 4 and 5 to almost surely, and strong consstency of the NL estmator follows. Q.E.D. ROOSITION 7: Suppose that Assumpton 2 holds. Then, there exsts a neghborhood N 1 of 0 such that θ j ˆθ NL = O( j 1 ˆ NL ) a.s. and j ˆ NL = M Ψθ Ψ 0 ( j 1 ˆ NL ) + O(M 1/2 j 1 ˆ NL + j 1 ˆ NL 2 ) a.s. unformly n j 1 N 1. ROOF: We suppress the subscrpt NL from ˆ NL and ˆθ NL.Forɛ>0, defne a neghborhood N (ɛ) ={(θ ) : θ θ <ɛ}. Then, there exsts ɛ 1 > 0 such that N (ɛ 1 ) N and sup (θ ) N (ɛ1 ) θθ Q 0(θ ) 1 < because θθ Q 0 (θ ) s contnuous and θθ Q 0 (θ 0 0 ) s nonsngular. Frst, we assume that ( θ j j 1 ) N (ɛ 1 ) and derve the stated representaton of θ j ˆθ and j ˆ. We later show that ( θ j j 1 ) N (ɛ 1 ) a.s. f N 1 s suffcently small. The frst-order condton for θ j s θ Q M ( θ j j 1 ) = 0. Expandng t around ( ˆθ ˆ) and usng θ Q M ( ˆθ ˆ) = 0 gves (12) 0 = θθ Q M ( θ )( θ j ˆθ) + θ Q M ( θ )( j 1 ˆ) where ( θ ) le between ( θ j j 1 ) and ( ˆθ ˆ). Wrte (12) as θ j ˆθ = θθ Q M ( θ ) 1 θ Q M ( θ )( j 1 ˆ); then the stated unform bound of θ j ˆθ follows because () ( θ ) N (ɛ 1 ) a.s. snce ( θ j j 1 ) N (ɛ 1 ) and ( ˆθ ˆ) s strongly consstent from roposton 6, and () sup (θ ) N (ɛ1 ) θθ Q M(θ ) 1 θ Q M (θ ) = O(1) a.s. snce sup (θ ) N (ɛ1 ) θθ Q 0(θ ) 1 < and sup (θ ) N 2 Q M (θ ) 2 Q 0 (θ ) =o(1) a.s., where the latter follows from Kolmogorov s strong law of large numbers and Theorem 2 and Lemma 1 of Andrews (1992). For the bound of j ˆ, frst we collect the followng results, whch follow from the Taylor expanson around (θ 0 0 ), root-m consstency of ( ˆθ ˆ),and the nformaton matrx equalty: (13) θθ Q M ( ˆθ ˆ) = Ω θθ + O ( M 1/2) a.s. θ Q M ( ˆθ ˆ) = Ω θ + O ( M 1/2) a.s. θ Ψ(ˆθ ˆ) = Ψ 0 + O( θ M 1/2) a.s. Ψ(ˆθ ˆ) = Ψ 0 + O( M 1/2) a.s. Expand the rght hand sde of j = Ψ( θ j j 1 ) twce around ( ˆθ ˆ) and use Ψ(ˆθ ˆ) = ˆ and θ j ˆθ = O( j 1 ˆ ) a.s.; then we obtan j
7 ESTIMATION OF STRUCTURAL MODELS 7 ˆ = θ Ψ(ˆθ ˆ)( θ j ˆθ) + Ψ(ˆθ ˆ)( j 1 ˆ) + O( j 1 ˆ 2 ) a.s. snce sup (θ ) N (ɛ1 ) 3 Ψ(θ )<. Applyng (13)and θ j ˆθ = O( j 1 ˆ ) a.s. to the rght hand sde gves (14) j ˆ = Ψ θ ( θ j ˆθ) + Ψ 0 ( j 1 ˆ) + O( j 1 ˆ 2 ) + O ( M 1/2 j 1 ˆ ) a.s. We proceed to refne (12) towrte θ j ˆθ n terms of j 1 ˆ and substtute t nto (14). Expandng θθ Q M ( θ ) n (12) around( ˆθ ˆ), notng that θ ˆθ θ j ˆθ and ˆ j 1 ˆ,andusng θ j ˆθ = O( j 1 ˆ ) a.s., we obtan θθ Q M ( θ ) = θθ Q M ( ˆθ ˆ)+ O( j 1 ˆ ) a.s. Further, applyng (13) gves θθ Q M ( θ ) = Ω θθ + O(M 1/2 ) + O( j 1 ˆ ) a.s. Smlarly, we obtan θ Q M ( θ ) = Ω θ + O(M 1/2 ) + O( j 1 ˆ ) a.s. Usng these results, refne (12) as θ j ˆθ = Ω 1 θθ Ω θ ( j 1 ˆ) + O(M 1/2 j 1 ˆ + j 1 ˆ 2 ) a.s. Substtutng ths nto (14) n conjuncton wth Ω 1 θθ Ω θ = (Ψ 0 Δ θ Ψ 0 θ ) 1 Ψ 0 Δ θ Ψ 0 gves the stated result. It remans to show ( θ j j 1 ) N (ɛ 1 ) a.s. f N 1 s suffcently small. Let N θ {θ : θ θ 0 <ɛ 1 /2} and defne Δ = Q 0 (θ 0 0 ) sup θ N c Q θ Θ 0(θ 0 )>0, where the last nequalty follows from nformaton nequalty, compactness of N c Θ, and contnuty of Q θ 0(θ ). It follows that { θ j / N θ } {Q 0 (θ 0 0 ) Q 0 ( θ j 0 ) Δ}. Further, observe that Q 0 (θ 0 0 ) Q 0 ( θ j 0 ) Q M (θ 0 j 1 ) Q M ( θ j j 1 ) + 2sup θ Θ Q 0 (θ 0 ) Q 0 (θ j 1 ) + 2sup (θ ) Θ B Q M (θ ) Q 0 (θ ) 2sup θ Θ Q 0 (θ 0 ) Q 0 (θ j 1 ) + 2sup (θ ) Θ B Q M (θ ) Q 0 (θ ), where the second nequalty follows from the defnton of θ j. From contnuty of Q 0 (θ ), there exsts ɛ Δ > 0 such that the frst term on the rght s smaller than Δ/2 f 0 j 1 ɛ Δ. The second term on the rght s o(1) a.s. from Kolmogorov s strong law of large numbers and Theorem 2 and Lemma 1 of Andrews (1992). Hence, r( θ j / N θ o ) = 0 f 0 j 1 ɛ Δ, and settng N 1 ={ : 0 mn{ɛ 1 /2 ɛ Δ }} gves ( θ j j 1 ) N (ɛ 1 ) a.s. Q.E.D. AENDIX C: ADDITIONAL ALTERNATIVE SEQUENTIAL ALGORITHMS C.1. Recursve rojecton Method In ths subsecton, we construct a mappng that has a better local contracton property than Ψ, buldng upon the Recursve rojecton Method (RM) of Shroff and Keller (1993; henceforth SK). Frst, fx θ.let θ denote an element of M θ ={ B : = Ψ(θ )}, so that θ s one of the fxed ponts of Ψ(θ ) when there are multple fxed ponts.
8 8 H. KASAHARA AND K. SHIMOTSU Consder fndng θ by teratng j = Ψ( j 1 θ)startng from a neghborhood of θ. If some egenvalues of Ψ(θ θ ) are outsde the unt crcle, ths teraton does not converge to θ n general. Suppose that, countng multplcty, there are r egenvalues of Ψ(θ θ ) that are larger than δ (0 1) n modulus: (15) λ 1 λ r >δ λ r+1 λ L Defne R L as the maxmum nvarant subspace of Ψ(θ θ ) belongng to {λ k } r k=1,andletq RL be the orthogonal complement of.letπ θ denote the orthogonal projector from R L on. WemaywrteΠ θ = Z θ Z θ,where Z θ R L r s an orthonormal bass of. Then, for each R L, we have the unque decomposton = u + v,whereu Π θ and v (I Π θ ) Q. Now apply Π θ and I Π θ to = Ψ(θ ), and decompose the system as follows: u = f(u v θ) Π θ Ψ(θ u+ v) v = g(u v θ) (I Π θ )Ψ (θ u + v) For a gven j 1, decompose t nto u j 1 = Π θ j 1 and v j 1 = (I Π θ ) j 1. Snce g(u v θ) s contractve n v (see Lemma 2.10 of SK), we can update v j 1 by the recurson v j = g(u v j 1 θ). On the other hand, when the domnant egenvalue of Ψ 0 s outsde the unt crcle, the recurson u j = f(u j 1 v θ)cannot be used to update u j 1 because f(u v θ)s not a contracton n u. Instead, the RM performs a sngle Newton step on the system u = f(u v θ),leadng to the followng updatng procedure: (16) u j = u j 1 + (I Π θ Ψ(θ j 1 )Π θ ) 1 (f (u j 1 v j 1 θ) u j 1 ) h(u j 1 v j 1 θ) v j = g(u j 1 v j 1 θ) Lemma 3.11 of SK shows that the spectral radus of the Jacoban of the stablzed teraton (16) s no larger than δ, and thus the teraton j = h(π θ j 1 (I Π θ ) j 1 θ)+ g(π θ j 1 (I Π θ ) j 1 θ) converges locally. In the followng, we develop a sequental algorthm buldng upon the updatng procedure (16). Let Π(θ ) be the orthogonal projector from R L onto the maxmum nvarant subspace of Ψ(θ )belongng to ts r largest (n modulus) egenvalues, countng multplcty. Defne u, v, h (u v θ),andg (u v θ)by replacng Π θ n u, v, h(u v θ),andg(u v θ) wth Π(θ ), and defne (17) Γ(θ ) h (u v θ)+ g (u v θ) = Ψ(θ )+ [ (I Π(θ ) Ψ (θ )Π(θ )) 1 I ] Π(θ )(Ψ (θ ) )
9 ESTIMATION OF STRUCTURAL MODELS 9 0 s a fxed pont of Γ(θ 0 ), because all the fxed ponts of Ψ(θ ) are also fxed ponts of Γ(θ ). The followng proposton shows two mportant propertes of Γ(θ ): local contracton and the equvalence of fxed ponts of Γ(θ )and Ψ(θ ). ROOSITION 8: (a) Suppose that I Π(θ ) Ψ (θ )Π(θ ) s nonsngular and hence Γ(θ )s well defned. Then Γ(θ )and Ψ(θ ) have the same fxed ponts; that s, Γ(θ ) = f and only f Ψ(θ ) =. (b) ρ( Γ(θ 0 0 )) δ 0, where δ 0 s defned by (15) n terms of the egenvalues of Ψ(θ 0 0 ). Hence, Γ(θ )s locally contractve. Defne Q Γ (θ ) M 1 M T ln Γ (θ )(a M m=1 t=1 mt x mt ). Defne an RM fxed pont as a par ( ˇθ ˇ) that satsfes ˇθ = arg max θ Θ Q Γ (θ M ˇ) and ˇ = Γ(ˇθ ˇ).TheRM estmator, denoted by ( ˆθ RM ˆ RM ), s defned as the RM fxed pont wth the hghest value of the pseudo lkelhood among all the RM fxed ponts. Defne the RM algorthm by the same sequental algorthm as the NL algorthm except that t uses Γ(θ )n place of Ψ(θ ). roposton 9 shows the asymptotc propertes of the RM estmator and the convergence propertes of the RM algorthm. Defne the RM counterparts of θ 0 (), φ 0 (), Ω θθ,andω θ as θ Γ () arg max 0 θ Θ EQΓ (θ ), M φγ () 0 Γ( θ Γ () ), 0 ΩΓ E( θθ θs Γ mt θ sγ mt ),andωγ E( θ θs Γ mt sγ mt ),wheresγ = mt T ln t=1 Γ(θ0 0 )(a mt x mt ).DefneΓ 0 Γ(θ0 0 ) and Γ 0 θ θ Γ(θ0 0 ). We outlne the assumptons frst. ASSUMTION 4: (a) Assumpton 1 holds. (b) Ψ(θ ) s four tmes contnuously dfferentable n N.(c)I Π(θ ) Ψ (θ )Π(θ ) s nonsngular. (d) Γ(θ )>0 for any (a x) A X and (θ ) Θ B.(e)The operator φ Γ 0 () has a nonsngular Jacoban matrx at 0. Assumpton 4(c) s requred for Γ(θ )to be well defned. It would be possble to drop Assumpton 4(d) by consderng a trmmed verson of Γ(θ ), but for brevty we do not pursue t. ROOSITION 9: Suppose that Assumpton 4 holds. Then (a) ˆ RM 0 = O(M 1/2 ) a.s. and M 1/2 ( ˆθ RM θ 0 ) d N(0 V RM ), where V RM =[Ω Γ + θθ Ω Γ (I Γ 0 θ ) 1 Γ 0 θ ] 1 Ω Γ θθ {[ΩΓ + θθ ΩΓ (I Γ 0 θ ) 1 Γ 0 θ ] 1 }. (b) Suppose we obtan ( θ j j ) from j 1 by the RM algorthm. Then, there exsts a neghborhood N 1 of 0 such that θ j ˆθ RM = O( j 1 ˆ RM ) and j ˆ RM = M Γθ Γ 0( j 1 ˆ RM ) + O(M 1/2 j 1 ˆ RM + j 1 ˆ RM 2 ) a.s. unformly n j 1 N 1, where M Γθ I Γ 0 0 θ (Γ Δ θ Γ 0 θ ) 1 Γ 0 Δ θ.
10 10 H. KASAHARA AND K. SHIMOTSU C.2. Approxmate RM Algorthm Implementng the RM algorthm s costly because t requres evaluatng Π(θ ) and Ψ(θ ) for all the tral values of θ. We reduce the computatonal burden by evaluatng Π(θ ) and Ψ(θ ) outsde the optmzaton routne by usng a prelmnary estmate of θ. Ths modfcaton has only a second-order effect on the convergence of the algorthm because the dervatves of Γ(θ )wth respect to Π(θ ) and Ψ(θ ) are zero when evaluated at = Ψ(θ ); see the second term n (17). Let η be a prelmnary estmate of θ. Replacng θ n Π(θ ) and Ψ(θ ) wth η, we defne the followng mappng: Γ(θ η) Ψ(θ )+ [ (I Π(η ) Ψ (η )Π(η )) 1 I ] Π(η )(Ψ (θ ) ) Once Π(η ) and Ψ(η ) are computed, the computatonal cost of evaluatng Γ(θ η)across dfferent values of θ would be smlar to that of evaluatng Ψ(θ ). Let ( θ 0 0 ) be an ntal estmator of (θ 0 0 ). For nstance, θ 0 can be the ML estmator. The approxmate RM algorthm terates the followng steps untl j = k: Step 1.Gven( θ j 1 j 1 ), update θ by θ j = arg max θ Θ j M 1 M m=1 t=1 T ln Γ(θ j 1 θ j 1 )(a mt x mt ) where Θ j {θ Θ : Γ(θ j 1 θ j 1 )(a x) [ξ 1 ξ] for all (a x) A X} for an arbtrary small ξ>0. We mpose ths restrcton to avod computng ln(0). 1 Step 2. Update usng the obtaned estmate θ j by j = Γ( θ j j 1 θ j 1 ). The followng proposton shows that the approxmate RM algorthm acheves the same convergence rate as the orgnal RM algorthm n the frst order. ROOSITION 10: Suppose that Assumpton 4 holds and that we obtan ( θ j j ) from ( θ j 1 j 1 ) by the approxmate RM algorthm. Then, there exsts a neghborhood N 2 of (θ 0 0 ) such that θ j ˆθ RM = O( j 1 ˆ RM + M 1/2 θ j 1 ˆθ RM + θ j 1 ˆθ RM 2 ) a.s. and j ˆ RM = M Γθ Γ 0( j 1 ˆ RM )+O(M 1/2 θ j 1 ˆθ RM + θ j 1 ˆθ RM 2 +M 1/2 j 1 ˆ RM + j 1 ˆ RM 2 ) a.s. unformly n ( θ j 1 j 1 ) N 2. 1 In practce, we may consder a penalzed objectve functon by truncatng Γ(θ j 1 θ j 1 ) so that t takes a value between ξ and 1 ξ, and addng a penalty term that penalzes θ such that Γ(θ j 1 θ j 1 )/ [ξ 1 ξ].
11 ESTIMATION OF STRUCTURAL MODELS 11 By choosng δ suffcently small, the domnant egenvalue of M Γθ Γ les nsde the unt crcle, and the approxmate RM algorthm can converge to a consstent estmator even when the NL algorthm dverges away from the true value. The followng proposton states the local convergence of the approxmate RM algorthm when ρ(m Γθ Γ )<1. ROOSITION 11: Suppose that Assumpton 4 holds, ρ(m Γθ Γ 0 )<1, and { θ k k } s generated by the approxmate RM algorthm startng from ( θ 0 0 ). Then, there exsts a neghborhood N 3 of (θ 0 0 ) such that, for any ntal value ( θ 0 0 ) N 3, we have lm k ( θ k k ) = ( ˆθ RM ˆ RM ) a.s. C.3. Numercal Implementaton of the Approxmate RM Algorthm Implementng the approxmate RM algorthm requres evaluatng (I Π( θ j 1 j 1 ) Ψ( θ j 1 j 1 )Π( θ j 1 j 1 )) 1 as well as computng an orthonormal bass Z( θ j 1 j 1 ) from the egenvectors of Ψ( θ j 1 j 1 ) for j = 1 k. Ths s potentally costly when the analytcal expresson of Ψ(θ ) s not avalable. In ths secton, we dscuss how to reduce the computatonal cost of mplementng the approxmate RM algorthm by updatng (I Π( θ j 1 j 1 ) Ψ( θ j 1 j 1 )Π( θ j 1 j 1 )) 1 and Z( θ j 1 j 1 ) wthout explctly computng Ψ(θ ) n each teraton. Frst, we provde theoretcal underpnnng. The followng corollary shows that, f an alternatve prelmnary consstent estmator (θ ) s used n formng Π(θ ) and Ψ(θ ), t only affects the remander terms n roposton 10. Therefore, f we use a root-m consstent (θ ) to evaluate Π(θ ) and Ψ(θ ) and keep these estmates unchanged throughout teratons, the resultng sequence of estmators s only O(M 1 ) away a.s. from the correspondng estmators generated by the approxmate RM algorthm. COROLLARY 1: Suppose that Assumpton 4 holds. Let (θ ) be a strongly consstent estmator of (θ 0 0 ), and suppose we obtan ( θ j j ) by the approxmate RM algorthm wth Π(θ ) and Ψ(θ ) n place of Π( θ j 1 j 1 ) and Ψ( θ j 1 j 1 ). Then, there exsts a neghborhood N 4 of (θ 0 0 ) such that θ j ˆθ RM = O( j 1 ˆ RM +r Mj ) a.s. and j ˆ RM = M Γθ Γ ( j 1 ˆ RM ) + O(M 1/2 j 1 ˆ RM + j 1 ˆ RM 2 + r Mj ) a.s. unformly n ( θ j 1 j 1 ) N 4, where r Mj = M 1/2 θ j 1 ˆθ RM + θ j 1 ˆθ RM 2 +M 1/2 θ ˆθ RM + θ ˆθ RM 2 + M 1/2 ˆ RM + ˆ RM 2. Usng Corollary 1, n the followng we dscuss how to reduce the computatonal cost of mplementng the RM algorthm by updatng (I Π( θ j 1
12 12 H. KASAHARA AND K. SHIMOTSU j 1 ) Ψ( θ j 1 j 1 )Π( θ j 1 j 1 )) 1 and Z( θ j 1 j 1 ) wthout explctly computng Ψ(θ ) n each teraton. Denote Π j 1 = Π( θ j 1 j 1 ), Z j 1 = Z( θ j 1 j 1 ),and Ψ j 1 = Ψ( θ j 1 j 1 ). Frst, usng Π j 1 = Z j 1 ( Z j 1 ) and ( Z j 1 ) Z j 1 = I, we may verfy that (I Π j 1 Ψ j 1 Π j 1 ) 1 Π j 1 = Z j 1 (I ( Z j 1 ) Ψ j 1 Z j 1 ) 1 ( Z j 1 ) Let Z j 1 =[ z 1 j 1 zr ] and ξ>0. The th column of j 1 Ψ j 1 Z j 1 can be approxmated by Ψ j 1 z (1/ξ)[Ψ( θ j 1 j 1 j 1 + ξ z ) Ψ( θ j 1 j 1 j 1 )], whch requres (r + 1) functon evaluatons of Ψ(θ ). Further, evaluatng (I Π j 1 Ψ j 1 Π j 1 ) 1 only requres the nverson of the r r matrx I ( Z j 1 ) Ψ j 1 Z j 1 nstead of an nverson of an L L matrx. Thus, when r s small, numercally evaluatng (I Π j 1 Ψ j 1 Π j 1 ) 1 s not computatonally dffcult. Second, t s possble to use Ψ j Z j 1 to update an estmate of the orthogonal bass Z. Namely, gven a prelmnary estmate Z j 1,wemayobtan Z j by performng one step of an orthogonal power teraton (see Shroff and Keller (1993), p. 1107, Golub and Van Loan (1996)) by computng Z j = orth( Ψ j Z j 1 ), where orth(b) denotes an orthonormal bass for the columns of B computed by Gram Schmdt orthogonalzaton. Our numercal mplementaton of the RM sequental algorthm s summarzed as follows. Step 0 Intalzaton. (a) Fnd the egenvalues of Ψ 0 Ψ( 0 θ 0 ) for whch the modulus s larger than δ. Let{ λ 0 1 λ 0 r } denote them. 2 (b) Fnd the egenvectors of Ψ 0 assocated wth λ 0 1 λ 0 r. (c) Usng Gram Schmdt orthogonalzaton, compute an orthonormal bass of the space spanned by these egenvectors. Let { z 1 0 zr } denote the bass. (d) Compute 0 Z 0 (I Z Ψ 0 0 Z 0 ) 1 Z and Π 0 0 = Z 0 Z,where 0 Z 0 =[ z 1 0 zr ]. 0 Step 1 Update θ. Gven Z j 1 (I Z Ψ j 1 j 1 Z j 1 ) 1 Z and Π j 1 j 1 = Z j 1 ( Z j 1 ), update θ by θ j = arg max θ Θj M 1 M T ln Γ(θ m=1 t=1 j 1 θ j 1 Z j 1 )(a mt x mt ),whereγ(θ j 1 θ j 1 Z j 1 ) = Π j 1 j 1 + Z j 1 (I Z Ψ j 1 j 1 Z j 1 ) 1 Z (Ψ (θ j 1 j 1 ) j 1 )+(I Π j 1 )Ψ (θ j 1 ) wth Ψ j 1 Ψ( θ j 1 j 1 ). Step 2 Update. Gven( θ j j 1 θ j 1 Z j 1 ), update by j = Γ( θ j j 1 θ j 1 Z j 1 ). 2 Computng the r domnant egenvalues of Ψ 0 s potentally costly. We follow the numercal procedure based on the power teraton method as dscussed n Secton 4.1 of SK.
13 ESTIMATION OF STRUCTURAL MODELS 13 Step 3 Update Z. (a) Update the orthonormal bass Z by Z j = orth( Ψ j Z j 1 ), where the th column of Ψ j Z j 1 s computed by Ψ j z j 1 (1/ξ)[Ψ( θ j j +ξ z j 1 ) Ψ( θ j j )] for small ξ>0, wth Z j 1 =[ z 1 j 1 zr j 1 ]. (b) Compute Π j = Z j ( Z j ) and Z j (I Z Ψ j j Z j ) 1 Z j, where the th row of Ψ j Z j s gven by Ψ j z (1/ξ)[Ψ( θ j j j + ξ z ) Ψ( θ j j j )]. (c) Every J teratons, update the orthonormal bass Z usng the algorthm of Step 0, where ( θ 0 0 ) s replaced wth ( θ j j ). Step 4. Iterate Steps 1 3 k tmes. When an ntal estmate s not precse, the domnant egenspace of Ψ j wll change as teratons proceed. In Step 3(a), the orthonormal bass s updated to mantan the accuracy of the bass wthout changng the sze of the orthonormal bass. If an ntal estmate of the sze of the orthonormal bass s smaller than the true sze, however, the estmated subspace = ΠR L may not contan all the bases for whch egenvalues are outsde the unt crcle. In such a case, the algorthm may not converge. To safeguard aganst such a possblty, the bass sze s updated every J teratons n Step 3(c). In our Monte Carlo experments, we chose J = 10. Corollary 1 mples that ths modfed algorthm wll converge. C.4. Applyng RM to the Example of esendorfer and Schmdt-Dengler (2010) Ths subsecton llustrates how the RM algorthm can be appled to the example of esendorfer and Schmdt-Dengler (2010). We frst derve the relaton between (Γ + θ Γ + ) and (Ψ + + θ Ψ + ). Defne Π + (θ + ) as the + orthogonal projector from R dm(+ ) onto the maxmum nvarant subspace of + Ψ(θ + ) belongng to ts r largest (n modulus) egenvalues, and let Z(θ + ) be an orthonormal bass of the column space of Π + (θ + ), so that Π + (θ + ) = Z(θ + )Z(θ + ). From the proof of roposton 6, we have Γ + (θ + ) + = A(θ + )(Ψ + (θ + ) + ),wherea(θ + ) = Z(θ + )[I Z(θ + ) + Ψ(θ + )Z(θ + )] 1 Z(θ + ) + I Π(θ + ). Consequently, Γ + θ = A(θ 0 0+ )Ψ + θ and Γ + = A(θ 0 0+ )(Ψ + + I) + I. + We proceed to derve M + Γ θ Γ +. Recall + ( ) 0 θ Ψ + = θ p0 1 2 Ψ + 0 = + θ 0 M 0 + Ψ θ = 1 ( ) The egenvectors and egenvalues of Ψ + are gven by + z 1 = 1 ( ) 1 λ = θ 0 z 2 = 1 ( ) λ 2 = θ 0 Because the egenvector z 1 s annhlated by M + Ψ θ,wemaytakez(θ 0 0+ ) = z 2. Suppress (θ 0 0+ ) from Z(θ 0 0+ ), Π(θ 0 0+ ),anda(θ 0 0+ ).SnceZ s the
14 14 H. KASAHARA AND K. SHIMOTSU egenvector of Ψ + + wth egenvalue θ 0,wehaveZ Ψ + + Z = θ 0 Z Z = θ 0 and hence A = Z(1 Z Ψ + + Z) 1 Z + (I Π) = (1 + θ 0 ) 1 Π + (I Π) = I θ 0 (1 + θ 0 ) 1 Π Because Ψ + s symmetrc, we may apply the egenvalue decomposton to t + and wrte Ψ + = θ 0 z + 1 z 1 θ0 z 2 z = 2 θ0 z 1 z 1 θ0 Π. In vew of Az 1 = z 1 and AΠ = (1 + θ 0 ) 1 Π,wehaveΓ + = A(Ψ + + I) + I = θ 0 z + 1 z 1 θ0 (1 + θ 0 ) 1 Π A + I = θ 0 z 1 z. Further, from Ψ + 1 θ = p 0 2z 1,wehaveΓ + θ = AΨ + θ = Ψ + θ and hence M + Γ θ = I z 1 (z 1 z 1 ) 1 z. It follows that 1 M+ Γ θ Γ + = 0, and the local convergence + condton holds. C.5. q-nl Algorthm and Approxmate q-nl Algorthm When the spectral radus of Λ 0 or Ψ 0 s smaller than but close to 1, the convergence of the NL algorthm could be slow and the generated sequence could behave erratcally. Furthermore, n such a case, the effcency loss from usng the NL estmator compared to the MLE s substantal. To overcome these problems, consder a q-fold operator of Λ as Λ q (θ ) Λ ( θ ( Λ ( θ Λ(θ Λ(θ )) ))) }{{} q tmes We may defne Γ q (θ ) and Ψ q (θ ) analogously. Defne the q-nl (q- RM) algorthm by usng a q-fold operator Λ q, Γ q,orψ q n place of Λ, Γ, or Ψ n the orgnal NL (RM) algorthm. In the followng, we focus on Λ q, but the same argument apples to Γ q and Ψ q. If the sequence of estmators generated by the q-nl algorthm converges, ts lmt satsfes ˇθ = arg max θ Θ M 1 M T ln m=1 t=1 Λq (θ ˇ)(a mt x mt ) and ˇθ = Λ q ( ˇθ ˇ). Among the pars ( ˆθ ˆ) that satsfy these two condtons, the one that maxmzes the value of the pseudo lkelhood s called the q-nl estmator and denoted by ( ˆθ qnl ˆ qnl ). Snce the result of roposton 7 also apples here by replacng Ψ wth Λ q, the local convergence property of the q-nl algorthm s prmarly determned by the spectral radus of Λ q Λ q (θ 0 0 ).Whenρ(Λ 0 ) s less than 1, the q-nl algorthm converges faster than the NL algorthm because ρ(λ q ) = (ρ(λ 0 ))q. Moreover, the varance of the q-nl estmator approaches that of the MLE as q. Applyng the q-nl algorthm, as defned above, s computatonally ntensve because the q-nl Step 1 requres evaluatng Λ q at many dfferent values of θ. We reduce the computatonal burden by ntroducng a lnear approxmaton of Λ q (θ ) around (η ), whereη s a prelmnary estmate of θ: Λ q (θ η) Λ q (η ) + θ Λ q (η )(θ η).
15 ESTIMATION OF STRUCTURAL MODELS 15 Gven an ntal estmator ( θ 0 0 ), the approxmate q-nl algorthm terates the followng steps untl j = k: Step 1. Gven ( θ j 1 j 1 ), update θ by θ j = arg max θ Θ q j M 1 M m=1 t=1 T ln Λ q (θ j 1 θ j 1 )(a mt x mt ) where Θ q j {θ Θ : Λ q (θ j 1 θ j 1 )(a x) [ξ 1 ξ] for all (a x) A X} for an arbtrary small ξ>0. Step 2. Gven ( θ j j 1 ), update usng the obtaned estmate θ j by j = Λ q ( θ j j 1 ). Implementng Step 1 requres evaluatng Λ q ( θ j 1 j 1 ) and θ Λ q ( θ j 1 j 1 ) only once outsde of the optmzaton routne for θ and thus nvolves far fewer evaluatons of Λ(θ ) across dfferent values of and θ, compared to the orgnal q-nl algorthm. 3 Defne the q-nl counterparts of θ 0 (), φ 0 (), and Ω θθ as θ q () 0 arg max θ Θ E[ T t=1 ln Λq (θ )(a mt x mt )], φ q 0 () Λq ( θ q 0 () ), and Ωq θθ E( θ s Λ mt θ sλ mt ) wth sλ mt = T t=1 ln Λq (θ 0 0 )(a mt x mt ), respectvely. Defne Ω q θ analogously. ASSUMTION 5: (a) Assumpton 1 holds. (b) Ψ(θ ) s four tmes contnuously dfferentable n N.(c)There s a unque θ 0 such that Λ q (θ 0 0 ) = 0. (d) I (αψ 0 +(1 α)i)q and I Ψ 0 are nonsngular.(e)the operator φq 0 () has a nonsngular Jacoban matrx at 0. Assumpton 5(c) s necessary for dentfyng θ 0 when the condtonal probablty s gven by Λ q (θ ). Ths assumpton rules out θ 1 θ 0 that satsfes Λ q (θ 1 0 ) = 0 even f Λ(θ 1 0 ) 0. Ths occurs, for example, f Λ(θ 1 0 ) = 1 and Λ(θ 1 1 ) = 0 hold for θ 1 θ 0 and 1 0. Assumpton 5(d) s necessary for Ω q θθ to be nonsngular. Snce Λ q = (αψ 0 + (1 α)i)q, the frst condton holds f ρ(λ q )<1 from of Seber (2007). The followng proposton establshes the asymptotcs of the q-nl estmator and the convergence property of the approxmate q-nl algorthm. roposton 12(c) mples that, when q s suffcently large, the q-nl estmator s more effcent than the NL estmator, provded that addtonal condtons n Assumpton 5 hold. roposton 12(d) corresponds to roposton 1. ROOSITION 12: Suppose that Assumpton 5 holds. Then (a) ˆ qnl 0 = O(M 1/2 ) a.s. and M 1/2 ( ˆθ qnl θ 0 ) d N(0 V qnl ), where V qnl = 3 Usng one-sded numercal dervatves, evaluatng θ Λ q ( θ j j ) requres (K + 1)q functon evaluatons of Ψ(θ ).
16 16 H. KASAHARA AND K. SHIMOTSU [Ω q θθ + Ω q θ(i Λ 0 ) 1 Λ q θ] 1 Ω q θθ{[ω q θθ + Ω q θ(i Λ 0 ) 1 Λ q θ] 1 }. (b) Suppose we obtan ( θ j j ) from ( θ j 1 j 1 ) by the approxmate q-nl algorthm. Then, there exsts a neghborhood N 6 of (θ 0 0 ) such that θ j ˆθ qnl = O( j 1 ˆ qnl +M 1/2 θ j 1 ˆθ qnl + θ j 1 ˆθ qnl 2 ) a.s. and j ˆ qnl = M q Λ Λq θ ( j 1 ˆ qnl ) + O(M 1/2 θ j 1 ˆθ qnl + θ j 1 ˆθ qnl 2 + M 1/2 j 1 ˆ qnl + j 1 ˆ qnl 2 ) a.s. unformly n ( θ j 1 j 1 ) N 6, where M q I Λ Λq θ θ(λ q θ Δ Λ q θ) 1 Λ q θ Δ wth Λ q θ θ Λ q (θ 0 0 ).(c)if ρ(λ 0 )<1, then V qnl V MLE as q.(d)suppose { θ k k } s generated by the approxmate q-nl algorthm startng from ( θ 0 0 ) and ρ(m Λ q θ Λq )<1. Then, there exsts a neghborhood N 7 of (θ 0 0 ) such that, for any startng value ( θ 0 0 ) N 7, we have lm k ( θ k k ) = ( ˆθ qnl ˆ qnl ) a.s. C.6. roof of ropostons n Appendx C ROOF OF ROOSITION 8: For part (a), wrte Γ(θ ) as Γ(θ ) = A(θ )(Ψ (θ ) ),wherea(θ ) (I Π(θ ) Ψ (θ )Π(θ )) 1 Π(θ ) + (I Π(θ )).LetZ(θ ) denote an orthonormal bass of the column space of Π(θ ), so that Z(θ )Z(θ ) = Π(θ ) and Z(θ ) Z(θ ) = I r. Suppress (θ ) from Π(θ ), Z(θ ), and Ψ(θ ). A drect calculaton gves (I Π ΨΠ) 1 Π = Z(I Z ΨZ) 1 Z,sowecanwrte A(θ ) as A(θ ) = Z(I Z ΨZ) 1 Z + (I Π). The stated result follows snce A(θ ) s nonsngular because rank[z(i Z ΨZ) 1 Z ]=r, rank(i Π) = L r, andz(i Z ΨZ) 1 Z and I Π are orthogonal to each other. For part (b), defne Γ 0 Γ(θ0 0 ) and Π 0 Π(θ 0 0 ). Defne wth respect to Ψ 0 Ψ(θ0 0 ). Computng Γ(θ ) and notng that Ψ(θ 0 0 ) = 0,wefndΓ 0 = Π0 + (I Π 0 Ψ 0 Π0 ) 1 Π 0 (Ψ 0 I)+ (I Π0 )Ψ 0. Observe that Γ 0 Π0 = (I Π 0 )Ψ 0 Π0 = 0, where the last equalty follows because Ψ 0 Π0 for any R L by the defnton of Π 0. Hence, Γ 0 = Γ 0(I Π0 ).Wealsohave(I Π 0 )Γ 0 = (I Π0 )Ψ 0 because a drect calculaton gves (I Π 0 Ψ 0 Π0 ) 1 Π 0 = Z 0 (I (Z 0 ) Ψ 0 Z0 ) 1 (Z 0 ),wherez 0 = Z(θ 0 0 ), and hence (I Π 0 )(I Π 0 Ψ 0 Π0 ) 1 Π 0 = 0. Then, n conjuncton wth Γ 0 = Γ 0(I Π0 ),weobtan(i Π 0 )Γ 0 = (I Π0 )Ψ 0(I Π0 ).SnceΓ 0(I Π0 ) has the same egenvalues as (I Π 0 )Γ 0 (see Theorem of Horn and Johnson (1985)), we have ρ(γ 0) = ρ(γ 0(I Π0 )) = ρ((i Π 0 )Γ 0) = ρ[(i Π 0 )Ψ 0(I Π0 )] δ 0, where the last nequalty follows from Lemma 2.10 of SK:, Q,andF n SK correspond to our u Π0, I Π 0,andΨ 0. Q.E.D. ROOF OF ROOSITION 9: The stated results follow from roposton 2 of AM07 and our roposton 7 f Assumptons 1(b), 1(c), 1(e) 1(h), and 2(b) and 2(c) hold when Ψ(θ ) s replaced wth Γ(θ ).
17 ESTIMATION OF STRUCTURAL MODELS 17 We check Assumptons 2(b) and 2(c) frst because they are used n showng the other condtons. Frst, note that Chu (1990, Secton4.2;npartcular, lne 17 on p. 1377) proved the followng: f a matrx A(t) s l tmes contnuously dfferentable wth respect to t, andfx(t) spans the nvarant subspace correspondng to a subset of egenvalues of A(t), then X(t) s also l tmes contnuously dfferentable wth respect to t. Consequently, Π(θ ) s three tmes contnuously dfferentable n N (we suppress n N henceforth), snce Ψ(θ ) s three tmes contnuously dfferentable from Assumpton 4(b). Further, I Π(θ ) Ψ (θ )Π(θ ) s nonsngular and three tmes contnuously dfferentable from Assumptons 4(b) and 4(c), and hence Assumpton 2(b) holds for Γ(θ ). For Assumpton 2(c), a drect calculaton gves Ω Γ = Ψ 0 θθ θ A(θ0 0 ) Δ A(θ 0 0 )Ψ 0 θ,wherea(θ ) s defned n the proof of roposton 2 and shown to be nonsngular. Snce rank(ψ 0 θ ) = K from nonsngularty of Ω θθ = Ψ 0 Δ θ Ψ 0, postve defnteness of θ ΩΓ follows. θθ We proceed to confrm that Assumptons 1(b), 1(c), and 1(e) 1(h) hold for Γ(θ ). Assumpton 1(b) for Γ(θ )follows from Assumpton 4(d). Assumpton 1(c) holds because we have already shown that Γ(θ )s three tmes contnuously dfferentable. Assumpton 1(e) holds because Ψ(θ ) and Γ(θ ) have the same fxed ponts by roposton 8. As dscussed on page 21 of AM07, Assumpton 1(f) s mpled by Assumpton 4(e). Assumpton 1(g) for θ Γ () 0 follows from the postve defnteness of Ω Γ θθ and by the mplct functon theorem appled to the frst-order condton for θ. Assumpton 1(h) follows from Assumpton 4(e). Q.E.D. ROOF OF ROOSITION 10: Wrte the objectve functon as Q Γ (θ η) M M 1 M T ln Γ (θ η)(a m=1 t=1 mt x mt ), and defne Q Γ (θ η) 0 EQΓ (θ M η).forɛ>0, defne a neghborhood N 3 (ɛ) ={(θ η):max{ θ θ 0 0 η θ 0 } <ɛ}. Then, there exsts ɛ 1 > 0 such that () Ψ(θ ) s four tmes contnuously dfferentable n (θ ) f (θ η) N 3 (ɛ 1 ), () sup (θ η) N3 (ɛ 1 ) θθ QΓ 0 (θ η) 1 <, and () sup (θ η) N3 (ɛ 1 ) 3 Q Γ (θ 0 η) < because Γ(θ 0 0 θ 0 )(a x) = 0 (a x) > 0, Γ(θ η) s three tmes contnuously dfferentable (see the proof of roposton 9), and θθ Q Γ 0 (θ0 0 θ 0 ) = θθ Q Γ 0 (θ0 0 ) s nonsngular. Frst, we assume ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) and derve the stated representaton of θ j ˆθ and j ˆ. We later show that ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) a.s. f N 2 s taken suffcently small. Henceforth, we suppress the subscrpt RM from ˆθ RM and ˆ RM. Expandng the frst-order condton θ Q Γ ( M θ j j 1 θ j 1 ) = 0 around ( ˆθ j 1 θ j 1 ) gves (18) 0 = θ Q Γ M ( ˆθ j 1 θ j 1 ) + θθ Q Γ M ( θ j 1 θ j 1 )( θ j ˆθ)
18 18 H. KASAHARA AND K. SHIMOTSU where θ [ θ j ˆθ]. Wrtng θ = θ( θ j ),weobtan sup ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) θθ Q Γ M ( θ( θ j ) j 1 θ j 1 ) 1 =O(1) a.s. because () θ( θ j ) θ 0 <ɛ 1 a.s. snce θ j θ 0 <ɛ 1 and ˆθ s strongly consstent, and () sup (θ η) N3 (ɛ 1 ) θθ QΓ M (θ η) 1 = O(1) a.s. snce sup (θ η) N3 (ɛ 1 ) θθ QΓ 0 (θ η) 1 < and sup (θ η) N3 (ɛ 1 ) 2 Q Γ M (θ η) 2 Q Γ 0 (θ η) =o(1) a.s. Therefore, the stated representaton of θ j ˆθ follows f we show that (19) θ Q Γ M ( ˆθ j 1 θ j 1 ) = Ω Γ θ ( j 1 ˆ)+ r Mj where r denotes a generc remander term that s Mj O(M 1/2 θ j 1 ˆθ + θ j 1 ˆθ 2 + M 1/2 j 1 ˆ + j 1 ˆ 2 ) a.s. unformly n ( θ j 1 j 1 ) N 2. We proceed to show (19). Expandng θ Q Γ ( M ˆθ j 1 θ j 1 ) twce around ( ˆθ ˆ ˆθ) gves θ Q Γ ( M ˆθ j 1 θ j 1 ) = θ Q Γ ( M ˆθ ˆ ˆθ) + θ Q Γ ( M ˆθ ˆ ˆθ)( j 1 ˆ)+ θη Q Γ ( M ˆθ ˆ ˆθ)( θ j 1 ˆθ) + O( θ j 1 ˆθ 2 + j 1 ˆ 2 ) a.s. For the frst term on the rght, the RM estmator satsfes θ Q Γ ( M ˆθ ˆ ˆθ) = 0 a.s. because θ Q Γ ( M ˆθ ˆ) = 0 from the frst-order condton, and roposton 8(a) mples Ψ(ˆθ ˆ) = ˆ a.s. and hence θ Γ(ˆθ ˆ ˆθ) = θ Γ(ˆθ ˆ) a.s. For the second and thrd terms on the rght, we have E[ T t=1 θ ln Γ(θ0 0 θ 0 )(a mt x mt )]= Ω Γ and E[ T θ t=1 θη ln Γ(θ0 0 θ 0 )(a mt x mt )]=0 by the nformaton matrx equalty because Γ(θ 0 0 θ 0 ) = Γ(θ 0 0 ), θ Γ(θ 0 0 θ 0 ) = θ Γ(θ 0 0 ), Γ(θ 0 0 θ 0 ) = Γ(θ 0 0 ), and η Γ(θ 0 0 θ 0 ) = 0 from 0 = Ψ(θ 0 0 ). Therefore, (19) follows from the root-m consstency of ( ˆθ ˆ). For the representaton of j ˆ,frstwehave (20) j = ˆ + Γ 0 θ ( θ j ˆθ) + Γ 0 ( j 1 ˆ)+ r Mj by expandng j = Γ( θ j j 1 θ j ) around ( ˆθ ˆ ˆθ) and usng Γ(ˆθ ˆ ˆθ) = ˆ. Next, refne (18) as0= θ Q Γ ( M ˆθ j 1 θ j 1 ) Ω Γ ( θθ θ j ˆθ) + r Mj by expandng θθ Q Γ ( M ˆθ j 1 θ j 1 ) n (18) around( ˆθ ˆ ˆθ) to wrte t as θθ Q Γ ( M ˆθ j 1 θ j 1 ) = Ω Γ + θθ O(M 1/2 ) + O( θ j 1 ˆθ ) + O( j 1 ˆ ) a.s. and usng the bound of θ j ˆθ obtaned above. Substtutng ths nto (19) gves (21) θ j ˆθ = (Ω Γ θθ ) 1 Ω Γ θ ( j 1 ˆ)+ r Mj The stated result follows from substtutng ths nto (20) n conjuncton wth (Ω Γ θθ ) 1 Ω Γ 0 θ = (Γ Δ θ Γ 0 θ ) 1 Γ 0 Δ θ Γ 0.
19 ESTIMATION OF STRUCTURAL MODELS 19 It remans to show that ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) a.s. f N 2 s taken suffcently small. We frst show that (22) sup Q Γ (θ η) (θ η ) Θ M QΓ (θ η) =o(1) 0 j N 2 Q Γ 0 (θ η)s contnuous n (θ η ) Θ j N 2 a.s. Take N 2 suffcently small; then t follows from the strong consstency of ( θ j 1 j 1 ) and the contnuty of Γ(θ η) that Γ (θ η)(a x) [ξ/2 1 ξ/2] for all (a x) A X and (θ η) Θ j N a.s. Observe that () Θ j N s compact because t s an ntersecton of the compact set Θ and A X closed sets, () ln Γ(θ η)s contnuous n (θ η) Θ j N,and () E sup ln Γ (θ η)(a (θ η) Θj N x ) ln(ξ/2) + ln(1 ξ/2) < because of the way we choose N. Therefore, (22) follows from Kolmogorov s strong law of large numbers and Theorem 2 and Lemma 1 of Andrews (1992). Fnally, we show ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) a.s. under (22) by applyng the argument n the proof of roposton 7. Defne Δ = Q Γ 0 (θ0 0 θ 0 ) sup θ Nθ (ɛ 1 ) c Θ QΓ (θ 0 0 θ 0 )>0, where the last nequalty follows from the nformaton nequalty because Q Γ (θ 0 0 θ 0 ) s unquely maxmzed at θ 0 and N θ (ɛ 1 ) c Θ s compact. It follows that { θ j / N θ (ɛ 1 )} {Q Γ 0 (θ0 0 θ 0 ) Q Γ ( 0 θ j 0 θ 0 ) Δ}. roceedng as n the proof of roposton 7, we fnd that, f N 2 s taken suffcently small, then Q Γ 0 (θ0 0 θ 0 ) Q Γ ( 0 θ j 0 θ 0 ) Δ/2+o(1) a.s. and hence ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) a.s. Q.E.D. ROOF OF ROOSITION 11: The proof closely follows the proof of roposton 1. We suppress the subscrpt RM from ˆθ RM and ˆ RM.Defne ( ) 0 (Ω Γ D = θθ ) 1 Ω (23) Γ θ 0 M Γθ Γ 0 Note that ρ(d) = ρ(m Γθ Γ ) and that there exsts a matrx norm α such that D α ρ(d) + b = ρ(m Γθ Γ ) + b. We defne the vector norm for x R k+l as x β = [x 0 0] α ; then Ax β A α x β for any matrx A. From the representaton of j ˆ and θ j ˆθ n roposton 10 and (21), there exsts a neghborhood N ζ of ζ 0 such that ζ j ˆζ = D( ζ j 1 ˆζ) + O(M 1/2 ζ j 1 ˆζ β + ζ j 1 ˆζ 2 ) holds a.s. unformly n β ζ j 1 N ζ.thestated result then follows from repeatng the proof of roposton 1. Q.E.D. ROOF OF COROLLARY 1: The proof closely follows the proof of roposton 10. DefneΓ(θ η Q) Ψ(θ ) +[(I Π(η Q) Ψ (η Q)Π(η Q)) 1 I]Π(η Q)(Ψ (θ ) ), so that the objectve functon n Step 1 s wrtten as Q Γ M (θ j 1 θ ) = M 1 M m=1 T t=1 ln Γ(θ j 1 θ )(a mt x mt ).
20 20 H. KASAHARA AND K. SHIMOTSU For ɛ 1 > 0, defne a neghborhood N 5 (ɛ 1 ) ={(θ η Q):max{ θ θ 0 0 η θ 0 Q 0 } <ɛ 1 }. Then, for any ɛ 1 > 0, we have ( θ j j 1 θ ) N 5 (ɛ 1 ) a.s. f N 4 s chosen suffcently small by the same argument as n the proof of roposton 10. Assumng ( θ j j 1 θ ) N 5 (ɛ 1 ), the stated result follows from startng from the frst order condton θ Q Γ ( M θ j j 1 θ ) = 0, expandng t around ( ˆθ j 1 θ ), and followng the proof of roposton 10 usng Q Γ(θ 0 0 θ 0 0 ) = 0. Q.E.D. ROOF OF ROOSITION 12: art (a) follows from roposton 2 of AM07 f Assumptons 1(b), 1(c), 1(e) 1(h), and 2(b) and 2(c) hold when Ψ(θ ) s replaced wth Λ q (θ ). Smlarly to the proof of roposton 10, we check Assumptons 2(b) and 2(c) frst. Assumpton 2(b) holds for Λ q (θ ) because Ψ(θ ) s three tmes contnuously dfferentable n N from Assumpton 5(b). For Assumpton 2(c), a drect calculaton gves Ω q θθ = ( θ Λ q (θ 0 0 )) Δ θ Λ q (θ 0 0 ) = Λ 0 (I θ (Λ0 )q ) (I Λ 0 ) 1 Δ (I Λ 0 ) 1 (I (Λ 0 )q )Λ θ = Ψ 0 (I (αψ 0 θ +(1 α)i)q ) (I Ψ 0 ) 1 Δ (I Ψ 0 ) 1 (I (αψ 0 +(1 α)i)q )Ψ 0, θ where the second equalty follows from θ Λ q (θ 0 0 ) = ( q 1 j=0 (Λ0 )j )Λ 0 = (I θ Λ 0 ) 1 (I (Λ 0 )q )Λ 0, and the thrd equalty follows from θ Λ0 = αψ 0 and θ θ Λ0 = αψ 0 + (1 α)i. Sncerank(Ψ 0) = K from nonsngularty of Ω θ θθ = Ψ 0 Δ θ Ψ 0, θ postve defnteness of Ω q θθ follows from Assumpton 5(d). The proof of part (a) s completed by confrmng that Assumptons 1(b), 1(c), and 1(e) 1(h) hold for Λ q (θ ). Assumptons 1(b) and 1(c) hold for Λ q (θ ) because Assumptons 1(b) and 1(c) hold for Ψ(θ ). Assumpton 1(e) for Λ q (θ ) follows from Assumpton 5(c). As dscussed on page 21 of AM07, Assumpton 1(f) for Λ q (θ ) s mpled by Assumpton 5(e). Assumpton 1(g) for θ q () follows from the postve defnteness of 0 Ωq θθ and applyng the mplct functon theorem to the frst-order condton for θ. Assumpton 1(h) follows from Assumpton 5(e). Ths completes the proof of part (a). We proceed to prove part (b). Defne the objectve functon and ts lmt as QM(θ η) q M 1 M T ln m=1 t=1 Λq (θ η)(a mt x mt ) and Q q (θ η) 0 EQM(θ η).forɛ>0, q defne a neghborhood N 3 (ɛ) ={(θ η): max{ θ θ 0 0 η θ 0 } <ɛ}. Then, there exsts ɛ 1 > 0 such that () Ψ(θ ) s four tmes contnuously dfferentable n (θ ) f (θ η) N 3 (ɛ 1 ), () sup (θ η) N3 (ɛ 1 ) θθ Qq 0 (θ η) 1 <, and () sup (θ η) N3 (ɛ 1 ) 3 Q q (θ 0 η) < because Λ q (θ 0 0 θ 0 )(a x) = 0 (a x) > 0, Λ q (θ η) s three tmes contnuously dfferentable, and θθ Q q 0 (θ0 0 θ 0 ) = θθ Q q 0 (θ0 0 ) s nonsngular. Frst, we assume that ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) and derve the stated representaton of θ j ˆθ and j ˆ. We later show that ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) a.s. f N 6 s taken suffcently small. Henceforth, we suppress the subscrpt qnl from ˆθ qnl and ˆ qnl. The proof s smlar to the proof of the up-
21 ESTIMATION OF STRUCTURAL MODELS 21 datng formula of roposton 10. For the representaton of θ j ˆθ, expandng the frst-order condton 0 = θ QM( q θ j j 1 θ j 1 ) around ( ˆθ j 1 θ j 1 ) gves 0 = θ QM( q ˆθ j 1 θ j 1 ) + θθ QM( q θ( θ j ) j 1 θ j 1 )( θ j ˆθ), whch corresponds to (18) n the proof of roposton 10. roceedng as n the proof of roposton 10, weobtansup ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) θθ Qq M( θ( θ j ) j 1 θ j 1 ) 1 = O(1) a.s. Therefore, the stated representaton of θ j ˆθ follows f we show θ QM( q ˆθ j 1 θ j 1 ) = Ω q θ( j 1 ˆ) + r Mj,wherer Mj denotes a remander term of O(M 1/2 θ j 1 ˆθ + θ j 1 ˆθ 2 + M 1/2 j 1 ˆ + j 1 ˆ 2 ) a.s. unformly n ( θ j 1 j 1 ) N 6. Ths representaton corresponds to (19) n the proof of roposton 10 and follows from the same argument. Namely, expandng θ QM( q ˆθ j 1 θ j 1 ) twce around ( ˆθ ˆ ˆθ), and notng that () the q-nl estmator satsfes θ QM( q ˆθ ˆ ˆθ) = 0, () Λ q (θ 0 0 θ 0 ) = Λ q (θ 0 0 ), θ Λ q (θ 0 0 θ 0 ) = θ Λ q (θ 0 0 ), Λ q (θ 0 0 θ 0 ) = Λ q (θ 0 0 ), and η Λ q (θ 0 0 θ 0 ) = 0, and usng the nformaton matrx equalty and the root- M consstency of ( ˆθ ˆ), gves the requred result. The proof of the representaton of j ˆ follows from the proof of roposton 10, because () j = ˆ +Λ q θ( θ j ˆθ)+Λ q ( j 1 ˆ)+r Mj, whch corresponds to (20) n the proof of roposton 10, from expandng Λ q ( θ j j 1 ) twce around ( ˆθ ˆ) and usng ˆ = Λ q ( ˆθ ˆ), () θθ QM( q ˆθ j 1 θ j 1 )( θ j ˆθ) = Ω q θθ( θ j ˆθ) + r Mj from expandng θθ QM( q ˆθ j 1 θ j 1 ) around ( ˆθ ˆ ˆθ) and usng the bound of θ j ˆθ obtaned above, and () (Ω q θθ) 1 Ω q θ = (Λ q θ Δ Λ q θ) 1 Λ q θ Δ Λ q. The proof of part (b) s completed by showng that ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) a.s. f N 6 s taken suffcently small. Frst, observe that (22) n the proof of roposton 10 holds wth Q Γ (θ η) and M QΓ (θ η) replacng 0 Qq M(θ η) and Q q (θ η) f we take N 0 6 suffcently small. Therefore, ( θ j j 1 θ j 1 ) N 3 (ɛ 1 ) a.s. follows from repeatng the argument n the last paragraph of the proof of roposton 10 f we show that θ 0 unquely maxmzes Q q (θ 0 0 θ 0 ). Note that (24) Q q (θ 0 0 θ 0 ) Q q 0 (θ0 0 θ 0 ) = TEln( θ Λ q (θ 0 0 )(θ θ 0 ) + 0 )(a mt x mt ) TEln 0 (a mt x mt ) ( ) θ Λ q (θ 0 0 )(a mt x mt )(θ θ 0 ) = TEln (a mt x mt ) Recall that ln(y + 1) y for all y > 1, where the nequalty s strct f y 0. Snce rank( θ Λ q (θ 0 0 )) = K from the postve defnteness of Ω q θθ, t follows that θ Λ q (θ 0 0 )ν 0 for any K-vector ν 0. Therefore, θ Λ q (θ 0 0 )(a mt x mt )(θ θ 0 ) 0 for at least one (a mt x mt ),forall
22 22 H. KASAHARA AND K. SHIMOTSU θ θ 0. Consequently, the rght hand sde of (24) s strctly smaller than TE[ θ Λ q (θ 0 0 )(a mt x mt )(θ θ 0 )/ 0 (a mt x mt )] for all θ θ 0. Because E[ θ Λ q (θ 0 0 )(a mt x mt )/ 0 (a mt x mt )]=0, we have Q q (θ 0 0 θ 0 ) Q q 0 (θ0 0 θ 0 )<0forallθ θ 0. Therefore, θ 0 unquely maxmzes Q q (θ 0 0 θ 0 ),andwe complete the proof of part (b). We prove part (c). From the proof of part (a) n conjuncton wth the relaton Λ 0 = αψ 0 + (1 α)i, wemaywrteωq θθ as Ω q θθ = TΨ 0 (I θ (Λ0 )q ) (I Ψ 0 ) 1 Δ (I Ψ 0 ) 1 (I (Λ 0 )q )Ψ 0. Smlarly, usng the relaton θ Λq (θ 0 0 ) = (Λ 0 )q,weobtanω q θ = TΛ 0 (I θ (Λ0 )q ) (I Λ 0 ) 1 Δ (Λ 0 )q. Therefore, f ρ(λ 0 )<1, then Ωq θθ TΨ 0 0 θ (I Ψ ) 1 Δ (I Ψ 0 ) 1 Ψ 0 and θ Ωq θ 0as q, and t follows that V qnl [TΨ 0 0 θ (I Ψ ) 1 Δ (I Ψ 0 ) 1 Ψ 0 θ ] 1 as q. Ths lmt s the same as V MLE = (T E[ θ ln (θ 0 )(a mt x mt ) θ ln (θ 0 )(a mt x mt )]) 1, where (θ) arg max Mθ E ln (a mt x mt ) wth M θ { B : = Ψ(θ )}, because θ (θ) = (I Ψ (θ (θ))) 1 θ Ψ(θ (θ)) holds n a neghborhood of θ = θ 0. We omt the proof of part (d) because t s dentcal to the proof of roposton 11 except that ˆθ RM, ˆ RM, (Ω Γ θθ ) 1 Ω Γ,andM θ Γ θ Γ are replaced wth ˆθ qnl, ˆ qnl, (Ω q θθ) 1 Ω q θ, andm Λ q θ Λq, respectvely. Q.E.D. AENDIX D: UNOBSERVED HETEROGENEITY Ths secton extends our analyss to models wth unobserved heterogenety. The NL algorthm has an mportant advantage over two-step methods n estmatng models wth unobserved heterogenety because t s dffcult to obtan a relable ntal estmate of n ths context. Suppose that there are K types of agents, where type k s characterzed by a type-specfc parameter θ k, and the probablty of beng type k s π k, wth K k=1 πk = 1. These types capture tme-nvarant state varables that are unobserved by researchers. Wth a slght abuse of notaton, denote θ = (θ 1 θ K ) Θ K and π = (π 1 π K ) Θ π. Then, ζ = (θ π ) s the parameter to be estmated, and let Θ ζ = Θ K Θ π denote the set of possble values of ζ. The true parameter s denoted by ζ 0. Consder a panel data set {{a mt x mt x m t+1 } T t=1 }M such that w m=1 m ={a mt x mt x m t+1 } T t=1 s randomly drawn across m s from the populaton. The condtonal probablty dstrbuton of a mt gven x mt for a type k agent s gven by a fxed pont of θ k = Ψ(θ k θ k). To smplfy our analyss, we assume that the transton probablty functon of x mt s ndependent of types and gven by f x (x m t+1 a mt x mt ) and s known to researchers. 4 4 When the transton probablty functon s ndependent of types, t can be drectly estmated from transton data wthout solvng the fxed pont problem. Kasahara and Shmotsu (2008) analyzed the case n whch the transton probablty functon s also type-dependent n the context of a sngle-agent dynamc programmng model wth unobserved heterogenety.
23 ESTIMATION OF STRUCTURAL MODELS 23 In ths framework, the ntal state x m1 s correlated wth the unobserved type (.e., the ntal condtons problem of Heckman (1981)). We assume that x m1 for type k s randomly drawn from the type k statonary dstrbuton characterzed by a fxed pont of the equaton p (x) = x X p (x )( a A θ k(a x ) f x (x a x )) [T(p θ k)](x). Snce solvng the fxed pont of T( )for gven s often less computatonally ntensve than computng the fxed pont of Ψ(θ ), we assume the full soluton of the fxed pont of T( ) s avalable gven. Let k denote type k s condtonal choce probabltes, stack the k s as = ( 1 K ),andlet 0 denote ts true value. Defne Ψ(θ ) = (Ψ (θ 1 1 ) Ψ(θ K K ) ). Then, for a value of θ, the set of possble condtonal choce probabltes consstent wth the fxed pont constrants s gven by M ={ θ BK : = Ψ(θ )}. The maxmum lkelhood estmator for a model wth unobserved heterogenety s { (25) ˆζ MLE = arg max ζ Θ ζ max M θ M 1 M ln ( [L(π )](w m ) )} m=1 where [L(π )](w m ) = K k=1 πk p (x k m1 ) T t=1 k (a mt x mt )f x (x m t+1 a mt x mt ), and p = T(p k ) s the type k statonary dstrbuton of x when the condtonal choce probablty s k.if 0 s the true condtonal choce probablty k k dstrbuton and π 0 s the true mxng dstrbuton, then L 0 = L(π 0 0 ) represents the true probablty dstrbuton of w. We consder a verson of the NL algorthm for models wth unobserved heterogenety orgnally developed by AM07 as follows. Assume that an ntal consstent estmator 0 = ( 1 0 K 0 ) s avalable. Startng from j = 1, terate the followng steps untl j = l: Step 1. Gven j 1, update ζ = (θ π ) by ζ j = arg max ζ Θ ζ M 1 M ln ([ L(π Ψ (θ j 1 )) ] (w m ) ) m=1 Step 2. Update usng the obtaned estmate θ j by j = Ψ( θ j j 1 ). If teratons converge, the lmt satsfes ˆζ = arg max ζ Θζ M 1 M ln([l(π m=1 Ψ(θ ˆ))](w m )) and ˆ = Ψ(ˆθ ˆ). Among the pars that satsfy these two condtons, the one that maxmzes the pseudo lkelhood s called the NL estmator, whchwedenoteby(ˆζ NL ˆ NL ). Let us ntroduce the assumptons requred for the consstency and asymptotc normalty of the NL estmator. They are analogous to the assumptons used n AM07. Defne ζ 0 () and φ 0 () smlarly to θ 0 () and φ 0 () n the man paper.
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Supporting information for: Functional Mixed Effects Model for Small Area Estimation
 Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Symplecticity of the Störmer-Verlet algorithm for coupling between the shallow water equations and horizontal vehicle motion
 Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Solutions for Mathematical Physics 1 (Dated: April 19, 2015)
 Solutons for Mathematcal Physcs 1 Dated: Aprl 19, 215 3.2.3 Usng the vectors P ê x cos θ + ê y sn θ, Q ê x cos ϕ ê y sn ϕ, R ê x cos ϕ ê y sn ϕ, 1 prove the famlar trgonometrc denttes snθ + ϕ sn θ cos
Solutons for Mathematcal Physcs 1 Dated: Aprl 19, 215 3.2.3 Usng the vectors P ê x cos θ + ê y sn θ, Q ê x cos ϕ ê y sn ϕ, R ê x cos ϕ ê y sn ϕ, 1 prove the famlar trgonometrc denttes snθ + ϕ sn θ cos
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Derivation for Input of Factor Graph Representation
 Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
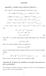 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Supplementary materials for Statistical Estimation and Testing via the Sorted l 1 Norm
 Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
2 Lagrangian and Green functions in d dimensions
 Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ. ICA: συναρτήσεις κόστους & εφαρμογές
 8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)
![2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p) 2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)](/thumbs/40/21364883.jpg) Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Constant Elasticity of Substitution in Applied General Equilibrium
 Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Phasor Diagram of an RC Circuit V R
 ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Non polynomial spline solutions for special linear tenth-order boundary value problems
 ISSN 746-7233 England UK World Journal of Modellng and Smulaton Vol. 7 20 No. pp. 40-5 Non polynomal splne solutons for specal lnear tenth-order boundary value problems J. Rashdna R. Jallan 2 K. Farajeyan
ISSN 746-7233 England UK World Journal of Modellng and Smulaton Vol. 7 20 No. pp. 40-5 Non polynomal splne solutons for specal lnear tenth-order boundary value problems J. Rashdna R. Jallan 2 K. Farajeyan
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
arxiv: v2 [math.ap] 6 Dec 2015
![arxiv: v2 [math.ap] 6 Dec 2015 arxiv: v2 [math.ap] 6 Dec 2015](/thumbs/85/91973743.jpg) Unform Regularty Estmates n Homogenzaton Theory of Ellptc System wth Lower Order Terms arxv:1507.06050v2 math.ap] 6 Dec 2015 Qang Xu School of Mathematcs and Statstcs, Lanzhou Unversty, Lanzhou, Gansu
Unform Regularty Estmates n Homogenzaton Theory of Ellptc System wth Lower Order Terms arxv:1507.06050v2 math.ap] 6 Dec 2015 Qang Xu School of Mathematcs and Statstcs, Lanzhou Unversty, Lanzhou, Gansu
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
THE SECOND WEIGHTED MOMENT OF ζ. S. Bettin & J.B. Conrey
 THE SECOND WEIGHTED MOMENT OF ζ by S. Bettn & J.B. Conrey Abstract. We gve an explct formula for the second weghted moment of ζs) on the crtcal lne talored for fast computatons wth any desred accuracy.
THE SECOND WEIGHTED MOMENT OF ζ by S. Bettn & J.B. Conrey Abstract. We gve an explct formula for the second weghted moment of ζs) on the crtcal lne talored for fast computatons wth any desred accuracy.
Neutralino contributions to Dark Matter, LHC and future Linear Collider searches
 Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Space-Time Symmetries
 Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Duals of the QCQP and SDP Sparse SVM. Antoni B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckriet
 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckret SVCL-TR 007-0 v Aprl 007 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R.
Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckret SVCL-TR 007-0 v Aprl 007 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R.
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
w o = R 1 p. (1) R = p =. = 1
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequality for metrics: Let (X, d) be a metric space and let x, y, z X.
 Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
8.323 Relativistic Quantum Field Theory I
 MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
Lecture 21: Properties and robustness of LSE
 Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER
 ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
The Probabilistic Method - Probabilistic Techniques. Lecture 7: The Janson Inequality
 The Probabilistic Method - Probabilistic Techniques Lecture 7: The Janson Inequality Sotiris Nikoletseas Associate Professor Computer Engineering and Informatics Department 2014-2015 Sotiris Nikoletseas,
The Probabilistic Method - Probabilistic Techniques Lecture 7: The Janson Inequality Sotiris Nikoletseas Associate Professor Computer Engineering and Informatics Department 2014-2015 Sotiris Nikoletseas,
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
MINIMAL CLOSED SETS AND MAXIMAL CLOSED SETS
 MINIMAL CLOSED SETS AND MAXIMAL CLOSED SETS FUMIE NAKAOKA AND NOBUYUKI ODA Received 20 December 2005; Revised 28 May 2006; Accepted 6 August 2006 Some properties of minimal closed sets and maximal closed
MINIMAL CLOSED SETS AND MAXIMAL CLOSED SETS FUMIE NAKAOKA AND NOBUYUKI ODA Received 20 December 2005; Revised 28 May 2006; Accepted 6 August 2006 Some properties of minimal closed sets and maximal closed
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Exam Statistics 6 th September 2017 Solution
 Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
Pricing of Options on two Currencies Libor Rates
 Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
 CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
The one-dimensional periodic Schrödinger equation
 The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly
The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Bounding Nonsplitting Enumeration Degrees
 Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
