8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ. ICA: συναρτήσεις κόστους & εφαρμογές
|
|
|
- Ξενία Μακρής
- 8 χρόνια πριν
- Προβολές:
Transcript
1 8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές
2 ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x] = E[ x 4 ] 3 Γκαουσίανές μεταβλητές έχουν κύρτωση=0 Υπεργκαουσιανές.τ.μ τ.μ. με κύρτωση>0 Υπογκαουσιανές τ.μ. τ.μ. με κύρτωση<0 Αν οι τ.μ. έχουν σταθερή διασπορά τότε η κύρτωση μπορεί να υπολογιστεί μέσω της 4 ης ροπής
3 ΥΠΟΛΟΓΙΣΜΌΣ ICA ΜΈΣΩ ΚΎΡΤΩΣΗΣ gradent ascent στην απόλυτη τιμή της κύρτωσης kurt( w w Μέθοδος προβολής z) = 4sgn( kurt( w ( για whtened data E[( w z) z))( E[ z( w ] = w ) z) 3 ] 3w w 3 Δ w sgn( kurt( w z))( E[ z( w z) ] w w w Σχόλια: δεν είναι ευσταθής ευαίσθητη σε παρεκτρεπόμενες τιμές 3
4 ΑΡΝΗΤΙΚΉ ΕΝΤΡΟΠΊΑ (NEGENROPY) J( y) = H( y gauss ) H( y) όπου Η(.): διαφορική εντροπία και y gauss : γκαουσιανικό άνυσμα τ.μ. με ίδιο πίνακα συσχέτισης με το y. J(y)>0 και J(y)=0 μόνο όταν y είναι γκαουσιανή. ΑΕ είναι στατιστικά πολύ καλή μέθοδος υπολογισμου της μη-γκαουσιανότητας Ευσταθής. Όμως υπολογισμικά περίπλοκη χρησιμοποίηση προσέγγισης, π.χ. J( y) E[ G( y)] E[ G( v όπου G: ένα οποιοδήποτε μη-τετραγωνική συνάρτηση και v: κανονική τ.μ. )] 4
5 Καλή επιλογή του G οδηγεί σε ευσταθείς εκτιμητές G ( y ) = Μετά gradent ascent projecton ICA Δw γe[ zg( w w Υπολογισμός σε πραγματικό χρόνο: g g ( y) w w όπου γ = ( y) = ye y / and a log cosh( ay ) a G ( y ) = e z)] y) ( y / ) γ : Δ γ ( w z) E[ G( v)] γ E[ G( y)] E[ G( v)] και g είναι dervatve του G, δηλ. = tanh( a G 5
6 ΜΈΓΙΣΤΗ ΠΙΘΑΝΌΤΗΤΑ (ΜΠ) ICA (MAXIMUM LIKELIHOOD ML ICA) Η ΣΚΠ των μικτών τ.μ. x = As είναι p x ( x) = ps ( s) det B = p όπου B = A και p ( s ) det B είναι ΣΚΠ των ICs. Υποθέτοντας ένα δείγμα παρατηρηθέντος μίγματος x(),,x() έχουμε λογαριθμική ΜΠ (log Lkelhood): log L( B) όπου B = n = t = = ( b,..., b ) logp ( b x( t)) + n log det B 6
7 Ή: log L( B) = E[ = n log p ( b x( t)) + log det B όπου Ε: υπολογισμός της μέσης τιμής ημιπαραμετρική εκτίμηση - ΜΠ εξαρτάται από παραμέτρους: στοιχεία του B; και ΣΚΠ των πηγών λύσεις: προηγούμενη γνώση των ΣΚΠ πηγών ή προσέγγιση των ΣΚΠ μέσω απλής παραμετρικής οικογένειας τιμών ΣΚΠ. 7
8 Ο ΑΛΓΌΡΙΘΜΟΣ BELL-SEJNOWSKI gradent descent για ML ICA log lkelhood gradent log L B = ( B όπου g( y) = ( g( y ),..., g( y ) + E[ g( Bx) x n ] )) και g = (log p )' = p p ' Ο αλγόριθμος: ΔB ( B ) + E[ g( Bx) x ] Αρκετά αργός Στην πράξη χρησιμοποιείται το λεγόμενο «natural gradent» Δ B ( I + E [ g ( Bx ) x ]) B 8
9 PCA VS ICA PCA Στατιστική ης τάξεως Ορθογώνιος μετασχηματισμός Μη-συσχέτιση: E[ ss ] = I ICA Στατιστική υψηλών τάξεων Μη-ορθ. μετασχηματισμός Στατιστική ανεξαρτησία: p (s) = p ( s ) 9
10 0
11
12 ΕΠΕΚΤΆΣΕΙΣ ICA Πληροφορίες χρονικής συσχέτισης τ.μ. Μη-γραμμική ICA ICA με θόρυβο Μιγαδική ICA κλπ.
13 ΕΦΑΡΜΟΓΈΣ ΣΕ ΔΕΥ Διαχωρισμός ΗΕΓ. ΗΕΓ είναι μικτά σήματα από: (α) δραστηριότητας από διάφορες εγκεφαλικές πηγές η οποία έχει αναμιχτεί στα διάφορα στρώματα του εγκεφάλου, το υγρό του εγκεφάλου, και το κρανίο. (β) δραστηριότητα μη εγκεφαλικής προέλευσης, π.χ. κίνηση ματιών ICA χρησιμοποιείται για αφαίρεση σημάτων μηεγκεφαλικής δραστηριότητας και για διαχωρισμό εγκεφαλικής δραστηριότητας διαφορετικής προέλευσης 3
14 4
15 5
16 ΕΠΌΜΕΝΟ ΜΆΘΗΜΑ: 6 Επανάληψη
17 MAXIMUM LIKELIHOOD ESIMAION assumes that the unknown parameters are constant; no pror nformaton avalable; good statstcal propertes; works well when there s a lot of data; ML soluton chooses the parameters defnng the model under whch the data are most lkely. he lkelhood functon p( x / Θ) = p( x(),..., x( )/ Θ) has the same form as the jont densty of the measurements. Often, the log lkelhood s used: ln p( x / Θ) 7
18 he lkelhood equaton ln p( x / Θ) = 0 Θ enables to fnd the maxmum of the lkelhood functon. Assumng that the measurements are ndependent, the lkelhood factors out p ( x / Θ ) = j = p ( x j / where p(xj/q) s a condtonal pdf of a measurement xj. In ths case, the log lkelhood conssts of a sum of logs of condtonal pdfs. he vector lkelhood equaton conssts of m scalar equatons Θ ) Θ ln p( x / Θ) = 0, =,..., m Usually these are nonlnear and coupled - need numercal soluton methods 8
19 GRADIEN DESCEN Gradent descent s a method of mnmsaton of a gven cost or objectve functon J(w): start at some ntal pont w(0); calculate gradent of J(w) at w(0); move n the drecton of the negatve gradent or steepest descent by some dstance; repeat above untl consecutve ponts are suffcently close. 9
20 In mathematcal notaton the above procedure reads J( w) Δw( t) = α ( t) w J( w) or Δw w gradent descent moves always downwards n a hlly landscape local mnma can trap the movement ntalsaton s mportant to avod local mnma choce of the learnng rate s crucal for speed of convergence; 0
7. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ
 7. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ 1 Principal & Independent Component Analysis (PCA, ICA) PRINCIPAL COMPONENT ANALYSIS (PCA) Principal Component Analysis (PCA): ορθογώνιος μετασχηματισμός κατά τον οποίο αφαιρείται
7. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ 1 Principal & Independent Component Analysis (PCA, ICA) PRINCIPAL COMPONENT ANALYSIS (PCA) Principal Component Analysis (PCA): ορθογώνιος μετασχηματισμός κατά τον οποίο αφαιρείται
4. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ
 4. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ Συσχέτιση Εντροπία Αμοιβαία Πληροφορία ΣΤΑΤΙΣΤΙΚΉ ΟΡΟΣ Μέση τιμή (epectato) th Ροπή (momet), μ: μέση τιμή η ροπή ( d momet): διασπορά (varace) Στατιστική ανεξαρτησία (statstcal depedece)
4. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ Συσχέτιση Εντροπία Αμοιβαία Πληροφορία ΣΤΑΤΙΣΤΙΚΉ ΟΡΟΣ Μέση τιμή (epectato) th Ροπή (momet), μ: μέση τιμή η ροπή ( d momet): διασπορά (varace) Στατιστική ανεξαρτησία (statstcal depedece)
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Αναγνώριση Προτύπων (Pattern Recognition) Μπεϋζιανή Θεωρία Αποφάσεων (Bayesian Decision Theory) Π. Τσακαλίδης
 Αναγνώριση Προτύπων (Pattern Recognton Μπεϋζιανή Θεωρία Αποφάσεων (Bayesan Decson Theory Π. Τσακαλίδης ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Μπεϋζιανή Θεωρία Αποφάσεων (Bayes Decson theory Στατιστικά
Αναγνώριση Προτύπων (Pattern Recognton Μπεϋζιανή Θεωρία Αποφάσεων (Bayesan Decson Theory Π. Τσακαλίδης ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Μπεϋζιανή Θεωρία Αποφάσεων (Bayes Decson theory Στατιστικά
ΚΑΤΗΓΟΡΙΕΣ ΤΑΞΙΝΟΜΗΣΗΣ
 ΚΑΤΗΓΟΡΙΕΣ ΤΑΞΙΝΟΜΗΣΗΣ Κατευθυνόμενη ταξινόμηση (supervsed cassfcaton) Μη-κατευθυνόμενη ταξινόμηση (unsupervsed cassfcaton) Γραμμική: Lnear Dscrmnant Anayss Μη- Γραμμική: Νευρωνικά δίκτυα κλπ. Ιεραρχική
ΚΑΤΗΓΟΡΙΕΣ ΤΑΞΙΝΟΜΗΣΗΣ Κατευθυνόμενη ταξινόμηση (supervsed cassfcaton) Μη-κατευθυνόμενη ταξινόμηση (unsupervsed cassfcaton) Γραμμική: Lnear Dscrmnant Anayss Μη- Γραμμική: Νευρωνικά δίκτυα κλπ. Ιεραρχική
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 4 Διαχωριστικές συναρτήσεις Ταξινόμηση Γκαουσιανών μεταβλητών Bayesan decson Mnmum msclassfcaton rate decson: διαλέγουμε την κατηγορίαck για την οποία η εκ των υστέρων
HMY 795: Αναγνώριση Προτύπων Διάλεξη 4 Διαχωριστικές συναρτήσεις Ταξινόμηση Γκαουσιανών μεταβλητών Bayesan decson Mnmum msclassfcaton rate decson: διαλέγουμε την κατηγορίαck για την οποία η εκ των υστέρων
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
ΝΕΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΣΧΕΤΙΚΑ ΜΕ ΤΗΝ ΥΠΑΡΞΗ ΕΚΤΙΜΗΤΩΝ ΜΕΓΙΣΤΗΣ ΠΙΘΑΝΟΦΑΝΕΙΑΣ ΓΙΑ ΤΗΝ 3-ΠΑΡΑΜΕΤΡΙΚΗ ΓΑΜΜΑ ΚΑΤΑΝΟΜΗ
 Ελληνικό Στατιστικό Ινστιτούτο Πρακτικά ου Πανελληνίου Συνεδρίου Στατιστικής 008, σελ 9-98 ΝΕΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΣΧΕΤΙΚΑ ΜΕ ΤΗΝ ΥΠΑΡΞΗ ΕΚΤΙΜΗΤΩΝ ΜΕΓΙΣΤΗΣ ΠΙΘΑΝΟΦΑΝΕΙΑΣ ΓΙΑ ΤΗΝ 3-ΠΑΡΑΜΕΤΡΙΚΗ ΓΑΜΜΑ ΚΑΤΑΝΟΜΗ Γεώργιος
Ελληνικό Στατιστικό Ινστιτούτο Πρακτικά ου Πανελληνίου Συνεδρίου Στατιστικής 008, σελ 9-98 ΝΕΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΣΧΕΤΙΚΑ ΜΕ ΤΗΝ ΥΠΑΡΞΗ ΕΚΤΙΜΗΤΩΝ ΜΕΓΙΣΤΗΣ ΠΙΘΑΝΟΦΑΝΕΙΑΣ ΓΙΑ ΤΗΝ 3-ΠΑΡΑΜΕΤΡΙΚΗ ΓΑΜΜΑ ΚΑΤΑΝΟΜΗ Γεώργιος
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας. Version 2
 Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson Σχεδιαζόντας ταξινομητές: Τα δεδομένα Στην πράξη η γνώση σχετικά διαδικασία γέννεσης των δεδομένων είναι πολύ σπάνια γνωστή. Το μόνο που έχουμε στη διάθεσή
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson Σχεδιαζόντας ταξινομητές: Τα δεδομένα Στην πράξη η γνώση σχετικά διαδικασία γέννεσης των δεδομένων είναι πολύ σπάνια γνωστή. Το μόνο που έχουμε στη διάθεσή
ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ
 ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙΔΡΑΣΗ Μ.Β ΣΤΙΣ ΙΔΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ (ΔΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙΔΡΑΣΗ Μ.Β ΣΤΙΣ ΙΔΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ (ΔΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.outras@e.aegea.gr Τηλ: 7035468 Μέθοδος Υπολογισμού
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.outras@e.aegea.gr Τηλ: 7035468 Μέθοδος Υπολογισμού
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
Phasor Diagram of an RC Circuit V R
 ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
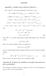 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
8.323 Relativistic Quantum Field Theory I
 MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 2 Επισκόπηση θεωρίας πιθανοτήτων Τυχαίες μεταβλητές: Βασικές έννοιες Τυχαία μεταβλητή: Μεταβλητή της οποίας δε γνωρίζουμε με βεβαιότητα την τιμή (σε αντίθεση με τις
HMY 795: Αναγνώριση Προτύπων Διάλεξη 2 Επισκόπηση θεωρίας πιθανοτήτων Τυχαίες μεταβλητές: Βασικές έννοιες Τυχαία μεταβλητή: Μεταβλητή της οποίας δε γνωρίζουμε με βεβαιότητα την τιμή (σε αντίθεση με τις
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
Constant Elasticity of Substitution in Applied General Equilibrium
 Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Γνωστές κατανομές συνεχών μεταβλητών (συν.) (Δ). Γάμμα κατανομή
 Γνωστές κατανομές συνεχών μεταβλητών (συν.) (Δ). Γάμμα κατανομή Συνάρτηση Γάμμα: Ιδιότητες o d Γ(α+)=αΓ(α) - αναδρομική συνάρτηση Γ(α+) = α! αν α ακέραιος. Πιθανότητες & Στατιστική 5 Τμήμα Μηχανικών Η/Υ
Γνωστές κατανομές συνεχών μεταβλητών (συν.) (Δ). Γάμμα κατανομή Συνάρτηση Γάμμα: Ιδιότητες o d Γ(α+)=αΓ(α) - αναδρομική συνάρτηση Γ(α+) = α! αν α ακέραιος. Πιθανότητες & Στατιστική 5 Τμήμα Μηχανικών Η/Υ
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
HMY 795: Αναγνώριση Προτύπων. Διάλεξη 2
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 2 Επισκόπηση θεωρίας πιθανοτήτων Θεωρία πιθανοτήτων Τυχαία μεταβλητή: Μεταβλητή της οποίας δε γνωρίζουμε με βεβαιότητα την τιμή (αντίθετα με τις ντετερμινιστικές μεταβλητές)
HMY 795: Αναγνώριση Προτύπων Διάλεξη 2 Επισκόπηση θεωρίας πιθανοτήτων Θεωρία πιθανοτήτων Τυχαία μεταβλητή: Μεταβλητή της οποίας δε γνωρίζουμε με βεβαιότητα την τιμή (αντίθετα με τις ντετερμινιστικές μεταβλητές)
Διάστημα εμπιστοσύνης της μέσης τιμής
 Διάστημα εμπιστοσύνης της μέσης τιμής Συντελεστής εμπιστοσύνης Όταν : x z c s < μ < x +z s c Ν>30 Στον πίνακα δίνονται κρίσιμες τιμές z c και η αντιστοίχισή τους σε διάφορους συντελεστές εμπιστοσύνης:
Διάστημα εμπιστοσύνης της μέσης τιμής Συντελεστής εμπιστοσύνης Όταν : x z c s < μ < x +z s c Ν>30 Στον πίνακα δίνονται κρίσιμες τιμές z c και η αντιστοίχισή τους σε διάφορους συντελεστές εμπιστοσύνης:
Στατιστική Συμπερασματολογία
 Στατιστική Συμπερασματολογία Διαφάνειες 1 ου κεφαλαίου Βιβλίο: Κολυβά Μαχαίρα, Φ. & Χατζόπουλος Στ. Α. (2016). Μαθηματική Στατιστική, Έλεγχοι Υποθέσεων. [ηλεκτρ. βιβλ.] Αθήνα: Σύνδεσμος Ελληνικών Ακαδημαϊκών
Στατιστική Συμπερασματολογία Διαφάνειες 1 ου κεφαλαίου Βιβλίο: Κολυβά Μαχαίρα, Φ. & Χατζόπουλος Στ. Α. (2016). Μαθηματική Στατιστική, Έλεγχοι Υποθέσεων. [ηλεκτρ. βιβλ.] Αθήνα: Σύνδεσμος Ελληνικών Ακαδημαϊκών
ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ
 ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙ ΡΑΣΗ Μ.Β ΣΤΙΣ Ι ΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ ( ΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙ ΡΑΣΗ Μ.Β ΣΤΙΣ Ι ΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ ( ΙΑΦΟΡΙΚΗ) Probablty Densty Functon
3 ο Μέρος Χαρακτηριστικά τυχαίων μεταβλητών
 3 ο Μέρος Χαρακτηριστικά τυχαίων μεταβλητών Βασικά χαρακτηριστικά τυχαίας μεταβλητής: Μέση Τιμή (Me Vlue) Διακύμανση (Vrice) Γενικά χαρακτηριστικά: Ροπές μεταβλητών / Ροπογεννήτριες Χαρακτηριστικές συναρτήσεις
3 ο Μέρος Χαρακτηριστικά τυχαίων μεταβλητών Βασικά χαρακτηριστικά τυχαίας μεταβλητής: Μέση Τιμή (Me Vlue) Διακύμανση (Vrice) Γενικά χαρακτηριστικά: Ροπές μεταβλητών / Ροπογεννήτριες Χαρακτηριστικές συναρτήσεις
Symplecticity of the Störmer-Verlet algorithm for coupling between the shallow water equations and horizontal vehicle motion
 Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Πολλαπλή παλινδρόμηση (Multivariate regression)
 ΜΑΘΗΜΑ 3 ο 1 Πολλαπλή παλινδρόμηση (Multivariate regression) Η συμπεριφορά των περισσότερων οικονομικών μεταβλητών είναι συνάρτηση όχι μιας αλλά πολλών μεταβλητών Υ = f ( X 1, X 2,... X n ) δηλαδή η Υ
ΜΑΘΗΜΑ 3 ο 1 Πολλαπλή παλινδρόμηση (Multivariate regression) Η συμπεριφορά των περισσότερων οικονομικών μεταβλητών είναι συνάρτηση όχι μιας αλλά πολλών μεταβλητών Υ = f ( X 1, X 2,... X n ) δηλαδή η Υ
27-Ιαν-2009 ΗΜΥ 429. 2. (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό
 ΗΜΥ 429 2. (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 1 (i) Βασική στατιστική 2 Στατιστική Vs Πιθανότητες Στατιστική: επιτρέπει μέτρηση και αναγνώριση θορύβου και
ΗΜΥ 429 2. (ι) Βασική στατιστική (ιι) Μετατροπές: αναλογικό-σεψηφιακό και ψηφιακό-σε-αναλογικό 1 (i) Βασική στατιστική 2 Στατιστική Vs Πιθανότητες Στατιστική: επιτρέπει μέτρηση και αναγνώριση θορύβου και
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Q- ΔΙΑΓΡΑΜΜΑΤΑ ΓΙΑ ΤΗΝ ΠΑΡΑΜΕΤΡΟ p ΤΗΣ ΔΙΩΝΥΜΙΚΗΣ ΚΑΤΑΝΟΜΗΣ
 Ελληνικό Στατιστικό Ινστιτούτο Πρακτικά 20 ου Πανελληνίου Συνεδρίου Στατιστικής (2007), σελ 249-258 Q- ΔΙΑΓΡΑΜΜΑΤΑ ΓΙΑ ΤΗΝ ΠΑΡΑΜΕΤΡΟ p ΤΗΣ ΔΙΩΝΥΜΙΚΗΣ ΚΑΤΑΝΟΜΗΣ Μανώλης Μανατάκης Τμήμα Μηχανολόγων και Αεροναυπηγών
Ελληνικό Στατιστικό Ινστιτούτο Πρακτικά 20 ου Πανελληνίου Συνεδρίου Στατιστικής (2007), σελ 249-258 Q- ΔΙΑΓΡΑΜΜΑΤΑ ΓΙΑ ΤΗΝ ΠΑΡΑΜΕΤΡΟ p ΤΗΣ ΔΙΩΝΥΜΙΚΗΣ ΚΑΤΑΝΟΜΗΣ Μανώλης Μανατάκης Τμήμα Μηχανολόγων και Αεροναυπηγών
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ: ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 13
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ: ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 20 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 20 2.1.1 Αβεβαιότητα
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ: ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 20 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 20 2.1.1 Αβεβαιότητα
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Εκτιμητές Μεγίστης Πιθανοφάνειας (Maximum Likelihood Estimators MLE)
 Εκτιμητές Μεγίστης Πιθανοφάνειας (Maximum Likelihood Estimators MLE) Εστω τ.δ. X={x, x,, x } με κατανομή με σ.π.π. f(x;θ). Η από-κοινού σ.π.π. των δειγμάτων είναι η συνάρτηση L f x, x,, x; f x i ; και
Εκτιμητές Μεγίστης Πιθανοφάνειας (Maximum Likelihood Estimators MLE) Εστω τ.δ. X={x, x,, x } με κατανομή με σ.π.π. f(x;θ). Η από-κοινού σ.π.π. των δειγμάτων είναι η συνάρτηση L f x, x,, x; f x i ; και
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας. Version 2
 Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson 2 1 ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥ ΧΩΡΟΥ ΤΩΝ ΤΑΞΙΝΟΜΗΤΩΝ Ταξινομητές Ταξινομητές συναρτ. διάκρισης Ταξινομητές επιφανειών απόφ. Παραμετρικοί ταξινομητές Μη παραμετρικοί
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson 2 1 ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥ ΧΩΡΟΥ ΤΩΝ ΤΑΞΙΝΟΜΗΤΩΝ Ταξινομητές Ταξινομητές συναρτ. διάκρισης Ταξινομητές επιφανειών απόφ. Παραμετρικοί ταξινομητές Μη παραμετρικοί
Χρονοσειρές - Μάθημα 9 Aνάλυση χρονοσειρών και δυναμικά συστήματα
 Χρονοσειρές - Μάθημα 9 Aνάλυση χρονοσειρών και δυναμικά συστήματα - Ανακατασκευή του χώρου καταστάσεων παρατήρηση της πολυπλοκότητας / στοχαστικότητας / δομής του συστήματος - Εκτίμηση χαρακτηριστικών
Χρονοσειρές - Μάθημα 9 Aνάλυση χρονοσειρών και δυναμικά συστήματα - Ανακατασκευή του χώρου καταστάσεων παρατήρηση της πολυπλοκότητας / στοχαστικότητας / δομής του συστήματος - Εκτίμηση χαρακτηριστικών
Συνεχείς Τυχαίες Μεταβλητές
 Συνεχείς Τυχαίες Μεταβλητές Η σ.κ.π. F() είναι παντού συνεχής F PX t dt H σ.π.π. df d Ισχύει ότι d F Πιθανότητες & Στατιστική 07 Τμήμα Μηχανικών Η/Υ & Πληροφορικής, Παν. Ιωαννίνων Δ0 () Πιθανότητες & Στατιστική
Συνεχείς Τυχαίες Μεταβλητές Η σ.κ.π. F() είναι παντού συνεχής F PX t dt H σ.π.π. df d Ισχύει ότι d F Πιθανότητες & Στατιστική 07 Τμήμα Μηχανικών Η/Υ & Πληροφορικής, Παν. Ιωαννίνων Δ0 () Πιθανότητες & Στατιστική
ΕΝΤΥΠΟ ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ
 F3W.PR09 Όνομα: Επίθετο: Ημερομηνία: 7/0/07 Πρωί: Απόγευμα: Θεματική ενότητα: Αναλογιστικά Πρότυπα Επιβίωσης Ερώτηση Εάν η τυχαία μεταβλητή Τ έχει συνάρτηση πυκνότητας f ep 3 3 να υπολογίσετε το 90 ο εκατοστημόριο
F3W.PR09 Όνομα: Επίθετο: Ημερομηνία: 7/0/07 Πρωί: Απόγευμα: Θεματική ενότητα: Αναλογιστικά Πρότυπα Επιβίωσης Ερώτηση Εάν η τυχαία μεταβλητή Τ έχει συνάρτηση πυκνότητας f ep 3 3 να υπολογίσετε το 90 ο εκατοστημόριο
ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ: ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ. Διπλωματική Εργασία
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ: ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ Διπλωματική Εργασία του Φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ: ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ Διπλωματική Εργασία του Φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας. Version 2
 Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΜΗ ΓΡΑΜΜΙΚΟΙ ΤΑΞΙΝΟΜΗΤΕΣ ΝΕΥΡΩΝΙΚΑ ΔΙΚΤΥΑ Η παραπάνω ανάλυση ήταν χρήσιμη προκειμένου να κατανοήσουμε τη λογική των δικτύων perceptrons πολλών επιπέδων
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΜΗ ΓΡΑΜΜΙΚΟΙ ΤΑΞΙΝΟΜΗΤΕΣ ΝΕΥΡΩΝΙΚΑ ΔΙΚΤΥΑ Η παραπάνω ανάλυση ήταν χρήσιμη προκειμένου να κατανοήσουμε τη λογική των δικτύων perceptrons πολλών επιπέδων
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας. Version 2
 Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson 2 1 C MH ΠΑΡΑΜΕΤΡΙΚΟΙ ΤΑΞΙΝΟΜΗΤΕΣ ΒΑΣΙΣΜΕΝΟΙ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΑΠΟΦΑΣΗΣ Υπενθύμιση: είναι το σύνολο δεδομένων που περιέχει τα διαθέσιμα δεδομένα από όλες
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson 2 1 C MH ΠΑΡΑΜΕΤΡΙΚΟΙ ΤΑΞΙΝΟΜΗΤΕΣ ΒΑΣΙΣΜΕΝΟΙ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΑΠΟΦΑΣΗΣ Υπενθύμιση: είναι το σύνολο δεδομένων που περιέχει τα διαθέσιμα δεδομένα από όλες
Πιθανότητες & Τυχαία Σήματα. Διγαλάκης Βασίλης
 Πιθανότητες & Τυχαία Σήματα Διγαλάκης Βασίλης Τυχαία Σήματα Γενίκευση τυχαίων διανυσμάτων Άπειρο σύνολο πιθανά αριθμήσιμο από τυχαίες μεταβλητές Παραδείγματα τυχαίων σημάτων: Τηλεπικοινωνίες: Σήμα πληροφορίας
Πιθανότητες & Τυχαία Σήματα Διγαλάκης Βασίλης Τυχαία Σήματα Γενίκευση τυχαίων διανυσμάτων Άπειρο σύνολο πιθανά αριθμήσιμο από τυχαίες μεταβλητές Παραδείγματα τυχαίων σημάτων: Τηλεπικοινωνίες: Σήμα πληροφορίας
Άσκηση 1: Λύση: Για το άθροισμα ισχύει: κι επειδή οι μέσες τιμές των Χ και Υ είναι 0: Έτσι η διασπορά της Ζ=Χ+Υ είναι:
 Άσκηση 1: Δύο τυχαίες μεταβλητές Χ και Υ έχουν στατιστικές μέσες τιμές 0 και διασπορές 25 και 36 αντίστοιχα. Ο συντελεστής συσχέτισης των 2 τυχαίων μεταβλητών είναι 0.4. Να υπολογισθούν η διασπορά του
Άσκηση 1: Δύο τυχαίες μεταβλητές Χ και Υ έχουν στατιστικές μέσες τιμές 0 και διασπορές 25 και 36 αντίστοιχα. Ο συντελεστής συσχέτισης των 2 τυχαίων μεταβλητών είναι 0.4. Να υπολογισθούν η διασπορά του
ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ ΔΙΔΑΚΤΟΡΙΚΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ ΔΙΔΑΚΤΟΡΙΚΗ
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
CRAMER-RAO ΚΑΤΩ ΦΡΑΓΜΑ - ΑΠΟ ΟΤΙΚΟΙ ΕΚΤΙΜΗΤΕΣ
 CRAMER-RAO ΚΑΤΩ ΦΡΑΓΜΑ - ΑΠΟ ΟΤΙΚΟΙ ΕΚΤΙΜΗΤΕΣ Τµήµα Μαθηµατικών, Πανεπιστήµιο Πατρών Θεώρηµα Cramer-Rao Θεώρηµα Cramer-Rao Εστω X = (X 1, X,...,X n ) ένα δείγµα µε από κοινού πυκνότητα πιθανότητας f X
CRAMER-RAO ΚΑΤΩ ΦΡΑΓΜΑ - ΑΠΟ ΟΤΙΚΟΙ ΕΚΤΙΜΗΤΕΣ Τµήµα Μαθηµατικών, Πανεπιστήµιο Πατρών Θεώρηµα Cramer-Rao Θεώρηµα Cramer-Rao Εστω X = (X 1, X,...,X n ) ένα δείγµα µε από κοινού πυκνότητα πιθανότητας f X
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ 3 ΔΕΣΜΕΥΜΕΝΗ ΠΙΘΑΝΟΤΗΤΑ, ΟΛΙΚΗ ΠΙΘΑΝΟΤΗΤΑ ΘΕΩΡΗΜΑ BAYES, ΑΝΕΞΑΡΤΗΣΙΑ ΚΑΙ ΣΥΝΑΦΕΙΣ ΕΝΝΟΙΕΣ 71
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 11 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 13 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 5 Κατανομές πιθανότητας και εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές Bayesian decision Minimum misclassificaxon rate decision: διαλέγουμε την κατηγορία Ck για
HMY 795: Αναγνώριση Προτύπων Διάλεξη 5 Κατανομές πιθανότητας και εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές Bayesian decision Minimum misclassificaxon rate decision: διαλέγουμε την κατηγορία Ck για
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
Έλεγχος και Διασφάλιση Ποιότητας
 Έλεγχος και Διασφάλιση Ποιότητας Ενότητα 6: Κουππάρης Μιχαήλ Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας General Successfully carry out the Preventive Maintenance Procedure and complete the Maintenance
Έλεγχος και Διασφάλιση Ποιότητας Ενότητα 6: Κουππάρης Μιχαήλ Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας General Successfully carry out the Preventive Maintenance Procedure and complete the Maintenance
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας. Version 2
 Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥ ΧΩΡΟΥ ΤΩΝ ΤΑΞΙΝΟΜΗΤΩΝ Ταξινομητές Ταξινομητές συναρτ. διάκρισης Ταξινομητές επιφανειών απόφ. Παραμετρικοί ταξινομητές Μη παραμετρικοί
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥ ΧΩΡΟΥ ΤΩΝ ΤΑΞΙΝΟΜΗΤΩΝ Ταξινομητές Ταξινομητές συναρτ. διάκρισης Ταξινομητές επιφανειών απόφ. Παραμετρικοί ταξινομητές Μη παραμετρικοί
Stochastic Signals Class Estimation Theory. Andreas Polydoros University of Athens Dept. of Physics Electronics Laboratory
 Stochastic Signals Class Estimation Theory Andreas Polydoros University of Athens Dept. of Physics Electronics Laboratory 1 Τι ειναι «Εκτιμηση» (Estimation)? Γενικο Πλαισιο: Θεωρια και Πραξη Συμπερασματων
Stochastic Signals Class Estimation Theory Andreas Polydoros University of Athens Dept. of Physics Electronics Laboratory 1 Τι ειναι «Εκτιμηση» (Estimation)? Γενικο Πλαισιο: Θεωρια και Πραξη Συμπερασματων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 07-08 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 07-08 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegea.gr Τηλ: 7035468 Θα μελετήσουμε
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Διάλεξη 1: Στατιστική Συμπερασματολογία - Εκτίμηση Σημείου
 Διάλεξη 1: Στατιστική Συμπερασματολογία - Εκτίμηση Σημείου Στατιστική Συμπερασματολογία Εκτιμητική Έλεγχος Στατιστικών Υποθέσεων εκτιμήτρια συνάρτηση, ˆ θ σημειακή εκτίμηση εκτίμηση με διάστημα εμπιστοσύνης
Διάλεξη 1: Στατιστική Συμπερασματολογία - Εκτίμηση Σημείου Στατιστική Συμπερασματολογία Εκτιμητική Έλεγχος Στατιστικών Υποθέσεων εκτιμήτρια συνάρτηση, ˆ θ σημειακή εκτίμηση εκτίμηση με διάστημα εμπιστοσύνης
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 6 Κατανομές πιθανότητας και εκτίμηση παραμέτρων Κατανομές πιθανότητας και εκτίμηση παραμέτρων κανονικές τυχαίες μεταβλητές Εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές
HMY 795: Αναγνώριση Προτύπων Διάλεξη 6 Κατανομές πιθανότητας και εκτίμηση παραμέτρων Κατανομές πιθανότητας και εκτίμηση παραμέτρων κανονικές τυχαίες μεταβλητές Εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές
The following are appendices A, B1 and B2 of our paper, Integrated Process Modeling
 he followng ae appendes A, B1 and B2 of ou pape, Integated Poess Modelng and Podut Desgn of Bodesel Manufatung, that appeas n the Industal and Engneeng Chemsty Reseah, Deembe (2009). Appendx A. An Illustaton
he followng ae appendes A, B1 and B2 of ou pape, Integated Poess Modelng and Podut Desgn of Bodesel Manufatung, that appeas n the Industal and Engneeng Chemsty Reseah, Deembe (2009). Appendx A. An Illustaton
Στατιστική. Εκτιμητική
 Στατιστική Εκτιμητική Χατζόπουλος Σταύρος 28/2/2018 και 01 /03/2018 Εισαγωγή Το αντικείμενο της Στατιστικής είναι η εξαγωγή συμπερασμάτων που αφορούν τον πληθυσμό ή το φαινόμενο που μελετάμε, με τη βοήθεια
Στατιστική Εκτιμητική Χατζόπουλος Σταύρος 28/2/2018 και 01 /03/2018 Εισαγωγή Το αντικείμενο της Στατιστικής είναι η εξαγωγή συμπερασμάτων που αφορούν τον πληθυσμό ή το φαινόμενο που μελετάμε, με τη βοήθεια
Ορίζουμε την τυπική πολυδιάστατη κανονική, σαν την κατανομή του τυχαίου (,, T ( ) μεταξύ τους ανεξάρτητα. Τότε
 Η πολυδιάστατη κανονική κατανομή Ορίζουμε την τυπική πολυδιάστατη κανονική, σαν την κατανομή του τυχαίου (,, διανύσματος X X X ), όπου X ~ N (,) και όλα τα X μεταξύ τους ανεξάρτητα Τότε ( ) (,, ) (, )
Η πολυδιάστατη κανονική κατανομή Ορίζουμε την τυπική πολυδιάστατη κανονική, σαν την κατανομή του τυχαίου (,, διανύσματος X X X ), όπου X ~ N (,) και όλα τα X μεταξύ τους ανεξάρτητα Τότε ( ) (,, ) (, )
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
HMY 795: Αναγνώριση Προτύπων
 HMY 795: Αναγνώριση Προτύπων Διάλεξη 5 Κατανομές πιθανότητας και εκτίμηση παραμέτρων Κατανομές πιθανότητας και εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές Διαχωριστικές συναρτήσεις Ταξινόμηση κανονικών
HMY 795: Αναγνώριση Προτύπων Διάλεξη 5 Κατανομές πιθανότητας και εκτίμηση παραμέτρων Κατανομές πιθανότητας και εκτίμηση παραμέτρων δυαδικές τυχαίες μεταβλητές Διαχωριστικές συναρτήσεις Ταξινόμηση κανονικών
Βέλτιστη παρεμβολή και πρόγνωση άγνωστης συνάρτησης με τη μέθοδο της σημειακής προσαρμογής
 Ειδικά Θέματα Συνορθώσεων & Εφαρμογές 8 ο εξάμηνο, Ακαδημαϊκό έτος 2016-2017 Βέλτιστη παρεμβολή και πρόγνωση άγνωστης συνάρτησης με τη μέθοδο της σημειακής προσαρμογής (Least squares collocation) Χριστόφορος
Ειδικά Θέματα Συνορθώσεων & Εφαρμογές 8 ο εξάμηνο, Ακαδημαϊκό έτος 2016-2017 Βέλτιστη παρεμβολή και πρόγνωση άγνωστης συνάρτησης με τη μέθοδο της σημειακής προσαρμογής (Least squares collocation) Χριστόφορος
Βιοστατιστική ΒΙΟ-309
 Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2015-2016 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2015-2016 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
ΕΠΕΞΕΡΓΑΣΙΑ & ΑΝΑΛΥΣΗ ΙΑΤΡΙΚΩΝ ΣΗΜΑΤΩΝ
 BIOMIG Medical Image Processing, Algorithms and Applications http://biomig.ntua.gr ΕΠΕΞΕΡΓΑΣΙΑ & ΑΝΑΛΥΣΗ ΙΑΤΡΙΚΩΝ ΣΗΜΑΤΩΝ Εισαγωγή στην MRI και στην fmri ΔΡ. Γ. ΜΑΤΣΟΠΟΥΛΟΣ ΑΝ. ΚΑΘΗΓΗΤΗΣ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ
BIOMIG Medical Image Processing, Algorithms and Applications http://biomig.ntua.gr ΕΠΕΞΕΡΓΑΣΙΑ & ΑΝΑΛΥΣΗ ΙΑΤΡΙΚΩΝ ΣΗΜΑΤΩΝ Εισαγωγή στην MRI και στην fmri ΔΡ. Γ. ΜΑΤΣΟΠΟΥΛΟΣ ΑΝ. ΚΑΘΗΓΗΤΗΣ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ
Εφαρμοσμένη Στατιστική: Συντελεστής συσχέτισης. Παλινδρόμηση απλή γραμμική, πολλαπλή γραμμική
 ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΜΕΡΟΣ B Δημήτρης Κουγιουμτζής e-mal: dkugu@auth.gr Ιστοσελίδα αυτού του τμήματος του μαθήματος: http://uer.auth.gr/~dkugu/teach/cvltraport/dex.html Εφαρμοσμένη Στατιστική:
ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΜΕΡΟΣ B Δημήτρης Κουγιουμτζής e-mal: dkugu@auth.gr Ιστοσελίδα αυτού του τμήματος του μαθήματος: http://uer.auth.gr/~dkugu/teach/cvltraport/dex.html Εφαρμοσμένη Στατιστική:
Εφαρμοσμένη Στατιστική Δημήτριος Μπάγκαβος Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπισ τήμιο Κρήτης 13 Μαρτίου /31
 Εφαρμοσμένη Στατιστική Δημήτριος Μπάγκαβος Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπιστήμιο Κρήτης 13 Μαρτίου 2017 1/31 Βασικοί ορισμοί. Ορισμός 1: Τυχαίο δείγμα. Τυχαίο δείγμα μεγέθους n από
Εφαρμοσμένη Στατιστική Δημήτριος Μπάγκαβος Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπιστήμιο Κρήτης 13 Μαρτίου 2017 1/31 Βασικοί ορισμοί. Ορισμός 1: Τυχαίο δείγμα. Τυχαίο δείγμα μεγέθους n από
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής
 ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής Υποθέσεις του Απλού γραμμικού υποδείγματος της Παλινδρόμησης Η μεταβλητή ε t (διαταρακτικός όρος) είναι τυχαία μεταβλητή με μέσο όρο
ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τραπεζικής & Χρηματοοικονομικής Υποθέσεις του Απλού γραμμικού υποδείγματος της Παλινδρόμησης Η μεταβλητή ε t (διαταρακτικός όρος) είναι τυχαία μεταβλητή με μέσο όρο
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών. Χρόνου (Ι)
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Χρόνου (Ι) Στοχαστικά σήματα Στα προηγούμενα: Ντετερμινιστικά
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Διάλεξη 5: Στοχαστικά/Τυχαία Σήματα Διακριτού Χρόνου (Ι) Στοχαστικά σήματα Στα προηγούμενα: Ντετερμινιστικά
Παρεμβολή & πρόγνωση άγνωστης συνάρτησης μέσω σημειακής προσαρμογής
 Ειδικά Θέματα Συνορθώσεων & Εφαρμογές 8 ο εξάμηνο, Ακαδημαϊκό έτος 2018-2019 Παρεμβολή & πρόγνωση άγνωστης συνάρτησης μέσω σημειακής προσαρμογής (Least squares collocation) Χριστόφορος Κωτσάκης Τμήμα Αγρονόμων
Ειδικά Θέματα Συνορθώσεων & Εφαρμογές 8 ο εξάμηνο, Ακαδημαϊκό έτος 2018-2019 Παρεμβολή & πρόγνωση άγνωστης συνάρτησης μέσω σημειακής προσαρμογής (Least squares collocation) Χριστόφορος Κωτσάκης Τμήμα Αγρονόμων
2 Lagrangian and Green functions in d dimensions
 Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ
 Π E Ρ IEXOMENA Πρόλογος... xiii ΜΕΡΟΣ ΠΡΩΤΟ ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΠΑΡΟΥΣΙΑΣΗ ΤΩΝ ΣΤΑΤΙΣΤΙΚΩΝ Ε ΟΜΕΝΩΝ 1.1 Εισαγωγή... 3 1.2 Ορισµός και αντικείµενο της στατιστικής... 3
Π E Ρ IEXOMENA Πρόλογος... xiii ΜΕΡΟΣ ΠΡΩΤΟ ΠΕΡΙΓΡΑΦΙΚΗ ΣΤΑΤΙΣΤΙΚΗ ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΠΑΡΟΥΣΙΑΣΗ ΤΩΝ ΣΤΑΤΙΣΤΙΚΩΝ Ε ΟΜΕΝΩΝ 1.1 Εισαγωγή... 3 1.2 Ορισµός και αντικείµενο της στατιστικής... 3
Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500
 Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500 Πληθυσμός Δείγμα Δείγμα Δείγμα Ο ρόλος της Οικονομετρίας Οικονομική Θεωρία Διατύπωση της
Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500 Πληθυσμός Δείγμα Δείγμα Δείγμα Ο ρόλος της Οικονομετρίας Οικονομική Θεωρία Διατύπωση της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών. HY-217: Πιθανότητες - Χειµερινό Εξάµηνο 2015 ιδάσκων : Π. Τσακαλίδης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-27: Πιθανότητες - Χειµερινό Εξάµηνο 205 ιδάσκων : Π. Τσακαλίδης Φροντιστήριο 8 Επιµέλεια : Κατερίνα Καραγιαννάκη Ασκηση. Η τυχαία µεταβλητή X έχει αθροιστική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-27: Πιθανότητες - Χειµερινό Εξάµηνο 205 ιδάσκων : Π. Τσακαλίδης Φροντιστήριο 8 Επιµέλεια : Κατερίνα Καραγιαννάκη Ασκηση. Η τυχαία µεταβλητή X έχει αθροιστική
Βιοστατιστική ΒΙΟ-309
 Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2017-2018 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
Βιοστατιστική ΒΙΟ-309 Χειμερινό Εξάμηνο Ακαδ. Έτος 2017-2018 Ντίνα Λύκα lika@biology.uoc.gr 1. Εισαγωγή Εισαγωγικές έννοιες Μεταβλητότητα : ύπαρξη διαφορών μεταξύ ομοειδών μετρήσεων Μεταβλητή: ένα χαρακτηριστικό
ΘΕΩΡΗΤΙΚΗ ΚΑΙ ΠΕΙΡΑΜΑΤΙΚΗ ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΙΕΡΓΑΣΙΑΣ ΣΚΛΗΡΥΝΣΗΣ ΙΑ ΛΕΙΑΝΣΕΩΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΑΥΤΟΜΑΤΙΣΜΟΥ / ΥΝΑΜΙΚΗΣ & ΘΕΩΡΙΑΣ ΜΗΧΑΝΩΝ ΙΕΥΘΥΝΤΗΣ: Καθηγητής Γ. ΧΡΥΣΟΛΟΥΡΗΣ Ι ΑΚΤΟΡΙΚΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΑΥΤΟΜΑΤΙΣΜΟΥ / ΥΝΑΜΙΚΗΣ & ΘΕΩΡΙΑΣ ΜΗΧΑΝΩΝ ΙΕΥΘΥΝΤΗΣ: Καθηγητής Γ. ΧΡΥΣΟΛΟΥΡΗΣ Ι ΑΚΤΟΡΙΚΗ
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Πραγματικοί κυματισμοί
 Πραγματικοί κυματισμοί Οι κυματισμοί που δημιουργεί η επίδραση του ανέμου στην επιφάνεια της θάλασσας, δεν είναι «μονοχρωματικοί». Η επιφάνεια της θάλασσας μπορεί να προσεγγιστεί με σύνθεση περισσοτέρων
Πραγματικοί κυματισμοί Οι κυματισμοί που δημιουργεί η επίδραση του ανέμου στην επιφάνεια της θάλασσας, δεν είναι «μονοχρωματικοί». Η επιφάνεια της θάλασσας μπορεί να προσεγγιστεί με σύνθεση περισσοτέρων
Στατιστική Συμπερασματολογία
 Στατιστική Συμπερασματολογία Διαφάνειες 5 ου κεφαλαίου Ελεγχοσυναρτήσεις για τις Παραμέτρους της Κανονικής Κατανομής Σταύρος Χατζόπουλος 08/05/207, 5/05/207 Εισαγωγή Στις παραγράφους που ακολουθούν παρουσιάζονται
Στατιστική Συμπερασματολογία Διαφάνειες 5 ου κεφαλαίου Ελεγχοσυναρτήσεις για τις Παραμέτρους της Κανονικής Κατανομής Σταύρος Χατζόπουλος 08/05/207, 5/05/207 Εισαγωγή Στις παραγράφους που ακολουθούν παρουσιάζονται
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΕΚΤΙΜΙΣΗ ΜΕΓΙΣΤΗΣ ΠΙΘΑΝΟΦΑΝΕΙΑΣ
 3.1 Εισαγωγή ΕΚΤΙΜΙΣΗ ΜΕΓΙΣΤΗΣ ΠΙΘΑΝΟΦΑΝΕΙΑΣ Στο κεφ. 2 είδαμε πώς θα μπορούσαμε να σχεδιάσουμε έναν βέλτιστο ταξινομητή εάν ξέραμε τις προγενέστερες(prior) πιθανότητες ( ) και τις κλάση-υπό όρους πυκνότητες
3.1 Εισαγωγή ΕΚΤΙΜΙΣΗ ΜΕΓΙΣΤΗΣ ΠΙΘΑΝΟΦΑΝΕΙΑΣ Στο κεφ. 2 είδαμε πώς θα μπορούσαμε να σχεδιάσουμε έναν βέλτιστο ταξινομητή εάν ξέραμε τις προγενέστερες(prior) πιθανότητες ( ) και τις κλάση-υπό όρους πυκνότητες
ΟΙΚΟΝΟΜΕΤΡΙΑ. Παπάνα Αγγελική
 ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 13: Επανάληψη Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana 1 Γιατί μελετούμε την Οικονομετρία;
ΟΙΚΟΝΟΜΕΤΡΙΑ Ενότητα 13: Επανάληψη Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ E-mail: angeliki.papana@gmail.com, agpapana@auth.gr Webpage: http://users.auth.gr/agpapana 1 Γιατί μελετούμε την Οικονομετρία;
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Τεχνικές Μείωσης Διαστάσεων. Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας
 Τεχνικές Μείωσης Διαστάσεων Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας 1 Εισαγωγή Το μεγαλύτερο μέρος των δεδομένων που καλούμαστε να επεξεργαστούμε είναι πολυδιάστατα.
Τεχνικές Μείωσης Διαστάσεων Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας 1 Εισαγωγή Το μεγαλύτερο μέρος των δεδομένων που καλούμαστε να επεξεργαστούμε είναι πολυδιάστατα.
Μάθημα 2: Mη-στάσιμη χρονοσειρά, έλεγχος μοναδιαίας ρίζας και έλεγχος ανεξαρτησίας
 close index close index Μάθημα : Mη-στάσιμη χρονοσειρά, έλεγχος μοναδιαίας ρίζας και έλεγχος ανεξαρτησίας Σταθεροποίηση διασποράς Απαλοιφή τάσης και περιοδικότητας / εποχικότητας Έλεγχοι μοναδιαίας ρίζας
close index close index Μάθημα : Mη-στάσιμη χρονοσειρά, έλεγχος μοναδιαίας ρίζας και έλεγχος ανεξαρτησίας Σταθεροποίηση διασποράς Απαλοιφή τάσης και περιοδικότητας / εποχικότητας Έλεγχοι μοναδιαίας ρίζας
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 13 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 15 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 13 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 15 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ΠΡΩΤΟ ΠΙΘΑΝΟΤΗΤΕΣ 13 ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΗ 15 ΚΕΦΑΛΑΙΟ 2 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΙΘΑΝΟΤΗΤΑΣ 19 2.1 Αβεβαιότητα, Τυχαία Διαδικασία, και Συναφείς Έννοιες 21 2.1.1 Αβεβαιότητα και Τυχαίο Πείραμα
Queensland University of Technology Transport Data Analysis and Modeling Methodologies
 Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας. Version 2
 Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥ ΧΩΡΟΥ ΤΩΝ ΤΑΞΙΝΟΜΗΤΩΝ Ταξινομητές Ταξινομητές συναρτ. διάκρισης Ταξινομητές επιφανειών απόφ. Παραμετρικοί ταξινομητές Μη παραμετρικοί
Σέργιος Θεοδωρίδης Κωνσταντίνος Κουτρούμπας Verson ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥ ΧΩΡΟΥ ΤΩΝ ΤΑΞΙΝΟΜΗΤΩΝ Ταξινομητές Ταξινομητές συναρτ. διάκρισης Ταξινομητές επιφανειών απόφ. Παραμετρικοί ταξινομητές Μη παραμετρικοί
ΠΡΟΣΟΧΗ : Νέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι. Για το 1ο εξάμηνο. ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι -ΜΗΧΑΝΙΚΗ
 στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι -ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί Lorentz 3. Δυναμική ενός σωματιδίου (Νόμοι της δυναμικής-ορμή-στροφορμήσυστήματα
στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι -ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί Lorentz 3. Δυναμική ενός σωματιδίου (Νόμοι της δυναμικής-ορμή-στροφορμήσυστήματα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.koutras@fme.aegea.gr Τηλ: 7035468 Εκτίμηση Διαστήματος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΔΙΟΙΚΗΣΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΣΤΑΤΙΣΤΙΚΗ Ακαδ. Έτος 06-07 Διδάσκων: Βασίλης ΚΟΥΤΡΑΣ Λέκτορας v.koutras@fme.aegea.gr Τηλ: 7035468 Εκτίμηση Διαστήματος
ΜΑΘΗΜΑ 3ο. Υποδείγματα μιας εξίσωσης
 ΜΑΘΗΜΑ 3ο Υποδείγματα μιας εξίσωσης Οι βασικές υποθέσεις 1. Ο διαταρακτικός όρος u t είναι μια τυχαία μεταβλητή με μέσο το μηδέν. Eu t = 0 για t = 1,2,3..n 2. Η διακύμανση της τυχαίας μεταβλητής u t είναι
ΜΑΘΗΜΑ 3ο Υποδείγματα μιας εξίσωσης Οι βασικές υποθέσεις 1. Ο διαταρακτικός όρος u t είναι μια τυχαία μεταβλητή με μέσο το μηδέν. Eu t = 0 για t = 1,2,3..n 2. Η διακύμανση της τυχαίας μεταβλητής u t είναι
ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΣΤΑΤΙΣΤΙΚΗ Ι ΜΕΡΟΣ Α (Σ. ΧΑΤΖΗΣΠΥΡΟΣ) . Δείξτε ότι η στατιστική συνάρτηση T = X( n)
 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΣΤΑΤΙΣΤΙΚΗ Ι ΜΕΡΟΣ Α (Σ. ΧΑΤΖΗΣΠΥΡΟΣ) Θέμα ο (Παρ..3.4, Παρ..4.3, Παρ..4.8.) Εάν = ( ) τυχαίο δείγμα από την ομοιόμορφη ( 0, ) X X,, X. Δείξτε ότι η στατιστική συνάρτηση T = X = το δειγματικό
ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΣΤΑΤΙΣΤΙΚΗ Ι ΜΕΡΟΣ Α (Σ. ΧΑΤΖΗΣΠΥΡΟΣ) Θέμα ο (Παρ..3.4, Παρ..4.3, Παρ..4.8.) Εάν = ( ) τυχαίο δείγμα από την ομοιόμορφη ( 0, ) X X,, X. Δείξτε ότι η στατιστική συνάρτηση T = X = το δειγματικό
