ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ.
|
|
|
- Ευτροπια Δοξαράς
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014 ΕΡΩΤΗΣΗ 1 Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. ΕΡΩΤΗΣΗ 2 Οριζόντιος ομογενής δίσκος μάζας και ακτίνας περιστρέφεται γύρω από ακλόνητο κατακόρυφο άξονα που διέρχεται από το κέντρο του και είναι κάθετος σε αυτόν. Πάνω στο δίσκο είναι στερεωμένο ένα υλικό σημείο μάζας σε απόσταση από τον άξονα περιστροφής. Αν το υλικό σημείο μεταφερθεί και τοποθετηθεί στο άκρο του δίσκου, η ροπή αδράνειας του συστήματος ως προς τον άξονα περιστροφής : α) μειώνεται. β) μένει η ίδια. γ) αυξάνεται. ΕΡΩΤΗΣΗ 3 Στο παρακάτω σχήμα φαίνεται μια οριζόντια λεπτή ράβδος, που αποτελείται από δύο τμήματα, ίσου μήκους, κολλημένα στο μέσο Μ της ράβδου. Το αριστερό είναι ξύλινο ενώ το δεξιό σιδερένιο. Η ράβδος μπορεί να στρέφεται γύρω από κατακόρυφο άξονα, που διέρχεται είτε από το άκρο Α είτε από το Β. Για να θέσουμε πιο εύκολα σε περιστροφή τη ράβδο πρέπει να την στρέψουμε, γύρω από τον άξονα, που διέρχεται από το: α) Α. β) Β. 1
2 ΕΡΩΤΗΣΗ 4 Ένας οριζόντιος δίσκος, στρέφεται με γωνιακή ταχύτητα μέτρου γύρω από σταθερό άξονα, που διέρχεται από το κέντρο του και είναι κάθετος σ' αυτόν. Στο δίσκο ασκείται ροπή δύναμης μέτρου, οπότε η γωνιακή ταχύτητα περιστροφής του μεταβάλλεται με το χρόνο όπως φαίνεται στο διάγραμμα του σχήματος. Η σωστή γραφική παράσταση της ροπής σε συνάρτηση με το χρόνο είναι το: Να επιλέξτε το σωστό διάγραμμα και να αιτιολογήσετε την επιλογή σας ΕΡΩΤΗΣΗ 5 Ένας ομογενής τροχός, με μικρό αριθμό ακτίνων και ένας ομογενής δίσκος, ίδιας ακτίνας R, μπορούν να περιστρέφονται χωρίς τριβές γύρω από κατακόρυφο, ακλόνητο άξονα που διέρχεται από το κέντρο μάζας τους και είναι κάθετος στο επίπεδο του καθενός. Η ροπή αδράνειας του τροχού ως προς τον άξονα περιστροφής του είναι μεγαλύτερη της ροπής αδράνειας του δίσκου ως προς το δικό του άξονα περιστροφής. Αρχικά τα δύο σώματα είναι ακίνητα και τη χρονική στιγμή αρχίζουμε να ασκούμε ταυτόχρονα στην περιφέρεια κάθε σώματος ίδια οριζόντια, εφαπτομενική, σταθερή κατά μέτρο δύναμη. Θεωρήστε αμελητέες οποιεσδήποτε άλλες επιδράσεις ροπών. Για το μέτρο της γωνιακής επιτάχυνσης του τροχού ( ) και το μέτρο της γωνιακής επιτάχυνσης του δίσκου ( ) ισχύει η σχέση: α). β). γ). ΕΡΩΤΗΣΗ 6 Ένας ομογενής δίσκος μάζας και ακτίνας κυλίεται χωρίς να ολισθαίνει σε οριζόντιο δάπεδο με τη βοήθεια οριζόντιας σταθερής δύναμης η οποία ασκείται στο κέντρο μάζας του. Ο δίσκος 2
3 κινείται επιταχυνόμενος ομαλά προς τα δεξιά. Η φορά της στατικής τριβής, που δέχεται, από το οριζόντιο δάπεδο, έχει φορά: α) ίδια με την. β) αντίθετη από την. ΕΡΩΤΗΣΗ 7 Ένας ομογενής οριζόντιος δίσκος, μάζας και ακτίνας, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα, ο οποίος διέρχεται από το κέντρο του δίσκου. Ένα μικρό σώμα, μάζας, τοποθετείται πολύ κοντά στο κέντρο και αρχίζει να ολισθαίνει αργά προς την περιφέρεια του δίσκου. Κατά τη διάρκεια της κίνησης του μικρού σώματος προς την περιφέρεια, η ροπή αδράνειας του συστήματος δίσκος μικρό σώμα: α) μειώνεται. β) μένει σταθερή. γ) αυξάνεται. ΕΡΩΤΗΣΗ 8 Ένας ομογενής ξύλινος δίσκος (1) και ένας ομογενής μεταλλικός δακτύλιος (2) έχουν την ίδια μάζα και την ίδια ακτίνα. Αν και είναι αντίστοιχα η ροπή αδράνειας του δίσκου και του δακτυλίου ως προς άξονα κάθετο στο επίπεδό τους, που διέρχεται από το κέντρο μάζας τους, τότε ισχύει η σχέση: α). β). γ). ΕΡΩΤΗΣΗ 9 Μία ομογενής ξύλινη ράβδος (1) και μια ομογενής μεταλλική ράβδος (2) έχουν ίδιες διαστάσεις και μπορούν να περιστρέφονται γύρω από κατακόρυφο άξονα, που διέρχεται από το μέσον τους και είναι κάθετος σ αυτές. Δίνεται ότι η ροπή αδράνειας μιας ομογενούς ράβδου ως προς άξονα κάθετο σ αυτήν που διέρχεται από το κέντρο μάζας της είναι:.αρχίζουμε να τις περιστρέφουμε ασκώντας οριζόντια δύναμη σταθερού μέτρου και αντίστοιχα στο άκρο τους και κάθετα στη ράβδο. Παρατηρούμε ότι οι δύο ράβδοι αποκτούν την ίδια γωνιακή επιτάχυνση. Για τα μέτρα των δύο δυνάμεων ισχύει ότι: α). β). γ). ΕΡΩΤΗΣΗ 10 Δύο οριζόντιοι τροχοί Α και Β, με ακτίνες αμελητέας μάζας, έχουν την ίδια μάζα και όλη η μάζα τους είναι ομοιόμορφα κατανεμημένη στην περιφέρειά τους. Ο τροχός Α έχει τη διπλάσια ακτίνα απ τον τροχό Β. Οι δύο τροχοί μπορούν να περιστρέφονται γύρω από κατακόρυφο άξονα, που διέρχεται από το κέντρο μάζας τους. Δίνεται η ροπή αδράνειας ενός τροχού ως προς άξονα, που 3
4 διέρχεται από το κέντρο μάζας του:. Ασκούμε εφαπτομενικά στην περιφέρεια κάθε τροχού δύναμη ίδιου μέτρου. Για τα μέτρα των γωνιακών επιταχύνσεων που θα αποκτήσουν οι δύο τροχοί, ισχύει ότι: α).β).γ). ΕΡΩΤΗΣΗ 11 Δύο ομογενείς κύλινδροι (1) και (2), ίδιας μάζας και ίδιας ακτίνας, αφήνονται από την κορυφή ενός κεκλιμένου επιπέδου και κατεβαίνουν κυλιόμενοι χωρίς ολίσθηση, δεχόμενοι την ίδια επιταχύνουσα ροπή. Ο ένας εκ των δύο κυλίνδρων είναι συμπαγής και ο άλλος κούφιος.η γραφική παράσταση του μέτρου της γωνιακής τους ταχύτητας σε συνάρτηση με το χρόνο, φαίνεται στο παρακάτω σχήμα. Ο κούφιος κύλινδρος είναι ο: α) (1). β) (2). ΕΡΩΤΗΣΗ 12 Ένας κατακόρυφος ομογενής κύλινδρος, στρέφεται αριστερόστροφα με γωνιακή ταχύτητα μέτρου γύρω από σταθερό άξονα, που διέρχεται από τον άξονά του. Στον κύλινδρο ασκείται κατάλληλη ροπή δύναμης μέτρου, οπότε η γωνιακή ταχύτητα περιστροφής του μεταβάλλεται με το χρόνο όπως φαίνεται στο διάγραμμα του σχήματος. Η σωστή γραφική παράσταση της ροπής είναι το: σε συνάρτηση με το χρόνο t Να επιλέξτε το σωστό διάγραμμα και να αιτιολογήσετε την επιλογή σας. ΑΣΚΗΣΗ 1 Ένας ομογενής και ισοπαχής δίσκος μάζας και ακτίνας μπορεί να περιστρέφεται γύρω από σταθερό άξονα, ο οποίος είναι κάθετος στο επίπεδό του και περνά από ένα σημείο Α της περιφέρειάς του. Στο αντιδιαμετρικό σημείο Β ασκείται μια δύναμη σταθερού μέτρου, η οποία είναι συνεχώς εφαπτόμενη στο 4
5 δίσκο και η διεύθυνσή της είναι επάνω στο επίπεδο που ορίζει ο δίσκος. α) Να βρείτε το μέτρο της ροπής που προκαλεί η δύναμη και να σχεδιάσετε το διάνυσμά της. β) Να υπολογίσετε τη ροπή αδράνειας του δίσκου ως προς τον άξονα περιστροφής. γ) Να υπολογίσετε το μέτρο της γωνιακής επιτάχυνσης με την οποία στρέφεται ο δίσκος και να σχεδιάσετε το διάνυσμά της. Δίνεται ότι η ροπή αδράνειας ομογενούς δίσκου ως προς άξονα που περνά από το κέντρο του και είναι κάθετος στο επίπεδό του, είναι. ΑΣΚΗΣΗ 2 Ένας οριζόντιος ομογενής δίσκος μάζας και ακτίνας περιστρέφεται αριστερόστροφα (δηλαδή με φορά αντίθετη των δεικτών του ρολογιού) χωρίς τριβές με γωνιακή συχνότητα Από τη χρονική στιγμή, γύρω από κατακόρυφο άξονα που διέρχεται από το κέντρο του. και μετά ο δίσκος δέχεται εφαπτομενικά στην περιφέρειά του δύο σταθερές κατά μέτρο δυνάμεις αριστερόστροφα και δεξιόστροφα, που τα μέτρα τους ικανοποιούν τη σχέση και οι οποίες προσδίδουν στο δίσκο γωνιακή επιτάχυνση μέτρου. Δίνεται η ροπή αδράνειας του δίσκου ως προς τον άξονα περιστροφής του. Να υπολογίσετε: α) τα μέτρα των δύο δυνάμεων. β) το μέτρο της γωνιακής ταχύτητας τη χρονική στιγμή. Τη χρονική στιγμή καταργούμε ακαριαία τη δύναμη, οπότε ο δίσκος σταματά τη χρονική στιγμή. γ) Να υπολογίσετε τη νέα γωνιακή επιτάχυνση. δ) Να σχεδιάστε τη γραφική παράσταση γωνιακής ταχύτητας χρόνου σε βαθμολογημένους άξονες, από τη χρονική στιγμή έως τη χρονική στιγμή. 5
6 ΑΣΚΗΣΗ 3 Μια ομογενής ράβδος ΑΒ, μάζας και μήκους, μπορεί να στρέφεται σε κατακόρυφο επίπεδο γύρω από έναν οριζόντιο άξονα που διέρχεται από το άκρο της Α. α) Να υπολογίσετε τη ροπή αδράνειάς της ως προς άξονα κάθετο στη ράβδο, που διέρχεται από το άκρο Α. Από την οριζόντια θέση αφήνουμε ελεύθερη τη ράβδο, να περιστραφεί γύρω απ το άκρο Α.β) Να υπολογίσετε τη γωνιακή επιτάχυνσή της τη στιγμή που την αφήνουμε ελεύθερη. γ) Να υπολογίσετε τη γωνιακή επιτάχυνσή της στη θέση όπου αυτή έχει στραφεί κατά γωνία φ, τέτοια ώστε. δ) Να υπολογίσετε το ρυθμό μεταβολής του μέτρου της γραμμικής ταχύτητας του σημείου Κ, που είναι το κέντρο μάζας cm της ράβδου, στη θέση όπου αυτή έχει στραφεί κατά γωνία φ, τέτοια ώστε. Δίνονται η ροπή αδράνειας της ράβδου ως προς άξονα κάθετο στην ράβδο που διέρχεται από το κέντρο μάζας της και η επιτάχυνση της βαρύτητας. ΑΣΚΗΣΗ 4 Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο άξονα που διέρχεται από το κέντρο του. Ο δίσκος είναι αρχικά ακίνητος και τη χρονική στιγμή αριστερόστροφη δύναμη μέτρου δέχεται εφαπτομενικά στην περιφέρειά του και η οποία του προσδίδει γωνιακή επιτάχυνση μέτρου. Α. Να υπολογίσετε: α) Τη ροπή αδράνειας του δίσκου ως προς τον άξονα περιστροφής του. β) Τη μάζα του δίσκου. γ) Το μέτρο της γωνιακής ταχύτητας του δίσκου τη χρονική στιγμή. Β. Τη χρονική στιγμή καταργούμε ακαριαία τη δύναμη. δ) Να υπολογίσετε τον αριθμό των περιστροφών που θα κάνει ο δίσκος από τη χρονική στιγμή έως τη χρονική στιγμή.δίνεται η ροπή αδράνειας του δίσκου ως προς τον άξονα περιστροφής του. 6
7 ΑΣΚΗΣΗ 5 Μια ομογενής λεπτή δοκός ΚΑ, μάζας και μήκους, μπορεί να στρέφεται σε οριζόντιο επίπεδο γύρω από έναν κατακόρυφο άξονα που διέρχεται από το άκρο της Κ. Στο άκρο Α της δοκού ασκείται οριζόντια δύναμη σταθερού κάθετα στη δοκό και η δοκός αρχίζει να περιστρέφεται αριστερόστροφα. Κατά την περιστροφή της δοκού υπάρχουν τριβές, που δημιουργούν ροπή ως προς τον άξονα περιστροφής μέτρου. Να υπολογίσετε: α) Το μέτρο της συνισταμένης των ροπών, ως προς τον άξονα περιστροφής, κατά τη διάρκεια της περιστροφής της δοκού. β) Τη ροπή αδράνειας της δοκού ως προς τον άξονα περιστροφής της. γ) Το μέτρο της γωνιακής επιτάχυνσης.δ) Το μέτρο της γραμμικής ταχύτητας του κέντρου μάζας της, όταν η δοκός έχει διαγράψει περιστροφές. Δίνεται η ροπή αδράνειας της δοκού ως προς άξονα κάθετο στη δοκό, που διέρχεται από το κέντρο μάζας της. ΑΣΚΗΣΗ 6 Ομογενής συμπαγής κύλινδρος ακτίνας, μπορεί να στρέφεται (τριβές αμελητέες) γύρω από κατακόρυφο άξονα, που συμπίπτει με τον άξονα συμμετρίας του. Στην περιφέρειά του έχουμε τυλίξει αβαρές μη εκτατό νήμα. Τη χρονική στιγμή νήματος, ασκώντας εφαπτομενική δύναμη μέτρου στιγμή, αρχίζουμε να σύρουμε το άκρο του. Τη χρονική, ο κύλινδρος περιστρέφεται αριστερόστροφα και έχει αποκτήσει γωνιακή ταχύτητα μέτρου. Να υπολογίσετε: α) Το μέτρο της γωνιακής επιτάχυνσης του κυλίνδρου. β) Τη ροπή αδράνειας του κυλίνδρου, χωρίς να θεωρήσετε γνωστό τον τύπο της ροπής αδράνειας κυλίνδρου. γ) Το μέτρο της γωνιακής μετατόπισης του κυλίνδρου τη χρονική στιγμή. δ) Το μήκος του νήματος, που ξετυλίχθηκε μέχρι τη χρονική στιγμή πάνω στην επιφάνεια του κυλίνδρου., θεωρώντας ότι αυτό δεν ολισθαίνει ΑΣΚΗΣΗ 7 Ο τροχός ενός αναποδογυρισμένου ποδηλάτου, αποτελείται από ομογενή στεφάνη αμελητέου πάχους, 7
8 με μάζα και ακτίνα, και τις ακτίνες του, μάζας η καθεμία και μήκους. Ο τροχός στρέφεται αρχικά γύρω από τον άξονά του, στο κέντρο του, έχοντας γωνιακή ταχύτητα μέτρου. Τη χρονική στιγμή, πατάμε το φρένο, οπότε ο τροχός ακινητοποιείται με σταθερό ρυθμό σε. Να υπολογίσετε: α) τη ροπή αδράνειας της στεφάνης ως προς άξονα κάθετο στο επίπεδό της, που διέρχεται από το κέντρο μάζας της. β) τον αριθμό των ακτίνων του τροχού. γ) τον αριθμό των στροφών, που έκανε ο τροχός μέχρι να ακινητοποιηθεί. δ) το μέτρο της δύναμης της τριβής, που εφαρμόστηκε από το φρένο στη στεφάνη. Δίνονται η ροπή αδράνειας της κάθε ακτίνας ως προς κάθετο σ αυτήν άξονα διερχόμενο απ το άκρο της:, η ροπή αδράνειάς ολόκληρου του τροχού ως προς άξονα κάθετο στο επίπεδό του, που διέρχεται από τον άξονά του είναι. ΑΣΚΗΣΗ 8 Μια ομογενής ράβδος, μάζας και μήκους, ισορροπεί σε οριζόντια θέση, στηριζόμενη με το αριστερό άκρο της Α σε κατακόρυφο τοίχο με άρθρωση και δεμένη στο σημείο Δ στο κάτω άκρο κατακόρυφου νήματος, του οποίου το πάνω άκρο είναι ακλόνητα στερεωμένο. Αν η τάση του νήματος είναι, να υπολογίσετε: α) την απόσταση του σημείου Δ, από το άκρο Α. β) τη δύναμη στήριξης από την άρθρωση. Τη χρονική στιγμή κόβουμε το νήμα, οπότε η ράβδος πέφτει στρεφόμενη γύρω από την άρθρωση. Αν η ροπή αδράνειας της ράβδου ως προς κάθετο σ αυτήν άξονα διερχόμενο απ το κέντρο μάζας της είναι στιγμή: γ) της εκκίνησης., να υπολογίσετε το μέτρο της γωνιακής επιτάχυνσης της ράβδου τη δ) την οποία η ράβδος σχηματίζει με την αρχική θέση γωνία, τέτοια ώστε. Δίνεται η επιτάχυνση της βαρύτητας. ΑΣΚΗΣΗ 9 Ομογενής λεπτή ράβδος μήκους και μάζας μπορεί να στραφεί χωρίς τριβές γύρω από οριζόντιο άξονα, κάθετο σε αυτήν στο άκρο της Ο. Ένα σωματίδιο, μάζας, 8
9 είναι στερεωμένο στο άλλο άκρο της Α. Αρχικά η ράβδος ισορροπεί σε οριζόντια θέση και τη χρονική στιγμή αφήνεται ελεύθερη, οπότε περιστρέφεται ως προς τον άξονα στο Ο σε κατακόρυφο επίπεδο.α. Να υπολογίσετε: α) την ολική ροπή αδράνειας του συστήματος.β) το μέτρο της συνισταμένης των ροπών, ως προς τον άξονα στο Ο τη χρονική στιγμή, που η ράβδος έχει διαγράψει γωνία, τέτοια ώστε.γ) το μέτρο της γωνιακής επιτάχυνση τη χρονική στιγμή. Β. Να σχεδιάσετε τη γραφική παράσταση της γωνιακής επιτάχυνσης σε συνάρτηση του συνημιτόνου της γωνίας, που σχηματίζει η ράβδος με τον οριζόντιο ημιάξονα Οχ, κατά την περιστροφή της από την αρχική οριζόντια θέση έως την κατακόρυφη θέση. Δίνονται η ροπή αδράνειας της ράβδου ως προς άξονα κάθετο στην ράβδο, που διέρχεται από το κέντρο μάζας της και η επιτάχυνση της βαρύτητας. ΑΣΚΗΣΗ 10 Μια ομογενής τροχαλία δίσκος, μάζας και ακτίνας, μπορεί να στρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο της χωρίς τριβές. Στο αυλάκι της τροχαλίας έχει τυλιχθεί αβαρές μη εκτατό νήμα, στο ελεύθερο άκρο του οποίου έχει δεθεί σώμα Σ μάζας. Αφήνουμε το σώμα ελεύθερο να κινηθεί, οπότε διαπιστώνουμε ότι μετά από χρόνο έχει ξετυλιχθεί σχοινί μήκους. Να υπολογίσετε: α) το μέτρο της επιτάχυνσης του σώματος. β) το μέτρο της γωνιακής επιτάχυνσης της τροχαλίας. γ) τη ροπή αδράνειας ως προς το κέντρο μάζας της και τη μάζα της τροχαλίας. δ) το μέτρο της δύναμης, που δέχεται η τροχαλία από τον άξονα περιστροφής της. Δίνονται η ροπή αδράνειας της τροχαλίας, ως προς τον άξονα περιστροφής της: και η επιτάχυνση της βαρύτητας. ΠΡΟΒΛΗΜΑ 1 Ένα σύστημα διπλής τροχαλίας αποτελείται από δύο ομογενείς λεπτούς δίσκους Α και Β με ακτίνες και αντίστοιχα. Το σύστημα μπορεί να περιστρέφεται γύρω από οριζόντιο σταθερό άξονα, που περνά από το κέντρο του και είναι κάθετος στο επίπεδό του. Ο άξονας αυτός, αποτελεί μέρος άρθρωσης, με την οποία το σύστημα είναι στερεωμένο ακλόνητα στην οροφή, όπως φαίνεται στο σχήμα. Γύρω από τους δίσκους είναι τυλιγμένα αβαρή νήματα, τα οποία δεν 9
10 ολισθαίνουν πάνω στους δίσκους. Στις ελεύθερες άκρες των νημάτων των τροχαλιών Α και Β έχουν δεθεί σώματα,, με μάζες και αντίστοιχα. Το σώμα βρίσκεται πάνω σε λείο οριζόντιο επίπεδο. Τη χρονική στιγμή ελεύθερο να κινηθεί. το σύστημα αφήνεται α) Να σχεδιάσετε τις δυνάμεις που ασκούνται στη διπλή τροχαλία και στα σώματα,. β) Να γράψετε και να εφαρμόσετε το θεμελιώδη νόμο στροφικής κίνησης για την τροχαλία και το θεμελιώδη νόμο της μηχανικής για τη μεταφορική κίνηση των σωμάτων,.(δε ζητείται αριθμητική αντικατάσταση) γ) Να βρείτε τις σχέσεις που συνδέουν τη γωνιακή επιτάχυνση της τροχαλίας με τις μεταφορικές επιταχύνσεις των σωμάτων,. δ) Να υπολογίσετε το μέτρο της γωνιακής επιτάχυνσης της διπλής τροχαλίας και να δείξετε την κατεύθυνσή της στο σχήμα. Η ροπή αδράνειας της διπλής τροχαλίας ως προς τον άξονα περιστροφής της είναι. Δίνεται:. ΠΡΟΒΛΗΜΑ 2 Ένας ομογενής και συμπαγής κύλινδρος μάζας και ακτίνας αφήνεται να κυλίσει κατά μήκος ενός πλάγιου επιπέδου γωνίας κλίσης φ, με, όπως φαίνεται στο σχήμα: Ο κύλινδρος κυλίεται χωρίς να ολισθαίνει. α) Να σχεδιάσετε τις δυνάμεις που ασκούνται στον κύλινδρο, να γράψετε και να εφαρμόσετε το Θεμελιώδη Νόμο της Μηχανικής για τη μεταφορική κίνηση και το Θεμελιώδη Νόμο της Μηχανικής για τη Στροφική Κίνηση του κυλίνδρου. (Δε ζητείται αριθμητική αντικατάσταση) β) Να υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας του κυλίνδρου καθώς αυτός κυλίεται. γ) Να υπολογίσετε το μέτρο της δύναμης της στατικής τριβής που ασκείται στον κύλινδρο από το 10
11 πλάγιο επίπεδο. δ) Να βρείτε το μέτρο της γωνιακής ταχύτητας του κυλίνδρου όταν το κέντρο μάζας του μετατοπιστεί 8m από το σημείο που αυτός αφέθηκε ελεύθερος.δίνονται: Η ροπή αδράνειας του κυλίνδρου ως προς τον άξονά του και η επιτάχυνση της βαρύτητας. ΠΡΟΒΛΗΜΑ 3 Δύο σώματα Σ 1 και Σ 2, με μάζες και αντίστοιχα, συνδέονται με αβαρές μη εκτατό νήμα, που είναι τυλιγμένο σε ομογενή δίσκο τροχαλίας, ακτίνας μάζας. Τα σώματα συγκρατούνται αρχικά στο ίδιο οριζόντιο επίπεδο. Τη χρονική στιγμή, αφήνουμε το σύστημα ελεύθερο, οπότε αρχίζει περιστρέφεται χωρίς το νήμα να ολισθαίνει στην τροχαλία. α) Να βρείτε αν το σύστημα θα περιστραφεί δεξιόστροφα ή αριστερόστροφα. β) Να υπολογίσετε τα μέτρα της επιτάχυνσης των σωμάτων. γ) Να υπολογίσετε τα μέτρα των τάσεων, που ασκεί το νήμα στα δύο σώματα. δ) Να υπολογίσετε το μέτρο της δύναμης στήριξης της τροχαλίας από τον άξονα. ε) Να υπολογίσετε το μήκος του νήματος, που ξετυλίγεται απ την τροχαλία, σε χρόνο. και Δίνονται και η ροπή αδράνειας της τροχαλίας ως προς τον άξονα περιστροφής της: ΠΡΟΒΛΗΜΑ 4. Σφαίρα ακτίνας και μάζας εκτοξεύεται προς τα πάνω από τη βάση κεκλιμένου επιπέδου, γωνίας κλίσης, με αρχική ταχύτητα και κυλίεται χωρίς να ολισθαίνει. Να υπολογίσετε: α) Το μέτρο της επιτάχυνσης του κέντρου μάζας της σφαίρας. β) Το μέτρο της στατικής τριβής, αν η μάζα της σφαίρας είναι. γ) τη χρονική διάρκεια και τη μετατόπιση της σφαίρας μέχρι να σταματήσει στιγμιαία. δ) για ποιες τιμές του συντελεστή στατικής τριβής, η σφαίρα κυλίεται χωρίς να ολισθαίνει. Δίνονται για τη σφαίρα: η επιτάχυνση της βαρύτητας και. 11
12 ΠΡΟΒΛΗΜΑ 5 Στο κυρτό μέρος της περιφέρειας ενός ομογενούς κυλίνδρου μικρού πάχους, έχει τυλιχτεί πολλές φορές ένα αβαρές, μη εκτατό νήμα. Σταθεροποιούμε το ελεύθερο άκρο του νήματος και αφήνουμε τον κύλινδρο να πέσει κατακόρυφα. Το νήμα ξετυλίγεται και ο κύλινδρος εκτελεί σύνθετη κίνηση: μετατοπίζεται κατακόρυφα προς τα κάτω και περιστρέφεται γύρω από ένα νοητό οριζόντιο άξονα x'x, που περνά από το κέντρο του. Σε όλη τη διάρκεια της κίνησης του κυλίνδρου το νήμα παραμένει κατακόρυφο. α) Να αποδείξετε ότι η επιτάχυνση του κέντρου μάζας του κυλίνδρου και η γωνιακή επιτάχυνσή του συνδέονται με τη σχέση:.να υπολογίσετε: β) τη γωνιακή επιτάχυνση του κυλίνδρου καθώς και την επιτάχυνση του κέντρου μάζας του. γ) την τάση του νήματος. δ) το μήκος του νήματος, που έχει ξετυλιχτεί όταν ο κύλινδρος έχει αποκτήσει γωνιακή ταχύτητα.δίνονται: η μάζα του κυλίνδρου, η ακτίνα του, η ροπή αδράνειάς του ως προς το κέντρο μάζας του και η επιτάχυνση της βαρύτητας ΠΡΟΒΛΗΜΑ 6. Μια μπάλα, μάζας και ακτίνας, αφήνεται από την κορυφή κεκλιμένου επιπέδου, γωνίας κλίσης, οπότε κυλίεται χωρίς να ολισθαίνει προς τη βάση του κεκλιμένου επιπέδου. α) Να σχεδιάσετε τις δυνάμεις, που ασκούνται στη μπάλα και να αιτιολογήσετε το σχεδιασμό της στατικής τριβής.να υπολογίσετε: β) το μέτρο της επιτάχυνσης του κέντρου μάζας της μπάλας. γ) το μέτρο της στατικής τριβής, αν η μάζα της μπάλας είναι.δ) τις επιτρεπτές τιμές του συντελεστή στατικής τριβής για τις οποίες η μπάλα μπορεί να κυλίεται χωρίς να ολισθαίνει. Δίνονται ότι, και η επιτάχυνση της βαρύτητας, η μπάλα θεωρείται κοίλη σφαίρα με ροπή αδράνειας ως προς άξονα διερχόμενο από το κέντρο μάζας της:. ΠΡΟΒΛΗΜΑ 7 Η διπλή τροχαλία του σχήματος αποτελείται από δύο ενωμένους ομόκεντρους δίσκους, που μπορούν να περιστρέφονται ενιαία γύρω από οριζόντιο άξονα περιστροφής, που διέρχεται από το κέντρο τους. Η ακτίνα του εξωτερικού δίσκου είναι και του 12
13 εσωτερικού. Η ροπή αδράνειας της διπλής τροχαλίας ως προς τον άξονα περιστροφής της είναι. Στα αυλάκια, που φέρουν οι δύο δίσκοι είναι τυλιγμένα δύο λεπτά αβαρή μεγάλου μήκους και μη εκτατά νήματα, στα κάτω άκρα των οποίων είναι δεμένα δύο σώματα Σ 1 και Σ 2, με μάζες και αντίστοιχα. Τα σώματα συγκρατούνται αρχικά στο ίδιο οριζόντιο επίπεδο και τη χρονική στιγμή, αφήνουμε το σύστημα ελεύθερο, οπότε αρχίζει να περιστρέφεται χωρίς τα νήματα να ολισθαίνουν στα αυλάκια των δίσκων. α) Να βρείτε αν το σύστημα θα περιστραφεί δεξιόστροφα ή αριστερόστροφα. β) Να υπολογίσετε: 1) το μέτρο της γωνιακής επιτάχυνσης της τροχαλίας. 2) το μέτρο της δύναμης στήριξης της τροχαλίας από τον άξονα, αν η μάζα της τροχαλίας είναι. 3) την κατακόρυφη απόσταση των σωμάτων, σε χρόνο. Δίνεται η επιτάχυνση βαρύτητας. ΠΡΟΒΛΗΜΑ 8 Ομογενής κύλινδρος μάζας και ακτίνας κυλίεται χωρίς να ολισθαίνει και χωρίς παραμόρφωση σε οριζόντιο δάπεδο (Α) με ταχύτητα μέτρου ο κύλινδρος δέχεται οριζόντια δύναμη μέτρου. Τη χρονική στιγμή, που ασκείται στο κέντρο μάζας του. Ο κύλινδρος συνεχίζει να κυλίεται χωρίς να ολισθαίνει και μετά την άσκηση της δύναμης. α) Να σχεδιάσετε τη στατική τριβή που δέχεται ο κύλινδρος από το δάπεδο, σε κατάλληλο σχήμα και να δικαιολογήσετε τη φορά της.β) Να υπολογίσετε το μέτρο: β1) της στατικής τριβής. β2) της επιτάχυνσης του κέντρου μάζας καθώς και της γωνιακής επιτάχυνσης του κυλίνδρου. β3) της γωνιακής ταχύτητας του κυλίνδρου τη χρονική στιγμή. γ) Στη συνέχεια τη χρονική στιγμή, ο κύλινδρος εισέρχεται σε λείο δάπεδο (Β), το οποίο είναι συνέχεια του προηγούμενου. Τη χρονική στιγμή, να υπολογίσετε την ταχύτητα του σημείου του κυλίνδρου, που είναι εκείνη τη στιγμή σ επαφή με το λείο δάπεδο.δίνεται η ροπή αδράνειας ομογενούς κυλίνδρου ως προς άξονά του:. ΠΡΟΒΛΗΜΑ 9 Ένας ομογενής δίσκος, μάζας και ακτίνας, που βρίσκεται σε οριζόντιο δάπεδο, φέρει στην περιφέρειά του αυλάκι, στο οποίο έχουμε τυλίξει αβαρές και μη εκτατό νήμα. Τη χρονική στιγμή 13
14 , ασκούμε στο δίσκο μέσω του νήματος σταθερή κατακόρυφη δύναμη μέτρου. Καθώς ξετυλίγεται το νήμα χωρίς να ολισθαίνει στο αυλάκι του δίσκου, ο δίσκος κυλίεται επίσης χωρίς να ολισθαίνει και χωρίς παραμόρφωση, πάνω σε οριζόντιο δάπεδο. α) Να σχεδιάσετε τη στατική τριβή που δέχεται ο δίσκος από το δάπεδο, σε κατάλληλο σχήμα και να δικαιολογήσετε τη φορά της. β) Να υπολογίσετε: β1) το μέτρο της στατικής τριβής, που δέχεται ο δίσκος. β2) το μέτρο της επιτάχυνσης του κέντρου μάζας καθώς και το μέτρο της γωνιακής επιτάχυνσης του δίσκου.β3) το μήκος του νήματος, που έχει ξετυλιχτεί από τη στιγμή, μέχρι τη στιγμή, κατά την οποία το ανώτερο σημείο του δίσκου έχει αποκτήσει ταχύτητα. Δίνεται η ροπή αδράνειας του δίσκου ως προς άξονά του:. ΠΡΟΒΛΗΜΑ 10 Γύρω από ένα ομογενή δίσκο, ακτίνας, μάζας και ροπής αδράνειας μέσω του οποίου, τη χρονική στιγμή, είναι τυλιγμένο αβαρές νήμα,, ασκούμε στο ανώτερο σημείο Γ οριζόντια δύναμη σταθερoύ μέτρου. Ο τροχός κυλίεται χωρίς παραμόρφωση σε οριζόντιο δάπεδο, που έχει τέτοια τιμή συντελεστή στατικής τριβής, ώστε οριακά να αποφεύγεται η ολίσθηση. Να υπολογίσετε: α) το μέτρο της επιτάχυνσης του κέντρου μάζας Ο. β) το μέτρο της επιτάχυνσης του ανώτερου σημείου Γ. γ) τη δύναμη της στατικής τριβής, που δέχεται ο δίσκος από το δάπεδο. δ) το συντελεστή στατικής τριβής. ΠΡΟΒΛΗΜΑ 11 Ένας κύλινδρος ακτίνας έχει μάζα. Στο εσωτερικό του υπάρχει μία κυλινδρική εγκοπή, ακτίνας πολύ μικρού πάχους, στην οποία έχουμε τυλίξει αβαρές μη εκτατό νήμα. Τη χρονική στιγμή, στο άκρο του νήματος και πάνω από το κέντρο μάζας, ασκείται σταθερή οριζόντια δύναμη, όπως φαίνεται στο σχήμα. Έτσι ο κύλινδρος κυλίεται χωρίς να ολισθαίνει πάνω σε οριζόντιο επίπεδο. Θεωρήστε τον κύλινδρο ομογενή με ροπή 14
15 αδράνειας ως προς τον άξονά του. Να υπολογίσετε: α) το μέτρο της επιτάχυνσης του κέντρου μάζας του κυλίνδρου. β) το μέτρο της στατικής τριβής, που δέχεται ο κύλινδρος από το οριζόντιο επίπεδο και να την σχεδιάσετε σε κατάλληλο σχήμα. γ) το μέτρο της οριζόντιας επιτάχυνσης του σημείου επαφής Γ νήματος - κυλίνδρου. δ) το μήκος του νήματος, που ξετυλίχτηκε, έως τη χρονική στιγμή. 15
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 3: ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ - ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 12. Ένας οριζόντιος ομογενής δίσκος ακτίνας μπορεί να περιστρέφεται χωρίς τριβές, γύρω από κατακόρυφο
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης)
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση. (Ροπή αδράνειας - Θεμελιώδης νόμος στροφικής κίνησης) Ένας ομογενής οριζόντιος δίσκος, μάζας Μ και ακτίνας R, περιστρέφεται γύρω από κατακόρυφο ακλόνητο άξονα z, ο οποίος διέρχεται
ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
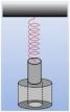
 1. Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. 2. Ένας ομογενής
1. Ο κύλινδρος και ο δίσκος του σχήματος, έχουν την ίδια μάζα και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω. Ποιό σώμα θα σταματήσει πιο δύσκολα; α) Το Α. β) Το Β. γ) Και τα δύο το ίδιο. 2. Ένας ομογενής
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου]
![ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου] ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ [Υποκεφάλαιο 4.2 Οι κινήσεις των στερεών σωμάτων του σχολικού βιβλίου]](/thumbs/52/29790189.jpg) ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]
![[1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s] [1kgm 2, 5m/s, 3,2cm, 8rad/s][1kgm 2, 5m/s, 3,2cm, 8rad/s]](/thumbs/61/46095927.jpg) ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ 34. Μία κατακόρυφη ράβδος μάζας μήκους, μπορεί να περιστρέφεται στο κατακόρυφο επίπεδο γύρω από
γ) το μέτρο της γωνιακής ταχύτητας του δίσκου τη στιγμή κατά την οποία έχει ξετυλιχθεί όλο το σχοινί.
 1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
το άκρο Β έχει γραμμική ταχύτητα μέτρου.
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ 1. Μια ράβδος ΑΒ περιστρέφεται με σταθερή γωνιακή ταχύτητα γύρω από έναν σταθερό οριζόντιο άξονα που περνάει από ένα σημείο πάνω
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ 1. Μια ράβδος ΑΒ περιστρέφεται με σταθερή γωνιακή ταχύτητα γύρω από έναν σταθερό οριζόντιο άξονα που περνάει από ένα σημείο πάνω
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΑΥΕΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/04 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Άσκηση 1. (Κινητική ενέργεια λόγω περιστροφής. Έργο και ισχύς σταθερής ροπής)
 ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΕΚΦΩΝΗΣΕΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 (Κινητική ενέργεια λόγω περιστροφής Έργο και ισχύς σταθερής ροπής) Ένας κύβος και ένας δίσκος έχουν ίδια μάζα και αφήνονται από το ίδιο ύψος να κινηθούν κατά μήκος δύο κεκλιμένων
ΣΤΕΡΕΟ. 1. Στο σχήμα φαίνεται πως μεταβάλλεται η γωνιακή ταχύτητα ενός δίσκου που εκτελεί στροφική κίνηση γύρω από σταθερό άξονα περιστροφής.
 1. Στο σχήμα φαίνεται πως μεταβάλλεται η γωνιακή ταχύτητα ενός δίσκου που εκτελεί στροφική κίνηση γύρω από σταθερό άξονα περιστροφής. Δίνεται ακτίνα δίσκου 0,5 m. α) Να βρεθούν οι γωνιακές επιταχύνσεις
1. Στο σχήμα φαίνεται πως μεταβάλλεται η γωνιακή ταχύτητα ενός δίσκου που εκτελεί στροφική κίνηση γύρω από σταθερό άξονα περιστροφής. Δίνεται ακτίνα δίσκου 0,5 m. α) Να βρεθούν οι γωνιακές επιταχύνσεις
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ 2013 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Σάββατο 24 Φεβρουαρίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
Διαγώνισμα Μηχανική Στερεού Σώματος Σάββατο 24 Φεβρουαρίου 2018 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Ένας δίσκος στρέφεται γύρω από άξονα που
γ) το μέτρο της γωνιακής ταχύτητας του δίσκου τη στιγμή κατά την οποία έχει ξετυλιχθεί όλο το σχοινί.
 1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
1. Ο ομογενής και ισοπαχής δίσκος του σχήματος έχει ακτίνα και μάζα, είναι οριζόντιος και μπορεί να περιστρέφεται, χωρίς τριβές, γύρω από κατακόρυφο ακλόνητο άξονα που διέρχεται από το κέντρο του. Ο δίσκος
% ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου
![% ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου % ] Βαγγέλης Δημητριάδης 4 ο ΓΕΛ Ζωγράφου](/thumbs/53/30956495.jpg) 1. Ομογενής και ισοπαχής ράβδος μήκους L= 4 m και μάζας M= 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου
1. Ομογενής και ισοπαχής ράβδος μήκους L= 4 m και μάζας M= 2 kg ισορροπεί οριζόντια. Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Σε σημείο Κ της ράβδου έχει προσδεθεί το ένα άκρο κατακόρυφου
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/014 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 09/03/014 ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΟΡΟΣΗΜΟ >Ι 3. δ. Ι Οι τροχοί (1) και (2) του σχήματος είναι ίδιοι. Τότε: και Ι 2
 ΚΕΦΑΛΑΙΟ 4 Ροπή αδράνειας - Θεμελιώδης νόμος της στροφικής κίνησης 4.1 Η ροπή αδράνειας ενός σώματος εξαρτάται: α. μόνο από τη μάζα του σώματος β. μόνο τη θέση του άξονα γύρω από τον οποίο μπορεί να περιστρέφεται
ΚΕΦΑΛΑΙΟ 4 Ροπή αδράνειας - Θεμελιώδης νόμος της στροφικής κίνησης 4.1 Η ροπή αδράνειας ενός σώματος εξαρτάται: α. μόνο από τη μάζα του σώματος β. μόνο τη θέση του άξονα γύρω από τον οποίο μπορεί να περιστρέφεται
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
Ασκήσεις. Φυσική Γ Λυκείου - Μηχανική στερεού σώματος
 - Μηχανική στερεού σώματος Ασκήσεις 1. Στερεό στρέφεται γύρω Ένας δίσκος μπορεί να περιστρέφεται γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο και είναι κάθετος στο επίπεδο του. Ο δίσκος είναι
- Μηχανική στερεού σώματος Ασκήσεις 1. Στερεό στρέφεται γύρω Ένας δίσκος μπορεί να περιστρέφεται γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο και είναι κάθετος στο επίπεδο του. Ο δίσκος είναι
Μηχανική Στερεού Ασκήσεις Εμπέδωσης
 Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
Για τις παραπάνω ροπές αδράνειας ισχύει: α. β. γ. δ. Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 01-03-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ M-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 01-03-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ M-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας
Διαγώνισμα Γ Λυκείου Θετικού προσανατολισμού. Διαγώνισμα Μηχανική Στερεού Σώματος. Τετάρτη 12 Απριλίου Θέμα 1ο
 Διαγώνισμα Μηχανική Στερεού Σώματος Τετάρτη 12 Απριλίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Η γωνιακή επιτάχυνση ενός ομογενούς δίσκου που
Διαγώνισμα Μηχανική Στερεού Σώματος Τετάρτη 12 Απριλίου 2017 Θέμα 1ο Στις παρακάτω προτάσεις 1.1 1.4 να επιλέξτε την σωστή απάντηση (4 5 = 20 μονάδες ) 1.1. Η γωνιακή επιτάχυνση ενός ομογενούς δίσκου που
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 206-207 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/03/207 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 206-207 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/03/207 (ΑΠΑΝΤΗΣΕΙΣ) ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 2016-2017 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 2016-2017 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β ΛΥΚΕΙΟΥ (ΠΡΟΕΤΟΙΜΑΣΙΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Διαγώνισμα: Μηχανική Στερεού Σώματος
 Διαγώνισμα: Μηχανική Στερεού Σώματος Θέμα Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τη συμπληρώνει σωστά
Διαγώνισμα: Μηχανική Στερεού Σώματος Θέμα Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τη συμπληρώνει σωστά
ταχύτητα μέτρου. Με την άσκηση κατάλληλης σταθερής ροπής, επιτυγχάνεται
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 4: ΣΤΡΟΦΟΡΜΗ 26. Δύο σημειακές σφαίρες που η καθεμιά έχει μάζα συνδέονται μεταξύ τους με οριζόντια αβαρή ράβδο. Το σύστημα περιστρέφεται γύρω από κατακόρυφο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 4: ΣΤΡΟΦΟΡΜΗ 26. Δύο σημειακές σφαίρες που η καθεμιά έχει μάζα συνδέονται μεταξύ τους με οριζόντια αβαρή ράβδο. Το σύστημα περιστρέφεται γύρω από κατακόρυφο
ΘΕΜΑ Γ, Δ. γ. 0,3 m δ. 112,5 rad] 3. Η ράβδος του σχήματος περιστρέφεται με σταθερή γωνιακή
![ΘΕΜΑ Γ, Δ. γ. 0,3 m δ. 112,5 rad] 3. Η ράβδος του σχήματος περιστρέφεται με σταθερή γωνιακή ΘΕΜΑ Γ, Δ. γ. 0,3 m δ. 112,5 rad] 3. Η ράβδος του σχήματος περιστρέφεται με σταθερή γωνιακή](/thumbs/65/53083887.jpg) ΘΕΜΑ Γ, Δ 1. Μια ευθύγραμμη ράβδος ΑΒ αρχίζει από την ηρεμία να περιστρέφεται με σταθερή γωνιακή επιτάχυνση 4 rad/s. Η ράβδος έχει μήκος l 1 m. 0 άξονας περιστροφής της ράβδου είναι κάθετος στη ράβδο και
ΘΕΜΑ Γ, Δ 1. Μια ευθύγραμμη ράβδος ΑΒ αρχίζει από την ηρεμία να περιστρέφεται με σταθερή γωνιακή επιτάχυνση 4 rad/s. Η ράβδος έχει μήκος l 1 m. 0 άξονας περιστροφής της ράβδου είναι κάθετος στη ράβδο και
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. (Θέμα Δ) Άσκηση 2. (Κύλιση χωρίς ολίσθηση, σχέση υ cm και ω, σχέση α cm και a γων )
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. (Γωνιακή ταχύτητα, γωνιακή επιτάχυνση, σύνθετη κίνηση, κέντρο μάζας) Δύο δίσκοι οριζόντιοι Δ 1 και Δ εκτελούν περιστροφική κίνηση γύρω από κατακόρυφο άξονα που περνά από το
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. (Γωνιακή ταχύτητα, γωνιακή επιτάχυνση, σύνθετη κίνηση, κέντρο μάζας) Δύο δίσκοι οριζόντιοι Δ 1 και Δ εκτελούν περιστροφική κίνηση γύρω από κατακόρυφο άξονα που περνά από το
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού Σώµατος Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Σάββατο 24 Φλεβάρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ : ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση. Tο γιο-γιο του σχήματος έχει ακτίνα R και αρχικά είναι ακίνητο. Την t=0 αφήνουμε ελεύθερο το δίσκο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ : ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση. Tο γιο-γιο του σχήματος έχει ακτίνα R και αρχικά είναι ακίνητο. Την t=0 αφήνουμε ελεύθερο το δίσκο
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1. ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση
 ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση Α.1 Το στερεό του σχήματος δέχεται αντίρροπες δυνάμεις F 1 kαι F 2 που έχουν ίσα μέτρα. Το μέτρο
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ 1 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις Α1-Α.5 να σημειώσετε την σωστή απάντηση Α.1 Το στερεό του σχήματος δέχεται αντίρροπες δυνάμεις F 1 kαι F 2 που έχουν ίσα μέτρα. Το μέτρο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 4: ΣΤΡΟΦΟΡΜΗ [Υποκεφάλαια 4.7: Στροφορμή του σχολικού βιβλίου]
![ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 4: ΣΤΡΟΦΟΡΜΗ [Υποκεφάλαια 4.7: Στροφορμή του σχολικού βιβλίου] ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 4: ΣΤΡΟΦΟΡΜΗ [Υποκεφάλαια 4.7: Στροφορμή του σχολικού βιβλίου]](/thumbs/63/49022859.jpg) ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Ομογενής δίσκος ροπής αδράνειας, με μάζα και ακτίνας θα χρησιμοποιηθεί σε 3 διαφορετικά πειράματα.
 Δίσκος Σύνθετη Τρίτη 01 Μαϊου 2012 ΑΣΚΗΣΗ 5 Ομογενής δίσκος ροπής αδράνειας, με μάζα και ακτίνας θα χρησιμοποιηθεί σε 3 διαφορετικά πειράματα. ΠΕΙΡΑΜΑ Α Θα εκτοξευθεί με ταχύτητα από τη βάση του κεκλιμένου
Δίσκος Σύνθετη Τρίτη 01 Μαϊου 2012 ΑΣΚΗΣΗ 5 Ομογενής δίσκος ροπής αδράνειας, με μάζα και ακτίνας θα χρησιμοποιηθεί σε 3 διαφορετικά πειράματα. ΠΕΙΡΑΜΑ Α Θα εκτοξευθεί με ταχύτητα από τη βάση του κεκλιμένου
ΘΕΜΑ Α Ι. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Ι. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1.
ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Ι. Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1.
3,6. sec. h a. Το μέτρο της επιτάχυνσης του κέντρου μάζας κάθε τροχού b. Τον αριθμό των περιστροφών κάθε τροχού στο χρόνο t=5 sec.
 ΚΙΝΗΣΕΙΣ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ. Ένας δίσκος στρέφεται γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδο του. Η γωνιακή ταχύτητα περιστροφής του δίσκου σε συνάρτηση με
ΚΙΝΗΣΕΙΣ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ. Ένας δίσκος στρέφεται γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδο του. Η γωνιακή ταχύτητα περιστροφής του δίσκου σε συνάρτηση με
Για τις παραπάνω ροπές αδράνειας ισχύει: α. β. γ. δ. Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ-A ΗΜΕΡΟΜΗΝΙΑ: 01-03-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ M-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΘΕΡΙΝΑ-A ΗΜΕΡΟΜΗΝΙΑ: 01-03-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ M-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ.-ΠΟΥΛΗ Κ. ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ. Δίνεται ότι η ροπή αδράνειας του δίσκου ως προς τον άξονα Κ είναι Ι= M R
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 1 Η ράβδος ΟΑ του σχήματος μπορεί να στρέφεται γύρω από τον άξονα z z χωρίς τριβές Tη στιγμή t=0 δέχεται την εφαπτομενική δύναμη F σταθερού μέτρου 0 Ν, με φορά όπως φαίνεται στο σχήμα
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 1 Η ράβδος ΟΑ του σχήματος μπορεί να στρέφεται γύρω από τον άξονα z z χωρίς τριβές Tη στιγμή t=0 δέχεται την εφαπτομενική δύναμη F σταθερού μέτρου 0 Ν, με φορά όπως φαίνεται στο σχήμα
ΦΥΕ 14 5η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Aσκηση 2 :
 ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθμολογικά ισοδύναμες) Άσκηση 1 : Συμπαγής κύλινδρος μάζας Μ συνδεδεμένος σε ελατήριο σταθεράς k = 3. N / και αμελητέας μάζας, κυλίεται, χωρίς να
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 3 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 01: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το
3 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 01: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το
6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι. Θέµα Α
 6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι Ηµεροµηνία : 10 Μάρτη 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστη απάντηση [4 5 = 20 µονάδες] Α.1. Στερεό
6ο ιαγώνισµα - Μηχανική Στερεού Σώµατος Ι Ηµεροµηνία : 10 Μάρτη 2013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστη απάντηση [4 5 = 20 µονάδες] Α.1. Στερεό
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. = 2r, τότε:
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. (Διατήρηση της στροφορμής) Η Γη στρέφεται σε ελλειπτική τροχιά γύρω από τον Ήλιο. Το κοντινότερο σημείο στον Ήλιο ονομάζεται Περιήλιο (π) και το πιο απομακρυσμένο Αφήλιο (α).
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. (Διατήρηση της στροφορμής) Η Γη στρέφεται σε ελλειπτική τροχιά γύρω από τον Ήλιο. Το κοντινότερο σημείο στον Ήλιο ονομάζεται Περιήλιο (π) και το πιο απομακρυσμένο Αφήλιο (α).
Διαγώνισμα Μηχανική Στερεού Σώματος
 Διαγώνισμα Μηχανική Στερεού Σώματος Θέμα Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τη συμπληρώνει σωστά
Διαγώνισμα Μηχανική Στερεού Σώματος Θέμα Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τη συμπληρώνει σωστά
ΚΕΦΑΛΑΙΟ 4ο: ΚΙΝΗΣΕΙΣ ΣΤΕΡΕΩΝ ΣΩΜΑΤΩΝ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Α ΕΡΩΤΗΣΕΙΣ
 Α ΕΡΩΤΗΣΕΙΣ Ερώτηση 1 Σε ένα ρολόι θέλουμε το άκρο του ωροδείκτη και το άκρο του λεπτοδείκτη να έχουν την ίδια ταχύτητα λόγω περιστροφής (γραμμική ταχύτητα). Αν συμβολίσουμε με το μήκος του ωροδείκτη και
Α ΕΡΩΤΗΣΕΙΣ Ερώτηση 1 Σε ένα ρολόι θέλουμε το άκρο του ωροδείκτη και το άκρο του λεπτοδείκτη να έχουν την ίδια ταχύτητα λόγω περιστροφής (γραμμική ταχύτητα). Αν συμβολίσουμε με το μήκος του ωροδείκτη και
Τίτλος Κεφαλαίου: Στερεό σώµα. Ασκήσεις που δόθηκαν στις εξετάσεις των Πανελληνίων ως. Γεώργιος Μακεδών, Φυσικός Ρ/Η Σελίδα 1
 Τίτλος Κεφαλαίου: Στερεό σώµα ιδακτική Ενότητα: Κινηµατική του Στερεού Σώµατος Ασκήσεις που δόθηκαν στις εξετάσεις των Πανελληνίων ως Θέµα 3ο: Γεώργιος Μακεδών, Φυσικός Ρ/Η Σελίδα 1 ιδακτική Ενότητα: Ροπή
Τίτλος Κεφαλαίου: Στερεό σώµα ιδακτική Ενότητα: Κινηµατική του Στερεού Σώµατος Ασκήσεις που δόθηκαν στις εξετάσεις των Πανελληνίων ως Θέµα 3ο: Γεώργιος Μακεδών, Φυσικός Ρ/Η Σελίδα 1 ιδακτική Ενότητα: Ροπή
ΡΟΠΗ ΔΥΝΑΜΗΣ ΙΣΟΡΡΟΠΙΑ ΣΤΕΡΕΟΥ ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ
 ΡΟΠΗ ΔΥΝΑΜΗΣ ΙΣΟΡΡΟΠΙΑ ΣΤΕΡΕΟΥ ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ 1. Ένας ελαιοχρωματιστής βάρους w 1 =700 N βρίσκεται σε μια οριζόντια σανίδα AB, μήκους l =5m και βάρους w=300 N. Η σανίδα κρέμεται από δυο κατακόρυφα σχοινιά
ΡΟΠΗ ΔΥΝΑΜΗΣ ΙΣΟΡΡΟΠΙΑ ΣΤΕΡΕΟΥ ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ 1. Ένας ελαιοχρωματιστής βάρους w 1 =700 N βρίσκεται σε μια οριζόντια σανίδα AB, μήκους l =5m και βάρους w=300 N. Η σανίδα κρέμεται από δυο κατακόρυφα σχοινιά
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 24 Γενάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 24 Γενάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ 4 Ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση. ΘΕΜΑ Β Ένα ομογενές σώμα με κανονικό γεωμετρικό σχήμα κυλίεται, χωρίς να
ΚΕΦΑΛΑΙΟ 4 Ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ 5: ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΙ ΕΡΓΟ ΔΥΝΑΜΗΣ ΣΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση. ΘΕΜΑ Β Ένα ομογενές σώμα με κανονικό γεωμετρικό σχήμα κυλίεται, χωρίς να
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ. ΘΕΜΑ Α (μοναδες 25)
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ ΘΕΜΑ Α (μοναδες 25) Α1. Σε στερεό που περιστρέφεται γύρω από σταθερό κατακόρυφο άξονα ενεργεί σταθερή ροπή. Τότε αυξάνεται με σταθερό ρυθμό: α. η ροπή αδράνειας του β. η
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΕΡΕΟ ΘΕΜΑ Α (μοναδες 25) Α1. Σε στερεό που περιστρέφεται γύρω από σταθερό κατακόρυφο άξονα ενεργεί σταθερή ροπή. Τότε αυξάνεται με σταθερό ρυθμό: α. η ροπή αδράνειας του β. η
2) Ομογενής δίσκος μάζας m και ακτίνας R κυλίεται χωρίς να ολισθαίνει πάνω σε οριζόντιο
 - 1 - Επώνυμο.. Όνομα.. Αγρίνιο 22/3/2015 Ζήτημα 1 0 Να επιλεγεί η σωστή πρόταση 1) Ομογενής δίσκος μάζας m και ακτίνας R κυλίεται χωρίς να ολισθαίνει πάνω σε οριζόντιο επίπεδο. Ο δίσκος στρέφεται γύρω
- 1 - Επώνυμο.. Όνομα.. Αγρίνιο 22/3/2015 Ζήτημα 1 0 Να επιλεγεί η σωστή πρόταση 1) Ομογενής δίσκος μάζας m και ακτίνας R κυλίεται χωρίς να ολισθαίνει πάνω σε οριζόντιο επίπεδο. Ο δίσκος στρέφεται γύρω
ΦΥΣΙΚΗ Β'Λ προετ. Γ'Λ
 ΦΥΣΙΚΗ Β'Λ προετ. Γ'Λ 18/03/018 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α1.
ΦΥΣΙΚΗ Β'Λ προετ. Γ'Λ 18/03/018 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α1.
Γ ΤΑΞΗ ΤΜΗΜΑ ΟΝΟΜΑ. ΘΕΜΑ 1ο. 7 mr 5. 1 mr. Μονάδες 5. α. 50 W β. 100 W γ. 200 W δ. 400 W
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΟΝΟΜΑ ΤΜΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΤΕΤΑΡΤΗ 8 ΜΑΡΤΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΟΝΟΜΑ ΤΜΗΜΑ ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΤΕΤΑΡΤΗ 8 ΜΑΡΤΙΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε
. α. περιστροφή σώματος με σταθερή γωνιακή ταχύτητα. και 0
 Επανάληψη: Περιστροφή στερεού σώματος (Φ25) 1. Να αποδείξετε ότι, για τροχό ακτίνας R που κυλίεται χωρίς να ολισθαίνει, ισχύει α cm =Rα γων. 2. Τροχός ακτίνας R έχει α cm =0 και α γων =0. Τι είδους κίνηση
Επανάληψη: Περιστροφή στερεού σώματος (Φ25) 1. Να αποδείξετε ότι, για τροχό ακτίνας R που κυλίεται χωρίς να ολισθαίνει, ισχύει α cm =Rα γων. 2. Τροχός ακτίνας R έχει α cm =0 και α γων =0. Τι είδους κίνηση
ΟΡΟΣΗΜΟ. Ισχύει: α. L 1. και Κ 1 β. 2L 1 =2L 2 =L 2. και 2Κ 1 γ. L 1
 61 Η κινητική ενέργεια ενός δίσκου μάζας m και ακτίνας R που εκτελεί στροφική κίνηση, εξαρτάται: α Μόνο από την γωνιακή του ταχύτητα β Μόνο από την μάζα και την ακτίνα του γ Μόνο από την γωνιακή του ταχύτητα,
61 Η κινητική ενέργεια ενός δίσκου μάζας m και ακτίνας R που εκτελεί στροφική κίνηση, εξαρτάται: α Μόνο από την γωνιακή του ταχύτητα β Μόνο από την μάζα και την ακτίνα του γ Μόνο από την γωνιακή του ταχύτητα,
Δυναμική στερεού. Ομάδα Δ
 Δυναμική στερεού. Ομάδα Δ 3.3.41. Ανεμιστήρες. Κατασκευαστής ανεμιστήρων έδωσε 4 σχεδιαστές την εντολή να σχεδιάσουν ανεμιστήρες με βάση έναν κύλινδρο μάζας Μ ακτίνας R και ροπής αδράνειας ως προς το κέντρο
Δυναμική στερεού. Ομάδα Δ 3.3.41. Ανεμιστήρες. Κατασκευαστής ανεμιστήρων έδωσε 4 σχεδιαστές την εντολή να σχεδιάσουν ανεμιστήρες με βάση έναν κύλινδρο μάζας Μ ακτίνας R και ροπής αδράνειας ως προς το κέντρο
7. Ένα σώμα εκτελεί Α.Α.Τ. Η σταθερά επαναφοράς συστήματος είναι.
 ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΦΥΣΙΚΗ Β'Λ προετ. Γ'Λ
 ΦΥΣΙΚΗ Β'Λ προετ. Γ'Λ 8/03/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Ζεύγος
ΦΥΣΙΚΗ Β'Λ προετ. Γ'Λ 8/03/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Ζεύγος
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ
 ΕΠΝΛΗΠΤΙΚΟ ΙΓΩΝΙΣΜ ΣΤΗ ΜΗΧΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΤΟΣ ΘΕΜ Για να απαντήσετε στις παρακάτω ερωτήσεις 1-4 πολλαπλής επιλογής, αρκεί να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δεξιά απ αυτόν, μέσα σε
ΕΠΝΛΗΠΤΙΚΟ ΙΓΩΝΙΣΜ ΣΤΗ ΜΗΧΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΤΟΣ ΘΕΜ Για να απαντήσετε στις παρακάτω ερωτήσεις 1-4 πολλαπλής επιλογής, αρκεί να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δεξιά απ αυτόν, μέσα σε
ΣΙΤΣΑΝΛΗΣ ΗΛΙΑΣ ΣΕΛΙΔΑ 1
 1. Ένα βλήμα μάζας 0,1 kg που κινείται οριζόντια με ταχύτητα 100 m/s σφηνώνεται σε ακίνητο ξύλο μάζας 1,9 kg. Να βρεθεί η απώλεια ενέργειας που οφείλεται στην κρούση, όταν το ξύλο είναι: α. πακτωμένο στο
1. Ένα βλήμα μάζας 0,1 kg που κινείται οριζόντια με ταχύτητα 100 m/s σφηνώνεται σε ακίνητο ξύλο μάζας 1,9 kg. Να βρεθεί η απώλεια ενέργειας που οφείλεται στην κρούση, όταν το ξύλο είναι: α. πακτωμένο στο
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΠΕΝΤΕ (15) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΠΕΝΤΕ (15) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας
3.3. Δυναμική στερεού.
 3.3.. 3.3.1. Ροπή και γωνιακή επιτάχυνση Μια οριζόντια τετράγωνη πλάκα ΑΒΓΔ, πλευράς 1m και μάζας 20kg μπορεί να στρέφεται γύρω από σταθερό άξονα z που περνά από το κέντρο της. Η πλάκα αποκτά γωνιακή ταχύτητα
3.3.. 3.3.1. Ροπή και γωνιακή επιτάχυνση Μια οριζόντια τετράγωνη πλάκα ΑΒΓΔ, πλευράς 1m και μάζας 20kg μπορεί να στρέφεται γύρω από σταθερό άξονα z που περνά από το κέντρο της. Η πλάκα αποκτά γωνιακή ταχύτητα
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Στερεό (Μέχρι Ροπή Αδράνειας) Γ ΛΥΚΕΙΟΥ. Α)Σε κάθε μια από τις ερωτήσεις (1-4) να σημειώσετε στο τετράδιό σας τη σωστή απάντηση.
 ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ Στερεό (Μέχρι Ροπή δράνειας) Γ ΛΥΚΕΙΟΥ ΘΕΜ 1 Ο : )Σε κάθε μια από τις ερωτήσεις (1-4) να σημειώσετε στο τετράδιό σας τη σωστή απάντηση. 1. Για ένα ζεύγος δυνάμεων Η ροπή του, εξαρτάται
ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ Στερεό (Μέχρι Ροπή δράνειας) Γ ΛΥΚΕΙΟΥ ΘΕΜ 1 Ο : )Σε κάθε μια από τις ερωτήσεις (1-4) να σημειώσετε στο τετράδιό σας τη σωστή απάντηση. 1. Για ένα ζεύγος δυνάμεων Η ροπή του, εξαρτάται
ΘΕΜΑΤΑ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 23/2/2014 ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 3-4
 ΚΕΝΤΡΟ Αγίας Σοφίας 39 3 ΝΤΕΠΩ Β Όλγας 3 38 ΕΥΟΣΜΟΣ ΜΑλεξάνδρου 5 37736 ΘΕΜΑΤΑ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3// ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 3- ΘΕΜΑ A Στις ερωτήσεις - να γράψετε
ΚΕΝΤΡΟ Αγίας Σοφίας 39 3 ΝΤΕΠΩ Β Όλγας 3 38 ΕΥΟΣΜΟΣ ΜΑλεξάνδρου 5 37736 ΘΕΜΑΤΑ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 3// ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 3- ΘΕΜΑ A Στις ερωτήσεις - να γράψετε
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 4 (ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ) ΚΥΡΙΑΚΗ 15 ΜΑΡΤΙΟΥ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 5
 ΑΡΧΗ 1 ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 4 (ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ) ΚΥΡΙΑΚΗ 15 ΜΑΡΤΙΟΥ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 5 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον
ΑΡΧΗ 1 ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 4 (ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ) ΚΥΡΙΑΚΗ 15 ΜΑΡΤΙΟΥ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 5 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον
6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο:
 6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο
6ο Πρόχειρο Τεστ Γ Τάξης Λυκείου Θεµελιώδης Νόµος Στροφικής Κίνησης Σύνολο Σελίδων: πέντε (5) - ιάρκεια Εξέτασης: 90 min Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο
ΘΕΜΑΤΑ ΑΠΟ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 4 ΘΕΜΑΤΑ ΑΠΟ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 3ο, 4ο ΘΕΜΑ Πανελληνίων εξετάσεων -O.Ε.Φ.Ε 196 ΘΕΜΑ 4 ο 00 Δύο ίδιες, λεπτές, ισοπαχείς και ομογενείς ράβδοι ΟΑ και ΟΒ, που έχουν μάζα Μ = 4 Κg και μήκος L =
ΚΕΦΑΛΑΙΟ 4 ΘΕΜΑΤΑ ΑΠΟ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 3ο, 4ο ΘΕΜΑ Πανελληνίων εξετάσεων -O.Ε.Φ.Ε 196 ΘΕΜΑ 4 ο 00 Δύο ίδιες, λεπτές, ισοπαχείς και ομογενείς ράβδοι ΟΑ και ΟΒ, που έχουν μάζα Μ = 4 Κg και μήκος L =
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΕΞΙ (16) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΕΞΙ (16) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 2017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 017 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΦΥΣΙΚΗ. α) έχουν κάθε χρονική στιγμή την ίδια οριζόντια συνιστώσα ταχύτητας, και την ίδια κατακόρυφη συνιστώσα ταχύτητας.
 Β Λυκείου 14 / 04 / 2019 ΦΥΣΙΚΗ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις A1 A4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση: Α1. Η ορμή ενός σώματος :
Β Λυκείου 14 / 04 / 2019 ΦΥΣΙΚΗ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις A1 A4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση: Α1. Η ορμή ενός σώματος :
ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 25/02/2018 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 25/02/2018 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
Ερωτήσεις. 2. Η ροπή αδράνειας μιας σφαίρας μάζας Μ και ακτίνας R ως προς άξονα που διέρχεται
 - Μηχανική στερεού σώματος Ερωτήσεις 1. Στερεό στρέφεται γύρω από σταθερό άξονα. Η γωνιακή ταχύτητα του στερεού μεταβάλλεται με το χρόνο όπως στο διπλανό διάγραμμα ω -. Να χαρακτηρίσετε τις παρακάτω προτάσεις
- Μηχανική στερεού σώματος Ερωτήσεις 1. Στερεό στρέφεται γύρω από σταθερό άξονα. Η γωνιακή ταχύτητα του στερεού μεταβάλλεται με το χρόνο όπως στο διπλανό διάγραμμα ω -. Να χαρακτηρίσετε τις παρακάτω προτάσεις
κατά την οποία το μέτρο της ταχύτητας του κέντρου μάζας του τροχού είναι ίσο με
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 06/0/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 06/0/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
3.6. Σύνθετα θέματα στερεού. Ομάδα Δ.
 3.5.61. Μια κινούμενη τροχαλία. 3.6. Σύνθετα θέματα στερεού. Ομάδα Δ. Γύρω από μια τροχαλία μάζας Μ=0,8kg έχουμε τυλίξει ένα αβαρές νήμα, στο άκρο του οποίου έχουμε δέσει ένα σώμα Σ μάζας m=0,1kg. Συγκρατούμε
3.5.61. Μια κινούμενη τροχαλία. 3.6. Σύνθετα θέματα στερεού. Ομάδα Δ. Γύρω από μια τροχαλία μάζας Μ=0,8kg έχουμε τυλίξει ένα αβαρές νήμα, στο άκρο του οποίου έχουμε δέσει ένα σώμα Σ μάζας m=0,1kg. Συγκρατούμε
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
κατά την οποία το μέτρο της ταχύτητας του κέντρου μάζας του τροχού είναι ίσο με
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ ΗΜΕΡΟΜΗΝΙΑ: 06/0/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ ΗΜΕΡΟΜΗΝΙΑ: 06/0/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΦΥΕ 14 5η ΕΡΓΑΣΙΑ Παράδοση 19-05-08 ( Οι ασκήσεις είναι βαθµολογικά ισοδύναµες) Άσκηση 1 : Aσκηση 2 :
 ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθµολογικά ισοδύναµες) Άσκηση 1 : Συµπαγής κύλινδρος µάζας Μ συνδεδεµένος σε ελατήριο σταθεράς k = 3. N / και αµελητέας µάζας, κυλίεται, χωρίς να
ΦΥΕ 14 5 η ΕΡΓΑΣΙΑ Παράδοση 19-5-8 ( Οι ασκήσεις είναι βαθµολογικά ισοδύναµες) Άσκηση 1 : Συµπαγής κύλινδρος µάζας Μ συνδεδεµένος σε ελατήριο σταθεράς k = 3. N / και αµελητέας µάζας, κυλίεται, χωρίς να
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος. και Α 2
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Ένα σύστημα ελατηρίου σταθεράς = 0 π N/ και μάζας = 0, g τίθεται σε εξαναγκασμένη ταλάντωση. Αν είναι Α 1 και Α τα πλάτη της ταλάντωσης
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α Α.1. Η γωνιακή επιτάχυνση ενός οµογενούς δίσκου που στρέφεται γύρω από σταθερό άξονα, που διέρχεται από το κέντρο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος Ι Ενδεικτικές Λύσεις Θέµα Α Α.1. Η γωνιακή επιτάχυνση ενός οµογενούς δίσκου που στρέφεται γύρω από σταθερό άξονα, που διέρχεται από το κέντρο
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΡΕΥΣΤΑ -ΣΤΕΡΕΟ 24/02/2019
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΡΕΥΣΤΑ -ΣΤΕΡΕΟ 24/02/2019 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΡΕΥΣΤΑ -ΣΤΕΡΕΟ 24/02/2019 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε.
 ΚΕΦΑΛΑΙΟ 4 3ο, 4ο ΘΕΜΑ Πανελληνίων εξετάσεων -OΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ ΘΕΜΑ 3 o 00 Ομογενής και ισοπαχής ράβδος ΑΓ, μήκους L=1 m και μάζας m=10 kg, μπορεί να στρέφεται γύρω από ακλόνητο οριζόντιο
ΚΕΦΑΛΑΙΟ 4 3ο, 4ο ΘΕΜΑ Πανελληνίων εξετάσεων -OΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ ΘΕΜΑ 3 o 00 Ομογενής και ισοπαχής ράβδος ΑΓ, μήκους L=1 m και μάζας m=10 kg, μπορεί να στρέφεται γύρω από ακλόνητο οριζόντιο
Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα.
 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΕΡΕΟΎ ΣΏΜΑΤΟΣ Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα. Ένα υλικό σημείο μπορεί να κάνει μόνο μεταφορική
ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΕΡΕΟΎ ΣΏΜΑΤΟΣ Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα. Ένα υλικό σημείο μπορεί να κάνει μόνο μεταφορική
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΤΡΙΩΡΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤO ΣΤΕΡΕΟ
 ΠΡΤΥΠ ΠΕΙΡΑΜΑΤΙΚ ΛΥΚΕΙ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΤΡΙΩΡ ΕΠΑΝΑΛΗΠΤΙΚ ΔΙΑΓΩΝΙΣΜΑ ΣΤO ΣΤΕΡΕ Μαθητής/Μαθήτρια -----------------------------------------------
ΠΡΤΥΠ ΠΕΙΡΑΜΑΤΙΚ ΛΥΚΕΙ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΤΡΙΩΡ ΕΠΑΝΑΛΗΠΤΙΚ ΔΙΑΓΩΝΙΣΜΑ ΣΤO ΣΤΕΡΕ Μαθητής/Μαθήτρια -----------------------------------------------
ΟΡΟΣΗΜΟ. 12 της στροφορμής της ράβδ ου ως προς παράλληλο άξονα, που περνά από το ένα άκρο της, με ίδια ω, είναι: ω 3
 5.1 Oι σφαίρες του σχήματος έχουν ίσες μάζες και ακτίνες. Η σφαίρα (1) είναι συμπαγής και η σφαίρα () κοίλη. Οι ροπές αδράνειάς τους είναι Ι 1 και Ι αντίστοιχα. Και οι δύο σφαίρες περιστρέφονται με γωνιακές
5.1 Oι σφαίρες του σχήματος έχουν ίσες μάζες και ακτίνες. Η σφαίρα (1) είναι συμπαγής και η σφαίρα () κοίλη. Οι ροπές αδράνειάς τους είναι Ι 1 και Ι αντίστοιχα. Και οι δύο σφαίρες περιστρέφονται με γωνιακές
ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 28/2/2016
 ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 8//06 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΣΤΕΡΕΟ ΚΑΙ Doppler ΘΕΜΑ Α Α Μικρότερη συχνότητα ακούει ένας παρατηρητής σε σχέση με την πραγματική συχνότητα
ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 8//06 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΣΤΕΡΕΟ ΚΑΙ Doppler ΘΕΜΑ Α Α Μικρότερη συχνότητα ακούει ένας παρατηρητής σε σχέση με την πραγματική συχνότητα
ΦΥΣΙΚΗ Ο.Π. ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Γ ΓΕΛ / 04 / 09 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Σώμα εκτελεί απλή αρμονική ταλάντωση
Γ ΓΕΛ / 04 / 09 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Στις ερωτήσεις Α Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Σώμα εκτελεί απλή αρμονική ταλάντωση
Β. Συµπληρώστε τα κενά των παρακάτω προτάσεων
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΟ ΣΤΕΡΕΟ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΘΕΜΑ Α Α. Στις ερωτήσεις 1 έως 3 επιλέξτε τη σωστή απάντηση 1. Δυο δακτύλιοι µε διαφορετικές ακτίνες αλλά ίδια µάζα κυλάνε χωρίς ολίσθηση σε οριζόντιο έδαφος µε την
ΔΙΑΓΩΝΙΣΜΑ ΣΤΟ ΣΤΕΡΕΟ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΘΕΜΑ Α Α. Στις ερωτήσεις 1 έως 3 επιλέξτε τη σωστή απάντηση 1. Δυο δακτύλιοι µε διαφορετικές ακτίνες αλλά ίδια µάζα κυλάνε χωρίς ολίσθηση σε οριζόντιο έδαφος µε την
F r. www.ylikonet.gr 1
 3.5. Έργο Ενέργεια. 3.5.1. Έργο δύναµης- ροπής και Κινητική Ενέργεια. Το οµοαξονικό σύστηµα των δύο κυλίνδρων µε ακτίνες R 1 =0,1m και R =0,5m ηρεµεί σε οριζόντιο επίπεδο. Τυλίγουµε γύρω από τον κύλινδρο
3.5. Έργο Ενέργεια. 3.5.1. Έργο δύναµης- ροπής και Κινητική Ενέργεια. Το οµοαξονικό σύστηµα των δύο κυλίνδρων µε ακτίνες R 1 =0,1m και R =0,5m ηρεµεί σε οριζόντιο επίπεδο. Τυλίγουµε γύρω από τον κύλινδρο
ΘΕΜΑ Α Α. Στις ερωτήσεις 1-5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση
 ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Α. Στις ερωτήσεις 1-5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση 1.
ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Α. Στις ερωτήσεις 1-5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και το γράμμα που αντιστοιχεί στη σωστή απάντηση 1.
ΦΥΣ. 111 Τελική Εξέταση: 17-Δεκεµβρίου-2017
 ΦΥΣ. 111 Τελική Εξέταση: 17-Δεκεµβρίου-2017 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός ταυτότητας Απενεργοποιήστε τα κινητά σας. Σας δίνονται
ΦΥΣ. 111 Τελική Εξέταση: 17-Δεκεµβρίου-2017 Πριν αρχίσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο και αριθµό ταυτότητας). Ονοµατεπώνυµο Αριθµός ταυτότητας Απενεργοποιήστε τα κινητά σας. Σας δίνονται
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΙΑΝΟΥΑΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό
ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 5/0/018 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π/Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 5/0/018 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
Προτεινόμενα ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ
 ΘΕΜΑΤΑ Β. Β1. Από ύψος h (σημείο Α) αφήνουμε να κυλίσει δακτύλιος μάζας m 1 =m χωρίς ολίσθηση σε οδηγό που καταλήγει σε τεταρτοκύκλιο. Στο σημείο Β και όταν η u cm είναι κατακόρυφη ο δακτύλιος εγκαταλείπει
ΘΕΜΑΤΑ Β. Β1. Από ύψος h (σημείο Α) αφήνουμε να κυλίσει δακτύλιος μάζας m 1 =m χωρίς ολίσθηση σε οδηγό που καταλήγει σε τεταρτοκύκλιο. Στο σημείο Β και όταν η u cm είναι κατακόρυφη ο δακτύλιος εγκαταλείπει
Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο
 Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο ) Οµογενής κύλινδρος µάζας m, ακτίνας R φέρει λεπτή εγκοπή βάθους είναι τυλιγµένο νήµα αµελητέου πάχους. R r=, στην οποία Το άλλο άκρο του νήµατος έχει δεθεί σε οροφή όπως στο
Όταν υπάρχει ΑΚΙΝΗΤΟ σηµείο ) Οµογενής κύλινδρος µάζας m, ακτίνας R φέρει λεπτή εγκοπή βάθους είναι τυλιγµένο νήµα αµελητέου πάχους. R r=, στην οποία Το άλλο άκρο του νήµατος έχει δεθεί σε οροφή όπως στο
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 3 να γράψετε στο τετράδιό
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΦΕΒΡΟΥΑΡΙΟΣ 016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 6 Στις παρακάτω ερωτήσεις 1 έως 3 να γράψετε στο τετράδιό
7ο ιαγώνισµα - Μηχανική Στερεού Σώµατος ΙΙ
 Σχολική Χρονιά 01-013 7ο ιαγώνισµα - Μηχανική Στερεού Σώµατος ΙΙ Ηµεροµηνία : 4 Μάρτη 013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστή απάντηση [4 5 = 0
Σχολική Χρονιά 01-013 7ο ιαγώνισµα - Μηχανική Στερεού Σώµατος ΙΙ Ηµεροµηνία : 4 Μάρτη 013 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα Α Στις ερωτήσεις Α.1 Α.4 επιλέξτε την σωστή απάντηση [4 5 = 0
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 28 Φλεβάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Μηχανική Στερεού - µέρος ΙΙ Σύνολο Σελίδων: οκτώ (8) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 28 Φλεβάρη 2016 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1
