This process is shown in Figure 1.1.
|
|
|
- Τισιφόνη Κομνηνός
- 6 χρόνια πριν
- Προβολές:
Transcript
1 1 When you have completed study of this chapter you should be able to: Understand the main elements of the data communication process Understand the difference between analog and digital transmission Explain how data transfer is affected by attenuation, bandwidth and noise in the channel Know the importance of synchronization of digital data systems Describe the basic synchronization concepts used with asynchronous and synchronous systems Explain the following types of encoding: Manchester RZ NRZ MLT-3 4B/5B Describe the basic error detection principles. Communications systems exist to transfer information from one location to another. The components of the information or message are usually known as data (derived from the Latin word for items of information). All data are made up of unique code symbols or other entities on which the sender and receiver of the messages have agreed. For example binary data is represented by two states 0 and 1. These are referred to as Binary digits or bits. These bits are represented inside our computers by the level of the electrical
2 signals within storage elements; a high level could represent a 1, and a low-level represent a 0. Alternatively, the data may be represented by the presence or absence of light in an optical fiber cable. A communications process requires the following components: A source of the information A transmitter to convert the information into data signals compatible with the communications channel A communications channel A receiver to convert the data signals back into a form the destination can understand The destination of the information This process is shown in Figure 1.1. Figure 1.1 Communications process The transmitter encodes the information into a suitable form to be transmitted over the communications channel. The communications channel moves this signal as electromagnetic energy from the source to one or more destination receivers. The channel may convert this energy from one form to another, such as electrical to optical signals, whilst maintaining the integrity of the information so the recipient can understand the message sent by the transmitter. For the communications to be successful the source and destination must use a mutually agreed method of conveying the data. The main factors to be considered are: The form of signaling and the magnitude(s) of the signals to be used The type of communications link (twisted pair, coaxial, optic fiber, radio etc) The arrangement of signals to form character codes from which the message can be constructed The methods of controlling the flow of data The procedures for detecting and correcting errors in the transmission The form of the physical connections is defined by interface standards, some agreed coding is applied to the message and the rules controlling the data flow and detection and correction of errors are known as the protocol. An interface standard defines the electrical and mechanical aspects of the interface to allow the communications equipment from different manufacturers to operate together. A typical example is the EIA/TIA-232-E interface standard. This specifies the following three components:
3 Electrical signal characteristics defining the allowable voltage levels, grounding characteristics etc Mechanical characteristics defining the connector arrangements and pin assignments Functional description of the interchange circuits defining the function of the various data, timing and control signals used at the interface It should be emphasized that the interface standard only defines the electrical and mechanical aspects of the interface between devices and does not cover how data is transferred between them. A wide variety of codes have been used for communications purposes. Early telegraph communications used Morse code with human operators as transmitter and receiver. The Baudot code introduced a constant 5-bit code length for use with mechanical telegraph transmitters and receivers. The commonly used codes for data communications today are the Extended Binary Coded Decimal Interchange Code (EBCIDIC) and the American Standards Committee for Information Interchange (ASCII). A protocol is essential for defining the common message format and procedures for transferring data between all devices on the network. It includes the following important features: Initialization: Initializes the protocol parameters and commences the data transmission Framing and synchronization: Defines the start and end of the frame and how the receiver can synchronize to the data stream Flow control: Ensures that the receiver is able to advise the transmitter to regulate the data flow and ensure no data is lost. Line control: Used with half-duplex links to reverse the roles of transmitter and receiver and begin transmission in the other direction. Error control: Provides techniques to check the accuracy of the received data to identify transmission errors. These include Block Redundancy checks and cyclic redundancy checks Time out control: Procedures for transmitters to retry or abort transmission when acknowledgments are not received within agreed time limits Xmodem or Kermit for asynchronous file transmission Binary synchronous protocol (BSC), synchronous data link control (SDLC) or high level data link control (HDLC) for synchronous transmissions Industrial protocols such as manufacturing automation protocol (MAP), technical office protocol (TOP), Modbus, Data Highway Plus, HART, Profibus, Foundation Fieldbus, etc
4 An analog communications channel conveys analog signals that are changing continuously in both frequency and amplitude. These signals are commonly used for audio and video communication as illustrated in Figure 1.2 and Figure 1.3. Figure 1.2 Analog signal Figure 1.3 Digital signal As the signal travels along a communications channel its amplitude decreases as the physical medium resists the flow of the electromagnetic energy. This effect is known as signal attenuation. With electrical signaling some materials such as copper are very efficient conductors of electrical energy. However, all conductors contain impurities that
5 resist the movement of the electrons that constitute the electric current. The resistance of the conductors causes some of the electrical energy of the signal to be converted to heat energy as the signal progresses along the cable resulting in a continuous decrease in the electrical signal. The signal attenuation is measured in terms of signal loss per unit length of the cable, typically db/km. Figure 1.4 Signal attenuation To allow for attenuation, a limit is set for the maximum length of the communications channel. This is to ensure that the attenuated signal arriving at the receiver is of sufficient amplitude to be reliably detected and correctly interpreted. If the channel is longer than this maximum length, amplifiers or repeaters must be used at intervals along the channel to restore the signal to acceptable levels. Figure 1.5 Signal repeaters Signal attenuation increases as the frequency increases. This causes distortion to practical signals containing a range of frequencies. This is illustrated in Figure 1.4 where the rise-times of the attenuated signals progressively decrease as the signal travels through the channel, caused by the greater attenuation of the high frequency components. This problem can be overcome by the use of amplifiers that amplify the higher frequencies by greater amounts.
6 The quantity of information a channel can convey over a given period is determined by its ability to handle the rate of change of the signal, that is its frequency. An analog signal varies between a minimum and maximum frequency and the difference between those frequencies is the bandwidth of that signal. The bandwidth of an analog channel is the difference between the highest and lowest frequencies that can be reliably received over the channel. These frequencies are often those at which the signal has fallen to half the power relative to the mid-band frequencies, referred to as 3 db points. In which case the bandwidth is known as the 3 db bandwidth. Figure 1.6 Channel bandwidth Digital signals are made up of a large number of frequency components, but only those within the bandwidth of the channel will be able to be received. It follows that the larger the bandwidth of the channel, the higher the data transfer rate can be and more high frequency components of the digital signal can be transported, and so a more accurate reproduction of the transmitted signal can be received. Figure 1.7 Effect of channel bandwidth on digital signal
7 The maximum data transfer rate (C) of the transmission channel can be determined from its bandwidth, by use of the following formula derived by Shannon. C= 2Blog 2 M bps Where B = bandwidth in hertz and M levels are used for each signaling element. In the special case where only two levels, ON and OFF are used (binary), M = 2 and C = 2 B. As an example, the maximum data transfer rate for a PSTN channel of bandwidth 3200 hertz carrying a binary signal would be = 6400 bps. The achievable data transfer rate is reduced to ½ of 6400 because of the Nyquist rate. It is further reduced in practical situations because of the presence of noise on the channel to approximately 2400 bps unless some modulation system is used. As the signals pass through a communications channel the atomic particles and molecules in the transmission medium vibrate and emit random electromagnetic signals as noise. The strength of the transmitted signal is normally large relative to the noise signal. However, as the signal travels through the channel and is attenuated, its level can approach that of the noise. When the wanted signal is not significantly higher than the background noise, the receiver cannot separate the data from the noise and communication errors occur. An important parameter of the channel is the ratio of the power of the received signal (S) to the power of the noise signal (N). The ratio S/N is called the signal to noise ratio, which is normally expressed in decibels, abbreviated to db. S/N = 10 log 10 (S/N) db A high signal to noise ratio means that the wanted signal power is high compared to the noise level, resulting in good quality signal reception. The theoretical maximum data transfer rate for a practical channel can be calculated using the Shannon-Hartley law, which states: C = B log 2 (1+S/N) bps Where C = data rate in bps B = bandwidth of the channel in hertz S = signal power in watts and N is the noise power in watts It can be seen from this formula that increasing the bandwidth or increasing the signal to noise ratio will allow increases to the data rate, and that a relatively small increase in bandwidth is equivalent to a much greater increase in signal to noise ratio. Digital transmission channels make use of higher bandwidths and digital repeaters or regenerators to regenerate the signals at regular intervals and maintain acceptable signal to noise ratios. The degraded signals received at the regenerator are detected, then retimed and retransmitted as nearly perfect replicas of the original digital signals, as shown in Figure 1.8. Provided the signal to noise ratios are maintained in each link, there is no accumulated noise on the signal, even when transmitted thousands of kilometers.
8 Figure 1.8 Digital link A simplex channel is unidirectional and allows data to flow in one direction only, as shown in Figure 1.9. Public radio broadcasting is an example of a simplex transmission. The radio station transmits the broadcast program, but does not receive any signals back from your radio receiver. Figure 1.9 Simplex transmission This has limited use for data transfer purposes, as we invariably require the flow of data in both directions to control the transfer process, acknowledge data etc. Half-duplex transmission allows us to provide simplex communication in both directions over a single channel, as shown in Figure Here the transmitter at station A sends data to a receiver at station B. A line turnaround procedure takes place whenever transmission is required in the opposite direction. The station B transmitter is then enabled and communicates with the receiver at station A. The delay in the line turnaround procedures reduces the available data throughput of the communications channel.
9 Figure 1.10 Half-duplex transmission A full-duplex channel gives simultaneous communications in both directions, as shown in Figure Figure 1.11 Full-duplex transmission Data communications depends on the timing of the signal generation and reception being kept correct throughout the message transmission. The receiver needs to look at the incoming data at the correct instants before determining whether a 1 or 0 was transmitted. The process of selecting and maintaining these sampling times is called synchronization. In order to synchronize their transmissions, the transmitting and receiving devices need to agree on the length of the code elements to be used, known as the bit time. The receiver needs to extract the transmitted clock signal encoded into the received data stream. By synchronizing the bit time of the receiver s clock with that encoded by the sender, the receiver is able to determine the right times to detect the data transitions in the message and correctly receive the message. The devices at both ends of a digital channel can synchronize themselves using either asynchronous or synchronous transmission as outlined below.
10 Here the transmitter and receiver operate independently, and exchange a synchronizing pattern at the start of each message code element (frame). There is no fixed relationship between one message frame and the next, such as a computer keyboard input with potentially long random pauses between keystrokes. Figure 1.12 Asynchronous data transmission At the receiver the channel is sampled at a high rate, typically in excess of 16 times the bit rate of the data channel, to accurately determine the centers of the synchronizing pattern (start bit) and its duration (bit time). Figure 1.13 Clock estimation at receiver The data bits are then determined by the receiver sampling the channel at intervals corresponding to the centers of each transmitted bit. These are estimated by delaying multiples of the bit time from the centers of the start bit. For an eight-bit serial transmission, this sampling is repeated for each of the eight data bits then a final sample is made during the ninth time interval. This sample is to identify the stop bit and confirm that the synchronization has been maintained to the end of the message frame. Figure 1.14 illustrates the asynchronous data reception process.
11 Figure 1.14 Asynchronous data reception The receiver here is initially synchronized to the transmitter then maintains this synchronization throughout the continuous transmission. This is achieved by special data coding schemes, such as Manchester encoding, which ensure that the transmitted clock is continuously encoded into the transmitted data stream. This enables the synchronization to be maintained at any receiver right to the last bit of the message, which could be as large as 4500 bytes ( bits). This allows larger frames of data to be efficiently transferred at higher data rates. The synchronous system packs many characters together and sends them as a continuous stream, called a block. For each transmission block there is a preamble, containing the start delimiter for initial synchronization purposes and information about the block, and a post-amble, to give error checking, etc. An example of a synchronous transmission block is shown in Figure Understandably all highspeed data transfer systems utilize synchronous transmission systems to achieve fast, accurate transfers of large blocks of data. Figure 1.15 Synchronous transmission block
12 Manchester is a bi-phase signal-encoding scheme used in Ethernet LANs. The direction of the transition in mid-interval (negative to positive or positive to negative) indicates the value (1 or 0, respectively) and provides the clocking. The Manchester codes have the advantage that they are self-clocking. Even a sequence of one thousand 0s will have a transition in every bit; hence the receiver will not lose synchronization. The price paid for this is a bandwidth requirement double that which is required by the RZ-type methods. The Manchester scheme follows these rules: +V and V voltage levels are used There is a transition from one to the other voltage level halfway through each bit interval There may or may not be a transition at that start of each bit interval, depending on whether the bit value is a 0 or 1 For a 1 bit, the transition is always from a V to +V; for a 0 bit, the transition is always from a +V to a V In Manchester encoding, the beginning of a bit interval is used merely to set the stage. The activity in the middle of each bit interval determines the bit value: upward transition for a 1 bit, downward for a 0 bit. Differential Manchester is a bi-phase signal-encoding scheme used in token ring LANs. The presence or absence of a transition at the beginning of a bit interval indicates the value; the transition in mid-interval just provides the clocking. For electrical signals, bit values will generally be represented by one of three possible voltage levels: positive (+V), zero (0 V), or negative ( V). Any two of these levels are needed for example, + V and V. There is a transition in the middle of each bit interval. This makes the encoding method self-clocking, and helps avoid signal distortion due to DC signal components. For one of the possible bit values but not the other, there will be a transition at the start of any given bit interval. For example, in a particular implementation, there may be a signal transition for a 1 bit. In differential Manchester encoding, the presence or absence of a transition at the beginning of the bit interval determines the bit value. In effect, 1 bit produces vertical signal patterns; 0 bits produce horizontal patterns. The transition in the middle of the interval is just for timing. The RZ-type codes consume only half the bandwidth taken up by the Manchester codes. However, they are not self-clocking since a sequence of a thousand 0s will result in no movement on the transmission medium at all. RZ is a bipolar signal-encoding scheme that uses transition coding to return the signal to a zero voltage during part of each bit interval. It is self-clocking.
13 In the differential version, the defining voltage (the voltage associated with the first half of the bit interval) changes for each 1 bit, and remains unchanged for each 0 bit. In the non-differential version, the defining voltage changes only when the bit value changes, so that the same defining voltages are always associated with 0 and 1. For example, +5 volts may define a 1, and 5 volts may define a 0. NRZ is a bipolar encoding scheme. In the non-differential version it associates, for example, +5 V with 1 and 5 V with 0. In the differential version, it changes voltages between bit intervals for 1 values but not for 0 values. This means that the encoding changes during a transmission. For example, 0 may be a positive voltage during one part, and a negative voltage during another part, depending on the last occurrence of a 1. The presence or absence of a transition indicates a bit value, not the voltage level. MLT-3 is a three-level encoding scheme that can also scramble data. This scheme is one proposed for use in FDDI networks. The MLT-3 signal-encoding scheme uses three voltage levels (including a zero level) and changes levels only when a 1 occurs. It follows these rules: +V, 0 V, and V voltage levels are used The voltage remains the same during an entire bit interval; that is, there are no transitions in the middle of a bit interval The voltage level changes in succession; from +V to 0 V to V to 0 V to +V, and so on The voltage level changes only for a 1 bit MLT-3 is not self-clocking, so that a synchronization sequence is needed to make sure the sender and receiver are using the same timing. The Manchester codes, as used for 10 Mbps Ethernet, are self-clocking but consume unnecessary bandwidth. For this reason, it is not possible to use it for 100 Mbps Ethernet over CAT5 cable. A solution to the problem is to revert back to one of the more bandwidth efficient methods such as NRZ or RZ. The problem with these, however, is that they are not self-clocking and hence the receiver loses synchronization if several zeros are transmitted sequentially. This problem, in turn, is overcome by using the 4B/5B technique. The 4B/5B technique codes each group of four bits into a five-bit code. For example, the binary pattern 0110 is coded into the five-bit pattern This code table has been designed in such a way that no combination of data can ever be encoded with more than 3 zeros on a row. This allows the carriage of 100 Mbps data by transmitting at 125 MHz, as opposed to the 200 Mbps required by Manchester encoding.
14 Table 1.1 4B/5B data coding All practical data communications channels are subject to noise, particularly where equipment is situated in industrial environments with high electrical noise, such as electromagnetic radiation from adjacent equipment or electromagnetic induction from adjacent cables. As a consequence the received data may contain errors. To ensure reliable data communication we need to check the accuracy of each message. Asynchronous systems often use a single bit checksum, the parity bit, for each message, calculated from the seven or eight data bits in the message. Longer messages require more complex checksum calculations to be effective. For example the longitudinal redundancy check (LRC) calculates an additional byte covering the content of the message (up to 15 bytes) while an arithmetic checksum (calculates two additional bytes) can be used for messages up to 50 bytes in length. Most high-speed local area networks uses a 32-bit cyclic redundancy check (CRC). The cyclic redundancy check (CRC) enables detection of errors with very high accuracy in messages of any length. So, for example, we can detect the presence of a single bit in error in a synchronous data frame containing bits. The CRC works by treating all the bits of the message block as one binary number that is then divided by a known polynomial. For a 32-bit CRC this is a specific 32-bit generator, specially chosen to detect very high percentages of errors, including all error sequences of less than 32 bits. The remainder found after this division process is the CRC. Calculation of the CRC is carried out by the hardware in the transmission interface of LAN adapter cards.
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1 [1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg) 1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
(1) Describe the process by which mercury atoms become excited in a fluorescent tube (3)
 Q1. (a) A fluorescent tube is filled with mercury vapour at low pressure. In order to emit electromagnetic radiation the mercury atoms must first be excited. (i) What is meant by an excited atom? (1) (ii)
Q1. (a) A fluorescent tube is filled with mercury vapour at low pressure. In order to emit electromagnetic radiation the mercury atoms must first be excited. (i) What is meant by an excited atom? (1) (ii)
Strain gauge and rosettes
 Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
the total number of electrons passing through the lamp.
 1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
6.003: Signals and Systems. Modulation
 6.003: Signals and Systems Modulation May 6, 200 Communications Systems Signals are not always well matched to the media through which we wish to transmit them. signal audio video internet applications
6.003: Signals and Systems Modulation May 6, 200 Communications Systems Signals are not always well matched to the media through which we wish to transmit them. signal audio video internet applications
Calculating the propagation delay of coaxial cable
 Your source for quality GNSS Networking Solutions and Design Services! Page 1 of 5 Calculating the propagation delay of coaxial cable The delay of a cable or velocity factor is determined by the dielectric
Your source for quality GNSS Networking Solutions and Design Services! Page 1 of 5 Calculating the propagation delay of coaxial cable The delay of a cable or velocity factor is determined by the dielectric
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Information Theory Θεωρία της Πληροφορίας. Vasos Vassiliou
 Information Theory Θεωρία της Πληροφορίας Vasos Vassiliou Network/Link Design Factors Transmission media Signals are transmitted over transmission media Examples: telephone cables, fiber optics, twisted
Information Theory Θεωρία της Πληροφορίας Vasos Vassiliou Network/Link Design Factors Transmission media Signals are transmitted over transmission media Examples: telephone cables, fiber optics, twisted
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Elements of Information Theory
 Elements of Information Theory Model of Digital Communications System A Logarithmic Measure for Information Mutual Information Units of Information Self-Information News... Example Information Measure
Elements of Information Theory Model of Digital Communications System A Logarithmic Measure for Information Mutual Information Units of Information Self-Information News... Example Information Measure
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Δίκτυα Δακτυλίου. Token Ring - Polling
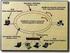 Δίκτυα Δακτυλίου Token Ring - Polling Όλοι οι κόμβοι είναι τοποθετημένοι σε ένα δακτύλιο. Εκπέμπει μόνο ο κόμβος ο οποίος έχει τη σκυτάλη (token). The token consists of a number of octets in a specific
Δίκτυα Δακτυλίου Token Ring - Polling Όλοι οι κόμβοι είναι τοποθετημένοι σε ένα δακτύλιο. Εκπέμπει μόνο ο κόμβος ο οποίος έχει τη σκυτάλη (token). The token consists of a number of octets in a specific
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Modbus basic setup notes for IO-Link AL1xxx Master Block
 n Modbus has four tables/registers where data is stored along with their associated addresses. We will be using the holding registers from address 40001 to 49999 that are R/W 16 bit/word. Two tables that
n Modbus has four tables/registers where data is stored along with their associated addresses. We will be using the holding registers from address 40001 to 49999 that are R/W 16 bit/word. Two tables that
Block Ciphers Modes. Ramki Thurimella
 Block Ciphers Modes Ramki Thurimella Only Encryption I.e. messages could be modified Should not assume that nonsensical messages do no harm Always must be combined with authentication 2 Padding Must be
Block Ciphers Modes Ramki Thurimella Only Encryption I.e. messages could be modified Should not assume that nonsensical messages do no harm Always must be combined with authentication 2 Padding Must be
Capacitors - Capacitance, Charge and Potential Difference
 Capacitors - Capacitance, Charge and Potential Difference Capacitors store electric charge. This ability to store electric charge is known as capacitance. A simple capacitor consists of 2 parallel metal
Capacitors - Capacitance, Charge and Potential Difference Capacitors store electric charge. This ability to store electric charge is known as capacitance. A simple capacitor consists of 2 parallel metal
Mean bond enthalpy Standard enthalpy of formation Bond N H N N N N H O O O
 Q1. (a) Explain the meaning of the terms mean bond enthalpy and standard enthalpy of formation. Mean bond enthalpy... Standard enthalpy of formation... (5) (b) Some mean bond enthalpies are given below.
Q1. (a) Explain the meaning of the terms mean bond enthalpy and standard enthalpy of formation. Mean bond enthalpy... Standard enthalpy of formation... (5) (b) Some mean bond enthalpies are given below.
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Monolithic Crystal Filters (M.C.F.)
 Monolithic Crystal Filters (M.C.F.) MCF (MONOLITHIC CRYSTAL FILTER) features high quality quartz resonators such as sharp cutoff characteristics, low loss, good inter-modulation and high stability over
Monolithic Crystal Filters (M.C.F.) MCF (MONOLITHIC CRYSTAL FILTER) features high quality quartz resonators such as sharp cutoff characteristics, low loss, good inter-modulation and high stability over
ΚΥΠΡΙΑΚΟΣ ΣΥΝΔΕΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY 21 ος ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ Δεύτερος Γύρος - 30 Μαρτίου 2011
 Διάρκεια Διαγωνισμού: 3 ώρες Απαντήστε όλες τις ερωτήσεις Μέγιστο Βάρος (20 Μονάδες) Δίνεται ένα σύνολο από N σφαιρίδια τα οποία δεν έχουν όλα το ίδιο βάρος μεταξύ τους και ένα κουτί που αντέχει μέχρι
Διάρκεια Διαγωνισμού: 3 ώρες Απαντήστε όλες τις ερωτήσεις Μέγιστο Βάρος (20 Μονάδες) Δίνεται ένα σύνολο από N σφαιρίδια τα οποία δεν έχουν όλα το ίδιο βάρος μεταξύ τους και ένα κουτί που αντέχει μέχρι
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Assalamu `alaikum wr. wb.
 LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump
LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump
Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών: OSPF Cost
 Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών: OSPF Cost Πανεπιστήμιο Πελοποννήσου Τμήμα Επιστήμης & Τεχνολογίας Τηλεπικοινωνιών Ευάγγελος Α. Κοσμάτος Basic OSPF Configuration Υλοποίηση Δικτυακών Υποδομών
Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών: OSPF Cost Πανεπιστήμιο Πελοποννήσου Τμήμα Επιστήμης & Τεχνολογίας Τηλεπικοινωνιών Ευάγγελος Α. Κοσμάτος Basic OSPF Configuration Υλοποίηση Δικτυακών Υποδομών
Potential Dividers. 46 minutes. 46 marks. Page 1 of 11
 Potential Dividers 46 minutes 46 marks Page 1 of 11 Q1. In the circuit shown in the figure below, the battery, of negligible internal resistance, has an emf of 30 V. The pd across the lamp is 6.0 V and
Potential Dividers 46 minutes 46 marks Page 1 of 11 Q1. In the circuit shown in the figure below, the battery, of negligible internal resistance, has an emf of 30 V. The pd across the lamp is 6.0 V and
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
(C) 2010 Pearson Education, Inc. All rights reserved.
 Connectionless transmission with datagrams. Connection-oriented transmission is like the telephone system You dial and are given a connection to the telephone of fthe person with whom you wish to communicate.
Connectionless transmission with datagrams. Connection-oriented transmission is like the telephone system You dial and are given a connection to the telephone of fthe person with whom you wish to communicate.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ιπλωµατική Εργασία του φοιτητή του τµήµατος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Ηλεκτρονικών
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ιπλωµατική Εργασία του φοιτητή του τµήµατος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Ηλεκτρονικών
Code Breaker. TEACHER s NOTES
 TEACHER s NOTES Time: 50 minutes Learning Outcomes: To relate the genetic code to the assembly of proteins To summarize factors that lead to different types of mutations To distinguish among positive,
TEACHER s NOTES Time: 50 minutes Learning Outcomes: To relate the genetic code to the assembly of proteins To summarize factors that lead to different types of mutations To distinguish among positive,
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων. Εξάμηνο 7 ο
 Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής
 Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
UNIVERSITY OF CALIFORNIA. EECS 150 Fall ) You are implementing an 4:1 Multiplexer that has the following specifications:
 UNIVERSITY OF CALIFORNIA Department of Electrical Engineering and Computer Sciences EECS 150 Fall 2001 Prof. Subramanian Midterm II 1) You are implementing an 4:1 Multiplexer that has the following specifications:
UNIVERSITY OF CALIFORNIA Department of Electrical Engineering and Computer Sciences EECS 150 Fall 2001 Prof. Subramanian Midterm II 1) You are implementing an 4:1 Multiplexer that has the following specifications:
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΙΣΧΥΟΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΙΣΧΥΟΣ Προοπτικές Εναρμόνισης της Ελληνικής Αγοράς Ηλεκτρικής Ενέργειας με τις Προδιαγραφές του Μοντέλου
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΙΣΧΥΟΣ Προοπτικές Εναρμόνισης της Ελληνικής Αγοράς Ηλεκτρικής Ενέργειας με τις Προδιαγραφές του Μοντέλου
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Right Rear Door. Let's now finish the door hinge saga with the right rear door
 Right Rear Door Let's now finish the door hinge saga with the right rear door You may have been already guessed my steps, so there is not much to describe in detail. Old upper one file:///c /Documents
Right Rear Door Let's now finish the door hinge saga with the right rear door You may have been already guessed my steps, so there is not much to describe in detail. Old upper one file:///c /Documents
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
ΜΕΛΕΤΗ ΚΑΙ ΠΡΟΣΟΜΟΙΩΣΗ ΙΑΜΟΡΦΩΣΕΩΝ ΣΕ ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΕΠΙΚΟΙΝΩΝΙΩΝ.
 Τµήµα Ηλεκτρονικής ΜΕΛΕΤΗ ΚΑΙ ΠΡΟΣΟΜΟΙΩΣΗ ΙΑΜΟΡΦΩΣΕΩΝ ΣΕ ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΕΠΙΚΟΙΝΩΝΙΩΝ. Σπουδαστής: Γαρεφαλάκης Ιωσήφ Α.Μ. 3501 Επιβλέπων καθηγητής : Ασκορδαλάκης Παντελής. -Χανιά 2010- ΠΕΡΙΛΗΨΗ : Η παρούσα
Τµήµα Ηλεκτρονικής ΜΕΛΕΤΗ ΚΑΙ ΠΡΟΣΟΜΟΙΩΣΗ ΙΑΜΟΡΦΩΣΕΩΝ ΣΕ ΨΗΦΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΕΠΙΚΟΙΝΩΝΙΩΝ. Σπουδαστής: Γαρεφαλάκης Ιωσήφ Α.Μ. 3501 Επιβλέπων καθηγητής : Ασκορδαλάκης Παντελής. -Χανιά 2010- ΠΕΡΙΛΗΨΗ : Η παρούσα
ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ. του φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και. Τεχνολογίας Υπολογιστών της Πολυτεχνικής Σχολής του. Πανεπιστημίου Πατρών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΜΗΧΑΝΙΚΗΣ ΜΕΤΑΤΡΟΠΗΣ ΕΝΕΡΓΕΙΑΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ του φοιτητή του
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΜΗΧΑΝΙΚΗΣ ΜΕΤΑΤΡΟΠΗΣ ΕΝΕΡΓΕΙΑΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ του φοιτητή του
Démographie spatiale/spatial Demography
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Démographie spatiale/spatial Demography Session 1: Introduction to spatial demography Basic concepts Michail Agorastakis Department of Planning & Regional Development Άδειες Χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Démographie spatiale/spatial Demography Session 1: Introduction to spatial demography Basic concepts Michail Agorastakis Department of Planning & Regional Development Άδειες Χρήσης
10.7 Performance of Second-Order System (Unit Step Response)
 Lecture Notes on Control Systems/D. Ghose/0 57 0.7 Performance of Second-Order System (Unit Step Response) Consider the second order system a ÿ + a ẏ + a 0 y = b 0 r So, Y (s) R(s) = b 0 a s + a s + a
Lecture Notes on Control Systems/D. Ghose/0 57 0.7 Performance of Second-Order System (Unit Step Response) Consider the second order system a ÿ + a ẏ + a 0 y = b 0 r So, Y (s) R(s) = b 0 a s + a s + a
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Γιπλυμαηική Δπγαζία. «Ανθπυποκενηπικόρ ζσεδιαζμόρ γέθςπαρ πλοίος» Φοςζιάνηρ Αθανάζιορ. Δπιβλέπυν Καθηγηηήρ: Νηθφιανο Π. Βεληίθνο
 ΔΘΝΙΚΟ ΜΔΣΟΒΙΟ ΠΟΛΤΣΔΥΝΔΙΟ ΥΟΛΗ ΝΑΤΠΗΓΩΝ ΜΗΥΑΝΟΛΟΓΩΝ ΜΗΥΑΝΙΚΩΝ Γιπλυμαηική Δπγαζία «Ανθπυποκενηπικόρ ζσεδιαζμόρ γέθςπαρ πλοίος» Φοςζιάνηρ Αθανάζιορ Δπιβλέπυν Καθηγηηήρ: Νηθφιανο Π. Βεληίθνο Σπιμελήρ Δξεηαζηική
ΔΘΝΙΚΟ ΜΔΣΟΒΙΟ ΠΟΛΤΣΔΥΝΔΙΟ ΥΟΛΗ ΝΑΤΠΗΓΩΝ ΜΗΥΑΝΟΛΟΓΩΝ ΜΗΥΑΝΙΚΩΝ Γιπλυμαηική Δπγαζία «Ανθπυποκενηπικόρ ζσεδιαζμόρ γέθςπαρ πλοίος» Φοςζιάνηρ Αθανάζιορ Δπιβλέπυν Καθηγηηήρ: Νηθφιανο Π. Βεληίθνο Σπιμελήρ Δξεηαζηική
CMOS Technology for Computer Architects
 CMOS Technology for Computer Architects Iakovos Mavroidis Giorgos Passas Manolis Katevenis Lecture 13: On chip SRAM Technology FORTH ICS / EURECCA & UoC GREECE ABC A A E F A BCDAECF A AB C DE ABCDAECF
CMOS Technology for Computer Architects Iakovos Mavroidis Giorgos Passas Manolis Katevenis Lecture 13: On chip SRAM Technology FORTH ICS / EURECCA & UoC GREECE ABC A A E F A BCDAECF A AB C DE ABCDAECF
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS
 CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική»
 Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική» Μεταπτυχιακή Διατριβή Τίτλος Διατριβής Επίκαιρα Θέματα Ηλεκτρονικής Διακυβέρνησης Ονοματεπώνυμο Φοιτητή Σταμάτιος
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική» Μεταπτυχιακή Διατριβή Τίτλος Διατριβής Επίκαιρα Θέματα Ηλεκτρονικής Διακυβέρνησης Ονοματεπώνυμο Φοιτητή Σταμάτιος
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 11/3/2006
 ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 11/3/26 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι το 1 εκτός αν ορίζεται διαφορετικά στη διατύπωση
ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 11/3/26 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι το 1 εκτός αν ορίζεται διαφορετικά στη διατύπωση
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΥΨΗΛΩΝ ΤΑΣΕΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΥΨΗΛΩΝ ΤΑΣΕΩΝ Διπλωµατική Εργασία Της Φοιτήτριας του Τµήµατος Ηλεκτρολόγων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΥΨΗΛΩΝ ΤΑΣΕΩΝ Διπλωµατική Εργασία Της Φοιτήτριας του Τµήµατος Ηλεκτρολόγων
«Χρήσεις γης, αξίες γης και κυκλοφοριακές ρυθμίσεις στο Δήμο Χαλκιδέων. Η μεταξύ τους σχέση και εξέλιξη.»
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ: «Χρήσεις γης, αξίες γης και κυκλοφοριακές ρυθμίσεις στο Δήμο Χαλκιδέων.
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ: «Χρήσεις γης, αξίες γης και κυκλοφοριακές ρυθμίσεις στο Δήμο Χαλκιδέων.
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
PhysicsAndMathsTutor.com 1
 PhysicsAndMathsTutor.com 1 Q1. The magnetic flux through a coil of N turns is increased uniformly from zero to a maximum value in a time t. An emf, E, is induced across the coil. What is the maximum value
PhysicsAndMathsTutor.com 1 Q1. The magnetic flux through a coil of N turns is increased uniformly from zero to a maximum value in a time t. An emf, E, is induced across the coil. What is the maximum value
Αναερόβια Φυσική Κατάσταση
 Αναερόβια Φυσική Κατάσταση Γιάννης Κουτεντάκης, BSc, MA. PhD Αναπληρωτής Καθηγητής ΤΕΦΑΑ, Πανεπιστήµιο Θεσσαλίας Περιεχόµενο Μαθήµατος Ορισµός της αναερόβιας φυσικής κατάστασης Σχέσης µε µηχανισµούς παραγωγής
Αναερόβια Φυσική Κατάσταση Γιάννης Κουτεντάκης, BSc, MA. PhD Αναπληρωτής Καθηγητής ΤΕΦΑΑ, Πανεπιστήµιο Θεσσαλίας Περιεχόµενο Μαθήµατος Ορισµός της αναερόβιας φυσικής κατάστασης Σχέσης µε µηχανισµούς παραγωγής
Surface Mount Multilayer Chip Capacitors for Commodity Solutions
 Surface Mount Multilayer Chip Capacitors for Commodity Solutions Below tables are test procedures and requirements unless specified in detail datasheet. 1) Visual and mechanical 2) Capacitance 3) Q/DF
Surface Mount Multilayer Chip Capacitors for Commodity Solutions Below tables are test procedures and requirements unless specified in detail datasheet. 1) Visual and mechanical 2) Capacitance 3) Q/DF
Δίκτυα Καθοριζόμενα από Λογισμικό
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δίκτυα Καθοριζόμενα από Λογισμικό Exercise Session 4: Familiarization with GNU Radio Τμήμα Επιστήμης Υπολογιστών SDR Assignment using GNU Radio Manolis Surligas
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Δίκτυα Καθοριζόμενα από Λογισμικό Exercise Session 4: Familiarization with GNU Radio Τμήμα Επιστήμης Υπολογιστών SDR Assignment using GNU Radio Manolis Surligas
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Διπλωματική Εργασία του φοιτητή του τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Ηλεκτρονικών
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Διπλωματική Εργασία του φοιτητή του τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Ηλεκτρονικών
Εγκατάσταση λογισμικού και αναβάθμιση συσκευής Device software installation and software upgrade
 Για να ελέγξετε το λογισμικό που έχει τώρα η συσκευή κάντε κλικ Menu > Options > Device > About Device Versions. Στο πιο κάτω παράδειγμα η συσκευή έχει έκδοση λογισμικού 6.0.0.546 με πλατφόρμα 6.6.0.207.
Για να ελέγξετε το λογισμικό που έχει τώρα η συσκευή κάντε κλικ Menu > Options > Device > About Device Versions. Στο πιο κάτω παράδειγμα η συσκευή έχει έκδοση λογισμικού 6.0.0.546 με πλατφόρμα 6.6.0.207.
Δίκτυα Επικοινωνιών ΙΙ: OSPF Configuration
 Δίκτυα Επικοινωνιών ΙΙ: OSPF Configuration Δρ. Απόστολος Γκάμας Διδάσκων 407/80 gkamas@uop.gr Δίκτυα Επικοινωνιών ΙΙ Διαφάνεια 1 1 Dynamic Routing Configuration Router (config) # router protocol [ keyword
Δίκτυα Επικοινωνιών ΙΙ: OSPF Configuration Δρ. Απόστολος Γκάμας Διδάσκων 407/80 gkamas@uop.gr Δίκτυα Επικοινωνιών ΙΙ Διαφάνεια 1 1 Dynamic Routing Configuration Router (config) # router protocol [ keyword
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Physical DB Design. B-Trees Index files can become quite large for large main files Indices on index files are possible.
 B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
Nuclear Physics 5. Name: Date: 8 (1)
 Name: Date: Nuclear Physics 5. A sample of radioactive carbon-4 decays into a stable isotope of nitrogen. As the carbon-4 decays, the rate at which the amount of nitrogen is produced A. decreases linearly
Name: Date: Nuclear Physics 5. A sample of radioactive carbon-4 decays into a stable isotope of nitrogen. As the carbon-4 decays, the rate at which the amount of nitrogen is produced A. decreases linearly
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
 9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Section 1: Listening and responding. Presenter: Niki Farfara MGTAV VCE Seminar 7 August 2016
 Section 1: Listening and responding Presenter: Niki Farfara MGTAV VCE Seminar 7 August 2016 Section 1: Listening and responding Section 1: Listening and Responding/ Aκουστική εξέταση Στο πρώτο μέρος της
Section 1: Listening and responding Presenter: Niki Farfara MGTAV VCE Seminar 7 August 2016 Section 1: Listening and responding Section 1: Listening and Responding/ Aκουστική εξέταση Στο πρώτο μέρος της
Precision Metal Film Fixed Resistor Axial Leaded
 Features EIA standard colour-coding Non-Flame type available Low noise and voltage coefficient Low temperature coefficient range Wide precision range in small package Too low or too high ohmic value can
Features EIA standard colour-coding Non-Flame type available Low noise and voltage coefficient Low temperature coefficient range Wide precision range in small package Too low or too high ohmic value can
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
EPL 603 TOPICS IN SOFTWARE ENGINEERING. Lab 5: Component Adaptation Environment (COPE)
 EPL 603 TOPICS IN SOFTWARE ENGINEERING Lab 5: Component Adaptation Environment (COPE) Performing Static Analysis 1 Class Name: The fully qualified name of the specific class Type: The type of the class
EPL 603 TOPICS IN SOFTWARE ENGINEERING Lab 5: Component Adaptation Environment (COPE) Performing Static Analysis 1 Class Name: The fully qualified name of the specific class Type: The type of the class
Solutions to the Schrodinger equation atomic orbitals. Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz
 Solutions to the Schrodinger equation atomic orbitals Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz ybridization Valence Bond Approach to bonding sp 3 (Ψ 2 s + Ψ 2 px + Ψ 2 py + Ψ 2 pz) sp 2 (Ψ 2 s + Ψ 2 px + Ψ 2 py)
Solutions to the Schrodinger equation atomic orbitals Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz ybridization Valence Bond Approach to bonding sp 3 (Ψ 2 s + Ψ 2 px + Ψ 2 py + Ψ 2 pz) sp 2 (Ψ 2 s + Ψ 2 px + Ψ 2 py)
Galatia SIL Keyboard Information
 Galatia SIL Keyboard Information Keyboard ssignments The main purpose of the keyboards is to provide a wide range of keying options, so many characters can be entered in multiple ways. If you are typing
Galatia SIL Keyboard Information Keyboard ssignments The main purpose of the keyboards is to provide a wide range of keying options, so many characters can be entered in multiple ways. If you are typing
Bounding Nonsplitting Enumeration Degrees
 Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
Aluminum Electrolytic Capacitors (Large Can Type)
 Aluminum Electrolytic Capacitors (Large Can Type) Snap-In, 85 C TS-U ECE-S (U) Series: TS-U Features General purpose Wide CV value range (33 ~ 47,000 µf/16 4V) Various case sizes Top vent construction
Aluminum Electrolytic Capacitors (Large Can Type) Snap-In, 85 C TS-U ECE-S (U) Series: TS-U Features General purpose Wide CV value range (33 ~ 47,000 µf/16 4V) Various case sizes Top vent construction
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΟΔΟΝΤΙΑΤΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΟΔΟΝΤΙΚΗΣ ΚΑΙ ΑΝΩΤΕΡΑΣ ΠΡΟΣΘΕΤΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΟΔΟΝΤΙΑΤΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΟΔΟΝΤΙΚΗΣ ΚΑΙ ΑΝΩΤΕΡΑΣ ΠΡΟΣΘΕΤΙΚΗΣ ΣΥΓΚΡΙΤΙΚΗ ΜΕΛΕΤΗ ΤΗΣ ΣΥΓΚΡΑΤΗΤΙΚΗΣ ΙΚΑΝΟΤΗΤΑΣ ΟΡΙΣΜΕΝΩΝ ΠΡΟΚΑΤΑΣΚΕΥΑΣΜΕΝΩΝ ΣΥΝΔΕΣΜΩΝ ΑΚΡΙΒΕΙΑΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΟΔΟΝΤΙΑΤΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΟΔΟΝΤΙΚΗΣ ΚΑΙ ΑΝΩΤΕΡΑΣ ΠΡΟΣΘΕΤΙΚΗΣ ΣΥΓΚΡΙΤΙΚΗ ΜΕΛΕΤΗ ΤΗΣ ΣΥΓΚΡΑΤΗΤΙΚΗΣ ΙΚΑΝΟΤΗΤΑΣ ΟΡΙΣΜΕΝΩΝ ΠΡΟΚΑΤΑΣΚΕΥΑΣΜΕΝΩΝ ΣΥΝΔΕΣΜΩΝ ΑΚΡΙΒΕΙΑΣ
Επιβλέπουσα Καθηγήτρια: ΣΟΦΙΑ ΑΡΑΒΟΥ ΠΑΠΑΔΑΤΟΥ
 EΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΚΠΑΙΔΕΥΤΙΚΟ ΤΕΧΝΟΛΟΓΙΚΟ ΙΔΡΥΜΑ ΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ ΤΜΗΜΑ ΔΗΜΟΣΙΩΝ ΣΧΕΣΕΩΝ & ΕΠΙΚΟΙΝΩΝΙΑΣ Ταχ. Δ/νση : Λεωφ. Αντ.Τρίτση, Αργοστόλι Κεφαλληνίας Τ.Κ. 28 100 τηλ. : 26710-27311 fax : 26710-27312
EΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΚΠΑΙΔΕΥΤΙΚΟ ΤΕΧΝΟΛΟΓΙΚΟ ΙΔΡΥΜΑ ΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ ΤΜΗΜΑ ΔΗΜΟΣΙΩΝ ΣΧΕΣΕΩΝ & ΕΠΙΚΟΙΝΩΝΙΑΣ Ταχ. Δ/νση : Λεωφ. Αντ.Τρίτση, Αργοστόλι Κεφαλληνίας Τ.Κ. 28 100 τηλ. : 26710-27311 fax : 26710-27312
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
