Πειράματα Φυσικής Β Γυμνασίου
|
|
|
- Ἄδραστος Γιάνναρης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΕΚΦΕ Α Αν. Αττικής - Υπεύθυνος Κ. Παπαμιχάλης Εργαστηριακές ασκήσεις Φυσικής Β - Εισαγωγή ΕΙΣΑΓΩΓΗ 1. Πείραμα και θεωρία Πειράματα Φυσικής Β Γυμνασίου Η Φυσική είναι η επιστήμη που διαμόρφωσε και συνεχίζει να διαμορφώνει ο άνθρωπος, στην προσπάθειά του να κατανοήσει και να ερμηνεύσει τα φυσικά φαινόμενα, δηλαδή τις μεταβολές του φυσικού κόσμου που τον περιβάλλει. Για να πετύχει σ αυτή του την προσπάθεια, επινοεί και χρησιμοποιεί κατάλληλες φυσικές έννοιες, και φυσικά μεγέθη, όπως για παράδειγμα, «υλικό σώμα», «βαρύτητα», «ηλεκτρικό πεδίο», ή ακόμα, «μήκος», «ταχύτητα», «ενέργεια», «θερμοκρασία», «φορτίο» κ.ά. Στη συνέχεια, στηριζόμενος στην εμπειρία του, επιχειρεί να βρει και να διατυπώσει σχέσεις μεταξύ των φυσικών μεγεθών, που είναι γνωστές ως φυσικοί νόμοι. Τέλος εντάσσει τους φυσικούς νόμους σε ευρύτερες λογικές κατασκευές, τις φυσικές θεωρίες. Παραδείγματα φυσικών νόμων: α) «Αν αυξήσεις τη θερμοκρασία μιας μεταλλικής ράβδου, αυξάνεται το μήκος της». β) «Αν προσφέρεις θερμότητα στο νερό και η θερμοκρασία του φτάσει τους C, σε ατμοσφαιρική πίεση 1atm, τότε μετατρέπεται από υγρό σε αέριο». γ) «Η μετατόπιση ενός σώματος, όταν κινείται με σταθερή ταχύτητα, είναι ανάλογη με το χρόνο της κίνησής του». Οι νόμοι και οι θεωρίες που διατυπώνονται στο πλαίσιο της Φυσικής δεν είναι αυθαίρετοι. Πρέπει να συμφωνούν με την «πραγματικότητα». Για να ελέγξεις αν αυτό πραγματικά συμβαίνει, πρέπει να καταφύγεις στο πείραμα. Πείραμα ονομάζουμε μια «καλοσχεδιασμένη ερώτηση που κάνει ο άνθρωπος στη φύση», με στόχο να επαληθεύσει ή να διαψεύσει ένα νόμο ή μια εικασία, ή για να ανακαλύψει έναν καινούργιο. Για παράδειγμα, για να ελέγξεις το παράδειγμα (β), δεν έχεις παρά να κάνεις το εξής: Μια μέρα που η ατμοσφαιρική πίεση είναι 1atm να ζεστάνεις νερό σ ένα δοχείο, παρακολουθώντας τη θερμοκρασία του με ένα θερμόμετρο και να ελέγξεις αν πραγματικά μετατρέπεται σε αέριο όταν η ένδειξη του θερμομέτρου φτάσει τους C. Το πείραμα παίζει κυρίαρχο ρόλο στη Φυσική. Αυτό είναι που επιβεβαιώνει ή διαψεύδει τις υποθέσεις, νόμους και τις θεωρίες που διατυπώνει ο άνθρωπος στην προσπάθειά του να κατανοήσει τα φαινόμενα που συμβαίνουν γύρω του. Για το λόγο αυτό η Φυσική χαρακτηρίζεται ως πειραματική επιστήμη. 2. Μέτρα ασφαλείας στο εργαστήριο Όπως και στην καθημερινή μας ζωή, οι κίνδυνοι που μπορεί να παρουσιαστούν κατά τη διενέργεια των πειραμάτων είναι πολλοί. Γι αυτό κατά την εκτέλεση κάθε εργαστηριακής άσκησης πρέπει να είσαι ιδιαίτερα προσεκτικός και πειθαρχημένος. Να ελέγχεις απόλυτα τις κινήσεις σου και να ακολουθείς πιστά τις οδηγίες του καθηγητή σου. Μια από τις δεξιότητες που πρέπει να αποκτήσεις μέσα στο εργαστήριο είναι η ικανότητα να εργάζεσαι με ασφάλεια. Ειδικότερα, όταν είσαι μέσα στο εργαστήριο Φυσικής, είναι απαραίτητο να γνωρίζεις και να εφαρμόζεις τους κανόνες ασφαλείας όπως διατυπώνονται παρακάτω: 1
2 1) Δεν χρησιμοποιώ καμιά συσκευή αν δεν μάθω καλά τον τρόπο λειτουργίας της και αν δεν ζητήσω άδεια από τον καθηγητή μου. 2) Έχω μελετήσει και γνωρίζω τι πρέπει να κάνω για να διεξαχθεί σωστά η εργαστηριακή άσκηση. Για κάθε απορία απευθύνομαι στον καθηγητή μου. 3) Φορώ προστατευτικά γυαλιά και ποδιά, εφ όσον προβλέπεται από τους κανόνες ασφαλείας της άσκησης ή μου το ζητήσει ο καθηγητής μου. 4) Μόλις ολοκληρώσω τη συναρμολόγηση της διάταξης μιας εργαστηριακής άσκησης, καλώ τον καθηγητή μου να την ελέγξει. Σε καμιά περίπτωση δεν αρχίζω την εκτέλεση του πειράματος προτού πραγματοποιηθεί έλεγχος. 5) Ποτέ δεν τροφοδοτώ μια διάταξη με ηλεκτρική τάση αν δεν έχει προηγηθεί έλεγχος από τον καθηγητή μου και δεν έχει δοθεί η άδειά του. 6) Ποτέ δεν ανάβω μια εστία θέρμανσης, χωρίς την άδεια και την επίβλεψη του καθηγητή μου. Θυμάμαι να τη σβήνω αμέσως μετά την εκτέλεση της εργασίας. 7) Δεν πιάνω ποτέ χωρίς αντιθερμικό γάντι σκεύη ή συσκευές που έχουν θερμανθεί είτε από κάποια εστία θέρμανσης είτε λόγω της διέλευσης ηλεκτρικού ρεύματος. 8) Είμαι ιδιαίτερα προσεκτικός όταν χρησιμοποιώ γυάλινα σκεύη. Δεν τα πιέζω και τα κρατώ ή τα τοποθετώ με προσοχή για να μη σπάσουν και με τραυματίσουν. 9) Δεν πιάνω χημικές ουσίες. Όταν έρθει σε επαφή το δέρμα μου ή τα μάτια μου με κάποια χημική ουσία, αμέσως τα ξεπλένω με άφθονο νερό και ειδοποιώ τον καθηγητή μου. 10) Δεν μετακινούμαι άσκοπα από τη θέση μου χωρίς την άδεια του καθηγητή μου. Εργάζομαι υπεύθυνα και δεν κάνω αστεία με τους συμμαθητές μου. Όταν ολοκληρώσεις μια εργαστηριακή άσκηση και καταγράψεις τα πειραματικά αποτελέσματα, δεν πρέπει να ξεχάσεις να κάνεις μια τελευταία εργασία: Να αποσυναρμολογήσεις προσεκτικά τη διάταξη, να καθαρίσεις τον πάγκο και να τακτοποιήσεις τα όργανα και τα υλικά στις θέσεις που θα σου υποδείξει ο καθηγητής σου.
3 ΜΕΤΡΗΣΗ - ΣΦΑΛΜΑΤΑ - ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ 1. Πώς μετράμε ένα μέγεθος; Τι θα κάνεις αν θελήσεις να μετρήσεις το πλάτος του βιβλίου σου; Το πιο πιθανό είναι ότι θα εφαρμόσεις διαδοχικά τις ακόλουθες ενέργειες: Παίρνεις ένα χάρακα (υποδεκάμετρο). Τοποθετείς τη χαραγή του χάρακα που αντιστοιχεί στο μηδέν στο ένα άκρο του βιβλίου. Ευθυγραμμίζεις το χάρακα με την ακμή του βιβλίου. Διαβάζεις την υποδιαίρεση του χάρακα που αντιστοιχεί στο άλλο άκρο της ακμής του βιβλίου. Έστω ότι βρήκες 20,92cm. Μπορείς να ονομάσεις το μήκος της ακμής που μέτρησες με ένα γράμμα (για παράδειγμα το α) και να καταγράψεις το αποτέλεσμα της μέτρησής σου ως εξής: α=20,92cm Αν πάλι θέλεις να μετρήσεις τη μάζα του σώματός σου, αρκεί να ανέβεις πάνω σε μια ζυγαριά. Ο δείκτης ή η ψηφιακή της οθόνη θα σου δείξουν αμέσως ότι η μάζα σου είναι, για παράδειγμα, 53,45 Kg. Αν συμβολίσεις τη μάζα με το γράμμα m, μπορείς τότε να γράψεις: m=53,45kg Στην πρώτη περίπτωση πραγματοποιήσαμε μια μέτρηση μήκους. Στη δεύτερη μια μέτρηση μάζας. Είναι ολοφάνερο ότι ενεργήσαμε με πολύ διαφορετικό τρόπο για να πραγματοποιήσουμε τις δύο παραπάνω μετρήσεις. Ωστόσο και οι δύο διαδικασίες χαρακτηρίζονται με τον ίδιο όρο. Ονομάζονται μετρήσεις. Γιατί άραγε; Ποια είναι τα κοινά τους χαρακτηριστικά; Κατά τη μέτρηση του μήκους, αν ξεχάσουμε τις λεπτομέρειες των ενεργειών μας, αυτό που κάναμε ουσιαστικά ήταν η σύγκριση του μήκους της ακμής του βιβλίου με ένα άλλο μήκος που έχουμε συμφωνήσει να το λέμε εκατοστό του μέτρου (cm). Το cm είναι η μονάδα μέτρησης μήκους που χρησιμοποιήσαμε. Προσδιορίζεται από το χάρακα που διαθέτουμε και από τους κάθε είδους χάρακες, κανόνες, μετροταινίες και άλλα όργανα μέτρησης μήκους που είναι βαθμονομημένα με τη συγκεκριμένη μονάδα. Έτσι βρήκαμε ότι το πλάτος του βιβλίου είναι 20,92 φορές το μήκος του ενός εκατοστού (cm). Το ίδιο όμως κάναμε και κατά τη μέτρηση της μάζας. Η μηχανή (ζυγαριά) έχει κατασκευαστεί έτσι ώστε να μπορεί να συγκρίνει τη μάζα του σώματός μας με μια συγκεκριμένη μάζα (την ίδια για όλες τις παρόμοιες ζυγαριές) που ονομάζεται κιλό (kg). Στην περίπτωση αυτή το αποτέλεσμα που προέκυψε από τη σύγκριση της μάζας του σώματός μας με το κιλό το πληροφορηθήκαμε αυτόματα από το δείκτη και την κλίμακα της μηχανής ή από τη ψηφιακή της οθόνη: Το σώμα που ζυγίσαμε έχει μάζα 53,45 φορές τη μάζα του ενός κιλού. Καταλήγουμε λοιπόν σε έναν ορισμό: Κάθε διαδικασία σύγκρισης δύο ομοειδών μεγεθών (ανεξαρτήτως του τρόπου με τον οποίο πραγματοποιείται και του πόσο εύκολα ή δύσκολα μπορεί να γίνει) ονομάζεται μέτρηση. Από τη μέτρηση ενός μεγέθους προκύπτει πάντοτε ένας αριθμός. Είναι το αποτέλεσμα της σύγκρισης του μεγέθους με τη μονάδα μέτρησης που χρησιμοποιούμε. Αν επιλέξουμε άλλη μονάδα, το αποτέλεσμα της μέτρησης θα είναι διαφορετικό. Για
4 παράδειγμα, αν χρησιμοποιήσουμε ως μονάδα το μέτρο (m) αντί του cm, το αποτέλεσμα της μέτρησης της ακμής του βιβλίου θα είναι: α=0,209m και αν χρησιμοποιήσουμε ως μονάδα την ίντσα (in), το ίδιο μήκος θα το βρούμε: α=8,2in Για να έχουν οι άνθρωποι έναν ενιαίο τρόπο σύγκρισης των μεγεθών που μετράνε, συμφώνησαν να χρησιμοποιούν ένα κοινό «σύστημα μονάδων μέτρησης». Δηλαδή συμφώνησαν με ποιο τρόπο θα ορίσουν το μέτρο (m) για τη μέτρηση του μήκους, πώς θα ορίσουν το δευτερόλεπτο (s) για τη μέτρηση του χρόνου, το κιλό (kg) για τη μέτρηση της μάζας κλπ. Έτσι, κάθε μέγεθος έχει τη δική του μονάδα μέτρησης ως προς την οποία το μετράμε. Μέτρηση και Σφάλματα Σε κάθε μέτρηση υπεισέρχεται πάντοτε ένα σφάλμα, μικρό ή μεγάλο. Το σφάλμα αυτό, όπως είδες και στα πειράματα που έκανες στην Α Γυμνασίου, μπορεί να οφείλεται: α) Σε ατέλειες της κατασκευής του οργάνου που χρησιμοποιούμε (ακρίβεια του οργάνου, κατάλληλη κλίμακα, κατασκευαστικές ατέλειες κλπ). β) Σε υποκειμενικές εκτιμήσεις που μπορεί να κάνουμε κατά τη μέτρηση (στην τοποθέτηση των οργάνων μέτρησης, στην ανάγνωση της ένδειξης κλπ). γ) Σε βαθύτερες αιτίες που είναι συνυφασμένες με την ίδια την δομή και τη λειτουργία του φυσικού κόσμου. [Για παράδειγμα, δεν μπορούμε να μετρήσουμε ταυτόχρονα και με απεριόριστη ακρίβεια τη θέση και την ταχύτητα ενός ηλεκτρονίου, όσο περίπλοκες συσκευές και αν επινοήσουμε!] Τα υποκειμενικά σφάλματα, που είναι αναπόφευκτα σε κάθε μέτρηση, μπορούμε να τα υπολογίσουμε. Το πετυχαίνουμε επαναλαμβάνοντας την ίδια μέτρηση πολλές φορές (του ίδιου μεγέθους, με τον ίδιο τρόπο και με το ίδιο όργανο). Η τιμή που προσεγγίζει με τη μεγαλύτερη ακρίβεια το μετρούμενο μέγεθος είναι η μέση τιμή όλων των αποτελεσμάτων των μετρήσεων που πραγματοποιήσαμε. Ακρίβεια ενός οργάνου μέτρησης - Σημαντικά ψηφία Ας προσπαθήσουμε να μετρήσουμε το πάχος ενός φύλλου του βιβλίου μας με ένα χάρακα. Διαπιστώνουμε ότι αυτό δεν είναι δυνατό. Δεν μπορούμε να είμαστε βέβαιοι για το αποτέλεσμα της μέτρησης. Ο χάρακας δεν είναι ένα όργανο αρκετά ακριβές για να κάνουμε μετρήσεις τόσο μικρών μηκών. Πώς θα προσδιορίσουμε και θα εκφράσουμε την ακρίβεια ενός οργάνου μέτρησης; Ας υποθέσουμε ότι τέσσερεις μαθητές, οι Α, Β, Γ και Δ, μετρούν με το χάρακά τους το πλάτος (α) ενός βιβλίου και ανακοινώνουν τα αποτελέσματα: Α: 20,35cm, ο Β: 20cm, ο Γ: 20,34624cm, ο Δ: 20,4cm. Κάθε μαθητής κατέγραψε το αποτέλεσμα της μέτρησής του με ένα αριθμό που έχει ένα συγκεκριμένο αριθμό ψηφίων. Τι σημαίνουν τα αριθμητικά ψηφία που προέκυψαν από κάθε μέτρηση; Ο Α έκανε τη μέτρησή του (20,35cm) με ακρίβεια τεσσάρων ψηφίων: Ισχυρίζεται ότι είναι σίγουρος για τα τρία πρώτα (το 2, το 0, και το 3), σχεδόν σίγουρος για το τελευταίο (το 5) και αβέβαιος για τα επόμενα ψηφία. Ο Β έκανε τη μέτρησή του (20cm) με ακρίβεια δύο ψηφίων: Ισχυρίζεται ότι είναι σίγουρος για το 2, σχεδόν σίγουρος (ή σίγουρος) για το 0 και αβέβαιος για τα επόμενα ψηφία.
5 Ο Γ έκανε τη μέτρησή του (20,34624cm) με ακρίβεια 7 ψηφίων (!!): Ισχυρίζεται ότι είναι σίγουρος για το 2, το 0, το 3, το 4, το 6, το 2, σχεδόν σίγουρος για το τελευταίο ψηφίο (το 4) και αβέβαιος για τα επόμενα ψηφία. Ο Δ έκανε τη μέτρησή του (20,4cm) με ακρίβεια τριών ψηφίων: Ισχυρίζεται ότι είναι σίγουρος για το 2, και το 0, σχεδόν σίγουρος (ή σίγουρος) για το 4 και αβέβαιος για τα επόμενα ψηφία. Τα ψηφία του αριθμητικού αποτελέσματος κάθε μέτρησης, για τα οποία είμαστε σίγουροι (ή σχεδόν σίγουροι) θα τα ονομάζουμε σημαντικά ψηφία της μέτρησης. Ο αριθμός των σημαντικών ψηφίων προσδιορίζει την ακρίβεια της μέτρησης. Έτσι, λέμε ότι: Ο Α έκανε τη μέτρησή του με ακρίβεια τεσσάρων σημαντικών ψηφίων. Ο Β έκανε τη μέτρησή του με ακρίβεια δύο σημαντικών ψηφίων. Ο Γ έκανε τη μέτρησή του με ακρίβεια επτά σημαντικών ψηφίων. Ο Δ έκανε τη μέτρησή του με ακρίβεια τριών σημαντικών ψηφίων. Η ακρίβεια μιας μέτρησης εξαρτάται από το είδος των οργάνων μέτρησης που χρησιμοποιούμε. Για παράδειγμα, άλλη ακρίβεια έχει μια μέτρηση που γίνεται με το χάρακα, άλλη (μεγαλύτερη ακρίβεια) μια μέτρηση που γίνεται με το διαστημόμετρο και διαφορετική μια μέτρηση που γίνεται με δέσμη laser. Είναι δυνατό με το χάρακα να κάνουμε μέτρηση με την ακρίβεια που ισχυρίζεται ο Γ; Ασφαλώς ΟΧΙ. Με το χάρακα μπορούμε να κάνουμε τις μετρήσεις του πλάτους του βιβλίου το πολύ με τέσσερα σημαντικά ψηφία. Η μέγιστη ακρίβεια στη μέτρηση εκφράζεται από το αποτέλεσμα που ανακοίνωσε ο Α: α=20,35cm. Ωστόσο, μπορεί να μη χρειάζεται να εκφράσουμε το αποτέλεσμα μιας μέτρησης με τη μέγιστη ακρίβεια που μας παρέχει το όργανο μέτρησης που χρησιμοποιούμε. Στο παράδειγμά μας, είναι πιθανό να θέλουμε να εκφράσουμε το αποτέλεσμα με τρία ή με δύο σημαντικά ψηφία. Στη περίπτωση αυτή στρογγυλοποιούμε κατάλληλα το αριθμητικό αποτέλεσμα: έτσι, αν θέλουμε να εκφράσουμε το αποτέλεσμα της μέτρησης του πλάτους του βιβλίου με τρία σημαντικά ψηφία, το αποτέλεσμα θα είναι α=20,4cm και με δύο σημαντικά ψηφία α=20cm. Συμπεραίνουμε ότι οι μετρήσεις των μαθητών Α, Β και Δ είναι αξιόπιστες: τα αποτελέσματα που ανακοίνωσαν διαφέρουν ως προς τον αριθμό των σημαντικών ψηφίων, αλλά βρίσκονται μέσα στα περιθώρια της ακρίβειας που μας παρέχει ο χάρακας. Το αποτέλεσμα όμως που ανακοίνωσε ο Γ είναι αναξιόπιστο: ο χάρακας δεν μας παρέχει δυνατότητα μέτρησης με τόσα πολλά σημαντικά ψηφία. Σημείωση: Αν εκφράσουμε το αποτέλεσμα α=20,35cm της μέτρηση του πλάτους του βιβλίου σε μέτρα, πρέπει να γράψουμε: α=0,2035m. Αν το εκφράσουμε σε χιλιόμετρα, θα γράψουμε: α=0, km. Βλέπουμε ότι στο αριθμητικό αποτέλεσμα εμφανίστηκαν μερικά μηδενικά, πριν το πρώτο μη μηδενικό ψηφίο της αρχικής έκφρασης (πριν από το 2). Πώς θα μετρήσουμε σε τέτοιες περιπτώσεις τα σημαντικά ψηφία της μέτρησης; Είναι φανερό ότι ο αριθμός των μηδενικών αριστερά του πρώτου μη μηδενικού ψηφίου (αριστερά του 2 στα παραδείγματά μας) δεν επηρεάζει την ακρίβεια της μέτρησης, αλλά εξαρτάται από τις μονάδες ως προς τις οποίες εκφράζουμε το αποτέλεσμα. Επομένως για να βρούμε τον αριθμό των σημαντικών ψηφίων αγνοούμε όλα τα μηδενικά αριστερά του πρώτου μη μηδενικού ψηφίου του αριθμητικού αποτελέσματος.
6 2. Πώς προκύπτουν τα σφάλματα στις μετρήσεις των φυσικών μεγεθών; Ας γυρίσουμε στο παράδειγμα της μέτρησης της ακμής του βιβλίου. Αν ζητούσαμε από δέκα συμμαθητές σου να κάνουν με τον ίδιο χάρακα την ίδια μέτρηση, θα κατέληγαν άραγε όλοι στο ίδιο αποτέλεσμα; Είναι εξαιρετικά απίθανο! Το πιθανότερο είναι ότι τα αποτελέσματα των μετρήσεών τους θα διέφεραν λίγο μεταξύ τους. Στον πίνακα Α καταγράφονται οι τιμές του μήκους μιας πλευράς ενός συγκεκριμένου βιβλίου που προέκυψαν από τις μετρήσεις δέκα μαθητών. ΠΙΝΑΚΑΣ Α Μήκος της ακμής (α) α/α Μαθητές του βιβλίου του Κώστα σε cm 1 Κώστας 20,92 2 Γιάννης 20,90 3 Μαρία 20,89 4 Βασιλική 20,93 5 Γιώργος 20,88 6 Ελένη 20,90 7 Ηλίας 20,91 8 Σάββας 20,92 9 Άννα 20,90 10 Μαργαρίτα 20,89 Μέση τιμή του α= 20,90 Κάτι ανάλογο θα συμβεί αν εσύ ο ίδιος επαναλάβεις, για παράδειγμα, δέκα φορές την ίδια μέτρηση και τοποθετήσεις τα αποτελέσματα σ ένα πίνακα παρόμοιο με τον πίνακα Α. Θα παρατηρήσεις ότι κάθε φορά που μετράς μια συγκεκριμένη απόσταση ή μια ορισμένη διάσταση ενός σώματος δεν καταλήγεις απαραίτητα στην ίδια τιμή. Οι διαφοροποιήσεις αυτές οφείλονται στα σφάλματα που γίνονται κατά τη διεξαγωγή κάθε μέτρησης. Ποιες είναι άραγε οι αιτίες των σφαλμάτων που επηρεάζουν το αποτέλεσμα μιας μέτρησης; Ποιο από τα αποτελέσματα που καταγράφουμε είναι το πλέον αξιόπιστο; Αν επαναλάβεις πολλές φορές τη μέτρηση του ίδιου μήκους (για παράδειγμα του πλάτους του βιβλίου), δεν είναι δύσκολο να ανακαλύψεις αρκετές αιτίες που ευθύνονται για τις μικρές διαφοροποιήσεις των αποτελεσμάτων που διαπιστώνεις. Παραθέτουμε μερικές από τις συνηθέστερες: α) Κάθε φορά που διεξάγουμε τη μέτρηση, η αρχή του χάρακα δεν τοποθετείται πάντοτε ακριβώς στο ίδιο σημείο (βλ. σχήμα 1). β) Αν το τέλος της ακμής του βιβλίου βρίσκεται μεταξύ δύο χαραγών του χάρακα, δεν μπορούμε να γνωρίζουμε με βεβαιότητα το τελευταίο ψηφίο του μετρούμενου μήκους. Έτσι αναγκαζόμαστε να καταφύγουμε σε υποκειμενική εκτίμηση. Για παράδειγμα, το αποτέλεσμα της μέτρησης του πλάτους του βιβλίου, που φαίνεται στο σχήμα 1, μπορεί να είναι 20,50, 20,55 ή 20,60cm.
7 Σχήμα 1 γ) Δεν είναι δυνατή η απόλυτη ευθυγράμμιση του χάρακα με το μετρούμενο αντικείμενο: Η καμπύλωση του χάρακα ή ο σχηματισμός μικρής γωνίας με την ακμή του βιβλίου μπορεί να επηρεάσουν τη μέτρηση και επομένως αποτελούν μια ακόμα αιτία σφαλμάτων (σχήμα 1). Αντίστοιχες αιτίες σφαλμάτων μπορούμε να ανακαλύψουμε στη μέτρηση οποιουδήποτε φυσικού μεγέθους. Με βάση λοιπόν τις παραπάνω διαπιστώσεις καταλήγουμε στη διατύπωση ενός συμπεράσματος: Η διαφοροποίηση των αποτελεσμάτων που προκύπτουν από πολλές μετρήσεις του ίδιου, σταθερού μεγέθους οφείλονται είτε σε αστάθμητους παράγοντες είτε σε υποκειμενικές εκτιμήσεις του παρατηρητή. Βέβαια όλοι αυτοί οι τυχαίοι ή υποκειμενικοί παράγοντες που επηρεάζουν τις μετρήσεις μας, δεν είναι δυνατό να ελεγχθούν και να αποφευχθούν πλήρως. Επομένως μπορούμε να ισχυριστούμε ότι όλες οι μετρήσεις ενός μεγέθους είναι μεταξύ τους ισοδύναμες και έχουν την ίδια αξιοπιστία, εφ όσον τηρούνται κάποιες προϋποθέσεις: Γίνονται με την ίδια προσοχή και κάτω από τις ίδιες οδηγίες. Οι συνθήκες του περιβάλλοντος διατηρούνται (κατά το δυνατόν) σταθερές και (περίπου) κοινές για όλες τις μετρήσεις. Πραγματοποιούνται με το ίδιο ή με πανομοιότυπα όργανα μέτρησης. Με δεδομένες αυτές τις προϋποθέσεις όλες οι μετρήσεις που καταγράφονται στον πίνακα Α θεωρούνται ισοδύναμες. Καμία τους δεν μπορεί να χαρακτηριστεί «καλύτερη» ή «πιο πιθανή» από τις άλλες. Κάθε αποτέλεσμα προσεγγίζει με την ίδια πιθανότητα το «πραγματικό» μήκος της ακμής του βιβλίου. Επομένως αποδεχόμαστε ότι η τιμή που προσεγγίζει με τη μεγαλύτερη ακρίβεια το μετρούμενο μήκος είναι η μέση τιμή (μέσος όρος) όλων των αποτελεσμάτων των μετρήσεων που πραγματοποιήσαμε. Δηλαδή: α=(20,92+20,90+20,89+20,93+20,88+20,90+20,91+20,92+20,90+20,89)/10 =20,90cm Το αποτέλεσμα αυτό καταγράφεται στην τελευταία σειρά του πίνακα Α. Πρέπει να τονιστεί ότι κατά τον υπολογισμό της μέσης τιμής κρατάμε στο τελικό αποτέλεσμα, τον ίδιο αριθμό σημαντικών ψηφίων με εκείνο των επιμέρους μετρήσεων. Αν προκύπτουν περισσότερα ψηφία, τα διαγράφουμε στρογγυλοποιώντας κατάλληλα το
8 τελευταίο σημαντικό ψηφίο. Για παράδειγμα, η μέση τιμή που προκύπτει για το α, με βάση τις τιμές του πίνακα Α είναι: α=20,904cm Επειδή οι μετρήσεις έχουν γίνει με προσέγγιση τεσσάρων σημαντικών ψηφίων, στρογγυλοποιούμε την τιμή του α και γράφουμε: α=20,90cm Τα σφάλματα των μετρήσεων που μελετήσαμε μέχρι τώρα μπορεί να οφείλονται σε τυχαίους Σχήμα 2: Σύμφωνα με τον χάρακα (1) που έχει λανθασμένη βαθμολόγηση, το μήκος του στυλογράφου του σχήματος είναι 14,5cm, ενώ το πραγματικό του μήκος είναι 15,5cm. [Ο χάρακας 2 είναι σωστά βαθμονομημένος] παράγοντες ή στις υποκειμενικές εκτιμήσεις του παρατηρητή. Ωστόσο υπάρχει και μια άλλη πιθανή αιτία σφαλμάτων: Η λανθασμένη κατασκευή ή η μη σωστή λειτουργία των οργάνων μέτρησης. Φαντάσου, για παράδειγμα, ότι οι υποδιαιρέσεις του ενός cm του χάρακα με τον οποίο μέτρησες το πλάτος του βιβλίου σου δεν έχουν πραγματικά μήκος ένα cm. Τότε οι μετρήσεις σου θα είναι εσφαλμένες λόγω της κακής κατασκευής του οργάνου (βλ. σχήμα 2). Τα σφάλματα που επηρεάζουν τις μετρήσεις μας και προέρχονται από λάθη στην κατασκευή ή τη λειτουργία των οργάνων μέτρησης, ονομάζονται συστηματικά. Τα συστηματικά σφάλματα σε αντίθεση με τα τυχαία μπορούμε να τα εξουδετερώσουμε και να τα αποφύγουμε. Αρκεί να κάνουμε προσεκτικό έλεγχο και δοκιμή των οργάνων μέτρησης πριν από τη χρήση τους. 3. Πώς σχεδιάζουμε πειραματικά τη γραφική παράσταση δύο φυσικών μεγεθών που σχετίζονται μεταξύ τους; Ας ξεκινήσουμε πάλι με ένα παράδειγμα: Γνωρίζεις ότι όσο περισσότερο χρόνο θερμαίνεις μια ορισμένη μάζα νερού (προτού αρχίσει να βράζει) τόσο περισσότερο αυξάνεται η θερμοκρασία του. Η θερμοκρασία του νερού σχετίζεται με το χρόνο θέρμανσής του. Πώς μπορούμε να βρούμε πειραματικά και να παραστήσουμε με ένα διάγραμμα τη σχέση μεταξύ της θερμοκρασίας του νερού και του χρόνου που το θερμαίνουμε; Αρκεί να σχεδιάσουμε και να εκτελέσουμε ένα κατάλληλο πείραμα. Μια πειραματική διαδικασία χωρίς ιδιαίτερες απαιτήσεις, θα μπορούσε να περιλαμβάνει τα εξής βήματα: α) Ρίχνουμε σ ένα δοχείο ζέσεως μια ποσότητα (~200 g) νερού και το τοποθετούμε σε μια ήπια εστία θέρμανσης. β) Φέρνουμε ένα θερμόμετρο σε επαφή με το νερό έτσι ώστε να μας δείχνει διαρκώς τη θερμοκρασία του. γ) Χρησιμοποιούμε ένα χρονόμετρο για να μετράμε το χρόνο θέρμανσης του νερού. δ) Ανάβουμε την εστία και μετά από λίγο θέτουμε σε λειτουργία το χρονόμετρο, καταγράφοντας ταυτόχρονα και την ένδειξη του θερμομέτρου. Σημειώνουμε σ ένα πίνακα τις τιμές της θερμοκρασίας ανά μισό ή ένα λεπτό. ε) Όταν η θερμοκρασία φτάσει τους 60-70C, κλείνουμε την εστία και σταματούμε τις μετρήσεις.
9 χρόνος θέρμανσης t min ΠΙΝΑΚΑΣ Β θερμοκρασία του νερού θ C μεταβολή της θερμοκρασίας από την αρχική της τιμή Δθ C , ,5 7,5 1, ,5 16,5 2, ,5 23,5 3, ,5 32,5 Ας υποθέσουμε ότι τα αποτελέσματα του συγκεκριμένου πειράματος είναι αυτά που περιέχουν οι δύο πρώτες στήλες του πίνακα Β. Παρατηρούμε, όπως εξ άλλου ήταν αναμενόμενο, ότι καθώς μεταβάλλεται ο χρόνος θέρμανσης, η θερμοκρασία του νερού αυξάνεται. Εμείς όμως επιδιώκουμε κάτι περισσότερο: θέλουμε να ανακαλύψουμε με ποια μαθηματική σχέση σχετίζονται και να διατυπώσουμε τον αντίστοιχο φυσικό νόμο. Για να πετύχουμε το στόχο μας αυτό, αρκεί να σχεδιάσουμε τη γραφική παράσταση της θερμοκρασίας του νερού σε συνάρτηση με το χρόνο θέρμανσης με βάση τα πειραματικά δεδομένα του πίνακα Β. Ο σωστός και μεθοδικός σχεδιασμός μιας γραφικής παράστασης, με βάση κάποια πειραματικά δεδομένα, απαιτεί την εφαρμογή ορισμένων απλών οδηγιών: Σχήμα 3 α) Με ένα χάρακα σχεδιάζουμε πάνω σε ένα χιλιοστομετρικό (μιλιμετρέ) φύλλο ένα σύστημα ορθογωνίων αξόνων. Επιλέγουμε κατάλληλη κλίμακα και στον οριζόντιο άξονα τοποθετούμε τις τιμές του χρόνου από 0 έως 5 min. Αντίστοιχα, στον κατακόρυφο άξονα τοποθετούμε τις τιμές της θερμοκρασίας, από 10 έως 50 C. β) Εντοπίζουμε και σημειώνουμε πάνω στο φύλλο τα σημεία με συντεταγμένες τις τιμές χρόνου και θερμοκρασίας που αναγράφονται σε κάθε σειρά του πίνακα Β (βλ. σχήμα 3).
10 γ) Με τη βοήθεια του χάρακα παρατηρούμε ότι όλα τα σημεία που έχουμε τοποθετήσει (με βάση τις πειραματικές τιμές του πίνακα Β) βρίσκονται περίπου επάνω ή πολύ κοντά σε μια ευθεία γραμμή (βλ. σχήμα 3). Γιατί άραγε συμβαίνει αυτό; Την απάντηση μπορείς να τη μαντέψεις αν συνδυάσεις ό,τι έχεις ήδη μάθει σχετικά με τα σφάλματα των μετρήσεων. Θυμήσου ότι κάθε σημείο που σημειώσαμε πάνω στο χιλιοστομετρικό χαρτί έχει προκύψει από τη μέτρηση δύο φυσικών μεγεθών: του χρόνου θέρμανσης (που τον μετρήσαμε με το χρονόμετρο) και της θερμοκρασίας του νερού (που τη μετρήσαμε με το θερμόμετρο). Γνωρίζεις όμως ότι κάθε μέτρηση περιέχει σφάλμα. Επομένως όλες οι τιμές του χρόνου και της θερμοκρασίας που έχουν καταγραφεί στον πίνακα Β (εφ όσον έχουν προκύψει από μετρήσεις) περιέχουν κάποιο σφάλμα. Άρα και οι θέσεις των αντίστοιχων πειραματικών σημείων στο διάγραμμα δεν είναι απόλυτα ακριβείς. Πώς θα σκεφτούμε λοιπόν για να σχεδιάσουμε τη γραφική παράσταση θερμοκρασίας - χρόνου που προσδιορίζεται από το σύνολο των πειραματικών μας σημείων; Αφού η θέση τους δεν είναι απόλυτα σωστή, δεν είναι απαραίτητο να βρίσκονται όλα επάνω στη γραμμή που παριστάνει τη σχέση των παραπάνω μεγεθών. Πρέπει ωστόσο να βρίσκονται πολύ κοντά σε αυτή. Σχεδιάζουμε επομένως μια απλή συνεχή γραμμή που περνάει όσο γίνεται πιο κοντά από το σύνολο των σημείων. Αφήνουμε έξω από τη γραμμή, δεξιά και αριστερά της, περίπου τον ίδιο αριθμό σημείων (βλ. σχήμα 3). 4. Μεταβολές μεγεθών Ας παρατηρήσουμε πάλι τις τιμές της θερμοκρασίας και του χρόνου που έχουν καταγραφεί στον πίνακα Β: Τη στιγμή t 1 =0,5min, η θερμοκρασία του νερού ήταν θ 1 =24 0 C. Τη χρονική στιγμή t 2 =1,5min η θερμοκρασία του νερού ήταν θ 2 =32 0 C. Πώς θα απαντήσεις στο ερώτημα «Πόσο μεταβλήθηκε η θερμοκρασία του νερού από τη στιγμή t 1 έως τη στιγμή t 2 ;», ή στο ισοδύναμο ερώτημα «Πόση είναι η μεταβολή της θερμοκρασίας στο χρονικό διάστημα που προσδιορίζεται από τις χρονικές στιγμές t 1 και t 2 ;» Η απάντηση προκύπτει αμέσως από την καθημερινή μας εμπειρία: Δεν έχεις παρά να αφαιρέσεις από τη θερμοκρασία θ 2 =32 0 C τη θερμοκρασία θ 1 =24 0 C. Δηλαδή η μεταβολή της θερμοκρασίας του νερού από τη στιγμή t 1 =0,5min μέχρι τη στιγμή t 2 =1,5 min είναι θ 2 -θ 1 =(32-24)C=8 0 C Τη μεταβολή της θερμοκρασίας τη συμβολίζουμε με το σύμβολο Δθ και γράφουμε: Δθ=θ 2 -θ 1 οπότε στο προηγούμενο παράδειγμα η μεταβολή της θερμοκρασίας είναι Δθ=8 0 C Πολλές φορές μας ενδιαφέρει να υπολογίζουμε τη μεταβολή ενός μεγέθους (για παράδειγμα της θερμοκρασίας) από την αρχική του τιμή, δηλαδή από τη χρονική στιγμή t=0, που αρχίσαμε τις μετρήσεις. Έτσι σύμφωνα με τις τιμές του πίνακα Β διαπιστώνουμε ότι: Τη στιγμή t=0,5min η θερμοκρασία του νερού έχει μεταβληθεί από την αρχική της τιμή κατά Δθ=(24-20)C=4 0 C. Τη στιγμή t=1min η θερμοκρασία του νερού έχει μεταβληθεί από την αρχική της τιμή κατά Δθ=(27,5-20) 0 C =7,5 0 C κλπ.
11 Όλες αυτές τις μεταβολές της θερμοκρασίας από την αρχική της τιμή μπορούμε να τις καταχωρίσουμε στην τρίτη στήλη του πίνακα Β, όπως φαίνεται στην αντίστοιχη εικόνα. Με βάση τις τιμές αυτές κατασκευάζουμε τη γραφική παράσταση της μεταβολής της θερμοκρασίας του νερού σε συνάρτηση με το χρόνο θέρμανσης. Αν ακολουθήσεις τους γνωστούς σου πλέον, κανόνες σχεδιασμού της, θα καταλήξεις σε ένα γράφημα παρόμοιο με αυτό του σχήματος 4. Παρατήρησε ότι σύμφωνα με το γράφημα του σχήματος 4 η μεταβολή της θερμοκρασίας του νερού σε Σχήμα 4 συνάρτηση με το χρόνο θέρμανσης παριστάνεται με μια ευθεία που διέρχεται από την αρχή των αξόνων. Επομένως, όπως γνωρίζεις από τα Μαθηματικά, τα δύο αυτά μεγέθη είναι ανάλογα. Ώστε από την επεξεργασία των πειραματικών μας δεδομένων καταλήξαμε στη διατύπωση ενός φυσικού νόμου: Αν η παροχή θερμότητας από την εστία θέρμανσης είναι σταθερή, τότε, η μεταβολή της θερμοκρασίας του νερού είναι ανάλογη του χρόνου που το θερμαίνουμε. Αναφορά Φυσική Β Γυμνασίου, Ν. Αντωνίου - Π. Δημητριάδης - Κ. Καμπούρης - Κ. Παπαμιχάλης - Λ. Παπατσίμπα, Υπ. Παιδείας - Ινστ. Εκπ. Πολιτικής, Αθήνα 2013
Ν. Αντωνίου, καθηγητής ΕΚΠΑ - Π. Δημητριάδης, Δρ. Φυσικής - Κ. Καμπούρης, Msc. Φυσικής - Κ. Παπαμιχάλης, Δρ. Φυσικής - Λ. Παπατσίμπα, Δρ.
 1 Συγγραφική ομάδα Ν. Αντωνίου, καθηγητής ΕΚΠΑ - Π. Δημητριάδης, Δρ. Φυσικής - Κ. Καμπούρης, Msc. Φυσικής - Κ. Παπαμιχάλης, Δρ. Φυσικής - Λ. Παπατσίμπα, Δρ. Φυσικής Επεξεργασία εικόνων Θεόφιλος Χατζητσοπάνης
1 Συγγραφική ομάδα Ν. Αντωνίου, καθηγητής ΕΚΠΑ - Π. Δημητριάδης, Δρ. Φυσικής - Κ. Καμπούρης, Msc. Φυσικής - Κ. Παπαμιχάλης, Δρ. Φυσικής - Λ. Παπατσίμπα, Δρ. Φυσικής Επεξεργασία εικόνων Θεόφιλος Χατζητσοπάνης
ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΕΜΒΑΔΟΥ ΟΓΚΟΥ ΕΠΙΣΗΜΑΝΣΕΙΣ ΠΡΟΣ ΤΟΝ ΚΑΘΗΓΗΤΗ
 ΕΚΦΕ Αν. Αττικής Υπεύθυνος: Κ. Παπαμιχάλης ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΕΜΒΑΔΟΥ ΟΓΚΟΥ ΕΠΙΣΗΜΑΝΣΕΙΣ ΠΡΟΣ ΤΟΝ ΚΑΘΗΓΗΤΗ Κεντρική επιδίωξη των εργαστηριακών ασκήσεων φυσικής στην Α Γυμνασίου, είναι οι μαθητές να οικοδομήσουν
ΕΚΦΕ Αν. Αττικής Υπεύθυνος: Κ. Παπαμιχάλης ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΕΜΒΑΔΟΥ ΟΓΚΟΥ ΕΠΙΣΗΜΑΝΣΕΙΣ ΠΡΟΣ ΤΟΝ ΚΑΘΗΓΗΤΗ Κεντρική επιδίωξη των εργαστηριακών ασκήσεων φυσικής στην Α Γυμνασίου, είναι οι μαθητές να οικοδομήσουν
Ε Ρ ΓΑ Σ Τ Η Ρ Ι Α Κ Ο Σ Ο Δ Η Γ Ο Σ. Νικόλαος Αντωνίου Παναγιώτης Δημητριάδης Κωνσταντίνος Καμπούρης Κωνσταντίνος Παπαμιχάλης Λαμπρινή Παπατσίμπα
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ Ε Ρ ΓΑ Σ Τ Η Ρ Ι Α Κ Ο Σ Ο Δ Η Γ Ο Σ Νικόλαος Αντωνίου Παναγιώτης Δημητριάδης Κωνσταντίνος Καμπούρης Κωνσταντίνος Παπαμιχάλης Λαμπρινή
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ Ε Ρ ΓΑ Σ Τ Η Ρ Ι Α Κ Ο Σ Ο Δ Η Γ Ο Σ Νικόλαος Αντωνίου Παναγιώτης Δημητριάδης Κωνσταντίνος Καμπούρης Κωνσταντίνος Παπαμιχάλης Λαμπρινή
Μια από τις σημαντικότερες δυσκολίες που συναντά ο φυσικός στη διάρκεια ενός πειράματος, είναι τα σφάλματα.
 Εισαγωγή Μετρήσεις-Σφάλματα Πολλές φορές θα έχει τύχει να ακούσουμε τη λέξη πείραμα, είτε στο μάθημα είτε σε κάποια είδηση που αφορά τη Φυσική, τη Χημεία ή τη Βιολογία. Είναι όμως γενικώς παραδεκτό ότι
Εισαγωγή Μετρήσεις-Σφάλματα Πολλές φορές θα έχει τύχει να ακούσουμε τη λέξη πείραμα, είτε στο μάθημα είτε σε κάποια είδηση που αφορά τη Φυσική, τη Χημεία ή τη Βιολογία. Είναι όμως γενικώς παραδεκτό ότι
Ν. Αντωνίου, καθηγητής ΕΚΠΑ - Π. Δημητριάδης, Δρ. Φυσικής - Κ. Καμπούρης, Msc. Φυσικής - Κ. Παπαμιχάλης, Δρ. Φυσικής - Λ. Παπατσίμπα, Δρ.
 1 Συγγραφική ομάδα Ν. Αντωνίου, καθηγητής ΕΚΠΑ - Π. Δημητριάδης, Δρ. Φυσικής - Κ. Καμπούρης, Msc. Φυσικής - Κ. Παπαμιχάλης, Δρ. Φυσικής - Λ. Παπατσίμπα, Δρ. Φυσικής Επεξεργασία εικόνων Θεόφιλος Χατζητσοπάνης
1 Συγγραφική ομάδα Ν. Αντωνίου, καθηγητής ΕΚΠΑ - Π. Δημητριάδης, Δρ. Φυσικής - Κ. Καμπούρης, Msc. Φυσικής - Κ. Παπαμιχάλης, Δρ. Φυσικής - Λ. Παπατσίμπα, Δρ. Φυσικής Επεξεργασία εικόνων Θεόφιλος Χατζητσοπάνης
Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2009 Πανελλήνιος προκαταρκτικός διαγωνισμός στη Φυσική
 ΠΑΝΕΚΦΕ Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 009 Πανελλήνιος προκαταρκτικός διαγωνισμός στη Φυσική 16-01-010 Σχολείο: Ονόματα των μαθητών της ομάδας: 1) ) 3) Σκοπός και κεντρική ιδέα της άσκησης Ο βασικός
ΠΑΝΕΚΦΕ Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 009 Πανελλήνιος προκαταρκτικός διαγωνισμός στη Φυσική 16-01-010 Σχολείο: Ονόματα των μαθητών της ομάδας: 1) ) 3) Σκοπός και κεντρική ιδέα της άσκησης Ο βασικός
Πειραματικός υπολογισμός της ειδικής θερμότητας του νερού. Σκοπός και κεντρική ιδέα της άσκησης
 Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης, Δ. Τριανταφύλλου Πειραματικός υπολογισμός της ειδικής θερμότητας του νερού Σκοπός και κεντρική ιδέα της άσκησης Σκοπός της άσκησης είναι ο πειραματικός
Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης, Δ. Τριανταφύλλου Πειραματικός υπολογισμός της ειδικής θερμότητας του νερού Σκοπός και κεντρική ιδέα της άσκησης Σκοπός της άσκησης είναι ο πειραματικός
ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ
 ΕΚΦΕ Α Αν. Αττικής - Υπεύθυνος Κ. Παπαμιχάλης Εργαστηριακές ασκήσεις Φυσικής Β Γυμνασίου ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 7 ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ Βασικές έννοιες: Θέση - μετατόπιση - χρόνος - χρονικό διάστημα - ταχύτητα
ΕΚΦΕ Α Αν. Αττικής - Υπεύθυνος Κ. Παπαμιχάλης Εργαστηριακές ασκήσεις Φυσικής Β Γυμνασίου ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 7 ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ Βασικές έννοιες: Θέση - μετατόπιση - χρόνος - χρονικό διάστημα - ταχύτητα
Μελέτη της ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης σώματος με χρήση συστήματος φωτοπύλης-χρονομέτρου. Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός
 Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης Μελέτη της ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης σώματος με χρήση συστήματος φωτοπύλης-χρονομέτρου Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός
Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης Μελέτη της ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης σώματος με χρήση συστήματος φωτοπύλης-χρονομέτρου Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός
Πειραματικός σχεδιασμός της χαρακτηριστικής καμπύλης παθητικής διπολικής συσκευής ηλεκτρικού κυκλώματος. Σκοπός και κεντρική ιδέα της άσκησης
 Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης, Δρ Φυσικής Πειραματικός σχεδιασμός της χαρακτηριστικής καμπύλης παθητικής διπολικής συσκευής ηλεκτρικού κυκλώματος Σκοπός και κεντρική ιδέα της άσκησης
Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης, Δρ Φυσικής Πειραματικός σχεδιασμός της χαρακτηριστικής καμπύλης παθητικής διπολικής συσκευής ηλεκτρικού κυκλώματος Σκοπός και κεντρική ιδέα της άσκησης
Α και Β ΕΡΓΑΣΤΗΡΙΑΚΟ ΚΕΝΤΡΟ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ
 Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 03-4 Τοπικός διαγωνισμός στη Φυσική 07--03 Σχολείο: Ονόματα των μαθητών της ομάδας: ) ) 3) Ιδανικά αέρια: o νόμος του Boyle Κεντρική ιδέα της άσκησης Στην άσκηση αυτή
Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 03-4 Τοπικός διαγωνισμός στη Φυσική 07--03 Σχολείο: Ονόματα των μαθητών της ομάδας: ) ) 3) Ιδανικά αέρια: o νόμος του Boyle Κεντρική ιδέα της άσκησης Στην άσκηση αυτή
ΧΑΡΑΚΤΗΡΙΣΜΟΣ ΥΛΙΚΩΝ. Μετρήσεις με Διαστημόμετρο και Μικρόμετρο
 ΧΑΡΑΚΤΗΡΙΣΜΟΣ ΥΛΙΚΩΝ Σκοπός της άσκησης Σε αυτή την άσκηση θα μετρήσουμε διαστάσεις στερεών σωμάτων χρησιμοποιώντας όργανα ακριβείας και θα υπολογίσουμε την πυκνότητα τους. Θα κάνουμε εφαρμογή της θεωρίας
ΧΑΡΑΚΤΗΡΙΣΜΟΣ ΥΛΙΚΩΝ Σκοπός της άσκησης Σε αυτή την άσκηση θα μετρήσουμε διαστάσεις στερεών σωμάτων χρησιμοποιώντας όργανα ακριβείας και θα υπολογίσουμε την πυκνότητα τους. Θα κάνουμε εφαρμογή της θεωρίας
ΜΕΛΕΤΗ ΤΗΣ ΚΙΝΗΣΗΣ ΡΑΒΔΟΥ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ ΜΕΤΡΗΣΗ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΤΗΣ ΡΑΒΔΟΥ
 ΜΕΛΕΤΗ ΤΗΣ ΚΙΝΗΣΗΣ ΡΑΒΔΟΥ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ ΜΕΤΡΗΣΗ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΤΗΣ ΡΑΒΔΟΥ Συνοπτική περιγραφή Μελετάμε την κίνηση μιας ράβδου που μπορεί να περιστρέφεται γύρω από σταθερό οριζόντιο άξονα,
ΜΕΛΕΤΗ ΤΗΣ ΚΙΝΗΣΗΣ ΡΑΒΔΟΥ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ ΜΕΤΡΗΣΗ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΤΗΣ ΡΑΒΔΟΥ Συνοπτική περιγραφή Μελετάμε την κίνηση μιας ράβδου που μπορεί να περιστρέφεται γύρω από σταθερό οριζόντιο άξονα,
25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗ 25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Το πρόβλημα Ένας φίλος σας βρήκε ένα μικρό, πολύ όμορφο τεμάχιο διαφανούς στερεού και ζητά τη γνώμη
ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗ 25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Το πρόβλημα Ένας φίλος σας βρήκε ένα μικρό, πολύ όμορφο τεμάχιο διαφανούς στερεού και ζητά τη γνώμη
1. Τίτλος εργαστηριακής άσκησης «Βαθμονόμηση θερμομέτρου»
 1. Τίτλος εργαστηριακής άσκησης «Βαθμονόμηση θερμομέτρου» 2. Εμπλεκόμενες γνωστικές περιοχές Γνωστικό αντικείμενο του μαθήματος Φυσική Β Γυμνασίου Ιδιαίτερη περιοχή του γνωστικού αντικειμένου Θερμότητα
1. Τίτλος εργαστηριακής άσκησης «Βαθμονόμηση θερμομέτρου» 2. Εμπλεκόμενες γνωστικές περιοχές Γνωστικό αντικείμενο του μαθήματος Φυσική Β Γυμνασίου Ιδιαίτερη περιοχή του γνωστικού αντικειμένου Θερμότητα
Θέματα Παγκύπριων Εξετάσεων
 Θέματα Παγκύπριων Εξετάσεων 2009 2014 Σελίδα 1 από 24 Ταλαντώσεις 1. Το σύστημα ελατήριο-σώμα εκτελεί απλή αρμονική ταλάντωση μεταξύ των σημείων Α και Β. (α) Ο χρόνος που χρειάζεται το σώμα για να κινηθεί
Θέματα Παγκύπριων Εξετάσεων 2009 2014 Σελίδα 1 από 24 Ταλαντώσεις 1. Το σύστημα ελατήριο-σώμα εκτελεί απλή αρμονική ταλάντωση μεταξύ των σημείων Α και Β. (α) Ο χρόνος που χρειάζεται το σώμα για να κινηθεί
Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών Προκαταρκτικός Διαγωνισμός Ανατολικής Αττικής. Φυσική
 Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 017-18 Προκαταρκτικός Διαγωνισμός Ανατολικής Αττικής Φυσική Σχολείο: Ονόματα των μαθητών της ομάδας: 1) ) 3) Οι στόχοι του πειράματος 1. Η μέτρηση της επιτάχυνσης
Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 017-18 Προκαταρκτικός Διαγωνισμός Ανατολικής Αττικής Φυσική Σχολείο: Ονόματα των μαθητών της ομάδας: 1) ) 3) Οι στόχοι του πειράματος 1. Η μέτρηση της επιτάχυνσης
Γνωριμία με το Σχολικό Εργαστήριο Φυσικών Επιστημών
 Φυσική Α Γενικού Λυκείου Γνωριμία με το Σχολικό Εργαστήριο Φυσικών Επιστημών (Μετρήσεις, αβεβαιότητα, επεξεργασία δεδομένων) Υποστηρικτικό υλικό 20 Οκτωβρίου 2016 Μαρίνα Στέλλα, Υπεύθυνη ΕΚΦΕ Σχολικό Εργαστήριο
Φυσική Α Γενικού Λυκείου Γνωριμία με το Σχολικό Εργαστήριο Φυσικών Επιστημών (Μετρήσεις, αβεβαιότητα, επεξεργασία δεδομένων) Υποστηρικτικό υλικό 20 Οκτωβρίου 2016 Μαρίνα Στέλλα, Υπεύθυνη ΕΚΦΕ Σχολικό Εργαστήριο
ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ. Σχεδιασμός - Περιγραφή
 ΕΚΦΕ Α Αν. Αττικής - Υπεύθυνος Κ. Παπαμιχάλης Εργαστηριακές ασκήσεις Φυσικής Β ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ Η εικόνα έχει ληφθεί από τον ιστότοπο: http://www.vbhelper.co/vbgptoc.ht Πώς θα μετρήσουμε
ΕΚΦΕ Α Αν. Αττικής - Υπεύθυνος Κ. Παπαμιχάλης Εργαστηριακές ασκήσεις Φυσικής Β ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ Η εικόνα έχει ληφθεί από τον ιστότοπο: http://www.vbhelper.co/vbgptoc.ht Πώς θα μετρήσουμε
Ένωση Ελλήνων Φυσικών ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ ΓΥΜΝΑΣΙΟΥ 2014 Πανεπιστήμιο Αθηνών Εργαστήριο Φυσικών Επιστημών, Τεχνολογίας, Περιβάλλοντος.
 A Γυμνασίου 29 Μαρτίου 2014 Όνομα και Επώνυμο:.. Όνομα Πατέρα: Όνομα Μητέρας:... Σχολείο:... Τάξη/Τμήμα:. Εξεταστικό Κέντρο:. Πειραματικό Μέρος Θέμα 1 ο H μέτρηση του μήκους γίνεται, συνήθως, με μετροταινία
A Γυμνασίου 29 Μαρτίου 2014 Όνομα και Επώνυμο:.. Όνομα Πατέρα: Όνομα Μητέρας:... Σχολείο:... Τάξη/Τμήμα:. Εξεταστικό Κέντρο:. Πειραματικό Μέρος Θέμα 1 ο H μέτρηση του μήκους γίνεται, συνήθως, με μετροταινία
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ B ΓΥΜΝΑΣΙΟΥ Κυριακή, 17 Μαΐου 2009 Ώρα: 10:00 12:30 Προτεινόμενες Λύσεις θεμα - 1 (5 μον.) Στον πίνακα υπάρχουν δύο στήλες με ασυμπλήρωτες προτάσεις. Στο τετράδιο των απαντήσεών
5 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ B ΓΥΜΝΑΣΙΟΥ Κυριακή, 17 Μαΐου 2009 Ώρα: 10:00 12:30 Προτεινόμενες Λύσεις θεμα - 1 (5 μον.) Στον πίνακα υπάρχουν δύο στήλες με ασυμπλήρωτες προτάσεις. Στο τετράδιο των απαντήσεών
Άσκηση Σ1 Άμεσες μετρήσεις σφάλματα
 Συμπλήρωμα Σ1.ΠΕΙΡΑΜΑΤΙΚΟ ΜΕΡΟΣ Άσκηση Σ1 Άμεσες μετρήσεις σφάλματα (Αφορά το 1ο εργαστήριο. Η αντίστοιχη θεωρία είναι στις σελίδες 13-20 του βιβλίου ενώ εδώ βλέπεις το πειραματικό μέρος επειδή δεν υπάρχει
Συμπλήρωμα Σ1.ΠΕΙΡΑΜΑΤΙΚΟ ΜΕΡΟΣ Άσκηση Σ1 Άμεσες μετρήσεις σφάλματα (Αφορά το 1ο εργαστήριο. Η αντίστοιχη θεωρία είναι στις σελίδες 13-20 του βιβλίου ενώ εδώ βλέπεις το πειραματικό μέρος επειδή δεν υπάρχει
Σφάλματα Είδη σφαλμάτων
 Σφάλματα Σφάλματα Κάθε μέτρηση ενός φυσικού μεγέθους χαρακτηρίζεται από μία αβεβαιότητα που ονομάζουμε σφάλμα, το οποίο αναγράφεται με τη μορφή Τιμή ± αβεβαιότητα π.χ έστω ότι σε ένα πείραμα μετράμε την
Σφάλματα Σφάλματα Κάθε μέτρηση ενός φυσικού μεγέθους χαρακτηρίζεται από μία αβεβαιότητα που ονομάζουμε σφάλμα, το οποίο αναγράφεται με τη μορφή Τιμή ± αβεβαιότητα π.χ έστω ότι σε ένα πείραμα μετράμε την
 Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
ΦΕ1. Περιεχόμενα. Η φυσική. Υπόθεση και φυσικό μέγεθος
 Περιεχόμενα ΦΕ1 ΤΑ ΦΥΣΙΚΑ ΜΕΓΕΘΗ ΚΑΙ Η ΜΕΤΡΗΣΗ ΤΟΥΣ ΤΟ ΜΗΚΟΣ 2015-16 6 ο ΓΥΜΝΑΣΙΟ ΑΘΗΝΑΣ Τα φυσικά μεγέθη Η Μέτρηση των φυσικών μεγεθών Μια μονάδα μέτρησης για όλους Το φυσικό μέγεθος Μήκος Όργανα μέτρησης
Περιεχόμενα ΦΕ1 ΤΑ ΦΥΣΙΚΑ ΜΕΓΕΘΗ ΚΑΙ Η ΜΕΤΡΗΣΗ ΤΟΥΣ ΤΟ ΜΗΚΟΣ 2015-16 6 ο ΓΥΜΝΑΣΙΟ ΑΘΗΝΑΣ Τα φυσικά μεγέθη Η Μέτρηση των φυσικών μεγεθών Μια μονάδα μέτρησης για όλους Το φυσικό μέγεθος Μήκος Όργανα μέτρησης
Τοπικός Διαγωνισμός EUSO2019 Πειραματική δοκιμασία Φυσικής
 ΕΚΦΕ Νέας Ιωνίας ΕΚΦΕ Χαλανδρίου Τοπικός Διαγωνισμός EUSO2019 Πειραματική δοκιμασία Φυσικής Ένα «ακατάλληλο» δυναμόμετρο! 8 Δεκεμβρίου 2018 ΣΧΟΛΙΚΗ ΜΟΝΑΔΑ: ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1) 2). 3).. Τα δυναμόμετρα Το
ΕΚΦΕ Νέας Ιωνίας ΕΚΦΕ Χαλανδρίου Τοπικός Διαγωνισμός EUSO2019 Πειραματική δοκιμασία Φυσικής Ένα «ακατάλληλο» δυναμόμετρο! 8 Δεκεμβρίου 2018 ΣΧΟΛΙΚΗ ΜΟΝΑΔΑ: ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1) 2). 3).. Τα δυναμόμετρα Το
Α και Β ΕΡΓΑΣΤΗΡΙΑΚΟ ΚΕΝΤΡΟ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ
 Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2011-12 Τοπικός διαγωνισμός στη Φυσική 10-12-2011 Σχολείο: Ονόματα των μαθητών της ομάδας: 1) 2) 3) Κεντρική ιδέα της άσκησης Στην άσκηση μελετάμε την κίνηση ενός
Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2011-12 Τοπικός διαγωνισμός στη Φυσική 10-12-2011 Σχολείο: Ονόματα των μαθητών της ομάδας: 1) 2) 3) Κεντρική ιδέα της άσκησης Στην άσκηση μελετάμε την κίνηση ενός
Μελέτη της κίνησης σώματος πάνω σε πλάγιο επίπεδο. Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός
 Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης Μελέτη της κίνησης σώματος πάνω σε πλάγιο επίπεδο Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός Βασικές έννοιες, σχέσεις και διαδικασίες Αδρανειακό
Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης Μελέτη της κίνησης σώματος πάνω σε πλάγιο επίπεδο Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός Βασικές έννοιες, σχέσεις και διαδικασίες Αδρανειακό
Περί σφαλμάτων και γραφικών παραστάσεων
 Περί σφαλμάτων και γραφικών παραστάσεων Σφάλμα ανάγνωσης οργάνου Το σφάλμα αυτό αναφέρεται σε αβεβαιότητες στη μέτρηση που προκαλούνται από τις πεπερασμένες ιδιότητες του οργάνου μέτρησης και/ή από τις
Περί σφαλμάτων και γραφικών παραστάσεων Σφάλμα ανάγνωσης οργάνου Το σφάλμα αυτό αναφέρεται σε αβεβαιότητες στη μέτρηση που προκαλούνται από τις πεπερασμένες ιδιότητες του οργάνου μέτρησης και/ή από τις
2. ΑΝΑΛΥΣΗ ΣΦΑΛΜΑΤΩΝ
 1. ΑΝΑΛΥΣΗ ΣΦΑΛΜΑΤΩΝ 1. Σφάλματα Κάθε μέτρηση ενός φυσικού μεγέθους χαρακτηρίζεται από μία αβεβαιότητα που ονομάζουμε σφάλμα, το οποίο αναγράφεται με τη μορφή Τιμή ± αβεβαιότητα π.χ έστω ότι σε ένα πείραμα
1. ΑΝΑΛΥΣΗ ΣΦΑΛΜΑΤΩΝ 1. Σφάλματα Κάθε μέτρηση ενός φυσικού μεγέθους χαρακτηρίζεται από μία αβεβαιότητα που ονομάζουμε σφάλμα, το οποίο αναγράφεται με τη μορφή Τιμή ± αβεβαιότητα π.χ έστω ότι σε ένα πείραμα
Φυσική Α Γυμνασίου. Για να καταφέρουμε λοιπόν να εξομαλύνουμε τα σφάλματα κάνουμε πολλές μετρήσεις και υπολογίζουμε την μέση τιμή.
 Φυσική Α Γυμνασίου Επιμέλεια: Αγκανάκης Α. Παναγιώτης Φυσικά Μεγέθη ονομάζουμε τις ποσότητες που μπορούμε να μετρήσουμε. Η μέτρηση τους γίνεται με την χρήση διαφόρων οργάνων, τα οποία θα δούμε αναλυτικά
Φυσική Α Γυμνασίου Επιμέλεια: Αγκανάκης Α. Παναγιώτης Φυσικά Μεγέθη ονομάζουμε τις ποσότητες που μπορούμε να μετρήσουμε. Η μέτρηση τους γίνεται με την χρήση διαφόρων οργάνων, τα οποία θα δούμε αναλυτικά
Α u. u cm. = ω 1 + α cm. cm cm
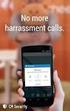 ΕΚΦΕ Ν.ΚΙΛΚΙΣ η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΠΕΞΕΡΓΑΣΙΑ : Κ. ΚΟΥΚΟΥΛΑΣ, ΦΥΣΙΚΟΣ - ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΟΣ [ Ε.Λ. ΠΟΛΥΚΑΣΤΡΟΥ ] ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΚΥΛΙΝΔΡΟΥ
ΕΚΦΕ Ν.ΚΙΛΚΙΣ η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΠΕΞΕΡΓΑΣΙΑ : Κ. ΚΟΥΚΟΥΛΑΣ, ΦΥΣΙΚΟΣ - ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΟΣ [ Ε.Λ. ΠΟΛΥΚΑΣΤΡΟΥ ] ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΚΥΛΙΝΔΡΟΥ
11 η ΕΥΡΩΠΑΙΚΗ ΟΛΥΜΠΙΑ Α ΕΠΙΣΤΗΜΩΝ EUSO 2013
 11 η ΕΥΡΩΠΑΙΚΗ ΟΛΥΜΠΙΑ Α ΕΠΙΣΤΗΜΩΝ EUSO 2013 ΤΟΠΙΚΟΣ ΜΑΘΗΤΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΠΕΙΡΑΜΑΤΙΚΗ ΟΚΙΜΑΣΙΑ ΣΤΗ ΦΥΣΙΚΗ Σάββατο 8 ΕΚΕΜΒΡΙΟΥ 2012 ΕΚΦΕ ΑΧΑΪΑΣ (ΑΙΓΙΟΥ) (Διάρκεια εξέτασης 60 min) Μαθητές: Σχολική Μονάδα
11 η ΕΥΡΩΠΑΙΚΗ ΟΛΥΜΠΙΑ Α ΕΠΙΣΤΗΜΩΝ EUSO 2013 ΤΟΠΙΚΟΣ ΜΑΘΗΤΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΠΕΙΡΑΜΑΤΙΚΗ ΟΚΙΜΑΣΙΑ ΣΤΗ ΦΥΣΙΚΗ Σάββατο 8 ΕΚΕΜΒΡΙΟΥ 2012 ΕΚΦΕ ΑΧΑΪΑΣ (ΑΙΓΙΟΥ) (Διάρκεια εξέτασης 60 min) Μαθητές: Σχολική Μονάδα
Η φυσική με πειράματα Α Γυμνασίου
 Εργαστήριο Φυσικών Επιστημών Γυμνασίου Δρεπάνου Η φυσική με πειράματα Α Γυμνασίου Φύλλο Εργασίας 5 Από τη Θερμότητα στη θερμοκρασία Η θερμική Ισορροπία Επεξεργασία-Απαντήσεις των δραστηριοτήτων και των
Εργαστήριο Φυσικών Επιστημών Γυμνασίου Δρεπάνου Η φυσική με πειράματα Α Γυμνασίου Φύλλο Εργασίας 5 Από τη Θερμότητα στη θερμοκρασία Η θερμική Ισορροπία Επεξεργασία-Απαντήσεις των δραστηριοτήτων και των
Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2011 Πανελλήνιος προκαταρκτικός διαγωνισμός στη Φυσική. Σχολείο: Ονόματα των μαθητών της ομάδας: 1) 2) 3)
 ΠΑΝΕΚΦΕ Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2011 Πανελλήνιος προκαταρκτικός διαγωνισμός στη Φυσική Σχολείο: Ονόματα των μαθητών της ομάδας: 1) 2) 3) Σχήμα 1 Εργαστηριακή Άσκηση: Μέτρηση της μάζας κινούμενου
ΠΑΝΕΚΦΕ Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2011 Πανελλήνιος προκαταρκτικός διαγωνισμός στη Φυσική Σχολείο: Ονόματα των μαθητών της ομάδας: 1) 2) 3) Σχήμα 1 Εργαστηριακή Άσκηση: Μέτρηση της μάζας κινούμενου
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ
 Ονομ/μο:.... Τμήμα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ Πώς θα μετρήσουμε την επιφάνεια ενός θρανίου, ενός φύλλου, ή του πουκάμισου που φοράμε; Την έννοια της «επιφάνειας» τη συναντάμε στα αντικείμενα
Ονομ/μο:.... Τμήμα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ Πώς θα μετρήσουμε την επιφάνεια ενός θρανίου, ενός φύλλου, ή του πουκάμισου που φοράμε; Την έννοια της «επιφάνειας» τη συναντάμε στα αντικείμενα
Με ποιο όργανο μετριέται το βάρος;
 Φύλλο Εργασίας 3 Μετρήσεις μάζας - τα διαγράμματα Τι είναι η μάζα; H μάζα ενός σώματος εκφράζει την ποσότητα της ύλης που περιέχεται στο σώμα αυτό. Συμβολίζεται με το γράμμα m. Η μάζα ενός σώματος είναι
Φύλλο Εργασίας 3 Μετρήσεις μάζας - τα διαγράμματα Τι είναι η μάζα; H μάζα ενός σώματος εκφράζει την ποσότητα της ύλης που περιέχεται στο σώμα αυτό. Συμβολίζεται με το γράμμα m. Η μάζα ενός σώματος είναι
Φύλλο Εργασίας 4 ο Μετρήσεις Θερμοκρασίας Η Βαθμονόμηση
 ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ Φύλλο Εργασίας 4 ο Μετρήσεις Θερμοκρασίας Η Βαθμονόμηση Εξακολουθούμε να μιλάμε για διαδικασίες μέτρησης, συγκεκριμένα της μέτρησης θερμοκρασίας. η μέτρηση είναι μία διαδικασία σύγκρισης
ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ Φύλλο Εργασίας 4 ο Μετρήσεις Θερμοκρασίας Η Βαθμονόμηση Εξακολουθούμε να μιλάμε για διαδικασίες μέτρησης, συγκεκριμένα της μέτρησης θερμοκρασίας. η μέτρηση είναι μία διαδικασία σύγκρισης
ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ. 5 - Δεκεμβρίου Χριστόφορος Στογιάννος
 ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ 5 - Δεκεμβρίου - 2015 Χριστόφορος Στογιάννος 1 ΕΚΦΕ ΑΛΙΜΟΥ ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 Eξεταζόμενο μάθημα: ΦΥΣΙΚΗ ΟΜΑΔΑ..... 1 η Δραστηριότητα Σκοπός της άσκησης
ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ 5 - Δεκεμβρίου - 2015 Χριστόφορος Στογιάννος 1 ΕΚΦΕ ΑΛΙΜΟΥ ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 Eξεταζόμενο μάθημα: ΦΥΣΙΚΗ ΟΜΑΔΑ..... 1 η Δραστηριότητα Σκοπός της άσκησης
ΕΡΩΤΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΓΥΜΝΑΣΙΟΥ. ΦΕ1. Μετρήσεις μήκους Η μέση τιμή. ΦΕ2. Μετρήσεις χρόνου Η ακρίβεια
 ΦΕ1. Μετρήσεις μήκους Η μέση τιμή. 1. Ποια μεγέθη λέγονται φυσικά μεγέθη; Πως γίνεται η μέτρησή τους; Οι ποσότητες που μπορούν να μετρηθούν ονομάζονται φυσικά μεγέθη. Η μέτρησή τους γίνεται με σύγκριση
ΦΕ1. Μετρήσεις μήκους Η μέση τιμή. 1. Ποια μεγέθη λέγονται φυσικά μεγέθη; Πως γίνεται η μέτρησή τους; Οι ποσότητες που μπορούν να μετρηθούν ονομάζονται φυσικά μεγέθη. Η μέτρησή τους γίνεται με σύγκριση
Για τη δραστηριότητα χρησιμοποιούνται τέσσερεις χάρακες του 1 m. Στο σχήμα φαίνεται το πρώτο δέκατο κάθε χάρακα.
 Σημαντικά ψηφία Η ταχύτητα διάδοσης του φωτός είναι 2.99792458 x 10 8 m/s. Η τιμή αυτή είναι δοσμένη σε 9 σημαντικά ψηφία. Τα 9 σημαντικά ψηφία είναι 299792458. Η τιμή αυτή μπορεί να δοθεί και με 5 σημαντικά
Σημαντικά ψηφία Η ταχύτητα διάδοσης του φωτός είναι 2.99792458 x 10 8 m/s. Η τιμή αυτή είναι δοσμένη σε 9 σημαντικά ψηφία. Τα 9 σημαντικά ψηφία είναι 299792458. Η τιμή αυτή μπορεί να δοθεί και με 5 σημαντικά
Η αβεβαιότητα στη μέτρηση.
 Η αβεβαιότητα στη μέτρηση. 1. Εισαγωγή. Κάθε μέτρηση, όσο προσεκτικά και αν έχει γίνει, περικλείει κάποια αβεβαιότητα. Η ανάλυση των σφαλμάτων είναι η μελέτη και ο υπολογισμός αυτής της αβεβαιότητας στη
Η αβεβαιότητα στη μέτρηση. 1. Εισαγωγή. Κάθε μέτρηση, όσο προσεκτικά και αν έχει γίνει, περικλείει κάποια αβεβαιότητα. Η ανάλυση των σφαλμάτων είναι η μελέτη και ο υπολογισμός αυτής της αβεβαιότητας στη
Εργαστηριακή άσκηση 12 ΜΕΤΑΤΡΟΠΗ ΦΑΣΗΣ ΒΡΑΣΜΟΣ
 Μιχαήλ Μιχαήλ, Φυσικός 1 Εργαστηριακή άσκηση 12 ΜΕΤΑΤΡΟΠΗ ΦΑΣΗΣ ΒΡΑΣΜΟΣ ΣΤΟΧΟΙ Οι στόχοι αυτής της εργαστηριακής άσκησης είναι: 1. Να επιβεβαιώνεις πειραµατικά ότι κατά τη διάρκεια του βρασµού ενός σώµατος
Μιχαήλ Μιχαήλ, Φυσικός 1 Εργαστηριακή άσκηση 12 ΜΕΤΑΤΡΟΠΗ ΦΑΣΗΣ ΒΡΑΣΜΟΣ ΣΤΟΧΟΙ Οι στόχοι αυτής της εργαστηριακής άσκησης είναι: 1. Να επιβεβαιώνεις πειραµατικά ότι κατά τη διάρκεια του βρασµού ενός σώµατος
26 Ιανουαρίου 2019 ΜΟΝΑΔΕΣ: ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ:
 ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΒΟΡΕΙΑΣ ΕΛΛΑΔΑΣ ΦΥΣΙΚΗ 26 Ιανουαρίου 2019 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Η βασική ιδέα Θα αναλάβετε το ρόλο ενός οργανοποιού με επιστημονικές ανησυχίες: Θέλετε
ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΒΟΡΕΙΑΣ ΕΛΛΑΔΑΣ ΦΥΣΙΚΗ 26 Ιανουαρίου 2019 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Η βασική ιδέα Θα αναλάβετε το ρόλο ενός οργανοποιού με επιστημονικές ανησυχίες: Θέλετε
Επισημάνσεις από τη θεωρία
 13 η ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΚΦΕ Ν.ΙΩΝΙΑΣ Τοπικός διαγωνισμός στη Φυσική 13 Δεκεμβρίου2014 α. β. γ. Ονοματεπώνυμο μαθητών Επισημάνσεις από τη θεωρία Σχολείο Ηλεκτρικό δίπολο ονομάζουμε κάθε ηλεκτρική
13 η ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΚΦΕ Ν.ΙΩΝΙΑΣ Τοπικός διαγωνισμός στη Φυσική 13 Δεκεμβρίου2014 α. β. γ. Ονοματεπώνυμο μαθητών Επισημάνσεις από τη θεωρία Σχολείο Ηλεκτρικό δίπολο ονομάζουμε κάθε ηλεκτρική
Με τους τρόπους της Φυσικής
 ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ Με τους τρόπους της Φυσικής Η Φυσική όπως και οι άλλες επιστήμες ασχολείται και μελετά τα Φαινόμενα. Φαινόμενα είναι οι αλλαγές που συμβαίνουν στον Κόσμο που ζεις, π.χ. η συνεχής εναλλαγή
ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ Με τους τρόπους της Φυσικής Η Φυσική όπως και οι άλλες επιστήμες ασχολείται και μελετά τα Φαινόμενα. Φαινόμενα είναι οι αλλαγές που συμβαίνουν στον Κόσμο που ζεις, π.χ. η συνεχής εναλλαγή
0,00620 = 6, ΣΗΜΑΝΤΙΚΑ ΨΗΦΙΑ. Γενικοί Κανόνες για τα Σημαντικά Ψηφία
 ΣΗΜΑΝΤΙΚΑ ΨΗΦΙΑ Είναι απαραίτητο να πούμε μερικά πράγματα για μια επαναλαμβανόμενη πηγή προβλημάτων και δυσκολιών: τα σημαντικά ψηφία. Τα μαθηματικά είναι μια επιστήμη όπου οι αριθμοί και οι σχέσεις μπορούν
ΣΗΜΑΝΤΙΚΑ ΨΗΦΙΑ Είναι απαραίτητο να πούμε μερικά πράγματα για μια επαναλαμβανόμενη πηγή προβλημάτων και δυσκολιών: τα σημαντικά ψηφία. Τα μαθηματικά είναι μια επιστήμη όπου οι αριθμοί και οι σχέσεις μπορούν
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ - 6 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 6 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ Κυριακή, 16 Μαΐου 2010 Ώρα : 10:00-12:30 Οδηγίες: 1) Το δοκίμιο αποτελείται από επτά (7) θέματα. 2) Να απαντήσετε σε όλα τα θέματα. 3)
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 6 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ Κυριακή, 16 Μαΐου 2010 Ώρα : 10:00-12:30 Οδηγίες: 1) Το δοκίμιο αποτελείται από επτά (7) θέματα. 2) Να απαντήσετε σε όλα τα θέματα. 3)
Φυσική Α Τάξης Φ.Ε. 1: Μετρήσεις μήκους - Η μέση τιμή
 Φυσική Α Τάξης Φ.Ε. 1: Μετρήσεις μήκους - Η μέση τιμή Α. Ερωτήσεις θεωρίας με απαντήσεις 1. Τι είναι τα φυσικά μεγέθη; Τα φυσικά μεγέθη είναι μετρήσιμες ποσότητες που υπεισέρχονται στα διάφορα φυσικά φαινόμενα
Φυσική Α Τάξης Φ.Ε. 1: Μετρήσεις μήκους - Η μέση τιμή Α. Ερωτήσεις θεωρίας με απαντήσεις 1. Τι είναι τα φυσικά μεγέθη; Τα φυσικά μεγέθη είναι μετρήσιμες ποσότητες που υπεισέρχονται στα διάφορα φυσικά φαινόμενα
ΓΥΜΝΑΣΙΟ ΚΑΘΟΛΙΚΗΣ ΛΕΜΕΣΟΥ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2018
 ΓΥΜΝΑΣΙΟ ΚΑΘΟΛΙΚΗΣ ΛΕΜΕΣΟΥ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2017-2018 ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2018 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΑΞΗ: Γ ΗΜΕΡΟΜΗΝΙΑ: 08/06/2018 ΧΡΟΝΙΚΗ ΔΙΑΡΚΕΙΑ: 1,5 ώρα ΩΡΑ: 07:45-09:15 ΒΑΘΜΟΣ Αριθμητικώς:...
ΓΥΜΝΑΣΙΟ ΚΑΘΟΛΙΚΗΣ ΛΕΜΕΣΟΥ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2017-2018 ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2018 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΑΞΗ: Γ ΗΜΕΡΟΜΗΝΙΑ: 08/06/2018 ΧΡΟΝΙΚΗ ΔΙΑΡΚΕΙΑ: 1,5 ώρα ΩΡΑ: 07:45-09:15 ΒΑΘΜΟΣ Αριθμητικώς:...
ΕΚΦΕ Τρικάλων. Πειραματική Δοκιμασία στη Φυσική. Τοπικός Μαθητικός Διαγωνισμός. Τρίκαλα, Σάββατο, 8 Δεκεμβρίου 2012
 1 Τοπικός Μαθητικός Διαγωνισμός 11η Ευρωπαϊκή Ολυμπιάδα Επιστημών EUSO 2013 11Η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2013 ΕΚΦΕ Τρικάλων Πειραματική Δοκιμασία στη Φυσική Τοπικός Μαθητικός Διαγωνισμός Τρίκαλα,
1 Τοπικός Μαθητικός Διαγωνισμός 11η Ευρωπαϊκή Ολυμπιάδα Επιστημών EUSO 2013 11Η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2013 ΕΚΦΕ Τρικάλων Πειραματική Δοκιμασία στη Φυσική Τοπικός Μαθητικός Διαγωνισμός Τρίκαλα,
Θέματα Παγκύπριων Εξετάσεων
 Θέματα Παγκύπριων Εξετάσεων 2009-2015 Σελίδα 1 από 13 Μηχανική Στερεού Σώματος 1. Στο πιο κάτω σχήμα φαίνονται δύο όμοιες πλατφόρμες οι οποίες μπορούν να περιστρέφονται χωρίς τριβές, γύρω από κατακόρυφο
Θέματα Παγκύπριων Εξετάσεων 2009-2015 Σελίδα 1 από 13 Μηχανική Στερεού Σώματος 1. Στο πιο κάτω σχήμα φαίνονται δύο όμοιες πλατφόρμες οι οποίες μπορούν να περιστρέφονται χωρίς τριβές, γύρω από κατακόρυφο
ΕΚΦΕ Α ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ. Φύλλο αξιολόγησης 1
 Φύλλο αξιολόγησης 1 1) Με ένα νήμα μήκους περίπου 60 εκατοστών και ένα βαρίδι φτιάχνουμε ένα εκκρεμές. Πέντε μαθητές μέτρησαν με το ίδιο χρονόμετρο το χρόνο 10 πλήρων ταλαντώσεων του εκκρεμούς. Οι μετρήσεις
Φύλλο αξιολόγησης 1 1) Με ένα νήμα μήκους περίπου 60 εκατοστών και ένα βαρίδι φτιάχνουμε ένα εκκρεμές. Πέντε μαθητές μέτρησαν με το ίδιο χρονόμετρο το χρόνο 10 πλήρων ταλαντώσεων του εκκρεμούς. Οι μετρήσεις
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2014 ΟΝΟΜΑΤΕΠΩΝΥΜΟ: 29/5/2014
 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΑΞΗ: Α ΟΝΟΜΑΤΕΠΩΝΥΜΟ: 29/5/2014 ΘΕΜΑ 1 Ο (ΥΠΟΧΡΕΩΤΙΚΟ) Στο ελατήριο του σχήματος, αναρτήσαμε κυλινδρικές μάζες και μετρήσαμε την αντίστοιχη
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΤΑΞΗ: Α ΟΝΟΜΑΤΕΠΩΝΥΜΟ: 29/5/2014 ΘΕΜΑ 1 Ο (ΥΠΟΧΡΕΩΤΙΚΟ) Στο ελατήριο του σχήματος, αναρτήσαμε κυλινδρικές μάζες και μετρήσαμε την αντίστοιχη
Προετοιμασία των ομάδων για τον τοπικό διαγωνισμό.
 Προετοιμασία των ομάδων για τον τοπικό διαγωνισμό. Φυσική 1. Επεξεργασία πειραματικών δεδομένων: α) Καταγραφή δεδομένων σε πίνακα μετρήσεων, β) Επιλογή συστήματος αξόνων με τις κατάλληλες κλίμακες και
Προετοιμασία των ομάδων για τον τοπικό διαγωνισμό. Φυσική 1. Επεξεργασία πειραματικών δεδομένων: α) Καταγραφή δεδομένων σε πίνακα μετρήσεων, β) Επιλογή συστήματος αξόνων με τις κατάλληλες κλίμακες και
ΦΥΛΛΟ ΑΠΑΝΤΗΣΗΣ 3 ης ΕΡΓΑΣΙΑΣ
 1 η θεματική ενότητα: Εφαρμογές του εκπαιδευτικού λογισμικού IP 2005 ΦΥΛΛΟ ΑΠΑΝΤΗΣΗΣ 3 ης ΕΡΓΑΣΙΑΣ Θέμα δραστηριότητας: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ Μάθημα και Τάξη στην Φυσική Γενικής Παιδείας Β Λυκείου οποία
1 η θεματική ενότητα: Εφαρμογές του εκπαιδευτικού λογισμικού IP 2005 ΦΥΛΛΟ ΑΠΑΝΤΗΣΗΣ 3 ης ΕΡΓΑΣΙΑΣ Θέμα δραστηριότητας: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ Μάθημα και Τάξη στην Φυσική Γενικής Παιδείας Β Λυκείου οποία
Το παρακάτω διάγραμμα παριστάνει την απομάκρυνση y ενός σημείου Μ (x Μ =1,2 m) του μέσου σε συνάρτηση με το χρόνο.
 ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα ζητούνται στο Θεωρητικό
ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα ζητούνται στο Θεωρητικό
ΜΕΤΡΗΣΗ ΤΗΣ ΔΙΑΜΕΤΡΟΥ ΚΥΛΙΝΔΡΙΚΟΥ ΣΥΡΜΑΤΟΣ
 14 η ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΚΦΕ ΧΑΛΑΝΔΡΙΟΥ και ΝΕΑΣ ΙΩΝΙΑΣ Τοπικός διαγωνισμός στη ΦΥΣΙΚΗ 05 Δεκεμβρίου 2015 Μαθητές Σχολείο 1. 2. 3. ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΦΥΣΙΚΗΣ ΜΕΤΡΗΣΗ ΤΗΣ ΔΙΑΜΕΤΡΟΥ ΚΥΛΙΝΔΡΙΚΟΥ
14 η ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΚΦΕ ΧΑΛΑΝΔΡΙΟΥ και ΝΕΑΣ ΙΩΝΙΑΣ Τοπικός διαγωνισμός στη ΦΥΣΙΚΗ 05 Δεκεμβρίου 2015 Μαθητές Σχολείο 1. 2. 3. ΤΙΤΛΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΦΥΣΙΚΗΣ ΜΕΤΡΗΣΗ ΤΗΣ ΔΙΑΜΕΤΡΟΥ ΚΥΛΙΝΔΡΙΚΟΥ
23 Ιανουαρίου 2016 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΒΟΡΕΙΑΣ ΕΛΛΑΔΑΣ ΦΥΣΙΚΗ 3 Ιανουαρίου 016 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1....... 3..... ΜΟΝΑΔΕΣ: Α. ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - Η ΙΔΕΑ Εικόνα 1: Ελεύθερη πτώση Ελεύθερη πτώση ονομάζεται η κίνηση
ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΒΟΡΕΙΑΣ ΕΛΛΑΔΑΣ ΦΥΣΙΚΗ 3 Ιανουαρίου 016 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1....... 3..... ΜΟΝΑΔΕΣ: Α. ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - Η ΙΔΕΑ Εικόνα 1: Ελεύθερη πτώση Ελεύθερη πτώση ονομάζεται η κίνηση
Φύλλο Εργασίας 1 Μετρήσεις Μήκους Η Μέση Τιμή
 Φύλλο Εργασίας 1 Μετρήσεις Μήκους Η Μέση Τιμή α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Όπως θα μάθεις αναλυτικότερα στη Β και Γ γυμνασίου: Η μέτρηση είναι πρωταρχική και σημαντική διαδικασία για τη φυσική
Φύλλο Εργασίας 1 Μετρήσεις Μήκους Η Μέση Τιμή α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Όπως θα μάθεις αναλυτικότερα στη Β και Γ γυμνασίου: Η μέτρηση είναι πρωταρχική και σημαντική διαδικασία για τη φυσική
ΣΧΕΔΙΟ ΥΠΟΒΟΛΗΣ ΔΗΜΙΟΥΡΓΙΚΗΣ ΕΡΓΑΣΙΑΣ των μαθητών ΣΤΟΙΧΕΙΑ ΥΠΕΥΘΥΝΟΥ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΑΝΤΙΚΕΙΜΕΝΟ ΜΩΡΑΪΤΑΚΗΣ ΗΛΙΑΣ ΠΕ04.01 ΦΥΣΙΚΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΣΧΕΔΙΟ ΥΠΟΒΟΛΗΣ ΔΗΜΙΟΥΡΓΙΚΗΣ ΕΡΓΑΣΙΑΣ των μαθητών ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΣΤΟΙΧΕΙΑ ΥΠΕΥΘΥΝΟΥ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ ΘΕΜΑΤΙΚΟΣ ΠΥΛΩΝΑΣ ΜΩΡΑΪΤΑΚΗΣ ΗΛΙΑΣ ΠΕ04.01 ΦΥΣΙΚΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΤΟΙΧΕΙΑ ΣΥΜΜΕΤΕΧΟΝΤΩΝ
ΣΧΕΔΙΟ ΥΠΟΒΟΛΗΣ ΔΗΜΙΟΥΡΓΙΚΗΣ ΕΡΓΑΣΙΑΣ των μαθητών ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΣΤΟΙΧΕΙΑ ΥΠΕΥΘΥΝΟΥ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ ΘΕΜΑΤΙΚΟΣ ΠΥΛΩΝΑΣ ΜΩΡΑΪΤΑΚΗΣ ΗΛΙΑΣ ΠΕ04.01 ΦΥΣΙΚΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΤΟΙΧΕΙΑ ΣΥΜΜΕΤΕΧΟΝΤΩΝ
8. Σύνθεση και ανάλυση δυνάμεων
 8. Σύνθεση και ανάλυση δυνάμεων Βασική θεωρία Σύνθεση δυνάμεων Συνισταμένη Σύνθεση δυνάμεων είναι η διαδικασία με την οποία προσπαθούμε να προσδιορίσουμε τη δύναμη εκείνη που προκαλεί τα ίδια αποτελέσματα
8. Σύνθεση και ανάλυση δυνάμεων Βασική θεωρία Σύνθεση δυνάμεων Συνισταμένη Σύνθεση δυνάμεων είναι η διαδικασία με την οποία προσπαθούμε να προσδιορίσουμε τη δύναμη εκείνη που προκαλεί τα ίδια αποτελέσματα
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλή Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscorses.wordpress.com/ Βασικές Έννοιες Ένα σώμα καθώς κινείται περνάει από διάφορα σημεία.
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλή Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscorses.wordpress.com/ Βασικές Έννοιες Ένα σώμα καθώς κινείται περνάει από διάφορα σημεία.
Εργαστηριακή άσκηση 10 Βαθµονόµηση θερµοµέτρου
 Μιχαήλ Μιχαήλ, Φυσικός 1 Εργαστηριακή άσκηση 10 Βαθµονόµηση θερµοµέτρου ΣΤΟΧΟΙ Οι στόχοι αυτής της εργαστηριακής άσκησης είναι: - Να κατασκευάζεις µια κλίµακα θερµοκρασίας Κελσίου. - Να µπορείς να χρησιµοποιείς
Μιχαήλ Μιχαήλ, Φυσικός 1 Εργαστηριακή άσκηση 10 Βαθµονόµηση θερµοµέτρου ΣΤΟΧΟΙ Οι στόχοι αυτής της εργαστηριακής άσκησης είναι: - Να κατασκευάζεις µια κλίµακα θερµοκρασίας Κελσίου. - Να µπορείς να χρησιµοποιείς
Φυσική: Ασκήσεις. Β Γυμνασίου. Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd
 0 Β Γυμνασίου Φυσική: Ασκήσεις Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 0 1 Ασκήσεις στο 1 ο Κεφάλαιο Ασκήσεις με κενά 1. Να συμπληρώσεις τα κενά στις παρακάτω προτάσεις:
0 Β Γυμνασίου Φυσική: Ασκήσεις Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 0 1 Ασκήσεις στο 1 ο Κεφάλαιο Ασκήσεις με κενά 1. Να συμπληρώσεις τα κενά στις παρακάτω προτάσεις:
ΕΝΩΣΗ ΕΛΛΗΝΩΝ ΦΥΣΙΚΩΝ 7 ος Πανελλήνιος Διαγωνισμός Φυσικής Β Γυμνασίου. ΘΕΜΑΤΑ 7 ου ΠΑΝΕΛΛΗΝΙΟΥ ΔΙΑΓΩΝΙΣΜΟΥ Β ΓΥΜΝΑΣΙΟΥ.
 ΘΕΜΑΤΑ 7 ου ΠΑΝΕΛΛΗΝΙΟΥ ΔΙΑΓΩΝΙΣΜΟΥ Β ΓΥΜΝΑΣΙΟΥ Σελίδα 1 από 11 ΘΕΜΑ Α ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ Να χαρακτηρίσετε στο απαντητικό φύλλο, χωρίς αιτιολόγηση, καθεμία από τις παρακάτω προτάσεις ως Σωστή (Σ) ή ως Λάθος
ΘΕΜΑΤΑ 7 ου ΠΑΝΕΛΛΗΝΙΟΥ ΔΙΑΓΩΝΙΣΜΟΥ Β ΓΥΜΝΑΣΙΟΥ Σελίδα 1 από 11 ΘΕΜΑ Α ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ Να χαρακτηρίσετε στο απαντητικό φύλλο, χωρίς αιτιολόγηση, καθεμία από τις παρακάτω προτάσεις ως Σωστή (Σ) ή ως Λάθος
Φύλλο Εργασίας 5 Από τη Θερμότητα στη Θερμοκρασία - Η Θερμική Ισορροπία
 Φύλλο Εργασίας 5 Από τη Θερμότητα στη Θερμοκρασία - Η Θερμική Ισορροπία α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Στο βιβλίο των φυσικών του δημοτικού σχολείου της Ε τάξης υπάρχει η παρακάτω αναφορά στη
Φύλλο Εργασίας 5 Από τη Θερμότητα στη Θερμοκρασία - Η Θερμική Ισορροπία α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Στο βιβλίο των φυσικών του δημοτικού σχολείου της Ε τάξης υπάρχει η παρακάτω αναφορά στη
ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ - ΑΞΙΟΛΟΓΗΣΗ
 ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ - ΑΞΙΟΛΟΓΗΣΗ 1 ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ Επιδιώκεται οι μαθητές: 1. Να συζητούν και να προβληματίζονται για τα μετρήσιμα και τα μη μετρήσιμα μεγέθη. 2. Να πειραματιστούν και να καταλήξουν σε
ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ - ΑΞΙΟΛΟΓΗΣΗ 1 ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ Επιδιώκεται οι μαθητές: 1. Να συζητούν και να προβληματίζονται για τα μετρήσιμα και τα μη μετρήσιμα μεγέθη. 2. Να πειραματιστούν και να καταλήξουν σε
ΓΥΜΝΑΣΙΟ ΑΡΧ. ΜΑΚΑΡΙΟΥ Γ - ΠΛΑΤΥ ΣΧΟΛΙΚΟ ΕΤΟΣ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΜΗΜΑ:... Αρ...
 ΓΥΜΝΑΣΙΟ ΑΡΧ. ΜΑΚΑΡΙΟΥ Γ - ΠΛΑΤΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 2013-2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΒΑΘΜΟΣ ΗΜΕΡΟΜΗΝΙΑ: 16/6/2014 Αριθμητικά ΒΑΘΜΟΣ:..... ΤΑΞΗ: Β ΧΡΟΝΟΣ: 2 ώρες Ολογράφως:...
ΓΥΜΝΑΣΙΟ ΑΡΧ. ΜΑΚΑΡΙΟΥ Γ - ΠΛΑΤΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 2013-2014 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΝΙΟΥ 2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΒΑΘΜΟΣ ΗΜΕΡΟΜΗΝΙΑ: 16/6/2014 Αριθμητικά ΒΑΘΜΟΣ:..... ΤΑΞΗ: Β ΧΡΟΝΟΣ: 2 ώρες Ολογράφως:...
Άσκηση 3 Υπολογισμός του μέτρου της ταχύτητας και της επιτάχυνσης
 Άσκηση 3 Υπολογισμός του μέτρου της ταχύτητας και της επιτάχυνσης Σύνοψη Σκοπός της συγκεκριμένης άσκησης είναι ο υπολογισμός του μέτρου της στιγμιαίας ταχύτητας και της επιτάχυνσης ενός υλικού σημείου
Άσκηση 3 Υπολογισμός του μέτρου της ταχύτητας και της επιτάχυνσης Σύνοψη Σκοπός της συγκεκριμένης άσκησης είναι ο υπολογισμός του μέτρου της στιγμιαίας ταχύτητας και της επιτάχυνσης ενός υλικού σημείου
Φύλλο Εργασίας 4 Μετρήσεις Θερμοκρασίας-Η βαθμονόμηση
 Φύλλο Εργασίας 4 Μετρήσεις Θερμοκρασίας-Η βαθμονόμηση Οι άνθρωποι προσπαθούν να εκτιμήσουν κατά προσέγγιση ή να μετρήσουν με ακρίβεια τη θερμοκρασία του περιβάλλοντος, των διαφόρων σωμάτων ή και τη θερμοκρασία
Φύλλο Εργασίας 4 Μετρήσεις Θερμοκρασίας-Η βαθμονόμηση Οι άνθρωποι προσπαθούν να εκτιμήσουν κατά προσέγγιση ή να μετρήσουν με ακρίβεια τη θερμοκρασία του περιβάλλοντος, των διαφόρων σωμάτων ή και τη θερμοκρασία
ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO Ε.Κ.Φ.Ε. Νέας Σμύρνης
 ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 14-15 Ε.Κ.Φ.Ε. Νέας Σμύρνης Εξέταση στη Φυσική ΛΥΚΕΙΟ: Τριμελής ομάδα μαθητών: 1.. 3. Αναπληρωματικός: Θέματα: Ηλ. Μαυροματίδης Β Σειρά Θεμάτων (Φυσική) Μέτρηση της
ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 14-15 Ε.Κ.Φ.Ε. Νέας Σμύρνης Εξέταση στη Φυσική ΛΥΚΕΙΟ: Τριμελής ομάδα μαθητών: 1.. 3. Αναπληρωματικός: Θέματα: Ηλ. Μαυροματίδης Β Σειρά Θεμάτων (Φυσική) Μέτρηση της
ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΧΡΟΝΟΥ ΜΑΖΑΣ ΔΥΝΑΜΗΣ
 1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΧΡΟΝΟΥ ΜΑΖΑΣ ΔΥΝΑΜΗΣ Α. ΣΤΟΧΟΙ Η συνειδητή χρήση των κανόνων ασφαλείας στο εργαστήριο. Η εξοικείωση στη χρήση του υποδεκάμετρου και του διαστημόμετρου
1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΧΡΟΝΟΥ ΜΑΖΑΣ ΔΥΝΑΜΗΣ Α. ΣΤΟΧΟΙ Η συνειδητή χρήση των κανόνων ασφαλείας στο εργαστήριο. Η εξοικείωση στη χρήση του υποδεκάμετρου και του διαστημόμετρου
Γ Γυμνασίου Τμήμα. Ημερομηνία. ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 2 Νόμος του Ohm. Θεωρία που πρέπει να γνωρίζεις
 Ονοματεπώνυμο Καθηγήτρια: Εγγλεζάκη Φρίντα Γ Γυμνασίου Τμήμα Βαθμός Ημερομηνία ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 2 Νόμος του Ohm. Θεωρία που πρέπει να γνωρίζεις Η ένταση (Ι) του ηλεκτρικού ρεύματος που διαρρέει έναν μεταλλικό
Ονοματεπώνυμο Καθηγήτρια: Εγγλεζάκη Φρίντα Γ Γυμνασίου Τμήμα Βαθμός Ημερομηνία ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 2 Νόμος του Ohm. Θεωρία που πρέπει να γνωρίζεις Η ένταση (Ι) του ηλεκτρικού ρεύματος που διαρρέει έναν μεταλλικό
Τοπικός διαγωνισμός EUSO2018
 ΕΚΦΕ Νέας Ιωνίας ΕΚΦΕ Χαλανδρίου Τοπικός διαγωνισμός EUSO2018 Πειραματική δοκιμασία Φυσικής Η τριβή και η μηχανική ενέργεια 9 Δεκεμβρίου 2017 ΣΧΟΛΙΚΗ ΜΟΝΑΔΑ: ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1) 2). 3).. Aριθμός ομάδας Η
ΕΚΦΕ Νέας Ιωνίας ΕΚΦΕ Χαλανδρίου Τοπικός διαγωνισμός EUSO2018 Πειραματική δοκιμασία Φυσικής Η τριβή και η μηχανική ενέργεια 9 Δεκεμβρίου 2017 ΣΧΟΛΙΚΗ ΜΟΝΑΔΑ: ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1) 2). 3).. Aριθμός ομάδας Η
ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΩΝ ΠΑΡΑΣΤΑΣΕΩΝ
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΣΧΟΛ. ΕΤΟΣ 2014-15 1. Εισαγωγή ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΩΝ ΠΑΡΑΣΤΑΣΕΩΝ Οι γραφικές παραστάσεις (ή διαγράμματα) χρησιμεύουν για την απεικόνιση της εξάρτησης
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΣΧΟΛ. ΕΤΟΣ 2014-15 1. Εισαγωγή ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΩΝ ΠΑΡΑΣΤΑΣΕΩΝ Οι γραφικές παραστάσεις (ή διαγράμματα) χρησιμεύουν για την απεικόνιση της εξάρτησης
Φύλλο Εργασίας 3 Μετρήσεις μάζας Τα διαγράμματα
 Φύλλο Εργασίας 3 Μετρήσεις μάζας Τα διαγράμματα α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Τι πρέπει να κάνουμε για να μετρήσουμε οποιοδήποτε μέγεθος; Πρέπει να ορίσουμε: 1. Μια ομοειδή ποσότητα ως μονάδα
Φύλλο Εργασίας 3 Μετρήσεις μάζας Τα διαγράμματα α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Τι πρέπει να κάνουμε για να μετρήσουμε οποιοδήποτε μέγεθος; Πρέπει να ορίσουμε: 1. Μια ομοειδή ποσότητα ως μονάδα
Φύλλο Εργασίας 6 Οι Αλλαγές Κατάστασης του Νερού Ο "Κύκλος" του Νερού
 Φύλλο Εργασίας 6 Οι Αλλαγές Κατάστασης του Νερού Ο "Κύκλος" του Νερού α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Παρατήρησε την παρακάτω εικόνα. Αναγνώρισε τα φαινόμενα που σχετίζονται με το νερό και ονόμασέ
Φύλλο Εργασίας 6 Οι Αλλαγές Κατάστασης του Νερού Ο "Κύκλος" του Νερού α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Παρατήρησε την παρακάτω εικόνα. Αναγνώρισε τα φαινόμενα που σχετίζονται με το νερό και ονόμασέ
kg(χιλιόγραμμο) s(δευτερόλεπτο) Ένταση ηλεκτρικού πεδίου Α(Αμπέρ) Ένταση φωτεινής πηγής cd (καντέλα) Ποσότητα χημικής ουσίας mole(μόλ)
 ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
Άσκηση 2: Εργαστηριακα σκεύ η χημει ας. Μετρη σεις ό γκων και μαζων 1
 Σκόπός της άσκησης: Άσκηση : Εργαστηριακα σκεύ η χημει ας. Μετρη σεις ό γκων και μαζων Να εξοικειωθούν οι φοιτητές με τα συνήθη σκεύη της Χημείας και την ορθή ανάγνωση όγκων και μαζών από αντίστοιχα κατάλληλα
Σκόπός της άσκησης: Άσκηση : Εργαστηριακα σκεύ η χημει ας. Μετρη σεις ό γκων και μαζων Να εξοικειωθούν οι φοιτητές με τα συνήθη σκεύη της Χημείας και την ορθή ανάγνωση όγκων και μαζών από αντίστοιχα κατάλληλα
1 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ
 ΑΕΙ ΠΕΙΡΑΙΑ ΤΤ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ Σκοπός της άσκησης 1 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Σκοπός αυτής της άσκησης είναι η εξοικείωση των σπουδαστών με τα σφάλματα που
ΑΕΙ ΠΕΙΡΑΙΑ ΤΤ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ Σκοπός της άσκησης 1 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Σκοπός αυτής της άσκησης είναι η εξοικείωση των σπουδαστών με τα σφάλματα που
Ευρωπαϊκή Ολυµπιάδα Φυσικών Επιστηµών 2010 Προκαταρκτικός διαγωνισµός στη Φυσική. Σχολείο:
 ΕΚΦΕ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ Ευρωπαϊκή Ολυµπιάδα Φυσικών Επιστηµών 010 Προκαταρκτικός διαγωνισµός στη Φυσική Σχολείο: Ονόµατα των µαθητών της οµάδας 1) ) 3) Οι στόχοι του πειράµατος 1. Η µέτρηση της επιτάχυνσης
ΕΚΦΕ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ Ευρωπαϊκή Ολυµπιάδα Φυσικών Επιστηµών 010 Προκαταρκτικός διαγωνισµός στη Φυσική Σχολείο: Ονόµατα των µαθητών της οµάδας 1) ) 3) Οι στόχοι του πειράµατος 1. Η µέτρηση της επιτάχυνσης
Ο ΝΟΜΟΣ ΤΟΥ HOOKE ΣΤΟΧΟΙ
 Ο ΝΟΜΟΣ ΤΟΥ HOOKE ΣΤΟΧΟΙ Να αποδείξεις πειραματικά ότι η επιμήκυνση ενός ελατηρίου είναι ανάλογη της δύναμης που την προκαλεί. Να υπολογίσεις την σταθερά k (σκληρότητα) του ελατηρίου. Να γίνει κατανοητή
Ο ΝΟΜΟΣ ΤΟΥ HOOKE ΣΤΟΧΟΙ Να αποδείξεις πειραματικά ότι η επιμήκυνση ενός ελατηρίου είναι ανάλογη της δύναμης που την προκαλεί. Να υπολογίσεις την σταθερά k (σκληρότητα) του ελατηρίου. Να γίνει κατανοητή
Μέτρηση μηκών και ακτίνων καμπυλότητας σφαιρικών επιφανειών
 Μ7 Μέτρηση μηκών και ακτίνων καμπυλότητας σφαιρικών επιφανειών 1. Σκοπός Τα διαστημόμετρα, τα μικρόμετρα και τα σφαιρόμετρα είναι όργανα που χρησιμοποιούνται για την μέτρηση της διάστασης του μήκους, του
Μ7 Μέτρηση μηκών και ακτίνων καμπυλότητας σφαιρικών επιφανειών 1. Σκοπός Τα διαστημόμετρα, τα μικρόμετρα και τα σφαιρόμετρα είναι όργανα που χρησιμοποιούνται για την μέτρηση της διάστασης του μήκους, του
Άσκηση 4 Θεμελιώδης νόμος της Μηχανικής
 Άσκηση 4 Θεμελιώδης νόμος της Μηχανικής Σύνοψη Η άσκηση αυτή διαφέρει από όλες τις άλλες. Σκοπός της είναι η πειραματική επαλήθευση του θεμελιώδους νόμου της Μηχανικής. Αυτό θα γίνει με τη γραφική ανάλυση
Άσκηση 4 Θεμελιώδης νόμος της Μηχανικής Σύνοψη Η άσκηση αυτή διαφέρει από όλες τις άλλες. Σκοπός της είναι η πειραματική επαλήθευση του θεμελιώδους νόμου της Μηχανικής. Αυτό θα γίνει με τη γραφική ανάλυση
Πειραματική διάταξη μελέτης, της. χαρακτηριστικής καμπύλης διπόλου
 Πειραματική διάταξη μελέτης, της χαρακτηριστικής καμπύλης διπόλου Επισημάνσεις από τη θεωρία. 1 Ηλεκτρικό δίπολο ονομάζουμε κάθε ηλεκτρική συσκευή που έχει δύο πόλους (άκρα) και όταν συνδεθεί σε ηλεκτρικό
Πειραματική διάταξη μελέτης, της χαρακτηριστικής καμπύλης διπόλου Επισημάνσεις από τη θεωρία. 1 Ηλεκτρικό δίπολο ονομάζουμε κάθε ηλεκτρική συσκευή που έχει δύο πόλους (άκρα) και όταν συνδεθεί σε ηλεκτρικό
Η ΦΥΣΙΚΗ ΜΕ ΠΕΙΡΑΜΑΤΑ
 ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ Η ΦΥΣΙΚΗ ΜΕ ΠΕΙΡΑΜΑΤΑ ΣΥΜΠΕΡΑΣΜΑΤΑ ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ ΕΠΙΜΕΛΕΙΑ: ΞΑΝΘΟΣ ΧΡΗΣΤΟΣ ΦΥΣΙΚΟΣ ΠΕ0401 0 1 o κεφάλαιο Συμπεράσματα 1. Για τη μέτρηση του μήκους με μετροταινία θα πρέπει
ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ Η ΦΥΣΙΚΗ ΜΕ ΠΕΙΡΑΜΑΤΑ ΣΥΜΠΕΡΑΣΜΑΤΑ ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ ΕΠΙΜΕΛΕΙΑ: ΞΑΝΘΟΣ ΧΡΗΣΤΟΣ ΦΥΣΙΚΟΣ ΠΕ0401 0 1 o κεφάλαιο Συμπεράσματα 1. Για τη μέτρηση του μήκους με μετροταινία θα πρέπει
ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ. Φύλλο Εργασίας 5 ο Από τη Θερμότητα στη Θερμοκρασία Η Θερμική Ισορροπία
 ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ Φύλλο Εργασίας 5 ο Από τη Θερμότητα στη Θερμοκρασία Η Θερμική Ισορροπία Φύλλο Εργασίας 5ο: Από τη Θερμότητα στη Θερμοκρασία Η Θερμική Ισορροπία Στόχος μας είναι: να διακρίνουμε τη διαφορά
ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ Φύλλο Εργασίας 5 ο Από τη Θερμότητα στη Θερμοκρασία Η Θερμική Ισορροπία Φύλλο Εργασίας 5ο: Από τη Θερμότητα στη Θερμοκρασία Η Θερμική Ισορροπία Στόχος μας είναι: να διακρίνουμε τη διαφορά
Πα.Δα. Τμήμα Μηχανικών Πληροφορικής και Υπολογιστών ΣΦΑΛΜΑΤΑ ΜΕΤΡΗΣΕΩΝ
 Πα.Δα. Τμήμα Μηχανικών Πληροφορικής και Υπολογιστών Εισαγωγή στην Εργαστηριακή Φυσική ΣΦΑΛΜΑΤΑ ΜΕΤΡΗΣΕΩΝ Δημήτριος Ν.Νικολόπουλος Καθηγητής Περιβαλλοντική και Ιατρική Φυσική Μέτρηση Η σύγκριση ενός μεγέθους
Πα.Δα. Τμήμα Μηχανικών Πληροφορικής και Υπολογιστών Εισαγωγή στην Εργαστηριακή Φυσική ΣΦΑΛΜΑΤΑ ΜΕΤΡΗΣΕΩΝ Δημήτριος Ν.Νικολόπουλος Καθηγητής Περιβαλλοντική και Ιατρική Φυσική Μέτρηση Η σύγκριση ενός μεγέθους
ΦΥΣΙΚΗ. 13 η Ευρωπαϊκή Ολυμπιάδα επιστημών EUSO 2015 ΕΚΦΕ Λευκάδας - Τοπικός Διαγωνισμός. Λευκάδα
 ΠΑΝΕΛΛΗΝΙΑ ΕΝΩΣΗ ΥΠΕΥΘΥΝΩΝ ΕΡΓΑΣΤΗΡΙΑΚΩΝ ΚΕΝΤΡΩΝ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ «ΠΑΝΕΚΦE» 13 η Ευρωπαϊκή Ολυμπιάδα επιστημών EUSO 15 ΕΚΦΕ Λευκάδας - Τοπικός Διαγωνισμός Λευκάδα 6-1-14 ΣΧΟΛΙΚΗ ΜΟΝΑΔΑ:. ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ:.
ΠΑΝΕΛΛΗΝΙΑ ΕΝΩΣΗ ΥΠΕΥΘΥΝΩΝ ΕΡΓΑΣΤΗΡΙΑΚΩΝ ΚΕΝΤΡΩΝ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ «ΠΑΝΕΚΦE» 13 η Ευρωπαϊκή Ολυμπιάδα επιστημών EUSO 15 ΕΚΦΕ Λευκάδας - Τοπικός Διαγωνισμός Λευκάδα 6-1-14 ΣΧΟΛΙΚΗ ΜΟΝΑΔΑ:. ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ:.
Άσκηση 1 Μέτρηση του συντελεστή γραμμικής διαστολής του υλικού μιας μεταλλικής ράβδου
 Άσκηση 1 Μέτρηση του συντελεστή γραμμικής διαστολής του υλικού μιας μεταλλικής ράβδου Σύνοψη Αυτή είναι μια από τις πρώτες ασκήσεις που κάνεις στο εργαστήριο Φυσικής Ι, γι αυτό καλό είναι να μάθεις ότι
Άσκηση 1 Μέτρηση του συντελεστή γραμμικής διαστολής του υλικού μιας μεταλλικής ράβδου Σύνοψη Αυτή είναι μια από τις πρώτες ασκήσεις που κάνεις στο εργαστήριο Φυσικής Ι, γι αυτό καλό είναι να μάθεις ότι
ΦΥΛΛΟ ΕΞΟΙΚΕΙΩΣΗΣ ΜΕ ΤΟ ΕΙΚΟΝΙΚΟ ΕΡΓΑΣΤΗΡΙΟ
 ΦΥΛΛΟ ΕΞΟΙΚΕΙΩΣΗΣ ΜΕ ΤΟ ΕΙΚΟΝΙΚΟ ΕΡΓΑΣΤΗΡΙΟ Βρίσκεσαι μπροστά σε ένα φύλλο εργασίας. Ακολούθησε τις οδηγίες που σου δίνει για να πραγματοποιήσεις μια σειρά από δραστηριότητες. Έτσι θα μάθεις να δουλεύεις
ΦΥΛΛΟ ΕΞΟΙΚΕΙΩΣΗΣ ΜΕ ΤΟ ΕΙΚΟΝΙΚΟ ΕΡΓΑΣΤΗΡΙΟ Βρίσκεσαι μπροστά σε ένα φύλλο εργασίας. Ακολούθησε τις οδηγίες που σου δίνει για να πραγματοποιήσεις μια σειρά από δραστηριότητες. Έτσι θα μάθεις να δουλεύεις
ΥΠΟΥΡΓΕΙΟ ΠΑΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΛΕΥΚΩΣΙΑ ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΛΥΚΕΙΑΚΟΣ ΚΥΚΛΟΣ Β ΣΕΙΡΑ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΥΡΓΕΙΟ ΠΑΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΛΕΥΚΩΣΙΑ ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΛΥΚΕΙΑΚΟΣ ΚΥΚΛΟΣ Β ΣΕΙΡΑ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑ: ΧΡΟΝΟΣ: ΦΥΣΙΚΗ 3 ΩΡΕΣ ΗΜΕΡΟΜΗΝΙΑ: 27/05/2014 ΩΡΑ ΕΝΑΡΞΗΣ:
ΥΠΟΥΡΓΕΙΟ ΠΑΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΛΕΥΚΩΣΙΑ ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2014 ΛΥΚΕΙΑΚΟΣ ΚΥΚΛΟΣ Β ΣΕΙΡΑ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑ: ΧΡΟΝΟΣ: ΦΥΣΙΚΗ 3 ΩΡΕΣ ΗΜΕΡΟΜΗΝΙΑ: 27/05/2014 ΩΡΑ ΕΝΑΡΞΗΣ:
ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑΔΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO 2017
 1ο και 2ο ΕΚΦΕ Ηρακλείου ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑΔΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO 2017 Σάββατο 3 Δεκεμβρίου 2016 Διαγωνισμός στη Φυσική (Διάρκεια 1 ώρα) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΩΝ 1)... 2)...
1ο και 2ο ΕΚΦΕ Ηρακλείου ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑΔΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO 2017 Σάββατο 3 Δεκεμβρίου 2016 Διαγωνισμός στη Φυσική (Διάρκεια 1 ώρα) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΩΝ 1)... 2)...
Β Γυμνασίου Σελ. 1 από 10
 ΟΔΗΓΙΕΣ: 1. Οι απαντήσεις σε όλα τα ερωτήματα θα πρέπει να αναγραφούν στο Φύλλο Απαντήσεων που θα σας δοθεί μαζί με τις εκφωνήσεις. 2. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε φύλλα Α4 ή σε τετράδιο
ΟΔΗΓΙΕΣ: 1. Οι απαντήσεις σε όλα τα ερωτήματα θα πρέπει να αναγραφούν στο Φύλλο Απαντήσεων που θα σας δοθεί μαζί με τις εκφωνήσεις. 2. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε φύλλα Α4 ή σε τετράδιο
Q 40 th International Physics Olympiad, Merida, Mexico, July 2009
 ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΟΥ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΦΩΤΟΣ ASER ΥΛΙΚΑ ΚΑΙ ΟΡΓΑΝΑ Επιπρόσθετα με τα υλικά 1), 2) και 3), αναμένεται να χρησιμοποιήσετε τα ακόλουθα: 4) Φακός ενσωματωμένος μέσα σε
ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΟΥ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΦΩΤΟΣ ASER ΥΛΙΚΑ ΚΑΙ ΟΡΓΑΝΑ Επιπρόσθετα με τα υλικά 1), 2) και 3), αναμένεται να χρησιμοποιήσετε τα ακόλουθα: 4) Φακός ενσωματωμένος μέσα σε
Μετρήσεις σε ράβδους γραφίτη.
 13 η ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΚΦΕ ΧΑΛΑΝΔΡΙΟΥ Τοπικός διαγωνισμός στη ΦΥΣΙΚΗ 13 Δεκεμβρίου2014 Σχολείο: Ονόματα μαθητών:1) 2) 3) Μετρήσεις σε ράβδους γραφίτη. Για να γράψουμε χρησιμοποιούμε τα μολύβια,
13 η ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΚΦΕ ΧΑΛΑΝΔΡΙΟΥ Τοπικός διαγωνισμός στη ΦΥΣΙΚΗ 13 Δεκεμβρίου2014 Σχολείο: Ονόματα μαθητών:1) 2) 3) Μετρήσεις σε ράβδους γραφίτη. Για να γράψουμε χρησιμοποιούμε τα μολύβια,
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΗΣ ΤΗΣ ΥΛΗΣ ΚΑΙ ΦΥΣΙΚΗΣ ΛΕΪΖΕΡ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ.
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΗΣ ΤΗΣ ΥΛΗΣ ΚΑΙ ΦΥΣΙΚΗΣ ΛΕΪΖΕΡ http://www.physicslab.tuc.gr https://www.eclass.tuc.gr/courses/sci123/ Επιμέλεια παρουσίασης: Ά.Καλλιατάκη,
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΗΣ ΤΗΣ ΥΛΗΣ ΚΑΙ ΦΥΣΙΚΗΣ ΛΕΪΖΕΡ http://www.physicslab.tuc.gr https://www.eclass.tuc.gr/courses/sci123/ Επιμέλεια παρουσίασης: Ά.Καλλιατάκη,
Άνοιξε τη μικροεφαρμογή (applet) PhET "Πίεση και ροή υγρού". Κάνε κλικ στην οθόνη "Πίεση" και βρες:
 1. ΜΕΛΕΤΗ ΤΗΣ ΥΔΡΟΣΤΑΤΙΚΗΣ ΠΙΕΣΗΣ Το 1ο μέρος του φύλλου εργασίας του Applet PhET "Πίεση και Ροή ρευστού" προτείνεται σε μαθητές που έχουν διδαχθεί από το Γυμνάσιο το νόμο της υδροστατικής πίεσης και θέλουν
1. ΜΕΛΕΤΗ ΤΗΣ ΥΔΡΟΣΤΑΤΙΚΗΣ ΠΙΕΣΗΣ Το 1ο μέρος του φύλλου εργασίας του Applet PhET "Πίεση και Ροή ρευστού" προτείνεται σε μαθητές που έχουν διδαχθεί από το Γυμνάσιο το νόμο της υδροστατικής πίεσης και θέλουν
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΗΣ ΤΗΣ ΥΛΗΣ ΚΑΙ ΦΥΣΙΚΗΣ ΛΕΪΖΕΡ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ.
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΗΣ ΤΗΣ ΥΛΗΣ ΚΑΙ ΦΥΣΙΚΗΣ ΛΕΪΖΕΡ http://www.physicslab.tuc.gr https://www.eclass.tuc.gr/courses/sci123/ Επιμέλεια παρουσίασης: Ά.Καλλιατάκη,
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΡΓΑΣΤΗΡΙΟ ΔΟΜΗΣ ΤΗΣ ΥΛΗΣ ΚΑΙ ΦΥΣΙΚΗΣ ΛΕΪΖΕΡ http://www.physicslab.tuc.gr https://www.eclass.tuc.gr/courses/sci123/ Επιμέλεια παρουσίασης: Ά.Καλλιατάκη,
