Mechanical Behaviour of Materials Chapter 5 Plasticity Theory
|
|
|
- Ιπποκράτης Καλάρης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Mechanical Behaviour of Materials Chapter 5 Plasticity Theory Dr.-Ing. 郭瑞昭
2 Yield criteria Question: For what combinations of loads will the cylinder begin to yield plastically? The criteria for deciding which combination of multiaxial stresses will cause yielding are called yield criteria. f (,,,,, ) C x y z xy yz zx 0 y f (,, ) C y 0
3 Rankine Criteria (Maximum normal stress) Yielding occurs when the largest principal normal stress is equal to the yield strength 0 in simple tension, or - 0 in compression. 0 Yielding will occur the state of stress is on the boundary of the rectangle.
4 Tresca Criteria Maximum-shear stress criterion: plastic flow takes place when the maximum shear stress in a complex state of stress reaches the maximum shear stress at the onset of flow in uniaxial tension. Yielding occurs when the maximum shear stress reaches a critical. Yielding will occur when one of the following six conditions is reached: ± ± ± 0 0 0
5 Tresca Criteria 0) ( 0) ( 0) ( 0) ( 0) 0, ( 0) 0, ( < < < < > > > > > < < >
6 von Mises Criteria Yielding occurs when the distortion energy equals the distortion energy at yield in simple tension. y +
7 von Mises Criteria Maximum-Distortion-Energy Criterion: The maximum-distortion energy theory is founded on the concept of strain energy. It assumes that only the strain energy that produces a change of shape is responsible for the plastic flow of the material. [( ) ( ) ( ) ] the total energy a volume change energy a distortion energy
8 von Mises Criteria [ ] p p p p p p u ε ε ε + + the total energy the volume change energy the distortion energy ε v v p u [ ] ε ε + ε + ε v p p p p p p d p u
9 von Mises Criteria u the total energy u E [ ε + ε + ε ] { [ ν( + )] + [ ν( + )] + [ ν( + )]} u E { + + ν( + + )}
10 von Mises Criteria: the energy of volume change ) ( + + p ( ) ν ε E p u v v p E v ) ( ν ε
11 von Mises Criteria: The distortion energy u E { + + ν( + + )} u v pεv ν 6E ( + + ) u d 6 E [ ( ) ( ) ] ( + + ) 6ν + + ( ν + + ) u d + ν 6E [ ( ) ( ) ] ( + + ) 6ν + + ( ν + + )
12 von Mises Criteria: The distortion energy ( ) ( ) ( ) [ ] ν E u d J E G J u d ν + ( ) ( ) ( ) [ ] J
13 von Mises Criteria: The distortion energy For tensile test ( ) ( ) ( ) [ ] y y y J + + ( ) ( ) ( ) [ ] + + y 0 y
14 von Mises Criteria: The distortion energy For pure shear y 0 J 6 [( ) ( ) ( )] y y y 0 y y y 6 [( ) ( ) ( ) ] + +
15 von Mises Criteria: The distortion energy y J For biaxial stress y 0 ( ) ( ) ( ) [ ] J + + y ( ) ( ) ( ) [ ] + + y
16 Comparison of Rankine, von Mises, and Tresca Criteria
17 Comparison of Rankine, von Mises, and Tresca Criteria Al, Cu Cast iron (a) Rankine, von Mises, and Tresca criteria. (b) Comparison of failure criteria with experimental results. (Reprinted with permission from E. P. Popov, Mechanics of Materials, nd ed. (Englewood Cliffs, NJ: Prentice-Hall, 976), and G. Murphy, Advanced. Mechanics of Materials (New York: McGraw-Hill, 964), p. 8.)
18 Tresca maximum shear stress criterion Example problem 5.
19 Tresca maximum shear stress criterion Example problem 5.
20 Von Mises criterion Example problem 5.
21 Von Mises criterion Example problem 5.
22 Von Mises criterion Example problem 5.
23 Von Mises criterion Example problem 5.
24 Flow rules The general relations between plastic strains and the stress states dε ij dλ f ij Levy-Mises eqs [ ( ) ( ) ] 4 dλ [ ( ) ] [ ( ) ] dε dλ + dε dλ + [ ( ) ] dε dλ + d ε : dε : dε : 0 :
25 Flow rules Example problem 5.4
26 Flow rules Example problem 5.4
27 Flow rules Example problem 5.5
28 Flow rules Example problem 5.5
29 Flow rules Example problem 5.6
30 Flow rules Example problem 5.6
31 Flow rules Example problem 5.7
32 Flow rules Example problem 5.7
33 Principle of normality dε d ε
34 Effective stress and effective strain d d d d d ε ε ε ε + + w For loading paths other than uniaxial tension ( ) ( ) ( ) [ ] + + y eff ( ) ε ε ε ε + + eff ε dw d
35 Effective stress and effective strain Example problem 5.8
36 Effective stress and effective strain Example problem 5.8
37 Effective stress and effective strain If straining is proportional ε ( ) ( ) ε +ε +ε In terms of non-principal strains (von Mises) ε ( ) ( ε x +ε y +ε z )+ ( y ) z + z x ( ) ( ) γ yz ( +γ +γ ) zx xy ( ) + ( x ) y +6 τ yz ( +τ +τ ) zx xy Tresca dε dε i max Tresca v. von Mises dε i max dε Mises.5 dε i max Strain hardening depends only on strain rate f ( ε)
38 Effective stress and effective strain Example problem 5.9
39 Effective stress and effective strain Example problem 5.9
40 Other isotropic yield criteria a + a + a Y a a, 4 a, von Mises Tresca For a even integer a a a a ( ) + ( ) + ( ) Y
41 Other isotropic yield criteria Example problem 5.0
42 Other isotropic yield criteria Example problem 5.0
43 Anisotropic plasticity Hill criterion (generalized von Mises) F ( y ) + G z z x If principal stress on symm. axes; planar isotropy ( y ) + z z x ( x ) + Lτ y yz ( ) + H ( x ) R + y ( ) + R ( )X + Mτ zx + Nτ xy Flow rules dε x : dε y : dε z R + ( ) x R y z ( ) y R x z : R + : z y x
44 Anisotropic plasticity
45 Anisotropic plasticity (cont.) ρ ( R + )α R ( R + ) Rα α ( R + )ρ + R ( R + )+ Rρ If R High-exponent criterion dε x : dε y : dε z R { ( y ) z + ( z x ) +R( x ) y ( R+) } { x ( α ) ( R+) } a a ( x y ) + ( x z ) α ++R ε ε x ( )+ αρ ( ) a a a ( y z ) + ( z x ) + R( x y ) R + a a ( y z ) ( + R y x ) ( )X a : : { a ( a y ) a a z + ( z x ) +R( x ) y ( R+) } ε ( x ) + αρ ( ) aeven integer, a> ( ) a a ( z x ) + z y
46 Anisotropic plasticity
47 Anisotropic plasticity Example problem 5.
48 Anisotropic plasticity Example problem 5.
49 Effect of strain-hardening on the yield locus
Dr. D. Dinev, Department of Structural Mechanics, UACEG
 Lecture 4 Material behavior: Constitutive equations Field of the game Print version Lecture on Theory of lasticity and Plasticity of Dr. D. Dinev, Department of Structural Mechanics, UACG 4.1 Contents
Lecture 4 Material behavior: Constitutive equations Field of the game Print version Lecture on Theory of lasticity and Plasticity of Dr. D. Dinev, Department of Structural Mechanics, UACG 4.1 Contents
MECHANICAL PROPERTIES OF MATERIALS
 MECHANICAL PROPERTIES OF MATERIALS! Simple Tension Test! The Stress-Strain Diagram! Stress-Strain Behavior of Ductile and Brittle Materials! Hooke s Law! Strain Energy! Poisson s Ratio! The Shear Stress-Strain
MECHANICAL PROPERTIES OF MATERIALS! Simple Tension Test! The Stress-Strain Diagram! Stress-Strain Behavior of Ductile and Brittle Materials! Hooke s Law! Strain Energy! Poisson s Ratio! The Shear Stress-Strain
Chapter 2. Stress, Principal Stresses, Strain Energy
 Chapter Stress, Principal Stresses, Strain nergy Traction vector, stress tensor z z σz τ zy ΔA ΔF A ΔA ΔF x ΔF z ΔF y y τ zx τ xz τxy σx τ yx τ yz σy y A x x F i j k is the traction force acting on the
Chapter Stress, Principal Stresses, Strain nergy Traction vector, stress tensor z z σz τ zy ΔA ΔF A ΔA ΔF x ΔF z ΔF y y τ zx τ xz τxy σx τ yx τ yz σy y A x x F i j k is the traction force acting on the
Strain gauge and rosettes
 Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
University of Waterloo. ME Mechanical Design 1. Partial notes Part 1
 University of Waterloo Department of Mechanical Engineering ME 3 - Mechanical Design 1 Partial notes Part 1 G. Glinka Fall 005 1 Forces and stresses Stresses and Stress Tensor Two basic types of forces
University of Waterloo Department of Mechanical Engineering ME 3 - Mechanical Design 1 Partial notes Part 1 G. Glinka Fall 005 1 Forces and stresses Stresses and Stress Tensor Two basic types of forces
ADVANCED STRUCTURAL MECHANICS
 VSB TECHNICAL UNIVERSITY OF OSTRAVA FACULTY OF CIVIL ENGINEERING ADVANCED STRUCTURAL MECHANICS Lecture 1 Jiří Brožovský Office: LP H 406/3 Phone: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
VSB TECHNICAL UNIVERSITY OF OSTRAVA FACULTY OF CIVIL ENGINEERING ADVANCED STRUCTURAL MECHANICS Lecture 1 Jiří Brožovský Office: LP H 406/3 Phone: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
Constitutive Equation for Plastic Behavior of Hydrostatic Pressure Dependent Polymers
 1/5 Constitutive Equation for Plastic Behavior of Hydrostatic Pressure Deendent Polymers by Yukio SANOMURA Hydrostatic ressure deendence in mechanical behavior of olymers is studied for the constitutive
1/5 Constitutive Equation for Plastic Behavior of Hydrostatic Pressure Deendent Polymers by Yukio SANOMURA Hydrostatic ressure deendence in mechanical behavior of olymers is studied for the constitutive
Mechanics of Materials Lab
 Mechanics of Materials Lab Lecture 9 Strain and lasticity Textbook: Mechanical Behavior of Materials Sec. 6.6, 5.3, 5.4 Jiangyu Li Jiangyu Li, Prof. M.. Tuttle Strain: Fundamental Definitions "Strain"
Mechanics of Materials Lab Lecture 9 Strain and lasticity Textbook: Mechanical Behavior of Materials Sec. 6.6, 5.3, 5.4 Jiangyu Li Jiangyu Li, Prof. M.. Tuttle Strain: Fundamental Definitions "Strain"
Fundamentals of Metal Forming. 1. Overview 2. Material Behavior 3. Temperature Effects 4. Strain Rate Effect 5. Friction and Lubrication
 Fundamentals o Metal Forming. Overview. Material Behavior. Temperature Eects. Strain Rate Eect 5. Friction and Lubrication ntroduction Metal Forming uses plastic deormation to change the shape o metal
Fundamentals o Metal Forming. Overview. Material Behavior. Temperature Eects. Strain Rate Eect 5. Friction and Lubrication ntroduction Metal Forming uses plastic deormation to change the shape o metal
Introduction to Theory of. Elasticity. Kengo Nakajima Summer
 Introduction to Theor of lasticit Summer Kengo Nakajima Technical & Scientific Computing I (48-7) Seminar on Computer Science (48-4) elast Theor of lasticit Target Stress Governing quations elast 3 Theor
Introduction to Theor of lasticit Summer Kengo Nakajima Technical & Scientific Computing I (48-7) Seminar on Computer Science (48-4) elast Theor of lasticit Target Stress Governing quations elast 3 Theor
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Μηχανουργική Τεχνολογία & Εργαστήριο Ι
 Μηχανουργική Τεχνολογία & Εργαστήριο Ι Mechanics in Deforming Processes - Διεργασίες Διαμόρφωσης Καθηγητής Χρυσολούρης Γεώργιος Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών Mechanics in deforming processes
Μηχανουργική Τεχνολογία & Εργαστήριο Ι Mechanics in Deforming Processes - Διεργασίες Διαμόρφωσης Καθηγητής Χρυσολούρης Γεώργιος Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών Mechanics in deforming processes
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Chapter 7 Transformations of Stress and Strain
 Chapter 7 Transformations of Stress and Strain INTRODUCTION Transformation of Plane Stress Mohr s Circle for Plane Stress Application of Mohr s Circle to 3D Analsis 90 60 60 0 0 50 90 Introduction 7-1
Chapter 7 Transformations of Stress and Strain INTRODUCTION Transformation of Plane Stress Mohr s Circle for Plane Stress Application of Mohr s Circle to 3D Analsis 90 60 60 0 0 50 90 Introduction 7-1
Chapter 8: Mechanical Properties of Metals
 Chapter8:MechanicalPropertiesofMetals ISSUESTOADDRESS 1 LECTURER: PRO. SEUNGTAE CHOI 8.1Introduction Mechanicalbehaviorofamaterialreflectsitsresponseordeformationin relationtoanappliedloadorforce. Keymechanicaldesignproperties:stiffness,strength,hardness,ductilityand
Chapter8:MechanicalPropertiesofMetals ISSUESTOADDRESS 1 LECTURER: PRO. SEUNGTAE CHOI 8.1Introduction Mechanicalbehaviorofamaterialreflectsitsresponseordeformationin relationtoanappliedloadorforce. Keymechanicaldesignproperties:stiffness,strength,hardness,ductilityand
Using the Jacobian- free Newton- Krylov method to solve the sea- ice momentum equa<on
 Using the Jacobian- free Newton- Krylov method to solve the sea- ice momentum equa
Using the Jacobian- free Newton- Krylov method to solve the sea- ice momentum equa
Διπλωματική Εργασία. Μελέτη των μηχανικών ιδιοτήτων των stents που χρησιμοποιούνται στην Ιατρική. Αντωνίου Φάνης
 Διπλωματική Εργασία Μελέτη των μηχανικών ιδιοτήτων των stents που χρησιμοποιούνται στην Ιατρική Αντωνίου Φάνης Επιβλέπουσες: Θεοδώρα Παπαδοπούλου, Ομότιμη Καθηγήτρια ΕΜΠ Ζάννη-Βλαστού Ρόζα, Καθηγήτρια
Διπλωματική Εργασία Μελέτη των μηχανικών ιδιοτήτων των stents που χρησιμοποιούνται στην Ιατρική Αντωνίου Φάνης Επιβλέπουσες: Θεοδώρα Παπαδοπούλου, Ομότιμη Καθηγήτρια ΕΜΠ Ζάννη-Βλαστού Ρόζα, Καθηγήτρια
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
ΚΕΦΑΛΑΙΟ 1 Ο 1.1. ΕΛΑΣΤΙΚΟ ΣΤΕΡΕΟ
 ΚΕΦΑΛΑΙΟ Ο.. ΕΛΑΣΤΙΚΟ ΣΤΕΡΕΟ Ο Robert Hooke έγρψε το 678, "he power of any spring is in the same proportion with the tension thereof". Αυτή η δήλωση είνι η βάση του πρώτου ρεολογικού νόµου γι ιδνικά ελστικά
ΚΕΦΑΛΑΙΟ Ο.. ΕΛΑΣΤΙΚΟ ΣΤΕΡΕΟ Ο Robert Hooke έγρψε το 678, "he power of any spring is in the same proportion with the tension thereof". Αυτή η δήλωση είνι η βάση του πρώτου ρεολογικού νόµου γι ιδνικά ελστικά
Overview. Transition Semantics. Configurations and the transition relation. Executions and computation
 Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Macromechanics of a Laminate. Textbook: Mechanics of Composite Materials Author: Autar Kaw
 Macromechanics of a Laminate Tetboo: Mechanics of Composite Materials Author: Autar Kaw Figure 4.1 Fiber Direction θ z CHAPTER OJECTIVES Understand the code for laminate stacing sequence Develop relationships
Macromechanics of a Laminate Tetboo: Mechanics of Composite Materials Author: Autar Kaw Figure 4.1 Fiber Direction θ z CHAPTER OJECTIVES Understand the code for laminate stacing sequence Develop relationships
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
 katoh@kuraka.co.jp okaken@kuraka.co.jp mineot@fukuoka-u.ac.jp 4 35 3 Normalized stress σ/g 25 2 15 1 5 Breaking test Theory 1 2 Shear tests Failure tests Compressive tests 1 2 3 4 5 6 Fig.1. Relation between
katoh@kuraka.co.jp okaken@kuraka.co.jp mineot@fukuoka-u.ac.jp 4 35 3 Normalized stress σ/g 25 2 15 1 5 Breaking test Theory 1 2 Shear tests Failure tests Compressive tests 1 2 3 4 5 6 Fig.1. Relation between
(Mechanical Properties)
 109101 Engineering Materials (Mechanical Properties-I) 1 (Mechanical Properties) Sheet Metal Drawing / (- Deformation) () 3 Force -Elastic deformation -Plastic deformation -Fracture Fracture 4 Mode of
109101 Engineering Materials (Mechanical Properties-I) 1 (Mechanical Properties) Sheet Metal Drawing / (- Deformation) () 3 Force -Elastic deformation -Plastic deformation -Fracture Fracture 4 Mode of
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Stresses in a Plane. Mohr s Circle. Cross Section thru Body. MET 210W Mohr s Circle 1. Some parts experience normal stresses in
 ME 10W E. Evans Stresses in a Plane Some parts eperience normal stresses in two directions. hese tpes of problems are called Plane Stress or Biaial Stress Cross Section thru Bod z angent and normal to
ME 10W E. Evans Stresses in a Plane Some parts eperience normal stresses in two directions. hese tpes of problems are called Plane Stress or Biaial Stress Cross Section thru Bod z angent and normal to
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
the total number of electrons passing through the lamp.
 1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
TRIAXIAL TEST, CORPS OF ENGINEERS FORMAT
 TRIAXIAL TEST, CORPS OF ENGINEERS FORMAT .5 C, φ, deg Tan(φ) Total.7 2.2 Effective.98 8.33 Shear,.5.5.5 2 2.5 3 Total Normal, Effective Normal, Deviator,.5.25.75.5.25 2.5 5 7.5 Axial Strain, % Type of
TRIAXIAL TEST, CORPS OF ENGINEERS FORMAT .5 C, φ, deg Tan(φ) Total.7 2.2 Effective.98 8.33 Shear,.5.5.5 2 2.5 3 Total Normal, Effective Normal, Deviator,.5.25.75.5.25 2.5 5 7.5 Axial Strain, % Type of
= l. = l. (Hooke s Law) Tensile: Poisson s ratio. σ = Εε. τ = G γ. Relationships between Stress and Strain
 Relationships between tress and train (Hooke s Law) When strains are small, most of materials are linear elastic. Tensile: Ε hear: Poisson s ratio Δl l Δl l Nominal lateral strain (transverse strain) Poisson
Relationships between tress and train (Hooke s Law) When strains are small, most of materials are linear elastic. Tensile: Ε hear: Poisson s ratio Δl l Δl l Nominal lateral strain (transverse strain) Poisson
Contents. Preface... xv Acknowledgments... xix About the Authors... xxi Nomenclature... xxiii
 Preface... xv Acknowledgments... xix About the Authors... xxi Nomenclature... xxiii Chapter 1: Road Load Analysis Techniques in Automotive Engineering... 1 Xiaobo Yang, Peijun Xu Introduction... 1 Fundamentals
Preface... xv Acknowledgments... xix About the Authors... xxi Nomenclature... xxiii Chapter 1: Road Load Analysis Techniques in Automotive Engineering... 1 Xiaobo Yang, Peijun Xu Introduction... 1 Fundamentals
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής
 Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Ξενόγλωσση Τεχνική Ορολογία
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ξενόγλωσση Τεχνική Ορολογία Ενότητα: Principles of an Internal Combustion Engine Παναγιώτης Τσατσαρός Τμήμα Μηχανολόγων Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ξενόγλωσση Τεχνική Ορολογία Ενότητα: Principles of an Internal Combustion Engine Παναγιώτης Τσατσαρός Τμήμα Μηχανολόγων Μηχανικών
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1 [1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg) 1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
3+1 Splitting of the Generalized Harmonic Equations
 3+1 Splitting of the Generalized Harmonic Equations David Brown North Carolina State University EGM June 2011 Numerical Relativity Interpret general relativity as an initial value problem: Split spacetime
3+1 Splitting of the Generalized Harmonic Equations David Brown North Carolina State University EGM June 2011 Numerical Relativity Interpret general relativity as an initial value problem: Split spacetime
Capacitors - Capacitance, Charge and Potential Difference
 Capacitors - Capacitance, Charge and Potential Difference Capacitors store electric charge. This ability to store electric charge is known as capacitance. A simple capacitor consists of 2 parallel metal
Capacitors - Capacitance, Charge and Potential Difference Capacitors store electric charge. This ability to store electric charge is known as capacitance. A simple capacitor consists of 2 parallel metal
Nuclear Physics 5. Name: Date: 8 (1)
 Name: Date: Nuclear Physics 5. A sample of radioactive carbon-4 decays into a stable isotope of nitrogen. As the carbon-4 decays, the rate at which the amount of nitrogen is produced A. decreases linearly
Name: Date: Nuclear Physics 5. A sample of radioactive carbon-4 decays into a stable isotope of nitrogen. As the carbon-4 decays, the rate at which the amount of nitrogen is produced A. decreases linearly
DETERMINATION OF DYNAMIC CHARACTERISTICS OF A 2DOF SYSTEM. by Zoran VARGA, Ms.C.E.
 DETERMINATION OF DYNAMIC CHARACTERISTICS OF A 2DOF SYSTEM by Zoran VARGA, Ms.C.E. Euro-Apex B.V. 1990-2012 All Rights Reserved. The 2 DOF System Symbols m 1 =3m [kg] m 2 =8m m=10 [kg] l=2 [m] E=210000
DETERMINATION OF DYNAMIC CHARACTERISTICS OF A 2DOF SYSTEM by Zoran VARGA, Ms.C.E. Euro-Apex B.V. 1990-2012 All Rights Reserved. The 2 DOF System Symbols m 1 =3m [kg] m 2 =8m m=10 [kg] l=2 [m] E=210000
A Bonus-Malus System as a Markov Set-Chain. Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics
 A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
Ingenieurbüro Frank Blasek - Beratender Ingenieur Am Kohlhof 10, Osterholz-Scharmbeck Tel: 04791/ Fax: 04791/
 Page: 10 CONTENTS Contents... 10 General Data... 10 Structural Data des... 10 erials... 10 Sections... 10 ents... 11 Supports... 11 Loads General Data... 12 LC 1 - Vollast 120 km/h 0,694 kn/qm... 12 LC,
Page: 10 CONTENTS Contents... 10 General Data... 10 Structural Data des... 10 erials... 10 Sections... 10 ents... 11 Supports... 11 Loads General Data... 12 LC 1 - Vollast 120 km/h 0,694 kn/qm... 12 LC,
Ingenieurbüro Frank Blasek - Beratender Ingenieur Am Kohlhof 10, Osterholz-Scharmbeck Tel: 04791/ Fax: 04791/
 Page: 1 CONTENTS Contents... 1 General Data... 1 Structural Data des... 1 erials... 1 Sections... 1 ents... 2 Supports... 2 Loads General Data... 3 LC 1 - Vollast 90 km/h 0,39 kn/qm... 3 LC, LG Results
Page: 1 CONTENTS Contents... 1 General Data... 1 Structural Data des... 1 erials... 1 Sections... 1 ents... 2 Supports... 2 Loads General Data... 3 LC 1 - Vollast 90 km/h 0,39 kn/qm... 3 LC, LG Results
PRESENTATION TITLE PRESENTATION SUBTITLE
 COURSE TUTORS : Advanced Materials Processing : D. Mataras, C. Galiotis PRESENTATION TITLE PRESENTATION SUBTITLE A. Student Outline 2 What is my material and why is it interesting? My Application Detailed
COURSE TUTORS : Advanced Materials Processing : D. Mataras, C. Galiotis PRESENTATION TITLE PRESENTATION SUBTITLE A. Student Outline 2 What is my material and why is it interesting? My Application Detailed
Delhi Noida Bhopal Hyderabad Jaipur Lucknow Indore Pune Bhubaneswar Kolkata Patna Web: Ph:
 Seria : 0. T_ME_(+B)_Strength of Materia_9078 Dehi Noida Bhopa Hyderabad Jaipur Luckno Indore une Bhubanesar Kokata atna Web: E-mai: info@madeeasy.in h: 0-56 CLSS TEST 08-9 MECHNICL ENGINEERING Subject
Seria : 0. T_ME_(+B)_Strength of Materia_9078 Dehi Noida Bhopa Hyderabad Jaipur Luckno Indore une Bhubanesar Kokata atna Web: E-mai: info@madeeasy.in h: 0-56 CLSS TEST 08-9 MECHNICL ENGINEERING Subject
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
IIT JEE (2013) (Trigonomtery 1) Solutions
 L.K. Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 677 (+) PAPER B IIT JEE (0) (Trigoomtery ) Solutios TOWARDS IIT JEE IS NOT A JOURNEY, IT S A BATTLE, ONLY THE TOUGHEST WILL SURVIVE
L.K. Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 677 (+) PAPER B IIT JEE (0) (Trigoomtery ) Solutios TOWARDS IIT JEE IS NOT A JOURNEY, IT S A BATTLE, ONLY THE TOUGHEST WILL SURVIVE
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 8η: Producer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 8η: Producer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Firm Behavior GOAL: Firms choose the maximum possible output (technological
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 8η: Producer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Firm Behavior GOAL: Firms choose the maximum possible output (technological
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 10η: Basics of Game Theory part 2 Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 0η: Basics of Game Theory part 2 Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Best Response Curves Used to solve for equilibria in games
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 0η: Basics of Game Theory part 2 Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Best Response Curves Used to solve for equilibria in games
Ψηφιακή Οικονομία. Διάλεξη 11η: Markets and Strategic Interaction in Networks Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 11η: Markets and Strategic Interaction in Networks Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Course Outline Part II: Mathematical Tools
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 11η: Markets and Strategic Interaction in Networks Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Course Outline Part II: Mathematical Tools
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
θ p = deg ε n = με ε t = με γ nt = μrad
 IDE 110 S08 Test 7 Name: 1. The strain components ε x = 946 με, ε y = -294 με and γ xy = -362 με are given for a point in a body subjected to plane strain. Determine the strain components ε n, ε t, and
IDE 110 S08 Test 7 Name: 1. The strain components ε x = 946 με, ε y = -294 με and γ xy = -362 με are given for a point in a body subjected to plane strain. Determine the strain components ε n, ε t, and
Aluminum Electrolytic Capacitors
 Aluminum Electrolytic Capacitors Snap-In, Mini., 105 C, High Ripple APS TS-NH ECE-S (G) Series: TS-NH Features Long life: 105 C 2,000 hours; high ripple current handling ability Wide CV value range (47
Aluminum Electrolytic Capacitors Snap-In, Mini., 105 C, High Ripple APS TS-NH ECE-S (G) Series: TS-NH Features Long life: 105 C 2,000 hours; high ripple current handling ability Wide CV value range (47
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Calculating the propagation delay of coaxial cable
 Your source for quality GNSS Networking Solutions and Design Services! Page 1 of 5 Calculating the propagation delay of coaxial cable The delay of a cable or velocity factor is determined by the dielectric
Your source for quality GNSS Networking Solutions and Design Services! Page 1 of 5 Calculating the propagation delay of coaxial cable The delay of a cable or velocity factor is determined by the dielectric
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Aluminum Electrolytic Capacitors (Large Can Type)
 Aluminum Electrolytic Capacitors (Large Can Type) Snap-In, 85 C TS-U ECE-S (U) Series: TS-U Features General purpose Wide CV value range (33 ~ 47,000 µf/16 4V) Various case sizes Top vent construction
Aluminum Electrolytic Capacitors (Large Can Type) Snap-In, 85 C TS-U ECE-S (U) Series: TS-U Features General purpose Wide CV value range (33 ~ 47,000 µf/16 4V) Various case sizes Top vent construction
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Themistoklis Tsalkatidis Lecturer Democritus University of Thrace Xanthi, Greece
 COMPUTATIONAL SIMULATION OF COMPOSITE STEEL- CONCRETE SHEAR WALLS WITH VERTICAL STEEL ENCASED PROFILES. COMPARATIVE EVALUATION WITH EXPERIMENTAL RESULTS. Themistoklis Tsalkatidis Lecturer Democritus University
COMPUTATIONAL SIMULATION OF COMPOSITE STEEL- CONCRETE SHEAR WALLS WITH VERTICAL STEEL ENCASED PROFILES. COMPARATIVE EVALUATION WITH EXPERIMENTAL RESULTS. Themistoklis Tsalkatidis Lecturer Democritus University
ΚΑΘΟΡΙΣΜΟΣ ΠΑΡΑΓΟΝΤΩΝ ΠΟΥ ΕΠΗΡΕΑΖΟΥΝ ΤΗΝ ΠΑΡΑΓΟΜΕΝΗ ΙΣΧΥ ΣΕ Φ/Β ΠΑΡΚΟ 80KWp
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΚΑΘΟΡΙΣΜΟΣ ΠΑΡΑΓΟΝΤΩΝ ΠΟΥ ΕΠΗΡΕΑΖΟΥΝ ΤΗΝ ΠΑΡΑΓΟΜΕΝΗ ΙΣΧΥ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΜΕΤΑΔΟΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΚΑΘΟΡΙΣΜΟΣ ΠΑΡΑΓΟΝΤΩΝ ΠΟΥ ΕΠΗΡΕΑΖΟΥΝ ΤΗΝ ΠΑΡΑΓΟΜΕΝΗ ΙΣΧΥ
New bounds for spherical two-distance sets and equiangular lines
 New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 9η: Basics of Game Theory Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 9η: Basics of Game Theory Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Course Outline Part II: Mathematical Tools Firms - Basics of Industrial
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 9η: Basics of Game Theory Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Course Outline Part II: Mathematical Tools Firms - Basics of Industrial
ΜΔΛΔΣΖ ΔΝΓΟΣΡΑΥΤΝΖ Δ ΥΑΛΤΒΔ ΘΔΡΜΖ ΔΛΑΖ
 ΔΘΝΗΚΟ ΜΔΣΟΒΗΟ ΠΟΛΤΣΔΥΝΔΗΟ ΔΙΑΣΜΗΜΑΣΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΣΑΠΣΤΥΙΑΚΩΝ ΠΟΤΔΩΝ (Δ.Π.Μ..): "ΔΠΗΣΖΜΖ ΚΑΗ ΣΔΥΝΟΛΟΓΗΑ ΤΛΗΚΧΝ" ΜΔΛΔΣΖ ΔΝΓΟΣΡΑΥΤΝΖ Δ ΥΑΛΤΒΔ ΘΔΡΜΖ ΔΛΑΖ ΜΕΣΑΠΣΤΥΙΑΚΗ ΕΡΓΑΙΑ ΕΔΡΒΑ ΑΗΜΗΛΗΑΝΟ Διπλωματούτος
ΔΘΝΗΚΟ ΜΔΣΟΒΗΟ ΠΟΛΤΣΔΥΝΔΗΟ ΔΙΑΣΜΗΜΑΣΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΣΑΠΣΤΥΙΑΚΩΝ ΠΟΤΔΩΝ (Δ.Π.Μ..): "ΔΠΗΣΖΜΖ ΚΑΗ ΣΔΥΝΟΛΟΓΗΑ ΤΛΗΚΧΝ" ΜΔΛΔΣΖ ΔΝΓΟΣΡΑΥΤΝΖ Δ ΥΑΛΤΒΔ ΘΔΡΜΖ ΔΛΑΖ ΜΕΣΑΠΣΤΥΙΑΚΗ ΕΡΓΑΙΑ ΕΔΡΒΑ ΑΗΜΗΛΗΑΝΟ Διπλωματούτος
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
1. Ηλεκτρικό μαύρο κουτί: Αισθητήρας μετατόπισης με βάση τη χωρητικότητα
 IPHO_42_2011_EXP1.DO Experimental ompetition: 14 July 2011 Problem 1 Page 1 of 5 1. Ηλεκτρικό μαύρο κουτί: Αισθητήρας μετατόπισης με βάση τη χωρητικότητα Για ένα πυκνωτή χωρητικότητας ο οποίος είναι μέρος
IPHO_42_2011_EXP1.DO Experimental ompetition: 14 July 2011 Problem 1 Page 1 of 5 1. Ηλεκτρικό μαύρο κουτί: Αισθητήρας μετατόπισης με βάση τη χωρητικότητα Για ένα πυκνωτή χωρητικότητας ο οποίος είναι μέρος
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
ΜΕΛΕΤΗ ΤΗΣ ΠΛΑΣΤΙΚΟΤΗΤΑΣ ΑΡΓΙΛΟΥΧΩΝ ΜΙΓΜΑΤΩΝ ΜΕ ΠΡΟΣΘΗΚΗ ΣΙΔΗΡΑΛΟΥΜΙΝΑΣ ΑΠΟ ΤΗ ΔΙΕΡΓΑΣΙΑ BAYER
 Πρακτικά 1ου Πανελληνίου Συνεδρίου για την Αξιοποίηση των Βιομηχανικών Παραπροϊόντων στη Δόμηση, ΕΒΙΠΑΡ, Θεσσαλονίκη, 24-26 Νοεμβρίου 2005 ΜΕΛΕΤΗ ΤΗΣ ΠΛΑΣΤΙΚΟΤΗΤΑΣ ΑΡΓΙΛΟΥΧΩΝ ΜΙΓΜΑΤΩΝ ΜΕ ΠΡΟΣΘΗΚΗ ΣΙΔΗΡΑΛΟΥΜΙΝΑΣ
Πρακτικά 1ου Πανελληνίου Συνεδρίου για την Αξιοποίηση των Βιομηχανικών Παραπροϊόντων στη Δόμηση, ΕΒΙΠΑΡ, Θεσσαλονίκη, 24-26 Νοεμβρίου 2005 ΜΕΛΕΤΗ ΤΗΣ ΠΛΑΣΤΙΚΟΤΗΤΑΣ ΑΡΓΙΛΟΥΧΩΝ ΜΙΓΜΑΤΩΝ ΜΕ ΠΡΟΣΘΗΚΗ ΣΙΔΗΡΑΛΟΥΜΙΝΑΣ
Solutions to the Schrodinger equation atomic orbitals. Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz
 Solutions to the Schrodinger equation atomic orbitals Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz ybridization Valence Bond Approach to bonding sp 3 (Ψ 2 s + Ψ 2 px + Ψ 2 py + Ψ 2 pz) sp 2 (Ψ 2 s + Ψ 2 px + Ψ 2 py)
Solutions to the Schrodinger equation atomic orbitals Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz ybridization Valence Bond Approach to bonding sp 3 (Ψ 2 s + Ψ 2 px + Ψ 2 py + Ψ 2 pz) sp 2 (Ψ 2 s + Ψ 2 px + Ψ 2 py)
CHAPTER 70 DOUBLE AND TRIPLE INTEGRALS. 2 is integrated with respect to x between x = 2 and x = 4, with y regarded as a constant
 CHAPTER 7 DOUBLE AND TRIPLE INTEGRALS EXERCISE 78 Page 755. Evaluate: dxd y. is integrated with respect to x between x = and x =, with y regarded as a constant dx= [ x] = [ 8 ] = [ ] ( ) ( ) d x d y =
CHAPTER 7 DOUBLE AND TRIPLE INTEGRALS EXERCISE 78 Page 755. Evaluate: dxd y. is integrated with respect to x between x = and x =, with y regarded as a constant dx= [ x] = [ 8 ] = [ ] ( ) ( ) d x d y =
Grey Cast Irons. Technical Data
 Grey Cast Irons Standard Material designation Grey Cast Irons BS EN 1561 EN-GJL-200 EN-GJL-250 EN-GJL-300 EN-GJL-350-1997 (EN-JL1030) (EN-JL1040) (EN-JL1050) (EN-JL1060) Characteristic SI unit Tensile
Grey Cast Irons Standard Material designation Grey Cast Irons BS EN 1561 EN-GJL-200 EN-GJL-250 EN-GJL-300 EN-GJL-350-1997 (EN-JL1030) (EN-JL1040) (EN-JL1050) (EN-JL1060) Characteristic SI unit Tensile
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
RECIPROCATING COMPRESSOR CALCULATION SHEET
 Gas properties, flowrate and conditions 1 Gas name Air RECIPRCATING CMPRESSR CALCULATIN SHEET WITH INTERCLER ( Sheet : 1. f 4.) Item or symbol Quantity Unit Item or symbol Quantity Unit 2 Suction pressure,
Gas properties, flowrate and conditions 1 Gas name Air RECIPRCATING CMPRESSR CALCULATIN SHEET WITH INTERCLER ( Sheet : 1. f 4.) Item or symbol Quantity Unit Item or symbol Quantity Unit 2 Suction pressure,
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
stability and aromaticity in the benzonitrile H 2 O complex with Na+ or Cl
 Electronic Supplementary Data A theoretical investigation on the cooperativity effect, reduced density gradient, stability and aromaticity in the benzonitrile H 2 O complex with Na+ or Cl Jiang-Bo Xie
Electronic Supplementary Data A theoretical investigation on the cooperativity effect, reduced density gradient, stability and aromaticity in the benzonitrile H 2 O complex with Na+ or Cl Jiang-Bo Xie
(C) 2010 Pearson Education, Inc. All rights reserved.
 Connectionless transmission with datagrams. Connection-oriented transmission is like the telephone system You dial and are given a connection to the telephone of fthe person with whom you wish to communicate.
Connectionless transmission with datagrams. Connection-oriented transmission is like the telephone system You dial and are given a connection to the telephone of fthe person with whom you wish to communicate.
Electronic Supplementary Information (ESI)
 Electronic Supplementary Material (ESI) for RSC Advances. This journal is The Royal Society of Chemistry 2016 Electronic Supplementary Information (ESI) Cyclopentadienyl iron dicarbonyl (CpFe(CO) 2 ) derivatives
Electronic Supplementary Material (ESI) for RSC Advances. This journal is The Royal Society of Chemistry 2016 Electronic Supplementary Information (ESI) Cyclopentadienyl iron dicarbonyl (CpFe(CO) 2 ) derivatives
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
 v R = c v 2 v P = R v = v 3 v n P = n 3 v 1 v = n 1 n P 1 P = c 1 c P 1 P = n 1 c 1 n 3 c = v 1 v 3 3 3 c P P = c v 4.5 P = c v 4 P = c v 3.5 v 1 = 24 v 2 = 18 c 1 c 1 4.5 = v 1 c 2 v 4.5 2 = 244.5 = 3.65
v R = c v 2 v P = R v = v 3 v n P = n 3 v 1 v = n 1 n P 1 P = c 1 c P 1 P = n 1 c 1 n 3 c = v 1 v 3 3 3 c P P = c v 4.5 P = c v 4 P = c v 3.5 v 1 = 24 v 2 = 18 c 1 c 1 4.5 = v 1 c 2 v 4.5 2 = 244.5 = 3.65
Distances in Sierpiński Triangle Graphs
 Distances in Sierpiński Triangle Graphs Sara Sabrina Zemljič joint work with Andreas M. Hinz June 18th 2015 Motivation Sierpiński triangle introduced by Wac law Sierpiński in 1915. S. S. Zemljič 1 Motivation
Distances in Sierpiński Triangle Graphs Sara Sabrina Zemljič joint work with Andreas M. Hinz June 18th 2015 Motivation Sierpiński triangle introduced by Wac law Sierpiński in 1915. S. S. Zemljič 1 Motivation
Volume of a Cuboid. Volume = length x breadth x height. V = l x b x h. The formula for the volume of a cuboid is
 Volume of a Cuboid The formula for the volume of a cuboid is Volume = length x breadth x height V = l x b x h Example Work out the volume of this cuboid 10 cm 15 cm V = l x b x h V = 15 x 6 x 10 V = 900cm³
Volume of a Cuboid The formula for the volume of a cuboid is Volume = length x breadth x height V = l x b x h Example Work out the volume of this cuboid 10 cm 15 cm V = l x b x h V = 15 x 6 x 10 V = 900cm³
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCourseWare http://ocw.mit.edu 6.03/ESD.03J Electromagnetics and Applications, Fall 005 Please use the following citation format: Markus Zahn, 6.03/ESD.03J Electromagnetics and Applications, Fall
MIT OpenCourseWare http://ocw.mit.edu 6.03/ESD.03J Electromagnetics and Applications, Fall 005 Please use the following citation format: Markus Zahn, 6.03/ESD.03J Electromagnetics and Applications, Fall
Study of In-vehicle Sound Field Creation by Simultaneous Equation Method
 Study of In-vehicle Sound Field Creation by Simultaneous Equation Method Kensaku FUJII Isao WAKABAYASI Tadashi UJINO Shigeki KATO Abstract FUJITSU TEN Limited has developed "TOYOTA remium Sound System"
Study of In-vehicle Sound Field Creation by Simultaneous Equation Method Kensaku FUJII Isao WAKABAYASI Tadashi UJINO Shigeki KATO Abstract FUJITSU TEN Limited has developed "TOYOTA remium Sound System"
Thin Film Chip Resistors
 FEATURES PRECISE TOLERANCE AND TEMPERATURE COEFFICIENT EIA STANDARD CASE SIZES (0201 ~ 2512) LOW NOISE, THIN FILM (NiCr) CONSTRUCTION REFLOW SOLDERABLE (Pb FREE TERMINATION FINISH) Type Size EIA PowerRating
FEATURES PRECISE TOLERANCE AND TEMPERATURE COEFFICIENT EIA STANDARD CASE SIZES (0201 ~ 2512) LOW NOISE, THIN FILM (NiCr) CONSTRUCTION REFLOW SOLDERABLE (Pb FREE TERMINATION FINISH) Type Size EIA PowerRating
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
Εγχειρίδια Μαθηµατικών και Χταποδάκι στα Κάρβουνα
 [ 1 ] Πανεπιστήµιο Κύπρου Εγχειρίδια Μαθηµατικών και Χταποδάκι στα Κάρβουνα Νίκος Στυλιανόπουλος, Πανεπιστήµιο Κύπρου Λευκωσία, εκέµβριος 2009 [ 2 ] Πανεπιστήµιο Κύπρου Πόσο σηµαντική είναι η απόδειξη
[ 1 ] Πανεπιστήµιο Κύπρου Εγχειρίδια Μαθηµατικών και Χταποδάκι στα Κάρβουνα Νίκος Στυλιανόπουλος, Πανεπιστήµιο Κύπρου Λευκωσία, εκέµβριος 2009 [ 2 ] Πανεπιστήµιο Κύπρου Πόσο σηµαντική είναι η απόδειξη
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
ECTS ΕΥΡΩΠΑΪΚΟ ΣΥΣΤΗΜΑ ΜΕΤΑΦΟΡΑΣ ΑΚΑΔΗΜΑΪΚΩΝ ΜΟΝΑΔΩΝ ΣΤΗΝ ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ. (Α) Λίστα με τα στοιχεία των μαθημάτων στα ελληνικά
 ECTS ΕΥΡΩΠΑΪΚΟ ΣΥΣΤΗΜΑ ΜΕΤΑΦΟΡΑΣ ΑΚΑΔΗΜΑΪΚΩΝ ΜΟΝΑΔΩΝ ΣΤΗΝ ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ (Α) Λίστα με τα στοιχεία των μαθημάτων στα ελληνικά Γενικές πληροφορίες μαθήματος: Τίτλος μαθήματος: Προχωρημένη Εδαφομηχανική
ECTS ΕΥΡΩΠΑΪΚΟ ΣΥΣΤΗΜΑ ΜΕΤΑΦΟΡΑΣ ΑΚΑΔΗΜΑΪΚΩΝ ΜΟΝΑΔΩΝ ΣΤΗΝ ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ (Α) Λίστα με τα στοιχεία των μαθημάτων στα ελληνικά Γενικές πληροφορίες μαθήματος: Τίτλος μαθήματος: Προχωρημένη Εδαφομηχανική
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Investigation of Different Material Distributions and Thermal Boundary Conditions on Stress Field of FGM Rotating Hollow Disk
 8./0-0 5. ( 67 -(4 *+(,-.( / 0 -+ (3) :; 0. +. ( 64-5 $%& 35 46 75 ) &!&! % ( '!%&! $ #! ) &! &!% ( '!- %&!+,* $ # % */- 8.. =
8./0-0 5. ( 67 -(4 *+(,-.( / 0 -+ (3) :; 0. +. ( 64-5 $%& 35 46 75 ) &!&! % ( '!%&! $ #! ) &! &!% ( '!- %&!+,* $ # % */- 8.. =
Comparison of Evapotranspiration between Indigenous Vegetation and Invading Vegetation in a Bog
 J. Jpn. Soc. Soil Phys. No. +*-, p.-3.1,**0 ** * *** Comparison of Evapotranspiration between Indigenous Vegetation and Invading Vegetation in a Bog Toshiki FUJIMOTO*, Ippei IIYAMA*, Mai SAKAI*, Osamu
J. Jpn. Soc. Soil Phys. No. +*-, p.-3.1,**0 ** * *** Comparison of Evapotranspiration between Indigenous Vegetation and Invading Vegetation in a Bog Toshiki FUJIMOTO*, Ippei IIYAMA*, Mai SAKAI*, Osamu
σ zz Stresses in 3-D σ yy τ yx σ xx z τ zy τ zx τ yz τ xz τ xy
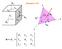 zz Stresses in -D z z z z z z zz ij z z z z z Matrices Review Matri Multiplication : When the number of columns of the first matri is the same as the number of rows in the second matri then matri multiplication
zz Stresses in -D z z z z z z zz ij z z z z z Matrices Review Matri Multiplication : When the number of columns of the first matri is the same as the number of rows in the second matri then matri multiplication
