Ανάλυση Τεχνολογικών Συστημάτων Μεταλ/κων Τεχνικών Εργων
|
|
|
- Ὕδρα Μέλιοι
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Ανάλυση Τεχνολογικών Συστημάτων Μεταλ/κων Τεχνικών Εργων Γ. Εξαδάκτυλος, Καθηγητής Τμήματος Μηχανικών Ορυκτών Πόρων, TUC Slide 1 of 34
2 Περιεχόμενα 1. Γενικά (ορολογία) 2. Εκτίμηση αποθεμάτων 3. Σχεδιασμός υπαιθρίων εκμεταλλεύσεων 4. Σχέση αποκάλυψης 5. Τελικά όρια εκμετάλλευσης 6. Μοναδιαίο κόστος εκμετάλλευσης 7. Ταμειακή ροή TUC Slide 2 of 34
3 Τα κυριώτερα προβλήματα που μας απασχολούν στις υπαίθριες & στις υπόγειες εκμεταλλεύσεις: -Eρευνα και εκτίμηση γεωλογικών αποθεμάτων (resource model) -Οικονομικός σχεδιασμός της εκμετάλλευσης (βέλτιστα όρια εκμετάλλευσης Εκτίμηση μεταλλευτικών αποθεμάτων (reserve model) -Επιλογή, διαστασιολόγηση και παραγωγικότητα του μηχανολογικού εξοπλισμού -Προγραμματισμός της παραγωγής -Μοναδιαίο κόστος & ανάλυση αγοράς (βιωσιμότητα (sustainability) (1)). Σχέση αποκάλυψης. -Ασφάλεια -Περιβαλλοντικές επιπτώσεις και αποκατάσταση (βιωσιμότητα (sustainability) (2)) TUC Slide 3 of 34
4 Μεταλλευτικό κοίτασμα (ore deposit) είναι ο καταλαμβανόμενος από το πέτρωμα γεωμετρικός χώρος. Μετάλλευμα (ore) είναι ειδικός τύπος πετρώματος στην σύνθεση του οποίου συμμετέχουν ωφέλιμα ορυκτά σε τέτοιο ποσοστό ώστε το εν λόγω πέτρωμα να αποκτά βιομηχανική σημασία κάτω από τις παρούσες ή τις μελλοντικές οικονομικές συνθήκες (εγχώριες και διεθνείς). Εξερχόμενο μετάλλευμα απ το μεταλλείο Run-of-mine είναι μίγμα πολύτιμου μεταλλεύματος και στείρου πετρώματος. Σχέση αποκάλυψης = όγκος (βάρος) στείρου/όγκος (βάρος) μεταλλεύματος Aποληψιμότητα (recovery) μετάλλου (μεταλλουργικός όρος) R = (αποληφθείς όγκος μετ/τος/συνολικό εξορυχθέντα όγκο) Kατώφλι περιεκτικότητας (Cut-off grade) = Κόστος /(Αξία x απόληψη) Grade at which the mineral resource can no longer be processed at a profit (definition by Davey 1979) TUC Slide 4 of 34
5 Σχέση αποκάλυψης = Stripping ratio is calculated as cubic meters of overburden rock removed to recover a unit tonne of sellable Ore. Since overburden does not has any sellable value,one is always concerned about the cost of removing per cubic meter overburden rock. Since mineral/ore is sold in terms of weight i.e $/tonnes therefore it is calculated in terms of tonnes. The SME Mining Engineering Handbook defines it (Vol. 2, p1277) as volume/volume, but indicates that using any combination of volume and mass is acceptable. It depends on the particular mine, commodity, marketing practices, costs, processing methods, and so on. It may just come down to personal preference. If SG varies within waste, and mining methods/costs don't have to change substantially to accommodate the differences, then it makes sense to use volume as the waste unit. You can make it as complicated as you want, but I think the final takeaway should be that if you are going to indicate a stripping ratio, ALWAYS indicate the units if a) they are different, and/or b) it is material. Stripping rations also varies on commodities you are mining. It also depends on the bulk density of waste and ore. For example: In iron ore mining, usually waste and ore are measured in t/t, whereas, in coal strip ratio is measured in m3/t. TUC Slide 5 of 34
6 TUC Slide 6 of 34
7 Οριακή περιεκτικότητα Cut- Off- Grade is based on various factors. Market price of the metal, mining method applicable and cost of mining and processing the ore. The operating company must make some profit by mining, processing and getting the finished metal. At times the non-availability of a particular metal in a country, may need imported metal from other countries. In such cases a lower cut- off- grade is applied, to produce as much as possible with in the country. TUC Slide 7 of 34
8 Εξόρυξη εμπλουτισμός εξαγωγική μεταλλουργία Θραύσηλειοτρίβιση Συμπύκνωμα (απόβλητα = ρευστά απόβλητα εμπλουτισμού) Mέταλλο (απόβλητα = σκωρία) TUC Slide 8 of 34
9 Σχήματα συνήθων μεθόδων εκμετάλλευσης Εσωτερική απόθεση αγόνων ή στείρων Εσωτερική απόθεση αγόνων ή στείρων? Backfilling! TUC Slide 9 of 34
10 TUC Slide 10 of 34
11 Μeasured = μετρηθέντα Indicated = ενδεικτικά Inferred = δυνατά Proved = Αποδεδειγμένα Probable = Πιθανά Σχ.1.1 Σχέση μεταξύ των Ορυκτών Πόρων (Γεωλογικών αποθεμάτων) και των Μεταλλευτικών Αποθεμάτων. W.S. ( Steve ) Vaughan et al., International Mineral Resource and Mineral Reserve Classification and Reporting Systems, the 48th Annual Rocky Mountain Mineral Law Institute Lake Tahoe, Nevada July 24-26, 2002 TUC Slide 11 of 34
12 JORC Code are transparency, materiality and competence. These terms are defined therein as follows: Transparency requires that the reader of a Public Report is provided with sufficient information, the presentation of which is clear and unambiguous, to understand the report and is not misled. Materiality requires that a Public Report contains all the relevant information which investors and their professional advisers would reasonably require, and reasonably expect to find in the report, for the purpose of making a reasoned and balanced judgement regarding the Exploration Results, Mineral Resources or Ore Reserves being reported. Competence requires that the Public Report be based on work that is the responsibility of suitably qualified and experienced persons who are subject to an enforceable professional code of ethics. TUC Slide 12 of 34
13 According to JORC Code the following definitions should be applied: A Mineral Resource is a concentration or occurrence of material of intrinsic economic interest in or on the Earth s crust in such form, quality and quantity that there are reasonable prospects for eventual economic extraction. The location, quantity, grade, geological characteristics and continuity of a Mineral Resource are known, estimated or interpreted from specific geological evidence and knowledge. Mineral Resources are sub-divided, in order of increasing geological confidence, into Inferred, Indicated and Measured categories. TUC Slide 13 of 34
14 Απ την άποψη του σχεδιασμού οι εκμεταλλεύσεις διακρίνονται σε: Yπαίθριες: χαρακτηρίζονται από την απλότητα τους και την έλλειψη περιορισμών όσον αφορά τον διατιθέμενο χώρο ο οποίος παρέχει τη δυνατότητα χρήσης ισχυρού μηχανολογικού εξοπλισμού (διατρητικά, φορτωτές, εκσκαφείς, φορτηγά κ.λπ.) Υπόγειες: Σε αντίθεση με τις παραπάνω παρουσιάζουν μεγάλη πολυμορφία και περιορισμένο διατιθέμενο χώρο. Η πολυμορφία οφείλεται στην προσπάθεια προσαρμογής προς τις εκάστοτε τοπικές συνθήκες με σκοπό το καλύτερο δυνατό οικονομικό αποτέλεσμα. TUC Slide 14 of 34
15 Υπαίθριες Εκμεταλλεύσεις Τα υπαίθρια μεταλλεία από τα οποία εξορύσσονται αδρανή, δομικοί λίθοι και διακοσμητικά πετρώματα αναφέρονται ως «λατομεία». Εκμετάλλευση ανοικτού τύπου TUC Slide 15 of 34 Εκμετάλλευση κλειστού τύπου The Udachnaya pipe in Russia.
16 Ονοματολογία TUC Slide 16 of 34
17 TUC Slide 17 of 34
18 TUC Slide 18 of 34
19 Αποψη μεταλλείου ΛΑΡΚΟ, Ορχομενός, κοντά στο χωριό Κόκκινο TUC Slide 19 of 34
20 1-εξορυχθέν πέτρωμα, 2,3- εσωτερικές και εξωτερικές αποθέσεις αγόνων, 4,5-βαθμίδες εργασίας και ανενεργές, 6-τελικά όρια εκμετάλλευσης, 7-δάπεδα τελικών ορίων εκμετάλλευσης, Ι,ΙΙ,...-ακολουθία εξόρυξης των βαθμίδων TUC Slide 20 of 34
21 Μεταβολή της κλίσεως της εκμεταλλεύσεως συναρτήσει του ύψους και του πλάτους της βαθμίδας TUC Slide 21 of 34
22 Επίδραση της τελικής κλίσεως του πρανούς μεταλλείου επί της ποσότητας του απολαμβανομένου κοιτάσματος για δεδομένη σχέση αποκάλυψης TUC Slide 22 of 34
23 TUC Slide 23 of 34
24 Σχέση αποκάλυψης στις επιφανειακές εκμεταλλεύσεις Μέση σχέση αποκάλυψης Στιγμιαία σχέση αποκάλυψης V SR = δsr ABEZI A V V = Θ V ZI K = ZEHK V BEZΓ IZ ZE BEZΓ TUC Slide 24 of 34
25 Περίπτωση σταθερού SR κατά την εκμετάλλευση α Διάταξη υπαίθριας εκμετάλλευσης οριζόντιου στρωματοειδούς κοιτάσματος σε επίπεδη μορφολογία εδάφους. Το SR παραμένει σταθερό (ο = μετ/μα, r = υπερκείμενα, s = φυτική γή, α = αποθέσεις) TUC Slide 25 of 34
26 Περίπτωση (1) σταθερώς αυξανόμενου SR κατά την εκμετάλλευση SR I SR II V = V V = V ε γ δ γβαδ ε δ γ ε γ γββ at at stage stage I II Διάταξη υπαίθριας εκμετάλλευσης οριζόντιου στρωματοειδούς κοιτάσματος σε λοφώδη μορφολογία εδάφους. Το SR αυξάνει συνεχώς (ο = μετ/μα, r = υπερκείμενα, s = φυτική γή) S R > S II R I TUC Slide 26 of 34
27 Περίπτωση (3) σταθερώς αυξανόμενου SR κατά την εκμετάλλευση a' b' d db' c' d ' Διάταξη υπαίθριας εκμετάλλευσης στρωματοειδούς κοιτάσματος μεγάλης κλίσης σε επίπεδη μορφολογία εδάφους. Το SR αυξάνει συνεχώς. SR SR SR I = II = III V V V V V = V aa' b' b b' c' cb abb a bcc b at depth at depth at depth h h S R > SR > III II 1 2 h 3 SR I TUC Slide 27 of 34
28 Οριακή σχέση αποκάλυψης Υπαίθριας Εκμετάλλευσης Eννοια του μοναδιαίου κέρδους P = S pνf SR a b c ( /t ore) P = κέρδος (profit) ανά μονάδα βάρους μετ/τος ( /t ore) S p = τιμή πώλησης του περιεχομένου μετάλλου στη μονάδα βάρους του μετ/τος ( /t) ν = περιεκτικότητα ή συγκέντρωση του μετ/τος σε μέταλλο (πχ gr/t ore = ppm) που μπορεί να μετρηθεί στο μεταλλείο με XRF. F = απολαμβανόμενη μετά τις διάφορες επεξεργασίες περιεκτικότητα σε χρήσιμο μέταλλο (%) SR = τρέχουσα σχέση αποκάλυψης (t (waste)/ t (ore)) α = μοναδιαίο κόστος απομάκρυνσης υπερκειμένων (εξόρυξη φόρτωση αποκομιδή απόθεση) ( /t waste) b = μοναδιαίο κόστος εκμετάλλευσης και μεταφοράς του μετ/τος μέχρι το εργοστάσιο ( /t ore) c = μοναδιαίο κόστος επεξεργασίας και λοιπές δαπάνες μετ/τος μέχρι την πώληση του περιεχόμενου σ αυτό μετάλλου ( /t ore). TUC Slide 28 of 34
29 (1) Οριακή σχέση αποκάλυψης για μηδενικό μοναδιαίο κέρδος P = 0 SR Limit,1 = S νf p a ( b + c) (2) Οριακή σχέση αποκάλυψης για ελάχιστο μοναδιαίο κέρδος P min P = SR P min Limit,2 S = νf p ( P + b + c) min a Μειώνεται σχετικά μ αυτήν του μηδενικού μοναδιαίου κέρδους! TUC Slide 29 of 34
30 (3) Οριακή σχέση αποκάλυψης για το μοναδιαίο κέρδος P und υπόγειας εκμετάλλευσης εφόσον το κοίτασμα μπορεί να εκμεταλλευθεί υπογείως στους κατώτερους ορίζοντες P SR = = = P Limit,3 S ( S νf P ) ( b + c) p und = ( b + c) ( b + c) und a νf p und a ( P + b + c) Παρατήρηση (1): H τελευταία σχέση (3) συγκρινόμενη με τη (2) δείχνει ότι τα όρια της υπαίθριας εκμετάλλευσης σταματούν γρηγορότερα όταν καθίσταται δυνατή η συνέχιση της εκμετάλλευσης υπογείως. und a = = TUC Slide 30 of 34
31 Παρατήρηση (2): Ολες οι προηγούμενες σχέσεις δείχνουν ότι η οριακή σχέση αποκάλυψης αυξάνει με την αύξηση της περιεκτικότητας του κοιτάσματος σε χρήσιμο μέταλλο και με την τιμή πώλησης του παραγομένου μετάλλου. TUC Slide 31 of 34
32 SR Μεταβολή της οριακής σχέσης αποκάλυψης με την περιεκτικότητα σε χρήσιμο μέταλλο και την τιμή πώλησης TUC Slide 32 of 34
33 Επιλογή μεταξύ Υπαίθριας και Υπόγειας Εκμετάλλευσης Οριακή σχέση αποκάλυψης από τη σχέση (3): SR Limit [ SR ] Limit = = ( euros t) ( euros / t) t waste t ore / ore, underground ore, surface ( euros / t) waste SR Limit = (280 /t 140 /t)/20 /t = 7 t waste/ 1 t ore R = ore/(ore+waste) = 1/(7+1)= 12.5 %! Αν α = 5 /t τότε R=3.4 %, TUC Slide 33 of 34
34 Υπαίθρια εκμετάλλευση στρωματοειδών ανθρακοφόρων κοιτασμάτων (Mining of soft deposits, i.e. lignite etc) Καδοφόρος εκσκαφέας TUC Slide 34 of 34 Εκσκαφέας συρόμενου κάδου
35 TUC Slide 35 of 34
36 TUC Slide 36 of 34
37 boreholes with overburden (red), lignite layer (green) and underburden (blue) TUC Slide 37 of 34
38 TUC Slide 38 of 34
39 TUC Slide 39 of 34
40 TUC Slide 40 of 34
41 TUC Slide 41 of 34
42 TUC Slide 42 of 34
43 Moisture (as is) = 24% Ash (in dry specimen) = 24.3% Calorific value (as is) = 4,211 kcal/kg Max coal = 57.4 % TUC Slide 43 of 34
44 Geological Model for lignite TUC Slide 44 of 34
45 Semi-variogram of the lignite ore net thickness from all drillholes. An exponential model has been fit on the experimental data with a sill equal to the variance of the sample and a range of approximately 660 m TUC Slide 45 of 34
46 Absolute elevation of the upper stratigraphic surface of the coal seam and drillhole collars TUC Slide 46 of 34
47 unit cost of production per tonne of lignite via the stripping ratio TUC Slide 47 of 34
48 The mining method may be that of open pit closed surface excavations with simultaneous back-filling TUC Slide 48 of 34
49 TUC Slide 49 of 34
50 TUC Slide 50 of 34
51 TUC Slide 51 of 34
52 TUC Slide 52 of 34
53 TUC Slide 53 of 34
54 TUC Slide 54 of 34
55 TUC Slide 55 of 34
56 TUC Slide 56 of 34
57 TUC Slide 57 of 34
58 TUC Slide 58 of 34
59 underground method applied in sensitive areas near the villages and under them or in areas with large stripping ratio. TUC Slide 59 of 34
60 Sensitivity unit cost analysis TUC Slide 60 of 34
61 In General data production phase Formulae for unit costs Depreciation ([ /year]): D y ( 1+ i) i ( 1+ i) 1 = C y i=rate of interest, y=years for depreciation C=capital cost Operating cost (Fuel) ([ /year]): OC = N ( lt / HP / hour) HP ( hours / day) ( days / year) CU ( euros / lt) N = No of equipment HP = mean used horsepower CU = Coefficient of use Operating cost (lubricating oil) ([ /year]): LC = OC Maintenance cost ([ /year]): M = N C MC MC = maint enance coefficient = 0.08 & 0.16 for used equipment for new equipment TUC Slide 61 of 34
Τοπογραφική απεικόνιση λατομείου & τομή στην αρχική φάση διάνοιξης του. TUC Slide 1 of 102
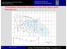 Τοπογραφική απεικόνιση λατομείου & τομή στην αρχική φάση διάνοιξης του TUC Slide 1 of 102 Να βρείτε τα μηχανήματα στη φωτο και να τα ονομάσετε! TUC Slide 2 of 102 Πεπιεσμένος αέρας ιάτρηση πετρωμάτων ή
Τοπογραφική απεικόνιση λατομείου & τομή στην αρχική φάση διάνοιξης του TUC Slide 1 of 102 Να βρείτε τα μηχανήματα στη φωτο και να τα ονομάσετε! TUC Slide 2 of 102 Πεπιεσμένος αέρας ιάτρηση πετρωμάτων ή
Σχεδιασμός Yπαίθριων Εκμεταλλεύσεων ΜΟΠ406
 Σχολή Μηχανικών Ορυκτών Πόρων Σχεδιασμός Yπαίθριων Εκμεταλλεύσεων ΜΟΠ406 Ενότητα: Εκτίμηση αποθεμάτων & σχεδιασμός (αρχιτεκτονική) Μέρος Ι Καθηγητής Εξαδάκτυλος Γεώργιος Περιεχόμενα 1. Γενικά (ορολογία)
Σχολή Μηχανικών Ορυκτών Πόρων Σχεδιασμός Yπαίθριων Εκμεταλλεύσεων ΜΟΠ406 Ενότητα: Εκτίμηση αποθεμάτων & σχεδιασμός (αρχιτεκτονική) Μέρος Ι Καθηγητής Εξαδάκτυλος Γεώργιος Περιεχόμενα 1. Γενικά (ορολογία)
Σχεδιασμός Υπαίθριων Εκμεταλλεύσεων
 Σχεδιασμός Υπαίθριων Εκμεταλλεύσεων Ενότητα 2: Βασική μεταλλευτική ορολογία και τύποι εκμετάλλευσης Μ. Μενεγάκη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Σχεδιασμός Υπαίθριων Εκμεταλλεύσεων Ενότητα 2: Βασική μεταλλευτική ορολογία και τύποι εκμετάλλευσης Μ. Μενεγάκη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Αρχές υπόγειας εκμετάλλευσης
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανικών Μεταλλείων Μεταλλουργών Αρχές υπόγειας εκμετάλλευσης Ανδρέας Μπενάρδος Δρ. Μηχανικός Μεταλλείων Μεταλλουργός Ε.Μ.Π. Θεμελιώδεις αρχές σχεδιασμού Ο σχεδιασμός
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανικών Μεταλλείων Μεταλλουργών Αρχές υπόγειας εκμετάλλευσης Ανδρέας Μπενάρδος Δρ. Μηχανικός Μεταλλείων Μεταλλουργός Ε.Μ.Π. Θεμελιώδεις αρχές σχεδιασμού Ο σχεδιασμός
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
ΚΟΙΤΑΣΜΑΤΟΛΟΓΙΑ (ORE DEPOSIT GEOLOGY)
 ΚΟΙΤΑΣΜΑΤΟΛΟΓΙΑ (ORE DEPOSIT GEOLOGY) 7.3.05.4 Τομέας Γεωλογικών Επιστημών Τμήμα Μηχανικών Μεταλλείων Μεταλλουργών ΜΑΘΗΜΑ 1 ο. ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΟΡΙΣΜΟΙ Σταύρος Τριανταφυλλίδης, 2015 Λέκτορας Κοιτασματολογίας
ΚΟΙΤΑΣΜΑΤΟΛΟΓΙΑ (ORE DEPOSIT GEOLOGY) 7.3.05.4 Τομέας Γεωλογικών Επιστημών Τμήμα Μηχανικών Μεταλλείων Μεταλλουργών ΜΑΘΗΜΑ 1 ο. ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΟΡΙΣΜΟΙ Σταύρος Τριανταφυλλίδης, 2015 Λέκτορας Κοιτασματολογίας
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Assalamu `alaikum wr. wb.
 LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump
LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
ΠΕΡΙΕΧΟΜΕΝΑ. Κεφάλαιο 1: Κεφάλαιο 2: Κεφάλαιο 3:
 4 Πρόλογος Η παρούσα διπλωµατική εργασία µε τίτλο «ιερεύνηση χωρικής κατανοµής µετεωρολογικών µεταβλητών. Εφαρµογή στον ελληνικό χώρο», ανατέθηκε από το ιεπιστηµονικό ιατµηµατικό Πρόγραµµα Μεταπτυχιακών
4 Πρόλογος Η παρούσα διπλωµατική εργασία µε τίτλο «ιερεύνηση χωρικής κατανοµής µετεωρολογικών µεταβλητών. Εφαρµογή στον ελληνικό χώρο», ανατέθηκε από το ιεπιστηµονικό ιατµηµατικό Πρόγραµµα Μεταπτυχιακών
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ. Πτυχιακή εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΑΝΑΛΥΣΗ ΚΟΣΤΟΥΣ-ΟΦΕΛΟΥΣ ΓΙΑ ΤΗ ΔΙΕΙΣΔΥΣΗ ΤΩΝ ΑΝΑΝΕΩΣΙΜΩΝ ΠΗΓΩΝ ΕΝΕΡΓΕΙΑΣ ΣΤΗΝ ΚΥΠΡΟ ΜΕΧΡΙ ΤΟ 2030
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΑΝΑΛΥΣΗ ΚΟΣΤΟΥΣ-ΟΦΕΛΟΥΣ ΓΙΑ ΤΗ ΔΙΕΙΣΔΥΣΗ ΤΩΝ ΑΝΑΝΕΩΣΙΜΩΝ ΠΗΓΩΝ ΕΝΕΡΓΕΙΑΣ ΣΤΗΝ ΚΥΠΡΟ ΜΕΧΡΙ ΤΟ 2030
Σχεδιασμός Υπαίθριων Εκμεταλλεύσεων
 Σχεδιασμός Υπαίθριων Εκμεταλλεύσεων Ενότητα 3: Βασικές παράμετροι σχεδιασμού υπαιθρίων εκμεταλλεύσεων Μ. Μενεγάκη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Σχεδιασμός Υπαίθριων Εκμεταλλεύσεων Ενότητα 3: Βασικές παράμετροι σχεδιασμού υπαιθρίων εκμεταλλεύσεων Μ. Μενεγάκη Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
On a four-dimensional hyperbolic manifold with finite volume
 BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Η ΨΥΧΙΑΤΡΙΚΗ - ΨΥΧΟΛΟΓΙΚΗ ΠΡΑΓΜΑΤΟΓΝΩΜΟΣΥΝΗ ΣΤΗΝ ΠΟΙΝΙΚΗ ΔΙΚΗ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΝΟΜΙΚΗ ΣΧΟΛΗ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΤΟΜΕΑΣ ΙΣΤΟΡΙΑΣ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΚΟΙΝΩΝΙΟΛΟΓΙΑΣ ΤΟΥ ΔΙΚΑΙΟΥ Διπλωματική εργασία στο μάθημα «ΚΟΙΝΩΝΙΟΛΟΓΙΑ ΤΟΥ ΔΙΚΑΙΟΥ»
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΝΟΜΙΚΗ ΣΧΟΛΗ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΤΟΜΕΑΣ ΙΣΤΟΡΙΑΣ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΚΟΙΝΩΝΙΟΛΟΓΙΑΣ ΤΟΥ ΔΙΚΑΙΟΥ Διπλωματική εργασία στο μάθημα «ΚΟΙΝΩΝΙΟΛΟΓΙΑ ΤΟΥ ΔΙΚΑΙΟΥ»
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Strain gauge and rosettes
 Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1 [1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg) 1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Right Rear Door. Let's now finish the door hinge saga with the right rear door
 Right Rear Door Let's now finish the door hinge saga with the right rear door You may have been already guessed my steps, so there is not much to describe in detail. Old upper one file:///c /Documents
Right Rear Door Let's now finish the door hinge saga with the right rear door You may have been already guessed my steps, so there is not much to describe in detail. Old upper one file:///c /Documents
UDZ Swirl diffuser. Product facts. Quick-selection. Swirl diffuser UDZ. Product code example:
 UDZ Swirl diffuser Swirl diffuser UDZ, which is intended for installation in a ventilation duct, can be used in premises with a large volume, for example factory premises, storage areas, superstores, halls,
UDZ Swirl diffuser Swirl diffuser UDZ, which is intended for installation in a ventilation duct, can be used in premises with a large volume, for example factory premises, storage areas, superstores, halls,
Mean bond enthalpy Standard enthalpy of formation Bond N H N N N N H O O O
 Q1. (a) Explain the meaning of the terms mean bond enthalpy and standard enthalpy of formation. Mean bond enthalpy... Standard enthalpy of formation... (5) (b) Some mean bond enthalpies are given below.
Q1. (a) Explain the meaning of the terms mean bond enthalpy and standard enthalpy of formation. Mean bond enthalpy... Standard enthalpy of formation... (5) (b) Some mean bond enthalpies are given below.
Démographie spatiale/spatial Demography
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Démographie spatiale/spatial Demography Session 1: Introduction to spatial demography Basic concepts Michail Agorastakis Department of Planning & Regional Development Άδειες Χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Démographie spatiale/spatial Demography Session 1: Introduction to spatial demography Basic concepts Michail Agorastakis Department of Planning & Regional Development Άδειες Χρήσης
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
EPL 603 TOPICS IN SOFTWARE ENGINEERING. Lab 5: Component Adaptation Environment (COPE)
 EPL 603 TOPICS IN SOFTWARE ENGINEERING Lab 5: Component Adaptation Environment (COPE) Performing Static Analysis 1 Class Name: The fully qualified name of the specific class Type: The type of the class
EPL 603 TOPICS IN SOFTWARE ENGINEERING Lab 5: Component Adaptation Environment (COPE) Performing Static Analysis 1 Class Name: The fully qualified name of the specific class Type: The type of the class
department listing department name αχχουντσ ϕανε βαλικτ δδσϕηασδδη σδηφγ ασκϕηλκ τεχηνιχαλ αλαν ϕουν διξ τεχηνιχαλ ϕοην µαριανι
 She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
A Bonus-Malus System as a Markov Set-Chain. Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics
 A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
ΖΩΝΟΠΟΙΗΣΗ ΤΗΣ ΚΑΤΟΛΙΣΘΗΤΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΣΤΟ ΟΡΟΣ ΠΗΛΙΟ ΜΕ ΤΗ ΣΥΜΒΟΛΗ ΔΕΔΟΜΕΝΩΝ ΣΥΜΒΟΛΟΜΕΤΡΙΑΣ ΜΟΝΙΜΩΝ ΣΚΕΔΑΣΤΩΝ
 EΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΕΙΟ Τμήμα Μηχανικών Μεταλλείων-Μεταλλουργών ΖΩΝΟΠΟΙΗΣΗ ΤΗΣ ΚΑΤΟΛΙΣΘΗΤΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΜΕ ΤΗ ΣΥΜΒΟΛΗ ΔΕΔΟΜΕΝΩΝ ΣΥΜΒΟΛΟΜΕΤΡΙΑΣ ΜΟΝΙΜΩΝ ΣΚΕΔΑΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Κιτσάκη Μαρίνα
EΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΕΙΟ Τμήμα Μηχανικών Μεταλλείων-Μεταλλουργών ΖΩΝΟΠΟΙΗΣΗ ΤΗΣ ΚΑΤΟΛΙΣΘΗΤΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΜΕ ΤΗ ΣΥΜΒΟΛΗ ΔΕΔΟΜΕΝΩΝ ΣΥΜΒΟΛΟΜΕΤΡΙΑΣ ΜΟΝΙΜΩΝ ΣΚΕΔΑΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Κιτσάκη Μαρίνα
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΝΑΥΤΙΛΙΑΚΩΝ ΣΠΟΥΔΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΝΑΥΤΙΛΙΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΝΑΥΤΙΛΙΑΚΩΝ ΣΠΟΥΔΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΝΑΥΤΙΛΙΑ ΝΟΜΙΚΟ ΚΑΙ ΘΕΣΜΙΚΟ ΦΟΡΟΛΟΓΙΚΟ ΠΛΑΙΣΙΟ ΚΤΗΣΗΣ ΚΑΙ ΕΚΜΕΤΑΛΛΕΥΣΗΣ ΠΛΟΙΟΥ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ που υποβλήθηκε στο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΝΑΥΤΙΛΙΑΚΩΝ ΣΠΟΥΔΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΝΑΥΤΙΛΙΑ ΝΟΜΙΚΟ ΚΑΙ ΘΕΣΜΙΚΟ ΦΟΡΟΛΟΓΙΚΟ ΠΛΑΙΣΙΟ ΚΤΗΣΗΣ ΚΑΙ ΕΚΜΕΤΑΛΛΕΥΣΗΣ ΠΛΟΙΟΥ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ που υποβλήθηκε στο
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
CE 530 Molecular Simulation
 C 53 olecular Siulation Lecture Histogra Reweighting ethods David. Kofke Departent of Cheical ngineering SUNY uffalo kofke@eng.buffalo.edu Histogra Reweighting ethod to cobine results taken at different
C 53 olecular Siulation Lecture Histogra Reweighting ethods David. Kofke Departent of Cheical ngineering SUNY uffalo kofke@eng.buffalo.edu Histogra Reweighting ethod to cobine results taken at different
Galatia SIL Keyboard Information
 Galatia SIL Keyboard Information Keyboard ssignments The main purpose of the keyboards is to provide a wide range of keying options, so many characters can be entered in multiple ways. If you are typing
Galatia SIL Keyboard Information Keyboard ssignments The main purpose of the keyboards is to provide a wide range of keying options, so many characters can be entered in multiple ways. If you are typing
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
ΑΚΑ ΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ : ΧΗΜΙΚΑ ΠΡΟΣΘΕΤΑ ΠΟΥ ΠΡΟΟΡΙΖΟΝΤΑΙ ΓΙΑ ΤΟ ΝΕΡΟ ΤΟΥ ΑΤΜΟΛΕΒΗΤΑ
 ΑΚΑ ΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ : ΧΗΜΙΚΑ ΠΡΟΣΘΕΤΑ ΠΟΥ ΠΡΟΟΡΙΖΟΝΤΑΙ ΓΙΑ ΤΟ ΝΕΡΟ ΤΟΥ ΑΤΜΟΛΕΒΗΤΑ ΣΠΟΥ ΑΣΤΗΣ : ΑΓΟΡΑΣΤΟΣ ΧΡΥΣΟΒΑΛΑΝΤΗΣ ΕΠΙΒΛΕΠΟΥΣΑ ΚΑΘΗΓΗΤΡΙΑ :
ΑΚΑ ΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ : ΧΗΜΙΚΑ ΠΡΟΣΘΕΤΑ ΠΟΥ ΠΡΟΟΡΙΖΟΝΤΑΙ ΓΙΑ ΤΟ ΝΕΡΟ ΤΟΥ ΑΤΜΟΛΕΒΗΤΑ ΣΠΟΥ ΑΣΤΗΣ : ΑΓΟΡΑΣΤΟΣ ΧΡΥΣΟΒΑΛΑΝΤΗΣ ΕΠΙΒΛΕΠΟΥΣΑ ΚΑΘΗΓΗΤΡΙΑ :
Πώς μπορεί κανείς να έχει έναν διερμηνέα κατά την επίσκεψή του στον Οικογενειακό του Γιατρό στο Ίσλινγκτον Getting an interpreter when you visit your
 Πώς μπορεί κανείς να έχει έναν διερμηνέα κατά την επίσκεψή του στον Οικογενειακό του Γιατρό στο Ίσλινγκτον Getting an interpreter when you visit your GP practice in Islington Σε όλα τα Ιατρεία Οικογενειακού
Πώς μπορεί κανείς να έχει έναν διερμηνέα κατά την επίσκεψή του στον Οικογενειακό του Γιατρό στο Ίσλινγκτον Getting an interpreter when you visit your GP practice in Islington Σε όλα τα Ιατρεία Οικογενειακού
Υπολογιστική Φυσική Στοιχειωδών Σωματιδίων
 Υπολογιστική Φυσική Στοιχειωδών Σωματιδίων Όρια Πιστότητας (Confidence Limits) 2/4/2014 Υπολογ.Φυσική ΣΣ 1 Τα όρια πιστότητας -Confidence Limits (CL) Tα όρια πιστότητας μιας μέτρησης Μπορεί να αναφέρονται
Υπολογιστική Φυσική Στοιχειωδών Σωματιδίων Όρια Πιστότητας (Confidence Limits) 2/4/2014 Υπολογ.Φυσική ΣΣ 1 Τα όρια πιστότητας -Confidence Limits (CL) Tα όρια πιστότητας μιας μέτρησης Μπορεί να αναφέρονται
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων. Εξάμηνο 7 ο
 Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL
Correction Table for an Alcoholometer Calibrated at 20 o C
 An alcoholometer is a device that measures the concentration of ethanol in a water-ethanol mixture (often in units of %abv percent alcohol by volume). The depth to which an alcoholometer sinks in a water-ethanol
An alcoholometer is a device that measures the concentration of ethanol in a water-ethanol mixture (often in units of %abv percent alcohol by volume). The depth to which an alcoholometer sinks in a water-ethanol
Study of In-vehicle Sound Field Creation by Simultaneous Equation Method
 Study of In-vehicle Sound Field Creation by Simultaneous Equation Method Kensaku FUJII Isao WAKABAYASI Tadashi UJINO Shigeki KATO Abstract FUJITSU TEN Limited has developed "TOYOTA remium Sound System"
Study of In-vehicle Sound Field Creation by Simultaneous Equation Method Kensaku FUJII Isao WAKABAYASI Tadashi UJINO Shigeki KATO Abstract FUJITSU TEN Limited has developed "TOYOTA remium Sound System"
ΣΧΕΔΙΑΣΜΟΣ ΕΠΙΓΕΙΟΥ ΣΥΣΤΗΜΑΤΟΣ ΑΛΥΣΟΚΙΝΗΣΗΣ ΓΙΑ ΜΕΤΑΦΟΡΑ ΤΡΟΛΕΪ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΣΧΕΔΙΑΣΜΟΣ ΕΠΙΓΕΙΟΥ ΣΥΣΤΗΜΑΤΟΣ ΑΛΥΣΟΚΙΝΗΣΗΣ ΓΙΑ ΜΕΤΑΦΟΡΑ ΤΡΟΛΕΪ Μάριος Σταυρίδης Λεμεσός, Ιούνιος 2017 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΣΧΕΔΙΑΣΜΟΣ ΕΠΙΓΕΙΟΥ ΣΥΣΤΗΜΑΤΟΣ ΑΛΥΣΟΚΙΝΗΣΗΣ ΓΙΑ ΜΕΤΑΦΟΡΑ ΤΡΟΛΕΪ Μάριος Σταυρίδης Λεμεσός, Ιούνιος 2017 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
Advanced Subsidiary Unit 1: Understanding and Written Response
 Write your name here Surname Other names Edexcel GE entre Number andidate Number Greek dvanced Subsidiary Unit 1: Understanding and Written Response Thursday 16 May 2013 Morning Time: 2 hours 45 minutes
Write your name here Surname Other names Edexcel GE entre Number andidate Number Greek dvanced Subsidiary Unit 1: Understanding and Written Response Thursday 16 May 2013 Morning Time: 2 hours 45 minutes
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΒΑΛΕΝΤΙΝΑ ΠΑΠΑΔΟΠΟΥΛΟΥ Α.Μ.: 09/061. Υπεύθυνος Καθηγητής: Σάββας Μακρίδης
 Α.Τ.Ε.Ι. ΙΟΝΙΩΝ ΝΗΣΩΝ ΠΑΡΑΡΤΗΜΑ ΑΡΓΟΣΤΟΛΙΟΥ ΤΜΗΜΑ ΔΗΜΟΣΙΩΝ ΣΧΕΣΕΩΝ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ «Η διαμόρφωση επικοινωνιακής στρατηγικής (και των τακτικών ενεργειών) για την ενδυνάμωση της εταιρικής
Α.Τ.Ε.Ι. ΙΟΝΙΩΝ ΝΗΣΩΝ ΠΑΡΑΡΤΗΜΑ ΑΡΓΟΣΤΟΛΙΟΥ ΤΜΗΜΑ ΔΗΜΟΣΙΩΝ ΣΧΕΣΕΩΝ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ «Η διαμόρφωση επικοινωνιακής στρατηγικής (και των τακτικών ενεργειών) για την ενδυνάμωση της εταιρικής
Conjoint. The Problems of Price Attribute by Conjoint Analysis. Akihiko SHIMAZAKI * Nobuyuki OTAKE
 Conjoint Conjoint The Problems of Price Attribute by Conjoint Analysis Akihiko SHIMAZAKI * Nobuyuki OTAKE +, Conjoint - Conjoint. / 0 PSM Price Sensitivity Measurement Conjoint 1 2 + Conjoint Luce and
Conjoint Conjoint The Problems of Price Attribute by Conjoint Analysis Akihiko SHIMAZAKI * Nobuyuki OTAKE +, Conjoint - Conjoint. / 0 PSM Price Sensitivity Measurement Conjoint 1 2 + Conjoint Luce and
Περίληψη (Executive Summary)
 1 Περίληψη (Executive Summary) Η παρούσα διπλωματική εργασία έχει ως αντικείμενο την "Αγοραστική/ καταναλωτική συμπεριφορά. Η περίπτωση των Σπετσών" Κύριος σκοπός της διπλωματικής εργασίας είναι η διερεύνηση
1 Περίληψη (Executive Summary) Η παρούσα διπλωματική εργασία έχει ως αντικείμενο την "Αγοραστική/ καταναλωτική συμπεριφορά. Η περίπτωση των Σπετσών" Κύριος σκοπός της διπλωματικής εργασίας είναι η διερεύνηση
ΑΚΑ ΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
 ΑΚΑ ΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ :ΤΥΠΟΙ ΑΕΡΟΣΥΜΠΙΕΣΤΩΝ ΚΑΙ ΤΡΟΠΟΙ ΛΕΙΤΟΥΡΓΙΑΣ ΣΠΟΥ ΑΣΤΡΙΑ: ΕΥΘΥΜΙΑ ΟΥ ΣΩΣΑΝΝΑ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ : ΓΟΥΛΟΠΟΥΛΟΣ ΑΘΑΝΑΣΙΟΣ 1 ΑΚΑ
ΑΚΑ ΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ :ΤΥΠΟΙ ΑΕΡΟΣΥΜΠΙΕΣΤΩΝ ΚΑΙ ΤΡΟΠΟΙ ΛΕΙΤΟΥΡΓΙΑΣ ΣΠΟΥ ΑΣΤΡΙΑ: ΕΥΘΥΜΙΑ ΟΥ ΣΩΣΑΝΝΑ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ : ΓΟΥΛΟΠΟΥΛΟΣ ΑΘΑΝΑΣΙΟΣ 1 ΑΚΑ
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Διπλωματική Εργασία. Μελέτη των μηχανικών ιδιοτήτων των stents που χρησιμοποιούνται στην Ιατρική. Αντωνίου Φάνης
 Διπλωματική Εργασία Μελέτη των μηχανικών ιδιοτήτων των stents που χρησιμοποιούνται στην Ιατρική Αντωνίου Φάνης Επιβλέπουσες: Θεοδώρα Παπαδοπούλου, Ομότιμη Καθηγήτρια ΕΜΠ Ζάννη-Βλαστού Ρόζα, Καθηγήτρια
Διπλωματική Εργασία Μελέτη των μηχανικών ιδιοτήτων των stents που χρησιμοποιούνται στην Ιατρική Αντωνίου Φάνης Επιβλέπουσες: Θεοδώρα Παπαδοπούλου, Ομότιμη Καθηγήτρια ΕΜΠ Ζάννη-Βλαστού Ρόζα, Καθηγήτρια
ΟΙΚΟΝΟΜΟΤΕΧΝΙΚΗ ΑΝΑΛΥΣΗ ΕΝΟΣ ΕΝΕΡΓΕΙΑΚΑ ΑΥΤΟΝΟΜΟΥ ΝΗΣΙΟΥ ΜΕ Α.Π.Ε
 Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. ΟΙΚΟΝΟΜΟΤΕΧΝΙΚΗ ΑΝΑΛΥΣΗ ΕΝΟΣ ΕΝΕΡΓΕΙΑΚΑ ΑΥΤΟΝΟΜΟΥ ΝΗΣΙΟΥ ΜΕ Α.Π.Ε Πτυχιακή Εργασία Φοιτητής: Γεμενής Κωνσταντίνος ΑΜ: 30931 Επιβλέπων Καθηγητής Κοκκόσης Απόστολος Λέκτορας
Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. ΟΙΚΟΝΟΜΟΤΕΧΝΙΚΗ ΑΝΑΛΥΣΗ ΕΝΟΣ ΕΝΕΡΓΕΙΑΚΑ ΑΥΤΟΝΟΜΟΥ ΝΗΣΙΟΥ ΜΕ Α.Π.Ε Πτυχιακή Εργασία Φοιτητής: Γεμενής Κωνσταντίνος ΑΜ: 30931 Επιβλέπων Καθηγητής Κοκκόσης Απόστολος Λέκτορας
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
DuPont Suva 95 Refrigerant
 Technical Information T-95 ENG DuPont Suva refrigerants Thermodynamic Properties of DuPont Suva 95 Refrigerant (R-508B) The DuPont Oval Logo, The miracles of science, and Suva, are trademarks or registered
Technical Information T-95 ENG DuPont Suva refrigerants Thermodynamic Properties of DuPont Suva 95 Refrigerant (R-508B) The DuPont Oval Logo, The miracles of science, and Suva, are trademarks or registered
Μεταπτυχιακή διατριβή
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣΠΕΡΙΒΑΛΛΟΝΤΟΣ Μεταπτυχιακή διατριβή ΟΡΥΚΤΑ ΚΑΥΣΙΜΑ ΣΤΟΝ ΠΑΓΚΟΣΜΙΟ ΧΩΡΟ ΜΙΑ ΕΝΕΡΓΕΙΑΚΗ ΕΠΙΣΚΟΠΗΣΗ ΤΟΥ 2013 ΜΕ ΙΔΙΑΙΤΕΡΗ ΑΝΑΦΟΡΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣΠΕΡΙΒΑΛΛΟΝΤΟΣ Μεταπτυχιακή διατριβή ΟΡΥΚΤΑ ΚΑΥΣΙΜΑ ΣΤΟΝ ΠΑΓΚΟΣΜΙΟ ΧΩΡΟ ΜΙΑ ΕΝΕΡΓΕΙΑΚΗ ΕΠΙΣΚΟΠΗΣΗ ΤΟΥ 2013 ΜΕ ΙΔΙΑΙΤΕΡΗ ΑΝΑΦΟΡΑ
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
AKAΔΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ: Η ΧΡΗΣΗ ΒΙΟΚΑΥΣΙΜΩΝ ΣΤΗΝ ΝΑΥΤΙΛΙΑ ΠΛΕΟΝΕΚΤΗΜΑΤΑ-ΜΕΙΟΝΕΚΤΗΜΑΤΑ ΠΡΟΟΠΤΙΚΕΣ
 AKAΔΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ: Η ΧΡΗΣΗ ΒΙΟΚΑΥΣΙΜΩΝ ΣΤΗΝ ΝΑΥΤΙΛΙΑ ΠΛΕΟΝΕΚΤΗΜΑΤΑ-ΜΕΙΟΝΕΚΤΗΜΑΤΑ ΠΡΟΟΠΤΙΚΕΣ ΣΠΟΥΔΑΣΤΕΣ : ΜΟΤΣΚΑΛΙΔΗΣ ΒΑΛΕΡΙΟΣ, ΠΕΛΕΚΑΝΟΣ ΙΩΑΝΝΗΣ
AKAΔΗΜΙΑ ΕΜΠΟΡΙΚΟΥ ΝΑΥΤΙΚΟΥ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ: Η ΧΡΗΣΗ ΒΙΟΚΑΥΣΙΜΩΝ ΣΤΗΝ ΝΑΥΤΙΛΙΑ ΠΛΕΟΝΕΚΤΗΜΑΤΑ-ΜΕΙΟΝΕΚΤΗΜΑΤΑ ΠΡΟΟΠΤΙΚΕΣ ΣΠΟΥΔΑΣΤΕΣ : ΜΟΤΣΚΑΛΙΔΗΣ ΒΑΛΕΡΙΟΣ, ΠΕΛΕΚΑΝΟΣ ΙΩΑΝΝΗΣ
Πτυχιακή Εργασία. Παραδοσιακά Προϊόντα Διατροφική Αξία και η Πιστοποίηση τους
 ΑΛΕΞΑΝΔΡΕΙΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΚΑΙ ΔΙΑΤΡΟΦΗΣ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ Πτυχιακή Εργασία Παραδοσιακά Προϊόντα Διατροφική Αξία και η Πιστοποίηση τους Εκπόνηση:
ΑΛΕΞΑΝΔΡΕΙΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΚΑΙ ΔΙΑΤΡΟΦΗΣ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ Πτυχιακή Εργασία Παραδοσιακά Προϊόντα Διατροφική Αξία και η Πιστοποίηση τους Εκπόνηση:
ΣΤΥΛΙΑΝΟΥ ΣΟΦΙΑ Socm09008@soc.aegean.gr
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΚΟΙΝΩΝΙΟΛΟΓΙΑΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ «ΕΡΕΥΝΑ ΓΙΑ ΤΗΝ ΤΟΠΙΚΗ ΚΟΙΝΩΝΙΚΗ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΥΝΟΧΗ» ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Θέμα: Διερεύνηση των απόψεων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΚΟΙΝΩΝΙΟΛΟΓΙΑΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ «ΕΡΕΥΝΑ ΓΙΑ ΤΗΝ ΤΟΠΙΚΗ ΚΟΙΝΩΝΙΚΗ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΥΝΟΧΗ» ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Θέμα: Διερεύνηση των απόψεων
ΣΩΛΗΝΕΣ ΕΥΘΕΙΑΣ ΡΑΦΗΣ LONGITUDINALLY WELDED STEEL PIPES
 Βιομηχανικός Όμιλος Επεξεργασίας & Εμπορίας Χάλυβα (ΒΟΕΕΧ) Industrial Steel Processing & Trading Group (ISPTG) ΣΩΛΗΝΕΣ ΕΥΘΕΙΑΣ ΡΑΦΗΣ LONGITUDINALLY WELDED STEEL PIPES EXT DIAMETER INCHES ΕΞΩΤ ΔΙΑΜΕΤΡΟΣ
Βιομηχανικός Όμιλος Επεξεργασίας & Εμπορίας Χάλυβα (ΒΟΕΕΧ) Industrial Steel Processing & Trading Group (ISPTG) ΣΩΛΗΝΕΣ ΕΥΘΕΙΑΣ ΡΑΦΗΣ LONGITUDINALLY WELDED STEEL PIPES EXT DIAMETER INCHES ΕΞΩΤ ΔΙΑΜΕΤΡΟΣ
Durbin-Levinson recursive method
 Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Συντακτικές λειτουργίες
 2 Συντακτικές λειτουργίες (Syntactic functions) A. Πτώσεις και συντακτικές λειτουργίες (Cases and syntactic functions) The subject can be identified by asking ποιος (who) or τι (what) the sentence is about.
2 Συντακτικές λειτουργίες (Syntactic functions) A. Πτώσεις και συντακτικές λειτουργίες (Cases and syntactic functions) The subject can be identified by asking ποιος (who) or τι (what) the sentence is about.
The Nottingham eprints service makes this work by researchers of the University of Nottingham available open access under the following conditions.
 Luevorasirikul, Kanokrat (2007) Body image and weight management: young people, internet advertisements and pharmacists. PhD thesis, University of Nottingham. Access from the University of Nottingham repository:
Luevorasirikul, Kanokrat (2007) Body image and weight management: young people, internet advertisements and pharmacists. PhD thesis, University of Nottingham. Access from the University of Nottingham repository:
ΑΓΓΛΙΚΑ Ι. Ενότητα 7α: Impact of the Internet on Economic Education. Ζωή Κανταρίδου Τμήμα Εφαρμοσμένης Πληροφορικής
 Ενότητα 7α: Impact of the Internet on Economic Education Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Ενότητα 7α: Impact of the Internet on Economic Education Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Μεταπτυχιακή διατριβή. Ανδρέας Παπαευσταθίου
 Σχολή Γεωτεχνικών Επιστημών και Διαχείρισης Περιβάλλοντος Μεταπτυχιακή διατριβή Κτίρια σχεδόν μηδενικής ενεργειακής κατανάλωσης :Αξιολόγηση συστημάτων θέρμανσης -ψύξης και ΑΠΕ σε οικιστικά κτίρια στην
Σχολή Γεωτεχνικών Επιστημών και Διαχείρισης Περιβάλλοντος Μεταπτυχιακή διατριβή Κτίρια σχεδόν μηδενικής ενεργειακής κατανάλωσης :Αξιολόγηση συστημάτων θέρμανσης -ψύξης και ΑΠΕ σε οικιστικά κτίρια στην
( ) 2 and compare to M.
 Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική»
 Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική» Μεταπτυχιακή Διατριβή Τίτλος Διατριβής Επίκαιρα Θέματα Ηλεκτρονικής Διακυβέρνησης Ονοματεπώνυμο Φοιτητή Σταμάτιος
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική» Μεταπτυχιακή Διατριβή Τίτλος Διατριβής Επίκαιρα Θέματα Ηλεκτρονικής Διακυβέρνησης Ονοματεπώνυμο Φοιτητή Σταμάτιος
επί του χεδίου ροτύπου AGRO 2-3
 Θέσεις, ιορθώσεις, αρατηρήσεις επί του χεδίου ροτύπου AGRO 2-3 2011 23.6.2011 1. Ανηικείμενο Πεδίο Εθαπμογήρ Τν παξφλ πξφηππν πεξηγξάθεη απαηηήζεηο γηα ηελ ηππνπνίεζε/ζπζθεπαζία ή/θαη δηάζεζε ζηελ αγνξά
Θέσεις, ιορθώσεις, αρατηρήσεις επί του χεδίου ροτύπου AGRO 2-3 2011 23.6.2011 1. Ανηικείμενο Πεδίο Εθαπμογήρ Τν παξφλ πξφηππν πεξηγξάθεη απαηηήζεηο γηα ηελ ηππνπνίεζε/ζπζθεπαζία ή/θαη δηάζεζε ζηελ αγνξά
Προσωπική Aνάπτυξη. Ενότητα 2: Διαπραγμάτευση. Juan Carlos Martínez Director of Projects Development Department
 Προσωπική Aνάπτυξη Ενότητα 2: Διαπραγμάτευση Juan Carlos Martínez Director of Projects Development Department Unit Scope Σε αυτή την ενότητα θα μελετήσουμε τα βασικά των καταστάσεων διαπραγμάτευσης winwin,
Προσωπική Aνάπτυξη Ενότητα 2: Διαπραγμάτευση Juan Carlos Martínez Director of Projects Development Department Unit Scope Σε αυτή την ενότητα θα μελετήσουμε τα βασικά των καταστάσεων διαπραγμάτευσης winwin,
ΑΞΙΟΛΟΓΗΣΗ ΦΥΣΙΚΟΧΗΜΙΚΩΝ ΧΑΡΑΚΤΗΡΙΣΤΗΚΩΝ ΑΠΟΒΛΗΤΟΥ (DRILL CUTTING) ΠΟΥ ΠΡΟΕΡΧΕΤΑΙ ΑΠΟ ΥΠΕΡΑΚΤΙΕΣ ΓΕΩΤΡΗΣΕΙΣ
 Σχολή Γεωτεχνικών Επιστημών και Διαχείρισης Περιβάλλοντος Πτυχιακή εργασία ΑΞΙΟΛΟΓΗΣΗ ΦΥΣΙΚΟΧΗΜΙΚΩΝ ΧΑΡΑΚΤΗΡΙΣΤΗΚΩΝ ΑΠΟΒΛΗΤΟΥ (DRILL CUTTING) ΠΟΥ ΠΡΟΕΡΧΕΤΑΙ ΑΠΟ ΥΠΕΡΑΚΤΙΕΣ ΓΕΩΤΡΗΣΕΙΣ Φυλακτής Κωνσταντίνου
Σχολή Γεωτεχνικών Επιστημών και Διαχείρισης Περιβάλλοντος Πτυχιακή εργασία ΑΞΙΟΛΟΓΗΣΗ ΦΥΣΙΚΟΧΗΜΙΚΩΝ ΧΑΡΑΚΤΗΡΙΣΤΗΚΩΝ ΑΠΟΒΛΗΤΟΥ (DRILL CUTTING) ΠΟΥ ΠΡΟΕΡΧΕΤΑΙ ΑΠΟ ΥΠΕΡΑΚΤΙΕΣ ΓΕΩΤΡΗΣΕΙΣ Φυλακτής Κωνσταντίνου
ΠΡΟΣΤΑΣΙΑ ΑΤΜΟΣΦΑΙΡΙΚΗΣ ΔΙΑΒΡΩΣΗΣ ΑΛΟΥΜΙΝΙΟΥ/ΑΝΟΔΙΩΣΗ Al
 Σχολή Μηχανικής και Τεχνολογίας Πτυχιακή εργασία ΠΡΟΣΤΑΣΙΑ ΑΤΜΟΣΦΑΙΡΙΚΗΣ ΔΙΑΒΡΩΣΗΣ ΑΛΟΥΜΙΝΙΟΥ/ΑΝΟΔΙΩΣΗ Al Ανδρέας Παπαχριστοδούλου Λεμεσός, Μάιος 2017 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ
Σχολή Μηχανικής και Τεχνολογίας Πτυχιακή εργασία ΠΡΟΣΤΑΣΙΑ ΑΤΜΟΣΦΑΙΡΙΚΗΣ ΔΙΑΒΡΩΣΗΣ ΑΛΟΥΜΙΝΙΟΥ/ΑΝΟΔΙΩΣΗ Al Ανδρέας Παπαχριστοδούλου Λεμεσός, Μάιος 2017 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
1) Formulation of the Problem as a Linear Programming Model
 1) Formulation of the Problem as a Linear Programming Model Let xi = the amount of money invested in each of the potential investments in, where (i=1,2, ) x1 = the amount of money invested in Savings Account
1) Formulation of the Problem as a Linear Programming Model Let xi = the amount of money invested in each of the potential investments in, where (i=1,2, ) x1 = the amount of money invested in Savings Account
Mean-Variance Analysis
 Mean-Variance Analysis Jan Schneider McCombs School of Business University of Texas at Austin Jan Schneider Mean-Variance Analysis Beta Representation of the Risk Premium risk premium E t [Rt t+τ ] R1
Mean-Variance Analysis Jan Schneider McCombs School of Business University of Texas at Austin Jan Schneider Mean-Variance Analysis Beta Representation of the Risk Premium risk premium E t [Rt t+τ ] R1
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΣΕΞΟΥΑΛΙΚΗΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ ΤΩΝ ΓΥΝΑΙΚΩΝ ΚΑΤΑ ΤΗ ΔΙΑΡΚΕΙΑ ΤΗΣ ΕΓΚΥΜΟΣΥΝΗΣ ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή Εργασία ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΣΕΞΟΥΑΛΙΚΗΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ ΤΩΝ ΓΥΝΑΙΚΩΝ ΚΑΤΑ ΤΗ ΔΙΑΡΚΕΙΑ ΤΗΣ ΕΓΚΥΜΟΣΥΝΗΣ ΑΝΔΡΕΟΥ ΣΤΕΦΑΝΙΑ Λεμεσός 2012 i ii ΤΕΧΝΟΛΟΓΙΚΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή Εργασία ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΣΕΞΟΥΑΛΙΚΗΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ ΤΩΝ ΓΥΝΑΙΚΩΝ ΚΑΤΑ ΤΗ ΔΙΑΡΚΕΙΑ ΤΗΣ ΕΓΚΥΜΟΣΥΝΗΣ ΑΝΔΡΕΟΥ ΣΤΕΦΑΝΙΑ Λεμεσός 2012 i ii ΤΕΧΝΟΛΟΓΙΚΟ
Appendix to On the stability of a compressible axisymmetric rotating flow in a pipe. By Z. Rusak & J. H. Lee
 Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
