Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY463 - Συστήματα Ανάκτησης Πληροφοριών Εαρινό Εξάμηνο. Φροντιστήριο 3.
|
|
|
- Νατάσα Δημητρίου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY6 - Συστήματα Ανάκτησης Πληροφοριών Εαρινό Εξάμηνο Φροντιστήριο Retrieval Models Άσκηση Θεωρείστε μια συλλογή κειμένων που περιέχει τα ακόλουθα έγγραφα: Έγγραφο : «Computer Games» Έγγραφο : «Computer Games Computer Games» Έγγραφο : «Games Theory and Computer» Έγγραφο : «Computer for Computer» Έγγραφο : «Cheap Games Computer Games» ) Δώστε τη διανυσματική παράσταση του κάθε εγγράφου με βάρη TF-IF. Θεωρείστε ότι η θέση της κάθε λέξης στα διανύσματα γίνεται κατά αλφαβητική σειρά. ) Θεωρείστε την επερώτηση =«Computer Games». Υπολογίστε το TF-IF διάνυσμα αυτής της επερώτησης και δώστε την διάταξη των εγγράφων που θα επιστρέψει ένα σύστημα που βασίζεται στο διανυσματικό μοντέλο. Σχεδιάστε το ανεστραμμένο ευρετήριο για αυτή τη συλλογή. Λύση ) Έγγραφο : «Computer Games» Έγγραφο : «Computer Games Computer Games» Έγγραφο : «Games Theory and Computer» Έγγραφο : «Computer for Computer» Έγγραφο : «Cheap Games Computer Games» And Cheap Computer for Games Theory MAXk{FREQ} F IF / / / / / / FREQ =το πλήθος των εμφανίσεων του όρου i στο έγγραφο j IF = N / F MAX k {FREQ } = συχνότητα της λέξης με τη μέγιστη συχνότητα στο κείμενο
2 TF-IF And Cheap Computer for Games Theory MAXk{FREQ} 0 0 /*/ 0 /*/ /*/ 0 /*/ 0 /*/ 0 /*/ 0 /*/ /*/ 0 0 /*/ /*/ /*/ /*/ 0 /*/ 0 F IF / / / / / / TF = FREQ / MAX k {FREQ } V = TF * IF i Οι διανυσματικές παραστάσεις των κειμένων είναι : V = {0, 0,, 0,., 0}, V =,6 V = {0, 0,, 0,., 0}, V =,6 V = {, 0,, 0,., }, V =,6 V = {0, 0,,., 0, 0}, V = 7, V = {0,., 0., 0,., 0}, V = 8,06 ) And Cheap Computer For Games Theory =Computer Games 0 0 /*/ 0 /*/ 0 IF / / / / / / = {0, 0,, 0,., 0}, =,6 V * =*+,*,=+,6=,6 V * =,6 V * =*0+*+,*,+*0=,6 V * = V * =0,*+,*,=,06
3 Με βάση τον παρπάνω τύπο, υπολογίζουμε το μέτρο ομοιότητας συνημίτονου για κάθε έγγραφο j R(, ) =,6/(,6*,6) / => R(, ) = R(, ) =,6/(,6*,6) / => R(, ) = R(, ) =,6/(,6*,6) / =,6/(,6906),6/,60667 => R(, ) = 0,9889 ½ = R(, ) = /(7,*,6) / =/(8,78) / = /,09 => R(, ) = 0,009 R(, ) =,06/(8,06*,6) / =,06/(0,6606) / =,06/, => R(, ) = 0,76099 Με βάση το διανυσματικό μοντέλο η διάταξη των εγγράφων είναι : < {, },,, > Θα περιμέναμε το έγγραφο να έρθει στη σειρά πριν το,επειδή περιέχει όλους τους όρους της επερώτησης, όμως περιέχει και τον όρο Theory ο οποίος εμφανίζεται μόνο σε αυτό το έγγραφο και αυτό επηρέασε το βάρος του. Ανεστραμμένο ευρετήριο Μία μορφή του ανεστραμμένου ευρετηρίου στο οποίο εμφανίζονται μόνο οι θέσεις των όρων είναι : Term < ocument Freuency, (ocument; Position) > Computer < ( ;), ( ;), ( ;), ( ;), ( ;), ( ;), ( ;)> Games < ( ;), ( ;), ( ;), ( ;), ( ;), ( ;) > Theory < ( ;) > Cheap < ( ;) > and < ( ;)> for < ( ;)> Μία άλλη μορφή του ανεστραμμένου ευρετηρίου στο οποίο εμφανίζεται το TF του κάθε όρου σε κάθε έγγραφο είναι :
4 Term < ocument : Term Freuency : { Position } > Computer < : : { } > < : : {, } > < : : { } > < : : {, } > < : 0. : { } > Games < :. : { } > < :. : {, } > < :. : { } > < :. : { } > Theory < : : { } > Cheap < :. : { } > and < : : { } > for < :. : { } > Άσκηση Έστω μια συλλογή από κείμενα, και έστω Α ένα διατεταγμένο υποσύνολο αυτής. Έστω ότι μας δίνουν το Α και μας ζητούν να βρούμε αν υπάρχει επερώτηση τ.ω. η απάντηση της να έχει στην αρχή της το διατεταγμένο σύνολο Α. Για παράδειγμα, αν A=<d, d, d> και βρούμε μια επερώτηση τ.ω. Answer() = <d, d, d, d8, > τότε αυτή είναι μια λύση του προβλήματος μας. Θεωρώντας ότι το σύστημα σας βασίζεται στο διανυσματικό μοντέλο, απαντήστε τα παρακάτω ερωτήματα. (α) Πως μπορούμε να βρούμε αν υπάρχει τέτοια επερώτηση; (β) Αν υπάρχει ποια είναι; (γ) Αν δεν υπάρχει τέτοια επερώτηση, πως θα χαλαρώνατε το πρόβλημα και τι θα μπορούσατε να επιστρέψετε; Μπορείτε να αναπτύξετε τις σκέψεις σας όσο θέλετε. Σημείωση: Προσέξτε ώστε το υπολογιστικό κόστος των λύσεων που θα προτείνετε για τα (α) και (β) να μην είναι απαγορευτικό. Λύση (α) Για να υπάρχει μία τέτοια επερώτηση θα πρέπει να ισχύουν οι δύο παρακάτω συνθήκες: (α) Έστω η επερώτηση που ψάχνουμε. Για να επιστρέφει η όλα τα έγγραφα του Α και μάλιστα με την σχετική διάταξη που έχουν στο Α, θα πρέπει το μέτρο ομοιότητας του συνημίτονου μεταξύ της και του πρώτου εγγράφου στο Α να είναι μεγαλύτερο από το μέτρο του δευτέρου εγγράφου και εκείνο μεγαλύτερο από του τρίτου εγγράφου κ.o.κ., και όλα να είναι μεγαλύτερα του μηδενός Δηλαδή αν Α = < d,d,d > τότε θα έπρεπε Sim (d, ) > Sim (d, ) > Sim (d, ) > 0 ()
5 (α) Για να μας επιστρέφει η όλα τα έγγραφα που ανήκουν στο Α, με την διάταξη που έχουν σε αυτό και πριν από οποιοδήποτε άλλο έγγραφο θα πρέπει όλα τα έγγραφα που μας επιστρέφει η επερώτηση και δεν ανήκουν στο Α, να έχουν μέτρο ομοιότητας του συνημίτονου μικρότερο από την τιμή του τελευταίου εγγράφου που ανήκει στο Α. Δηλαδή αν Α = < d,d,d > τότε θα έπρεπε Sim (d, ) > Sim (d, ) > Sim (d, ) > Sim (d x, ) για κάθε d x που δεν ανήκει στο Α. (β) Εύκολα μπορούμε να δείξουμε ότι αν ικανοποιούνται οι παραπάνω συνθήκες τότε το =d είναι μια επιθυμητή απάντηση (από τις ενδεχομένως πολλές). Ο έλεγχος της συνθήκης (α) είναι απλός και όχι ιδιαίτερα ακριβός. Συγκεκριμένα απαιτεί Α - υπολογισμούς βαθμού ομοιότητας. Ένας εύκολος τρόπος για να δούμε αν ισχύει η συνθήκη (α) είναι να υπολογίσουμε το Answer(d) και να δούμε εάν τα πρώτα A στοιχεία του είναι τα στοιχεία του Α. (γ) Μια χαλάρωση του προβλήματος είναι η εξής: Η συνθήκη (α) ικανοποιείται αλλά δεν ικανοποιείται η συνθήκη (α). Και σε αυτήν την περίπτωση το =d θα ήταν μια πιθανή λύση του προβλήματος. Απλά η απάντηση του θα μπορούσε θα είχε τη μορφή: Α() = < d, d, d6, d, d, d8, d9, d, d0, d7 > Μια άλλη χαλάρωση του προβλήματος θα ήταν να μειώσουμε το σύνολο των εγγράφων του συνόλου Α αρχίζοντας από το τέλος. Δηλαδή αντί για Α = < d, d, d > να δούμε αν υπάρχει λύση για το σύνολο Α = < d, d >. Αν δεν υπάρχει ούτε για το Α να δούμε αν υπάρχει για το Α =<d>. Για περισσότερα δείτε τις διαφάνειες του Μαθήματος (007) καθώς και το άρθρο: Άσκηση Στο μάθημα είδαμε δύο μοντέλα ανάκτησης του βασίζονται στη Θεωρία Ασαφών Συνόλων. To πρώτο θεωρεί βάρυνση TF*IF, ενώ το δεύτερο είναι εκείνο που προτάθηκε από τους [Ogawa, Morita, Kobayashi, 99]. Θεωρείστε έναν όρο t i ενός εγγράφου d j. Συγκρίνετε την συμπεριφορά των δύο αυτών μοντέλων για διάφορες περιπτώσεις, π.χ.: για μικρές και μεγάλες τιμές του tf, για μικρές και μεγάλες τιμές του idf i, για μικρές και μεγάλες τιμές του w αν προκύπτει από tf*idf. Λύση Για το πρώτο μοντέλο που βασίζεται σε βάρυνση ΤF-IF ξέρουμε ότι: d j = ( w,j, w,j,, w t,j ) όπου w i,j є [0,] R(d j, t i ) = μ ti (d j ) = w i,j = tf * idf i όπου tf = fre / MAX k { fre κj }, idf i = log ( N / df i ) και Ν ο αριθμός των εγγράφων. Για το μοντέλο που προτάθηκε από τους [Ogawa, Morita, and Kobayashi,99] ξέρουμε ότι: d j = ( w,j, w,j,, w t,j ) όπου w i,j є {0,} και
6 w i,j = όταν ο όρος t i εμφανίζεται στο κείμενο d j. (αλλιώς w i,j = 0) R(d j,t i ) = μ ti (d j ) το οποίο ορίζεται ως εξής: Αρχικά ορίζεται η εγγύτητα μεταξύ των όρων με τον εξής τύπο: c(i,j) = n(i,j) / ni + nj n(i,j) όπου n(i,j) : το πλήθος των εγγράφων που περιέχουν τον όρο k i και τον k l. ni : το πλήθος των εγγράφων που περιέχουν τον όρο k i. nj : το πλήθος των εγγράφων που περιέχουν τον όρο k l. Κατόπιν θέτουμε μ i (j) = Σ c(i,w), t w є d j μ i (j) = Π(- c(i,w) ), t w є d j Έστω ότι θέλουμε να κάνουμε μία επερώτηση σε μία σύλλογη εγγράφων και η επερώτηση αποτελείται από ένα όρο κ, δηλαδή = k. Μικρές τιμές tf Έστω ένα έγγραφο j. Αν το tf του όρου ki είναι μικρό, αυτό σημαίνει ότι ο όρος ki εμφανίζεται λίγες φορές στο έγγραφο αυτό άρα η κατάταξη του εγγράφου θα είναι χαμηλή σύμφωνα με το πρώτο μοντέλο ανάκτησης. Το δεύτερο μοντέλο ([Ogawa, Morita, Kobayashi, 99]) αγνοεί το πλήθος των εμφανίσεων ενός όρου σε ένα έγγραφο Λαμβάνει όμως υπόψη τον βαθμό συνεμφάνισης των όρων στη συλλογή. Αυτό σημαίνει ότι αν το έγγραφο j περιέχει πολλούς όρους οι οποίοι έχουν μεγάλη εγγύτητα (συνεμφάνιση) με τον όρο ki, τότε το έγγραφο αυτό μπορεί να σταθμιστεί υψηλά. Μεγάλες τιμές tf Έστω ένα έγγραφο j. Αν το tf του όρου ki είναι μεγάλο, αυτό σημαίνει ότι ο όρος ki εμφανίζεται πολλές φορές στο έγγραφο αυτό άρα η κατάταξη του εγγράφου θα είναι υψηλή σύμφωνα με το πρώτο μοντέλο ανάκτησης. Στο δεύτερο μοντέλο (που αγνοεί το tf) το έγγραφο αυτό θα μπορούσε να σταθμιστεί χαμηλά αν περιέχει λίγους όρους που έχουν εγγύτητα (συνεμφάνιση) με τον όρο ki. Μικρές τιμές idf i Αν το idf του όρου ki είναι μικρό αυτό σημαίνει ότι το πλήθος των εγγράφων που περιέχουν τον όρο ki είναι μεγάλο (αφού idf = Ν/df). Έστω ένα έγγραφο j που περιέχει τον όρο ki. Aν λαμβάναμε υπόψη μόνο το idf τότε το o μοντέλο, θα έδινε μικρό βαθμό συνάφειας στο έγγραφο j (καθώς και σε όλα τα υπόλοιπα έγγραφα). Αντίθετα το o μοντέλο ενδεχομένως να έδινε μεγαλύτερο βαθμό συνάφειας στο έγγραφο j διότι από τη στιγμή που ο όρος ki εμφανίζεται σε πολλά κείμενα μπορεί να έχει υψηλό βαθμό συνεμφάνισης με άλλους όρους που περιέχει το έγγραφο j. Μεγάλες τιμές idf i Αν το idf του όρου ki είναι μεγάλο αυτό σημαίνει ότι το πλήθος των εγγράφων που περιέχουν τον όρο ki είναι μικρό (αφού idf = Ν/df). Έστω ένα έγγραφο j που περιέχει τον όρο ki. Aν λαμβάναμε υπόψη μόνο το idf τότε το o μοντέλο, θα έδινε μεγάλο βαθμό συνάφειας στο έγγραφο j (καθώς και σε όλα τα υπόλοιπα έγγραφα). Αντίθετα το o μοντέλο ενδεχομένως να έδινε μικρότερο βαθμό συνάφειας στο έγγραφο j διότι από τη στιγμή που ο όρος ki εμφανίζεται σε λίγα κείμενα μπορεί να έχει μικρό βαθμό συνεμφάνισης με άλλους όρους που περιέχει το έγγραφο j.
7 Mικρές και μεγάλες τιμές του w Θα μπορούσαμε να διακρίνουμε τις παρακάτω περιπτώσεις: ) Μικρό TF*IF λόγω πολύ μικρού TF Έστω ένα έγγραφο j. Αν το tf του όρου ki είναι πολύ μικρό, αυτό σημαίνει ότι ο όρος ki εμφανίζεται πολύ λίγες φορές στο έγγραφο αυτό άρα η κατάταξη του εγγράφου θα είναι χαμηλή σύμφωνα με το πρώτο μοντέλο ανάκτησης. Το δεύτερο μοντέλο αγνοεί το πλήθος των εμφανίσεων ενός όρου σε ένα έγγραφο Λαμβάνει όμως υπόψη τον βαθμό συνεμφάνισης των όρων στη συλλογή. Αυτό σημαίνει ότι αν το έγγραφο j περιέχει πολλούς όρους οι οποίοι έχουν μεγάλη εγγύτητα (συνεμφάνιση) με τον όρο ki, τότε το έγγραφο αυτό μπορεί να σταθμιστεί υψηλά. ) Μικρό TF*IF λόγω πολύ μικρού IF Αν το idf του όρου ki είναι πολύ μικρό αυτό σημαίνει ότι το πλήθος των εγγράφων που περιέχουν τον όρο ki είναι πολύ μεγάλο (αφού idf = Ν/df). Έστω ένα έγγραφο j που περιέχει τον όρο ki. Aν λαμβάναμε υπόψη μόνο το idf τότε το o μοντέλο, θα έδινε πολύ μικρό βαθμό συνάφειας στο έγγραφο j (καθώς και σε όλα τα υπόλοιπα έγγραφα). Αντίθετα το o μοντέλο ενδεχομένως να έδινε πολύ μεγαλύτερο βαθμό συνάφειας στο έγγραφο j διότι από τη στιγμή που ο όρος ki εμφανίζεται σε πολλά κείμενα μπορεί να έχει υψηλό βαθμό συνεμφάνισης με άλλους όρους που περιέχει το έγγραφο j. ) Μικρό TF*IF λόγω μικρού ΤF και μικρού IF Έστω ένα έγγραφο j. Αν το tf του όρου ki είναι μικρό, αυτό σημαίνει ότι ο όρος ki εμφανίζεται λίγες φορές στο έγγραφο αυτό και αν το idf του όρου ki είναι μικρό αυτό σημαίνει ότι το πλήθος των εγγράφων που περιέχουν τον όρο ki είναι μεγάλο (αφού idf = Ν/df). Επομένως, το πρώτο μοντέλο θα έδινε μικρό βαθμό συνάφειας στο έγγραφο j. Αντίθετα το o μοντέλο ενδεχομένως να έδινε πολύ μεγαλύτερο βαθμό συνάφειας στο έγγραφο j διότι από τη στιγμή που ο όρος ki εμφανίζεται σε πολλά κείμενα μπορεί να έχει υψηλό βαθμό συνεμφάνισης με άλλους όρους που περιέχει το έγγραφο j. ) Μεγάλο TF*IF λόγω πολύ μεγάλου TF Έστω ένα έγγραφο j. Αν το tf του όρου ki είναι πολύ μεγάλο, αυτό σημαίνει ότι ο όρος ki εμφανίζεται πολλές φορές στο έγγραφο αυτό άρα η κατάταξη του εγγράφου θα είναι πολύ υψηλή σύμφωνα με το πρώτο μοντέλο ανάκτησης. Στο δεύτερο μοντέλο (που αγνοεί το tf) το έγγραφο αυτό θα μπορούσε να σταθμιστεί χαμηλά αν περιέχει λίγους όρους που έχουν εγγύτητα (συνεμφάνιση) με τον όρο ki. ) Μεγάλο TF*IF λόγω πολύ μεγάλου IF Αν το idf του όρου ki είναι πολύ μεγάλο αυτό σημαίνει ότι το πλήθος των εγγράφων που περιέχουν τον όρο ki είναι πολύ μικρό (αφού idf = Ν/df). Έστω ένα έγγραφο j που περιέχει τον όρο ki. Aν λαμβάναμε υπόψη μόνο το idf τότε το o μοντέλο, θα έδινε πολύ μεγάλο βαθμό συνάφειας στο έγγραφο j (καθώς και σε όλα τα υπόλοιπα έγγραφα). Αντίθετα το o
8 μοντέλο ενδεχομένως να έδινε πολύ μικρότερο βαθμό συνάφειας στο έγγραφο j διότι από τη στιγμή που ο όρος ki εμφανίζεται σε πολλά κείμενα μπορεί να έχει υψηλό βαθμό συνεμφάνισης με άλλους όρους που περιέχει το έγγραφο j. 6) Μεγάλο TF*IF λόγω μεγάλου ΤF και μεγάλου IF Έστω ένα έγγραφο j. Αν το tf του όρου ki είναι μεγάλο, αυτό σημαίνει ότι ο όρος ki εμφανίζεται πολλές φορές στο έγγραφο αυτό και αν το idf του όρου ki είναι μεγάλο αυτό σημαίνει ότι το πλήθος των εγγράφων που περιέχουν τον όρο ki είναι μικρό (αφού idf = Ν/df). Επομένως, το πρώτο μοντέλο θα έδινε μεγάλο βαθμό συνάφειας στο έγγραφο j. Αντίθετα το o μοντέλο ενδεχομένως να έδινε πολύ μικρότερο βαθμό συνάφειας στο έγγραφο j διότι από τη στιγμή που ο όρος ki εμφανίζεται σε λίγα κείμενα μπορεί να έχει μικρό βαθμό συνεμφάνισης με άλλους όρους που περιέχει το έγγραφο j. Άσκηση Θεωρείστε μια συλλογή κειμένων που περιέχει τα ακόλουθα έγγραφα: Έγγραφο : «New York Times» Έγγραφο : «New Times» Έγγραφο : «Financial Times» Έγγραφο : «High High Times» Έγγραφο : «New Financial Times» ) Δώστε τη διανυσματική παράσταση του κάθε εγγράφου με βάρη TF-IF (για ευκολία θεωρήστε ότι IF=N/F και όχι IF=log(N/F)). Θεωρείστε ότι η θέση της κάθε λέξης στα διανύσματα γίνεται αλφαβητικά. ) Θεωρείστε την επερώτηση =«high financial». Υπολογίστε το TF-IF διάνυσμα αυτής της επερώτησης και δώστε την διάταξη των εγγράφων που θα επιστρέψει ένα σύστημα που βασίζεται στο διανυσματικό μοντέλο. ) Θεωρείστε τις επερωτήσεις =«high AN financial» =«high OR financial» και δώστε τις απαντήσεις που θα επιστρέψει ένα σύστημα που βασίζεται στο Extended Boolean μοντέλο. Λύση ) Term Occurrence Table
9 FREQ = το πλήθος των εμφανίσεων του όρου i στο έγγραφο j N = IF = N/F MAX k { FREQ } = συχνότητα της λέξης με τη μέγιστη συχνότητα στο κείμενο Term Weight Table ) TF = FREQ / MAX k {FREQ } W = TF *IF i *d = (/,,0,0,0)*(0,0,/,,) = 0 *d = (/,,0,0,0)*(0,0,/,,0) = 0 *d = (/,,0,0,0)*(/,0,0,,0) = / *d = (/,,0,0,0)*(0,,0,/,0) = *d = (/,,0,0,0)*(/,0,/,,0) = / Άρα η διάταξη των εγγράφων που θα επιστρέψει η ερώτηση Q είναι:,,
10 ) Κανονικοποίηση των διανυσμάτων maxifi=: d =(0,0,/,,)/=(0,0,/,/,) d =(0,0,/,,0)/=(0,0,/,/,0) d =(/,0,0,,0)/=(/,0,0,/,0) d =(0,,0,/,0)/=(0,,0,/0,0) d =(/,0,/,,0)/=(/,0,/,/,0) Q = high AN financial Με βάση τον παραπάνω τύπο, υπολογίζουμε την ομοιότητα της επερώτησης Q με κάθε έγγραφο. Sim(,d ) = -srt(((-0)^+(-0)^)/) = 0 Sim(,d ) = -srt(((-0)^+(-0)^)/) = 0 Sim(,d ) = -srt(((-/)^+(-0)^)/) = 0. Sim(,d ) = -srt(((-0)^+(-)^)/) = 0.9 Sim(,d ) = -srt(((-/)^+(-0)^)/) = 0. Άρα η διάταξη των εγγράφων που θα επιστρέψει η ερώτηση Q είναι:,, Q= high OR financial Με βάση τον παραπάνω τύπο, υπολογίζουμε την ομοιότητα της επερώτησης Q με κάθε έγγραφο. Sim(,d ) = srt((0^+0^)/) = 0 Sim(,d ) = srt((0^+0^)/) = 0 Sim(,d ) = srt(((/)^+0^)/) = /(srt()) Sim(,d ) = srt((0^+^)/) = /(srt()) Sim(,d ) = srt(((/)^+0^)/) = /(srt())
11 Άρα η διάταξη των εγγράφων που θα επιστρέψει η ερώτηση Q είναι:,, Άσκηση (συνάρτηση διαβάθμισης) Θεωρείστε ένα Σύστημα Ανάκτησης Πληροφοριών (ΣΑΠ) από μια μεγάλη συλλογή κειμένων. Θέλουμε να δώσουμε τη δυνατότητα χρήσης του ΣΑΠ μέσω κινητού τηλεφώνου. Για το λόγο αυτό θέλουμε να ορίσουμε μια συνάρτηση διαβάθμισης (ranking function) η οποία να ευνοεί τα μικρά κείμενα, αφενός για να κρατήσουμε σε χαμηλά επίπεδα τον όγκο δεδομένων που θα μεταφέρονται και αφετέρου διότι οι χρήστες κινητών τηλεφώνων προτιμούν τα μικρά κείμενα (ένεκα του μικρού μεγέθους της οθόνης). Θεωρείστε ότι οι επερωτήσεις των χρηστών είναι σάκοι λέξεων (bag of words). Σχεδιάστε μια συνάρτηση διαβάθμισης για το σκοπό αυτό για κάθε μια από τις παρακάτω περιπτώσεις (α) Το ευρετήριο του ΣΑΠ έχει δυαδικά (0,) βάρη (όπως για παράδειγμα το ευρετήριο του Boolean μοντέλου) (β) Το ευρετήριο έχει βάρη TF-IF. Τεκμηριώστε τις προτάσεις σας (με αποδείξεις ή παραδείγματα). Λύση α) Θέλουμε να τροποποιήσουμε το Boolean μοντέλο έτσι ώστε να ευνοεί τα μικρότερα κείμενα. Η συνάρτηση που θα χρησιμοποιήσουμε είναι η R(d,) = d / d η οποία κανονικοποιεί την συνάρτηση που εκφράζει τη συσχέτιση ενός κειμένου με μια επερώτηση με βάση το μέγεθος του κειμένου. Γνωρίζουμε ότι R(d,) = d / d = d /( d + d\ ). Αν η τομή d είναι σταθερή, δηλαδή n έγγραφα έχουν την ίδια συνάφεια, τότε αυτό που έχει μεγαλύτερο μέγεθος θα διαβαθμιστεί πιο χαμηλά, διότι θα μεγαλώσει ο παρανομαστής άρα η συνάρτηση θα επιστρέψει μικρότερη τιμή διαβάθμισης. Στη γενική περίπτωση που έχουμε διαφορετικές συνάφειες τα μικρότερα έγγραφα ευνοούνται έναντι των μεγαλύτερων. Πειραματικά αυτό σημαίνει: = a b R(d,) = d / d d = a /= d = a c /=0. d = a c d /=0. d = a b c /=0.66 d = a b c d a / = 0. Διάταξη εγγράφων <d, d, d, d, d> β) Γενικεύουμε την ιδέα του (α) για την περίπτωση που έχουμε μη δυαδικά βάρη. Συγκεκριμένα μπορούμε να ορίσουμε: R(d,) = d* / d (όπου το * είναι το
12 εσωτερικό γινόμενο) όπου το εσωτερικό γινόμενο υπολογίζεται από τον τύπο: και τα w i,j =tf *idf i και w i, = tf i *idf i a b c MAX k {FREQ } F IF /= /=. /=. /=. A b C MAX k {FREQ } /*/= /*/= 0 /*/=. 0 /*/= 0 /*/=. /*/=. /*/= /*/=. /*/=. 0 /*/= /*/=. /*/=0.6 /*/=. Q /*/= /*/=. 0 0 F IF /= /=. /=. /=. W *Q = (,0,0,0)*(,.,0,0) = W *Q = (,0,.,0)*(,.,0,0) = W *Q = (,0,.,.)*(,.,0,0) = W *Q = (,.,.,0)*(,.,0,0) =7. W *Q = (,.,0.6,.)*(,.,0,0) =. Εφαρμόζουμε τη συνάρτηση για τον υπολογισμό της συνάφειας: R(,Q )=/= * Q / = R(,Q )=/=0. R(,Q )=/=0. R(,Q )=7./=.6 R(,Q )=./=0.8 Επομένως η διάταξη που επιστρέφει η συνάρτηση μας είναι η,,,,. Παρατηρούμε ότι από τα κείμενα που είναι ποιο σχετικά στο ερώτημα μας (δηλαδή περιέχουν και τους δύο όρους) ευνοήθηκε αυτό με το μικρότερο πλήθος όρων.
ΛΥΣΕΙΣ 2 ης ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ
 ΛΥΣΕΙΣ 2 ης ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 Θεωρείστε μια συλλογή κειμένων που περιέχει τα ακόλουθα 5 έγγραφα: Έγγραφο 1: «Computer Games» Έγγραφο 2: «Computer Games Computer Games» Έγγραφο 3: «Games Theory and
ΛΥΣΕΙΣ 2 ης ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 Θεωρείστε μια συλλογή κειμένων που περιέχει τα ακόλουθα 5 έγγραφα: Έγγραφο 1: «Computer Games» Έγγραφο 2: «Computer Games Computer Games» Έγγραφο 3: «Games Theory and
1. Financial New Times Year MAXk {FREQij} D D D D
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY46 - Συστήματα Ανάκτησης Πληροφοριών 2004-2005 Εαρινό Εξάμηνο 2 η Σειρά ασκήσεων (Μοντέλα Ανάκτησης Πληροφοριών και Ευρετήρια) Ανάθεση: 6 Μαρτίου Παράδοση:
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY46 - Συστήματα Ανάκτησης Πληροφοριών 2004-2005 Εαρινό Εξάμηνο 2 η Σειρά ασκήσεων (Μοντέλα Ανάκτησης Πληροφοριών και Ευρετήρια) Ανάθεση: 6 Μαρτίου Παράδοση:
Θέμα : Retrieval Models. Ημερομηνία : 9 Μαρτίου 2006
 ΗΥ-464: Συστήματα Ανάκτησης Πληροφορίας Informaton Retreval Systems Πανεπιστήμιο Κρήτης Άνοιξη 2006 Φροντιστήριο 2 Θέμα : Retreval Models Ημερομηνία : 9 Μαρτίου 2006 Outlne Prevous Semester Exercses Set
ΗΥ-464: Συστήματα Ανάκτησης Πληροφορίας Informaton Retreval Systems Πανεπιστήμιο Κρήτης Άνοιξη 2006 Φροντιστήριο 2 Θέμα : Retreval Models Ημερομηνία : 9 Μαρτίου 2006 Outlne Prevous Semester Exercses Set
Προτεινόμενες Λύσεις 1 ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσματικότητας της Ανάκτησης & Μοντέλα Ανάκτησης)
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών ΗΥ463 Συστήματα Ανάκτησης Πληροφοριών 28-29 Εαρινό Εξάμηνο Προτεινόμενες Λύσεις 1 ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσματικότητας της Ανάκτησης &
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών ΗΥ463 Συστήματα Ανάκτησης Πληροφοριών 28-29 Εαρινό Εξάμηνο Προτεινόμενες Λύσεις 1 ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσματικότητας της Ανάκτησης &
Ανάκτηση Πληροφορίας
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #05 Ακρίβεια vs. Ανάκληση Extended Boolean Μοντέλο Fuzzy Μοντέλο 1 Άδεια χρήσης Το παρόν εκπαιδευτικό
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #05 Ακρίβεια vs. Ανάκληση Extended Boolean Μοντέλο Fuzzy Μοντέλο 1 Άδεια χρήσης Το παρόν εκπαιδευτικό
Ανάκτηση Πληροφορίας
 Ανάκτηση Πληροφορίας Το μοντέλο Boolean Το μοντέλο Vector Ταξινόμηση Μοντέλων IR Ανάκτηση Περιήγηση Κλασικά Μοντέλα Boolean Vector Probabilistic Δομικά Μοντέλα Non-Overlapping Lists Proximal Nodes Browsing
Ανάκτηση Πληροφορίας Το μοντέλο Boolean Το μοντέλο Vector Ταξινόμηση Μοντέλων IR Ανάκτηση Περιήγηση Κλασικά Μοντέλα Boolean Vector Probabilistic Δομικά Μοντέλα Non-Overlapping Lists Proximal Nodes Browsing
HΥ463 - Συστήματα Ανάκτησης Πληροφοριών Information Retrieval (IR) Systems. Μοντέλα Ανάκτησης Ι
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών Άνοιξη 009 HΥ463 - Συστήματα Ανάκτησης Πληροφοριών Information Retrieval (IR) Systems Μοντέλα Ανάκτησης Ι (Retrieval Models) Γιάννης Τζίτζικας άλ ιάλεξη
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών Άνοιξη 009 HΥ463 - Συστήματα Ανάκτησης Πληροφοριών Information Retrieval (IR) Systems Μοντέλα Ανάκτησης Ι (Retrieval Models) Γιάννης Τζίτζικας άλ ιάλεξη
Ανάκτηση Πληροφορίας
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #04 Εισαγωγή στα Μοντέλα Ανάκτησης Πληροφορίας Boolean Μοντέλο 1 Άδεια χρήσης Το παρόν εκπαιδευτικό
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #04 Εισαγωγή στα Μοντέλα Ανάκτησης Πληροφορίας Boolean Μοντέλο 1 Άδεια χρήσης Το παρόν εκπαιδευτικό
Πιθανοκρατικό μοντέλο
 Πιθανοκρατικό μοντέλο Το μοντέλο MAP Αλέξανδρος Γκιμπερίτης Βασίλης Μπούργος Δημήτρης Σουραβλιάς 1 Εισαγωγικές έννοιες Κάθε έγγραφο d της συλλογής παριστάνεται από το δυαδικό διάνυσμα x = (x 1, x 2,...,
Πιθανοκρατικό μοντέλο Το μοντέλο MAP Αλέξανδρος Γκιμπερίτης Βασίλης Μπούργος Δημήτρης Σουραβλιάς 1 Εισαγωγικές έννοιες Κάθε έγγραφο d της συλλογής παριστάνεται από το δυαδικό διάνυσμα x = (x 1, x 2,...,
ΓΛΩΣΣΙΚΗ ΤΕΧΝΟΛΟΓΙΑ. Μάθημα 7 ο : Ανάκτηση πληροφορίας. Γεώργιος Πετάσης. Ακαδημαϊκό Έτος:
 ΓΛΩΣΣΙΚΗ ΤΕΧΝΟΛΟΓΙΑ Μάθημα 7 ο : Ανάκτηση πληροφορίας Γεώργιος Πετάσης Ακαδημαϊκό Έτος: 2012 2013 ΤMHMA MHXANIKΩΝ Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ, Πανεπιστήμιο Πατρών, 2012 2013 Οι διαφάνειες αυτού του μαθήματος βασίζονται
ΓΛΩΣΣΙΚΗ ΤΕΧΝΟΛΟΓΙΑ Μάθημα 7 ο : Ανάκτηση πληροφορίας Γεώργιος Πετάσης Ακαδημαϊκό Έτος: 2012 2013 ΤMHMA MHXANIKΩΝ Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ, Πανεπιστήμιο Πατρών, 2012 2013 Οι διαφάνειες αυτού του μαθήματος βασίζονται
Φροντιστήριο 5. Το πρώτο πράγµα λοιπόν που πρέπει να κάνουµε είναι να βρούµε τις πιθανότητες εµφάνισης των συµβόλων. Έτσι έχουµε:
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2006-2007 Εαρινό Εξάµηνο Φροντιστήριο 5 Άσκηση 1 Θεωρείστε το αλφάβητο {α,β,γ,δ,ε} και την εξής φράση: «α α β γ
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2006-2007 Εαρινό Εξάµηνο Φροντιστήριο 5 Άσκηση 1 Θεωρείστε το αλφάβητο {α,β,γ,δ,ε} και την εξής φράση: «α α β γ
6. Βαθμολόγηση, Στάθμιση Όρων, και το Μοντέλο Διανυσματικού Χώρου
 Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 6. Βαθμολόγηση, Στάθμιση Όρων, και το Μοντέλο Διανυσματικού Χώρου Ανάκτηση Πληροφοριών Χρήστος ουλκερίδης
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 6. Βαθμολόγηση, Στάθμιση Όρων, και το Μοντέλο Διανυσματικού Χώρου Ανάκτηση Πληροφοριών Χρήστος ουλκερίδης
ΑΣΚΗΣΗ. Δημιουργία Ευρετηρίων Συλλογής Κειμένων
 Γλωσσική Τεχνολογία Ακαδημαϊκό Έτος 2011-2012 Ημερομηνία Παράδοσης: Στην εξέταση του μαθήματος ΑΣΚΗΣΗ Δημιουργία Ευρετηρίων Συλλογής Κειμένων Σκοπός της άσκησης είναι η υλοποίηση ενός συστήματος επεξεργασίας
Γλωσσική Τεχνολογία Ακαδημαϊκό Έτος 2011-2012 Ημερομηνία Παράδοσης: Στην εξέταση του μαθήματος ΑΣΚΗΣΗ Δημιουργία Ευρετηρίων Συλλογής Κειμένων Σκοπός της άσκησης είναι η υλοποίηση ενός συστήματος επεξεργασίας
Ανάκτηση Πληροφορίας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4: Μοντελοποίηση: Διανυσματικό μοντέλο Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4: Μοντελοποίηση: Διανυσματικό μοντέλο Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ανάκτηση Πληροφορίας
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #06 Πιθανοτικό Μοντέλο 1 Άδεια χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #06 Πιθανοτικό Μοντέλο 1 Άδεια χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Διαχείριση εγγράφων. Αποθήκες και Εξόρυξη Δεδομένων Διδάσκων: Μ. Χαλκίδη
 Διαχείριση εγγράφων Αποθήκες και Εξόρυξη Δεδομένων Διδάσκων: Μ. Χαλκίδη Απεικόνιση κειμένων για Information Retrieval Δεδομένου ενός κειμένου αναζητούμε μια μεθοδολογία απεικόνισης του γραμματικού χώρου
Διαχείριση εγγράφων Αποθήκες και Εξόρυξη Δεδομένων Διδάσκων: Μ. Χαλκίδη Απεικόνιση κειμένων για Information Retrieval Δεδομένου ενός κειμένου αναζητούμε μια μεθοδολογία απεικόνισης του γραμματικού χώρου
Θα μιλήσουμε για ΜΟΝΤΕΛΑ ΑΝΑΚΤΗΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ. Διαφάνειες του καθ. Γιάννη Τζίτζικα (Παν. Κρήτης) http://www.ics.forth.
 Θα μιλήσουμε για ΜΟΝΤΕΛΑ ΑΝΑΚΤΗΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Διαφάνειες του καθ. Γιάννη Τζίτζικα (Παν. Κρήτης) http://www.ics.forth.gr/~tzitzik/ Γιατοπιθανοτικότουκαθ. Απ. Παπαδόπουλου (Αριστοτέλειο Παν.) Κεφάλαιο 2
Θα μιλήσουμε για ΜΟΝΤΕΛΑ ΑΝΑΚΤΗΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Διαφάνειες του καθ. Γιάννη Τζίτζικα (Παν. Κρήτης) http://www.ics.forth.gr/~tzitzik/ Γιατοπιθανοτικότουκαθ. Απ. Παπαδόπουλου (Αριστοτέλειο Παν.) Κεφάλαιο 2
Μοντέλα Ανάκτησης Ι (Retrieval Models)
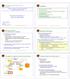 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών Άνοιξη 006 Διάρθρωση HΥ463 - Συστήματα Ανάκτησης Πληροφοριών Informaion Rerieval (IR) Sysems Μοντέλα Ανάκτησης Ι (Rerieval Models) Εισαγωγή στα Μοντέλα
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών Άνοιξη 006 Διάρθρωση HΥ463 - Συστήματα Ανάκτησης Πληροφοριών Informaion Rerieval (IR) Sysems Μοντέλα Ανάκτησης Ι (Rerieval Models) Εισαγωγή στα Μοντέλα
Ανάκτηση Πληροφορίας
 Το Πιθανοκρατικό Μοντέλο Κλασικά Μοντέλα Ανάκτησης Τρία είναι τα, λεγόμενα, κλασικά μοντέλα ανάκτησης: Λογικό (Boolean) που βασίζεται στη Θεωρία Συνόλων Διανυσματικό (Vector) που βασίζεται στη Γραμμική
Το Πιθανοκρατικό Μοντέλο Κλασικά Μοντέλα Ανάκτησης Τρία είναι τα, λεγόμενα, κλασικά μοντέλα ανάκτησης: Λογικό (Boolean) που βασίζεται στη Θεωρία Συνόλων Διανυσματικό (Vector) που βασίζεται στη Γραμμική
Λύση (από: Τσιαλιαμάνης Αναγνωστόπουλος Πέτρος) (α) Το trie του λεξιλογίου είναι
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY463 - Συστήματα Ανάκτησης Πληροφοριών 2006-2007 Εαρινό Εξάμηνο 3 η Σειρά ασκήσεων (Ευρετηρίαση, Αναζήτηση σε Κείμενα και Άλλα Θέματα) (βαθμοί 12: όποιος
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY463 - Συστήματα Ανάκτησης Πληροφοριών 2006-2007 Εαρινό Εξάμηνο 3 η Σειρά ασκήσεων (Ευρετηρίαση, Αναζήτηση σε Κείμενα και Άλλα Θέματα) (βαθμοί 12: όποιος
Θα μιλήσουμε για ΜΟΝΤΕΛΑ ΑΝΑΚΤΗΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ. Διαφάνειες του καθ. Γιάννη Τζίτζικα (Παν. Κρήτης)
 Θα μιλήσουμε για ΜΟΝΤΕΛΑ ΑΝΑΚΤΗΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Διαφάνειες του καθ. Γιάννη Τζίτζικα (Παν. Κρήτης) http://www.ics.forth.gr/~tzitzik/ Για το πιθανοκρατικό του καθ. Απ. Παπαδόπουλου (Αριστοτέλειο Παν.) Κεφάλαιο
Θα μιλήσουμε για ΜΟΝΤΕΛΑ ΑΝΑΚΤΗΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Διαφάνειες του καθ. Γιάννη Τζίτζικα (Παν. Κρήτης) http://www.ics.forth.gr/~tzitzik/ Για το πιθανοκρατικό του καθ. Απ. Παπαδόπουλου (Αριστοτέλειο Παν.) Κεφάλαιο
Δημιουργία Ευρετηρίων Συλλογής Κειμένων
 Γλωσσική Τεχνολογία Ακαδημαϊκό Έτος 2011-2012 - Project Σεπτεμβρίου Ημερομηνία Παράδοσης: Στην εξέταση του μαθήματος Εξέταση: Προφορική, στο τέλος της εξεταστικής. Θα βγει ανακοίνωση στο forum. Ομάδες
Γλωσσική Τεχνολογία Ακαδημαϊκό Έτος 2011-2012 - Project Σεπτεμβρίου Ημερομηνία Παράδοσης: Στην εξέταση του μαθήματος Εξέταση: Προφορική, στο τέλος της εξεταστικής. Θα βγει ανακοίνωση στο forum. Ομάδες
Information Retrieval
 Introduction to Information Retrieval ΠΛΕ70: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Διάλεξη 7: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου. 1 Κεφ. 6 Τι θα δούμε σήμερα; Βαθμολόγηση
Introduction to Information Retrieval ΠΛΕ70: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Διάλεξη 7: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου. 1 Κεφ. 6 Τι θα δούμε σήμερα; Βαθμολόγηση
Part A. CS-463 Information Retrieval Systems. Yannis Tzitzikas. University of Crete. CS-463,Spring 05 PART (A) PART (C):
 CS-463 Information Systems Μοντέλα Ανάκτησης ( Models) Part A Yannis Tzitzikas University of Crete CS-463,Spring 05 Lecture : 3 Date : 1-3- ιάρθρωση PART (A) Ανάκτηση και Φιλτράρισµα Εισαγωγή στα Μοντέλα
CS-463 Information Systems Μοντέλα Ανάκτησης ( Models) Part A Yannis Tzitzikas University of Crete CS-463,Spring 05 Lecture : 3 Date : 1-3- ιάρθρωση PART (A) Ανάκτηση και Φιλτράρισµα Εισαγωγή στα Μοντέλα
Τι (άλλο) θα δούμε σήμερα;
 Introduction to Information Retrieval ΠΛΕ70: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Διάλεξη6: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου. 1 Κεφ. 6 Τι (άλλο) θα δούμε σήμερα;
Introduction to Information Retrieval ΠΛΕ70: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Διάλεξη6: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου. 1 Κεφ. 6 Τι (άλλο) θα δούμε σήμερα;
ΜΥΕ003: Ανάκτηση Πληροφορίας. Διδάσκουσα: Ευαγγελία Πιτουρά Κεφάλαιο 11: Πιθανοτική ανάκτηση πληροφορίας.
 ΜΥΕ003: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Κεφάλαιο : Πιθανοτική ανάκτηση πληροφορίας. Κεφ. Πιθανοτική Ανάκτηση Πληροφορίας Βασική ιδέα: Διάταξη εγγράφων με βάση την πιθανότητα να είναι
ΜΥΕ003: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Κεφάλαιο : Πιθανοτική ανάκτηση πληροφορίας. Κεφ. Πιθανοτική Ανάκτηση Πληροφορίας Βασική ιδέα: Διάταξη εγγράφων με βάση την πιθανότητα να είναι
Λύσεις 1 ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης)
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών ΗΥ-6 Συστήµατα Ανάκτησης Πληροφοριών 7-8 Εαρινό Εξάµηνο Άσκηση Λύσεις ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης) Θεωρείστε µια
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών ΗΥ-6 Συστήµατα Ανάκτησης Πληροφοριών 7-8 Εαρινό Εξάµηνο Άσκηση Λύσεις ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης) Θεωρείστε µια
Φροντιστήριο 4. Άσκηση 1. Λύση. Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών Εαρινό Εξάµηνο
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2007-2008 Εαρινό Εξάµηνο Άσκηση 1 Φροντιστήριο 4 Θεωρείστε ένα έγγραφο με περιεχόμενο «αυτό είναι ένα κείμενο και
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2007-2008 Εαρινό Εξάµηνο Άσκηση 1 Φροντιστήριο 4 Θεωρείστε ένα έγγραφο με περιεχόμενο «αυτό είναι ένα κείμενο και
4 η Σειρά ασκήσεων (Συμπίεση, Ομαδοποίηση, Ευρετηρίαση Πολυμέσων, Κατανεμημένη Ανάκτηση)
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY463 -Συστήματα Ανάκτησης Πληροφοριών 2005-2006 Εαρινό Εξάμηνο 4 η Σειρά ασκήσεων (Συμπίεση, Ομαδοποίηση, Ευρετηρίαση Πολυμέσων, Κατανεμημένη Ανάκτηση)
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY463 -Συστήματα Ανάκτησης Πληροφοριών 2005-2006 Εαρινό Εξάμηνο 4 η Σειρά ασκήσεων (Συμπίεση, Ομαδοποίηση, Ευρετηρίαση Πολυμέσων, Κατανεμημένη Ανάκτηση)
ΓΛΩΣΣΙΚΗ ΤΕΧΝΟΛΟΓΙΑ. Μάθημα 10 ο : Αποσαφήνιση εννοιών λέξεων. Γεώργιος Πετάσης. Ακαδημαϊκό Έτος:
 ΓΛΩΣΣΙΚΗ ΤΕΧΝΟΛΟΓΙΑ Μάθημα 10 ο : Αποσαφήνιση εννοιών λέξεων Γεώργιος Πετάσης Ακαδημαϊκό Έτος: 2012 2013 ΤMHMA MHXANIKΩΝ Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ, Πανεπιστήμιο Πατρών, 2012 2013 Οι διαφάνειες αυτού του μαθήματος
ΓΛΩΣΣΙΚΗ ΤΕΧΝΟΛΟΓΙΑ Μάθημα 10 ο : Αποσαφήνιση εννοιών λέξεων Γεώργιος Πετάσης Ακαδημαϊκό Έτος: 2012 2013 ΤMHMA MHXANIKΩΝ Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ, Πανεπιστήμιο Πατρών, 2012 2013 Οι διαφάνειες αυτού του μαθήματος
Ανάκτηση πληροφορίας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ανάκτηση πληροφορίας Ενότητα 3: Μοντελοποίηση: Boolean μοντέλο Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ανάκτηση πληροφορίας Ενότητα 3: Μοντελοποίηση: Boolean μοντέλο Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Παλαιότερες ασκήσεις
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY6 - Συστήµατα Ανάκτησης Πληροφοριών Παλαιότερες ασκήσεις η Σειρά Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης) Άσκηση ( η σειρά ασκήσεων
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY6 - Συστήµατα Ανάκτησης Πληροφοριών Παλαιότερες ασκήσεις η Σειρά Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης) Άσκηση ( η σειρά ασκήσεων
Η ακρίβεια ορίζεται σαν το πηλίκο των ευρεθέντων συναφών εγγράφων προς τα ευρεθέντα έγγραφα. Άρα για τα τρία συστήµατα έχουµε τις εξής τιµές:
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2005-2006 Εαρινό Εξάµηνο 1 η Σειρά Ασκήσεων (Αξιολόγηση Αποτελεσµατικότητας Ανάκτησης) Άσκηση 1 (4 βαθµοί) Θεωρείστε
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2005-2006 Εαρινό Εξάµηνο 1 η Σειρά Ασκήσεων (Αξιολόγηση Αποτελεσµατικότητας Ανάκτησης) Άσκηση 1 (4 βαθµοί) Θεωρείστε
Επεξεργασία & Οργάνωση Δεδομένων Κειμένου
 Επεξεργασία & Οργάνωση Δεδομένων Εφαρμογές Γλωσσικής Τεχνολογίας Σοφία Στάμου Γλώσσα και Επικοινωνία Κάθε γλωσσικό σύστημα διέπεται από κανόνες για τη χρήση, τη σύνταξη και την ερμηνεία των λέξεων Γιατί
Επεξεργασία & Οργάνωση Δεδομένων Εφαρμογές Γλωσσικής Τεχνολογίας Σοφία Στάμου Γλώσσα και Επικοινωνία Κάθε γλωσσικό σύστημα διέπεται από κανόνες για τη χρήση, τη σύνταξη και την ερμηνεία των λέξεων Γιατί
ΑΣΚΗΣΗ Α. Δεικτοδότηση Συλλογής Κειμένων σε Ανεστραμμένο Ευρετήριο
 Γλωσσική Τεχνολογία Ακαδημαϊκό Έτος 2009-2010 ΑΣΚΗΣΗ Α Δεικτοδότηση Συλλογής Κειμένων σε Ανεστραμμένο Ευρετήριο Τα ανεστραμμένα αρχεία αποτελούν μια βασική μορφή ευρετηρίου και μας επιτρέπουν να εντοπίσουμε
Γλωσσική Τεχνολογία Ακαδημαϊκό Έτος 2009-2010 ΑΣΚΗΣΗ Α Δεικτοδότηση Συλλογής Κειμένων σε Ανεστραμμένο Ευρετήριο Τα ανεστραμμένα αρχεία αποτελούν μια βασική μορφή ευρετηρίου και μας επιτρέπουν να εντοπίσουμε
Πίνακες Διασποράς. Χρησιμοποιούμε ένα πίνακα διασποράς T και μια συνάρτηση διασποράς h. Ένα στοιχείο με κλειδί k αποθηκεύεται στη θέση
 Πίνακες Διασποράς Χρησιμοποιούμε ένα πίνακα διασποράς T και μια συνάρτηση διασποράς h Ένα στοιχείο με κλειδί k αποθηκεύεται στη θέση κλειδί k T 0 1 2 3 4 5 6 7 U : χώρος πιθανών κλειδιών Τ : πίνακας μεγέθους
Πίνακες Διασποράς Χρησιμοποιούμε ένα πίνακα διασποράς T και μια συνάρτηση διασποράς h Ένα στοιχείο με κλειδί k αποθηκεύεται στη θέση κλειδί k T 0 1 2 3 4 5 6 7 U : χώρος πιθανών κλειδιών Τ : πίνακας μεγέθους
ΜΥΕ003: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά. Κεφάλαια 6, 7: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου.
 ΜΥΕ003: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Κεφάλαια 6, 7: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου. 1 Κεφ. 6 Τι θα δούμε σήμερα; Βαθμολόγηση και κατάταξη εγγράφων Στάθμιση
ΜΥΕ003: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Κεφάλαια 6, 7: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου. 1 Κεφ. 6 Τι θα δούμε σήμερα; Βαθμολόγηση και κατάταξη εγγράφων Στάθμιση
[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)
![[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x) [1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)](/thumbs/52/30132893.jpg) [] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
[] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
Μία αξιωματική προσέγγιση για τη διαφοροποίηση των αποτελεσμάτων
 Μία αξιωματική προσέγγιση για τη διαφοροποίηση των αποτελεσμάτων ΜΑΘΗΜΑ Ανάκτηση Πληροφορίας Παππάς Χρήστος Ιωάννινα, Ιανουάριος 2010 Διάρθρωση Εισαγωγή Πρόβλημα Σημαντικότητα Ενδιαφέροντα θέματα Τεχνικό
Μία αξιωματική προσέγγιση για τη διαφοροποίηση των αποτελεσμάτων ΜΑΘΗΜΑ Ανάκτηση Πληροφορίας Παππάς Χρήστος Ιωάννινα, Ιανουάριος 2010 Διάρθρωση Εισαγωγή Πρόβλημα Σημαντικότητα Ενδιαφέροντα θέματα Τεχνικό
Εισαγωγή στην Επεξεργασία Ερωτήσεων. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα 2 Βήματα Επεξεργασίας Τα βασικά βήματα στην επεξεργασία
Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα 2 Βήματα Επεξεργασίας Τα βασικά βήματα στην επεξεργασία
Εργασία Μαθήματος Αξία: 40% του τελικού σας βαθμού Ανάθεση: Παράδοση:
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών ΗΥ463 Συστήματα Ανάκτησης Πληροφοριών 2009-2010 Φθινοπωρινό Εξάμηνο Εργασία Μαθήματος Αξία: 40% του τελικού σας βαθμού Ανάθεση: Παράδοση: Σκοπός αυτής της
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών ΗΥ463 Συστήματα Ανάκτησης Πληροφοριών 2009-2010 Φθινοπωρινό Εξάμηνο Εργασία Μαθήματος Αξία: 40% του τελικού σας βαθμού Ανάθεση: Παράδοση: Σκοπός αυτής της
Ανάκτηση Πληροφορίας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Μοντελοποίηση: Πιθανοκρατικό Μοντέλο Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Μοντελοποίηση: Πιθανοκρατικό Μοντέλο Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος
 9/6/5 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 5 Δίνεται ο πίνακας A 5. Αν διαγωνοποιείται να τον διαγωνοποιήσετε και στη συνέχεια να k υπολογίσετε το A όπου k θετικός
9/6/5 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 5 Δίνεται ο πίνακας A 5. Αν διαγωνοποιείται να τον διαγωνοποιήσετε και στη συνέχεια να k υπολογίσετε το A όπου k θετικός
Ανάκτηση Πληροφορίας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Ανάδραση Σχετικότητας (Relevance Feedback ή RF) Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Ανάδραση Σχετικότητας (Relevance Feedback ή RF) Απόστολος Παπαδόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
i) Για να δείξουμε την επιθυμητή ισότητα, δείχνουμε πως A B {A x : x B} και πως {A x : x B} A B. Για τον πρώτο εγκλεισμό, έστω a A B, δηλάδη a A και a
 Θεωρία Συνόλων Χειμερινό Εξάμηνο 2016 2017 Λύσεις 1. Άσκηση 1.9 (σελ. 17), από τις σημειώσεις του Σκανδάλη. Εστω A, B δεδομένα σύνολα. Θα χρησιμοποιήσουμε τα αξιώματα αλλά αναφερόμενοι, αποκλειστικά, είτε
Θεωρία Συνόλων Χειμερινό Εξάμηνο 2016 2017 Λύσεις 1. Άσκηση 1.9 (σελ. 17), από τις σημειώσεις του Σκανδάλη. Εστω A, B δεδομένα σύνολα. Θα χρησιμοποιήσουμε τα αξιώματα αλλά αναφερόμενοι, αποκλειστικά, είτε
Information Retrieval
 Introduction to Information Retrieval ΠΛΕ70: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Διάλεξη 8: Θέματα Υλοποίησης. Περίληψη Αποτελεσμάτων. 1 Κεφ. 6 Τι είδαμε στο προηγούμενο μάθημα Βαθμολόγηση
Introduction to Information Retrieval ΠΛΕ70: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Διάλεξη 8: Θέματα Υλοποίησης. Περίληψη Αποτελεσμάτων. 1 Κεφ. 6 Τι είδαμε στο προηγούμενο μάθημα Βαθμολόγηση
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Εφαρμοσμένη Θεωρία Πινάκων. Quiz 2. Σύντομες Λύσεις
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Εφαρμοσμένη Θεωρία Πινάκων Γ. Καραγιώργος ykarag@aegean.gr Quiz 2 Σύντομες Λύσεις Άσκηση 1. Βρείτε μία βάση και τη διάσταση, για τους διανυσματικούς χώρους M 3
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Εφαρμοσμένη Θεωρία Πινάκων Γ. Καραγιώργος ykarag@aegean.gr Quiz 2 Σύντομες Λύσεις Άσκηση 1. Βρείτε μία βάση και τη διάσταση, για τους διανυσματικούς χώρους M 3
Παραδείγματα (2) Διανυσματικοί Χώροι
 Παραδείγματα () Διανυσματικοί Χώροι Παράδειγμα 7 Ελέγξτε αν τα ακόλουθα σύνολα διανυσμάτων είναι γραμμικά ανεξάρτητα ή όχι: α) v=(,4,6), v=(,,), v=(7,,) b) v=(,4), v=(,), v=(4,) ) v=(,,), v=(5,,), v=(5,,)
Παραδείγματα () Διανυσματικοί Χώροι Παράδειγμα 7 Ελέγξτε αν τα ακόλουθα σύνολα διανυσμάτων είναι γραμμικά ανεξάρτητα ή όχι: α) v=(,4,6), v=(,,), v=(7,,) b) v=(,4), v=(,), v=(4,) ) v=(,,), v=(5,,), v=(5,,)
ΜΟΝΤΕΛΑ ΑΝΑΚΤΗΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 2 του βιβλίου. 2 ο ΜΕΡΟΣ
 ΜΟΝΤΕΛΑ ΑΝΑΚΤΗΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Διαφάνειες του καθ. Γιάννη Τζίτζικα (Παν. Κρήτης) http://www.ics.forth.gr/~tzitzik/ Για το πιθανοκρατικό του καθ. Απ. Παπαδόπουλου (Αριστοτέλειο Παν.) Κεφάλαιο 2 του βιβλίου
ΜΟΝΤΕΛΑ ΑΝΑΚΤΗΣΗΣ ΠΛΗΡΟΦΟΡΙΑΣ Διαφάνειες του καθ. Γιάννη Τζίτζικα (Παν. Κρήτης) http://www.ics.forth.gr/~tzitzik/ Για το πιθανοκρατικό του καθ. Απ. Παπαδόπουλου (Αριστοτέλειο Παν.) Κεφάλαιο 2 του βιβλίου
Σειρά Προβλημάτων 1 Λύσεις
 ΕΠΛ: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Θεωρείστε τις γλώσσες Α = { n n } και Β = {w η w είναι λέξη επί του αλφαβήτου {,} τ.ώ. w }. (α) Για κάθε μια από τις πιο κάτω γλώσσες
ΕΠΛ: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Θεωρείστε τις γλώσσες Α = { n n } και Β = {w η w είναι λέξη επί του αλφαβήτου {,} τ.ώ. w }. (α) Για κάθε μια από τις πιο κάτω γλώσσες
HY380 Αλγόριθμοι και πολυπλοκότητα Hard Problems
 HY380 Αλγόριθμοι και πολυπλοκότητα Hard Problems Ημερομηνία Παράδοσης: 0/1/017 την ώρα του μαθήματος ή με email: mkarabin@csd.uoc.gr Γενικές Οδηγίες α) Επιτρέπεται η αναζήτηση στο Internet και στην βιβλιοθήκη
HY380 Αλγόριθμοι και πολυπλοκότητα Hard Problems Ημερομηνία Παράδοσης: 0/1/017 την ώρα του μαθήματος ή με email: mkarabin@csd.uoc.gr Γενικές Οδηγίες α) Επιτρέπεται η αναζήτηση στο Internet και στην βιβλιοθήκη
N(F I G) = = N N(F ) N(I ) N(G)+N(FI ) + N(FG)+N(IG) N(FIG) = = = 200
 Διακριτά Μαθηματικά Ι Φροντιστήριο Αρχή Εγκλεισμού-Αποκλεισμού 1 / 9 Σε ένα σχολείο υπάρχουν 1000 μαθητές. Απ αυτούς οι 400 μιλάνε Γαλλικά, οι 300 Ιταλικά και 200 μιλάνε Γερμανικά. Εάν υπάρχουν 200 μαθητές,που
Διακριτά Μαθηματικά Ι Φροντιστήριο Αρχή Εγκλεισμού-Αποκλεισμού 1 / 9 Σε ένα σχολείο υπάρχουν 1000 μαθητές. Απ αυτούς οι 400 μιλάνε Γαλλικά, οι 300 Ιταλικά και 200 μιλάνε Γερμανικά. Εάν υπάρχουν 200 μαθητές,που
Δυναμικός Κατακερματισμός. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Δυναμικός Κατακερματισμός Βάσεις Δεδομένων 2018-2019 1 Κατακερματισμός Πρόβλημα στατικού κατακερματισμού: Έστω Μ κάδους και r εγγραφές ανά κάδο - το πολύ Μ * r εγγραφές (αλλιώς μεγάλες αλυσίδες υπερχείλισης)
Δυναμικός Κατακερματισμός Βάσεις Δεδομένων 2018-2019 1 Κατακερματισμός Πρόβλημα στατικού κατακερματισμού: Έστω Μ κάδους και r εγγραφές ανά κάδο - το πολύ Μ * r εγγραφές (αλλιώς μεγάλες αλυσίδες υπερχείλισης)
Διακριτός Μετασχηματισμός Fourier
 Διακριτός Μετασχηματισμός Fourier 1 Διακριτός Μετασχηματισμός Fourier Ο μετασχηματισμός Fourier αποτελεί τον ακρογωνιαίο λίθο της επεξεργασίας σήματος αλλά και συχνή αιτία πονοκεφάλου για όσους πρωτοασχολούνται
Διακριτός Μετασχηματισμός Fourier 1 Διακριτός Μετασχηματισμός Fourier Ο μετασχηματισμός Fourier αποτελεί τον ακρογωνιαίο λίθο της επεξεργασίας σήματος αλλά και συχνή αιτία πονοκεφάλου για όσους πρωτοασχολούνται
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Διδάσκων : Επίκ Καθ Κολάσης Χαράλαμπος Άδειες Χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Διδάσκων : Επίκ Καθ Κολάσης Χαράλαμπος Άδειες Χρήσης
Μηχανική Μάθηση: γιατί;
 Μηχανική Μάθηση Μηχανική Μάθηση: γιατί; Απαραίτητη για να μπορεί ο πράκτορας να ανταπεξέρχεται σε άγνωστα περιβάλλοντα Δεν είναι δυνατόν ο σχεδιαστής να προβλέψει όλα τα ενδεχόμενα περιβάλλοντα. Χρήσιμη
Μηχανική Μάθηση Μηχανική Μάθηση: γιατί; Απαραίτητη για να μπορεί ο πράκτορας να ανταπεξέρχεται σε άγνωστα περιβάλλοντα Δεν είναι δυνατόν ο σχεδιαστής να προβλέψει όλα τα ενδεχόμενα περιβάλλοντα. Χρήσιμη
7. Υπολογισμός Βαθμολογιών σε ένα Πλήρες Σύστημα Αναζήτησης
 Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 7. Υπολογισμός Βαθμολογιών σε ένα Πλήρες Σύστημα Αναζήτησης Ανάκτηση Πληροφοριών Χρήστος ουλκερίδης Τμήμα
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 7. Υπολογισμός Βαθμολογιών σε ένα Πλήρες Σύστημα Αναζήτησης Ανάκτηση Πληροφοριών Χρήστος ουλκερίδης Τμήμα
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
 Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
ΠΑΡΑΡΤΗΜΑ Γ. Επικαμπύλια και Επιφανειακά Ολοκληρώματα. Γ.1 Επικαμπύλιο Ολοκλήρωμα
 ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
BΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ ΕΞΕΤΑΣΗ ΦΕΒΡΟΥΑΡΙΟΥ 2005
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ BΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ ΕΞΕΤΑΣΗ ΦΕΒΡΟΥΑΡΙΟΥ 2005 ΛΥΣΕΙΣ Ι. Βασιλείου -----------------------------------------------------------------------------------------------------
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ BΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ ΕΞΕΤΑΣΗ ΦΕΒΡΟΥΑΡΙΟΥ 2005 ΛΥΣΕΙΣ Ι. Βασιλείου -----------------------------------------------------------------------------------------------------
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Εφαρμοσμένη Θεωρία Πινάκων. Quiz 3. Σύντομες Λύσεις
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Εφαρμοσμένη Θεωρία Πινάκων Γ. Καραγιώργος ykarag@aegean.gr Quiz Σύντομες Λύσεις Άσκηση. Δείξτε ότι η απεικόνιση u, v = u v + 5u v, όπου u = (u, u ), v = (v, v ),
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Εφαρμοσμένη Θεωρία Πινάκων Γ. Καραγιώργος ykarag@aegean.gr Quiz Σύντομες Λύσεις Άσκηση. Δείξτε ότι η απεικόνιση u, v = u v + 5u v, όπου u = (u, u ), v = (v, v ),
Συνοπτική Μεθοδολογία Ασκήσεων IP Fragmentation. Ασκήσεις στο IP Fragmentation
 Συνοπτική Μεθοδολογία Ασκήσεων IP Fragmentation Οι σημειώσεις που ακολουθούν περιγράφουν τις ασκήσεις IP Fragmentation που θα συναντήσετε στο κεφάλαιο 3. Η πιο συνηθισμένη και βασική άσκηση αναφέρεται
Συνοπτική Μεθοδολογία Ασκήσεων IP Fragmentation Οι σημειώσεις που ακολουθούν περιγράφουν τις ασκήσεις IP Fragmentation που θα συναντήσετε στο κεφάλαιο 3. Η πιο συνηθισμένη και βασική άσκηση αναφέρεται
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ
 Proslipsis.gr ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 006 ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος: ΠΕ 0 ΜΑΘΗΜΑΤΙΚΩΝ ΕΞΕΤΑΣΗ ΣΤΗΝ ΠΡΩΤΗ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ (Γνωστικό αντικείμενο)
Proslipsis.gr ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 006 ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος: ΠΕ 0 ΜΑΘΗΜΑΤΙΚΩΝ ΕΞΕΤΑΣΗ ΣΤΗΝ ΠΡΩΤΗ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ (Γνωστικό αντικείμενο)
ΤΕΙ ΣΕΡΡΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ «ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ ΝΕΥΡΩΝΙΚΑ ΔΙΚΤΥΑ» ΠΑ. 7 ΣΕΠΤΕΜΒΡΙΟΥ 2012
 ΠΑ. 7 ΣΕΠΤΕΜΒΡΙΟΥ Δίνονται τα εξής πρότυπα: [ ] [ ] [ ] [ ] Άσκηση η (3 μονάδες) Χρησιμοποιώντας το κριτήριο της ομοιότητας να απορριφθεί ένα χαρακτηριστικό με βάση το συντελεστή συσχέτισης. (γράψτε ποιο
ΠΑ. 7 ΣΕΠΤΕΜΒΡΙΟΥ Δίνονται τα εξής πρότυπα: [ ] [ ] [ ] [ ] Άσκηση η (3 μονάδες) Χρησιμοποιώντας το κριτήριο της ομοιότητας να απορριφθεί ένα χαρακτηριστικό με βάση το συντελεστή συσχέτισης. (γράψτε ποιο
ph αραιωμένου ρυθμιστικού διαλύματος.
 αραιωμένου ρυθμιστικού διαλύματος. Ρυθμιστικό διάλυμα HA NA με συγκεντρώσεις και αντίστοιχα, αρχικού όγκου V, αραιώνεται με προσθήκη νερού. Να βρεθεί η σχέση που συνδέει το του διαλύματος με τον όγκο V
αραιωμένου ρυθμιστικού διαλύματος. Ρυθμιστικό διάλυμα HA NA με συγκεντρώσεις και αντίστοιχα, αρχικού όγκου V, αραιώνεται με προσθήκη νερού. Να βρεθεί η σχέση που συνδέει το του διαλύματος με τον όγκο V
ΜΥΕ003: Ανάκτηση Πληροφορίας
 ΜΥΕ003: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Κεφάλαια 6, 7, 8.7: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου. Περιλήψεις. 1 Κεφ. 6 Τι θα δούμε σήμερα; Βαθμολόγηση και κατάταξη
ΜΥΕ003: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Κεφάλαια 6, 7, 8.7: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου. Περιλήψεις. 1 Κεφ. 6 Τι θα δούμε σήμερα; Βαθμολόγηση και κατάταξη
Εαρινό Εξάμηνο ΗΥ111 Απειροστικός Λογισμός ΙΙ
 ΗΥ-111 Απειροστικός Λογισμός ΙΙ Εαρινό Εξάμηνο 2010-2011 Εισαγωγή Διδάσκων: (cpanag@csd.uoc.gr), Επισκέπτης Καθηγητής www.csd.uoc.gr/~cpanag Γραφείο: Δ215 - Τηλέφωνο: 2810 393588 Ώρες γραφείου: Δευτέρα
ΗΥ-111 Απειροστικός Λογισμός ΙΙ Εαρινό Εξάμηνο 2010-2011 Εισαγωγή Διδάσκων: (cpanag@csd.uoc.gr), Επισκέπτης Καθηγητής www.csd.uoc.gr/~cpanag Γραφείο: Δ215 - Τηλέφωνο: 2810 393588 Ώρες γραφείου: Δευτέρα
ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο
 ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο 2014-2015 Πρώτη Σειρά Ασκήσεων (Υποχρεωτική, 25% του συνολικού βαθμού στο μάθημα) Ημερομηνία Ανακοίνωσης: 22/10/2014 Ημερομηνία Παράδοσης: Μέχρι 14/11/2014 23:59
ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο 2014-2015 Πρώτη Σειρά Ασκήσεων (Υποχρεωτική, 25% του συνολικού βαθμού στο μάθημα) Ημερομηνία Ανακοίνωσης: 22/10/2014 Ημερομηνία Παράδοσης: Μέχρι 14/11/2014 23:59
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 11: Διανύσματα (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων &
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 11: Διανύσματα (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων &
X = {(x 1, x 2 ) x 1 + 2x 2 = 0}.
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 4 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 26/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 4 26/2/2014 1 / 12 Υποσύνολα ενός διανυσματικού χώρου. Πότε είναι ένα υποσύνολο X ενός
Γραμμική Άλγεβρα ΙΙ Διάλεξη 4 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 26/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 4 26/2/2014 1 / 12 Υποσύνολα ενός διανυσματικού χώρου. Πότε είναι ένα υποσύνολο X ενός
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Διακριτά Μαθηματικά Ι Ενότητα 4: Θεωρία Μέτρησης Po lya Μέρος 1 Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Διακριτά Μαθηματικά Ι Ενότητα 4: Θεωρία Μέτρησης Po lya Μέρος 1 Διδάσκων: Χ. Μπούρας (bouras@cti.gr) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
1. Για καθένα από τους ακόλουθους διανυσματικούς χώρους βρείτε μια βάση και τη διάσταση. 3. U x y z x y z x y. {(,, ) } a b. c d
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
ΑΣΚΗΣΗ. Συγκομιδή και δεικτοδότηση ιστοσελίδων
 Γλωσσική Τεχνολογία Ακαδημαϊκό Έτος 2010-2011 ΑΣΚΗΣΗ Συγκομιδή και δεικτοδότηση ιστοσελίδων Σκοπός της άσκησης είναι η υλοποίηση ενός ολοκληρωμένου συστήματος συγκομιδής και δεικτοδότησης ιστοσελίδων.
Γλωσσική Τεχνολογία Ακαδημαϊκό Έτος 2010-2011 ΑΣΚΗΣΗ Συγκομιδή και δεικτοδότηση ιστοσελίδων Σκοπός της άσκησης είναι η υλοποίηση ενός ολοκληρωμένου συστήματος συγκομιδής και δεικτοδότησης ιστοσελίδων.
Συστήματα Ανάκτησης Πληροφοριών ΗΥ-463
 ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ COMPUTER SCIENCE DEPARTMENT UNIVERSITY OF CRETE Συστήματα Ανάκτησης Πληροφοριών ΗΥ-463 4 η Σειρά Ασκήσεων Ψαράκη Μαρία-Γεωργία ΜΕΤ 556 psaraki@csd.uoc.gr Εαρινό Εξάμηνο 2008-2009
ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ COMPUTER SCIENCE DEPARTMENT UNIVERSITY OF CRETE Συστήματα Ανάκτησης Πληροφοριών ΗΥ-463 4 η Σειρά Ασκήσεων Ψαράκη Μαρία-Γεωργία ΜΕΤ 556 psaraki@csd.uoc.gr Εαρινό Εξάμηνο 2008-2009
Κατ οίκον Εργασία 1 Σκελετοί Λύσεων
 ΕΠΛ 1 Δομές Δεδομένων και Αλγόριθμοι Σεπτέμβριος 009 Κατ οίκον Εργασία 1 Σκελετοί Λύσεων Άσκηση 1 Αρχικά θα πρέπει να υπολογίσουμε τον αριθμό των πράξεων που μπορεί να εκτελέσει ο υπολογιστής σε μια ώρα,
ΕΠΛ 1 Δομές Δεδομένων και Αλγόριθμοι Σεπτέμβριος 009 Κατ οίκον Εργασία 1 Σκελετοί Λύσεων Άσκηση 1 Αρχικά θα πρέπει να υπολογίσουμε τον αριθμό των πράξεων που μπορεί να εκτελέσει ο υπολογιστής σε μια ώρα,
Λογισμός 3. Ενότητα 1: Τοπολογία των Ευκλείδειων χώρων. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Τοπολογία των Ευκλείδειων χώρων. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Τοπολογία των Ευκλείδειων χώρων. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Σύντομες εισαγωγικές σημειώσεις για την. Matlab
 Σύντομες εισαγωγικές σημειώσεις για την Matlab Δήλωση Μεταβλητών Για να εισάγει κανείς δεδομένα στη Matlab υπάρχουν πολλοί τρόποι. Ο πιο απλός είναι στη γραμμή εντολών να εισάγουμε αυτό που θέλουμε και
Σύντομες εισαγωγικές σημειώσεις για την Matlab Δήλωση Μεταβλητών Για να εισάγει κανείς δεδομένα στη Matlab υπάρχουν πολλοί τρόποι. Ο πιο απλός είναι στη γραμμή εντολών να εισάγουμε αυτό που θέλουμε και
Εντολή Δεδομένα Περιεχόμενα μετά την εκτέλεση 1 read(x) 122 x= 2 read(a,b,c) 133 244 355 a= b= c= 3 read(d,e) 166 277 3888
 ΕΡΩΤΗΣΕΙΣ 1. Να αναφέρετε μερικά από τα ιδιαίτερα χαρακτηριστικά της Pascal. 2. Ποιο είναι το αλφάβητο της Pascal; 3. Ποια είναι τα ονόματα-ταυτότητες και σε τι χρησιμεύουν; 4. Σε τι χρησιμεύει το συντακτικό
ΕΡΩΤΗΣΕΙΣ 1. Να αναφέρετε μερικά από τα ιδιαίτερα χαρακτηριστικά της Pascal. 2. Ποιο είναι το αλφάβητο της Pascal; 3. Ποια είναι τα ονόματα-ταυτότητες και σε τι χρησιμεύουν; 4. Σε τι χρησιμεύει το συντακτικό
Επεξεργασία Ερωτήσεων
 Εισαγωγή Επεξεργασία Ερωτήσεων Σ Β Βάση εδομένων Η ομή ενός ΣΒ Βάσεις Δεδομένων 2006-2007 Ευαγγελία Πιτουρά 1 Βάσεις Δεδομένων 2006-2007 Ευαγγελία Πιτουρά 2 Εισαγωγή Εισαγωγή ΜΕΡΟΣ 1 (Χρήση Σ Β ) Γενική
Εισαγωγή Επεξεργασία Ερωτήσεων Σ Β Βάση εδομένων Η ομή ενός ΣΒ Βάσεις Δεδομένων 2006-2007 Ευαγγελία Πιτουρά 1 Βάσεις Δεδομένων 2006-2007 Ευαγγελία Πιτουρά 2 Εισαγωγή Εισαγωγή ΜΕΡΟΣ 1 (Χρήση Σ Β ) Γενική
Ασκήσεις μελέτης της 19 ης διάλεξης
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 19 ης διάλεξης 19.1. Δείξτε ότι το Perceptron με (α) συνάρτηση ενεργοποίησης
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 19 ης διάλεξης 19.1. Δείξτε ότι το Perceptron με (α) συνάρτηση ενεργοποίησης
Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης. Διανύσματα ΚΑΤΗΓΟΡΙΑ 8. Εσωτερικό γινόµενο διανυσµάτων. Ασκήσεις προς λύση 1-50
 Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης Διανύσματα Εσωτερικό γινόµενο διανυσµάτων. ΚΑΤΗΓΟΡΙΑ 8 Ασκήσεις προς λύση 1-50 1. Θεωρούμε τα σημεία Α(1,2), Β(4,1). Να βρείτε σημείο Μ του άξονα
Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης Διανύσματα Εσωτερικό γινόµενο διανυσµάτων. ΚΑΤΗΓΟΡΙΑ 8 Ασκήσεις προς λύση 1-50 1. Θεωρούμε τα σημεία Α(1,2), Β(4,1). Να βρείτε σημείο Μ του άξονα
Query-Driven Indexing for Scalable Peer-to-Peer Text Retrieval. Gleb Skobeltsyn, Toan Luu, Ivana Podnar Zarko, Martin Rajman, Karl Aberer
 Query-Driven Indexing for Scalable Peer-to-Peer Text Retrieval Gleb Skobeltsyn, Toan Luu, Ivana Podnar Zarko, Martin Rajman, Karl Aberer Περιγραφή του προβλήματος Ευρετηριοποίηση μεγάλων συλλογών εγγράφων
Query-Driven Indexing for Scalable Peer-to-Peer Text Retrieval Gleb Skobeltsyn, Toan Luu, Ivana Podnar Zarko, Martin Rajman, Karl Aberer Περιγραφή του προβλήματος Ευρετηριοποίηση μεγάλων συλλογών εγγράφων
Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β.
 Η έννοια της ακολουθίας Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β. Δηλαδή: f : A B Η ακολουθία είναι συνάρτηση.
Η έννοια της ακολουθίας Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β. Δηλαδή: f : A B Η ακολουθία είναι συνάρτηση.
2.1 2.2 ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ
 ΚΕΦΑΛΑΙΟ Ο : ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ - ΕΝΟΤΗΤΕΣ :.... ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΜΕΘΟΔΟΛΟΓΙΑ : ΠΡΑΓΜΑΤΙΚΟ & ΦΑΝΤΑΣΤΙΚΟ ΜΕΡΟΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Έστω ένας μιγαδικός αριθμός,
ΚΕΦΑΛΑΙΟ Ο : ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ - ΕΝΟΤΗΤΕΣ :.... ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΜΕΘΟΔΟΛΟΓΙΑ : ΠΡΑΓΜΑΤΙΚΟ & ΦΑΝΤΑΣΤΙΚΟ ΜΕΡΟΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Έστω ένας μιγαδικός αριθμός,
ΤΕΙ ΣΕΡΡΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ «ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ ΝΕΥΡΩΝΙΚΑ ΔΙΚΤΥΑ» ΔΕ. 11 ΙΟΥΝΙΟΥ 2012
 ΔΕ. ΙΟΥΝΙΟΥ Δίνονται τα εξής πρότυπα: [ ] [ ] [ ] [ ] Άσκηση η ( μονάδες) Χρησιμοποιώντας το κριτήριο της ομοιότητας να απορριφθεί ένα χαρακτηριστικό με βάσει το συντελεστή συσχέτισης. (γράψτε ποιο χαρακτηριστικό
ΔΕ. ΙΟΥΝΙΟΥ Δίνονται τα εξής πρότυπα: [ ] [ ] [ ] [ ] Άσκηση η ( μονάδες) Χρησιμοποιώντας το κριτήριο της ομοιότητας να απορριφθεί ένα χαρακτηριστικό με βάσει το συντελεστή συσχέτισης. (γράψτε ποιο χαρακτηριστικό
Τεχνητή Νοημοσύνη. 18η διάλεξη ( ) Ίων Ανδρουτσόπουλος.
 Τεχνητή Νοημοσύνη 18η διάλεξη (2016-17) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται: στο βιβλίο Machine Learning του T. Mitchell, McGraw- Hill, 1997,
Τεχνητή Νοημοσύνη 18η διάλεξη (2016-17) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται: στο βιβλίο Machine Learning του T. Mitchell, McGraw- Hill, 1997,
Λογική Δημήτρης Πλεξουσάκης Ασκήσεις στον Κατηγορηματικό Λογισμό Τμήμα Επιστήμης Υπολογιστών
 Λογική Δημήτρης Πλεξουσάκης Ασκήσεις στον Κατηγορηματικό Λογισμό Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια χρήσης Creative Commons και ειδικότερα Αναφορά
Λογική Δημήτρης Πλεξουσάκης Ασκήσεις στον Κατηγορηματικό Λογισμό Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια χρήσης Creative Commons και ειδικότερα Αναφορά
1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
Information Retrieval
 Introduction to Information Retrieval ΜΥΕ003-ΠΛΕ70: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Διάλεξη 6-7: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου. 1 Κεφ. 6 Τι θα δούμε σήμερα;
Introduction to Information Retrieval ΜΥΕ003-ΠΛΕ70: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Διάλεξη 6-7: Βαθμολόγηση. Στάθμιση όρων. Το μοντέλο διανυσματικού χώρου. 1 Κεφ. 6 Τι θα δούμε σήμερα;
1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
Άσκηση 1 (ανακοινώθηκε στις 20 Μαρτίου 2017, προθεσμία παράδοσης: 24 Απριλίου 2017, 12 τα μεσάνυχτα).
 Κ08 Δομές Δεδομένων και Τεχνικές Προγραμματισμού Διδάσκων: Μανόλης Κουμπαράκης Εαρινό Εξάμηνο 2016-2017. Άσκηση 1 (ανακοινώθηκε στις 20 Μαρτίου 2017, προθεσμία παράδοσης: 24 Απριλίου 2017, 12 τα μεσάνυχτα).
Κ08 Δομές Δεδομένων και Τεχνικές Προγραμματισμού Διδάσκων: Μανόλης Κουμπαράκης Εαρινό Εξάμηνο 2016-2017. Άσκηση 1 (ανακοινώθηκε στις 20 Μαρτίου 2017, προθεσμία παράδοσης: 24 Απριλίου 2017, 12 τα μεσάνυχτα).
Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών
 Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών Συμβολισμοί Σε αναλογία με τους ορισμούς συμβολίζουμε μια ακολουθία: 1 είτε μέσω του διανυσματικού ορισμού, παραθέτοντας αναγκαστικά
Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών Συμβολισμοί Σε αναλογία με τους ορισμούς συμβολίζουμε μια ακολουθία: 1 είτε μέσω του διανυσματικού ορισμού, παραθέτοντας αναγκαστικά
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ
 Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
ΠΕΡΙΛΗΨΗ ΘΕΩΡΙΑΣ ΣΤΗΝ ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ
 ΠΕΡΙΛΗΨΗ ΘΕΩΡΙΑΣ ΣΤΗΝ ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ Αλγεβρική τιμή διανύσματος Όταν ένα διάνυσμα είναι παράλληλο σε έναν άξονα (δηλαδή μια ευθεία στην οποία έχουμε ορίσει θετική φορά), τότε αλγεβρική τιμή του διανύσματος
ΠΕΡΙΛΗΨΗ ΘΕΩΡΙΑΣ ΣΤΗΝ ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ Αλγεβρική τιμή διανύσματος Όταν ένα διάνυσμα είναι παράλληλο σε έναν άξονα (δηλαδή μια ευθεία στην οποία έχουμε ορίσει θετική φορά), τότε αλγεβρική τιμή του διανύσματος
ΚΕΦΑΛΑΙΟ 3. Περιγραφή της Μεθόδου ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΜΕΘΟΔΟΥ
 ΚΕΦΑΛΑΙΟ 3 Περιγραφή της Μεθόδου Το αντικείμενο αυτής της εργασίας είναι η χρήση μιας μεθόδου προσέγγισης συναρτήσεων που έχει προταθεί από τον hen-ha huang και ονομάζεται Ασαφώς Σταθμισμένη Παλινδρόμηση
ΚΕΦΑΛΑΙΟ 3 Περιγραφή της Μεθόδου Το αντικείμενο αυτής της εργασίας είναι η χρήση μιας μεθόδου προσέγγισης συναρτήσεων που έχει προταθεί από τον hen-ha huang και ονομάζεται Ασαφώς Σταθμισμένη Παλινδρόμηση
