Conjugate Bayesian analysis of the Gaussian distribution
|
|
|
- Κύνθια Δελή
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Conjugate Bayesan analyss of the Gaussan dstrbuton Kevn P. Murphy Last updated October 3, 7 Introducton The Gaussan or normal dstrbuton s one of the most wdely used n statstcs. Estmatng ts parameters usng Bayesan nference and conjugate prors s also wdely used. The use of conjugate prors allows all the results to be derved n closed form. Unfortunately, dfferent books use dfferent conventons on how to parameterze the varous dstrbutons e.g., put the pror on the precson or the varance, use an nverse gamma or nverse ch-squared, etc, whch can be very confusng for the student. In ths report, we summarze all of the most commonly used forms. We provde detaled dervatons for some of these results; the rest can be obtaned by smple reparameterzaton. See the appendx for the defnton the dstrbutons that are used. Normal pror Let us consder Bayesan estmaton of the mean of a unvarate Gaussan, whose varance s assumed to be known. We dscuss the unknown varance case later.. Lkelhood Let D = x,..., x n be the data. The lkelhood s { n pd µ, σ = px µ, σ = πσ n/ exp σ = Let us defne the emprcal mean and varance x = n s = n } x µ = x = x x 3 = Note that other authors e.g., [GCSR4] defne s = n n = x x. We can rewrte the term n the exponent as follows x µ = [x x µ x] 4 snce = x x + x µ x xµ x 5 = ns + nx µ 6 x xµ x = µ x Thanks to Hoyt Koepke for proof readng. x nx = µ xnx nx = 7
2 Hence pd µ, σ = π n/ σ σ n exp [ ns σ + nx µ ] n/ exp n σ x µ exp ns σ 8 9 If σ s a constant, we can wrte ths as pd µ exp n σ x µ Nx µ, σ n snce we are free to drop constant factors n the defnton of the lkelhood. Thus n observatons wth varance σ and mean x s equvalent to observaton x = x wth varance σ /n.. Pror Snce the lkelhood has the form pd µ the natural conjugate pror has the form pµ exp n σ x µ Nx µ, σ n exp σ µ µ Nµ µ, σ Do not confuse σ, whch s the varance of the pror, wth σ, whch s the varance of the observaton nose. A natural conjugate pror s one that has the same form as the lkelhood..3 Posteror Hence the posteror s gven by pµ D pd µ, σpµ µ, σ 3 [ ] exp [ σ x µ exp ] σ µ µ 4 [ ] = exp σ x + µ x µ + µ + µ µ µ 5 Snce the product of two Gaussans s a Gaussan, we wll rewrte ths n the form pµ D exp [ µ σ + n µ σ + µ σ + x ] µ σ σ + x σ [ def = exp ] [ σn µ µµ n + µ n = exp ] σn µ µ n Matchng coeffcents of µ, we fnd σn s gven by µ σ n σ n σ n = = µ σ + n σ σ = σ + n σ 9 σ σ nσ + = σ n σ + σ
3 5 N = N = N = N = Fgure : Sequentally updatng a Gaussan mean startng wth a pror centered on µ =. The true parameters are µ =.8 unknown, σ =. known. Notce how the data quckly overwhelms the pror, and how the posteror becomes narrower. Source: Fgure. [Bs6]. Matchng coeffcents of µ we get µµ n σ n n = = µ x σ + µ σ µ n σ n = n = x σ + µ σ = σ nx + σ µ σ σ 3 Hence µ n = σ nσ + µ σ + nσ nσ + x = µ σ σ n σ + nx σ 4 Ths operaton of matchng frst and second powers of µ s called completng the square. Another way to understand these results s f we work wth the precson of a Gaussan, whch s /varance hgh precson means low varance, low precson means hgh varance. Let Then we can rewrte the posteror as λ = /σ 5 λ = /σ 6 λ n = /σ n 7 pµ D, λ = Nµ µ n, λ n 8 λ n = λ + nλ 9 µ n = xnλ + µ λ λ n = wµ ML + wµ 3 3
4 pror lk post pror sgma pror sgma. pror lk post a b Fgure : Bayesan estmaton of the mean of a Gaussan from one sample. a Weak pror N,. b Strong pror N,. In the latter case, we see the posteror mean s shrunk towards the pror mean, whch s. Fgure produced by gaussbayesdemo. where nx = n = x and w = nλ λ n. The precson of the posteror λ n s the precson of the pror λ plus one contrbuton of data precson λ for each observed data pont. Also, we see the mean of the posteror s a convex combnaton of the pror and the MLE, wth weghts proportonal to the relatve precsons. To gan further nsght nto these equatons, consder the effect of sequentally updatng our estmate of µ see Fgure. After observng one data pont x so n =, we have the followng posteror mean µ = σ σ + σ µ + σ σ + σ x 3 σ = µ + x µ σ + σ σ = x x µ σ + σ The frst equaton s a convex combnaton of the pror and MLE. The second equaton s the pror mean ajusted towards the data x. The thrd equaton s the data x adjusted towads the pror mean; ths s called shrnkage. These are all equvalent ways of expressng the tradeoff between lkelhood and pror. See Fgure for an example..4 Posteror predctve The posteror predctve s gven by px D = = 3 33 px µpµ Ddµ 34 Nx µ, σ Nµ µ n, σn dµ 35 = Nx µ n, σ n + σ 36 Ths follows from general propertes of the Gaussan dstrbuton see Equaton.5 of [Bs6]. An alternatve proof s to note that x = x µ + µ 37 x µ N, σ 38 µ Nµ n, σ n 39 Snce E[X + X ] = E[X ] + E[X ] and Var [X + X ] = Var [X ] + Var [X ] f X, X are ndependent, we have X Nµ n, σ n + σ 4 4
5 snce we assume that the resdual error s condtonally ndependent of the parameter. Thus the predctve varance s the uncertanty due to the observaton nose σ plus the uncertanty due to the parameters, σ n..5 Margnal lkelhood Wrtng m = µ and τ = σ for the hyper-parameters, we can derve the margnal lkelhood as follows: n l = pd m, σ, τ = [ Nx µ, σ ]Nµ m, τ dµ 4 = = σ πσ n nτ + σ exp x σ τ m n x σ + σ m τ exp τ + nxm nτ + σ 4 The proof s below, based on the on the appendx of [DMP + 6]. We have n l = pd m, σ, τ = [ Nx µ, σ ]Nµ m, τ dµ 43 = = σ π n τ π exp σ x µ µ m dµ 44 τ Let us defne S = /σ and T = /τ. Then l = π/s n exp S π/t x + nµ µ x T µ + m µm dµ 45 = c exp S nµ S x + T µ T µm dµ 46 where So Now l = c [ exp S n + T c = exp S x + T m π/s n π/t µ µ S x + T m S n + T S nx + T m [ = c exp S n + T exp S n + T S nx + T m = c exp S n + T = exp S x + T m S π/s n nx + T m exp π/t S n + T π/t 47 ] dµ 48 µ S nx + T ] m S n + T dµ 49 π S n + T 5 π S n + T = π S n + T 5 σ Nτ + σ 5 and nx σ + m τ n σ + τ = nxτ + mσ σ τ nτ + σ = n x τ /σ + σ m /τ + nxm nτ + σ
6 So pd = σ πσ n nτ + σ exp x σ To check ths, we should ensure that we get To be completed.6 Condtonal pror pµ σ px D = px, D pd τ m n x σ + σ m τ exp τ + nxm nτ + σ 55 = Nx µ n, σ n + σ 56 Note that the prevous pror s not, strctly speakng, conjugate, snce t has the form pµ whereas the posteror has the form pµ D, σ,.e., σ occurs n the posteror but not the pror. We can rewrte the pror n condtonal form as follows pµ σ = Nµ µ, σ /κ 57 Ths means that f σ s large, the varance on the pror of µ s also large. Ths s reasonable snce σ defnes the measurement scale of x, so the pror belef about µ s equvalent to κ observatons of µ on ths scale. Hence a nonnformatve pror s κ =. Then the posteror s pµ D = Nµ µ n, σ /κ n 58 where κ n = κ + n. In ths form, t s clear that κ plays a role analogous to n. Hence κ s the equvalent sample sze of the pror..7 Reference analyss To get an unnformatve pror, we just set the pror varance to nfnty to smulate a unform pror on µ. 3 Normal-Gamma pror pµ = Nµ, 59 pµ D = Nµ x, σ /n 6 We wll now suppose that both the mean m and the precson λ = σ are unknown. We wll mostly follow the notaton n [DeG7, p69]. 3. Lkelhood The lkelhood can be wrtten n ths form pd µ, λ = π n/ λn/ exp λ 3. Pror The conjugate pror s the normal-gamma: = NGµ, λ µ, κ, α, β π n/ λn/ exp def λ x µ = [ nµ x + ] x x = 6 6 = Nµ µ, κ λ Gaλ α, rate = β 63 = Z NG µ, κ, α, β λ exp κ λ µ µ λ α e λβ 64 = λ α exp λ [ κ µ µ ] + β 65 Z NG Z NG µ, κ, α, β = Γα β α π κ 66 6
7 NGκ=., a=., b=. NGκ=., a=3., b= λ µ 4 λ µ NGκ=., a=5., b=. NGκ=., a=5., b= λ µ 4 λ µ Fgure 3: Some Normal-Gamma dstrbutons. Produced by NGplot. See Fgure 3 for some plots. We can compute the pror margnal on µ as follows: pµ = pµ, λdλ 67 λ α+ exp λβ + κ µ µ dλ 68 We recognze ths as an unnormalzed Gaa = α +, b = β + κµ µ dstrbuton, so we can just wrte down whch we recognze as as a T α µ µ, β /α κ dstrbuton. pµ Γa b a 69 b a 7 = β + κ µ µ α 7 = + α α κ µ µ β α+/ 7 7
8 3.3 Posteror The posteror can be derved as follows. pµ, λ D NGµ, λ µ, κ, α, β pd µ, λ 73 λ e κλµ µ / λ α e βλ λ n/ e λ P n = x µ 74 λ λ α+n/ e βλ e λ/[κµ µ + P x µ ] 75 From Equaton 6 we have Also, t can be shown that x µ = nµ x + x x 76 = = where Hence κ µ µ + nµ x = κ + nµ µ n + κ nx µ µ n = κ µ + nx κ + n κ + n κ µ µ + x µ = κ µ µ + nµ x + x x 79 = κ + nµ µ n + κ nx µ + κ + n x x 8 So pµ, λ D λ e λ/κ+nµ µn 8 λ α+n/ e βλ e λ/ P x x e λ/ κ nx µ κ +n 8 Nµ µ n, κ + nλ Gaλ α + n/, β n 83 where In summary, β n = β + = x x + κ nx µ κ + n 84 pµ, λ D = NGµ, λ µ n, κ n, α n, β n 85 µ n = κ µ + nx 86 κ + n κ n = κ + n 87 α n = α + n/ 88 β n = β + x x + κ nx µ κ + n 89 = We see that the posteror sum of squares, β n, combnes the pror sum of squares, β, the sample sum of squares, x x, and a term due to the dscrepancy between the pror mean and sample mean. As can be seen from Fgure 3, the range of probable values for µ and σ can be qute large even after for moderate n. Keep ths pcture n mnd whenever someones clams to have ft a Gaussan to ther data. 8
9 3.3. Posteror margnals The posteror margnals are usng Equaton 7 pλ D = Gaλ α n, β n 9 pµ D = T αn µ µ n, β n /α n κ n Margnal lkelhood To derve the margnal lkelhood, we just dererve the posteror, but ths tme we keep track of all the constant factors. Let NG µ, λ µ, κ, α, β denote an unnormalzed Normal-Gamma dstrbuton, and let Z = Z NG µ, κ, α, β be the normalzaton constant of the pror; smlarly let Z n be the normalzaton constant of the posteror. Let N x µ, λ denote an unnormalzed Gaussan wth normalzaton constant / π. Then pµ, λ D = n/ NG µ, λ µ, κ, α, β N x µ, λ 9 pd Z π The NG and N terms combne to make the posteror NG : Hence 3.5 Posteror predctve pµ, λ D = Z n NG µ, λ µ n, κ n, α n, β n 93 pd = Z n Z π n/ 94 = Γα n Γα The posteror predctve for m new observatons s gven by β α β αn n κ κ n π n/ 95 pd new D = pd new, D pd 96 = Z n+m Z π n+m/ Z Z n π n/ 97 = Z n+m π m/ 98 Z n = Γα n+m Γα n β αn n β αn+m n+m κn κ n+m π m/ 99 In the specal case that m =, t can be shown see below that ths s a T-dstrbuton px D = t αn x µ n, β nκ n + α n κ n To derve the m = result, we proceed as follows. Ths proof s by Xang Xuan, and s based on [GH94, p]. When m =, the posteror parameters are α n+ = α n + / κ n+ = κ n + β n+ = β n + x x + κ n x µ n 3 κ n + = 9
10 Use the fact that when m =, we have x = x snce there s only one observaton, hence we have = x x =. Let s use x denote D new, then β n+ s β n+ = β n + κ nx µ n κ n + 4 Substtutng, we have the followng, pd new D = Γα n+ Γα n β αn n β αn+ n+ = Γα n + / Γα n = Γα n + / Γα n / = Γα n + / Γα n / κn κ n+ π / β αn n β n + κnx µn = π / Γα n + / Γα n / κ n+ αn+/ β n β n + κnx µn κ n+ + κnx µn β nκ n+ κn π / κ n + α n+/ α n+/ α n κ n α n β n κ n + β n κ n π / κ n + κ n π / β n κ n + + α nκ n x µ n α n β n κ n + αn+/ Let Λ = αnκn β nκ n+, then we have, pd new D = π / Γα n + / Γα n / Λ α n + Λx µ n α n αn+/ We can see ths s a T-dstrbuton wth center at µ n, precson Λ = 3.6 Reference analyss The reference pror for NG s So the posteror s αnκn β, and degree of freedom α nκ n+ n. pm, λ λ = NGm, λ µ =, κ =, α =, β = pm, λ D = NGµ n = x, κ n = n, α n = n /, β n = So the posteror margnal of the mean s x x = pm D = t n m x, x x 3 nn whch corresponds to the frequentst samplng dstrbuton of the MLE ˆµ. Thus n ths case, the confdence nterval and credble nterval concde. 4 Gamma pror If µ s known, and only λ s unknown e.g., when mplementng Gbbs samplng, we can use the followng results, whch can be derved by smplfyng the results for the Normal-NG model.
11 4. Lkelhood pd λ λ n/ exp λ x µ = 4 4. Pror pλ = Gaλ α, β λ α e λβ Posteror pλ D = Gaλ α n, β n 6 α n = α + n/ 7 β n = β + x µ 8 = 4.4 Margnal lkelhood To be completed. 4.5 Posteror predctve px D = t αn x µ, σ = β n /α n Reference analyss pλ λ = Gaλ, m pλ D = Gaλ n/, x µ = 5 Normal-nverse-ch-squared NIX pror We wll see that the natural conjugate pror for σ s the nverse-ch-squared dstrbuton. 5. Lkelhood The lkelhood can be wrtten n ths form pd µ, σ = π n/ σ n/ exp σ [ n ] x x + nx µ = 5. Pror The normal-nverse-ch-squared pror s pµ, σ = NIχ µ, κ, ν, σ 3 = Nµ µ, σ /κ χ σ ν, σ 4 = Z p µ, κ, ν, σ σ ν/+ exp σ σ [ν σ + κ µ µ ] 5 ν/ π Z p µ, κ, ν, σ = Γν / κ ν σ 6
12 NIXµ =., κ =., ν =., σ =. NIXµ =., κ =5., ν =., σ = sgma µ sgma µ.5 a NIXµ =., κ =., ν =5., σ =. b NIXµ =.5, κ =5., ν =5., σ = sgma µ sgma µ.5 c d Fgure 4: The NIχ µ, κ, ν, σ dstrbuton. µ s the pror mean and κ s how strongly we beleve ths; σ s the pror varance and ν s how strongly we beleve ths. a µ =, κ =, ν =, σ =. Notce that the contour plot underneath the surface s shaped lke a squashed egg. b We ncrease the strenght of our belef n the mean, so t gets narrower: µ =, κ = 5, ν =, σ =. c We ncrease the strenght of our belef n the varance, so t gets narrower: µ =, κ =, ν = 5, σ =. d We strongly beleve the mean and varance are.5: µ =.5, κ = 5, ν = 5, σ =.5. These plots were produced wth NIXdemo. See Fgure 4 for some plots. The hyperparameters µ and σ /κ can be nterpreted as the locaton and scale of µ, and the hyperparameters u and σ as the degrees of freedom and scale of σ. For future reference, t s useful to note that the quadratc term n the pror can be wrtten as where S = ν σ s the pror sum of squares. Q µ = S + κ µ µ 7 = κ µ κ µ µ + κ µ + S 8
13 5.3 Posteror The followng dervaton s based on [Lee4, p67]. The posteror s pµ, σ D Nµ µ, σ /κ χ σ ν, σpd µ, σ 9 [ σ σ ν/+ exp ] σ [ν σ + κ µ µ ] 3 [ σ n/ exp [ ns σ + nx µ ] ] 3 σ 3 σ νn/ exp σ [ν nσn + κ nµ n µ ] = NIχ µ n, κ n, ν n, σn 3 Matchng powers of σ, we fnd ν n = ν + n 33 To derve the other terms, we wll complete the square. Let S = ν σ and S n = ν n σn for brevty. Groupng the terms nsde the exponental, we have S + κ µ µ + ns + nx µ = S + κ µ + ns + nx + µ κ + n κ µ + nxµ34 Comparng to Equaton 8, we have One can rearrange ths to get κ n = κ + n 35 κ n µ n = κ µ + nx 36 S n + κ n µ n = S + κ µ + ns + nx 37 S n S n = S + ns + κ µ + nx κ n µ n 38 = S + ns + κ + n µ x 39 = S + ns + nκ κ + n µ x 4 We see that the posteror sum of squares, S n = ν n σ n, combnes the pror sum of squares, S = ν σ, the sample sum of squares, ns, and a term due to the uncertanty n the mean. In summary, The posteror mean s gven by The posteror mode s gven by Equaton 4 of [BL]: µ n = κ µ + nx κ n 4 κ n = κ + n 4 ν n = ν + n 43 σn = ν σ + x x + nκ ν n κ + n µ x 44 E[µ D] = µ n 45 E[σ ν n D] = ν n σ n 46 mode[µ D] = µ n 47 mode[σ D] = 3 ν nσ n ν n 48
14 The modes of the margnal posteror are mode[µ D] = µ n 49 mode[σ D] = ν nσ n ν n Margnal posteror of σ Frst we ntegrate out µ, whch s just a Gaussan ntegral. pσ D = pσ, µ Ddµ 5 σ σ νn/+ exp σ [ν nσn] exp κ n σ µ n µ ] dµ 5 σ σ νn/+ exp σ π σ [ν nσn ] 53 κn σ νn/+ exp σ [ν nσn ] 54 = χ σ ν n, σ n Margnal posteror of µ Let us rewrte the posteror as pµ, σ D = Cφ α φ exp φ [ν nσn + κ nµ n µ ] 56 where φ = σ and α = ν n + /. Ths follows snce Now make the substtutons σ σ νn/+ = σ σ νn σ = φ νn+ φ = φ α 57 A = ν n σ n + κ n µ n µ 58 x = A φ 59 so dφ dx = A x 6 pµ D = Cφ α+ e A/φ dφ 6 = A/ C A x α+ e x x dx 6 A α x α e x dx 63 A α 64 = ν n σn + κ n µ n µ νn+/ 65 [ + κ ] νn+/ n ν n σn µ µ n 66 t νn µ µ n, σn /κ n 67 4
15 5.4 Margnal lkelhood Repeatng the dervaton of the posteror, but keepng track of the normalzaton constants, gves the followng. pd = PD µ, σ Pµ, σ dµdσ Posteror predctve = Z pµ n, κ n, ν n, σn Z p µ, κ, ν, σ Zl N κ Γν n / ν σ = κn Γν / = Γν n/ Γν / ν/ νn/ 69 π n/ 7 ν n σn κ ν σ ν/ 7 κ n ν n σn νn/ π n/ px D = px µ, σ pµ, σ Ddµdσ Reference analyss = px, D pd = Γν n + / Γν n / = Γν n + / Γν n / κn 73 ν n σn νn/ κ n + ν n σn + κn κ x µ 74 n+ n νn+/ π / κ n κ n + πν n σn + κ nx µ n νn+/ κ n + ν n σn 75 = t νn µ n, + κ nσ n κ n 76 The reference pror s pµ, σ σ whch can be modeled by κ =, ν =, σ =, snce then we get See also [DeG7, p97] and [GCSR4, p88]. Wth the reference pror, the posteror s The posteror margnals are pµ, σ σ σ + e = σ σ / = σ 77 µ n = x 78 ν n = n 79 κ n = n 8 σn = x x 8 n pµ, σ D σ n exp σ [ x x + nx µ ] 8 pσ D = χ σ n, x x 83 n pµ D = t n µ x, x x 84 nn 5
16 whch are very closely related to the samplng dstrbuton of the MLE. The posteror predctve s px D = t n x, + x x nn 85 Note that [Mn] argues that Jeffrey s prncple says the unnformatve pror should be of the form lm Nµ µ, σ /kχ σ k, σ k πσ σ σ 3 86 Ths can be acheved by settng ν = nstead of ν =. 6 Normal-nverse-Gamma NIG pror Another popular parameterzaton s the followng: pµ, σ = NIGm, V, a, b 87 = Nµ m, σ V IGσ a, b Lkelhood The lkelhood can be wrtten n ths form pd µ, σ = π n/ σ n/ exp [ ns σ + nx µ ] Pror pµ, σ = NIGm, V, a, b 9 = Nµ m, σ V IGσ a, b 9 Ths s equvalent to the NIχ pror, where we make the followng substtutons. m = µ 9 V = κ 93 a = ν b = ν σ Posteror We can show that the posteror s also NIG: pµ, σ D = NIGm n, V n, a n, b n 96 Vn = V + n 97 m n V n = V m + nx 98 a n = a + n/ 99 b n = b + [m V + x m n V n ] The NIG posteror follows drectly from the NIχ results usng the specfed substtutons. The b n term requres some tedous algebra... 6
17 6.3. Posteror margnals To be derved. 6.4 Margnal lkelhood For the margnal lkelhood, substtutng nto Equaton 7 we have pd = Γa n Vn b a Γa V b n an π n/ = V n b a Γa n V b an n Γa π n/ a an = V n b a Γa n V 3 b an n Γa π n/ n 6.5 Posteror predctve For the predctve densty, substtutng nto Equaton 76 we have κ n + κ n σ n = = κ n + σn a n b n + V n 4 5 So py D = t an m n, b n + V n a n 6 These results follow from [DHMS, p4] by settng x =, β = µ, B T B = n, B T X = nx, X T X = x. Note that we use a dfference parameterzaton of the student-t. Also, our equatons for pd dffer by a n term. 7 Multvarate Normal pror If we assume Σ s known, then a conjugate analyss of the mean s very smple, snce the conjugate pror for the mean s Gaussan, the lkelhood s Gaussan, and hence the posteror s Gaussan. The results are analogous to the scalar case. In partcular, we use the general result from [Bs6, p9] wth the followng substtutons: 7. Pror 7. Lkelhood x = µ, y = x, Λ = Σ, A = I, b =, L = Σ/N 7 pµ = Nµ µ, Σ Posteror pd µ, Σ Nx µ, Σ 9 N pµ D, Σ = Nµ µ N, Σ N Σ N = Σ + NΣ µ N = Σ N NΣ x + Σ µ 7
18 7.4 Posteror predctve px D = Nx µ N, Σ + Σ N Reference analyss 8 Normal-Wshart pror pµ = Nµ, I 4 pµ D = Nx, Σ/n 5 The multvarate analog of the normal-gamma pror s the normal-wshart pror. Here we just state the results wthout proof; see [DeG7, p78] for detals. We assume X s a d-dmensonal. 8. Lkelhood 8. Pror pd µ, Λ = π nd/ Λ n/ exp = x µ T Λx µ 6 pµ, Λ = NWµ, Λ µ, κ, ν, T = Nµ µ, κλ W ν Λ T 7 = Z Λ exp κ µ µ T Λµ µ Λ κ d / exp trt Λ 8 κ d/ Z = T κ/ dκ/ Γ d κ/ 9 π Here T s the pror covarance. To see the connecton to the scalar case, make the substtutons α = ν, β = T 8.3 Posteror pµ, Λ D = Nµ µ n, κ n Λ W νn Λ T n µ n = κµ + nx κ + n T n = T + S + κn κ + n µ xµ x T 3 S = x xx x T 4 = ν n = ν + n 5 κ n = κ + n 6 Posteror margnals pλ D = W νn T n 7 pµ D = T n t νn d+µ µ n, κ n ν n d + 8 8
19 The MAP estmates are gven by ˆµ, ˆΛ = ˆµ = ˆΣ = argmax pd µ, ΛNWµ, Λ 9 µ,λ x + κ µ N + κ 3 = n = x ˆµx ˆµ T + κ ˆµ µ ˆµ µ T + T N + ν d 3 Ths reduces to the MLE f κ =, ν = d and T =. 8.4 Posteror predctve If d =, ths reduces to Equaton. 8.5 Margnal lkelhood px D = t νn d+µ n, Ths can be computed as a rato of normalzaton constants. T n κ n + κ n ν n d + 3 pd = Z n 33 Z π nd/ Γ d ν n / T ν/ d/ κ = 34 π nd/ Γ d ν / T n νn/ κ n Ths reduces to Equaton 95 f d =. 8.6 Reference analyss We set to gve µ =, κ =, ν =, T = 35 pµ, Λ Λ d+/ 36 Then the posteror parameters become the posteror margnals become and the posteror predctve becomes µ n = x, T n = S, κ n = n, ν n = n 37 S pµ D = t n d µ x, nn d 38 pλ D = W n d Λ S 39 px D = t n d x, Sn + nn d 4 9 Normal-Inverse-Wshart pror The multvarate analog of the normal nverse ch-squared NIX dstrbuton s the normal nverse Wshart NIW see also [GCSR4, p85]. 9
20 9. Lkelhood The lkelhood s pd µ, Σ Σ n exp x µ T Σ x µ = = Σ n exp trσ S where S s the matrx of sum of squares scatter matrx 9. Pror S = N x xx x T 44 = The natural conjugate pror s normal-nverse-wshart 9.3 Posteror The posteror s Σ IW ν Λ 45 µ Σ Nµ, Σ/κ 46 pµ, Σ The margnals are def = NIWµ, κ, Λ, ν 47 = Z Σ ν+d/+ exp trλ Σ κ µ µ T Σ µ µ 48 Z = vd/ Γ d ν /π/κ d/ Λ ν/ 49 pµ, Σ D, µ, κ, Λ, ν = NIWµ, Σ µ n, κ n, Λ n, ν n 5 µ n = κ µ + + ny = κ κ n κ + n µ + n κ + n y 5 κ n = κ + n 5 ν n = ν + n 53 Λ n = Λ + S + κ n κ + n x µ x µ T 54 Σ D IWΛ n, ν n 55 µ D = Λ n t νn d+µ n, κ n ν n d + 56 To see the connecton wth the scalar case, note that Λ n plays the role of ν n σn posteror sum of squares, so Λ n κ n ν n d + = Λ n κ n ν n = σ κ n 57
21 9.4 Posteror predctve px D = t νn d+µ n, To see the connecton wth the scalar case, note that 9.5 Margnal lkelhood The posteror s gven by where Λ n κ n + κ n ν n d + 58 Λ n κ n + κ n ν n d + = Λ nκ n + = σ κ n + 59 κ n ν n κ n pµ, Σ D = NIW µ, Σ α pd Z π N D µ, Σ 6 nd/ = NIW µ, Σ α n 6 Z n Σ ν+d/+ exp NIW µ, Σ α = trλ Σ κ N D µ, Σ = Σ n exp trσ S s the unnormalzed pror and lkelhood. Hence µ µ T Σ µ µ 6 63 pd = Z n Z π nd/ = νnd/ Γ d ν n /π/κ n d/ Λ n νn/ Λ ν/ νd/ Γ d ν /π/κ d/ π nd/ 64 = = Ths reduces to Equaton 7 f d =. 9.6 Reference analyss νnd/ π/κ n d/ Γ d ν n / π nd/ νd/ π/κ d/ Γ d ν / 65 Γ d ν n / Λ ν/ d/ κ π nd/ Γ d ν / Λ n νn/ 66 κ n A nonnformatve Jeffrey s pror s pµ, Σ Σ d+/ whch s the lmt of κ, ν, Λ [GCSR4, p88]. Then the posteror becomes µ n = x 67 κ n = n 68 ν n = n 69 Λ n = S = x xx x T 7 pσ D = IW n Σ S 7 pµ D = S t n d µ x, nn d 7 px D = t n d x x, Sn + nn d 73 Note that [Mn] argues that Jeffrey s prncple says the unnformatve pror should be of the form lm Nµ µ, Σ/kIW k Σ kσ πσ Σ d+/ Σ d + 74 k Ths can be acheved by settng ν = nstead of ν =.
22 Gammashape=a,rate=b a=.5, b=. a=., b=. a=.5, b=. a=., b=. a=5., b=. 3.5 Gammashape=a,rate=b a=.5, b=3. a=., b=3. a=.5, b=3. a=., b=3. a=5., b= Fgure 5: Some Gaa, b dstrbutons. If a <, the peak s at. As we ncrease b, we squeeze everythng leftwards and upwards. Fgures generated by gammadstplot. Appendx: some standard dstrbutons. Gamma dstrbuton The gamma dstrbuton s a flexble dstrbuton for postve real valued rv s, x >. It s defned n terms of two parameters. There are two common parameterzatons. Ths s the one used by Bshop [Bs6] and many other authors: Gax shape = a, rate = b = b a Γa xa e xb, x, a, b > 75 The second parameterzaton and the one used by Matlab s gampdf s Gax shape = α, scale = β = β α Γα xα e x/β = Ga rate x α, /β 76 Note that the shape parameter controls the shape; the scale parameter merely defnes the measurement scale the horzontal axs. The rate parameter s just the nverse of the scale. See Fgure 5 for some examples. Ths dstrbuton has the followng propertes usng the rate parameterzaton:. Inverse Gamma dstrbuton mean = a 77 b mode = a for a 78 b var = a b 79 Let X Gashape = a, rate = b and Y = /X. Then t s easy to show that Y IGshape = a, scale = b, where the nverse Gamma dstrbuton s gven by IGx shape = a, scale = b = b a Γa x a+ e b/x, x, a, b > 8
23 .4. IGa,b a=., b=. a=., b=. a=., b=. a=., b=. a=., b=. a=., b= Fgure 6: Some nverse gamma dstrbutons a=shape, b=rate. These plots were produced by nvchplot. The dstrbuton has these propertes mean = mode = var = b a, a > 8 b a + 8 b a a, a > 83 See Fgure 6 for some plots. We see that ncreasng b just stretches the horzontal axs, but ncreasng a moves the peak up and closer to the left. There s also another parameterzaton, usng the rate nverse scale:.3 Scaled Inverse-Ch-squared IGx shape = α, rate = β = β a Γax α+ e /βx, x, α, β > 84 The scaled nverse-ch-squared dstrbuton s a reparameterzaton of the nverse Gamma [GCSR4, p575]. χ x ν, σ = Γν/ νσ ν/ x ν exp[ νσ ], x > 85 x = IGx shape= ν, scale=νσ 86 where the parameter ν > s called the degrees of freedom, and σ > s the scale. See Fgure 7 for some plots. We see that ncreasng ν lfts the curve up and moves t slghtly to the rght. Later, when we consder Bayesan parameter estmaton, we wll use ths dstrbuton as a conjugate pror for a scale parameter such as the varance of a Gaussan; ncreasng ν corresponds to ncreasng the effectve strength of the pror. 3
24 .5 χ ν,σ ν=., σ =.5 ν=., σ =. ν=., σ =. ν=5., σ =.5 ν=5., σ =. ν=5., σ = Fgure 7: Some nverse scaled χ dstrbutons. These plots were produced by nvchplot. The dstrbuton has these propertes mean = νσ for ν > 87 ν mode = νσ 88 ν + ν σ 4 var = ν for ν > 4 89 ν 4 The nverse ch-squared dstrbuton, wrtten χ ν x, s the specal case where νσ =.e., σ = /ν. Ths corresponds to IGa = ν/, b = scale = /..4 Wshart dstrbuton Let X be a p dmensonal symmetrc postve defnte matrx. The Wshart s the multdmensonal generalzaton of the Gamma. Snce t s a dstrbuton over matrces, t s hard to plot as a densty functon. However, we can easly sample from t, and then use the egenvectors of the resultng matrx to defne an ellpse. See Fgure 8. There are several possble parameterzatons. Some authors e.g., [Bs6, p693], [DeG7, p.57],[gcsr4, p574], wkpeda as well as WnBUGS and Matlab wshrnd, defne the Wshart n terms of degrees of freedom ν p and the scale matrx S as follows: W ν X S = Z X ν p / exp[ trs X] 9 Z = νp/ Γ p ν/ S ν/ 9 where Γ p a s the generalzed gamma functon p α + Γ p α = π pp /4 Γ So Γ α = Γα. The mean and mode are gven by see also [Pre5] = 9 mean = νs 93 mode = ν p S, ν > p
25 Wshartdof=.,S=[4 3; 3 4] Wshartdof=.,S=[4 3; 3 4] Fgure 8: Some samples from the Wshart dstrbuton. Left: ν =, rght: ν =. We see that f f ν = the smallest vald value n dmensons, we often sample nearly sngular matrces. As ν ncreases, we put more mass on the S matrx. If S = I, the samples would look on average lke crcles. Generated by wshplot. In D, ths becomes Gashape = ν/, rate = S/. Note that f X WuS, and Y = X, then Y IW ν S and E[Y ] = S ν d. In [BS94, p.38], and the wshpdf n Tom Mnka s lghtspeed toolbox, they use the followng parameterzaton WX a,b = B a Γ p a X a p+/ exp[ trbx] 95 We requre that B s a p p symmetrc postve defnte matrx, and a > p. If p =, so B s a scalar, ths reduces to the Gashape = a, rate= b densty. To get some ntuton for ths dstrbuton, recall that trab s a vector whch contans the nner product of the rows of A and the columns of B. In Matlab notaton we have tracea B = [a,:*b:,,..., an,:*b:,n] If X W ν S, then we are performng a knd of template matchng between the columns of X and S recall that both X and S are symmetrc. Ths s a natural way to defne the dstance between two matrces..5 Inverse Wshart Ths s the multdmensonal generalzaton of the nverse Gamma. Consder a d d postve defnte covarance matrx X and a dof parameter ν > d and psd matrx S. Some authors eg [GCSR4, p574] use ths parameterzaton: IW ν X S = Z X ν+d+/ exp TrSX 96 Z = S ν/ νd/ Γ d ν/ 97 where Γ d ν/ = π dd /4 d = Γ ν
26 The dstrbuton has mean In Matlab, use wshrnd. In the d case, we have E X = S ν d 99 χ Σ ν, σ = IW ν Σ ν σ 3 Other authors e.g., [Pre5, p7] use a slghtly dfferent formulaton wth d < ν d IW ν X Q = ν d d/ π dd /4 Γν d j/ whch has mean.6 Student t dstrbuton The generalzed t-dstrbuton s gven as j= Q ν d / X ν/ exp E X = t ν x µ, σ = c = Q ν d TrX Q [ c + ν x µ ] ν+ σ 34 Γν/ + / Γν/ νπσ 35 where c s the normalzaton consant. µ s the mean, ν > s the degrees of freedom, and σ > s the scale. Note that the ν parameter s often wrtten as a subscrpt. In Matlab, use tpdf. The dstrbuton has the followng propertes: mean = µ, ν > 36 mode = µ 37 var = νσ ν, ν > 38 Note: f x t ν µ, σ, then x µ t ν 39 σ whch corresponds to a standard t-dstrbuton wth µ =, σ = : t ν x = Γν + / νπγν/ + x /ν ν+/ 3 In Fgure 9, we plot the densty for dfferent parameter values. As ν, the T approaches a Gaussan. T- dstrbutons are lke Gaussan dstrbutons wth heavy tals. Hence they are more robust to outlers see Fgure. If ν =, ths s called a Cauchy dstrbuton. Ths s an nterestng dstrbuton snce f X Cauchy, then E[X] does not exst, snce the correspondng ntegral dverges. Essentally ths s because the tals are so heavy that samples from the dstrbuton can get very far from the center µ. It can be shown that the t-dstrbuton s lke an nfnte sum of Gaussans, where each Gaussan has a dfferent precson: px µ, a, b = Nx µ, τ Gaτ a, rate = bdτ 3 See exercse.46 of [Bs6]. = t a x µ, b/a 3 6
27 Student T dstrbutons tν=. tν=. tν=5. N, Fgure 9: Student t-dstrbutons Tµ, σ, ν for µ =. The effect of σ s just to scale the horzontal axs. As ν, the dstrbuton approaches a Gaussan. See studenttplot a 5 5 b Fgure : Fttng a Gaussan and a Student dstrbuton to some data left and to some data wth outlers rght. The Student dstrbuton red s much less affected by outlers than the Gaussan green. Source: [Bs6] Fgure.6. 7
28 T dstrbuton, dof. Gaussan Fgure : Left: T dstrbuton n d wth dof= and Σ =.I. Rght: Gaussan densty wth Σ =.I and µ =, ; we see t goes to zero faster. Produced by multvartplot..7 Multvarate t dstrbutons The multvarate T dstrbuton n d dmensons s gven by t ν x µ, Σ = Γν/ + d/ Γν/ Σ / v d/ π d/ [ + ] ν+d ν x µt Σ x µ 33 where Σ s called the scale matrx snce t s not exactly the covarance matrx. Ths has fatter tals than a Gaussan: see Fgure. In Matlab, use mvtpdf. The dstrbuton has the followng propertes 34 E x = µ f ν > 35 mode x = µ 36 Cov x = ν Σ for ν > ν 37 The followng results are from [Koo3, p38]. Suppose Y Tµ, Σ, ν and we partton the varables nto blocks. Then the margnals are Y Tµ, Σ, ν 38 and the condtonals are We can also show lnear combnatons of Ts are Ts: Y y Tµ, Σ, ν + d 39 µ = µ + Σ Σ y µ 3 Σ = h Σ Σ Σ ΣT 3 h = [ ν + y µ T Σ ν + d µ ] 3 Y Tµ, Σ, ν AY TAµ, AΣA, ν 33 We can sample from a y Tµ, Σ, ν by samplng x T,, ν and then transformng y = µ + R T x, where R = cholσ, so R T R = Σ. 8
29 References [Bs6] C. Bshop. Pattern recognton and machne learnng. Sprnger, 6. [BL] P. Bald and A. Long. A Bayesan framework for the analyss of mcroarray expresson data: regularzed t-test and statstcal nferences of gene changes. Bonformatcs, 76:59 59,. [BS94] J. Bernardo and A. Smth. Bayesan Theory. John Wley, 994. [DeG7] M. DeGroot. Optmal Statstcal Decsons. McGraw-Hll, 97. [DHMS] D. Denson, C. Holmes, B. Mallck, and A. Smth. Bayesan methods for nonlnear classfcaton and regresson. Wley,. [DMP + 6] F. Demchels, P. Magn, P. Pergorg, M. Rubn, and R. Bellazz. A herarchcal Nave Bayes model for handlng sample heterogenety n classfcaton problems: an applcaton to tssue mcroarrays. BMC Bonformatcs, 7:54, 6. [GCSR4] A. Gelman, J. Carln, H. Stern, and D. Rubn. Bayesan data analyss. Chapman and Hall, 4. nd edton. [GH94] D. Geger and D. Heckerman. Learnng Gaussan networks. Techncal Report MSR-TR-94-, Mcrosoft Research, 994. [Koo3] Gary Koop. Bayesan econometrcs. Wley, 3. [Lee4] Peter Lee. Bayesan statstcs: an ntroducton. Arnold Publshng, 4. Thrd edton. [Mn] T. Mnka. Inferrng a Gaussan dstrbuton. Techncal report, MIT,. [Pre5] S. J. Press. Appled multvarate analyss, usng Bayesan and frequentst methods of nference. Dover, 5. Second edton. 9
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
A Sequential Experimental Design based on Bayesian Statistics for Online Automatic Tuning. Reiji SUDA,
 Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng
Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
Derivation for Input of Factor Graph Representation
 Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
( ) 2 and compare to M.
 Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
8.323 Relativistic Quantum Field Theory I
 MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Supporting information for: Functional Mixed Effects Model for Small Area Estimation
 Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
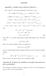 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ. ICA: συναρτήσεις κόστους & εφαρμογές
 8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
5 Haar, R. Haar,. Antonads 994, Dogaru & Carn Kerkyacharan & Pcard 996. : Haar. Haar, y r x f rt xβ r + ε r x β r + mr k β r k ψ kx + ε r x, r,.. x [,
 4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Generalized Linear Model [GLM]
![Generalized Linear Model [GLM] Generalized Linear Model [GLM]](/thumbs/93/113885699.jpg) Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
Symplecticity of the Störmer-Verlet algorithm for coupling between the shallow water equations and horizontal vehicle motion
 Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
An Inventory of Continuous Distributions
 Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Solutions for Mathematical Physics 1 (Dated: April 19, 2015)
 Solutons for Mathematcal Physcs 1 Dated: Aprl 19, 215 3.2.3 Usng the vectors P ê x cos θ + ê y sn θ, Q ê x cos ϕ ê y sn ϕ, R ê x cos ϕ ê y sn ϕ, 1 prove the famlar trgonometrc denttes snθ + ϕ sn θ cos
Solutons for Mathematcal Physcs 1 Dated: Aprl 19, 215 3.2.3 Usng the vectors P ê x cos θ + ê y sn θ, Q ê x cos ϕ ê y sn ϕ, R ê x cos ϕ ê y sn ϕ, 1 prove the famlar trgonometrc denttes snθ + ϕ sn θ cos
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Exam Statistics 6 th September 2017 Solution
 Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES. Reading: QM course packet Ch 5 up to 5.6
 SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES Readig: QM course packet Ch 5 up to 5. 1 ϕ (x) = E = π m( a) =1,,3,4,5 for xa (x) = πx si L L * = πx L si L.5 ϕ' -.5 z 1 (x) = L si
SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES Readig: QM course packet Ch 5 up to 5. 1 ϕ (x) = E = π m( a) =1,,3,4,5 for xa (x) = πx si L L * = πx L si L.5 ϕ' -.5 z 1 (x) = L si
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Supplementary materials for Statistical Estimation and Testing via the Sorted l 1 Norm
 Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
TMA4115 Matematikk 3
 TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
Durbin-Levinson recursive method
 Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C
 DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Notes on the Open Economy
 Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Pricing of Options on two Currencies Libor Rates
 Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Concomitants of Dual Generalized Order Statistics from Bivariate Burr III Distribution
 Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Suppose Mr. Bump observes the selling price and sales volume of milk gallons for 10 randomly selected weeks as follows
 Albert Ludwgs Unverst Freburg Department of Emprcal Research and Econometrcs Appled Econometrcs Dr Kestel ummer 9 EXAMPLE IMPLE LINEAR REGREION ANALYI uppose Mr Bump observes the sellng prce and sales
Albert Ludwgs Unverst Freburg Department of Emprcal Research and Econometrcs Appled Econometrcs Dr Kestel ummer 9 EXAMPLE IMPLE LINEAR REGREION ANALYI uppose Mr Bump observes the sellng prce and sales
FORMULAS FOR STATISTICS 1
 FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
 9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
2 Lagrangian and Green functions in d dimensions
 Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Parametrized Surfaces
 Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Solution Set #2
 . For the followng two harmon waves: (a) Show on a phasor dagram: 05-55-007 Soluton Set # phasor s the omplex vetor evaluated at t 0: f [t] os[ω 0 t] h f [t] 7os ω 0 t π f [t] exp[ 0] + 0 h f [t] 7exp
. For the followng two harmon waves: (a) Show on a phasor dagram: 05-55-007 Soluton Set # phasor s the omplex vetor evaluated at t 0: f [t] os[ω 0 t] h f [t] 7os ω 0 t π f [t] exp[ 0] + 0 h f [t] 7exp
Duals of the QCQP and SDP Sparse SVM. Antoni B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckriet
 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckret SVCL-TR 007-0 v Aprl 007 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R.
Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckret SVCL-TR 007-0 v Aprl 007 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R.
Exercise 2: The form of the generalized likelihood ratio
 Stats 2 Winter 28 Homework 9: Solutions Due Friday, March 6 Exercise 2: The form of the generalized likelihood ratio We want to test H : θ Θ against H : θ Θ, and compare the two following rules of rejection:
Stats 2 Winter 28 Homework 9: Solutions Due Friday, March 6 Exercise 2: The form of the generalized likelihood ratio We want to test H : θ Θ against H : θ Θ, and compare the two following rules of rejection:
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Theorem 8 Let φ be the most powerful size α test of H
 Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ
 ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙΔΡΑΣΗ Μ.Β ΣΤΙΣ ΙΔΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ (ΔΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙΔΡΑΣΗ Μ.Β ΣΤΙΣ ΙΔΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ (ΔΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ
 ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙ ΡΑΣΗ Μ.Β ΣΤΙΣ Ι ΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ ( ΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙ ΡΑΣΗ Μ.Β ΣΤΙΣ Ι ΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ ( ΙΑΦΟΡΙΚΗ) Probablty Densty Functon
