High order transmission conditions for conductive thin sheets Asymptotic Expansions versus Thin Sheet Bases

Transcript

1 High order transmission conditions for conductive thin sheets Asymptotic Expansions versus Thin Sheet Bases Kersten Schmidt, Sébastien Tordeux 2 Project POEMS, INRIA Paris-Rocquencourt, 2 Toulouse Mathematics Institute Workshop Asymptotic methods, mechanics and other applications, ENS Cachan Bretagne, September st 29

2 Outline Introduction Applications The meshing problem Model problem Geometry for the transmission problem and different frameworks Thin sheet basis First order impedance boundary condition Bound of modelling error by best approximation error Derivation of basis to any order Numerical results Asymptotic Expansions Derivation of the iterative models Existence, uniqueness, regularity and convergence Decoupling and models only exterior field Numerical experiments with high-order FEM Collectively computed model of order Collectively computed models of higher orders Comparison of thin sheet basis and asymptotic expansions Conclusion K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 2/ 43

3 Introduction Applications Transformator inside a conducting casing. Protection of integrated circuits. Cable with a foil shield. Thin conducting sheets for electromagnetic shielding, for mechanical stability, as casing for liquids and gases, with little material wastage. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 3/ 43

4 Introduction The meshing problem Difficult to create by most mesh generators. High number of triangles. Even more triangles for resolving the sheet. Triangle mesh inside the sheet. Conforming triangle mesh resolving the sheet. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 4/ 43

5 Introduction The meshing problem Difficult to create by most mesh generators. High number of triangles. Even more triangles for resolving the sheet. Triangle mesh inside the sheet. Conforming triangle mesh resolving the sheet. Quadrilateral cells with large aspect ratio. Thin sheet basis functions inside the sheet (and no lateral refinement). Conforming quadrilateral mesh resolving a thin sheet. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 4/ 43

6 Introduction The meshing problem Difficult to create by most mesh generators. High number of triangles. Even more triangles for resolving the sheet. Triangle mesh inside the sheet. Conforming triangle mesh resolving the sheet. Quadrilateral cells with large aspect ratio. Thin sheet basis functions inside the sheet (and no lateral refinement). Replace the thin sheet by an interface. Replace its behaviour by transmission conditions resulting from asymptotic expansions. Conforming quadrilateral mesh resolving a thin sheet. Conforming triangle mesh resolving an interface. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 4/ 43

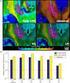
7 Introduction The Model Time-harmonic Eddy-current model for low frequency applications Two important effects curle = iωµh, curlh = σe + j Shielding effect in conductors induced currents diminish electromagnetic fields (behind the conductors) Skin effect major current flow in a boundary layer (skins of the conductor) Without conducting sheet. With conducting sheet. Field generated by an alternating current inside a cylindrical conductor. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 5/ 43

8 Introduction Model Time-harmonic Eddy-current model for low frequency applications Two important effects curle = iωµh, curlh = σe + j Shielding effect in conductors induced currents diminish electromagnetic fields (behind the conductors) Skin effect major current flow in a boundary layer (skins of the conductor) δ q δ = 2 δ d δ d δ d µσω Skin depth in solid body. Skin effect in thin conducting sheets. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 6/ 43

9 Introduction Model Time-harmonic Eddy-current model for low frequency applications Two important effects curle = iωµh, curlh = σe + j Shielding effect in conductors induced currents diminish electromagnetic fields (behind the conductors) Skin effect major current flow in a boundary layer (skins of the conductor) Time-harmonic Eddy-current model in 2D (TM mode) e(x) + iωµ σe(x) = iωµ j (x) Consider the Model problem in 2D including these effects u + cu = f, with conductivity c(x) vanishing outside the thin conductive sheet. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 7/ 43

10 Introduction Geometry for the transmission problem Geometry Ω ε int... thin conducting sheet of thickness ε Ω ε ext... non-conducting domain ε t Ω = Ω ε int Ωε ext Ω ε int n Ω ε ext s Γ m... midline of Ω ε int smooth mapping b Γ R Γ m Ω Ω local orthogonal coordinate system in Ω ε int local coordinates (t, s) b Γ [ ε 2, ε 2 ] n... left unit normal vector Goal : Description of thin conducting sheets of higher order. Two strategies A. Approximation of the solution inside the sheet by an optimal basis. B. Asymptotic analysis of the solution inside and outside the sheet. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 8/ 43

11 Introduction Geometry for the transmission problem and different frameworks Ω ε int n Ω ε ext ε s t Geometry Ω ε int... thin conducting sheet of thickness ε Ω ε ext... non-conducting domain Ω = Ω ε int Ωε ext Γ m... midline of Ω ε int smooth mapping b Γ R Γ m Ω Ω local orthogonal coordinate system in Ω ε int local coordinates (t, s) b Γ [ ε 2, ε 2 ] n... left unit normal vector Frameworks with ε varying conductivity u ε + c(ε) u ε == f c(ε) = c... compare sheets of constant material c(ε) = c ε... compare sheets of constant shielding Modelling error in ε related to a particular framework K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 8/ 43

12 Outline Introduction Applications The meshing problem Model problem Geometry for the transmission problem and different frameworks Thin sheet basis First order impedance boundary condition Bound of modelling error by best approximation error Derivation of basis to any order Numerical results Asymptotic Expansions Derivation of the iterative models Existence, uniqueness, regularity and convergence Decoupling and models only exterior field Numerical experiments with high-order FEM Collectively computed model of order Collectively computed models of higher orders Comparison of thin sheet basis and asymptotic expansions Conclusion K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 9/ 43

13 Thin sheet basis First order impedance boundary condition.8 First order impedance boundary conditions (e. g. Igarashi et. al., 998) use fundamental solutions of the ODE in thickness direction after neglecting longitudinal variations and the curvature. u ε int + cuε int = 2 s u ε int + cuε int e± cs ε 2 φ ε int, φ ε int, ε s 2 ε t Ω ε int Ω ε ext s n Ω Ω K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. / 43

14 Thin sheet basis First order impedance boundary condition.8 First order impedance boundary conditions (e. g. Igarashi et. al., 998) use fundamental solutions of the ODE in thickness direction after neglecting longitudinal variations and the curvature. u ε int + cuε int = 2 s u ε int + cuε int e± cs ε 2 φ ε int, φ ε int, ε s 2 Dirichlet-to-Neumann map is derived on Γ ε nuint ε (t, + ε 2 ) «u ε nuint ε (t, ε 2 ) int (t, + ε 2 ) «uint ε (t, ε 2 ) Ω ε int n Ω ε ext ε s t Ω Ω K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. / 43

15 Thin sheet basis First order impedance boundary condition.8 First order impedance boundary conditions (e. g. Igarashi et. al., 998) use fundamental solutions of the ODE in thickness direction after neglecting longitudinal variations and the curvature. u ε int + cuε int = 2 s u ε int + cuε int e± cs ε 2 φ ε int, φ ε int, ε s 2 Dirichlet-to-Neumann map is derived on Γ ε nuint ε (t, + ε 2 ) «u ε nuint ε (t, ε 2 ) int (t, + ε 2 ) «uint ε (t, ε 2 ) Ω ε int n Ω ε ext ε s t and used for transmission conditions on the mid-line Γ m nuext ε ««(t, +) u ε nuext ε (t, ) ext (t, +) uext ε (t, ) Ω Ω Condition at Γ ε used at Γ m Modelling error of O(ε) independent of any improvement in the interior Γ m n Ω ext Ω Ω K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. / 43

16 Thin sheet basis Extension to higher orders Approximation of higher order without reduction to an interface Ansatz for the solution inside the sheet N uint ε (t, s) uε int,n (t, s) = X φ ε int,i (s, t)uε int,i (t). i= Ω ε int n Ω ε ext ε s t with N 2 linear independent basis functions φ ε int,i spanning V ε N, and uε int,i H ( b Γ). Ω Ω Estimate of the overall modelling error only that in the sheet WN nu ε := : u ext H (Ω ε ext ),u int VN ε H ( b o Γ), u ext = u int H (Γ ε ) H (Ω) H (Ω)-ellipticity estimate by best-approximation by Cea s Lemma u ε u ε N H (Ω) C inf u N W ε N u ε u N H (Ω) K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. / 43

17 Thin sheet basis Extension to higher orders Approximation of higher order without reduction to an interface Ansatz for the solution inside the sheet N uint ε (t, s) uε int,n (t, s) = X φ ε int,i (s, t)uε int,i (t). i= Ω ε int n Ω ε ext ε s t with N 2 linear independent basis functions φ ε int,i spanning V ε N, and uε int,i H ( b Γ). Ω Ω Estimate of the overall modelling error only that in the sheet fw N nu ε := : u ext H (Ω ε ext ),u int VN ε H ( b o Γ), u ext = u int = u ε H (Γ ε ) WN ε H (Ω)-ellipticity estimate by best-approximation by Cea s Lemma u ε u ε N H (Ω) C inf u N W ε N = C inf u N f W ε N u ε u N H (Ω) C u ε u N H (Ω ε ext ) {z } inf u N f W ε N u ε u N H (Ω) +C inf u ε u N H u N W f N ε (Ω ε int ) K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. / 43

18 Thin sheet basis Extension to higher orders Approximation of higher order without reduction to an interface Ansatz for the solution inside the sheet N uint ε (t, s) uε int,n (t, s) = X φ ε int,i (s, t)uε int,i (t). i= Ω ε int n Ω ε ext ε s t with N 2 linear independent basis functions φ ε int,i spanning V ε N, and uε int,i H ( b Γ). Ω Ω Estimate of the overall modelling error only that in the sheet fw N nu ε := : u ext H (Ω ε ext ),u int VN ε H ( b o Γ), u ext = u int = u ε H (Γ ε ) WN ε H (Ω)-ellipticity estimate by best-approximation by Cea s Lemma u ε u ε N H (Ω) C inf u N W ε N = C inf u N f W ε N u ε u N H (Ω) C u ε u N H (Ω ε ext ) {z } inf u N f W ε N u ε u N H (Ω) +C inf u ε u N H u N W f N ε (Ω ε int ) C u ε w ε N H (Ω ε int ) for some candidate function w ε N K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. / 43

19 Thin sheet basis Extension to higher orders for the circular sheet Dirichlet boundary value problem in Ω ε int u ε int + c(ε) uε int = in Ωε int. Circular sheet + c(ε) = ( 2 s κ +sκ s + c(ε)) (+sκ) 2 2 t Corresponding bilinear form (v H (Ωε int )) a int (u, v) := ( su su + c(ε)uv) ( + sκ) + tu tv ds dt Ω ε + sκ int Error of candidate function in H (Ω ε int )-seminorm u ε wn ε 2 H (Ω ε int ) a int(u ε wn ε,uε wn ε ) = a int(wn ε,uε wn ε ) min K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 2/ 43

20 Thin sheet basis Extension to higher orders for the circular sheet Error of candidate function in H (Ω ε int )-seminorm u ε wn ε 2 H (Ω ε int ) a int(u ε wn ε,uε wn ε ) = a int(wn ε,uε wn ε ) min Bilinear form (u H 2 (Ω ε int ), v H (Ωε int )) a int (u, v) := Ω ε int ( + sκ)( s 2 κ s + c(ε)) + sκ {z } scales with ε uv + sκ 2 t uv ds dt Candidate function for N = 2 satisfying boundary data with φ ε int, (± ε 2 ) =, φε int, (± ε 2 ) = ± 2 a int (w ε 2, v) = Ω ε int w2 ε (s, t) = φε int, (s){uε }(t) + φ ε int, (s) [uε ](t). {z } for illustration (+sκ){u ε }(t)( s 2 κ +sκ s + c(ε))φε int, (s) 2 t {uε }(t) +sκ φε int, (s)v ds dt {z } Choose basis functions φ ε int,, φε int, in the kernel of ( 2 s κ +sκ + c(ε)) K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 3/ 43

21 Thin sheet basis Extension to higher orders for the circular sheet Error of candidate function in H (Ω ε int )-seminorm u ε wn ε 2 H (Ω ε int ) a int(u ε wn ε,uε wn ε ) = a int(wn ε,uε wn ε ) min Bilinear form (u H 2 (Ω ε int ), v H (Ωε int )) a int (u, v) := ( + sκ)( Ω ε s 2 κ s + c(ε)) uv + sκ + sκ 2 t uv ds dt int {z } scales with ε Candidate function for N = 4 satisfying boundary data with φ ε int,2 (± ε 2 ) = φε int,3 (± ε 2 ) = w ε 4 (s, t) = wε 2 (s, t) + φε int,2 (s)uε int,2 (t). a int (w4 ε,v) = 2 t {uε }(t) Ω ε +sκ φε int, (s)v + (+sκ)uε int,2 (t)( 2 s κ +sκ s + c(ε))φε int,2 (s)v ds dt int + 2 t uε int,2 (t) +sκ φε int,2(s) v ds dt Ω ε int Choose basis functions φ ε int,2, φε int,3 such that ( 2 s κ +sκ + c(ε))φε int,2 (s) = ε2 φ ε int, (s) K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 3/ 43

22 Thin sheet basis Extension to higher orders for the circular sheet Error of candidate function in H (Ω ε int )-seminorm u ε wn ε 2 H (Ω ε int ) a int(u ε wn ε,uε wn ε ) = a int(wn ε,uε wn ε ) min Bilinear form (u H 2 (Ω ε int ), v H (Ωε int )) a int (u, v) := ( + sκ)( Ω ε s 2 κ s + c(ε)) + sκ int {z } scales with ε uv + sκ 2 t uv ds dt Choose basis functions ( 2 s κ + sκ + c(ε))φε int, (s) = ( 2 s κ + sκ + c(ε))φε int,2 (s) = ε2 φ ε int, (s) Candidate function for N = 2, N = 4 satisfying boundary data w ε 2 (s, t) = {uε }(t)φ ε int, (s) it remains a int (w ε 2, v) = wε 4 (s,t) = wε 2 (s, t) ε2 2 t {uε }(t) (+sκ) 2 φε int,2 (s) Ω ε int a int (w ε 4, v) = ε2 2 t {uε }(t) +sκ φε int, (s)v ds dt Ω ε int t 4{uε }(t) (+sκ) 3 φε int,2 (s)v ds dt K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 3/ 43

23 Thin sheet basis Extension to higher orders for the circular sheet Error of candidate function in H (Ω ε int )-seminorm u ε wn ε 2 H (Ω ε int ) a int(u ε wn ε,uε wn ε ) = a int(wn ε,uε wn ε ) min Bilinear form (u H 2 (Ω ε int ), v H (Ωε int )) a int (u, v) := ( + sκ)( Ω ε s 2 κ s + c(ε)) uv + sκ + sκ 2 t uv ds dt int {z } scales with ε Choose basis functions ( s 2 κ + sκ + c(ε))φε int,j (s) = j =, ( s 2 κ + sκ + c(ε))φε int,j (s) = ε2 φ ε int,j 2 (s), j = 2,..., N Candidate function satisfying boundary data it remains N 2 wn ε (s, t) = X a int (w ε N, v) = εn 2 Ω ε int i= ε 2i ( t) 2i (+sκ) 2i {u ε }(t)φ ε int,2i (s) + [uε ](t)φ ε int,2i+ (s) ( t 2) N 2 (+sκ) N+ {u ε }(t)φ ε int,n 2 (s) + [uε ](t)φ ε int,n (s) v ds dt K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 3/ 43

24 Thin sheet basis Extension to higher orders for the circular sheet Error of candidate function in H (Ω ε int )-seminorm u ε wn ε 2 H (Ω ε int ) a int(u ε wn ε,uε wn ε ) = a int(wn ε,uε wn ε ) min Bilinear form (u H 2 (Ω ε int ), v H (Ωε int )) a int (u, v) := ( + sκ)( Ω ε s 2 κ s + c(ε)) uv + sκ + sκ 2 t uv ds dt int {z } scales with ε Choose basis functions ( s 2 κ + sκ + c(ε))φε int,j (s) = j =, ( s 2 κ + sκ + c(ε))φε int,j (s) = ε2 φ ε int,j 2 (s), j = 2,..., N it remains a int (w ε N,v) = εn 2 = ε N Ω ε int ( t 2) N 2 (+sκ) N+ {u ε }(t)φ ε int,n 2 (s) + [uε ](t)φ ε int,n (s) v ds dt (+sκ) N+ ( 2 s κ +sκ s + c(ε)) ( 2 t ) N 2 {u ε }(t)φ ε int,n (s) +... {z } rn ε (s, t)(+sκ) Ω ε int Scaling of φ ε int,j (s) with O( ε) in the L 2 ([ ε 2, ε ])-norm and Cauchy-Schwarz 2 K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 3/ 43

25 Thin sheet basis Extension to higher orders for the circular sheet Error of candidate function in H (Ω ε int )-seminorm u ε w ε N 2 H (Ω ε int ) a int(u ε w ε N,uε w ε N ) = a int(w ε N, uε w ε N ) O(ε2N ) Bilinear form (u H 2 (Ω ε int ), v H (Ωε int )) a int (u, v) := ( + sκ)( Ω ε s 2 κ s + c(ε)) uv + sκ + sκ 2 t uv ds dt int {z } scales with ε Choose basis functions ( s 2 κ + sκ + c(ε))φε int,j (s) = j =, ( s 2 κ + sκ + c(ε))φε int,j (s) = ε2 φ ε int,j 2 (s), j = 2,..., N it remains a int (w ε N,v) = εn 2 = ε N Ω ε int ( t 2) N 2 (+sκ) N+ {u ε }(t)φ ε int,n 2 (s) + [uε ](t)φ ε int,n (s) v ds dt (+sκ) N+ ( 2 s κ +sκ s + c(ε)) ( 2 t ) N 2 {u ε }(t)φ ε int,n (s) +... {z } rn ε (s, t)(+sκ) Ω ε int Scaling of φ ε int,j (s) with O( ε) in the L 2 ([ ε 2, ε ])-norm and Cauchy-Schwarz 2 K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 3/ 43

26 Thin sheet basis Extension to higher orders for the circular sheet Theorem (The modelling error of a candidate function) Let N be an even integer. There exists a function wn ε W f int,n ε such that w ε N uε int H (Ω ε int ) C Nε N /2, w ε N uε int L 2 (Ω ε int ) C Nε N+/2, with a constant C N independent of ε and the choice of c(ε). This result transfers to the overall modelling error due to Cea s lemma. u ε u ε N H (Ω) C inf u N f W ε N u ε u N H (Ω) = C inf u N f W ε int,n Corollary (The modelling error for the circular sheet) Let N be an even integer, κ (t) = and un ε W N ε the solution of un ε v dx + un ε v + c(ε)uε N v dx = Ω ε ext Ω ε int Then, there exists a constant C N independent of ε such that u ε u ε N H (Ω) C Nε N 2. u ε u N H (Ω ε int ). Ω ε ext fv dx, K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 4/ 43

27 Thin sheet basis Extension to higher orders curved sheet Circular sheet + c(ε) = ( s 2 κ s + c(ε)) + sκ {z } scales with ε Choose basis functions φ ε 2j, φε 2j+ in the kernel of ( 2 s p p Basis I c(ε) +sκ p(s), K κ c(ε) +sκ κ +sκ t +sκ t κ +sκ s + c(ε))j+, j N p(s) instable for small curvatures K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 5/ 43

28 Thin sheet basis Extension to higher orders curved sheet Circular sheet + c(ε) = ( s 2 κ s + c(ε)) + sκ {z } scales with ε Choose basis functions φ ε 2j, φε 2j+ in the kernel of ( 2 s p p Basis I c(ε) +sκ p(s), K κ c(ε) +sκ κ + c(ε) = s 2 κ «2 + sκ s + c(ε) + κ +sκ {z } scales with ε Choose basis functions φ ε 2j, φε 2j+ in the kernel of 2 s +sκ t +sκ t κ +sκ s + c(ε))j+, j N p(s) instable for small curvatures Basis e± c(ε) s +sκ p(s) stable for small curvatures 2 +sκ t +sκ t κ +sκ «κ(t) 2 j+ +sκ(t) s + c(ε) + κ +sκ φ ε int,.5.5 φ ε int,2.5 φ ε int,4 κ = +8 κ = 8 φ ε int, ε ε 2 s 2 φ ε int, ε ε 2 s 2 φ ε int, ε ε 2 s 2 K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 5/ 43

29 Thin sheet basis Numerical results for a circular sheet ε 2.5 φ = /R ΓD,2 4 Ω ε ext Ω ε ext Ω ε int 6 ΓD, φ = r = R R R + Semianalytical study with f =, g = sin(πt) on Γ D, Γ D,2, otherwise g = Error in H -seminorm inside the sheet ε N = N = 2 N = 3 N = 4 N = (a) Constant conductivity c =. κ = N = N = 2 N = 3 N = N = N = 2 N = 3 N = (b) Conductivity c(ε) = ε. κ = 2. ε ε (c) Conductivity c(ε) = ε 2. κ = 2. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 6/ 43

30 Thin sheet basis Numerical results for a circular sheet ε φ = /R ΓD,2 5 Ω ε ext Ω ε ext Ω ε int ΓD, φ = r = R R R + Semianalytical study with f =, g = sin(πt) on Γ D, Γ D,2, otherwise g = Error in H -seminorm outside the sheet. 5 N = N = 2 N = 3 N = 4 N = 5 N = (a) Constant conductivity c =. κ = 2. ε N = N = 2 N = 3 N = 4 N = 5 N = N = N = 2 N = 3 N = ε (b) Conductivity c(ε) = ε. κ = 2. (c) Conductivity c(ε) = ε 2. κ = 2. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 7/ 43 ε

31 Thin sheet basis Numerical results for a straight sheet Dependance of the number of basis functions in comparison with polynomial basis c = 4 c = 4 c = 4 c = 4 5 c = 4 5 ε = (a) Error in the H -norm inside the sheet. N c = 4 c = 4 c = 4 c = 4 5 c = (b) Error in the H -norm outside the sheet. N K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 8/ 43

32 Outline Introduction Applications The meshing problem Model problem Geometry for the transmission problem and different frameworks Thin sheet basis First order impedance boundary condition Bound of modelling error by best approximation error Derivation of basis to any order Numerical results Asymptotic Expansions Derivation of the iterative models Existence, uniqueness, regularity and convergence Decoupling and models only exterior field Numerical experiments with high-order FEM Collectively computed model of order Collectively computed models of higher orders Comparison of thin sheet basis and asymptotic expansions Conclusion K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 9/ 43

33 Asymptotic Expansions Choice of the asymptotics α = ε R 2R asymptotically no shielding for ε α =.5 ε = 2 ε = 3 ε = 4 ε Families of problems with c(ε) = c ε α Choose α = (borderline case) asymptotically constant shielding for ε α = 2 asymptotically impermeable sheet for ε.5 ε = 2 ε = 3 ε = 4 ε K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 2/ 43

34 Asymptotic Expansions Expansion of u ε t b Γ Ω ε int Ω ε ext ε s t Γ m Ω ext bω n n Ω Ω Ω Ω 2 2 S Stretched variable in Ω ε int S = ε s normalised domain b Ω := b Γ [ 2, 2 ]. Notation v(x) = v(t,s) = V(t, S) for a function v in Ω ε int. (t, S) b Ω. Expansion of uext ε (x) and Uε int (t, S) : We seek the exact solution with the form u ε ext(x) = X i= ε i u i ext(x) + o (ε ) ε, U ε int (t, S) = X where the terms uext i (x) and Ui int (t, S) do not depend on ε. i= ε i U i int (t, S) + o (ε ) ε K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 2/ 43

35 Asymptotic Expansions Taylor expansion of u i (t, ±ε/2) t b Γ Ω ε int Ω ε ext ε s t Γ m Ω ext bω n n Ω Ω Ω Ω 2 2 S Dirichlet transmission condition for expansion coefficient = uext ε (t, ± ε 2 ) Uε int (t, ± 2 ) = X ix ε j `± 2 j! j s ui j ext (t, ±) Ui int (t, ± 2 ) A + o (ε ). i= j= ε Neumann transmission condition = ε su ε ext (t, ± ε 2 ) SU ε int (t, ± 2 ) = X Xi ε i i= j= j `± 2 j! j+ s «u i j ext (t, ±) S Uint i (t, ± 2 ) + o (ε ). ε K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 22/ 43

36 Asymptotic Expansions Expansion of Laplace operator = 2 s + κ(t) + sκ(t) s + + sκ(t) t = ε 2 2 S + ε κ(t) + εsκ(t) S + + εsκ(t) t Laplacian () can be expanded in powers of ε = ε 2 where for l, L there are defined ba l (t) := ( κ(t))l 2 (l ) + sκ(t) t «, in Ω ε int + εsκ(t) t «. in b Ω ()! L S 2 + X ε l A l + ε L R L ε, for all L, (2) l= 2 t + l 2 2 A l (t, S) := b A l (t)sl 2 + b A l (t)sl S, κ «(t) κ(t) t, A b l (t) := ( κ(t)) l, K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 23/ 43

37 Asymptotic Expansions Hierarchical coupled problem 8 >< >: Hierarchical definition of external and internal expansion functions. c 2 2 u i ext = f δi in Ω ext, u i ext = gδi ix 2 S Ui int (t, S) = cui int (t, S) l= ix U i int (t, ± 2 ) ui ext (t, ± ) = U i int (t, S) ds k(t) hu i int ix 2 l= Jumps and mean values l= S U i int (t, ± 2 ) = ix 2 l= i h i (t) su i ext (t) = on Ω, A l U i l int (t, S) in b Ω. ± «l 2 l! l s ui l ext (t, ± ) on Γ m, ± «l 2 (l )! l s ui l ext (t, ± ) «l/2 «A l+ U i l int (t, S) ds + 4 l! [ l+ s u i l ext ]l (t) on Γ m on Γ m (3) [V](t) := V(t, /2) V(t, /2), {V }(t) := 2 (V(t, /2) + V(t, /2)), [v](t) := v(t, + ) v(t, ), {v}(t) := `v(t, + ) + v(t, ). 2 j [v] n [v](t) n even (t) := {v}(t) n odd. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 24/ 43

38 Asymptotic Expansions Existence, Uniqueness and Regularity Existence, Uniqueness and Regularity of the hierarchical problem Theorem The sequences (uext i ) and (Ui int ) exist and are uniquely defined. Ui int are polynomials in S of degree 2i with monomial coefficients Uint,j i, j =,..., 2i. For any k N and i N there exists a constant C i,k < + such that u i ext (x) H k ( e Ω ext ) C i,k, U i int,j (t) H k+/2 (Γ m ) C i,k, given that Γ m is C. Convergence of the modelling error Lemma The remainder r ε,n+ (x) := uext/int ε (x) uε,n (x) satisfies ext/int r ε,n+ H (Ω ε ext ) + ε r ε,n+ H (Ω ε int ) C Nε N+. Are the expansion functions u i ext and so uε,n ext computable? K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 25/ 43

39 Asymptotic Expansions Uncoupled problems for the first three exterior expansion functions Solving the equation for U e int i (t, s) and {Ui int }(t) interface conditions yields. Problem in Ω ext for ui ext (x) 8 u ext (x) = f in Ω ext Γ m n Ω ext Ω Ω Order Order 8 >< >: >< >: uext (x) = g i (t) = h u ext h nuext i (t) c uext (t, ) = u ext (x) = uext (x) = h uext i (t) =, on Ω on Γ m on Γm in Ω ext on Ω on Γ m h nu i ext (t) c u ext (t) = c2 6 u ext (t, ) on Γm 8 u 2 ext (x) = in Ω ext Order 2 >< >: uext 2 (x) = h u 2 i ext (t) = c 24 κ(t)u ext (t, ) c 2 n 24 κ(t) nu ext 7 + c 24 c2! 2 t uext (t, ) 2 h nu 2 i ext (t) c nu 2 o ext (t) = c2 6 u ext (t) + c on Ω n nu o ext (t) on Γ m, o (t) on Γm K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 26/ 43

40 Asymptotic Expansions Numerical Results computations for an ellipsoidal sheet with Concepts C++ class library Concepts Started by Christian Lage during his Ph.D. studies (995). Used and improved by Frauenfelder, Matache, Schmidlin, Schmidt, Kauf and severals students. Concept Oriented Design using mathematical principles []. Currently two parts: hp-fem (nodal and edge elements), BEM (wavelet and multipole methods). most of it is released under GPL, Features used and/or implemented in this project quadrilateral elements with high-order tensor product basis functions, elements on edges with high-order basis functions, bilinear and linear forms on these respective elements, exact mapping of curved boundaries, various functions of finite element solutions (trace, jump, extension, gradient,...). [] Ph. Frauenfelder and Ch. Lage, Concepts An Object Oriented Software Package for Partial Differential Equations, Math. Model. Numer. Anal. 36 (5), pp (22). K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 27/ 43

41 Asymptotic Expansions Numerical Results computations for an ellipsoidal sheet with Concepts Ω ε int Γ m Meshes M ε resolving the thin sheets of thickness ε for the reference solutions u ε (x). Limit mesh M for the computation of the asymptotic expansion functions u i ext (x). Following computation of the polynomials Uint i (t, S), representation of u ε,n (x) = P N i= εi u i (x) on meshes M ε to calculate the modelling error in dependence of ε. K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 28/ 43

42 Asymptotic Expansions Numerical Results computations for an ellipsoidal sheet with Concepts uε uext -2-2 y y - - x x 2 c = 2 2 (c) ε = /8 2 (d) Order y y - - x x (e) Order K. Schmidt, S. Tordeux 2 uext -. - uext -2 ENS Cachan Bretagne, September st 29 2 (f) Order 2 p. 29/ 43

43 Asymptotic Expansions Numerical Results computations for an ellipsoidal sheet with Concepts 2 Order Order Order 2 3 u ε u ε,i H (Ω ε ext ) H -seminorm in the exterior sub-domain Ω ε ext. ε K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 3/ 43

44 Asymptotic Expansions Numerical Results computations for an ellipsoidal sheet with Concepts Order Order Order u ε u ε,i H (Ω ε int ) H -seminorm in the sheet Ω ε int. ε K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 3/ 43

45 Asymptotic Expansions Collectively computed model of order Transmission condition of order N = 8 >< h >: nũ ε, ext Stability for Ic > and Rc ũ ε, ext (x) = f in Ω ext h i, ũ ε, ext (t) = on Γ m, i(t) c + c 6 ε ũ ε, ext (t, ) = on Γm, ũ ε, ext (x) = g ũ ε, H (Ω ext ) C f L 2 (Ω ext ). on Ωext. Modelling error ũ ε, u ε H (Ω ε ext ) C ε2 2 4 L2-norm H-seminorm 2 L 2 -norm H -seminorm error error ε (a) Errors in the exterior sub-domain Ω ε ext (b) Errors in the sheet Ω ε int. ε K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 3/ 43

46 Asymptotic Expansions Collectively computed models of higher orders Rewrite the systems in general form u i ext (x) = f δi, in Ω ext, h i u i ext (t) = h i n o nu i ext (t) c u i ext (t) = with the operators (up to order 3) ix l=2 ix l= u i ext (x) = gδi (γ l u j l ext )(t), on Γm, (ζ l u j l ext )(t), on Γm, on Ω (γ 2 u)(t) := c `κ(t){u}(t) + 2{ nu}(t), (γ 3 u)(t) := c2 `κ(t){u}(t) + 2{ nu}(t), (ζ u)(t) := c2 6 {u}(t), (ζ 2 u)(t) := c 2 (ζ 3 u)(t) := c c2 7 κ2 (t) 2 t 7 2 c2 2 t «{u}(t) c2 24 κ(t){ nu}(t). «{u}(t) + c 24 κ(t){ nu}(t) K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 32/ 43

47 Asymptotic Expansions Collectively computed models for higher orders Transmission condition of order N > h with γ ε,n l nũ ε,n ext h i u i ext (t) γ ε,n {ũ ε,n ext n ũ ε,n ext i (t) (c + ζ ε,n ) ũ ε,n ext (x) = f, in Ω ext, }(t) γε,n { nũ ε,n ext }(t) =, on Γm, o (t) ζ ε,n { nũ ε,n ext }(t) =, on Γm, ũ ε,n ext (x) = g on Ω := P N j=2 εj γ j,l and ζ ε,n l := P N j= εj ζ j,l and the operators (up to order 3) γ ε,2 = ε 2 c κ(t), γε,3 = γ ε,2 + ε 3 c κ(t) γ ε,2 = ε 2 c ζ ε,2 = ε c2 6 + ε2 c 2 2, γε,3 = γ ε,2 + ε 3 c 2 2, «7 2 c2 2 t, ζ ε,3 = ζ ε,2 + ε 3 c 2 4 ζ ε,2 = ε 2 c κ(t), ζε,3 = ζ ε,2 ε 3 c κ(t) 7 4 c2 7 κ2 (t) 2 t Greens formula gives ũ ε,n Ω ext v dx + { nũ ε,n ext Γ m ext {z } [v] + [ nũ ε,n ext } ]{v} dt = λ Ω ext fv dx K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 33/ 43 «

48 Asymptotic Expansions Collectively computed models for higher orders Transmission condition of order N > h nũ ε,n ext Ω ext h i ũ ε,n ext (t) γ ε,n i (t) (c + ζ ε,n ) {ũ ε,n ext n ũ ε,n ext }(t) γε,n { nũ ε,n ũ ε,n ext (x) = f, in Ω ext, ext }(t) =, on Γm, o (t) ζ ε,n { nũ ε,n ext }(t) =, on Γm, ũ ε,n ext (x) = g on Ω Mixed variational formulation Seek (ũ ε,n ext, λ) HT, (Ω ext, g) L2 (Γ m ) such that for all (v, λ ) HT, (Ω ext, ) L2 (Γ m ) ũ ε,n ext v dx + (c + ζ ε,n Γ m ){ũ ε,n ext }{v} + λ[v]dt = fv dx Γ m ([ũ ε,n ext Stability for N = 2, 3, Ic > and Rc ](t) γε,n {ũ ε,n ext }(t))λ γ ε,n λλ dt =. Ω ext ũ ε,n H (Ω ext ) + ε λ L 2 (Γ m ) + ε [ũ ε,n ] L 2 (Γ m ) C f L 2 (Ω ext ). Modelling error ũ ε,n u ε H (Ω ε ext ) C εn+ K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 34/ 43

49 Comparison of thin sheet basis and asymptotic expansions Thin sheet basis Order Mesh Usability Any for circular sheets. Sheet has to be resolved. Simple definition of basis to any order. Condition Local. Computation In one step. Convergence For ε and for N. DOF Additional variable for each function. Discretisation H -continuous elements. Ω ε int K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 35/ 43

50 Comparison of thin sheet basis and asymptotic expansions Thin sheet basis Asymptotic expansions Order Any for circular sheets. Any proven order for C -sheets. Mesh Sheet has to be resolved. Only interface. Usability Simple definition of basis to any order. Practically limited order, more and more terms (derived up to order 4). Condition Local. Local. Computation In one step. Iteratively or in one step. Convergence For ε and for N. For ε. DOF Additional variable for each function. No additional variable. Discretisation H -continuous elements. High order tangential continuity on Γ m needed with increasing order. Ω ε int Γ m K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 35/ 43

51 Conclusions Introduction Applications like casings or shielding layer. Difficult to create meshes for thin sheets and expensive to use. Model problem considering shielding and skin effects. Thin sheet basis First order impedance boundary conditions based on fundamental solutions of an ODE in thickness direction Resolving the sheet for higher order approximations. Derivation of the basis for circular sheet in kernel of 2 s j. κ +sκ s + c(ε) Proof of convergence: Best-approximation, candidate function, cancelling of low order terms. Validation by semi-analytical studies. Convergence for ε and N Asymptotic Expansions Expansion for c(ε) = c ε (asymptotically constant shielding). Derived (coupled) model by asymptotic expansions of arbitrary order. Showed existence, uniqueness, regularity and consistency. Models only for exterior field for order, and 2. Validation by numerical results with high-order FEM (Concepts). Collectively computed model of order N =. Same formulation. Collectively computed models of order N >. Mixed formulation. Showed existence, uniqueness and convergence up to order 3. Comparison K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 36/ 43

52 Asymptotic Expansions Collectively computed models for higher orders Problem with this structure u(x) = f, in Ω ext, [u] (t) + ε 2 c { nu}(t) =, on Γ m, [ nu] (t) c {u}(t) =, on Γ m, u = and the associated variational formulation u v dx + c {u}{v} + λ[v]dt = Ω ext Γ m [u]λ + ε 2 c λλ dt =. Γ m on Ω Ω ext fv dx Ellipticity?? Testing with v = u and λ = λ and substracting second from first eq. u 2 dx + c ` {u} 2 ε 2 λ 2 dt Γ m Ω ext K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 37/ 43

53 Asymptotic Expansions Collectively computed models for higher orders Lemma (Stability) Let N = 2, 3, Ic > and Rc. It holds ũ ε,n H (Ω ext ) + ε λ L 2 (Γ m ) + ε [ũ ε,n ] L 2 (Γ m ) C f L 2 (Ω ext ). Proof. u v dx + c {u}{v} + λ[v] + [u]λ + ε 2 c λλ dt = fv dx. Ω ext Γ m Ω ext. Testing with v = u and λ such that ε 2 c λ = [u]. u 2 dx + c {u} 2 ε 2 c λ 2 dt = Γ m Ω ext and taking imaginary part Ic {u} Γ 2 + ε 2 λ 2 dt = I m Ω ext Ω ext f u dx f u dx, and we have {u} L 2 (Γ m ) C f L 2 (Ω ext ), [u] L 2 (Γ m ) Cε f L 2 (Ω ext ). K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 38/ 43

54 Asymptotic Expansions Collectively computed models for higher orders Lemma (Stability) Let N = 2, 3, Ic > and Rc. It holds ũ ε,n H (Ω ext ) + ε λ L 2 (Γ m ) + ε [ũ ε,n ] L 2 (Γ m ) C f L 2 (Ω ext ). Proof. u v dx + c {u}{v} + λ[v] + [u]λ + ε 2 c λλ dt = fv dx. Ω ext Γ m Ω ext. We have {u} L 2 (Γ m ) C f L 2 (Ω ext ), [u] L 2 (Γ m ) Cε f L 2 (Ω ext ). 2. Testing with v = and λ such that ε 2 c λ = [u] λ[u]dt Γ m c ε 2 [u] 2 L 2 (Γ m ) C f 2 L 2 (Ω ). ext 3. Testing with v = u and λ =, multiplying with ( + i) and taking real part γ u 2 H (Ω ext ) u 2 dx + R (( + i)c ) {u} 2 Ω ext Γ m «= R `( + i) f u dx λ[u]dt C f 2 Γ m L 2 (Ω ). ext Ω ext K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 39/ 43

55 Asymptotic Expansions Collectively computed models for higher orders Lemma (Stability) Let N = 2, 3, Ic > and Rc. It holds ũ ε,n H (Ω ext ) + ε λ L 2 (Γ m ) + ε [ũ ε,n ] L 2 (Γ m ) C f L 2 (Ω ext ). Proof. u v dx + c {u}{v} + λ[v] + [u]λ + ε 2 c λλ dt = fv dx. Ω ext Γ m Ω ext. We have {u} L 2 (Γ m ) C f L 2 (Ω ext ), [u] L 2 (Γ m ) Cε f L 2 (Ω ext ). 2. We have RΓ m λ[u]dt C f 2 L 2 (Ω ext ). 3. We have u H (Ω ext ) C f L 2 (Ω ext ). 4. Testing with v = and λ such that ε 2 c λ = λ λ 2 dt ε 2 λ[u] dt Cε 2 f 2 Γ m c Γ m L 2 (Ω ). ext K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 4/ 43

56 Asymptotic Expansions Collectively computed models for higher orders System for order N = 2, 3 and general right hand sides. h nũ ε,n ext h i ũ ε,n ext (t) γ ε,n i (t) (c + ζ ε,n ) {ũ ε,n ext n ũ ε,n ext }(t) γε,n { nũ ε,n ũ ε,n ext (x) = f, in Ω ext, ext }(t) = g(t), on Γm, o (t) ζ ε,n { nũ ε,n ext }(t) = g2(t), on Γm, ũ ε,n ext (x) = on Ω Lemma (Stability) Let N = 2, 3, Ic > and Rc. It holds ũ ε,n H (Ω ext ) + ε λ L 2 (Γ m ) C f L 2 (Ω ext ) + ε 2 g L 2 (Γ m ) + g 2 H /2 (Γ m ). Error r ε,n+ ext = ũ ε,n ext uε,n ext solves system of the same structure with f =, g = O(ε N+ ) and g 2 = O(ε N+ ). Attention: Error only O(ε N )?? K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 4/ 43

57 Asymptotic Expansions Collectively computed models for higher orders System for order N = 2, 3 and general right hand sides. h nũ ε,n ext h i ũ ε,n ext (t) γ ε,n i (t) (c + ζ ε,n ) {ũ ε,n ext n ũ ε,n ext Lemma (Stability) Let N = 2, 3, Ic > and Rc. It holds }(t) γε,n { nũ ε,n ũ ε,n ext (x) = f, in Ω ext, ext }(t) = g(t), on Γm, o (t) ζ ε,n { nũ ε,n ext }(t) = g2(t), on Γm, ũ ε,n ext (x) = on Ω ũ ε,n H (Ω ext ) + ε λ L 2 (Γ m ) C f L 2 (Ω ext ) + ε 2 g L 2 (Γ m ) + g 2 H /2 (Γ m ). However, we can find functions v N,j ext solving similar system than un ext and r ε,n+,k ext = ũ ε,n ext uε,n ext P N+k j=n+ εj v {z} N,j solves system of the above structure with O() f =, g = O(ε N++k ), g 2 = O(ε N++k ). Result: r ε,n+,k ext is O(ε N+k ) and so with k = 2 ũ ε,n ext uε,n ext H (Ω ext ) rε,n+,2 ext Cε N+ H (Ω ext ) + εn+ v N,N+ ext H (Ω ext ) + εn+2 v N,N+2 ext H (Ω ext ) K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 42/ 43

58 Asymptotic Expansions Asymptotic expansion N uext ε (x) uε,n ext (x) := X ε i uext i (x), i= N uε int (t, s) uε,n int (t, s) := X ε i Uint i (t, s ε ) i= Hierarchical partly uncoupled problem Existence, Uniqueness and Regularity for any order Convergence of asymptotic expansion u ε u ε,n ext H (Ω ε ext ) + ε u ε u ε,n ext H (Ω ε int ) C Nε N+ Hierarchical uncoupled problem for u i ext derived up to order 4, numerical experiments up to order 2 Collective computation for ũ ε,n ext uε,n ext system for order like for uext i, well-posed, regularity, convergence mixed variational system for order higher than well-posedness and convergence for Ic > for order 2 and 3 K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 43/ 43

59 Thin sheet basis Extension to higher orders Dirichlet-to-Neumann-map of high-order, Extension of the outer solution up to the mid-line Power loss Jump in normal derivative L 2 -norm ε 2 R 2R relative error Consider resolved sheets for methods of higher order thickness ε K. Schmidt, S. Tordeux ENS Cachan Bretagne, September st 29 p. 44/ 43