Concomitants of generalized order statistics from bivariate Lomax distribution
|
|
|
- Κυριακή Γιαννόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ProbStat Forum, Volume 6, October 23, Pages ISSN ProbStat Forum s an e-ournal. For detals please vst Concomtants of generalzed order statstcs from bvarate Lomax dstrbuton Nayabuddn Abstract. In ths paper probablty densty functon (pdf for rth, r n and the ont (pdf of rth and sth, r < s n, concomtants of generalzed order statstcs from bvarate Lomax dstrbuton s obtaned. Also sngle and product moments are derved. Further the results are deduced for moments of kth upper record values and order statstcs. Also ther means and product moments are tabulated.. Introducton The Lomax dstrbuton ntroduced and studed by Lomax (954. He used ths dstrbuton to analyze busness falure data. Lomax dstrbuton has been studed by several authors n lterature. Balkema and de Haan (974 showed that the (df of Lomax dstrbuton arses as a lmt dstrbuton of resdual lfetme at great age. Accordng to Arnold (983, the Lomax dstrbuton s well adapted for modelng relablty problems. Nayak (987 used multvarate Lomax dstrbuton n relablty theory. Balakrshnan and Ahsanullah (994 derved the relatons for sngle and product moments of record values from Lomax dstrbuton. The Lomax dstrbuton s also known as the Pareto dstrbuton of second knd. In ths paper, we consder the bvarate Lomax dstrbuton (Sankaran and Nar, 993 wth probablty dstrbuton functon (pdf f(x, y α α 2 c(c + ( + α x + α 2 y (c+2, x, y, c, α, α 2 >, ( and correspondng df F (x, y ( + α x + α 2 y c, x, y, c, α, α 2 >. The condtonal pdf of Y gven X s f(y x α 2(c + ( + α x (c+ ( + α x + α 2 y (c+2, y >. (2 The margnal pdf of X s f(x cα, x >, (3 ( + α x (c+ Keywords. Generalzed order statstcs, concomtants of generalzed order statstcs, order statstcs, record values, bvarate Lomax dstrbuton, sngle and product moments Receved: 9 August 22; Revsed: 3 May 23; Re-revsed: 2 September 23; Accepted: 7 September 23 Emal address: nayabstats@gmal.com (Nayabuddn
2 and the margnal df of X s Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages F (x ( + α x c, x >. (4 The concept of generalzed order statstcs (gos was gven by Kamps (995. Several authors utlzed the concept of (gos n ther work for detaled survey one may refer to Khan et al. (26, Ahsanullah and beg (26, Anwar et al. (27, Beg and Ahsanullah (28, Fazan and Athar (28, Tavangar and Asad (28, Khan et al. (29, Tahmaseb and Behboodan (22, Athar et al. (22, Athar et al. (23, Athar and Nayabuddn (23, Athar and Nayabuddn (23, among others. Let n N, n 2, k >, m (m, m 2,..., m n R n, M r n r m, such that γ r k + n r + M r > for all r {, 2,..., n }. Then X(r, n, m, k, r {, 2,..., n} are called gos f ther ont pdf s gven by k ( n ( n γ [ F (x ] m f(x [ F (xn ] k f(xn (5 on the cone F ( < x x 2... x n < F ( of R n. Choosng the parameters approprately, models such as ordnary order statstcs (γ n + ;, 2,..., n,.e. m m 2... m n, k, kth record values (γ k,.e. m m 2... m n, k N, sequental order statstcs (γ (n + α ; α, α 2,..., α n >, order statstcs wth non-ntegral sample sze (γ (α + ; α >, Pfefers record values (γ β ; β, β 2,..., β n > and progressve type II censored order statstcs (m N, k N are obtaned (Kamps, 995, 2. In vew of (5 wth m m;, 2,..., n, the pdf of rth gos, X(r, n, m, k s f X(r,n,m,k C r (r! [ F (x] γr f(xg r m (F (x (6 and ont pdf of X(s, n, m, k and X(r, n, m, k, r < s n, s where and f X(r,s,n,m,k (x, y C r C s (r!(s r! [ F (x] m f(xgm r ( ( ( F (x [hm F (y hm F (x ] s r [ F (y] γs f(y, α x < y β, (7 r γ, γ k + (n (m +, ( xm+, h m (x m + log( x g m (x h m (x h m (, x (,. m, m Let (X, Y,, 2,..., n, be n pars of ndependent random varables from some bvarate populaton wth dstrbuton functon F (x, y. If we arrange the X varates n ascendng order as X(, n, m, k X(2, n, m, k X(n, n, m, k, then Y varates pared (not necessarly n ascendng order wth these generalzed ordered statstcs are called the concomtants of generalzed order statstcs and are denoted by Y [,n,m,k], Y [2,n,m,k],..., Y [n,n,m,k]. The pdf of Y [r,n,m,k], the rth concomtant of generalzed order statstcs s gven as g [r,n,m,k] f Y X (y xf X(r,n,m,k (xdx (8
3 Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages and the ont pdf of Y [r,n,m,k] and Y [s,n,m,k] s g [r,s,n,m,k] (y, y 2 x2 f Y X (y x f Y X (y 2 x 2 f X(r,s,n,m,k (x, x 2 dx dx 2. (9 It s well known that the dstrbuton functon of order statstcs are connected by the relatons (Davd, 98 n ( ( n F r:n (x ( n+r F : (x n r n r+ where F r:n (x s the df of rth order statstcs. Thus the pdf of rth concomtants of order statstcs Y [r:n] s g [r:n] (y n n r+ and the kth moments of Y [r:n] s µ k [r:n] (y n n r+ ( ( n ( n+r g [:] (y n r ( ( n ( n+r µ (k n r [:](y. ( Here some mportant transformaton and formulas are presented, whch wll be used n the subsequent sectons (Prudnkov et al., 986; Srvastava and Karlsson, 985 (λ n ( + z a ( n ( λ n, n, 2, 3,..., λ, ±, ±2,..., ( ( p (a p z p, (2 p! p (λ + m λ(λ + m (λ m, where (λ m Γ(λ+m Γ(λ, λ,, 2,... (3 (λ + m + n λ(λ + m+n (λ m+n, (4 (λ m+n (λ m (λ + m n. Important denttes/result n hypergeometrc functon are a, b 2F ; z (a p (b p ( z p (c c p p p! (5 (6 s condtonally convergent for z, z f < Re(ω, 2F a, b ; Γ(cΓ(c a b, Re(c a b >, c,,, 2,..., (7 Γ(c aγ(c b c a, b x p 2F ; mx dx (m p Γ(cΓ(pΓ(a pγ(b p, (8 Γ(aΓ(bΓ(c p c
4 Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages f < Re p < a, Re b; arg m < π (a, (a 2, (a 3 x s 3F 2 ; x dx Γ(b Γ(b 2 Γ(sΓ(a sγ(a 2 sγ(a 3 s, (9 Γ(a (b, (b 2 Γ(a 2 Γ(a 3 Γ(b sγ(b 2 s f < Re < s < Re a ;, 2, 3 3F 2 N,, a m,, 2 b, (b (a m F 2, (b + N (a b, a m, 3 2 b N, 2 a, (2 N,, N, m, 3F 2, (l F 2,, (N + l l, m 3 m, 2 N l (2 for m, 2,..., l N, N, N,... For real postve k, c and a postve nteger b b ( b ( a B(a + k, c B(k, c + b. (22 a a Note that (Erdély et al., 954 y x λ (x y µ Γ(λ µγµ dx y (µ λ, < Reµ < Re < λ Γλ (23 µ, v x v (a + x µ (x + y ρ ΓvΓ(µ v + ρ dx Γ(µ + ρa µ y (v ϱ 2F ; y a µ + ρ (24 f arg a < Π, Rev >, arg y < Π, Reρ > Re(v µ. Note that (Srvastava and Karlsson, 985 F p:q;k (a p; (b q ; (c k p l:m;n ; x, y (a q r+s (b k r (c s x r l (α l ; (β m ; (γ n ; r s (α m r+s (β n r (γ s r! s known as Kampé de Féret s seres. Note that (Prudnkov et al., 986 pf q α, α 2,..., α p ; z β β 2,..., β q k (α k (α 2 k...(α p k (z k (β k (β 2 k...(β q k k! y s s! (25 (26 s known as generalzed hypergeometrc seres. 2. Probablty densty functon of Y [r,n,m,k] For the bvarate Lomax dstrbuton as gven n (, usng (2, (3, (4 and (6 n (8, the pdf of rth concomtants of gos Y [r,n,m,k] s gven as g [r,n,m,k] (y α 2C r c(c + r ( r (r!(m + r ( α ( + α x + α 2 y c+2 dx. (27 ( + α x c(γr
5 Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages Let t α x, then the R.H.S. of (27 reduces to α 2 C r (r!(m + r r c(c + Usng relaton (24 n (28, we get g [r,n,m,k] (y ( r ( ( + t + α 2 y (c+2 ( + t c(γr dt. (28 C r (r!(m + r c(c + (α 2 r ( ( + α 2 y (c+ ( (cγ r r c, (cγ r + 2 F ; α 2 y. (29 (cγ r + 2 We now prove that g [r,n,m,k] (ydy. We have, g [r,n,m,k] (ydy Usng relaton (6 n (3, we get C r (r!(m + r r c(c + α 2 ( + α 2 y (c+ 2 F α 2C r c(c + r ( r ( (r!(m + r cγ r + Let t + α 2 y, then R.H.S. of (3 becomes C r c(c + r (r!(m + r ( r ( Now usng relaton (23 n (32, we get C r (r!(m + r r c(c + p cγ r + ( r ( ( r ( (cγ r c, (cγ r + 2 (cγ r c p ( p ( p (cγ r + 2 p p! p cγ r + cγ r + (cγ r c p ( p ( p (cγ r + 2 p p! p ; α 2 y dy. (3 ( + α 2 y (c+ (α 2y p dy. (3 t (c+ (t p dt. (32 (cγ r c p ( p ( p Γ(c p. (cγ r + 2 p Γ(c + In vew of (, we have C r (r!(m + r r (c + ( r ( cγ r + 3 F 2 (cγ r c,, (cγ r + 2, ( c,. (33 Usng relaton (2 n (33, we get C r r ( r (r!(m + r ( 2F (cγ r c, ( c ;. (34 Now n vew of (7 n (34, we have n vew of (22. g [r,n,m,k] (ydy C r r ( r ( k (r!(m + r ( B m + + (n r +,
6 Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages Moment of Y [r,n,m,k] In vew of (29, we have ( E Y (a [r,n,m,k] y a g [r,n,m,k] (ydy C r (r!(m + (r!(m + p Lettng t + α 2 y n (35 we have r r c(c + ( r ( (cγ y a α r c, 2 ( + α 2 y (c+ 2 F (cγ r + 2 C r r r c(c + (cγ r c p ( p (cγ r + 2p! C r c(c + r ( r ( (α 2 a (r!(m + r cγ r + In vew of relaton (23, (36, becomes (α 2 a C r c(c + r ( r ( (r!(m + r cγ r + p ( ( r cγ r + ; α 2 y cγ r + dy y a (α 2 ( + α 2 y (c+ ( α 2y p dy. (35 p (cγ r c p ( p ( p (cγ r + 2p! (cγ r c p ( p ( p (cγ r + 2 p p! t (c+ ( t (p+a dt. (36 Γ(c a pγ(p + + a. (37 Γ(c + Now on usng ( n (37, we get after smplfcaton α a 2 C r ( r c(c + r ( (cγ Γ(c aγ( + a r c,, ( + a (r!(m + r 3F 2 cγ r + Γ(c + (cγ r + 2, ( c + a After applcaton of (2 n (38, we have cα2 a C r (c aγ(c a Γ( + a r ( r (r!(m + r ( 2F Γ(c + a, ( cγ r ( a Applyng (7 n (39, we get C r Γ(c + aγ( + a r ( r (α 2 a (r!(m + r ( cγ(c γ r a c, ;. (38. (39 α2 a C r Γ(c + aγ( + a r ( r ( k (r!(m + r ( a sb + (n r + Γ(c + m + c(m +,, whch after applcaton of (22, yelds ( E y (a [r,n,m,k] C r Γ(c + a Γ( + a Γ( k+(n r(m+ a c (α 2 a (m + r m+ cγ(c Γ( k+n(m+ a c Γ(c + a Γ( + a (α 2 a cγ(c r ( a cγ m+ (4 (4
7 Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages Remark 3.. Set m, k n (4, to get moments of concomtants of order statstcs from bvarate Lomax dstrbuton ( E y (a [r:n] n! (α 2 a (n r! and at r, we get ( E y (a [:n] n (α 2 a (nc a Further, n vew of (, (42 becomes ( E y (a [r:n] n n r+ Γ(c + a Γ( + a Γ(n r + a c cγ(c Γ(n + a c Γ(c + a Γ( + a. (42 Γ(c ( ( n ( n+r Γ(c + a Γ( + a n r (c a(α 2 a. Γ(c Remark 3.2. At m n (4, we get moment of concomtants of kth upper record value from bvarate Lomax dstrbuton ( E y (a [r,n,,k] Γ(c + a Γ( + a (α 2 a cγ(c ( a. ck r Here n Table 3, t may be noted that the well known property of order statstcs n E(X :n ne(x (Davd and Nagaraa, 23 s satsfed. 4. Jont probablty densty functon of Y [r,n,m,k] and Y [s,n,m,k] For the bvarate Lomax dstrbuton as gven n (, usng (2, (3, (4 and (7 n (9, the ont pdf of rth and sth concomtants of gos Y [r,n,m,k] and Y [s,n,m,k] s gven as g [r,s,n,m,k] (y, y 2 C s c 2 (c + 2 (α (α 2 2 (r!(s r!(m + s 2 r s r ( + ( r ( s r ( + α x 2 c(γs ( + α x 2 + α 2 y 2 c+2 I(x 2, y dx 2 (43 where I(x 2, y x2 α ( + α x c(s r+ (m+ c ( + α x + α 2 y c+2 dx. (44 Let t ( + α x, then the R.H.S. of (44 reduces to I(x 2, y (λ β +αx 2 t α ( + t λ β dt, (45 where α c(s r + (m + c, β (c + 2 and λ α 2 y. Now on usng (2 n (45, and smplfyng, we get I(x 2, y (λ β p ( p (β p( λ p p! [ ] ( + α x 2 (α p. ( α + p +
8 Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages Table : Mean of the concomtant of order statstcs n r α 2, c 2 α 2 2, c 3 α 2 3, c Table 2: Mean of the concomtant of record statstcs r α 2, c 2, k α 2 2, c 3, k 2 α 2 3, c 4, k
9 Therefore, n vew of (43, we have Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages g [r,s,n,m,k] (y, y 2 c 2 (c + 2 (α (α 2 2 C s (r!(s r!(m + s 2 r s r ( + ( r ( s r (λ β p α ( + α x 2 (cγs c ( + α x 2 + α 2 y 2 c+2 [ ( + α x 2 (α p ( p (β p ( λ p ( α + p + p! ] dx. (46 Lettng t 2 ( + α x 2 n (46, and usng relaton (2, we get g [r,s,n,m,k] (y, y 2 c 2 (c + 2 (α 2 2 C s (r!(s r!(m + s 2 (λ β (δ β p where δ α 2 y 2 and θ cγ s c. Set d θ and g 2 θ α n (47, to get c2 (c + 2 (α 2 2 C s λ β δ β r (r!(s r!(m + s 2 s r (β p ( λ p p! After substtutng the value of λ and δ n (48, we get c 2 (c + 2 (α 2 2 C s (r!(s r!(m + s 2 l (β l ( l (d + ll! p r l s r (β l ( δ l l! ( ( ( + r s r r Usng relaton (3 and (4 n (49, t becomes Therefore c 2 (c + 2 C s (r!(s r!(m + s 2 (α 2 (α 2 y β (α 2 (α 2 y 2 β s r ( + ( r ( + ( r p ( s r ( θ + l(2 θ α + l + p, (47 (β p ( λ p (g + p + lp! ( s r l (β l ( δ l (d + ll!. (48 (α 2 y 2 β (α 2 y β (β p ( α 2y p (g + p + lp!. (49 l p r s r ( + ( r (g p+l (g + p+l (β l (d l (β p ( s r ( α 2y p (d + l p! ( l l! dg. g [r,s,n,m,k] (y, y 2 c 2 (c + 2 C s (r!(s r!(m + s 2 (α 2 (α 2 (α 2 y β (α 2 y 2 β F :; :2; r s r ( + ( r ( s r (g; (β; (d; (β; ;, α 2y (g + ; (d + ; dg (5 where F :; :2; [ ] s as defned n (25.
10 Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages We now prove that g [r,s,n,m,k] (y, y 2 dy dy 2 A g [r,s,n,m,k] (y, y 2 dy dy 2. We have F :; :2; (α 2 (α 2 y β (α 2 (α 2 y 2 β (g; (β; (d; (β; ;, α 2y (g + ; (d + ; dy dy 2 where Then, A c 2 (c + 2 C s (r!(s r!(m + s 2 r g [r,s,n,m,k] (y, y 2 dy dy 2 A On applyng (5 n (5, we can wrte (α 2 A (α 2 y 2 β l s r (g l (β l (d l ( (g + l (d + l l! ( + ( r p l l { ( s r (α 2 (α 2 y β (α 2 (α 2 y 2 β (g l+p (g + l+p (β l (d l (β p (α 2 (α 2 y β dg. ( α 2y p (d + l p! (g + l p (β p ( (g + l + p p! p ( α 2y p l l! dy dy 2. (5 dy }dy 2. (52 Now usng relaton (26 n (52, we have α 2 A (α 2 y 2 β (g l (β l (d l ( (g + l (d + l l! l l (α 2 (α 2 y β 2 F (β; (g + l (g + + l ; α 2y dy dy 2. (53 Now lettng t α 2y (α 2 y 2 A (α 2 y 2 β n (53, to get (g l (β l (d l ( (g + l (d + l l! l l t (β 2F (β; (g + l (g + + l ; t dt dy 2. Now n vew of relaton (8, we have (α 2 A (α 2 y 2 β (g l (β l (d l ( (g + l (d + l l! l Further, usng relaton (3 n (54, to get ga (α 2 (g β + (α 2 y 2 β l (g β + l (β l (d l ( (g β + 2 l (d + l l! l (g + l (β (g + l + β dy 2. (54 l dy 2. (55 Now usng relaton (26 n (55, we have ga (g + β; (β; (d (α 2 (g β + (α 2 y 2 β 3 F 2 ; dy 2. (56 (g + 2 β; (d +
11 Set t 2 ga (g β + Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages n (56, to get (t 2 (β 3F 2 Now on usng relaton (9 n (57, we have (g + β; (β; (d ; t 2 (g + 2 β; (d + dt 2. (57 Agd (β 2 (g + 2 2β(d + β. (58 Now after puttng the value of g, d, β, A n (58, we get Therefore, C s (r!(s r!(m + s n vew of (22. r s r g [r,s,n,m,k] (y, y 2 dy dy 2 s r ( + ( r ( s r [ k C s (r!(s r!(m + s ( ( + r ( k B m + + (n r +, B m+ + (n s + ] k [ m+ + (n r + ]. r ( s r ( k m + + (n s +,. 5. Product moments of two concomtants Y [r,n,m,k] and Y [s,n,m,k] The product moments of two concomtants Y [r,n,m,k] and Y [s,n,m,k] s gven by ( E Y (a [r,n,m,k] Y (b [s,n,m,k] In vew of (5 and (59, we have ( E Y (a [r,n,m,k] Y (b [s,n,m,k] A yy a 2 b (α 2 (α 2 (α 2 y β (α 2 y 2 β F :; :2; A On applyng (5 n (6, we have A y2 b (α 2 (α 2 y 2 β yy a 2 b (α 2 (α 2 (α 2 y β (α 2 y 2 β l y a y b 2 g [r,s,n,m,k] (y, y 2 dy dy 2. (59 (g l (β l (d l ( (g + l (d + l l! p l l (g; (β; (d; (β; ;, α 2y (g + ; (d + ; (g l+p (g + l+p (β l (d l (β p { Usng relaton (26 n (6, we have A y b (α 2 (g l (β l (d l ( l 2 (α 2 y 2 β (g + l (d + l l! l (β; (g + l y a (α 2 (α 2 y β 2 F (g + l + y a (α 2 (α 2 y β ( α 2y p (d + l p! ( l l! (β p (g + l p ( (g + + l p p! p ; α 2y α 2y p dy dy 2. dy dy 2. (6 dy }dy 2. (6 dy dy 2. (62
12 Settng t α 2y Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages n (62, to get A (α 2 a y2 b (α 2 (g l (β l (d l ( l (α 2 y 2 β (g + l (d + l l! l (β; (g + l t (β a 2F ; t (g + l + dt dy 2. (63 On usng relaton (8 n (63, we have A (g + lγ(β a Γ(a + (α 2 a Γ(β(g + l + β + a y2 b (α 2 (α 2 y 2 β l (g l (β l (d l ( l (g + l (d + l l! dy 2. Now n vew of relaton (3 and (26, we have Let t 2 Γ(β a Γ(a + (g + β + a Γ(β (d; (g + β + a; (β 3 F 2 (d + ; (g + 2 β + a A (α 2 a g n (64, we have A g (α 2 a+b 3 F 2 (g + β + a Usng relaton (9 n (65, to get A Γ(β a Γ(a + (α 2 a+b Γ(β Γ(β a Γ(a + Γ(β y2 b ; (d; (g + β + a; (β ; t 2 (d + ; (g + 2 β + a Γ(β b Γ(b + Γ(β (α 2 (α 2 y 2 β dy 2. (64 t (β b 2 dt 2. (65 dg (d β + b + (g 2β + a + b + 2. (66 Now puttng the value of A, d, g and β n (66, we have ( E Y (a [r,n,m,k] Y (b c 2 (c + 2 C s Γ(c a + Γ(a + [s,n,m,k] (α 2 (a+b (r!(s r!(m + s 2 Γ(c + 2 Γ(c b + Γ(b + Γ(c + 2 r s r [c{k + (n s + (m + } b] ( + ( r ( s r [c{k + (n r + (m + } a b] (c + 2 C s Γ(c a + Γ(a + (α 2 (a+b (r!(s r!(m + s 2 Γ(c + 2 ( k r Γ(c b + Γ(b + Γ(c + 2 s r ( ( s r ( ( r B ( k b B + (n s + m + + (n r + a m + c(m +,. + b c(m +, (67
13 In vew of relaton (22, we get Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages (c + 2 C s Γ(c a + Γ(a + Γ(c b + Γ(b + (α 2 (a+b (r!(s r!(m + s 2 Γ(c + 2 Γ(c + 2 ( k B + (n r a + b ( k m + c(m +, r b B + (n s m + c(m +, s r, whch after smplfcaton yelds ( E Y (a [r,n,m,k] Y (b C s [s,n,m,k] (α 2 (a+b Γ( k (m+ + (n r a+b Γ( k (m+ + n c(m+ a+b c(m+ Γ(c a + Γ(a + (m + s 2 Γ(c + k Γ( (m+ + (n s b + (n r b Γ( k (m+ c(m+ c(m+. Γ(c b + Γ(b + Γ(c + ( E Y (a [r,n,m,k] Y (b Γ(c a + Γ(a + Γ(c b + Γ(b + [s,n,m,k] (α 2 (a+b Γ(c + Γ(c + r a+b ( cγ s r+ ( b cγ. (68 Remark 5.. Set m, k n (67, to get product moments of concomtants of order statstcs from bvarate Lomax dstrbuton ( E Y (a [r:n] Y (b [s:n] C r,s:n r s r Γ(c a + Γ(a + Γ(c b + Γ(b + (α 2 (a+b Γ(c Γ(c ( ( r s r ( + [sc nc c c + b] [rc nc c c + a + b]. ( E Y (a [r:n] Y (b [s:n] (α 2 (a+b n! (n s! a+b Γ(n r + c b Γ(n s + c Γ(n + a+b c Γ(n r + b c. Γ(c a + Γ(a + Γ(c b + Γ(b + Γ(c + Γ(c + Remark 5.2. If m, n (68, then we get product moment of concomtants of kth upper record value from bvarate Lomax dstrbuton as ( E Y (a [r,n,,k] Y (b [s,n,,k] Γ(c a + Γ(a + (α 2 (a+b Γ(c + Γ(c b + Γ(b + Γ(c + ( a+b ck r ( b. ck (s r Acknowledgement Authors are grateful to Dr. Haseeb Athar, Algarh Muslm Unversty, Algarh, Inda, for hs help and suggestons throughout the preparaton of ths manuscrpt. The authors are also thankful to learned referee for hs/her comments whch led mprovement n the manuscrpt.
14 Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages Table 3: Product moments between the concomtants of order statstcs: α 2 c 3 n s \ r Table 4: Product moments between the concomtants of order statstcs: α 2 2 c 4 n s \ r
15 Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages Table 5: Product moments between the concomtants of order statstcs: α 2 3 c 5 n s \ r Table 6: Product moments between the concomtants of record statstcs: s r α 2, c 3 α 2 2, c 4 α 2 3, c
16 Nayabuddn / ProbStat Forum, Volume 6, October 23, Pages References Ahsanullah, M., Beg, M.I. (26 Concomtant of generalzed order statstcs n Gumbel s bvarate exponental dstrbuton, Journal of Statstcal Theory and Applcatons 6, Anwar Z., Athar H., Khan R.U. (27 Expectaton denttes based on recurrence relatons of functon of generalzed order statstcs, J. Statst. Res. 4(2, Arnold, B.C. (983 Pareto Dstrbutons, Internatonal Cooperatve Publshng House, Farland, Maryland. Athar H., Nayabuddn (22 On moment generatng functon of generalzed order statstcs from extended generalzed half logstc dstrbuton and ts characterzaton, South Pacfc Journal of Pure and Appled Mathematcs (,. Athar H., Nayabuddn (23 Recurrence relatons for sngle and product moments of generalzed order statstcs from Marshall- Olkn extended general class of dstrbutons, J. Stat. Appl. Prob. 2(2, Athar H., Nayabuddn, Saba Khald Khwaa (23 Relatons for moments of generalzed order statstcs from Marshall-Olkn extended Webull dstrbuton and ts characterzaton, ProbStat Forum 5, Athar H., Saba Khald Khwaa, Nayabuddn (22 Expectaton denttes of Pareto dstrbuton based on generalzed order statstcs and ts characterzaton, AJAMMS (, Balakrshnan, N., Ahsanullah, M. (994 Relatons for sngle and product moments of record values from Lomax dstrbuton, Sankhya B(56, Balkema, A.A., de Haan, L. (974 Resdual lfe tme at great age, Ann. Probab. 2, Beg, M.I., Ahsanullah, M. (28 Concomtants of generalzed order statstcs from Farle-Gumbel-Morgenstern dstrbutons, Statstcal Methodology 5, 2. Davd, H.A. (98 Order Statstcs, 2nd edn, John Wley and Sons, New York. Davd, H.A., Nagaraa, H.N. (23 Order Statstcs, John Wley, New York. Erdély, A., Magnus, W., Oberhetnger, F., Trcom, F.G. (954 Tables of Integral Transforms Vol. I and Vol. II, MC Graw-Hll, New York. Fazan M., Athar H. (28 Moments of generalzed order statstcs from a general class of dstrbutons, Journal of Statstcs 5, Kamps, U. (995 A concept of generalzed order statstcs, B.G. Teubner Stuttgart, Germany (Ph. D. Thess. Kamps, U., Cramer, E. (2 On dstrbuton of generalzed order statstcs, Statstcs 35, Khan, A.H., Khan R.U., Yaqub, M. (26 Characterzaton of contnuous dstrbutons through condtonal expectaton of generalzed order statstcs, J. Appl. Prob. Statst, 5 3. Khan A.H., Anwar Z., Athar, H. (29 Exact moments of generalzed and dual generalzed order statstcs from a general form of dstrbutons, J. Statst. Sc (, Lomax, K.S. (954 Busness falures. Another example of the analyss of falure data, J. Amer. Statst. Assoc. 49, Nayak, T.K. (987 Multvarate Lomax dstrbuton: Propertes and usefulness n relablty theory, J. Appl. Prob. 24, Prudnkov, A.P., Brychkov, Y.A., Marchev, I. (986 Integral and seres Vol. 3, More Specal Functons, Gordon and Breach Scence Publsher, New York. Sankaran, P.G., Nar, N.U. (993 A bvarate Pareto model and ts applcatons to relablty, Naval Research Logstcs 4, 3 2. Srvastava, H.M., Karlsson, P.W. (985 Multple Gaussan Hypergeometrc seres, John Wley and Sons, New York. Tahmaseb, S., Behboodan, J. (22 Shannon nformaton for concomtants of generalzed order statstcs n Farle-Gumbel- Morgenstern (FGM famly, Bull. Malays. Math. Sc. Soc. 34(4, Tavangar M., Asad M. (28 On a characterzaton of generalzed Pareto dstrbuton based on generalzed order statstcs, Commun. Statst. Theory Meth. 37,
Concomitants of Dual Generalized Order Statistics from Bivariate Burr III Distribution
 Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
5 Haar, R. Haar,. Antonads 994, Dogaru & Carn Kerkyacharan & Pcard 996. : Haar. Haar, y r x f rt xβ r + ε r x β r + mr k β r k ψ kx + ε r x, r,.. x [,
 4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A summation formula ramified with hypergeometric function and involving recurrence relation
 South Asian Journal of Mathematics 017, Vol. 7 ( 1): 1 4 www.sajm-online.com ISSN 51-151 RESEARCH ARTICLE A summation formula ramified with hypergeometric function and involving recurrence relation Salahuddin
South Asian Journal of Mathematics 017, Vol. 7 ( 1): 1 4 www.sajm-online.com ISSN 51-151 RESEARCH ARTICLE A summation formula ramified with hypergeometric function and involving recurrence relation Salahuddin
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Commutative Monoids in Intuitionistic Fuzzy Sets
 Commutative Monoids in Intuitionistic Fuzzy Sets S K Mala #1, Dr. MM Shanmugapriya *2 1 PhD Scholar in Mathematics, Karpagam University, Coimbatore, Tamilnadu- 641021 Assistant Professor of Mathematics,
Commutative Monoids in Intuitionistic Fuzzy Sets S K Mala #1, Dr. MM Shanmugapriya *2 1 PhD Scholar in Mathematics, Karpagam University, Coimbatore, Tamilnadu- 641021 Assistant Professor of Mathematics,
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
Generalized Linear Model [GLM]
![Generalized Linear Model [GLM] Generalized Linear Model [GLM]](/thumbs/93/113885699.jpg) Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
SPECIAL FUNCTIONS and POLYNOMIALS
 SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Neutralino contributions to Dark Matter, LHC and future Linear Collider searches
 Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
An Inventory of Continuous Distributions
 Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).
![Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ). Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).](/thumbs/91/105872052.jpg) Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
The one-dimensional periodic Schrödinger equation
 The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly
The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly
DiracDelta. Notations. Primary definition. Specific values. General characteristics. Traditional name. Traditional notation
 DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Homomorphism in Intuitionistic Fuzzy Automata
 International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
Vidyamandir Classes. Solutions to Revision Test Series - 2/ ACEG / IITJEE (Mathematics) = 2 centre = r. a
 Per -.(D).() Vdymndr lsses Solutons to evson est Seres - / EG / JEE - (Mthemtcs) Let nd re dmetrcl ends of crcle Let nd D re dmetrcl ends of crcle Hence mnmum dstnce s. y + 4 + 4 6 Let verte (h, k) then
Per -.(D).() Vdymndr lsses Solutons to evson est Seres - / EG / JEE - (Mthemtcs) Let nd re dmetrcl ends of crcle Let nd D re dmetrcl ends of crcle Hence mnmum dstnce s. y + 4 + 4 6 Let verte (h, k) then
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ
 ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙΔΡΑΣΗ Μ.Β ΣΤΙΣ ΙΔΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ (ΔΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙΔΡΑΣΗ Μ.Β ΣΤΙΣ ΙΔΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ (ΔΙΑΦΟΡΙΚΗ) Probablty Densty Functon
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ
 ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙ ΡΑΣΗ Μ.Β ΣΤΙΣ Ι ΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ ( ΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙ ΡΑΣΗ Μ.Β ΣΤΙΣ Ι ΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ ( ΙΑΦΟΡΙΚΗ) Probablty Densty Functon
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Some generalization of Cauchy s and Wilson s functional equations on abelian groups
 Aequat. Math. 89 (2015), 591 603 c The Author(s) 2013. Ths artcle s publshed wth open access at Sprngerlnk.com 0001-9054/15/030591-13 publshed onlne December 6, 2013 DOI 10.1007/s00010-013-0244-4 Aequatones
Aequat. Math. 89 (2015), 591 603 c The Author(s) 2013. Ths artcle s publshed wth open access at Sprngerlnk.com 0001-9054/15/030591-13 publshed onlne December 6, 2013 DOI 10.1007/s00010-013-0244-4 Aequatones
Technical Report: A Unified Framework for Analysis of Path Selection Based Decode-and-Forward (DF) Cooperation in Wireless Systems
 Techncal Report: A Unfed Framework for Analyss of ath Selecton Based Decode-and-Forward DF Cooperaton n Wreless Systems Neeraj Varshney Student ember, IEEE and Adtya K. Jagannatham, ember, IEEE I. VALUES
Techncal Report: A Unfed Framework for Analyss of ath Selecton Based Decode-and-Forward DF Cooperaton n Wreless Systems Neeraj Varshney Student ember, IEEE and Adtya K. Jagannatham, ember, IEEE I. VALUES
ΣΔΥΝΟΛΟΓΗΚΟ ΔΚΠΑΗΓΔΤΣΗΚΟ ΗΓΡΤΜΑ ΗΟΝΗΧΝ ΝΖΧΝ «ΗΣΟΔΛΗΓΔ ΠΟΛΗΣΗΚΖ ΔΠΗΚΟΗΝΧΝΗΑ:ΜΔΛΔΣΖ ΚΑΣΑΚΔΤΖ ΔΡΓΑΛΔΗΟΤ ΑΞΗΟΛΟΓΖΖ» ΠΣΤΥΗΑΚΖ ΔΡΓΑΗΑ ΔΤΑΓΓΔΛΗΑ ΣΔΓΟΤ
 [Type the abstract of the document here. The abstract is typically a short summary of the contents of the document. Type the abstract of the document here. The abstract is typically a short summary of
[Type the abstract of the document here. The abstract is typically a short summary of the contents of the document. Type the abstract of the document here. The abstract is typically a short summary of
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Homomorphism of Intuitionistic Fuzzy Groups
 International Mathematical Forum, Vol. 6, 20, no. 64, 369-378 Homomorphism o Intuitionistic Fuzz Groups P. K. Sharma Department o Mathematics, D..V. College Jalandhar Cit, Punjab, India pksharma@davjalandhar.com
International Mathematical Forum, Vol. 6, 20, no. 64, 369-378 Homomorphism o Intuitionistic Fuzz Groups P. K. Sharma Department o Mathematics, D..V. College Jalandhar Cit, Punjab, India pksharma@davjalandhar.com
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Trigonometry 1.TRIGONOMETRIC RATIOS
 Trigonometry.TRIGONOMETRIC RATIOS. If a ray OP makes an angle with the positive direction of X-axis then y x i) Sin ii) cos r r iii) tan x y (x 0) iv) cot y x (y 0) y P v) sec x r (x 0) vi) cosec y r (y
Trigonometry.TRIGONOMETRIC RATIOS. If a ray OP makes an angle with the positive direction of X-axis then y x i) Sin ii) cos r r iii) tan x y (x 0) iv) cot y x (y 0) y P v) sec x r (x 0) vi) cosec y r (y
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Aquinas College. Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET
 Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Solve the difference equation
 Solve the differece equatio Solutio: y + 3 3y + + y 0 give tat y 0 4, y 0 ad y 8. Let Z{y()} F() Taig Z-trasform o both sides i (), we get y + 3 3y + + y 0 () Z y + 3 3y + + y Z 0 Z y + 3 3Z y + + Z y
Solve the differece equatio Solutio: y + 3 3y + + y 0 give tat y 0 4, y 0 ad y 8. Let Z{y()} F() Taig Z-trasform o both sides i (), we get y + 3 3y + + y 0 () Z y + 3 3y + + y Z 0 Z y + 3 3Z y + + Z y
A General Note on δ-quasi Monotone and Increasing Sequence
 International Mathematical Forum, 4, 2009, no. 3, 143-149 A General Note on δ-quasi Monotone and Increasing Sequence Santosh Kr. Saxena H. N. 419, Jawaharpuri, Badaun, U.P., India Presently working in
International Mathematical Forum, 4, 2009, no. 3, 143-149 A General Note on δ-quasi Monotone and Increasing Sequence Santosh Kr. Saxena H. N. 419, Jawaharpuri, Badaun, U.P., India Presently working in
Coefficient Inequalities for a New Subclass of K-uniformly Convex Functions
 International Journal of Computational Science and Mathematics. ISSN 0974-89 Volume, Number (00), pp. 67--75 International Research Publication House http://www.irphouse.com Coefficient Inequalities for
International Journal of Computational Science and Mathematics. ISSN 0974-89 Volume, Number (00), pp. 67--75 International Research Publication House http://www.irphouse.com Coefficient Inequalities for
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Constant Elasticity of Substitution in Applied General Equilibrium
 Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Noriyasu MASUMOTO, Waseda University, Okubo, Shinjuku, Tokyo , Japan Hiroshi YAMAKAWA, Waseda University
 A Study on Predctve Control Usng a Short-Term Predcton Method Based on Chaos Theory (Predctve Control of Nonlnear Systems Usng Plural Predcted Dsturbance Values) Noryasu MASUMOTO, Waseda Unversty, 3-4-1
A Study on Predctve Control Usng a Short-Term Predcton Method Based on Chaos Theory (Predctve Control of Nonlnear Systems Usng Plural Predcted Dsturbance Values) Noryasu MASUMOTO, Waseda Unversty, 3-4-1
Estimators when the Correlation Coefficient. is Negative
 It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
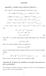 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Modelling Lifetime Dependence for Older Ages using a Multivariate Pareto Distribution
 Modellng Lfetme Dependence for Older Ages usng a Multvarate Pareto Dstrbuton Danel H Ala Znovy Landsman Mchael Sherrs 3 School of Mathematcs, Statstcs and Actuaral Scence Unversty of Kent, Canterbury,
Modellng Lfetme Dependence for Older Ages usng a Multvarate Pareto Dstrbuton Danel H Ala Znovy Landsman Mchael Sherrs 3 School of Mathematcs, Statstcs and Actuaral Scence Unversty of Kent, Canterbury,
Stochastic Finite Element Analysis for Composite Pressure Vessel
 * ** ** Stochastc Fnte Element Analyss for Composte Pressure Vessel Tae Kyung Hwang Young Dae Doh and Soon Il Moon Key Words : Relablty Progressve Falure Pressure Vessel Webull Functon Abstract ABAQUS
* ** ** Stochastc Fnte Element Analyss for Composte Pressure Vessel Tae Kyung Hwang Young Dae Doh and Soon Il Moon Key Words : Relablty Progressve Falure Pressure Vessel Webull Functon Abstract ABAQUS
Quadratic Expressions
 Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Supplementary materials for Statistical Estimation and Testing via the Sorted l 1 Norm
 Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Differentiation exercise show differential equation
 Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
On a four-dimensional hyperbolic manifold with finite volume
 BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
SOLVING CUBICS AND QUARTICS BY RADICALS
 SOLVING CUBICS AND QUARTICS BY RADICALS The purpose of this handout is to record the classical formulas expressing the roots of degree three and degree four polynomials in terms of radicals. We begin with
SOLVING CUBICS AND QUARTICS BY RADICALS The purpose of this handout is to record the classical formulas expressing the roots of degree three and degree four polynomials in terms of radicals. We begin with
ON NEGATIVE MOMENTS OF CERTAIN DISCRETE DISTRIBUTIONS
 Pa J Statist 2009 Vol 25(2), 135-140 ON NEGTIVE MOMENTS OF CERTIN DISCRETE DISTRIBUTIONS Masood nwar 1 and Munir hmad 2 1 Department of Maematics, COMSTS Institute of Information Technology, Islamabad,
Pa J Statist 2009 Vol 25(2), 135-140 ON NEGTIVE MOMENTS OF CERTIN DISCRETE DISTRIBUTIONS Masood nwar 1 and Munir hmad 2 1 Department of Maematics, COMSTS Institute of Information Technology, Islamabad,
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
A Sequential Experimental Design based on Bayesian Statistics for Online Automatic Tuning. Reiji SUDA,
 Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng
Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng
MathCity.org Merging man and maths
 MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
M a t h e m a t i c a B a l k a n i c a. On Some Generalizations of Classical Integral Transforms. Nina Virchenko
 M a t h e m a t i c a B a l k a n i c a New Series Vol. 26, 212, Fasc. 1-2 On Some Generalizations of Classical Integral Transforms Nina Virchenko Presented at 6 th International Conference TMSF 211 Using
M a t h e m a t i c a B a l k a n i c a New Series Vol. 26, 212, Fasc. 1-2 On Some Generalizations of Classical Integral Transforms Nina Virchenko Presented at 6 th International Conference TMSF 211 Using
CAPM. VaR Value at Risk. VaR. RAROC Risk-Adjusted Return on Capital
 C RAM 3002 C RAROC Rsk-Adjusted Return on Captal C C RAM Rsk-Adjusted erformance Measure C RAM RAM Bootstrap RAM C RAROC RAM Bootstrap F830.9 A CAM 2 CAM 3 Value at Rsk RAROC Rsk-Adjusted Return on Captal
C RAM 3002 C RAROC Rsk-Adjusted Return on Captal C C RAM Rsk-Adjusted erformance Measure C RAM RAM Bootstrap RAM C RAROC RAM Bootstrap F830.9 A CAM 2 CAM 3 Value at Rsk RAROC Rsk-Adjusted Return on Captal
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Additional Results for the Pareto/NBD Model
 Additional Results for the Pareto/NBD Model Peter S. Fader www.petefader.com Bruce G. S. Hardie www.brucehardie.com January 24 Abstract This note derives expressions for i) the raw moments of the posterior
Additional Results for the Pareto/NBD Model Peter S. Fader www.petefader.com Bruce G. S. Hardie www.brucehardie.com January 24 Abstract This note derives expressions for i) the raw moments of the posterior
On the Galois Group of Linear Difference-Differential Equations
 On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
Solutions for Mathematical Physics 1 (Dated: April 19, 2015)
 Solutons for Mathematcal Physcs 1 Dated: Aprl 19, 215 3.2.3 Usng the vectors P ê x cos θ + ê y sn θ, Q ê x cos ϕ ê y sn ϕ, R ê x cos ϕ ê y sn ϕ, 1 prove the famlar trgonometrc denttes snθ + ϕ sn θ cos
Solutons for Mathematcal Physcs 1 Dated: Aprl 19, 215 3.2.3 Usng the vectors P ê x cos θ + ê y sn θ, Q ê x cos ϕ ê y sn ϕ, R ê x cos ϕ ê y sn ϕ, 1 prove the famlar trgonometrc denttes snθ + ϕ sn θ cos
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
