Modelling Lifetime Dependence for Older Ages using a Multivariate Pareto Distribution
|
|
|
- Νύξ Μαυρίδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Modellng Lfetme Dependence for Older Ages usng a Multvarate Pareto Dstrbuton Danel H Ala Znovy Landsman Mchael Sherrs 3 School of Mathematcs, Statstcs and Actuaral Scence Unversty of Kent, Canterbury, Kent CT 7NF, UK Department of Statstcs, Unversty of Hafa Mount Carmel, Hafa 3905, Israel CEPAR, Rsk and Actuaral Studes, UNSW Busness School UNSW, Sydney NSW 05, Australa DRAFT ONLY DO NOT CIRCULATE WITHOUT AUTHORS PERMISSION Abstract In order to solate the longevty component n lfe-beneft products, we focus our attenton on deferred annutes These products are drven by older age mortalty, where lttle s known about potental dependence structures We propose to nvestgate a multvarate Pareto dstrbuton, whch wll allow us to explore a varety of applcatons, from large portfolos of standard annutes to jont-last survvor annuty products for couples In past work, t has been shown that even a lttle dependence between lves can lead to much hgher uncertanty Therefore, the ablty to assess and ncorporate the approprate dependence structure wll sgnfcantly mprove the prcng and rsk management of deferred annuty products Keywords: Longevty Rsk, Lfetme Dependence, Multvarate Pareto Dstrbuton dhala@kentacuk landsman@stathafaacl 3 msherrs@unsweduau
2 Introducton The study of lfetme dependence s hghly mportant n actuaral scence We consder a pool of lves where the ndvdual lfetmes follow a Pareto dstrbuton The dependence among the lves s determned by the nature of the multvarate dstrbuton We consder a multvarate constructon of the type II Pareto dstrbuton such that the correlaton between lves s governed by the Pareto shape parameter The nature of the problem s determned by the sze of the pool For example, for a pool of sze two, an applcaton of ths model wll help determne the prcng and rsk management of jont annuty products On the other hand, where the pool ncludes a natonal cohort, an applcaton of ths model wll help quantfy systematc longevty rsk Both ends of the spectrum are hghly relevant to ether prvate nsurance or publc polcy In the work of Ala et al 03, 05a,b, lfetme dependence modellng was consdered for members of the exponental dsperson famly, specfcally for the Tweede subclass Dependence was nduced va a common stochastc component, rather than governed parametrcally The Pareto dstrbuton represents an nterestng and relevant dstrbuton for modellng heavy-taled data It s chosen here to more accurately model old-age dependence, whether the applcaton of nterest s a jont-last survvor annuty or a pool of deferred annuty products The ssue of dependence has also been studed n Dhaene et al 000, Denut et al 00, Denut 008 and Dhaene and Denut 007, among others Snce the focus s on older age-mortalty, lfetmes are necessarly left-truncated Ths represents a non-trval ssue wth respect to parameter calbraton; one that we nvestgate on two fronts The frst of whch consders matchng observed wth theoretcal moments, and the second, observed wth theoretcal quantles mnmum and maxmum Organzaton of the paper: In Secton we ntroduce some basc notaton and provde some results for the unvarate Pareto dstrbuton The multvarate Pareto dstrbuton s ntroduced n Secton 3, where we derve certan mean and varance as well as mnmum and maxmum results These results are necessary for establshng parameter estmaton procedures, whch wll be consdered n subsequent sectons We provde some temporary conclusons n Secton 4 Notaton and the Type II Pareto Dstrbuton Notaton We begn by provdng some notaton concernng moments We denote wth k X and µ k X the k th, k Z +, raw and central theoretcal moments of random varable X, respectvely k X E[X k ], µ k X E[X X k ] The raw sample moments for random sample X X,, X n are gven by a k X X k, k Z + n
3 The raw sample moments of an dentcally dstrbuted sample are unbased estmators of the correspondng raw moments of X E[a k X] k X Fnally, adjusted second central sample moment s gven by m X X a X n The adjusted central sample moment of an ndependent and dentcally dstrbuted sample s an unbased and consstent estmator of the correspondng central moment of X E[ m X] µ X The Type II Pareto Dstrbuton We consder the type II Pareto dstrbuton wth scale and shape parameters > 0 and, respectvely The densty functon s gven by fy y +, y > 0 The survval functon s gven by F y The raw moments of nterest are gven by Y Y or, generally, for k Z + and > k, The varance s gven by µ Y y, y > 0, >,, > k Γ k k Y Γk + Γ, > 3 Mean and Varance for the Truncated Pareto Theorem Consder Y dstrbuted type II Pareto, Defne the assocated truncated random varable Y Y Y > The mean and varance of Y are gven by Y +, µ Y + 3
4 Proof F y; denotes the survval functon of a type II Pareto dstrbuton wth shape parameter Y F y y + dy Applyng partal fractons produces Y F y y dy + F y dy F F ; F ; F F F ; F + y + dy Y F F F + F y y y y + y + + dy y dy F y F ; F ; F F dy F F dy y dy
5 We presently use the fact that µ Y Y Y µ Y A Multvarate Pareto Dstrbuton We now consder a multvarate constructon of the type II Pareto dstrbuton Scale and shape parameters are gven by > 0 and, respectvely Let Y Y,, Y n be an n-dmensonal multvarate Pareto dstrbuton; the survval functon s gven by n F y y, where y y,, y n It s known that the margnal dstrbuton of Y,,, n follows a unvarate type II Pareto dstrbuton wth parameters and Furthermore, the dependence structure of the margnals s characterzed by the parameter ; that s, the correlaton between Y and Y j, for j s gven by / We provde some detal; for Y Y,, Y n multvarate Pareto, the covarance of Y and Y s gven by CovY, Y E[Y Y ] E[Y ]E[Y ] 3 Mean, Varance and Covarance Results We presently consder mean, varance, and covarance results for the margnal dstrbutons after applyng truncaton to the multvarate dstrbuton Note that ths s dfferent from consderng truncaton on a subset of the multvarate dstrbuton only For example, one may consder mean and varance results on the margnal dstrbuton when t alone s truncated, or even covarance results when the two margnals n queston are truncated Incdentally, we acheve the latter results as a by-product of multvarate truncaton by trvally allowng n and n To avod confuson, we ntroduce precse notaton Let Y Y,, Y n be the multvarate dstrbuton of nterest Let n be an n-dmensonal vector where each entry takes value Then, let Y Y Y > Theorem Consder Y Y,, Y n Multvarate P areto, wth survval functon denoted F y;, Defne the assocated truncated multvarate dstrbuton 5
6 Y Y Y > The mean and varance of Y are gven by Y µ Y + n +, + n The covarance between Y and Y j, j remans Cov Y, Y j, but the correlaton between Y and Y j, j s now gven by Corr Y, Y j + n Proof The densty of the multvarate dstrbuton s found by approprately dfferentatng the jont survval functon fy n n F y y y y 3 y n The truncated margnal densty s found by, frst, ntegratng ths jont densty; snce we are dealng wth a truncated multvarate dstrbuton, lower ntegraton ndces are set to And second, by normalzng wth constant F Note that the survval functon of the n-dmensonal jont Pareto evaluated at pont, F, s equvalent to the survval functon of a unvarate Pareto evaluated at pont n, F n For completeness, whenever F takes a sngle argument, a unvarate Pareto survval functon, otherwse, a multvarate Pareto survval functon, s mpled We consequently have that Y F n y dy y n + Apply partal fractons to obtan Y F n y n n y +n + dy Fnally, apply substtuton z y n and recognze that ntegrals are scaled survval functons of Pareto dstrbutons Y F n n z n z + dz F n F n; n F n n n n n + + n + 6
7 Apply a smlar approach to obtan the second raw moment Y Y F n y dy y n + Apply partal fractons and substtuton z y n Y F n n z n z + n z + dz F n; n F n; F n + n F n Ths mples Y / n n n + n n [ ] + + n [ ] + [ ] n + n + Rewrte the above as a quadratc of to obtan Y + n + + n + n + To derve the varance, we agan use the fact that µ Y Y Y Usng a common denomnator of, the expresson reduces very ncely to the one gven above To derve the covarance, we requre E[ Y Y ] Agan, we take expectaton wth respect to the the jont densty After ntegratng out the remanng n varables, we have E[ Y Y ] F n y y + dy dy y y +n + Although fndng an expresson for ths term s more complcated, t s based on the same prncples as before; we provde some detals Let z y y + n and 7
8 z y + n E[ Y Y ] + F n + F n + F n y y y [ y y +n dy y y +n + dy y +n z + z + dz dy y +n + y +n + ]dy y +n Havng dealt wth y, collect the y terms, notng the presence of y [ + y E[ Y Y ] F n y +n y n + y +n + y y +n + ]dy + Apply partal fractons and pull out scaled Pareto survval functons [ + E[ Y Y ] F n n z n z n n + z z + + z n n ] z + z + dz [ + F n F n; n F n; n n F n; F n + n F n; F n; + n ] + F n The rato of two Pareto survval functons reduces dependng on the dfference n shape parameters Collect terms based on these ratos, usng common denomnator 8
9 ; a lot of terms cancel out! [ n E[ Y Y ] + + n n n n n + [ n + n Rewrte as a quadratc n to obtan n n + ] + E[ Y Y ] + n + + n + n + Notce the smlarty of ths expresson wth that of Y In order to derve the covarance, we now take E[ Y Y ], rather than Y, and subtract Y Cov Y, Y E[ Y Y ] Y CovY, Y Clearly the varance of the margnal from the truncated multvarate dstrbuton dffers from the varance of the margnal from the un-truncated dstrbuton Hence, we obtan a dfferent correlaton coeffcent, one that goes to zero as n ncreases Corr Y, Y + n ] Remark It s convenent to note that Y E[ Y Y ] 3 Mnmum and Maxmum Results + n We presently consder the mnmum and maxmum element of our n-dmensonal truncated multvarate Pareto dstrbuton wth shape and scale parameters and As before, we have Y Y,, Y n and Y Y Y > Let Y mn Y and Y n max Y It s easy to demonstrate that Y follows a Pareto dstrbuton wth shape and scale /n, and hence that Y follows a truncated Pareto dstrbuton wth the same parameters In some detal, we have Pr[Y > y] Pr[Y > y,, Y n > y] F y,, y F ny 9 ny
10 Therefore, adjustng the scale parameter by /n results n a Pareto survval functon Furthermore, t s rrelevant whether you ether: fnd the mnmum of a truncated multvarate Pareto, or truncate the mnmum of an un-truncated multvarate Pareto Both lead to the same result, the latter beng more convenent We may apply Theorem to obtan the mean and varance of Y Y µ Y /n +, /n + For the maxmum, we have a less straght-forward result We start wth the dstrbuton functon of the maxmum of the truncated multvarate Pareto Pr[ < Y y] Pr[ Y n y] Pr[Y n y Y > ] Pr[Y > ] F n + n n F y F n n F y F n Dfferentate to fnd the densty f Y n y n F n y The expectaton s gven by n E[ Y n ] + y dy F n y + n + F n y n + F n n + F F n n + F F n n F + / + F n +, y > dy y + F ; F F F n Remark It s nterestng to note that when 0, we obtan the followng n / E[Y n ] + n + n! + γ, where γ s Euler s constant 0
11 It s also of nterest to know the varance of the truncated maxmum For ths, we begn wth the second raw moment Y n n + y dy F n y + n + F n y y + y dy + n + F ; F n F ; + F n + F + F n n + F + F n n + F + + F n n F F n Consequently, we have that µ Y n n F + F n n F + F n + + / + Remark 3 It s nterestng to note that when 0, we obtan the followng n µ Y n + / n / + n + n + n + n + [ ] n n + + [ n ] n The frst square-bracketed term appears to converge; t s equal to for n 600, reachng 6 at n 0 The second square-bracketed term appears to go to nfnty, but very slowly, for n 600, the term s 35, for n 0, t s 57
12 4 Concluson Lfetme dependence s studed usng a multvarate constructon of the type II Pareto dstrbuton We am to apply ths model to nvestgate older age mortalty, specfcally for jont-last survvor annutes and portfolos of deferred annuty products Gven the nature of the data, parameter estmaton technques need to ncorporate lefttruncaton We derve the necessary results for two estmaton procedures, one that uses mean-varance results, a second based on mnmum-maxmum We am to test the performance of both procedures usng smulaton We antcpate that one wll perform better for a large collecton of small pools of lves, say, one thousand jontlast survvor polces; the other for a small collecton of large pools of lves, say, ten portfolos of fve hundred deferred annutes References Ala, D H, Landsman, Z, and Sherrs, M 03 Lfetme dependence modellng usng a multvarate gamma dstrbuton Insurance: Mathematcs and Economcs, 53, Ala, D H, Landsman, Z, and Sherrs, M 05a A multvarate Tweede lfetme model: Censorng and truncaton Workng Paper Ala, D H, Landsman, Z, and Sherrs, M 05b Multvarate Tweede lfetmes: The mpact of dependence To appear n Scandnavan Actuaral Journal Denut, M 008 Comonotonc approxmatons to quantles of lfe annuty condtonal expected present value Insurance: Mathematcs and Economcs, 4, Denut, M, Dhaene, J, Le Bally de Tlleghem, C, and Teghem, S 00 Measurng the mpact of a dependence among nsured lfelengths Belgan Actuaral Bulletn,, 8 39 Dhaene, J and Denut, M 007 Comonotonc bounds on the survval probabltes n the Lee-Carter model for mortalty projectons Journal of Computatonal and Appled Mathematcs, 03, Dhaene, J, Vanneste, M, and Wolthus, H 000 A note on dependences n multple lfe statuses Bulletn of the Swss Assocaton of Actuares,, 9 34
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
Concomitants of Dual Generalized Order Statistics from Bivariate Burr III Distribution
 Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
Symplecticity of the Störmer-Verlet algorithm for coupling between the shallow water equations and horizontal vehicle motion
 Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Neutralino contributions to Dark Matter, LHC and future Linear Collider searches
 Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
35 90% 30 35 85% 2000 2008 + 2 2008 22-37 1997 26 1953- 2000 556 888 0.63 2001 0.58 2002 0.60 0.55 2004 0.51 2005 0.47 0.45 0.43 2009 0.
 184 C913.7 A 1672-616221 2-21- 7 Vol.7 No.2 Apr., 21 1 26 1997 26 25 38 35 9% 8% 3 35 85% 2% 3 8% 21 1 2 28 + 2 1% + + 2 556 888.63 21 572 986.58 22 657 1 97 23 674 1 229.55 24 711 1 48.51 25 771 1 649.47
184 C913.7 A 1672-616221 2-21- 7 Vol.7 No.2 Apr., 21 1 26 1997 26 25 38 35 9% 8% 3 35 85% 2% 3 8% 21 1 2 28 + 2 1% + + 2 556 888.63 21 572 986.58 22 657 1 97 23 674 1 229.55 24 711 1 48.51 25 771 1 649.47
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
A Two Sample Test for Mean Vectors with Unequal Covariance Matrices
 A Two Sample Test for Mean Vectors wth Unequal Covarance Matrces Tamae Kawasak 1 and Takash Seo 2 1 Department of Mathematcal Informaton Scence Graduate School of Scence, Tokyo Unversty of Scence, Tokyo,
A Two Sample Test for Mean Vectors wth Unequal Covarance Matrces Tamae Kawasak 1 and Takash Seo 2 1 Department of Mathematcal Informaton Scence Graduate School of Scence, Tokyo Unversty of Scence, Tokyo,
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Estimators when the Correlation Coefficient. is Negative
 It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
Supplementary materials for Statistical Estimation and Testing via the Sorted l 1 Norm
 Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
CAPM. VaR Value at Risk. VaR. RAROC Risk-Adjusted Return on Capital
 C RAM 3002 C RAROC Rsk-Adjusted Return on Captal C C RAM Rsk-Adjusted erformance Measure C RAM RAM Bootstrap RAM C RAROC RAM Bootstrap F830.9 A CAM 2 CAM 3 Value at Rsk RAROC Rsk-Adjusted Return on Captal
C RAM 3002 C RAROC Rsk-Adjusted Return on Captal C C RAM Rsk-Adjusted erformance Measure C RAM RAM Bootstrap RAM C RAROC RAM Bootstrap F830.9 A CAM 2 CAM 3 Value at Rsk RAROC Rsk-Adjusted Return on Captal
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Generalized Linear Model [GLM]
![Generalized Linear Model [GLM] Generalized Linear Model [GLM]](/thumbs/93/113885699.jpg) Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
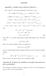 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
An Inventory of Continuous Distributions
 Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Pricing of Options on two Currencies Libor Rates
 Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
ECE Spring Prof. David R. Jackson ECE Dept. Notes 2
 ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Right Rear Door. Let's now finish the door hinge saga with the right rear door
 Right Rear Door Let's now finish the door hinge saga with the right rear door You may have been already guessed my steps, so there is not much to describe in detail. Old upper one file:///c /Documents
Right Rear Door Let's now finish the door hinge saga with the right rear door You may have been already guessed my steps, so there is not much to describe in detail. Old upper one file:///c /Documents
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Supporting information for: Functional Mixed Effects Model for Small Area Estimation
 Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
2 Lagrangian and Green functions in d dimensions
 Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
5 Haar, R. Haar,. Antonads 994, Dogaru & Carn Kerkyacharan & Pcard 996. : Haar. Haar, y r x f rt xβ r + ε r x β r + mr k β r k ψ kx + ε r x, r,.. x [,
 4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
= λ 1 1 e. = λ 1 =12. has the properties e 1. e 3,V(Y
 Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Constant Elasticity of Substitution in Applied General Equilibrium
 Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Commutative Monoids in Intuitionistic Fuzzy Sets
 Commutative Monoids in Intuitionistic Fuzzy Sets S K Mala #1, Dr. MM Shanmugapriya *2 1 PhD Scholar in Mathematics, Karpagam University, Coimbatore, Tamilnadu- 641021 Assistant Professor of Mathematics,
Commutative Monoids in Intuitionistic Fuzzy Sets S K Mala #1, Dr. MM Shanmugapriya *2 1 PhD Scholar in Mathematics, Karpagam University, Coimbatore, Tamilnadu- 641021 Assistant Professor of Mathematics,
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
 9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
THE SECOND WEIGHTED MOMENT OF ζ. S. Bettin & J.B. Conrey
 THE SECOND WEIGHTED MOMENT OF ζ by S. Bettn & J.B. Conrey Abstract. We gve an explct formula for the second weghted moment of ζs) on the crtcal lne talored for fast computatons wth any desred accuracy.
THE SECOND WEIGHTED MOMENT OF ζ by S. Bettn & J.B. Conrey Abstract. We gve an explct formula for the second weghted moment of ζs) on the crtcal lne talored for fast computatons wth any desred accuracy.
ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ ΔΙΔΑΚΤΟΡΙΚΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΕΛΕΤΗ ΤΗΣ ΜΑΚΡΟΧΡΟΝΙΑΣ ΠΑΡΑΜΟΡΦΩΣΗΣ ΤΟΥ ΦΡΑΓΜΑΤΟΣ ΚΡΕΜΑΣΤΩΝ ΜΕ ΒΑΣΗ ΑΝΑΛΥΣΗ ΓΕΩΔΑΙΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΜΕΤΑΒΟΛΩΝ ΣΤΑΘΜΗΣ ΤΑΜΙΕΥΤΗΡΑ ΔΙΔΑΚΤΟΡΙΚΗ
arxiv: v1 [stat.me] 20 Jun 2015
![arxiv: v1 [stat.me] 20 Jun 2015 arxiv: v1 [stat.me] 20 Jun 2015](/thumbs/87/95713260.jpg) Combnng cluster sampg and k-tracng sampg to estmate the sze of a hdden populaton: asymptotc propertes of the estmators arxv:56.69v stat.me 2 Jun 25 Martín H. Fél Medna Techncal report Number: FCFM-UAS-25-
Combnng cluster sampg and k-tracng sampg to estmate the sze of a hdden populaton: asymptotc propertes of the estmators arxv:56.69v stat.me 2 Jun 25 Martín H. Fél Medna Techncal report Number: FCFM-UAS-25-
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
On a four-dimensional hyperbolic manifold with finite volume
 BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)
![MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3) MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)](/thumbs/81/84712331.jpg) 1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
w o = R 1 p. (1) R = p =. = 1
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Risk! " #$%&'() *!'+,'''## -. / # $
 Risk! " #$%&'(!'+,'''## -. / 0! " # $ +/ #%&''&(+(( &'',$ #-&''&$ #(./0&'',$( ( (! #( &''/$ #$ 3 #4&'',$ #- &'',$ #5&''6(&''&7&'',$ / ( /8 9 :&' " 4; < # $ 3 " ( #$ = = #$ #$ ( 3 - > # $ 3 = = " 3 3, 6?3
Risk! " #$%&'(!'+,'''## -. / 0! " # $ +/ #%&''&(+(( &'',$ #-&''&$ #(./0&'',$( ( (! #( &''/$ #$ 3 #4&'',$ #- &'',$ #5&''6(&''&7&'',$ / ( /8 9 :&' " 4; < # $ 3 " ( #$ = = #$ #$ ( 3 - > # $ 3 = = " 3 3, 6?3
LESSON 14 (ΜΑΘΗΜΑ ΔΕΚΑΤΕΣΣΕΡΑ) REF : 202/057/34-ADV. 18 February 2014
 LESSON 14 (ΜΑΘΗΜΑ ΔΕΚΑΤΕΣΣΕΡΑ) REF : 202/057/34-ADV 18 February 2014 Slowly/quietly Clear/clearly Clean Quickly/quick/fast Hurry (in a hurry) Driver Attention/caution/notice/care Dance Σιγά Καθαρά Καθαρός/η/ο
LESSON 14 (ΜΑΘΗΜΑ ΔΕΚΑΤΕΣΣΕΡΑ) REF : 202/057/34-ADV 18 February 2014 Slowly/quietly Clear/clearly Clean Quickly/quick/fast Hurry (in a hurry) Driver Attention/caution/notice/care Dance Σιγά Καθαρά Καθαρός/η/ο
Exam Statistics 6 th September 2017 Solution
 Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
Derivation for Input of Factor Graph Representation
 Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Duals of the QCQP and SDP Sparse SVM. Antoni B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckriet
 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckret SVCL-TR 007-0 v Aprl 007 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R.
Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckret SVCL-TR 007-0 v Aprl 007 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R.
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
