ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ
|
|
|
- Άλκηστις Μακρή
- 5 χρόνια πριν
- Προβολές:
Transcript
1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Λογισμός Ι Ενότητα 2: Ακολουθίες - Σειρές Κ. Δασκαλογιάννης Τμήμα Μαθηματικών Α.Π.Θ. (Α.Π.Θ.) Λογισμός Ι 1 / 83
2 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,όπως εικόνες,που υπόκειται σε άλλου τύπου άδειας χρήσης, η άδεια χρήσης αναφέρεται ρητώς. (Α.Π.Θ.) Λογισμός Ι 2 / 83
3 Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το έργο Ἁνοικτά Ακαδημαικά Μαθήματα στο Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης έχει χρηματοδοτήσει μόνο την αναδιαμόρφωση του εκπαιδευτικού υλικού. Το έργο υλοποιείται στο πλαίσιο του Επιχειρησιακού Προγράμματος Εκπαίδευση και Δια Βίου Μάθηση και συγχρηματοδοτείται απο την Ευρωπαική Ενωση (Ευρωπαικό Κοινωνικό Ταμείο) και από εθνικούς πόρους. (Α.Π.Θ.) Λογισμός Ι 3 / 83
4 Περιεχόμενα Ενότητας Σημεία Συσσώρευσης και Απομονωμένα Σημεία Θεώρημα Bolzano-Weierstrass Ακολουθία Σύγκλιση ακολουθιών Υπακολουθίες Μονότονες ακολουθίες Ακολουθίες Cauchy Αποκλίνουσες ακολουθίες Σύγκλιση Σειράς Κριτήρια Σύγκλισης (Α.Π.Θ.) Λογισμός Ι 4 / 83
5 Σκοποί Ενότητας Σε αυτή την ενότητα θα μελετήσουμε τις ακολουθίες, τις σειρές και τις ιδιότητές τους. (Α.Π.Θ.) Λογισμός Ι 5 / 83
6 Ανοικτή περιοχή Ανοικτό διάστημα (a, b) = x R : a < x < b Ορισμός ανοικτής περιοχής ή σφαίρας ή μπάλας (x 0 ɛ, x 0 + ɛ) B(x 0, ɛ) (ανοικτή) περιοχή του x 0 ακτίνας ɛ B(x,ε)=(x -ε,x +ε) ο ο ο x -ε ο x o x +ε ο ( ) ε ε (Α.Π.Θ.) Λογισμός Ι 6 / 83
7 Σημεία συσσώρευσης και απομονωμένα σημεία Σημείο συσσώρευσης x 0 σημείο συσσώρευσης του A ɛ > 0 (B(x 0, ɛ) x 0 ) A ή ɛ > 0 x A και x x 0 x x 0 < ɛ Παράδειγμα: A = 1 n, n N, το 0 A είναι σημείο συσσώρευσης του A. Απομονωμένο ή μεμονωμένο σημείο x 0 απομονωμένο ή μεμονωμένο σημείο του A το x 0 δεν είναι σημείο συσσώρευσης ɛ > 0 B (x 0, ɛ) A = x 0 ή ɛ > 0 x A και x x 0 x x 0 ɛ Παράδειγμα: A = 1 n, n N, το 1 5 A είναι απομονωμένο σημείο του A. (Α.Π.Θ.) Λογισμός Ι 7 / 83
8 Θεώρημα Bolzano Weierstrass Πρόταση Αν a είναι σημείο συσσώρευσης του A Το A έχει άπειρο αριθμό στοιχείων (τουλάχιστον αριθμήσιμο). Θεώρημα Bolzano Weierstrass Κάθε (άνω και κάτω) φραγμένο απειροσύνολο A έχει τουλάχιστον ένα σημείο συσσώρευσης Συμπέρασμα A φραγμένο απειροσύνολο σημείο συσσώρευσης (Α.Π.Θ.) Λογισμός Ι 8 / 83
9 Σχήμα 1 m n M n d n d n+1 =d n /2 m n+1 M n+1 (Α.Π.Θ.) Λογισμός Ι 9 / 83
10 Σχήμα 2 m n M n d n d n+1 =d n /2 m n+1 (Α.Π.Θ.) Λογισμός Ι 10 / 83
11 Σχήμα 3 (Α.Π.Θ.) Λογισμός Ι 11 / 83
12 Πρόταση 1 Πρόταση Αν a είναι σημείο συσσώρευσης του A Το A έχει άπειρο αριθμό στοιχείων. Απόδειξη Εστω A = a 1, a 2,..., a n έχει n στοιχεία και σημείο συσσώρευσης το a θέτουμε Ατοπο 1 ɛ = min 2 a k a, k = 1, 2,..., n x A a x > ɛ a όχι σημ. συσσώρευσης (Α.Π.Θ.) Λογισμός Ι 12 / 83
13 Θεώρημα Bolzano Weierstrass (Απόδειξη) Θεώρημα Bolzano Weierstrass Κάθε (άνω και κάτω) φραγμένο απειροσύνολο A έχει τουλάχιστον ένα σημείο συσσώρευσης Απόδειξη x A inf A = m0 x M0 = sup A d0 = M0 m0 d1 = d0 M0 m0 = 2 2 ή Χωρίζουμε το διάστημα [m0, M0] σε δύο ίσα μέρη, σε κάποιο από αυτά υπάρχουν άπειρα στοιχεία του A αυτό το διάστημα το ονομάζουμε [m1, M1] d2 = d1 2 = d0 22. Επαναλαμβάνουμε την διαδικασία n φορές. m0 m1 mn Mn M1 M0 Mn 1 mn 1 dn = = d0 2 2 n sup mn, n N = ξ η = inf Mn, n N d0 d0 Υποθ ξ < η k N : < η ξ < Mk mk = άτοπο 2k 2k Αρα ξ = η k N ξ mk d0 2 k και Mk ξ d0 d0 [mk, Mk] B(ξ, 2k 2 k ) ɛ > 0 k N : ɛ > d0 k > d0 d0 [mk, Mk] B(ξ, ) B(ξ, ɛ) 2k 2k [mk, Mk] A B(ξ, ɛ) A Το B(ξ, ɛ) A έχει άπειρα στοιχεία του A επομένως το ξ είναι σημείο συσσώρευσης του A (Α.Π.Θ.) Λογισμός Ι 13 / 83
14 Ακολουθία (1/3) Ορισμός Ακολουθία x n n N λίστα στοιχείων (x 1, x 2,..., x n,...). x n είναι ο γενικός όρος Ισοδύναμος ορισμός Ακολουθία είναι μια απεικόνιση του N στο R Παράδειγμα: Δίδεται ο γενικός όρος x n = N n f f(n) = x n R 1 n(n + 1) x n n N = Παράδειγμα: Αναδρομική σχέση ( 1 2, 1 6, 1 12, 1 ) 20,... x 1 = 1, x n = n 2 x n 1 x n = n! 2 n 1 (Α.Π.Θ.) Λογισμός Ι 14 / 83
15 Ακολουθία (2/3) Παράδειγμα: Αναδρομική σχέση Fibonacci x 1 = 1, x 2 = 1 x n = x n 1 + x n 2 x n n N = (1, 1, 2, 3, 5, 8, 13, 21,...) ( ) n ( ) n x n = 2 n 5 Παράδειγμα: Εναλλασσομένη ακολουθία 1 γιά n = 2k x n = 1 γιά n = 2k + 1 x n = ( 1) n+1 = cos nπ x n n N = (1, 1, 1, 1, 1, 1,...) (Α.Π.Θ.) Λογισμός Ι 15 / 83
16 Ακολουθία (3/3) Παράδειγμα: x n = 1 n x n = 1 n 1 + ( 1)n 2 x n n N = γιά n = 2k n 1 n γιά n = 2k n 1 n ( 0, 1 2, 2 3, 1 4, 4 5,..., 1 2k, 1 ( 1)n 2 2k 2k + 1,... ) (Α.Π.Θ.) Λογισμός Ι 16 / 83
17 οριακά σημεία 2 και 1 (Α.Π.Θ.) Λογισμός Ι 17 / 83 Οριακό Σημείο Ακολουθίας Οριακό Σημείο x = οριακό σημείο της x n n N Το x είναι σημείο συσσώρευσης της x n n N ή Υπάρχουν άπειροι όροι = x Παράδειγμα: Ακολουθία με ( γενικό όρο ) x n = sin2 nπ 2 + (n + 1) ( ) cos2 nπ 2, n N n n (1, 32, 13, 54, 15, 76, 17 ),... οριακά σημεία 0 και 1 Παράδειγμα: Ακολουθία με γενικό όρο x n = 1 + (n + 1) ( cos2 nπ 2, n N n (1, 52, 1, 94, 1, 136 ), 1,... )
18 Μιά συγλίνουσα ακολουθία έχει μόνο ένα οριακό σημείο. (Α.Π.Θ.) Λογισμός Ι 18 / 83 Σύγκλιση ακολουθιών Ορισμός: ΣΥΓΚΛΙΝΟΥΣΑ ΑΚΟΛΟΥΘΙΑ Η ακολουθία x n n N συγκλίνει στο x lim x n = x ή x n για κάθε περιοχή του x τελικά όλοι οι όροι της ακολουθίας περιέχονται σε αυτή x αν lim x n = x ɛ > 0 N(ɛ) > 0 : n > N(ɛ) x n B(x, ɛ) Εψιλοντικός ορισμός lim x n = x ɛ > 0 N(ɛ) > 0 : n > N(ɛ) x n x < ɛ
19 Παράδειγμα 1 lim x n = x ɛ > 0 N(ɛ) > 0 : n > N(ɛ) x n x < ɛ Παράδειγμα: x n = 1 n lim x n = 0 n n ΠΡΟΧΕΙΡΟ n > N x n x = 1 n 0 = 1 < 1 n N = ɛ φθίνουσα; 1 N = ɛ, N(ɛ) = 1 ɛ ɛ > 0 N(ɛ) = 1 ɛ : n > N(ɛ) x n < ɛ (Α.Π.Θ.) Λογισμός Ι 19 / 83
20 Παράδειγμα 2 lim x n = x ɛ > 0 N(ɛ) > 0 : n > N(ɛ) x n x < ɛ Παράδειγμα: ΠΡΟΧΕΙΡΟ x n = 1 n 2 +e n n > N x n x = 1 e N = ɛ lim n n x n = 0 1 n 2 + e n 1 e n < 1 e N = ɛ φθίνουσα; N(ɛ) = ln 1 ɛ ɛ > 0 N(ɛ) = ln 1 ɛ : n > N(ɛ) x n < ɛ (Α.Π.Θ.) Λογισμός Ι 20 / 83
21 Παράδειγμα 3 a > 1, lim n a = x > 0 (1 + x) n 1 + nx ( Bernoulli) a > 1 a = n a n n a 1 x x n a 1 a 1 n Πρόχειρο n > N n a 1 a 1 < a 1 a 1 = ɛ N(ɛ) = n N ɛ ɛ > 0 N(ɛ) = a 1 ɛ : n > N(ɛ) n a 1 a 1 n n < a 1 N = ɛ (Α.Π.Θ.) Λογισμός Ι 21 / 83
22 Παράδειγμα 4 Πρόχειρο n! n n = n! lim n n = (n 2) (n 1) n n n = 1 n 2 n (1 2 n ) (1 1 n ) ( = 1 n n 2 1 k ) < 1 k=1 n n <1 n! n n < 1 n < 1 N = ɛ N(ɛ) = 1 ɛ n > N(ɛ) ɛ > 0 N(ɛ) = 1 ɛ : n! n n 1 n < 1 N(ɛ) = ɛ (Α.Π.Θ.) Λογισμός Ι 22 / 83
23 Παράδειγμα 5 n 3 lim 2 n = 0 2 n = (1 + 1) n = n ( n ) ( k = + n ) 4 + = k=0 = + n(n 1)(n 2)(n 3) 4! + 2 n > n(n 1)(n 2)(n 3) 4! n > 6 n k > n 2 για k = 1, 2, 3 Πρόχειρο 2 n > n ! 23 4! n > n3 2 n n 3 2 n < 23 4! < 23 4! n N = ɛ N(ɛ) = 23 4! ɛ n > N(ɛ) ɛ > 0 N(ɛ) = 23 4! n3 2 < 2 3 4! n ɛ : n < 23 4! N(ɛ) = ɛ (Α.Π.Θ.) Λογισμός Ι 23 / 83
24 ΜΗΔΕΝΙΚΕΣ ΑΚΟΛΟΥΘΙΕΣ Ορισμός x n n N είναι μηδενική ακολουθία lim x n = 0 ή x n 0 ɛ > 0, N(ɛ) > 0 : n > N(ɛ) x n < ɛ Μηδ. 1: x n Μηδ. 2: x n Μηδ. 3: Μηδ. 4: Μηδ. 5: x n x n 0 x n 0 0 λ x n 0 και y n και y n < M x n y n και y n 0 Μηδ. 6: x n 0 x n n N x n + y n x n y n x n φραγμένη C > 0 : n x n < C (Α.Π.Θ.) Λογισμός Ι 24 / 83
25 ΣΥΓΚΛΙΝΟΥΣΕΣ ΑΚΟΛΟΥΘΙΕΣ (1/2) Ορισμός συγκλίνουσας ακολουθίας Πρ. 1 x n x n n N συγκλίνει στο x lim x n = x ή x n x ɛ > 0, N(ɛ) > 0 : n > N(ɛ) x n x < ɛ (x n x) n N μηδενική ακολουθία x x n x Πρ. 2 x n x λ x n λx Πρ. 3 x n x x n n N φραγμένη C, D > 0 και N > 0 : n > N D < x n < C Πρ. 4 x n Πρ. 5 x n x και y n x και y n y x n + y n y x n y n x + y x y (Α.Π.Θ.) Λογισμός Ι 25 / 83
26 ΣΥΓΚΛΙΝΟΥΣΕΣ ΑΚΟΛΟΥΘΙΕΣ (2/2) Πρ. 6α: Πρ. 6β: Πρ. 7: Πρ. 8α: Πρ. 8β: Πρ. 9α: Πρ. 9β: 0 x n και x n x x n y n και x n z n x n y n z n x n x n και a, y n a x και x 0 x, y n a < 1 a n 0 x y x, y n x n 1 x n y και y 0, 0 x n 0, x n+1 x n k < 1 a 1 x x n x y xn y n 0 x y (Α.Π.Θ.) Λογισμός Ι 26 / 83
27 ΜΗΔΕΝΙΚΕΣ ΑΚΟΛΟΥΘΙΕΣ-αποδείξεις Ορισμός x n n N είναι μηδενική ακολουθία lim x n = 0 ή x n 0 ɛ > 0, N(ɛ) > 0 : n > N(ɛ) x n < ɛ Πρόταση Μηδ.1 x n 0 x n 0 Πρόταση Μηδ.2 x n 0 λ x n 0 Απόδ: ɛ > 0, N(ɛ) > 0 : x n 0 n > N(ɛ) x n < ɛ ( ) Πρόχειρο: x n < ɛ λ x n = λ x n < λ ɛ = ɛ ( ɛ > ) 0, N (ɛ ) = N ɛ λ = N(ɛ) > 0 : n > N (ɛ ) = N(ɛ) x n < ɛ λ x n < ɛ λ x n 0 (Α.Π.Θ.) Λογισμός Ι 27 / 83
28 Αποδείξεις για μηδενικές ακολουθίες (1/3) Πρόταση Μηδ. 3 Απόδ: x n y n x n y n 0 0 x n + y n 0 ɛ > 0, N1 (ɛ) > 0 : 0 n > N 1 (ɛ) x n < ɛ 0 ɛ > 0, N2 (ɛ) > 0 : n > N 2 (ɛ) y n < ɛ (Πρόχειρο : x n + y n x n + y n < 2ɛ = ɛ ) ( ) ɛ > 0, N (ɛ ) = max N ɛ 1 ( ) 2 n > N (ɛ ) N ɛ 1 Επομένως x n + y n n > N (ɛ ) N 2 ( ɛ 2 2, N 2 ( ɛ 2 ) > 0 : = N 1 (ɛ) x n < ɛ 2 ) = N 2 (ɛ) y n < ɛ 2 Αρα x n + y n = x n + y n < ɛ 0 (Α.Π.Θ.) Λογισμός Ι 28 / 83
29 Αποδείξεις για μηδενικές ακολουθίες (2/3) Πρόταση Μηδ. 4 x n 0 y n < M x n y n 0 Απόδ: x n 0 ɛ > 0, N1 (ɛ) > 0 : n > N 1 (ɛ) x n < ɛ (Πρόχειρο : x n y n x n y n < ɛm = ɛ ) ɛ > 0, N (ɛ ) = N 1 (ɛ /M) : n > N (ɛ )) = N 1 (ɛ /M) x n < ɛ /M Αρα x n y n = x n y n < ɛ Επομένως x n y n 0 (Α.Π.Θ.) Λογισμός Ι 29 / 83
30 Αποδείξεις για μηδενικές ακολουθίες (3/3) Πρόταση Μηδ. 5 x n y n και y n 0 x n 0 Απόδ: y n 0 ɛ > 0, N(ɛ) > 0 : n > N(ɛ) x n y n < ɛ Απόδειξη Μη. 6 x n 0 x n n N φραγμένη C > 0 : n x n < C Απόδ: x n 0 ɛ = 1, N(1) : n > N(1) x n < 1 C = 1 + max x k, k x n n x n < C (Α.Π.Θ.) Λογισμός Ι 30 / 83
31 ΣΥΓΚΛΙΝΟΥΣΕΣ ΑΚΟΛΟΥΘΙΕΣ-Αποδείξεις (1/5) Ορισμός Πρ. 1 x n x n n N συγκλίνει στο x lim x n = x ή x n x ɛ > 0, N(ɛ) > 0 : n > N(ɛ) x n x < ɛ x x n x Απόδ: x n x ɛ > 0, N(ɛ) > 0 : n > N(ɛ) x n x < ɛ Επειδή ( x n x ) x n x < ɛ ɛ > 0, N(ɛ) > 0 : n > N(ɛ) ( x n x ) x n x < ɛ Πρ. 2 x n x λ x n λx x n x (Α.Π.Θ.) Λογισμός Ι 31 / 83
32 ΣΥΓΚΛΙΝΟΥΣΕΣ ΑΚΟΛΟΥΘΙΕΣ-Αποδείξεις (2/5) Πρ. 3 x n x x n n N φραγμένη C, D > 0 και N > 0 : n > N D < x n < C Απόδ: Για n > N x n x ( ) x 2 η τριγωνική ιδιότητα δίνει ( ) για ɛ = x 2, N x 2 > 0 : ( ) n > N x 2 x n x < x 2 x n = (x n x) + x x n x + x < 3 2 x = C D = x 2 < x (x n x) (x n x) + x = x n (Α.Π.Θ.) Λογισμός Ι 32 / 83
33 ΣΥΓΚΛΙΝΟΥΣΕΣ ΑΚΟΛΟΥΘΙΕΣ-Αποδείξεις (3/5) Πρ. 4: xn yn x y xn + yn x + y Πρ. 5: xn x yn Απόδ: Πρόχειρο: y xn yn x y ɛ > 0, N1(ɛ) > 0 : xn x n > N1(ɛ) xn x < ɛ Πρ. 3 yn n > N1 y ( ) x xn x < 3 x 2 2 ɛ > 0, N2(ɛ) > 0 : n > N2(ɛ) yn y < ɛ xnyn xy = xn(yn y) + (xn x)y xn yn y + xn x y 3 x 2 ɛ + y ɛ = ɛ ( ɛ ) N (ɛ ( ) = ) ( ɛ = maxn1 ɛ y +3 x /2, N2 x y +3 x /2.N1 2 n > N (ɛ ) xnyn xy < ɛ xnyn xy ) (Α.Π.Θ.) Λογισμός Ι 33 / 83
34 ΣΥΓΚΛΙΝΟΥΣΕΣ ΑΚΟΛΟΥΘΙΕΣ-Αποδείξεις (4/5) Πρ. 6α 0 x n και x n x 0 x Απόδ: Εστω x < 0 N ( ) n > N x 2 Πρ. 6β x n Πρ. 7 z n ( ) x 2 : x n x < x 2 x n < 0 άτοπο. x n y n και x, y n y z n x n y n και a, y n a x y xn a Απόδ: Είναι μια άμεση εφαρμογή της προηγούμενης πρότασης. Αλλη απόδειξη με εψιλοντικό ορισμό: ɛ > 0, N y n a 1(ɛ) > 0 : n > N 1(ɛ) a ɛ < y n < a + ɛ ɛ > 0, N z n a 2(ɛ) > 0 : n > N 2(ɛ) a ɛ < z n < a + ɛ n > maxn 1(ɛ), N 2(ɛ) a ɛ < z n x n y n < a + ɛ x n a (Α.Π.Θ.) Λογισμός Ι 34 / 83
35 ΣΥΓΚΛΙΝΟΥΣΕΣ ΑΚΟΛΟΥΘΙΕΣ-Αποδείξεις (5/5) Πρ. 8 xn x και x 0 1 xn Πρ. 9α a < 1 a n 0 1 x Απόδ: a < 1 a = 1 1+x, x > 0 (1 + x) n 1 + nx 1 a 1 + n( 1 n a 1) a n 1 1+n( 1 a 1) a n 0 Πρ. 9β xn 0, xn+1 Απόδ: xn k < 1 xn 0 xn+1 xn xn+1 k < 1 xn ɛ = 1 k 2, N ( ) 1 k ) [ ( 2 : > N 1 k )] 2 = m 2 xn+1 n > N ( 1 k 2 1 k k < xm+1 < 1+k 2 xm xn xm+2 < 1+k 2 xm+1 < ( 1+k 2 xn = x m+(n m) < < ( 1+k 2 ) n m xm = ( 1+k 2 ( ) 1 + k n lim xn lim n 0 n 0 2 =0 < k + 1 k 2 = 1+k 2 ) 2 xm ) n ( 1+k ) m 2 xm ) m xm = 0 ( 1 + k 2 (Α.Π.Θ.) Λογισμός Ι 35 / 83
36 Διάφορες ιδιότητες ακολουθιών n Ιδ. 1 : a > 0, a 1 n Ιδ. 2 : n 1 Ιδ. 3 : x n > 0, x n x k x n k x Ιδ. 4 : P (n) = a 0 n p + a 1 n p a p 1 n + a p, Q(n) = b 0 n q + b 1 n q a q 1 n + a q Αν p = q τότε P (n) Q(n) a 0 b 0 Αν p < q τότε P (n) Q(n) 0 (Α.Π.Θ.) Λογισμός Ι 36 / 83
37 ΥΠΑΚΟΛΟΥΘΙΕΣ (1/2) Ορισμός Μια επιλογή y k k N = x nk k N από άπειρους όρους της ακολουθίας, με n 1 < n 2 < n 3 < ονομάζεται υπακολουθία της x n n N ( ) x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9,... ( ) x 1 x 2, x 3, x 4 x 5 x 6, x 7, x 8 x 9,... ( ( ) x n1, x n2, x n3, x n4, x n5,... ) y 1, y 2, y 3, y 4, y 5,... Σημείωση για τους δείκτες: k n k και k < l n k < n l (Α.Π.Θ.) Λογισμός Ι 37 / 83
38 ΥΠΑΚΟΛΟΥΘΙΕΣ (2/2) Υπακ.1 x n συγκλίνει στο x Παράδειγμα: n n 1 κάθε υπακολουθία y k = x nk συγκλίνει στο x Θεώρημα Bolzano Weierstrass n 2 n2 1 Κάθε (άνω και κάτω) φραγμένο απειροσύνολο A έχει τουλάχιστον ένα σημείο συσσώρευσης Υπακ. 2 Κάθε (άνω και κάτω) φραγμένη ακολουθία έχει τουλάχιστον μια συγκλίνουσα υπακολουθία (Α.Π.Θ.) Λογισμός Ι 38 / 83
39 Αποδείξεις για τις υπακολουθίες (1/2) Υπακ. 1 x n συγκλίνει στο x Παράδειγμα: n n 1 Απόδ: x n x κάθε υπακολουθία y k = x nk συγκλίνει στο x n 2 n 2 1 ɛ > 0, N(ɛ) > 0 : k > N(ɛ) x k x < ɛ Επειδή n k k > N(ɛ) τότε x nk x < ɛ ɛ > 0, N(ɛ) > 0 : n k > N(ɛ) x nk x < ɛ (Α.Π.Θ.) Λογισμός Ι 39 / 83
40 Αποδείξεις για τις υπακολουθίες (2/2) Θεώρημα Bolzano Weierstrass Κάθε (άνω και κάτω) φραγμένο απειροσύνολο A έχει τουλάχιστον ένα σημείο συσσώρευσης Υπ. 2 Κάθε (άνω και κάτω) φραγμένη ακολουθία έ- χει τουλάχιστον μια συγκλίνουσα υπακολουθία Απόδ: Αν η ακολουθία έχει μια απειρία από σταθερούς όρους τότε διαλέγουμε την υπακολουθία από τους σταθερούς όρους και είναι συκλίνουσα αν η ακολουθία έχει άπειρους μη ίσους όρους τότε έχουμε ένα φραγμένο απειροσύνολο υπάρχει ένα σημείο συσσώρευσης x n N, x kn : x 1 n < x k n < x + 1 n Αρα x kn x. (Α.Π.Θ.) Λογισμός Ι 40 / 83
41 ΜΟΝΟΤΟΝΕΣ ΑΚΟΛΟΥΘΙΕΣ x n είναι αύξουσα ακολουθία x n x n+1 x n είναι φθίνουσα ακολουθία x n x n+1 x n είναι μονότονη ακολουθία φθίνουσα ή αύξουσα ακολουθία Μον. 1α x n είναι αύξουσα και φραγμένη ακολουθία x n Μον. 1β x n είναι φθίνουσα και φραγμένη ακολουθία x n supx k k N infx m m N Μον. 2 x n είναι μονότονη ακολουθία και έχει μια συγκλίνουσα υπακολουθία lim x n k = x η ακολουθία x n συγκλίνει στο ίδιο όριο δηλ x n x k (Α.Π.Θ.) Λογισμός Ι 41 / 83
42 ΜΟΝΟΤΟΝΕΣ ΑΚΟΛΟΥΘΙΕΣ - αποδείξεις (1/2) x n είναι αύξουσα ακολουθία x n x n+1 x n είναι φθίνουσα ακολουθία x n x n+1 x n είναι x n είναι μονότονη ακολουθία φθίνουσα ή αύξουσα ακολουθία Μον. 1α x n είναι αύξουσα και φραγμένη ακολουθία x n supx k k N Απόδ: Εχουμε xn xn+1 K. Υπάρχουν δύο περιπτώσεις, είτε υπάρχει κάποιος δείκτης l τέτοιος ώστε για κάθε n l xn = L R, στην περίπτωση αυτή L = lim xk = maxx1, x2,..., xm k είτε η ακολουθία έχει απειρους διαφορετικούς όρους. Εστω R M = supxkk N (υπάρχει το Μ λόγω του αξιώματος ΙΙΙ του συνόλου R!) τότε από τον ορισμό του sup ɛ > 0, k N : M ɛ < xk M Επομένως xn αύξουσα n > k xk xn M < M + ɛ ɛ > 0, k = N(ɛ) : n > N(ɛ) M ɛ < xn < M + ɛ άρα xn M Μον. 1β x n είναι φθίνουσα και φραγμένη ακολουθία x n infx m m N (Α.Π.Θ.) Λογισμός Ι 42 / 83
43 ΜΟΝΟΤΟΝΕΣ ΑΚΟΛΟΥΘΙΕΣ - αποδείξεις (2/2) Μον. 2 x n είναι μονότονη ακολουθία και έχει μια συγκλίνουσα υπακολουθία lim x n k = x η ακολουθία x n συγκλίνει στο ίδιο όριο δηλ x n x k Απόδειξη. Η υπακολουθία x nk είναι μια μονότονη (πχ αύξουσα) ακολουθία, επομένως x = sup x nk. Το x είναι επίσης supremum της k N υπαακολουθίας x nk (βλ. Μον. 1α). Θέτουμε A = x nk, k N και B = x n, n N, z A z B επομένως z sup B δηλαδή x = sup A sup B. Αν sup A < sup B l : x l > x αλλά τότε υπάρχει κάποιο m έτσι ώστε x nm x l > x πράγμα άτοπο. Οπότε sup A = sup B. (Α.Π.Θ.) Λογισμός Ι 43 / 83
44 Παράδειγμα 6.1 ( Ορ. x n = ) n n x n = = ( n) n = n l=0 n l=0 ( ) n 1 l n l = 1 + n n(n 1) + n n n(n 1)(n 2) (n l + 1) l! n l = n(n 1)(n 2) 2!n 2 + 3!n n n ( ) ( 1 2 ) ( 1 3 ) l! n n n l=0 ( 1 l x n+1 > x n n+1 x n+1 = = l=0 n l=0 + 1 l! 1 l! αύξουσα ακολουθία ( 1 1 n + 1 ( 1 1 n + 1 ) ( 1 2 n + 1 ) ( 1 2 n + 1 ) ( 1 3 n + 1 ) ( 1 3 n (n + 1) ( n+1 1 k ) ( > 1 k ) x n+1 > x n n + 1 n ) ( 1 l 1 n + 1 ) ( 1 l 1 n + 1 ) ) + (Α.Π.Θ.) Λογισμός Ι 44 / 83
45 Παράδειγμα 6.2 Ορ. y n = n l=0 1 l! y n+1 > y n αύξουσα ακολουθία x n y n y n φραγμένη ακολουθία x n φραγμένη ακολουθία x n e και y n k ( 1 γ n,k = 1 1 l! n l=0 γ n,k x n e γ n,k 1 l! = l 1 2 l 1 x n < y n = ! ( n! = = ) 2 n 1 < < = 3 2 e e e ) ( 1 2 n ) ( 1 3 n ) ( 1 l 1 ) n y k (Α.Π.Θ.) Λογισμός Ι 45 / 83
46 Παράδειγμα 6.3 y k e lim y k = e e k ( e = e lim ) n = 1 n k= k! 1 (1 1n ) n 2 1 n 1n ( ) n n 2 1 ( 1 n) 1 n (1 1n ) n = ( ) n e 1 ( n k N ( 1 + k l n 1 + k n) n ) n ek/l ek ( 1 + α n ) n = e α = sup e q, q Q, q α, α > 0 (Α.Π.Θ.) Λογισμός Ι 46 / 83
47 ΑΚΟΛΟΥΘΙΕΣ CAUCHY (1/3) Ορισμός x n Cauchy ɛ > 0 N(ɛ) : n > m > N(ɛ) x n x m < ɛ x n x x n Cauchy x n x n Cauchy ΚΑΙ Cauchy x n x nk x k x x n x θεώρημα πληρότητας x n Cauchy x n x (Α.Π.Θ.) Λογισμός Ι 47 / 83
48 Θεώρημα πληρότητας θεώρημα πληρότητας x n Cauchy x n x x n δεν συγκλίνει x n όχι Cauchy ɛ, N > 0 : n > m > N x n x m > ɛ πχ. x n = δεν συγκλίνει n x n = n 2 συγκλίνει Συστολή ακολουθίας Αν x n+1 x n < k x n x n 1 και k < 1 Η x n είναι συστολή η x n είναι Cauchy (Α.Π.Θ.) Λογισμός Ι 48 / 83
49 ΑΚΟΛΟΥΘΙΕΣ CAUCHY (2/3) Ορισμός x n Πρόταση x n x Απόδειξη. x n x n Cauchy x n ɛ > 0 N(ɛ) : n > m > N(ɛ) x n x m < ɛ Cauchy x ɛ > 0 N(ɛ) > 0 : m > N(ɛ) x x m < ɛ n > m x n x < ɛ x n x m x n x + x x m < 2ɛ = ɛ ( ) ɛ > 0 N (ɛ ) = N ɛ 2 : n > m > N (ɛ ) x n x m < ɛ Cauchy (Α.Π.Θ.) Λογισμός Ι 49 / 83
50 ΑΚΟΛΟΥΘΙΕΣ CAUCHY (3/3) Λήμμα xn Cauchy xn x ΚΑΙ xnk x k Απόδειξη. xn Cauchy ɛ > 0 N1(ɛ) : n > m > N1(ɛ) xn xm < ɛ ɛ > 0 N2(ɛ) : xnk k k > N2(ɛ) xnk x < ɛ Αν ɛ = 2ɛ και N (ɛ ) = max N1(ɛ), N2(ɛ) τότε n > nk > N (ɛ ) xn x xn + xnk x < 2ɛ = ɛ xnk ɛ > 0 N (ɛ ) > 0 : n > N (ɛ ) x xn < ɛ xn x Πρόταση xn Cauchy xn x Απόδειξη. xn Cauchy ɛ = 1 n0 > N(1) : n > n0 xn xn xn0 + xn0 < 1 + xn0 xn τελικά φραγμένη υπακολουθία που συγκλίνει Bolzano Λήμμα xn συγκλίνει. (Α.Π.Θ.) Λογισμός Ι 50 / 83
51 Προτάσεις xn ΘΕΩΡΗΜΑ ΠΛΗΡΟΤΗΤΑΣ xn Cauchy xn x δεν συγκλίνει xn όχι Cauchy ɛ, N > 0 : n > m > N xn xm > ɛ πχ. Πρόταση xn = δεν συγκλίνει n Απόδειξη. x2n xn = 1 n n n + n > n n + n = 1 2 Πρόταση xn = n 2 συγκλίνει Απόδειξη. 1 xn xm = (m + 1) (m + 2) n 2 1 m(m+1) + 1 (m+1)(m+2) n(n 1) = = 1 m 1 m m+1 1 m n 1 1 n = 1 m 1 m+1 + m+1 m n 1 1 n = 1 m 1 n < 1 m ɛ > 0 N(ɛ) = 1 ɛ : n > m > N(ɛ) xn xm < 1 m < ɛ (Α.Π.Θ.) Λογισμός Ι 51 / 83
52 Πλήρης χώρος και ακολουθίες Cauchy κάθε ακολουθία Πλήρης χώρος Cauchy συγκλίνει Το R είναι πλήρης χώρος Το Q δεν είναι πλήρης χώρος ( ) πχ. Η ακολουθία x 1 = 2, x n+1 = 1 2 x n + 2 x n x n Q αλλά x n 2 Q Αν γνωρίζουμε μόνο το Q μπορούμε να πάρουμε το σύνολο ακολουθιών Cauchy και το σύνολο αυτό είναι ένα ολικά διατεταγμένο πεδίο/σώμα που κάθε ταυτίζεται με το R. R= Cauchy- πλήρωση του Q (Α.Π.Θ.) Λογισμός Ι 52 / 83
53 Αξιώματα Constructive Αξιώματα Peano N προσθετική ομάδα Z πολλαπλασιαστική ομάδα Q Cauchy- πλήρωση R Axiomatic Αξιώματα Ι, ΙΙ, ΙΙΙ R μέγιστο 1-hereditary σύνολο N προσθετική ομάδα Z πολλαπλασιαστική ομάδα Q (Α.Π.Θ.) Λογισμός Ι 53 / 83
54 Πρόταση (Stolz) Πρ. (Stolz) b k > 0 a n b n και n x n k=1 l n b k k=1 πχ x n x n n n n n k N 1 + 2k + 3 k + n k n k+1 Πρόταση x n+1 x n l x n x n l 1 k + 1 n a k k=1 n b k k=1 l π.χ. lim n n5 3n = 1 (Α.Π.Θ.) Λογισμός Ι 54 / 83
55 Συμπληρωματικά κριτήρια σύγκλισης (1/2) Πρ (Stolz): Απόδ: an bn bk > 0 l an bn και l n k=1 bk n k=1 n k=1 ak bk ɛ > 0 N1(ɛ) > 0 : k > m > N1(ɛ) l ɛ < ak bk l < l + ɛ (l ɛ) bk < ak < (l + ɛ) bk n (l ɛ) bk < n n ak < (l + ɛ) bk k=m+1 k=m+1 k=m+1 m n ak + (l ɛ) bk < n ak < m ak + (l + ɛ) k=1 k=m+1 k=1 k=1 m ak (l ɛ) m bk + (l ɛ) n bk < n ak < k=1 k=1 k=1 k=1 m < ak (l + ɛ) m bk + (l + ɛ) n bk k=1 k=1 k=1 m ak (l ɛ) m n bk ak k=1 k=1 k=1 n + (l ɛ) < n < bk bk k=1 k=1 m ak (l+ɛ) m bk k=1 k=1 < n + (l + ɛ) bk k=1 n k=m+1 Για ένα σταθερό ɛ > 0, διαλέγουμε ένα m = [N1(ɛ)] + 1 > N1(ɛ), που είναι σταθερό (και εξαρτάται από το ɛ). Τότε m ak (l ɛ) m n bk ak k=1 k=1 k=1 lim + (l ɛ) lim n n bk bk k=1 k=1 m ak (l + ɛ) m bk k=1 k=1 lim + (l + ɛ) n bk k=1 Οι παραστάσεις μεταξύ δεν εξαρτώνται από το n τότε επειδή n lim bk = + θά έχουμε ότι για το συγκεκριμένο ɛ k=1 Επομένως n k=1 n k=1 ak bk (l ɛ) lim l n k=1 n k=1 ak bk (l + ɛ) bk (Α.Π.Θ.) Λογισμός Ι 55 / 83
56 Συμπληρωματικά κριτήρια σύγκλισης (2/2) Πρ: x n+1 x n l n x n l Απόδ: x n+1 x n l ɛ > 0 N 1 (ɛ) > 0 : m > N 1 (ɛ) l ɛ < x m+1 < l + ɛ x m Για n = m + k > m έχουμε (l ɛ) x m < x m+1 < (l + ɛ) x m (l ɛ) k x m < x m+k < (l + ɛ) k x m (l ɛ) m+k xm m+k xm (l ɛ) m < x m+k < (l + ɛ) (l+ɛ) m (l ɛ) n xm (l ɛ) m < x n < (l + ɛ) n xm (l+ɛ) m (l ɛ) n xm (l ɛ) m < n x n < (l + ɛ) n xm (l+ɛ) m n (l ɛ) lim (l ɛ) lim xm (l ɛ) m n lim xn (l + ɛ) n xn (l + ɛ) lim n xm (l+ɛ) m Επομένως n x n l (Α.Π.Θ.) Λογισμός Ι 56 / 83
57 ΑΠΟΚΛΙΝΟΥΣΕΣ ΑΚΟΛΟΥΘΙΕΣ Ορισμός x n R > 0, N(R) > 0 : n > N(R) x n > R x n Κάθε αύξουσα μη φραγμένη ακολουθία αποκλίνει + 1 x n 0 Ορισμός x n R > 0, N(R) > 0 : n > N(R) x n < R Κάθε φθίνουσα μη φραγμένη ακολουθία αποκλίνει (Α.Π.Θ.) Λογισμός Ι 57 / 83
58 Συμπεράσματα 1 x n συγκλίνει x n είναι ακολουθία Cauchy 2 x n 0 x n n N φραγμένη C > 0 : n x n < C 3 a < 1 a n 0 4 (Συστολή) x n 0, xn+1 xn k < 1 xn 0 5 x n x Καθε υπακολουθία x nk συγκλίνει στο x 6 (Bolzano-Weierstrass): Κάθε (άνω και κάτω) φραγμένη ακολουθία έχει τουλάχιστον μια συγκλίνουσα υπακολουθία 7 x n είναι αύξουσα και φραγμένη ακολουθία x n supx k k N 8 x n είναι μονότονη ακολουθία και έχει μια συγκλίνουσα υπακολουθία lim xnk = x η ακολουθία xn συγκλίνει στο ίδιο k όριο δηλ x n x ( 9 lim 1 + x ) n = e x = x l n l=0 l! 10 (Stolz): b k > 0 και x n+1 x n l 11 a n l b n n b k k=1 n x n l n a k k=1 n b k k=1 l (Α.Π.Θ.) Λογισμός Ι 58 / 83
59 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ (1/4) Ορισμός S n = n k=1 a k μερικό άθροισμα, Αν S n S τότε συγκλίνει απλά η σειρά S a k η k=1 ακολουθία S N είναι Cauchy ɛ > 0 N(ɛ) : n > m > N(ɛ) S n S m = Παράδειγμα: Η σειρά k=1 1 k 2 συγκλίνει. n k=m+1 a k < ɛ (Α.Π.Θ.) Λογισμός Ι 59 / 83
60 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ (2/4) Η σειρά συγκλίνει ɛ > 0 N(ɛ) : n > m > N(ɛ) n a k <ɛ k=m+1 Η σειρά ΔΕΝ συγκλίνει ɛ > 0 N : n > m > N Παράδειγμα: Η σειρά Πρόταση k=1 συγκλίνει απλά η σειρά n=1 n k=m+1 a k ɛ 1 ΔΕΝ συγκλίνει. k a n a n 0 ΠΡΟΣΟΧΗ: Αν a n 0 τότε ΔΕΝ ΣΥΓΚΛΙΝΕΙ ΠΑΝΤΑ η σειρά n πχ. a n = 1 n 0 αλλά 1 n = (Α.Π.Θ.) n=1 Λογισμός Ι 60 / 83 a n
61 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ (3/4) Ορισμός συγκλίνει απόλυτα η σειρά συγκλίνει η σειρά των απόλυτων τιμών a k k=1 Πρόταση Απόλυτη σύγκλιση σειράς Απλή σύγκλιση σειράς Κριτήριο Σύγκρισης (Comparison test) b n a n, a n συγκλίνει b n συγκλίνει n=1 Πρόταση 0 a n b n, n=1 n=1 a n = αποκλίνει n=1 b n = αποκλίνει (Α.Π.Θ.) Λογισμός Ι 61 / 83
62 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ (4/4) Η σειρά k=0 t k συγκλίνει μόνο για t < 1 και τότε k=0 t k = 1 1 t Η απόδειξη στηρίζεται στο γεγονός ότι n 1 k=0 t k = 1 tn 1 t (Α.Π.Θ.) Λογισμός Ι 62 / 83
63 Κριτήρια Σύγκλισης Σειρών (1/3) Κριτήριο των λόγων (Ratio test) Η σειρά a n n=1 1 συγκλίνει απόλυτα αν lim a n+1 a n < 1 2 αποκλίνει αν lim a n+1 a n > 1 3 δεν μπορούμε να αποφασίσουμε αν lim Κριτήριο των ριζών (Root test) Η σειρά a n n=1 1 συγκλίνει απόλυτα αν lim 2 n αποκλίνει αν lim an > 1 n an < 1 3 δεν μπορούμε να αποφασίσουμε αν lim a n+1 a n = 1 n an = 1 (Α.Π.Θ.) Λογισμός Ι 63 / 83
64 Κριτήρια Σύγκλισης Σειρών (2/3) Λόγος ακολουθιών a n και b n θετικές ακολουθίες. Αν lim a n b n = l 0 τότε n=1 b n υπάρχει n=1 a n υπάρχει Μηδενικός Λόγος ακολουθιών a n και b n θετικές ακολουθίες. Αν lim a n b n = 0 τότε b n υπάρχει n=1 n=1 a n υπάρχει (Α.Π.Θ.) Λογισμός Ι 64 / 83
65 Κριτήρια Σύγκλισης Σειρών (3/3) Κριτήριο συμπύκνωσης (Condensation test) Αν 0 < a n+1 < a n φθίνουσα θετική ακολουθία τότε: a n υπάρχει 2 k a 2 k υπάρχει n=1 Παραδείγματα: p > 1 p > 1 n=1 n=2 1 n < p 1 n(ln n) < p k=1 Κριτήριο σύγκλισης εναλλασσομένης σειράς (Alternating Series Test) Αν 0 < a n+1 < a n φθίνουσα θετική ακολουθία και a n ( 1) n+1 a n υπάρχει n=1 0 τότε: (Α.Π.Θ.) Λογισμός Ι 65 / 83
66 Αναδιάταξη των Φυσικών αριθμών Αναδιάταξη των Φυσικών αριθμών (1, 2,..., k,...) σ (σ 1, σ 2,..., σ k,...) σ k n k N : max σ 1, σ 2,... σ k < n k Αναδιάταξη ακολουθίας b m = a σm Αν η σειρά a n συγκλίνει απόλυτα τότε κάθε αναδιάταξη της σειράς n b n συγκλίνει απόλυτα στο ίδιο όριο. n (Α.Π.Θ.) Λογισμός Ι 66 / 83
67 ΔΙΠΛΕΣ ΣΕΙΡΕΣ a 11 a 12 a 13 a 14 a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 Ορισμός a mn = l συγκλίνει απόλυτα m,n=0 ( ) a mn = l συγκλίνει απόλυτα m=0 n=0 (Α.Π.Θ.) Λογισμός Ι 67 / 83
68 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ-αποδείξεις (1/7) Ορισμός S n = n a k μερικό άθροισμα, k=1 Αν S n S τότε συγκλίνει απλά η σειρά S a k η k=1 ακολουθία S N είναι Cauchy n ɛ > 0 N(ɛ) : n > m > N(ɛ) S n S m = a k < ɛ k=m+1 Παράδειγμα: Η σειρά Πρόταση k=1 1 k 2 συγκλίνει. συγκλίνει απλά η σειρά a n a n 0 n=1 Απόδειξη. συγκλίνει απλά η σειρά η ακολουθία μερικών αθροισμάτων είναι Cauchy Επομένως a n ɛ > 0, N(ɛ) : n > N(ɛ) S n S n 1 = a n < ɛ 0 ΠΡΟΣΟΧΗ: Αν a n 0 τότε ΔΕΝ ΣΥΓΚΛΙΝΕΙ ΠΑΝΤΑ η σειρά a n n πχ. a n = 1 n 0 αλλά 1 n = n=1 (Α.Π.Θ.) Λογισμός Ι 68 / 83
69 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ-αποδείξεις (2/7) Ορισμός συγκλίνει απόλυτα η σειρά συγκλίνει η σειρά των απόλυτων τιμών a k k=1 Πρόταση Απόλυτη σύγκλιση σειράς Απλή σύγκλιση σειράς Απόδειξη. συγκλίνει απόλυτα η σειρά ɛ > 0, ɛ > 0, N(ɛ) : n > m > N(ɛ) n k=m+1 n n a k a k < ɛ k=m+1 k=m+1 n N(ɛ) : n > m > N(ɛ) k=m+1 a k < ɛ a k < ɛ (Α.Π.Θ.) Λογισμός Ι 69 / 83
70 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ-αποδείξεις (3/7) Κριτήριο Σύγκρισης (Comparison test) bn an, an συγκλίνει bn συγκλίνει n=1 n=1 Απόδειξη. ɛ > 0, N(ɛ) : an n=1 n συγκλίνει n > m > N(ɛ) ak k=m+1 < ɛ n n bk ak k=m+1 k=m+1 ɛ > 0, N(ɛ) : bn n > m > N(ɛ) n bk < ɛ n=1 συγκλίνει k=m+1 απόλυτα Πρόταση 0 an bn, an = αποκλίνει bn = αποκλίνει n=1 n=1 Απόδειξη. an = R > 0, N(R) > 0 : n > N(R) n n=1 k=1 n n bk ak > R bn = k=1 k=1 n=1 ak > R (Α.Π.Θ.) Λογισμός Ι 70 / 83
71 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ-αποδείξεις (4/7) Κριτήριο των λόγων (Ratio test) Η σειρά an n=1 (i) συγκλίνει απόλυτα αν lim an+1 < 1 an (ii) αποκλίνει αν lim an+1 > 1 an (iii) δεν μπορούμε να αποφασίσουμε αν lim an+1 = 1 an Απόδ (i) lim a n+1 an = c < 1 για ɛ = 1 c 2, n0 : Απόδ (ii) Επειδή c+1 2 a lim n+1 an n > n0 an < a n+1 < (c + 1 c ( c + 1 < 1 ( κριτήριο σύγκρισης) η σειρά n = f > 1 για ɛ = f 1 2, n0 : 2 ) n an0 ( c ) an ) n0 an συγκλίνει απόλυτα. Επειδή f+1 2 n > n0 a n+1 > (f f 1 an > ( f ) n an0 ( f ) an ) n0 > 1 η ακολουθία an δεν είναι μηδενική δεν συγκλίνει η σειρά n an Κριτήριο των ριζών (Root test) Η σειρά an n=1 n an < 1 (i) συγκλίνει απόλυτα αν lim n (ii) αποκλίνει αν lim an > 1 (iii) δεν μπορούμε να αποφασίσουμε αν n lim an = 1 (Α.Π.Θ.) Λογισμός Ι 71 / 83
72 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ-αποδείξεις (5/7) Κριτήριο συμπύκνωσης (Condensation test) Αν 0 < an+1 < an φθίνουσα θετική ακολουθία τότε: an υπάρχει 2 k a 2 k υπάρχει n=1 k=1 Απόδειξη. S 2 k+1 1 = a1 + (a2 + a3) + (a4 + a5 + a6 + a7) + 2 όροι 4 όροι + (a8 + a9 + a10 + a11 + a12 + a13 + a14 + a15) 8 όροι ( ) a 2 k + a 2 k +1 + a10 + a 2 k a 2 k k όροι a1 + 2a2 + 4a4 + 8a k a 2 k = Tk η ακολουθία Tk συγκλίνει η υπακολουθία S 2 k+1 1 συγκλίνει και η ακολουθία Sn είναι αύξουσα η Sn συγκλίνει. Tk 2 = a1 2 + a2 + 2a4 + 4a k 1 a 2 k a1 + a2 + (a3 + a4) + (a5 + a6 + a7 + a8) ( a 2 k a 2 k a 2 k) = S2 k η ακολουθίαsn συγκλίνει και είναι αύξουσα η υπακολουθία S 2 k συγκλίνει η ακολουθία Tk συγκλίνει. πχ 1 δεν συγκλίνει n=2 n ln n 1 n=2 n(ln n) 2 συγκλίνει 1 συγκλίνει για r > 1, n=1 nr δεν συγκλίνει για r 1 (Α.Π.Θ.) Λογισμός Ι 72 / 83
73 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ-αποδείξεις (6/7) Κριτήριο σύγκλισης εναλλασσομένης σειράς (Alternating Series Test) Αν 0 < an+1 < an φθίνουσα θετική ακολουθία και an ( 1) n+1 an υπάρχει n=1 Απόδειξη. 0 τότε: Sn = n k=1 ( 1) k+1 ak Sm+2 Sm = ( 1) m+3 am+2 ( 1) m+2 am+1 = ( 1) m+2 (am+1 am+2) Sm+2 Sm = am+1 am+2 0 Sm+4 Sm+2 = am+3 am+4 Sm+6 Sm+4 = am+5 am Sm+2p S m+2(p 1) = am+2p 1 am+2p Sm+2p Sm Sm+2p Sm+2p 2 + Sm+2p 2 Sm+2p Sm+2 Sm Sm+2p Sm am+2p 1 am+2p + am+2p 3 am+2p am+3 am+4 + am+1 am+2 Sm+2p Sm am+1 am+2p < am+1 Sm+2p+1 Sm Sm+2p+1 Sm+2p + Sm+2p Sm am+2p+1 + am+1 am+2p < am+1 n > m Sn Sm < am+1 lim an = 0 ɛ > 0 N(ɛ) : m > N(ɛ) am+1 < am < ɛ Sn Sm < ɛ Sn Cauchy πχ ( 1) n συγκλίνει n n ( 1) n n ln n συγκλίνει ( 1) n sin π n n συγκλίνει (Α.Π.Θ.) Λογισμός Ι 73 / 83
74 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ-αποδείξεις (7/7) Σύγκλιση αναδιατεταγμένης σειράς Αν η σειρά a n συγκλίνει απόλυτα τότε κάθε αναδιάταξη της σειράς n b n συγκλίνει απόλυτα στο ίδιο όριο. n Απόδειξη. Θεωρούμε την αναδιάταξη των Φυσικών αριθμών: Εστω τα μερικά αθροίσματα: (1, 2,..., k,...) σ (σ 1, σ 2,..., σ k,...) σ k n k N : max σ 1, σ 2,... σ k < n k S l = a 1 + a a l, T k = b 1 + b b k όπου b m = a σm επομένως T k S nk. Η υπακολουθία S nk συγκλινει δηλαδή είναι μια ακολουθία Cauchy η ακολουθία T k είναι μια ακολουθία Cauchy, δηλαδή συγκλίνει. Επειδή έχουν αύξουσες ακολουθίες που συγκλίνουν, τότε το όριο της υπακολουθίας είναι και το όριο της ακολουθίας. Αρα T k S nk lim Tk lim k k Snk b n a n n n Η ακολουθία a n μια αναδιάταξη της ακολουθίας b n, επομένως a n b n n n Αρα οι δύο σειρές συγκλίνουν στο ίδιο όριο. (Α.Π.Θ.) Λογισμός Ι 74 / 83
75 ( Οριακά Σημεία X = lim sup n N σύνολο των οριακών σημείων της φραγμένης ακολουθίας x n x n = lim n N x n = sup X= μεγαλύτερο οριακό σημείο ΟΡΙΑΚΑ ΣΗΜΕΙΑ ( limsup xn (Α.Π.Θ.) Λογισμός Ι 75 / 83
76 Λήμμα X = lim inf n N σύνολο των οριακών σημείων της φραγμένης ακολουθίας x n x n = lim n N x n = inf X= m = lim inf n N x n μικρότερο οριακό σημείο ɛ > 0 x nk k N : m + ɛ > x nk Λήμμα Αν x n τελικά μικρότερο (ή μεγαλύτερο) του c lim sup x n c (ή lim inf x n c) n n (Α.Π.Θ.) Λογισμός Ι 76 / 83
77 Πρόταση 2 Πρόταση lim inf x n+1 x n lim inf n x n lim sup n x n lim sup Απόδ: lim sup x n+1 n x n = c ɛ > 0 n 0 : n n 0 x n+1 x n < c + ɛ n xn0 c n0 x n x n0 < cn n0 n x n < (c + ɛ) n xn0 1 n 1 : n > n 1 n c n0 x n+1 x n xn0 < 1 + ɛ c n0 c τελικά n x n < c + 2ɛ + ɛ2 c lim sup n n xn c γιατί αν θέσουμε ɛ = 2ɛ + ɛ2 c και N = maxn 0, n 1 έχουμε ότι ɛ, N : n > N n x n < c + ɛ δηλαδή πέραν του c + ɛ βρίσκεται ένας πεπερασμένος αριθμός μελών της ακολουθίας (Α.Π.Θ.) Λογισμός Ι 77 / 83
78 Πρόταση 3 Πρόταση x n+1 x n l n x n l n n! πχ n Απόδ: π.χ. lim lim 1 e x n = n! = n n 1 (n + 1) n n n n xn = ( xn+1 (n + 1)! x n = (n + 1) n+1 1 n n! n = ( n 1 e n n 5 3n = 1 n 5 n 2 n = 5 1 ) n e ) ( ) / n! n n = (Α.Π.Θ.) Λογισμός Ι 78 / 83
79 ΒΙΒΛΙΟΓΡΑΦΙΑ Απειροστικός Λογισμός-Τόμος Α Σ.Κ. Ντούγιας, LEADER BOOKS, 2003 Διαφορικός Ολοκληρωτικός Λογισμός, M. Spivak, Παν. Εκδ. Κρήτης, Απειροστικός Λογισμός, THOMAS-FINLEY, Παν. Εκδ. Κρήτης Μαθήματα στο δίκτυο: Μαθήματα Μ. Παπαδημητράκη (Παν. Κρήτης) papadim/apeirostikos1.pdf Μαθήματα στο δίκτυο: Μαθήματα Α. Γιαννόπολου (Παν. Αθηνών) apgiannop Διαφάνειες: daskalo
80 Σημείωμα Αναφοράς Copyright Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης, Δασκαλογιάννης Κωνσταντίνος. Λογισμός Ι. Ενότητα 2: Ακολουθίες - Σειρές. Εκδοση: 1.0. Θεσσαλονίκη Διαθέσιμο από τη δικτυακή διεύθυνση: (Α.Π.Θ.) Λογισμός Ι 80 / 83
81 Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Παρόμοια Διανομή 4.0[1] ή μεταγενέστερη, Διεθνής Εκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο Σημείωμα Χρήσης Εργων Τρίτων. Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί. [1] (Α.Π.Θ.) Λογισμός Ι 81 / 83
82 Διατήρηση Σημειωμάτων Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει: το Σημείωμα Αναφοράς το Σημείωμα Αδειοδότησης τη δήλωση Διατήρησης Σημειωμάτων το Σημείωμα Χρήσης Εργων Τρίτων (εφόσον υπάρχει) μαζί με τους συνοδευόμενους υπερσυνδέσμους. (Α.Π.Θ.) Λογισμός Ι 82 / 83
83 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Τέλος Ενότητας Επεξεργασία: Αναστασία Γ. Γρηγοριάδου Θεσσαλονίκη, Χειμερινό Εξάμηνο (Α.Π.Θ.) Λογισμός Ι 83 / 83
Γενικά Μαθηματικά Ι. Ενότητα 12: Κριτήρια Σύγκλισης Σειρών. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Κριτήρια Σύγκλισης Σειρών Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Κριτήρια Σύγκλισης Σειρών Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ. Ορισμός. S n = a k μερικό άθροισμα, Αν S n S τότε συγκλίνει απλά η σειρά S. a k η. a k. 1 k 2 συγκλίνει. Παράδειγμα: Η σειρά k=1.
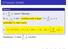 ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ Ορισμός S = a k μερικό άθροισμα, Αν S S τότε συγκλίνει απλά η σειρά S ακολουθία S N είναι Cauchy a k η ɛ > 0 N(ɛ) : > m > N(ɛ) S S m = a k < ɛ Παράδειγμα: Η σειρά 1 k 2 συγκλίνει. Η σειρά
ΣΥΓΚΛΙΣΗ ΣΕΙΡΑΣ Ορισμός S = a k μερικό άθροισμα, Αν S S τότε συγκλίνει απλά η σειρά S ακολουθία S N είναι Cauchy a k η ɛ > 0 N(ɛ) : > m > N(ɛ) S S m = a k < ɛ Παράδειγμα: Η σειρά 1 k 2 συγκλίνει. Η σειρά
ΑΡΙΣΤΟΤΕΛΕΙΟ ΑΝΟΙΚΤΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΚΑΔΗΜΑΪΚΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΜΑΘΗΜΑΤΑ Γενικά Μαθηματικά Ι Ενότητα 11 : Ακολουθίες και Σειρές Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα : Ακολουθίες και Σειρές Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative Commos. Για
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα : Ακολουθίες και Σειρές Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative Commos. Για
Infimum. Ορισμός κάτω φράγματος συνόλου A. Ορισμός infimum του συνόλου A. Το σύνολο A R είναι κάτω φραγμένο αν. k R : x A k x.
 Infimum Ορισμός κάτω φράγματος συνόλου A Το σύνολο A R είναι κάτω φραγμένο αν k R : x A k x k = κάτω φράγμα Ορισμός infimum του συνόλου A inf A = infimum του συνόλου A Το μεγαλύτερο από τα κάτω φράγματα
Infimum Ορισμός κάτω φράγματος συνόλου A Το σύνολο A R είναι κάτω φραγμένο αν k R : x A k x k = κάτω φράγμα Ορισμός infimum του συνόλου A inf A = infimum του συνόλου A Το μεγαλύτερο από τα κάτω φράγματα
Γενικά Μαθηματικά Ι. Ενότητα 15: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 4. Ενότητα 2: Ορισμός του ολοκληρώματος. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Ορισμός του ολοκληρώματος. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Ορισμός του ολοκληρώματος. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Μαθηματική Ανάλυση Ι
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 2: Ακολουθίες Πραγματικών Αριθμών Επίκ. Καθηγητής Θ. Ζυγκιρίδης e-mail: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 2: Ακολουθίες Πραγματικών Αριθμών Επίκ. Καθηγητής Θ. Ζυγκιρίδης e-mail: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 4. Ενότητα 3: Το Θεώρημα του Lebesgue. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Το Θεώρημα του Lebesgue. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Το Θεώρημα του Lebesgue. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Μαθηματική Ανάλυση Ι
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 5: Όρια και Συνέχεια Επίκ. Καθηγητής Θ. Ζυγκιρίδης e-mail: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 5: Όρια και Συνέχεια Επίκ. Καθηγητής Θ. Ζυγκιρίδης e-mail: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Λογισμός 3. Ενότητα 19: Θεώρημα Πεπλεγμένων (γενική μορφή) Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 19: Θεώρημα Πεπλεγμένων (γενική μορφή) Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 19: Θεώρημα Πεπλεγμένων (γενική μορφή) Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Μαθηματική Ανάλυση Ι
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 3: Σειρές Πραγματικών Αριθμών Επίκ. Καθηγητής Θ. Ζυγκιρίδης e-mail: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 3: Σειρές Πραγματικών Αριθμών Επίκ. Καθηγητής Θ. Ζυγκιρίδης e-mail: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Λογισμός 4 Ενότητα 10
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10: Διαιρέσεις της μονάδας και επέκταση του ολοκληρώματος. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10: Διαιρέσεις της μονάδας και επέκταση του ολοκληρώματος. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Εκκλησιαστικό Δίκαιο. Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Τμήμα Νομικής Α.Π.Θ.
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 4. Ενότητα 5: Το Θεώρημα του Fubini. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Το Θεώρημα του Fubini. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Το Θεώρημα του Fubini. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γενικά Μαθηματικά Ι. Ενότητα 13: Ακτίνα Σύγκλισης, Αριθμητική Ολοκλήρωση, Ολοκλήρωση Κατά Παράγοντες. Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Ακτίνα Σύγκλισης, Αριθμητική Ολοκλήρωση, Ολοκλήρωση Κατά Παράγοντες Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Ακτίνα Σύγκλισης, Αριθμητική Ολοκλήρωση, Ολοκλήρωση Κατά Παράγοντες Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Πρόταση. f(x) ομοιόμορφα συνεχής στο I. δ (ɛ) > 0 : x, ξ I, x ξ < δ (ɛ, ξ) f(x) f(ξ) < ɛ. ɛ > 0, δ > 0 : ΜΗ ομοιόμορφα συνεχής.
 f(x) ομοιόμορφα συνεχής στο I ɛ > 0, δ (ɛ) > 0 : x, ξ I, x ξ < δ (ɛ, ξ) f(x) f(ξ) < ɛ f(x) ΜΗ ομοιόμορφα συνεχής ɛ > 0, δ > 0 : x, ξ I, x ξ < δ f(x) f(ξ) ɛ f(x) συνεχής στο [a, b] f(x) ομοιόμορφα συνεχής
f(x) ομοιόμορφα συνεχής στο I ɛ > 0, δ (ɛ) > 0 : x, ξ I, x ξ < δ (ɛ, ξ) f(x) f(ξ) < ɛ f(x) ΜΗ ομοιόμορφα συνεχής ɛ > 0, δ > 0 : x, ξ I, x ξ < δ f(x) f(ξ) ɛ f(x) συνεχής στο [a, b] f(x) ομοιόμορφα συνεχής
Ιστορία της μετάφρασης
 ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Θεωρία μέτρου και ολοκλήρωσης
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεωρία μέτρου και ολοκλήρωσης Ενότητα 5: Οι χώροι L p Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεωρία μέτρου και ολοκλήρωσης Ενότητα 5: Οι χώροι L p Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Γενικά Μαθηματικά Ι. Ενότητα 16: Ολοκλήρωση Τριγωνομετρικών Συναρτήσεων, Γενικευμένα Ολοκληρώματα Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 16: Ολοκλήρωση Τριγωνομετρικών Συναρτήσεων, Γενικευμένα Ολοκληρώματα Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 16: Ολοκλήρωση Τριγωνομετρικών Συναρτήσεων, Γενικευμένα Ολοκληρώματα Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Λογισμός 3. Ενότητα 1: Τοπολογία των Ευκλείδειων χώρων. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Τοπολογία των Ευκλείδειων χώρων. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Τοπολογία των Ευκλείδειων χώρων. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Μαθηματικά Και Στατιστική Στη Βιολογία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαθηματικά Και Στατιστική Στη Βιολογία Ενότητα 8 : Μιγαδικοί Αριθμοί & Ακολουθίες Αριθμών Στέφανος Σγαρδέλης Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαθηματικά Και Στατιστική Στη Βιολογία Ενότητα 8 : Μιγαδικοί Αριθμοί & Ακολουθίες Αριθμών Στέφανος Σγαρδέλης Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Λογισμός 3. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Γενικά Μαθηματικά Ι. Ενότητα 14: Ολοκλήρωση Κατά Παράγοντες, Ολοκλήρωση Ρητών Συναρτήσεων Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Ολοκλήρωση Κατά Παράγοντες, Ολοκλήρωση Ρητών Συναρτήσεων Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Ολοκλήρωση Κατά Παράγοντες, Ολοκλήρωση Ρητών Συναρτήσεων Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 7η: Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 7η: Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Λογισμός 4 Ενότητα 12
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Μη γνήσια ολοκληρώματα. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Μη γνήσια ολοκληρώματα. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos.
Εκκλησιαστικό Δίκαιο
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11η: Οργανισμοί της Εκκλησίας της Ελλάδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11η: Οργανισμοί της Εκκλησίας της Ελλάδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2)
 Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Μηχανολογικό Σχέδιο Ι
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα # 8: Άτρακτοι και σφήνες Μ. Γρηγοριάδου Μηχανολόγων Μηχανικών Α.Π.Θ. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα # 8: Άτρακτοι και σφήνες Μ. Γρηγοριάδου Μηχανολόγων Μηχανικών Α.Π.Θ. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Λογισμός Ι Ενότητα 4: Παράγωγοι Κ. Δασκαλογιάννης Τμήμα Μαθηματικών Α.Π.Θ. (Α.Π.Θ.) Λογισμός Ι 1 / 68 Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Λογισμός Ι Ενότητα 4: Παράγωγοι Κ. Δασκαλογιάννης Τμήμα Μαθηματικών Α.Π.Θ. (Α.Π.Θ.) Λογισμός Ι 1 / 68 Άδειες Χρήσης Το παρόν εκπαιδευτικό
mail:
 Λογισμός Ι - Τμήμα 1Β Κ. Δασκαλογιάννης Γραφείο 18, 3ος όροφος ΣΘΕ τηλ: 2310-998074 mail: daskalo@math.auth.gr ιστοσελίδα: users.auth.gr/daskalo 2014 ΛΟΓΙΣΜΟΣ CALCULUS (Διαφορικός Λογισμός, Απειροστικός
Λογισμός Ι - Τμήμα 1Β Κ. Δασκαλογιάννης Γραφείο 18, 3ος όροφος ΣΘΕ τηλ: 2310-998074 mail: daskalo@math.auth.gr ιστοσελίδα: users.auth.gr/daskalo 2014 ΛΟΓΙΣΜΟΣ CALCULUS (Διαφορικός Λογισμός, Απειροστικός
Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 10η: Απεσταλμένοι του Ρωμαίου Ποντίφικα και Ρωμαϊκή Κουρία Κυριάκος Κυριαζόπουλος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 10η: Απεσταλμένοι του Ρωμαίου Ποντίφικα και Ρωμαϊκή Κουρία Κυριάκος Κυριαζόπουλος
Λογισμός 3. Ενότητα 5:Θεώρημα ακραίων τιμών και θεώρημα ενδιάμεσων τιμών- Ομοιόμορφη συνέχεια. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5:Θεώρημα ακραίων τιμών και θεώρημα ενδιάμεσων τιμών- Ομοιόμορφη συνέχεια. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5:Θεώρημα ακραίων τιμών και θεώρημα ενδιάμεσων τιμών- Ομοιόμορφη συνέχεια. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό
Εκκλησιαστικό Δίκαιο
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8η: Ο νέος αντιρατσιστικός νόμος και ο ν.4301/2014 Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8η: Ο νέος αντιρατσιστικός νόμος και ο ν.4301/2014 Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Γενικά Μαθηματικά Ι. Ενότητα 9: Κίνηση Σε Πολικές Συντεταγμένες. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Κίνηση Σε Πολικές Συντεταγμένες Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Κίνηση Σε Πολικές Συντεταγμένες Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative
Λογισμός 4 Ενότητα 15
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 15: Αρμονικές συναρτήσεις. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 15: Αρμονικές συναρτήσεις. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γενικά Μαθηματικά Ι. Ενότητα 5: Παράγωγος Πεπλεγμένης Συνάρτησης, Κατασκευή Διαφορικής Εξίσωσης. Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Παράγωγος Πεπλεγμένης Συνάρτησης, Κατασκευή Διαφορικής Εξίσωσης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Παράγωγος Πεπλεγμένης Συνάρτησης, Κατασκευή Διαφορικής Εξίσωσης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Οικονομία των ΜΜΕ. Ενότητα 7: Μορφές αγοράς και συγκέντρωση των ΜΜΕ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Οικονομία των ΜΜΕ Ενότητα 7: Μορφές αγοράς και συγκέντρωση των ΜΜΕ Γιώργος Τσουρβάκας, Αναπληρωτής Καθηγητής Τμήμα Δημοσιογραφίας και
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Οικονομία των ΜΜΕ Ενότητα 7: Μορφές αγοράς και συγκέντρωση των ΜΜΕ Γιώργος Τσουρβάκας, Αναπληρωτής Καθηγητής Τμήμα Δημοσιογραφίας και
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
Γενικά Μαθηματικά Ι. Ενότητα 17: Αριθμητική Ολοκλήρωση, Υπολογισμός Μήκους Καμπύλης Λουκάς Βλάχος Τμήμα Φυσικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Αριθμητική Ολοκλήρωση, Υπολογισμός Μήκους Καμπύλης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Αριθμητική Ολοκλήρωση, Υπολογισμός Μήκους Καμπύλης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Γενικά Μαθηματικά Ι. Ενότητα 8: Εφαρμογές Σειρών Taylor. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Εφαρμογές Σειρών Tylor Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Εφαρμογές Σειρών Tylor Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons.
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός
 Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.4: Ολοκλήρωση με Αντικατάσταση Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.4: Ολοκλήρωση με Αντικατάσταση Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Λογισμός 4. Ενότητα 4: Ιδιότητες του Ολοκληρώματος. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΑΝΕΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4: Ιδιότητες του Ολοκληρώματος. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΑΝΕΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4: Ιδιότητες του Ολοκληρώματος. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Παράκτια Τεχνικά Έργα
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΔΙΑΘΕΣΗ ΥΓΡΩΝ ΣΤΗ ΘΑΛΑΣΣΑ ΥΠΟΒΡΥΧΙΟΙ ΑΓΩΓΟΙ Ενότητα 5 η : Κατασκευαστικά παραδείγματα Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΔΙΑΘΕΣΗ ΥΓΡΩΝ ΣΤΗ ΘΑΛΑΣΣΑ ΥΠΟΒΡΥΧΙΟΙ ΑΓΩΓΟΙ Ενότητα 5 η : Κατασκευαστικά παραδείγματα Γιάννης Ν. Κρεστενίτης Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 4. Ενότητα 1: Εισαγωγή. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Εισαγωγή. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Εισαγωγή. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Γενικά Μαθηματικά Ι. Ενότητα 1: Συναρτήσεις και Γραφικές Παραστάσεις. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Συναρτήσεις και Γραφικές Παραστάσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Συναρτήσεις και Γραφικές Παραστάσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 4. Ενότητα 6: Εφαρμογές του Fubini. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Εφαρμογές του Fubini. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Εφαρμογές του Fubini. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Εργαστήριο Χημείας Ενώσεων Συναρμογής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 4: Τοποθέτηση d ηλεκτρονίων σε οκτάεδρα Σύμπλοκα Περικλής Ακρίβος Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 4: Τοποθέτηση d ηλεκτρονίων σε οκτάεδρα Σύμπλοκα Περικλής Ακρίβος Άδειες Χρήσης Το παρόν
ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 3. Ενότητα 13: Τύπος του Taylor. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 13: Τύπος του Taylor. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 13: Τύπος του Taylor. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Λογισμός 3. Ενότητα 8: Ιδιότητες της κλίσης, Κανόνας της αλυσίδας. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Ιδιότητες της κλίσης, Κανόνας της αλυσίδας. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Ιδιότητες της κλίσης, Κανόνας της αλυσίδας. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης
Ιστορία της μετάφρασης
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η μετάφραση των εβδομήκοντα, η εκπαίδευση των μεταφραστών κατά Κικέρωνα, η τέχνη της μετάφρασης από την αρχαιότητα μέχρι τα
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η μετάφραση των εβδομήκοντα, η εκπαίδευση των μεταφραστών κατά Κικέρωνα, η τέχνη της μετάφρασης από την αρχαιότητα μέχρι τα
mail:
 Λογισμός ΙΙΙ - Τμήμα Α Κ. Δασκαλογιάννης Γραφείο 18, 3ος όροφος ΣΘΕ τηλ: 2310-998074 mail: daskalo@math.auth.gr ιστοσελίδα: users.auth.gr/daskalo 2014 Βιβλιογραφία Ν. Δανίκας - Μ. Μαριάς Μαθήματα Διαφορικού
Λογισμός ΙΙΙ - Τμήμα Α Κ. Δασκαλογιάννης Γραφείο 18, 3ος όροφος ΣΘΕ τηλ: 2310-998074 mail: daskalo@math.auth.gr ιστοσελίδα: users.auth.gr/daskalo 2014 Βιβλιογραφία Ν. Δανίκας - Μ. Μαριάς Μαθήματα Διαφορικού
Γενικά Μαθηματικά Ι. Ενότητα 7: Σειρές Taylor, Maclaurin. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Σειρές Taylor, Maclaurin Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Σειρές Taylor, Maclaurin Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Λογιστική Κόστους Ενότητα 8: Κοστολογική διάρθρωση Κύρια / Βοηθητικά Κέντρα Κόστους.
 Λογιστική Κόστους Ενότητα 8: Κοστολογική διάρθρωση Κύρια / Βοηθητικά Κέντρα Κόστους. Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Λογιστική Κόστους Ενότητα 8: Κοστολογική διάρθρωση Κύρια / Βοηθητικά Κέντρα Κόστους. Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Αξιολόγηση μεταφράσεων ιταλικής ελληνικής γλώσσας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Αξιολόγηση μεταφράσεων ιταλικής ελληνικής γλώσσας Ενότητα 1: Αυτοαξιολόγηση μεταφραστών Κασάπη Ελένη Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Αξιολόγηση μεταφράσεων ιταλικής ελληνικής γλώσσας Ενότητα 1: Αυτοαξιολόγηση μεταφραστών Κασάπη Ελένη Άδειες Χρήσης Το παρόν εκπαιδευτικό
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Λογισμός 3. Ενότητα 10: Παραγώγιση Διανυσματικών Συναρτήσεων. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10: Παραγώγιση Διανυσματικών Συναρτήσεων. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10: Παραγώγιση Διανυσματικών Συναρτήσεων. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative
Λογισμός 4. Ενότητα 9: Παραδείγματα από άλλες αλλαγές. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Παραδείγματα από άλλες αλλαγές. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Παραδείγματα από άλλες αλλαγές. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ Ενότητα # 17: Ταχύτητα Αντιδράσεων Ακρίβος Περικλής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ Ενότητα # 17: Ταχύτητα Αντιδράσεων Ακρίβος Περικλής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Λογισμός 3. Ενότητα 12:Οι κλασικοί μετασχηματισμοί και ο κανόνας της αλυσίδας. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 12:Οι κλασικοί μετασχηματισμοί και ο κανόνας της αλυσίδας. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 12:Οι κλασικοί μετασχηματισμοί και ο κανόνας της αλυσίδας. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Λογισμός 3. Ενότητα 17: Απόδειξη Θεωρήματος Αντιστροφής. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 17: Απόδειξη Θεωρήματος Αντιστροφής. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 17: Απόδειξη Θεωρήματος Αντιστροφής. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative
Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 11η: Σύγκριση Ρωσικής Ορθόδοξης Εκκλησίας και Καθολικής Εκκλησίας Κυριάκος Κυριαζόπουλος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 11η: Σύγκριση Ρωσικής Ορθόδοξης Εκκλησίας και Καθολικής Εκκλησίας Κυριάκος Κυριαζόπουλος
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Β. Διαφορικός Λογισμός
 Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Β. Διαφορικός Λογισμός Κεφάλαιο Β.9: Το Διαφορικό Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Γεώργιος Νικ. Μπροδήμας Κεφάλαιο Β.9: Το Διαφορικό 1 Άδειες
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Β. Διαφορικός Λογισμός Κεφάλαιο Β.9: Το Διαφορικό Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Γεώργιος Νικ. Μπροδήμας Κεφάλαιο Β.9: Το Διαφορικό 1 Άδειες
ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 3. Ενότητα 6: Μερικές παράγωγοι. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μερικές παράγωγοι. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative Commons. Για
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μερικές παράγωγοι. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative Commons. Για
Διοικητική Λογιστική
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 10: Προσφορά και κόστος Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 10: Προσφορά και κόστος Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Εκκλησιαστικό Δίκαιο
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6η: Ελληνική νομολογία Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6η: Ελληνική νομολογία Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Πίνακες Νερού σε κατάσταση Κορεσμού. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Μαθηματική Ανάλυση ΙI
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση ΙI Ενότητα 3: Συναρτήσεις πολλών μεταβλητών Επίκουρος Καθηγητής Θ. Ζυγκιρίδης e-mail: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση ΙI Ενότητα 3: Συναρτήσεις πολλών μεταβλητών Επίκουρος Καθηγητής Θ. Ζυγκιρίδης e-mail: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και
Θέματα Αρμονικής Ανάλυσης
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θέματα Αρμονικής Ανάλυσης Ενότητα 3: Αρμονικές Συναρτήσεις Μιχ. Μ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θέματα Αρμονικής Ανάλυσης Ενότητα 3: Αρμονικές Συναρτήσεις Μιχ. Μ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 3. Ενότητα 11: Κανόνας της αλυσίδας. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11: Κανόνας της αλυσίδας. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11: Κανόνας της αλυσίδας. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative Commons.
Κλασσική Θεωρία Ελέγχου
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 15: Επίλυση διοφαντικών εξισώσεων πολυωνύμων Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 15: Επίλυση διοφαντικών εξισώσεων πολυωνύμων Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Υπόγεια Υδραυλική και Υδρολογία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Συστήματα πηγαδιών Μέθοδος εικόνων Καθηγητής Κωνσταντίνος Λ. Κατσιφαράκης Αναπληρωτής Καθηγητής Νικόλαος Θεοδοσίου ΑΠΘ Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Συστήματα πηγαδιών Μέθοδος εικόνων Καθηγητής Κωνσταντίνος Λ. Κατσιφαράκης Αναπληρωτής Καθηγητής Νικόλαος Θεοδοσίου ΑΠΘ Άδειες
Εισαγωγή στην Διοίκηση Επιχειρήσεων
 Εισαγωγή στην Διοίκηση Επιχειρήσεων Ενότητα 7: ΑΣΚΗΣΕΙΣ ΜΕΓΕΘΟΥΣ ΕΠΙΧΕΙΡΗΣΗΣ Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εισαγωγή στην Διοίκηση Επιχειρήσεων Ενότητα 7: ΑΣΚΗΣΕΙΣ ΜΕΓΕΘΟΥΣ ΕΠΙΧΕΙΡΗΣΗΣ Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση - Συγχώνευση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση - Συγχώνευση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Φ 619 Προβλήματα Βιοηθικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Ο Πλάτων και ο Αριστοτέλης ως ιατροί. Οι ιατροφιλόσοφοι (Ιπποκράτης, Γαληνός, Κέλσος). Ελένη Καλοκαιρινού Φιλοσοφίας-Παιδαγωγικής
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Ο Πλάτων και ο Αριστοτέλης ως ιατροί. Οι ιατροφιλόσοφοι (Ιπποκράτης, Γαληνός, Κέλσος). Ελένη Καλοκαιρινού Φιλοσοφίας-Παιδαγωγικής
Λογισμός 3. Ενότητα 18: Θεώρημα Πεπλεγμένων (Ειδική περίπτωση) Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 18: Θεώρημα Πεπλεγμένων (Ειδική περίπτωση) Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 18: Θεώρημα Πεπλεγμένων (Ειδική περίπτωση) Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Διεθνείς Οικονομικές Σχέσεις και Ανάπτυξη
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διεθνείς Οικονομικές Σχέσεις και Ανάπτυξη Ενότητα 8: Η Οικονομική πολιτική της Ευρωπαϊκής Ένωσης Γρηγόριος Ζαρωτιάδης Άδειες Χρήσης Το
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Διεθνείς Οικονομικές Σχέσεις και Ανάπτυξη Ενότητα 8: Η Οικονομική πολιτική της Ευρωπαϊκής Ένωσης Γρηγόριος Ζαρωτιάδης Άδειες Χρήσης Το
Μαθηματική Ανάλυση Ι
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 10: Δυναμοσειρές Επίκουρος Καθηγητής Θ. Ζυγκιρίδης e-mail: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 10: Δυναμοσειρές Επίκουρος Καθηγητής Θ. Ζυγκιρίδης e-mail: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Οικονομία των ΜΜΕ. Ενότητα 9: Εταιρική διασπορά και στρατηγικές τιμολόγησης
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Εταιρική διασπορά και στρατηγικές τιμολόγησης Γιώργος Τσουρβάκας, Αναπληρωτής Καθηγητής Τμήμα Δημοσιογραφίας και ΜΜΕ Σχολή
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Εταιρική διασπορά και στρατηγικές τιμολόγησης Γιώργος Τσουρβάκας, Αναπληρωτής Καθηγητής Τμήμα Δημοσιογραφίας και ΜΜΕ Σχολή
Συνταγματικό Δίκαιο Ενότητα 11:Εκτελεστική Λειτουργία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11:Εκτελεστική Λειτουργία Λίνα Παπαδοπούλου Αν. Καθηγήτρια Συνταγματικού Δικαίου Τμήμα Νομικής Σχολής ΑΠΘ Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11:Εκτελεστική Λειτουργία Λίνα Παπαδοπούλου Αν. Καθηγήτρια Συνταγματικού Δικαίου Τμήμα Νομικής Σχολής ΑΠΘ Άδειες Χρήσης Το παρόν
Εργαστήριο Χημείας Ενώσεων Συναρμογής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 9: Μέτρηση Αγωγιμότητας Διαλυμάτων Περικλής Ακρίβος Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 9: Μέτρηση Αγωγιμότητας Διαλυμάτων Περικλής Ακρίβος Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 3. Ενότητα 7: Κλίση και παράγωγος. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Κλίση και παράγωγος. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative Commons. Για
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Κλίση και παράγωγος. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative Commons. Για
Εργαστήριο Χημείας Ενώσεων Συναρμογής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 6: Προσδιορισμός δ0 σε οκτάεδρα σύμπλοκα Περικλής Ακρίβος Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εργαστήριο Χημείας Ενώσεων Συναρμογής Ενότητα 6: Προσδιορισμός δ0 σε οκτάεδρα σύμπλοκα Περικλής Ακρίβος Άδειες Χρήσης Το παρόν εκπαιδευτικό
Φ 619 Προβλήματα Βιοηθικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η Βιοηθική στη σύγχρονη εποχή. Ελένη Καλοκαιρινού Φιλοσοφίας-Παιδαγωγικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Η Βιοηθική στη σύγχρονη εποχή. Ελένη Καλοκαιρινού Φιλοσοφίας-Παιδαγωγικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Λογισμός 3. Ενότητα 4:Συνέχεια διανυσματικών συναρτήσεων-ιδιότητες της συνέχειας. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4:Συνέχεια διανυσματικών συναρτήσεων-ιδιότητες της συνέχειας. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4:Συνέχεια διανυσματικών συναρτήσεων-ιδιότητες της συνέχειας. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Συμπεριφορά Καταναλωτή
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9 : Ομάδες αναφοράς Χριστίνα Μπουτσούκη Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9 : Ομάδες αναφοράς Χριστίνα Μπουτσούκη Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γεωργική Εκπαίδευση Ενότητα 9
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Σχεδιασμός εκπαιδευτικών προγραμμάτων για τον αγροτικό χώρο Αφροδίτη Παπαδάκη-Κλαυδιανού Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Σχεδιασμός εκπαιδευτικών προγραμμάτων για τον αγροτικό χώρο Αφροδίτη Παπαδάκη-Κλαυδιανού Άδειες Χρήσης Το παρόν εκπαιδευτικό
Διπλωματική Ιστορία Ενότητα 2η:
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2η: Η εμφάνιση των εθνών-κρατών και οι συνέπειες στο διεθνές σύστημα Ιωάννης Στεφανίδης, Καθηγητής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2η: Η εμφάνιση των εθνών-κρατών και οι συνέπειες στο διεθνές σύστημα Ιωάννης Στεφανίδης, Καθηγητής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 3. Ενότητα 16: Θεώρημα Αντιστροφής. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 16: Θεώρημα Αντιστροφής. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 16: Θεώρημα Αντιστροφής. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σεάδειες χρήσης Creative Commons.
Υπόγεια Υδραυλική και Υδρολογία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4: Αναλυτική επίλυση του μαθηματικού ομοιώματος: Σύμμορφη Απεικόνιση Καθηγητής Κωνσταντίνος Λ. Κατσιφαράκης Αναπληρωτής Καθηγητής
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4: Αναλυτική επίλυση του μαθηματικού ομοιώματος: Σύμμορφη Απεικόνιση Καθηγητής Κωνσταντίνος Λ. Κατσιφαράκης Αναπληρωτής Καθηγητής
Μαθηματική Ανάλυση Ι
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 8: Ολοκληρώματα Επίκουρος Καθηγητής Θ. Ζυγκιρίδης e-mil: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μαθηματική Ανάλυση Ι Ενότητα 8: Ολοκληρώματα Επίκουρος Καθηγητής Θ. Ζυγκιρίδης e-mil: tzygiridis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Επιμέλεια μεταφράσεων και εκδοτικός χώρος
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Επιμέλεια μεταφράσεων και εκδοτικός χώρος 13 η ενότητα: Ημερίδα «οι δρόμοι των μεταφραστών» Ελένη Κασάπη Τμήμα Ιταλικής Γλώσσας και Φιλολογίας
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Επιμέλεια μεταφράσεων και εκδοτικός χώρος 13 η ενότητα: Ημερίδα «οι δρόμοι των μεταφραστών» Ελένη Κασάπη Τμήμα Ιταλικής Γλώσσας και Φιλολογίας
Κλασσική Θεωρία Ελέγχου
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ο μετασχηματισμός Laplace Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ο μετασχηματισμός Laplace Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Μαθηματικά Και Στατιστική Στη Βιολογία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαθηματικά Και Στατιστική Στη Βιολογία Ενότητα : Λύση διαφορικών εξισώσεων & εξισώσεων διαφορών Μελέτη Ισορροπίας Στέφανος Σγαρδέλης Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαθηματικά Και Στατιστική Στη Βιολογία Ενότητα : Λύση διαφορικών εξισώσεων & εξισώσεων διαφορών Μελέτη Ισορροπίας Στέφανος Σγαρδέλης Άδειες
Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 12η: Αυτόνομες και ημιαυτόνομες εκκλησίες κ.ά. διατάξεις Κυριάκος Κυριαζόπουλος Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 12η: Αυτόνομες και ημιαυτόνομες εκκλησίες κ.ά. διατάξεις Κυριάκος Κυριαζόπουλος Άδειες
Οδοποιία IΙ. Ενότητα 14: Υπόδειγμα σύνταξης τευχών θέματος Οδοποιίας. Γεώργιος Μίντσης ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Οδοποιία IΙ Ενότητα 14: Υπόδειγμα σύνταξης τευχών θέματος Οδοποιίας Γεώργιος Μίντσης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Οδοποιία IΙ Ενότητα 14: Υπόδειγμα σύνταξης τευχών θέματος Οδοποιίας Γεώργιος Μίντσης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Λογισμός 4 Ενότητα 17
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 17: Το επί-επιφάνειο ολοκλήρωμα διανυσματικών πεδίων. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 17: Το επί-επιφάνειο ολοκλήρωμα διανυσματικών πεδίων. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Λογισμός 4 Ενότητα 11
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11: Θεώρημα αλλαγής μεταβλητών. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11: Θεώρημα αλλαγής μεταβλητών. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Γενικά Μαθηματικά Ι. Ενότητα 6: Ακρότατα Συνάρτησης. Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Ακρότατα Συνάρτησης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Ακρότατα Συνάρτησης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
