Magnetic bubble refraction in inhomogeneous antiferromagnets

Transcript

1 Magnetic bubble refraction in inhomogeneous antiferromagnets Martin Speight University of Leeds Nonlinearity 19 (006)

2 Plan Planar isotropic inhomogeneous antiferromagnetic spin lattices Continuum limit: O(3) sigma model on curved space Magnetic bubbles Doping domain walls, Snell s law of refraction The geodesic approximation, reduction to geometry Circular lenses, bubble guides

3 Antiferromagnets: Isotropic Heisenberg model Classical spins: S : Z R 3, S ij = s, ds ij dτ = S ij H S ij, H := i,j J ij S ij (S i,j+1 + S i+1,j ) J > 0 is a constant called the exchange integral H minimized when spins anti-align Doping: enrich part of AFM with different species J position dependent

4 Antiferromagnets: Isotropic Heisenberg model Classical spins: S : Z R 3, S ij = s, ds ij dτ = S ij H S ij, H := i,j J ij S ij (S i,j+1 + S i+1,j ) J > 0 is a constant called the exchange integral H minimized when spins anti-align Doping: enrich part of AFM with different species J position dependent

5 Antiferromagnets: Isotropic Heisenberg model Classical spins: S : Z R 3, S ij = s, ds ij dτ = S ij H S ij, H := i,j J ij S ij (S i,j+1 + S i+1,j ) J > 0 is a constant called the exchange integral H minimized when spins anti-align Doping: enrich part of AFM with different species J position dependent

6 The continuum limit: dimerization

7 The continuum limit: dimerization

8 The continuum limit: dimerization β α

9 The continuum limit: dimerization β α (-,1) dimer { B -,1 A -,1

10 The continuum limit: dimerization δ ε

11 The continuum limit: dimerization δ ε x = iε, y = jε, λ = αδ, ξ = βδ Assumption: A α,β B α,β J ij have continuum limits A(λ, ξ) B(λ, ξ) J(λ, ξ) as δ 0

12 The continuum limit: dimerization da αβ dτ db αβ dτ = J α β,α+β (B α,β 1 + B αβ + B α 1,β + B α 1,β 1 ) = J α β,α+β+1 (A α+1,β + A α+1,β+1 + A α,β+1 + A α,β ) Replace A α+1,β by A + δa λ + δ A λλ + etc Work to order δ J α β,α+β = J(λ, ξ) J α β,α+β+1 = J(λ + 1 δ, ξ + 1 δ) = J(λ, ξ) + δ (J λ + J ξ ) + δ 8 (J λλ + J ξξ + J λξ ) + Define rescaled time t = sδτ sδa t = JA [4B δ(b λ + B ξ ) + δ (B λλ + B ξξ + B λξ )] sδb t = JB [4A + δ(a λ + A ξ ) + δ (A λλ + A ξξ + A λξ )] B [δ(j λ + J ξ )A + δ (J λ + J ξ )(A λ + A ξ ) + δ (J λλ + J ξξ + J λξ )A]

13 The continuum limit: dimerization da αβ dτ db αβ dτ = J α β,α+β (B α,β 1 + B αβ + B α 1,β + B α 1,β 1 ) = J α β,α+β+1 (A α+1,β + A α+1,β+1 + A α,β+1 + A α,β ) Replace A α+1,β by A + δa λ + δ A λλ + etc Work to order δ J α β,α+β = J(λ, ξ) J α β,α+β+1 = J(λ + 1 δ, ξ + 1 δ) = J(λ, ξ) + δ (J λ + J ξ ) + δ 8 (J λλ + J ξξ + J λξ ) + Define rescaled time t = sδτ sδa t = JA [4B δ(b λ + B ξ ) + δ (B λλ + B ξξ + B λξ )] sδb t = JB [4A + δ(a λ + A ξ ) + δ (A λλ + A ξξ + A λξ )] B [δ(j λ + J ξ )A + δ (J λ + J ξ )(A λ + A ξ ) + δ (J λλ + J ξξ + J λξ )A]

14 The continuum limit: dimerization da αβ dτ db αβ dτ = J α β,α+β (B α,β 1 + B αβ + B α 1,β + B α 1,β 1 ) = J α β,α+β+1 (A α+1,β + A α+1,β+1 + A α,β+1 + A α,β ) Replace A α+1,β by A + δa λ + δ A λλ + etc Work to order δ J α β,α+β = J(λ, ξ) J α β,α+β+1 = J(λ + 1 δ, ξ + 1 δ) = J(λ, ξ) + δ (J λ + J ξ ) + δ 8 (J λλ + J ξξ + J λξ ) + Define rescaled time t = sδτ sδa t = JA [4B δ(b λ + B ξ ) + δ (B λλ + B ξξ + B λξ )] sδb t = JB [4A + δ(a λ + A ξ ) + δ (A λλ + A ξξ + A λξ )] B [δ(j λ + J ξ )A + δ (J λ + J ξ )(A λ + A ξ ) + δ (J λλ + J ξξ + J λξ )A]

15 The continuum limit: dimerization sδa t = JA [4B δ(b λ + B ξ ) + δ (B λλ + B ξξ + B λξ )] sδb t = JB [4A + δ(a λ + A ξ ) + δ (A λλ + A ξξ + A λξ )] B [δ(j λ + J ξ )A + δ (J λ + J ξ )(A λ + A ξ ) + δ (J λλ + J ξξ + J λξ )A] New fields: m = 1 1 (A + B), n = (A B) s s m n = 0 and m + n = 1 neighbouring spins almost anti-align m small assume m = O(δ) whence n = 1 + O(δ ) m t = ( λ + ξ )[Jm n] + δ 4 [Jn (n λλ + n ξξ + n λξ ) + (J λ + J ξ )n (n λ + n ξ )] δ n t = 4Jm n δjn (n λ + n ξ ) δ(j λ + J ξ )m n δ 4 (J λ + J ξ )n (n λ + n ξ )

16 The continuum limit: dimerization sδa t = JA [4B δ(b λ + B ξ ) + δ (B λλ + B ξξ + B λξ )] sδb t = JB [4A + δ(a λ + A ξ ) + δ (A λλ + A ξξ + A λξ )] B [δ(j λ + J ξ )A + δ (J λ + J ξ )(A λ + A ξ ) + δ (J λλ + J ξξ + J λξ )A] New fields: m = 1 1 (A + B), n = (A B) s s m n = 0 and m + n = 1 neighbouring spins almost anti-align m small assume m = O(δ) whence n = 1 + O(δ ) m t = ( λ + ξ )[Jm n] + δ 4 [Jn (n λλ + n ξξ + n λξ ) + (J λ + J ξ )n (n λ + n ξ )] δ n t = 4Jm n δjn (n λ + n ξ ) δ(j λ + J ξ )m n δ 4 (J λ + J ξ )n (n λ + n ξ )

17 The continuum limit: dimerization sδa t = JA [4B δ(b λ + B ξ ) + δ (B λλ + B ξξ + B λξ )] sδb t = JB [4A + δ(a λ + A ξ ) + δ (A λλ + A ξξ + A λξ )] B [δ(j λ + J ξ )A + δ (J λ + J ξ )(A λ + A ξ ) + δ (J λλ + J ξξ + J λξ )A] New fields: m = 1 1 (A + B), n = (A B) s s m n = 0 and m + n = 1 neighbouring spins almost anti-align m small assume m = O(δ) whence n = 1 + O(δ ) m t = ( λ + ξ )[Jm n] + δ 4 [Jn (n λλ + n ξξ + n λξ ) + (J λ + J ξ )n (n λ + n ξ )] δ n t = 4Jm n δjn (n λ + n ξ ) δ(j λ + J ξ )m n δ 4 (J λ + J ξ )n (n λ + n ξ )

18 The continuum limit: dimerization m t = ( λ + ξ )[Jm n] + δ 4 [Jn (n λλ + n ξξ + n λξ ) + (J λ + J ξ )n (n λ + n ξ )] ( ) δ n t = 4Jm n δjn (n λ + n ξ ) δ(j λ + J ξ )m n δ 4 (J λ + J ξ )n (n λ + n ξ )

19 The continuum limit: dimerization m t = ( λ + ξ )[Jm n] + δ 4 [Jn (n λλ + n ξξ + n λξ ) + (J λ + J ξ )n (n λ + n ξ )] ( ) δ n t = 4Jm n δjn (n λ + n ξ ) + O(δ ) δ 4 Solve ( ) for m: m = δ 4 ( ) [ 1 J n n t n λ n ξ ] + O(δ )

20 The continuum limit: dimerization m t = ( λ + ξ )[Jm n] + δ 4 [Jn (n λλ + n ξξ + n λξ ) + (J λ + J ξ )n (n λ + n ξ )] ( ) δ n t = 4Jm n δjn (n λ + n ξ ) + O(δ ) δ 4 Solve ( ) for m: Subst in ( ): All terms involving J λ, J ξ cancel! m = δ 4 ( ) [1 J n n t n λ n ξ ] + O(δ ) n n tt = J n (n λλ + n ξξ ) + O(δ)

21 The continuum limit: dimerization m t = ( λ + ξ )[Jm n] + δ 4 [Jn (n λλ + n ξξ + n λξ ) + (J λ + J ξ )n (n λ + n ξ )] ( ) δ n t = 4Jm n δjn (n λ + n ξ ) + O(δ ) δ 4 Solve ( ) for m: Subst in ( ): All terms involving J λ, J ξ cancel! m = δ 4 ( ) [1 J n n t n λ n ξ ] + O(δ ) n n tt = J n (n λλ + n ξξ ) + O(δ) Limit δ 0: ( ) n n t n J λ n J = 0 }{{ ξ } Dn

22 ( ) D = J(x, y) t x + y The O(3) sigma model ( ) n n t n J λ n J = 0 }{{ ξ } Dn where J(x, y) = J( λ ξ, λ+ξ )

23 ( ) D = J(x, y) t x + y The O(3) sigma model ( ) n n t n J λ n J = 0 }{{ ξ } Dn where Wave operator on spacetime R +1 with inhomogeneous metric J(x, y) = J( λ ξ, λ+ξ ) η = dt J(x, y) (dx + dy )

24 ( ) D = J(x, y) t x + y The O(3) sigma model ( ) n n t n J λ n J = 0 }{{ ξ } Dn where Wave operator on spacetime R +1 with inhomogeneous metric J(x, y) = J( λ ξ, λ+ξ ) η = dt J(x, y) (dx + dy ) n Dn = 0 n Dn Dn (n Dn)n = 0 Variational equation for S = 1 R +1 dt dx dy η η µν µ n ν n

25 Magnetic bubbles n [n tt J(x, y) (n xx + n yy )] = 0 Static solutions are independent of J (conformal invariance) S R x + iy = z n(z) u(z) Belavin-Polyakov: u(z) = rational map Choose u( ) =, that is, n( ) = (0, 0, 1) Unit bubble : u(z) = χ 1 e iψ (z a) =: u 0 (z; χ, ψ, a) gradient energy χ R + width ψ [0, π] internal phase a C position z χ a

26 Doping domain walls J J + J - J + dope this end (suppress J ) J y x v θ

27 Doping domain walls Noether s Theorem conservation of E = 1 ( nt ) dx dy J(x) + n x + n y and P = dx dy n t n y J(x) Minkowski space speed of light = J v θ v + θ + Minkowski space speed of light = J + Mγ + = Mγ and v +γ + sinθ + J + where γ ± = Snell s Law: ( ) 1 1 v ± J± 1 J + sinθ + = 1 J sinθ M = v γ sinθ J M J 1 = refractive index Total internal reflexion if θ 1 > sin 1 (J /J + ) Crucial fact: bubble rest energy M = M + = M = 4π (conformal invariance)

28 Doping domain walls Noether s Theorem conservation of E = 1 ( nt ) dx dy J(x) + n x + n y and P = dx dy n t n y J(x) Minkowski space speed of light = J v θ v + θ + Minkowski space speed of light = J + Mγ + = Mγ and v +γ + sinθ + J + where γ ± = Snell s Law: ( ) 1 1 v ± J± 1 J + sinθ + = 1 J sinθ M = v γ sinθ J M J 1 = refractive index Total internal reflexion if θ 1 > sin 1 (J /J + ) Crucial fact: bubble rest energy M = M + = M = 4π (conformal invariance)

29 Doping domain walls Noether s Theorem conservation of E = 1 ( nt ) dx dy J(x) + n x + n y and P = dx dy n t n y J(x) Minkowski space speed of light = J v θ v + θ + Minkowski space speed of light = J + Mγ + = Mγ and v +γ + sinθ + J + where γ ± = Snell s Law: ( ) 1 1 v ± J± 1 J + sinθ + = 1 J sinθ M = v γ sinθ J M J 1 = refractive index Total internal reflexion if θ 1 > sin 1 (J /J + ) Crucial fact: bubble rest energy M = M + = M = 4π (conformal invariance)

30 Doping domain walls Noether s Theorem conservation of E = 1 ( nt ) dx dy J(x) + n x + n y and P = dx dy n t n y J(x) Minkowski space speed of light = J v θ v + θ + Minkowski space speed of light = J + Mγ + = Mγ and v +γ + sinθ + J + where γ ± = Snell s Law: ( ) 1 1 v ± J± 1 J + sinθ + = 1 J sinθ M = v γ sinθ J M J 1 = refractive index Total internal reflexion if θ 1 > sin 1 (J /J + ) Crucial fact: bubble rest energy M = M + = M = 4π (conformal invariance)

31 Slow bubble dynamics: the geodesic approximation Bubble u 0 (z; χ, ψ, a): 4 parameter family of energy minimizers Parameter space: M 1 = C C u 0 (χe iψ, a) = (q 1 + iq, q 3 + iq 4 ) Approximation: u(z, t) = u 0 (z; χ(t), ψ(t), a(t)) S ( ) 1 = dt g ij(q) q i q j 4π. Variational equations for q i (t): geodesic equation on M 1 with metric g = g ij dq i dq j

32 Slow bubble dynamics: the geodesic approximation J(x, y) bounded χ = ψ = χ, ψ frozen by infinite inertia Can assume ψ = 0. Width χ is a free but frozen parameter Metric on width χ phase 0 leaf M χ 1 : g = f χ (a)(da 1 + da ) where f χ(a) = the integral of J(χu + a) over the standard unit sphere 4 du dū 1 (1 + u ) J(χu + a), lim χ 0 g = 4π J(a) (da 1 + da ) = 4π metric on physical plane g = smeared out metric on R due to finite bubble core size

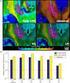
33 Doping domain walls J J J - x 30 5 [ f χ (a) = π J 1 a 1 χ + a 1 ] + π J + interpolates smoothly between 4π J [ 1 + a 1 χ + a 1 and 4π J + ]} J + J = solid: χ = 0.5 dashed: χ = 0.1

34 Circular lenses Have geometric optics model of bubble trajectories Should be able to focus bubbles with thin lenses Simple test case: sharp circular lens J + J - J + J - J(z) = { J+, z > 1 J, z 1 Can write down f χ ( a ) explicitly (but it s complicated)

35 Circular lenses (M χ 1, g) can be isometrically embedded as a surface of revolution in R3 (for χ not too small) χ = 1 χ = 1 χ = 1 4 χ = 1 5

36 Circular lenses 1.5 χ= J = 1, J + = χ= J = 1, J + =

37 Circular lenses

38 Circular lenses

39 Circular lenses

40 Circular lenses

41 Circular lenses

42 Bubble guides low J high J χ = χ =

43 Prospects Snell s law follows direct from elastic scattering (should hold for low velocities) and field theoretic conservation laws......provided scattering off walls does not cause bubble collapse Numerics: simulate spin lattice directly, not sigma model Practical problem: spins anti-align magnetization (almost) zero. Very hard to observe and manipulate bubbles experimentally Refraction relies only on conformal invariance: should happen to instantons in dimensional Yang-Mills, for example Laboratory model of soliton dynamics in exotic spacetimes! Nonlinearity 19 (006)