Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών. ΗΥ-561 Διαχείριση Δεδομένων στο Παγκόσμιο Ιστό Βασίλης Χριστοφίδης
|
|
|
- Ἀγαυή Παπαϊωάννου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-561 Διαχείριση Δεδομένων στο Παγκόσμιο Ιστό Βασίλης Χριστοφίδης Ονοματεπώνυμο: Αριθμός Μητρώου: Τελική Εξέταση (3 ώρες) Ημερομηνία: Παρασκευή 14 Ιουλίου 2006 Άσκηση 1 (50 μονάδες) Σας δίνεται το παρακάτω μοντέλο οντοτήτων-συσχετίσεων (ΟΣ) για την αναπαράσταση πληροφορίας σχετικής με ασθενείς και τους θεράποντες γιατρούς τους. 1.(15 μονάδες) Μεταφράστε το παραπάνω μοντέλο ΟΣ σε σχήμα XML. Σχεδιάστε κατάλληλους τύπους στοιχείων XML (σε δύο αρχεία patients.xsd και doctors.xsd) για κάθε οντότητα λαμβάνοντας υπόψη τους περιορισμούς ακεραιότητας (κλειδιά, εξωτερικά κλειδιά) καθώς και ότι: Α) Για κάθε Ασθενή (Patient): SSN (1 occurrence, required) Name (1 occurrence, required)
2 Insurance Plan (1 or more occurrence, required) Address (0 or 1 occurrence, optional) Phone Number (1 occurrence, required) Β) Για κάθε Γιατρό (Doctor): ID (1 occurrence, required) Name (1 occurrence, required) SSN (1 occurrence, required) Office visit fee (values from 10 to 115, required) Specialty (1 occurrence, required) Accepted Insurance plans (0 or more occurrence, optional) <?xml version="1.0"?> <xsd:schema xmlns:xsd= xmlns:msdata="urn:schemas-microsoft-com:xml-msdata" xsd:nonamespaceschemalocation="doctors.xsd"> <xsd:element name="doctors"> <xsd:complextype> <xsd:sequence> <xsd:element name="doctor" maxoccurs="unbounded"> <xsd:complextype> <xsd:sequence> <xsd:element name="id" type="xsd:string" minoccurs="1" maxoccurs="1" nillable="false"/> <xsd:key name="doctorskey"> <xsd:selector xpath=".//doctor" /> <xsd:field xpath="id" /> </xsd:key> <xsd:element name="name" type="xsd:string" minoccurs="1" maxoccurs="1" nillable="false"/> <xsd:element name="ssn" type="xsd:string" minoccurs="1" maxoccurs="1" nillable="false"/> <xsd:element name="visitfee" nillable="false"> <xsd:simpletype> <xsd:restriction base="xsd:integer"> <xsd:mininclusive value="10"/> <xsd:maxinclusive value="115"/> </xsd:restriction> </xsd:simpletype> </xsd:element> <xsd:element name="specialty" type="xsd:string" minoccurs="1" maxoccurs="1" nillable="false"/> <xsd:element name="acceptableplan" type="xsd:string" minoccurs="0" maxoccurs="unbounded"/> </xsd:sequence> </xsd:complextype> </xsd:element> </xsd:sequence> </xsd:complextype> </xsd:element> </xsd:schema> <?xml version="1.0"?> <xsd:schema xmlns:xsd= xmlns:msdata="urn:schemas-microsoft-com:xml-msdata" xmlns:doc="./doctors.xsd" xsd:nonamespaceschemalocation="patients.xsd"> <xsd:element name="patients"> <xsd:complextype> <xsd:sequence> <xsd:element name="patient" maxoccurs="unbounded"> <xsd:complextype> <xsd:sequence> <xsd:element name="name" type="xsd:string"nillable="false"/> <xsd:element name="ssn" type="xsd:string" nillable="false"
3 minoccurs="1" maxoccurs="1"/> <xsd:key name="patientskey"> <xsd:selector xpath=".//patient" /> <xsd:field xpath="ssn" /> </xsd:key> <xsd:element name="phone" nillable="false" minoccurs="1" maxoccurs="1"> <xsd:complextype> <xsd:sequence> <xsd:element name="areacode" type="xsd:string"/> <xsd:element name="phoneno" type="xsd:string"/> </xsd:sequence> </xsd:complextype> </xsd:element> <xsd:element name="address" maxoccurs="1"> <xsd:complextype> <xsd:sequence> <xsd:element name="streetno" type="xsd:string"/> <xsd:element name="streetname" type="xsd:string"/> <xsd:element name="city" type="xsd:string"/> <xsd:element name="state" type="xsd:string"/> <xsd:element name="zip" type="xsd:string" /> </xsd:sequence> </xsd:complextype> </xsd:element> <! Here we translate the relationship has_appointment --!> <xsd:element name="id" type="xsd:string" minoccurs="0" maxoccurs="unbounded"/> <xsd:keyref name="has_appointment" msdata:refrencekey="true" refer="doc:doctorskey"> <xsd:selector xpath=".//patient" /> <xsd:field xpath="id" /> </xs:keyref> <xsd:element name="insuranceplan" minoccurs="1" maxoccurs="unbounded"/> </xsd:sequence> </xsd:complextype> </xsd:element> </xsd:sequence> </xsd:complextype> </xsd:element> </xsd:schema> 2.(35 μονάδες) Δώστε τις εκφράσεις XQuery καθώς και τον τύπο του αποτελέσματός τους για τις παρακάτω επερωτήσεις, υποθέτοντας ότι σας δίνονται δύο σχετικά έγγραφα XML patient.xml και doctor.xml. Σημείωση: Οι ασθενείς διακρίνονται από τον αριθμό κοινωνικής ασφάλισης (SSN) (και για ευκολία θεωρείστε ότι τα ονόματά τους είναι μοναδικά στα δεδομένα του αρχείου patient.xml) ενώ οι γιατροί διακρίνονται από τις ταυτότητές τους (ID). Έτσι στις ακόλουθες επερωτήσεις: Όποτε σας ζητείται να επιστρέψετε μια συγκεκριμένη τιμή για τους ασθενείς, δώστε το όνομα καθώς και τη ζητούμενη τιμή για κάθε ασθενή. Όποτε σας ζητείται να επιστρέψετε μια συγκεκριμένη τιμή για τους γιατρούς, δώστε το όνομα καθώς και τη ζητούμενη τιμή για κάθε γιατρό. a) Δώστε τα ασφαλιστικά ταμεία (insurance plans) για κάθε ασθενή (κάθε ασφαλιστικό ταμείο πρέπει να διαχωρίζεται από ","). Ταξινομήστε το αποτέλεσμα σε αύξουσα σειρά ως προς το όνομα των ασθενών.
4 FOR $p IN distinct-values(document("patient.xml")//patients/patient) ORDER BY $p/name ascending RETURN <Patient> {$p/name} { Let $d := count($p/insuranceplan) return if($d = 1) then <InsurancePlans>{$p/InsurancePlan[1]/text()}</InsurancePlans> else <InsurancePlans>{$p/InsurancePlan[position() <$d]/text(),", "}, {$p/insuranceplan[position() = $d]/text()}</insuranceplans> } </Patient> element Patient { element Name {xsd:string}, element s {{text}*} }* b) Δώστε τον αριθμό ασθενών για κάθε ταχυδρομικό κώδικα (zip). Ταξινομήστε το αποτέλεσμα σε φθίνουσα σειρά ως προς τον αριθμό των ασθενών. FOR $z IN distinct-values(document("patient.xml")// Patients/Patient/Address/Zip) LET $n := count(document("patient.xml")//patients/patient/ [Address/Zip=$z]) ORDER BY $n descending RETURN <Patients zip = "{$z}"> <PatientNum>{$n}</PatientNum> </Patients> element Patients { attribute zip {xdt:untypedatomic}, element PatientNum {xsd:integer} }* c) Δώστε τον αριθμό ασθενών για κάθε γιατρό με την προϋπόθεση ότι ο ασθενής ανήκει σ ένα ασφαλιστικό ταμείο με το οποίο ο γιατρός είναι συμβεβλημένος. Ταξινομήστε το αποτέλεσμα σε φθίνουσα σειρά ως προς τον αριθμό των ασθενών. FOR $d IN document("doctor.xml")//doctors/doctor LET $n := count( for $p IN document("patient.xml")//patients/patient Where exists(for $docid IN $p/id where $docid = $d/id and exists(for $dplan IN $d/acceptableplan for $pplan IN $p/insuranceplan where $dplan = $pplan return $dplan) return $docid) return $p) ORDER BY $n descending RETURN <Doctors> <DoctorID>{$d/ID}, <PatientNum>{$n}</PatientNum> </Doctors> element Doctors { element DoctorID {xsd:string}, element PatientNum {xsd:integer} }*
5 d) Δώστε τους ασθενείς που πρέπει να καταβάλουν αμοιβή (fee) σε τουλάχιστον δύο γιατρούς που έχουν επισκεφτεί (δηλ., τουλάχιστον δύο από τους γιατρούς στον κατάλογό τους δεν είναι συμβεβλημένοι με κανένα από τα ασφαλιστικά ταμεία του ασθενούς). Ταξινομήστε το αποτέλεσμα σε αύξουσα σειρά ως προς το όνομα των ασθενών. FOR $p IN document("patient.xml")//patients/patient WHERE count($p/id) - count( for $docid IN $p/id where exists( for $d IN document("doctor.xml")//doctors/doctor where $d/id = $docid and exists(for $dplan IN $d/acceptableplan where $dplan = $p/insuranceplan[position() <= count($p/insuranceplan)] return $dplan) return $d) return $docid) >=2 ORDER BY $p/name ascending RETURN <Patients>{$p/Name}</Patients> element Patients { element Name {xsd:string} }* e) Δώστε τους ασθενείς που έχουν καταβάλει σ ένα γιατρό αμοιβή (fee) επίσκεψης μεγαλύτερη ή ίση του 100 γιατί ο γιατρός δεν είναι συμβεβλημένος με τα ασφαλιστικά τους ταμεία. Ταξινομήστε το αποτέλεσμα σε αύξουσα σειρά ως προς το όνομα των ασθενών. FOR $p IN document("patient.xml")//patients/patient WHERE exists( for $dd IN $p/id for $d in document("doctor.xml")//doctors/doctor where $d/id = $dd and $d/visitfee > 100 and empty(for $plan IN $d/acceptableplan where $plan = $p/insuranceplan[position() <= count($p/insuranceplan)] return $plan) return $d) ORDER BY $p/name ascending RETURN <Patients>{$p/Name}</Patients> element Patients { element Name {xsd:string} }* f) Δώστε τους ασθενείς που έχουν κλείσει τουλάχιστον μια συνάντηση με έναν δερματολόγο. Ταξινομήστε το αποτέλεσμα σε αύξουσα σειρά ως προς το όνομα των ασθενών. LET $d := document("doctor.xml")//doctors/doctor FOR $p IN document("patient.xml")//patients/patient WHERE count($d[id = $p/id[position()<=count($p/id)] and Specialty = "Dermatology"])!= 0 ORDER BY $p/name ascending RETURN <Patients> {$p/name} </Patients> element Patients { element Name {xsd:string} }*
6 g) Δώστε τους ασθενείς που έχουν κλείσει συνάντηση με τουλάχιστον δύο γιατρούς της ίδιας ειδικότητας. Ταξινομήστε το αποτέλεσμα σε φθίνουσα σειρά ως προς το όνομα των ασθενών. For $p IN document("patient.xml")//patients/patient Where count(distinct-values( for $dd IN $p/id for $d in document("doctor.xml")//doctors/doctor where $d/id = $dd return $d/specialty)) < count($p/id) ORDER BY $p/name descending RETURN <Patients> {$p/name} </Patients> element Patients { element Name {xsd:string} }* Άσκηση 2 (33 μονάδες) Ο εγκλεισμός (containment) και η ισοδυναμία (equivalence) είναι δύο σημαντικά προβλήματα για δηλωτικές γλώσσες επερωτήσεων XML (όπως και στις σχεσιακές βάσεις δεδομένων). Υποθέστε ότι έχουμε δύο εκφράσεις XPath Q1 και Q2. Η αποτίμηση της Q1 στο έγγραφο XML D, που συμβολίζεται Q1(D), είναι ένα σύνολο κόμβων από το D (χωρίς διάταξη). Ορίζουμε τον εγκλεισμό δύο εκφράσεων XPath ως εξής: Q1 Q2 εάν για κάθε έγγραφο XML D Q1(D) Q2(D) (δηλ. τα αποτελέσματα της Q1 περιέχονται πάντα στα αποτελέσματα της Q2). Εάν Q1 Q2 και Q2 Q1, τότε Q1 και Q2 είναι δύο ισοδύναμες εκφράσεις. α) (18 μονάδες) Σας δίνονται οι ακόλουθες εκφράσεις XPath: Q1: /a[*]/b Q2: /a//b Q3: /a[b][g] Q4: /a[g][b] Q5: /a[b]/*//g Q6: /a[b]//*/g Ποιες από τις παρακάτω σχέσεις εγκλεισμού ισχύουν (απαντήστε με ένα ναι ή όχι) i) Q1 Q2? Yes ii) Q2 Q1? No iii) Q3 Q4? Yes iv) Q4 Q3? Yes v) Q5 Q6? Yes vi) Q6 Q5? Yes
7 β) (15 μονάδες) Εστιάζοντας σε απλές εκφράσεις XPath, όπως αυτές του προηγούμενου ερωτήματος (δηλ. που χρησιμοποιούν μόνο τούς άξονες child και descendent-or-self καθώς και απλά κατηγορήματα και μπαλαντέρ *), μια έκφραση XPath Q είναι ελάχιστη εάν όλες οι ισοδύναμες εκφράσεις που υπάρχουν είναι τουλάχιστον τόσο μεγάλες όσο και η Q (μετρώντας όλες τις δοκιμές κόμβων (node tests), συμπεριλαμβανομένου του μπαλαντέρ *, και των κατηγορημάτων). i) Είναι ελάχιστη κάποια από τις παραπάνω εκφράσεις XPath Q1... Q6? Στην αντίθετη περίπτωση, δώστε μια μικρότερη ισοδύναμη έκφραση. The only non-minimal expression is Q1. It can be written as /a/b. ii) Υπάρχει μόνο μια μοναδική ελάχιστη μορφή μιας έκφρασης XPath? Δικαιολογήστε γιατί ή δώστε ένα αντι-παράδειγμα. No. Expressions Q5 and Q6 above are two different but equivalent expressions and both are minimal. iii) Ποια είναι η ελάχιστη μορφή της ακόλουθης έκφρασης XPath: /a[b/*][b//g]/b/g A: Equivalent to: a/b/g Άσκηση 3 (30 μονάδες) Σας δίνεται η παρακάτω επερώτηση XQuery η οποία επιστρέφει τα αεροδρόμια με την μεγαλύτερη κίνηση στις 26/06/2006 (βασισμένη στον αριθμό των αφίξεων και αναχωρήσεων κάθε αεροδρομίου): LET $results := ( <traffic> { for $a in doc('flights.xml')//airport let $c :=count( doc('flights.xml')//flight[((/source/text() eq $a/@airid) or (./destination/text() eq $a/@airid)) and (date/text() eq ' ') ] ) return <result> {$a} <count>{$c}</count> </result> } </traffic>) RETURN $results/result[xs:integer(./count/text()) eq xs:integer(max($results//count/text()))] Σημείωση: Για την αλγεβρική μετάφραση μιας επερώτησης XQuery χρειαζόμαστε τελεστές που αναπαριστούν τις εκφράσεις πλοήγησης XPath (στους άξονες child, descendant or self) καθώς και τις εκφράσεις XQuery για τον έλεγχο ροής (ifthenelse), το ταίριασμα (match) μονοπατιών και την κατασκευή κόμβων (nodeconstructor) στο αποτέλεσμα. 1. Μια έκφραση XPath μπορεί να αναπαρασταθεί με μια γραμμική δομή που εκφράζει όλα τα βήματα πλοήγησης σε ένα μονοπάτι και η οποία διαβάζεται από κάτω προς τα επάνω: children, descendant-or-self είναι λειτουργίες που αντιστοιχούν στα /,// Λειτουργία ταιριάσματος.
8 - match(text()) επιστρέφει όλους τους κόμβους κειμένου από ένα δεδομένο σύνολο κόμβων, - match(count) επιστρέφει όλους τους κόμβους με όνομα count από ένα δεδομένο σύνολο κόμβων. 2. Οι σταθερές αναπαριστώνται χρησιμοποιώντας τη λειτουργία constant 3. Οι λειτουργίες και οι τελεστές αναπαριστώνται σαν δέντρα, όπου η παράμετρός τους είναι τα παιδιά του δέντρου. 4. Κάθε λειτουργία έχει μια τιμή επιστροφής την οποία περνούν στους κόμβους προγόνους του δέντρου. α) (10 μονάδες) Κατασκευάστε ένα πλάνο εκτέλεσης για την παραπάνω επερώτηση μεταφράζοντας τις εκφράσεις XQuery σε αλγεβρικές εκφράσεις ως ακολούθως: Εκφράσεις LET/RETURN: (a return belongs to a let or for ) let $result := <order>abc</order> return $result/text() Notes: we represent the let variable as a label on the left edge; the right edge gives the result; the right edge(corresponding to the initial return ) cannot be executed before the left edge. Εκφράσεις FOR : for $a in doc( flights.xml )//Airport let $c:= 5 return $result <result>{$c}</result> Notes: - The for variable is a label of the left edge. The left edge evaluates to a sequence of nodes. - For each mapping of $a to one of the items in the sequence generated by the left size, the right edge is executed - the result of the for is the union of all results returned on the right side for each mapping - the return belongs to the let statement, so the result returned at each iteration is the right edge of the let node
9 Εκφράσεις ifthenelse: let $results := [ ] return $results/result[xs:integer(. /count/text())eq2] Note: the expression is equivalent to : for $r in $results/result where xs:integer($r/count/text()) eq 2 return $r - a temporary variable, $r, is introduced - an ifthenelse function takes a Boolean expression, and returns the result of the second branch when the expression is true, and the result of the thirds branch when the result is false (in our case, we return the empty sequence)
10 ( )
11 β) (20 μονάδες) Διαλέγοντας σαν συνάρτηση κόστους τον αριθμό των λειτουργιών του πλάνου εκτέλεσης, βελτιστοποιήστε το πλάνο που δώσατε στο προηγούμενο ερώτημα. Σημείωση: Ο στόχος αυτής της επαναδιατύπωσης (rewriting) του πλάνου είναι να προσδιορίσουμε τις λειτουργίες που μπορούν να αφαιρεθούν (δηλ. που δεν είναι απαραίτητες) ή να βελτιστοποιηθούν (π.χ. μερικές διαδικασίες μπορούν να εκτελεσθούν μόνο μία φορά, έξω από έναν βρόχο, αντί της εκτέλεσής τους σε κάθε επανάληψη του βρόχου), κλπ. προκειμένου να πετύχουμε αποδοτικότερη αποτίμηση της επερώτησης. Ιδιαίτερα μας ενδιαφέρει να αναγνωρίσουμε κοινές υποεκφράσεις (δηλ., εκφράσεις που είναι ίδιες και γι αυτό δεν χρειάζεται να εκτελεστούν πολλές φορές σε διαφορετικά σημεία της ίδιας ερώτησης). Οι σταθερές επίσης είναι μια ειδική περίπτωση των κοινών υποεκφράσεων οι οποίες αποτιμώνται μόνο μία φορά έξω από όλους τούς βρόχους. Query rewriting: We will eliminate common subexpressions from the initial query (expressions which can be evaluated once instead of each time they appear). Depending on the query engine, several other optimization steps might be applied to the expression. The common subexpressions do not depend on the variable of the for expression where they appear: 1. Identifying common subexpressions: - all constants: flights.xml, doc( flights.xml ) : evaluated both: for getting the Flights and getting the Airports doc( flights.xml )//Flights doc( flights.xml )//Airports - doc( flights.xml )//Flight: currently, executed for each iteration of for number 1 - $a/airid: computed for each Flight in for number 2 - max($results//count/text()): computed for each iteration of for number 3 2. Rewriting the query plan - For each common subexpression, we introduce a let statement and a temporary variable. The new let statement computes the value of the expression once for each context where it was executed several times. - We use the temporary variable wherever the common sub-expression previously appeared. NOTE: For simplification, we will only rewrite the expressions without rewriting the descendantor-self axis. Figure below shows the common subexpressions (in red) and where the new let statements should be introduced. Figure 3 shows the rewritten query plan.
12 ( )
13 Figure below shows the rewritten query plan where sub-expressions are optimized ( )
14 The rewritten query is equivalent to the following XQuery: (new variables appear in red and bold; the usage of new variables appears in blue) let $results := (<traffic> { (: all descendants :) let $_doc := doc('flights.xml')//descendant-or-self::* let $_flights := $_doc/flight for $a in $_doc/airport let $_airid := $a/@airid let $c := count($_flights[((./source/text() eq $_airid) or (./destination/text() eq $_airid)) and (date/text() eq ' ') ] ) return <result> {$a} <count>{$c}</count> </result> } </traffic>) let $_max := xs:integer(max($results//count/text())) return $results/result[xs:integer(./count/text()) eq $_max] One way to compute the cost of the initial query plan is to add 1 for each node in the query plan (for uniformity, we add 1 for the let nodes, also for the root of the for). The cost of the for expressions is computed as : 1 (=cost of the root node) + Cost of left part + count(number of items in left part) * cost(right part) In the following computation, we take into account the number of Airports and number of Flights : Flights: 41 Airports: 10 Initial Cost (before rewrite) Cost(Q1_initial) = 2 + cost(for1) + cost(for3) = , = 12,601 Cost(for1) = (=left side) + no_of_airports * cost(right_side) = * (7 + cost(for2)) = * (7+1235) = 12,425 Cost(for2) = (= left side) + no_of_flights * 30 = * 30 = 1235 Cost(for3) = (= left side) + no_of_<result>_elements * (cost(right_side)) = * 17 = 174 Cost after Query Rewrite Cost(Q1_rewrite) = 9 + cost(for1) cost(for3) = = Cost(for1) = no_airports * cost(right_side) = = * (6 + cost(for2) + 5) = = * (11 + cost (for2)) = = * ( ) = * 1079 = cost(for2) = no_flights * cost(right_side) = * 26 = 1068 cost(for3) = no_of_<result>_elements * (cost(right_side)) = = * 11 = 114 Of course, cost (Q1_rewrite) < cost(q1_initial), so the rewrite helps to gain the cost. This computation included actually all operations, even though the Boolean operations might not be always executed. However, it gives an impression on the technique of query rewriting.
15
Πανεπιστήµιο Κρήτης Τµήµα Επιστήµης Υπολογιστών. ΗΥ-561 ιαχείριση εδοµένων στο Παγκόσµιο Ιστό Βασίλης Χριστοφίδης
 Πανεπιστήµιο Κρήτης Τµήµα Επιστήµης Υπολογιστών ΗΥ-561 ιαχείριση εδοµένων στο Παγκόσµιο Ιστό Βασίλης Χριστοφίδης Ονοµατεπώνυµο: Αριθµός Μητρώου: Άσκηση 1 (55 µονάδες) Τελική Εξέταση (3 ώρες) Ηµεροµηνία:
Πανεπιστήµιο Κρήτης Τµήµα Επιστήµης Υπολογιστών ΗΥ-561 ιαχείριση εδοµένων στο Παγκόσµιο Ιστό Βασίλης Χριστοφίδης Ονοµατεπώνυµο: Αριθµός Μητρώου: Άσκηση 1 (55 µονάδες) Τελική Εξέταση (3 ώρες) Ηµεροµηνία:
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών. ΗΥ-561 Διαχείριση Δεδομένων στο Παγκόσμιο Ιστό Βασίλης Χριστοφίδης
 Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-561 Διαχείριση Δεδομένων στο Παγκόσμιο Ιστό Βασίλης Χριστοφίδης Ονοματεπώνυμο : Αριθμός Μητρώου: Τελική Εξέταση (3 ώρες) Ημερομηνία: Πέμπτη 19 Ιουλίου
Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-561 Διαχείριση Δεδομένων στο Παγκόσμιο Ιστό Βασίλης Χριστοφίδης Ονοματεπώνυμο : Αριθμός Μητρώου: Τελική Εξέταση (3 ώρες) Ημερομηνία: Πέμπτη 19 Ιουλίου
5. Επερώτηση XML Εγγράφων: Εισαγωγή στη Γλώσσα XQuery
 Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 5. Επερώτηση XML Εγγράφων: Εισαγωγή στη Γλώσσα XQuery ιαχείριση εδομένων στον Παγκόσμιο Ιστό Χρήστος ουλκερίδης
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 5. Επερώτηση XML Εγγράφων: Εισαγωγή στη Γλώσσα XQuery ιαχείριση εδομένων στον Παγκόσμιο Ιστό Χρήστος ουλκερίδης
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής
 Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ. ΕΠΛ342: Βάσεις Δεδομένων. Χειμερινό Εξάμηνο Φροντιστήριο 10 ΛΥΣΕΙΣ. Επερωτήσεις SQL
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ342: Βάσεις Δεδομένων Χειμερινό Εξάμηνο 2013 Φροντιστήριο 10 ΛΥΣΕΙΣ Επερωτήσεις SQL Άσκηση 1 Για το ακόλουθο σχήμα Suppliers(sid, sname, address) Parts(pid, pname,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ342: Βάσεις Δεδομένων Χειμερινό Εξάμηνο 2013 Φροντιστήριο 10 ΛΥΣΕΙΣ Επερωτήσεις SQL Άσκηση 1 Για το ακόλουθο σχήμα Suppliers(sid, sname, address) Parts(pid, pname,
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
3. Επερώτηση XML Εγγράφων: Η Γλώσσα XPath
 Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 3. Επερώτηση XML Εγγράφων: Η Γλώσσα XPath ιαχείριση εδομένων στον Παγκόσμιο Ιστό Χρήστος ουλκερίδης Τμήμα
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 3. Επερώτηση XML Εγγράφων: Η Γλώσσα XPath ιαχείριση εδομένων στον Παγκόσμιο Ιστό Χρήστος ουλκερίδης Τμήμα
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
ΑΝΑΠΑΡΑΣΤΑΣΗ ΓΝΩΣΗΣ ΣΤΟΝ ΠΑΓΚΟΣΜΙΟ ΙΣΤΟ
 ΑΝΑΠΑΡΑΣΤΑΣΗ ΓΝΩΣΗΣ ΣΤΟΝ ΠΑΓΚΟΣΜΙΟ ΙΣΤΟ XML-XPath Ι. Χατζηλυγερούδης Ερωτήματα σε έγγραφα XML Αντίστοιχα των ερωτημάτων (queries) σε βάσεις δεδομένων Γλώσσες ερωτημάτων (αντίστοιχες της SQL) XQL (XML Query
ΑΝΑΠΑΡΑΣΤΑΣΗ ΓΝΩΣΗΣ ΣΤΟΝ ΠΑΓΚΟΣΜΙΟ ΙΣΤΟ XML-XPath Ι. Χατζηλυγερούδης Ερωτήματα σε έγγραφα XML Αντίστοιχα των ερωτημάτων (queries) σε βάσεις δεδομένων Γλώσσες ερωτημάτων (αντίστοιχες της SQL) XQL (XML Query
Βάσεις Δεδομένων ΙΙ. Διάλεξη 5 η XML και ΒΔ στο Διαδίκτυο
 Βάσεις Δεδομένων ΙΙ Διάλεξη 5 η XML και ΒΔ στο Διαδίκτυο Δ. Χριστοδουλάκης - Α. Φωκά Τμήμα Μηχανικών Η/Υ & Πληροφορικής - Εαρινό Εξάμηνο 2007 Εισαγωγή Πολλές εφαρμογές διαδικτύου υποστηρίζουν web διεπαφές
Βάσεις Δεδομένων ΙΙ Διάλεξη 5 η XML και ΒΔ στο Διαδίκτυο Δ. Χριστοδουλάκης - Α. Φωκά Τμήμα Μηχανικών Η/Υ & Πληροφορικής - Εαρινό Εξάμηνο 2007 Εισαγωγή Πολλές εφαρμογές διαδικτύου υποστηρίζουν web διεπαφές
Μορφοποίηση υπό όρους : Μορφή > Μορφοποίηση υπό όρους/γραμμές δεδομένων/μορφοποίηση μόο των κελιών που περιέχουν/
 Μορφοποίηση υπό όρους : Μορφή > Μορφοποίηση υπό όρους/γραμμές δεδομένων/μορφοποίηση μόο των κελιών που περιέχουν/ Συνάρτηση round() Περιγραφή Η συνάρτηση ROUND στρογγυλοποιεί έναν αριθμό στον δεδομένο
Μορφοποίηση υπό όρους : Μορφή > Μορφοποίηση υπό όρους/γραμμές δεδομένων/μορφοποίηση μόο των κελιών που περιέχουν/ Συνάρτηση round() Περιγραφή Η συνάρτηση ROUND στρογγυλοποιεί έναν αριθμό στον δεδομένο
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων. Εξάμηνο 7 ο
 Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL
1. Αφετηρία από στάση χωρίς κριτή (self start όπου πινακίδα εκκίνησης) 5 λεπτά µετά την αφετηρία σας από το TC1B KALO LIVADI OUT
 Date: 21 October 2016 Time: 14:00 hrs Subject: BULLETIN No 3 Document No: 1.3 --------------------------------------------------------------------------------------------------------------------------------------
Date: 21 October 2016 Time: 14:00 hrs Subject: BULLETIN No 3 Document No: 1.3 --------------------------------------------------------------------------------------------------------------------------------------
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Partial Trace and Partial Transpose
 Partial Trace and Partial Transpose by José Luis Gómez-Muñoz http://homepage.cem.itesm.mx/lgomez/quantum/ jose.luis.gomez@itesm.mx This document is based on suggestions by Anirban Das Introduction This
Partial Trace and Partial Transpose by José Luis Gómez-Muñoz http://homepage.cem.itesm.mx/lgomez/quantum/ jose.luis.gomez@itesm.mx This document is based on suggestions by Anirban Das Introduction This
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Notes on the Open Economy
 Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Πανεπιστήµιο Κρήτης Τµήµα Επιστήµης Υπολογιστών. ΗΥ-561 ιαχείριση εδοµένων στο Παγκόσµιο Ιστό Βασίλης Χριστοφίδης
 Πανεπιστήµιο Κρήτης Τµήµα Επιστήµης Υπολογιστών ΗΥ-561 ιαχείριση εδοµένων στο Παγκόσµιο Ιστό Βασίλης Χριστοφίδης Ονοµατεπώνυµο: Αριθµός Μητρώου: Άσκηση 1 (40 µονάδες) Τελική Εξέταση (3 ώρες) Ηµεροµηνία:
Πανεπιστήµιο Κρήτης Τµήµα Επιστήµης Υπολογιστών ΗΥ-561 ιαχείριση εδοµένων στο Παγκόσµιο Ιστό Βασίλης Χριστοφίδης Ονοµατεπώνυµο: Αριθµός Μητρώου: Άσκηση 1 (40 µονάδες) Τελική Εξέταση (3 ώρες) Ηµεροµηνία:
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Dynamic types, Lambda calculus machines Section and Practice Problems Apr 21 22, 2016
 Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Dynamic types, Lambda calculus machines Apr 21 22, 2016 1 Dynamic types and contracts (a) To make sure you understand the
Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Dynamic types, Lambda calculus machines Apr 21 22, 2016 1 Dynamic types and contracts (a) To make sure you understand the
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
10 MERCHIA. 10. Starting from standing position (where the SIGN START ) without marshal (self start) 5 minutes after TC4 KALO LIVADI OUT
 Date: 22 October 2016 Time: 09:00 hrs Subject: BULLETIN No 5 Document No: 1.6 --------------------------------------------------------------------------------------------------------------------------------------
Date: 22 October 2016 Time: 09:00 hrs Subject: BULLETIN No 5 Document No: 1.6 --------------------------------------------------------------------------------------------------------------------------------------
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
ΚΥΠΡΙΑΚΟΣ ΣΥΝΔΕΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY 21 ος ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ Δεύτερος Γύρος - 30 Μαρτίου 2011
 Διάρκεια Διαγωνισμού: 3 ώρες Απαντήστε όλες τις ερωτήσεις Μέγιστο Βάρος (20 Μονάδες) Δίνεται ένα σύνολο από N σφαιρίδια τα οποία δεν έχουν όλα το ίδιο βάρος μεταξύ τους και ένα κουτί που αντέχει μέχρι
Διάρκεια Διαγωνισμού: 3 ώρες Απαντήστε όλες τις ερωτήσεις Μέγιστο Βάρος (20 Μονάδες) Δίνεται ένα σύνολο από N σφαιρίδια τα οποία δεν έχουν όλα το ίδιο βάρος μεταξύ τους και ένα κουτί που αντέχει μέχρι
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
SQL Data Manipulation Language
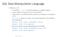 SQL Data Manipulation Language Τελεστής union συνδυάζει subselects τα οποία παράγουν συμβατές σχέσεις γενική μορφή: subselect {union [all] subselect} περιορισμός: τα subselects δεν μπορούν να περιέχουν
SQL Data Manipulation Language Τελεστής union συνδυάζει subselects τα οποία παράγουν συμβατές σχέσεις γενική μορφή: subselect {union [all] subselect} περιορισμός: τα subselects δεν μπορούν να περιέχουν
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Overview. Transition Semantics. Configurations and the transition relation. Executions and computation
 Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
1 String with massive end-points
 1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
Οδηγίες Αγοράς Ηλεκτρονικού Βιβλίου Instructions for Buying an ebook
 Οδηγίες Αγοράς Ηλεκτρονικού Βιβλίου Instructions for Buying an ebook Βήμα 1: Step 1: Βρείτε το βιβλίο που θα θέλατε να αγοράσετε και πατήστε Add to Cart, για να το προσθέσετε στο καλάθι σας. Αυτόματα θα
Οδηγίες Αγοράς Ηλεκτρονικού Βιβλίου Instructions for Buying an ebook Βήμα 1: Step 1: Βρείτε το βιβλίο που θα θέλατε να αγοράσετε και πατήστε Add to Cart, για να το προσθέσετε στο καλάθι σας. Αυτόματα θα
MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)
![MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3) MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)](/thumbs/81/84712331.jpg) 1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Εργαστήριο Σημασιολογικού Ιστού
 Εργαστήριο Σημασιολογικού Ιστού Ενότητα 8: Εισαγωγή στη SPARQL Βασική Χρήση Μ.Στεφανιδάκης 3-5-2015. Η γλώσσα ερωτημάτων SPARQL Ερωτήσεις (και ενημερώσεις) σε σετ δεδομένων RDF Και σε δεδομένα άλλης μορφής
Εργαστήριο Σημασιολογικού Ιστού Ενότητα 8: Εισαγωγή στη SPARQL Βασική Χρήση Μ.Στεφανιδάκης 3-5-2015. Η γλώσσα ερωτημάτων SPARQL Ερωτήσεις (και ενημερώσεις) σε σετ δεδομένων RDF Και σε δεδομένα άλλης μορφής
ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ. ΘΕΜΑ: «ιερεύνηση της σχέσης µεταξύ φωνηµικής επίγνωσης και ορθογραφικής δεξιότητας σε παιδιά προσχολικής ηλικίας»
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΠΡΟΣΧΟΛΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΤΟΥ ΕΚΠΑΙ ΕΥΤΙΚΟΥ ΣΧΕ ΙΑΣΜΟΥ «ΠΑΙ ΙΚΟ ΒΙΒΛΙΟ ΚΑΙ ΠΑΙ ΑΓΩΓΙΚΟ ΥΛΙΚΟ» ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ που εκπονήθηκε για τη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΑΝΘΡΩΠΙΣΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΠΡΟΣΧΟΛΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΤΟΥ ΕΚΠΑΙ ΕΥΤΙΚΟΥ ΣΧΕ ΙΑΣΜΟΥ «ΠΑΙ ΙΚΟ ΒΙΒΛΙΟ ΚΑΙ ΠΑΙ ΑΓΩΓΙΚΟ ΥΛΙΚΟ» ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ που εκπονήθηκε για τη
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
A ΜΕΡΟΣ. 1 program Puppy_Dog; 2 3 begin 4 end. 5 6 { Result of execution 7 8 (There is no output from this program ) 9 10 }
 A ΜΕΡΟΣ 1 program Puppy_Dog; begin 4 end. 5 6 { Result of execution 7 (There is no output from this program ) 10 } (* Κεφάλαιο - Πρόγραµµα EX0_.pas *) 1 program Kitty_Cat; begin 4 Writeln('This program');
A ΜΕΡΟΣ 1 program Puppy_Dog; begin 4 end. 5 6 { Result of execution 7 (There is no output from this program ) 10 } (* Κεφάλαιο - Πρόγραµµα EX0_.pas *) 1 program Kitty_Cat; begin 4 Writeln('This program');
Physical DB Design. B-Trees Index files can become quite large for large main files Indices on index files are possible.
 B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Εισαγωγή στον Προγραμματισμό
 Εισαγωγή στον Προγραμματισμό Έλεγχος Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ακ. Έτος 2012-2013 Σχεσιακοί Τελεστές και Ισότητας Ένα πρόγραμμα εκτός από αριθμητικές πράξεις
Εισαγωγή στον Προγραμματισμό Έλεγχος Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ακ. Έτος 2012-2013 Σχεσιακοί Τελεστές και Ισότητας Ένα πρόγραμμα εκτός από αριθμητικές πράξεις
HY380 Αλγόριθμοι και πολυπλοκότητα Hard Problems
 HY380 Αλγόριθμοι και πολυπλοκότητα Hard Problems Ημερομηνία Παράδοσης: 0/1/017 την ώρα του μαθήματος ή με email: mkarabin@csd.uoc.gr Γενικές Οδηγίες α) Επιτρέπεται η αναζήτηση στο Internet και στην βιβλιοθήκη
HY380 Αλγόριθμοι και πολυπλοκότητα Hard Problems Ημερομηνία Παράδοσης: 0/1/017 την ώρα του μαθήματος ή με email: mkarabin@csd.uoc.gr Γενικές Οδηγίες α) Επιτρέπεται η αναζήτηση στο Internet και στην βιβλιοθήκη
Differential equations
 Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
 Υποερωτήματα στην SQL Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr 1 / 31 Η ανάγκη για υποερώτημα Ποιος υπάλληλος παίρνει το μεγαλύτερο μισθό; Αν ξέραμε το μεγαλύτερο μισθό, πχ 2000, θα γράφαμε:
Υποερωτήματα στην SQL Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr 1 / 31 Η ανάγκη για υποερώτημα Ποιος υπάλληλος παίρνει το μεγαλύτερο μισθό; Αν ξέραμε το μεγαλύτερο μισθό, πχ 2000, θα γράφαμε:
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Μέρος 2 Κατασκευή Συντακτικού Αναλυτή
 Αντίρριο, 05/04/2017 Προδιαγραφές Εργαστηριακής Εργασίας για το μάθημα «Μεταγλωττιστές» To δεύτερο μέρος της εργασίας έχει ως στόχο την ανάπτυξη του συντακτικού αναλυτή με χρήση του bison / byacc. Στο
Αντίρριο, 05/04/2017 Προδιαγραφές Εργαστηριακής Εργασίας για το μάθημα «Μεταγλωττιστές» To δεύτερο μέρος της εργασίας έχει ως στόχο την ανάπτυξη του συντακτικού αναλυτή με χρήση του bison / byacc. Στο
ΕΓΧΕΙΡΙΔΙΟ ΧΡΗΣΗΣ ΕΤΑΙΡΕΙΩΝ ΔΙΑΜΕΣΟΛΑΒΗΣΗΣ ΣΤΗ ΜΕΤΑΦΟΡΑ ΚΕΦΑΛΑΙΩΝ
 ΕΓΧΕΙΡΙΔΙΟ ΧΡΗΣΗΣ ΕΤΑΙΡΕΙΩΝ ΔΙΑΜΕΣΟΛΑΒΗΣΗΣ ΣΤΗ ΜΕΤΑΦΟΡΑ ΚΕΦΑΛΑΙΩΝ ΠΕΡΙΕΧΟΜΕΝΑ 1.Γενικές παρατηρήσεις... 2 1.2 Είσοδος στην εφαρμογή... 3 2. Πίνακας αναφορών... 3 2.1 Περιγραφή του πίνακα αναφορών... 4
ΕΓΧΕΙΡΙΔΙΟ ΧΡΗΣΗΣ ΕΤΑΙΡΕΙΩΝ ΔΙΑΜΕΣΟΛΑΒΗΣΗΣ ΣΤΗ ΜΕΤΑΦΟΡΑ ΚΕΦΑΛΑΙΩΝ ΠΕΡΙΕΧΟΜΕΝΑ 1.Γενικές παρατηρήσεις... 2 1.2 Είσοδος στην εφαρμογή... 3 2. Πίνακας αναφορών... 3 2.1 Περιγραφή του πίνακα αναφορών... 4
ES440/ES911: CFD. Chapter 5. Solution of Linear Equation Systems
 ES440/ES911: CFD Chapter 5. Solution of Linear Equation Systems Dr Yongmann M. Chung http://www.eng.warwick.ac.uk/staff/ymc/es440.html Y.M.Chung@warwick.ac.uk School of Engineering & Centre for Scientific
ES440/ES911: CFD Chapter 5. Solution of Linear Equation Systems Dr Yongmann M. Chung http://www.eng.warwick.ac.uk/staff/ymc/es440.html Y.M.Chung@warwick.ac.uk School of Engineering & Centre for Scientific
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
 9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Section 1: Listening and responding. Presenter: Niki Farfara MGTAV VCE Seminar 7 August 2016
 Section 1: Listening and responding Presenter: Niki Farfara MGTAV VCE Seminar 7 August 2016 Section 1: Listening and responding Section 1: Listening and Responding/ Aκουστική εξέταση Στο πρώτο μέρος της
Section 1: Listening and responding Presenter: Niki Farfara MGTAV VCE Seminar 7 August 2016 Section 1: Listening and responding Section 1: Listening and Responding/ Aκουστική εξέταση Στο πρώτο μέρος της
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Matrices and vectors. Matrix and vector. a 11 a 12 a 1n a 21 a 22 a 2n A = b 1 b 2. b m. R m n, b = = ( a ij. a m1 a m2 a mn. def
 Matrices and vectors Matrix and vector a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn def = ( a ij ) R m n, b = b 1 b 2 b m Rm Matrix and vectors in linear equations: example E 1 : x 1 + x 2 + 3x 4 =
Matrices and vectors Matrix and vector a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn def = ( a ij ) R m n, b = b 1 b 2 b m Rm Matrix and vectors in linear equations: example E 1 : x 1 + x 2 + 3x 4 =
From the finite to the transfinite: Λµ-terms and streams
 From the finite to the transfinite: Λµ-terms and streams WIR 2014 Fanny He f.he@bath.ac.uk Alexis Saurin alexis.saurin@pps.univ-paris-diderot.fr 12 July 2014 The Λµ-calculus Syntax of Λµ t ::= x λx.t (t)u
From the finite to the transfinite: Λµ-terms and streams WIR 2014 Fanny He f.he@bath.ac.uk Alexis Saurin alexis.saurin@pps.univ-paris-diderot.fr 12 July 2014 The Λµ-calculus Syntax of Λµ t ::= x λx.t (t)u
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
department listing department name αχχουντσ ϕανε βαλικτ δδσϕηασδδη σδηφγ ασκϕηλκ τεχηνιχαλ αλαν ϕουν διξ τεχηνιχαλ ϕοην µαριανι
 She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
1. Ηλεκτρικό μαύρο κουτί: Αισθητήρας μετατόπισης με βάση τη χωρητικότητα
 IPHO_42_2011_EXP1.DO Experimental ompetition: 14 July 2011 Problem 1 Page 1 of 5 1. Ηλεκτρικό μαύρο κουτί: Αισθητήρας μετατόπισης με βάση τη χωρητικότητα Για ένα πυκνωτή χωρητικότητας ο οποίος είναι μέρος
IPHO_42_2011_EXP1.DO Experimental ompetition: 14 July 2011 Problem 1 Page 1 of 5 1. Ηλεκτρικό μαύρο κουτί: Αισθητήρας μετατόπισης με βάση τη χωρητικότητα Για ένα πυκνωτή χωρητικότητας ο οποίος είναι μέρος
Use Cases: μια σύντομη εισαγωγή. Heavily based on UML & the UP by Arlow and Neustadt, Addison Wesley, 2002
 Use Cases: μια σύντομη εισαγωγή Heavily based on UML & the UP by Arlow and Neustadt, Addison Wesley, 2002 (γενικές εισαγωγικές ιδέες) ΣΥΛΛΟΓΗ ΑΠΑΙΤΗΣΕΩΝ 2 Ανάλυση απαιτήσεων Λειτουργικές απαιτήσεις: τι
Use Cases: μια σύντομη εισαγωγή Heavily based on UML & the UP by Arlow and Neustadt, Addison Wesley, 2002 (γενικές εισαγωγικές ιδέες) ΣΥΛΛΟΓΗ ΑΠΑΙΤΗΣΕΩΝ 2 Ανάλυση απαιτήσεων Λειτουργικές απαιτήσεις: τι
Εισαγωγή στην Επεξεργασία Ερωτήσεων. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα 2 Βήματα Επεξεργασίας Τα βασικά βήματα στην επεξεργασία
Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα 2 Βήματα Επεξεργασίας Τα βασικά βήματα στην επεξεργασία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 133: ΑΝΤΙΚΕΙΜΕΝΟΣΤΡΕΦΗΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΡΓΑΣΤΗΡΙΟ 3 Javadoc Tutorial
 ΕΡΓΑΣΤΗΡΙΟ 3 Javadoc Tutorial Introduction Το Javadoc είναι ένα εργαλείο που παράγει αρχεία html (παρόμοιο με τις σελίδες στη διεύθυνση http://docs.oracle.com/javase/8/docs/api/index.html) από τα σχόλια
ΕΡΓΑΣΤΗΡΙΟ 3 Javadoc Tutorial Introduction Το Javadoc είναι ένα εργαλείο που παράγει αρχεία html (παρόμοιο με τις σελίδες στη διεύθυνση http://docs.oracle.com/javase/8/docs/api/index.html) από τα σχόλια
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ. Πτυχιακή εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΑΝΑΛΥΣΗ ΚΟΣΤΟΥΣ-ΟΦΕΛΟΥΣ ΓΙΑ ΤΗ ΔΙΕΙΣΔΥΣΗ ΤΩΝ ΑΝΑΝΕΩΣΙΜΩΝ ΠΗΓΩΝ ΕΝΕΡΓΕΙΑΣ ΣΤΗΝ ΚΥΠΡΟ ΜΕΧΡΙ ΤΟ 2030
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΑΝΑΛΥΣΗ ΚΟΣΤΟΥΣ-ΟΦΕΛΟΥΣ ΓΙΑ ΤΗ ΔΙΕΙΣΔΥΣΗ ΤΩΝ ΑΝΑΝΕΩΣΙΜΩΝ ΠΗΓΩΝ ΕΝΕΡΓΕΙΑΣ ΣΤΗΝ ΚΥΠΡΟ ΜΕΧΡΙ ΤΟ 2030
SOAP API. https://bulksmsn.gr. Table of Contents
 SOAP API https://bulksmsn.gr Table of Contents Send SMS...2 Query SMS...3 Multiple Query SMS...4 Credits...5 Save Contact...5 Delete Contact...7 Delete Message...8 Email: sales@bulksmsn.gr, Τηλ: 211 850
SOAP API https://bulksmsn.gr Table of Contents Send SMS...2 Query SMS...3 Multiple Query SMS...4 Credits...5 Save Contact...5 Delete Contact...7 Delete Message...8 Email: sales@bulksmsn.gr, Τηλ: 211 850
Τελική Εξέταση (3 ώρες) Ηµεροµηνία: Πέµπτη 12 Ιουνίου 2009
 Πανεπιστήµιο Κρήτης Τµήµα Επιστήµης Υπολογιστών ΗΥ-561 ιαχείριση εδοµένων στο Παγκόσµιο Ιστό Ειρήνη Φουντουλάκη Βασίλης Χριστοφίδης Ονοµατεπώνυµο: Αριθµός Μητρώου: Τελική Εξέταση (3 ώρες) Ηµεροµηνία: Πέµπτη
Πανεπιστήµιο Κρήτης Τµήµα Επιστήµης Υπολογιστών ΗΥ-561 ιαχείριση εδοµένων στο Παγκόσµιο Ιστό Ειρήνη Φουντουλάκη Βασίλης Χριστοφίδης Ονοµατεπώνυµο: Αριθµός Μητρώου: Τελική Εξέταση (3 ώρες) Ηµεροµηνία: Πέµπτη
