Προηγμένες ικτυακές Τεχνολογίες
|
|
|
- Ήρα Ἀθήνη Γαλάνης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Προηγμένες ικτυακές Τεχνολογίες εαρινό εξάμηνο 016 Καθ. Ιωάννης Σταυρακάκης Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Υλικό μαθήματος Διαλέξεις.ppt διαφάνειες, επιπλέον papers συνοδευτικά γράψιμο στον πίνακα Ε-class link γραφτείτε αν δεν τo έχετε κάνει ήδη! Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016
2 Εξέταση/αξιολόγηση Ερευνητικές εργασίες παρουσίαση άρθρων (0-30% Γραπτές εξετάσεις (70-80% στο τέλος του εξαμήνου, καλύπτουν τις παρουσιάσεις από τους διδάσκοντες του μαθήματος. Κατά κανόνα, γίνονται με κλειστά άββλί βιβλία. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Course Outline PART A: Routing in Mobile Adhoc Networks (5 Asymptotic Scalability of mobile ad hoc networks (MANET (3 Fundamental aspects of network and routing protocol scalability Asymptotic scalability of basic routing protocols (Standard Link State, Dynamic Source Routing, Plain Flooding, Zone Routing Protocol, etc Asymptotic scalability of Hierarchical Routing Protocols (under various location management approaches The family of Hazy Sighted Link Statet protocols: asymptotically ti scalable lbl flat routing protocols Delay Tolerant Networking (scalable wrt network size (1 multi copy li message spreading, impact of cooperation performance analysis of hop message relaying Adaptive Routing and Information Acquisition in Dynamically Changing Mobile Networking Environments (1 Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 4
3 Topics PART B: Resource Competition in a Highly Networked World of Humans and Things / Decision Making i Mki in Distributedib Competitive i Environments (4 Motivation (environment early study Decision making in uncoordinated competitive environment formulation rational case Price of Anarchy limited info case human driven case Prospect Thy alternative models heuristics Alternative, partially coordinated approaches Auctioning resources ICT supported distributed apps Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Topics PART C: Information centric networking Content Placement / Replication (3 Content/Service Placement Distributed Facility Location problem Cooperative Caching Distributed Selfish Replication Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 6
4 Mobile Networks: MANET - DTN MANET t 1 DTN t > t 1 t 1 7 t > t 1 Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 Mobile Networks: MANET - DTN MANET t 1 t > t 1 DTN 8 Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016
5 Scalability of Ad Hoc Routing Protocols (wrt mobility, size, load, etc References: C. Santivanez, R. Ramanathan, I. Stavrakakis, Making Link-State Routing Scale for Ad Hoc Networks, MobiHoc 001, Oct. 4-5, 001, Long Beach, CA, USA. C. Santivanez, B. McDonald, I. Stavrakakis, R. Ramanathan, On the Scalability of Ad hoc Routing Protocols, IEEE INFOCOM 0, N. York, USA. C.Santivarez, R. Ramanathan, "Scalability of Routing in Ad Hoc Networks: Principles and Practise", in AD HOC WIRELESS NETWORKING, X. Chieng, X. Huang, D.-Z. Du (eds., klywer Academic Publishers, 003. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης ROUTING ALGORITHMS PROACTIVE (table-driven REACTIVE (on-demand SLS AODV DSR HYBRID ZRP Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
6 Proactive/Table-Driven Maintain routes (paths for all possible destinations + Minimum route discovery delay Additional induced control overhead Meaningless in highly mobile environments Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Proactive Algorithms Routing tables constructed through: Neighborhood Discovery: Each node learns: every neighbor s address cost to communicate with each neighbor Applying an algorithm for routing path construction Distance vector Link state Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 1
7 Proactive Algorithms: Standard Link State (SLS Every node sends Link State Updates (LSUs in case of a link status change periodically Every node stores a copy of the latest LSU in a topology table that provides connectivity info for the entire network The source node may apply Dijkstra s Shortest Path First (SPF algorithm to find a route Typical representative of proactive routing algorithms Simple, predictable dynamics, quick convergence Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Reactive/On-Demand Acquisition of routing info only when it is needed + Lower bandwidth consumption - Dramatic increase of delay for specific applications Generally better than proactive for highly mobile environments, but still rather inefficient Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
8 Reactive/On-Demand: Dynamic Source Routing (DSR A reactive algorithm - consists of two main processes: Route Discovery: a source node S wishing to send a packet to a destination node D obtains a source route to D. It is used only when S attempts to send a packet to D and does not already know a route to it. Route Maintenance: while using a source route to D, a source node S is able to detect errors that prohibit the use of its route to D because a link along the route no longer works. In such case, S can attempt to use any other route to D it happens to know, or it can invoke a new Route Discovery to find a new one. It is used only when S is actually sending packets to D. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Proactive/Table-Driven Maintain routes (paths for all possible destinations + Minimum route discovery delay Additional induced control overhead Meaningless in highly mobile environments Reactive/On-Demand Acquisition of routing info only when it is needed + Lower bandwidth consumption - Dramatic increase of delay for specific applications Generally better than proactive for highly mobile environments, but still rather inefficient Development of hybrid algorithms Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
9 Hybrid routing algorithms Trying to take advantage of the efficiencies of proactive and reactive schemes Advantage of proactive algorithms: low delay Advantage of reactive algorithms: high efficiency Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Zone Routing Protocol (ZRP A typical representative of hybrid routing algorithms A set of k-hop neighbors constitute the node s zone The size of a zone is given by a radius of length r, where r is the number of hops to the perimeter of the zone The zones may be overlapping and of variable size (proactive function : A node disseminates event-driven Link State Updates LSUs to its k-hop neighbors (up to k hops Proactive discovery within a node s local neighborhood ood (zones Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
10 Zone Routing Protocol (ZRP (reactive function : Reactive protocol for communication between the zones Use of peripheral nodes for efficient flooding To forward packets outside its zone, it sends route request to a subset of nodes (peripheral nodes, reducing overhead K E D L H G I A C B Routing zone of node A with r = F J Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Components of ZRP ZRP NDP IARP IERP ICMP BRP IP NDP - Neighborhood Discovery Protocol: A node needs to know about its neighbors IARP - Intrazone Routing Protocol: Determine the routes to peripheral nodes (proactive IERP - Interzone Routing Protocol: Communication between different zones (reactive BRP - Bordercast Resolution Protocol: Efficient use of peripheral nodes ICMP - Internet t Control lmessage Protocol: Existing protocol to support tip-routing Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 0
11 Plain Flooding g( (PF The source node broadcasts the packet to be transmitted The neighbors of the source node rebroadcast it once to their neighbors, and this is repeated until it reaches the destination Nodes must keep track of the packets previously sent, to avoid sending a packet more than once PF is not used for data packet delivery due to increased useless retransmissions Meaningful in cases of control traffic, small traffic load, small network size and high mobility rate Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Scalability of Ad Hoc Routing Protocols References: C. Santivanez, R. Ramanathan, I. Stavrakakis, Making Link-State Routing Scale for Ad Hoc Networks, MobiHoc 001, Oct. 4-5, 001, Long Beach, CA, USA. C. Santivanez, B. McDonald, I. Stavrakakis, R. Ramanathan, On the Scalability of Ad hoc Routing Protocols, IEEE INFOCOM 0, N. York, USA. C.Santivarez, R. Ramanathan, "Scalability of Routing in Ad Hoc Networks: Principles and Practise", in AD HOC WIRELESS NETWORKING, X. Chieng, X. Huang, D.-Z. Du (eds., klywer Academic Publishers, 003. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016
12 Communication overhead Traditionally: overhead control overhead ( = amount of bandwidth required to construct and maintain a route o In proactive approaches: number of packets exchanged in order to maintain the node s forwarding tables up-to-date o In reactive approaches: bandwidth consumed by the route request/reply messages (global or local control overhead fails to include the impact of suboptimal routes Suboptimal routes not only increase the end-to-end delay but also result in a greater bandwidth usage than required. As the network size increases keeping route optimality imposes an unacceptable cost. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Communication overhead reactive protocols introduce suboptimal routes because: o they try to maintain the current source-destination path for as long as it is valid, although it may no longer be optimal o local repair techniques try to reduce the overhead induced by the protocol at the expense of longer, non optimal paths proactive protocols introduce suboptimal routes by: o limiting the scope of topology information dissemination (e.g. hierarchical routing and/or o limiting the time between successive topology information updates dissemination (topology updates are no longer instantaneously t event-driven Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 4
13 Communication overhead revise the concept of overhead so that it includes the effect of suboptimal routes The minimum traffic load of a network, is the minimum amount of bandwidth required to forward packets over the shortest distance (in number of fh hops paths available, ilbl assuming all the nodes have instantaneous a priori i full topology information. routing protocol-independent metric assumes that all the nodes are provided a priori global information o possible in fixed networks o inmobilescenariosthisishardlypossible is hardly (even if static routes are provided it is unlikely that these remain optimal motivates the definition of the total overhead of a routing protocol Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Minimum traffic load Total overhead Total amount of bandwidth = minimum traffic load + total overhead routing protocol dependent routing protocol independent routing protocol dependent The total overhead induced by a routing protocol is the difference between the total amount of bandwidth actually consumed by the network operating under such routing protocol, minus the minimum traffic load that would have been required should the nodes had a priori full topology information. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 6
14 Minimum traffic load Total overhead The total overhead : provides an unbiased metric for performance comparison that reflects bandwidth consumption may not fully characterize all the performance aspects relevant to specific applications, but o bandwidth is likely to remain a limiting factor in terms of scalability o bandwidth is proportional to factors including energy consumption, memory and processing requirements The different sources of overhead may be expressed in terms of o Reactive routing overhead o Proactive routing overhead o suboptimal routing overhead Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Proactive, Reactive & Suboptimal overhead The reactive overhead of a protocol is the amount of bandwidth consumed by the specific protocol to build paths from a source to a destination, after a traffic flow to that destination has been generated at the source. In static ti networks is a function of the rate of generation of new flows. In dynamic (mobile networks is a function of both the traffic and the rate topology change. (paths are (rebuilt not only due to new flows but also due to link failures in an already active path Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 8
15 Proactive, Reactive & Suboptimal overhead The proactive overhead of a protocol is the amount of bandwidth consumed by the protocol in order to propagate route information before it is needed. The suboptimal routing overhead of a protocol is the difference between the bandwidth consumed when transmitting data from all the sources to their destinations using the routes determined by the specific protocol, and the bandwidth that would have been consumed should the data have fll followed dthe shortest tavailable ilbl path(s. th( Example: a source that is 3 hops away from its destination a protocol chooses to deliver one packet following a k ( k 3 hop path (for example, due to out-of-date information ( k 3 packet_length bits will be added to the suboptimal RO Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Achievable Regions & Operating points The 3 different overhead sources are locked in a 3-way trade-off in an already efficient algorithm, the reduction of one of them will most likely cause the increase of one of the others For example, reducing the zone size in ZRP: will reduce ZRP s proactive overhead, but will increase ZRP s reactive overhead achievable region of overhead: The three dimensional region formed by all the values of proactive, reactive, and suboptimal routing overheads that can be induced by any protocol under the same scenario (traffic, mobility, etc. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
16 Achievable Regions & Operating points Figure: -dimensional transformation of the achievable region horizontal axis: proactive overhead induced by a protocol vertical axis: reactive + suboptimal routing overheads ra bandwidth ptimal routes, Extr (sub-op usage per no ode route reques st,etc. Achievable Region Proactive cost (per node Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Achievable Regions & Operating points the achievable region is convex o consider the points P 1 and P achieved by protocols P 1 and P o any point P1(1 P can be achieved by engaging protocol P 3 that behaves as protocol P 1 a fraction of a (long time as protocol P the remaining of the time is lower-bounded by the curve of overhead points achieved by the efficient protocols ( efficient protocols: minimize some source of overhead given a condition imposed on the others Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 3
17 Achievable Regions & Operating points P best pure proactive approach (reactive overhead = 0 given that optimal routes are required (suboptimal overhead= 0 P moves to the right as mobility increases R best protocol that does not use any proactive information R moves upward as traffic increases or diversifies the best protocol (in terms of overhead minimizes total overhead point Opt : point tangent to the curve x y constant achieves point Opt Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Effect of increasing the network size B B B B B R B B the boundary region is pulled up the region displacement is not uniform P Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
18 Effect of increasing the network size points P and R increase proportionally to ( N Pure proactive protocols (SLS [Pure reactive algorithms (DSR without the route cache option] generate a control message [a route request (RREQ message] each time a link changes (worst case [a new session is initiated] Each control message [RREQ message] is retransmitted by each node The generation rate of control messages [RREQ messages] increases linearly with network size ( N The number of message retransmissions increases linearly with N The total overhead increases as rapidly as N Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Effect of increasing the network size R B B B B Protocols &ri αiviznb inducing m,hvmkb mαfr5f,meαf intermediate υim-αneab Hierarchical link state (HierLS: 166 ZRP: N 15 N B B B P As size increases, the best operating point is far from the extreme points P and R and in the region where the proactive, reactive, and suboptimal routing overheads are balanced. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
19 Network s scalability (Qualitatively Scalability is the ability of a network to support the increase of its limiting parameters. Limiting parameters of a network are those parameter whose increase causes the network performance to degrade. For example: mobility rate traffic rate network size network density Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Network s scalability (Quantitatively Let Tr ( 1 be the minimum traffic load experienced by a network under parameters 1. Then, the network scalability factor of such a network, with respect to a parameter i ( i is: def log Tr ( 1 lim i i log relates the increase in network load to the different network parameters may be used to compare the scalability properties of different networks (wireline, mobile ad hoc, etc. For the class of mobile ad hoc networks defined by assumptions 15 a.1-a.8 the minimum traffic load Tr( N = ( 0, 1,and 15 lc t N lc i t t N Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
20 Network s scalability (Quantitatively Define the network rate to assess network scalability w.r.t. i network The network rate R of a network is the maximum number of bits that can be simultaneously transmitted in a unit of time. network To compute the network rate ( R, ALL successful link layer transmissions must be counted, regardless of whether the link layer recipient is the final network-layer destination or not. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Network s scalability (Quantitatively A network is said to be scalable with respect to the parameter i if and only if, as the parameter i increases, the network s minimum traffic load does not increase faster than the network network rate ( R can support. That is, if and only if: i network log R ( 1 lim i log i Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
21 Network s scalability (Quantitatively Scalability of Mobile Ad Hoc Networks (with respect to N: It has been shown [Gupta, Kumar 000] that in mobile ad hoc networks Θ(Ν successful transmissions can be scheduled simultaneously. I.E., the network rate is Θ(Ν log R / log N 1. Thus, to be regarded as scalable with respect tto network size N 1 For example, for the class of networks considered here (assumptions a.1- a.8 15 N networks under study are not scalable wrt w.r.t. tonetwork size Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Network s scalability (Quantitatively Scalability of Mobile Ad Hoc Networks (with respect to N Delay Tolerant Networks: average path length may be reduced to ( Θ(1 provided that applications can tolerate infinite delivery delays and mobility pattern is random ([Groossglauser&TSE, Infocom 001] thus, network scalability factor with respect to network size Ψ Ν is equal to 1. (N nodes X traffic rate X constant path length Thus, those ad hoc networks (random mobility and capable of accepting infinitely long delays are the only class of ad hoc networks that are scalable with respect to network size. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 4
22 Network s scalability (Quantitatively Scalability of Wireline fully connected Networks (with respect to N They may have 1, thus potentially scalable w.r.t. N N (1li link-load kl dis needed d for any transmission; i thus, the network rate is Θ(Ν (However, this scalability requires the nodes degree to grow without bound, which may be prohibitively expensive epesve Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Network s scalability (Quantitatively mobile networks: the network rate does not increase with mobility or traffic load Recall: [Gupta, Kumar 000]in mobile ad hoc networks Θ(Ν successful transmissions can be scheduled simultaneously. I.E., the network rate is Θ(N --> logr/log* = 0, *=mobility or traffic load the network will be scalable w.r.t. mobility lc 0 (=network rate w.r.t. traffic t 0 (=network rate the networks considered here ( lc 0, t 1, and N 15 o are scalable w.r.t. mobility o but are not scalable w.r.t. traffic Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
23 Network s scalability (Quantitatively Similar conclusions for scalability w.r.t. other parameters: For example, w.r.t. transmission range as transmission range l increases the spatial reuse decreases (assuming an infinite size network with regular density network rate decreases as rapidly as (reduction of space available for additional, non-interfering transmissions should be lower than for the network to be scalable (to compensate for the above network rate reduction Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Network s scalability (Quantitatively should be lower than for the network to be scalable (to compensate for the above network rate reduction ad hoc networks are not scalable w.r.t. transmission range (since the length of a path has linear dependence on the transmission range, a transmission range l increase leads to a path reduction that is linear with l the minimum traffic load decreases only linearly w.r.t. => 1 focus on networks with power control (the transmission range changes so that the network degree is kept bounded Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
24 Routing Protocol s scalability (Qualitatively mobile ad hoc networks are not scalable with respect to size How about routing gprotocol scalability? Routing protocol s scalability is the ability of a routing protocol to support the continuous increase of the network parameters without degrading network performance. the network s own scalabilty properties provide the reference level as to what to expect of a routing protocol If the overhead induced by a routing protocol grows slower than the minimum traffic load (network property then the routing protocol is not degrading network performance, even if the overhead happens to grow faster than the network rate. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Routing Protocol s scalability (Quantitatively Let X ( ov 1 be the total overhead induced by routing protocol X, dependent on parameters 1 (e.g. network size, mobility rate, data generation rate, etc.. Then, the Protocol X s routing protocol scalability factor X with respect to a parameter i ( is defined to be : i def X log X ov( 1 lim i i log provides a basis for comparison among different routing protocols i Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
25 Routing Protocol s scalability (Quantitatively (to assess whether a routing protocol is scalable the following definition is used A routing protocol X is said to be scalable with respect to parameter i if and only if, as i increases, the total overhead induced by such protocol ( X ov does not increase faster than the network s minimum traffic load. That is, if and only if: X i i For the class of network under study, a routing protocol X is: X o scalable w.r.t. network size 15 X o scalable w.r.t. traffic 1 X o scalable w.r.t. mobility rate 0 t N lc Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Scalability dimensions network size is a key parameter, but not the only one (mobility, network density, network diameter, traffic diversity, energy etc. Examples : diameter => latency for control => inconsistent routes, instability density spatial reuse => capacity dimension Size Mobility Density Diameter layer Transport Network Link/MAC Physical Key scalability dimensions and their effect on the lower four layers (in addition to traffic Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
26 Scalability dimensions size, density, diameter, and transmission range are related. Given size & density, different transmission power levels ( result in different (node degree (, network diameter ( in order to increase the overall network performance, the average node degree must remain bounded d( (provided d (bi-connectivity it density dimension can be addressed by means of effective topology (transmission power control algorithms Focus on: network size, mobility & traffic load assuming topology control Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Network model: Notations N : number of nodes in the network d : average in-degree L : average path length over all source destination pairs lc : expected number of link status changes that a node detects (/sec t : average traffic rate that a node generates in a second (in bps s : average number of new sessions generated by a node in a second Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 5
27 Standard asymptotic notations f ( n ( g( n if c 1, n 1 : c1 g( n f ( n, n n1 f ( n O( g( n if c, n : f ( n c g( n, n n f ( n ( g( n if c 1 c, and n 0 : cg 1 ( n f( n cg ( n, n n0 c1 cconstants Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Assumptions o a.1 As the network size increases, the average in-degree remains constant. d imposing a fixed degree in a network is: o desirable (density increase jeopardizes the achievable throughput h t o achievable (through effective power control mechanisms a topology control algorithm should: o make the density as small as possible o without compromising (biconnectivity Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
28 Assumptions a. : Let A be the area covered by the N nodes of the network, and NA be the network average density. Then, the expected (average number of nodes inside id an area A 1 is approximately A1. on large scales uniformity is expected to increase (for example, it is expected that half the area contains approx. ½ of the nodes focus on expected (mean behavior (for a specific network topology this assumption may not hold Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Assumptions a. Let A be the area covered by the N nodes of the network, and NA be the network average density. Then, the expected (average number of nodes inside an area A 1 is approximately A1. One can talk about the `geographical' and `topological' regions. In the `geographical' (large-scale region, geographical-based reasoning shapes routing decisions. In the `topological' region, it is the actual link connectivity (topology that drives the routing decisions, and geographical insights are less useful. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
29 Assumptions a.3 : The number of nodes that are at distance of k or less hops away from a source node increases (on average as ( d k. The number of nodes exactly at k hops away increases as ( d k. a.4 : The maximum and average path length (in hops among nodes in a connected subset of n nodes both increase as ( n. In particular, the maximum and the average ( L path length across the network increase as ( N. a.3 and a.4 are based on a. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Assumptions a.3, a.4 R S a.3 and a.4 are based on a. R example: a circular area centered at node S of radius R with n nodes If R R o covered area, number of nodes inside the area 4R* o distance (in meters from S to the farthest tnodes R o distance (in hops from S to the farthest nodes R (assuming that the transmission range of the nodes does not change o `boundary' area (where the nodes farthest away from S are R Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
30 Assumptions a.5 : The traffic that a node generates in a second ( t, is independent of the network size N (number of possible destinations. As the network size increases, the total amount of data transmitted/received by a single node will remain constant but the number of destinations will increase (the destinations diversity will increase. a.6 : For a given source node, all possible destinations ( N 1 nodes are equiprobable e and as a consequence ce of a.5 the traffic from one node to every destination decreases as (1 N. a.5 & a.6 : As the network size increases the total amount of traffic generated by a single user typically diversifies rather than increases. a.5 & a.6 are first order approximations motivated by observed behavior with existing networks (human users some other networks may violate these assumptions Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Assumptions a.5 & a6 Examples: low-cost long distance service: a user speaks with more friends (wherever they are, but does not increase the total time the user has to spare for personal phone calls increase in size and content of the Internet: a user may find more web pages (destination set diversifies but he/she will limit the total time (and traffic spent on the Internet Sensor networks may violate these assumptions o each node may broadcast its information i to all other nodes increases as ( ( t o or, may transmit to a central node (causing the destination set to consist of only 1 node, violating a.6 Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
31 Assumptions a.6 Traffic assumption largely determines the effect of suboptimal routing on performance. o limited to the locality of the source hierarchical routing, ZRP, and NSLS will benefit o small set of destinations will favor algorithms such as DSR o uniform traffic tends to favor proactive approaches such as link state Equally distributed traffic (a.6 tends to pose the most demanding requirements on a routing protocol. A protocol that is scalable (with respect to traffic under a.6, will also be scalable under any other traffic pattern. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Assumptions a.7 : Link status changes are due to mobility. lc is directly proportional to the relative node speed. assumption: short-lived link degradation will not trigger updates short-term variations in link quality can be offset by link control mechanisms for example: by requiring a high fading margin before declaring a link up by waiting for several seconds before declaring a link down wireless channel is quite unpredictable and long-lived link degradation is possible without mobility Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 6
32 Assumptions a.8 : Mobility models : time scaling. Let f ( x y 10 be the probability distribution function of a node position at time 1 second, given that the node was at the origin (0 0 at time 0. Then, the probability distribution function of a node position at time t given that the node was at the position ( x t y t at time t 0 is given by xx yy tt t t tt tt f xyx y f. 1 t0 t0 ( ( 10( tt motivated by mobility models where the velocity of a mobile over time is highly correlated for example, this is the case if the unknown speed and direction are constant does not hold for a random walk model induces smaller node displacements over time ( ( t, t : elapsed time focus on the most demanding scenario (larger displacements Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Routing protocol scalability conditions for the networks subject to assumptions a For the class of mobile ad hoc networks defined by assumptions a.1-a.8 the 15 minimum traffic load Tr( N = ( and thus : lc t t N 0, 1, and 15 lc t N Consequently, for the class of network considered here, a routing protocol X is: X o scalable w.r.t. mobility rate 0 X o scalable w.r.t. traffic 1 X o scalable w.r.t. network size 15 t N lc Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
33 Plain Flooding (PF PF reactive RO = PF proactive RO = 0 15 PF suboptimal RO / sec = ( ( N N ( N t N t data packets are generated / sec N 1 transmissions / packet (is (retransmitted by every node, except the destination optimal value (on average = L, L ( N (a.4 (up to L hops broadcast needed, the rest is OH additional bandwidth required = data ( N 1 L t N bps t PF total t RO /sec = ( t N PF PF 0, 1, PF lc t N Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Standard Link State (SLS SLS reactive RO = SLS suboptimal RO = 0 SLS proactive RO / sec = lsu N bps = N lc ( lc lsu := size of the LSU (Link State Update packet N lc lc N LSUs are generated /sec (on average (each node generates an LSU at a rate of lc / sec overhead of lsu N bits / LSU (each hlsu is transmitted at least N times (once/node lc SLS total RO /sec= lsu bps = ( N lc lc N bps = SLS SLS SLS 1, 0,. lc t N Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
34 Dynamic Source Routing (DSR no proactive information is exchanged A node (source reaches a destination by flooding the network with a route request (RREQ message. When an RREQ message reaches the destination (or a node with a cached route towards the destination a route reply message is sent back to the source, including the newly found route The source attaches the new route to the header of all subsequent packets to that destination, and any intermediate node along the route uses this attached information to determine the next hop in the route. focus on DSR without the route cache option (DSR-noRC Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης DSR without Route Cache (DSR-noRC DSR-noRC reactive RO RREQ (route request messages are generated by: new session requests (at a rate s per second per node failures in links that are part of a path currently in use only new requests are considered a lower bound is obtained s N RREQ messages are generated / sec (new session requests overhead of size_ of_ RREQ ( N 1 bits / RREQ message (each RREQ message is flooded N 1 retransmissions DSR-noRC reactive RO / sec = ( N s upper bound O(( s lc N (assumption: each link failure has the same effect as a new session request (local repair fails Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
35 DSR without Route Cache (DSR-noRC DSR-noRC suboptimal RO only the extra bandwidth required for appending the source-route in each data packet is considered a lower bound is obtained number of bits appended in each packet ~ length L i of path i opt opt L L (optimal path length, L instead of L i lower bound i i i t d extra bits for a packet delivered using a path i : (log N( L opt i opt opt o at least L i retransmissions of at least Li log N bits log N is the minimum length of a node address o Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης DSR without Route Cache (DSR-noRC extra bits for a packet delivered using a path i : (log N( L opt i extra bits / packet over all paths (average: opt opt E{(log N( L } (log N E{ L } (log N L bits i i N t packets are transmitted / sec t suboptimal RO at least (log N L bps, L ( N (a.4 t N DSR-noRC RC suboptimal lro / sec = t N N ( log bps Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
36 DSR without Route Cache (DSR-noRC DSR-noRC reactive RO / sec = ( N s = O(( N DSR-noRC suboptimal RO / sec = s lc ( N log N t bps DSR-noRC total overhead / sec = ( sn tn log N DSRnoRC DSRnoRC DSRnoRC 1, 0 1, t lc N Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Zone Routing Protocol (ZRP lower bound for ZRP total overhead (can be proved ZRP = ( n N N n ov k lc s k where: n k = average number of nodes inside node s zone o proactive overhead: ( n N o reactive overhead: ( N n (For the sub-optimal routing overhead an upper bound can be proved that shows that it is (asymptotically dominated by the reactive overhead Minimizing this lower bound by properly choosing the value n k 3 s N k (( ( n k lc s k lc 1 lc s N k 5 Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 016 7
37 Can hierarchies enhance scalability? Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Hierarchical Routing Protocols Classical approach to improving routing scalability Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
38 Outline 1. Hierarchical Routing Techniques. Cluster and Cluster Leader Selection Methods Cluster Radius Cluster Affiliation Method Performance Objective Cluster Leader Selection 3. Topology Abstraction Methods Virtual Node Abstraction Virtual Link Abstraction 4. Location Management Methods LM1, LM, LM3 Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Hierarchical Routing Techniques Characteristics of Hierarchical Routing Techniques 1. Basic idea: organize nodes in groups and assign to nodes different functionalities inside and outside the group [1]. Recursive grouping of nodes: nodes are grouped into clusters (level-1, clusters into superclusters (level-, and so on 3. A cluster-leader (among the cluster nodes is elected to coordinate the cluster Nodes need to have or exchange only partial knowledge of the network Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
39 Hierarchical Routing Techniques Characteristics of Hierarchical Routing Techniques 4. A formal abstraction method is used to form the virtual network topology 5. A location management scheme is necessary to handle mobility that is constantly changing the physical network topology. 6. Routing if information about tfar away nodes is aggregated td Bandwidth / memory / processing / etc requirements are lower Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Hierarchical Routing Techniques Components of Hierarchical Routing Schemes Cluster and Cluster Leader Selection Algorithm Topology Abstraction Method Location Management Technique Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
40 Cluster and Cluster Leader Selection Methods Cluster Radius Criterion 1. 1-hop clusters All cluster nodes are 1-hop neighbors of the cluster leader (simple and reliable Adjacent clusters have cluster leaders at most two hops away (via gateway nodes. More than 1-hop clusters Cluster radius is below a maximum Cluster radius can be adjusted based on conditions and performance objectives (flexibility Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Cluster and Cluster Leader Selection Methods Cluster Affiliation Method Criterion (refers to the way nodes are assigned to clusters 1. Cluster nodes decide Allows for distributed algorithm implementation Lack of centralized control Latency in propagating control information unpredictable dynamics. Cluster leader decides Grabs nodes sequentially: slow convergence Grabs nodes in large sets: faster, but requires information from outside the cluster Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
41 Cluster and Cluster Leader Selection Methods Performance Objective Criterion 1. Clusters with balanced size Clusters with a minimum or maximum number of nodes E.g. MMWN[6] protocol uses join or split procedures if a cluster population exceeds certain limits Clusters with a fixed number of nodes (almost [8]. Cluster nodes with k-connectivity degree Increased robustness against link failures 3. Minimum level of affiliation Affiliation: Composite bandwidth between a node and all other nodes in the cluster, or Distance to the cluster leader, or Linear combinations of the above Commonalities in interests of locality [9] Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Cluster and Cluster Leader Selection Methods Cluster Leader Selection Criterion 1. In homogeneous networks Nodes with the lowest ids Equivalent to randomized cluster leader election. In non-homogeneous networks Election based on extra knowledge about the scenario, e.g. known mobility patterns in LANMAR[4] Other extra knowledge about power, memory, etc. 3. Maximization of some gain function Gain function example: node degree Other gain functions exist, definitions vary accordingly, e.g. SOAP[, 7] protocol Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 015 8
42 Topology Abstraction Methods Objective: To reduce the topology information that needs to be propagated inside the network Some existing techniques: Virtual node abstraction, in HierLS[7] Virtual gateway abstraction, in MMWN[6] Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Virtual Node Abstraction Algorithm 1. Network nodes are level-1 nodes. Level-i nodes are grouped into level-i clusters 3. Level-i clusters become level-(i+1 nodes Example i=1: level-1 clusters level- nodes i=: level- clusters level-3 nodes i=m-1: level-(m-1 clusters level-m nodes [ stands for become] Link state information inside a level i cluster is aggregated and transmitted only to other level i nodes belonging in the same level i cluster. Thus a node link change may not be sent outside the level 1 cluster thus reducing the proactive overhead. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
43 Virtual Node Abstraction Example: Routing with the Virtual Node Abstraction Routing relies on Location Management service (providing to source S the highest level cluster containing D and not S Nd Node S will only build a high-levelh lroute towards D: [ S n n4 X.1. X. Y Z D ] in the 4-level net hierarchy below S n1 X.1.1 n3 n n4 n5 X.1.3 X.1. X.1 X X.3 X. Y V Z D Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Virtual Node Abstraction Example: Routing with the Virtual Node Abstraction Intermediate nodes will produce the same high-level route Intermediate nodes will expand the high-level links that traverse their cluster using lower level information (more detailed links This expansion can be seen graphically in the last segment of the route, Z D Z D Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
44 Virtual Node Abstraction Conclusions on the Virtual node abstraction method Intuitive method Easy to analyze, implement, debug Clusters aren't able to properly estimate the virtual link cost Note on the Virtual gateway abstraction method Provides better aggregation of link information Produces routes of better quality Extra complexity in maintaining the virtual gateway structure Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Location Management (LM Methods Main purpose p of hierarchical routing: to efficiently aggregate routing information by using the network hierarchy Source nodes need to know the identity of a cluster associated with the destination node LM provides this information LM is needed only in mobile networks, not in wireline, static networks Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
45 Location Management Methods LM implementation methodologies Proactive (using Location Update Messages Reactive (using Paging Techniques a combination of both Some basic/typical LM techniqueses 1. LM1 (pure proactive. LM (local paging 3. LM3 (global paging Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Location Management Method LM1 X.1 Proactive method using Location Update Messages (LUMs S X.1.1 n3 n n4 X1 X.1. n1 n5 X.1.3 Algorithm When a node changes its level-i clustering membership, but not its level-(i+1 membership, it sends an LUM to all the nodes inside its level-(i+1 cluster. Example Node n moves from cluster X.1.1 to X.1.3 Node n sends updates to all nodes in cluster X.1 Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
46 Location Management Method LM Each level-i cluster elects one level-i LM server among its participating i nodes, up to the level-m cluster X.1.1 X.1 X.1. LM servers form a hierarchical tree of servers Location Update Messages are propagated only between LM servers Nodes requiring location information about other nodes in the network, page their local level-1 LM server (local paging X.1.3 O Level-1 LM server O Level-1 LM server AND level- LM server Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Location Management Method LM X X. X.1 X..1 X.. X.1.1 X.1. X..3 X.1.3 BLUE move: X.1.3 receiving, informs X.1 X.1 informs X.1.1, X.1.3 RED move: X X.. receiving, i informs X X. X. informs X..1, X..3 X. informs X X informs all X.x (here, X.1 except X. X.1 informs all X.1.1, X.1., X.1.3 O Level-1 LM server O Level-1 LM server AND level- LM server Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 015 9
47 Location Management Method LM LM Algorithm The level-i LM server in the new cluster of a moving node will send an LUM to its level-(i+1 LM server The level-(i+1 server will check if the moving node is new in the level-(i+1 cluster and inform the level-(i+ LM server accordingly The level-(i+1 server will forward the LUM to all level-i LM servers inside this level (i+1 cluster Each such level-i LM server will forward LUMs to all of its level-(i-1 LM servers The previous step repeats all the way until all such level-1 LU servers are updated Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Location Management Method LM3 Same as LM, with LM servers exchanging LMUs, with one exception: Level-i LM servers receiving LUMs from higher level servers do not forward this information to the lower level servers A mechanism for removing outdated location information about nodes that left a level-i cluster is needed Nodes requiring location information about other nodes in the network page their local level-1 LM server If it is not updated, d then the level-l LM server is paged, then the level-3 server, and so on (global paging Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
48 Comparison of LM1, LM, and LM3 LM1 is the simplest of the three Consumes significant bandwidth for propagating the LUMs LM reduces the bandwidth consumption in thenetworkt Induces increased complexity and latency in route building LM1 and LM techniques do not alter the asymptotic characteristics of the hierarchical routing protocol used Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης Comparison of LM1, LM, and LM3 LM3 is the most complex to implement and analyze It can significantly reduce the amount of overhead induced by mobility Latency is increased High paging cost under high traffic load More susceptible to single points of failure Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
49 Hierarchical Link State (HierLS The network organized in m level clusters, each of equal size k m ( N k, k is predefined while m increases with N. Location Management (LM service choices: LM1 Pure proactive. LM Local paging. pg g LM3 Global paging. Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης HierLS-LM1 Total Overhead HierLS-LM1 proactive RO = HierLS-LM1 suboptimal RO / sec = 15 ( sn lc N 15 ( N t HierLS-LM1 total overhead / sec = ( sn N N lc t HierLS LM 1 t HierLS LM 1 HierLS LM1 1, 1, and lc N (HierLS is almost scalable w.r.t. network size Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
50 HierLS-LM Total Overhead HierLS-LM suboptimal RO / sec = 15 = HierLS-LM1 suboptimal RO / sec = ( N t HierLS-LM proactive RO = 15 = HierLS-LM1 proactive RO = ( s N N HierLS-LM reactive RO = O( N t lc HierLS-LM total overhead = ( sn lcn t N same asymptotic scalability factors as HierLS-LM1 Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης HierLS-LM3 Total Overhead HierLS-LM3 suboptimal RO / sec = = HierLS-LM1 suboptimal RO / sec = HierLS-LM3 proactive RO = ( s Nlog N N lc N t 15 ( HierLS-LM3 reactive RO = O N 15 ( t 15 HierLS-LM3 total overhead = ( s Nlog N N N lc t same asymptotic scalability factors as HierLS-LM1 Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης
Hierarchical Routing Protocols
 Hierarchical Routing Protocols Classical approach to improving scalability of routing for Mobile Ad Hoc Networks Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 2015 1 Outline
Hierarchical Routing Protocols Classical approach to improving scalability of routing for Mobile Ad Hoc Networks Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 2015 1 Outline
Προηγμένες ικτυακές Τεχνολογίες
 Προηγμένες ικτυακές Τεχνολογίες εαρινό εξάμηνο 015 Καθ. Ιωάννης Σταυρακάκης Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 015 1 Υλικό μαθήματος Διαλέξεις.ppt διαφάνειες,
Προηγμένες ικτυακές Τεχνολογίες εαρινό εξάμηνο 015 Καθ. Ιωάννης Σταυρακάκης Τμήμα Πληρ. & Τηλεπ. ΕΚΠΑ : Προηγμένες ικτυακές Τεχνολογίες ίκτυα Ευρείας Ζώνης 015 1 Υλικό μαθήματος Διαλέξεις.ppt διαφάνειες,
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Démographie spatiale/spatial Demography
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Démographie spatiale/spatial Demography Session 1: Introduction to spatial demography Basic concepts Michail Agorastakis Department of Planning & Regional Development Άδειες Χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ Démographie spatiale/spatial Demography Session 1: Introduction to spatial demography Basic concepts Michail Agorastakis Department of Planning & Regional Development Άδειες Χρήσης
Physical DB Design. B-Trees Index files can become quite large for large main files Indices on index files are possible.
 B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Block Ciphers Modes. Ramki Thurimella
 Block Ciphers Modes Ramki Thurimella Only Encryption I.e. messages could be modified Should not assume that nonsensical messages do no harm Always must be combined with authentication 2 Padding Must be
Block Ciphers Modes Ramki Thurimella Only Encryption I.e. messages could be modified Should not assume that nonsensical messages do no harm Always must be combined with authentication 2 Padding Must be
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
the total number of electrons passing through the lamp.
 1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Μειέηε θαη αλάιπζε επίδνζεο πξσηνθόιισλ δξνκνιόγεζεο ζε θηλεηά ad hoc δίθηπα κε βάζε ελεξγεηαθά θξηηήξηα ΓΗΠΛΩΜΑΣΗΚΖ ΔΡΓΑΗΑ
 ΔΘΝΗΚΟ ΜΔΣΟΒΗΟ ΠΟΛΤΣΔΥΝΔΗΟ ΥΟΛΖ ΖΛΔΚΣΡΟΛΟΓΩΝ ΜΖΥΑΝΗΚΩΝ ΚΑΗ ΜΖΥΑΝΗΚΩΝ ΤΠΟΛΟΓΗΣΩΝ ΣΟΜΔΑ ΤΣΖΜΑΣΩΝ ΜΔΣΑΓΟΖ ΠΛΖΡΟΦΟΡΗΑ ΚΑΗ ΣΔΥΝΟΛΟΓΗΑ ΤΛΗΚΩΝ Μειέηε θαη αλάιπζε επίδνζεο πξσηνθόιισλ δξνκνιόγεζεο ζε θηλεηά ad
ΔΘΝΗΚΟ ΜΔΣΟΒΗΟ ΠΟΛΤΣΔΥΝΔΗΟ ΥΟΛΖ ΖΛΔΚΣΡΟΛΟΓΩΝ ΜΖΥΑΝΗΚΩΝ ΚΑΗ ΜΖΥΑΝΗΚΩΝ ΤΠΟΛΟΓΗΣΩΝ ΣΟΜΔΑ ΤΣΖΜΑΣΩΝ ΜΔΣΑΓΟΖ ΠΛΖΡΟΦΟΡΗΑ ΚΑΗ ΣΔΥΝΟΛΟΓΗΑ ΤΛΗΚΩΝ Μειέηε θαη αλάιπζε επίδνζεο πξσηνθόιισλ δξνκνιόγεζεο ζε θηλεηά ad
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Assalamu `alaikum wr. wb.
 LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump
LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Δίκτυα Επικοινωνιών ΙΙ: OSPF Configuration
 Δίκτυα Επικοινωνιών ΙΙ: OSPF Configuration Δρ. Απόστολος Γκάμας Διδάσκων 407/80 gkamas@uop.gr Δίκτυα Επικοινωνιών ΙΙ Διαφάνεια 1 1 Dynamic Routing Configuration Router (config) # router protocol [ keyword
Δίκτυα Επικοινωνιών ΙΙ: OSPF Configuration Δρ. Απόστολος Γκάμας Διδάσκων 407/80 gkamas@uop.gr Δίκτυα Επικοινωνιών ΙΙ Διαφάνεια 1 1 Dynamic Routing Configuration Router (config) # router protocol [ keyword
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Calculating the propagation delay of coaxial cable
 Your source for quality GNSS Networking Solutions and Design Services! Page 1 of 5 Calculating the propagation delay of coaxial cable The delay of a cable or velocity factor is determined by the dielectric
Your source for quality GNSS Networking Solutions and Design Services! Page 1 of 5 Calculating the propagation delay of coaxial cable The delay of a cable or velocity factor is determined by the dielectric
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Προσομοίωση BP με το Bizagi Modeler
 Προσομοίωση BP με το Bizagi Modeler Α. Τσαλγατίδου - Γ.-Δ. Κάπος Πρόγραμμα Μεταπτυχιακών Σπουδών Τεχνολογία Διοίκησης Επιχειρησιακών Διαδικασιών 2017-2018 BPMN Simulation with Bizagi Modeler: 4 Levels
Προσομοίωση BP με το Bizagi Modeler Α. Τσαλγατίδου - Γ.-Δ. Κάπος Πρόγραμμα Μεταπτυχιακών Σπουδών Τεχνολογία Διοίκησης Επιχειρησιακών Διαδικασιών 2017-2018 BPMN Simulation with Bizagi Modeler: 4 Levels
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1 [1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg) 1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών: OSPF Cost
 Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών: OSPF Cost Πανεπιστήμιο Πελοποννήσου Τμήμα Επιστήμης & Τεχνολογίας Τηλεπικοινωνιών Ευάγγελος Α. Κοσμάτος Basic OSPF Configuration Υλοποίηση Δικτυακών Υποδομών
Υλοποίηση Δικτυακών Υποδομών και Υπηρεσιών: OSPF Cost Πανεπιστήμιο Πελοποννήσου Τμήμα Επιστήμης & Τεχνολογίας Τηλεπικοινωνιών Ευάγγελος Α. Κοσμάτος Basic OSPF Configuration Υλοποίηση Δικτυακών Υποδομών
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
Bounding Nonsplitting Enumeration Degrees
 Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων. Εξάμηνο 7 ο
 Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL
Εργαστήριο Ανάπτυξης Εφαρμογών Βάσεων Δεδομένων Εξάμηνο 7 ο Procedures and Functions Stored procedures and functions are named blocks of code that enable you to group and organize a series of SQL and PL/SQL
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Potential Dividers. 46 minutes. 46 marks. Page 1 of 11
 Potential Dividers 46 minutes 46 marks Page 1 of 11 Q1. In the circuit shown in the figure below, the battery, of negligible internal resistance, has an emf of 30 V. The pd across the lamp is 6.0 V and
Potential Dividers 46 minutes 46 marks Page 1 of 11 Q1. In the circuit shown in the figure below, the battery, of negligible internal resistance, has an emf of 30 V. The pd across the lamp is 6.0 V and
Pg The perimeter is P = 3x The area of a triangle is. where b is the base, h is the height. In our case b = x, then the area is
 Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
(1) Describe the process by which mercury atoms become excited in a fluorescent tube (3)
 Q1. (a) A fluorescent tube is filled with mercury vapour at low pressure. In order to emit electromagnetic radiation the mercury atoms must first be excited. (i) What is meant by an excited atom? (1) (ii)
Q1. (a) A fluorescent tube is filled with mercury vapour at low pressure. In order to emit electromagnetic radiation the mercury atoms must first be excited. (i) What is meant by an excited atom? (1) (ii)
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
EPL324: Tutorials* on Communications and Networks Tutorial 2: Chapter 1 Review Questions
 EPL324: Tutorials* on Communications and Networks Tutorial 2: Chapter 1 Review Questions Pavlos Antoniou University of Cyprus Department of Computer Science * The material is taken from J.F. Kurose & K.W.
EPL324: Tutorials* on Communications and Networks Tutorial 2: Chapter 1 Review Questions Pavlos Antoniou University of Cyprus Department of Computer Science * The material is taken from J.F. Kurose & K.W.
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Internet protocol stack Encapsulation Connection oriented VS connectionless services Circuit Switching Packet Switching Store-and-forward switches
 Internet protocol stack Encapsulation Connection oriented VS connectionless services Circuit Switching Packet Switching Store-and-forward switches ultiplexing: TD, FD, Statistical multiplexing, CDA OSI
Internet protocol stack Encapsulation Connection oriented VS connectionless services Circuit Switching Packet Switching Store-and-forward switches ultiplexing: TD, FD, Statistical multiplexing, CDA OSI
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 8η: Producer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 8η: Producer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Firm Behavior GOAL: Firms choose the maximum possible output (technological
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 8η: Producer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Firm Behavior GOAL: Firms choose the maximum possible output (technological
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Χρήση συστημάτων πληροφορικής στην οδική υποδομή
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΕΜΠ Εργαστήριο Συγκοινωνιακής Τεχνικής Χρήση συστημάτων πληροφορικής στην οδική υποδομή Συσχέτιση δεδομένων GPS και χάρτη Βύρωνας Νάκος Καθηγήτης ΕΜΠ bnakos@central.ntua.gr
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΕΜΠ Εργαστήριο Συγκοινωνιακής Τεχνικής Χρήση συστημάτων πληροφορικής στην οδική υποδομή Συσχέτιση δεδομένων GPS και χάρτη Βύρωνας Νάκος Καθηγήτης ΕΜΠ bnakos@central.ntua.gr
EPL 603 TOPICS IN SOFTWARE ENGINEERING. Lab 5: Component Adaptation Environment (COPE)
 EPL 603 TOPICS IN SOFTWARE ENGINEERING Lab 5: Component Adaptation Environment (COPE) Performing Static Analysis 1 Class Name: The fully qualified name of the specific class Type: The type of the class
EPL 603 TOPICS IN SOFTWARE ENGINEERING Lab 5: Component Adaptation Environment (COPE) Performing Static Analysis 1 Class Name: The fully qualified name of the specific class Type: The type of the class
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 10η: Basics of Game Theory part 2 Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 0η: Basics of Game Theory part 2 Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Best Response Curves Used to solve for equilibria in games
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 0η: Basics of Game Theory part 2 Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Best Response Curves Used to solve for equilibria in games
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΒΑΛΕΝΤΙΝΑ ΠΑΠΑΔΟΠΟΥΛΟΥ Α.Μ.: 09/061. Υπεύθυνος Καθηγητής: Σάββας Μακρίδης
 Α.Τ.Ε.Ι. ΙΟΝΙΩΝ ΝΗΣΩΝ ΠΑΡΑΡΤΗΜΑ ΑΡΓΟΣΤΟΛΙΟΥ ΤΜΗΜΑ ΔΗΜΟΣΙΩΝ ΣΧΕΣΕΩΝ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ «Η διαμόρφωση επικοινωνιακής στρατηγικής (και των τακτικών ενεργειών) για την ενδυνάμωση της εταιρικής
Α.Τ.Ε.Ι. ΙΟΝΙΩΝ ΝΗΣΩΝ ΠΑΡΑΡΤΗΜΑ ΑΡΓΟΣΤΟΛΙΟΥ ΤΜΗΜΑ ΔΗΜΟΣΙΩΝ ΣΧΕΣΕΩΝ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ «Η διαμόρφωση επικοινωνιακής στρατηγικής (και των τακτικών ενεργειών) για την ενδυνάμωση της εταιρικής
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Ad-hoc Networks. Επίκ. Καθηγητής Συμεών Παπαβασιλείου
 Ad-hoc Networks Επίκ. Καθηγητής Συμεών Παπαβασιλείου Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Τομέας Επικοινωνιών, Ηλεκτρονικής & Συστημάτων Πληροφορικής (papavass@mail.ntua.gr
Ad-hoc Networks Επίκ. Καθηγητής Συμεών Παπαβασιλείου Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Τομέας Επικοινωνιών, Ηλεκτρονικής & Συστημάτων Πληροφορικής (papavass@mail.ntua.gr
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
CMOS Technology for Computer Architects
 CMOS Technology for Computer Architects Iakovos Mavroidis Giorgos Passas Manolis Katevenis Lecture 13: On chip SRAM Technology FORTH ICS / EURECCA & UoC GREECE ABC A A E F A BCDAECF A AB C DE ABCDAECF
CMOS Technology for Computer Architects Iakovos Mavroidis Giorgos Passas Manolis Katevenis Lecture 13: On chip SRAM Technology FORTH ICS / EURECCA & UoC GREECE ABC A A E F A BCDAECF A AB C DE ABCDAECF
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 6η: Basics of Industrial Organization Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 6η: Basics of Industrial Organization Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Course Outline Part II: Mathematical Tools Firms - Basics
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 6η: Basics of Industrial Organization Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Course Outline Part II: Mathematical Tools Firms - Basics
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 9η: Basics of Game Theory Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 9η: Basics of Game Theory Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Course Outline Part II: Mathematical Tools Firms - Basics of Industrial
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 9η: Basics of Game Theory Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Course Outline Part II: Mathematical Tools Firms - Basics of Industrial
department listing department name αχχουντσ ϕανε βαλικτ δδσϕηασδδη σδηφγ ασκϕηλκ τεχηνιχαλ αλαν ϕουν διξ τεχηνιχαλ ϕοην µαριανι
 She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
(C) 2010 Pearson Education, Inc. All rights reserved.
 Connectionless transmission with datagrams. Connection-oriented transmission is like the telephone system You dial and are given a connection to the telephone of fthe person with whom you wish to communicate.
Connectionless transmission with datagrams. Connection-oriented transmission is like the telephone system You dial and are given a connection to the telephone of fthe person with whom you wish to communicate.
Γιπλυμαηική Δπγαζία. «Ανθπυποκενηπικόρ ζσεδιαζμόρ γέθςπαρ πλοίος» Φοςζιάνηρ Αθανάζιορ. Δπιβλέπυν Καθηγηηήρ: Νηθφιανο Π. Βεληίθνο
 ΔΘΝΙΚΟ ΜΔΣΟΒΙΟ ΠΟΛΤΣΔΥΝΔΙΟ ΥΟΛΗ ΝΑΤΠΗΓΩΝ ΜΗΥΑΝΟΛΟΓΩΝ ΜΗΥΑΝΙΚΩΝ Γιπλυμαηική Δπγαζία «Ανθπυποκενηπικόρ ζσεδιαζμόρ γέθςπαρ πλοίος» Φοςζιάνηρ Αθανάζιορ Δπιβλέπυν Καθηγηηήρ: Νηθφιανο Π. Βεληίθνο Σπιμελήρ Δξεηαζηική
ΔΘΝΙΚΟ ΜΔΣΟΒΙΟ ΠΟΛΤΣΔΥΝΔΙΟ ΥΟΛΗ ΝΑΤΠΗΓΩΝ ΜΗΥΑΝΟΛΟΓΩΝ ΜΗΥΑΝΙΚΩΝ Γιπλυμαηική Δπγαζία «Ανθπυποκενηπικόρ ζσεδιαζμόρ γέθςπαρ πλοίος» Φοςζιάνηρ Αθανάζιορ Δπιβλέπυν Καθηγηηήρ: Νηθφιανο Π. Βεληίθνο Σπιμελήρ Δξεηαζηική
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Mean bond enthalpy Standard enthalpy of formation Bond N H N N N N H O O O
 Q1. (a) Explain the meaning of the terms mean bond enthalpy and standard enthalpy of formation. Mean bond enthalpy... Standard enthalpy of formation... (5) (b) Some mean bond enthalpies are given below.
Q1. (a) Explain the meaning of the terms mean bond enthalpy and standard enthalpy of formation. Mean bond enthalpy... Standard enthalpy of formation... (5) (b) Some mean bond enthalpies are given below.
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
Business English. Ενότητα # 9: Financial Planning. Ευαγγελία Κουτσογιάννη Τμήμα Διοίκησης Επιχειρήσεων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Business English Ενότητα # 9: Financial Planning Ευαγγελία Κουτσογιάννη Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Business English Ενότητα # 9: Financial Planning Ευαγγελία Κουτσογιάννη Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το παρόν εκπαιδευτικό
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική»
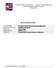 Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική» Μεταπτυχιακή Διατριβή Τίτλος Διατριβής Επίκαιρα Θέματα Ηλεκτρονικής Διακυβέρνησης Ονοματεπώνυμο Φοιτητή Σταμάτιος
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική» Μεταπτυχιακή Διατριβή Τίτλος Διατριβής Επίκαιρα Θέματα Ηλεκτρονικής Διακυβέρνησης Ονοματεπώνυμο Φοιτητή Σταμάτιος
"ΦΟΡΟΛΟΓΙΑ ΕΙΣΟΔΗΜΑΤΟΣ ΕΤΑΙΡΕΙΩΝ ΣΥΓΚΡΙΤΙΚΑ ΓΙΑ ΤΑ ΟΙΚΟΝΟΜΙΚΑ ΕΤΗ 2011-2013"
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Επιμέλεια Κρανιωτάκη Δήμητρα Α.Μ. 8252 Κωστορρίζου Δήμητρα Α.Μ. 8206 Μελετίου Χαράλαμπος Α.Μ.
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Επιμέλεια Κρανιωτάκη Δήμητρα Α.Μ. 8252 Κωστορρίζου Δήμητρα Α.Μ. 8206 Μελετίου Χαράλαμπος Α.Μ.
«Χρήσεις γης, αξίες γης και κυκλοφοριακές ρυθμίσεις στο Δήμο Χαλκιδέων. Η μεταξύ τους σχέση και εξέλιξη.»
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ: «Χρήσεις γης, αξίες γης και κυκλοφοριακές ρυθμίσεις στο Δήμο Χαλκιδέων.
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ: «Χρήσεις γης, αξίες γης και κυκλοφοριακές ρυθμίσεις στο Δήμο Χαλκιδέων.
Adaptive Message Routing and Information Acquisition in Dynamic Mobile Networking Environments
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών, ΕΚΠΑ - Προηγμένες ικτυακές Τεχνολογίες - 2016 1 Adaptive Message Routing and Information Acquisition in Dynamic Mobile Networking Environments I. Manolopoulos, K.
Τμήμα Πληροφορικής και Τηλεπικοινωνιών, ΕΚΠΑ - Προηγμένες ικτυακές Τεχνολογίες - 2016 1 Adaptive Message Routing and Information Acquisition in Dynamic Mobile Networking Environments I. Manolopoulos, K.
Finite difference method for 2-D heat equation
 Finite difference method for 2-D heat equation Praveen. C praveen@math.tifrbng.res.in Tata Institute of Fundamental Research Center for Applicable Mathematics Bangalore 560065 http://math.tifrbng.res.in/~praveen
Finite difference method for 2-D heat equation Praveen. C praveen@math.tifrbng.res.in Tata Institute of Fundamental Research Center for Applicable Mathematics Bangalore 560065 http://math.tifrbng.res.in/~praveen
Strain gauge and rosettes
 Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
σχεδιαστικές προκλήσεις, θεωρία γράφων
 Δομή παρουσίασης 1. Εισαγωγή στις κατανεμημένες εφαρμογές: σχεδιαστικές προκλήσεις, θεωρία γράφων 2. Χαρακτηριστικά και πεδία εφαρμογών: ιδιαιτερότητες και χαρακτηριστικά που απαιτούν τη χρήση αλγορίθμων
Δομή παρουσίασης 1. Εισαγωγή στις κατανεμημένες εφαρμογές: σχεδιαστικές προκλήσεις, θεωρία γράφων 2. Χαρακτηριστικά και πεδία εφαρμογών: ιδιαιτερότητες και χαρακτηριστικά που απαιτούν τη χρήση αλγορίθμων
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
 9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
Πέτσιος Στέφανος Κων/νος Α.Μ. #47. Οι απαντήσεις του paper:
 Πέτσιος Στέφανος Κων/νος Α.Μ. #47 Οι απαντήσεις του paper: D. S. Milojicic, V. Kalogeraki, R. Lukose, K. Nagaraja, J. Pruyne, B. Richard, S. Rollins, and Z. Xu "Peer-to-Peer Computing", HP Technical Report,
Πέτσιος Στέφανος Κων/νος Α.Μ. #47 Οι απαντήσεις του paper: D. S. Milojicic, V. Kalogeraki, R. Lukose, K. Nagaraja, J. Pruyne, B. Richard, S. Rollins, and Z. Xu "Peer-to-Peer Computing", HP Technical Report,
