Probability theory STATISTICAL METHODS FOR SAFETY ANALYSIS FMS065 TABLE OF FORMULÆ (2016) Basic probability theory. One-dimensional random variables
|
|
|
- Ἁλκυόνη Φιλιππίδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Lund University Centre for Mthemticl Sciences Mthemticl Sttistics STATISTICAL METHODS FOR SAFETY ANALYSIS FMS065 TABLE OF FORMULÆ (06) Probbility theory Bsic probbility theory Let S be smple spce, nd let P be probbility on S. Then, for ll events A, B, A, A,..., A n S, () Kolmogorov s xioms (.) 0 P(A) (.) P(S) = (.3) P(A B) = P(A) + P(B), if A nd B re disjoint. () P(A B) = P(A) + P(B) P(A B) (3) A nd B re independent P(A B) = P(A) P(B). (4) Conditionl probbility: P(B A) = (5) Lw of totl probbility: P(B) = P(A B). P(A) P(B A i ) P(A i ), whenever A,..., A n re pirwise disjoint nd stisfy (6) Byes theorem: P(A i B) = P(B A i) P(A i ) P(B) whenever A,..., A n re pirwise disjoint nd stisfy One-dimensionl rndom vribles = n A i = S. P(B A i ) P(A i ) n j= P(B A j) P(A j ), n A k = S. (7) Distribution function for the rndom vrible X : F X (x) = P(X x). (8) Probbility-mss function for the discrete rndom vrible X : p X (x) = P(X = x). k= (9) Density function for the continuous rndom vrible X : f X (x) = df X (x) dx differentible. for ll x where F X is (0) If X is discrete, then P( < X b) = F X (b) F X () = p X (x) x ],b] If there is no element x in ], b] such tht p X (x) 0, then F X (b) F X () = 0.
2 ii TABLE OF FORMULÆ, FMS065, 06 () If X is continuous, then P( < X b) = F X (b) F X () = Two-dimensionl rndom vribles b f X (x) dx () oint distribution function for the two rndom vribles X nd Y : F X,Y (x, y) = P(X x Y y) (3) oint probbility-mss function for the two discrete rndom vribles X nd Y : p X,Y (x, y) = P(X = x Y = y) (4) oint density function for the two continuous rndom vribles X nd Y : f X,Y (x, y) = F X,Y (x, y) x y for ll (x, y) where the derivtive exists. (5) If X nd Y both re discrete: P ( (X, Y ) A ) = (x,y) A p X,Y (x, y) If there is no pir (x, y) in A such tht p X (x) 0, then P ( (X, Y ) A ) = 0. (6) If X nd Y both re continuous: P ( (X, Y ) A ) = f X,Y (x, y) d(x, y) Conditionl distributions (x,y) A (7) Conditionl distribution function: F X Y (x y) = P(X x Y = y). (8) Conditionl probbility-mss function for the discrete rndom vrible X : p X Y (x y) = P(X = x Y = y) p X,Y (x, y), p Y (y) 0 If Y is lso discrete, then p X Y (x y) = p Y (y) 0, p Y (y) = 0. (9) Conditionl density function for the continuous rndom vrible X : f X Y (x y) = F X Y (x y) x f X,Y (x, y), f Y (y) 0 If Y is lso continuous, then f X Y (x y) = f Y (y) 0, f Y (y) = 0.
3 TABLE OF FORMULÆ, FMS065, 06 iii (0) Byes theorem: p X Y (x y) p Y (y), p X (x) 0, (0.) X discrete nd Y discrete: p Y X (y x) = p X (x) 0, p X (x) = 0. (0.) Y continuous: replce p Y X (y x) by f Y X (y x) nd p Y (y) by f Y (y). (0.3) X continuous: replce p X Y (x y) by f X Y (x y) nd p X (x) by f X (x). () Mrginl probbility-mss function for the discrete rndom vrible X : (.) Y is discrete: p X (x) = y p X Y (x y) p Y (y) = y p X,Y (x, y) (.) Y is continuous: p X (x) = p X Y (x y) f Y (y) dy () Mrginl density function for the continuous rndom vrible X : (.) Y is discrete: f X (x) = f X Y (x y) p Y (y) (.) Y is continuous: f X (x) = y; p Y (y) 0 f X Y (x y) f Y (y) dy = (3) If X nd Y re independent, (3.) then F X,Y (x, y) = F X (x) F Y (y), (3.) then p X,Y (x, y) = p X (x) p Y (y) if X nd Y re discrete, (3.3) then f X,Y (x, y) = f X (x) f Y (y) if X nd Y re continuous, (3.4) then F X Y (x y) = F X (x), (3.5) then p X Y (x y) = p X (x) if X is discrete, (3.6) then f X Y (x y) = f X (x) if X is continuous. Lw of totl probbility gin Lw of totl probbility: Let A be n event. f X,Y (x, y) dy (4) If X is discrete rndom vrible, then P(A) = x P(A X = x) p X (x). (5) If X is continuous rndom vrible, then P(A) = Expecttion, vrince, nd the like P(A X = x) f X (x) dx. (6) Let g be rel-vlued function x g(x). Then the expecttion of g(x ) is given by (6.) E ( g(x ) ) = g(x) p X (x), if X is discrete, (6.) E ( g(x ) ) = p X (x) 0 g(x) f X (x) dx, if X is continuous.
4 iv TABLE OF FORMULÆ, FMS065, 06 (7) Let g be rel-vlued function (x, y) g(x, y). Then the expecttion of g(x, Y ) is given by (7.) E ( g(x, Y ) ) = x,y g(x, y) p X,Y (x, y), if X nd Y re discrete, (7.) E ( g(x, Y ) ) = g(x, y) f X,Y (x, y) d(x, y), ( (X ) ) (8) Vrince: V(X ) = E E(X ) = E(X ) ( E(X ) ). (9) Stndrd devition: D(X ) = V(X ). (30) Coefficient of vrition: R(X ) = D(X )/E(X ). if X nd Y re continuous. (3) Covrince: C(X ; Y ) = E( (X E(X ) )( Y E(Y ) ) ) = E(XY ) E(X ) E(Y ). (3) C(X, X ) = V(X ). (33) Coefficient of correltion: r(x, Y ) = C(X, Y ) D(X ) D(Y ). (34) Expecttion is liner, i.e. E(X + by + c) = E(X ) + be(y ) + c. (35) V(X ± by ± c) = V(X ) + b V(Y ) ± b C(X, Y ) (36) Covrince is biliner, i.e. C(X ± by, cz) = cc(x, Z) ± bcc(y, Z). (37) For independent rndom vribles X, Y : E(XY ) = E(X ) E(Y ). (38) Guss pproximtions: Let g be rel-vlued function (x, x,..., x n ) g(x, x,..., x n ). Then E(g(X,..., X n )) g(e(x ),..., E(X n )). V(g(X,..., X n )) ci V(X i ) + c i c j C(X i, X j ), i n j n i<j where c i = g x i (E(X ),..., E(X n )) = g x i (E(X ),..., E(X n )). Norml (Gussin) distribution (39) Univrite norml (Gussin) distribution (s > 0): X N(m, s ) X m s N(0, ) (40) Bivrite norml (Gussin) distribution: Let m, m, s, s, nd r be rel numbers (s > 0, s > 0, < r < ). If (X, Y ) N(m, m, s, s, r), then (40.) f X,Y (x, y) = ps s r e (x m ) s + (y m ) s r x m s y m s «,
5 TABLE OF FORMULÆ, FMS065, 06 v (40.) X N(m, s ), Y N(m, s ), C(X, Y ) = rs s, r(x, Y ) = r, ( ( ) ) (40.3) f X Y (x y) = ps r e s x m ( r +r s ) s (y m ), i.e. N ( m + r s s (y m ), s ( r ) ) (40.4) X + by N(m + bm, s + b s + b r s s ) for ll rel numbers nd b. Limit theorems (4) Lw of Lrge Numbers (LLN): Let X, X,... be independent nd identiclly distributed rndom vribles with existing expecttion E(X i ) = m. Then Y n = X X n n E(X i ), when n. (4) Centrl Limit Theorem: Let X, X,..., X n be independent nd identiclly distributed rndom vribles with existing expecttion E(X i ) nd existing stndrd devition D(X i ) = s <. Then Y n = X X n AsN(n m, n s ), when n. (43) We hve pproximtely (43.) Bin(n, p) Po(np) if p 0. nd n 0. (43.) Bin(n, p) N(np, np( p)) if np( p) 0. (43.3) Po(m) N(m, m) if m 5. Sums of rndom vribles (44) Let X N(m, s ),..., X n N(m n, s n ) be n independent, normlly distributed rndom vribles. For ny set c,..., c n of n rel numbers, we hve ( c i X i N c i m i, c i si ). (45) If X nd X re independent, then (45.) X Bin(n, p), X Bin(n, p) X + X Bin(n + n, p) (45.) X Po(m ), X Po(m ) X + X Po(m + m ). (45.3) X Gmm(, b), X Gmm(, b) X + X Gmm( +, b). (45.4) X q (f ), X q (f ) X + X q (f + f )
6 vi TABLE OF FORMULÆ, FMS065, 06 Sttistics Point estimtion Let x,...,x n be observtions of n independent, identiclly distributed rndom vribles with expecttion m nd stndrd devition s. Then unbised estimtions of m nd s re given by (46) m = n x i = x (47) (s ) = n (x i m), m known. (48) (s ) = s = n Confidence intervls (x i x), m unknown. (49) Let j be some prmeter, nd let (r.v.) be n estimtor of j such tht is (pproximtely) normlly distributed with expecttion j. Let j be the estimte of j, i.e. let j be the observtion of. Then I j = [j l ( g)/ d( ); j + l ( g)/ d( )] I j = [j l g d( ); ] I j = [; j + l g d( )] (two-sided), (one-sided, bounded below), (one-sided, bounded bove) re confidence intervls for j with pproximtive confidence level g (g is typiclly lrge, g = 0.95, g = 0.99,... ). Here, d( ) is the stndrd error of the estimtor. d( ) = Hypothesis testing D( ) if D( ) is known nd independent of j, ( D( ) ) if D( ) is unknown or dependent on j. (50) Let j be prmeter. We wnt to test the simple hypothesis H 0 : j = j 0 on the significnce level ( is typiclly smll, = 0.05, = 0.0,... ). Then the test will be Reject H0 j 0 I j Do not reject H 0 j 0 I j where I j is confidence intervl of j with (pproximtive) confidence level. If H : j j 0, then choose I j to be two-sided. If H : j > j 0, then choose I j to be one-sided nd bounded below. If H : j < j 0, then choose I j to be one-sided nd bounded bove.
7 TABLE OF FORMULÆ, FMS065, 06 vii (5) The q test. Let H 0 be hypothesis bout the expressed by probbilities p,..., p r. We hve n observtions. Clculte r (x i np i ) Q =. np i Reject H 0 if Q > q (r ). Byesin updting (5) Let be the prmeter modelled s rndom vrible. Let X be the observed rndom vrible with observed vlue x. (5.) is discrete, X is discrete: p post (j) = c P(X = x = j) pprior (j), where c = P(X = x) = j P(X = x = j) p prior (j). (5.) is continuous, X is discrete: f post prior (j) = c P(X = x = j) f (j), where c = P(X = x) = P(X = x = j) f prior (j) dj. (5.3) If X is continuous: replce P(X = x = j) by f X (x j) nd P(X = x) by f X (x). (53) Prticulrly, Prior distribution of Conditionl distribution of X, given = j Posterior distribution of (x is the observtion of X ) (53.) Gmm(, b) Po(j t) Gmm( + x, b + t) (53.) Bet(, b) Bin(n, j) Bet( + x, b + n x) (54) If the event A nd the rndom vrible X re independent on condition tht is known, then we hve the lw of totl probbility: (54.) P post (A) = (j), if is discrete, (54.) P post (A) = p post (j) 0 P(A = j) p post P(A = j) f post (j) dj, if is continuous. (55) If we hve observed the occurrence of n event B (insted of hving observed the rndom vrible X ), then: (55.) p post (j) = P(B = j) pprior(j), if is discrete, (55.) f post prior (j) = P(B = j) f (j), if is continuous. If the event A nd the event B re independent on condition tht is known, then (54.) nd (54.) still re vlid.
8 viii TABLE OF FORMULÆ, FMS065, 06 Miscellneous The Poisson process Let N (t) be the number of events tking plce in the time intervl ]0, t]. If N (t) is Poisson process with constnt intensity l, then (56) N (t) Po(lt). (57) Time lgs between consecutive events re independent nd exponentilly distributed with expecttion /l. (58) The number of events occurring in time intervl I nd the number of events occurring in nother time intervl I re independent if I nd I re disjoint. Filure rte Let T be positive, continuous rndom vrible with density function f T nd distribution function F T. (59) l(t) = f T (t) F T (t), t 0 nd F T (t). (60) P(T > t) = exp ( t ) l(s) ds, t 0. 0 (6) P(t < T t + D T > t) l(t) D, if D is smll (D > 0). Quntiles Quntiles is the sme s frctiles. Let be rel number such tht 0 < <. Let X be continuous rndom vrible with distribution function F X. (6) The -quntile (denoted x ) is defined to be ny number such tht P(X > x ) = or, equivlently, F X (x ) =. (63) x /4 = x 0.5 is clled the upper (distribution) qurtile. x / = x 0.5 is clled the (distribution) medin. x 3/4 = x 0.75 is clled the lower (distribution) qurtile. x 0.0, x 0.0,..., x 0.98, x 0.99 re clled the (distribution) percentiles. (64) Quntiles l bsed on the stndrd-norml distribution re denoted l : If X N(0; ), then P(X > l ) = F(l ) = l = F ( ), where F (...) is the inverse function of F. (So, F (...) hs nothing to do with (64.) l = l (for ll such tht 0 < < ) (64.) l for some vlues of re found in (99) F(...).)
9 TABLE OF FORMULÆ, FMS065, 06 ix Cornell s relibility index Let h(r,..., R k, S,..., S n ) be the filure function of k rndom strength vribles R,..., R k nd n rndom lod vribles S,..., S n. Let E ( h(r,..., R k, S,..., S n ) ) > 0. (65) Cornell s sfety index b C is defined s b C = E( h(r,..., R k, S,..., S n ) ) D ( h(r,..., R k, S,..., S n ) ). (66) If h(r,..., R k, S,..., S n ) is normlly distributed, then the probbility P f of filure is P f = P ( h(r,..., R k, S,..., S n ) 0 ) = F(b C ). (67) An upper bound for the probbility P f of filure is P f = P ( h(r,..., R k, S,..., S n ) 0 ) Log-norml distribution + b C (68) Let X be log-normlly distributed rndom vrible, i.e. ln X N(m, s ) or ln( X ) x / N(0, s ). Then the coefficient of vrition is given by D(X ) E(X ) = e s (69) Let X nd X be two independent rndom vribles. Then ln X N(m, s ), ln X N(m, s ) ln(x k X k ) N(k m +k m, k s +k s ) Mximum nd minimum Let X,..., X n be n independent, identiclly distributed rndom vribles with distribution function F X (x). If we define then X mx = mx(x,..., X n ) nd X min = min(x,..., X n ), (70) F Xmx (z) = ( F X (z) ) n, (7) F Xmin (z) = ( F X (z) ) n. Some functions (7) The gmm function is defined (for p > 0) by (7.) G(p) = 0 x p e x dx, p > 0 Some properties of the gmm function: (7.) G(p) = (p )!, p ; ; 3;...} (7.3) G( ) = p (7.4) G(p + ) = p G(p); p > 0
10 x TABLE OF FORMULÆ, FMS065, 06 (73) The incomplete gmm function is defined (for p > 0, x 0) by (73.) G(p, x) = x x p e x dx, x 0, p > 0 A property of the incomplete gmm function: (73.) G(p, 0) = G(p), p > 0 (74) The incomplete bet function is defined (for > 0, b > 0, 0 x ) by (74.) B(x,, b) = x 0 A property of the incomplete bet function: x ( x) b dx, 0 x, > 0, b > 0 (74.) B(,, b) = G() G(b) G( + b), > 0, b > 0 Tble of distributions Distribution (75) Hypergeometric distribution (76) Binomil Bin(n, p) (77) Poisson Po(m) ( N )( N ) x n x ( p(x) = N+N ), x Z [n min(n,n), min(n,n )] n 0, otherwise ( ) n p x ( p) n x, x = 0,,..., n p(x) = x 0, otherwise m mx e, x = 0,,... p(x) = x! 0, otherwise Prmeter restrictions N =,,... N =,,... n = =,..., N +N n =,,... 0 < p < Expecttion n N Vrince N + N N +N n N +N n N N (N +N ) np np( p) m > 0 m m (78) Geometric Ge(p) p(x) = p( p) x, x = 0,,... 0, otherwise 0 < p < p p p p (79) First success distribution (80) Uniform U(, b) p(x) = p( p) x, x =,,... 0, otherwise f (x) = b, < x < b 0, otherwise 0, x x b, < x < b, x b 0 < p < < b p + b p p ( b)
11 TABLE OF FORMULÆ, FMS065, 06 xi Distribution (8) Bet Bet(, b) Γ( + b) f (x) = Γ() Γ(b) x ( x) b, 0 < x < 0, otherwise 0, x 0 Γ( + b) B(x,, b), 0 < x < Γ() Γ(b), x Prmeter restrictions > 0, b > 0 Expecttion Vrince + b b ( + b) ( + b + ) (8) Norml (Gussin) distribution, N(m, σ ) f (x) = (x m) e s πσ ( ) σ > 0 m σ x m Φ σ (83) Log-norml distribution, ln X N(m, σ ) 0, x 0 Φ( ln x m ), x > 0 σ σ > 0 e m+s / e m+s e m+s (84) Log-norml 0, ( x 0 distribution, Φ ln X x / N(0, σ ) σ ln x ), x > 0 x / (85) Gmm Gmm(, b) 0, x 0 f (x) = b Γ() x e b x, x 0 0, x 0 Γ(, b x), x > 0 Γ() x / > 0, σ > 0 x / e s / x / (e s e s ) > 0, b > 0 b b (86) Exponentil Exp() 0, x 0 e x/, x > 0 > 0 (87) Gumbel (type I extreme vlue) distribution e e (x b)/ > 0 b + γ π 6 (88) Fréchet (type II extreme vlue) distribution 0, x b e x b c, x > b (89) Type III e x b c, x < b extreme vlue, x b distribution > 0, c > 0 > 0, c > 0 b + Γ( /c) [ Γ( c ) ( Γ( c ) ) ] b Γ( + /c) [ Γ( + c ) ( Γ( + c ) ) ] ) Φ(x) is tbulted in (98). ) Here, x / denotes the distribution medin of the rndom vrible X. ) γ is Euler s constnt. γ = lim n ( ( n k= k ) ln n) = ) Expecttion exists if nd only if c >. Vrince exists if nd only if c >. ) If X is type III extreme vlue distributed rndom vrible, then X (i.e. the negtive of X ) is Weibull distributed. Therefore the type III extreme vlue distribution now nd then is clled the extreme vlue distribution of Weibull type.
12 xii TABLE OF FORMULÆ, FMS065, 06 Distribution Prmeter restrictions Expecttion Vrince (90) Weibull distribution 0, x b e x b c, x > b > 0, c > 0 b + Γ( + /c) [ Γ( + c ) ( Γ( + c ) ) ] (9) Ryleigh distribution (9) Chi-squre χ (n), Gmm( n, ) 0, x b e x b, x > b 0, x 0 f (x) = / Γ( n ) (x/)(n/) e x/, x > 0 0, x 0 Γ( n, x ) Γ( n ), x > 0 > 0 b + π ( π 4 ) n =,,... n n (93) Student s t-distribution, t(n) (94) Fisher s F-distribution, F(n, n ) (95) Preto (c > 0) f (x) = n Γ( n+ ) π Γ( n ) ( + x n )(n+)/ B( n n+x, n, ) B(, n, ), x < 0 B( n n+x, n, ) B(, n, ) ; x 0 [x 0] = 0 f (x) = [x > 0] = n+n Γ( ) = Γ( n n ) Γ( ) n n/ n n/ x n (n + n x) (n+n)/ 0; x 0 B( n n, n +n x, n ) B(, n, n ), x > 0 0, x 0 ( c x )/c, 0 < x < c, x c n =,,... 0 n =,,... n =,,... > 0, c > 0 n n c + n n n (n + n ) n (n ) (n 4) (c + )(c + ) (96) Preto distribution, (c < 0) 0, x 0 ( + c x ) / c, x > 0 > 0, c < 0 c + (c + )(c + ) (97) Preto distribution, (c = 0) 0, x 0 e x/, x > 0 > 0 ) Vrince exists if nd only if n 3. ) Expecttion exists if nd only if n 3. Vrince exists if nd only if n 5. ) Expecttion exists if nd only if c >. Vrince exists if nd only if c >. ) This is n exponentil Exp().
13 TABLE OF FORMULÆ, FMS065, 06 xiii Tble of the stndrd-norml distribution function (98) If X N(0; ), then P(X x) = F(x), where F( ) is non-elementry function given by x p e u du. This tble gives the function vlues F(x) for x = 0.00, 0.0,..., For negtive vlues of x, use tht F( x) = F(x) Tble of some quntiles of the stndrd norml distribution (99) l = F ( ), l = l α λ
14 xiv TABLE OF FORMULÆ, FMS065, 06 Tble of quntiles of Student s t-distribution (00) If X t(n), then the -quntile t (n) is defined by P ( X > t (n) ) =, 0 < < This tble gives the -quntile t (n) for = 0., 0.05, 0.05, 0.0, 0.005, 0.00, nd for n =,,..., 9, 30, 40, 60, 0. For vlues of 0.9, use tht t (n) = t (n), 0 < < n
15 TABLE OF FORMULÆ, FMS065, 06 xv Tble of quntiles of the q distribution (0) If X q (n), then the -quntile q (n) is defined by P ( X > q (n) ) =, 0 < < This tble gives the -quntile q (n) for = , 0.999, 0.99, 0.975, 0.95, 0.05, 0.05, 0.0, 0.005, 0.00, nd for n =,,..., 9, 30, 40, 50,..., 90, 00. n α This is version
Oscillatory integrals
 Oscilltory integrls Jordn Bell jordn.bell@gmil.com Deprtment of Mthemtics, University of Toronto August, 0 Oscilltory integrls Suppose tht Φ C R d ), ψ DR d ), nd tht Φ is rel-vlued. I : 0, ) C by Iλ)
Oscilltory integrls Jordn Bell jordn.bell@gmil.com Deprtment of Mthemtics, University of Toronto August, 0 Oscilltory integrls Suppose tht Φ C R d ), ψ DR d ), nd tht Φ is rel-vlued. I : 0, ) C by Iλ)
APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 651 APPENDIX B. BIBLIOGRAPHY 677 APPENDIX C. ANSWERS TO SELECTED EXERCISES 679
 APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 1 Table I Summary of Common Probability Distributions 2 Table II Cumulative Standard Normal Distribution Table III Percentage Points, 2 of the Chi-Squared
APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 1 Table I Summary of Common Probability Distributions 2 Table II Cumulative Standard Normal Distribution Table III Percentage Points, 2 of the Chi-Squared
Solutions 3. February 2, Apply composite Simpson s rule with m = 1, 2, 4 panels to approximate the integrals:
 s Februry 2, 216 1 Exercise 5.2. Apply composite Simpson s rule with m = 1, 2, 4 pnels to pproximte the integrls: () x 2 dx = 1 π/2, (b) cos(x) dx = 1, (c) e x dx = e 1, nd report the errors. () f(x) =
s Februry 2, 216 1 Exercise 5.2. Apply composite Simpson s rule with m = 1, 2, 4 pnels to pproximte the integrls: () x 2 dx = 1 π/2, (b) cos(x) dx = 1, (c) e x dx = e 1, nd report the errors. () f(x) =
FORMULAS FOR STATISTICS 1
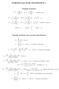 FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Aquinas College. Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET
 Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών. Εθνικό Μετσόβιο Πολυτεχνείο. Thales Workshop, 1-3 July 2015.
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Thles Worksho, 1-3 July 015 The isomorhism function from S3(L(,1)) to the free module Boštjn Gbrovšek Άδεια Χρήσης Το παρόν
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Thles Worksho, 1-3 July 015 The isomorhism function from S3(L(,1)) to the free module Boštjn Gbrovšek Άδεια Χρήσης Το παρόν
Notes on Tobin s. Liquidity Preference as Behavior toward Risk
 otes on Tobin s Liquidity Preference s Behvior towrd Risk By Richrd McMinn Revised June 987 Revised subsequently Tobin (Tobin 958 considers portfolio model in which there is one sfe nd one risky sset.
otes on Tobin s Liquidity Preference s Behvior towrd Risk By Richrd McMinn Revised June 987 Revised subsequently Tobin (Tobin 958 considers portfolio model in which there is one sfe nd one risky sset.
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Solutions_3. 1 Exercise Exercise January 26, 2017
 s_3 Jnury 26, 217 1 Exercise 5.2.3 Apply composite Simpson s rule with m = 1, 2, 4 pnels to pproximte the integrls: () x 2 dx = 1 π/2 3, (b) cos(x) dx = 1, (c) e x dx = e 1, nd report the errors. () f(x)
s_3 Jnury 26, 217 1 Exercise 5.2.3 Apply composite Simpson s rule with m = 1, 2, 4 pnels to pproximte the integrls: () x 2 dx = 1 π/2 3, (b) cos(x) dx = 1, (c) e x dx = e 1, nd report the errors. () f(x)
Review-2 and Practice problems. sin 2 (x) cos 2 (x)(sin(x)dx) (1 cos 2 (x)) cos 2 (x)(sin(x)dx) let u = cos(x), du = sin(x)dx. = (1 u 2 )u 2 ( du)
 . Trigonometric Integrls. ( sin m (x cos n (x Cse-: m is odd let u cos(x Exmple: sin 3 (x cos (x Review- nd Prctice problems sin 3 (x cos (x Cse-: n is odd let u sin(x Exmple: cos 5 (x cos 5 (x sin (x
. Trigonometric Integrls. ( sin m (x cos n (x Cse-: m is odd let u cos(x Exmple: sin 3 (x cos (x Review- nd Prctice problems sin 3 (x cos (x Cse-: n is odd let u sin(x Exmple: cos 5 (x cos 5 (x sin (x
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
Biostatistics for Health Sciences Review Sheet
 Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
AMS 212B Perturbation Methods Lecture 14 Copyright by Hongyun Wang, UCSC. Example: Eigenvalue problem with a turning point inside the interval
 AMS B Perturbtion Methods Lecture 4 Copyright by Hongyun Wng, UCSC Emple: Eigenvlue problem with turning point inside the intervl y + λ y y = =, y( ) = The ODE for y() hs the form y () + λ f() y() = with
AMS B Perturbtion Methods Lecture 4 Copyright by Hongyun Wng, UCSC Emple: Eigenvlue problem with turning point inside the intervl y + λ y y = =, y( ) = The ODE for y() hs the form y () + λ f() y() = with
CHAPTER (2) Electric Charges, Electric Charge Densities and Electric Field Intensity
 CHAPTE () Electric Chrges, Electric Chrge Densities nd Electric Field Intensity Chrge Configurtion ) Point Chrge: The concept of the point chrge is used when the dimensions of n electric chrge distriution
CHAPTE () Electric Chrges, Electric Chrge Densities nd Electric Field Intensity Chrge Configurtion ) Point Chrge: The concept of the point chrge is used when the dimensions of n electric chrge distriution
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Probability theory STATISTICAL MODELING OF MULTIVARIATE EXTREMES, FMSN15/MASM23 TABLE OF FORMULÆ. Basic probability theory
 Lud Istitute of Techology Cetre for Mathematical Scieces Mathematical Statistics STATISTICAL MODELING OF MULTIVARIATE EXTREMES, FMSN5/MASM3 Probability theory Basic probability theory TABLE OF FORMULÆ
Lud Istitute of Techology Cetre for Mathematical Scieces Mathematical Statistics STATISTICAL MODELING OF MULTIVARIATE EXTREMES, FMSN5/MASM3 Probability theory Basic probability theory TABLE OF FORMULÆ
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
An Inventory of Continuous Distributions
 Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
Vidyamandir Classes. Solutions to Revision Test Series - 2/ ACEG / IITJEE (Mathematics) = 2 centre = r. a
 Per -.(D).() Vdymndr lsses Solutons to evson est Seres - / EG / JEE - (Mthemtcs) Let nd re dmetrcl ends of crcle Let nd D re dmetrcl ends of crcle Hence mnmum dstnce s. y + 4 + 4 6 Let verte (h, k) then
Per -.(D).() Vdymndr lsses Solutons to evson est Seres - / EG / JEE - (Mthemtcs) Let nd re dmetrcl ends of crcle Let nd D re dmetrcl ends of crcle Hence mnmum dstnce s. y + 4 + 4 6 Let verte (h, k) then
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Υπολογιστική Φυσική Στοιχειωδών Σωματιδίων
 Υπολογιστική Φυσική Στοιχειωδών Σωματιδίων Όρια Πιστότητας (Confidence Limits) 2/4/2014 Υπολογ.Φυσική ΣΣ 1 Τα όρια πιστότητας -Confidence Limits (CL) Tα όρια πιστότητας μιας μέτρησης Μπορεί να αναφέρονται
Υπολογιστική Φυσική Στοιχειωδών Σωματιδίων Όρια Πιστότητας (Confidence Limits) 2/4/2014 Υπολογ.Φυσική ΣΣ 1 Τα όρια πιστότητας -Confidence Limits (CL) Tα όρια πιστότητας μιας μέτρησης Μπορεί να αναφέρονται
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Stationary Stochastic Processes Table of Formulas, 2017
 Stationary Stochastic Processes, 07 Stationary Stochastic Processes Table of Formulas, 07 Basics of probability theory The following is valid for probabilities: P(Ω), where Ω is all possible outcomes 0
Stationary Stochastic Processes, 07 Stationary Stochastic Processes Table of Formulas, 07 Basics of probability theory The following is valid for probabilities: P(Ω), where Ω is all possible outcomes 0
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Stationary Stochastic Processes Table of Formulas, 2016
 Stationary Stochastic Processes, 06 Stationary Stochastic Processes Table of Formulas, 06 Basics of probability theory The following is valid for probabilities: P(Ω), where Ω is all possible outcomes 0
Stationary Stochastic Processes, 06 Stationary Stochastic Processes Table of Formulas, 06 Basics of probability theory The following is valid for probabilities: P(Ω), where Ω is all possible outcomes 0
ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ
 ΗΜΥ ΔΙΑΚΡΙΤΗ ΑΝΑΛΥΣΗ ΚΑΙ ΔΟΜΕΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΗΜΥ Διακριτή Ανάλυση και Δομές Χειμερινό Εξάμηνο 6 Σειρά Ασκήσεων Ακέραιοι και Διαίρεση, Πρώτοι Αριθμοί, GCD/LC, Συστήματα
ΗΜΥ ΔΙΑΚΡΙΤΗ ΑΝΑΛΥΣΗ ΚΑΙ ΔΟΜΕΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΗΜΥ Διακριτή Ανάλυση και Δομές Χειμερινό Εξάμηνο 6 Σειρά Ασκήσεων Ακέραιοι και Διαίρεση, Πρώτοι Αριθμοί, GCD/LC, Συστήματα
LAPLACE TYPE PROBLEMS FOR A DELONE LATTICE AND NON-UNIFORM DISTRIBUTIONS
 Dedicted to Professor Octv Onicescu, founder of the Buchrest School of Probbility LAPLACE TYPE PROBLEMS FOR A DELONE LATTICE AND NON-UNIFORM DISTRIBUTIONS G CARISTI nd M STOKA Communicted by Mrius Iosifescu
Dedicted to Professor Octv Onicescu, founder of the Buchrest School of Probbility LAPLACE TYPE PROBLEMS FOR A DELONE LATTICE AND NON-UNIFORM DISTRIBUTIONS G CARISTI nd M STOKA Communicted by Mrius Iosifescu
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Quadratic Expressions
 Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
1. If log x 2 y 2 = a, then dy / dx = x 2 + y 2 1] xy 2] y / x. 3] x / y 4] none of these
![1. If log x 2 y 2 = a, then dy / dx = x 2 + y 2 1] xy 2] y / x. 3] x / y 4] none of these 1. If log x 2 y 2 = a, then dy / dx = x 2 + y 2 1] xy 2] y / x. 3] x / y 4] none of these](/thumbs/52/30390275.jpg) 1. If log x 2 y 2 = a, then dy / dx = x 2 + y 2 1] xy 2] y / x 3] x / y 4] none of these 1. If log x 2 y 2 = a, then x 2 + y 2 Solution : Take y /x = k y = k x dy/dx = k dy/dx = y / x Answer : 2] y / x
1. If log x 2 y 2 = a, then dy / dx = x 2 + y 2 1] xy 2] y / x 3] x / y 4] none of these 1. If log x 2 y 2 = a, then x 2 + y 2 Solution : Take y /x = k y = k x dy/dx = k dy/dx = y / x Answer : 2] y / x
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
SPECIAL FUNCTIONS and POLYNOMIALS
 SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
If ABC is any oblique triangle with sides a, b, and c, the following equations are valid. 2bc. (a) a 2 b 2 c 2 2bc cos A or cos A b2 c 2 a 2.
 etion 6. Lw of osines 59 etion 6. Lw of osines If is ny oblique tringle with sides, b, nd, the following equtions re vlid. () b b os or os b b (b) b os or os b () b b os or os b b You should be ble to
etion 6. Lw of osines 59 etion 6. Lw of osines If is ny oblique tringle with sides, b, nd, the following equtions re vlid. () b b os or os b b (b) b os or os b () b b os or os b b You should be ble to
ON NEGATIVE MOMENTS OF CERTAIN DISCRETE DISTRIBUTIONS
 Pa J Statist 2009 Vol 25(2), 135-140 ON NEGTIVE MOMENTS OF CERTIN DISCRETE DISTRIBUTIONS Masood nwar 1 and Munir hmad 2 1 Department of Maematics, COMSTS Institute of Information Technology, Islamabad,
Pa J Statist 2009 Vol 25(2), 135-140 ON NEGTIVE MOMENTS OF CERTIN DISCRETE DISTRIBUTIONS Masood nwar 1 and Munir hmad 2 1 Department of Maematics, COMSTS Institute of Information Technology, Islamabad,
The tables gives expressions for VaR p (X) and ES p (X) when X is an absolutely continuous random variable specified by the stated pdf and cdf.
 The tbles gies eressions for VR X nd ES X when X is n bsolutely continuous rndom rible secified by the stted df nd cdf. Eonentil Kumrswmy eonentil df cdf VR X ES X e b e e e b e e b /b / /b / Eonentited
The tbles gies eressions for VR X nd ES X when X is n bsolutely continuous rndom rible secified by the stted df nd cdf. Eonentil Kumrswmy eonentil df cdf VR X ES X e b e e e b e e b /b / /b / Eonentited
Homomorphism of Intuitionistic Fuzzy Groups
 International Mathematical Forum, Vol. 6, 20, no. 64, 369-378 Homomorphism o Intuitionistic Fuzz Groups P. K. Sharma Department o Mathematics, D..V. College Jalandhar Cit, Punjab, India pksharma@davjalandhar.com
International Mathematical Forum, Vol. 6, 20, no. 64, 369-378 Homomorphism o Intuitionistic Fuzz Groups P. K. Sharma Department o Mathematics, D..V. College Jalandhar Cit, Punjab, India pksharma@davjalandhar.com
F19MC2 Solutions 9 Complex Analysis
 F9MC Solutions 9 Complex Analysis. (i) Let f(z) = eaz +z. Then f is ifferentiable except at z = ±i an so by Cauchy s Resiue Theorem e az z = πi[res(f,i)+res(f, i)]. +z C(,) Since + has zeros of orer at
F9MC Solutions 9 Complex Analysis. (i) Let f(z) = eaz +z. Then f is ifferentiable except at z = ±i an so by Cauchy s Resiue Theorem e az z = πi[res(f,i)+res(f, i)]. +z C(,) Since + has zeros of orer at
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Exercise 2: The form of the generalized likelihood ratio
 Stats 2 Winter 28 Homework 9: Solutions Due Friday, March 6 Exercise 2: The form of the generalized likelihood ratio We want to test H : θ Θ against H : θ Θ, and compare the two following rules of rejection:
Stats 2 Winter 28 Homework 9: Solutions Due Friday, March 6 Exercise 2: The form of the generalized likelihood ratio We want to test H : θ Θ against H : θ Θ, and compare the two following rules of rejection:
Theorem 8 Let φ be the most powerful size α test of H
 Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
12. Radon-Nikodym Theorem
 Tutorial 12: Radon-Nikodym Theorem 1 12. Radon-Nikodym Theorem In the following, (Ω, F) is an arbitrary measurable space. Definition 96 Let μ and ν be two (possibly complex) measures on (Ω, F). We say
Tutorial 12: Radon-Nikodym Theorem 1 12. Radon-Nikodym Theorem In the following, (Ω, F) is an arbitrary measurable space. Definition 96 Let μ and ν be two (possibly complex) measures on (Ω, F). We say
Homomorphism in Intuitionistic Fuzzy Automata
 International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
( )( ) La Salle College Form Six Mock Examination 2013 Mathematics Compulsory Part Paper 2 Solution
 L Slle ollege Form Si Mock Emintion 0 Mthemtics ompulsor Prt Pper Solution 6 D 6 D 6 6 D D 7 D 7 7 7 8 8 8 8 D 9 9 D 9 D 9 D 5 0 5 0 5 0 5 0 D 5. = + + = + = = = + = =. D The selling price = $ ( 5 + 00)
L Slle ollege Form Si Mock Emintion 0 Mthemtics ompulsor Prt Pper Solution 6 D 6 D 6 6 D D 7 D 7 7 7 8 8 8 8 D 9 9 D 9 D 9 D 5 0 5 0 5 0 5 0 D 5. = + + = + = = = + = =. D The selling price = $ ( 5 + 00)
Errata for Introduction to Statistical Signal Processing by R.M. Gray and L.D. Davisson
 Errt for Introduction to Sttisticl Signl Processing by R.M. Gry nd L.D. Dvisson Errors not cught in the corrected 2 edition re noted with n sterisk *. Updted October 2, 24 hnks to In Lee, Michel Gutmnn,
Errt for Introduction to Sttisticl Signl Processing by R.M. Gry nd L.D. Dvisson Errors not cught in the corrected 2 edition re noted with n sterisk *. Updted October 2, 24 hnks to In Lee, Michel Gutmnn,
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
An Introduction to Signal Detection and Estimation - Second Edition Chapter II: Selected Solutions
 An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
INTEGRAL INEQUALITY REGARDING r-convex AND
 J Koren Mth Soc 47, No, pp 373 383 DOI 434/JKMS47373 INTEGRAL INEQUALITY REGARDING r-convex AND r-concave FUNCTIONS WdAllh T Sulimn Astrct New integrl inequlities concerning r-conve nd r-concve functions
J Koren Mth Soc 47, No, pp 373 383 DOI 434/JKMS47373 INTEGRAL INEQUALITY REGARDING r-convex AND r-concave FUNCTIONS WdAllh T Sulimn Astrct New integrl inequlities concerning r-conve nd r-concve functions
Gaussian related distributions
 Gaussian related distributions Santiago Aja-Fernández June 19, 009 1 Gaussian related distributions 1. Gaussian: ormal PDF: MGF: Main moments:. Rayleigh: PDF: MGF: Raw moments: Main moments: px = 1 σ π
Gaussian related distributions Santiago Aja-Fernández June 19, 009 1 Gaussian related distributions 1. Gaussian: ormal PDF: MGF: Main moments:. Rayleigh: PDF: MGF: Raw moments: Main moments: px = 1 σ π
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
SOME PROPERTIES OF FUZZY REAL NUMBERS
 Sahand Communications in Mathematical Analysis (SCMA) Vol. 3 No. 1 (2016), 21-27 http://scma.maragheh.ac.ir SOME PROPERTIES OF FUZZY REAL NUMBERS BAYAZ DARABY 1 AND JAVAD JAFARI 2 Abstract. In the mathematical
Sahand Communications in Mathematical Analysis (SCMA) Vol. 3 No. 1 (2016), 21-27 http://scma.maragheh.ac.ir SOME PROPERTIES OF FUZZY REAL NUMBERS BAYAZ DARABY 1 AND JAVAD JAFARI 2 Abstract. In the mathematical
Chapter 7b, Torsion. τ = 0. τ T. T τ D'' A'' C'' B'' 180 -rotation around axis C'' B'' D'' A'' A'' D'' 180 -rotation upside-down C'' B''
 Chpter 7b, orsion τ τ τ ' D' B' C' '' B'' B'' D'' C'' 18 -rottion round xis C'' B'' '' D'' C'' '' 18 -rottion upside-down D'' stright lines in the cross section (cross sectionl projection) remin stright
Chpter 7b, orsion τ τ τ ' D' B' C' '' B'' B'' D'' C'' 18 -rottion round xis C'' B'' '' D'' C'' '' 18 -rottion upside-down D'' stright lines in the cross section (cross sectionl projection) remin stright
ON CONVERGENCE THEOREMS FOR FUZZY HENSTOCK INTEGRALS
 Irnin Journl of Fuzzy Systems Vol. 14, No. 6, 2017 pp. 87-102 87 ON CONVERGENCE THEOREMS FOR FUZZY HENSTOCK INTEGRALS B. M. UZZAL AFSAN Abstrct. The min purpose of this pper is to estblish different types
Irnin Journl of Fuzzy Systems Vol. 14, No. 6, 2017 pp. 87-102 87 ON CONVERGENCE THEOREMS FOR FUZZY HENSTOCK INTEGRALS B. M. UZZAL AFSAN Abstrct. The min purpose of this pper is to estblish different types
Κεφάλαιο 1 Πραγματικοί Αριθμοί 1.1 Σύνολα
 x + = 0 N = {,, 3....}, Z Q, b, b N c, d c, d N + b = c, b = d. N = =. < > P n P (n) P () n = P (n) P (n + ) n n + P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + ) P (n) n m P n P (n) P () P (), P (),...,
x + = 0 N = {,, 3....}, Z Q, b, b N c, d c, d N + b = c, b = d. N = =. < > P n P (n) P () n = P (n) P (n + ) n n + P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + ) P (n) n m P n P (n) P () P (), P (),...,
Solution to Review Problems for Midterm III
 Solution to Review Problems for Mierm III Mierm III: Friday, November 19 in class Topics:.8-.11, 4.1,4. 1. Find the derivative of the following functions and simplify your answers. (a) x(ln(4x)) +ln(5
Solution to Review Problems for Mierm III Mierm III: Friday, November 19 in class Topics:.8-.11, 4.1,4. 1. Find the derivative of the following functions and simplify your answers. (a) x(ln(4x)) +ln(5
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Limit theorems under sublinear expectations and probabilities
 Limit theorems under sublinear expectations and probabilities Xinpeng LI Shandong University & Université Paris 1 Young Researchers Meeting on BSDEs, Numerics and Finance 4 July, Oxford 1 / 25 Outline
Limit theorems under sublinear expectations and probabilities Xinpeng LI Shandong University & Université Paris 1 Young Researchers Meeting on BSDEs, Numerics and Finance 4 July, Oxford 1 / 25 Outline
Elements of Information Theory
 Elements of Information Theory Model of Digital Communications System A Logarithmic Measure for Information Mutual Information Units of Information Self-Information News... Example Information Measure
Elements of Information Theory Model of Digital Communications System A Logarithmic Measure for Information Mutual Information Units of Information Self-Information News... Example Information Measure
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 5: Numerical Integration
 Lecture notes on Vritionl nd Approximte Metods in Applied Mtemtics - A Peirce UBC 1 Lecture 5: Numericl Integrtion Compiled 15 September 1 In tis lecture we introduce tecniques for numericl integrtion,
Lecture notes on Vritionl nd Approximte Metods in Applied Mtemtics - A Peirce UBC 1 Lecture 5: Numericl Integrtion Compiled 15 September 1 In tis lecture we introduce tecniques for numericl integrtion,
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
STAT200C: Hypothesis Testing
 STAT200C: Hypothesis Testing Zhaoxia Yu Spring 2017 Some Definitions A hypothesis is a statement about a population parameter. The two complementary hypotheses in a hypothesis testing are the null hypothesis
STAT200C: Hypothesis Testing Zhaoxia Yu Spring 2017 Some Definitions A hypothesis is a statement about a population parameter. The two complementary hypotheses in a hypothesis testing are the null hypothesis
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
1. (a) (5 points) Find the unit tangent and unit normal vectors T and N to the curve. r(t) = 3cost, 4t, 3sint
 1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P, π, rt) cost, t, sint ). b) 5 points) Find curvature of the curve at the point P. Solution: a) r t) sint,,
1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P, π, rt) cost, t, sint ). b) 5 points) Find curvature of the curve at the point P. Solution: a) r t) sint,,
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Chapter 3: Ordinal Numbers
 Chapter 3: Ordinal Numbers There are two kinds of number.. Ordinal numbers (0th), st, 2nd, 3rd, 4th, 5th,..., ω, ω +,... ω2, ω2+,... ω 2... answers to the question What position is... in a sequence? What
Chapter 3: Ordinal Numbers There are two kinds of number.. Ordinal numbers (0th), st, 2nd, 3rd, 4th, 5th,..., ω, ω +,... ω2, ω2+,... ω 2... answers to the question What position is... in a sequence? What
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
A Bonus-Malus System as a Markov Set-Chain. Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics
 A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequality for metrics: Let (X, d) be a metric space and let x, y, z X.
 Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =
 Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
P AND P. P : actual probability. P : risk neutral probability. Realtionship: mutual absolute continuity P P. For example:
 (B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
(B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
HOMEWORK#1. t E(x) = 1 λ = (b) Find the median lifetime of a randomly selected light bulb. Answer:
 HOMEWORK# 52258 李亞晟 Eercise 2. The lifetime of light bulbs follows an eponential distribution with a hazard rate of. failures per hour of use (a) Find the mean lifetime of a randomly selected light bulb.
HOMEWORK# 52258 李亞晟 Eercise 2. The lifetime of light bulbs follows an eponential distribution with a hazard rate of. failures per hour of use (a) Find the mean lifetime of a randomly selected light bulb.
