ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ
|
|
|
- Ἥβη Καρράς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ Έννοιες που πρέπει να γνωρίζετε Ισορροπία φάσεων, εξίσωση Clauiu-Clapeyron Θέμα ασκήσεως Προσρόφηση ουσίας από αραιά διαλύματα. Προσδιορισμός ισόθερμων προσροφήσεως. Υπολογισμός ειδικής επιφάνειας στερεού. Θεωρία Σ ένα ετερογενές σύστημα από δύο φάσεις, π.χ. στερεού-αερίου. παρατηρείται στην επιφάνεια του στερεού μία αυξημένη συγκέντρωση αερίου οφειλόμενη στις ελκτικές δυνάμεις των ατόμων ή μορίων του στερεού. Η ιδιαίτερη αυτή φάση ονομάζεται προσροφημένη φάση και το φαινόμενο προσρόφηση. Εάν τα μόρια της προσροφημένης φάσης συνδέονται με τα μόρια της στερεάς επιφάνειας, που ονομάζεται προσροφητής, με ασθενείς ηλεκτρομαγνητικές δυνάμεις, το φαινόμενο χαρακτηρίζεται ως φυσική προσρόφηση, ενώ εάν συνδέονται με χημικό δεσμό, το φαινόμενο χαρακτηρίζεται ως χημική προσρόφηση. Στο κεφάλαιο αυτό θα αναφερθούμε στην φυσική προσρόφηση. Κατά την ισορροπία της προσροφημένης φάσεως με την αέρια (μη προσροφημένη) φάση ισχύει το κριτήριο ισορροπίας που είναι η ισότητα των χημικών δυναμικών του αερίου στις δύο φάσεις, δηλ. μ = μ g όπου ο δείκτης αφορά την προσροφημένη και g την αέρια φάση. Το χημικό δυναμικό της αέριας φάσης εκφράζεται ως συνάρτηση μ g (P,T), της δε προσροφημένης ως συνάρτηση μ (P,T,θ), όπου θ το ποσοστό της επιφάνειας που καταλαμβάνεται από προσροφημένο αέριο. Μεταβάλλοντας τις συνθήκες του πειράματος μία νέα κατάσταση ισορροπίας θα αποκατασταθεί. Στις φασικές αυτές μεταβολές ισχύει η εξίσωση Clauiu-Clapeyron: d ln P H (1) dt RT όπου ΔΗ η ισοστερική (δηλ. υπό σταθερό θ) ενθαλπία προσροφήσεως, δηλ. η μεταβολή της ενθαλπίας υπό σταθερό ποσοστό καλύψεως θ. Η προσρόφηση είναι εξώθερμη διεργασία, οπότε ΔH < 0. Από τις πειραματικές μετρήσεις της προσροφημένης συγκέντρωσης ουσίας και της αντίστοιχης συγκέντρωσης στην μη προσροφημένη φάση υπό σταθερή θερμοκρασία λαμβάνονται σχέσεις της μορφής V = f(p i ) στην περίπτωση αερίων, όπου V ο προσροφημένος όγκος και P i η πίεση ισορροπίας ή γενικά n = f(c i ) όπου n ο αριθμός των γραμμομορίων της προσροφημένης ουσίας ανά g προσροφητή και c i η συγκέντρωση της μη προσροφημένης ουσίας στην ισορροπία. Οι σχέσεις αυτές ονομάζονται ισόθερμες προσροφήσεως. Οι ισόθερμες που χρησιμοποιούνται ευρέως για μονομοριακές στιβάδες είναι του Langmuir και του Freundlich, ενώ για πολυστρωματικές προσροφήσεις των Brunauer, Emmet και Teller (BET). Ο Langmuir έδωσε την πρώτη μαθηματική έκφραση της ισοθέρμου με εφαρμογή της κινητικής θεωρίας η οποία στην απλή περίπτωση των αερίων δίνεται από την εξίσωση: n bp () 1 bp και γενικά: 10-1
2 n bci (3) 1 bci όπου n m ο αριθμός των προσροφημένων γραμμομορίων για τον σχηματισμό μονοστιβάδας ανά g προσροφητή και b σταθερά της εξισώσεως εξαρτώμενη από την φύση του αερίου και την θερμοκρασία. Η εξίσωση αυτή αποτελεί την ισόθερμο Langmuir που περιγράφει ικανοποιητικά μεγάλο αριθμό συστημάτων στερεού αερίου, αλλά εφαρμόζεται εξ ίσου καλά στην προσρόφηση ουσίας από διαλύματα. Το ποσοστό καλύψεως της επιφάνειας θ ισούται με το ποσοστό των προσροφηθέντων mol από το σύνολο των mol που αντιστοιχούν στην κορεσμένη μονοστιβάδα. Η εξαγωγή της σχέσης αυτής στηρίζεται σε μια σειρά παραδοχών όπως ότι: i. η ενέργεια προσροφήσεως είναι ίδια σ' όλα τα σημεία του προσροφητή, ii. κατά την προσρόφηση σχηματίζεται μονομοριακή στιβάδα, iii. η μη προσροφημένη φάση συμπεριφέρεται ιδανικά, iv. τα προσροφημένα μόρια δεν αλληλεπιδρούν μεταξύ τους. Για να διαπιστώσουμε την ισχύ της εξισώσεως Langmuir, η εξίσωση (3) μετασχηματίζεται στην: ci ci 1 (4) n b και ελέγχεται η γραμμικότητα της γραφικής παράστασης c i /n = f(c i ). Μία άλλη ισόθερμος που χρησιμοποιείται ευρέως είναι η ισόθερμος Freundlich που δίνεται από την εμπειρική σχέση : 1 n n kc i (5) όπου n ο αριθμός των γραμμομορίων της προσροφημένης ουσίας ανά g προσροφητή, c i η συγκέντρωση της μη προσροφημένης ουσίας στην ισορροπία και k, n σταθερές χαρακτηριστικές του συστήματος. Η σχέση αυτή γράφεται: 1 ln n ln k ln c i (6) n Από την γραφική παράσταση n = f(ln c i ), υπολογίζονται οι σταθερές n και k από την κλίση και την τεταγμένη επί την αρχή αντίστοιχα. Η εξίσωση Freundlich περιγράφει ικανοποιητικά την προσρόφηση από υδατικά διαλύματα. Από τις ισόθερμες προσροφήσεως προσδιορίζεται η ειδική επιφάνεια Α του στερεού (προσροφητή), δηλ. η επιφάνεια του προσροφητή ανά μονάδα μάζας που συνήθως εκφράζεται σε m /g. Εάν ένα μόριο καταλαμβάνει επιφάνεια σ, ο αριθμός των μορίων που μπορούν να προσροφηθούν σ' ένα στερεό με ειδική επιφάνεια Α σχηματίζοντας μία μονοστιβάδα είναι N Α n m = A/σ, δηλ. A N n A m (7) όπου n m ο αριθμός των προσροφημένων γραμμομορίων για τον σχηματισμό μονοστιβάδας ανά g προσροφητή και Ν ο αριθμός Avogadro (Ν Α = μόρια/mol). Η επιφάνεια που καταλαμβάνει 1 μόριο στην μονοστιβάδα προσεγγίζεται ικανοποιητικά αν δεχθούμε ότι είναι ίδια με την διατομή του μορίου στην συμπυκνωμένη φάση: M (8) N A όπου Μ το γραμμομοριακή μοριακή μάζα και ρ η πυκνότητα της συμπυκνωμένης φάσεως. Κατά την προσρόφηση ουσίας από διάλυμα σε στερεό προσροφητή, θεωρούμε ότι η προσρόφηση του διαλύτη είναι αμελητέα σε σχέση με την διαλυμένη ουσία. Οι εξισώσεις των ισοθέρμων που αναφέρθησαν ισχύουν και στην περίπτωση προσρόφησης από διάλυμα
3 Η ενέργεια προσροφήσεως υπολογίζεται συνήθως σε ποσοστό καλύψεως της επιφάνειας 0.5 (n = 0.5 n m ) από την γραφική παράσταση της εξισώσεως lnc i = f(1/t), όπως προκύπτει, από την ανάλογη προς την (1), εξίσωση: d ln ci H (9) dt RT Από την κλίση της εξισώσεως αυτής υπολογίζεται η ισοστερική ενθαλπία προσροφήσεως υπό σταθερό ποσοστό καλύψεως. c ln i H (10) 1 R T n0. 5 Πείραμα Προσρόφηση ασθενούς οργανικού οξέος σε ενεργό άνθρακα Στο πείραμα αυτό μελετάται η προσρόφηση ασθενούς οξέος σε ενεργό άνθρακα, από σειρά διαλυμάτων διαφόρων συγκεντρώσεων. Η πειραματική μέθοδος βασίζεται στον ογκομετρικό προσδιορισμό της συγκεντρώσεως του οξέος με πρότυπο διάλυμα NaOH 0.1 M πριν και μετά την προσρόφηση και υπολογισμό από αυτές της ποσότητας του προσροφηθέντος οξέος. Η πειραματική εργασία έχει ως ακολούθως: Από αρχικό διάλυμα 0.5 M οξέος (HCOOH, CH 3 COOH, C H 5 COOH) παρασκευάζονται διαλύματα συγκεντρώσεων 0.4, 0.3, 0., 0.1 και 0.05 M. Λαμβάνονται 100 ml από κάθε ένα από τα 5 διαλύματα που παρασκευάστηκαν και από το αρχικό (0.5 M) και φέρονται αντίστοιχα σε 6 στεγνές κωνικές φιάλες των 500 ml οι οποίες αριθμούνται. Ζυγίζονται 6 δείγματα ενεργού άνθρακα 1 g περίπου το καθένα με ακρίβεια 0.01 g σε αριθμημένα χαρτιά ζυγίσεως και προστίθενται αντίστοιχα στις αριθμημένες φιάλες. Η προσθήκη του ενεργού άνθρακα δεν γίνεται ταυτόχρονα σ' όλες τις φιάλες αλλά ανά 10 min, αρχίζοντας από το πυκνότερο, δηλ. αφήνεται τόσος χρόνος όσος περίπου θα απαιτηθεί αργότερα για την διήθηση του διαλύματος (με στόχο πάντα ο ενεργός άνθρακας να παραμένει σε επαφή με το διάλυμα τον ίδιο χρόνο σ' όλα τα διαλύματα). Είναι προφανές ότι εάν τα διαλύματα με τον ενεργό άνθρακα αφεθούν για πολύ χρόνο (συνήθως όλη την νύκτα) για να αποκατασταθεί ισορροπία, δεν υπάρχει θέμα στην ακρίβεια των μετρήσεων για μικρές διαφορές στους χρόνους αυτούς. Στο πλαίσιο της εργαστηριακής άσκησης, αν και οι ώρες δεν είναι αρκετές για την αποκατάσταση πλήρους ισορροπίας, είναι όμως ικανοποιητικές για την εξαγωγή συμπερασμάτων. Τα διαλύματα τοποθετούνται διαδοχικά σε υδατόλουτρο του οποίου η θερμοκρασία διατηρείται σταθερή στους 0 C (±0.1 C) ή άλλη που προτείνει ο υπεύθυνος της ασκήσεως και αναδεύονται επί h το κάθε ένα. Όπως αναφέρεται και προηγουμένως ο χρόνος προσρόφησης πρέπει να είναι ίδιος σ' όλα τα διαλύματα. Κατά την διάρκεια της παραμονής των φιαλών στο υδατόλουτρο για την ολοκλήρωση της προσρόφησης γίνονται οι τιτλοδοτήσεις των αρχικών διαλυμάτων σε δύο τουλάχιστον δείγματα όπως αναφέρεται παρακάτω. Ακολούθως τα διαλύματα ανασύρονται από το υδατόλουτρο με την σειρά που τοποθετήθηκαν διηθούνται και τα διηθήματα τιτλοδοτούνται όπως τα αρχικά διαλύματα. Τα πρώτα 1- ml του διηθήματος απορρίπτονται προς αποφυγή σφαλμάτων λόγω προσροφήσεως οξέος από το χαρτί. Επισημαίνεται ότι η λήψη του δείγματος για την τιτλοδότηση γίνεται μετά την ολοκλήρωση της διηθήσεως ώστε να εξασφαλίζεται η ομοιογένεια της συγκεντρώσεως στο διήθημα λόγω μικρής προσροφήσεως του οξέος από το διηθητικό χαρτί κατά τα πρώτα λεπτά της διηθήσεως. 10-3
4 Οι τιτλοδοτήσεις των διαλυμάτων πριν και μετά την προσρόφηση γίνονται με πρότυπο διάλυμα ΝaOH 0.1 M προσθέτοντας σταγόνες δείκτη φαινολοφθαλεΐνης. Τα δείγματα που λαμβάνονται από κάθε συγκέντρωση και ο τρόπος γραφής των μετρήσεων αναγράφονται στις πρώτες 5 στήλες του ακόλουθου πίνακα: Πίνακας Προσροφημένη ουσία : Θερμοκρασία : c β V δείγμα V α V τ V α -V τ c i n c i /n lnc i lnn (mol/l) (g) (ml) (ml) (ml) (ml) (mol/l) (mol/g) (g/l) β: ζυγισθείσα ποσότητα ενεργού άνθρακα V α : όγκος διαλύματος NaOH 0.1 M που καταναλώθηκε για την τιτλοδότηση του αρχικού διαλύματος V τ : όγκος διαλύματος NaOH 0.1 M που καταναλώθηκε για την τιτλοδότηση του διαλύματος μετά την διήθηση (προσρόφηση) Οι πυκνότητες των οξέων που χρησιμοποιούνται στο εργαστήριο είναι: ρ HCOOH = 1.00 g/cm 3, ρ CH3 COOH = g/cm 3, ρ C H 5 COOH = g/cm 3. Αποτελέσματα-Υπολογισμοί Υπολογίζεται η συγκέντρωση του οξέος c i στην ισορροπία προσροφήσεως σε mol/l από την σχέση c i = V τ /V δειγμ 0.1 M και τα γραμμομόρια του οξέος που προσροφήθηκαν (ανά 1 g ενεργού άνθρακα) από την σχέση: V V mol 100 ml n 0.1 V 1000 ml Οι μετρήσεις και οι υπολογιζόμενες ποσότητες τοποθετούνται στον πίνακα. Σχεδιάζεται η γραφική παράσταση της ισόθερμης προσροφήσεως, n = f(c i ). Η μορφή που θα έχουν οι ισόθερμες φαίνεται στην επόμενη σελίδα. Σημειώστε ότι θα πρέπει να διέρχονται από το σημείο (0,0). Διερευνάται εάν η ισόθερμη Freundlich ή Langmuir περιγράφει ικανοποιητικότερα το σύστημα δηλ. ελέγχεται η γραμμικότητα των συναρτήσεων lnn = f(lnc i ) και c i /n = f(c i ). Τα υπολογιζόμενα μεγέθη αναγράφονται επίσης στον πίνακα. Υπολογίζεται η κλίση και η τεταγμένη επί την αρχή της συναρτήσεως lnn = f(lnc i ) και από αυτές οι σταθερές της εξισώσεως Freundlich. Επίσης υπολογίζονται η κλίση και η τεταγμένη επί την αρχή της συναρτήσεως c i /n = f(c i ) και από αυτές ο αριθμός των γραμμομορίων που καταλαμβάνουν μία μονομοριακή στιβάδα ανά g προσροφητή n m και η σταθερά b της εξισώσεως Langmuir. Υπολογίζεται η ειδική επιφάνεια Α του ενεργού άνθρακα, σε m /g,από την σχέση (7). Εάν το πείραμα πραγματοποιηθεί, κατόπιν υποδείξεως του υπευθύνου, σε δύο ή τρεις θερμοκρασίες, υπολογίζεται η ισοστερική ενθαλπία προσροφήσεως από την γραφική παράσταση της lnc i = f(1/t) για δεδομένο ποσοστό καλύψεως (θ = 0.5). 10-4
5 Παράδείγμα προσαρμογής των μετρήσεων σε ισόθερμες Langmuir και Freundlich. 10-5
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις Άσκηση 10: Φαινόμενα προσροφήσεως Προσρόφηση ουσίας από διαλύματα Βασιλική Χαβρεδάκη Τμήμα Χημείας 1. Θεωρία... 3 2. Μετρήσεις... 5 3. Επεξεργασία Μετρήσεων... 6 Σελίδα
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις Άσκηση 10: Φαινόμενα προσροφήσεως Προσρόφηση ουσίας από διαλύματα Βασιλική Χαβρεδάκη Τμήμα Χημείας 1. Θεωρία... 3 2. Μετρήσεις... 5 3. Επεξεργασία Μετρήσεων... 6 Σελίδα
2). i = n i - n i - n i (2) 9-2
 ΕΠΙΦΑΝΕΙΑΚΗ ΤΑΣΗ ΙΑΛΥΜΑΤΩΝ Έννοιες που πρέπει να γνωρίζετε: Εξίσωση Gbbs-Duhem, χηµικό δυναµικό συστατικού διαλύµατος Θέµα ασκήσεως: Μελέτη της εξάρτησης της επιφανειακής τάσης διαλυµάτων από την συγκέντρωση,
ΕΠΙΦΑΝΕΙΑΚΗ ΤΑΣΗ ΙΑΛΥΜΑΤΩΝ Έννοιες που πρέπει να γνωρίζετε: Εξίσωση Gbbs-Duhem, χηµικό δυναµικό συστατικού διαλύµατος Θέµα ασκήσεως: Μελέτη της εξάρτησης της επιφανειακής τάσης διαλυµάτων από την συγκέντρωση,
ΦΥΣΙΚΗ ΧΗΜΕΙΑ ΙΙΙ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΕΠΙΔΡΑΣΗ ΘΕΡΜΟΚΡΑΣΙΑΣ ΣΤΗ ΣΤΑΘΕΡΑ ΤΑΧΥΤΗΤΑΣ ΑΝΤΙΔΡΑΣΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΟΧΗΜΕΙΑΣ Γραφείο 211 Επίκουρος Καθηγητής: Δ. Τσιπλακίδης Τηλ.: 2310 997766 e mail: dtsiplak@chem.auth.gr url:
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΟΧΗΜΕΙΑΣ Γραφείο 211 Επίκουρος Καθηγητής: Δ. Τσιπλακίδης Τηλ.: 2310 997766 e mail: dtsiplak@chem.auth.gr url:
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2018 Β ΦΑΣΗ ΧΗΜΕΙΑ
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ Ημερομηνία: Τετάρτη 11 Απριλίου 2018 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α1. Η σωστή τετράδα κβαντικών αριθμών για το μονήρες
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ Ημερομηνία: Τετάρτη 11 Απριλίου 2018 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α1. Η σωστή τετράδα κβαντικών αριθμών για το μονήρες
Στόχοι της εργαστηριακής άσκησης
 ΕΡΓΑΣΤΗΡΙΑΚΑ ΚΕΝΤΡΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2013-2014 Τοπικός διαγωνισμός στη Χημεία Ονόματα των μαθητών της ομάδας: 1) 2) 3) Στόχοι της εργαστηριακής
ΕΡΓΑΣΤΗΡΙΑΚΑ ΚΕΝΤΡΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2013-2014 Τοπικός διαγωνισμός στη Χημεία Ονόματα των μαθητών της ομάδας: 1) 2) 3) Στόχοι της εργαστηριακής
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 9: Επιφανειακή τάση διαλυμάτων Βασιλική Χαβρεδάκη Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 7 3. Επεξεργασία Μετρήσεων... 7 Σελίδα 1. Θεωρία Η επιφάνεια ενός
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 9: Επιφανειακή τάση διαλυμάτων Βασιλική Χαβρεδάκη Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 7 3. Επεξεργασία Μετρήσεων... 7 Σελίδα 1. Θεωρία Η επιφάνεια ενός
Προσδιορισμός της Γραμμομοριακής Μάζας ουσίας με την μέθοδο της Κρυοσκοπίας
 Προσδιορισμός της Γραμμομοριακής Μάζας ουσίας με την μέθοδο της Κρυοσκοπίας ΙΣΟΡΡΟΠΙΑΙ ΙΔΑΝΙΚΟΥ ΔΙΑΛΥΜΑΤΟΣ ΜΕΘ ΕΤΕΡΑΣ ΦΑΣΕΩΣ ΕΚ ΚΑΘΑΡΟΥ ΔΙΑΛΥΤΟΥ Προσδιορισμός μοριακού βάρους κρυοσκοπικώς Γραμμομοριακή
Προσδιορισμός της Γραμμομοριακής Μάζας ουσίας με την μέθοδο της Κρυοσκοπίας ΙΣΟΡΡΟΠΙΑΙ ΙΔΑΝΙΚΟΥ ΔΙΑΛΥΜΑΤΟΣ ΜΕΘ ΕΤΕΡΑΣ ΦΑΣΕΩΣ ΕΚ ΚΑΘΑΡΟΥ ΔΙΑΛΥΤΟΥ Προσδιορισμός μοριακού βάρους κρυοσκοπικώς Γραμμομοριακή
Διάλυμα καλείται κάθε ομογενές σύστημα, το οποίο αποτελείται από δύο ή περισσότερες χημικές ουσίες, και έχει την ίδια σύσταση σε όλη του τη μάζα.
 1. ΔΙΑΛΥΜΑ Διάλυμα καλείται κάθε ομογενές σύστημα, το οποίο αποτελείται από δύο ή περισσότερες χημικές ουσίες, και έχει την ίδια σύσταση σε όλη του τη μάζα. Ετερογενές σύστημα καλείται αυτό, το οποίο αποτελείται
1. ΔΙΑΛΥΜΑ Διάλυμα καλείται κάθε ομογενές σύστημα, το οποίο αποτελείται από δύο ή περισσότερες χημικές ουσίες, και έχει την ίδια σύσταση σε όλη του τη μάζα. Ετερογενές σύστημα καλείται αυτό, το οποίο αποτελείται
CH COOC H H O CH COOH C H OH
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΤΟΜΕΑΣ ΦΥΣΙΚΟΧΗΜΕΙΑΣ ΠΕΙΡΑΜΑ 2 ΧΗΜΙΚΗΣ ΚΙΝΗΤΙΚΗΣ (ΧΚ2) ΜΑΘΗΜΑ: ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΟΧΗΜΕΙΑΣ ΙΙ ΑΚΑΔ. ΕΤΟΣ: 2013-14 ΤΜΗΜAΤΑ TΡΙΤΗΣ ΚΑΙ ΤΕΤΑΡΤΗΣ Τίτλος Πειράματος: ΚΙΝΗΤΙΚΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΤΟΜΕΑΣ ΦΥΣΙΚΟΧΗΜΕΙΑΣ ΠΕΙΡΑΜΑ 2 ΧΗΜΙΚΗΣ ΚΙΝΗΤΙΚΗΣ (ΧΚ2) ΜΑΘΗΜΑ: ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΟΧΗΜΕΙΑΣ ΙΙ ΑΚΑΔ. ΕΤΟΣ: 2013-14 ΤΜΗΜAΤΑ TΡΙΤΗΣ ΚΑΙ ΤΕΤΑΡΤΗΣ Τίτλος Πειράματος: ΚΙΝΗΤΙΚΗ
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 4: Μερικός γραμμομοριακός όγκος Αθανάσιος Τσεκούρας Τμήμα Χημείας . Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 4. Τελικά αποτελέσματα... 7 Σελίδα
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 4: Μερικός γραμμομοριακός όγκος Αθανάσιος Τσεκούρας Τμήμα Χημείας . Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 4. Τελικά αποτελέσματα... 7 Σελίδα
Ατομική μονάδα μάζας (amu) ορίζεται ως το 1/12 της μάζας του ατόμου του άνθρακα 12 6 C.
 4.1 Βασικές έννοιες Ατομική μονάδα μάζας (amu) ορίζεται ως το 1/12 της μάζας του ατόμου του άνθρακα 12 6 C. Σχετική ατομική μάζα ή ατομικό βάρος λέγεται ο αριθμός που δείχνει πόσες φορές είναι μεγαλύτερη
4.1 Βασικές έννοιες Ατομική μονάδα μάζας (amu) ορίζεται ως το 1/12 της μάζας του ατόμου του άνθρακα 12 6 C. Σχετική ατομική μάζα ή ατομικό βάρος λέγεται ο αριθμός που δείχνει πόσες φορές είναι μεγαλύτερη
ΧΗΜΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ I (Ar, Mr, mol, N A, V m, νόμοι αερίων)
 ΧΗΜΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ I (Ar, Mr, mol, N A, V m, νόμοι αερίων) 1. Να εξηγήσετε ποιες από τις παρακάτω προτάσεις είναι σωστές. i. H σχετική ατομική μάζα μετριέται σε γραμμάρια. ii. H σχετική ατομική μάζα είναι
ΧΗΜΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ I (Ar, Mr, mol, N A, V m, νόμοι αερίων) 1. Να εξηγήσετε ποιες από τις παρακάτω προτάσεις είναι σωστές. i. H σχετική ατομική μάζα μετριέται σε γραμμάρια. ii. H σχετική ατομική μάζα είναι
1.1 Να επιλέξετε τη σωστή απάντηση σε καθεμιά από τις επόμενες ερωτήσεις:
 ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 21-4-2016 ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΔΙΑΡΚΕΙΑ 3 ΩΡΕΣ ΘΕΜΑ 1 1.1 Να επιλέξετε τη σωστή απάντηση σε καθεμιά από τις επόμενες ερωτήσεις: α. Σε κάθε εξώθερμη αντίδραση
ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 21-4-2016 ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΔΙΑΡΚΕΙΑ 3 ΩΡΕΣ ΘΕΜΑ 1 1.1 Να επιλέξετε τη σωστή απάντηση σε καθεμιά από τις επόμενες ερωτήσεις: α. Σε κάθε εξώθερμη αντίδραση
ΚΕΦΑΛΑΙΟ 3 Ο ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΤΩΝ ΙΔΑΝΙΚΩΝ ΑΕΡΙΩΝ
 Σχολικό Έτος 016-017 67 ΚΕΦΑΛΑΙΟ Ο ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΤΩΝ ΙΔΑΝΙΚΩΝ ΑΕΡΙΩΝ Α. ΕΙΣΑΓΩΓΗ ΣΤΑ ΑΕΡΙΑ 1. Σχετικές Ατομικές και Μοριακές Μάζες Σχετική Ατομική Μάζα (Α r) του ατόμου ενός στοιχείου, ονομάζεται ο αριθμός
Σχολικό Έτος 016-017 67 ΚΕΦΑΛΑΙΟ Ο ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΤΩΝ ΙΔΑΝΙΚΩΝ ΑΕΡΙΩΝ Α. ΕΙΣΑΓΩΓΗ ΣΤΑ ΑΕΡΙΑ 1. Σχετικές Ατομικές και Μοριακές Μάζες Σχετική Ατομική Μάζα (Α r) του ατόμου ενός στοιχείου, ονομάζεται ο αριθμός
ΦΥΣΙΚΟΧΗΜΕΙΑ Ι Ακαδ. έτος Εαρινό εξάμηνο Δ Σειρά Ασκήσεων
 Παράδοση : Παρασκευή 20 Μαΐου 2005 Κεφάλαιο : Επιφανειακή τάση ΦΥΣΙΚΟΧΗΜΕΙΑ Ι Ακαδ. έτος 2004-05 Εαρινό εξάμηνο Δ Σειρά Ασκήσεων. Δύο παράλληλες γυάλινες πλάκες εμβαπτίζονται σε δοχείο με νερό στους 20
Παράδοση : Παρασκευή 20 Μαΐου 2005 Κεφάλαιο : Επιφανειακή τάση ΦΥΣΙΚΟΧΗΜΕΙΑ Ι Ακαδ. έτος 2004-05 Εαρινό εξάμηνο Δ Σειρά Ασκήσεων. Δύο παράλληλες γυάλινες πλάκες εμβαπτίζονται σε δοχείο με νερό στους 20
ΣΧΟΛΕΙΟ: ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ. ΧΡΟΝΟΣ: 2,5 ώρες ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΧΡΗΣΙΜΑ ΔΕΔΟΜΕΝΑ
 ΣΧΟΛΕΙΟ: ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2014 2015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΚΑΤΕΥΘΥΝΣΗΣ ΗΜΕΡΟΜΗΝΙΑ : ΧΡΟΝΟΣ: 2,5 ώρες ΤΑΞΗ: Β Ενιαίου Λυκείου ΩΡΑ ΕΝΑΡΞΗΣ:. ΟΝΟΜΑΤΕΠΩΝΥΜΟ: Τμήμα: Aρ.:.
ΣΧΟΛΕΙΟ: ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2014 2015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΚΑΤΕΥΘΥΝΣΗΣ ΗΜΕΡΟΜΗΝΙΑ : ΧΡΟΝΟΣ: 2,5 ώρες ΤΑΞΗ: Β Ενιαίου Λυκείου ΩΡΑ ΕΝΑΡΞΗΣ:. ΟΝΟΜΑΤΕΠΩΝΥΜΟ: Τμήμα: Aρ.:.
ΣΧΟΛΕΙΟ: ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ. ΧΡΟΝΟΣ: 2,5 ώρες ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΧΡΗΣΙΜΑ ΔΕΔΟΜΕΝΑ
 ΣΧΟΛΕΙΟ: ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2014 2015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΚΑΤΕΥΘΥΝΣΗΣ ΗΜΕΡΟΜΗΝΙΑ : ΧΡΟΝΟΣ: 2,5 ώρες ΤΑΞΗ: Β Ενιαίου Λυκείου ΩΡΑ ΕΝΑΡΞΗΣ:. ΟΝΟΜΑΤΕΠΩΝΥΜΟ: Τμήμα: Aρ.:.
ΣΧΟΛΕΙΟ: ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ: 2014 2015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ - ΙΟΥΝΙΟΥ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΚΑΤΕΥΘΥΝΣΗΣ ΗΜΕΡΟΜΗΝΙΑ : ΧΡΟΝΟΣ: 2,5 ώρες ΤΑΞΗ: Β Ενιαίου Λυκείου ΩΡΑ ΕΝΑΡΞΗΣ:. ΟΝΟΜΑΤΕΠΩΝΥΜΟ: Τμήμα: Aρ.:.
ΠΑΓΚΥΠΡΙΑ ΕΝΩΣΗ ΕΠΙΣΤΗΜΟΝΩΝ ΧΗΜΙΚΩΝ ΔΙΑΓΩΝΙΣΜΟΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΤΗ ΔΙΕΘΝΗ ΟΛΥΜΠΙΑΔΑ ΧΗΜΕΙΑΣ 2012 Γ ΦΑΣΗ (ΕΡΓΑΣΤΗΡΙΑΚΗ ΕΞΕΤΑΣΗ)
 Ονοματεπώνυμο: Αριθμός Εργ. Θέσης:. Σχολείο: Ημερομ. Γέννησης: Αριθμός Ταυτότητας: Διεύθυνση:..τηλ.. ΠΑΓΚΥΠΡΙΑ ΕΝΩΣΗ ΕΠΙΣΤΗΜΟΝΩΝ ΧΗΜΙΚΩΝ ΔΙΑΓΩΝΙΣΜΟΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΤΗ ΔΙΕΘΝΗ ΟΛΥΜΠΙΑΔΑ ΧΗΜΕΙΑΣ 2012 Γ ΦΑΣΗ
Ονοματεπώνυμο: Αριθμός Εργ. Θέσης:. Σχολείο: Ημερομ. Γέννησης: Αριθμός Ταυτότητας: Διεύθυνση:..τηλ.. ΠΑΓΚΥΠΡΙΑ ΕΝΩΣΗ ΕΠΙΣΤΗΜΟΝΩΝ ΧΗΜΙΚΩΝ ΔΙΑΓΩΝΙΣΜΟΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΤΗ ΔΙΕΘΝΗ ΟΛΥΜΠΙΑΔΑ ΧΗΜΕΙΑΣ 2012 Γ ΦΑΣΗ
Ονοματεπώνυμο: Χημεία Γ Λυκείου Υλη: Χημική Κινητική Χημική Ισορροπία Ιοντισμός (K a K b ) Επιμέλεια διαγωνίσματος: Τσικριτζή Αθανασία Αξιολόγηση :
 Ονοματεπώνυμο: Μάθημα: Χημεία Γ Λυκείου Υλη: Χημική Κινητική Χημική Ισορροπία Ιοντισμός (K a K b ) Επιμέλεια διαγωνίσματος: Τσικριτζή Αθανασία Αξιολόγηση : Θέμα Α Να επιλέξετε τη σωστή απάντηση σε καθεμία
Ονοματεπώνυμο: Μάθημα: Χημεία Γ Λυκείου Υλη: Χημική Κινητική Χημική Ισορροπία Ιοντισμός (K a K b ) Επιμέλεια διαγωνίσματος: Τσικριτζή Αθανασία Αξιολόγηση : Θέμα Α Να επιλέξετε τη σωστή απάντηση σε καθεμία
Γενική Χημεία. Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής
 Γενική Χημεία Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής Πολυτεχνείο Κρήτης Τμήμα Μηχανικών Περιβάλλοντος Γραφείο Κ2.125, τηλ.: 28210-37772 e-mail:nikosxek@gmail.com Περιεχόμενα Διαλύματα Γραμμομοριακή
Γενική Χημεία Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής Πολυτεχνείο Κρήτης Τμήμα Μηχανικών Περιβάλλοντος Γραφείο Κ2.125, τηλ.: 28210-37772 e-mail:nikosxek@gmail.com Περιεχόμενα Διαλύματα Γραμμομοριακή
Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών Τοπικός διαγωνισμός στη Φυσική και Χημεία Στόχοι της εργαστηριακής άσκησης
 ΕΡΓΑΣΤΗΡΙΑΚΑ ΚΕΝΤΡΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2012-13 Τοπικός διαγωνισμός στη Φυσική και Χημεία 08-12-2012 Σχολείο: Ονόματα των μαθητών της ομάδας: 1) 2)
ΕΡΓΑΣΤΗΡΙΑΚΑ ΚΕΝΤΡΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2012-13 Τοπικός διαγωνισμός στη Φυσική και Χημεία 08-12-2012 Σχολείο: Ονόματα των μαθητών της ομάδας: 1) 2)
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 7: Κατανομή ουσίας μεταξύ δύο διαλυτών και προσδιορισμός σταθεράς ισορροπίας αντιδράσεως Βασιλική Χαβρεδάκη Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 5 3. Επεξεργασία
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 7: Κατανομή ουσίας μεταξύ δύο διαλυτών και προσδιορισμός σταθεράς ισορροπίας αντιδράσεως Βασιλική Χαβρεδάκη Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 5 3. Επεξεργασία
Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2014 Τοπικός διαγωνισμός στη Χημεία Ονοματεπώνυμο μαθητών. Το σενάριο
 ΕΡΓΑΣΤΗΡΙΑΚΑ ΚΕΝΤΡΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Β' ΑΘΗΝΑΣ Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2014 Τοπικός διαγωνισμός στη Χημεία 07-12-2013 α. β. γ. Ονοματεπώνυμο μαθητών Σχολείο Το σενάριο Δυο μαθητές βγαίνοντας
ΕΡΓΑΣΤΗΡΙΑΚΑ ΚΕΝΤΡΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Β' ΑΘΗΝΑΣ Ευρωπαϊκή Ολυμπιάδα Φυσικών Επιστημών 2014 Τοπικός διαγωνισμός στη Χημεία 07-12-2013 α. β. γ. Ονοματεπώνυμο μαθητών Σχολείο Το σενάριο Δυο μαθητές βγαίνοντας
Ομογενή μίγματα χημικών ουσιών τα οποία έχουν την ίδια χημική σύσταση και τις ίδιες ιδιότητες (χημικές και φυσικές) σε οποιοδήποτε σημείο τους.
 ΔΙΑΛΥΜΑΤΑ Ομογενή μίγματα χημικών ουσιών τα οποία έχουν την ίδια χημική σύσταση και τις ίδιες ιδιότητες (χημικές και φυσικές) σε οποιοδήποτε σημείο τους. Διαλύτης: η ουσία που βρίσκεται σε μεγαλύτερη αναλογία
ΔΙΑΛΥΜΑΤΑ Ομογενή μίγματα χημικών ουσιών τα οποία έχουν την ίδια χημική σύσταση και τις ίδιες ιδιότητες (χημικές και φυσικές) σε οποιοδήποτε σημείο τους. Διαλύτης: η ουσία που βρίσκεται σε μεγαλύτερη αναλογία
Στοιχειομετρικοί Υπολογισμοί στη Χημεία
 Στοιχειομετρικοί Υπολογισμοί στη Χημεία Δομικές μονάδες της ύλης ΑΤΟΜΑ ΜΟΡΙΑ ΣΤΟΙΧΕΙΑ ΕΝΩΣΕΙΣ Αριθμός Avogadro N A = 6,02 10 23 mol -1 Δηλαδή αυτός ο αριθμός παριστάνει την ποσότητα μιας ουσίας που περιέχει
Στοιχειομετρικοί Υπολογισμοί στη Χημεία Δομικές μονάδες της ύλης ΑΤΟΜΑ ΜΟΡΙΑ ΣΤΟΙΧΕΙΑ ΕΝΩΣΕΙΣ Αριθμός Avogadro N A = 6,02 10 23 mol -1 Δηλαδή αυτός ο αριθμός παριστάνει την ποσότητα μιας ουσίας που περιέχει
Συντάκτης: Τζαμτζής Αθανάσιος Σελίδα 1
 ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ Παρασκευή διαλύματος ορισμένης συγκέντρωσης Αραίωση διαλυμάτων ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΟΜΑΔΑ ΜΑΘΗΤΩΝ 1 2
ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ Παρασκευή διαλύματος ορισμένης συγκέντρωσης Αραίωση διαλυμάτων ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΟΜΑΔΑ ΜΑΘΗΤΩΝ 1 2
Παρασκευαστικό διαχωρισμό πολλών ουσιών με κατανομή μεταξύ των δύο διαλυτών.
 1. ΕΚΧΥΛΙΣΗ Η εκχύλιση είναι μία από τις πιο συνηθισμένες τεχνικές διαχωρισμού και βασίζεται στην ισορροπία κατανομής μιας ουσίας μεταξύ δύο φάσεων, που αναμιγνύονται ελάχιστα μεταξύ τους. Η ευρύτητα στη
1. ΕΚΧΥΛΙΣΗ Η εκχύλιση είναι μία από τις πιο συνηθισμένες τεχνικές διαχωρισμού και βασίζεται στην ισορροπία κατανομής μιας ουσίας μεταξύ δύο φάσεων, που αναμιγνύονται ελάχιστα μεταξύ τους. Η ευρύτητα στη
ΥΠΟΛΟΓΙΣΜΟΣ ΘΕΡΜΟΤΗΤΑΣ ΑΝΤΙΔΡΑΣΗΣ ΕΞΟΥΔΕΤΕΡΩΣΗΣ ΜΕ ΤΗ ΧΡΗΣΗ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ ΣΥΓΧΡΟΝΙΚΗΣ ΛΗΨΗΣ ΚΑΙ ΑΠΕΙΚΟΝΙΣΗΣ MultiLog
 ΥΠΟΛΟΓΙΣΜΟΣ ΘΕΡΜΟΤΗΤΑΣ ΑΝΤΙΔΡΑΣΗΣ ΕΞΟΥΔΕΤΕΡΩΣΗΣ ΜΕ ΤΗ ΧΡΗΣΗ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ ΣΥΓΧΡΟΝΙΚΗΣ ΛΗΨΗΣ ΚΑΙ ΑΠΕΙΚΟΝΙΣΗΣ MultiLog Αντωνίου Κωνσταντίνος ΠΕ04-02 (χημικός) ΓΕ.Λ Ζωσιμαίας Σχολής Ιωαννίνων. Το MultiLog
ΥΠΟΛΟΓΙΣΜΟΣ ΘΕΡΜΟΤΗΤΑΣ ΑΝΤΙΔΡΑΣΗΣ ΕΞΟΥΔΕΤΕΡΩΣΗΣ ΜΕ ΤΗ ΧΡΗΣΗ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ ΣΥΓΧΡΟΝΙΚΗΣ ΛΗΨΗΣ ΚΑΙ ΑΠΕΙΚΟΝΙΣΗΣ MultiLog Αντωνίου Κωνσταντίνος ΠΕ04-02 (χημικός) ΓΕ.Λ Ζωσιμαίας Σχολής Ιωαννίνων. Το MultiLog
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Χημική Τεχνολογία. Εργαστηριακό Μέρος
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Χημική Τεχνολογία Εργαστηριακό Μέρος Ενότητα 4: Ογκομετρική Ανάλυση Ευάγγελος Φουντουκίδης Τμήμα Μηχανολόγων Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Χημική Τεχνολογία Εργαστηριακό Μέρος Ενότητα 4: Ογκομετρική Ανάλυση Ευάγγελος Φουντουκίδης Τμήμα Μηχανολόγων Μηχανικών Τ.Ε. Άδειες
Καθηγητής : ΓΕΩΡΓΙΟΣ ΔΑΝΙΗΛ ΠΛΑΪΝΑΚΗΣ. Χημεία ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΑΣΠΡΟΠΥΡΓΟΣ
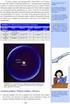 ΑΕΝ / ΑΣΠΡΟΠΥΡΓΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ Καθηγητής : ΓΕΩΡΓΙΟΣ ΔΑΝΙΗΛ ΠΛΑΪΝΑΚΗΣ Χημεία ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΑΣΠΡΟΠΥΡΓΟΣ 2 Ογκομέτρηση προχοϊδα διάλυμα HCl ΕΔΩ ακριβώς μετράμε τον όγκο ( στην εφαπτομένη της καμπύλης
ΑΕΝ / ΑΣΠΡΟΠΥΡΓΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ Καθηγητής : ΓΕΩΡΓΙΟΣ ΔΑΝΙΗΛ ΠΛΑΪΝΑΚΗΣ Χημεία ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΑΣΠΡΟΠΥΡΓΟΣ 2 Ογκομέτρηση προχοϊδα διάλυμα HCl ΕΔΩ ακριβώς μετράμε τον όγκο ( στην εφαπτομένη της καμπύλης
2 ο Διαγώνισμα Χημείας Γ Λυκείου Θ Ε Μ Α Τ Α. Θέμα Α
 Θέμα 2 ο Διαγώνισμα Χημείας Γ Λυκείου Στα θέματα 1 έως 4 να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Η μεταβολή της οξειδωτικής ικανότητας. α. Συμβαδίζει με τη μεταβολή της ενέργειας
Θέμα 2 ο Διαγώνισμα Χημείας Γ Λυκείου Στα θέματα 1 έως 4 να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Η μεταβολή της οξειδωτικής ικανότητας. α. Συμβαδίζει με τη μεταβολή της ενέργειας
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2014 ÊÏÑÕÖÁÉÏ ÅÕÏÓÌÏÓ
 ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΧΗΜΕΙΑ Ηµεροµηνία: Τετάρτη 3 Απριλίου 014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ Για τις ερωτήσεις Α1 έως και Α4 να γράψετε στο τετράδιό σας τον αριθµό
ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΧΗΜΕΙΑ Ηµεροµηνία: Τετάρτη 3 Απριλίου 014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ Για τις ερωτήσεις Α1 έως και Α4 να γράψετε στο τετράδιό σας τον αριθµό
Ε.Κ.Φ.Ε. ΔΙ.Δ.Ε Α ΑΘΗΝΑΣ ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 2016 ΠΡΟΚΑΤΑΡΚΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΣΤΗ ΧΗΜΕΙΑ
 Ε.Κ.Φ.Ε. ΔΙ.Δ.Ε Α ΑΘΗΝΑΣ ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 2016 ΠΡΟΚΑΤΑΡΚΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΣΤΗ ΧΗΜΕΙΑ Ονόματα διαγωνιζομένων: 1) 2) 3) Σχολείο: Όνομα Υπεύθυνου Καθηγητή: 1 η ΠΕΙΡΑΜΑΤΙΚΗ ΔΡΑΣΤΗΡΙΟΤΗΤΑ
Ε.Κ.Φ.Ε. ΔΙ.Δ.Ε Α ΑΘΗΝΑΣ ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 2016 ΠΡΟΚΑΤΑΡΚΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΣΤΗ ΧΗΜΕΙΑ Ονόματα διαγωνιζομένων: 1) 2) 3) Σχολείο: Όνομα Υπεύθυνου Καθηγητή: 1 η ΠΕΙΡΑΜΑΤΙΚΗ ΔΡΑΣΤΗΡΙΟΤΗΤΑ
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 6 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΠΟΥ ΥΠΗΡΕΤΟΥΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 7 ΣΕΠΤΕΜΒΡΙΟΥ 2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΠΟΥ ΥΠΗΡΕΤΟΥΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 7 ΣΕΠΤΕΜΒΡΙΟΥ 2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ
ΜΕΡΟΣ Α : Ερωτήσεις 1-6 Να απαντήσετε σε όλες τις ερωτήσεις 1-6. Κάθε ορθή απάντηση βαθμολογείται με πέντε (5) μονάδες.
 ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2008-2009 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΔΕΙΓΜΑΤΙΚΟ ΕΞΕΤΑΣΤΙΚΟ ΔΟΚΙΜΙΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΤΑΞΗ: Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΧΡΟΝΟΣ: 2 ώρες και 30 λεπτά Το εξεταστικό δοκίμιο αποτελείται από
ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2008-2009 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΔΕΙΓΜΑΤΙΚΟ ΕΞΕΤΑΣΤΙΚΟ ΔΟΚΙΜΙΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΤΑΞΗ: Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΧΡΟΝΟΣ: 2 ώρες και 30 λεπτά Το εξεταστικό δοκίμιο αποτελείται από
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Διαλύματα Παρασκευή Διαλυμάτων
 ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Διαλύματα Παρασκευή Διαλυμάτων Ιωάννης Πούλιος Ιωάννης Ζιώγας Αθανάσιος Κούρας Ευαγγελία Μανώλη ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Διαλύματα Παρασκευή Διαλυμάτων Ιωάννης Πούλιος Ιωάννης Ζιώγας Αθανάσιος Κούρας Ευαγγελία Μανώλη ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
Όνομα :... Ημερομηνία:... /... /...
 Όνομα :... Ημερομηνία:... /... /... Επαναληπτικό Διαγώνισμα Χημείας Γ Λυκείου Ομάδας Προσανατολισμού Θετικών Σπουδών (1 ο + 2 ο + 3 ο + 4 ο + 5 ο ΚΕΦ.) Διάρκεια 180 min ΘΕΜΑ Α Στις ερωτήσεις Α1 εως Α4
Όνομα :... Ημερομηνία:... /... /... Επαναληπτικό Διαγώνισμα Χημείας Γ Λυκείου Ομάδας Προσανατολισμού Θετικών Σπουδών (1 ο + 2 ο + 3 ο + 4 ο + 5 ο ΚΕΦ.) Διάρκεια 180 min ΘΕΜΑ Α Στις ερωτήσεις Α1 εως Α4
Συντάκτης: Τζαμτζής Αθανάσιος Σελίδα 1
 ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ Παρασκευή διαλύματος ορισμένης συγκέντρωσης Αραίωση διαλυμάτων ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΟΜΑΔΑ ΜΑΘΗΤΩΝ 1 2
ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ Παρασκευή διαλύματος ορισμένης συγκέντρωσης Αραίωση διαλυμάτων ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ ΗΜΕΡΟΜΗΝΙΑ ΟΜΑΔΑ ΜΑΘΗΤΩΝ 1 2
Συντάκτης: Τζαμτζής Αθανάσιος Σελίδα 1
 ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 3 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Γ ΛΥΚΕΙΟΥ Υπολογισμός της περιεκτικότητας του ξιδιού σε οξικό οξύ με την κλασική μέθοδο. ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ Γ θετ ΗΜΕΡΟΜΗΝΙΑ
ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 3 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Γ ΛΥΚΕΙΟΥ Υπολογισμός της περιεκτικότητας του ξιδιού σε οξικό οξύ με την κλασική μέθοδο. ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ Γ θετ ΗΜΕΡΟΜΗΝΙΑ
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 24 ΜΑΪΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 24 ΜΑΪΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1.1-1.4, να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 24 ΜΑΪΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1.1-1.4, να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
P 1 V 1 = σταθ. P 2 V 2 = σταθ.
 ΝΟΜΟΙ ΤΩΝ ΑΕΡΙΩΝ 83 Την κατάσταση ενός αερίου μέσα σε ένα δοχείο μπορούμε να την κατανοήσουμε, άρα και να την περιγράψουμε πλήρως, αν γνωρίζουμε τις τιμές των παραμέτρων εκείνων που επηρεάζουν την συμπεριφορά
ΝΟΜΟΙ ΤΩΝ ΑΕΡΙΩΝ 83 Την κατάσταση ενός αερίου μέσα σε ένα δοχείο μπορούμε να την κατανοήσουμε, άρα και να την περιγράψουμε πλήρως, αν γνωρίζουμε τις τιμές των παραμέτρων εκείνων που επηρεάζουν την συμπεριφορά
ΓΑΛΒΑΝΙΚΑ ΣΤΟΙΧΕΙΑ II
 4-1 ΓΑΛΒΑΝΙΚΑ ΣΤΟΙΧΕΙΑ II Θέμα ασκήσεως: Ποτενσιομετρική τιτλοδότηση, προσδιορισμός κανονικού δυναμικού ηλεκτροδίου, πειραματική επαλήθευση της εξισώσεως Nernst. Αρχή μεθόδου: Μετρείται η ΗΕΔ γαλβανικού
4-1 ΓΑΛΒΑΝΙΚΑ ΣΤΟΙΧΕΙΑ II Θέμα ασκήσεως: Ποτενσιομετρική τιτλοδότηση, προσδιορισμός κανονικού δυναμικού ηλεκτροδίου, πειραματική επαλήθευση της εξισώσεως Nernst. Αρχή μεθόδου: Μετρείται η ΗΕΔ γαλβανικού
ΔΙΔΑΚΤΕΑ ΥΛΗ ΣΤΟΧΟΙ ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ
 ΑΝΑΛΥΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΧΗΜΕΙΑΣ B ΤΑΞΗ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΓΡΑΦΕΙΑ ΕΠΙΘΕΩΡΗΤΩΝ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΛΕΥΚΩΣΙΑ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2007-2008 ΔΙΔΑΚΤΕΑ ΥΛΗ ΣΤΟΧΟΙ ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ 1. Ταξινόμηση
ΑΝΑΛΥΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΧΗΜΕΙΑΣ B ΤΑΞΗ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΓΡΑΦΕΙΑ ΕΠΙΘΕΩΡΗΤΩΝ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΛΕΥΚΩΣΙΑ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2007-2008 ΔΙΔΑΚΤΕΑ ΥΛΗ ΣΤΟΧΟΙ ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ 1. Ταξινόμηση
1. Ο ατμοσφαιρικός αέρας, ως αέριο μίγμα, είναι ομογενές. Άρα, είναι διάλυμα.
 2.8 Διαλύματα Υπόδειξη: Στα αριθμητικά προβλήματα, τα πειραματικά μεγέθη που δίνονται με ένα ή δύο σημαντικά ψηφία θεωρούνται ότι πρακτικά έχουν 3 ή 4 σημαντικά ψηφία. 1. Ο ατμοσφαιρικός αέρας, ως αέριο
2.8 Διαλύματα Υπόδειξη: Στα αριθμητικά προβλήματα, τα πειραματικά μεγέθη που δίνονται με ένα ή δύο σημαντικά ψηφία θεωρούνται ότι πρακτικά έχουν 3 ή 4 σημαντικά ψηφία. 1. Ο ατμοσφαιρικός αέρας, ως αέριο
ΣΥΓΚΕΝΤΡΩΣΗ ΔΙΑΛΥΜΑΤΟΣ (Μolarity)
 ΣΥΓΚΕΝΤΡΩΣΗ ΔΙΑΛΥΜΑΤΟΣ (Μolarity) ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σημειώστε με Σωστό ή Λάθος. i) Η συγκέντρωση ενός διαλύματος είναι ίδια για ολόκληρο το διάλυμα ή για ένα μέρος αυτού. ii) Σε 50 ml διαλύματος
ΣΥΓΚΕΝΤΡΩΣΗ ΔΙΑΛΥΜΑΤΟΣ (Μolarity) ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σημειώστε με Σωστό ή Λάθος. i) Η συγκέντρωση ενός διαλύματος είναι ίδια για ολόκληρο το διάλυμα ή για ένα μέρος αυτού. ii) Σε 50 ml διαλύματος
Ισορροπία (γενικά) Ισορροπίες σε διαλύματα. Εισαγωγική Χημεία
 Ισορροπία (γενικά) Ισορροπίες σε διαλύματα Εισαγωγική Χημεία 2013-14 1 Χημική Ισορροπία Εισαγωγική Χημεία 2013-14 2 Ισορροπία: Βαθμός συμπλήρωσης αντίδρασης Ν 2 (g) + 3H 2(g) 2NH 3 (g) Όταν αναφερόμαστε
Ισορροπία (γενικά) Ισορροπίες σε διαλύματα Εισαγωγική Χημεία 2013-14 1 Χημική Ισορροπία Εισαγωγική Χημεία 2013-14 2 Ισορροπία: Βαθμός συμπλήρωσης αντίδρασης Ν 2 (g) + 3H 2(g) 2NH 3 (g) Όταν αναφερόμαστε
Εργαστηριακή άσκηση 1: ΠΑΡΑΓΟΝΤΕΣ ΠΟΥ ΕΠΗΡΕΑΖΟΥΝ ΤΗΝ ΤΑΧΥΤΗΤΑ ΔΙΑΛΥΣΗΣ
 ΧΗΜΕΙΑ Α ΛΥΚΕΙΟΥ ΣΤΟΧΟΙ Εργαστηριακή άσκηση 1: ΠΑΡΑΓΟΝΤΕΣ ΠΟΥ ΕΠΗΡΕΑΖΟΥΝ ΤΗΝ ΤΑΧΥΤΗΤΑ ΔΙΑΛΥΣΗΣ Στο τέλος του πειράματος αυτού θα πρέπει να μπορείς : 1. Να αναγνωρίζεις ότι το φαινόμενο της διάλυσης είναι
ΧΗΜΕΙΑ Α ΛΥΚΕΙΟΥ ΣΤΟΧΟΙ Εργαστηριακή άσκηση 1: ΠΑΡΑΓΟΝΤΕΣ ΠΟΥ ΕΠΗΡΕΑΖΟΥΝ ΤΗΝ ΤΑΧΥΤΗΤΑ ΔΙΑΛΥΣΗΣ Στο τέλος του πειράματος αυτού θα πρέπει να μπορείς : 1. Να αναγνωρίζεις ότι το φαινόμενο της διάλυσης είναι
Συντάκτης: Τζαμτζής Αθανάσιος Σελίδα 1
 ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 3 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Γ ΛΥΚΕΙΟΥ Υπολογισμός της περιεκτικότητας του ξιδιού σε οξικό οξύ με την κλασική μέθοδο. ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ Γ θετ ΗΜΕΡΟΜΗΝΙΑ
ΒΑΘΜΟΛΟΓΙΑ ΟΜΑΔΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 3 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ Γ ΛΥΚΕΙΟΥ Υπολογισμός της περιεκτικότητας του ξιδιού σε οξικό οξύ με την κλασική μέθοδο. ΣΧΟΛΕΙΟ 1 ο ΓΕΛ ΑΜΠΕΛΟΚΗΠΩΝ ΤΜΗΜΑ Γ θετ ΗΜΕΡΟΜΗΝΙΑ
ΘΕΜΑ 1ο Στις ερωτήσεις , να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 24 ΜΑΪΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ ΘΕΜΑ 1ο Στις ερωτήσεις 1.1-1.4, να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 24 ΜΑΪΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ ΘΕΜΑ 1ο Στις ερωτήσεις 1.1-1.4, να γράψετε
Φυσικοί μετασχηματισμοί καθαρών ουσιών
 Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2015
 ΛΥΚΕΙΟ ΑΡΧ. ΜΑΚΑΡΙΟΥ Γ - ΔΑΣΟΥΠΟΛΗ ΣΧΟΛΙΚΟ ΕΤΟΣ 2014-2015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2015 ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΗΜΕΡΟΜΗΝΙΑ: 25/5/2015 ΒΑΘΜΟΣ:... ΤΑΞΗ: Β ΧΡΟΝΟΣ: 2.5 ώρες ΥΠ. ΚΑΘΗΓΗΤΗ:... ΟΝΟΜΑΤΕΠΩΝΥΜΟ:...
ΛΥΚΕΙΟ ΑΡΧ. ΜΑΚΑΡΙΟΥ Γ - ΔΑΣΟΥΠΟΛΗ ΣΧΟΛΙΚΟ ΕΤΟΣ 2014-2015 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2015 ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΗΜΕΡΟΜΗΝΙΑ: 25/5/2015 ΒΑΘΜΟΣ:... ΤΑΞΗ: Β ΧΡΟΝΟΣ: 2.5 ώρες ΥΠ. ΚΑΘΗΓΗΤΗ:... ΟΝΟΜΑΤΕΠΩΝΥΜΟ:...
Άσκηση 3η. Μέθοδοι Διαχωρισμού. Τμήμα ΔΕΑΠΤ - Εργαστήριο Γενικής Χημείας
 Άσκηση 3η Μέθοδοι Διαχωρισμού 1 2 Θεωρητικό μέρος Χρήση των μεταβολών των φάσεων στην ανάλυση Οι ουσίες λειώνουν και βράζουν σε ορισμένες θερμοκρασίες, αλλάζοντας έτσι μορφή από στερεή σε υγρή ή από υγρή
Άσκηση 3η Μέθοδοι Διαχωρισμού 1 2 Θεωρητικό μέρος Χρήση των μεταβολών των φάσεων στην ανάλυση Οι ουσίες λειώνουν και βράζουν σε ορισμένες θερμοκρασίες, αλλάζοντας έτσι μορφή από στερεή σε υγρή ή από υγρή
Ιοντική Ισορροπία: Ανάμιξη διαλυμάτων 27 επαναληπτικές ασκήσεις
 Ιοντική Ισορροπία: Ανάμιξη διαλυμάτων 27 επαναληπτικές ασκήσεις 1) Υδατικό διάλυμα Δ 1 ασθενούς μονοπρωτικού οξέος ΗΑ έχει ph=3 και όγκο 200 ml. Στο διάλυμα Δ 1 προστίθενται 100 ml υδατικού διαλύματος
Ιοντική Ισορροπία: Ανάμιξη διαλυμάτων 27 επαναληπτικές ασκήσεις 1) Υδατικό διάλυμα Δ 1 ασθενούς μονοπρωτικού οξέος ΗΑ έχει ph=3 και όγκο 200 ml. Στο διάλυμα Δ 1 προστίθενται 100 ml υδατικού διαλύματος
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 6 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ & Δ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 7 ΣΕΠΤΕΜΒΡΙΟΥ 2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ & Δ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 7 ΣΕΠΤΕΜΒΡΙΟΥ 2017 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
Για τις προτάσεις Α1 έως και Α5 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή επιλογή.
 ΘΕΜΑ Α Για τις προτάσεις Α1 ές και Α5 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σστή επιλογή. Α1. Στη χημική αντίδραση C(s) O 2 (g) CO 2 (g) α. Ο αριθμός
ΘΕΜΑ Α Για τις προτάσεις Α1 ές και Α5 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σστή επιλογή. Α1. Στη χημική αντίδραση C(s) O 2 (g) CO 2 (g) α. Ο αριθμός
ΕΚΦΩΝΗΣΕΙΣ. o o o f f 3 o o o f 3 f o o o o o f 3 f 2 f 2 f H = H ( HCl ) H ( NH ) 2A + B Γ + 3
 ΘΕΜΑ ο Β' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΧΗΜΕΙΑ ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις 4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Η πρότυπη ενθαλπία ( ο
ΘΕΜΑ ο Β' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΧΗΜΕΙΑ ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις 4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Η πρότυπη ενθαλπία ( ο
Enrico Fermi, Thermodynamics, 1937
 I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ
 1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ ΗΛΙΑΣ ΝΟΛΗΣ-ΚΩΝΣΤΑΝΤΙΝΙΔΗΣ ΘΕΟΔΩΡΟΣ 2012 Διαλύματα Διάλυμα ονομάζεται κάθε ομογενές μείγμα δύο ή περισσοτέρων συστατικών. Κάθε
1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ ΗΛΙΑΣ ΝΟΛΗΣ-ΚΩΝΣΤΑΝΤΙΝΙΔΗΣ ΘΕΟΔΩΡΟΣ 2012 Διαλύματα Διάλυμα ονομάζεται κάθε ομογενές μείγμα δύο ή περισσοτέρων συστατικών. Κάθε
ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΧΗΜΕΙΑ. 5 - Δεκεμβρίου Ερρίκος Γιακουμάκης
 ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΧΗΜΕΙΑ 5 - Δεκεμβρίου - 2015 Ερρίκος Γιακουμάκης 1 ΕΚΦΕ ΑΛΙΜΟΥ ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 Εξεταζόμενο μάθημα: ΧΗΜΕΙΑ ΟΜΑΔΑ...... Εισαγωγικό σημείωμα Θεωρία Brőnsted- Lowry
ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΧΗΜΕΙΑ 5 - Δεκεμβρίου - 2015 Ερρίκος Γιακουμάκης 1 ΕΚΦΕ ΑΛΙΜΟΥ ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 Εξεταζόμενο μάθημα: ΧΗΜΕΙΑ ΟΜΑΔΑ...... Εισαγωγικό σημείωμα Θεωρία Brőnsted- Lowry
σύμφωνα με τη θεωρία της μεταβατικής κατάστασης. Ισχύει ότι: Α. E 1 ΔH = E 3 Σελίδα 1 από 7 g g g Δ g
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 4 ΜΑΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) ΘΕΜΑ Α Στις ερωτήσεις Α.1. έως Α.4. να γράψετε στο τετράδιο
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 4 ΜΑΙΟΥ 2017 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) ΘΕΜΑ Α Στις ερωτήσεις Α.1. έως Α.4. να γράψετε στο τετράδιο
4. Πόσο οξικό οξύ περιέχει το ξίδι;
 4. Πόσο οξικό οξύ περιέχει το ξίδι; Σκοπός Σκοπός αυτού του πειράματος είναι να προσδιορίσετε την ποσότητα (γραμμομοριακή συγκέντρωση) του οξικού οξέος που υπάρχει σε ένα λευκό ξίδι μέσω ογκομέτρησης με
4. Πόσο οξικό οξύ περιέχει το ξίδι; Σκοπός Σκοπός αυτού του πειράματος είναι να προσδιορίσετε την ποσότητα (γραμμομοριακή συγκέντρωση) του οξικού οξέος που υπάρχει σε ένα λευκό ξίδι μέσω ογκομέτρησης με
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 3: Προσδιορισμός συντελεστή ενεργότητας μέσω μετρήσεων διαλυτότητας Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων...
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση 3: Προσδιορισμός συντελεστή ενεργότητας μέσω μετρήσεων διαλυτότητας Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων...
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 Β ΦΑΣΗ ΧΗΜΕΙΑ
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ Ημερομηνία: Σάββατο 20 Απριλίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Για τις προτάσεις Α1 έως και Α4 να γράψετε στο τετράδιό
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ Ημερομηνία: Σάββατο 20 Απριλίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Για τις προτάσεις Α1 έως και Α4 να γράψετε στο τετράδιό
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις. Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι
 Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
ΥΠΟΛΟΓΙΣΜΟΣ ΘΕΡΜΟΤΗΤΑΣ ΑΝΤΙΔΡΑΣΗΣ
 33 Πείραμα 1 Πείραμα 1 ΥΠΟΛΟΓΙΣΜΟΣ ΘΕΡΜΟΤΗΤΑΣ ΑΝΤΙΔΡΑΣΗΣ ΣΤΟΧΟΙ Στο τέλος του πειράματος αυτού θα πρέπει να μπορείς: 1. Να μετράς τη θερμότητα μιας αντίδρασης. 2. Να αναγνωρίζεις την έννοια της περίσσειας
33 Πείραμα 1 Πείραμα 1 ΥΠΟΛΟΓΙΣΜΟΣ ΘΕΡΜΟΤΗΤΑΣ ΑΝΤΙΔΡΑΣΗΣ ΣΤΟΧΟΙ Στο τέλος του πειράματος αυτού θα πρέπει να μπορείς: 1. Να μετράς τη θερμότητα μιας αντίδρασης. 2. Να αναγνωρίζεις την έννοια της περίσσειας
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ ΤΜΗΜΑΤΟΣ ΧΗΜΕΙΑΣ
 1 ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ ΤΜΗΜΑΤΟΣ ΧΗΜΕΙΑΣ Ιωάννης Πούλιος ΝΟΜΟΣ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 54124 ΘΕΣΣΑΛΟΝΙΚΗ ΝΟΜΟΣ ΤΗΣ ΚΑΤΑΝΟΜΗΣ
1 ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ ΤΜΗΜΑΤΟΣ ΧΗΜΕΙΑΣ Ιωάννης Πούλιος ΝΟΜΟΣ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 54124 ΘΕΣΣΑΛΟΝΙΚΗ ΝΟΜΟΣ ΤΗΣ ΚΑΤΑΝΟΜΗΣ
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 A ΦΑΣΗ
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ Ημερομηνία: Πέμπτη 3 Ιανουαρίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Για τις προτάσεις Α1 έως και Α4 να γράψετε στο τετράδιό
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ Ημερομηνία: Πέμπτη 3 Ιανουαρίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Για τις προτάσεις Α1 έως και Α4 να γράψετε στο τετράδιό
ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ. κινητική + + δυναμική
 ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ Εσωτερική ενέργεια: Το άθροισμα της κινητικής (εσωτερική κινητική ενέργεια ή θερμική ενέργεια τυχαία, μη συλλογική κίνηση) και δυναμικής ενέργειας (δεσμών κλπ) όλων των σωματιδίων (ατόμων
ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ Εσωτερική ενέργεια: Το άθροισμα της κινητικής (εσωτερική κινητική ενέργεια ή θερμική ενέργεια τυχαία, μη συλλογική κίνηση) και δυναμικής ενέργειας (δεσμών κλπ) όλων των σωματιδίων (ατόμων
ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΟΞΥΤΗΤΑΣ ΣΕ ΚΡΑΣΙ (ΛΕΥΚΟ)
 ΠΑΝΕΛΛΗΝΙΑ ΕΝΩΣΗ ΥΠΕΥΘΥΝΩΝ ΕΡΓΑΣΤΗΡΙΑΚΩΝ ΚΕΝΤΡΩΝ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ - «ΠΑΝΕΚΦE» email:panekfe@yahoo.gr www.ekfe.gr ΠΑΝΕΛΛΗΝΙΟΣ ΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑ ΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO 2010 ΑΞΙΟΛΟΓΗΣΗ ΜΑΘΗΤΩΝ ΣΤΗ
ΠΑΝΕΛΛΗΝΙΑ ΕΝΩΣΗ ΥΠΕΥΘΥΝΩΝ ΕΡΓΑΣΤΗΡΙΑΚΩΝ ΚΕΝΤΡΩΝ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ - «ΠΑΝΕΚΦE» email:panekfe@yahoo.gr www.ekfe.gr ΠΑΝΕΛΛΗΝΙΟΣ ΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑ ΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO 2010 ΑΞΙΟΛΟΓΗΣΗ ΜΑΘΗΤΩΝ ΣΤΗ
Διατύπωση μαθηματικών εκφράσεων για τη περιγραφή του εγγενούς ρυθμού των χημικών αντιδράσεων.
 25/9/27 Εισαγωγή Διατύπωση μαθηματικών εκφράσεων για τη περιγραφή του εγγενούς ρυθμού των χημικών αντιδράσεων. Οι ρυθμοί δεν μπορούν να μετρηθούν απευθείας => συγκεντρώσεις των αντιδρώντων και των προϊόντων
25/9/27 Εισαγωγή Διατύπωση μαθηματικών εκφράσεων για τη περιγραφή του εγγενούς ρυθμού των χημικών αντιδράσεων. Οι ρυθμοί δεν μπορούν να μετρηθούν απευθείας => συγκεντρώσεις των αντιδρώντων και των προϊόντων
ΕΚΦΩΝΗΣΕΙΣ. 2NH + 3Cl N + 6HCl. 3 (g) 2 (g) 2 (g) (g) 2A + B Γ + 3. (g) (g) (g) (g) ποια από τις παρακάτω εκφράσεις είναι λανθασµένη;
 Επαναληπτικά Θέµατα ΟΕΦΕ ΘΕΜΑ ο Β' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΧΗΜΕΙΑ ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις..4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
Επαναληπτικά Θέµατα ΟΕΦΕ ΘΕΜΑ ο Β' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΧΗΜΕΙΑ ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις..4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
8. Μελέτη ρυθμιστικών διαλυμάτων
 8. Μελέτη ρυθμιστικών διαλυμάτων Σκοπός Σκοπός της παρούσας εργαστηριακής άσκησης είναι να γνωρίσουμε τον τρόπο παρασκευής ενός ρυθμιστικού διαλύματος και ακολούθως να μελετήσουμε τη δράση του, δηλαδή
8. Μελέτη ρυθμιστικών διαλυμάτων Σκοπός Σκοπός της παρούσας εργαστηριακής άσκησης είναι να γνωρίσουμε τον τρόπο παρασκευής ενός ρυθμιστικού διαλύματος και ακολούθως να μελετήσουμε τη δράση του, δηλαδή
Αρχή της μεθόδου: MAΘΗΜΑ 7 ο MEΘΟ ΟΙ ΙΑΧΩΡΙΣΜΟΥ ΟΡΓΑΝΙΚΩΝ ΕΝΩΣΕΩΝ ΕΚΧΥΛΙΣΗ
 MAΘΗΜΑ 7 ο MEΘΟ ΟΙ ΙΑΧΩΡΙΣΜΟΥ ΟΡΓΑΝΙΚΩΝ ΕΝΩΣΕΩΝ ΕΚΧΥΛΙΣΗ Αρχή της μεθόδου: Η μέθοδος στηρίζεται στις διαφορετικές διαλυτότητες των ουσιών σε δύο μη μιγνυομένους διαλύτες Δρα. Κουκουλίτσα Αικατερίνη Χημικός
MAΘΗΜΑ 7 ο MEΘΟ ΟΙ ΙΑΧΩΡΙΣΜΟΥ ΟΡΓΑΝΙΚΩΝ ΕΝΩΣΕΩΝ ΕΚΧΥΛΙΣΗ Αρχή της μεθόδου: Η μέθοδος στηρίζεται στις διαφορετικές διαλυτότητες των ουσιών σε δύο μη μιγνυομένους διαλύτες Δρα. Κουκουλίτσα Αικατερίνη Χημικός
ΕΚΦΩΝΗΣΕΙΣ. 2NH + 3Cl N + 6HCl. 3 (g) 2 (g) 2 (g) (g) 2A + B Γ + 3. (g) (g) (g) (g) ποια από τις παρακάτω εκφράσεις είναι λανθασµένη;
 Επαναληπτικά Θέµατα ΟΕΦΕ Β' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΘΕΜΑ ο ΧΗΜΕΙΑ ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις..4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
Επαναληπτικά Θέµατα ΟΕΦΕ Β' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΘΕΜΑ ο ΧΗΜΕΙΑ ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις..4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
HF + OHˉ. Διάλυμα ΝΗ 4 Βr και NH 3 : ΝΗ 4 Βr NH Brˉ, NH 3 + H 2 O NH OHˉ NH H 2 O NH 3 + H 3 O +
 α) Υπολογίζουμε την αρχική συγκέντρωση c M κάθε ηλεκτρολύτη που περιέχεται στο διάλυμα. Αν η αρχική συγκέντρωση κάποιου ηλεκτρολύτη δεν μπορεί να υπολογιστεί, την ορίζουμε ως άγνωστο c. β) Γράφουμε τις
α) Υπολογίζουμε την αρχική συγκέντρωση c M κάθε ηλεκτρολύτη που περιέχεται στο διάλυμα. Αν η αρχική συγκέντρωση κάποιου ηλεκτρολύτη δεν μπορεί να υπολογιστεί, την ορίζουμε ως άγνωστο c. β) Γράφουμε τις
Άσκηση 3η. Μέθοδοι Διαχωρισμού. Τμήμα ΔΕΑΠΤ - Εργαστήριο Γενικής Χημείας
 Άσκηση 3η Μέθοδοι Διαχωρισμού 1 2 Θεωρητικό μέρος Χρήση των μεταβολών των φάσεων στην ανάλυση Οι ουσίες λειώνουν και βράζουν σε ορισμένες θερμοκρασίες, αλλάζοντας έτσι μορφή από στερεή σε υγρή ή από υγρή
Άσκηση 3η Μέθοδοι Διαχωρισμού 1 2 Θεωρητικό μέρος Χρήση των μεταβολών των φάσεων στην ανάλυση Οι ουσίες λειώνουν και βράζουν σε ορισμένες θερμοκρασίες, αλλάζοντας έτσι μορφή από στερεή σε υγρή ή από υγρή
ΑΣΚΗΣΗ 2. ΜΕΘΟΔΟΙ ΔΙΑΧΩΡΙΣΜΟΥ Α. Θεωρητικό μέρος 1. Χρήση των μεταβολών των φάσεων στην ανάλυση Η μελέτη της χημικής ανάλυσης αρχίζει με μια από τις
 ΑΣΚΗΣΗ 2. ΜΕΘΟΔΟΙ ΔΙΑΧΩΡΙΣΜΟΥ Α. Θεωρητικό μέρος 1. Χρήση των μεταβολών των φάσεων στην ανάλυση Η μελέτη της χημικής ανάλυσης αρχίζει με μια από τις παλιότερες παρατηρήσεις : Οι ουσίες λειώνουν και βράζουν
ΑΣΚΗΣΗ 2. ΜΕΘΟΔΟΙ ΔΙΑΧΩΡΙΣΜΟΥ Α. Θεωρητικό μέρος 1. Χρήση των μεταβολών των φάσεων στην ανάλυση Η μελέτη της χημικής ανάλυσης αρχίζει με μια από τις παλιότερες παρατηρήσεις : Οι ουσίες λειώνουν και βράζουν
Αυτoϊοντισμός του νερού ph
 Αυτoϊοντισμός του νερού ph Το καθαρό νερό είναι ηλεκτρολύτης; Το καθαρό νερό είναι ομοιοπολική ένωση και θα περιμέναμε να είναι μην εμφανίζει ηλεκτρική αγωγιμότητα. Μετρήσεις μεγάλης ακρίβειας όμως έδειξαν
Αυτoϊοντισμός του νερού ph Το καθαρό νερό είναι ηλεκτρολύτης; Το καθαρό νερό είναι ομοιοπολική ένωση και θα περιμέναμε να είναι μην εμφανίζει ηλεκτρική αγωγιμότητα. Μετρήσεις μεγάλης ακρίβειας όμως έδειξαν
l R= ρ Σε ηλεκτρικό αγωγό µήκους l και διατοµής A η αντίσταση δίνεται από την εξίσωση: (1)
 ΑΓΩΓΙΜΟΤΗΤΑ ΗΕΚΤΡΟΥΤΩΝ Θέµα ασκήσεως Μελέτη της µεταβολής της αγωγιµότητας ισχυρού και ασθενούς ηλεκτρολύτη µε την συγκέντρωση, προσδιορισµός της µοριακής αγωγιµότητας σε άπειρη αραίωση ισχυρού οξέος,
ΑΓΩΓΙΜΟΤΗΤΑ ΗΕΚΤΡΟΥΤΩΝ Θέµα ασκήσεως Μελέτη της µεταβολής της αγωγιµότητας ισχυρού και ασθενούς ηλεκτρολύτη µε την συγκέντρωση, προσδιορισµός της µοριακής αγωγιµότητας σε άπειρη αραίωση ισχυρού οξέος,
1 ο Διαγώνισμα Χημείας Γ Λυκείου Θ Ε Μ Α Τ Α. Θέμα Α
 Θέμα 1 ο Διαγώνισμα Χημείας Γ Λυκείου Στις ερωτήσεις 1 ως 5 να επιλέξετε τη σωστή απάντηση. 1. Η αντίδραση ενός στοιχείου Σ με το υδρογόνο είναι. α. ντίδραση οξείδωσης. β. ντίδραση αναγωγής. γ. ντίδραση
Θέμα 1 ο Διαγώνισμα Χημείας Γ Λυκείου Στις ερωτήσεις 1 ως 5 να επιλέξετε τη σωστή απάντηση. 1. Η αντίδραση ενός στοιχείου Σ με το υδρογόνο είναι. α. ντίδραση οξείδωσης. β. ντίδραση αναγωγής. γ. ντίδραση
1o ΘΕΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΧΗΜΕΙΑ B ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ
 1o ΘΕΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΧΗΜΕΙΑ B ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Για τις ερωτήσεις Α1 έως και Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
1o ΘΕΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΧΗΜΕΙΑ B ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Για τις ερωτήσεις Α1 έως και Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
1 η Εργαστηριακή άσκηση. Παρασκευή Αραίωση. διαλύματος. Δρ. Άρης Γιαννακάς - Ε.ΔΙ.Π.
 1 η Εργαστηριακή άσκηση Παρασκευή Αραίωση διαλύματος 1 Θεωρητικό Μέρος Εισαγωγικές έννοιες Όπως είναι γνωστό η ύλη διαχωρίζεται σε δύο βασικές κατηγορίες: Τις καθαρές ουσίες (στοιχεία, χημικές ενώσεις)
1 η Εργαστηριακή άσκηση Παρασκευή Αραίωση διαλύματος 1 Θεωρητικό Μέρος Εισαγωγικές έννοιες Όπως είναι γνωστό η ύλη διαχωρίζεται σε δύο βασικές κατηγορίες: Τις καθαρές ουσίες (στοιχεία, χημικές ενώσεις)
Γ.Κονδύλη 1 & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο: , /
 Γ.Κονδύλη 1 & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο:210-61.24.000, http:/ / www.akadimos.gr ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 2016 ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Επιμέλεια θεμάτων: Βελαώρας Βασίλειος, Χημικός ΘΕΜΑ Α Για
Γ.Κονδύλη 1 & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο:210-61.24.000, http:/ / www.akadimos.gr ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 2016 ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Επιμέλεια θεμάτων: Βελαώρας Βασίλειος, Χημικός ΘΕΜΑ Α Για
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2018 ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2018 ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ ΘΕΜΑ Α Για τις προτάσεις Α1 έως Α5 να γράψετε τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή επιλογή Α1. ι) To S στις διάφορες
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2018 ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ ΘΕΜΑ Α Για τις προτάσεις Α1 έως Α5 να γράψετε τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή επιλογή Α1. ι) To S στις διάφορες
Φάσμα group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο
 σύγχρονο Φάσμα group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο Μάθημα: ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Καθηγητής: ΟΜΑΔΑ ΧΗΜΙΚΩΝ ΦΡΟΝΤΙΣΤΗΡΙΩΝ ΦΑΣΜΑ Τάξη: Γ ΛΥΚΕΙΟΥ Ημερομηνία: 08/12/2018
σύγχρονο Φάσμα group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο Μάθημα: ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Καθηγητής: ΟΜΑΔΑ ΧΗΜΙΚΩΝ ΦΡΟΝΤΙΣΤΗΡΙΩΝ ΦΑΣΜΑ Τάξη: Γ ΛΥΚΕΙΟΥ Ημερομηνία: 08/12/2018
n i i = n i - n i - n i (2) (3) A = Γ (4) (5) (6) (7) (8)
 ΕΠΙΦΑΝΕΙΑΚΗ ΤΑΣΗ ΙΑΛΥΜΑΤΩΝ Θέµα ασκήσεως: Μελέτη της εξάρτησης της επιφανειακής τάσης διαλυµάτων από την συγκέντρωση, υπολογισµός επιφανειακής περίσσειας της ουσίας, υπολογισµός επιφάνειας ανά mole και
ΕΠΙΦΑΝΕΙΑΚΗ ΤΑΣΗ ΙΑΛΥΜΑΤΩΝ Θέµα ασκήσεως: Μελέτη της εξάρτησης της επιφανειακής τάσης διαλυµάτων από την συγκέντρωση, υπολογισµός επιφανειακής περίσσειας της ουσίας, υπολογισµός επιφάνειας ανά mole και
ΦΥΛΛΟ ΑΠΑΝΤΗΣΗΣ 3 ης ΕΡΓΑΣΙΑΣ
 2 η θεματική ενότητα: Εργαστηριακές εφαρμογές Συγχρονικού Συστήματος Λήψης και Απεικόνισης (Σ.Σ.Λ.Α.) ΦΥΛΛΟ ΑΠΑΝΤΗΣΗΣ 3 ης ΕΡΓΑΣΙΑΣ Θέμα δραστηριότητας: Μάθημα και Τάξη στην οποία απευθύνεται: Εκπαιδευτικοί:
2 η θεματική ενότητα: Εργαστηριακές εφαρμογές Συγχρονικού Συστήματος Λήψης και Απεικόνισης (Σ.Σ.Λ.Α.) ΦΥΛΛΟ ΑΠΑΝΤΗΣΗΣ 3 ης ΕΡΓΑΣΙΑΣ Θέμα δραστηριότητας: Μάθημα και Τάξη στην οποία απευθύνεται: Εκπαιδευτικοί:
ΧΗΜΕΙΑ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 Κανάρη 36, Δάφνη Τηλ. 210 9713934 & 210 9769376 ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΧΗΜΕΙΑ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ Α. Σε καθεμιά από τις παρακάτω ερωτήσεις να επιλέξετε τη σωστή απάντηση. Α.1. Στη χημική αντίδραση:
Κανάρη 36, Δάφνη Τηλ. 210 9713934 & 210 9769376 ΔΙΑΓΩΝΙΣΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΧΗΜΕΙΑ Ο.Π. ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ Α. Σε καθεμιά από τις παρακάτω ερωτήσεις να επιλέξετε τη σωστή απάντηση. Α.1. Στη χημική αντίδραση:
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΥΠΟΛΟΓΙΣΜΟΣ ΤΗΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΤΟΥ ΞΙΔΙΟΥ ΣΕ ΟΞΙΚΟ ΟΞΥ
 ΜΙΝΟΠΕΤΡΟΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΦΥΣΙΚΟΣ - Ρ/Η ΚΑΘΗΓΗΤΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΥΠΕΥΘΥΝΟΣ ΣΕΦΕ 2 ου ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΡΑΜΑΤΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΥΠΟΛΟΓΙΣΜΟΣ ΤΗΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΤΟΥ
ΜΙΝΟΠΕΤΡΟΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΦΥΣΙΚΟΣ - Ρ/Η ΚΑΘΗΓΗΤΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΥΠΕΥΘΥΝΟΣ ΣΕΦΕ 2 ου ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΡΑΜΑΤΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΧΗΜΕΙΑΣ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΥΠΟΛΟΓΙΣΜΟΣ ΤΗΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ ΤΟΥ
ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑΤΑ ΘΕΜΑ Α Για τις ερωτήσεις Α1 έως και Α5 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και, δίπλα, το γράμμα που αντιστοιχεί στη σωστή επιλογή. Α1. Ποια
ΧΗΜΕΙΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑΤΑ ΘΕΜΑ Α Για τις ερωτήσεις Α1 έως και Α5 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και, δίπλα, το γράμμα που αντιστοιχεί στη σωστή επιλογή. Α1. Ποια
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Τράπεζα θεμάτων. Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ
 ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ 16111 Ένα παιδί κρατάει στο χέρι του ένα μπαλόνι γεμάτο ήλιο που καταλαμβάνει όγκο 4 L (σε πίεση
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ 16111 Ένα παιδί κρατάει στο χέρι του ένα μπαλόνι γεμάτο ήλιο που καταλαμβάνει όγκο 4 L (σε πίεση
3. Υπολογισμοί με Χημικούς Τύπους και Εξισώσεις
 3. Υπολογισμοί με Χημικούς Τύπους και Εξισώσεις ΠΕΡΙΕΧΟΜΕΝΑ: Μοριακή μάζα και τυπική μάζα μιας ουσίας Η έννοια του mole Εκατοστιαία περιεκτικότητα από το χημικό τύπο Στοιχειακή ανάλυση: Εκατοστιαία περιεκτικότητα
3. Υπολογισμοί με Χημικούς Τύπους και Εξισώσεις ΠΕΡΙΕΧΟΜΕΝΑ: Μοριακή μάζα και τυπική μάζα μιας ουσίας Η έννοια του mole Εκατοστιαία περιεκτικότητα από το χημικό τύπο Στοιχειακή ανάλυση: Εκατοστιαία περιεκτικότητα
Θερμόχήμεία Κεφάλαιό 2 ό
 Θερμόχήμεία Κεφάλαιό 2 ό Επιμέλεια: Χημικός Διδάκτωρ Πανεπιστημίου Πατρών 11 12 Τι είναι η χημική ενέργεια των χημικών ουσιών; Που οφείλεται; Μπορεί να αποδοθεί στο περιβάλλον; Πότε μεταβάλλεται η χημική
Θερμόχήμεία Κεφάλαιό 2 ό Επιμέλεια: Χημικός Διδάκτωρ Πανεπιστημίου Πατρών 11 12 Τι είναι η χημική ενέργεια των χημικών ουσιών; Που οφείλεται; Μπορεί να αποδοθεί στο περιβάλλον; Πότε μεταβάλλεται η χημική
Πείραμα 4 ο. Προσδιορισμός Οξύτητας Τροφίμων
 Πείραμα 4 ο Προσδιορισμός Οξύτητας Τροφίμων Εισαγωγή Τα οργανικά οξέα που υπάρχουν ως συστατικά σε διάφορα τρόφιμα επηρεάζουν το άρωμα, το χρώμα, τη μικροβιακή σταθερότητα και τη διατήρηση της ποιότητας
Πείραμα 4 ο Προσδιορισμός Οξύτητας Τροφίμων Εισαγωγή Τα οργανικά οξέα που υπάρχουν ως συστατικά σε διάφορα τρόφιμα επηρεάζουν το άρωμα, το χρώμα, τη μικροβιακή σταθερότητα και τη διατήρηση της ποιότητας
Διαλύματα ασθενών οξέων ασθενών βάσεων.
 Διαλύματα ασθενών οξέων ασθενών βάσεων. Η ισχύς ενός οξέος σε υδατικό διάλυμα περιγράφεται από τη σταθερά ισορροπίας ιοντισμού του οξέος. Σε ένα αραιό υδατικό διάλυμα ασθενούς μονοπρωτικού οξέος ΗΑ, έχουμε
Διαλύματα ασθενών οξέων ασθενών βάσεων. Η ισχύς ενός οξέος σε υδατικό διάλυμα περιγράφεται από τη σταθερά ισορροπίας ιοντισμού του οξέος. Σε ένα αραιό υδατικό διάλυμα ασθενούς μονοπρωτικού οξέος ΗΑ, έχουμε
ΘΕΜΑΤΑ ΧΗΜΕΙΑΣ Γ ΛΥΚΕΙΟΥ 31/03/2019
 ΘΕΜΑΤΑ ΧΗΜΕΙΑΣ Γ ΛΥΚΕΙΟΥ 31/03/2019 ΘΕΜΑ Α Στις παρακάτω ημιτελείς προτάσεις Α1 Α5 να μεταφέρετε στο τετράδιο σας τη σωστή απάντηση Α1. Η ακόλουθη γραφική παράσταση αναφέρεται στην ισορροπία η οποία περιγράφεται
ΘΕΜΑΤΑ ΧΗΜΕΙΑΣ Γ ΛΥΚΕΙΟΥ 31/03/2019 ΘΕΜΑ Α Στις παρακάτω ημιτελείς προτάσεις Α1 Α5 να μεταφέρετε στο τετράδιο σας τη σωστή απάντηση Α1. Η ακόλουθη γραφική παράσταση αναφέρεται στην ισορροπία η οποία περιγράφεται
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ NEO ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ NEO ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 30 ΜΑΪΟΥ 016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ Π Ρ Ο Σ Α Ν Α Τ Ο Λ Ι Σ Μ Ο Υ (Ν Ε Ο Σ Υ Σ Τ Η Μ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ NEO ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 30 ΜΑΪΟΥ 016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ Π Ρ Ο Σ Α Ν Α Τ Ο Λ Ι Σ Μ Ο Υ (Ν Ε Ο Σ Υ Σ Τ Η Μ
ΤΕΣΤ 30 ΕΡΩΤΗΣΕΩΝ ΓΝΩΣΤΙΚΟΥ ΧΗΜΕΙΑΣ
 ΤΕΣΤ 30 ΕΡΩΤΗΣΕΩΝ ΓΝΩΣΤΙΚΟΥ ΧΗΜΕΙΑΣ ο αριθμός Avogadro, N A, L = 6,022 10 23 mol -1 η σταθερά Faraday, F = 96 487 C mol -1 σταθερά αερίων R = 8,314 510 (70) J K -1 mol -1 = 0,082 L atm mol -1 K -1 μοριακός
ΤΕΣΤ 30 ΕΡΩΤΗΣΕΩΝ ΓΝΩΣΤΙΚΟΥ ΧΗΜΕΙΑΣ ο αριθμός Avogadro, N A, L = 6,022 10 23 mol -1 η σταθερά Faraday, F = 96 487 C mol -1 σταθερά αερίων R = 8,314 510 (70) J K -1 mol -1 = 0,082 L atm mol -1 K -1 μοριακός
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση : Προσδιορισμός μοριακής μάζας με ζεσεοσκοπία Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 4 Σελίδα 1. Θεωρία
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση : Προσδιορισμός μοριακής μάζας με ζεσεοσκοπία Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 4 Σελίδα 1. Θεωρία
ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 8 ΥΔΑΤΙΚΑ ΔΙΑΛΥΜΑΤΑ ΑΣΘΕΝΩΝ ΗΛΕΚΤΡΟΛΥΤΩΝ
 ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 8 ΥΔΑΤΙΚΑ ΔΙΑΛΥΜΑΤΑ ΑΣΘΕΝΩΝ ΗΛΕΚΤΡΟΛΥΤΩΝ 1. Να βρεθεί το ph διαλύματος CH 3 COOH συγκέντρωσης 0,1Μ στους 25 ο C. Δίνεται για το CH 3 COOH στους 25 ο C Κ α =10-5.
ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 8 ΥΔΑΤΙΚΑ ΔΙΑΛΥΜΑΤΑ ΑΣΘΕΝΩΝ ΗΛΕΚΤΡΟΛΥΤΩΝ 1. Να βρεθεί το ph διαλύματος CH 3 COOH συγκέντρωσης 0,1Μ στους 25 ο C. Δίνεται για το CH 3 COOH στους 25 ο C Κ α =10-5.
