arxiv: v1 [stat.me] 20 Jun 2015
|
|
|
- Νάρκισσα Κοσμόπουλος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Combnng cluster sampg and k-tracng sampg to estmate the sze of a hdden populaton: asymptotc propertes of the estmators arxv:56.69v stat.me 2 Jun 25 Martín H. Fél Medna Techncal report Number: FCFM-UAS-25- Class: Research June, 25 Facultad de Cencas Físco-Matemátcas Unversdad Autónoma de Snaloa Cudad Unverstara, Culacán Snaloa Méco
2 Combnng cluster sampg and k-tracng sampg to estmate the sze of a hdden populaton: asymptotc propertes of the estmators Martín H. Fél Medna Facultad de Cencas Físco-Matemátcas de la Unversdad Autónoma de Snaloa Abstract Fél-Medna and Thompson 24 proposed a varant of k-tracng sampg to estmate the sze of a hdden populaton such as drug users, seual workers or homeless people. In ther varant a sampg frame of stes where the members of the populaton tend to gather s constructed. The frame s not assumed to cover the whole populaton, but only a porton of t. A smple random sample of stes s selected; the people n the sampled stes are dentfed and are asked to name other members of the populaton whch are added to the sample. Those authors proposed mamum lkelhood estmators of the populaton sze whch derved from a multnomal model for the numbers of people found n the sampled stes and a model that consders that the probablty that a person s named by any element n a partcular sampled ste k-probablty does not depend on the named person, that s, that the probabltes are homogeneous. Later, Fél-Medna et al. 25 proposed uncondtonal and condtonal mamum lkelhood estmators of the populaton sze whch derved from a model that takes nto account the heterogenety of the k-probabltes. In ths work we consder ths sampg desgn and set condtons for a general model for the k-probabltes that guarantee the consstency and asymptotc normalty of the estmators of the populaton sze and of the estmators of the parameters of the model for the k-probabltes. In partcular we showed that both the uncondtonal and condtonal mamum lkelhood estmators of the populaton sze are consstent and have asymptotc normal dstrbutons whch are dfferent from each other. Key words: Asymptotc normalty, capture-recapture, chan referral sampg, hard-todetect populaton, mamum lkelhood estmator, snowball sampg mhfel@uas.edu.m
3 Introducton Conventonal sampg methods are not approprate for sampg hdden or hard-to-reach human populatons, such as drug users, seual-workers and homeless people, because of the lack of sutable sampg frames. For ths reason, several specfc sampg methods for ths type of populaton have been proposed. See Magnan et al. 25 and Kalton 29 for revews of some of them. One of ths methods s snowball sampg, also known as ktracng sampg LTS or chan referral sampg. In LTS an ntal sample of members of the populaton s selected and the sample sze s ncreased by askng the people n the ntal sample to name other members of the populatons. The named people who are not n the ntal sample are added to the sample and they are asked to name other members of the populaton. The sampg process mght contnue n ths way untl a stoppng rule s satsfed. For revews of several varants of LTS see Spreen 992, Thompson and Frank 2 and Johnston and Sabn 2. Fél-Medna and Thompson 24 proposed a varant of k-tracng sampg LTS to estmate the sze of a hdden populaton. In ther varant they supposed that a sampg frame of stes where the members of the target populaton tend to gather can be constructed. As a eamples of stes are publc parks, bars and blocks. It s worth nothng that they do not supposed that the frame covers the whole populaton, but only a porton of t. Then an ntal sample of stes s selected by a smple random sampg wthout replacement desgn and the members of the populaton who belong to the sampled stes are dentfed. Fnally the people n the ntal sample are asked to named other members of the populaton and the named persons who are not n the ntal sample are ncluded n the sample. Those authors proposed models to descrbe the number of members of the populaton who belong to each ste n the frame and to descrbe the probablty that a person s ked to a sampled ste, that s, that he or she was named by at least one person who belongs to that ste. From those models they derved mamum lkelhood estmators of the populaton sze. In that work those authors consdered that the probablty that a person s ked to a ste k-probablty does not depend on the person, but does on the ste, that s, they consder homogeneous k-probabltes. Fél-Medna and Monardn 26 consdered ths same varant of LTS and derved estmators of the populaton sze usng a Bayesan-asssted approach, that s, they derved the estmators usng the Bayesan approach, but the nferences were made under a frequentst approach. Those authors consdered an homogeneous two-stage normal model for the logts of the k-probabltes. Later Fél-Medna et al. 25 etended the work by Fél-Medna and Thompson 24 to the case n whch the k-probabltes are heterogeneous, that s, that they depend on the named people. Those authors modeled the heterogenety of the k-probabltes by means of a med logstc normal model proposed by Coull and Agrest 999 n the contet of capture-recapture studes. From ths model they derved uncondtonal and condtonal mamum lkelhood estmators of the populaton sze. In ths work we consder the varant of the LTS proposed by Fél-Medna and Thompson 24 and a general model for the k-probabltes from whch we derve the forms of the 2
4 uncondtonal and condtonal mamum lkelhood estmators of the populaton sze. We state condtons that guarantee the consstency and asymptotc normalty of both types of estmators, and we proposed estmators of the varances of the estmators of the populaton sze. It s worth notng that our work s based on that by Sanathanan 972 n whch she derved asymptotc propertes of both uncondtonal and condtonal mamum lkelhood estmators of the sze of a multnomal dstrbuton from an ncomplete observaton of the cell totals whch s a stuaton that occurs n capture-recapture studes. Thus, our work s bascally an adaptaton of that by Sanathanan 972 to the estmators used n the sampg varant proposed by Fél-Medna and Thompson 24. The structure of ths document s the followng. In secton 2 we descrbe the varant of LTS proposed by Fél-Medna and Thompson 24. In secton 3 we present probablty models that descrbe the numbers of people that belong to the stes n the frame and the probabltes of ks between the members of the populaton and the stes. From these models we construct the lkelhood functon that allows us to derve the uncondtonal and condtonal mamum lkelhood estmators of the parameters of the assumed model for the k-probabltes and of the populaton sze. In addton, we present condtons that guarantee the consstency of the proposed estmators. In secton 4, whch s the central part of ths paper, we defne the asymptotc framework under whch are derved the asymptotc propertes of the proposed estmators. In secton 5 we proposed a method for estmatng the varancecovarance matrces of the estmators of the dfferent vectors of parameters that appear n the assumed models. Fnally, n secton 6 we dscuss some ponts to be consdered whenever the results of ths paper want to be used n actual stuatons. 2 Lnk-tracng sampg desgn In ths secton we wll descrbe the LTS varant proposed by Fél-Medna and Thompson 24. Thus, let U be a fnte populaton of τ people. Let U be the porton of U that s covered by a sampg frame of N stes A,...,A N, whch are places where members of the populaton tend to gather. We wll assume that each one of the τ persons who are n U belongs to only one stea n the frame. Notce that ths does not mply that a person cannot be found n dstnct places, but that, as n ordnary cluster sampg, the researcher has a crteron that allows hm or her to assgn a person to only one ste. Let M be the number of people n U that belong to the ste A, =,...,N. The prevous assumpton mples that τ = N M. Letτ 2 = τ τ be the number of people that belong to the portonu 2 = U U ofu that s not covered by the sampg frame. The sampg procedure s as follows. An ntal smple random sample wthout replacement SRSWOR S A of n stes A,...,A n s selected from the frame and the members of the populaton who belong to each sampled ste are dentfed. Let S be the set of people n the ntal sample. Notce that the sze of S s M = n M. Then from each sampled stea, =,...,n, the people who belong to that ste are asked to name other members of the populaton. A person and a sampled ste are sad to be ked f any of the persons who belong to that ste names that person. Let S and S 2 be the sets of people n U S and n 3
5 U 2, respectvely, who are ked to at least one ste n S A. Fnally, from each named person the followng nformaton s obtaned: the porton of U where that person s located, that s, U S,A S A oru 2, and the subset of sampled stes that are ked to hm or her. 3 Uncondtonal and condtonal mamum lkelhood estmators 3. Probablty models As n Fél-Medna and Thompson 24, we wll suppose that the numbers M,..., M N of people who belong to the stesa,...,a N are ndependent Posson random varables wth mean λ. Therefore, the ont condtonal dstrbuton of M,...,M n,τ M gven that N M = τ s multnomal wth probablty mass functon pmf: fm,...,m n,τ m τ = τ! m n m n τ m.!τ m! N N To model the ks between the members of the populaton and the sampled stes we wll defne for person nu k S the vector of k-ndcator varablesx k = X k,...,xk n, where X k = f person s ked to ste A and X k = otherwse. Notce that X k ndcates whch stes n S A are ked to person. We wll suppose that gven S A, and consequently the values M s of the sampled stes, the X k s are Bernoull random varables wth means p k s and that the vectors Xk are ndependent. Let Ω = {,..., n : =, ; =,..., n}, that s, the set of all the n-dmensonal vectors such that each one of ther elements s or. For =,..., n Ω we wll denote by π k the probablty that the vector of k-ndcator varables assocated wth a randomly selected person from U k S equals, that s, the probablty that the person s ked only to the stesa such that the-th element of equals. We wll suppose that π k depends on a q k -dmensonal parameter θ k = θ k,...,θk q k Θ k R q k k, that s, π = π k θ k, k =,2. In ths work we wll assume thatθ k does not depend on the observed M s. Smlarly, for person n A S A, we wll defne the vector of k-ndcator varables X A = X A,..., X A,XA,...,XA n, where X A = f person s ked to ste A, =,...,n, and X k = otherwse. We wll suppose that gven S A the X A s are Bernoull random varables wth means p s and that the vectors XA are ndependent. For eacha S A, letω = {,...,,,..., n : =,;, =,...,n}, that s, the set of all n -dmensonal vectors obtaned from the vectors n Ω by omttng ther -th coordnate. For =,...,,,..., n Ω we wll denote by π A the probablty that the vector of k-ndcator varables assocated wth a randomly selected person froma equals. We wll suppose thatπ A depends on theq -dmensonal parameter θ = θ,...,θ q Θ, that s, π A = π A θ, =,...,n. 4
6 For nstance, Fél-Medna and Monardn 26 modeled the k-probablty between person nu k A and stea S A byp k =Pr X k = S A =ep α k / ep α k, where the condtonal dstrbuton of α k gven ψ k s normal wth mean ψ k and varance σk 2, whch we denote by αk ψ k N ψ k,σk 2 and ψ k N µ k,γk 2. Thus, n ths case θ k = µ k,γ k,σ k Θ k = R,,, and t π k θ epα k= epα f kα ψf k ψdαdψ epα f kα ψf k ψdαdψ n t, where =,..., n Ω, t = n, and f k α ψ and f k ψ denote the probablty densty functons of the dstrbutons N ψ k,σk 2 and N µ k,γk 2, respectvely. It s worth notng that those authors dd not computeπ k θ k because they followed a Bayesan approach and focused on computng the posteror dstrbuton of the parameters. As another eample, Fél-Medna et al. 25 modeled the k-probablty between person nu k A and stea S A by the followng Rasch model: p k =Pr X k = S A = ep α k β k / ep α k β k, where α k s a fed not random effect assocated wth the ste A and β k s a normal random effect wth mean zero and varance σk 2 assocated wth person nu k A. Therefore π k θ n k = = ep ep α k σ k z φzdz, α k σ k z where =,..., n Ω,θ k = α k,...,αk n,σ k Θ k = R n, andφ denotes the probablty densty functon of the standard normal dstrbuton. Those authors compute π k θ k by means of Gaussan quadrature formula. Notce that n the frst eample the parameter θ k s defned prevously to the selecton of the ntal sample because the α k s are a random sample from a probablty dstrbuton ndeed by θ k and consequently ths parameter does not represent characterstcs of the partcular selected sample. On the other hand, n the second eample the parameterθ k s defned once the ntal sample of stes s selected because the α k s represent characterstcs of the partcular stes ns A. Therefore, as long asθ k does not depend on them s the results derved n ths work are vald for both cases. 3.2 Lkelhood functon To compute the lkelhood functon we wll factorze t nto dfferent components. One component, L MULT τ, s gven by the probablty of observng the partcular szes m,...,m n of the stes ns A ; therefore, t s specfed by the multnomal dstrbuton. Two addtonal 5
7 factors are gven by the probabltes of the confguratons of the ks between the people n U k S, k =,2, and the stes A S A. To obtan those factors we wll denote by R k, =,..., n Ω, the random varable that ndcates the number of dstnct people n U k S whose vectors of k-ndcator varables are equal to, and by R k the random varable that ndcates the number of dstnct people nu k S who are ked to at least one ste A S A. Notce that R k = Ω {} Rk, where denotes the n-dmensonal vector of zeros. Because of the assumptons we made about the vectors X k of k-ndcator varables we have that the condtonal ont probablty dstrbuton of the varables{r } Ω gvens A s a multnomal dstrbuton wth parameter of sze τ m and probabltes{π θ } Ω, whereas that of the varables{r 2 } Ω s a multnomal dstrbuton wth parameter of szeτ 2 and probabltes {π 2 θ 2 } Ω. Therefore, the factors of the lkelhood functon assocated wth the probabltes of the confguratons of ks between the people nu k S, k =,2, and the stesa S A are and L τ,θ = L 2 τ 2,θ 2 = τ m! τ m r! Ω r! τ 2! τ 2 r 2! Ω r2! Ω Ω π θ r π 2 θ 2 r 2. Notce that r = τ m r andr 2 = τ 2 r 2. The last factor of the lkelhood functon s gven by the probablty of the confguraton of ks between the people ns and the stesa S A. To obtan ths factor, we wll denote by R A, =,...,,,..., n Ω, the random varable that ndcates the number of dstnct people n A S A such that ther vectors of k-ndcator varables equal and byr A the random varable that ndcates the number of dstnct people na S A who are ked to at least one ste A S A,. Notce that R A = Ω {} RA, where denotes then -dmensonal vector of zeros andr A = m R A. Then, as n the prevous cases, the condtonal ont probablty dstrbuton of the varables{r A } Ω gvens A s a multnomal dstrbuton wth parameter of sze m and probabltes {π A θ } Ω. Therefore, the probablty of the confguraton of ks between the people n S and the stes A S A s gven by the product of the prevous multnomal probabltes one for each A S A, and consequently the factor of the lkelhood functon assocated wth that probablty s L θ = n = m! Ω ra! π A θ r A Ω π A θ m ra. From the prevous results we have that the mamum lkelhood functon s gven by Lτ,τ 2,θ,θ 2 = L τ,θ L 2 τ 2,θ 2, 6 2
8 where L τ,θ = L MULT τ L τ,θ L θ and 3 L 2 τ 2,θ 2 = L 2 τ 2,θ Uncondtonal and condtonal mamum lkelhood estmators of τ k,θ k In ths secton we wll derve uncondtonal and condtonal mamum lkelhood estmators of the parameters of the prevously specfed models. Henceforth we wll suppose that condtonal on the ntal samples A of stes the followng regularty condtons are satsfed: θ k s the true value ofθ k. 2 θ k s an nteror pont ofθ k. 3 π k θ k >, Ω and πa θ >, Ω, =,...,n. 4 π k θ k / θ k, Ω and π A θ / θ, Ω, =,...,n; =,...,q k, est at anyθ k Θ k and θ Θ, and are contnuous n neghborhoods ofθ k and θ, respectvely. 5 Gven aδ >, t s possble to fnd an ε > such that nf θ θ >δ Ω {} π N n π θ π θ θ n π A = Ω π θ / π θ / θ θ θ θ ε π A. θ π π π A 6 Gven aδ 2 >, t s possble to fnd an ε 2 > such that nf π 2 θ 2 θ 2 θ 2 >δ 2 Ω {} π 2 θ 2 π 2 θ 2 / π 2 θ 2 / π 2 θ 2 ε 2. π 2 θ 2 Remark. For a dfferentable functon f : R q R, the notaton f / represents f/ =. 7
9 The regularty condtons -4 and 6 or condtons equvalent to them have been assumed by several authors such as Brch 964, Rao 973, Ch. 5, Bshop et al. 975, Ch. 4, Sanathanan 972 and Agrest 22, Ch. 4, among others, n the contet of dervng asymptotc propertes of estmators of the parameters of models for the probabltes of a multnomal dstrbuton. The partcular form of condton 6 comes from Sanathanan 972 who took t from the frst edton of Rao 973, Ch. 5 and t s known as a strong dentfablty condton. Condton 5 s a modfcaton of 6 to meet the requrements of our partcular sampg desgn. In general, these condtons mply the estence and consstency of the UMLEs and CMLEs of θ and θ 2, and that they can be obtaned dervng the lkelhood functon wth respect toθ andθ Uncondtonal and condtonal mamum lkelhood estmators ofτ andθ Let us frstly consder the uncondtonal mamum lkelhood estmators UMLEs ˆτ U and ˆθ U ofτ and θ. The log-lkelhood functon ofτ and θ s l τ,θ = L τ,θ = τ! τ m r!τ n/n Ω r π θ n r A π A θ C, = Ω where C does not depend on τ and θ, and recall that r = τ m r and r A m r A U. Then, the UMLE ˆθ ofθ s the soluton to the followng equatons: l τ,θ = r π θ θ Ω π θ θ n = Ω = A r π A θ =, =,...,q π A θ θ. 4 Snceτ s an nteger we wll use the rato method to mamzel τ,θ. See Feller 968, Ch. 3. Thus L τ,θ L τ,θ = τ n/nπ θ. τ m r Snce ths rato s greater than or equal to f τ mr / n/nπ θ and t s smaller than or equal tofτ s greater than or equal to that quantty, t follows that ˆτ U s gven by ˆτ U = M R n/nπ ˆθ U, 5 where denotes the largest nteger not greater than. Notce that the rght hand-sde of 5 s not a closed form for ˆτ U U snce ths epresson depends on ˆθ. In fact, ˆτ U U and ˆθ are 8
10 obtaned by smultaneously solvng the set of equatons 4 and 5, whch s generally done by numercal methods. Let us now consder the condtonal mamum lkelhood estmators CMLEs ˆτ C and ˆθ C ofτ and θ. It s worth notng that ths type of estmators was proposed by Sanathanan 972 n the contet of estmatng the parameter of sze of a multnomal dstrbuton from an ncomplete observaton of the cell frequences. The approach we wll follow to derve ˆτ C C and ˆθ s an adaptaton of Sanathanan s 972 approach to our case. Thus, from 2 we have that L τ,θ =f {r } Ω {m },τ,θ =f {r } Ω {} r,{m },τ,θ f r {m },τ,θ r! π r θ = Ω {} r! Ω {} π θ τ m! π τ m r!r! θ r π θ τ m r =L θ L 2 τ,θ 6 Notce that the frst factor L θ s gven{ by the ont pmf of the multnomal } dstrbuton wth parameter of sze r and probabltes π θ / π θ and that ths Ω {} dstrbuton does not depend onτ. Note also that the second factorl 2 τ,θ s gven by the pmf of the bnomal dstrbuton wth parameter of szeτ mand probablty π θ. C Thus, the CMLE ˆθ ofθ s the soluton to the followng system of equatons: θ L θ L θ = Ω {} n = Ω r π θ r π θ π θ θ π θ θ The CMLE ˆτ C ofτ s obtaned by the rato method. Thus, snce A r π A θ =, =,...,q π A θ θ. 7 L MULT τ L 2 τ,θ L MULT τ L 2 τ,θ = τ n/nπ θ, τ m r t follows that ˆτ C = M R n/nπ ˆθC. 8 Note that 8 s a closed form for ˆτ C C snce ˆθ s frstly obtaned from 7. 9
11 3.3.2 Uncondtonal and condtonal mamum lkelhood estmators ofτ 2 andθ 2 By a smlar analyss as that conducted n the prevous subsecton we have that the UMLEs ˆτ U U 2 and ˆθ 2 ofτ 2 and θ 2 are the soluton to the followng equatons: Ω r 2 π 2 θ 2 =, =,...,q π 2 θ 2 θ 2 2 and ˆτ U 2 = π 2 R 2 ˆθU 2. 9 where recall thatr 2 = τ 2 r 2. Wth respect to the condtonal estmators, we have that the CMLE ˆθ C 2 of θ 2 soluton to the followng equatons: Ω {} r 2 π 2 θ 2 r 2 π 2 θ 2 π 2 θ 2 θ 2 π 2 θ 2 θ 2 =, =,...,q 2. s the The CMLE ˆτ C 2 ofτ 2 s gven by 9, but replacng a closed form for ˆτ C 2. U C ˆθ 2 by ˆθ 2. Note that n ths case 9 s Uncondtonal and condtonal mamum lkelhood estmators ofτ = τ τ 2 The UMLE and CMLE ofτ = τ τ 2 are gven by ˆτ U = ˆτ U ˆτ U 2 and ˆτ C = ˆτ C ˆτ C 2, respectvely. 4 Asymptotc propertes of the uncondtonal and condtonal mamum lkelhood estmators The structure of ths secton s as follows. Frstly we wll defne the asymptotc framework under whch we wll derve the asymptotc propertes of the estmators. Net we wll state and proof a theorem that guarantees the asymptotc multvarate normal dstrbuton of any estmator of τ,θ that satsfes the condtons epressed n the theorem. Snce not any estmator ofτ,θ satsfes the condtons of the theorem, n partcular the CMLE does not, we wll state and proof another theorem that guarantees the asymptotc multvarate normal dstrbuton of any estmator of θ that satsfes the condtons of that theorem. Then, we wll prove that the UMLE of τ,θ satsfes the condtons of the frst theorem, whereas the CMLE of θ satsfes those of the second one. In addton, we wll prove that n spte of that result, the CMLE ˆτ C does have an asymptotc normal dstrbuton although t s not the same as that of ˆτ U. After that we wll consder the asymptotc propertes of estmators of
12 τ 2,θ 2. Snce ths problem s eactly the same as that consdered by Sanathanan 972, we wll only state a theorem that guarantees the asymptotc multvarate normal dstrbuton of any estmator of τ 2,θ 2 that satsfes the condtons epressed n the theorem, but we wll omt ts proof, as well as the proofs that both the UMLE and the CMLE ofτ 2,θ 2 satsfy the condtons of that theorem. Fnally, we wll obtan the asymptotc propertes of the estmators ˆτ U and ˆτ C ofτ. 4. Basc assumptons To derve the asymptotc propertes of the UMLEs and CMLEs of τ k and θ k, k =,2, we wll make the followng assumptons: A. τ k, k =,2. B. τ k /τ α k, < α k <,k =,2. C. N andnare fed postve nteger numbers. For convenence of notaton, we wll put τ k ether as a subscrpt or a superscrpt of every term that depends onτ k,k =,2. In addton, convergence n dstrbuton wll be denoted by D and convergence n probablty by. P Notce that from t follows that the condtonal dstrbuton of M τ gvenτ s bnomal wth parameter of sze τ and probablty /N, that s M τ τ Bnτ,/N; consequently M τ /τ s stochastcally bounded, that s, M τ = O p τ. Ths means that the sze of U τ s ncreased by ncreasng the szes of the clusters, even though ther number N s kept fed. In the same manner, the number of people n the ntal sample S τ, gven by M τ = n Mτ τ Bnτ,n/N, s ncreased because of the ncreasng of M τ, =,...,n, even though n s kept fed. On the other hand, snce τ M τ τ Bnτ, n/n,r τ S τ A Bnτ M τ, π andrτ 2 2 S τ A Bnτ 2, π 2, t follows that R τ τ Bn τ, n/n π and R τ 2 2 τ 2 Bnτ 2, π 2 ; therefore R τ = O p τ and R τ 2 2 = O p τ 2. Thus, the szes of the sets S τ and S τ 2 2 are ncreased because τ and τ 2 are ncreased even though the probabltes {π } Ω and {π 2 } Ω are kept fed. We wll end ths subsecton presentng the condtonal and uncondtonal dstrbutons of the varables R τ, R A and R τ 2 whch wll be used later n ths work. Thus, from the multnomal dstrbutons ndcated n Subsecton 3. t follows that R τ S τ A Bnτ M τ,π,r A M τ BnM τ,π A andr τ 2 S τ A Bnτ 2,π 2 ; thereforer τ τ Bn τ, n/nπ, R A τ Bn τ,π A /N and R τ 2 τ 2 Bnτ 2,π 2.
13 4.2 Asymptotc multvarate normal dstrbuton of estmators ofτ,θ Theorem. Let θ = θ,...,θ q be the true value of θ. Let ˆτ τ and ˆθ τ = ˆθ τ,..., ˆθ τ q be estmators ofτ andθ, such that ˆθ τ τ /2 P τ /2 θ. { ˆτ τ θ M τ R τ l τ ˆττ, ˆθ τ / n/nπ P, =,...,q. } ˆθτ P. In addton, letσ be theq q matr whose elements are Σ n/nπ, = θ / n/nπ θ, = Σ, /π, = θ π θ / θ, =,...,q,, = Σ, = n /π θ N π θ / θ Σ Σ N n l= Ω /π A l θ π A l θ Ω / θ l and whch s assumed to be a non-sngular matr. Then τ /2 ˆτ τ τ,τ /2 ˆθτ θ D N q,σ, whereσ s the nverse of Σ and =,..., R q. π θ / θ π A l θ / θ,, =,...,q, 2
14 Proof. Evaluatng equaton 4 at ˆτ τ, ˆθ τ we get θ = Ω n l τ ˆτ τ, ˆθ τ R τ π ˆθ τ l= Ω l R τ = Ω n = Ω π ˆθ τ l= Ω l R τ π ˆθ τ ˆττ θ A R l,τ π A l ˆθ τ π ˆθ τ π ˆθ τ θ A R l,τ π A l ˆθ τ π ˆθ τ θ π A l ˆθ τ θ M τ R τ π ˆθ τ ˆτ τ M τ R τ π A l ˆθ τ θ ˆττ τ π ˆθ τ π ˆθ τ θ π ˆθ τ π ˆθ τ θ τ M τ R τ n l= Ω l A R l,τ π A l ˆθ τ π ˆθ τ θ π A l ˆθ τ. θ Snce Ω from we get that π ˆθ τ / θ = and Ω l π Al ˆθ τ / θ =, τ /2 n l= { Ω R τ τ M τ π π ˆθ τ A R l,τ M τ l π A l Ω l π A l = τ /2 ˆτ τ τ τ /2 n l= { τ M τ M τ l τ τ ˆθ τ π ˆθ τ Ω A π l ˆθ τ Ω l θ θ π ˆθ τ θ π ˆθ τ π π ˆθ τ π A l π A l ˆθ τ π ˆθ τ θ π A l ˆθ τ θ θ θ τ /2 π ˆθ τ θ π A l ˆθ τ θ θ l τ ˆτ τ, ˆθ τ. 2 3
15 Let Y τ = R τ τ M τ π θ, Y A l,τ = R A l,τ M τ l π A l θ and Z τ = τ /2 = τ /2 Ω Ω R τ π θ π Y τ π θ π θ θ θ θ n R l= Ω l π A l n A l,τ A Y l,τ l= Ω l π A l A l π θ θ θ A π l θ, θ θ where the last equalty s obtaned usng but replacng ˆθ τ by θ. Then, the dfference between the left-hand sde of 2 and Z τ s gven by τ /2 τ /2 = τ /2 n l= τ /2 Ω θ { Ω Y τ π ˆθ τ l τ Y τ π ˆθ τ θ ˆτ τ, ˆθ τ Y Al,τ Ω l θ π ˆθ τ π A l ˆθ τ l τ ˆτ τ, ˆθ τ Z τ n l= Ω l π ˆθ τ θ Y A l,τ π A l ˆθ τ π θ π A l ˆθ τ θ π π A l ˆθ τ θ θ π A l θ π A l θ θ θ. 3 Snce uncondtonally EY τ = and VY τ = τ n/nπ θ π θ, and also EY A l,τ = and VY A l,τ = τ /Nπ A l θ πa l θ, t follows that τ /2 Y τ = O p and τ /2 Y A l,τ = O p. Consequently, these results along wth condtons 3-4 and condtons and of the theorem mply that 3 converges to zero n probablty. On the other hand, by the mean value theorem for functons of several varables we have that π ˆθ τ π θ = q = π A l ˆθ τ π A l θ = q = ˆθτ θ ˆθτ θ π θ τ / θ and 4 π A l θ τ A l / θ, where θ τ and θτ A l are between ˆθ τ and θ. Snce the dfference between the rght-hand 4
16 sde of 2 and Z τ also converges to zero n probablty, we have that = where τ /2 ˆτ τ τ τ /2 n l= ˆΣ { τ M τ M τ l τ, τ π ˆθ τ Ω π ˆθ τ Ω l π A l ˆθ τ τ /2 ˆτ τ τ π ˆθ τ θ π ˆθ τ θ π A l ˆθ τ θ q = ˆΣ q = q =, ˆθτ π θ θ τ θ ˆθτ A π l θ θ τ A l θ τ /2 ˆθτ θ Zτ Z τ P, 5 ˆΣ, ˆΣ, = π ˆθ τ = τ M τ τ n l= M τ l τ π ˆθ τ θ Ω π ˆθ τ and Ω l π A l ˆθ τ π ˆθ τ θ π A l ˆθ τ θ π θ τ θ π A l θ τ A l θ. 6 π Epresson 5 suggests the followng equalty n terms of ˆτ τ τ and π ˆθ τ θ : { τ /2 ˆτ τ n/nπ τ /2 n/n n/nπ ˆθ τ ˆθ τ τ /2 π ˆθ τ π θ. } M τ R τ { M τ R τ = τ /2 ˆτ τ τ } τ n/nπ θ By condton of the theorem t follows that the left hand-sde of the prevous equaton converges to zero n probablty. Therefore, f we dvde the rght hand-sde of ths equaton by n/nπ θ and use 4, we wll get that the followng epresson also converges to zero n probablty, that s 5
17 τ /2 ˆτ τ n/nπ τ n/nπ θ M τ R τ τ /2 q = = ˆΣ τ /2, ˆθτ θ τ /2 ˆθ τ τ n/nπ θ n/nπ θ π π θ θ ˆτ τ τ q whereθ τ s between ˆθ τ and θ and and ˆΣ, θ τ = = n/nπ ˆθ τ n/nπ θ, Z τ = τ /2 ˆΣ,, ˆΣ, τ /2 ˆθτ θ Z τ P, 7 = π π θ θ τ M τ R τ τ n/nπ θ n/nπ θ. θ Let W τ = τ /2 ˆτ τ τ,τ /2 ˆθ τ θ and Z τ = Z τ,z τ 2,...,Z τ q, by the prevous results we have that 8 ˆΣ Wτ Z τ P, 9 where ˆΣ s theq q matr whose elements are defned n 6 and 8. Notce that from the defntons of the matrcesσ and ˆΣ, condtons 3-4 and condton of the theorem along wth the fact that τ M τ /τ P n/n and M τ l /τ P /N, t follows that ˆΣ P Σ. We wll show that Z τ D Z N q,σ as τ. To do ths, we wll assocate wth each element t U, t =,...,τ, a random vector V t = V t,,...,v t,q such that a V t, = and V t, = π θ π θ / θ assocated vectorx t b V t, = π n/nπ θ, =,...,q, f t U S and ts of k-ndcator varables equals the vector Ω {}; / n/nπ θ and V t, = π θ θ / θ, =,...,q, f t U S and ts assocated vector X t of k-ndcator varables equals the vector Ω, and 6
18 c V t, = and V t, = πa l θ π A l θ / θ, =,...,q, f t A l S A and ts assocated vectorx t of k-ndcator varables equals the vector Ω l. τ /2 and τ /2 Snce τ t= τ t= V t =τ /2 =Z τ, V t, =τ /2 M τ R τ Ω R τ π θ π θ θ t follows that Z τ = τ /2 τ t= V t. From the defnton ofv t, we have that { Pr V t, = } = n/n { Pr V t, = n/nπ { } Pr V t, = π θ π θ / θ θ / τ M τ R τ n A R l,τ l= Ω l π A l n/nπ θ n/nπ θ θ π θ n/n, θ π A l θ = Z τ =,...,q ; n/nπ θ } = n/nπ θ, = n/nπ θ, Ω, =,...,q, and { } Pr V t, = πa l θ π A l θ / θ =/Nπ A l θ, Ω l, =,...,q, l =,...,n; therefore, the epected values of the varablesv t, are E V t, = n/n π θ n/n n/nπ θ = and E V t, = Ω because of. Thus,E V V t, π θ / θ n/n V t n l= Ω l π Al θ / θ /N =, =,...,q, =, t =,...,τ. Furthermore, ther varances are = n/n π θ n/n = n/nπ θ n/nπ θ 7 2 n/nπ θ n/nπ θ
19 and V V t, = n/n Ω N n l= π θ Ω l π A l θ π θ θ π A l 2 θ 2, =,...,q, θ and ther covarances are Cov Cov V t,,v t, = π Ω {} θ θ n/n = π θ π n/n n/nπ θ n/nπ n l= Ω l π A l θ N θ θ, =,...,q, and θ V t,,v t, = n/n Ω n N l= π θ θ π Ω l π A l θ θ π A l θ θ π θ θ π A l θ, θ, =,...,q,. θ π θ θ Therefore, the varance-covarance matr ofv t sσ. Fnally, snce the V t, t =,...,τ, are ndependent and dentcally dstrbuted random vectors, by the central lmt theorem t follows that Consequently by 9, as ˆΣ P Σ. W τ = Z τ = τ /2 τ /2 τ t= V t D Z N q,σ. ˆτ τ τ,τ /2 ˆθ τ θ D Σ Z N q,σ 4.3 Asymptotc multvarate normal dstrbuton of estmators ofθ Theorem 2. Let θ = θ,...,θ q be the true value of θ. Let ˆθ τ = ˆθ τ,..., ˆθ τ q be an estmator of θ, such that ˆθ τ P θ. 8
20 { τ /2 θ L τ ˆθ τ L τ ˆθ τ } P, =,...,q. In addton, letψ be theq q matr whose elements are Ψ = Ψ,, = n/n π θ Ω {} n N l= / π θ π θ / θ π θ / θ /π A l θ π A l θ Ω / θ π A l θ / θ, l, =,...,q, where π θ = π θ / π θ, Ω {}, and suppose that Ψ s a nonsngular matr. Then τ /2 ˆθτ θ D N q,ψ, whereψ s the nverse of Ψ and =,..., R q. Furthermore, f ˆτ τ s an estmator ofτ such that { } τ /2 ˆτ τ M τ R τ / n/nπ ˆθτ P, then where σ 2 = n/n n/nπ θ 2 θ / θ,..., π θ / θ q s the gradent of π θ eval- and π θ = uated atθ. π τ /2 ˆτ τ τ D N,σ 2, π θ Ψ n/n π θ π n/nπ θ θ, Proof. From the defntons ofl τ θ and L τ θ we have that Snce θ L τ ˆθ τ L τ ˆθ τ Ω {} = Ω π ˆθ τ / θ = and 9 n R τ π ˆθ τ l= Ω l π ˆθ τ θ A R l,τ π A l ˆθ τ π A l ˆθ τ θ. 2 Ω l π Al ˆθ τ / θ =, 22
21 from 2 we get that τ /2 n l= = τ /2 θ n l= Ω {} Ω l R R τ τ M τ l τ Let Y τ = R τ R τ Z τ = τ /2 = τ /2 π Ω {} Ω {} R τ R τ π π ˆθ τ A l,τ M τ l π A l π A l ˆθ τ θ θ L τ ˆθ τ L τ ˆθ τ Ω {} π ˆθ τ π A π l ˆθ τ Ω l π ˆθ τ π A l π A l ˆθ τ θ,y A l,τ = R A l,τ R τ π θ π θ θ Y τ π θ π θ θ π ˆθ τ θ π A l ˆθ τ θ θ θ π ˆθ τ θ π A l ˆθ τ θ M τ l π A l n A R l,τ l= Ω l π A l n Y l= Ω l π A l where the last equalty s obtaned usng 22 but replacng ˆθ τ by θ between the left-hand sde of 23 and Z τ s gven by τ /2 τ /2 = τ /2 n l= τ /2 Ω {} θ Ω {} Y τ π ˆθ τ π ˆθ τ θ L τ ˆθ τ L τ ˆθ τ Y τ Y Al,τ Ω l θ π ˆθ τ π A l ˆθ τ L τ ˆθ τ L τ ˆθ τ n l= Ω l Z τ π ˆθ τ θ π A l ˆθ τ θ 2 Y. 23 θ and π A l θ θ θ A l,τ π A l θ, θ A l,τ π A l ˆθ τ π θ π θ. Then, the dfference π A l ˆθ τ θ θ θ A π l θ θ π A l θ. 24
22 Snceτ /2 Y τ = O p andτ /2 Y A l,τ = O p, these results along wth condtons 3-4 and condtons and of the theorem mply that 24 converges to zero n probablty. On the other hand, by the mean value theorem of several varables we have that π ˆθ τ π θ = q = π A l ˆθ τ π A l θ = q = ˆθτ θ ˆθτ θ π θτ / θ and 25 π A l θ τ A l / θ, where θ τ and θ τ A l are between ˆθ τ and θ. Snce the dfference between the rght-hand sde of 23 and Z τ also converges to zero n probablty, we have that = where τ /2 q = n l= R τ τ M τ l τ ˆΨ, ˆΨ, Ω {} π ˆθ τ Ω l π A l ˆθ τ τ /2 ˆθτ θ = Rτ τ n l= Ω {} M τ l τ π ˆθ τ θ π A l ˆθ τ θ Z τ π ˆθ τ q = q = ˆθτ π θ θ τ θ ˆθτ A π l θ θ τ A l θ Zτ P, 26 π ˆθ τ Ω l π A l ˆθ τ θ π A l ˆθ τ π θ τ θ θ Notce that from the defntons of the matrces Ψ and ˆΨ π A l θ τ A l θ. 27, condtons 3-4 and θ and condton of the theorem along wth the fact thatr τ /τ P n/n π /τ P /N, t follows that ˆΨ P Ψ M τ l. By condton of the theorem and usng eactly the same procedure as that used to obtan epresson 7 we wll get that epresson whch we wll put n the followng terms: â τ /2 ˆτ τ τ q τ /2 ˆθτ θ Z τ P, 28 where â = n/nπ ˆθ τ n/nπ Z τ = τ /2 =â θ, â = π θ τ π θ, =,...,q θ, M τ R τ τ n/nπ θ n/nπ θ, 29 2
23 and θ τ s between ˆθ τ and θ theorem mply that â P a, =,..., q, where a = n/nπ θ, anda = Let Z τ =. Notce that condtons 3-4 and condton of the n/nπ θ / π θ / θ /π θ, =,...,q. Z τ,z τ 2,...,Z τ q, then by the prevous results we have that ˆΨ τ /2 ˆθτ θ Z τ P, 3 where ˆΨ s theq q matr whose elements are defned n 27. We wll show thatz τ D Z N q,ψ asτ, wherez = Z,...,Z q, and that Z τ D Z N,a, where Z τ s gven by 29. To do ths, we wll assocate wth each element t U, t =,...,τ, a random vector V t = V t, varablev t such that,...,v t,q and a random a V t, = π θ π θ / θ, =,...,q, and V t =, f t U S and ts assocated vectorx t of k-ndcator varables equals the vector Ω {}; b V t, =, =,...,q, and V t = n/nπ θ / n/nπ θ, ft U S and ts assocated vectorx t of k-ndcator varables equals the vector Ω, and c V t, = π A l θ π A l θ / θ, =,...,q, and V t =, f t A l S A and ts assocated vectorx t of k-ndcator varables equals the vector Ω l. Snce τ /2 τ t= V t, =τ /2 Ω {} R τ π =Z τ, =,...,q, θ π θ θ n A R l,τ l= Ω l π A l A π l θ θ θ t follows that Z τ = τ /2 τ /2 τ t= V t =τ /2 =Z τ. τ t= V t, and M τ R τ τ M τ R τ n/nπ θ n/nπ θ 22
24 From the defnton ofv t, and V t we have that { } Pr V t, = π θ π θ / θ = n/nπ θ, Ω {}, { } Pr V t, = { Pr V t, = π A l θ π A l θ / θ and { Pr V t = and { } Pr V t = n/nπ θ / = n/n =,...,q, = n/nπ θ, =,...,q, } =/Nπ A l θ, Ω l, =,...,q, l =,...,n, π θ n/n and } n/nπ θ = n/nπ θ ; therefore, the epected values of the varablesv t, and V t are = E E V t V t, Ω {} because of 22. Thus, E varances are V n l= π θ / θ n/n π θ Ω l π Al θ / θ /N =, =,...,q, = n/n π θ n/n n/nπ θ = V t, V t = and E V t = n/n π θ N n l= Ω l π A l θ =, t =,...,τ. Furthermore, ther Ω {} π π θ θ 2 θ θ 2, =,...,q, π A l θ and V V t 2 n/nπ = n/n π θ θ n/n n/nπ θ = n/nπ θ, n/nπ θ 23
25 and ther covarances are Cov V t,,v t, = n N and Cov N n l= π θ Ω l π A l Ω {} π A π l θ θ θ V t,v t, = n π N θ π Ω {} π θ θ θ π θ θ π A l θ,, =,...,q θ,, θ N θ n l= Ω l π A l θ θ Therefore, the varance-covarance matr ofv t sψ. Fnally, snce the V t,v t, t =,...,τ, are ndependent and dentcally dstrbuted random vectors, by the central lmt theorem t follows that Z τ,z τ = τ /2 τ τ /2 t= V t,v t D Z,Z N q q, Ψ a Thus,Z τ D Z N q,ψ and Zτ D Z N,a. Consequently by 3 ˆθτ θ D Ψ Z N q,ψ as ˆΨ P Ψ. At last, from 28 and the prevous results ˆτ τ D τ { Z q a τ /2 = n/nπ θ n/nπ θ Z whereψ Z s the-th element ofψ Z and σ 2 = n/n n/nπ θ π θ = a Ψ Z } π θ π θ Ψ Z N,σ 2, Ψ n/n π θ π n/nπ θ =.. θ. 4.4 Consstency of the UMLE and CMLE ofτ,θ To prove the consstency of the UMLE and CMLE we wll use condton 5 and the followng nequalty of nformaton theory: If a and b are convergent seres of postve numbers such that a b, then a logb a loga, and the equalty s attaned f and only fa = b. See Rao 973, p
26 4.4. Consstency of the UMLE Let us frst consder get that l ˆτ U, n = Ω {} ˆθ U. Usng 3 and 6 and the defnton of the UMLE U ˆθ = { R τ Ω {} R A,τ Ω R τ π A ˆθU π ˆθU / π L MULT { π θ / π θ } n = ˆθU } ˆτ U, ˆτ U L 2 ˆτ U, L MULT τ L 2 τ,θ C = l τ,θ, R A,τ π A θ Ω U ˆθ we U ˆθ C where C depends only on observable varables. Snce L MULT ˆτ U and L 2 ˆτ U, ˆθ U are nonpostve we have that Ω {} Ω {} R τ R τ R τ R τ π π ˆθU ˆθU π θ π θ n = n = M τ R τ M τ R τ A R,τ Ω M τ A R,τ Ω M τ π A π A θ ˆθU L MULT τ /R τ L 2 τ,θ /R τ. 3 Now, snce = Ω {} R τ R τ = Ω {} π π ˆθU ˆθ U and = Ω R A,τ M τ ˆθU π A Ω = =,...,n,, usng n tmes the prevously ndcated nformaton theory nequalty we have that Ω {} Ω {} R τ R τ R τ /Rτ R τ R τ π π ˆθU ˆθU n = M τ R τ n = M τ R τ Ω R A,τ M τ Ω R A,τ M τ R A,τ /M τ π A ˆθU.32 25
27 Thus, by 3 and 32 we get that Ω {} n = Ω {} R τ R τ M τ R τ R τ R τ π ˆθU A R,τ Ω M τ π A θ R A,τ /M τ / π R /R τ πa π θ / π R /R τ ˆθU ˆθU R A,τ /M τ θ n = M τ R τ A R,τ Ω M τ L MULT τ /R τ L 2 τ,θ /R τ. 33 From the uncondtonal dstrbutons ofm τ,m τ andr τ,r A,τ andr A,τ n Subsecton 4., t follows that R τ /R τ P π θ / π θ, R A,τ π A θ andmτ /R τ P /{N n π θ ndcated /M τ }. Therefore, the frst two summands of the last term of the double nequalty 33 converges to zero n probablty, In addton, snce R τ /τ P π θ, and from well known results of large devatons theory see Varadhan, 28, we have that for the bnomal probabltyl 2 τ,θ : L 2 τ,θ R τ R τ { = τ M τ R τ τ R τ R τ τ M τ /τ M τ π θ R τ /τ M τ } π θ P π θ π θ =, π θ and for the multnomal probabltyl MULT τ : { n L MULT τ = τ M τ M τ /τ τ /N τ R τ o p P R τ { n = = N n/n τ M τ o R τ p τ M τ τ τ R τ τ M τ P } τ M τ /τ n/n } { } / π θ n/n =. The prevous results mply that the last term of the double nequalty 33 converges to zero n probablty, and consequently so does the mddle term. 26
28 Thus, { as M τ Ω {} π = N n Ω {} π θ θ R τ R τ n M τ = R τ Ω {} n = Ω π θ π Ω {} π A R,τ Ω M τ π θ θ π n ˆθU / π ˆθU π θ / π θ π A θ = Ω ˆθ U / π ˆθ U R τ /R τ πa ˆθU R A,τ /M τ π θ π θ R τ π R τ π A θ R N n π θ N n π θ π ˆθU / π ˆθU π θ / n ˆθU A R τ R τ /R τ π A = Ω π πa π A ˆθU θ / π R τ /R τ πa θ ˆθU ˆθU R A,τ /M τ θ R A,τ /M τ π A θ } / R τ /R τ and π A ˆθU P / R A,τ / are bounded as τ otherwse the mddle term of the nequalty 33 would not{ converge to zero. } Fnally, condton 5 mples that for any δ > we have that ˆθU Pr θ U P δ, that s, ˆθ θ. Straghtforward results of the prevous one are the followng: π ˆθU P π θ, ˆθU Ω, and π A assumed to be contnuous functons ofθ. P π A θ, Ω, =,...,n, as π θ and π A θ are Wth respect to ˆτ U, from epresson 5 we have that the dfference { between ˆτ U and M τ R τ / n/nπ ˆθU s less than. Thus, ˆτ U M τ R τ / } n/nπ ˆθU / τ = ˆτ U /τ M τ R τ /τ / n/n 27
29 π ˆθU P, and snce the second term of the last dfference converges to n probablty so does ˆτ U /τ Consstency of the CMLE By the defnton of the CMLE L ˆθ C L ˆθ C R τ ˆθ C, we have that = Ω {} n = Ω {} n = R τ R τ M τ R τ R τ R τ M τ R τ π π A R,τ Ω M τ π θ ˆθC ˆθC π θ A R,τ Ω M τ = L θ L θ, R τ π A ˆθC π A θ C wherec depends only on observable varables. Usng the same procedure as that used n the case of the UMLE ˆθ U C we wll get the double C U nequalty 33 but n terms of ˆθ nstead of ˆθ and wthout the termsl MULT τ /R τ and L 2 τ,θ /R τ C P. Consequently, we wll also have that ˆθ θ, π ˆθC P π θ, Ω, πa ˆθ C P π A θ, Ω, =,...,n, and ˆτ C /τ P, where the last result s obtaned by usng epresson 8 and the same arguments as those used to prove that ˆτ U /τ P. 4.5 Asymptotc dstrbutons of the UMLEs and CMLEs ofτ andθ 4.5. Asymptotc multvarate normal dstrbuton of the UMLE ofτ,θ We wll prove the asymptotc multvarate normal dstrbuton of τ /2 ˆτ U,τ /2 ˆθ U by provng that ths estmator satsfes the condtons of Theorem. Condton was already proved n the prevous secton. From epresson 5 t follows that ˆτ U, ˆθ U satsfes condton. Fnally, by the defnton of the UMLEs we have that condton s also satsfed. Thus, by Theorem, τ /2 ˆτ U τ,τ /2 ˆθU θ D N q,σ. Ths result 28
30 mples thatτ /2 ˆτ U ˆθU D τ N,σU 2 and τ/2 θ D N q,σ 22, where σ 2 U = Σ 22 = n/n n/nπ θ { π θ n/n n/nπ θ π θ Σ 22 π θ }, 34 Σ 22 n/n π π θ n/nπ θ θ π θ π θ s the gradent of π θ evaluated at θ and Σ Σ obtaned by removng ts frst row and frst column s the q q submatr of U Asymptotc multvarate normal dstrbuton of the CMLE ˆθ and asymptotc normal dstrbuton of the CMLE ˆτ C The CMLE τ /2 ˆτ C,τ /2 ˆθ C does not have an asymptotc multvarate normal dstrbuton snce ths estmator { does not satsfy condton } of Theorem. To see ths, notce that ˆθC ˆθC by 7 t follows that L L / θ =. Therefore, τ /2 θ l ˆτ C, C ˆθ =τ /2 θ π =τ /2 L 2 ˆτ C, ˆθC θ ˆτC C ˆθ M τ R τ π ˆθC By usng epresson 8 and after some algebrac steps we get that ˆθC τ /2 l ˆτ C C, ˆθ = π τ /2 θ ˆτ C M τ R τ / τ /2 π θ n/nπ ˆθ C M τ /τ n/n π n/nπ ˆθC ˆθC π ˆθC R τ π R τ ˆθC,. /τ n/n. 36 ˆθC 29
31 From 8 and the fact that π ˆθC P π θ, t follows that the order of magntude of the frst term n the curly brackets of 36 so p τ /2. On the other hand, sncem τ /τ = n/no p τ /2,R τ /τ = n/n π θ O p τ /2 and, as we wll show C n the net paragraph, ˆθ = θ O p τ /2, t follows that the order of the second term n the curly brackets of 36 so p ; therefore 36 does not converge to zero n probablty. Nevertheless, although τ /2 ˆτ C τ,τ /2 ˆθC θ does not have an asymptotc multvarate normal dstrbuton, τ /2 ˆθ C θ does have. To prove ths, we wll show that condtons and of Theorem 2 are satsfed. In the prevous secton we proved C C ˆθ ˆθ satsfes condton. Thus that satsfes condton, and from 7 we have that by Theorem 2,τ ˆθ /2 C θ D N q,ψ. Now, τ /2 ˆθ C ˆθC θ ˆτ C τ has also an asymptotc normal dstrbuton because n addton that satsfes condtons and of Theorem 2, ˆτ C satsfes condton. Thus by Theorem 2, τ /2 ˆτ C D τ N,σC 2, whereσ2 C s gven by 2. It s worth notng that the asymptotc margnal dstrbutons of τ /2 ˆτ C τ and τ /2 are not the same as those of τ /2 ˆτ U τ and τ /2. To show ths, we wll frstly prove that Ψ = Σ 22 π θ n/n π θ ˆθU θ π θ π θ, 37 whereψ s theq q matr defned n the statement of Theorem 2 andσ 22 s theq q submatr of the matr Σ, defned n the statement of Theorem, obtaned by removng ts frst row and frst column. Snce π θ = π θ / π θ, t follows that π θ θ = = π θ / θ π θ π θ θ θ π θ π θ / θ 2 π θ π π θ 2 π θ π θ θ. 3
32 Then n/n π θ Ω {} = n/n π θ π θ 2 π θ = n/n Ω {} θ π θ = n/n π Ω {} π π θ θ π θ θ Ω {} π n/n π π θ θ θ Ω {} π θ θ θ n/n π Ω {} π θ π π θ θ π θ π θ π θ π θ π θ π θ θ θ θ θ π θ θ π θ θ θ θ π θ θ θ π θ π θ θ n/n π Ω {} π θ θ π θ θ π θ 2 π θ π θ π θ θ 2 n/n π θ θ π θ π θ θ n/n 2 π θ θ θ π θ θ = n/n = n/n Ω θ π θ Ω {} π π θ π θ θ θ. π π θ θ θ θ π θ θ π θ θ Therefore, from the defntons ofψ and Σ 22 we have that and 37 s proved. Ψ = Σ, 22, n/n π θ π 3 n/n π π θ θ θ n/n π θ π θ π θ θ θ π θ θ π θ θ,
33 From 34 and 37 t follows thatσ 2 C σ2 U, and henceτ /2 ˆτ U τ andτ /2 ˆτ C τ do not have the same asymptotc normal dstrbuton. In addton, 35 and 37 mply that Ψ Σ 22, and consequently that τ /2 ˆθU θ and τ /2 ˆθC θ do not have the same asymptotc normal dstrbuton. Notce also that even though the asymptotc margnal dstrbutons of the UMLEs and CMLEs of τ and θ are not the same, from 37 t follows that fn/n were small enough so that n/nπ θ π θ, thenψ Σ 22 and ther asymptotc margnal dstrbutons would be very smlar to each other. 4.6 Asymptotc propertes of uncondtonal and condtonal mamum lkelhood estmators of τ 2,θ 2 The uncondtonal and condtonal mamum lkelhood estmators of τ 2,θ 2 are eactly the same as those used n capture-recapture studes. Sanathanan 972 assumed condtons smlar to -4 and 6 and proved the followng results: ˆθ U 2 P θ C 2 and ˆθ 2 P θ 2 as τ 2. ˆτ U 2 /τ P 2 and ˆτ C τ /2 2 ˆτ U 2 τ 2 2 /τ 2 P as τ 2.,τ /2 2 θ 2 D N q2,σ 2 as τ 2, ˆθU 2 θ 2 D N q2,σ 2 and τ /2 2 ˆτ C 2 τ 2,τ /2 2 ˆθC 2 whereσ 2 s the nverse of theq 2 q 2 matrσ 2 defned by Σ 2 π, = 2 θ 2 /π 2 θ 2, Σ 2 = Σ, 2 /π, = 2 θ 2 π 2 θ 2 / θ2, =,...,q 2, Σ 2 = Σ, 2 =, /π 2 θ 2 π 2 θ 2/ θ 2 π 2 θ 2/ θ 2, Ω, =,...,q 2, and whch s assumed to be a non-sngular matr. Because the proofs of these results are eactly the same as those gven by Sanathanan 972, we wll omt them. It s worth notng that unlke the CMLE τ /2 ˆτ C,τ /2 ˆθ C, the estmator τ /2 2 ˆτ C 2,τ /2 2 ˆθ C 2 does have an asymptotc multvarate normal dstrbuton. 32
34 The prevous results mply that τ /2 2 ˆτ U D 2 τ 2 N,σ2 2 N,σ2 2, where σ 2 2 = π 2 θ 2 { π 2 θ 2 π 2 θ 2 π 2 θ 2 π 2 θ 2 π 2 θ 2 π 2 and τ /2 2 π 2 θ 2 Σ 2 22 θ 2 π 2 ˆτ C 2 τ 2 D θ 2, where π 2 θ 2 s the gradent ofπ2 θ 2 evaluated atθ 2 andσ 2 22 s theq 2 q 2 submatr ofσ 2 obtaned by removng ts frst row and frst column. 4.7 Consstency and asymptotc normalty of the uncondtonal and condtonal mamum lkelhood estmators of τ = τ τ 2 The UMLE and CMLE of τ = τ τ 2 were defned n Subsecton by ˆτ U = ˆτ U ˆτ U 2 and ˆτ C = ˆτ C ˆτ C 2. From assumptons A and B and the prevous results we have that ˆτ U /τ = τ /τ ˆτ U /τ τ 2 /τ ˆτ U P 2 /τ 2 α α 2 =, as τ and τ 2. Smlarly, ˆτ C /τ P as τ and τ 2. Furthermore, τ /2ˆτ U τ =τ/τ /2 τ /2 ˆτ U τ τ/τ 2 /2 τ /2 2 ˆτ U D 2 τ 2 N,σU 2, as τ and τ 2, where σ 2 U = α σ 2 U α 2σ 2 2. Lkewse, τ /2ˆτ C τ D N,σ 2 C, whereσ2 C = α σ 2 C α 2σ Estmaton of the matrcesσ k andψ Although estmates of Σ k, k =,2, and Ψ can be obtaned by replacng the parameters θ k and θ by ther respectve estmates n the epressons for these matrces, ths procedure requres the computaton of sums of 2 n terms. Ths s not a problem f n s small, but f n s large enough, say greater than or equal to2, the number of these terms s very large and the calculaton of the estmates ofσ k and Ψ could be computatonally epensve. A procedure that requres a much smaller number of calculatons s based on estmates of the vectors V k t, t =,...,τ k, k =,2. Vectors V t s were defned n the proofs of Theorems and 2, whereas vectors V 2 t s are defned n Sanathanan 972 and we wll gve ther defnton later n ths secton. As was shown n the proofs of Theorem and 2, the vectors V t s are ndependent and equally dstrbuted wth mean vector equal to the vector zero and covarance matr equal to Σ n the case of Theorem, and Ψ n the case of Theorem 2. The same result holds n the case of the vectorsv 2 t s, but the covarance matr s Σ 2. Therefore, the sample covarance matr of the vectors V k t s s an estmate of ther covarance matr Σ k orψ based only onτ k observatons. 33
35 To mplement ths procedure we need to estmate the V k t s they are unknown because depend on θ k and τ k. In the case of the V t s defned n Theorem an estmate ˆV t of V t could be obtaned by replacng θ by ˆθ U n the epresson for V t, and τ could be estmated by ˆτ U. In the case of the V t s defned n Theorem 2 estmates of V t could be obtaned by replacng θ by ˆθ C n the epresson for V t, and τ could be estmated by ˆτ C. Estmates of V 2 t s and τ 2 could be obtaned as n the case of Theorem, and n ths stuaton both UMLE and CMLE could be used. Thus, once ˆτ k and the vectors ˆV k t s are obtaned, ther sample covarance matr can be computed and used as an estmate ofσ k or Ψ. The vectorsv 2 t = V 2 t,,...,v 2 t,q 2, t =,...,τ 2, are defned as follows: a V 2 t, = and V 2 t, = π2 θ 2 π 2 θ 2 / θ2, =,...,q 2, f the vector X 2 t of k-ndcator varables assocated wth the t-th element n U 2 equals the vector Ω {}; b V 2 t, = π 2 θ 2 / π 2 θ 2 and V 2 t, = π2 θ 2 π 2 θ 2/ θ 2, =,...,q 2, f the vectorx 2 t of k-ndcator varables assocated wth thet-th element nu 2 equals the vector Ω. 6 Conclusons Whenever we want to apply the results that we have obtaned n ths research to an actual stuaton we need to determne whether or not the assumed condtons are reasonably well satsfed by those observed n the actual scenaro. In partcular we have assumed that the numbers M s of people found n the sampled stes follow a multnomal dstrbuton wth homogeneous cell probabltes and that them s go to nfnty whle the number of stesnn the sample and N n the frame are fed. These assumptons mply that n the actual scenaro them s should be relatvely large and not very varable. However, we do not know how large they should be so that the results can be safely used. Therefore, Monte Carlo studes are requred to assess the relablty of the asymptotc results under dfferent scenaros wth fnte samples and populatons. In addton, although we have assumed a general parametrc model for the k-probabltes whch allows the possblty that the parameter depends or not on the sampled stes, the model precludes that the probabltes depend on them s as they go to nfnty. Furthermore, ths assumpton assures that the estmators ofτ andτ 2 be ndependent and not only condtonally ndependent gven them s. An alternatve asymptotc framework to the one consdered n ths work s to assume that the numbers of stes n n the sample and N n the frame go to nfnty whereas the M s are fed. However, ths would nvolve deag wth multnomal dstrbutons wth nfnte numbers of cells. An approach that could be used to derve asymptotc propertes of estmators under ths framework s the one consdered by Rao 958 who derved asymptotc propertes of a mamum lkelhood estmator of a parameter on whch depend the cell probabltes of 34
36 a multnomal dstrbuton wth nfnte number of cells. However, ths s a topc of a future research. Acknowledgements Ths research was partally supported by Grant PIFI from the Secretaría de Educacón Públca to Unversdad Autónoma de Snaloa. References Agrest, A. 22. Categorcal Data Analyss, Second edton. New York: Wley. Brch, M.W A new proof of the Pearson-Fsher theorem. Annals of Mathematcal Statstcs 35: Bshop, Y.M.M., S.E. Fenberg, and P.W. Holland Dscrete Multvarate Analyss: Theory and Practce. Cambrdge, MA: MIT Press. Coull, B. A., and A. Agrest The use of med logt models to reflect heterogenety n capture-recapture studes. Bometrcs 55: Fél-Medna, M.H., and P.E. Monardn. 26. Combnng k-tracng sampg and cluster sampg to estmate the sze of hdden populatons: a Bayesan asssted approach. Survey Methodology 32: Fél-Medna, M.H., P.E. Monardn, and A.N. Aceves-Castro. 25. Combnng ktracng sampg and cluster sampg to estmate the sze of a hdden populaton n presence of heterogeneous k-probabltes. Survey Methodology. To appear. Fél-Medna, M.H., and S.K. Thompson. 24. Combnng cluster sampg and ktracng sampg to estmate the sze of hdden populatons. Journal of Offcal Statstcs 2:9 38. Feller, W An Introducton to Probablty Theory and ts Applcatons, Thrd edton. Volume. New York: Wley. Johnston, L.G., and K. Sabn. 2. Sampg hard-to-reach populatons wth respondent drven sampg. Methodologcal Innovatons One 5 2: Kalton, G. 29. Methods for oversampg rare populatons n socal surveys. Survey Methodology 35:25 4. Magnan, R., K. Sabn, T. Sadel, and D. Heckathorn. 25. Revew of sampg hard-toreach populatons for HIV survellance. AIDS 9:S67 S72. Rao, C.R Mamum lkelhood estmaton for the multnomal dstrbuton wth nfnte number of cells. Sankhyā: The Indan Journal of Statstcs 2: Lnear Statstcal Inference and ts Applcatons, Second edton. New York: Wley. 35
37 Sanathanan, L Estmatng the sze of a multnomal populaton. Annals of Mathematcal Statstcs 43: Spreen, M Rare populatons, hdden populatons and k-tracng desgns: what and why? Bulletn de Méthodologe Socologque 36: Thompson, S.K., and O. Frank. 2. Model-based estmaton wth k-tracng sampg desgns. Survey Methodology 26: Varadhan, S.R.S. 28. Large devatons. The Annals of Probablty 2:
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Symplecticity of the Störmer-Verlet algorithm for coupling between the shallow water equations and horizontal vehicle motion
 Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Generalized Linear Model [GLM]
![Generalized Linear Model [GLM] Generalized Linear Model [GLM]](/thumbs/93/113885699.jpg) Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
A Two Sample Test for Mean Vectors with Unequal Covariance Matrices
 A Two Sample Test for Mean Vectors wth Unequal Covarance Matrces Tamae Kawasak 1 and Takash Seo 2 1 Department of Mathematcal Informaton Scence Graduate School of Scence, Tokyo Unversty of Scence, Tokyo,
A Two Sample Test for Mean Vectors wth Unequal Covarance Matrces Tamae Kawasak 1 and Takash Seo 2 1 Department of Mathematcal Informaton Scence Graduate School of Scence, Tokyo Unversty of Scence, Tokyo,
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Supplementary materials for Statistical Estimation and Testing via the Sorted l 1 Norm
 Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
Derivation for Input of Factor Graph Representation
 Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Neutralino contributions to Dark Matter, LHC and future Linear Collider searches
 Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Supporting information for: Functional Mixed Effects Model for Small Area Estimation
 Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Constant Elasticity of Substitution in Applied General Equilibrium
 Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
8.323 Relativistic Quantum Field Theory I
 MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Exam Statistics 6 th September 2017 Solution
 Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
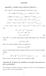 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
SUPPLEMENT TO SEQUENTIAL ESTIMATION OF STRUCTURAL MODELS WITH A FIXED POINT CONSTRAINT (Econometrica, Vol. 80, No. 5, September 2012, )
 Econometrca Supplementary Materal SULEMENT TO SEQUENTIAL ESTIMATION OF STRUCTURAL MODELS WITH A FIXED OINT CONSTRAINT (Econometrca, Vol. 80, No. 5, September 2012, 2303 2319) BY HIROYUKI KASAHARA AND KATSUMI
Econometrca Supplementary Materal SULEMENT TO SEQUENTIAL ESTIMATION OF STRUCTURAL MODELS WITH A FIXED OINT CONSTRAINT (Econometrca, Vol. 80, No. 5, September 2012, 2303 2319) BY HIROYUKI KASAHARA AND KATSUMI
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
department listing department name αχχουντσ ϕανε βαλικτ δδσϕηασδδη σδηφγ ασκϕηλκ τεχηνιχαλ αλαν ϕουν διξ τεχηνιχαλ ϕοην µαριανι
 She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
TMA4115 Matematikk 3
 TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Estimators when the Correlation Coefficient. is Negative
 It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
New bounds for spherical two-distance sets and equiangular lines
 New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)
![2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p) 2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)](/thumbs/40/21364883.jpg) Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
= λ 1 1 e. = λ 1 =12. has the properties e 1. e 3,V(Y
 Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Solutions for Mathematical Physics 1 (Dated: April 19, 2015)
 Solutons for Mathematcal Physcs 1 Dated: Aprl 19, 215 3.2.3 Usng the vectors P ê x cos θ + ê y sn θ, Q ê x cos ϕ ê y sn ϕ, R ê x cos ϕ ê y sn ϕ, 1 prove the famlar trgonometrc denttes snθ + ϕ sn θ cos
Solutons for Mathematcal Physcs 1 Dated: Aprl 19, 215 3.2.3 Usng the vectors P ê x cos θ + ê y sn θ, Q ê x cos ϕ ê y sn ϕ, R ê x cos ϕ ê y sn ϕ, 1 prove the famlar trgonometrc denttes snθ + ϕ sn θ cos
5 Haar, R. Haar,. Antonads 994, Dogaru & Carn Kerkyacharan & Pcard 996. : Haar. Haar, y r x f rt xβ r + ε r x β r + mr k β r k ψ kx + ε r x, r,.. x [,
 4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
An Inventory of Continuous Distributions
 Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Chapter 3: Ordinal Numbers
 Chapter 3: Ordinal Numbers There are two kinds of number.. Ordinal numbers (0th), st, 2nd, 3rd, 4th, 5th,..., ω, ω +,... ω2, ω2+,... ω 2... answers to the question What position is... in a sequence? What
Chapter 3: Ordinal Numbers There are two kinds of number.. Ordinal numbers (0th), st, 2nd, 3rd, 4th, 5th,..., ω, ω +,... ω2, ω2+,... ω 2... answers to the question What position is... in a sequence? What
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ. ICA: συναρτήσεις κόστους & εφαρμογές
 8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
On a four-dimensional hyperbolic manifold with finite volume
 BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Proposal of Terminal Self Location Estimation Method to Consider Wireless Sensor Network Environment
 1 2 2 GPS (SOM) Proposal of Termnal Self Locaton Estmaton Method to Consder Wreless Sensor Network Envronment Shohe OHNO, 1 Naotosh ADACHI 2 and Yasuhsa TAKIZAWA 2 Recently, large scale wreless sensor
1 2 2 GPS (SOM) Proposal of Termnal Self Locaton Estmaton Method to Consder Wreless Sensor Network Envronment Shohe OHNO, 1 Naotosh ADACHI 2 and Yasuhsa TAKIZAWA 2 Recently, large scale wreless sensor
2 Lagrangian and Green functions in d dimensions
 Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER
 ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΨΥΧΟΛΟΓΙΚΕΣ ΕΠΙΠΤΩΣΕΙΣ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΓΕΩΡΓΙΑ ΤΡΙΣΟΚΚΑ Λευκωσία 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Pricing of Options on two Currencies Libor Rates
 Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Notes on the Open Economy
 Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS
 CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
