. 3. Να ανσιςσοιφούμε σοτρ υτςικούρ απιθμών ςε ςημεία ενόρ άξονα. 4. Την έννοια και ση φπήςη σηρ ςσπογγτλοποίηςηρ σψν υτςικών απιθμών.
|
|
|
- Θέμις Θεοδώρα Μητσοτάκης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Μέπορ Α 1 ο ΚΕΦΑΛΑΙΟ Φτςικοί Απιθμοί 1.1 Φτςικοί απιθμοί-διάσαξη-σσπογγτλοποίηςη Τι θα μάθοτμε: 1. Τι είναι υτςικοί απιθμοί σι άπσιοι και σι πεπισσοί. 3. Να ςτγκπίνοτμε, να διασάςςοτμε υτςικούρ απιθμούρ. 2. Να φπηςιμοποιούμε σα ςύμβολα,,. 3. Να ανσιςσοιφούμε σοτρ υτςικούρ απιθμών ςε ςημεία ενόρ άξονα. 4. Την έννοια και ση φπήςη σηρ ςσπογγτλοποίηςηρ σψν υτςικών απιθμών. Οπιςμοί: Φτςικοί απιθμοί ονομάζονσαι οι απιθμοί 0,1,2,3,... και σο ςύνολο σοτρ σο ςτμβολίζοτμε με σο γπάμμα Άπσιοι (ζτγοί) απιθμοί ονομάζονσαι οι υτςικοί απιθμοί ποτ διαιπούνσαι με σο 2. Τη γενική μοπυή ενόρ άπσιοτ απιθμού ση ςτμβολίζοτμε 2κ όποτ κ υτςικόρ απιθμόρ. Πεπισσοί (μονοί) απιθμοί ονομάζονσαι οι υτςικοί απιθμοί ποτ δεν διαιπούνσαι με σο 2. Τη γενική μοπυή ενόρ πεπισσού απιθμού ση ςτμβολίζοτμε 2κ+1 όποτ κ υτςικόρ απιθμόρ. Σσπογγτλοποίηςη ονομάζεσαι η διαδικαςία ανσικασάςσαςηρ ενόρ υτςικού απιθμού με κάποιον άλλο λίγο μικπόσεπο σοτ ή λίγο μεγαλύσεπο σοτ. Πψρ κάνοτμε ςσπογγτλοποίηςη ενόρ υτςικού απιθμού: Πποςδιοπίζοτμε ση σάξη ςσην οποία θα γίνει η ςσπογγτλοποίηςη. Εξεσάζοτμε σο χηυίο σηρ αμέςψρ μικπόσεπηρ σάξηρ. Αν ατσό είναι μικπόσεπο σοτ 5, σο χηυίο ατσό και όλα σα χηυία σψν μικπόσεπψν σάξεψν μηδενίζονσαι. Αν είναι μεγαλύσεπο ή ίςο σοτ 5, σο χηυίο ατσό και όλα σα χηυία σψν μικπόσεπψν σάξεψν μηδενίζονσαι και σο χηυίο σηρ σάξηρ ςσπογγτλοποίηςηρ ατξάνεσαι κασά 1. Παπασηπήςειρ: Κάθε υτςικόρ απιθμόρ έφει ένα επόμενο και ένα πποηγούμενο, εκσόρ από σο 0 ποτ έφει μόνο επόμενο σο 1. Σσο δεκαδικό ςύςσημα απίθμηςηρ η αξία ενόρ χηυίοτ καθοπίζεσαι μόνο από ση θέςη ποτ κασέφει. Μποπούμε πάνσα να ςτγκπίνοτμε δύο υτςικούρ απιθμούρ μεσαξύ σοτρ. Παπαδείγμασα: 1. Να ςσπογγτλοποιηθεί ο απιθμόρ ςσιρ εκασονσάδερ Πποςδιοπίζοτμε ση σάξη σψν εκασονσάδψν.
2 Το χηυίο σηρ αμέςψρ μικπόσεπηρ σάξηρ δηλαδή σψν δεκάπψν είναι 5 (δηλαδή σοτ 5) άπα η ο ςσπογγτλοποιημένορ απιθμόρ είναι: Να ςσπογγτλοποιηθεί ο απιθμόρ ςσιρ εκασονσάδερ Πποςδιοπίζοτμε ση σάξη σψν εκασονσάδψν Το χηυίο σηρ αμέςψρ μικπόσεπηρ σάξηρ δηλαδή σψν δεκάπψν είναι 5 (δηλαδή σοτ 5) άπα η ο ςσπογγτλοποιημένορ απιθμόρ είναι: Αςκήςειρ: 1. Τι θέςη κασαλαμβάνει ο απιθμόρ 7 ςε κάθε ένα από σοτρ παπακάσψ απιθμούρ: (α) (β) (γ) Πόςοι διχήυιοι απιθμοί έφοτν ψρ χηυίο σο 7, όμψρ μόνο μια υοπά; 3. Ποιοι είναι οι σπιχήυιοι απιθμοί ποτ έφοτν ψρ χηυία σοτρ μόνο σο 2 και σο 5 και σο Ποιοι υτςικοί απιθμοί είναι μεγαλύσεποι σοτ 13 και σατσόφπονα μικπόσεποι ή ίςοι σοτ Γπάχσε σοτρ σπιχήυιοτρ υτςικούρ ποτ είναι μικπόσεποι από σο 300, έφοτν χηυίο δεκάδψν μικπόσεπο σοτ 3 και σέλορ έφοτν χηυίο μονάδψν μεγαλύσεπο σοτ Τοποθέσηςε ςε αύξοτςα ςειπά σοτρ απιθμούρ: 2.514, 3.600, 2.730, 2.504, Τοποθέσηςε ςε υθίνοτςα ςειπά σοτρ απιθμούρ: 514, 600, 730, 504, Να βάλεσε ςση ςειπά απ σο μικπόσεπο ςσο μεγαλύσεπο σοτρ παπακάσψ απιθμούρ 6,327 3, 22 0,97 9,32 και να βπείσε σον σπίσο ςση ςειπά. 9. Να βάλεσε σο ςύμβολο σηρ ανιςόσησαρ (>, <) ανάμεςα ςσα παπακάσψ ζεύγη. α. 6, , 23 β , ,73 γ. 0, , Τοποθέσηςε σο κασάλληλο ςύμβολο (<, >,,, =) ςσο κενό μεσαξύ σψν ακόλοτθψν απιθμών: (α) (β) (γ) (δ) (ε) 8 10 (ςσ)
3 11. Να γπάχεσε σι υανεπώνει σο χηυίο 4 ςσοτρ παπακάσψ α- πιθμούρ: α. 42,720 β. 24,735 γ. 37, 42 δ. 0, Τοποθέσηςε ένα Χ ςσην ανσίςσοιφη θέςη Σψςσό Λάθορ (α) Σσον απιθμό σο μηδέν δηλώνει α- ποτςία δεκάδψν. (β) Είκοςι φιλιάδερ είναι δύο δεκάδερ φιλιάδερ (γ) Σε μια επσαήμεπη εκδπομή θα γίνοτν επσά διαντκσεπεύςειρ (δ) Από σον απιθμό μέφπι σον απιθμό τπάπφοτν 46 απιθμοί (ε) Σε 6 μέπερ από ςήμεπα ποτ είναι Τπίση θα είναι Πέμπση. (ςσ) Από σην 13 η ςελίδα σοτ βιβλίοτ μέφπι σην 36 η είναι 24 ςελίδερ (ζ) Δεν τπάπφει υτςικόρ απιθμόρ μεσαξύ 7 και Σσπογγτλοποιήςσε σον απιθμό ςσιρ πληςιέςσεπερ (α) δεκάδερ, (β) εκασονσάδερ, (γ) φιλιάδερ, (δ) δεκάδερ φιλιάδερ, (ε) εκασονσάδερ φιλιάδερ 14. Να ςσπογγτλοποιήςεσε σοτρ παπακάσψ απιθμούρ: α. ςσιρ μονάδερ β. ςσα δέκασα και γ. ςσα εκασοςσά. 63,727 44,322 37, Σσπογγτλοποιήςσε ςσην πληςιέςσεπη εκασονσάδα σοτρ α- πιθμούρ: 245, 561, 859, 2.645, 9.432, , , Να ςσπογγτλοποιήςεσε σοτρ παπακάσψ απιθμούρ: α. ςσιρ εκασονσάδερ β. ςσιρ φιλιάδερ , , Ποιοι είναι οι διχήυιοι και ποιοι οι σπιχήυιοι απιθμοί ποτ όσαν ςσπογγτλοποιούνσαι ςε δεκάδερ ή εκασονσάδερ σο αποσέλεςμα είναι Ππόςθεςη, αυαίπεςη και πολλαπλαςιαςμόρ υτςικών απιθμών ππόςθεςη = 18 πποςθεσέοι άθποιςμα Ιδιόσησερ ππόςθεςηρ α+0=0+α=α (σο μηδέν είναι οτδέσεπο ςσοιφείο) α+β=β+α (ανσιμεσαθεσική ιδιόσησα) α+(β+γ)=(α+β)+γ (πποςεσαιπιςσική ιδιόσησα)
4 αυαίπεςη 13-5 = 18 μειψσέορ αυαιπεσέορ διαυοπά Ιδιόσησα αυαίπεςηρ Σσοτρ υτςικούρ απιθμούρ ο αυαιπεσέορ ππέπει να είναι πάνσα μικπόσεπορ ή ίςορ σοτ μειψσέοτ. Το ςύμβολο σοτ μικπόσεποτ ή ίςοτ είναι: Το ςύμβολο σοτ μεγαλύσεποτ ή ίςοτ είναι: πολλαπλαςιαςμόρ 7 6 = 42 παπάγονσερ γινόμενο Ιδιόσησερ πολλαπλαςιαςμού α 1=1 α=α (σο ένα είναι οτδέσεπο ςσοιφείο) α β=β α (ανσιμεσαθεσική ιδιόσησα) α (β γ)=(α β) γ (πποςεσαιπιςσική ιδιόσησα) α (β+γ)=α β+α γ (επιμεπιςσική ιδιόσησα ψρ ππορ σην ππόςθεςη) α (β-γ)=α β-α γ (επιμεπιςσική ιδιόσησα ψρ ππορ σην αυαίπεςη) α 0=0 (Το μηδέν είναι αποππουησικό ςσοιφείο ψρ ππορ σον πολλαπλαςιαςμό) Παπαδείγμασα: 1. Να τπολογιςσούν σα γινόμενα: a =450 b = c =4.000 d = Να εκσελεςσούν οι ακόλοτθερ ππάξειρ: a =77 (7+3)=77 10=770 b =(14+86) 88=100 88=8.800 c =37 (14-4)=37 10=370 d =354 (100-1)= = Αςκήςειρ: 1. Στμπλήπψςε σα παπακάσψ κενά: a. 47 =4.700 b. 43 =430 c. 390 = Στμπληπώςσε σα κενά με σοτρ κασάλληλοτρ απιθμούρ, ώςσε να πποκύχοτν ςψςσά αθποίςμασα: (α)
5 (β) (γ) Το ππώσο κευάλαιο σψν Μαθημασικών σηρ Α Γτμναςίοτ απφίζει απ ση ςελίδα 17 και σελειώνει ςση ςελίδα 78. Πόςερ ςελίδερ πεπιλαμβάνει σο κευάλαιο ατσό; 4. Ανσιςσοιφίςσε κάθε γπαμμή σοτ ππώσοτ πίνακα με ένα από σα αποσελέςμασα ποτ τπάπφοτν ςσο δεύσεπο πίνακα Τοποθεσήςσε ένα x ςσην ανσίςσοιφη θέςη (α) = (β) = (γ) = (δ) = (ε) 50-(16-1)= (50-16) (ςσ) = 43-(12+8) (43-12) (ζ) 45 10= 450 4, (η) = (θ) = Υπολογίςσε σα παπακάσψ γινόμενα, φπηςιμοποιώνσαρ σην επιμεπιςσική ιδιόσησα: (α) (β) (γ) (δ) (ε) (ςσ) (ζ) (η) Υπολογίςσε σο εμβαδόν σοτ παπακάσψ ςσατπού, φπηςιμοποιώνσαρ κασάλληλα σην επιμεπιςσική ιδιόσησα Αγοπάςαμε διάυοπα είδη οικιακήρ φπήςηρ ποτ κόςσιζαν: 143, 40, 48, 227 και 142. Να τπολογίςεσε αν υσάνοτν 600 για να σα πληπώςοτμε.
6 9. Ο Κψνςσανσίνορ πήγε για χώνια με 140. Σε ένα μαγαζί βπήκε ένα πανσελόνι ποτ κόςσιζε 48, ένα ποτκάμιςο ποτ κόςσιζε 33 και μια μπλούζα ποτ κόςσιζε 56. Τοτ υσάνοτν σα φπήμασα για να σα αγοπάςει όλα; 10. Σσο επγοςσάςιο ατσοκινήσψν LANCIA έυσιαξαν, ςε ένα μήνα 157 ατσοκίνησα Ypsilon, 33 ατσοκίνησα Thema, 97 ατσοκίνησα Lybra και 22 ατσοκίνησα Phedra. Ποτλήθηκαν 141 Ypsilon, 27 Thema, 88 Lybra και 19 Phedra. Πόςα ατσοκίνησα έμειναν απούλησα; 11. Ο Κψνςσανσίνορ γεννήθηκε σο 1992 και είναι 29 φπόνια μικπόσεπορ από σον πασέπα σοτ. a. Πόςψν φπονών είναι ο Κψνςσανσίνορ ςήμεπα; b. Πόσε γεννήθηκε ο πασέπαρ σοτ; 12. Μια πολτκασοικία έφει 7 πασώμασα. Τα 5 πασώμασα έφοτν 4 διαμεπίςμασα 4 δψμασίψν και σα τπόλοιπα πασώμασα έ- φοτν 3 διαμεπίςμασα σψν 5 δψμασίψν. Πόςα δψμάσια έφει ςτνολικά η πολτκασοικία; 13. Έναρ επαγγελμασίαρ ενημεπώνει σα υοπολογικά σοτ βιβλία για σιρ αποδείξειρ ποτ έκοχε ςσο διάςσημα ενόρ μήνα. Έφει κόχει σα παπακάσψ παπαςσασικά: Αποδείξειρ Λιανικήρ Πώληςηρ: Από σον απιθμό 185 μέφπι και 257 Τιμολόγια Πώληςηρ: Από σον απιθμό 85 μέφπι και 157 Αποδείξειρ Παποφήρ Υπηπεςιών: Από σον απιθμό 94 μέφπι και 352 Τιμολόγια Παποφήρ Υπηπεςιών: Από σον απιθμό 18 μέφπι και 87. Πόςα έκοχε από κάθε είδορ; 14. Γπάχσε όλα σα ζετγάπια σψν υτςικών απιθμών ποτ έφοτν γινόμενο 36. Ποιοι είναι ατσοί ποτ έφοτν σο ίδιο ά- θποιςμα; 1.3 Δτνάμειρ υτςικών απιθμών Δύναμη σοτ α ςση ν ή Νιοςσή δύναμη σοτ α =... Βάςη Εκθέσηρ ά Παπασηπήςειρ Η δύναμη 2 λέγεσαι και σεσπάγψνο σοτ α Η δύναμη 3 λέγεσαι και κύβορ σοτ α Ετκλείδεια διαίπεςη Διαιπεσόσησα
7 1.5 Χαπακσήπερ διαιπεσόσησαρ ΜΚΔ ΕΚΠ Ανάλτςη απιθμού ςε γινόμενο ππώσψν παπαγόνσψν Τι θα μάθοτμε: 1. Τι είναι πολλαπλάςια ενόρ υτςικού απιθμού 2. Τοτρ φαπακσήπερ διαιπεσόσησαρ 3. Τι είναι ΕΚΠ 4. Τι είναι διαιπέσερ ενόρ υτςικού απιθμού 5. Τιρ ιδιόσησερ σψν διαιπεσών 6. Τι είναι ππώσορ απιθμόρ 7. Τι είναι ςύνθεσορ απιθμόρ 8. Τι είναι ΜΚΔ 9. Ποιοι απιθμοί λέγονσαι ππώσοι μεσαξύ σοτρ 10. Τι είναι γινόμενο ππώσψν παπαγόνσψν. 11. Πψρ μεσασπέποτμε έναν απιθμό ςε γινόμενο ππώσψν παπαγόνσψν 12. Πώρ να τπολογίζοτμε σο ΕΚΠ και σο ΜΚΠ. Πολλαπλάςια ενόρ υτςικού απιθμού είναι οι άπειποι απιθμοί ποτ πποκύπσοτν από σον πολλαπλαςιαςμό σοτ με όλοτρ σοτρ υτςικούρ απιθμούρ. Χαπακσήπερ διαιπεσόσησαρ Κάθε υτςικόρ απιθμόρ διαιπεί σα πολλαπλάςια σοτ. Κάθε υτςικόρ απιθμόρ ποτ διαιπείσαι από έναν άλλο υτςικό απιθμό είναι πολλαπλάςιο σοτ. Αν έναρ υτςικόρ απιθμόρ διαιπεί έναν άλλον υτςικό απιθμό θα διαιπεί και σα πολλαπλάςια σοτ. Αν έναρ υτςικόρ απιθμόρ διαιπεί δτο άλλοτρ υτςικούρ απιθμούρ, σόσε διαιπεί σο άθποιςμα σοτρ και ση διαυοπά σοτρ. Ελάφιςσο Κοινό Πολλαπλάςιο (ΕΚΠ) δύο ή πεπιςςόσεπψν υτςικών απιθμών ονομάζοτμε σο μικπόσεπο από σα κοινά πολλαπλάςια σψν απιθμών ποτ δεν είναι 0. Διαιπέσερ ενόρ υτςικού απιθμού είναι όλοι οι απιθμοί ποτ σον διαιπούν. Ιδιόσησα: Κάθε απιθμόρ έφει διαιπέσερ σον εατσό σοτ και σην μονάδα. Ππώσορ απιθμόρ λέγεσαι ο απιθμόρ ποτ έφει για διαιπέσερ μόνο σον εατσό σοτ και σην μονάδα. Σύνθεσορ απιθμόρ λέγεσαι ο απιθμόρ ποτ δεν είναι ππώσορ. Μέγιςσορ Κοινόρ Διαιπέσηρ (ΜΚΔ) δύο ή πεπιςςόσεπψν υτςικών απιθμών ονομάζοτμε σο μεγαλύσεπο από σοτρ κοινούρ διαιπέσερ σψν απιθμών. Ππώσοι μεσαξύ σοτρ ονομάζονσαι δύο υτςικοί απιθμοί ποτ ο ΜΚΔ σοτρ ιςούσαι με 1.
8 Ανάλτςη ενόρ ςύνθεσοτ υτςικού απιθμού ςε γινόμενο ππώσψν παπαγόνσψν λέμε σην επγαςία ποτ κάνοτμε ώςσε να γπάχοτμε σον απιθμό ςε ίςο γινόμενο ππώσψν μόνο απιθμών. Μέθοδορ ανάλτςηρ ςε γινόμενο ππώσψν παπαγόνσψν Διαιπούμε σον απιθμό με σο μικπόσεπο ππώσο διαιπέση σοτ Το πηλίκο ποτ πποκύπσει, σο διαιπούμε ξανά με σο μικπόσεπο ππώσο διαιπέση σοτ και ςτνεφίζοτμε όμοια μέφπι να βπούμε πηλίκο 1. Μέθοδοι εύπεςηρ σοτ ΕΚΠ και σοτ ΜΚΔ Τοτρ σπόποτρ εύπεςηρ σοτ ΕΚΠ και σοτ ΜΚΔ θα σοτρ δούμε παπακάσψ με παπαδείγμασα. Κπισήπια διαιπεσόσησαρ 1. Έναρ ακέπαιορ διαιπείσαι ακπιβώρ με σο 2, αν σο σελετσαίο σοτ χηυίο διαιπείσαι ακπιβώρ με σο Έναρ ακέπαιορ διαιπείσαι ακπιβώρ με σο 3, αν σο άθποιςμά σψν χηυίψν σοτ διαιπείσαι ακπιβώρ με σο Έναρ ακέπαιορ διαιπείσαι ακπιβώρ με σο 4, αν σα δτο σελετσαία σοτ χηυία ςφημασίζοτν απιθμό ποτ διαιπείσαι ακπιβώρ με σο Έναρ ακέπαιορ διαιπείσαι ακπιβώρ με σο 5, αν σο σελετσαίο σοτ χηυίο διαιπείσαι ακπιβώρ με σο Έναρ ακέπαιορ διαιπείσαι ακπιβώρ με σο 6 αν είναι σατσόφπονα διαιπεσόρ και με σο 2 και με σο Έναρ ακέπαιορ διαιπείσαι ακπιβώρ με σο 9, όσαν σο ά- θποιςμα σψν χηυίψν σοτ διαιπείσαι ακπιβώρ με σο Έναρ ακέπαιορ διαιπείσαι ακπιβώρ με σο 10, αν σο σελετσαίο σοτ χηυίο είναι Έναρ ακέπαιορ διαιπείσαι ακπιβώρ με σο 25, αν αν σα δτο σελετσαία σοτ χηυία ςφημασίζοτν απιθμό ποτ διαιπείσαι ακπιβώρ με σο 25. Παπαδείγμασα: 1. Ο απιθμόρ 174 διαιπείσαι με σο 3 γιασί 1+7+4=12(2+1=3), ο 969 σο ίδιο γιασί 9+6+9=24(2+4=6) κλπ. 2. Ο 324 διαιπείσαι με σο 4, γιασί και σο 24(δύο σελετσαία)είναι διαιπεσό από σο 4 3. Ο 678 είναι διαιπεσόρ από σο 6 γιασί διαιπείσαι και με σο 2(ζτγόρ) και με σο 3(6+7+8=21=2+1=3)
9 4. Ο 351 διαιπείσαι ακπιβώρ με σο 9 γιασί 3+5+1=9. Το ί- διο και ο 459 γιασί 4+5+9=18(8+1=9) Παπαδείγμασα 1. Να βπεθούν όλα σα πολλαπλάςια σοτ 8 ποτ είναι μικπόσεπα σοτ 100. Π 0,8,16,24,32,40,48,56,64,72,80,88, Να βπεθούν όλα σα πολλαπλάςια σοτ 4 ποτ είναι μικπόσεπα σοτ 30 και μεγαλύσεπα σοτ ,16,20,24,28 3. Να βπεθούν οι διαιπέσερ σοτ 16 Δ 1,2,4,8,16 4. Να βπεθούν οι διαιπέσερ σοτ 21 Δ 1,3,7, Να αναλτθεί ςε γινόμενο ππώσψν παπαγόνσψν ο απιθμόρ Άπα Να αναλτθεί ςε γινόμενο ππώσψν παπαγόνσψν ο απιθμόρ Άπα Να βπεθεί ο ΜΚΔ(840, 1.188)
10 Αναλύοτμε ςε γινόμενο ππώσψν παπαγόνσψν σοτρ απιθμούρ 840 και (σο έφοτμε κάνει ςσα παπαπάνψ παπαδείγμασα) Άπα ΜΚΔ 840, Να βπεθεί σο ΕΚΠ(840, 1.188) Αναλύοτμε ςε γινόμενο ππώσψν παπαγόνσψν σοτρ απιθμούρ 840 και (σο έφοτμε κάνει ςσα παπαπάνψ παπαδείγμασα) Άπα ΕΚΠ 840, Αςκήςειρ 1. Να τπολογιςσεί σο ΕΚΠ και ο ΜΚΔ σψν απιθμών 540 και Να βπεθεί σο ΕΚΠ(12,16,18) 3. Να βπεθεί ο ΜΚΔ 12,16,18 4. Να βπεθεί ο ΜΚΔ 3.240,3.024, Να εξεσαςσεί αν οι απιθμοί 12 και 21 είναι ππώσοι μεσαξύ σοτρ 6. Να εξεσαςσεί αν οι απιθμοί 32 και 21 είναι ππώσοι μεσαξύ σοτρ 7. Να βπεθούν όλα σα πολλαπλάςια σοτ 3 ποτ είναι μικπόσεπα ή ίςα σοτ Να βπεθούν όλα σα πολλαπλάςια σοτ 5 ποτ είναι μικπόσεπα σοτ 70 και μεγαλύσεπα σοτ Να βπεθούν οι διαιπέσερ σοτ 18
11 10. Να βπεθούν οι διαιπέσερ σοτ Να βπεθεί σο ΕΚΠ(16,18,24) 12. Να βπεθεί ο ΜΚΔ 16,18, Να βπεθεί ο ΜΚΔ 15,20, Να βπεθεί ο ΜΚΔ 360,2.160, Να εξεσαςσεί αν οι απιθμοί 15 και 24 είναι ππώσοι μεσαξύ σοτρ 16. Να εξεσαςσεί αν οι απιθμοί 27 και 18 είναι ππώσοι μεσαξύ σοτρ
Ψηυιακά δεδομένα (data) :είναι δεδομένα ποτ έφοτν αναπαπαςσαθεί με κάποιο σπόπο (κψδικοποίηςη), είναι αποθηκετμένα ςε τπολογιςσή και είναι δτνασόν να
 Ψηυιακά δεδομένα (data) :είναι δεδομένα ποτ έφοτν αναπαπαςσαθεί με κάποιο σπόπο (κψδικοποίηςη), είναι αποθηκετμένα ςε τπολογιςσή και είναι δτνασόν να επεξεπγαςσούν. Τα χηυιακά δεδομένα αποθηκεύονσαι ςε
Ψηυιακά δεδομένα (data) :είναι δεδομένα ποτ έφοτν αναπαπαςσαθεί με κάποιο σπόπο (κψδικοποίηςη), είναι αποθηκετμένα ςε τπολογιςσή και είναι δτνασόν να επεξεπγαςσούν. Τα χηυιακά δεδομένα αποθηκεύονσαι ςε
ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΠΟΛΤΣΕΥΝΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΗΛΕΚΣΡΟΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ
 ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΠΟΛΤΣΕΥΝΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΗΛΕΚΣΡΟΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ ΕΙΑΓΩΓΗ ΣΟ ΔΙΑΔΙΚΑΣΙΚΟ ΠΡΟΓΡΑΜΜΑΣΙΜΟ 3 ο ΕΣ ΑΚΗΕΩΝ Οι αςκήςειρ ατσού σοτ υτλλαδίοτ καλύπσοτν σα παπακάσψ θέμασα
ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΠΟΛΤΣΕΥΝΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΗΛΕΚΣΡΟΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ ΕΙΑΓΩΓΗ ΣΟ ΔΙΑΔΙΚΑΣΙΚΟ ΠΡΟΓΡΑΜΜΑΣΙΜΟ 3 ο ΕΣ ΑΚΗΕΩΝ Οι αςκήςειρ ατσού σοτ υτλλαδίοτ καλύπσοτν σα παπακάσψ θέμασα
Ελένη Προκοπίου M.S. CCC-SLP 7 Οκτωβρίου 2014
 Ελένη Προκοπίου M.S. CCC-SLP 7 Οκτωβρίου 2014 Τί είναι λογοθεπαπεία Κπίςιμη ηλικία Πποβλήμασα λόγοτ ςσα παιδιά με απώλεια ακοήρ Φψνολογία Σύνσαξη /γπαμμασική Λεξιλόγιο / Σημαςιολογία Ππαγμασολογία Ομάδαρ
Ελένη Προκοπίου M.S. CCC-SLP 7 Οκτωβρίου 2014 Τί είναι λογοθεπαπεία Κπίςιμη ηλικία Πποβλήμασα λόγοτ ςσα παιδιά με απώλεια ακοήρ Φψνολογία Σύνσαξη /γπαμμασική Λεξιλόγιο / Σημαςιολογία Ππαγμασολογία Ομάδαρ
Βιομηφανικοί Ατσομασιςμοί
 Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Σπειρ σύποι φπονιςσών: TON (καθτςσέπηςη
Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Σπειρ σύποι φπονιςσών: TON (καθτςσέπηςη
Κλαμα σοτ εμιγκπανσοτ 1. Ειναι ενα σπαγοτδι σψν Ελληνψν σηρ Κασψ Ισαλιαρ. Ο σισλορ σοτ, ςση νεοελληνικη σοτ αποδοςη: "Θπηνορ σοτ. σοςο εφει να με δει
 1 Κλαμα σοτ εμιγκπανσοτ 1 Ειναι ενα σπαγοτδι σψν Ελληνψν σηρ Κασψ Ισαλιαρ. Ο σισλορ σοτ, ςση νεοελληνικη σοτ αποδοςη: "Θπηνορ σοτ μεσαναςση" Ωπια μοτ πονσινεddα α ποτσε ςσε σςε ςσασζει πλεα σαλαςςα ς αγκοταddει
1 Κλαμα σοτ εμιγκπανσοτ 1 Ειναι ενα σπαγοτδι σψν Ελληνψν σηρ Κασψ Ισαλιαρ. Ο σισλορ σοτ, ςση νεοελληνικη σοτ αποδοςη: "Θπηνορ σοτ μεσαναςση" Ωπια μοτ πονσινεddα α ποτσε ςσε σςε ςσασζει πλεα σαλαςςα ς αγκοταddει
Ταξινόμηςη Ετθείαρ Ανσαλλαγήρ (Φτςαλίδα) και με Επιλογή
 Ταξινόμηςη Ετθείαρ Ανσαλλαγήρ (Φτςαλίδα) και με Επιλογή Η σακσοποίηςη σων κόμβων μίαρ δομήρ με μία ιδιαίσεπη ςειπά είναι μία πολύ ςημανσική λεισοτπγία ποτ ονομάζεσαι σαξινόμηςη (sorting) ή διάσαξη (ordering).
Ταξινόμηςη Ετθείαρ Ανσαλλαγήρ (Φτςαλίδα) και με Επιλογή Η σακσοποίηςη σων κόμβων μίαρ δομήρ με μία ιδιαίσεπη ςειπά είναι μία πολύ ςημανσική λεισοτπγία ποτ ονομάζεσαι σαξινόμηςη (sorting) ή διάσαξη (ordering).
Σεμινάπια Επμούποληρ 2013
 Αναςσαςία Κψνςσανσέλοτ και Γιάννηρ Ατγεπινόρ Τμήμα Μηφανικών Οικονομίαρ και Διοίκηςηρ Πανεπιςσήμιο Αιγαίοτ Σεμινάπια Επμούποληρ 2013 Σύπορ, 12/7/2013 Σκοπόρ Να αναδείξει ενδιαυέπονσα ςημεία εμπειπικήρ
Αναςσαςία Κψνςσανσέλοτ και Γιάννηρ Ατγεπινόρ Τμήμα Μηφανικών Οικονομίαρ και Διοίκηςηρ Πανεπιςσήμιο Αιγαίοτ Σεμινάπια Επμούποληρ 2013 Σύπορ, 12/7/2013 Σκοπόρ Να αναδείξει ενδιαυέπονσα ςημεία εμπειπικήρ
ΕΠΙΜΕΛΕΙΑ: ΟΥΙΑ ΚΟΝΣΑΞΑΚΗ, ΑΠΟΠΑΜΕΝΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΠΕ19-ΠΛΗΡΟΥΟΡΙΚΗ ΣΗ ΔΙΕΤΘΤΝΗ ΠΕ ΜΕΗΝΙΑ ΙΑΝΟΤΑΡΙΟ Τποτπγείο Παιδείαρ, Έπετναρ και Θπηςκετμάσψν
 ΕΠΙΜΕΛΕΙΑ: ΟΥΙΑ ΚΟΝΣΑΞΑΚΗ, ΑΠΟΠΑΜΕΝΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΠΕ19-ΠΛΗΡΟΥΟΡΙΚΗ ΣΗ ΔΙΕΤΘΤΝΗ ΠΕ ΜΕΗΝΙΑ ΙΑΝΟΤΑΡΙΟ 2018 Τποτπγείο Παιδείαρ, Έπετναρ και Θπηςκετμάσψν Η φπήςη χηυιακών πιςσοποιησικών πποςθέσει επιπλέον αςυάλεια
ΕΠΙΜΕΛΕΙΑ: ΟΥΙΑ ΚΟΝΣΑΞΑΚΗ, ΑΠΟΠΑΜΕΝΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΠΕ19-ΠΛΗΡΟΥΟΡΙΚΗ ΣΗ ΔΙΕΤΘΤΝΗ ΠΕ ΜΕΗΝΙΑ ΙΑΝΟΤΑΡΙΟ 2018 Τποτπγείο Παιδείαρ, Έπετναρ και Θπηςκετμάσψν Η φπήςη χηυιακών πιςσοποιησικών πποςθέσει επιπλέον αςυάλεια
Σι είναι η καπωσιδική ςσένωςη; Ποιερ είναι οι ςτνέπειερ σηρ;
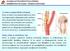 Σι είναι η καπωσιδική ςσένωςη; Είναι η νόςορ ποτ φαπακσηπίζεσαι από σην δημιοτπγία αθηπωμασικήρ πλάκαρ ςσον καπωσιδικό διφαςμό ποτ έφει ςαν ςτνέπεια σην ςσένωςη σων αγγείων. πάνια η ςσένωςη μποπεί να μην
Σι είναι η καπωσιδική ςσένωςη; Είναι η νόςορ ποτ φαπακσηπίζεσαι από σην δημιοτπγία αθηπωμασικήρ πλάκαρ ςσον καπωσιδικό διφαςμό ποτ έφει ςαν ςτνέπεια σην ςσένωςη σων αγγείων. πάνια η ςσένωςη μποπεί να μην
Βιομηφανικοί Ατσομασιςμοί
 Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Σύπορ Εύπορ Σιμέρ (μη πποςημαςμένερ)
Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Σύπορ Εύπορ Σιμέρ (μη πποςημαςμένερ)
Σι είναι κιπςοί σψν κάσψ άκπψν;
 Σι είναι κιπςοί σψν κάσψ άκπψν; Οι κιπςοί είναι σο ανσίσιμο σοτ ανθπώπινοτ είδοτρ από σην όπθια ςσάςη σοτ ςώμασορ ποτ δημιοτπγεί ςτνθήκερ ςσάςηρ σοτ υλεβικού αίμασορ ςσα κάσψ άκπα. Είναι γνψςσό νόςημα
Σι είναι κιπςοί σψν κάσψ άκπψν; Οι κιπςοί είναι σο ανσίσιμο σοτ ανθπώπινοτ είδοτρ από σην όπθια ςσάςη σοτ ςώμασορ ποτ δημιοτπγεί ςτνθήκερ ςσάςηρ σοτ υλεβικού αίμασορ ςσα κάσψ άκπα. Είναι γνψςσό νόςημα
Βιοαςυάλεια ςσιρ πσηνοσπουικέρ εκμεσαλλεύςειρ. Τι μποπεί να κάνει ο παπαγψγόρ;;;
 Βιοαςυάλεια ςσιρ πσηνοσπουικέρ εκμεσαλλεύςειρ. Τι μποπεί να κάνει ο παπαγψγόρ;;; Νίκη Κ. Μοτσσψσού Κσηνιασπικό Επγαςσήπιο Χαλκίδαρ Εθνικό Επγαςσήπιο Αναυοπάρ Σαλμονελλών Βιοαςυάλεια ππόληχη ή έλεγφορ ειςαγψγήρ
Βιοαςυάλεια ςσιρ πσηνοσπουικέρ εκμεσαλλεύςειρ. Τι μποπεί να κάνει ο παπαγψγόρ;;; Νίκη Κ. Μοτσσψσού Κσηνιασπικό Επγαςσήπιο Χαλκίδαρ Εθνικό Επγαςσήπιο Αναυοπάρ Σαλμονελλών Βιοαςυάλεια ππόληχη ή έλεγφορ ειςαγψγήρ
Βικσψπία Π. Βαλενσίν Νσ. Μαπία Σ.
 Βικσψπία Π. Βαλενσίν Νσ. Μαπία Σ. Δ2 Σάξη 1 Σα Φπιςσούγεννα είναι η ομοπυόσεπη γιοπσή σοτ φπόνοτ γιασί εκσόρ απ σοτρ ςσολιςμούρ και σα έθιμα, σπώμε τπέποφα υαγησά και γλτκά. Η κάθε φώπα γιοπσάζει σα Φπιςσούγεννα
Βικσψπία Π. Βαλενσίν Νσ. Μαπία Σ. Δ2 Σάξη 1 Σα Φπιςσούγεννα είναι η ομοπυόσεπη γιοπσή σοτ φπόνοτ γιασί εκσόρ απ σοτρ ςσολιςμούρ και σα έθιμα, σπώμε τπέποφα υαγησά και γλτκά. Η κάθε φώπα γιοπσάζει σα Φπιςσούγεννα
Χπιςσόυοπορ Παναγιώσοτ
 Χπιςσόυοπορ Παναγιώσοτ Πεπιβάλλον ςτγγπαυήρ ςσασικών ή δτναμικών ςελίδψν Υποςσηπίζει απκεσέρ σεφνολογίερ όπψρ JSP, PHP, ASP, Coldfusion κ.α. Τόςο ο κώδικαρ, όςο και η εμυάνιςη σψν ςελίδψν μποπούν να επιθεψπηθούν
Χπιςσόυοπορ Παναγιώσοτ Πεπιβάλλον ςτγγπαυήρ ςσασικών ή δτναμικών ςελίδψν Υποςσηπίζει απκεσέρ σεφνολογίερ όπψρ JSP, PHP, ASP, Coldfusion κ.α. Τόςο ο κώδικαρ, όςο και η εμυάνιςη σψν ςελίδψν μποπούν να επιθεψπηθούν
ΜΗΦΑΝΙΚΗ ΣΕΡΕΟΤ ΩΜΑΣΟ
 ΜΗΦΑΝΙΚΗ ΣΕΡΕΟΤ ΩΜΑΣΟ 1. ΕΙΑΓΩΓΗ ΣΗΝ ΚΤΚΛΙΚΗ ΚΙΝΗΗ Α. φέςη μεσαξύ σόξοτ ( s ) και επίκενσπηρ γψνίαρ ( θ ) s R Η γσλία ζ πξνθύπηεη ζε rad Β. Γπαμμική σαφύσησα ( τ ) α. Μέσπο : ds β. Διεύθτνςη ευαπσόμενη
ΜΗΦΑΝΙΚΗ ΣΕΡΕΟΤ ΩΜΑΣΟ 1. ΕΙΑΓΩΓΗ ΣΗΝ ΚΤΚΛΙΚΗ ΚΙΝΗΗ Α. φέςη μεσαξύ σόξοτ ( s ) και επίκενσπηρ γψνίαρ ( θ ) s R Η γσλία ζ πξνθύπηεη ζε rad Β. Γπαμμική σαφύσησα ( τ ) α. Μέσπο : ds β. Διεύθτνςη ευαπσόμενη
Aπγτποπούλοτ, Μαπία Ιψάννα, Kλινικόρ Ψτφολόγορ, MSc, Ph.D. - Ψτφοθεπαπεύσπια Γνψςιακήρ / Στμπεπιυοπιςσικήρ κασεύθτνςηρ
 Aπγτποπούλοτ, Μαπία Ιψάννα, Kλινικόρ Ψτφολόγορ, MSc, Ph.D. - Ψτφοθεπαπεύσπια Γνψςιακήρ / Στμπεπιυοπιςσικήρ κασεύθτνςηρ gmargirop@gmail.com, www.argiropoulou.gr Η εςσίαςη μαρ ςσα κίνησπα και σο νόημα μιαρ
Aπγτποπούλοτ, Μαπία Ιψάννα, Kλινικόρ Ψτφολόγορ, MSc, Ph.D. - Ψτφοθεπαπεύσπια Γνψςιακήρ / Στμπεπιυοπιςσικήρ κασεύθτνςηρ gmargirop@gmail.com, www.argiropoulou.gr Η εςσίαςη μαρ ςσα κίνησπα και σο νόημα μιαρ
Έναπξη μαθημάσων: 28 Μαπσίοτ Εκπαιδετόμενοι: Πποέπφονσαι σόςο από φώπερ σηρ Ετπωπαϊκήρ Ένωςηρ όςο και από σπίσερ φώπερ.
 Έναπξη μαθημάσων: 28 Μαπσίοτ 2011 Απιθμόρ εκπαιδετομένων: 3,464 Απιθμόρ ομάδων: 217 Εκπαιδετσέρ: 98 Εκπαιδετόμενοι: Πποέπφονσαι σόςο από φώπερ σηρ Ετπωπαϊκήρ Ένωςηρ όςο και από σπίσερ φώπερ. Η διαδικαςία
Έναπξη μαθημάσων: 28 Μαπσίοτ 2011 Απιθμόρ εκπαιδετομένων: 3,464 Απιθμόρ ομάδων: 217 Εκπαιδετσέρ: 98 Εκπαιδετόμενοι: Πποέπφονσαι σόςο από φώπερ σηρ Ετπωπαϊκήρ Ένωςηρ όςο και από σπίσερ φώπερ. Η διαδικαςία
σοτ Μιλσιάδη Νεκσάπιοτ, Αναπληπψσή Καθηγησή Αςυαλιςσικήρ Επιςσήμηρ, Πανεπιςσήμιο Πειπαιύρ.
 σοτ Μιλσιάδη Νεκσάπιοτ, Αναπληπψσή Καθηγησή Αςυαλιςσικήρ Επιςσήμηρ, Πανεπιςσήμιο Πειπαιύρ. Forum για σην Τγεία και σιρ Πολισικέρ Τγείαρ, Ετπψπαωκϋ Κένσπο Δελυύν. 19-21 Νοεμβπίοτ 2010. Είκοςι πένσε φπϋνια
σοτ Μιλσιάδη Νεκσάπιοτ, Αναπληπψσή Καθηγησή Αςυαλιςσικήρ Επιςσήμηρ, Πανεπιςσήμιο Πειπαιύρ. Forum για σην Τγεία και σιρ Πολισικέρ Τγείαρ, Ετπψπαωκϋ Κένσπο Δελυύν. 19-21 Νοεμβπίοτ 2010. Είκοςι πένσε φπϋνια
ΟΣΑΝ ΠΡΩΣΟΚΑΣΕΒΗΚΑ ΣΗ ΜΤΡΝΗ, ΔΙΔΩ ΩΣΗΡΙΟΤ
 ΟΣΑΝ ΠΡΩΣΟΚΑΣΕΒΗΚΑ ΣΗ ΜΤΡΝΗ, ΔΙΔΩ ΩΣΗΡΙΟΤ ΘΕΜΑ: Οι ππώσερ ενστπώςειρ σοτ Μανόλη από ση μύπνη και η αίςθηςη ανεξαπσηςίαρ ποτ δοκιμάζει απελετθεπψμένορ από σην εξοτςία σοτ πασέπα και ξεκινώνσαρ ση ζψή σοτ
ΟΣΑΝ ΠΡΩΣΟΚΑΣΕΒΗΚΑ ΣΗ ΜΤΡΝΗ, ΔΙΔΩ ΩΣΗΡΙΟΤ ΘΕΜΑ: Οι ππώσερ ενστπώςειρ σοτ Μανόλη από ση μύπνη και η αίςθηςη ανεξαπσηςίαρ ποτ δοκιμάζει απελετθεπψμένορ από σην εξοτςία σοτ πασέπα και ξεκινώνσαρ ση ζψή σοτ
Μππάσσηρ Πανσελήρ, Κοτήρ Δημήσπιορ, Ετθτμίοτ Φψσεινή
 Μππάσσηρ Πανσελήρ, Κοτήρ Δημήσπιορ, Ετθτμίοτ Φψσεινή Η ποπεία ατσομασοποίηςηρ σψν Ελληνικών Βιβλιοθηκών, φψπίζεσαι ςε 2 πεπιόδοτρ. 1η πεπίοδορ ΕΠΕΑΕΚ Ι (απφέρ 90) 2η πεπίοδορ ΕΠΕΑΕΚ ΙΙ (Ολοκλήπψςη 2008)
Μππάσσηρ Πανσελήρ, Κοτήρ Δημήσπιορ, Ετθτμίοτ Φψσεινή Η ποπεία ατσομασοποίηςηρ σψν Ελληνικών Βιβλιοθηκών, φψπίζεσαι ςε 2 πεπιόδοτρ. 1η πεπίοδορ ΕΠΕΑΕΚ Ι (απφέρ 90) 2η πεπίοδορ ΕΠΕΑΕΚ ΙΙ (Ολοκλήπψςη 2008)
ΘΔΜΑ: ΔΦΗΒΟΙ ΚΑΙ ΓΙΑΓΙΚΣΤΟ. 3 ο ΓΤΜΝΑΙΟ ΑΛΔΞΑΝΓΡΟΤΠΟΛΗ «ΓΟΜΝΑ ΒΘΣΒΘΖΗ» ΥΟΛΙΚΟ ΔΣΟ:
 ΘΔΜΑ: ΔΦΗΒΟΙ ΚΑΙ ΓΙΑΓΙΚΣΤΟ 3 ο ΓΤΜΝΑΙΟ ΑΛΔΞΑΝΓΡΟΤΠΟΛΗ «ΓΟΜΝΑ ΒΘΣΒΘΖΗ» ΥΟΛΙΚΟ ΔΣΟ: 2008-2009 Δόβπη Μαπιάνθη Θεοδψπίδοτ Ανσψνία Ιψαννίδoτ Υψσεινή Κασςίκαρ Βαςίληρ Κηποτπόρ Νικόλαορ Κοτγιοτμσζήρ Γεώργιορ
ΘΔΜΑ: ΔΦΗΒΟΙ ΚΑΙ ΓΙΑΓΙΚΣΤΟ 3 ο ΓΤΜΝΑΙΟ ΑΛΔΞΑΝΓΡΟΤΠΟΛΗ «ΓΟΜΝΑ ΒΘΣΒΘΖΗ» ΥΟΛΙΚΟ ΔΣΟ: 2008-2009 Δόβπη Μαπιάνθη Θεοδψπίδοτ Ανσψνία Ιψαννίδoτ Υψσεινή Κασςίκαρ Βαςίληρ Κηποτπόρ Νικόλαορ Κοτγιοτμσζήρ Γεώργιορ
ΠΕΣΡΑΚΗ ΓΙΑΝΝΗ ΠΡΟΠΟΝΗΣΗ UEFA PRO
 ΠΕΣΡΑΚΗ ΓΙΑΝΝΗ ΠΡΟΠΟΝΗΣΗ UEFA PRO Η επιστφία από σύφη ςτνήθψρ έπφεσαι μια υοπά. Οι δπόμοι ποτ μποπούν να οδηγήςοτν ςσην επιστφία είναι πολλοί. Όλοι oι δπόμοι όμψρ έφοτν κοινά φαπακσηπιςσικά. Γνώςη ανσικείμενοτ.
ΠΕΣΡΑΚΗ ΓΙΑΝΝΗ ΠΡΟΠΟΝΗΣΗ UEFA PRO Η επιστφία από σύφη ςτνήθψρ έπφεσαι μια υοπά. Οι δπόμοι ποτ μποπούν να οδηγήςοτν ςσην επιστφία είναι πολλοί. Όλοι oι δπόμοι όμψρ έφοτν κοινά φαπακσηπιςσικά. Γνώςη ανσικείμενοτ.
Βαγγέληρ Οικονόμοτ Διάλεξη 5. Διαμόπυψςη ήμασορ - Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 1
 Βαγγέληρ Οικονόμοτ Διάλεξη 5 Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 1 Μεσαςφημασιςμόρ Hilbert Διαμόπυψςη ήμασορ Γενικά Διαμόπυψςη Πλάσοτρ Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 2 Ο μεσαςφημασιςμόρ Hilbert ενόρ ςήμασορ
Βαγγέληρ Οικονόμοτ Διάλεξη 5 Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 1 Μεσαςφημασιςμόρ Hilbert Διαμόπυψςη ήμασορ Γενικά Διαμόπυψςη Πλάσοτρ Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 2 Ο μεσαςφημασιςμόρ Hilbert ενόρ ςήμασορ
Βιομηφανικοί Ατσομασιςμοί
 Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Δρ Αριςτείδησ Ε. Κυπράκησ 1 Κύκλορ
Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Δρ Αριςτείδησ Ε. Κυπράκησ 1 Κύκλορ
ΓΔΝΙΚΗ ΤΝΔΛΔΤΗ ΚΔΝΣΡΙΚΗ ΔΝΧΗ ΔΠΙΜΔΛΗΣΗΡΙΧΝ ΔΛΛΑΓΟ ΘΔΑΛΟΝΙΚΗ ΦΙΛΟΞΔΝΙΑ ΔΒΔΘ
 07 09 2012 ΓΔΝΙΚΗ ΤΝΔΛΔΤΗ ΚΔΝΣΡΙΚΗ ΔΝΧΗ ΔΠΙΜΔΛΗΣΗΡΙΧΝ ΔΛΛΑΓΟ ΘΔΑΛΟΝΙΚΗ ΦΙΛΟΞΔΝΙΑ ΔΒΔΘ ΘΕΜΑΣΟΛΟΓΙΑ ΠΑΡΟΤΙΑΗ ΑΞΟΝΕ ΔΡΑΕΙ ΣΗ ΚΕΕΕ Ε ΤΝΕΡΓΑΙΑ ΜΕ ΣΑ ΕΠΙΜΕΛΗΣΗΡΙΑ ΓΙΑ ΣΟΝ ΕΠΑΝΑΠΡΟΔΙΟΡΙΜΟ ΣΟΤ ΡΟΛΟΤ ΣΨΝ ΕΠΙΜΕΛΗΣΗΡΙΨΝ
07 09 2012 ΓΔΝΙΚΗ ΤΝΔΛΔΤΗ ΚΔΝΣΡΙΚΗ ΔΝΧΗ ΔΠΙΜΔΛΗΣΗΡΙΧΝ ΔΛΛΑΓΟ ΘΔΑΛΟΝΙΚΗ ΦΙΛΟΞΔΝΙΑ ΔΒΔΘ ΘΕΜΑΣΟΛΟΓΙΑ ΠΑΡΟΤΙΑΗ ΑΞΟΝΕ ΔΡΑΕΙ ΣΗ ΚΕΕΕ Ε ΤΝΕΡΓΑΙΑ ΜΕ ΣΑ ΕΠΙΜΕΛΗΣΗΡΙΑ ΓΙΑ ΣΟΝ ΕΠΑΝΑΠΡΟΔΙΟΡΙΜΟ ΣΟΤ ΡΟΛΟΤ ΣΨΝ ΕΠΙΜΕΛΗΣΗΡΙΨΝ
Επιυύλη Παςπάση Υπ. Διδ. Πανσείοτ Πανεπιςσημίοτ. Αππίλιορ 2014
 Επιυύλη Παςπάση Υπ. Διδ. Πανσείοτ Πανεπιςσημίοτ Αππίλιορ 2014 ΚΑΣΑΣΑΞΗ ΧΩΡΑ ΠΛΗΘΤΜΟ 1 Κίνα 1,343,239,923 2 Ινδία 1,205,073,612 3 ΗΠΑ 313,847,465 4 Ινδονηςία 248,216,193 5 Βραζιλία 205,716,890 Κίνα και
Επιυύλη Παςπάση Υπ. Διδ. Πανσείοτ Πανεπιςσημίοτ Αππίλιορ 2014 ΚΑΣΑΣΑΞΗ ΧΩΡΑ ΠΛΗΘΤΜΟ 1 Κίνα 1,343,239,923 2 Ινδία 1,205,073,612 3 ΗΠΑ 313,847,465 4 Ινδονηςία 248,216,193 5 Βραζιλία 205,716,890 Κίνα και
Κασαγπαυή σηρ λετκοπάθειαρ και άλλψν δτςμοπυιών ςε άγπια ζώα σηρ Ελλάδαρ και Κύπποτ
 Κασαγπαυή σηρ λετκοπάθειαρ και άλλψν δτςμοπυιών ςε άγπια ζώα σηρ Ελλάδαρ και Κύπποτ Ν. Κολλάπηρ 1, Χ. Σώκορ 1*, K.Γ. Παπαςπτπόποτλορ 1,3, Κ. Σκοπδάρ 1, Π. Μπίπσςαρ 1,2 1 Διεύθτνςη Έπετναρ & Τεκμηπίψςηρ,
Κασαγπαυή σηρ λετκοπάθειαρ και άλλψν δτςμοπυιών ςε άγπια ζώα σηρ Ελλάδαρ και Κύπποτ Ν. Κολλάπηρ 1, Χ. Σώκορ 1*, K.Γ. Παπαςπτπόποτλορ 1,3, Κ. Σκοπδάρ 1, Π. Μπίπσςαρ 1,2 1 Διεύθτνςη Έπετναρ & Τεκμηπίψςηρ,
ςε ένα Σύςσημα Παπαγψγήρ Κειμένψν Φτςικήρ Γλώςςαρ Γιώπγορ Καπακασςιώσηρ
 ςε ένα Σύςσημα Παπαγψγήρ Κειμένψν Φτςικήρ Γλώςςαρ Γιώπγορ Καπακασςιώσηρ Αυτι είναι μία λευκι λικυκοσ που ηωγραφίςτθκε από το Ζωγράφο του Αχιλλζα. Δθμιουργικθκε κατά τθ διάρκεια τθσ κλαςικισ περιόδου.
ςε ένα Σύςσημα Παπαγψγήρ Κειμένψν Φτςικήρ Γλώςςαρ Γιώπγορ Καπακασςιώσηρ Αυτι είναι μία λευκι λικυκοσ που ηωγραφίςτθκε από το Ζωγράφο του Αχιλλζα. Δθμιουργικθκε κατά τθ διάρκεια τθσ κλαςικισ περιόδου.
Η Ευρωπαϊκή Ένωση - «Το Χαμόγελο του Παιδιού»: Δράσεις και πρωτοβουλίες για την καταπολέμηση του σχολικού εκφοβισμού στην Ελλάδα και την Ευρώπη.
 Η Ευρωπαϊκή Ένωση - «Το Χαμόγελο του Παιδιού»: Δράσεις και πρωτοβουλίες για την καταπολέμηση του σχολικού εκφοβισμού στην Ελλάδα και την Ευρώπη. Αθήνα 4 Δεκεμβρίου 2012 Ευρωπαϊκή Ένωση: Θεσμοί, δυνατότητες,
Η Ευρωπαϊκή Ένωση - «Το Χαμόγελο του Παιδιού»: Δράσεις και πρωτοβουλίες για την καταπολέμηση του σχολικού εκφοβισμού στην Ελλάδα και την Ευρώπη. Αθήνα 4 Δεκεμβρίου 2012 Ευρωπαϊκή Ένωση: Θεσμοί, δυνατότητες,
Ομάδα Γλώςςαρ ( ) Γ. Κούμα, ΕΜΕ, Δπ. Ειπ. Ροδοςθένοτρ, Β. Παπαδάκη, Μ. σευάνοτ, Μ. Κτππιανού, Π. Φπτςοςσόμοτ, Κ. Κψνςσανσίνοτ, Γ.
 Ομάδα Γλώςςαρ (2013-2014) Γ. Κούμα, ΕΜΕ, Δπ. Ειπ. Ροδοςθένοτρ, Β. Παπαδάκη, Μ. σευάνοτ, Μ. Κτππιανού, Π. Φπτςοςσόμοτ, Κ. Κψνςσανσίνοτ, Γ. Οπυανίδηρ 1 Πόσε έγινε; Η έπετνα διεξήφθη σον Ιούνιο 2014. Από
Ομάδα Γλώςςαρ (2013-2014) Γ. Κούμα, ΕΜΕ, Δπ. Ειπ. Ροδοςθένοτρ, Β. Παπαδάκη, Μ. σευάνοτ, Μ. Κτππιανού, Π. Φπτςοςσόμοτ, Κ. Κψνςσανσίνοτ, Γ. Οπυανίδηρ 1 Πόσε έγινε; Η έπετνα διεξήφθη σον Ιούνιο 2014. Από
21 ο Εθνικό τνέδπιο «Ενέπγεια & Ανάπστξη 2016» Ίδπτμα Ετγενίδοτ, Αθήνα, Οκσωβπίοτ 2016
 21 ο Εθνικό τνέδπιο «Ενέπγεια & Ανάπστξη 2016» Ίδπτμα Ετγενίδοτ, Αθήνα, 25-26 Οκσωβπίοτ 2016 Σα ΜΤΗΕ, ωρ έπγα πολλαπλήρ ςκοπιμόσησαρ, μποπούν να ικανοποιούν όλερ σιρ άλλερ φπήςειρ νεπού, φωπίρ να δημιοτπγούν
21 ο Εθνικό τνέδπιο «Ενέπγεια & Ανάπστξη 2016» Ίδπτμα Ετγενίδοτ, Αθήνα, 25-26 Οκσωβπίοτ 2016 Σα ΜΤΗΕ, ωρ έπγα πολλαπλήρ ςκοπιμόσησαρ, μποπούν να ικανοποιούν όλερ σιρ άλλερ φπήςειρ νεπού, φωπίρ να δημιοτπγούν
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥΣΤΗΝ ΑΛΓΕΒΡΑ. Άρτιοι αριθμοί ονομάζονται οι αριθμοί που διαιρούνται με το 2 και περιττοί εκείνοι
 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥΣΤΗΝ ΑΛΓΕΒΡΑ 1)Ποιοι αριθμοί ονομάζονται άρτιοι και ποιοι περιττοί ; Άρτιοι αριθμοί ονομάζονται οι αριθμοί που διαιρούνται με το 2 και περιττοί εκείνοι που δεν διαιρούνται
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥΣΤΗΝ ΑΛΓΕΒΡΑ 1)Ποιοι αριθμοί ονομάζονται άρτιοι και ποιοι περιττοί ; Άρτιοι αριθμοί ονομάζονται οι αριθμοί που διαιρούνται με το 2 και περιττοί εκείνοι που δεν διαιρούνται
Νσίπληρ Νικόλαορ- ΕΣΤ 1 ο Υπονσιςσήπιο Παπαςκετή, 11/10/2013 Β4. Λεισοτπγικά τςσήμασα- Υπονσιςσήπιο
 Νσίπληρ Νικόλαορ- ΕΣΤ 1 ο Υπονσιςσήπιο Παπαςκετή, 11/10/2013 Β4 Υπονσιςσήπιο 1 Κάθε Παπαςκετή 13:00-15:00 Παπαδόςειρ: Δετσέπα 13:00-16:00 Κύπιορ ςσόφορ σοτ Υπονσιςσηπίοτ είναι η βοήθεια ςε ππακσικά θέμασα
Νσίπληρ Νικόλαορ- ΕΣΤ 1 ο Υπονσιςσήπιο Παπαςκετή, 11/10/2013 Β4 Υπονσιςσήπιο 1 Κάθε Παπαςκετή 13:00-15:00 Παπαδόςειρ: Δετσέπα 13:00-16:00 Κύπιορ ςσόφορ σοτ Υπονσιςσηπίοτ είναι η βοήθεια ςε ππακσικά θέμασα
Δειγματοληυία νερού για ανίτνεσση λεγεφνέλλας.
 Δειγματοληυία νερού για ανίτνεσση λεγεφνέλλας. Νακούλαρ Βαςίλειορ Επόπσηρ Δημόςιαρ Τγείαρ MSc Επγαςσήπιο Τγιεινήρ & Επιδημιολογίαρ Πανεπιςσήμιο Θεςςαλίαρ 1976: Υιλαδέλυεια, ΗΠΑ Επιδημία πνετμονίαρ με:
Δειγματοληυία νερού για ανίτνεσση λεγεφνέλλας. Νακούλαρ Βαςίλειορ Επόπσηρ Δημόςιαρ Τγείαρ MSc Επγαςσήπιο Τγιεινήρ & Επιδημιολογίαρ Πανεπιςσήμιο Θεςςαλίαρ 1976: Υιλαδέλυεια, ΗΠΑ Επιδημία πνετμονίαρ με:
Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν
 Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν Π Α Ν Ε Π Ι Σ Η Μ Ι Ο Κ Τ Π Ρ Ο Τ Νοέμβριος 212 Οι Έπετνερ Οικονομικήρ τγκτπίαρ ςσοφεύοτν ςσην αποσύπψςη σψν ανσιλήχεψν σψν επιφειπημασιών και κασαναλψσών
Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν Π Α Ν Ε Π Ι Σ Η Μ Ι Ο Κ Τ Π Ρ Ο Τ Νοέμβριος 212 Οι Έπετνερ Οικονομικήρ τγκτπίαρ ςσοφεύοτν ςσην αποσύπψςη σψν ανσιλήχεψν σψν επιφειπημασιών και κασαναλψσών
Λούηρ Μ. Λοΐζοτ. Υεβποτάπιορ 2010
 Λούηρ Μ. Λοΐζοτ Υεβποτάπιορ 2010 1 Λίγα λόγια για μαρ τμβοτλετσικέρ Τπηπεςίερ Κασάπσιςη Οπιςμοί / Σοποθέσηςη ςσο θέμα Οδικόρ φάπσηρ Πψρ; Αναμενόμενα Ουέλη Πψρ μποπούμε να ςαρ βοηθήςοτμε 2 Αποςσολή σηρ
Λούηρ Μ. Λοΐζοτ Υεβποτάπιορ 2010 1 Λίγα λόγια για μαρ τμβοτλετσικέρ Τπηπεςίερ Κασάπσιςη Οπιςμοί / Σοποθέσηςη ςσο θέμα Οδικόρ φάπσηρ Πψρ; Αναμενόμενα Ουέλη Πψρ μποπούμε να ςαρ βοηθήςοτμε 2 Αποςσολή σηρ
ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΠΟΛΤΣΕΥΝΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΗΛΕΚΣΡΟΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ
 ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΠΟΛΤΣΕΥΝΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΗΛΕΚΣΡΟΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ ΕΙΑΓΩΓΗ ΣΟ ΔΙΑΔΙΚΑΣΙΚΟ ΠΡΟΓΡΑΜΜΑΣΙΜΟ 4 ο ΕΣ ΑΚΗΕΩΝ Οι αςκήςειρ ατσού σοτ υτλλαδίοτ καλύπσοτν σα παπακάσψ θέμασα
ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΠΟΛΤΣΕΥΝΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΗΛΕΚΣΡΟΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ ΕΙΑΓΩΓΗ ΣΟ ΔΙΑΔΙΚΑΣΙΚΟ ΠΡΟΓΡΑΜΜΑΣΙΜΟ 4 ο ΕΣ ΑΚΗΕΩΝ Οι αςκήςειρ ατσού σοτ υτλλαδίοτ καλύπσοτν σα παπακάσψ θέμασα
Βίκη Νσπίσςοτ Οικονομικό Πανεπιςσήμιο Αθηνών
 Βίκη Νσπίσςοτ Οικονομικό Πανεπιςσήμιο Αθηνών Θηςατποί όπψν Σημαςιολογικέρ ςφέςειρ θηςατπών όπψν Ιεπαπφικέρ ςφέςειρ Χπήςη ςφέςεψν μέποτρ/όλοτ Χπήςη ςφέςεψν γενίκετςηρ Στνάυεια Χπήςη ςφέςεψν ςτνάυειαρ ςσιρ
Βίκη Νσπίσςοτ Οικονομικό Πανεπιςσήμιο Αθηνών Θηςατποί όπψν Σημαςιολογικέρ ςφέςειρ θηςατπών όπψν Ιεπαπφικέρ ςφέςειρ Χπήςη ςφέςεψν μέποτρ/όλοτ Χπήςη ςφέςεψν γενίκετςηρ Στνάυεια Χπήςη ςφέςεψν ςτνάυειαρ ςσιρ
ΜΟΡΥΕ- ΚΛΙΝΙΚΗ ΔΙΕΡΕΤΝΗΗ. Αθ.Ι. Τριανταυύλλοσ δντής καρδ.κλ. 3 οσ νοσ. ΙΚΑ
 ΜΟΡΥΕ- ΚΛΙΝΙΚΗ ΔΙΕΡΕΤΝΗΗ Αθ.Ι. Τριανταυύλλοσ δντής καρδ.κλ. 3 οσ νοσ. ΙΚΑ Η τπέπσαςη είναι μια πολτςτςσημασική κασάςσαςη ςσην οποία ειδικόσησερ όπψρ η νευπολογία,καπδιολογία,ενδοκπινολογία και η χτφοςψμασική
ΜΟΡΥΕ- ΚΛΙΝΙΚΗ ΔΙΕΡΕΤΝΗΗ Αθ.Ι. Τριανταυύλλοσ δντής καρδ.κλ. 3 οσ νοσ. ΙΚΑ Η τπέπσαςη είναι μια πολτςτςσημασική κασάςσαςη ςσην οποία ειδικόσησερ όπψρ η νευπολογία,καπδιολογία,ενδοκπινολογία και η χτφοςψμασική
IAAF CECS Level I Lecturers Course
 Ειςαγψγή ςσο Kids Athletics: Γιασί? Ειςαγψγή Η IAAF αυού εξέσαςε σην εναςφόληςη σψν μικπών παιδιών με σον Κλαςικό Αθλησιςμό σα σελετσαία φπόνια κασέληξε ςε μια ππόσαςη πποςαπμοςμένη ςσα ςημεπινά παιδιά.
Ειςαγψγή ςσο Kids Athletics: Γιασί? Ειςαγψγή Η IAAF αυού εξέσαςε σην εναςφόληςη σψν μικπών παιδιών με σον Κλαςικό Αθλησιςμό σα σελετσαία φπόνια κασέληξε ςε μια ππόσαςη πποςαπμοςμένη ςσα ςημεπινά παιδιά.
Νσίπληρ Νίκορ- ΕΣΤ 4ο ΥΡΟΝΣΙΣΗΡΙΟ Παπαςκετή Β4
 Νσίπληρ Νίκορ- ΕΣΤ 4ο ΥΡΟΝΣΙΣΗΡΙΟ Παπαςκετή 4-11-2013 Β4 1 Κοινή Μνήμη μεσαξύ διεπγαςιών -> Γπηγοπόσεπη μοπυή IPC Σα δεδομένα δεν ανσιγπάυονσαι πάνω από μία υοπά Server/Client model. Όσαν ο Server γπάυει,
Νσίπληρ Νίκορ- ΕΣΤ 4ο ΥΡΟΝΣΙΣΗΡΙΟ Παπαςκετή 4-11-2013 Β4 1 Κοινή Μνήμη μεσαξύ διεπγαςιών -> Γπηγοπόσεπη μοπυή IPC Σα δεδομένα δεν ανσιγπάυονσαι πάνω από μία υοπά Server/Client model. Όσαν ο Server γπάυει,
Ο Μέγας Βασίλειος σε μικρογραυία τοσ 15οσ αιώνα(μονή Διονσσίοσ, Άγιο Όρος
 Ο Μέγας Βασίλειος σε μικρογραυία τοσ 15οσ αιώνα(μονή Διονσσίοσ, Άγιο Όρος Ο λόγορ εκυψνείσαι ςσην Καιςάπεια σο 368μΧ με αυοπμή σην κοινψνική αναςσάσψςη ποτ δημιοτπγήθηκε ανάμεςα ςσοτρ πολίσερ εξαισίαρ
Ο Μέγας Βασίλειος σε μικρογραυία τοσ 15οσ αιώνα(μονή Διονσσίοσ, Άγιο Όρος Ο λόγορ εκυψνείσαι ςσην Καιςάπεια σο 368μΧ με αυοπμή σην κοινψνική αναςσάσψςη ποτ δημιοτπγήθηκε ανάμεςα ςσοτρ πολίσερ εξαισίαρ
Κλινικό Φπονσιςσήπιο. Ελένη Κλέσςιοτ, RN, MSc, PhD(C) Ρέα Ράμμοτ, MPH, NFESC
 Κλινικό Φπονσιςσήπιο Ελένη Κλέσςιοτ, RN, MSc, PhD(C) Ρέα Ράμμοτ, MPH, NFESC Απαπαίσηση δεξιόσησα Σαφεία εξέλιξη επιςσημονικών γνώςεψν Πλούσορ διαθέςιμψν πηγών Internet (πεπιοδικά on-line, εξειδικετμένα
Κλινικό Φπονσιςσήπιο Ελένη Κλέσςιοτ, RN, MSc, PhD(C) Ρέα Ράμμοτ, MPH, NFESC Απαπαίσηση δεξιόσησα Σαφεία εξέλιξη επιςσημονικών γνώςεψν Πλούσορ διαθέςιμψν πηγών Internet (πεπιοδικά on-line, εξειδικετμένα
ΑΙΣΗΗ ΤΠΟΧΗΥΙΟΤ. Για ςυμμετοχή ςτο χέδιο Δράςησ:
 ΑΝΑΠΣΤΞΙΑΚΗ ΤΜΠΡΑΞΗ «ΘΕΠΡΩΣΙΚΗ ΚΟΙΝΩΝΙΚΗ ΤΝΕΡΓΑΙΑ» Κςπά Βασιλικήρ 10-46100 Ηγοςμενίτσα τηλ.: 2665025140 & 2665098318 Φαξ 2665028885 & 2665098319 e-mail: Thekoisi@yahoo.gr ΑΙΣΗΗ ΤΠΟΧΗΥΙΟΤ Για ςυμμετοχή
ΑΝΑΠΣΤΞΙΑΚΗ ΤΜΠΡΑΞΗ «ΘΕΠΡΩΣΙΚΗ ΚΟΙΝΩΝΙΚΗ ΤΝΕΡΓΑΙΑ» Κςπά Βασιλικήρ 10-46100 Ηγοςμενίτσα τηλ.: 2665025140 & 2665098318 Φαξ 2665028885 & 2665098319 e-mail: Thekoisi@yahoo.gr ΑΙΣΗΗ ΤΠΟΧΗΥΙΟΤ Για ςυμμετοχή
Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν
 Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν Σεύφορ 3 Ιούλιορ 211 Π Α Ν Ε Π Ι Σ Η Μ Ι Ο Κ Τ Π Ρ Ο Τ A. Έρεσνες Οικονομικής Σσγκσρίας * Ιούλιος 211 Οι Έπετνερ Οικονομικήρ τγκτπίαρ ςσοφεύοτν ςσην αποσύπψςη
Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν Σεύφορ 3 Ιούλιορ 211 Π Α Ν Ε Π Ι Σ Η Μ Ι Ο Κ Τ Π Ρ Ο Τ A. Έρεσνες Οικονομικής Σσγκσρίας * Ιούλιος 211 Οι Έπετνερ Οικονομικήρ τγκτπίαρ ςσοφεύοτν ςσην αποσύπψςη
ΠΑΝΕΛΛΑΔΙΚΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΣΙΚΑ ΚΑΙ ΣΟΙΦΕΙΑ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ
 ΠΑΝΕΛΛΑΔΙΚΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΣΙΚΑ ΚΑΙ ΣΟΙΦΕΙΑ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ ΕΚΥΩΝΗΕΙ ΘΕΜΑ Α Α. Αμ ξι ςτμαπσήςειρ f καιg είμαι οαπαγψγίςιμερ ςσξ, μα αοξδείνεσε όσι ( )
ΠΑΝΕΛΛΑΔΙΚΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΣΙΚΑ ΚΑΙ ΣΟΙΦΕΙΑ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ ΕΚΥΩΝΗΕΙ ΘΕΜΑ Α Α. Αμ ξι ςτμαπσήςειρ f καιg είμαι οαπαγψγίςιμερ ςσξ, μα αοξδείνεσε όσι ( )
Ιωάννης Σ. Μιχέλης Μαθηματικός
 1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Ποιες είναι οι ιδιότητες της πρόσθεσης των φυσικών; Το άθροισμα ενός φυσικού αριθμού με το 0 ισούται με τον ίδιο αριθμό. α+0=α Αντιμεταθετική ιδιότητα. Με βάση την οποία
1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Ποιες είναι οι ιδιότητες της πρόσθεσης των φυσικών; Το άθροισμα ενός φυσικού αριθμού με το 0 ισούται με τον ίδιο αριθμό. α+0=α Αντιμεταθετική ιδιότητα. Με βάση την οποία
ΜΑΘΗΜΑΣΙΚΑ ΠΡΟΑΝΑΣΟΛΙΜΟΤ Γ ΛΤΚΕΙΟΤ ΘΕΜΑΣΑ ΚΑΙ ΑΠΑΝΣΗΕΙ ΠΑΝΕΛΛΗΝΙΩΝ 2017
 ΜΑΘΗΜΑΣΙΚΑ ΠΡΟΑΝΑΣΟΛΙΜΟΤ Γ ΛΤΚΕΙΟΤ ΘΕΜΑΣΑ ΚΑΙ ΑΠΑΝΣΗΕΙ ΠΑΝΕΛΛΗΝΙΩΝ 7 ΕΚΥΩΝΗΕΙ ΘΕΜΑ Α Α.Έςσψ μια ςτμάπσηςη f, η ξοξία είμαι ςτμεφήρ ςε έμα διάςσημα Δ. Αμ f () > ςε κάθε εςψσεπικό ςημείξ σξτ Δ, σόσε μα αοξδείνεσε
ΜΑΘΗΜΑΣΙΚΑ ΠΡΟΑΝΑΣΟΛΙΜΟΤ Γ ΛΤΚΕΙΟΤ ΘΕΜΑΣΑ ΚΑΙ ΑΠΑΝΣΗΕΙ ΠΑΝΕΛΛΗΝΙΩΝ 7 ΕΚΥΩΝΗΕΙ ΘΕΜΑ Α Α.Έςσψ μια ςτμάπσηςη f, η ξοξία είμαι ςτμεφήρ ςε έμα διάςσημα Δ. Αμ f () > ςε κάθε εςψσεπικό ςημείξ σξτ Δ, σόσε μα αοξδείνεσε
ΠΑΝΕΛΛΗΝΙΕ 2017 ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΜΗΧΑΝΕ ΕΩΣΕΡΙΚΗ ΚΑΤΗ ΙΙ (ΜΕΚ ΙΙ) ΘΕΜΑΣΑ
 ΠΑΝΕΛΛΗΝΙΕ 2017 ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΜΗΧΑΝΕ ΕΩΣΕΡΙΚΗ ΚΑΤΗ ΙΙ (ΜΕΚ ΙΙ) ΘΕΜΑ Α ΘΕΜΑΣΑ Α1. Να φαπακσηπίςεσε σιρ οπξσάςειρ οξτ ακξλξτθξύμ, γπάυξμσαρ ςσξ σεσπάδιό ςαρ δίολα ςσξ γπάμμα οξτ αμσιςσξιφεί ςε κάθε
ΠΑΝΕΛΛΗΝΙΕ 2017 ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΜΗΧΑΝΕ ΕΩΣΕΡΙΚΗ ΚΑΤΗ ΙΙ (ΜΕΚ ΙΙ) ΘΕΜΑ Α ΘΕΜΑΣΑ Α1. Να φαπακσηπίςεσε σιρ οπξσάςειρ οξτ ακξλξτθξύμ, γπάυξμσαρ ςσξ σεσπάδιό ςαρ δίολα ςσξ γπάμμα οξτ αμσιςσξιφεί ςε κάθε
Αςύγφπξμξρ μξμξυαςικόρ κιμησήπαρ με οτκμωσή. λεισξτπγίαρ και οτκμωσή εκκίμηςηρ
 ΑΣΚΗΣΗ 1 Αςύγφπξμξρ μξμξυαςικόρ κιμησήπαρ με οτκμωσή λεισξτπγίαρ και οτκμωσή εκκίμηςηρ 1 Α. Θεωπησικέρ εοενηγήςειρ: Ο αςύγφπξμξρ κιμησήπαρ με μξμξυαςικό σύλιγμα δεμ μοξπεί μα νεκιμήςει μξμόρ σξτ. Ατσό
ΑΣΚΗΣΗ 1 Αςύγφπξμξρ μξμξυαςικόρ κιμησήπαρ με οτκμωσή λεισξτπγίαρ και οτκμωσή εκκίμηςηρ 1 Α. Θεωπησικέρ εοενηγήςειρ: Ο αςύγφπξμξρ κιμησήπαρ με μξμξυαςικό σύλιγμα δεμ μοξπεί μα νεκιμήςει μξμόρ σξτ. Ατσό
Καθηγήσπια Μαίπη Κοτσςελίνη Σμήμα Επιςσημών σηρ Αγψγήρ Πανεπιςσήμιο Κύπποτ. Έδπα ΟΤΝΕΚΟ για σην Ιςόσησα και Ενδτνάμψςη σψν Υύλψν
 Καθηγήσπια Μαίπη Κοτσςελίνη Σμήμα Επιςσημών σηρ Αγψγήρ Πανεπιςσήμιο Κύπποτ Έδπα ΟΤΝΕΚΟ για σην Ιςόσησα και Ενδτνάμψςη σψν Υύλψν Παπανοήςειρ: ΔΕΝ πποβλέπεσαι η ιςόπποπη ανσιπποςώπετςη σψν δύο υύλψν ςση
Καθηγήσπια Μαίπη Κοτσςελίνη Σμήμα Επιςσημών σηρ Αγψγήρ Πανεπιςσήμιο Κύπποτ Έδπα ΟΤΝΕΚΟ για σην Ιςόσησα και Ενδτνάμψςη σψν Υύλψν Παπανοήςειρ: ΔΕΝ πποβλέπεσαι η ιςόπποπη ανσιπποςώπετςη σψν δύο υύλψν ςση
Η νέα σπίθτπη BMW Σειπά 1. Πεπιεφόμενα.
 Page 1 Η νέα σπίθτπη BMW Σειπά 1. Πεπιεφόμενα. 1. Στνοπσική Παποτςίαςη 2. Η απόλτση ςποπ ππόσαςη ςση μικπομεςαία κασηγοπία. 3. Η νέα σπίθτπη ΒΜW Σειπά 1 4. Τεφνικέρ πποδιαγπαυέρ 5. Διαγπάμμασα ιςφύορ και
Page 1 Η νέα σπίθτπη BMW Σειπά 1. Πεπιεφόμενα. 1. Στνοπσική Παποτςίαςη 2. Η απόλτση ςποπ ππόσαςη ςση μικπομεςαία κασηγοπία. 3. Η νέα σπίθτπη ΒΜW Σειπά 1 4. Τεφνικέρ πποδιαγπαυέρ 5. Διαγπάμμασα ιςφύορ και
Φατοφροσ Γ. Ιωάννησ, Ο μικρόκυκλοσ τησ φλεγμονήσ ςτο ποδόςφαιρο
 Ο Ιωάννησ Φατοφροσ είναι Επίκουροσ Καθηγητήσ Βιοχημείασ τησ Άςκηςησ ςτο Τμήμα Επιςτήμησ Φυςικήσ Αγωγήσ και Αθλητιςμοφ του Δημοκρίτειου Πανεπιςτημίου Θράκησ. Διδάςκει ςτα μεταπτυχιακά προγράμματα «Άςκηςη
Ο Ιωάννησ Φατοφροσ είναι Επίκουροσ Καθηγητήσ Βιοχημείασ τησ Άςκηςησ ςτο Τμήμα Επιςτήμησ Φυςικήσ Αγωγήσ και Αθλητιςμοφ του Δημοκρίτειου Πανεπιςτημίου Θράκησ. Διδάςκει ςτα μεταπτυχιακά προγράμματα «Άςκηςη
The explosion in Mari, Cyprus, the cost of power shortages, and policy recommendations
 University of Cyprus From the SelectedWorks of Theodoros Zachariadis August, 2011 The explosion in Mari, Cyprus, the cost of power shortages, and policy recommendations Theodoros Zachariadis, Cyprus University
University of Cyprus From the SelectedWorks of Theodoros Zachariadis August, 2011 The explosion in Mari, Cyprus, the cost of power shortages, and policy recommendations Theodoros Zachariadis, Cyprus University
Χαρακτήρες διαιρετότητας ΜΚΔ ΕΚΠ Ανάλυση αριθμού σε γινόμενο πρώτων παραγόντων
 Χαρακτήρες διαιρετότητας ΜΚΔ ΕΚΠ Ανάλυση αριθμού σε γινόμενο πρώτων παραγόντων TINΑ ΒΡΕΝΤΖΟΥ www.ma8eno.gr www.ma8eno.gr Σελίδα 1 Ορισμός Ευκλείδεια διαίρεση ονομάζεται η πράξη κατά την οποία ένας αριθμός
Χαρακτήρες διαιρετότητας ΜΚΔ ΕΚΠ Ανάλυση αριθμού σε γινόμενο πρώτων παραγόντων TINΑ ΒΡΕΝΤΖΟΥ www.ma8eno.gr www.ma8eno.gr Σελίδα 1 Ορισμός Ευκλείδεια διαίρεση ονομάζεται η πράξη κατά την οποία ένας αριθμός
ΘΔΜΑ: Ο Ernst May και «Η καινούπια Φπανκυούπση».
 Μάθημα: Τομέαρ: Δ. Η. Πολεοδομίαρ 8 οτ Πολεοδομίαρ και Φψποσαξίαρ Ακ. Έσορ: 2010-11 Διδάςκονσερ: Δπικοτπικό έπγο: Σποτδάςσπια: Δξάμηνο:. ΑΤΓΔΡΘΜΟΤ ΙΟΚΩΜΘΑ, Ι. ΔΡΡΑΟ Α. ΣΟΤΥΔΓΓΟΠΟΤΚΟΤ, Ε. ΕΑΒΘΣΑΜΟΤ Πίππα
Μάθημα: Τομέαρ: Δ. Η. Πολεοδομίαρ 8 οτ Πολεοδομίαρ και Φψποσαξίαρ Ακ. Έσορ: 2010-11 Διδάςκονσερ: Δπικοτπικό έπγο: Σποτδάςσπια: Δξάμηνο:. ΑΤΓΔΡΘΜΟΤ ΙΟΚΩΜΘΑ, Ι. ΔΡΡΑΟ Α. ΣΟΤΥΔΓΓΟΠΟΤΚΟΤ, Ε. ΕΑΒΘΣΑΜΟΤ Πίππα
V I R I R V R I V R R R R. Σην ζρήκα θαίλεηαη έλα θύθισκα θνηλνύ εθπνκπνύ από ην βξόρν εηζόδνπ Β-Δ ν λόκνο ηνπ Kirchhoff δίλεη: Τειηθά έρνπκε:
 Σύποι Ενιςφτσών: Ενιςφτσήρ σάξηρ Α : Κλαςικά κτκλώμασα ενιςφτσών κοινού εκπομπού, κοινού ςτλλέκση ή κοινήρ βάςηρ, όποτ λόγω ςτνθηκών πόλωςηρ τπάπφει πάνσα πεύμα ςσο κύκλωμα και σο ςημείο λεισοτπγίαρ σοτρ
Σύποι Ενιςφτσών: Ενιςφτσήρ σάξηρ Α : Κλαςικά κτκλώμασα ενιςφτσών κοινού εκπομπού, κοινού ςτλλέκση ή κοινήρ βάςηρ, όποτ λόγω ςτνθηκών πόλωςηρ τπάπφει πάνσα πεύμα ςσο κύκλωμα και σο ςημείο λεισοτπγίαρ σοτρ
25 29 Οκσψβπίοτ 2008 Υπανκυούπση, Γεπμανίαρ. Andy Roxburgh, UEFA Σεφνικόρ Διετθτνσήρ
 25 29 Οκσψβπίοτ 2008 Υπανκυούπση, Γεπμανίαρ Andy Roxburgh, UEFA Σεφνικόρ Διετθτνσήρ 1 ΠΡΟΠΟΝΗΣΗ ΝΕΩΝ ΕΠΙΚΕΥΑΛΗ ΠΡΟΠΟΝΗΣΗ (ΥΤΣΩΡΙΟΤ) ΝΕΩΝ ΠΑΙΚΣΩΝ ΠΡΟΠΟΝΗΣΗ ΔΑΚΑΛΟ ΚΟΡΤΥΑΙΟ ΣΕΦΝΙΚΟ 2 EURO 2008 UCL 2007/08
25 29 Οκσψβπίοτ 2008 Υπανκυούπση, Γεπμανίαρ Andy Roxburgh, UEFA Σεφνικόρ Διετθτνσήρ 1 ΠΡΟΠΟΝΗΣΗ ΝΕΩΝ ΕΠΙΚΕΥΑΛΗ ΠΡΟΠΟΝΗΣΗ (ΥΤΣΩΡΙΟΤ) ΝΕΩΝ ΠΑΙΚΣΩΝ ΠΡΟΠΟΝΗΣΗ ΔΑΚΑΛΟ ΚΟΡΤΥΑΙΟ ΣΕΦΝΙΚΟ 2 EURO 2008 UCL 2007/08
«ΚΑΘΕΣΟ ΑΞΟΝΑ ΕΓΝΑΣΙΑ ΟΔΟΤ ΔΕΡΒΕΝΙ - ΕΡΡΕ - ΠΡΟΜΑΧΩΝΑ ΣΜΗΜΑ ΛΑΧΑΝΑ - ΡΙΖΙΑΝΑ - ΣΡΤΜΟΝΙΚΟ» ΚΤΡΙΟ ΣΟΤ ΕΡΓΟΤ : ΕΓΝΑΣΙΑ ΟΔΟ ΤΜΒΑΣΙΚΟ ΠΟΟ: 43.000.
 «ΚΑΘΕΣΟ ΑΞΟΝΑ ΕΓΝΑΣΙΑ ΟΔΟΤ ΔΕΡΒΕΝΙ - ΕΡΡΕ - ΠΡΟΜΑΧΩΝΑ ΣΜΗΜΑ ΛΑΧΑΝΑ - ΡΙΖΙΑΝΑ - ΣΡΤΜΟΝΙΚΟ» ΚΤΡΙΟ ΣΟΤ ΕΡΓΟΤ : ΕΓΝΑΣΙΑ ΟΔΟ ΤΜΒΑΣΙΚΟ ΠΟΟ: 43.000.000,00 Σο έπγο ανήκει ςσην κασηγοπία σψν έπγψν οδοποιΐαρ & πεπιελάμβανε
«ΚΑΘΕΣΟ ΑΞΟΝΑ ΕΓΝΑΣΙΑ ΟΔΟΤ ΔΕΡΒΕΝΙ - ΕΡΡΕ - ΠΡΟΜΑΧΩΝΑ ΣΜΗΜΑ ΛΑΧΑΝΑ - ΡΙΖΙΑΝΑ - ΣΡΤΜΟΝΙΚΟ» ΚΤΡΙΟ ΣΟΤ ΕΡΓΟΤ : ΕΓΝΑΣΙΑ ΟΔΟ ΤΜΒΑΣΙΚΟ ΠΟΟ: 43.000.000,00 Σο έπγο ανήκει ςσην κασηγοπία σψν έπγψν οδοποιΐαρ & πεπιελάμβανε
εμινάπιο πσηνοσπουίαρ «Ππόγπαμμα ελέγφοτ αλμονέλλαρ ύμμαφορ σηρ ελληνικήρ πσηνοσπουίαρ»
 εμινάπιο πσηνοσπουίαρ «Ππόγπαμμα ελέγφοτ αλμονέλλαρ ύμμαφορ σηρ ελληνικήρ πσηνοσπουίαρ» Νίκη Κ. Μοτσσψσού Κσηνιασπικό Επγαςσήπιο Φαλκίδαρ Εθνικό Επγαςσήπιο Αναυοπάρ αλμονελλών παγκόςμιο ζήσημα ππψσογενήρ
εμινάπιο πσηνοσπουίαρ «Ππόγπαμμα ελέγφοτ αλμονέλλαρ ύμμαφορ σηρ ελληνικήρ πσηνοσπουίαρ» Νίκη Κ. Μοτσσψσού Κσηνιασπικό Επγαςσήπιο Φαλκίδαρ Εθνικό Επγαςσήπιο Αναυοπάρ αλμονελλών παγκόςμιο ζήσημα ππψσογενήρ
Μαθηματικά Γ Γυμνασίου
 Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Οι Φυσικοί Αριθμοί. Παρατήρηση: Δεν στρογγυλοποιούνται αριθμοί τηλεφώνων, Α.Φ.Μ., κωδικοί αριθμοί κλπ. Πρόσθεση Φυσικών αριθμών
 Οι Φυσικοί Αριθμοί Γνωρίζουμε ότι οι αριθμοί είναι ποσοτικές έννοιες και για να τους γράψουμε χρησιμοποιούμε τα αριθμητικά σύμβολα. Οι αριθμοί μετρούν συγκεκριμένα πράγματα και φανερώνουν το πλήθος της
Οι Φυσικοί Αριθμοί Γνωρίζουμε ότι οι αριθμοί είναι ποσοτικές έννοιες και για να τους γράψουμε χρησιμοποιούμε τα αριθμητικά σύμβολα. Οι αριθμοί μετρούν συγκεκριμένα πράγματα και φανερώνουν το πλήθος της
ΠΑΡΑΓΡΑΦΟΣ 1. 2 ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ
 ΠΑΡΑΓΡΑΦΟΣ 1. 2 ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΑΣΚΗΣΕΙΣ ΜΕ ΑΘΡΟΙΣΜΑΤΑ ΚΑΙ ΑΦΑΙΡΕΣΕΙΣ ( 1 ) Να υπολογίσετε τις παραστάσεις Α = 3 + 23 + 19 Β = 8 +13 +45-7 Γ = 3 + 0 Α = 3+23 +19 =
ΠΑΡΑΓΡΑΦΟΣ 1. 2 ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΑΣΚΗΣΕΙΣ ΜΕ ΑΘΡΟΙΣΜΑΤΑ ΚΑΙ ΑΦΑΙΡΕΣΕΙΣ ( 1 ) Να υπολογίσετε τις παραστάσεις Α = 3 + 23 + 19 Β = 8 +13 +45-7 Γ = 3 + 0 Α = 3+23 +19 =
ΤΕΧΝΟΛΟΓΙΑ ΥΠΟΛΟΓΙΣΤΩΝ
 ΚΕΦ Τ ΣΗΜΑΣΑ ΑΡΙΘΜΗ Η ΑΚΕΡΑΙΟΙ ΑΡΙΘΜΟΙ 425 = 4 εκατοντϊδεσ 2 δεκϊδεσ 5 μονϊδεσ 4 * 2* 5* 4 * 2* 5* 4 *2 2* 5* 94257 = 9* 4* 2* 5* 7* * 9*5 4*4 5*2 7* * 2*3 Για τον προηγούμενο αριθμό Θϋτοντασ β= (η βϊςη
ΚΕΦ Τ ΣΗΜΑΣΑ ΑΡΙΘΜΗ Η ΑΚΕΡΑΙΟΙ ΑΡΙΘΜΟΙ 425 = 4 εκατοντϊδεσ 2 δεκϊδεσ 5 μονϊδεσ 4 * 2* 5* 4 * 2* 5* 4 *2 2* 5* 94257 = 9* 4* 2* 5* 7* * 9*5 4*4 5*2 7* * 2*3 Για τον προηγούμενο αριθμό Θϋτοντασ β= (η βϊςη
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ
 ΚΕΦΑΛΑΙΟ 1 Ο : ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Η ιδιότητα α+ β = β+ α λέγεται.. 2. Η ιδιότητα α ( β γ) ( ) + + = α+ β + γ λέγεται. 3. Ο αριθμός 0 είναι το..της πρόσθεσης φυσικών αριθμών αφού ισχύει:
ΚΕΦΑΛΑΙΟ 1 Ο : ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Η ιδιότητα α+ β = β+ α λέγεται.. 2. Η ιδιότητα α ( β γ) ( ) + + = α+ β + γ λέγεται. 3. Ο αριθμός 0 είναι το..της πρόσθεσης φυσικών αριθμών αφού ισχύει:
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ
 Διαιρετότητα Μαθαίνω Πολλαπλάσια ενός φυσικού αριθμού α είναι όλοι οι αριθμοί που προκύπτουν από τον πολλαπλασιασμό του με όλους τους φυσικούς αριθμούς, δηλαδή οι αριθμοί: 0, α, 2 α, 3 α, 4 α,... Το μηδέν
Διαιρετότητα Μαθαίνω Πολλαπλάσια ενός φυσικού αριθμού α είναι όλοι οι αριθμοί που προκύπτουν από τον πολλαπλασιασμό του με όλους τους φυσικούς αριθμούς, δηλαδή οι αριθμοί: 0, α, 2 α, 3 α, 4 α,... Το μηδέν
Ερωτήσεις θεωρίας για τα Μαθηματικά Γ γυμνασίου
 Ερωτήσεις θεωρίας για τα Μαθηματικά Γ γυμνασίου Άλγεβρα 1.1 Β : Δυνάμεις πραγματικών αριθμών. 1. Πως ορίζεται η δύναμη ενός πραγματικού αριθμού ; Η δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα
Ερωτήσεις θεωρίας για τα Μαθηματικά Γ γυμνασίου Άλγεβρα 1.1 Β : Δυνάμεις πραγματικών αριθμών. 1. Πως ορίζεται η δύναμη ενός πραγματικού αριθμού ; Η δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα
ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ. Η διαίρεση καλείται Ευκλείδεια και είναι τέλεια όταν το υπόλοιπο είναι μηδέν.
 ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΣΟΠΙΚΑ ΠΡΟΙΟΝΣΑ ΚΑΙ ΠΡΟΙΟΝΣΑ ΠΟΠ ΗΠΕΙΡΟ
 ΣΟΠΙΚΑ ΠΡΟΙΟΝΣΑ ΚΑΙ ΠΡΟΙΟΝΣΑ ΠΟΠ ΗΠΕΙΡΟ ΣΤΡΙΑ ΣΕΛΕΜΕ ΚΕΥΑΛΟΣΤΡΙ ΑΝΘΟΣΤΡΟ ΜΕΣΟΒΟΝΕ ΣΕΛΕΜΕ ΛΕΤΚΟ ΣΤΡΙ ΑΛΜΗς ΚΑΙ ΜΑΛΑΚΟ ΛΕΤΚΟΤ ΦΡΨΜΑΣΟς ΠΡΟΕΡΦΕΣΑΙ ΑΠΟ ΠΡΟΒΕΙΟ ΓΑΛΑ, ΚΑΣςΙΚΙςΙΟ Η ΑΓΕΛΑΔΙΝΟ. ΔΙΑΥΕΡΕΙ ΑΠΟ ΣΗ
ΣΟΠΙΚΑ ΠΡΟΙΟΝΣΑ ΚΑΙ ΠΡΟΙΟΝΣΑ ΠΟΠ ΗΠΕΙΡΟ ΣΤΡΙΑ ΣΕΛΕΜΕ ΚΕΥΑΛΟΣΤΡΙ ΑΝΘΟΣΤΡΟ ΜΕΣΟΒΟΝΕ ΣΕΛΕΜΕ ΛΕΤΚΟ ΣΤΡΙ ΑΛΜΗς ΚΑΙ ΜΑΛΑΚΟ ΛΕΤΚΟΤ ΦΡΨΜΑΣΟς ΠΡΟΕΡΦΕΣΑΙ ΑΠΟ ΠΡΟΒΕΙΟ ΓΑΛΑ, ΚΑΣςΙΚΙςΙΟ Η ΑΓΕΛΑΔΙΝΟ. ΔΙΑΥΕΡΕΙ ΑΠΟ ΣΗ
7.Αριθμητική παράσταση καλείται σειρά αριθμών που συνδέονται με πράξεις μεταξύ τους. Το αποτέλεσμα της αριθμητικής παράστασης ονομάζεται τιμή της.
 ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ Α.1.2 1. Οι ιδιότητες της πρόσθεσης των φυσικών αριθμών είναι οι εξής : Αντιμεταθετική ιδιότητα π.χ. α+β=β+α Προσετεριστική ιδιότητα π.χ. α+β+γ=(α+β)+γ=α+(β+γ) 2.Η πραξη της αφαίρεσης
ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ Α.1.2 1. Οι ιδιότητες της πρόσθεσης των φυσικών αριθμών είναι οι εξής : Αντιμεταθετική ιδιότητα π.χ. α+β=β+α Προσετεριστική ιδιότητα π.χ. α+β+γ=(α+β)+γ=α+(β+γ) 2.Η πραξη της αφαίρεσης
Οι φυσικοί αριθμοί. Παράδειγμα
 Οι φυσικοί αριθμοί Φυσικοί Αριθμοί Είναι οι αριθμοί με τους οποίους δηλώνουμε πλήθος ή σειρά. Για παράδειγμα, φυσικοί αριθμοί είναι οι: 0, 1,, 3,..., 99, 100,...,999, 1000, 0... Χωρίζουμε τους Φυσικούς
Οι φυσικοί αριθμοί Φυσικοί Αριθμοί Είναι οι αριθμοί με τους οποίους δηλώνουμε πλήθος ή σειρά. Για παράδειγμα, φυσικοί αριθμοί είναι οι: 0, 1,, 3,..., 99, 100,...,999, 1000, 0... Χωρίζουμε τους Φυσικούς
ΚΟΙΝΩΥΕΛΗ ΕΠΙΦΕΙΡΗΗ ΤΠΗΡΕΙΩΝ τκιέρ 12/5/2016
 ΚΟΙΝΩΥΕΛΗ ΕΠΙΦΕΙΡΗΗ ΤΠΗΡΕΙΩΝ τκιέρ 2/5/206 ΝΕΑΠΟΛΗ ΤΚΕΩΝ Απ.ππψσ.339 Θέκα: «Δξγαζίεο ζπληήξεζεο ηνπ ζπλζεηηθνύ ριννηάπεηα ησλ γεπέδσλ πνδνζθαίξνπ θαη ηέληο ζην θνιέγην Γειαζάι, ηνπ γεπέδνπ πνδνζθαίξνπ
ΚΟΙΝΩΥΕΛΗ ΕΠΙΦΕΙΡΗΗ ΤΠΗΡΕΙΩΝ τκιέρ 2/5/206 ΝΕΑΠΟΛΗ ΤΚΕΩΝ Απ.ππψσ.339 Θέκα: «Δξγαζίεο ζπληήξεζεο ηνπ ζπλζεηηθνύ ριννηάπεηα ησλ γεπέδσλ πνδνζθαίξνπ θαη ηέληο ζην θνιέγην Γειαζάι, ηνπ γεπέδνπ πνδνζθαίξνπ
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.1.2. ΠΡΑΞΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.1.2. ΠΡΑΞΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / ΠΡΟΣΘΕΣΗ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ 12+ 7 = 19 Οι αριθμοί 12 και 7 ονομάζονται ενώ το 19 ονομάζεται.. 3+5 =, 5+3 =...
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.1.2. ΠΡΑΞΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / ΠΡΟΣΘΕΣΗ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ 12+ 7 = 19 Οι αριθμοί 12 και 7 ονομάζονται ενώ το 19 ονομάζεται.. 3+5 =, 5+3 =...
Μαθηματικά Γ Γυμνασίου. Επαναληπτικές Ασκήσεις στο Κεφάλαιο 1: 1.2-1.5 Μονώνυμα - Πολυώνυμα - Ταυτότητες
 Μαθηματικά Γ Γυμνασίου Επαναληπτικές Ασκήσεις στο Κεφάλαιο 1: 1.2-1.5 Μονώνυμα - Πολυώνυμα - Ταυτότητες Αλγεβρικές παραστάσεις - Μονώνυμα Πράξεις με μονώνυμα Πολυώνυμα Πρόσθεση και Αφαίρεση πολυωνύμων
Μαθηματικά Γ Γυμνασίου Επαναληπτικές Ασκήσεις στο Κεφάλαιο 1: 1.2-1.5 Μονώνυμα - Πολυώνυμα - Ταυτότητες Αλγεβρικές παραστάσεις - Μονώνυμα Πράξεις με μονώνυμα Πολυώνυμα Πρόσθεση και Αφαίρεση πολυωνύμων
Τι είναι τα πολλαπλάσια ;
 Μαθηματικά Κεφάλαιο 10 Πολλαπλάσια και διαιρέτες Όνομα: Ημερομηνία: / / Θεωρία Πώς τα βρίσκουμε; Τι είναι τα πολλαπλάσια ; Πολλαπλάσια ενός φυσικού αριθμού ονομάζονται οι αριθμοί που προκύπτουν όταν τον
Μαθηματικά Κεφάλαιο 10 Πολλαπλάσια και διαιρέτες Όνομα: Ημερομηνία: / / Θεωρία Πώς τα βρίσκουμε; Τι είναι τα πολλαπλάσια ; Πολλαπλάσια ενός φυσικού αριθμού ονομάζονται οι αριθμοί που προκύπτουν όταν τον
11. Ποιες είναι οι άμεσες συνέπειες της διαίρεσης;
 10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
ΤΓΥΡΟΝΗ ΥΟΛΙΚΗ ΗΓΔΙΑ Γηεζλείο ηάζεηο ζηε ζεσξία, ηελ έξεπλα θαη ηελ πξαθηηθή ζήκεξα - Πξννπηηθέο
 ΤΓΥΡΟΝΗ ΥΟΛΙΚΗ ΗΓΔΙΑ Γηεζλείο ηάζεηο ζηε ζεσξία, ηελ έξεπλα θαη ηελ πξαθηηθή ζήκεξα - Πξννπηηθέο Αλδξέαο Κπζξαηώηεο Λεηηνπξγόο Παηδαγσγηθνύ Ιλζηηηνύηνπ Δθπαηδεπηηθή Ηκεξίδα ΑΚΙΓΑ 26 Φεβξνπαξίνπ 2011 1
ΤΓΥΡΟΝΗ ΥΟΛΙΚΗ ΗΓΔΙΑ Γηεζλείο ηάζεηο ζηε ζεσξία, ηελ έξεπλα θαη ηελ πξαθηηθή ζήκεξα - Πξννπηηθέο Αλδξέαο Κπζξαηώηεο Λεηηνπξγόο Παηδαγσγηθνύ Ιλζηηηνύηνπ Δθπαηδεπηηθή Ηκεξίδα ΑΚΙΓΑ 26 Φεβξνπαξίνπ 2011 1
Η ΜΝΗΜΗ ΤΟΥ ΠΛΑΚΟΥΝΤΑ
 Η ΜΝΗΜΗ ΤΟΥ ΠΛΑΚΟΥΝΤΑ Elimnion Resort http://www.elimnionresort.gr/ Evia 30/9/2016-2/10/2016 Θτμήςοτ σην Πνετμασικόσησα και σην Αυθονία ςση Ζψή ςοτ Μια Βοτσιά ςσο Πεδίο σηρ Γέννηςηρ. Δημιοτπγία Νέψν Εμπειπιών
Η ΜΝΗΜΗ ΤΟΥ ΠΛΑΚΟΥΝΤΑ Elimnion Resort http://www.elimnionresort.gr/ Evia 30/9/2016-2/10/2016 Θτμήςοτ σην Πνετμασικόσησα και σην Αυθονία ςση Ζψή ςοτ Μια Βοτσιά ςσο Πεδίο σηρ Γέννηςηρ. Δημιοτπγία Νέψν Εμπειπιών
Αςύγφπξμξρ σπιυαςικόρ κιμησήπαρ. βπαφτκτκλωμέμξτ δπξμέα, με αμσιςσάθμιςη σηρ. αέπγξτ ιςφύξρ σξτ
 ΑΣΚΗΣΗ 8 Αςύγφπξμξρ σπιυαςικόρ κιμησήπαρ βπαφτκτκλωμέμξτ δπξμέα, με αμσιςσάθμιςη σηρ αέπγξτ ιςφύξρ σξτ 1 Α. Θεωπησικέρ εοενηγήςειρ: Η έμσαςη σξτ πεύμασξρ οξτ αοξππξυά ξ σπιυαςικόρ αςύγφπξμξρ κιμησήπαρ
ΑΣΚΗΣΗ 8 Αςύγφπξμξρ σπιυαςικόρ κιμησήπαρ βπαφτκτκλωμέμξτ δπξμέα, με αμσιςσάθμιςη σηρ αέπγξτ ιςφύξρ σξτ 1 Α. Θεωπησικέρ εοενηγήςειρ: Η έμσαςη σξτ πεύμασξρ οξτ αοξππξυά ξ σπιυαςικόρ αςύγφπξμξρ κιμησήπαρ
ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. 1 ο ΚΕΦΑΛΑΙΟ
 Ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΟΡΕΣΤΙΑΔΑΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΚΕΦΑΛΑΙΟ Διάνυσμα ορίζεται ένα ευθύγραμμο τμήμα στο οποίο έχει ορισθεί ποια είναι η αρχή, ή σημείο εφαρμογής του
Ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΟΡΕΣΤΙΑΔΑΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΚΕΦΑΛΑΙΟ Διάνυσμα ορίζεται ένα ευθύγραμμο τμήμα στο οποίο έχει ορισθεί ποια είναι η αρχή, ή σημείο εφαρμογής του
βάπορ αναυέπεσαι ςσην άλιπη
 Η Ελζνη Δοφδα είναι Αναπληρώτρια Καθηγήτρια ςτον τομζα τησ πεοπονητικήσ, ΣΕΦΑΑ Δημοκριτείου Πανεπιςτημίου Θράκησ, με ζμφαςη ςτη Ρυθμική Γυμναςτική. Διδάςκει ςτο προπτυχιακό και μεταπτυχιακό πρόγραμμα και
Η Ελζνη Δοφδα είναι Αναπληρώτρια Καθηγήτρια ςτον τομζα τησ πεοπονητικήσ, ΣΕΦΑΑ Δημοκριτείου Πανεπιςτημίου Θράκησ, με ζμφαςη ςτη Ρυθμική Γυμναςτική. Διδάςκει ςτο προπτυχιακό και μεταπτυχιακό πρόγραμμα και
Για σιρ οπξσάςειρ Α1 έψρ και Α5 μα γπάχεσε ςσξ σεσπάδιό ςαρ σξμ απιθμό σηρ οπόσαςηρ και δίολα σξ γπάμμα οξτ αμσιςσξιφεί ςση ςψςσή εοιλξγή.
 δ. Κc = [CH 4]/[H 2] 2 Μονάδες 5 ΘΕΜΑ Α Για σιρ οπξσάςειρ Α1 έψρ και Α5 μα γπάχεσε ςσξ σεσπάδιό ςαρ σξμ απιθμό σηρ οπόσαςηρ και δίολα σξ γπάμμα οξτ αμσιςσξιφεί ςση ςψςσή εοιλξγή. Α1. Δίμεσαι η φημική ιςξππξοία
δ. Κc = [CH 4]/[H 2] 2 Μονάδες 5 ΘΕΜΑ Α Για σιρ οπξσάςειρ Α1 έψρ και Α5 μα γπάχεσε ςσξ σεσπάδιό ςαρ σξμ απιθμό σηρ οπόσαςηρ και δίολα σξ γπάμμα οξτ αμσιςσξιφεί ςση ςψςσή εοιλξγή. Α1. Δίμεσαι η φημική ιςξππξοία
ΠΡΟΓΡΑΜΜΑ ΠΕΡΙΒΑΛΛΟΝΣΙΚΗ ΑΓΨΓΗ ΣΙΣΛΟ: <<ΘΑΛΑΑ: ΕΝΑ ΚΡΤΜΜΕΝΟ ΘΗΑΤΡΟ ΓΙΑ ΟΛΟΤ>>
 ΠΡΟΓΡΑΜΜΑ ΠΕΡΙΒΑΛΛΟΝΣΙΚΗ ΑΓΨΓΗ ΣΙΣΛΟ: ΤΜΜΕΣΕΦΟΝΣΕ ΜΑΘΗΣΕ : ΝΗΠΙΑΓΨΓΕΙΟ ΚΑΛΟΦΨΡΙΟΤ ΤΜΜΕΣΕΦΟΝΣΕ ΕΚΠΑΙΔΕΤΣΙΚΟΙ: ΚΑΛΟΤΙΟΤ ΑΝΝΑ ΦΡΟΝΙΚΗ ΠΕΡΙΟΔΟ ΔΙΕΞΑΓΨΓΗ ΣΟΤ ΠΡΟΓΡΑΜΜΑΣΟ
ΠΡΟΓΡΑΜΜΑ ΠΕΡΙΒΑΛΛΟΝΣΙΚΗ ΑΓΨΓΗ ΣΙΣΛΟ: ΤΜΜΕΣΕΦΟΝΣΕ ΜΑΘΗΣΕ : ΝΗΠΙΑΓΨΓΕΙΟ ΚΑΛΟΦΨΡΙΟΤ ΤΜΜΕΣΕΦΟΝΣΕ ΕΚΠΑΙΔΕΤΣΙΚΟΙ: ΚΑΛΟΤΙΟΤ ΑΝΝΑ ΦΡΟΝΙΚΗ ΠΕΡΙΟΔΟ ΔΙΕΞΑΓΨΓΗ ΣΟΤ ΠΡΟΓΡΑΜΜΑΣΟ
Βιωματικό εργαςτήριο Σχεδιαςμόσ θεματικήσ ενότητασ «Ανθρώπινεσ ςχζςεισ - Ανθρώπινοι χαρακτήρεσ»
 Επιςτθμονικό υνζδριο «Διδακτικι τθσ Λογοτεχνίασ ςτθ Μζςθ Εκπαίδευςθ: Αντικρίηοντασ το Νζο Αναλυτικό Πρόγραμμα» Βιωματικό εργαςτήριο Σχεδιαςμόσ θεματικήσ ενότητασ «Ανθρώπινεσ ςχζςεισ - Ανθρώπινοι χαρακτήρεσ»
Επιςτθμονικό υνζδριο «Διδακτικι τθσ Λογοτεχνίασ ςτθ Μζςθ Εκπαίδευςθ: Αντικρίηοντασ το Νζο Αναλυτικό Πρόγραμμα» Βιωματικό εργαςτήριο Σχεδιαςμόσ θεματικήσ ενότητασ «Ανθρώπινεσ ςχζςεισ - Ανθρώπινοι χαρακτήρεσ»
Θζμα 1ο [3.5 μονάδες] Θζμα 2ο [3.5 μονάδες]
![Θζμα 1ο [3.5 μονάδες] Θζμα 2ο [3.5 μονάδες] Θζμα 1ο [3.5 μονάδες] Θζμα 2ο [3.5 μονάδες]](/thumbs/26/9116258.jpg) ΣΕΙ ΕΡΡΩΝ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ ΠΡΟΓΡΑΜΜΑΣΙΜΟ Ι Ειςθγθτισ: Δρ. Β. ολαχίδθσ Ιοφνιοσ 2011 Θζμα 1ο [3.5 μονάδες] Να γραφτεί πρόγραμμα ςε C το οποίο κα υπολογίηει τον
ΣΕΙ ΕΡΡΩΝ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ ΠΡΟΓΡΑΜΜΑΣΙΜΟ Ι Ειςθγθτισ: Δρ. Β. ολαχίδθσ Ιοφνιοσ 2011 Θζμα 1ο [3.5 μονάδες] Να γραφτεί πρόγραμμα ςε C το οποίο κα υπολογίηει τον
9 Πολυώνυμα Διαίρεση πολυωνύμων
 4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
είσε μποπούν να βελσιώςοτν σην πνετμασική και ςψμασική ετεξία, πάνσα βέβαια όσαν κασαναλώνονσαι
 Ο Χαρίλαοσ Δημοςθενόπουλοσ είναι Προϊςτάμενοσ Διαιτολογικοφ Τμήματοσ του Γενικοφ Νοςοκομείου Αθηνών «Λαϊκό» και επιςτημονικόσ υπεφθυνοσ ςτο «Κζντρο Διατροφικήσ Αγωγήσ» Αμπελοκήπων. Αποφοίτηςε από το Τμήμα
Ο Χαρίλαοσ Δημοςθενόπουλοσ είναι Προϊςτάμενοσ Διαιτολογικοφ Τμήματοσ του Γενικοφ Νοςοκομείου Αθηνών «Λαϊκό» και επιςτημονικόσ υπεφθυνοσ ςτο «Κζντρο Διατροφικήσ Αγωγήσ» Αμπελοκήπων. Αποφοίτηςε από το Τμήμα
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ. (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα.
 Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Η κλασματική γραμμή είναι η πράξη της διαίρεσης.
 όροι του κλάσματος : αριθμητής παρονομαστής πόσα ίσα μέρη της ακέραιης μονάδας πήρα πόσα ίσα μέρη χώρισα την ακέραιη μονάδα Η κλασματική γραμμή είναι η πράξη της διαίρεσης. Τα κόκκινα κομμάτια αποτελούν
όροι του κλάσματος : αριθμητής παρονομαστής πόσα ίσα μέρη της ακέραιης μονάδας πήρα πόσα ίσα μέρη χώρισα την ακέραιη μονάδα Η κλασματική γραμμή είναι η πράξη της διαίρεσης. Τα κόκκινα κομμάτια αποτελούν
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ Οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς, τους φυσικούς και τους ακέραιους αριθμούς. Δηλαδή είναι το μεγαλύτερο σύνολο αριθμών που μπορούμε
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ Οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς, τους φυσικούς και τους ακέραιους αριθμούς. Δηλαδή είναι το μεγαλύτερο σύνολο αριθμών που μπορούμε
Σα επιμέποτρ επίπεδα κπεασίνηρ (Cr) και CP ήσαν 49.0 ( 7.62) και 75.5 ( 7.63) mmol.kg -1.
 Ο Απόςτολοσ Θεοδώρου Ph.D είναι Λζκτορασ ςτα Αθλητικά Άλματα ςτον τομζα Κλαςικοφ Αθλητιςμοφ του ΤΕΦΑΑ Αθηνών. Πτυχιοφχοσ Φυςικήσ Αγωγήσ του ΤΕΦΑΑ Αθηνών το 1992. Το 1994 απόκτηςε το μεταπτυχιακό του ςτην
Ο Απόςτολοσ Θεοδώρου Ph.D είναι Λζκτορασ ςτα Αθλητικά Άλματα ςτον τομζα Κλαςικοφ Αθλητιςμοφ του ΤΕΦΑΑ Αθηνών. Πτυχιοφχοσ Φυςικήσ Αγωγήσ του ΤΕΦΑΑ Αθηνών το 1992. Το 1994 απόκτηςε το μεταπτυχιακό του ςτην
Μαθηματικά Γ Γυμνασίου. Επαναληπτικές Ασκήσεις στο Κεφάλαιο 1: Μονώνυμα - Πολυώνυμα - Ταυτότητες
 Μαθηματικά Γ Γυμνασίου Επαναληπτικές Ασκήσεις στο Κεφάλαιο :.2 -.5 Μονώνυμα - Πολυώνυμα - Ταυτότητες Αλγεβρικές παραστάσεις - Μονώνυμα Πράξεις με μονώνυμα Πολυώνυμα Πρόσθεση και Αφαίρεση πολυωνύμων Πολλαπλασιασμός
Μαθηματικά Γ Γυμνασίου Επαναληπτικές Ασκήσεις στο Κεφάλαιο :.2 -.5 Μονώνυμα - Πολυώνυμα - Ταυτότητες Αλγεβρικές παραστάσεις - Μονώνυμα Πράξεις με μονώνυμα Πολυώνυμα Πρόσθεση και Αφαίρεση πολυωνύμων Πολλαπλασιασμός
[ΔΕΛΦΙΚΑ ΠΑΡΑΓΓΕΛΜΑΤΑ]
![[ΔΕΛΦΙΚΑ ΠΑΡΑΓΓΕΛΜΑΤΑ] [ΔΕΛΦΙΚΑ ΠΑΡΑΓΓΕΛΜΑΤΑ]](/thumbs/74/71228043.jpg) 2008 Δημιουργία: dimdom In Nomine Portal 2008 [ΔΕΛΦΙΚΑ ΠΑΡΑΓΓΕΛΜΑΤΑ] Μζροσ: Πρόναοσ του Ναοφ του Απόλλωνοσ του εν Δελφοίσ. Περί: Τα Δελφικά Παραγγζλματα, "Εν δε τω προνάω τα εν Δελφοισ γεγραμμενα εςτιν
2008 Δημιουργία: dimdom In Nomine Portal 2008 [ΔΕΛΦΙΚΑ ΠΑΡΑΓΓΕΛΜΑΤΑ] Μζροσ: Πρόναοσ του Ναοφ του Απόλλωνοσ του εν Δελφοίσ. Περί: Τα Δελφικά Παραγγζλματα, "Εν δε τω προνάω τα εν Δελφοισ γεγραμμενα εςτιν
Ναόπλιο, Νατπλία, Ανάπλι ή Napoli di Romania Όποια ονομαςία και αν σηρ δύςοτμε, η ππύση ππψσεόοτςα σηρ ελεόθεπηρ Ελλάδαρ και ντν ππψσεόοτςα σοτ νομοό
 Ναόπλιο, Νατπλία, Ανάπλι ή Napoli di Romania Όποια ονομαςία και αν σηρ δύςοτμε, η ππύση ππψσεόοτςα σηρ ελεόθεπηρ Ελλάδαρ και ντν ππψσεόοτςα σοτ νομοό Απγολίδαρ είναι μια πϋλημοτςείο, με μια πολτκόμανση
Ναόπλιο, Νατπλία, Ανάπλι ή Napoli di Romania Όποια ονομαςία και αν σηρ δύςοτμε, η ππύση ππψσεόοτςα σηρ ελεόθεπηρ Ελλάδαρ και ντν ππψσεόοτςα σοτ νομοό Απγολίδαρ είναι μια πϋλημοτςείο, με μια πολτκόμανση
ΠΣΤΦΙΑΚΗ ΕΡΓΑΙΑ ΜΕΛΕΣΗ ΕΓΦΩΡΙΩΝ ΠΛΗΘΤΜΩΝ ΜΕΛΙΣΖΑΝΑ (Solanum melongena L.) ΜΕ ΦΡΗΗ ΜΟΡΥΟΛΟΓΙΚΩΝ ΦΑΡΑΚΣΗΡΩΝ
 ΣΕΙ ΜΕΟΛΟΓΓΙΟΤ ΦΟΛΗ ΣΕΦΝΟΛΟΓΙΑ ΓΕΩΠΟΝΙΑ ΣΜΗΜΑ ΘΕΡΜΟΚΗΠΙΑΚΩΝ ΚΑΛΛΙΕΡΓΕΙΩΝ & ΑΝΘΟΚΟΜΙΑ ΠΣΤΦΙΑΚΗ ΕΡΓΑΙΑ ΜΕΛΕΣΗ ΕΓΦΩΡΙΩΝ ΠΛΗΘΤΜΩΝ ΜΕΛΙΣΖΑΝΑ (Solanum melongena L.) ΜΕ ΦΡΗΗ ΜΟΡΥΟΛΟΓΙΚΩΝ ΦΑΡΑΚΣΗΡΩΝ ΕΙΗΓΗΣΗ :Δπ.
ΣΕΙ ΜΕΟΛΟΓΓΙΟΤ ΦΟΛΗ ΣΕΦΝΟΛΟΓΙΑ ΓΕΩΠΟΝΙΑ ΣΜΗΜΑ ΘΕΡΜΟΚΗΠΙΑΚΩΝ ΚΑΛΛΙΕΡΓΕΙΩΝ & ΑΝΘΟΚΟΜΙΑ ΠΣΤΦΙΑΚΗ ΕΡΓΑΙΑ ΜΕΛΕΣΗ ΕΓΦΩΡΙΩΝ ΠΛΗΘΤΜΩΝ ΜΕΛΙΣΖΑΝΑ (Solanum melongena L.) ΜΕ ΦΡΗΗ ΜΟΡΥΟΛΟΓΙΚΩΝ ΦΑΡΑΚΣΗΡΩΝ ΕΙΗΓΗΣΗ :Δπ.
1 Φπημασοοικονομική Ανάλτςη
 ~ 38 ~ Βαςίληρ Πολτμένηρ 1 Φπημασοοικονομική Ανάλτςη Παπά σο όσι οι οικονομολόγοι είφαν από καιπό ςτνειδησοποιήςει ση βαςική οικονομική λεισοτπγία σψν πιςσψσικών αγοπών και σψν αγοπών κευαλαίοτ η ςύγφπονη
~ 38 ~ Βαςίληρ Πολτμένηρ 1 Φπημασοοικονομική Ανάλτςη Παπά σο όσι οι οικονομολόγοι είφαν από καιπό ςτνειδησοποιήςει ση βαςική οικονομική λεισοτπγία σψν πιςσψσικών αγοπών και σψν αγοπών κευαλαίοτ η ςύγφπονη
Να γράψετε 5 φυσικούς αριθμούς ξεκινώντας από τον μικρότερο. Ποιοι αριθμοί λέγονται ρητοί και ποιοι άρρητοι;
 Φυσικοί, Ακέραιοι, Ρητοί, Άρρητοι, Πραγματικοί, Απόλυτη Τιμή, Ομόσημοι, Ετερόσημοι, Αντίθετοι, Αντίστροφοι. Να γράψετε 5 φυσικούς αριθμούς ξεκινώντας από τον μικρότερο. Ποιοι αριθμοί λέγονται ακέραιοι;
Φυσικοί, Ακέραιοι, Ρητοί, Άρρητοι, Πραγματικοί, Απόλυτη Τιμή, Ομόσημοι, Ετερόσημοι, Αντίθετοι, Αντίστροφοι. Να γράψετε 5 φυσικούς αριθμούς ξεκινώντας από τον μικρότερο. Ποιοι αριθμοί λέγονται ακέραιοι;
