Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός
|
|
|
- Βασιλική Αλιβιζάτος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
2 Ηλεκτρικό δυναμικό Ηλεκτρικό δυναμικό Σε προηγούμενα κεφάλαια συνδέσαμε τη μελέτη του ηλεκτρομαγνητισμού με τις προγενέστερες γνώσεις μας σχετικά με τις δυνάμεις. Σε αυτό το κεφάλαιο, θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα προβλήματα μηχανικής, τα οποία δεν είναι δυνατόν να λυθούν με μεθόδους που χρησιμοποιούν την έννοια της δύναμης. Η έννοια της δυναμικής ενέργειας είναι πολύ χρήσιμη και στη μελέτη του ηλεκτρισμού. Επειδή η ηλεκτροστατική δύναμη είναι συντηρητική, μπορούμε να περιγράψουμε τα ηλεκτροστατικά φαινόμενα χρησιμοποιώντας την έννοια της ηλεκτρικής δυναμικής ενέργειας. Αυτή η έννοια μας επιτρέπει να ορίσουμε το μέγεθος του ηλεκτρικού δυναμικού. Εισαγωγή Ηλεκτρική δυναμική ενέργεια Ηλεκτρική δυναμική ενέργεια (συνέχεια) Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη. Fe qoe Η ηλεκτρική δύναμη είναι συντηρητική. Αν το δοκιμαστικό φορτίο μετακινείται μέσα στο πεδίο υπό την επίδραση κάποιου εξωτερικού παράγοντα, τότε το έργο που παράγει το πεδίο στο φορτίο είναι ίσο κατά μέτρο και αντίθετο με το έργο που παράγει ο εξωτερικός παράγοντας. Με το σύμβολο ds συμβολίζουμε το απειροστό διάνυσμα μετατόπισης, το οποίο εφάπτεται σε μια διαδρομή στον χώρο. Η διαδρομή αυτή μπορεί να είναι ευθεία ή καμπύλη και το ολοκλήρωμα σε αυτή τη διαδρομή ονομάζεται επικαμπύλιο ολοκλήρωμα. Στο σύστημα φορτίου-πεδίου, το έργο που παράγει το ηλεκτρικό πεδίο στο φορτίο είναι F ds q E ds o Επειδή το έργο αυτό παράγεται από το πεδίο, η δυναμική ενέργεια του συστήματος φορτίου-πεδίου μεταβάλλεται κατά ΔU = q. oeds Για μια πεπερασμένη μετατόπιση του φορτίου από το σημείο A στο σημείο B, η μεταβολή της δυναμικής ενέργειας του συστήματος είναι U UB U B qo d A A Επειδή η δύναμη είναι συντηρητική, το επικαμπύλιο ολοκλήρωμα δεν εξαρτάται από τη διαδρομή που ακολουθεί το φορτίο. Ενότητα Η3.1 Ενότητα Η3.1 Ηλεκτρικό δυναμικό (1) Ηλεκτρικό δυναμικό (2) Η δυναμική ενέργεια ανά μονάδα φορτίου, U/q o, ονομάζεται ηλεκτρικό δυναμικό. Το δυναμικό είναι χαρακτηριστικό μόνο του πεδίου. Η δυναμική ενέργεια είναι χαρακτηριστικό του συστήματος φορτίου-πεδίου. Το δυναμικό είναι ανεξάρτητο από την τιμή του φορτίου q o. Το δυναμικό έχει τιμή σε κάθε σημείο του ηλεκτρικού πεδίου. Το ηλεκτρικό δυναμικό είναι U V q o Το δυναμικό είναι βαθμωτό μέγεθος. Επειδήη ενέργεια είναι βαθμωτό μέγεθος. Όταν ένα φορτισμένο σωματίδιο κινείται μέσα σε ένα ηλεκτρικό πεδίο, το δυναμικό μεταβάλλεται κατά U B V d q E s A o Η απειροστή μετατόπιση μπορεί να εκληφθεί ως απόσταση μεταξύ δύο σημείων του χώρου αντί ως μετατόπιση ενός σημειακού φορτίου. Ενότητα Η3.1 Ενότητα Η3.1 1
3 Ηλεκτρικό δυναμικό (τελική διαφάνεια) Έργο και ηλεκτρικό δυναμικό Το μέγεθος που έχει σημασία είναι η διαφορά του ηλεκτρικού δυναμικού. Συχνά θεωρούμε αυθαίρετα ότι σε κάποιο κατάλληλο σημείο του ηλεκτρικού πεδίου η τιμή του ηλεκτρικού δυναμικού είναι ίση με μηδέν. Το ηλεκτρικό δυναμικό είναι ένα βαθμωτό μέγεθος που χαρακτηρίζει το ηλεκτρικό πεδίο και είναι ανεξάρτητο από το όποιο φορτίο ενδέχεται να βρεθεί μέσα στο πεδίο. Η διαφορά δυναμικού μεταξύ δύο σημείων οφείλεται αποκλειστικά στην ύπαρξη ενός φορτίου-πηγής και εξαρτάται από την κατανομή του φορτίουπηγής. Για να υπάρχει δυναμική ενέργεια, πρέπει να έχουμε ένα σύστημα με δύο ή περισσότερα φορτία. Η δυναμική ενέργεια ανήκει στο σύστημα και μεταβάλλεται μόνο όταν ένα φορτίο μετακινείται σε σχέση με το υπόλοιπο σύστημα. Έστω ότι ένα φορτίο κινείται μέσα σε ένα ηλεκτρικό πεδίο χωρίς να μεταβάλλεται η κινητική ενέργειά του. Το έργο που παράγεται στο φορτίο είναι: W = ΔU = q ΔV Μονάδα μέτρησης: 1 V 1 J/C Το V είναι το αρχικό του volt. Χρειάζεται 1 joule έργου για να μετακινήσουμε ένα φορτίο 1 coulomb μεταξύ δύο σημείων που έχουν διαφορά δυναμικού 1 volt. Επιπλέον, 1 N/C = 1 V/m. Συνεπώς, μπορούμε να εκλάβουμε το ηλεκτρικό πεδίο ως ένα μέτρο του ρυθμού μεταβολής του ηλεκτρικού δυναμικού συναρτήσει της απόστασης. Ενότητα Η3.1 Ενότητα Η3.1 Τάση και βολτάζ Ηλεκτρονιοβόλτ Το ηλεκτρικό δυναμικό περιγράφεται με διάφορους όρους. Οι πιο κοινοί είναι η τάση και το βολτάζ. Η τάση που εφαρμόζεται σε μια συσκευή ή στα άκρα μιας συσκευής είναι ίδια με τη διαφορά δυναμικού στα άκρα της συσκευής. Παρά το γεγονός ότι οι εκφράσεις αυτές υποδηλώνουν κίνηση, η τάση δεν είναι κάτι που κινείται διαμέσου της συσκευής. Μια άλλη μονάδα ενέργειας που χρησιμοποιείται συνήθως στην ατομική και πυρηνική φυσική είναι το ηλεκτρονιοβόλτ. Ένα ηλεκτρονιοβόλτ είναι η ενέργεια που προσλαμβάνει ή χάνει ένα σύστημα φορτίου-πεδίου όταν ένα φορτίο με τιμή e (δηλαδή ένα ηλεκτρόνιο ή πρωτόνιο) κινείται μεταξύ δύο θέσεων με διαφορά δυναμικού 1 volt. 1 ev = 1.60 x J Ενότητα Η3.1 Ενότητα Η3.1 Διαφορά δυναμικού σε ομογενές ηλεκτρικό πεδίο Αν το ηλεκτρικό πεδίο είναι ομογενές, οι εξισώσεις που δίνουν τη διαφορά δυναμικού μεταξύ δύο σημείων A και B μπορούν να αναχθούν σε πιο απλή μορφή: V B B B V A V E d s E d Ed A s A Η μετατόπιση γίνεται από το σημείο A στο σημείο B, παράλληλα στις γραμμές του ηλεκτρικού πεδίου. Το αρνητικό πρόσημο δείχνει ότι το ηλεκτρικό δυναμικό είναι μικρότερο στο σημείο B απ ό,τι στο σημείο A. Οι γραμμές του ηλεκτρικού πεδίου πάντα δείχνουν προς την κατεύθυνση στην οποία μειώνεται το ηλεκτρικό δυναμικό. Η ενέργεια και η κατεύθυνση του ηλεκτρικού πεδίου Όταν το ηλεκτρικό πεδίο έχει κατεύθυνση προς τα κάτω, το σημείο B έχει χαμηλότερο δυναμικό από το A. Όταν ένα θετικό δοκιμαστικό φορτίο μετακινείται από το σημείο A στο B, το σύστημα φορτίου-πεδίου χάνει δυναμική ενέργεια. Οι γραμμές του ηλεκτρικού πεδίου πάντα δείχνουν προς την κατεύθυνση στην οποία μειώνεται το ηλεκτρικό δυναμικό. Ενότητα Η3.2 Ενότητα Η3.2 2
4 Περισσότερα σχετικά με την κατεύθυνση του πεδίου Σε ένα σύστημα που αποτελείται από ένα θετικό φορτίο και ένα ηλεκτρικό πεδίο, η ηλεκτρική δυναμική ενέργεια του συστήματος μειώνεται όταν το φορτίο κινείται με κατεύθυνση ίδια με αυτή του πεδίου. Το ηλεκτρικό πεδίο παράγει έργο σε ένα θετικό φορτίο όταν το φορτίο κινείται στην κατεύθυνση του πεδίου. Η αύξηση της κινητικής ενέργειας του φορτισμένου σωματιδίου συνοδεύεται από ισόποση μείωση της δυναμικής ενέργειας του συστήματος φορτίου-πεδίου. Ένα ακόμα παράδειγμα της αρχής διατήρησης της ενέργειας. Κατεύθυνση του ηλεκτρικού πεδίου (συνέχεια) Αν το φορτίο q o είναι αρνητικό, τότε η μεταβολή της ηλεκτρικής δυναμικής ενέργειας ΔU είναι θετική. Σε ένα σύστημα που αποτελείται από ένα αρνητικό φορτίο και ένα ηλεκτρικό πεδίο, η ηλεκτρική δυναμική ενέργεια του συστήματος αυξάνεται όταν το φορτίο κινείται με κατεύθυνση ίδια με αυτή του πεδίου. Για να κινηθεί το αρνητικό φορτίο στην κατεύθυνση του πεδίου, πρέπει να δεχτεί μια εξωτερική δύναμη η οποία θα παραγάγει θετικό έργο στο φορτίο. Ενότητα Η3.2 Ενότητα Η3.2 Ισοδυναμικές επιφάνειες Το σημείο B έχει χαμηλότερο δυναμικό από το A. Τα σημεία A και Γ έχουν το ίδιο δυναμικό. Όλα τα σημεία που ανήκουν σε ένα επίπεδο το οποίο είναι κάθετο σε ένα ομογενές ηλεκτρικό πεδίο έχουν το ίδιο ηλεκτρικό δυναμικό. Κάθε επιφάνεια που αποτελείται από μια συνεχή κατανομή σημείων, τα οποία έχουν το ίδιο ηλεκτρικό δυναμικό, ονομάζεται ισοδυναμική επιφάνεια. Φορτισμένο σωματίδιο σε ομογενές πεδίο Παράδειγμα Ένα θετικό φορτίο, που βρίσκεται σε κατάσταση ηρεμίας,αφήνεται ελεύθερο και κινείται σε κατεύθυνση ίδια με αυτή του ηλεκτρικού πεδίου. Η μεταβολή του δυναμικού είναι αρνητική. Η μεταβολή της δυναμικής ενέργειας είναι αρνητική. Η δύναμη και η επιτάχυνση έχουν κατεύθυνση ίδια με αυτή του πεδίου. Μπορούμε να υπολογίσουμε το μέτρο της ταχύτητας του φορτίου χρησιμοποιώντας την αρχή διατήρησης της ενέργειας. Ενότητα Η3.2 Ενότητα Η3.2 Ηλεκτρικό δυναμικό και σημειακά φορτία Ένα απομονωμένο θετικό σημειακό φορτίο δημιουργεί ηλεκτρικό πεδίο με ακτινική κατεύθυνση προς τα έξω. Η διαφορά δυναμικού μεταξύ των σημείων A και B είναι: 1 1 VB VA keq r B r A Ηλεκτρικό δυναμικό και σημειακά φορτία (συνέχεια) Το ηλεκτρικό δυναμικό είναι ανεξάρτητο από τη διαδρομή που ακολουθεί το φορτίο για να μετακινηθεί από το σημείο A στο B. Ως τιμή αναφοράς του ηλεκτρικού δυναμικού συνήθως επιλέγουμε τη V = 0 στο r A =. Έτσι, το ηλεκτρικό δυναμικό ενός σημειακού φορτίου σε απόσταση r από αυτό είναι ίσο με: q V ke r Ενότητα Η3.3 Ενότητα Η3.3 3
5 Το ηλεκτρικό δυναμικό ενός σημειακού φορτίου Στην εικόνα φαίνεται το γράφημα του ηλεκτρικού δυναμικού στον κατακόρυφο άξονα για ένα θετικό φορτίο, το οποίο βρίσκεται στο επίπεδο xy. Η καφέ καμπύλη δείχνει ότι το δυναμικό είναι αντιστρόφως ανάλογο του r. Το ηλεκτρικό δυναμικό που οφείλεται σε πολλά φορτία Το συνολικό ηλεκτρικό δυναμικό λόγω πολλώνσημειακών φορτίων σε ένα σημείο Σ ισούται με το άθροισμα των δυναμικών των επιμέρους φορτίων. Ένα ακόμα παράδειγμα της αρχής της υπέρθεσης. Πρόκειται για αλγεβρικό άθροισμα. qi V ke i ri V = 0 στο r =. Ενότητα Η3.3 Ενότητα Η3.3 Το ηλεκτρικό δυναμικό ενός ηλεκτρικού διπόλου Στον κατακόρυφο άξονα y του γραφήματος απεικονίζεται το δυναμικό ενός ηλεκτρικού διπόλου. Η απότομη κλίση μεταξύ των φορτίων αντιπροσωπεύει το ισχυρό ηλεκτρικό πεδίο σε αυτή την περιοχή. Δυναμική ενέργεια πολλών φορτίων qq 1 2 Η δυναμική ενέργεια του συστήματος είναι U ke. r 12 Αν τα δύο φορτία είναι ομόσημα, τότε η δυναμική ενέργεια U είναι θετική και πρέπει να παραχθεί έργο για να πλησιάσουν τα φορτία το ένα στο άλλο. Αν τα δύο φορτία είναι ετερόσημα, τότε η δυναμική ενέργεια U είναι αρνητική και πρέπει να παραχθεί έργο για να μην πλησιάσουν τα φορτία το ένα στο άλλο. Ενότητα Η3.3 Ενότητα Η3.3 Δυναμική ενέργεια πολλών φορτίων (συνέχεια) Αν υπάρχουν περισσότερα από δύο φορτία, τότε βρίσκουμε τη δυναμική ενέργεια U για κάθε ζεύγος φορτίων και αθροίζουμε αλγεβρικά τους όρους. Για τρία φορτία: qq 1 2 q1q 3 q2q 3 U ke r12 r13 r23 Το αποτέλεσμα δεν εξαρτάται από τη σειρά πρόσθεσης των φορτίων. Υπολογισμός του ηλεκτρικού πεδίου E από το ηλεκτρικό δυναμικό V Αρχικά υποθέτουμε ότι το πεδίο έχει μόνο μια οριζόντια συνιστώσα x. dv Ex dx Μπορούμε να γράψουμε παρόμοιες σχέσεις και για τις συνιστώσες y και z. Οι ισοδυναμικές επιφάνειες πρέπει πάντα να είναι κάθετες στις γραμμές του ηλεκτρικού πεδίου που διέρχονται από αυτές. Ενότητα Η3.3 Ενότητα Η3.4 4
6 Τα E και V για ένα φορτισμένο φύλλο άπειρων διαστάσεων Οι ισοδυναμικές είναι οι διακεκομμένες μπλε γραμμές. Οι γραμμές του ηλεκτρικού πεδίου είναι οι καφέ γραμμές. Οι ισοδυναμικές είναι κάθετες σε κάθε σημείο των γραμμών του ηλεκτρικού πεδίου. Τα E και V για ένα σημειακό φορτίο Οι ισοδυναμικές είναι οι διακεκομμένες μπλε γραμμές. Οι γραμμές του ηλεκτρικού πεδίου είναι οι καφέ γραμμές. Οι γραμμές του ηλεκτρικού πεδίου έχουν ακτινική διεύθυνση. E r = dv / dr Οι ισοδυναμικές είναι κάθετες σε κάθε σημείο των γραμμών του ηλεκτρικού πεδίου. Ενότητα Η3.4 Ενότητα Η3.4 Τα E και V για ένα ηλεκτρικό δίπολο Οι ισοδυναμικές είναι οι διακεκομμένες μπλε γραμμές. Οι γραμμές του ηλεκτρικού πεδίου είναι οι καφέ γραμμές. Οι ισοδυναμικές είναι κάθετες σε κάθε σημείο των γραμμών του ηλεκτρικού πεδίου. Υπολογισμός του ηλεκτρικού πεδίου από το ηλεκτρικό δυναμικό Γενικά Γενικά, το ηλεκτρικό δυναμικό είναι συνάρτηση και των τριών χωρικών συντεταγμένων. Αν η συνάρτηση V εκφράζεται με βάση τις καρτεσιανές συντεταγμένες, τότε οι συνιστώσες E x, E y, και E z του ηλεκτρικού πεδίου προκύπτουν εύκολα από τις μερικές παραγώγους της V(x, y, z). V V V Ex Ey Ez x y z Ενότητα Η3.4 Ενότητα Η3.4 Ηλεκτρικό δυναμικό συνεχούς κατανομής φορτίου Μέθοδος 1: Η κατανομή φορτίου είναι γνωστή. Θεωρούμε ένα μικρό στοιχειώδες φορτίο dq. Εκλαμβάνουμε το φορτίο ως σημειακό. Το δυναμικό σε οποιοδήποτε σημείο λόγω αυτού του στοιχειώδους φορτίου είναι: Ηλεκτρικό δυναμικό συνεχούς κατανομής φορτίου (συνέχεια) Για να βρούμε το συνολικό δυναμικό, ολοκληρώνουμε την προηγούμενη εξίσωση ώστε να συμπεριλάβουμε τις συνεισφορές όλων των στοιχείων της κατανομής φορτίου. dq V ke r Σε αυτή τη σχέση για το V, το ηλεκτρικό δυναμικό θεωρείται ίσο με το μηδέν όταν το σημείο Σ βρίσκεται σε άπειρη απόσταση από την κατανομή φορτίου. dq dv ke r 5
7 Ηλεκτρικό δυναμικό συνεχούς κατανομής φορτίου (τελική διαφάνεια) Μεθοδολογία επίλυσης προβλημάτων (1) Αν γνωρίζουμε ήδη το ηλεκτρικό πεδίο, τότε μπορούμε να υπολογίσουμε το ηλεκτρικό δυναμικό από την αρχική σχέση: B E A V d s Αν η κατανομή φορτίου χαρακτηρίζεται από επαρκή βαθμό συμμετρίας, τότε πρώτα υπολογίζουμε το ηλεκτρικό πεδίο με τον νόμο του Gauss και έπειτα τη διαφορά δυναμικού μεταξύ δύο τυχαίων σημείων. Επιλέγουμε V = 0 σε ένα κατάλληλο σημείο. Μοντελοποίηση Φανταστείτε τα επιμέρους φορτία ή την κατανομή φορτίου. Φανταστείτε τον τύπο του δυναμικού που δημιουργούν. Λάβετε υπόψη τη συμμετρία (αν υπάρχει) στη διάταξη των φορτίων. Κατηγοριοποίηση Πρόκειται για ένα σύνολο από μεμονωμένα φορτία ή για μια συνεχή κατανομή φορτίων; Η απάντηση σε αυτή την ερώτηση θα καθορίσει τη διαδικασία που θα ακολουθήσετε στο βήμα της Ανάλυσης. Μεθοδολογία επίλυσης προβλημάτων (2) Μεθοδολογία επίλυσης προβλημάτων (3) Ανάλυση Γενικά Το ηλεκτρικό δυναμικό είναι βαθμωτό μέγεθος, άρα δεν χρειάζεται να βρείτε συνιστώσες. Χρησιμοποιήστε την αρχή της υπέρθεσης και αθροίστε αλγεβρικά τα δυναμικά των επιμέρους φορτίων. Προσοχή στα πρόσημα. Μόνο οι μεταβολές του ηλεκτρικού δυναμικού έχουν σημασία. Θεωρήστε ότι V = 0 σε ένα σημείο που βρίσκεται πολύ μακριά από τα φορτία. Αν η κατανομή εκτείνεται ως το άπειρο, επιλέξτε κάποιο άλλο σημείο ως σημείο αναφοράς. Ανάλυση (συνέχεια) Αν δίνεται μια ομάδα μεμονωμένων φορτίων: Χρησιμοποιήστε την αρχή της υπέρθεσης και αθροίστε αλγεβρικά τα δυναμικά των επιμέρους φορτίων. Αν δίνεται μια συνεχής κατανομή φορτίου: Υπολογίστε το συνολικό δυναμικό σε κάποιο σημείο χρησιμοποιώντας ολοκληρώματα. Θεωρήστε κάθε στοιχειώδες τμήμα της κατανομής φορτίου ως σημειακό φορτίο. Αν δίνεται το ηλεκτρικό πεδίο: Ξεκινήστε από τον ορισμό του ηλεκτρικού δυναμικού. Αν χρειαστεί, υπολογίστε το πεδίο χρησιμοποιώντας τον νόμο του Gauss (ή κάποιον άλλο τρόπο). Μεθοδολογία επίλυσης προβλημάτων (4) Ηλεκτρικό δυναμικό ομοιόμορφα φορτισμένου δακτυλίου Ολοκλήρωση Βεβαιωθείτε ότι η σχέση του ηλεκτρικού δυναμικού που βρήκατε συμφωνεί με τη νοητική σας αναπαράσταση. Η τελική σχέση αντικατοπτρίζει την όποια συμμετρία υπάρχει; Μεταβάλλετε νοητικά παραμέτρους για να εξακριβώσετε αν το μαθηματικό αποτέλεσμα αλλάζει με εύλογο τρόπο. Το σημείο Σ βρίσκεται στον κάθετο κεντρικό άξονα του ομοιόμορφα φορτισμένου δακτυλίου. Με βάση τη συμμετρία της περίπτωσης, όλα τα φορτία του δακτυλίου ισαπέχουν από το σημείο Σ. Ο δακτύλιος έχει ακτίνα α και συνολικό φορτίο Q. Το δυναμικό και το πεδίο δίνονται από τις σχέσεις: dq kq e V ke r 2 2 α x Ex kx e Q 3/2 2 α x 2 6
8 Ηλεκτρικό δυναμικό ομοιόμορφα φορτισμένου δίσκου Ο δακτύλιος έχει ακτίνα R και επιφανειακή πυκνότητα φορτίου σ. Το σημείο Σ βρίσκεται στον κάθετο κεντρικό άξονα του ομοιόμορφα φορτισμένου δακτυλίου. Επειδή το σημείο Σ βρίσκεται επάνω στον κεντρικό άξονα του δίσκου, συνάγεται λόγω συμμετρίας ότι όλα τα σημεία κάθε δακτυλίου ισαπέχουν από το Σ. Το δυναμικό και το πεδίο δίνονται από τις σχέσεις: V 2πkeσ R x x x Ex 2πkeσ R x 1/2 Ηλεκτρικό δυναμικό πεπερασμένης φορτισμένης ευθείας Μια ράβδος μήκους l έχει συνολικό φορτίο Q και γραμμική πυκνότητα φορτίου λ. Δεν υπάρχει συμμετρία, αλλά η γεωμετρία του προβλήματος είναι απλή. 2 2 kq e α V ln α Ηλεκτρικό δυναμικό φορτισμένου αγωγού Θεωρούμε δύο σημεία επί της επιφάνειας του φορτισμένου αγωγού, όπως φαίνεται στην εικόνα. Το πεδίο E είναι πάντα κάθετο στη μετατόπιση ds. Άρα, Eds 0 Επομένως, η διαφορά δυναμικού μεταξύ των σημείων A και B είναι επίσης μηδενική. Ηλεκτρικό δυναμικό φορτισμένου αγωγού (συνέχεια) Σε κάθε σημείο της επιφάνειας ενός φορτισμένου αγωγού, ο οποίος βρίσκεται σε ισορροπία, V = σταθερό. ΔV = 0 μεταξύ οποιουδήποτε ζεύγους σημείων της επιφάνειας. Η επιφάνεια κάθε φορτισμένου αγωγού που βρίσκεται σε ηλεκτροστατική ισορροπία είναι ισοδυναμική. Κάθε σημείο της επιφάνειας ενός φορτισμένου αγωγού που είναι σε ισορροπία έχει το ίδιο ηλεκτρικό δυναμικό. Επειδή στο εσωτερικό του αγωγού το ηλεκτρικό πεδίο είναι ίσο με μηδέν, συμπεραίνουμε ότι το ηλεκτρικό δυναμικό παντού στο εσωτερικό του αγωγού είναι σταθερό και ίσο με την τιμή του στην επιφάνεια. Ενότητα Η3.6 Ενότητα Η3.6 Σώματα με ακανόνιστο σχήμα Κοιλότητα στο εσωτερικό ενός αγωγού Όπου η ακτίνα καμπυλότητας είναι μικρή, η πυκνότητα φορτίου είναι μεγάλη. Και όπου η ακτίνα καμπυλότητας είναι μεγάλη, η πυκνότητα φορτίου είναι μικρή. Το ηλεκτρικό πεδίο είναι ισχυρό κοντά σε κυρτά σημεία με μικρή ακτίνα καμπυλότητας και φτάνει σε πολύ μεγάλες τιμές σε αιχμηρά σημεία. Έστω ότι ένας αγωγός περιέχει μια κοιλότητα ακανόνιστου σχήματος. Υποθέτουμε ότι μέσα στην κοιλότητα δεν υπάρχουν φορτία. Το ηλεκτρικό πεδίο στο εσωτερικό του αγωγού πρέπει να είναι ίσο με μηδέν. Ενότητα Η3.6 Ενότητα Η3.6 7
9 Κοιλότητα στο εσωτερικό ενός αγωγού (συνέχεια) Το ηλεκτρικό πεδίο στο εσωτερικό του αγωγού δεν εξαρτάται από την κατανομή φορτίου στην εξωτερική επιφάνεια του αγωγού. Για κάθε διαδρομή μεταξύ των σημείων A και B, B VB VA E d s 0 A Σε μια κοιλότητα η οποία περιβάλλεται από αγώγιμα τοιχώματα δεν υπάρχει πεδίο, υπό την προϋπόθεση ότι στο εσωτερικό της δεν υπάρχει φορτίο. Στεμματόμορφη εκκένωση Αν το ηλεκτρικό πεδίο στην περιοχή κοντά στον αγωγό είναι αρκετά ισχυρό, τα ηλεκτρόνια που προκύπτουν από τον τυχαίο ιοντισμό μορίων του αέρα κοντά στον αγωγό απομακρύνονται επιταχυνόμενα από τα μόρια από τα οποία προήλθαν. Αυτά τα ηλεκτρόνια μπορούν να ιοντίσουν και άλλα μόρια που βρίσκονται κοντά στον αγωγό. Έτσι δημιουργούνται κι άλλα ελεύθερα ηλεκτρόνια. Η λάμψη που παρατηρείται η στεμματόμορφη εκκένωση οφείλεται στην επανένωση αυτών των ελεύθερων ηλεκτρονίων με τα ιοντισμένα μόρια του αέρα. Η πιθανότητα να συμβεί ιοντισμός και στεμματόμορφη εκκένωση είναι μεγάλη σε αιχμηρά σημεία ή στις ακμές του αγωγού. Ενότητα Η3.6 Το πείραμα των σταγονιδίων λαδιού του Millikan Το πείραμα των σταγονιδίων λαδιού του Millikan Πειραματική διάταξη (1) Ο Robert Millikan μέτρησε το e, την τιμή του στοιχειώδους φορτίου του ηλεκτρονίου. Επίσης απέδειξε ότι το φορτίο αυτό είναι κβαντισμένο. Τα σταγονίδια λαδιού διέρχονται από μια μικρή οπή και φωτίζονται από μια φωτεινή πηγή. Ενότητα Η3.7 Ενότητα Η3.7 Το πείραμα των σταγονιδίων λαδιού του Millikan (2) Αν μεταξύ των πλακών δεν υπάρχει ηλεκτρικό πεδίο, τότε στο σταγονίδιο ασκούνται η βαρυτική δύναμη και η δύναμη τριβής. Το σταγονίδιο φτάνει στην οριακή του ταχύτητα όταν F mg D Το πείραμα των σταγονιδίων λαδιού του Millikan (3) Μεταξύ των πλακών δημιουργείται ένα ηλεκτρικό πεδίο. Η άνω πλάκα έχει υψηλότερο δυναμικό από την κάτω. Το σταγονίδιο φτάνει σε μια νέα οριακή ταχύτητα, όταν η ηλεκτρική δύναμη γίνει ίση με το άθροισμα της δύναμης αντίστασης του αέρα και της βαρυτικής δύναμης. Ενότητα Η3.7 Ενότητα Η3.7 8
10 Το πείραμα των σταγονιδίων λαδιού του Millikan (4) Ενεργοποιώντας και απενεργοποιώντας το ηλεκτρικό πεδίο μπορούμε να παρακολουθούμε το σταγονίδιο να ανυψώνεται και να πέφτει πολλές φορές. Μετά από πολλά πειράματα, ο Millikan προσδιόρισε τα εξής: q = ne όπου n = 0, 1, 2, 3, e = 1.60 x C Αυτό αποτελεί αδιάσειστη απόδειξη ότι το φορτίο είναι κβαντισμένο. Η ηλεκτροστατική γεννήτρια Van de Graaff Ένα ηλεκτρόδιο υψηλής τάσης τροφοδοτείται συνεχώς με φορτίο μέσω ενός κινούμενου ιμάντα από μονωτικό υλικό. Το ηλεκτρόδιο υψηλής τάσης είναι ένας κοίλος μεταλλικός θολωτός αγωγός, ο οποίος είναι τοποθετημένος επάνω σε μια μονωτική στήλη. Με τη συνεχή κίνηση του ιμάντα αναπτύσσεται υψηλή διαφορά δυναμικού μεταξύ της σφαίρας και της γης. Τα πρωτόνια που επιταχύνονται μέσα από τόσο μεγάλες διαφορές δυναμικού, προσλαμβάνουν επαρκή ενέργεια ώστε να μπορούν να προκαλέσουν πυρηνικές αντιδράσεις. Ενότητα Η3.7 Ενότητα Η3.8 Ο ηλεκτροστατικός διαχωριστής Ο ηλεκτροστατικός διαχωριστής αποτελεί μια σημαντική εφαρμογή της ηλεκτρικής εκκένωσης στα αέρια. Αφαιρεί τα σωματίδια ύλης από τα καυσαέρια. Ο αέρας που πρέπει να καθαριστεί εισέρχεται στον αεραγωγό και κινείται προς το σύρμα. Καθώς τα ηλεκτρόνια και τα αρνητικά ιόντα που δημιουργούνται από την εκκένωση επιταχύνονται εξαιτίας του ηλεκτρικού πεδίου προς το τοίχωμα του αγωγού, συγκρούονται και προσκολλώνται στα σωματίδια σκόνης του αέρα, προσδίδοντας τους φορτίο. Επειδή τα περισσότερα από τα φορτισμένα σωματίδια σκόνης είναι αρνητικά φορτισμένα, έλκονται λόγω του ηλεκτρικού πεδίου προς τα τοιχώματα του αεραγωγού. Ενότητα Η3.8 9
11 Τέλος Ηλεκτρικό δυναμικό
12 Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στo πλαίσιo του εκπαιδευτικού έργου του διδάσκοντα. Το έργο «Ανοικτά Ακαδημαϊκά Μαθήματα στο Πανεπιστήμιο Αθηνών» έχει χρηματοδοτήσει μόνο την αναδιαμόρφωση του εκπαιδευτικού υλικού. Το έργο υλοποιείται στο πλαίσιο του Επιχειρησιακού Προγράμματος «Εκπαίδευση και Δια Βίου Μάθηση» και συγχρηματοδοτείται από την Ευρωπαϊκή Ένωση (Ευρωπαϊκό Κοινωνικό Ταμείο) και από εθνικούς πόρους. Ηλεκτρομαγνητισμός 3
13 Σημειώματα
14 Σημείωμα Ιστορικού Εκδόσεων Έργου Το παρόν έργο αποτελεί την έκδοση 1.0. Ηλεκτρομαγνητισμός 5
15 Σημείωμα Αναφοράς Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Βαρουτάς Δημήτρης. «Ηλεκρομαγνητισμός - Οπτική - Σύγχρονη Φυσική. Ηλεκτρομαγνητισμός». Έκδοση: 1.0. Αθήνα Διαθέσιμο από τη δικτυακή διεύθυνση: Ηλεκτρομαγνητισμός 6
16 Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων». [1] Ως Μη Εμπορική ορίζεται η χρήση: που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί. Ηλεκτρομαγνητισμός 7
17 Διατήρηση Σημειωμάτων Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει: το Σημείωμα Αναφοράς το Σημείωμα Αδειοδότησης τη δήλωση Διατήρησης Σημειωμάτων το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει) μαζί με τους συνοδευόμενους υπερσυνδέσμους. Ηλεκτρομαγνητισμός 8
Ηλεκτρομαγνητισμός. Ηλεκτρικό δυναμικό. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Κεφάλαιο Η3. Ηλεκτρικό δυναµικό
 Κεφάλαιο Η3 Ηλεκτρικό δυναµικό Ηλεκτρικό δυναµικό Σε προηγούµενα κεφάλαια συνδέσαµε τη µελέτη του ηλεκτροµαγνητισµού µε τις προγενέστερες γνώσεις µας σχετικά µε τις δυνάµεις. Σε αυτό το κεφάλαιο, θα συνδέσουµε
Κεφάλαιο Η3 Ηλεκτρικό δυναµικό Ηλεκτρικό δυναµικό Σε προηγούµενα κεφάλαια συνδέσαµε τη µελέτη του ηλεκτροµαγνητισµού µε τις προγενέστερες γνώσεις µας σχετικά µε τις δυνάµεις. Σε αυτό το κεφάλαιο, θα συνδέσουµε
Ηλεκτρικό δυναμικό. Κεφάλαιο Η3
 Ηλεκτρικό δυναμικό Κεφάλαιο Η3 Ηλεκτρικό δυναμικό Σε προηγούμενα κεφάλαια συνδέσαμε τη μελέτη του ηλεκτρομαγνητισμού με τις προγενέστερες γνώσεις μας σχετικά με τις δυνάμεις. Σε αυτό το κεφάλαιο, θα συνδέσουμε
Ηλεκτρικό δυναμικό Κεφάλαιο Η3 Ηλεκτρικό δυναμικό Σε προηγούμενα κεφάλαια συνδέσαμε τη μελέτη του ηλεκτρομαγνητισμού με τις προγενέστερες γνώσεις μας σχετικά με τις δυνάμεις. Σε αυτό το κεφάλαιο, θα συνδέσουμε
Ηλεκτρική δυναμική ενέργεια
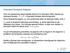 Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική.
 Ηλεκτρική δυναµική ενέργεια Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική. e o Έστω δοκιµαστικό φορτίο,
Ηλεκτρική δυναµική ενέργεια Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική. e o Έστω δοκιµαστικό φορτίο,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ. Ενότητα 3: Ηλεκτρικό δυναμικό. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 3: Ηλεκτρικό δυναμικό Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 3: Ηλεκτρικό δυναμικό Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών 7/15/2014 Ο νόμος του Gauss Νόμος Gauss Ο νόμος
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών 7/15/2014 Ο νόμος του Gauss Νόμος Gauss Ο νόμος
ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ
 ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ Ημερομηνία:. ΤΜΗΜΑ:.. ΟΜΑΔΑ:. Ονομ/νυμο: Α.Μ. Συνεργάτες Ονομ/νυμο: Α.Μ. Ονομ/νυμο: Α.Μ. ΠΕΡΙΛΗΨΗ ΤΗΣ ΑΣΚΗΣΗΣ (καθένας με δικά του λόγια, σε όλες τις γραμμές) ΒΑΘΜΟΣ#1: ΥΠΟΓΡΑΦΗ:
ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ Ημερομηνία:. ΤΜΗΜΑ:.. ΟΜΑΔΑ:. Ονομ/νυμο: Α.Μ. Συνεργάτες Ονομ/νυμο: Α.Μ. Ονομ/νυμο: Α.Μ. ΠΕΡΙΛΗΨΗ ΤΗΣ ΑΣΚΗΣΗΣ (καθένας με δικά του λόγια, σε όλες τις γραμμές) ΒΑΘΜΟΣ#1: ΥΠΟΓΡΑΦΗ:
ΦΥΣΙΚΗ ΙΙΙ. Ενότητα: Ηλεκτροστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ
 ΦΥΣΙΚΗ ΙΙΙ Ενότητα: Ηλεκτροστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ Σελίδα 2 ΑΣΚΗΣΕΙΣ... 4 Σελίδα 3 ΑΣΚΗΣΕΙΣ Ηλεκτροστατική 1. Στις κορυφές κανονικού n-πλεύρου τοποθετούνται ίδια φορτία q. Να δειχθεί ότι η
ΦΥΣΙΚΗ ΙΙΙ Ενότητα: Ηλεκτροστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ Σελίδα 2 ΑΣΚΗΣΕΙΣ... 4 Σελίδα 3 ΑΣΚΗΣΕΙΣ Ηλεκτροστατική 1. Στις κορυφές κανονικού n-πλεύρου τοποθετούνται ίδια φορτία q. Να δειχθεί ότι η
Κλασική Hλεκτροδυναμική
 Κλασική Hλεκτροδυναμική Ενότητα 1: Εισαγωγή Ανδρέας Τερζής Σχολή Θετικών επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι μια σύντομη επανάληψη στις βασικές έννοιες της ηλεκτροστατικής.
Κλασική Hλεκτροδυναμική Ενότητα 1: Εισαγωγή Ανδρέας Τερζής Σχολή Θετικών επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι μια σύντομη επανάληψη στις βασικές έννοιες της ηλεκτροστατικής.
Γενική Φυσική. Ενότητα 5: Έργο, ενέργεια. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών
 Γενική Φυσική Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Έργο - Ενέργεια Βασική έννοια. Μηχανική, Ηλεκτρομαγνητική, Χημική, Θερμική, Πυρηνική, κ.α. Δυνατότητα μετατροπής της μίας μορφής
Γενική Φυσική Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Έργο - Ενέργεια Βασική έννοια. Μηχανική, Ηλεκτρομαγνητική, Χημική, Θερμική, Πυρηνική, κ.α. Δυνατότητα μετατροπής της μίας μορφής
Γενική Φυσική Ενότητα: Δυναμική Άκαμπτου Σώματος
 Γενική Φυσική Ενότητα: Δυναμική Άκαμπτου Σώματος Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ερωτήσεις Δυναμικής Άκαμπτου Σώματος... 4 1.1 Ερώτηση 1... 4 1.2 Ερώτηση 2... 4 1.3 Ερώτηση
Γενική Φυσική Ενότητα: Δυναμική Άκαμπτου Σώματος Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ερωτήσεις Δυναμικής Άκαμπτου Σώματος... 4 1.1 Ερώτηση 1... 4 1.2 Ερώτηση 2... 4 1.3 Ερώτηση
Γενική Φυσική Ενότητα: Ταλαντώσεις
 Γενική Φυσική Ενότητα: Ταλαντώσεις Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ερωτήσεις Ταλαντώσεων... 4 1.1 Ερώτηση 1... 4 2. Ασκήσεις Ταλαντώσεων... 4 2.1 Άσκηση 1... 4 2.2 Άσκηση
Γενική Φυσική Ενότητα: Ταλαντώσεις Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ερωτήσεις Ταλαντώσεων... 4 1.1 Ερώτηση 1... 4 2. Ασκήσεις Ταλαντώσεων... 4 2.1 Άσκηση 1... 4 2.2 Άσκηση
Φυσική ΙΙΙ. Ενότητα 4: Ηλεκτρικά Κυκλώματα. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Γ. Βούλγαρης 2 Ταχύτητα ολίσθησης σε σύρμα από χαλκό. Διάμετρος δ=1,6 mm Ρεύμα 10 Α Πυκνότητα
Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Γ. Βούλγαρης 2 Ταχύτητα ολίσθησης σε σύρμα από χαλκό. Διάμετρος δ=1,6 mm Ρεύμα 10 Α Πυκνότητα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Νόμος Ampere Το ολοκλήρωμα του μαγνητικού
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Νόμος Ampere Το ολοκλήρωμα του μαγνητικού
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Γενική Φυσική Ενότητα: Εισαγωγή στην Ειδική Θεωρία της Σχετικότητας
 Γενική Φυσική Ενότητα: Εισαγωγή στην Ειδική Θεωρία της Σχετικότητας Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ασκήσεις στην Εισαγωγή στην Ειδική Θεωρία της Σχετικότητας... 4 1.1
Γενική Φυσική Ενότητα: Εισαγωγή στην Ειδική Θεωρία της Σχετικότητας Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ασκήσεις στην Εισαγωγή στην Ειδική Θεωρία της Σχετικότητας... 4 1.1
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Χωρικές σχέσεις και Γεωμετρικές Έννοιες στην Προσχολική Εκπαίδευση
 Χωρικές σχέσεις και Γεωμετρικές Έννοιες στην Προσχολική Εκπαίδευση Ενότητα 7: Κανονικότητες, συμμετρίες και μετασχηματισμοί στο χώρο Δημήτρης Χασάπης Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία
Χωρικές σχέσεις και Γεωμετρικές Έννοιες στην Προσχολική Εκπαίδευση Ενότητα 7: Κανονικότητες, συμμετρίες και μετασχηματισμοί στο χώρο Δημήτρης Χασάπης Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ. Ενότητα 2: Ο νόμος του Gauss. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 2: Ο νόμος του Gauss Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 2: Ο νόμος του Gauss Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23)
 ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
Γενική Φυσική Ενότητα: Κινητική
 Γενική Φυσική Ενότητα: Κινητική Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ασκήσεις κινητικής... 4 1.1 Άσκηση 1... 4 1.2 Άσκηση 2... 4 1.3 Άσκηση 3... 4 1.4 Άσκηση 4... 4 1.5 Άσκηση
Γενική Φυσική Ενότητα: Κινητική Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ασκήσεις κινητικής... 4 1.1 Άσκηση 1... 4 1.2 Άσκηση 2... 4 1.3 Άσκηση 3... 4 1.4 Άσκηση 4... 4 1.5 Άσκηση
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική ΙΙΙ. Ενότητα 3: Επαγωγή. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 3: Επαγωγή Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Χρονικά μεταβαλλόμενο πεδίο. Κυκλικό πηνίο με 100 σπείρες και αντίσταση =5 Ω, τοποθετείται γύρω από σωληνοειδές όπως
Φυσική ΙΙΙ Ενότητα 3: Επαγωγή Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Χρονικά μεταβαλλόμενο πεδίο. Κυκλικό πηνίο με 100 σπείρες και αντίσταση =5 Ω, τοποθετείται γύρω από σωληνοειδές όπως
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής
 Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 11: Μεγιστοποίηση κέρδους Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Οικονομικό κέρδος Μια
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 11: Μεγιστοποίηση κέρδους Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Οικονομικό κέρδος Μια
Γενική Φυσική. Ενότητα 1: Κινητική. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών
 Γενική Φυσική Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Τι είναι το διαφορικό (1 από 2) Η μεταβολή μίας συνάρτησης f(x), όταν το x αυξάνεται κατά Δx γράφεται : Δy AΔx B( Δx ) 2 Αν οι
Γενική Φυσική Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Τι είναι το διαφορικό (1 από 2) Η μεταβολή μίας συνάρτησης f(x), όταν το x αυξάνεται κατά Δx γράφεται : Δy AΔx B( Δx ) 2 Αν οι
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Νόμος Faraday Η μεταβαλλόμενη μαγνητική
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Νόμος Faraday Η μεταβαλλόμενη μαγνητική
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα
 Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Ασκήσεις 1 Ανδριανός Ε. Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής Σελίδα 2 1. Σκοποί ενότητας... 5 2.
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Ασκήσεις 1 Ανδριανός Ε. Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής Σελίδα 2 1. Σκοποί ενότητας... 5 2.
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 13 Ηλεκτρικό (Βαθμωτό) δυναμικό ΦΥΣ102 1 Διαφορά δυναμικού Η Ηλεκτροστατική Δύναμη
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 13 Ηλεκτρικό (Βαθμωτό) δυναμικό ΦΥΣ102 1 Διαφορά δυναμικού Η Ηλεκτροστατική Δύναμη
Φυσική ΙΙΙ. Ενότητα 4: Ηλεκτρικά Κυκλώματα. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ηλεκτρεγερτική δύναμη. emf Ιστορική ονομασία που δόθηκε από τον Faraday. (Η αιτία που τείνει να δημιουργήσει
Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ηλεκτρεγερτική δύναμη. emf Ιστορική ονομασία που δόθηκε από τον Faraday. (Η αιτία που τείνει να δημιουργήσει
Ορισμός κανονικής τ.μ.
 Πιθανότητες και Στατιστική Ενότητα 4: Τυχαίες τυχαίες μεταβλητές Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Αθήνα 2015 Ορισμός κανονικής τ.μ. Ορισμός κανονικής τ.μ. Μια συνεχής τ.μ.
Πιθανότητες και Στατιστική Ενότητα 4: Τυχαίες τυχαίες μεταβλητές Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Αθήνα 2015 Ορισμός κανονικής τ.μ. Ορισμός κανονικής τ.μ. Μια συνεχής τ.μ.
ΦΥΣΙΚΗ. Ενότητα 2: ΔΙΑΝΥΣΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΦΥΣΙΚΗ Ενότητα 2: ΔΙΑΝΥΣΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΦΥΣΙΚΗ Ενότητα 2: ΔΙΑΝΥΣΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Φυσική IΙ. Ενότητα 3: Ο Νόμος του Gauss. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική IΙ Ενότητα 3: Ο Νόμος του Gauss Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Ορισμός και ερμηνεία των δυναμικών γραμμών Παραδείγματα δυναμικών γραμμών σημειακού φορτίου,
Φυσική IΙ Ενότητα 3: Ο Νόμος του Gauss Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Ορισμός και ερμηνεία των δυναμικών γραμμών Παραδείγματα δυναμικών γραμμών σημειακού φορτίου,
Φυσική ΙΙΙ. Ενότητα 4: Ηλεκτρικά Κυκλώματα. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ηλεκτρικό ρεύμα Ι 2 Ηλεκτρικό ρεύμα ΙΙ μe v D 3 Φορά ρεύματος Συμβατική φορά ρεύματος, η φορά της κίνησης
Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ηλεκτρικό ρεύμα Ι 2 Ηλεκτρικό ρεύμα ΙΙ μe v D 3 Φορά ρεύματος Συμβατική φορά ρεύματος, η φορά της κίνησης
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 14: Ολοκλήρωση πολυπολικής ανάπτυξης και διηλεκτρικά Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει την πολυπολική
Κλασική Ηλεκτροδυναμική Ενότητα 14: Ολοκλήρωση πολυπολικής ανάπτυξης και διηλεκτρικά Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει την πολυπολική
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα
 Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Ασκήσεις 11 Ανδριανός Ε. Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής Σελίδα 2 1. Σκοποί ενότητας... 5
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Ασκήσεις 11 Ανδριανός Ε. Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής Σελίδα 2 1. Σκοποί ενότητας... 5
Φυσική ΙΙΙ. Ενότητα 4: Ηλεκτρικά Κυκλώματα. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Ηλεκτρικά Κυκλώματα Γ. Βούλγαρης 2 Ασκήσεις κατανομές φορτίου 1) Ένα γραμμικό φορτίο με
Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Ηλεκτρικά Κυκλώματα Γ. Βούλγαρης 2 Ασκήσεις κατανομές φορτίου 1) Ένα γραμμικό φορτίο με
Κεφάλαιο Η2. Ο νόµος του Gauss
 Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Γενική Φυσική. Ενότητα 4: Εισαγωγή στην ειδική θεωρία της σχετικότητας. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών
 Γενική Φυσική Ενότητα 4: Εισαγωγή στην ειδική θεωρία της σχετικότητας Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Εισαγωγή στη Eιδική Θεωρία της Σχετικότητας - Διδακτικοί στόχοι Οι Νόμοι
Γενική Φυσική Ενότητα 4: Εισαγωγή στην ειδική θεωρία της σχετικότητας Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Εισαγωγή στη Eιδική Θεωρία της Σχετικότητας - Διδακτικοί στόχοι Οι Νόμοι
Κλασική Hλεκτροδυναμική
 Κλασική Hλεκτροδυναμική Ενότητα 3: Η συνάρτηση Green σε επίπεδη γεωμετρία και η μέθοδος των ειδώλων σε σφαιρική Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας
Κλασική Hλεκτροδυναμική Ενότητα 3: Η συνάρτηση Green σε επίπεδη γεωμετρία και η μέθοδος των ειδώλων σε σφαιρική Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 9: Ολοκληρώματα (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 9: Ολοκληρώματα (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων
 Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα : Περιγραφή Δυναμικών Συστημάτων Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα : Περιγραφή Δυναμικών Συστημάτων Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική. Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΟΠΤΙΚΗ (Ηλεκτροµαγνητισµός-Οπτική) Γεωµετρική Οπτική (Μάθηµα
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΟΠΤΙΚΗ (Ηλεκτροµαγνητισµός-Οπτική) Γεωµετρική Οπτική (Μάθηµα
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Πίνακες Νερού σε κατάσταση Κορεσμού. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού. Ιωάννης Γκιάλας 14 Μαρτίου 2014
 Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
ΦΥΣΙΚΗ ΙΙΙ. Ενότητα: Μαγνητοστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ
 ΦΥΣΙΚΗ ΙΙΙ Ενότητα: Μαγνητοστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ Σελίδα 2 ΑΣΚΗΣΕΙΣ... 4 Σελίδα 3 ΑΣΚΗΣΕΙΣ Μαγνητοστατική. Σωματίδιο μάζας m φορτίου Q βρίσκεται αρχικά ακίνητο μέσα σε ομογενές μαγνητικό
ΦΥΣΙΚΗ ΙΙΙ Ενότητα: Μαγνητοστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ Σελίδα 2 ΑΣΚΗΣΕΙΣ... 4 Σελίδα 3 ΑΣΚΗΣΕΙΣ Μαγνητοστατική. Σωματίδιο μάζας m φορτίου Q βρίσκεται αρχικά ακίνητο μέσα σε ομογενές μαγνητικό
Διοικητική Λογιστική
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 10: Προσφορά και κόστος Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Διοικητική Λογιστική Ενότητα 10: Προσφορά και κόστος Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά
Γενική Φυσική Ενότητα: Ορμή, Κέντρο Μάζας
 Γενική Φυσική Ενότητα: Ορμή, Κέντρο Μάζας Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ερωτήσεις Ορμής... 4 1.1 Ερώτηση 1... 4 1.2 Ερώτηση 2... 4 1.3 Ερώτηση 3... 4 2. Ασκήσεις Ορμής...
Γενική Φυσική Ενότητα: Ορμή, Κέντρο Μάζας Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ερωτήσεις Ορμής... 4 1.1 Ερώτηση 1... 4 1.2 Ερώτηση 2... 4 1.3 Ερώτηση 3... 4 2. Ασκήσεις Ορμής...
Βέλτιστος Έλεγχος Συστημάτων
 Βέλτιστος Έλεγχος Συστημάτων Ενότητα 7: Βέλτιστος έλεγχος συστημάτων διακριτού χρόνου Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
Βέλτιστος Έλεγχος Συστημάτων Ενότητα 7: Βέλτιστος έλεγχος συστημάτων διακριτού χρόνου Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 12: Συνάρτηση Green από ιδιοσυναρτήσεις Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να μελετήσει την συνάρτηση Green από
Κλασική Ηλεκτροδυναμική Ενότητα 12: Συνάρτηση Green από ιδιοσυναρτήσεις Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να μελετήσει την συνάρτηση Green από
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
Λογισμός 4 Ενότητα 13
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Το επικαμπύλιο ολοκλήρωμα. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Το επικαμπύλιο ολοκλήρωμα. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 8: Εφαρμογές παραγώγων Μελέτη και βελτιστοποίηση συναρτήσεων μιας μεταβλητής (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 8: Εφαρμογές παραγώγων Μελέτη και βελτιστοποίηση συναρτήσεων μιας μεταβλητής (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός
 Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.08.1: Μήκος Τόξου Καμπύλης Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.08.1: Μήκος Τόξου Καμπύλης Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Κβαντική Επεξεργασία Πληροφορίας
 Κβαντική Επεξεργασία Πληροφορίας Ενότητα 12: Ιδιοτιμές και Ιδιοδιανύσματα Σγάρμπας Κυριάκος Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Ιδιοτιμές και Ιδιοδιανύσματα
Κβαντική Επεξεργασία Πληροφορίας Ενότητα 12: Ιδιοτιμές και Ιδιοδιανύσματα Σγάρμπας Κυριάκος Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Ιδιοτιμές και Ιδιοδιανύσματα
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
Σχεδίαση Ολοκληρωμένων Κυκλωμάτων Ασκήσεις Μικροηλεκτρονικής
 Σχεδίαση Ολοκληρωμένων Κυκλωμάτων Ασκήσεις Μικροηλεκτρονικής Αραπογιάννη Αγγελική Τμήμα Πληροφορικής και Τηλεπικοινωνιών. Σελίδα 2 1. Εισαγωγή... 4 2. Ανάπτυξη Κρυστάλλων... 4 3. Οξείδωση του πυριτίου...
Σχεδίαση Ολοκληρωμένων Κυκλωμάτων Ασκήσεις Μικροηλεκτρονικής Αραπογιάννη Αγγελική Τμήμα Πληροφορικής και Τηλεπικοινωνιών. Σελίδα 2 1. Εισαγωγή... 4 2. Ανάπτυξη Κρυστάλλων... 4 3. Οξείδωση του πυριτίου...
Γενική Φυσική. Ενότητα 8: Ταλαντώσεις. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών
 Γενική Φυσική Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Ταλάντωση με απόσβεση Η δύναμη τριβής δίνεται από τη σχέση : -kυ. ΣF x =-kx-υ=a x kx dx dt d x dt x Ae d x dt dx dt t k x 0 cos
Γενική Φυσική Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Ταλάντωση με απόσβεση Η δύναμη τριβής δίνεται από τη σχέση : -kυ. ΣF x =-kx-υ=a x kx dx dt d x dt x Ae d x dt dx dt t k x 0 cos
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων
 Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα 6: Δυναμική μηχανής συνεχούς ρεύματος Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα 6: Δυναμική μηχανής συνεχούς ρεύματος Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 11: Διανύσματα (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων &
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 11: Διανύσματα (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων &
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας. Βιοστατιστική (Ε) Ενότητα 3: Έλεγχοι στατιστικών υποθέσεων
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 3: Έλεγχοι στατιστικών υποθέσεων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 3: Έλεγχοι στατιστικών υποθέσεων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ηλεκτρισμός και μαγνητισμός Ηλεκτρικά Πεδία Οι
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ηλεκτρισμός και μαγνητισμός Ηλεκτρικά Πεδία Οι
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας. Βιοστατιστική (Ε) Ενότητα 1: Καταχώρηση δεδομένων
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 1: Καταχώρηση δεδομένων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 1: Καταχώρηση δεδομένων Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος διατίθεται
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων
 Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα 4: Παραδείγματα Περιγραφής Δυναμικών Συστημάτων II Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα 4: Παραδείγματα Περιγραφής Δυναμικών Συστημάτων II Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Φυσική (Ε) Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 4: Προσδιορισμός της σταθεράς ενός ελατηρίου. Αικατερίνη Σκουρολιάκου. Τμήμα Ενεργειακής Τεχνολογίας
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική (Ε) Ενότητα 4: Προσδιορισμός της σταθεράς ενός ελατηρίου Αικατερίνη Σκουρολιάκου Τμήμα Ενεργειακής Τεχνολογίας Το περιεχόμενο του
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική (Ε) Ενότητα 4: Προσδιορισμός της σταθεράς ενός ελατηρίου Αικατερίνη Σκουρολιάκου Τμήμα Ενεργειακής Τεχνολογίας Το περιεχόμενο του
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής
 Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 2: Εισοδηματικοί και άλλοι περιορισμοί στην επιλογή Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 2: Εισοδηματικοί και άλλοι περιορισμοί στην επιλογή Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής
 Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 13: Καμπύλες κόστους Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Μορφές καμπυλών κόστους Καμπύλη
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 13: Καμπύλες κόστους Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Μορφές καμπυλών κόστους Καμπύλη
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας. Βιοστατιστική (Ε) Ενότητα 2: Περιγραφική στατιστική
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 2: Περιγραφική στατιστική Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Βιοστατιστική (Ε) Ενότητα 2: Περιγραφική στατιστική Δρ.Ευσταθία Παπαγεωργίου, Αναπληρώτρια Καθηγήτρια Τμήμα Ιατρικών Εργαστηρίων Το περιεχόμενο του μαθήματος
Φυσική ΙΙΙ. Ενότητα 4: Ηλεκτρικά Κυκλώματα. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Ασκήσεις κυκλωμάτων συνεχούς ρεύματος. Κανόνες Kirchhoff. Γ. Βούλγαρης 2 Ο Νόμος των Ρευμάτων
Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Ασκήσεις κυκλωμάτων συνεχούς ρεύματος. Κανόνες Kirchhoff. Γ. Βούλγαρης 2 Ο Νόμος των Ρευμάτων
Υπολογιστική άλγεβρα Ενότητα 10: Βάσεις Groebner ενός ιδεώδους ΙΙΙ
 Υπολογιστική άλγεβρα Ενότητα 10: Βάσεις Groebner ενός ιδεώδους ΙΙΙ Ράπτης Ευάγγελος Σχολή Θετικών επιστημών Τμήμα Μαθηματικών Κεφάλαιο 10 Βάσεις Groebner ενός ιδεώδους 10.1 Τρίτο μέρος Επαναλαμβάνουμε
Υπολογιστική άλγεβρα Ενότητα 10: Βάσεις Groebner ενός ιδεώδους ΙΙΙ Ράπτης Ευάγγελος Σχολή Θετικών επιστημών Τμήμα Μαθηματικών Κεφάλαιο 10 Βάσεις Groebner ενός ιδεώδους 10.1 Τρίτο μέρος Επαναλαμβάνουμε
Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2)
 Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Εισαγωγή στους Η/Υ. Ενότητα 2β: Αντίστροφο Πρόβλημα. Δημήτρης Σαραβάνος, Καθηγητής Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών
 Εισαγωγή στους Η/Υ Ενότητα 2β: Δημήτρης Σαραβάνος, Καθηγητής Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών Σκοποί ενότητας Εύρεση συνάρτησης Boole όταν είναι γνωστός μόνο ο πίνακας αληθείας.
Εισαγωγή στους Η/Υ Ενότητα 2β: Δημήτρης Σαραβάνος, Καθηγητής Πολυτεχνική Σχολή Τμήμα Μηχανολόγων & Αεροναυπηγών Μηχανικών Σκοποί ενότητας Εύρεση συνάρτησης Boole όταν είναι γνωστός μόνο ο πίνακας αληθείας.
ΦΥΣΙΚΗ. Ενότητα 7: ΠΕΡΙΣΤΡΟΦΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΦΥΣΙΚΗ Ενότητα 7: ΠΕΡΙΣΤΡΟΦΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΦΥΣΙΚΗ Ενότητα 7: ΠΕΡΙΣΤΡΟΦΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Γενικά Μαθηματικά Ι. Ενότητα 17: Αριθμητική Ολοκλήρωση, Υπολογισμός Μήκους Καμπύλης Λουκάς Βλάχος Τμήμα Φυσικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Αριθμητική Ολοκλήρωση, Υπολογισμός Μήκους Καμπύλης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Αριθμητική Ολοκλήρωση, Υπολογισμός Μήκους Καμπύλης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός
 Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.08.4: Υπολογισμός Όγκων Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.08.4: Υπολογισμός Όγκων Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Κεφάλαιο 23 Ηλεκτρικό Δυναµικό. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 23 Ηλεκτρικό Δυναµικό Διαφορά Δυναµικού-Δυναµική Ενέργεια Σχέση Ηλεκτρικού Πεδίου και Ηλεκτρικού Δυναµικού Ηλεκτρικό Δυναµικό Σηµειακών Φορτίων Δυναµικό Κατανοµής Φορτίων Ισοδυναµικές Επιφάνειες
Κεφάλαιο 23 Ηλεκτρικό Δυναµικό Διαφορά Δυναµικού-Δυναµική Ενέργεια Σχέση Ηλεκτρικού Πεδίου και Ηλεκτρικού Δυναµικού Ηλεκτρικό Δυναµικό Σηµειακών Φορτίων Δυναµικό Κατανοµής Φορτίων Ισοδυναµικές Επιφάνειες
Εφαρμοσμένη Βελτιστοποίηση
 Εφαρμοσμένη Βελτιστοποίηση Ενότητα 2: Συναρτήσεις Χώροι - Μεταβλητές Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το
Εφαρμοσμένη Βελτιστοποίηση Ενότητα 2: Συναρτήσεις Χώροι - Μεταβλητές Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 1: Συναρτήσεις (Θεωρία) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 1: Συναρτήσεις (Θεωρία) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα
 Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Ασκήσεις 10 Ανδριανός Ε. Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής Σελίδα 2 1. Σκοποί ενότητας... 5
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Ασκήσεις 10 Ανδριανός Ε. Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής Σελίδα 2 1. Σκοποί ενότητας... 5
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση - Συγχώνευση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση - Συγχώνευση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Πρακτική Άσκηση σε σχολεία της δευτεροβάθμιας εκπαίδευσης
 Πρακτική Άσκηση σε σχολεία της δευτεροάθμιας εκπαίδευσης Ενότητα : Κρίσιμα συμάντα Δέσποινα Πόταρη, Γιώργος Ψυχάρης Σχολή Θετικών επιστημών Τμήμα Μαθηματικό 3.4. H συνάρτηση = α + Η ευθεία με εξίσωση =
Πρακτική Άσκηση σε σχολεία της δευτεροάθμιας εκπαίδευσης Ενότητα : Κρίσιμα συμάντα Δέσποινα Πόταρη, Γιώργος Ψυχάρης Σχολή Θετικών επιστημών Τμήμα Μαθηματικό 3.4. H συνάρτηση = α + Η ευθεία με εξίσωση =
Κβαντική Επεξεργασία Πληροφορίας
 Κβαντική Επεξεργασία Πληροφορίας Ενότητα 4: Κλασσική και Κβαντική Πιθανότητα Σγάρμπας Κυριάκος Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Σκοπός της ενότητας
Κβαντική Επεξεργασία Πληροφορίας Ενότητα 4: Κλασσική και Κβαντική Πιθανότητα Σγάρμπας Κυριάκος Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Σκοπός της ενότητας
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική. Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΟΠΤΙΚΗ (Πεδία και Κύµατα) Φύση του φωτός Γεωµετρική Οπτική
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΟΠΤΙΚΗ (Πεδία και Κύµατα) Φύση του φωτός Γεωµετρική Οπτική
Ενδεικτικές λύσεις ασκήσεων διαχείρισης έργου υπό συνθήκες αβεβαιότητας
 Ενδεικτικές λύσεις ασκήσεων διαχείρισης έργου υπό συνθήκες αβεβαιότητας 1 Περιεχόμενα 1 η Άσκηση... 4 2 η Άσκηση... 7 3 η Άσκηση... 10 Χρηματοδότηση... 12 Σημείωμα Αναφοράς... 13 Σημείωμα Αδειοδότησης...
Ενδεικτικές λύσεις ασκήσεων διαχείρισης έργου υπό συνθήκες αβεβαιότητας 1 Περιεχόμενα 1 η Άσκηση... 4 2 η Άσκηση... 7 3 η Άσκηση... 10 Χρηματοδότηση... 12 Σημείωμα Αναφοράς... 13 Σημείωμα Αδειοδότησης...
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής
 Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 14: Προσφορά επιχείρησης Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Προσφορά επιχείρησης
Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Διάλεξη 14: Προσφορά επιχείρησης Ανδρέας Παπανδρέου Σχολή Οικονομικών και Πολιτικών Επιστημών Τμήμα Οικονομικών Επιστημών Προσφορά επιχείρησης
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι. Ενότητα 4: Πρώτος Θερμοδυναμικός Νόμος. Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι Ενότητα 4: Πρώτος Θερμοδυναμικός Νόμος Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Σκοπός της ενότητας αυτής είναι η περιγραφή των ορισμών και των θεμελιωδών
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι Ενότητα 4: Πρώτος Θερμοδυναμικός Νόμος Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Σκοπός της ενότητας αυτής είναι η περιγραφή των ορισμών και των θεμελιωδών
Κβαντική Φυσική Ι. Ενότητα 2: Σύστημα δύο σωματιδίων-αρχή της αντιστοιχίας. Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Κβαντική Φυσική Ι Ενότητα 2: Σύστημα δύο σωματιδίων-αρχή της αντιστοιχίας Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοπός ενότητας Σκοπός της ενότητας είναι η σύντομη παρουσίαση μελέτης της
Κβαντική Φυσική Ι Ενότητα 2: Σύστημα δύο σωματιδίων-αρχή της αντιστοιχίας Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοπός ενότητας Σκοπός της ενότητας είναι η σύντομη παρουσίαση μελέτης της
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών
 Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 2: Γραμμικές συναρτήσεις (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Μαθηματικά Διοικητικών & Οικονομικών Επιστημών Ενότητα 2: Γραμμικές συναρτήσεις (Φροντιστήριο) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
