Ηλεκτρικό δυναμικό. Κεφάλαιο Η3
|
|
|
- ΣoφпїЅα Δουρέντης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Ηλεκτρικό δυναμικό Κεφάλαιο Η3
2 Ηλεκτρικό δυναμικό Σε προηγούμενα κεφάλαια συνδέσαμε τη μελέτη του ηλεκτρομαγνητισμού με τις προγενέστερες γνώσεις μας σχετικά με τις δυνάμεις. Σε αυτό το κεφάλαιο, θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα προβλήματα μηχανικής, τα οποία δεν είναι δυνατόν να λυθούν με μεθόδους που χρησιμοποιούν την έννοια της δύναμης. Η έννοια της δυναμικής ενέργειας είναι πολύ χρήσιμη και στη μελέτη του ηλεκτρισμού. Επειδή η ηλεκτροστατική δύναμη είναι συντηρητική, μπορούμε να περιγράψουμε τα ηλεκτροστατικά φαινόμενα χρησιμοποιώντας την έννοια της ηλεκτρικής δυναμικής ενέργειας. Αυτή η έννοια μας επιτρέπει να ορίσουμε το μέγεθος του ηλεκτρικού δυναμικού.
3 Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη. F e q o E Η ηλεκτρική δύναμη είναι συντηρητική. Αν το δοκιμαστικό φορτίο μετακινείται μέσα στο πεδίο υπό την επίδραση κάποιου εξωτερικού παράγοντα, τότε το έργο που παράγει το πεδίο στο φορτίο είναι ίσο κατά μέτρο και αντίθετο με το έργο που παράγει ο εξωτερικός παράγοντας. Με το σύμβολο ds συμβολίζουμε το απειροστό διάνυσμα μετατόπισης, το οποίο εφάπτεται σε μια διαδρομή στον χώρο. Η διαδρομή αυτή μπορεί να είναι ευθεία ή καμπύλη και το ολοκλήρωμα σε αυτή τη διαδρομή ονομάζεται επικαμπύλιο ολοκλήρωμα. 3
4 Ηλεκτρική δυναμική ενέργεια (συνέχεια) Στο σύστημα φορτίου-πεδίου, το έργο που παράγει το ηλεκτρικό πεδίο στο φορτίο είναι Fds q Eds o Επειδή το έργο αυτό παράγεται από το πεδίο, η δυναμική ενέργεια του συστήματος φορτίου-πεδίου μεταβάλλεται κατά Για μια πεπερασμένη μετατόπιση του φορτίου από το σημείο A στο σημείο B, η μεταβολή της δυναμικής ενέργειας του συστήματος είναι U U U q E ds B A o A U = q E ds B o Επειδή η δύναμη είναι συντηρητική, το επικαμπύλιο ολοκλήρωμα δεν εξαρτάται από τη διαδρομή που ακολουθεί το φορτίο. 4
5 Ηλεκτρικό δυναμικό (1) U Η δυναμική ενέργεια ανά μονάδα φορτίου,, ονομάζεται ηλεκτρικό δυναμικό. qo Το δυναμικό είναι χαρακτηριστικό μόνο του πεδίου. Η δυναμική ενέργεια είναι χαρακτηριστικό του συστήματος φορτίου-πεδίου. Το δυναμικό είναι ανεξάρτητο από την τιμή του φορτίου q o. Το δυναμικό έχει τιμή σε κάθε σημείο του ηλεκτρικού πεδίου. Το ηλεκτρικό δυναμικό είναι V U q o Το δυναμικό είναι βαθμωτό μέγεθος. Επειδή η ενέργεια είναι βαθμωτό μέγεθος. Όταν ένα φορτισμένο σωματίδιο κινείται μέσα σε ένα ηλεκτρικό πεδίο, το δυναμικό μεταβάλλεται κατά U B V d q E s A o Η απειροστή μετατόπιση μπορεί να εκληφθεί ως απόσταση μεταξύ δύο σημείων του χώρου αντί ως μετατόπιση ενός σημειακού φορτίου. 5
6 Ηλεκτρικό δυναμικό Το μέγεθος που έχει σημασία είναι η διαφορά του ηλεκτρικού δυναμικού. Συχνά θεωρούμε αυθαίρετα ότι σε κάποιο κατάλληλο σημείο του ηλεκτρικού πεδίου η τιμή του ηλεκτρικού δυναμικού είναι ίση με μηδέν. Το ηλεκτρικό δυναμικό είναι ένα βαθμωτό μέγεθος που χαρακτηρίζει το ηλεκτρικό πεδίο και είναι ανεξάρτητο από το όποιο φορτίο ενδέχεται να βρεθεί μέσα στο πεδίο. Η διαφορά δυναμικού μεταξύ δύο σημείων οφείλεται αποκλειστικά στην ύπαρξη ενός φορτίου-πηγής και εξαρτάται από την κατανομή του φορτίουπηγής. Για να υπάρχει δυναμική ενέργεια, πρέπει να έχουμε ένα σύστημα με δύο ή περισσότερα φορτία. Η δυναμική ενέργεια ανήκει στο σύστημα και μεταβάλλεται μόνο όταν ένα φορτίο μετακινείται σε σχέση με το υπόλοιπο σύστημα. 6
7 Έργο και ηλεκτρικό δυναμικό Έστω ότι ένα φορτίο κινείται μέσα σε ένα ηλεκτρικό πεδίο χωρίς να μεταβάλλεται η κινητική ενέργειά του. Το έργο που παράγεται στο φορτίο είναι: W = ΔU = q ΔV Μονάδα μέτρησης: 1 V = 1 J/C Το V είναι το αρχικό του volt. Χρειάζεται 1 joule έργου για να μετακινήσουμε ένα φορτίο 1 coulomb μεταξύ δύο σημείων που έχουν διαφορά δυναμικού 1 volt. Επιπλέον, 1 V = 1 J/C 1 V = 1 N.m/C 1 V/m = 1 N/C Συνεπώς, μπορούμε να εκλάβουμε το ηλεκτρικό πεδίο ως ένα μέτρο του ρυθμού μεταβολής του ηλεκτρικού δυναμικού συναρτήσει της απόστασης. 7
8 Τάση και βολτάζ Το ηλεκτρικό δυναμικό περιγράφεται με διάφορους όρους. Οι πιο κοινοί είναι η τάση και το βολτάζ. Η τάση που εφαρμόζεται σε μια συσκευή ή στα άκρα μιας συσκευής είναι ίδια με τη διαφορά δυναμικού στα άκρα της συσκευής. Παρά το γεγονός ότι οι εκφράσεις αυτές υποδηλώνουν κίνηση, η τάση δεν είναι κάτι που κινείται διαμέσου της συσκευής. Ηλεκτρονιοβόλτ Μια άλλη μονάδα ενέργειας που χρησιμοποιείται συνήθως στην ατομική και πυρηνική φυσική είναι το ηλεκτρονιοβόλτ. Ένα ηλεκτρονιοβόλτ είναι η ενέργεια που προσλαμβάνει ή χάνει ένα σύστημα φορτίου-πεδίου όταν ένα φορτίο με τιμή e (δηλαδή ένα ηλεκτρόνιο ή πρωτόνιο) κινείται μεταξύ δύο θέσεων με διαφορά δυναμικού 1 volt. 1 ev = 1.60 x J 8
9 Διαφορά δυναμικού σε ομογενές ηλεκτρικό πεδίο Αν το ηλεκτρικό πεδίο είναι ομογενές, οι εξισώσεις που δίνουν τη διαφορά δυναμικού μεταξύ δύο σημείων A και B μπορούν να αναχθούν σε πιο απλή μορφή: B A B V V V E d s E d s Ed A B A Η μετατόπιση γίνεται από το σημείο A στο σημείο B, παράλληλα στις γραμμές του ηλεκτρικού πεδίου. Το αρνητικό πρόσημο δείχνει ότι το ηλεκτρικό δυναμικό είναι μικρότερο στο σημείο B απ ό,τι στο σημείο A. Οι γραμμές του ηλεκτρικού πεδίου πάντα δείχνουν προς την κατεύθυνση στην οποία μειώνεται το ηλεκτρικό δυναμικό. 9
10 Η ενέργεια και η κατεύθυνση του ηλεκτρικού πεδίου Όταν το ηλεκτρικό πεδίο έχει κατεύθυνση προς τα κάτω, το σημείο B έχει χαμηλότερο δυναμικό από το A. Όταν ένα θετικό δοκιμαστικό φορτίο μετακινείται από το σημείο A στο B, το σύστημα φορτίου-πεδίου χάνει δυναμική ενέργεια. Οι γραμμές του ηλεκτρικού πεδίου πάντα δείχνουν προς την κατεύθυνση στην οποία μειώνεται το ηλεκτρικό δυναμικό. 10
11 Κατεύθυνση του ηλεκτρικού πεδίου (συνέχεια) Σε ένα σύστημα που αποτελείται από ένα θετικό φορτίο και ένα ηλεκτρικό πεδίο, η ηλεκτρική δυναμική ενέργεια του συστήματος μειώνεται όταν το φορτίο κινείται με κατεύθυνση ίδια με αυτή του πεδίου. Το ηλεκτρικό πεδίο παράγει έργο σε ένα θετικό φορτίο όταν το φορτίο κινείται στην κατεύθυνση του πεδίου. Η αύξηση της κινητικής ενέργειας του φορτισμένου σωματιδίου συνοδεύεται από ισόποση μείωση της δυναμικής ενέργειας του συστήματος φορτίου-πεδίου. Ένα ακόμα παράδειγμα της αρχής διατήρησης της ενέργειας. Αν το φορτίο q o είναι αρνητικό, τότε η μεταβολή της ηλεκτρικής δυναμικής ενέργειας ΔU είναι θετική. Σε ένα σύστημα που αποτελείται από ένα αρνητικό φορτίο και ένα ηλεκτρικό πεδίο, η ηλεκτρική δυναμική ενέργεια του συστήματος αυξάνεται όταν το φορτίο κινείται με κατεύθυνση ίδια με αυτή του πεδίου. Για να κινηθεί το αρνητικό φορτίο στην κατεύθυνση του πεδίου, πρέπει να δεχτεί μια εξωτερική δύναμη η οποία θα παραγάγει θετικό έργο στο φορτίο. 11
12 Ισοδυναμικές επιφάνειες Το σημείο B έχει χαμηλότερο δυναμικό από το A. Τα σημεία B και Γ έχουν το ίδιο δυναμικό. Όλα τα σημεία που ανήκουν σε ένα επίπεδο το οποίο είναι κάθετο σε ένα ομογενές ηλεκτρικό πεδίο έχουν το ίδιο ηλεκτρικό δυναμικό. Κάθε επιφάνεια που αποτελείται από μια συνεχή κατανομή σημείων, τα οποία έχουν το ίδιο ηλεκτρικό δυναμικό, ονομάζεται ισοδυναμική επιφάνεια. 1
13 Παράδειγμα Φορτισμένο σωματίδιο σε ομογενές πεδίο Η μεταβολή του δυναμικού είναι αρνητική. Η μεταβολή της δυναμικής ενέργειας είναι αρνητική. 13
14 Ηλεκτρικό δυναμικό και σημειακά φορτία Ένα απομονωμένο θετικό σημειακό φορτίο δημιουργεί ηλεκτρικό πεδίο με ακτινική κατεύθυνση προς τα έξω. Η διαφορά δυναμικού μεταξύ των σημείων A και B είναι: 1 1 VB VA keq r B r A Το ηλεκτρικό δυναμικό είναι ανεξάρτητο από τη διαδρομή που ακολουθεί το φορτίο για να μετακινηθεί από το σημείο A στο B. Ως τιμή αναφοράς του ηλεκτρικού δυναμικού συνήθως επιλέγουμε τη V = 0 στο r A =. Έτσι, το ηλεκτρικό δυναμικό ενός σημειακού φορτίου σε απόσταση r από αυτό είναι ίσο με: q V ke r 14
15 Το ηλεκτρικό δυναμικό ενός σημειακού φορτίου Στην εικόνα φαίνεται το γράφημα του ηλεκτρικού δυναμικού στον κατακόρυφο άξονα για ένα θετικό φορτίο, το οποίο βρίσκεται στο επίπεδο xy. Η καφέ καμπύλη δείχνει ότι το δυναμικό είναι αντιστρόφως ανάλογο του r. Το συνολικό ηλεκτρικό δυναμικό λόγω πολλών σημειακών φορτίων σε ένα σημείο Σ ισούται με το άθροισμα των δυναμικών των επιμέρους φορτίων. Ένα ακόμα παράδειγμα της αρχής της υπέρθεσης. Πρόκειται για αλγεβρικό άθροισμα. V k V = 0 στο r =. e i q r i i 15
16 Το ηλεκτρικό δυναμικό ενός ηλεκτρικού διπόλου Στον κατακόρυφο άξονα y του γραφήματος απεικονίζεται το δυναμικό ενός ηλεκτρικού διπόλου. Η απότομη κλίση μεταξύ των φορτίων αντιπροσωπεύει το ισχυρό ηλεκτρικό πεδίο σε αυτή την περιοχή. 16
17 Δυναμική ενέργεια πολλών φορτίων qq Η δυναμική ενέργεια του συστήματος είναι U k. e r Αν τα δύο φορτία είναι ομόσημα, τότε η δυναμική ενέργεια U είναι θετική και πρέπει να παραχθεί έργο για να πλησιάσουν τα φορτία το ένα στο άλλο. Αν τα δύο φορτία είναι ετερόσημα, τότε η δυναμική ενέργεια U είναι αρνητική και πρέπει να παραχθεί έργο για να μην πλησιάσουν τα φορτία το ένα στο άλλο
18 Δυναμική ενέργεια πολλών φορτίων (συνέχεια) Αν υπάρχουν περισσότερα από δύο φορτία, τότε βρίσκουμε τη δυναμική ενέργεια U για κάθε ζεύγος φορτίων και αθροίζουμε αλγεβρικά τους όρους. Για τρία φορτία: U qq q q q q ke r1 r13 r3 Το αποτέλεσμα δεν εξαρτάται από τη σειρά πρόσθεσης των φορτίων. Υπολογισμός του ηλεκτρικού πεδίου E από το ηλεκτρικό δυναμικό V Αρχικά υποθέτουμε ότι το πεδίο έχει μόνο μια οριζόντια συνιστώσα x. E x dv dx Μπορούμε να γράψουμε παρόμοιες σχέσεις και για τις συνιστώσες y και z. Οι ισοδυναμικές επιφάνειες πρέπει πάντα να είναι κάθετες στις γραμμές του ηλεκτρικού πεδίου που διέρχονται από αυτές. 18
19 Τα E και V για ένα φορτισμένο φύλλο άπειρων διαστάσεων Οι ισοδυναμικές είναι οι διακεκομμένες μπλε γραμμές. Οι γραμμές του ηλεκτρικού πεδίου είναι οι καφέ γραμμές. Οι ισοδυναμικές είναι κάθετες σε κάθε σημείο των γραμμών του ηλεκτρικού πεδίου. 19
20 Τα E και V για ένα σημειακό φορτίο Οι ισοδυναμικές είναι οι διακεκομμένες μπλε γραμμές. Οι γραμμές του ηλεκτρικού πεδίου είναι οι καφέ γραμμές. Οι γραμμές του ηλεκτρικού πεδίου έχουν ακτινική διεύθυνση. E r = dv / dr Οι ισοδυναμικές είναι κάθετες σε κάθε σημείο των γραμμών του ηλεκτρικού πεδίου. 0
21 Τα E και V για ένα ηλεκτρικό δίπολο Οι ισοδυναμικές είναι οι διακεκομμένες μπλε γραμμές. Οι γραμμές του ηλεκτρικού πεδίου είναι οι καφέ γραμμές. Οι ισοδυναμικές είναι κάθετες σε κάθε σημείο των γραμμών του ηλεκτρικού πεδίου. 1
22 Υπολογισμός του ηλεκτρικού πεδίου από το ηλεκτρικό δυναμικό Γενικά Γενικά, το ηλεκτρικό δυναμικό είναι συνάρτηση και των τριών χωρικών συντεταγμένων. Αν η συνάρτηση V εκφράζεται με βάση τις καρτεσιανές συντεταγμένες, τότε οι συνιστώσες E x, E y, και E z του ηλεκτρικού πεδίου προκύπτουν εύκολα από τις μερικές παραγώγους της V(x, y, z). V V V Ex Ey Ez x y z E V iˆ jˆ kˆ V x y z Εξίσωση Poisson E q Εξίσωση Laplace (χωρίς φορτία q=0) V 0 0 EV E V V q 0
23 Παράδειγμα Λύση q i q q V ke ke i ri α y α y 0 q i q q kqα V e T ke ke i r x α x α x α i 3
24 (γ) Υπολογίστε τα V και E x σε ένα σημείο του άξονα x που βρίσκεται σε μεγάλη απόσταση από το δίπολο Για το σημείο Τ, σε μεγάλη απόσταση από το δίπολο x >> α, θεωρήστε αμελητέο το α στον παρονομαστή της λύσης του σκέλους (β), άρα το V γράφετε σε αυτό το όριο: kqα e keqα VT lim xα x α x α x E x dv d kqα e dx dx x d 1 4kqα e Ex keqα x α 3 dx x x 4
25 Παράδειγμα Το ηλεκτρικό δίπολο βρίσκεται στον άξονα y. Το μέτρο της ροπής του ηλεκτρικού διπόλου ορίζεται από την σχέση p = αq. (α) στο σημείο Σ, το οποίο βρίσκεται σε μεγάλη απόσταση από το δίπολου (r >> α), δείξτε ότι το ηλεκτρικό δυναμικό ισούται με kp e cosθ V Λύση r keq keq keq V r r r r r r 1 r a 1 r r r a ra cos r a 1 cos r 1 1 a 1 cos r r r kq e V αcosθ rr r r a ra cos r r a r a 1 cos r 1 1 a 1 cos r r r Για r >> α και χρησιμοποιούμε το ανάπτυγμα Taylor a 1 1 a 1 1 a 1 cos, 1 cos cos r r r r r r r r r 1 1 V kpcosθ e r 1 1x 1 x 5
26 Δευτερός τρόπος keq keq keq V r r r r r r Αν r >> α r r 1 α cos V kpcosθ e r (β) Υπολογίστε την ακτινική συνιστώσα E r και την κάθετη σε αυτήν συνιστώσα E θ του ηλεκτρικού πεδίου. Λάβετε υπόψη ότι E 1/ /. Αυτά τα αποτελέσματα είναι λογικά για θ=90 o και 0 o θ r V θ ; E V r kpcosθ e r V r kpcosθ e r 3 E θ 1V kp e sinθ 3 r θ r Για r >> α E r kp kp 0 0, 90 e3 r o e o 0 0 0, E r Eθ Eθ r 6
27 Ηλεκτρικό δυναμικό συνεχούς κατανομής φορτίου Μέθοδος 1: Η κατανομή φορτίου είναι γνωστή. Θεωρούμε ένα μικρό στοιχειώδες φορτίο dq. Εκλαμβάνουμε το φορτίο ως σημειακό. Το δυναμικό σε οποιοδήποτε σημείο λόγω αυτού του στοιχειώδους φορτίου είναι: dq dv ke r Για να βρούμε το συνολικό δυναμικό, ολοκληρώνουμε την προηγούμενη εξίσωση ώστε να συμπεριλάβουμε τις συνεισφορές όλων των στοιχείων της κατανομής φορτίου. Σε αυτή τη σχέση για το V, το ηλεκτρικό δυναμικό θεωρείται ίσο με το μηδέν όταν το σημείο Σ βρίσκεται σε άπειρη απόσταση από την κατανομή φορτίου. Αν γνωρίζουμε ήδη το ηλεκτρικό πεδίο, τότε μπορούμε να υπολογίσουμε το ηλεκτρικό δυναμικό από την αρχική σχέση: V d s B E A Αν η κατανομή φορτίου χαρακτηρίζεται από επαρκή βαθμό συμμετρίας, τότε πρώτα υπολογίζουμε το ηλεκτρικό πεδίο με τον νόμο του Gauss και έπειτα τη διαφορά δυναμικού μεταξύ δύο τυχαίων σημείων. Επιλέγουμε V = 0 σε ένα κατάλληλο σημείο. V k e dq r 7
28 Μεθοδολογία επίλυσης προβλημάτων Μοντελοποίηση 8 Φανταστείτε τα επιμέρους φορτία ή την κατανομή φορτίου. Φανταστείτε τον τύπο του δυναμικού που δημιουργούν. Λάβετε υπόψη τη συμμετρία (αν υπάρχει) στη διάταξη των φορτίων. Κατηγοριοποίηση Πρόκειται για ένα σύνολο από μεμονωμένα φορτία ή για μια συνεχή κατανομή φορτίων; Η απάντηση σε αυτή την ερώτηση θα καθορίσει τη διαδικασία που θα ακολουθήσετε στο βήμα της Ανάλυσης. Γενικά Το ηλεκτρικό δυναμικό είναι βαθμωτό μέγεθος, άρα δεν χρειάζεται να βρείτε συνιστώσες. Χρησιμοποιήστε την αρχή της υπέρθεσης και αθροίστε αλγεβρικά τα δυναμικά των επιμέρους φορτίων. Προσοχή στα πρόσημα. Μόνο οι μεταβολές του ηλεκτρικού δυναμικού έχουν σημασία. Θεωρήστε ότι V = 0 σε ένα σημείο που βρίσκεται πολύ μακριά από τα φορτία. Αν η κατανομή εκτείνεται ως το άπειρο, επιλέξτε κάποιο άλλο σημείο ως σημείο αναφοράς.
29 Μεθοδολογία επίλυσης προβλημάτων Ανάλυση Αν δίνεται μια ομάδα μεμονωμένων φορτίων: Χρησιμοποιήστε την αρχή της υπέρθεσης και αθροίστε αλγεβρικά τα δυναμικά των επιμέρους φορτίων. Αν δίνεται μια συνεχής κατανομή φορτίου: Υπολογίστε το συνολικό δυναμικό σε κάποιο σημείο χρησιμοποιώντας ολοκληρώματα. Θεωρήστε κάθε στοιχειώδες τμήμα της κατανομής φορτίου ως σημειακό φορτίο. Αν δίνεται το ηλεκτρικό πεδίο: Ξεκινήστε από τον ορισμό του ηλεκτρικού δυναμικού. Αν χρειαστεί, υπολογίστε το πεδίο χρησιμοποιώντας τον νόμο του Gauss (ή κάποιον άλλο τρόπο). Ολοκλήρωση Βεβαιωθείτε ότι η σχέση του ηλεκτρικού δυναμικού που βρήκατε συμφωνεί με τη νοητική σας αναπαράσταση. Η τελική σχέση αντικατοπτρίζει την όποια συμμετρία υπάρχει; Μεταβάλλετε νοητικά παραμέτρους για να εξακριβώσετε αν το μαθηματικό αποτέλεσμα αλλάζει με εύλογο τρόπο. 9
30 Παράδειγμα Ηλεκτρικό δυναμικό ομοιόμορφα φορτισμένου δακτυλίου Με βάση τη συμμετρία της περίπτωσης, όλα τα φορτία του δακτυλίου ισαπέχουν από το σημείο Σ. Ο δακτύλιος έχει ακτίνα α και συνολικό φορτίο Q. Το δυναμικό και το πεδίο δίνονται από τις σχέσεις: dq ke keq V ke dq r α x α x dv d 1 E k Q α x k Q α x x x e e dx dx E x 1/ 3 / α kx e x 3 / Q 30
31 Παράδειγμα Ηλεκτρικό δυναμικό ομοιόμορφα φορτισμένου δίσκου Το σημείο Σ βρίσκεται στον κάθετο κεντρικό άξονα του ομοιόμορφα φορτισμένου δακτυλίου. Επειδή το σημείο Σ βρίσκεται επάνω στον κεντρικό άξονα του δίσκου, συνάγεται λόγω συμμετρίας ότι όλα τα σημεία κάθε δακτυλίου ισαπέχουν από το Σ. 1 V πkeσ R x x Το δυναμικό και το πεδίο δίνονται από τις σχέσεις: E x dv x πkeσ 1 dx R x 1/ 31
32 Ηλεκτρικό δυναμικό πεπερασμένης φορτισμένης ευθείας Δεν υπάρχει συμμετρία, αλλά η γεωμετρία του προβλήματος είναι απλή. V kq e α ln α 3
33 Παράδειγμα Ένας ομοιόμορφο φορτισμένο κυλινδρικό κέλυφος με ανοιχτές βάσεις έχει συνολικό φορτίο Q, ακτίνας R, και μήκος h. Προσδιορίστε το ηλεκτρικό δυναμικό σε ένα σημείο που απέχει d από το δεξιό άκρο του κυλίνδρου. Λύση Θεωρούμε τον κυλινδρικό κέλυφος ως ένα σύνολο δακτυλίων ο καθένας έχει ακτίνα R και συνολικό φορτίο dq. Για να βρούμε το φορτίο,dq, αυτού του τμήματος παρατηρούμε πως αν το φορτίο κατανέμεται ομογενώς, ο λόγος του dq προς το ολικό φορτίο Q ισούται με το λόγο dx προς το ολικό μήκος h. Έτσι dq dx dq Q dx Q h h keqdx dh k dv eqdx keq V h R x dv ln x R x d h R x h ' ολα τα φορτία dh d V kq d h R d h e ln h d R d 33
34 Παράδειγμα 34
35 Παράδειγμα Στην αρχή των αξόνων ενός συστήματος συντεταγμένων xyz που βρίσκεται μέσα σε ένα αρχικά ομογενές ηλεκτρικό πεδίο E E 0 kˆ τοποθετείται μια αφόρτιστη αγώγιμη σφαίρα ακτίνας α. τότε το ηλεκτρικό δυναμικό για σημεία που βρίσκονται μέσα στη σφαίρα είναι V(x,y,z) = V 0 ενώ για σημεία έξω 3 από τη σφαίρα ίσο με E0αz V x,y,z V E z 0 0 3/ x y z Όπου V 0 είναι το σταθερό ηλεκτρικό δυναμικό του αγωγού. Χρησιμοποιώντας αυτή την εξίσωση, προσδιορίστε τις συνιστώσες x,y, και z του συνολικού ηλεκτρικού πεδίου (α) μέσα στη σφαίρα και (β) έξω από τη σφαίρα. Μέσα στη σφαίρα E x = E y = E z = 0. Έξω από τη σφαίρα. V 3 3 x E 0 0 E αz x 0 5/ x x y z 3 5/ E 3E α xz x y z x 0 35
36 Ηλεκτρικό δυναμικό φορτισμένου αγωγού Θεωρούμε δύο σημεία επί της επιφάνειας του φορτισμένου αγωγού, όπως φαίνεται στην εικόνα. Το πεδίο E είναι πάντα κάθετο στη μετατόπιση ds. Άρα, Eds 0 Επομένως, η διαφορά δυναμικού μεταξύ των σημείων A και B είναι επίσης μηδενική. Σε κάθε σημείο της επιφάνειας ενός φορτισμένου αγωγού, ο οποίος βρίσκεται σε ισορροπία, V = σταθερό. ΔV = 0 μεταξύ οποιουδήποτε ζεύγους σημείων της επιφάνειας. Η επιφάνεια κάθε φορτισμένου αγωγού που βρίσκεται σε ηλεκτροστατική ισορροπία είναι ισοδυναμική. Κάθε σημείο της επιφάνειας ενός φορτισμένου αγωγού που είναι σε ισορροπία έχει το ίδιο ηλεκτρικό δυναμικό. Επειδή στο εσωτερικό του αγωγού το ηλεκτρικό πεδίο είναι ίσο με μηδέν, συμπεραίνουμε ότι το ηλεκτρικό δυναμικό παντού στο εσωτερικό του αγωγού είναι σταθερό και ίσο με την τιμή του στην επιφάνεια. 36
37 Σώματα με ακανόνιστο σχήμα Όπου η ακτίνα καμπυλότητας είναι μικρή, η πυκνότητα φορτίου είναι μεγάλη. Και όπου η ακτίνα καμπυλότητας είναι μεγάλη, η πυκνότητα φορτίου είναι μικρή. Το ηλεκτρικό πεδίο είναι ισχυρό κοντά σε κυρτά σημεία με μικρή ακτίνα καμπυλότητας και φτάνει σε πολύ μεγάλες τιμές σε αιχμηρά σημεία. 37
38 Κοιλότητα στο εσωτερικό ενός αγωγού Έστω ότι ένας αγωγός περιέχει μια κοιλότητα ακανόνιστου σχήματος. Υποθέτουμε ότι μέσα στην κοιλότητα δεν υπάρχουν φορτία. Το ηλεκτρικό πεδίο στο εσωτερικό του αγωγού πρέπει να είναι ίσο με μηδέν. Το ηλεκτρικό πεδίο στο εσωτερικό του αγωγού δεν εξαρτάται από την κατανομή φορτίου στην εξωτερική επιφάνεια του αγωγού. Για κάθε διαδρομή μεταξύ των σημείων A και B, VB VA E d s B A 0 Σε μια κοιλότητα η οποία περιβάλλεται από αγώγιμα τοιχώματα δεν υπάρχει πεδίο, υπό την προϋπόθεση ότι στο εσωτερικό της δεν υπάρχει φορτίο. 38
39 Στεμματόμορφη εκκένωση Αν το ηλεκτρικό πεδίο στην περιοχή κοντά στον αγωγό είναι αρκετά ισχυρό, τα ηλεκτρόνια που προκύπτουν από τον τυχαίο ιοντισμό μορίων του αέρα κοντά στον αγωγό απομακρύνονται επιταχυνόμενα από τα μόρια από τα οποία προήλθαν. Αυτά τα ηλεκτρόνια μπορούν να ιοντίσουν και άλλα μόρια που βρίσκονται κοντά στον αγωγό. Έτσι δημιουργούνται κι άλλα ελεύθερα ηλεκτρόνια. Η λάμψη που παρατηρείται η στεμματόμορφη εκκένωση οφείλεται στην επανένωση αυτών των ελεύθερων ηλεκτρονίων με τα ιοντισμένα μόρια του αέρα. Η πιθανότητα να συμβεί ιοντισμός και στεμματόμορφη εκκένωση είναι μεγάλη σε αιχμηρά σημεία ή στις ακμές του αγωγού. 39
40 Το πείραμα των σταγονιδίων λαδιού του Millikan Ο Robert Millikan μέτρησε το e, την τιμή του στοιχειώδους φορτίου του ηλεκτρονίου. Επίσης απέδειξε ότι το φορτίο αυτό είναι κβαντισμένο. Τα σταγονίδια λαδιού διέρχονται από μια μικρή οπή και φωτίζονται από μια φωτεινή πηγή. 40
41 Το πείραμα των σταγονιδίων λαδιού του Millikan () Αν μεταξύ των πλακών δεν υπάρχει ηλεκτρικό πεδίο, τότε στο σταγονίδιο ασκούνται η βαρυτική δύναμη και η δύναμη τριβής. Το σταγονίδιο φτάνει στην οριακή του ταχύτητα όταν F mg D 41
42 Το πείραμα των σταγονιδίων λαδιού του Millikan Μεταξύ των πλακών δημιουργείται ένα ηλεκτρικό πεδίο. Η άνω πλάκα έχει υψηλότερο δυναμικό από την κάτω. Το σταγονίδιο φτάνει σε μια νέα οριακή ταχύτητα, όταν η ηλεκτρική δύναμη γίνει ίση με το άθροισμα της δύναμης αντίστασης του αέρα και της βαρυτικής δύναμης. Ενεργοποιώντας και απενεργοποιώντας το ηλεκτρικό πεδίο μπορούμε να παρακολουθούμε το σταγονίδιο να ανυψώνεται και να πέφτει πολλές φορές. Μετά από πολλά πειράματα, ο Millikan προσδιόρισε τα εξής: q = ne όπου n = 0, 1,, 3, e = 1.60 x C Αυτό αποτελεί αδιάσειστη απόδειξη ότι το φορτίο είναι κβαντισμένο. 4
43 Παράδειγμα Δύο μεγάλες παράλληλες κατακόρυφες αγώγιμες πλάκες που βρίσκονται σε απόσταση d μεταξύ τους, είναι φορτισμένες έτσι ώστε τα δυναμικά τους να είναι +V 0 και V 0. Στο μέσο μεταξύ των πλακών κρέμεται μια μικρή αγώγιμη σφαίρα μάζας m και ακτίνας R (όπου R << d). Το νήμα μήκους L από το οποίο κρέμεται η σφαίρα είναι ένα γειωμένο αγώγιμο σύρμα, οπότε το δυναμικό της σφαίρας είναι σταθερό και ίσο με V = 0. Όταν το V 0 είναι μικρό, η σφαίρα κρέμεται κατακόρυφα προς τα κάτω και βρίσκεται σε ευσταθή ισορροπία. Δείξτε ότι η ισορροπία της σφαίρας θα είναι ασταθής αν το V 0 υπερβεί την κρίσιμη τιμή (k e d mg/(4rl)) 1/ Λύση Οι πλάκες δημιουργούν ομοιόμορφο ηλεκτρικό πεδίο προς τα δεξιά V V V E d d Ας υποθέσουμε ότι η μπάλα ταλαντεύεται σε μικρή απόσταση x προς τα δεξιά. Κινείται σε ένα μέρος όπου η τάση που δημιουργείται από τις πλάκες είναι χαμηλότερη από V 0 Ex x V x k d V = 0 (γείωση), άρα 0 eq V xr 0 q 0 d R ked 4V 0 xr Στη συνέχεια η μπάλα αισθάνεται ηλεκτρική δύναμη προς τα δεξιά F qe kd Για την ισορροπία αυτή πρέπει να αντισταθμίζεται από την οριζόντια συνιστώσα της τάσης της χορδής σύμφωνα με Τcosθ = mg (1) και 4V 0 xr T sin () kd e 1/ 4V 0 xr x k ed mg Από (1) και () tan V 0 ked mg L 4LR e 43
Ηλεκτρομαγνητισμός. Ηλεκτρικό δυναμικό. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Κεφάλαιο Η3. Ηλεκτρικό δυναµικό
 Κεφάλαιο Η3 Ηλεκτρικό δυναµικό Ηλεκτρικό δυναµικό Σε προηγούµενα κεφάλαια συνδέσαµε τη µελέτη του ηλεκτροµαγνητισµού µε τις προγενέστερες γνώσεις µας σχετικά µε τις δυνάµεις. Σε αυτό το κεφάλαιο, θα συνδέσουµε
Κεφάλαιο Η3 Ηλεκτρικό δυναµικό Ηλεκτρικό δυναµικό Σε προηγούµενα κεφάλαια συνδέσαµε τη µελέτη του ηλεκτροµαγνητισµού µε τις προγενέστερες γνώσεις µας σχετικά µε τις δυνάµεις. Σε αυτό το κεφάλαιο, θα συνδέσουµε
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ηλεκτρικό δυναμικό Ηλεκτρικό δυναμικό Σε προηγούμενα
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ηλεκτρικό δυναμικό Ηλεκτρικό δυναμικό Σε προηγούμενα
Ηλεκτρική δυναμική ενέργεια
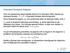 Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική.
 Ηλεκτρική δυναµική ενέργεια Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική. e o Έστω δοκιµαστικό φορτίο,
Ηλεκτρική δυναµική ενέργεια Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική. e o Έστω δοκιµαστικό φορτίο,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ. Ενότητα 3: Ηλεκτρικό δυναμικό. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 3: Ηλεκτρικό δυναμικό Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 3: Ηλεκτρικό δυναμικό Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ
 ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ Ημερομηνία:. ΤΜΗΜΑ:.. ΟΜΑΔΑ:. Ονομ/νυμο: Α.Μ. Συνεργάτες Ονομ/νυμο: Α.Μ. Ονομ/νυμο: Α.Μ. ΠΕΡΙΛΗΨΗ ΤΗΣ ΑΣΚΗΣΗΣ (καθένας με δικά του λόγια, σε όλες τις γραμμές) ΒΑΘΜΟΣ#1: ΥΠΟΓΡΑΦΗ:
ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ Ημερομηνία:. ΤΜΗΜΑ:.. ΟΜΑΔΑ:. Ονομ/νυμο: Α.Μ. Συνεργάτες Ονομ/νυμο: Α.Μ. Ονομ/νυμο: Α.Μ. ΠΕΡΙΛΗΨΗ ΤΗΣ ΑΣΚΗΣΗΣ (καθένας με δικά του λόγια, σε όλες τις γραμμές) ΒΑΘΜΟΣ#1: ΥΠΟΓΡΑΦΗ:
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 13 Ηλεκτρικό (Βαθμωτό) δυναμικό ΦΥΣ102 1 Διαφορά δυναμικού Η Ηλεκτροστατική Δύναμη
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 13 Ηλεκτρικό (Βαθμωτό) δυναμικό ΦΥΣ102 1 Διαφορά δυναμικού Η Ηλεκτροστατική Δύναμη
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23)
 ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού. Ιωάννης Γκιάλας 14 Μαρτίου 2014
 Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία. Ιωάννης Γκιάλας 7 Μαρτίου 2014
 Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Κεφάλαιο Η2. Ο νόµος του Gauss
 Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
Ορίζοντας την δυναμική ενέργεια σαν: Για μετακίνηση του φορτίου ανάμεσα στις πλάκες: Ηλεκτρικό Δυναμικό 1
 Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
Κεφάλαιο 23 Ηλεκτρικό Δυναµικό. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 23 Ηλεκτρικό Δυναµικό Διαφορά Δυναµικού-Δυναµική Ενέργεια Σχέση Ηλεκτρικού Πεδίου και Ηλεκτρικού Δυναµικού Ηλεκτρικό Δυναµικό Σηµειακών Φορτίων Δυναµικό Κατανοµής Φορτίων Ισοδυναµικές Επιφάνειες
Κεφάλαιο 23 Ηλεκτρικό Δυναµικό Διαφορά Δυναµικού-Δυναµική Ενέργεια Σχέση Ηλεκτρικού Πεδίου και Ηλεκτρικού Δυναµικού Ηλεκτρικό Δυναµικό Σηµειακών Φορτίων Δυναµικό Κατανοµής Φορτίων Ισοδυναµικές Επιφάνειες
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ, Αγωγοί Διηλεκτρικά. Ν. Τράκας, Ι. Ράπτης Ζωγράφου 27.3.
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ
 ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΒΙΒΛΙΟΓΡΑΦΙΑ H.D. H.D. Young Πανεπιστημιακή Φυσική Εκδόσεις Παπαζήση Alonso Alonso / Finn Θεμελιώδης Πανεπιστημιακή Φυσική Α. Φίλιππας, Λ. Ρεσβάνης (Μετ.) R. A. Seway Φυσική
ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΒΙΒΛΙΟΓΡΑΦΙΑ H.D. H.D. Young Πανεπιστημιακή Φυσική Εκδόσεις Παπαζήση Alonso Alonso / Finn Θεμελιώδης Πανεπιστημιακή Φυσική Α. Φίλιππας, Λ. Ρεσβάνης (Μετ.) R. A. Seway Φυσική
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο. Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 2014
 ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Υπενθύμιση (από τη Μηχανική) /Εισαγωγή:
 ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ Υπενθύμιση (από τη Μηχανική) /Εισαγωγή: Είχαμε πει ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος
ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ Υπενθύμιση (από τη Μηχανική) /Εισαγωγή: Είχαμε πει ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος
W Bά. Υπενθύμιση από την Α τάξη. Το έργο του βάρους κατά την ανύψωση του κουτιού από τη θέση A στη θέση Γ είναι ίσο με W=-mgh
 Υπενθύμιση από την Α τάξη Το έργο του βάρους κατά την ανύψωση του κουτιού από τη θέση A στη θέση Γ είναι ίσο με W=-mgh Η h Γ W ά mgh mg( H h1) mgh1 W ά mgh1 mgh mgh h 1 A ποσότητα που σχετίζεται με την
Υπενθύμιση από την Α τάξη Το έργο του βάρους κατά την ανύψωση του κουτιού από τη θέση A στη θέση Γ είναι ίσο με W=-mgh Η h Γ W ά mgh mg( H h1) mgh1 W ά mgh1 mgh mgh h 1 A ποσότητα που σχετίζεται με την
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ
 Δυνάμεις Μεταξύ Ηλεκτρικών Φορτίων σελ. 1 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ 1. Ο νόμος του Coulomb. Ηλεκτρικό πεδίο 3. Ηλεκτρική δυναμική ενέργεια 4. Δυναμικό
Δυνάμεις Μεταξύ Ηλεκτρικών Φορτίων σελ. 1 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ 1. Ο νόμος του Coulomb. Ηλεκτρικό πεδίο 3. Ηλεκτρική δυναμική ενέργεια 4. Δυναμικό
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών 7/15/2014 Ο νόμος του Gauss Νόμος Gauss Ο νόμος
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών 7/15/2014 Ο νόμος του Gauss Νόμος Gauss Ο νόμος
1η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1. Λύσεις Ασκήσεων 1 ου Κεφαλαίου
 1η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Λύσεις Ασκήσεων 1 ου Κεφαλαίου 1. Στον άξονα βρίσκονται δύο σημειακά φορτία q A = 1 μ και q Β = 45 μ, καθώς και ένα τρίτο σωματίδιο με άγνωστο φορτίο
1η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Λύσεις Ασκήσεων 1 ου Κεφαλαίου 1. Στον άξονα βρίσκονται δύο σημειακά φορτία q A = 1 μ και q Β = 45 μ, καθώς και ένα τρίτο σωματίδιο με άγνωστο φορτίο
ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ
 ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα
ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
(α) 1. (β) Το σύστημα βρίσκεται υπό διαφορά δυναμικού 12 V: U ολ = 1 2 C ολ(δv) 2 = J.
 4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
Κεφάλαιο M4. Κίνηση σε δύο διαστάσεις
 Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23
 ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
Ισχύει όταν κινούνται ; Ισχύει όταν κινείται μόνο το ένα δηλαδή η δύναμη αλληλεπίδρασης περιγράφεται σωστά από το νόμο Coulomb
 Σημαντικό!!!!!!!! Με βάση το νόμο Coulomb υπολογίζουμε τη δύναμη ανάμεσα σε δύο φορτισμένα σωματίδια οποία είναι ακίνητα Ισχύει όταν κινούνται ; Ισχύει όταν κινείται μόνο το ένα δηλαδή η δύναμη αλληλεπίδρασης
Σημαντικό!!!!!!!! Με βάση το νόμο Coulomb υπολογίζουμε τη δύναμη ανάμεσα σε δύο φορτισμένα σωματίδια οποία είναι ακίνητα Ισχύει όταν κινούνται ; Ισχύει όταν κινείται μόνο το ένα δηλαδή η δύναμη αλληλεπίδρασης
Κεφάλαιο 21 Ηλεκτρικά Φορτία και Ηλεκτρικά Πεδία. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 21 Ηλεκτρικά Φορτία και Ηλεκτρικά Πεδία Στατικός Ηλεκτρισμός, Ηλεκτρικό Φορτίο και η διατήρηση αυτού Ηλεκτρικό φορτίο στο άτομο Αγωγοί και Μονωτές Επαγόμενα Φορτία Ο Νόμος του Coulomb Το Ηλεκτρικό
Κεφάλαιο 21 Ηλεκτρικά Φορτία και Ηλεκτρικά Πεδία Στατικός Ηλεκτρισμός, Ηλεκτρικό Φορτίο και η διατήρηση αυτού Ηλεκτρικό φορτίο στο άτομο Αγωγοί και Μονωτές Επαγόμενα Φορτία Ο Νόμος του Coulomb Το Ηλεκτρικό
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. Ν. Τράκας, Ι. Ράπτης 2/4/2018
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 7-8 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Ν. Τράκας Ι. Ράπτης /4/8 Παράδοση των 3 4 5 μέχρι /4/8 [Σε χειρόγραφη μορφή στο μάθημα ή σε μορφή ενιαίου αρχείου PDF στις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 7-8 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Ν. Τράκας Ι. Ράπτης /4/8 Παράδοση των 3 4 5 μέχρι /4/8 [Σε χειρόγραφη μορφή στο μάθημα ή σε μορφή ενιαίου αρχείου PDF στις
Δομή Διάλεξης. Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο
 Ηλεκτρικό Δυναμικό Δομή Διάλεξης Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο Ιδιότητες ηλεκτρικού δυναμικού (χρησιμότητα σε υπολογισμούς, σημείο αναφοράς, αρχή υπέρθεσης) Διαφορικές
Ηλεκτρικό Δυναμικό Δομή Διάλεξης Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο Ιδιότητες ηλεκτρικού δυναμικού (χρησιμότητα σε υπολογισμούς, σημείο αναφοράς, αρχή υπέρθεσης) Διαφορικές
Ασκήσεις 6 ου Κεφαλαίου
 Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
1η ΠΑΡΟΥΣΙΑΣΗ. Ηλεκτρικά πεδία
 1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε με τις αισθήσεις μας οφείλονται
1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε με τις αισθήσεις μας οφείλονται
1η ΠΑΡΟΥΣΙΑΣΗ. Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία
 1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε
1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε
Ενημέρωση. Η διδασκαλία του μαθήματος, όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή
 Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
To θετικό πρόσημο σημαίνει ότι το πεδίο προσφέρει την ενέργεια για τη μετακίνηση αυτή.
 Ασκήσεις 3 ου Κεφαλαίου, Ηλεκτρικό Δυναμικό 23.21.Δύο σημειακά φορτία q 1 =+2,4 nc q 2 =-6,5 nc βρίσκονται σε απόσταση 0,1 m το ένα από το άλλο. Το σημείο Α βρίσκεται στο μέσον της απόστασής τους και το
Ασκήσεις 3 ου Κεφαλαίου, Ηλεκτρικό Δυναμικό 23.21.Δύο σημειακά φορτία q 1 =+2,4 nc q 2 =-6,5 nc βρίσκονται σε απόσταση 0,1 m το ένα από το άλλο. Το σημείο Α βρίσκεται στο μέσον της απόστασής τους και το
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Μονάδα μέτρησης του ηλεκτρικού φορτίου στο Διεθνές Σύστημα (S.I.) είναι το προς τιμήν του Γάλλου φυσικού Charles Augustin de Coulomb.
 Βασικές έννοιες Τα σώματα μπορούν να αλληλεπιδράσουν ηλεκτρικά. Ο Θαλής ο Μιλήσιος παρατήρησε πρώτος την έλξη μικρών αντικειμένων από ήλεκτρο, αφού πρώτα τριφτεί σε ξηρό ύφασμα. Το φαινόμενο αυτό ονομάστηκε
Βασικές έννοιες Τα σώματα μπορούν να αλληλεπιδράσουν ηλεκτρικά. Ο Θαλής ο Μιλήσιος παρατήρησε πρώτος την έλξη μικρών αντικειμένων από ήλεκτρο, αφού πρώτα τριφτεί σε ξηρό ύφασμα. Το φαινόμενο αυτό ονομάστηκε
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 - ΖΩΓΡΑΦΟΥ, 157 73 ΑΘΗΝΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 - ΖΩΓΡΑΦΟΥ, 157 73 ΑΘΗΝΑ
Εξίσωση Laplace Θεωρήματα Μοναδικότητας
 Εξίσωση Laplace Θεωρήματα Μοναδικότητας Δομή Διάλεξης Εξίσωση Laplace πλεονεκτήματα μεθόδου επίλυσης της για εύρεση ηλεκτρικού δυναμικού Ιδιότητες λύσεων εξίσωσης Laplace σε 1, 2 και 3 διαστάσεις Θεώρημα
Εξίσωση Laplace Θεωρήματα Μοναδικότητας Δομή Διάλεξης Εξίσωση Laplace πλεονεκτήματα μεθόδου επίλυσης της για εύρεση ηλεκτρικού δυναμικού Ιδιότητες λύσεων εξίσωσης Laplace σε 1, 2 και 3 διαστάσεις Θεώρημα
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
Ηλεκτρική ροή. Εμβαδόν=Α
 Ηλεκτρική ροή Hλεκτρική ροή: φυσικό μέγεθος (μονόμετρο) που δηλώνει τον αριθμό των δυναμικών γραμών ενός ηλεκτρικού πεδίου που διαπερνούν μία επιφάνεια. Εμβαδόν=Α Για παράδειγμα, η ηλεκτρική ροή για την
Ηλεκτρική ροή Hλεκτρική ροή: φυσικό μέγεθος (μονόμετρο) που δηλώνει τον αριθμό των δυναμικών γραμών ενός ηλεκτρικού πεδίου που διαπερνούν μία επιφάνεια. Εμβαδόν=Α Για παράδειγμα, η ηλεκτρική ροή για την
7.1 Τα πρώτα πειράματα της χρονιάς.
 7.1 Τα πρώτα πειράματα της χρονιάς. 7.Β. Μπορείτε να ερμηνεύσετε τις παρακάτω πειραματικές παρατηρήσεις; i) Μια αφόρτιστη μεταλλική ράβδος κρέμεται όπως στο σχήμα από μονωτικό νήμα και ηρεμεί. Όταν πλησιάσουμε
7.1 Τα πρώτα πειράματα της χρονιάς. 7.Β. Μπορείτε να ερμηνεύσετε τις παρακάτω πειραματικές παρατηρήσεις; i) Μια αφόρτιστη μεταλλική ράβδος κρέμεται όπως στο σχήμα από μονωτικό νήμα και ηρεμεί. Όταν πλησιάσουμε
ΕΡΓΑΣΙΑ 6. Ημερομηνία Παράδοσης: 29/6/09
 ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 120 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει:
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
Hλεκτρικό. Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Hλεκτρικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SRWAY, Physics fo scientists nd enginees YOUNG H.D., Univesity
Hλεκτρικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SRWAY, Physics fo scientists nd enginees YOUNG H.D., Univesity
Πυκνότητα φορτίου. dq dv. Μικρή Περιοχή. φορτίου. Χωρική ρ Q V. Επιφανειακή σ. dq da Γραµµική λ Q A. σ = dq dl. Q l. Γ.
 Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
ΘΕΜΑΤΑ ΠΑΛΑΙΟΤΕΡΩΝ ΕΞΕΤΑΣΕΩΝ
 ΘΕΜΑΤΑ ΠΑΛΑΙΟΤΕΡΩΝ ΕΞΕΤΑΣΕΩΝ Όπως θα παρατηρήσετε, τα θέματα αφορούν σε θεωρία που έχει διδαχθεί στις παραδόσεις και σε ασκήσεις που είτε προέρχονται από τα λυμένα παραδείγματα του βιβλίου, είτε έχουν
ΘΕΜΑΤΑ ΠΑΛΑΙΟΤΕΡΩΝ ΕΞΕΤΑΣΕΩΝ Όπως θα παρατηρήσετε, τα θέματα αφορούν σε θεωρία που έχει διδαχθεί στις παραδόσεις και σε ασκήσεις που είτε προέρχονται από τα λυμένα παραδείγματα του βιβλίου, είτε έχουν
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Τάξης ΓΕΛ 4 ο ΓΕΛ ΚΟΖΑΝΗΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Τάξης ΓΕΛ 4 ο ΓΕΛ ΚΟΖΑΝΗΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ - ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ Δυναμική ενέργεια δυο φορτίων Δυναμική ενέργεια τριών ή περισσοτέρων
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Τάξης ΓΕΛ 4 ο ΓΕΛ ΚΟΖΑΝΗΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ - ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ Δυναμική ενέργεια δυο φορτίων Δυναμική ενέργεια τριών ή περισσοτέρων
Κεφάλαιο 21 Ηλεκτρικά Φορτία και Ηλεκτρικά Πεδία. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 21 Ηλεκτρικά Φορτία και Ηλεκτρικά Πεδία Στατικός Ηλεκτρισµός, Ηλεκτρικό Φορτίο και η διατήρηση αυτού Ηλεκτρικό φορτίο στο άτοµο Αγωγοί και Μονωτές Επαγόµενα Φορτία Ο Νόµος του Coulomb Το Ηλεκτρικό
Κεφάλαιο 21 Ηλεκτρικά Φορτία και Ηλεκτρικά Πεδία Στατικός Ηλεκτρισµός, Ηλεκτρικό Φορτίο και η διατήρηση αυτού Ηλεκτρικό φορτίο στο άτοµο Αγωγοί και Μονωτές Επαγόµενα Φορτία Ο Νόµος του Coulomb Το Ηλεκτρικό
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Κίνηση σε Ηλεκτρικό Πεδίο.
 Κίνηση σε Ηλεκτρικό Πεδίο. 3.01. Έργο κατά την μετακίνηση φορτίου. Στις κορυφές Β και Γ ενός ισοπλεύρου τριγώνου ΒΓ πλευράς α= 2cm, βρίσκονται ακλόνητα δύο σημειακά ηλεκτρικά φορτία 1 =2μC και 2 αντίστοιχα.
Κίνηση σε Ηλεκτρικό Πεδίο. 3.01. Έργο κατά την μετακίνηση φορτίου. Στις κορυφές Β και Γ ενός ισοπλεύρου τριγώνου ΒΓ πλευράς α= 2cm, βρίσκονται ακλόνητα δύο σημειακά ηλεκτρικά φορτία 1 =2μC και 2 αντίστοιχα.
ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ 3.1 ΝΟΜΟΣ ΤΟΥ COULOMB
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ 3.1 ΝΟΜΟΣ ΤΟΥ COULOMB Η δύναμη που ασκείται μεταξύ σημειακών ηλεκτρικών φορτιών 1, είναι ανάλογη του γινομένου των φορτίων, και αντιστρόφως
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ 3.1 ΝΟΜΟΣ ΤΟΥ COULOMB Η δύναμη που ασκείται μεταξύ σημειακών ηλεκτρικών φορτιών 1, είναι ανάλογη του γινομένου των φορτίων, και αντιστρόφως
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Εισαγωγή Ο νόµος του Gauss: Μπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού της έντασης του ηλεκτρικού πεδίου. Βασίζεται
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Εισαγωγή Ο νόµος του Gauss: Μπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού της έντασης του ηλεκτρικού πεδίου. Βασίζεται
Κεφάλαιο Η1. Ηλεκτρικά πεδία
 Κεφάλαιο Η1 Ηλεκτρικά πεδία Ηλεκτρισµός και µαγνητισµός Οι νόµοι του ηλεκτρισµού και του µαγνητισµού έχουν πρωταρχικό ρόλο στη λειτουργία πολλών σύγχρονων συσκευών. Οι ενδοατοµικές και ενδοµοριακές δυνάµεις,
Κεφάλαιο Η1 Ηλεκτρικά πεδία Ηλεκτρισµός και µαγνητισµός Οι νόµοι του ηλεκτρισµού και του µαγνητισµού έχουν πρωταρχικό ρόλο στη λειτουργία πολλών σύγχρονων συσκευών. Οι ενδοατοµικές και ενδοµοριακές δυνάµεις,
Κεφάλαιο 5. Ενέργεια συστήματος
 Κεφάλαιο 5 Ενέργεια συστήματος Εισαγωγή στην ενέργεια Οι νόμοι του Νεύτωνα και οι αντίστοιχες αρχές μας επιτρέπουν να λύνουμε μια ποικιλία προβλημάτων. Ωστόσο, μερικά προβλήματα, που θεωρητικά μπορούν
Κεφάλαιο 5 Ενέργεια συστήματος Εισαγωγή στην ενέργεια Οι νόμοι του Νεύτωνα και οι αντίστοιχες αρχές μας επιτρέπουν να λύνουμε μια ποικιλία προβλημάτων. Ωστόσο, μερικά προβλήματα, που θεωρητικά μπορούν
ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο 30-03-014 ΘΕΜΑ 1 ο Α) Να επιλέξετε τη σωστή απάντηση σε καθεμία από τις επόμενες προτάσεις
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο 30-03-014 ΘΕΜΑ 1 ο Α) Να επιλέξετε τη σωστή απάντηση σε καθεμία από τις επόμενες προτάσεις
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
2. Οι νόµοι της κίνησης, οι δυνάµεις και οι εξισώσεις κίνησης
 Οι νόµοι της κίνησης, οι δυνάµεις και οι εξισώσεις κίνησης Βιβλιογραφία C Kittel, W D Knight, A Rudeman, A C Helmholz και B J oye, Μηχανική (Πανεπιστηµιακές Εκδόσεις ΕΜΠ, 1998) Κεφ, 3 R Spiegel, Θεωρητική
Οι νόµοι της κίνησης, οι δυνάµεις και οι εξισώσεις κίνησης Βιβλιογραφία C Kittel, W D Knight, A Rudeman, A C Helmholz και B J oye, Μηχανική (Πανεπιστηµιακές Εκδόσεις ΕΜΠ, 1998) Κεφ, 3 R Spiegel, Θεωρητική
Λύση Α. Σωστή η επιλογή α. Β.
 1) Αρνητικά φορτισμένο σωμάτιο κινείται σε ομογενές ηλεκτρικό πεδίο μεγάλης έκτασης. Να επιλέξετε τη σωστή πρόταση. Αν η κατεύθυνση της κίνησης του σωματίου παραμένει σταθερή, τότε: α. Συμπίπτει με την
1) Αρνητικά φορτισμένο σωμάτιο κινείται σε ομογενές ηλεκτρικό πεδίο μεγάλης έκτασης. Να επιλέξετε τη σωστή πρόταση. Αν η κατεύθυνση της κίνησης του σωματίου παραμένει σταθερή, τότε: α. Συμπίπτει με την
Δυνάμεις μεταξύ ηλεκτρικών φορτίων ΘΕΜΑ Δ
 Δυνάμεις μεταξύ ηλεκτρικών φορτίων ΘΕΜΑ Δ 4_15580 Δύο σημειακά ηλεκτρικά φορτία Q 1 = μc και Q = 8 μc, συγκρατούνται ακλόνητα πάνω σε οριζόντιο μονωτικό δάπεδο, στα σημεία Α και Β αντίστοιχα, σε απόσταση
Δυνάμεις μεταξύ ηλεκτρικών φορτίων ΘΕΜΑ Δ 4_15580 Δύο σημειακά ηλεκτρικά φορτία Q 1 = μc και Q = 8 μc, συγκρατούνται ακλόνητα πάνω σε οριζόντιο μονωτικό δάπεδο, στα σημεία Α και Β αντίστοιχα, σε απόσταση
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΦΥΣΙΚΗ ΓΙΑ ΜΗΧΑΝΙΚΟΥΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΗΛΕΚΤΡΙΣΜΟΣ ΜΑΓΝΗΤΙΣΜΟΣ
 ΦΥΣΙΚΗ ΓΙΑ ΜΗΧΑΝΙΚΟΥΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΗΛΕΚΤΡΙΣΜΟΣ ΜΑΓΝΗΤΙΣΜΟΣ Μοντέλο ατόμου m p m n =1,7x10-27 Kg m e =9,1x10-31 Kg Πυρήνας: πρωτόνια (p + ) και νετρόνια (n) Γύρω από τον πυρήνα νέφος ηλεκτρονίων (e -
ΦΥΣΙΚΗ ΓΙΑ ΜΗΧΑΝΙΚΟΥΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΗΛΕΚΤΡΙΣΜΟΣ ΜΑΓΝΗΤΙΣΜΟΣ Μοντέλο ατόμου m p m n =1,7x10-27 Kg m e =9,1x10-31 Kg Πυρήνας: πρωτόνια (p + ) και νετρόνια (n) Γύρω από τον πυρήνα νέφος ηλεκτρονίων (e -
3 + O. 1 + r r 0. 0r 3 cos 2 θ 1. r r0 M 0 R 4
 Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 8-9 Ν. Βλαχάκης. (α) Ποια είναι η ένταση και το δυναμικό του βαρυτικού πεδίου που δημιουργεί μια ομογενής σφαίρα πυκνότητας ρ και ακτίνας σε όλο το χώρο; Σχεδιάστε
Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 8-9 Ν. Βλαχάκης. (α) Ποια είναι η ένταση και το δυναμικό του βαρυτικού πεδίου που δημιουργεί μια ομογενής σφαίρα πυκνότητας ρ και ακτίνας σε όλο το χώρο; Σχεδιάστε
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
sin(30 o ) 4 cos(60o ) = 3200 Nm 2 /C (7)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ Η ηλεκτρική ϱοή διαµέσου µιας επιφάνειας A είναι
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ Η ηλεκτρική ϱοή διαµέσου µιας επιφάνειας A είναι
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ 1. Δύο ακίνητα σημειακά ηλεκτρικά φορτία q 1 = - 2 μc και q 2 = + 3 μc, βρίσκονται αντίστοιχα
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ 1. Δύο ακίνητα σημειακά ηλεκτρικά φορτία q 1 = - 2 μc και q 2 = + 3 μc, βρίσκονται αντίστοιχα στις θέσεις x 1 = - 3 m και x 2 = + 6 m ενός άξονα x'x, όπως φαίνεται στο παρακάτω
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ 1. Δύο ακίνητα σημειακά ηλεκτρικά φορτία q 1 = - 2 μc και q 2 = + 3 μc, βρίσκονται αντίστοιχα στις θέσεις x 1 = - 3 m και x 2 = + 6 m ενός άξονα x'x, όπως φαίνεται στο παρακάτω
Πεδίο, ονομάζεται μια περιοχή του χώρου, όπου σε κάθε σημείο της ένα ορισμένο φυσικό μέγεθος
 ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ Πεδίο, ονομάζεται μια περιοχή του χώρου, όπου σε κάθε σημείο της ένα ορισμένο φυσικό μέγεθος παίρνει καθορισμένη τιμή. Ηλεκτρικό πεδίο Ηλεκτρικό πεδίο ονομάζεται ο χώρος, που σε κάθε σημείο
ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ Πεδίο, ονομάζεται μια περιοχή του χώρου, όπου σε κάθε σημείο της ένα ορισμένο φυσικό μέγεθος παίρνει καθορισμένη τιμή. Ηλεκτρικό πεδίο Ηλεκτρικό πεδίο ονομάζεται ο χώρος, που σε κάθε σημείο
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Κεφάλαιο 5: Στατικός Ηλεκτρισμός
 Κεφάλαιο 5: Στατικός Ηλεκτρισμός Ο Θαλής ο Μιλήσιος (600 π.χ) παρατήρησε ότι αν τρίψουμε το ήλεκτρο (κεχριμπάρι) με ένα στεγνό μάλλινο ύφασμα αποκτά την ιδιότητα να έλκει μικρά κομματάκια από χαρτί, τρίχες
Κεφάλαιο 5: Στατικός Ηλεκτρισμός Ο Θαλής ο Μιλήσιος (600 π.χ) παρατήρησε ότι αν τρίψουμε το ήλεκτρο (κεχριμπάρι) με ένα στεγνό μάλλινο ύφασμα αποκτά την ιδιότητα να έλκει μικρά κομματάκια από χαρτί, τρίχες
ΚΕΦΑΛΑΙΟ 1 Ο ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ
 15 Α. ΝΟΜΟΣ ΤΟΥ COULOMB ΚΕΦΑΛΑΙΟ 1 Ο ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ 1. Στο χλωριούχο νάτριο (NaCl) η ελάχιστη απόσταση μεταξύ του ιόντος Να + και του ιόντος του Cl - είναι 2,3.10-10 m. Πόση είναι η
15 Α. ΝΟΜΟΣ ΤΟΥ COULOMB ΚΕΦΑΛΑΙΟ 1 Ο ΔΥΝΑΜΕΙΣ ΜΕΤΑΞΥ ΗΛΕΚΤΡΙΚΩΝ ΦΟΡΤΙΩΝ 1. Στο χλωριούχο νάτριο (NaCl) η ελάχιστη απόσταση μεταξύ του ιόντος Να + και του ιόντος του Cl - είναι 2,3.10-10 m. Πόση είναι η
Ηλεκτρικό φορτίο Ηλεκτρικό Πεδίο
 Ηλεκτρικό Φορτίο Ν.Coulomb Όπου χρειάζεται στις παρακάτω ασκήσεις θεωρείστε δεδομένες τις τιμές των μεγεθών: k ηλ = 9.10 9 Nm 2 /C 2, e = 1,6.10-19 C, m e = 9,1.10-31 kg, m p = 1,7.10-27 kg, g = 10 m/s
Ηλεκτρικό Φορτίο Ν.Coulomb Όπου χρειάζεται στις παρακάτω ασκήσεις θεωρείστε δεδομένες τις τιμές των μεγεθών: k ηλ = 9.10 9 Nm 2 /C 2, e = 1,6.10-19 C, m e = 9,1.10-31 kg, m p = 1,7.10-27 kg, g = 10 m/s
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ. Ενότητα 2: Ο νόμος του Gauss. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 2: Ο νόμος του Gauss Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 2: Ο νόμος του Gauss Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Επαναληπτικές Σημειώσεις για τη Φυσική Γενικής Παιδείας Β Λυκείου Κεφάλαιο 3.1 Δυνάμεις μεταξύ ηλεκτρικών φορτίων
 Επαναληπτικές Σημειώσεις για τη Φυσική Γενικής Παιδείας Β Λυκείου Κεφάλαιο 3.1 Δυνάμεις μεταξύ ηλεκτρικών φορτίων 3.1.1 Ο Νόμος του Coulomb Στη φύση εμφανίζονται δύο ειδών φορτία. Θετικό (+) και αρνητικό
Επαναληπτικές Σημειώσεις για τη Φυσική Γενικής Παιδείας Β Λυκείου Κεφάλαιο 3.1 Δυνάμεις μεταξύ ηλεκτρικών φορτίων 3.1.1 Ο Νόμος του Coulomb Στη φύση εμφανίζονται δύο ειδών φορτία. Θετικό (+) και αρνητικό
Λυμένες ασκήσεις. Ηλεκτρική δυναμική ενέργεια
 Λυμένες ασκήσεις Ηλεκτρική δυναμική ενέργεια 1. Στις κορυφές οριζόντιου ισόπλευρου τριγώνου Α,Β,Γ πλευράς α βρίσκονται τα φόρτια,όπου. α. Ποια η δυναμική ηλεκτρική ενέργεια του συστήματος; β. Ποιο το φυσικό
Λυμένες ασκήσεις Ηλεκτρική δυναμική ενέργεια 1. Στις κορυφές οριζόντιου ισόπλευρου τριγώνου Α,Β,Γ πλευράς α βρίσκονται τα φόρτια,όπου. α. Ποια η δυναμική ηλεκτρική ενέργεια του συστήματος; β. Ποιο το φυσικό
Κίνηση σε Ηλεκτρικό Πεδίο.
 Κίνηση σε Ηλεκτρικό Πεδίο. 3.01. Έργο κατά την μετακίνηση φορτίου. Στις κορυφές Β και Γ ενόςισοπλεύρου τριγώνου ΑΒΓ πλευράς α= 2cm, βρίσκονται ακλόνητα δύο σηµειακά ηλεκτρικά φορτία q 1 =2µC και q 2 αντίστοιχα.
Κίνηση σε Ηλεκτρικό Πεδίο. 3.01. Έργο κατά την μετακίνηση φορτίου. Στις κορυφές Β και Γ ενόςισοπλεύρου τριγώνου ΑΒΓ πλευράς α= 2cm, βρίσκονται ακλόνητα δύο σηµειακά ηλεκτρικά φορτία q 1 =2µC και q 2 αντίστοιχα.
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Χωρητικότητα Εικόνα: Όλες οι παραπάνω συσκευές είναι πυκνωτές, οι οποίοι αποθηκεύουν ηλεκτρικό φορτίο και ενέργεια. Ο πυκνωτής είναι ένα είδος κυκλώματος που μπορούμε να συνδυάσουμε
Φυσική για Μηχανικούς Χωρητικότητα Εικόνα: Όλες οι παραπάνω συσκευές είναι πυκνωτές, οι οποίοι αποθηκεύουν ηλεκτρικό φορτίο και ενέργεια. Ο πυκνωτής είναι ένα είδος κυκλώματος που μπορούμε να συνδυάσουμε
