Υυςικοχημικό Μελϋτη Σησ ταθερότητασ Γαλακτωμϊτων Πρωτεώνών Γϊλακτοσ Με Σην Σεχνικό Σησ Μονοφαςικόσ Φρωματογραφύασ Πεδύου
|
|
|
- Ῥεβέκκα Αλαφούζος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΣΜΗΜΑ ΧΗΜΕΙΑ Μεταπτυχιακό Δύπλωμα Ειδύκευςησ «ΦΗΜΕΙΑ ΤΛΙΚΨΝ ΠΡΟΗΓΜΕΝΗ ΣΕΦΝΟΛΟΓΙΑ» Υυςικοχημικό Μελϋτη Σησ ταθερότητασ Γαλακτωμϊτων Πρωτεώνών Γϊλακτοσ Με Σην Σεχνικό Σησ Μονοφαςικόσ Φρωματογραφύασ Πεδύου ΚΕΝΣΑ ΣΕΛΛΑ Επιβλζπων Κακθγθτισ: Γεώργιοσ Καραϊςκάκθσ ΠΑΣΡΑ 2011
2 Στους γονείς μου Ανδρζα και Ελζνη, στα αδζρφια μου Γιώργο και Χριστόφορο, στον Τάσο μου και στους φίλους μου! 1
3 Ευχαριστίες Η παρούςα διπλωματικό εργαςύα εκπονόθηκε ςτο Εργαςτόριο Υυςικοχημεύασ του Σμόματοσ Φημεύασ του Πανεπιςτημύου Πατρών υπό την επύβλεψη του Καθηγητό κ. Γεώργιου Καραώςκϊκη, τον οπούο ευχαριςτώ θερμϊ για τη ςυνεχό καθοδόγηςη και τισ πολύτιμεσ ςυμβουλϋσ του καθ όλη την διϊρκεια τησ μελϋτησ αυτόσ. Θα όθελα επύςησ να ευχαριςτόςω την Επύκουρο Καθηγότρια κα Αθαναςύα Κολιαδόμα για την καθοριςτικό ςυμβολό τησ ςτην διεκπεραύωςη τησ διπλωματικόσ μου εργαςύασ. Ευχαριςτώ θερμϊ τον Αναπληρωτό Καθηγητό του ΣΕΙ Καλαμϊτασ κ. Γιϊννη Καπόλο γιατύ η ςυμβολό και το ενδιαφϋρον του όταν πϊντα καθοριςτικϊ ςε κϊθε τεχνικό δυςκολύα που αντιμετωπύςαμε. Ευχαριςτώ επύςησ, τον Δρ. Βαςύλη Ρϊικο για την απύςτευτη βοόθεια που μου πρόςφερε ςε όλη την διϊρκεια των πειραμϊτων και για την τϋλεια ςυνεργαςύα μασ. Ευχαριςτώ πϊρα πολύ τον Δημότρη εβαςτό για την αςτεύρευτη ενϋργειϊ του και την καθημερινό και ϊψογη ςυνεργαςύα μασ. Σον ευχαριςτώ επύςησ, καθώσ και την Γεωργύα Λαώνιώτη και την Ωρτεμισ Βαγενϊ για το ευχϊριςτο κλύμα ςτον χώρο του εργαςτηρύου μασ. Ευχαριςτώ μϋςα από όλη μου την καρδιϊ τισ φύλεσ μου Ϊλενα, Ευδοκύα, Μϊρα, Δϋςποινα και Αγγελικό και τουσ φύλουσ μου Φρόςτο, Νύκο και Γιαννϊκη που όταν δύπλα μου πϊντα, για όλη την βοόθεια που μου προςϋφεραν, όποτε το χρειϊςτηκα, καθώσ και για την απαραύτητη ψυχικό δύναμη που αντλούςα από αυτούσ κϊθε ςτιγμό! Θα όθελα να πω ϋνα πολύ μεγϊλο ευχαριςτώ ςτον Σϊςο Καμπανό γιατύ εύναι μαζύ μου κϊθε ςτιγμό, ςτηρύζει την κϊθε μου κύνηςη, ϋχει υπομονό και κατανόηςη και που χϊρη ς αυτόν, η ολοκλόρωςη του μεταπτυχιακού μου ϋγινε πιο εύκολη και η διϊρκεια των ςπουδών μου πιο ευχϊριςτη! Σϋλοσ θα όθελα να ευχαριςτόςω ολόψυχα τουσ γονεύσ μου για την υπομονό τουσ, τουσ κόπουσ και τισ θυςύεσ που ϋκαναν για μϋνα και την ηθικό ςτόριξη που μου προςϋφεραν. Ευχαριςτώ τα αδερφϊκια μου γιατύ υπϊρχουν ςτη ζωό μου και με κϊνουν χαρούμενη και περόφανη! την οικογϋνειϊ μου αφιερώνω την εργαςύα αυτό για την αγϊπη που ϋδωςαν χωρύσ κανϋνα αντϊλλαγμα 2
4 Περιεχόμενα Ι. ΘΕΨΡΗΣΙΚΟ ΜΕΡΟ ΚΟΛΛΟΕΙΔΗ ΜΑΚΡΟΜΟΡΙΑ Γενικά Ηλεκτρικές ιδιότητες των κολλοειδών σωματιδίων ΓΑΛΑΚΣΨΜΑΣΑ Γενικά Αποσταθεροποίηση των γαλακτωμάτων Κρεμοποίηση υσσωμάτωση υγχώνευση Γαλακτωματοποιητές και μηχανισμός δράσης τους Πρωτεΐνες ως γαλακτωματοποιητές Καζεΐνες Πρωτεΐνες Ορού Γάλακτος (WP) υνθετικοί γαλακτωματοποιητές ΜΟΝΟΥΑΙΚΗ ΦΡΨΜΑΣΟΓΡΑΥΙΑ ΠΕΔΙΟΤ Γενικές αρχές της Μονοφασικής Φρωματογραφίας Πεδίου Μηχανισμός συγκράτησης και κλασικό μοντέλο συστήματος Μονοφασικής Φρωματογραφίας Πεδίου Μοντέλα λειτουργίας της Μονοφασικής Φρωματογραφίας Πεδίου Εγκάρσια συγκέντρωση δείγματος Η κλασική εξίσωση συγκράτησης Ύψος θεωρητικών πλακών
5 3.6.1 υνεισφορές στο ισοδύναμο ύψος θεωρητικών πλακών Επιμέρους τεχνικές της Μονοφασικής Φρωματογραφίας Πεδίου Γενικά Μονοφασική Φρωματογραφία Υυγοκεντρικού Πεδίου τερική Μονοφασική Φρωματογραφία Πεδίου Μονοφασική Φρωματογραφία Διασταυρούμενου Πεδίου Ροής Μονοφασική Φρωματογραφία Ηλεκτρικού Πεδίου Μονοφασική Φρωματογραφία Θερμικού Πεδίου Μονοφασική Φρωματογραφία Πεδίου και Δυναμικού Υράγματος ΤΓΚΡΙΗ ΜΟΝΟΥΑΙΚΗ ΦΡΨΜΑΣΟΓΡΑΥΙΑ ΠΕΔΙΟΤ ΜΕ ΑΛΛΕ ΣΕΦΝΙΚΕ ύγκριση της Μονοφασικής Φρωματογραφίας Πεδίου με άλλες τεχνικές μέτρησης μεγέθους σωματιδίων ύγκριση της Μονοφασικής Φρωματογραφίας Πεδίου με την κλασική Φρωματογραφία ΔΤΝΑΜΕΙ ΑΛΛΗΛΕΠΙΔΡΑΗ Δυνάμεις ανύψωσης Ολίσθηση σωματιδίου Δυνάμεις Van der Waals Ηλεκτροστατικές δυνάμεις ΗΛΕΚΣΡΟΝΙΚΗ ΜΙΚΡΟΚΟΠΙΑ ΑΡΨΗ ΑΝΣΙΚΕΙΜΕΝΟ ΣΗ ΠΑΡΟΤΑ ΕΡΓΑΙΑ ΙΙ. ΠΕΙΡΑΜΑΣΙΚΟ ΜΕΡΟ ΓΕΝΙΚΗ ΠΕΡΙΓΡΑΥΗ ΣΟΤ ΤΣΗΜΑΣΟ ΜΟΝΟΥΑΙΚΗ ΦΡΨΜΑΣΟΓΡΑΥΙΑ ΥΤΓΟΚΕΝΣΡΙΚΟΤ ΠΕΔΙΟΤ ΤΛΙΚΑ ΚΑΙ ΜΕΘΟΔΟΙ ΠΕΙΡΑΜΑΣΙΚΗ ΔΙΑΔΙΚΑΙΑ Προετοιμασία γαλακτωμάτων ελαίου νερού (o/w)
6 9.2 ύστημα της Μονοφασικής Φρωματογραφίας Υυγοκεντρικού Πεδίου Ηλεκτροφόρηση SDS-PAGE Οπτικό μικροσκόπιο Ηλεκτρονικό Μικροσκόπιο άρωσης ΤΝΘΗΚΕ ΠΕΙΡΑΜΑΣΙΚΗ ΔΙΑΔΙΚΑΙΑ Μεταβολή της πίεσης ομογενοποίησης των γαλακτωμάτων Μεταβολή της συγκέντρωσης των πρωτεϊνών του γάλακτος Μεταβολή της αναλογίας του τύπου των πρωτεϊνών γάλακτος Κινητική μελέτη συσσωμάτωσης των γαλακτωμάτων από πρωτεΐνες γάλακτος Προσθήκη συνθετικού γαλακτωματοποιητή (Tween 80) ΣΑΣΙΣΙΚΗ ΑΝΑΛΤΗ ΠΕΙΡΑΜΑΣΙΚΨΝ ΑΠΟΣΕΛΕΜΑΣΨΝ ΙIΙ. ΑΠΟΣΕΛΕΜΑΣΑ EΠΙΔΡΑΗ ΣΗ ΠΙΕΗ ΟΜΟΓΕΝΟΠΟΙΗΗ ΣΨΝ ΓΑΛΑΚΣΨΜΑΣΨΝ ΠΡΨΣΕΩΝΨΝ ΓΑΛΑΚΣΟ ΣΟ ΜΕΓΕΘΟ ΣΨΝ ΛΙΠΟΥΑΙΡΙΔΙΨΝ ΣΨΝ ΓΑΛΑΚΣΨΜΑΣΨΝ EΠΙΔΡΑΗ ΣΗ ΤΓΚΕΝΣΡΨΗ ΣΨΝ ΠΡΨΣΕΩΝΨΝ ΣΟΤ ΓΑΛΑΚΣΟ ΣΟ ΜΕΓΕΘΟ ΣΨΝ ΛΙΠΟΥΑΙΡΙΔΙΨΝ ΣΨΝ ΓΑΛΑΚΣΨΜΑΣΨΝ EΠΙΔΡΑΗ ΣΟΤ ΣΤΠΟΤ ΣΨΝ ΠΡΨΣΕΩΝΨΝ ΓΑΛΑΚΣΟ ΣΟ ΜΕΓΕΘΟ ΣΨΝ ΛΙΠΟΥΑΙΡΙΔΙΨΝ ΣΨΝ ΓΑΛΑΚΣΨΜΑΣΨΝ ΚΙΝΗΣΙΚΗ ΜΕΛΕΣΗ ΤΨΜΑΣΨΗ ΣΨΝ ΓΑΛΑΚΣΨΜΑΣΨΝ ΑΠΟ ΠΡΨΣΕΩΝΕ ΓΑΛΑΚΣΟ Ποιοτική μελέτη της κινητικής της συσσωμάτωσης των γαλακτωμάτων από πρωτεΐνες γάλακτος Μελέτη της κινητικής της συσσωμάτωσης των γαλακτωμάτων από καζεΐνες
7 15.3 Προσδιορισμός της σταθεράς ταχύτητας της συσσωμάτωσης των λιποσφαιριδίων των γαλακτωμάτων από καζεΐνες EΠΙΔΡΑΗ ΤΝΘΕΣΙΚΟΤ ΓΑΛΑΚΣΨΜΑΣΟΠΟΙΗΣΗ (TWEEN 80) ΣΟ ΜΕΓΕΘΟ ΣΨΝ ΛΙΠΟΥΑΙΡΙΔΙΨΝ ΣΨΝ ΓΑΛΑΚΣΨΜΑΣΨΝ ΠΡΨΣΕΩΝΨΝ ΓΑΛΑΚΣΟ ΙV. ΓΕΝΙΚΑ ΤΜΠΕΡΑΜΑΣΑ V. ΠΕΡΙΛΗΧΗ VI. ABSTRACT VΙΙ. ΒΙΒΛΙΟΓΡΑΥΙΑ
8 Ι. ΘΕΨΡΗΣΙΚΟ ΜΕΡΟ 7
9 1. ΚΟΛΛΟΕΙΔΗ ΜΑΚΡΟΜΟΡΙΑ 1.1 Γενικά Σα διαλύματα των κολλοειδών είναι συστήματα ετερογενή, που αποτελούνται από δύο φάσεις. Η μία είναι το μέσο διασποράς και η άλλη η διεσπαρμένη ουσία, οι οποίες βρίσκονται σε αναλογία με τους όρους διαλύτης και διαλυμένη ουσία που χρησιμοποιούνται στα κοινά διαλύματα. Σο μέσο διασποράς αποτελεί τη συνεχή φάση, ενώ η διεσπαρμένη ουσία την ασυνεχή φάση, η οποία κατανέμεται ομοιόμορφα. Ένα από τα βασικά χαρακτηριστικά των κολλοειδών διαλυμάτων είναι το γεγονός ότι το μέγεθος των σωματιδίων που αποτελούν τη διασπαρμένη ουσία είναι μεγαλύτερο του μεγέθους των μορίων, αλλά όχι σε σημείο που να διακρίνονται είτε με γυμνό μάτι είτε με το οπτικό μικροσκόπιο, όπως συμβαίνει στην περίπτωση των αιωρημάτων. Πιο συγκεκριμένα, το μέγεθος των κολλοειδών σωματιδίων κυμαίνεται από 1nm έως 1μm. Σα όρια αυτά δεν είναι αυστηρά, καθώς υπάρχουν περιπτώσεις όπου συναντώνται σωματίδια μεγαλύτερου μεγέθους (γαλακτώματα, μερικά αιωρήματα). το σημείο αυτό θα πρέπει να σημειωθεί πως δεν είναι απαραίτητο και οι τρεις διαστάσεις των σωματιδίων να βρίσκονται κάτω του ορίου του 1μm, καθώς η κολλοειδής συμπεριφορά έχει παρατηρηθεί και σε συστήματα ινών, όπου μόνο οι δύο διαστάσεις βρίσκονται στην περιοχή των κολλοειδών. Ένα σημαντικό στοιχείο, βάσει του οποίου χαρακτηρίζονται και ταξινομούνται τα διάφορα κολλοειδή, αποτελεί η σχέση τους ως προς το μέσο διασποράς. Αν τα σωματίδια της διασπαρμένης ουσίας προσροφούν μόρια από το μέσο διασποράς έχουμε τα λυόφιλα κολλοειδή, ενώ όταν δεν προσροφούν μόρια του μέσου διασποράς έχουμε τα λυόφοβα. την περίπτωση όπου το μέσο 8
10 διασποράς είναι το νερό, τα κολλοειδή διακρίνονται σε υδρόφοβα και υδρόφιλα, αντίστοιχα. Όσον αφορά στα κολλοειδή και λαμβάνοντας υπόψη τις μικρές διαστάσεις των σωματιδίων των κολλοειδών, ο λόγος της επιφάνειας προς τον όγκο είναι μεγάλος, με αποτέλεσμα να εμφανίζονται διαφορές στις ιδιότητες των μορίων τα οποία βρίσκονται στη διαφασική επιφάνεια από τις αντίστοιχες των μορίων της κύριας φάσης του αιωρήματος. Έτσι, κατά την περιγραφή ενός κολλοειδούς συστήματος, τα μόρια που βρίσκονται στη διαχωριστική μεταξύ των δύο φάσεων επιφάνεια, παίζουν σημαντικό ρόλο. υνεπώς, η χημεία των κολλοειδών συνδέεται με τη χημεία των επιφανειών. Ένα μέγεθος που χαρακτηρίζει τα κολλοειδή σωματίδια είναι η επιφάνεια ανά μονάδα μάζας (ειδική επιφάνεια). Πρόκειται ουσιαστικά για την επιφάνεια που αντιστοιχεί σε μάζα στερεού, που αποτελείται από ισομεγέθη σωματίδια και αυξάνεται με αντίστροφο τρόπο από τις γραμμικές διαστάσεις των σωματιδίων. Η ειδική επιφάνεια δίδεται από το λόγο δ/ρd, με δ να είναι το εμβαδόν της επιφάνειας, ρ η πυκνότητα του υλικού και d το μήκος της ακμής, προκειμένου για κυβικού σχήματος σωματίδια ή η διάμετρος για σφαιρικά σωματίδια. Ψς ενδεικτικά παραδείγματα κολλοειδών συστημάτων αναφέρονται: γάλα (αιώρημα σταγονιδίων λίπους σε υδατική φάση), χρώματα, μπογιές, λάσπες, ζελέ (αιωρήματα μακρομορίων σε υγρά-πηκτή), ομίχλες και καπνοί (αιωρήματα σταγονιδίων υγρών ή στερεών σωματιδίων, σε αέρια φάση). τα κολλοειδή συστήματα, μπορούν να συμπεριληφθούν και τα διαλύματα μακρομορίων υπό την προϋπόθεση ότι, το μέγεθος ενός μακρομορίου έχει διαστάσεις μεταξύ 1nm και 1μm. Tα διαλύματα των μακρομορίων σχηματίζονται αυθόρμητα και παρουσιάζονται θερμοδυναμικά σταθερά. Παρουσιάζουν παρόμοιες αθροιστικές ιδιότητες και ανάλογη συμπεριφορά με τα κολλοειδή συστήματα με την συνηθέστερα μετρούμενη ιδιότητα να είναι η ωσμωτική πίεση. 9
11 Άλλες βασικές ιδιότητες των μακρομορίων είναι η καθίζηση που υφίστανται με υπερφυγοκέντρηση καθώς και η σκέδαση του φωτός. Σα κολλοειδή συστήματα διασποράς, στα οποία όλα τα σωματίδια έχουν παρεμφερείς διαστάσεις, καλούνται μονοδιεσπαρμένα ή ομογενή συστήματα. την αντίθετη περίπτωση, όπου τα σωματίδια έχουν διαφορετικά μεγέθη, έχουμε τα πολυδιεσπαρμένα ή ετερογενή συστήματα. υχνά, παρατηρούνται και καταστάσεις κατά τις οποίες, σε ένα αιώρημα, τα σωματίδια ενώνονται το ένα με το άλλο, δημιουργώντας συσσωματώματα. Η φύση των συσσωματωμάτων συνδέεται άμεσα με τον τρόπο και τις συνθήκες κάτω από τις οποίες σχηματίζονται και είναι δυνατό να μεταβληθεί με την πάροδο του χρόνου. Σα συσσωματώματα αυτά καθιζάνουν υπό την επίδραση της βαρύτητας. Για την ακρίβεια, αν το σχηματιζόμενο συσσωμάτωμα είναι μεγαλύτερης πυκνότητας από το μέσο διασποράς, καθιζάνει, ενώ εάν είναι λιγότερο πυκνό, επιπλέει. Επιπρόσθετα, έχει παρατηρηθεί, ότι τα κολλοειδή συστήματα εμφανίζουν μεγάλη επιφάνεια στο όριο της διαχωριστικής επιφάνειας μεταξύ της συνεχούς και ασυνεχούς φάσεως. Αυτό έχει ως αποτέλεσμα, τόσο οι θερμοδυναμικές ιδιότητες, όσο και η ελεύθερη επιφάνειά τους, να καθορίζονται σε μεγάλο βαθμό από τα μόρια που βρίσκονται στην επιφάνεια των σωματιδίων των κολλοειδών [1]. 1.2 Ηλεκτρικές ιδιότητες των κολλοειδών σωματιδίων Επειδή τα κολλοειδή σωματίδια είναι φορτισμένα και το όλο σύστημα είναι ηλεκτρικά ουδέτερο, το μέσο διασποράς θα πρέπει να φέρει φορτίο αντίθετο από εκείνο των σωματιδίων. Έτσι με την εφαρμογή ενός ηλεκτρικού πεδίου στο σύστημα, τα κολλοειδή σωματίδια μετακινούνται προς την άνοδο ή την κάθοδο, ανάλογα με το φορτίο που φέρουν. Η μετακίνηση αυτή των κολλοειδών σωματιδίων, με την επίδραση ενός ηλεκτρικού πεδίου, είναι το γνωστό φαινόμενο της ηλεκτροφόρησης. Με τη βοήθεια κατάλληλων συσκευών που επιτρέπουν την 10
12 εφαρμογή εξωτερικού ηλεκτρικού πεδίου σε κολλοειδή συστήματα και την παρακολούθηση της κίνησης των σωματιδίων, είναι δυνατός ο πειραματικός προσδιορισμός της ηλεκτροφορητικής ευκινησία τους, u (cm 2 V -1 s -1 ). H ηλεκτροφορητική ευκινησία δίνεται από τη σχέση: u E (1) όπου με υ συμβολίζεται η ταχύτητα με την οποία κινούνται τα σωματίδια και με Ε η ένταση του εφαρμοζόμενου εξωτερικού ηλεκτρικού πεδίου. Σο φορτίο των κολλοειδών σωματιδίων (θετικό ή αρνητικό) προσδιορίζεται από τη διεύθυνση προς την οποία αυτά τα σωματίδια μετακινούνται. Οι ηλεκτροφορητικές ευκινησίες των κολλοειδών σωματιδίων σε υδατικά διαλύματα είναι της τάξης 10-4 cm 2 V -1 s -1. Αν και μικρά ποσά ηλεκτρολυτών σε κολλοειδή διαλύματα σταθεροποιούν τα τελευταία, τουλάχιστον σε νερό, εντούτοις μεγαλύτερα ποσά από αυτά συντελούν στην καταβύθισή τους. Σο φαινόμενο αυτό ονομάζεται κροκίδωση ή καταβύθιση. Έχει αποδειχθεί πειραματικά ότι, τα ιόντα που είναι υπεύθυνα για τη συσσωμάτωση και συνεπώς για την καταβύθιση ενός κολλοειδούς συστήματος, είναι εκείνα που τα φορτία τους είναι αντίθετα από εκείνο των κολλοειδών σωματιδίων και ότι, η ταχύτητα της καταβύθισης αυξάνεται με την αύξηση του σθένους αυτών των ιόντων. ε κάθε διεπιφάνεια στερεού-υγρού και συνεπώς και στην επιφάνεια κάθε κολλοειδούς σωματιδίου, που είναι η επαφή του στερεού σωματιδίου με το υγρό μέσο διασποράς, σχηματίζεται μία ηλεκτρική διπλοστοιβάδα από θετικά και αρνητικά φορτία. ύμφωνα με το μοντέλο της ηλεκτρικής διπλοστοιβάδας του Stern, πάνω στην επιφάνεια του στερεού υπάρχει στρώμα διπόλων νερού και μη εφυδατωμένων ιόντων. Ο γεωμετρικός τόπος των κέντρων αυτών των ιόντων συνιστά το εσωτερικό επίπεδο Helmholtz. Κοντά στην επιφάνεια του στερεού σχηματίζεται μια στοιβάδα από ιόντα που έχουν το αντίθετο φορτίο από αυτό της 11
13 επιφάνειας του στερεού. Η παρουσία των ιόντων αυτών εντοπίζεται σε ένα επίπεδο, το λεγόμενο εξωτερικό επίπεδο Helmholtz (outer Helmholtz plame, OHP). Αμέσως μετά υπάρχει η κινητή στοιβάδα διάχυσης, που εκτείνεται μέχρι την κύρια μάζα του διαλύματος. Σο ολικό φορτίο της στοιβάδας διάχυσης είναι ίσο και αντίθετο με εκείνο του σταθερού στρώματος. Λόγω των ηλεκτρικών φορτίων υπάρχει μία διαφορά δυναμικού μεταξύ της διαχωριστικής γραμμής του σταθερού στρώματος και της κινητής στοιβάδας διάχυσης και της κύριας μάζας του διαλύματος. Σο δυναμικό αυτό ονομάζεται ηλεκτροκινητικό δυναμικό ή δυναμικό ζήτα, ζ. τα κολλοειδή σωματίδια το σταθερό τμήμα της διπλοστοιβάδας αντιστοιχεί στα ιόντα που προσροφώνται από τα σωματίδια, ενώ η κινητή στοιβάδα διάχυσης αντιπροσωπεύεται από τα αντίθετα φορτισμένα ιόντα του διαλύματος. Η αμοιβαία άπωση των ηλεκτρικών διπλοστοιβάδων, που περιβάλλουν όλα τα κολλοειδή σωματίδια, πιθανόν να είναι υπεύθυνη και για τη σταθερότητα των τελευταίων, αφού τα εμποδίζει να πλησιάζουν μεταξύ τους και να συσσωματωθούν. Όταν στα κολλοειδή σωματίδια προσροφάται ένα ιόν με φορτίο αντίθετο από εκείνο των σωματιδίων, το δυναμικό ζ ελαττώνεται. Αυτό έχει σαν συνέπεια την ελάττωση της αμοιβαίας άπωσης των σωματιδίων και την πιθανή καταβύθισή τους. Σο δυναμικό ζ συνδέεται με την ηλεκτροφορητική ευκινησία, u, των σωματιδίων σύμφωνα με τις σχέσεις: 6u για (2α) 4u για (2β) τις παραπάνω σχέσεις συμβολίζουμε με η το ιξώδες και με ε τη διηλεκτρική σταθερά του μέσου διασποράς, r είναι η ακτίνα των σωματιδίων και κ -1 είναι το αντίστροφο μήκος Debye-Hückel [1]. 12
14 2. ΓΑΛΑΚΣΨΜΑΣΑ 2.1 Γενικά Γαλάκτωμα είναι η κολλοειδής διασπορά ενός υγρού σε ένα άλλο υγρό, μη αναμίξιμο με το πρώτο. τα γαλακτώματα τροφίμων οι δυο μη αναμίξιμες φάσεις είναι συνήθως το έλαιο και το νερό. Ο τύπος του γαλακτώματος εξαρτάται από την σχετική αναλογία των δύο υγρών του μίγματος. Σα γαλακτώματα διακρίνονται σε δύο κατηγορίες: στα γαλακτώματα ελαίου σε νερό (o/w) και στα γαλακτώματα νερού σε έλαιο (w/o), όπου η συνεχής φάση είναι το νερό ή το έλαιο, αντίστοιχα. Σο γάλα και η μαγιονέζα αποτελούν παραδείγματα τροφίμων που ανήκουν στην πρώτη κατηγορία (o/w), ενώ οι μαργαρίνες και το βούτυρο είναι τρόφιμα που ανήκουν στη δεύτερη κατηγορία (w/o). Για τον σχηματισμό ενός γαλακτώματος σημαντική επίδραση έχει η διεπιφάνεια, δηλαδή η επιφάνεια (Α) που διαχωρίζει την υδατική φάση από τη φάση του ελαίου. τα συστήματα ελαίου σε νερό, τα μη-πολικά μόρια του ελαίου δεν μπορούν να σχηματίσουν δεσμούς υδρογόνου με τα μόρια του νερού, λόγω του υψηλού υδρόφοβου χαρακτήρα τους, με αποτέλεσμα τα δυο υγρά να μην μπορούν να αναμιχθούν. Αυτό έχει ως αποτέλεσμα να μειώνεται το μέγεθος των σωματιδίων του ελαίου, που είναι διασκορπισμένα στο νερό, με σκοπό να ελαττωθεί η επιφάνεια επαφής τους με το νερό, δηλαδή η διεπιφάνεια, και επομένως ο αριθμός των ανεπιθύμητων αλληλεπιδράσεων μεταξύ των μορίων των δύο φάσεων. Αυτή η τάση μείωσης του μεγέθους των λιποσωματιδίων είναι το αποτέλεσμα της διεπιφανειακής τάσης, η τιμή της οποίας καθορίζεται από την έλλειψη ισορροπίας μεταξύ των μοριακών δυνάμεων. Εκφράζει το απαραίτητο ποσό ενέργειας (ΔG) που πρέπει να προσφερθεί στο σύστημα του γαλακτώματος, ώστε να αυξηθεί το εμβαδό της διεπιφάνειας μεταξύ των δυο μη αναμίξιμων υγρών 13
15 και το σύστημα να επανέλθει στην κατάσταση ισορροπίας. Η σχέση ανάμεσα στην απαιτούμενη ενέργεια ΔG και τη διεπιφανειακή τάση (γ), υπολογίζεται από τη σχέση: ΔG = γ ΔΑ (3) Από τη σχέση (3) προκύπτει ότι όσο λιγότερο αναμίξιμα είναι τα δυο υγρά τόσο πιο μεγάλη είναι η διεπιφανειακή τάση και άρα τόσο πιο μεγάλη είναι η απαιτούμενη ποσότητα ενέργειας για την επίτευξη της κατάστασης ισορροπίας. Η ενέργεια που απαιτείται ώστε τα σωματίδια της ασυνεχούς φάσης να διατμηθούν σε μικρότερα σωματίδια, προκαλώντας έτσι αύξηση του εμβαδού της διεπιφάνειας ανάμεσα στα δυο μη αναμίξιμα υγρά, παρέχεται κατά την έντονη ανάδευση του συστήματος με τη χρησιμοποίηση κατάλληλων συσκευών, όπως είναι οι ομογενοποιητές με πίεση ή υπερήχους κ.α. Η μείωση της απαιτούμενης ποσότητας ενέργειας επιτυγχάνεται με την προσθήκη στο σύστημα κατάλληλων ουσιών, των γαλακτωματοποιητών, οι οποίοι προκαλούν μείωση της διεπιφανειακής τάσης. 2.2 Αποσταθεροποίηση των γαλακτωμάτων Σα γαλακτώματα είναι θερμοδυναμικά ασταθή συστήματα γιατί η ανάμιξη ελαίου με νερό δεν ευνοείται ενεργειακά. Η αστάθειά τους οφείλεται σε μια σειρά από φυσικούς μηχανισμούς, όπως είναι η κρεμοποίηση, η συσσωμάτωση και η συγχώνευση. 14
16 χήμα 2.1: Υυσικοί μηχανισμοί αποσταθεροποίησης γαλακτωμάτων: (α) κρεμοποίηση, (β) συσσωμάτωση και (γ) συγχώνευση Κρεμοποίηζη Σα λιποσφαιρίδια του γαλακτώματος έχουν μικρότερη πυκνότητα από αυτή της υδατικής φάσης και έτσι έχουν την τάση να κινούνται ανοδικά χωρίς να παρατηρείται κάποια μεταβολή στο μέγεθός τους. τα γαλακτώματα ελαίου σε νερό παρατηρείται αρχικά μια μεταβολή της συγκέντρωσης του ελαίου με την απόσταση από τον πυθμένα του δοχείου, χωρίς να γίνεται αντιληπτό οπτικά. Με την πάροδο του χρόνου διακρίνονται δύο ξεχωριστές στοιβάδες, μια υδατική και μια εμπλουτισμένη με σταγονίδια ελαίου (χήμα 2.1α). Σο φαινόμενο αυτό είναι αντιστρεπτό γιατί με απλή ανάδευση επιτυγχάνεται ομοιόμορφη ανακατανομή των λιποσφαιριδίων σε όλο τον όγκο του γαλακτώματος. Ο βαθμός συσσωμάτωσης και η πολυδιασπορά του μεγέθους των λιποσφαιριδίων επιδρούν σημαντικά στην ταχύτητα της κρεμοποίησης του γαλακτώματος. Σα συσσωματώματα είναι μη ομοιογενή σφαιρίδια που συμπεριφέρονται ως σωματίδια μεγάλης διαμέτρου και κινούνται ταχύτερα από τα μεμονωμένα λιποσφαιρίδια μικρότερου μεγέθους συμπαρασύροντάς τα προς τα πάνω. Έτσι επιταχύνεται το φαινόμενο της κρεμοποίησης [2]. 15
17 2.2.2 σζζφμάηφζη Η συσσωμάτωση είναι επίσης μια αντιστρεπτή διαδικασία κατά την οποία τα λιποσφαιρίδια πλησιάζουν και δημιουργούν ένα τρισδιάστατο πλέγμα. Μέσα στα πλέγματα αυτά τα λιποσφαιρίδια συνδέονται χαλαρά με ελκτικές δυνάμεις, ακολουθώντας την κίνηση Brown, με αποτέλεσμα να συγκρούονται συχνά, κάτι που οδηγεί τελικά στην συσσωμάτωσή τους (χήμα 2.1β). ε αυτή την αλληλεπίδραση των λιποσφαιριδίων, κυριότερο ρόλο παίζουν οι ηλεκτροστατικές δυνάμεις, οι δυνάμεις Van der Waals και οι πολυμερικές δυνάμεις (steric forces) που οφείλονται στα προσροφημένα μόρια των γαλακτωματοποιητών [3] σγτώνεσζη Η συγχώνευση περιλαμβάνει τη διάσπαση του διεπιφανειακού υμενίου και τη συνένωση στη συνέχεια δύο ή περισσότερων λιποσφαιριδίων προς λιποσφαιρίδια μεγαλύτερου μεγέθους. Είναι μια μη αντιστρεπτή διαδικασία η οποία οδηγεί τελικά σε ολική κατάρρευση του γαλακτώματος και διαχωρισμό των δύο φάσεων, με αποτέλεσμα να παρατηρείται μακροσκοπικά η δημιουργία ελαιώδους στοιβάδας στο πάνω μέρος του γαλακτώματος. Σο φαινόμενο της συγχώνευσης εμφανίζεται κυρίως σε γαλακτώματα με λιποσφαιρίδια που έχουν παραμείνει συσσωματωμένα για μεγάλο χρονικό διάστημα [4]. 16
18 2.3 Γαλακτωματοποιητές και μηχανισμός δράσης τους Ψς γαλακτωματοποιητές ορίζονται οι ουσίες εκείνες οι οποίες διευκολύνουν το σχηματισμό ενός γαλακτώματος συμβάλλοντας ταυτόχρονα και στη σταθεροποίησή του. Για να δράσει μια ουσία ως γαλακτωματοποιητής, απαραίτητη προϋπόθεση είναι η παρουσία στο μόριό της τόσο υδρόφιλων όσο και υδρόφοβων ομάδων, πρέπει δηλαδή να έχει αμφιφιλική δράση. Ο μηχανισμός δράσης των γαλακτωματοποιητών στηρίζεται στην ικανότητά τους να προσροφώνται στη διεπιφάνεια ελαίου νερού, αντικαθιστώντας έτσι την άμεση και ανεπιθύμητη επαφή των μορίων του ελαίου με τα μόρια του νερού. Αυτό συμβαίνει με την έμμεση επαφή των μορίων του ελαίου με τις υδρόφοβες ομάδες του γαλακτωματοποιητή και των υδρόφιλων ομάδων του γαλακτωματοποιητή με τα μόρια του νερού. Ο βαθμός προσρόφησης ενός γαλακτωματοποιητή στη διεπιφάνεια είναι καθοριστικής σημασίας για το σχηματισμό και τη σταθεροποίηση ενός γαλακτώματος. Τπάρχουν πολλοί γαλακτωματοποιητές οι οποίοι κατατάσσονται σε δύο βασικές κατηγορίες: α) τους συνθετικούς γαλακτωματοποιητές (ή surfactants), και β) τις πρωτεΐνες. Ανάλογα με τις φυσικοχημικές τους ιδιότητες και τη μοριακή δομή τους, εμφανίζουν διαφορετικό μηχανισμό προσρόφησης Πρφηεΐνες φς γαλακηφμαηοποιηηές Οι πρωτεΐνες είναι αμφίφιλα μόρια, περιέχουν δηλαδή στο μόριό τους τόσο υδρόφοβες όσο και υδρόφιλες ομάδες, με αποτέλεσμα να έχουν μια «έμφυτη» ικανότητα να μεταναστεύουν εξαιρετικά γρήγορα στη διεπιφάνεια αέρα - νερού ή ελαίου - νερού. Αυτή η στιγμιαία μετακίνηση των πρωτεϊνών από το εσωτερικό της συνεχούς φάσης στη διεπιφάνεια είναι ενδεικτική του γεγονότος ότι η ελεύθερη ενέργεια των πρωτεϊνών είναι χαμηλότερη στη διεπιφάνεια από ό,τι στη συνεχή 17
19 φάση. Επομένως, όταν επέλθει η ισορροπία, η συγκέντρωση της πρωτεΐνης είναι μεγαλύτερη στη διεπιφάνεια από ότι στην υδατική φάση [5-7]. Οι πρωτεΐνες, σε αντίθεση με τους γαλακτωματοποιητές μικρού μοριακού βάρους, έχουν την ικανότητα να σχηματίζουν στη διεπιφάνεια ένα ισχυρό ιξωδοελαστικό υμένιο, με αποτέλεσμα τα γαλακτώματα να εμφανίζουν μεγαλύτερη σταθερότητα και ανθεκτικότητα σε τυχόν αλλαγές που λαμβάνουν χώρα στις συνθήκες που επικρατούν κατά την παρασκευή και την αποθήκευσή τους. Για το λόγο αυτό, άλλωστε, οι πρωτεΐνες χρησιμοποιούνται σε μεγαλύτερο βαθμό απ ότι οι γαλακτωματοποιητές μικρού μοριακού βάρους. Παρά το γεγονός ότι όλες οι πρωτεΐνες εμφανίζουν αμφιφιλική δράση, διαφοροποιούνται σημαντικά ως προς την επιφανειοδραστικότητά τους, με αποτέλεσμα να εμφανίζουν διαφορετικό βαθμό προσρόφησης. Οι διαφορές αυτές οφείλονται στη δευτεροταγή και τριτοταγή δομή τους και πιο συγκεκριμένα στην ελαστικότητα του πρωτεϊνικού μορίου, καθώς και στην κατανομή και αναλογία των υδρόφοβων και υδρόφιλων ομάδων της πρωτεΐνης στην επιφάνεια του μορίου. Γενικά, μια πρωτεΐνη για να εμφανίζει ικανοποιητική επιφανειακή δράση, θα πρέπει να φέρει τα εξής χαρακτηριστικά: α) να προσροφάται γρήγορα στη διεπιφάνεια, β) να ξεδιπλώνεται και να επανοριοθετείται γρήγορα σε αυτήν, και γ) να αλληλεπιδρά στη διεπιφάνεια με γειτονικά μόρια, σχηματίζοντας ένα ισχυρό και συνεκτικό ιξωδοελαστικό υμένιο, ανθεκτικό στη θερμική και μηχανική κίνηση των πρωτεϊνικών μορίων. Σο πόσο γρήγορα θα προσροφηθεί μια πρωτεΐνη στη ανασχηματισμένη διεπιφάνεια εξαρτάται από τα χαρακτηριστικά του μορίου της και πιο συγκεκριμένα από τον τρόπο κατανομής των υδρόφοβων και υδρόφιλων ομάδων στην επιφάνεια του. Αν η επιφάνεια είναι εξαιρετικά υδρόφιλη και δεν περιέχει διακριτές υδρόφοβες περιοχές, η πρωτεΐνη εμφανίζει μικρή πιθανότητα προσρόφησης, καθώς η 18
20 ελεύθερη ενέργειά της είναι χαμηλότερη στην υδατική φάση από ότι στη διεπιφάνεια. Όσο ο αριθμός των υδρόφοβων περιοχών στην επιφάνεια του πρωτεϊνικού μορίου αυξάνει, τόσο αυξάνει και η πιθανότητα της γρήγορης προσρόφησής του στη διεπιφάνεια. Κατά την προσρόφηση μιας πρωτεΐνης σε μια διεπιφάνεια, το μεγαλύτερο τμήμα του μορίου της παραμένει στη συνεχή φάση και μόνο ένα μικρό τμήμα αυτού προσροφάται σε αυτή. Σο αν η πρωτεΐνη θα παραμείνει ή όχι προσροφημένη στη διεπιφάνεια εξαρτάται από τον αριθμό των υδρόφοβων περιοχών του μορίου της που είναι προσροφημένες στη διεπιφάνεια. Όσο μεγαλύτερος είναι ο αριθμός των προσροφημένων υδρόφοβων περιοχών τόσο πιο ισχυρή είναι η δέσμευση του πρωτεϊνικού μορίου στη διεπιφάνεια και άρα και το υμένιο που σχηματίζεται. Η αύξηση του αριθμού των υδρόφοβων περιοχών εξαρτάται από την ελαστικότητα του μορίου της πρωτεΐνης. ε αντίθεση με τις σφαιροπρωτεΐνες, μόρια με μεγάλη ευελιξία, όπως είναι για παράδειγμα αυτά των καζεΐνών, μπορούν να υποστούν γρήγορες αλλαγές της δομής τους όταν προσροφηθούν σε μια διεπιφάνεια. Ο σχηματισμός τόσο υδρόφοβων και δισουλφιδικών δεσμών όσο και δεσμών υδρογόνου, ενισχύουν τη μηχανική ισχύ και τις ιξωδοελαστικές ιδιότητες του διεπιφανειακού υμενίου συμβάλλοντας έτσι στη σταθερότητα του συστήματος. Οι πρωτεΐνες χρησιμοποιούνται ευρέως στην παρασκευή τροφίμων τόσο για τα οργανοληπτικά χαρακτηριστικά και τη θρεπτική αξία που προσδίδουν στο τρόφιμο, όσο και για τις λειτουργικές ιδιότητές τους, όπως π.χ τη γαλακτωματοποιητική. Για να χρησιμοποιηθεί μια πρωτεΐνη στην παρασκευή τροφίμων θα πρέπει να πληρεί κάποιες προϋποθέσεις: να μην είναι τοξική, να είναι εύπεπτη, να βρίσκεται σε αφθονία, να έχει μεγάλη θρεπτική αξία και τέλος να φέρει τις κατάλληλες κάθε φορά λειτουργικές ιδιότητες ανάλογα με το τρόφιμο. Από όλες τις πρωτεΐνες που χρησιμοποιούνται στα τρόφιμα, ιδιαίτερο ενδιαφέρον παρουσιάζει η μελέτη των πρωτεϊνών του γάλακτος, λόγω της χρήσης τους σε ένα μεγάλο αριθμό προϊόντων, όπως γαλακτώματα, προϊόντα κρέατος και αρτοποιίας 19
21 κ.α. Σo γάλα περιέχει πρωτεΐνες υψηλής διατροφικής αξίας σε συγκέντρωση g/l. Οι πρωτεΐνες του γάλακτος χωρίζονται σε δυο κατηγορίες, τις καζεΐνες (caseins) και τις πρωτεΐνες ορού γάλακτος ή whey proteins (WP). τον Πίνακα 2.1 δίνεται η σύσταση (%) του γάλακτος σε πρωτεΐνες. Πίνακας 2.1 : Πρωτεϊνική σύσταση του γάλακτος. Πρωτεΐνη υγκέντρωση ύσταση (%) του συνόλου των (g/l) πρωτεϊνών Καζεΐνες α-καζεΐνες ας1-καζεΐνες ας2-καζεΐνες β-καζεΐνες κ-καζεΐνες γ-καζεΐνες Πρωτεΐνες ορού γάλακτος β-λακτογλοβουλίνη α-λακταλβουμίνη Πρωτεάσες Πρωτεΐνες Αίματος Αλβουμίνη ερίνης Ανοσογλοβουλίνη
22 Καζεΐνες Οι καζεΐνες αποτελούν το 80% των συνολικών πρωτεϊνών του γάλακτος (Πίνακας 2.1). Ο διαχωρισμός τους από τις υπόλοιπες πρωτεΐνες που περιέχει το γάλα γίνεται με τη μέθοδο της ισοηλεκτρικής καταβύθισης (pi 4.6). Η γνώση της πρωτοταγούς δομής τους παρέχει τη δυνατότητα εξαγωγής πολλών πληροφοριών, σχετικά με τις φυσικοχημικές και λειτουργικές τους ιδιότητες [8]. Μελέτες, ως προς την αλληλουχία των αμινοξέων των καζεϊνών, έδειξαν την παρουσία πολλών υδρόφοβων αμινοξέων στο μόριό τους, γεγονός που δικαιολογεί τη μεγάλη σταθερότητα της δομής τους σε υψηλές θερμοκρασίες. Επιπλέον, η κατανομή των υδρόφοβων και υδρόφιλων ομάδων αποκάλυψε ένα ακόμα μοναδικό χαρακτηριστικό των καζεϊνών. Σόσο τα υδρόφιλα όσο και τα υδρόφοβα αμινοξέα βρίσκονται συγκεντρωμένα σε ξεχωριστές ομάδες στην πρωτοταγή δομή τους, με συνέπεια το σχηματισμό ευδιάκριτων υδρόφιλων και υδρόφοβων περιοχών. Οι περιοχές αυτές θεωρούνται υπεύθυνες για τον ισχυρά πολικό και αμφίφιλο χαρακτήρα των καζεϊνών, στον οποίο αποδίδεται και η υψηλή γαλακτωματοποιητική ικανότητά τους. Ένα ακόμα χαρακτηριστικό των καζεϊνών είναι ότι εμφανίζουν στην τιμή ενεργού οξύτητας του γάλακτος (ph 6.8) υψηλό αρνητικό φορτίο και άρα υψηλή διαλυτότητα. Αυτό οφείλεται στο ότι στην πλειοψηφία τους οι πολικές περιοχές του μορίου αποτελούνται από φωσφορυλιωμένες σερίνες. Σέλος, η ύπαρξη στο μόριό τους, σε μεγάλο ποσοστό, του αμινοξέος προλίνη, έχει ως αποτέλεσμα οι δευτεροταγείς διαμορφώσεις των καζεϊνών να διακόπτονται, και οι καζεΐνες να μην εμφανίζονται οργανωμένες με τη μορφή τριτοταγών και τεταρτοταγών διαμορφώσεων, αλλά αντίθετα να υιοθετούν τη δομή πολυπεπτιδίων τυχαίας διαμόρφωσης. Αυτό έχει σαν συνέπεια το μόριο να εμφανίζει μια ιδιαίτερα ανοιχτή και ευέλικτη δομή, γεγονός που το καθιστά ικανό να προσροφάται στη διεπιφάνεια και να σχηματίζει διεπιφανειακά υμένια. Επιπλέον, η ιδιαιτερότητα αυτή 21
23 της δευτεροταγούς δομής, φαίνεται ότι συμβάλει σημαντικά στη μεγάλη σταθερότητα των μορίων των καζεϊνών σε υψηλές θερμοκρασίες [9]. Οι καζεΐνες, λόγω της φωσφορυλιωμένης και αμφιφιλικής τους δομής, εμφανίζουν την τάση να αλληλεπιδρούν σε υδατικά διαλύματα, παρουσία Ca 2+, σχηματίζοντας ενυδατωμένα σφαιρικά συστήματα, γνωστά ως μικκύλια (χήμα 2.2). Οι δυνάμεις που συγκρατούν τα διάφορα είδη καζεϊνών ενωμένα σε αυτή τη δομή είναι κυρίως υδρόφοβες. Σο γεγονός, όμως, ότι σε χαμηλές θερμοκρασίες η δομή των μικκυλίων δεν καταστρέφεται είναι ενδεικτικό ότι και άλλα είδη δεσμών συμμετέχουν στο σχηματισμό τους. Η παρουσία, στην επιφάνεια των σχηματιζόμενων μικκυλίων, της κ-καζεΐνης εμποδίζει τη συσσωμάτωσή τους λόγω στερεοχημικών παρεμποδίσεων. Επιπλέον, οι καζεΐνες που βρίσκονται με τη μορφή μικκυλίων εμφανίζουν μεγάλη θερμική σταθερότητα σε σύγκριση με την πλειοψηφία των πρωτεϊνών που χρησιμοποιούνται στα τρόφιμα. χήμα 2.2: Μικκύλιο καζεΐνης, A: υπομικκύλιο, B: προεξοχές αλυσίδας, C: Υωσφορικό ασβέστιο, D: κ-καζεΐνη, E: φωσφορικές ομάδες. 22
24 το εμπόριο κυκλοφορούν διάφορα προϊόντα καζεϊνών, οι ιδιότητες των οποίων διαφέρουν λόγω της διαφορετικής μεθόδου παραλαβής τους. Η επιλογή του κατάλληλου κάθε φορά προϊόντος γίνεται σύμφωνα με τις λειτουργικές ιδιότητες που απαιτούνται κατά την παρασκευή ενός συγκεκριμένου τροφίμου. την παρούσα εργασία χρησιμοποιήθηκε το άλας της καζεΐνης με νάτριο, γνωστό ως sodium caseinate (Na-cas). Σο προϊόν αυτό εμφανίζει βελτιωμένες φυσικοχημικές ιδιότητες έναντι των άλλων καζεϊνικών αλάτων, όπως εξαιρετική διαλυτότητα σε υδατικά διαλύματα και μεγάλη θερμική σταθερότητα. Ακόμη, η αμφιφιλική του δομή σε συνδυασμό με την υψηλή επιφανειακή του δράση, λόγω του μικρού βαθμού συσσωμάτωσης που παρουσιάζει, του προσδίδουν μεγάλη ικανότητα σχηματισμού γαλακτωμάτων [10,11] Πρωτεΐνες Ορού Γάλακτος (WP) Οι πρωτεΐνες ορού του γάλακτος (whey proteins, WP) αποτελούν τη δεύτερη μεγάλη κατηγορία πρωτεϊνών που περιέχονται στο γάλα και βρίσκονται σε ποσοστό 20% (Πίνακας 2.1). Λόγω της υψηλής περιεκτικότητάς τους σε θειούχα αμινοξέα είναι ιδιαίτερα επιθυμητές ως θρεπτικά συστατικά. Παραλαμβάνονται από τη συμπύκνωση του τυρογάλακτος, και προκύπτει το συμπυκνωμένο (whey protein concentrate, WPC) και το υπερσυμπυκνωμένο κλάσμα (whey protein isolate, WPI) με 59-80% και 80 92% πρωτεΐνη επί ξηρού, αντίστοιχα. Σο κλάσμα των πρωτεϊνών ορού περιλαμβάνει σε μεγάλο ποσοστό τις σφαιροπρωτεΐνες β- λακτογλοβουλίνη (χήμα 2.3) και α-λακταλβουμίνη (χήμα 2.4) [8]. 23
25 χήμα 2.3: Σρισδιάστατη δομή της β λακτογλοβουλίνης. χήμα 2.4: Σρισδιάστατη δομή της α λακταλβουμίνης. Οι πρωτεΐνες ορού του γάλακτος, σε αντίθεση με τις καζεΐνες, εμφανίζουν μια ομοιομορφία ως προς την κατανομή των υδρόφοβων και υδρόφιλων περιοχών στην επιφάνεια των μορίων τους, με τις υδρόφιλες να υπερτερούν έναντι των υδρόφοβων. Έτσι, οι πρωτεΐνες αυτές έχουν την ικανότητα να αναδιπλώνονται στο χώρο σχηματίζοντας τρισδιάστατες δομές, στο εσωτερικό των οποίων είναι «θαμμένες» οι υδρόφοβες ομάδες. Αυτό έχει ως αποτέλεσμα τα πρωτεϊνικά μόρια να εμφανίζουν έντονα την τάση να αλληλεπιδρούν με υδρόφοβα μόρια μικρού 24
26 μοριακού βάρους, ενώ η μεταξύ τους αλληλεπίδραση, προς σχηματισμό συσσωματωμάτων, είναι σημαντικά μειωμένη. Όπως οι καζεΐνες, έτσι και οι πρωτεΐνες ορού, εμφανίζουν μεγάλη διαλυτότητα στην τιμή ενεργού οξύτητας του γάλακτος. Αυτό οφείλεται στο υψηλό αρνητικό φορτίο που παρατηρείται στην επιφάνεια των μορίων τους, εξαιτίας της ιδιαιτερότητάς τους ως προς την κατανομή των υδρόφοβων και υδρόφιλων ομάδων. Επιπλέον, στην ιδιαιτερότητά τους αυτή οφείλεται και το μοναδικό χαρακτηριστικό τους να παραμένουν ευδιάλυτες ακόμα και στο ισοηλεκτρικό τους σημείο (pi ), καθώς λόγω του αυξημένου αριθμού υδρόφιλων ομάδων εμφανίζουν, ακόμα και στο ισοηλεκτρικό σημείο, ένα μεγάλο αριθμό φορτισμένων υδρόφιλων αμινοξέων. Έτσι, η ενυδάτωση αυτών των πολικών ομάδων δημιουργεί απωστικές δυνάμεις ικανές να εμποδίσουν τη συσσωμάτωση των μορίων λόγω υδρόφοβων αλληλεπιδράσεων. ε αντίθεση με τις καζεΐνες, οι πρωτεΐνες ορού του γάλακτος εμφανίζουν μειωμένη σταθερότητα, ως προς τη δομή τους, σε υψηλές θερμοκρασίες. Γενικά, η αύξηση της θερμοκρασίας προκαλεί μη αντιστρεπτές μεταβολές στη δομή των μορίων, με αποτέλεσμα να εμφανίζονται στην επιφάνεια υδρόφοβες ομάδες, το ποσοστό των οποίων αυξάνει σημαντικά σε υψηλότερες θερμοκρασίες. Αυτό έχει ως συνέπεια την ανάπτυξη υδρόφοβων αλληλεπιδράσεων, οι οποίες οδηγούν στο σχηματισμό συσσωματωμάτων και σε μείωση της διαλυτότητάς τους. Οι πρωτεΐνες ορού είναι, λοιπόν, ιδιαίτερα επιρρεπείς στην αποδιοργάνωση της δομής τους και για το λόγο αυτό είναι απαραίτητος ο προσεκτικός χειρισμός τους κατά το στάδιο της παραλαβής τους. ύμφωνα με τη βιβλιογραφία [8,12], η γαλακτωματοποιητική ικανότητα των πρωτεϊνών ορού βελτιώνεται αν λάβει χώρα μερική αποδιοργάνωση της δομής τους. Αυτό οφείλεται στο γεγονός ότι οι πρωτεΐνες αυτές στερούνται της αμφιφιλικής δομής των καζεϊνών, με αποτέλεσμα να έχουν μειωμένη ικανότητα αποδιοργάνωσης στη διεπιφάνεια. 25
27 2.3.2 σνθεηικοί γαλακηφμαηοποιηηές Οι συνθετικοί γαλακτωματοποιητές είναι επιφανειοδραστικές ουσίες χαμηλού μοριακού βάρους. υγκεκριμένα είναι μικρά αμφίφιλα μόρια τα οποία φέρουν μια υδρόφιλη ομάδα στο ένα άκρο («κεφαλή») και μια υδρόφοβη ομάδα στο άλλο άκρο («ουρά»). Σο υδρόφοβο τμήμα τους αποτελείται συνήθως από μια ή περισσότερες ανθρακικές αλυσίδες 10 έως 20 ατόμων άνθρακα. Οι αλυσίδες αυτές μπορεί να είναι είτε κορεσμένες είτε ακόρεστες, ενώ συνήθως είναι αλειφατικές. Σο υδρόφιλο τμήμα τους διαφοροποιείται και, ανάλογα με τη φύση του, οι γαλακτωματοποιητές χαμηλού μοριακού βάρους διακρίνονται σε ανιονικούς, κατιονικούς και ουδέτερους. Οι λειτουργικές ιδιότητες κάθε γαλακτωματοποιητή μικρού μοριακού βάρους καθορίζονται από τη χημική του δομή, η οποία είναι χαρακτηριστική για τον καθένα. Για το λόγο αυτό, είναι απαραίτητη η επιλογή του καταλληλότερου κάθε φορά γαλακτωματοποιητή ανάλογα με τη χρήση για την οποία προορίζεται. Η πλειοψηφία των γαλακτωματοποιητών χαμηλού μοριακού βάρους δεν εμφανίζει μεγάλη διαλυτότητα ούτε στο νερό ούτε στη φάση του ελαίου. Αντίθετα, εμφανίζουν μια βέλτιστη διαλυτότητα όταν βρίσκονται σε ένα μερικώς υδρόφιλο και μερικώς υδρόφοβο περιβάλλον, όπως είναι αυτό της διεπιφάνειας ελαίου νερού. ε υδατικά διαλύματα βρίσκονται με την μορφή μικκυλίων, σχηματίζουν δηλ. μια υδρόφιλη επιφάνεια και μια υδρόφοβη κοιλότητα που συμβάλλουν στη ελάττωση των απωστικών αλληλεπιδράσεων με τα μόρια του διαλύτη. Οι δομές αυτές είναι θερμοδυναμικά σταθερές, ενώ το σχήμα τους εξαρτάται από την πολικότητα του γαλακτωματοποιητή, καθώς και από τη μοριακή γεωμετρία του. Οι αλληλεπιδράσεις που σταθεροποιούν αυτές τις δομές είναι σχετικά ασθενείς σε σχέση με τη θερμική ενέργεια, με αποτέλεσμα οι διαμορφώσεις αυτές να είναι ιδιαίτερα ευέλικτες, αλλά και ευαίσθητες σε αλλαγές των συνθηκών του περιβάλλοντός τους, όπως η θερμοκρασία, η ενεργός οξύτητα, η ιονική ισχύς κ.α. 26
28 Η γαλακτωματοποιητική ικανότητα των μορίων αυτών οφείλεται, όπως και στην περίπτωση των πρωτεϊνών, στην αμφιφιλική τους δομή. Παρόλα αυτά, όμως, ο μηχανισμός προσρόφησης των γαλακτωματοποιητών μικρού μοριακού βάρους στη διεπιφάνεια, είναι διαφορετικός από αυτόν των πρωτεϊνών. Αυτό οφείλεται στο γεγονός ότι, στην περίπτωση των γαλακτωματοποιητών μικρού μοριακού βάρους, οι υδρόφιλες και υδρόφοβες ομάδες βρίσκονται στα άκρα των μορίων σε αντίθεση με τις πρωτεΐνες που βρίσκονται σε όλο το μόριο. Για το λόγο αυτό δεν υφίστανται παρεμποδίσεις στην προσρόφηση με αποτέλεσμα να προσροφώνται με τη μορφή ενός μονομοριακού στρώματος στο οποίο η υδρόφιλη «ουρά» εκτείνεται προς την υδατική φάση ενώ το υδρόφοβο τμήμα προς τη φάση του ελαίου (χήμα 2.5). Αυτό έχει ως αποτέλεσμα τη μείωση των ανεπιθύμητων αλληλεπιδράσεων, καθώς και τη μείωση της διεπιφανειακής τάσης, γεγονός που διευκολύνει το σχηματισμό του γαλακτώματος. Μετά την προσρόφηση στη διεπιφάνεια, ο γαλακτωματοποιητής πρέπει να σταθεροποιήσει το σύστημα εμποδίζοντας τη συσσωμάτωση των λιποσφαιριδίων. Ο τρόπος με τον οποίο επιτυγχάνεται αυτό διαφοροποιείται ανάλογα με την κατηγορία στην οποία ανήκει ο γαλακτωματοποιητής. Έτσι, μπορεί να σταθεροποιεί το γαλάκτωμα είτε με το να παρέχει σε όλα τα λιποσφαιρίδια το ίδιο ηλεκτρικό φορτίο (ανιονικός), είτε με το σχηματισμό ενός πολυστρωματικού διεπιφανειακού υμενίου (αντί ενός μονοστρωματικού), είτε λόγω στερεοχημικών αλληλεπιδράσεων και άλλων απωστικών δυνάμεων (ουδέτερος). χήμα 2.5: χηματική αναπαράσταση προσρόφησης του γαλακτωματοποιητή στη διεπιφάνεια ελαίου-νερού. 27
29 3. ΜΟΝΟΥΑΙΚΗ ΦΡΨΜΑΣΟΓΡΑΥΙΑ ΠΕΔΙΟΤ 3.1 Γενικές αρχές της Μονοφασικής Φρωματογραφίας Πεδίου Η Μονοφασική Φρωματογραφία Πεδίου (Μ.Φ.Π.) είναι μία σχετικά νέα οικογένεια τεχνικών εκλεκτικής προσρόφησης, ικανών για ταυτόχρονο διαχωρισμό και ανάλυση μακρομορίων και κολλοειδών υλικών. Η μέθοδος αυτή, που ανακαλύφθηκε από τον J.C.Giddings στο Σμήμα Φημείας του Πανεπιστημίου της Utah (ΗΠΑ) το 1966, καλείται επίσης και «χρωματογραφία σε μία φάση». Έχει κοινά χαρακτηριστικά με την κλασική χρωματογραφία, με τη διαφορά ότι ο μηχανισμός συγκράτησης απαιτεί την εφαρμογή εξωτερικού πεδίου[13]. Η περιοχή δειγμάτων της μεθόδου εκτείνεται από περίπου 1nm σε περισσότερα από 100μm με συνέπεια να ενσωματώνει και τα απλά και σύνθετα μακρομόρια με βιολογικές, βιοϊατρικές, βιομηχανικές και περιβαλλοντικές εφαρμογές. Η Μ.Φ.Π. διαχωρίζει τις ουσίες με βάση το μοριακό βάρος, το μέγεθος, το συντελεστή διάχυσης ή το ηλεκτρικό τους φορτίο. υγχρόνως με το διαχωρισμό μετρούνται φυσικοχημικές ιδιότητες των συστατικών, όπως η μάζα, το μέγεθος, η πυκνότητα, το φορτίο, η διάχυση και η ηλεκτροφορητική κινητικότητα. Ο διαχωρισμός των συστατικών συμβαίνει από τη διαφορετική συγκράτηση σε ένα ρεύμα υγρού που διατρέχει τη στήλη του συστήματος. Αντί ακίνητης φάσης στη Μ.Φ.Π., η στήλη που χρησιμοποιείται είναι κενή και η εκλεκτική προσρόφηση, και συνεπώς ο διαχωρισμός των συστατικών, προκαλούνται από μία εξωτερικά εφαρμοζόμενη δύναμη, η οποία είναι η μόνη υπεύθυνη για το φαινόμενο του διαχωρισμού. Σα διαχωρισμένα συστατικά εξέρχονται στη συνέχεια από τη στήλη και μέσω ενός κατάλληλου ανιχνευτή λαμβάνεται το χρωματογράφημα, το οποίο είναι η καταγραφή του σήματος του ανιχνευτή έναντι του χρόνου από την είσοδο του δείγματος. Ο παρατηρηθείς χρόνος συγκράτησης συσχετίζεται με τις διάφορες φυσικοχημικές ιδιότητες των συγκρατούμενων ειδών και η μέτρηση των τιμών του 28
30 μπορεί επομένως να αποδώσει αυτές τις ιδιότητες για κάθε διαχωρισμένο συστατικό[14]. 3.2 Μηχανισμός συγκράτησης και κλασικό μοντέλο συστήματος Μονοφασικής Φρωματογραφίας Πεδίου Ο μηχανισμός της Μ.Φ.Π. συνδυάζει τα στοιχεία της χρωματογραφίας και των τεχνικών που χρησιμοποιούν πεδίο (π.χ. ηλεκτροφόρηση, υπερφυγοκέντρηση), όπως θα αναφερθεί στη συνέχεια. Σο εξωτερικά εφαρμοζόμενο πεδίο δεν οδηγεί άμεσα σε διαχωρισμό. Αντ' αυτού, το πεδίο εφαρμόζεται κάθετα στη ροή του διαλύτη και αλληλεπιδρώντας με τη διεσπαρμένη ουσία, ωθεί τα συστατικά της προς το ένα τοίχωμα της στήλης. Όταν αυτά συγκεντρωθούν τότε μία άλλη παράμετρος εμφανίζεται, η λεγόμενη διάχυση, η οποία παρεμποδίζει την προαναφερθείσα συγκέντρωση των μορίων δρώντας σε αντίθετη κατεύθυνση από εκείνη του εξωτερικού πεδίου. Έτσι δημιουργείται μία λεπτή στοιβάδα από μόρια (ή σωματίδια) της ουσίας, που ονομάζεται «στοιβάδα στατικής κατάστασης»[2]. χεδόν πάντα, η στήλη διαχωρισμού της Μ.Φ.Π. δημιουργείται μεταξύ δύο παράλληλων επίπεδων τοιχωμάτων-πλακών, ορθογώνιου σχήματος με τις επιθυμητές διαστάσεις. Είναι κενή με τα άκρα της να είναι ενωμένα ώστε να είναι εφικτή η ροή του φέροντος διαλύτη, όπως φαίνεται και στο χήμα 3.1. Έχει τη μορφή ενός παραλληλεπιπέδου με τυπικό μήκος L, περίπου cm, πλάτος b, περίπου 1-2 cm και πάχος w, περίπου 0,1-0,25 mm. Σο γεγονός ότι το πλάτος b, έτσι όπως είναι διαμορφωμένη η στήλη διαχωρισμού, είναι πολύ μεγάλο σε σχέση με το πάχος w, καθιστά επιτρεπτή τη χρησιμοποίηση της θεωρίας των παράλληλων πλακών για την περιγραφή της συμπεριφοράς του προς ανάλυση δείγματος. 29
31 Οι άνισες ταχύτητες που αποκτούν τα χημικά είδη της διεσπαρμένης ουσίας εξαιτίας του παραβολικού μετώπου της ροής του διαλύτη, προκαλούν έπειτα το διαχωρισμό, ο οποίος εκτυλίσσεται κατά μήκος του άξονα ροής του διαλύτη. Σο προς ανάλυση δείγμα εισάγεται στη στήλη με τη βοήθεια κατάλληλης συσκευής ένεσης (μικροσύριγγας). Tα σωματίδια που βρίσκονται κοντά στο κέντρο της στήλης εκλούονται πρώτα, ενώ τα σωματίδια που βρίσκονται πιο κοντά στα τοιχώματα της στήλης εκλούονται αργότερα. την αρχή αυτή στηρίζεται και η εκλεκτική συγκράτηση. χήμα 3.1: χηματική αναπαράσταση της στήλης ενός συστήματος Μ.Φ.Π. όπου φαίνεται αναλυτικά το παραβολικό μέτωπο της ροής του διαλύτη. 30
32 3.3 Μοντέλα λειτουργίας της Μονοφασικής Φρωματογραφίας Πεδίου Η λειτουργία της Μ.Φ.Π., όπως προαναφέρθηκε, χαρακτηρίζεται από την εφαρμογή ενός πεδίου κάθετα στην κατεύθυνση ροής του φέροντα διαλύτη στη στήλη διαχωρισμού. Με αυτόν τον τρόπο προκαλείται μία διασπορά των σωματιδίων που αναλύονται κατά μήκος της διατομής της στήλης με αποτέλεσμα το διαχωρισμό τους. Τπάρχουν διάφοροι μηχανισμοί αλληλεπίδρασης του πεδίου με τα σωματίδια που ρέουν σ έναν κλειστό αγωγό, οι οποίοι οδηγούν σε μια χαρακτηριστική μορφή εγκάρσιας διασποράς των σωματιδίων του δείγματος. Κάθε μηχανισμός αλληλεπίδρασης οδηγεί και σε συγκεκριμένο τρόπο λειτουργίας της Μ.Φ.Π. Οι εξισώσεις συγκράτησης είναι συγκεκριμένες για κάθε μηχανισμό και οι ερμηνείες των δεδομένων για το αναλυόμενο δείγμα είναι διαφορετικές ανάλογα με την τεχνική που χρησιμοποιείται. Με βάση τις πειραματικές συνθήκες λειτουργίας, οι οποίες μπορούν να καθοριστούν και να εισάγουν έναν συγκεκριμένο μηχανισμό διαχωρισμού, δύναται να γίνει γνωστός ο τρόπος λειτουργίας. Βέβαια δεν αποκλείεται και η περίπτωση να υπάρχουν και περισσότεροι του ενός μηχανισμοί, οι οποίοι να δρουν ταυτόχρονα και να καθιστούν δύσκολη την ερμηνεία μεταφοράς των σωματιδίων του δείγματος. Παρ όλα αυτά, υπάρχει γενικά ένα κυρίαρχο μοντέλο λειτουργίας που καθορίζει τη γενική μορφή της εγκάρσιας διασποράς των σωματιδίων του δείγματος και με βάση αυτό θα χρησιμοποιηθούν οι εξισώσεις που το αφορούν, ούτως ώστε να περιγραφεί η διαδικασία συγκράτησης στη Μ.Φ.Π. Ο σαφής προσδιορισμός του κυρίαρχου αυτού μοντέλου λειτουργίας είναι αναγκαίος για την αποφυγή κάθε είδους σφαλμάτων και παρερμηνειών κατά την επεξεργασία των δεδομένων. Σο μοντέλο λειτουργίας που συναντάται πιο συχνά στη Μ.Φ.Π., είναι το μοντέλο Βrown, καθότι εφαρμόζεται κυρίως σε μακρομοριακά και κολλοειδή υλικά, για τα οποία η επίδραση στην κίνηση Brown είναι σημαντική. Κύριο χαρακτηριστικό αυτού του μοντέλου είναι η σταθερή μείωση που παρατηρείται στη συγκέντρωση 31
33 του δείγματος με την αύξηση της απόστασης από το ένα τοίχωμα. τη βιβλιογραφία παρατηρείται η αναφορά αυτού του μοντέλου ως η «κανονική περιοχή λειτουργίας» της Μ.Φ.Π.[15] 3.4 Εγκάρσια συγκέντρωση δείγματος Όπως έχει προαναφερθεί (Παρ. 3.2), τα προς ανάλυση σωματίδια του δείγματος, υπό την επίδραση του εξωτερικού πεδίου, σχηματίζουν μία «στοιβάδα στατικής κατάστασης» στο ένα τοίχωμα της στήλης διαχωρισμού. Έχει αποδειχθεί ότι στην κατάσταση αυτή, που είναι κατάσταση ισορροπίας, η συγκέντρωση των σωματιδίων του δείγματος είναι συγκέντρωση ισορροπίας. Για να υπολογιστεί αυτή η συγκέντρωση θα πρέπει να μελετηθεί η συμπεριφορά του δείγματος στη διεύθυνση του πεδίου. Έστω J(x) ο ρυθμός ροής των σωματιδίων της διεσπαρμένης ουσίας κατά τη διεύθυνση εφαρμογής του εξωτερικού πεδίου, δηλ. ο αριθμός των σωματιδίων που διασχίζουν μία μονάδα επιφάνειας στη διεύθυνση x, κάθετα στον άξονα x (όπως αυτός ορίζεται στο χ. 3.1) ανά μονάδα χρόνου. Αυτός ο ρυθμός ροής αποτελείται από έναν παράγοντα συγκέντρωσης, Jc, που οφείλεται στη δύναμη που ασκεί το πεδίο στα σωματίδια, καθώς και από έναν παράγοντα διάχυσης, Jd. Αν θεωρήσουμε Uf την ταχύτητα των σωματιδίων λόγω του πεδίου, ή αλλιώς την απόσταση που διανύουν τα σωματίδια στη διεύθυνση του πεδίου ανά μονάδα χρόνου, τότε ο αριθμός των σωματιδίων που διασχίζουν μία επιφάνεια Α στη μονάδα του χρόνου είναι ο αριθμός αυτών των σωματιδίων που περιέχονται σε όγκο Uf A. Αν c είναι η συγκέντρωση των σωματιδίων σ αυτόν τον όγκο, τότε ο αριθμός τους θα είναι Uf A c. Για μία όμως μοναδιαία επιφάνεια (Α=1), ο αριθμός των σωματιδίων γίνεται Uf c, που είναι ο παράγοντας συγκέντρωσης. Ο ρυθμός διάχυσης, Jd, που σύμφωνα με τον πρώτο νόμο του Fick για τη διάχυση είναι ανάλογος με τη συγκέντρωση, δίνεται από τη σχέση D dc/dx, η οποία ορίζει το 32
34 συντελεστή διάχυσης του δείγματος, D. ύμφωνα με τα παραπάνω ο ρυθμός ροής θα έχει τη μορφή: J(x)=Uf c D(dc/dx) (4) ύμφωνα με την κατεύθυνση που έχει επιλεγεί για τον άξονα x, η δύναμη του εξωτερικού πεδίου Ff και η ταχύτητα Uf θα είναι αρνητικές. Όταν το εξωτερικό πεδίο δρα για μεγάλο χρονικό διάστημα στα σωματίδια της ουσίας και αυτά βρεθούν σε κατάσταση ισορροπίας, ο ρυθμός διάχυσης βρίσκεται σε πλήρη ισορροπία με το ρυθμό συγκέντρωσης και επομένως ο ρυθμός ροής J(x) της διαλυμένης ουσίας είναι ίσος με το μηδέν. Άρα, η κατανομή της συγκέντρωσης του δείγματος στην κατάσταση ισορροπίας δίνεται από τη σχέση: c( x) exp c o x 0 U f D dx (5) όπου c0 είναι η συγκέντρωση του δείγματος στο τοίχωμα συσσώρευσης της στήλης (x=0). την περίπτωση κατά την οποία ο λόγος Uf /D είναι σταθερός κατά μήκος του πάχους της αναλυτικής στήλης, τότε η Εξ.(5) μετασχηματίζεται σε: ή αλλιώς: με: c( x) U f exp c o D c( x) x exp c l o U f x (6) (7) D l (8) 33
35 Θα πρέπει να διευκρινιστεί ότι στις Εξ.(6) και (8) χρησιμοποιείται η απόλυτη τιμή της ποσότητας Uf διότι η ταχύτητα των αναλυόμενων σωματιδίων είναι αρνητική, σύμφωνα με τον τρόπο με τον οποίο ορίστηκε η διεύθυνση του άξονα x. Τπό αυτές τις συνθήκες, η συγκέντρωση των σωματιδίων φαίνεται να μειώνεται εκθετικά με την αύξηση των αποστάσεων από το τοίχωμα συσσώρευσης του δείγματος. Η παράμετρος l που υπεισέρχεται στην Εξ.(8) και έχει διαστάσεις μήκους, αποτελεί τη χωρική σταθερά της εκθετικής διασποράς της εγκάρσιας συγκέντρωσης του δείγματος ή αλλιώς το μέσο πάχος της στοιβάδας στατικής κατάστασης των σωματιδίων του δείγματος που σχηματίζεται κοντά στο τοίχωμα της στήλης και είναι χαρακτηριστική των θεωρούμενων σωματιδίων. Πιο αναλυτικά, για σωματίδια τα οποία επηρεάζονται ισχυρά από το εξωτερικά εφαρμοζόμενο πεδίο, η παράμετρος l θα λαμβάνει μικρές τιμές και επομένως αυτά θα συγκεντρώνονται σε μια στενή ζώνη έκλουσης κοντά στο τοίχωμα συσσώρευσης της στήλης. Η στοιβάδα των σωματιδίων για μεγάλες τιμές του συντελεστή διάχυσης, D, θα εκτείνεται σχετικά μακριά από το τοίχωμα της στήλης. την οριακή περίπτωση, κατά την οποία το l τείνει στο άπειρο, η κατανομή της συγκέντρωσης γίνεται σταθερή, αφού τα σωματίδια του δείγματος δεν επηρεάζονται από τη δύναμη του εξωτερικού πεδίου, με αποτέλεσμα να παραμένουν ανομοιόμορφα διασκορπισμένα κατά μήκος της στήλης. Η παράμετρος l μπορεί να θεωρηθεί σαν αριθμητής του αδιάστατου κλάσματος: l D (9) w U w f όπου w είναι το πάχος της στήλης. 34
36 Σο λ είναι η σπουδαιότερη παράμετρος στη Μ.Φ.Π., επειδή ελέγχει τη συγκράτηση και τη διεύρυνση των κορυφών έκλουσης. Είναι χαρακτηριστική για κάθε είδος σωματιδίων και προκύπτει απευθείας από δεδομένα συγκράτησης σε αυτό το κλασικό μοντέλο συγκράτησης της Μ.Φ.Π., όπου η αντίθετη δράση των δυνάμεων λόγω του εξωτερικού πεδίου και της διαχύσεως οδηγεί στο σχηματισμό εκθετικά κατανεμημένων στοιβάδων των σωματιδίων κοντά στο τοίχωμα συσσώρευσης της στήλης. Η παράμετρος λ είναι επίσης ο λόγος της θερμικής ενέργειας προς την ενέργεια αλληλεπίδρασης πεδίου-ουσίας. Σο τελευταίο εκφράζεται από τη σχέση: Ff U f (10) f όπου f είναι ο γραμμομοριακός συντελεστής τριβής. Ο συντελεστής διάχυσης συνδέεται με τον προαναφερθέντα συντελεστή τριβής με την εξίσωση του Einstein[16]: kt D (11) f όπου k η σταθερά Boltzmann και Σ η απόλυτη θερμοκρασία. Από τις Εξ.(10) και (11) προκύπτει η σχέση: kt (12) F w f η οποία είναι ο λόγος της θερμικής ενέργειας (kt) προς το μηχανικό έργο (Ff w) που καταναλώνεται από το πεδίο για τη μεταφορά του σωματιδίου κατά μήκος της απόστασης w. Επειδή στην πράξη, για να επιτύχουμε έναν ικανοποιητικό διαχωρισμό με τη Μ.Φ.Π., απαιτούνται μικρές τιμές του λ (συνήθως μικρότερες του 0,2), με βάση την Εξ.(12) θα πρέπει να ισχύει kt>>ff w. υνεπώς, ο τύπος και η ισχύς του πεδίου πρέπει να επιλέγονται πάντα με τέτοιο τρόπο, ώστε η ενέργεια 35
37 αλληλεπίδρασης του πεδίου με την ουσία, Ff w, να είναι αρκετά μεγαλύτερη από τη θερμική ενέργεια, kt[17]. 3.5 Η κλασική εξίσωση συγκράτησης Ο χαρακτηρισμός στη Μ.Φ.Π. βασίζεται σε μία μέθοδο διαχωρισμού η οποία εφαρμόζεται όπως και στην περίπτωση της κλασικής χρωματογραφίας. Έτσι, ορίζεται ο λόγος συγκράτησης, R, ως ο λόγος της ταχύτητας της ζώνης των σωματιδίων του δείγματος, V, προς τη μέση ταχύτητα ροής του διαλύτη, <u>: V R (13) u Λαμβάνοντας υπόψη ότι <u>=l/tm και V=L/tR, όπου L είναι το μήκος της αναλυτικής στήλης, tm είναι ο νεκρός χρόνος της στήλης και tr ο χρόνος συγκράτησης του δείγματος, ο λόγος συγκράτησης μπορεί να αποδοθεί ως: t t M R (14) R Η Εξ.(14) χρησιμοποιείται, κατά κύριο λόγο, για τον πειραματικό προσδιορισμό του λόγου συγκράτησης. Μία άλλη απόδοση του λόγου συγκράτησης είναι και ο λόγος του νεκρού όγκου της στήλης, VM, προς τον όγκο συγκράτησης του δείγματος, VR, σύμφωνα με τη σχέση[18,19]: V V M R (15) R O λόγος συγκράτησης που αντιστοιχεί σε μία εκθετική κατανομή συγκέντρωσης και ένα παραβολικό μέτωπο ροής σχετίζεται με το λ σύμφωνα με τη σχέση [20]: 1 R 6coth 2 (16) 2 Η Εξ.(16) καλείται κλασική εξίσωση διαχωρισμού και δείχνει ότι, στην κατάσταση Brown, ο λόγος συγκράτησης εξαρτάται μόνο από τη θεμελιώδη 36
38 παράμετρο λ. Ο λόγος συγκράτησης, R, αυξάνει με την αύξηση του λ και τα όριά του για σχετικά χαμηλές και υψηλές τιμές λ είναι: 2 R 6 12 (17) lim 1 Για πολύ μικρές τιμές του λ: lim R 6 (18) 0 Για πολύ μεγάλες τιμές του λ: 1 lim R (19) Η μεταβολή του R έναντι του λ απεικονίζεται στο χήμα 3.2. χήμα 3.2: Μεταβολή του λόγου συγκράτησης, R, του δείγματος με τη θεμελιώδη παράμετρο λ στη Μ.Φ.Π. όπου φαίνονται, η ακριβής καμπύλη έκλουσης καθώς και οι προσεγγίσεις στην περίπτωση υψηλής συγκράτησης. 37
39 Επομένως, για μικρές τιμές του λ, όπου η στοιβάδα των σωματιδίων συσσωρεύεται κοντά στο τοίχωμα σαν μία λεπτή ζώνη, όπου η κατανομή της ταχύτητας είναι σχεδόν γραμμική και ίση με 6<u>x /w, η ζώνη αυτή βρίσκεται σε απόσταση l από το τοίχωμα της στήλης. Για πολύ μικρές τιμές του λ, η ζώνη αυτή μετατοπίζεται σε αποστάσεις στις οποίες η ταχύτητα είναι ίση με 6<u >l/w, ενώ ο λόγος συγκράτησης δίνεται από τη σχέση R=6λ, κατά την οποία επιτυγχάνεται ο καλύτερος δυνατός διαχωρισμός, εφόσον έχουμε τη μεγαλύτερη διακριτική ικανότητα. 3.6 Ύψος θεωρητικών πλακών Η άνιση κατανομή των ταχυτήτων, όπως και η διαφορετική θερμική κίνηση των σωματιδίων του δείγματος, έχει ως αποτέλεσμα οι ζώνες έκλουσης να διασπείρονται σε κάποια έκταση κατά μήκος της αναλυτικής στήλης. ε συγκεκριμένο χρόνο, η διασπορά των αποστάσεων που διανύουν τα σωματίδια αποδίδεται μέσω της διασποράς σz 2. Με την πάροδο ενός μικρού χρονικού διαστήματος, όταν το κέντρο βάρους της ζώνης έχει μετακινηθεί κατά μια απόσταση δz, αυτή η ζώνη έχει υποστεί διεύρυνση με συνέπεια η διασπορά της να έχει αυξηθεί κατά δσz 2. Η διαδικασία διεύρυνσης της ζώνης έκλουσης, όπως και στη χρωματογραφία, περιγράφεται μέσω του ισοδύναμου ύψους θεωρητικής πλάκας, το οποίο ορίζεται ως [21]: 2 z H lim 0 z 2 d z dz (20) Η ολοκλήρωση της Εξ.(20) δίνει την ολική διασπορά σz 2 (z=l) της ζώνης, η οποία συμβολίζεται ως σl 2, όταν το κέντρο βάρους εξέρχεται της στήλης στο χρόνο έκλουσης της ζώνης. Αν οι τιμές των φυσικών παραμέτρων που ελέγχουν τη μεταφορά, όπως π.χ. η θερμοκρασία, η δύναμη του εξωτερικά εφαρμοζόμενου 38
Αιωρήματα & Γαλακτώματα
 Αιωρήματα & Γαλακτώματα Εαρινό εξάμηνο Ακ. Έτους 2015-16 Μάθημα 9ο 5 May 2017 Αιωρήματα Γαλακτώματα 1 Στρατηγική δοσολογίας (Για άλατα μετάλλων τα οποία υδρολύονται ) Περιοχές δραστικότητας: Περιοχή 1:
Αιωρήματα & Γαλακτώματα Εαρινό εξάμηνο Ακ. Έτους 2015-16 Μάθημα 9ο 5 May 2017 Αιωρήματα Γαλακτώματα 1 Στρατηγική δοσολογίας (Για άλατα μετάλλων τα οποία υδρολύονται ) Περιοχές δραστικότητας: Περιοχή 1:
Κροκίδωση Συσσωμάτωση Χημική κατακρήμνιση Πηγή: Μαρία Λοϊζίδου, ΕΜΠ, Αθήνα 2006
 Κροκίδωση Συσσωμάτωση Χημική κατακρήμνιση Πηγή: Μαρία Λοϊζίδου, ΕΜΠ, Αθήνα 2006 Η χημική κατακρήμνιση βασίζεται στη λειτουργία της συσσωμάτωσης και κροκίδωσης των κολλοειδών σωματιδίων που υπάρχουν αρχικά
Κροκίδωση Συσσωμάτωση Χημική κατακρήμνιση Πηγή: Μαρία Λοϊζίδου, ΕΜΠ, Αθήνα 2006 Η χημική κατακρήμνιση βασίζεται στη λειτουργία της συσσωμάτωσης και κροκίδωσης των κολλοειδών σωματιδίων που υπάρχουν αρχικά
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΕΘΟΔΟΥΣ ΧΡΩΜΑΤΟΓΡΑΦΙΑΣ ΧΡΩΜΑΤΟΓΡΑΦΙΑ:
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΕΘΟΔΟΥΣ ΧΡΩΜΑΤΟΓΡΑΦΙΑΣ ΧΡΩΜΑΤΟΓΡΑΦΙΑ: ΜΕΘΟΔΟΙ ΔΙΑΧΩΡΙΣΜΟΥ οργανικών, οργανομεταλλικών και ανόργανων ουσιών. Ο ΔΙΑΧΩΡΙΣΜΟΣ ΕΠΙΤΥΓΧΑΝΕΤΑΙ ΕΞΑΙΤΙΑΣ ΤΩΝ ΔΙΑΦΟΡΩΝ ΣΤΗ ΦΥΣΙΚΟΧΗΜΙΚΗ ΣΥΓΓΕΝΕΙΑ ΤΩΝ
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΕΘΟΔΟΥΣ ΧΡΩΜΑΤΟΓΡΑΦΙΑΣ ΧΡΩΜΑΤΟΓΡΑΦΙΑ: ΜΕΘΟΔΟΙ ΔΙΑΧΩΡΙΣΜΟΥ οργανικών, οργανομεταλλικών και ανόργανων ουσιών. Ο ΔΙΑΧΩΡΙΣΜΟΣ ΕΠΙΤΥΓΧΑΝΕΤΑΙ ΕΞΑΙΤΙΑΣ ΤΩΝ ΔΙΑΦΟΡΩΝ ΣΤΗ ΦΥΣΙΚΟΧΗΜΙΚΗ ΣΥΓΓΕΝΕΙΑ ΤΩΝ
Απομόνωση Καζεΐνης ΆΣΚΗΣΗ 6 Η ΕΡΓΑΣΤΗΡΙΟ ΧΗΜΕΙΑΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ
 Απομόνωση Καζεΐνης ΆΣΚΗΣΗ 6 Η ΕΡΓΑΣΤΗΡΙΟ ΧΗΜΕΙΑΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ Θεωρητικό μέρος ΠΡΩΤΕΪΝΕΣ ΚΑΖΕΪΝΗ Πρωτεΐνες Είναι μεγάλα σύνθετα βιομόρια. Έχουν μοριακό βάρος από 10.000 μέχρι πάνω από 1 εκατομμύριο.
Απομόνωση Καζεΐνης ΆΣΚΗΣΗ 6 Η ΕΡΓΑΣΤΗΡΙΟ ΧΗΜΕΙΑΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ Θεωρητικό μέρος ΠΡΩΤΕΪΝΕΣ ΚΑΖΕΪΝΗ Πρωτεΐνες Είναι μεγάλα σύνθετα βιομόρια. Έχουν μοριακό βάρος από 10.000 μέχρι πάνω από 1 εκατομμύριο.
Γενικά. Εικόνα 1. Πείραµα κροκίδωσης
 ΕΠΕΞΕΡΓΑΣΙΑ ΝΕΡΟΥ ΚΑΙ ΥΓΡΩΝ ΑΠΟΒΛΗΤΩΝ Αχαρνών 364 & Γλαράκι 10Β, Αθήνα, 11145 Τηλ: 211 1820 163-4-5 Φαξ: 211 1820 166 e-mail: enerchem@enerchem.gr web site: www.enerchem.gr ΚΡΟΚΙΔΩΣΗ ΣΥΣΣΩΜΑΤΩΣΗ ΧΗΜΙΚΗ
ΕΠΕΞΕΡΓΑΣΙΑ ΝΕΡΟΥ ΚΑΙ ΥΓΡΩΝ ΑΠΟΒΛΗΤΩΝ Αχαρνών 364 & Γλαράκι 10Β, Αθήνα, 11145 Τηλ: 211 1820 163-4-5 Φαξ: 211 1820 166 e-mail: enerchem@enerchem.gr web site: www.enerchem.gr ΚΡΟΚΙΔΩΣΗ ΣΥΣΣΩΜΑΤΩΣΗ ΧΗΜΙΚΗ
Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd Email : stvrentzou@gmail.com
 1 2.4 Παράγοντες από τους οποίους εξαρτάται η αντίσταση ενός αγωγού Λέξεις κλειδιά: ειδική αντίσταση, μικροσκοπική ερμηνεία, μεταβλητός αντισ ροοστάτης, ποτενσιόμετρο 2.4 Παράγοντες που επηρεάζουν την
1 2.4 Παράγοντες από τους οποίους εξαρτάται η αντίσταση ενός αγωγού Λέξεις κλειδιά: ειδική αντίσταση, μικροσκοπική ερμηνεία, μεταβλητός αντισ ροοστάτης, ποτενσιόμετρο 2.4 Παράγοντες που επηρεάζουν την
Αγωγιμότητα στα μέταλλα
 Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Σκοπός: Περιγραφή της συμπεριφοράς των νευρικών κυττάρων και ποσοτικά και ποιοτικά.
 Σκοπός: Περιγραφή της συμπεριφοράς των νευρικών κυττάρων και ποσοτικά και ποιοτικά. Τα νευρικά κύτταρα περιβάλλονται από μία πλασματική μεμβράνη της οποίας κύρια λειτουργία είναι να ελέγχει το πέρασμα
Σκοπός: Περιγραφή της συμπεριφοράς των νευρικών κυττάρων και ποσοτικά και ποιοτικά. Τα νευρικά κύτταρα περιβάλλονται από μία πλασματική μεμβράνη της οποίας κύρια λειτουργία είναι να ελέγχει το πέρασμα
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
Αγωγιμότητα στα μέταλλα
 Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
ΧΡΩΜΑΤΟΓΡΑΦΙΚΕΣ ΤΕΧΝΙΚΕΣ ΑΝΑΛΥΣΗΣ
 ΧΡΩΜΑΤΟΓΡΑΦΙΚΕΣ ΤΕΧΝΙΚΕΣ ΑΝΑΛΥΣΗΣ Με τον όρο χρωματογραφία εννοούμε ένα πλήθος τεχνικών διαχωρισμού που βασίζονται στη διαφορετική κατανομή των συστατικών ενός μίγματος μεταξύ μια κινητής και μιας στατικής
ΧΡΩΜΑΤΟΓΡΑΦΙΚΕΣ ΤΕΧΝΙΚΕΣ ΑΝΑΛΥΣΗΣ Με τον όρο χρωματογραφία εννοούμε ένα πλήθος τεχνικών διαχωρισμού που βασίζονται στη διαφορετική κατανομή των συστατικών ενός μίγματος μεταξύ μια κινητής και μιας στατικής
Κεφάλαιο 7 Κολλοειδή
 Κεφάλαιο 7 Κολλοειδή Σύνοψη Τα κολλοειδή είναι μορφή μείγματος με διεσπαρμένα σωματίδια, τα οποία έχουν διαστάσεις από 1 ως 1000 nm. Τα σωματίδια αυτά παραμένουν διεσπαρμένα στον διαλύτη και δεν καταβυθίζονται.
Κεφάλαιο 7 Κολλοειδή Σύνοψη Τα κολλοειδή είναι μορφή μείγματος με διεσπαρμένα σωματίδια, τα οποία έχουν διαστάσεις από 1 ως 1000 nm. Τα σωματίδια αυτά παραμένουν διεσπαρμένα στον διαλύτη και δεν καταβυθίζονται.
ΜΑΘΗΜΑ: Τεχνολογία Μετρήσεων ΙΙ
 ΜΑΘΗΜΑ: Τεχνολογία Μετρήσεων ΙΙ ΔΙΔΑΣΚΩΝ: Αν. Καθ. Δρ Μαρία Α. Γούλα ΤΜΗΜΑ: Μηχανικών Περιβάλλοντος & Μηχανικών Αντιρρύπανσης 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΜΑΘΗΜΑ: Τεχνολογία Μετρήσεων ΙΙ ΔΙΔΑΣΚΩΝ: Αν. Καθ. Δρ Μαρία Α. Γούλα ΤΜΗΜΑ: Μηχανικών Περιβάλλοντος & Μηχανικών Αντιρρύπανσης 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 8 η : Υγρά, Στερεά & Αλλαγή Φάσεων. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 8 η : Υγρά, Στερεά & Αλλαγή Φάσεων Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Πολικοί Ομοιοπολικοί Δεσμοί & Διπολικές Ροπές 2 Όπως έχει
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 8 η : Υγρά, Στερεά & Αλλαγή Φάσεων Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Πολικοί Ομοιοπολικοί Δεσμοί & Διπολικές Ροπές 2 Όπως έχει
Ε. Μήτσου, Γ. Ταβαντζής, Α. Ξενάκης, Β. Παπαδημητρίου
 ΙΝΣΤΙΤΟΥΤΟ ΒΙΟΛΟΓΙΑΣ, ΦΑΡΜΑΚΕΥΤΙΚΗΣ ΧΗΜΕΙΑΣ ΚΑΙ ΒΙΟΤΕΧΝΟΛΟΓΙΑΣ ΤΜΗΜΑ ΒΙΟΜΙΜΗΤΙΚΗΣ ΚΑΙ ΝΑΝΟΒΙΟΤΕΧΝΟΛΟΓΙΑΣ «Σύνθεση βιοσυμβατών νανοδιασπορών και χρήση τους ως αντικαταστάτες της υδατικής/λιπαρής φάσης μακρογαλακτωμάτων»
ΙΝΣΤΙΤΟΥΤΟ ΒΙΟΛΟΓΙΑΣ, ΦΑΡΜΑΚΕΥΤΙΚΗΣ ΧΗΜΕΙΑΣ ΚΑΙ ΒΙΟΤΕΧΝΟΛΟΓΙΑΣ ΤΜΗΜΑ ΒΙΟΜΙΜΗΤΙΚΗΣ ΚΑΙ ΝΑΝΟΒΙΟΤΕΧΝΟΛΟΓΙΑΣ «Σύνθεση βιοσυμβατών νανοδιασπορών και χρήση τους ως αντικαταστάτες της υδατικής/λιπαρής φάσης μακρογαλακτωμάτων»
F el = z k e 0 (3) F f = f k v k (4) F tot = z k e 0 x f kv k (5)
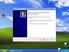 Κίνηση των ιόντων υπό την επίδραση ηλεκτρικού πεδίου Αντώνης Καραντώνης 15 Μαρτίου 2011 1 Σκοπός της άσκησης Σκοπός της άσκησης είναι ο προσδιορισμός της οριακής ταχύτητας των ιόντων υπό την επίδραση ηλεκτρικού
Κίνηση των ιόντων υπό την επίδραση ηλεκτρικού πεδίου Αντώνης Καραντώνης 15 Μαρτίου 2011 1 Σκοπός της άσκησης Σκοπός της άσκησης είναι ο προσδιορισμός της οριακής ταχύτητας των ιόντων υπό την επίδραση ηλεκτρικού
Χρωµατογραφικές µέθοδοι διαχωρισµού
 Χρωµατογραφικές µέθοδοι διαχωρισµού Εισαγωγή Ε. Μπακέας 2011 Χρωµατογραφία: ποικιλία µεθόδων διαχωρισµού µίγµατος ουσιών µε παραπλήσιες χηµικές ιδιότητες Βασίζεται στη διαφορετική κατανοµή των ουσιών µεταξύ
Χρωµατογραφικές µέθοδοι διαχωρισµού Εισαγωγή Ε. Μπακέας 2011 Χρωµατογραφία: ποικιλία µεθόδων διαχωρισµού µίγµατος ουσιών µε παραπλήσιες χηµικές ιδιότητες Βασίζεται στη διαφορετική κατανοµή των ουσιών µεταξύ
ΑΛΕΞΑΝΔΡΕΙΟ ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ
 ΑΛΕΞΑΝΔΡΕΙΟ ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΚΡΟΚΙΔΩΣΗ ΓΑΛΑΚΤΩΜΑΤΩΝ ΥΠΟ ΤΗΝ ΕΠΙΔΡΑΣΗ ΜΥΞΙΝΗΣ: ΡΕΟΛΟΓΙΑ & ΜΙΚΡΟΔΟΜΗ ΕΠΙΜΕΛΕΙΑ: ΞΕΝΤΕ ΕΛΕΝΗ
ΑΛΕΞΑΝΔΡΕΙΟ ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΚΡΟΚΙΔΩΣΗ ΓΑΛΑΚΤΩΜΑΤΩΝ ΥΠΟ ΤΗΝ ΕΠΙΔΡΑΣΗ ΜΥΞΙΝΗΣ: ΡΕΟΛΟΓΙΑ & ΜΙΚΡΟΔΟΜΗ ΕΠΙΜΕΛΕΙΑ: ΞΕΝΤΕ ΕΛΕΝΗ
Γεωργικά Φάρμακα ΙΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Έλεγχος φυτοπροστατευτικών προϊόντων Διαχωριστικές τεχνικές: χρωματογραφία Ουρανία Μενκίσογλου-Σπυρούδη Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Έλεγχος φυτοπροστατευτικών προϊόντων Διαχωριστικές τεχνικές: χρωματογραφία Ουρανία Μενκίσογλου-Σπυρούδη Άδειες Χρήσης Το παρόν
Άσκηση 3η. Μέθοδοι Διαχωρισμού. Τμήμα ΔΕΑΠΤ - Εργαστήριο Γενικής Χημείας
 Άσκηση 3η Μέθοδοι Διαχωρισμού 1 2 Θεωρητικό μέρος Χρήση των μεταβολών των φάσεων στην ανάλυση Οι ουσίες λειώνουν και βράζουν σε ορισμένες θερμοκρασίες, αλλάζοντας έτσι μορφή από στερεή σε υγρή ή από υγρή
Άσκηση 3η Μέθοδοι Διαχωρισμού 1 2 Θεωρητικό μέρος Χρήση των μεταβολών των φάσεων στην ανάλυση Οι ουσίες λειώνουν και βράζουν σε ορισμένες θερμοκρασίες, αλλάζοντας έτσι μορφή από στερεή σε υγρή ή από υγρή
v = 1 ρ. (2) website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Θρεπτικές ύλες Τρόφιµα - Τροφή
 ΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ 1 Θρεπτικές ύλες Τι καλούµε θρεπτικές ύλες; Ποιες είναι; Τρόφιµα Τι καλούµε τρόφιµο; Χηµεία Τροφίµων Θρεπτικές ύλες Τρόφιµα - Τροφή Προϋπόθεση για να χαρακτηριστεί ένα προϊόν τρόφιµο; 2
ΧΗΜΕΙΑ ΤΡΟΦΙΜΩΝ 1 Θρεπτικές ύλες Τι καλούµε θρεπτικές ύλες; Ποιες είναι; Τρόφιµα Τι καλούµε τρόφιµο; Χηµεία Τροφίµων Θρεπτικές ύλες Τρόφιµα - Τροφή Προϋπόθεση για να χαρακτηριστεί ένα προϊόν τρόφιµο; 2
Από πού προέρχεται η θερμότητα που μεταφέρεται από τον αντιστάτη στο περιβάλλον;
 3. ΗΛΕΚΤΡΙΚΗ ΕΝΕΡΓΕΙΑ Ένα ανοικτό ηλεκτρικό κύκλωμα μετατρέπεται σε κλειστό, οπότε διέρχεται από αυτό ηλεκτρικό ρεύμα που μεταφέρει ενέργεια. Τα σπουδαιότερα χαρακτηριστικά της ηλεκτρικής ενέργειας είναι
3. ΗΛΕΚΤΡΙΚΗ ΕΝΕΡΓΕΙΑ Ένα ανοικτό ηλεκτρικό κύκλωμα μετατρέπεται σε κλειστό, οπότε διέρχεται από αυτό ηλεκτρικό ρεύμα που μεταφέρει ενέργεια. Τα σπουδαιότερα χαρακτηριστικά της ηλεκτρικής ενέργειας είναι
ΜΙΚΡΟΓΑΛΑΚΤΩΜΑΤΑ ΠΑΡΑΣΚΕΥΗ ΚΑΙ ΜΕΛΕΤΗ ΦΥΣΙΚΩΝ ΙΔΙΟΤΗΤΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΣΥΝΘΕΣΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΕΡΓΑΣΤΗΡΙΟ ΧΗΜΕΙΑΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΜΙΚΡΟΓΑΛΑΚΤΩΜΑΤΑ ΠΑΡΑΣΚΕΥΗ ΚΑΙ ΜΕΛΕΤΗ ΦΥΣΙΚΩΝ ΙΔΙΟΤΗΤΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΣΥΝΘΕΣΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΕΡΓΑΣΤΗΡΙΟ ΧΗΜΕΙΑΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΤΡΟΦΙΜΩΝ ΜΙΚΡΟΓΑΛΑΚΤΩΜΑΤΑ ΠΑΡΑΣΚΕΥΗ ΚΑΙ ΜΕΛΕΤΗ ΦΥΣΙΚΩΝ ΙΔΙΟΤΗΤΩΝ
Άσκηση 3η. Μέθοδοι Διαχωρισμού. Τμήμα ΔΕΑΠΤ - Εργαστήριο Γενικής Χημείας
 Άσκηση 3η Μέθοδοι Διαχωρισμού 1 2 Θεωρητικό μέρος Χρήση των μεταβολών των φάσεων στην ανάλυση Οι ουσίες λειώνουν και βράζουν σε ορισμένες θερμοκρασίες, αλλάζοντας έτσι μορφή από στερεή σε υγρή ή από υγρή
Άσκηση 3η Μέθοδοι Διαχωρισμού 1 2 Θεωρητικό μέρος Χρήση των μεταβολών των φάσεων στην ανάλυση Οι ουσίες λειώνουν και βράζουν σε ορισμένες θερμοκρασίες, αλλάζοντας έτσι μορφή από στερεή σε υγρή ή από υγρή
ΗΛΕΚΤΡΟΤΕΧΝΙΚΑ Υλικα 3ο μεροσ. Θεωρητικη αναλυση
 ΗΛΕΚΤΡΟΤΕΧΝΙΚΑ Υλικα 3ο μεροσ Θεωρητικη αναλυση μεταλλα Έχουν κοινές φυσικές ιδιότητες που αποδεικνύεται πως είναι αλληλένδετες μεταξύ τους: Υψηλή φυσική αντοχή Υψηλή πυκνότητα Υψηλή ηλεκτρική και θερμική
ΗΛΕΚΤΡΟΤΕΧΝΙΚΑ Υλικα 3ο μεροσ Θεωρητικη αναλυση μεταλλα Έχουν κοινές φυσικές ιδιότητες που αποδεικνύεται πως είναι αλληλένδετες μεταξύ τους: Υψηλή φυσική αντοχή Υψηλή πυκνότητα Υψηλή ηλεκτρική και θερμική
ηλεκτρικό ρεύμα ampere
 Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Μεταλλικός δεσμός - Κρυσταλλικές δομές Ασκήσεις
 Μεταλλικός δεσμός - Κρυσταλλικές δομές Ασκήσεις Ποια από τις ακόλουθες προτάσεις ισχύει για τους μεταλλικούς δεσμούς; α) Οι μεταλλικοί δεσμοί σχηματίζονται αποκλειστικά μεταξύ ατόμων του ίδιου είδους μετάλλου.
Μεταλλικός δεσμός - Κρυσταλλικές δομές Ασκήσεις Ποια από τις ακόλουθες προτάσεις ισχύει για τους μεταλλικούς δεσμούς; α) Οι μεταλλικοί δεσμοί σχηματίζονται αποκλειστικά μεταξύ ατόμων του ίδιου είδους μετάλλου.
ΚΕΦΑΛΑΙΟ ΕΚΤΟ ΤΕΧΝΟΛΟΓΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ. Περιληπτική θεωρητική εισαγωγή
 ΚΕΦΑΛΑΙΟ ΕΚΤΟ ΤΕΧΝΟΛΟΓΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Περιληπτική θεωρητική εισαγωγή α) Τεχνική zchralski Η πιο συχνά χρησιμοποιούμενη τεχνική ανάπτυξης μονοκρυστάλλων πυριτίου (i), αρίστης ποιότητας,
ΚΕΦΑΛΑΙΟ ΕΚΤΟ ΤΕΧΝΟΛΟΓΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Περιληπτική θεωρητική εισαγωγή α) Τεχνική zchralski Η πιο συχνά χρησιμοποιούμενη τεχνική ανάπτυξης μονοκρυστάλλων πυριτίου (i), αρίστης ποιότητας,
Κεφάλαιο 2 Χημικοί Δεσμοί
 Κεφάλαιο 2 Χημικοί Δεσμοί Σύνοψη Παρουσιάζονται οι χημικοί δεσμοί, ιοντικός, μοριακός, ατομικός, μεταλλικός. Οι ιδιότητες των υλικών τόσο οι φυσικές όσο και οι χημικές εξαρτώνται από το είδος ή τα είδη
Κεφάλαιο 2 Χημικοί Δεσμοί Σύνοψη Παρουσιάζονται οι χημικοί δεσμοί, ιοντικός, μοριακός, ατομικός, μεταλλικός. Οι ιδιότητες των υλικών τόσο οι φυσικές όσο και οι χημικές εξαρτώνται από το είδος ή τα είδη
Τα χημικά στοιχεία που είναι επικρατέστερα στους οργανισμούς είναι: i..
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΤΟ 1 ο ΚΕΦΑΛΑΙΟ «XHMIKH ΣΥΣΤΑΣΗ ΤΟΥ ΚΥΤΤΑΡΟΥ» ΕΙΣΑΓΩΓΗ ΚΑΙ Η ΧΗΜΕΙΑ ΤΗΣ ΖΩΗΣ Α. ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΜΕΣΑ ΣΤΗΝ ΤΑΞΗ 1. Όταν αναφερόμαστε στον όρο «Χημική Σύσταση του Κυττάρου», τί νομίζετε ότι
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΤΟ 1 ο ΚΕΦΑΛΑΙΟ «XHMIKH ΣΥΣΤΑΣΗ ΤΟΥ ΚΥΤΤΑΡΟΥ» ΕΙΣΑΓΩΓΗ ΚΑΙ Η ΧΗΜΕΙΑ ΤΗΣ ΖΩΗΣ Α. ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΜΕΣΑ ΣΤΗΝ ΤΑΞΗ 1. Όταν αναφερόμαστε στον όρο «Χημική Σύσταση του Κυττάρου», τί νομίζετε ότι
ΜΗΧΑΝΙΣΜΟΙ ΚΥΤΤΑΡΙΚΗΣ ΜΕΤΑΦΟΡΑΣ ΚΑΙ ΔΙΑΠΕΡΑΤΟΤΗΤΑ
 ΜΗΧΑΝΙΣΜΟΙ ΚΥΤΤΑΡΙΚΗΣ ΜΕΤΑΦΟΡΑΣ ΚΑΙ ΔΙΑΠΕΡΑΤΟΤΗΤΑ Διάχυση Η διάχυση είναι το κύριο φαινόμενο με το οποίο γίνεται η παθητική μεταφορά διαμέσου ενός διαχωριστικού φράγματος Γενικά στη διάχυση ένα αέριο ή
ΜΗΧΑΝΙΣΜΟΙ ΚΥΤΤΑΡΙΚΗΣ ΜΕΤΑΦΟΡΑΣ ΚΑΙ ΔΙΑΠΕΡΑΤΟΤΗΤΑ Διάχυση Η διάχυση είναι το κύριο φαινόμενο με το οποίο γίνεται η παθητική μεταφορά διαμέσου ενός διαχωριστικού φράγματος Γενικά στη διάχυση ένα αέριο ή
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις. Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι
 Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ - ΒΙΟΧΗΜΕΙΑ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 ΗΜΕΡΟΜΗΝΙΑ: 21 / 09 /2014
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ - ΒΙΟΧΗΜΕΙΑ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 ΗΜΕΡΟΜΗΝΙΑ: 21 / 09 /2014 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Για τις ερωτήσεις Α1 έως και Α3 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ - ΒΙΟΧΗΜΕΙΑ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 ΗΜΕΡΟΜΗΝΙΑ: 21 / 09 /2014 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Για τις ερωτήσεις Α1 έως και Α3 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα
ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΘΕΩΡΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΘΕΩΡΙΑ Περιεχόμενα 1. Όρια καταστατικής εξίσωσης ιδανικού αερίου 2. Αποκλίσεις των Ιδιοτήτων των πραγματικών αερίων από τους Νόμους
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΘΕΩΡΙΑ Περιεχόμενα 1. Όρια καταστατικής εξίσωσης ιδανικού αερίου 2. Αποκλίσεις των Ιδιοτήτων των πραγματικών αερίων από τους Νόμους
ΕΡΓΑΣΤΗΡΙΑΚΟ ΚΕΝΤΡΟ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Ν. ΜΑΓΝΗΣΙΑΣ ( Ε.Κ.Φ.Ε ) ΕΡΓΑΣΤΗΡΙΟ ΒΙΟΛΟΓΙΑΣ
 ΕΡΓΑΣΤΗΡΙΑΚΟ ΚΕΝΤΡΟ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Ν. ΜΑΓΝΗΣΙΑΣ ( Ε.Κ.Φ.Ε ) ΕΡΓΑΣΤΗΡΙΟ ΒΙΟΛΟΓΙΑΣ Θέμα: ΜΕΤΟΥΣΙΩΣΗ ΠΡΩΤΕΪΝΩΝ (άσκηση 7 του εργαστηριακού οδηγού) Μέσος χρόνος πειράματος: 45 λεπτά Α. ΑΝΑΛΩΣΙΜΑ Εργαλεία
ΕΡΓΑΣΤΗΡΙΑΚΟ ΚΕΝΤΡΟ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Ν. ΜΑΓΝΗΣΙΑΣ ( Ε.Κ.Φ.Ε ) ΕΡΓΑΣΤΗΡΙΟ ΒΙΟΛΟΓΙΑΣ Θέμα: ΜΕΤΟΥΣΙΩΣΗ ΠΡΩΤΕΪΝΩΝ (άσκηση 7 του εργαστηριακού οδηγού) Μέσος χρόνος πειράματος: 45 λεπτά Α. ΑΝΑΛΩΣΙΜΑ Εργαλεία
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
ΤΕΧΝΟΛΟΓΙΑ ΚΑΙ ΑΡΧΕΣ ΠΑΡΑΣΚΕΥΗΣ ΤΡΟΦΙΜΩΝ ΤΡΟΦΙΜΑ ΚΑΙ ΓΑΛΑΚΤΩΜΑΤΑ
 ΤΕΧΝΟΛΟΓΙΑ ΚΑΙ ΑΡΧΕΣ ΠΑΡΑΣΚΕΥΗΣ ΤΡΟΦΙΜΩΝ ΤΡΟΦΙΜΑ ΚΑΙ ΓΑΛΑΚΤΩΜΑΤΑ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στη φύση επικρατεί η βασική αρχή: Τα όμοια διαλύονται σε όμοια Πολικές ενώσεις σε πολικούς διαλύτες (π.χ. Αιθανόλη (πολική
ΤΕΧΝΟΛΟΓΙΑ ΚΑΙ ΑΡΧΕΣ ΠΑΡΑΣΚΕΥΗΣ ΤΡΟΦΙΜΩΝ ΤΡΟΦΙΜΑ ΚΑΙ ΓΑΛΑΚΤΩΜΑΤΑ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στη φύση επικρατεί η βασική αρχή: Τα όμοια διαλύονται σε όμοια Πολικές ενώσεις σε πολικούς διαλύτες (π.χ. Αιθανόλη (πολική
Υλικά Ηλεκτρονικής & Διατάξεις
 Τμήμα Ηλεκτρονικών Μηχανικών Υλικά Ηλεκτρονικής & Διατάξεις 2 η σειρά διαφανειών Δημήτριος Λαμπάκης ΜΟΡΙΑΚΗ ΔΟΜΗ Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια Μόρια: Τα υπόλοιπα άτομα σχηματίζουν μόρια, γιατί
Τμήμα Ηλεκτρονικών Μηχανικών Υλικά Ηλεκτρονικής & Διατάξεις 2 η σειρά διαφανειών Δημήτριος Λαμπάκης ΜΟΡΙΑΚΗ ΔΟΜΗ Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια Μόρια: Τα υπόλοιπα άτομα σχηματίζουν μόρια, γιατί
Ενόργανη Ανάλυση II. Ενότητα 2: Εισαγωγή στις μεθόδους χρωματογραφίας 1η Διάλεξη. Θωμαΐδης Νικόλαος Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας
 Ενόργανη Ανάλυση II Ενότητα 2: Εισαγωγή στις μεθόδους χρωματογραφίας 1η Διάλεξη Θωμαΐδης Νικόλαος Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας ΧΡΩΜΑΤΟΓΡΑΦΙΑ: ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΕΘΟΔΟΥΣ ΧΡΩΜΑΤΟΓΡΑΦΙΑΣ ΜΕΘΟΔΟΙ
Ενόργανη Ανάλυση II Ενότητα 2: Εισαγωγή στις μεθόδους χρωματογραφίας 1η Διάλεξη Θωμαΐδης Νικόλαος Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας ΧΡΩΜΑΤΟΓΡΑΦΙΑ: ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΕΘΟΔΟΥΣ ΧΡΩΜΑΤΟΓΡΑΦΙΑΣ ΜΕΘΟΔΟΙ
πρωτεΐνες πολυμερείς ουσίες δομούν λειτουργούν λευκώματα 1.Απλές πρωτεΐνες 2.Σύνθετες πρωτεΐνες πρωτεΐδια μη πρωτεϊνικό μεταλλοπρωτεΐνες
 ΠΡΩΤΕΙΝΕΣ Οι πρωτεΐνες είναι πολυμερείς ουσίες με κυρίαρχο και πρωταρχικό ρόλο στη ζωή. Πρωτεΐνες είναι οι ουσίες που κυρίως δομούν και λειτουργούν τους οργανισμούς. Λέγονται και λευκώματα λόγω του λευκού
ΠΡΩΤΕΙΝΕΣ Οι πρωτεΐνες είναι πολυμερείς ουσίες με κυρίαρχο και πρωταρχικό ρόλο στη ζωή. Πρωτεΐνες είναι οι ουσίες που κυρίως δομούν και λειτουργούν τους οργανισμούς. Λέγονται και λευκώματα λόγω του λευκού
Η βαθμίδα του ηλεκτρικού πεδίου της μεμβράνης τείνει να συγκρατήσει τα θετικά φορτισμένα ιόντα.
 Τα ιόντα χλωρίου βρίσκονται σε πολύ μεγαλύτερη πυκνότητα στο εξωτερικό παρά στο εσωτερικό του κυττάρου, με αποτέλεσμα να εμφανίζεται παθητικό ρεύμα εισόδου τους στο κύτταρο. Τα αρνητικά φορτισμένα ιόντα
Τα ιόντα χλωρίου βρίσκονται σε πολύ μεγαλύτερη πυκνότητα στο εξωτερικό παρά στο εσωτερικό του κυττάρου, με αποτέλεσμα να εμφανίζεται παθητικό ρεύμα εισόδου τους στο κύτταρο. Τα αρνητικά φορτισμένα ιόντα
ηλεκτρικό ρεύµα ampere
 Ηλεκτρικό ρεύµα Το ηλεκτρικό ρεύµα είναι ο ρυθµός µε τον οποίο διέρχεται ηλεκτρικό φορτίο από µια περιοχή του χώρου. Η µονάδα µέτρησης του ηλεκτρικού ρεύµατος στο σύστηµα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύµα Το ηλεκτρικό ρεύµα είναι ο ρυθµός µε τον οποίο διέρχεται ηλεκτρικό φορτίο από µια περιοχή του χώρου. Η µονάδα µέτρησης του ηλεκτρικού ρεύµατος στο σύστηµα SI είναι το ampere (A). 1 A =
Ανόργανη Χημεία. Τμήμα Τεχνολογίας Τροφίμων. Ενότητα 5 η : Ομοιοπολικοί δεσμοί & μοριακή δομή. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 5 η : Ομοιοπολικοί δεσμοί & μοριακή δομή Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Ο Ομοιοπολικός Δεσμός 2 Ο δεσμός Η Η στο μόριο Η
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 5 η : Ομοιοπολικοί δεσμοί & μοριακή δομή Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Ο Ομοιοπολικός Δεσμός 2 Ο δεσμός Η Η στο μόριο Η
αποτελούν το 96% κ.β Ποικιλία λειτουργιών
 ΧΗΜΙΚΑ ΣΤΟΙΧΕΙΑ ΠΟΥ ΣΥΝΘΕΤΟΥΝ ΤΟΥΣ ΟΡΓΑΝΙΣΜΟΥΣ 92 στοιχεία στο φλοιό της Γης 27 απαραίτητα για τη ζωή H, Ο, Ν, C αποτελούν το 96% κ.β S, Ca, P, Cl, K, Na, Mg αποτελούν το 4% κ.β. Fe, I Ιχνοστοιχεία αποτελούν
ΧΗΜΙΚΑ ΣΤΟΙΧΕΙΑ ΠΟΥ ΣΥΝΘΕΤΟΥΝ ΤΟΥΣ ΟΡΓΑΝΙΣΜΟΥΣ 92 στοιχεία στο φλοιό της Γης 27 απαραίτητα για τη ζωή H, Ο, Ν, C αποτελούν το 96% κ.β S, Ca, P, Cl, K, Na, Mg αποτελούν το 4% κ.β. Fe, I Ιχνοστοιχεία αποτελούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
Ενόργανη Ανάλυση II. Ενότητα 1: Θεωρία Χρωματογραφίας 3 η Διάλεξη. Θωμαΐδης Νικόλαος Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας
 Ενόργανη Ανάλυση II Ενότητα 1: 3 η Διάλεξη Θωμαΐδης Νικόλαος Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας ΘΕΩΡΙΑ ΤΑΧΥΤΗΤΑΣ Πως επηρεάζει η ταχύτητα ροής της κινητής φάσης την αποδοτικότητα της στήλης (Η,
Ενόργανη Ανάλυση II Ενότητα 1: 3 η Διάλεξη Θωμαΐδης Νικόλαος Τμήμα Χημείας Εργαστήριο Αναλυτικής Χημείας ΘΕΩΡΙΑ ΤΑΧΥΤΗΤΑΣ Πως επηρεάζει η ταχύτητα ροής της κινητής φάσης την αποδοτικότητα της στήλης (Η,
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Αέρια & Πίεση Αερίων 2 Ο αέρας είναι ένα τυπικό αέριο
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 7 η : Αέρια Ιδιότητες & συμπεριφορά Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Αέρια & Πίεση Αερίων 2 Ο αέρας είναι ένα τυπικό αέριο
Ξεκινώντας από την εξίσωση Poisson για το δυναμικό V στο στατικό ηλεκτρικό πεδίο:
 1 2. Διοδος p-n 2.1 Επαφή p-n Στο σχήμα 2.1 εικονίζονται δύο μέρη ενός ημιαγωγού με διαφορετικού τύπου αγωγιμότητες. Αριστερά ο ημιαγωγός είναι p-τύπου και δεξια n-τύπου. Και τα δύο μέρη είναι ηλεκτρικά
1 2. Διοδος p-n 2.1 Επαφή p-n Στο σχήμα 2.1 εικονίζονται δύο μέρη ενός ημιαγωγού με διαφορετικού τύπου αγωγιμότητες. Αριστερά ο ημιαγωγός είναι p-τύπου και δεξια n-τύπου. Και τα δύο μέρη είναι ηλεκτρικά
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 9 η : Διαλύματα & οι ιδιότητές τους. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 9 η : Διαλύματα & οι ιδιότητές τους Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Διαλύματα 2 Τα ομοιογενή μίγματα μπορούν να ταξινομηθούν
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 9 η : Διαλύματα & οι ιδιότητές τους Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Διαλύματα 2 Τα ομοιογενή μίγματα μπορούν να ταξινομηθούν
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα. Φαινόμενα μεταφοράς Ορισμοί. Ενεργός διατομή 3. Ενεργός διατομή στο μοντέλο των σκληρών σφαιρών
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα. Φαινόμενα μεταφοράς Ορισμοί. Ενεργός διατομή 3. Ενεργός διατομή στο μοντέλο των σκληρών σφαιρών
Η κίνηση του νερού εντός των φυτών (Soil-Plant-Atmosphere Continuum) Δημήτρης Κύρκας
 Η κίνηση του νερού εντός των φυτών (Soil-Plant-Atmosphere Continuum) Δημήτρης Κύρκας Η Σεκόγια (Sequoia) «Redwood» είναι το ψηλότερο δέντρο στο κόσμο και βρίσκεται στην Καλιφόρνια των ΗΠΑ 130 μέτρα ύψος
Η κίνηση του νερού εντός των φυτών (Soil-Plant-Atmosphere Continuum) Δημήτρης Κύρκας Η Σεκόγια (Sequoia) «Redwood» είναι το ψηλότερο δέντρο στο κόσμο και βρίσκεται στην Καλιφόρνια των ΗΠΑ 130 μέτρα ύψος
Τμήμα Τεχνολογίας Τροφίμων. Ανόργανη Χημεία. Ενότητα 11 η : Χημική ισορροπία. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής.
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 11 η : Χημική ισορροπία Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Η Κατάσταση Ισορροπίας 2 Πολλές αντιδράσεις δεν πραγματοποιούνται
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 11 η : Χημική ισορροπία Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Η Κατάσταση Ισορροπίας 2 Πολλές αντιδράσεις δεν πραγματοποιούνται
Περιεχόμενο της άσκησης
 Προαπαιτούμενες γνώσεις Επαφή p- Στάθμη Fermi Χαρακτηριστική ρεύματος-τάσης Ορθή και ανάστροφη πόλωση Περιεχόμενο της άσκησης Οι επαφές p- παρουσιάζουν σημαντικό ενδιαφέρον επειδή βρίσκουν εφαρμογή στη
Προαπαιτούμενες γνώσεις Επαφή p- Στάθμη Fermi Χαρακτηριστική ρεύματος-τάσης Ορθή και ανάστροφη πόλωση Περιεχόμενο της άσκησης Οι επαφές p- παρουσιάζουν σημαντικό ενδιαφέρον επειδή βρίσκουν εφαρμογή στη
Διάλεξη 7: Μοριακή Δομή
 Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια Μόρια: Τα υπόλοιπα άτομα σχηματίζουν μόρια Γιατί; Διότι η ολική ενέργεια ενός ευσταθούς μορίου είναι μικρότερη από την ολική ενέργεια των μεμονωμένων ατόμων που αποτελούν
Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια Μόρια: Τα υπόλοιπα άτομα σχηματίζουν μόρια Γιατί; Διότι η ολική ενέργεια ενός ευσταθούς μορίου είναι μικρότερη από την ολική ενέργεια των μεμονωμένων ατόμων που αποτελούν
Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών ΤΜΗΜΑ ΦΑΡΜΑΚΕΥΤΙΚΗΣ Τομέας Φαρμακευτικής Χημείας. Ιωάννης Ντότσικας. Επικ.
 Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών ΤΜΗΜΑ ΦΑΡΜΑΚΕΥΤΙΚΗΣ Τομέας Φαρμακευτικής Χημείας Ιωάννης Ντότσικας Επικ. Καθηγητής 1 Οι κυκλοδεξτρίνες (Cyclodextrins, CDs) είναι κυκλικοί ολιγοσακχαρίτες
Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών ΤΜΗΜΑ ΦΑΡΜΑΚΕΥΤΙΚΗΣ Τομέας Φαρμακευτικής Χημείας Ιωάννης Ντότσικας Επικ. Καθηγητής 1 Οι κυκλοδεξτρίνες (Cyclodextrins, CDs) είναι κυκλικοί ολιγοσακχαρίτες
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 13 Ηλεκτρικό (Βαθμωτό) δυναμικό ΦΥΣ102 1 Διαφορά δυναμικού Η Ηλεκτροστατική Δύναμη
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 13 Ηλεκτρικό (Βαθμωτό) δυναμικό ΦΥΣ102 1 Διαφορά δυναμικού Η Ηλεκτροστατική Δύναμη
Αιωρήματα & Γαλακτώματα
 Αιωρήματα & Γαλακτώματα Εαρινό εξάμηνο Ακ. Έτους 2014-15 Μάθημα 3ο 1 March 2015 Αιωρήματα Γαλακτώματα 1 Σχηματισμός Λυοφιλικών Κολλοειδών Φάση Αιώρημα Διάλυμα Αύξηση επιφάνειας (δεν ευνοείται) Αύξηση του
Αιωρήματα & Γαλακτώματα Εαρινό εξάμηνο Ακ. Έτους 2014-15 Μάθημα 3ο 1 March 2015 Αιωρήματα Γαλακτώματα 1 Σχηματισμός Λυοφιλικών Κολλοειδών Φάση Αιώρημα Διάλυμα Αύξηση επιφάνειας (δεν ευνοείται) Αύξηση του
Κεφάλαιο 3. Διεργασίες στη διεπιφάνεια υγρούστερεού
 Κεφάλαιο 3 Διεργασίες στη διεπιφάνεια υγρούστερεού Εισαγωγή Η προσρόφηση δηλαδή η συσσώρευση στη διεπαφή στερεού-υγρού είναι η βάση των περισσοτέρων επιφανειακών-χημικών διαδικασιών 1. Επηρεάζει την κατανομή
Κεφάλαιο 3 Διεργασίες στη διεπιφάνεια υγρούστερεού Εισαγωγή Η προσρόφηση δηλαδή η συσσώρευση στη διεπαφή στερεού-υγρού είναι η βάση των περισσοτέρων επιφανειακών-χημικών διαδικασιών 1. Επηρεάζει την κατανομή
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Aγωγιμομετρία
 ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Aγωγιμομετρία Ιωάννης Πούλιος Αθανάσιος Κούρας Ευαγγελία Μανώλη ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 54124 ΘΕΣΣΑΛΟΝΙΚΗ
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑΤΟΣ ΒΙΟΛΟΓΙΑΣ Aγωγιμομετρία Ιωάννης Πούλιος Αθανάσιος Κούρας Ευαγγελία Μανώλη ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 54124 ΘΕΣΣΑΛΟΝΙΚΗ
ΠΡΩΤΕΪΝΕΣ. Φατούρος Ιωάννης Αναπληρωτής Καθηγητής
 ΠΡΩΤΕΪΝΕΣ Φατούρος Ιωάννης Αναπληρωτής Καθηγητής Θέματα Διάλεξης Δομή, αριθμός και διαχωρισμός των αμινοξέων Ένωση αμινοξέων με τον πεπτιδικό δεσμό για τη δημιουργία πρωτεΐνης Λειτουργίες των πρωτεϊνών
ΠΡΩΤΕΪΝΕΣ Φατούρος Ιωάννης Αναπληρωτής Καθηγητής Θέματα Διάλεξης Δομή, αριθμός και διαχωρισμός των αμινοξέων Ένωση αμινοξέων με τον πεπτιδικό δεσμό για τη δημιουργία πρωτεΐνης Λειτουργίες των πρωτεϊνών
ΤΕΧΝΟΛΟΓΙΑ & ΕΠΙΣΤΗΜΗ ΤΩΝ ΥΛΙΚΩΝ
 Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνσης Συντήρησης Πολιτισμικής Κληρονομιάς ΤΕΧΝΟΛΟΓΙΑ & ΕΠΙΣΤΗΜΗ ΤΩΝ ΥΛΙΚΩΝ 3 η Ενότητα ΔΕΣΜΟΙ Δημήτριος Λαμπάκης ΜΟΡΙΑΚΗ ΔΟΜΗ Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια
Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνσης Συντήρησης Πολιτισμικής Κληρονομιάς ΤΕΧΝΟΛΟΓΙΑ & ΕΠΙΣΤΗΜΗ ΤΩΝ ΥΛΙΚΩΝ 3 η Ενότητα ΔΕΣΜΟΙ Δημήτριος Λαμπάκης ΜΟΡΙΑΚΗ ΔΟΜΗ Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια
ΥΔΡΑΥΛΙΚΕΣ ΑΠΩΛΕΙΕΣ ΚΑΤΑ ΤΗΝ ΡΟΗ ΝΕΡΟΥ ΣΕ ΚΛΕΙΣΤΟ ΑΓΩΓΟ
 Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 8 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΥΔΡΑΥΛΙΚΕΣ ΑΠΩΛΕΙΕΣ ΚΑΤΑ ΤΗΝ ΡΟΗ ΝΕΡΟΥ ΣΕ ΚΛΕΙΣΤΟ ΑΓΩΓΟ Σκοπός του πειράματος είναι να μελετηθεί
Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 8 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΥΔΡΑΥΛΙΚΕΣ ΑΠΩΛΕΙΕΣ ΚΑΤΑ ΤΗΝ ΡΟΗ ΝΕΡΟΥ ΣΕ ΚΛΕΙΣΤΟ ΑΓΩΓΟ Σκοπός του πειράματος είναι να μελετηθεί
Οργανική Χημεία. Κεφάλαια 12 &13: Φασματοσκοπία μαζών και υπερύθρου
 Οργανική Χημεία Κεφάλαια 12 &13: Φασματοσκοπία μαζών και υπερύθρου 1. Γενικά Δυνατότητα προσδιορισμού δομών με σαφήνεια χρησιμοποιώντας τεχνικές φασματοσκοπίας Φασματοσκοπία μαζών Μέγεθος, μοριακός τύπος
Οργανική Χημεία Κεφάλαια 12 &13: Φασματοσκοπία μαζών και υπερύθρου 1. Γενικά Δυνατότητα προσδιορισμού δομών με σαφήνεια χρησιμοποιώντας τεχνικές φασματοσκοπίας Φασματοσκοπία μαζών Μέγεθος, μοριακός τύπος
Βιοχημεία Τροφίμων Ι. Ενότητα 5 η Γάλα ΙI (μέρος α) Όνομα καθηγητή: Έφη Τσακαλίδου. Τμήμα: Επιστήμης Τροφίμων & Διατροφής του Ανθρώπου
 Βιοχημεία Τροφίμων Ι Ενότητα 5 η Γάλα ΙI (μέρος α) Όνομα καθηγητή: Έφη Τσακαλίδου Τμήμα: Επιστήμης Τροφίμων & Διατροφής του Ανθρώπου Στόχοι ενότητας Κατανόηση της δομής των πρωτεϊνών του γάλακτος. Κατανόηση
Βιοχημεία Τροφίμων Ι Ενότητα 5 η Γάλα ΙI (μέρος α) Όνομα καθηγητή: Έφη Τσακαλίδου Τμήμα: Επιστήμης Τροφίμων & Διατροφής του Ανθρώπου Στόχοι ενότητας Κατανόηση της δομής των πρωτεϊνών του γάλακτος. Κατανόηση
ΦΥΣΙΚΟΧΗΜΙΚΗ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΜΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΤΟΜΕΑΣ ΦΥΣΙΚΟΧΗΜΕΙΑΣ, ΑΝΟΡΓΑΝΗΣ ΚΑΙ ΠΥΡΗΝΙΚΗΣ ΧΗΜΕΙΑΣ Μεταπτυχιακό Δίπλωμα Ειδίκευσης: «ΑΝΑΛΥΤΙΚΗ ΧΗΜΕΙΑ ΚΑΙ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ» ΘΕΜΑ ΔΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ ΦΥΣΙΚΟΧΗΜΙΚΗ ΜΕΛΕΤΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΧΗΜΕΙΑΣ ΤΟΜΕΑΣ ΦΥΣΙΚΟΧΗΜΕΙΑΣ, ΑΝΟΡΓΑΝΗΣ ΚΑΙ ΠΥΡΗΝΙΚΗΣ ΧΗΜΕΙΑΣ Μεταπτυχιακό Δίπλωμα Ειδίκευσης: «ΑΝΑΛΥΤΙΚΗ ΧΗΜΕΙΑ ΚΑΙ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ» ΘΕΜΑ ΔΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ ΦΥΣΙΚΟΧΗΜΙΚΗ ΜΕΛΕΤΗ
ΤΕΧΝΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΚΑΤΑ ΤΗΝ ΑΞΙΟΠΟΙΗΣΗ ΤΗΣ ΓΕΩΘΕΡΜΙΑΣ
 ΤΕΧΝΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΚΑΤΑ ΤΗΝ ΑΞΙΟΠΟΙΗΣΗ ΤΗΣ ΓΕΩΘΕΡΜΙΑΣ Η αξιοποίηση της γεωθερμικής ενέργειας συναντά ορισμένα τεχνικά προβλήματα, Τα προβλήματα αυτά είναι: (α) ο σχηματισμός επικαθίσεων (ή καθαλατώσεις
ΤΕΧΝΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΚΑΤΑ ΤΗΝ ΑΞΙΟΠΟΙΗΣΗ ΤΗΣ ΓΕΩΘΕΡΜΙΑΣ Η αξιοποίηση της γεωθερμικής ενέργειας συναντά ορισμένα τεχνικά προβλήματα, Τα προβλήματα αυτά είναι: (α) ο σχηματισμός επικαθίσεων (ή καθαλατώσεις
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Νευτώνια και μη Νευτώνια ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 15 Απριλίου 2019 1 Καταστατικές εξισώσεις Νευτώνιου ρευστού Νευτώνια ή Νευτωνικά
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Νευτώνια και μη Νευτώνια ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 15 Απριλίου 2019 1 Καταστατικές εξισώσεις Νευτώνιου ρευστού Νευτώνια ή Νευτωνικά
ΔΠΘ - Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων ΦΥΣΙΟΛΟΓΙΑ ΦΥΤΩΝ ΠΡΟΣΛΗΨΗ ΚΑΙ ΜΕΤΑΦΟΡΑ ΤΟΥ ΝΕΡΟΥ ΣΤΑ ΦΥΤΑ
 ΔΠΘ - Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων ΦΥΣΙΟΛΟΓΙΑ ΦΥΤΩΝ ΠΡΟΣΛΗΨΗ ΚΑΙ ΜΕΤΑΦΟΡΑ ΤΟΥ ΝΕΡΟΥ ΣΤΑ ΦΥΤΑ Θερινό εξάμηνο 2011 Ο ρόλος του νερού στο φυτό Βασικότερο συστατικό των ιστών
ΔΠΘ - Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων ΦΥΣΙΟΛΟΓΙΑ ΦΥΤΩΝ ΠΡΟΣΛΗΨΗ ΚΑΙ ΜΕΤΑΦΟΡΑ ΤΟΥ ΝΕΡΟΥ ΣΤΑ ΦΥΤΑ Θερινό εξάμηνο 2011 Ο ρόλος του νερού στο φυτό Βασικότερο συστατικό των ιστών
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανολόγων Μηχανικών. Χημεία. Ενότητα 15: Διαλύματα
 Τμήμα Μηχανολόγων Μηχανικών Χημεία Ενότητα 15: Διαλύματα Αν. Καθηγητής Γεώργιος Μαρνέλλος e-mail: gmarnellos@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Τμήμα Μηχανολόγων Μηχανικών Χημεία Ενότητα 15: Διαλύματα Αν. Καθηγητής Γεώργιος Μαρνέλλος e-mail: gmarnellos@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Κεφάλαιο 4 Καταστάσεις της Ύλης: Αέρια, Υγρά και Στερεά
 Κεφάλαιο 4 Καταστάσεις της Ύλης: Αέρια, Υγρά και Στερεά Σύνοψη Η ύλη χαρακτηρίζεται από μεγάλη ποικιλία φυσικών καταστάσεων όπως αέρια, υγρή, στερεή. Οι διάφορες αυτές φάσεις που μπορεί να έχει μία ουσία
Κεφάλαιο 4 Καταστάσεις της Ύλης: Αέρια, Υγρά και Στερεά Σύνοψη Η ύλη χαρακτηρίζεται από μεγάλη ποικιλία φυσικών καταστάσεων όπως αέρια, υγρή, στερεή. Οι διάφορες αυτές φάσεις που μπορεί να έχει μία ουσία
ΔΙΕΘΝΕΣ ΣΥΣΤΗΜΑ ΜΟΝΑΔΩΝ (S.I.)
 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΔΙΕΘΝΕΣ ΣΥΣΤΗΜΑ ΜΟΝΑΔΩΝ (S.I.) Το 1960 καθορίστηκε μετά από διεθνή συμφωνία το Διεθνές Σύστημα Μονάδων S.I. (από τα αρχικά των γαλλικών λέξεων Système International d Unités). Το σύστημα
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΔΙΕΘΝΕΣ ΣΥΣΤΗΜΑ ΜΟΝΑΔΩΝ (S.I.) Το 1960 καθορίστηκε μετά από διεθνή συμφωνία το Διεθνές Σύστημα Μονάδων S.I. (από τα αρχικά των γαλλικών λέξεων Système International d Unités). Το σύστημα
ΗΛΕΚΤΡΟΦΟΡΗΣΗ ΠΡΩΤΕΙΝΩΝ
 ΗΛΕΚΤΡΟΦΟΡΗΣΗ ΠΡΩΤΕΙΝΩΝ Άννα-Μαρία Ψαρρά ΤΒΒ, Παν/μιο Θεσσαλίας Λάρισα 2015 ΗΛΕΚΤΡΟΦΟΡΗΣΗ Αναλυτικός τρόπος διαχωρισμού πρωτεϊνών και άλλων μακρομορίων όπως πρωτεϊνών DNA, RNA Αρχή της μεθόδου Μόρια που
ΗΛΕΚΤΡΟΦΟΡΗΣΗ ΠΡΩΤΕΙΝΩΝ Άννα-Μαρία Ψαρρά ΤΒΒ, Παν/μιο Θεσσαλίας Λάρισα 2015 ΗΛΕΚΤΡΟΦΟΡΗΣΗ Αναλυτικός τρόπος διαχωρισμού πρωτεϊνών και άλλων μακρομορίων όπως πρωτεϊνών DNA, RNA Αρχή της μεθόδου Μόρια που
Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων.
 Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων. Θεωρώντας τα αέρια σαν ουσίες αποτελούμενες από έναν καταπληκτικά μεγάλο αριθμό μικροσκοπικών
Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων. Θεωρώντας τα αέρια σαν ουσίες αποτελούμενες από έναν καταπληκτικά μεγάλο αριθμό μικροσκοπικών
6 ο Μάθημα. Επιφανειακή Τάση
 6 ο Μάθημα Επιφανειακή Τάση 1 Επιφανειακή τάση του νερού Επιμέλεια: Γ. Ζαρδαλίδης, Θ. Κουκούλης Καθημερινές παρατηρήσεις Έντομα επιπλέουν στο νερό. Αντικείμενα μεγάλης πυκνότητας επιπλέουν στο νερό. Ανύψωση
6 ο Μάθημα Επιφανειακή Τάση 1 Επιφανειακή τάση του νερού Επιμέλεια: Γ. Ζαρδαλίδης, Θ. Κουκούλης Καθημερινές παρατηρήσεις Έντομα επιπλέουν στο νερό. Αντικείμενα μεγάλης πυκνότητας επιπλέουν στο νερό. Ανύψωση
ΑΣΚΗΣΗ ΦΑΣΜΑΤΟΜΕΤΡΙΑΣ ΜΑΖΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΤΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ
 ΑΣΚΗΣΗ ΦΑΣΜΑΤΟΜΕΤΡΙΑΣ ΜΑΖΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΤΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ Τίτλος Εργαστηριακής Άσκησης: Προσδιορισμός Σχετικής Μοριακής Μάζας (Μ r ) Πρωτεΐνης με την Xρησιμοποίηση Φασματομετρίας Μάζας Ηλεκτροψεκασμού
ΑΣΚΗΣΗ ΦΑΣΜΑΤΟΜΕΤΡΙΑΣ ΜΑΖΑΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΤΙΚΗΣ ΧΗΜΕΙΑΣ ΙΙ Τίτλος Εργαστηριακής Άσκησης: Προσδιορισμός Σχετικής Μοριακής Μάζας (Μ r ) Πρωτεΐνης με την Xρησιμοποίηση Φασματομετρίας Μάζας Ηλεκτροψεκασμού
2η Εργαστηριακή Άσκηση Εξάρτηση της ηλεκτρικής αντίστασης από τη θερμοκρασία Θεωρητικό μέρος
 2η Εργαστηριακή Άσκηση Εξάρτηση της ηλεκτρικής αντίστασης από τη θερμοκρασία Θεωρητικό μέρος Όπως είναι γνωστό από την καθημερινή εμπειρία τα περισσότερα σώματα που χρησιμοποιούνται στις ηλεκτρικές ηλεκτρονικές
2η Εργαστηριακή Άσκηση Εξάρτηση της ηλεκτρικής αντίστασης από τη θερμοκρασία Θεωρητικό μέρος Όπως είναι γνωστό από την καθημερινή εμπειρία τα περισσότερα σώματα που χρησιμοποιούνται στις ηλεκτρικές ηλεκτρονικές
ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ
 ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ Έννοιες που πρέπει να γνωρίζετε Ισορροπία φάσεων, εξίσωση Clauiu-Clapeyron Θέμα ασκήσεως Προσρόφηση ουσίας από αραιά διαλύματα. Προσδιορισμός ισόθερμων
ΦΑΙΝΟΜΕΝΑ ΠΡΟΣΡΟΦΗΣΕΩΣ ΠΡΟΣΡΟΦΗΣΗ ΟΥΣΙΑΣ ΑΠΟ ΔΙΑΛΥΜΑΤΑ Έννοιες που πρέπει να γνωρίζετε Ισορροπία φάσεων, εξίσωση Clauiu-Clapeyron Θέμα ασκήσεως Προσρόφηση ουσίας από αραιά διαλύματα. Προσδιορισμός ισόθερμων
ΤΕΧΝΟΛΟΓΙΑ ΚΑΙ ΠΟΙΟΤΙΚΟΣ ΕΛΕΓΧΟΣ ΠΡΟΣΘΕΤΩΝ ΚΑΙ ΓΛΥΚΑΝΤΙΚΩΝ ΥΛΩΝ. 6 ο ΕΡΓΑΣΤΗΡΙΟ Γαλακτωματοποιητές Παρασκευή Γαλακτώματος.
 ΤΕΧΝΟΛΟΓΙΑ ΚΑΙ ΠΟΙΟΤΙΚΟΣ ΕΛΕΓΧΟΣ ΠΡΟΣΘΕΤΩΝ ΚΑΙ ΓΛΥΚΑΝΤΙΚΩΝ ΥΛΩΝ 6 ο ΕΡΓΑΣΤΗΡΙΟ Γαλακτωματοποιητές Παρασκευή Γαλακτώματος Εισηγητής: Πρόδρομος Σκενδερίδης Γαλακτώματα Γαλάκτωμα ονομάζεται ένα κολλοειδές
ΤΕΧΝΟΛΟΓΙΑ ΚΑΙ ΠΟΙΟΤΙΚΟΣ ΕΛΕΓΧΟΣ ΠΡΟΣΘΕΤΩΝ ΚΑΙ ΓΛΥΚΑΝΤΙΚΩΝ ΥΛΩΝ 6 ο ΕΡΓΑΣΤΗΡΙΟ Γαλακτωματοποιητές Παρασκευή Γαλακτώματος Εισηγητής: Πρόδρομος Σκενδερίδης Γαλακτώματα Γαλάκτωμα ονομάζεται ένα κολλοειδές
ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2018 Β ΦΑΣΗ ΦΥΣΙΚΗ ΣΥΝΕΙΡΜΟΣ
 ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ημερομηνία: Τετάρτη Απριλίου 08 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό
ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ημερομηνία: Τετάρτη Απριλίου 08 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό
Ανόργανη Χημεία. Τμήμα Τεχνολογίας Τροφίμων. Ενότητα 4 η : Ιοντικοί Δεσμοί Χημεία Κύριων Ομάδων. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 4 η : Ιοντικοί Δεσμοί Χημεία Κύριων Ομάδων Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Δόμηση Ηλεκτρονίων στα Ιόντα 2 Για τα στοιχεία
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 4 η : Ιοντικοί Δεσμοί Χημεία Κύριων Ομάδων Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Δόμηση Ηλεκτρονίων στα Ιόντα 2 Για τα στοιχεία
ΜΟΡΦΟΠΟΙΗΣΗ ΜΕ ΤΕΧΝΙΚΕΣ ΚΟΝΙΟΜΕΤΑΛΛΟΥΡΓΙΑΣ
 ΜΟΡΦΟΠΟΙΗΣΗ ΜΕ ΤΕΧΝΙΚΕΣ ΚΟΝΙΟΜΕΤΑΛΛΟΥΡΓΙΑΣ Η πρώτη ύλη με τη μορφή σωματιδίων (κόνεως) μορφοποιείται μέσα σε καλούπια, με μηχανισμό που οδηγεί σε δομική διασύνδεση των σωματιδίων με πρόσδοση θερμότητας.
ΜΟΡΦΟΠΟΙΗΣΗ ΜΕ ΤΕΧΝΙΚΕΣ ΚΟΝΙΟΜΕΤΑΛΛΟΥΡΓΙΑΣ Η πρώτη ύλη με τη μορφή σωματιδίων (κόνεως) μορφοποιείται μέσα σε καλούπια, με μηχανισμό που οδηγεί σε δομική διασύνδεση των σωματιδίων με πρόσδοση θερμότητας.
ΔΙΕΛΑΣΗ. Το εργαλείο διέλασης περιλαμβάνει : το μεταλλικό θάλαμο, τη μήτρα, το έμβολο και το συμπληρωματικό εξοπλισμό (δακτυλίους συγκράτησης κλπ.).
 ΔΙΕΛΑΣΗ Κατά τη διέλαση (extrusion) το τεμάχιο συμπιέζεται μέσω ενός εμβόλου μέσα σε μεταλλικό θάλαμο, στο άλλο άκρο του οποίου ευρίσκεται κατάλληλα διαμορφωμένη μήτρα, και αναγκάζεται να εξέλθει από το
ΔΙΕΛΑΣΗ Κατά τη διέλαση (extrusion) το τεμάχιο συμπιέζεται μέσω ενός εμβόλου μέσα σε μεταλλικό θάλαμο, στο άλλο άκρο του οποίου ευρίσκεται κατάλληλα διαμορφωμένη μήτρα, και αναγκάζεται να εξέλθει από το
Κροκίδωση - Συσσωµάτωση
 ΕΠΕΞΕΡΓΑΣΙΑ ΝΕΡΟΥ ΚΑΙ ΥΓΡΩΝ ΑΠΟΒΛΗΤΩΝ Αχαρνών 364 & Γλαράκι 10Β, Αθήνα, 11145 Τηλ: 211 1820 163-4-5 Φαξ: 211 1820 166 e-mail: enerchem@enerchem.gr web site: www.enerchem.gr Κροκίδωση - Συσσωµάτωση Πηγή:
ΕΠΕΞΕΡΓΑΣΙΑ ΝΕΡΟΥ ΚΑΙ ΥΓΡΩΝ ΑΠΟΒΛΗΤΩΝ Αχαρνών 364 & Γλαράκι 10Β, Αθήνα, 11145 Τηλ: 211 1820 163-4-5 Φαξ: 211 1820 166 e-mail: enerchem@enerchem.gr web site: www.enerchem.gr Κροκίδωση - Συσσωµάτωση Πηγή:
γ ρ α π τ ή ε ξ έ τ α σ η σ τ ο μ ά θ η μ α Φ Υ Σ Ι Κ Η Γ Ε Ν Ι Κ Η Σ Π Α Ι Δ Ε Ι Α Σ B Λ Υ Κ Ε Ι Ο Υ
 η εξεταστική περίοδος από 9//5 έως 9//5 γ ρ α π τ ή ε ξ έ τ α σ η σ τ ο μ ά θ η μ α Φ Υ Σ Ι Κ Η Γ Ε Ν Ι Κ Η Σ Π Α Ι Δ Ε Ι Α Σ B Λ Υ Κ Ε Ι Ο Υ Τάξη: Β Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητής: Θ
η εξεταστική περίοδος από 9//5 έως 9//5 γ ρ α π τ ή ε ξ έ τ α σ η σ τ ο μ ά θ η μ α Φ Υ Σ Ι Κ Η Γ Ε Ν Ι Κ Η Σ Π Α Ι Δ Ε Ι Α Σ B Λ Υ Κ Ε Ι Ο Υ Τάξη: Β Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητής: Θ
6η Εργαστηριακή Άσκηση Μέτρηση διηλεκτρικής σταθεράς σε κύκλωµα RLC
 6η Εργαστηριακή Άσκηση Μέτρηση διηλεκτρικής σταθεράς σε κύκλωµα RLC Θεωρητικό µέρος Αν µεταξύ δύο αρχικά αφόρτιστων αγωγών εφαρµοστεί µία συνεχής διαφορά δυναµικού ή τάση V, τότε στις επιφάνειές τους θα
6η Εργαστηριακή Άσκηση Μέτρηση διηλεκτρικής σταθεράς σε κύκλωµα RLC Θεωρητικό µέρος Αν µεταξύ δύο αρχικά αφόρτιστων αγωγών εφαρµοστεί µία συνεχής διαφορά δυναµικού ή τάση V, τότε στις επιφάνειές τους θα
ΕΙΣΑΓΩΓΗ ΔΙΑΧΩΡΙΣΜΟΣ ΠΡΩΤΕΙΝΩΝ ΜΕ ΒΑΣΗ ΤΟ ΜΕΓΕΘΟΣ ΚΑΙ ΤΗ ΔΙΑΛΥΤΟΤΗΤΑ. ΑΝΝΑ-ΜΑΡΙΑ ΨΑΡΡΑ Τμήμα Βιοχημείας κ Βιοτεχνολογίας
 ΕΙΣΑΓΩΓΗ ΔΙΑΧΩΡΙΣΜΟΣ ΠΡΩΤΕΙΝΩΝ ΜΕ ΒΑΣΗ ΤΟ ΜΕΓΕΘΟΣ ΚΑΙ ΤΗ ΔΙΑΛΥΤΟΤΗΤΑ Τμήμα Βιοχημείας κ Βιοτεχνολογίας 1 ΔΙΑΧΩΡΙΣΜΟΣ ΠΡΩΤΕΙΝΩΝ ΒΑΣΕΙ ΔΙΑΛΥΤΟΤΗΤΑΣ ΜΕΓΕΘΟΥΣ ΦΟΡΤΙΟΥ ΧΗΜΙΚΗ ΣΥΓΓΕΝΕΙΑΣ ΜΕ ΣΥΓΚΕΚΡΙΜΕΝΑ ΜΟΡΙΑ
ΕΙΣΑΓΩΓΗ ΔΙΑΧΩΡΙΣΜΟΣ ΠΡΩΤΕΙΝΩΝ ΜΕ ΒΑΣΗ ΤΟ ΜΕΓΕΘΟΣ ΚΑΙ ΤΗ ΔΙΑΛΥΤΟΤΗΤΑ Τμήμα Βιοχημείας κ Βιοτεχνολογίας 1 ΔΙΑΧΩΡΙΣΜΟΣ ΠΡΩΤΕΙΝΩΝ ΒΑΣΕΙ ΔΙΑΛΥΤΟΤΗΤΑΣ ΜΕΓΕΘΟΥΣ ΦΟΡΤΙΟΥ ΧΗΜΙΚΗ ΣΥΓΓΕΝΕΙΑΣ ΜΕ ΣΥΓΚΕΚΡΙΜΕΝΑ ΜΟΡΙΑ
(Από το βιβλίο Γενική Χημεία των Ebbing, D. D., Gammon, S. D., Εκδόσεις Παπασωτηρίου )
 Δυνάμεις διπόλου διπόλου (Από το βιβλίο Γενική Χημεία των Ebbing, D. D., Gammon, S. D., Εκδόσεις Παπασωτηρίου ) Τα πολικά μόρια μπορούν να έλκονται αμοιβαία μέσω δυνάμεων διπόλου διπόλου. Η δύναμη διπόλου
Δυνάμεις διπόλου διπόλου (Από το βιβλίο Γενική Χημεία των Ebbing, D. D., Gammon, S. D., Εκδόσεις Παπασωτηρίου ) Τα πολικά μόρια μπορούν να έλκονται αμοιβαία μέσω δυνάμεων διπόλου διπόλου. Η δύναμη διπόλου
Αιωρήματα & Γαλακτώματα
 Αιωρήματα & Γαλακτώματα Εαρινό εξάμηνο Ακ. Έτους 2014-15 Μάθημα 2ο 25 February 2015 Αιωρήματα Γαλακτώματα 1 Παρασκευή αιωρημάτων Οι μέθοδοι παρασκευής αιωρημάτων κατατάσσονται σε δύο μεγάλες κατηγορίες
Αιωρήματα & Γαλακτώματα Εαρινό εξάμηνο Ακ. Έτους 2014-15 Μάθημα 2ο 25 February 2015 Αιωρήματα Γαλακτώματα 1 Παρασκευή αιωρημάτων Οι μέθοδοι παρασκευής αιωρημάτων κατατάσσονται σε δύο μεγάλες κατηγορίες
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
Κεφάλαιο 23 Ηλεκτρικό Δυναµικό. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 23 Ηλεκτρικό Δυναµικό Διαφορά Δυναµικού-Δυναµική Ενέργεια Σχέση Ηλεκτρικού Πεδίου και Ηλεκτρικού Δυναµικού Ηλεκτρικό Δυναµικό Σηµειακών Φορτίων Δυναµικό Κατανοµής Φορτίων Ισοδυναµικές Επιφάνειες
Κεφάλαιο 23 Ηλεκτρικό Δυναµικό Διαφορά Δυναµικού-Δυναµική Ενέργεια Σχέση Ηλεκτρικού Πεδίου και Ηλεκτρικού Δυναµικού Ηλεκτρικό Δυναµικό Σηµειακών Φορτίων Δυναµικό Κατανοµής Φορτίων Ισοδυναµικές Επιφάνειες
Γενική Χημεία. Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής
 Γενική Χημεία Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής Πολυτεχνείο Κρήτης Τμήμα Μηχανικών Περιβάλλοντος Γραφείο Κ2.125, τηλ.: 28210-37772 e-mail:nikosxek@gmail.com Περιεχόμενα Διαλύματα Γραμμομοριακή
Γενική Χημεία Νίκος Ξεκουκουλωτάκης Επίκουρος Καθηγητής Πολυτεχνείο Κρήτης Τμήμα Μηχανικών Περιβάλλοντος Γραφείο Κ2.125, τηλ.: 28210-37772 e-mail:nikosxek@gmail.com Περιεχόμενα Διαλύματα Γραμμομοριακή
ΙΑΤΡΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΚΑΤΑΤΑΚΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΑΚ.ΕΤΟΥΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ
 ΙΑΤΡΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΚΑΤΑΤΑΚΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΑΚ.ΕΤΟΥΣ 2017-2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ 1. Σε ποια μορφή της αιμοσφαιρίνης συνδέεται το 2,3, BPG, ποιο είναι το ηλεκτρικό του φορτίο, με
ΙΑΤΡΙΚΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΚΑΤΑΤΑΚΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΑΚ.ΕΤΟΥΣ 2017-2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ 1. Σε ποια μορφή της αιμοσφαιρίνης συνδέεται το 2,3, BPG, ποιο είναι το ηλεκτρικό του φορτίο, με
τα βιβλία των επιτυχιών
 Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Διατάξεις ημιαγωγών. Δίοδος, δίοδος εκπομπής φωτός (LED) Τρανζίστορ. Ολοκληρωμένο κύκλωμα
 Δίοδος, δίοδος εκπομπής φωτός (LED) Διατάξεις ημιαγωγών p n Άνοδος Κάθοδος Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Άνοδος Κάθοδος dpapageo@cc.uoi.gr http://pc64.materials.uoi.gr/dpapageo
Δίοδος, δίοδος εκπομπής φωτός (LED) Διατάξεις ημιαγωγών p n Άνοδος Κάθοδος Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Άνοδος Κάθοδος dpapageo@cc.uoi.gr http://pc64.materials.uoi.gr/dpapageo
Εργαστήριο Μηχανικής Ρευστών. Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής
 Εργαστήριο Μηχανικής Ρευστών Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής Ονοματεπώνυμο:Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημερομηνία εκτέλεσης Πειράματος : 12/4/2000 Ημερομηνία
Εργαστήριο Μηχανικής Ρευστών Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής Ονοματεπώνυμο:Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημερομηνία εκτέλεσης Πειράματος : 12/4/2000 Ημερομηνία
Παράγοντες που εξηγούν τη διαλυτότητα. Είδη διαλυμάτων
 Παράγοντες που εξηγούν τη διαλυτότητα 1. Η φυσική τάση των ουσιών να αναμιγνύονται μεταξύ τους. 2. Οι σχετικές ελκτικές δυνάμεις μεταξύ των χημικών οντοτήτων του διαλύματος Είδη διαλυμάτων Στα διαλύματα
Παράγοντες που εξηγούν τη διαλυτότητα 1. Η φυσική τάση των ουσιών να αναμιγνύονται μεταξύ τους. 2. Οι σχετικές ελκτικές δυνάμεις μεταξύ των χημικών οντοτήτων του διαλύματος Είδη διαλυμάτων Στα διαλύματα
Σύσταση του αυγού Λευκό Κρόκος Βάρος 38 g 17 g Πρωτείνη 3,9 g 2,7 g Υδατάνθρακες 0,3 g 0,3 g Λίπος 0 6 g Χοληστερόλη 0 213 mg
 Αυγό Τα αυγά αποτελούνται από το κέλυφος (10 %), το ασπράδι ή λευκό (50-60 %), τον κρόκο ή κίτρινο (30 %). Το κέλυφος αποτελείται κατά 95 % από ανόργανα συστατικά όπως ανθρακικό ασβέστιο, ανθρακικό μαγνήσιο
Αυγό Τα αυγά αποτελούνται από το κέλυφος (10 %), το ασπράδι ή λευκό (50-60 %), τον κρόκο ή κίτρινο (30 %). Το κέλυφος αποτελείται κατά 95 % από ανόργανα συστατικά όπως ανθρακικό ασβέστιο, ανθρακικό μαγνήσιο
Ασκήσεις Ακ. Έτους 2014 15 (επιλύθηκαν συζητήθηκαν κατά τη διδασκαλία) Όπου χρειάζεται ο Αριθμός Avogadro λαμβάνεται 0.6023 1024
 Ασκήσεις Ακ. Έτους 014 15 (επιλύθηκαν συζητήθηκαν κατά τη διδασκαλία) Όπου χρειάζεται ο Αριθμός Avoadro λαμβάνεται 0.603 10 4 και τα ατομικά βάρη θεωρείται ότι ταυτίζονται με τον μαζικό αριθμό σε 1. Το
Ασκήσεις Ακ. Έτους 014 15 (επιλύθηκαν συζητήθηκαν κατά τη διδασκαλία) Όπου χρειάζεται ο Αριθμός Avoadro λαμβάνεται 0.603 10 4 και τα ατομικά βάρη θεωρείται ότι ταυτίζονται με τον μαζικό αριθμό σε 1. Το
