ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
|
|
|
- Νικηφόρος Ζυγομαλάς
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ Οι ηλεκτρικές µηχανές συνεχούς ρεύµατος που εξετάσαµε ως γεννήτριες, µπορούν να χρησιµοποιηθούν και ως κινητήρες, αν τροφοδοτήσουµε το τύλιγµα του οπλισµού µε συνεχή τάση. Όταν το τύλιγµα του δροµέα, ευρισκόµενο εντός του κύριου πεδίου του στάτη, διαρρέετε από ρεύµα, αναπτύσσεται ροπή η οποία τείνει να στρέψει το δροµέα. Εποµένως, η µηχανή λειτουργεί ως κινητήρας µετατρέποντας την ηλεκτρική ενέργεια εισόδου σε µηχανική. Παρόλο που οι γεννήτριες συνεχούς ρεύµατος άρχισαν να εκτοπίζονται από τις γεννήτριες εναλλασσόµενου ρεύµατος πριν από το 19, οι κινητήρες συνεχούς ρεύµατος είναι ακόµη και σήµερα αρκετά διαδεδοµένοι. Ο κύριος λόγος που καθιστά τους κινητήρες συνεχούς ρεύµατος δηµοφιλείς, είναι η ευκολία στον έλεγχο της ταχύτητάς τους µέχρι το µηδέν και η εξαιρετική δυναµική τους συµπεριφορά. Έτσι, υπάρχουν εφαρµογές πολύ υψηλών απαιτήσεων στις οποίες οι κινητήρες συνεχούς ρεύµατος είναι αναντικατάστατοι. Η συµπεριφορά των κινητήρων περιγράφεται από τη χαρακτηριστική ταχύτητας ροπής. Αυτή περιγράφει τη µεταβολή της ταχύτητας του κινητήρα, καθώς µεταβάλλεται η ροπή του φορτίου που εφαρµόζεται στον άξονά του. Στη συνέχεια εξετάζουµε τα χαρακτηριστικά λειτουργίας των µηχανών συνεχούς ρεύµατος µε ανεξάρτητη διέγερση και αυτοδιέγερση, όταν χρησιµοποιούνται ως κινητήρες. 4.2 ΚΙΝΗΤΗΡΕΣ ΜΕ ΑΝΕΞΑΡΤΗΤΗ ΙΕΓΕΡΣΗ Το ισοδύναµο κύκλωµα του κινητήρα µε ανεξάρτητη διέγερση, είναι αντίστοιχο µ εκείνο της γεννήτριας συνεχούς ρεύµατος και εικονίζεται στο Σχ Στο Σχ. 4.1 µε E a συµβολίζεται η αντιηλεκτρεγερτική δύναµη (ΑΗΕ ) του κινητήρα. Η ΑΗΕ είναι η τάση που αναπτύσσεται στο τύλιγµα του οπλισµού καθώς αυτός στρέφεται µέσα στο κύριο µαγνητικό πεδίο του στάτη.
2 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 a = a Ε a R R' R = R R t Σχ. 4.1 Ισοδύναµο κύκλωµα του κινητήρα µε ανεξάρτητη διέγερση Εποµένως, το φαινόµενο της γεννήτριας εκδηλώνεται και στον κινητήρα, µε τον ίδιο ακριβώς τρόπο. Έτσι, η ΑΗΕ στους κινητήρες Ε a υπολογίζεται από την ίδια σχέση, που ορίζεται η ηλεκτρεγερτική δύναµη Ε στις γεννήτριες E = C φω (4.1) a r Από το ισοδύναµο κύκλωµα ισχύει η σχέση, = Ea ara (4.2) όπου είναι η τάση τροφοδοσίας του κινητήρα. Η τάση τροφοδοσίας είναι µεγαλύτερη από την ΑΗΕ του κινητήρα και η διαφορά των δύο τάσεων καθορίζει το µέγεθος του ρεύµατος στο δροµέα. Για δεδοµένη φορά περιστροφής, το ρεύµα του δροµέα στον κινητήρα έχει αντίθετη φορά από εκείνο στη γεννήτρια. Στις γεννήτριες, όπου η ροή της ισχύος είναι αντίθετη, η ηλε κτρεγερτική δύναµη Ε είναι µεγαλύτερη από την τάση εξόδου. Η ροπή που αναπτύσσεται στον άξονα των µηχανών συνεχούς ρεύµατος, όλων των κατηγοριών, ορίζεται από τη σχέση T = C φ (4.3) T a Οι σταθερές C και C T στις Εξ. (4.1), (4.3) είναι ίσες, C = C T. Από τις Εξ. (4.1), (4.2) προκύπτει µια έκφραση της ταχύτητας του κινητήρα µε ανεξάρτητη διέγερση ω r ara = (4.4) C φ( ) Η κύρια µαγνητική ροή στην Εξ. (4.4) ορίζεται από το ρεύµα διέγερσης, το οποίο ρυθµίζεται από την ανεξάρτητη πηγή συνεχούς τάσης. Αντικαθιστώντας στην Εξ. (4.4) το ρεύµα του δροµέα από την Εξ. (4.3), προκύπτει η παρακάτω έκφραση της ταχύτητας ως προς τη ροπή ω r = Ra T 2 C φ ( C φ) (4.5) Από την Εξ. (4.5), όταν η τάση τροφοδοσίας του κινητήρα και η µαγνητική ροή είναι σταθερές, η ταχύτητα µειώνεται γραµµικά µε την αύξηση της ροπής φορτίου T L (Σχ. 4.2). Στην κατάσταση ισορροπίας ισχύει, Τ =T L. 4 2
3 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Χωρίς τύλιγµα αντιστάθµισης o 1 2 Με τύλιγµα αντιστάθµισης = ratd Ι =,ratd Τ 1 = Τ L1 Τ 2 = Τ L2 Σχ. 4.2 Φυσική χαρακτηριστική ταχύτητας ροπής του κινητήρα µε ανεξάρτητη διέγερση Η γραµµική µεταβολή της ταχύτητας ισχύει µόνο όταν ο κινητήρας διαθέτει τύλιγµα αντιστάθµισης. Αν αυτό δεν συµβαίνει, µε την αύξηση της ροπής φορτίου η αντίδραση του οπλισµού προκαλεί τη µείωση της ροής, καθώς από την Εξ. (4.3) αυξάνει το ρεύµα a. Έτσι, η µείωση της ταχύτητας είναι µικρότερη από αυτή που ορίζει η Εξ. (4.5) και εικονίζεται στο Σχ. 4.2 µε διακεκοµµένη γραµµή. Η χαρακτηριστική ταχύτητας ροπής του κινητήρα που αντιστοιχεί στην ονοµαστική τάση οπλισµού = ratd και την ονοµαστική ροή φ = φratd ονοµάζεται φυσική (natural). Η χαρακτηριστική ταχύτητας ροπής του κινητήρα εξηγείται ως εξής: Θεωρούµε ότι ο κινητήρας στρέφεται µε ταχύτητα 1 και αναπτύσσει ροπή T 1, η οποία είναι ίση µε τη ροπή του φορτίου T L1 (T 1 = T L1 ). Αν η ροπή του φορτίου αυξηθεί στην τιµή T L2, η ταχύτητα του κινητήρα τείνει να µειωθεί. Με τη µείωση της ταχύτητας, από την Εξ. (4.1) µε σταθερή ροή, η ΑΗΕ µειώνεται. Εφόσον η τάση τροφοδοσίας είναι σταθερή, µε τη µείωση της E a το ρεύµα στο δροµέα αυξάνεται. Το αυξηµένο Ι a από την Εξ. (4.3) προκαλεί την αύξηση της παραγόµενης ροπής, στην τιµή T 2, η οποία είναι ίση µε τη νέα ροπή φορτίου T L2. Η µειωµένη ταχύτητα του κινητήρα 2 στο νέο σηµείο ισορροπίας, εξαρτάται αποκλειστικά από τη ροπή του φορτίου. Από την Εξ. (4.5), προκύπτουν οι τρεις µέθοδοι για τον έλεγχο της ταχύτητας ενός κινητήρα µε ανεξάρτητη διέγερση: Ρύθµιση της τάσης στο τύλιγµα του οπλισµού (armatur voltag control). Ρύθµιση της µαγνητικής ροής (fild control) φ. Ρυθµιζόµενη αντίσταση στο κύκλωµα του δροµέα (armatur rsistanc control). Τ Έλεγχος της Ταχύτητας µε Ρύθµιση της Τάσης Οπλισµού Η ταχύτητα ενός κινητήρα µε ανεξάρτητη διέγερση, µπορεί να ρυθµιστεί µε τον έλεγχο της τάσης που εφαρµόζεται στο τύλιγµα του οπλισµού. Η τάση διέγερσης διατηρείται σταθερή. Έτσι, το ρεύµα διέγερσης και η µαγνητική ροή είναι επίσης σταθερές. Προκειµένου να ερµηνεύσουµε τη διαδικασία µεταβολής της ταχύτητας, θεωρούµε ότι ο κινητήρας αρχικά τροφοδοτείται µε τάση 1, στρέφεται µε ταχύτητα 1 και αναπτύσσει ροπή T 1, η οποία είναι ίση µε τη ροπή του φορτίου T L (T 1 = T L ). Μια αύξηση της τάσης του τυλίγµατος οπλισµού, από την τιµή 1 στην 2, προκαλεί την αύξηση του ρεύµατος οπλισµού a, καθώς a2 = ( 2 Ea)/ Ra. Η αύξηση του a, από την τιµή a1 στην τιµή a2, προκαλεί την αύξηση της αναπτυσσόµενης ροπής, στην τιµή T = C φ > T (Σχ. 4.3). 2 a2 L 4 3
4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 Φυσική φ = φ ratd 1 < 2 < 3 < ratd atd ratd Τ L T ratd Σχ. 4.3 Έλεγχος της ταχύτητας του κινητήρα µε ανεξάρτητη διέγερση, µε τη ρύθµιση της τάσης οπλισµού Εφόσον η ροπή T 2 είναι µεγαλύτερη της ροπής φορτίου, ο κινητήρας επιταχύνεται. Η αύξηση της ταχύτητας προκαλεί την αύξηση της ΑΗΕ από τη σχέση Ea = Cφωr, οπότε το ρεύµα του οπλισµού ελαττώνεται ξανά. Έτσι, η ροπή επανέρχεται στην αρχική της τιµή T 1 = T L, σε µια ταχύτητα 2 µεγαλύτερη της αρχικής. Η ροπή του φορτίου έχει θεωρηθεί σταθερή και ανεξάρτητη της ταχύτητας. Οι χαρακτηριστικές ταχύτητας ροπής του κινητήρα, µε τη ρύθµιση της τάσης οπλισµού, εικονίζονται στο Σχ Οι χαρακτηριστικές είναι παράλληλες µεταξύ τους, δηλαδή η κλίση τους είναι σταθερή, όπως ορίζει η Εξ. (4.5). Αυτή η µέθοδος ελέγχου εφαρµόζεται µόνο για τη ρύθµιση της ταχύτητας του κινητήρα σε τιµές µικρότερες της ονοµαστικής. Ο κινητήρας στρέφεται µε την ονοµαστική του ταχύτητα atd, όταν τροφοδοτείται µε την ονοµαστική του τάση ratd, το ονοµαστικό ρεύµα διέγερσης και το ονοµαστικό φορτίο. Η ταχύτητα του κινητήρα είναι ανάλογη µε την τάση του δροµέα. Όσο µεγαλύτερη είναι η τάση του οπλισµού, τόσο µεγαλύτερη είναι η ταχύτητα του κινητήρα. Εποµένως, για την αύξηση της ταχύτητας σε τιµές µεγαλύτερες της ονοµαστικής, πρέπει και η τάση στο τύλιγµα του δροµέα να υπερβεί την ratd. Όµως αυτό δεν είναι επιτρεπτό, καθώς µπορεί να καταστραφεί το κύκλωµα του οπλισµού. Έτσι, η µέθοδος της ρύθµισης της τάσης οπλισµού, χρησιµοποιείται στον έλεγχο της ταχύτητας σε τιµές µικρότερες από την ονοµαστική. Τ Έλεγχος της Ταχύτητας µε Ρύθµιση της Μαγνητικής Ροής Η µαγνητική ροή του κινητήρα ελέγχεται µε τη ρύθµιση του ρεύµατος διέγερσης, µέσω της τάσης ή της αντίστασης R. Θεωρούµε όπως και προηγούµενα, ότι ο κινητήρας στρέφεται αρχικά µε ταχύτητα 1 και αναπτύσσει ροπή T 1, η οποία είναι ίση µε τη ροπή του φορτίου T L (T 1 = T L ). Η µαγνητική ροή είναι ίση µε φ 1. Η τάση στο τύλιγµα του δροµέα είναι σταθερή και ίση µε την ονοµαστική. Μια µείωση στο ρεύµα διέγερσης και αντίστοιχα στη µαγνητική ροή, από την τιµή φ 1 στην τιµή φ 2, προκαλεί την ελάττωση της ΑΗΕ Ea = Cφωr. Η µείωση της ΑΗΕ έχει ως αποτέλεσµα την αύξηση του ρεύµατος οπλισµού a = ( Ea)/ Ra. Όταν η ταχύ τητα του κινητήρα 1 είναι κοντά στην ονοµαστική, η ΑΗΕ έχει µεγάλη τιµή. Έτσι, ακόµη και µια ελάχιστη µείωση στη ροή και την ΑΗΕ, προκαλεί µια εξαιρετικά µεγάλη αύξηση του ρεύµατος οπλισµού, καθώς η είναι πολύ µικρή. Επειδή η αύξηση του a είναι πολύ µεγαλύ τερη της µείωσης της ροής, η αναπτυσσόµενη ροπή αυξάνει T = CTφ a. 4 4
5 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ φ 3 φ 2 2 φ 1 1 φ ratd Φυσική = ratd φ > φ > φ > φ ratd Τ L Σχ. 4.4 Έλεγχος της ταχύτητας του κινητήρα µε ανεξάρτητη διέγερση, µε τη ρύθµιση της µαγνητικής ροής Σηµειώνουµε ότι, σε µικρές ταχύτητες η αύξηση του ρεύµατος οπλισµού µε τη µείωση της ροής περιορίζεται. Έτσι, σε εξαιρετικά µικρές ταχύτητες είναι δυνατό η µείωση της ροής να υπερισχύει της αύξησης του a και η ροπή να µειώνεται µε τη µείωση ροής. Όµως, αυτή η συνθήκη λειτουργίας δεν έχει πρακτικό ενδιαφέρον. Εξαιτίας της αύξησης της ροπής που προκαλεί η µείωση της ροής, ο κινητήρας επιταχύνει. Όµως, καθώς αυξάνει η ταχύτητα, µειώνεται η ΑΗΕ, το ρεύµα του δροµέα και η παραγόµενη ροπή. Τελικά ο κινητήρας ισορροπεί σε µια µεγαλύτερη ταχύτητα 2 από την αρχική, στην οποία η ροπή του είναι και πάλι ίση µε τη ροπή του φορτίου. Οι χαρακτηριστικές ταχύτητας ροπής του κινητήρα, µε τη ρύθµιση της µαγνητικής ροής, εικονίζονται στο Σχ Οι χαρακτηριστικές δεν έχουν την ίδια κλίση, όπως στην προηγούµενη µέθοδο. Όσο µειώνεται η ροή, τόσο µεγαλύτερη είναι η κλίση των χαρακτηριστικών. Αυτή η συµπεριφορά ερµηνεύεται από την Εξ. (4.5), στην οποία ο δεύτερος όρος (κλίση), είναι αντι στρόφως ανάλογος µε το τετράγωνο της µαγνητικής ροής. Η ταχύτητα του κινητήρα στο κενό, είναι αντιστρόφως ανάλογη της µαγνητικής ροής. Με τη ρύθµιση της µαγνητικής ροής, η ταχύτητα του κινητήρα ελέγχεται σε τιµές µεγαλύ τερες από την ονοµαστική. Για τη λειτουργία του κινητήρα σε ταχύτητες µικρότερες από την ονοµαστική, το ρεύµα διέγερσης πρέπει να γίνει µεγαλύτερο από το ονοµαστικό. Θεωρούµε ότι = ratd. Όµως, ένα ρεύµα διέγερσης µεγαλύτερο από το ονοµαστικό, θα προκαλέσει υπερ θέρµανση του τυλίγµατος, µε κίνδυνο την καταστροφή του. Στους κινητήρες συνεχούς ρεύµατος είναι κρίσιµο το ρεύµα διέγερσης να ρέει συνεχώς. Αν για κάποιο λόγο το ρεύµα διέγερσης διακοπεί, ενώ ο κινητήρας λειτουργεί, η µαγνητική ροή θα γίνει ίση µε την παραµένουσα φ r. Η ΑΗΕ θα γίνει πολύ µικρή Ea = Cφω r r και το ρεύµα του οπλισµού θα αυξηθεί υπερβολικά. Έτσι, η παραγόµενη ροπή θα γίνει µεγαλύτερη της ροπής φορτίου και η ταχύτητα του κινητήρα θα αυξάνει συνεχώς. Τ Έλεγχος της Ταχύτητας µε Ρυθµιζόµενη Αντίσταση στο ροµέα Από την Εξ. (4.5) προκύπτει ότι, η ταχύτητα του κινητήρα ανεξάρτητης διέγερσης µπορεί να ρυθµιστεί µε την εισαγωγή µιας µεταβλητής αντίστασης σε σειρά µε το τύλιγµα του δροµέα. Όσο µεγαλύτερη είναι η τιµή της αντίστασης, τόσο µικρότερη είναι η ταχύτητα του κινητήρα, όταν λειτουργεί µε φορτίο. Η µέθοδος αυτή χρησιµοποιείται σπάνια, εξαιτίας των µεγάλων απωλειών 4 5
6 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 ισχύος στην αντίσταση ρύθµισης, από το µεγάλο ρεύµα του οπλισµού. Ένα δεύτερο µειονέκτηµα είναι ότι, η ταχύτητα του κινητήρα στο κενό δεν µπορεί να ελεγχθεί Περιοχές Λειτουργίας Μέγιστης Ροπής και Μέγιστης Ισχύος Οι µέθοδοι ελέγχου της ταχύτητας του κινητήρα ανεξάρτητης διέγερσης, µε ρύθµιση της τάσης οπλισµού και ρύθµιση της µαγνητικής ροής, δρουν συµπληρωµατικά. Όταν απαιτείται η ρύθµιση της ταχύτητας του κινητήρα σε µεγάλο εύρος, οι δύο µέθοδοι χρησιµοποιούνται ταυτό χρονα. Σε ταχύτητες µικρότερες της ονοµαστικής, η µαγνητική ροή διατηρείται στην ονοµαστική τιµή και η ταχύτητα ελέγχεται µε τη ρύθµιση της τάσης του οπλισµού. Σε ταχύτητες µεγαλύτερες της ονοµαστικής, η τάση του οπλισµού διατηρείται στην ονοµαστική τιµή και η µαγνητική ροή µειώνεται από την ονοµαστική. Στο Σχ. 4.5 εικονίζεται η µεταβολή της µέγιστης ροπής και της µέγιστης ισχύος, που µπορεί να αναπτύξει ένας κινητήρας µε ανεξάρτητη διέγερση, όταν η ταχύτητα του ελέγχεται µε τις δύο µεθόδους. Σε ταχύτητες µικρότερες της ονοµαστικής, όπου φ = φratd, η µέγιστη ροπή που µπορεί να αναπτύξει ο κινητήρας εξαρτάται από το µέγιστο ρεύµα του οπλισµού a,max T = C φ (4.6),max a,max Η τιµή της µέγιστης ροπής διατηρείται σταθερή µε τη µείωση της ταχύτητας, µέχρι τη µηδενική (περιοχή σταθερής ροπής). Η µέγιστη ισχύς εξόδου είναι ίση µε P = T ω (4.7) o,max,max r Εποµένως, η τιµή της µέγιστης ισχύος µεταβάλλεται γραµµικά µε την ταχύτητα. Σε ταχύτητες µεγαλύτερες από την ονοµαστική, η ροή µειώνεται από την ονοµαστική. Επειδή το ρεύµα του οπλισµού διατηρείται στη µέγιστη τιµή a,max, η µέγιστη ροπή µειώνεται µε την αύξηση της ταχύτητας, Εξ. (4.6). Η µέγιστη ισχύς εξόδου διατηρείται σταθερή, στην τιµή που αντιστοιχεί στην ονοµαστική ταχύτητα (περιοχή σταθερής ισχύος). T,max a = a,max P o,max P o,max T,max φ = φ ratd = ratd < ratd φ < φratd Ρύθµιση της τάσης οπλισµού. Περιοχή σταθερής ροπής atd Ρύθµιση της µαγνητικής ροής. Περιοχή σταθερής ισχύος,max Σχ. 4.5 Περιοχές λειτουργίας του κινητήρα ανεξάρτητης διέγερσης µε σταθερή µέγιστη ροπή σε ταχύ τητες µικρότερες της ονοµαστικής και σταθερή µέγιστη ισχύ σε ταχύτητες µεγαλύτερες της ονοµαστικής 4 6
7 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ a Ε a R R' R = R R t Σχ. 4.6 Ισοδύναµο κύκλωµα του κινητήρα παράλληλης διέγερσης 4.3 ΚΙΝΗΤΗΡΕΣ ΠΑΡΑΛΛΗΛΗΣ ΙΕΓΕΡΣΗΣ Το ισοδύναµο κύκλωµα του κινητήρα παράλληλης διέγερσης εικονίζεται στο Σχ Η διαφορά του κινητήρα παράλληλης διέγερσης από τον κινητήρα µε ανεξάρτητη διέγερση, είναι ότι το κύκλωµα του δροµέα και το κύκλωµα της διέγερσης τροφοδοτούνται από την ίδια πηγή συνεχούς τάσης. Οι Εξ. (4.1) (4.5) και η χαρακτηριστική ταχύτητας ροπής του Σχ. 4.2, ισχύουν και στους κινητήρες µε παράλληλη διέγερση. Έτσι, η συµπεριφορά των κινητήρων παράλληλης διέγερσης, δεν διαφέρει από εκείνη των κινητήρων µε ανεξάρτητη διέγερση. Οι κινητήρες ανεξάρτητης διέγερσης, προτιµώνται από τους κινητήρες µε παράλληλη διέγερση, σε εφαρµογές όπου απαιτείται ο έλεγχος της ταχύτητας σε ευρεία περιοχή µε υψηλή ακρίβεια. 4.4 ΚΙΝΗΤΗΡΕΣ ΜΕ ΙΕΓΕΡΣΗ ΣΕΙΡΑΣ Στους κινητήρες µε διέγερση σειράς, το τύλιγµα της διέγερσης συνδέεται σε σειρά µε το κύκλωµα του δροµέα, όπως εικονίζεται στο Σχ Έτσι, το ρεύµα της διέγερσης είναι ίσο µε το ρεύµα του οπλισµού και η µαγνητική ροή είναι συνάρτηση του ρεύµατος στο δροµέα ( = a = ). Στη µη κορεσµένη περιοχή της καµπύλης µαγνήτισης του κινητήρα, η ροή µπορεί να θεωρηθεί ότι µεταβάλλεται γραµµικά µε το ρεύµα του οπλισµού φ= C (4.8) f a Ε a a R = a = Σχ. 4.7 Ισοδύναµο κύκλωµα του κινητήρα µε διέγερση σειράς 4 7
8 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 Αντικαθιστώντας την Εξ. (4.8) στις Εξ. (4.1) και (4.3), οι οποίες ισχύουν σ όλους τους κινη τήρες συνεχούς ρεύµατος, έχουµε E = C C ω (4.9) a f a r T = C C (4.1) 2 f a Από το ισοδύναµο κύκλωµα (Σχ. 4.7), ισχύει η σχέση = E ( R R ) (4.11) a a a Συνδυάζοντας τις Εξ. (4.9) (4.11), προκύπτει η σχέση της ταχύτητας του κινητήρα ως προς τη ροπή ω r Ra R 1 Ra R = = (4.12) CC CC CC T CC f a f f f Από την Εξ. (4.12) παρατηρούµε ότι, η ταχύτητα του ακόρεστου κινητήρα µε διέγερση σειράς, µεταβάλλεται αντιστρόφως ανάλογα µε την τετραγωνική ρίζα της ροπής του. Η χαρακτη ριστική ταχύτητας ροπής που προκύπτει από την Εξ. (4.12) εικονίζεται στο Σχ. 4.8, µε σταθερή τάση τροφοδοσίας ίση µε την ονοµαστική (φυσική χαρακτηριστική). Η απότοµη µεταβολή της ταχύτητας µε τη ροπή, οφείλεται στη µεταβολή της µαγνητικής ροής µε το φορτίο. Έτσι, µια αύξηση της ροπής φορτίου προκαλεί την αύξηση του ρεύµατος οπλισµού Εξ. (4.1) και της µαγνητικής ροής Εξ. (4.8). Επειδή η ροή αυξάνεται µε τη ροπή, η ταχύτητα πρέπει να µειωθεί σηµαντικά ώστε να διατηρηθεί η ισορροπία µεταξύ της σταθερής τάσης τροφοδοσίας και της ΑΗΕ του κινητήρα, Εξ. (4.9) και (4.11). Από το Σχ. 4.8 παρατηρούµε ότι, η ταχύτητα του κινητήρα αποκτά πολύ µεγάλες τιµές όταν η ροπή του φορτίου τείνει στο µηδέν. Έτσι, οι κινητήρες µε διέγερση σειράς δεν πρέπει ποτέ να λειτουργούν χωρίς φορτίο. Οι κινητήρες σειράς δίνουν τη µεγαλύτερη ροπή ανά µονάδα ρεύ µατος, από κάθε άλλο κινητήρα συνεχούς ρεύµατος, εξαιτίας της αύξησης της ροής µε τη ροπή και µάλιστα σε µικρή ταχύτητα. Εποµένως, χρησιµοποιούνται σε εφαρµογές όπου απαιτείται υψηλή ροπή εκκίνησης και µεγάλες υπερφορτίσεις. Τέτοιες εφαρµογές είναι οι κινητήρες των ανελκυστήρων, των γερανών και των συστηµάτων έλξης (τρένα). = ratd Σχ. 4.8 Φυσική χαρακτηριστική ταχύτητας ροπής του κινητήρα µε διέγερση σειράς Τ 4 8
9 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Φυσική ratd Μείωση της Σχ. 4.9 Έλεγχος της ταχύτητας του κινητήρα διέγερσης σειράς, µε ρύθµιση της τάσης τροφοδοσίας Έλεγχος της Ταχύτητας Από την Εξ. (4.12) προκύπτει ότι, η µόνη βολική µέθοδος για τον έλεγχο της ταχύτητας του κινητήρα µε διέγερση σειράς, είναι η ρύθµιση της τάσης τροφοδοσίας. Μειώνοντας την τάση από την ονοµαστική της τιµή, µειώνεται και η ταχύτητα του κινητήρα, ανεξάρτητα από την ροπή του φορτίου (Σχ. 4.9). Επειδή η µαγνητική ροή δεν µπορεί να ελεγχθεί, η ονοµαστική ταχύτητα του κινητήρα σειράς πρέπει να επιλέγεται ίση µε τη µέγιστη επιθυµητή ταχύτητα του συστήµατος. 4.5 ΚΙΝΗΤΗΡΕΣ ΜΕ ΣΥΝΘΕΤΗ ΙΕΓΕΡΣΗ Στους κινητήρες µε αθροιστική σύνθετη διέγερση, το τύλιγµα σειράς και το παράλληλο τύλιγµα συνδέονται µε τέτοιο τρόπο, έτσι ώστε οι µαγνητικές ροές που αναπτύσσουν να προστί θενται. Ανάλογα µε τον τρόπο σύνδεσης των δύο τυλιγµάτων, διακρίνουµε τα ισοδύναµα κυκλώ µατα του Σχ Οι τάσεις και τα ρεύµατα στη σύνδεση long shunt δίνονται από τις σχέσεις a Τ = (4.13) = E ( R R ) (4.14) a a a s = (4.15) R tp Στη σύνδεση short shunt, ισχύουν οι σχέσεις = (4.16) a p = Ea ara (4.17) = R (4.18) p s p = (4.19) R tp 4 9
10 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 a E a R s a R p R' p R = R R tp p p a p (α) E a R p R' p Rtp = Rp R p R s (β) Σχ. 4.1 Ισοδύναµο κύκλωµα του κινητήρα αθροιστικής σύνθετης διέγερσης σε σύνδεση long shunt (α) και σε σύνδεση short shunt (β) Η χαρακτηριστική ταχύτητας ροπής του κινητήρα µε αθροιστική σύνθετη διέγερση εικο νίζεται στο Σχ Στο ίδιο σχήµα έχουν σχεδιαστεί για σύγκριση, οι φυσικές χαρακτηριστικές ταχύτητας ροπής των κινητήρων µε ανεξάρτητη ή παράλληλη διέγερση και διέγερσης σειράς. Όλοι οι κινητήρες έχουν την ίδια ονοµαστική ταχύτητα και ισχύ (ροπή). Σε µικρές ροπές φορτίου, η επίδραση του τυλίγµατος σειράς είναι ασθενής. Έτσι, ο κινητήρας παρουσιάζει τη συµπεριφορά ενός κινητήρα µε παράλληλη διέγερση. Η ταχύτητα του κινητήρα στο κενό έχει µια σαφώς καθορισµένη τιµή, όπως οι κινητήρες παράλληλης και ανεξάρτητης διέγερσης. Σε µεγάλες ροπές του φορτίου, η επίδραση του τυλίγµατος σειράς είναι έντονη, εξαιτίας του υψηλού ρεύµατος δροµέα. Εποµένως, ο κινητήρας αθροιστικής σύνθετης διέγερσης τείνει να συµπερι φέρεται ως κινητήρας µε διέγερση σειράς, εµφανίζοντας µεγάλη ροπή εκκίνησης. Αθροιστική σύνθετη διέγερση ιέγερση σειράς = ratd atd Ανεξάρτητη ή παράλληλη διέγερση Τ ratd Σχ Φυσική χαρακτηριστική ταχύτητας ροπής του κινητήρα αθροιστικής σύνθετης διέγερσης, σε συνδυασµό µε τις χαρακτηριστικές των κινητήρων παράλληλης διέγερσης και διέγερσης σειράς Τ 4 1
11 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ = ratd Σχ Χαρακτηριστική ταχύτητας ροπής του κινητήρα διαφορικής σύνθετης διέγερσης Οι κινητήρες στο Σχ. 4.1 µετατρέπονται σε κινητήρες διαφορικής σύνθετης διέγερσης, αλλάζοντας τη φορά σύνδεσης του τυλίγµατος σειράς (θέση της τελείας). Στους κινητήρες µε διαφορική σύνθετη διέγερση, η µαγνητική ροή µειώνεται µε την αύξηση της ροπής φορτίου. Έτσι, η ταχύτητα του κινητήρα αυξάνεται µε την αύξηση της ροπής, όπως εικονίζεται στο Σχ. 4.12, µε αποτέλεσµα την ασταθή λειτουργία της µηχανής. Εποµένως, οι κινητήρες µε διαφορική σύνθετη διέγερση δεν έχουν πρακτικές εφαρµογές. Τ 4.6 ΕΚΚΙΝΗΣΗ ΤΩΝ ΚΙΝΗΤΗΡΩΝ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Κατά την εκκίνηση των κινητήρων συνεχούς ρεύµατος µε την ονοµαστική τάση, το ρεύµα του οπλισµού αποκτά πολύ µεγάλες τιµές. Τη στιγµή της εκκίνησης, η ΑΗΕ του κινητήρα είναι µηδενική. Έτσι, το αρχικό ρεύµα εκκίνησης είναι ίσο µε /. Η ωµική αντίσταση του οπλισµού είναι πολύ µικρή, µε αποτέλεσµα το ρεύµα εκκίνησης των τυπικών κινητήρων συνεχούς ρεύµατος να είναι περίπου 2 φορές µεγαλύτερο από το ονοµαστικό. Το µεγάλο ρεύµα εκκίνη σης οφείλεται στο ότι η ΑΗΕ είναι µηδενική, επειδή ο κινητήρας δεν στρέφεται, =. Καθώς η ταχύτητα του κινητήρα αυξάνεται, η ΑΗΕ ενισχύεται και περιορίζει το ρεύµα του οπλισµού. Αν και η χρονική διάρκεια του ρεύµατος εκκίνησης είναι µικρή, η εξαιρετικά µεγάλη τιµή του µπορεί να προκαλέσει βλάβη στη µηχανή. Για τον περιορισµό του ρεύµατος εκκίνησης, τοποθετείται σε σειρά µε το τύλιγµα του οπλισµού µια αντίσταση εκκίνησης. Η αντίσταση εκκίνησης βραχυκυκλώνεται µε διακόπτες, όταν η ταχύτητα του κινητήρα αποκτήσει µια επαρκώς µεγάλη τιµή. Στο Σχ εικονίζεται η διάταξη εκκίνησης ενός κινητήρα παράλληλης διέγερσης. S 1 S 2 S 3 S 4 a R s1 R s2 R s3 R s4 Ε a R R' Σχ ιάταξη εκκίνησης του κινητήρα µε παράλληλη διέγερση 4 11
12 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 Η αντίσταση εκκίνησης αποτελείται από τέσσερα στάδια, µε τις κατάλληλες τιµές, τα οποία βραχυκυκλώνονται σταδιακά από τους διακόπτες S 1, S 2, S 3, S 4. Ένα κύκλωµα ελέγχου ενεργοποιεί αυτόµατα τους διακόπτες την κατάλληλη χρονική στιγµή, για τη βέλτιστη εκκίνηση του κινητήρα. Η εκκίνηση του κινητήρα είναι τόσο ποιο οµαλή, όσο µεγαλύτερος είναι ο αριθµός των βηµάτων της αντίστασης εκκίνησης. 4.7 ΠΕ ΗΣΗ ΤΩΝ ΚΙΝΗΤΗΡΩΝ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Πέδηση ονοµάζεται η διαδικασία επιβράδυνσης, µείωσης της ταχύτητας, ενός ηλεκτρικού κινητήρα. Κατά τη διάρκεια της πέδησης, ο κινητήρας λειτουργεί ως γεννήτρια. ηλαδή, ο κινητήρας µετατρέπει κατά το διάστηµα της πέδησης τη µηχανική ενέργεια από το φορτίο, σε ηλεκτρική. Η µηχανική ενέργεια παρέχεται, στην περίπτωση του παθητικού φορτίου, από την κινητική ενέργεια που είναι αποθηκευµένη στην αδράνεια του συστήµατος κινητήρας φορτίο, είτε απευθείας από το ενεργό φορτίο. Τα είδη των φορτίων αναφέρονται στην παρ Για την πέδηση των κινητήρων συνεχούς ρεύµατος, το ρεύµα του οπλισµού πρέπει να αντιστραφεί, ενώ η φορά της κύριας µαγνητικής ροής διατηρείται σταθερή. Τότε, η φορά της αναπτυσσόµενης ροπής αντιστρέφεται T = CTφ a και η ισχύς γίνεται αρνητική P = Tω r. Η αρνητική ισχύς σηµαίνει ότι, η µηχανή µετατρέπει τη µηχανική ενέργεια σε ηλεκτρική, δηλαδή λειτουργεί ως γεννήτρια. ιακρίνουµε τρεις µεθόδους πέδησης των ηλεκτρικών κινητήρων όλων των κατηγοριών, ανάλογα µε τον τρόπο διάθεσης της ισχύος που ανακτάται από τη µηχανή (rgnratd powr): Πέδηση µε ανάκτηση της ισχύος (rgnrativ braking) υναµική πέδηση (dynamic braking) Πέδηση µε αναστροφή της τάσης (plugging) Πέδηση µε Ανάκτηση της Ισχύος Στη µέθοδο πέδησης µε ανάκτηση της ισχύος, η ενέργεια που παράγεται από τη µηχανή κατά το διάστηµα της επιβράδυνσής της, επιστρέφει στην πηγή τροφοδοσίας. Εποµένως, η πηγή τροφοδοσίας πρέπει να έχει την ικανότητα αποθήκευσης, ή διάθεσης σ άλλα φορτία, της παραγόµενης από τη µηχανή ενέργειας. Αν η δυνατότητα αυτή δεν υπάρχει, τότε η µέθοδος της πέδησης µε ανάκτηση της ισχύος δεν µπορεί να χρησιµοποιηθεί. Ε a a 1 > E a R 1 ΜΕΤΑΤΡΟΠΕΑΣ ΙΣΧΥΟΣ ratd Ε a a 2 R 2 < E a ΜΕΤΑΤΡΟΠΕΑΣ ΙΣΧΥΟΣ ratd (α) (β) Σχ Πέδηση του κινητήρα µε ανεξάρτητη διέγερση. Λειτουργία κινητήρα µε 1 > E a (α) και λειτουργία γεννήτριας 2 < E a (β) 4 12
13 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Φυσική φ = φ ratd 2 < 1 < ratd ratd T braking Σχ Χαρακτηριστικές ταχύτητας ροπής του κινητήρα µε ανεξάρτητη διέγερση, κατά τη λειτουργία κινητήρα (πρώτο τεταρτηµόριο) και κατά την πέδηση µε τη µέθοδο της ανάκτησης ισχύος (δεύτερο τεταρτηµόριο) Στο Σχ εικονίζεται ένας κινητήρας µε ανεξάρτητη διέγερση. Το τύλιγµα διέγερσης του κινητήρα τροφοδοτείται από µια πηγή σταθερής τάσης και ο κινητήρας λειτουργεί µε την ονοµαστική µαγνητική ροή. Το κύκλωµα του οπλισµού τροφοδοτείται από ένα µετατροπέα ισχύος, µε τάση που µπορεί να ρυθµιστεί από το µηδέν έως την ονοµαστική τιµή (<< ratd ). Μέσω του µετατροπέα ισχύος είναι δυνατός ο έλεγχος της ταχύτητας του κινητήρα, από το µηδέν έως την ονοµαστική τιµή και ταυτόχρονα η πέδησή του, µε τη µέθοδο της ανάκτησης ισχύος. Για την πέδηση του κινητήρα, ο µετατροπέας ισχύος µειώνει την τάση τροφοδοσίας του κινητήρα από την τιµή 1 (Σχ. 4.14α), στην τιµή 2 (Σχ. 4.14β). Στο Σχ. 4.14α είναι 1 > E a έτσι, το ρεύµα του οπλισµού είναι θετικό και η µηχανή απορροφά ισχύ από την ηλεκτρική πηγή εισόδου. Στο Σχ. 4.14β, ο µετατροπέας επιβάλλει την τάση 2 < E a. Επειδή η ΑΗΕ του κινητήρα είναι µεγα λύτερη από την τάση εισόδου του, το ρεύµα του οπλισµού και η ροπή λαµβάνουν αρνητικές τιµές. Εποµένως, η µηχανή λειτουργεί ως γεννήτρια. Ο µετατροπέας ισχύος πρέπει να έχει την ικανότητα να φέρει ρεύµα και προς τις δύο κατευθύνσεις και η πηγή να απορροφά την ενέργεια της πέδησης. Αυτές οι συνθήκες εκπληρώνονται στα ηλεκτρικά αυτοκίνητα, όπου η ενέργεια που παράγεται σε κάθε πέδηση του οχήµατος, χρησιµοποιείται στη φόρτιση των συσσωρευτών του. Οι χαρακτηριστικές ταχύτητας ροπής του κινητήρα προκύπτουν από την Εξ. (4.5) και εικο νίζονται στο Σχ Οι χαρακτηριστικές αυτές αποτελούν µια επέκταση των χαρακτηριστικών του κινητήρα από το Σχ. 4.3, στο δεύτερο τεταρτηµόριο, όπου η ροπή είναι αρνητική. Τ L Τ υναµική Πέδηση Η πέδηση ενός κινητήρα συνεχούς ρεύµατος µε τη δυναµική µέθοδο, σηµαίνει την αποσύνδεση του κυκλώµατος οπλισµού από την πηγή τροφοδοσίας και τον παραλληλισµό του µε µια αντίσταση (Σχ. 4.16). Επειδή η τάση τροφοδοσίας της µηχανής είναι µηδέν (Σχ. 4.16β), η ΑΗΕ προκαλεί τη ροή ενός ρεύµατος οπλισµού µε την αντίθετη φορά από εκείνη στη λειτουρ γία του κινητήρα (Σχ. 4.16α). Εποµένως, η µηχανή λειτουργεί ως γεννήτρια αναπτύσσοντας αρνητική ροπή. Η αντίσταση πέδησης R br που συνδέεται στο κύκλωµα του δροµέα πρέπει να έχει κατάλληλη τιµή, έτσι ώστε το αρχικό ρεύµα πέδησης, για τη µέγιστη ταχύτητα άρα και τη µέγιστη ΑΗΕ max του κινητήρα = E max /( R R ), να περιορίζεται σε ασφαλή τιµή. a a br 4 13
14 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 a a Ε a R R br Ε a R R br (α) Σχ υναµική πέδηση του κινητήρα µε ανεξάρτητη διέγερση. Λειτουργία κινητήρα (α), λειτουργία γεννήτριας (β) Στο δεύτερο τεταρτηµόριο του Σχ εικονίζονται οι χαρακτηριστικές ταχύτητας ροπής του κινητήρα ανεξάρτητης διέγερσης µε δυναµική πέδηση, για δύο τιµές της αντίστασης πέδησης. Οι χαρακτηριστικές αυτές λαµβάνονται από την Εξ. (4.5) θέτοντας, = και στη θέση της αντίστασης οπλισµού το άθροισµα R br. (β) ω r Ra Rbr = ( T ) 2 (4.2) ( C φ) Παρατηρούµε ότι, το µέγεθος της αρνητικής ροπής είναι τόσο µεγαλύτερο, όσο µικρότερη είναι η τιµή της αντίστασης πέδησης. Έτσι, το χρονικό διάστηµα της πέδησης ελαττώνεται, µε τη µείωση της αντίστασης R br. Ακόµη, η ροπή πέδησης µειώνεται µε τη µείωση της ταχύτητας και µηδενίζεται στη µηδενική ταχύτητα. Έτσι, σε εφαρµογές όπου απαιτείται ταχεία πέδηση, η τιµή της αντίστασης R br µειώνεται έως το µηδέν, καθώς ελαττώνεται η ταχύτητα του κινητήρα. Η δυναµική πέδηση είναι µια αναποτελεσµατική µέθοδος πέδησης των κινητήρων, καθώς η ενέργεια που παράγει η µηχανή σπαταλάτε υπό µορφή θερµότητας, στην αντίσταση πέδησης. υναµική Πέδηση Λειτουργία κινητήρα R br2 R br1 R br1 > R br2 2 1 φ = φ ratd T braking2 T braking1 Σχ Χαρακτηριστικές ταχύτητας ροπής του κινητήρα µε ανεξάρτητη διέγερση, κατά τη λειτουργία κινητήρα (πρώτο τεταρτηµόριο) και κατά τη δυναµική πέδηση (δεύτερο τεταρτηµόριο) 4 14 Τ L Τ
15 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ a a Ε a R Ε a R (α) Σχ Πέδηση του κινητήρα ανεξάρτητης διέγερσης µε αναστροφή της τάσης τροφοδοσίας. Λειτουργία κινητήρα (α), λειτουργία γεννήτριας (β) Πέδηση µε Αναστροφή της Τάσης (plugging) Σ αυτή τη µέθοδο πέδησης, αντιστρέφεται η φορά της τάσης τροφοδοσίας στο τύλιγµα του οπλισµού (Σχ. 4.18). Έτσι, αντιστρέφεται η φορά του ρεύµατος στον οπλισµό και η µηχανή λειτουργεί ως γεννήτρια. Η ενέργεια που παράγεται από τη µηχανή, µαζί µε την ισχύ που η µηχανή απορροφά από την πηγή τροφοδοσίας, καταναλώνονται στην ωµική αντίσταση του δροµέα. Το ρεύµα στον οπλισµό αποκτά µια εξαιρετικά µεγάλη τιµή a = (E a )/, η οποία συχνά περιορίζεται µε τη σύνδεση µιας εξωτερικής αντίστασης, σε σειρά µε το κύκλωµα του δροµέα. Εποµένως, η πέδηση µε plugging είναι µια εξαιρετικά αναποτελεσµατική µέθοδος. Η χαρακτηριστική ταχύτητας ροπής του κινητήρα µε plugging, εικονίζεται στο δεύτερο τεταρτηµόριο του Σχ Η χαρακτηριστική λαµβάνεται από την Εξ. (4.5) αντικαθιστώντας την τάση µε την. Η ροπή πέδησης της µηχανής στη µηδενική ταχύτητα είναι σηµαντική. Έτσι, όταν ο σκοπός της πέδησης είναι το σταµάτηµα του κινητήρα, απαιτούνται πρόσθετες διατάξεις για την αποσύνδεση του κινητήρα από την πηγή. Αν δεν γίνει αυτό, ο κινητήρας επιταχύνει προς την αντίθετη κατεύθυνση. (β) ω r Ra = ( T ) 2 (4.21) C φ ( C φ) Πέδηση µε αναστροφή της τάσης (plugging) Λειτουργία κινητήρα 2 1 φ = φ ratd Τ braking Σχ Χαρακτηριστική ταχύτητας ροπής του κινητήρα µε ανεξάρτητη διέγερση, κατά τη λειτουργία κινητήρα (πρώτο τεταρτηµόριο) και κατά τη πέδηση µε αναστροφή της τάσης (δεύτερο τεταρτηµόριο) 4 15 Τ L Τ
16 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ ΛΕΙΤΟΥΡΓΙΑ ΣΕ ΤΕΣΣΕΡΑ ΤΕΤΑΡΤΗΜΟΡΙΑ Ένας κινητήρας συνεχούς ρεύµατος µε ανεξάρτητη διέγερση, µπορεί να ελεγχθεί σε τέσσερα τεταρτηµόρια του επιπέδου ταχύτητας ροπής, µε πέδηση ανάκτησης ισχύος, όταν το τύλιγµα του οπλισµού τροφοδοτείται από τον κατάλληλο µετατροπέα ισχύος. Ο µετατροπέας ισχύος πρέπει να παρέχει τάση τροφοδοσίας µε θετική και αρνητική πολικότητα και ταυτόχρονα να επιτρέπει την αµφίδροµη ροή του ρεύµατος οπλισµού (µετατροπέας τεσσάρων τεταρτηµορίων). Σύµφωνα µε το Σχ. 4.2, η µηχανή λειτουργεί ως κινητήρας στο πρώτο τεταρτηµόριο καθώς η ισχύς, η οποία είναι ίση µε το γινόµενο της ταχύτητας µε τη ροπή P=T, είναι θετική. Ο κινητήρας θεωρούµε ότι στρέφεται µε την ορθή (θετική) φορά στο πρώτο τεταρτηµόριο, όταν η τάση τροφοδοσίας είναι θετική και > E a (forward motoring). Στο δεύτερο τεταρτηµόριο, όπου < E a, η ισχύς είναι αρνητική και η µηχανή λειτουργεί ως γεννήτρια (πέδηση κατά την ορθή φορά, forward braking). Η φορά του ρεύµατος οπλισµού και η ροπή είναι αντεστραµµένες, σε σχέση µε το πρώτο τεταρτηµόριο. Η ροπή του παθητικού φορτίου και η αρνητική ροπή πέδησης, επιβραδύνουν τη µηχανή. Έτσι, η µηχανή µπορεί να λειτουργήσει στο δεύτερο τεταρτηµόριο µόνο κατά το µεταβατικό χρονικό διάστηµα της πέδησης. Η µηχανή λειτουργεί σε µόνιµη κατά σταση ισορροπίας στο δεύτερο τεταρτηµόριο, µόνο όταν το φορτίο είναι ενεργό µε αρνητική ροπή. Παράδειγµα τέτοιου φορτίου είναι ένα ηλεκτρικό τρένο που κινείται σε κατωφέρεια. Τότε, η ροπή της βαρύτητας υποστηρίζει την κίνηση, ενώ το µέγεθος της ροπής πέδησης ρυθµίζει την ταχύτητα. Πέδηση ορθής φοράς (forward braking) Λειτουργία κινητήρα ορθής φοράς (forward motoring) a a 2 1 <E a E a >E a E a Τ a a 3 4 > E a E a < E a E a Λειτουργία κινητήρα ανάστροφης φοράς (rvrs motoring) Πέδηση ανάστροφης φοράς (rvrs braking) Σχ. 4.2 Λειτουργία του κινητήρα συνεχούς ρεύµατος µε ανεξάρτητη διέγερση, σε τέσσερα τεταρτηµόρια 4 16
17 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Η µηχανή λειτουργεί ως κινητήρας στο τρίτο τεταρτηµόριο. Η ταχύτητα και η ροπή θεω ρούνται αρνητικές. Εποµένως, η ισχύς είναι θετική και η µηχανή απορροφά ισχύ από την πηγή τροφοδοσίας (rvrs motoring). Η τάση τροφοδοσίας, η ΑΗΕ και το ρεύµα του οπλισµού, είναι αρνητικά σε σχέση µε το πρώτο τεταρτηµόριο. Για την πέδηση της µηχανής κατά την ανάστροφη (αρνητική) φορά περιστροφή, πρέπει < Ea. Τότε, αντιστρέφεται η φορά του ρεύµατος οπλισµού και η ροπή γίνεται θετική, τέταρτο τεταρτηµόριο (rvrs braking). 4.9 ΡΟΠΗ ΤΟΥ ΦΟΡΤΙΟΥ Οι δυνατότητες των ηλεκτρικών κινητήρων περιγράφονται από τη χαρακτηριστική ταχύτητας ροπής. Η χαρακτηριστική ταχύτητας ροπής που λαµβάνεται όταν ο κινητήρας τροφοδοτείται µε τα ονοµαστικά του ηλεκτρικά µεγέθη, ονοµάζεται φυσική (natural). Η επιλογή κάποιου είδους κινητήρα, συνεχούς ή εναλλασσόµενου ρεύµατος που θα εξετάσουµε στη συνέχεια, εξαρτάται από το αν η χαρακτηριστική ταχύτητας ροπής του κινητήρα, ταιριάζει µε τη χαρακτηριστική ταχύτητας ροπής του φορτίου. Εποµένως, η χαρακτηριστική ταχύτητας ροπής του φορτίου πρέπει να είναι γνωστή, για την επιλογή του κατάλληλου κινητήρα οδήγησης του φορτίου. Ένας κινητήρας είναι συµβατός µε το φορτίο, αν ικανοποιεί τις απαιτήσεις ταχύτητας και ροπής του φορτίου, χωρίς να υπερβαίνει τους περιορισµούς ρεύµατος που επιβάλλονται είτε από τον ίδιο τον κινητήρα, ή από την πηγή τροφοδοσίας του. Συχνά, η φυσική χαρακτηριστική ταχύτητας ροπής οποιοδήποτε κινητήρα, δεν είναι συµβατή µε τις απαιτήσεις του φορτίου. Τότε, ένας µετατροπέας ισχύος (powr smiconductor convrtr), παρεµβάλλεται µεταξύ της πηγής τροφοδοσίας και του κινητήρα. Ο µετατροπέας ελέγχει τη ροή της ισχύος από την πηγή προς τον κινητήρα µε τέτοιο τρόπο, έτσι ώστε η χαρακτηριστική ταχύτητας ροπής του κινητήρα να προσαρµοστεί στις απαιτήσεις του φορτίου. Επιπλέον, µε το µετατροπέα ισχύος επιτυγχάνεται ο έλεγχος των µεταβατικών ρευµάτων στην πηγή (δίκτυο), έτσι ώστε να πληρούνται οι κανονισµοί που επιβάλλουν τη χρήση του υναµική Ροπή Η ροπή που αναπτύσσει ο κινητήρας T και ροπή του φορτίου T L, συνδέονται µε τη σχέση dω T T J dt r = L (4.22) όπου, J είναι η αδράνεια του συστήµατος κινητήρας φορτίο σε kg m 2. Ο δεύτερος όρος J dωr / dt στην Εξ. (4.22) ονοµάζεται δυναµική ροπή (dynamic torqu), επειδή υφίσταται µόνο κατά τη διάρκεια των µεταβατικών χρονικών διαστηµάτων. Η δυναµική ροπή είναι µηδέν στην κατάσταση ισορροπίας. Στην κατάσταση ισορροπίας, η ροπή που αναπτύσσει ο κινητήρας είναι ίση µε τη ροπή του φορτίου. Όταν η ροπή του κινητήρα είναι µεγαλύτερη από τη ροπή του φορτίου, ο κινητήρας επιταχύνει. Κατά την επιτάχυνση, ο κινητήρας πρέπει να παρέχει εκτός από τη ροπή φορτίου T L και τη δυναµική ροπή, για να υπερνικήσει την αδράνεια των στρεφόµενων µαζών. Έτσι, σε εφαρµογές όπου η αδράνεια είναι µεγάλη και απαιτούνται µικροί χρόνοι απόκρισης, ο κινητήρας πρέπει να παρέχει µια ροπή πολύ µεγαλύτερη από τη στατική ροπή του φορτίου. Ο κινητήρας επιβραδύνεται όταν η ροπή που παράγει είναι µικρότερη από τη ροπή του φορτίου. Κατά την επιβράδυνση (πέδηση), η δυναµική ροπή αλλάζει πρόσηµο. Αυτό σηµαίνει ότι η ενέργεια που είναι αποθηκευµένη στις στρεφόµενες µάζες του συστήµατος ανακτάται και µετατρέπεται σε ηλεκτρική (λειτουργία γεννήτριας). Αν η ροπή του κινητήρα T απλά µηδενιστεί κατά την πέδηση, µε την αποσύνδεση του κινητήρα από την πηγή τροφοδοσίας, ο ρυθµός της 4 17
18 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 επιβράδυνσης εξαρτάται µόνο από την αδράνεια και τη ροπή T L. Όταν η αδράνεια είναι µεγάλη, είτε η ροπή φορτίου µικρή, ο χρόνος πέδησης είναι υψηλός. Για τη µείωση του χρόνου πέδησης, ο κινητήρας τροφοδοτείται από το µετατροπέα ισχύος µε τέτοιο τρόπο, έτσι ώστε να αναπτύξει αρνητική ροπή, οπότε λειτουργεί ως γεννήτρια. ηλαδή, χρησιµοποιούνται ηλεκτρικά µέσα για την πέδηση του κινητήρα. Η ηλεκτρική πέδηση εξασφαλίζει ταχεία και µε υψηλή ακρίβεια επιβράδυνση των κινητήρων Χαρακτηριστικές Ταχύτητας Ροπής από Συνήθη Φορτία Οι χαρακτηριστικές ταχύτητας ροπής κάποιων φορτίων που χρησιµοποιούνται συχνά σε πρακτικές εφαρµογές, εικονίζονται στο Σχ Η ροπή του φορτίου µεταβάλλεται ανάλογα µε το τετράγωνο της ταχύτητας στις αντλίες (cntrifugal pumps) και τους ανεµιστήρες (blowrs, fans), όπως δείχνει το Σχ. 4.21α. Στα συστήµατα έλξης, όπως τα ηλεκτρικά τρένα και τα αυτοκίνητα, η µεταβολή της ροπής µε την ταχύτητα παρουσιάζεται στο Σχ. 4.21β. Στη χαρακτηριστική αυτή δεν έχει συµπεριληφθεί η ροπή που οφείλεται στη βαρύτητα. Στους εκσκαφείς, οι χαρακτηριστικές ταχύτητας ροπής έχουν τη µορφή του Σχ. 4.21γ. Όταν ο εκσκαφέας συναντήσει κάποιο εµπόδιο, η ταχύτητα του κινητήρα πρέπει να µηδενιστεί και η ροπή, όπως και το ρεύµα να περιοριστούν σε κάποια ασφαλή τιµή (τµήµα ΒΓ της χαρακτηρι στικής). Τα τµήµατα ΑΒ, Α Β και Α Β σχετίζονται µε τη σκληρότητα του εδάφους. Στα ανυψωτικά συστήµατα, όπως οι γερανοί, η ροπή του φορτίου εξαρτάται κυρίως από τη βαρύτητα και είναι ανεξάρτητη της ταχύτητας. Στα ανυψωτικά υψηλής ταχύτητας, εξαιτίας των τριβών και του αερισµού, η ροπή αποκτά µια µικρή εξάρτηση από την ταχύτητα. (α) Τ (β) Τ Α Α Α Β Β Β Μικρή Ταχύτητα Μεγάλη Ταχύτητα Τ (γ) Γ Τ (δ) Σχ Χαρακτηριστικές ταχύτητας ροπής µερικών τυπικών φορτίων. Αντλιών, ανεµιστήρων (α), συστηµάτων έλξης (β), εκσκαφέων (γ), ανυψωτικών (δ) 4 18
19 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Κατηγορίες Φορτίων Τα φορτία διακρίνονται σε δύο µεγάλες κατηγορίες: τα παθητικά φορτία και τα ενεργά φορτία. Ως παθητικά φορτία χαρακτηρίζουµε εκείνα, που πάντοτε αντιτίθενται στην κίνηση της µηχανής. Η ροπή των παθητικών φορτίων αλλάζει πρόσηµο, µε την αντιστροφή της φοράς του κινητήρα. Αντίθετα, τα ενεργά φορτία έχουν τη δυνατότητα να οδηγήσουν τον κινητήρα, κατά τη φορά της κίνησής του. Η ροπή των ενεργών φορτίων δεν αλλάζει πρόσηµο, µε την αλλαγή της φοράς περιστροφής. Η ροπή που προκαλείται από τη βαρύτητα είναι µια ενεργός ροπή. Έτσι, όταν ένα ηλεκτρικό όχηµα κινείται σε µια ανηφόρα, η ενεργός ροπή από τη βαρύτητα αντιτίθενται στην κίνηση. Εποµένως, ο κινητήρας του οχήµατος πρέπει να αναπτύξει επιπλέον ροπή, για να υπερνικήσει τη ροπή της βαρύτητας. Όταν το ίδιο όχηµα κινείται σε µια κατωφέρεια µε έντονη κλίση, η ροπή της βαρύτητας είναι αυτή που το κινεί. Ο κινητήρας πρέπει τώρα να αναπτύξει ροπή πέδησης, για τον έλεγχο της ταχύτητας στην επιθυµητή τιµή. Το ίδιο ισχύει και σε ένα γερανό, ο οποίος κατεβάζει κάποιο φορτίο. 4.1 ΚΙΝΗΤΗΡΙΑ ΣΥΣΤΗΜΑΤΑ Όταν η φυσική χαρακτηριστική του ηλεκτρικού κινητήρα δεν ταιριάζει µε τη χαρακτηρι στική ταχύτητας ροπής του φορτίου, είναι αναγκαία η εισαγωγή µεταξύ του κινητήρα και της πηγής τροφοδοσίας ενός µετατροπέα ισχύος. Ο µετατροπέας ισχύος ελέγχει τη ροή της ενέργειας από την πηγή, µε σταθερή συνεχή ή εναλλασσόµενη τάση, στον κινητήρα. Έτσι, σχηµατίζεται ένα κινητήριο σύστηµα (motor driv), το λειτουργικό διάγραµµα του οποίου εικονίζεται στο Σχ Ο µετατροπέας ισχύος αποτελείται από ηµιαγωγούς διακόπτες ισχύος (MOSFET, GBT, SCR), µε συνέπεια να παρουσιάζει πολύ µεγάλο βαθµό απόδοσης. Με το κινητήριο σύστηµα επιτυγχάνεται η ρύθµιση της ταχύτητας περιστροφής του κινητήρα, στην επιθυµητή τιµή αναφο * ράς ω r. Όταν απαιτείται η ρύθµιση της ταχύτητας µε µεγάλη ακρίβεια, χρησιµοποιείται ένας αισθητήρας µέτρησης της ταχύτητας, ή οποία σ ένα σύστηµα κλειστού βρόχου αναγκάζεται να * ακολουθεί την τιµή αναφοράς ω r. Οι µετατροπείς ισχύος διακρίνονται σε διάφορες κατηγορίες, ανάλογα µε τον αριθµό των τεταρτηµορίων που επιτρέπουν τη λειτουργία του κινητήρα. Κάθε ηλεκτρικός κινητήρας, όπως ο κινητήρας συνεχούς ρεύµατος στο Σχ. 4.2, µπορεί να λειτουργεί και στα τέσσερα τεταρτηµόρια του επιπέδου ταχύτητας ροπής. Αν ο κινητήρας στο κινητήριο σύστηµα θα λειτουργεί και στα τέσσερα τεταρτηµόρια ή σε λιγότερα, όπως σε δύο είτε σε ένα, εξαρτάται από τη δοµή του µετατροπέα ισχύος. ΠΗΓΗ ΜΕΤΑΤΡΟΠΕΑΣ ΙΣΧΥΟΣ ΚΙΝΗΤΗΡΑΣ ΦΟΡΤΙΟ ΜΟΝΑ Α ΕΛΕΓΧΟΥ ΑΙΣΘΗΤΗΡA ω * r Σχ Γενικό λειτουργικό διάγραµµα των κινητήριων συστηµάτων 4 19
20 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 Μέγιστη ορθή ταχύτητα 2 atd Μέγιστη συνεχής ισχύς 1 Μέγιστη συνεχής ροπή Μέγιστη µεταβατική ισχύς Μέγιστη µεταβατική ροπή T 3 4 -atd Ι=Ι ratd Ι=cΙ ratd c>1 Μέγιστη ανάστροφη ταχύτητα Σχ Λειτουργία του κινητήριου συστήµατος σε τέσσερα τεταρτηµόρια. Εικονίζονται οι περιοχές σταθερής µέγιστης ροπής και ισχύος στη µόνιµη κατάσταση λειτουργίας (συνεχής γραµµή) και οι αντίστοιχες περιοχές για λειτουργία στα µεταβατικά χρονικά διαστήµατα (διακεκοµµένη γραµµή) Στο Σχ θεωρούµε ότι, ο κινητήρας οδηγείται από ένα µετατροπέα ισχύος τεσσάρων τεταρτηµορίων. Η εσωτερική επιφάνεια ορίζει την περιοχή λειτουργίας του κινητήρα στη µόνιµη κατάσταση ισορροπίας. Η συνεχής γραµµή που περιβάλλει την επιφάνεια αυτή, αντιστοιχεί στη λειτουργία του κινητήρα µε το ονοµαστικό του ρεύµα. Έτσι, σε ταχύτητες µικρότερες από την ονοµαστική ο κινητήρας λειτουργεί µε σταθερή µέγιστη ροπή. Σε ταχύτητες µεγαλύτερες από την ονοµαστική, έχουµε τη λειτουργία µε σταθερή µέγιστη ισχύ, ίση µε την ονοµαστική. Ο κινητήρας λειτουργεί µε την ονοµαστική ροή, σε ταχύτητες µικρότερες από την ονοµαστική. Η ροή µειώνεται σε µεγαλύτερες ταχύτητες. Όταν το ρεύµα είναι µικρότερο από το ονοµαστικό, το σηµείο λειτουργίας του κινητήρα βρίσκεται στο εσωτερικό της επιφάνειας που περικλείεται από τη συνεχή γραµµή. Κατά τη διάρκεια των µεταβατικών καταστάσεων αλλαγής της ταχύτητας του κινητήρα, το ρεύµα µπορεί να λάβει τιµές σηµαντικά µεγαλύτερες από το ονοµαστικό c ratd. Αυτό οφείλεται στη µεγάλη θερµική σταθερά χρόνου του κινητήρα και το µικρό χρονικό διάστηµα που διαρκεί η ροή του µεταβατικού ρεύµατος. Η ροή ενός ρεύµατος µεγαλύτερου από το ονοµαστικό, επιτρέπει την ανάπτυξη µιας ροπής που υπερβαίνει την ονοµαστική. Έτσι, το χρονικό διάστηµα της µετα βατικής λειτουργίας περιορίζεται και η δυναµική συµπεριφορά του συστήµατος βελτιώνεται. Στο Σχ η διακεκοµµένη γραµµή ορίζει τη µέγιστη ροπή και ισχύ που µπορεί να αναπτύξει ο κινητήρας, όταν τροφοδοτείται µε το αυξηµένο ρεύµα c ratd στα µεταβατικά χρονικά διαστή µατα. Εποµένως, ο κινητήρας µπορεί να λειτουργεί στα µεταβατικά διαστήµατα, στην περιοχή που ορίζεται µεταξύ της διακεκοµµένης και της συνεχούς γραµµής. Όµως, η λειτουργία στην περιοχή αυτή σηµαίνει ότι, οι ηµιαγωγοί διακόπτες του µετατροπέα ισχύος πρέπει να επιλεγούν µε βάση τα αυξηµένο µεταβατικό ρεύµα, αντί για το ονοµαστικό. Αυτό οφείλεται στη µικρή θερµική σταθερά χρόνου των ηµιαγωγών ισχύος. Έτσι, το κόστος του µετατροπέα ισχύος αυξά νεται σηµαντικά. Στο Σχ περιγράφεται η µεταβατική συµπεριφορά των κινητήριων συστηµάτων, σε τρεις διαφορετικές συνθήκες λειτουργίας. 4 2
21 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ α 1 m1 Μέγιστη ισχύς β γ 2 atd 2 m2 Τ L 1 Μέγιστη ροπή T (α) α 1 m1 Μέγιστη ισχύς β γ 2 atd Τ L 1 Μέγιστη ροπή T δ 3 4 Τ L -atd ε m2-2 (β) 2 2 atd 1 m1 Τ L m2 1 γ Μέγιστη ισχύς β α Μέγιστη ροπή (γ) Σχ Μεταβατική λειτουργία του κινητήριου συστήµατος. Μείωση της ταχύτητας (α), αντιστροφή της φοράς περιστροφής (β), αύξηση της ταχύτητας (γ) T 4 21
22 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 Στο Σχ. 4.24α παρουσιάζεται η διαδικασία µείωσης της ταχύτητας του κινητήρα από την τιµή 1 στην τιµή 2. Ο κινητήρας αρχικά λειτουργεί στη µόνιµη κατάσταση ισορροπίας στο σηµείο m1, όπου η ροπή του κινητήρα είναι ίση µε τη ροπή του φορτίου. Όταν το σήµα αναφοράς ταχύτητας στο κινητήριο σύστηµα λάβει την τιµή ω * r2, το σηµείο λειτουργίας µεταβαίνει από το m1 στο α. Η µετάβαση γίνεται σε ελάχιστο χρονικό διάστηµα, γι αυτό η ταχύτητα δεν µεταβάλλεται. Το σηµείο α βρίσκεται στο δεύτερο τεταρτηµόριο, όπου η µηχανή λειτουργεί ως γεννήτρια και αναπτύσσει τη µέγιστη ισχύ πέδησης. Επειδή η ταχύτητα 1 είναι µεγαλύτερη από την ονοµαστική, ο κινητήρας αρχικά υφίσταται πέδηση µε τη µέγιστη ισχύ, έως το σηµείο β και στη συνέχεια µε τη µέγιστη ροπή έως το σηµείο γ. Ανάλογα µε τη µέγιστη επιτρεπόµενη τιµή του ρεύµατος, η τροχιά α β γ αντιστοιχεί στη συνεχή ή τη διακεκοµµένη γραµµή του Σχ Το σηµείο γ αντιστοιχεί στη νέα επιθυµητή ταχύτητα 2 και η λειτουργία του κινητήρα µεταβαίνει στο νέο σηµείο ισορροπίας m2, στο πρώτο τεταρτηµόριο. Στο Σχ. 4.24β εικονίζεται η διαδικασία αντιστροφής της ταχύτητας του κινητήρα, από την τιµή 1 στην τιµή 2. Από το αρχικό σηµείο ισορροπίας m1, ο κινητήρας µεταβαίνει στο δεύτερο τεταρτηµόριο, σηµείο α. Ο κινητήρας αρχικά υφίσταται πέδηση µε τη µέγιστη ισχύ, έως το σηµείο β και κατόπιν µε τη µέγιστη ισχύ, έως τη µηδενική ταχύτητα γ. Στη συνέχεια η λειτουργία µεταβαίνει στο τρίτο τεταρτηµόριο, όπου η µηχανή λειτουργεί ως κινητήρας και επιταχύνει µε τη µέγιστη ροπή ως το σηµείο δ και τη µέγιστη ισχύ ως το σηµείο ε. Στο σηµείο ε, όπου η ταχύτητα είναι ίση µε την επιθυµητή 2, µειώνεται το ρεύµα και ο κινητήρας µεταβαί νει στο νέο σηµείο ισορροπίας m2. Η διαδικασία αύξησης της ταχύτητας από την τιµή 1 στην τιµή 2, φαίνεται στο Σχ. 4.24γ. Ο κινητήρας επιταχύνει αρχικά µε τη µέγιστη ροπή, τµήµα α β, και στη συνέχεια µε τη µέγιστη ισχύ, τµήµα β γ. Η διαδικασία επιτελείται στο πρώτο τεταρτηµόριο. Οι µετατροπείς ισχύος τεσσάρων τεταρτηµορίων χρησιµοποιούνται όταν είναι επιθυµητή η περιστροφή του κινητήρα και προς τις δύο φορές. Όταν η περιστροφή του κινητήρα σε µια φορά είναι επαρκής, χρησιµοποιούνται οι µετατροπείς δύο τεταρτηµορίων. Η λειτουργία στο δεύτερο τεταρτηµόριο, παρέχει την ταχεία ηλεκτρική πέδηση της µηχανής (Σχ. 4.24α). Όταν η ροπή του φορτίου είναι υψηλή, τότε µπορεί να χρησιµοποιηθούν οι µετατροπείς ενός τεταρτηµορίου. Οι µετατροπείς αυτοί δεν παρέχουν ροπή πέδησης, Τ =. Έτσι, ο κινητήρας επιβραδύνεται µόνο µε την επίδραση της ροπής του φορτίου, µε συνέπεια η απόκρισή του να είναι αργή ΠΑΡΑ ΕΙΓΜΑΤΑ Παράδειγµα 4.1 Κινητήρας συνεχούς ρεύµατος µε παράλληλη διέγερση έχει τάση τροφοδοσίας 22 και στρέφεται µε ταχύτητα 14rpm, όταν το ρεύµα του δροµέα είναι 25A. Η αντίσταση του δροµέα είναι.3ω. Να βρεθούν: α) Η ΑΗΕ του κινητήρα. β) Η ταχύτητα του κινητήρα όταν το ρεύµα του δροµέα αυξηθεί στα 5A και η ροή κατά 1%. γ) Η ισχύς εξόδου στις δύο περιπτώσεις. Η ΑΗΕ του κινητήρα για ρεύµα δροµέα Ι a1 = 25A είναι η E a1 και για ρεύµα Ι a2 = 5A η E a2, οι οποίες υπολογίζονται από τις σχέσεις = Ea 1 Raa1 Ea1 = = = Ea2 Raa2 Ea1 = =
23 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ a Ε a R R' Ισοδύναµο κύκλωµα του κινητήρα παράλληλης διέγερσης Η ΑΕΗ συνδέεται µε την ταχύτητα από τη σχέση Ea = Cφωr, η οποία για τις δύο περιπτώσεις γράφεται ως εξής 2π E = C φω = C φ n 6 a1 1 r π E = C 1.1φω 25 = C 1.1φ n 6 a2 1 r2 1 2 ιαιρώντας κατά µέλη τις παραπάνω εξισώσεις έχουµε n = n2 = = n2 1228rpm Η ισχύς εξόδου για τα ρεύµατα Ι a1 = 25A και Ι a2 = 5A είναι Po 1 = Ea 1a1 = = 5.3kW Po2 = Ea2a2 = 25 5 = 1.25kW Παράδειγµα 4.2 Κινητήρας συνεχούς ρεύµατος µε παράλληλη διέγερση, έχει τα εξής ονοµαστικά στοιχεία: =22, P =15kW, η =88%, n =1rpm, =.5Ω, P =22W, J =.5Kgm 2. Υπολογίστε: α) Την αντίσταση εκκίνησης, έτσι ώστε a,max = 2 a,ratd, β) την ονοµαστική ροπή, γ) το χρόνο εκκίνησης, όταν η µέση ροπή εκκίνησης είναι 3Nm. Η ισχύς των 15kW είναι η ισχύς εξόδου του κινητήρα. Εποµένως, η ισχύς εισόδου είναι ίση µε P in Po 15 = = = 17kW η.88 Το ρεύµα τροφοδοσίας είναι P in 17 = = = 77.5A
24 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 a R start Ε a R Ισοδύναµο κύκλωµα του κινητήρα παράλληλης διέγερσης, µε την αντίσταση εκκίνησης Το ρεύµα στο τύλιγµα παράλληλης διέγερσης είναι P 22 = = = 1A 22 και το ονοµαστικό ρεύµα στον οπλισµό a, ratd = = = 76.5A Η µέγιστη επιτρεπόµενη τιµή του ρεύµατος εκκίνησης είναι ίση µε a,max = 2 a,ratd = 153Α. Τη στιγµή της εκκίνησης, η ΑΗΕ είναι µηδέν, καθώς ο κινητήρας δεν στρέφεται. Έτσι, η ολική αντίσταση του κυκλώµατος οπλισµού, η οποία είναι ίση µε το άθροισµα της αντίστασης του δροµέα και της άγνωστης αντίστασης εκκίνησης R start, ορίζεται από τη σχέση 22 = ( Ea = ) a,max ( Ra Rstart) Ra Rstart = = = 1.44Ω 153 a,max Εποµένως, η αντίσταση εκκίνησης είναι ίση µε R start = =.94Ω. Η ονοµαστική ροπή υπολογίζεται από την ονοµαστική ισχύ εξόδου 2π 15 6 Po = Tratdωratd = Tratd n Tratd = = 143.3Nm 6 2π 1 Ο χρόνος εκκίνησης υπολογίζεται από την παρακάτω διαφορική εξίσωση, στην οποία θεωρούµε προσεγγιστικά ότι η ροπή που αναπτύσσει ο κινητήρας Τ, έχει µια σταθερή µέση τιµή 3Nm dωr 2π1 / 6 T = TL J 3 = tstart =.33s dt t start Παράδειγµα 4.3 Κινητήρας συνεχούς ρεύµατος µε διέγερση σειράς, έχει την παρακάτω καµπύλη µαγνήτισης, όταν στρέφεται µε ταχύτητα 7rpm. Ι [A] E 7 []
25 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Η αντίσταση του δροµέα είναι.45ω και του τυλίγµατος σειράς.35ω. Όταν η τάση λειτουργίας του κινητήρα είναι 4, σχεδιάστε τη χαρακτηριστική ταχύτητας ροπής του κινητήρα, υπολογίζοντας πέντε σηµεία της καµπύλης. Η καµπύλη µαγνήτισης του κινητήρα έχει ληφθεί λειτουργώντας τη µηχανή ως γεννήτρια µε ανεξάρτητη διέγερση. Η µηχανή στρέφεται µε 7rpm και το ρεύµα διέγερσης λαµβάνει διαδοχικά τις τιµές του πίνακα. Η ΗΕ είναι ίση µε την τάση στα άκρα της µηχανής. Στα παρακάτω σχήµατα εικονίζονται το ισοδύναµο κύκλωµα της µηχανής για τη µέτρηση της καµπύλης µαγνήτισης και το ισοδύναµο κύκλωµα του κινητήρα σειράς. a E R R' Ισοδύναµο κύκλωµα της µηχανής για τη λήψη της καµπύλης µαγνήτισης. Ο κινητήρας σειράς συνδέεται ως γεννήτρια µε ανεξάρτητη διέγερση και στρέφεται µε 7rpm a = a = Ε a R Ισοδύναµο κύκλωµα του κινητήρα σειράς Για την εύρεση της χαρακτηριστικής ταχύτητας ροπής, αρχικά υπολογίζουµε την ΑΗΕ του κινητήρα, ανάλογα µε το ρεύµα τροφοδοσίας, το οποίο είναι ίσο µε το ρεύµα διέγερσης. Η ΑΗΕ ορίζεται από τη σχέση E = ( R R ) = 4 (.45.35) = 4.8 a a Η ΑΗΕ του κινητήρα ορίζεται από τη γενική σχέση 2π Ea = Cφωr = C φn 6 Η ταχύτητα του κινητήρα υπολογίζεται από το λόγο της ΗΕ από την καµπύλη µαγνήτισης, προς την πραγµατική ΑΗΕ του κινητήρα 4 25
26 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦ. 4 E7 7 7Ea = n = E n E a 7 Η ροπή και η ισχύς εξόδου συνδέονται µε τη σχέση Po = Ea = Tω r. Έτσι, η ροπή του κινητήρα είναι ίση µε T 6E a = 2π n Από τις παραπάνω εξισώσεις συµπληρώνουµε τον πίνακα Ι [A] E 7 [] E = 4.8 [] a 7 n = 7 E / E [rpm] a T = 6 E /(2 π n) [Nm] a Η χαρακτηριστική ταχύτητας ροπής n = f(t ), σχεδιάζεται από τα ζεύγη τιµών στις δύο τελευταίες σειρές του πίνακα. Παράδειγµα 4.4 Κινητήρας συνεχούς ρεύµατος µε παράλληλη διέγερση έχει τα εξής ονοµαστικά στοιχεία: Ρ = 5kW, = 4, n = 1rpm, η = 9%, =.2Ω, R = 2Ω. Ζητούνται: α) Οι επιµέρους απώλειες της µηχανής στην ονοµαστική λειτουργία, όταν οι απώλειες σιδήρου είναι διπλάσιες από τις απώλειες τριβών και αερισµού. Οι απώλειες ψηκτρών και οι κατανεµηµένες απώλειες αγνοούνται. β) Η ταχύτητα του κινητήρα στο κενό. γ) Η αδράνεια του κινητήρα, όταν ο χρόνος εκκίνησης στο κενό είναι.7s και η µέση ροπή εκκίνησης 5Nm. Οι απώλειες χαλκού εξαρτώνται από τα ρεύµατα στον οπλισµό και το τύλιγµα διέγερσης 4 = = = 2A R 2 Pin Po / η 5 / = = = = = 138.9A 4 4 = = = 136.9A a P = R R = = = 4548W cu a a Οι ολικές απώλειες είναι ίσες µε P loss = = 5555W. Εποµένως, οι απώλειες σιδήρου µαζί µε τις απώλειες τριβών και αερισµού είναι P P = P P 3P = P = 336W και P = 2P = 672W iron fw loss cu fw fw iron fw 4 26
27 ΚΕΦ. 4 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Στο κενό η ΑΗΕ του κινητήρα Ε anl είναι ίση µε την τάση τροφοδοσίας του, καθώς το ρεύµα του οπλισµού είναι µηδενικό. Στην ονοµαστική λειτουργία, η ΑΗΕ είναι ίση µε Ea = Raa = = Από το λόγο των ΑΗΕ στο κενό και την ονοµαστική λειτουργία έχουµε Ea nl n Ea nln nl 4 1 = nnl = = = 173.5rpm E n E a a Όταν ο κινητήρας λειτουργεί στο κενό, η µόνη ροπή φορτίου είναι η ροπή τριβών και αερισµού. Η ροπή αυτή υπολογίζεται στην ονοµαστική ταχύτητα και θεωρείται καταχρηστικά σταθερή T Lfw = Pfw 336 3Nm ω = 2π173.5/ 6 = r nl Η αδράνεια του κινητήρα υπολογίζεται από τη σχέση ωr 2π173.5/ 6 T = TL J 5 = 3 J J = 3.1kgm t.7 2 Παράδειγµα 4.5 Ένας κινητήρας συνεχούς ρεύµατος µε σύνθετη διέγερση, έχει τα εξής ονοµαστικά στοιχεία: P = 7kW, = 22, =.2Ω, R s =.3Ω, R p = 5Ω. Το τύλιγµα παράλληλης διέγερσης διαθέτει 1 σπείρες ανά πόλο και το τύλιγµα σειράς 4 σπείρες ανά πόλο. Η καµπύλη µαγνήτισης ορίζεται στις 1rpm από τον παρακάτω πίνακα, όπου Ι t είναι το ισοδύναµο ρεύµα διέγερσης από τα δύο τυλίγµατα διέγερσης. Υπολογίστε: α) Την τιµή της αντίστασης R p έτσι ώστε ο κινητήρας να στρέφεται στο κενό µε 1rpm. β) Την ταχύτητα του κινητήρα µε αθροιστική σύνθετη διέγερση, όταν το ρεύµα του οπλισµού είναι 2A. γ) Την ταχύτητα του κινητήρα µε διαφορική σύνθετη διέγερση, όταν το ρεύµα του οπλισµού είναι 2A. Ι t [A] E 1 [] a Αθροιστική σύνθετη διέγερση ιαφορική σύνθετη διέγερση E a R s a R p R' p Ισοδύναµο κύκλωµα του κινητήρα σύνθετης διέγερσης Στη λειτουργία χωρίς φορτίο, το ρεύµα του οπλισµού είναι µηδέν. Έτσι, η ΑΗΕ του κινητήρα είναι ίση µε την τάση τροφοδοσίας E = 22. Το ολικό ρεύµα διέγερσης είναι ίσο µε το ρεύµα διέγερσης στο a nl 4 27
ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦΑΛΑΙΟ 3 3.1 ΕΙΣΑΓΩΓΗ Μια ηλεκτρική µηχανή συνεχούς ρεύµατος χρησιµοποιείται ως γεννήτρια, όταν ο άξονάς της στρέφεται από µια κινητήρια µηχανή (prim movr). Η κινητήρια µηχανή
ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΚΕΦΑΛΑΙΟ 3 3.1 ΕΙΣΑΓΩΓΗ Μια ηλεκτρική µηχανή συνεχούς ρεύµατος χρησιµοποιείται ως γεννήτρια, όταν ο άξονάς της στρέφεται από µια κινητήρια µηχανή (prim movr). Η κινητήρια µηχανή
ΓΚΙΟΚΑΣ ΠΑΝΑΓΙΩΤΗΣ. ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας μιας ηλεκτρικής γεννήτριας Σ.Ρ. με διέγερση σειράς.
 ΓΚΙΟΚΑΣ ΠΑΝΑΓΙΩΤΗΣ ΑΜ:6749 ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας μιας ηλεκτρικής γεννήτριας Σ.Ρ. με διέγερση σειράς. ΣΚΟΠΟΣ: Για να λειτουργήσει μια γεννήτρια, πρέπει να πληρούνται οι παρακάτω βασικές
ΓΚΙΟΚΑΣ ΠΑΝΑΓΙΩΤΗΣ ΑΜ:6749 ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας μιας ηλεκτρικής γεννήτριας Σ.Ρ. με διέγερση σειράς. ΣΚΟΠΟΣ: Για να λειτουργήσει μια γεννήτρια, πρέπει να πληρούνται οι παρακάτω βασικές
ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας του κινητήρα συνεχούς
ΑΣΚΗΣΗ 8 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας του κινητήρα συνεχούς
3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
 Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
 Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτροµηχανικών Συστηµάτων Μετατροπής Ενέργειας 3η Εργαστηριακή Άσκηση: Εύρεση χαρακτηριστικής και συντελεστή απόδοσης κινητήρα συνεχούς ρεύµατος
Δίνεται η επαγόμενη τάση στον δρομέα συναρτήσει του ρεύματος διέγερσης στις 1000στρ./λεπτό:
 ΑΣΚΗΣΗ 1 Η Ένας κινητήρας συνεχούς ρεύματος ξένης διέγερσης, έχει ονομαστική ισχύ 500kW, τάση 1000V και ρεύμα 560Α αντίστοιχα, στις 1000στρ/λ. Η αντίσταση οπλισμού του κινητήρα είναι RA=0,09Ω. Το τύλιγμα
ΑΣΚΗΣΗ 1 Η Ένας κινητήρας συνεχούς ρεύματος ξένης διέγερσης, έχει ονομαστική ισχύ 500kW, τάση 1000V και ρεύμα 560Α αντίστοιχα, στις 1000στρ/λ. Η αντίσταση οπλισμού του κινητήρα είναι RA=0,09Ω. Το τύλιγμα
Τμήμα Ηλεκτρολόγων Μηχανικών ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΚΑΤΆ ΤΗ ΛΕΙΤΟΥΡΓΙΑ ΣΓ
 Όταν κατά τη λειτουργία μιας ΣΓ η ροπή στον άξονα της ή το φορτίο της μεταβληθούν απότομα, η λειτουργία της παρουσιάζει κάποιο μεταβατικό φαινόμενο για κάποια χρονική διάρκεια μέχρι να επανέλθει στη στάσιμη
Όταν κατά τη λειτουργία μιας ΣΓ η ροπή στον άξονα της ή το φορτίο της μεταβληθούν απότομα, η λειτουργία της παρουσιάζει κάποιο μεταβατικό φαινόμενο για κάποια χρονική διάρκεια μέχρι να επανέλθει στη στάσιμη
ΙΤ=ΙS RT RS. Uεπ. Άσκηση 5 Ηλεκτρικοί κινητήρες DC
 Άσκηση 5 Ηλεκτρικοί κινητήρες DC 5.1 Σκοπός της Άσκησης Σκοπός την Άσκησης είναι η μελέτη του τρόπου λειτουργίας και ελέγχου των ηλεκτρικών κινητήρων DC. Αναλύονται ο τρόπος εκκίνησης και ρύθμισης της
Άσκηση 5 Ηλεκτρικοί κινητήρες DC 5.1 Σκοπός της Άσκησης Σκοπός την Άσκησης είναι η μελέτη του τρόπου λειτουργίας και ελέγχου των ηλεκτρικών κινητήρων DC. Αναλύονται ο τρόπος εκκίνησης και ρύθμισης της
Διατάξεις εκκίνησης κινητήρων ΣΡ
 Διατάξεις εκκίνησης κινητήρων ΣΡ Η διάταξη ελέγχου και προστασίας του κινητήρα ΣΡ πρέπει: 1. Να προστατεύει τον κινητήρα από βραχυκυκλώματα στην ίδια τη διάταξη προστασίας 2. Να προστατεύει τον κινητήρα
Διατάξεις εκκίνησης κινητήρων ΣΡ Η διάταξη ελέγχου και προστασίας του κινητήρα ΣΡ πρέπει: 1. Να προστατεύει τον κινητήρα από βραχυκυκλώματα στην ίδια τη διάταξη προστασίας 2. Να προστατεύει τον κινητήρα
Κινητήρας παράλληλης διέγερσης
 Κινητήρας παράλληλης διέγερσης Ισοδύναμο κύκλωμα V = E + I T V = I I T = I F L R F I F R Η διέγερση τοποθετείται παράλληλα με το κύκλωμα οπλισμού Χαρακτηριστική φορτίου Έλεγχος ταχύτητας Μεταβολή τάσης
Κινητήρας παράλληλης διέγερσης Ισοδύναμο κύκλωμα V = E + I T V = I I T = I F L R F I F R Η διέγερση τοποθετείται παράλληλα με το κύκλωμα οπλισμού Χαρακτηριστική φορτίου Έλεγχος ταχύτητας Μεταβολή τάσης
ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι γεννήτριες συνεχούς ρεύματος διαχωρίζονται στις ακόλουθες κατηγορίες: Ανεξάρτητης (ξένης) διέγερσης. Παράλληλης διέγερσης. Διέγερσης σειράς. Αθροιστικής σύνθετης διέγερσης.
ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι γεννήτριες συνεχούς ρεύματος διαχωρίζονται στις ακόλουθες κατηγορίες: Ανεξάρτητης (ξένης) διέγερσης. Παράλληλης διέγερσης. Διέγερσης σειράς. Αθροιστικής σύνθετης διέγερσης.
Γεννήτρια συνεχούς ρεύματος ξένης διέγερσης
 ΑΣΚΗΣΗ 5 Γεννήτρια συνεχούς ρεύματος ξένης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Μια ηλεκτρική μηχανή συνεχούς ρεύματος παράγει τάση συνεχούς μορφής όταν χρησιμοποιείται ως γεννήτρια, ενώ ένας κινητήρας
ΑΣΚΗΣΗ 5 Γεννήτρια συνεχούς ρεύματος ξένης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Μια ηλεκτρική μηχανή συνεχούς ρεύματος παράγει τάση συνεχούς μορφής όταν χρησιμοποιείται ως γεννήτρια, ενώ ένας κινητήρας
ΑΣΚΗΣΗ 11 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 11 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση των τρόπων ελέγχου της ταχύτητας
ΑΣΚΗΣΗ 11 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση των τρόπων ελέγχου της ταχύτητας
Κινητήρες ΣΡ Διέγερσης Σειράς
 Διέγερσης Σειράς Ισοδύναμο κύκλωμα: Τα τυλίγματα διέγερσης διαθέτουν σχετικά λίγες σπείρες και συνδέονται σε σειρά με το κύκλωμα οπλισμού Εδώ το ρεύμα οπλισμού, το ρεύμα διέγερσης και το ρεύμα φορτίου
Διέγερσης Σειράς Ισοδύναμο κύκλωμα: Τα τυλίγματα διέγερσης διαθέτουν σχετικά λίγες σπείρες και συνδέονται σε σειρά με το κύκλωμα οπλισμού Εδώ το ρεύμα οπλισμού, το ρεύμα διέγερσης και το ρεύμα φορτίου
Ηλεκτρικές Μηχανές ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 7: Μέθοδοι Εκκίνησης και Πέδησης Ασύγχρονων Τριφασικών Κινητήρων Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 7: Μέθοδοι Εκκίνησης και Πέδησης Ασύγχρονων Τριφασικών Κινητήρων Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων
ΑΣΚΗΣΗ 7 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 7 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας της γεννήτριας συνεχούς
ΑΣΚΗΣΗ 7 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΣΥΝΘΕΤΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας της γεννήτριας συνεχούς
ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της αρχής λειτουργίας των μηχανών συνεχούς ρεύματος, β) η ανάλυση της κατασκευαστικών
ΑΣΚΗΣΗ 4 η ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της αρχής λειτουργίας των μηχανών συνεχούς ρεύματος, β) η ανάλυση της κατασκευαστικών
ΑΣΚΗΣΗ 4 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ
 ΑΣΚΗΣΗ 4 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ Σκοπός της άσκησης: Σκοπός της άσκησης είναι: 1. Να εξοικειωθεί ο σπουδαστής με την διαδικασία εκκίνησης ενός σύγχρονου τριφασικού
ΑΣΚΗΣΗ 4 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ Σκοπός της άσκησης: Σκοπός της άσκησης είναι: 1. Να εξοικειωθεί ο σπουδαστής με την διαδικασία εκκίνησης ενός σύγχρονου τριφασικού
ΑΣΚΗΣΗ 6 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 6 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α), η κατανόηση της λειτουργίας της γεννήτριας
ΑΣΚΗΣΗ 6 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α), η κατανόηση της λειτουργίας της γεννήτριας
ΑΣΚΗΣΗ 5 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΚΑΜΠΥΛΕΣ
 ΑΣΚΗΣΗ 5 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΚΑΜΠΥΛΕΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας της γεννήτριας συνεχούς ρεύματος
ΑΣΚΗΣΗ 5 η ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ ΔΙΕΓΕΡΣΗΣ ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΚΑΜΠΥΛΕΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση της λειτουργίας της γεννήτριας συνεχούς ρεύματος
ΑΣΚΗΣΗ 10 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΔΙΕΓΕΡΣΗΣ ΣΕΙΡΑΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 10 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΔΙΕΓΕΡΣΗΣ ΣΕΙΡΑΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση των τρόπων ελέγχου της ταχύτητας ενός
ΑΣΚΗΣΗ 10 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΔΙΕΓΕΡΣΗΣ ΣΕΙΡΑΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι α) η κατανόηση των τρόπων ελέγχου της ταχύτητας ενός
Ροή ισχύος στις γεννήτριες συνεχούς ρεύματος
 Ροή ισχύος στις γεννήτριες συνεχούς ρεύματος Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών, Μέτρο 1.2., Κοινωνία της Πληροφορίας 51 Ροή ισχύος στους κινητήρες συνεχούς ρεύματος Προηγμένες Υπηρεσίες
Ροή ισχύος στις γεννήτριες συνεχούς ρεύματος Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών, Μέτρο 1.2., Κοινωνία της Πληροφορίας 51 Ροή ισχύος στους κινητήρες συνεχούς ρεύματος Προηγμένες Υπηρεσίες
ΑΣΚΗΣΗ 7 η ΧΑΡΑΚΤΗΡΙΣΤΙΚΗ ΡΟΠΗΣ ΣΤΡΟΦΩΝ ΑΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ
 ΑΣΚΗΣΗ 7 η ΧΑΡΑΚΤΗΡΙΣΤΙΚΗ ΡΟΠΗΣ ΣΤΡΟΦΩΝ ΑΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ Σκοπός της άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: 1. Η μελέτη του τρόπου εκκίνησης και λειτουργίας
ΑΣΚΗΣΗ 7 η ΧΑΡΑΚΤΗΡΙΣΤΙΚΗ ΡΟΠΗΣ ΣΤΡΟΦΩΝ ΑΣΥΓΧΡΟΝΟΥ ΤΡΙΦΑΣΙΚΟΥ ΚΙΝΗΤΗΡΑ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ Σκοπός της άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: 1. Η μελέτη του τρόπου εκκίνησης και λειτουργίας
2. ΓΕΝΝΗΤΡΙΕΣ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ
 28 2. ΓΕΝΝΗΤΡΙΕΣ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ Οι γεννήτριες εναλλασσόµενου ρεύµατος είναι δύο ειδών Α) οι σύγχρονες γεννήτριες ή εναλλακτήρες και Β) οι ασύγχρονες γεννήτριες Οι σύγχρονες γεννήτριες παράγουν
28 2. ΓΕΝΝΗΤΡΙΕΣ ΕΝΑΛΛΑΣΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ Οι γεννήτριες εναλλασσόµενου ρεύµατος είναι δύο ειδών Α) οι σύγχρονες γεννήτριες ή εναλλακτήρες και Β) οι ασύγχρονες γεννήτριες Οι σύγχρονες γεννήτριες παράγουν
Τμήμα Ηλεκτρολόγων Μηχανικών ΕΛΕΓΧΟΣ ΤΑΧΥΤΗΤΑΣ ΣΤΟΥΣ ΕΠΑΓΩΓΙΚΟΥΣ ΚΙΝΗΤΗΡΕΣ
 Το κανονικό εύρος λειτουργίας ενός τυπικού επαγωγικού κινητήρα (κλάσης Α, Β και C) περιορίζεται κάτω από 5% για την ολίσθηση ενώ η μεταβολή της ταχύτητας πέρα από αυτό το εύρος είναι σχεδόν ανάλογη του
Το κανονικό εύρος λειτουργίας ενός τυπικού επαγωγικού κινητήρα (κλάσης Α, Β και C) περιορίζεται κάτω από 5% για την ολίσθηση ενώ η μεταβολή της ταχύτητας πέρα από αυτό το εύρος είναι σχεδόν ανάλογη του
ΑΣΚΗΣΗ 6 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ
 ΑΣΚΗΣΗ 6 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ Σκοπός της άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: 1. Ο πειραματικός προσδιορισμός των απωλειών σιδήρου και των μηχανικών απωλειών
ΑΣΚΗΣΗ 6 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ ΒΡΑΧΥΚΥΚΛΩΜΕΝΟΥ ΔΡΟΜΕΑ Σκοπός της άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: 1. Ο πειραματικός προσδιορισμός των απωλειών σιδήρου και των μηχανικών απωλειών
ΑΣΚΗΣΗ 1 η ΜΕΛΕΤΗ ΛΕΙΤΟΥΡΓΙΑΣ ΤΡΙΦΑΣΙΚΗΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΝΗΤΡΙΑΣ (ΕΝΑΛΛΑΚΤΗΡΑ) ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ ΤΟΥ ΙΣΟΔΥΝΑΜΟΥ ΚΥΚΛΩΜΑΤΟΣ
 ΑΣΚΗΣΗ 1 η ΜΕΛΕΤΗ ΛΕΙΤΟΥΡΓΙΑΣ ΤΡΙΦΑΣΙΚΗΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΝΗΤΡΙΑΣ (ΕΝΑΛΛΑΚΤΗΡΑ) ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ ΤΟΥ ΙΣΟΔΥΝΑΜΟΥ ΚΥΚΛΩΜΑΤΟΣ Σκοπός της άσκησης: 1. Ο πειραματικός προσδιορισμός της χαρακτηριστικής λειτουργίας
ΑΣΚΗΣΗ 1 η ΜΕΛΕΤΗ ΛΕΙΤΟΥΡΓΙΑΣ ΤΡΙΦΑΣΙΚΗΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΝΗΤΡΙΑΣ (ΕΝΑΛΛΑΚΤΗΡΑ) ΓΙΑ ΤΟΝ ΠΡΟΣΔΙΟΡΙΣΜΟ ΤΟΥ ΙΣΟΔΥΝΑΜΟΥ ΚΥΚΛΩΜΑΤΟΣ Σκοπός της άσκησης: 1. Ο πειραματικός προσδιορισμός της χαρακτηριστικής λειτουργίας
ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ. Κινητήρες ΣΡ. Άγγελος Μπουχουράς - Μηχανές Ι
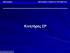 Το ισοδύναμο κύκλωμα ενός κινητήρα ΣΡ: Το κύκλωμα οπλισμού παριστάνεται με μια ιδανική πηγή τάσης ΕΑ και μία αντίσταση RA Στην ουσία πρόκειται για το ισοδύναμο κύκλωμα του δρομέα που περιλαμβάνει: τους
Το ισοδύναμο κύκλωμα ενός κινητήρα ΣΡ: Το κύκλωμα οπλισμού παριστάνεται με μια ιδανική πηγή τάσης ΕΑ και μία αντίσταση RA Στην ουσία πρόκειται για το ισοδύναμο κύκλωμα του δρομέα που περιλαμβάνει: τους
Ηλεκτρικές Μηχανές ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 3: Εξισώσεις Μόνιμης Κατάστασης Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 3: Εξισώσεις Μόνιμης Κατάστασης Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Άδειες Χρήσης
Στο στάτη της μηχανής εφαρμόζεται ένα 3-φασικό σύστημα ρευμάτων το οποίο παράγει στο εσωτερικό της στρεφόμενο ομογενές μαγνητικό πεδίο
 Στον ΣΚ 2 πόλων το μαγνητικό πεδίο του δρομέα BR παράγεται από το ρεύμα διέγερσης IF Στο στάτη της μηχανής εφαρμόζεται ένα 3-φασικό σύστημα ρευμάτων το οποίο παράγει στο εσωτερικό της στρεφόμενο ομογενές
Στον ΣΚ 2 πόλων το μαγνητικό πεδίο του δρομέα BR παράγεται από το ρεύμα διέγερσης IF Στο στάτη της μηχανής εφαρμόζεται ένα 3-φασικό σύστημα ρευμάτων το οποίο παράγει στο εσωτερικό της στρεφόμενο ομογενές
Γεννήτριες ΣΡ Ξένης Διέγερσης
 Γεννήτριες ΣΡ Ξένης Διέγερσης Γεννήτριες ΣΡ Γεννήτριες ανεξάρτητης διέγερσης: το κύκλωμα που παράγει το κύριο πεδίο (κύκλωμα διέγερσης) τροφοδοτείται από μία ξεχωριστή πηγή, ανεξάρτητη από τη γεννήτρια
Γεννήτριες ΣΡ Ξένης Διέγερσης Γεννήτριες ΣΡ Γεννήτριες ανεξάρτητης διέγερσης: το κύκλωμα που παράγει το κύριο πεδίο (κύκλωμα διέγερσης) τροφοδοτείται από μία ξεχωριστή πηγή, ανεξάρτητη από τη γεννήτρια
Κινητήρας συνεχούς ρεύματος σύνθετης διέγερσης. α) αθροιστικής σύνθετης διέγερσης
 ΑΣΚΗΣΗ 10 Κινητήρας συνεχούς ρεύματος σύνθετης διέγερσης α) αθροιστικής σύνθετης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Ο κινητήρας συνεχούς ρεύματος σύνθετης διέγερσης συνδυάζει τα πλεονεκτήματα του κινητήρα
ΑΣΚΗΣΗ 10 Κινητήρας συνεχούς ρεύματος σύνθετης διέγερσης α) αθροιστικής σύνθετης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Ο κινητήρας συνεχούς ρεύματος σύνθετης διέγερσης συνδυάζει τα πλεονεκτήματα του κινητήρα
Τμήμα Ηλεκτρολόγων Μηχανικών ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΡΟΠΗΣ ΤΑΧΥΤΗΤΑΣ ΕΠΑΓΩΓΙΚΩΝ ΚΙΝΗΤΗΡΩΝ
 Αν είναι γνωστή η συμπεριφορά των μαγνητικών πεδίων στη μηχανή, είναι δυνατός ο προσεγγιστικός προσδιορισμός της χαρακτηριστικής ροπής-ταχύτητας του επαγωγικού κινητήρα Όπως είναι γνωστό η επαγόμενη ροπή
Αν είναι γνωστή η συμπεριφορά των μαγνητικών πεδίων στη μηχανή, είναι δυνατός ο προσεγγιστικός προσδιορισμός της χαρακτηριστικής ροπής-ταχύτητας του επαγωγικού κινητήρα Όπως είναι γνωστό η επαγόμενη ροπή
ΟΝΟΜ/ΩΝΥΜΟ:ΣΤΕΦΑΝΟΣ ΓΚΟΥΝΤΟΥΣΟΥΔΗΣ Α.Μ:6750 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ:ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ (ΕΡΓΑΣΤΗΡΙΟ)
 ΟΝΟΜ/ΩΝΥΜΟ:ΣΤΕΦΑΝΟΣ ΓΚΟΥΝΤΟΥΣΟΥΔΗΣ Α.Μ:6750 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ:ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ (ΕΡΓΑΣΤΗΡΙΟ) Περιγραφή Λειτουργίας Σύγχρονου Κινητήρα Σκοπός: Η παρούσα εργασία έχει σκοπό να περιγράψει τη λειτουργία ενός
ΟΝΟΜ/ΩΝΥΜΟ:ΣΤΕΦΑΝΟΣ ΓΚΟΥΝΤΟΥΣΟΥΔΗΣ Α.Μ:6750 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ:ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ (ΕΡΓΑΣΤΗΡΙΟ) Περιγραφή Λειτουργίας Σύγχρονου Κινητήρα Σκοπός: Η παρούσα εργασία έχει σκοπό να περιγράψει τη λειτουργία ενός
Γεννήτρια συνεχούς ρεύματος παράλληλης. διέγερσης
 ΑΣΚΗΣΗ 6 Γεννήτρια συνεχούς ρεύματος παράλληλης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Στις γεννήτριες παράλληλης διέγερσης το τύλιγμα διέγερσης συνδέεται παράλληλα με το κύκλωμα του δρομέα, όπως φαίνεται
ΑΣΚΗΣΗ 6 Γεννήτρια συνεχούς ρεύματος παράλληλης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Στις γεννήτριες παράλληλης διέγερσης το τύλιγμα διέγερσης συνδέεται παράλληλα με το κύκλωμα του δρομέα, όπως φαίνεται
Αυτά τα πειράµατα έγιναν από τους Michael Faraday και Joseph Henry.
 Επαγόµενα πεδία Ένα µαγνητικό πεδίο µπορεί να µην είναι σταθερό, αλλά χρονικά µεταβαλλόµενο. Πειράµατα που πραγµατοποιήθηκαν το 1831 έδειξαν ότι ένα µεταβαλλόµενο µαγνητικό πεδίο µπορεί να επάγει ΗΕΔ σε
Επαγόµενα πεδία Ένα µαγνητικό πεδίο µπορεί να µην είναι σταθερό, αλλά χρονικά µεταβαλλόµενο. Πειράµατα που πραγµατοποιήθηκαν το 1831 έδειξαν ότι ένα µεταβαλλόµενο µαγνητικό πεδίο µπορεί να επάγει ΗΕΔ σε
5. ΜΟΝΟΦΑΣΙΚΟΙ ΚΑΙ ΑΛΛΟΙ ΚΙΝΗΤΗΡΕΣ
 73 5. ΜΟΝΟΦΑΣΙΚΟΙ ΚΑΙ ΑΛΛΟΙ ΚΙΝΗΤΗΡΕΣ Στην συνέχεια εξετάζονται οι µονοφασικοί επαγωγικοί κινητήρες αλλά και ορισµένοι άλλοι όπως οι τριφασικοί σύγχρονοι κινητήρες που υπάρχουν σε µικρό ποσοστό σε βιοµηχανικές
73 5. ΜΟΝΟΦΑΣΙΚΟΙ ΚΑΙ ΑΛΛΟΙ ΚΙΝΗΤΗΡΕΣ Στην συνέχεια εξετάζονται οι µονοφασικοί επαγωγικοί κινητήρες αλλά και ορισµένοι άλλοι όπως οι τριφασικοί σύγχρονοι κινητήρες που υπάρχουν σε µικρό ποσοστό σε βιοµηχανικές
ΑΣΚΗΣΗ 2 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΑΥΤΟΝΟΜΗΣ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΗΣ ΤΡΙΦΑΣΙΚΗΣ ΓΕΝΝΗΤΡΙΑΣ ΜΕ ΦΟΡΤΙΟ
 ΑΣΚΗΣΗ 2 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΑΥΤΟΝΟΜΗΣ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΗΣ ΤΡΙΦΑΣΙΚΗΣ ΓΕΝΝΗΤΡΙΑΣ ΜΕ ΦΟΡΤΙΟ Σκοπός της άσκησης: Σκοπός της άσκησης είναι η μελέτη των χαρακτηριστικών λειτουργίας μιας σύγχρονης γεννήτριας
ΑΣΚΗΣΗ 2 η ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΑΥΤΟΝΟΜΗΣ ΛΕΙΤΟΥΡΓΙΑΣ ΣΥΓΧΡΟΝΗΣ ΤΡΙΦΑΣΙΚΗΣ ΓΕΝΝΗΤΡΙΑΣ ΜΕ ΦΟΡΤΙΟ Σκοπός της άσκησης: Σκοπός της άσκησης είναι η μελέτη των χαρακτηριστικών λειτουργίας μιας σύγχρονης γεννήτριας
ΑΣΚΗΣΗ 1 η ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ ΙΣΧΥΟΣ ΕΙΣΑΓΩΓΗ. Στόχοι της εργαστηριακής άσκησης είναι η εξοικείωση των σπουδαστών με την:
 Σκοπός της Άσκησης: ΑΣΚΗΣΗ η ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ ΙΣΧΥΟΣ ΕΙΣΑΓΩΓΗ Στόχοι της εργαστηριακής άσκησης είναι η εξοικείωση των σπουδαστών με την: α. Κατασκευή μετασχηματιστών. β. Αρχή λειτουργίας μετασχηματιστών.
Σκοπός της Άσκησης: ΑΣΚΗΣΗ η ΜΕΤΑΣΧΗΜΑΤΙΣΤΕΣ ΙΣΧΥΟΣ ΕΙΣΑΓΩΓΗ Στόχοι της εργαστηριακής άσκησης είναι η εξοικείωση των σπουδαστών με την: α. Κατασκευή μετασχηματιστών. β. Αρχή λειτουργίας μετασχηματιστών.
Οι μηχανές ΕΡ είναι γεννήτριες που μετατρέπουν τη μηχανική ισχύ σε ηλεκτρική και κινητήρες που μετατρέπουν την ηλεκτρική σε μηχανική
 Οι μηχανές ΕΡ είναι γεννήτριες που μετατρέπουν τη μηχανική ισχύ σε ηλεκτρική και κινητήρες που μετατρέπουν την ηλεκτρική σε μηχανική Υπάρχουν 2 βασικές κατηγορίες μηχανών ΕΡ: οι σύγχρονες και οι επαγωγικές
Οι μηχανές ΕΡ είναι γεννήτριες που μετατρέπουν τη μηχανική ισχύ σε ηλεκτρική και κινητήρες που μετατρέπουν την ηλεκτρική σε μηχανική Υπάρχουν 2 βασικές κατηγορίες μηχανών ΕΡ: οι σύγχρονες και οι επαγωγικές
ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΙΙ
 ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΙΙ ΣΥΓΧΡΟΝΕΣ ΜΗΧΑΝΕΣ Ε.Ρ. 1. Μια σύγχρονη γεννήτρια με ονομαστικά στοιχεία: 2300V, 1000kV, 60Hz, διπολική με συντελεστής ισχύος 0,8 επαγωγικό και σύνδεση σε αστέρα έχει σύγχρονη
ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΙΙ ΣΥΓΧΡΟΝΕΣ ΜΗΧΑΝΕΣ Ε.Ρ. 1. Μια σύγχρονη γεννήτρια με ονομαστικά στοιχεία: 2300V, 1000kV, 60Hz, διπολική με συντελεστής ισχύος 0,8 επαγωγικό και σύνδεση σε αστέρα έχει σύγχρονη
10 - ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ
 10 - ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Ηλεκτρική μηχανή ονομάζεται κάθε διάταξη η οποία μετατρέπει τη μηχανική ενεργεια σε ηλεκτρική ή αντίστροφα ή μετατρεπει τα χαρακτηριστικά του ηλεκτρικού ρεύματος. Οι ηλεκτρικες
10 - ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Ηλεκτρική μηχανή ονομάζεται κάθε διάταξη η οποία μετατρέπει τη μηχανική ενεργεια σε ηλεκτρική ή αντίστροφα ή μετατρεπει τα χαρακτηριστικά του ηλεκτρικού ρεύματος. Οι ηλεκτρικες
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: 2 η
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: 2 η Τίτλος Άσκησης: ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ και ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ «Λειτουργία Γεννήτριας Συνεχούς Ρεύματος Ξένης διέγερσης και σχεδίαση της χαρακτηριστικής φορτίου» «Λειτουργία
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: 2 η Τίτλος Άσκησης: ΓΕΝΝΗΤΡΙΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΞΕΝΗΣ και ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ «Λειτουργία Γεννήτριας Συνεχούς Ρεύματος Ξένης διέγερσης και σχεδίαση της χαρακτηριστικής φορτίου» «Λειτουργία
ΑΣΚΗΣΗ 9 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ
 ΑΣΚΗΣΗ 9 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: α) η ασφαλής εκκίνηση β) η χάραξη της χαρακτηριστικής
ΑΣΚΗΣΗ 9 η ΚΙΝΗΤΗΡΑΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΠΑΡΑΛΛΗΛΗΣ ΔΙΕΓΕΡΣΗΣ ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΛΕΙΤΟΥΡΓΙΑΣ Σκοπός της Άσκησης: Σκοπός της εργαστηριακής άσκησης είναι: α) η ασφαλής εκκίνηση β) η χάραξη της χαρακτηριστικής
Απαντήσεις Θεμάτων Τελικής Αξιολόγησης (Εξετάσεις Ιουνίου) στο Μάθημα «Ηλεκτροτεχνία Ηλεκτρικές Μηχανές» ΕΕ 2013/2014, Ημερομηνία: 24/06/2014
 Θέμα ο Απαντήσεις Θεμάτων Τελικής Αξιολόγησης (Εξετάσεις Ιουνίου) στο Μάθημα «Ηλεκτροτεχνία Ηλεκτρικές Μηχανές» ΕΕ 03/04, Ημερομηνία: 4/06/04 Σε μονοφασικό Μ/Σ ονομαστικής ισχύος 60kA, 300/30, 50Hz, ελήφθησαν
Θέμα ο Απαντήσεις Θεμάτων Τελικής Αξιολόγησης (Εξετάσεις Ιουνίου) στο Μάθημα «Ηλεκτροτεχνία Ηλεκτρικές Μηχανές» ΕΕ 03/04, Ημερομηνία: 4/06/04 Σε μονοφασικό Μ/Σ ονομαστικής ισχύος 60kA, 300/30, 50Hz, ελήφθησαν
Τμήμα Ηλεκτρολόγων Μηχανικών ΜΟΝΟΦΑΣΙΚΟΙ ΚΙΝΗΤΗΡΕΣ
 Το βασικό μειονέκτημα που εμφανίζεται στη σχεδίαση των μονοφασικών επαγωγικών κινητήρων είναι ότι αντίθετα από τις 3-φασικές πηγές ισχύος οι 1-φασικές πηγές δεν παράγουν στρεφόμενο μαγνητικό πεδίο Το μαγνητικό
Το βασικό μειονέκτημα που εμφανίζεται στη σχεδίαση των μονοφασικών επαγωγικών κινητήρων είναι ότι αντίθετα από τις 3-φασικές πηγές ισχύος οι 1-φασικές πηγές δεν παράγουν στρεφόμενο μαγνητικό πεδίο Το μαγνητικό
Στον άπειρο ζυγό και μέσω μιας γραμμής μεταφοράς ισχύος συνδέεται κάποια βιομηχανία
 ΣΥΓΧΡΟΝΟΙ ΚΙΝΗΤΗΡΕΣ Στον άπειρο ζυγό και μέσω μιας γραμμής μεταφοράς ισχύος συνδέεται κάποια βιομηχανία Οι 2 από τους 3 κινητήρες αυτής της βιομηχανίας είναι επαγωγικοί και διαθέτουν επαγωγικούς συντελεστές
ΣΥΓΧΡΟΝΟΙ ΚΙΝΗΤΗΡΕΣ Στον άπειρο ζυγό και μέσω μιας γραμμής μεταφοράς ισχύος συνδέεται κάποια βιομηχανία Οι 2 από τους 3 κινητήρες αυτής της βιομηχανίας είναι επαγωγικοί και διαθέτουν επαγωγικούς συντελεστές
Τμήμα Ηλεκτρολόγων Μηχανικών ΧΑΡΑΚΤΗΡΙΣΤΙΚΕΣ ΡΟΠΗΣ ΤΑΧΥΤΗΤΑΣ ΕΠΑΓΩΓΙΚΩΝ ΚΙΝΗΤΗΡΩΝ
 Ένας που κατασκευάζεται ώστε να παρουσιάζει μεγάλη αντίσταση δρομέα η ροπή εκκίνησης του είναι αρκετά υψηλή αλλά το ίδιο υψηλή είναι και η ολίσθηση του στις κανονικές συνθήκες λειτουργίας Όμως επειδή Pconv=(1-s)PAG,
Ένας που κατασκευάζεται ώστε να παρουσιάζει μεγάλη αντίσταση δρομέα η ροπή εκκίνησης του είναι αρκετά υψηλή αλλά το ίδιο υψηλή είναι και η ολίσθηση του στις κανονικές συνθήκες λειτουργίας Όμως επειδή Pconv=(1-s)PAG,
Άσκηση 4 Αρχή λειτουργίας Μηχανών DC
 Άσκηση 4 Αρχή λειτουργίας Μηχανών DC 4.1 Σκοπός της Άσκησης Σκοπός την Άσκησης είναι η μελέτη της αρχής λειτουργίας των μηχανών DC. Οι μηχανές DC μπορούν να λειτουργήσουν είτε ως γεννήτριες είτε ως κινητήρες.
Άσκηση 4 Αρχή λειτουργίας Μηχανών DC 4.1 Σκοπός της Άσκησης Σκοπός την Άσκησης είναι η μελέτη της αρχής λειτουργίας των μηχανών DC. Οι μηχανές DC μπορούν να λειτουργήσουν είτε ως γεννήτριες είτε ως κινητήρες.
Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Τομέας Μηχανολογικών Κατασκευών και Αυτομάτου Ελέγχου 2.3.26.3 Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας Εξέταση 3 ου Eξαμήνου (20 Φεβρουαρίου
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Τομέας Μηχανολογικών Κατασκευών και Αυτομάτου Ελέγχου 2.3.26.3 Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας Εξέταση 3 ου Eξαμήνου (20 Φεβρουαρίου
Ηλεκτροκινητήρας Εναλλασσόμενου Ρεύματος τύπου κλωβού. Άσκηση 9. Ηλεκτροκινητήρας εναλλασσόμενου ρεύματος τύπου κλωβού
 ANTIKEIMENO: Άσκηση 9 Ηλεκτροκινητήρας εναλλασσόμενου ρεύματος τύπου κλωβού ΣΤΟΧΟΙ ΑΥΤΟΥ ΤΟΥ ΠΕΙΡΑΜΑΤΟΣ: Κατανόηση της λειτουργίας του ηλεκτροκινητήρα εναλλασσόμενου ρεύματος τύπου κλωβού Υπολογισμός μηχανικών
ANTIKEIMENO: Άσκηση 9 Ηλεκτροκινητήρας εναλλασσόμενου ρεύματος τύπου κλωβού ΣΤΟΧΟΙ ΑΥΤΟΥ ΤΟΥ ΠΕΙΡΑΜΑΤΟΣ: Κατανόηση της λειτουργίας του ηλεκτροκινητήρα εναλλασσόμενου ρεύματος τύπου κλωβού Υπολογισμός μηχανικών
Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας.
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
«Προηγµένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών»,
 «Προηγµένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών», Μέτρο: «Εισαγωγή και Αξιοποίηση των νέων Τεχνολογιών στην Εκπαίδευση» του Επιχειρησιακού Προγράµµατος Κοινωνία της Πληροφορίας ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ
«Προηγµένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών», Μέτρο: «Εισαγωγή και Αξιοποίηση των νέων Τεχνολογιών στην Εκπαίδευση» του Επιχειρησιακού Προγράµµατος Κοινωνία της Πληροφορίας ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ
ΚΕΦΑΛΑΙΟ 2 ΜΑΘΗΜΑ : Ηλεκτρικές Μηχανές ΚΕΦΑΛΑΙΟ : Ηλεκτρικές Μηχανές Σ.Ρ. ΕΝΟΤΗΤΑ : Αρχή Λειτουργίας Γεννητριών και Κινητήρων Σ.Ρ.
 ΚΕΦΑΛΑΙΟ 2 ΜΑΘΗΜΑ : Ηλεκτρικές Μηχανές ΚΕΦΑΛΑΙΟ : Ηλεκτρικές Μηχανές Σ.Ρ. ΕΝΟΤΗΤΑ : Αρχή Λειτουργίας Γεννητριών και Κινητήρων Σ.Ρ. Α. ΑΡΧΗ ΛΕΙΤΟΥΡΓΙΑΣ ΓΕΝΝΗΤΡΙΩΝ Σ.Ρ. Η λειτουργία της γεννήτριας, βασίζεται
ΚΕΦΑΛΑΙΟ 2 ΜΑΘΗΜΑ : Ηλεκτρικές Μηχανές ΚΕΦΑΛΑΙΟ : Ηλεκτρικές Μηχανές Σ.Ρ. ΕΝΟΤΗΤΑ : Αρχή Λειτουργίας Γεννητριών και Κινητήρων Σ.Ρ. Α. ΑΡΧΗ ΛΕΙΤΟΥΡΓΙΑΣ ΓΕΝΝΗΤΡΙΩΝ Σ.Ρ. Η λειτουργία της γεννήτριας, βασίζεται
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 7: Μεταβατική απόκριση κυκλωμάτων RL και RC Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 7: Μεταβατική απόκριση κυκλωμάτων RL και RC Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΣΗΕ I ΣΥΓΧΡΟΝΗ ΓΕΝΝΗΤΡΙΑ ΘΕΣΣΑΛΟΝΙΚΗ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΣΗΕ I ΣΥΓΧΡΟΝΗ ΓΕΝΝΗΤΡΙΑ ΘΕΣΣΑΛΟΝΙΚΗ
Ηλεκτροτεχνία Ηλ. Μηχανές & Εγκαταστάσεις πλοίου Στρεφόμενες ηλεκτρικές μηχανές Μηχανές Σ.Ρ.
 Βασική περιγραφή στρεφόμενων ηλεκτρικών μηχανών Αποτελεί το βασικό στοιχείο μετατροπής ενέργειας από ηλεκτρική σε μηχανική και αντίστροφα Κατηγοριοποιούνται σε : Σύγχρονες μηχανές Μηχανές συνεχούς ρεύματος
Βασική περιγραφή στρεφόμενων ηλεκτρικών μηχανών Αποτελεί το βασικό στοιχείο μετατροπής ενέργειας από ηλεκτρική σε μηχανική και αντίστροφα Κατηγοριοποιούνται σε : Σύγχρονες μηχανές Μηχανές συνεχούς ρεύματος
Τμήμα Ηλεκτρολόγων Μηχανικών ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΠΑΡΑΜΕΤΡΩΝ ΣΤΟ ΙΣΟΔΥΝΑΜΟ ΚΥΚΛΩΜΑ
 Το ισοδύναμο κύκλωμα ενός επαγωγικού κινητήρα αποτελεί ένα πολύ σημαντικό εργαλείο για τον προσδιορισμό της απόκρισης του κινητήρα στις αλλαγές του φορτίου του Για να χρησιμοποιηθεί αυτό το ισοδύναμο θα
Το ισοδύναμο κύκλωμα ενός επαγωγικού κινητήρα αποτελεί ένα πολύ σημαντικό εργαλείο για τον προσδιορισμό της απόκρισης του κινητήρα στις αλλαγές του φορτίου του Για να χρησιμοποιηθεί αυτό το ισοδύναμο θα
Εργαστήριο Ανάλυσης Συστημάτων Ηλεκτρικής Ενέργειας
 Εργαστήριο Ανάλυσης Συστημάτων Ηλεκτρικής Ενέργειας Ενότητα: Άσκηση 5: Η σύγχρονη μηχανή (γεννήτρια/κινητήρας ) Νικόλαος Βοβός, Γαβριήλ Γιαννακόπουλος, Παναγής Βοβός Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Εργαστήριο Ανάλυσης Συστημάτων Ηλεκτρικής Ενέργειας Ενότητα: Άσκηση 5: Η σύγχρονη μηχανή (γεννήτρια/κινητήρας ) Νικόλαος Βοβός, Γαβριήλ Γιαννακόπουλος, Παναγής Βοβός Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Γεννήτριες ΣΡ Κινητήρες ΣΡ
 Κινητήρες ΣΡ Ως γεννήτρια ΣΡ χαρακτηρίζεται η ηλεκτρική μηχανή που κατά τη λειτουργία της λαμβάνει κινητική ενέργεια και τη μετατρέπει σε ηλεκτρική με τη μορφή συνεχούς ρεύματος Η ΗΕΔ που δημιουργείται
Κινητήρες ΣΡ Ως γεννήτρια ΣΡ χαρακτηρίζεται η ηλεκτρική μηχανή που κατά τη λειτουργία της λαμβάνει κινητική ενέργεια και τη μετατρέπει σε ηλεκτρική με τη μορφή συνεχούς ρεύματος Η ΗΕΔ που δημιουργείται
ΛΕΙΤΟΥΡΓΙΑ ΗΛΕΚΤΡΙΚΟΥ ΚΙΝΗΤΗΡΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΜΕ ΔΙΕΓΕΡΣΗ ΣΕΙΡΑΣ ΣΕ ΔΙΚΤΥΟ ΕΝΑΛΛΑΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ
 ΛΕΙΤΟΥΡΓΙΑ ΗΛΕΚΤΡΙΚΟΥ ΚΙΝΗΤΗΡΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΜΕ ΔΙΕΓΕΡΣΗ ΣΕΙΡΑΣ ΣΕ ΔΙΚΤΥΟ ΕΝΑΛΛΑΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ ΕΡΓΑΣΙΑ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΛΑΜΠΡΟΥ ΑΡΓΥΡΙΟΣ, Α.Μ : 7021 ΣΚΟΠΟΣ Σκοπός της
ΛΕΙΤΟΥΡΓΙΑ ΗΛΕΚΤΡΙΚΟΥ ΚΙΝΗΤΗΡΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΜΕ ΔΙΕΓΕΡΣΗ ΣΕΙΡΑΣ ΣΕ ΔΙΚΤΥΟ ΕΝΑΛΛΑΣΟΜΕΝΟΥ ΡΕΥΜΑΤΟΣ ΕΡΓΑΣΙΑ ΗΛΕΚΤΡΙΚΩΝ ΜΗΧΑΝΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΛΑΜΠΡΟΥ ΑΡΓΥΡΙΟΣ, Α.Μ : 7021 ΣΚΟΠΟΣ Σκοπός της
ΑΣΚΗΣΗ 1 ΜΟΝΟΦΑΣΙΚΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΤΗΣ
 ΑΣΚΗΣΗ 1 ΜΟΝΟΦΑΣΙΚΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΤΗΣ Α.1 ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΜΟΝΟΦΑΣΙΚΟ ΜΕΤΑΣΧΗΜΑΤΙΣΤΗ Ο μετασχηματιστής είναι μια ηλεκτρική διάταξη που μετατρέπει εναλλασσόμενη ηλεκτρική ενέργεια ενός επιπέδου τάσης
ΑΣΚΗΣΗ 1 ΜΟΝΟΦΑΣΙΚΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΤΗΣ Α.1 ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΜΟΝΟΦΑΣΙΚΟ ΜΕΤΑΣΧΗΜΑΤΙΣΤΗ Ο μετασχηματιστής είναι μια ηλεκτρική διάταξη που μετατρέπει εναλλασσόμενη ηλεκτρική ενέργεια ενός επιπέδου τάσης
Λειτουργικά χαρακτηριστικά γεννητριών
 Λειτουργικά χαρακτηριστικά γεννητριών Η φασική τάση στο εσωτερικό μιας μηχανής (στα τυλίγματα του στάτη) δίνεται από τη σχέση: E 2 N φ f A = π C Συχνότητα περιστροφής μηχανής Πλήθος σπειρών στο τύλιγμα
Λειτουργικά χαρακτηριστικά γεννητριών Η φασική τάση στο εσωτερικό μιας μηχανής (στα τυλίγματα του στάτη) δίνεται από τη σχέση: E 2 N φ f A = π C Συχνότητα περιστροφής μηχανής Πλήθος σπειρών στο τύλιγμα
Κινητήρας συνεχούς ρεύματος παράλληλης. διέγερσης
 ΑΣΚΗΣΗ 9 Κινητήρας συνεχούς ρεύματος παράλληλης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Σε μια ηλεκτρική μηχανή συνεχούς ρεύματος αν τροφοδοτήσουμε το τύλιγμα οπλισμού με συνεχή τάση τότε μπορεί να χρησιμοποιηθεί
ΑΣΚΗΣΗ 9 Κινητήρας συνεχούς ρεύματος παράλληλης διέγερσης 1 Α. Θεωρητικές επεξηγήσεις: Σε μια ηλεκτρική μηχανή συνεχούς ρεύματος αν τροφοδοτήσουμε το τύλιγμα οπλισμού με συνεχή τάση τότε μπορεί να χρησιμοποιηθεί
Πείραμα επαγόμενου ρεύματος
 Επαγόμενα πεδία Ένα μαγνητικό πεδίο μπορεί να μην είναι σταθερό, αλλά χρονικά μεταβαλλόμενο. Πειράματα που πραγματοποιήθηκαν το 1831 (από τους Michael Faraday και Joseph Henry) έδειξαν ότι ένα μεταβαλλόμενο
Επαγόμενα πεδία Ένα μαγνητικό πεδίο μπορεί να μην είναι σταθερό, αλλά χρονικά μεταβαλλόμενο. Πειράματα που πραγματοποιήθηκαν το 1831 (από τους Michael Faraday και Joseph Henry) έδειξαν ότι ένα μεταβαλλόμενο
ΣΥΓΧΡΟΝΕΣ ΓΕΝΝΗΤΡΙΕΣ
 ΣΥΓΧΡΟΝΕΣ ΓΕΝΝΗΤΡΙΕΣ Για τη λειτουργία των σύγχρονων γεννητριών (που ονομάζονται και εναλλακτήρες) απαραίτητη προϋπόθεση είναι η τροοδοσία του τυλίγματος του δρομέα με συνεχές ρεύμα Καθώς περιστρέεται
ΣΥΓΧΡΟΝΕΣ ΓΕΝΝΗΤΡΙΕΣ Για τη λειτουργία των σύγχρονων γεννητριών (που ονομάζονται και εναλλακτήρες) απαραίτητη προϋπόθεση είναι η τροοδοσία του τυλίγματος του δρομέα με συνεχές ρεύμα Καθώς περιστρέεται
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α Β ) ΕΥΤΕΡΑ 6
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΚΑΙ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΑ Α Β ) ΕΥΤΕΡΑ 6
Τρόπος λειτουργίας ενός ηλεκτρικού κινητήρα Σ.Ρ σύνθετης διέγερσης
 Τρόπος λειτουργίας ενός ηλεκτρικού κινητήρα Σ.Ρ σύνθετης διέγερσης [1] Περιεχόμενα Τίτλος (σελ 1) Σκοπός (σελ 3) Περίληψη (σελ 4) Εισαγωγή (σελ 5) Κύριο μέρος (σελ 7) Επίλογος (σελ 12) Βιβλιογραφία (σελ
Τρόπος λειτουργίας ενός ηλεκτρικού κινητήρα Σ.Ρ σύνθετης διέγερσης [1] Περιεχόμενα Τίτλος (σελ 1) Σκοπός (σελ 3) Περίληψη (σελ 4) Εισαγωγή (σελ 5) Κύριο μέρος (σελ 7) Επίλογος (σελ 12) Βιβλιογραφία (σελ
Ηλεκτρικές Ταλαντώσεις 2ο Σετ Ασκήσεων - Φθινόπωρο 2012
 Ηλεκτρικές Ταλαντώσεις - Φθινόπωρο 2012 Επιµέλεια: Μιχάλης Ε. Καραδηµητρίου, M Sc Φυσικός http://perifysikhs.wordpress.com Α. Ερωτήσεις πολλαπλής επιλογής Α.1. Ποια µεταβολή ϑα έχουµε στην περίοδο ηλεκτρικών
Ηλεκτρικές Ταλαντώσεις - Φθινόπωρο 2012 Επιµέλεια: Μιχάλης Ε. Καραδηµητρίου, M Sc Φυσικός http://perifysikhs.wordpress.com Α. Ερωτήσεις πολλαπλής επιλογής Α.1. Ποια µεταβολή ϑα έχουµε στην περίοδο ηλεκτρικών
ΘΕΜΑ 1ο Για τις ερωτήσεις να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 2010 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Κακαζιάνης Πέτρος ΘΕΜΑ 1ο Για τις ερωτήσεις 1.1 1.13 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 2010 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Κακαζιάνης Πέτρος ΘΕΜΑ 1ο Για τις ερωτήσεις 1.1 1.13 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΟΥΝΙΟΥ 2007
 ΤΕΙ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΣΤΕΦ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΔΙΔΑΣΚΩΝ: Δρ. Π. Β. Μαλατέστας, Καθηγητής ΗΜΕΡΟΜΗΝΙΑ : 5//7 Μάθημα : Ηλεκτρική Κίνηση ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΟΥΝΙΟΥ 7 ΘΕΜΑ ο (4%) Κινητήρας με γραμμική χαρακτηριστική
ΤΕΙ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΣΤΕΦ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΔΙΔΑΣΚΩΝ: Δρ. Π. Β. Μαλατέστας, Καθηγητής ΗΜΕΡΟΜΗΝΙΑ : 5//7 Μάθημα : Ηλεκτρική Κίνηση ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΟΥΝΙΟΥ 7 ΘΕΜΑ ο (4%) Κινητήρας με γραμμική χαρακτηριστική
ΗΜΥ 340 Μηχανική Ηλεκτρικής Ισχύος Μηχανές συνεχούς έντασης
 ΗΜΥ 340 Μηχανική Ηλεκτρικής Ισχύος Μηχανές συνεχούς έντασης Δρ. Ηλίας Κυριακίδης Αναπληρωτής Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ 2006
ΗΜΥ 340 Μηχανική Ηλεκτρικής Ισχύος Μηχανές συνεχούς έντασης Δρ. Ηλίας Κυριακίδης Αναπληρωτής Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ 2006
Τμήμα Ηλεκτρολόγων Μηχανικών ΑΥΤΟΝΟΜΗ ΛΕΙΤΟΥΡΓΙΑ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ
 ΑΥΤΟΝΟΜΗ ΛΕΙΤΟΥΡΓΙΑ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ Οι βασικοί παράγοντες που επηρεάζουν τη συμπεριφορά μιας ΣΓ όταν αυτή λειτουργεί με κάποιο φορτίο είναι αφενός ο συντελεστής ισχύος του φορτίου και αφετέρου το αν
ΑΥΤΟΝΟΜΗ ΛΕΙΤΟΥΡΓΙΑ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ Οι βασικοί παράγοντες που επηρεάζουν τη συμπεριφορά μιας ΣΓ όταν αυτή λειτουργεί με κάποιο φορτίο είναι αφενός ο συντελεστής ισχύος του φορτίου και αφετέρου το αν
Τμήμα Ηλεκτρολόγων Μηχανικών ΑΝΑΛΥΣΗ ΣΓ ΠΟΥ ΛΕΙΤΟΥΡΓΟΥΝ ΠΑΡΑΛΛΗΛΑ
 Πολύ συχνά όταν μία ΣΓ συνδεθεί σε κάποιο μεγάλο σύστημα ισχύος, καμία μεταβολή στα χαρακτηριστικά της γεννήτριας δεν μπορεί να προκαλέσει εμφανή αλλαγή στη συχνότητα του συστήματος Η παρατήρηση αυτή εκφράζει
Πολύ συχνά όταν μία ΣΓ συνδεθεί σε κάποιο μεγάλο σύστημα ισχύος, καμία μεταβολή στα χαρακτηριστικά της γεννήτριας δεν μπορεί να προκαλέσει εμφανή αλλαγή στη συχνότητα του συστήματος Η παρατήρηση αυτή εκφράζει
Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Τομέας Μηχανολογικών Κατασκευών και Αυτομάτου Ελέγχου 2.3.26.3 Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας Επαναληπτική Εξέταση 3 ου Eξαμήνου
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Τομέας Μηχανολογικών Κατασκευών και Αυτομάτου Ελέγχου 2.3.26.3 Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας Επαναληπτική Εξέταση 3 ου Eξαμήνου
ΑΣΚΗΣΗ 5 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ. 1. Η μελέτη της δομής και της αρχής λειτουργίας ενός ασύγχρονου τριφασικού κινητήρα.
 Σκοπός της άσκησης: ΑΣΚΗΣΗ 5 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ Σκοπός της εργαστηριακής άσκησης είναι: 1. Η μελέτη της δομής και της αρχής λειτουργίας ενός ασύγχρονου τριφασικού κινητήρα. 1. Γενικά Οι
Σκοπός της άσκησης: ΑΣΚΗΣΗ 5 η ΑΣΥΓΧΡΟΝΟΣ ΤΡΙΦΑΣΙΚΟΣ ΚΙΝΗΤΗΡΑΣ Σκοπός της εργαστηριακής άσκησης είναι: 1. Η μελέτη της δομής και της αρχής λειτουργίας ενός ασύγχρονου τριφασικού κινητήρα. 1. Γενικά Οι
1. ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΣΗΜΕΙΩΣΕΙΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ 11 1. ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ 1.1 Συγκρότηση κατασκευή Μια µηχανή συνεχούς ρεύµατος αποτελείται από ένα ακίνητο τµήµα που λέγεται στάτης και ένα
ΣΗΜΕΙΩΣΕΙΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ 11 1. ΜΗΧΑΝΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ 1.1 Συγκρότηση κατασκευή Μια µηχανή συνεχούς ρεύµατος αποτελείται από ένα ακίνητο τµήµα που λέγεται στάτης και ένα
Θέµατα Εξετάσεων 94. δ. R
 Θέµατα Εξετάσεων 94 Συνεχές ρεύµα 42) Ο ρόλος µιας ηλεκτρικής πηγής σ' ένα κύκλωµα είναι: α) να δηµιουργεί διαφορά δυναµικού β) να παράγει ηλεκτρικά φορτία γ) να αποθηκεύει ηλεκτρικά φορτία δ) να επιβραδύνει
Θέµατα Εξετάσεων 94 Συνεχές ρεύµα 42) Ο ρόλος µιας ηλεκτρικής πηγής σ' ένα κύκλωµα είναι: α) να δηµιουργεί διαφορά δυναµικού β) να παράγει ηλεκτρικά φορτία γ) να αποθηκεύει ηλεκτρικά φορτία δ) να επιβραδύνει
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΙΣΑΓΩΓΙΚΑ Η ηλεκτρική μηχανή είναι μια διάταξη μετατροπής μηχανικής ενέργειας σε ηλεκτρική και αντίστροφα. απώλειες Μηχανική ενέργεια Γεννήτρια Κινητήρας Ηλεκτρική ενέργεια
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΙΣΑΓΩΓΙΚΑ Η ηλεκτρική μηχανή είναι μια διάταξη μετατροπής μηχανικής ενέργειας σε ηλεκτρική και αντίστροφα. απώλειες Μηχανική ενέργεια Γεννήτρια Κινητήρας Ηλεκτρική ενέργεια
Γεννήτριες ΣΡ Παράλληλης Διέγερσης
 Παράλληλης Διέγερσης Το κύκλωμα διέγερσης συνδέεται στα άκρα της και τροφοδοτείται από την τάση εξόδου της μηχανής Σε αυτό το κύκλωμα το ρεύμα οπλισμού τροφοδοτεί τόσο το κύκλωμα διέγερσης όσο και το φορτίο
Παράλληλης Διέγερσης Το κύκλωμα διέγερσης συνδέεται στα άκρα της και τροφοδοτείται από την τάση εξόδου της μηχανής Σε αυτό το κύκλωμα το ρεύμα οπλισμού τροφοδοτεί τόσο το κύκλωμα διέγερσης όσο και το φορτίο
4. ΤΡΙΦΑΣΙΚΟΙ ΑΣΥΓΧΡΟΝΟΙ ΚΙΝΗΤΗΡΕΣ
 56 4. ΤΡΙΦΑΣΙΚΟΙ ΑΣΥΓΧΡΟΝΟΙ ΚΙΝΗΤΗΡΕΣ Οι ασύγχρονοι κινητήρες που ονοµάζονται και επαγωγικοί κινητήρες διακρίνονται σε µονοφασικούς και τριφασικούς. Στην συνέχεια θα εξετασθούν οι τριφασικοί ασύγχρονοι
56 4. ΤΡΙΦΑΣΙΚΟΙ ΑΣΥΓΧΡΟΝΟΙ ΚΙΝΗΤΗΡΕΣ Οι ασύγχρονοι κινητήρες που ονοµάζονται και επαγωγικοί κινητήρες διακρίνονται σε µονοφασικούς και τριφασικούς. Στην συνέχεια θα εξετασθούν οι τριφασικοί ασύγχρονοι
ΜΕΤΑΤΡΟΠΕΙΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΜΑΘ.. 12 ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΜΕΤΑΤΡΟΠΕΙΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ 1. ΓΕΝΙΚΑ Οι μετατροπείς συνεχούς ρεύματος επιτελούν τη μετατροπή μιας τάσης συνεχούς μορφής, σε συνεχή τάση με ρυθμιζόμενο σταθερό πλάτος ή και πολικότητα.
ΜΑΘ.. 12 ΕΙΣΑΓΩΓΗ ΣΤΟΥΣ ΜΕΤΑΤΡΟΠΕΙΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ 1. ΓΕΝΙΚΑ Οι μετατροπείς συνεχούς ρεύματος επιτελούν τη μετατροπή μιας τάσης συνεχούς μορφής, σε συνεχή τάση με ρυθμιζόμενο σταθερό πλάτος ή και πολικότητα.
ΟΝΟΜ/ΝΥΜΟ: ΜΠΑΛΑΜΠΑΝΗ ΓΕΩΡΓΙΑ ΑΜ:6105 ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΡΓΑΣΙΑ ΤΙΤΛΟΣ: ΤΡΟΠΟΣ ΛΕΙΤΟΥΡΓΙΑΣ ΜΙΑΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ
 ΟΝΟΜ/ΝΥΜΟ: ΜΠΑΛΑΜΠΑΝΗ ΓΕΩΡΓΙΑ ΑΜ:6105 ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΡΓΑΣΙΑ ΤΙΤΛΟΣ: ΤΡΟΠΟΣ ΛΕΙΤΟΥΡΓΙΑΣ ΜΙΑΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ 1 Η γεννήτρια ή ηλεκτρογεννήτρια είναι μηχανή που βασίζεται στους νόμους της
ΟΝΟΜ/ΝΥΜΟ: ΜΠΑΛΑΜΠΑΝΗ ΓΕΩΡΓΙΑ ΑΜ:6105 ΜΑΘΗΜΑ: ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΡΓΑΣΙΑ ΤΙΤΛΟΣ: ΤΡΟΠΟΣ ΛΕΙΤΟΥΡΓΙΑΣ ΜΙΑΣ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ 1 Η γεννήτρια ή ηλεκτρογεννήτρια είναι μηχανή που βασίζεται στους νόμους της
Ηλεκτρικές Μηχανές ΙΙ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 2: Ασύγχρονος Τριφασικός Κινητήρας Αρχή Λειτουργίας Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ηλεκτρικές Μηχανές ΙΙ Ενότητα 2: Ασύγχρονος Τριφασικός Κινητήρας Αρχή Λειτουργίας Ηρακλής Βυλλιώτης Τμήμα Ηλεκτρολόγων Μηχανικών
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΣΤΟΙΧΕΙΑ ΠΡΑΓΜΑΤΙΚΩΝ ΜΗΧΑΝΩΝ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΣΤΟΙΧΕΙΑ ΠΡΑΓΜΑΤΙΚΩΝ ΜΗΧΑΝΩΝ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΒΑΣΙΚΑ ΤΜΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΜΗΧΑΝΗΣ ΣΡ Αναλύοντας τη δομή μιας πραγματικής μηχανής ΣΡ, αναφέρουμε τα ακόλουθα βασικά μέρη: Στάτης: αποτελεί το ακίνητο τμήμα
ΣΤΟΙΧΕΙΑ ΠΡΑΓΜΑΤΙΚΩΝ ΜΗΧΑΝΩΝ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ ΒΑΣΙΚΑ ΤΜΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΜΗΧΑΝΗΣ ΣΡ Αναλύοντας τη δομή μιας πραγματικής μηχανής ΣΡ, αναφέρουμε τα ακόλουθα βασικά μέρη: Στάτης: αποτελεί το ακίνητο τμήμα
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΣΗΕ I ΣΥΓΧΡΟΝΗ ΓΕΝΝΗΤΡΙΑ ΘΕΣΣΑΛΟΝΙΚΗ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΣΗΕ I ΣΥΓΧΡΟΝΗ ΓΕΝΝΗΤΡΙΑ ΘΕΣΣΑΛΟΝΙΚΗ
ηλεκτρικό ρεύµα ampere
 Ηλεκτρικό ρεύµα Το ηλεκτρικό ρεύµα είναι ο ρυθµός µε τον οποίο διέρχεται ηλεκτρικό φορτίο από µια περιοχή του χώρου. Η µονάδα µέτρησης του ηλεκτρικού ρεύµατος στο σύστηµα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύµα Το ηλεκτρικό ρεύµα είναι ο ρυθµός µε τον οποίο διέρχεται ηλεκτρικό φορτίο από µια περιοχή του χώρου. Η µονάδα µέτρησης του ηλεκτρικού ρεύµατος στο σύστηµα SI είναι το ampere (A). 1 A =
Γεννήτριες ΣΡ Κινητήρες ΣΡ
 Γεννήτριες ΣΡ Κινητήρες ΣΡ - Στοιχειώδεις Ηλεκτρικές Μηχανές Επαγωγή λέγεται το φαινόμενο κατά το οποίο αναπτύσσεται ΗΕΔ: a. Στα άκρα αγωγού όταν αυτός κινείται με ταχύτητα υ μέσα σε μαγνητικό πεδίο επαγωγής
Γεννήτριες ΣΡ Κινητήρες ΣΡ - Στοιχειώδεις Ηλεκτρικές Μηχανές Επαγωγή λέγεται το φαινόμενο κατά το οποίο αναπτύσσεται ΗΕΔ: a. Στα άκρα αγωγού όταν αυτός κινείται με ταχύτητα υ μέσα σε μαγνητικό πεδίο επαγωγής
ΕΝ ΕΙΚΤΙΚΑ ΠΑΡΑ ΕΙΓΜΑΤΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ
 ΕΝ ΕΙΚΤΙΚΑ ΠΑΡΑ ΕΙΓΜΑΤΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ 1ο Παράδειγµα κριτηρίου (εξέταση στο µάθηµα της ηµέρας) ΣΤΟΙΧΕΙΑ ΜΑΘΗΤΗ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΑΞΗ:... ΤΜΗΜΑ:... ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:... ΗΜΕΡΟΜΗΝΙΑ:... Σκοπός της
ΕΝ ΕΙΚΤΙΚΑ ΠΑΡΑ ΕΙΓΜΑΤΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ 1ο Παράδειγµα κριτηρίου (εξέταση στο µάθηµα της ηµέρας) ΣΤΟΙΧΕΙΑ ΜΑΘΗΤΗ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΑΞΗ:... ΤΜΗΜΑ:... ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:... ΗΜΕΡΟΜΗΝΙΑ:... Σκοπός της
Εργαστήριο Ελέγχου και Ευστάθειας Συστημάτων Ηλεκτρικής Ενέργειας
 Εργαστήριο Ελέγχου και Ευστάθειας Συστημάτων Ηλεκτρικής Ενέργειας Ενότητα: Άσκηση 4 Συμπεριφορά σύγχρονου κινητήρα υπό φορτίο Νικόλαος Βοβός, Γαβριήλ Γιαννακόπουλος, Παναγής Βοβός Τμήμα Ηλεκτρολόγων Μηχανικών
Εργαστήριο Ελέγχου και Ευστάθειας Συστημάτων Ηλεκτρικής Ενέργειας Ενότητα: Άσκηση 4 Συμπεριφορά σύγχρονου κινητήρα υπό φορτίο Νικόλαος Βοβός, Γαβριήλ Γιαννακόπουλος, Παναγής Βοβός Τμήμα Ηλεκτρολόγων Μηχανικών
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΗΠΙΩΝ ΜΟΡΦΩΝ ΕΝΕΡΓΕΙΑΣ. Μελέτη Ηλεκτρικού Κινητήρα
 ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΗΠΙΩΝ ΜΟΡΦΩΝ ΕΝΕΡΓΕΙΑΣ Μελέτη Ηλεκτρικού Κινητήρα Τύπος Ηλεκτρικού Κινητήρα Ασύγχρονος μονοφασικός ηλεκτρικός κινητήρας βραχυκυκλωμένου δρομέα. Α. Γενική Θεωρητική
ΤΕΙ ΠΑΤΡΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΗΠΙΩΝ ΜΟΡΦΩΝ ΕΝΕΡΓΕΙΑΣ Μελέτη Ηλεκτρικού Κινητήρα Τύπος Ηλεκτρικού Κινητήρα Ασύγχρονος μονοφασικός ηλεκτρικός κινητήρας βραχυκυκλωμένου δρομέα. Α. Γενική Θεωρητική
ΗΛΕΚΤΡΟΝΙΚΑ ΙΣΧΥΟΣ ΗΜΥ 444
 ΗΛΕΚΤΡΟΝΙΚΑ ΙΣΧΥΟΣ ΗΜΥ 444 ΕΛΕΓΧΟΣ ΚΙΝΗΤΗΡΩΝ DC ΚΑΙ AC ΣΥΣΤΗΜΑΤΑ ΑΔΙΑΛΕΙΠΤΗΣ ΠΑΡΟΧΗΣ Δρ Ανδρέας Σταύρου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τα Θέματα
ΗΛΕΚΤΡΟΝΙΚΑ ΙΣΧΥΟΣ ΗΜΥ 444 ΕΛΕΓΧΟΣ ΚΙΝΗΤΗΡΩΝ DC ΚΑΙ AC ΣΥΣΤΗΜΑΤΑ ΑΔΙΑΛΕΙΠΤΗΣ ΠΑΡΟΧΗΣ Δρ Ανδρέας Σταύρου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τα Θέματα
Απαραίτητη προϋπόθεση για να λειτουργήσει μία σύγχρονη γεννήτρια είναι η τροφοδοσία του τυλίγματος του δρομέα με ΣΡ
 ΣΥΓΧΡΟΝΕΣ ΓΕΝΝΗΤΡΙΕΣ Απαραίτητη προϋπόθεση για να λειτουργήσει μία σύγχρονη γεννήτρια είναι η τροφοδοσία του τυλίγματος του δρομέα με ΣΡ Αυτό το ρεύμα δημιουργεί μαγνητικό πεδίο στο εσωτερικό της γεννήτριας
ΣΥΓΧΡΟΝΕΣ ΓΕΝΝΗΤΡΙΕΣ Απαραίτητη προϋπόθεση για να λειτουργήσει μία σύγχρονη γεννήτρια είναι η τροφοδοσία του τυλίγματος του δρομέα με ΣΡ Αυτό το ρεύμα δημιουργεί μαγνητικό πεδίο στο εσωτερικό της γεννήτριας
Το μηδέν και το τετράγωνο.
 Το μηδέν και το τετράγωνο. Στο κύκλωµα του σχήµατος, ο διακόπτης (δ ) είναι κλειστός ενώ ο (δ ) ανοικτός. Θεωρούµε γνωστές τις τιµές της ΗΕ της πηγής Ε, των αντιστάσεων,, του συντελεστή αυτεπαγωγής του
Το μηδέν και το τετράγωνο. Στο κύκλωµα του σχήµατος, ο διακόπτης (δ ) είναι κλειστός ενώ ο (δ ) ανοικτός. Θεωρούµε γνωστές τις τιµές της ΗΕ της πηγής Ε, των αντιστάσεων,, του συντελεστή αυτεπαγωγής του
ΗΛΕΚΤΡΙΚΑ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ Α. ΑΣΚΗΣΕΙΣ ΕΛΕΓΧΟΥ ΤΑΧΥΤΗΤΑΣ D.C. ΚΙΝΗΤΗΡΑ
 ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ. ΓΕΝΙΚΑ ΗΛΕΚΤΡΙΚΑ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ Α. ΑΣΚΗΣΕΙΣ ΕΛΕΓΧΟΥ ΤΑΧΥΤΗΤΑΣ D.C. ΚΙΝΗΤΗΡΑ Σε ένα ανοιχτό σύστημα με συνάρτηση μεταφοράς G η έξοδος Υ και είσοδος Χ συνδέονται με τη σχέση: Y=G*Χ
ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ. ΓΕΝΙΚΑ ΗΛΕΚΤΡΙΚΑ ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ Α. ΑΣΚΗΣΕΙΣ ΕΛΕΓΧΟΥ ΤΑΧΥΤΗΤΑΣ D.C. ΚΙΝΗΤΗΡΑ Σε ένα ανοιχτό σύστημα με συνάρτηση μεταφοράς G η έξοδος Υ και είσοδος Χ συνδέονται με τη σχέση: Y=G*Χ
Κινητήρες μιας νέας εποχής
 Κινητήρες μιας νέας εποχής H ABB παρουσιάζει μια νέα γενιά κινητήρων υψηλής απόδοσης βασισμένη στην τεχνολογία σύγχρονης μαγνητικής αντίστασης. Η ΑΒΒ στρέφεται στην τεχνολογία κινητήρων σύγχρονης μαγνητικής
Κινητήρες μιας νέας εποχής H ABB παρουσιάζει μια νέα γενιά κινητήρων υψηλής απόδοσης βασισμένη στην τεχνολογία σύγχρονης μαγνητικής αντίστασης. Η ΑΒΒ στρέφεται στην τεχνολογία κινητήρων σύγχρονης μαγνητικής
Εξεταστική περίοδος χειμερινού εξαμήνου
 Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ Διδάσκων: Δρ. Π. Β. Μαλατέστας, Καθηγητής Ημερομηνία : 06/0/0 Διάρκεια: h 5in Ονοματεπώνυμο σπουδαστή: Αριθμός μητρώου: Μάθημα : Ηλεκτρική
Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ Διδάσκων: Δρ. Π. Β. Μαλατέστας, Καθηγητής Ημερομηνία : 06/0/0 Διάρκεια: h 5in Ονοματεπώνυμο σπουδαστή: Αριθμός μητρώου: Μάθημα : Ηλεκτρική
Τ.Ε.Ι. ΠΑΤΡΑΣ / Σ.Τ.ΕΦ. Πάτρα Τμήμα: ΜΗΧΑΝΟΛΟΓΙΑΣ. Εξέταση στο μάθημα «Ηλεκτρικές Μηχανές»
 Τ.Ε.Ι. ΠΑΤΡΑΣ / Σ.Τ.ΕΦ. Πάτρα 26-1-2012 Τμήμα: ΜΗΧΑΝΟΛΟΓΙΑΣ Εξέταση στο μάθημα «Ηλεκτρικές Μηχανές» ΠΡΟΣΟΧΗ: Για οποιοδήποτε σύμβολο χρησιμοποιήσετε στις πράξεις σας, να γράψετε ξεκάθαρα τι αντιπροσωπεύει
Τ.Ε.Ι. ΠΑΤΡΑΣ / Σ.Τ.ΕΦ. Πάτρα 26-1-2012 Τμήμα: ΜΗΧΑΝΟΛΟΓΙΑΣ Εξέταση στο μάθημα «Ηλεκτρικές Μηχανές» ΠΡΟΣΟΧΗ: Για οποιοδήποτε σύμβολο χρησιμοποιήσετε στις πράξεις σας, να γράψετε ξεκάθαρα τι αντιπροσωπεύει
Στο μαγνητικό πεδίο του πηνίου αποθηκεύεται ενέργεια. Το μαγνητικό πεδίο έχει πυκνότητα ενέργειας.
 Αυτεπαγωγή Αυτεπαγωγή Ένα χρονικά μεταβαλλόμενο ρεύμα που διαρρέει ένα κύκλωμα επάγει ΗΕΔ αντίθετη προς την ΗΕΔ από την οποία προκλήθηκε το χρονικά μεταβαλλόμενο ρεύμα.στην αυτεπαγωγή στηρίζεται η λειτουργία
Αυτεπαγωγή Αυτεπαγωγή Ένα χρονικά μεταβαλλόμενο ρεύμα που διαρρέει ένα κύκλωμα επάγει ΗΕΔ αντίθετη προς την ΗΕΔ από την οποία προκλήθηκε το χρονικά μεταβαλλόμενο ρεύμα.στην αυτεπαγωγή στηρίζεται η λειτουργία
