Οι μηχανές εξωτερικής καύσεως διαχωρίζονται σε δύο κατηγορίες : - μηχανές με χρήση ατμού - σε μηχανές με χρήση αερίου.
|
|
|
- Άποφις Βασιλείου
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΚΥΚΛΟΙ ΙΣΧΥΟΣ ΑΤΜΟΥ Οι εγκαταστάσεις παραγωγής έργου με ατμό λειτουργούν με μηχανές που ονομάζονται μηχανές εξωτερικής καύσης, δεδομένου ότι το ρευστό φορέας ενέργειας δεν συμμετέχει στην χημική αντίδραση της καύσης, αλλά το ποσό θερμότητας που παράγεται από την καύση μεταδίδεται από το περιβάλλον στο ρευστό σύστημα. Η θερμότητα προσδίδεται στο ρευστό σε μια διάταξη ξεχωριστή από τη μηχανή. Η διάταξη αυτή αποτελείται από την εστία (διάταξη για την κάυση και πρόσδοση της θερμότητας), το δοχείο μέσα στο οποίο το νερό μετατρέπεται σε ατμό (κοινώς λέβητας), και από τα διάφορα εξαρτήματα μηχανήματα που είναι απαραίτητα για τη λειτουργία της εγκατάστασης. Χαρακτηριστικό γνώρισμα των μηχανών εξωτερικής καύσης είναι ότι η χημική σύσταση του εργαζόμενου μέσου δεν αλλάζει, οπότε δεν χρειάζεται να ανανεώνεται σε κάθε κύκλο. Απλώς συμπληρώνεται εάν η στάθμη πέσει κάτω από την πίεση λειτουργίας. Οι μηχανές εξωτερικής καύσεως διαχωρίζονται σε δύο κατηγορίες : - μηχανές με χρήση ατμού - σε μηχανές με χρήση αερίου. Στην πρώτη κατηγορία το ρευστό σύστημα κατά τη διάρκεια του κύκλου, υπόκειται σε αλλαγή καταστάσεων. Αρχικά ευρίσκεται σε υγρή κατάσταση, ακολούθως σε κατάσταση μίγματος και στη συνέχεια σε κατάσταση υπέρθερμου ατμού. Μετά την ολοκήρωση του κύκλου επανέρχεται στην αρχική κατάσταση. Στην δεύτερη κατηγορία το σύστημα είναι αέριο, κυρίως αέρας που δέχεται θερμότητα από εξωτερική πηγή, εκτονώνεται σε ένα στρόβιλο και στη συνέχεια αποβάλει θερμότητα. Στις εγκαταστάσεις αυτές το σύστημα δεν υπόκειται σε αλλαγή φάσεων και στην κατηγορία αυτή ανήκουν οι στρόβιλοι ανοικτού κυκλώματος. Θεωρητικά κάθε στοιχείο θα μπορούσε να χρησιμοποιηθεί σαν σύστημα σε μια εγκατάσταση με μηχανή ατμού, διατηρώντας βέβαια την χημική του ισορροπία σε όλο το διάστημα της θερμοκρασίας κατά τη διάρκεια των μεταβολών που υπόκειται. Στην πράξη όμως οι περιορισμοί είναι πολύ περισσότεροι οπότε μια ουσία για να χρησιμοποιηθεί σε μια τέτοια εγκατάσταση πρέπει να έχει τα ακόλουθα χαρακτηριστικά :. το σημείο τήξης να είναι χαμηλώτερο από την ελάχιστη θερμοκρασία του κύκλου 2. η πίεση κορεσμού του ατμού δεν πρέπει να είναι πολύ μικρή ως προς την ελάχιστη θερμοκρασία του κύκλου. 3. η πίεση κορεσμού του ατμού δεν πρέπει να είναι πολύ μεγάλη ως προς τη μέγιστη θερμοκρασία του κύκλου 4. το σύστημα ( ουσία, φορέας της ενέργειας που συμμετέχει στον κύκλο) πρέπει να έχει μεγάλη κρίσιμη θερμοκρασία και η θερμότητα ατμοποίησης πρέπει να είναι η μέγιστη δυνατή 5. η ανώτερη οριακή καμπύλη (καμπύλη δρόσου, καμπύλη που αναπτύσσεται δεξιά τιυ κρίσιμου σημείου Κ) στο διάγραμμα (T S) πρέπει να είναι πολύ κεκλιμένη. Αυτό σημαίνει ότι το ρευστό πρέπει να παρουσιάζει μικρές μεταβολές εντροπίας όταν η θερμοκρασία μεταβάλλεται. 6. στις χαμηλές πιέσεις ο ειδικός όγκος του ατμού πρέπει να είναι πολύ μεγάλος 202 Σελίδα 239
2 7. εκτός από τη χημική σταθερότητα στις περιοχές της θερμοκρασίας που εξελλίσσεται ο κύκλος, πρέπει το σύστημα (συνθήκη τεχνολογικά απαραίτητη) να μην συνδυάζεται ή να μην αντιδρά χημικά με τα εξαρτήματα που αποτελούν τα όργανα της εγκατάστασης. Οι προαναφερόμενες συνθήκες είναι απαραίτητες στην πράξη και σε ότι αφορά στην μηχανική αντίσταση των υλικών και σε ότι αφορά σε πρακτική ωφέλεια. Συγκεκριμένα, κυρίως με αναφορά στο νερό : Η πρώτη συνθήκη είναι απαραίτητη για την απρόσκοπτη διέλευση του ρευστού μέσα από τα όργανα της εγκατάστασης. Για να εξασφαλίζεται αυτό, πρέπει το σύστημα να μην στερεοποιείται κατά την πορεία του στα όργανα της εγκατάστασης, κάτι που το νερό το ικανοποιεί. Η δεύτερη συνθήκη είναι απαραίτητη ώστε να διατηρηθεί στον συμπυκνωτή η πίεση ισορροπίας με τη θερμοκρασία της συμπύκνωσης : όσο μικρότερη είναι η πίεση (και εδώ οι πιέσεις είναι μικρότερες από την ατμοσφαιρική) τόσο μεγαλύτερη δυσκολία στην πραγματοποίηση και διατήρηση της ισορροπίας κατά τη συμπύκνωση. Επίσης, όσο μικραίνει η πίεση τόσο μεγαλώνει ο ειδικός όγκος και αυτό προξενεί προβλήματα όγκου στις μεγαλύτερες διαστάσεις της μηχανής. Σε αυτό το θέμα, το νερό δεν παρουσιάζει ευνοικά χαρακτηριστικά, όμως οι απαιτούμενες συνθήκες πίεσης στον συμπυκνωτή μπορούν να πραγματοποιηθούν. Η τρίτη συνθήκη επιβάλλεται από τις ανάγκες της εφαρμογής. Όσο αυξάνεται η θερμοκρασία μειώνονται οι μηχανικές αντιστάσεις των υλικών. Είναι επομένως απαραίτητο η μέγιστη πίεση του κύκλου να μην είναι πολύ αυξημένη γεγονός που οδηγεί για λόγους βελτίωσης του βαθμού αποδόσεως στην αύξηση της μέγιστης θερμοκρασίας. Εδώ το νερό δεν έχει ευνοικά χαρακτηριστικά. Εάν η κρίσιμη θερμοκρασία (4 η συνθήκη) είναι αυξημένη, τότε μπορεί να δοθεί θερμότητα στις συνήκες κορεσμού, δηλαδή p και T σταθερές και αντίστοιχες, ακόμα και σε υψηλές θερμοκρασίες με ευνοικό πρακτικό αποτέλεσμα. Το νερό έχει κρίσιμη θερμοκρασία μάλλον χαμηλή (374, 0 C), οπότε δεν ικανοποιεί πλήρως αυτή τη συνθήκη. Επιπροσθέτως εάν η θερμότητα ατμοποίησης είναι μεγάλη, μειώνεται (με ίση εναλλαγή ποσού θερμότητας) το βάρος του ρευστού που κυκλοφορεί στον κύκλο. Στο τέλος της εκτόνωσης του ατμού το σύστημα συνήθως ευρίσκεται στην περιοχή του μίγματος. Με ίδια αρχική και τελική πίεση (σημεία και 2 στο παρακάτω διάγραμμα) ο βαθμός ξηρότητας του συστήματος είναι μικρότερος όσο περισσότερο μεταβάλλεται η εντροπία του ξηρού ατμού στη χαμηλή πίεση, δηλαδή όσο μικρότερη κλίση ως προς τον άξονα της εντροπίας έχει η κατώτερη οριακή καμπύλη. Το νερό στην περίπτωση αυτή έχει πλεονέκτημα, δεδομένου ότι η κατώτερη οριακή του καμπύλη παρουσιάζει μεγάλη κλίση (αριστερό διάγραμμα στο παρακάτω σχήμα). 202 Σελίδα 240
3 ΣΧΗΜΑ 06 Όσον αφορά στην 6 η συνθήκη, μπορεί να παρατηρηθεί ότι το σύστημα στο τέλος της εκτόνωσης βρίσκεται σε χαμηλή πίεση (στις μοντένες εγκαταστάσεις και κάτω από την ατμοσφαιρική). Εάν ο αντίστοιχος ειδικός όγκος είναι μεγάλος, τότε ο εκτομωτής έχει μεγάλες διαστάσεις. Το νερό στην περίπτωση αυτή έχει σαφές μειονέκτημα, γι α 3 παράδειγμα σε p 0,2 ata ο ειδικός όγκος του ξηρού ατμού είναι υ 2,60( m kp). Η τελευταία συνθήκη για τη χημική σταθερότητα στην περιοχή θερμοκρασιών που ενδιαφέρουν τον κύκλο, ικανοποιείται όταν το σύστημα είναι ατμός, αλλά δεν ικανοποιείται όταν το σύστημα είναι στην κατάσταση μίγματος ή στην καθαρά υγρή κατάσταση, δεδομένου ότι το νερό διαβρώνει τα σιδηρούχα υλικά. Υπάρχουν σήμερα μέθοδες για την αντιμετώπιση της διάβρωσης με κατάλληλη επεξεργασία του νερού τροφοδοσίας του λέβητα. Συμπερασματικά, μπορεί να ειπωθεί ότι το νερό δεν έχει πλήρως όλα τα απαραίτητα χαρακτηριστικά ώστε να χρησιμοποιείται σε μια εγκατάσταση παραγωγής έργου με ατμό. Παγκοσμίως όμως είναι το πλέον χρησιμοποιούμενο σύστημα. Αυτό συμβαίνει διότι υπάρχει άφθονο και ότι έχει σχετικά μικρό κόστος. ΘΕΡΜΟΔΥΝΑΜΙΚΟΙ ΚΥΚΛΟΙ ΙΣΧΥΟΣ ΑΤΜΟΥ για εγκαταστάσεις παραγωγής έργου με ατμό νερού Εξετάζεται ο κύκλος παραγωγής έργου, όπου σαν εργαζόμενο μέσο είναι το νερό σε υγρή φάση, σε μίγμα και υπέρθερμο ατμό. Ο κύκλος ισχύος ατμού αποτελεί τη βάση λειτουργίας των ναυτικών ατμοστροβίλων που χρησιμοποιούνται για την πρόωση των πλοίων, αλλά και για εγκαταστάσεις παραγωγής ηλεκτρικής ενέργειας. Η ποσότητα του εργαζόμενου μέσου δεν μεταβάλλεται (εκτός από τις περιπτώσεις απωλειών) κατά τη διάρκεια του κύκλου και την πορεία του μέσα από τα μηχανήματα. Στο τέλος κάθε κύκλου το σύστημα όχι μόνο χαρακτηρίζεται από τα καταστατικά μεγέθη που είχε στην αρχική του κατάσταση, δεν έχει υποστεί μεταβολές στη χημική του σύσταση 202 Σελίδα 24
4 δεδομένου ότι δεν συμμετέχει σε χημικές αντιδράσεις, αλλά θα έχει την ίδια ποσότητα για να εκτελέσει τον επόμενο κύκλο. Ο κύκλος αποτελείται από μια σειρά διαδοχικών μεταβολών στις οποίες υποβάλεται το κλειστό σύστημα (σταθερή ποσότητα), όπου σε κάθε μια από αυτές ευρίσκεται σε συγκεκριμένη φυσική κατάσταση. Οι διαδοχικές αυτές μεταβολές θεωρούνται κατ αρχήν ιδανικές (αντιστρέψιμες) χωρίς να λαμβάνονται υπ όψιν απώλειες οπότε προκύπτει ο ιδανικός κύκλος αναφοράς, στον οποίο βεβαίως δεν αποτυπώνονται τα προβλήματα που υπάρχουν στην πραγματικότητα. Για παράδειγμα, ο στρόβιλος θεωρείται αδιαβατικό σύστημα, οπότε ενεργώντας σε κύκλο με ιδανικές ( αντιστρέψιμες) μεταβολές, η εκτόνωση είναι μια μεταβολή αδιαβατική ισοεντροπική (απεικονίζεται δηλαδή κατακόρυφα σε ένα διάγραμμα T S). Στην πραγματικότητα, παρ ότι ο στρόβιλος εξακολουθεί να θεωρείται αδιαβατικό σύστημα (επομένως δεν εναλλάσσονται ποσά θερμότητας μεταξύ του στροβίλου και του περιβάλλοντος), κατά τη διάρκεια της εκτόνωσης υπάρχουν τριβές οπότε η εκτόνωση πρέπει να παρασταθεί σαν μια μεταβολή αδιαβατική πραγματική επομένως μεταβολή αυξανόμενης εντροπίας. Ο ιδανικός κύκλος αναφοράς, δίδει τη δυνατότητα υπολογισμού του βαθμού απόδοσης αναφοράς, δηλαδή του μέγιστου δυνατού από ένα κύκλο με τις συγκεκριμένες θεωρητικές μεταβολές. Στη συνέχεια αντικαθιστώνται οι δυναμικές μεταβολές, δηλαδή η εκτόνωση και η συμπίεση, με τις αδιαβατικές πραγματικές μεταβολές, οπότε στον υπολογισμό του βαθμού απόδοσης λαμβάνονται υπ όψιν οι απώλειες, κυρίως λόγω τριβών, κατά τις μεταβολές αυτές. Πρίν την αναφορά και την περιγραφή του θερμοδυναμικού κύκλου, δίδεται μια περιγραφή των μηχανημάτων που συνθέτουν μια εγκατάσταση παραγωγής έργου με ατμό νερού, η οποία αποτελείται από τα εξής στοιχεία : - ΛΕΒΗΤΑΣ ή ΑΤΜΟΠΟΙΗΤΗΣ : το νερό ατμοποιείται υπό σταθερή πίεση και η απαιτούμενη θερμότητα προσφέρεται στο νερό από την καύση του χρησιμοποιούμενου καυσίμου σε χώρο εκτός του θαλάμου που το νερό περιέχεται. - ΕΚΤΟΝΩΤΗΣ ή ΣΤΡΟΒΙΛΟΣ : ο ατμός εκτονώνεται και προσφέρει έργο στον άξονα του στροβίλου. - ΣΥΜΠΥΚΝΩΤΗΣ ή ΨΥΓΕΙΟ : ο ατμός μετά την εκτόνωση στο στρόβιλο, σε κατάσταση μίγματος, διοχετεύεται στο συμπυκνωτή όπου αποβάλει τη λανθάνουσα θερμότητα στο νερό ψύξεως του συμπυκνωτή και μετατρέπεται σε κεκορεσμένο υγρό. - ΑΝΤΛΙΑ ΣΥΜΠΥΚΝΩΜΑΤΟΣ : συμπιέζει το κεκορεσμένο υγρό από την πίεση του συμπυκνωτή μέχρι την πίεση του λέβητα, ώστε ν αγίνει πάλι οκύκλος. 202 Σελίδα 242
5 Δεδομένου ότι ο κύκλος του Carnot έχει το μεγαλύτερο βαθμό απόδοσης από όλους τους κύκλους που λειτουργούν μεταξύ δύο θερμικών πηγών με συγκεκριμένες θερμοκρασίες,, γίνεται προσπάθεια υλοποίησης κύκλου ατμού με βάση τον κύκλο αυτό : Έστω ένας κύκλος Carnot για ένα ανοικτό σύστημα στην περιοχή του μίγματος ατμού νερού. Το νερό συμπιέζεται ισοεντροπικά στο συμπιεστή (μεταβολή 2), ατμοποιείται αντιστρεπτά και ισόθερμα στο λέβητα (μεταβολή 23), εκτονώνεται ισοεντροπικά στο στρόβιλο (μεταβολή 34), και τέλος αποδίδει τη λανθάνουσα θερμότητα ατμοποίησης αντιστρεπτά και ισόθερμα στο συμπυκνωτή (μεταβολή 4). ΣΧΗΜΑ 07 Η υλοποίηση του κύκλου ισχύος ατμού με βάση τον κύκλο του Carnot, παρουσιάζει προβλήματα :. δύσκολα ελέγχεται ο βαθμός ξηρότητας του μίγματος στο τέλος της εκτόνωσης. Πάντως ο βαθμός ξηρότητας μειώνεται κατά την εκτόνωση, οπότε ο στρόβιλος λειτουργεί με αυξημένη ποσότητα υγρασίας γεγονός που έχει σαν συνέπεια τη σπηλαίωση, φαινόμενο που δημιουργεί βλάβες στα πτερύγια του στροβίλου και μείωση του βαθμού απόδοσης αυτού. Για τις εγκαταστάσεις αυτές, ο βαθμός ξηρότητας στο τέλος της εκτόνωσης δεν πρέπει να είναι μικρότερος από 0,88 0, η συμπίεση υγρού ατμού, δηλαδή η μεταβολή -2, είναι πρακτικά αδύνατη, δεδομένου ότι είναι πολύ δύσκολη η λειτουργία ενός συμπιεστή με ρευστό που ευρίσκεται ταυτόχρονα σε δύο φάσεις (υγρό και ατμός). 3. η Τ max περιορίζεται από το κρίσιμο σημείο, οπότε είναι χαμηλός ο βαθμός απόδοσης. Μια πρώτη σκέψη για βελτίωση του θερμικού βαθμού απόδοσης είναι η συνέχιση της συμπίεσης πάνω από την καμπύλη του κεκορεσμένου υγρού, δημιουργώντας τον κύκλο του επόμενου σχήματος. Στη λύση αυτή παρουσιάζονται προβλήματα, αφ ενός στην ισοεντροπική συμπίεση του συστήματος (αρχικά δύο φάσεων, μεταβολή ) μέχρι πολύ υψηλές πιέσεις, και αφ ετέρου στη θέρμανση του συστήματος κατά μια μεταβολή ισόθερμη αλλά με μεταβλητή πίεση (μεταβολή 2 3 ). 202 Σελίδα 243
6 ΣΧΗΜΑ 08 Για τη βελτίωση της κατάστασης, συνεχίσθηκε η συμπύκνωση μέχρι το σύστημα να γίνει κεκορεσμένο υγρό στη χαμηλή πίεση, δηλαδή το σημείο ευρίσκεται επάνω στην καμπύλη του κεκορεσμένου υγρού, οπότε προέκυψε ο ΚΥΚΛΟΣ RANKINE ΣΧΗΜΑ 09 όπου λύθηκε μεν το πρόβλημα της συμπίεσης - 2 δεδομένου ότι τώρα συμπιέζεται υγρό χωρίς παρουσία ατμού, όπως όταν ήταν μίγμα, παρέμεινε όμως το πρόβλημα στην εκτόνωση, διότι εξακολουθεί η έντονη παρουσία υγρού στο στρόβιλο, μεταβολή 3-4, αλλά και η μειωμένη μετατροπή της θερμικής ενέργειας σε έργο κατά την εκτόνωση 3-4. Τα προβλήματα αυτά ξεπεράσθηκαν, συνεχίζοντας τη θέρμανση του συστήματος από κεκορεσμένο (ξηρό) ατμό στην ίδια πίεση και παράγοντας υπέρθερμο ατμό. 202 Σελίδα 244
7 Προέκυψε έτσι ο ΚΥΚΛΟΣ RANKINE ΜΕ ΥΠΕΡΘΕΡΜΑΝΣΗ ή ΚΥΚΛΟΣ ΗΙRΝ Παρατηρήσεις : ΣΧΗΜΑ 0. σημειώνεται ότι κατά την εκτόνωση διαπιστώνεται αύξηση της υγρασίας στη μάζα του ατμού που εκτονώνεται. Η αύξηση αυτή συνεχίζεται όσο μειώνεται η πίεση οπότε τα υγρά μόρια κτυπούν τα πτερύγια του στροβίλου και προκαλούν φθορές, εξ αιτίας του φαινομένου της σπηλάιωσης. Για την παοφυγή αυτών των προβλημάτων, ο βαθμός ξηρότητας στο τέλος της εκτόνωσης στη χαμηλή πίεση πρέπει να έχει τιμή τουλάχιστον x 0, σημειώνεται επίσης ότι το ίδιο πρόβλημα παρουσιάζεται στις αντλίες του συστήματος. Για να είναι λοιπόν ομοιογενής η υγρή φάση, η συμπύκνωση 5- διαρκεί τόσο ώστε το συμπυκνούμενο σύστημα να γίνει κεκορεσμένο υγρό, δηλαδή να είναι καταστάσεως, με βαθμό ξηρότητας x 0. Περιγραφή του θεωρητικού κύκλου Στο παρακάτω σχήμα παρουσιάζεται ο θερμοδυναμικός κύκλος σε διάγραμμα (T-S) και διάγραμμα (I-S), καθώς και ένα σχήμα με τα όργανα μηχανήματα που συνθέτουν την 202 Σελίδα 245
8 εγκατάσταση. ΣΧΗΜΑ Στις εγκαταστάσεις αυτού του τύπου, τα όργανα όπου γίνονται οι θερμικές εναλλαγές, δηλαδή :. λέβητας που αποτελείται από : - προθερμαντήρας (ΠΡ) - ατμοποιητής (ΑΤ) - υπερθερμαντήρας (ΥΠ) 2. συμπυκνωτής (ΣΥΜ., ή Ψ) ξεχωρίζουν από τα όργανα όπου γίνονται οι μηχανικές εναλλαγές, δηλαδή :. εκτονωτής ή στρόβιλος (ΣΤΡ.) 2. συμπιεστής ή αντλία (Ρ). Εξετάζονται τώρα οι επιμέρους μεταβολές : Στο σημείο το σύστημα ευρίσκεται στην κατάσταση κεκορεσμένου υγρού στη χαμηλή πίεση p (πίεση συνήθως μικρότερη από την ατμοσφαιρική πίεση)και στην αντίστοιχη θερμοκρασία ισορροπίας (συνθήκη κορεσμού) Τ. Η αντλία Ρ συμπιέζει το υγρό από τον συμπυκνωτή Ψ στην πίεση p 2 που είναι η μέγιστη του κύκλου και το τροφοδοεί στο λέβητα. Στις πραγματικές εφαρμογές, μια αντλία απορροφά το υγρό από το συμπυκνωτή σε πίεση μικρότερη από την ατμοσφαιρική και το μεταφέρει σε μια δεξαμενή ανοικτή στην ατμόσφαιρα από όπου μια δεύτερη αντλία το μεταφέρει στο λέβητα συμπιέζοντάς το από την ατμοσφαιρική πίεση μέχρι την μέγιστη πίεση του κύκλου. Στο τέλος της συμπίεσης το υγρό ευρίσκεται στην πίεση p 2 αλλά σε μια θερμοκρασία, Τ μικρότερη από εκείνη του κορεσμού που αντιστοιχεί σε αυτή την πίεση. Στον προθερμαντήρα (ΠΡ) το υγρό θερμαίνεται υπό σταθερή πίεση ( την πίεση p 2 ) μέχρι την αντίστοιχη (στην πίεση p 2 ) θερμοκρασία κορεσμού Τ Σελίδα 246
9 Οπότε τώρα το σύστημα βρίσκεται στην κατάσταση κορεσμού στην μέγιστη πίεση του κύκλου και στο διάγραμμα αυτή η κατάσταση παριστάνεται από το σημείο 2. Τα ποσά θερμότητας που εναλλάσσονται κατά την πραγματοποίηση του κύκλου, παριστάνονται από τα εμβαδά : (Α 2 Γ) θερμότητα προθέρμανσης του υγρού (q) (Γ 2 3 Δ) θερμότητα για την ατμοποίηση ( r) (Δ Β) θερμότητα για την υπερθέρμανση T3 Q c dt T 3 ' p (Α 5 Β) θερμότητα που αφαιρείται στον συμπυκνωτή κατά τη συμπύκνωση ( ) θερμικό ισοδύναμο του έργου που εναλλάσσεται κατά τηην πραγματοποίηση ενός κύκλου (αυτό το εμβαδόν μόνο στο θεωρητικό κύκλο) Στη συνέχεια, εξετάζεται ο ΠΡΑΓΜΑΤΙΚΟΣ ΚΥΚΛΟΣ με αναφορά στο παρακάτω διάγραμμα : ΣΧΗΜΑ 2 - Στο τμήμα ( 2 ) που αντιστοιχεί στη συμπίεση του υγρού στην αντλία και το οποίο στον θεωρητικό κύκλο αυτή προσδιορίζεται από μια ΑΔΙΑΒΑΤΙΚΗ ΙΣΟΕΝΤΡΟΠΙΚΗ, τώρα στον πραγματικό κύκλο η συμπίεση παριστάνεται από τη μεταβολή ( ) δηλαδή μια ΑΔΙΑΒΑΤΙΚΗ ΠΡΑΓΜΑΤΙΚΗ μεταβολή, στην οποία το σημείο ( τέλος πραγματικής συμπίεσης) βρίσκεται δεξιότερα του σημείου ( τέλος της ιδανικής συμπίεσης) λόγω του ότι τώρα, υπάρχει αύξηση εντροπίας. - Η φάση της εκτόνωσης, στον πραγματικό κύκλο παριστάνεται από μια ΑΔΙΑΒΑΤΙΚΗ ΠΡΑΓΜΑΤΙΚΗ μεταβολή, την (4 5 ) όπου το σημείο 5 είναι δεξιότερα του 5, λόγω της αυξημένης εντροπίας. 202 Σελίδα 247
10 Είναι : (Α Β) θερμότητα που προσφέρεται στο ρευστό (Α 5 Β ) θερμότητα που αφαιρείται από το ρευστό Το εμβαδόν ( ) δεν παριστάνει πλέον το έργο L r που εναλλάσσεται (ισχύει πάντα Lr Q Q2), όπου Lr είναι το άθροισμα όλων των έργων που εναλλάσσονται μεταξύ του ρευστού και των οργάνων της μηχανής σε επαφή με το ρευστό, αλλά είναι το έργο στον άξονα της μηχανής, ή όπως συνηθίζεται να ονομάζεται, το ΠΡΑΓΜΑΤΙΚΟ ΕΡΓΟ L πρ < L. r Το χρήσιμο έργο L u μπορεί να είναι Lu L, οπότε ορίζεται ο r ΜΗΧΑΝΙΚΟΣ ΒΑΘΜΟΣ ΑΠΟΔΟΣΗΣ L η. m u L πρ Τέλος, ορίζεται ο ΟΛΙΚΟΣ ΒΑΘΜΟΣ ΑΠΟΔΟΣΗΣ ή ΤΗΣ ΕΓΚΑΤΑΣΤΑΣΗΣ, ως : η η η η, ολ b ϑ m όπου : Q η b βαθμός απόδοσης της καύσεως M c Hi L Q Q2 η θ θερμικός βαθμός απόδοσης Q Q L u η m μηχανικός βαθμός απόδοσης L πρ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΝΑΛΥΣΗ ΜΗΧΑΝΗΜΑΤΩΝ ΤΟΥ ΚΥΚΛΟΥ ΣΤΡΟΒΙΛΟΣ Είναι ένα ανοικτό σύστημα που θεωρείται αδιαβατικό και η εκτ λονωση μπορεί να είναι ιδανική αδιαβατική ( αντιστρέψιμη) άρα και ισοεντροπική, ή αδιαβατική πραγματική με αυξημένη εντροπία στο τέλος της εκτόνωσης λόγω της μη αντιστρεψιμότητας. Εάν θεωρηθούν αμελητέες η κινητική και η δυναμική ενέργεια του συστήματος στο στρόβιλο, τότε : ( ) ( ) ( L ) I M V Δ I M V I I στρ Δ IΔ Σελίδα 248
11 ή ( ) ( ) ( L ) MV Δ I MV I I στρ πραγμ. πραγμ 4 5 ' ΣΥΜΠΥΚΝΩΤΗΣ (εναλλάκτης θερμότητας) Σε έναν εναλλάκτη θερμότητας η θερμότητα που έχει το σύστημα μετά την εκτόνωση (μίγμα επιθυμητού βαθμού ξηρότητας x > 0,90) μεταδίδεται στο νερό ψύξεως του εναλλάκτη λόγω διαφοράς θερμοκρασίας. Ο θερμικός ισολογισμός είναι : ( 5 ) 2 ΣΧΗΜΑ 3 θερμότητα που αποβάλλεται θερμότητα που παραλαμβάνει από τομγμα ί τονερό ψύξεωςτουεναλλάκτη Μ I I M I I V H O ( εξόδου εισ όδου ) M ( c ) ( ΔΤ) HO 2 p HO HO 2 2 Στις προηγούμενες σχέσεις η εκτόνωση θεωρείται ιδανική. Εάν η εκτόνωση αντιμετωπιστεί ως πραγματική, τότε στο τέλος της εκτόνωσης υπολογίζεται η ενθαλπία της πραγματικής μεταβολής, δηλαδή η προηγούμενη σχέση γράφεται : ( I ' I ) M ( Iεξ δου Iεισ δου ) M ( c ) ( ) Μ ΔΤ V 5 H2O ό ό HO 2 p HO H 2 2O ΑΝΤΛΙΑ Η θερμική ισχύς της αντλίας υπολογίζεται από την παρακάτω σχέση : ( ' ) N M I I όταν θεωρείται ιδανική η συμπίεση αντλ. V ( ) N M I I όταν θεωρείται πραγματική η συμπίεση αντλ. V '' 202 Σελίδα 249
12 Γίνονται δύο υποθέσεις : α) δεν μεταβάλλεται κατά τη συμπίεση η εσωτερική ενέργεια του νερού : U U U όταν θεωρείται ιδανική η συμπίεση ' U όταν θεωρείται πραγματική η συμπίεση '' β) δεν μεταβάλλεται ο ειδικός όγκος του νερού : υ υ όταν θεωρείται ιδανική η συμπίεση ' υ υ όταν θεωρείται πραγματική η συμπίεση '' Οπότε : N M I I M υ p p όταν θεωρείται ιδανική η συμπίεση ( ' ) V ( ) αντλ. V ' και : I I + υ ( p p ) ' ' Nαντλ. MV ( I'' I ) MV υ' ( p'' p ) και : I I + υ ( p p ) ΛΕΒΗΤΑΣ όταν θεωρείται πραγματική η συμπίεση '' ' '' Στο λέβητα περιέχεται η απαραίτητη για την εγκατάσταση ποσότητα νερού, το οποίο μετατρέπεται σε υπέρθερμο ατμό. Για το σκοπό αυτό προσδίδεται η αναγκαία θερμότητα που προέρχεται από τη μετατροπή της χημικής ενέργειας του καυσίμου σε θερμοκή ενέργεια. Η πρόσδοση της θερμότητας στο νερό γίνεται υπό σταθερή πίεση, το νερό μετατρέπεται σε κεκοκρεσμένο, στη συνέχεια ατμοποιείται και μετατρέπεται σε κεκορεσμένο ατμό. ΣΧΗΜΑ 4 Η ανάλυση λειτουργίας του λέβητα είναι πολύπλοκη, μια απλή όμως σχέση για την ανάλυση του κύκλου Rankine, είναι η ακόλουθη : 202 Σελίδα 250
13 Q+ M I m I θεωρώντας ιδανική τη συμπίεση V V ' 4 Q+ M I m I θεωρώντας πραγματική τη συμπίεση '' 4 όπου : I η ενθαλπία στο τέλος της ιδανικής αδιαβατικής συμπίεσης ' I η ενθαλπία στο τέλος της πραγματικής αδιαβατικής συμπίεσης '' I η ενθαλπία του υπέρθερμου ατμού 4 M V η ποσότητα του νερού στον κύκλο Q η προσφερόμενη από το καύσιμο θερμότητα ΠΑΡΑΔΕΙΓΜΑ ΚΥΚΛΟΥ RANKINE Σε ένα κύκλο RANKINE, το σύστημα ( kg) εισέρχεται στο στρόβιλο σε κατάσταση υπέρθερμου ατμού σε πίεση 40 bar και θερμοκρασία C, η δε πίεση στο συμπυκνωτή είναι 0,05 bar. Να υπολογισθούν : α) το χορηγούμενο ποσό θερμότητας, β) το αποβαλλόμενο ποσό θερμότητας, γ) το παραγόμενο έργο, δ) το έργο της αντλίας, ε) ο θερμικός βαθμός απόδοσης, στ) η μέση θερμοκρασία κατά την οποία χορηγείται η θερμότητα. Λύση Α. Στο παρακάτω σχήμα παρουσιάζεται το διαγραμματικό της εγκατάστασης και η απεικόνηση αυτής στο διάγραμμα (T-S) και στο διάγραμμα (I-S).θεωρώντας ιδανικές μεταβολές τη συμπίεση και την εκτόνωση. 202 Σελίδα 25
14 ΣΧΗΜΑ 5 Ακολουθούν οι υπολογισμοί των ζητούμενων στοιχείων. α) Το ποσό θερμότητας που πρέπει να χορηγηθεί στην εγκατάσταση δίδεται από την παρακάτω σχέση : Q I4 I ' Από το διάγραμμα (I-S) για πίεση 40 bar και θερμοκρασία C, είναι : I4 32, τιμή που αναγράφεται και στον πίνακα του υπέρθερμου ατμού (ΠΙΝΑΚΑΣ 8). Η τιμή της ενθαλπίας I ' υπολογίζεται από τη σχέση της αντλίας : ( ) ( ) ( ) ' ' ' ' N m I I m p p I I + p p αντλ. υ υ Από τον πίνακα -5- για πίεση κορεσμού 0,05 bar είναι : 3 m I 37,83, υ 0,000053, οπότε η ενθαλπία στο τέλος της συμπίεσης είναι : 2 37,83 0, ( 40 0,05) 0 4,846 KJoule I + ' Οπότε το ποσό θερμότητας είναι : Q ( 32 4,846 ) 3069,54 KJoule β) Το ποσό θερμότητας που αποβάλλεται, ευρίσκεται από τη μεταβολή της συμπύκνωσης, ήτοι : 202 Σελίδα 252
15 q I I I I τελ. αρχ. 5 Η ενθαλπία I 5 είναι η ενθαλπία του μίγματος στην κατάσταση 5. Η κατάσταση αυτή είναι το τέλος της εκτόνωσης στο στρόβιλο και μπορεί να προσδιοριστεί γραφικά και αναλυτικά. Γραφικός προσδιορισμός : Χρησιμοποιείται το διάγραμμα (Ι-S), δεδομένου ότι στο διάγραμμμα αυτό δίδονται απ ευθείας οι τιμές της ενθαλπίας στον άξονα. Ο προσδιορισμός γίνεται ως εξής : Από το σημείο 4 (κατάσταση υπέρθερμου ατμού) χαράσσεται κατακόρυφη γραμμή (κατακόρυφη διότι η εκτόνωση είναι ιδανική, άρα μεταβολή σταθερής εντροπίας) και το σημείο τομής αυτής με την οριζόντιο p 0,05 bar είναι το ζητούμενο σημείο 5. Στον κατακόρυφο άξονα του διαγράμματος δίδονται οι τιμές της ενθαλπίας και στη συγκεκριμένη περίπτωση είναι : I Αναλυτικός υπολογισμός : Η κατακόρυφη από το σημείο 4 [είτε χαραχθεί στο διάγραμμα (T-S) είτε στο διάγραμμα (I-S)], τέμνει την ισοβαρή 0,05 bar στην περιοχή του μίγματος. Η ενθαλπία του μίγματος δίδεται από την παρακάτω σχέση : I5 I+ r x5 Ο βαθμός ξηρότητας στο σημείο -5- δεν δίδεται. Εάν από το σημείο -5- επί της ισοβαρούς 0,05 bar διέρχεται κάποια καμπύλη βαθμού ξηρότητας, τότε αυτή η τιμή είναι το x 5. Εάν δεν είναι εφικτό να προσδιοριστεί το x5 από το διάγραμμα, τότε υπολογίζεται αναλυτικά ως εξής : Η εκτόνωση 45 έχει θεωρηθεί ιδανική, οπότε είναι και ισοεντροπική, δηλαδή : Η τιμή της εντροπίας του υπέρθερμου ατμού (πίεση 40 bar και θερμοκρασία C) υπολογίζεται από τον πίνακα -8-, ήτοι S 4 6,762 0 και αυτή η εντροπία ισούται kg K με την εντροπία στο σημείο 5 : S4 S5 6, Στο σημείο 5 το σύστημα είναι kg K μίγμα και η εντροπία μίγματος σούται με : r S5 S S4 S5 S+ x5 και λύνοντας ως προς βαθμό ξηρότητας είναι : x5 T, r T όπου για πίεση κορεσμού 0,05 bar από τον πίνακα νερού ατμού σε συνθήκες κορεσμού (ΠΙΝΑΚΑΣ 5) είναι : S r T K kg K 0 0, 476, 2423, 32, ,5 306, 03 ( ) Σελίδα 253
16 και αντικαθιστώντας προκύπτει : x 5 0,794 Οπότε η ενθαλπία του μίγματος είναι : KJoule I5 I+ r x5 37, , ,692 Και το ζητούμενο ποσό θερμότητας είναι : q I I I I τελ. αρχ. 5 37,83 206, ,862 Σημ. : το σημείο (-) δικαιολογείται διότι σύμφωνα με τη σύμβαση το ποσό θερμότητας που αποβάλλεται από το σύστημα θεωρείται αρνητικό. γ) Το ποσό θερμικής ενέργειας στην εκτόνωση που διατίθεται για μηχανική ενέργεια, δίδεται από τη σχέση : L45 I4 I ,692 49,308 δ) Το απαιτούμενο έργο για τη λειτουργία της αντλίας, είναι : Lαντλ. I ' I 4,846 37,830 4,06 ε) Ο θερμικός βαθμός απόδοσης, είναι : ( I4 I5) ( I ' I) 49,308 4, 06 45, 292 I I 32 4, ,54 η θ 4 ' 0,373, ή 37,3 % στ) Η θερμότητα χορηγείται κατά τη μεταβολή ( εντροπίας, είναι : 4). Από τη σχέση ορισμού της T Q I I 32 4, ,26 ΔS S S 6,762 0,476 4 ' 0 4 ' K Β. Θεωρώντας πραγματικές την εκτόνωση και τη συμπίεση, με βαθμούς απόδοσης 0,85 και 0,80, επαναλαμβάνονται οι υπολογισμοί των ίδιων μεγεθών σε κάθε ερώτημα. 202 Σελίδα 254
17 Στο παρακάτω σχήμα παρουσιάζεται το διαγραμματικό της εγκατάστασης και η απεικόνηση αυτής στο διάγραμμα (T-S) και στο διάγραμμα (I-S).θεωρώντας τώρα πραγματικές μεταβολές τη συμπίεση και την εκτόνωση. ΣΧΗΜΑ 6 α) Το ποσό θερμότητας που πρέπει να χορηγηθεί στην εγκατάσταση δίδεται από την παρακάτω σχέση : Q I4 I ' ' Για την εύρεση της I ' ' χρησιμοποιείται η σχέση του εσωτερικού βαθμού απόδοσης της αντλίας : I ' I I ' I 4,846 37,830 ηαντλ. I ' ' I + 37, ,85 I ' ' I ηαντλ. 0,80 Οπότε το ποσό θερμότητας είναι : 32 42, ,5 Q 202 Σελίδα 255
18 β) Το ποσό θερμότητας που αποβάλλεται, ευρίσκεται από τη μεταβολή της συμπύκνωσης, ήτοι : q I I I I τελ. αρχ. ' 5 Η ενθαλπία η στρ I ' χρησιμοποιείται ο εσωτεροκός βαθμός απόδοσης του στροβίλου : 5 I I ( ) η 32 ( ,692) 0, ,088 I I 4 ' 5. I ' I4 I 5 4 I5 στρ. 4 5 Οπότε είναι : q 37, , ,258 Η θέση του σημείου 5 που αντιστοιχεί στο τέλος της πραγματικής εκτόνωσης, μπορεί να προσδιοριστεί ως εξής : Συγκρίνοντας την τιμή της ενθαλπίας I ' 5 με την τιμή της ενθαλπίας του κεκορεσμένου(ξηρού) ατμού στην πίεση p 0,50 bar μέχρι την οποία γίνεται η εκτόνωση, φαίνεται η θέση του σημείου 5, δηλαδή : I 2234, ,00 ( I ) 5 < ' V p 0,05 bar συνεπώς το σημείο 5 ευρίσκεται στην περιοχή του μίγματος. Ο βαθμός ξηρότητας που αντιστοιχεί στο σημείο 5 ευρίσκεται ως εξής : I ' I , ,83 I ' I + r x ' x ' x ' r ,865 Ο βαθμός ξηρότητας μπορεί να βρεθεί και γραφικά : Με την τιμή της ενθαλπίας I ' 2234,088 5 στο διάγραμμα του Mollier από τον άξονα των ενθαλπιών χαράσσεται ευθεία παράλληλη προς τον άξονα της εντροπίας μέχρι να βρεθεί η καμπύλη p 0,05 bar οπότε το σημείο αυτής της τομής είναι το σημείο 5 και η καμπύλη του βαθμού ξηρότητας που περνά από το σημείο αυτό είναι η ζητούμενη τιμή του x '. Εάν δεν διέρχεται κάποια καμπύλη, τότε υπολογίζεται με αναλογίες η τιμή 5 αυτή ή υπολογίζεται με τον αναλυτικό τρόπο που προηγουμένως περιράφηκε. γ) Το ποσό θερμικής ενέργειας στην εκτόνωση που διατίθεται για μηχανική ενέργεια, δίδεται από τη σχέση : 202 Σελίδα 256
19 L ' I4 I ' , , δ) Το απαιτούμενο έργο για τη λειτουργία της αντλίας, είναι : Lαντλ. I'' I 42,85 37,830 5,02 ε) Ο θερμικός βαθμός απόδοσης, είναι : ( I4 I ' ) ( I'' I) 5 η θ 0,37 I I 4 '' 97, ,5 3,7 %. στ) Η θερμότητα χορηγείται κατά τη μεταβολή ( εντροπίας, είναι : Q I4 I '' 32 42,85 0 T 488,2 K ΔS S S 6,762 0, '' 4). Από τη σχέση ορισμού της ΙΣΧΥΣ ΕΓΚΑΤΑΣΤΑΣΕΩΝ ΑΤΜΟΥ - ΒΑΘΜΟΣ ΑΠΟΔΟΣΗΣ Στα δύο παρακάτω σχήματα παρουσιάζεται ο κύκλος Hirn (Rankine με υπερθέρμανση). ΣΧΗΜΑ 7 Θεωρητική ισχύς : είναι η ισχύς που ο ατμός θα μπορούσε να αποδώση στον άξονα του στροβίλου, εάν το ρευστό ελάμβανε μέρος σε αντιστρέψιμες μεταβολές και εάν υπήρχε έλλειψη τριβών οιασδήποτε μορφής. Η πτώση ενθαλπίας στη φάση της εκτόνωσης είναι (στην ιδανική κατάσταση) : 202 Σελίδα 257
20 ( Δ I ) ( I I ) ΙΔ. 4 5 Η σχέση που δίδει την ισχύ διαμορφώνεται ανάλογα με το σύστημα μονάδων. Α. Τεχνικό Σύστημα Εάν από το στρόβιλο διέρχωνται ισχύς είναι : M V kp h και η ενθαλπία δίδεται σε Kcal kp, τότε η ( ) N M I I ΙΔ. V 4 5 Kcal h είναι : N 632,2 και επειδή : α) Kcal ( PS h) β) Kcal 860, : l IΔ. M V ( ) ΔΙ 632,2 ( ) ΙΔ. ( PS) ( ) V ΙΔ. KW εναι ί NIΔ. KW M ΔΙ 860 Β. Διεθνές Σύστημα Εάν από το στρόβιλο διέρχωνται ισχύς είναι : ( ) N M I I ΙΔ. V 4 5 h M V kg h και η ενθαλπία δίδεται σε kg, τότε η και επειδή : α) KW 3600 h ( ) είναι : MV ΔΙ NIΔ ΙΔ. ( KW) Λαμβάνοντας υπ όψιν την ισχύ της αντλίας τροφοδοσίας η οποία συμπιέζει το κεκορεσμένο υγρό από τη χαμηλή πίεση στην υψηλή πίεση του κύκλου, είναι : Α) Τεχνικό Σύστημα : N N ΙΔ ΙΔ ( 4 5) ( ' ) I I I I M 860 ( 4 5) ( ' ) I I I I M 632,2 V V ( KW) ( PS) 202 Σελίδα 258
21 Β) Διεθνές Σύστημα : N ΙΔ ( 4 5) ( ' ) I I I I M V 3600 ( KW) Θεωρώντας τώρα τις πραγματικές μεταβολές (συμπίεση και εκτόνωση), οι προηγούμενες σχέσεις είναι : Α) Τεχνικό Σύστημα : Β) Διεθνές Σύστημα : N N N Πραγμ. Πραγμ. Πραγμ. ( 4 ') ( '' ) I I I I M ( 4 ') ( '' ) I I I I M 5 632,2 ( 4 ') ( '' ) I I I I M 5 V 3600 V V ( KW) ( PS) ( KW) ΘΕΡΜΙΚΟΣ ΒΑΘΜΟΣ ΑΠΟΔΟΣΗΣ Διαχωρίζοντας τις ιδανικές και τις πραγματικές μεταβολές, ο θερμικός βαθμός απόδοσης είναι : Α) Ιδανικές μεταβολές : η θ. Β) Πραγματικές μεταβολές : η θ. ( I4 I5) ( I ' I) ( I I ) 4 ( I4 I ') ( I '' I 5 ) ( I I '' ) 4 Για να προσδοθεί στο υγρό μια θερμική ισχύς : Kcal KJoule M I4 I ή h h Kcal KJoule MV I4 I '' ή h h α) V ( ' ) β) ( ) με ιδανική συμπίεση με πραγματική συμπίεση πρέπει να δοθεί στο λέβητα (για να αντιμετωπιστούν οι απώλειες εξ αιτίας μη πλήρους καύσεως, οι απώλειες στην καπνοδόχο και εν γένει οι θερμικές απώλειες προς το περιβάλλον) ποσό θερμικής ενέργειας μεγαλύτερο από το προαναφερόμενο, ήτοι ποσό θερμότητας που προσφέρει το καύσιμο : καυσ. i V 4 καυσ. i V 4 ( ' ) ( ιδανικ συμπ εση ) ( '' ) ( πραγματικ συμπ εση ) M H > M I I ή ί M H > M I I ή ί 202 Σελίδα 259
22 Οπότε ορίζεται ΒΑΘΜΟΣ ΑΠΟΔΟΣΗΣ της ΚΑΥΣΕΩΣ : ( ' ) ( '' ) M I I M I I ηg ( ιδανική συμπ ίεση ) η ( πραγματικ ή συμπ ίεση ) M H M H V 4 V 4, g καυσ ίμου i καυσ ίμου i Ο βαθμός απόδοσης της καύσεως λαμβάνει τιμές : 0,60 < η g < 0,92 ΟΛΙΚΟΣ ΒΑΘΜΟΣ ΑΠΟΔΟΣΗΣ Ο ολικός βαθμός απόδοσης της εγκατάστασης, δίδεται από την παρακάτω σχέση : η η η η με τιμές που κυμαίνονται : 0,20 <. < 0,35 ολ. θερμ. g m η ολ Διακρίνονται οι περιπτώσεις : α) Θερμοηλεκτρική εγκατάσταση Στην περίπτωση αυτή, η σχέση του ολικού βαθμού απόδοσης είναι : η η η ( η, όπου η η ). 0,98 ολ. θερμ. g m ηηλ.) ( m ηλ β) Εγκατάσταση ναυτικής πρόωσης : η. η. ηg ηm ( πρόωσης), όπου η πρόωσης (0,50 0,65), ολ θερμ η ή μπορεί να χρησθμοποιηθεί η σχέση : 6 η 0,836 0,00065 D, όπου η αριθμός στροφών της έλικας, πρόωσης D όγκος της γάστρας σε (m 3 ). Σημείωση Στην έκφραση του ολικού βαθμού απόδοσης, εμφανίζεται ο βαθμός απόδοσης της καύσης : Q η g <, δεδομένου ότι το ποσό της θερμότητα που μπορεί να δώσει το Μ καυσ. H κάυσιμο είναι ( Μκαυσ. H ) και είναι πάντοτε μεγαλύτερο από το ποσό θερμότητας που χρησιμοποιείται στην εγκατάσταση δηλαδή το Q, γιας λόγους ατελούς καύσης, απώλεια στα καυσαέρια, και άλλεε αιτίες απωλειών. Καύσιμο, είναι η ουσία η οποία κάτω από συγκεκριμένες συνθήκες (διαφορετικές για κάθε ουσία) αντιδρά με το οξυγόνο παράγοντας θερμότητα. 202 Σελίδα 260
23 Χαρακτηριστικό κάθε καυσίμου είναι η θερμαντική ικανότητα Η ή θερμογόνος δύναμη. Ορίζεται θερμογόνος δύναμη ή θερμαντική ικανότητα, το ποσό της θερμότητας που ελευθερώνεται κατά την πλήρη καύση ενός kg ή kp καυσίμου. Κατά την καύση παράγεται ατμός νερού, που οφείλεται :. στην αντίδραση οξείδωσης του υδρογόνου 2. στην παρουσία νερού υπό μορφή υγρασίας σε όλα τα κάυσιμα Εάν υπολογισθεί η θερμογόνος δύναμη με τρόπον ώστε ο ατμός που περιέχεται στα καυσαέρια να έχει συμπυκνωθε πλήρως, τότε ορίζεταιο η ανωτέρα θερμογόνος δύναμη H S στην οποία περιλαμβάνεται και το ποσό της θερμότητας που απαιτείται για τη συμπύκνωση. Εάν ο ατμός δεν είναι συμπυκνωμένος κατά τον υπολογισμό της Η, τότε ορίζεται η κατωτέρα θερμογόνος δύναμη H που υπολογίζεται από την : i Hi HS m r, όπου : m το βάρος του νερού που παράγεται από kg ή kp καυσίμου r συντελεστής που μεταβάλλεται με την ποσοστιαία αναλογία του υδρογόνου στο κάυσιμο, την υγρασία του αέρα και τη θερμοκρασία στην οποία ψύχονται τα παράγωγα της καύσης. Είναι : 600 ( U% + 9 H %) H 00 2 O2 % HS C% H2% S% 8 σχέση του DOYLONG 2 i HS, όπου U% ποσοστιαία παρουσία της υγρασίας, και ΠΑΡΑΔΕΙΓΜΑ Να υπολογιστεί η ανωτέρα και η κατωτέρα θερμογόνος δύναμη καυσίμου με την παρακάτω σύνθεση : C 83,5% H 4, 6% O 4, 7% S 0, 2% U 2,5% ( υγρασία) 2 2 Λύση Εφαρμοζοντας τη σχέση του DOYLONG είναι : 2 4,7 kcal H S , , , kp 600 ( 2, ,6) kcal Οπότε : Hi kp 202 Σελίδα 26
24 202 Σελίδα 262
Οι µηχανές εξωτερικής καύσεως διαχωρίζονται σε δύο κατηγορίες : - µηχανές µε χρήση ατµού - σε µηχανές µε χρήση αερίου.
 ΚΥΚΛΟΙ ΙΣΧΥΟΣ ΑΤΜΟΥ Οι εγκαταστάσεις παραγωγής έργου µε ατµό λειτουργούν µε µηχανές που ονοµάζονται µηχανές εξωτερικής καύσης, δεδοµένου ότι το ρευστό φορέας ενέργειας δεν συµµετέχει στην χηµική αντίδραση
ΚΥΚΛΟΙ ΙΣΧΥΟΣ ΑΤΜΟΥ Οι εγκαταστάσεις παραγωγής έργου µε ατµό λειτουργούν µε µηχανές που ονοµάζονται µηχανές εξωτερικής καύσης, δεδοµένου ότι το ρευστό φορέας ενέργειας δεν συµµετέχει στην χηµική αντίδραση
ΠΑΡΑ ΕΙΓΜΑ ΚΥΚΛΟΥ RANKINE
 ΠΑΡΑ ΕΙΓΜΑ ΚΥΚΛΟΥ RANKINE Σε ένα κύκλο RANKINE, το σύστηµα ( kg) εισέρχεται στο στρόβιλο σε κατάσταση υπέρθερµου ατµού σε πίεση 0 bar και θερµοκρασία 00 0 C, η δε πίεση στο συµπυκνωτή είναι 0,0 bar Να
ΠΑΡΑ ΕΙΓΜΑ ΚΥΚΛΟΥ RANKINE Σε ένα κύκλο RANKINE, το σύστηµα ( kg) εισέρχεται στο στρόβιλο σε κατάσταση υπέρθερµου ατµού σε πίεση 0 bar και θερµοκρασία 00 0 C, η δε πίεση στο συµπυκνωτή είναι 0,0 bar Να
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 5: Παράδειγμα 1. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενότητα : Παράδειγμα Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση Ποιότητας,
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενότητα : Παράδειγμα Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση Ποιότητας,
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 6: Παράδειγμα Κύκλου με αναθέρμανση. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενότητα 6: Παράδειγμα Κύκλου με αναθέρμανση Γεώργιος Κ Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ Ναυπηγός Μηχανολόγος Μηχανικός MSc Διασφάλιση
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενότητα 6: Παράδειγμα Κύκλου με αναθέρμανση Γεώργιος Κ Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ Ναυπηγός Μηχανολόγος Μηχανικός MSc Διασφάλιση
ΑΥΞΗΣΗ ΤΟΥ ΒΑΘΜΟΥ ΑΠΟΔΟΣΗΣ ΜΕ ΑΝΑΘΕΡΜΑΝΣΗ
 ΑΥΞΗΣΗ ΤΟΥ ΒΑΘΜΟΥ ΑΠΟΔΟΣΗΣ ΜΕ ΑΝΑΘΕΡΜΑΝΣΗ Με τ μέθοδο τς αναθέρμανσς (ή δεύτερς υπερθέρμανσς) αυξάνεται ο βαθμός απόδοσς. Η διαδικασία παρουσιάζεται στο παρακάτω σχήμα, όπου υπάρχουν τα διαγράμματα (I-S),
ΑΥΞΗΣΗ ΤΟΥ ΒΑΘΜΟΥ ΑΠΟΔΟΣΗΣ ΜΕ ΑΝΑΘΕΡΜΑΝΣΗ Με τ μέθοδο τς αναθέρμανσς (ή δεύτερς υπερθέρμανσς) αυξάνεται ο βαθμός απόδοσς. Η διαδικασία παρουσιάζεται στο παρακάτω σχήμα, όπου υπάρχουν τα διαγράμματα (I-S),
ΣΤΑΘΜΟΙ ΠΑΡΑΓΩΓΗΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΣΤΑΘΜΟΙ ΠΑΡΑΓΩΓΗΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Ενότητα 11: Κύκλα ατμού Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΣΤΑΘΜΟΙ ΠΑΡΑΓΩΓΗΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Ενότητα 11: Κύκλα ατμού Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και
ΥΛΙΚΑ ΓΙΑ ΕΝΕΡΓΕΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ
 ΥΛΙΚΑ ΓΙΑ ΕΝΕΡΓΕΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΤΜΟΣΤΡΟΒΙΛΟΙ Σημειώσεις Δ. Κουζούδη Εαρινό Εξάμηνο 2017 ΑΤΜΟ-ΣΤΡΟΒΙΛΟΙ (ΑΤΜΟ-ΤΟΥΡΜΠΙΝΕΣ) Που χρησιμοποιούνται; Για παραγωγή ηλεκτρικής ς σε μεγάλη κλίμακα. Εκτός από τα
ΥΛΙΚΑ ΓΙΑ ΕΝΕΡΓΕΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΤΜΟΣΤΡΟΒΙΛΟΙ Σημειώσεις Δ. Κουζούδη Εαρινό Εξάμηνο 2017 ΑΤΜΟ-ΣΤΡΟΒΙΛΟΙ (ΑΤΜΟ-ΤΟΥΡΜΠΙΝΕΣ) Που χρησιμοποιούνται; Για παραγωγή ηλεκτρικής ς σε μεγάλη κλίμακα. Εκτός από τα
Εφηρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 8: Θερμοδυναμικά κύκλα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 8: Θερμοδυναμικά κύκλα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
1. ΡΥΘΜΙΣΗ ΜΕ ΣΤΡΑΓΓΑΛΙΣΜΟ ΤΟΥ ΑΤΜΟΥ
 1. ΡΥΘΜΙΣΗ ΜΕ ΣΤΡΑΓΓΑΛΙΣΜΟ ΤΟΥ ΑΤΜΟΥ Ο στραγγαλισμός του ατμού υλοποιείται εξαναγκάζοντας τον ατμό, πριν παροχετευθεί στο στρόβιλο, να περάσει μέσα από κατάλληλη βαλβίδα όπου μικραίνει η διατομή διέλευσης
1. ΡΥΘΜΙΣΗ ΜΕ ΣΤΡΑΓΓΑΛΙΣΜΟ ΤΟΥ ΑΤΜΟΥ Ο στραγγαλισμός του ατμού υλοποιείται εξαναγκάζοντας τον ατμό, πριν παροχετευθεί στο στρόβιλο, να περάσει μέσα από κατάλληλη βαλβίδα όπου μικραίνει η διατομή διέλευσης
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
V (β) Αν κατά τη μεταβολή ΓΑ μεταφέρεται θερμότητα 22J από το αέριο στο περιβάλλον, να βρεθεί το έργο W ΓA.
 Άσκηση 1 Ιδανικό αέριο εκτελεί διαδοχικά τις αντιστρεπτές μεταβολές ΑΒ, ΒΓ, ΓΑ που παριστάνονται στο διάγραμμα p V του σχήματος. (α) Αν δίνονται Q ΑΒΓ = 30J και W BΓ = 20J, να βρεθεί η μεταβολή της εσωτερικής
Άσκηση 1 Ιδανικό αέριο εκτελεί διαδοχικά τις αντιστρεπτές μεταβολές ΑΒ, ΒΓ, ΓΑ που παριστάνονται στο διάγραμμα p V του σχήματος. (α) Αν δίνονται Q ΑΒΓ = 30J και W BΓ = 20J, να βρεθεί η μεταβολή της εσωτερικής
ΘΕΡΜΙΚΕΣ & ΨΥΚΤΙΚΕΣ ΜΗΧΑΝΕΣ ΘΕΩΡΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 www.pmoiras.weebly.om ΘΕΡΜΙΚΕΣ & ΨΥΚΤΙΚΕΣ ΜΗΧΑΝΕΣ ΘΕΩΡΙΑ Περιεχόμενα 1. Κυκλικές διαδικασίες 2. O 2ος Θερμοδυναμικός Νόμος- Φυσική Ερμηνεία 2.1 Ισοδυναμία
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 www.pmoiras.weebly.om ΘΕΡΜΙΚΕΣ & ΨΥΚΤΙΚΕΣ ΜΗΧΑΝΕΣ ΘΕΩΡΙΑ Περιεχόμενα 1. Κυκλικές διαδικασίες 2. O 2ος Θερμοδυναμικός Νόμος- Φυσική Ερμηνεία 2.1 Ισοδυναμία
Παραγωγή Ηλεκτρικής Ενέργειας. 6ο Εξάμηνο Ηλεκτρολόγων Μηχανικών και Μηχανικών Ηλεκτρονικών Υπολογιστών. 1η Σειρά Ασκήσεων.
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Ηλεκτρολόγων Μηχ. και Μηχ. Υπολογιστών Ακαδ. Έτος 00- Τομέας Ηλεκτρικής Ισχύος Αθήνα 5//0 Κ. Βουρνάς, Κ. Ντελκής, Π. Γεωργιλάκης Παράδοση,,,4: //0 Παράδοση 5, 6: 5/4/0
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Ηλεκτρολόγων Μηχ. και Μηχ. Υπολογιστών Ακαδ. Έτος 00- Τομέας Ηλεκτρικής Ισχύος Αθήνα 5//0 Κ. Βουρνάς, Κ. Ντελκής, Π. Γεωργιλάκης Παράδοση,,,4: //0 Παράδοση 5, 6: 5/4/0
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 6: Παράδειγμα Κύκλου με Απομάστευση. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενότητα : Παράδειγμα Κύκλου με Απομάστευση Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc.
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενότητα : Παράδειγμα Κύκλου με Απομάστευση Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc.
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Τράπεζα θεμάτων. Δ Θέμα ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Δ Θέμα ΘΕΡΜΟΔΥΝΑΜΙΚΗ 15949 Ποσότητα ιδανικού αέριου ίση με /R mol, βρίσκεται αρχικά σε κατάσταση ισορροπίας στην οποία έχει
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Δ Θέμα ΘΕΡΜΟΔΥΝΑΜΙΚΗ 15949 Ποσότητα ιδανικού αέριου ίση με /R mol, βρίσκεται αρχικά σε κατάσταση ισορροπίας στην οποία έχει
E. ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ. 2. Β2.26 Με ποιόν τρόπο αποβάλλεται θερµότητα κατά τη λειτουργία της µηχανής του αυτοκινήτου;
 E. ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ 1. Β2.25 Θερµική µηχανή είναι, α) το τρόλεϊ; β) ο φούρνος; γ) το ποδήλατο; δ) ο κινητήρας του αεροπλάνου; Επιλέξτε τη σωστή απάντηση. 2. Β2.26 Με ποιόν τρόπο αποβάλλεται θερµότητα κατά
E. ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ 1. Β2.25 Θερµική µηχανή είναι, α) το τρόλεϊ; β) ο φούρνος; γ) το ποδήλατο; δ) ο κινητήρας του αεροπλάνου; Επιλέξτε τη σωστή απάντηση. 2. Β2.26 Με ποιόν τρόπο αποβάλλεται θερµότητα κατά
ΚΕΦΑΛΑΙΟ 4 Ο ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 103 Α. ΠΡΩΤΟΣ ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ ΚΕΦΑΛΑΙΟ 4 Ο ΘΕΡΜΟΔΥΝΑΜΙΚΗ 1. Ιδανικό αέριο εκτελεί διαδοχικά τις αντιστρεπτές μεταβολές ΑΒ, ΒΓ, ΓΑ που παριστάνονται στο ακόλουθο διάγραμμα P-V. α. Αν δίνονται Q ΑΒΓ
103 Α. ΠΡΩΤΟΣ ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ ΚΕΦΑΛΑΙΟ 4 Ο ΘΕΡΜΟΔΥΝΑΜΙΚΗ 1. Ιδανικό αέριο εκτελεί διαδοχικά τις αντιστρεπτές μεταβολές ΑΒ, ΒΓ, ΓΑ που παριστάνονται στο ακόλουθο διάγραμμα P-V. α. Αν δίνονται Q ΑΒΓ
ΕΝΤΡΟΠΙΑ-2ος ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ-ΚΥΚΛΟΣ CARNOT
 ΕΝΤΡΟΠΙΑ-ος ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ-ΚΥΚΛΟΣ CARNO Η εντροπία είναι το φυσικό µέγεθος το οποίο εκφράζει ποσοτικά το βαθµό αταξίας µιας κατάστασης ενός θερµοδυναµικού συστήµατος. ΣΤΑΤΙΣΤΙΚΟΣ ΟΡΙΣΜΟΣ Η εντροπία
ΕΝΤΡΟΠΙΑ-ος ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ-ΚΥΚΛΟΣ CARNO Η εντροπία είναι το φυσικό µέγεθος το οποίο εκφράζει ποσοτικά το βαθµό αταξίας µιας κατάστασης ενός θερµοδυναµικού συστήµατος. ΣΤΑΤΙΣΤΙΚΟΣ ΟΡΙΣΜΟΣ Η εντροπία
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 4: Ατμοί. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής. Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενότητα 4: Ατμοί Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση Ποιότητας, Τμήμα
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενότητα 4: Ατμοί Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση Ποιότητας, Τμήμα
Το παραγόµενο έργο είναι µεγαλύτερο στη µεταβολή β. Η προσφερόµενη θερµότητα είναι µεγαλύτερη στη µεταβολή β
 1 η Άσκηση : Στο παρακάτω σχήµα απεικονίζονται δύο διαφορετικές µεταβολές α και β ενός ιδανικού αερίου, µεταξύ των καταστάσεων 1 και 2. Η µεταβολή α παριστάνει µια ισόθερµη εκτόνωση ενώ η β αποτελείται
1 η Άσκηση : Στο παρακάτω σχήµα απεικονίζονται δύο διαφορετικές µεταβολές α και β ενός ιδανικού αερίου, µεταξύ των καταστάσεων 1 και 2. Η µεταβολή α παριστάνει µια ισόθερµη εκτόνωση ενώ η β αποτελείται
ΑΤΜΟΛΕΒΗΤΕΣ-ΑΤΜΟΣΤΡΟΒΙΛΟΙ ΑΣΚΗΣΕΙΣ ΠΡΑΞΗΣ
 Α. Κύκλος Rankine ΑΤΜΟΛΕΒΗΤΕΣ-ΑΤΜΟΣΤΡΟΒΙΛΟΙ ΑΣΚΗΣΕΙΣ ΠΡΑΞΗΣ. Ατμοστροβιλοεγκατάσταση λειτουργεί μεταξύ των πιέσεων 30 bar και 0,08 bar.η θερμοκρασία του υπέρθερμου ατμού είναι 400 C. Να υπολογιστεί ο θεωρητικός
Α. Κύκλος Rankine ΑΤΜΟΛΕΒΗΤΕΣ-ΑΤΜΟΣΤΡΟΒΙΛΟΙ ΑΣΚΗΣΕΙΣ ΠΡΑΞΗΣ. Ατμοστροβιλοεγκατάσταση λειτουργεί μεταξύ των πιέσεων 30 bar και 0,08 bar.η θερμοκρασία του υπέρθερμου ατμού είναι 400 C. Να υπολογιστεί ο θεωρητικός
ΘΕΡΜΑΝΣΗ-ΨΥΞΗ-ΚΛΙΜΑΤΙΣΜΟΣ Ι ΑΣΚΗΣΕΙΣ
 ΘΕΡΜΑΝΣΗ-ΨΥΞΗ-ΚΛΙΜΑΤΙΣΜΟΣ Ι ΑΣΚΗΣΕΙΣ 1. Ψυκτική εγκατάσταση που ακολουθεί στοιχειώδη ψυκτικό κύκλο συμπίεσης ατμών με ψυκτικό μέσο R134a, εργάζεται μεταξύ των ορίων πίεσης 0,12 MΡa και 1 MΡa. Αν η παροχή
ΘΕΡΜΑΝΣΗ-ΨΥΞΗ-ΚΛΙΜΑΤΙΣΜΟΣ Ι ΑΣΚΗΣΕΙΣ 1. Ψυκτική εγκατάσταση που ακολουθεί στοιχειώδη ψυκτικό κύκλο συμπίεσης ατμών με ψυκτικό μέσο R134a, εργάζεται μεταξύ των ορίων πίεσης 0,12 MΡa και 1 MΡa. Αν η παροχή
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 7: Ρύθμιση Ισχύος Στροβίλων. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενότητα 7: Ρύθμιση Ισχύος Στροβίλων Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενότητα 7: Ρύθμιση Ισχύος Στροβίλων Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Παραγωγή Ηλεκτρικής Ενέργειας 6ο Εξάμηνο Ηλεκτρολόγων Μηχανικών και Μηχανικών Ηλεκτρονικών Υπολογιστών Ροή Ε. 1η Σειρά Ασκήσεων
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Ηλεκτρολόγων Μηχ. και Μηχ. Υπολογιστών Ακαδ. Έτος 0- Τομέας Ηλεκτρικής Ισχύος Αθήνα, 0 Μαρτίου 0 Καθηγητής Κ.Βουρνάς Παράδοση,,5: 8// Λέκτωρ Σ. Καβατζά 6,,4: /4/ Παραγωγή
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Ηλεκτρολόγων Μηχ. και Μηχ. Υπολογιστών Ακαδ. Έτος 0- Τομέας Ηλεκτρικής Ισχύος Αθήνα, 0 Μαρτίου 0 Καθηγητής Κ.Βουρνάς Παράδοση,,5: 8// Λέκτωρ Σ. Καβατζά 6,,4: /4/ Παραγωγή
Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ (Ασκήσεις πράξης) ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ
 ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ 1. Να υπολογιστεί η πυκνότητα του αέρα σε πίεση 0,1 MPa και θερμοκρασία 20 ο C. (R air =0,287 kj/kgk) 2. Ποσότητα αέρα 1 kg εκτελεί τις παρακάτω διεργασίες: Διεργασία 1-2: Αδιαβατική
ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ 1. Να υπολογιστεί η πυκνότητα του αέρα σε πίεση 0,1 MPa και θερμοκρασία 20 ο C. (R air =0,287 kj/kgk) 2. Ποσότητα αέρα 1 kg εκτελεί τις παρακάτω διεργασίες: Διεργασία 1-2: Αδιαβατική
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 4-1 Ο ΨΥΚΤΙΚΟΣ ΚΥΚΛΟΣ, ΤΟ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΗΧΑΝΟΛΟΓΙΑ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 4-1 Ο ΨΥΚΤΙΚΟΣ ΚΥΚΛΟΣ, ΤΟ
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Τράπεζα θεμάτων. Β Θέμα ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΘΕΡΜΟΔΥΝΑΜΙΚΗ 16111 Στο πιο κάτω διάγραμμα παριστάνονται τρεις περιπτώσεις Α, Β και Γ αντιστρεπτών μεταβολών τις οποίες
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΘΕΡΜΟΔΥΝΑΜΙΚΗ 16111 Στο πιο κάτω διάγραμμα παριστάνονται τρεις περιπτώσεις Α, Β και Γ αντιστρεπτών μεταβολών τις οποίες
. ΠΡΩΤΟΣ ΘΕΡΜΟ ΥΝΑΜΙΚΟΣ ΝΟΜΟΣ
 . ΠΡΩΤΟΣ ΘΕΡΜΟ ΥΝΑΜΙΚΟΣ ΝΟΜΟΣ 1. Σε µια ισόθερµη µεταβολή : α) Το αέριο µεταβάλλεται µε σταθερή θερµότητα β) Η µεταβολή της εσωτερικής ενέργειας είναι µηδέν V W = PV ln V γ) Το έργο που παράγεται δίνεται
. ΠΡΩΤΟΣ ΘΕΡΜΟ ΥΝΑΜΙΚΟΣ ΝΟΜΟΣ 1. Σε µια ισόθερµη µεταβολή : α) Το αέριο µεταβάλλεται µε σταθερή θερµότητα β) Η µεταβολή της εσωτερικής ενέργειας είναι µηδέν V W = PV ln V γ) Το έργο που παράγεται δίνεται
P. kpa T, C v, m 3 /kg u, kj/kg Περιγραφή κατάστασης και ποιότητα (αν εφαρμόζεται) , ,0 101,
 Ασκήσεις Άσκηση 1 Να συμπληρώσετε τα κενά κελιά στον επόμενο πίνακα των ιδιοτήτων του νερού εάν παρέχονται επαρκή δεδομένα. Στην τελευταία στήλη να περιγράψετε την κατάσταση του νερού ως υπόψυκτο υγρό,
Ασκήσεις Άσκηση 1 Να συμπληρώσετε τα κενά κελιά στον επόμενο πίνακα των ιδιοτήτων του νερού εάν παρέχονται επαρκή δεδομένα. Στην τελευταία στήλη να περιγράψετε την κατάσταση του νερού ως υπόψυκτο υγρό,
ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ-2 ος ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ
 ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ-2 ος ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ Θερμικες μηχανες 1. Το ωφελιμο εργο μπορει να υπολογιστει με ένα από τους παρακατω τροπους: Α.Υπολογιζουμε το αλγεβρικο αθροισμα των εργων ( μαζι με τα προσημα
ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ-2 ος ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ Θερμικες μηχανες 1. Το ωφελιμο εργο μπορει να υπολογιστει με ένα από τους παρακατω τροπους: Α.Υπολογιζουμε το αλγεβρικο αθροισμα των εργων ( μαζι με τα προσημα
Προσανατολισμού Θερμοδυναμική
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ 60 Ον/μο:.. Β Λυκείου Ύλη: Κινητική θεωρία αερίων Προσανατολισμού Θερμοδυναμική 8-2-2015 Θέμα 1 ο : 1. Η απόλυτη θερμοκρασία ορισμένης ποσότητας αερίου διπλασιάζεται υπό σταθερό όγκο.
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ 60 Ον/μο:.. Β Λυκείου Ύλη: Κινητική θεωρία αερίων Προσανατολισμού Θερμοδυναμική 8-2-2015 Θέμα 1 ο : 1. Η απόλυτη θερμοκρασία ορισμένης ποσότητας αερίου διπλασιάζεται υπό σταθερό όγκο.
2. Ορισµένη µάζα ενός ιδανικού αερίου πραγµατοποιεί τις παρακάτω
 Θ Ε Ρ Μ Ο Υ Ν Α Μ Ι Κ Η Α Σ Κ Η Σ Ε Ι Σ 1. Ένα αέριο βρίσκεται στην κατάσταση Α (P 0,V 0,T 0 ) και παθαίνει τις εξής διαδοχικές µεταβολές: Α Β :ισόθερµη εκτόνωση µέχρι τριπλασιασµού του όγκου του, Β Γ
Θ Ε Ρ Μ Ο Υ Ν Α Μ Ι Κ Η Α Σ Κ Η Σ Ε Ι Σ 1. Ένα αέριο βρίσκεται στην κατάσταση Α (P 0,V 0,T 0 ) και παθαίνει τις εξής διαδοχικές µεταβολές: Α Β :ισόθερµη εκτόνωση µέχρι τριπλασιασµού του όγκου του, Β Γ
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Δ ΘΕΜΑΤΑ ΘΕΡΜΟΔΥΝΑΜΙΚΗ» ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 1. ΘΕΜΑ Δ Ορισμένη
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Δ ΘΕΜΑΤΑ ΘΕΡΜΟΔΥΝΑΜΙΚΗ» ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 1. ΘΕΜΑ Δ Ορισμένη
ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΘΕΜΑ 4
 ΘΕΜΑ 4 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ 15984 Ποσότητα μονατομικού ιδανικού αερίου βρίσκεται στην κατάσταση θερμοδυναμικής ισορροπίας Α (ρ0, V0, To). Το αέριο εκτελεί αρχικά ισόθερμη αντιστρεπτή μεταβολή
ΘΕΜΑ 4 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ 15984 Ποσότητα μονατομικού ιδανικού αερίου βρίσκεται στην κατάσταση θερμοδυναμικής ισορροπίας Α (ρ0, V0, To). Το αέριο εκτελεί αρχικά ισόθερμη αντιστρεπτή μεταβολή
Energy resources: Technologies & Management
 Energy resources: Technologies & Management Θερμοδυναμικοί κύκλοι παραγωγής ισχύος με ατμό Αν. Καθηγητής Γ. Σκόδρας Περιεχόμενα Ορισμοί Ιδανικό υγρό και ατμός Ενθαλπία και εντροπία μίγματος νερού /ατμού
Energy resources: Technologies & Management Θερμοδυναμικοί κύκλοι παραγωγής ισχύος με ατμό Αν. Καθηγητής Γ. Σκόδρας Περιεχόμενα Ορισμοί Ιδανικό υγρό και ατμός Ενθαλπία και εντροπία μίγματος νερού /ατμού
Ο «TRANSCRITICAL» ΨΥΚΤΙΚΟΣ ΚΥΚΛΟΣ ΤΟΥ CO2
 6--5 Ο «TRANSCRITICAL» ΨΥΚΤΙΚΟΣ ΚΥΚΛΟΣ ΤΟΥ CO2 Στα συνηθισμένα ψυκτικά ρευστά, η απόρριψη θερμότητας γίνεται υπό σταθερά θερμοκρασία, που είναι η θερμοκρασία συμπύκνωσης του ψυκτικού ρευστού. Όπως φαίνεται
6--5 Ο «TRANSCRITICAL» ΨΥΚΤΙΚΟΣ ΚΥΚΛΟΣ ΤΟΥ CO2 Στα συνηθισμένα ψυκτικά ρευστά, η απόρριψη θερμότητας γίνεται υπό σταθερά θερμοκρασία, που είναι η θερμοκρασία συμπύκνωσης του ψυκτικού ρευστού. Όπως φαίνεται
Διαγώνισμα B Λυκείου Σάββατο 09 Μαρτίου 2019
 Διαγώνισμα B Λυκείου Σάββατο 09 Μαρτίου 019 Διάρκεια Εξέτασης ώρες Ονοματεπώνυμο. Αξιολόγηση : Θέμα Α Στις ημιτελείς προτάσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα
Διαγώνισμα B Λυκείου Σάββατο 09 Μαρτίου 019 Διάρκεια Εξέτασης ώρες Ονοματεπώνυμο. Αξιολόγηση : Θέμα Α Στις ημιτελείς προτάσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα
3ο ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Θερµοδυναµική/Ιδανικά Αέρια. Ενδεικτικές Λύσεις. Θέµα Α
 3ο ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Θερµοδυναµική/Ιδανικά Αέρια Ενδεικτικές Λύσεις Θέµα Α Α.1 Ορισµένη ποσότητα ιδανικού αερίου πραγµατοποιεί ισοβαρή ϑέρµανση κατά την διάρκεια της οποίας η ϑερµοκρασία
3ο ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Θερµοδυναµική/Ιδανικά Αέρια Ενδεικτικές Λύσεις Θέµα Α Α.1 Ορισµένη ποσότητα ιδανικού αερίου πραγµατοποιεί ισοβαρή ϑέρµανση κατά την διάρκεια της οποίας η ϑερµοκρασία
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Β ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 04/01/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Β ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 04/01/2014 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιο σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1 Α4 και δίπλα το γράμμα που αντιστοιχεί
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Β ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 04/01/2014 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιο σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1 Α4 και δίπλα το γράμμα που αντιστοιχεί
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ. α. Χρησιμοποιώντας τον πρώτο θερμοδυναμικό νόμο έχουμε : J J J
 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ος θερμοδυναμικός νόμος 1. α. Αέριο απορροφά θερμότητα 2500 και παράγει έργο 1500. Να υπολογισθεί η μεταβολή της εσωτερικής του ενέργειας. β. Αέριο συμπιέζεται ισόθερμα και αποβάλλει
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ος θερμοδυναμικός νόμος 1. α. Αέριο απορροφά θερμότητα 2500 και παράγει έργο 1500. Να υπολογισθεί η μεταβολή της εσωτερικής του ενέργειας. β. Αέριο συμπιέζεται ισόθερμα και αποβάλλει
ΕΞΙΣΩΣΗ CLAUSIUS-CLAPEYRON ΘΕΩΡΙΑ
 ΕΞΙΣΩΣΗ CLAUSIUS-CLAEYRON ΘΕΩΡΙΑ Περιεχόμενα 1. 3D Διάγραμμα Φάσης 2. Λανθάνουσα θερμότητα 3. Εξίσωση Clausius Clapeyron 4. Συμπιεστότητα 5. Θερμική διαστολή 6. Θερμοχωρητικότητα 1 στερεό στερεό+υγρό υγρό
ΕΞΙΣΩΣΗ CLAUSIUS-CLAEYRON ΘΕΩΡΙΑ Περιεχόμενα 1. 3D Διάγραμμα Φάσης 2. Λανθάνουσα θερμότητα 3. Εξίσωση Clausius Clapeyron 4. Συμπιεστότητα 5. Θερμική διαστολή 6. Θερμοχωρητικότητα 1 στερεό στερεό+υγρό υγρό
(διαγώνισµα Θερµοδυναµική Ι)
 0.06.000 (διαγώνισµα Θερµοδυναµική Ι) Θερµοκινητήρας CARNOT λειτουργεί µεταξύ θερµοκρασίας, T υ =640 K και θερµοκρασίας περιβάλλοντος Τ π =0 Κ προσφέροντας εξολοκλήρου την παραγόµενη µηχανική ισχύ του
0.06.000 (διαγώνισµα Θερµοδυναµική Ι) Θερµοκινητήρας CARNOT λειτουργεί µεταξύ θερµοκρασίας, T υ =640 K και θερµοκρασίας περιβάλλοντος Τ π =0 Κ προσφέροντας εξολοκλήρου την παραγόµενη µηχανική ισχύ του
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 6: Αναθέρμανση - Απομάστευση. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδμαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενόττα 6: Αναθέρμανσ - Απομάστευσ Γεώργιος Κ. Χατζκωνσταντής Επίκουρος Καθγτής Διπλ. Ναυπγός Μχανολόγος Μχανικός M.Sc. Διασφάλισ Ποιόττας,
Ανοικτά Ακαδμαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ενόττα 6: Αναθέρμανσ - Απομάστευσ Γεώργιος Κ. Χατζκωνσταντής Επίκουρος Καθγτής Διπλ. Ναυπγός Μχανολόγος Μχανικός M.Sc. Διασφάλισ Ποιόττας,
2. Ασκήσεις Θερµοδυναµικής
 1) Πολλά Έργα σε εποχές αν-εργείας. 2. Ασκήσεις ς Α) ίνεται η µεταβολή του πρώτου σχήµατος. Να υπολογιστούν τα έργα σε κάθε επιµέρους µεταβολή, καθώς και το συνολικό έργο στη διάρκεια του κύκλου. Β) ίνεται
1) Πολλά Έργα σε εποχές αν-εργείας. 2. Ασκήσεις ς Α) ίνεται η µεταβολή του πρώτου σχήµατος. Να υπολογιστούν τα έργα σε κάθε επιµέρους µεταβολή, καθώς και το συνολικό έργο στη διάρκεια του κύκλου. Β) ίνεται
ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ 1. Πώς ορίζεται η περίσσεια αέρα και η ισχύς μίγματος σε μία καύση; 2. Σε ποιές περιπτώσεις παρατηρείται μή μόνιμη μετάδοση της θερμότητας; 3. Τί είναι η αντλία
ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ 1. Πώς ορίζεται η περίσσεια αέρα και η ισχύς μίγματος σε μία καύση; 2. Σε ποιές περιπτώσεις παρατηρείται μή μόνιμη μετάδοση της θερμότητας; 3. Τί είναι η αντλία
ΜΕΤΑΒΟΛΕΣ ΚΑΤΑΣΤΑΣΗΣ ΑΕΡΙΩΝ. 1. Δώστε τον ορισμό τον τύπο και το διάγραμμα σε άξονες P v της ισόθερμης μεταβολής. σελ. 10. και
 ΜΕΤΑΒΟΛΕΣ ΚΑΤΑΣΤΑΣΗΣ ΑΕΡΙΩΝ 1. Δώστε τον ορισμό τον τύπο και το διάγραμμα σε άξονες P v της ισόθερμης μεταβολής. σελ. 10 ορισμός : Ισόθερμη, ονομάζεται η μεταβολή κατά τη διάρκεια της οποίας η θερμοκρασία
ΜΕΤΑΒΟΛΕΣ ΚΑΤΑΣΤΑΣΗΣ ΑΕΡΙΩΝ 1. Δώστε τον ορισμό τον τύπο και το διάγραμμα σε άξονες P v της ισόθερμης μεταβολής. σελ. 10 ορισμός : Ισόθερμη, ονομάζεται η μεταβολή κατά τη διάρκεια της οποίας η θερμοκρασία
ΔΙΑΓΩΝΙΣΜΑ Α. και d B οι πυκνότητα του αερίου στις καταστάσεις Α και Β αντίστοιχα, τότε
 ΔΙΑΓΩΝΙΣΜΑ Α Θέµα ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Σύµφωνα µε την κινητική θεωρία των ιδανικών αερίων, η πίεση
ΔΙΑΓΩΝΙΣΜΑ Α Θέµα ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Σύµφωνα µε την κινητική θεωρία των ιδανικών αερίων, η πίεση
Διάρκεια εξέτασης 75 λεπτά
 Α.Ε.Ν ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΟΝΟΜΑ... ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 2017 ΕΚΠΑΙΔΕΥΤΙΚΟ ΕΤΟΣ 2016-2017 ΕΠΩΝΗΜΟ.. ΕΞΑΜΗΝΟ B ΝΑΥΤΙΚΕΣ ΜΗΧΑΝΕΣ ΑΡΙΘΜΟΣ ΜΗΤΡΩΟΥ... Οι απαντήσεις να συμπληρωθούν στο πίνακα
Α.Ε.Ν ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΟΝΟΜΑ... ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 2017 ΕΚΠΑΙΔΕΥΤΙΚΟ ΕΤΟΣ 2016-2017 ΕΠΩΝΗΜΟ.. ΕΞΑΜΗΝΟ B ΝΑΥΤΙΚΕΣ ΜΗΧΑΝΕΣ ΑΡΙΘΜΟΣ ΜΗΤΡΩΟΥ... Οι απαντήσεις να συμπληρωθούν στο πίνακα
Υπεύθυνοι Καθηγητές: Γκαραγκουνούλης Ι., Κοέν Ρ., Κυριτσάκας Β. B ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 1 Ονοματεπώνυμο.., τμήμα:. Υπεύθυνοι Καθηγητές: Γκαραγκουνούλης Ι., Κοέν Ρ., Κυριτσάκας Β. B ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ >
1 Ονοματεπώνυμο.., τμήμα:. Υπεύθυνοι Καθηγητές: Γκαραγκουνούλης Ι., Κοέν Ρ., Κυριτσάκας Β. B ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ >
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 26 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ ΚΑΙ ΚΛΙΜΑΤΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 26 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ ΚΑΙ ΚΛΙΜΑΤΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Τράπεζα θεμάτων. Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ
 ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ 16111 Ένα παιδί κρατάει στο χέρι του ένα μπαλόνι γεμάτο ήλιο που καταλαμβάνει όγκο 4 L (σε πίεση
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ 16111 Ένα παιδί κρατάει στο χέρι του ένα μπαλόνι γεμάτο ήλιο που καταλαμβάνει όγκο 4 L (σε πίεση
εύτερος Θερμοδυναμικός Νόμος Εντροπία ιαθέσιμη ενέργεια Εξέργεια
 εύτερος Θερμοδυναμικός Νόμος Εντροπία ιαθέσιμη ενέργεια Εξέργεια Χαρακτηριστικά Θερμοδυναμικών Νόμων 0 ος Νόμος Εισάγει την έννοια της θερμοκρασίας Αν Α Γ και Β Γ τότε Α Β, όπου : θερμική ισορροπία ος
εύτερος Θερμοδυναμικός Νόμος Εντροπία ιαθέσιμη ενέργεια Εξέργεια Χαρακτηριστικά Θερμοδυναμικών Νόμων 0 ος Νόμος Εισάγει την έννοια της θερμοκρασίας Αν Α Γ και Β Γ τότε Α Β, όπου : θερμική ισορροπία ος
Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί:
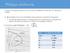 Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Β ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 04/01/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Β ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 04/01/2014 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιο σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1 Α4 και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Β ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΑΠΑΝΤΗΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 04/01/2014 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιο σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1 Α4 και δίπλα το γράμμα
ΘΕΡΜΟΔΥΝΑΜΙΚΗ. Χαροκόπειο Πανεπιστήμιο. 11 Μαΐου 2006
 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Χαροκόπειο Πανεπιστήμιο 11 Μαΐου 2006 Κλάδοι της Θερμοδυναμικής Χημική Θερμοδυναμική: Μελετά τις μετατροπές ενέργειας που συνοδεύουν φυσικά ή χημικά φαινόμενα Θερμοχημεία: Κλάδος της Χημικής
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Χαροκόπειο Πανεπιστήμιο 11 Μαΐου 2006 Κλάδοι της Θερμοδυναμικής Χημική Θερμοδυναμική: Μελετά τις μετατροπές ενέργειας που συνοδεύουν φυσικά ή χημικά φαινόμενα Θερμοχημεία: Κλάδος της Χημικής
2. Ασκήσεις Θερμοδυναμικής. Ομάδα Γ.
 . σκήσεις ς. Ομάδα..1. Ισοβαρής θέρμανση και έργο. Ένα αέριο θερμαίνεται ισοβαρώς από θερμοκρασία Τ 1 σε θερμοκρασία Τ, είτε κατά την μεταβολή, είτε κατά την μεταβολή Δ. i) Σε ποια μεταβολή παράγεται περισσότερο
. σκήσεις ς. Ομάδα..1. Ισοβαρής θέρμανση και έργο. Ένα αέριο θερμαίνεται ισοβαρώς από θερμοκρασία Τ 1 σε θερμοκρασία Τ, είτε κατά την μεταβολή, είτε κατά την μεταβολή Δ. i) Σε ποια μεταβολή παράγεται περισσότερο
διαιρούμε με το εμβαδό Α 2 του εμβόλου (1)
 1)Συνήθως οι πτήσεις των αεροσκαφών γίνονται στο ύψος των 15000 m, όπου η θερμοκρασία του αέρα είναι 210 Κ και η ατμοσφαιρική πίεση 10000 N / m 2. Σε αεροδρόμιο που βρίσκεται στο ίδιο ύψος με την επιφάνεια
1)Συνήθως οι πτήσεις των αεροσκαφών γίνονται στο ύψος των 15000 m, όπου η θερμοκρασία του αέρα είναι 210 Κ και η ατμοσφαιρική πίεση 10000 N / m 2. Σε αεροδρόμιο που βρίσκεται στο ίδιο ύψος με την επιφάνεια
Ζήτημα 1 0. Επώνυμο... Όνομα... Αγρίνιο 1/3/2015. Επιλέξτε τη σωστή απάντηση
 1 Επώνυμο... Όνομα... Αγρίνιο 1/3/2015 Ζήτημα 1 0 Επιλέξτε τη σωστή απάντηση 1) Η θερμότητα που ανταλλάσει ένα αέριο με το περιβάλλον θεωρείται θετική : α) όταν προσφέρεται από το αέριο στο περιβάλλον,
1 Επώνυμο... Όνομα... Αγρίνιο 1/3/2015 Ζήτημα 1 0 Επιλέξτε τη σωστή απάντηση 1) Η θερμότητα που ανταλλάσει ένα αέριο με το περιβάλλον θεωρείται θετική : α) όταν προσφέρεται από το αέριο στο περιβάλλον,
ΛΥΣΕΙΣ. µεταφορική κινητική ενέργεια του K η θερµοκρασία του αερίου πρέπει να: β) τετραπλασιαστεί δ) υποτετραπλασιαστεί (Μονάδες 5) δ) 0 J
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 0-0 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Β ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 30// ΛΥΣΕΙΣ ΘΕΜΑ ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω ερωτήσεις Α.- Α.4
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 0-0 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Β ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 30// ΛΥΣΕΙΣ ΘΕΜΑ ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω ερωτήσεις Α.- Α.4
12 η Διάλεξη Θερμοδυναμική
 12 η Διάλεξη Θερμοδυναμική Φίλιππος Φαρμάκης Επ. Καθηγητής 1 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Εισαγωγικά Προσέγγιση των μεγεθών όπως πίεση, θερμοκρασία, κλπ. με άλλο τρόπο (διαφορετικό από την στατιστική φυσική) Ασχολείται
12 η Διάλεξη Θερμοδυναμική Φίλιππος Φαρμάκης Επ. Καθηγητής 1 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Εισαγωγικά Προσέγγιση των μεγεθών όπως πίεση, θερμοκρασία, κλπ. με άλλο τρόπο (διαφορετικό από την στατιστική φυσική) Ασχολείται
ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ 1. Να υπολογιστεί η μαζική παροχή του ατμού σε (kg/h) που χρησιμοποιείται σε ένα θερμαντήρα χυμού με τα παρακάτω στοιχεία: αρχική θερμοκρασία χυμού 20 C, τελική θερμοκρασία
ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ 1. Να υπολογιστεί η μαζική παροχή του ατμού σε (kg/h) που χρησιμοποιείται σε ένα θερμαντήρα χυμού με τα παρακάτω στοιχεία: αρχική θερμοκρασία χυμού 20 C, τελική θερμοκρασία
ΣΥΜΠΑΡΑΓΩΓΗ ΘΕΡΜΟΤΗΤΑΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥ ΕΡΓΟΥ
 ΣΥΜΠΑΡΑΓΩΓΗ ΘΕΡΜΟΤΗΤΑΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥ ΕΡΓΟΥ ΒΑΘΜΟΙ ΑΠΟΔΟΣΗΣ Συντελεστής διάθεσης ενέργειας - EUF (Energy Utilisation Factor) ΒΑΘΜΟΙ ΑΠΟΔΟΣΗΣ ΚΑΙ ΑΛΛΟΙ ΟΡΙΣΜΟΙ P ch-s : η συνολική χημική ισχύς των καυσίμων
ΣΥΜΠΑΡΑΓΩΓΗ ΘΕΡΜΟΤΗΤΑΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥ ΕΡΓΟΥ ΒΑΘΜΟΙ ΑΠΟΔΟΣΗΣ Συντελεστής διάθεσης ενέργειας - EUF (Energy Utilisation Factor) ΒΑΘΜΟΙ ΑΠΟΔΟΣΗΣ ΚΑΙ ΑΛΛΟΙ ΟΡΙΣΜΟΙ P ch-s : η συνολική χημική ισχύς των καυσίμων
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ
 ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ΑΣΚΗΣΗ 1 Το δοχείο του σχήματος είναι απομονωμένο (αδιαβατικά τοιχώματα). Το διάφραγμα χωρίζει το δοχείο σε δύο μέρη. Το αριστερό μέρος έχει όγκο 1 και περιέχει ιδανικό αέριο
ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ΑΣΚΗΣΗ 1 Το δοχείο του σχήματος είναι απομονωμένο (αδιαβατικά τοιχώματα). Το διάφραγμα χωρίζει το δοχείο σε δύο μέρη. Το αριστερό μέρος έχει όγκο 1 και περιέχει ιδανικό αέριο
ΜΕΤΑΒΟΛΕΣ ΙΣΟΧΩΡΗ ΜΕΤΑΒΟΛΗ
 Δοχείο περιέχει ιδανικό αέριο υπό πίεση Ρ 1 =2atm και θερμοκρασία Τ 1 =300Κ. Αφαιρούμε με κάποιο τρόπο από το δοχείο 0,8Kg αερίου οπότε η πίεση στο δοχείο γίνεται Ρ 2 =0,95atm και η θερμοκρασία Τ 2 =285Κ.
Δοχείο περιέχει ιδανικό αέριο υπό πίεση Ρ 1 =2atm και θερμοκρασία Τ 1 =300Κ. Αφαιρούμε με κάποιο τρόπο από το δοχείο 0,8Kg αερίου οπότε η πίεση στο δοχείο γίνεται Ρ 2 =0,95atm και η θερμοκρασία Τ 2 =285Κ.
Δύναμη F F=m*a kgm/s 2. N = W / t 1 J / s = 1 Watt ( W ) 1 HP ~ 76 kp*m / s ~ 746 W. 1 PS ~ 75 kp*m / s ~ 736 W. 1 τεχνική ατμόσφαιρα 1 at
 Δύναμη F F=m*a kgm/s 2 1 kg*m/s 2 ~ 1 N 1 N ~ 10 5 dyn Ισχύς Ν = Έργο / χρόνος W = F*l 1 N*m = 1 Joule ( J ) N = W / t 1 J / s = 1 Watt ( W ) 1 1 kp*m / s 1 HP ~ 76 kp*m / s ~ 746 W 1 PS ~ 75 kp*m / s
Δύναμη F F=m*a kgm/s 2 1 kg*m/s 2 ~ 1 N 1 N ~ 10 5 dyn Ισχύς Ν = Έργο / χρόνος W = F*l 1 N*m = 1 Joule ( J ) N = W / t 1 J / s = 1 Watt ( W ) 1 1 kp*m / s 1 HP ~ 76 kp*m / s ~ 746 W 1 PS ~ 75 kp*m / s
Μεταβολή Q, W, ΔU Παρατηρήσεις (3) ) Q = nrt ln V 1. W = Q = nrt ln U = 0 (5). Q = nc V T (8) W = 0 (9) U = nc V T (10)
 Θερμοδυναμική 1 1 Θερμοδυναμική 11 Τυπολόγιο Θερμοδυναμικής Πίνακας 1: Οι Μεταβολές Συνοπτικά Μεταβολή Q, W, ΔU Παρατηρήσεις Ισόθερμη Μεταβολή Νόμος oyle = σταθερό (1) 1 1 = 2 2 (2) Q = nrt ln ( 2 W =
Θερμοδυναμική 1 1 Θερμοδυναμική 11 Τυπολόγιο Θερμοδυναμικής Πίνακας 1: Οι Μεταβολές Συνοπτικά Μεταβολή Q, W, ΔU Παρατηρήσεις Ισόθερμη Μεταβολή Νόμος oyle = σταθερό (1) 1 1 = 2 2 (2) Q = nrt ln ( 2 W =
Επανάληψη των Κεφαλαίων 1 και 2 Φυσικής Γ Έσπερινού Κατεύθυνσης
 Επανάληψη των Κεφαλαίων 1 και Φυσικής Γ Έσπερινού Κατεύθυνσης Φυσικά µεγέθη, µονάδες µετρήσεως (S.I) και µετατροπές P: Η πίεση ενός αερίου σε N/m (1atm=1,013 10 5 N/m ). : Ο όγκος τουαερίου σε m 3 (1m
Επανάληψη των Κεφαλαίων 1 και Φυσικής Γ Έσπερινού Κατεύθυνσης Φυσικά µεγέθη, µονάδες µετρήσεως (S.I) και µετατροπές P: Η πίεση ενός αερίου σε N/m (1atm=1,013 10 5 N/m ). : Ο όγκος τουαερίου σε m 3 (1m
ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ ΚΛΙΜΑΤΙΣΜΟΥ
 ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ ΚΛΙΜΑΤΙΣΜΟΥ 2/12/2018 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1. Να γράψετε στο τετράδιό σας το γράμμα καθεμιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή ή τη λέξη ΛΑΘΟΣ,
ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ ΚΛΙΜΑΤΙΣΜΟΥ 2/12/2018 ΚΑΡΑΓΚΙΑΟΥΡΗΣ ΝΙΚΟΛΑΟΣ ΘΕΜΑ 1 ο 1. Να γράψετε στο τετράδιό σας το γράμμα καθεμιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή ή τη λέξη ΛΑΘΟΣ,
Φυσική Προσανατολισμού Β Λυκείου Κεφάλαιο 2 ο. Σύντομη Θεωρία
 Φυσική Προσανατολισμού Β Λυκείου 05-06 Κεφάλαιο ο Σύντομη Θεωρία Θερμοδυναμικό σύστημα είναι το σύστημα το οποίο για να το περιγράψουμε χρησιμοποιούμε και θερμοδυναμικά μεγέθη, όπως τη θερμοκρασία, τη
Φυσική Προσανατολισμού Β Λυκείου 05-06 Κεφάλαιο ο Σύντομη Θεωρία Θερμοδυναμικό σύστημα είναι το σύστημα το οποίο για να το περιγράψουμε χρησιμοποιούμε και θερμοδυναμικά μεγέθη, όπως τη θερμοκρασία, τη
Μεταβολή Q, W, ΔU Παρατηρήσεις (3) ) Q = nrt ln V 1. W = Q = nrt ln U = 0 (5). Q = nc V T (8) W = 0 (9) U = nc V T (10)
 Θερμοδυναμική 1 1 Θερμοδυναμική 11 Τυπολόγιο Θερμοδυναμικής Πίνακας 1: Οι Μεταβολές Συνοπτικά Μεταβολή Q, W, ΔU Παρατηρήσεις Ισόθερμη Μεταβολή Νόμος oyle = σταθερό (1) 1 1 = 2 2 (2) Q = nrt ln ( 2 W =
Θερμοδυναμική 1 1 Θερμοδυναμική 11 Τυπολόγιο Θερμοδυναμικής Πίνακας 1: Οι Μεταβολές Συνοπτικά Μεταβολή Q, W, ΔU Παρατηρήσεις Ισόθερμη Μεταβολή Νόμος oyle = σταθερό (1) 1 1 = 2 2 (2) Q = nrt ln ( 2 W =
3ο ιαγώνισµα Β Τάξης Ενιαίου Λυκείου ευτέρα 2 Μάρτη 2015 Θερµοδυναµική/Ιδανικά Αέρια
 3ο ιαγώνισµα Β Τάξης Ενιαίου Λυκείου ευτέρα 2 Μάρτη 2015 Θερµοδυναµική/Ιδανικά Αέρια Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
3ο ιαγώνισµα Β Τάξης Ενιαίου Λυκείου ευτέρα 2 Μάρτη 2015 Θερµοδυναµική/Ιδανικά Αέρια Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
Εφηρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 10: Ψυκτικά κύκλα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 10: Ψυκτικά κύκλα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΔΙΑΓΩΝΙΣΜΑ ΙΔΑΝΙΚΑ ΑΕΡΙΑ/ΘΕΡΜΟΔΥΝΑΜΙΚΗ Φυσική Προσανατολισμού Β Λυκείου Κυριακή 6 Μαρτίου 2016 Θέμα Α
 ΔΙΑΓΩΝΙΣΜΑ ΙΔΑΝΙΚΑ ΑΕΡΙΑ/ΘΕΡΜΟΔΥΝΑΜΙΚΗ Φυσική Προσανατολισμού Β Λυκείου Κυριακή 6 Μαρτίου 2016 Θέμα Α Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα
ΔΙΑΓΩΝΙΣΜΑ ΙΔΑΝΙΚΑ ΑΕΡΙΑ/ΘΕΡΜΟΔΥΝΑΜΙΚΗ Φυσική Προσανατολισμού Β Λυκείου Κυριακή 6 Μαρτίου 2016 Θέμα Α Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα
Επαναληπτικό Χριστουγέννων Β Λυκείου
 Επαναληπτικό Χριστουγέννων Β Λυκείου 1.Ποιά από τις παρακάτω προτάσεις είναι σωστή ; Σύµφωνα µε τον 1ο θερµοδυναµικό νόµο το ποσό της θερµότητας που απορροφά η αποβάλει ένα θερµοδυναµικό σύστηµα είναι
Επαναληπτικό Χριστουγέννων Β Λυκείου 1.Ποιά από τις παρακάτω προτάσεις είναι σωστή ; Σύµφωνα µε τον 1ο θερµοδυναµικό νόµο το ποσό της θερµότητας που απορροφά η αποβάλει ένα θερµοδυναµικό σύστηµα είναι
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΓΩΝΙΣΜΑ ΚΡΟΥΣΕΙΣ- ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ-ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΓΩΝΙΣΜΑ ΚΡΟΥΣΕΙΣ- ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ-ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ημερομηνία: 15/2/15 Διάρκεια διαγωνίσματος: 18 Υπεύθυνος καθηγητής: Τηλενίκης Ευάγγελος ΖΗΤΗΜΑ 1 Ο Στις
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΓΩΝΙΣΜΑ ΚΡΟΥΣΕΙΣ- ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ-ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ημερομηνία: 15/2/15 Διάρκεια διαγωνίσματος: 18 Υπεύθυνος καθηγητής: Τηλενίκης Ευάγγελος ΖΗΤΗΜΑ 1 Ο Στις
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 Θέμα 1 Επιλέγοντας το κατάλληλο διάγραμμα φάσεων για ένα πραγματικό
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 Θέμα 1 Επιλέγοντας το κατάλληλο διάγραμμα φάσεων για ένα πραγματικό
Θερμοδυναμική. Ερωτήσεις πολλαπλής επιλογής
 Ερωτήσεις πολλαπλής επιλογής Θερμοδυναμική 1. Η εσωτερική ενέργεια ορισμένης ποσότητας ιδανικού αερίου α) Είναι αντιστρόφως ανάλογη της απόλυτης θερμοκρασίας του αερίου. β) Είναι ανάλογη της απόλυτης θερμοκρασίας
Ερωτήσεις πολλαπλής επιλογής Θερμοδυναμική 1. Η εσωτερική ενέργεια ορισμένης ποσότητας ιδανικού αερίου α) Είναι αντιστρόφως ανάλογη της απόλυτης θερμοκρασίας του αερίου. β) Είναι ανάλογη της απόλυτης θερμοκρασίας
ΘΕΡΜΟΔΥΝΑΜΙΚΕΣ ΜΕΤΑΒΟΛΕΣ Η ΚΑΤΑΣΤΑΤΙΚΗ ΕΞΙΣΩΣΗ ΤΩΝ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ
 ΘΕΡΜΟΔΥΝΑΜΙΚΕΣ ΜΕΤΑΒΟΛΕΣ Η ΚΑΤΑΣΤΑΤΙΚΗ ΕΞΙΣΩΣΗ ΤΩΝ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ Η εξίσωση αυτή εκφράζει μια σχέση μεταξύ της πίεσης, της θερμοκρασίας και του ειδικού όγκου. P v = R Όπου P = πίεση σε Pascal v = Ο ειδικός
ΘΕΡΜΟΔΥΝΑΜΙΚΕΣ ΜΕΤΑΒΟΛΕΣ Η ΚΑΤΑΣΤΑΤΙΚΗ ΕΞΙΣΩΣΗ ΤΩΝ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ Η εξίσωση αυτή εκφράζει μια σχέση μεταξύ της πίεσης, της θερμοκρασίας και του ειδικού όγκου. P v = R Όπου P = πίεση σε Pascal v = Ο ειδικός
EΡΓΟ-ΘΕΡΜΟΤΗΤΑ-ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ
 EΡΓΟ-ΘΕΡΜΟΤΗΤΑ-ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Διαδοση θερμοτητας και εργο είναι δυο τροποι με τους οποιους η ενεργεια ενός θερμοδυναμικου συστηματος μπορει να αυξηθει ή να ελαττωθει. Δεν εχει εννοια
EΡΓΟ-ΘΕΡΜΟΤΗΤΑ-ΕΣΩΤΕΡΙΚΗ ΕΝΕΡΓΕΙΑ ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Διαδοση θερμοτητας και εργο είναι δυο τροποι με τους οποιους η ενεργεια ενός θερμοδυναμικου συστηματος μπορει να αυξηθει ή να ελαττωθει. Δεν εχει εννοια
Τμήμα: Γοχημάτων ΑΘ.ΚΕΡΜΕΛΙΔΗΣ ΠΕ 12.04
 Είναι θερμικές μηχανές που μετατρέπουν την χημική ενέργεια του καυσίμου σε θερμική και μέρος αυτής για την παραγωγή μηχανικού έργου, προκαλώντας την περιστροφή του στροφαλοφόρου άξονα. α) ανάλογα με το
Είναι θερμικές μηχανές που μετατρέπουν την χημική ενέργεια του καυσίμου σε θερμική και μέρος αυτής για την παραγωγή μηχανικού έργου, προκαλώντας την περιστροφή του στροφαλοφόρου άξονα. α) ανάλογα με το
ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΟΛΟΓΙΑΣ (7 Ο ΕΞΑΜΗΝΟ)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΟΛΟΓΙΑΣ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 2-1 ΔΙΕΡΓΑΣΙΕΣ ΑΕΡΙΩΝ Εισαγωγικά
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ - ΜΕΤΑΛΛΟΥΡΓΩΝ ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΟΛΟΓΙΑΣ (7 Ο ΕΞΑΜΗΝΟ) Νίκος Μ. Κατσουλάκος Μηχανολόγος Μηχανικός Ε.Μ.Π., PhD, Msc ΜΑΘΗΜΑ 2-1 ΔΙΕΡΓΑΣΙΕΣ ΑΕΡΙΩΝ Εισαγωγικά
2 mol ιδανικού αερίου, η οποία
 ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΕΡΓΑΣΙΑ 7 ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ 1. Μια μηχανή Carnot λειτουργεί μεταξύ των θερμοκρασιών Τ h =400Κ και Τ c =300Κ. Αν στη διάρκεια ενός κύκλου, η μηχανή αυτή απορροφά
ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΕΡΓΑΣΙΑ 7 ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ 1. Μια μηχανή Carnot λειτουργεί μεταξύ των θερμοκρασιών Τ h =400Κ και Τ c =300Κ. Αν στη διάρκεια ενός κύκλου, η μηχανή αυτή απορροφά
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΑΕΡΙΑ
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ. ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΑΕΡΙΑ 1) Η αντιστρεπτή θερµοδυναµική µεταβολή ΑΒ που παρουσιάζεται στο διάγραµµα πίεσης όγκου (P V) του σχήµατος περιγράφει: α. ισόθερµη εκτόνωση β. ισόχωρη ψύξη γ. ισοβαρή
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ. ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΑΕΡΙΑ 1) Η αντιστρεπτή θερµοδυναµική µεταβολή ΑΒ που παρουσιάζεται στο διάγραµµα πίεσης όγκου (P V) του σχήµατος περιγράφει: α. ισόθερµη εκτόνωση β. ισόχωρη ψύξη γ. ισοβαρή
Θερμοδυναμική. Ενότητα 3: Ασκήσεις στη Θερμοδυναμική. Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ
 Θερμοδυναμική Ενότητα 3: Ασκήσεις στη Θερμοδυναμική Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Θερμοδυναμική Ενότητα 3: Ασκήσεις στη Θερμοδυναμική Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΘΕΡΜΟΔΥΝΑΜΙΚΗ» ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 Νόμοι αερίων,
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΘΕΡΜΟΔΥΝΑΜΙΚΗ» ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 Νόμοι αερίων,
Enrico Fermi, Thermodynamics, 1937
 I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΤΕΤΑΡΤΗ 22 ΙΟΥΝΙΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ ΚΑΙ ΚΛΙΜΑΤΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΤΕΤΑΡΤΗ 22 ΙΟΥΝΙΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ ΚΑΙ ΚΛΙΜΑΤΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
1. Τι είναι οι ΜΕΚ και πώς παράγουν το μηχανικό έργο ; 8
 ΚΕΦΑΛΑΙΟ 1 ο 1. Τι είναι οι ΜΕΚ και πώς παράγουν το μηχανικό έργο ; 8 Είναι θερμικές μηχανές που μετατρέπουν την χημική ενέργεια του καυσίμου σε θερμική και μέρος αυτής για την παραγωγή μηχανικού έργου,
ΚΕΦΑΛΑΙΟ 1 ο 1. Τι είναι οι ΜΕΚ και πώς παράγουν το μηχανικό έργο ; 8 Είναι θερμικές μηχανές που μετατρέπουν την χημική ενέργεια του καυσίμου σε θερμική και μέρος αυτής για την παραγωγή μηχανικού έργου,
ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ 2 ΕΡΓΟ ΑΕΡΙΟΥ
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ ΕΡΓΟ ΑΕΡΙΟΥ Κατά την εκτόνωση ενός αερίου, το έρο του είναι θετικό ( δηλαδή παραόμενο). Κατά την συμπίεση ενός
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ ΚΕΦΑΛΑΙΟΥ ΕΡΓΟ ΑΕΡΙΟΥ Κατά την εκτόνωση ενός αερίου, το έρο του είναι θετικό ( δηλαδή παραόμενο). Κατά την συμπίεση ενός
ΤΥΠΟΛΟΓΙΟ-ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ
 ΤΥΠΟΛΟΓΙΟ-ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο ΚΑΙ ο : 1. ΝΟΜΟΣ ΤΟΥ oyle:.=σταθ. για Τ =σταθ. για δύο καταστάσεις Α και Β : Α. Α = Β. Β (α)ισόθερμη εκτόνωση:αύξηση όγκου > και μείωση της πίεσης
ΤΥΠΟΛΟΓΙΟ-ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΗ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο ΚΑΙ ο : 1. ΝΟΜΟΣ ΤΟΥ oyle:.=σταθ. για Τ =σταθ. για δύο καταστάσεις Α και Β : Α. Α = Β. Β (α)ισόθερμη εκτόνωση:αύξηση όγκου > και μείωση της πίεσης
Διεργασίες Καύσης & Ατμολέβητες
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Διεργασίες Καύσης & Ατμολέβητες Σκοπός Παρουσίαση των βασικών αρχών λειτουργίας των διεργασιών καύσης
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Διεργασίες Καύσης & Ατμολέβητες Σκοπός Παρουσίαση των βασικών αρχών λειτουργίας των διεργασιών καύσης
7. Πως πραγµατοποιείται σύµφωνα µε το διάγραµµα ενθαλπίας εντροπίας η ενθαλπιακή πτώση του ατµού κατά την εκτόνωσή του χωρίς απώλειες α. Με σταθερή τη
 ΑΕΝ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 2012 ΝΑΥΤΙΚΕΣ ΜΗΧΑΝΕΣ Β ΕΞΑΜ. ΚΑΘΗΓΗΤΗΣ Ξ. ΒΟΥΒΑΛΙ ΗΣ ΘΕΜΑΤΑ ΟΝΟΜΑ: ΕΠΩΝΥΜΟ: ΜΗΤΡΩΟ: ΒΑΘΜΟΛΟΓΙΑ: Κάθε ερώτηση βαθµολογείται µε 0,25 1. Με ποια σειρά
ΑΕΝ ΜΑΚΕ ΟΝΙΑΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 2012 ΝΑΥΤΙΚΕΣ ΜΗΧΑΝΕΣ Β ΕΞΑΜ. ΚΑΘΗΓΗΤΗΣ Ξ. ΒΟΥΒΑΛΙ ΗΣ ΘΕΜΑΤΑ ΟΝΟΜΑ: ΕΠΩΝΥΜΟ: ΜΗΤΡΩΟ: ΒΑΘΜΟΛΟΓΙΑ: Κάθε ερώτηση βαθµολογείται µε 0,25 1. Με ποια σειρά
ΚΕΦΑΛΑΙΟ 2 ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΚΕΦΑΛΑΙΟ 2 ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΠΟ ΤΗ ΒΕΡΩΝΗ ΕΙΡΗΝΗ ΜΗΧΑΝΙΚΗ Ο κλάδος της Φυσικής που εξετάζει μόνο όσες ενεργειακές ανταλλαγές γίνονται με την εκτέλεση έργου. ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ο κλάδος της Φυσικής που εξετάζει
ΚΕΦΑΛΑΙΟ 2 ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΠΟ ΤΗ ΒΕΡΩΝΗ ΕΙΡΗΝΗ ΜΗΧΑΝΙΚΗ Ο κλάδος της Φυσικής που εξετάζει μόνο όσες ενεργειακές ανταλλαγές γίνονται με την εκτέλεση έργου. ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ο κλάδος της Φυσικής που εξετάζει
ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ & ΚΛΙΜΑΤΙΣΜΟΥ ΕΠΑΛ
 ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ & ΚΛΙΜΑΤΙΣΜΟΥ ΕΠΑΛ Απαντήσεις Πανελλήνιων Εξετάσεων 2017-2018 ΕΚΠΑΙΔΕΥΤΙΚΟΣ: ΒΑΝΤΣΗΣ Β. ΓΕΩΡΓΙΟΣ ΜΗΧΑΝΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ ΠΕ17 ΘΕΜΑ Α. Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας
ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ & ΚΛΙΜΑΤΙΣΜΟΥ ΕΠΑΛ Απαντήσεις Πανελλήνιων Εξετάσεων 2017-2018 ΕΚΠΑΙΔΕΥΤΙΚΟΣ: ΒΑΝΤΣΗΣ Β. ΓΕΩΡΓΙΟΣ ΜΗΧΑΝΟΛΟΓΟΣ ΜΗΧΑΝΙΚΟΣ ΠΕ17 ΘΕΜΑ Α. Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας
Περιεχόμενα. 2ος ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ. Περιορισμοί του 1ου νόμου. Γένεση - Καταστροφή ενέργειας
 ΘΕΡΜΟΔΥΝΑΜΙΚΗ I Περιεχόμενα This 1000 hp engine photo is courtesy of Bugatti automobiles. 2ος ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ Εισαγωγή στον 2ο Θερμοδυναμικό Νόμο Θερμικές Μηχανές: Χαρακτηριστικά-
ΘΕΡΜΟΔΥΝΑΜΙΚΗ I Περιεχόμενα This 1000 hp engine photo is courtesy of Bugatti automobiles. 2ος ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ ΘΕΡΜΙΚΕΣ ΜΗΧΑΝΕΣ Εισαγωγή στον 2ο Θερμοδυναμικό Νόμο Θερμικές Μηχανές: Χαρακτηριστικά-
Θερμοδυναμική. Ενότητα 5: 2 ος Νόμος Θερμοδυναμικής. Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ
 Θερμοδυναμική Ενότητα 5: 2 ος Νόμος Θερμοδυναμικής Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Θερμοδυναμική Ενότητα 5: 2 ος Νόμος Θερμοδυναμικής Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση α: Συντελεστής Joule Thomson (Τζουλ Τόμσον ) Αθανάσιος Τσεκούρας Τμήμα Χημείας Θεωρία 3 Μετρήσεις 6 3 Επεξεργασία Μετρήσεων 6 Σελίδα Θεωρία Η καταστατική εξίσωση
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση α: Συντελεστής Joule Thomson (Τζουλ Τόμσον ) Αθανάσιος Τσεκούρας Τμήμα Χημείας Θεωρία 3 Μετρήσεις 6 3 Επεξεργασία Μετρήσεων 6 Σελίδα Θεωρία Η καταστατική εξίσωση
ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΚΑΥΣΙΜΩΝ ΘΕΡΜΟΤΗΤΑ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ ΗΛΕΚΤΡΙΣΜΟΣ
 ΣΤΟΧΟΣ Ο μαθητής να μπορεί να (α) αναφέρει πως εφαρμόζεται στη πράξη ο ενεργειακός κύκλος για τη μετατροπή της δυναμικής ενέργειας των καυσίμων, σε ηλεκτρική ενέργεια. (β) διακρίνει σε ποίες κατηγορίες
ΣΤΟΧΟΣ Ο μαθητής να μπορεί να (α) αναφέρει πως εφαρμόζεται στη πράξη ο ενεργειακός κύκλος για τη μετατροπή της δυναμικής ενέργειας των καυσίμων, σε ηλεκτρική ενέργεια. (β) διακρίνει σε ποίες κατηγορίες
ΑΝΤΙΣΤΡΕΠΤΕΣ ΘΕΡΜΟΔΥΝΑΜΙΚΕΣ ΜΕΤΑΒΟΛΕΣ ΘΕΩΡΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΑΝΤΙΣΤΡΕΠΤΕΣ ΘΕΡΜΟΔΥΝΑΜΙΚΕΣ ΜΕΤΑΒΟΛΕΣ ΘΕΩΡΙΑ Περιεχόμενα 1. Μελέτη Ισόχωρης μεταβολής 2. Μελέτη Ισοβαρής μεταβολής 3. Μελέτη Ισόθερμης μεταβολής 4.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΑΝΤΙΣΤΡΕΠΤΕΣ ΘΕΡΜΟΔΥΝΑΜΙΚΕΣ ΜΕΤΑΒΟΛΕΣ ΘΕΩΡΙΑ Περιεχόμενα 1. Μελέτη Ισόχωρης μεταβολής 2. Μελέτη Ισοβαρής μεταβολής 3. Μελέτη Ισόθερμης μεταβολής 4.
Ψυκτικοί Κύκλοι Κύκλοι παραγωγής Ψύξης
 Ψυγεία και Αντλίες Θερμότητας Ο στόχος του ψυγείου είναι η μεταφορά θερμότητας ( L ) από τον ψυχρό χώρο; Ψυκτικοί Κύκλοι Κύκλοι παραγωγής Ψύξης Ο στόχος της αντλίας θερμότητας είναι η μεταφορά θερμότητας
Ψυγεία και Αντλίες Θερμότητας Ο στόχος του ψυγείου είναι η μεταφορά θερμότητας ( L ) από τον ψυχρό χώρο; Ψυκτικοί Κύκλοι Κύκλοι παραγωγής Ψύξης Ο στόχος της αντλίας θερμότητας είναι η μεταφορά θερμότητας
