9 2 T 9 t 2 = 9 t ( 9 t t c 2 t. .,Gurtin Pipkin [6 ],Coleman [7 ] , Guyer Krumhansl [9 ] . Tavernier [8 ] . Tzou [13,14], .

Transcript

1 Π2008Π57 (07) Π ACTA PHYSICA SINICA Vol. 57,No. 7,July,2008 ν 2008 Chin. Phys. Soc. g (, ) ( ; ),,. (). (),,.,,,,,,,.,, CV,,,. :,,, PACC: 4410, 6370, 0340G [1 ],, [2 ].,.,,,, [3 ].,,,,,.,. Cattaneo [4 ],Vernotte [5 ]., q + 9 q = - K T, (1) (1) CV, q, T, K, t,. (1),,. 1 9 T + 1 c 2 t 9 2 T 2 = 2 T, (2) = KΠ( c p ), c t = Π.,,.,Gurtin Pipkin [6 ],Coleman [7 ] CV. Tavernier [8 ], Guyer Krumhansl [9 ] Maurer [10 ] Boltzmann, CV., Bai Lavine [11 ] Kgrner Bergmann [12 ] CV. Tzou [13,14],, q T, q q = - K q T - K ( T 9 T), (3) g E2mail : edu. cn

2 T + q 9 2 T 2 = 2 T + 9 ( 2 T) T. (4) ( s), (4),,,.,Π,,Xu Guo [15 ],Masuda [16 ],Antaki [17 ],Cho Juhng [18 ], Fan Lu [19 ] Zhang [20 ].,Brorson [21 ], Tang Araki [22 ].,, Lepri [23 ],, ( ),Narayan [24 ],. Maruyama [25 ],. Livi [26 ],. 21, ,19 40,,, [27 ].,, [1 ],,,.,,.. [28 ],, E = Mc 2 = M v 2 Πc 2 c2 = E v 2 Πc 2, (5), M,, M 0,, c, v, E, E 0. (5),,. ( ), (5) E k = E - E 0 g 1 2 M 0 v 2, (6a) M k = M - M 0 g 1 2 M 0 v 2 c 2, (6b) E k = 1 2 M 0 v 2, M k.,v ν c M M 0 M k..,,,, M = M 0 + M h, (7a) M h = E h c 2 = V h, (7b) M 0, E h,,,,, M h,, h,. 31 [29 ] (5), (6).,,,

3 7 : 4275, m = m 0 + m h, gm = m 0 + gm h, (8) m h = 1 2 m 0 v 2 3 c 2, gm h = 1 2 m 0 v 2 3 c 2, (9) m 0, m h, gm, v 2 3, 1 2 m 0 v 2 3, m h.,:1),. v 3, v 2 3.,.,,.. 2),,,,,. [29 ].,., p = 1 3 n mv 3 v 3 = 1 3 n m 0 v n m h v 2 3 = p 0 + p h, (10) p 0, p h, p. (8) (10) p h = 5 18 h =C v TΠc 2. p h p h ν p 0, nm 0 c 2 ( v 2 3 ) 2. (11) = 5 3 h RT, (12) p = p 0 + p h = h RT. (13) p p 0 = 0 RT. (14),, p h ν p 0,.,.,, ( ),( ).. 41 [30 ] p = - 9 E 0 9V + E D0 V, (15), p V, E D0,,.,,, [31 ], [32 ] (15), p 0 = E D0 V. (16), Dulong2Pefit, E D0 = M 0 CT = 3 R mol T = 3 M 0 RT, (17) M 0, R. (17),M 0 ( ) E D0, CT, (, ). (17) (16) p 0 = 3 0 RT = 0 CT, (18) C, 0,, (18),.,.,,.., M h = E D0 c 2 = M 0 CT c 2. (19),CT,

4 , d E h = M h d ( CT) = M 0 C 2 c 2 Td T, (20a) T E h = d E h = 1 2 M h ( CT). (20b) 0 (18), ( ) p h = E h V = 3 2 h RT = 0 ( CT) 2 2 c 2, (21) h =CTΠc 2,.,, p = p 0 + p h, p h ν p 0. (22),,,, ,,. ( ) q = 0 CTu h, (23) q, 0 CT, u h., q h = q c 2 = 0 CT c 2 u h = h u h, (24) q h, u h.,,,.,, 9 h + div( 9 h U h ) = 0. (25) t (25).,1 ( T 1 > T 2 ), (25) 1 h u h = q h = const, (26) ( ), h,, u h2 u h1 = h1 = T 1, h2 T 2 u h2 > u h1, (27)., ( ) [32 ] 9 U h h + U h U h + P h + f h = 0, (28),,,., ( ),,. (23) 9 u h 9 u h 9 x = = 1 9 q q 9 T - 0 CT 0 CT 2, (29a) 1 9 q 0 CT 9 x - q 9 T 0 CT 2 9 x. (29b) 9 p h 9 x = 0 C 2 T 9 T 9 x = h C 9 T 9 x. (29c) c 2 ().

5 7 : 4277,,,. f = u h, (30),(29), (30) (28), K C h K 9 q Kq 9 T 0 C 2 - T 0 C 2 T 2 - Kq 2 9 T 2 0 C 3 T 3 9 x Kq 9 q C 3 T 2 9 x =K 9 T 9 x - Kc C 3 T 2 q. (31a) CV, K 0 C 2 T = a = (32) CT,(31a) 9 q t 9 ( 0 CT) - u h = - K 9 T 9 x - Kc C 3 T 2 q, + t u h 9 q 9 x - u h 9 ( 0 CT) 9 x (31b),,,, (31b). ( ) ( ), (31) ( ),. 5131,,,,., (28) p h + f h = 0, (33a). (30) (31), (33a) K d T d x + K 2 h Cc 2 q = 0. (33b),, = K c2 C 2 h, (34) (31b) () 9 q 9 ( 0 CT) t - u 9 h t = K 9 T 9 x + t u h 9 q 9 x - u h 9 ( 0 CT) 9 x - q. (31c), (31c) q = - K d T d x - q K = d T d x. (35) :.,,, ( ) (28) (,, )., () ( 1),, CV,,(31c),,,,. C u d u h h d x = - K d T d x - q, (36a), K d T d x + q = Kq 2 d T 2 0 C 3 T 3 d x, q = q C 3 T 3 K d T d x. (36b) (36c), q 2. K a = C 3 T 3 K, q = - K a d T d x, (36d)

6 q2 2 0 C 3 T 3.,, T 1 = 400 K, T 2 = 300 K, q = 10 6 WΠm 2, q2 2 0 C 3 T ν 1,,.,,,,,,, (36d)., 20 K,70 K, K = 5000 WΠmK, m., WΠm 2,,,,. (36c) 2.,,,,... Onsager [33 ], Kaliski,CV [34 ].,,,, ( ),( (31c) ),, (31c),q T,. (1) (31c) CV,, ( ) ( ). (31c) 9 2 T T 2 qk 9 2 T + t t 2 0 C 3 v T 2 9 x = 1 - K 9 2 T 2 0 C 3 v T 3 (37) 0 C v t 9 x 2 q 2 CV (2),,. CV,, 3, y z, x L, T 0,T w., :x 3 = xπl,t 3 = TΠT 0, t 3 = tπ CV,(1),,(2), (2),,,, s, 3 T 3 w = 013,

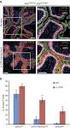
7 7 : 4279 CV 4,4 (a), (b), (c) (d) 013,016, (a), CV,,CV,,,.,, 4 (b),, 4 (c) (d)., CV,, [11,12 ], CV,,, CV,CV (), (, ),.,,,.,CV,. 21,,.,, ( ). 31,,,,,

8 ,.,,,,,,. 41,,. CV,,. [1] Fourier J 1955 Analytical Theory of Heat ( New York : Dover Publications) [2] Eckert E R G, Drake R M; Hang Q ( Trans) 1983 Heat and Mass Transfer (Beijing : Science Press) (in Chinese) [, ; () 1983 ( : ) ] [3] Dampier W C 2001 A History of Science and Its Relatios with Philosophy and Religion ( Guilin : Guangxi Normal University Press) [ ; 2001 ( : ) ] [4] Cattaneo C 1948 Atti. Sem. Mat. Fis. Univ. Modena 3 3 [5] Vernotte P 1958 C. R. Acad. Sci [6] Gurtin M E, Pipkin A C 1968 Arch. Ration Mech. Anal [7] Coleman B D, Fabrizio M, Owen D R 1982 Arch. Ration Mech. Anal [8] Tavernier J 1962 C. R. Acad. Sci [9] Guyer R A, Krumhansl JA 1966 Phys. Rev [10] Maurer M J 1969 J. Appl. Phys [11] Bai C, Lavine A S 1995 J. Heat Transfer [12] Kgrner C, Bergmann H W 1998 Appl. Phys. A [13] Tzou D Y 1995 ASME J. Heat Transfer [14] Tzou D Y 1997 Macro to microscale heat transfer : the lagging behavior (Washington : Taylor & Francis) [15] Xu Y S, Guo Z Y 1995 Int. J. Heat Mass Transfer [16] Masuda K, Okuma O, Nishizawa T, Kanaji M, Matsumura T, Tang D W, Araki N 1996 Int. J. Heat Mass Transfer [17] Antaki P J 1998 Int. J. Heat Mass Transfer [18] Cho C J, Juhng W N 2000 J. Korean Phys. Soc [19] Fan Q M, Lu W Q 2002 Int. J. Heat Mass Transfer [20] Zhang H W, Zhang S, Guo X, Bi J Y 2005 Int. J. Solids Struct [21] Brorson S D, Fujimoto J G, Ippen E P 1987 Phys. Rev. Lett [22] Tang D W, Araki N 1996 Int. J. Heat Mass Transfer [23] Lepri S, Livi R, Politi A 1997 Phys. Rev. Lett [24] Narayan O, Ramaswamy S 2002 Phys. Rev. Lett [25] Maruyama S 2002 Physica B [26] Livi R, Lepri S 2001 Nature [27] Shen X J 1985 Probe into the Essence of Heat (Beijing : Beijing Publishing House) (in Chinese) [ 1985 ( : ) ] [28] Einstein A, Lorentz H A, Minkowski H, Weyl H 1952 The principle of relativity (New York : Dover Publications) [29] Guo Z Y 2006 J. Eng. Thermophys (in Chinese) [ ] [30] Tien C L ; Gu Y Q ( Trans) 1987 Statistical thermodynamics (Beijing : Tsinghua University Press) (in Chinese) [; 1987 ( :) ] [31] Du L J, Xi T G; Wang M H ( Trans) 1987 Introduction to solid thermophysical properties : theory and measurement (Beijing : China Metrology Publishing House) (in Chinese) [,; 1987 :( : ) ] [32] Guo Z Y, Cao B Y, Zhu H Y, Zhang Q G 2007 Acta Phys. Sin (in Chinese) [ ] [33] Onsager L 1931 Phys. Rev [34] Kaliski S 1965 Bull. Acad. Pol. Sci. XIII 211

9 7 : 4281 A general heat conduction law ba sed on the concept of motion of thermal ma ss Guo Zeng2Yuan g Cao Bing2Yang ( Department of Engineering Mechanics, Tsinghua University, Beijing , China) (Received 1 November 2007 ; revised manuscript received 5 December 2007) Abstract Based on the mass2energy relation in Einstein s relativity theory, thermal energy has equivalent mass, which is referred to as thermal mass. The concepts of phonon gas mass in solids and thermon gas mass in gases are then introduced. Based on these concepts, the momentum conservation equation, including driving force, resistance and inertial force, for the thermal mass motion is established using Newtonian mechanics. Since the heat conduction is just the motion of the thermal mass (phonon gas or thermon gas) in a medium, the momentum conservation equation for thermal mass is a general heat conduction law which can unify the description of heat conduction under various conditions. The momentum conservation equation reduces to Fourier s heat conduction law when the heat flux is not very high so that the inertial force of the thermal mass can be ignored. For micro2πnano2 scale heat conduction, the heat flux may be very high and the inertial force due to the spatial velocity variation can not be ignored. Therefore, the heat conduction deviates from Fourier s law, i. e. non2fourier phenomenon takes place even under steady state conditions. In such cases, the thermal conductivity can not be calculated by the ratio of the heat flux to the temperature gradient. Under ultra fast heat conduction conditions, the inertial force of the thermal mass must be taken into consideration and the momentum conservation equation for the thermal mass motion leads to a damped wave equation. Compared with the CV model, the general heat conduction law includes the inertial force due to the spatial velocity variation. Thus the physically impossible phenomenon of negative temperatures induced by the thermal wave superposition described by CV model, is elliminated, which demonstrates that the present general law of heat conduction based on thermal mass motion is more reasonable. Keywords : Fourier heat conduction law, general heat conduction law, motion of thermal mass, non2fourier heat conduction PACC: 4410, 6370, 0340G g E2mail : edu. cn