Introduction Introduction
|
|
|
- Ονησίφορος Παπακωνσταντίνου
- 6 χρόνια πριν
- Προβολές:
Transcript
1 EW OOLS FOR BAYESIA IFERECE: HE VARIAIOAL AROXIAIO olaos. Galatsanos ECE Dept. Unv. of atras, Greece. Dmtrs zas CS Dept. Unv. of Ioannna, Greece. Outlne Introducton Bayesan Inference Bascs A Estmaton Conugate Dstrbutons Graphcal odels E Algorthm An Alternatve Vew of the E he Varatonal E framewor Examples Lnear Regresson Blnd Image Deconvoluton Image Restoraton. Constraned. Bounded Gaussan xture odelng Conclusons Introducton Introducton homas Bayes (7 76, left, frst dscovered Bayes theorem n 764. However, Bayes n hs theorem used unform prors. erre Smon Laplace (749 87, rght, unaware of Bayes wor, dscovered the same theorem n more general form n a memor he wrote at the age of 5 and showed ts wde applcablty. (a (b (a: # of papers /year n IEEE Journals E Algorthm (b: # of papers /year n IEEE Journals Varatonal ethodology Applcatons of Varatonal Approxmaton. xture odelng of pdfs & Clusterng. ICA & CA Analyss 3. Learnng RFs 4. Dynamc Systems odelng 5. Image Recovery 6. Vsual racng 7. Dgtal Communcatons 8. Acoustcs and Speech rocessng 9. Learnng from Data Bases Sample of US atents that Use US atent Varatonal relevance vector machne, Issued on Aprl, 5 US atent Varatonal nference engne for probablstc graphcal models, Issued on Aprl 9, 3 US atent 8567 Removng camera shae from a sngle photograph US atent ethod and apparatus for denosng and deverberaton usng varatonal nference and Strong Speech odels, Issue date: Jan 4, 6. US atent ethod for learnng swtchng lnear dynamc system models from data, Issue date: Jul 8, 3 US atent ethod of speech recognton usng varatonal nference wth swtchng state space models, Issue date: Aug 6, 5. US atent 4/6548 Varatonal nference and learnng for segmental swtchng state space models of hdden speech dynamcs, US atent 4/5493 A Systems and methods for tractable varatonal approxmaton for nference n decson graph Bayesan networs, Issue Feb 7, 7 ublcaton number US 7/8398 Data securty and ntruson detecton, ublcaton number: US 5/7657 A Dagnostc marers of mood dsorders and methods of use thereof ublcaton number: US 7/3339 A opulaton sequencng ublcaton number: US 6/846 A layer ranng wth partal nformaton ublcaton number: US 7/6578 A eam matchng ublcaton number: US 7/9854 A Detectng humans va ther pose
2 Bayesan Inference Bascs Estmaton > arameter Observatons: x arameters: Lelhood Functon: p x; axmum Lelhood Estmaton ( ( parameter ( ˆ arg max p x; L Bayesan Inference Bascs Inference > Random Varable Fnd osteror p ( x osteror ORE nformaton than pont estmate E( x SE estmate Var x accuracy of estmates ( Bayesan Inference Bascs Hdden Varables z: Descrbe data generaton mechansm (graphcal model lns between observatons and parameters Easy to compute p( x z Introduce prors p( z; Bayesan Inference Bascs Fnd Lelhood, argnalze Hdden Varables ( ; (, ; ( ; ( ; p x p x z dz p x z p z dz Fnd osteror p x z p z x; ( ( ; p( z; p( x; In most cases of nterest Cannot argnalze Bayesan Inference Bascs an effort n Bayesan Inference technques bypass or approxmate margnalzaton ntegral. Random samplng methods onte Carlo Determnstc approxmatons Laplace Varatonal A Estmaton Defned as mode of posteror : ˆ A argmax p x Based on Bayes theorem p( x p( p( x p x Can be found as: ( ˆ A argmax px ( p( (
3 A Estmaton o need for p( x no margnalzaton A Estmator uch easer to fnd ode of posteror o nformaton about shape of posteror Uses Bayes heorem, however posteror not found Aoor an s Bayesan Inference Conugate rors Fnd pror whch allows closed form margnalzaton of hdden varables ( (, ( ( p x p x z dz p x z p z dz Conugate rors Example #: μ hdden varable ( μ; σ ( ; μσ,, ( μ; μ, σ ( ; μ, σ ( ; μ, σ, σ ( μσ ; ( μ; μ, σ μ px x p x px px p d Conugate rors px ( μσ ; f ( μ exp ( μ μx σ p ( σ ( μμ ;, σ g( μ exp ( μ μμ px μ; σ, and pμμ ;, σ conugate ( ;, w.r.t. to μ both p x μ; σ and p μ μ σ have the same form (Gaussan. ( ( Conugate rors argnalzng μ possble (Gaussan Integral: ( ; ( (,, ; ;, p x μ σ σ p x μ σ p μμ σ dμ x; μ, + σ σ osteror: σx + σ μ p( μ x; σ, μ, σ μ;, + σ σ + σ σ Conugate rors Example #: a hdden varable ( ( p x a x;, a, b b ca exp p( abc ;, Gamma( abc ;, Γ ( ca ( b
4 Conugate rors p( x a and p ( abc ;, w.r.t. to a both have the same form (Gamma. / ax p( x a f ( a a exp p abc g a a ac b ( ;, ( exp( p( x a ( and p abc ;, conugate Conugate rors argnalze a possble / Γ ( b + / b x p( x; b, c c c+ Γ( b π b/ Can wrte as Student s t wth ν, b λ b/ c / Γ ( ν /+ / λ λx px ( ; λν, Stx ( ; λν, + Γ( ν/ πν ν osteror x p( a x; b, c Gamma a; b+, c+ ν // Lelhood Conugate ror Dstrbuton Conugate rors osteror Dstrbuton ( σ ab Gamma σ + n /, + n ( / μ n Σ ν V Wshart ( Σ ν + n, V+ ( X ( μ X μ ( X μσ, ( μμ, Σ μ ( Σ + nσ ( Σ μ + nσ x,( Σ + nσ ( x μ σ, (, Gamma(, X μσ Wshart (, ultn ( X π Dr( π a n + Dr( π a X Graphcal odels Represent dependences between rv.s n a statstcal model Graph nodes represent rv.s and edges dependences Drected and undrected graphs. Undrected arov Random Felds Rest of presentaton: drected, no cycles graphs Graphcal odels x rv assocated node s, π ( s parents of s s ( p xs x π ( s condtonal pdf Graphcal odels Example: pabcd,,, ; pa; pba; pca ; pdbc, ; ( ( ( ( 3 ( 4 Jont pdf over all varables p( x p( xs x π ( s s
5 E Algorthm x- observatons, z hdden varables, -parameters. Defne: old Q, E ln p x, z; old ln p( x, z; p( z x; dz ( ( old pzx ( ; E Algorthm old. Intal selecton. E step: Evaluate p(z x; old new 3. step: Evaluate new arg max Q, old ( 4. Chec for convergence parameters of log lelhood, f not satsfed, go to. An Alternatve Vew of the E Algorthm Can wrte: ln p( x; F( q, + KL( q p pxz (, ; Fq (, qz ( ln dz qz ( pz ( x; KL( q p q( zln dz qz ( q( z any pdf, KL( q p Kullbac Lebler Dvergence An Alternatve Vew of the E Algorthm *** KL( q p ln px ( ; Fq (, ln px ( ; Fq (, when KLq ( p or qz ( pz ( x; An Alternatve Vew of the E Algorthm *** OLD Substtute qz ( pz ( x ; Can wrte: OLD Fq (, pz ( x; ln pxz (, ; dz Same as before: OLD OLD p( z x; ln p( x z; dz OLD Q(, ant [ ] p ( z x ( OLD Q, E ln p ( x, z; ; OLD he Varatonal E framewor *** Assume p(z x; unnown F(q, functonal n terms of q(z Varatonal E Varatonal E step: Varatonal step: OLD ( EW ( q EW ( z max F q, EW arg max F q,
6 he Varatonal E framewor *** Key ssue: maxmze F(q, w.r.t. q(z? Assume parametrc form for q(z q(z approxmates unnown posteror p(z x ln p( x; F( q, + KL( q p max F(q, >mn KL(q p ean Feld Approxmaton*** Assumpton: q(z factorzes qz ( q( z ean Feld approxmaton, statstcal physcs ean Feld Approxmaton*** hen optmal factor q( z s: wth exp ln pxz (, ; exp ln pxz (, ; q ( z ln p( xz, ; ln pxz (, ; qdz dz Conugate Exponental models ror dstrbutons belong to the exponental famly p( X Y exp φ( Y u( X + f( X + g( Y Graphcal model wth conugate prors at each level hdden z, parents π ( z p ( z π ( z conugate to p( π( z π( π( z ( ( ( p z ππ ( ( z p z π( z p π( z ππ ( ( z dπ( z Conugate Exponental models p(x z,p(z z,p(z exponental dstrbutons p(z conugate to p(z z p( x z p( x z p( z z dz (x z conugate to p(z z z p( z p( z z p( z dz Cannot evaluate margnal z ( ( ( p x p x z p z z p( z dzdz x Conugate Exponental models ractable Varatonal computatons qz ( exp ln pxz (, ; ln qz ( ln px ( z; + ln pz ( z; q z ( ln qz ( ln pz ( z; + ln pz ( ; q( z
7 Lnear Regresson Examples Lnear Regresson Observatons at t n fnd y(x tn y( xn + ε n, n,, Sgnal y(x modeled by Lnear Regresson y( xw ; wmφm( x m Observaton model t y ( x ; w + ε, Φ X desgn matrx n n n n t Φw + ε φ φ φ ( φ x φ x Φ (,,, (,, ( m m m p β p Lnear Regresson Gaussan addtve nose ( ε ( ε, I Lelhood of observatons (; tw, β ( t Φw, β I Lnear Regresson: Least Squares (w parameters Graphcal odel Lnear Regresson: arameter Estmaton nmze mean square error E [ ] LS ( w t Φw tn y( xn; w n Soluton w LS ( ΦΦ Φt β t Φw axmum Lelhood Estmaton wl p t w t Φw, I arg max ( ;, β arg max ( β w w
8 Lnear Regresson: roblems wth Least Squares (w parameters axmum Lelhood Lmtatons: observatons parameters to estmate, >> Otherwse ΦΦ Ill condtoned L estmates large varance Assume constrants on the parameters w Bayesan: Use pror dstrbuton p(w Bayesan Lnear Regresson: odel (w Gaussan d dstrbuted Gaussan weght pror p w α wm, α ( ; ( m Why Gaussan? Conugate to lelhood Bayesan Lnear Regresson: Inference osteror gven by Bayes s law p( t w; β p( w; α p( w t; αβ, p( t; αβ, Can be found n closed form p( w t; αβ, ( w μ, Σ μ β ΣΦ t Σ ( βφ Φ+ αi Bayesan Lnear Regresson: arameter Estmaton axmum Lelhood αβ, { β I α ΦΦ t ( β I α ΦΦ t} ( αl, βl argmn p( t; α, β p( t w; β p( w; α dw argmn log αβ, ot straght forward constraned optmzaton because α>, β>. Resort to E algorthm! Bayesan Lnear Regresson: E Algorthm Observatons t, parameters α, β; hdden varables w. Key for the applcaton of E: p(w t explctly nown E step: p(w t; α, β obtaned, nference of hdden varables step: L estmates of parameters Bayesan Lnear Regresson: E algorthm ( t Q ( twαβ ln p( twαβ ( t ( t p( wt ; α, β, ;,, ;, ln p( t w; αβ, p( w; αβ, ( t ( t p( wt ; α, β ( α ( t Φw α α ( w Q ( tw, ; αβ, β ln β t Φw + lnα w ( t β ln β + ln ( tr ( ( t ( t μ tr Σ ( t β ( t ( t Q ( tw, ; αβ, ln β t Φμ + [ Φ Σ Φ] α + ln α + [ ]
9 Lnear Regresson: E algorthm, E step E step: Evaluate p(w t;α (t,β (t (μ (t,σ (t Σ ( β Φ Φ+ α I μ ( t ( t ( t β Σ Φ t ( t ( t ( t Bayesan Lnear Regresson: arameter Estmaton: step step ( t ( t ( t ( α +, β + argmax( αβ, Q ( tw, ; α, β ( t Q, ;, ( ( t [ ( t μ tr Σ ] ( ( t [ ( t t Φμ tr ΦΣ Φ] ( twαβ + α α ( t Q ( tw, ; αβ, + β β ( t α + μ ( t ( t + tr[ Σ ] ( t β + ( t ( t t Φμ + tr[ ΦΣ Φ] Sparse Bayesan Lnear Regresson Lmted model: w d How to select bass functons? Sparse Lnear odel Consder many bass functons Estmatons use only few bass functons Advantages Small varance (good generalzaton Fast Evaluaton of estmaton Sparse Bayesan Lnear Regresson: ror Dstrbuton ew ror: w not dentcally dstrbuted ( w α ( m, m m p w α parameters to estmate, observatons Use Conugate Hyperprors p( α; a, b Gamma( α a, b m p( β; c, d Gamma( β c, d m Sparse Bayesan Lnear Regresson: ror Dstrbuton Graphcal odel: w, α hdden varables, a,b,c,d, parameters Sparse Bayesan Lnear Regresson: ror Dstrbuton rue weght pror s Student s t p( wa ;, b p( w α p( α; a, b dα m m m w, α Gamma α a, b dα ( ( m m m m St( w λν, m
10 Sparse Bayesan Lnear Regresson: osteror: p( t w, β p( w α p( α p( β p( w, α, β t p( t Cannot compute p( t p( t w, β p( w α p( α p( β dwdαdβ Varatonal ean Feld Approxmaton p( w, α, β t q( w, α, β q( w q( α q( β Sparse Bayesan Lnear Regresson: ln q( w ln p( t, w, α, β q α q ( ( β ln pt ( w, β p( w α q α q ( ( β ln pt ( w, β + ln p( w α q( α q ( β β ( t Φw ( tφw α mw m m α q q β ( ( β [ tt tφw + wφφw ] α m m w m w ( β Φ Φ + A w β w Φt+ const w Σ w w Σ μ+ const q( w ( w μσ, Σ β Φ Φ+ A μ β ΣΦ t ( Sparse Bayesan Lnear Regresson: ln q( α ln p( twα,,, β q( w q( β ln p( w α p( α w + a b a w + b q( w ln αm αm m ( lnαm αm m m m m ln m m m α α m m lnαm b mαm const m m a + q( α Gamma( α a, b a a+ / m m m bm b+ wm Sparse Bayesan Lnear Regresson: ln q( β ln p( twα,,, β q( w q( α ln p( t w p( β q( w q( α ln β β t Φw + ( c ln β dβ c + lnβ + d β+ const t Φw c ln β d β q( β Gamma( β c, d c c+ / d d + t Φw Sparse Bayesan Lnear Regresson: Fndng the requred expectatons q( β Gamma( β c, d, β c / d q( α Gamma( α a, b, α a / b m m m m m q w ( w ( w μσ,, m μm + Σmm { } t t t t t Φw t + tr ΦΣΦ + μ Φ Φμ t Φμ Sparse Bayesan Lnear Regresson: arameter Estmaton arameters a,b,c,d? Use fxed values that defne unnformatve prors Estmate parameters n Varatonal step For fxed a,b,c,d terate only between VE step for q(α, q(β and q(w
11 Lnear Regresson Example Lnear Regresson Example orgnal observatons L(SE7.4e- Bayesan(SE4.9e-.5 Sgnal estmate Bass functons. Varatonal(SE3.7e- RVs( Blnd Image Deconvoluton Examples Blnd Image Deconvoluton Unnown: Blur SF h rue Image f g h f + n g Hf + n Fh + n Convoluton Observed Image g Blnd Image Deconvoluton Restored Image Blnd Image Deconvoluton Unnown quanttes (f,h twce than nown (g ropertes that model should mpose: SF: smooth, lmted support Image: smooth, preserve edges ose: robustness Blnd Image Deconvoluton: ose odel Robust nose model Student s t pdf ( n β (, p n β β β p( β Gamma( β a, b pn ( pn ( β p( β dβ Student's t
12 Blnd Image Deconvoluton: SF odel SF: Sparse Lnear model Bass functons are Gaussan ernels hx ( wφ ( x h Φw φ ( x K( x, x Φ, K( x, x Sparseness weght pror α α p( w α ( w, α, p( α Gamma( α; a, b p( w p( w α p( α dα Student's t Blnd Image Deconvoluton: Image odel Drectonal mage dfferences ε ( x, y f( x, y f( x+, y ε ( xy, f( xy, f( xy, + ε γ γ γ ( ( p( γ Gamma ( γ a, b p( f γ f, ( Q ΓQ p( ε, γ ( Jont pdf Blnd Image Deconvoluton: Graphcal odel p( gf,, wαβγ,,, ; p( g f, w, β p( f γ p( w α p( β p( γ p( α Blnd Image Deconvoluton: Varatonal Bound ean feld approxmaton q( fwαβγ,,,, q( f q( w q( α q( β q( γ axmzaton of Varatonal Bound results n: log q( f log p( g, f, w, αβγ,, ; q( w q( α q( β q( γ log q( w log p( g, f, w, αβγ,, ; log q( α log p( gf,, wαβγ,,, ; q( w q( f q( β q( γ log q( β log p( gf,, wαβγ,,, ; q( w q( α q( f q( γ log q( γ log p( gfwαβγ,,,,, ; q ( w q ( α q ( f q ( β q( f q( α q( β q( γ Blnd Image Deconvoluton: Fnd approxmate posteror q(f ean Feld Optmzaton log q( f ( ΦWf g B( ΦWf g f Q ΓQf ( w q( β q( γ q f ( Φ W BWΦ + Q ΓQ f+ f Φ W Bg ( w q( β q( γ q f ( Φ W BW Φ + Q Γ Qf + f Φ W B g Completng Square results n q( f ( f μ f, Σ f μ Σ fφ < WB> g f Σ Φ < WBW> Φ + Q < Γ > Q f ( Blnd Image Deconvoluton: Approxmate posteror q(w Smlar calculatons log q( w ( FΦwg B( FΦwg w Aw q( f q( β q( α w ( Φ FBFΦ+ A w+ w Φ FBg+ const q( w ( w μ, Σ w ( w w w < > μ Σ Φ FB g Σ Φ < FBF> Φ+< A > w
13 Blnd Image Deconvoluton: Approxmate posteror q(α Based on the mean feld approxmaton log q( α log p( w α + log p( α q( w logα α w + ( a α logα b α α q( w ( a log α α ( b w α const α Whch mples α α q( α Gamma( α a, b α α a a + / + < > b α α b w Blnd Image Deconvoluton: Approxmate posterors q(β and q(γ Smlarly we get β β q( β Gamma( β a, b K γ γ q( γ Gamma( γ a, b β β a a + / β β b b + < nn > n FΦwg γ γ a a + / b γ γ b + ( < > ( Q ff Q Blnd Image Deconvoluton: Statstcs of Approxmate osterors Blnd Image Deconvoluton: Statstcs of Approxmate osterors ae dagonal and crculant approxmatons hs results n Blnd Image Deconvoluton: Overall V E Algorthm Fx parameters { a α, b α, a β, b. β a γ, b γ } to yeld unnformatve hyperprors (no Varatonal step. Blnd Image Deconvoluton: Example SF: Square 7x7, 4db nose Iterate between estmates of statstcs of q(f, q(w, q(α, q(β and q(γ (only Varatonal E step.
14 Blnd Image Deconvoluton: Examples true V StStSt Example: Image Restoraton (Constraned * G. Chantas,. Galatsanos, A. Las and. Saunders, "Varatonal Bayesan Image Restoraton * Based on a roduct of Dstrbutons Image ror", IEEE rans. on Image rocessng, to appear. (avalable on lne Image Restoraton Image Restoraton: roblem Defnton Known SF h: ose Observed Degraded Image g Imagng odel ( pxels g h* f + n Hf + n Convoluton * rue Image f + g: ( : Degraded (Observatons h: (,H:( : ont Spread Functon (nown f: ( : Orgnal Image (unnown n~, β I : ose (unnown ( Image Restoraton: f arameter Lelhood of Observatons p( g; f, β ( Hf, β I ( ˆ f H H H g { p ( β } fˆ arg max g; f, arg mn g Hf Graphcal odel f roblematc too many parameters g β Image Restoraton: f arameter Example f SR log n Double crcled observed r.v. SR~8dB SR~dB
15 Image Restoraton: Bayesan Inference (f: hdden r.v., Image Restoraton: Bayesan Inference (f: hdden r.v. Error from Local Lnear redctor fˆ ( f ( ( f( + f( + ε ( Assume Gaussan..d. redcton Errors ( ε ( (, α p ( ε ( ε ( p p Smultaneously Autoregressve (SAR ror Qf ε, Q Operator that descrbes ε ff -ˆ p( f; a α exp α f Q Qf Graphcal odel a f g Double crcled observed rv β Image Restoraton: Bayesan Inference (f: hdden r.v. Image Restoraton: Bayesan Inference (f hdden r.v. Observaton Lelhood (computed analytcally ( β ( β ( p g;, a p g f; p f; a df osteror of Hdden (computed analytcally ( f g;, β ( μf g, Σf g p a Bayesan Inference va E Small α/β Amplfes ose Large α/β Smoothes Edges Image Restoraton: Spatally Varyng Bayesan odel Image Restoraton: Spatally Varyng, Bayesan Inference Spatally Varyng ( ε ( (, Use many ε,, n pror Qf p a α hdden varables Bayesan Inference Conugate pdf p ( α Gamma( a ; αβ, roduct ror p( f a p f a, p f a exp f QAQf ( ( ( Z a ( (, ( ( A dag a a a ror: Enforces many propertes smultaneously
16 Image Restoraton: Spatally Varyng Bayesan Inference Graphcal odel α,,β α,β α,β α α α Image Restoraton: Spatally Varyng, Bayesan Inference Dffculty: Compute normalzaton of pror Z ( a K det QAQ Q,A (Νx, 5-6 f β g Image Restoraton: Spatally Varyng, Bayesan Inference Image Restoraton: Spatallyvaryng, Bayesan Inference Change Observatons Doman QgQHf+Qn, y Hε +n,,..., Hdden Varables: l [ ε, ε ε ], a [ a, a a ] [ ε (, ε ( ε ( ], a [ a (, a ( a ( ] ε ε l l l l l l l β v λ α ε β v λ α ε... β v λ α ε ε κ Q f,,.. y y y Image Restoraton: Spatally Varyng Bayesan Inference ror on ε O dffculty normalzng p( ε a p( ε ( a(, ( ( ε ( (; λ ε (;, λ ( ν ν ( (; ν (;, p a a p a Gamma a Cannot margnalze hdden varables Resort to Varatonal ethodology Image Restoraton: Spatally Varyng, Bayesan Inference osterors ean Feld Approxmaton ( ε a ( ε ( a q, q q,,..., axmze Var. Bound q( ε ( μ, Σ, μ β ΣHg, Σ HH+ QAQ ( β λ ew problem: Dfferent f for each μ
17 Image Restoraton: Constraned Defne Constraned osteror q( ε ( QmQRQ, Consstent wth ( ( ( ( ε Qf, m E f, R E fm fm axmze the Varatonal Bound w.r.t. m and R Image Restoraton: Constraned t+ ( t+ ( t VE-step: q, arg max F q α,, q ( α, [ Rm] ( ( α ( t+ ( t+ ( t+ F q ( α ( ( ( ( ( V-step: arg max,,,, [ β, λ,..., λ, ν,..., ν ] Image Restoraton: Constraned VE Step Fq (, q( ε; q( a log p( y, ε, a ; dd ε a q( ε; q( a log q( ε; q( a dε da, F F ( F ( q( ε; q( a log p( y ε; p( ε a; dεda q( ε; log q( ε; dε. Image Restoraton: Constraned q( ε ; q( a log p( y ε; p( ε a; dεda - β( Hε -y Q Q ( Hε -y λε Aε q( ε ; q ( a β λ trace β + λ q ( ε; log q ( ε; d ε logdet R Image Restoraton: Constraned ˆ trace β + λ logdet F HHR ( QAQR R R R ˆ β λ ˆ HH+ QAQ R R βhh+ λqaq F ( m βrh g m Image Restoraton: Constraned q( a exp log p( y, ε, a q( ε ν + ν ( ( a exp a( λ( ( m ( + C (, a( ( ν ν ( ( (;, ( ( q a Gamma a + + λ m + C (, m Q m, and C Q RQ
18 Image Restoraton: Constraned V step ( t+ ( t+ df ( q ( a, log (,, ; ( (, d p y ε a t+ t+ q( ε ;, q ( a d d β ( Hm - g trace{ H HR } + t t t ( + ( + ( + ( ( (, a ( ( t m + C q ( a ( ( t λ + ( t ( t + ( t ( log a ( a ( ( t ( ψ ν + + ( t ( + + q q a a ( t ν ν log ν + ψ + log + d ψ ( x log Γ( x dx Image Restoraton: Constraned. Intalze, m statonary model.. Repeat untl convergence: VE step: Update, m and R, calculate m and C. Calculate expected value w.r.t. q(a (, needed for V step and the next VE step. V step: Update β, λ κ, ν κ,, Use m as restored mage estmate. Image Restoraton: Constraned Example: Image Restoraton (Bounded * Babacan, S.D.; olna, R.; Katsaggelos, A.K.; arameter Estmaton n V Image Restoraton * Usng Varatonal Dstrbuton Approxmaton, IEEE rans. on Image rocessng, Volume 7, Issue 3, arch 8 age(s: Image Restoraton: Bounded Imagng odel ( pxels g h* f + n Hf + n Observatons Lelhood ( β p( g/ f; β~ Hf, I Image Restoraton: Bounded V Based Image ror p( f a α exp( αv( f V( f ([ Qf] + ([ Qf], [ ] [ ] Qf f(, f(,, Qf f(, f(, Conugate Hyperpror p ( α; ab, Gamma( α; ab,
19 Image Restoraton: Bounded Graphcal odel a, b α f Image Restoraton: Bounded Dffculty n VE step log q( α log p( gf,, α; β, a, b q( f β Hf g α, ([ Qf] + ([ Qf] Due to q( f cannot Compute Expectaton β g Image Restoraton: Bounded Bypass dffculty: axmze a Lower Bound of Varatonal Bound w+ u Use Upper Bound: f( w w g( u, w, u> u Image Restoraton: Bounded Defne Functon w ([ ] ([ ] u + + p( f α ( f, α, u α exp a Qf Qf u p( gf,, α ; p( g/ f ( f, α, u p( α ( gfu,,, α ; Bound gets tght : f ( w g( u, w, u w Lower Bound of Varatonal Bound F( q q, ln d d F ( q, ( gfu,,, α ; b, ( f α f α, u q ( f, α Image Restoraton: Bounded VE Step q (, f q ( α argmax F (( q f, q( α, u, ( t+ ( t+ b ( t ( t q( f, q( α V Step Bound ghtenng u ( t+ b ( t+ ( t+ ( t arg max F ( q ( f, q ( α, u, u ( t b ( t ( t ( t + arg max F ( q + (, q + ( α, +, f u Image Restoraton: Bounded ghtest Bound f( w g( u, w, u w ([ ] ([ ] ( t+ + ( t+ q ( f ( t+ ( t+ ( t+ ( t+ Qμ + Qμ + QΣ Q + QΣ Q ( t+ ( t+ ( t+ u Qf Q f,, wth q ( f f; μ, Σ ( u Captures Local Spatal Actvty
20 Gaussan xture odels Example: Gaussan xture odels.4 p( x; π ( x; μ, Σ.35.3 odel any pdf.5. Soft clusterng.5. arameters.5 { π, μ, Σ},, axmum Lelhood Estmaton Dffcult arg max log π ( x; μ, Σ L Gaussan xture odels: Data Generaton echansm Introduce bnary hdden varable z. Select component z, z (,,,,,, z z p ( z; π π multnomal. Generate sample from selected component x p ( x ( x; μ, Σ Gaussan xture odels: Data Generaton echansm Jont pdf p( xz, ; p( x z p( z ( x; μ, Σ argnal pdf p( x p ; ( xz, ; z ( π z z π ( ;, x μ Σ Gaussan xture odels: osteror osteror (responsblty can be computed analytcally p( x z p( z π ( x μ, Σ z ( x ( ( p( z x; p x π l l x μ l, Σl π (, π ( l l x μ l, Σl x μ Σ z Gaussan xture odels: arameter Estmaton axmum lelhood L argmax log p( X; arg max log π ( x; μ, Σ Use E Smplfes optmzaton roved convergence Satsfes postvty constrants π >, π
21 Gaussan xture odels: arameter Estmaton E z z n p( XZ, ; ( xn; μ, Σ ( π n ( t Q(, log p( XZ, ; ( t p( zx ; ( t ( t zn π + zn xn; μ, Σ n n log log ( n Gaussan xture odels: arameter Estmaton E E step z z n ( t ( t ( t ( t ( t ( t π ( ( ( xn; μ, Σ π x t n; μ, Σ n ( t ( t ( t ( t ( t ( t z n π xn; μ, Σ π x n; μ, Σ step ( ( ( t ( t π + z n n μ ( t z ( t+ n n ( t z n n x n Σ z ( xn μ ( xn μ ( ( ( n n t ( + z ( t n n Gaussan xture odels: Lmtatons How many components? Ill condtoned covarance matrces 6 Varatonal Bayesan Gaussan xture odels 4 4 H. Attas, "A Varatonal Bayesan Framewor for Graphcal odels", roc. IS, pp. 9 6, I ress, Varatonal Bayesan Gaussan xture odels: ror Dstrbuton reat parameters as hdden varables h { Z, πμ,, } Introduce conugate prors p ( π α Dr( π,, Γ( α α α α π Γ( α Varatonal Bayesan Gaussan xture odels: ean Feld Approxmaton Exact Bayesan Inference Intractable Varatonal ean Feld Approxmaton q( h qz( Z qπ( π qμ( μ, q ( μ, q ( μ q ( μ μ p( μ ( μ ; μ, β ( ν d / ν, ν, d ν d/ / n/ d( d 4 p( V W( V exptr V π V Γ (( ν + /
22 Varatonal Bayesan Gaussan xture odels: Approxmate osterors Varatonal Bayesan Gaussan xture odels: Approxmate osterors Z n z n q ( Z r n d log rn logπ + log ( yn μ ( y n μ β β ( β / ( β q ( μ ( μ ; m, μ m μ + μ + β + β μ z nyn n q ( π Dr( π { λ } π λ + α z n n q ( W( ; η, U η + ν ( ( / ( β U Σ + β μ μ μ μ + + n( n ( n n Σ z y μ y μ Varatonal Bayesan Gaussan xture odels: Dscusson Select arameters that defne unnformatve prors (e.g. α / Advantages Dsallow sngular covarance matrce Bayesan model selecton Drchlet dstrbuton for mxng coeffcents π dsallows prunng of unnecessary components Varatonal Bayesan Gaussan xture odels: Removng the pror from the mxng weghts A. Corduneanu and C. Bshop, Varatonal Bayesan odel Selecton for xture Dstrbutons, roc. AI and Statstcs Conference, January Varatonal Bayesan G: Removng the pror from the mxng weghts reat π as parameter Include step to update π r n n π r n n r n rn r n r π exp log tr x x x μ + μ x + μμ n n n n n Advantage Elmnates rrelevant components Varatonal Bayesan G: Example
23 Incremental Varatonal Bayesan Gaussan xture odels Incremental Varatonal Bayesan Gaussan xture odels Solutons depend on: maxmum ntal number of components ntalzaton of component parameters specfcaton of the scale matrx V of p( Wshart(v, V Constantnopoulos C. and Las, A., "Unsupervsed Learnng of Gaussan xtures Based on Varatonal Component Splttng", IEEE rans. on eural etwors, vol. 8, no. 3, pp , 7. Incremental Varatonal Bayesan Gaussan xture odels Dvde components as fxed and free Restrct competton among free components only α + s s ( Γ α s π + p( π π π s Γ( α s s + π + s μ X Z π ~ Js π s Incremental Varatonal Bayesan Gaussan xture odels We start by tranng a G wth two components At each step: Select a component Set, V dλi, where λ the max egenvalue of Splt the component n two subcomponents Apply VB learnng consderng the two components as free Incremental Varatonal Bayesan Gaussan xture odels If the data n the regon of component suggest the exstence of more than two components then the two components wll be retaned Otherwse one of the two components wll be removed from the model Incremental Varatonal Bayesan Gaussan xture odels
24 Conclusons Varatonal Approxmaton ros:. Very Flexble ool. ce heoretcal ropertes 3. Gves ractable Algorthms 4. Appled to any roblems * Varatonal Approxmaton Cons:. ghtness of Bound. Sometmes Dffcult Calculatons
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Generalized Linear Model [GLM]
![Generalized Linear Model [GLM] Generalized Linear Model [GLM]](/thumbs/93/113885699.jpg) Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
CS 1675 Introduction to Machine Learning Lecture 7. Density estimation. Milos Hauskrecht 5329 Sennott Square
 CS 675 Itroducto to Mache Learg Lecture 7 esty estmato Mlos Hausrecht mlos@cs.tt.edu 539 Seott Square ata: esty estmato {.. } a vector of attrbute values Objectve: estmate the model of the uderlyg robablty
CS 675 Itroducto to Mache Learg Lecture 7 esty estmato Mlos Hausrecht mlos@cs.tt.edu 539 Seott Square ata: esty estmato {.. } a vector of attrbute values Objectve: estmate the model of the uderlyg robablty
5 Haar, R. Haar,. Antonads 994, Dogaru & Carn Kerkyacharan & Pcard 996. : Haar. Haar, y r x f rt xβ r + ε r x β r + mr k β r k ψ kx + ε r x, r,.. x [,
 4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
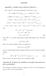 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Derivation for Input of Factor Graph Representation
 Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Dervaton for Input of actor Graph Representaton Sum-Product Prmal Based on the orgnal LP formulaton b x θ x + b θ,x, s.t., b, b,, N, x \ b x = b we defne V as the node set allocated to the th core. { V
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Symplecticity of the Störmer-Verlet algorithm for coupling between the shallow water equations and horizontal vehicle motion
 Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Supplementary materials for Statistical Estimation and Testing via the Sorted l 1 Norm
 Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ. ICA: συναρτήσεις κόστους & εφαρμογές
 8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
Neutralino contributions to Dark Matter, LHC and future Linear Collider searches
 Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
ΕΝΟΤΗΤΑ 2: Αυτόνομα Ευφυή Κινούμενα Ρομποτικά Συστήματα
 Ε.Μ.Π., ΣΗΜΜΥ, Ακαδημαϊκό Έτος 200-, 8ο Εξάμηνο Μάθημα: Ρομποτική ΙΙ. Διδάσκων: Κ.Τζαφέστας ΕΝΟΤΗΤΑ 2: Αυτόνομα Ευφυή Κινούμενα Ρομποτικά Συστήματα Σύνθεση αισθητηριακών πληροφοριών (data / sensor fuson)
Ε.Μ.Π., ΣΗΜΜΥ, Ακαδημαϊκό Έτος 200-, 8ο Εξάμηνο Μάθημα: Ρομποτική ΙΙ. Διδάσκων: Κ.Τζαφέστας ΕΝΟΤΗΤΑ 2: Αυτόνομα Ευφυή Κινούμενα Ρομποτικά Συστήματα Σύνθεση αισθητηριακών πληροφοριών (data / sensor fuson)
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
The one-dimensional periodic Schrödinger equation
 The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly
The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
2 Lagrangian and Green functions in d dimensions
 Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Exam Statistics 6 th September 2017 Solution
 Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ
 ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙΔΡΑΣΗ Μ.Β ΣΤΙΣ ΙΔΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ (ΔΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ΜΕΡΟΣ ΙΙΙ ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙΔΡΑΣΗ Μ.Β ΣΤΙΣ ΙΔΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ (ΔΙΑΦΟΡΙΚΗ) Probablty Densty Functon
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Estimators when the Correlation Coefficient. is Negative
 It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
Concomitants of Dual Generalized Order Statistics from Bivariate Burr III Distribution
 Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Proposal of Terminal Self Location Estimation Method to Consider Wireless Sensor Network Environment
 1 2 2 GPS (SOM) Proposal of Termnal Self Locaton Estmaton Method to Consder Wreless Sensor Network Envronment Shohe OHNO, 1 Naotosh ADACHI 2 and Yasuhsa TAKIZAWA 2 Recently, large scale wreless sensor
1 2 2 GPS (SOM) Proposal of Termnal Self Locaton Estmaton Method to Consder Wreless Sensor Network Envronment Shohe OHNO, 1 Naotosh ADACHI 2 and Yasuhsa TAKIZAWA 2 Recently, large scale wreless sensor
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
: Monte Carlo EM 313, Louis (1982) EM, EM Newton-Raphson, /. EM, 2 Monte Carlo EM Newton-Raphson, Monte Carlo EM, Monte Carlo EM, /. 3, Monte Carlo EM
 2008 6 Chinese Journal of Applied Probability and Statistics Vol.24 No.3 Jun. 2008 Monte Carlo EM 1,2 ( 1,, 200241; 2,, 310018) EM, E,,. Monte Carlo EM, EM E Monte Carlo,. EM, Monte Carlo EM,,,,. Newton-Raphson.
2008 6 Chinese Journal of Applied Probability and Statistics Vol.24 No.3 Jun. 2008 Monte Carlo EM 1,2 ( 1,, 200241; 2,, 310018) EM, E,,. Monte Carlo EM, EM E Monte Carlo,. EM, Monte Carlo EM,,,,. Newton-Raphson.
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
A Sequential Experimental Design based on Bayesian Statistics for Online Automatic Tuning. Reiji SUDA,
 Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng
Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Matrices and vectors. Matrix and vector. a 11 a 12 a 1n a 21 a 22 a 2n A = b 1 b 2. b m. R m n, b = = ( a ij. a m1 a m2 a mn. def
 Matrices and vectors Matrix and vector a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn def = ( a ij ) R m n, b = b 1 b 2 b m Rm Matrix and vectors in linear equations: example E 1 : x 1 + x 2 + 3x 4 =
Matrices and vectors Matrix and vector a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn def = ( a ij ) R m n, b = b 1 b 2 b m Rm Matrix and vectors in linear equations: example E 1 : x 1 + x 2 + 3x 4 =
V. Finite Element Method. 5.1 Introduction to Finite Element Method
 V. Fnte Element Method 5. Introducton to Fnte Element Method 5. Introducton to FEM Rtz method to dfferental equaton Problem defnton k Boundary value problem Prob. Eact : d d, 0 0 0, 0 ( ) ( ) 4 C C * 4
V. Fnte Element Method 5. Introducton to Fnte Element Method 5. Introducton to FEM Rtz method to dfferental equaton Problem defnton k Boundary value problem Prob. Eact : d d, 0 0 0, 0 ( ) ( ) 4 C C * 4
Suppose Mr. Bump observes the selling price and sales volume of milk gallons for 10 randomly selected weeks as follows
 Albert Ludwgs Unverst Freburg Department of Emprcal Research and Econometrcs Appled Econometrcs Dr Kestel ummer 9 EXAMPLE IMPLE LINEAR REGREION ANALYI uppose Mr Bump observes the sellng prce and sales
Albert Ludwgs Unverst Freburg Department of Emprcal Research and Econometrcs Appled Econometrcs Dr Kestel ummer 9 EXAMPLE IMPLE LINEAR REGREION ANALYI uppose Mr Bump observes the sellng prce and sales
Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).
![Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ). Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).](/thumbs/91/105872052.jpg) Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
8.323 Relativistic Quantum Field Theory I
 MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ
 ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙ ΡΑΣΗ Μ.Β ΣΤΙΣ Ι ΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ ( ΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ΜΕΡΟΣ ΙΙI ΜΟΡΙΑΚΟ ΒΑΡΟΣ ΠΟΛΥΜΕΡΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΕΠΙ ΡΑΣΗ Μ.Β ΣΤΙΣ Ι ΙΟΤΗΤΕΣ ΠΟΛΥΜΕΡΩΝ ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΚΑΤΑΝΟΜΗΣ ΜΟΡΙΑΚΟΥ ΒΑΡΟΥΣ ΣΥΝΑΡΤΗΣΗ ΠΙΘΑΝΟΤΗΤΟΣ ( ΙΑΦΟΡΙΚΗ) Probablty Densty Functon
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Noriyasu MASUMOTO, Waseda University, Okubo, Shinjuku, Tokyo , Japan Hiroshi YAMAKAWA, Waseda University
 A Study on Predctve Control Usng a Short-Term Predcton Method Based on Chaos Theory (Predctve Control of Nonlnear Systems Usng Plural Predcted Dsturbance Values) Noryasu MASUMOTO, Waseda Unversty, 3-4-1
A Study on Predctve Control Usng a Short-Term Predcton Method Based on Chaos Theory (Predctve Control of Nonlnear Systems Usng Plural Predcted Dsturbance Values) Noryasu MASUMOTO, Waseda Unversty, 3-4-1
CMOS Technology for Computer Architects
 CMOS Technology for Computer Architects Iakovos Mavroidis Giorgos Passas Manolis Katevenis Lecture 13: On chip SRAM Technology FORTH ICS / EURECCA & UoC GREECE ABC A A E F A BCDAECF A AB C DE ABCDAECF
CMOS Technology for Computer Architects Iakovos Mavroidis Giorgos Passas Manolis Katevenis Lecture 13: On chip SRAM Technology FORTH ICS / EURECCA & UoC GREECE ABC A A E F A BCDAECF A AB C DE ABCDAECF
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Conjugate Bayesian analysis of the Gaussian distribution
 Conjugate Bayesan analyss of the Gaussan dstrbuton Kevn P. Murphy murphyk@cs.ubc.ca Last updated October 3, 7 Introducton The Gaussan or normal dstrbuton s one of the most wdely used n statstcs. Estmatng
Conjugate Bayesan analyss of the Gaussan dstrbuton Kevn P. Murphy murphyk@cs.ubc.ca Last updated October 3, 7 Introducton The Gaussan or normal dstrbuton s one of the most wdely used n statstcs. Estmatng
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
Answer sheet: Third Midterm for Math 2339
 Answer sheet: Third Midterm for Math 339 November 3, Problem. Calculate the iterated integrals (Simplify as much as possible) (a) e sin(x) dydx y e sin(x) dydx y sin(x) ln y ( cos(x)) ye y dx sin(x)(lne
Answer sheet: Third Midterm for Math 339 November 3, Problem. Calculate the iterated integrals (Simplify as much as possible) (a) e sin(x) dydx y e sin(x) dydx y sin(x) ln y ( cos(x)) ye y dx sin(x)(lne
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
The ε-pseudospectrum of a Matrix
 The ε-pseudospectrum of a Matrix Feb 16, 2015 () The ε-pseudospectrum of a Matrix Feb 16, 2015 1 / 18 1 Preliminaries 2 Definitions 3 Basic Properties 4 Computation of Pseudospectrum of 2 2 5 Problems
The ε-pseudospectrum of a Matrix Feb 16, 2015 () The ε-pseudospectrum of a Matrix Feb 16, 2015 1 / 18 1 Preliminaries 2 Definitions 3 Basic Properties 4 Computation of Pseudospectrum of 2 2 5 Problems
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
ECE Spring Prof. David R. Jackson ECE Dept. Notes 2
 ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C
 DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
DERIVATION OF MILES EQUATION FOR AN APPLIED FORCE Revision C By Tom Irvine Email: tomirvine@aol.com August 6, 8 Introduction The obective is to derive a Miles equation which gives the overall response
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
THE SECOND WEIGHTED MOMENT OF ζ. S. Bettin & J.B. Conrey
 THE SECOND WEIGHTED MOMENT OF ζ by S. Bettn & J.B. Conrey Abstract. We gve an explct formula for the second weghted moment of ζs) on the crtcal lne talored for fast computatons wth any desred accuracy.
THE SECOND WEIGHTED MOMENT OF ζ by S. Bettn & J.B. Conrey Abstract. We gve an explct formula for the second weghted moment of ζs) on the crtcal lne talored for fast computatons wth any desred accuracy.
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Stochastic Finite Element Analysis for Composite Pressure Vessel
 * ** ** Stochastc Fnte Element Analyss for Composte Pressure Vessel Tae Kyung Hwang Young Dae Doh and Soon Il Moon Key Words : Relablty Progressve Falure Pressure Vessel Webull Functon Abstract ABAQUS
* ** ** Stochastc Fnte Element Analyss for Composte Pressure Vessel Tae Kyung Hwang Young Dae Doh and Soon Il Moon Key Words : Relablty Progressve Falure Pressure Vessel Webull Functon Abstract ABAQUS
Bayesian random effects model for disease mapping of relative risks
 Avalable onlne at www.scholarsresearchlbrary.com Scholars Research Lbrary Annals of Bologcal Research, 014, 5 (1):3-31 (http://scholarsresearchlbrary.com/archve.html) ISS 0976-133 CODE (USA): ABRBW Bayesan
Avalable onlne at www.scholarsresearchlbrary.com Scholars Research Lbrary Annals of Bologcal Research, 014, 5 (1):3-31 (http://scholarsresearchlbrary.com/archve.html) ISS 0976-133 CODE (USA): ABRBW Bayesan
Durbin-Levinson recursive method
 Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Latent variable models Variational approximations.
 CS 3750 Mache Learg Lectre 9 Latet varable moel Varatoal appromato. Mlo arecht mlo@c.ptt.e 539 Seott Sqare CS 750 Mache Learg Cooperatve vector qatzer Latet varable : meoalty bary var Oberve varable :
CS 3750 Mache Learg Lectre 9 Latet varable moel Varatoal appromato. Mlo arecht mlo@c.ptt.e 539 Seott Sqare CS 750 Mache Learg Cooperatve vector qatzer Latet varable : meoalty bary var Oberve varable :
Power allocation under per-antenna power constraints in multiuser MIMO systems
 33 0 Vol.33 No. 0 0 0 Journal on Councatons October 0 do:0.3969/.ssn.000-436x.0.0.009 IO 009 IO IO N94 A 000-436X(0)0-007-06 Power allocaton under er-antenna ower constrants n ultuser IO systes HAN Sheng-qan,
33 0 Vol.33 No. 0 0 0 Journal on Councatons October 0 do:0.3969/.ssn.000-436x.0.0.009 IO 009 IO IO N94 A 000-436X(0)0-007-06 Power allocaton under er-antenna ower constrants n ultuser IO systes HAN Sheng-qan,
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
