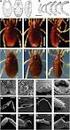
aab aabb aaabb aaaabb aaaabb aaaabb

Transcript

1 Κεφάλαιο 4 Γλώσσες & Γραμματικές Χωρίς Συμφραζόμενα Σύνοψη Η κλάση των Γλωσσών Χωρίς Συμφραζόμενα (ΓΧΣ) είναι εκφραστικά αρκετά ισχυρή, ώστε να επιτρέπει την περιγραφή γλωσσών, όπως οι γλώσσες προγραμματισμού, που δεν μπορούν να εκφραστούν ως κανονικές γλώσσες. Οι ΓΧΣ χαρακτηρίζονται από μία μορφή αναδρομικής δομής. Στο κεφάλαιο αυτό θα εισάγουμε ένα μηχανισμό παραγωγής ΓΧΣ, που θα τον ονομάσουμε Γραμματική Χωρίς Συμφραζόμενα. Θα δούμε πώς ακριβώς παράγονται οι συμβολοσειρές των ΓΧΣ από τις γραμματικές και θα αναφερθούμε σε διάφορα προβλήματα ορισμού γλωσσών με γραμματικές χωρίς συμφραζόμενα. Προαπαιτούμενη γνώση Για την κατανόηση του κεφαλαίου θα πρέπει ο αναγνώστης να έχει αφομοιώσει τις μαθηματικές έννοιες του Παραρτήματος I, καθώς και τους ορισμούς και τα αποτελέσματα από το Κεφάλαιο 2. Για καλύτερη εξοικείωση με τις αναπαραστάσεις γλωσσών, προτείνεται η διαδραστική προσομοίωση των εφαρμογών με το ανοικτό λογισμικό JFLAP. Στο Παράρτημα II γίνεται μία εισαγωγή στη χρήση του λογισμικού JFLAP. 135

2 136 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ 4.1 Γραμματικές Χωρίς Συμφραζόμενα Αρχίζουμε με ένα παράδειγμα. Ας θεωρήσουμε τους πέντε κανόνες αντικατάστασης που φαίνονται παρακάτω: AB A a A aa B b B bb Εδώ τα, A και B είναι μη τερματικά σύμβολα (μεταβλητές), είναι η αρχή (μεταβλητή εκκίνησης), ενώ τα a και b λέμε ότι είναι τερματικά σύμβολα. Αυτοί οι κανόνες χρησιμοποιούνται στην παραγωγή συμβολοσειρών, που αποτελούνται από τερματικά σύμβολα (δηλαδή στοιχείων του {a, b} ) με τον εξής τρόπο: 1. Αρχικά η τρέχουσα συμβολοσειρά αποτελείται από την αρχή. 2. Για μία μεταβλητή της τρέχουσας συμβολοσειράς μπορεί να χρησιμοποιηθεί ένας κανόνας αντικατάστασης στον οποίο αυτή εμφανίζεται στο αριστερό του μέρος. Τότε, στην τρέχουσα συμβολοσειρά αντικαθίσταται το συγκεκριμένο μη τερματικό σύμβολο με το δεξί μέρος του κανόνα. 3. Επαναλαμβάνεται το βήμα 2 μέχρις ότου η τρέχουσα συμβολοσειρά να αποτελείται μόνο από τερματικά σύμβολα. Ετσι, για παράδειγμα η συμβολοσειρά aaaabb μπορεί να παραχθεί με τον εξής τρόπο: AB aab aabb aaabb aaaabb aaaabb aaaabb Οι πέντε κανόνες αντικατάστασης, που χρησιμοποιήσαμε αποτελούν μία γραμματική χωρίς συμφραζόμενα. Η γλώσσα της γραμματικής είναι το σύνολο

3 4.1. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ 137 όλων των συμβολοσειρών, που μπορούν να παραχθούν από την αρχή και περιέχουν μόνο τερματικά σύμβολα. Για το συγκεκριμένο παράδειγμα, η γλώσσα αυτή είναι η {a m b n : m 1, n 1} επειδή κάθε συμβολοσειρά της μορφής a m b n, για κάποια m 1 και n 1 μπορεί να παραχθεί από την αρχή, ενώ καμία άλλη συμβολοσειρά με αλφάβητο {a, b} δε μπορεί να παραχθεί από την αρχή. Ορισμός 4.1 Μία Γραμματική Χωρίς Συμφραζόμενα ορίζεται από μία τετράδα G = (V, Σ, R, ), όπου: V είναι ένα πεπερασμένο σύνολο με στοιχεία, που λέγονται μη τερματικά σύμβολα ή αλλιώς μεταβλητές, Σ είναι ένα πεπερασμένο σύνολο, που τα στοιχεία του λέγονται τερματικά σύμβολα, V Σ =, είναι ένα στοιχείο του V, που λέγεται μεταβλητή εκκίνησης ή αλλιώς αρχή της γραμματικής και R είναι ένα πεπερασμένο σύνολο, που τα στοιχεία του λέγονται κανόνες, με καθένα από αυτά να έχει τη μορφή A w, όπου A V και w (V Σ). Στο παράδειγμα που χρησιμοποιήσαμε έχουμε V = {, A, B}, Σ = {a, b} και R = { AB, A a, A aa, B b, B bb} Ορισμός 4.2 Εστω μία γραμματική χωρίς συμφραζόμενα G = (V, Σ, R, ). Ας υποθέσουμε ότι A είναι ένα στοιχείο του V και u, v και w είναι τρεις συμβολοσειρές του (V Σ), τέτοιες ώστε το A w να είναι ένας κανόνας του R. Τότε λέμε ότι η συμβολοσειρά uvw παράγεται σε ένα βήμα από τη συμβολοσειρά uav και αυτό γράφεται ως uav uvw Με άλλα λόγια, με την εφαρμογή του κανόνα A w στη συμβολοσειρά uav παίρνουμε τη συμβολοσειρά uwv. Στο παράδειγμα, που χρησιμοποιήσαμε, παρατηρούμε ότι aaabb aaaabb.

4 138 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ Ορισμός 4.3 Εστω μία γραμματική χωρίς συμφραζόμενα G = (V, Σ, R, ) και u, v συμβολοσειρές του (V Σ). Θα λέμε ότι η v παράγεται από την u και αυτό θα γράφεται ως u v, αν ισχύει μία από τις εξής δύο συνθήκες: 1. u = v ή 2. υπάρχει ένας ακέραιος k 2 και μία ακολουθία συμβολοσειρών u 1, u 2,... u k του (V Σ), τέτοιων ώστε i. u = u 1 ii. v = u k και iii. u 1 u 2... u k. Με άλλα λόγια, ξεκινώντας από τη συμβολοσειρά u και εφαρμόζοντας κανόνες για μηδέν ή περισσότερες φορές παίρνουμε τελικά η συμβολοσειρά v. Στο παράδειγμα που χρησιμοποιήσαμε, παρατηρούμε ότι aaabb aaaabbbb. Ορισμός 4.4 Εστω μία γραμματική χωρίς συμφραζόμενα G = (V, Σ, R, ). Η γλώσσα της γραμματικής G ορίζεται ως το σύνολο όλων των συμβολοσειρών του Σ, που παράγονται από την αρχή της γραμματικής: L(G) = {w Σ : w} Ορισμός 4.5 Μία γλώσσα L λέμε ότι είναι χωρίς συμφραζόμενα, αν υπάρχει μία γραμματική χωρίς συμφραζόμενα G, τέτοια ώστε L(G) = L. Παράδειγμα 4.1 (Επαλήθευση πρόσθεσης) Ας εξετάσουμε τη γλώσσα L = {a n b m c n+m : n 0, m 0} Εφαρμόζοντας το λήμμα της άντλησης (Θεώρημα 3.4) διαπιστώνεται ότι η L δεν είναι κανονική γλώσσα. Θα ορίσουμε μία γραμματική χωρίς συμφραζόμενα G, που παράγει τη γλώσσα L δείχνοντας με αυτό τον τρόπο ότι η L είναι ΓΧΣ. Αρχικά παρατηρούμε ότι ɛ L και γι αυτό θα συμπεριλάβουμε ως έναν από τους κανόνες της γραμματικής τον ɛ. Ας δούμε το πώς μπορεί να παράγονται όλες οι συμβολοσειρές της L από την αρχή της γραμματικής που ορίζουμε: 1. Κάθε φορά που προσθέτουμε στη συμβολοσειρά ένα a θα πρέπει να προσθέσουμε ταυτόχρονα και ένα c. Ετσι θα παίρνουμε όλες τις συμβολοσειρές της μορφής a n c n, όπου n 0.

5 4.1. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ Δεδομένης μιας συμβολοσειράς της μορφής a n c n ξεκινάμε να προσθέτουμε b. Παρατηρούμε ότι κάθε b θα πρέπει να παρεμβάλλεται μεταξύ των a και των c. Γι αυτό, θα χρησιμοποιήσουμε ένα μη τερματικό σύμβολο B, ως ένα «δείκτη» της θέσης της τρέχουσας συμβολοσειράς, όπου μπορεί να προστεθεί ένα b: αντί λοιπόν να παράγουμε από το συμβολοσειρές της μορφής a n c n, θα παράγουμε τη συμβολοσειρά a n Bc n. Τότε, από το B θα παράγονται όλες οι συμβολοσειρές της μορφής b m c m, όπου m 0. Προκύπτει λοιπόν η γραμματική G = (V, Σ, R, ), όπου V = {, A, B}, Σ = {a, b, c} και το R περιλαμβάνει τους κανόνες: Από το γεγονός ότι ɛ A A ɛ aac B B ɛ bbc A a n Bc n, για κάθε n 0, B b m c m, για κάθε m 0, συνεπάγεται ότι από την αρχή της γραμματικής παράγονται οι εξής συμβολοσειρές: a n Bc n a n b m c m c n = a n b m c n+m, για κάθε n 0 και m 0 Στην πραγματικότητα καμία άλλη συμβολοσειρά του {a, b, c} δε μπορεί να παραχθεί από το και έτσι προκύπτει ότι L(G) = L. Καθώς A B ɛ η γραμματική G είναι δυνατό να απλοποιηθεί απαλείφοντας τους κανόνες ɛ και A ɛ. Αυτό δίνει ως αποτέλεσμα τη γραμματική G = (V, Σ, R, ), όπου V = {, A, B}, Σ = {a, b, c} και το R να αποτελείται από τους κανόνες A A aac B B ɛ bbc Τέλος παρατηρούμε ότι δε χρειαζόμαστε το, αφού μπορούμε να χρησιμοποιήσουμε ως αρχή το μη τερματικό σύμβολο A. Αυτή η απλοποίηση δίνει τελικά

6 140 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ τη γραμματική G = (V, Σ, R, A), με V = {A, B}, Σ = {a, b, c} και το R να αποτελείται από τους κανόνες A aac B B ɛ bbc Θεώρημα 4.1 (Οι κανονικές γλώσσες είναι ΓΧΣ) Εστω Σ ένα αλφάβητο και έστω L Σ μία κανονική γλώσσα. Τότε η L είναι επίσης ΓΧΣ. Απόδειξη: Αφού η L είναι κανονική γλώσσα, τότε υπάρχει ένα ντεντερμινιστικό πεπερασμένο αυτόματο M = (K, Σ, δ, s, F ), που αποδέχεται την L. Για να αποδείξουμε ότι η L είναι ΓΧΣ θα πρέπει να ορίσουμε μία γραμματική χωρίς συμφραζόμενα G = (V, Σ, R, ), τέτοια ώστε L = L(M) = L(G). Κατά συνέπεια θα πρέπει για την G να έχουμε για κάθε w Σ, που μπορεί να αναδιατυπωθεί ως w L(M) αν και μόνο αν w L(G) το M αποδέχεται την w αν και μόνο αν w Θα ορίσουμε τη γραμματική χωρίς συμφραζόμενα G, έτσι ώστε για οποιαδήποτε συμβολοσειρά w = w 1 w 2... w n να ισχύει η εξής αντιστοίχιση: Το M θα βρίσκεται στην κατάσταση A K, όταν θα έχει ολοκληρωθεί η ανάγνωση της υποσυμβολοσειράς w 1 w 2... w i. Τότε για την G θα έχουμε w 1 w 2... w i A. Στο επόμενο βήμα, το M θα διαβάσει το σύμβολο w i+1 και θα εκτελέσει μετάβαση από την κατάσταση A σε μία κατάσταση, έστω B, οπότε δ(a, w i+1 ) = B. Για να μπορούμε να εγγυηθούμε ότι εξακολουθεί να διατηρείται η παραπάνω αντιστοίχιση, θα πρέπει να προσθέσουμε στη γραμματική G τον κανόνα A w i+1 B. Ας δούμε τώρα τι συμβαίνει τη στιγμή που το αυτόματο M έχει διαβάσει ολόκληρη τη συμβολοσειρά w. Εστω ότι εκείνη τη στιγμή το M βρίσκεται στην κατάσταση A. Από την αντιστοίχιση που ορίσαμε θα ισχύει: w 1 w 2... w n A = wa

7 4.1. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ 141 Υπενθυμίζουμε ότι για την G θα πρέπει να ισχύει η ιδιότητα, που είναι ισοδύναμη με την Το M αποδέχεται την w αν και μόνο αν w A F αν και μόνο αν w Αυτή την ιδιότητα την εγγυόμαστε με την προσθήκη στην G ενός κανόνα A ɛ για κάθε κατάσταση αποδοχής A του M. Τώρα είμαστε σε θέση να ορίσουμε τυπικά τη γραμματική χωρίς συμφραζόμενα G = (V, Σ, R, ). V = K, δηλαδή τα μη τερματικά σύμβολα της G θα είναι οι καταστάσεις του M. = s, δηλαδή η αρχή της G θα είναι η αρχική κατάσταση s του M. Το σύνολο R αποτελείται από τους κανόνες: και A ab, όπου A K, a Σ, B K και δ(a, a) = B A ɛ, για κάθε A F Ισχυριζόμαστε ότι L(G) = L. Για να αποδειχθεί αυτός ο ισχυρισμός, πρέπει να δείξουμε ότι L(G) L και L L(G). Αποδεικνύουμε καταρχήν ότι L L(G). Εστω w = w 1 w 2... w n μία οποιαδήποτε συμβολοσειρά της L. Οταν το πεπερασμένο αυτόματο M διαβάζει τη συμβολοσειρά w, επισκέπτεται με τη σειρά τις καταστάσεις r 0, r 1,..., r n, όπου r 0 = s και r i+1 = δ(r i, w i+1 ) για i = 0, 1,..., n 1. Εφόσον w L = L(M), γνωρίζουμε ότι r n F. Ως συνέπεια του τρόπου με τον οποίο ορίστηκε η γραμματική G έχουμε: για κάθε i = 0, 1,..., n 1, ο r i w i+1 r i+1 είναι ένας κανόνας του R και ο r n ɛ είναι ένας κανόνα του R.

8 142 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ Γι αυτό τον λόγο θα έχουμε την παραγωγή: = s = r 0 w 1 r 1 w 1 w 2 r 2... w 1 w 2 r 2... w n r n w 1 w 2... w n = w Ετσι αποδεικνύεται ότι w L(G). Η απόδειξη του ισχυρισμού L(G) L αφήνεται ως άσκηση. Στην Ενότητα 3.2 αποδείξαμε ότι η γλώσσα {0 n 1 n : n 0} δεν είναι κανονική, αν και μπορούμε εύκολα να ορίσουμε μία γραμματική που να την παράγει και άρα είναι ΓΧΣ. Με αυτό τον τρόπο επαληθεύεται η σχέση μεταξύ των δύο κλάσεων γλωσσών, που αναφέρθηκε στην Ενότητα 1.4, ότι δηλαδή το σύνολο των κανονικών γλωσσών είναι γνήσιο υποσύνολο των ΓΧΣ. Παράδειγμα 4.2 (Κανονική γλώσσα ως ΓΧΣ) Ας εξετάσουμε τη γλώσσα L = {w {0, 1} : η 101 είναι υποσυμβολοσειρά της w} Το παρακάτω ντεντερμινιστικό πεπερασμένο αυτόματο M αποδέχεται την L και επομένως η L είναι κανονική γλώσσα A 0 0 0, 1 B 1 C Εφαρμόζουμε την κατασκευή, που περιγράφηκε στην απόδειξη του Θεωρήματος 4.1, για να μετατρέψουμε το αυτόματο M σε μία γραμματική χωρίς συμφραζόμενα G με γλώσσα L, αυτή που γίνεται αποδεκτή από το M. Σύμφωνα με αυτή την κατασκευή έχουμε G = (V, Σ, R, ), όπου V = {, A, B, C}, Σ = {0, 1}, το σύμβολο της αρχής είναι το, δηλαδή η αρχική κατάσταση του M και το R αποτελείται από τους κανόνες: 0 1A

9 4.1. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ 143 A 0B 1A B 0 1C C 0C 1C ɛ Ας εξετάσουμε τη συμβολοσειρά , που ανήκει στη γλώσσα L. Οταν το πεπερασμένο αυτόματο M διαβάζει τη συμβολοσειρά, επισκέπτεται με τη σειρά τις καταστάσεις,, A, B,, A, A, B, C, C Για τη γραμματική G, αυτός ο υπολογισμός αντιστοιχεί στην παραγωγή: Επομένως έχουμε: 0 01A 010B A A B C C που σημαίνει ότι η συμβολοσειρά ανήκει στη γλώσσα της γραμματικής G. Από την άλλη μεριά, η συμβολοσειρά δεν ανήκει στη γλώσσα L. Για τη συγκεκριμένη συμβολοσειρά το αυτόματο M επισκέπτεται διαδοχικά τις καταστάσεις, A, B,, A, A δηλαδή εκτελεί έναν υπολογισμό, που δεν καταλήγει σε μία κατάσταση αποδοχής. Για τη γραμματική G, η ανάγνωση της συμβολοσειράς αντιστοιχεί στην παραγωγή: 1A

10 144 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ 10B A 10011A Επειδή το σύμβολο A δεν αντιστοιχεί σε μία κατάσταση αποδοχής του M, η γραμματική G δεν περιέχει τον κανόνα A ɛ. Αυτό έχει ως συνέπεια η συμβολοσειρά να μη μπορεί να παραχθεί από την αρχή της γραμματικής και άρα / L(G). 4.2 Παραγωγές και Συντακτικά Δέντρα Οι γραμματικές χωρίς συμφραζόμενα δε χρησιμοποιούνται μόνο για να περιγράψουν τις συμβολοσειρές μιας γλώσσας, αλλά παρέχουν επίσης και ένα μέσο για την καταγραφή της δομής των συμβολοσειρών, που παράγονται. Η δομή των συμβολοσειρών της γλώσσας είναι σημαντική, επειδή αυτή αποτελεί το σημείο εκκίνησης για την απόδοση σημασίας στις συμβολοσειρές της γλώσσας. Η δομή μιας συμβολοσειράς ως προς τη γραμματική αναπαριστάται από ένα συντακτικό δέντρο, που καταγράφει τους κανόνες της γραμματικής και το πώς αυτοί εφαρμόζονται στα διάφορα μη τερματικά σύμβολα κατά την παραγωγή μιας συμβολοσειράς. Ενα συντακτικό δέντρο, που παράγεται από μία γραμματική G = (V, Σ, R, ) είναι ένα διατεταγμένο δέντρο με ρίζα, στο οποίο: κάθε φύλλο επιγράφεται με ένα στοιχείο του Σ {ɛ}, ο κόμβος της ρίζας επιγράφεται με το σύμβολο, όλοι οι άλλοι κόμβοι επιγράφονται με κάποιο στοιχείο του V Σ και αν υπάρχει εσωτερικός κόμβος (όχι φύλλο), που επιγράφεται με X και οι απόγονοι του κόμβου αυτού επιγράφονται με x 1, x 2,..., x n, τότε το R περιλαμβάνει τον κανόνα X x 1 x 2... x n. Για τη γραμματική AB A a A aa

11 4.2. ΠΑΡΑΓΩΓΕΣ - ΣΥΝΤΑΚΤΙΚΑ ΔΕΝΤΡΑ 145 B b B bb που χρησιμοποιήσαμε ως παράδειγμα στην Ενότητα 4.1, η παραγωγή AB aab aabb aaabb aaaabb aaaabb aaaabb μπορεί επίσης να αναπαρασταθεί από το συντακτικό δέντρο: A B a A b B a A b a A a Τα συντακτικά δέντρα καταγράφουν τις δομικές σχέσεις των συμβολοσειρών μιας παραγωγής χωρίς τις λεπτομέρειες για τη σειρά με την οποία αντικαθίστανται τα μη τερματικά σύμβολα. Αν και η σειρά με την οποία αντικαθίστανται τα μη τερματικά σύμβολα, που εμφανίζονται σε μία παραγωγή, δε σχετίζεται με τη γραμματική δομή της συμβολοσειράς, είναι σε κάποιες περιπτώσεις χρήσιμο να διακρίνουμε δύο συγκεκριμένες προσεγγίσεις παραγωγών: Σε μία αριστερή παραγωγή, σε κάθε βήμα αντικαθίσταται στην τρέχουσα συμβολοσειρά πάντα το πρώτο μη τερματικό σύμβολο από αριστερά (συμβολίζεται με τον προσδιορισμό lm). Σε μία δεξιά παραγωγή, σε κάθε βήμα αντικαθίσταται στην τρέχουσα συμβολοσειρά πάντα το πρώτο μη τερματικό σύμβολο από δεξιά (συμβολίζεται με τον προσδιορισμό rm).

12 146 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ Μία αριστερή παραγωγή της συμβολοσειράς aaaabb του παραδείγματος είναι η: lm AB lm aab lm aaab lm aaaab lm aaaab lm aaaabb lm aaaabb Αντίστοιχα, μία δεξιά παραγωγή της συμβολοσειράς aaaabb του παραδείγματος είναι η: rm AB rm AbB rm Abb rm aabb rm aaabb rm aaaabb rm aaaabb 4.3 Διφορούμενες Γραμματικές Κάποιες γραμματικές μπορεί να παράγουν περισσότερα από ένα συντακτικά δέντρα για κάποιες ή όλες τις συμβολοσειρές της γλώσσας τους. Οταν για μία γραμματική συμβαίνει κάτι τέτοιο, τότε λέμε ότι αυτή είναι διφορούμενη. Πιο συγκεκριμένα, μία γραμματική G είναι διφορούμενη αν και μόνο αν υπάρχει τουλάχιστο μία συμβολοσειρά της L(G), για την οποία η G παράγει περισσότερα από ένα συντακτικά δέντρα. Παράδειγμα 4.3 (Διφορούμενη γραμματική παρενθέσεων) Η γλώσσα L bal = {w {), (} : οι παρενθέσεις είναι ισοσκελισμένες} παράγεται από τη γραμματική G = ({, ), (}, {), (}, R, ), με το R να αποτελείται από τους κανόνες: () ɛ Ομως η γραμματική G μπορεί να παράγει για τη συμβολοσειρά (())() τα εξής δύο συντακτικά δέντρα: ( ( ) ) ( ɛ ) ɛ ( ) ( ɛ ) ɛ ( ɛ )

13 4.3. ΔΙΦΟΡΟΥΜΕΝΕΣ ΓΡΑΜΜΑΤΙΚΕΣ 147 Στην πραγματικότητα, η G μπορεί να παράγει άπειρα συντακτικά δέντρα για τη συμβολοσειρά (())() και όχι μόνο δύο. Μία γραμματική G δε μπορεί να είναι διφορούμενη, αν και μόνο αν για όλες τις συμβολοσειρές w και σε κάθε βήμα μιας αριστερής (ή δεξιάς) παραγωγής της w μπορεί να εφαρμοστεί μόνο ένας κανόνας της G. Η γραμματική του Παραδείγματος 4.3 είναι σαφές ότι δεν εκπληρώνει αυτή την απαίτηση. Ετσι, θα μπορούσαμε εύκολα να σχηματίσουμε δύο αριστερές παραγωγές για τη συμβολοσειρά (())(): lm lm () lm (()) lm (()) lm (())() lm (())() lm lm lm lm () lm (()) lm (()) lm (())() lm (())() Σε πολλές περιπτώσεις, όταν έχουμε μία διφορούμενη γραμματική G είναι δυνατό να οριστεί μία νέα γραμματική G, που παράγει την L(G), ενώ είναι απαλλαγμένη με κάποια (ή και όλα) από τα προβλήματα της διφορούμενης γραμματικής G. Δυστυχώς όμως αυτό δεν είναι πάντα εφικτό. Υπάρχουν ΓΧΣ γι τις οποίες δεν είναι δυνατό να οριστούν γραμματικές, που δεν είναι διφορούμενες. Αυτές οι γλώσσες λέγονται εγγενώς διφορούμενες. Παράδειγμα 4.4 (Εγγενώς διφορούμενη ΓΧΣ) Ας εξετάσουμε τη γλώσσα L = {a n b n c m, n, m 0} {a n b m c m, n, m 0} Κάθε συμβολοσειρά της L είτε έχει τον ίδιο αριθμό a και b, είτε τον ίδιο αριθμό b και c, είτε ισχύουν και τα δύο. Η L είναι εγγενώς διφορούμενη. Μία γραμματική, που παράγει αυτή τη γλώσσα είναι η G δ = ({, 1, 2, A, B, a, b, c}, {a, b, c}, R, ), όπου R αποτελείται από τους κανόνες: c A A aab ɛ 2 a 2 B B bbc ɛ Ας επικεντρωθούμε τώρα στις συμβολοσειρές {a n b n c n : n 0}. Αυτές οι συμβολοσειρές έχουν δύο διακριτές παραγωγές, τη μία μέσω του συμβόλου

14 148 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ 1 και την άλλη μέσω του 2. Μπορεί να αποδειχθεί ότι η γραμματική G δ είναι εγγενώς διφορούμενη: δοθείσης οποιασδήποτε γραμματικής που μπορεί να παράγει την L υπάρχει τουλάχιστο μία συμβολοσειρά με δύο διαφορετικές παραγωγές βάση αυτής της γραμματικής. Για να μπορεί μία ΓΧΣ να δώσει λύση σε ένα πρακτικό πρόβλημα, θα πρέπει αυτή να μην είναι εγγενώς διφορούμενη και να βρεθεί μία γραμματική, που δεν είναι διφορούμενη. Παρόλο που δεν υπάρχει ένας γενικός αλγόριθμος για να ελέγχεται αν μία γραμματική είναι διφορούμενη ή για να απομακρύνονται τα προβλήματα της γραμματικής, όταν αυτά εντοπίζονται, υπάρχουν εμπειρικές τεχνικές, που εφαρμόζονται για κάποιες από τις πιο κοινές περιπτώσεις διφορούμενης γραμματικής. Αναφέρουμε δύο συγκεκριμένα δομικά χαρακτηριστικά μιας γραμματικής, που αποτελούν τις πιο συνηθισμένες αιτίες για να είναι αυτή διφορούμενη. 1. Κανόνες-ɛ της μορφής ɛ 2. Αναδρομικοί κανόνες, που το δεξί τους μέρος είναι συμμετρικό και περιέχει τουλάχιστο δύο εμφανίσεις του μη τερματικού συμβόλου του αριστερού μέρους. Τέτοιοι κανόνες είναι για παράδειγμα οι και E E + E. Ας δούμε πρώτα το πώς μπορεί να απομακρυνθούν οι κανόνες-ɛ, που καθιστούν μία γραμματική διφορούμενη. Μία περίπτωση διφορούμενης γραμματικής με αυτό το πρόβλημα είναι η γραμματική των παρενθέσεων του Παραδείγματος 4.3. Το μεγαλύτερο πρόβλημα αυτής της γραμματικής είναι ότι μπορεί να χρησιμοποιηθεί ο κανόνας για έναν οποιοδήποτε αριθμό φορών δημιουργώντας έτσι περιττές εμφανίσεις του συμβόλου, που μπορούν στη συνέχεια να απαλειφθούν με χρήση του κανόνα ɛ. Αν μπορούσαμε να απομακρύνουμε τον κανόνα ɛ, τότε δε θα υπήρχε πια αυτός ο λόγος, που κάνει τη γραμματική διφορούμενη. Για να γίνει όμως κάτι τέτοιο θα πρέπει ο μετασχηματισμός, που θα εφαρμοστεί στη γραμματική G να μην επηρεάζει τη γλώσσα που αυτή παράγει. Αν ɛ L(G), τότε θα πρέπει να γίνει κατάλληλος χειρισμός αυτής της περίπτωσης. Μετά από την απομάκρυνση του προβληματικού κανόνα-ɛ θα πρέπει να επισυναφθεί ένας νέος κανόνας-ɛ, που θα αποκαθιστά τη γλώσσα της γραμματικής, αλλά θα έχει διαφορετική μορφή από τον κανόνα-ɛ, που έκανε τη γραμματική διφορούμενη. Εστω G = (V, Σ, R, ) μία οποιαδήποτε γραμματική χωρίς συμφραζόμενα. Ο παρακάτω μετασχηματισμός δημιουργεί μία νέα γραμματική G, τέτοια ώστε L(G ) = L(G) {ɛ} και η G δεν περιέχει κανόνες-ɛ:

15 4.3. ΔΙΦΟΡΟΥΜΕΝΕΣ ΓΡΑΜΜΑΤΙΚΕΣ Αρχικά G = G. 2. Εστω N το σύνολο των απαλείψιμων μη τερματικών συμβόλων. Ενα μη τερματικό σύμβολο X είναι απαλείψιμο αν και μόνο αν: i. υπάρχει ένας κανόνας X ɛ ή ii. υπάρχει ένα κανόνας τη μορφής X P QR..., τέτοιος ώστε τα P, Q, R,... να είναι όλα απαλείψιμα. 3. Λέμε ότι ένας κανόνας μπορεί να τροποποιηθεί, αν και μόνο αν είναι της μορφής P aqβ για κάποιο Q N και για οποιαδήποτε a, β V. Αφού το Q είναι απαλείψιμο, θα μπορούσε να απαλειφθεί με την εφαρμογή κανόνων-ɛ, δηλαδή των κανόνων που πρόκειται να αφαιρεθούν. Μία δυνατότητα για να παρακαμφθεί ο συγκεκριμένος περιορισμός είναι το να μην παράγεται καταρχήν το Q, αλλά για να συμβεί αυτό θα πρέπει να προστεθούν νέοι κανόνες. Ετσι, η παρακάτω διαδικασία ε- παναλαμβάνεται μέχρι τη στιγμή, που η G δε θα περιέχει κανόνες, που μπορούν να τροποποιηθούν και δεν έχει γίνει ακόμη η επεξεργασία τους: i. Δοθέντος του κανόνα P aqβ με Q N, προσθέτουμε τον P aβ, αν δεν υπάρχει ήδη και αν aβ ɛ και P aβ. Αυτός ο τελευταίος έλεγχος εμποδίζει την εισαγωγή άχρηστων κανόνων P P, που θα δημιουργούνταν αν η πρωτότυπη γραμματική περιείχε, για παράδειγμα, τον κανόνα P P Q με το Q να είναι απαλείψιμο. 4. Διαγράφονται από την G όλοι οι κανόνες της μορφής X ɛ. Με την παραπάνω διαδικασία παίρνουμε μία γραμματική G χωρίς κανόνες-ɛ, τέτοια ώστε L(G ) = L(G) {ɛ}. Στην περίπτωση που η L(G) περιέχει το ɛ, θα πρέπει να δημιουργηθεί στη συνέχεια μία γραμματική G, που θα περιέχει ένα μοναδικό κανόνα-ɛ με αποκλειστικό σκοπό την παραγωγή της συμβολοσειράς ɛ, χωρίς όμως ο κανόνας αυτός να αλληλεπιδρά με τους άλλους κανόνες. Αυτό γίνεται ως εξής: 1. Εστω ότι με τη διαδικασία που περιγράψαμε δημιουργείται από την G η νέα γραμματική G χωρίς κανόνες-ɛ. 2. Αν η αρχή της G ήταν απαλείψιμη, τότε, i. Δημιουργείται στην G ένα νέο σύμβολο αρχής. ii. Προστίθενται στην G δύο νέοι κανόνες, οι ɛ και.

16 150 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ Παράδειγμα 4.5 (Επιδιόρθωση γραμματικής παρενθέσεων) Επανερχόμαστε στη γραμματική της γλώσσας L bal = {w {), (} : οι παρενθέσεις είναι ισοσκελισμένες}, που επεξεργαστήκαμε στο Παράδειγμα 4.3, δηλαδή στη γραμματική G = ({, ), (}, {), (}, R, ), όπου R να αποτελείται από τους κανόνες: () (1) (2) ɛ (3) Για να μετασχηματίσουμε την G σε μία μη διφορούμενη γραμματική, που θα παράγει την ίδια γλώσσα, αρχικά απομακρύνουμε τον κανόνα-ε και αφού ɛ L(G) στη συνέχεια ενσωματώνουμε ένα νέο κανόνα-ε, που θα παράγει τη συμβολοσειρά ɛ χωρίς να αλληλεπιδρά με τους υπόλοιπους κανόνες. Εφαρμόζοντας τα βήματα της διαδικασίας αφαίρεσης του κανόνα-epsilon, που περιγράψαμε, έχουμε: Στο βήμα 2, N = {}. Στο βήμα 3, εξαιτίας του κανόνα (1) προσθέτουμε το νέο κανόνα (). Εξαιτίας του κανόνα (2), θεωρητικά εξετάζεται και η προσθήκη του κανόνα, αλλά επειδή το αριστερό και το δεξί μέρος του κανόνα είναι ίδιο, τελικά δεν το συμπεριλαμβάνουμε στη νέα γραμματική. Στο βήμα 4, διαγράφεται ο κανόνας ɛ. Επειδή όμως ɛ L bal και N είναι απαραίτητο να προσθέσουμε ένα νέο κανόνα-ɛ και γι αυτό ορίζουμε μία νέα αρχή και εισάγουμε τους κανόνες ɛ και. Συνολικά, ο συγκεκριμένος μετασχηματισμός μας δίνει τη γραμματική G = ({,, ), (}, {), (}, R, ), όπου R να αποτελείται από τους κανόνες: ɛ () () Τώρα η συμβολοσειρά (())() παράγεται με ένα μόνο τρόπο από τη γραμματική G. Παρόλα αυτά, η νέα γραμματική εξακολουθεί να είναι διφορούμενη, αλλά αυτή τη φορά για άλλο λόγο. Οπως φαίνεται στο σχήμα που ακολουθεί, για τη συμβολοσειρά ()()() έχουμε δύο διαφορετικά συντακτικά δέντρα:

17 4.3. ΔΙΦΟΡΟΥΜΕΝΕΣ ΓΡΑΜΜΑΤΙΚΕΣ 151 ( ) ( ) ( ) ( ) ( ) ( ) Σε αυτή την περίπτωση το πρόβλημα είναι ο κανόνας, που πρέπει να εφαρμοστεί n 1 φορές για να παράξει n ισοσκελισμένες συμβολοσειρές παρενθέσεων. Ομως μετά από την πρώτη εφαρμογή του κανόνα, υπάρχει κάθε φορά μία επιλογή ως προς το ποιο πρόκειται να αναπτυχθεί. Εχουμε λοιπόν μία περίπτωση συμμετρικού αναδρομικού κανόνα, δηλαδή του δεύτερου από τα τρία πιθανά δομικά προβλήματα μιας διφορούμενης γραμματικής, που αναφέραμε. Η λύση σε ένα τέτοιο πρόβλημα είναι να μετασχηματιστεί η γραμματική, έτσι ώστε να μη διατίθεται πλέον μία τέτοια επιλογή. Αντικαθιστούμε λοιπόν τον κανόνα με έναν από τους κανόνες, 1 1 όπου στην πρώτη περίπτωση επιβάλλεται διακλάδωση στα αριστερά και στη δεύτερη περίπτωση έχουμε διακλάδωση στα δεξιά. Στη συνέχεια προσθέτουμε τον κανόνα 1 και αντικαθιστούμε τους κανόνες () και () με τους κανόνες 1 () και 1 (). Ουσιαστικά η γραμματική έχει μετασχηματιστεί, έτσι ώστε η διακλάδωση να γίνεται πάντα μόνο κατά μία κατεύθυνση. Κάθε που παράγεται μπορεί να διακλαδωθεί, αλλά κανένα 1 δε μπορεί. Οταν έχουν συμβεί όλες οι απαραίτητες διακλαδώσεις, τότε το γράφεται ως 1 και στη συνέχεια έχουμε το υπόλοιπο της παραγωγής. Ετσι, μία μη διφορούμενη γραμματική για τη γλώσσα L bal είναι η G = ({,, 1, ), (}, {), (}, R, ), όπου R να αποτελείται από τους κανόνες: ɛ () 1 ()

18 152 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ Η τεχνική που περιγράψαμε για το μετασχηματισμό της γραμματικής G του Παραδείγματος 4.5 είναι γενικά εφαρμόσιμη σε κάθε περίπτωση διφορούμενης γραμματικής, λόγω ενός αναδρομικού κανόνα, που στο δεξί του μέρος περιέχει δύο ή περισσότερες εμφανίσεις του συμβόλου του αριστερού μέρους. Το πρόβλημα του αν μία γραμματική G είναι διφορούμενη είναι γενικά μη αποφασίσιμο, αλλά σε κάποιες περιπτώσεις μπορεί να είναι εφικτή μία απόδειξη ότι η G δεν είναι διφορούμενη. Αρκεί τότε να δειχθεί ότι για κάθε συμβολοσειρά, που αυτή παράγει υπάρχει μία μοναδική αριστερή παραγωγή. Ετσι, αν μπορούμε να δείξουμε ότι για μία αριστερή παραγωγή οποιασδήποτε συμβολοσειράς w L(G) μπορεί να εφαρμοστεί σε κάθε βήμα μόνο ένας κανόνας, τότε η G σίγουρα δεν είναι διφορούμενη. Παράδειγμα 4.6 (Μη διφορούμενη γραμματική παρενθέσεων) Επανερχόμαστε στη γραμματική G για τη L bal, στην οποία καταλήξαμε στο Παράδειγμα 4.5 σε μία προσπάθεια να απαλλαγούμε από τα προβλήματα της διφορούμενης γραμματικής G. Θα αποδείξουμε ότι η G = ({,, 1, ), (}, {), (}, R, ), με R : ɛ (1) (2) 1 (3) 1 (4) 1 () (5) 1 () (6) δεν είναι διφορούμενη. Δοθείσης της αριστερής παραγωγής μιας οποιασδήποτε συμβολοσειράς w L(G ), σε κάθε βήμα της παραγωγής υπάρχει ένα μοναδικό σύμβολο, έστω X, που είναι το πρώτο μη τερματικό σύμβολο από αριστερά. Οποιο και αν είναι το X, θα πρέπει να αντικατασταθεί με την εφαρμογή ενός κανόνα της γραμματικής και γι αυτό μπορεί να χρησιμοποιηθεί μόνο ένας από τους κανόνες, που έχει X στο αριστερό του μέρος. Στη γραμματική G έχουμε μόνο τρία μη τερματικά σύμβολα. Θα δείξουμε, για καθένα από αυτά, ότι δεν υπάρχει περίπτωση να μπορεί να εφαρμοστούν εναλλακτικοί κανόνες στην αριστερή παραγωγή της συγκεκριμένης συμβολοσειράς w. Ξεκινάμε αρχικά με τις δύο απλούστερες περιπτώσεις:

19 4.3. ΔΙΦΟΡΟΥΜΕΝΕΣ ΓΡΑΜΜΑΤΙΚΕΣ 153 Το σύμβολο μπορεί να εμφανιστεί σε μία παραγωγή μόνο στην αρχή της. Αν w = ɛ, τότε ο κανόνας (1) είναι ο μόνος που μπορεί να εφαρμοστεί. Από την άλλη, αν w ɛ, τότε ο κανόνας (2) είναι και πάλι ο μοναδικός που μπορεί να εφαρμοστεί. Το σύμβολο 1, αν η παραγωγή συνεχίζει με (), θα πρέπει να αντικατασταθεί σύμφωνα με τον κανόνα (6), ενώ σε διαφορετική περίπτωση έχουμε και πάλι ένα μόνο δυνατό κανόνα και αυτός είναι ο (5). Σχετικά με το, ορίζουμε αρχικά για κάθε ισοσκελισμένο σύνολο παρενθέσεων m οι αδερφοί του m να είναι το μικρότερο σύνολο, που περιλαμβάνει το σύνολο p ακριβώς στα δεξιά του m και όλους τους αδερφούς του p. Ετσι, αν υποθέσουμε ότι έχουμε τη συμβολοσειρά ( () 1 5 ) () 2 () () τότε το σύνολο παρενθέσεων () με επιγραφή 1 έχει ένα μόνο αδερφό σύνολο, δηλαδή αυτό με επιγραφή 2. Το σύνολο (()()) με επιγραφή 5 έχει δύο αδέρφια, δηλαδή αυτά με τις επιγραφές 3 και 4. Σχετικά λοιπόν με το σύμβολο παρατηρούμε ότι: 3 Το πρέπει να παράγει μία συμβολοσειρά της L bal και επομένως πρέπει να δημιουργεί ένα ισοσκελισμένο σύνολο παρενθέσεων, που μπορεί να συνοδεύεται και από αδέρφια. Συνεπώς το πρώτο τερματικό σύμβολο οποιασδήποτε από τις συμβολοσειρές, που παράγει το είναι (. Ας καλέσουμε s τη συμβολοσειρά, που αρχίζει με ( και τελειώνει με ένα ), που ταιριάζει με το αρχικό (. Από το 1 μπορεί να παράγεται μόνο ένα ισοσκελισμένο σύνολο παρενθέσεων χωρίς αδέρφια. Εστω n ο αριθμός των αδερφών συνόλων της συμβολοσειράς s. Για να παραχθούν αυτά τα σύνολα θα πρέπει να εφαρμοστεί για το ο κανόνας (3) ακριβώς n φορές (δημιουργώντας n αντίγραφα του 1 ) πριν από την εφαρμογή του κανόνα (4), που θα παράξει μόνο ένα 1, δηλαδή αυτό που τελικά θα αποδώσει την s. Ετσι, για κάθε βήμα μιας παραγωγής έστω p ο αριθμός των εμφανίσεων του 1 στα δεξιά του. Αν p < n, το θα πρέπει να αντικατασταθεί με εφαρμογή του κανόνα (3). Αν p = n, τότε το πρέπει να αντικατασταθεί με εφαρμογή του κανόνα (4). 4

20 154 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ Για όλες τις περιπτώσεις, που εξετάσαμε, δεν είναι δυνατό να να μπορούν να εφαρμοστούν εναλλακτικοί κανόνες σε ένα βήμα της αριστερής παραγωγής της συμβολοσειράς w. 4.4 Κανονική Μορφή Chomsky Σε μία γραμματική χωρίς συμφραζόμενα G = (V, Σ, R, ), κάθε κανόνας είναι της μορφής A w όπου το A είναι ένα μη τερματικό σύμβολο και η w είναι μία συμβολοσειρά από το αλφάβητο V Σ. Θα δείξουμε ότι κάθε γραμματική χωρίς συμφραζόμενα G μπορεί να μετασχηματιστεί σε μία γραμματική χωρίς συμφραζόμενα G, τέτοια ώστε L(G) = L(G ) και οι κανόνες της G είναι της μορφής, που περιγράφει ο παρακάτω ορισμός. Ορισμός 4.6 Μία γραμματική χωρίς συμφραζόμενα G = (V, Σ, R, ) λέμε ότι είναι διατυπωμένη σε κανονική μορφή Chomsky, αν κάθε κανόνας του R έχει μία από τις εξής τρεις μορφές: 1. A BC, όπου A, B και C είναι στοιχεία του V, B και C. 2. A a, όπου A είναι ένα στοιχείο του V και a είναι ένα στοιχείο του Σ. 3. ɛ, όπου είναι το μη τερματικό σύμβολο της αρχής της γραμματικής. Είναι σημαντικό να επισημανθεί ότι σε μία τέτοια γραμματική το R περιλαμβάνει τον κανόνα ɛ, αν και μόνο αν ɛ L(G). Θεώρημα 4.2 (ΓΧΣ σε κανονική μορφή Chomsky) Εστω Σ ένα αλφάβητο και έστω L Σ μία ΓΧΣ. Τότε υπάρχει μία γραμματική χωρίς συμφραζόμενα σε κανονική μορφή Chomsky που παράγει την L. Απόδειξη: Αφού η L είναι ΓΧΣ, θα υπάρχει μία γραμματική χωρίς συμφραζόμενα G = (V, Σ, R, ), τέτοια ώστε L(G) = L. Θα μετασχηματίσουμε την G σε μία γραμματική σε κανονική μορφή Chomsky, που η γλώσσα της είναι η L(G). Ο μετασχηματισμός επιτυγχάνεται σε πέντε βήματα.

21 4.4. ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ CHOM KY 155 Βήμα 1: απαλείφεται το μη τερματικό σύμβολο της αρχής από το δεξί μέρος των κανόνων. Ορίζουμε τη γραμματική G 1 = (V 1, Σ, R 1, 1 ), με αρχή το 1, V 1 = V { 1 } και R 1 = R { 1 }. Η συγκεκριμένη γραμματική θα έχει την ιδιότητα: η αρχή της 1 να μην εμφανίζεται στο δεξί μέρος οποιουδήποτε κανόνα του R 1 και L(G 1 ) = L(G). Βήμα 2: απαλείφονται όλοι οι κανόνες-ɛ της μορφής A ɛ, όπου A είναι μη τερματικό σύμβολο διαφορετικό από την αρχή. Για όλους τους κανόνες-ɛ της μορφής A ɛ με A V 1 και A 1 γίνεται η εξής επεξεργασία: 1. Αφαιρείται ο κανόνας A ɛ από το σύνολο R Για κάθε κανόνα από το τρέχον σύνολο R 1 με μορφή α. B A, προστίθεται ο κανόνας B ɛ στο R 1, εκτός και αν αυτός ο κανόνας έχει ήδη διαγραφεί παρατηρήστε ότι με αυτό τον τρόπο αντικαθίσταται η παραγωγή δύο βημάτων B A ɛ με την παραγωγή ενός βήματος B ɛ β. B uav (με u και v συμβολοσειρές, που συμβαίνει να μην είναι και οι δύο κενές), προστίθεται στο R 1 ο κανόνας B uv παρατηρήστε ότι με αυτό τον τρόπο αντικαθίσταται η παραγωγή δύο βημάτων B uav uv με την παραγωγή ενός βήματος B uv γ. B uavaw (με u, v και w συμβολοσειρές), προστίθενται στο R 1 οι κανόνες B uvw, B uavw και B uvaw αν u = v = w = ɛ και ο κανόνας B ɛ έχει ήδη διαγραφεί από το R 1, τότε δεν προστίθεται ο κανόνας B ɛ δ. αν το A εμφανίζεται περισσότερες από δύο φορές στο δεξί μέρος, ο κανόνας αντιμετωπίζεται με ανάλογο τρόπο. Η διαδικασία αυτή επαναλαμβάνεται μέχρι να έχουν απαλειφθεί όλοι οι κανόνεςɛ. Εστω R 2 το σύνολο των κανόνων μετά από την απαλοιφή όλων των κανόνωνɛ. Ορίζουμε τη γραμματική G 2 = (V 2, Σ, R 2, 2 ), όπου V 2 = V 1 και 2 = 1. Αυτή η γραμματική έχει την εξής ιδιότητα: η αρχή 2 δεν εμφανίζεται στο δεξί μέρος κάποιου κανόνα του R 2,

22 156 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ το R 2 δεν περιέχει κανόνα-ɛ (μπορεί να περιέχει τον κανόνα 2 ɛ) και L(G 2 ) = L(G 1 ) = L(G). Βήμα 3: απαλείφονται όλοι οι μοναδιαίοι κανόνες A B, με A και B δύο μη τερματικά σύμβολα της γραμματικής. Για κάθε κανόνα A B και εφόσον ισχύει B 2, η G 2 τροποποιείται ως εξής: 1. Απομακρύνεται ο κανόνας A B από το τρέχον σύνολο κανόνων R Για κάθε κανόνα της μορφής B u στο τρέχον σύνολο R 2, όπου u (V 2 Σ), προστίθεται ο κανόνας A u, εκτός και ο συγκεκριμένος μοναδιαίος κανόνας έχει ήδη απαλειφθεί. Παρατηρήστε ότι με αυτό τον τρόπο αντικαθίσταται η παραγωγή δύο βημάτων A B u με την παραγωγή ενός βλήματος A u. Η διαδικασία αυτή επαναλαμβάνεται μέχρι να έχουν απαλειφθεί όλοι οι μοναδιαίοι κανόνες. Εστω R 3 το σύνολο των κανόνων που προκύπτει μετά από την απαλοιφή όλων των μοναδιαίων κανόνων. Η γραμματική G 3 = (V 3, Σ, R 3, 3 ), όπου V 3 = V 2 και 3 = 2 έχει την εξής ιδιότητα: η αρχή 3 δεν εμφανίζεται στο δεξί μέρος κάποιου κανόνα του R 3, το R 3 δεν περιέχει κανόνα-ɛ (μπορεί να περιέχει τον κανόνα 3 ɛ), το R 3 δεν περιέχει μοναδιαίο κανόνα και L(G 3 ) = L(G 2 ) = L(G 1 ) = L(G). Βήμα 4: απαλείφονται όλοι οι κανόνες με περισσότερα από δύο σύμβολα στο δεξί τους μέρος. Για κάθε κανόνα της μορφής A u 1 u 2... u k, όπου k 3 και u i V 3 Σ για όλα τα i, η G 3 τροποποιείται ως εξής: 1. Αφαιρείται ο κανόνας A u 1 u 2... u k από το τρέχον σύνολο κανόνων R Ενσωματώνονται στο τρέχον σύνολο R 3 οι κανόνες A u 1 A 1 A 1 u 2 A 2 A 2 u 3 A 3

23 4.4. ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ CHOM KY 157. A k 3 u k 2 A k 2 A k 2 u k 1 u k όπου A 1, A 2,..., A k 2 είναι νέα μη τερματικά σύμβολα, που προστίθενται στο τρέχον σύνολο V 3. Παρατηρήστε ότι με αυτό τον τρόπο αντικαθίσταται η παραγωγή ενός βήματος A u 1 u 2... u k με την παραγωγή k 1 βημάτων A u 1 A 1 u 1 u 2 A 2... u 1 u 2... u k 2 A k 2 u 1 u 2... u k Εστω R 4 το σύνολο των κανόνων και V 4 το σύνολο των μη τερματικών συμβόλων, που προκύπτουν μετά από την απαλοιφή όλων των κανόνων με περισσότερα από δύο σύμβολα στο δεξί τους μέρος. Η γραμματική G 4 = (V 4, Σ, R 4, 4 ), όπου 4 = 3 έχει την εξής ιδιότητα: η αρχή 4 δεν εμφανίζεται στο δεξί μέρος κάποιου κανόνα του R 4, το R 4 δεν περιέχει κανόνα-ɛ (μπορεί να περιέχει τον κανόνα 4 ɛ), το R 4 δεν περιέχει μοναδιαίο κανόνα, το R 4 δεν περιέχει κανόνα με περισσότερα από δύο σύμβολα στο δεξί του μέρος και L(G 4 ) = L(G 3 ) = L(G 2 ) = L(G 1 ) = L(G). Βήμα 5: απαλείφονται όλοι οι κανόνες της μορφής A u 1 u 2, όπου u 1 και u 2 συμβαίνει να μην είναι και τα δύο μη τερματικά σύμβολα. Για κάθε κανόνα της μορφής A u 1 u 2, όπου u 1, u 2 V 4 Σ χωρίς όμως να περιέχονται και τα δύο στο V 4, η G 4 τροποποιείται ως εξής: 1. Αν u 1 Σ και u 2 V 4, τότε αντικαθίσταται ο κανόνας A u 1 u 2 στο τρέχον σύνολο R 4 με τους κανόνες A U 1 u 2 και U 1 u 1, όπου U 1 είναι ένα νέο μη τερματικό σύμβολο, που προστίθεται στο τρέχον V 4. Παρατηρήστε ότι με αυτό τον τρόπο αντικαθίσταται η παραγωγή ενός βήματος A u 1 u 2 με την παραγωγή δύο βημάτων A U 1 u 2 u 1 u Αν u 1 V 4 και u 2 Σ, τότε αντικαθίσταται ο κανόνας A u 1 u 2 στο τρέχον σύνολο R 4 με τους κανόνες A u 1 U 2 και U 2 u 2, όπου U 2 είναι ένα νέο μη τερματικό σύμβολο, που προστίθεται στο τρέχον V 4. Παρατηρήστε ότι έτσι αντικαθίσταται η παραγωγή ενός βήματος A u 1 u 2 με την παραγωγή δύο βημάτων A u 1 U 2 u 1 u 2.

24 158 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ 3. Αν u 1 Σ, u 2 Σ και u 1 u 2, τότε αντικαθίσταται ο κανόνας A u 1 u 2 στο τρέχον σύνολο R 4 με τους κανόνες A U 1 U 2, U 1 u 1 και U 2 u 2, όπου U 1 και U 2 είναι νέα μη τερματικά σύμβολα, που προστίθενται στο τρέχον V 4. Παρατηρήστε ότι έτσι αντικαθίσταται η παραγωγή ενός βήματος A u 1 u 2 με την παραγωγή τριών βημάτων A U 1 U 2 u 1 U 2 u 1 u Αν u 1 Σ, u 2 Σ και u 1 = u 2, τότε αντικαθίσταται ο κανόνας A u 1 u 2 = u 1 u 1 στο τρέχον σύνολο R 4 με τους κανόνες A U 1 U 1 και U 1 u 1, όπου U 1 είναι νέα μη τερματικό σύμβολο, που προστίθεται στο τρέχον V 4. Παρατηρήστε ότι έτσι αντικαθίσταται η παραγωγή ενός βήματος A u 1 u 2 = u 1 u 1 με την παραγωγή τριών βημάτων A U 1 U 1 u 1 U 1 u 1 u 1. Εστω R 5 το σύνολο των κανόνων και V 5 το σύνολο των μη τερματικών συμβόλων, που προκύπτουν μετά από την εφαρμογή του βήματος 5. Η γραμματική G 5 = (V 5, Σ, R 5, 5 ), όπου 5 = 4 έχει την εξής ιδιότητα: η αρχή 5 δεν εμφανίζεται στο δεξί μέρος κάποιου κανόνα του R 5, το R 5 δεν περιέχει κανόνα-ɛ (μπορεί να περιέχει τον κανόνα 5 ɛ), το R 5 δεν περιέχει μοναδιαίο κανόνα, το R 5 δεν περιέχει κανόνα με περισσότερα από δύο σύμβολα στο δεξί του μέρος το R 5 δεν περιέχει κανόνα της μορφής A u 1 u 2, όπου τα u 1, u 2 δεν είναι και τα δύο μη τερματικά σύμβολα του V 5 και L(G 5 ) = L(G 4 ) = L(G 3 ) = L(G 2 ) = L(G 1 ) = L(G). Αφού η γραμματική G 5 είναι σε κανονική μορφή Chomsky, η απόδειξη έχει ολοκληρωθεί. Παράδειγμα 4.7 (Μετασχηματισμός σε καν. μορφή Chomsky) Ας θεωρήσουμε τη γραμματική χωρίς συμφραζόμενα G = (V, Σ, R, A), όπου V = {A, B}, Σ = {0, 1}, A είναι το μη τερματικό σύμβολο της αρχής και R αποτελείται από τους κανόνες: A BAB B ɛ

25 4.4. ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ CHOM KY 159 B 00 ɛ Εφαρμόζουμε την κατασκευή της απόδειξης του Θεωρήματος 4.2 για να μετασχηματίσουμε τη γραμματική G σε μία γραμματική κανονικής μορφής Chomsky με την ίδια γλώσσα. Κατά τον μετασχηματισμό, χρησιμοποιούμε κεφαλαίους χαρακτήρες για την αναπαράσταση μη τερματικών συμβόλων. Βήμα 1: απαλείφεται το μη τερματικό σύμβολο της αρχής από το δεξί μέρος των κανόνων. Εισάγουμε ένα νέο μη τερματικό σύμβολο και προσθέτουμε τον κανόνα A, οπότε έχουμε τη γραμματική: A A BAB B ɛ B 00 ɛ Βήμα 2: απαλείφονται όλοι οι κανόνες-ɛ. Αρχικά αφαιρείται ο κανόνας A ɛ, οπότε εξετάζονται όλοι οι κανόνες που περιέχουν A στο δεξί τους μέρος. Υπάρχουν δύο τέτοιοι κανόνες: ο A, για τον οποίο προστίθεται ο ɛ και ο A BAB, για τον οποίο προστίθεται ο A BB. Ετσι, προκύπτει η γραμματική: A ɛ A BAB B BB B 00 ɛ Στη συνέχεια απαλείφεται ο κανόνας B ɛ και εξετάζονται όλοι οι κανόνες, που στο δεξί τους μέρος έχουν B. Υπάρχουν τρεις τέτοιοι κανόνες: ο A BAB, για τον οποίο προστίθενται οι κανόνες A AB, A BA και A A, ο A B, για τον οποίο δε χρειάζεται να προστεθεί ο A ɛ, αφού ο συγκεκριμένος κανόνας έχει ήδη αφαιρεθεί και ο A BB, για τον οποίο προστίθεται ο A B, αλλά όχι ο A ɛ, που έχει ήδη αφαιρεθεί.

26 160 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ Ετσι, προκύπτει η γραμματική: A ɛ A BAB B BB AB BA A B 00 Αφού έχουν απομακρυνθεί όλοι οι κανόνες-ɛ ολοκληρώνεται ο μετασχηματισμός του βήματος 2 (ο κανόνας ɛ παραμένει, επειδή το είναι αρχή). Βήμα 3: απαλείφονται όλοι οι μοναδιαίοι κανόνες. Απομακρύνεται ο μοναδιαίος κανόνας A A χωρίς να χρειάζεται να προστεθεί κάποιος νέος κανόνας. Ετσι, προκύπτει η γραμματική: A ɛ A BAB B BB AB BA B 00 Απαλείφεται ο μοναδιαίος κανόνας A και στη θέση του προστίθενται οι κανόνες: Ετσι, προκύπτει η γραμματική: BAB B BB AB BA ɛ BAB B BB AB BA A BAB B BB AB BA B 00 Μετά αφαιρείται ο μοναδιαίος κανόνας B, για τον οποίο προστίθεται ο κανόνας 00, οπότε η γραμματική γίνεται: ɛ BAB BB AB BA 00 A BAB B BB AB BA B 00 Τέλος αφαιρείται ο μοναδιαίος κανόνας A B, για τον οποίο προστίθεται ο κανόνας A 00, οπότε η γραμματική γίνεται: ɛ BAB BB AB BA 00 A BAB BB AB BA 00 B 00

27 4.4. ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ CHOM KY 161 Αφού έχουν απομακρυνθεί όλοι οι μοναδιαίοι κανόνες ολοκληρώνεται ο μετασχηματισμός του βήματος 3. Βήμα 4: απαλείφονται όλοι οι κανόνες με περισσότερα από δύο σύμβολα στο δεξί τους μέρος. Υπάρχουν δύο τέτοιοι κανόνες, που αφαιρούνται: ο κανόνας BAB, για τον οποίο προστίθενται οι BA 1 και A 1 AB και ο κανόνας A BAB, για τον οποίο προστίθενται οι A BA 2 και A 2 AB. Ο συγκεκριμένος μετασχηματισμός μας δίνει τη γραμματική: ɛ BB AB BA 00 BA 1 A BB AB BA 00 BA 2 B 00 A 1 AB A 2 AB Σε αυτό το σημείο ολοκληρώνεται η εφαρμογή του βήματος 4. Βήμα 5: απαλείφονται όλοι οι κανόνες, που στο δεξί τους μέρος περιέχουν ακριβώς δύο σύμβολα, που δεν είναι όλα μη τερματικά. Υπάρχουν τρεις τέτοιοι κανόνες, που αφαιρούνται: ο κανόνας 00, που αντικαθίσταται από τους A 3 A 3, A 3 0, ο κανόνας A 00, που αντικαθίσταται από τους A A 4 A 4, A 4 0 και ο κανόνας B 00, που αντικαθίσταται από τους B A 5 A 5, A 5 0. Τελικά προκύπτει η παρακάτω γραμματική, που είναι σε κανονική μορφή Chomsky: ɛ BB AB BA BA 1 A 3 A 3 A BB AB BA BA 2 A 4 A 4 B A 5 A 5 A 1 AB A 2 AB A 3 0

28 162 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ A 4 0 A Εφαρμογές Σύνταξη Γλωσσών Προγραμματισμού Κάθε γλώσσα προγραμματισμού περιγράφεται από τη σημασία της και από τη σύνταξή της. Η σημασία μιας γλώσσας προγραμματισμού προσδιορίζει το νόημα όλων των πιθανών προγραμμάτων με ορθή σύνταξη. Η σημασία ενός προγράμματος δεν είναι ανεξάρτητη από τη σύνταξη της γλώσσας. Αν και υπάρχουν πολλές διαφορετικές προσεγγίσεις για την περιγραφή της σημασίας των γλωσσών προγραμματισμού, η σύνταξή τους περιγράφεται αποκλειστικά και μόνο με γραμματικές χωρίς συμφραζόμενα [1]. Η παρακάτω γραμματική, όπου τα τερματικά σύμβολα εμφανίζονται με έντονη γραφή, είναι ένα παράδειγμα σύνταξης δηλώσεων σε μία υποθετική γλώσσα προγραμματισμού: decl list decl list decl ; decl ; decl ID : type type INT REAL CHAR ARRAY CONT.. CONT OF type RECORD decl list END Στη γραμματική αυτή το ID αντιστοιχεί στη συμβολοσειρά ενός οποιουδήποτε ονόματος μεταβλητής, το CONT στη συμβολοσειρά μιας οποιασδήποτε σταθεράς και τα REAL, INT, CHAR σε δεσμευμένες λέξεις για τους βασικούς τύπους δεδομένων της γλώσσας. Τα ARRAY, OF, RECORD και END χρησιμοποιούνται σε δηλώσεις μεταβλητών πίνακα και δομών, ενώ τα ; και.. χρησιμοποιούνται αντίστοιχα για το διαχωρισμό εντολών και αριθμητικών σταθερών. Μία συντακτικά σωστή δήλωση, δηλαδή μία συμβολοσειρά που παράγεται από την παραπάνω γραμματική είναι η:

29 4.5. ΕΦΑΡΜΟΓΕΣ 163 foo:record a: CHAR; b: ARRAY 1..2 OF REAL; END; Στοχαστικές Γραμματικές Χωρίς Συμφραζόμενα Ορισμός 4.7 Μία στοχαστική γραμματική χωρίς συμφραζόμενα G ορίζεται από μία πεντάδα (V, Σ, R,, D) όπου: 1. V είναι ένα πεπερασμένο σύνολο με μη τερματικά σύμβολα, 2. Σ είναι ένα πεπερασμένο σύνολο από τερματικά σύμβολα, 3. V Σ =, 4. το V είναι η αρχή της γραμματικής και 5. το D είναι μία συνάρτηση από το R στο [0 1], που αντιστοιχίζει μία τιμή πιθανότητας σε κάθε κανόνα του R. Για κάθε μη τερματικό σύμβολο, το άθροισμα των πιθανοτήτων όλων των κανόνων γι αυτό πρέπει να είναι 1. Δοθείσας μιας γραμματικής G και μιας συμβολοσειράς s, η πιθανότητα ενός συγκεκριμένου συντακτικού δέντρου t είναι το γινόμενο των πιθανοτήτων των κανόνων, που χρησιμοποιούνται στην παραγωγή του. Αν C είναι η σειρά των κανόνων, που χρησιμοποιούνται στην παραγωγή του t και P r(r) είναι η πιθανότητα του κανόνα r, τότε: P r(t) = r C P r(r) Οι στοχαστικές γραμματικές χωρίς συμφραζόμενα έχουν πολλές εφαρμογές στην επεξεργασία φυσικής γλώσσας [2]. Για παράδειγμα, σε ένα περιβάλλον με θόρυβο μπορεί να μην είμαστε βέβαιοι για το ποια συμβολοσειρά πρέπει να αναλυθεί. Σε αυτή την περίπτωση είναι πιθανό να υπάρχουν ορθογραφικά λάθη σε μία συμβολοσειρά παρόμοια με αυτή, που υποτίθεται ότι εκφράζει ή μπορεί ακόμη να υπάρχουν και λάθη μετάδοσης. Σε κάθε τέτοια περίσταση μας ενδιαφέρει να επιλύσουμε το εξής πρόβλημα: δοθέντος ενός συνόλου πιθανών συμβολοσειρών, έστω X και μιας παρατηρούμενης συμβολοσειράς o να βρεθεί η συμβολοσειρά s, που είναι η πιο πιθανή

30 164 ΚΕΦ ΑΛΑΙΟ 4. ΓΡΑΜΜΑΤΙΚΕΣ ΧΩΡΙΣ ΣΥΜΦΡΑΖΟΜΕΝΑ από τις συμβολοσειρές του X. Η πιθανότητα παραγωγής μιας συγκεκριμένης συμβολοσειράς w δίνεται ως το άθροισμα των πιθανοτήτων παραγωγής κάθε πιθανού συντακτικού δέντρου για την w. Δηλαδή, αν T είναι το σύνολο των πιθανών συντακτικών δέντρων για την w, τότε η συνολική πιθανότητα να παραχθεί η συμβολοσειρά w είναι: P r(w) = t T P r(t) Η συμβολοσειρά s, που είναι πιο πιθανό να έχει παραχθεί δεδομένης της παρατηρούμενης συμβολοσειράς o είναι αυτή με τη μεγαλύτερη υπό συνθήκη πιθανότητα δεδομένης της o. Άρα, s = argmaxp r(w o) w X = argmax w X P r(o w)p r(w) P r(o) όπου το argmax επιστρέφει την παράμετρο w, που μεγιστοποιεί την τιμή της συνάρτησης πιθανότητας. 4.6 Βιντεοδιαλέξεις Στην ενότητα αυτή, ο αναγνώστης μπορεί να παρακολουθήσει... βιντεοδιαλέξεις 4.7 Διαδραστικό τεστ Στο διαδραστικό τεστ, που ακολουθεί καλείστε να απαντήσετε σε μία ερώτηση πολλαπλής επιλογής πάνω στην ύλη του Κεφαλαίου 4. Αν επιλέξετε λάθος απάντηση, τότε μπορείτε να επαναλάβετε την προσπάθεια. Ο βαθμός με τον οποίο αξιολογείστε σε κάθε ερώτηση εξαρτάται από το πόσες προσπάθειες θα χρειαστείτε για να βρείτε τη σωστή απάντηση. Για κάθε σωστή απάντηση, εμφανίζεται στην οθόνη ο μέσος όρος των επιδόσεων σας στις ερωτήσεις, που έχουν απαντηθεί μέχρι εκείνη τη στιγμή. Πατήστε εδώ για να ξεκινήσετε το τεστ.

31 ΒΙΒΛΙΟΓΡΑΦ ΙΑ - ΑΝΑΦΟΡ ΕΣ 165 Βιβλιογραφία - Αναφορές [1] Κωνσταντίνος Λάζος, Παναγιώτης Κατσαρός, Ζαφείρης Καραίσκος. Μεταγλωττιστές Γλωσσών Προγραμματισμού: Θεωρία και Πράξη. 3η έκδοση, Θεσσαλονίκη, [2] Elaine A. Rich. Automata Theory and Applications. Prentice-Hall, Inc., Upper addle River, NJ, UA, IBN