КУЋА ГРЧКОГ ОБРАЗОВНОГ БРАТСТВА ПОСЛАСТИЧАРА АБИЈАНА
|
|
|
- Χριστόφορος Αγγελόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 КУЋА ГРЧКОГ ОБРАЗОВНОГ БРАТСТВА ПОСЛАСТИЧАРА АБИЈАНА УДК (497.11) МИОДРАГ ДАБИЖИЋ КУЋА ГРЧКОГ ОБРАЗОВНОГ БРАТСТВА ПОСЛАСТИЧАРА АБИЈАНА U старом језгру Земуна, у зидном платну на источној, парној страни Главне улице, од једноспратнице Катарине Марковић (бр. 12) до спратне зграде трговца Стевана Капамаџије (бр. 24), налазе се још три спратне зграде и једна високопартерна кућа посластичара Фердинанда Абијана (Abian). Она је у штампаном Попису кућа у граду Земуну са новом нумерациjом и нацртом нових назива улица из године уписана на име удове Абијан, a у Попису кућа из године назначено је име (удове) Каролина. 1 Међутим, кућа има дугу прошлост и везује се за два пређашња века. Писац Историје Земуна Петар Марковић у сачуваном рукописном раду Грађевине у Земуну, почевши од године, који је урадио 1911, указао је суграђанима, поред осталог, и на кућу познатог посластичара, власника, који је у њој становао и који је у истој улици имао радњу у старој спратној згради бр. 13 породице Oпел (Oppel). 2 За Абијана се зна да је своје производе (посластице и пециво) достављао и двору кнеза Михаила, кнеза па краља Милана, a у време српско-турског рата (1876) посредством српског коморџије (лиферант) снабдевао је пецивом, шампањцем и разним ликерима и српски логор руског и српског генерала Михаила Черњајева. Може се поменути да Ф. Абијан није био староседелац Земуна и да je године стекао завичајност или, како се званично говорило, да је примљен у завичајну свезу тада пограничног краљевског слободног града на Дунаву. 3 Грађење куће године У рукописном раду П. Марковића забележени су подаци о стању на поменутом земљишту (плац). На уличној страни била je једна стара, пониска, проста кућа с два прозора и улазом и цео плац био је ограђен циглом. Иза куће, у дворишту, налазила се стара чатмара (Riegelbau) с доксатом на првом кату по турском кроју 77
2 МИОДРАГ ДАБИЖИЋ Сл. 1. Факсимил темељне повеље куће Грчког образовног братства из године с печатом инвеститора СПОМЕНИЧКО НАСЛЕЂЕ 78
3 КУЋА ГРЧКОГ ОБРАЗОВНОГ БРАТСТВА ПОСЛАСТИЧАРА АБИЈАНА Сл. 2. Земун, Главна улица око 1906: кућа Фердинанда Абијана (бр. 22), једноспратнице градоначелника Константина Петровића, па фотографа Рудолфа Гатера (бр. 20), Гине Вулка (бр. 18) са спомен-плочом о боравку аустријског цара Франца Првог 1817) и посластичара Фрање Блауенштајнера (бр. 16) (извесно балканском, прим. а.) и у њеном приземљу налазила се чувена гостионица Fassel Fasselwirt. Занимљиво je навести да се назив гостионице помиње у попису земунских домаћина породица и њихових занимања из 1736/1737. године, који је објавио историчар Душан Поповић. У списку је и извесни Гашпар (Caspar Prosek), који је имао Würth beim Fassel. 4 Према томе, може се прихватити мишљење о старој чатмари и гостионици јер је Петар Марковић описано видео. Земљиште је касније дошло у посед Грчког образовног братства и оно је на једном делу плаца (према кући бр. 24) саградило уздигнуту приземну кућу. О времену подизања куће зна се захваљујући добро очуваној темељној повељи, која je пронађена приликом адаптације постојећег локала године, када је рушен фронтални зид. На висини једног метра од пода извађена је метална кутија са стакленом теглицом у којој се налазио табак хартије (34 x 21 сm) са записом на првој страни. У правилно савијеном табаку била су приложена три новчића, међу њима 1 / 4 FL (флорин, форинта) с ликом цара Франца Јозефа I, који је емитован 1860, и три крајцаре с ликом цара Фердинанда I, који је искован године. 5 Темељна повеља почиње свечаним речима да чувени потомци Платона прилажу овај дом Грчкој школи (елиномусион), која се гради у време моћног императора Франца Јозефа Првог и племенитих чланова Димитрија Бијала, Георгија пл. (фон) Спирта и Паусанија Димитријадиса, према пројекту уметничког (вештог) градитеља Јозефа Маркса (Маrx) лета Господњег (спасоносне) и овде основане грчке заједнице њених представника: Димитрије Бијало (Βιαλλоς), Георгије пл. Спирта, Константин пл. Спирта, Паусаније Димитријадис (Δημητριάδης), Григорије Харис, Константин А. Петровић (Пετροβίк), Петар З. Леко (Λεκος), Константин Спида, Стеван Гешос (Гεσσιоς), Никола Валко (Βαλκος), Антоније Златкос. Текст записа завршава се податком да је Грчко образовно братство имало једног учитеља Одисеја Мавракиса (Μαυράκης). 6 Испод рукописа повеље стоји округли печат утиснут у црвени восак, на којем је у плитком рељефу приказан Силазак Светог Духа на апостоле, 7 а на периферном кружном венцу великим грчким словима исписан je текст: ЕΛΛНNIКН ЕКПАIΔЕУТIКН ЕNОТНΣ ЕN ZЕ- МОNI (Грчко образовно братство у Земуну). 8 Међу именима наведених у повељи има неколико значајних за локалну историју града. Браћа Георгије Ђорђе ( 1909) и Константин Спирта ( 1881) преузели су после смрти оца Павла ( 1858) послове куће и као образовани привредници стекли су углед и поштовање грађана. О њима jе писано, 9 нарочито о Ђорђу који је био члан Градског заступства и његових одбора. У грчкој заједници имао је низ функција и не изненађује да је учествовао у раду Српске православне црквене општине, да је приложник Српског црквено-школског фонда и да је у време оснивања и легализације Српске црквене 79
4 МИОДРАГ ДАБИЖИЋ певачке задруге (1866), заједно с Константином, био дејствителни (извршни) члан њеног мешовитог хора. Ђорђе је забележен као први тенор, док је брат певао први бас, односно баритон. 10 Име врло образованог трговца Константина Коче Петровића повезано јe с променама у тадашњој Аустрији (од Аустро-Угарска). Војни комунитет Земун добио је године статус краљевског слободног града. Крајем исте године одржани су избори за градску управу и на њима је, из редова грађана, К. Петровић изабран за начелника града, који је, од почетка године до почетка године, успешно обавио прелаз војне управе у грађанску. 11 Глас угледног грађанина пратио je и Григорија, члана трговачке породице Харис/Хариш, који je учествовао и у јавном раду у граду. Угледу је допринело и једно грађевинско дело. Наиме, после смрти супруге Марије, рођене Петровић, остварио је њену жељу и на земљишту у непосредној близини православног гробља саграђени су ( ) црква с криптом за умрле чланове породице Петровић-Хариш (Харишева црква) и партерна кућа са станом за свештеника. Према повељи, поменути градитељ Јозеф Маркс обавио је све грађевинске радове (црква, кућа и ограда). 12 Паусаније Димитријадис такође се помиње као заступник. У време кад се комунитетска и градска управа борила за грађење железничке пругe, у једној земунској делегацији која је ради остварења ове жеље упућена у Будимпешту и Беч, био је и П. Димитријадис. 13 Доградња куће и садашње стање Кад је кућа дошла у посед посластичара Абијана, њој је дограђено крило (П+П) с три дућана, тако да је спојена с једноспратницом Константина Петровића (бр. 20). Тада je фасада обрађена у духу историцизма, првенствено неоренесансе. Према картографском извору, у исто време изграђено je и дворишно крило с аркадним тремом. 14 После Првог светског рата у делу стамбеног крила према згради бр. 24 уређена је продавница боја и лакова браће Бихали, која је ратне године постала немачка продавница затвореног типа Место за расподелу животних намирница (Lebensmittelverteilungstelle). Приликом авионског бомбардовања града године кућа није теже оштећена, али су после године обављене мање преправке. Последњи, велики радови обављени су 1983/1984. године, кад су темељито уређене данашње две продавнице. Том приликом повећени су отвори за излагање робе и двоја врата, тако да je зграда, изузимајући станове у дворишту, коначно претворена у пословну. 15 Сад већ стара кућа с измењеним изгледом прочеља, ипак је сачувала изглед поткровног венца с плитком Сл. 3. Садашњи изглед Абијанове куће (април 2009) СПОМЕНИЧКО НАСЛЕЂЕ 80
5 КУЋА ГРЧКОГ ОБРАЗОВНОГ БРАТСТВА ПОСЛАСТИЧАРА АБИЈАНА малтерском профилацијом и округлим отворима (розете), смањени броj пиластара, капију и медаљон. Уска, висока дрвена капија с полукружним светларником заштићена је гитерима од кованог гвожђа. Она показује умеће домаћих занатлија и укус грађана који су овом детаљу посвећивали посебну пажњу. Нажалост, она је у непримереном стању: давно није бојена и недостаје joj брава. Изнад капије jе медаљон урађен у гипсу или малтеру с иницијалима имена и презимена бивше власнице испреплетена слова СA (Carolina Abian). За стару партерну кућу приликом последње валоризације, стручњак Завода за заштиту споменика културе града Београда, који ју је обавио, у обрасцу за поједине објекте уписао је да је грађевина изменила првобитни изглед и да није карактеристична за развој блока који је од постанка тендирао ка једноспратности. Што се тиче степена заштите, оцењено је да је због амбијенталног интегритета треба слободно третирати. Ипак, њено постојање треба забележити јер je повезана за бившу колониjу Грка и Цинцара, која је од године до почетка XX века дала значајан допринос напретку Земуна. Исто тако, она не подсећа само на Ф. Абиjана него и на друге врсне земунске посластичаре, као што су Фрања Блауенштајнер, који је имао радњу у непосредном суседству, у својој једноспратници бр. 16, и који је радионицу и продавницу године предао свом ученику Петру Глумцу ( 3емун 1966). Њихове посластичарнице посећивали су многобројни гости а поруџбине су стизале са разних страна, из Београда, Народног позоришта, на пример. 16 Сл. 4. Стилска капија и медаљон са иницијалима CA. Фотограф: мајстор Зденко Штромар 81
6 МИОДРАГ ДАБИЖИЋ НАПОМЕНЕ: 1] Попис кућа и Попис кућа, Земун, 1906, 8. 2] П. Марковић, Грађевине у Земуну (рукопис), Земун, 1911, 8. 3] Извештај Поглаварства града Земуна за управну годину 1888, Земун, 1890, 28. 4] Д. Ј. Поповић, Срби у Срему до 1736/7, САН, Београд, 1950, ] Архива М. Д. Фас. о Абијановој кући, белешка о пронађеној повељи. 6] Исто, писмо и превод проф. др Ј. Пападријаноса (март 2007). 7] Други дан Духова била је слава Грка и њихових установа. 8] Грчки школски фонд основан је 1793, а основано је Грчко образовно братство / Грчко школско друштво. 9] О грчкој колонији писали су Ј. Пападријанос, П. Марковић, И. Сопрон, Г. Kopaћ, земунска породица Спирта, Београд, 2007, М. Дабижић и други. 10] Д. М., Српска певачка задруга земунска, Народни гласник, бр. 44, Земун, 9/22. јун 1907, 1 2. Д. М. je протојереј Душан Марковић ( 1935). 11] В. Николић, Знаменити земунски Срби у XIX веку, Земун, 1913, ; П. Марковић, Земун, Земун, 1896, ] B. Hиколић, Димитрије Петровић и Григорије Хариш, Мали гласник, бр. 44, Земун, 27. октобар/9. новембар 1913, 1 2; М. Дабижић, Успомене на Хеленску колонију у Земуну, Београд Земун, 1996, 14 и др. 13] П. Марковић, Земун, ] А. М. Дабижић, Старо језгро Земуна Блок између улица Главне, Господске, Трга победе и Прерадовићеве у просторној културноисторијској целини, Наслеђе, I, Београд, 1997, 40 (План блока I IV) и 52 (Абијанова кућа). 15] Oбразац ЗЗСКГБ о Абијановој кући, испунио Жељко Шкаламера. 16] Попис кућа 1906, 8; Писана изјава Виде Глумац ( 1993) о брату Петру. Фас. породица Глумац. Проверавани су подаци о кући и стога захваљујем професорима др Јоанису Пападријаносу ( Солун, 2009), др Миодрагу Стојановићу и грађевинару Славку Коњевићу, који је запис сачувао. Summary: MIODRAG DABIŽIĆ THE HOUSE OF THE GREEK EDUCATIONAL FRATERNITY THE CONFECTIONER ABIAN S HOUSE The house at 22 Glavna Street in the historic core of Zemun has a long history. In the eighteenth century and until 1877, the site was occupied by two modest houses, one of which accommodated the well-known Beym Fassel inn. In 1877 the Greek Educational Fraternity had a building erected there for their purposes. Later on, it changed ownership and was acquired by the confectioner Ferdinand Abian, i.e. his wife Karolina. Abian had it enlarged and its façade redone in the neo-renaissance style. The residential-commercial building was remodelled several times. During the last remodelling, in 1983/4, when its use became commercial, the foundation charter in Greek and three coins were discovered. Apart from the patron, the charter specifies the builder (Joseph Marx), the purpose (educational), twelve representatives of the Greek- Tzintzar community, two of them members of the distinguished patrician Spirta family, and the year The charter was authenticated with a red-wax seal. The remodelling of 1983/4 converted the street-facing wing into two commercial-purpose units, thus altering the earlier façade of which some fragments have been retained. The value of the house is reduced to an ambience one. As for the level of protection, it is to be treated freely. In the view of the author of this paper, the house should be recorded in local history because of its association with the former colony of Greeks and Tzintzars who contributed significantly to the prosperity of Zemun (Semlin), a border town until ILLUSTRATIONS Fig. 1 Facsimile of the foundation charter for the building of the Greek Educational Fraternity with the patron s seal Fig. 2 Zemun, Glavna Street ca 1906: House of Ferdinand Abian (No 22), two-storey houses of the mayor Konstantin Petrović, the photographer Rudolph Gatter (No 20), Gino Vulko (No 18) with the plate commemorating the stay of the Austrian emperor Franz I in 1817, and of the confectioner Blauensteiner (No 16) Fig. 3 Abian s house today (April 2009) Fig. 4 Period gate and medallion with the initials SA (by master photographer Zdenko Štromar) СПОМЕНИЧКО НАСЛЕЂЕ 82
Теорија електричних кола
 др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
налазе се у диелектрику, релативне диелектричне константе ε r = 2, на међусобном растојању 2 a ( a =1cm
 1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
г) страница aa и пречник 2RR описаног круга правилног шестоугла јесте рац. бр. јесу самерљиве
 в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
I Наставни план - ЗЛАТАР
 I Наставни план - ЗЛААР I РАЗРЕД II РАЗРЕД III РАЗРЕД УКУО недељно годишње недељно годишње недељно годишње годишње Σ А1: ОАЕЗНИ ОПШЕОРАЗОНИ ПРЕДМЕИ 2 5 25 5 2 1. Српски језик и књижевност 2 2 4 2 2 1.1
I Наставни план - ЗЛААР I РАЗРЕД II РАЗРЕД III РАЗРЕД УКУО недељно годишње недељно годишње недељно годишње годишње Σ А1: ОАЕЗНИ ОПШЕОРАЗОНИ ПРЕДМЕИ 2 5 25 5 2 1. Српски језик и књижевност 2 2 4 2 2 1.1
Tестирање хипотеза. 5.час. 30. март Боjана Тодић Статистички софтвер март / 10
 Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
1.2. Сличност троуглова
 математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
K ад се говори о првим просветним активностима међу
 УДК 930.85(497.11 Земун) 17/18 ; 792.071/.072:929 Вујић Ј. ; 727.112(497.11) 17/18 МИОДРАГ ДАБИЖИЋ ЗГРАДЕ СРПСКЕ ШКОЛЕ И ОБЕЛЕЖЈЕ О ЈОАКИМУ ВУЈИЋУ K ад се говори о првим просветним активностима међу земунским
УДК 930.85(497.11 Земун) 17/18 ; 792.071/.072:929 Вујић Ј. ; 727.112(497.11) 17/18 МИОДРАГ ДАБИЖИЋ ЗГРАДЕ СРПСКЕ ШКОЛЕ И ОБЕЛЕЖЈЕ О ЈОАКИМУ ВУЈИЋУ K ад се говори о првим просветним активностима међу земунским
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ
 7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
(од 4. до 155. стране) (од 4. до 73. стране) ДРУГИ, ТРЕЋИ И ЧЕТВРТИ РАЗРЕД - Европа и свет у другој половини 19. и почетком 20.
 Драгољуб М. Кочић, Историја за први разред средњих стручних школа, Завод за уџбенике Београд, 2007. година * Напомена: Ученици треба да се припремају за из уџбеника обајвљених од 2007 (треће, прерађено
Драгољуб М. Кочић, Историја за први разред средњих стручних школа, Завод за уџбенике Београд, 2007. година * Напомена: Ученици треба да се припремају за из уџбеника обајвљених од 2007 (треће, прерађено
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
Писмени испит из Теорије површинских носача. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама.
 Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2. За плочу
Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2. За плочу
ТРАПЕЗ РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ. Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце
 РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
Први корак у дефинисању случајне променљиве је. дефинисање и исписивање свих могућих eлементарних догађаја.
 СЛУЧАЈНА ПРОМЕНЉИВА Једнодимензионална случајна променљива X је пресликавање у коме се сваки елементарни догађај из простора елементарних догађаја S пресликава у вредност са бројне праве Први корак у дефинисању
СЛУЧАЈНА ПРОМЕНЉИВА Једнодимензионална случајна променљива X је пресликавање у коме се сваки елементарни догађај из простора елементарних догађаја S пресликава у вредност са бројне праве Први корак у дефинисању
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ
 СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
Положај сваке тачке кружне плоче је одређен са поларним координатама r и ϕ.
 VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА
 ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА 1. Допуни шта недостаје: а) 5m = dm = cm = mm; б) 6dm = m = cm = mm; в) 7cm = m = dm = mm. ПОЈАМ ПОВРШИНЕ. Допуни шта недостаје: а) 10m = dm = cm = mm ; б) 500dm = a
ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА 1. Допуни шта недостаје: а) 5m = dm = cm = mm; б) 6dm = m = cm = mm; в) 7cm = m = dm = mm. ПОЈАМ ПОВРШИНЕ. Допуни шта недостаје: а) 10m = dm = cm = mm ; б) 500dm = a
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Тест Математика Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 00/0. година ТЕСТ МАТЕМАТИКА
Тест Математика Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 00/0. година ТЕСТ МАТЕМАТИКА
Предмет: Задатак 4: Слика 1.0
 Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
КРУГ. У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице.
 КРУГ У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице. Архимед (287-212 г.п.н.е.) 6.1. Централни и периферијски угао круга Круг
КРУГ У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице. Архимед (287-212 г.п.н.е.) 6.1. Централни и периферијски угао круга Круг
2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ
 2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ 2.1. МАТЕМАТИЧКИ РЕБУСИ Најједноставније Диофантове једначине су математички ребуси. Метод разликовања случајева код ових проблема се показује плодоносним, јер је раздвајање
2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ 2.1. МАТЕМАТИЧКИ РЕБУСИ Најједноставније Диофантове једначине су математички ребуси. Метод разликовања случајева код ових проблема се показује плодоносним, јер је раздвајање
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
ОБЛАСТИ: 1) Тачка 2) Права 3) Криве другог реда
 ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
Количина топлоте и топлотна равнотежа
 Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
6.5 Површина круга и његових делова
 7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
Θέμα διπλωματικής εργασίας: «Από το «φρενοκομείο» στη Λέρο και την Ψυχιατρική Μεταρρύθμιση: νομικό πλαίσιο και ηθικοκοινωνικές διαστάσεις»
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΕΣ ΙΑΤΡΙΚΗΣ & ΟΔΟΝΤΙΑΤΡΙΚΗΣ ΤΜΗΜΑΤΑ ΝΟΜΙΚΗΣ & ΘΕΟΛΟΓΙΑΣ ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΣΥΓΧΡΟΝΕΣ ΙΑΤΡΙΚΕΣ ΠΡΑΞΕΙΣ: ΔΙΚΑΙΙΚΗ ΡΥΘΜΙΣΗ ΚΑΙ ΒΙΟΗΘΙΚΗ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΕΣ ΙΑΤΡΙΚΗΣ & ΟΔΟΝΤΙΑΤΡΙΚΗΣ ΤΜΗΜΑΤΑ ΝΟΜΙΚΗΣ & ΘΕΟΛΟΓΙΑΣ ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΣΥΓΧΡΟΝΕΣ ΙΑΤΡΙΚΕΣ ΠΡΑΞΕΙΣ: ΔΙΚΑΙΙΚΗ ΡΥΘΜΙΣΗ ΚΑΙ ΒΙΟΗΘΙΚΗ
6.2. Симетрала дужи. Примена
 6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ПРОБНИ ЗАВРШНИ ИСПИТ школска 016/017. година ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ПРОБНИ ЗАВРШНИ ИСПИТ школска 016/017. година ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
10.3. Запремина праве купе
 0. Развијени омотач купе је исечак чији је централни угао 60, а тетива која одговара том углу је t. Изрази површину омотача те купе у функцији од t. 0.. Запремина праве купе. Израчунај запремину ваљка
0. Развијени омотач купе је исечак чији је централни угао 60, а тетива која одговара том углу је t. Изрази површину омотача те купе у функцији од t. 0.. Запремина праве купе. Израчунај запремину ваљка
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције. Diffie-Hellman размена кључева
 ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2/13 Diffie-Hellman размена кључева први алгоритам са јавним
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2/13 Diffie-Hellman размена кључева први алгоритам са јавним
L кплп (Калем у кплу прпстпперипдичне струје)
 L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
b) Израз за угиб дате плоче, ако се користи само први члан реда усвојеног решења, је:
 Пример 1. III Савијање правоугаоних плоча За правоугаону плочу, приказану на слици, одредити: a) израз за угиб, b) вредност угиба и пресечних сила у тачки 1 ако се користи само први члан реда усвојеног
Пример 1. III Савијање правоугаоних плоча За правоугаону плочу, приказану на слици, одредити: a) израз за угиб, b) вредност угиба и пресечних сила у тачки 1 ако се користи само први члан реда усвојеног
2.3. Решавање линеарних једначина с једном непознатом
 . Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
. Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 01/01. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 01/01. година ТЕСТ
Примена првог извода функције
 Примена првог извода функције 1. Одреди дужине страница два квадрата тако да њихов збир буде 14 а збир површина тих квадрата минималан. Ре: x + y = 14, P(x, y) = x + y, P(x) = x + 14 x, P (x) = 4x 8 Први
Примена првог извода функције 1. Одреди дужине страница два квадрата тако да њихов збир буде 14 а збир површина тих квадрата минималан. Ре: x + y = 14, P(x, y) = x + y, P(x) = x + 14 x, P (x) = 4x 8 Први
Анализа Петријевих мрежа
 Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА
 Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
Георгиос Нектариос Лоис
 Ni{ i Vizantija XIV 645 Георгиос Нектариос Лоис ГРЧКА ПРАВОСЛАВНА ЗАЈЕДНИЦА У АДРИАНУПОЉУ (ЈЕДРЕНУ) ПО ОСНОВИ ПРАВИЛНИКА НАРОДНО-СТАРЕШИНСТВА ИЗ 1904 Град Адрианупољ изграђен је око 125. године после Христа
Ni{ i Vizantija XIV 645 Георгиос Нектариос Лоис ГРЧКА ПРАВОСЛАВНА ЗАЈЕДНИЦА У АДРИАНУПОЉУ (ЈЕДРЕНУ) ПО ОСНОВИ ПРАВИЛНИКА НАРОДНО-СТАРЕШИНСТВА ИЗ 1904 Град Адрианупољ изграђен је око 125. године после Христа
1. 2. МЕТОД РАЗЛИКОВАЊА СЛУЧАЈЕВА 1
 1. 2. МЕТОД РАЗЛИКОВАЊА СЛУЧАЈЕВА 1 Метод разликовања случајева је један од најексплоатисанијих метода за решавање математичких проблема. У теорији Диофантових једначина он није свемогућ, али је сигурно
1. 2. МЕТОД РАЗЛИКОВАЊА СЛУЧАЈЕВА 1 Метод разликовања случајева је један од најексплоатисанијих метода за решавање математичких проблема. У теорији Диофантових једначина он није свемогућ, али је сигурно
Универзитет у Крагујевцу Факултет за машинство и грађевинарство у Краљеву Катедра за основне машинске конструкције и технологије материјала
 Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Теорија електричних кола
 Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
Тест за 7. разред. Шифра ученика
 Министарство просвете Републике Србије Српско хемијско друштво Окружно/градско/међуокружно такмичење из хемије 28. март 2009. године Тест за 7. разред Шифра ученика Пажљиво прочитај текстове задатака.
Министарство просвете Републике Србије Српско хемијско друштво Окружно/градско/међуокружно такмичење из хемије 28. март 2009. године Тест за 7. разред Шифра ученика Пажљиво прочитај текстове задатака.
У к у п н о :
 ГОДИШЊИ (ГЛОБАЛНИ) ПЛАН РАДА НАСТАВНИКА Наставни предмет: ФИЗИКА Разред: Седми Ред.број Н А С Т А В Н А Т Е М А / О Б Л А С Т Број часова по теми Број часова за остале обраду типове часова 1. КРЕТАЊЕ И
ГОДИШЊИ (ГЛОБАЛНИ) ПЛАН РАДА НАСТАВНИКА Наставни предмет: ФИЗИКА Разред: Седми Ред.број Н А С Т А В Н А Т Е М А / О Б Л А С Т Број часова по теми Број часова за остале обраду типове часова 1. КРЕТАЊЕ И
Слава или Крсно име код Срба
 DOI: 10.2298/GEI1501123P УДК: 398.332:271.222(497.11) Примљено за штампу на седници Редакције 05. 03. 2015. Никола Ф. Павковић Проф. Универзитета у Београду npavkovi@eunet.rs Слава или Крсно име код Срба
DOI: 10.2298/GEI1501123P УДК: 398.332:271.222(497.11) Примљено за штампу на седници Редакције 05. 03. 2015. Никола Ф. Павковић Проф. Универзитета у Београду npavkovi@eunet.rs Слава или Крсно име код Срба
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
6.1. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре
 0 6.. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре У обичном говору се често каже да су неки предмети симетрични. Примери таквих објеката, предмета, геометријских
0 6.. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре У обичном говору се често каже да су неки предмети симетрични. Примери таквих објеката, предмета, геометријских
7.3. Површина правилне пирамиде. Површина правилне четворостране пирамиде
 математик за VIII разред основне школе 4. Прво наћи дужину апотеме. Како је = 17 cm то је тражена површина P = 18+ 4^cm = ^4+ cm. 14. Основа четворостране пирамиде је ромб чије су дијагонале d 1 = 16 cm,
математик за VIII разред основне школе 4. Прво наћи дужину апотеме. Како је = 17 cm то је тражена површина P = 18+ 4^cm = ^4+ cm. 14. Основа четворостране пирамиде је ромб чије су дијагонале d 1 = 16 cm,
3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни
 ТАЧКА. ПРАВА. РАВАН Талес из Милета (624 548. пре н. е.) Еуклид (330 275. пре н. е.) Хилберт Давид (1862 1943) 3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни Настанак геометрије повезује
ТАЧКА. ПРАВА. РАВАН Талес из Милета (624 548. пре н. е.) Еуклид (330 275. пре н. е.) Хилберт Давид (1862 1943) 3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни Настанак геометрије повезује
Хомогена диференцијална једначина је она која може да се напише у облику: = t( x)
 ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ Штa треба знати пре почетка решавања задатака? Врсте диференцијалних једначина. ДИФЕРЕНЦИЈАЛНА ЈЕДНАЧИНА КОЈА РАЗДВАЈА ПРОМЕНЉИВЕ Код ове методе поступак је следећи: раздвојити
ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ Штa треба знати пре почетка решавања задатака? Врсте диференцијалних једначина. ДИФЕРЕНЦИЈАЛНА ЈЕДНАЧИНА КОЈА РАЗДВАЈА ПРОМЕНЉИВЕ Код ове методе поступак је следећи: раздвојити
TAЧКАСТА НАЕЛЕКТРИСАЊА
 TЧКАСТА НАЕЛЕКТРИСАЊА Два тачкаста наелектрисања оптерећена количинама електрицитета и налазе се у вакууму као што је приказано на слици Одредити: а) Вектор јачине електростатичког поља у тачки А; б) Електрични
TЧКАСТА НАЕЛЕКТРИСАЊА Два тачкаста наелектрисања оптерећена количинама електрицитета и налазе се у вакууму као што је приказано на слици Одредити: а) Вектор јачине електростатичког поља у тачки А; б) Електрични
Универзитет у Београду, Саобраћајни факултет Предмет: Паркирање. 1. вежба
 Универзитет у Београду, Саобраћајни факултет Предмет: Паркирање ОРГАНИЗАЦИЈА ПАРКИРАЛИШТА 1. вежба Место за паркирање (паркинг место) Део простора намењен, технички опремљен и уређен за паркирање једног
Универзитет у Београду, Саобраћајни факултет Предмет: Паркирање ОРГАНИЗАЦИЈА ПАРКИРАЛИШТА 1. вежба Место за паркирање (паркинг место) Део простора намењен, технички опремљен и уређен за паркирање једног
6. ЛИНЕАРНА ДИОФАНТОВА ЈЕДНАЧИНА ах + by = c
 6. ЛИНЕАРНА ДИОФАНТОВА ЈЕДНАЧИНА ах + by = c Ако су а, b и с цели бројеви и аb 0, онда се линеарна једначина ах + bу = с, при чему су х и у цели бројеви, назива линеарна Диофантова једначина. Очигледно
6. ЛИНЕАРНА ДИОФАНТОВА ЈЕДНАЧИНА ах + by = c Ако су а, b и с цели бројеви и аb 0, онда се линеарна једначина ах + bу = с, при чему су х и у цели бројеви, назива линеарна Диофантова једначина. Очигледно
ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΘΕΜΕΛΙΩΔΗΣ ΚΛΑΔΙΚΗ ΑΝΑΛΥΣΗ ΤΩΝ ΕΙΣΗΓΜΕΝΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΑΓΟΡΑΣ
 ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ Διπλωματική Εργασία ΘΕΜΕΛΙΩΔΗΣ ΚΛΑΔΙΚΗ ΑΝΑΛΥΣΗ ΤΩΝ ΕΙΣΗΓΜΕΝΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΑΓΟΡΑΣ Του ΚΩΣΤΟΥΛΗ ΔΗΜΗΤΡΙΟΥ ΤΟΥ ΒΑΣΙΛΕΙΟΥ
ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ Διπλωματική Εργασία ΘΕΜΕΛΙΩΔΗΣ ΚΛΑΔΙΚΗ ΑΝΑΛΥΣΗ ΤΩΝ ΕΙΣΗΓΜΕΝΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΑΓΟΡΑΣ Του ΚΩΣΤΟΥΛΗ ΔΗΜΗΤΡΙΟΥ ΤΟΥ ΒΑΣΙΛΕΙΟΥ
Штампарске грешке у петом издању уџбеника Основи електротехнике, 1. део, Електростатика
 Штампарске грешке у петом издању уџбеника Основи електротехнике део Страна пасус први ред треба да гласи У четвртом делу колима променљивих струја Штампарске грешке у четвртом издању уџбеника Основи електротехнике
Штампарске грешке у петом издању уџбеника Основи електротехнике део Страна пасус први ред треба да гласи У четвртом делу колима променљивих струја Штампарске грешке у четвртом издању уџбеника Основи електротехнике
8. ПИТАГОРИНА ЈЕДНАЧИНА х 2 + у 2 = z 2
 8. ПИТАГОРИНА ЈЕДНАЧИНА х + у = z Један од најзанимљивијих проблема теорије бројева свакако је проблем Питагориних бројева, тј. питање решења Питагорине Диофантове једначине. Питагориним бројевима или
8. ПИТАГОРИНА ЈЕДНАЧИНА х + у = z Један од најзанимљивијих проблема теорије бројева свакако је проблем Питагориних бројева, тј. питање решења Питагорине Диофантове једначине. Питагориним бројевима или
ОДЛУКУ. I Народна скупштина Републике Српске усваја Измјене и допуне Развојног програма Републике Српске, година.
 1102 На основу члана 70. став 1. тачка 2. Устава Републике Српске, члана 183. и члана 187. ст. 1. и 2. Пословника Народне скупштине Републике Српске - Пречишћени текст ( Службени гласник Републике Српске,
1102 На основу члана 70. став 1. тачка 2. Устава Републике Српске, члана 183. и члана 187. ст. 1. и 2. Пословника Народне скупштине Републике Српске - Пречишћени текст ( Службени гласник Републике Српске,
Μεταπτυχιακή διατριβή. Ανδρέας Παπαευσταθίου
 Σχολή Γεωτεχνικών Επιστημών και Διαχείρισης Περιβάλλοντος Μεταπτυχιακή διατριβή Κτίρια σχεδόν μηδενικής ενεργειακής κατανάλωσης :Αξιολόγηση συστημάτων θέρμανσης -ψύξης και ΑΠΕ σε οικιστικά κτίρια στην
Σχολή Γεωτεχνικών Επιστημών και Διαχείρισης Περιβάλλοντος Μεταπτυχιακή διατριβή Κτίρια σχεδόν μηδενικής ενεργειακής κατανάλωσης :Αξιολόγηση συστημάτων θέρμανσης -ψύξης και ΑΠΕ σε οικιστικά κτίρια στην
Мониторинг квалитета ваздуха Града Новог Сада у години
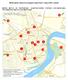 Мониторинг квалитета ваздуха Града Новог Сада у 2010. години МЕРНА МЕСТА ЗА УЗОРКОВАЊЕ ЈЕДНОЧАСОВНИХ УЗОРАКА АЗОТДИОКСИДA, УГЉЕНМОНОКСИДА И УГЉЕНДИОКСИДА А1. Поликлиника, Хајдук Вељкова 2, Нови Сад NO
Мониторинг квалитета ваздуха Града Новог Сада у 2010. години МЕРНА МЕСТА ЗА УЗОРКОВАЊЕ ЈЕДНОЧАСОВНИХ УЗОРАКА АЗОТДИОКСИДA, УГЉЕНМОНОКСИДА И УГЉЕНДИОКСИДА А1. Поликлиника, Хајдук Вељкова 2, Нови Сад NO
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x,
 РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
Η ΨΥΧΙΑΤΡΙΚΗ - ΨΥΧΟΛΟΓΙΚΗ ΠΡΑΓΜΑΤΟΓΝΩΜΟΣΥΝΗ ΣΤΗΝ ΠΟΙΝΙΚΗ ΔΙΚΗ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΝΟΜΙΚΗ ΣΧΟΛΗ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΤΟΜΕΑΣ ΙΣΤΟΡΙΑΣ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΚΟΙΝΩΝΙΟΛΟΓΙΑΣ ΤΟΥ ΔΙΚΑΙΟΥ Διπλωματική εργασία στο μάθημα «ΚΟΙΝΩΝΙΟΛΟΓΙΑ ΤΟΥ ΔΙΚΑΙΟΥ»
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΝΟΜΙΚΗ ΣΧΟΛΗ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΤΟΜΕΑΣ ΙΣΤΟΡΙΑΣ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΚΟΙΝΩΝΙΟΛΟΓΙΑΣ ΤΟΥ ΔΙΚΑΙΟΥ Διπλωματική εργασία στο μάθημα «ΚΟΙΝΩΝΙΟΛΟΓΙΑ ΤΟΥ ΔΙΚΑΙΟΥ»
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
Скупови (наставак) Релације. Професор : Рака Јовановић Асиситент : Јелена Јовановић
 Скупови (наставак) Релације Професор : Рака Јовановић Асиситент : Јелена Јовановић Дефиниција дуалне скуповне формуле За скуповне формулу f, која се састоји из једног или више скуповних симбола и њихових
Скупови (наставак) Релације Професор : Рака Јовановић Асиситент : Јелена Јовановић Дефиниција дуалне скуповне формуле За скуповне формулу f, која се састоји из једног или више скуповних симбола и њихових
ΑΛΕΞΑΝΔΡΟΣ ΠΑΛΛΗΣ SCHOOLTIME E-BOOKS
 ΟΜΗΡΟΥ ΙΛΙΑΔΑ ΑΛΕΞΑΝΔΡΟΣ ΠΑΛΛΗΣ SCHOOLTIME E-BOOKS www.scooltime.gr [- 2 -] The Project Gutenberg EBook of Iliad, by Homer This ebook is for the use of anyone anywhere at no cost and with almost no restrictions
ΟΜΗΡΟΥ ΙΛΙΑΔΑ ΑΛΕΞΑΝΔΡΟΣ ΠΑΛΛΗΣ SCHOOLTIME E-BOOKS www.scooltime.gr [- 2 -] The Project Gutenberg EBook of Iliad, by Homer This ebook is for the use of anyone anywhere at no cost and with almost no restrictions
6.3. Паралелограми. Упознајмо још нека својства паралелограма: ABD BCD (УСУ), одакле је: а = c и b = d. Сл. 23
 6.3. Паралелограми 27. 1) Нацртај паралелограм чији је један угао 120. 2) Израчунај остале углове тог четвороугла. 28. Дат је паралелограм (сл. 23), при чему је 0 < < 90 ; c и. c 4 2 β Сл. 23 1 3 Упознајмо
6.3. Паралелограми 27. 1) Нацртај паралелограм чији је један угао 120. 2) Израчунај остале углове тог четвороугла. 28. Дат је паралелограм (сл. 23), при чему је 0 < < 90 ; c и. c 4 2 β Сл. 23 1 3 Упознајмо
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Διπλωματική Εργασία του φοιτητή του τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Ηλεκτρονικών
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΥΣΤΗΜΑΤΩΝ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Διπλωματική Εργασία του φοιτητή του τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Ηλεκτρονικών
Могућности и планови ЕПС на пољу напонско реактивне подршке. Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије
 Могућности и планови ЕПС на пољу напонско реактивне подршке Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије 1 Обавезе ЈП ЕПС као КПС... ЗАКОН О ЕНЕРГЕТИЦИ ЧЛАН 94. Енергетски
Могућности и планови ЕПС на пољу напонско реактивне подршке Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије 1 Обавезе ЈП ЕПС као КПС... ЗАКОН О ЕНЕРГЕТИЦИ ЧЛАН 94. Енергетски
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΝΑΥΤΙΛΙΑΚΩΝ ΣΠΟΥΔΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΝΑΥΤΙΛΙΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΝΑΥΤΙΛΙΑΚΩΝ ΣΠΟΥΔΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΝΑΥΤΙΛΙΑ ΝΟΜΙΚΟ ΚΑΙ ΘΕΣΜΙΚΟ ΦΟΡΟΛΟΓΙΚΟ ΠΛΑΙΣΙΟ ΚΤΗΣΗΣ ΚΑΙ ΕΚΜΕΤΑΛΛΕΥΣΗΣ ΠΛΟΙΟΥ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ που υποβλήθηκε στο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΝΑΥΤΙΛΙΑΚΩΝ ΣΠΟΥΔΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΝΑΥΤΙΛΙΑ ΝΟΜΙΚΟ ΚΑΙ ΘΕΣΜΙΚΟ ΦΟΡΟΛΟΓΙΚΟ ΠΛΑΙΣΙΟ ΚΤΗΣΗΣ ΚΑΙ ΕΚΜΕΤΑΛΛΕΥΣΗΣ ΠΛΟΙΟΥ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ που υποβλήθηκε στο
ttl КОНСТРУИСАЊЕ МОБИЛНИХ МАШИНА манипулатори машина, полужни погонски механизми Конструисање мобилних машина Седмо предавање
 КОНСТРУИСАЊЕ МОБИЛНИХ МАШИНА Седмо предавање манипулатори машина, полужни погонски механизми проф. др Драгослав Јаношевић Кнематички ланци: манипулатори а) L 3 L n L n+1 Ez { L1,L2 a) прости, б) разгранати,
КОНСТРУИСАЊЕ МОБИЛНИХ МАШИНА Седмо предавање манипулатори машина, полужни погонски механизми проф. др Драгослав Јаношевић Кнематички ланци: манипулатори а) L 3 L n L n+1 Ez { L1,L2 a) прости, б) разгранати,
4.4. Паралелне праве, сечица. Углови које оне одређују. Углови са паралелним крацима
 50. Нацртај било које унакрсне углове. Преношењем утврди однос унакрсних углова. Какво тврђење из тога следи? 51. Нацртај угао чија је мера 60, а затим нацртај њему унакрсни угао. Колика је мера тог угла?
50. Нацртај било које унакрсне углове. Преношењем утврди однос унакрсних углова. Какво тврђење из тога следи? 51. Нацртај угао чија је мера 60, а затим нацртај њему унакрсни угао. Колика је мера тог угла?
ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
КА КО КОД НАС ЦР КВЕ И ДА ЉЕ ЛЕ ТЕ
 Н И КО Л И Н А Т У Т У Ш КА КО КОД НАС ЦР КВЕ И ДА ЉЕ ЛЕ ТЕ Мо тив ле те ће цр кве чест је у на род ним пре да њи ма и ле генда ма о на с т а н к у по је д и н и х ц р к а в а и ма на с т и ра. 1 Ро ма
Н И КО Л И Н А Т У Т У Ш КА КО КОД НАС ЦР КВЕ И ДА ЉЕ ЛЕ ТЕ Мо тив ле те ће цр кве чест је у на род ним пре да њи ма и ле генда ма о на с т а н к у по је д и н и х ц р к а в а и ма на с т и ра. 1 Ро ма
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή Εργασία "Η ΣΗΜΑΝΤΙΚΟΤΗΤΑ ΤΟΥ ΜΗΤΡΙΚΟΥ ΘΗΛΑΣΜΟΥ ΣΤΗ ΠΡΟΛΗΨΗ ΤΗΣ ΠΑΙΔΙΚΗΣ ΠΑΧΥΣΑΡΚΙΑΣ" Ειρήνη Σωτηρίου Λεμεσός 2014 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή Εργασία "Η ΣΗΜΑΝΤΙΚΟΤΗΤΑ ΤΟΥ ΜΗΤΡΙΚΟΥ ΘΗΛΑΣΜΟΥ ΣΤΗ ΠΡΟΛΗΨΗ ΤΗΣ ΠΑΙΔΙΚΗΣ ΠΑΧΥΣΑΡΚΙΑΣ" Ειρήνη Σωτηρίου Λεμεσός 2014 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 1 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 1 МАТЕМАТИКА УПУТСТВО
ΕΘΝΙΚΗ ΣΧΟΛΗ ΤΟΠΙΚΗΣ ΑΥΤΟ ΙΟΙΚΗΣΗΣ Β ΕΚΠΑΙ ΕΥΤΙΚΗ ΣΕΙΡΑ ΤΜΗΜΑ: ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΙΟΙΚΗΣΗΣ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ. Θέµα:
 Ε ΕΘΝΙΚΗ ΣΧΟΛΗ ΤΟΠΙΚΗΣ ΑΥΤΟ ΙΟΙΚΗΣΗΣ Β ΕΚΠΑΙ ΕΥΤΙΚΗ ΣΕΙΡΑ ΤΜΗΜΑ: ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΙΟΙΚΗΣΗΣ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ Θέµα: Πολιτιστική Επικοινωνία και Τοπική ηµοσιότητα: Η αξιοποίηση των Μέσων Ενηµέρωσης, ο ρόλος των
Ε ΕΘΝΙΚΗ ΣΧΟΛΗ ΤΟΠΙΚΗΣ ΑΥΤΟ ΙΟΙΚΗΣΗΣ Β ΕΚΠΑΙ ΕΥΤΙΚΗ ΣΕΙΡΑ ΤΜΗΜΑ: ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΙΟΙΚΗΣΗΣ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ Θέµα: Πολιτιστική Επικοινωνία και Τοπική ηµοσιότητα: Η αξιοποίηση των Μέσων Ενηµέρωσης, ο ρόλος των
ΠΑΝΔΠΗΣΖΜΗΟ ΠΑΣΡΩΝ ΣΜΖΜΑ ΖΛΔΚΣΡΟΛΟΓΩΝ ΜΖΥΑΝΗΚΩΝ ΚΑΗ ΣΔΥΝΟΛΟΓΗΑ ΤΠΟΛΟΓΗΣΩΝ ΣΟΜΔΑ ΤΣΖΜΑΣΩΝ ΖΛΔΚΣΡΗΚΖ ΔΝΔΡΓΔΗΑ
 ΠΑΝΔΠΗΣΖΜΗΟ ΠΑΣΡΩΝ ΣΜΖΜΑ ΖΛΔΚΣΡΟΛΟΓΩΝ ΜΖΥΑΝΗΚΩΝ ΚΑΗ ΣΔΥΝΟΛΟΓΗΑ ΤΠΟΛΟΓΗΣΩΝ ΣΟΜΔΑ ΤΣΖΜΑΣΩΝ ΖΛΔΚΣΡΗΚΖ ΔΝΔΡΓΔΗΑ Γηπισκαηηθή Δξγαζία ηνπ Φνηηεηή ηνπ ηκήκαηνο Ζιεθηξνιόγσλ Μεραληθώλ θαη Σερλνινγίαο Ζιεθηξνληθώλ
ΠΑΝΔΠΗΣΖΜΗΟ ΠΑΣΡΩΝ ΣΜΖΜΑ ΖΛΔΚΣΡΟΛΟΓΩΝ ΜΖΥΑΝΗΚΩΝ ΚΑΗ ΣΔΥΝΟΛΟΓΗΑ ΤΠΟΛΟΓΗΣΩΝ ΣΟΜΔΑ ΤΣΖΜΑΣΩΝ ΖΛΔΚΣΡΗΚΖ ΔΝΔΡΓΔΗΑ Γηπισκαηηθή Δξγαζία ηνπ Φνηηεηή ηνπ ηκήκαηνο Ζιεθηξνιόγσλ Μεραληθώλ θαη Σερλνινγίαο Ζιεθηξνληθώλ
НАСТАВНИ ПЛАН И ПРОГРАМ
 НАСТАВНИ ПЛАН И ПРОГРАМ I НАСТАВНИ ПЛАН за образовни профил Техничар мехатронике I РАЗРЕД II РАЗРЕД III РАЗРЕД IV РАЗРЕД УКУПНО недељно годишње недељно годишње недељно годишње недељно годишње годишње Т
НАСТАВНИ ПЛАН И ПРОГРАМ I НАСТАВНИ ПЛАН за образовни профил Техничар мехатронике I РАЗРЕД II РАЗРЕД III РАЗРЕД IV РАЗРЕД УКУПНО недељно годишње недељно годишње недељно годишње недељно годишње годишње Т
ΣΤΥΛΙΑΝΟΥ ΣΟΦΙΑ Socm09008@soc.aegean.gr
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΚΟΙΝΩΝΙΟΛΟΓΙΑΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ «ΕΡΕΥΝΑ ΓΙΑ ΤΗΝ ΤΟΠΙΚΗ ΚΟΙΝΩΝΙΚΗ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΥΝΟΧΗ» ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Θέμα: Διερεύνηση των απόψεων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΚΟΙΝΩΝΙΟΛΟΓΙΑΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ «ΕΡΕΥΝΑ ΓΙΑ ΤΗΝ ΤΟΠΙΚΗ ΚΟΙΝΩΝΙΚΗ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΥΝΟΧΗ» ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Θέμα: Διερεύνηση των απόψεων
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΟΔΟΝΤΙΑΤΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΟΔΟΝΤΙΚΗΣ ΚΑΙ ΑΝΩΤΕΡΑΣ ΠΡΟΣΘΕΤΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΟΔΟΝΤΙΑΤΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΟΔΟΝΤΙΚΗΣ ΚΑΙ ΑΝΩΤΕΡΑΣ ΠΡΟΣΘΕΤΙΚΗΣ ΣΥΓΚΡΙΤΙΚΗ ΜΕΛΕΤΗ ΤΗΣ ΣΥΓΚΡΑΤΗΤΙΚΗΣ ΙΚΑΝΟΤΗΤΑΣ ΟΡΙΣΜΕΝΩΝ ΠΡΟΚΑΤΑΣΚΕΥΑΣΜΕΝΩΝ ΣΥΝΔΕΣΜΩΝ ΑΚΡΙΒΕΙΑΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΟΔΟΝΤΙΑΤΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΟΔΟΝΤΙΚΗΣ ΚΑΙ ΑΝΩΤΕΡΑΣ ΠΡΟΣΘΕΤΙΚΗΣ ΣΥΓΚΡΙΤΙΚΗ ΜΕΛΕΤΗ ΤΗΣ ΣΥΓΚΡΑΤΗΤΙΚΗΣ ΙΚΑΝΟΤΗΤΑΣ ΟΡΙΣΜΕΝΩΝ ΠΡΟΚΑΤΑΣΚΕΥΑΣΜΕΝΩΝ ΣΥΝΔΕΣΜΩΝ ΑΚΡΙΒΕΙΑΣ
Саборност 6 (2012) УДК Инок Исаија 091(=163.41)"13" DOI: /sabornost Оригинални научни рад. Живорад Јанковић *
 Саборност 6 (2012) Α Ω 51 61 УДК 821.163.41.09 Инок Исаија 091(=163.41)"13" DOI:10.5937/sabornost6-2977 Оригинални научни рад Живорад Јанковић * Биб иотека Српске патријаршије, Београ Поводом записа инока
Саборност 6 (2012) Α Ω 51 61 УДК 821.163.41.09 Инок Исаија 091(=163.41)"13" DOI:10.5937/sabornost6-2977 Оригинални научни рад Живорад Јанковић * Биб иотека Српске патријаршије, Београ Поводом записа инока
ТЕХНИЧАР ЗА ДИГИТАЛНУ ГРАФИКУ И ИНТЕРЕНЕТ ОБЛИКОВАЊЕ
 План наставе и учења: ТЕХНИЧАР ЗА ДИГИТАЛНУ ГРАФИКУ И ИНТЕРЕНЕТ ОБЛИКОВАЊЕ I РАЗРЕД I УКУПНО недељно годишње недељно годишње недељно годишње недељно годишње годишње Т В Т В Б Т В Т В Б Т В Т В Б Т В Т
План наставе и учења: ТЕХНИЧАР ЗА ДИГИТАЛНУ ГРАФИКУ И ИНТЕРЕНЕТ ОБЛИКОВАЊЕ I РАЗРЕД I УКУПНО недељно годишње недељно годишње недељно годишње недељно годишње годишње Т В Т В Б Т В Т В Б Т В Т В Б Т В Т
Упутство за избор домаћих задатака
 Упутство за избор домаћих задатака Студент од изабраних задатака области Математике 2: Комбинаторика, Вероватноћа и статистика бира по 20 задатака. Студент може бирати задатке помоћу програмског пакета
Упутство за избор домаћих задатака Студент од изабраних задатака области Математике 2: Комбинаторика, Вероватноћа и статистика бира по 20 задатака. Студент може бирати задатке помоћу програмског пакета
ВОЈИСЛАВ АНДРИЋ МАЛА ЗБИРКА ДИОФАНТОВИХ ЈЕДНАЧИНА
 ВОЈИСЛАВ АНДРИЋ МАЛА ЗБИРКА ДИОФАНТОВИХ ЈЕДНАЧИНА ВАЉЕВО, 006 1 1. УВОД 1.1. ПОЈАМ ДИОФАНТОВЕ ЈЕДНАЧИНЕ У једној земљи Далеког истока живео је некад један краљ, који је сваке ноћи узимао нову жену и следећег
ВОЈИСЛАВ АНДРИЋ МАЛА ЗБИРКА ДИОФАНТОВИХ ЈЕДНАЧИНА ВАЉЕВО, 006 1 1. УВОД 1.1. ПОЈАМ ДИОФАНТОВЕ ЈЕДНАЧИНЕ У једној земљи Далеког истока живео је некад један краљ, који је сваке ноћи узимао нову жену и следећег
ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΣΕΞΟΥΑΛΙΚΗΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ ΤΩΝ ΓΥΝΑΙΚΩΝ ΚΑΤΑ ΤΗ ΔΙΑΡΚΕΙΑ ΤΗΣ ΕΓΚΥΜΟΣΥΝΗΣ ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή Εργασία ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΣΕΞΟΥΑΛΙΚΗΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ ΤΩΝ ΓΥΝΑΙΚΩΝ ΚΑΤΑ ΤΗ ΔΙΑΡΚΕΙΑ ΤΗΣ ΕΓΚΥΜΟΣΥΝΗΣ ΑΝΔΡΕΟΥ ΣΤΕΦΑΝΙΑ Λεμεσός 2012 i ii ΤΕΧΝΟΛΟΓΙΚΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή Εργασία ΔΙΕΡΕΥΝΗΣΗ ΤΗΣ ΣΕΞΟΥΑΛΙΚΗΣ ΔΡΑΣΤΗΡΙΟΤΗΤΑΣ ΤΩΝ ΓΥΝΑΙΚΩΝ ΚΑΤΑ ΤΗ ΔΙΑΡΚΕΙΑ ΤΗΣ ΕΓΚΥΜΟΣΥΝΗΣ ΑΝΔΡΕΟΥ ΣΤΕΦΑΝΙΑ Λεμεσός 2012 i ii ΤΕΧΝΟΛΟΓΙΚΟ
Територија на којој се данас простиру кучевачке парохије била је насељена
 Саборнос 4 (2010) Α Ω 311 345 УДК 271.222(497.11)-523.4-9"1898/2010" 726.54(497.11)"1898/2010" Сања Николић Кучево Црква Светог Вазнесења Господњег у Кучеву Abstract: Црква у Кучеву била је и остала место
Саборнос 4 (2010) Α Ω 311 345 УДК 271.222(497.11)-523.4-9"1898/2010" 726.54(497.11)"1898/2010" Сања Николић Кучево Црква Светог Вазнесења Господњег у Кучеву Abstract: Црква у Кучеву била је и остала место
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 2004
 РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 004 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор 100 VA има напон и реактансу кратког споја u 4% и x % респективно При номиналном оптерећењу
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 004 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор 100 VA има напон и реактансу кратког споја u 4% и x % респективно При номиналном оптерећењу
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Το franchising ( δικαιόχρηση ) ως µέθοδος ανάπτυξης των επιχειρήσεων λιανικού εµπορίου
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Το franchising ( δικαιόχρηση ) ως µέθοδος ανάπτυξης των επιχειρήσεων λιανικού εµπορίου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΒΑΛΚΑΝΙΚΩΝ, ΣΛΑΒΙΚΩΝ & ΑΝΑΤΟΛΙΚΩΝ ΣΠΟΥΔΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΒΑΛΚΑΝΙΚΩΝ, ΣΛΑΒΙΚΩΝ & ΑΝΑΤΟΛΙΚΩΝ ΣΠΟΥΔΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΑΙ ΠΟΛΙΤΙΚΗ ΔΙΑΚΥΒΕΡΝΗΣΗ ΤΗΣ ΝΟΤΙΟΑΝΑΤΟΛΙΚΗΣ ΕΥΡΩΠΗΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ "Η ΕΛΛΑΔΑ ΚΑΙ ΤΑ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΒΑΛΚΑΝΙΚΩΝ, ΣΛΑΒΙΚΩΝ & ΑΝΑΤΟΛΙΚΩΝ ΣΠΟΥΔΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΑΙ ΠΟΛΙΤΙΚΗ ΔΙΑΚΥΒΕΡΝΗΣΗ ΤΗΣ ΝΟΤΙΟΑΝΑΤΟΛΙΚΗΣ ΕΥΡΩΠΗΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ "Η ΕΛΛΑΔΑ ΚΑΙ ΤΑ
Површине неких равних фигура
 Природно-математички факултет, Универзитет у Нишу, Србија http://www.pmf.ni.ac.rs/mii Математика и информатика 3() (5), -6 Површине неких равних фигура Жарко Ђурић Париске комуне 4-/8, Врање zarkocr@gmail.com
Природно-математички факултет, Универзитет у Нишу, Србија http://www.pmf.ni.ac.rs/mii Математика и информатика 3() (5), -6 Површине неких равних фигура Жарко Ђурић Париске комуне 4-/8, Врање zarkocr@gmail.com
СЛУЖБЕНИ БИЛТЕН број / јануар 2018.
 СЛУЖБЕНИ БИЛТЕН број 15. 2017/2018. 08. јануар 2018. ПОЛУФИНАЛЕ КУПА СРБИЈЕ 26. децембар 817 ЦРВЕНА ЗВЕЗДА - ЈЕДИНСТВО (СП) 3:0 (25:18, 25:23, 25:21) 75:62 Поповић А., Баланџић П. Дел. Ћато Г. 818 ЖЕЛЕЗНИЧАР
СЛУЖБЕНИ БИЛТЕН број 15. 2017/2018. 08. јануар 2018. ПОЛУФИНАЛЕ КУПА СРБИЈЕ 26. децембар 817 ЦРВЕНА ЗВЕЗДА - ЈЕДИНСТВО (СП) 3:0 (25:18, 25:23, 25:21) 75:62 Поповић А., Баланџић П. Дел. Ћато Г. 818 ЖЕЛЕЗНИЧАР
Technical Research Report, Earthquake Research Institute, the University of Tokyo, No. +-, pp. 0 +3,,**1. No ,**1
 No. +- 0 +3,**1 Technical Research Report, Earthquake Research Institute, the University of Tokyo, No. +-, pp. 0 +3,,**1. * Construction of the General Observation System for Strong Motion in Earthquake
No. +- 0 +3,**1 Technical Research Report, Earthquake Research Institute, the University of Tokyo, No. +-, pp. 0 +3,,**1. * Construction of the General Observation System for Strong Motion in Earthquake
Τμήμα Πολιτικών και Δομικών Έργων
 Τμήμα Πολιτικών και Δομικών Έργων Πτυχιακή Εργασία: Τοπογραφικό διάγραμμα σε ηλεκτρονική μορφή κεντρικού λιμένα Κέρκυρας και κτιρίου νέου επιβατικού σταθμού σε τρισδιάστατη μορφή και σχεδίαση με AutoCAD
Τμήμα Πολιτικών και Δομικών Έργων Πτυχιακή Εργασία: Τοπογραφικό διάγραμμα σε ηλεκτρονική μορφή κεντρικού λιμένα Κέρκυρας και κτιρίου νέου επιβατικού σταθμού σε τρισδιάστατη μορφή και σχεδίαση με AutoCAD
ЛИНЕАРНА ФУНКЦИЈА. k, k 0), осна и централна симетрија и сл. 2, x 0. У претходном примеру неке функције су линеарне а неке то нису.
 ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
Решења задатака са првог колоквиjума из Математике 1Б II група задатака
 Решења задатака са првог колоквиjума из Математике Б II група задатака Пре самих решења, само да напоменем да су решења детаљно исписана у нади да ће помоћи студентима у даљоj припреми испита, као и да
Решења задатака са првог колоквиjума из Математике Б II група задатака Пре самих решења, само да напоменем да су решења детаљно исписана у нади да ће помоћи студентима у даљоj припреми испита, као и да
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΠΟΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΒΙΟΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΤΡΟΦΙΜΩΝ. Πτυχιακή εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΠΟΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΒΙΟΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΤΡΟΦΙΜΩΝ Πτυχιακή εργασία ΜΕΛΕΤΗ ΠΟΛΥΦΑΙΝΟΛΩΝ ΚΑΙ ΑΝΤΙΟΞΕΙΔΩΤΙΚΗΣ ΙΚΑΝΟΤΗΤΑΣ ΣΟΚΟΛΑΤΑΣ Αναστασία Σιάντωνα Λεμεσός
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΠΟΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΒΙΟΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΤΡΟΦΙΜΩΝ Πτυχιακή εργασία ΜΕΛΕΤΗ ΠΟΛΥΦΑΙΝΟΛΩΝ ΚΑΙ ΑΝΤΙΟΞΕΙΔΩΤΙΚΗΣ ΙΚΑΝΟΤΗΤΑΣ ΣΟΚΟΛΑΤΑΣ Αναστασία Σιάντωνα Λεμεσός
Писмени испит из Метода коначних елемената
 Београд,.0.07.. За приказани билинеарни коначни елемент (Q8) одредити вектор чворног оптерећења услед задатог линијског оптерећења p. Користити природни координатни систем (ξ,η).. На слици је приказан
Београд,.0.07.. За приказани билинеарни коначни елемент (Q8) одредити вектор чворног оптерећења услед задатог линијског оптерећења p. Користити природни координатни систем (ξ,η).. На слици је приказан
