Συστήµατα Πολυµέσων και Εικονική Πραγµατικότητα Εργασία
|
|
|
- Ἀκύλας Κοντόσταυλος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Συστήµατα Πολυµέσων και Εικονική Πραγµατικότητα Εργασία Οµάδα Κατανόησης Πολυµέσων Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Αριστοτέλειο Πανεπιστήµιο Θεσσαλονίκης 1 Εισαγωγικές Παρατηρήσεις Η παρακάτω εργασία αποτελεί προαιρετικό µέρος του µαθήµατος Συστήµατα Πολυµέσων και Εικονική Πραγµατικότητα και η εκτέλεσή της συνεισφέρει 2,3 ή και 4 επιπλέον µονάδες στην τελική ϐαθµολογία. Η εργασία ϑα πρέπει να εκτελεστεί σε οµάδες µέχρι και δύο ατόµων. Η εργασία αποτελείται από 3 ενότητες. Η υλοποίηση της εργασίας µπορεί κατ επιλογή να περιλάβει την πρώτη ενότητα, την πρώτη και τη δεύτερη, κ.ο.κ. συνεισφέροντας τις αντίστοιχες µονάδες για κάθε ενότητα. εν µπορεί όµως να εκτελεστεί µία ενότητα χωρίς να έχει ορθά εκτελεστεί η προηγούµενή της. Η προτεινόµενη εργασία στοχεύει στην υλοποίηση ενός κωδικοποιητή/ αποκωδικοποιητή video κατά το open source πρότυπο Theora του Xiph.org foundation. 2 ιάρθρωση και Παραδοτέα Η εργασία ϑα περιλαµβάνει τις συναρτήσεις που περιγράφονται στη συνέχεια, υλοποιηµένες σε matlab. Θα συνοδεύεται υποχρεωτικά από γραπτή αναφορά η οποία ϑα περιγράφει τον τρόπο χρήσης των προγραµµάτων και ϑα επιδεικνύει ενδεικτικά αποτελέσµατα. Για τον έλεγχο του κωδικοποιητή/ αποκωδικοποιητή που ϑα κατασκευαστεί ϑα χρησιµοποιηθεί ενδεικτική ακολουθία ασυµπίεστων εικόνων σε µορφή RGB CCIR 2.1 Theora Library (2 µονάδες) Σκοπός του πρώτου παραδοτέου είναι η δηµιουργία µιας ϐιβλιοθήκης συναρτήσεων που ϑα χρησιµοποιηθούν αργότερα για την κατασκευή του κωδικοποιητή. Κάθε συνάρτηση της ϐιβλιοθήκης συνοδεύεται και από την αντίστροφή της που ανακατασκευάζει την είσοδο της πρώτης και που ϑα αποτελέσει µέρος του αποκωδικοποιητή. Προεπεξεργασία Η ακολουθία των εικόνων εισόδου περνά αρχικά από ένα στάδιο προεπεξεργασίας µε σκοπό τη µετατροπή της σε κατάλληλο format, αλλάζοντας το χρωµατικό χώρο σε YCrCb και επιλέγοντας την υποδειγµατοληψία χρώµατος. Κατασκευάστε τη συνάρτηση και την αντίστροφή της [frame] = preproc(framergb,pf) [framergb] = postproc(frame,pf) frame: Το επεξεργασµένο frame. οµή (struct) του matlab που αποτελείται από τρία στοιχεία: frame.y, frame.cr, frame.cb τα οποία αντιστοιχούν στο Y, Cr, Cb component του frame. framergb: Το frame προς επεξεργασία. Είναι πίνακας της µορφής M N 3 ( Μ και Ν είναι το ύψος και το πλάτος του frame αντίστοιχα σε pixels). Σύµφωνα µε την ονοµατολογία του προτύπου M = FMBH 16 και N = FMBW 16. 1
2 PF: Ο τρόπος υποδειγµατοληψίας χρώµατος. Ακέραιος αριθµός µε δυνατές τιµές: 0, 2, 3, για τα formats 4:2:0, 4:2:2 και 4:4:4 αντίστοιχα (όπως ϕαίνεται στον πίνακα 6.4 του προτύπου). Αντίστροφα, η postproc ανακατασκευάζει την είσοδο σε format RGB 4:4:4. Εκτίµηση και Αντιστάθµιση Κίνησης Για την εκτίµηση κίνησης κατασκευάστε τη συνάρτηση [resframe,mv ECTS,MBMODES,BCODED] = motest(frame,pframe,gframe, PF,mbSearchOffset,bSearchOffset,errThres) και την αντίστροφή της [frame] = imotest(resframe,mv ECTS,MBMODES,BCODED,pFrame,gFrame,PF) resframe: οµή µε τα Y, Cr, Cb components του frame σφάλµατος πρόβλεψης. MVECTS: Ο πίνακας µε τα motion vectors που αντιστοιχούν στα blocks της εικόνας. Είναι ένα cell array 1 NBS ( NBS ο αριθµός blocks στο frame) και κάθε στοιχείο MVECTS(bi) είναι µια δοµή µε στοιχεία MVECTS(bi).MVX 1 και MVECTS(bi).MVY τα οποία εκφράζουν την οριζόντια και κατακόρυφη συνιστώσα των motion vectors για κάθε block. Σηµειώστε ότι ο πίνακας MVECTS είναι ϕλύαρος γιατί εκτός από την περίπτωση INTER_MV_FOUR τα blocks του ίδιου macroblock έχουν τα ίδια motion vectors. MBMODES: Περιλαµβάνει πληροφορία για τον τρόπο κωδικοποίησης των macroblocks της εικόνας. Πίνακας από ακέραιους µε διαστάσεις 1 NMBS ( NMBS ο αριθµός των macroblock στο frame). Κάθε στοιχείο του παίρνει τιµές στο διάστηµα [0, 7]. Για την αντιστοιχία τους µε τα modes της κωδικοποίησης δείτε τους πίνακες 7.18 και 7.46 του προτύπου. BCODED: Πίνακας που υποδηλώνει το αν κωδικοποιήθηκε ή όχι κάθε block της εικόνας. Εχει διαστάσεις 1 N BS και παίρνει τιµές 0 ( δεν κωδικοποιήθηκε ) ή 1( κωδικοποιήθηκε ). Η απόφαση για τη µη κωδικοποίηση ενός block έχει νόηµα µόνο για blocks που έχουν προβλεφθεί από το previous frame και έχουν µηδενικά motion vectors και λαµβάνεται ελέγχοντας αν το σφάλµα πρόβλεψης έχει µικρότερη ενέργεια 2 από το κατώφλι σφάλµατος (errthres). Προσέξτε ότι ο πίνακας αυτός είναι σε coded order. Αυτό σηµαίνει ότι η εικόνα χωρίζεται σε superblocks 16x16, αρχίζοντας τη µέτρηση από κάτω αριστερά, ενώ µέσα σε κάθε superblock, τα blocks διατάσσονται µε hilbert order. Επίσης παρατηρήστε ότι η δεικτοδότηση αφορά και τα chroma blocks της εικόνας. Για περισσότερες πληροφορίες δείτε στη σελ. 7 του προτύπου. frame: οµή µε τα Y, Cr, Cb components του τρέχοντος frame. pframe: οµή µε τα Y, Cr, Cb components του προηγούµενου frame. gframe: οµή µε τα Y, Cr, Cb components του golden frame. PF: Ο τρόπος υποδειγµατοληψίας χρώµατος. mbsearchoffset: Η αναζήτηση του αντίστοιχου macroblock στην εικόνα αναφοράς γίνεται µε υποψήφια motion vectors που ϐρίσκονται στο διάστηµα [ mbsearchoffset, mbsearchoffset] για κάθε κατεύθυνση. bsearchoffset: Είδικά στην περίπτωση της κωδικοποίησης INTER_MV_FOUR η αναζήτηση ενός καλύτερου αντίστοιχου block για κάθε luminance block του macroblock γίνεται σε µια περιοχή [ bsearchoffset, bsearchoffset] για κάθε κατεύθυνση ώς προς τη ϑέση που είχε αρχικά επιλεγεί σε επίπεδο macroblock. errthres: Το κατώφλι σφάλµατος που χρησιµοποιείται για την απόφαση κωδικοποίησης ή όχι ενός block. Μετασχηµατισµός DCT και Zig zag scanning Κατασκευάστε τη συνάρτηση [dctblockcoef f s] = blockdct(block) 1 Η µεταβλητή bi δεικτοδοτεί τα blocks εντός του τρέχοντος frame και παίρνει τιµές από 1 ως NBS. Υπονοείται ότι η δεικτοδότηση αυτή ακολουθεί το coded order, όπως περιγράφεται στην ενότητα 2.3 του προτύπου. 2 άθροισµα τετραγώνων των τιµών του σφάλµατος πρόβλεψης. 2
3 και την αντίστροφή της [block] = iblockdct(dctblockcoef f s) dctblockcoeffs: Οι DCT coefficients του block 8x8 σε διάταξη zig zag. Πίνακας µε διαστάσεις block: Το block της εισόδου. Πίνακας 8x8. Για την υλοποίηση αυτού του ϐήµατος συνίσταται η χρήση της συνάρτησης dct2 της matlab. Υπενθυµίζεται ότι ο µετασχηµατισµός εφαρµόζεται σε επίπεδο block 8x8. Κβαντισµός Για τον κβαντισµό των blocks κατασκευάστε τις συναρτήσεις [blockcoef F S] = blockquantize(dctblockcoef f s, BM, DCSCALE, DCSCALE, qti, qi) [DQC] = iblockquantize(blockcoef F S, BM, DCSCALE, DCSCALE, qti, qi) blockcoeffs: Τα σύµβολα κβαντισµού των DCT coefficients του block. dctblockcoeffs: Οι DCT coefficients εισόδου σε διάταξη zig zag. BM: Ο πίνακας κβαντισµού σε διάταξη zig zag και έχει διαστάσεις DCSCALE: Πίνακας 1x64 µε τις κλίµακες κβαντισµού για τον DC συντελεστή. Η κλίµακα κβαντισµού του συγκεκριµένου block επιλέγεται, από αυτόν τον πίνακα, ως DCSCALE(qi). ACSCALE: Πίνακας 1x64 µε τις κλίµακες κβαντισµού για τους AC συντελεστές. Η κλίµακα κβαντισµού του συγκεκριµένου block επιλέγεται, από αυτόν τον πίνακα, ως ACSCALE(qi). DQC: Οι ανακατασκευασµένοι DCT coefficients του block σε διάταξη zig zag. qti: Quantization type index. Αριθµός που παίρνει τις τιµές 0 ή 1 ανάλογα µε το αν το block είναι κωδικοποιηµένο κατά INTRA ή όχι, αντίστοιχα. qi: Quantization index. Αριθµός που χρησιµοποιείται για να επιλεγούν οι πίνακες κβαντισµού ac και dc και κυµαίνεται από το 1 ως το 64 (για λόγους δεικτοδότησης στο matlab). Πρόκειται για έναν αριθµό που εκφράζει την ποιότητα της κβάντισης. Οσο µικρότερος είναι, τόσο πιο χονδρικοί είναι οι πίνακες κβαντισµού κάτι που οδηγεί σε µειωµένη ποιότητα, αλλά και σε µεγαλύτερη συµπίεση. Για περισσότερες πληροφορίες δείτε στη σελίδα 13 του προτύπου. Ο κβαντισµός γίνεται µε διαίρεση των συντελεστών DCT µε τα αντίστοιχα στοιχεία ενός πίνακα QMAT και στη συνέχεια στρογγυλοποίηση στον πλησιέστερο ακέραιο στο διάστηµα [ 580, 580]. Ετσι blockcoeffs(ci) = fix( dctblockcoeffs(ci) ) QMAT(ci) Οι τιµές που είναι εκτός του διαστήµατος [ 580,580] αποκόπτονται. Ο αποκβαντισµός γίνεται µε την αντίστροφη διαδικασία: Οι τιµές του QMAT δίνονται από τη σχέση: DQC(ci) = blockcoeffs(ci) QMAT(ci) QMAT(ci) = max(qmin,min(fix( QSCALE BM(ci) ) 4,4096)) 100 Ο συντελεστής QSCALE αντιστοιχεί στα DCSCALE(qi) και ACSCALE(qi) ανάλογα µε το είδος του συντελεστή ενώ το QMIN υπολογίζεται σύµφωνα µε τον πίνακα 6.18 του προτύπου. Υπενθυµίζεται ότι, κατά τον κβαντισµό, το αποτέλεσµα που προκύπτει από το ακέραιο µέρος της διαίρεσης µε το ϐήµα κβαντισµού είναι σύµβολο και όχι νούµερο (τιµή ϕωτεινότητας ή χρω- µατικότητας). 3
4 Run Length Encoding των συντελεστών DCT Το πρότυπο χρησιµοποιεί δύο κατηγορίες µηκών διαδροµής. Η πρώτη κωδικοποιεί α) µεµονω- µένους συντελεστές DCT ϐ) n-άδες µηδενικών όπως εµφανίζονται σε διάταξη zig zag και γ) n-άδες µηδενικών ακολουθούµενες από έναν κβαντισµένο (µη-µηδενικό) συντελεστή DCT. Η δεύτερη κατηγορία κωδικοποιεί τα σύµβολα τερµατισµού των blocks (EOB), όπως ϑα δούµε παρακάτω. Τα µήκη διαδροµής ονοµάζονται tokens και κάθε token χαρακτηρίζεται από µια τριάδα ακε- ϱαίων: (ti, token_value, extra_bits) Οπου ti (token index): δηλώνει τη ϑέση του πρώτου συντελεστή που αφορά το token. Στην περίπτωση της πρώτης κατηγορίας, ο συνδυασµός του token value και των extra bits σηµαίνει το συνδυασµό µήκους διαδροµής µηδενικών ή/και συντελεστών που ακολουθούν (ϐλέπε πίνακα 7.38 του προτύπου). Στην περίπτωση της δεύτερης κατηγορίας, ο συνδυασµός του token value και των extra bits σηµαίνει το πλήθος των EOBs που κωδικοποιεί το token (ϐλέπε πίνακα 7.33 του προτύπου). Ο υπολογισµός των tokens της πρώτης κατηγορίας γίνεται σε επίπεδο block. Τα tokens που αντιστοιχούν σε σύµβολα µηδενικών στο τέλος του block παραλείπονται. Η λίστα των tokens συµπληρώνεται µε ένα προσωρινό σύµβολο EOB. Στη συνέχεια, τα tokens που έχουν παραχθεί από τα blocks ολόκληρου του frame διατάσσονται κατά αύξουσα σειρά των ti τους. Αν στη διάταξη αυτή ανιχνευθούν ακολουθίες από EOB, αυτές κωδικοποιούνται µε tokens της δεύτερης κατηγορίας. Η αποκωδικοποίηση µήκους διαδροµής ενός frame γίνεται παράλληλα για όλα τα blocks και για κάθε ένα από αυτά ϕυλάσσεται στη µνήµη ένα current token index (TIS(bi)). Βλέπε ενότητα 7.7 του προτύπου. Παράδειγµα: Εστω ότι έχουµε να κωδικοποιήσουµε τα εξής blockcoeffs: b1 : [2,,3,0,4, 5,0,1, ] 8 49 b2 : [ 3,3,4,5,,5, ] και b3 : [7,,9,420,, 1, ] Στο πρώτο ϐήµα υπολογίζονται τα tokens για κάθε block 3 : block element token b1: 2 (0,11,b) (1,7,b111) } {{ } 8 3 (9,13,b0) 0 (10,7,b000) 4 (11,14,b0) 5 (12,15,b1) 0, 1 (13,23,b0, EOB (15,EOB) 49 3 τα extra bits κάθε token αναπαρίστανται σε δυαδική µορφή. Ετσι το b101 συµβολίζει τη δυαδική λέξη 101 ενώ το b σηµαίνει ότι δεν υπάρχουν extra bits 4
5 block element token 3 (0,13,b1), 3 (1,31,b011) 3 4 (5,14,b0) b2: 5 (6,15,b0) (7,8,b011101) 30 5 (37,15,b0), EOB (38,EOB) 26 block element token 7 (0,17,b00), 3 (1,8,b001001) 10 9 (11,18,b000) b3: 420 (12,22,b ), 1 (13,28,b110) 8, EOB (22,EOB) 42 Στο δεύτερο ϐήµα διατάσσονται σύµφωνα µε το ti τους και για το ίδιο ti σύµφωνα µε τον αύξοντα αριθµό block, bi. Οπότε, ϑεωρώντας για λόγους συντοµίας ότι το frame περιέχει µόνο αυτά τα τρία blocks, προκύπτει ο κάτωθι πίνακας: no ti bi Ανιχνεύοντας τώρα ακολουθίες από EOBs σε αυτή τη λίστα, παρατηρούµε ότι οι στήλες 18 και 19 αντιστοιχούν σε δύο διαδοχικά EOBs ενώ η στήλη 21 περιέχει ένα µεµονωµένο EOB. Κατά συνέπεια, εφαρµόζοντας την κωδικοποίηση του πίνακα 7.33, τα δύο διαδοχικά EOB tokens κωδικοποιούνται ως (1,b) και το τελευταίο ως (0,b). Με ϐάση τα παραπάνω κατασκευάστε τη συνάρτηση υπολογισµού των κωδικοποιηµένων κατά huffman συµβόλων µήκους διαδροµής tokens για τους κβαντισµένους συντελεστές DCT. και την αντίστροφή της [tokenstream] = runlengthf rame(coef F S, BCODED) [COEF F S] = irunlengthf rame(tokenstream, BCODED) tokenstream: Πίνακας από bits που περιέχει τα κωδικοποιηµένα tokens για το συγκεκριµένο frame. Επίσης περιέχει τις τιµές των htil και htic, που ϑα χρησιµοποιηθούν για να υπολογίσουµε στην αποκωδικοποίηση τους επιλεγέντες πίνακες κβαντισµού (ϐλ. σελ του προτύπου), τοποθετηµένες ακριβώς πριν από από τα στοιχεία που αντιστοιχούν σε ti=0 (htil_dc και htic_dc) και ti=1 (htil_ac και htic_ac). COEFFS: Τα σύµβολα κβαντισµού των DCT coefficients. Cell array που περιέχει τα blockcoeffs για τα κωδικοποιηµένα blocks και κενούς πίνακες για τις ϑέσεις που αντιστοιχούν σε µη-κωδικοποιηµένα blocks (BCODED(bi)=0). BCODED: Πίνακας που υποδηλώνει το αν κωδικοποιήθηκε ή όχι κάθε block της εικόνας. Χρησιµοποιείται για να παρακάµπτονται τα blocks που δεν κωδικοποιήθηκαν. Επίσης, κατασκευάστε τη συνάρτηση και την αντίστροφή της [vlct oken] = vlc(token, ti, blockt ype) [token] = iv LC(vlcToken,ti,blockType) 5
6 vlctoken: Πίνακας από bits. Ενα token κωδικοποιηµένο µε huffman. ti: Πίνακας µε τις τιµές των token indices (ti). token: οµή της µορφής token.tokenvalue και token.extrabits και περιέχει δύο στοιχεία: τον ακέραιο token value και µια δυαδική συµβολοσειρά µε τα extra bits στο ϕορµά της υποσηµείωσης.. Για την κωδικοποίηση µεταβλητού µήκους διαδροµής, η συνάρτηση runlengthframe ϑα καλεί την υποσυνάρτηση vlc και ϑα προσθέτει το αποτέλεσµά της στο tokenstream. Αντίστοιχα, στην αποκωδικοποίηση, η συνάρτηση ivlc καλείται από την irunlengthframe. Οι συναρτήσεις αυτές πρέπει να (απο-)κωδικοποιούν τα σύµβολα µήκους διαδροµής σύµφωνα µε τους κώδικες που περιλαµβάνονται στους πίνακες της ενότητας Β.4 του προτύπου οι οποίοι πρέπει να είναι προσβάσιµοι σαν global µεταβλητές. Παρατηρήσεις: 1. Για την υλοποίησή µας ϑα ϑεωρήσουµε (για λόγους απλούστευσης) ότι οι προς κωδικοποίηση εικόνες έχουν διαστάσεις πολλαπλάσιες του 32. Με αυτόν τον τρόπο εξασφαλίζουµε ότι περιέχουν ακέραιο αριθµό από superblocks, ενώ έτσι επίσης το picture region ταυτίζεται µε το frame (ϐλ. σελ του προτύπου). 2. Για τις συνάρτησεις κωδικοποίησης/αποκωδικοποίησης huffman (vlc ivlc) ϑα χρειαστούν οι πίνακες του παραρτήµατος Β.4 (σελ. 145) του προτύπου 4, ενώ µέσα σε αυτές µπορείτε να καλείτε τις συναρτήσεις του matlab (huffmanenco, huffmandeco, huffmandict). 2.2 Theora Processing (+1 µονάδα) Σε αυτό το ϐήµα ϑα χρησιµοποιηθούν οι προηγούµενες συναρτήσεις για την κατασκευή ενός codec, ο οποίος ϑα είναι δοµηµένος σε επίπεδα, όπως αυτά ορίζονται από το πρότυπο. Συγκεκριµένα, υπάρχουν τα επίπεδα κωδικοποίησης Sequence και Frame, τα οποία ϑα χειρίζονται οι αντίστοιχες συναρτήσεις οµή Αποθήκευσης Το αποτέλεσµα της διαδικασίας encodetheora ϑα αποθηκευθεί σε δοµή τύπου struct του matlab. Αυτή παρουσιάζεται στους πίνακες που ακολουθούν. οµή Στοιχείο Σχόλια SeqEntity SeqHeader (1) Sequence Header FrameEntityArray(1,*) Πίνακας από δοµές τύπου FrameEntity FrameEntity FrameHeader (1) Frame Header FrameData (1) Τα πραγµατικά δεδοµένα του Frame 4 Θα ήταν καλή ιδέα, αντί να τους αντιγράψει καθένας από το πρότυπο, να συνεννοηθείτε και να µοιράσετε τη δουλεία. 6
7 οµή Στοιχεία Σχόλια SeqHeader IDHeader (1) Identification Header CommentHeader (1) Comment Header SetupHeader (1) Setup Header IDHeader VMAJ*, VMIN*, VREV*, FMBW, FMBH Οπως αυτά περιγράφονται στις NSBS, NBS, NMBS, PICW, PICH, PICX* σελίδες του προτύπου. PICY*, FRN*, FRD*, PARN*, PARD*, CS, PF NOMBR*, QUAL*, KFGSHIFT* CommentHeader VENDOR, NCOMMENTS Βλέπε σελ. 47 του προτύπου. COMMENTS Cell array που περιέχει NCOMMENTS συµβολοσειρές σχολίων SetupHeader LFLIMS*, ACSCALE, DCSCALE, NBMS Βλέπε σελ του προτύπου. BMS, NQRS, QRSIZES, QRBMIS, HTS FrameHeader FTYPE, NQIS, QIS Βλέπε σελ. 61 του προτύπου. FrameData BCODED Οπως στο πρώτο µέρος της εργασίας MBMODES MVECTS QIIS Βλέπε σελ. 79 του προτύπου vlcstream Το αποτέλεσµα της κωδικοποίησης µεταβλητού µήκους λέξης Να σηµειωθεί ότι οι µεταβλητές που χρησιµοποιούνται στη δική µας, απλουστευµένη, υλοποίηση υπάρχουν αλλά µπορούν να αφεθούν κενές σε αυτό το επίπεδο καθώς αγνοούνται στην αποκωδικοποίηση. Αυτές οι µεταβλητές σηµειώνονται µε έναν αστερίσκο (*). Επίσης, στη δική µας υλοποίηση χρησιµοποιούµε µόνο ένα quantization index (qi) για όλη την ακολουθία. Συνεπώς το στοιχείο NQIS του FrameHeader είναι πάντα 1, ενώ ο πίνακας QIS περιέχει µόνο ένα στοιχείο: το ίδιο το qi Ορισµοί Συναρτήσεων και οµών εδοµένων Κύριες Συναρτήσεις function SeqEntity=encodeTheora(fName, fextension, startframe,... GoPFrames, stopframe, seqheader, outfname, qi) fname: Το πρόθεµα της σειράς των αρχείων εικόνων. fextension: Η επέκταση της σειράς των αρχείων εικόνων. startframe: Ο αύξων αριθµός της πρώτης εικόνας. GoPFrames: Ο αριθµός των frames κωδικοποιούνται σαν οµάδα (Group of Pictures GoP), µε αναφορά στο ίδιο Golden (INTRA) frame. Θεωρούµε, δηλαδή, ότι κάθε INTRA frame ακολουθείται από (GoPFrames 1) INTER frames, ενώ µετά ξεκινά ένα νέο GoP κ.ο.κ. stopframe: Ο αύξων αριθµός της τελευταίας εικόνας. seqheader: Μια δοµή τύπου seqheader όπως ορίστηκε παραπάνω. Περιέχει τα µεταδεδοµένα που ϑα χρειαστούν στην κωδικοποίηση. outfname: Το όνοµα του αρχείου (.mat στο οποίο αποθηκεύεται η έξοδος). qi: Ο δείκτης στους πίνακες κβαντισµού DCSCALE, ACSCALE, όπως περιγράφεται στη συνάρτηση blockquantize του πρώτου µέρους. Αποτελεί µέτρο της ποιότητας κωδικοποίησης και χρησιµοποιείται για τον έλεγχο µεγέθους/ποιότητας. Στο πρότυπο µπορεί να είναι διαφορετικός για κάθε frame, αλλά εµείς επιλέγουµε να είναι σταθερός για όλη την ακολουθία εικόνων. SeqEntity: οµή τύπου SeqEntity που περιέχει το κωδικοποιηµένο ϐίντεο. function FrameEntityArray=encodeSeq(fName, fextension, startframe,... GoPFrames, stopframe, seqheader, qi) fname: Το πρόθεµα της σειράς των αρχείων εικόνων. fextension: Η επέκταση της σειράς των αρχείων εικόνων. startframe: Ο αύξων αριθµός της πρώτης εικόνας. GoPFrames: Ο αριθµός των frames κωδικοποιούνται σαν οµάδα. stopframe: Ο αύξων αριθµός της τελευταίας εικόνας. 7
8 qi: Ο δείκτης στους πίνακες κβαντισµού DCSCALE, ACSCALE. FrameEntityArray: Πίνακας από δοµές τύπου GoPEntity. function FrameData=encodeFrame(frame, gframe, pframe, SeqHeader, qi) frame: οµή µε τα Y, Cr, Cb components του frame προς κωδικοποίηση. gframe: οµή µε τα Y, Cr, Cb components του τρέχοντος golden frame. pframe: οµή µε τα Y, Cr, Cb components του τρέχοντος previous frame. qi: Ο δείκτης στους πίνακες κβαντισµού DCSCALE, ACSCALE. SeqHeader: οµή τύπου SeqHeader. function decodetheora(fname,outfname) fname: Το όνοµα του αρχείου τύπου mat είναι αποθηκευµένη η δοµή του ϐίντεο. outfname: Η ϐάση του ονόµατος µε το οποίο ϑα αποθηκευτούν οι αποκωδικοποιηµένες RGB εικόνες. Το όνοµα ϑα έχει τη µορφή [όνοµα ϐάσης, αριθµός καρέ,.tiff ]. function decodeseq(seqentity,outfname) SeqEntity: οµή τύπου SeqEntity. outfname: Η ϐάση του ονόµατος µε το οποίο ϑα αποθηκευτούν οι αποκωδικοποιηµένες RGB εικόνες. Το όνοµα ϑα έχει τη µορφή [όνοµα ϐάσης, αριθµός καρέ,.tiff ]. function frame=decodeframe(frameentity, gframe, pframe, SeqHeader) FrameEntity: οµή τύπου FrameEntity. frame: Η αποκωδικοποιηµένη εικόνα. οµή µε τα Y,Cr,Cb components. gframe: οµή µε τα Y, Cr, Cb components του τρέχοντος golden frame. pframe: οµή µε τα Y, Cr, Cb components του τρέχοντος previous frame. SeqHeader: οµή τύπου SeqHeader. 2.3 Theora Evaluation (+1 µονάδα) Το τελευταίο µέρος της εργασίας είναι µια αξιολόγηση της συµπίεσης που έχει επιτευχθεί. Τα κοµµάτια που περιέχουν την κυρίως πληροφορία του κωδικοποιηµένου ϐίντεο είναι τα motion vectors και ϕυσικά τα tokens των κβαντισµένων dct συντελεστών. Για να υπολογίσει κανείς την εντροπία τους, χρειάζεται να µετρήσει τις σχετικές συχνότητες εµφάνισης όλων των συµβόλων που αυτά παράγουν. Συγκεκριµένα, τα σύµβολα των motion vectors είναι όλοι οι εµφανιζόµενοι συνδυασµοί των Ϲευγαριών (x, y). Ο αριθµός των πιθανών συνδυασµών εξαρτάται από το εύρος των τιµών που µπορούν να πάρουν τα x και y (ϐλ. µεταβλητές mbsearchoffset, bsearchoffset στη συνάρτηση motest). Αντίστοιχα, τα πιθανά σύµβολα στα tokens είναι όλοι οι συνδυασµοί των δυάδων token value, extra bits που προκύπτουν από την runlengthframe. Για τον υπολογισµό της εντροπίας, ϑα δηµιουργηθούν δύο global µεταβλητές που ϑα περιέχουν µετρητές εµφάνισης κάθε συµβόλου: mvcounts: cell array διάστασης 2x(αρ. συµβόλων). Η πρώτη στήλη περιλαµβάνει όλα τα δυνατά σύµβολα σε µορφή συµβολοσειράς και η δεύτερη τον αριθµό εµφάνισής τους. tokencounts: Οµοια µε την mvcounts, που όµως αναφέρεται στα σύµβολα των tokens. Στο σηµείο αυτό ϑα γίνουν µερικές τροποποιήσεις στις συναρτήσεις motest και runlengthframe, οι οποίες, επιπλέον από τις λειτουργίες τους, ϑα επιδρούν στις παραπάνω global µεταβλητές, αυξάνοντας κατά ένα τον αντίστοιχο µετρητή για κάθε σύµβολο που συναντούν. Επιπλέον, για την αξιολόγηση της διαδικασίας, κατασκευάστε τη συνάρτηση: [tsize, rsize, huffratio] = huffstats(seqentity) 8
9 SeqEntity: Το κωδικοποιηµένο ϐίντεο του δεύτερου ϐήµατος σε µορφή SeqEntity. tsize: Το ϑεωρητικό ελάχιστο µέγεθος των motion vectors και των tokens. Υπολογίζεται από το άθροισµα της εντροπίας τους. rsize: Το πραγµατικό µέγεθος των motion vectors και των tokens, µετά την κωδικοποίηση huffman. huffratio: Ο λόγος του ϑεωρητικού προς το µέγεθος που επιτεύχθηκε µέσω huffman. Μας δείχνει την επίδοση του huffman (πόσο καλά προσεγγίζει την κωδικοποίηση εντροπίας) και ισούται µε huffratio = tsize rsize Η συνάρτηση αυτή µετρά την εντροπία των motion vectors και των tokens χρησιµοποιώντας τους µετρητές των µεταβλητών tokencounts και mvcounts (των οποίων και η ύπαρξη στη µνήµη προϋποτίθεται) και το ελάχιστο µέγεθος της ακολουθίας πολλαπλασιάζοντας µε τον αριθµό των motion vectors και των tokens αντίστοιχα και προσθέτοντας τα extra bits για κάθε token. Το πραγµατικό µέγεθος αντιστοιχεί στο µήκος των ακολουθιών, όπως αυτές είναι αποθηκευµένες σε κάθε FrameEntity της ακολουθίας. Για τον υπολογισµό της συµπίεσης ϑα ληφθούν υπόψη και οι headers. Το µέγεθός τους ϑα εκτιµηθεί προσεγγιστικά, ανάλογα µε τον τρόπο συµπίεσης της ακολουθίας και σύµφωνα µε το κεφάλαιο 6 του προτύπου. Για το σκοπό αυτό, ϑα κατασκευαστεί η παρακάτω συνάρτηση η οποία ϑα καλεί την huffstats και ϑα υπολογίζει το ϐαθµό συµπίεσης λαµβάνοντας υπόψη και τους headers. [theorasize,rawsize,theoraratio,tsize,rsize,huffratio] =... theorastats(seqentity) SeqEntity: Το κωδικοποιηµένο ϐίντεο του δεύτερου ϐήµατος σε µορφή SeqEntity. theorasize: Το µέγεθος του συµπιεσµένου ϐίντεο. rawsize: Το µέγεθος του ασυµπίεστου ϐίντεο. theoraratio: Ο λόγος της συµπίεσης που επιτεύχθηκε µέσω του theora και ισούται µε theoraratio = theorasize rawsize tsize: Το ϑεωρητικό ελάχιστο µέγεθος των motion vectors και των tokens. rsize: Το πραγµατικό µέγεθος των motion vectors και των tokens, µετά την κωδικοποίηση huffman. huffratio: Ο λόγος του ϑεωρητικού ελάχιστου προς το µέγεθος που επιτεύχθηκε µέσω huffman 9
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ,
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση αποτελείται από δύο µέρη. Το πρώτο περιλαµβάνει
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση αποτελείται από δύο µέρη. Το πρώτο περιλαµβάνει
χωρίςναδηµιουργείταιαίσθησηαπώλειαςτηςποιότηταςτηςανακατασκευασµένηςεικόνας.
 Το πρότυπο JPEG για κωδικοποίησηση εικόνας Το JPEG, που υιοθετήθηκε από την Joint Photographic Experts Group, είναι ένα πρότυπο που χρησιµοποιείταιευρέωςγιατησυµπίεσηακίνητωνεικόνων, µε µέσο λόγο συµπίεσης
Το πρότυπο JPEG για κωδικοποίησηση εικόνας Το JPEG, που υιοθετήθηκε από την Joint Photographic Experts Group, είναι ένα πρότυπο που χρησιµοποιείταιευρέωςγιατησυµπίεσηακίνητωνεικόνων, µε µέσο λόγο συµπίεσης
Συµπίεση Εικόνας: Το πρότυπο JPEG
 ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων ΒΕΣ Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση Εικόνας: Το πρότυπο JPEG ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Εισαγωγή Σχεδιάστηκε από την οµάδα Joint Photographic Experts
ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων ΒΕΣ Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση Εικόνας: Το πρότυπο JPEG ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Εισαγωγή Σχεδιάστηκε από την οµάδα Joint Photographic Experts
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 9 : Κωδικοποίηση βίντεο Πρότυπο συμπίεσης MPEG Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 9 : Κωδικοποίηση βίντεο Πρότυπο συμπίεσης MPEG Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Θεωρητικές Ασκήσεις (# ): ειγµατοληψία, κβαντοποίηση και συµπίεση σηµάτων. Στην τηλεφωνία θεωρείται ότι το ουσιαστικό περιεχόµενο της
Κωδικοποίηση βίντεο (H.261 / DVI)
 Κωδικοποίηση βίντεο (H.261 / DVI) Αρχές κωδικοποίησης βίντεο Εισαγωγή στο H.261 Κωδικοποίηση βίντεο Ροή δεδοµένων Εισαγωγή στο DVI Κωδικοποίηση ήχου και εικόνων Κωδικοποίηση βίντεο Ροή δεδοµένων Τεχνολογία
Κωδικοποίηση βίντεο (H.261 / DVI) Αρχές κωδικοποίησης βίντεο Εισαγωγή στο H.261 Κωδικοποίηση βίντεο Ροή δεδοµένων Εισαγωγή στο DVI Κωδικοποίηση ήχου και εικόνων Κωδικοποίηση βίντεο Ροή δεδοµένων Τεχνολογία
Group (JPEG) το 1992.
 Μέθοδοι Συμπίεσης Εικόνας Πρωτόκολλο JPEG Συμπίεση Εικόνας: Μείωση αποθηκευτικού χώρου Ευκολία στη μεταφορά αρχείων Δημιουργήθηκε από την ομάδα Joint Photographic Experts Group (JPEG) το 1992. Ονομάστηκε
Μέθοδοι Συμπίεσης Εικόνας Πρωτόκολλο JPEG Συμπίεση Εικόνας: Μείωση αποθηκευτικού χώρου Ευκολία στη μεταφορά αρχείων Δημιουργήθηκε από την ομάδα Joint Photographic Experts Group (JPEG) το 1992. Ονομάστηκε
Η κωδικοποίηση των συντελεστών DC
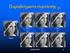 Η κωδικοποίηση των συντελεστών DC Γιακάθευποπίνακαηδιαφορά, d,του DC συντελεστήτουαπότοσυντελεστή DC τουπροηγούµενουυποπίνακαοδηγούνταιστονκωδικοποιητήεντροπίας (variable length coding VLC). Στονκωδικοποιητήηδιαφοράκατατάσσεταιανάλογαµετοµέγεθόςτηςστοακόλουθοπίνακα,
Η κωδικοποίηση των συντελεστών DC Γιακάθευποπίνακαηδιαφορά, d,του DC συντελεστήτουαπότοσυντελεστή DC τουπροηγούµενουυποπίνακαοδηγούνταιστονκωδικοποιητήεντροπίας (variable length coding VLC). Στονκωδικοποιητήηδιαφοράκατατάσσεταιανάλογαµετοµέγεθόςτηςστοακόλουθοπίνακα,
Περιεχόµενα. ΕΠΛ 422: Συστήµατα Πολυµέσων. Βιβλιογραφία. Εισαγωγή. Συµπίεση εικόνων: Το πρότυπο JPEG. Εισαγωγή. Ευθύς µετασχηµατισµός DCT
 Περιεχόµενα ΕΠΛ : Συστήµατα Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση ηµιουργία
Περιεχόµενα ΕΠΛ : Συστήµατα Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση ηµιουργία
Συστήματα Πολυμέσων. Ενότητα 15: Συμπίεση Ψηφιακού Βίντεο. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 15: Συμπίεση Ψηφιακού Βίντεο Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 15: Συμπίεση Ψηφιακού Βίντεο Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΙΔΗ ΠΛΑΙΣΙΩΝ Ενδο-πλαισιακή κωδικοποίηση (Intra- frame Coding): Δια-πλαισιακή κωδικοποίηση (Inter-frame Coding):
 ΕΙΔΗ ΠΛΑΙΣΙΩΝ Ενδο-πλαισιακή κωδικοποίηση (Intraframe Coding): κάθε εικόνα αντιμετωπίζεται και κωδικοποιείται ανεξάρτητα από τις υπόλοιπες (όπως στο JPEG) Δια-πλαισιακή κωδικοποίηση (Inter-frame Coding):
ΕΙΔΗ ΠΛΑΙΣΙΩΝ Ενδο-πλαισιακή κωδικοποίηση (Intraframe Coding): κάθε εικόνα αντιμετωπίζεται και κωδικοποιείται ανεξάρτητα από τις υπόλοιπες (όπως στο JPEG) Δια-πλαισιακή κωδικοποίηση (Inter-frame Coding):
ΒΕΣ 04: Συµπίεση και Μετάδοση Πολυµέσων. Περιεχόµενα. Βιβλιογραφία. Συµπίεση εικόνων: Το πρότυπο JPEG. Εισαγωγή. Ευθύς µετασχηµατισµός DCT
 ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Περιεχόµενα Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση
ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Περιεχόµενα Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση
Συστήµατα και Αλγόριθµοι Πολυµέσων
 Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #5: Αρχές Επεξεργασίας Σηµάτων Πολυµέσων 7 Νοεµβρίου 2005 Επανάληψη Θεωρία Πληροφορίας Εντροπία: H ( P) i= 0 Κωδικοποίηση Huffman 3
Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #5: Αρχές Επεξεργασίας Σηµάτων Πολυµέσων 7 Νοεµβρίου 2005 Επανάληψη Θεωρία Πληροφορίας Εντροπία: H ( P) i= 0 Κωδικοποίηση Huffman 3
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Θεωρητικές Ασκήσεις (# 3): 1. Ο διακριτός µετασχηµατισµός συνηµίτονου (Discrete Cosine Transform)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Θεωρητικές Ασκήσεις (# 3): 1. Ο διακριτός µετασχηµατισµός συνηµίτονου (Discrete Cosine Transform)
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ. Κωδικοποίηση εικόνας
 ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 2 Κωδικοποίηση εικόνας Ακολουθία από ψηφιοποιημένα καρέ (frames) που έχουν συλληφθεί σε συγκεκριμένο ρυθμό frame rate (π.χ. 10fps,
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 2 Κωδικοποίηση εικόνας Ακολουθία από ψηφιοποιημένα καρέ (frames) που έχουν συλληφθεί σε συγκεκριμένο ρυθμό frame rate (π.χ. 10fps,
Αρχές κωδικοποίησης. Τεχνολογία Πολυµέσων 08-1
 Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Βασικές τεχνικές κωδικοποίησης Κωδικοποίηση Huffman Κωδικοποίηση µετασχηµατισµών Κβαντοποίηση διανυσµάτων ιαφορική κωδικοποίηση Τεχνολογία
Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Βασικές τεχνικές κωδικοποίησης Κωδικοποίηση Huffman Κωδικοποίηση µετασχηµατισµών Κβαντοποίηση διανυσµάτων ιαφορική κωδικοποίηση Τεχνολογία
Δ11 Δ12. Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2013-2014 Κωδικοποιητές εικονοροής (Video) Δρ. Ν. Π. Σγούρος 2 Κωδικοποιητές Εικονοροών ITU-T VCEG H.261 (1990) ISO/IEC MPEG H.263 (1995/9 6) MPEG-2 (H.262) (1994/9 5) H.263+ (1997/98)
Συμπίεση Δεδομένων 2013-2014 Κωδικοποιητές εικονοροής (Video) Δρ. Ν. Π. Σγούρος 2 Κωδικοποιητές Εικονοροών ITU-T VCEG H.261 (1990) ISO/IEC MPEG H.263 (1995/9 6) MPEG-2 (H.262) (1994/9 5) H.263+ (1997/98)
Συµπίεση Ψηφιακών Εικόνων: Συµπίεση µε Απώλειες. Πρότυπα Συµπίεσης Εικόνων
 ΤΨΣ 5: Ψηφιακή Επεξεργασία Εικόνας ΤΨΣ 5 Ψηφιακή Επεξεργασία Εικόνας Συµπίεση Ψηφιακών Εικόνων: Συµπίεση µε απώλειες Πρότυπα Συµπίεσης Εικόνων Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο
ΤΨΣ 5: Ψηφιακή Επεξεργασία Εικόνας ΤΨΣ 5 Ψηφιακή Επεξεργασία Εικόνας Συµπίεση Ψηφιακών Εικόνων: Συµπίεση µε απώλειες Πρότυπα Συµπίεσης Εικόνων Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 04: ΣΥΜΠΙΕΣΗ ΚΑΙ ΜΕΤΑ ΟΣΗ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2007 2008, Χειµερινό Εξάµηνο 6 Νοεµβρίου 2007 Φροντιστηριακή Άσκηση 2: (I) Εντροπία,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 04: ΣΥΜΠΙΕΣΗ ΚΑΙ ΜΕΤΑ ΟΣΗ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2007 2008, Χειµερινό Εξάµηνο 6 Νοεµβρίου 2007 Φροντιστηριακή Άσκηση 2: (I) Εντροπία,
Κωδικοποίηση βίντεο (MPEG)
 (MEG) Εισαγωγή στο MEG-1 Κωδικοποίηση βίντεο οµή βίντεο Κωδικοποίηση ήχου Ροή δεδοµένων Τεχνολογία Πολυµέσων 11-1 Εισαγωγή στο MEG-1 MEG (Motion ictures Experts Group) ίντεο και ήχος υψηλής ποιότητας ιανοµή
(MEG) Εισαγωγή στο MEG-1 Κωδικοποίηση βίντεο οµή βίντεο Κωδικοποίηση ήχου Ροή δεδοµένων Τεχνολογία Πολυµέσων 11-1 Εισαγωγή στο MEG-1 MEG (Motion ictures Experts Group) ίντεο και ήχος υψηλής ποιότητας ιανοµή
Συμπίεση Πολυμεσικών Δεδομένων
 Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο
 Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Κωδικοποίηση εικόνων κατά JPEG
 Κωδικοποίηση εικόνων κατά JPEG Εισαγωγή Προετοιµασία της εικόνας ρυθµός Ακολουθιακός απωλεστικός ρυθµός Εκτεταµένος απωλεστικός ρυθµός Μη απωλεστικός ρυθµός Ιεραρχικός ρυθµός Τεχνολογία Πολυµέσων 09-1
Κωδικοποίηση εικόνων κατά JPEG Εισαγωγή Προετοιµασία της εικόνας ρυθµός Ακολουθιακός απωλεστικός ρυθµός Εκτεταµένος απωλεστικός ρυθµός Μη απωλεστικός ρυθµός Ιεραρχικός ρυθµός Τεχνολογία Πολυµέσων 09-1
Πολυμέσα. Συμπίεση δεδομένων Κωδικοποίηση JPEG. Δρ. Γεώργιος Π. Παυλίδης ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ
 Πολυμέσα Συμπίεση δεδομένων Δρ. Γεώργιος Π. Παυλίδης Συμπίεση Δεδομένων Περιεχόμενα Γνωστοίαλγόριθμοισυμπίεσης JPEG, Οικογένεια H.26x, H.32x Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη
Πολυμέσα Συμπίεση δεδομένων Δρ. Γεώργιος Π. Παυλίδης Συμπίεση Δεδομένων Περιεχόμενα Γνωστοίαλγόριθμοισυμπίεσης JPEG, Οικογένεια H.26x, H.32x Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη
Μάθημα 7 ο. Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
Αρχές κωδικοποίησης. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 08-1
 Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Κωδικοποίηση εντροπίας Διαφορική κωδικοποίηση Κωδικοποίηση μετασχηματισμών Στρωματοποιημένη κωδικοποίηση Κβαντοποίηση διανυσμάτων Τεχνολογία
Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Κωδικοποίηση εντροπίας Διαφορική κωδικοποίηση Κωδικοποίηση μετασχηματισμών Στρωματοποιημένη κωδικοποίηση Κβαντοποίηση διανυσμάτων Τεχνολογία
Τεχνολογία Πολυμέσων. Ενότητα # 11: Κωδικοποίηση εικόνων: JPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 11: Κωδικοποίηση εικόνων: JPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Τεχνολογία Πολυμέσων Ενότητα # 11: Κωδικοποίηση εικόνων: JPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας. Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στη συμπίεση εικόνας Μη απωλεστικες
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στη συμπίεση εικόνας Μη απωλεστικες
ιαφορική εντροπία Σεραφείµ Καραµπογιάς
 ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
ιαφορική εντροπία Σεραφείµ Καραµπογιάς Για πηγές διακριτού χρόνου µε συνεχές αλφάβητο, των οποίων οι έξοδοι είναι πραγµατικοί αριθµοί, ορίζεται µια άλλη ποσότητα που µοιάζει µε την εντροπία και καλείται
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2013-2014 JPEG 2000 Δρ. Ν. Π. Σγούρος 2 JPEG 2000 Βασικά χαρακτηριστικά Επιτρέπει συμπίεση σε εξαιρετικά χαμηλούς ρυθμούς όπου η συμπίεση με το JPEG εισάγει μεγάλες παραμορφώσεις Ενσωμάτωση
Συμπίεση Δεδομένων 2013-2014 JPEG 2000 Δρ. Ν. Π. Σγούρος 2 JPEG 2000 Βασικά χαρακτηριστικά Επιτρέπει συμπίεση σε εξαιρετικά χαμηλούς ρυθμούς όπου η συμπίεση με το JPEG εισάγει μεγάλες παραμορφώσεις Ενσωμάτωση
Πολυμέσα. Συμπίεση δεδομένων Κωδικοποίηση MPEG. Δρ. Γεώργιος Π. Παυλίδης ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ
 Πολυμέσα Συμπίεση δεδομένων Κωδικοποίηση MPEG Δρ. Γεώργιος Π. Παυλίδης Συμπίεση Δεδομένων Περιεχόμενα Γνωστοίαλγόριθμοισυμπίεσης MPEG Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη Υπηρεσίες
Πολυμέσα Συμπίεση δεδομένων Κωδικοποίηση MPEG Δρ. Γεώργιος Π. Παυλίδης Συμπίεση Δεδομένων Περιεχόμενα Γνωστοίαλγόριθμοισυμπίεσης MPEG Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη Υπηρεσίες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 422: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2004 2005, Χειµερινό Εξάµηνο Φροντιστηριακή Άσκηση 3: Εντροπία, κωδικοποίηση Quadtree 1. Εντροπία 22 Σεπτεµβρίου 2004
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 422: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2004 2005, Χειµερινό Εξάµηνο Φροντιστηριακή Άσκηση 3: Εντροπία, κωδικοποίηση Quadtree 1. Εντροπία 22 Σεπτεµβρίου 2004
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ. Ενότητα 9: Πρότυπο Συμπίεσης Βίντεο MPEG
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ενότητα 9: Πρότυπο Συμπίεσης Βίντεο MPEG Ιωάννης Έλληνας Τμήμα Υπολογιστικών Συστημάτων Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ενότητα 9: Πρότυπο Συμπίεσης Βίντεο MPEG Ιωάννης Έλληνας Τμήμα Υπολογιστικών Συστημάτων Άδειες Χρήσης Το παρόν
Η ανάγκη για συμπίεση
 Πρότυπα συμπίεσης Η ανάγκη για συμπίεση High-Definition Television (HDTV) 1920x1080 30 frames per second (full motion) 8 bits για κάθε κανάλι χρώματος 1.5 Gb/sec! Κάθε κανάλι 6 MHz Max data rate: 19.2
Πρότυπα συμπίεσης Η ανάγκη για συμπίεση High-Definition Television (HDTV) 1920x1080 30 frames per second (full motion) 8 bits για κάθε κανάλι χρώματος 1.5 Gb/sec! Κάθε κανάλι 6 MHz Max data rate: 19.2
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΥΓΚΡΙΣΗ ΜΕΘΟΔΩΝ ΠΡΟΒΛΕΨΗΣ ΜΕΤΑΞΥ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΥΓΚΡΙΣΗ ΜΕΘΟΔΩΝ ΠΡΟΒΛΕΨΗΣ ΜΕΤΑΞΥ
Τεχνολογία Πολυμέσων. Ενότητα # 12: Κωδικοποίηση βίντεο: H.26x Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
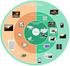 Τεχνολογία Πολυμέσων Ενότητα # 12: Κωδικοποίηση βίντεο: H.26x Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Τεχνολογία Πολυμέσων Ενότητα # 12: Κωδικοποίηση βίντεο: H.26x Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Δομές Δεδομένων και Αλγόριθμοι
 Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 20 Huffman codes 1 / 12 Κωδικοποίηση σταθερού μήκους Αν χρησιμοποιηθεί κωδικοποίηση σταθερού μήκους δηλαδή
Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 20 Huffman codes 1 / 12 Κωδικοποίηση σταθερού μήκους Αν χρησιμοποιηθεί κωδικοποίηση σταθερού μήκους δηλαδή
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ. MPEG 2 bitstream και πολυπλεξία
 ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 3 MPEG 2 bitstream και πολυπλεξία 2 Μικρότερο δομικό στοιχείο: Το block 8x8 με τους συντελεστές DCT είτε για τη φωτεινότητα ή
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 3 MPEG 2 bitstream και πολυπλεξία 2 Μικρότερο δομικό στοιχείο: Το block 8x8 με τους συντελεστές DCT είτε για τη φωτεινότητα ή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ ΕΠΛ 035 - ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΗΛΕΚΤΡΟΛΟΓΟΥΣ ΜΗΧΑΝΙΚΟΥΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥΣ ΥΠΟΛΟΓΙΣΤΩΝ Ακαδηµαϊκό έτος 2017-2018 Υπεύθυνος εργαστηρίου: Γεώργιος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ ΕΠΛ 035 - ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΗΛΕΚΤΡΟΛΟΓΟΥΣ ΜΗΧΑΝΙΚΟΥΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥΣ ΥΠΟΛΟΓΙΣΤΩΝ Ακαδηµαϊκό έτος 2017-2018 Υπεύθυνος εργαστηρίου: Γεώργιος
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
Συστήματα Πολυμέσων. Ενότητα 3: Εισαγωγικά θέματα Συμπίεσης. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
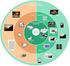 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Εισαγωγικά θέματα Συμπίεσης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Εισαγωγικά θέματα Συμπίεσης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Συστήματα Πολυμέσων. Ενότητα 7: Συμπίεση Εικόνας κατά JPEG. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Συμπίεση Εικόνας κατά JPEG Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Συμπίεση Εικόνας κατά JPEG Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Τεχνολογία Πολυμέσων. Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Τεχνολογία Πολυμέσων Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Δ13b. Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Εκτίμηση ποιότητας Εικόνας Ι Αντικειμενική Αξιολόγηση Χρήση μετρικών εκτίμησης ποιότητας Βασίζονται στη σύγκριση μεταξύ εικονοστοιχείων αρχικής και ανασυσταμένης εικόνας Υποκειμενική
Συμπίεση Δεδομένων 2014-2015 Εκτίμηση ποιότητας Εικόνας Ι Αντικειμενική Αξιολόγηση Χρήση μετρικών εκτίμησης ποιότητας Βασίζονται στη σύγκριση μεταξύ εικονοστοιχείων αρχικής και ανασυσταμένης εικόνας Υποκειμενική
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο
 Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Ραδιοτηλεοπτικά Συστήματα Ενότητα 4: Ψηφιοποίηση και συμπίεση σημάτων εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ραδιοτηλεοπτικά Συστήματα Ενότητα 4: Ψηφιοποίηση και συμπίεση σημάτων εικόνας Δρ. Νικόλαος- Αλέξανδρος Τάτλας Τμήμα Ηλεκτρονικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ραδιοτηλεοπτικά Συστήματα Ενότητα 4: Ψηφιοποίηση και συμπίεση σημάτων εικόνας Δρ. Νικόλαος- Αλέξανδρος Τάτλας Τμήμα Ηλεκτρονικών
Ακαδηµαϊκό Έτος , Χειµερινό Εξάµηνο ιδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
Συστήματα Πολυμέσων. Ενότητα 16: Διαμορφώσεις και Πρότυπα Ψηφιακού Βίντεο. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής
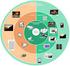 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 16: Διαμορφώσεις και Πρότυπα Ψηφιακού Βίντεο Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 16: Διαμορφώσεις και Πρότυπα Ψηφιακού Βίντεο Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν
Υπάρχουν δύο τύποι μνήμης, η μνήμη τυχαίας προσπέλασης (Random Access Memory RAM) και η μνήμη ανάγνωσης-μόνο (Read-Only Memory ROM).
 Μνήμες Ένα από τα βασικά πλεονεκτήματα των ψηφιακών συστημάτων σε σχέση με τα αναλογικά, είναι η ευκολία αποθήκευσης μεγάλων ποσοτήτων πληροφοριών, είτε προσωρινά είτε μόνιμα Οι πληροφορίες αποθηκεύονται
Μνήμες Ένα από τα βασικά πλεονεκτήματα των ψηφιακών συστημάτων σε σχέση με τα αναλογικά, είναι η ευκολία αποθήκευσης μεγάλων ποσοτήτων πληροφοριών, είτε προσωρινά είτε μόνιμα Οι πληροφορίες αποθηκεύονται
Αρχιτεκτονική Μηχανής. Αποθήκευση εδοµένων
 Αρχιτεκτονική Μηχανής Αποθήκευση εδοµένων Οι πράξεις AND, OR, και Αλγεβρας Boole XOR (exclusive or) της Μία απεικόνιση των πυλών AND, OR, XOR, και NOT καθώς και των τιµών εισόδου (inputs) και εξόδου (output)
Αρχιτεκτονική Μηχανής Αποθήκευση εδοµένων Οι πράξεις AND, OR, και Αλγεβρας Boole XOR (exclusive or) της Μία απεικόνιση των πυλών AND, OR, XOR, και NOT καθώς και των τιµών εισόδου (inputs) και εξόδου (output)
Συστήµατα και Αλγόριθµοι Πολυµέσων
 Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #3: Αρχές Επεξεργασίας Σηµάτων Πολυµέσων 10 Οκτωβρίου 005 Επανάλειψη (1) ειγµατοληψία επανα-δειγµατοληψία Τεχνικές φίλτρων (συνέλειξη)
Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #3: Αρχές Επεξεργασίας Σηµάτων Πολυµέσων 10 Οκτωβρίου 005 Επανάλειψη (1) ειγµατοληψία επανα-δειγµατοληψία Τεχνικές φίλτρων (συνέλειξη)
Δημιουργία Περιλήψεων από Ακολουθίες Βίντεο στο Συμπιεσμένο Πεδίο
 Εργαστήριο Ηλεκτρονικής Τομέας Ηλεκτρονικής και Υπολογιστών Τμήμα Φυσικής Πανεπιστήμιο Πατρών Ειδική Επιστημονική Εργασία Δημιουργία Περιλήψεων από Ακολουθίες Βίντεο στο Συμπιεσμένο Πεδίο Ρήγας Ιωάννης
Εργαστήριο Ηλεκτρονικής Τομέας Ηλεκτρονικής και Υπολογιστών Τμήμα Φυσικής Πανεπιστήμιο Πατρών Ειδική Επιστημονική Εργασία Δημιουργία Περιλήψεων από Ακολουθίες Βίντεο στο Συμπιεσμένο Πεδίο Ρήγας Ιωάννης
Ακαδηµαϊκό Έτος , Χειµερινό Εξάµηνο ιδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 04: ΣΥΜΠΙΕΣΗ ΚΑΙ ΜΕΤΑ ΟΣΗ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2005 2006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση αποτελείται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 04: ΣΥΜΠΙΕΣΗ ΚΑΙ ΜΕΤΑ ΟΣΗ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2005 2006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση αποτελείται
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο
 Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Επεξεργασία Χαρτογραφικής Εικόνας
 Επεξεργασία Χαρτογραφικής Εικόνας ιδάσκων: Αναγνωστόπουλος Χρήστος Αρχές συµπίεσης δεδοµένων Ήδη συµπίεσης Συµπίεση εικόνων Αλγόριθµος JPEG Γιατί χρειαζόµαστε συµπίεση; Τα σηµερινά αποθηκευτικά µέσα αδυνατούν
Επεξεργασία Χαρτογραφικής Εικόνας ιδάσκων: Αναγνωστόπουλος Χρήστος Αρχές συµπίεσης δεδοµένων Ήδη συµπίεσης Συµπίεση εικόνων Αλγόριθµος JPEG Γιατί χρειαζόµαστε συµπίεση; Τα σηµερινά αποθηκευτικά µέσα αδυνατούν
Θεωρία Πληροφορίας. Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Τεράστιες ανάγκες σε αποθηκευτικό χώρο
 ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 7 : Πρότυπο συμπίεσης JPEG Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 7 : Πρότυπο συμπίεσης JPEG Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
DIP_06 Συμπίεση εικόνας - JPEG. ΤΕΙ Κρήτης
 DIP_06 Συμπίεση εικόνας - JPEG ΤΕΙ Κρήτης Συμπίεση εικόνας Το μέγεθος μιας εικόνας είναι πολύ μεγάλο π.χ. Εικόνα μεγέθους Α4 δημιουργημένη από ένα σαρωτή με 300 pixels ανά ίντσα και με χρήση του RGB μοντέλου
DIP_06 Συμπίεση εικόνας - JPEG ΤΕΙ Κρήτης Συμπίεση εικόνας Το μέγεθος μιας εικόνας είναι πολύ μεγάλο π.χ. Εικόνα μεγέθους Α4 δημιουργημένη από ένα σαρωτή με 300 pixels ανά ίντσα και με χρήση του RGB μοντέλου
Συστήµατα Πολυµέσων Ενδιάµεση Εξέταση: Οκτώβριος 2004
 Ενδιάµεση Εξέταση: Οκτώβριος 4 ΜΕΡΟΣ Β: ΑΣΚΗΣΕΙΣ Άσκηση (25 µονάδες): Μια εικόνα αποχρώσεων του γκρι και διαστάσεων 25 x pixel έχει κωδικοποιηθεί κατά PCM µε βάθος χρώµατος 3 bits /pixel. Οι τιµές φωτεινότητας
Ενδιάµεση Εξέταση: Οκτώβριος 4 ΜΕΡΟΣ Β: ΑΣΚΗΣΕΙΣ Άσκηση (25 µονάδες): Μια εικόνα αποχρώσεων του γκρι και διαστάσεων 25 x pixel έχει κωδικοποιηθεί κατά PCM µε βάθος χρώµατος 3 bits /pixel. Οι τιµές φωτεινότητας
Επεξεργασία Πολυµέσων. Δρ. Μαρία Κοζύρη Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας
 Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 3: Επισκόπηση Συµπίεσης 2 Θεωρία Πληροφορίας Κωδικοποίηση Θεµελιώθηκε απο τον Claude
Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 3: Επισκόπηση Συµπίεσης 2 Θεωρία Πληροφορίας Κωδικοποίηση Θεµελιώθηκε απο τον Claude
Πληροφορική Ι. Μάθημα 9 ο Συμπίεση δεδομένων. Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας. Δρ.
 Οι διαφάνειες έχουν βασιστεί στο βιβλίο «Εισαγωγή στην επιστήμη των υπολογιστών» του B. Forouzanκαι Firoyz Mosharraf(2 η έκδοση-2010) Εκδόσεις Κλειδάριθμος Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου
Οι διαφάνειες έχουν βασιστεί στο βιβλίο «Εισαγωγή στην επιστήμη των υπολογιστών» του B. Forouzanκαι Firoyz Mosharraf(2 η έκδοση-2010) Εκδόσεις Κλειδάριθμος Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου
Κωδικοποίηση και αποκωδικοποίηση µε χρήση του H.264/MPEG-4 για βίντεο µε µία ή περισσότερες λήψεις
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Κωδικοποίηση και αποκωδικοποίηση µε χρήση του H.264/MPEG-4 για βίντεο µε µία
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Κωδικοποίηση και αποκωδικοποίηση µε χρήση του H.264/MPEG-4 για βίντεο µε µία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ. ΑΣΚΗΣΗ 5 Ανάπτυξη Προγράμματος Συμπίεσης/Αποσυμπίεσης Αρχείων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 035: Δομές Δεδομένων και Αλγόριθμοι για Ηλεκτρολόγους Μηχανικούς και Μηχανικούς Υπολογιστών Χειμερινό Εξάμηνο 2012 ΑΣΚΗΣΗ 5 Ανάπτυξη Προγράμματος Συμπίεσης/Αποσυμπίεσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 035: Δομές Δεδομένων και Αλγόριθμοι για Ηλεκτρολόγους Μηχανικούς και Μηχανικούς Υπολογιστών Χειμερινό Εξάμηνο 2012 ΑΣΚΗΣΗ 5 Ανάπτυξη Προγράμματος Συμπίεσης/Αποσυμπίεσης
7ο ΕΡΓΑΣΤΗΡΙΟ AAAABBBBAAAAABBBBBBCCCCCCCCCCCCCCBBABAAAABBBBBBCCCCD
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΛΑΜΙΑΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2010 11 Ιστοσελίδα μαθήματος: http://eclass.teilam.gr/di288 1 Συμπίεση
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΛΑΜΙΑΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2010 11 Ιστοσελίδα μαθήματος: http://eclass.teilam.gr/di288 1 Συμπίεση
Κεφάλαιο 3 Συμπίεση Βίντεο
 Κεφάλαιο 3 Συμπίεση Βίντεο Σύνοψη Στο κεφάλαιο αυτό εξετάζουμε τους βασικούς τρόπους με τους οποίους το πρότυπο MPEG (και συγκεκριμένα το MPEG-2) προβλέπει τη συμπίεση του σήματος βίντεο. Η ανάγκη για
Κεφάλαιο 3 Συμπίεση Βίντεο Σύνοψη Στο κεφάλαιο αυτό εξετάζουμε τους βασικούς τρόπους με τους οποίους το πρότυπο MPEG (και συγκεκριμένα το MPEG-2) προβλέπει τη συμπίεση του σήματος βίντεο. Η ανάγκη για
Περιεχόµενα. ΕΠΛ 422: Συστήµατα Πολυµέσων. Συµπίεση Βίντεο. Βιβλιογραφία. Αρχές συµπίεσης βίντεο
 Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Συµπίεση Βίντεο Αρχές Συµπίεσης Τύποι πλαισίων Εκτίµηση και αντιστάθµιση κίνησης Θέµατα υλοποίησης Η261 Η263 MEG MEG-1 MEG-2 MEG-4 Βιβλιογραφία Καγιάφας [2000]:
Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Συµπίεση Βίντεο Αρχές Συµπίεσης Τύποι πλαισίων Εκτίµηση και αντιστάθµιση κίνησης Θέµατα υλοποίησης Η261 Η263 MEG MEG-1 MEG-2 MEG-4 Βιβλιογραφία Καγιάφας [2000]:
Συµπίεση Ψηφιακών Εικόνων:
 ΤΨΣ 5 Ψηφιακή Επεξεργασία Εικόνας Συµπίεση Ψηφιακών Εικόνων: Συµπίεση χωρίς απώλειες Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο Πειραιώς Περιεχόµενα Βιβλιογραφία Περιεχόµενα Ενότητας
ΤΨΣ 5 Ψηφιακή Επεξεργασία Εικόνας Συµπίεση Ψηφιακών Εικόνων: Συµπίεση χωρίς απώλειες Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο Πειραιώς Περιεχόµενα Βιβλιογραφία Περιεχόµενα Ενότητας
3ο σετ σημειώσεων - Πίνακες, συμβολοσειρές, συναρτήσεις
 3ο σετ σημειώσεων - Πίνακες, συμβολοσειρές, συναρτήσεις 5 Απριλίου 01 1 Πίνακες Είδαμε ότι δηλώνοντας μία μεταβλητή κάποιου συγκεκριμένου τύπου δεσμεύουμε μνήμη κατάλληλη για να αποθηκευτεί μία οντότητα
3ο σετ σημειώσεων - Πίνακες, συμβολοσειρές, συναρτήσεις 5 Απριλίου 01 1 Πίνακες Είδαμε ότι δηλώνοντας μία μεταβλητή κάποιου συγκεκριμένου τύπου δεσμεύουμε μνήμη κατάλληλη για να αποθηκευτεί μία οντότητα
Θεωρία πληροφοριών. Τεχνολογία Πολυµέσων 07-1
 Θεωρία πληροφοριών Εισαγωγή Αµοιβαία πληροφορία Εσωτερική πληροφορία Υπό συνθήκη πληροφορία Παραδείγµατα πληροφορίας Μέση πληροφορία και εντροπία Παραδείγµατα εντροπίας Εφαρµογές Τεχνολογία Πολυµέσων 07-
Θεωρία πληροφοριών Εισαγωγή Αµοιβαία πληροφορία Εσωτερική πληροφορία Υπό συνθήκη πληροφορία Παραδείγµατα πληροφορίας Μέση πληροφορία και εντροπία Παραδείγµατα εντροπίας Εφαρµογές Τεχνολογία Πολυµέσων 07-
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Εισαγωγή στην επιστήμη των υπολογιστών. Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 2.1 Τύποι Δεδομένων Τα δεδομένα σήμερα συναντώνται σε διάφορες μορφές, στις οποίες περιλαμβάνονται αριθμοί,
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 2.1 Τύποι Δεδομένων Τα δεδομένα σήμερα συναντώνται σε διάφορες μορφές, στις οποίες περιλαμβάνονται αριθμοί,
3. ΤΕΧΝΙΚΕΣ ΣΥΜΠΙΕΣΗΣ ΠΟΛΥΜΕΣΩΝ
 3. ΤΕΧΝΙΚΕΣ ΣΥΜΠΙΕΣΗΣ ΠΟΛΥΜΕΣΩΝ ΑΝΑΓΚΗ ΣΥΜΠΙΕΣΗΣ ΔΕΔΟΜΕΝΩΝ Local Multimedia Π.χ. Μία ταινία 90 min απαιτεί 120 GB, και τα σημερινά μέσα αποθήκευσης < 25 GB. Άρα σήμερα είναι αδύνατη η αποθήκευση και η
3. ΤΕΧΝΙΚΕΣ ΣΥΜΠΙΕΣΗΣ ΠΟΛΥΜΕΣΩΝ ΑΝΑΓΚΗ ΣΥΜΠΙΕΣΗΣ ΔΕΔΟΜΕΝΩΝ Local Multimedia Π.χ. Μία ταινία 90 min απαιτεί 120 GB, και τα σημερινά μέσα αποθήκευσης < 25 GB. Άρα σήμερα είναι αδύνατη η αποθήκευση και η
Θέματα Συστημάτων Πολυμέσων. Ενότητα # 8: MPEG Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών
 Θέματα Συστημάτων Πολυμέσων Ενότητα # 8: MPEG Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Θέματα Συστημάτων Πολυμέσων Ενότητα # 8: MPEG Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
MPEG-4: Βασικά Χαρακτηριστικά
 MPEG-4 MPEG-4: Βασικά Χαρακτηριστικά Σχεδιάστηκε ώστε να καλύπτει ευρύ φάσμα ρυθμών, από 5 kbps εώς 10 Mbps Εκτός από τη συμπίεση δίνει έμφαση και στην αλληλεπίδραση με το χρήστη Χρησιμοποιεί αντικείμενα
MPEG-4 MPEG-4: Βασικά Χαρακτηριστικά Σχεδιάστηκε ώστε να καλύπτει ευρύ φάσμα ρυθμών, από 5 kbps εώς 10 Mbps Εκτός από τη συμπίεση δίνει έμφαση και στην αλληλεπίδραση με το χρήστη Χρησιμοποιεί αντικείμενα
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
Συστήµατα και Αλγόριθµοι Πολυµέσων
 Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #12: Αρχιτεκτονική Texas Instruments OMAP (διπλού πυρήνα ARM + DSP) και Intel XScale 29 Νοεµβρίου 2005 Επανάληψη ιεθνές στάνταρ H.264/MPEG4-10/AVC
Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #12: Αρχιτεκτονική Texas Instruments OMAP (διπλού πυρήνα ARM + DSP) και Intel XScale 29 Νοεµβρίου 2005 Επανάληψη ιεθνές στάνταρ H.264/MPEG4-10/AVC
Δύο είναι οι κύριες αιτίες που μπορούμε να πάρουμε από τον υπολογιστή λανθασμένα αποτελέσματα εξαιτίας των σφαλμάτων στρογγυλοποίησης:
 Ορολογία bit (binary digit): δυαδικό ψηφίο. Τα δυαδικά ψηφία είναι το 0 και το 1 1 byte = 8 bits word: η θεμελιώδης μονάδα σύμφωνα με την οποία εκπροσωπούνται οι πληροφορίες στον υπολογιστή. Αποτελείται
Ορολογία bit (binary digit): δυαδικό ψηφίο. Τα δυαδικά ψηφία είναι το 0 και το 1 1 byte = 8 bits word: η θεμελιώδης μονάδα σύμφωνα με την οποία εκπροσωπούνται οι πληροφορίες στον υπολογιστή. Αποτελείται
Συστήματα Πολυμέσων & Εικονική Πραγματικότητα Εργασία
 Συστήματα Πολυμέσων & Εικονική Πραγματικότητα Εργασία 2015-2016 Α. Ντελόπουλος, Β. Παπαπαναγιώτου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης 5 Δεκεμβρίου,
Συστήματα Πολυμέσων & Εικονική Πραγματικότητα Εργασία 2015-2016 Α. Ντελόπουλος, Β. Παπαπαναγιώτου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης 5 Δεκεμβρίου,
Επεξεργασία Χαρτογραφικής Εικόνας
 Επεξεργασία Χαρτογραφικής Εικόνας ιδάσκων: Αναγνωστόπουλος Χρήστος Αλγόριθµος JPEG για έγχρωµες εικόνες Είδη αρχείων εικόνων Συµπίεση video και ήχου Μπλόκ x Τιµές - 55 Αρχική πληροφορία, 54 54 75 6 7 75
Επεξεργασία Χαρτογραφικής Εικόνας ιδάσκων: Αναγνωστόπουλος Χρήστος Αλγόριθµος JPEG για έγχρωµες εικόνες Είδη αρχείων εικόνων Συµπίεση video και ήχου Μπλόκ x Τιµές - 55 Αρχική πληροφορία, 54 54 75 6 7 75
( ) log 2 = E. Σεραφείµ Καραµπογιάς
 Παρατηρούµε ότι ο ορισµός της Η βασίζεται στη χρονική µέση τιµή. Για να ισχύει ο ορισµός αυτός και για µέση τιµή συνόλου πρέπει η πηγή να είναι εργοδική, δηλαδή H ( X) ( ) = E log 2 p k Η εντροπία µιας
Παρατηρούµε ότι ο ορισµός της Η βασίζεται στη χρονική µέση τιµή. Για να ισχύει ο ορισµός αυτός και για µέση τιµή συνόλου πρέπει η πηγή να είναι εργοδική, δηλαδή H ( X) ( ) = E log 2 p k Η εντροπία µιας
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων
 Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Αριθµητική Ανάλυση 1 εκεµβρίου / 43
 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 1 / 43 Κεφ.5. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ίνεται ένας πίνακας A C n n και Ϲητούνται να προσδιορισθούν οι
Αριθµητική Ανάλυση 1 εκεµβρίου 2014 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 1 / 43 Κεφ.5. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ίνεται ένας πίνακας A C n n και Ϲητούνται να προσδιορισθούν οι
ITU-T : H.261 (1990), H.262 (1996), H.263 (1995) MPEG-1, MPEG-2, MPEG-4. Αποθήκευση, Μετάδοση, Επικοινωνίες, ίκτυα
 Συµπίεση/κωδικοποίηση βίντεο ITU-T : H.261 (1990), H.262 (1996), H.263 (1995) Συνδιάσκεψη : ISDN, ATM, LANs, Internet, PSTN MPEG-1, MPEG-2, MPEG-4 Αποθήκευση, Μετάδοση, Επικοινωνίες, ίκτυα 1 H.261 : εισαγωγή
Συµπίεση/κωδικοποίηση βίντεο ITU-T : H.261 (1990), H.262 (1996), H.263 (1995) Συνδιάσκεψη : ISDN, ATM, LANs, Internet, PSTN MPEG-1, MPEG-2, MPEG-4 Αποθήκευση, Μετάδοση, Επικοινωνίες, ίκτυα 1 H.261 : εισαγωγή
ΣΕΤ ΑΣΚΗΣΕΩΝ 3. Προθεσµία: 18/12/12, 22:00
 ΣΕΤ ΑΣΚΗΣΕΩΝ 3 ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ I, ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2012-2013 Προθεσµία: 18/12/12, 22:00 Περιεχόµενα Διαβάστε πριν ξεκινήσετε Εκφώνηση άσκησης 1 Οδηγίες αποστολής άσκησης Διαδικαστικά Η εργασία
ΣΕΤ ΑΣΚΗΣΕΩΝ 3 ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ I, ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2012-2013 Προθεσµία: 18/12/12, 22:00 Περιεχόµενα Διαβάστε πριν ξεκινήσετε Εκφώνηση άσκησης 1 Οδηγίες αποστολής άσκησης Διαδικαστικά Η εργασία
Τεχνικές Συµπίεσης Βίντεο. Δρ. Μαρία Κοζύρη Τµήµα Πληροφορικής Πανεπιστήµιο Θεσσαλίας
 Τεχνικές Συµπίεσης Βίντεο Δρ. Μαρία Κοζύρη Τµήµα Πληροφορικής Πανεπιστήµιο Θεσσαλίας Ενότητα 3: Entropy Coding Δρ. Μαρία Κοζύρη Τεχνικές Συµπίεσης Βίντεο Ενότητα 3 2 Θεωρία Πληροφορίας Κωδικοποίηση Θεµελιώθηκε
Τεχνικές Συµπίεσης Βίντεο Δρ. Μαρία Κοζύρη Τµήµα Πληροφορικής Πανεπιστήµιο Θεσσαλίας Ενότητα 3: Entropy Coding Δρ. Μαρία Κοζύρη Τεχνικές Συµπίεσης Βίντεο Ενότητα 3 2 Θεωρία Πληροφορίας Κωδικοποίηση Θεµελιώθηκε
Συστήματα Πολυμέσων και Εικονική Πραγματικότητα Εργασία
 Συστήματα Πολυμέσων και Εικονική Πραγματικότητα Εργασία 2014-15 Α. Ντελόπουλος Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης 4 Δεκεμβρίου 2014 1 Εισαγωγικές
Συστήματα Πολυμέσων και Εικονική Πραγματικότητα Εργασία 2014-15 Α. Ντελόπουλος Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης 4 Δεκεμβρίου 2014 1 Εισαγωγικές
ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ, ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΑΙ ΔΙΚΤΥΩΝ, ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ
 ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ, ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΑΙ ΔΙΚΤΥΩΝ, ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ I, ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2011-2012 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ Ποιος πρέπει να ολοκληρώσει αυτή την εργασία? Φοιτητές έτους >=2 που
ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ, ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΑΙ ΔΙΚΤΥΩΝ, ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ I, ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2011-2012 ΕΡΓΑΣΙΑ ΕΞΑΜΗΝΟΥ Ποιος πρέπει να ολοκληρώσει αυτή την εργασία? Φοιτητές έτους >=2 που
Επεξεργασία Πολυµέσων. Δρ. Μαρία Κοζύρη Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας
 Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 4: Συµπίεση Εικόνας 2 Συµπίεση Εικόνας Μείωση Πλεονασµού: Το σήµα εικόνας παρουσιάζει
Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 4: Συµπίεση Εικόνας 2 Συµπίεση Εικόνας Μείωση Πλεονασµού: Το σήµα εικόνας παρουσιάζει
Συνοπτική Μεθοδολογία Ασκήσεων IP Fragmentation. Ασκήσεις στο IP Fragmentation
 Συνοπτική Μεθοδολογία Ασκήσεων IP Fragmentation Οι σημειώσεις που ακολουθούν περιγράφουν τις ασκήσεις IP Fragmentation που θα συναντήσετε στο κεφάλαιο 3. Η πιο συνηθισμένη και βασική άσκηση αναφέρεται
Συνοπτική Μεθοδολογία Ασκήσεων IP Fragmentation Οι σημειώσεις που ακολουθούν περιγράφουν τις ασκήσεις IP Fragmentation που θα συναντήσετε στο κεφάλαιο 3. Η πιο συνηθισμένη και βασική άσκηση αναφέρεται
Οργάνωση αρχείων: πως είναι τοποθετηµένες οι εγγραφές ενός αρχείου όταν αποθηκεύονται στο δίσκο
 Κατακερµατισµός 1 Οργάνωση Αρχείων (σύνοψη) Οργάνωση αρχείων: πως είναι τοποθετηµένες οι εγγραφές ενός αρχείου όταν αποθηκεύονται στο δίσκο 1. Αρχεία Σωρού 2. Ταξινοµηµένα Αρχεία Φυσική διάταξη των εγγραφών
Κατακερµατισµός 1 Οργάνωση Αρχείων (σύνοψη) Οργάνωση αρχείων: πως είναι τοποθετηµένες οι εγγραφές ενός αρχείου όταν αποθηκεύονται στο δίσκο 1. Αρχεία Σωρού 2. Ταξινοµηµένα Αρχεία Φυσική διάταξη των εγγραφών
o AND o IF o SUMPRODUCT
 Πληροφοριακά Εργαστήριο Management 1 Information Συστήματα Systems Διοίκησης ΤΕΙ Τμήμα Ελεγκτικής Ηπείρου Χρηματοοικονομικής (Παράρτημα Πρέβεζας) και Αντικείµενο: Μοντελοποίηση προβλήµατος Θέµατα που καλύπτονται:
Πληροφοριακά Εργαστήριο Management 1 Information Συστήματα Systems Διοίκησης ΤΕΙ Τμήμα Ελεγκτικής Ηπείρου Χρηματοοικονομικής (Παράρτημα Πρέβεζας) και Αντικείµενο: Μοντελοποίηση προβλήµατος Θέµατα που καλύπτονται:
Εισαγωγή στην επιστήµη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ
 Εισαγωγή στην επιστήµη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ 1 Αριθµητικό Σύστηµα! Ορίζει τον τρόπο αναπαράστασης ενός αριθµού µε διακεκριµένα σύµβολα! Ένας αριθµός αναπαρίσταται διαφορετικά σε κάθε σύστηµα,
Εισαγωγή στην επιστήµη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ 1 Αριθµητικό Σύστηµα! Ορίζει τον τρόπο αναπαράστασης ενός αριθµού µε διακεκριµένα σύµβολα! Ένας αριθµός αναπαρίσταται διαφορετικά σε κάθε σύστηµα,
Κώδικες µεταβλητού µήκους
 6 Κώδικες µεταβλητού µήκους Στο κεφάλαιο αυτό µελετώνται οι κώδικες µεταβλητού µήκους, στους οποίους όλες οι λέξεις δεν έχουν το ίδιο µήκος και δίνονται οι µέ- ϑοδοι Fano-Shannon και Huffman για την κατασκευή
6 Κώδικες µεταβλητού µήκους Στο κεφάλαιο αυτό µελετώνται οι κώδικες µεταβλητού µήκους, στους οποίους όλες οι λέξεις δεν έχουν το ίδιο µήκος και δίνονται οι µέ- ϑοδοι Fano-Shannon και Huffman για την κατασκευή
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Αριθμητική Ανάλυση & Εφαρμογές
 Αριθμητική Ανάλυση & Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Υπολογισμοί και Σφάλματα Παράσταση Πραγματικών Αριθμών Συστήματα Αριθμών Παράσταση Ακέραιου
Αριθμητική Ανάλυση & Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Υπολογισμοί και Σφάλματα Παράσταση Πραγματικών Αριθμών Συστήματα Αριθμών Παράσταση Ακέραιου
19/3/2007 Πολυµέσα και Συµπίεση εδοµένων
 ΓΤΠ 61 Ηλεκτρονικοί Υπολογιστές στις Γραφικές Τέχνες Πολυµέσα και Συµπίεση εδοµένων Εισαγωγή Βασικές Έννοιες Ταξινόµηση Τεχνικών Συµπίεσης Συµπίεση Κειµένου Συµπίεση Εικόνας Συµπίεση Ήχου Συµπίεση Video
ΓΤΠ 61 Ηλεκτρονικοί Υπολογιστές στις Γραφικές Τέχνες Πολυµέσα και Συµπίεση εδοµένων Εισαγωγή Βασικές Έννοιες Ταξινόµηση Τεχνικών Συµπίεσης Συµπίεση Κειµένου Συµπίεση Εικόνας Συµπίεση Ήχου Συµπίεση Video
Θεώρημα κωδικοποίησης πηγής
 Κωδικοποίηση Kωδικοποίηση πηγής Θεώρημα κωδικοποίησης πηγής Καθορίζει ένα θεμελιώδες όριο στον ρυθμό με τον οποίο η έξοδος μιας πηγής πληροφορίας μπορεί να συμπιεσθεί χωρίς να προκληθεί μεγάλη πιθανότητα
Κωδικοποίηση Kωδικοποίηση πηγής Θεώρημα κωδικοποίησης πηγής Καθορίζει ένα θεμελιώδες όριο στον ρυθμό με τον οποίο η έξοδος μιας πηγής πληροφορίας μπορεί να συμπιεσθεί χωρίς να προκληθεί μεγάλη πιθανότητα
ΤΗΛΕΜΑΤΙΚΗ ΚΑΙ ΝΕΕΣ ΥΠΗΡΕΣΙΕΣ
 ΤΗΛΕΜΑΤΙΚΗ ΚΑΙ ΝΕΕΣ ΥΠΗΡΕΣΙΕΣ Ενότητα #1: Κωδικοποίηση Πολυμεσικών Δεδομένων Καθηγητής Χρήστος Ι. Μπούρας Τμήμα μηχανικών Η/Υ & Πληροφορικής, Πανεπιστήμιο Πατρών email: bouras@cti.gr, site: http://ru6.cti.gr/ru6/bouras?language=el
ΤΗΛΕΜΑΤΙΚΗ ΚΑΙ ΝΕΕΣ ΥΠΗΡΕΣΙΕΣ Ενότητα #1: Κωδικοποίηση Πολυμεσικών Δεδομένων Καθηγητής Χρήστος Ι. Μπούρας Τμήμα μηχανικών Η/Υ & Πληροφορικής, Πανεπιστήμιο Πατρών email: bouras@cti.gr, site: http://ru6.cti.gr/ru6/bouras?language=el
