Solutions Ph 236a Week 2
|
|
|
- Ἀρτεμᾶς Αἰνέας Δεσποτόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Solutions Ph 236a Week 2 Page 1 of 13 Solutions Ph 236a Week 2 Kevin Bakett, Jonas Lippune, and Mak Scheel Octobe 6, 2015 Contents Poblem Pat (a Pat (b Pat (c Poblem Pat (a Pat (b Pat (c Pat (d Poblem Pat (a Pat (b Pat (c Pat (d Pat (e Poblem Pat (a Pat (b Pat (c Pat (d Poblem Pat (a Pat (b
2 Solutions Ph 236a Week 2 Page 2 of 13 Pat (a Poblem 1 Fo a paticle in its est fame, we know that its 4-velocity is given by u = (1, 0 and we ae given in the poblem statement that its spin vecto is S = (0, s. Thus Pat (b S u = 0, d dτ ( S u = 0 (1.1 Fist, let us examine the deivative spatial components of S while in the paticles est fame so that d s dτ = A 1F i js j (1.2 Whee i, j ae spatial indices that un ove 1, 2, 3. To see what happens, let us pick a spin component and expand (fo example, the z-diection ds z dτ = A 1F z js j = A 1 (s x B y s y B x (1.3 But this is just the fom we expect of the usual 3-vecto coss poduct. So using that esult with equation (1 fom the poblem set, we get To get A 2, we stat with d s dτ = A 1 s B, A 1 = ge 2m d dτ ( S u = 0 S d u dτ = u d S dτ (1.4 (1.5 Note, that d u dτ is an acceleation, which is foce divided by mass. Since the electomagnetic foce is given by qf α β uβ, we can wite S d u dτ = q m S αf α βu β = A 1 S α F α βu β + A 2 (1.6 whee we used the fact that A 2 u u = A 2. Now we can plug in the esult of A 1 fom above and solve fo A 2 and we get A 1 = ge 2m, A 2 = F α βs α u β e m (g 1 (1.7 2
3 Solutions Ph 236a Week 2 Page 3 of 13 Pat (c Let Ẽ = 0 and s = (s 0, S. Thus the paticle s 4-velocity is given by u = γ(1, ṽ. Then S u = 0 = γ( s 0 + s ṽ s ṽ = s 0 (1.8 Now note that since Ẽ = 0 F α β = 0 if eithe α o β = 0. So then ds 0 dτ = A 1F 0 βs β + A 2 u 0 = γa 2 (1.9 and fom that, in the lab fame with time coodinate t, the time ate of change of the helicity is, d dt ( s ṽ = ds0 dt = ds dτ dτ dt = A 2 = F α βs α u β e m (g 2 1 = γf i js i v j e m (g 2 1 = γv j e ( s j B m (g 1 ( In the case whee g = 2, the quantity ( g 2 1 = 0 which implies the time ate of change of the helicity is 0, so the helicity is constant. Poblem 2 Pat (a Stat by evaluating v = P( v = P αβ v β = g αβ v β + u α u β v β = v α + u α u β v β (2.1 To show that it is othogonal to u, v u = (v α + u α u β v β u α = v α v α + u α u α u β v β = v α u α (1 + u α u α = 0 (2.2 since u is a 4-velocity. Thus v is othogonal to u.
4 Solutions Ph 236a Week 2 Page 4 of 13 Pat (b We want to show that v = P( v and we know fom above that v = v α + u α u β v β so then P( v = (g αβ + u α u β (v β + u β u γ v γ = g αβ v β + g αβ u β u γ v γ + u α u β v β + u α u β u β u γ v γ = v α + u α u γ v γ + u α u β v β u α u γ v γ = v α + u α u β v β = v (2.3 Thus we have shown that P is unique. Pat (c Since we ae given a non-null vecto q we can define q 2 = q q and we don t need to be afaid of dividing by q 2. Now define ou pojection tenso fo q as P q = g αβ 1 q 2 q αq β (2.4 It can be shown using the same aguments as in pats (a and (b that P q is indeed the pojection tenso and that it is unique. Pat (d Fo a null vecto k, constuct its pojection tenso as P k = ck α k β fo an abitay eal numbe c. Thus, fo an abitay vecto v, we have k P k ( v = k α ck α k β v β = ck β v β (0 = 0 (2.5 Thus P k is indeed the pojection opeato, howeve it is not unique because c is abitay. Poblem 3 Pat (a Using the usual spheical coodinates, the Catesian coodinates ae given by x = sin θ cos φ, y = sin θ sin φ, z = cos θ. (3.1
5 Solutions Ph 236a Week 2 Page 5 of 13 Since e is the tangent vecto of the cuves paametized by with constant θ and φ, we find e = = xi x i = sin θ cos φ e x + sin θ sin φ e y + cos θ e z, (3.2 whee i = 1, 2, 3 and we used x 1 = x, x 2 = y, and x 3 = z. Similaly, we find Pat (b e θ = θ = xi θ e φ = φ = xi φ x i = cos θ cos φ e x + cos θ sin φ e y sin θ e z, x i = sin θ sin φ e x + sin θ cos φ e y. (3.3 Recall that the spheical coodinates ae given by = x 2 + y 2 + z 2, ( z θ = accos, x2 + y 2 + z 2 φ = { accot(x/y if y 0 accot(x/y + π if y < 0, (3.4 whee accos etuns a value in [0, π] and accot etuns a value in [0, π] (when extending its domain to include ±. We find that d = i dx i = x dx i 1 ( i = 2 2x dx + 2y dy + 2z dz x 2 + y 2 + z 2 = sin θ cos φ dx + sin θ sin φ dy + cos θ dz, (3.5
6 Solutions Ph 236a Week 2 Page 6 of 13 and dθ = i θ dx i = = = 1 1 z 2 x 2 + y 2 + z 2 ( 2xz dx 2(x 2 + y 2 + z 2 3/2 2yz dy 2(x 2 + y 2 + z 2 + dz 3/2 x2 + y 2 + z 2 x 2 + y 2 + z 2 xz dx zy dy + (x 2 + y 2 dz x 2 + y 2 (x 2 + y 2 + z 2 3/2 2z 2 dz 2(x 2 + y 2 + z 2 3/2 xz zy dx + dy x2 + y 2 (x 2 + y 2 + z 2 x2 + y 2 (x 2 + y 2 + z 2 and finally x2 + y 2 x 2 + y 2 + z 2 dz = 2 sin θ cos φ cos θ dx sin θ sin φ cos θ sin θ 3 sin θ cos θ cos φ cos θ sin φ = dx + dy sin θ dφ = i φ x i 1 = 1 + x 2 /y 2 = Pat (c 1 2 sin 2 θ ( dx y x dy y 2 = ( sin θ sin φ dx + sin θ cos φ dy dy sin θ 2 dz dz, (3.6 1 ( x 2 + y 2 y dx + x dy = sin φ sin θ dx + cos φ sin θ dy. (3.7 We have found in pat (a that and in pat (b we found that e = sin θ cos φ e x + sin θ sin φ e y + cos θ e z, e θ = cos θ cos φ e x + cos θ sin φ e y sin θ e z, e φ = sin θ sin φ e x + sin θ cos φ e y, (3.8 d = sin θ cos φ dx + sin θ sin φ dy + cos θ dz, dθ = cos θ cos φ dx + cos θ sin φ dy sin θ dφ = sin φ sin θ dx + cos φ sin θ dy. (3.9 dz,
7 Solutions Ph 236a Week 2 Page 7 of 13 Recall that ( e x, e y, e z ae basis vectos and thus they ae linealy independent. It can be shown (but is not necessay that ( e, e θ, e φ ae also linealy independent. And since these ae 3 vectos in a 3-dimensional space, it follows that they fom a basis. Similaly, it can be shown that ( d, dθ, dφ ae linealy independent and since the space of 1-foms is also 3-dimensional, it follows that they fom a basis too. Thus it emains to be shown that ( d, dθ, dφ ae dual to ( e, e θ, e φ. Since ( dx, dy, dz ae dual to ( e x, e y, e z, we have that dx i, e j = δ i j, (3.10 whee dx 1 = dx, dx 2 = dy, dx 3 = dz, e 1 = e x, e 2 = e y, and e 3 = e z. We find and and finally d, e = sin 2 θ cos 2 φ + sin 2 θ sin 2 φ + cos 2 θ = 1, d, e θ = sin θ cos θ cos 2 φ + sin θ cos θ sin 2 φ sin θ cos θ = 0, d, e φ = sin 2 θ sin φ cos φ + sin 2 θ sin φ cos φ = 0, (3.11 dθ, e = sin θ cos θ cos2 φ + sin θ cos θ sin2 φ sin θ cos θ = 0, dθ, e θ = cos 2 θ cos 2 φ + cos 2 θ sin 2 φ + sin 2 θ = 1, dθ, e φ = sin θ cos θ sin φ cos φ + sin θ cos θ sin φ cos φ = 0, (3.12 Thus we have shown that dφ, sin φ cos φ sin φ cos φ e = + = 0, dφ, cos θ sin φ cos φ cos θ sin φ cos φ e θ = + = 0, sin θ sin θ dφ, e φ = sin 2 φ + cos 2 φ = 1. (3.13 dxī, e j = δī j, (3.14 whee dx 1 = d, dx 2 = dθ, dx 3 = dφ, e 1 = e, e 2 = e θ, and e 3 = e φ, and so we have shown that ( d, dθ, dφ ae dual to ( e, e θ, e φ. Pat (d Recall that the components of the metic tenso ae given by g ī j = e ī e j. (3.15
8 Solutions Ph 236a Week 2 Page 8 of 13 Using (3.8 we find g 1 1 = e e = sin 2 θ cos 2 φ + sin 2 θ sin 2 φ + cos 2 θ = 1, g 1 2 = g 2 1 = e e θ = sin θ cos θ cos 2 φ + sin θ cos θ sin 2 φ = 0, sin θ cos θ g 1 3 = g 3 1 = e e φ = sin 2 θ sin φ cos φ + sin 2 θ sin φ cos φ = 0, g 2 2 = e θ e θ = 2 cos 2 θ cos 2 φ + 2 cos 2 θ sin 2 φ + 2 sin 2 θ = 2, g 2 3 = g 3 2 = 2 sin θ cos θ sin φ cos φ + 2 sin θ cos θ sin φ cos φ = 0, g 3 3 = 2 sin 2 θ sin 2 φ + 2 sin 2 θ cos 2 φ = 2 sin 2 θ. (3.16 Hence the components of the metic tenso in spheical coodinates ae g ī j = ( sin 2 θ The full metic tenso in all its gloy is Pat (e g = g ī j dxī dx j = d d + 2 dθ dθ + 2 sin 2 θ dφ dφ. (3.18 Since gîĵ = e î e ĵ, it is obvious that g îĵ = δ îĵ if the vecto e î ae othonomal. We have aleady found in (3.16 that e ī ae othogonal, so we can make them othonomal by scaling them with the invese of thei lengths. Thus we obtain e eˆ = = e e e 1 = sin θ cos φ e x + sin θ sin φ e y + cos θ e z, e θ eˆθ = = e θ eθ e θ = cos θ cos φ e x + cos θ sin φ e y sin θ e z, e φ e ˆφ = = e φ eφ e φ sin θ = sin φ e x + cos φ e y. (3.19 Poblem 4 Pat (a If A µν is antisymmetic and S µν is symmetic, then S µν = g µα g νβ S αβ = g νβ g µα S βα = S νµ (4.1
9 Solutions Ph 236a Week 2 Page 9 of 13 so we know that S µν is also symmetic. So finally A µν S µν = A νµ S µν = A νµ S νµ = A µν S µν. (4.2 Hee the fist step used antisymmety of A µν, the second step used symmety of S µν, and the thid step elabeled dummy indices. Since A µν S µν is equal to minus itself, it must be zeo. Pat (b Let A µν and S µν be as above and let V µν be an abitay tenso. Fo equation (4 in the poblem set, we can see that V µν A µν = 1 2 (V µν A µν + V µν A µν = 1 2 (V µν A µν V µν A νµ = 1 2 (V µν A µν V νµ A µν = 1 2 (V µν V νµ A µν (4.3 Similaly to get equation (5 in the poblem set V µν S µν = 1 2 (V µν S µν + V µν S µν = 1 2 (V µν S µν V µν S νµ = 1 2 (V µν S µν + V νµ S µν = 1 2 (V µν + V νµ S µν (4.4 Pat (c To show that these tansfomation maticies ae inveses of each othe, simply opeate with both of them in succession. e µ = Λ µ µ e µ = Λ µ µ(λ ν µ e ν (4.5 Since we ae tansfoming back into the baed fame, that means e µ = δ ν µ e ν Λ µ µλ ν µ = δ ν µ (4.6
10 Solutions Ph 236a Week 2 Page 10 of 13 The evese can be shown be doing the same thing except with 1-foms instead. Now we know by definition that tensos can be witten as T α γ β = T( w α, e β, w γ (4.7 We also know that it a linea opeato and so plugging in the tansfomation matices we have T ᾱ γ β = T( wᾱ, e β, w γ = T(Λᾱα w α, Λ β β e β, Λ γ γ w γ = ΛᾱαΛ β βλ γ γt( w α, e β, w γ = ΛᾱαΛ β βλ γ γt α γ β (4.8 Pat (d Since g µν is a tenso, its indices can be aised and loweed as any othe tenso. g αβ = g αµ g βν g µν (4.9 g αβ = g αµ g βν g µν (4.10 To show that g α β = δα β, just aise o lowe one of the indices and use equation (8 fom the homewok set. g α β = g αγ g γβ = δ α β (4.11 Pat (a Poblem 5 Case 1: Fist conside the case whee α, β, and γ ae not unique. In that case ɛ αβγρ = 0 fo all ρ, which means the ight-hand side will be 0. If α, β, and γ ae not unique, it makes no sense to talk about even o odd pemutations of them and so this case falls unde othewise. The same agument holds if µ, ν, and λ ae not unique. Case 2: Thus we ae left with the cases whee α, β, and γ ae unique and also µ, ν, and λ ae unique. Howeve, since each index can be 0, 1, 2, o 3, the two sets of indices do not necessaily have to be the same (e.g. we could have α, β, γ = 0, 1, 2 and µ, ν, λ = 1, 2, 3. Conside a case like this (i.e. the set {α, β, γ} is diffeent fom the set {µ, ν, λ}. Since the Levi-Civita tenso is only non-zeo if all fou indices ae distinct, thee is only one value of ρ, say ρ 1, that makes ɛ αβγρ non-zeo. Similaly, thee is only one value of ρ, say ρ 2, that makes
11 Solutions Ph 236a Week 2 Page 11 of 13 ɛ µνλρ non-zeo. Since {µ, ν, λ} is diffeent fom {α, β, γ}, it follows that ρ 1 ρ 2 and thus all fou tems in the sum ove ρ ae 0 and so the total sum is 0. Since the two sets of indices ae not the same, one is not a pemutation of the othe and so this case also falls unde othewise. Thus we ae left with the cases whee the two sets of indices ae the same. In that case (α, β, γ is always eithe an even o odd pemutation of (µ, ν, λ. Recall that the Levi-Civita tenso does not change unde an even pemutation of its indices. Case 3: Conside the case whee (α, β, γ is an even pemutation of (µ, ν, λ. Since we can pefom any even pemutations we like without changing the Levi- Civita tenso, we can conside the specific case (α, β, γ = (µ, ν, λ without loss of geneality. Thee is only one value of ρ, say ρ 0 that is diffeent fom α, β, and γ. This is the only value of ρ fo which ɛ αβγρ is non-zeo. Thus the sum ove ρ educes to one non-zeo tem, namely δ αβγ µνλ = ɛαβγρ ɛ µνλρ = ɛ αβγρ0 ɛ αβγρ0 = (±1( 1 = +1, (5.1 since ɛ αβγδ = ɛ αβγδ. Case 4: The only emaining case now is whee (α, β, γ is an odd pemutation of (µ, ν, λ. In that case we can take (α, β, γ = (ν, µ, λ without loss of geneality, because even pemutations do not change the Levi-Civita tensos. Again, we only have one value of ρ, say ρ 0 fo which ɛ αβγρ is non-zeo. The sum ove ρ again educes to one tem, namely δ αβγ µνλ = ɛαβγρ ɛ µνλρ = ɛ αβγρ0 ɛ βαγρ0 = +ɛ αβγρ0 ɛ αβγρ0 = +(±1( 1 = 1. (5.2 Thus we have shown that +1 if (α, β, γ is an even pemutation of (µ, ν, λ δ αβγ µνλ = 1 if (α, β, γ is an odd pemutation of (µ, ν, λ 0 othewise. (5.3 Note that δ αβ µν = 1 2 δαβγ µνγ (5.4 Fom what we found above, it is obvious that δ αβ µν = 0 if α = β, µ = ν, o {α, β} {µ, ν}, which fall unde othewise. If (α, β is an even pemutation of (µ, ν, then we must have that (α, β = (µ, ν, and thee ae only two values of γ, say γ 1 and γ 2, fo which δ αβγ is non-zeo. Thus the sum ove γ educes to two tems, namely δ αβ µν = 1 2 δαβγ µνγ = 1 2 (δ αβγ1αβγ1 + δ αβγ2αβγ2 = 1 (1 + 1 = +1. (5.5 2
12 Solutions Ph 236a Week 2 Page 12 of 13 Finally, if (α, β is an odd pemutation of (µ, ν, then we must have that (α, β = (ν, µ, and thee ae again only two values of γ, say γ 1 and γ 2, fo which δ αβγ is non-zeo. Thus the sum ove γ again educes to two tems, namely δ αβ µν = 1 2 δαβγ µνγ = 1 (δ αβγ1βαγ1 + δ αβγ2βαγ2 = 1 ( = 1. (5.6 Thus we have shown that +1 if (α, β is an even pemutation of (µ, ν δ αβ µν = 1 if (α, β is an odd pemutation of (µ, ν 0 othewise. (5.7 Pat (b Since J is a 3-index antisymmetic tenso, J is a 1-index tenso. We find J αβγ = J µ ɛ µαβγ = J µ ɛ µ αβγ = 1 3! J νλρ ɛ νλρµ ɛ µ αβγ = 1 3! J νλρɛ νλρµ ɛ µαβγ = 1 3! J νλρɛ νλρµ ɛ αβγµ = 1 3! J νλρ( δ νλρ αβγ = 1 6 J νλρδ νλρ αβγ. (5.8 Now ecall that J is an antisymmetic tenso. Thus J αβγ = 0 if the 3 indices ae not distinct. Similaly, δ νλρ αβγ = 0 if α, β, and γ ae not distinct. Similaly, the tems in the sum above ae 0 if ν, λ, and ρ ae not distinct. Also δ νλρ αβγ = 0 if {ν, λ, ρ} {α, β, γ}. Thus thee ae only 6 tems in the sum fo which δ νλρ αβγ 0, namely the tems whee (ν, λ, ρ is a pemutation of (α, β, γ. We find J αβγ = 1 6 J νλρδ νλρ αβγ = 1 6 (J αβγ J αγβ + J γαβ J γβα + J βγα J βαγ = 1 6 (J αβγ + J αβγ + J αβγ + J αβγ + J αβγ + J αβγ = 1 6 (6J αβγ = J αβγ, (5.9 whee we have used that J is antisymmetic, hence J αγβ J αβγ, fo example. Fo the 2-index antisymmetic tenso F we find F αβ = 1 F µν ɛ µναβ = 1 F µν ɛ µν αβ 2! 2! = 1 2! 1 2! F λρ ɛ λρµν ɛ µν αβ = 1 4 F λρɛ λρµν ɛ µναβ = 1 4 F λρɛ λρµν ɛ αβµν = 1 4 F λρ ( 2δ λρ αβ = 1 2 F λρδ λρ αβ. (5.10
13 Solutions Ph 236a Week 2 Page 13 of 13 Fom pat (a we know that δ λρ αβ Thus we find = 0 unless (λ, ρ = (α, β o (λ, ρ = (β, α. F αβ = 1 2 F λρδ λρ αβ = 1 2 (F αβ F βα = 1 2 (F αβ + F αβ = F αβ, (5.11 whee we have used that F is antisymmetic, hence F αβ = F βα. Finally, fo the 1-index antisymmetic tenso B we find B α = 1 B µνλ ɛ µνλα = 1 B µνλ ɛ µνλ α = 1 3! 3! 3! Bρ ɛ ρµνλ ɛ µνλ α = 1 3! B ρɛ ρµνλ ɛ µνλα = 1 3! B ρɛ ρµνλ ɛ αµνλ = 1 6 B ( ρ 2δ ρµ αµ = 1 3 B ρδ ρµ αµ. (5.12 Note that δ ρµ αµ = 0 if ρ α because in that case the two sets of indices ae always diffeent. Thus δ ρµ αµ is only non-zeo if ρ = α, in that case we find δ ρµ αµ = δ ρ0 ρ0 + δρ1 ρ1 + δρ2 ρ2 + δρ3 ρ3 = 3, (5.13 because ρ will be 0, 1, 2, o 3. Thus we found that δ ρµ αµ = 3δ ρ α, (5.14 whee δ ρ α is the usual Konecke delta. Thus (5.12 becomes B α = 1 3 B ρδ ρµ αµ = 1 3 B ρ3δ ρ α = B α, (5.15 which is what we need to show.
Laplace s Equation in Spherical Polar Coördinates
 Laplace s Equation in Spheical Pola Coödinates C. W. David Dated: Januay 3, 001 We stat with the pimitive definitions I. x = sin θ cos φ y = sin θ sin φ z = cos θ thei inveses = x y z θ = cos 1 z = z cos1
Laplace s Equation in Spheical Pola Coödinates C. W. David Dated: Januay 3, 001 We stat with the pimitive definitions I. x = sin θ cos φ y = sin θ sin φ z = cos θ thei inveses = x y z θ = cos 1 z = z cos1
Analytical Expression for Hessian
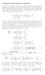 Analytical Expession fo Hessian We deive the expession of Hessian fo a binay potential the coesponding expessions wee deived in [] fo a multibody potential. In what follows, we use the convention that
Analytical Expession fo Hessian We deive the expession of Hessian fo a binay potential the coesponding expessions wee deived in [] fo a multibody potential. In what follows, we use the convention that
Example 1: THE ELECTRIC DIPOLE
 Example 1: THE ELECTRIC DIPOLE 1 The Electic Dipole: z + P + θ d _ Φ = Q 4πε + Q = Q 4πε 4πε 1 + 1 2 The Electic Dipole: d + _ z + Law of Cosines: θ A B α C A 2 = B 2 + C 2 2ABcosα P ± = 2 ( + d ) 2 2
Example 1: THE ELECTRIC DIPOLE 1 The Electic Dipole: z + P + θ d _ Φ = Q 4πε + Q = Q 4πε 4πε 1 + 1 2 The Electic Dipole: d + _ z + Law of Cosines: θ A B α C A 2 = B 2 + C 2 2ABcosα P ± = 2 ( + d ) 2 2
e t e r Cylindrical and Spherical Coordinate Representation of grad, div, curl and 2
 Cylindical and Spheical Coodinate Repesentation of gad, div, cul and 2 Thus fa, we have descibed an abitay vecto in F as a linea combination of i, j and k, which ae unit vectos in the diection of inceasin,
Cylindical and Spheical Coodinate Repesentation of gad, div, cul and 2 Thus fa, we have descibed an abitay vecto in F as a linea combination of i, j and k, which ae unit vectos in the diection of inceasin,
r = x 2 + y 2 and h = z y = r sin sin ϕ
 Homewok 4. Solutions Calculate the Chistoffel symbols of the canonical flat connection in E 3 in a cylindical coodinates x cos ϕ, y sin ϕ, z h, b spheical coodinates. Fo the case of sphee ty to make calculations
Homewok 4. Solutions Calculate the Chistoffel symbols of the canonical flat connection in E 3 in a cylindical coodinates x cos ϕ, y sin ϕ, z h, b spheical coodinates. Fo the case of sphee ty to make calculations
Tutorial Note - Week 09 - Solution
 Tutoial Note - Week 9 - Solution ouble Integals in Pola Coodinates. a Since + and + 5 ae cicles centeed at oigin with adius and 5, then {,θ 5, θ π } Figue. f, f cos θ, sin θ cos θ sin θ sin θ da 5 69 5
Tutoial Note - Week 9 - Solution ouble Integals in Pola Coodinates. a Since + and + 5 ae cicles centeed at oigin with adius and 5, then {,θ 5, θ π } Figue. f, f cos θ, sin θ cos θ sin θ sin θ da 5 69 5
Matrix Hartree-Fock Equations for a Closed Shell System
 atix Hatee-Fock Equations fo a Closed Shell System A single deteminant wavefunction fo a system containing an even numbe of electon N) consists of N/ spatial obitals, each occupied with an α & β spin has
atix Hatee-Fock Equations fo a Closed Shell System A single deteminant wavefunction fo a system containing an even numbe of electon N) consists of N/ spatial obitals, each occupied with an α & β spin has
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
(a,b) Let s review the general definitions of trig functions first. (See back cover of your book) sin θ = b/r cos θ = a/r tan θ = b/a, a 0
 TRIGONOMETRIC IDENTITIES (a,b) Let s eview the geneal definitions of tig functions fist. (See back cove of you book) θ b/ θ a/ tan θ b/a, a 0 θ csc θ /b, b 0 sec θ /a, a 0 cot θ a/b, b 0 By doing some
TRIGONOMETRIC IDENTITIES (a,b) Let s eview the geneal definitions of tig functions fist. (See back cove of you book) θ b/ θ a/ tan θ b/a, a 0 θ csc θ /b, b 0 sec θ /a, a 0 cot θ a/b, b 0 By doing some
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
The Laplacian in Spherical Polar Coordinates
 Univesity of Connecticut DigitalCommons@UConn Chemisty Education Mateials Depatment of Chemisty -6-007 The Laplacian in Spheical Pola Coodinates Cal W. David Univesity of Connecticut, Cal.David@uconn.edu
Univesity of Connecticut DigitalCommons@UConn Chemisty Education Mateials Depatment of Chemisty -6-007 The Laplacian in Spheical Pola Coodinates Cal W. David Univesity of Connecticut, Cal.David@uconn.edu
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines
![Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines](/thumbs/51/28406191.jpg) Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the
Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the
ANTENNAS and WAVE PROPAGATION. Solution Manual
 ANTENNAS and WAVE PROPAGATION Solution Manual A.R. Haish and M. Sachidananda Depatment of Electical Engineeing Indian Institute of Technolog Kanpu Kanpu - 208 06, India OXFORD UNIVERSITY PRESS 2 Contents
ANTENNAS and WAVE PROPAGATION Solution Manual A.R. Haish and M. Sachidananda Depatment of Electical Engineeing Indian Institute of Technolog Kanpu Kanpu - 208 06, India OXFORD UNIVERSITY PRESS 2 Contents
Curvilinear Systems of Coordinates
 A Cuvilinea Systems of Coodinates A.1 Geneal Fomulas Given a nonlinea tansfomation between Catesian coodinates x i, i 1,..., 3 and geneal cuvilinea coodinates u j, j 1,..., 3, x i x i (u j ), we intoduce
A Cuvilinea Systems of Coodinates A.1 Geneal Fomulas Given a nonlinea tansfomation between Catesian coodinates x i, i 1,..., 3 and geneal cuvilinea coodinates u j, j 1,..., 3, x i x i (u j ), we intoduce
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Strain and stress tensors in spherical coordinates
 Saeanifolds.0 Stain and stess tensos in spheical coodinates This woksheet demonstates a few capabilities of Saeanifolds (vesion.0, as included in Saeath 7.5) in computations eadin elasticity theoy in Catesian
Saeanifolds.0 Stain and stess tensos in spheical coodinates This woksheet demonstates a few capabilities of Saeanifolds (vesion.0, as included in Saeath 7.5) in computations eadin elasticity theoy in Catesian
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Fundamental Equations of Fluid Mechanics
 Fundamental Equations of Fluid Mechanics 1 Calculus 1.1 Gadient of a scala s The gadient of a scala is a vecto quantit. The foms of the diffeential gadient opeato depend on the paticula geomet of inteest.
Fundamental Equations of Fluid Mechanics 1 Calculus 1.1 Gadient of a scala s The gadient of a scala is a vecto quantit. The foms of the diffeential gadient opeato depend on the paticula geomet of inteest.
1 String with massive end-points
 1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
VEKTORANALYS. CURVILINEAR COORDINATES (kroklinjiga koordinatsytem) Kursvecka 4. Kapitel 10 Sidor
 VEKTORANALYS Kusvecka 4 CURVILINEAR COORDINATES (koklinjiga koodinatstem) Kapitel 10 Sido 99-11 TARGET PROBLEM An athlete is otating a hamme Calculate the foce on the ams. F ams F F ma dv a v dt d v dt
VEKTORANALYS Kusvecka 4 CURVILINEAR COORDINATES (koklinjiga koodinatstem) Kapitel 10 Sido 99-11 TARGET PROBLEM An athlete is otating a hamme Calculate the foce on the ams. F ams F F ma dv a v dt d v dt
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
21. Stresses Around a Hole (I) 21. Stresses Around a Hole (I) I Main Topics
 I Main Topics A Intoducon to stess fields and stess concentaons B An axisymmetic poblem B Stesses in a pola (cylindical) efeence fame C quaons of equilibium D Soluon of bounday value poblem fo a pessuized
I Main Topics A Intoducon to stess fields and stess concentaons B An axisymmetic poblem B Stesses in a pola (cylindical) efeence fame C quaons of equilibium D Soluon of bounday value poblem fo a pessuized
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Oscillating dipole system Suppose we have two small spheres separated by a distance s. The charge on one sphere changes with time and is described by
 5 Radiation (Chapte 11) 5.1 Electic dipole adiation Oscillating dipole system Suppose we have two small sphees sepaated by a distance s. The chage on one sphee changes with time and is descibed by q(t)
5 Radiation (Chapte 11) 5.1 Electic dipole adiation Oscillating dipole system Suppose we have two small sphees sepaated by a distance s. The chage on one sphee changes with time and is descibed by q(t)
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
1 3D Helmholtz Equation
 Deivation of the Geen s Funtions fo the Helmholtz and Wave Equations Alexande Miles Witten: Deembe 19th, 211 Last Edited: Deembe 19, 211 1 3D Helmholtz Equation A Geen s Funtion fo the 3D Helmholtz equation
Deivation of the Geen s Funtions fo the Helmholtz and Wave Equations Alexande Miles Witten: Deembe 19th, 211 Last Edited: Deembe 19, 211 1 3D Helmholtz Equation A Geen s Funtion fo the 3D Helmholtz equation
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
dx x ψ, we should find a similar expression for rθφ L ψ. From L = R P and our knowledge of momentum operators, it follows that + e y z d
 PHYS851 Quantum Mechanics I, Fall 2009 HOMEWORK ASSIGNMENT 11 Topics Coveed: Obital angula momentum, cente-of-mass coodinates Some Key Concepts: angula degees of feedom, spheical hamonics 1. [20 pts] In
PHYS851 Quantum Mechanics I, Fall 2009 HOMEWORK ASSIGNMENT 11 Topics Coveed: Obital angula momentum, cente-of-mass coodinates Some Key Concepts: angula degees of feedom, spheical hamonics 1. [20 pts] In
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Slide 1 of 18 Tensors in Mathematica 9: Built-In Capabilities. George E. Hrabovsky MAST
 Slide of 8 Tensos in Mathematica 9: Built-In Capabilities eoge E. Habovsky MAST This Talk I intend to cove fou main topics: How to make tensos in the newest vesion of Mathematica. The metic tenso and how
Slide of 8 Tensos in Mathematica 9: Built-In Capabilities eoge E. Habovsky MAST This Talk I intend to cove fou main topics: How to make tensos in the newest vesion of Mathematica. The metic tenso and how
Problems in curvilinear coordinates
 Poblems in cuvilinea coodinates Lectue Notes by D K M Udayanandan Cylindical coodinates. Show that ˆ φ ˆφ, ˆφ φ ˆ and that all othe fist deivatives of the cicula cylindical unit vectos with espect to the
Poblems in cuvilinea coodinates Lectue Notes by D K M Udayanandan Cylindical coodinates. Show that ˆ φ ˆφ, ˆφ φ ˆ and that all othe fist deivatives of the cicula cylindical unit vectos with espect to the
Higher Derivative Gravity Theories
 Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
General Relativity (225A) Fall 2013 Assignment 5 Solutions
 Univesity of Califonia at San Diego Depatment of Physics Pof. John McGeevy Geneal Relativity 225A Fall 2013 Assignment 5 Solutions Posted Octobe 23, 2013 Due Monday, Novembe 4, 2013 1. A constant vecto
Univesity of Califonia at San Diego Depatment of Physics Pof. John McGeevy Geneal Relativity 225A Fall 2013 Assignment 5 Solutions Posted Octobe 23, 2013 Due Monday, Novembe 4, 2013 1. A constant vecto
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
4.2 Differential Equations in Polar Coordinates
 Section 4. 4. Diffeential qations in Pola Coodinates Hee the two-dimensional Catesian elations of Chapte ae e-cast in pola coodinates. 4.. qilibim eqations in Pola Coodinates One wa of epesg the eqations
Section 4. 4. Diffeential qations in Pola Coodinates Hee the two-dimensional Catesian elations of Chapte ae e-cast in pola coodinates. 4.. qilibim eqations in Pola Coodinates One wa of epesg the eqations
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Lecture 13 - Root Space Decomposition II
 Lecture 13 - Root Space Decomposition II October 18, 2012 1 Review First let us recall the situation. Let g be a simple algebra, with maximal toral subalgebra h (which we are calling a CSA, or Cartan Subalgebra).
Lecture 13 - Root Space Decomposition II October 18, 2012 1 Review First let us recall the situation. Let g be a simple algebra, with maximal toral subalgebra h (which we are calling a CSA, or Cartan Subalgebra).
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER
 ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Problem Set 9 Solutions. θ + 1. θ 2 + cotθ ( ) sinθ e iφ is an eigenfunction of the ˆ L 2 operator. / θ 2. φ 2. sin 2 θ φ 2. ( ) = e iφ. = e iφ cosθ.
 Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
 CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
Lecture 15 - Root System Axiomatics
 Lecture 15 - Root System Axiomatics Nov 1, 01 In this lecture we examine root systems from an axiomatic point of view. 1 Reflections If v R n, then it determines a hyperplane, denoted P v, through the
Lecture 15 - Root System Axiomatics Nov 1, 01 In this lecture we examine root systems from an axiomatic point of view. 1 Reflections If v R n, then it determines a hyperplane, denoted P v, through the
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequality for metrics: Let (X, d) be a metric space and let x, y, z X.
 Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS
 CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Tutorial problem set 6,
 GENERAL RELATIVITY Tutorial problem set 6, 01.11.2013. SOLUTIONS PROBLEM 1 Killing vectors. a Show that the commutator of two Killing vectors is a Killing vector. Show that a linear combination with constant
GENERAL RELATIVITY Tutorial problem set 6, 01.11.2013. SOLUTIONS PROBLEM 1 Killing vectors. a Show that the commutator of two Killing vectors is a Killing vector. Show that a linear combination with constant
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Spherical Coordinates
 Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
 9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
Forced Pendulum Numerical approach
 Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Lecture VI: Tensor calculus
 Lectue VI: Tenso calculus Chistophe M. Hiata Caltech M/C 350-7, Pasadena CA 925, USA (Dated: Octobe 4, 20) I. OVERVIEW In this lectue, we will begin with some examples fom vecto calculus, and then continue
Lectue VI: Tenso calculus Chistophe M. Hiata Caltech M/C 350-7, Pasadena CA 925, USA (Dated: Octobe 4, 20) I. OVERVIEW In this lectue, we will begin with some examples fom vecto calculus, and then continue
Pg The perimeter is P = 3x The area of a triangle is. where b is the base, h is the height. In our case b = x, then the area is
 Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Orbital angular momentum and the spherical harmonics
 Orbital angular momentum and the spherical harmonics March 8, 03 Orbital angular momentum We compare our result on representations of rotations with our previous experience of angular momentum, defined
Orbital angular momentum and the spherical harmonics March 8, 03 Orbital angular momentum We compare our result on representations of rotations with our previous experience of angular momentum, defined
Orbital angular momentum and the spherical harmonics
 Obital angula momentum and the spheical hamonics Apil 2, 207 Obital angula momentum We compae ou esult on epesentations of otations with ou pevious expeience of angula momentum, defined fo a point paticle
Obital angula momentum and the spheical hamonics Apil 2, 207 Obital angula momentum We compae ou esult on epesentations of otations with ou pevious expeience of angula momentum, defined fo a point paticle
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)
![2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p) 2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)](/thumbs/40/21364883.jpg) Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
= {{D α, D α }, D α }. = [D α, 4iσ µ α α D α µ ] = 4iσ µ α α [Dα, D α ] µ.
![= {{D α, D α }, D α }. = [D α, 4iσ µ α α D α µ ] = 4iσ µ α α [Dα, D α ] µ. = {{D α, D α }, D α }. = [D α, 4iσ µ α α D α µ ] = 4iσ µ α α [Dα, D α ] µ.](/thumbs/93/113370452.jpg) PHY 396 T: SUSY Solutions for problem set #1. Problem 2(a): First of all, [D α, D 2 D α D α ] = {D α, D α }D α D α {D α, D α } = {D α, D α }D α + D α {D α, D α } (S.1) = {{D α, D α }, D α }. Second, {D
PHY 396 T: SUSY Solutions for problem set #1. Problem 2(a): First of all, [D α, D 2 D α D α ] = {D α, D α }D α D α {D α, D α } = {D α, D α }D α + D α {D α, D α } (S.1) = {{D α, D α }, D α }. Second, {D
Parametrized Surfaces
 Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Geodesic Equations for the Wormhole Metric
 Geodesic Equations for the Wormhole Metric Dr R Herman Physics & Physical Oceanography, UNCW February 14, 2018 The Wormhole Metric Morris and Thorne wormhole metric: [M S Morris, K S Thorne, Wormholes
Geodesic Equations for the Wormhole Metric Dr R Herman Physics & Physical Oceanography, UNCW February 14, 2018 The Wormhole Metric Morris and Thorne wormhole metric: [M S Morris, K S Thorne, Wormholes
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
1 Full derivation of the Schwarzschild solution
 EPGY Summe Institute SRGR Gay Oas 1 Full deivation of the Schwazschild solution The goal of this document is to povide a full, thooughly detailed deivation of the Schwazschild solution. Much of the diffeential
EPGY Summe Institute SRGR Gay Oas 1 Full deivation of the Schwazschild solution The goal of this document is to povide a full, thooughly detailed deivation of the Schwazschild solution. Much of the diffeential
On a four-dimensional hyperbolic manifold with finite volume
 BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Variational Wavefunction for the Helium Atom
 Technische Universität Graz Institut für Festkörperphysik Student project Variational Wavefunction for the Helium Atom Molecular and Solid State Physics 53. submitted on: 3. November 9 by: Markus Krammer
Technische Universität Graz Institut für Festkörperphysik Student project Variational Wavefunction for the Helium Atom Molecular and Solid State Physics 53. submitted on: 3. November 9 by: Markus Krammer
