Various types of likelihood
|
|
|
- Μνάσων Ανδρέου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Various types of likelihood 1. likelihood, marginal likelihood, conditional likelihood, profile likelihood, adjusted profile likelihood, Bayesian asymptotics 2. quasi-likelihood, composite likelihood 3. semi-parametric likelihood, partial likelihood 4. empirical likelihood, penalized likelihood 5. bootstrap likelihood, h-likelihood, weighted likelihood, pseudo-likelihood, local likelihood, sieve likelihood, simulated likelihood STA 4508: Topics in Likelihood Inference January 14, /57
2 Nuisance parameters: notation θ = (ψ, λ) = (ψ 1,..., ψ q, λ 1,..., λ d q ) ( ) Uψ (θ) U(θ) =, U U λ (θ) λ (ψ, ˆλ ψ ) = 0 ( ) ( ) iψψ i i(θ) = ψλ jψψ j j(θ) = ψλ i λψ i λλ ( i i 1 (θ) = ψψ i ψλ ) i λψ i λλ j λψ j λλ ( j j 1 (θ) = ψψ j ψλ ). j λψ i ψψ (θ) = {i ψψ (θ) i ψλ (θ)i 1 λλ (θ)i λψ(θ)} 1, l p (ψ) = l(ψ, ˆλ ψ ), j p (ψ) = l p(ψ) j λλ STA 4508: Topics in Likelihood Inference January 14, /57
3 Nuisance parameters: approximate pivots w u (ψ) = U ψ (ψ, ˆλ ψ ) T {i ψψ (ψ, ˆλ ψ )}U ψ (ψ, ˆλ ψ ). χ 2 q w e (ψ) = ( ˆψ ψ) T {i ψψ ( ˆψ, ˆλ)} 1 ( ˆψ ψ). χ 2 q w(ψ) = 2{l( ˆψ, ˆλ) l(ψ, ˆλ ψ )} = 2{l p ( ˆψ) l p (ψ)}. χ 2 q; r u (ψ) = l p(ψ)j 1/2 p ( ˆψ) r e (ψ) = ( ˆψ ψ)j 1/2 p ( ˆψ). N(0, 1),. N(0, 1), r(ψ) = sign( ˆψ ψ)[2{l p ( ˆψ) l p (ψ)}] 1/2. N(0, 1) STA 4508: Topics in Likelihood Inference January 14, /57
4
5 Nuisance parameters: properties of likelihood maximum likelihood estimates are equivariant: ĥ(θ) = h(ˆθ) for one-to-one h( ) question: which of w e, w u, w are invariant under reparametrization of the full parameter: ϕ(θ)? question: which of r e, r u, r are invariant under interest-respecting reparameterizations (ψ, λ) {ψ, η(ψ, λ)}? consistency of maximum likelihood estimate equivalence of maximum likelihood estimate and root of score equation observed vs. expected information STA 4508: Topics in Likelihood Inference January 14, /57
6
7 Various types of likelihood 1. likelihood, marginal likelihood, conditional likelihood, profile likelihood, adjusted profile likelihood 2. quasi-likelihood, composite likelihood 3. semi-parametric likelihood, partial likelihood 4. empirical likelihood, penalized likelihood 5. bootstrap likelihood, h-likelihood, weighted likelihood, pseudo-likelihood, local likelihood, sieve likelihood, simulated likelihood STA 4508: Topics in Likelihood Inference January 14, /57
8 Marginal and conditional likelihoods Example: Y N(Xβ, σ 2 ), Y R n Example: Y ij N(µ i, σ 2 ), Example: Y ij N(µ, σ 2 i ), j = 1,..., k; i = 1,..., m j = 1,..., k i ; i = 1,..., m Example: Y i1, Y i2 Bernoulli(p i1, p i2 ), i = 1,..., n Example: Y i1, Y i2 Exponential(λ i ψ, λ i /ψ) or ψλ i, ψ/λ i STA 4508: Topics in Likelihood Inference January 14, /57
9
10 Frequentist inference, nuisance parameters first-order pivotal quantities r u (ψ) = l P (ψ)j P( ˆψ) 1/2. N(0, 1), r e (ψ) = ( ˆψ ψ)j P ( ˆψ) 1/2. N(0, 1), r(ψ) = sign( ˆψ ψ)[2{l P ( ˆψ) l P (ψ)}] 1/2. N(0, 1) all based on treating profile log-likelihood as a one-parameter log-likelihood example y = Xβ + ɛ, ɛ N(0, σ 2 ) ˆσ 2 = (y X ˆβ) T (y X ˆβ)/n STA 4508: Topics in Likelihood Inference January 14, /57
11 log-likelihood ψ 1 2
12 Eliminating nuisance parameters by using marginal density f (y; ψ, λ) f m (t 1 ; ψ)f c (t 2 t 1 ; ψ, λ) Example N(Xβ, σ 2 I) : f (y; β, σ 2 ) f m (RSS; σ 2 )f c ( ˆβ RSS; β, σ 2 ) by using conditional density f (y; ψ, λ) f c (t 1 t 2 ; ψ)f m (t 2 ; ψ, λ) Example N(Xβ, σ 2 I) : f (y; β, σ 2 ) f c (RSS ˆβ; σ 2 )f m ( ˆβ; β, σ 2 ) STA 4508: Topics in Likelihood Inference January 14, /57
13 Linear exponential families conditional density free of nuisance parameter f (y i ; ψ, λ) = exp{ψ T s(y i ) + λ T t(y i ) k(ψ, λ)}h(y i ) f (y; ψ, λ) = s = t = f (s, t; ψ, λ) = f (s t; ψ) = STA 4508: Topics in Likelihood Inference January 14, /57
14 Adjusted profile log-likelihood l A (ψ) = l p (ψ) + A(ψ) = l(ψ, ˆλ ψ ) + A(ψ) A(ψ) assumed to be O p (1) generic form is A FR (ψ) = log j λλ(ψ, ˆλ ψ ) log d(λ) d ˆλ ψ Fraser, 2003 closely related A BN (ψ) = 1 2 log j λλ(ψ, ˆλ ψ ) + log d ˆλ d ˆλ ψ SM , BN 1983 if i ψλ (θ) = 0, then ˆλ ψ = ˆλ + O p (n 1 ), suggesting we ignore last term if ψ is scalar, then in principle we can find a parametrization (ψ, λ) in which i ψλ (θ) = 0 SM STA 4508: Topics in Likelihood Inference January 14, /57
15 Asymptotics for Bayesian inference exp{l(θ; y)}π(θ) π(θ y) = exp{l(θ; y)}π(θ)dθ expand numerator and denominator about ˆθ, assuming l (ˆθ) = 0 π(θ y). = N{ˆθ, j 1 (ˆθ)} expand denominator only about ˆθ result π(θ y). = 1 (2π) d/2 j(ˆθ) +1/2 exp{l(θ; y) l(ˆθ; y)} π(θ) π(ˆθ) STA 4508: Topics in Likelihood Inference January 14, /57
16 Posterior is asymptotically normal π(θ y). N{ˆθ, j 1 (ˆθ)} θ R, y = (y 1,..., y n ) careful statement STA 4508: Topics in Likelihood Inference January 14, /57
17 ... posterior is asymptotically normal π(θ y). N{ˆθ, j 1 (ˆθ)} θ R, y = (y 1,..., y n ) equivalently l π (θ) = STA 4508: Topics in Likelihood Inference January 14, /57
18 ... posterior is asymptotically normal In fact, If π(θ) > 0 and π (θ) is continuous in a neighbourhood of θ 0, there exist constants D and n y s.t. F n (ξ) Φ(ξ) < Dn 1/2, for all n > n y, on an almost-sure set with respect to π(θ 0 )f (y; θ 0 ), where y = (y 1,..., y n ) is a sample from f (y; θ 0 ), and θ 0 is an observation from the prior density π(θ). F n (ξ) = Pr{(θ ˆθ)j 1/2 (ˆθ) ξ y} Johnson (1970); Datta & Mukerjee (2004) STA 4508: Topics in Likelihood Inference January 14, /57
19 Laplace approximation π(θ y). = 1 (2π) 1/2 j(ˆθ) +1/2 exp{l(θ; y) l(ˆθ; y)} π(θ) π(ˆθ) π(θ y) = π(θ y) = 1 (2π) 1/2 j(ˆθ) +1/2 exp{l(θ; y) l(ˆθ; y)} π(θ) π(ˆθ) {1+O p(n 1 )} y = (y 1,..., y n ), θ R 1 1 (2π) 1/2 j π(ˆθ π ) +1/2 exp{l π (θ; y) l π (ˆθ π ; y)}{1+o p (n 1 )} STA 4508: Topics in Likelihood Inference January 14, /57
20 Posterior tail area θ π(ϑ y)dϑ. = θ 1 (2π) 1/2 el(ϑ;y) l( ˆϑ;y) 1/2 π(ϑ) j( ˆϑ) π( ˆϑ) dϑ STA 4508: Topics in Likelihood Inference January 14, /57
21 Posterior cdf θ π(ϑ y)dϑ. = θ 1 (2π) 1/2 el(ϑ;y) l( ˆϑ;y) 1/2 π(ϑ) j( ˆϑ) π( ˆϑ) dϑ SM, 11.3 STA 4508: Topics in Likelihood Inference January 14, /57
22
23 BDR, Ch.3, Cauchy with flat prior
24 Nuisance parameters y = (y 1,..., y n ) f (y; θ), θ = (ψ, λ) π m (ψ y) = π(ψ, λ y)dλ = exp{l(ψ, λ; y)π(ψ, λ)dλ exp{l(ψ, λ; y)π(ψ, λ)dψdλ STA 4508: Topics in Likelihood Inference January 14, /57
25 ... nuisance parameters y = (y 1,..., y n ) f (y; θ), θ = (ψ, λ) π m (ψ y) = π(ψ, λ y)dλ = exp{l(ψ, λ; y)π(ψ, λ)dλ exp{l(ψ, λ; y)π(ψ, λ)dψdλ j(ˆθ) = j ψψ (ˆθ) j λλ (ˆθ) STA 4508: Topics in Likelihood Inference January 14, /57
26 Posterior marginal cdf, d = 1 Π m (ψ y) =. = ψ ψ π m (ξ y)dξ 1 (2π) 1/2 elp(ξ) lp(ˆξ) j 1/2 p (ˆξ) π(ξ, ˆλ ξ ) j λλ (ˆξ, ˆλ) 1/2 π(ˆξ, ˆλ) j λλ (ξ, ˆλ ξ ) 1/2 dξ STA 4508: Topics in Likelihood Inference January 14, /57
27 ... posterior marginal cdf, d = 1 Π m (ψ y) r = r(ψ) =. = Φ(r B ) = Φ{r + 1 r log(q B r )} q B = q B (ψ) = STA 4508: Topics in Likelihood Inference January 14, /57
28 normal circle, k=2 p value STA 4508: Topics in Likelihood Inference January 14, /57 ψ
29 normal circle, k=2 p value STA 4508: Topics in Likelihood Inference January 14, /57 ψ
30 normal circle, k=2 p value STA 4508: Topics in Likelihood Inference January 14, /57 ψ
31 normal circle, k = 2, 5, 10 p value STA 4508: Topics in Likelihood Inference January 14, /57 ψ
32 normal circle, k = 2, 5, 10 p value STA 4508: Topics in Likelihood Inference January 14, /57 ψ
33 normal circle, k = 2, 5, 10 p value STA 4508: Topics in Likelihood Inference January 14, /57 ψ
34 normal circle, k = 2, 5, 10 p value STA 4508: Topics in Likelihood Inference January 14, /57 ψ
35 Link to adjusted log-likelihoods π m (ψ y). = 1 (2π) d/2 elp(ψ) lp( ˆψ) j 1/2 p ( ˆψ) π(ψ, ˆλ ψ ) π( ˆψ, ˆλ) j λλ ( ˆψ, ˆλ) 1/2 j λλ (ψ, ˆλ ψ ) 1/2 π m (ψ y) =. c exp{l p (ψ) 1 2 log j λλ(ψ, ˆλ ψ ) + log π(ψ, ˆλ ψ )} l A (ψ) = l p (ψ) 1 2 log j d ˆλ λλ(ψ, ˆλ ψ ) + log d ˆλ ψ if i ψλ (θ) = 0, then ˆλ ψ = ˆλ + O p (n 1 ) STA 4508: Topics in Likelihood Inference January 14, /57
36 Composite likelihood Vector observation: Y f (y; θ), Y Y R m, θ R d Set of events: {A k, k K } Composite Likelihood: (Lindsay, 1988) CL(θ; y) = k K L k (θ; y) w k L k (θ; y) = f ({y A k }; θ) likelihood for an event {w k, k K } a set of weights STA 4508: Topics in Likelihood Inference January 14, /57
37 Examples Composite Conditional Likelihood: (Besag, 1974) L C (θ; y) = s S f s s c(y s y s c) ws, and variants by modifying events Composite Marginal Likelihood: CML(θ; y) = s S f s(y s ; θ) ws, f s (y s ; θ): marginal density of the subvector y s induced by f Independence Likelihood: Pairwise Likelihood: STA 4508: Topics in Likelihood Inference January 14, /57
38 Derived quantities log composite likelihood: cl(θ; y) = log CL(θ; y) score function: U(θ; y) = θ cl(θ; y) = s S w su s (θ; y) U s (θ; y) = θ log f s (y s ; θ) variability matrix: J(θ) = var θ {U(θ; Y )} sensitivity matrix: H(θ) = E θ { θ U(θ; Y )} Godambe information (or sandwich information): G(θ) = H(θ)J(θ) 1 H(θ) STA 4508: Topics in Likelihood Inference January 14, /57
39 Inference Sample: Y 1,..., Y n, i.i.d., CL(θ; y) = n i=1 CL(θ; y i) n(ˆθ CL θ). N{0, G 1 (θ)} G(θ) = H(θ)J(θ) 1 H(θ) STA 4508: Topics in Likelihood Inference January 14, /57
40 ... inference w(θ) = 2{cl(ˆθ CL ) cl(θ)}. d a=1 µ az 2 a Z a N(0, 1) µ 1,..., µ d eigenvalues of J(θ)H(θ) 1 STA 4508: Topics in Likelihood Inference January 14, /57
41 ... inference w(θ) = 2{cl(ˆθ CL ) cl(θ)}. d a=1 µ az 2 a Z a N(0, 1) µ 1,..., µ d eigenvalues of J(θ)H(θ) 1 w(θ). = (ˆθ CL θ){nh(θ)}(ˆθ CL θ) ˆθ CL. N{θ, G 1 (θ)} STA 4508: Topics in Likelihood Inference January 14, /57
42 Nuisance parameters θ = (ψ, λ) constrained estimator: θ ψ = sup θ=θ(ψ) cl(θ; y) n( ˆψ CL ψ). N{0, G ψψ (θ)} G(θ) = H(θ)J(θ) 1 H(θ) w(ψ) = 2{cl(ˆθ CL ) cl( θ ψ )}. d 0 a=1 µ az 2 a µ 1,..., µ d0 eigenvalues of (H ψψ ) 1 G ψψ Kent, 1982 STA 4508: Topics in Likelihood Inference January 14, /57
43 Model selection Akaike s information criterion Varin and Vidoni, 2005 AIC = 2cl(ˆθ CL ; y) 2 dim(θ) Bayesian information criterion Gao and Song, 2009 BIC = 2cl(ˆθ CL ; y) log n dim(θ) effective number of parameters (?) dim(θ) = tr{h(θ)g 1 (θ)} these criteria used for model averaging Hjort and Claeskens, 2008 or for selection of tuning parameters Gao and Song, 2009 STA 4508: Topics in Likelihood Inference January 14, /57
44 Example: symmetric normal Y i N(0, R), var(y ir ) = 1, corr (Y ir, Y is ) = ρ compound bivariate normal densities to form pairwise likelihood nm(m 1) cl(ρ; y 1,..., y n ) = log(1 ρ 2 ) m 1 + ρ 4 2(1 ρ 2 ) SS w (m 1)(1 ρ) SS b 2(1 ρ 2 ) m SS w = n i=1 s=1 m (y is ȳ i. ) 2, SS b = n(m 1) l(ρ; y 1,..., y n ) = log(1 ρ) n log{1 + (m 1)ρ} (1 ρ) SS 1 SS w b 2{1 + (m 1)ρ} m n i=1 y 2 i. STA 4508: Topics in Likelihood Inference January 14, /57
45 ... symmetric normal a. var(ˆρ) = a. var(ˆρ CL ) = 2 {1 + (m 1)ρ} 2 (1 ρ) 2 nm(m 1) 1 + (m 1)ρ 2 2 (1 ρ) 2 c(m, ρ) nm(m 1) (1 + ρ 2 ) 2 c(m, ρ) = (1 ρ) 2 (3ρ 2 + 1) + mρ( 3ρ 3 + 8ρ 2 3ρ + 2) + m 2 ρ 2 (1 ρ) 2 2 (1 ρ) 2 a.var(ˆρ CL ) = nm(m 1) (1 + ρ 2 c(m, ρ) ) 2 O( 1 n ) O(1) n m STA 4508: Topics in Likelihood Inference January 14, /57
46 ... symmetric normal a.var(ˆρ ), m = 3, 5, 8, 10 a.var(ˆρ CL ) (Cox & Reid, 2004) efficiency ρ STA 4508: Topics in Likelihood Inference January 14, /57
47 Likelihood ratio test log likelihoods rho=0.5, n=10, q=5 log likelihoods rho=0.8, n=10, q= rho rho log likelihoods rho=0.2, n=10, q=5 log likelihoods rho=0.2, n=7, q= rho rho STA 4508: Topics in Likelihood Inference January 14, /57
48 ... symmetric normal + Y i N(µ1, σ 2 R) R st = ρ ˆµ = ˆµ CL, ˆσ 2 = ˆσ 2 CL, ˆρ = ˆρ CL G(θ) = H(θ)J(θ) 1 H(θ) = i(θ) expected Fisher information pairwise likelihood is fully efficient also true for Y i N(µ, Σ) (Mardia, Hughes, Taylor 2007; Jin 2009) because U CL (θ) = J(θ)H(θ)U full (θ) Pagui; Pace et al., 2011 STA 4508: Topics in Likelihood Inference January 14, /57
49 Example: dichotomized MV Normal Y ir = 1{Z ir > 0} Z N(0, R) r = 1,..., m; i = 1, l 2 (ρ) = n {y ir y is log P(y r = 1, y s = 1) + y ir (1 y is ) log P 10 i=1 s<r + (1 y ir )y is log P 01 + (1 y ir )(1 y is ) log P 00 } a.var(ˆρ CL ) = 1 n 4π 2 m 2 (1 ρ 2 ) (m 1) 2 var(t ) T = i (2y ir y is y ir y is ) s<r var(t ) = nm 4 (p p p 11 p )+ m 3 ( 6p ) + m 2 (...) + m(...) STA 4508: Topics in Likelihood Inference January 14, /57
50 a. variance pairwise full rho ρ ARE ρ ARE
51 Example: multi-level probit model latent variable: z ir = x ir β + b i + ɛ ir, ɛ ir N(0, 1) binary observations: y ir = 1(z ir > 0); r = 1,... m i ; i = 1,... n probit model: Pr(y ir = 1 b i ) = Φ(x ir β + b i); b i N(0, σ 2 b ) likelihood L(β, σ b ) = n i=1 m i pairwise likelihood CL(β, σ b ) = r=1 i=1 r<s Φ(x ir β+b i) y ir {1 Φ(x ir β+b i)} 1 y ir φ(b i, σ 2 b )db i n P y ir y is 11 P y ir (1 y is ) 10 P (1 y ir )y is 01 P (1 y ir )(1 y is ) 00 each Pr(y ir = j, y is = k) evaluated using Φ 2 (, ; ρ irs ) (Renard et al., 2004) STA 4508: Topics in Likelihood Inference January 14, /57
52 ... multi-level probit (Renard et al. 2004) computational effort doesn t increase with the number of random effects pairwise likelihood numerically stable efficiency losses, relative to maximum likelihood, of about 20% for estimation of β somewhat larger for estimation of σ 2 b STA 4508: Topics in Likelihood Inference January 14, /57
53 ... Example
54 Markov chains Hjort and Varin, 2008 comparison of likelihood L(θ; y) = pr(y r = y r Y r 1 = y r 1 ; θ) adjoining pairs CML CML(θ; y) = pr(y r = y r, Y r 1 = y r 1 ; θ) composite conditional likelihood (= Besag s PL) CCL(θ; y) = pr(y r = y r neighbours ; θ) STA 4508: Topics in Likelihood Inference January 14, /57
55 ... Markov chain example Random walk with p states and two reflecting barriers Transition matrix P = ρ 0 ρ ρ 0 ρ STA 4508: Topics in Likelihood Inference January 14, /57
56 ... Markov chain example Reflecting barrier with five states: efficiency of pairwise likelihood (dashed line) and Besag s pseudolikelihood (solid line) STA 4508: Topics in Likelihood Inference January 14, /57
57 Example: longitudinal count data subjects i = 1,..., n observations counts y ir, r = 1,... m i model y ir Poisson(u ir x T u i1,..., u imi ir β) gamma-distributed random effects but correlated corr(u ir, u is ) = ρ r s joint density has combinatorial number of terms in m i ; impractical weighted pairwise composite likelihood L pair (β) = n i=1 1 m i 1 m i m i r=1 s=r+1 f (y ir, y is ; β) weights chosen so that L pair = full likelihood if ρ = 0 Henderson & Shimura, 2003 STA 4508: Topics in Likelihood Inference January 14, /57
Various types of likelihood
 Various types of likelihood 1. likelihood, marginal likelihood, conditional likelihood, profile likelihood, adjusted profile likelihood, Bayesian asymptotics 2. quasi-likelihood, composite likelihood 3.
Various types of likelihood 1. likelihood, marginal likelihood, conditional likelihood, profile likelihood, adjusted profile likelihood, Bayesian asymptotics 2. quasi-likelihood, composite likelihood 3.
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Theorem 8 Let φ be the most powerful size α test of H
 Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Asymptotic distribution of MLE
 Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
Asymptotic distribution of MLE Theorem Let {X t } be a causal and invertible ARMA(p,q) process satisfying Φ(B)X = Θ(B)Z, {Z t } IID(0, σ 2 ). Let ( ˆφ, ˆϑ) the values that minimize LL n (φ, ϑ) among those
Introduction to the ML Estimation of ARMA processes
 Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
5.4 The Poisson Distribution.
 The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Tutorial on Multinomial Logistic Regression
 Tutorial on Multinomial Logistic Regression Javier R Movellan June 19, 2013 1 1 General Model The inputs are n-dimensional vectors the outputs are c-dimensional vectors The training sample consist of m
Tutorial on Multinomial Logistic Regression Javier R Movellan June 19, 2013 1 1 General Model The inputs are n-dimensional vectors the outputs are c-dimensional vectors The training sample consist of m
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
FORMULAS FOR STATISTICS 1
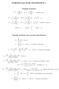 FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Lecture 7: Overdispersion in Poisson regression
 Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 12: Pseudo likelihood approach
 Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Description of the PX-HC algorithm
 A Description of the PX-HC algorithm Let N = C c= N c and write C Nc K c= i= k= as, the Gibbs sampling algorithm at iteration m for continuous outcomes: Step A: For =,, J, draw θ m in the following steps:
A Description of the PX-HC algorithm Let N = C c= N c and write C Nc K c= i= k= as, the Gibbs sampling algorithm at iteration m for continuous outcomes: Step A: For =,, J, draw θ m in the following steps:
Survival Analysis: One-Sample Problem /Two-Sample Problem/Regression. Lu Tian and Richard Olshen Stanford University
 Survival Analysis: One-Sample Problem /Two-Sample Problem/Regression Lu Tian and Richard Olshen Stanford University 1 One sample problem T 1,, T n 1 S( ), C 1,, C n G( ) and T i C i Observations: (U i,
Survival Analysis: One-Sample Problem /Two-Sample Problem/Regression Lu Tian and Richard Olshen Stanford University 1 One sample problem T 1,, T n 1 S( ), C 1,, C n G( ) and T i C i Observations: (U i,
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data
 Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data Rahim Alhamzawi, Haithem Taha Mohammad Ali Department of Statistics, College of Administration and Economics,
Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data Rahim Alhamzawi, Haithem Taha Mohammad Ali Department of Statistics, College of Administration and Economics,
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
More Notes on Testing. Large Sample Properties of the Likelihood Ratio Statistic. Let X i be iid with density f(x, θ). We are interested in testing
 Ulrich Müller Economics 2110 Fall 2008 More Notes on Testing Large Sample Properties of the Likelihood Ratio Statistic Let X i be iid with density f(x, θ). We are interested in testing H 0 : θ = θ 0 against
Ulrich Müller Economics 2110 Fall 2008 More Notes on Testing Large Sample Properties of the Likelihood Ratio Statistic Let X i be iid with density f(x, θ). We are interested in testing H 0 : θ = θ 0 against
Empirical best prediction under area-level Poisson mixed models
 Noname manuscript No. (will be inserted by the editor Empirical best prediction under area-level Poisson mixed models Miguel Boubeta María José Lombardía Domingo Morales eceived: date / Accepted: date
Noname manuscript No. (will be inserted by the editor Empirical best prediction under area-level Poisson mixed models Miguel Boubeta María José Lombardía Domingo Morales eceived: date / Accepted: date
An Introduction to Signal Detection and Estimation - Second Edition Chapter II: Selected Solutions
 An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Local Approximation with Kernels
 Local Approximation with Kernels Thomas Hangelbroek University of Hawaii at Manoa 5th International Conference Approximation Theory, 26 work supported by: NSF DMS-43726 A cubic spline example Consider
Local Approximation with Kernels Thomas Hangelbroek University of Hawaii at Manoa 5th International Conference Approximation Theory, 26 work supported by: NSF DMS-43726 A cubic spline example Consider
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
: Monte Carlo EM 313, Louis (1982) EM, EM Newton-Raphson, /. EM, 2 Monte Carlo EM Newton-Raphson, Monte Carlo EM, Monte Carlo EM, /. 3, Monte Carlo EM
 2008 6 Chinese Journal of Applied Probability and Statistics Vol.24 No.3 Jun. 2008 Monte Carlo EM 1,2 ( 1,, 200241; 2,, 310018) EM, E,,. Monte Carlo EM, EM E Monte Carlo,. EM, Monte Carlo EM,,,,. Newton-Raphson.
2008 6 Chinese Journal of Applied Probability and Statistics Vol.24 No.3 Jun. 2008 Monte Carlo EM 1,2 ( 1,, 200241; 2,, 310018) EM, E,,. Monte Carlo EM, EM E Monte Carlo,. EM, Monte Carlo EM,,,,. Newton-Raphson.
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Queensland University of Technology Transport Data Analysis and Modeling Methodologies
 Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
Queensland University of Technology Transport Data Analysis and Modeling Methodologies Lab Session #7 Example 5.2 (with 3SLS Extensions) Seemingly Unrelated Regression Estimation and 3SLS A survey of 206
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Biostatistics for Health Sciences Review Sheet
 Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
ESTIMATION OF SYSTEM RELIABILITY IN A TWO COMPONENT STRESS-STRENGTH MODELS DAVID D. HANAGAL
 ESTIMATION OF SYSTEM RELIABILITY IN A TWO COMPONENT STRESS-STRENGTH MODELS DAVID D. HANAGAL Department of Statistics, University of Poona, Pune-411007, India. Abstract In this paper, we estimate the reliability
ESTIMATION OF SYSTEM RELIABILITY IN A TWO COMPONENT STRESS-STRENGTH MODELS DAVID D. HANAGAL Department of Statistics, University of Poona, Pune-411007, India. Abstract In this paper, we estimate the reliability
Supplementary Appendix
 Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Abstract Storage Devices
 Abstract Storage Devices Robert König Ueli Maurer Stefano Tessaro SOFSEM 2009 January 27, 2009 Outline 1. Motivation: Storage Devices 2. Abstract Storage Devices (ASD s) 3. Reducibility 4. Factoring ASD
Abstract Storage Devices Robert König Ueli Maurer Stefano Tessaro SOFSEM 2009 January 27, 2009 Outline 1. Motivation: Storage Devices 2. Abstract Storage Devices (ASD s) 3. Reducibility 4. Factoring ASD
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
 22 .5 Real consumption.5 Real residential investment.5.5.5 965 975 985 995 25.5 965 975 985 995 25.5 Real house prices.5 Real fixed investment.5.5.5 965 975 985 995 25.5 965 975 985 995 25.3 Inflation
22 .5 Real consumption.5 Real residential investment.5.5.5 965 975 985 995 25.5 965 975 985 995 25.5 Real house prices.5 Real fixed investment.5.5.5 965 975 985 995 25.5 965 975 985 995 25.3 Inflation
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Overview. Transition Semantics. Configurations and the transition relation. Executions and computation
 Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Partial Trace and Partial Transpose
 Partial Trace and Partial Transpose by José Luis Gómez-Muñoz http://homepage.cem.itesm.mx/lgomez/quantum/ jose.luis.gomez@itesm.mx This document is based on suggestions by Anirban Das Introduction This
Partial Trace and Partial Transpose by José Luis Gómez-Muñoz http://homepage.cem.itesm.mx/lgomez/quantum/ jose.luis.gomez@itesm.mx This document is based on suggestions by Anirban Das Introduction This
Introduction to Bayesian Statistics
 Introduction to Bayesian Statistics Lecture 9: Hierarchical Models Rung-Ching Tsai Department of Mathematics National Taiwan Normal University May 6, 2015 Example Data: Weekly weights of 30 young rats
Introduction to Bayesian Statistics Lecture 9: Hierarchical Models Rung-Ching Tsai Department of Mathematics National Taiwan Normal University May 6, 2015 Example Data: Weekly weights of 30 young rats
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
HW 3 Solutions 1. a) I use the auto.arima R function to search over models using AIC and decide on an ARMA(3,1)
 HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Generalized additive models in R
 www.nr.no Generalized additive models in R Magne Aldrin, Norwegian Computing Center and the University of Oslo Sharp workshop, Copenhagen, October 2012 Generalized Linear Models - GLM y Distributed with
www.nr.no Generalized additive models in R Magne Aldrin, Norwegian Computing Center and the University of Oslo Sharp workshop, Copenhagen, October 2012 Generalized Linear Models - GLM y Distributed with
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
The Profile Likelihood
 Chapter 6 he Profile Likelihood 6.1 he Profile Likelihood See also Section 4.5., Davison (). 6.1.1 he method of profiling Let us suppose that the unknown parameters can be partitioned as (ψ λ ), where
Chapter 6 he Profile Likelihood 6.1 he Profile Likelihood See also Section 4.5., Davison (). 6.1.1 he method of profiling Let us suppose that the unknown parameters can be partitioned as (ψ λ ), where
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
An Inventory of Continuous Distributions
 Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
ECE598: Information-theoretic methods in high-dimensional statistics Spring 2016
 ECE598: Information-theoretic methods in high-dimensional statistics Spring 06 Lecture 7: Information bound Lecturer: Yihong Wu Scribe: Shiyu Liang, Feb 6, 06 [Ed. Mar 9] Recall the Chi-squared divergence
ECE598: Information-theoretic methods in high-dimensional statistics Spring 06 Lecture 7: Information bound Lecturer: Yihong Wu Scribe: Shiyu Liang, Feb 6, 06 [Ed. Mar 9] Recall the Chi-squared divergence
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
 1 1 1 2 1 2 2 1 43 123 5 122 3 1 312 1 1 122 1 1 1 1 6 1 7 1 6 1 7 1 3 4 2 312 43 4 3 3 1 1 4 1 1 52 122 54 124 8 1 3 1 1 1 1 1 152 1 1 1 1 1 1 152 1 5 1 152 152 1 1 3 9 1 159 9 13 4 5 1 122 1 4 122 5
1 1 1 2 1 2 2 1 43 123 5 122 3 1 312 1 1 122 1 1 1 1 6 1 7 1 6 1 7 1 3 4 2 312 43 4 3 3 1 1 4 1 1 52 122 54 124 8 1 3 1 1 1 1 1 152 1 1 1 1 1 1 152 1 5 1 152 152 1 1 3 9 1 159 9 13 4 5 1 122 1 4 122 5
Mean-Variance Analysis
 Mean-Variance Analysis Jan Schneider McCombs School of Business University of Texas at Austin Jan Schneider Mean-Variance Analysis Beta Representation of the Risk Premium risk premium E t [Rt t+τ ] R1
Mean-Variance Analysis Jan Schneider McCombs School of Business University of Texas at Austin Jan Schneider Mean-Variance Analysis Beta Representation of the Risk Premium risk premium E t [Rt t+τ ] R1
A Lambda Model Characterizing Computational Behaviours of Terms
 A Lambda Model Characterizing Computational Behaviours of Terms joint paper with Silvia Ghilezan RPC 01, Sendai, October 26, 2001 1 Plan of the talk normalization properties inverse limit model Stone dualities
A Lambda Model Characterizing Computational Behaviours of Terms joint paper with Silvia Ghilezan RPC 01, Sendai, October 26, 2001 1 Plan of the talk normalization properties inverse limit model Stone dualities
w o = R 1 p. (1) R = p =. = 1
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Lecture 21: Properties and robustness of LSE
 Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Aquinas College. Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET
 Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
The ε-pseudospectrum of a Matrix
 The ε-pseudospectrum of a Matrix Feb 16, 2015 () The ε-pseudospectrum of a Matrix Feb 16, 2015 1 / 18 1 Preliminaries 2 Definitions 3 Basic Properties 4 Computation of Pseudospectrum of 2 2 5 Problems
The ε-pseudospectrum of a Matrix Feb 16, 2015 () The ε-pseudospectrum of a Matrix Feb 16, 2015 1 / 18 1 Preliminaries 2 Definitions 3 Basic Properties 4 Computation of Pseudospectrum of 2 2 5 Problems
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)
![MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3) MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)](/thumbs/81/84712331.jpg) 1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Assalamu `alaikum wr. wb.
 LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump
LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump
Space-Time Symmetries
 Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Modern Bayesian Statistics Part III: high-dimensional modeling Example 3: Sparse and time-varying covariance modeling
 Modern Bayesian Statistics Part III: high-dimensional modeling Example 3: Sparse and time-varying covariance modeling Hedibert Freitas Lopes 1 hedibert.org 13 a amostra de Estatística IME-USP, October
Modern Bayesian Statistics Part III: high-dimensional modeling Example 3: Sparse and time-varying covariance modeling Hedibert Freitas Lopes 1 hedibert.org 13 a amostra de Estatística IME-USP, October
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
= λ 1 1 e. = λ 1 =12. has the properties e 1. e 3,V(Y
 Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Additional Results for the Pareto/NBD Model
 Additional Results for the Pareto/NBD Model Peter S. Fader www.petefader.com Bruce G. S. Hardie www.brucehardie.com January 24 Abstract This note derives expressions for i) the raw moments of the posterior
Additional Results for the Pareto/NBD Model Peter S. Fader www.petefader.com Bruce G. S. Hardie www.brucehardie.com January 24 Abstract This note derives expressions for i) the raw moments of the posterior
( ) 2 and compare to M.
 Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Notes on the Open Economy
 Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
SECTION II: PROBABILITY MODELS
 SECTION II: PROBABILITY MODELS 1 SECTION II: Aggregate Data. Fraction of births with low birth weight per province. Model A: OLS, using observations 1 260 Heteroskedasticity-robust standard errors, variant
SECTION II: PROBABILITY MODELS 1 SECTION II: Aggregate Data. Fraction of births with low birth weight per province. Model A: OLS, using observations 1 260 Heteroskedasticity-robust standard errors, variant
Solutions: Homework 3
 Solutios: Homework 3 Suppose that the radom variables Y,, Y satisfy Y i = βx i + ε i : i,, where x,, x R are fixed values ad ε,, ε Normal0, σ ) with σ R + kow Fid ˆβ = MLEβ) IND Solutio: Observe that Y
Solutios: Homework 3 Suppose that the radom variables Y,, Y satisfy Y i = βx i + ε i : i,, where x,, x R are fixed values ad ε,, ε Normal0, σ ) with σ R + kow Fid ˆβ = MLEβ) IND Solutio: Observe that Y
