arxiv: v1 [math.na] 16 Apr 2017
|
|
|
- Λυσίμαχος Ανδρέου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Energy estmates for two-dmensonal space-resz fractonal wave equaton Mnghua Chen, Wenshan Yu arxv:17.716v1 math.na 16 Apr 17 School of Mathematcs and Statstcs, Gansu Key Laboratory of Appled Mathematcs and Complex Systems, Lanzhou Unversty, Lanzhou 73, P.R. Chna Abstract The fractonal wave equaton governs the propagaton of mechancal dffusve waves n vscoelastc meda whch exhbts a power-law creep, and consequently provded a physcal nterpretaton of ths equaton n the framework of dynamc vscoelastcty. In ths paper, we frst develop the energy method to estmate the one-dmensonal space-resz fractonal wave equaton. For two-dmensonal cases wth the varable coeffcents, the dscretzed matrces are proved to be commutatve, whch ensures to carry out of the pror error estmates. The uncondtonal stablty and convergence wth the global truncaton error Oτ +h are theoretcally proved and numercally verfed. In partculary, the framework of the pror error estmates and convergence analyss are stll vald for the compact fnte dfference scheme and the nonlocal wave equaton. Keywords: Resz fractonal wave equaton; Nonlocal wave equaton; Pror error estmates; Energy method; Numercal stablty and convergence 1. Introducton The fractonal wave equaton s obtaned from the classcal wave equaton by replacng the secondorder dervatve wth a fractonal dervatve of order, 1 <. Manard 18 ponted out that the fractonal wave equaton governs the propagaton of mechancal dffusve waves n vscoelastc meda whch exhbts a power-law creep, and consequently provded a physcal nterpretaton of ths equaton n the framework of dynamc vscoelastcty. In ths paper, we study a second-order accurate numercal method n both space and tme for the two-dmensonal space-resz fractonal wave equaton wth the varable coeffcents whose prototype s, for 1 <,β, ux,y,t t = ax,y ux,y,t x +bx,y β ux,y,t y β +fx,y,t. 1.1 The ntal condtons are ux,y, = ϕx,y for x,y Ω, u t x,y, = ψx,y for x,y Ω, 1. and the Drchlet boundary condton ux,y,t = for x,y Ω Correspondng author. E-mal: chenmh@lzu.edu.cn; yuwsh1@lzu.edu.cn
2 wth Ω =,x r,y r. The functon fx,y,t s a source term and all the coeffcents are postve,.e., < a ax,y a 1 and < b bx,y b 1. The space-resz fractonal dervatve appears n the contnuous lmt of lattce models wth long-range nteractons 9, for n N, n 1 < n, whch s defned as where ux,y,t x = κ Dx + x Dx 1 r ux,y,t wth κ = cosπ/, 1.3 n Dx ux,y,t = 1 Γn x n xdx r ux,y,t = 1n Γn x n x n xr x x ξ n 1 uξ,y,tdξ, ξ x n 1 uξ,y,tdξ. For the Caputo-Resz tme-space fractonal wave equaton c D γ t ux,t = ux,t x wth 1 <,γ, Manard 1 et al. obtaned the fundamental soluton of the space-tme fractonal dffuson equaton 19. Metzler and Nonnenmacher nvestgated the physcal backgrounds and mplcatons of a space-and tme-fractonal dffuson and wave equaton 1. The numercal soluton of space-tme fractonal dffuson-wave equatons are dscussed n 1, 11, but they are lack of the stablty and convergence analyss. To rewrte the fractonal dffuson-wave equaton as the the Volterra type ntegro-dfferental equatons, the stablty and convergence analyss are gven wth the zero ntal condtons 5. For 1 < γ < and =, t has been proposed by varous authors 6, 7, 16,,, 3, 33, 3, 35. For example, based on the second-order fractonal Lubch s methods 17, Cuesta 6 et al. derved the second-order error bounds of the tme dscretzaton n a Banach space wth the u x a sectoral operator 7 and Yang 1 et al. obtaned the second-order convergence schemes wth 1 γ For γ = and 1 < <, t seems that achevng a second-order accurate scheme for 1.1 s not an easy task wth the nonzero ntal condtons. Ths paper focuses on provdng the weghted numercal scheme to solve the space-resz fractonal wave equaton wth the nonzero ntal condtons and the varable coeffcents n one-dmensonal and two-dmensonal cases. The uncondtonal stablty and convergence wth the global truncaton error Oτ + h are theoretcally proved and numercally verfed by the energy method, whch can be easly extended to the nonlocal wave equaton 1. The rest of the paper s organzed as follows. The next secton proposes the second-order accurate scheme for 1.1. In Secton 3, we carry out a detaled stablty and convergence analyss wth the second order accuracy n both tme and space drectons for the derved schemes. To show the effectveness of the schemes, we perform the numercal experments to verfy the theoretcal results n Secton. The paper s concluded wth some remarks n the last secton.. Dscretzaton Schemes Let the mesh ponts x = h, =,1,...,N x, and t k = kτ, k N t wth h = x r /N x, τ = T/N t,.e., h s the unform space stepsze and τ the tme stepsze. And u k denotes the approxmated value of ux,t k, a = ax, f k = fx,t k. Nowadays, there are already many types of hgh order dscretzaton schemes for the Remann-Louvlle space fractonal dervatves, 1, 1, 3, 6, 8, 31. Here, we take the followng schemes to approach
3 1.3, see n 3, 31 D x ux = δ x,+ ux +Oh wth δ x,+ ux = 1 h +1 m= ϕ m ux m+1, xdx r ux = δx, ux +Oh wth δx, ux = 1 N x +1 h ϕ mux +m 1, m=.1 where ϕ = g, ϕ m = g m + g m 1, m 1, and g m = 1m m,.e., g = 1, g m = 1 +1 gm 1 m, m 1. wth Usng 1.3 and.1, we obtan the approxmaton operator of the space-resz fractonal dervatve ux x = hux +Oh. hux = κ δ x,+ +δx, ux = κ h N x ϕ,lux l, where = 1,...,N x 1 together wth the zero Drchlet boundary condtons and ϕ l+1, l < 1, ϕ +ϕ, l = 1, ϕ,l = ϕ 1, l =, ϕ +ϕ, l = +1, ϕ l +1, l > +1. Takng u = ux 1,ux,,ux N T, and usng.1,., there exsts t yelds Nx 1 N x N T x h ϕ 1,lux l, ϕ,lux l,..., ϕ N,lux l = δ l= l= l= l= x,+ +δ x, 1 u = h A u, hu = κ δ x,+ +δ x, u = κ h A u,.3
4 where the matrx ϕ 1 ϕ ϕ 3 ϕ N x ϕ N ϕ ϕ 1 ϕ ϕ 3 ϕ N x A = B +B T ϕ ϕ 1 ϕ.... wth B = ϕ 3... ϕ 1 ϕ ϕ ϕ 1.1. Numercal scheme for one-dmensonal space-resz fractonal wave equaton We now examne the full dscretzaton scheme to the one-dmensonal space-resz fractonal wave equaton,.e, ux,t t = ax ux,t x +fx,t.5 wth < a ax a 1 and the zero Drchlet boundary condton. The ntal condtons are ux, = ϕx for x Ω, u t x, = ψx for x Ω..6 In the tme drecton dervatve, we use the followng center dfference scheme ux,t t = δt ux,t k +Oτ wth δt ux,t k = uk+1 u k +uk 1 τ..7 In order to acheve an uncondtonal stable algorthm, we use the weghted algorthm for the space- Resz fractonal dervatve,.e., θ +1 θu k +θu k 1, 1 θ 1, to approxmate ux,t k. From. and the above equatons, we can rewrte.5 as ux,t k+1 ux,t k +ux,t k 1 τ = ax h θux,t k+1 +1 θux,t k +θux,t k 1 +fx,t k +R k.8 wth the local truncaton error R k C u, τ +h,.9 where the constant C u, s ndependent of h and τ. Therefore, the full dscretzaton of.5 has the followng form δ t uk = θa h uk+1 +1 θa h uk +θa h uk 1 +f k,.1
5 .e., +1 +θ τ h κ a ϕ m m= = u k 1 θτ h κ a u k 1 m+1 + Nx m= +1 θ τ h κ a ϕ m uk 1 m= m= ϕ m +m 1 N x +1 ϕ m uk m+1 + m+1 + Nx +1 m= m= ϕ m uk +m 1 ϕ m uk 1 +m 1 +τ f k..11 Usng.5,.6 and Taylor expanson wth ntegral form of the remander, there exsts ux,τ = ux,+τ ux, t = ϕx +τψx + τ + τ ux, t + 1 τ ax ux, x +fx, τ t 3 ux,t t 3 dt + 1 τ τ t 3 ux,t t 3 dt..1 Then we can obtan u 1,.e., u 1 = ϕx +τψx + τ ax hux,+fx,.13 wth the local truncaton error Oτ 3 +τ h, see Secton 3. For the convenence of mplementaton, we use the matrx form of the grd functons U k = u k 1,u k,...,u k N T, F k = f k 1,f k,...,f k N T. Hence, the fnte dfference scheme.11 can be recast as I +θ τ h κ DA U k+1 = I 1 θ τ h κ DA U k I +θ τ h κ DA U k 1 +τf k,.1 where A s defned by. and the dagonal matrx a 1 a D =... a N Numercal scheme for two-dmensonal space-resz fractonal wave equaton Let the mesh ponts x = h x, =,1,...,N x and y j = jh y, j =,1,...,N y and t k = kτ, k N t wthh x = x r /N x,h y = y r /N y,τ = T/N t. Smlarly,wetakeu k,j astheapproxmatedvalueofux,y j,t k, a,j = ax,y j, b,j = bx,y j, f k,j = fx,y j,t k. We use the center dfference scheme to do the dscretzaton n tme drecton dervatve, ux,y,t t = uk+1,j u k,j +uk 1,j τ +Oτ,
6 and the weghted schemes for the space-resz fractonal dervatve,.e., θ,j +1 θu k,j +θuk 1,j to approxmate ux,y j,t k. Therefore 1.1 can be rewrtten as ux,y j,t k+1 ux,y j,t k +ux,y j,t k 1 τ = ax,y j h x θux,y j,t k+1 +1 θux,y j,t k +θux,y j,t k 1 +bx,y j β h y θux,y j,t k+1 +1 θux,y j,t k +θux,y j,t k 1 +fx,y j,t k +R,j k,.16 where the local truncaton error s R,j k C u,,βτ +h x +h y..17 Smlarly, we denote h x ux,y j = κ δ x,+ +δx, ux,y j and β h y ux,y j = κ β δ β y,+ +δ β y, ux,y j..18 Therefore, the resultng dscretzaton of 1.1 has the followng form δt uk,j = θa,j h x,j +1 θa,j h x u k,j +θa,j h x u,j k 1 +θb,j β h y,j +1 θb,j β h y u k,j +θb,j β h y u k 1,j +f k,j,.19.e., 1 θτ a,j h x +b,j β h y,j = +1 θτ a,j +b hx,j βhy u k,j 1 θτ a,j h x +b,j β. h y u,j k 1 +τ f,j k. Usng.1 and.13, we can obtan u 1,j = ϕx,y j +τψx,y j + τ a,j +b hx,j β h y u,j +f,j.1 wth the local truncaton error Oτ 3 +τ h x +τ h y, see Secton 3. For the two-dmensonal space-resz fractonal wave equaton1.1, the relevant perturbaton equaton of. s of the form 1 θτ a,j hx 1 θτ b,j βhy,j = 1 θτ a,j hx 1 θτ b,j +τ βhy a,j hx +τ b,j βhy 1 θτ a,j 1 θτ b hx,j βhy u,j k 1 +τ f,j k. Comparng. wth., the splttng term s gven by u k,j. θ τ a,j b,j h x β h y u k+1,j u k,j +uk 1,j, snce,j u k,j +uk 1,j s an Oτ term, t mples that the perturbaton contrbutes an Oτ 6 error
7 component to the truncaton error of.. Thus we can rewrte 1.1 as ux,y j,t k+1 ux,y j,t k +ux,y j,t k 1 τ +θ τ a,j b,j h x β h ux y,y j,t k+1 ux,y j,t k +ux,y j,t k 1 = ax,y j h x θux,y j,t k+1 +1 θux,y j,t k +θux,y j,t k 1 +bx,y j β h y θux,y j,t k+1 +1 θux,y j,t k +θux,y j,t k 1 +fx,y j,t k + R,j k.3 where R k,j = R k,j +θ τ a,j b,j h x β h y ux,y j,t k+1 ux,y j,t k +ux,y j,t k 1 C u,,β τ +h x +h y.. Hence, the system. can be solved by the alternatng drecton mplct method D-ADI 8, 9: 1 θτ a,j hx u,j = u k,j uk 1,j +τ a,j h x 1 θu k,j +θu k 1,j +τ b,j β h y u k,j +τ f,j k 1 θτ,.5 b,j βhy,j = u,j +θτ b,j β h y u k,j +u k 1,j, where u,j s an ntermedate soluton. Take and denote U k = u k 1,1,uk,1,...,uk N,1,uk 1,,uk,,...,uk N,,...,uk 1,N y 1,uk,N y 1,...,uk N,N y 1 T, F k = f k 1,1,f k,1,...,f k N,1,f k 1,,f k,,...,f k N,,...,f k 1,N y 1,f k,n y 1,...,f k N,N y 1 T, A x = I A and A y = A β I,.6 where I denotes the unt matrx and the symbol the Kronecker product 15, and A, A β are defned by.. Therefore, we can rewrte.5 as the followng form I +θ τ h κ DA x U = I 1 θ τ x I +θ τ h x I +θ τ h β κ β EA y U k+1 = y h x κ DA x τ h β κ β EA y U k y κ DA x U k 1 +τ F k, θ τ h β κ β EA y U k y θ τ h β κ β EA y U k 1 +U, y.7 where D 1 D D =... a 1,j a,j wth D j =... D Ny 1 a N,j
8 and E 1 E E =... b 1,j b,j wth E j =.... E Ny 1 b N,j 3. Convergence and Stablty Analyss To rewrte the fractonal dffuson-wave equaton as the the Volterra type ntegro-dfferental equatons, the stablty and convergence analyss are gven wth the zero ntal condtons 5. Here, we frst develop the energy method to estmate the space-resz fractonal wave equaton wth the nonzero ntal condtons. For two-dmensonal cases wth the varable coeffcents, the dscretzed matrces are proved to be commutatve, whch ensures to carry out of the pror error estmates. Lemma Let h be gven n.3 and 1 <. Then there exsts an symmetrc postve defnte matrx Λ h such that h u,u > and h u,v = Λ h u,λ h v wth h = Λ h Λ h. Lemma 3.. Dscrete Gronwall Lemma 5 Assume that {a k } and {b k } s a nonnegatve sequence, and the sequence ϕ k satsfes where c. Then the sequence {ϕ k } satsfes k 1 k 1 ϕ c, ϕ k c + b l + a l ϕ l, k 1, l= k 1 ϕ k c + b l exp l= l= k 1 a l, k 1. Lemma , p.11 Let A R n n have egenvalues {λ } n and B Rm m have egenvalues {µ j } m j=1. Then the mn egenvalues of A B are l= λ 1 µ 1,...,λ 1 µ m,λ µ 1,...,λ µ m,...,λ n µ 1...,λ n µ m. Lemma , p.1 Let A R m n, B R r s, C R n p, and D R s t. Then A BC D = AC BD R mr pt. Moreover, for all A and B, A B T = A T B T. Lemma 3.5. Let A x = I A and A y = A β I be defned by.6. Then A x A y = A y A x, Λ x A y = A y Λ x and Λ x Λ y = Λ y Λ x wth A = Λ Λ, A β = Λ β Λ β where we denote Λ x := I Λ and Λ y := Λ β I. Proof. From 3 or Lemma 3.1, there exsts A = Λ Λ and A β = Λ β Λ β, snce A and A β
9 are the symmetrc postve defnte matrces. Takng Λ x := I Λ and Λ y := Λ β I and usng Lemma 3., the results are obtaned. Lemma 3.6. Let h x and β h y be gven n.18 wth 1 <,β. Then there exst the symmetrc postve defnte matrces Λ h x and, respectvely, such that h x U,U > and h x U,V = Λ h x U,Λ h x V wth h x = Λ h x Λ h x, and β h y U,U > and β h y U,V = U, V wth β h y =. Proof. Accordng to.18 and.6, t mpled that h x U = κ δ x,+ +δx, κ U = A x U. From Lemmas 3.3 and 3.5, we know that A x = I A s a symmetrc negatve defnte, whch leads to h x or β h y s the symmetrc postve defnte. The proof s completed Convergence and stablty for one-dmensonal space-resz fractonal wave equaton Frst, we ntroduce some relevant notatons and propertes of dscretzed nner product gven n13, 7. Denote u k = {u k N x, k N t } and v k = {v k N x, k N t }, whch are grd functons. And N u k t, = uk u k 1 /τ, u k,v k = h u k v, k u k = u k,u k 1/. 3.1 Lemma 3.7. Let 1 θ 1, 1 < and {uk } be the soluton of the dfference scheme h x δ t uk = θa h uk+1 +1 θa h uk +θa h uk 1 wth the ntal condtons and the Drchlet boundary condtons u = ϕ, N x, u 1 = ψ, N x, u k =, uk N x =, k N t 1. +f k Then E k e 3 kτ E + 3 k τ f l, l=1 where the energy norm s defned by E k = + 1 aλ h +Λ hu k + 1 θ 1 aλ h Λ hu k. Proof. Multplyng.1 by h δ tu k h u k 1, respectvely, t yelds u k +hu k u k 1 = h, hu k,,
10 and θa h uk+1 +1 θa h uk +θa h uk 1 +f k hu k+1 u k 1. Then summng up for from 1 to N x 1 for the above equatons, respectvely, there exsts and h, hu k, = u k, 3. θa h = I 1 +I +f k, u k 1, +1 θa hu k +θa hu k 1 +f k hu k+1 u k where I 1 = θa h uk+1 +a h uk 1, u k 1, I = 1 θa h uk, u k 1. Accordng to Lemma 3.1, whch leads to I 1 = θ aλ h uk+1 +u k 1,Λ h uk+1 u k 1 = θ aλ h uk+1 aλ h uk 1, and I = 1 θ aλ h uk,λ h uk+1 aλ h uk,λ h uk 1 = 1 θ aλ hu k +aλ h,λ hu k +Λ h aλ hu k aλ h,λ hu k Λ h aλ h uk +aλ h uk 1,Λ h uk +Λ h uk 1 +aλ h uk aλ h uk 1,Λ h uk Λ h uk 1 = 1 θ aλ h +Λ hu k aλ h Λ hu k aλ h uk +Λ h uk 1 + aλ h uk Λ h uk 1. Combne.1, 3. and 3.3, we obtan.e., u k I 1 I = f k, u k 1, 3. +θ aλ h uk θ = u k +θ aλ h uk θ +f k, u k 1. aλ h +Λ h uk aλ h uk+1 Λ h uk aλ h u k +Λ h uk 1 aλ h uk Λ h uk 1
11 Addng θ aλ h uk on both sdes of the above equaton, there exsts Denotng.e., +θ aλ h uk+1 + aλ h uk + 1 θ aλ h uk+1 +Λ h uk aλ h uk+1 Λ h uk = u k +θ aλ hu k + aλ hu k θ aλ hu k +Λ hu k 1 aλ hu k Λ hu k 1 +f k, u k 1. E k = +θ aλ h + aλ hu k + 1 θ aλ h +Λ hu k aλ h Λ hu k, E k = + 1 aλ h +Λ hu k + 1 θ 1 aλ h Λ hu k, 3.5 where we use aλ hu k + aλ hu k 1 = 1 aλ h u k +Λ hu k 1 + aλ hu k Λ hu k 1. From f k, u k 1 = hτ hτ τ f k f k u k 1 τ + + u k +τ f k, u k +uk uk 1 τ 3.6 and 3.5, 3., we obtan E k E k 1 = f k, u k 1 τ Ek +E k 1 +τ f k,.e, 1 τ E k 1+ τ E k 1 +τ f k. Therefore, for τ /3, t yelds E k 1+ 3τ E k τ fk. Usng the dscrete Gronwall nequalty see Lemma 3., we have E k e 3 kτ E + 3 k τ f l. l=1
12 The proof s completed. Theorem 3.1. Let ux,t k be the exact soluton of.5 wth 1 <, 1 θ 1; uk of the fnte dfference scheme.1 and e k = ux,t k u k. Then be the soluton E k = Oτ +h, where the energy norm s defned by E k = e k aλ he k+1 +Λ he k + 1 θ 1 aλ he k+1 Λ he k. Proof. Subtractng.1 from.8, t yelds δ t ek = θa h ek+1 +1 θa h ek +θa h ek 1 +R k. 3.7 Usng Lemma 3.7, we obtan E k e 3 kτ E + 3 k τ R l, 3.8 l=1 where E k = e k aλ he k+1 +Λ he k + 1 θ 1 aλ he k+1 Λ he k. 3.9 Next we estmate the local error truncaton of E. Snce e = and e 1 = τ where ξ,x r and t mples that ux, ax x h ϕx = τ ax C 1, + uξ,t x + h + 1 C, = max x x r, t T τ + 1 τ τ t 3 ux,t t 3 dt τ t 3 ux,t t 3 dt C, τ 3 +τ h, { 1 1 a + uξ,t, 1 τ C 1, x ux,t t 3 dt }, e 1 t = e1 e τ N x 1h 1 τ C,τ 3 +τ h C, τ 3 +τ h C,x r τ +τh. 3.1 Here, the coeffcents C l,,1 l are the constants ndependent of h and τ.
13 Accordng to. and the above equatons, there exsts aλ he 1 = a he 1,e 1 = h a h e 1 1 e = h N x a l= a C 1, = h a h a τ κ a C 1, + uξ,t h ϕ,l x + τ h + 1 τ + uξ,t x + τ h + uξ +C,t 3, x + τ h τ t +3 ux,t t 3 x C 5, τ 3 +τ h C, τ 3 +τ h, +5 u ξ,t +C, t 3 h x + τ t 3 ux,t t 3 dt e 1 e 1 dt e 1 where ξ,ξ, ξ,x r and C l,,1 l 5 are the constants ndependent of h and τ. Usng 3.9, 3.1 and the above equaton, we have wth a constant C. From.9, 3.8 and 3.11, t means that E C x rτ +τh 3.11 E k e 3 kτ C x r τ +τh + 3 kτc u,τ +h C e 3 T τ +h wth C = max{c x r, 3 C u,t}. The proof s completed. Theorem 3.. The dfference scheme.1 wth 1 < and 1 θ 1 s uncondtonally stable. Proof. From Lemma 3.7, the proof s completed. 3.. Convergence and stablty for two-dmensonal space-resz fractonal wave equaton Denote u k = {u k,j N x, j N y, k N t } and v k = {v k,j N x, j N y, k N t }, whch are grd functons. And u k t,,j = uk,j u k 1,j /τ, u k,v k = h x h y N y 1 j=1 u k,jv k,j, u k = u k,u k 1/. 3.1 Lemma 3.8. Let 1 θ 1, 1 <,β and {uk j } be the soluton of the dfference scheme δt uk,j +θ τ a,j b,j h x β h y u k+1,j u k,j +uk 1,j = θa,j h x,j +1 θa,j h x u k,j +θa,j h x u k 1,j +θb,j β h y,j +1 θb,j β h y u k,j +θb,j β h y u k 1,j +f k,j 3.13 wth the ntal condtons and the Drchlet boundary condtons u,j = ϕ,j, N x, j N y, u 1,j = ψ,j, N x, j N y, u k,j =, x,y j Ω, k N t 1.
14 Then E k e 3 kτ E + 3 k τ f l, l=1 where the energy norm s defned by E k = + 1 aλ h x +Λ h x u k + 1 θ 1 aλ h x Λ h x u k + 1 b + u k + 1 θ 1 b u k +θ τ 6 abλ h x t. Proof. Multplyng 3.13 by h x h y,j u k 1,j and usng Lemmas 3.5, 3.6, there exsts δtu k,j +θ τ a,j b,j h x β h y,j u k,j +u k 1,j h x h y,j u k,j+h x h y u k,j u k 1,j =h x h y,,j h x h y u k,,j +h x h y θ τ 6 a,j b,j Λ h x t,,j h x h y θ τ 6 a,j b,j Λ h x u k t,,j, and θa,j h x,j +1 θa,j h x u k,j +θa,j h x u,j k 1 +θ,j +1 θb,j β h y u k,j +θb,j β h y u k 1,j +f k,j h x h y,j u k 1,j. Then summng up for from 1 to N x 1 and for j from 1 to N y 1, we have N y 1 j=1 N y 1 j=1 h x h y,,j h x h y u k,,j = u k, h x h y θ τ 6 a,j b,j Λ h x t,,j h x h y θ τ 6 a,j b,j Λ h x u k t,,j = θ τ 6 abλ h x t θ τ 6 abλ h x u k t, 3.1 and N y 1 j=1 θa,j h x,j +1 θa,j h x u k,j +θa,j h x u k 1,j +θb,j,j +1 θb,j u k,j +θb,j u k 1,j +f,j k h x h y,j u k 1,j = I 1 +I +I 3 +I +f k, u k 1, 3.15 where I 1 = θ a h x +a h x u k 1, u k 1, I = 1 θ a h x u k, u k 1, I 3 = θ b β h y +b β h y u k 1, u k 1, I = 1 θ b β h y u k, u k 1.
15 Accordng to Lemma 3.6, we have I 1 = θ aλ h x aλ h x u k 1 I = 1 θ aλ h x +Λ h x u k aλ h x Λ h x u k aλ h x u k +Λ h x u k 1 + aλ h x u k Λ h x u k 1, and I 3 = θ b b u k 1, I = 1 θ b + u k b u k b u k + u k 1 + b u k u k 1. From 3.1 and 3.15, we obtan.e., u k +θ τ 6 abλ h x θ τ 6 abλ t h x u k t I 1 I I 3 I = f k, u k 1, +θ τ 6 abλ h x +θ aλ t h x + 1 θ aλ h x +Λ h x u k aλ h x Λ h x u k +θ b + 1 θ bλ β h y + u k b u k = u k +θ τ 6 abλ h x u k t +θ aλ h x u k θ aλ h x u k +Λ h x u k 1 aλ h x u k Λ h x u k 1 +θ b u k + 1 θ bλ β h y u k + u k 1 b u k u k 1 +f k, u k 1. Addng θ aλ h x u k +θ b u k on both sdes of the above equaton, we have +θ aλ h x + aλ h x u k + 1 θ aλ h x +Λ h x u k aλ h x Λ h x u k +θ b + b u k + 1 θ bλ β h y + u k b u k +θ τ 6 abλ h x t = u k +θ aλ h x u k + aλ h x u k θ aλ h x u k +Λ h x u k 1 aλ h x u k Λ h x u k 1 +θ b u k + b u k θ bλ β h y u k + u k 1 b u k u k 1 +θ τ 6 abλ h x u k t +f k, u k 1.
16 Denotng E k = +θ aλ h x + aλ h x u k + 1 θ aλ h x +Λ h x u k aλ h x Λ h x u k +θ b + b u k + 1 θ bλ β h y + u k b u k +θ τ 6 abλ h x, t 3.16 we have E k = E k 1 +f k, u k We rewrte 3.16 as the followng form E k = + 1 aλ h x +Λ h x u k + 1 θ 1 aλ h x Λ h x u k + 1 b + u k + 1 θ 1 b u k 3.18 where we use +θ τ 6 abλ h x t, aλ h x + aλ h x u k = 1 aλ h x +Λ h x u k + aλ h x Λ h x u k, and b + b u k = 1 b + u k + b u k. Accordng to f k, u k 1 = h x h y τ and 3.18, 3.17, there exsts h x h y τ τ N y 1 j=1 N y 1 j=1 f k,j f k,j + u k +τ f k, u k+1,j u k 1,j τ u k+1,j u k,j +uk,j uk 1,j + τ E k E k 1 = f k, u k 1 τ Ek +E k 1 +τ f k,.e., 1 τ E k 1+ τ E k 1 +τ f k. For τ /3, whch leads to E k 1+ 3τ E k τ fk.
17 From Lemma 3., there exsts E k e 3 kτ E + 3 k τ f l. l=1 The proof s completed. Theorem 3.3. Let ux,y j,t k be the exact soluton of 1.1 wth 1 <,β, u k,j. and e k j = ux,y j,t k u k j. Then be the soluton of E k = Oτ +h x +h y, where the energy norm s defned by E k = e k aλ h x e k+1 +Λ h x e k + 1 θ 1 aλ h x e k+1 Λ h x e k + 1 b e k+1 + e k + 1 θ 1 b e k+1 e k +θ τ 6 abλ h x e k+1 t. Proof. Subtractng. from.3, t yelds 1 τ δ t ek,j +θ τ a,j b,j h x β h y e k+1,j e k,j +ek 1,j = θa,j h x e k+1,j +1 θa,j h x e k,j +θa,j h x e k 1,j +θb,j β h y e k+1,j +1 θb,j β h y e k,j +θb,j β h y e k 1,j + R k,j. Usng Lemma 3.8, there exsts wth the energy norm E k e 3 kτ E + 3 k τ R l l= E k = e k aλ h x e k+1 +Λ h x e k + 1 θ 1 aλ h x e k+1 Λ h x e k + 1 b e k+1 + e k + 1 θ 1 b e k+1 e k 3. +θ τ 6 abλ h x e k+1 t. Next we estmate the local error truncaton of E. Snce e,j =, θ τ 6 abλ h x e 1 t = Oτ 6 n
18 3.1 and e 1,j = τ ux,y j, ax,y j x h x ϕx,y j β ux,y j, +bx,y j y β β h y ϕx,y j + 1 = τ uξ,y j,t ax,y j C 1, x + τ τ τ t 3 ux,y j,t t 3 dt h β+ ux,η j,t x +bx,y j C 1,β y β+ h y τ t 3 ux,y j,t t 3 dt C 1,,β τ 3 +τ h x +τ h y. Here the coeffcents C 1, and C 1,β are the constants ndependent of h, τ and Then we obtan C 1,,β = { 1 1 a + uξ,y j,t, C 1, x + 1 b β+ ux,η j,t, 1 τ 3 ux,y j,t } 1 C 1,β y β+ 6 t 3 dt. max x x r, y y r, t T e 1 t = e1 e τ N x 1h x N y 1h y 1 τ C 1,,βτ 3 +τ h x +τ h y C 1,,β τ 3 +τ h x +τ h y C 1,,βx r y r τ +τh x +τh y. 3.1 From 1.1 and the above equatons, there exsts aλ h x e 1 = a h x e 1,e 1 = h x h y = h x h y + b,jc 1,β = h x h y + b,jc 1,β h x h y N y 1 j=1 N x a,j l= κ h ϕ a,j C 1,,l x β+ ux,η j,t y β+ τ h y + 1 y 1 j=1 a,j a,j C 1, τ N y 1 j=1 a,j hx e 1,j e 1,j + uξ,y j,t x + τ h x τ t 3 ux,y j,t t 3 dt e 1,j + uξ,y j,t x + τ h x +C + u ξ,y j,t, x + τ h x +β+ ux,η j,t x y β+ τ h +β+ uξ,η j,t y +C,,β N y 1 j=1 a,j τ τ t +3 ux,y j,t t 3 x C 3,,β τ 3 +τ h x +τ h y C 1,,β τ 3 +τ h x +τ h y, x + y β+ τ h xh y e 1,j +5 u ξ,y j,t +C 3, t 3 x + h x dt e 1,j where ξ, ξ,ξ, ξ,x r and C l, and C l,,β,1 l 3 are the constants. Smlarly, we have b e 1 C 3,,β τ 3 +τ h x +τ h y C 1,,β τ 3 +τ h x +τ h y wth the constants C 1,,β and C 3,,β.
19 Accordng to 3., 3.1 and the above equatons, we get E C,β x ry r τ +τh x +τh y, 3. where C,β s a constant. Hence, usng.17, 3.19 and 3., there exsts E k e 3 kτ C,β x ry r τ +τh x +τh y + 3 kτc u,,β τ +h x +h y C,β e 3 T τ +h x +h y wth C,β = max{c,β x ry r, 3 C u,,βt}. The proof s completed. Theorem 3.. The dfference scheme.7 wth 1 <,β and 1 θ 1 s uncondtonally stable. Proof. From Lemma 3.7, the result s obtaned. Remark 3.1. The operator L appears n the nonlocal wave equaton 1 ux,t t L δ ux,t = f δ x,t on Ω, t >, ux, = u on Ω Ω I, u = g on Ω I,t >. From, we known that the approxmaton operator of L δ s also the symmetrc postve defnte. Hence, the framework of the stablty and convergence analyss are stll vald for the nonlocal wave equaton.. Numercal results In ths secton, we numercally verfy the above theoretcal results and the l norm s used to measure the numercal errors. Example.1. Consder the space-resz fractonal wave equaton.5, on a fnte doman < x < 1, < t 1 wth the coeffcent dx = x, the forcng functon s fx,t =e t x 1 x + x e t cosπ/ Γ5 x +1 x Γ5 Γ x3 +1 x 3 Γ +Γ3 x +1 x Γ3 wth the ntal condtons ux, = x 1 x, t ux, = x 1 x, and the boundary condtons u,t = u1,t =. The exact soluton of the fractonal PDEs s ux,t = e t x 1 x. Table 1 shows that the scheme.1 s second order convergent n both space and tme drectons. Example.. Consder the two-dmensonal space-resz fractonal wave equaton 1.1, on a fnte doman < x < 1, < y < 1, < t 1/ wth the varable coeffcents dx,y = x y, ex,y = xy β,
20 Table 1: The maxmum errors and convergent orders for.1 wth τ = h. τ = 1.3,θ =.5 Rate = 1.6,θ =.5 Rate = 1.9,θ = 1 Rate 1/ e e e-5 1/8.156e e e /16 5.5e e e / e e e Table : The maxmum errors and convergent orders for.7 wth τ = h x = h y and θ =.75. τ = 1.3,β = 1.7 Rate = 1.5,β = 1.5 Rate = 1.7,β = 1.3 Rate 1/ 1.66e- 1.66e- 1.5e- 1/ 3.89e e e /8 9.99e e e /16.9e e e and the ntal condtons ux,y, = sn1x 1 x y 1 y, t ux,y, = cos1x 1 x y 1 y wth the zero Drchlet boundary condtons on the rectangle. The exact soluton of the PDEs s ux,y,t = snt+1x 1 x y 1 y. Usng the above condtons, t s easy to obtan the forcng functon fx,y,t. Table shows that the scheme.7 s second order convergent n both space and tme drectons. 5. Concluson In ths work we have developed the energy method to estmate the two-dmensonal space-resz fractonal wave equaton wth the varable coeffcents. To the best of our knowledge, the convergence and stablty are lack of study for the one-dmensonal space-resz fractonal wave equaton wth the nonzero condtons. In ths paper, the pror error estmates have been establshed and the convergence analyss and stablty of the proposed method have been proved. For two-dmensonal cases wth the varable coeffcents, the dscretzed matrces are proved to be commutatve, whch ensures to carry out of the pror error estmates. Numercal results have been gven to llustrate the robustness and effcency of the presented method wth the second order convergence. We remark that though ths current paper focus on the space-resz fractonal wave equaton, the energy estmates s stll vald for the compact fnte dfference schemes and the nonlocal wave equaton 1. Acknowledgments Ths work was supported by NSFC 11616, the Fundamental Research Funds for the Central Unverstes under Grant No. lzujbky-16-15, and SIETP References 1 Bhrawy, A.H., Zaky, M.A., Van Gorder, R.A.: A space-tme Legendre spectral tau method for the two-sded space Caputo fractonal dffuson-wave equaton. Numer. Algor. 71,
21 Chen, M.H., Deng, W.H.: Fourth order accurate scheme for the space fractonal dffuson equatons. SIAM J. Numer. Anal. 5, Chen, M.H., Deng, W.H.: Hgh order algorthm for the tme-tempered fractonal Feynman-Kac equaton. arxv: Chen, M.H., Deng, W.H.: Convergence proof for the multgrd method of the nonlocal model. SIAM J. Matrx Anal. Appl mnor revsed. arxv: Chen, M.H., Deng, W.H.: A second-order accurate numercal method for the space-tme tempered fractonal dffuson-wave equaton. Appl. Math. Lett. 68, Chen, C., Thomée. V., Wahlbn. L.B.: Fnte element approxmaton of a parabolc ntegrodfferental equaton wth a weakly sngular kernel. Math. Comput. 198, Cuesta, E., Lubch, Ch., Palenca, C.: Convoluton quadrature tme dscretzaton of fractonal dffuson-wave equatons. Math. Comput. 75, Dougls, J.: On the numercal ntegraton of u xx + u yy = u tt by mplct methods. J. Soc. Indust. Appl. Math. 3, Dougls, J.: Alternatng drecton methods for three space varables. Numer. Math. 6, Du, Q., Gunzburger, M., Lehoucq, R., Zhou, K.: Analyss and approxmaton of nonlocal dffuson problems wth volume constrants. SIAM Rev. 56, Garg, M., Manohar, P.: Matrx method for numercal soluton of space-tme fractonal dffuson-wave equatons wth three space varables. Afr. Mat. 5, Hao, Z.P., Ln, G., Sun, Z.Z: A hgh-order dfference scheme for the fractonal sub-dffuson equaton. Int. J. Comput. Math. 9, Hu, J.W., Tang, H.M.: Numercal Methods for Dfferental Equatons. Scence Press, Bejng, J, C.C., Sun, Z.Z.: A hgh-order compact fnte dfference shcemes for the fractonal sub-dffuson equaton. J. Sc. Comput. 6, Laub, A.J.: Matrx Analyss for Scentsts and Engneers. SIAM, Lu, F., Meerschaert, M., McGough, R. Zhuang, P., Lu, Q.: Numercal methods for solvng the mult-term tme-fractonal wave-dffuson equaton. Fract. Calc. Appl. Anal. 16, Lubch, Ch.: Dscretzed fractonal calculus. SIAM J. Math. Anal. 17, Manard, F.: Fractal calculus: some basc problems n contnuum and statstcal mechancs, In: Carpnter, A., Manard, F. Eds., Fractals and Fractonal Calculus n Contnuum Mechancs. Sprnger, Manard, F., Luchko, Y., Pagnn G.: The fundamental soluton of the space-tme fractonal dffuson equaton. Fract. Calc. Appl. Anal., McLean, W., Thomée. V.: Numercal soluton of an evoluton equaton wth a postve-type memory term. J. Austral. Math. Soc. Ser. B 35, Metzler, R., Nonnenmacher, T.F.: Space-and tme-fractonal dffuson and wave equatons, fractonal Fokker-Planck equatons, and physcal motvaton. Chem. Phys. 8, Mustapha, K., Mclean, W.: Superconvergence of a dscontnous galerkn method for fractonal dffuson and wave equatons. SIAM J. Numer. Anal. 51, Ortguera, M.D.: Resz potental operators and nverses va fractonal centred dervatves. Int. J. Math. Math. Sc Podlubny, I.: Fractonal Dfferental Equatons. Academc Press, New York, Quarteron, A., Vall, A.: Numercal Approxmaton of Partal Dfferental Equatons. Sprnger, 8.
22 6 Sousa, E., L, C.: A weghted fnte dfference method for the fractonal dffuson equaton based on the Remann-Louvlle drvatve. Appl. Numer. Math. 9, Sun, Z.Z.: Numercal Methods for Partal Dfferental Equatons. Scence Press, Bejng, 5. 8 Tadjeran, C., Meerschaert, M.M., Scheffler, H.P.: A second-order accurate numercal approxmaton for the fractonal dffuson equaton. J. Comput. Phys. 13, Tarasov, V.E.: Fractonal Dynamcs: Applcatons of Fractonal Calculus to Dynamcs of Partcles, Felds and Meda. Hgher Educaton Press, Bejng and Sprnger-Verlag Berln Hedelberg, 1. 3 Sun, Z.Z., Wu, X.N.: A fully dscrete dfference scheme for a dffuson-wave system. Appl. Numer. Math. 56, Tan, W.Y., Zhou, H., Deng, W.H.: A class of second order dfference approxmatons for Solvng space fractonal dffuson equatons. Math. Comput. 8, Wang, P.D., Huang, C.M.: An energy conservatve dfference scheme for the nonlnear fractonal Schrödnger equatons. J. Comput. Phys. 93, Yang, J.Y., Huang, J.F., Lang, D.M., Tang, Y.F.: Numercal soluton of fractonal dffuson-wave equaton based on fractonal multstep method. Appl. Math. Modell. 38, Zeng, F.H.: Second-order stable fnte dfference schemes for the tme-fractonal dffuson-wave equaton. J. Sc. Comput. 65, Zhang, Y.N., Sun, Z.Z., Zhao, X.: Compact alternatng drecton mplct scheme for the twodmensonal fractonal dffuson-wave equaton. SIAM J. Numer. Anal. 5,
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Symplecticity of the Störmer-Verlet algorithm for coupling between the shallow water equations and horizontal vehicle motion
 Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
5 Haar, R. Haar,. Antonads 994, Dogaru & Carn Kerkyacharan & Pcard 996. : Haar. Haar, y r x f rt xβ r + ε r x β r + mr k β r k ψ kx + ε r x, r,.. x [,
 4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
4 Chnese Journal of Appled Probablty and Statstcs Vol.6 No. Apr. Haar,, 6,, 34 E-,,, 34 Haar.., D-, A- Q-,. :, Haar,. : O.6..,..,.. Herzberg & Traves 994, Oyet & Wens, Oyet Tan & Herzberg 6, 7. Haar Haar.,
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
V. Finite Element Method. 5.1 Introduction to Finite Element Method
 V. Fnte Element Method 5. Introducton to Fnte Element Method 5. Introducton to FEM Rtz method to dfferental equaton Problem defnton k Boundary value problem Prob. Eact : d d, 0 0 0, 0 ( ) ( ) 4 C C * 4
V. Fnte Element Method 5. Introducton to Fnte Element Method 5. Introducton to FEM Rtz method to dfferental equaton Problem defnton k Boundary value problem Prob. Eact : d d, 0 0 0, 0 ( ) ( ) 4 C C * 4
Non polynomial spline solutions for special linear tenth-order boundary value problems
 ISSN 746-7233 England UK World Journal of Modellng and Smulaton Vol. 7 20 No. pp. 40-5 Non polynomal splne solutons for specal lnear tenth-order boundary value problems J. Rashdna R. Jallan 2 K. Farajeyan
ISSN 746-7233 England UK World Journal of Modellng and Smulaton Vol. 7 20 No. pp. 40-5 Non polynomal splne solutons for specal lnear tenth-order boundary value problems J. Rashdna R. Jallan 2 K. Farajeyan
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
Πεπερασμένες διαφορές για την ελλειπτική εξίσωση στις δύο διαστάσεις
 Κεφάλαιο 9 Πεπερασμένες διαφορές για την ελλειπτική εξίσωση στις δύο διαστάσεις Σε αυτό το κεφάλαιο θεωρούμε μια απλή ελλειπτική εξίσωση, στις δύο διαστάσεις. Θα κατασκευάσουμε μεθόδους πεπερασμένων διαφορών
Κεφάλαιο 9 Πεπερασμένες διαφορές για την ελλειπτική εξίσωση στις δύο διαστάσεις Σε αυτό το κεφάλαιο θεωρούμε μια απλή ελλειπτική εξίσωση, στις δύο διαστάσεις. Θα κατασκευάσουμε μεθόδους πεπερασμένων διαφορών
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).
![Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ). Vol. 34 ( 2014 ) No. 4. J. of Math. (PRC) : A : (2014) Frank-Wolfe [7],. Frank-Wolfe, ( ).](/thumbs/91/105872052.jpg) Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
Vol. 4 ( 214 ) No. 4 J. of Math. (PRC) 1,2, 1 (1., 472) (2., 714) :.,.,,,..,. : ; ; ; MR(21) : 9B2 : : A : 255-7797(214)4-759-7 1,,,,, [1 ].,, [4 6],, Frank-Wolfe, Frank-Wolfe [7],.,,.,,,., UE,, UE. O-D,,,,,
A domain decomposition method for the Oseen-viscoelastic flow equations
 A doman decomposton method for the Oseen-vscoelastc flow equatons Eleanor Jenkns Hyesuk Lee Abstract We study a non-overlappng doman decomposton method for the Oseen-vscoelastc flow problem. The data on
A doman decomposton method for the Oseen-vscoelastc flow equatons Eleanor Jenkns Hyesuk Lee Abstract We study a non-overlappng doman decomposton method for the Oseen-vscoelastc flow problem. The data on
8.323 Relativistic Quantum Field Theory I
 MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
MIT OpenCourseWare http://ocwmtedu 8323 Relatvstc Quantum Feld Theory I Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocwmtedu/terms 1 The Lagrangan: 8323 Lecture
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
2 Lagrangian and Green functions in d dimensions
 Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Renormalzaton of φ scalar feld theory December 6 Pdf fle generated on February 7, 8. TODO Examne ε n the two-pont functon cf Sterman. Lagrangan and Green functons n d dmensons In these notes, we ll use
Noriyasu MASUMOTO, Waseda University, Okubo, Shinjuku, Tokyo , Japan Hiroshi YAMAKAWA, Waseda University
 A Study on Predctve Control Usng a Short-Term Predcton Method Based on Chaos Theory (Predctve Control of Nonlnear Systems Usng Plural Predcted Dsturbance Values) Noryasu MASUMOTO, Waseda Unversty, 3-4-1
A Study on Predctve Control Usng a Short-Term Predcton Method Based on Chaos Theory (Predctve Control of Nonlnear Systems Usng Plural Predcted Dsturbance Values) Noryasu MASUMOTO, Waseda Unversty, 3-4-1
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Supplementary materials for Statistical Estimation and Testing via the Sorted l 1 Norm
 Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Duals of the QCQP and SDP Sparse SVM. Antoni B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckriet
 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckret SVCL-TR 007-0 v Aprl 007 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R.
Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R. G. Lanckret SVCL-TR 007-0 v Aprl 007 Duals of the QCQP and SDP Sparse SVM Anton B. Chan, Nuno Vasconcelos, and Gert R.
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
The one-dimensional periodic Schrödinger equation
 The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly
The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly
Supporting information for: Functional Mixed Effects Model for Small Area Estimation
 Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
Supportng nformaton for: Functonal Mxed Effects Model for Small Area Estmaton Tapabrata Mat 1, Samran Snha 2 and Png-Shou Zhong 1 1 Department of Statstcs & Probablty, Mchgan State Unversty, East Lansng,
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Finite difference method for 2-D heat equation
 Finite difference method for 2-D heat equation Praveen. C praveen@math.tifrbng.res.in Tata Institute of Fundamental Research Center for Applicable Mathematics Bangalore 560065 http://math.tifrbng.res.in/~praveen
Finite difference method for 2-D heat equation Praveen. C praveen@math.tifrbng.res.in Tata Institute of Fundamental Research Center for Applicable Mathematics Bangalore 560065 http://math.tifrbng.res.in/~praveen
J. of Math. (PRC) Banach, , X = N(T ) R(T + ), Y = R(T ) N(T + ). Vol. 37 ( 2017 ) No. 5
 Vol. 37 ( 2017 ) No. 5 J. of Math. (PRC) 1,2, 1, 1 (1., 225002) (2., 225009) :. I +AT +, T + = T + (I +AT + ) 1, T +. Banach Hilbert Moore-Penrose.. : ; ; Moore-Penrose ; ; MR(2010) : 47L05; 46A32 : O177.2
Vol. 37 ( 2017 ) No. 5 J. of Math. (PRC) 1,2, 1, 1 (1., 225002) (2., 225009) :. I +AT +, T + = T + (I +AT + ) 1, T +. Banach Hilbert Moore-Penrose.. : ; ; Moore-Penrose ; ; MR(2010) : 47L05; 46A32 : O177.2
Some generalization of Cauchy s and Wilson s functional equations on abelian groups
 Aequat. Math. 89 (2015), 591 603 c The Author(s) 2013. Ths artcle s publshed wth open access at Sprngerlnk.com 0001-9054/15/030591-13 publshed onlne December 6, 2013 DOI 10.1007/s00010-013-0244-4 Aequatones
Aequat. Math. 89 (2015), 591 603 c The Author(s) 2013. Ths artcle s publshed wth open access at Sprngerlnk.com 0001-9054/15/030591-13 publshed onlne December 6, 2013 DOI 10.1007/s00010-013-0244-4 Aequatones
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
A Two Sample Test for Mean Vectors with Unequal Covariance Matrices
 A Two Sample Test for Mean Vectors wth Unequal Covarance Matrces Tamae Kawasak 1 and Takash Seo 2 1 Department of Mathematcal Informaton Scence Graduate School of Scence, Tokyo Unversty of Scence, Tokyo,
A Two Sample Test for Mean Vectors wth Unequal Covarance Matrces Tamae Kawasak 1 and Takash Seo 2 1 Department of Mathematcal Informaton Scence Graduate School of Scence, Tokyo Unversty of Scence, Tokyo,
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Solutions for Mathematical Physics 1 (Dated: April 19, 2015)
 Solutons for Mathematcal Physcs 1 Dated: Aprl 19, 215 3.2.3 Usng the vectors P ê x cos θ + ê y sn θ, Q ê x cos ϕ ê y sn ϕ, R ê x cos ϕ ê y sn ϕ, 1 prove the famlar trgonometrc denttes snθ + ϕ sn θ cos
Solutons for Mathematcal Physcs 1 Dated: Aprl 19, 215 3.2.3 Usng the vectors P ê x cos θ + ê y sn θ, Q ê x cos ϕ ê y sn ϕ, R ê x cos ϕ ê y sn ϕ, 1 prove the famlar trgonometrc denttes snθ + ϕ sn θ cos
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
THE SECOND WEIGHTED MOMENT OF ζ. S. Bettin & J.B. Conrey
 THE SECOND WEIGHTED MOMENT OF ζ by S. Bettn & J.B. Conrey Abstract. We gve an explct formula for the second weghted moment of ζs) on the crtcal lne talored for fast computatons wth any desred accuracy.
THE SECOND WEIGHTED MOMENT OF ζ by S. Bettn & J.B. Conrey Abstract. We gve an explct formula for the second weghted moment of ζs) on the crtcal lne talored for fast computatons wth any desred accuracy.
New bounds for spherical two-distance sets and equiangular lines
 New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
Quantum annealing inversion and its implementation
 49 2 2006 3 CHINESE JOURNAL OF GEOPHYSICS Vol. 49, No. 2 Mar., 2006,,..,2006,49 (2) :577 583 We C, Zhu P M, Wang J Y. Quantum annealng nverson and ts mplementaton. Chnese J. Geophys. (n Chnese), 2006,49
49 2 2006 3 CHINESE JOURNAL OF GEOPHYSICS Vol. 49, No. 2 Mar., 2006,,..,2006,49 (2) :577 583 We C, Zhu P M, Wang J Y. Quantum annealng nverson and ts mplementaton. Chnese J. Geophys. (n Chnese), 2006,49
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ. ICA: συναρτήσεις κόστους & εφαρμογές
 8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Estimators when the Correlation Coefficient. is Negative
 It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
It J Cotemp Math Sceces, Vol 5, 00, o 3, 45-50 Estmators whe the Correlato Coeffcet s Negatve Sad Al Al-Hadhram College of Appled Sceces, Nzwa, Oma abur97@ahoocouk Abstract Rato estmators for the mea of
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
u i t=0 = u i0 (x) 0, (1.2)
 Electronc Journal of Dfferental Euatons, Vol. 8 (8), No. 9, pp. 3. ISSN: 7-669. URL: http://ede.math.txstate.edu or http://ede.math.unt.edu NONEXISTENCE OF GLOBAL SOLUTIONS TO THE SYSTEM OF SEMILINEAR
Electronc Journal of Dfferental Euatons, Vol. 8 (8), No. 9, pp. 3. ISSN: 7-669. URL: http://ede.math.txstate.edu or http://ede.math.unt.edu NONEXISTENCE OF GLOBAL SOLUTIONS TO THE SYSTEM OF SEMILINEAR
Phasor Diagram of an RC Circuit V R
 ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
IF(Ingerchange Format) [7] IF C-STAR(Consortium for speech translation advanced research ) [8] IF 2 IF
![IF(Ingerchange Format) [7] IF C-STAR(Consortium for speech translation advanced research ) [8] IF 2 IF IF(Ingerchange Format) [7] IF C-STAR(Consortium for speech translation advanced research ) [8] IF 2 IF](/thumbs/91/106522878.jpg) 100080 e-mal:{gdxe, cqzong, xubo}@nlpr.a.ac.cn tel:(010)82614468 IF 1 1 1 IF(Ingerchange Format) [7] IF C-STAR(Consortum for speech translaton advanced research ) [8] IF 2 IF 2 IF 69835003 60175012 [6][12]
100080 e-mal:{gdxe, cqzong, xubo}@nlpr.a.ac.cn tel:(010)82614468 IF 1 1 1 IF(Ingerchange Format) [7] IF C-STAR(Consortum for speech translaton advanced research ) [8] IF 2 IF 2 IF 69835003 60175012 [6][12]
A General Note on δ-quasi Monotone and Increasing Sequence
 International Mathematical Forum, 4, 2009, no. 3, 143-149 A General Note on δ-quasi Monotone and Increasing Sequence Santosh Kr. Saxena H. N. 419, Jawaharpuri, Badaun, U.P., India Presently working in
International Mathematical Forum, 4, 2009, no. 3, 143-149 A General Note on δ-quasi Monotone and Increasing Sequence Santosh Kr. Saxena H. N. 419, Jawaharpuri, Badaun, U.P., India Presently working in
Pricing of Options on two Currencies Libor Rates
 Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
ECE Spring Prof. David R. Jackson ECE Dept. Notes 2
 ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
Journal of Theoretics Vol.4-5
 Journal of Theoretcs Vol.4- A Unfed Feld Theory Peter Hckman peter.hckman@ntlworld.com Abstract: In ths paper, the extenson of Remann geometry to nclude an asymmetrc metrc tensor s presented. A new co-varant
Journal of Theoretcs Vol.4- A Unfed Feld Theory Peter Hckman peter.hckman@ntlworld.com Abstract: In ths paper, the extenson of Remann geometry to nclude an asymmetrc metrc tensor s presented. A new co-varant
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Differentiation exercise show differential equation
 Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
Discrete Fourier Transform { } ( ) sin( ) Discrete Sine Transformation. n, n= 0,1,2,, when the function is odd, f (x) = f ( x) L L L N N.
 Dscrete Fourer Trasform Refereces:. umercal Aalyss of Spectral Methods: Theory ad Applcatos, Davd Gottleb ad S.A. Orszag, Soc. for Idust. App. Math. 977.. umercal smulato of compressble flows wth smple
Dscrete Fourer Trasform Refereces:. umercal Aalyss of Spectral Methods: Theory ad Applcatos, Davd Gottleb ad S.A. Orszag, Soc. for Idust. App. Math. 977.. umercal smulato of compressble flows wth smple
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
arxiv: v2 [math.ap] 6 Dec 2015
![arxiv: v2 [math.ap] 6 Dec 2015 arxiv: v2 [math.ap] 6 Dec 2015](/thumbs/85/91973743.jpg) Unform Regularty Estmates n Homogenzaton Theory of Ellptc System wth Lower Order Terms arxv:1507.06050v2 math.ap] 6 Dec 2015 Qang Xu School of Mathematcs and Statstcs, Lanzhou Unversty, Lanzhou, Gansu
Unform Regularty Estmates n Homogenzaton Theory of Ellptc System wth Lower Order Terms arxv:1507.06050v2 math.ap] 6 Dec 2015 Qang Xu School of Mathematcs and Statstcs, Lanzhou Unversty, Lanzhou, Gansu
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Pseudo Almost Periodic Solutions for HCNNs with Time-Varying Leakage Delays
 DOI 1.763/s4956-15-4-7 Moroccan J. Pure and Appl. Anal.(MJPAA) Volume 1(1), 215, Pages 51 69 ISSN: 2351-8227 RESEARCH ARTICLE Pseudo Almost Perodc Solutons for HCNNs wth Tme-Varyng Leakage Delays Ceml
DOI 1.763/s4956-15-4-7 Moroccan J. Pure and Appl. Anal.(MJPAA) Volume 1(1), 215, Pages 51 69 ISSN: 2351-8227 RESEARCH ARTICLE Pseudo Almost Perodc Solutons for HCNNs wth Tme-Varyng Leakage Delays Ceml
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
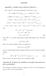 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Constant Elasticity of Substitution in Applied General Equilibrium
 Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
NON-HOMOGENEOUS BOUNDARY-VALUE PROBLEMS OF HIGHER ORDER DIFFERENTIAL EQUATIONS WITH p-laplacian
 Electronc Journal of Dfferental Equatons, Vol. 2828, No. 2, pp. 43. ISSN: 72-669. URL: http://ejde.ath.txstate.edu or http://ejde.ath.unt.edu ftp ejde.ath.txstate.edu logn: ftp NON-HOMOGENEOUS BOUNDARY-VALUE
Electronc Journal of Dfferental Equatons, Vol. 2828, No. 2, pp. 43. ISSN: 72-669. URL: http://ejde.ath.txstate.edu or http://ejde.ath.unt.edu ftp ejde.ath.txstate.edu logn: ftp NON-HOMOGENEOUS BOUNDARY-VALUE
Nonlinear problem with subcritical exponent in Sobolev space
 Jebrl Journal of Inequaltes and Applcatons 06 06:305 DOI 0.86/s3660-06-5-3 R E S E A R C H Open Access Nonlnear problem wth subcrtcal exponent n Sobolev space Iqbal H Jebrl * * Correspondence: qbal50@hotmal.com
Jebrl Journal of Inequaltes and Applcatons 06 06:305 DOI 0.86/s3660-06-5-3 R E S E A R C H Open Access Nonlnear problem wth subcrtcal exponent n Sobolev space Iqbal H Jebrl * * Correspondence: qbal50@hotmal.com
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
arxiv: v1 [math.ca] 6 Dec 2012
![arxiv: v1 [math.ca] 6 Dec 2012 arxiv: v1 [math.ca] 6 Dec 2012](/thumbs/91/105692162.jpg) arxv:.v [math.ca] 6 Dec Pontwse strong approxmaton of almost perodc functons n S W lodzmerz Lensk and Bogdan Szal Unversty of Zelona Góra Faculty of Mathematcs, Computer Scence and Econometrcs 65-56 Zelona
arxv:.v [math.ca] 6 Dec Pontwse strong approxmaton of almost perodc functons n S W lodzmerz Lensk and Bogdan Szal Unversty of Zelona Góra Faculty of Mathematcs, Computer Scence and Econometrcs 65-56 Zelona
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Local Approximation with Kernels
 Local Approximation with Kernels Thomas Hangelbroek University of Hawaii at Manoa 5th International Conference Approximation Theory, 26 work supported by: NSF DMS-43726 A cubic spline example Consider
Local Approximation with Kernels Thomas Hangelbroek University of Hawaii at Manoa 5th International Conference Approximation Theory, 26 work supported by: NSF DMS-43726 A cubic spline example Consider
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
A Two-Sided Laplace Inversion Algorithm with Computable Error Bounds and Its Applications in Financial Engineering
 Electronic Companion A Two-Sie Laplace Inversion Algorithm with Computable Error Bouns an Its Applications in Financial Engineering Ning Cai, S. G. Kou, Zongjian Liu HKUST an Columbia University Appenix
Electronic Companion A Two-Sie Laplace Inversion Algorithm with Computable Error Bouns an Its Applications in Financial Engineering Ning Cai, S. G. Kou, Zongjian Liu HKUST an Columbia University Appenix
Concomitants of Dual Generalized Order Statistics from Bivariate Burr III Distribution
 Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
Journal of Statstcal Theory and Applcatons, Vol. 4, No. 3 September 5, 4-56 Concomtants of Dual Generalzed Order Statstcs from Bvarate Burr III Dstrbuton Haseeb Athar, Nayabuddn and Zuber Akhter Department
1 String with massive end-points
 1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
THREE-DIMENSIONAL VISCO-ELASTIC ARTIFICIAL BOUNDARIES IN TIME DOMAIN FOR WAVE MOTION PROBLEMS
 6 Vol. No.6 005 ENGNEENG MEHANS Dec. 005 000-4750(005)06-0046-06 * (. 00084. 000) O47.4, P5. A THEE-DMENSONAL VSO-ELAST ATFAL BOUNDAES N TME DOMAN FO WAVE MOTON POBLEMS * LU Jng-bo, WANG Zhen-yu, DU Xu-l,
6 Vol. No.6 005 ENGNEENG MEHANS Dec. 005 000-4750(005)06-0046-06 * (. 00084. 000) O47.4, P5. A THEE-DMENSONAL VSO-ELAST ATFAL BOUNDAES N TME DOMAN FO WAVE MOTON POBLEMS * LU Jng-bo, WANG Zhen-yu, DU Xu-l,
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
On homeomorphisms and C 1 maps
 arxv:1804.10691v1 [mah.gm] 7 Apr 018 On homeomorphsms and C 1 maps Nkolaos E. Sofronds Deparmen of Economcs, Unversy of Ioannna, Ioannna 45110, Greece. nsofron@oene.gr, nsofron@cc.uo.gr Absrac Our purpose
arxv:1804.10691v1 [mah.gm] 7 Apr 018 On homeomorphsms and C 1 maps Nkolaos E. Sofronds Deparmen of Economcs, Unversy of Ioannna, Ioannna 45110, Greece. nsofron@oene.gr, nsofron@cc.uo.gr Absrac Our purpose
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
SPECIAL FUNCTIONS and POLYNOMIALS
 SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
