ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ

Transcript

1 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ενότητα: Αναγνώριση Διεργασίας - Προσαρμοστικός Έλεγχος (Process Identification) Αλαφοδήμος Κωνσταντίνος Τμήμα Μηχανικών Αυτοματισμού Τ.Ε.

2 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας χρήσης, η άδεια χρήσης αναφέρεται ρητώς. Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το έργο «Ανοικτά Ακαδημαϊκά Μαθήματα στο Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα» έχει χρηματοδοτήσει μόνο την αναδιαμόρφωση του εκπαιδευτικού υλικού. Το έργο υλοποιείται στο πλαίσιο του Επιχειρησιακού Προγράμματος «Εκπαίδευση και Δια Βίου Μάθηση» και συγχρηματοδοτείται από την Ευρωπαϊκή Ένωση (Ευρωπαϊκό Κοινωνικό Ταμείο) και από εθνικούς πόρους.

3 1. Σκοποί ενότητας Περιεχόμενα ενότητας ΑΝΑΓΝΩΡΙΣΗ ΔΙΕΡΓΑΣΙΑΣ-ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ (Process Identification) Αναγνώριση Διεργασίας Παράδειγμα1: Αναγνώριση παραμέτρων του μοντέλου διεργασίας Παράδειγμα 2: Αναγνώριση διεργασίας και προσαρμοστικός έλεγχος Παράδειγμα 3: Σχεδιασμός Αυτοπροσαρμοζόμενου Ρυθμιστή για Διεργασία 2ης Τάξεως

4 1. Σκοποί ενότητας Απόκτηση γνώσεων στη μεθοδολογία υπολογισμού της διεργασίας για μεταβαλλόμενες συνθήκες. 2. Περιεχόμενα ενότητας ΑΝΑΓΝΩΡΙΣΗ ΔΙΕΡΓΑΣΙΑΣ-ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ (Process Identification) o Αναγνώριση Διεργασίας Παράδειγμα1: Αναγνώριση παραμέτρων του μοντέλου διεργασίας Παράδειγμα 2 o Αναγνώριση διεργασίας και προσαρμοστικός έλεγχος Παράδειγμα 3: Σχεδιασμός Αυτοπροσαρμοζόμενου Ρυθμιστή για Διεργασία 2ης Τάξεως.

5 3. ΑΝΑΓΝΩΡΙΣΗ ΔΙΕΡΓΑΣΙΑΣ-ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ (Process Identification) Στο κεφάλαιο αυτό γίνεται παρουσίαση της στοχαστικής μεθόδου για την ανεύρεση ενός αξιόπιστου μοντέλου πριν ή κατά την λειτουργία της διεργασίας. Επί πλέον, παρουσιάζεται μέθοδος χρήσης της αναγνώρισης διεργασίας σε διάφορα συστήματα ελέγχου για την ανάπτυξη online στρατηγικών προσαρμοστικού ελέγχου. Αξίζει να επισημανθεί πως αναγνώριση διεργασίας και online προσαρμοστικός έλεγχος απαιτούν πολλούς υπολογισμούς, που μπορούν να εκτελεστούν ταχύτατα και με ακρίβεια μόνο με Η/Υ. Για το λόγο αυτό, online αναγνώριση διεργασίας, άρχισε να εφαρμόζεται μετά την είσοδο των Η/Υ στον βιομηχανικό έλεγχο. Είναι γνωστό πως η προσπάθεια για να βρεθεί το μοντέλο διεργασίας εκ των προτέρων είχε μικρή επιτυχία, λόγω μη γραμμικότητας και λόγω μεταβολής των δυναμικών χαρακτηριστικών της διεργασίας με το χρόνο. Δηλαδή λόγω αλλαγής στις τιμές φυσικών παραμέτρων της διεργασίας. Χρειάζεται ένας πειραματικός τρόπος για τον υπολογισμό ενός αξιόπιστου μοντέλου πριν ή κατά την διάρκεια λειτουργίας της διεργασίας που ονομάζεται αναγνώριση διεργασίας (process identification). Επίσης γίνεται παρουσίαση πώς τα διάφορα συστήματα ελέγχου συνδέονται με την αναγνώριση για online στρατηγικές προσαρμοστικού ελέγχου. 3.1 Αναγνώριση Διεργασίας Η άγνωστος διεργασία στο διακριτό χρόνο περιγράφεται από εξίσωση n τάξεως. y n = α 1 y n-1 + α 2 y n α k y n-k + b 1 m n-1 + b 2 m n b k m n-k (5.1) όπου y και m είναι οι τιμές εισόδου και εξόδου αντίστοιχα τη στιγμή i και α 0, α 1,.... α k, b 0, b 1,..., b k είναι παράμετροι ελάχιστα γνωστές και πρέπει να υπολογιστούν. Η τάξη του μοντέλου μπορεί να είναι γνωστός ή όχι. Υποθέτουμε πως m n είναι οι μετρούμενες τιμές της μεταβλητής εισόδου και y n οι μετρούμενες τιμές της μεταβλητής εξόδου της διεργασίας την n στιγμή για n=0,1,2... Οι παραπάνω τιμές υπολογίζονται από τα πειραματικά δεδομένα της εξόδου που συλλέγονται σε δοκιμαστική μεταβολή της εισόδου. Για την εκτίμηση των τιμών των παραμέτρων a και b χρησιμοποιείται η μέθοδος των ελαχίστων τετραγώνων για πλήθος μετρήσεων Ν. Οι εκτιμώμενες τιμές των a και b συμβολίζονται με και και δεν είναι πλέον σταθερές αλλά τυχαίες μεταβλητές. Επομένως αντικειμενικός σκοπός της μεθόδου αυτής είναι η βέλτιστη εκτίμηση των παραμέτρων a και b. Η εκτιμώμενη τιμή της y n συμβολίζεται με και δίνεται από την εξίσωση: (5.2) Η διαφορά μεταξύ πραγματικής και εκτιμώμενης τιμής του y ονομάζεται εκτίμηση σφάλματος και υπολογίζεται από την εξίσωση: ) (5.3)

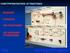
6 Οι βέλτιστες τιμές των αγνώστων παραμέτρων a και b χρησιμοποιούνται για να υπολογιστεί το ελάχιστο μέσο σφάλμα μεταξύ πραγματικών και εκτιμώμενων τιμών της μεταβλητής εξόδου y της διεργασίας. Έτσι η βέλτιστη εκτίμηση των παραμέτρων της διεργασίας υπολογίζεται από την λύση του προβλήματος: ) (5.4) Η λύσης του παραπάνω προβλήματος γίνεται με τη χρήση μερικών παραγώγων της P ως προς a και b και εξίσωσής τους με το μηδέν οπότε βρίσκεται ένα σύστημα εξισώσεων ως εξής: Το μοντέλο επιλογής μας είναι αποδεκτό αν το μέσο σφάλμα είναι μηδέν (P=0) διαφορετικά συμπεραίνουμε ότι η τάξη του επιλεγόμενου μοντέλου είναι μη αποδεκτή και επομένως χρειάζεται να επιλέξουμε ένα μοντέλο υψηλότερης τάξης. Στη συνέχεια δίνονται τα απαραίτητα βήματα που πρέπει να ακολουθούνται για την πειραματική αναγνώριση της διεργασίας (Σχ.5.1). 1. Επιλέγεται το μοντέλο της διεργασίας. Η άγνωστη διεργασία δεν είναι ένα μαύρο κουτί. Μερικές πληροφορίες σχετικά με τη δυναμική της συμπεριφορά είναι γνωστές από βασικές αρχές ή/και εμπειρία. Έτσι μερικές εκτιμήσεις (estimate) όπως τάξη του μοντέλου και αρχικές τιμές της άγνωστης διεργασίας θα υπάρχουν. Όσο πιο πολλά γνωρίζουμε σχετικά με την διεργασία τόσο πιο αποτελεσματικό θα είναι το επιλεγόμενο μοντέλο. Συνεπώς, πρέπει να χρησιμοποιήσουμε όλες τις πληροφορίες που υπάρχουν στην διάθεση μας. Αξίζει να επισημανθεί πως σύνθετα μοντέλα υψηλού βαθμού δεν προδικάζουν απαραίτητα το σχεδιασμό καλύτερου ελεγκτή και επιπλέον απαιτούνται πιο πολύπλοκοι υπολογισμοί. Η τάξη του μοντέλου παίζει σημαντικό ρόλο και για μερικές διεργασίες είναι δύσκολο να προσδιοριστεί, όπως του σωλήνα αποστάξεως. Σαν αρχικό σημείο μπορούμε να χρησιμοποιήσουμε ένα μοντέλο πρώτης ή δεύτερης τάξης, με ή χωρίς χρονική καθυστέρηση. Πολλές διεργασίες περιγράφονται αποτελεσματικά και από χαμηλής τάξης μοντέλα. 2. Εισάγεται γνωστή μεταβολή στην είσοδο της διεργασίας (step, pulse, sine) και καταγράφεται η έξοδός της. Το ερέθισμα (ξαφνική μεταβολή) της εισόδου της διεργασίας θα προκαλέσει μεταβολή στην μεταβλητή εξόδου. Έτσι συλλέγονται σημαντικές πληροφορίες σχετικά με τη δυναμική της διεργασίας. Πρέπει να ληφθεί όμως υπ' όψη πως ξαφνικές αλλαγές στην είσοδο ίσως έχει σοβαρές επιπτώσεις στη λειτουργία της διεργασίας. Ο υπολογισμός όμως των παραμέτρων με την μέθοδο των ελαχίστων τετραγώνων εξαρτάται από τον τρόπο που εφαρμόζεται το τεστ στην είσοδο. 3. Υπολογισμός με εκτίμηση (estimate )των "άριστων" τιμών των αγνώστων παραμέτρων της διεργασίας. Η μέθοδος των ελαχίστων τετραγώνων είναι επίσης γνωστή σαν μέθοδος παλινδρόμησης (regression ανάλυση). Αν το μοντέλο

7 επιλογής είναι γραμμικό, έχουμε την μέθοδο γραμμικής παλινδρόμησης (linear regression analysis), διαφορετικά ονομάζεται μη γραμμική μέθοδος παλινδρόμησης. O πειραματικός τρόπος φαίνεται στο Σχ.5.1. Σχ.5.1 Πειραματικός τρόπος Αναγνώρισης Διεργασίας Παράδειγμα1: Αναγνώριση παραμέτρων του μοντέλου διεργασίας Να υπολογισθούν οι παράμετροι του μοντέλου διεργασίας για τα δεδομένα του Πίνακα1. Σημειώνεται πώς για αρνητικές στιγμές, δηλ. n < 0 έχουμε μηδενικές τιμές. 1. Αρχικά υποθέτουμε μοντέλο 1 ης τάξεως: y n = α 1 y n-1 +b 1 m n-1 Υπολογίζονται οι παράμετροι α, b που ελαχιστοποιούν το μέσο τετράγωνο του σφάλματος (mean-square error): { } (5.4) Οι βέλτιστες τιμές α 1, b 1 πρέπει να ικανοποιούν τις απαραίτητες συνθήκες για ελάχιστο: ) ) ) ) (5.5) ) ) ) ) (5.6)

8 ΠΙΝΑΚΑΣ 5.1 ΔΕΔΟΜΕΝΑ ΑΝΑΓΝΩΡΙΣΗΣ ΔΙΕΡΓΑΣΙΑΣ Στιγμή Μεταβλητή εισόδου Μεταβλητή εξόδου Δειγματοληψίας N m n y n n< από τις εξισώσεις (5.5), (5.6)και τις τιμές των y, y n-1, m n-1 (n=1,2,.....,15) του Πίνακα 5.1. Βρίσκουμε: α1= 0.86, b1= 0.57 Οι τιμές αυτές δίδουν: ελάχιστο P = Το ελάχιστο, σχεδόν, πλησιάζει το μηδέν, επομένως το μοντέλο 1ης τάξεως ικανοποιητικά περιγράφει την άγνωστη διεργασία. Η εξίσωση που θα χρησιμοποιηθεί για τον υπολογισμό του ελεγκτή είναι: y n =0.864y n m n-1 2. Υποθέτουμε μοντέλο 2ας τάξεως: y = α 1 y n-1 +α 2 y n-2 +b 1 m n-1 +b 2 m n-2 Η συνάρτηση ελαχίστου τετραγώνου του σφάλματος είναι: { } ακολουθώντας την ίδια διαδικασία όπως παραπάνω έχουμε: και βρίσκουμε: α 1 =0.6, α 2 =0.2, b 1 =0.5, b 2 =0.3.

9 και οι τιμές αυτές δίνουν: ελάχιστο P = 0 Επομένως το μοντέλο δευτέρας τάξεως περιγράφει επακριβώς τη δυναμική συμπεριφορά της διεργασίας. Η εξίσωση διακριτού χρόνου που θα χρησιμοποιηθεί για σχεδιασμό του ελεγκτή είναι: y n = 0.6y n y n m n m n Παράδειγμα 2: Να υπολογιστεί το μοντέλο της διεργασίας για τα δεδομένα εισόδου/εξόδου του Πίνακα 5.2 για μοντέλο 1 ης τάξεως. Στιγμή Δειγματοληψίας n ΠΙΝΑΚΑΣ 5.2 Μεταβλητή Εξόδου m n Μεταβλητή Εισόδου y n n< Για πρώτης τάξεως μοντέλο: y n = α 1 y n-1 b 1 m n-1 ) (1) ) ) (2) ) ) (3) από την (2) βρίσκεται η εξίσωση: 70,03 α 1 +12,871 b 1 = 78,785 (4) και από την (3) η εξίσωση: 12,879 α ,3358 b 1 = 35,555 (5) Επομένως από την (4) λύνουμε ως προς α 1 οπότε: α 1 = 1,125 0,183 b 1 Στη συνέχεια θέτουμε την εξίσωση α 1 στην (5) και λύνουμε ως προς b 1 οπότε b 1 = 0,527 Οπότε από την (5) βρίσκεται α 1 = 1,028 Επομένως η διεργασία περιγράφεται από την εξίσωση: y n = 1.028y n m n-1

10 Από την εξίσωση (1) βρίσκουμε το σφάλμα Ρ, που πρέπει να είναι μηδέν ή περίπου μηδέν. Στη συνέχεια ερευνάται αν η τάξη του μοντέλου είναι αποδεκτή. ) Επομένως Ρ 0 ( 2% ) και το μοντέλο είναι αποδεκτό. 3.2 Αναγνώριση διεργασίας και προσαρμοστικός έλεγχος Είναι γνωστό πως η δυναμική συμπεριφορά της διεργασίας μεταβάλλεται κατά την διάρκεια της λειτουργίας. Για την αντιμετώπιση αυτού του προβλήματος χρειάζεται ένας ελεγκτής που θα προσαρμόζει τις παραμέτρους του κατά βέλτιστο τρόπο. Άρα οδηγούμαστε στους σχηματισμούς που αναφέραμε σε προηγούμενο κεφάλαιο. Βέλτιστη προσαρμογή των παραμέτρων του ελεγκτή επιτυγχάνεται μόνο αν έχουμε στη διάθεση μας ένα καλό μοντέλο που περιγράφει τη δυναμική συμπεριφορά της διεργασίας κατά την διάρκεια των διαφόρων φάσεων λειτουργίας της. Επομένως η αναγνώριση διεργασίας αποτελεί μέρος όλων των σχεδιασμών προσαρμοστικού ελέγχου και περιγράφεται στο μπλοκ διάγραμμα του Σχ ) Σχ.5.2 Λογικό περίγραμμα Προσαρμοστικού Ελέγχου

11 Η διεργασία περιγράφεται από το μοντέλο διακριτού χρόνου: Yn = a 1 y n-1 + a 2 y n a κ y n-κ + b 1 m n-1 + b 2 m n b κ m n-κ (5.6) Οι συντελεστές α 1, α 2,...α k, b 1, b 2,..., b k είναι σταθερές παράμετροι. Στόχος του ελεγκτή είναι να διατηρήσει την έξοδο της διεργασίας όσο το δυνατό πλησίον στην επιθυμητή τιμή (set point) y sp, παρουσία διαταραχών (μεταβολών φορτίου). Η απόκλιση (σφάλμα) υπολογίζεται από μία από τις παρακάτω μεθόδους: ) έλεγχος μιας κατάστασης ) έλεγχος πολλαπλών καταστάσεων Επομένως το πρόβλημα μπορεί να διατυπωθεί ως εξής: Να σχεδιαστεί ένας ελεγκτής που θα ελαχιστοποιεί τους δείκτες P 1 και P 2 σε περιβάλλον με διαταραχές (μεταβολές φορτίου). Επομένως η ενέργεια ελέγχου που ελαχιστοποιεί το P 1 στοχεύει στο να διατηρήσει την έξοδο πλησίον του σημείου αναφοράς λαμβάνοντας αποφάσεις ελέγχου σε κάθε στάδιο. Αντίθετα, ελαχιστοποίηση του P 2 σημαίνει άσκηση ελέγχου στον μεγαλύτερο χρονικό ορίζοντα. Εμείς θα επικεντρώσουμε το ενδιαφέρον μας στην πρώτη περίπτωση και η λύση του προβλήματος έχει ως εξής: Υποθέτουμε ότι την n th στιγμή επιθυμούμε να υπολογιστεί το σήμα ελέγχου m n έτσι ώστε η τιμή της μεταβλητής εξόδου την στιγμή n+1,y n+1 να είναι πολύ κοντά στην επιθυμητή τιμή y sp. Επομένως : ) ) Το ελάχιστο του P 1 βρίσκεται από την: ( ) ) Και το βέλτιστο σήμα ελέγχου m n την n th στιγμή δίνεται από την εξίσωση : (5.7) )

12 Ο ελεγκτής που ορίζεται από την εξίσωση αυτή είναι υλοποιήσιμος διότι χρησιμοποιεί τις τωρινές και τις προηγούμενες τιμές των m και y (m n-1,m n-2, και y n, y n-1,. κ.λπ). Η ενέργεια ελέγχου που ελαχιστοποιεί το τετράγωνο του σφάλματος στην επόμενη περίοδο ή τη μέση τιμή του τετραγώνου του σφάλματος σε Ν περιόδους δειγματοληψίας, δίδεται από την εξίσωση: m n =1/b 1 [y sp -y n ]= 1/b 1 {y sp - α 1 y n - α 2 y n α κ y n-κ+1 b 2 m n b κ m n-κ+1 } (5.8) Αν οι παράμετροι α 1, α 2,..., α κ, b 1, b 2,..., bκ είναι γνωστές τότε η (5.8) περιγράφει τον βέλτιστο έλεγχο που εφαρμόζεται την n th χρονική στιγμή για να διατηρήσει την έξοδο όσο το δυνατό πιο κοντά στην επιθυμητή (set point)τιμή. Αλλά τα α 1, α 2,..., α κ, b 1, b 2,..., b k δεν είναι σταθερές αλλά μεταβάλλονται είτε διότι μετακινούμε τη λειτουργία της διεργασίας σε νέο set point (επίδραση της μη γραμμικότητας) είτε διότι η διεργασία μόνη της μεταβάλλεται με την πάροδο του χρόνου. Χρειαζόμαστε λοιπόν και στις δύο περιπτώσεις να γίνει μια νέα εκτίμηση (υπολογισμός )των τιμών των παραμέτρων. Αυτό γίνεται με την μέθοδο της γραμμικής παλινδρόμησης, χρησιμοποιώντας πειραματικά δεδομένα εισόδουεξόδου. Άρα εφαρμόζεται η παρακάτω μεθοδολογία προσαρμοστικού έλεγχου σε πραγματικό χρόνο (on-line) : 1. Υποθέτουμε πως η διεργασία λειτουργεί στο set point ).Το σήμα ελέγχου που δίδεται από την (5.9) προσαρμόζει την έξοδο στην τιμή του set point y sp για κάθε αλλαγή του φορτίου: ) ) ) ) ) ) ) ) (5.9) όπου ο δείκτης (i) συμβολίζει τις εκτιμούμενες τιμές των παραμέτρων της διεργασίας κατά την παρούσα στάθμη λειτουργίας i, και ο δείκτης " " υποδηλώνει μετρούμενες τιμές. 2. Αν θελήσουμε να μετακινηθεί η έξοδος σε νέο set point, y sp, σημείο λειτουργίας όπου οι παράμετροι της διεργασίας έχουν διαφορετικές τιμές. Χρησιμοποιείται η ) εξίσωση (5.9) με για να φέρουμε την διεργασία στο νέο set point. 3. Κατά την διάρκεια της μεταφοράς από το παλαιό στο νέο set point, καταγράφονται οι τιμές των μεταβλητών στη είσοδο και στην υπό έλεγχο έξοδο. Χρησιμοποιούνται αυτά τα δεδομένα εισόδου-εξόδου για να υπολογισθούν (estimate) οι νέες τιμές των παραμέτρων με την βοήθεια της γραμμικής regression ανάλυσης. Τότε ο νέος ελεγκτής γίνεται: ) ) ) ) ) ) ) ) (5.10) Στο Σχ.5.3 φαίνεται η επίδραση της on-line προσαρμογής στην ποιότητα της απόκρισης κλειστού βρόγχου σε σύγκριση με έλεγχο χωρίς προσαρμοζόμενο ελεγκτή.

13 Σx.5.3 Απόκριση διεργασίας κλειστού βρόγχου με (συνεχής γραμμή) και χωρίς (διακοπτόμενη γραμμή) προσαρμοστικό έλεγχο Παράδειγμα 3: Σχεδιασμός Αυτοπροσαρμοζόμενου Ρυθμιστή για Διεργασία 2ης Τάξεως. Για τα δεδομένα του Πίνακα 5.3 να σχεδιαστεί αυτοπροσαρμοζόμενος ρυθμιστής. Εδώ περιγράφεται πώς ένας ψηφιακός ελεγκτής μπορεί να προσαρμόσει τις παραμέτρους του αυτόματα, on-line, κατά την διάρκεια της λειτουργίας. Υποθέτουμε πως μια πολύ γνωστή διεργασία είναι δυνατόν να προσομοιωθεί με μοντέλο 2 ας τάξεως: y n = α 1 y n-1 +α 2 y n-2 +b 1 m n-1 +b 2 m n-2 Πριν την λειτουργία της διεργασίας πρέπει να υπολογισθούν οι τιμές των παραμέτρων της, χρησιμοποιώντας τα πειραματικά δεδομένα εισόδου-εξόδου. Επομένως έχουμε το μοντέλο: y n = 0.5y n y n m n m n-2 Από την εξίσωση 5.7 μπορούμε να βρούμε πως η επίδραση του βέλτιστου ελέγχου για την διατήρηση της εξόδου της διεργασίας όσο το δυνατόν πλησίον στην επιθυμητή τιμή (set point) (y sp =1)δίδεται από την εξίσωση: m n = 1/0.6 {1-0.5y n - 0.3y n-1-0.4m n-1 } (5.11) Χρησιμοποιώντας την (5.11) η έξοδος της διεργασίας διατηρεί την τιμή ίση με την επιθυμητή τιμή δηλαδή 1 παρά την επίδραση των διαταραχών (π.χ. αλλαγές φορτίου). Έστω ότι επιθυμούμε να γίνει έλεγχος (regulate) διεργασίας σε νέα στάθμη για y sp =5. Μπορούμε να χρησιμοποιήσουμε τον παρακάτω αλγόριθμο ελέγχου με τις παλαιές τιμές των παραμέτρων της διεργασίας. m n = 1/0.6 {5-0.5y n - 0.3y n-1-0.4m n-1 } (5.12)

14 Κατά την μετάβαση από το παλαιό στο νέο επιθυμητό σημείο, καταγράφουμε τις τιμές των μεταβλητών εισόδου και εξόδου. Οι πληροφορίες δίνονται στον Πίνακα 5.2. Η ανάλυση γραμμικής παλινδρόμησης με τα δεδομένα του Πίνακα 2 παράγει τις παρακάτω τιμές για τις παραμέτρους της διεργασίας. α 1 =0.58, α 2 =0.35, b 1 =0.52, b 2 =0.48 και επομένως το μοντέλο έχει τη μορφή y n =0.58 y n y n m n m n-2 Στιγμή Δειγματοληψίας n ΠΙΝΑΚΑΣ 5.3 INPUT-OUTPUT DATA Μεταβλητή εισόδου m n Μεταβλητή Εξόδου y n n< H βέλτιστη ρύθμιση για y sp =5, υπό την παρουσία εξωτερικών μεταβολών φορτίου (διαταραχές), δίδεται από την εξίσωση: m n = 1/0.52 ( y n y n m n-1 ) (5.13) Στο Σχ.5.4 φαίνεται η βελτίωση της απόκρισης κλειστού βρόγχου όταν χρησιμοποιηθεί έλεγχος με προσαρμογή (adaptive) σε σύγκριση με απόκριση χωρίς προσαρμογή (αλλά με ελεγκτή). Άλλα κριτήρια θα μπορούσαν επίσης να χρησιμοποιηθούν για τον σχεδιασμό των ελεγκτών ή την προσαρμογή on-line των παραμέτρων αλγορίθμου ελέγχου. Σχ.5.4 Επίδραση της προσαρμογής παραμέτρων στην ποιότητα της απόκρισης κλειστού βρόγχου