ΠΡΟΣΟΜΟΙΩΣΗ ΦΟΡΗΤΟΥ ΑΝΙΧΝΕΥΤΗ ΓΕΡΜΑΝΙΟΥ ΜΕ ΤΗΝ ΜΕΘΟ Ο MONTE CARLO ΓΙΑ ΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΤΗΣ ΡΟΗΣ ΤΗΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ Γ-ΑΚΤΙΝΟΒΟΛΙΑΣ
|
|
|
- Μελαινη Παπακώστας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΡΟΣΟΜΟΙΩΣΗ ΦΟΡΗΤΟΥ ΑΝΙΧΝΕΥΤΗ ΓΕΡΜΑΝΙΟΥ ΜΕ ΤΗΝ ΜΕΘΟ Ο MONTE CARLO ΓΙΑ ΤΟΝ ΥΠΟΛΟΓΙΣΜΟ ΤΗΣ ΡΟΗΣ ΤΗΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ Γ-ΑΚΤΙΝΟΒΟΛΙΑΣ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΚΥΡΙΑΝΑΚΗΣ ΓΕΩΡΓΙΟΣ ΑΕΜ : 3926 Επιβλέπων : Καθηγητής Α. Κλούβας ΘΕΣΣΑΛΟΝΙΚΗ 2005
2 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΕΙΣΑΓΩΓΗ ΟΙ ΑΝΙΧΝΕΥΤΕΣ ΓΕΡΜΑΝΙΟΥ ΣΤΙΣ Γ-ΦΑΣΜΑΤΟΣΚΟΠΙΚΕΣ ΜΕΤΡΗΣΕΙΣ ΜΗΧΑΝΙΣΜΟΙ ΑΛΛΗΛΕΠΙ ΡΑΣΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ Γ ΜΕ ΤΗΝ ΥΛΗ ΚΑΙ Η ΕΠΙΡΡΟΗ ΤΟΥΣ ΣΤΗΝ ΑΠΟΚΡΙΣΗ ΤΩΝ ΑΝΙΧΝΕΥΤΩΝ Γενικά Φωτοηλεκτρικό Φαινόµενο Σκέδαση Compton ίδυµη Γένεση Απόκριση Ανιχνευτών Σύµφωνα Με Το Μέγεθός Τους "Μικροί Ανιχνευτές" Πολύ "Μεγάλοι" Ανιχνευτές Ανιχνευτές Μεσαίου Μεγέθους ΜΕΘΟ ΟΣ MONTE CARLO Γενικά Ο Κώδικας MCNP 4A Γενικά Στοιχεία Για Τον Κώδικα Απαριθµητής Ύψους Παλµών (Pulse Height Tally, f8) ΠΡΟΣΟΜΟΙΩΣΗ ΑΝΙΧΝΕΥΤΗ HPGE Περιγραφή Του Ανιχνευτή Και Του Αντίστοιχου Εξοπλισµού Υλοποίηση Της Προσοµοίωσης Προσδιορισµός Απόδοσης Ανιχνευτή Μεταβατική Ζώνη Στον Κρύσταλλο Του Ανιχνευτή ΕΦΑΡΜΟΓΗ ΤΗΣ ΜΕΘΟ ΟΥ ΚΑΘΑΡΙΣΜΟΥ ΦΑΣΜΑΤΟΣ ΥΠΟΛΟΓΙΣΜΟΣ ΤΗΣ ΡΟΗΣ ΦΩΤΟΝΙΩΝ ΣΥΜΠΕΡΑΣΜΑΤΑ...40 ΒΙΒΛΙΟΓΡΑΦΙΑ ΑΝΑΦΟΡΕΣ.42 ΠΑΡΑΡΤΗΜΑ 43 1
3 1. ΕΙΣΑΓΩΓΗ Η γ-ακτινοβολία εκτός από το ότι είναι ένα µέρος της ιοντίζουσας ακτινοβολίας αποτελεί και ένα κοµµάτι της ηλεκτροµαγνητικής ακτινοβολίας. Η ηλεκτροµαγνητική ακτινοβολία χαρακτηρίζεται από τη συχνότητα της ακτινοβολίας ή από το µήκος κύµατός της. Υπάρχει εξάρτηση της συχνότητας µε το µήκος κύµατος και γενικά η αύξηση της συχνότητας οδηγεί σε ελάττωση του µήκους κύµατος. Παρακάτω δίνεται το φάσµα της ηλεκτροµαγνητικής ακτινοβολίας εξηγώντας παράλληλα τα είδη των ηλεκτροµαγνητικών ακτινοβολιών. ίνονται οι συχνότητες και τα µήκη κύµατος εντός των οποίων βρίσκονται οι διάφορες ακτινοβολίες καθώς και οι συνήθεις εφαρµογές τους ή η προέλευσή τους. Τέλος το φάσµα της ηλεκτροµαγνητικής ακτινοβολίας χωρίζεται σε δύο µεγάλα µέρη, την ιοντίζουσα ακτινοβολία που προκαλεί ιονισµό των µορίων των κυττάρων και τη µη ιοντίζουσα που προκαλεί συνήθως θερµικά φαινόµενα στα κύτταρα των ζώντων οργανισµών. γραµµές µεταφοράς φούρνοι λαµπτήρες θερµότητας φωνή-µουσική ΑΜ radio FM radio, TV µικροκυµάτων υπέρυθρες κάµερες ακτινογραφικά µηχανήµατα ραδιενεργά στοιχεία ΕΞΑΙΡΕΤΙΚΑ ΧΑΜΗΛΕΣ ΣΥΧΝΟΤΗΤΕΣ ΦΩΝΗΤΙΚΕΣ ΣΥΧΝΟΤΗΤΕΣ ΠΟΛΥ ΧΑΜΗΛΕΣ ΣΥΧΝΟΤΗΤΕΣ ΧΑΜΗΛΕΣ ΣΥΧΝΟΤΗΤΕΣ ΜΕΣΑΙΕΣ ΣΥΧΝΟΤΗΤΕΣ ΥΨΗΛΕΣ ΣΥΧΝΟΤΗΤΕΣ ΠΟΛΥ ΥΨΗΛΕΣ ΣΥΧΝΟΤΗΤΕΣ ΠΛΕΟΝ ΥΨΗΛΕΣ ΣΥΧΝΟΤΗΤΕΣ ΚΥΜΑΤΑ ΕΚΑΤΟΣΤΩΝ ΚΥΜΑΤΑ ΧΙΛΙΟΣΤΩΝ ΥΠΕΡ ΥΨΗΛΕΣ ΣΥΧΝΟΤΗΤΕΣ ΕΞΑΙΡΕΤΙΚΑ ΥΨΗΛΕΣ ΣΥΧΝΟΤΗΤΕΣ ELF VF VLF LF MF HF VHF UHF SHF EHF ITU ITU ITU ITU ITU ITU ITU ITU BAND BAND BAND BAND BAND BAND BAND BAND ΚΥΜΑΤΑ ΜΙΚΡΟΤΕΡΑ ΧΙΛΙΟΣΤΩΝ ITU BAND 12 ΜΑΚΡΙΝΕΣ ΥΠΕΡΥΘΡΕΣ ΕΝ ΙΑΜΕΣΕΣ ΥΠΕΡΥΘΡΕΣ ΚΟΝΤΙΝΕΣ ΥΠΕΡΥΘΡΕΣ ΟΡΑΤΟ ΦΩΣ ΚΟΝΤΙΝΕΣ ΥΠΕΡΙΩ ΕΙΣ ΜΑΚΡΙΝΕΣ ΥΠΕΡΙΩ ΕΙΣ ΑΚΤΙΝΕΣ-Χ ΑΚΤΙΝΕΣ-γ ΕΥΤΕΡΕΥΟΥΣΑ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΑΚΤΙΝΕΣ-γ ΠΟΥ ΠΑΡΗΧΘΗΣΑΝ ΑΠΟ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ HERTZ KILOHERTZ MEGAHERTZ GIGAHERTZ TERAHERTZ ΕΝΕΡΓΕΙΑ ΦΩΤΟΝΙΩΝ ΣΕ ELECTRON VOLTS (ev) kev MeV ev GeV ΣΥΧΝΟΤΗΤΑ ΣΕ HERTZ (κύκλοι ανά δευτερόλεπτο) ΜΗΚΟΣ ΚΥΜΑΤΟΣ ΣΕ ΜΕΤΡΑ ΜΗ ΙΟΝΤΙΖΟΥΣΑ ΑΚΤΙΝΟΒΟΛΙΑ ΙΟΝΤΙΖΟΥΣΑ ΑΚΤΙΝΟΒΟΛΙΑ µή θερµική θερµική οπτική θραύση δεσµών (µικρά επαγώµενα ρεύµατα) (µεγάλα επαγώµενα ρεύµατα) (διέγερση ηλεκτρονίων) (βλάβη του DNA) Σχήµα 1-1. Ηλεκτροµαγνητικό φάσµα. Η πιο διαδεδοµένη µέθοδος για τη µέτρηση της γ-ακτινοβολίας είναι η γ- φασµατοσκοπία. Όλα σχεδόν τα υλικά περιέχουν έστω και ελάχιστες ποσότητες ραδιενεργών ισοτόπων που εκπέµπουν γ-ακτινοβολία. Το ενεργειακό φάσµα ακτινοβολίας είναι χαρακτηριστικό (αποτελεί ταυτότητα) του νουκλιδίου που την 2
4 εκπέµπει. Από το χαρακτηριστικό φάσµα που εκπέµπει το ραδιενεργό ισότοπο µπορούµε να διαγνώσουµε την παρουσία ακόµα και ελάχιστων ποσοτήτων κάποιου στοιχείου σε υλικό. Αν πάλι το υλικό δεν περιέχει ραδιενεργό ισότοπο του υπόψη στοιχείου, χρησιµοποιείται η µέθοδος της ενεργοποίησης (πχ µε νετρόνια, δείγµα του υλικού βοµβαρδίζεται µε νετρόνια) οπότε παράγονται ραδιενεργά ισότοπα που συνήθως εκπέµπουν γ-ακτινοβολία. Από τα φάσµατα των ακτινοβολιών αυτών προσδιορίζεται η παρουσία συγκεκριµένων στοιχείων στο υλικό. Η γ-φασµατοσκοπία λοιπόν εφαρµόζεται ευρύτατα ως ένα εργαλείο για την ανάλυση ενός ραδιενεργού δείγµατος και συγκεκριµένα τον ποιοτικό και ποσοτικό προσδιορισµό των ισοτόπων που υπάρχουν σ αυτό. Οι εφαρµογές της περιλαµβάνουν τοµείς όπως: παρακολούθηση πυρηνικών εγκαταστάσεων, ακτινοφυσική, πυρηνική ιατρική, επιστήµη περιβάλλοντος, έρευνα υλικών, βιοεπιστήµες και βιοµηχανικές εφαρµογές ραδιοϊσοτόπων. Μία συντηρητική εκτίµηση δείχνει ότι περισσότερα από συστήµατα γ-φασµατοµετρίας χρησιµοποιούνται σε ακαδηµαϊκό αλλά και βιοµηχανικό επίπεδο παγκοσµίως. Κατά τη διάρκεια των τελευταίων 10 µε 15 χρόνων έχουν κατασκευαστεί ανιχνευτές, ηλεκτρονικά και λογισµικό µεταφοράς και απεικόνισης δεδοµένων για διατάξεις γ-φασµατοσκοπίας που µπορούν µε ευκολία να αναπτυχθούν σε εξωτερικούς χώρους. Στον χώρο των ανιχνευτών, τα συστήµατα φορητών ανιχνευτών γερµανίου γνωρίζουν ιδιαίτερη άνθιση στις µέρες µας, µε χρήση κρυστάλλων υπερκαθαρού γερµανίου HPGe (Ηigh Purity Ge), που εξασφαλίζουν πέρα από τη δυνατότητα επιτόπου φασµατοσκοπίας, την πολύ καλή διακριτική ικανότητα, αλλά και τη δυνατότητα θέρµανσης του κρυστάλλου χωρίς να υπάρξει καταστροφή αυτού. Τα φορητά αυτά συστήµατα χρησιµοποιήθηκαν σε ευρύτατη κλίµακα µετά το ατύχηµα του Chernobyl για τον επί τόπου ποιοτικό και ποσοτικό προσδιορισµό των ραδιονουκλιδίων που ρύπαιναν το περιβάλλον. Τα µεγέθη που µπορούν να προσδιοριστούν µε τη µέθοδο της in-situ γ-φασµατοσκοπίας είναι: η συγκέντρωση των ραδιονουκλιδίων και ο ρυθµός απορροφούµενης δόσης. Η βαθµονόµηση εργαστηριακού συστήµατος γ-φασµατοσκοπίας είναι ευρύτατα γνωστή και γίνεται µε πρότυπες πηγές. Στην επί τόπου (in situ) γ-φασµατοσκοπία, η οποία πραγµατοποιείται σε ανοιχτό χώρο, στοχεύοντας στον προσδιορισµό της ραδιενέργειας ή του ρυθµού απορροφούµενης δόσης του πεδίου 3
5 και όχι κάποιου δείγµατος, η βαθµονόµηση είναι πιο περίπλοκη και γι αυτόν το λόγο έχουν προταθεί διάφορες τεχνικές. Ο στόχος αυτής της διπλωµατικής είναι η συµβολή στον προσδιορισµό του ρυθµού απορροφούµενης δόσης ανεξάρτητα από την γεωµετρία της πηγής. Για την επίτευξη όµως αυτού του στόχου απαιτείται η εξαγωγή της ενεργειακής κατανοµής ροής των φωτονίων από το µετρούµενο in-situ φάσµα. Καθώς όµως το λαµβανόµενο φάσµα παρουσιάζει µία παραµορφωµένη εικόνα της ενεργειακής κατανοµής των προσπιπτόντων φωτονίων, εξαιτίας κυρίως των σκεδάσεων Compton στο εσωτερικό του κρύσταλλου γερµανίου, ακολουθήθηκε η µέθοδος καθαρισµού φάσµατος (spetrum stripping). Για το σκοπό αυτό πραγµατοποιήθηκε προσοµοίωση του ανιχνευτή µε µεθόδους Monte Carlo µε στόχο την αναπαραγωγή των φασµάτων που προέρχονται από φωτόνια διάφορων ενεργειών και τον προσδιορισµό του υποβάθρου Compton. Με τη χρήση λοιπόν αυτών των φασµάτων γίνεται ο καθαρισµός των χτύπων που οφείλονται σε µερική απορρόφηση. 2. ΟΙ ΑΝΙΧΝΕΥΤΕΣ ΓΕΡΜΑΝΙΟΥ ΣΤΙΣ Γ-ΦΑΣΜΑΤΟΣΚΟΠΙΚΕΣ ΜΕΤΡΗΣΕΙΣ. Οι ηµιαγωγοί ανιχνευτές κατασκευάζονται συνήθως από πυρίτιο (Si) ή γερµάνιο(ge). Οι απολύτως καθαροί ηµιαγωγοί, αυτοί δηλαδή χωρίς την παραµικρή πρόσµιξη ονοµάζονται ενδογενείς (intrinsi) ηµιαγωγοί. Σε αυτούς όλα τα ηλεκτρόνια στη ζώνη αγωγιµότητας προκύπτουν από θερµική διέγερση, εφόσον δεν έχουν παραχθεί από αλληλεπίδραση µε ιοντίζουσες ακτινοβολίες. Εφόσον κάθε ηλεκτρόνιο που διεγείρεται στη ζώνη αγωγιµότητας αφήνει πίσω του µία θετική οπή έπεται ότι στους ενδογενείς ηµιαγωγούς η πυκνότητα των ηλεκτρονίων αγωγιµότητας είναι ίση µε την πυκνότητα των οπών. Όπως φαίνεται από τη σχέση : p(t) = CT 3\2. exp(-e g \2kT) (2) (2-1) όπου Τ η απόλυτη θερµοκρασία του κρυστάλλου, k η σταθερά του Boltzmann, C σταθερά αναλογίας και E g το εύρος της απαγορευµένης ζώνης, οι πυκνότητες αυτές µειώνονται για αυξανόµενο εύρος της απαγορευµένης ζώνης και για µειούµενη θερµοκρασία του κρυστάλλου. Οι πυκνότητες αυτές σε θερµοκρασία δωµατίου είναι 4
6 2, m -3 στο γερµάνιο και 1, m -3 στο πυρίτιο. Στην ηλεκτρική αγωγιµότητα συµβάλλον τόσο τα ηλεκτρόνια όσο και οι οπές. Είναι αδύνατον να παρασκευασθούν ενδογενείς ηµιαγωγοί. Τα πραγµατικά υλικά περιέχουν πάντα πολύ µικρές ποσότητες προσµίξεων, που καθορίζουν τις ηλεκτρικές ιδιότητες των ηµιαγωγών. Τα ουδέτερα άτοµα τουge και του Si έχουν 4 ηλεκτρόνια σθένους και στη συνήθη κρυσταλλική δοµή κάθε άτοµο, π.χ. Ge, διαµορφώνει δεσµούς µε τα 4 πλησιέστερα προς αυτό άτοµα γερµανίου. Ας υποθέσουµε τώρα ότι ο κρύσταλλος,έστω του Ge,περιέχει µικρή συγκέντρωση (π.χ. της τάξης µερικών ατόµων ανά εκατοµµύριο άτοµα) πρόσµιξης πεντασθενών ατόµων, π.χ. φωσφόρου (Ρ). Τότε σε κάποιες θέσεις της κρυσταλλικής δοµής θα υπάρχουν άτοµα του πεντασθενούς Ρ, αντί ατόµων του τετρασθενούς Ge. Από τα 5 ηλεκτρόνια σθένους κάθε ατόµου Ρ, τα 4 σχηµατίζουν δεσµό µε ηλεκτρόνια σθένους 4 γειτονικών ατόµων Ge και θα περισσεύει ένα ηλεκτρόνιο του ατόµου του Ρ το οποίο θα είναι ασθενώς συνδεδεµένο µε τη θέση της κρυσταλλικής δοµής που βρίσκεται που βρίσκεται το άτοµο του Ρ. Τα ηλεκτρόνια αυτά έχουν επιτρεπόµενη ενέργεια πολύ κοντά στη στάθµη αγωγιµότητας, σχήµα 2-1 και µε πολύ µικρή ενέργεια µπορούν να διεγερθούν στη ζώνη αγωγιµότητας. Προσµίξεις αυτού του είδους ονοµάζονται προσµίξεις-δότες, διότι συνεισφέρουν εύκολα ηλεκτρόνια αγωγιµότητας, δεδοµένου ότι η ενεργειακή απόσταση της στάθµης του ηλεκτρονίου του δότη από τη ζώνη αγωγιµότητας είναι αρκετά µικρή, σχήµα 2-1(α), ώστε µεγάλο ποσοστό (πιθανότητα, σχέση 2-1) των δοτών να δώσουν µε θερµική διέγερση ηλεκτρόνια αγωγιµότητας. Σχήµα 2-1 Ενεργειακές στάθµες (α) δότη και (β) δέκτη. 5
7 Κάθε τέτοιο ηλεκτρόνιο αφήνει πίσω του στη θέση του ατόµου-πρόσµιξης θετικό ηλεκτρικό φορτίο. Αυτό το φορτίο ευρισκόµενο στο άτοµο-πρόσµιξη που συνιστά µέρος της κρυσταλλικής δοµής είναι µη µετακινήσιµο, δεν µπορεί να µετατοπιστεί υπό τη επίδραση ηλεκτρικού πεδίου, δεδοµένου ότι οι 4 δεσµοί των ηλεκτρονίων του ατόµου-πρόσµιξης µε τα 4 γειτονικά άτοµα είναι πλήρεις και δεν χωράει εκεί άλλο ηλεκτρόνιο. Κατά συνέπεια τα θετικά ηλεκτρικά φορτία στις θέσεις των ατόµων πρόσµιξης δεν συνιστούν οπές, είναι δεσµευµένα στην κρυσταλλική δοµή και δεν µπορούν να διακινηθούν, δεν συνεισφέρουν στην ηλεκτρική αγωγιµότητα του κρυστάλλου. Ο κρύσταλλος παραµένει ηλεκτρικά ουδέτερος, αφού κάθε ηλεκτρόνιο µου µεταβαίνει στη ζώνη αγωγιµότητας αφήνει ένα άτοµο µε ίσο και αντίθετο ηλεκτρικό φορτίο. εδοµένου ότι, στις περισσότερες περιπτώσεις η πυκνότητα των προσµίξεων και κατά συνέπεια η πυκνότητα των ηλεκτρονίων αγωγιµότητας που συνεισφέρουν είναι πολύ µεγαλύτερη από την πυκνότητα ηλεκτρονίων αγωγιµότητας που διατίθενται από το ενδογενές υλικό, έπεται ότι : α) ο αριθµός των ηλεκτρονίων αγωγιµότητας καθορίζεται πλήρως από τη συµβολή των δοτών και β) η πυκνότητα των ηλεκτρονίων αγωγιµότητας είναι πολύ µεγαλύτερη από την πυκνότητα των οπών, δεδοµένου ότι οι οπές αφήνουν µόνο τα ηλεκτρόνια αγωγιµότητας του ενδογενούς υλικού και αυτά των δοτών. Ως εκ τούτων, η ηλεκτρική αγωγιµότητα τέτοιων ηµιαγωγών καθορίζεται σχεδόν αποκλειστικά από τα ηλεκτρόνια και σε πολύ µικρότερο βαθµό από τις οπές. Τέτοιοι ηµιαγωγοί ονοµάζονται ηµιαγωγοί τύπου-n. Ας υποθέσουµε τώρα ότι πχ σε κρύσταλλο Ge προστίθεται µικρή ποσότητα πρόσµιξης τρισθενούς ατόµου (π.χ. βορίου, Β), οπότε κάποιες θέσεις της κρυσταλλικής δοµής καταλαµβάνονται από άτοµα της τρισθενούς πρόσµιξης, αντί των ατόµων του τετρασθενούς Ge. Σε κάθε µία από τις θέσεις αυτές υπάρχει ένα λιγότερο ηλεκτρόνιο σθένους απ ότι στις γειτονικές θέσεις που καταλαµβάνονται από άτοµα Ge. Αυτή η "άδεια υποδοχή" ηλεκτρονίου συνιστά οπή. Η επιτρεπόµενη ενεργειακά στάθµη σε αυτή τη θέση βρίσκεται µέσα στην απαγορευµένη ζώνη του κρυστάλλου και πολύ κοντά στη ζώνη σθένους, σχήµα 2-1(β). Τέτοιες προσµίξεις ονοµάζονται δέκτες. Η πιθανότητα να πληρωθεί η οπή αυτή από θερµικά διεγερµένα ηλεκτρόνια είναι µεγάλη και έτσι ένα µεγάλο ποσοστό των οπών των δεκτών πληρούνται µε θερµικά διεγερµένα ηλεκτρόνια. Αυτά προέρχονται από άλλες θέσεις οπών στον κρύσταλλο και κατά συνέπεια αφήνουν πίσω τους οπές. Έτσι για κάθε 6
8 δέκτη δηµιουργείται µία οπή. Τέτοιοι ηµιαγωγοί ονοµάζονται ηµιαγωγοί τύπου-p και σε αυτούς η ροή των οπών καθορίζει την ηλεκτρική αγωγιµότητα του κρυστάλλου. Οι πληρωµένες µε ηλεκτρόνια θέσεις των δεκτών συνιστούν ακίνητα ηλεκτρικά φορτία τα οποία ισοσταθµίζουν τα ηλεκτρικά φορτία των αντίστοιχων οπών. Ας φαντασθούµε ότι έρχονται σε "τέλεια επαφή" ηµιαγωγός τύπου-n µε ηµιαγωγό τύπου-p, όπως φαίνεται στο σχηµατικό διάγραµµα 2-2. Τέτοια διάταξη ονοµάζεται ζεύξη p-n (p-n juntion). Σχήµα 2-2 (α) ζεύξη p-n, (β) δεσµευµένα ηλεκτρικά φορτία q(x), (γ) ηλεκτρικό δυναµικό V(x) και (δ) ένταση του ηλεκτρικού πεδίου E(x). Στην επιφάνεια επαφής των δύο ηµιαγωγών συµβαίνουν τα εξής : Αριστερά της επιφάνειας όπου βρίσκεται ο κρύσταλλος τύπου n υπάρχει µεγάλη πυκνότητα ηλεκτρονίων αγωγιµότητας ενώ στα δεξιά, όπου ευρίσκεται ο κρύσταλλος τύπου-p, υπάρχει πρακτικά µηδενική πυκνότητα ηλεκτρονίων αγωγιµότητας. Υπάρχει δηλαδή στην επιφάνεια αυτή µεγάλη κλίση dn/dx, από τα αριστερά προς τα δεξιά, της πυκνότητας των ηλεκτρονίων αγωγιµότητας. Κατά συνέπεια θα υπάρξει διάχυση ηλεκτρονίων αγωγιµότητας από τον κρύσταλλο τύπου-n προς τον κρύσταλλο τύπου-p. Η έξοδος των ηλεκτρονίων αγωγιµότητας από τον κρύσταλλο τύπο-n αφήνει πίσω της δεσµευµένα, δηλαδή µη δυνάµενα να διακινηθούν, θετικά ηλεκτρικά φορτία στις θέσεις των ιοντισµένων δοτών. Ενώ προηγουµένως αυτά τα θετικά φορτία εξισορροπούνταν από τα αρνητικά φορτία των αντίστοιχων ηλεκτρονίων αγωγιµότητας, µετά την έξοδο των τελευταίων από τον κρύσταλλο τύπου-n 7
9 δηµιουργείται στον κρύσταλλο τύπου-n, αριστερά της επιφάνειας ζεύξης, στατικό, µη µετακινίσιµο θετικό ηλεκτρικό φορτίο. Τα ηλεκτρόνια που εισέρχονται στον κρύσταλλο τύπου-p συνδυάζονται γρήγορα µε οπές, συλλαµβάνονται από κάποιες από τις κενές θέσεις σθένους στον κρύσταλλο τύπου-p. Παρόµοια στην επιφάνεια ζεύξης υπάρχει κλίση dp/dx της πυκνότητας p των οπών, τώρα από τα δεξιά προς τα αριστερά, δεδοµένου ότι οι οπές υπάρχουν πρακτικά µόνο στον κρύσταλλο τύπου-p. Κατά συνέπεια θα υπάρχει διάχυση οπών από τον κρύσταλλο τύπου-p προς τον κρύσταλλο τύπου-n. Κάθε οπή που φεύγει έξω από τον κρύσταλλο τύπου-p αφήνει πίσω της µια θέση δέκτη που έχει συλλάβει ένα επιπλέον ηλεκτρόνιο και κατά συνέπεια συνιστά ένα δεσµευµένο, δηλαδή µη µετακινήσιµο, αρνητικό ηλεκτρονικό φορτίο. Έτσι ο συνδυασµός διάχυσης ηλεκτρονίων και οπών αναπτύσσει θετικό φορτίο χώρου στην πλευρά-n αριστερά της επιφάνειας της ζεύξης και αρνητικό φορτίο χώρου στην πλευρά-p δεξιά της ζεύξης. Αυτά τα φορτία χώρου αντιτίθενται στην περαιτέρω διάχυση ηλεκτρονίων και οπών και τελικά αποκαθίσταται ισορροπία, ευσταθής κατάσταση φορτίου q(x) στο χώρο, περίπου της µορφής του σχήµατος 2-2 (β). Η περιοχή στην οποία υπάρχουν αυτά τα φορτία χώρου ονοµάζεται περιοχή απεµπλουτισµού (depletion region) διότι σε αυτήν οι πυκνότητες ηλεκτρονίων και οπών είναι εξαιρετικά µικρές. Το ηλεκτρικό πεδίο που αναπτύσσεται από τα φορτία χώρου της περιοχής απεµπλουτισµού ωθεί οποιοδήποτε ηλεκτρόνιο αγωγιµότητας που εµφανίζεται εκεί προς τον κρύσταλλο τύπου-n και οποιαδήποτε οπή προς τον κρύσταλλο τύπου-p. Έτσι στην περιοχή απεµπλουτισµού εξαφανίζονται, πρακτικά δεν υπάρχουν, φορείς ηλεκτρικού ρεύµατος. Τα µόνα φορτία που υπάρχουν στην περιοχή απεµπλουτισµού είναι τα αµετακίνητα φορτία χώρου. εδοµένου ότι αυτά δεν συµβάλλουν στην ηλεκτρική αγωγιµότητα η περιοχή απεµπλουτισµού έχει µεγάλη ειδική ηλεκτρική αντίσταση σε σχέση µε τις γειτονικές της περιοχές. Το δυναµικό V(x) και η ένταση Ε(x) του ηλεκτρικού πεδίου είναι περίπου της µορφής των σχηµάτων 2-2(γ) και 2-2(δ) αντίστοιχα. Το δυναµικό V της επαφής της ζεύξης είναι της τάξης του ενός Volt. Εφόσον ιοντίζον σωµατίδιο αλληλεπιδράσει µε το υλικό εντός της απεµπλουτισµένης περιοχής, θα παραχθούν ζεύγη ηλεκτρονίων-οπών τα οποία θα ωθηθούν από το ηλεκτρικό πεδίο έξω από την απεµπλουτισµένη περιοχή, οπότε η κίνηση τους συνιστά ηλεκτρικό σήµα. Το εγγενές δυναµικό V =1Volt είναι ανεπαρκές για να προκληθεί γρήγορη κίνηση των φορτίων, οπότε φορτία µπορούν 8
10 εύκολα να χαθούν µε επανασύνδεση ηλεκτρονίων και οπών, µε αποτέλεσµα το συλλεγόµενο ηλεκτρικό φορτίο από την αλληλεπίδραση του ιοντίζοντος σωµατιδίου να µην επαρκεί για τη διάκρισή του από το υπόβαθρο που π.χ µπορεί να προέρχεται από θερµική διέγερση. Ως εκ τούτου εφαρµόζεται στη ζεύξη αυτό που ονοµάζεται αντίστροφη πόλωση µε την έννοια ότι το p-άκρο της ζεύξης καθίσταται αρνητικό σε σχέση µε το n-άκρο, η δε εφαρµοζόµενη διαφορά δυναµικού µπορεί να είναι από µερικές εκατοντάδες ως µερικές χιλιάδες Volt. ηµιουργία ζευγών ηλεκτρονίωνοπών από αλληλεπίδραση ιοντίζοντος σωµατιδίου έξω από την απεµπλουτισµένη περιοχή δεν θα δώσει σήµα διότι, σχήµα 2-2 (δ), η ένταση του ηλεκτρικού πεδίου εκεί είναι µηδενική και τα ηλεκτρόνια-οπές θα επανασυνδεθούν. Είναι λοιπόν προφανές ότι είναι επιθυµητή η αύξηση του όγκου της απεµπλουτισµένης περιοχής. Σε µονοδιάστατο πρόβληµα όπως αυτό που παριστάνεται στο σχήµα 2-2 αποδεικνύεται ότι το πάχος d της απεµπλουτισµένης περιοχής είναι ανάλογο της τετραγωνικής ρίζας του λόγου V/N, όπου V η τάση αντίστροφης πόλωσης και Ν η πυκνότητα προσµίξεων στον ηµιαγωγό. V d ~ N Πολλοί ανιχνευτές λειτουργούν µε τάσεις αντίστροφης πόλωσης τόσο µεγάλες, ώστε η περιοχή απεµπλουτισµού εκτείνεται σε ολόκληρο τον όγκο του κρυστάλλου οπότε ο ανιχνευτής ονοµάζεται πλήρως απεµπλουτισµένος. Βεβαίως αν η τάση αυτή υπερβεί κάποια τιµή, δηµιουργείται κατάρρευση της διόδου και διέλευση µεγάλων ρευµάτων, συχνά µε καταστροφικά για τον ανιχνευτή αποτελέσµατα Για δεδοµένη τάση V µπορεί να επιτευχθεί µεγαλύτερος όγκος απεµπλουτισµού µε µείωση της πυκνότητας N της πρόσµιξης. Η αναγκαίες µειώσεις έχουν επιτευχθεί µόνο σε κρυστάλλους γερµανίου, όπου πραγµατοποιούνται προσµίξεις της τάξης άτοµα αν m 3 που αντιστοιχούν σε επίπεδα µικρότερα του ενός ατόµου πρόσµιξης ανά άτοµα του κρυστάλλου. Ανιχνευτές κατασκευασµένοι από τέτοιο υπερκαθαρό γερµάνιο ονοµάζονται ενδογενείς (intrinsi) ανιχνευτές γερµανίου ή ανιχνευτές γερµανίου υψηλής καθαρότητας (HPGe). Τέτοιοι ανιχνευτές είναι διαθέσιµοι από τις αρχές τις δεκαετίας του 80 και είναι πλέον οι µοναδικοί που χρησιµοποιούνται για φασµατοµετρία υψηλής διακριτικής ικανότητας ακτινοβολιών µε µεγάλη εµβέλεια, όπως η ακτινοβολία γ. Λειτουργούν ως πλήρως απεµπλουτισµένοι ανιχνευτές, µε τυπικές τάσεις 3-5KV. Εξαιτίας του µικρού εύρους της απαγορευµένης ζώνης (Ε g = 0,7eV) είναι αδύνατη η 9
11 λειτουργία του ανιχνευτή σε θερµοκρασία δωµατίου, διότι το ρεύµα που προκύπτει από θερµική διέγερση είναι µεγάλο µε αποτέλεσµα του λόγου σήµατος προς θόρυβο. Ως εκ τούτου λειτουργούν σε θερµοκρασία υγρού αζώτου (77 ο Κ) µε χρήση µονωµένου δοχείου υγρού αζώτου και κατάλληλη διάταξη ψύξης του κρυστάλλου. Μεγάλοι ανιχνευτές υπερκαθαρού γερµανίου έχουν τιµές FWHM (Full Width Half Maximum) από 0,8 ως 1,2keV για φωτόνια 122keV και από 1,7 ως 2,3keV για φωτόνια 1333keV. Στο σχήµα 2-3 συγκρίνονται οι διακριτικές ικανότητες ανιχνευτών NaI (TI) και HPGe. Η πολύ καλύτερη διακριτική ικανότητα του HPGe φαίνεται π.χ. από το γεγονός ότι στις δύο "αιχµηρές κορυφές" που διακρίνει ο HPGe στις ενέργειες 1086keV και 112keV ο NaI(TI) δεν τις διακρίνει, τις "βλέπει" ως µια ευρεία κορυφή. Σχήµα 2-3 γ-φάσµα Εu 152. Το επάνω φάσµα µε ανιχνευτή NaI (TI), το κάτω φάσµα µε ανιχνευτή HPGe Πολύ σηµαντικό πλεονέκτηµα των ανιχνευτών του υπερκαθαρού γερµανίου που συνέβαλε αποφασιστικά στην επικράτησή τους στην γ-φασµατοµετρία υψηλής διακριτικής ικανότητας αποτελεί το γεγονός ότι µπορούν να αφεθούν µεταξύ των χρήσεων να θερµανθούν µέχρι θερµοκρασίες δωµατίου χωρίς να υποστούν βλάβες. Οι ηµιαγωγοί ανιχνευτές γερµανίου λιθίου (Ge(Li)) έχουν παρόµοιες ιδιότητες µε τους ανιχνευτές HPGe, αλλά ένα σοβαρό µειονέκτηµα : ο κρύσταλλος πρέπει να διατηρείται συνεχώς σε χαµηλή θερµοκρασία (77 ο Κ), διαφορετικά, αν 10
12 θερµανθεί σε θερµοκρασία δωµατίου συµβαίνει καταστροφική ανακατανοµή του λιθίου. Αυτός είναι ο λόγος που έχουν πλέον εγκαταληφθεί. 3. ΜΗΧΑΝΙΣΜΟΙ ΑΛΛΗΛΕΠΙ ΡΑΣΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ Γ ΜΕ ΤΗΝ ΥΛΗ ΚΑΙ Η ΕΠΙΡΡΟΗ ΤΟΥΣ ΣΤΗΝ ΑΠΟΚΡΙΣΗ ΤΩΝ ΑΝΙΧΝΕΥΤΩΝ 3.1. ΓΕΝΙΚΑ Παρά τον µεγάλο αριθµό των µηχανισµών µε τους οποίους µπορούν να αλληλεπιδράσουν τα φωτόνια µε την ύλη, µόνο τρεις είναι αυτοί που παίζουν κυρίαρχο ρόλο στη φασµατοσκοπία της ακτινοβολίας γ. Το φωτοηλεκτρικό φαινόµενο, η σκέδαση Compton και η δίδυµη γένεση. Και οι τρεις αυτές διαδικασίες οδηγούν στην ολική ή µερική µετατροπή της ενέργειας του φωτονίου σε ενέργεια ηλεκτρονίου, καταλήγοντας στην εξαφάνιση ή στη σκέδαση µέσω µιας µεγάλης µέσης γωνίας του αρχικού φωτονίου. Στις χαµηλές ενέργειες, µέχρι µερικές εκατοντάδες kev, το φωτοηλεκτρικό φαινόµενο είναι αυτό που κυριαρχεί ενώ στις ενέργειες πάνω από 5MeV επικρατεί η δίδυµη γένεση. Ανάµεσα σ αυτές τις τιµές η σκέδαση Compton είναι η πιο πιθανή εξέλιξη. Σηµαντικό ρόλο παίζει επίσης και ο ατοµικός αριθµός του υλικού µε το οποίο συµβαίνει η αλληλεπίδραση, ασκώντας ισχυρή επιρροή στις σχετικές πιθανότητες µεταξύ των τριών φαινοµένων. Οι βασικές αρχές των τριών µηχανισµών αναλύονται αµέσως παρακάτω ΦΩΤΟΗΛΕΚΤΡΙΚΟ ΦΑΙΝΟΜΕΝΟ Το φωτοηλεκτρικό φαινόµενο, που αναφέρεται συνήθως και ως φωτοηλεκτρική απορρόφηση (photoeletri absorption), αποτελεί την αλληλεπίδραση που οδηγεί στην ολική εξαφάνιση του αρχικού φωτονίου και στη θέση αυτού την εµφάνιση ενός φωτοηλεκτρονίου που προέρχεται από µία από τις ηλεκτρονιακές στοιβάδες του ατόµου-απορροφητή. Για συνηθισµένες ενέργειες η πιθανότερη στοιβάδα που θα δώσει το ηλεκτρόνιο είναι η Κ, για την οποία οι τυπικές τιµές για την ενέργεια σύνδεσης κυµαίνονται από µερικά kev, για υλικά µε µικρό ατοµικό αριθµό, µέχρι µερικές δεκάδες kev για υλικά µε µεγαλύτερο ατοµικό αριθµό. Αξίζει να σηµειωθεί πως η αλληλεπίδραση έχει να κάνει συνολικά µε ολόκληρο το άτοµο και δεν µπορεί να πραγµατοποιηθεί µε κάποιο ελεύθερο ηλεκτρόνιο. 11
13 Σχήµα Φωτοηλεκτρική απορρόφηση. Η κινητική ενέργεια του ηλεκτρονίου που αποδεσµεύεται είναι ίση µε την ενέργεια του προσπίπτοντος φωτονίου, µειωµένη κατά την ενέργεια σύνδεσης της στοιβάδας από την οποία προήλθε, δηλαδή : E = e 1 2 m u 2 = h. v - E b όπου, E b η ενέργεια σύνδεσης του φωτοηλεκτρονίου στην αρχική του στοιβάδα m η µάζα του ηλεκτρονίου και u η ταχύτητά του h η σταθερά του Plank v η συχνότητα του φωτονίου. Από αυτήν τη σχέση γίνεται φανερό πως για την πραγµατοποίηση του φαινοµένου υπάρχει κατώφλι ενέργειας του φωτονίου, δηλαδή θα πρέπει h.v E b. Για ενέργειες λοιπόν της ακτινοβολίας µερικών εκατοντάδων kev το φωτοηλεκτρόνιο φέρει το µεγαλύτερο µέρος του αρχικού φωτονίου. Το κενό, τώρα, που έχει δηµιουργηθεί από την εκποµπή του ηλεκτρονίου αναπληρώνεται σύντοµα από κάποιο ελεύθερο ηλεκτρόνιο ή από την ανακατανοµή των ηλεκτρονίων στο άτοµο. Γι αυτόν το λόγο το φωτοηλεκτρικό φαινόµενο συνοδεύεται και από την εκποµπή µιας ή και περισσότερων χαρακτηριστικών ακτίνων Χ. Στις περισσότερες περιπτώσεις, αυτές οι ακτινοβολίες απορροφούνται ξανά κοντά στην περιοχή δηµιουργίας τους µέσω φωτοηλεκτρικής απορρόφησης, εµπλέκοντας στοιβάδες χαµηλότερων ενεργειών σύνδεσης. Όπως προαναφέρθηκε, το φωτοηλεκτρικό φαινόµενο αποτελεί τον κυρίαρχο µηχανισµό της αλληλεπίδρασης των ακτίνων γ µε σχετικά χαµηλές ενέργειες, και εντείνεται µε την παρουσία υλικών µε µεγάλο ατοµικό αριθµό. Αν και γενικά δεν υπάρχει για κάθε άτοµο ξεχωριστά µία αναλυτική έκφραση της σχέσης µεταξύ της πιθανότητας του φαινοµένου µε τον ατοµικό του αριθµό (Ζ) και την ενέργεια της ακτινοβολίας (Ε γ ), κατά προσέγγιση ισχύει : 12
14 τ Z n onst (3) 3 Eγ όπου ο εκθέτης n κυµαίνεται µεταξύ του 4 και του 5, εξαρτώµενος από την περιοχή των ενεργειών που εξετάζουµε. Αυτή λοιπόν η επιρροή του ατοµικού αριθµού στην πιθανότητα πραγµατοποίησης της φωτοηλεκτρικής απορρόφησης οδηγεί στην επιλογή υλικών µε µεγάλο ατοµικό αριθµό (όπως ο µόλυβδος) ως θωράκιση έναντι της ακτινοβολίας γ, καθώς και για την κατασκευή ανιχνευτών. Συµπερασµατικά, θα µπορούσαµε να πούµε πως το φωτοηλεκτρικό φαινόµενο αποτελεί τον ιδανικό µηχανισµό αλληλεπίδρασης αν κάποιος θέλει να µετρήσει την ενέργεια του αρχικού φωτονίου. Το άθροισµα των κινητικών ενεργειών του φωτοηλεκτρονίου και των υπόλοιπων ηλεκτρονίων που ίσως ακολουθήσουν το αρχικό φαινόµενο πρέπει να ισούται µε την ενέργεια του προσπίπτοντος φωτονίου, µε την προϋπόθεση ότι εµπλέκονται µονοενεργειακά φωτόνια. Στην ιδανική περίπτωση λοιπόν που κανένα από τα ηλεκτρόνια δεν θα ξεφύγει από τον ανιχνευτή, η µορφή του φάσµατος θα είναι µία απλή συνάρτηση δέλτα και η κορυφή αυτή θα αντιπροσωπεύει την ενέργεια του αρχικού φωτονίου. Σχήµα Κατανοµή της κινητικής ενέργειας των ηλεκτρονίων του φωτοηλεκτρικού φαινοµένου, συνεπώς και της ενέργειας των προσπιπτόντων φωτονίων ΣΚΕ ΑΣΗ COMPTON Ο µηχανισµός της σκέδασης Compton λαµβάνει χώρα µεταξύ του προσπίπτοντος φωτονίου (inident photon) και ενός ηλεκτρονίου από το υλικό πρόσπτωσης. Το αποτέλεσµα είναι η κίνηση του σκεδασµένου φωτονίου (sattered photon), µε µικρότερη πλέον ενέργεια από αυτή που είχε αρχικά, κατά µία γωνία θ σε σχέση µε την αρχική του κατεύθυνση και η εκτίναξη του ηλεκτρονίου (reoil eletron), που αρχικά θεωρείται ακίνητο, απορροφώντας µέρος από την ενέργεια του φωτονίου. 13
15 Σχήµα Σκέδαση Compton. Το φαινόµενο µπορεί να θεωρηθεί σαν ελαστική σκέδαση του φωτονίου µε ελεύθερο ηλεκτρόνιο και χρησιµοποιώντας τις αρχές διατήρησης της ορµής και της ενέργειας, η ενέργεια του σκεδασµένου φωτονίου, χρησιµοποιώντας τα σύµβολα του σχήµατος, αποδεικνύεται πως δίνεται από τη σχέση : h v h v' = h v 1+ (1 osθ ) 2 m 0 (3) (3-1) όπου m. 0 2 η ενέργεια του ηλεκτρονίου σε κατάσταση ηρεµίας, µε τιµή 0,511ΜeV. Εποµένως η κινητική ενέργεια που αποδίδεται στο ηλεκτρόνιο ισούται µε : h v (1 osθ ) 2 m 0 E e = = h v h v' h v (3-2) h v 1+ (1 osθ ) 2 m0 Στις ακραίες περιπτώσεις, δηλαδή για θ 0 rad όπου το φωτόνιο συνεχίζει να κινείται στην ίδια σχεδόν διεύθυνση η ενέργεια που µεταφέρεται είναι η ελάχιστη, ενώ για θ=π rad όπου το φωτόνιο οπισθοσκεδάζεται παρατηρείται η µέγιστη δυνατή µεταφορά ενέργειας που µπορεί να συµβεί µέσω του µηχανισµού Compton (Compton edge). Έτσι, από τις σχέσεις 3-1, 3-2 προκύπτει : hv hv] θ =π = και hv m 0 14 E e ] θ = π 2hv 2 m0 = hv 2hv 1+ m0 2
16 Για τον λόγο ότι είναι πιθανό να συµβούν όλες οι γωνίες σκέδασης, η ενέργεια που µεταφέρεται στο ηλεκτρόνιο κυµαίνεται ανάµεσα στις ακραίες τιµές που βρέθηκαν παραπάνω. Μία τυπική λοιπόν µορφή υποβάθρου Compton για µονοενεργειακά φωτόνια δίνεται στο σχήµα που ακολουθεί. Σχήµα Υπόβαθρο Compton για µονοενεργειακή δέσµη φωτονίων, ενέργειας hv. Η απόσταση ανάµεσα στην κορυφή Compton και την φωτοκορυφή που αντιστοιχεί στην ενέργεια των ολικά απορροφούµενων φωτονίων δίνεται από τη σχέση : E hv E ] θ = e π hv = 2hv 1+ m Ι ΥΜΗ ΓΕΝΕΣΗ Ο τρίτος σηµαντικός µηχανισµός αλληλεπίδρασης είναι η δίδυµη γένεση. Σύµφωνα µε αυτόν η αλληλεπίδραση του φωτονίου µε την ύλη οδηγεί στην εξαφάνιση του πρώτου και στην δηµιουργία ενός ζεύγους ηλεκτρονίου-ποζιτρονίου. Καθώς η απαιτούµενη ενέργεια για τη δηµιουργία αυτού του ζεύγους είναι 2m. 0 2 συνεπάγεται πως για να είναι ενεργειακά πιθανό αυτό το φαινόµενο, χρειάζεται η ενέργεια του φωτονίου να είναι τουλάχιστον 1,02MeV. Έτσι, στην περίπτωση που ικανοποιείται αυτή η συνθήκη, η επιπλέον ενέργεια του φωτονίου θα αποδοθεί στο ζεύγος ως κινητική ενέργεια, δηλαδή: E e + E + e = hv 2m
17 Μετά την γένεσή τους, το ηλεκτρόνιο και το ποζιτρόνιο επιβραδύνονται µε διαδοχικές συγκρούσεις µε τα άτοµα του υλικού και η απόσταση που διανύουν µέσα σ αυτό είναι το πολύ µερικά χιλιοστά. Η παράσταση της κινητικής ενέργειας του ζεύγους είναι και πάλι µία συνάρτηση δέλτα της οποίας όµως η κορυφή εντοπίζεται µετατοπισµένη κατά 2m 0 2 πριν την ενέργεια hv του προσπίπτοντος φωτονίου. Σχήµα Κατανοµή της ενέργειας του ζεύγους ηλεκτρονίου-ποζιτρονίου. Η δίδυµη γένεση αποτελεί µία διαδικασία σχετικά περίπλοκη από την άποψη πως το ποζιτρόνιο δεν είναι ένα σταθερό σωµατίδιο. Καθώς η κινητική του ενέργεια µειωθεί αρκετά, η σύγκρουση του ποζιτρονίου µε κάποιο ηλεκτρόνιο οδηγεί στην σύντηξη των δύο σωµατιδίων, οπότε εξαφανίζονται και στη θέση τους εµφανίζονται δύο φωτόνια ενέργειας m 0 2 το καθένα (εξαΰλωση). Ο χρόνος που απαιτείται για να επιβραδυνθεί το ποζιτρόνιο και να εξαϋλωθεί είναι µικρός και εποµένως η ενέργεια από την εξαΰλωση θεωρούµε πως εµφανίζεται στην πραγµατικότητα ταυτόχρονα µε την αρχική αλληλεπίδραση ΑΠΟΚΡΙΣΗ ΑΝΙΧΝΕΥΤΩΝ ΣΥΜΦΩΝΑ ΜΕ ΤΟ ΜΕΓΕΘΟΣ ΤΟΥΣ "ΜΙΚΡΟΙ ΑΝΙΧΝΕΥΤΕΣ" Ως µικροί χαρακτηρίζονται οι ανιχνευτές, των οποίων το µέγεθος είναι µικρό σε σχέση µε την µέση ελεύθερη διαδροµή των δευτερευόντων γ-ακτινοβολιών, δηλαδή αυτών που προέκυψαν µετά τις αρχικές αλληλεπιδράσεις των προσπιπτόντων φωτονίων. Αυτές περιλαµβάνουν λοιπόν τα σκεδασµένα φωτόνια µαζί µε τα φωτόνια που προέκυψαν από την εξαΰλωση του ποζιτρονίου της δίδυµης γένεσης. Επειδή η µέση ελεύθερη διαδροµή αυτών των ακτίνων είναι της τάξης των µερικών εκατοστών δεχόµαστε πως αυτές διαφεύγουν από τον ανιχνευτή, εποµένως σε έναν τέτοιο 16
18 ανιχνευτή έχουµε µόνο απλές αλληλεπιδράσεις. Η ενέργεια, όµως, των διάφορων φορέων, δηλαδή του φωτοηλεκτρονίου, του ηλεκτρονίου από σκέδαση Compton, του ηλεκτρονίου της δίδυµης γένεσης και του ποζιτρονίου δεχόµαστε πως απορροφάται πλήρως εντός του όγκου του ανιχνευτή. Με αυτές τις παραδοχές τα φάσµατα που αντιπροσωπεύουν την εναπόθεση ενέργειας των ηλεκτρονίων φαίνονται στο σχήµα που ακολουθεί : Σχήµα Σχηµατική παράσταση ενός µικρού µεγέθους ανιχνευτή (πάνω) και τα φάσµατα που προκύπτουν ανάλογα µε τη δυνατότητα της προσπίπτουσας ακτινοβολίας να προκαλέσει ή όχι δίδυνη γένεση. Στο πρώτο φάσµα όπου η ενέργεια του φωτονίου δεν είναι ικανή για δίδυµη γένεση παρατηρούµε πως το φάσµα αποτελείται από την φωτοκορυφή (photopeak) και το υπόβαθρο Compton, όπως αυτά σχολιάστηκαν σε προηγούµενη ενότητα. Στο δεύτερο φάσµα όπου η ενέργεια της ακτινοβολίας είναι αρκετά µεγάλη ώστε να µπορεί να προκαλέσει δίδυµη γένεση παρατηρούµε στο φάσµα και µία επιπλέον κορυφή στη θέση hv _ 2m 0 2, που αναφέρεται ως κορυφή διπλής διαφυγής (double esape peak). Ο όρος διπλή διαφυγή αναφέρεται στο γεγονός ότι και τα δύο φωτόνια της εξαΰλωσης διέφυγαν του ανιχνευτή χωρίς άλλη αλληλεπίδραση. 17
19 ΠΟΛΥ "ΜΕΓΑΛΟΙ" ΑΝΙΧΝΕΥΤΕΣ. Ως αντίθετη περίπτωση από την παραπάνω έχουµε τους ανιχνευτές που το µέγεθός τους είναι τόσο µεγάλο ώστε ακόµη και ακτινοβολίες που προκύπτουν από διαδοχικές αλληλεπιδράσεις να παραµένουν στον ενεργό όγκο του ανιχνευτή. Αυτό οδηγεί σε ανιχνευτές µε διαστάσεις µερικών δεκάδων εκατοστών, µέγεθος µη πρακτικό για τις περισσότερες εφαρµογές. Στο σχήµα φαίνεται η ιστορία κάποιων φωτονίων που εισέρχονται στον ανιχνευτή, δηλαδή η αρχική αλληλεπίδρασή τους µε το υλικό και όποια άλλη µπορεί να ακολουθήσει την πρώτη. Σχήµα Σχηµατική παράσταση ενός µεγάλου ανιχνευτή, των πιθανών αλληλεπιδράσεων που λαµβάνουν χώρα µέσα σ αυτόν (αριστερά), και της απόκριση του (δεξιά) Καθώς λοιπόν τίποτα δεν διαφεύγει από τον ανιχνευτή η απόκριση του είναι ένας παλµός στην θέση hv, που αντιστοιχεί στην ενέργεια της προσπίπτουσας ακτινοβολίας. Θα πρέπει να αναφερθεί πως ο χρόνος που διαρκεί η εξέλιξη καθενός από τα επιµέρους φαινόµενα µιας ολόκληρης ιστορίας, είναι πολύ µικρότερος σε σχέση µε τη δυνατή απόκριση του ανιχνευτή. Έτσι παρά το γεγονός πως η συνολική εναπόθεση ενέργειας είναι το άθροισµα των επιµέρους εναποθέσεων από κάθε φαινόµενο, ο ανιχνευτής αντιλαµβάνεται τη δράση ενός φωτονίου σαν µία φωτοηλεκτρική απορρόφηση που πραγµατοποιήθηκε σε ένα µόνο στάδιο. 18
20 ΑΝΙΧΝΕΥΤΕΣ ΜΕΣΑΙΟΥ ΜΕΓΕΘΟΥΣ. Οι ανιχνευτές που χρησιµοποιούνται για κοινές εφαρµογές δεν µπορούν να χαρακτηριστούν ούτε ως µικροί άλλα ούτε και ως µεγάλοι. Συνδυάζουν τις ιδιότητες και των δύο αυτών ανιχνευτών και επιπλέον εµφανίζουν και κάποια χαρακτηριστικά που οφείλονται σε µερική απορρόφηση των φωτονίων από δευτερεύουσες αλληλεπιδράσεις. Τα διάφορα πιθανά γεγονότα που µπορούν να συµβούν εντός του ανιχνευτή και τα αντίστοιχα φάσµατα που προκύπτουν φαίνονται στο σχήµα Σχήµα Σχηµατική παράσταση ενός µεσαίου µεγέθους ανιχνευτή (πάνω) και τα φάσµατα που προκύπτουν ανάλογα µε τη δυνατότητα της προσπίπτουσας ακτινοβολίας να προκαλέσει ή όχι δίδυνη γένεση. Επισηµαίνονται τα τµήµατα που προκύπτουν από φωτόνια που διέφυγαν κατόπιν πολλαπλών σκεδάσεων. Αυτό που παρατηρούµε είναι πως µετά την κορυφή Compton δεν υπάρχει το διάκενο που υπήρχε στους µικρούς ανιχνευτές. Η ύπαρξη αυτής της περιοχής στα φάσµατα προέρχεται από τα φωτόνια που έχουν υποστεί πολλαπλές σκεδάσεις (multiple sattered photons), εναπόθεσαν µεγάλο µέρος της ενέργειάς τους, µεγαλύτερο από αυτό που αντιστοιχεί στην κορυφή Compton, και στη συνέχεια διέφυγαν από τον ανιχνευτή. Επιπλέον, στην περίπτωση όπου είναι δυνατή η δίδυµη γένεση υπάρχει η πιθανότητα ένα από τα δύο φωτόνια της εξαΰλωσης να διαφύγει εκτός του ανιχνευτή. Το αποτέλεσµα αυτού είναι η ύπαρξη της κορυφής που 19
21 αναφέρεται ως κορυφή απλής διαφυγής (single esape peak) και η οποία βρίσκεται κατά m 0 2 (0,511MeV) χαµηλότερα της φωτοκορυφής. Σαφώς είναι πιθανή και η ύπαρξη της κορυφής διπλής διαφυγής η οποία εξετάστηκε στους µικρούς ανιχνευτές. Τέλος, ακόµη ένα πιθανό ενδεχόµενο είναι το ένα ή και τα δύο εξαϋλωµένα φωτόνια να υποστούν σκέδαση Compton και να εγκαταλείψουν τον ανιχνευτή µε αποτέλεσµα η συνεισφορά αυτού του φαινοµένου στο φάσµα να εντοπίζεται στην περιοχή ανάµεσα στην κορυφή διπλής διαφυγής και της φωτοκορυφής. 4. ΜΕΘΟ ΟΣ MONTE CARLO 4.1. ΓΕΝΙΚΑ Ως ορισµός µπορεί να ειπωθεί συνοπτικά πως η µέθοδος Monte Carlo είναι µια στοχαστική προσοµοίωση τις οποίας η στατιστική δειγµατοληψία βασίζεται στην επιλογή τυχαίων αριθµών, σε αναλογία µε το ρίξιµο του ζαριού σε ένα καζίνο στοιχηµάτων. Η οµοιότητα των µεθόδων Monte Carlo µε τα τυχερά παιχνίδια είναι µεγάλη, µόνο που εδώ το "παιχνίδι" είναι ένα φυσικό σύστηµα, και το αποτέλεσµα του παιχνιδιού δεν είναι χρήµατα ή µάρκες αλλά η λύση κάποιου προβλήµατος. Η µέθοδος Monte Carlo µπορεί να χρησιµοποιηθεί ώστε να αναπαράγει θεωρητικά µια στατιστική διαδικασία (όπως η αλληλεπίδραση των ατοµικών σωµατιδίων µε την ύλη), και είναι ιδιαίτερα χρήσιµη σε σύνθετα προβλήµατα που δεν µπορούν να σχεδιαστούν και να αναπαραχθούν από υπολογιστικούς κώδικες που χρησιµοποιούν ντετερµινιστικές µεθόδους. Τα διάφορα πιθανοτικά γεγονότα που συνθέτουν µια διαδικασία εξοµοιώνονται διαδοχικά, και η κατανοµές των πιθανοτήτων που διέπουν αυτά τα γεγονότα δειγµατοληπτούνται στατιστικά ώστε να περιγραφεί συνολικά κάποιο φαινόµενο. Γενικά, η εξοµοίωση πραγµατοποιείται µε τη βοήθεια ηλεκτρονικού υπολογιστή καθώς ο αριθµός των δοκιµών και των τυχαίων αριθµών που απαιτούνται για να περιγράψουν επαρκώς ή έστω ικανοποιητικά κάποιο φαινόµενο είναι πολύ µεγάλος. Οι µέθοδοι Monte Carlo χρησιµοποιούνται ευρύτατα τις τελευταίες δεκαετίες, λόγω της ανάπτυξης της τεχνολογίας των ηλεκτρονικών υπολογιστών, και αναπτύχθηκαν τόσο ώστε να θεωρούνται µια αριθµητική µέθοδος ικανή να εφαρµοστεί και στις πιο περίπλοκες εφαρµογές. Ενδεικτικά αναφέρουµε την 20
22 εφαρµογή της µεθόδου στον σχεδιασµό πυρηνικών αντιδραστήρων, στην εξελικτική πορεία των αστέρων, στην πρόβλεψη του δείκτη των χρηµατιστηρίων κ.α. Σε πολλές εφαρµογές Monte Carlo η φυσική διεργασία προσοµοιώνεται απ ευθείας, χωρίς να χρειάζεται να γράψουµε τις διαφορικές εξισώσεις που περιγράφουν την συµπεριφορά του συστήµατος. Η µόνη απαίτηση είναι το φυσικό ή µαθηµατικό σύστηµα να περιγράφεται από συναρτήσεις πυκνότητας πιθανότητας. Εφόσον αυτές είναι γνωστές η προσοµοίωση Monte Carlo µπορεί να προχωρήσει δειγµατοληπτώντας τυχαία από τις συναρτήσεις. Με αυτόν τον τρόπο διεξάγεται ένας αριθµός προσοµοιώσεων, τα λεγόµενα histories και το επιθυµητό αποτέλεσµα λαµβάνεται σαν ένας µέσος όρος από τον αριθµό των παρατηρήσεων. Σε πολλές πρακτικές εφαρµογές, µπορεί να προβλεφθεί το στατιστικό σφάλµα σε αυτό το µέσο αποτέλεσµα και εποµένως να υπολογισθεί και ο αριθµός των σεναρίων (histories) που χρειάζονται για να επιτευχθεί το επιθυµητό σφάλµα. Τυπικά, η ακρίβεια µιας προσοµοίωσης Monte Carlo είναι ανάλογη µε την τετραγωνική ρίζα των σεναρίων που χρησιµοποιήθηκαν. Καθώς οι δυνατότητες των σύγχρονων υπολογιστών είναι µεγάλες µπορούµε και εφαρµόζουµε την µέθοδο σε πολύπλοκα προβλήµατα µε µεγάλη ακρίβεια, µιας και µπορούµε να "τρέξουµε" έναν πολύ µεγάλο αριθµό σεναρίων. Όσων αφορά την εφαρµογή της µεθόδου για τη µελέτη της κίνησης των σωµατιδίων και τις διάφορες αλληλεπιδράσεις τους µε την ύλη αυτή θεωρείται εξαιρετικά ρεαλιστική. Συνίσταται στην ακριβή παρακολούθηση καθ όλη τη διάρκεια της ζωής καθενός από τα πολλά σωµατίδια, που εκπέµπονται από µια πηγή ή δηµιουργούνται κατά την πορεία κάποιου άλλου σωµατιδίου, από τη στιγµή της γέννησής του ως τον θάνατό του µε κάποια από τις καταληκτικές διαδικασίες, δηλαδή απορρόφηση, διαφυγή κτλ. Οι κατανοµές των διάφορων πιθανοτήτων δειγµατοληπτούνται τυχαία και χρησιµοποιώντας τα δεδοµένα κίνησης - µεταφοράς των σωµατιδίων προσδιορίζεται η έκβαση σε κάθε φάση της ζωής του. 21
23 Σχήµα 4.1 Παρακολούθηση ενός νετρονίου κατά την εισαγωγή του σε ένα υλικό που µπορεί να υποστεί διάσπαση. Το σχήµα 4.1 αντιπροσωπεύει την τυχαία "ιστορία" ενός νετρονίου σε ένα υλικό στο οποίο µπορεί να συµβεί κάποια διάσπαση. Τυχαίοι αριθµοί, επιλέγονται για να καθορίσουν ποιά θα είναι (αν ποτέ συµβεί) και πού θα λάβει χώρα µια αλληλεπίδραση µε το υλικό, βασιζόµενη στους κανόνες της φυσικής και στις πιθανότητες που διέπουν την συµπεριφορά του σωµατιδίου εντός του υλικού. Στο συγκεκριµένο παράδειγµα το νετρόνιο πραγµατοποιεί µια κρούση στο σηµείο 1 και κατόπιν σκεδάζεται προς την κατεύθυνση που δηλώνεται µε τη συνεχή γραµµή. Η κατεύθυνση στην οποία το νετρόνιο συνεχίζει την πορεία του προέκυψε τυχαία από την κατανοµή της πιθανότητας που αφορά την πορεία του νετρονίου µετά από µία σκέδαση. Ταυτόχρονα είχαµε και την παραγωγή ενός φωτονίου, το οποίο όµως αποθηκεύεται προσωρινά για να εξεταστεί και να αναλυθεί αργότερα. Στο σηµείο 2 λαµβάνει χώρα µία διάσπαση που οδηγεί στην εξαφάνιση του αρχικού νετρονίου και στην εκποµπή δύο νέων νετρονίων και ενός φωτονίου. Το ένα νετρόνιο και το φωτόνιο αποθηκεύονται για να αναλυθούν αργότερα. Το άλλο νετρόνιο απορροφάται στο σηµείο 3 και τερµατίζεται η ιστορία του. Στη συνέχεια το αποθηκευµένο νετρόνιο αποδεσµεύεται και κατόπιν τυχαίας δειγµατοληψίας εγκαταλείπει το υλικό στο σηµείο 4. Όσο για το φωτόνιο που προέκυψε από τη διάσπαση, αρχικά σκεδάζεται στο σηµείο 5 και στη συνέχεια διαφεύγει από το υλικό στο σηµείο 6. Τέλος, αποδεσµεύεται και το φωτόνιο που προέκυψε από την κρούση του αρχικού νετρονίου και σύµφωνα µε τυχαίες πάλι διαδικασίες απορροφάται στο σηµείο 7, ολοκληρώνοντας έτσι την ιστορία του αρχικού νετρονίου. 22
24 4.2. Ο ΚΩ ΙΚΑΣ MCNP 4A ΓΕΝΙΚΑ ΣΤΟΙΧΕΙΑ ΓΙΑ ΤΟΝ ΚΩ ΙΚΑ Για την διεξαγωγή των προσοµοιώσεων της παρούσας εργασίας χρησιµοποιήθηκε ο κώδικας Monte Carlo MCNP, έκδοση 4A. Ο MCNP είναι ένας κώδικας Monte Carlo γενικής χρήσης, µε δυνατότητες προσοµοίωσης προβληµάτων µεταφοράς νετρονίων, ηλεκτρονίων και φωτονίων, µε συνεχείς ενέργειες, σε γενικευµένες γεωµετρίες µε εξάρτηση από τον χρόνο. Μπορεί να χρησιµοποιηθεί σε αρκετά προβλήµατα αλληλεπίδρασης, νετρονίων µόνο, φωτονίων µόνο, ηλεκτρονίων µόνο, συνδυασµού φωτονίων και νετρονίων όπου τα φωτόνια παράγονται από αλληλεπιδράσεις των νετρονίων, νετρονίων - φωτονίων - ηλεκτρονίων, φωτονίων - ηλεκτρονίων, ηλεκτρονίων - φωτονίων, µε την ύλη. Η ενέργεια των νετρονίων µπορεί να κυµανθεί από MeV έως 20 MeV, ενώ των ηλεκτρονίων και φωτονίων από 1 kev έως 1000 MeV. Ο χρήστης δηµιουργεί ένα αρχείο εισόδου το οποίο στη συνέχεια διαβάζεται από τον MCNP. Αυτό το αρχείο περιέχει πληροφορίες σχετικά µε το πρόβληµα σε τοµείς όπως : Ο καθορισµός της γεωµετρίας. Η περιγραφή των υλικών και η επιλογή των µικροσκοπικών διατοµών. Η θέση και τα χαρακτηριστικά της πηγής νετρονίων, φωτονίων ή ηλεκτρονίων. Η µορφή και ο τύπος των αποτελεσµάτων. Οι τεχνικές ελαχιστοποίησης της διακύµανσης που χρησιµοποιούνται για την αύξηση της απόδοσης. Οι πληροφορίες αυτές διαβιβάζονται στον κώδικα και µε τον τρόπο αυτόν ξεκινά η επεξεργασία. Τα αποτελέσµατα της επεξεργασίας αποθηκεύονται σε ένα αρχείο εξόδου, και στη συνέχεια από την επεξεργασία των αποτελεσµάτων προκύπτουν τα ζητούµενα µεγέθη. Όσων αφορά τους τύπους των ανιχνευτών, ο MCNP παρέχει επτά καθορισµένους ανιχνευτές νετρονίων, έξι καθορισµένους ανιχνευτές φωτονίων και τέσσερις καθορισµένους ανιχνευτές ηλεκτρονίων, οι οποίοι όµως γενικά µπορούν να διαφοροποιηθούν από τον χρήστη. Επειδή το ενδιαφέρον µας επικεντρώνεται στη µελέτη φωτονίων θα αναφερθούµε αποκλειστικά στους ανιχνευτές φωτονίων και συγκεκριµένα στον απαριθµητή ύψους παλµών (pulse height tally). Οι υπόλοιποι πέντε τύποι ανιχνευτών υπολογίζουν τα εξής : 23
25 Ρεύµα επιφάνειας (σωµατίδια) Ροή από επιφάνεια (1/m 2 ) Ροή σε έναν όγκο (1/m 2 ) Ροή σε σηµείο (1/m 2 ) Εναπόθεση ενέργειας (MeV/g) ΑΠΑΡΙΘΜΗΤΗΣ ΎΨΟΥΣ ΠΑΛΜΩΝ (PULSE HEIGHT TALLY, F8) Ο απαριθµητής ύψους παλµών παρέχει την ενεργειακή κατανοµή των παλµών που δηµιουργούνται στο κελί που ορίζουµε ως ανιχνευτή, ενώ µπορεί επίσης να υπολογίζει την εναπόθεση ενέργειας σε κάποιο κελί. Γενικά, ο συγκεκριµένος τύπος ανιχνευτή είναι ανάλογος µε τον πραγµατικό ανιχνευτή, καθώς η διαµέριση των ενεργειών που ορίζουµε αντιστοιχεί στα κανάλια του πολυκαναλικού αναλυτή στα οποία καταµετρούνται τα σωµατίδια ανάλογα µε την ενέργεια που καθένα από αυτά εναποθέτει στον κρύσταλλο του ανιχνευτή. Για παράδειγµα, ας υποθέσουµε ότι από µία πηγή εκπέµπονται 100 φωτόνια ενέργειας 10 kev και 10 από αυτά εισέρχονται στο κελί του ανιχνευτή. Επιπλέον, υποθέτουµε πως το πρώτο φωτόνιο εναποθέτει ενέργεια 1 kev, το δεύτερο 2 kev, και ούτω καθ εξής µέχρι το δέκατο φωτόνιο που εναποθέτει 10 kev. Έτσι, το αποτέλεσµα της καταµέτρησης του ανιχνευτή θα είναι ένας παλµός στη διαµέριση του ενός kev, ένας παλµός στη διαµέριση των 2 kev, και συνεχίζοντας ανάλογα, ένας παλµός σε κάθε διαµέριση µέχρι τα 10 kev. 24
26 5. ΠΡΟΣΟΜΟΙΩΣΗ ΑΝΙΧΝΕΥΤΗ HPGE 5.1. ΠΕΡΙΓΡΑΦΗ ΤΟΥ ΑΝΙΧΝΕΥΤΗ ΚΑΙ ΤΟΥ ΑΝΤΙΣΤΟΙΧΟΥ ΕΞΟΠΛΙΣΜΟΥ Ο ανιχνευτής που προσοµοιώθηκε είναι ο φορητός ανιχνευτής υπερκαθαρού γερµανίου EGPC R της εταιρείας Eurisys Mesures. Πρόκειται για έναν κυλινδρικό, οµοαξονικό, τύπου-p ανιχνευτή υπερκαθαρού γερµανίου µε απόδοση 35% σε σχέση µε ανιχνευτή NaI, διαστάσεων 3x3, στα 1332keV. Ο κρύσταλλος του έχει διάµετρο 58mm και ύψος 62mm. Αµέσως µετά τον κρύσταλλο ακολουθούν ο προενισχυτής και τα διάφορα άλλα ηλεκτρονικά συστήµατα του ανιχνευτή. Επίσης ο κρύσταλλος ενώνεται µε ένα δοχείο, χωρητικότητας περίπου 5 λίτρων, που περιέχει υγρό άζωτο και το οποίο παρέχει την απαραίτητη ψύξη στον κρύσταλλο (σχήµα 5.1). Στις µετρήσεις που πραγµατοποιήθηκαν το φάσµα συλλέγεται στον φορητό πολυκαναλικό αναλυτή (MCA, MultiChannel Analyzer) InSpetor 2000 της εταιρείας Canberra, µε 8192 κανάλια, και στη συνέχεια µε τη χρήση του προγράµµατος Genie το φάσµα αποθηκεύεται σε φορητό υπολογιστή. Πιο συγκεκριµένα, ο αναλυτής δέχεται τους παλµούς που στέλνει ο κρύσταλλος και καθώς οι παλµοί αυτοί είναι ανάλογοι της ενέργειας του προσπίπτοντος φωτονίου τους ταξινοµεί στα αντίστοιχα κανάλια. Έτσι προκύπτει ένα φάσµα, αριθµού χτύπων συναρτήσει της ενέργειας. Ο πολυκαναλικός αναλυτής, τέλος, είναι αυτός που τροφοδοτεί τον κρύσταλλο µε θετική υψηλή τάση 4000V µέσω µιας µπαταρίας ή σύνδεσης µε ρευµατοδότη. Σχήµα 5.1 ύο απόψεις του ανιχνευτή υπερκαθαρού γερµανίου που χρησιµοποιήθηκε για τις µετρήσεις και που προσοµοιώθηκε µε τον κώδικα MCNP. Στο κάτω µέρος των φωτογραφιών φαίνεται και ο πολυκαναλικός αναλυτής. 25
27 5.2. ΥΛΟΠΟΙΗΣΗ ΤΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Για την προσοµοίωση του ανιχνευτή µε τον κώδικα MCNP χρησιµοποιήθηκε το µοντέλο του σχήµατος 5.2, και πρόκειται για ένα σχετικά απλό µοντέλο που δίνει τα βασικά χαρακτηριστικά του ανιχνευτή. Αξίζει να σηµειωθεί πως ενώ αρχικά χρησιµοποιήθηκε ένα µοντέλο που προσοµοίωνε µε µεγάλη λεπτοµέρεια τα διάφορα µέρη του ανιχνευτή διαπιστώθηκε πως η διαφορές που είχαµε στα λαµβανόµενα φάσµατα ήταν ασήµαντες. Καθώς όµως το πρόγραµµα του απλούστερου µοντέλου "έτρεχε" γρηγορότερα από αυτό του πολυπλοκότερου, µπορούσαµε να επιτύχουµε τον απαιτούµενο αριθµό προσοµοιώσεων σε µικρότερο χρονικό διάστηµα, γι αυτό και αποτέλεσε την τελική επιλογή µας. Σχήµα 5.2 Σκαρίφηµα του µοντέλου του ανιχνευτή όπως προσοµοιώθηκε µε τον κώδικα MCNP. Εισάγοντας λοιπόν στο πρόγραµµα τα χαρακτηριστικά του ανιχνευτή όπως αυτά δόθηκαν από τον κατασκευαστή έγινε προσπάθεια να προσοµοιωθεί το φάσµα του λάβαµε από σηµειακή πηγή 137 Cs. Να αναφέρουµε πως χρησιµοποιήθηκαν δύο είδη πηγών για τις διάφορες προσοµοιώσεις. Σηµειακές, για να αναπαράγουν όσο το δυνατόν καλύτερα τα πειραµατικά φάσµατα που προέκυψαν από σηµειακές πηγές και επίπεδες για τον προσδιορισµό της απόδοσης του ανιχνευτή. 26
28 5.3. ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΑΠΟ ΟΣΗΣ ΑΝΙΧΝΕΥΤΗ Για τον πειραµατικό προσδιορισµό της απόδοσης του ανιχνευτή χρησιµοποιήθηκε πηγή 152 Eu. Σύµφωνα µε τα στοιχεία της πηγής η ενεργότητά της στις ήταν 4,114 MBq. Για την εύρεση της ενεργότητας της πηγής στις , όπου πραγµατοποιήθηκε η µέτρηση, χρησιµοποιήθηκε η σχέση : Α(t) = A 0. e -λt, (5-1) όπου Α 0 η αρχική ενεργότητα της πηγής Α(t) η ενεργότητα της πηγής µετά από χρόνο t λ η σταθερά διάσπασης του υλικού, η οποία µε τη σειρά της ισούται µε ln 2 / t, όπου t 1/2 ο χρόνος ηµιζωής του υλικού. 1/ 2 Γνωρίζοντας το χρόνο ηµιζωής του 152 Eu (t 1/2 = 4933 ηµέρες) η ενεργότητα της πηγής βρέθηκε τελικά ίση µε 3,255 MBq. Η µέτρηση διήρκησε 1000s, χρόνος ικανοποιητικός για τη λήψη ενός καλοσχηµατισµένου φάσµατος και πραγµατοποιήθηκε σε χώρο όπου απουσίαζαν τα πολλά εµπόδια, ώστε να έχουµε όσο το δυνατόν µικρότερη επιρροή από σκεδασµένα φωτόνια. Επιπλέον η πηγή τοποθετήθηκε σε απόσταση τεσσάρων µέτρων µπροστά από το µπροστινό παράθυρο του ανιχνευτή για να µπορέσουµε να θεωρήσουµε πως στον ανιχνευτή καταµετρούνται µόνο τα ασκέδαστα, παράλληλης δέσµης φωτόνια πού πέφτουν κάθετα στον ανιχνευτή. Και αυτό γιατί, για φορητό ανιχνευτή Ge, η πειραµατική απόδοση σε κάποια ενέργεια ορίζεται ως το πηλίκο του ρυθµού των χτύπων της φωτοκορυφής προς τη ροή των ασκέδαστων φωτονίων της πηγής. Η ασκέδαστη προσπίπτουσα ροή στον ανιχνευτή σε απόσταση r από την πηγή δίνεται από τη σχέση : φ S r = e µ 2 4π r [γ. m -2. s -1 ] (5-2) όπου S η ένταση της πηγής σε φωτόνια/s r η απόσταση ανάµεσα στην πηγή και τον ανιχνευτή σε m µ ο συντελεστής εξασθένισης στον αέρα για τη συγκεκριµένη ενέργεια των ακτίνων γ σε m -1 27
29 Επειδή όµως συνήθως χρησιµοποιείται ο µαζικός συντελεστής εξασθένισης, δηλαδή το πηλίκο του συντελεστή εξασθένισης διά την πυκνότητα του υλικού µε µονάδες τα m 2 /gr, η παραπάνω σχέση 5-2 παίρνει τη µορφή : S φ = 4π r 2 e µ ( ) ρ r ρ Στις τιµές των ενεργειών για τις οποίες δεν υπήρχε απ ευθείας τιµή για τον µαζικό συντελεστή εξασθένησης (Πίνακας , Εισαγωγή στην πυρηνική τεχνολογία, Μ. Αντωνόπουλος-Ντόµης (1985)) πραγµατοποιήθηκε γραµµική παρεµβολή µεταξύ των κατάλληλων τιµών. Πρέπει να αναφερθεί πως η απόδοση του ανιχνευτή µετριέται για συγκεκριµένη διεύθυνση πρόσπτωσης της δέσµης των φωτονίων και στη δική µας περίπτωση πρόκειται για δέσµη κάθετη στο µπροστινό παράθυρο του ανιχνευτή. Λόγω της σηµαντικής διαφοράς µεταξύ των τιµών της πειραµατικής απόδοσης και της απόδοσης που προκύπτει από τον προσοµοιωµένο ανιχνευτή χρησιµοποιώντας τα χαρακτηριστικά που δόθηκαν από τον κατασκευαστή, θεωρήθηκε σκόπιµο να γίνουν κάποιες αλλαγές ώστε να προκύψει σύµπτωση των πειραµατικών τιµών και των τιµών που προέκυψαν από την προσοµοίωση pm/φωτόνια. m -2. s πειραµατικά νεκρή ζώνη 0.5mm Ενέργεια (kev) Σχήµα Σύγκριση της απόδοσης του προσοµοιωµένου ανιχνευτή για νεκρή ζώνη πάχους 0,5mm µε την πειραµατική απόδοση. 28
30 Πιο συγκεκριµένα, ορίζοντας αρχικά τη νεκρή ζώνη να εκτείνεται µέχρι τα 0,5mm παρατηρήθηκε µία υπερεκτίµηση της απόδοσης του ανιχνευτή (σχήµα 5.3-1). Θα έπρεπε λοιπόν να µειώσουµε την απόδοση του προσοµοιωµένου ανιχνευτή, δηλαδή να µειώσουµε τον ενεργό όγκο του κρύσταλλου ή αντίστοιχα να αυξήσουµε την νεκρή ζώνη εις βάρος του ενεργού όγκου. Αυξάνοντας λοιπόν την νεκρή ζώνη του κρύσταλλου µε βήµατα των 0.5mm και σχηµατίζοντας τις καµπύλες απόδοσης διαπιστώθηκε πως µέχρι περίπου τα 1000keV υπάρχει καλή σύµπτωση του πειραµατικού µε το προσοµοιωµένο φάσµα για εύρος νεκρής ζώνης στα 1.5mm, ενώ για τις ενέργειες πάνω από τα 1000 kev η πειραµατική καµπύλη συµπίπτει µε αυτή που προέκυψε για νεκρή ζώνη 1mm. Η εξήγηση που θα µπορούσε να δοθεί γι αυτό το γεγονός είναι πως γενικά η νεκρή ζώνη παίζει έναν σηµαντικό ρόλο στην απόδοση του ανιχνευτή για τις χαµηλότερες ενέργειες, σε αντίθεση µε τα φωτόνια υψηλότερων ενεργειών που θα διαπεράσουν την ζώνη αυτή χωρίς να προκαλέσουν σχεδόν καµία αλληλεπίδραση. Για τον λόγο λοιπόν ότι στις χαµηλές ενέργειες υπήρχε καλύτερη σύµπτωση των καµπυλών της απόδοσης για πάχος νεκρής ζώνης 1.5mm, η τιµή αυτή επιλέχθηκε τελικά για τον προσδιορισµό της νεκρής ζώνης. Στο σχήµα φαίνονται οι πειραµατικές τιµές της απόδοσης για διάφορες ενέργειες φωτονίων και αυτές που προέκυψαν από προσοµοιώσεις µε διαφορετικές νεκρές ζώνες χρησιµοποιώντας τον κώδικα ΜCNP pm/φωτόνια. m -2. s πειραµατικά χωρίς νεκρή ζώνη νεκρή ζώνη 0.5mm νεκρή ζώνη 1mm νεκρή ζώνη 1.5mm νεκρή ζώνη 2mm Ενέργεια (kev) Σχήµα Καµπύλες απόδοσης όπως προέκυψαν από τον προσοµοιωµένο ανιχνευτή, για διάφορες θεωρήσεις της νεκρής ζώνης, και από την πειραµατική µέτρηση µε χρήση σηµειακής πηγής 152 Εu. 29
31 Θα µπορούσαµε γενικά να αναφέρουµε πως η απόδοση που προκύπτει πειραµατικά διαφέρει από αυτήν της προσοµοίωσης και για κάποιους άλλους λόγους. Ένας από αυτούς έχει να κάνει µε την αδυναµία του πραγµατικού ανιχνευτή να ξεχωρίζει δύο γεγονότα τα οποία συµβαίνουν ταυτόχρονα ή σχεδόν ταυτόχρονα, όπως π.χ την έλευση δύο φωτονίων που έχουν εκπεµφθεί ταυτόχρονα από µία πηγή. Το αποτέλεσµα θα είναι η καταγραφή ενός συνολικού γεγονότος κάτι το οποίο δεν συµβαίνει στον MCNP διότι µε την τεχνική της αποθήκευσης (banking) εξετάζεται ξεχωριστά η εξέλιξη κάθε φαινόµενου. Ακόµη, εξαιτίας της µορφής του κρυστάλλου, το ηλεκτρικό πεδίο που εφαρµόζεται ενδέχεται να είναι χαµηλότερο σε κάποιες περιοχές του, και να οδηγεί µε αυτόν τον τρόπο σε µία µη αποδοτική συλλογή των φορέων που δηµιουργούνται από την επίδραση των διάφορων ακτινοβολιών. Επιπλέον, το γεγονός να µην έχει ψυχθεί ο κρύσταλλος για µεγάλο χρονικό διάστηµα µπορεί να οδηγήσει σε µία µικρή αύξηση της νεκρής ζώνης εξαιτίας της κίνησης του λιθίου προς το εσωτερικό του κρύσταλλου ΜΕΤΑΒΑΤΙΚΗ ΖΩΝΗ ΣΤΟΝ ΚΡΥΣΤΑΛΛΟ ΤΟΥ ΑΝΙΧΝΕΥΤΗ Ένα καλά προσοµοιωµένο φάσµα θα πρέπει όχι µόνο να προβλέπει σωστά την φωτοκορυφή των ολικά απορροφηµένων φωτονίων, δηλαδή αυτών που ορίζουν την απόδοση του ανιχνευτή, αλλά και τη µερική απορρόφηση των φωτονίων στον κρύσταλλο του ανιχνευτή. Τυπικά, το µεγαλύτερο µέρος ενός φάσµατος δηµιουργείται από µερικώς απορροφούµενα φωτόνια, δηλαδή φωτόνια που υπέστησαν µία ή και περισσότερες σκεδάσεις στο εσωτερικό του κρύσταλλου, εναπόθεσαν κάποιο ποσό ενέργειας και στη συνέχεια διέφυγαν από αυτόν. Στο σχήµα δίνεται το πειραµατικό φάσµα από µία πηγή 137 Cs που τοποθετήθηκε µπροστά από το µπροστινό παράθυρο του ανιχνευτή, και το αντίστοιχο φάσµα προσοµοίωσης µε χρήση του MCNP. Η νεκρή ζώνη στην συγκεκριµένη προσοµοίωση τέθηκε ίση µε 1.5mm και συνολικά πραγµατοποιήθηκε η παρακολούθηση και η καταγραφή του αποτελέσµατος από τη εκποµπή 10 εκατοµµυρίων φωτονίων από την πηγή. Η διαµέριση των ενεργειών ορίστηκε να γίνει ανά 0,25keV. Η συνεισφορά της σκεδασµένης ακτινοβολίας από τους τοίχους, το πάτωµα και γενικότερα από τα αντικείµενα του περιβάλλοντα χώρου θεωρούµε πως είναι αµελητέα, διότι η πηγή βρίσκεται σε πολύ µικρή απόσταση από τον ανιχνευτή. 30
32 χτύποι (κανονικοποιηµένοι στην κορυφή) πειραµατικό φάσµα φάσµα από MCNP Ενέργεια (kev) Σχήµα Σύγκριση πειραµατικού και προσοµοιωµένου φάσµατος για πηγή 137 Cs. Στο συγκεκριµένο φάσµα αλλά και σε όλα τα υπόλοιπα που ακολούθησαν έγινε κανονικοποίηση µεταξύ του πειραµατικού και του προσοµοιωµένου φάσµατος στο παράθυρο της φωτοκορυφής. Πιο συγκεκριµένα, έγινε διαίρεση του αριθµού χτύπων της φωτοκορυφής µε το πηλίκο της διαίρεσης του αθροίσµατος των χτύπων σε όλο το εύρος της φωτοκορυφής του προσοµοιωµένου φάσµατος προς το αντίστοιχο άθροισµα του πειραµατικού. Κατόπιν, µε αυτό το πηλίκο διαιρέθηκαν και όλοι οι υπόλοιποι χτύποι του φάσµατος. Ο λόγος που οδήγησε σ αυτό είναι για να µπορέσουµε να κάνουµε άµεση σύγκριση των φασµάτων και να διαπιστώσουµε τη διαφορά της µορφής του φάσµατος που αντιστοιχεί στο φαινόµενο Compton. Από το σχήµα που προηγήθηκε φαίνεται πως γενικά δεν υπάρχει σύµπτωση των δύο φασµάτων παρά µόνο µία καλή προσέγγιση από τα 300keV µέχρι τα 550keV. ιαπιστώθηκε λοιπόν ότι υπάρχει αδυναµία του κώδικα, έτσι όπως αυτός υλοποιήθηκε για την πρώτη προσοµοίωση, να περιγράψει το κοµµάτι του φάσµατος που αντιστοιχεί στις χαµηλές ενέργειες και το κοµµάτι πριν την φωτοκορυφή. Στους τύπου-p οµοαξονικούς ανιχνευτές Ge η παραδοσιακή µέθοδος κατασκευής της εξωτερικής επαφής είναι η εξάχνωση λιθίου στην επιφάνεια του κρυστάλλου για το σχηµατισµό του n στρώµατος. Αυτό αντιπροσωπεύει τη νεκρή ζώνη. Στην προσοµοίωση θεωρήθηκε ότι η συλλογή φορτίου από απορρόφηση φωτονίων στη νεκρή ζώνη είναι µηδενική, ενώ η απόδοση από τη συλλογή φορτίου στην ενεργό περιοχή, δηλαδή τον ενεργό όγκο του κρύσταλλου, ίση µε τη µονάδα. Όµως, η νεκρή ζώνη µπορεί να θεωρηθεί πως αποτελείται από δύο περιοχές. Μία µε µηδενική απόδοση συλλογής φορτίου και µία µε αυξανόµενη απόδοση. Αυτό 31
33 συµβαίνει διότι, εξαιτίας της διάχυσης, έστω και µικρής, του λιθίου προς το εσωτερικό του κρυστάλλου έχουµε την εµφάνιση µιας µεταβατικής ζώνης στην οποία ένα απορροφηµένο φωτόνιο δε θα εµφανιστεί µε την πραγµατική του ενέργεια αλλά µε µικρότερη. Επειδή όµως τα απορροφηµένα στην µεταβατική ζώνη φωτόνια δεν συνεισφέρουν στην φωτοκορυφή των ολικά απορροφηµένων χτύπων δεχόµαστε πως δεν υπάρχει µεταβολή στην απόδοση του ανιχνευτή. Έτσι, στη διαδικασία εύρεσης της απόδοσης του ανιχνευτή ενώ θεωρήσαµε ανενεργή ζώνη τα 1,5mm, χωρίς να λάβουµε υπόψη τη ζώνη µετάβασης, διαπιστώθηκε καλή σύµπτωση της πειραµατικής µε την καµπύλη της απόδοσης από την προσοµοίωση. Τελικά, ορίστηκε η νεκρή ζώνη ίση µε 0,5mm, όπως δηλαδή δόθηκε από τον κατασκευαστή, και η ζώνη µετάβασης ίση µε 1mm ώστε να έχουµε συνολικά τα 1,5mm που βρέθηκαν από την προσοµοίωση. Το επόµενο βήµα που έπρεπε να γίνει ήταν η εύρεση της συνάρτησης µετάβασης η οποία θα καθόριζε την µεταβολή της απόδοσης εντός της ζώνης µετάβασης. Η συνάρτηση αυτή πρέπει να έχει µηδενική τιµή εντός της νεκρής ζώνης, να αυξάνεται όσο προχωράµε εσωτερικά της ζώνης µετάβασης και να πλησιάζει την τιµή 1 στο τέλος της µεταβατικής περιοχής. Επιπλέον θα πρέπει να είναι αντιστρόφως ανάλογη της συγκέντρωσης του λιθίου στη ζώνη µετάβασης. Η συνάρτηση που προκύπτει από αυτές τις θεωρήσεις είναι µία σιγµοειδής συνάρτηση της οποίας όµως η βέλτιστη µορφή βρίσκεται κατόπιν δοκιµών και σύγκρισης των φασµάτων που προκύπτουν µε το πειραµατικό φάσµα. (1) Για τον λόγο ότι δεν ήταν δυνατόν να οριστεί µία συνάρτηση στο κείµενο του κώδικα που αυτόµατα θα έκανε την προσοµοίωση της ζώνης µετάβασης κατά το τρέξιµο του MCNP δόθηκε η εξής λύση. Τα πρώτα 0,5mm από την επιφάνεια του κρύσταλλου ορίστηκαν ως η ανενεργή περιοχή του λιθίου και το 1 χιλιοστό της ζώνης µετάβασης χωρίστηκε σε 10 επιµέρους ζώνες, µε πάχος 0,1mm η καθεµία. Σε κάθε µία από αυτές της ζώνες τοποθετήθηκε ένας ανιχνευτής που θα µετρούσε τους χτύπους που θα συνέβαιναν στην αντίστοιχη ζώνη. Σαφώς τοποθετήθηκε και ένας ανιχνευτής στον ενεργό όγκο του γερµανίου. Στη συνέχεια, από το αρχείο εξόδου δηµιουργούσαµε το φάσµα που αντιστοιχούσε στον κάθε ανιχνευτή, συνεπώς και στο αντίστοιχο κοµµάτι της ζώνης µετάβασης, και κατόπιν το πολλαπλασιάζαµε µε την κατάλληλη τιµή από την συνάρτηση µετάβασης. Αυτό που πετυχαίναµε ουσιαστικά ήταν η µετατόπιση των φασµάτων της ζώνης µετάβασης προς τις χαµηλότερες ενέργειες, καθώς,όπως αναφέρθηκε στην ανάλυση που προηγήθηκε, τα φωτόνια στη 32
34 ζώνη αυτή µετρούνται µε ενέργειες χαµηλότερες από την πραγµατική τους. Τα επεξεργασµένα αυτά φάσµατα προστιθέµενα στο φάσµα που προέκυπτε από τον ενεργό όγκο του γερµανίου µας έδιναν το τελικό φάσµα. Από τη σύγκριση ανάµεσα στο πειραµατικό και προσοµοιωµένο φάσµα για το 137 Cs, χρησιµοποιώντας διάφορες µορφές σιγµοειδών συναρτήσεων για την ζώνη µετάβασης, βρέθηκε ότι η συγκεκριµένη συνάρτηση θα πρέπει να αυξάνεται αργά κοντά στη νεκρή ζώνη και σε µικρή απόσταση από αυτήν να αυξάνεται απότοµα παίρνοντας τις τιµές που πλησιάζουν την µοναδιαία απόδοση. Με αυτήν την διαπίστωση χρησιµοποιήθηκε η συνάρτηση που φαίνεται στο σχήµα και το αντίστοιχο φάσµα φαίνεται στο αµέσως επόµενο σχήµα. 1,2 1 0,8 απόδοση 0,6 0,4 0, ,2 0,4 0,6 0,8 1 1,2 απόσταση από τη νεκρή ζώνη (mm) Σχήµα Σιγµοειδής συνάρτηση µετάβασης. Με κόκκινο σηµειώνονται οι τιµές µε τις οποίες πολλαπλασιάζονται τα φάσµατα των επιµέρους µεταβατικών ζωνών χτύποι (κανονικοποιηµένοι στην κορυφή) πειραµατικό φάσµα φάσµα από MCNP Ενέργεια (kev) Σχήµα Σύγκριση πειραµατικού και προσοµοιωµένου φάσµατος στο οποίο χρησιµοποιήθηκε η συνάρτηση µετάβασης του σχήµατος
35 Από το προηγούµενο σχήµα φαίνεται καθαρά η πολύ καλύτερη σύµπτωση των δύο φασµάτων σε σχέση µε αυτά στο οποίο δεν χρησιµοποιήθηκε συνάρτηση µετάβασης (σχήµα 5.4.1),και ειδικά στις ενέργειες από τα 100keV µέχρι τα 550keV µε εξαίρεση την κορυφή Compton. Αυτό όµως που εύκολα κάποιος διακρίνει και που αλλοιώνει την γενικά καλή εικόνα του φάσµατος είναι κάποιες αιχµές σε διάφορα σηµεία του φάσµατος. Αυτές αποτελούν ουσιαστικά τη µετατόπιση των φωτοκορυφών από τα φάσµατα των επιµέρους µεταβατικών ζωνών προς τις χαµηλότερες ενέργειες, καθώς καθένα από αυτά πολλαπλασιάζεται µε µία διακριτή τιµή από τη συνάρτηση µετάβασης (σχήµα 5.4-2). Όσο µεγαλύτερος είναι ο αριθµός που διαιρούµε τη ζώνη µετάβασης, τόσες περισσότερες τιµές χρησιµοποιούνται από τη συνάρτηση µετάβασης, και τόσο περισσότερο προσεγγίζεται η τελευταία µε συνεχείς τιµές, κάτι που θα αποτελούσε την ιδανική περίπτωση. Για να αποµακρυνθούν οι ανεπιθύµητες κορυφές από το φάσµα θεωρήθηκε συνάρτηση µετάβασης η οποία από τις αρχικές τις τιµές µεταπηδούσε απότοµα σ αυτές που πλησίαζαν τη µονάδα, µετατοπίζοντας έτσι στα άκρα τις ενδιάµεσες τιµές, οι οποίες ήταν υπεύθυνες για τις αιχµές. Η σιγµοειδής εποµένως συνάρτηση αντικαταστάθηκε από ένα είδος βηµατικής συνάρτησης της οποίας η µορφή φαίνεται µε πράσινη γραµµή στο αριστερό διάγραµµα, ενώ δεξιά φαίνονται σε µεγέθυνση τα τµήµατα που µας ενδιαφέρουν. Σχήµα Τροποποίηση της σιγµοειδούς συνάρτησης σε "βηµατική". 34
Η απορρόφηση των φωτονίων από την ύλη βασίζεται σε τρεις µηχανισµούς:
 AΣΚΗΣΗ 5 ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΑΚΤΙΝΩΝ-γ (1 o ΜΕΡΟΣ) - Βαθµονόµηση και εύρεση της απόδοσης του ανιχνευτή - Μέτρηση της διακριτικότητας ενέργειας του ανιχνευτή 1. Εισαγωγή Η ακτινοβολία -γ είναι ηλεκτροµαγνητική
AΣΚΗΣΗ 5 ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΑΚΤΙΝΩΝ-γ (1 o ΜΕΡΟΣ) - Βαθµονόµηση και εύρεση της απόδοσης του ανιχνευτή - Μέτρηση της διακριτικότητας ενέργειας του ανιχνευτή 1. Εισαγωγή Η ακτινοβολία -γ είναι ηλεκτροµαγνητική
Προσομοίωση Ανιχνευτή Γερμανίου με τη μέθοδο Monte Carlo.
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Προσομοίωση Ανιχνευτή
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Προσομοίωση Ανιχνευτή
Πρόοδος µαθήµατος «οµικής και Χηµικής Ανάλυσης Υλικών» Χρόνος εξέτασης: 3 ώρες
 21 Οκτωβρίου 2009 Πρόοδος µαθήµατος «οµικής και Χηµικής Ανάλυσης Υλικών» Χρόνος εξέτασης: 3 ώρες 1) α. Ποια είναι η διαφορά µεταξύ της ιονίζουσας και της µη ιονίζουσας ακτινοβολίας; β. Ποιες είναι οι γνωστότερες
21 Οκτωβρίου 2009 Πρόοδος µαθήµατος «οµικής και Χηµικής Ανάλυσης Υλικών» Χρόνος εξέτασης: 3 ώρες 1) α. Ποια είναι η διαφορά µεταξύ της ιονίζουσας και της µη ιονίζουσας ακτινοβολίας; β. Ποιες είναι οι γνωστότερες
ΒΙΟΦΥΣΙΚΗ. Αλληλεπίδραση ιοντίζουσας ακτινοβολίας και ύλης.
 ΒΙΟΦΥΣΙΚΗ Αλληλεπίδραση ιοντίζουσας ακτινοβολίας και ύλης http://eclass.uoa.gr/courses/md73/ Ε. Παντελής Επικ. Καθηγητής, Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών. Εργαστήριο προσομοίωσης 10-746
ΒΙΟΦΥΣΙΚΗ Αλληλεπίδραση ιοντίζουσας ακτινοβολίας και ύλης http://eclass.uoa.gr/courses/md73/ Ε. Παντελής Επικ. Καθηγητής, Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών. Εργαστήριο προσομοίωσης 10-746
«Συγκριτική μελέτη in-situ γ-φασματοσκοπίας και τεχνικών Monte
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ «Συγκριτική μελέτη
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ «Συγκριτική μελέτη
P = E /c. p γ = E /c. (p) 2 = (p γ ) 2 + (p ) 2-2 p γ p cosθ E γ. (pc) (E γ ) (E ) 2E γ E cosθ E m c Eγ
 Σκέδαση Compton Το φαινόμενο Compton περιγράφει ργρ τη σκέδαση ενός φωτονίου από ένα ελεύθερο ατομικό ηλεκτρόνιο: γ + e γ + e. To φωτόνιο δεν εξαφανίζεται μετά τη σκέδαση αλλά αλλάζει κατεύθυνση και ενέργεια.
Σκέδαση Compton Το φαινόμενο Compton περιγράφει ργρ τη σκέδαση ενός φωτονίου από ένα ελεύθερο ατομικό ηλεκτρόνιο: γ + e γ + e. To φωτόνιο δεν εξαφανίζεται μετά τη σκέδαση αλλά αλλάζει κατεύθυνση και ενέργεια.
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΑΚΤΙΝΩΝ-γ 1.
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΑΚΤΙΝΩΝ-γ 1.
Μελέτη της ακτινοβολίας γ µε τη βοήθεια απαριθµητή Geiger - Muller
 ΑΠ1 Μελέτη της ακτινοβολίας γ µε τη βοήθεια απαριθµητή Geiger - Muller 1. Σκοπός Στην άσκηση αυτή γίνεται µελέτη της εξασθενήσεως της ακτινοβολίας γ (ραδιενεργός πηγή Co 60 ) µε την βοήθεια απαριθµητή
ΑΠ1 Μελέτη της ακτινοβολίας γ µε τη βοήθεια απαριθµητή Geiger - Muller 1. Σκοπός Στην άσκηση αυτή γίνεται µελέτη της εξασθενήσεως της ακτινοβολίας γ (ραδιενεργός πηγή Co 60 ) µε την βοήθεια απαριθµητή
Ανακλώμενο ηλεκτρόνιο KE = E γ - E γ = E mc 2
 Σκέδαση Compton Το φαινόμενο Compton περιγράφει τη σκέδαση ενός φωτονίου από ένα ελεύθερο ατομικό ηλεκτρόνιο: γ + γ +. To φωτόνιο δεν εξαφανίζεται μετά τη σκέδαση αλλά αλλάζει κατεύθυνση και ενέργεια.
Σκέδαση Compton Το φαινόμενο Compton περιγράφει τη σκέδαση ενός φωτονίου από ένα ελεύθερο ατομικό ηλεκτρόνιο: γ + γ +. To φωτόνιο δεν εξαφανίζεται μετά τη σκέδαση αλλά αλλάζει κατεύθυνση και ενέργεια.
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ 1 Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε την ηλεκτροµαγνητική θεωρία
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ 1 Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε την ηλεκτροµαγνητική θεωρία
Ξεκινώντας από την εξίσωση Poisson για το δυναμικό V στο στατικό ηλεκτρικό πεδίο:
 1 2. Διοδος p-n 2.1 Επαφή p-n Στο σχήμα 2.1 εικονίζονται δύο μέρη ενός ημιαγωγού με διαφορετικού τύπου αγωγιμότητες. Αριστερά ο ημιαγωγός είναι p-τύπου και δεξια n-τύπου. Και τα δύο μέρη είναι ηλεκτρικά
1 2. Διοδος p-n 2.1 Επαφή p-n Στο σχήμα 2.1 εικονίζονται δύο μέρη ενός ημιαγωγού με διαφορετικού τύπου αγωγιμότητες. Αριστερά ο ημιαγωγός είναι p-τύπου και δεξια n-τύπου. Και τα δύο μέρη είναι ηλεκτρικά
Ανιχνευτές σωματιδίων
 Ανιχνευτές σωματιδίων Προκειμένου να κατανοήσουμε την φύση του πυρήνα αλλά και να καταγράψουμε τις ιδιότητες των στοιχειωδών σωματιδίων εκτός των επιταχυντικών συστημάτων και υποδομών εξίσου απαραίτητη
Ανιχνευτές σωματιδίων Προκειμένου να κατανοήσουμε την φύση του πυρήνα αλλά και να καταγράψουμε τις ιδιότητες των στοιχειωδών σωματιδίων εκτός των επιταχυντικών συστημάτων και υποδομών εξίσου απαραίτητη
ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2006 ΕΚΦΩΝΗΣΕΙΣ
 ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 6 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1 ο Στις ερωτήσεις 1- να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε την
ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 6 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1 ο Στις ερωτήσεις 1- να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε την
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΤΗΣ ΡΑ ΙΟΧΗΜΕΙΑΣ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΤΗΣ ΡΑ ΙΟΧΗΜΕΙΑΣ Ατοµικός αριθµός (Ζ): Μαζικός αριθµός (Α) : Ισότοπα : Ισοβαρή: Νοuκλίδιο: Ολικός αριθµός των πρωτονίων ενός πυρήνα. Χαρακτηρίζει το στοιχείο. Άθροισµα του αριθµού
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΤΗΣ ΡΑ ΙΟΧΗΜΕΙΑΣ Ατοµικός αριθµός (Ζ): Μαζικός αριθµός (Α) : Ισότοπα : Ισοβαρή: Νοuκλίδιο: Ολικός αριθµός των πρωτονίων ενός πυρήνα. Χαρακτηρίζει το στοιχείο. Άθροισµα του αριθµού
ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ. Εργαστήριο Φυσικής IΙ. Μελέτη της απόδοσης φωτοβολταϊκού στοιχείου με χρήση υπολογιστή. 1. Σκοπός. 2. Σύντομο θεωρητικό μέρος
 ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ 1. Σκοπός Το φωτοβολταϊκό στοιχείο είναι μία διάταξη ημιαγωγών η οποία μετατρέπει την φωτεινή ενέργεια που προσπίπτει σε αυτήν σε ηλεκτρική.. Όταν αυτή φωτιστεί με φωτόνια κατάλληλης συχνότητας
ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ 1. Σκοπός Το φωτοβολταϊκό στοιχείο είναι μία διάταξη ημιαγωγών η οποία μετατρέπει την φωτεινή ενέργεια που προσπίπτει σε αυτήν σε ηλεκτρική.. Όταν αυτή φωτιστεί με φωτόνια κατάλληλης συχνότητας
Οι ακτίνες Χ είναι ηλεκτροµαγνητική ακτινοβολία µε λ [10-9 -10-12 m] (ή 0,01-10Å) και ενέργεια φωτονίων kev.
![Οι ακτίνες Χ είναι ηλεκτροµαγνητική ακτινοβολία µε λ [10-9 -10-12 m] (ή 0,01-10Å) και ενέργεια φωτονίων kev. Οι ακτίνες Χ είναι ηλεκτροµαγνητική ακτινοβολία µε λ [10-9 -10-12 m] (ή 0,01-10Å) και ενέργεια φωτονίων kev.](/thumbs/28/12687661.jpg) Οι ακτίνες Χ είναι ηλεκτροµαγνητική ακτινοβολία µε λ [10-9 -10-12 m] (ή 0,01-10Å) και ενέργεια φωτονίων kev. To ορατό καταλαµβάνει ένα πολύ µικρό µέρος του ηλεκτροµαγνητικού φάσµατος: 1,6-3,2eV. Page 1
Οι ακτίνες Χ είναι ηλεκτροµαγνητική ακτινοβολία µε λ [10-9 -10-12 m] (ή 0,01-10Å) και ενέργεια φωτονίων kev. To ορατό καταλαµβάνει ένα πολύ µικρό µέρος του ηλεκτροµαγνητικού φάσµατος: 1,6-3,2eV. Page 1
ΑΛΛΗΛΕΠΙΔΡΑΣΕΙΣ ΑΚΤΙΝΩΝ Χ ΚΑΙ ΥΛΗΣ
 ΑΛΛΗΛΕΠΙΔΡΑΣΕΙΣ ΑΚΤΙΝΩΝ Χ ΚΑΙ ΥΛΗΣ Όταν οι ακτίνες Χ περνούν μέσα από την ύλη (πχ το σώμα του ασθενή) μπορεί να συμβεί οποιοδήποτε από τα 4 φαινόμενα που αναλύονται στις επόμενες σελίδες. Πρέπει να γίνει
ΑΛΛΗΛΕΠΙΔΡΑΣΕΙΣ ΑΚΤΙΝΩΝ Χ ΚΑΙ ΥΛΗΣ Όταν οι ακτίνες Χ περνούν μέσα από την ύλη (πχ το σώμα του ασθενή) μπορεί να συμβεί οποιοδήποτε από τα 4 φαινόμενα που αναλύονται στις επόμενες σελίδες. Πρέπει να γίνει
Απορρόφηση ακτινοβολίας-β από την ύλη
 ΑΣΚΗΣΗ 3 Απορρόφηση ακτινοβολίας-β από την ύλη 1. Εισαγωγή Η β-διάσπαση είναι το συλλογικό όνοµα τριών φαινοµένων, στα οποία εκπέµπονται ηλεκτρόνια και ποζιτρόνια υψηλής ενέργειας ή πραγµατοποιείται σύλληψη
ΑΣΚΗΣΗ 3 Απορρόφηση ακτινοβολίας-β από την ύλη 1. Εισαγωγή Η β-διάσπαση είναι το συλλογικό όνοµα τριών φαινοµένων, στα οποία εκπέµπονται ηλεκτρόνια και ποζιτρόνια υψηλής ενέργειας ή πραγµατοποιείται σύλληψη
ΑΡΧΕΣ ΜΕΤΡΗΣΗΣ ΠΥΡΗΝΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ
 ΑΡΧΕΣ ΜΕΤΡΗΣΗΣ ΠΥΡΗΝΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ 1. ΧΡΗΣΕΙΣ ΚΑΙ ΠΛΕΟΝΕΚΤΗΜΑΤΑ ΡΑΔΙΟΝΟΥΚΛΙΔΙΩΝ 2. ΠΡΟΪΟΝΤΑ ΡΑΔΙΕΝΕΡΓΟΥ ΔΙΑΣΠΑΣΗΣ 3. ΠΡΟΕΛΕΥΣΗ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΑΚΤΙΝΩΝ-γ 4. ΑΝΙΧΝΕΥΣΗ ΑΚΤΙΝΩΝ-γ (ΑΝΟΡΓΑΝΟΙ ΚΡΥΣΤΑΛΛΙΚΟΙ
ΑΡΧΕΣ ΜΕΤΡΗΣΗΣ ΠΥΡΗΝΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ 1. ΧΡΗΣΕΙΣ ΚΑΙ ΠΛΕΟΝΕΚΤΗΜΑΤΑ ΡΑΔΙΟΝΟΥΚΛΙΔΙΩΝ 2. ΠΡΟΪΟΝΤΑ ΡΑΔΙΕΝΕΡΓΟΥ ΔΙΑΣΠΑΣΗΣ 3. ΠΡΟΕΛΕΥΣΗ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΤΩΝ ΑΚΤΙΝΩΝ-γ 4. ΑΝΙΧΝΕΥΣΗ ΑΚΤΙΝΩΝ-γ (ΑΝΟΡΓΑΝΟΙ ΚΡΥΣΤΑΛΛΙΚΟΙ
ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝ. ΠΑΙ ΕΙΑΣ ΑΤΟΜΙΚΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο.
 ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝ. ΠΑΙ ΕΙΑΣ ΑΤΟΜΙΚΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο. Στις ερωτήσεις 1-5 επιλέξτε την πρόταση που είναι σωστή. 1) Το ηλεκτρόνιο στο άτοµο του υδρογόνου, το οποίο βρίσκεται στη θεµελιώδη κατάσταση: i)
ΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝ. ΠΑΙ ΕΙΑΣ ΑΤΟΜΙΚΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 ο. Στις ερωτήσεις 1-5 επιλέξτε την πρόταση που είναι σωστή. 1) Το ηλεκτρόνιο στο άτοµο του υδρογόνου, το οποίο βρίσκεται στη θεµελιώδη κατάσταση: i)
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 3 ΙΟΥΛΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 3 ΙΟΥΛΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 3 ΙΟΥΛΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης
ΗΛΕΚΤΡΟΝΙΚΑ Ι ΚΕΦΑΛΑΙΟ 1 Ο :ΗΜΙΑΓΩΓΟΙ
 ΗΛΕΚΤΡΟΝΙΚΑ Ι ΚΕΦΑΛΑΙΟ 1 Ο :ΗΜΙΑΓΩΓΟΙ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΟΜΗ. ΕΝΔΟΓΕΝΕΙΣ ΗΜΙΑΓΩΓΟΙ Δομή του ατόμου Σήμερα γνωρίζουμε ότι η ύλη αποτελείται από ενώσεις ατόμων, δημιουργώντας τις πολυάριθμες χημικές ενώσεις
ΗΛΕΚΤΡΟΝΙΚΑ Ι ΚΕΦΑΛΑΙΟ 1 Ο :ΗΜΙΑΓΩΓΟΙ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΟΜΗ. ΕΝΔΟΓΕΝΕΙΣ ΗΜΙΑΓΩΓΟΙ Δομή του ατόμου Σήμερα γνωρίζουμε ότι η ύλη αποτελείται από ενώσεις ατόμων, δημιουργώντας τις πολυάριθμες χημικές ενώσεις
ΕΚΦΩΝΗΣΕΙΣ. Στις παρακάτω ερωτήσεις 1-4, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 Γ' ΛΥΚΕΙΟΥ ΕΠΙΛΟΓΗΣ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ ΦΥΣΙΚΗ Στις παρακάτω ερωτήσεις, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ο λαµπτήρας φθορισµού:
Γ' ΛΥΚΕΙΟΥ ΕΠΙΛΟΓΗΣ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ ΦΥΣΙΚΗ Στις παρακάτω ερωτήσεις, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ο λαµπτήρας φθορισµού:
1.1 Ηλεκτρονικές ιδιότητες των στερεών. Μονωτές και αγωγοί
 1. Εισαγωγή 1.1 Ηλεκτρονικές ιδιότητες των στερεών. Μονωτές και αγωγοί Από την Ατομική Φυσική είναι γνωστό ότι οι επιτρεπόμενες ενεργειακές τιμές των ηλεκτρονίων είναι κβαντισμένες, όπως στο σχήμα 1. Σε
1. Εισαγωγή 1.1 Ηλεκτρονικές ιδιότητες των στερεών. Μονωτές και αγωγοί Από την Ατομική Φυσική είναι γνωστό ότι οι επιτρεπόμενες ενεργειακές τιμές των ηλεκτρονίων είναι κβαντισμένες, όπως στο σχήμα 1. Σε
I. ΜΕΤΡΗΣΗ ΑΚΤΙΝΟΒΟΛΙΑΣ ΥΠΟΒΑΘΡΟΥ ΘΩΡΑΚΙΣΗ ΤΟΥ ΑΝΙΧΝΕΥΤΗ
 I. ΜΕΤΡΗΣΗ ΑΚΤΙΝΟΒΟΛΙΑΣ ΥΠΟΒΑΘΡΟΥ ΘΩΡΑΚΙΣΗ ΤΟΥ ΑΝΙΧΝΕΥΤΗ Α. Ακτινοβολία υποβάθρου (Background radiation) Εξαιτίας της κοσµικής ακτινοβολίας που βοµβαρδίζει συνεχώς την ατµόσφαιρα της γης και της ύπαρξης
I. ΜΕΤΡΗΣΗ ΑΚΤΙΝΟΒΟΛΙΑΣ ΥΠΟΒΑΘΡΟΥ ΘΩΡΑΚΙΣΗ ΤΟΥ ΑΝΙΧΝΕΥΤΗ Α. Ακτινοβολία υποβάθρου (Background radiation) Εξαιτίας της κοσµικής ακτινοβολίας που βοµβαρδίζει συνεχώς την ατµόσφαιρα της γης και της ύπαρξης
Ηλεκτρονική Φυσική (Εργαστήριο) ρ. Κ. Ι. ηµητρίου ΙΟ ΟΙ
 Ηλεκτρονική Φυσική (Εργαστήριο) ρ. Κ. Ι. ηµητρίου ΙΟ ΟΙ Για να κατανοήσουµε τη λειτουργία και το ρόλο των διόδων µέσα σε ένα κύκλωµα, θα πρέπει πρώτα να µελετήσουµε τους ηµιαγωγούς, υλικά που περιέχουν
Ηλεκτρονική Φυσική (Εργαστήριο) ρ. Κ. Ι. ηµητρίου ΙΟ ΟΙ Για να κατανοήσουµε τη λειτουργία και το ρόλο των διόδων µέσα σε ένα κύκλωµα, θα πρέπει πρώτα να µελετήσουµε τους ηµιαγωγούς, υλικά που περιέχουν
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β )
 ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 13/04/2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΤΡΕΙΣ (13) ΟΔΗΓΙΕΣ ΑΥΤΟΔΙΟΡΘΩΣΗΣ Στις ερωτήσεις Α1
ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 13/04/2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΤΡΕΙΣ (13) ΟΔΗΓΙΕΣ ΑΥΤΟΔΙΟΡΘΩΣΗΣ Στις ερωτήσεις Α1
Κεφάλαιο 37 Αρχική Κβαντική Θεωρία και Μοντέλα για το Άτομο. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 37 Αρχική Κβαντική Θεωρία και Μοντέλα για το Άτομο Περιεχόμενα Κεφαλαίου 37 Η κβαντική υπόθεση του Planck, Ακτινοβολία του μέλανος (μαύρου) σώματος Θεωρία των φωτονίων για το φως και το Φωτοηλεκτρικό
Κεφάλαιο 37 Αρχική Κβαντική Θεωρία και Μοντέλα για το Άτομο Περιεχόμενα Κεφαλαίου 37 Η κβαντική υπόθεση του Planck, Ακτινοβολία του μέλανος (μαύρου) σώματος Θεωρία των φωτονίων για το φως και το Φωτοηλεκτρικό
ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ ΜΕ ΤΗΝ ΥΛΗ
 ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ ΜΕ ΤΗΝ ΥΛΗ Η σχέση της σ κάθε τρόπου απορρόφησης φωτονίων-γ από το νερό συναρτήσει της ενέργειας των φωτονίων φαίνεται στο σχήμα: ΑΠΟΤΕΛΕΣΜΑΤΑ ΤΗΣ ΑΛΛΗΛΕΠΙΔΡΑΣΗΣ
ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ ΜΕ ΤΗΝ ΥΛΗ Η σχέση της σ κάθε τρόπου απορρόφησης φωτονίων-γ από το νερό συναρτήσει της ενέργειας των φωτονίων φαίνεται στο σχήμα: ΑΠΟΤΕΛΕΣΜΑΤΑ ΤΗΣ ΑΛΛΗΛΕΠΙΔΡΑΣΗΣ
Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2000
 Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα 1ο Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα
Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα 1ο Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα
Γ' ΤΑΞΗ ΓΕΝ.ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΦΥΣΙΚΗ ΕΚΦΩΝΗΣΕΙΣ
 Γ' ΤΑΞΗ ΓΕΝ.ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΦΥΣΙΚΗ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό κάθε µιας από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Όταν
Γ' ΤΑΞΗ ΓΕΝ.ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΦΥΣΙΚΗ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό κάθε µιας από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Όταν
ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ eclass: PHYS215 Π. Παπαγιάννης
 ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ eclass: PHYS215 Π. Παπαγιάννης Αν. Καθηγητής, Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών. Γραφείο 21 210-746 2442 ppapagi@phys.uoa.gr Έμμεσα ιοντίζουσα ακτινοβολία: Πότε ισούται το
ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ eclass: PHYS215 Π. Παπαγιάννης Αν. Καθηγητής, Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών. Γραφείο 21 210-746 2442 ppapagi@phys.uoa.gr Έμμεσα ιοντίζουσα ακτινοβολία: Πότε ισούται το
Κανονικη Εξεταστικη
 Κανονικη Εξεταστικη 29-1-2015 1ο: - Ποιοι παραγοντες επηρεαζουν τη δοση που χορηγειται στον εξεταζομενο κατα την ακτινογραφια 2ο: - Που οφειλεται το γραμμικο φασμα ακτινων χ, και να κανουμε το σχημα της
Κανονικη Εξεταστικη 29-1-2015 1ο: - Ποιοι παραγοντες επηρεαζουν τη δοση που χορηγειται στον εξεταζομενο κατα την ακτινογραφια 2ο: - Που οφειλεται το γραμμικο φασμα ακτινων χ, και να κανουμε το σχημα της
Ιατρική Φυσική. Π. Παπαγιάννης Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών Γραφείο
 Ιατρική Φυσική Π. Παπαγιάννης Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών Γραφείο 21 210-746 2442 ppapagi@phys.uoa.gr PHYS215 Ιατρική Φυσική: Δοσιμετρία Ιοντίζουσας Ακτινοβολίας Βιολογικές επιδράσεις
Ιατρική Φυσική Π. Παπαγιάννης Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών Γραφείο 21 210-746 2442 ppapagi@phys.uoa.gr PHYS215 Ιατρική Φυσική: Δοσιμετρία Ιοντίζουσας Ακτινοβολίας Βιολογικές επιδράσεις
ΕΚΦΩΝΗΣΕΙΣ. Στις παρακάτω ερωτήσεις 1-4, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 Επαναληπτικά Θέµατα ΟΕΦΕ 008 Γ' ΛΥΚΕΙΟΥ ΕΠΙΛΟΓΗΣ ΦΥΣΙΚΗ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Στις παρακάτω ερωτήσεις -, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση..
Επαναληπτικά Θέµατα ΟΕΦΕ 008 Γ' ΛΥΚΕΙΟΥ ΕΠΙΛΟΓΗΣ ΦΥΣΙΚΗ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Στις παρακάτω ερωτήσεις -, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση..
Μια εισαγωγή στις Ακτίνες Χ. Πηγές ακτίνων Χ Φάσματα ακτίνων Χ O νόμος του Moseley Εξασθένηση ακτινοβολίας ακτίνων Χ
 Μια εισαγωγή στις Ακτίνες Χ Πηγές ακτίνων Χ Φάσματα ακτίνων Χ O νόμος του Moseley Εξασθένηση ακτινοβολίας ακτίνων Χ Πειράματα Φυσικής: Ακτινοβολία Ακτίνων Χ Πηγές Ακτίνων Χ Οι ακτίνες Χ ή ακτίνες Roetge,
Μια εισαγωγή στις Ακτίνες Χ Πηγές ακτίνων Χ Φάσματα ακτίνων Χ O νόμος του Moseley Εξασθένηση ακτινοβολίας ακτίνων Χ Πειράματα Φυσικής: Ακτινοβολία Ακτίνων Χ Πηγές Ακτίνων Χ Οι ακτίνες Χ ή ακτίνες Roetge,
δ. εξαρτάται µόνο από το υλικό του οπτικού µέσου. Μονάδες 4
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 7 ΙΟΥΛΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-5 να
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 7 ΙΟΥΛΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-5 να
Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2000
 Ζήτηµα 1ο Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε το πρότυπο
Ζήτηµα 1ο Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε το πρότυπο
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΤΡΙΤΗ 22 MAIΟΥ 2007 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ 1 o ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΤΡΙΤΗ 22 MAIΟΥ 2007 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση.
ΘΕΜΑ 1 o ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΤΡΙΤΗ 22 MAIΟΥ 2007 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση.
ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΣΧΕΤΙΚΙΣΤΙΚΗΣ ΥΝΑΜΙΚΗΣ Έλλειµµα µάζας και ενέργεια σύνδεσης του πυρήνα του ατόµου A
 ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΣΧΕΤΙΚΙΣΤΙΚΗΣ ΥΝΑΜΙΚΗΣ Έλλειµµα µάζας και ενέργεια σύνδεσης του πυρήνα του ατόµου A Ένα ισότοπο, το οποίο συµβολίζουµε µε Z X, έχει ατοµικό αριθµό Ζ και µαζικό αριθµό Α. Ο πυρήνας του ισοτόπου
ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΣΧΕΤΙΚΙΣΤΙΚΗΣ ΥΝΑΜΙΚΗΣ Έλλειµµα µάζας και ενέργεια σύνδεσης του πυρήνα του ατόµου A Ένα ισότοπο, το οποίο συµβολίζουµε µε Z X, έχει ατοµικό αριθµό Ζ και µαζικό αριθµό Α. Ο πυρήνας του ισοτόπου
Ε ι σ α γ ω γ ή στo Εργαστήριο Πυρηνικής Φυσικής
 Ε ι σ α γ ω γ ή στo Εργαστήριο Πυρηνικής Φυσικής Γενικές Πληροφορίες - I ιστοσελίδα μαθήματος http://eclass.uoa.gr Κωδικός μαθήματος στο eclass PHYS211 Γενικές Πληροφορίες - II χώρος άσκησης Εργαστήριο
Ε ι σ α γ ω γ ή στo Εργαστήριο Πυρηνικής Φυσικής Γενικές Πληροφορίες - I ιστοσελίδα μαθήματος http://eclass.uoa.gr Κωδικός μαθήματος στο eclass PHYS211 Γενικές Πληροφορίες - II χώρος άσκησης Εργαστήριο
αγωγοί ηµιαγωγοί µονωτές Σχήµα 1
 Η2 Μελέτη ηµιαγωγών 1. Σκοπός Στην περιοχή της επαφής δυο ηµιαγωγών τύπου p και n δηµιουργούνται ορισµένα φαινόµενα τα οποία είναι υπεύθυνα για τη συµπεριφορά της επαφής pn ή κρυσταλλοδιόδου, όπως ονοµάζεται,
Η2 Μελέτη ηµιαγωγών 1. Σκοπός Στην περιοχή της επαφής δυο ηµιαγωγών τύπου p και n δηµιουργούνται ορισµένα φαινόµενα τα οποία είναι υπεύθυνα για τη συµπεριφορά της επαφής pn ή κρυσταλλοδιόδου, όπως ονοµάζεται,
Λειτουργία και Απόδοση του Πρότυπου Ανιχνευτή ΝΕΣΤΩΡ
 12 Λειτουργία και Απόδοση του Πρότυπου Ανιχνευτή ΝΕΣΤΩΡ Εισαγωγή Στο παρόν Κεφάλαιο περιγράφεται η λειτουργία και απόδοση του πρότυπου ανιχνευτή ΝΕΣΤΩΡ κατά τη λειτουργία του στη βαθιά θάλασσα. Συγκεκριμένα
12 Λειτουργία και Απόδοση του Πρότυπου Ανιχνευτή ΝΕΣΤΩΡ Εισαγωγή Στο παρόν Κεφάλαιο περιγράφεται η λειτουργία και απόδοση του πρότυπου ανιχνευτή ΝΕΣΤΩΡ κατά τη λειτουργία του στη βαθιά θάλασσα. Συγκεκριμένα
ΠΕΙΡΑΜΑ FRANK-HERTZ ΜΕΤΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΔΙΕΓΕΡΣΗΣ ΕΝΟΣ ΑΤΟΜΟΥ
 ΠΕΙΡΑΜΑ FRANK-HERTZ ΜΕΤΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΔΙΕΓΕΡΣΗΣ ΕΝΟΣ ΑΤΟΜΟΥ Η απορρόφηση ενέργειας από τα άτομα γίνεται ασυνεχώς και σε καθορισμένες ποσότητες. Λαμβάνοντας ένα άτομο ορισμένα ποσά ενέργειας κάποιο
ΠΕΙΡΑΜΑ FRANK-HERTZ ΜΕΤΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΔΙΕΓΕΡΣΗΣ ΕΝΟΣ ΑΤΟΜΟΥ Η απορρόφηση ενέργειας από τα άτομα γίνεται ασυνεχώς και σε καθορισμένες ποσότητες. Λαμβάνοντας ένα άτομο ορισμένα ποσά ενέργειας κάποιο
Αγωγιμότητα στα μέταλλα
 Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
ΑΡΧΗ 2ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 5 ΙΟΥΛΙΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 5 ΙΟΥΛΙΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να
ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ
 ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΑΤΟΜΙΚΑ ΜΟΝΤΕΛΑ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 0-05 ΘΕΜΑ B Σχέσεις μεταξύ κινητικής,
ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΑΤΟΜΙΚΑ ΜΟΝΤΕΛΑ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 0-05 ΘΕΜΑ B Σχέσεις μεταξύ κινητικής,
Η ΕΝΕΡΓΕΙΑ ΤΟΥ ΑΤΟΜΟΥ ΤΟΥ ΥΔΡΟΓΟΝΟΥ
 Η ΕΝΕΡΓΕΙΑ ΤΟΥ ΑΤΟΜΟΥ ΤΟΥ ΥΔΡΟΓΟΝΟΥ ΑΣΚΗΣΗ 1 Άτομα αερίου υδρογόνου που βρίσκονται στη θεμελιώδη κατάσταση (n = 1), διεγείρονται με κρούση από δέσμη ηλεκτρονίων που έχουν επιταχυνθεί από διαφορά δυναμικού
Η ΕΝΕΡΓΕΙΑ ΤΟΥ ΑΤΟΜΟΥ ΤΟΥ ΥΔΡΟΓΟΝΟΥ ΑΣΚΗΣΗ 1 Άτομα αερίου υδρογόνου που βρίσκονται στη θεμελιώδη κατάσταση (n = 1), διεγείρονται με κρούση από δέσμη ηλεκτρονίων που έχουν επιταχυνθεί από διαφορά δυναμικού
ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ eclass: MED808 Π. Παπαγιάννης
 ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ eclass: MED808 Π. Παπαγιάννης Επικ. Καθηγητής, Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών. Γραφείο 21 210-746 2442 ppapagi@phys.uoa.gr Αλ/δραση Ιοντίζουσας H/M Ακτινοβολίας -Ύλης
ΙΑΤΡΙΚΗ ΦΥΣΙΚΗ eclass: MED808 Π. Παπαγιάννης Επικ. Καθηγητής, Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών. Γραφείο 21 210-746 2442 ppapagi@phys.uoa.gr Αλ/δραση Ιοντίζουσας H/M Ακτινοβολίας -Ύλης
Πειραματική Ενότητα I ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΑΚΤΙΝΟΒΟΛΙΑΣ ΓΑΜΜΑ ME ΤΗΝ YΛH
 Πειραματική Ενότητα I ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΑΚΤΙΝΟΒΟΛΙΑΣ ΓΑΜΜΑ ME ΤΗΝ YΛH Σκοπός To πείραμα αυτό έχει σχεδιαστεί ώστε να εξοικειώσει το φοιτητή με τις βασικές αρχές της Φασματοσκοπίας με Σπινθηριστή NaΙ(Tl). Κατά
Πειραματική Ενότητα I ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΑΚΤΙΝΟΒΟΛΙΑΣ ΓΑΜΜΑ ME ΤΗΝ YΛH Σκοπός To πείραμα αυτό έχει σχεδιαστεί ώστε να εξοικειώσει το φοιτητή με τις βασικές αρχές της Φασματοσκοπίας με Σπινθηριστή NaΙ(Tl). Κατά
Διάλεξη 10: Ακτίνες Χ
 Διάλεξη 10: Ακτίνες Χ Ένταση Roentgen (1895): Παρατήρησε ότι όταν ταχέα ηλεκτρόνια πέσουν σε υλικό στόχο παράγεται ακτινοβολία, που ονομάστηκε ακτίνες Χ, με τις εξής ιδιότητες: Ευθύγραμμη διάδοση ακόμη
Διάλεξη 10: Ακτίνες Χ Ένταση Roentgen (1895): Παρατήρησε ότι όταν ταχέα ηλεκτρόνια πέσουν σε υλικό στόχο παράγεται ακτινοβολία, που ονομάστηκε ακτίνες Χ, με τις εξής ιδιότητες: Ευθύγραμμη διάδοση ακόμη
Αγωγιμότητα στα μέταλλα
 Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ
 ΘΕΜΑ 1 ο ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύμφωνα με την ηλεκτρομαγνητική
ΘΕΜΑ 1 ο ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύμφωνα με την ηλεκτρομαγνητική
ηλεκτρικό ρεύµα ampere
 Ηλεκτρικό ρεύµα Το ηλεκτρικό ρεύµα είναι ο ρυθµός µε τον οποίο διέρχεται ηλεκτρικό φορτίο από µια περιοχή του χώρου. Η µονάδα µέτρησης του ηλεκτρικού ρεύµατος στο σύστηµα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύµα Το ηλεκτρικό ρεύµα είναι ο ρυθµός µε τον οποίο διέρχεται ηλεκτρικό φορτίο από µια περιοχή του χώρου. Η µονάδα µέτρησης του ηλεκτρικού ρεύµατος στο σύστηµα SI είναι το ampere (A). 1 A =
Φυσικά ή τεχνητά ραδιονουκλίδια
 ΠΗΓΕΣ ΙΟΝΤΙΖΟΥΣΩΝ ΑΚΤΙΝΟΒΟΛΙΩΝ Φυσικά ή τεχνητά ραδιονουκλίδια π.χ. 60 Co, 137 Cs, Sr, Επιταχυντικές μηχανές π.χ. επιταχυντές e, επιταχυντές ιόντων Y Πυρηνικοί αντιδραστήρες π.χ. ακτινοβολία-γ, νετρόνια
ΠΗΓΕΣ ΙΟΝΤΙΖΟΥΣΩΝ ΑΚΤΙΝΟΒΟΛΙΩΝ Φυσικά ή τεχνητά ραδιονουκλίδια π.χ. 60 Co, 137 Cs, Sr, Επιταχυντικές μηχανές π.χ. επιταχυντές e, επιταχυντές ιόντων Y Πυρηνικοί αντιδραστήρες π.χ. ακτινοβολία-γ, νετρόνια
Ανάστροφη πόλωση της επαφής p n
 Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
ΟΡΟΣΗΜΟ ΘΕΜΑ Δ. Δίνονται: η ταχύτητα του φωτός στο κενό c 0 = 3 10, η σταθερά του Planck J s και για το φορτίο του ηλεκτρονίου 1,6 10 C.
 Σε μια διάταξη παραγωγής ακτίνων X, η ηλεκτρική τάση που εφαρμόζεται μεταξύ της ανόδου και της καθόδου είναι V = 25 kv. Τα ηλεκτρόνια ξεκινούν από την κάθοδο με μηδενική ταχύτητα, επιταχύνονται και προσπίπτουν
Σε μια διάταξη παραγωγής ακτίνων X, η ηλεκτρική τάση που εφαρμόζεται μεταξύ της ανόδου και της καθόδου είναι V = 25 kv. Τα ηλεκτρόνια ξεκινούν από την κάθοδο με μηδενική ταχύτητα, επιταχύνονται και προσπίπτουν
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2007 ΕΚΦΩΝΗΣΕΙΣ
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΙ ΕΙΣ 007 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜ 1o Στις ερωτήσεις 1- να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση. 1. Η υπέρυθρη ακτινοβολία
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΙ ΕΙΣ 007 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜ 1o Στις ερωτήσεις 1- να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση. 1. Η υπέρυθρη ακτινοβολία
Μονάδες 5. 3. Η υπεριώδης ακτινοβολία. α. με πολύ μικρό μήκος κύματος δεν προκαλεί βλάβες στα κύτταρα του δέρματος. β. δεν προκαλεί φθορισμό.
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 3 ΙΟΥΛΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 3 ΙΟΥΛΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε
ΤΙΤΛΟΣ: Ποιοτικός και ποσοτικός προσδιορισμός ραδιοϊσοτόπων με την μέθοδο της γ φασματοσκοπίας. Γιαννούλης Ευάγγελος.
 1 ΤΙΤΛΟΣ: Ποιοτικός και ποσοτικός προσδιορισμός ραδιοϊσοτόπων με την μέθοδο της γ φασματοσκοπίας ΟΝΟΜΑΤΕΠΩΝΥΜΟ: Καραβαγγέλη Μαριάννα ΗΜΕΡΟΜΗΝΙΑ ΕΚΤΕΛΕΣΗΣ ΤΗΣ ΑΣΚΗΣΗΣ: 13.11.2015 ΕΡΓΑΣΤΗΡΙΑΚΗ ΟΜΑΔΑ: Αργυριάδου
1 ΤΙΤΛΟΣ: Ποιοτικός και ποσοτικός προσδιορισμός ραδιοϊσοτόπων με την μέθοδο της γ φασματοσκοπίας ΟΝΟΜΑΤΕΠΩΝΥΜΟ: Καραβαγγέλη Μαριάννα ΗΜΕΡΟΜΗΝΙΑ ΕΚΤΕΛΕΣΗΣ ΤΗΣ ΑΣΚΗΣΗΣ: 13.11.2015 ΕΡΓΑΣΤΗΡΙΑΚΗ ΟΜΑΔΑ: Αργυριάδου
Ανάστροφη πόλωση της επαφής p n
 Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
Ο Πυρήνας του Ατόμου
 1 Σκοποί: Ο Πυρήνας του Ατόμου 15/06/12 I. Να δώσει μία εισαγωγική περιγραφή του πυρήνα του ατόμου, και της ενέργειας που μπορεί να έχει ένα σωματίδιο για να παραμείνει δέσμιο μέσα στον πυρήνα. II. III.
1 Σκοποί: Ο Πυρήνας του Ατόμου 15/06/12 I. Να δώσει μία εισαγωγική περιγραφή του πυρήνα του ατόμου, και της ενέργειας που μπορεί να έχει ένα σωματίδιο για να παραμείνει δέσμιο μέσα στον πυρήνα. II. III.
Περιεχόµενα Παρουσίασης 2.1
 Πυρηνική Τεχνολογία - ΣΕΜΦΕ Κ ε φ ά λ α ι ο 2 ο Π α ρ ο υ σ ί α σ η 2. 1 1 Περιεχόµενα Παρουσίασης 2.1 1. Αρχή Λειτουργίας των ΠΑΙ : Η Σχάση 2. Πυρηνική Ηλεκτροπαραγωγή ΠΗΣ 3. Πυρηνικά Υλικά και Τύποι
Πυρηνική Τεχνολογία - ΣΕΜΦΕ Κ ε φ ά λ α ι ο 2 ο Π α ρ ο υ σ ί α σ η 2. 1 1 Περιεχόµενα Παρουσίασης 2.1 1. Αρχή Λειτουργίας των ΠΑΙ : Η Σχάση 2. Πυρηνική Ηλεκτροπαραγωγή ΠΗΣ 3. Πυρηνικά Υλικά και Τύποι
ΕΠΑ.Λ. Β ΟΜΑ ΑΣ ΦΥΣΙΚΗ I ΕΚΦΩΝΗΣΕΙΣ
 1 ΕΠΑ.Λ. Β ΟΜΑ ΑΣ ΦΥΣΙΚΗ I ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1- και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σχετικά µε τις ιδιότητες
1 ΕΠΑ.Λ. Β ΟΜΑ ΑΣ ΦΥΣΙΚΗ I ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1- και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σχετικά µε τις ιδιότητες
Περι - Φυσικής. ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Κυριακή 5 Απρίλη 2015 Φως - Ατοµικά Φαινόµενα - Ακτίνες Χ. Θέµα Α. Ενδεικτικές Λύσεις
 ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Κυριακή 5 Απρίλη 2015 Φως - Ατοµικά Φαινόµενα - Ακτίνες Χ Ενδεικτικές Λύσεις Θέµα Α Α.1 Ο Planck εισήγαγε τη ϑεωρία των κβάντα ϕωτός, για να ερµηνεύσει : (δ) την ακτινοβολία
ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Κυριακή 5 Απρίλη 2015 Φως - Ατοµικά Φαινόµενα - Ακτίνες Χ Ενδεικτικές Λύσεις Θέµα Α Α.1 Ο Planck εισήγαγε τη ϑεωρία των κβάντα ϕωτός, για να ερµηνεύσει : (δ) την ακτινοβολία
Εύρεση της περιοχής λειτουργίας και της τάσης εργασίας του απαριθµητή Geiger-Müller
 AΣΚΗΣΗ 1 Εύρεση της περιοχής λειτουργίας και της τάσης εργασίας του απαριθµητή Geiger-Müller 1. Εισαγωγή Ο ανιχνευτής Geiger-Müller, που είναι ένα από τα πιο γνωστά όργανα µέτρησης ιονίζουσας ακτινοβολίας,
AΣΚΗΣΗ 1 Εύρεση της περιοχής λειτουργίας και της τάσης εργασίας του απαριθµητή Geiger-Müller 1. Εισαγωγή Ο ανιχνευτής Geiger-Müller, που είναι ένα από τα πιο γνωστά όργανα µέτρησης ιονίζουσας ακτινοβολίας,
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. 3. Ισότοποι ονοµάζονται οι πυρήνες που ανήκουν στο ίδιο χηµικό στοιχείο και έχουν τον ίδιο: α. µαζικό αριθµό β.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΤΕΛΟΣ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 4 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΤΕΛΟΣ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 4 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
Ραδιενέργεια Ένα τρομακτικό όπλο ή ένα μέσον για την έρευνα και για καλλίτερη ποιότητα ζωής; Για πόσο μεγάλες ενέργειες μιλάμε; Κ.-Α. Θ.
 Ραδιενέργεια Ένα τρομακτικό όπλο ή ένα μέσον για την έρευνα και για καλλίτερη ποιότητα ζωής; Για πόσο μεγάλες ενέργειες μιλάμε; Ραδιενέργεια 1896: Ανακάλυψη από τον Henry Becquerel (βραβείο Nobel 1903)
Ραδιενέργεια Ένα τρομακτικό όπλο ή ένα μέσον για την έρευνα και για καλλίτερη ποιότητα ζωής; Για πόσο μεγάλες ενέργειες μιλάμε; Ραδιενέργεια 1896: Ανακάλυψη από τον Henry Becquerel (βραβείο Nobel 1903)
Μονάδες Η υπεριώδης ακτινοβολία. α. με πολύ μικρό μήκος κύματος δεν προκαλεί βλάβες στα κύτταρα του δέρματος. β. δεν προκαλεί φθορισμό.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 3 ΙΟΥΛΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 3 ΙΟΥΛΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1ο Στις ερωτήσεις 1-4 να γράψετε
Ιατρική Φυσική: Δοσιμετρία Ιοντίζουσας Ακτινοβολίας. Βιολογικές επιδράσεις. Ακτινοπροστασία
 Ιατρική Φυσική: Δοσιμετρία Ιοντίζουσας Ακτινοβολίας Βιολογικές επιδράσεις Ακτινοπροστασία Π. Παπαγιάννης Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών Γραφείο 21 210-746 2442 ppapagi@phys.uoa.gr PHYS215
Ιατρική Φυσική: Δοσιμετρία Ιοντίζουσας Ακτινοβολίας Βιολογικές επιδράσεις Ακτινοπροστασία Π. Παπαγιάννης Εργαστήριο Ιατρικής Φυσικής, Ιατρική Σχολή Αθηνών Γραφείο 21 210-746 2442 ppapagi@phys.uoa.gr PHYS215
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ Συζευγμένα ηλεκτρικά και μαγνητικά πεδία τα οποία κινούνται με την ταχύτητα του φωτός και παρουσιάζουν τυπική κυματική συμπεριφορά Αν τα φορτία ταλαντώνονται περιοδικά οι διαταραχές
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ Συζευγμένα ηλεκτρικά και μαγνητικά πεδία τα οποία κινούνται με την ταχύτητα του φωτός και παρουσιάζουν τυπική κυματική συμπεριφορά Αν τα φορτία ταλαντώνονται περιοδικά οι διαταραχές
ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ
 ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Δ ΘΕΜΑΤΑ ΑΤΟΜΙΚΕΣ ΘΕΩΡΙΕΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 2014-2015 1. ΘΕΜΑ Δ Ένα άτομο
ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Δ ΘΕΜΑΤΑ ΑΤΟΜΙΚΕΣ ΘΕΩΡΙΕΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 2014-2015 1. ΘΕΜΑ Δ Ένα άτομο
i. 3 ii. 4 iii. 16 Ε 1 = -13,6 ev. 1MeV= 1, J.
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ Θέµα Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει σωστά την ηµιτελή πρόταση.
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ Θέµα Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει σωστά την ηµιτελή πρόταση.
λ Ε Πχ. Ένα σωματίδιο α έχει φορτίο +2 όταν επιταχυνθεί από μια διαφορά Για ακτίνες Χ ή ακτινοβολία γ έχουμε συχνότητα
 Μονάδες Ενέργειας 1 ev = 1,602 10-19 J 1 fj(= 10-15 J) = 6,241 10 3 ev Πχ. Ένα σωματίδιο α έχει φορτίο +2 όταν επιταχυνθεί από μια διαφορά δυναμικού 1000 V αποκτά ενέργεια 2 kev Για ακτίνες Χ ή ακτινοβολία
Μονάδες Ενέργειας 1 ev = 1,602 10-19 J 1 fj(= 10-15 J) = 6,241 10 3 ev Πχ. Ένα σωματίδιο α έχει φορτίο +2 όταν επιταχυνθεί από μια διαφορά δυναμικού 1000 V αποκτά ενέργεια 2 kev Για ακτίνες Χ ή ακτινοβολία
Παραγωγή ακτίνων Χ. V e = h ν = h c/λ λ min = h c/v e λ min (Å) 12400/V
 Παραγωγή ακτίνων Χ Οι ακτίνες Χ είναι ηλεκτροµαγνητική ακτινοβολία µε µήκη κύµατος της τάξης των Å (=10-10 m). Στο ηλεκτροµαγνητικό φάσµα η ακτινοβολία Χ εκτείνεται µεταξύ της περιοχής των ακτίνων γ και
Παραγωγή ακτίνων Χ Οι ακτίνες Χ είναι ηλεκτροµαγνητική ακτινοβολία µε µήκη κύµατος της τάξης των Å (=10-10 m). Στο ηλεκτροµαγνητικό φάσµα η ακτινοβολία Χ εκτείνεται µεταξύ της περιοχής των ακτίνων γ και
Πηγές Πηγές Ταχέων Ηλεκτρονίων internal conversion internal conversion
 Πηγές Ταχέων Ηλεκτρονίων internal conversion Ένας πυρήνας σε διεγερμένη κατάσταση (πχ μετα από β-διάσπαση) που για διάφορους λόγους δεν μπορεί να διασπασθεί μέσω εκπομπής γ ακτινοβολίας. Η ενέργεια διέγερσης
Πηγές Ταχέων Ηλεκτρονίων internal conversion Ένας πυρήνας σε διεγερμένη κατάσταση (πχ μετα από β-διάσπαση) που για διάφορους λόγους δεν μπορεί να διασπασθεί μέσω εκπομπής γ ακτινοβολίας. Η ενέργεια διέγερσης
ΑΤΟΜΙΚΗ ΠΥΡΗΝΙΚΗ ΦΥΣΙΚΗ
 ΑΤΟΜΙΚΗ ΠΥΡΗΝΙΚΗ ΦΥΣΙΚΗ Περιεχόμενα ΦΩΤΟΗΛΕΚΤΡΙΚΟ ΦΑΙΝΟΜΕΝΟ, ΦΑΣΜΑΤΑ ΕΚΠΟΜΠΗΣ-ΑΠΟΡΡΟΦΗΣΗΣ, ΚΥΜΑΤΟΣΩΜΑΤΙΔΙΑΚΟΣ ΔΥΪΣΜΟΣ, ΑΡΧΕΣ ΚΒΑΝΤΙΚΗΣ ΘΕΩΡΙΑΣ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου...
ΑΤΟΜΙΚΗ ΠΥΡΗΝΙΚΗ ΦΥΣΙΚΗ Περιεχόμενα ΦΩΤΟΗΛΕΚΤΡΙΚΟ ΦΑΙΝΟΜΕΝΟ, ΦΑΣΜΑΤΑ ΕΚΠΟΜΠΗΣ-ΑΠΟΡΡΟΦΗΣΗΣ, ΚΥΜΑΤΟΣΩΜΑΤΙΔΙΑΚΟΣ ΔΥΪΣΜΟΣ, ΑΡΧΕΣ ΚΒΑΝΤΙΚΗΣ ΘΕΩΡΙΑΣ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου...
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα, που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 22 MAIΟΥ 2007 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 22 MAIΟΥ 2007 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 20 ΜΑΪΟΥ 2013 ΕΚΦΩΝΗΣΕΙΣ
 Θέµα Α ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 0 ΜΑΪΟΥ 013 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση, η οποία
Θέµα Α ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 0 ΜΑΪΟΥ 013 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση, η οποία
ηλεκτρικό ρεύμα ampere
 Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Ακτίνες Χ (Roentgen) Κ.-Α. Θ. Θωμά
 Ακτίνες Χ (Roentgen) Είναι ηλεκτρομαγνητικά κύματα με μήκος κύματος μεταξύ 10 nm και 0.01 nm, δηλαδή περίπου 10 4 φορές μικρότερο από το μήκος κύματος της ορατής ακτινοβολίας. ( Φάσμα ηλεκτρομαγνητικής
Ακτίνες Χ (Roentgen) Είναι ηλεκτρομαγνητικά κύματα με μήκος κύματος μεταξύ 10 nm και 0.01 nm, δηλαδή περίπου 10 4 φορές μικρότερο από το μήκος κύματος της ορατής ακτινοβολίας. ( Φάσμα ηλεκτρομαγνητικής
Άσκηση 1. 1s 2s 2p (δ) 1s 3 2s 1. (ε) 1s 2 2s 1 2p 7 (στ) 1s 2 2s 2 2p 6 3s 2 3p 6 3d 8 4s 2
 Άσκηση 1 Ποια από τα ακόλουθα διαγράµµατα τροχιακών και τις ηλεκτρονικές δοµές είναι επιτρεπτό και ποιο αδύνατο, σύµφωνα µε την απαγορευτική αρχή του Pauli; Εξηγήστε. (α) (β) (γ) 1s 2s 2p (δ) 1s 3 2s 1
Άσκηση 1 Ποια από τα ακόλουθα διαγράµµατα τροχιακών και τις ηλεκτρονικές δοµές είναι επιτρεπτό και ποιο αδύνατο, σύµφωνα µε την απαγορευτική αρχή του Pauli; Εξηγήστε. (α) (β) (γ) 1s 2s 2p (δ) 1s 3 2s 1
ΣΩΜΑΤΙ ΙΑΚΗ ΦΥΣΗ ΦΩΤΟΣ
 Μάθηµα 1 ο, 30 Σεπτεµβρίου 2008 (9:00-11:00). ΣΩΜΑΤΙ ΙΑΚΗ ΦΥΣΗ ΦΩΤΟΣ Ακτινοβολία µέλανος σώµατος (1900) Plank: έδωσε εξήγηση του φάσµατος (κβαντική ερµηνεία*) ΠΑΡΑ ΟΧΗ Το φως δεν είναι µόνο κύµα. Είναι
Μάθηµα 1 ο, 30 Σεπτεµβρίου 2008 (9:00-11:00). ΣΩΜΑΤΙ ΙΑΚΗ ΦΥΣΗ ΦΩΤΟΣ Ακτινοβολία µέλανος σώµατος (1900) Plank: έδωσε εξήγηση του φάσµατος (κβαντική ερµηνεία*) ΠΑΡΑ ΟΧΗ Το φως δεν είναι µόνο κύµα. Είναι
Άσκηση 5 ΦΩΤΟΒΟΛΤΑΪΚΟ ΦΑΙΝΟΜΕΝΟ
 Άσκηση 5 ΦΩΤΟΒΟΛΤΑΪΚΟ ΦΑΙΝΟΜΕΝΟ 1. ΓΕΝΙΚΑ Τα ηλιακά στοιχεία χρησιμοποιούνται για τη μετατροπή του φωτός (που αποτελεί μία μορφή ηλεκτρομαγνητικής ενέργειας) σε ηλεκτρική ενέργεια. Κατασκευάζονται από
Άσκηση 5 ΦΩΤΟΒΟΛΤΑΪΚΟ ΦΑΙΝΟΜΕΝΟ 1. ΓΕΝΙΚΑ Τα ηλιακά στοιχεία χρησιμοποιούνται για τη μετατροπή του φωτός (που αποτελεί μία μορφή ηλεκτρομαγνητικής ενέργειας) σε ηλεκτρική ενέργεια. Κατασκευάζονται από
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2014
 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α Ηµεροµηνία: Κυριακή 13 Απριλίου 2014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ 1. ύο µονοχρωµατικές ακτινοβολίες Α και Β µε µήκη κύµατος στο κενό
ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α Ηµεροµηνία: Κυριακή 13 Απριλίου 2014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ 1. ύο µονοχρωµατικές ακτινοβολίες Α και Β µε µήκη κύµατος στο κενό
Μελέτη των χαρακτηριστικών της β - ραδιενεργού εκποµπής
 ΑΠ2 Μελέτη των χαρακτηριστικών της β - ραδιενεργού εκποµπής 1. Σκοπός Η εργαστηριακή αυτή άσκηση µελετά τα χαρακτηριστικά της β - ακτινοβολίας. Πιο συγκεκριµένα υπολογίζεται πειραµατικά η εµβέλεια των
ΑΠ2 Μελέτη των χαρακτηριστικών της β - ραδιενεργού εκποµπής 1. Σκοπός Η εργαστηριακή αυτή άσκηση µελετά τα χαρακτηριστικά της β - ακτινοβολίας. Πιο συγκεκριµένα υπολογίζεται πειραµατικά η εµβέλεια των
ΑΤΟΜΙΚΑ ΠΡΟΤΥΠΑ. Θέμα B
 ΑΤΟΜΙΚΑ ΠΡΟΤΥΠΑ Θέμα B _70 Β. Το ηλεκτρόνιο ενός ατόμου υδρογόνου που βρίσκεται στη τρίτη διεγερμένη ενεργειακή κατάσταση (n = ), αποδιεγείρεται εκπέμποντας φωτόνιο ενέργειας Ε.Κατά τη συγκεκριμένη αποδιέγερση
ΑΤΟΜΙΚΑ ΠΡΟΤΥΠΑ Θέμα B _70 Β. Το ηλεκτρόνιο ενός ατόμου υδρογόνου που βρίσκεται στη τρίτη διεγερμένη ενεργειακή κατάσταση (n = ), αποδιεγείρεται εκπέμποντας φωτόνιο ενέργειας Ε.Κατά τη συγκεκριμένη αποδιέγερση
ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ 2 ΕΡΓΑΣΙΑ: Χρονική φασματοσκοπία- χρήση συστήματος TAC-μέτρηση μικρών χρόνων ζωής
 ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ 2 ΕΡΓΑΣΙΑ: Χρονική φασματοσκοπία- χρήση συστήματος TAC-μέτρηση μικρών χρόνων ζωής Αλέξανδρος Κετικίδης ΑΕΜ:13299 1/6/14 κ.χαρδάλας Περίληψη Σκοπός αυτής της εργασίας είναι η μέτρηση
ΕΡΓΑΣΤΗΡΙΟ ΠΥΡΗΝΙΚΗΣ 2 ΕΡΓΑΣΙΑ: Χρονική φασματοσκοπία- χρήση συστήματος TAC-μέτρηση μικρών χρόνων ζωής Αλέξανδρος Κετικίδης ΑΕΜ:13299 1/6/14 κ.χαρδάλας Περίληψη Σκοπός αυτής της εργασίας είναι η μέτρηση
ΑΝΑΛΟΓΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ
 ΑΝΑΛΟΓΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Διάλεξη 1: Ημιαγωγοί Δίοδος pn Δρ. Δ. ΛΑΜΠΑΚΗΣ 1 Ταλαντωτές. Πολυδονητές. Γεννήτριες συναρτήσεων. PLL. Πολλαπλασιαστές. Κυκλώματα μετατροπής και επεξεργασίας σημάτων. Εφαρμογές με
ΑΝΑΛΟΓΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Διάλεξη 1: Ημιαγωγοί Δίοδος pn Δρ. Δ. ΛΑΜΠΑΚΗΣ 1 Ταλαντωτές. Πολυδονητές. Γεννήτριες συναρτήσεων. PLL. Πολλαπλασιαστές. Κυκλώματα μετατροπής και επεξεργασίας σημάτων. Εφαρμογές με
ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Κυριακή 5 Απρίλη 2015 Φως - Ατοµικά Φαινόµενα - Ακτίνες Χ
 ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Κυριακή 5 Απρίλη 2015 Φως - Ατοµικά Φαινόµενα - Ακτίνες Χ Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις
ιαγώνισµα Β Τάξης Ενιαίου Λυκείου Κυριακή 5 Απρίλη 2015 Φως - Ατοµικά Φαινόµενα - Ακτίνες Χ Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις
1. ΤΟΜΟΓΡΑΦΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΜΕ ΙΣΟΤΟΠΑ ΕΦΑΡΜΟΓΕΣ ΙΟΝΤΙΖΟΥΣΩΝ ΑΚΤΙΝΟΒΟΛΙΩΝ
 1. ΤΟΜΟΓΡΑΦΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΜΕ ΙΣΟΤΟΠΑ 1 x y 1. γ-κάµερα ή Κύκλωµα Πύλης Αναλυτής Ύψους Παλµών z κάµερα Anger (H. Anger, Berkeley, 1958) Λογικό Κύκλωµα Θέσης ιάταξη Φωτοπολλαπλασιαστών Μολύβδινη Θωράκιση
1. ΤΟΜΟΓΡΑΦΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΜΕ ΙΣΟΤΟΠΑ 1 x y 1. γ-κάµερα ή Κύκλωµα Πύλης Αναλυτής Ύψους Παλµών z κάµερα Anger (H. Anger, Berkeley, 1958) Λογικό Κύκλωµα Θέσης ιάταξη Φωτοπολλαπλασιαστών Μολύβδινη Θωράκιση
ΠΥΡΗΝΙΚΗ ΙΑΤΡΙΚΗ ΚΑΙ ΤΟΜΟΓΡΑΦΙΑ SPECT
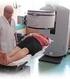 ΠΥΡΗΝΙΚΗ ΙΑΤΡΙΚΗ ΚΑΙ ΤΟΜΟΓΡΑΦΙΑ SPECT ΚΑΘΗΓΗΤΗΣ Δ. ΚΟΥΤΣΟΥΡΗΣ Εισαγωγή Πυρηνική Ιατρική: διαγνωστικές και θεραπευτικές διαδικασίες που απαιτούν την εισαγωγή ραδιενέργειας στον οργανισμό με ενδοφλέβια ένεση,
ΠΥΡΗΝΙΚΗ ΙΑΤΡΙΚΗ ΚΑΙ ΤΟΜΟΓΡΑΦΙΑ SPECT ΚΑΘΗΓΗΤΗΣ Δ. ΚΟΥΤΣΟΥΡΗΣ Εισαγωγή Πυρηνική Ιατρική: διαγνωστικές και θεραπευτικές διαδικασίες που απαιτούν την εισαγωγή ραδιενέργειας στον οργανισμό με ενδοφλέβια ένεση,
είναι τα μήκη κύματος του φωτός αυτού στα δύο υλικά αντίστοιχα, τότε: γ. 1 Β) Να δικαιολογήσετε την επιλογή σας.
 Β.1 Μονοχρωματικό φως, που διαδίδεται στον αέρα, εισέρχεται ταυτόχρονα σε δύο οπτικά υλικά του ίδιου πάχους d κάθετα στην επιφάνειά τους, όπως φαίνεται στο σχήμα. Οι χρόνοι διάδοσης του φωτός στα δύο υλικά
Β.1 Μονοχρωματικό φως, που διαδίδεται στον αέρα, εισέρχεται ταυτόχρονα σε δύο οπτικά υλικά του ίδιου πάχους d κάθετα στην επιφάνειά τους, όπως φαίνεται στο σχήμα. Οι χρόνοι διάδοσης του φωτός στα δύο υλικά
δ-ray με κινητική ενέργεια T e και ορμή p e παράγεται σε μια γωνία Θ q, p
 δ rays Κατά τον ιονισμό το εκπεμπόμενο θα έχει κινητική ενέργεια : 0 T T max q, p δ-ray με κινητική ενέργεια T και ορμή p παράγεται σε μια γωνία Θ T p cosθ = p T max max όπου p max η ορμή ενός με τη μέγιστη
δ rays Κατά τον ιονισμό το εκπεμπόμενο θα έχει κινητική ενέργεια : 0 T T max q, p δ-ray με κινητική ενέργεια T και ορμή p παράγεται σε μια γωνία Θ T p cosθ = p T max max όπου p max η ορμή ενός με τη μέγιστη
ETY-202. Εκπομπή και απορρόφηση ακτινοβολίας ETY-202 ΎΛΗ & ΦΩΣ 12. ΎΛΗ & ΦΩΣ. Στέλιος Τζωρτζάκης 21/12/2012
 stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 Εκπομπή και απορρόφηση ακτινοβολίας ΎΛΗ & ΦΩΣ 12. ΎΛΗ & ΦΩΣ Στέλιος Τζωρτζάκης 1 3 4 Ηλεκτρομαγνητικά πεδία Απορρόφηση είναι Σε αυτή τη διαδικασία το ηλεκτρόνιο
stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 Εκπομπή και απορρόφηση ακτινοβολίας ΎΛΗ & ΦΩΣ 12. ΎΛΗ & ΦΩΣ Στέλιος Τζωρτζάκης 1 3 4 Ηλεκτρομαγνητικά πεδία Απορρόφηση είναι Σε αυτή τη διαδικασία το ηλεκτρόνιο
Διάλεξη 4: Ραδιενέργεια
 Σύγχρονη Φυσική - 216: Πυρηνική Φυσική και Φυσική Στοιχειωδών Σωματιδίων 4/4/16 Διάλεξη 4: Ραδιενέργεια Βασικοί τρόποι αποδιέγερσης Όπως γνωρίζουμε στην φύση υπάρχουν σταθερές πυρηνικές καταστάσεις αλλά
Σύγχρονη Φυσική - 216: Πυρηνική Φυσική και Φυσική Στοιχειωδών Σωματιδίων 4/4/16 Διάλεξη 4: Ραδιενέργεια Βασικοί τρόποι αποδιέγερσης Όπως γνωρίζουμε στην φύση υπάρχουν σταθερές πυρηνικές καταστάσεις αλλά
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013
 ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηνία: Κυριακή 7 Απριλίου 201 ιάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας τον αριθµό
ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηνία: Κυριακή 7 Απριλίου 201 ιάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας τον αριθµό
ΦΥΣΙΚΕΣ ΜΕΘΟΔΟΙ ΣΤΗΝ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΕΣ ΜΕΘΟΔΟΙ ΣΤΗΝ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ Φασματοσκοπία Mossbauer ΠΕΡΙΚΛΗΣ ΑΚΡΙΒΟΣ Τμήμα Χημείας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΕΣ ΜΕΘΟΔΟΙ ΣΤΗΝ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ Φασματοσκοπία Mossbauer ΠΕΡΙΚΛΗΣ ΑΚΡΙΒΟΣ Τμήμα Χημείας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Άσκηση Ραδιοχηµείας. Ραδιενέργεια 8-1
 Άσκηση Ραδιοχηµείας Ραδιενέργεια Οι πυρήνες των ατόµων αποτελούνται από νουκλεόνια, δηλ. πρωτόνια και νετρόνια. Ο αριθµός Ζ των πρωτονίων χαρακτηρίζει τις χηµικές ιδιότητες των ατόµων γιατί καθορίζει το
Άσκηση Ραδιοχηµείας Ραδιενέργεια Οι πυρήνες των ατόµων αποτελούνται από νουκλεόνια, δηλ. πρωτόνια και νετρόνια. Ο αριθµός Ζ των πρωτονίων χαρακτηρίζει τις χηµικές ιδιότητες των ατόµων γιατί καθορίζει το
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2015 Β ΦΑΣΗ Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΕΚΦΩΝΗΣΕΙΣ
 ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηνία: Μ. Τετάρτη 8 Απριλίου 2015 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α1 Α4 να γράψετε στο τετράδιό σας τον
ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηνία: Μ. Τετάρτη 8 Απριλίου 2015 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α1 Α4 να γράψετε στο τετράδιό σας τον
