Program ΕΜΒΑ ΟΝ_ΚΥΚΛΟΥ Variables double: p, R, E Begin π 3.14 Print ώστε ακτίνα κύκλου Input R Print Εµβαδόν κύκλου Ε πrr Print Ε End program

Μέγεθος: px

Εμφάνιση ξεκινά από τη σελίδα:

Download "Program ΕΜΒΑ ΟΝ_ΚΥΚΛΟΥ Variables double: p, R, E Begin π 3.14 Print ώστε ακτίνα κύκλου Input R Print Εµβαδόν κύκλου Ε π*r*r Print Ε End program"

Μίδας Παχής
8 χρόνια πριν
Προβολές:

1 Άσκηση 1.1 Το εµβαδόν ενός κύκλου δίνεται από τον τύπο Ε=π*R 2 ; όπου R η ακτίνα του κύκλου. Να δοθεί αλγόριθµος ο οποίος να κάνει τα παρακάτω: 1) Εµφανίζει το µήνυµα «ώστε ακτίνα κύκλου» και διαβάζει την ακτίνα του κύκλου. 2) Εµφανίζει το µήνυµα «Εµβαδόν κύκλου» και στη συνέχεια υπολογίζει και εµφανίζει το εµβαδόν του σύµφωνα µε τον παραπάνω τύπο ( ίνεται π=3,14). Αλγόριθµος ΕΜΒΑ ΟΝ_ΚΥΚΛΟΥ πραγµατικός π, R, E αρχή π:=3,14; εµφάνισε ώστε ακτίνα κύκλου ; διάβασε R; εµφάνισε Εµβαδόν κύκλου ; Ε:=π*R*R; εµφάνισε Ε; τέλος Program ΕΜΒΑ ΟΝ_ΚΥΚΛΟΥ Variables double: p, R, E Begin π 3.14 Print ώστε ακτίνα κύκλου Input R Print Εµβαδόν κύκλου Ε π*r*r Print Ε End program Αρχή π:=3,14; εµφάνισε ώστε ακτίνα διάβασε R; εµφάνισε Εµβαδόν κύκλου ; Ε:=π*R*R; εµφάνισε Ε; Τέλος

2) Εµφανίζει το µήνυµα «Εµβαδόν κύκλου» και στη συνέχεια υπολογίζει και εµφανίζει το εµβαδόν του σύµφωνα µε τον παραπάνω τύπο ( ίνεται π=3,14).

2 Private Sub cmd_calc_click() Dim r As Double r = Val(txt_value.Text) txt_result.text = Str(r * r * 3.14) Private Sub cmd_exit_click() Unload Me Private Sub Form_Load() Private Sub txt_result_change() Άσκηση 1.2 Στο διαστηµικό κέντρο της ΝΑSA υπάρχει ένα ηλεκτρονικό ρόλοι που εµφανίζει το χρόνο σε δευτερόλεπτα που αποµένουν για την εκτόξευση του διαστηµικού λεωφορείου. ώστε ένα αλγόριθµο ο οποίος να διαβάζει τα δευτερόλεπτα που αναγράφονται στο ηλεκτρονικό ρολόι εµφανίζοντας το µήνυµα «ώστε τα δευτερόλεπτα που γράφει το ρολόι» και να εµφανίζει πόσες ώρες, λεπτά, και δευτερόλεπτα αποµένουν για την εκτόξευση, χρησιµοποιώντας την µορφή «ώρες:λεπτά:δευτερόλεπτα». Αλγόριθµος Μορφή_ώρες_λεπτά_δευτερόλεπτα ακέραιος Α_δεύτερα, δεύτερα, λεπτά, ώρες αρχή εµφάνισε ώστε τα δευτερόλεπτα που γράφει το ρολόι ; διάβασε Α_δεύτερα; ώρες:= Α_δεύτερα div 3600; λεπτά:= (Α_δεύτερα mod 3600) div 60; δεύτερα:= (Α_δεύτερα mod 3600) mod 60; εµφάνισε ώρες, :,λεπτά, :,δευτερόλεπτα; τέλος Program ΕΜΒΑ ΟΝ_ΚΥΚΛΟΥ Variables integer Α_δεύτερα, δεύτερα, λεπτά, ώρες Begin Print ώστε τα δευτερόλεπτα που γράφει το ρολόι Input Α_δεύτερα; ώρες Α_δεύτερα div 3600 λεπτά (Α_δεύτερα mod 3600) div 60 δεύτερα (Α_δεύτερα mod 3600) mod 60 Print ώρες, :,λεπτά, :,δευτερόλεπτα End program

2 Στο διαστηµικό κέντρο της ΝΑSA υπάρχει ένα ηλεκτρονικό ρόλοι που εµφανίζει το χρόνο σε δευτερόλεπτα που αποµένουν για την εκτόξευση του διαστηµικού λεωφορείου.

3 Αρχή εµφάνισε ώστε τα δευτερόλεπτα που γράφει το ρολόι ; διάβασε Α_δεύτερα; ώρες:=α_δεύτερα div 3600; λεπτά:= (Α_δεύτερα mod 3600) div 60; δεύτερα:= (Α_δεύτερα mod 3600) mod 60; εµφάνισε ώρες, :,λεπτά, :,δευτερόλεπτα; Τέλος

(Α_δεύτερα mod 3600) div 60; δεύτερα:= (Α_δεύτερα mod

4 Άσκηση 1.3 ίνονται τα παρακάτω τµήµατα ενός αλγορύθµου. Να κάνετε έναν πίνακα τιµών για όλες τις µεταβλητές και για όλα τα βήµατα καθενός από τα ακόλουθα τµήµατα αλγορίθµων. α) Α 10 Β Α+2 Α Α*10 Α Β+Α+Α*Α Β 2 Α Β-Α β) Χ 5 Χ Χ*Χ Α Χ Β Α+Χ C B/A X A*C A A+B+C+X Βήµα Α Β 1 10 απροσδιόριστο Βήµα Χ Α Β C 1 5 απροσδιόριστο απροσδιόριστο απροσδιόριστο

5 Άσκηση 1.4 Να δοθεί αλγόριθµος ο οποίος να υπολογίζει τον αριθµό των δισκετών των οποίων τα περιεχόµενα µπορεί να αποθηκεύσει ένας σκληρός δίσκος. Ο αλγόριθµος θα πρέπει να διαβάζει την χωρητικότητα του δίσκου σε GB εµφανίζοντας το µήνυµα «ώστε την χωρητικότητα του δίσκου σε GB» και τέλος να εµφανίζει το µήνυµα «ο δίσκος χωράει Χ δισκέτες»,όπου Χ είναι ο αριθµός των δισκετών που υπολογίστηκε. Θεωρείστε ότι: 1GB=1024MB Χωρητικότητα δισκέτας = 1,44ΜΒ.

6 Άσκηση 1.5 Να δοθεί αλγόριθµος που: Α) Να διαβάζει δύο ακέραιους αριθµούς εµφανίζοντας το µήνυµα «ώστε τους δύο αριθµούς». Β) Να υπολογίζει το άθροισµα, το γινόµενο, τη διαφορά και το µέσο όρο των δύο αριθµών Γ) Να τα εµφανίζει χρησιµοποιώντας κατάλληλα µηνύµατα. Program ΥΟ_ΑΡΙΘΜΟΙ Variables Integer Α,B,Ath,Gin,Diaf,MO Begin Print ώστε τους δύο αριθµούς Input Α Input B Ath Α+B Gin Α*B Diaf Α-B MO Ath/2 Print Αθροισµα Α+Β:,Ath Print ιαφορα Α-Β:,Diaf Print Γινόµενο Α*Β:,Gin Print M.O. Α,Β:,MO End program Private Sub cmdenter_click() A = InputBox(" ώσε τον αριθµό A") B = InputBox(" ώσε τον αριθµό B") ath = Val(A) + Val(B) gin = Val(A) * Val(B) diaf = Val(A) - Val(B) mo = ath / 2 Print "Άθροισµα Α+Β: "; ath Print "Γινόµενο Α*Β: "; gin Print " ιαφορά Α-Β: "; diaf Print "Μ.Ο. Α,Β: "; mo Private Sub cmdexit_click() End

Program ΥΟ_ΑΡΙΘΜΟΙ Variables Integer Α,B,Ath,Gin,Diaf,MO Begin Print ώστε τους δύο αριθµούς Input Α Input B Ath Α+B Gin Α*B Diaf Α-B MO Ath/2 Print Αθροισµα Α+Β:,Ath Print ιαφορα Α-Β:,Diaf Print

7 Άσκηση 1.6 Το µήκος της υποτείνουσας ενός ορθογωνίου τριγώνου υπολογίζεται από τον τύπο C 2 =A 2 +B 2 ;όπου Α,Β τα µήκη των καθέτων πλευρών και C το µήκος της υποτείνουσας. Να δοθεί αλγόριθµος ο οποίος: ιαβάζει τα µήκη των καθέτων πλευρών εµφανίζοντας το µήνυµα «ώσε µήκος πλευράς Α», «ώσε µήκος πλευράς Β». Υπολογίζει το µήκος της υποτείνουσας εµφανίζοντας το λεκτικό «Η υποτείνουσα έχει µήκος:» ακολουθούµενο από το µήκος που έχει υπολογιστεί. Private Sub cmdenter_click() A = InputBox("Dose mekos pleuras A") B = InputBox("Dose mekos pleuras B") C = (A ^ 2 + B ^ 2) ^ (1 / 2) Print "H ypoteinoysa exei mekos: "; C Private Sub cmdexit_click() End

υποτείνουσας. Να δοθεί αλγόριθµος ο οποίος: ιαβάζει τα µήκη των καθέτων πλευρών εµφανίζοντας το µήνυµα «ώσε µήκος πλευράς Α», «ώσε µήκος πλευράς Β».

8 Άσκηση 1.7 Να γραφεί αλγόριθµος ο οποίος: Να διαβάζει το αρχικό κεφάλαιο µιας κατάθεσης, το τρέχον επιτόκιο καταθέσεων µε µορφή δεκαδικού αριθµού, εµφανίζοντας τα µηνύµατα, «ώσε το αρχικό κεφάλαιο κατάθεσης», ώσε το επιτόκιο». Υπολογίζει τους τόκους καθώς και το συνολικό κεφάλαιο όπως αυτό έχει προσαυξηθεί µε τους τόκους, για χρονική περίοδο ενός έτους. Εµφανίζει το λεκτικό «Το σύνολο των τόκων είναι» ακολουθούµενο από τους τόκους και το λεκτικό «Το τελικό ποσό είναι:» ακολουθούµενο από το συνολικό κεφάλαιο. Private Sub cmd_enter_click() A_K = InputBox("Dose to arxiko kafalaio:") E = InputBox("Dose to epitokio:") tokos_a = A_K * (E / 2) / 100 tokos_b = (A_K + tokos_a) * (E / 2) / 100 s_tokos = tokos_a + tokos_b T_K = A_K + s_tokos Print "To synolo ton tokon einai: "; s_tokos Print "To teliko poso e;inai:"; T_K Private Sub cmd_exit_click() End

ώσε το επιτόκιο». Υπολογίζει τους τόκους καθώς και το συνολικό κεφάλαιο όπως αυτό έχει προσαυξηθεί µε τους τόκους, για χρονική περίοδο ενός έτους.

9 Άσκηση 1.8 Να υπολογιστούν οι παραστάσεις log(6) log( 6,2 + 1) e Private Sub cmd_enter_click() A = (1 + Abs(-10) ^ (1 / 2)) / (2 + Log(6)) b = (5 ^ (1 / 2) + Log(Abs(6.2 ^ 2 + 1))) / (Exp(4) + 1) Print "A= "; A Print "b=:"; b Private Sub cmd_exit_click() End

e 4 + 1 Private Sub cmd_enter_click() A = (1 + Abs(-10) ^ (1 / 2)) /

Σχετικά έγγραφα

Άσκηση 2.1 Να σχεδιαστεί το διάγραµµα ροής πρωτοβάθµιας εξίσωσης της µορφής:

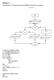Άσκηση 2.1 Να σχεδιαστεί το διάγραµµα ροής πρωτοβάθµιας εξίσωσης της µορφής: y = bx+ c Αρχή εµφάνισε " ώσε τιµές στα b,cι διάβασε b,c b=0 c=0 x=-c/b εµφάνισε A ΥΝΑΤΗ εµφάνισε AOPIΣΤΗ εµφάνισε Λύση x=:,x